No CrossRef data available.
Article contents
SCHRÖDINGER PROPAGATOR ON WIENER AMALGAM SPACES IN THE FULL RANGE
Published online by Cambridge University Press: 27 August 2024
Abstract
Using the technique of Gabor analysis, we characterize the boundedness of 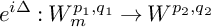 $e^{i\Delta }: W^{p_1,q_1}_m\rightarrow W^{p_2,q_2}$ with modulation and translation operators, where
$e^{i\Delta }: W^{p_1,q_1}_m\rightarrow W^{p_2,q_2}$ with modulation and translation operators, where 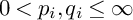 and m is a v-moderate weight. The sharp exponents for the boundedness are also characterized in the case of power weight.
and m is a v-moderate weight. The sharp exponents for the boundedness are also characterized in the case of power weight.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
Footnotes
This work was supported by the National Natural Foundation of China (Grant No. 12371100) and the Natural Science Foundation of Fujian Province (Grant Nos. 2021J011192 and 2022J011241).
References
Bényi, Á., Gröchenig, K., Okoudjou, K. A. and Rogers, L. G.,
Unimodular Fourier multipliers for modulation spaces
, J. Funct. Anal. 246 (2007), no. 2, 366–384.CrossRefGoogle Scholar
Bényi, A. and Okoudjou, K.,
Local well-posedness of nonlinear dispersive equations on modulation spaces
, Bull. Lond. Math. Soc. 41 (2009), 549–558.CrossRefGoogle Scholar
Bhimani, D. G. and Haque, S.,
Strong ill-posedness for fractional Hartree and cubic NLS equations
, J. Funct. Anal. 285 (2023), no. 11, 110157.CrossRefGoogle Scholar
Cordero, E. and Nicola, F.,
Boundedness of Schrödinger type propagators on modulation spaces
, J. Fourier Anal. Appl. 16 (2010), 311–339.CrossRefGoogle Scholar
Cunanan, J. and Sugimoto, M.,
Unimodular Fourier multipliers on Wiener amalgam spaces
, J. Math. Anal. Appl. 419 (2014), 738–747.CrossRefGoogle Scholar
Feichtinger, H. G.,
Gewichtsfunktionen auf lokalkompakten gruppen
, Österreich. Akad. Wiss. Math. Natur. Kl. Sitzungsber. II 188 (1979), no. 8, 451–471.Google Scholar
Feichtinger, H. G., Modulation spaces on locally compact abelian groups. Technical Report, University of Vienna, 1983.Google Scholar
Galperin, Y. V. and Samarah, S.,
Time-frequency analysis on modulation spaces
 ${M}_m^{p,q},$
${M}_m^{p,q},$
 , Appl. Comput. Harmon. Anal. 16 (2004), no. 1, pp. 1–18.CrossRefGoogle Scholar
, Appl. Comput. Harmon. Anal. 16 (2004), no. 1, pp. 1–18.CrossRefGoogle Scholar
Gröchenig, K., Foundations of time–frequency analysis, Applied and Numerical Harmonic Analysis, Birkhäuser, Boston, MA, 2001.CrossRefGoogle Scholar
Gröchenig, K. and Leinert, M.,
Wiener’s lemma for twisted convolution and Gabor frames
, J. Amer. Math. Soc. 17 (2004), no. 1, 1–18.CrossRefGoogle Scholar
Guo, W., Chen, J., Fan, D. and Zhao, G.,
Characterizations of some properties on weighted modulation and Wiener amalgam spaces
, Michigan Math. J. 68 (2019), no. 3, 451–482.CrossRefGoogle Scholar
Guo, W., Fan, D., Wu, H. and Zhao, G.,
Sharp weighted convolution inequalities and some applications
, Studia Math. 241 (2018), no. 3, 201–239.CrossRefGoogle Scholar
Guo, W. and Zhao, G.,
Sharp estimates of unimodular Fourier multipliers on Wiener amalgam spaces
, J. Funct. Anal. 278 (2020), no. 6, 108405.CrossRefGoogle Scholar
Heil, C., “An introduction to weighted Wiener amalgams” in Krishna, M., Radha, R. and Thangavelu, S. (eds.) Wavelets and their applications (Chennai, January 2002), Allied Publishers, New Delhi, 2003, pp. 183–216.Google Scholar
Kato, K., Kobayashi, M. and Ito, S.,
Representation of Schrödinger operator of a free particle via short-time Fourier transform and its applications
, Tohoku Math. J. Sec. Ser. 64 (2012), no. 2, 223–231.Google Scholar
Kato, T. and Tomita, N..
A remark on the Schrödinger propagator on Wiener amalgam spaces
. Mathematische Nachrichten, 292:350 – 357, 2018.CrossRefGoogle Scholar
Schippa, R..
On smoothing estimates in modulation spaces and the nonlinear Schrödinger equation with slowly decaying initial data
. Journal of Functional Analysis, 282(5):109352, 2022.CrossRefGoogle Scholar
Triebel, H..
Modulation Spaces on the Euclidean n-Space
. Zeitschrift für Analysis und ihre Anwendungen, 2(5):443–457, 1983.CrossRefGoogle Scholar
Walnut, D. F..
Continuity properties of the Gabor frame operator
. J. Math. Anal. Appl., 165(2):479–504, 1992.CrossRefGoogle Scholar
Wang, B. and Hudzik, H..
The global Cauchy problem for the NLS and NLKG with small rough data
. Journal of Differential Equations, 232(1):36–73, jan 2007.CrossRefGoogle Scholar
Wang, B., Zhao, L. and Guo, B.. Isometric decomposition operators, function spaces  and applications to nonlinear evolution equations. Journal of Functional Analysis, 233(1):1–39, 2006.Google Scholar
and applications to nonlinear evolution equations. Journal of Functional Analysis, 233(1):1–39, 2006.Google Scholar
Zhao, G., Chen, J., Fan, D. and Guo, W.,
Sharp estimates of unimodular multipliers on frequency decomposition spaces
, Nonlinear Anal. 142 (2016), 26–47.CrossRefGoogle Scholar


