1. Introduction
Capsules, which are fluid droplets protected by a thin elastic membrane, are encountered in nature (red blood cells, phospholipid vesicles, etc.) and in various industrial applications. In the last decade, major improvements have been made in cosmetics (Casanova & Santos Reference Casanova and Santos2016) and medicine (Huang et al. Reference Huang, Zhou, Chen, Li, Han and Wang2020; Lopez-Mendez et al. Reference Lopez-Mendez, Santos-Vizcaino, Pedraz, Hernandez and Orive2021) for the controlled delivery of active substances, the new generations of messenger ribonucleic acid (mRNA) vaccines being an example (Kowalski et al. Reference Kowalski, Rudra, Miao and Anderson2019).
When a capsule is placed in an external flow, it undergoes large deformations and potentially ruptures, which, depending on the application, is to be avoided to preserve the internal content or promoted to allow the release of the internal substance. The first experimental study on capsule burst was conducted in a simple shear flow by Chang & Olbricht (Reference Chang and Olbricht1993) on polyamide capsules. Breakup was initiated surprisingly from one of the major axis tips of the deformed capsule and propagated within the shear plane. The explanation provided by the authors is that, during deformation, the membrane thins out the most at these locations. More recent rupture studies were conducted by Husmann et al. (Reference Husmann, Rehage, Dhenin and Barthès-Biesel2005) and Koleva & Rehage (Reference Koleva and Rehage2012), who placed polysiloxane capsules in a spinning-drop apparatus and in a microrheometer, respectively. They showed that the rupture was observed rather at the tips of the flow vorticity axis, located on the capsule sides, which correspond to the zones of maximum elastic tensions. Joung, Song & Kim (Reference Joung, Song and Kim2020) also studied the rupture of human serum albumin (HSA) capsules in a rheoscope, suggesting that the initiation of rupture occurs within the shear plane. These results are consistent with those obtained by Grandmaison, Brancherie & Salsac (Reference Grandmaison, Brancherie and Salsac2021), who observed the same rupture phenomena using a novel fluid–structure interaction (FSI) numerical model, specifically developed to study capsule damage and rupture in Stokes flow. The novelty of the model is to describe the gradual weakening of the capsule membrane until rupture using the framework of continuum damage mechanics. Since then the model has been enriched by adding the propagation of rupture (Grandmaison Reference Grandmaison2021). The studies by Xie et al. (Reference Xie, de Loubens, Dubreuil, Gunes, Jaeger and Leonetti2017) and Chachanidze et al. (Reference Chachanidze, Xie, Lyu, Jaeger and Leonetti2022) on chitosan capsules placed in a hyperbolic flow similarly found that the initial rupture point corresponds to the area of maximum internal stress within the membrane.
The experimental studies of the last decades have thus mostly provided a common view on the occurrence of rupture. However, none of them provides insight on the evolution of the mechanical state leading to rupture. Using the numerical codes of Grandmaison et al. (Reference Grandmaison, Brancherie and Salsac2021) and Walter et al. (Reference Walter, Salsac, Barthès-Biesel and Le Tallec2010), we have computed the deformation of capsules with and without damage, respectively. We have been surprised not to see any effect on the capsule shape during damage build up, suggesting no visible rheological impact of damage on capsule suspension. An open question is thus how can one characterize damage/rupture mechanical properties experimentally. In this paper, we propose a protocol based on microrheometric measurements of the behaviour of ovalbumin microcapsules under simple shear flow coupled with a characterization of the mechanical properties of the membrane to follow their time evolution. Our objective is indeed to characterize damage by following the decrease of the capsule surface shear modulus over time. We then propose to determine capsule rupture varying the shear rate and time duration by comparing the number and size of capsules before and after exposure to shear.
In the following, we first present the experimental set-up and methods of our study in § 2. The damage is studied in § 3.2, in which we detail the effects of the capsule size and shear exposure time on the capsule surface shear modulus. To study the rupture mechanisms, we investigate in § 3.3 how the experimental parameters influence the probability and kinetics of rupture.
2. Experimental set-up and methods
2.1. Capsule preparation
A few hours before being tested in the microrheometer, spherical microcapsules are prepared by the interfacial cross-linking of ovalbumin with terephthaloyl chloride in a water-in-oil emulsion following the protocol described in Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021). A volume of 1 ml of a ![]() $10\,\%$ (w/v) ovalbumin (Sigma-Aldrich) in a phosphate-buffered aqueous solution (Sigma-Aldrich) having a pH of 7.4 is emulsified in 10 ml of sunflower oil using a laboratory vortex (Heidolph top-mix 94323) at 2400 r.p.m. for 15 s. To induce a cross-linking reaction at the water–oil interfaces, 10 ml of a
$10\,\%$ (w/v) ovalbumin (Sigma-Aldrich) in a phosphate-buffered aqueous solution (Sigma-Aldrich) having a pH of 7.4 is emulsified in 10 ml of sunflower oil using a laboratory vortex (Heidolph top-mix 94323) at 2400 r.p.m. for 15 s. To induce a cross-linking reaction at the water–oil interfaces, 10 ml of a ![]() $2.5\,\%$ (w/v) solution of terephthaloyl chloride (Sigma-Aldrich) in sunflower oil is added to the emulsion. After a reaction time of 15 min at room temperature, a batch of spherical capsules with radii ranging from a few tens to a few hundreds of microns is obtained. Capsules are then centrifuged at 800 r.p.m. for 1 min. The supernatant is removed and replaced by sunflower oil containing
$2.5\,\%$ (w/v) solution of terephthaloyl chloride (Sigma-Aldrich) in sunflower oil is added to the emulsion. After a reaction time of 15 min at room temperature, a batch of spherical capsules with radii ranging from a few tens to a few hundreds of microns is obtained. Capsules are then centrifuged at 800 r.p.m. for 1 min. The supernatant is removed and replaced by sunflower oil containing ![]() $2\,\%$ (v/v) of Tween 20 (Sigma-Aldrich). The sedimented capsules are resuspended into the oil inducing successive aspirations and ejections using a pipette. The suspension is centrifuged for the second time at 800 r.p.m. for 1 min. The supernatant is then removed and replaced by Milli-Q water with a
$2\,\%$ (v/v) of Tween 20 (Sigma-Aldrich). The sedimented capsules are resuspended into the oil inducing successive aspirations and ejections using a pipette. The suspension is centrifuged for the second time at 800 r.p.m. for 1 min. The supernatant is then removed and replaced by Milli-Q water with a ![]() $2\,\%$ (v/v) of Tween 20. The same resuspension and centrifugation procedures are used. After centrifugation, the pellet is resuspended in Milli-Q water for storage.
$2\,\%$ (v/v) of Tween 20. The same resuspension and centrifugation procedures are used. After centrifugation, the pellet is resuspended in Milli-Q water for storage.
2.2. Suspension preparation for microrheometric tests
To prepare the solution for the microrheometric tests with a minimal volume of water, the microcapsules are pipetted from the sediment (§ 2.1). They are then transferred into glycerol (Sigma-Aldrich) to maximize the shear stresses during the microrheometric tests.
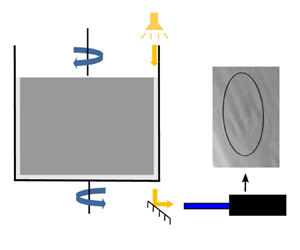
To avoid prestresses due to osmotic effects in the capsule membrane, we prepare in advance an ovalbumin–glycerol solution in two steps. We first mix 1.5 g of ovalbumin into 1 ml of water using a spatula until a homogeneous paste is obtained. The paste is then incorporated into 50 ml of glycerol and mixed using a rocking shaker providing a 3 % (w/v) ovalbumin–glycerol solution. Finally, to prepare a 2 % (v/v) capsule suspension in glycerol (left part of figure 1), 1 ml of capsule sediment is added to 50 ml of the 3 % ovalbumin–glycerol solution.

Figure 1. Description of production of the capsules-in-glycerol suspension and their test in the microrheometry set-up.
To find the osmotic equilibrium, we have tested various ovalbumin concentrations and found that 3 % (w/v) is optimal. Indeed, from 0 % to 3 % ovalbumin, the capsule size decreases (by at least 50 %) and above 3 %, capsules are no longer spherical and present large folds, indicating that they collapse onto themselves.
2.3. Microrheometry
Our study of capsule motion is carried out in a Couette flow, generated within a counter-rotating microrheometer (MCR 702, Anton Paar, Austria) in the coaxial cylinders configuration (figure 1). A volume of 10 ml of capsule-in-glycerol suspension (§ 2.2) is introduced in the 1 mm gap between the cylinders and sheared varying two parameters: the shear rate ![]() $\dot {\gamma }$ and the exposure time to shear
$\dot {\gamma }$ and the exposure time to shear ![]() $t_E$. Another parameter of the study is the viscosity of the capsule suspension, which is directly measured by the rheometer at each instant of time. The viscosity is mainly a function of the concentration in capsules of the suspension (which is not controlled precisely) and of the temperature. The temperature
$t_E$. Another parameter of the study is the viscosity of the capsule suspension, which is directly measured by the rheometer at each instant of time. The viscosity is mainly a function of the concentration in capsules of the suspension (which is not controlled precisely) and of the temperature. The temperature ![]() $T$ was set at
$T$ was set at ![]() $19\,^{\circ }$C during the microrheometric experiments, but seasonal variations have been measured, the temperature varying in practice between
$19\,^{\circ }$C during the microrheometric experiments, but seasonal variations have been measured, the temperature varying in practice between ![]() $16\,^{\circ }$C and
$16\,^{\circ }$C and ![]() $22\,^{\circ }$C. In the following, the given value of viscosity
$22\,^{\circ }$C. In the following, the given value of viscosity ![]() $\mu$ corresponds to the average over the experiment duration.
$\mu$ corresponds to the average over the experiment duration.
The capsule motion and deformation within the shear plane are viewed from the bottom using a ![]() $45^{\circ }$ mirror placed under the inter-cylinder gap (figure 1). The images are captured at a resolution of
$45^{\circ }$ mirror placed under the inter-cylinder gap (figure 1). The images are captured at a resolution of ![]() $800\times 600$ pixels and a frame rate of 23.95 f.p.s. by a video camera (LM165M, Lumenera, Canada) placed after a microscope tube. The light intensity is increased by illuminating the gap from the top with a spot light (KL 1600 LED, SCHOTT, Germany). We can only track the capsules whose centre of gravity is in the vicinity of the shear stationary plane of the counter-rotating cylinders and within the focal plane of the optical system. Their deformed profiles are extracted using ImageJ (National Institutes of Health, USA), by fitting them with an ellipse of semiaxes
$800\times 600$ pixels and a frame rate of 23.95 f.p.s. by a video camera (LM165M, Lumenera, Canada) placed after a microscope tube. The light intensity is increased by illuminating the gap from the top with a spot light (KL 1600 LED, SCHOTT, Germany). We can only track the capsules whose centre of gravity is in the vicinity of the shear stationary plane of the counter-rotating cylinders and within the focal plane of the optical system. Their deformed profiles are extracted using ImageJ (National Institutes of Health, USA), by fitting them with an ellipse of semiaxes ![]() $L_{1}$ and
$L_{1}$ and ![]() $L_{2}$ (right part of figure 1).
$L_{2}$ (right part of figure 1).
2.4. Identification of the membrane elasticity evolution
Capsule deformations are analysed by computing the Taylor parameter ![]() $D_{12}$ defined as
$D_{12}$ defined as ![]() $D_{12}={(L_{1}-L_{2})}/{(L_{1}+L_{2})}$, from the measured values of the capsule semiaxes
$D_{12}={(L_{1}-L_{2})}/{(L_{1}+L_{2})}$, from the measured values of the capsule semiaxes ![]() $L_{1}$ and
$L_{1}$ and ![]() $L_{2}$ in the shear plane. Note that the Taylor parameter of the undeformed capsule is 0, the microcapsules being nearly perfectly spherical (maximum difference between
$L_{2}$ in the shear plane. Note that the Taylor parameter of the undeformed capsule is 0, the microcapsules being nearly perfectly spherical (maximum difference between ![]() $L_{1}$ and
$L_{1}$ and ![]() $L_{2}$ of 1 %). For the purpose of characterizing mechanically the microcapsules from their deformed state, we only keep those for which
$L_{2}$ of 1 %). For the purpose of characterizing mechanically the microcapsules from their deformed state, we only keep those for which ![]() $D_{12} \geq 0.1$ in order to have substantial deformations. To identify the surface shear modulus
$D_{12} \geq 0.1$ in order to have substantial deformations. To identify the surface shear modulus ![]() $G_s$ of the capsule membrane, we use the numerical results from Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021), presented in figure 2, which link the Taylor parameter to the elastic capillary number
$G_s$ of the capsule membrane, we use the numerical results from Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021), presented in figure 2, which link the Taylor parameter to the elastic capillary number ![]() $Ca$ and to
$Ca$ and to ![]() $L_3/a$ (ratio of the capsule semiaxis in the outer plane direction
$L_3/a$ (ratio of the capsule semiaxis in the outer plane direction ![]() $L_3$ to the capsule initial radius
$L_3$ to the capsule initial radius ![]() $a$) for two constitutive laws. We consider the neo-Hookean (NH) law, which is strain-softening, and the generalized Hooke's (GH) law, which is strain-hardening. From the measured value of
$a$) for two constitutive laws. We consider the neo-Hookean (NH) law, which is strain-softening, and the generalized Hooke's (GH) law, which is strain-hardening. From the measured value of ![]() $D_{12}$, we deduce the values of
$D_{12}$, we deduce the values of ![]() $Ca$ and
$Ca$ and ![]() $L_3$, and hence of
$L_3$, and hence of ![]() $a$ considering that
$a$ considering that ![]() $a=\sqrt {L_{1}L_{2}L_{3}/a}$ from the volume conservation. With the values of
$a=\sqrt {L_{1}L_{2}L_{3}/a}$ from the volume conservation. With the values of ![]() $Ca$ and
$Ca$ and ![]() $a$ in hand, the expression of the surface shear modulus of the observed capsules is obtained as
$a$ in hand, the expression of the surface shear modulus of the observed capsules is obtained as
where ![]() $\mu$ and
$\mu$ and ![]() $\dot {\gamma }$ are the viscosity and shear rate taken from the experiment, respectively. The time evolution of the shear modulus is determined in order to study potential damage effect induced by the shear flow. Indeed, a decrease in
$\dot {\gamma }$ are the viscosity and shear rate taken from the experiment, respectively. The time evolution of the shear modulus is determined in order to study potential damage effect induced by the shear flow. Indeed, a decrease in ![]() $G_{s}$ with respect to exposure time to shear is a marker of damage.
$G_{s}$ with respect to exposure time to shear is a marker of damage.

Figure 2. Charts of the dependency of the Taylor parameter ![]() $D_{12}$ on (a) the elastic capillary number
$D_{12}$ on (a) the elastic capillary number ![]() $Ca$ and (b) the capsule semiaxis length
$Ca$ and (b) the capsule semiaxis length ![]() $L_{3}$ in the transverse direction. The numerical results are from Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021) and are provided for the NH and GH laws.
$L_{3}$ in the transverse direction. The numerical results are from Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021) and are provided for the NH and GH laws.
2.5. Experimental characterization of capsule rupture
After having studied the appearance of damage in the capsule membrane, we characterize capsule rupture by comparing the number and size of the capsules present before and after exposure to shear. To verify that the distribution of capsules suspended in the glycerol solution (§ 2.2) is homogeneous, three ![]() $10\ \mathrm {\mu }$l samples are extracted from the same capsules-in-glycerol suspension prior to being sheared. Each of them is placed on a glass slide for observation under an optical microscope (DMI8, Leica, Microsystems, Germany) with a magnification of 20 (left part of figure 3). The capsule radius
$10\ \mathrm {\mu }$l samples are extracted from the same capsules-in-glycerol suspension prior to being sheared. Each of them is placed on a glass slide for observation under an optical microscope (DMI8, Leica, Microsystems, Germany) with a magnification of 20 (left part of figure 3). The capsule radius ![]() $a$ is determined using ImageJ. In order to guarantee that we observe all the capsules in the drop, we screen the entire slide and move the focal plane to explore in the axial direction. The number of capsules before shearing
$a$ is determined using ImageJ. In order to guarantee that we observe all the capsules in the drop, we screen the entire slide and move the focal plane to explore in the axial direction. The number of capsules before shearing ![]() $N_{{before}}$ is calculated after having grouped the capsules over 6
$N_{{before}}$ is calculated after having grouped the capsules over 6 ![]() $\mathrm {\mu }$m size intervals. Figure 4 shows that the number and size distribution of capsules are almost identical for the three samples, validating the hypothesis of homogeneity within the same capsules-in-glycerol solution. Variations are, however, found from one batch of capsules to another (total number of capsules between 150 and 350). This must be due to the way capsules sediment at the bottom of the Eppendorf tube, before the volume is pipetted.
$\mathrm {\mu }$m size intervals. Figure 4 shows that the number and size distribution of capsules are almost identical for the three samples, validating the hypothesis of homogeneity within the same capsules-in-glycerol solution. Variations are, however, found from one batch of capsules to another (total number of capsules between 150 and 350). This must be due to the way capsules sediment at the bottom of the Eppendorf tube, before the volume is pipetted.

Figure 3. Schematic describing the method of characterization of capsule rupture.

Figure 4. Distribution of the radius ![]() $a$ of the microcapsules suspended in the ovalbumin–glycerol solution prior to exposure to shear (capsule suspension viscosity,
$a$ of the microcapsules suspended in the ovalbumin–glycerol solution prior to exposure to shear (capsule suspension viscosity, ![]() $\mu = 0.94$ Pa s). Comparison of the number of capsules
$\mu = 0.94$ Pa s). Comparison of the number of capsules ![]() $N_{{before}}$ measured on three samples of the same suspension and having the same volume (
$N_{{before}}$ measured on three samples of the same suspension and having the same volume (![]() $10\ \mathrm {\mu }$l).
$10\ \mathrm {\mu }$l).
The same procedure is applied on 10 ![]() $\mathrm {\mu }$l samples taken after exposure to shear, varying the shear rate
$\mathrm {\mu }$l samples taken after exposure to shear, varying the shear rate ![]() $\dot {\gamma }$ and exposure time
$\dot {\gamma }$ and exposure time ![]() $t_E$ (right part of figure 3). They are extracted after homogenization of the solution present in the rheometer. We then obtain
$t_E$ (right part of figure 3). They are extracted after homogenization of the solution present in the rheometer. We then obtain ![]() $N_{{after}}$, the number of capsules after shearing. In the perspective of comparing the results from one capsule batch to another, we compute
$N_{{after}}$, the number of capsules after shearing. In the perspective of comparing the results from one capsule batch to another, we compute ![]() $\Delta N =(N_{{before}} - N_{{after}})/N_{{before}}$, the percentage of ruptured capsules for each size interval.
$\Delta N =(N_{{before}} - N_{{after}})/N_{{before}}$, the percentage of ruptured capsules for each size interval.
To estimate the capillary number at rupture ![]() $Ca_{t_{E}}$, we would ideally need to visualize each of the capsules at their instant of rupture, which is not feasible, as it is very unlikely that any capsule will rupture while being in the focal plane of the camera. We have thus decided to rewind the image recording from the end and look for the first capsule with a radius lying in each 6
$Ca_{t_{E}}$, we would ideally need to visualize each of the capsules at their instant of rupture, which is not feasible, as it is very unlikely that any capsule will rupture while being in the focal plane of the camera. We have thus decided to rewind the image recording from the end and look for the first capsule with a radius lying in each 6 ![]() $\mathrm {\mu }$m radius interval. Using the identification method of § 2.4, we then determine its capillary number, and assume that it is equal to
$\mathrm {\mu }$m radius interval. Using the identification method of § 2.4, we then determine its capillary number, and assume that it is equal to ![]() $Ca_{t_{E}}$. By estimating
$Ca_{t_{E}}$. By estimating ![]() $Ca_{t_{E}}$ just prior to rupture, we obtain a fair estimate of the capsule rupture properties, the limit of rupture being most likely underestimated. This provides a safety margin, which will be useful when optimizing capsule design.
$Ca_{t_{E}}$ just prior to rupture, we obtain a fair estimate of the capsule rupture properties, the limit of rupture being most likely underestimated. This provides a safety margin, which will be useful when optimizing capsule design.
3. Results
3.1. Validation of the capsule constitutive law
To evaluate the nonlinear constitutive law that best characterizes the capsule membrane behaviour, we examine how the surface shear modulus ![]() $G_{s}$ varies with deformation. One searches for the constitutive law that provides constant values of
$G_{s}$ varies with deformation. One searches for the constitutive law that provides constant values of ![]() $G_{s}$ irrespective of the deformation level. As we will show in § 3.2.2 that the mechanical properties depend strongly on the capsule size and exposure time, one needs to select capsules within a small size range and a small exposure time to do the inverse analysis. The rheometry data, shown in figure 5 as a function of the Taylor parameter, provide the values of
$G_{s}$ irrespective of the deformation level. As we will show in § 3.2.2 that the mechanical properties depend strongly on the capsule size and exposure time, one needs to select capsules within a small size range and a small exposure time to do the inverse analysis. The rheometry data, shown in figure 5 as a function of the Taylor parameter, provide the values of ![]() $G_{s}$, obtained for capsule radii in the range 30–
$G_{s}$, obtained for capsule radii in the range 30–![]() $40\ \mathrm {\mu }$m and an exposure time
$40\ \mathrm {\mu }$m and an exposure time ![]() $t_E < 2$ min. The inverse analysis has been done for two membrane constitutive laws: the NH law and the GH law. The
$t_E < 2$ min. The inverse analysis has been done for two membrane constitutive laws: the NH law and the GH law. The ![]() $G_{s}$ values estimated with the GH law tend to monotonically decrease with deformation. Those estimated with the NH law, however, remain approximately constant with a mean value of
$G_{s}$ values estimated with the GH law tend to monotonically decrease with deformation. Those estimated with the NH law, however, remain approximately constant with a mean value of ![]() $0.034 \pm 0.003$ N m
$0.034 \pm 0.003$ N m![]() $^{-1}$, making it a good fit for the ovalbumin membrane. We retrieve the same law as Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021) and Chu et al. (Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011).
$^{-1}$, making it a good fit for the ovalbumin membrane. We retrieve the same law as Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021) and Chu et al. (Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011).

Figure 5. Values of the surface shear modulus ![]() $G_{s}$ determined on capsules with an exposure time
$G_{s}$ determined on capsules with an exposure time ![]() $t_E < 2$ min and a radius in the range
$t_E < 2$ min and a radius in the range ![]() $30\ \mathrm {\mu } {\rm m}\leq a \leq 40\ \mathrm {\mu }$m. They tend to decrease with the capsule deformation
$30\ \mathrm {\mu } {\rm m}\leq a \leq 40\ \mathrm {\mu }$m. They tend to decrease with the capsule deformation ![]() $D_{12}$ when fitted with the GH law, but remain constant with the NH law. This proves that the ovalbumin capsule membrane has a strain-softening behaviour following the NH law. The smaller variations of
$D_{12}$ when fitted with the GH law, but remain constant with the NH law. This proves that the ovalbumin capsule membrane has a strain-softening behaviour following the NH law. The smaller variations of ![]() $G_{s}$ values observed for
$G_{s}$ values observed for ![]() $D_{12} < 0.2$ can be explained by the sparcity of experimental results in this region.
$D_{12} < 0.2$ can be explained by the sparcity of experimental results in this region.
3.2. Capsule damage
3.2.1. Typical results for the time evolution of the surface shear modulus  $G_s$
$G_s$
We select a typical experiment conducted on a microcapsule suspension subjected to a shear rate ![]() $\dot {\gamma } = 150$ s
$\dot {\gamma } = 150$ s![]() $^{-1}$ (
$^{-1}$ (![]() $\mu =0.703$ Pa s,
$\mu =0.703$ Pa s, ![]() $T=18\,^{\circ }$C) to illustrate how capsule properties evolve over time. We first extract the capsules having a size between 30 and
$T=18\,^{\circ }$C) to illustrate how capsule properties evolve over time. We first extract the capsules having a size between 30 and ![]() $40\ \mathrm {\mu }$m from the images and determine the values of the apparent membrane surface shear modulus
$40\ \mathrm {\mu }$m from the images and determine the values of the apparent membrane surface shear modulus ![]() $G_s$ obtained with the identification method (§ 2.4). Figure 6(a) shows the evolution of
$G_s$ obtained with the identification method (§ 2.4). Figure 6(a) shows the evolution of ![]() $G_s$ with the exposure time
$G_s$ with the exposure time ![]() $t_E$. The surface shear modulus remains constant over the first minutes and then decreases reaching a lower plateau value following a sigmoidal regression law. Some data dispersion is observed, but it remains of the order of 20 % thanks to the fact that we have shown the results for capsules within a small range in size. We associate the decrease in material rigidity to damage, which is characterized by the gradual occurrence of irreversible phenomena affecting the material ability to resist to stress.
$t_E$. The surface shear modulus remains constant over the first minutes and then decreases reaching a lower plateau value following a sigmoidal regression law. Some data dispersion is observed, but it remains of the order of 20 % thanks to the fact that we have shown the results for capsules within a small range in size. We associate the decrease in material rigidity to damage, which is characterized by the gradual occurrence of irreversible phenomena affecting the material ability to resist to stress.

Figure 6. Evolution of ![]() $G_{s}$ as a function of the exposure time to shear
$G_{s}$ as a function of the exposure time to shear ![]() $t_{E}$ (
$t_{E}$ (![]() $\dot {\gamma }=150$ s
$\dot {\gamma }=150$ s![]() $^{-1}$,
$^{-1}$, ![]() $\mu =0.703$ Pa s,
$\mu =0.703$ Pa s, ![]() $T=18\,^{\circ }$C) for (a) capsules of size
$T=18\,^{\circ }$C) for (a) capsules of size ![]() $30\ \mathrm {\mu } {\rm m} \le a\le 40\ \mathrm {\mu }$m and (b) capsules of size
$30\ \mathrm {\mu } {\rm m} \le a\le 40\ \mathrm {\mu }$m and (b) capsules of size ![]() $55\ \mathrm {\mu } {\rm m}\le a \le 65\ \mathrm {\mu }$m.
$55\ \mathrm {\mu } {\rm m}\le a \le 65\ \mathrm {\mu }$m.
The values of ![]() $G_s$ are also shown in figure 6(b) for capsules having a radius between 55 and
$G_s$ are also shown in figure 6(b) for capsules having a radius between 55 and ![]() $65\ \mathrm {\mu }$m, in order to illustrate the effect of size. The mechanical resistance of the intact capsules (i.e. for an exposure time
$65\ \mathrm {\mu }$m, in order to illustrate the effect of size. The mechanical resistance of the intact capsules (i.e. for an exposure time ![]() $t_E=0$) are four times higher than those measured on the 35
$t_E=0$) are four times higher than those measured on the 35 ![]() $\mathrm {\mu }$m capsules. Such a dependence on the capsule size is consistent with what was previously shown by Gubspun et al. (Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Leonetti, Leclerc, Edwards-Lévy and Salsac2016) for cross-linked serum albumin microcapsules deformed in a microfluidic straight channel. The surface shear modulus then decreases following a sigmoidal curve like for the
$\mathrm {\mu }$m capsules. Such a dependence on the capsule size is consistent with what was previously shown by Gubspun et al. (Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Leonetti, Leclerc, Edwards-Lévy and Salsac2016) for cross-linked serum albumin microcapsules deformed in a microfluidic straight channel. The surface shear modulus then decreases following a sigmoidal curve like for the ![]() $35\, \mathrm {\mu } {\rm m}$ capsules, and it tends likewise towards a plateau value that is half the initial value.
$35\, \mathrm {\mu } {\rm m}$ capsules, and it tends likewise towards a plateau value that is half the initial value.
Having detailed some typical measurement results, we hereafter present the combined effects of the shear rate ![]() $\dot {\gamma }$, capsule size
$\dot {\gamma }$, capsule size ![]() $a$ and exposure time to shear
$a$ and exposure time to shear ![]() $t_{E}$.
$t_{E}$.
3.2.2. Effect of the capsule size and exposure time to shear  $t_{E}$
$t_{E}$
A large series of experiments have been conducted varying the shear rate from 40 to 350 s![]() $^{-1}$. The suspension viscosity is measured by the rheometer to vary between 0.45 and 0.9 Pa s. We determine the deformed profiles of the capsules that have crossed the focal plane of the camera over 10 min of exposure. We identify the initial size and current surface shear modulus for each of them following the method described in § 2.4. The values of
$^{-1}$. The suspension viscosity is measured by the rheometer to vary between 0.45 and 0.9 Pa s. We determine the deformed profiles of the capsules that have crossed the focal plane of the camera over 10 min of exposure. We identify the initial size and current surface shear modulus for each of them following the method described in § 2.4. The values of ![]() $G_s$ are provided in figure 7 as a function of the initial capsule size
$G_s$ are provided in figure 7 as a function of the initial capsule size ![]() $a$ and shear rate
$a$ and shear rate ![]() $\dot {\gamma }$, by splitting the time of the experiment (and thus exposure time
$\dot {\gamma }$, by splitting the time of the experiment (and thus exposure time ![]() $t_E$) in 2 minute intervals. Each data point on the graphs represents an individual capsule.
$t_E$) in 2 minute intervals. Each data point on the graphs represents an individual capsule.

Figure 7. Evolution of ![]() $G_{s}$ as a function of the capsule size for different exposure times
$G_{s}$ as a function of the capsule size for different exposure times ![]() $t_{E}$: (a)
$t_{E}$: (a) ![]() $t_{E}<2$ min, (b)
$t_{E}<2$ min, (b) ![]() $2\,{\rm min}\le t_{E}<4$ min, (c)
$2\,{\rm min}\le t_{E}<4$ min, (c) ![]() $4\,{\rm min}\le t_{E}<6$ min, (d)
$4\,{\rm min}\le t_{E}<6$ min, (d) ![]() $6\,{\rm min}\le t_{E}<8$ min, (e)
$6\,{\rm min}\le t_{E}<8$ min, (e) ![]() $8\,{\rm min}\le t_{E} \le 10$ min.
$8\,{\rm min}\le t_{E} \le 10$ min.
Figure 7 shows a large dependence of ![]() $G_s$ on the capsule size. For
$G_s$ on the capsule size. For ![]() $t_E < 2$ min,
$t_E < 2$ min, ![]() $G_s$ indeed varies between 0.03 N m
$G_s$ indeed varies between 0.03 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a<40\ \mathrm {\mu }$m and 0.51 N m
$a<40\ \mathrm {\mu }$m and 0.51 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a>220\ \mathrm {\mu }$m following a sigmoidal trend (figure 7a). When the capsules are produced at 2400 r.p.m., the initial sizes of the observed capsules are predominantly between 30 and 100
$a>220\ \mathrm {\mu }$m following a sigmoidal trend (figure 7a). When the capsules are produced at 2400 r.p.m., the initial sizes of the observed capsules are predominantly between 30 and 100 ![]() $\mathrm {\mu }$m, only a few capsules being found in the range
$\mathrm {\mu }$m, only a few capsules being found in the range ![]() $100\unicode{x2013}150\ \mathrm {\mu }$m. We have thus also generated capsule batches at 1400 r.p.m. to find the higher plateau of the sigmoidal curve. When the capsules are intact (
$100\unicode{x2013}150\ \mathrm {\mu }$m. We have thus also generated capsule batches at 1400 r.p.m. to find the higher plateau of the sigmoidal curve. When the capsules are intact (![]() $t_E < 2$ min), the
$t_E < 2$ min), the ![]() $G_s$ values plateau at 0.51 N m
$G_s$ values plateau at 0.51 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a>220\ \mathrm {\mu }$m.
$a>220\ \mathrm {\mu }$m.
The sigmoidal trend remains valid over the subsequent time intervals. The occurrence of damage is, however, visible through the decrease in ![]() $G_s$ of the higher plateau of the sigmoidal and its shift towards lower values of capsule size: 0.4 N m
$G_s$ of the higher plateau of the sigmoidal and its shift towards lower values of capsule size: 0.4 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a > 175\ \mathrm {\mu }$m (figure 7b), 0.25 N m
$a > 175\ \mathrm {\mu }$m (figure 7b), 0.25 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a > 150\ \mathrm {\mu }$m (figure 7c), 0.16 N m
$a > 150\ \mathrm {\mu }$m (figure 7c), 0.16 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a > 130\ \mathrm {\mu }$m (figure 7d) and 0.11 N m
$a > 130\ \mathrm {\mu }$m (figure 7d) and 0.11 N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a > 115\ \mathrm {\mu }$m (figure 7e).
$a > 115\ \mathrm {\mu }$m (figure 7e).
3.3. Capsule rupture
3.3.1. Example of results on capsule rupture
In figure 8, we first give evidence of the occurrence of breakup in the same case as in figure 6 (![]() $\dot {\gamma }=150$ s
$\dot {\gamma }=150$ s![]() $^{-1}$,
$^{-1}$, ![]() $\mu =0.703$ Pa s,
$\mu =0.703$ Pa s, ![]() $T=18\,^{\circ }$C,
$T=18\,^{\circ }$C, ![]() $t_E = 10$ min). The histogram (figure 8a) provides the values of the number of capsules present before (
$t_E = 10$ min). The histogram (figure 8a) provides the values of the number of capsules present before (![]() $N_{{before}}$) and after (
$N_{{before}}$) and after (![]() $N_{{after}}$) exposure to shear as a function of the capsule size
$N_{{after}}$) exposure to shear as a function of the capsule size ![]() $a$. An effect of the exposure to shear is observed for capsules of size
$a$. An effect of the exposure to shear is observed for capsules of size ![]() $25\ \mathrm {\mu }$m and above. We compute the percentage of ruptured capsules
$25\ \mathrm {\mu }$m and above. We compute the percentage of ruptured capsules ![]() $\Delta N =( N_{{before}} - N_{{after}})/N_{{before}}$ to quantify the probability of rupture. It increases with the capsule radius until reaching the value of 100 % for radii greater than
$\Delta N =( N_{{before}} - N_{{after}})/N_{{before}}$ to quantify the probability of rupture. It increases with the capsule radius until reaching the value of 100 % for radii greater than ![]() $80\ \mathrm {\mu }$m (figure 8b). All the capsules above
$80\ \mathrm {\mu }$m (figure 8b). All the capsules above ![]() $80\ \mathrm {\mu }$m are thus broken, and those below
$80\ \mathrm {\mu }$m are thus broken, and those below ![]() $25\ \mathrm {\mu }$m remain intact, which does not exclude the occurrence of damage processes. Following the work of Le Goff et al. (Reference Le Goff, Kaoui, Kurzawa, Haszon and Salsac2017), we have fitted the experimental points with a Weibull law and found a good fit. The increase of
$25\ \mathrm {\mu }$m remain intact, which does not exclude the occurrence of damage processes. Following the work of Le Goff et al. (Reference Le Goff, Kaoui, Kurzawa, Haszon and Salsac2017), we have fitted the experimental points with a Weibull law and found a good fit. The increase of ![]() $\Delta N$ with size indicates that the larger the radius, the higher the probability of rupture and the kinetics of crack propagation.
$\Delta N$ with size indicates that the larger the radius, the higher the probability of rupture and the kinetics of crack propagation.

Figure 8. Size dependency of the number of capsules before and after exposure to shear for the experiment of figure 6: (a) capsule number distribution; (b) percentage of ruptured capsules ![]() $\Delta N$ fitted with a Weibull law (left axis); Taylor parameter at rupture
$\Delta N$ fitted with a Weibull law (left axis); Taylor parameter at rupture ![]() $D_{12t_{E}}$ (right axis).
$D_{12t_{E}}$ (right axis).
Figure 8(b) also shows the evolution of the Taylor parameter at rupture ![]() $D_{12t_{E}}$, and that it is strongly correlated with
$D_{12t_{E}}$, and that it is strongly correlated with ![]() $\Delta N$. When studying rupture, it can also be of interest to know the corresponding values of the global deformation
$\Delta N$. When studying rupture, it can also be of interest to know the corresponding values of the global deformation ![]() $\varLambda = S/(4{\rm \pi} a^2)$, where
$\varLambda = S/(4{\rm \pi} a^2)$, where ![]() $S$ is approximated by
$S$ is approximated by ![]() $4{\rm \pi} ({((L_{1} L_{2})^p + (L_{1} L_{3})^p + (L_{2} L_{3})^p)}/{3})^{1/p}$ (
$4{\rm \pi} ({((L_{1} L_{2})^p + (L_{1} L_{3})^p + (L_{2} L_{3})^p)}/{3})^{1/p}$ ( ![]() $p=1.6$). This parameter, ratio of the current to initial capsule surfaces, increases with
$p=1.6$). This parameter, ratio of the current to initial capsule surfaces, increases with ![]() $D_{12t_{E}}$ and reaches 1.19 when
$D_{12t_{E}}$ and reaches 1.19 when ![]() $\Delta N$ is approximately 100 %. This shows that rupture occurs when the capsule membrane is subjected to large deformation.
$\Delta N$ is approximately 100 %. This shows that rupture occurs when the capsule membrane is subjected to large deformation.
3.3.2. Characterization of parameters affecting the percentage of rupture
We now further investigate how the percentage of ruptured capsules depends on the experimental parameters for the capsules fabricated at 2400 r.p.m. (capsule radius between 20 and ![]() $120\ \mathrm {\mu }$m). Figure 9 provides the values of
$120\ \mathrm {\mu }$m). Figure 9 provides the values of ![]() $\Delta N$ (through the colour code) as a function of the exposure time
$\Delta N$ (through the colour code) as a function of the exposure time ![]() $t_E$ and of the capillary number at rupture
$t_E$ and of the capillary number at rupture ![]() $Ca_{t_{E}}$, the capillary number classically governing capsule dynamics (Grandmaison et al. Reference Grandmaison, Brancherie and Salsac2021). They increase with
$Ca_{t_{E}}$, the capillary number classically governing capsule dynamics (Grandmaison et al. Reference Grandmaison, Brancherie and Salsac2021). They increase with ![]() $Ca_{t_{E}}$ following a Weibull law like that shown in figure 8(b) on the effect of size. But, contrary to what could have been expected, an effect of the values of shear rate is observed: for instance, the higher
$Ca_{t_{E}}$ following a Weibull law like that shown in figure 8(b) on the effect of size. But, contrary to what could have been expected, an effect of the values of shear rate is observed: for instance, the higher ![]() $\dot {\gamma }$, the lower the value
$\dot {\gamma }$, the lower the value ![]() $Ca_{t_{E}}(\Delta N>90\,\%$) for which all the capsules are broken. This value of
$Ca_{t_{E}}(\Delta N>90\,\%$) for which all the capsules are broken. This value of ![]() $Ca_{t_{E}}$ also decreases with the exposure time, the dependency being stronger at low
$Ca_{t_{E}}$ also decreases with the exposure time, the dependency being stronger at low ![]() $\dot {\gamma }$ (e.g.
$\dot {\gamma }$ (e.g. ![]() $\dot {\gamma }=100$ s
$\dot {\gamma }=100$ s![]() $^{-1}$). This could indicate a potential influence of the loading speed on the capsule membrane properties, which could modify the alignment of the membrane inner connections created during reticulation. It could also be due to fatigue phenomena, the number of cycles, to which the capsule is subjected to, decreasing as
$^{-1}$). This could indicate a potential influence of the loading speed on the capsule membrane properties, which could modify the alignment of the membrane inner connections created during reticulation. It could also be due to fatigue phenomena, the number of cycles, to which the capsule is subjected to, decreasing as ![]() $\dot {\gamma }$ decreases.
$\dot {\gamma }$ decreases.

Figure 9. Dependency of the percentage of capsule rupture on the capillary number at rupture ![]() $Ca_{t_{E}}$, shear rate
$Ca_{t_{E}}$, shear rate ![]() $\dot {\gamma }$ and exposure time
$\dot {\gamma }$ and exposure time ![]() $t_E$: (a)
$t_E$: (a) ![]() $t_{E}=5$ min, (b)
$t_{E}=5$ min, (b) ![]() $t_{E}=10$ min, (c)
$t_{E}=10$ min, (c) ![]() $t_{E}=15$ min, (d)
$t_{E}=15$ min, (d) ![]() $t_{E}=20$ min.
$t_{E}=20$ min.
4. Discussion and conclusion
We have conducted microrheometric experiments subjecting microcapsules to simple shear flow using a counter-rotating rheometer, with the objective to study the occurrence of damage and rupture on the capsule membrane. We have followed the time evolution of damage by acquiring the deformed profiles that the capsules take under the hydrodynamic forces.
We have used the deformation predicted by a numerical FSI model to determine the instantaneous capillary number and the initial radius from the experimental results (Wang et al. Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021). We have thus identified the initial radius ![]() $a$ and surface shear modulus
$a$ and surface shear modulus ![]() $G_{s}$ for the capsules that crossed the steady shear plane. We have used, for the comparison, numerical results based on the NH constitutive law, which had previously allowed us to obtain a good fit for ovalbumin microcapsules (Wang et al. Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021). The results first reveal that the membrane elastic properties depend on the capsule radius, the surface shear modulus increasing with the capsule size following a sigmoidal law. The surface shear modulus, however, also depends strongly on time and decreases with the exposure time over which the microcapsules are subjected to shear. Indeed, the surface shear modulus starts to decrease after 2 min of shearing and tends towards a plateau value. This decrease in
$G_{s}$ for the capsules that crossed the steady shear plane. We have used, for the comparison, numerical results based on the NH constitutive law, which had previously allowed us to obtain a good fit for ovalbumin microcapsules (Wang et al. Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021). The results first reveal that the membrane elastic properties depend on the capsule radius, the surface shear modulus increasing with the capsule size following a sigmoidal law. The surface shear modulus, however, also depends strongly on time and decreases with the exposure time over which the microcapsules are subjected to shear. Indeed, the surface shear modulus starts to decrease after 2 min of shearing and tends towards a plateau value. This decrease in ![]() $G_{s}$ is attributed to membrane damage.
$G_{s}$ is attributed to membrane damage.
We have then studied the occurrence of rupture (which causes the capsule disintegration), varying the shear rate to which the capsules are subjected and the exposure time to shear. We have assessed the capsule number and size within a ![]() $10\ \mathrm {\mu }$l sample before and after exposure to shear and estimated the probability of rupture as the normalized difference in capsule number for
$10\ \mathrm {\mu }$l sample before and after exposure to shear and estimated the probability of rupture as the normalized difference in capsule number for ![]() $6\ \mathrm {\mu }$m size intervals. The results show that the larger the capsule, the larger the capsule deformation, and thus the higher the probability of rupture, and that rupture is dictated not only by the capillary number at rupture but also by the exposure time to shear and shear rate. The shear rate indeed impacts the rate at which capsule damage occurs and the risk of brittle rupture due to local stress concentrations.
$6\ \mathrm {\mu }$m size intervals. The results show that the larger the capsule, the larger the capsule deformation, and thus the higher the probability of rupture, and that rupture is dictated not only by the capillary number at rupture but also by the exposure time to shear and shear rate. The shear rate indeed impacts the rate at which capsule damage occurs and the risk of brittle rupture due to local stress concentrations.
No comparison of the present results on damage to the literature is possible, as it is the first time that damage per se is estimated. Previous studies have provided values of surface shear modulus without considering that the exposure time could affect the results due to potential apparition of damage. Keeping this limitation in mind, we can still do a tentative comparison of our results at small exposure times (<2 min) to those of the literature. Wang et al. (Reference Wang, Merlo, Dupont, Salsac and Barthès-Biesel2021) determined the surface shear modulus of 10 % ovalbumin microcapsules of 30–![]() $46\ \mathrm {\mu }$m in radii and found a value of
$46\ \mathrm {\mu }$m in radii and found a value of ![]() $G_{s}=0.043 \pm 0.004$ N m
$G_{s}=0.043 \pm 0.004$ N m![]() $^{-1}$ when flowing the capsules in a microfluidic straight channel, which is close to the value they found placing the capsules in a counter-rotating rheometer (
$^{-1}$ when flowing the capsules in a microfluidic straight channel, which is close to the value they found placing the capsules in a counter-rotating rheometer (![]() $G_{s}=0.039 \pm 0.01$ N m
$G_{s}=0.039 \pm 0.01$ N m![]() $^{-1}$). These results are consistent with our own observations (
$^{-1}$). These results are consistent with our own observations (![]() $G_{s}=0.036 \pm 0.014$ N m
$G_{s}=0.036 \pm 0.014$ N m![]() $^{-1}$), but are lower by a factor of two than those of Chu et al. (Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011), who had measured
$^{-1}$), but are lower by a factor of two than those of Chu et al. (Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011), who had measured ![]() $G_{s}=0.072 \pm 0.019$ N m
$G_{s}=0.072 \pm 0.019$ N m![]() $^{-1}$. Our results are also in line with those of Gubspun et al. (Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Leonetti, Leclerc, Edwards-Lévy and Salsac2016), their 15 % HSA microcapsules having
$^{-1}$. Our results are also in line with those of Gubspun et al. (Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Leonetti, Leclerc, Edwards-Lévy and Salsac2016), their 15 % HSA microcapsules having ![]() $G_s \in [0.12, 0.3]$ N m
$G_s \in [0.12, 0.3]$ N m![]() $^{-1}$ for
$^{-1}$ for ![]() $a \in [50, 70]\ \mathrm {\mu }$m, which is close to our values (
$a \in [50, 70]\ \mathrm {\mu }$m, which is close to our values (![]() $G_s \in [0.1, 0.2]$ N m
$G_s \in [0.1, 0.2]$ N m![]() $^{-1}$ in this size range). Similarly to them, we find a sigmoidal dependence of the capsule mechanical resistance on size.
$^{-1}$ in this size range). Similarly to them, we find a sigmoidal dependence of the capsule mechanical resistance on size.
Contrary to Chang & Olbricht (Reference Chang and Olbricht1993), Husmann et al. (Reference Husmann, Rehage, Dhenin and Barthès-Biesel2005) and Koleva & Rehage (Reference Koleva and Rehage2012), we have not been able to follow individual microcapsules over sufficient time periods. We have therefore devised a method to estimate the chance of rupture on an entire capsule population. We have found that the probability of rupture follows a Weibull distribution, which aligns with Le Goff et al. (Reference Le Goff, Kaoui, Kurzawa, Haszon and Salsac2017) findings. The large datasets of experimental results presently collected now have to be translated into phenomenological constitutive laws of damage and rupture.
The advantage of this study is to open the way to the follow-up of capsule batches and the optimization of their design. It could have significant implications in areas such as pharmaceuticals, food processing and cosmetics, where capsule stability and integrity are crucial to ensure product quality.
Funding
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. ERC-2017-COG772191 – MultiphysMicroCaps).
Declaration of interests
The authors report no conflict of interest.