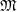Hostname: page-component-857557d7f7-fn92c Total loading time: 0 Render date: 2025-12-08T11:33:05.078Z Has data issue: false hasContentIssue false
  • English
  • Français

$R_\textrm{e}$. II. Understanding IC 3475 galaxy type (including ultra-diffuse galaxy) structural scaling relations

Published online by Cambridge University Press:  21 October 2025

Alister W. Graham Open the ORCID record for Alister W. Graham [Opens in a new window]
Alister W. Graham*
Affiliation:
Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, VIC, Australia
*
Email: AGraham@swin.edu.au
Rights & Permissions [Opens in a new window]

Abstract

It is explained why relatively gas-poor ultra-diffuse galaxies (UDGs), a subset of IC 3475 galaxy types, do not have unexpectedly large sizes but large sizes that are in line with expectations from the curved size-luminosity relation defined by brighter early-type galaxies (ETGs). These UDGs extend the faint end of the (absolute magnitude, $\mathfrak{M}$)-log(Sérsic index, n) and $\mathfrak{M}$-(central surface brightness, $\mu_\textrm{0}$) relations defined by ETGs, leading to the large effective half-light radii, $R_\textrm{e}$, in these UDGs. It is detailed how the scatter in $\mu_\textrm{0}$, at a given $\mathfrak{M}$, relates to variations in the galaxies’ values of n and effective surface brightness, $\mu_\textrm{e}$. These variations map into changes in $R_\textrm{e}$ and produce the scatter about the $\mathfrak{M}$-$R_\textrm{e}$ relation at fixed $\mathfrak{M}$. Similarly, the scatter in $\mathfrak{M}$, at fixed $\mu_\textrm{0}$ and n, can be mapped into changes in $R_\textrm{e}$. The suggestion that there may be two types of relatively gas-poor UDGs appears ill-founded, arising from the scatter about the $\mathfrak{M}$-$\mu_\textrm{0}$ relation. The increased scatter about the faint end of the $\mathfrak{M}$-$R_\textrm{e}$ relation and the smaller scatter about $\mathfrak{M}$-(isophotal radii, $R_\textrm{iso}$) relations are explained. Artificial and potentially misleading size-luminosity relations for UDGs are also addressed. Finally, expected trends with dynamical mass and evolutionary pathways towards relatively gas-rich galaxies are briefly discussed. Hopefully, the understanding presented here will prove helpful for interpreting the many low surface brightness galaxies that the Legacy Survey of Space and Time will detect.

Keywords

Galaxies: dwarfgalaxies: elliptical and lenticular, cDgalaxies: formationgalaxies: fundamental parametersgalaxies: structure

Information

Type
Research Article
Information
Publications of the Astronomical Society of Australia , Volume 42 , 2025 , e155
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (https://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is used to distribute the re-used or adapted article and the original article is properly cited. The written permission of Cambridge University Press must be obtained prior to any commercial use.
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Astronomical Society of Australia

1. Introduction

Reaves (Reference Reaves1956) introduced the IC 3475 (I) galaxy type after he analysed the large, low surface brightness (LSB) dwarf-mass early-type galaxy (ETG) IC 3475. Many such I-type galaxies, e.g. DDO 28 and DDO 29, were subsequently identified in the David Dunlap Observatory dwarf galaxy catalogue once distances became available (Fisher & Tully Reference Fisher and Tully1975), and many other IC 3475 types were reported (e.g. Reaves Reference Reaves1983; Sandage & Binggeli Reference Sandage and Binggeli1984; Vigroux et al. Reference Vigroux, Thuan, Vader and Lachieze-Rey1986). As noted by Reaves (Reference Reaves1983), these large LSB galaxies were designated by the letter ‘I’, encapsulating both ‘IC 3475’ and, to a degree, also their (weakly) ‘Irregular’ structure.Footnote a Sandage & Binggeli (Reference Sandage and Binggeli1984) noted that IC 3475 was a bright example of the huge [LSB] systems in their catalogue (Binggeli, Sandage, & Tammann Reference Binggeli, Sandage and Tammann1985). In recent years, a subset of these large LSB galaxies has been referred to as ultra-diffuse galaxies (UDGs: Koda et al. Reference Koda, Yagi, Yamanoi and Komiyama2015; van Dokkum et al. Reference van Dokkum, Abraham, Merritt, Zhang, Geha and Conroy2015) if their major-axis effective half-light radius, $R_\textrm{e,maj}$ , is larger than $\approx$ 1.5 kpc and their central B- or g-band surface brightness, $\mu_\textrm{0}$ , fainter than $\approx 24$ mag arcsec $^{-2}$ .

This study demonstrates how IC 3475 type galaxies and thus UDGs appear as the natural extension of dwarf ETGs (dETGs) in key photometric scaling diagrams, with the dETGs known to be the extension of ordinary high surface brightness ETGs (Graham & Guzmán Reference Graham and Guzmán2003; Graham Reference Graham2019, hereafter Paper I). UDGs, dETGs, and ordinary ETGs follow the same log-linear (absolute magnitude, $\mathfrak{M}$ )-log (Sérsic index, n) and $\mathfrak{M}$ -(central surface brightness, $\mu_\textrm{0}$ ) relations. In Graham (Reference Graham2023), it was mentioned that the UDGs may also follow the same curved size-luminosity relation (Graham et al. Reference Graham, Merritt, Moore and Diemand2006) as (dwarf and ordinary) ETGs, extending the sequence to fainter magnitudes (lower stellar masses) and larger $R_\textrm{e}$ sizes. Here, this prediction is shown and quantified.

Figure 1. Absolute magnitude versus central surface brightness (Equation (1), panel a), Sérsic index (Equation (2), panel b), and (equivalent axis) effective half-light radius (Equation (4), panel c). The dashed lines in panel a) ensnare roughly the $\pm2\sigma$ scatter about the ETGs, and they have been mapped into panel c). The arrows reveal how a change in absolute magnitude at fixed $\mu_\textrm{0,B}$ and n results in a corresponding change in $R_\textrm{e}$ , simultaneously explaining the low and high levels of scatter at bright and faint absolute magnitudes, respectively. For the curves in panel c), the central surface brightness (and Sérsic index) associated with points E and F (and the lower circle) are the same, but $R_\textrm{e}$ is different because the magnitude is different (see Equation (4)). Here, galaxies from Buzzo et al. (Reference Buzzo2024) and Buzzo et al. (Reference Buzzo2025) are designated UDGs if they have $R_\textrm{e,maj} \ge 1.5$ kpc and $\mu_\textrm{0,g} \ge 24$ mag arcsec $^{-2}$ , otherwise they are designated NUDGes. The ETG sample compiled by Graham & Guzmán (Reference Graham and Guzmán2003, see Section 2) contains a few (6–9) galaxies that would likely be considered UDGs using this definition.

Figure 2. Extension of Figure 1 with the addition of UDG and NUDG data from Buzzo et al. (Reference Buzzo2024) and (Reference Buzzo2025), and a slightly revised $\mathfrak{M}_B$ - $\mu_\textrm{0,B,obs}$ relation (Equation (9)) and thus a slightly revised $\mathfrak{M}_B$ - $R_\textrm{e,eq}$ relation (Equation (10)). The colour-coding tracks the two classes (A=blue filled star, B=red open star) assigned to the UDGs and ‘NUDGes’ by Buzzo et al. (Reference Buzzo2025). The two vertical lines of constant central surface brightness shown in the lower left of panel (a) map into the diagonal lines seen in panel (c), with the arrows in Figure 1c showing how this occurs. This reveals and explains the creation of the misleading size-luminosity relation for UDGs, relative to the ETG population at large.

This connection is crucial for assessing the applicability of suggested UDG formation scenarios, which have included disorganised star formation in gas-rich but quiescent systems (Gerola et al. Reference Gerola, Seiden and Schulman1980; Reaves Reference Reaves1983), or ‘failed’ massive galaxies formed in large dark matter haloes but quenched early, possibly due to feedback or environmental effects (White & Rees Reference White and Rees1978; Dekel & Birnboim Reference Dekel and Birnboim2006; van Dokkum et al. Reference van Dokkum, Abraham, Merritt, Zhang, Geha and Conroy2015). Alternatively, it has been proposed that UDGs may be low-mass dwarf galaxies that expanded through internal processes such as bursty star formation and strong stellar feedback (Larson Reference Larson1974; Dekel & Silk Reference Dekel and Silk1986; Di Cintio et al. Reference Di Cintio, Brook, Dutton, Macciò, Obreja and Dekel2017). Similarly, in dense environments, such as clusters, tidal interactions and ram-pressure stripping (Gunn & Gott Reference Gunn1972) might transform initially compact galaxies into diffuse systems by removing gas and inducing a puffing-up of the stellar distribution (Moore et al. Reference Moore, Katz, Lake, Dressler and Oemler1996; Mayer et al. Reference Mayer, Governato, Colpi, Moore, Quinn, Wadsley, Stadel and Lake2001, Reference Mayer, Mastropietro, Wadsley, Stadel and Moore2006; Yozin & Bekki Reference Yozin and Bekki2015; Carleton et al. Reference Carleton, Errani, Cooper, Kaplinghat, Peñarrubia and Guo2019). Another formation channel suggests that UDGs naturally form in high-spin haloes, leading to extended, LSB galaxies without requiring strong environmental effects (Fall & Efstathiou Reference Fall and Efstathiou1980; Amorisco & Loeb Reference Amorisco and Loeb2016).

Paper I explained how the value of $\mathfrak{M}$ associated with the bend in the size-magnitude relation depends on the arbitrary percentage of light enclosed within the scale radius, which is invariably set at 50 per cent to give $R_\textrm{e}$ . Consequently, this bend does not signify a physical division or unique formation processes operating above and below this magnitude, and care needs to be taken when interpreting slopes and bends in curved size-luminosity diagrams. Additional care is required when the sample selection is based on the galaxies’ central surface brightness, as this can slice the data in such a way that it is distributed nearly orthogonal to the underlying size-magnitude trend defined by the population at large, giving rise to some misleading results. This is addressed within.

Just as there is a continuity in structure between dETGs and ordinary ETGs, no distinct separation exists between IC 3475 type galaxies and UDGs and (dwarf and ordinary) ETGs in the $\mathfrak{M}$ - $R_\textrm{e}$ diagram. Here, UDGs are presented as the natural extension of the ETG sequence to lower luminosities and surface brightnesses. The curved size–luminosity relation, along with consistent trends in Sérsic index and surface brightness, suggests continuity rather than a new class of galaxy. This study reveals the reasons behind the increased scatter observed in the (size, $R_\textrm{e}$ )-luminosity relation at faint magnitudes. Furthermore, given that IC 3475 type galaxies have long been known to display a different behaviour – having smaller radii and less scatter – in diagrams using isophotal radii (e.g. Binggeli & Cameron Reference Binggeli and Cameron1991, their Figures 1 and 2, with $-20 \lt \mathfrak{M}_B \lt -12$ mag), the $\mathfrak{M}$ - $R_\textrm{iso}$ relation and its smaller leval of scatter is also presented and explained. Finally, the scatter about the above key scaling relations is used to explain trends in dynamical mass for dwarf galaxies, including UDGs.

The data used for this paper are described in Section 2, and the analysis is performed in Section 3, where the key results are presented. A review is provided in Section 4, along with a select discussion of some immediate and important implications and a recognition that the ETG sequence is one of mergers, from primaeval galaxies to wet-merger-built dust-rich S0 galaxies and dry-merger-built E galaxies.

2. Data

Two compilations of galaxy structural parameters have been used, one for (dwarf and ordinary) ETGs (Graham & Guzmán Reference Graham and Guzmán2003) and one for UDGs (Buzzo et al. Reference Buzzo2025).

The ETG sample comprises the alleged (dwarf and ordinary) elliptical galaxies from Caon et al. (Reference Caon, Capaccioli and D’Onofrio1993) and D’Onofrio et al. (Reference D’Onofrio, Capaccioli and Caon1994), Faber et al. (Reference Faber1997, no Sérsic indices), Binggeli & Jerjen (Reference Binggeli and Jerjen1998), Stiavelli et al. (Reference Stiavelli, Miller, Ferguson, Mack, Whitmore and Lotz2001, $R_\textrm{e}$ derived from the other Sérsic parameters), and the Coma cluster dwarf elliptical galaxies modelled in Graham & Guzmán (Reference Graham and Guzmán2003). The parameters displayed in this work pertain to the B-band on the Vega magnitude system and include the galaxies’ absolute magnitude, $\mathfrak{M}_B$ , and the central surface brightness, $\mu_\textrm{0,B}$ . For simplicity, no subscript B is assigned to the Sérsic index n or the effective half-light radii, $R_\textrm{e}$ , although, due to radial colour gradients, these parameters are slightly dependent on the filter used (e.g. Kelvin et al. Reference Kelvin2012; Häußler et al. Reference Häußler2013; Kennedy et al. Reference Kennedy2016 a,b).

The UDG sample consists of 36 ‘nearly UDGs’ (NUDGes)Footnote b presented in Buzzo et al. (Reference Buzzo2025), see also Marleau et al. (Reference Marleau2024), plus their remodelled data for another 28 UDGs previously studied by Buzzo et al. (Reference Buzzo2022), along with data for another 59 UDGs taken from Buzzo et al. (Reference Buzzo2024), see also Marleau et al. (Reference Marleau2021). The NUDGes have slightly smaller sizes and slightly brighter central surface brightnesses than UDGs and are regarded as mainly dwarf elliptical (dE) galaxies (Buzzo et al. Reference Buzzo2025). This UDG and NUDG data compilation spans stellar masses of $7 \lesssim \log(M_{\star}/M_\odot) \lesssim 8.5$ dex, and their g-band (AB) data is used here. These recent works are selected because they not only propogate the idea that UDGs should perhaps be separated from (dwarf and ordinary) ETGs – based on their sizes ( $R_\textrm{e,maj}=1.5$ kpc) and central surface brightnesses $\mu_\textrm{0,g}=24$ mag arcsec $^{-2}$ ) – but because they additionally suggest that there might be two classes of UDGs. While the former suggestion is addressed here by reviewing the extension of the size-luminosity relation to fainter luminosities, the latter development is addressed here by considering the scatter about the size-luminosity relation.

Given that the UDG $(g-z)_\textrm{AB}$ colours in the above works peak at $\approx 0.9$ –1 mag, this data is expected to have $(g-i)_\textrm{AB} \approx0.8\pm0.1$ and $(B-V)_\textrm{Vega} \approx 0.6\pm0.1$ . The g-band (AB) magnitudes are transformed into B-band (Vega) magnitudes using $B_\textrm{AB}=g_\textrm{AB} + 0.35$ (Jester et al. Reference Jester2005; Jordi, Grebel, & Ammon Reference Jordi, Grebel and Ammon2006), which should vary by only $\pm0.04$ mag due to the colour spread in the data, and then using $B_\textrm{Vega} = B_\textrm{AB}+0.12$ (Fukugita et al. Reference Fukugita, Ichikawa, Gunn, Doi, Shimasaku and Schneider1996, their Table 8). The UDGs and NUDGes were separated into one of two classes (A or B) by Buzzo et al. (Reference Buzzo2025, see their section 4.3), based on an array of galaxy and associated globular cluster system properties.Footnote c Key factors in separating galaxies into Class A and Class B turned out to be the offset from the classical dwarf galaxy mass–metallicity relation (e.g. Kirby et al. Reference Kirby, Cohen, Guhathakurta, Cheng, Bullock and Gallazzi2013), the number of associated globular clusters, and the axial ratio. Class A systems broadly resemble traditional dwarf ETGs, with structural and chemical properties consistent with formation through internal processes like supernova-driven feedback (Dekel & Silk Reference Dekel and Silk1986), supporting a ‘puffy dwarf’ origin (Di Cintio et al. Reference Di Cintio, Brook, Dutton, Macciò, Obreja and Dekel2017). In contrast, Class B galaxies show signs of early quenching of stars and high globular cluster richness, suggestive of more massive haloes that failed to form substantial stellar populations, consistent with a failed galaxy scenario (van Dokkum et al. Reference van Dokkum, Abraham, Merritt, Zhang, Geha and Conroy2015). Just five of the three dozen NUDGes were assigned to Class B.

As with the ETG sample, the most distant UDGs are located in the Coma cluster, which is $\sim$ 100 Mpc distant. Given this proximity, the cosmological correctionsFootnote d are minor, and only the $(1+z)^4$ surface brightness dimming correction is applied. Some dETGs, particularly in the field or low-density environments, can harbor gas and display recent or ongoing star formation (e.g. Chilingarian Reference Chilingarian2009; Grossi et al. Reference Grossi2009; Koleva et al. Reference Koleva, de Rijcke, Prugniel, Zeilinger and Michielsen2009; Oosterloo et al. Reference Oosterloo2010; Seo & Ann Reference Seo and Ann2023). Field and isolated UDGs often retain significant HI gas reservoirs and show evidence of ongoing or recent star formation, though at low efficiencies (Kado-Fong et al. Reference Kado-Fong, Greene, Huang and Goulding2022; Karunakaran et al. Reference Karunakaran, Motiwala, Spekkens, Zaritsky, Donnerstein and Dey2024). This is not surprising given they often have an irregular or knotty structure. These systems likely represent the actively evolving, gas-retaining counterparts of the quiescent Class A UDGs. In this context, Class A would span a continuum from still-forming, diffuse dwarfs in the field to faded, quiescent analogues in higher-density environments.

3. Analysis and relations

The data points in the left and central panel of Figure 1 reproduce the B-band (absolute magnitude, $\mathfrak{M}_B$ )–(central surface brightness, $\mu_\textrm{0,B}$ ) and $\mathfrak{M}_B$ –(Sérsic index, n) diagrams from Graham & Guzmán (Reference Graham and Guzmán2003, their Figure 9). The two empirical relations shown here are

(1) \begin{align}\mathfrak{M}_B = 0.63\mu_\textrm{0,B,obs} - 28.7, \sigma=0.8\, \textrm{mag} \end{align}

and

(2) \begin{align} \mathfrak{M}_B = -10.0\log(n) - 14.0, \end{align}

where $\sigma$ denotes the 1-sigma scatter in the $\mathfrak{M}_B$ -direction about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation. These slopes and intercepts include a slight (5 per cent) variation on the values reported by Graham & Guzmán (Reference Graham and Guzmán2003), yielding a slightly more symmetrical scatter of the ETG data about these lines. This will, nonetheless, soon be revisited once the IC 3475 galaxy types are added. The subscript ‘obs’ has been added to $\mu_\textrm{0,B}$ to differentiate this observed surface brightness from an upcoming adjusted value. Galaxies from Buzzo et al. (Reference Buzzo2024, Reference Buzzo2025) with $R_\textrm{e,maj} \ge 1.5$ kpc and central surface brightnesses $\mu_\textrm{0,g} \ge 24$ mag arcsec $^{-2}$ are designated as UDGs in Figure 1, while the remaining galaxies from these two works are denoted NUDGes.

Figure 3. Variant of Figure 2 showing $\mu_\textrm{0,B,adj}$ (see Equations (11) and (12)) in panel a) and $R_\textrm{e,maj}$ (see Equation (13)) in panel c). Symbols have the same meaning as in Figure 2. At fixed $\mathfrak{M}_B$ , the (horizontal) scatter $\delta\mu_\textrm{0,B}$ is directly related to the scatter $\delta\log(n)$ (panel b) and $\delta\mu_\textrm{e,B}$ (see Figure 4).

The curved line in Figure 1c is not a fit to the data; it is the solution for Sersic (Reference Sersic1968a) $R^{1/n}$ light profiles (Capaccioli Reference Capaccioli, Corwin and Bottinelli1989; Graham & Driver Reference Graham and Driver2005) based on Equations (1) and (2). This curve pertains to the radius equivalent to the geometric mean of the minor and major axis, $R_\textrm{e,eq} = \sqrt{R_\textrm{e,maj} R_\textrm{e,min}}$ , and stems from the analytical expression

(3) \begin{align}\mathfrak{M} = \langle \mu \rangle_\textrm{e,abs} - 2.5\log\big(2\pi R_\textrm{e,eq}^2\big)- 36.57, \end{align}

with $\langle \mu \rangle_\textrm{e,abs}$ the absolute mean effective surface brightness in units of mag arcsec $^{-2}$ and $R_\textrm{e,eq}$ in kpc (see Graham & Driver Reference Graham and Driver2005, their Equation 12). As such, $\langle \mu \rangle_\textrm{e,abs} = \langle \mu \rangle_\textrm{e} -10\log(1+z)$ . Equation (3) can be re-expressed as

(4) \begin{align}\log R_\textrm{e,eq} \textrm{(kpc)} = (\langle \mu \rangle_\textrm{e,B,abs} - \mathfrak{M}_B)/5.0-7.713 .\end{align}

The difference between $\langle \mu \rangle_\textrm{e}$ and $\mu_\textrm{0}$ (and $\langle \mu \rangle_\textrm{e,abs}$ and $\mu_\textrm{0,abs}$ ) is a (mathematical, not empirical) function of the Sérsic model, given by

(5) \begin{align}\mu (R)=\mu_\textrm{e}+\frac{2.5b_n}{\ln(10)}\left[\left(R/R_\textrm{e}\right)^{1/n}-1\right],\end{align}

and, in particular, the Sérsic index n, such that

(6) \begin{align}\langle \mu \rangle_\textrm{e} = \mu_\textrm{0} + 2.5b/\ln(10) - 2.5 \log[f(n)], \end{align}

with the effective surface brightness at $R_\textrm{e}$ denoted $\mu_\textrm{e}$ and

(7) \begin{align} \mu_\textrm{0} + 2.5b/\ln(10) = \mu_\textrm{e} \end{align}

(see Equations 7, 8 and 9 from Graham & Driver Reference Graham and Driver2005). One additionally has that

(8) \begin{align}f(n) = \frac{n \textrm{e}^b \Gamma(2n)}{b^{2n}},\end{align}

with b a function of n obtained by solving $\gamma(2n,b) / \Gamma(2n) = 1/2$ , and $\Gamma$ is the complete gamma function.

Therefore, knowing how n and $\mu_\textrm{0,B}$ vary with $\mathfrak{M}_B$ (Equations 1 and 2), one knows how $\langle \mu \rangle_\textrm{e,B}$ (and $\mu_\textrm{e}$ ) varies with $\mathfrak{M}_B$ , and hence, $R_\textrm{e,eq}$ can be derived as a function of $\mathfrak{M}_B$ . This derivation is shown by the central, solid curve in Figure 1c, explaining the trend in the data toward larger sizes at lower luminosities. Although this curved size-luminosity relation was presented in Graham et al. (Reference Graham, Merritt, Moore and Diemand2006) and Graham & Worley (Reference Graham and Worley2008), it is extended here to fainter magnitudes to show better the expected increase in size of fainter ETGs/UDGs. In this panel, and all others bearing the inset text ‘derived (not a fit)’, the curves are not a fit to the data but are derived from empirical fits to other galaxy parameters coupled with the Sérsic model.

The dashed lines in Figure 1a roughly capture the $\pm2\sigma$ scatter. These lines have been combined with Equation (2) to produce the dashed curves in Figure 1c. They are insightful because they show how, for a fixed n and $\mu_\textrm{0,B}$ , changes in luminosity are met by changes in size. This combination results in shifts roughly along the size-luminosity relation for galaxies with high Sérsic indices but perpendicular to it for galaxies with low Sérsic indices. At faint magnitudes, where the Sérsic index is low, a 2 $\sigma$ change in magnitude of 1.6 mag (or roughly a factor of 4 in luminosity) requires a roughly factor of 2 change in $R_\textrm{e,eq}$ . This explains the broadening of the size-luminosity relation for ETGs at low masses and is shown by the labels E and F in Figure 1.

Figure 2 introduces the UDGs, which appear to be the extension of (ordinary and dwarf) ETGs to fainter magnitudes. This is most immediately obvious in the $\mathfrak{M}_B$ – $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ – $\log(n)$ diagrams due to the roughly log-linear behaviour of these relations before the onset of core depletion in the massive elliptical galaxies built from gas-poor major mergers. The colour-coding assigned to the UDGs and ‘NUDGes’ shows the two classes (A=blue filled star, B=red open star) assigned by Buzzo et al. (Reference Buzzo2025).

The following slightly revised version of Equation (1) better matches the fuller ensemble of data shown in Figure 2a:

(9) \begin{align}\mathfrak{M}_B = 0.59\mu_\textrm{0,B,obs} - 28.1, \sigma=0.8\, \textrm{mag}. \end{align}

By feeding this empirical relation into Equations (4) and (6), one derives the following relation shown by the black curve in Figure 2c.

(10) \begin{align}\log R_\textrm{e,eq} \textrm{(kpc)} = 0.139\mathfrak{M}_B - 0.5\log[f(n)] + 0.217b + 1.812,\end{align}

with $n=10^{-(14.0+\mathfrak{M}_B)/10.0}$ coming from Equation (2).

It is noted that a sample collection gap is evident in Figure 2a at $\mathfrak{M}_B\gt-12$ mag and $\mu_\textrm{0,B} \lt 24$ mag arcsec $^{-2}$ , leading to a small triangular cutout that can be seen to propagate into Figure 2c (and Figure 3c). This creates the illusion of a trend for the UDGs and NUDGes in the $\mathfrak{M}_B$ - $R_\textrm{e}$ diagram that is roughly perpendicular to the actual trend for UDGs/NUDGes and (dwarf and ordinary) ETGs. That is, Figure 2c reveals how the arbitrary sample selection of the UDGs yields an artificial and misleading size-luminosity relation.

3.1. Major axis radii

If one uses the major axis radius, $R_\textrm{e,maj}$ ( $= R_\textrm{e,eq}\sqrt{b/a}$ , where $b/a$ is the minor-to-major axis ratio), in the size-luminosity diagram, then an adjustment to Figure 2a is required. Due to an increased size, a fainter surface brightness is required to balance the derivation of the magnitude (Equation (3)). The adjusted surface brightness affects $\langle \mu \rangle_\textrm{e}$ and $\mu_\textrm{0}$ equally and is given by

(11) \begin{align} \mu_\textrm{0,B,adj} = \mu_\textrm{0,B,obs} - 2.5\log(b/a). \end{align}

This is similar to a correction for disc galaxies where $b/a \approx cos(i)$ and i is the inclination of the disc such that $i=0$ denotes alignment of the galaxy’s polar axis with our line of sight, i.e. face-on. Although rotation and the presence of faint spiral patterns and bars in some dwarf galaxies reveal their disc-like nature, most are thought to be triaxial, and the brighter dETGs with regular isophotes are less triaxial and slightly more spherical (e.g. Sung et al. Reference Sung, Han, Ryden, Patterson, Chun, Kim, Lee and Kim1998). Basically, the rebalancing performed through Equation (3) accounts for the larger radii ( $R_\textrm{e,maj} \gt R_\textrm{e,eq}$ ) encapturing a fainter ‘mean effective surface brightness’, which is implemented here by making the central surface brightness fainter via Equation (11).

Figure 4. An example of how variations/offsets in $\mu_\textrm{e}$ and n for a surface brightness profile will result in the offset to $\mu_\textrm{0}$ . For a given $\mathfrak{M}$ , with an associated $\mu_\textrm{0}$ and n from the $\mathfrak{M}$ - $\mu_\textrm{0}$ and $\mathfrak{M}$ - $\log(n)$ relations, the horizontal offsets $\delta\mu_\textrm{0}$ seen in Figures 1a–3a are attributable to the offsets $\delta\mu_\textrm{e}$ and $\delta\log(n)$ .

Observed axis ratios for the dETG sample in Binggeli & Jerjen (Reference Binggeli and Jerjen1998) have come from the values reported by Binggeli & Cameron (Reference Binggeli and Cameron1993), while for the remaining UDG/NUDG and (dwarf and ordinary) ETG samples, they have come from the reported ratios or ellipticities in their respective papers. The result is shown in Figure 3a, along with the slightly revised line

(12) \begin{align}\mathfrak{M}_B = 0.59\mu_\textrm{0,B,adj} - 28.4, \sigma=0.8\, \textrm{mag}, \end{align}

and thus a new expression for the $\mathfrak{M}_B$ - $R_\textrm{e,maj}$ curve (Figure 3c) that differs slightly from Equation (10) shown in Figure 2c. This new equation for the major axis $R_\textrm{e}$ is given by

(13) \begin{align}\log R_\textrm{e,maj} \textrm{(kpc)} = 0.139\mathfrak{M}_B - 0.5\log[f(n)] + 0.217b +1.914.\end{align}

3.2. Min(d)ing the scatter

Understanding the intrinsic scatter in the scaling relations is beneficial for interpreting where UDGs and NUDGes sit relative to the brighter population of ETGs. Before assessing how LSB systems deviate from or extend these relations, it is helpful to examine the causes and implications of scatter across the full mass spectrum. In particular, the high-mass end of ETGs offers key insight into how systematic trends and physical diversity influence relation slopes and scatter, concepts equally important when analysing the faint, diffuse regime occupied by UDGs.

Dry major mergers between ETGs containing supermassive black holes can scour away the core of the newly-formed galaxy, producing the abrupt turn in the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation at $\mathfrak{M}_B\approx-20.5$ mag (Graham & Guzmán Reference Graham and Guzmán2003) rather than at the previously suggested $\mathfrak{M}_B\approx-18$ mag (Kormendy Reference Kormendy1985; Faber et al. Reference Faber1997, see their discussion of their Figure 4c based on the nucleated and stripped galaxy M32). Graham & Sahu (Reference Graham and Sahu2023) suggested that extensive scouring from the multiple mergers (aided by captured satellites: Goerdt et al. Reference Goerdt, Moore, Read and Stadel2010; Bonfini et al. Reference Bonfini, Dullo and Graham2015) that build brightest cluster galaxies, typically massive ETGs, leads to such a dramatic redistribution of stars that the galaxy’s reduced central concentration and stellar build-up at larger galactic radii changes the galaxy profile from having an obvious core, and thus a core-Sérsic light profile, to a low-n Sérsic profile that may additionally have an exponential-like envelope (e.g. Seigar et al. Reference Seigar, Graham and Jerjen2007). This transformation was termed ‘galforming’. While this explains large-scale departures of E galaxies at high masses from the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations, the scatter about these relations can be mined for insight into the formation and evolution of ETGs. As displayed in Figure 3, $\delta \mu_\textrm{0,B}$ and $\delta \log(n)$ shall denote the horizontal scatter/offset between the data and the ‘expected’ value (from the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations) at the same magnitude.

One can deduce a lot from coupling the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations with the properties of the 3-parameter Sérsic model used to describe ETG light profiles. The previous section showed how $\mathfrak{M}_B$ , $\mu_\textrm{0,B}$ , and n dictate the value of $R_\textrm{e}$ and $\langle\mu\rangle_\textrm{e,B}$ (and $\mu_\textrm{e,B}$ ). Conversely, $R_\textrm{e}$ , $\mu_\textrm{0,B}$ (or $\langle\mu\rangle_\textrm{e,B}$ or $\mu_\textrm{e,B}$ ), and n yield the value of $\mathfrak{M}_B$ for a given Sérsic light profile. Here, it is revealed how the scatter about the $\mathfrak{M}_B$ - $R_\textrm{e}$ relation can be traced back to the scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation, which is directly related to the galaxies’ variation in both $\mu_\textrm{e,B}$ and n at a given magnitude (see Figure 4).

Equation (3) reveals that, in a sense, a galaxy’s values of $\mathfrak{M}$ and $R_\textrm{e}$ depend on its value of $\langle\mu\rangle_\textrm{e}$ , and Equation (6) shows how $\langle\mu\rangle_\textrm{e}$ depends on $\mu_\textrm{e}$ and n. Therefore, for a given $\mathfrak{M}$ , the value of $R_\textrm{e}$ depends on $\mu_\textrm{e}$ and n. Consequently, at a given $\mathfrak{M}$ , the scatter about the $\mathfrak{M}$ - $R_\textrm{e}$ curve relates to the scatter in $\mu_\textrm{e}$ and n about their median expected value, as traced by the $\mathfrak{M}$ - $\mu_\textrm{e}$ and $\mathfrak{M}$ - $\log(n)$ relations. The latter horizontal scatter is seen in the $\mathfrak{M}$ - $\log(n)$ diagram (Figure 3b), while the former horizontal scatter is displayed in Figure 5.

Figure 5. Effective surface brightness, $\mu_\textrm{e,B}$ , at $R_\textrm{e}$ versus $\mathfrak{M}_B$ . Symbols have the same meaning as in Figure 2. The curve is not a fit but instead a derivation from the $\mathfrak{M}_B$ - $\mu_\textrm{0}$ and $\mathfrak{M}_B$ - $\log(n)$ relations (Equations (2) and (9)).

Figure 6. Breaking down the scatter in the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ diagram for ETGs. Symbols have the same meaning as in Figure 2. At fixed $\mathfrak{M}_B$ , the horizontal scatter $\delta\mu_\textrm{0,B}$ and $\delta\log(n)$ from Figures 2a and 2b are shown against each other in panel (a). The predictable contribution to $\delta\mu_\textrm{0,B}$ arises from offsets in $\log(n)$ and $\mu_\textrm{e,B}$ from their expected values (based on the scaling relations). These are shown in panels (b) and (c), respectively. The different behaviour of the UDGs from the (dwarf and ordinary) ETGs is explained in Section 3.2 and simply reflects their different Sérsic indices.

For each galaxy, with its observed values of $\mathfrak{M}_B$ and n, one additionally has the expected value of n from the $\mathfrak{M}_B$ - $\log(n)$ relation. One can then calculate $\mu_\textrm{0,B} -\mu_\textrm{e,B}$ for each of these two values of n (Equation 7) in order to explore how the difference/offset in the Sérsic index, $\delta \log(n)$ , propagates into a horizontal offset of central surface brightness about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation. The remaining scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation is due to the difference between the expected value of $\mu_\textrm{e,B}$ (based on the expected values of $\mu_\textrm{0,B}$ and n for any $\mathfrak{M}_B$ ) and the observed value of $\mu_\textrm{e,B}$ . These offsets are denoted $\delta \mu_\textrm{e}$ , with an example illustrated in Figure 4 using $n=1$ and $\mu_\textrm{e} = 26$ mag arcsec $^{-2}$ as the ‘expected’ values. From Figure 4, one can envisage how changes to n and $\mu_\textrm{e}$ alter $\mu_\textrm{0}$ .

Figure 6a reveals that, for a given $\mathfrak{M}_B$ , UDGs with a brighter $\mu_\textrm{0,B}$ than ‘expected’ (from the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation) also have a higher value of n (than expected from the $\mathfrak{M}_B$ - $\log(n)$ relation). In contrast, those with a fainter-than-expected value of $\mu_\textrm{0,B}$ have a lower-than-expected value of n for their absolute magnitude. This change in the Sérsic index accounts for some of the horizontal scatter in the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ diagram, as shown in Figure 6b. The offset in $\mu_\textrm{0,B}$ due to the differences between the observed and expected values of n is given by $(2.5/\ln(10))[b_\textrm{obs} - b_\textrm{expected}]$ , with $b\approx 1.9992n-0.3271$ , for $0.5{\lt}n{\lt}10$ (Capaccioli Reference Capaccioli, Corwin and Bottinelli1989). Figure 6b also reveals that, for UDGs with their small Sérsic indices, the offset in the observed value of n from the expected value accounts for about one-third of the UDGs’ offset between the observed value of $\mu_\textrm{0,B}$ and the expected value at that magnitude. For brighter ETGs, with their larger values of n, the difference between the observed and expected value of n accounts for most of their scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation. This is as expected given how the difference between $\mu_\textrm{e}$ and $\mu_\textrm{0}$ in the $R^{1/n}$ model increases roughly linearly with the Sérsic index while, and this is the key, the logarithmic scatter $\delta \log(n)$ about the $\mathfrak{M}_B$ - $\log(n)$ relation does not sufficiently decline as n increases. That is, the horizontal scatter $\delta n$ about the $\mathfrak{M}_B$ - $\log(n)$ relation increases with increasing n.

The difference between the observed value of $\mu_\textrm{e,B}$ and the expected value at each magnitude (see the curve in Figure 5) accounts for the remaining offset of the observed value of $\mu_\textrm{0,B}$ from the expected value of $\mu_\textrm{0,B}$ at that magnitude, i.e. the scatter. This component of the difference in $\mu_\textrm{0,B}$ is shown in Figure 6c, where it can be seen that differences in $\mu_\textrm{e,B}$ dominate the difference in $\mu_\textrm{0,B}$ for the UDGs. For the (brighter) ETGs, the contribution to the scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation stemming from the different $\mu_\textrm{e,B}$ values at a given $\mathfrak{M}_B$ is seen to be sub-dominant to the scatter arising from the difference between their observed and expected Sérsic index.

Figure 7. Variant of Figure 2a, in which the symbol size is now proportional to the ellipticity ( $=1-b/a$ ) such that galaxies that appear round have a small symbol size. In the inset panel, the grey triangles represent 28 UDGs predominantly in clusters, while the pink squares represent 59 UDGs in low-to-moderate density environments. UDGs with high $b/a$ ratios are prevalent in both environments and are thus not a product of the environment. At faint absolute magnitudes, the samples’ $b/a$ ratios are small, possibly a result of sample selection (see the discussion in Section 3.2.1).

In essence, the situation for the UDGs can be summarised as follows. UDGs with $\mu_\textrm{0,B}$ values fainter than expected for their magnitude (based on the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation) and with Sérsic indices smaller than expected (based on the $\mathfrak{M}_B$ - $\log(n)$ relation) will have effective half-light radii that are larger than expected, where ‘expected’ means the value coming from the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations. Equally, UDGs with brighter than expected $\mu_\textrm{0}$ values and larger than expected n values will have smaller than expected $R_\textrm{e}$ values. These shifts (in $R_\textrm{e}$ ) from expectation come on top of the curved $\mathfrak{M}_B$ - $R_\textrm{e}$ relation for ETGs, of which UDGs are a part.

3.2.1. Ellipticity

A factor that could contribute to some of the horizontal scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation is the line-of-sight through the ETGs, with longer sight lines potentially leading to brighter surface brightnesses. It is important to understand that this can arise in two distinct ways. If the (dust-free) ETGs are oblate or disc-like, then those ETGs viewed with a more edge-on orientation will appear to have higher ellipticities and brighter surface brightnesses. As such, one would expect to find a predominance of low $b/a$ galaxies occupying the right-hand side (high surface brightness side) of the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ distribution. If, on the other hand, ETGs are more prolate, with one long axis and two shorter axes, then the sightline depth through these galaxies will be greatest when the long axis aligns with our line-of-sight and the $b/a$ axis ratio is highest. Conversely, their surface brightness will be faintest when they appear most elongated, i.e. higher ellipticity. Figure 7 displays the ellipticity of the ETGs. There is no obvious trend for high-ellipticity galaxies to occupy either the left or right side of the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ distribution.

Cluster dETGs might be vertically-heated discs, which need not have ever hosted a spiral pattern. Should clusters be harassing disc galaxies to make them smaller and more ellipsoidal (Moore et al. Reference Moore, Katz, Lake, Dressler and Oemler1996), then the effect should be greater on the lower mass systems and, thus, there should be a difference between the mean ellipticity of field and cluster UDGs of the same absolute magnitude. Rong et al. (Reference Rong2020) reported that UDGs near the centres of clusters are rounder than those near the outskirts, but those near the outskirts were also fainter, thus convoluting any attribution to an environmental effect because this $\mathfrak{M}$ - $\epsilon$ trend is also seen with UDGs not in clusters (Figure 7).

Buzzo et al. (Reference Buzzo2025) report that the sample of 59 UDGs from Buzzo et al. (Reference Buzzo2024) reside in low-to-moderate density environments, whereas galaxies in clusters heavily dominate the remodelled sample from Buzzo et al. (Reference Buzzo2022). The inset panel in Figure 7 shows the range of observed $b/a$ axis ratios for these two UDG samples. It is informative. There is no clear environmental dependence for this sample. High $b/a$ values are observed in the field and cluster ETGs, ruling out an environmental driver for this sample’s shapes. What is also apparent is that at faint magnitudes, the ratios are low, that is, at faint magnitudes the ellipticity is high. If these are oblate disc-like galaxies at faint magnitudes, then some of this population should have a relatively face-on orientation and high $b/a$ ratio. Given the lack of such detections, it seems plausible that sample selection effects are at play such that at these faint magnitudes, only systems whose surface brightness has been enhanced by an increased line-of-sight depth have made it into the sample. Finally, if ordered rotation had produced oblate discs in the UDGs, impeding their initial gravitational collapse and resulting in larger sizes, then the larger UDGs would be associated with a more elliptical, rather than round, population, which is not observed.

In conclusion, the apparent ellipticity may contribute to some scatter, but it does not produce strong trends in the present $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ diagram. It is, however, noted that the brighter S0 galaxies with rather edge-on discs and thus higher ellipticity may have been filtered from the sample because, in the past, they were more readily identified as disc galaxies rather than elliptical galaxies. Dwarf mass ( $M_{\star},{\mathrm {gal}}/M_{\odot} \approx $ (2-5) $\times10^9$ , $\mathfrak{M}_B \approx -17.5\pm0.5$ mag) ETGs in clusters have the same kinematic properties as those in isolated field environments (Janz et al. Reference Janz, Penny, Graham, Forbes and Davies2017). This further undermines the notion that cluster-related processes have had a strong hand in shaping dETGs, implying that they are born as they are rather than transformed. This was the conclusion reached by Vigroux et al. (Reference Vigroux, Thuan, Vader and Lachieze-Rey1986) in the case of IC 3475.

3.3. Isophotal radii

Following Binggeli & Cameron (Reference Binggeli and Cameron1991), who used ETGs and UDGs from Binggeli et al. (Reference Binggeli, Sandage and Tammann1985), Figure 8 displays the geometric-mean ( $R_\textrm{eq}$ ) isophotal radii where $\mu_\textrm{B}=26$ mag arcsec $^{-2}$ versus the B-band absolute magnitude.Footnote e As shown by Binggeli & Cameron (Reference Binggeli and Cameron1991, their Figure 2, with $-20 \lt \mathfrak{M}_B \lt -12$ mag) and Cellone, Forte, & Geisler (Reference Cellone, Forte and Geisler1994, their Figure 7, with $\mathfrak{M}_B \lt -14.5$ mag), IC 3475 type galaxies have smaller isophotal radii than brighter ETGs. As shown since then, for example, Forbes et al. (Reference Forbes, Lasky, Graham and Spitler2008, their Figure 3) and Schombert & McGaugh (Reference Schombert and McGaugh2014, their Figure 1), and cleverly using (stellar mass)-density profiles (Chamba, Trujillo, & Knapen Reference Chamba, Trujillo and Knapen2020; Trujillo, Chamba, & Knapen Reference Trujillo, Chamba and Knapen2020), the $\mathfrak{M}_B$ -(isophotal radius, $R_\textrm{iso}$ ) relation (Heidmann Reference Heidmann1967, Reference Heidmann1969) has less scatter than the curved $\mathfrak{M}_B$ - $R_{\textrm{e}}$ relation (e.g. Graham et al. Reference Graham, Merritt, Moore and Diemand2006) when using specific outer surface brightness levels. This reduced scatter is explained here for the first time.

Figure 8. Absolute magnitude versus the ‘equivalent axis’ isophotal radius at $\mu_\textrm{B}=26$ mag arcsec $^{-2}$ obtained from each galaxy’s Sérsic profile. The central black curve is derived using Equations (2) and (9), while the outer grey curves denote a $\pm0.125$ dex offset in isophotal radius at fixed magnitude. The two diagonal lines pertain to a fixed B-band central surface brightness of 24 and 25 mag arcsec $^{-2}$ and reveal how $R_\textrm{iso}$ changes if $\mathfrak{M}_B$ changes by up to $\pm$ 1.6 mag while the associated Sérsic index is held fixed (at $n=0.986$ and 0.861). The faint/grey symbols in the lower-left have $\mu_\textrm{0,B} \gt 25$ mag arcsec $^{-2}$ . The outlier in the lower-middle is MATLAS-1408.

First, however, it is shown how the UDGs with $\mu_\textrm{0,B} \gtrsim 25$ mag arcsec $^{-2}$ tend to be impacted by the above isophotal level ( $\mu_\textrm{B}=26$ mag arcsec $^{-2}$ ), which is rather close to their central surface brightness value. This proximity causes some UDGs to scatter to small radii, as shown by the faint/grey symbols in Figure 8. Given that $\mu_\textrm{e}-\mu_\textrm{0}=1.822$ for an $n=1$ profile, one can immediately appreciate how such isophotal radii will be small for galaxies with $\mu_\textrm{0} \gtrsim 25$ mag arcsec $^{-2}$ because these isophotal radii barely sample the galaxy. Furthermore, those UDGs with $\mu_\textrm{0,B} \gt 26$ mag arcsec $^{-2}$ will have a meaningless isophotal radius of zero. Obviously, isophotal levels that are too bright, or stellar mass density levels that are too high, will be problematic. For example, the UDG MATLAS-1302 has $\mu_\textrm{0,B}=28.11$ mag arcsec $^{-2}$ , assuming $B_\textrm{Vega}=g_\textrm{AB}+0.47$ mag. For reference, adopting a B-band stellar mass-to-light ratio of 2.5 gives a central stellar mass surface density of 0.93 $M_\odot$ pc $^{-2}$ for this galaxy. Therefore, a fainter than traditionally-used isophotal level is additionally included below.

Recently, Graham (Reference Graham2024b) has revealed how galaxy mergers have led to the anti-truncation of discs in dust-rich merger-built S0 galaxies and, more generally, to the Sérsicification of massive ETGs. The extended nature of high-n galaxy light profiles at large radii was explained by the superposition of acquired progenitor galaxy ‘discs’ and the accumulation of accreted stellar material and stars flung to large radii. Such mergers, and tidally heated discs or UDGs, can push a galaxy’s outer stellar density below a gas disc’s threshhold density for star formation, thereby requiring rather faint isophotal levels or projected stellar densities to measure their sizes.

Before proceeding, the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations (Equations 9 and 2) are used to create five representative light profiles of ETGs and UDGs with values of $n=0.5$ , 1, 2, 4, and 8. The thick curves in Figure 9 show these profiles, and their $\mu_\textrm{e,B}$ and $R_\textrm{e}$ values are marked with a star. Joining these stars traces out the curved $\mu_\textrm{e,B}$ - $R_\textrm{e}$ relation for ETGs and UDGs. Next, accompanying each of these five light profiles are two offset profiles with the same $\mathfrak{M}_B$ . One has had $\delta\log(n)=0.2$ dex and $\delta\mu_\textrm{e}=-1.5$ mag arcsec $^{-2}$ applied, while the other has had $\delta\log(n)=-0.2$ dex and $\delta\mu_\textrm{e}=+1.5$ mag arcsec $^{-2}$ applied. Their offset values of $\mu_\textrm{e,B}$ and $R_\textrm{e}$ are calculated and marked with open circles. For each of the five cases, one can immediately see that the change to the isophotal radii from these perturbations is smaller than the change to $R_\textrm{e}$ . That is, the scatter at fixed $\mathfrak{M}_B$ about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ (and $\mathfrak{M}_B$ - $\log(n)$ ) relations will create a larger scatter about the $\mathfrak{M}_B$ - $R_\textrm{e}$ relation (Figure 2c) than it will about an $\mathfrak{M}_B$ - $R_\textrm{iso}$ relation (unless the isophotal level is close to the central surface brightness of the light profile, as witnessed in Figure 8).

Figure 9. Five representative B-band light profiles of ETGs with different Sérsic indices are shown (thick solid curves). For each value of n, an associated absolute magnitude and central surface brightness are assigned from Equations (2) and (9), from which the effective surface brightness and radius can then be calculated (Equation (10)). For each profile, the ‘effective’ parameters $\mu_\textrm{e,B}$ and $R_\textrm{e}$ are shown by the stars, and the dashed curve connecting them traces the $\mu_\textrm{e,B}$ - $R_\textrm{e}$ relation for ETGs. While keeping the absolute magnitude fixed, offsets of $\delta \mu_\textrm{e} = \pm1.5$ mag arcsec $^{-2}$ and $\delta\log(n)=\pm0.2$ dex are applied to each profile, thereby generating offsets in $\mu_\textrm{0,B}$ . This produces the dotted and dashed curves, whose $\mu_\textrm{e}$ and $R_\textrm{e}$ values are shown by the open circles. These offset profiles yield slight differences in the isophotal radii relative to the larger changes seen in $R_\textrm{e}$ , provided the chosen isophotal surface brightness is not too close to the light profile’s central surface brightness.

To circumvent the above problem for UDGs that an isophotal limit of $\mu_\textrm{B}=26$ mag (and $\mu_\textrm{B}=27$ –28 mag) causes, the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations have been used to derive the ‘expected’ isophotal radius where $\mu_\textrm{B}=31$ mag arcsec $^{-2}$ for different values of $\mathfrak{M}_B$ . This is shown in Figure 10 by the thick curve. For each galaxy from the data samples, which are overplotted in this figure, their Sérsic parameters have been used to compute the radius where $\mu_\textrm{B}=31$ mag arcsec $^{-2}$ . That is, the calculations assume that the galaxies’ Sérsic profiles can be extrapolated this far. This is a very faint surface brightness level, and where triaxial and disc galaxies actually end is a separate topic (Shull Reference Shull2014; Chamba et al. Reference Chamba, Trujillo and Knapen2022). Additional caveats beyond the scope of the current analysis include departures in the light profiles arising from truncated and anti-truncated discs in some ETGs (Eliche-Moral et al. Reference Eliche-Moral, Borlaff, Beckman and Gutiérrez2015; Graham Reference Graham2024b), tidal debris streams (van Dokkum Reference van Dokkum2005; Janowiecki et al. Reference Janowiecki, Mihos, Harding, Feldmeier, Rudick and Morrison2010; Miró-Carretero et al. Reference Miró-Carretero2024), and cluster light creating envelopes around brightest cluster galaxies (Seigar et al. Reference Seigar, Graham and Jerjen2007; Pierini et al. Reference Pierini, Zibetti, Braglia, Böhringer, Finoguenov, Lynam and Zhang2008). In practice, use of a brighter isophotal level may prove desirable. The Legacy Survey of Space and Time (LSST)Footnote f (Ivezić et al. Reference Ivezić2019) will probe most galaxies to new depths, and the European Space Agency’s ARRAKIHS (Analysis of Resolved Remnants of Accreted galaxies as a Key Instrument for Halo Surveys) missionFootnote g will reach a surface brightness of 31 AB mag arcsec $^{-2}$ (Guzman et al. Reference Guzman2022). Additional upcoming facilities capable of probing the very outskirts of galaxies include the Nancy Grace Roman Space Telescope (NGRST: Spergel et al. Reference Spergel2013; Akeson et al. Reference Akeson2019) and the Extremely Large Telescope (Padovani & Cirasuolo Reference Padovani and Cirasuolo2023).

Figure 10. Absolute magnitude versus the ‘equivalent axis’ isophotal radius at $\mu_\textrm{B}=31$ mag obtained from each galaxy’s Sérsic profile. The central black curve is derived using Equations (2) and (9), while the outer grey curves denote a $\pm0.25$ dex offset in isophotal radius at fixed $\mathfrak{M}_B$ . The two diagonal lines pertain to a fixed B-band central surface brightness of 24 and 27.5 mag arcsec $^{-2}$ and reveal how $R_\textrm{iso}$ changes if $\mathfrak{M}_B$ changes by up to $\pm$ 1.6 mag while the associated Sérsic index is held fixed (at $n=0.986$ and 0.613, respectively).

The slight curvature in the $\mathfrak{M}_B$ - $R_\textrm{iso}$ relations for ETGs has been known for decades, and it remains when using a range of different deprojected (internal) luminosity densities to define ETG sizes (Graham Reference Graham2019, his Figure 11). This is somewhat different to the magnitude- and (stellar-mass)-(isodensity radii) relations involving the stellar edges of thin spiral galaxy discs (e.g. Chamba et al. Reference Chamba, Marcum, Saintonge, Borlaff, Hayes, Le Gouellec, Chojnowski and Fanelli2024, and references therein), and conflating the two may hide key insight. For galaxies with thin discs, such as spiral galaxies, the outer surface brightness is closely tied to the local gas volume density (e.g. from HI or HII), and hence to the star formation threshold. This is because in such systems, the line of sight through the disc is short and well-defined, so the observed surface brightness is a good proxy for the local stellar volume density. In contrast, for ETGs that have triaxial or thick oblate/prolate stellar distributions, the relationship is more complex. The surface brightness in these galaxies represents the integrated light along extended lines of sight through the galaxy’s volume, making it a poor tracer of the local volume density at any given point. To estimate the internal density distribution in these systems, one must perform deprojections (e.g. Ciotti Reference Ciotti1991) – which differ from simple inclination corrections – in order to recover the three-dimensional structure. This has direct implications for UDGs with triaxial shapes: their surface brightness is often a result of geometric projection, and is not indicative of a local stellar density. Therefore, the surface brightness in such systems may not relate to the conditions needed for star formation.

Once again, the scatter in the data about the $\mathfrak{M}_B$ - $R_\textrm{iso}$ curve can be small compared to that of the $\mathfrak{M}_B$ - $R_\textrm{e}$ curve. Such behaviour has been known for decades. As with Figure 2c, two diagonal lines of constant central surface brightness have been added to Figures 8 and 10 to illustrate how the UDG/NUDG sample selection again results in a misleading luminosity-size relation for this sample, at odds with that (the thick curved line) from its parent sample. That is, the sample selection spawns a relation that deviates from the trend defined by the ETG population at large. This same sample selection bias was seen to arise in the luminosity-(effective radius) diagram (Figure 2c). Clearly, considerable care is needed when interpreting $\mathfrak{M}_B$ - $R_\textrm{iso}$ diagrams for UDGs: galaxies defined by an arbitrary slicing of the broader ETG population.

4. Discussion

Recent studies have presented a range of definitions for UDGs, often anchored to structural criteria such as a minimum effective radius (e.g. $R_\textrm{e,maj} \gtrsim 1.5$ –1.7 kpc) and a threshold central surface brightness (e.g. $\mu_\textrm{0,g} \gtrsim 24$ mag arcsec $^{-2}$ ), as originally outlined by van Dokkum et al. (Reference van Dokkum, Abraham, Merritt, Zhang, Geha and Conroy2015) and adopted in similar form by others (e.g. Koda et al. Reference Koda, Yagi, Yamanoi and Komiyama2015; Yagi et al. Reference Yagi, Koda, Komiyama and Yamanoi2016). Additional definitions of UDGs include outliers from linear (Li et al. Reference Li2023) or curved (Lim et al. Reference Lim2020) size–luminosity or surface brightness–luminosity relations. However such definitions can be arbitrary (see Van Nest et al. Reference Van Nest, Munshi, Wright, Tremmel, Brooks, Nagai and Quinn2022) and misleading when applied to a population following a curved trend with intrinsic scatter. Rather than identifying a physically distinct class, many of these criteria capture a portion of the continuous distribution of ETGs in structural parameter space. Therefore, care must be taken when drawing evolutionary conclusions based on classifications that may reflect observational bias or parameter slicing, rather than a genuine bifurcation in formation mechanisms or intrinsic galaxy properties. In passing, it is noted that not all UDGs should be considered ETGs, as a small number of UDGs have spiral structure, particularly among the bluer, gas-rich UDG population in the field and groups (Bothun et al. Reference Bothun, Impey, Malin and Mould1987; Leisman et al. Reference Leisman2017; Román & Trujillo Reference Román and Trujillo2017; Shi et al. Reference Shi2017; Prole et al. Reference Prole2019; Poulain et al. Reference Poulain2021). It is also noted that the galaxy sample used here does not include compact elliptical galaxies like NGC 4486B or M32 – considered to be the denser, more spherical bulge component of stripped disc galaxies (Bekki et al. Reference Bekki, Couch, Drinkwater and Gregg2001; Graham Reference Graham2002)Footnote h –, nor dwarf spheroidal galaxies (Mateo Reference Mateo1998; Martin et al. Reference Martin, de Jong and Rix2008), with their smaller and denser stellar distributions than UDGs. Therefore, their connections to or differences from ETGs and UDGs are not explored here.

4.1. Division of ETGs

The notion that there may be two distinct (dwarf and ordinary) types of ETG was perhaps first raised by Sérsic (Reference Sérsic1968b) upon inspecting the departure of the fainter ETGs from the $\mathfrak{M}_B$ – $R_\textrm{e}$ relation defined by the brighter ETGs. This departure is also seen in the $\mathfrak{M}_B$ – $\langle \mu \rangle_\textrm{e,B}$ diagram (e.g. Sandage et al. Reference Sandage, Binggeli, Tammann, Richter and Binggeli (Garching: ESO)1985, their Figure 3) and the $\mathfrak{M}_B$ – $\mu_\textrm{e}$ diagram (Figure 5). However, as detailed in Paper I, these departures (and departures in all diagrams involving ‘effective’ half-light parameters) arise from the systematically varying – with absolute magnitude – Sersic (Reference Sersic1968a) $R^{1/n}$ nature of their stellar distribution. The suggestion of a third (UDG) type of ETG due to their deviation to increasing sizes at yet fainter magnitudes in the $\mathfrak{M}_B$ – $R_\textrm{e}$ diagram is dispelled here because bends in diagrams involving effective half-light parameters should not be used as a diagnostic tool for galaxy formation. As Paper I explained, the magnitude associated with the ‘bend point’ in diagrams involving ‘effective’ parameters changes with the enclosed fraction of light used to define the ‘effective’ parameters. This voids any physical significance of the bend point in terms of galaxy formation scenarios.

There are, however, subtypes among the ETGs, which has undoubtedly added to the confusion when interpreting scaling relations involving effective half-light parameters. These subtypes are presented in Graham (Reference Graham2023) and encompass primordial/primaeval lenticular (S0) galaxies – including the UDGs at the faint end – that need not have once been spiral galaxies, plus major-merger-built S0 galaxies, which are dust-rich if a spiral galaxy was involved in the collision, ellicular (ES) galaxies with fully embedded discs, and discless elliptical (E) galaxies. Therefore, the dwarf-mass ETGs are not simply small versions of giant S0 or E galaxies in that they represent an earlier stage of evolution. This aspect has likely muddied the waters and given false support to interpretations of a division at $\mathfrak{M}_B \approx -18$ mag based on scaling diagrams involving $\mu_\textrm{e}$ , $\langle \mu \rangle_\textrm{e}$ , and $R_\textrm{e}$ .

The yet further division of UDGs and NUDGes into two classes by Buzzo et al. (Reference Buzzo2025) can be seen in Figure 2. It is immediately apparent that Class B (denoted by the open stars) is, on average, brighter than Class A (denoted by the filled stars). Therefore, the more massive Class B will have, on average, redder colours, given the colour-magnitude relation for dETGs (e.g. de Vaucouleurs & de Vaucouleurs Reference de Vaucouleurs and de Vaucouleurs1991; Forbes et al. Reference Forbes, Lasky, Graham and Spitler2008; Graham Reference Graham2024a). The redder colours will equate to a higher (stellar mass)-to-light ratio, $M_*/L$ , for Class B, given the well-known $M_*/L$ -colour trends (e.g. Bell & de Jong Reference Bell and de Jong2001). Class B will also have higher velocity dispersions, $\sigma$ , given the luminosity- $\sigma$ relation for dETGs (e.g. Davies et al. Reference Davies, Efstathiou, Fall, Illingworth and Schechter1983; Toloba et al. Reference Toloba2014). Furthermore, Figure 2 reveals why the galaxies in Class B have larger sizes and, therefore, higher inferred total masses when using $\sigma^2R_\textrm{e}/G$ as a proxy for dynamical mass. Consequently, Class B will have more globular clusters, given how this scales with the inferred halo mass (Spitler & Forbes Reference Spitler and Forbes2009), modulo the increased scatter at low-masses (Forbes et al. Reference Forbes, Read, Gieles and Collins2018). To summarise, a division among UDGs (and NUDGes) indirectly but heavily based on their distribution about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation will explain the offsets between the mean value of many parameters for Class A and B. This need not imply a second uniquely different origin story (e.g. ‘puffy dwarfs’: Errani, Penarrubia, & Tormen Reference Errani, Penarrubia and Tormen2015; Conselice Reference Conselice2018) for LSB ETGs unless one is to attribute the scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation to different formation scenarios.

The question of whether studies have identified two classes of UDG on either side of the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation or whether the effect of intrinsic scatter on the scaling relations has been missed appears to have been answered in Section 3. A greater level of spin, i.e. ordered rotation, does not appear to correlate with the larger UDGs. Given that galaxies with a higher spin would be supported by rotation, in addition to velocity dispersion, one would expect them to be relatively flatter systems. However, the larger UDGs, which reside on the fainter central surface brightness side of the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation, do not have smaller axis ratios (Figure 7). Equally, if there is a population of UDGs with edge-on discs yielding brightened $\mu_\textrm{0}$ values, Figure 2c (and 3c) require them to have smaller radii (both $R_\textrm{eq}$ and $R_\textrm{maj}$ ) than the other UDGs of the same magnitude. This is not observed; that is, they are not spun out to larger radii. What makes the first option even more problematic is that the scenario to preferentially place those UDGs assumed to have ‘puffed up’ after gas loss from stellar winds or ram pressure stripping (Saito Reference Saito1979; Dekel & Silk Reference Dekel and Silk1986; Vader Reference Vader1986; Di Cintio et al. Reference Di Cintio, Brook, Dutton, Macciò, Obreja and Dekel2017) on one side of the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation seems unlikely to preferentially operate on the higher mass UDGs that are more capable of retaining their gas. One might expect that the proposed processes to ‘puff up’ some UDGs should preferentially operate on fainter, lower mass systems, yet the brighter, higher mass UDGs have the larger sizes. This undermines the relevance of this proposed additional formation scenario. Furthermore, the observed size-luminosity trend is readily explained because brighter galaxies require larger sizes (Equation 4) for a given Sérsic profile with fixed values of $\mu_\textrm{0,B}$ and n. That is, no recourse to different formation scenarios is required to explain the increased sizes or many of the trends observed in UDG properties that can be traced back to their differing mass.

Figure 11. Given $\mathfrak{M}_B \propto \sigma^2$ for dETGs (Davies et al. Reference Davies, Efstathiou, Fall, Illingworth and Schechter1983; Graham Reference Graham, Oswalt and Keel2013, and references therein), one can appreciate how the scatter about the $\mathfrak{M}_B$ - $R_\textrm{e}$ relation, shown here, results in different dynamical masses ( $\sigma^2R_\textrm{e}/G$ ), and in turn, mass-dependent trends, that are subject to arbitrary divisions of the dETG (including UDG) sample. The green dots are ETGs not in the UDG sample but with $\mathfrak{M}_B \ge -15$ mag. As in Figure 1c, the curves are not a fit to the data but are derived from fits to other empirical relations coupled with the Sérsic $R^{1/n}$ function.

Due to the $\sim$ 3.2 mag of vertical scatter ( $\pm2\sigma$ ) about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ relation, selecting a sample of LSB ETGs with $24 \lt \mu_\textrm{0,B} \lt 27.5$ mag arcsec $^{-2}$ results in an $\mathfrak{M}_B$ - $R_\textrm{e}$ distribution that is roughly orthogonal to the wholesale $\mathfrak{M}_B$ - $R_\textrm{e}$ correlation for ETGs (Figures 2c and 3c). This behaviour is also somewhat true for the $\mathfrak{M}_B$ - $R_\textrm{iso}$ relation (Figure 10). As Sung et al. (Reference Sung, Han, Ryden, Patterson, Chun, Kim, Lee and Kim1998) noted, these misleading trends of brighter luminosities and larger sizes for samples with (a small range in) low central surface brightness had previously been used to separate LSB dwarf galaxies from blue compact dwarf galaxies.

As seen, faint galaxies with fainter surface brightnesses than other galaxies of the same faint magnitude have larger radii than those of the same faint magnitude. What causes this is unclear, although it is noted that those with larger radii also have smaller Sérsic indices. Rather than subsequently being puffed up after formation, these large galaxies may initially form this way. The ETG sequence may well be a primordial and merger-built sequence representing the long side of the TriangalFootnote i (Graham Reference Graham2023), encapsulating primaeval galaxies (UDG/IC 3475, dS0, dE), merger-built S0 galaxies, and multiple-merger-built E galaxies, with mass and Sérsic index increasing through mergers. This notion will be detailed further in a follow-up paper involving kinematical information. While there are several facets and intricacies to this problem, a broad overview is presented in Figure 11. It shows how the arbitrary and artificial division of LSB galaxies and regular-size dwarf-mass galaxies will result in a different average dynamical mass for each subdivision. The brighter UDGs have higher velocity dispersions due to the $\mathfrak{M}_B$ - $\sigma$ relation, and those with larger $R_\textrm{e}$ values will have bigger dynamical massses when using $\sigma^2R_\textrm{e}/G$ as a total mass indicator, thereby explaining why the dynamical masses of UDG samples correlates with the richness of their globular cluster system (Spitler & Forbes Reference Spitler and Forbes2009). However, they all belong to the ETG population with a continuous range of properties. Intrinsic scatter about the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ -n scaling relations will be addressed in terms of dark matter fractions in a follow-up paper.

Although Amorisco & Loeb (Reference Amorisco and Loeb2016) did not explore if their model for creating UDGs with larger $R_\textrm{e}$ due to a larger angular momentum reproduces the $\mathfrak{M}_B$ - $\log(n)$ relation for ETGs.Footnote j their conclusion that UDGs need not be shaped by their environment and that they are the natural extension of ordinary and dwarf ETGs agrees with this manuscript’s alternate analysis of the situation and sample in hand. The combination of lower n and fainter $\mu_\textrm{0,B}$ for a given absolute magnitude will result in a larger $R_\textrm{e}$ (Section 3). This differs somewhat from the statement by Amorisco & Loeb (Reference Amorisco and Loeb2016) that ‘the UDG population represents the tail of galaxies formed in dwarf-sized haloes with higher-than-average angular momentum’. If true, this would necessitate that, at fixed $\mathfrak{M}_B$ , the Sérsic index is lower (higher) for UDGs with higher (lower) angular momentum. This notion will be pursued in a follow-up paper.

4.2. Might some UDGs be (precursors to) discs?

The stellar discs in many local high surface brightness (HSB) ETGs (e.g. Capaccioli Reference Capaccioli, Jarvis and Terndrup1990; Rix & White Reference Rix and White1990) went overlooked for decades, with Graham et al. (Reference Graham, Colless, Busarello, Zaggia and Longo1998) concluding that the number of (discless) E galaxies is much lower than previously thought. This finding supported the view that low-luminosityFootnote k ETGs are S0 galaxies (van den Bergh Reference van den Bergh1990). With increased numbers of kinematic maps, it is now known that among galaxies that are more massive than $\sim10^9$ M $_\odot$ , true pressure-supported E galaxies are only found at the high mass end ( $\gtrsim 10^{11}$ M $_\odot$ : Emsellem et al. Reference Emsellem2011; Krajnović et al. Reference Krajnović2013). These systems are built from the merger and summation of many disc galaxies (Graham Reference Graham2024b), as required to erase the ordered orbital angular momentum.

Based on the distribution of ellipticities in galaxies deemed, from visual inspection, to be dE rather than dS0 or Im, it was reported (Sandage & Shaw Reference Sandage and Shaw1980; Sandage et al. Reference Sandage, Binggeli, Tammann, Richter and Binggeli (Garching: ESO)1985) that they are not discs but rather true elliptical systems. This view has been pervasive but was partly challenged by Ryden & Terndrup (Reference Ryden and Terndrup1994), who reported a greater flattening than previously recognised. Binggeli & Popescu (Reference Binggeli and Popescu1995) subsequently reported consistency among the ellipticity distributions of normal (non-nucleated) dEs, dS0s, late spirals (Sdm - Sms), smooth irregulars (Ims), and clumpy irregulars (Blue Compact Dwarfs) and a different distribution for nucleated dwarfs and a sample of giant ETGs containing ordinary S0 and E galaxies. For cluster UDGs, Mancera Piña et al. (Reference Mancera Piña, Aguerri, Peletier, Venhola, Trager and Choque Challapa2019a) report $\lt b/a\gt=0.67$ with a 2 $\sigma$ scatter (not to be confused with the uncertainty on the mean) of $\approx\pm0.2$ resembling their expected distribution for thick discs. More specifically, for UDGs projected within their clusters’ $R_\textrm{200}$ radius, they observe $\lt b/a\gt\approx 0.72\pm0.02$ if $R_\textrm{e,maj}\lesssim 3.5$ kpc, and more discy shapes ( $\lt b/a\gt\approx 0.5$ ) for the truly giant LSB galaxies not abundant in the present manuscript’s sample. Based on the $q \equiv b/a$ ratios in Lim et al. (Reference Lim2020, their Appendix B.1 and B.2) for 44 UDGs in the Coma cluster, they observe a distribution from 0.3 to 1, consistent with that of dETGs in the Virgo and Fornax clusters. They interpret this as evidence of triaxial or spheroidal shapes rather than preferentially edge-on discs, which would have a flat distribution ranging from the disc thickness to 1. While not disagreeing with this, it is remarked that given how the prevalence of discs – by which it is meant a substantial, somewhat flattenned, rotating component – was missed in many ordinary HSB ETGs for decades, it would not be surprising if some are still missed in large LSB galaxies.

As with some ordinary ETGs, some LSB dwarf ETGs reveal their disc nature by displaying bars or spiral patterns (e.g. Jerjen, Kalnajs, & Binggeli Reference Jerjen, Kalnajs and Binggeli2000; Barazza, Binggeli, & Jerjen Reference Barazza, Binggeli and Jerjen2002; Graham, Jerjen, & Guzmán Reference Graham, Jerjen and Guzmán2003b). Initially considered something of a novelty, the significance of these discoveries went somewhat over-looked as it was not appreciated how widespread the dS0 rather than dE population was, although, at that time, it was starting to be discovered that rotation in dwarf ETGs is common (Pedraz et al. Reference Pedraz, Gorgas, Cardiel, Sánchez-Blázquez and Guzmán2002; Geha, Guhathakurta, & van der Marel Reference Geha, Guhathakurta and van der Marel2003; Toloba et al. Reference Toloba2009). Rotational dominance over velocity dispersion has also been observed in the stellar kinematics of some UDGs (Buttitta et al. Reference Buttitta2025). The HI gas, when present, is also known to rotate in UDGs (e.g. Leisman et al. Reference Leisman2017), although at a slower than expected pace for some (Mancera Piña et al. Reference Mancera Piña2019b, 2020). Another reason why some UDGs are likely to be disc-like rather than spheroidal is that the internal (not projected) stellar luminosity density profile derived by deprojecting the Sérsic $R^{1/n}$ light profile leads to spheroids with holes in the middle if $n\lt0.5$ .

Given the declining bulge-to-disc stellar-mass ratio in ETGs with declining bulge stellar masses down to at least $2\times10^9$ M $_\odot$ ( $\mathfrak{M}_B\approx-$ 16 mag: Graham Reference Graham2023, his Figure A2), the continuity in the structural scaling relations shown here implies that UDGs might also be disc-like galaxies. Indeed, IC 3475 has a faint bar-like structure (Vigroux et al. Reference Vigroux, Thuan, Vader and Lachieze-Rey1986; Knezek, Sembach, & Gallagher Reference Knezek, Sembach and Gallagher1999) and HI rotation ( $W_{20}=114$ km s $^{-1}$ : Huchtmeier & Richter Reference Huchtmeier and Richter1989), revealing its possible disc nature.Footnote l These latter two studies struggled to identify what IC 3475 might have evolved from, rejecting the proposition that it is a disc-stripped dwarf spiral galaxy. More recently, the UDG NGVSUDG-A11 has been found to display a faint spiral pattern in its stellar distribution (Lim et al. Reference Lim2020).

The rather common IC 3475 types (Reaves Reference Reaves1983) may include dS0 galaxies with some knotty regions, with some displaying mild irregularities without apparent dust lanes or clear spiral structure. Once the irregularities and knots disperse or settle to the galaxy centre via dynamical friction – such sinking is more efficient in the brighter dwarf galaxies with their higher-n light profile and thus steeper gravitational potentials within $R_\textrm{e}$ (Terzić & Graham Reference Terzić and Graham2005) – they will resemble the so-called dE or nucleated dE,N systems. These need not be flat discs but thick (hot) discs that are somewhat rotationally supported structures, similar to the exponential components seen in HSB ETG light profiles.

4.3. Further musings

Explanations, whether through observation, theory, or simulation, for the $\mathfrak{M}$ - $\mu_\textrm{0}$ and $\mathfrak{M}$ - $\log(n)$ relations for ETGs would be welcome. For the low-n ETGs with faint central surface brightnesses, including the UDGs presented thus far, it is speculated here that they are somewhat primordial rather than a transformed population. They may have grown onto the $\mathfrak{M}_B$ - $\mu_\textrm{0,B}$ and $\mathfrak{M}_B$ - $\log(n)$ relations, with secondary processes (along with measurement error and arguably some disc presence and inclination effects) adding further scatter to these relations, beyond that arising from the randomness of the accretion and merger assembly that built the UDGs and ETGs.

If the growth results in a sufficient amount of high angular momentum gas accumulating and cooling in a disc, it may lead to knotty star formation, Irregular galaxies, and the formation of spiral structures. This progression in galaxy evolution is captured by the ‘Triangal’ evolutionary schema for HSB galaxies (Graham Reference Graham2023), with major ‘wet’ (gas-rich) mergers of spiral galaxies building bulges and creating massive dust-rich S0 galaxies, thereby returning spiral galaxies to the ETG classification. Subsequent major mergers further erase the ordered angular momentum of stellar discs and disc-like structures to build the elliptical galaxies with their greater central concentration of stars within the effective half light radius. ETGs can also collide with themselves to migrate along the ‘red sequence’, with major ’dry’ (gas-poor) mergers involving supermassive black holes leading to elliptical galaxies with core-Sérsic profiles (Begelman, Blandford, & Rees Reference Begelman, Blandford and Rees1980; Graham et al. Reference Graham, Erwin, Trujillo and Asensio Ramos2003a). This behaviour of accretion- and merger-driven galaxy evolution is apparent in the colour-magnitude diagram (Graham Reference Graham2024a) for HSB galaxies, including dETGs, and in the (stellar mass)-(star formation rate) diagram (Graham et al. Reference Graham, Jarrett and Cluver2024). Such speciation is supported by the distribution of galaxy types in the (black hole)-bulge mass scaling diagram (Graham Reference Graham2023), which illustrates how bulges and black holes grow in mass in a monotonic fashion.

In the past, S0 galaxies likely evolved into spiral galaxies when sufficient fuel was available and able to cool and form stars. Today, S0 galaxies generally remain S0 galaxies if their HI gas disc is either stable or has been removed. That is, the bulk of the S0 to spiral transformations may have already occurred when the Universe was more gas-rich. While Leaman et al. (Reference Leaman, Cole, Venn, Tolstoy, Irwin, Szeifert, Skillman and McConnachie2009) report the gas-disc in DDO 221, aka WLM (Wolf-Lundmark-Melotte), has a (rotation speed)-to-(velocity dispersion) ratio of $\approx$ 6.7, compared to $\approx$ 1.2 for the galaxy’s evolved red giant branch population, the scarcity of dS galaxies reveals that (gas discs built from the collapse of high angular momentum gas and the ensuing) spiral formation has been more common in the HSB galaxies, with their higher densities. This scenario (see Figure 12) does not suppose UDGs to be faded spiral galaxies, but instead failed spiral galaxies that did not experience sufficient cold gas accretion and mergers (from, say, satellites or dwarf spheroidal galaxies) to develop showy discs. For the relatively gas-poor UDGs and NUDGes depicted in Figure 12, the ‘Triangal’ suggests their evolution may occur through two pathways: (i) the acquisition of gas, which is collisional and leads to the formation of discs, dissipation, and star (and perhaps spiral) formation, or (ii) the acquisition of stars (and dark matter), resulting in a collisionless, dissipationless merger that results in a more massive ETG-like system. The balance between the amount of gas and star infall, along with factors such as orbital momentum and geometry, likely determines where the needle falls between each pathway.

Figure 12. B-band (Vega) central surface brightness versus effective half light radius for the UDGs, NUDGes and ETGs presented herein (Section 2), along with the disc-component of the S0 and spiral galaxies compiled by Graham & de Blok (Reference Graham and de Blok2001) and the exponential models fit to the UDGs and NUDGes detected in neutral hydrogen by Leisman et al. (Reference Leisman2017). The curve is not a fit but rather the derived expectation following on from Equations (2) and (12). Along this curve, the location of different absolute magnitudes and the associated Sérsic indices are marked with plus signs. Lines of constant absolute magnitude for exponential ( $n=1$ ) light profiles are also shown, and the dotted lines delineate the upper envelope and relation reported by Graham (Reference Graham2001), replacing the once-popular notion that spiral galaxies have a canonical central surface brightness of approximately 21.65 B-mag arcsec $^{-2}$ (Freeman Reference Freeman1970). The ‘Triangal’ evolutionary schematic (Graham Reference Graham2023) is illustrated in the lower left.

To better reveal the ‘Triangal’ in the size-surface brightness diagram, two additional samples are used. One consists of the UDGs and NUDGes detected in HI and modelled by Leisman et al. (Reference Leisman2017). The second sample includes the discs of HSB and LSB spiral (and a few S0) galaxies from Graham & de Blok (Reference Graham and de Blok2001). The scaling parameters for these relatively gas-rich, HI-bearing UDGs and NUDGes have come from Leisman et al. (Reference Leisman2017), who fit exponential ( $n=1$ ) models to their light profiles. Their g-band central surface brightnesses were corrected for Galactic extinction and also, here, cosmological surface brightness dimming. These values were then converted to the B-band using the Galactic extinction corrected $(g-r)_\textrm{AB}$ colours from Leisman et al. (Reference Leisman2017) and the relation $(B-V)_\textrm{Vega} = 0.98(g-r)_\textrm{AB} + 0.22$ (Jester et al. Reference Jester2005), along with $(g-B)_\textrm{AB} =-0.366(B-V)_\textrm{Vega} - 0.126$ (Jordi et al. Reference Jordi, Grebel and Ammon2006) and $B_\textrm{Vega} = B_\textrm{AB}+0.12$ . This conversion gives a $B_\textrm{Vega} - g_\textrm{AB}$ distribution peaking at $\approx$ 0.46 mag, with a FWHM of $\approx$ 0.06 mag and a slight blue excess noticed at $\approx$ 0.33 mag. From the predominantly spiral galaxy sample, the exponential galaxy discs have had their $\mu_\textrm{0,B}$ values and scalelengths, $h_\textrm{disc}$ , corrected following equations 1 and 2 in Graham & Worley (Reference Graham and Worley2008), and $h_\textrm{disc}$ was converted into $R_\textrm{e,maj}$ using the multiplier 1.678 (e.g. Graham & Driver Reference Graham and Driver2005, their equation 16).

For a given size, the isolated HI-bearing UDGs and NUDGes (Leisman et al. Reference Leisman2017) tend to have central surface brightnesses a couple of mag arcsec $^{-2}$ brighter than the average UDG presented thus far (see Marleau et al. Reference Marleau2021, their Figure 7). These HI-bearing UDGs bridge the UDG/NUDG samples from Buzzo et al. (Reference Buzzo2024) and Buzzo et al. (Reference Buzzo2025) and the spiral galaxies in the $\mu_\textrm{0,B}$ - $R_\textrm{e}$ diagram (Figure 12). The triangular shaped pathway shown in the lower left of Figure 12 reveals how accretion and minor and major mergers can build galaxies.

Acknowledgements

This paper is dedicated to Ena (née McKenzie) Graham (Reference Graham1931–2019), who adopted AWG long ago and graciously let him claim Scrabble victories during her multiple surgeries and lengthy hospital stays from 2017 to 2019. AWG is grateful to the Department of Astronomy at the University of Florida, Gainesville, USA, where he largely completed the figures during 2019. The delayed write-up has benefitted from an expanded UDG data set and updated entries in the figures. Publication costs were funded through the Australian and New Zealand Institutions (Council of Australian University Librarians affiliated) Open Access Agreement. This research has used the NASA/IPAC Extragalactic Database (NED) and the SAO/NASA Astrophysics Data System (ADS) bibliographic services.

Footnotes

a Use of the letter ‘I’ also encapsulated the presence of some Population I stars.

b This term was coined by Forbes & Gannon (Reference Forbes and Gannon2024) and snares galaxies often also considered by others (e.g. Lim et al. Reference Lim2020; Venhola et al. Reference Venhola2022; Li et al. Reference Li2023).

c For the sample from Buzzo et al. (Reference Buzzo2024), the class adopted here is that derived without the number of globular clusters used as a criterion; this was done as it resulted in a greater number of assigned classes. This does not imply an irrelevance of the globular cluster systems of UDGs (van Dokkum et al. Reference van Dokkum2017; Amorisco et al. Reference Amorisco, Monachesi, Agnello and White2018; Lim et al. Reference Lim2020; Marleau et al. Reference Marleau2024).

d These are the K-correction, evolutionary correction, and $(1+z)^4$ surface brightness dimming.

e For reference, the Third Reference Catalogue (RC3: de Vaucouleurs et al. Reference de Vaucouleurs and de Vaucouleurs1991) used $\mu_\textrm{B}=25$ mag arcsec $^{-2}$ , while Heidmann (Reference Heidmann1969) used $\mu_\textrm{V}=26$ mag arcsec $^{-2}$ .

f https://www.lsst.org/.

g https://www.arrakihs-mission.eu/.

h The (stellar mass)- $R_\textrm{e}$ relation for bulges/spheroids – with a galaxy’s disc, bar and other components removed – can be seen in Hon et al. (Reference Hon, Graham and Sahu2023). Compact elliptical galaxies, which are essentially the bulge component of disc-stripped S0 galaxies (Bekki et al. Reference Bekki, Couch, Drinkwater and Gregg2001; Graham Reference Graham2002), follow this distribution rather than the curved distribution of ETGs.

i The Triangal is a schematic showing the speciation of galaxies. Unlike galaxy morphology diagrams such as the Tuning Fork (Jeans Reference Jeans1928; Hubble Reference Hubble1936) or the Trident (van den Bergh Reference van den Bergh1976), the Triangal includes evolutionary pathways, such as major mergers of disc galaxies with strong spirals forming dust-rich lenticular galaxies.

j While Amorisco & Loeb (Reference Amorisco and Loeb2016) refer to models having different ‘concentrations’, they are not referring to a different radial concentration of stars as per the Sérsic model (Ciotti Reference Ciotti1991; Trujillo, Graham, & Caon Reference Trujillo, Graham and Caon2001; Graham, Trujillo, & Caon Reference Graham, Trujillo and Caon2001) but to a measure of the density contrast of the halo relative to the average background density of the Universe.

k $\mathfrak{M}_B \gt -20$ mag, H $_\textrm{0}$ =50 km s $^{-1}$ Mpc $^{-1}$ .

l The bar brightens the reported B-band central surface brightness to 23.3 mag arcsec $^{-2}$ .

References

Akeson, R., et al. 2019, arXiv e-prints, p. arXiv:1902.05569Google Scholar
Amorisco, N. C., & Loeb, A. 2016, MNRAS, 459, L51Google Scholar
Amorisco, N. C., Monachesi, A., Agnello, A., & White, S. D. M. 2018, MNRAS, 475, 4235Google Scholar
Barazza, F. D., Binggeli, B., & Jerjen, H. 2002, A&A, 391, 823Google Scholar
Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307Google Scholar
Bekki, K., Couch, W. J., Drinkwater, M. J., & Gregg, M. D. 2001, ApJ, 557, L39Google Scholar
Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212Google Scholar
Binggeli, B., & Cameron, L. M. 1991, A&A, 252, 27Google Scholar
Binggeli, B., & Cameron, L. M. 1993, A&AS, 98, 297Google Scholar
Binggeli, B., & Jerjen, H. 1998, A&A, 333, 17Google Scholar
Binggeli, B., & Popescu, C. C. 1995, A&A, 298, 63Google Scholar
Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681Google Scholar
Bonfini, P., Dullo, B. T., & Graham, A. W. 2015, ApJ, 807, 136Google Scholar
Bothun, G. D., Impey, C. D., Malin, D. F., & Mould, J. R. 1987, AJ, 94, 23Google Scholar
Buttitta, C., et al. 2025, A&A, 694, A276Google Scholar
Buzzo, M. L., et al. 2022, MNRAS, 517, 2231Google Scholar
Buzzo, M. L., et al. 2024, MNRAS, 529, 3210Google Scholar
Buzzo, M. L., et al. 2025, MNRAS, 536, 2536Google Scholar
Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013Google Scholar
Capaccioli, M. 1989, in World of Galaxies (Le Monde des Galaxies), ed. H. G. Corwin, Jr., & Bottinelli, L. (New York: Springer), 208Google Scholar
Capaccioli, M. 1990, in European Southern Observatory Conference and Workshop Proceedings, Vol. 35, European Southern Observatory Conference and Workshop Proceedings, ed. Jarvis, B. J., & Terndrup, D. M., 231Google Scholar
Carleton, T., Errani, R., Cooper, M., Kaplinghat, M., Peñarrubia, J., & Guo, Y. 2019, MNRAS, 485, 382Google Scholar
Cellone, S. A., Forte, J. C., & Geisler, D. 1994, ApJS, 93, 397Google Scholar
Chamba, N., Marcum, P. M., Saintonge, A., Borlaff, A. S., Hayes, M. J., Le Gouellec, V. J. M., Chojnowski, S. D., & Fanelli, M. N. 2024, ApJ, 974, 247Google Scholar
Chamba, N., Trujillo, I., & Knapen, J. H. 2020, A&A, 633, L3Google Scholar
Chamba, N., Trujillo, I., & Knapen, J. H. 2022, A&A, 667, A87Google Scholar
Chilingarian, I. V. 2009, MNRAS, 394, 1229Google Scholar
Ciotti, L. 1991, A&A, 249, 99Google Scholar
Conselice, C. J. 2018, Research Notes of the American Astronomical Society, 2, 43Google Scholar
D’Onofrio, M., Capaccioli, M., & Caon, N. 1994, MNRAS, 271, 523Google Scholar
Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41Google Scholar
de Vaucouleurs, G., & de Vaucouleurs, A. 1991, MmRAS, 77, 1Google Scholar
Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2Google Scholar
Dekel, A., & Silk, J. 1986, ApJ, 303, 39Google Scholar
Di Cintio, A., Brook, C. B., Dutton, A. A., Macciò, A. V., Obreja, A., & Dekel, A. 2017, MNRAS, 466, L1Google Scholar
Eliche-Moral, M. C., Borlaff, A., Beckman, J. E., & Gutiérrez, L. 2015, A&A, 580, A33Google Scholar
Emsellem, E., et al. 2011, MNRAS, 414, 888Google Scholar
Errani, R., Penarrubia, J., & Tormen, G. 2015, MNRAS, 449, L46Google Scholar
Ivezić, Ž., et al. 2019, ApJ, 873, 111Google Scholar
Faber, S. M., et al. 1997, AJ, 114, 1771Google Scholar
Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189Google Scholar
Fisher, J. R., & Tully, R. B. 1975, A&A, 44, 151Google Scholar
Forbes, D. A., & Gannon, J. 2024, MNRAS, 528, 608Google Scholar
Forbes, D. A., Lasky, P., Graham, A. W., & Spitler, L. 2008, MNRAS, 389, 1924Google Scholar
Forbes, D. A., Read, J. I., Gieles, M., & Collins, M. L. M. 2018, MNRAS, 481, 5592Google Scholar
Freeman, K. C. 1970, ApJ, 160, 811Google Scholar
Fukugita, M., Ichikawa, T., Gunn, J. E., Doi, M., Shimasaku, K., & Schneider, D. P. 1996, AJ, 111, 1748Google Scholar
Geha, M., Guhathakurta, P., & van der Marel, R. P. 2003, AJ, 126, 1794Google Scholar
Gerola, H., Seiden, P. E., & Schulman, L. S. 1980, ApJ, 242, 517Google Scholar
Goerdt, T., Moore, B., Read, J. I., & Stadel, J. 2010, ApJ, 725, 1707Google Scholar
Graham, A. W. 2001, MNRAS, 326, 543Google Scholar
Graham, A. W. 2002, ApJ, 568, L13Google Scholar
Graham, A. W. 2013, in Planets, Stars and Stellar Systems. Volume 6: Extragalactic Astronomy and Cosmology, Vol. 6, ed. Oswalt, T. D., & Keel, W. C. (Dordrecht: Springer Science+Business Media), 91, https://doi.org/10.1007/978-94-007-5609-0_2Google Scholar
Graham, A. W. 2019, PASA, 36, e035 (Paper I)Google Scholar
Graham, A. W. 2023, MNRAS, 522, 3588Google Scholar
Graham, A. W. 2024a, MNRAS, 531, 230Google Scholar
Graham, A. W. 2024b, MNRAS, 535, 299Google Scholar
Graham, A. W., Colless, M. M., Busarello, G., Zaggia, S., & Longo, G. 1998, A&AS, 133, 325Google Scholar
Graham, A. W., & de Blok, W. J. G. 2001, ApJ, 556, 177Google Scholar
Graham, A. W., & Driver, S. P. 2005, PASA, 22, 118Google Scholar
Graham, A. W., Erwin, P., Trujillo, I., & Asensio Ramos, A. 2003a, AJ, 125, 2951Google Scholar
Graham, A. W., & Guzmán, R. 2003, AJ, 125, 2936Google Scholar
Graham, A. W., Jarrett, T. H., & Cluver, M. E. 2024, MNRAS, 527, 10059Google Scholar
Graham, A. W., Jerjen, H., & Guzmán, R. 2003b, AJ, 126, 1787Google Scholar
Graham, A. W., Merritt, D., Moore, B., Diemand, J., & Terzić, B. 2006, AJ, 132, 2711Google Scholar
Graham, A. W., & Sahu, N. 2023, MNRAS, 520, 1975Google Scholar
Graham, A. W., Trujillo, I., & Caon, N. 2001, AJ, 122, 1707Google Scholar
Graham, A. W., & Worley, C. C. 2008, MNRAS, 388, 1708Google Scholar
Grossi, M., et al. 2009, A&A, 498, 407Google Scholar
Gunn, J. E., & Gott III J. R. 1972, ApJ, 176, 1Google Scholar
Guzman, R., et al. 2022, in EAS2022, European Astronomical Society Annual Meeting, 1507Google Scholar
Häußler, B., et al. 2013, MNRAS, 430, 330Google Scholar
Heidmann, J. 1967, CRAS, Paris, 265, 866Google Scholar
Heidmann, J. 1969, ApL, 3, 19Google Scholar
Hon, D. S. H., Graham, A. W., & Sahu, N. 2023, MNRAS, 519, 4651Google Scholar
Hubble, E. P. 1936, Realm of the Nebulae (New Haven: Yale University Press)Google Scholar
Huchtmeier, W. K., & Richter, O. G. 1989, A&A, 210, 1Google Scholar
Janowiecki, S., Mihos, J. C., Harding, P., Feldmeier, J. J., Rudick, C., & Morrison, H. 2010, ApJ, 715, 972Google Scholar
Janz, J., Penny, S. J., Graham, A. W., Forbes, D. A., & Davies, R. L. 2017, MNRAS, 468, 2850Google Scholar
Jeans, J. H. 1928, Astronomy and Cosmogony (Cambridge: Cambridge University Press)Google Scholar
Jerjen, H., Kalnajs, A., & Binggeli, B. 2000, A&A, 358, 845Google Scholar
Jester, S., et al. 2005, AJ, 130, 873Google Scholar
Jordi, K., Grebel, E. K., & Ammon, K. 2006, A&A, 460, 339Google Scholar
Kado-Fong, E., Greene, J. E., Huang, S., & Goulding, A. 2022, ApJ, 941, 11Google Scholar
Karunakaran, A., Motiwala, K., Spekkens, K., Zaritsky, D., Donnerstein, R. L., & Dey, A. 2024, ApJ, 975, 91Google Scholar
Kelvin, L. S., et al. 2012, MNRAS, 421, 1007Google Scholar
Kennedy, R., et al. 2016a, MNRAS, 460, 3458Google Scholar
Kennedy, R., Bamford, S. P., Häußler, B., Brough, S., Holwerda, B., Hopkins, A. M., Vika, M., & Vulcani, B. 2016b, A&A, 593, A84Google Scholar
Kirby, E. N., Cohen, J. G., Guhathakurta, P., Cheng, L., Bullock, J. S., & Gallazzi, A. 2013, ApJ, 779, 102Google Scholar
Knezek, P. M., Sembach, K. R., & GallagherIII, J. S. 1999, ApJ, 514, 119Google Scholar
Koda, J., Yagi, M., Yamanoi, H., & Komiyama, Y. 2015, ApJ, 807, L2Google Scholar
Koleva, M., de Rijcke, S., Prugniel, P., Zeilinger, W. W., & Michielsen, D. 2009, MNRAS, 396, 2133Google Scholar
Kormendy, J. 1985, ApJ, 295, 73Google Scholar
Krajnović, D., et al. 2013, MNRAS, 432, 1768Google Scholar
Larson, R. B. 1974, MNRAS, 169, 229Google Scholar
Leaman, R., Cole, A. A., Venn, K. A., Tolstoy, E., Irwin, M. J., Szeifert, T., Skillman, E. D., & McConnachie, A. W. 2009, ApJ, 699, 1Google Scholar
Leisman, L., et al. 2017, ApJ, 842, 133Google Scholar
Li, J., et al. 2023, ApJ, 955, 1Google Scholar
Lim, S., et al. 2020, ApJ, 899, 69Google Scholar
Mancera Piña, P. E., et al. 2019b, ApJ, 883, L33Google Scholar
Mancera Piña, P. E., et al. 2020, MNRAS, 495, 3636Google Scholar
Mancera Piña, P. E., Aguerri, J. A. L., Peletier, R. F., Venhola, A., Trager, S., & Choque Challapa, N. 2019a, MNRAS, 485, 1036Google Scholar
Marleau, F. R., et al. 2021, A&A, 654, A105Google Scholar
Marleau, F. R., et al. 2024, A&A, 690, A339Google Scholar
Martin, N. F., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075Google Scholar
Mateo, M. L. 1998, ARA&A, 36, 435Google Scholar
Mayer, L., Governato, F., Colpi, M., Moore, B., Quinn, T., Wadsley, J., Stadel, J., & Lake, G. 2001, ApJ, 547, L123Google Scholar
Mayer, L., Mastropietro, C., Wadsley, J., Stadel, J., & Moore, B. 2006, MNRAS, 369, 1021Google Scholar
Miró-Carretero, J., et al. 2024, A&A, 691, A196Google Scholar
Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Natur, 379, 613Google Scholar
Oosterloo, T., et al. 2010, MNRAS, 409, 500Google Scholar
Padovani, P., & Cirasuolo, M. 2023, Contemporary Physics, 64, 47Google Scholar
Pedraz, S., Gorgas, J., Cardiel, N., Sánchez-Blázquez, P., & Guzmán, R. 2002, MNRAS, 332, L59Google Scholar
Pierini, D., Zibetti, S., Braglia, F., Böhringer, H., Finoguenov, A., Lynam, P. D., & Zhang, Y. Y. 2008, A&A, 483, 727Google Scholar
Poulain, M., et al. 2021, MNRAS, 506, 5494Google Scholar
Prole, D. J., et al. 2019, MNRAS, 484, 4865Google Scholar
Reaves, G. 1956, AJ, 61, 69Google Scholar
Reaves, G. 1983, ApJS, 53, 375Google Scholar
Rix, H.-W., & White, S. D. M. 1990, ApJ, 362, 52Google Scholar
Román, J., & Trujillo, I. 2017, MNRAS, 468, 4039Google Scholar
Rong, Y., et al. 2020, ApJ, 899, 78Google Scholar
Ryden, B. S., & Terndrup, D. M. 1994, ApJ, 425, 43Google Scholar
Saito, M. 1979, PASJ, 31, 193Google Scholar
Sandage, A., & Binggeli, B. 1984, AJ, 89, 919Google Scholar
Sandage, A., Binggeli, B., & Tammann, G. A. 1985, in European Southern Observatory Conference and Workshop Proceedings, Vol. 20, ESO Workshop on the Virgo Cluster of Galaxies, ed. Richter, O. G., & Binggeli (Garching: ESO), B., 239Google Scholar
Sandage, A., & Shaw, R. 1980, Year Book 79. Year Book - Carnegie Institution of Washington, Vol. 79 (Washington, D.C.: Carnegie Institution of Washington), https://archive.org/details/yearbookcarne79197980carn/page/2/mode/2upGoogle Scholar
Schombert, J. M., & McGaugh, S. 2014, PASA, 31, e011Google Scholar
Seigar, M. S., Graham, A. W., & Jerjen, H. 2007, MNRAS, 378, 1575Google Scholar
Seo, M., & Ann, H. B. 2023, MNRAS, 520, 5521Google Scholar
Sersic, J. L. 1968a, Atlas de Galaxias Australes. Observatorio Astronomico, Cordoba, ArgentinaGoogle Scholar
Sérsic, J. L. 1968b, BAICz, 19, 105Google Scholar
Shi, D. D., et al. 2017, ApJ, 846, 26Google Scholar
Shull, J. M. 2014, ApJ, 784, 142Google Scholar
Spergel, D., et al. 2013, arXiv e-prints, p. arXiv:1305.5422Google Scholar
Spitler, L. R., & Forbes, D. A. 2009, MNRAS, 392, L1Google Scholar
Stiavelli, M., Miller, B. W., Ferguson, H. C., Mack, J., Whitmore, B. C., & Lotz, J. M. 2001, AJ, 121, 1385Google Scholar
Sung, E.-C., Han, C., Ryden, B. S., Patterson, R. J., Chun, M.-S., Kim, H.-I., Lee, W.-B., & Kim, D.-J. 1998, ApJ, 505, 199Google Scholar
Terzić, B., & Graham, A. W. 2005, MNRAS, 362, 197Google Scholar
Toloba, E., et al. 2009, ApJ, 707, L17Google Scholar
Toloba, E., et al. 2014, ApJS, 215, 17Google Scholar
Trujillo, I., Chamba, N., & Knapen, J. H. 2020, MNRAS, 493, 87Google Scholar
Trujillo, I., Graham, A. W., & Caon, N. 2001, MNRAS, 326, 869Google Scholar
Vader, J. P. 1986, ApJ, 305, 669Google Scholar
van den Bergh, S. 1976, ApJ, 206, 883Google Scholar
van den Bergh, S. 1990, ApJ, 348, 57Google Scholar
van Dokkum, P., et al. 2017, ApJ, 844, L11Google Scholar
van Dokkum, P. G. 2005, AJ, 130, 2647Google Scholar
van Dokkum, P. G., Abraham, R., Merritt, A., Zhang, J., Geha, M., & Conroy, C. 2015, ApJ, 798, L45Google Scholar
Van Nest, J. D., Munshi, F., Wright, A. C., Tremmel, M., Brooks, A. M., Nagai, D., & Quinn, T. 2022, ApJ, 926, 92Google Scholar
Venhola, A., et al. 2022, A&A, 662, A43Google Scholar
Vigroux, L., Thuan, T. X., Vader, J. P., & Lachieze-Rey, M. 1986, AJ, 91,70Google Scholar
White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341Google Scholar
Yagi, M., Koda, J., Komiyama, Y., & Yamanoi, H. 2016, ApJS, 225, 11Google Scholar
Yozin, C., & Bekki, K. 2015, MNRAS, 452, 937Google Scholar
Figure 0

Figure 1. Absolute magnitude versus central surface brightness (Equation (1), panel a), Sérsic index (Equation (2), panel b), and (equivalent axis) effective half-light radius (Equation (4), panel c). The dashed lines in panel a) ensnare roughly the $\pm2\sigma$ scatter about the ETGs, and they have been mapped into panel c). The arrows reveal how a change in absolute magnitude at fixed $\mu_\textrm{0,B}$ and n results in a corresponding change in $R_\textrm{e}$, simultaneously explaining the low and high levels of scatter at bright and faint absolute magnitudes, respectively. For the curves in panel c), the central surface brightness (and Sérsic index) associated with points E and F (and the lower circle) are the same, but $R_\textrm{e}$ is different because the magnitude is different (see Equation (4)). Here, galaxies from Buzzo et al. (2024) and Buzzo et al. (2025) are designated UDGs if they have $R_\textrm{e,maj} \ge 1.5$ kpc and $\mu_\textrm{0,g} \ge 24$ mag arcsec$^{-2}$, otherwise they are designated NUDGes. The ETG sample compiled by Graham & Guzmán (2003, see Section 2) contains a few (6–9) galaxies that would likely be considered UDGs using this definition.

Figure 1

Figure 2. Extension of Figure 1 with the addition of UDG and NUDG data from Buzzo et al. (2024) and (2025), and a slightly revised $\mathfrak{M}_B$-$\mu_\textrm{0,B,obs}$ relation (Equation (9)) and thus a slightly revised $\mathfrak{M}_B$-$R_\textrm{e,eq}$ relation (Equation (10)). The colour-coding tracks the two classes (A=blue filled star, B=red open star) assigned to the UDGs and ‘NUDGes’ by Buzzo et al. (2025). The two vertical lines of constant central surface brightness shown in the lower left of panel (a) map into the diagonal lines seen in panel (c), with the arrows in Figure 1c showing how this occurs. This reveals and explains the creation of the misleading size-luminosity relation for UDGs, relative to the ETG population at large.

Figure 2

Figure 3. Variant of Figure 2 showing $\mu_\textrm{0,B,adj}$ (see Equations (11) and (12)) in panel a) and $R_\textrm{e,maj}$ (see Equation (13)) in panel c). Symbols have the same meaning as in Figure 2. At fixed $\mathfrak{M}_B$, the (horizontal) scatter $\delta\mu_\textrm{0,B}$ is directly related to the scatter $\delta\log(n)$ (panel b) and $\delta\mu_\textrm{e,B}$ (see Figure 4).

Figure 3

Figure 4. An example of how variations/offsets in $\mu_\textrm{e}$ and n for a surface brightness profile will result in the offset to $\mu_\textrm{0}$. For a given $\mathfrak{M}$, with an associated $\mu_\textrm{0}$ and n from the $\mathfrak{M}$-$\mu_\textrm{0}$ and $\mathfrak{M}$-$\log(n)$ relations, the horizontal offsets $\delta\mu_\textrm{0}$ seen in Figures 1a–3a are attributable to the offsets $\delta\mu_\textrm{e}$ and $\delta\log(n)$.

Figure 4

Figure 5. Effective surface brightness, $\mu_\textrm{e,B}$, at $R_\textrm{e}$ versus $\mathfrak{M}_B$. Symbols have the same meaning as in Figure 2. The curve is not a fit but instead a derivation from the $\mathfrak{M}_B$-$\mu_\textrm{0}$ and $\mathfrak{M}_B$-$\log(n)$ relations (Equations (2) and (9)).

Figure 5

Figure 6. Breaking down the scatter in the $\mathfrak{M}_B$-$\mu_\textrm{0,B}$ diagram for ETGs. Symbols have the same meaning as in Figure 2. At fixed $\mathfrak{M}_B$, the horizontal scatter $\delta\mu_\textrm{0,B}$ and $\delta\log(n)$ from Figures 2a and 2b are shown against each other in panel (a). The predictable contribution to $\delta\mu_\textrm{0,B}$ arises from offsets in $\log(n)$ and $\mu_\textrm{e,B}$ from their expected values (based on the scaling relations). These are shown in panels (b) and (c), respectively. The different behaviour of the UDGs from the (dwarf and ordinary) ETGs is explained in Section 3.2 and simply reflects their different Sérsic indices.

Figure 6

Figure 7. Variant of Figure 2a, in which the symbol size is now proportional to the ellipticity ($=1-b/a$) such that galaxies that appear round have a small symbol size. In the inset panel, the grey triangles represent 28 UDGs predominantly in clusters, while the pink squares represent 59 UDGs in low-to-moderate density environments. UDGs with high $b/a$ ratios are prevalent in both environments and are thus not a product of the environment. At faint absolute magnitudes, the samples’ $b/a$ ratios are small, possibly a result of sample selection (see the discussion in Section 3.2.1).

Figure 7

Figure 8. Absolute magnitude versus the ‘equivalent axis’ isophotal radius at $\mu_\textrm{B}=26$ mag arcsec$^{-2}$ obtained from each galaxy’s Sérsic profile. The central black curve is derived using Equations (2) and (9), while the outer grey curves denote a $\pm0.125$ dex offset in isophotal radius at fixed magnitude. The two diagonal lines pertain to a fixed B-band central surface brightness of 24 and 25 mag arcsec$^{-2}$ and reveal how $R_\textrm{iso}$ changes if $\mathfrak{M}_B$ changes by up to $\pm$1.6 mag while the associated Sérsic index is held fixed (at $n=0.986$ and 0.861). The faint/grey symbols in the lower-left have $\mu_\textrm{0,B} \gt 25$ mag arcsec$^{-2}$. The outlier in the lower-middle is MATLAS-1408.

Figure 8

Figure 9. Five representative B-band light profiles of ETGs with different Sérsic indices are shown (thick solid curves). For each value of n, an associated absolute magnitude and central surface brightness are assigned from Equations (2) and (9), from which the effective surface brightness and radius can then be calculated (Equation (10)). For each profile, the ‘effective’ parameters $\mu_\textrm{e,B}$ and $R_\textrm{e}$ are shown by the stars, and the dashed curve connecting them traces the $\mu_\textrm{e,B}$-$R_\textrm{e}$ relation for ETGs. While keeping the absolute magnitude fixed, offsets of $\delta \mu_\textrm{e} = \pm1.5$ mag arcsec$^{-2}$ and $\delta\log(n)=\pm0.2$ dex are applied to each profile, thereby generating offsets in $\mu_\textrm{0,B}$. This produces the dotted and dashed curves, whose $\mu_\textrm{e}$ and $R_\textrm{e}$ values are shown by the open circles. These offset profiles yield slight differences in the isophotal radii relative to the larger changes seen in $R_\textrm{e}$, provided the chosen isophotal surface brightness is not too close to the light profile’s central surface brightness.

Figure 9

Figure 10. Absolute magnitude versus the ‘equivalent axis’ isophotal radius at $\mu_\textrm{B}=31$ mag obtained from each galaxy’s Sérsic profile. The central black curve is derived using Equations (2) and (9), while the outer grey curves denote a $\pm0.25$ dex offset in isophotal radius at fixed $\mathfrak{M}_B$. The two diagonal lines pertain to a fixed B-band central surface brightness of 24 and 27.5 mag arcsec$^{-2}$ and reveal how $R_\textrm{iso}$ changes if $\mathfrak{M}_B$ changes by up to $\pm$1.6 mag while the associated Sérsic index is held fixed (at $n=0.986$ and 0.613, respectively).

Figure 10

Figure 11. Given $\mathfrak{M}_B \propto \sigma^2$ for dETGs (Davies et al. 1983; Graham 2013, and references therein), one can appreciate how the scatter about the $\mathfrak{M}_B$-$R_\textrm{e}$ relation, shown here, results in different dynamical masses ($\sigma^2R_\textrm{e}/G$), and in turn, mass-dependent trends, that are subject to arbitrary divisions of the dETG (including UDG) sample. The green dots are ETGs not in the UDG sample but with $\mathfrak{M}_B \ge -15$ mag. As in Figure 1c, the curves are not a fit to the data but are derived from fits to other empirical relations coupled with the Sérsic $R^{1/n}$ function.

Figure 11

Figure 12. B-band (Vega) central surface brightness versus effective half light radius for the UDGs, NUDGes and ETGs presented herein (Section 2), along with the disc-component of the S0 and spiral galaxies compiled by Graham & de Blok (2001) and the exponential models fit to the UDGs and NUDGes detected in neutral hydrogen by Leisman et al. (2017). The curve is not a fit but rather the derived expectation following on from Equations (2) and (12). Along this curve, the location of different absolute magnitudes and the associated Sérsic indices are marked with plus signs. Lines of constant absolute magnitude for exponential ($n=1$) light profiles are also shown, and the dotted lines delineate the upper envelope and relation reported by Graham (2001), replacing the once-popular notion that spiral galaxies have a canonical central surface brightness of approximately 21.65 B-mag arcsec$^{-2}$ (Freeman 1970). The ‘Triangal’ evolutionary schematic (Graham 2023) is illustrated in the lower left.