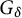1 Introduction
Shadowing is an important concept in the topological theory of dynamical systems (see [Reference Aoki and Hiraide5, Reference Pilyugin18] for background). It was derived from the study of hyperbolic differentiable dynamics [Reference Anosov4, Reference Bowen6] and generally refers to a situation in which coarse orbits, or pseudo-orbits, can be approximated by true orbits. Above all else, it is worth mentioning that the shadowing is known to be generic in the space of homeomorphisms or continuous self-maps of a closed differentiable manifold (see [Reference Pilyugin and Plamenevskaya19] and Theorem 1 of [Reference Mazur and Oprocha16]) and so plays a significant role in the study of topologically generic dynamics.
Chain components are basic objects for global understanding of dynamical systems [Reference Conley9]. In this paper, we focus on attractor-like, or terminal, chain components and the basins of them. By a result (Corollary 6.16) of [Reference Hurley11], if a continuous flow on a compact metric space has the so-called weak shadowing, then the union of the basins of terminal chain components is a dense
![]() $G_\delta $
-subset of the space. For any continuous self-map of a compact metric space, we strengthen it by assuming the standard shadowing (Theorem 1.1). Our proof is by a method related to but independent of a result (Proposition 22 in Section 7) of [Reference Akin1]. It is shown in [Reference Akin, Hurley and Kennedy3] that topologically generic homeomorphisms of a closed differentiable manifold are almost chain continuous (see Introduction of [Reference Akin, Hurley and Kennedy3] where the word “almost equicontinuous” is used). We also give an alternative proof of this fact by using the genericity of shadowing.
$G_\delta $
-subset of the space. For any continuous self-map of a compact metric space, we strengthen it by assuming the standard shadowing (Theorem 1.1). Our proof is by a method related to but independent of a result (Proposition 22 in Section 7) of [Reference Akin1]. It is shown in [Reference Akin, Hurley and Kennedy3] that topologically generic homeomorphisms of a closed differentiable manifold are almost chain continuous (see Introduction of [Reference Akin, Hurley and Kennedy3] where the word “almost equicontinuous” is used). We also give an alternative proof of this fact by using the genericity of shadowing.
First, we define the chain components. Throughout, X denotes a compact metric space endowed with a metric d.
Definition 1.1 Given a continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $\delta>0$
, a finite sequence
$\delta>0$
, a finite sequence
![]() $(x_i)_{i=0}^{k}$
of points in X, where
$(x_i)_{i=0}^{k}$
of points in X, where
![]() $k>0$
is a positive integer, is called a
$k>0$
is a positive integer, is called a
![]() $\delta $
-chain of f if
$\delta $
-chain of f if
![]() $d(f(x_i),x_{i+1})\le \delta $
for every
$d(f(x_i),x_{i+1})\le \delta $
for every
![]() $0\le i\le k-1$
. A
$0\le i\le k-1$
. A
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^{k}$
of f with
$(x_i)_{i=0}^{k}$
of f with
![]() $x_0=x_k$
is said to be a
$x_0=x_k$
is said to be a
![]() $\delta $
-cycle of f.
$\delta $
-cycle of f.
Let
![]() $f\colon X\to X$
be a continuous map. For any
$f\colon X\to X$
be a continuous map. For any
![]() $x,y\in X$
and
$x,y\in X$
and
![]() $\delta>0$
, the notation
$\delta>0$
, the notation
![]() $x\rightarrow _\delta y$
means that there is a
$x\rightarrow _\delta y$
means that there is a
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of f with
$(x_i)_{i=0}^k$
of f with
![]() $x_0=x$
and
$x_0=x$
and
![]() $x_k=y$
. We write
$x_k=y$
. We write
![]() $x\rightarrow y$
if
$x\rightarrow y$
if
![]() $x\rightarrow _\delta y$
for all
$x\rightarrow _\delta y$
for all
![]() $\delta>0$
. We say that
$\delta>0$
. We say that
![]() $x\in X$
is a chain recurrent point for f if
$x\in X$
is a chain recurrent point for f if
![]() $x\rightarrow x$
, or equivalently, for every
$x\rightarrow x$
, or equivalently, for every
![]() $\delta>0$
, there is a
$\delta>0$
, there is a
![]() $\delta $
-cycle
$\delta $
-cycle
![]() $(x_i)_{i=0}^{k}$
of f with
$(x_i)_{i=0}^{k}$
of f with
![]() $x_0=x_k=x$
. Let
$x_0=x_k=x$
. Let
![]() $CR(f)$
denote the set of chain recurrent points for f. We define a relation
$CR(f)$
denote the set of chain recurrent points for f. We define a relation
![]() $\leftrightarrow $
in
$\leftrightarrow $
in
by the following: for any
![]() $x,y\in CR(f)$
,
$x,y\in CR(f)$
,
![]() $x\leftrightarrow y$
if and only if
$x\leftrightarrow y$
if and only if
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
![]() $y\rightarrow x$
. Note that
$y\rightarrow x$
. Note that
![]() $\leftrightarrow $
is a closed equivalence relation in
$\leftrightarrow $
is a closed equivalence relation in
![]() $CR(f)^2$
and satisfies
$CR(f)^2$
and satisfies
![]() $x\leftrightarrow f(x)$
for all
$x\leftrightarrow f(x)$
for all
![]() $x\in CR(f)$
. An equivalence class C of
$x\in CR(f)$
. An equivalence class C of
![]() $\leftrightarrow $
is called a chain component for f. We regard the quotient space
$\leftrightarrow $
is called a chain component for f. We regard the quotient space
as a space of chain components.
A subset S of X is said to be f-invariant if
![]() $f(S)\subset S$
. For an f-invariant subset S of X, we say that
$f(S)\subset S$
. For an f-invariant subset S of X, we say that
![]() $f|_S\colon S\to S$
is chain transitive if for any
$f|_S\colon S\to S$
is chain transitive if for any
![]() $x,y\in S$
and
$x,y\in S$
and
![]() $\delta>0$
, there is a
$\delta>0$
, there is a
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of
$(x_i)_{i=0}^k$
of
![]() $f|_S$
with
$f|_S$
with
![]() $x_0=x$
and
$x_0=x$
and
![]() $x_k=y$
.
$x_k=y$
.
Remark 1.1 The following properties hold:
-
•
 $CR(f)=\bigsqcup _{C\in \mathcal {C}(f)}C$
,
$CR(f)=\bigsqcup _{C\in \mathcal {C}(f)}C$
, -
• every
 $C\in \mathcal {C}(f)$
is a closed f-invariant subset of
$C\in \mathcal {C}(f)$
is a closed f-invariant subset of
 $CR(f)$
,
$CR(f)$
, -
•
 $f|_C\colon C\to C$
is chain transitive for all
$f|_C\colon C\to C$
is chain transitive for all
 $C\in \mathcal {C}(f)$
,
$C\in \mathcal {C}(f)$
, -
• for any f-invariant subset S of X, if
 $f|_S\colon S\to S$
is chain transitive, then
$f|_S\colon S\to S$
is chain transitive, then
 $S\subset C$
for some
$S\subset C$
for some
 $C\in \mathcal {C}(f)$
.
$C\in \mathcal {C}(f)$
.
Next, we recall the definition of terminal chain components. For
![]() $x\in X$
and a subset S of X, we denote by
$x\in X$
and a subset S of X, we denote by
![]() $d(x,S)$
the distance of x from S:
$d(x,S)$
the distance of x from S:
Definition 1.2 We say that a closed f-invariant subset S of X is chain stable if for any
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta>0$
such that every
$\delta>0$
such that every
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of f with
$(x_i)_{i=0}^k$
of f with
![]() $x_0\in S$
satisfies
$x_0\in S$
satisfies
![]() $d(x_i,S)\le \epsilon $
for all
$d(x_i,S)\le \epsilon $
for all
![]() $0\le i\le k$
. Following [Reference Akin, Hurley and Kennedy3], we say that
$0\le i\le k$
. Following [Reference Akin, Hurley and Kennedy3], we say that
![]() $C\in \mathcal {C}(f)$
is terminal if C is chain stable. We denote by
$C\in \mathcal {C}(f)$
is terminal if C is chain stable. We denote by
![]() $\mathcal {C}_{\mathrm {ter}}(f)$
the set of terminal chain components for f.
$\mathcal {C}_{\mathrm {ter}}(f)$
the set of terminal chain components for f.
Remark 1.2 For any continuous map
![]() $f\colon X\to X$
, a partial order
$f\colon X\to X$
, a partial order
![]() $\le $
on
$\le $
on
![]() $\mathcal {C}(f)$
is defined by the following: for all
$\mathcal {C}(f)$
is defined by the following: for all
![]() $C,D\in \mathcal {C}(f)$
,
$C,D\in \mathcal {C}(f)$
,
![]() $C\le D$
if and only if
$C\le D$
if and only if
![]() $x\rightarrow y$
for some
$x\rightarrow y$
for some
![]() $x\in C$
and
$x\in C$
and
![]() $y\in D$
. We can easily show that for any
$y\in D$
. We can easily show that for any
![]() $C\in \mathcal {C}(f)$
,
$C\in \mathcal {C}(f)$
,
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
if and only if C is maximal with respect to
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
if and only if C is maximal with respect to
![]() $\le $
; that is,
$\le $
; that is,
![]() $C\le D$
implies
$C\le D$
implies
![]() $C=D$
for all
$C=D$
for all
![]() $D\in \mathcal {C}(f)$
.
$D\in \mathcal {C}(f)$
.
Given a continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $x\in X$
, the
$x\in X$
, the
![]() $\omega $
-limit set
$\omega $
-limit set
![]() $\omega (x,f)$
of x for f is defined as the set of
$\omega (x,f)$
of x for f is defined as the set of
![]() $y\in X$
such that
$y\in X$
such that
for some sequence
![]() $0\le i_1<i_2<\cdots $
. Note that
$0\le i_1<i_2<\cdots $
. Note that
![]() $\omega (x,f)$
is a closed f-invariant subset of X and
$\omega (x,f)$
is a closed f-invariant subset of X and
![]() $f|_{\omega (x,f)}\colon \omega (x,f)\to \omega (x,f)$
is chain transitive. We denote by
$f|_{\omega (x,f)}\colon \omega (x,f)\to \omega (x,f)$
is chain transitive. We denote by
![]() $C(x,f)$
the unique
$C(x,f)$
the unique
![]() $C(x,f)\in \mathcal {C}(f)$
such that
$C(x,f)\in \mathcal {C}(f)$
such that
![]() $\omega (x,f)\subset C(x,f)$
. For each
$\omega (x,f)\subset C(x,f)$
. For each
![]() $C\in \mathcal {C}(f)$
, we define the basin
$C\in \mathcal {C}(f)$
, we define the basin
![]() $W^s(C)$
of C by
$W^s(C)$
of C by
For every
![]() $x\in X$
, since
$x\in X$
, since
we have
![]() $x\in W^s(C)$
if and only if
$x\in W^s(C)$
if and only if
![]() $C=C(x,f)$
. This implies
$C=C(x,f)$
. This implies
We also define the chain
![]() $\omega $
-limit set
$\omega $
-limit set
![]() $\omega ^\ast (x,f)$
of x for f as the set of
$\omega ^\ast (x,f)$
of x for f as the set of
![]() $y\in X$
such that for any
$y\in X$
such that for any
![]() $\delta>0$
and
$\delta>0$
and
![]() $N>0$
, there is a
$N>0$
, there is a
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of f with
$(x_i)_{i=0}^k$
of f with
![]() $x_0=x$
,
$x_0=x$
,
![]() $x_k=y$
, and
$x_k=y$
, and
![]() $k\ge N$
. Note that
$k\ge N$
. Note that
![]() $\omega ^\ast (x,f)$
is a closed f-invariant subset of X and chain stable. We have
$\omega ^\ast (x,f)$
is a closed f-invariant subset of X and chain stable. We have
Remark 1.3 The chain
![]() $\omega $
-limit set is denoted in [Reference Akin, Hurley and Kennedy3] as
$\omega $
-limit set is denoted in [Reference Akin, Hurley and Kennedy3] as
![]() $\omega \mathcal {C}(x,f)$
instead of
$\omega \mathcal {C}(x,f)$
instead of
![]() $\omega ^\ast (x,f)$
.
$\omega ^\ast (x,f)$
.
The following lemma is obvious (see Section 1.4 of [Reference Akin, Hurley and Kennedy3]).
Lemma 1.1 Let
![]() $f\colon X\to X$
be a continuous map.
$f\colon X\to X$
be a continuous map.
-
(A) For any
 $x\in X$
, the following properties are equivalent:
$x\in X$
, the following properties are equivalent:-
–
 $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
,
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, -
–
 $\omega ^\ast (x,f)\subset C(x,f)$
,
$\omega ^\ast (x,f)\subset C(x,f)$
, -
–
 $\omega ^\ast (x,f)=C(x,f)$
,
$\omega ^\ast (x,f)=C(x,f)$
, -
–
 $f|_{\omega ^\ast (x,f)}\colon \omega ^\ast (x,f)\to \omega ^\ast (x,f)$
is chain transitive.
$f|_{\omega ^\ast (x,f)}\colon \omega ^\ast (x,f)\to \omega ^\ast (x,f)$
is chain transitive.
-
-
(B) For any
 $x\in X$
, the following properties are equivalent:
$x\in X$
, the following properties are equivalent:-
–
 $\omega (x,f)=C(x,f)=\omega ^\ast (x,f)$
,
$\omega (x,f)=C(x,f)=\omega ^\ast (x,f)$
, -
–
 $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
 $\omega (x,f)=C(x,f)$
.
$\omega (x,f)=C(x,f)$
.
-
We give the definition of shadowing.
Definition 1.3 Let
![]() $f\colon X\to X$
be a continuous map and let
$f\colon X\to X$
be a continuous map and let
![]() $\xi =(x_i)_{i\ge 0}$
be a sequence of points in X. For
$\xi =(x_i)_{i\ge 0}$
be a sequence of points in X. For
![]() $\delta>0$
,
$\delta>0$
,
![]() $\xi $
is called a
$\xi $
is called a
![]() $\delta $
-pseudo orbit of f if
$\delta $
-pseudo orbit of f if
![]() $d(f(x_i),x_{i+1})\le \delta $
for all
$d(f(x_i),x_{i+1})\le \delta $
for all
![]() $i\ge 0$
. For
$i\ge 0$
. For
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $\xi $
is said to be
$\xi $
is said to be
![]() $\epsilon $
-shadowed by
$\epsilon $
-shadowed by
![]() $x\in X$
if
$x\in X$
if
![]() $d(f^i(x),x_i)\leq \epsilon $
for all
$d(f^i(x),x_i)\leq \epsilon $
for all
![]() $i\ge 0$
. We say that f has the shadowing property if for any
$i\ge 0$
. We say that f has the shadowing property if for any
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta>0$
such that every
$\delta>0$
such that every
![]() $\delta $
-pseudo orbit of f is
$\delta $
-pseudo orbit of f is
![]() $\epsilon $
-shadowed by some point of X.
$\epsilon $
-shadowed by some point of X.
For a topological space Z, a subset S of Z is called a
![]() $G_\delta $
-subset of Z if S is a countable intersection of open subsets of Z. If Z is completely metrizable, then by Baire Category Theorem, every countable intersection of open dense subsets of Z is dense in Z. We know that a subspace Y of a completely metrizable space Z is completely metrizable if and only if Y is a
$G_\delta $
-subset of Z if S is a countable intersection of open subsets of Z. If Z is completely metrizable, then by Baire Category Theorem, every countable intersection of open dense subsets of Z is dense in Z. We know that a subspace Y of a completely metrizable space Z is completely metrizable if and only if Y is a
![]() $G_\delta $
-subset of Z (see Theorem 24.12 of [Reference Willard20]).
$G_\delta $
-subset of Z (see Theorem 24.12 of [Reference Willard20]).
For any continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $x\in X$
, let
$x\in X$
, let
![]() $\Omega (x,f)$
denote the set of
$\Omega (x,f)$
denote the set of
![]() $y\in X$
such that
$y\in X$
such that
for some sequence
![]() $0\le i_1<i_2<\cdots $
and
$0\le i_1<i_2<\cdots $
and
![]() $x_j\in X$
,
$x_j\in X$
,
![]() $j\ge 1$
, with
$j\ge 1$
, with
Note that
for all
![]() $x\in X$
. By Proposition 22 in Section 7 of [Reference Akin1], we know that
$x\in X$
. By Proposition 22 in Section 7 of [Reference Akin1], we know that
is a dense
![]() $G_{\delta }$
-subset of X. The proof of this result in [Reference Akin1] is based on a nontrivial fact that the set of continuity points of a lower semicontinuous (lsc) set-valued map is a dense
$G_{\delta }$
-subset of X. The proof of this result in [Reference Akin1] is based on a nontrivial fact that the set of continuity points of a lower semicontinuous (lsc) set-valued map is a dense
![]() $G_{\delta }$
-subset. If f has the shadowing property, then we have
$G_{\delta }$
-subset. If f has the shadowing property, then we have
for all
![]() $x\in X$
. This can be proved as follows. Let
$x\in X$
. This can be proved as follows. Let
![]() $(\epsilon _j)_{j\ge 1}$
be a sequence of positive numbers with
$(\epsilon _j)_{j\ge 1}$
be a sequence of positive numbers with
![]() $\lim _{j\to \infty }\epsilon _j=0$
. Since f has the shadowing property, for each
$\lim _{j\to \infty }\epsilon _j=0$
. Since f has the shadowing property, for each
![]() $j\ge 1$
, there is
$j\ge 1$
, there is
![]() $\delta _j>0$
such that every
$\delta _j>0$
such that every
![]() $\delta _j$
-pseudo orbit of f is
$\delta _j$
-pseudo orbit of f is
![]() $\epsilon _j$
-shadowed by some point of X. Let
$\epsilon _j$
-shadowed by some point of X. Let
![]() $x\in X$
and
$x\in X$
and
![]() $y\in \omega ^\ast (x,f)$
. Since
$y\in \omega ^\ast (x,f)$
. Since
![]() $y\in \omega ^\ast (x,f)$
, we have a sequence
$y\in \omega ^\ast (x,f)$
, we have a sequence
![]() $(x_i^{(j)})_{i=0}^{k_j}$
,
$(x_i^{(j)})_{i=0}^{k_j}$
,
![]() $j\ge 1$
, of
$j\ge 1$
, of
![]() $\delta _j$
-chains of f with
$\delta _j$
-chains of f with
![]() $x_0^{(j)}=x$
,
$x_0^{(j)}=x$
,
![]() $x_{k_j}^{(j)}=y$
, and
$x_{k_j}^{(j)}=y$
, and
![]() $k_j< k_{j+1}$
for all
$k_j< k_{j+1}$
for all
![]() $j\ge 1$
. By the choice of
$j\ge 1$
. By the choice of
![]() $\delta _j$
, we obtain
$\delta _j$
, we obtain
![]() $x_j\in X$
,
$x_j\in X$
,
![]() $j\ge 1$
, such that
$j\ge 1$
, such that
![]() $d(x_j,x)=d(x_j,x_0^{(j)})\le \epsilon _j$
and
$d(x_j,x)=d(x_j,x_0^{(j)})\le \epsilon _j$
and
![]() $d(f^{k_j}(x_j),y)=d(f^{k_j}(x_j),x_{k_j}^{(j)})\le \epsilon _j$
for all
$d(f^{k_j}(x_j),y)=d(f^{k_j}(x_j),x_{k_j}^{(j)})\le \epsilon _j$
for all
![]() $j\ge 1$
. It follows that
$j\ge 1$
. It follows that
![]() $0<k_1<k_2<\cdots $
,
$0<k_1<k_2<\cdots $
,
and
Thus,
![]() $y\in \Omega (x,f)$
. Since
$y\in \Omega (x,f)$
. Since
![]() $x\in X$
and
$x\in X$
and
![]() $y\in \omega ^\ast (x,f)$
are arbitrary, we conclude that
$y\in \omega ^\ast (x,f)$
are arbitrary, we conclude that
for all
![]() $x\in X$
, completing the proof. It follows that if a continuous map
$x\in X$
, completing the proof. It follows that if a continuous map
![]() $f\colon X\to X$
has the shadowing property, then
$f\colon X\to X$
has the shadowing property, then
is a dense
![]() $G_{\delta }$
-subset of X; therefore,
$G_{\delta }$
-subset of X; therefore,
is a dense
![]() $G_{\delta }$
-subset of X (see [Reference Hurley11] and [Reference Pilyugin17] for related results). The main aim of this paper is to give an alternative proof of the following statement.
$G_{\delta }$
-subset of X (see [Reference Hurley11] and [Reference Pilyugin17] for related results). The main aim of this paper is to give an alternative proof of the following statement.
Theorem 1.1 If a continuous map
![]() $f\colon X\to X$
has the shadowing property, then
$f\colon X\to X$
has the shadowing property, then
and
are dense
![]() $G_\delta $
-subsets of X.
$G_\delta $
-subsets of X.
Given a continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $x\in X$
, we say that f is chain continuous at x if for any
$x\in X$
, we say that f is chain continuous at x if for any
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta>0$
such that every
$\delta>0$
such that every
![]() $\delta $
-pseudo orbit
$\delta $
-pseudo orbit
![]() $(x_i)_{i\ge 0}$
of f with
$(x_i)_{i\ge 0}$
of f with
![]() $x_0=x$
is
$x_0=x$
is
![]() $\epsilon $
-shadowed by x [Reference Akin2]. We denote by
$\epsilon $
-shadowed by x [Reference Akin2]. We denote by
![]() $CC(f)$
the set of chain continuity points for f. The notion of chain continuity is closely related to odometers. An odometer (or an adding machine) is defined as follows. Let
$CC(f)$
the set of chain continuity points for f. The notion of chain continuity is closely related to odometers. An odometer (or an adding machine) is defined as follows. Let
![]() $m=(m_j)_{j\ge 1}$
be an increasing sequence of positive integers with
$m=(m_j)_{j\ge 1}$
be an increasing sequence of positive integers with
![]() $m_j|m_{j+1}$
for all
$m_j|m_{j+1}$
for all
![]() $j\ge 1$
. Let
$j\ge 1$
. Let
![]() $X_j$
,
$X_j$
,
![]() $j\ge 1$
, denote the quotient group
$j\ge 1$
, denote the quotient group
![]() $\mathbb {Z}/m_j\mathbb {Z}$
with the discrete topology. Let
$\mathbb {Z}/m_j\mathbb {Z}$
with the discrete topology. Let
![]() $\pi _j\colon X_{j+1}\to X_j$
,
$\pi _j\colon X_{j+1}\to X_j$
,
![]() $j\ge 1$
, be the natural projections and let
$j\ge 1$
, be the natural projections and let
As a closed subspace of
![]() $\prod _{j\ge 1}X_j$
with the product topology,
$\prod _{j\ge 1}X_j$
with the product topology,
![]() $X_m$
is a compact metrizable space. Consider the map
$X_m$
is a compact metrizable space. Consider the map
![]() $g_m\colon X_m\to X_m$
defined by
$g_m\colon X_m\to X_m$
defined by
for all
![]() $x=(x_j)_{j\ge 1}\in X_m$
and
$x=(x_j)_{j\ge 1}\in X_m$
and
![]() $j\ge 1$
. Note that
$j\ge 1$
. Note that
![]() $g_m$
is a homeomorphism. We say that
$g_m$
is a homeomorphism. We say that
![]() $(X_m,g_m)$
is an odometer with the periodic structure m. We say that a closed f-invariant subset S of X is an odometer if
$(X_m,g_m)$
is an odometer with the periodic structure m. We say that a closed f-invariant subset S of X is an odometer if
![]() $(S,f|_S)$
is topologically conjugate to an odometer. This is equivalent to that S is a Cantor space and
$(S,f|_S)$
is topologically conjugate to an odometer. This is equivalent to that S is a Cantor space and
is a minimal equicontinuous homeomorphism (see Theorem 4.4 of [Reference Kůrka15]). By Theorem 7.5 of [Reference Akin, Hurley and Kennedy3], we know that for any
![]() $x\in X$
,
$x\in X$
,
![]() $x\in CC(f)$
if and only if
$x\in CC(f)$
if and only if
and
![]() $C(x,f)$
is a periodic orbit or an odometer. By Lemma 1.1, this is equivalent to that
$C(x,f)$
is a periodic orbit or an odometer. By Lemma 1.1, this is equivalent to that
![]() $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
![]() $C(x,f)$
is a periodic orbit or an odometer. We say that X is locally connected if for any
$C(x,f)$
is a periodic orbit or an odometer. We say that X is locally connected if for any
![]() $x\in X$
and any open subset U of X with
$x\in X$
and any open subset U of X with
![]() $x\in U$
, we have
$x\in U$
, we have
![]() $x\in V\subset U$
for some open connected subset V of X. A subspace S of X is said to be totally disconnected if every connected component of S is a singleton. If X is locally connected and
$x\in V\subset U$
for some open connected subset V of X. A subspace S of X is said to be totally disconnected if every connected component of S is a singleton. If X is locally connected and
![]() $CR(f)$
is totally disconnected, then due to Theorem 5.1 of [Reference Buescu and Stewart8] or Theorem B of [Reference Hirsch and Hurley10], every
$CR(f)$
is totally disconnected, then due to Theorem 5.1 of [Reference Buescu and Stewart8] or Theorem B of [Reference Hirsch and Hurley10], every
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
is a periodic orbit or an odometer. By these facts, we obtain the following lemma.
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
is a periodic orbit or an odometer. By these facts, we obtain the following lemma.
Lemma 1.2 Let
![]() $f\colon X\to X$
be a continuous map. If X is locally connected and
$f\colon X\to X$
be a continuous map. If X is locally connected and
![]() $CR(f)$
is totally disconnected, then for any
$CR(f)$
is totally disconnected, then for any
![]() $x\in X$
, the following properties are equivalent:
$x\in X$
, the following properties are equivalent:
-
•
 $x\in CC(f)$
,
$x\in CC(f)$
, -
•
 $\omega (x,f)=C(x,f)=\omega ^\ast (x,f)$
,
$\omega (x,f)=C(x,f)=\omega ^\ast (x,f)$
, -
•
 $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
.
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
.
Let
![]() $f\colon X\to X$
be a continuous map. For any
$f\colon X\to X$
be a continuous map. For any
![]() $j,l\ge 1$
, let
$j,l\ge 1$
, let
![]() $C_{j,l}$
denote the set of
$C_{j,l}$
denote the set of
![]() $x\in X$
such that there is a neighborhood U of x for which every
$x\in X$
such that there is a neighborhood U of x for which every
![]() $\frac {1}{j}$
-pseudo orbit
$\frac {1}{j}$
-pseudo orbit
![]() $(x_i)_{i\ge 0}$
of f with
$(x_i)_{i\ge 0}$
of f with
![]() $x_0\in U$
is
$x_0\in U$
is
![]() $\frac {1}{l}$
-shadowed by
$\frac {1}{l}$
-shadowed by
![]() $x_0$
. We see that
$x_0$
. We see that
![]() $C_{j,l}$
is an open subset of X for all
$C_{j,l}$
is an open subset of X for all
![]() $j,l\ge 1$
and
$j,l\ge 1$
and
Thus,
![]() $CC(f)$
is a
$CC(f)$
is a
![]() $G_{\delta }$
-subset of X. We say that f is almost chain continuous if
$G_{\delta }$
-subset of X. We say that f is almost chain continuous if
![]() $CC(f)$
is a dense
$CC(f)$
is a dense
![]() $G_\delta $
-subset of X. By Theorem 1.1 and Lemma 1.2, we obtain the following theorem.
$G_\delta $
-subset of X. By Theorem 1.1 and Lemma 1.2, we obtain the following theorem.
Theorem 1.2 Let
![]() $f\colon X\to X$
be a continuous map. If X is locally connected, f has the shadowing property, and if
$f\colon X\to X$
be a continuous map. If X is locally connected, f has the shadowing property, and if
![]() $CR(f)$
is totally disconnected, then f is almost chain continuous.
$CR(f)$
is totally disconnected, then f is almost chain continuous.
We present a corollary of Theorem 1.2. For a closed differentiable manifold M, let
![]() $\mathcal {H}(M)$
(resp.
$\mathcal {H}(M)$
(resp.
![]() $\mathcal {C}(M)$
) denote the set of homeomorphisms (resp. continuous self-maps) of M, endowed with the
$\mathcal {C}(M)$
) denote the set of homeomorphisms (resp. continuous self-maps) of M, endowed with the
![]() $C^0$
-topology. It is shown in [Reference Akin, Hurley and Kennedy3] that generic
$C^0$
-topology. It is shown in [Reference Akin, Hurley and Kennedy3] that generic
![]() $f\in \mathcal {H}(M)$
(resp.
$f\in \mathcal {H}(M)$
(resp.
![]() $f\in \mathcal {C}(M)$
, if
$f\in \mathcal {C}(M)$
, if
![]() $\dim {M}>1$
) is almost chain continuous (see Introduction of [Reference Akin, Hurley and Kennedy3] where the word “almost equicontinuous” is used). Note that the shadowing is generic in
$\dim {M}>1$
) is almost chain continuous (see Introduction of [Reference Akin, Hurley and Kennedy3] where the word “almost equicontinuous” is used). Note that the shadowing is generic in
![]() $\mathcal {H}(M)$
[Reference Pilyugin and Plamenevskaya19] and also generic in
$\mathcal {H}(M)$
[Reference Pilyugin and Plamenevskaya19] and also generic in
![]() $\mathcal {C}(M)$
[Reference Mazur and Oprocha16, Theorem 1]. Moreover, by results of [Reference Akin, Hurley and Kennedy3, Reference Krupski, Omiljanowski and Ungeheuer14], we know that for generic
$\mathcal {C}(M)$
[Reference Mazur and Oprocha16, Theorem 1]. Moreover, by results of [Reference Akin, Hurley and Kennedy3, Reference Krupski, Omiljanowski and Ungeheuer14], we know that for generic
![]() $f\in \mathcal {H}(M)$
(resp.
$f\in \mathcal {H}(M)$
(resp.
![]() $f\in \mathcal {C}(M)$
),
$f\in \mathcal {C}(M)$
),
![]() $CR(f)$
is totally disconnected (see Introduction of [Reference Akin, Hurley and Kennedy3] and Theorem 3.3 of [Reference Krupski, Omiljanowski and Ungeheuer14]). Thus, by Theorem 1.2, we obtain the following corollary.
$CR(f)$
is totally disconnected (see Introduction of [Reference Akin, Hurley and Kennedy3] and Theorem 3.3 of [Reference Krupski, Omiljanowski and Ungeheuer14]). Thus, by Theorem 1.2, we obtain the following corollary.
Corollary 1.1 Generic
![]() $f\in \mathcal {H}(M)$
(resp.
$f\in \mathcal {H}(M)$
(resp.
![]() $f\in \mathcal {C}(M)$
) is almost chain continuous.
$f\in \mathcal {C}(M)$
) is almost chain continuous.
Our results also apply to the case where X is not a manifold. We say that X is a dendrite if X is connected, locally connected, and contains no simple closed curves. The shadowing is proved to be generic in the space of continuous self-maps of a dendrite (see [Reference Brian, Meddaugh and Raines7] and [Reference Kościelniak, Mazur, Oprocha and Kubica13, Theorem 19]). However, by Corollary 5.2 of [Reference Krupski, Omiljanowski and Ungeheuer14], a generic continuous self-map of a dendrite has the totally disconnected chain recurrent set. By Theorem 1.2, we conclude that a generic continuous self-map of a dendrite is almost chain continuous.
This paper consists of two sections. In the next section, we prove Theorem 1.1.
2 Proof of Theorem 1.1
In this section, we prove Theorem 1.1. The proof is based on the following lemma in [Reference Kawaguchi12].
Lemma 2.1 [Reference Kawaguchi12, Lemma 2.1]
For any continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $x\in X$
, there is
$x\in X$
, there is
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
such that for every
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
such that for every
![]() $\delta>0$
, there is a
$\delta>0$
, there is a
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of f with
$(x_i)_{i=0}^k$
of f with
![]() $x_0=x$
and
$x_0=x$
and
![]() $x_k\in C$
.
$x_k\in C$
.
We need one more lemma. In what follows, for
![]() $x\in X$
and a subset S of X, we denote by
$x\in X$
and a subset S of X, we denote by
![]() $d(x,S)$
the distance of x from S:
$d(x,S)$
the distance of x from S:
We also denote by
![]() $U_r(S)$
,
$U_r(S)$
,
![]() $r>0$
, the open r-neighborhood of S:
$r>0$
, the open r-neighborhood of S:
Lemma 2.2 For any continuous map
![]() $f\colon X\to X$
and
$f\colon X\to X$
and
![]() $x\in X$
, if
$x\in X$
, if
![]() $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, then
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, then
![]() $C(\cdot ,f)\colon X\to \mathcal {C}(f)$
is continuous at x.
$C(\cdot ,f)\colon X\to \mathcal {C}(f)$
is continuous at x.
Proof Let
![]() $x\in X$
and
$x\in X$
and
![]() $C=C(x,f)$
. If
$C=C(x,f)$
. If
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
(i.e., C is chain stable), then for any
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
(i.e., C is chain stable), then for any
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
![]() $\delta>0$
such that every
$\delta>0$
such that every
![]() $\delta $
-chain
$\delta $
-chain
![]() $(x_i)_{i=0}^k$
of f with
$(x_i)_{i=0}^k$
of f with
![]() $d(x_0,C)\le \delta $
satisfies
$d(x_0,C)\le \delta $
satisfies
![]() $d(x_i,C)\le \epsilon /2$
for all
$d(x_i,C)\le \epsilon /2$
for all
![]() $0\le i\le k$
. It follows that
$0\le i\le k$
. It follows that
![]() $d(y,C)\le \delta $
implies
$d(y,C)\le \delta $
implies
for all
![]() $y\in X$
. Since
$y\in X$
. Since
we have
![]() $d(f^i(x),C)\le \delta /2$
for some
$d(f^i(x),C)\le \delta /2$
for some
![]() $i\ge 0$
. By taking
$i\ge 0$
. By taking
![]() $\gamma>0$
such that
$\gamma>0$
such that
![]() $d(x,z)\le \gamma $
implies
$d(x,z)\le \gamma $
implies
![]() $d(f^i(x),f^i(z))\le \delta /2$
for all
$d(f^i(x),f^i(z))\le \delta /2$
for all
![]() $z\in X$
, we obtain
$z\in X$
, we obtain
![]() $d(f^i(z),C)\le \delta $
and so
$d(f^i(z),C)\le \delta $
and so
for all
![]() $z\in X$
with
$z\in X$
with
![]() $d(x,z)\le \gamma $
. Since
$d(x,z)\le \gamma $
. Since
![]() $\epsilon>0$
is arbitrary, this implies that
$\epsilon>0$
is arbitrary, this implies that
![]() $C(\cdot ,f)\colon X\to \mathcal {C}(f)$
is continuous at x, completing the proof.
$C(\cdot ,f)\colon X\to \mathcal {C}(f)$
is continuous at x, completing the proof.
By using these lemmas, we prove Theorem 1.1.
Proof of Theorem 1.1
First, we show that
![]() $V(f)$
is a dense
$V(f)$
is a dense
![]() $G_\delta $
-subset of X. Fix a sequence
$G_\delta $
-subset of X. Fix a sequence
![]() $(\epsilon _j)_{j\ge 1}$
of positive numbers such that
$(\epsilon _j)_{j\ge 1}$
of positive numbers such that
![]() $\epsilon _1>\epsilon _2>\cdots $
and
$\epsilon _1>\epsilon _2>\cdots $
and
For any
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
, we take
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
, we take
![]() $\delta _{j,C}>0$
such that
$\delta _{j,C}>0$
such that
![]() $x\in U_{\delta _{j,C}}(C)$
implies
$x\in U_{\delta _{j,C}}(C)$
implies
for all
![]() $x\in X$
. Let
$x\in X$
. Let
for all
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
. We define a subset V of X by
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
. We define a subset V of X by
Note that V is a
![]() $G_{\delta }$
-subset of X. Since f has the shadowing property, by Lemma 2.1, we see that for every
$G_{\delta }$
-subset of X. Since f has the shadowing property, by Lemma 2.1, we see that for every
![]() $x\in X$
, there is
$x\in X$
, there is
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
such that
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
such that
for all
![]() $j\ge 1$
. This can be proved as follows. For
$j\ge 1$
. This can be proved as follows. For
![]() $x\in X$
, fix
$x\in X$
, fix
![]() $C\in \mathcal {C}_{\mathrm {ter}}(f)$
as in Lemma 2.1 and
$C\in \mathcal {C}_{\mathrm {ter}}(f)$
as in Lemma 2.1 and
![]() $\gamma _l>0$
,
$\gamma _l>0$
,
![]() $l\ge 1$
, with
$l\ge 1$
, with
![]() $\lim _{l\to \infty }\gamma _l=0$
. There are
$\lim _{l\to \infty }\gamma _l=0$
. There are
![]() $\beta _l>0$
,
$\beta _l>0$
,
![]() $l\ge 1$
, and a sequence
$l\ge 1$
, and a sequence
![]() $(x_i^{(l)})_{i=0}^{k_l}$
,
$(x_i^{(l)})_{i=0}^{k_l}$
,
![]() $l\ge 1$
, of
$l\ge 1$
, of
![]() $\beta _l$
-chains of f such that for each
$\beta _l$
-chains of f such that for each
![]() $l\ge 1$
,
$l\ge 1$
,
-
• every
 $\beta _l$
-pseudo orbit of f is
$\beta _l$
-pseudo orbit of f is
 $\gamma _l$
-shadowed by some point of X,
$\gamma _l$
-shadowed by some point of X, -
•
 $x^{(l)}_0=x$
and
$x^{(l)}_0=x$
and
 $x_{k_l}^{(l)}\in C$
.
$x_{k_l}^{(l)}\in C$
.
By taking
![]() $x_l\in X$
,
$x_l\in X$
,
![]() $l\ge 1$
, with
$l\ge 1$
, with
![]() $d(x_l,x)=d(x_l,x^{(l)}_0)\le \gamma _l$
and
$d(x_l,x)=d(x_l,x^{(l)}_0)\le \gamma _l$
and
![]() $d(f^{k_l}(x_l),C)\le d(f^{k_l}(x_l),x_{k_l}^{(l)})\le \gamma _l$
, we obtain
$d(f^{k_l}(x_l),C)\le d(f^{k_l}(x_l),x_{k_l}^{(l)})\le \gamma _l$
, we obtain
![]() $\lim _{l\to \infty }x_l=x$
and
$\lim _{l\to \infty }x_l=x$
and
for any fixed
![]() $j\ge 1$
and all sufficiently large
$j\ge 1$
and all sufficiently large
![]() $l\ge 1$
, implying
$l\ge 1$
, implying
for all
![]() $j\ge 1$
. This proves the claim. It follows that
$j\ge 1$
. This proves the claim. It follows that
for all
![]() $j\ge 1$
. With the aid of Baire Category Theorem, this implies that V is a dense
$j\ge 1$
. With the aid of Baire Category Theorem, this implies that V is a dense
![]() $G_\delta $
-subset of X. It remains to prove that
$G_\delta $
-subset of X. It remains to prove that
![]() $V(f)=V$
. Given any
$V(f)=V$
. Given any
![]() $x\in V(f)$
, by
$x\in V(f)$
, by
![]() $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
and
we have
![]() $x\in V$
. It follows that
$x\in V$
. It follows that
![]() $V(f)\subset V$
. Conversely, let
$V(f)\subset V$
. Conversely, let
![]() $x\in V$
. For each
$x\in V$
. For each
![]() $j\ge 1$
, we take
$j\ge 1$
, we take
![]() $C_j\in \mathcal {C}_{\mathrm {ter}}(f)$
and
$C_j\in \mathcal {C}_{\mathrm {ter}}(f)$
and
![]() $m_j\ge 0$
such that
$m_j\ge 0$
such that
Then, because
![]() $\mathcal {C}(f)=CR(f)/{\leftrightarrow }$
is a compact metrizable space, there are a sequence
$\mathcal {C}(f)=CR(f)/{\leftrightarrow }$
is a compact metrizable space, there are a sequence
![]() $1\le j_1<j_2<\cdots $
and
$1\le j_1<j_2<\cdots $
and
![]() $C\in \mathcal {C}(f)$
such that
$C\in \mathcal {C}(f)$
such that
in
![]() $\mathcal {C}(f)$
. Note that for every
$\mathcal {C}(f)$
. Note that for every
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
for all sufficiently large
![]() $l\ge 1$
. For every
$l\ge 1$
. For every
![]() $l\ge 1$
, by
$l\ge 1$
, by
we have
By
we obtain
for all
![]() $\epsilon>0$
; thus,
$\epsilon>0$
; thus,
![]() $\omega ^\ast (x,f)\subset C$
. From Lemma 1.1, it follows that
$\omega ^\ast (x,f)\subset C$
. From Lemma 1.1, it follows that
![]() $C=C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, implying
$C=C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, implying
![]() $x\in V(f)$
. Since
$x\in V(f)$
. Since
![]() $x\in V$
is arbitrary, we conclude that
$x\in V$
is arbitrary, we conclude that
![]() $V\subset V(f)$
, proving the claim.
$V\subset V(f)$
, proving the claim.
Next, we show that
![]() $W(f)$
is a dense
$W(f)$
is a dense
![]() $G_\delta $
-subset of X. Since
$G_\delta $
-subset of X. Since
![]() $V(f)$
is a dense
$V(f)$
is a dense
![]() $G_\delta $
-subset of X, it suffices to show that
$G_\delta $
-subset of X, it suffices to show that
![]() $W(f)$
is a dense
$W(f)$
is a dense
![]() $G_\delta $
-subset of
$G_\delta $
-subset of
![]() $V(f)$
. Letting
$V(f)$
. Letting
we have
![]() $W=W(f)$
. Let
$W=W(f)$
. Let
for all
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $m\ge 0$
. Given any
$m\ge 0$
. Given any
![]() $x\in W_{j,m}$
,
$x\in W_{j,m}$
,
![]() $j\ge 1$
,
$j\ge 1$
,
![]() $m\ge 0$
, by compactness of
$m\ge 0$
, by compactness of
![]() $C(x,f)$
, there are
$C(x,f)$
, there are
![]() $0<r<\frac {1}{j}$
and
$0<r<\frac {1}{j}$
and
![]() $n\ge m$
such that
$n\ge m$
such that
We take
![]() $\epsilon>0$
with
$\epsilon>0$
with
![]() $r+2\epsilon <\frac {1}{j}$
. Since
$r+2\epsilon <\frac {1}{j}$
. Since
![]() $x\in V(f)$
and so
$x\in V(f)$
and so
![]() $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, by Lemma 2.2, there is
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, by Lemma 2.2, there is
![]() $a>0$
such that
$a>0$
such that
![]() $d(x,y)<a$
implies
$d(x,y)<a$
implies
for all
![]() $y\in X$
. By continuity of f, we have
$y\in X$
. By continuity of f, we have
![]() $b>0$
such that
$b>0$
such that
![]() $d(x,y)<b$
implies
$d(x,y)<b$
implies
for all
![]() $y\in X$
. It follows that
$y\in X$
. It follows that
![]() $d(x,y)<\min \{a,b\}$
implies
$d(x,y)<\min \{a,b\}$
implies
for all
![]() $y\in X$
. Since
$y\in X$
. Since
![]() $x\in W_{j,m}$
is arbitrary,
$x\in W_{j,m}$
is arbitrary,
![]() $W_{j,m}$
is an open subset of
$W_{j,m}$
is an open subset of
![]() $V(f)$
. Since
$V(f)$
. Since
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $m\ge 0$
are arbitrary, we conclude that W is a
$m\ge 0$
are arbitrary, we conclude that W is a
![]() $G_\delta $
-subset of
$G_\delta $
-subset of
![]() $V(f)$
. It remains to prove that W is a dense subset of
$V(f)$
. It remains to prove that W is a dense subset of
![]() $V(f)$
. Let
$V(f)$
. Let
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $m\ge 0$
. Given any
$m\ge 0$
. Given any
![]() $x\in V(f)$
and
$x\in V(f)$
and
![]() $\epsilon>0$
, since
$\epsilon>0$
, since
![]() $C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, by Lemma 2.2, there is
$C(x,f)\in \mathcal {C}_{\mathrm {ter}}(f)$
, by Lemma 2.2, there is
![]() $0<a<\epsilon /2$
such that
$0<a<\epsilon /2$
such that
![]() $d(x,y)<2a$
implies
$d(x,y)<2a$
implies
for all
![]() $y\in X$
. Since f has the shadowing property, we see that
$y\in X$
. Since f has the shadowing property, we see that
for some
![]() $p\in X$
with
$p\in X$
with
![]() $d(x,p)<a$
. By compactness of
$d(x,p)<a$
. By compactness of
![]() $C(x,f)$
, we obtain
$C(x,f)$
, we obtain
for some
![]() $n\ge m$
. By continuity of f, we have
$n\ge m$
. By continuity of f, we have
![]() $b>0$
such that
$b>0$
such that
![]() $d(p,q)<b$
implies
$d(p,q)<b$
implies
for all
![]() $q\in X$
. Since
$q\in X$
. Since
![]() $V(f)$
is a dense subset of X, we have
$V(f)$
is a dense subset of X, we have
![]() $d(p,q)<\min \{a,b\}$
for some
$d(p,q)<\min \{a,b\}$
for some
![]() $q\in V(f)$
. Note that
$q\in V(f)$
. Note that
It follows that
implying
![]() $q\in W_{j,m}$
. Since
$q\in W_{j,m}$
. Since
![]() $x\in V(f)$
and
$x\in V(f)$
and
![]() $\epsilon>0$
are arbitrary,
$\epsilon>0$
are arbitrary,
![]() $W_{j,m}$
is an open dense subset of
$W_{j,m}$
is an open dense subset of
![]() $V(f)$
. Since
$V(f)$
. Since
![]() $j\ge 1$
and
$j\ge 1$
and
![]() $m\ge 0$
are arbitrary, we conclude that W is a dense subset of
$m\ge 0$
are arbitrary, we conclude that W is a dense subset of
![]() $V(f)$
, proving the claim. Thus, the theorem has been proved.
$V(f)$
, proving the claim. Thus, the theorem has been proved.
We conclude with a remark on the proof.
Remark 2.1
-
• The proof shows that
 $V(f)$
and
$V(f)$
and
 $W(f)$
are
$W(f)$
are
 $G_\delta $
-subsets of X for every continuous map
$G_\delta $
-subsets of X for every continuous map
 $f\colon X\to X$
.
$f\colon X\to X$
. -
• For any continuous map
 $f\colon X\to X$
, we can show that if f has the shadowing property, then By this, since
$f\colon X\to X$
, we can show that if f has the shadowing property, then By this, since $$\begin{align*}V(f)=\{x\in X\colon C(\cdot,f)\colon X\to\mathcal{C}(f) \text{ is continuous at } x\}. \end{align*}$$
$$\begin{align*}V(f)=\{x\in X\colon C(\cdot,f)\colon X\to\mathcal{C}(f) \text{ is continuous at } x\}. \end{align*}$$
 $\mathcal {C}(f)$
is a compact metrizable space, we can show that
$\mathcal {C}(f)$
is a compact metrizable space, we can show that
 $V(f)$
is a
$V(f)$
is a
 $G_\delta $
-subset of X.
$G_\delta $
-subset of X.
-
• Let
 $f\colon X\to X$
be a continuous map and let
$f\colon X\to X$
be a continuous map and let
 $\xi =(x_i)_{i\ge 0}$
be a sequence of points in X. For
$\xi =(x_i)_{i\ge 0}$
be a sequence of points in X. For
 $\delta>0$
,
$\delta>0$
,
 $\xi $
is called a
$\xi $
is called a
 $\delta $
-limit-pseudo orbit of f if
$\delta $
-limit-pseudo orbit of f if
 $d(f(x_i),x_{i+1})\le \delta $
for all
$d(f(x_i),x_{i+1})\le \delta $
for all
 $i\ge 0$
, and For
$i\ge 0$
, and For $$\begin{align*}\lim_{i\to\infty}d(f(x_i),x_{i+1})=0. \end{align*}$$
$$\begin{align*}\lim_{i\to\infty}d(f(x_i),x_{i+1})=0. \end{align*}$$
 $\epsilon>0$
,
$\epsilon>0$
,
 $\xi $
is said to be
$\xi $
is said to be
 $\epsilon $
-limit shadowed by
$\epsilon $
-limit shadowed by
 $x\in X$
if
$x\in X$
if
 $d(f^i(x),x_i)\leq \epsilon $
for all
$d(f^i(x),x_i)\leq \epsilon $
for all
 $i\ge 0$
, and We say that f has the s-limit shadowing property if for any
$i\ge 0$
, and We say that f has the s-limit shadowing property if for any $$\begin{align*}\lim_{i\to\infty}d(f^i(x),x_i)=0. \end{align*}$$
$$\begin{align*}\lim_{i\to\infty}d(f^i(x),x_i)=0. \end{align*}$$
 $\epsilon>0$
, there is
$\epsilon>0$
, there is
 $\delta>0$
such that every
$\delta>0$
such that every
 $\delta $
-limit-pseudo orbit of f is
$\delta $
-limit-pseudo orbit of f is
 $\epsilon $
-limit shadowed by some point of X. When f has the s-limit shadowing property, by Lemma 2.1, we can easily show that
$\epsilon $
-limit shadowed by some point of X. When f has the s-limit shadowing property, by Lemma 2.1, we can easily show that
 $W(f)$
is a dense subset of X.
$W(f)$
is a dense subset of X.
Acknowledgements
The author would like to thank the reviewer for helpful suggestions.