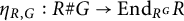1 Introduction
In [Reference Qin, Wang and Zhang18], Qin, Wang, and Zhang initiated a study of the McKay correspondence for nonconnected
![]() $\mathbb N$
-graded algebras in (global) dimension 2. An important component to this study is Auslander’s theorem. This project is an attempt to study this result in the context of preprojective algebras of type A.
$\mathbb N$
-graded algebras in (global) dimension 2. An important component to this study is Auslander’s theorem. This project is an attempt to study this result in the context of preprojective algebras of type A.
Let V be a finite-dimensional vector space, and let G be a finite group acting linearly on
![]() $R=\mathbb C[V]$
. The Auslander map
$R=\mathbb C[V]$
. The Auslander map
![]() $\gamma _{R,G}: R\# G \to \operatorname {\mathrm {End}}_{R^G} R$
is defined as
$\gamma _{R,G}: R\# G \to \operatorname {\mathrm {End}}_{R^G} R$
is defined as
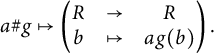 $$ \begin{align} a \# g &\mapsto \left(\begin{matrix}R & \to & R \\ b & \mapsto & ag(b)\end{matrix}\right). \end{align} $$
$$ \begin{align} a \# g &\mapsto \left(\begin{matrix}R & \to & R \\ b & \mapsto & ag(b)\end{matrix}\right). \end{align} $$
Auslander’s theorem, then, states that
![]() $\eta _{R,G}$
is an isomorphism if and only if G acts without reflections. That is, G is a small group [Reference Auslander1].
$\eta _{R,G}$
is an isomorphism if and only if G acts without reflections. That is, G is a small group [Reference Auslander1].
The Auslander map may be defined for any algebra R, commutative or noncommutative, and any subgroup G of
![]() $\operatorname {\mathrm {Aut}} R$
. However, in general, the map need not be injective or surjective. Bao, He, and Zhang introduced the pertinency invariant as a tool to study Auslander’s theorem in the noncommutative setting [Reference Bao, He and Zhang3, Reference Bao, He and Zhang4]. If
$\operatorname {\mathrm {Aut}} R$
. However, in general, the map need not be injective or surjective. Bao, He, and Zhang introduced the pertinency invariant as a tool to study Auslander’s theorem in the noncommutative setting [Reference Bao, He and Zhang3, Reference Bao, He and Zhang4]. If
![]() $\delta $
is any dimension function on an algebra R, G is a finite group acting on R, and
$\delta $
is any dimension function on an algebra R, G is a finite group acting on R, and
![]() $f_G=\sum _{g \in G} 1\# g \in R\#G$
, the pertinency of the G-action is defined as
$f_G=\sum _{g \in G} 1\# g \in R\#G$
, the pertinency of the G-action is defined as
Throughout this work, we take
![]() $\delta $
to be the Gelfand–Kirillov dimension. Under suitable hypotheses, the Auslander map is an isomorphism for the pair
$\delta $
to be the Gelfand–Kirillov dimension. Under suitable hypotheses, the Auslander map is an isomorphism for the pair
![]() $(R,G)$
if
$(R,G)$
if
![]() $\mathsf {p}(R,G) \geq 2$
.
$\mathsf {p}(R,G) \geq 2$
.
Kirkman, Moore, Won, and the second author proved that the Auslander map is an isomorphism for
![]() $(\mathbb C_{-1}[x_1,\ldots ,x_n],G)$
, where G is any subgroup of
$(\mathbb C_{-1}[x_1,\ldots ,x_n],G)$
, where G is any subgroup of
![]() $\mathcal S_n$
acting linearly as permutations of the generators (i.e.,
$\mathcal S_n$
acting linearly as permutations of the generators (i.e.,
![]() $\sigma (x_i)=x_{\sigma (i)}$
) [Reference Gaddis, Kirkman, Moore and Won11]. Chan, Young, and Zhang computed the explicit pertinency value for many cyclic subgroups of
$\sigma (x_i)=x_{\sigma (i)}$
) [Reference Gaddis, Kirkman, Moore and Won11]. Chan, Young, and Zhang computed the explicit pertinency value for many cyclic subgroups of
![]() $\mathcal S_n$
in search of noncommutative cyclic isolated singularities [Reference Chan, Young and Zhang8]. Crawford proved that the Auslander map is an isomorphism for any pair
$\mathcal S_n$
in search of noncommutative cyclic isolated singularities [Reference Chan, Young and Zhang8]. Crawford proved that the Auslander map is an isomorphism for any pair
![]() $(R,G)$
where R is a two-dimensional Artin–Schelter regular algebra and G is a small group, in which “smallness” is generalized to the noncommutative setting using the homological determinant [Reference Crawford10]. Further study of Auslander’s theorem and applications of the pertinency invariant can be found in [Reference Chan, Kirkman, Walton and Zhang7, Reference Chen, Kirkman and Zhang9, Reference Gaddis and Yee12, Reference He and Zhang14, Reference Mori and Ueyama17].
$(R,G)$
where R is a two-dimensional Artin–Schelter regular algebra and G is a small group, in which “smallness” is generalized to the noncommutative setting using the homological determinant [Reference Crawford10]. Further study of Auslander’s theorem and applications of the pertinency invariant can be found in [Reference Chan, Kirkman, Walton and Zhang7, Reference Chen, Kirkman and Zhang9, Reference Gaddis and Yee12, Reference He and Zhang14, Reference Mori and Ueyama17].
A natural generalization of the above is then to study the Auslander map in the context of nonconnected algebras. That is, to replace the condition of Artin–Schelter regularity with the twisted Calabi–Yau condition (see [Reference Ginzburg13]). By a result of Bocklandt, if R is Calabi–Yau of dimension 2, then R is the preprojective algebra of a non-Dynkin quiver [Reference Bocklandt6, Theorem 3.2]. More generally, Reyes and Rogalski have classified graded twisted Calabi–Yau algebras of global dimension 2 that are generated in degree 1 [Reference Reyes and Rogalski19].
We review the definition of preprojective algebras, as well as relevant ring-theoretic and homological definitions necessary to our study, in Section 2. Our main focus, however, will be the preprojective algebra
![]() $\Pi _{\widetilde {A_{n-1}}}$
, where
$\Pi _{\widetilde {A_{n-1}}}$
, where
![]() $\widetilde {A_{n-1}}$
is the extended Dynkin diagram of type A. In Theorem 2.6, we establish some cases where the Auslander map is an isomorphism for cyclic subgroups of scalar automorphisms on
$\widetilde {A_{n-1}}$
is the extended Dynkin diagram of type A. In Theorem 2.6, we establish some cases where the Auslander map is an isomorphism for cyclic subgroups of scalar automorphisms on
![]() $\Pi _{\widetilde {A_{n-1}}}$
.
$\Pi _{\widetilde {A_{n-1}}}$
.
In Section 3, we study dihedral group actions on
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
. Each graph automorphism of the underlying graph
$R=\Pi _{\widetilde {A_{n-1}}}$
. Each graph automorphism of the underlying graph
![]() $\Gamma _n$
of
$\Gamma _n$
of
![]() $\widetilde {A_{n-1}}$
extends to a graded algebra automorphism of R. From this, we obtain a subgroup of
$\widetilde {A_{n-1}}$
extends to a graded algebra automorphism of R. From this, we obtain a subgroup of
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
which is isomorphic to the graph automorphism group of
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
which is isomorphic to the graph automorphism group of
![]() $\Gamma _n$
, namely the dihedral group on n vertices
$\Gamma _n$
, namely the dihedral group on n vertices
![]() $D_n$
. We identify this group with
$D_n$
. We identify this group with
![]() $D_n$
itself. Our main result classifies the subgroups G of
$D_n$
itself. Our main result classifies the subgroups G of
![]() $D_n$
for which
$D_n$
for which
![]() $\eta _{R,G}$
is an isomorphism.
$\eta _{R,G}$
is an isomorphism.
Theorem 1.1 Let
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
and G a subgroup of
$R=\Pi _{\widetilde {A_{n-1}}}$
and G a subgroup of
![]() $D_n$
. The Auslander map
$D_n$
. The Auslander map
![]() $\eta _{R,G}$
is an isomorphism if and only if there exists a reflection
$\eta _{R,G}$
is an isomorphism if and only if there exists a reflection
![]() $\tau \in D_n$
that fixes a vertex and
$\tau \in D_n$
that fixes a vertex and
![]() $\tau \notin G$
.
$\tau \notin G$
.
A natural next question would be to study actions on preprojective algebras associated with other extended Dynkin types. However, as these exhibit significantly fewer symmetries, we do not consider them here.
2 Preprojective algebras
Throughout, we assume that
![]() ${\Bbb k}$
is an algebraically closed field of characteristic zero. All algebras are assumed to be
${\Bbb k}$
is an algebraically closed field of characteristic zero. All algebras are assumed to be
![]() ${\Bbb k}$
-algebras unless otherwise noted.
${\Bbb k}$
-algebras unless otherwise noted.
An algebra R is called (
![]() $\mathbb N$
-)graded if there exists a collection of
$\mathbb N$
-)graded if there exists a collection of
![]() ${\Bbb k}$
-vector subspaces
${\Bbb k}$
-vector subspaces
![]() $\{R_n\}_{n=0}^\infty $
of R such that
$\{R_n\}_{n=0}^\infty $
of R such that
![]() $R=\bigoplus _{n\in \mathbb N} R_n$
and
$R=\bigoplus _{n\in \mathbb N} R_n$
and
![]() $R_iR_j\subseteq R_{i+j}$
for all
$R_iR_j\subseteq R_{i+j}$
for all
![]() $i,j\in \mathbb N$
. We say that R is locally finite if
$i,j\in \mathbb N$
. We say that R is locally finite if
![]() $\dim _{\Bbb k}(R_n)<\infty $
for all
$\dim _{\Bbb k}(R_n)<\infty $
for all
![]() $n\in \mathbb N$
. If
$n\in \mathbb N$
. If
![]() $R_0={\Bbb k}$
, we say that R is connected. A
$R_0={\Bbb k}$
, we say that R is connected. A
![]() ${\Bbb k}$
-algebra automorphism
${\Bbb k}$
-algebra automorphism
![]() $\phi $
of R is called graded if
$\phi $
of R is called graded if
![]() $\phi (R_n)=R_n$
for all
$\phi (R_n)=R_n$
for all
![]() $n\in \mathbb N$
. We denote the group of
$n\in \mathbb N$
. We denote the group of
![]() $\mathbb N$
-graded automorphisms of R by
$\mathbb N$
-graded automorphisms of R by
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}} (R).$
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}} (R).$
Let R be an algebra, and let G be a finite subgroup of
![]() $\operatorname {\mathrm {Aut}}(R)$
. Let
$\operatorname {\mathrm {Aut}}(R)$
. Let
![]() $R\# G$
denote the set of formal sums
$R\# G$
denote the set of formal sums
Define a multiplication on
![]() $R\# G$
by
$R\# G$
by
extended linearly. We call
![]() $R\# G$
the skew group ring
$R\# G$
the skew group ring
![]() $R\# G$
. Note that, under this definition, the group ring
$R\# G$
. Note that, under this definition, the group ring
![]() ${\Bbb k} G$
is
${\Bbb k} G$
is
![]() ${\Bbb k} \#G$
with trivial G action.
${\Bbb k} \#G$
with trivial G action.
A quiver Q is a tuple
![]() $(Q_0,Q_1,s,t)$
consisting of a set of vertices
$(Q_0,Q_1,s,t)$
consisting of a set of vertices
![]() $Q_0=\{e_0,\dots ,e_n\}$
, a set of arrows
$Q_0=\{e_0,\dots ,e_n\}$
, a set of arrows
![]() $Q_1$
, and source and target functions
$Q_1$
, and source and target functions
![]() $s,t:Q_1\rightarrow Q_0$
. For any arrow
$s,t:Q_1\rightarrow Q_0$
. For any arrow
![]() $\alpha $
, we call the vertex
$\alpha $
, we call the vertex
![]() $s(\alpha )$
the source of
$s(\alpha )$
the source of
![]() $\alpha $
and the vertex
$\alpha $
and the vertex
![]() $t(\alpha )$
the target of
$t(\alpha )$
the target of
![]() $\alpha $
. We say Q is finite if
$\alpha $
. We say Q is finite if
![]() $Q_0$
and
$Q_0$
and
![]() $Q_1$
are finite, and Schurian if , given any two vertices i and j, there is at most one arrow with source i and target j. The adjacency matrix of a quiver Q is the matrix
$Q_1$
are finite, and Schurian if , given any two vertices i and j, there is at most one arrow with source i and target j. The adjacency matrix of a quiver Q is the matrix
![]() $M_Q$
in which
$M_Q$
in which
![]() $(M_Q)_{ij}$
denotes the number of arrows
$(M_Q)_{ij}$
denotes the number of arrows
![]() $i \to j$
.
$i \to j$
.
A path of length
![]() $\ell $
with source
$\ell $
with source
![]() $e_i$
and target
$e_i$
and target
![]() $e_j$
is a word of the form
$e_j$
is a word of the form
![]() $\alpha _1\alpha _2\cdots \alpha _\ell $
where
$\alpha _1\alpha _2\cdots \alpha _\ell $
where
![]() $\alpha _k\in Q_1$
for each
$\alpha _k\in Q_1$
for each
![]() $k=1,\dots ,\ell $
, and
$k=1,\dots ,\ell $
, and
![]() $s(\alpha _1)=e_i$
,
$s(\alpha _1)=e_i$
,
![]() $t(\alpha _\ell )=e_j$
, and
$t(\alpha _\ell )=e_j$
, and
![]() $t(\alpha _k)=s(\alpha _{k+1})$
for each
$t(\alpha _k)=s(\alpha _{k+1})$
for each
![]() $k=1,\dots ,\ell -1$
. If
$k=1,\dots ,\ell -1$
. If
![]() $p=\alpha _1\cdots \alpha _\ell $
, we extend the source and target functions to the set of all paths by the rule
$p=\alpha _1\cdots \alpha _\ell $
, we extend the source and target functions to the set of all paths by the rule
![]() $s(p)=s(\alpha _1)$
and
$s(p)=s(\alpha _1)$
and
![]() $t(p)=t(\alpha _\ell )$
. We denote the set of paths of length
$t(p)=t(\alpha _\ell )$
. We denote the set of paths of length
![]() $\ell $
by
$\ell $
by
![]() $Q_\ell $
, and treat the vertices
$Q_\ell $
, and treat the vertices
![]() $e_i$
as trivial paths of length 0 with
$e_i$
as trivial paths of length 0 with
![]() $s(e_i)=t(e_i)=e_i$
.
$s(e_i)=t(e_i)=e_i$
.
Let Q be a quiver. The path algebra of a quiver Q over the field
![]() ${\Bbb k}$
, denoted
${\Bbb k}$
, denoted
![]() ${\Bbb k} Q$
, is the algebra with
${\Bbb k} Q$
, is the algebra with
![]() ${\Bbb k}$
-basis the set of paths
${\Bbb k}$
-basis the set of paths
![]() $\bigcup _{\ell =0}^\infty Q_\ell $
and multiplication defined by concatenation. That is, given paths
$\bigcup _{\ell =0}^\infty Q_\ell $
and multiplication defined by concatenation. That is, given paths
![]() $p=\alpha _1\cdots \alpha _\ell $
and
$p=\alpha _1\cdots \alpha _\ell $
and
![]() $q=\beta _1\cdots \beta _k$
,
$q=\beta _1\cdots \beta _k$
,
![]() $pq=\alpha _1\cdots \alpha _\ell \beta _1\cdots \beta _k$
if
$pq=\alpha _1\cdots \alpha _\ell \beta _1\cdots \beta _k$
if
![]() $t(p)=s(q)$
and
$t(p)=s(q)$
and
![]() $pq=0$
otherwise. For any
$pq=0$
otherwise. For any
![]() $e\in Q_0$
and any path p, we also have the following:
$e\in Q_0$
and any path p, we also have the following:
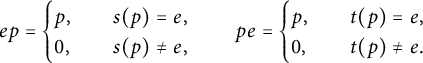 $$ \begin{align*} ep =\begin{cases} p, &\quad s(p)=e,\\ 0, &\quad s(p)\neq e, \end{cases} \qquad pe =\begin{cases} p, &\quad t(p)=e,\\ 0, &\quad t(p)\neq e. \end{cases} \end{align*} $$
$$ \begin{align*} ep =\begin{cases} p, &\quad s(p)=e,\\ 0, &\quad s(p)\neq e, \end{cases} \qquad pe =\begin{cases} p, &\quad t(p)=e,\\ 0, &\quad t(p)\neq e. \end{cases} \end{align*} $$
Note that a path algebra
![]() ${\Bbb k} Q$
on a finite quiver is graded by
${\Bbb k} Q$
on a finite quiver is graded by
![]() $\{({\Bbb k} Q)_\ell \}_{\ell =0}^\infty $
where
$\{({\Bbb k} Q)_\ell \}_{\ell =0}^\infty $
where
![]() $({\Bbb k} Q)_\ell =\operatorname {\mathrm {Span}}_{\Bbb k}(Q_\ell )$
, and there are only finitely many paths of any given length, so
$({\Bbb k} Q)_\ell =\operatorname {\mathrm {Span}}_{\Bbb k}(Q_\ell )$
, and there are only finitely many paths of any given length, so
![]() ${\Bbb k} Q$
is locally finite.
${\Bbb k} Q$
is locally finite.
The double of a quiver Q, denoted
![]() $\overline {Q}$
, is defined by setting
$\overline {Q}$
, is defined by setting
![]() $\overline {Q}_0=Q_0$
, and for every arrow
$\overline {Q}_0=Q_0$
, and for every arrow
![]() $\alpha \in Q_1$
with
$\alpha \in Q_1$
with
![]() $s(\alpha )=e_i$
and
$s(\alpha )=e_i$
and
![]() $t(\alpha )=e_j$
, we add an arrow
$t(\alpha )=e_j$
, we add an arrow
![]() $\alpha ^*$
with
$\alpha ^*$
with
![]() $s(\alpha ^*)=e_j$
and
$s(\alpha ^*)=e_j$
and
![]() $t(\alpha ^*)=e_i$
. We call
$t(\alpha ^*)=e_i$
. We call
![]() $Q_1$
the set of nonstar arrows and
$Q_1$
the set of nonstar arrows and
![]() $Q_1^*:=\overline {Q_1}\setminus Q_1$
the set of star arrows.
$Q_1^*:=\overline {Q_1}\setminus Q_1$
the set of star arrows.
Definition 2.1 Let Q be a finite quiver, and set
![]() $\Omega =\sum _{\alpha \in Q_1} \alpha \alpha ^*-\alpha ^*\alpha \in \overline {Q}$
. The preprojective algebra associated with Q, denoted
$\Omega =\sum _{\alpha \in Q_1} \alpha \alpha ^*-\alpha ^*\alpha \in \overline {Q}$
. The preprojective algebra associated with Q, denoted
![]() $\Pi _Q$
, is the quotient
$\Pi _Q$
, is the quotient
![]() ${\Bbb k} \overline {Q}/(\Omega )$
. We call
${\Bbb k} \overline {Q}/(\Omega )$
. We call
![]() $\Omega $
the preprojective relation.
$\Omega $
the preprojective relation.
The type A extended Dynkin quivers
![]() $\widetilde {A_{n-1}}$
,
$\widetilde {A_{n-1}}$
,
![]() $n\geq 3$
, are given by
$n\geq 3$
, are given by
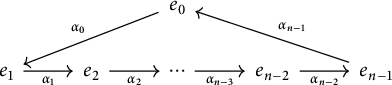
We focus on preprojective algebras corresponding to this type. If
![]() $Q=\widetilde {A_{n-1}}$
, then
$Q=\widetilde {A_{n-1}}$
, then
![]() $\overline {Q}$
can be characterized as follows. The vertex set
$\overline {Q}$
can be characterized as follows. The vertex set
![]() $\overline {Q_0}$
of
$\overline {Q_0}$
of
![]() $\overline {Q}$
is
$\overline {Q}$
is
![]() $\{e_0,\dots ,e_{n-1}\}$
, and there is exactly one nonstar arrow,
$\{e_0,\dots ,e_{n-1}\}$
, and there is exactly one nonstar arrow,
![]() $\alpha _i$
, from
$\alpha _i$
, from
![]() $e_i$
to
$e_i$
to
![]() $e_{i+1}$
and one star arrow,
$e_{i+1}$
and one star arrow,
![]() $\alpha _i^*$
, from
$\alpha _i^*$
, from
![]() $e_{i+1}$
to
$e_{i+1}$
to
![]() $e_{i}$
for each
$e_{i}$
for each
![]() $i=0,\dots ,n-1$
where the index is taken mod n. That is,
$i=0,\dots ,n-1$
where the index is taken mod n. That is,
![]() $\overline {Q}$
is Schurian. For example, the double of
$\overline {Q}$
is Schurian. For example, the double of
![]() $\widetilde {A_2}$
is presented below:
$\widetilde {A_2}$
is presented below:
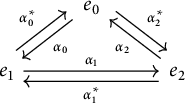
We note that
![]() $\widetilde {A_1}$
is also defined. However, as its double is not Schurian, it does not fit into the theory we have developed.
$\widetilde {A_1}$
is also defined. However, as its double is not Schurian, it does not fit into the theory we have developed.
The preprojective algebra
![]() $\Pi _{\widetilde {A_{n-1}}}$
has nice ring-theoretic properties, as discussed in the next proposition. Before this, we review some of the definitions. For others, such as graded injectively smooth and the generalized Gorenstein condition, we refer to [Reference Stafford and Zhang20, Reference Weispfenning22], respectively.
$\Pi _{\widetilde {A_{n-1}}}$
has nice ring-theoretic properties, as discussed in the next proposition. Before this, we review some of the definitions. For others, such as graded injectively smooth and the generalized Gorenstein condition, we refer to [Reference Stafford and Zhang20, Reference Weispfenning22], respectively.
Let
![]() $R = \bigoplus _{n \in \mathbb N} R_n$
be a locally finite graded algebra. The Gelfand–Kirillov (GK) dimension of R is defined as
$R = \bigoplus _{n \in \mathbb N} R_n$
be a locally finite graded algebra. The Gelfand–Kirillov (GK) dimension of R is defined as
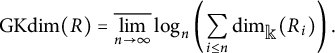 $$\begin{align*}\operatorname{\mathrm{GKdim}} (R) = \overline{\lim_{n\to\infty}}\log_n\left(\sum_{i\leq n}\dim_{\Bbb k}( R_i) \right).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{GKdim}} (R) = \overline{\lim_{n\to\infty}}\log_n\left(\sum_{i\leq n}\dim_{\Bbb k}( R_i) \right).\end{align*}$$
Now, let
![]() $\delta $
be a dimension function on R. For example, we may have
$\delta $
be a dimension function on R. For example, we may have
![]() $\delta =\operatorname {\mathrm {GKdim}}$
or
$\delta =\operatorname {\mathrm {GKdim}}$
or
![]() $\delta =\operatorname {\mathrm {Kdim}}$
, the Krull dimension. The ring R is
$\delta =\operatorname {\mathrm {Kdim}}$
, the Krull dimension. The ring R is
![]() $\delta $
-Cohen–Macaulay (
$\delta $
-Cohen–Macaulay (
![]() $\delta $
-CM) if
$\delta $
-CM) if
![]() $\delta (R)$
is finite, and for every nontrivial finitely generated right R-module M,
$\delta (R)$
is finite, and for every nontrivial finitely generated right R-module M,
![]() $j(M)+\delta (M) = \delta (R)$
, where
$j(M)+\delta (M) = \delta (R)$
, where
![]() $j(M)=\min \{i:\operatorname {\mathrm {Ext}}_R^i (M,R)\neq 0\}$
denotes the grade of M.
$j(M)=\min \{i:\operatorname {\mathrm {Ext}}_R^i (M,R)\neq 0\}$
denotes the grade of M.
The (total) Hilbert series of R is the formal power series
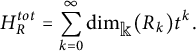 $$\begin{align*}H_R^{tot} = \sum_{k=0}^\infty \dim_{{\Bbb k}}(R_k) t^k.\end{align*}$$
$$\begin{align*}H_R^{tot} = \sum_{k=0}^\infty \dim_{{\Bbb k}}(R_k) t^k.\end{align*}$$
If
![]() $R_0 = {\Bbb k}^n$
with primitive idempotents
$R_0 = {\Bbb k}^n$
with primitive idempotents
![]() $\{e_0,\ldots ,e_{n-1}\}$
, then the matrix-valued Hilbert series is the matrix with entries
$\{e_0,\ldots ,e_{n-1}\}$
, then the matrix-valued Hilbert series is the matrix with entries
 $$\begin{align*}(H_R)_{ij} = \sum_{k=0}^\infty \dim_{{\Bbb k}}(e_{i+1} R_k e_{j+1} ) t^k.\end{align*}$$
$$\begin{align*}(H_R)_{ij} = \sum_{k=0}^\infty \dim_{{\Bbb k}}(e_{i+1} R_k e_{j+1} ) t^k.\end{align*}$$
Proposition 2.1 Let
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
. Then R is a locally finite graded Noetherian algebra of global and GK dimension 2. Moreover, R is
$R=\Pi _{\widetilde {A_{n-1}}}$
. Then R is a locally finite graded Noetherian algebra of global and GK dimension 2. Moreover, R is
![]() $\operatorname {\mathrm {GKdim}}$
-CM and
$\operatorname {\mathrm {GKdim}}$
-CM and
![]() $H_R = (1-M_{\overline {Q}} t)^{-2}$
.
$H_R = (1-M_{\overline {Q}} t)^{-2}$
.
Proof That R is locally finite graded follows because Q (and hence
![]() $\overline {Q}$
) is finite. By [Reference Baer, Geigle and Lenzing2, Theorem 6.5], R is a Noetherian polynomial identity ring. Furthermore, R satisfies the generalized Gorenstein condition [Reference Weispfenning21, Proposition 2.11], which implies that R is right graded injectively smooth. Then, by [Reference Stafford and Zhang20, Theorem 1.3], R is
$\overline {Q}$
) is finite. By [Reference Baer, Geigle and Lenzing2, Theorem 6.5], R is a Noetherian polynomial identity ring. Furthermore, R satisfies the generalized Gorenstein condition [Reference Weispfenning21, Proposition 2.11], which implies that R is right graded injectively smooth. Then, by [Reference Stafford and Zhang20, Theorem 1.3], R is
![]() $\operatorname {\mathrm {Kdim}}$
-CM, which implies that R is
$\operatorname {\mathrm {Kdim}}$
-CM, which implies that R is
![]() $\operatorname {\mathrm {GKdim}}$
-CM by [Reference Stafford and Zhang20, Lemma 4.3]. The statement on the Hilbert series follows from [Reference Bocklandt6].▪
$\operatorname {\mathrm {GKdim}}$
-CM by [Reference Stafford and Zhang20, Lemma 4.3]. The statement on the Hilbert series follows from [Reference Bocklandt6].▪
The next lemma gives a canonical form for paths in the preprojective algebra
![]() $\Pi _{\widetilde {A_{n-1}}}$
.
$\Pi _{\widetilde {A_{n-1}}}$
.
Lemma 2.2 (Structure Lemma)
Let
![]() $Q=\widetilde {A_{n-1}}$
, and let
$Q=\widetilde {A_{n-1}}$
, and let
![]() $R=\Pi _Q$
. Let p be a (nonconstant) monomial in R. Then there exist nonstar arrows
$R=\Pi _Q$
. Let p be a (nonconstant) monomial in R. Then there exist nonstar arrows
![]() $\beta _1,\dots ,\beta _\ell $
and star arrows
$\beta _1,\dots ,\beta _\ell $
and star arrows
![]() $\gamma _1,\dots ,\gamma _m$
such that
$\gamma _1,\dots ,\gamma _m$
such that
![]() $p=\beta _1\cdots \beta _\ell \gamma _1\cdots \gamma _m$
.
$p=\beta _1\cdots \beta _\ell \gamma _1\cdots \gamma _m$
.
Proof Given any idempotent
![]() $e_i \in Q_0$
,
$e_i \in Q_0$
,
![]() $e_i\Omega e_i \in (\Omega )$
and so the following relations hold in
$e_i\Omega e_i \in (\Omega )$
and so the following relations hold in
![]() $\Pi _{\widetilde {A_{n-1}}}$
:
$\Pi _{\widetilde {A_{n-1}}}$
:
where the indices are taken mod n.
Given any star arrow
![]() $\alpha _i^*$
, the only nonstar arrow
$\alpha _i^*$
, the only nonstar arrow
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha _i^*\beta \neq 0$
is
$\alpha _i^*\beta \neq 0$
is
![]() $\alpha _i$
. Consequently, whenever a star arrow is followed by a nonstar arrow, we can use (2) to obtain a nonstar arrow followed by a star arrow instead. By repeated use of (2), we have
$\alpha _i$
. Consequently, whenever a star arrow is followed by a nonstar arrow, we can use (2) to obtain a nonstar arrow followed by a star arrow instead. By repeated use of (2), we have
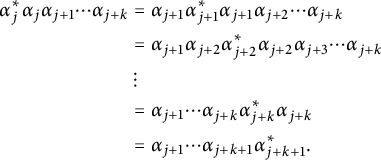 $$ \begin{align*} \alpha_j^*\alpha_j\alpha_{j+1}\cdots\alpha_{j+k} &= \alpha_{j+1}\alpha_{j+1}^*\alpha_{j+1}\alpha_{j+2}\cdots\alpha_{j+k}\\ &=\alpha_{j+1}\alpha_{j+2}\alpha_{j+2}^*\alpha_{j+2}\alpha_{j+3}\cdots\alpha_{j+k}\\ &\ \vdots\\ &=\alpha_{j+1}\cdots\alpha_{j+k}\alpha_{j+k}^*\alpha_{j+k}\\ &=\alpha_{j+1}\cdots\alpha_{j+k+1}\alpha_{j+k+1}^*. \end{align*} $$
$$ \begin{align*} \alpha_j^*\alpha_j\alpha_{j+1}\cdots\alpha_{j+k} &= \alpha_{j+1}\alpha_{j+1}^*\alpha_{j+1}\alpha_{j+2}\cdots\alpha_{j+k}\\ &=\alpha_{j+1}\alpha_{j+2}\alpha_{j+2}^*\alpha_{j+2}\alpha_{j+3}\cdots\alpha_{j+k}\\ &\ \vdots\\ &=\alpha_{j+1}\cdots\alpha_{j+k}\alpha_{j+k}^*\alpha_{j+k}\\ &=\alpha_{j+1}\cdots\alpha_{j+k+1}\alpha_{j+k+1}^*. \end{align*} $$
By induction on the number of star arrows, it follows that we can push all star arrows to the right.▪
The invariant theory of preprojective algebras was studied by Weispfenning, with particular interest toward a version of the Shephard–Todd–Chevalley theorem [Reference Weispfenning21, Reference Weispfenning22]. Our interest is in a version of Auslander’s theorem for group actions on the projective algebra
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
. Particularly relevant to the present investigation is the following theorem due to Bao, He, and Zhang.
$R=\Pi _{\widetilde {A_{n-1}}}$
. Particularly relevant to the present investigation is the following theorem due to Bao, He, and Zhang.
Theorem 2.3 [Reference Bao, He and Zhang4, Theorem 3.5]
Let R be a Noetherian locally finite graded algebra, and let G be a finite subgroup of
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
. Assume further that R is
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
. Assume further that R is
![]() $\operatorname {\mathrm {GKdim}}$
-CM of global dimension 2 with
$\operatorname {\mathrm {GKdim}}$
-CM of global dimension 2 with
![]() $\operatorname {\mathrm {GKdim}} R\geq 2$
. Then
$\operatorname {\mathrm {GKdim}} R\geq 2$
. Then
![]() $\eta _{R,G}$
is a graded algebra isomorphism if and only if
$\eta _{R,G}$
is a graded algebra isomorphism if and only if
![]() $\mathsf {p}(R,G)\geq 2$
.
$\mathsf {p}(R,G)\geq 2$
.
Let
![]() $R'$
be the image of R in the composition
$R'$
be the image of R in the composition
We call
![]() $R'$
the identity component of
$R'$
the identity component of
![]() $(R\# G)/(f_G)$
, which we can associate with R. By [Reference Bao, He and Zhang4, Lemma 5.2],
$(R\# G)/(f_G)$
, which we can associate with R. By [Reference Bao, He and Zhang4, Lemma 5.2],
![]() $\operatorname {\mathrm {GKdim}}(R') = \operatorname {\mathrm {GKdim}}((R\# G)/(f_G))$
.
$\operatorname {\mathrm {GKdim}}(R') = \operatorname {\mathrm {GKdim}}((R\# G)/(f_G))$
.
Theorem 2.4 Let
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
, let G be a finite subgroup of
$R=\Pi _{\widetilde {A_{n-1}}}$
, let G be a finite subgroup of
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
, and let
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
, and let
![]() $R'$
be the identity component of
$R'$
be the identity component of
![]() $(R\# G)/(f_G)$
. Then
$(R\# G)/(f_G)$
. Then
![]() $\eta _{R,G}$
is a graded algebra isomorphism if and only if
$\eta _{R,G}$
is a graded algebra isomorphism if and only if
![]() $\dim _{\Bbb k}(R')<\infty $
.
$\dim _{\Bbb k}(R')<\infty $
.
Proof By Proposition 2.1, R satisfies the conditions of Theorem 2.3. That is,
![]() $\eta _{R,G}$
is an isomorphism if and only if
$\eta _{R,G}$
is an isomorphism if and only if
![]() $\mathsf {p}(R,G)\geq 2$
. Since
$\mathsf {p}(R,G)\geq 2$
. Since
![]() $\operatorname {\mathrm {GKdim}}(R)=2$
, then
$\operatorname {\mathrm {GKdim}}(R)=2$
, then
![]() $\mathsf {p}(R,G)\geq 2$
if and only if
$\mathsf {p}(R,G)\geq 2$
if and only if
![]() $\operatorname {\mathrm {GKdim}} ((R\# G)/(f_G))=0$
, which is equivalent to
$\operatorname {\mathrm {GKdim}} ((R\# G)/(f_G))=0$
, which is equivalent to
![]() $(R\# G)/(f_G)$
being a finite-dimensional
$(R\# G)/(f_G)$
being a finite-dimensional
![]() ${\Bbb k}$
-vector space.▪
${\Bbb k}$
-vector space.▪
Since R is locally finite,
![]() ${\Bbb k}\cup \bigcup _{\ell < m} R_\ell $
is finite-dimensional for all
${\Bbb k}\cup \bigcup _{\ell < m} R_\ell $
is finite-dimensional for all
![]() $m\in \mathbb N$
. Consequently, if there exists
$m\in \mathbb N$
. Consequently, if there exists
![]() $m\in \mathbb N$
such that every path of length at least m is in
$m\in \mathbb N$
such that every path of length at least m is in
![]() $(f_G)$
, then
$(f_G)$
, then
![]() $R'$
has a complete set of coset representatives in
$R'$
has a complete set of coset representatives in
![]() ${\Bbb k}\cup \bigcup _{\ell < m} R_m$
. That is,
${\Bbb k}\cup \bigcup _{\ell < m} R_m$
. That is,
![]() $\dim _{\Bbb k}(R')<\infty $
.
$\dim _{\Bbb k}(R')<\infty $
.
We conclude this section with a discussion of graded automorphisms of
![]() $\Pi _{\widetilde {A_{n-1}}}$
.
$\Pi _{\widetilde {A_{n-1}}}$
.
Let Q be a quiver. A quiver automorphism
![]() $\sigma =(\sigma _0, \sigma _1)$
of Q is a pair of bijections
$\sigma =(\sigma _0, \sigma _1)$
of Q is a pair of bijections
![]() $\sigma _0:Q_0\to Q_0$
and
$\sigma _0:Q_0\to Q_0$
and
![]() $\sigma _1:Q_1\to Q_1$
such that for all
$\sigma _1:Q_1\to Q_1$
such that for all
![]() $\alpha \in Q_1$
,
$\alpha \in Q_1$
,
![]() $s(\sigma _1(\alpha ))=\sigma _0(s(\alpha ))$
and
$s(\sigma _1(\alpha ))=\sigma _0(s(\alpha ))$
and
![]() $t(\sigma _1(\alpha ))=\sigma _0(t(\alpha ))$
. Every quiver automorphism extends to a graded automorphism of
$t(\sigma _1(\alpha ))=\sigma _0(t(\alpha ))$
. Every quiver automorphism extends to a graded automorphism of
![]() ${\Bbb k} Q$
which, by an abuse of notation, we again denote by
${\Bbb k} Q$
which, by an abuse of notation, we again denote by
![]() $\sigma $
(see [Reference Kinser and Walton16]).
$\sigma $
(see [Reference Kinser and Walton16]).
Conversely, if
![]() $\sigma $
is a graded automorphism of
$\sigma $
is a graded automorphism of
![]() $\Pi _{\widetilde {A_{n-1}}}$
, then
$\Pi _{\widetilde {A_{n-1}}}$
, then
![]() $\sigma _0$
permutes the set
$\sigma _0$
permutes the set
![]() $Q_0$
. Since Q is Schurian, then for any
$Q_0$
. Since Q is Schurian, then for any
![]() $\alpha \in Q_1$
,
$\alpha \in Q_1$
,
![]() $\sigma (\alpha )$
is necessarily a nonzero scalar multiple of the unique arrow from
$\sigma (\alpha )$
is necessarily a nonzero scalar multiple of the unique arrow from
![]() $\sigma _0(s(\alpha ))$
to
$\sigma _0(s(\alpha ))$
to
![]() $\sigma _0(t(\alpha ))$
. First, we will consider automorphisms which fix the vertices of
$\sigma _0(t(\alpha ))$
. First, we will consider automorphisms which fix the vertices of
![]() $\widetilde {A_{n-1}}$
. In Section 3, we study automorphisms corresponding to dihedral automorphisms on
$\widetilde {A_{n-1}}$
. In Section 3, we study automorphisms corresponding to dihedral automorphisms on
![]() $\widetilde {A_{n-1}}$
.
$\widetilde {A_{n-1}}$
.
For the remainder of this section, let
![]() $Q=\widetilde {A_{n-1}}$
and
$Q=\widetilde {A_{n-1}}$
and
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
. Let
$R=\Pi _{\widetilde {A_{n-1}}}$
. Let
Fixed subrings of R under automorphisms in F were studied by Weispfenning [Reference Weispfenning21, Reference Weispfenning22].
Let
![]() $\sigma \in F$
. By the above discussion,
$\sigma \in F$
. By the above discussion,
![]() $\sigma (\alpha ) \in \operatorname {\mathrm {Span}}_{\Bbb k}\{\alpha \}$
for each
$\sigma (\alpha ) \in \operatorname {\mathrm {Span}}_{\Bbb k}\{\alpha \}$
for each
![]() $\alpha \in Q_1$
. Thus, there exists
$\alpha \in Q_1$
. Thus, there exists
![]() $\xi _i,\xi _i^* \in {\Bbb k}^\times $
such that
$\xi _i,\xi _i^* \in {\Bbb k}^\times $
such that
![]() $\sigma (\alpha _i)=\xi _i \alpha _i$
and
$\sigma (\alpha _i)=\xi _i \alpha _i$
and
![]() $\sigma (\alpha _i^*)=\xi _i^* \alpha _i^*$
for each
$\sigma (\alpha _i^*)=\xi _i^* \alpha _i^*$
for each
![]() $i=0,\ldots ,n-1$
. Since
$i=0,\ldots ,n-1$
. Since
![]() $\sigma $
is of finite order, each
$\sigma $
is of finite order, each
![]() $\xi _i,\xi _i^*$
must be a root of unity. On the other hand,
$\xi _i,\xi _i^*$
must be a root of unity. On the other hand,
![]() $\sigma (\Omega ) \in \operatorname {\mathrm {Span}}_{{\Bbb k}}(\Omega )$
and so
$\sigma (\Omega ) \in \operatorname {\mathrm {Span}}_{{\Bbb k}}(\Omega )$
and so
![]() $\sigma (\Omega )=\omega \Omega $
for some
$\sigma (\Omega )=\omega \Omega $
for some
![]() $\omega \in {\Bbb k}^\times $
. It is not difficult to show using the preprojective relation that
$\omega \in {\Bbb k}^\times $
. It is not difficult to show using the preprojective relation that
![]() $\xi _i\xi _i^*=\omega $
for all i. The value
$\xi _i\xi _i^*=\omega $
for all i. The value
![]() $\omega $
in this case is the homological determinant of the
$\omega $
in this case is the homological determinant of the
![]() $\sigma $
-action on R [Reference Jørgensen and Zhang15, Reference Weispfenning22]. We will consider cases in which
$\sigma $
-action on R [Reference Jørgensen and Zhang15, Reference Weispfenning22]. We will consider cases in which
![]() $\omega =1$
.
$\omega =1$
.
Our primary tool for studying the Auslander map for cyclic subgroups of F is the following result of He and Zhang, which we have rephrased for our purpose.
Lemma 2.5 [Reference He and Zhang14, Lemma 3.4]
Let
![]() $\sigma \in F$
, let
$\sigma \in F$
, let
![]() $G=\langle \sigma \rangle $
, and let
$G=\langle \sigma \rangle $
, and let
![]() $|\sigma |=m$
. Assume that there are elements
$|\sigma |=m$
. Assume that there are elements
![]() $a_0,\dots ,a_{m-1}\in R$
such that
$a_0,\dots ,a_{m-1}\in R$
such that
![]() $\sigma (a_i)=\zeta a_i$
for
$\sigma (a_i)=\zeta a_i$
for
![]() $i=0,\dots ,m-1$
, where
$i=0,\dots ,m-1$
, where
![]() $\zeta $
is an mth primitive root of unity. Then
$\zeta $
is an mth primitive root of unity. Then
![]() $a_0a_1\cdots a_{m-1}\# 1 \in (f_G)$
.
$a_0a_1\cdots a_{m-1}\# 1 \in (f_G)$
.
We now apply Lemma 2.5 to establish an isomorphism of the Auslander map for certain scalar automorphisms.
Theorem 2.6 Let
![]() $\sigma \in F$
with
$\sigma \in F$
with
![]() $m=|\sigma |$
,
$m=|\sigma |$
,
![]() $1 < m < \infty $
, and let
$1 < m < \infty $
, and let
![]() $G=\langle \sigma \rangle $
. As above, write
$G=\langle \sigma \rangle $
. As above, write
![]() $\sigma (\alpha _i)=\xi _i \alpha _i$
and
$\sigma (\alpha _i)=\xi _i \alpha _i$
and
![]() $\sigma (\alpha _i^*)=\xi _i^* \alpha _i^*$
,
$\sigma (\alpha _i^*)=\xi _i^* \alpha _i^*$
,
![]() $i=0,\ldots ,n-1$
, with
$i=0,\ldots ,n-1$
, with
![]() $\xi _1\xi _1^*=1$
. In each of the following cases,
$\xi _1\xi _1^*=1$
. In each of the following cases,
![]() $\eta _{R,G}$
is an isomorphism.
$\eta _{R,G}$
is an isomorphism.
-
(1) There is some primitive mth root of unity
 $\zeta $
such that
$\zeta $
such that
 $\xi _i=\zeta $
for
$\xi _i=\zeta $
for
 $i=0,\ldots ,n-1$
.
$i=0,\ldots ,n-1$
. -
(2) There is some primitive mth root of unity
 $\zeta $
such that
$\zeta $
such that
 $\xi _0\xi _1\cdots \xi _{n-1}=\zeta $
.
$\xi _0\xi _1\cdots \xi _{n-1}=\zeta $
. -
(3) For all
 $i,j=0,\ldots ,n-1$
with
$i,j=0,\ldots ,n-1$
with
 $i\neq j$
, we have
$i\neq j$
, we have
 $\gcd (|\xi _i|,|\xi _j|)=1$
.
$\gcd (|\xi _i|,|\xi _j|)=1$
.
Proof First, suppose that there exists a pure nonstar path q of length
![]() $\ell $
such that
$\ell $
such that
![]() $q\# 1 \in (f_G)$
. Then let p be a path containing at least
$q\# 1 \in (f_G)$
. Then let p be a path containing at least
![]() $2\ell $
nonstar arrows. Pushing all nonstar arrows to the left using the Structure Lemma (Lemma 2.2), it follows that p contains q, so
$2\ell $
nonstar arrows. Pushing all nonstar arrows to the left using the Structure Lemma (Lemma 2.2), it follows that p contains q, so
![]() $p\# 1 \in (f_G)$
. The same argument applies if
$p\# 1 \in (f_G)$
. The same argument applies if
![]() $q,p$
are pure star paths. Hence, if
$q,p$
are pure star paths. Hence, if
![]() $(f_G)$
contains both a pure nonstar path and a pure star path of length
$(f_G)$
contains both a pure nonstar path and a pure star path of length
![]() $\ell $
, then
$\ell $
, then
![]() $\dim _{{\Bbb k}}(R')<\infty $
and
$\dim _{{\Bbb k}}(R')<\infty $
and
![]() $\eta _{R,G}$
is an isomorphism by Theorem 2.4. Thus, in each case, we will attempt to produce such paths.
$\eta _{R,G}$
is an isomorphism by Theorem 2.4. Thus, in each case, we will attempt to produce such paths.
(1) Assuming
![]() $\xi _i=\zeta $
as in the hypothesis, take
$\xi _i=\zeta $
as in the hypothesis, take
![]() $a_i=\alpha _i$
and apply Lemma 2.5. Taking indices mod n, it follows that
$a_i=\alpha _i$
and apply Lemma 2.5. Taking indices mod n, it follows that
![]() $a_0\cdots a_{m-1} \in (f_G)$
is a pure nonstar path. One similarly obtains a pure star path. Hence,
$a_0\cdots a_{m-1} \in (f_G)$
is a pure nonstar path. One similarly obtains a pure star path. Hence,
![]() $\eta _{R,G}$
is an isomorphism by the above argument.
$\eta _{R,G}$
is an isomorphism by the above argument.
(2) Let p be any pure nonstar path of length n, and let q be any pure star path of length n. Since p contains each nonstar arrow exactly once,
![]() $\sigma (p)=\zeta p$
. No power of p is zero and so we apply Lemma 2.5 with
$\sigma (p)=\zeta p$
. No power of p is zero and so we apply Lemma 2.5 with
![]() $a_i=p$
to obtain
$a_i=p$
to obtain
![]() $p^m\# 1 \in (f_G)$
. Similarly, we obtain
$p^m\# 1 \in (f_G)$
. Similarly, we obtain
![]() $q^m\#1 \in (f_G)$
. Hence,
$q^m\#1 \in (f_G)$
. Hence,
![]() $\eta _{R,G}$
is an isomorphism.
$\eta _{R,G}$
is an isomorphism.
(3) The order of
![]() $\sigma $
is determined by its image on
$\sigma $
is determined by its image on
![]() $R_1$
, which in turn is determined by its image on
$R_1$
, which in turn is determined by its image on
![]() $\alpha _0,\dots ,\alpha _{n-1}$
. That is,
$\alpha _0,\dots ,\alpha _{n-1}$
. That is,
![]() $|\sigma |=k$
, where k is the least positive integer such that
$|\sigma |=k$
, where k is the least positive integer such that
![]() $\sigma ^k(\alpha _i)=\alpha _i$
for all
$\sigma ^k(\alpha _i)=\alpha _i$
for all
![]() $i=0,\dots ,n-1$
. Since the orders of the scalars
$i=0,\dots ,n-1$
. Since the orders of the scalars
![]() $\xi _i$
are relatively prime, then we have
$\xi _i$
are relatively prime, then we have
![]() $|\zeta | = |\xi _0|\cdot |\xi _1|\cdots |\xi _{n-1}| = |\sigma |$
. The result now follows from (2).▪
$|\zeta | = |\xi _0|\cdot |\xi _1|\cdots |\xi _{n-1}| = |\sigma |$
. The result now follows from (2).▪
3 Dihedral actions on
 $\Pi _{\widetilde {A_{n-1}}}$
$\Pi _{\widetilde {A_{n-1}}}$
In this section, we establish our main theorem regarding the Auslander map for dihedral actions on
![]() $\Pi _{\widetilde {A_{n-1}}}$
.
$\Pi _{\widetilde {A_{n-1}}}$
.
Let
![]() $\sigma $
be a quiver automorphism of a Schurian quiver Q. As discussed above, if
$\sigma $
be a quiver automorphism of a Schurian quiver Q. As discussed above, if
![]() $\alpha \in Q_1$
, then
$\alpha \in Q_1$
, then
![]() $\sigma (\alpha )$
is a scalar multiple of the unique arrow from
$\sigma (\alpha )$
is a scalar multiple of the unique arrow from
![]() $\sigma _0(s(\alpha ))$
to
$\sigma _0(s(\alpha ))$
to
![]() $\sigma _0(t(\alpha ))$
. Throughout this section, we assume that scalar is 1.
$\sigma _0(t(\alpha ))$
. Throughout this section, we assume that scalar is 1.
Proposition 3.1 Let Q be a quiver such that
![]() $\overline {Q}$
is Schurian, let
$\overline {Q}$
is Schurian, let
![]() $R=\Pi _Q$
, and let
$R=\Pi _Q$
, and let
![]() $\sigma \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}({\Bbb k} \overline {Q})$
be induced from a quiver automorphism of
$\sigma \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}({\Bbb k} \overline {Q})$
be induced from a quiver automorphism of
![]() $\overline {Q}$
as above. If one of the following holds, then
$\overline {Q}$
as above. If one of the following holds, then
![]() $\sigma \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
:
$\sigma \in \operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
:
-
(1)
 $\sigma $
is star-preserving:
$\sigma $
is star-preserving:
 $\sigma (Q_1)=Q_1$
and
$\sigma (Q_1)=Q_1$
and
 $\sigma (Q_1^*)=Q_1^*$
;
$\sigma (Q_1^*)=Q_1^*$
; -
(2)
 $\sigma $
is star-inverting:
$\sigma $
is star-inverting:
 $\sigma (Q_1)=Q_1^*$
and
$\sigma (Q_1)=Q_1^*$
and
 $\sigma (Q_1^*)=Q_1$
.
$\sigma (Q_1^*)=Q_1$
.
Proof Given a nonstar arrow
![]() $\alpha $
with source
$\alpha $
with source
![]() $e_i$
and target
$e_i$
and target
![]() $e_j$
,
$e_j$
,
![]() $\alpha ^*$
is the unique arrow with source
$\alpha ^*$
is the unique arrow with source
![]() $e_j$
and target
$e_j$
and target
![]() $e_i$
. In particular, this holds for
$e_i$
. In particular, this holds for
![]() $\sigma (\alpha )$
, so in case 1, we must have
$\sigma (\alpha )$
, so in case 1, we must have
![]() $\sigma (\alpha ^*)=\sigma (\alpha )^*$
. Then
$\sigma (\alpha ^*)=\sigma (\alpha )^*$
. Then
![]() $\sigma (\alpha \alpha ^*)=\sigma (\alpha )\sigma (\alpha )^*$
and
$\sigma (\alpha \alpha ^*)=\sigma (\alpha )\sigma (\alpha )^*$
and
![]() $\sigma (\alpha ^* \alpha )=\sigma (\alpha )^*\sigma (\alpha )$
, so
$\sigma (\alpha ^* \alpha )=\sigma (\alpha )^*\sigma (\alpha )$
, so
![]() $\sigma $
permutes the summands of both
$\sigma $
permutes the summands of both
![]() $\sum _{\alpha \in Q_1} \alpha \alpha ^*$
and
$\sum _{\alpha \in Q_1} \alpha \alpha ^*$
and
![]() $\sum _{\alpha \in Q_1} \alpha ^* \alpha $
. That is,
$\sum _{\alpha \in Q_1} \alpha ^* \alpha $
. That is,
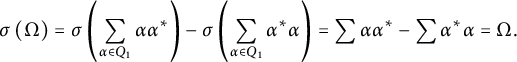 $$\begin{align*}\sigma\left(\Omega\right)=\sigma\left(\sum_{\alpha \in Q_1} \alpha\alpha^*\right) -\sigma\left(\sum_{\alpha \in Q_1} \alpha^* \alpha\right)= \sum \alpha\alpha^* - \sum \alpha^*\alpha = \Omega.\end{align*}$$
$$\begin{align*}\sigma\left(\Omega\right)=\sigma\left(\sum_{\alpha \in Q_1} \alpha\alpha^*\right) -\sigma\left(\sum_{\alpha \in Q_1} \alpha^* \alpha\right)= \sum \alpha\alpha^* - \sum \alpha^*\alpha = \Omega.\end{align*}$$
The argument is similar in case 2 except we obtain
![]() $\sigma (\Omega )=-\Omega $
, so again it preserves the ideal
$\sigma (\Omega )=-\Omega $
, so again it preserves the ideal
![]() $(\Omega )$
.▪
$(\Omega )$
.▪
For the remainder of this section, let
![]() $Q=\widetilde {A_{n-1}}$
and
$Q=\widetilde {A_{n-1}}$
and
![]() $R=\Pi _{\widetilde {A_{n-1}}}$
. We will show that there is a group of quiver automorphisms of
$R=\Pi _{\widetilde {A_{n-1}}}$
. We will show that there is a group of quiver automorphisms of
![]() $\overline {Q}$
that is isomorphic to the dihedral group on n vertices. We first identify two quiver automorphisms of
$\overline {Q}$
that is isomorphic to the dihedral group on n vertices. We first identify two quiver automorphisms of
![]() $\overline {Q}$
which extend to automorphisms of R.
$\overline {Q}$
which extend to automorphisms of R.
-
(1) Define
 $\rho :\overline {Q}\to \overline {Q}$
by
$\rho :\overline {Q}\to \overline {Q}$
by
 $\rho (e_i)=e_{i+1}$
, where the index is taken mod n. Then
$\rho (e_i)=e_{i+1}$
, where the index is taken mod n. Then
 $\rho (\alpha _i)$
is the unique arrow with source
$\rho (\alpha _i)$
is the unique arrow with source
 $\rho (s(\alpha _i))=e_{i+1}$
and target
$\rho (s(\alpha _i))=e_{i+1}$
and target
 $\rho (t(\alpha _i))=e_{i+2}$
, which is
$\rho (t(\alpha _i))=e_{i+2}$
, which is
 $\alpha _{i+1}$
. Consequently,
$\alpha _{i+1}$
. Consequently,
 $\rho (\alpha _i^*)=\rho (\alpha _i)^*=\alpha _{i+1}^*$
. Thus,
$\rho (\alpha _i^*)=\rho (\alpha _i)^*=\alpha _{i+1}^*$
. Thus,
 $\rho $
is a star-preserving automorphism of
$\rho $
is a star-preserving automorphism of
 $\overline {Q}$
, and has order n.
$\overline {Q}$
, and has order n. -
(2) Define
 $r:\overline {Q}\rightarrow \overline {Q}$
by
$r:\overline {Q}\rightarrow \overline {Q}$
by
 $r(e_i)=e_{n-i}$
. Since
$r(e_i)=e_{n-i}$
. Since
 $r(s(\alpha _i))=e_{n-i}$
and
$r(s(\alpha _i))=e_{n-i}$
and
 $r(t(\alpha _i))=e_{n-i-1}$
, we must have
$r(t(\alpha _i))=e_{n-i-1}$
, we must have
 $r(\alpha _i)=\alpha _{n-i-1}^*$
and
$r(\alpha _i)=\alpha _{n-i-1}^*$
and
 $r(\alpha _i^*)=\alpha _{n-i-1}$
. Thus, r is a star-inverting automorphism of
$r(\alpha _i^*)=\alpha _{n-i-1}$
. Thus, r is a star-inverting automorphism of
 $\overline {Q}$
order
$\overline {Q}$
order
 $2$
.
$2$
.
By Proposition 3.1,
![]() $G=\langle \rho , r\rangle $
extends to a subgroup of
$G=\langle \rho , r\rangle $
extends to a subgroup of
![]() $\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
where
$\operatorname {\mathrm {Aut}}_{\operatorname {\mathrm {gr}}}(R)$
where
![]() $R=\Pi _Q$
. It is clear that
$R=\Pi _Q$
. It is clear that
![]() $G \cong D_n$
, and so we identify
$G \cong D_n$
, and so we identify
![]() $D_n$
with the group G acting on R by graded automorphisms.
$D_n$
with the group G acting on R by graded automorphisms.
Theorem 3.2 Let G be a subgroup of
![]() $D_n$
. If there exists a reflection
$D_n$
. If there exists a reflection
![]() $\tau \in D_n$
that fixes a vertex and
$\tau \in D_n$
that fixes a vertex and
![]() $\tau \notin G$
, then
$\tau \notin G$
, then
![]() $\dim _{\Bbb k} (R')<\infty $
.
$\dim _{\Bbb k} (R')<\infty $
.
Proof Let
![]() $\tau $
be the reflection that fixes
$\tau $
be the reflection that fixes
![]() $e_i$
and suppose
$e_i$
and suppose
![]() $\tau \notin G$
. Since
$\tau \notin G$
. Since
![]() $\tau $
is the only nontrivial element of
$\tau $
is the only nontrivial element of
![]() $D_n$
that fixes
$D_n$
that fixes
![]() $e_i$
, we have
$e_i$
, we have
![]() $e_i g(e_i)=0$
for all
$e_i g(e_i)=0$
for all
![]() $g\in G\setminus \{1\}$
. Consequently,
$g\in G\setminus \{1\}$
. Consequently,
![]() $e_i(f_G) e_i=e_i\# 1$
. Let p be a path of length at least
$e_i(f_G) e_i=e_i\# 1$
. Let p be a path of length at least
![]() $2n+1$
, so p contains at least
$2n+1$
, so p contains at least
![]() $n+1$
nonstar arrows or at least
$n+1$
nonstar arrows or at least
![]() $n+1$
star arrows. Without loss of generality, suppose p has at least
$n+1$
star arrows. Without loss of generality, suppose p has at least
![]() $n+1$
nonstar arrows. By the Structure Lemma (Lemma 2.2), we may push all star arrows to the right, so that
$n+1$
nonstar arrows. By the Structure Lemma (Lemma 2.2), we may push all star arrows to the right, so that
for some path
![]() $p'$
and some
$p'$
and some
![]() $j=0,\dots ,n-1$
where the indices are taken mod n. Then, for some
$j=0,\dots ,n-1$
where the indices are taken mod n. Then, for some
![]() $0\leq k\leq n-1$
,
$0\leq k\leq n-1$
,
![]() $i=j+k+1$
mod n, so
$i=j+k+1$
mod n, so
Hence,
![]() $p\# 1\in (f_G)$
and so
$p\# 1\in (f_G)$
and so
![]() $q\# 1 \in (f_G)$
for all paths q of length at least
$q\# 1 \in (f_G)$
for all paths q of length at least
![]() $2m+1$
. Thus,
$2m+1$
. Thus,
![]() $\dim _{\Bbb k} (R')<\infty .$
▪
$\dim _{\Bbb k} (R')<\infty .$
▪
Theorem 3.2 shows that the Auslander map is an isomorphism for the pair
![]() $(R,G)$
so long as G is missing a reflection which fixes some vertex. In case n is odd, this includes all proper subgroups of
$(R,G)$
so long as G is missing a reflection which fixes some vertex. In case n is odd, this includes all proper subgroups of
![]() $D_n$
. However, in the case that n is even, there is one additional subgroup,
$D_n$
. However, in the case that n is even, there is one additional subgroup,
![]() $W_n$
. It remains to show that the Auslander map fails to be an isomorphism in the case of
$W_n$
. It remains to show that the Auslander map fails to be an isomorphism in the case of
![]() $W_n$
and the full dihedral group
$W_n$
and the full dihedral group
![]() $D_n$
.
$D_n$
.
3.1 The
 $D_n$
case
$D_n$
case
For
![]() $x \in R$
, we denote by the
$x \in R$
, we denote by the
![]() $\mathcal O(x)$
the orbit of x under
$\mathcal O(x)$
the orbit of x under
![]() $D_n$
. We begin by describing the orbits of R under the
$D_n$
. We begin by describing the orbits of R under the
![]() $D_n$
action so as to find a
$D_n$
action so as to find a
![]() ${\Bbb k}$
-basis of
${\Bbb k}$
-basis of
![]() $R^{D_n}$
.
$R^{D_n}$
.
Recall that for
![]() $k \geq 0$
, we let
$k \geq 0$
, we let
![]() $Q_k$
(resp.
$Q_k$
(resp.
![]() $Q_k^*$
) denote the set of paths of length k containing only nonstar (resp. star) arrows, and
$Q_k^*$
) denote the set of paths of length k containing only nonstar (resp. star) arrows, and
![]() $Q_0=Q_0^*$
is the set of trivial paths. Furthermore, let
$Q_0=Q_0^*$
is the set of trivial paths. Furthermore, let
![]() $Q_\ell Q_k^*$
denote the set of paths containing exactly
$Q_\ell Q_k^*$
denote the set of paths containing exactly
![]() $\ell $
nonstar arrows followed by k star arrows. Then, in the double quiver, we have
$\ell $
nonstar arrows followed by k star arrows. Then, in the double quiver, we have
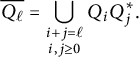 $$\begin{align*}\overline{Q_\ell} = \bigcup_{\substack{i+j=\ell \\ i,j\geq 0}} Q_iQ_j^*.\end{align*}$$
$$\begin{align*}\overline{Q_\ell} = \bigcup_{\substack{i+j=\ell \\ i,j\geq 0}} Q_iQ_j^*.\end{align*}$$
Clearly,
![]() $\overline {Q_\ell }$
is a generating set for the graded piece
$\overline {Q_\ell }$
is a generating set for the graded piece
![]() $R_\ell $
of R. Finally, for
$R_\ell $
of R. Finally, for
![]() $\ell \geq k \geq 0$
, set
$\ell \geq k \geq 0$
, set
![]() $B_{\ell ,k}=Q_\ell Q_k^*\cup Q_k Q_\ell ^*$
.
$B_{\ell ,k}=Q_\ell Q_k^*\cup Q_k Q_\ell ^*$
.
Lemma 3.3 For any
![]() $p\in B_{\ell ,k}$
,
$p\in B_{\ell ,k}$
,
![]() $\displaystyle \mathcal O(p)= B_{\ell ,k}$
.
$\displaystyle \mathcal O(p)= B_{\ell ,k}$
.
Proof By Structure Lemma (Lemma 2.2), a path p is uniquely determined by its source along with the number of nonstar and star arrows it contains. Consequently, each
![]() $p\in Q_\ell Q_k^*$
is uniquely determined by its source, as is each
$p\in Q_\ell Q_k^*$
is uniquely determined by its source, as is each
![]() $q\in Q_k Q_\ell ^*$
. Thus, for each
$q\in Q_k Q_\ell ^*$
. Thus, for each
![]() $i=0,\dots ,n-1$
, let
$i=0,\dots ,n-1$
, let
![]() $p_i$
(resp.
$p_i$
(resp.
![]() $q_i$
) denote the unique path in
$q_i$
) denote the unique path in
![]() $Q_\ell Q_k^*$
(resp.
$Q_\ell Q_k^*$
(resp.
![]() $Q_k Q_\ell ^*$
) with source
$Q_k Q_\ell ^*$
) with source
![]() $e_i$
. Then
$e_i$
. Then
![]() $B_{\ell ,k}=\{p_0,\dots ,p_{n-1},q_0,\dots ,q_{n-1}\}$
.
$B_{\ell ,k}=\{p_0,\dots ,p_{n-1},q_0,\dots ,q_{n-1}\}$
.
Let
![]() $x\in B_{\ell ,k}$
and
$x\in B_{\ell ,k}$
and
![]() $y\in \mathcal O(x)$
, so
$y\in \mathcal O(x)$
, so
![]() $y=g(x)$
for some
$y=g(x)$
for some
![]() $g\in D_n$
. If g is a rotation, then g bijectively maps
$g\in D_n$
. If g is a rotation, then g bijectively maps
![]() $Q_1$
to
$Q_1$
to
![]() $Q_1$
and
$Q_1$
and
![]() $Q_1^*$
to
$Q_1^*$
to
![]() $Q_1^*$
. Consequently,
$Q_1^*$
. Consequently,
![]() $g(x)$
has the same number of nonstar arrows as x, and the same number of star arrows as x. That is, if
$g(x)$
has the same number of nonstar arrows as x, and the same number of star arrows as x. That is, if
![]() $x\in Q_\ell Q_k^*$
, then
$x\in Q_\ell Q_k^*$
, then
![]() $y\in Q_\ell Q_k^*$
. Thus,
$y\in Q_\ell Q_k^*$
. Thus,
![]() $y\in B_{\ell ,k}$
. If g is a reflection, then g bijectively maps
$y\in B_{\ell ,k}$
. If g is a reflection, then g bijectively maps
![]() $Q_1$
to
$Q_1$
to
![]() $Q_1^*$
and
$Q_1^*$
and
![]() $Q_1^*$
to
$Q_1^*$
to
![]() $Q_1$
. Hence,
$Q_1$
. Hence,
![]() $g(x)$
has the same number of nonstar arrows as x has star arrows, and the same number of star arrows as x has nonstar arrows. That is, if
$g(x)$
has the same number of nonstar arrows as x has star arrows, and the same number of star arrows as x has nonstar arrows. That is, if
![]() $x\in Q_\ell Q_k^*$
, then
$x\in Q_\ell Q_k^*$
, then
![]() $y\in Q_k Q_\ell ^*$
. Once again,
$y\in Q_k Q_\ell ^*$
. Once again,
![]() $y\in B_{\ell ,k}$
, so
$y\in B_{\ell ,k}$
, so
![]() $\mathcal O(x)\subseteq B_{\ell ,k}.$
$\mathcal O(x)\subseteq B_{\ell ,k}.$
We have
![]() $|\mathcal O(x)|=|D_n|/|\operatorname {\mathrm {stab}}(x)|,$
and
$|\mathcal O(x)|=|D_n|/|\operatorname {\mathrm {stab}}(x)|,$
and
![]() $g\in \operatorname {\mathrm {stab}}(x)$
only if g fixes the source of x. Hence, g is the identity or the unique reflection r fixing
$g\in \operatorname {\mathrm {stab}}(x)$
only if g fixes the source of x. Hence, g is the identity or the unique reflection r fixing
![]() $s(x)$
. Now, if
$s(x)$
. Now, if
![]() $\ell \neq k$
, then
$\ell \neq k$
, then
![]() $Q_\ell Q_k^*\neq Q_k Q_\ell ^*$
so
$Q_\ell Q_k^*\neq Q_k Q_\ell ^*$
so
![]() $|B_{\ell ,k}|=2n$
, and r inverts the number of star and nonstar arrows, so
$|B_{\ell ,k}|=2n$
, and r inverts the number of star and nonstar arrows, so
![]() $r(x)\neq x$
. Consequently,
$r(x)\neq x$
. Consequently,
![]() $\operatorname {\mathrm {stab}}(x)=\{1\}$
, so
$\operatorname {\mathrm {stab}}(x)=\{1\}$
, so
![]() $|\mathcal O(x)|=|G|=2n$
. Thus,
$|\mathcal O(x)|=|G|=2n$
. Thus,
![]() $\mathcal O(x) = B_{\ell ,k}$
. If, on the other hand,
$\mathcal O(x) = B_{\ell ,k}$
. If, on the other hand,
![]() $\ell =k,$
then
$\ell =k,$
then
![]() $B_{\ell ,k}=B_{\ell ,\ell }=Q_\ell Q_\ell ^*$
, and
$B_{\ell ,k}=B_{\ell ,\ell }=Q_\ell Q_\ell ^*$
, and
![]() $r(x)=x$
, so
$r(x)=x$
, so
![]() $\operatorname {\mathrm {stab}}(x)=\{1,r\}$
. In this case, we have
$\operatorname {\mathrm {stab}}(x)=\{1,r\}$
. In this case, we have
![]() $|B_{\ell ,k}|=n=|D_n|/|\operatorname {\mathrm {stab}}(x)|=|\mathcal O(x)|$
, so
$|B_{\ell ,k}|=n=|D_n|/|\operatorname {\mathrm {stab}}(x)|=|\mathcal O(x)|$
, so
![]() $\mathcal O(x)=B_{\ell ,k}$
.▪
$\mathcal O(x)=B_{\ell ,k}$
.▪
Set
By Lemma 3.3, these are exactly the orbit sums of homogeneous elements in R, and hence form a
![]() ${\Bbb k}$
-basis for
${\Bbb k}$
-basis for
![]() $R^{D_n}$
. This shows that
$R^{D_n}$
. This shows that
![]() $R^{D_n}$
has Hilbert series
$R^{D_n}$
has Hilbert series
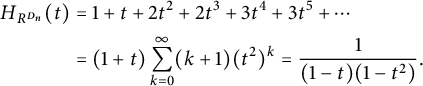 $$ \begin{align*} H_{R^{D_n}}(t) &= 1 + t + 2t^2 + 2t^3 + 3t^4 + 3t^5 + \cdots \\ &= (1+t)\sum_{k=0}^\infty (k+1) (t^2)^k = \frac{1}{(1-t)(1-t^2)}. \end{align*} $$
$$ \begin{align*} H_{R^{D_n}}(t) &= 1 + t + 2t^2 + 2t^3 + 3t^4 + 3t^5 + \cdots \\ &= (1+t)\sum_{k=0}^\infty (k+1) (t^2)^k = \frac{1}{(1-t)(1-t^2)}. \end{align*} $$
Lemma 3.4 The orbit sums
![]() $\mathbb O(\ell ,k)$
satisfy the following relations:
$\mathbb O(\ell ,k)$
satisfy the following relations:
 $$ \begin{align} \mathbb O(1,0)\mathbb O(\ell,k) &= \begin{cases} \mathbb O(\ell+1,k) + \mathbb O(\ell,k+1), & \text{ if } \ell> k, \\ \mathbb O(\ell+1,k), & \text{ if } \ell=k, \end{cases} \end{align} $$
$$ \begin{align} \mathbb O(1,0)\mathbb O(\ell,k) &= \begin{cases} \mathbb O(\ell+1,k) + \mathbb O(\ell,k+1), & \text{ if } \ell> k, \\ \mathbb O(\ell+1,k), & \text{ if } \ell=k, \end{cases} \end{align} $$
Proof To prove (3), we suppose that
![]() $\ell>k$
and then
$\ell>k$
and then
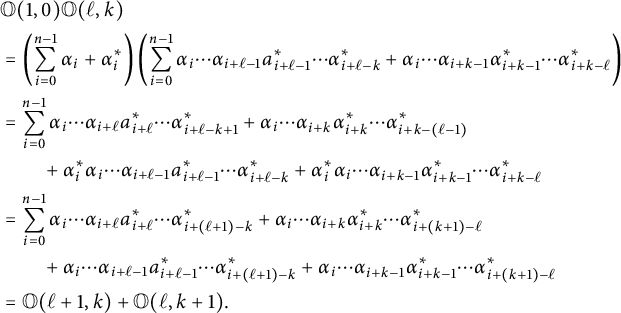 $$ \begin{align*} &\mathbb O(1,0)\mathbb O(\ell,k) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+\ell-k}^* + \alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^* \cdots\alpha_{i+k-\ell}^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^* \cdots \alpha_{i+\ell-k+1}^* + \alpha_i\cdots\alpha_{i+k}\alpha_{i+k}^* \cdots\alpha_{i+k-(\ell-1)}^* \\ &\qquad+ \alpha_i^*\alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+\ell-k}^* + \alpha_i^*\alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^*\cdots\alpha_{i+k-\ell}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^* \cdots \alpha_{i+(\ell+1)-k}^* + \alpha_i\cdots\alpha_{i+k}\alpha_{i+k}^* \cdots\alpha_{i+(k+1)-\ell}^* \\ &\qquad+ \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+(\ell+1)-k}^* + \alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^*\cdots\alpha_{i+(k+1)-\ell}^* \\ &= \mathbb O(\ell+1,k) + \mathbb O(\ell,k+1). \end{align*} $$
$$ \begin{align*} &\mathbb O(1,0)\mathbb O(\ell,k) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+\ell-k}^* + \alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^* \cdots\alpha_{i+k-\ell}^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^* \cdots \alpha_{i+\ell-k+1}^* + \alpha_i\cdots\alpha_{i+k}\alpha_{i+k}^* \cdots\alpha_{i+k-(\ell-1)}^* \\ &\qquad+ \alpha_i^*\alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+\ell-k}^* + \alpha_i^*\alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^*\cdots\alpha_{i+k-\ell}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^* \cdots \alpha_{i+(\ell+1)-k}^* + \alpha_i\cdots\alpha_{i+k}\alpha_{i+k}^* \cdots\alpha_{i+(k+1)-\ell}^* \\ &\qquad+ \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_{i+(\ell+1)-k}^* + \alpha_i\cdots\alpha_{i+k-1}\alpha_{i+k-1}^*\cdots\alpha_{i+(k+1)-\ell}^* \\ &= \mathbb O(\ell+1,k) + \mathbb O(\ell,k+1). \end{align*} $$
On the other hand, if
![]() $\ell =k$
, then
$\ell =k$
, then
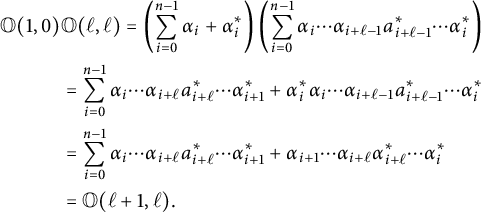 $$ \begin{align*} \mathbb O(1,0)&\mathbb O(\ell,\ell) = \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_i^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^*\cdots \alpha_{i+1}^* + \alpha_i^*\alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_i^* \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^*\cdots \alpha_{i+1}^* + \alpha_{i+1}\cdots \alpha_{i+\ell}\alpha_{i+\ell}^*\cdots \alpha_i^* \\ &= \mathbb O(\ell+1,\ell). \end{align*} $$
$$ \begin{align*} \mathbb O(1,0)&\mathbb O(\ell,\ell) = \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_i^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^*\cdots \alpha_{i+1}^* + \alpha_i^*\alpha_i\cdots \alpha_{i+\ell-1}a_{i+\ell-1}^* \cdots \alpha_i^* \\ &= \sum_{i=0}^{n-1} \alpha_i\cdots \alpha_{i+\ell}a_{i+\ell}^*\cdots \alpha_{i+1}^* + \alpha_{i+1}\cdots \alpha_{i+\ell}\alpha_{i+\ell}^*\cdots \alpha_i^* \\ &= \mathbb O(\ell+1,\ell). \end{align*} $$
For (4), the result is obvious if
![]() $m=1$
. Suppose that it holds for some m, then
$m=1$
. Suppose that it holds for some m, then
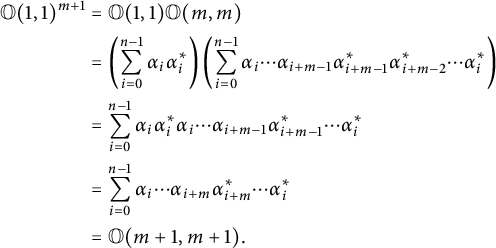 $$ \begin{align*} \mathbb O(1,1)^{m+1} &= \mathbb O(1,1)\mathbb O(m,m) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i\alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i \cdots \alpha_{i+m-1}\alpha_{i+m-1}^*\alpha_{i+m-2}^* \cdots \alpha_i^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_i^*\alpha_i \cdots \alpha_{i+m-1}\alpha_{i+m-1}^* \cdots \alpha_i^* \\ &= \sum_{i=0}^{n-1} \alpha_i \cdots \alpha_{i+m}\alpha_{i+m}^*\cdots \alpha_i^* \\ &= \mathbb O(m+1,m+1). \end{align*} $$
$$ \begin{align*} \mathbb O(1,1)^{m+1} &= \mathbb O(1,1)\mathbb O(m,m) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i\alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i \cdots \alpha_{i+m-1}\alpha_{i+m-1}^*\alpha_{i+m-2}^* \cdots \alpha_i^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_i^*\alpha_i \cdots \alpha_{i+m-1}\alpha_{i+m-1}^* \cdots \alpha_i^* \\ &= \sum_{i=0}^{n-1} \alpha_i \cdots \alpha_{i+m}\alpha_{i+m}^*\cdots \alpha_i^* \\ &= \mathbb O(m+1,m+1). \end{align*} $$
The result now follows by induction.▪
Set
![]() $s_0=\mathbb O(0,0) = 1$
,
$s_0=\mathbb O(0,0) = 1$
,
![]() $s_1 = \mathbb O(1,0)$
, and
$s_1 = \mathbb O(1,0)$
, and
![]() $s_2 = \mathbb O(2,0)$
. We claim that
$s_2 = \mathbb O(2,0)$
. We claim that
![]() $R^{D_n} = {\Bbb k}[s_1,s_2]$
.
$R^{D_n} = {\Bbb k}[s_1,s_2]$
.
Lemma 3.5 The orbit sums
![]() $s_1$
and
$s_1$
and
![]() $s_2$
commute.
$s_2$
commute.
Proof We recall first that, for every arrow
![]() $\alpha $
, there is exactly one nonstar arrow
$\alpha $
, there is exactly one nonstar arrow
![]() $\beta $
and one star arrow
$\beta $
and one star arrow
![]() $\gamma $
such that
$\gamma $
such that
![]() $\alpha \beta \neq 0$
and
$\alpha \beta \neq 0$
and
![]() $\alpha \gamma \neq 0$
. Using this fact and the preprojective relation, we have
$\alpha \gamma \neq 0$
. Using this fact and the preprojective relation, we have
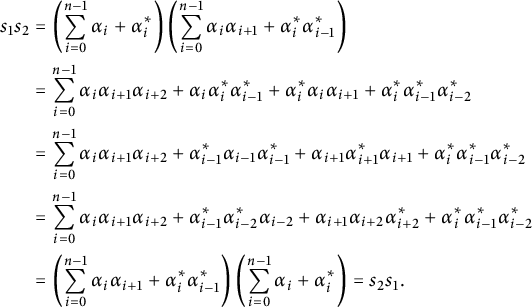 $$ \begin{align*} s_1s_2 &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i \alpha_{i+1} + \alpha_i^* \alpha_{i-1}^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_i\alpha_i^* \alpha_{i-1}^* + \alpha_i^*\alpha_i\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_{i-1}^*\alpha_{i-1} \alpha_{i-1}^* + \alpha_{i+1}\alpha_{i+1}^*\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_{i-1}^*\alpha_{i-2}^* \alpha_{i-2} + \alpha_{i+1}\alpha_{i+2}\alpha_{i+2}^* + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \left( \sum_{i=0}^{n-1} \alpha_i \alpha_{i+1} + \alpha_i^* \alpha_{i-1}^* \right)\left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) = s_2s_1.\\[-38pt] \end{align*} $$
$$ \begin{align*} s_1s_2 &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \left( \sum_{i=0}^{n-1} \alpha_i \alpha_{i+1} + \alpha_i^* \alpha_{i-1}^* \right) \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_i\alpha_i^* \alpha_{i-1}^* + \alpha_i^*\alpha_i\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_{i-1}^*\alpha_{i-1} \alpha_{i-1}^* + \alpha_{i+1}\alpha_{i+1}^*\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1}\alpha_{i+2} + \alpha_{i-1}^*\alpha_{i-2}^* \alpha_{i-2} + \alpha_{i+1}\alpha_{i+2}\alpha_{i+2}^* + \alpha_i^*\alpha_{i-1}^*\alpha_{i-2}^* \\ &= \left( \sum_{i=0}^{n-1} \alpha_i \alpha_{i+1} + \alpha_i^* \alpha_{i-1}^* \right)\left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) = s_2s_1.\\[-38pt] \end{align*} $$
▪
Lemma 3.6 For all
![]() $\ell \geq k \geq 0$
,
$\ell \geq k \geq 0$
,
![]() $\displaystyle \mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
.
$\displaystyle \mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
.
Proof We already have
![]() $\mathbb O(0,0), \mathbb O(1,0), \mathbb O(2,0) \in {\Bbb k}[s_1,s_2]$
. Then
$\mathbb O(0,0), \mathbb O(1,0), \mathbb O(2,0) \in {\Bbb k}[s_1,s_2]$
. Then
 $$ \begin{align*} s_1^2 &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right)\left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^* \right) + \left( \sum_{i=0}^{n-1} \alpha_i\alpha_i^* + \alpha_i^*\alpha_i \right) \\ &= s_2 + 2\mathbb O(1,1). \end{align*} $$
$$ \begin{align*} s_1^2 &= \left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right)\left( \sum_{i=0}^{n-1} \alpha_i + \alpha_i^* \right) \\ &= \left( \sum_{i=0}^{n-1} \alpha_i\alpha_{i+1} + \alpha_i^*\alpha_{i-1}^* \right) + \left( \sum_{i=0}^{n-1} \alpha_i\alpha_i^* + \alpha_i^*\alpha_i \right) \\ &= s_2 + 2\mathbb O(1,1). \end{align*} $$
Hence,
![]() $\mathbb O(1,1) \in {\Bbb k}[s_1,s_2]$
. Suppose inductively that
$\mathbb O(1,1) \in {\Bbb k}[s_1,s_2]$
. Suppose inductively that
![]() $\mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
for all
$\mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
for all
![]() $\ell ,k$
with
$\ell ,k$
with
![]() $\ell \geq k \geq 0$
and
$\ell \geq k \geq 0$
and
![]() $\ell +k \leq d$
for some
$\ell +k \leq d$
for some
![]() $d \geq 2$
. First, assume that d is even, so that
$d \geq 2$
. First, assume that d is even, so that
![]() $\mathbb O(\frac {d}{2},\frac {d}{2}) \in {\Bbb k}[s_1,s_2]$
. Then, by (3),
$\mathbb O(\frac {d}{2},\frac {d}{2}) \in {\Bbb k}[s_1,s_2]$
. Then, by (3),
![]() $\mathbb O(\frac {d}{2}+1,\frac {d}{2})=\mathbb O(1,0)\mathbb O(\frac {d}{2},\frac {d}{2})\in {\Bbb k}[s_1,s_2]$
. Furthermore, since
$\mathbb O(\frac {d}{2}+1,\frac {d}{2})=\mathbb O(1,0)\mathbb O(\frac {d}{2},\frac {d}{2})\in {\Bbb k}[s_1,s_2]$
. Furthermore, since
![]() $\mathbb O(\frac {d}{2}+1,\frac {d}{2}-1) \in {\Bbb k}[s_1,s_2]$
, then
$\mathbb O(\frac {d}{2}+1,\frac {d}{2}-1) \in {\Bbb k}[s_1,s_2]$
, then
By another induction, we have
![]() $\mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
with
$\mathbb O(\ell ,k) \in {\Bbb k}[s_1,s_2]$
with
![]() $\ell +k=d+1$
.
$\ell +k=d+1$
.
Now, assume that d is odd. Then
![]() $d+1$
is even, and since
$d+1$
is even, and since
![]() $\mathbb O(1,1) \in {\Bbb k}[s_1,s_2]$
, then, by (4),
$\mathbb O(1,1) \in {\Bbb k}[s_1,s_2]$
, then, by (4),
![]() $\mathbb O(1,1)^{(d+1)/2} = \mathbb O(\frac {d+1}{2}, \frac {d+1}{2})$
. Now, the argument proceeds as in the even case.▪
$\mathbb O(1,1)^{(d+1)/2} = \mathbb O(\frac {d+1}{2}, \frac {d+1}{2})$
. Now, the argument proceeds as in the even case.▪
We now proceed to our main result for this section.
Theorem 3.7 The Auslander map is not an isomorphism for the pair
![]() $(R,D_n)$
.
$(R,D_n)$
.
Proof Combining the previous two lemmas, there is a surjective map
![]() ${\Bbb k}[s_1,s_2] \to R^{D_n}$
. Since both algebras have the same Hilbert series, then it follows that this map is an isomorphism. It now suffices to show that the set
${\Bbb k}[s_1,s_2] \to R^{D_n}$
. Since both algebras have the same Hilbert series, then it follows that this map is an isomorphism. It now suffices to show that the set
is a basis for R over
![]() $R^{D_n}$
. That is, R is a rank
$R^{D_n}$
. That is, R is a rank
![]() $2n$
free module over
$2n$
free module over
![]() $R^{D_n}$
. Then we have
$R^{D_n}$
. Then we have
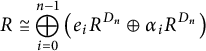 $$\begin{align*}R \cong \bigoplus_{i=0}^{n-1} \left( e_i R^{D_n} \oplus \alpha_i R^{D_n}\right)\end{align*}$$
$$\begin{align*}R \cong \bigoplus_{i=0}^{n-1} \left( e_i R^{D_n} \oplus \alpha_i R^{D_n}\right)\end{align*}$$
as
![]() $R^{D_n}$
-modules. Since
$R^{D_n}$
-modules. Since
![]() $\alpha _{n-1} R^{D_n} \cong e_0 R^{D_n}(-1)$
, then
$\alpha _{n-1} R^{D_n} \cong e_0 R^{D_n}(-1)$
, then
![]() $\operatorname {\mathrm {End}}_{R^{D_n}} R$
contains a map of negative degree and so the Auslander map is not an isomorphism for
$\operatorname {\mathrm {End}}_{R^{D_n}} R$
contains a map of negative degree and so the Auslander map is not an isomorphism for
![]() $(R,D_n)$
.
$(R,D_n)$
.
First, we show that the set S generates R as an
![]() $R^{D_n}$
-module. Clearly,
$R^{D_n}$
-module. Clearly,
![]() $R_0 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. Moreover, for all
$R_0 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. Moreover, for all
![]() $i=0,\ldots ,n-1$
,
$i=0,\ldots ,n-1$
,
![]() $\alpha _{i-1}^* = e_i (s_1) - \alpha _i (1)$
. Hence,
$\alpha _{i-1}^* = e_i (s_1) - \alpha _i (1)$
. Hence,
![]() $R_1 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
.
$R_1 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
.
Note that there are exactly three paths of degree 2 for each vertex. Consider the degree 2 paths based at vertex
![]() $0$
. We have
$0$
. We have
Hence,
![]() $\{ \alpha _0\alpha _0^*, \alpha _0\alpha _1, \alpha _{n-1}^*\alpha _{n-2}^* \} \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. A similar argument for the remaining vertices shows that
$\{ \alpha _0\alpha _0^*, \alpha _0\alpha _1, \alpha _{n-1}^*\alpha _{n-2}^* \} \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. A similar argument for the remaining vertices shows that
![]() $R_2 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
.
$R_2 \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
.
In particular, the above argument shows that
![]() $R_2 = S_1R_1^{D_n} + S_0R_2^{D_n}$
, which implies that
$R_2 = S_1R_1^{D_n} + S_0R_2^{D_n}$
, which implies that
![]() $R_2 = R_1R_1^{D_n} + R_0R_2^{D_n}$
. Multiplying by
$R_2 = R_1R_1^{D_n} + R_0R_2^{D_n}$
. Multiplying by
![]() $R_1$
on the left gives
$R_1$
on the left gives
![]() $R_3 = R_2R_1^{D_n} + R_1R_2^{D_n}$
, and by induction,
$R_3 = R_2R_1^{D_n} + R_1R_2^{D_n}$
, and by induction,
![]() $R_{m+1} = R_mR_1^{D_n} + R_{m-1}R_2^{D_n}$
for all m. Thus, R is generated as a right
$R_{m+1} = R_mR_1^{D_n} + R_{m-1}R_2^{D_n}$
for all m. Thus, R is generated as a right
![]() $R^{D_n}$
-module by
$R^{D_n}$
-module by
![]() $R_0$
and
$R_0$
and
![]() $R_1$
. It follows that
$R_1$
. It follows that
![]() $R \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. That is, S is a generating set for R as an
$R \subset \operatorname {\mathrm {Span}}_{R^{D_n}} S$
. That is, S is a generating set for R as an
![]() $R^{D_n}$
-module.
$R^{D_n}$
-module.
For independence, we note that, for every element of S, there is exactly one other element in S with the same source. Hence, it suffices to prove that
![]() $e_i R^{D_n} \cap \alpha _i R^{D_n} = \{0\}$
. We do this computation for
$e_i R^{D_n} \cap \alpha _i R^{D_n} = \{0\}$
. We do this computation for
![]() $i=0$
, and the other vertices follow similarly.
$i=0$
, and the other vertices follow similarly.
Suppose that
![]() $a \in e_i R^{D_n} \cap \alpha _i R^{D_n}$
. We may assume without loss of generality that a is homogeneous of degree d. Suppose first that d is even. Then there exist scalars
$a \in e_i R^{D_n} \cap \alpha _i R^{D_n}$
. We may assume without loss of generality that a is homogeneous of degree d. Suppose first that d is even. Then there exist scalars
![]() $k_i,k_i' \in {\Bbb k}$
such that
$k_i,k_i' \in {\Bbb k}$
such that
 $$ \begin{align*} a &= e_0 \left( k_0 \mathbb O(d,0) + k_1 \mathbb O(d-1,1) + \cdots + k_{d/2}(d/2,d/2) \right), \\ a &= \alpha_0 \left( k_0' \mathbb O(d-1,0) + k_1' \mathbb O(d-2,1) + \cdots + k_{d/2-1}'(d/2,d/2-1) \right). \end{align*} $$
$$ \begin{align*} a &= e_0 \left( k_0 \mathbb O(d,0) + k_1 \mathbb O(d-1,1) + \cdots + k_{d/2}(d/2,d/2) \right), \\ a &= \alpha_0 \left( k_0' \mathbb O(d-1,0) + k_1' \mathbb O(d-2,1) + \cdots + k_{d/2-1}'(d/2,d/2-1) \right). \end{align*} $$
From the second expression, we note that every path summand of a must contain at least one nonstarred arrow. Hence,
![]() $k_0=0$
. But then, from the first expression, we note that every path summand of a must contain at least one starred arrow, so
$k_0=0$
. But then, from the first expression, we note that every path summand of a must contain at least one starred arrow, so
![]() $k_0'=0$
. Continuing in this way, we see that
$k_0'=0$
. Continuing in this way, we see that
![]() $a=0$
.▪
$a=0$
.▪
3.2 The
 $W_n$
case
$W_n$
case
In case n is odd,
![]() $\eta _{R,G}$
is an isomorphism if and only if G is a proper subgroup of
$\eta _{R,G}$
is an isomorphism if and only if G is a proper subgroup of
![]() $D_n$
. In case n is even, there is one additional instance when
$D_n$
. In case n is even, there is one additional instance when
![]() $\eta _{R,G}$
fails to be an isomorphism, namely for the subgroup
$\eta _{R,G}$
fails to be an isomorphism, namely for the subgroup
![]() $W_n$
defined as
$W_n$
defined as
That is,
![]() $W_n$
is generated by the reflections in
$W_n$
is generated by the reflections in
![]() $D_n$
that pass through a vertex. If n is odd, then every reflection fixes a vertex, so
$D_n$
that pass through a vertex. If n is odd, then every reflection fixes a vertex, so
![]() $W_n$
contains every reflection and
$W_n$
contains every reflection and
![]() $W_n=D_n$
. If n is even, only half of the reflections fix a vertex, so
$W_n=D_n$
. If n is even, only half of the reflections fix a vertex, so
![]() $W_n$
is a proper subgroup of
$W_n$
is a proper subgroup of
![]() $D_n$
. Since
$D_n$
. Since
![]() $W_n$
is of index 2 in
$W_n$
is of index 2 in
![]() $D_n$
,
$D_n$
,
![]() $W_n$
is a maximal subgroup of
$W_n$
is a maximal subgroup of
![]() $D_n$
.
$D_n$
.
Throughout this section, we assume that n is even. Our strategy will be similar to the previous section. The key difference is that the invariant ring is no longer connected graded. In particular, there are exactly twice as many orbits in each graded piece as in the
![]() $D_n$
case.
$D_n$
case.
As in the previous section, for
![]() $\ell \geq k \geq 0$
, set
$\ell \geq k \geq 0$
, set
![]() $B_{\ell ,k}=Q_\ell Q_k^*\cup Q_k Q_\ell ^*$
. Then define
$B_{\ell ,k}=Q_\ell Q_k^*\cup Q_k Q_\ell ^*$
. Then define
Lemma 3.8 For any
![]() $p\in B_{\ell ,k}^{\mathrm {even}}$
(resp.
$p\in B_{\ell ,k}^{\mathrm {even}}$
(resp.
![]() $p\in B_{\ell ,k}^{\mathrm {odd}}$
),
$p\in B_{\ell ,k}^{\mathrm {odd}}$
),
![]() $\displaystyle \mathcal O(p)= B_{\ell ,k}^{\mathrm {even}}$
(resp.
$\displaystyle \mathcal O(p)= B_{\ell ,k}^{\mathrm {even}}$
(resp.
![]() $\mathcal O(p) = B_{\ell ,k}^{\mathrm {odd}}$
).
$\mathcal O(p) = B_{\ell ,k}^{\mathrm {odd}}$
).
Proof This is similar to the proof of Lemma 3.3. In particular, the
![]() $B_{\ell ,k}$
partition the paths of Q. However, since
$B_{\ell ,k}$
partition the paths of Q. However, since
![]() $g \in W_n$
preserves the parity of the idempotents
$g \in W_n$
preserves the parity of the idempotents
![]() $e_i$
, it follows that
$e_i$
, it follows that
![]() $g(B_{\ell ,k}^{\mathrm {even}}) \subset B_{\ell ,k}^{\mathrm {even}}$
. Because g is bijective, then, in fact, we have equality.
$g(B_{\ell ,k}^{\mathrm {even}}) \subset B_{\ell ,k}^{\mathrm {even}}$
. Because g is bijective, then, in fact, we have equality.
It remains to show that we have an equivalence with the orbits. If
![]() $p \in B_{\ell ,k}^{\mathrm {even}}$
, then clearly
$p \in B_{\ell ,k}^{\mathrm {even}}$
, then clearly
![]() $\mathcal O(p) \subset B_{\ell ,k}^{\mathrm {even}}$
. Since
$\mathcal O(p) \subset B_{\ell ,k}^{\mathrm {even}}$
. Since
![]() $|B_{\ell ,k}^{\mathrm {even}}|=\frac {1}{2} |B_{\ell ,k}|$
and
$|B_{\ell ,k}^{\mathrm {even}}|=\frac {1}{2} |B_{\ell ,k}|$
and
![]() $|W_n|=\frac {1}{2} |D_n|$
, then it follows from the argument in Lemma 3.3 that
$|W_n|=\frac {1}{2} |D_n|$
, then it follows from the argument in Lemma 3.3 that
![]() $|B_{\ell ,k}^{\mathrm {even}}|=|\mathcal O(p)|$
. A similar argument applies to
$|B_{\ell ,k}^{\mathrm {even}}|=|\mathcal O(p)|$
. A similar argument applies to
![]() $|B_{\ell ,k}^{\mathrm {odd}}|$
. ▪
$|B_{\ell ,k}^{\mathrm {odd}}|$
. ▪
Set
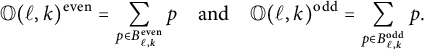 $$\begin{align*}\mathbb O(\ell,k)^{\mathrm{even}} = \sum_{p \in B_{\ell,k}^{\mathrm{even}}} p \quad\text{and}\quad \mathbb O(\ell,k)^{\mathrm{odd}} = \sum_{p \in B_{\ell,k}^{\mathrm{odd}}} p.\end{align*}$$
$$\begin{align*}\mathbb O(\ell,k)^{\mathrm{even}} = \sum_{p \in B_{\ell,k}^{\mathrm{even}}} p \quad\text{and}\quad \mathbb O(\ell,k)^{\mathrm{odd}} = \sum_{p \in B_{\ell,k}^{\mathrm{odd}}} p.\end{align*}$$
These form a
![]() ${\Bbb k}$
-basis for
${\Bbb k}$
-basis for
![]() $R^{W_n}$
. Thus,
$R^{W_n}$
. Thus,
![]() $R^{W_n}$
has total Hilbert series
$R^{W_n}$
has total Hilbert series
However, since
![]() $(R^{W_n})_0 = {\Bbb k}^2$
, then we can also record the matrix-valued Hilbert series. Let M be the
$(R^{W_n})_0 = {\Bbb k}^2$
, then we can also record the matrix-valued Hilbert series. Let M be the
![]() $2 \times 2$
matrix defined by
$2 \times 2$
matrix defined by
 $$ \begin{align*} M_{0,0} &= \#\{ p \in B_{\ell,k}^{\mathrm{even}} \text{ with target } e_i, i \text{ even} \}, \\ M_{0,1} &= \#\{ p \in B_{\ell,k}^{\mathrm{even}} \text{ with target } e_i, i \text{ odd} \}, \\ M_{1,0} &= \#\{ p \in B_{\ell,k}^{\mathrm{odd}} \text{ with target } e_i, i \text{ even} \}, \\ M_{1,1} &= \#\{ p \in B_{\ell,k}^{\mathrm{odd}} \text{ with target } e_i, i \text{ odd} \}. \end{align*} $$
$$ \begin{align*} M_{0,0} &= \#\{ p \in B_{\ell,k}^{\mathrm{even}} \text{ with target } e_i, i \text{ even} \}, \\ M_{0,1} &= \#\{ p \in B_{\ell,k}^{\mathrm{even}} \text{ with target } e_i, i \text{ odd} \}, \\ M_{1,0} &= \#\{ p \in B_{\ell,k}^{\mathrm{odd}} \text{ with target } e_i, i \text{ even} \}, \\ M_{1,1} &= \#\{ p \in B_{\ell,k}^{\mathrm{odd}} \text{ with target } e_i, i \text{ odd} \}. \end{align*} $$
Note that for
![]() $p \in B_{\ell ,k}$
, the parity of the target depends on the source and the parity of
$p \in B_{\ell ,k}$
, the parity of the target depends on the source and the parity of
![]() $\ell + k$
. Hence, it follows that the matrix-valued Hilbert series of
$\ell + k$
. Hence, it follows that the matrix-valued Hilbert series of
![]() $R^{W_n}$
is
$R^{W_n}$
is
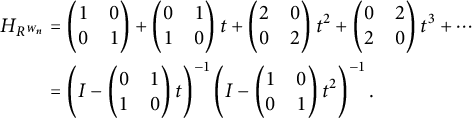 $$ \begin{align*} H_{R^{W_n}} &= \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} + \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}t + \begin{pmatrix}2 & 0 \\ 0 & 2\end{pmatrix}t^2 + \begin{pmatrix}0 & 2 \\ 2 & 0\end{pmatrix}t^3 + \cdots \\ &= \left( I - \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}t\right)^{-1} \left( I - \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}t^2\right)^{-1}. \end{align*} $$
$$ \begin{align*} H_{R^{W_n}} &= \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix} + \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}t + \begin{pmatrix}2 & 0 \\ 0 & 2\end{pmatrix}t^2 + \begin{pmatrix}0 & 2 \\ 2 & 0\end{pmatrix}t^3 + \cdots \\ &= \left( I - \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}t\right)^{-1} \left( I - \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}t^2\right)^{-1}. \end{align*} $$
Proofs of the relations in the next lemma are similar to the corresponding proofs in Lemma 3.4.
Lemma 3.9 Let
![]() $\bullet ,\dagger $
denote opposite parities. The orbit sums
$\bullet ,\dagger $
denote opposite parities. The orbit sums
![]() $\mathbb O(\ell ,k)$
satisfy the following relations:
$\mathbb O(\ell ,k)$
satisfy the following relations:
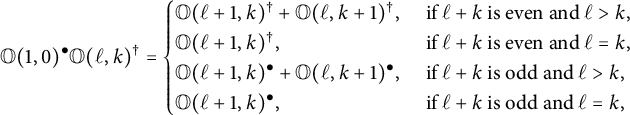 $$ \begin{align}\kern1pc \mathbb O(1,0)^{\bullet}\mathbb O(\ell,k)^{\dagger} &= \begin{cases} \mathbb O(\ell+1,k)^{\dagger} + \mathbb O(\ell,k+1)^{\dagger}, & \text{ if } \ell+k \text{ is even and } \ell> k, \\ \mathbb O(\ell+1,k)^{\dagger}, & \text{ if } \ell+k \text{ is even and } \ell=k, \\ \mathbb O(\ell+1,k)^{\bullet} + \mathbb O(\ell,k+1)^{\bullet}, & \text{ if } \ell+k \text{ is odd and } \ell > k, \\ \mathbb O(\ell+1,k)^{\bullet}, & \text{ if } \ell+k \text{ is odd and } \ell=k, \end{cases} \end{align} $$
$$ \begin{align}\kern1pc \mathbb O(1,0)^{\bullet}\mathbb O(\ell,k)^{\dagger} &= \begin{cases} \mathbb O(\ell+1,k)^{\dagger} + \mathbb O(\ell,k+1)^{\dagger}, & \text{ if } \ell+k \text{ is even and } \ell> k, \\ \mathbb O(\ell+1,k)^{\dagger}, & \text{ if } \ell+k \text{ is even and } \ell=k, \\ \mathbb O(\ell+1,k)^{\bullet} + \mathbb O(\ell,k+1)^{\bullet}, & \text{ if } \ell+k \text{ is odd and } \ell > k, \\ \mathbb O(\ell+1,k)^{\bullet}, & \text{ if } \ell+k \text{ is odd and } \ell=k, \end{cases} \end{align} $$
We set
![]() $s_0=\mathbb O(0,0)^{\mathrm {even}}$
,
$s_0=\mathbb O(0,0)^{\mathrm {even}}$
,
![]() $s_1=\mathbb O(1,0)^{\mathrm {even}}$
, and
$s_1=\mathbb O(1,0)^{\mathrm {even}}$
, and
![]() $s_2=\mathbb O(2,0)^{\mathrm {even}}$
. Similarly, we set
$s_2=\mathbb O(2,0)^{\mathrm {even}}$
. Similarly, we set
![]() $s_0'=\mathbb O(0,0)^{\mathrm {odd}}$
,
$s_0'=\mathbb O(0,0)^{\mathrm {odd}}$
,
![]() $s_1'=\mathbb O(1,0)^{\mathrm {odd}}$
, and
$s_1'=\mathbb O(1,0)^{\mathrm {odd}}$
, and
![]() $s_2'=\mathbb O(2,0)^{\mathrm {odd}}$
. Let C denote the subalgebra of
$s_2'=\mathbb O(2,0)^{\mathrm {odd}}$
. Let C denote the subalgebra of
![]() $R^{W_n}$
generated by these elements. Let Q be the following quiver:
$R^{W_n}$
generated by these elements. Let Q be the following quiver:
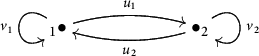
and let
![]() ${\Bbb k} Q$
denote its path algebra. We assign degree 1 to the arrows
${\Bbb k} Q$
denote its path algebra. We assign degree 1 to the arrows
![]() $u_1,u_2$
and degree 2 to
$u_1,u_2$
and degree 2 to
![]() $v_1,v_2$
. We will show that
$v_1,v_2$
. We will show that
![]() $C=R^{W_n}$
and that
$C=R^{W_n}$
and that
![]() $R^{W_n} \cong {\Bbb k} Q/ (v_1u_1-u_1v_2, v_2u_2-u_2v_1)$
.
$R^{W_n} \cong {\Bbb k} Q/ (v_1u_1-u_1v_2, v_2u_2-u_2v_1)$
.
Remark 3.10 The algebra
![]() ${\Bbb k} Q/ (v_1u_1-u_1v_2, v_2u_2-u_2v_1)$
is a quotient-derivation algebra appearing in the classification of graded twisted Calabi–Yau algebras of global dimension 2 [Reference Reyes and Rogalski19]. In particular, the matrix corresponding to the Nakayama automorphism
${\Bbb k} Q/ (v_1u_1-u_1v_2, v_2u_2-u_2v_1)$
is a quotient-derivation algebra appearing in the classification of graded twisted Calabi–Yau algebras of global dimension 2 [Reference Reyes and Rogalski19]. In particular, the matrix corresponding to the Nakayama automorphism
![]() $\mu $
is
$\mu $
is
![]() $\left (\begin {smallmatrix}0 & 1 \\ 1 & 0\end {smallmatrix}\right )$
, and the
$\left (\begin {smallmatrix}0 & 1 \\ 1 & 0\end {smallmatrix}\right )$
, and the
![]() $\mu $
-twisted superpotential is
$\mu $
-twisted superpotential is
![]() $v_1u_1-u_2v_1+v_2u_2-u_1v_2$
.
$v_1u_1-u_2v_1+v_2u_2-u_1v_2$
.
Lemma 3.11 The relations
![]() $s_2s_1 = s_1s_2'$
and
$s_2s_1 = s_1s_2'$
and
![]() $s_2's_1' = s_1's_2$
hold in C.
$s_2's_1' = s_1's_2$
hold in C.
Proof We prove the first relation. The second is similar.
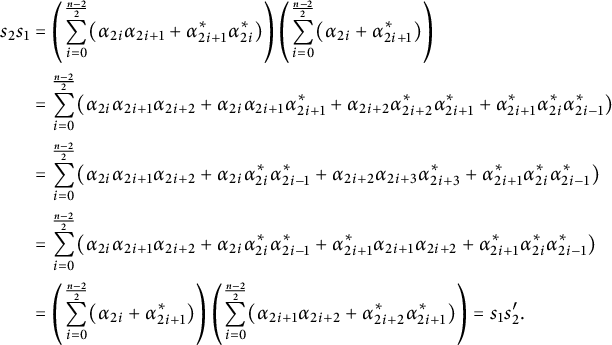 $$ \begin{align*} s_2s_1 &= \left( \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^* ) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i+1}\alpha_{2i+1}^* + \alpha_{2i+2} \alpha_{2i+2}^*\alpha_{2i+1}^* + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i}^*\alpha_{2i-1}^* + \alpha_{2i+2}\alpha_{2i+3}\alpha_{2i+3}^* + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i}^*\alpha_{2i-1}^* + \alpha_{2i+1}^*\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i+2}^*\alpha_{2i+1}^*) \right) = s_1s_2'.\\[-38pt] \end{align*} $$
$$ \begin{align*} s_2s_1 &= \left( \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^* ) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i+1}\alpha_{2i+1}^* + \alpha_{2i+2} \alpha_{2i+2}^*\alpha_{2i+1}^* + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i}^*\alpha_{2i-1}^* + \alpha_{2i+2}\alpha_{2i+3}\alpha_{2i+3}^* + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \sum_{i=0}^{\frac{n-2}{2}} ( \alpha_{2i}\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i}\alpha_{2i}^*\alpha_{2i-1}^* + \alpha_{2i+1}^*\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i+1}^*\alpha_{2i}^*\alpha_{2i-1}^* ) \\ &= \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i+1}\alpha_{2i+2} + \alpha_{2i+2}^*\alpha_{2i+1}^*) \right) = s_1s_2'.\\[-38pt] \end{align*} $$
▪
Lemma 3.12 We have
![]() $C=R^{W_n}$
.
$C=R^{W_n}$
.
Proof Clearly,
![]() $C \subset R^{W_n}$
. We claim
$C \subset R^{W_n}$
. We claim
![]() $R^{W_n} \subset C$
. By definition,
$R^{W_n} \subset C$
. By definition,
![]() $(R^{W_n})_0 \subset C$
and
$(R^{W_n})_0 \subset C$
and
![]() $(R^{W_n})_1 \subset C$
. Now,
$(R^{W_n})_1 \subset C$
. Now,
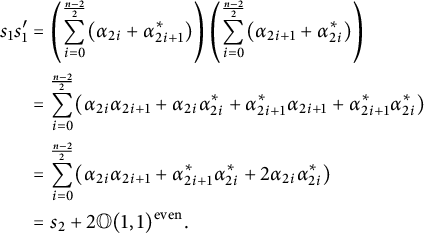 $$ \begin{align*} s_1s_1' &= \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i+1} + \alpha_{2i}^*) \right) \\ &= \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i}\alpha_{2i+1} + \alpha_{2i}\alpha_{2i}^* + \alpha_{2i+1}^*\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^*) \\ &= \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i}\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^* + 2\alpha_{2i}\alpha_{2i}^*) \\ &= s_2 + 2\mathbb O(1,1)^{\mathrm{even}}. \end{align*} $$
$$ \begin{align*} s_1s_1' &= \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i} + \alpha_{2i+1}^*) \right) \left( \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i+1} + \alpha_{2i}^*) \right) \\ &= \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i}\alpha_{2i+1} + \alpha_{2i}\alpha_{2i}^* + \alpha_{2i+1}^*\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^*) \\ &= \sum_{i=0}^{\frac{n-2}{2}} (\alpha_{2i}\alpha_{2i+1} + \alpha_{2i+1}^*\alpha_{2i}^* + 2\alpha_{2i}\alpha_{2i}^*) \\ &= s_2 + 2\mathbb O(1,1)^{\mathrm{even}}. \end{align*} $$
Thus,
![]() $\mathbb O(1,1)^{\mathrm {even}} \in C$
. A similar proof with
$\mathbb O(1,1)^{\mathrm {even}} \in C$
. A similar proof with
![]() $s_1's_1$
shows that
$s_1's_1$
shows that
![]() $\mathbb O(1,1)^{\mathrm {odd}} \in C$
so that
$\mathbb O(1,1)^{\mathrm {odd}} \in C$
so that
![]() $(R^{W_n})_2 \subset C$
. The remainder of the proof follows similarly to Lemma 3.6 with proper respect shown toward parity. In particular, we use (5) and (6).▪
$(R^{W_n})_2 \subset C$
. The remainder of the proof follows similarly to Lemma 3.6 with proper respect shown toward parity. In particular, we use (5) and (6).▪
Theorem 3.13 The Auslander map is not an isomorphism for the pair
![]() $(R,W_n)$
.
$(R,W_n)$
.
Proof Denote the trivial paths of Q by
![]() $f_0,f_1$
. There is a map
$f_0,f_1$
. There is a map
![]() $\phi :{\Bbb k} Q \to R^{W_n}$
defined by setting
$\phi :{\Bbb k} Q \to R^{W_n}$
defined by setting
It is easy to verify that this determines a well-defined surjective map
![]() ${\Bbb k} Q \to R^{W_n}$
and
${\Bbb k} Q \to R^{W_n}$
and
belongs to
![]() $\ker \phi $
. By comparing the matrix-valued Hilbert series, it is clear that
$\ker \phi $
. By comparing the matrix-valued Hilbert series, it is clear that
![]() ${\Bbb k} Q/K \cong R^{W_n}$
.
${\Bbb k} Q/K \cong R^{W_n}$
.
The remainder of the proof follows analogously to Theorem 3.7. In particular, R is a free
![]() $R^{W_n}$
-module with basis
$R^{W_n}$
-module with basis
![]() $S=\{ e_0,\ldots ,e_{n-1},\alpha _0,\ldots ,\alpha _{n-1} \}$
, and this gives rise to a map in
$S=\{ e_0,\ldots ,e_{n-1},\alpha _0,\ldots ,\alpha _{n-1} \}$
, and this gives rise to a map in
![]() $\operatorname {\mathrm {End}}_{R^{W_n}} R$
of negative degree.▪
$\operatorname {\mathrm {End}}_{R^{W_n}} R$
of negative degree.▪
Theorems 3.7 and 3.13 give instances of fixed rings of preprojective algebras which are graded Calabi–Yau. These examples are novel from those presented by Weispfenning in that they do not fix pointwise the degree zero part of
![]() $\Pi _{\widetilde {A_{n-1}}}$
.
$\Pi _{\widetilde {A_{n-1}}}$
.
Corollary 3.14 Let
![]() $G=D_n$
or
$G=D_n$
or
![]() $G=W_n$
. Then
$G=W_n$
. Then
![]() $\mathsf {p}(R,G)=1$
.
$\mathsf {p}(R,G)=1$
.
Proof Let
![]() $p=\alpha _0\alpha _1\cdots \alpha _{n-1}$
and
$p=\alpha _0\alpha _1\cdots \alpha _{n-1}$
and
![]() $q=\alpha _{n-1}^*\alpha _{n-2}^* \cdots \alpha _0^*$
. Set
$q=\alpha _{n-1}^*\alpha _{n-2}^* \cdots \alpha _0^*$
. Set
Then
![]() $(p-q) \# 1 = pf_1 - f_1q \in (f_G)$
. Consequently,
$(p-q) \# 1 = pf_1 - f_1q \in (f_G)$
. Consequently,
![]() $\mathsf {p}(R,W_n) \geq 1$
. By Theorems 2.3, 3.7, and 3.13,
$\mathsf {p}(R,W_n) \geq 1$
. By Theorems 2.3, 3.7, and 3.13,
![]() $\mathsf {p}(R,G) < 2$
. Thus,
$\mathsf {p}(R,G) < 2$
. Thus,
![]() $\mathsf {p}(R,G)=1$
by Bergman’s Gap Theorem [Reference Bergman5].▪
$\mathsf {p}(R,G)=1$
by Bergman’s Gap Theorem [Reference Bergman5].▪
Acknowledgment
The authors appreciate the referee’s comments and suggestions for improving this manuscript.