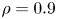1. Introduction
The Large Helical Device (LHD), a heliotron type stellarator, has achieved a volume-averaged normalised pressure, or beta value, $\langle \beta \rangle$![]() , of over 4 % at low magnetic field (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). Linear ideal magnetohydrodynamics (MHD) stability calculations have been carried out for this operational regime. These have found that MHD instabilities in the peripheral region do not cause drastic degradation of the plasma confinement (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). This is in stark contrast to tokamaks, where operational $\langle \beta \rangle$
, of over 4 % at low magnetic field (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). Linear ideal magnetohydrodynamics (MHD) stability calculations have been carried out for this operational regime. These have found that MHD instabilities in the peripheral region do not cause drastic degradation of the plasma confinement (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). This is in stark contrast to tokamaks, where operational $\langle \beta \rangle$![]() limits predicted by the linear ideal MHD theory can often be successfully confirmed by experiment (ITER Physics Basis Editors et al. 1999).
limits predicted by the linear ideal MHD theory can often be successfully confirmed by experiment (ITER Physics Basis Editors et al. 1999).
In order to sustain the high-beta plasma in the LHD, heating schemes including neutral beam injection (NBI), ion cyclotron resonance heating (ICRH) and electron cyclotron resonance heating (ECRH) are employed (Motojima et al. Reference Motojima, Ohyabu, Komori, Kaneko, Yamada, Kawahata, Nakamura, Ida, Akiyama and Ashikawa2003). These heating schemes sometimes produce a plasma with a non-Maxwellian velocity space distribution depending on the thermal equilibration, which then leads to a pressure anisotropic plasma. In the LHD, the ratio of parallel to perpendicular kinetic energy has been shown to exceed a value of 4 as a consequence of heating through NBI (Yamaguchi et al. Reference Yamaguchi, Watanabe, Sakakibara, Narushima, Narihara, Tokuzawa, Tanaka, Yamada, Osakabe and Yamada2005). Under low magnetic field conditions, the operational $\langle \beta \rangle$![]() regime of LHD has been shown to cross the theoretical threshold predicted by isotropic, linear MHD theory (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). Although MHD stability analyses have been carried out for LHD plasmas with an anisotropic pressure distribution (Cooper et al. Reference Cooper, Graves, Tran, Gruber, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki and Watanabe2006b, Reference Cooper, Graves, Jucker, Watanabe, Narushima and Yamaguchi2007, Reference Cooper, Asahi, Narushima, Suzuki, Watanabe, Graves and Isaev2012), the effect of anisotropic plasmas on the operational $\langle \beta \rangle$
regime of LHD has been shown to cross the theoretical threshold predicted by isotropic, linear MHD theory (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). Although MHD stability analyses have been carried out for LHD plasmas with an anisotropic pressure distribution (Cooper et al. Reference Cooper, Graves, Tran, Gruber, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki and Watanabe2006b, Reference Cooper, Graves, Jucker, Watanabe, Narushima and Yamaguchi2007, Reference Cooper, Asahi, Narushima, Suzuki, Watanabe, Graves and Isaev2012), the effect of anisotropic plasmas on the operational $\langle \beta \rangle$![]() regime has not been researched in detail.
regime has not been researched in detail.
The three-dimensional (3-D) equilibrium solver VMEC (variational moments equilibrium code) (Hirshman & Betancourt Reference Hirshman and Betancourt1991) has been expanded by separating the parallel and perpendicular components of the plasma pressure to a code called ANIMEC (anisotropic Neumann inverse moments equilibrium code) (Cooper et al. Reference Cooper, Hirshman, Merkel, Graves, Kisslinger, Wobig, Narushima, Okamura and Watanabe2009). The hot plasma particles are described in this code using either a variant of a bi-Maxwellian distribution (Cooper et al. Reference Cooper, Graves, Hirshman, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki, Watanabe and Yamada2006a) or a slowing-down distribution (Cooper et al. Reference Cooper, Hirshman, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki, Watanabe, Yamada and Yamazaki2005). The 3-D equilibria constructed by ANIMEC can be used to perform ideal linear MHD stability calculations using the TERPSICHORE code (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990). This code has been expanded to include two energy principles that extend beyond ideal MHD theory, which allows plasmas with a pressure anisotropy to be analysed. The Kruskal–Oberman (KO) principle models the hot-particle species as a fully interacting liquid, enabling it to contribute to pressure- and current-driven instabilities (Kruskal & Oberman Reference Kruskal and Oberman1958). The Johnson–Kulsrud–Weimer model, on the other hand, also known in the literature as the non-interacting (NI) model, simulates the hot-particle species as a non-interacting layer (Johnson, Kulsrud & Weimer Reference Johnson, Kulsrud and Weimer1969).
Building on the analysis of 3-D equilibria of pressure anisotropy in LHD carried out by Romba, Suzuki & Proll (Reference Romba, Suzuki and Proll2021), in this work, we analyse the effect of pressure anisotropy on linear 3-D MHD stability using both ANIMEC and TERPSICHORE. In particular, we provide both a qualitative and a quantitative analysis of pressure anisotropy on linear MHD stability for different hot-particle pressure profiles. We consider both on-axis and off-axis particle deposition profiles. For the off-axis profiles, both high field (HF) and low field (LF) deposition simulations are carried out and compared. The MHD stability corresponding to pressure anisotropic plasmas is analysed by investigating the plasma displacement, growth rate and Mercier criterion of global (low-n) MHD modes. This analysis is then used to investigate the effect of pressure anisotropy on plasma stability and the operational $\langle \beta \rangle$![]() regime of LHD.
regime of LHD.
Section 2 treats the theory associated with magnetic equilibria in the context of pressure anisotropy. Section 3 introduces the theory behind linear MHD stability for pressure anisotropic plasmas and discusses two energy principles that extend isotropic MHD theory. Section 4 describes the magnetic equilibrium of the plasmas that will be simulated. Next, in § 5, the result of the MHD stability calculations pertaining to the equilibria described in the previous section is analysed. Finally, § 6 summarises the results and looks at possible future research that could extend this work.
2. Numerical equilibrium theory
Magnetohydrodynamic equilibrium codes employ energy minimisation techniques to calculate a plasma equilibrium. The total energy minimised in VMEC and ANIMEC comprises a potential and kinetic energy part. The former is associated with magnetic pressure and the latter with plasma pressure. The total energy functional used in ANIMEC is given by (Cooper et al. Reference Cooper, Hirshman, Merazzi and Gruber1992),
where $B$![]() denotes the local magnetic field strength, $\mu _0$
denotes the local magnetic field strength, $\mu _0$![]() is the permeability of free space ($4{\rm \pi} \times 10^{-7}$
is the permeability of free space ($4{\rm \pi} \times 10^{-7}$![]() H m$^{-1}$
H m$^{-1}$![]() ) and $\varGamma$
) and $\varGamma$![]() is the adiabatic index, which is usually set to zero. The total parallel particle pressure $p_{\|}(s,B)$
is the adiabatic index, which is usually set to zero. The total parallel particle pressure $p_{\|}(s,B)$![]() , is a function of the flux surface coordinate $s\in [0,1]$
, is a function of the flux surface coordinate $s\in [0,1]$![]() , which is proportional to the toroidal magnetic flux $2{\rm \pi} \varPhi$
, which is proportional to the toroidal magnetic flux $2{\rm \pi} \varPhi$![]() enclosed, and of the magnetic field strength $B$
enclosed, and of the magnetic field strength $B$![]() . Note that the normalised radial coordinate $\rho$
. Note that the normalised radial coordinate $\rho$![]() relates to the flux surface coordinate $s$
relates to the flux surface coordinate $s$![]() as $s = \rho ^2$
as $s = \rho ^2$![]() . It has been shown that (2.1) can be manipulated such that the ideal MHD equilibrium force is recovered (Cooper et al. Reference Cooper, Hirshman, Merazzi and Gruber1992)
. It has been shown that (2.1) can be manipulated such that the ideal MHD equilibrium force is recovered (Cooper et al. Reference Cooper, Hirshman, Merazzi and Gruber1992)
In this equation, $\boldsymbol {P}$![]() is the pressure tensor given by (Chew et al. Reference Chew, Goldberger, Low and Chandrasekhar1956)
is the pressure tensor given by (Chew et al. Reference Chew, Goldberger, Low and Chandrasekhar1956)
where $p_\perp$![]() and $p_\|$
and $p_\|$![]() are the total perpendicular and parallel pressures, respectively, $\boldsymbol {I}$
are the total perpendicular and parallel pressures, respectively, $\boldsymbol {I}$![]() is the unit matrix, $\boldsymbol {b} = \boldsymbol {B}/B$
is the unit matrix, $\boldsymbol {b} = \boldsymbol {B}/B$![]() is the unit vector in the direction of the magnetic field lines and $\boldsymbol {j}$
is the unit vector in the direction of the magnetic field lines and $\boldsymbol {j}$![]() is the current density. Given that the parallel pressure is a function of $B$
is the current density. Given that the parallel pressure is a function of $B$![]() , this quantity, and by extension the perpendicular pressure, are not flux surface quantities, as opposed to the total pressure. The parallel pressure comprises a part due to thermal particles and a part due to hot particles. With the adiabatic index set to zero, the total parallel pressure takes the form (Cooper et al. Reference Cooper, Hirshman, Merazzi and Gruber1992)
, this quantity, and by extension the perpendicular pressure, are not flux surface quantities, as opposed to the total pressure. The parallel pressure comprises a part due to thermal particles and a part due to hot particles. With the adiabatic index set to zero, the total parallel pressure takes the form (Cooper et al. Reference Cooper, Hirshman, Merazzi and Gruber1992)
where $M(s)$![]() is the plasma mass, $p_h(s)$
is the plasma mass, $p_h(s)$![]() is the hot-particle pressure component and $H(s,B)$
is the hot-particle pressure component and $H(s,B)$![]() is a factor that describes the change in total parallel pressure around a magnetic flux surface. The hot-particle term in this equation introduces an anisotropy through the dependence of $H$
is a factor that describes the change in total parallel pressure around a magnetic flux surface. The hot-particle term in this equation introduces an anisotropy through the dependence of $H$![]() on the magnetic field. For completeness, the force balance describing the calculation of the total perpendicular pressure is given by
on the magnetic field. For completeness, the force balance describing the calculation of the total perpendicular pressure is given by
The hot particles modelled by ANIMEC are described by a variant of the bi-Maxwellian distribution (Cooper et al. Reference Cooper, Graves, Hirshman, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki, Watanabe and Yamada2006a)

In this equation $\mathcal {E}$![]() and $\mu$
and $\mu$![]() represent the total particle energy and the particle magnetic moment, respectively. These parameters can be rewritten to obtain an equivalent description in terms of $v_{\|}$
represent the total particle energy and the particle magnetic moment, respectively. These parameters can be rewritten to obtain an equivalent description in terms of $v_{\|}$![]() and $v_{\perp }$
and $v_{\perp }$![]() , the parallel and perpendicular particle velocity components. The parameters $\mathcal {N}(s)$
, the parallel and perpendicular particle velocity components. The parameters $\mathcal {N}(s)$![]() , $m_h$
, $m_h$![]() , $T_\perp (s)$
, $T_\perp (s)$![]() and $T_{\|}(s)$
and $T_{\|}(s)$![]() describe a density-like amplitude, the hot-particle mass and the perpendicular and parallel components of the plasma temperature, respectively. The parameter $B_C$
describe a density-like amplitude, the hot-particle mass and the perpendicular and parallel components of the plasma temperature, respectively. The parameter $B_C$![]() , called the critical magnetic field, determines the number of trapped particles in the fusion device. This is a consequence of the fact that most hot particles are deposited near the location where $B = B_C$
, called the critical magnetic field, determines the number of trapped particles in the fusion device. This is a consequence of the fact that most hot particles are deposited near the location where $B = B_C$![]() . This variant of the bi-Maxwellian distribution has been shown to satisfy the lowest-order solution to the Fokker–Planck equation $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\nabla } \mathcal {F}_{{h}} = 0$
. This variant of the bi-Maxwellian distribution has been shown to satisfy the lowest-order solution to the Fokker–Planck equation $\boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\nabla } \mathcal {F}_{{h}} = 0$![]() (Dendy et al. Reference Dendy, Hastie, McClements and Martin1995).
(Dendy et al. Reference Dendy, Hastie, McClements and Martin1995).
3. Linear MHD stability theory
Two energy principles have been implemented in the TERPSICHORE code: the fully interacting KO principle (Kruskal & Oberman Reference Kruskal and Oberman1958) and the non-interacting NI model (Johnson et al. Reference Johnson, Kulsrud and Weimer1969). These energy principles fundamentally differ in the way they treat hot-particle species in the context of pressure- and current-driven instabilities. The KO model incorporates the effect of hot particles on MHD instabilities, while the NI model describes hot particles as non-interacting, therefore affecting MHD instabilities only indirectly. In this research we focus on the KO energy principle, given that this model forms the most comprehensive framework for studying the effect that different hot-particle pressure profiles have on pressure- and current-driven instabilities.
The TERPSICHORE code solves the following eigenvalue equation:
where $\delta W_P$![]() , $\delta W_V$
, $\delta W_V$![]() and $\delta W_K$
and $\delta W_K$![]() denote the plasma potential energy, the vacuum energy and the kinetic energy. The variable $\langle W\rangle$
denote the plasma potential energy, the vacuum energy and the kinetic energy. The variable $\langle W\rangle$![]() denotes the volume average of the energy $W$
denotes the volume average of the energy $W$![]() . The plasma potential energy can be subdivided into the following components:
. The plasma potential energy can be subdivided into the following components:
where $W_{C^2}$![]() represents a positive definite stabilising component, which is associated with magnetic field line bending and compression as well as plasma compression; $W_{{\rm BI}}$
represents a positive definite stabilising component, which is associated with magnetic field line bending and compression as well as plasma compression; $W_{{\rm BI}}$![]() represents pressure driven instabilities such as ballooning and interchange modes and $W_{J}$
represents pressure driven instabilities such as ballooning and interchange modes and $W_{J}$![]() represents parallel current driven kink modes. In TERPSICHORE, the terms in (3.2) are evaluated in Boozer coordinates, which allows the eigenvalue problem to be separated into individual Fourier components (Boozer Reference Boozer1980).
represents parallel current driven kink modes. In TERPSICHORE, the terms in (3.2) are evaluated in Boozer coordinates, which allows the eigenvalue problem to be separated into individual Fourier components (Boozer Reference Boozer1980).
In ideal MHD theory with isotropic pressure, the term in (3.2) that describes pressure-driven instabilities is given by
where $\boldsymbol {\xi }$![]() denotes the plasma displacement vector, $p$
denotes the plasma displacement vector, $p$![]() the pressure and $\boldsymbol {\kappa }$
the pressure and $\boldsymbol {\kappa }$![]() the curvature vector of the magnetic flux surface. The asterisk denotes complex conjugation. By modelling the plasma as an incompressible fluid, the plasma displacement can be written as follows (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990):
the curvature vector of the magnetic flux surface. The asterisk denotes complex conjugation. By modelling the plasma as an incompressible fluid, the plasma displacement can be written as follows (Anderson et al. Reference Anderson, Cooper, Gruber, Merazzi and Schwenn1990):
where $\xi ^s$![]() and $\eta$
and $\eta$![]() are the radial and binormal components of $\boldsymbol {\xi }$
are the radial and binormal components of $\boldsymbol {\xi }$![]() , respectively, and $\sqrt {g}$
, respectively, and $\sqrt {g}$![]() is the Jacobian describing the transformation from Cartesian to Boozer coordinates. Due to the incompressibility constraint, the component of $\boldsymbol {\xi }$
is the Jacobian describing the transformation from Cartesian to Boozer coordinates. Due to the incompressibility constraint, the component of $\boldsymbol {\xi }$![]() parallel to the field lines vanishes.
parallel to the field lines vanishes.
The KO and NI energy principles expand on the equation above by introducing pressure anisotropy. When expressing the corresponding energy term in the KO energy principle in Boozer coordinates (Boozer Reference Boozer1980), the following expression is obtained (Grad Reference Grad1966; Cooper et al. Reference Cooper, Graves, Tran, Gruber, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki and Watanabe2006b):

In this equation $\tau$![]() and $\sigma$
and $\sigma$![]() refer to the mirror and firehose stability criteria, $2{\rm \pi} \varPsi$
refer to the mirror and firehose stability criteria, $2{\rm \pi} \varPsi$![]() , $2{\rm \pi} I$
, $2{\rm \pi} I$![]() and $2{\rm \pi} J$
and $2{\rm \pi} J$![]() refer, respectively, to the poloidal magnetic flux, the effective poloidal current flux and effective toroidal current flux and $L_s$
refer, respectively, to the poloidal magnetic flux, the effective poloidal current flux and effective toroidal current flux and $L_s$![]() refers to the number of field periods within one toroidal period. This equation shows that the hot-particle pressures, which are contained in the terms $p_{\|}$
refers to the number of field periods within one toroidal period. This equation shows that the hot-particle pressures, which are contained in the terms $p_{\|}$![]() and $p_\perp$
and $p_\perp$![]() , have a direct influence on the energy balance.
, have a direct influence on the energy balance.
The TERPSICHORE code is a linear MHD code which returns an eigenvalue corresponding to the growth rate of the most dominant linear MHD instability as well as the corresponding eigenvector which describes the plasma displacement. The TERPSICHORE code has, however, been expanded to return quasi-linear parameters such as physical values for the kinetic energy and a calculation of the Mercier criterion for both the KO and NI energy principles (Cooper Reference Cooper1992). Growth rates, plasma displacements and Mercier criteria are analysed in § 5.
4. Equilibrium calculations
The 3-D magnetic equilibria required to perform MHD stability analysis have been simulated using ANIMEC with fixed boundary conditions. In this work, the last closed magnetic flux surface has been chosen to represent the LHD standard configuration. The pressure anisotropy can be input in ANIMEC by specifying $T_\perp / T_{\|}$![]() as a function of $s$
as a function of $s$![]() . In this work we have set the ratio $T_\perp / T_{\|}$
. In this work we have set the ratio $T_\perp / T_{\|}$![]() to a constant value. In order to better capture the degree of pressure anisotropy in the plasma, the following parameter will be used to characterise magnetic equilibria:
to a constant value. In order to better capture the degree of pressure anisotropy in the plasma, the following parameter will be used to characterise magnetic equilibria:
The following definitions are employed:



We approximate the fraction $\langle \beta _{{h}} \rangle / \langle \beta \rangle \approx 1/3$![]() for all simulations in this work, unless otherwise specified. For all simulations $\langle \beta \rangle$
for all simulations in this work, unless otherwise specified. For all simulations $\langle \beta \rangle$![]() is scanned over the set $\langle \beta \rangle \in \{ 0.5\,\%,1.0\,\%,\ldots,3.5\,\% \}$
is scanned over the set $\langle \beta \rangle \in \{ 0.5\,\%,1.0\,\%,\ldots,3.5\,\% \}$![]() . The perpendicular to parallel pressure ratio was approximated to be $\langle \beta _{\perp / \|} \rangle \in \{1/4,1,4\}$
. The perpendicular to parallel pressure ratio was approximated to be $\langle \beta _{\perp / \|} \rangle \in \{1/4,1,4\}$![]() , corresponding to parallel dominant, isotropic and perpendicular dominant plasmas, respectively. It should be noted that this pressure ratio strongly depends on the thermal- and hot-pressure profiles. The thermal-pressure profile has been set to a parabolic profile $p_{{\rm th}} \propto 1-s$
, corresponding to parallel dominant, isotropic and perpendicular dominant plasmas, respectively. It should be noted that this pressure ratio strongly depends on the thermal- and hot-pressure profiles. The thermal-pressure profile has been set to a parabolic profile $p_{{\rm th}} \propto 1-s$![]() , which approximates experimental observations (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). The hot-particle pressure profiles used in this work are described in table 1. These hot-particle pressure profiles have been chosen to be able to simulate the effect of pressure anisotropy in the context of different heating schemes. The table lists the $B_C$
, which approximates experimental observations (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). The hot-particle pressure profiles used in this work are described in table 1. These hot-particle pressure profiles have been chosen to be able to simulate the effect of pressure anisotropy in the context of different heating schemes. The table lists the $B_C$![]() values for which simulations have been carried out and the heating methods that most accurately describe the corresponding hot-pressure profile. The values $B_C=2.3\,{\rm T},3.1\,{\rm T}$
values for which simulations have been carried out and the heating methods that most accurately describe the corresponding hot-pressure profile. The values $B_C=2.3\,{\rm T},3.1\,{\rm T}$![]() correspond to LF and HF deposition. Note that, for pressure isotropic simulations, a value of $B_C=1.0$
correspond to LF and HF deposition. Note that, for pressure isotropic simulations, a value of $B_C=1.0$![]() T has been used. For isotropic simulations, $T_\|(s) = T_\perp (s)$
T has been used. For isotropic simulations, $T_\|(s) = T_\perp (s)$![]() , which, in combination with the value of $B_C=1.0$
, which, in combination with the value of $B_C=1.0$![]() T, reduces the bi-Maxwellian given in (2.6) to a Maxwellian distribution. Figure 1 displays the hot-pressure profiles as a function of the flux surface coordinate $s$
T, reduces the bi-Maxwellian given in (2.6) to a Maxwellian distribution. Figure 1 displays the hot-pressure profiles as a function of the flux surface coordinate $s$![]() . The parabolic, peaked and broad profiles have a maximum at $s=0$
. The parabolic, peaked and broad profiles have a maximum at $s=0$![]() , corresponding to on-axis hot-particle deposition, whereas the hollow and realistic profiles correspond to off-axis deposition.
, corresponding to on-axis hot-particle deposition, whereas the hollow and realistic profiles correspond to off-axis deposition.
Table 1. The hot-particle pressure profiles for which MHD stability analysis has been performed, along with the values for $B_C$![]() chosen for simulation and the corresponding heating scheme.
chosen for simulation and the corresponding heating scheme.


Figure 1. The normalised hot-particle pressure profiles $p_{{h}}$![]() described in table 1, as a function of the flux surface coordinate $s$
described in table 1, as a function of the flux surface coordinate $s$![]() .
.
The magnetic equilibrium computed by ANIMEC can be analysed by investigating the parallel and perpendicular components of the hot-particle pressure distribution. For the example case of the perpendicular dominant realistic hot-particle profile, figures 2 and 3 show the parallel and perpendicular components of the hot-particle distribution, respectively, overlapped by flux surfaces. From these plots, it is observed that neither component of the hot-particle distribution is a flux surface quantity. The perpendicular hot-particle pressure shows two clear local maxima. This can be explained by the fact that the perpendicular component of the ion velocity is highest near the reflection points of trapped particles. The shape of the perpendicular hot-particle pressure distribution implies the existence of high pressure gradients which can negatively impact plasma stability. Also, these gradients impose a threshold on the maximum $\langle \beta \rangle$![]() value that can be simulated. Both the hot- and thermal-pressure distributions have an effect on the local effective magnetic field, which in turn affects the rotational transform profile, $\iota (s)$
value that can be simulated. Both the hot- and thermal-pressure distributions have an effect on the local effective magnetic field, which in turn affects the rotational transform profile, $\iota (s)$![]() . The rotational transform profile of two example cases and a vacuum simulation are shown in figure 4. The rotational transform of the LHD is negative everywhere inside the fusion device. In this work, however, the rotational transform will be presented as a positive value for readability of the figures. Note that, under specific conditions, the magnetic shear can vanish close to the magnetic axis.
. The rotational transform profile of two example cases and a vacuum simulation are shown in figure 4. The rotational transform of the LHD is negative everywhere inside the fusion device. In this work, however, the rotational transform will be presented as a positive value for readability of the figures. Note that, under specific conditions, the magnetic shear can vanish close to the magnetic axis.

Figure 2. Hot-particle parallel pressure distribution for the realistic hot-pressure profile with $B_C=2.3$![]() T and $\langle \beta \rangle \approx 3\,\%$
T and $\langle \beta \rangle \approx 3\,\%$![]() in a vertically elongated cross-section. The black curves indicate flux surfaces.
in a vertically elongated cross-section. The black curves indicate flux surfaces.

Figure 3. Hot-particle perpendicular pressure distribution for the realistic hot-pressure profile with $B_C=2.3$![]() T and $\langle \beta \rangle \approx 3\,\%$
T and $\langle \beta \rangle \approx 3\,\%$![]() in a vertically elongated cross-section. The black curves indicate flux surfaces.
in a vertically elongated cross-section. The black curves indicate flux surfaces.

Figure 4. Rotational transform $\iota (s)$![]() for a vacuum simulation and for the parabolic and realistic hot-pressure profiles at pressure isotropy. For the latter two profiles, $\langle \beta \rangle \approx 2.5\,\%$
for a vacuum simulation and for the parabolic and realistic hot-pressure profiles at pressure isotropy. For the latter two profiles, $\langle \beta \rangle \approx 2.5\,\%$![]() and $\langle \beta \rangle \approx 3\,\%$
and $\langle \beta \rangle \approx 3\,\%$![]() , respectively.
, respectively.
5. The MHD stability results
The MHD stability code TERPSICHORE will be used to analyse the $n=1$![]() mode family of instabilities (Cooper et al. Reference Cooper, Fu, Gruber, Merazzi, Schwenn and Anderson1990; Nührenberg née Schwab Reference Nührenberg(née Schwab)1993; Ardelea & Cooper Reference Ardelea and Cooper1997). The $n=1$
mode family of instabilities (Cooper et al. Reference Cooper, Fu, Gruber, Merazzi, Schwenn and Anderson1990; Nührenberg née Schwab Reference Nührenberg(née Schwab)1993; Ardelea & Cooper Reference Ardelea and Cooper1997). The $n=1$![]() mode family is analysed, because experiment shows that the most dominant MHD instabilities in LHD belong to this particular mode family (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). The growth rate, plasma displacement vector $\boldsymbol {\xi }$
mode family is analysed, because experiment shows that the most dominant MHD instabilities in LHD belong to this particular mode family (Watanabe et al. Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005). The growth rate, plasma displacement vector $\boldsymbol {\xi }$![]() and Mercier criterion corresponding to the KO energy principle (Cooper et al. Reference Cooper, Graves, Tran, Gruber, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki and Watanabe2006b) will be analysed in this section. The plasma displacement vector $\boldsymbol {\xi }$
and Mercier criterion corresponding to the KO energy principle (Cooper et al. Reference Cooper, Graves, Tran, Gruber, Yamaguchi, Narushima, Okamura, Sakakibara, Suzuki and Watanabe2006b) will be analysed in this section. The plasma displacement vector $\boldsymbol {\xi }$![]() will be analysed through its modal structure as a function of the flux surface coordinate $s$
will be analysed through its modal structure as a function of the flux surface coordinate $s$![]() . For every hot-particle pressure profile, the maximum $\langle \beta \rangle$
. For every hot-particle pressure profile, the maximum $\langle \beta \rangle$![]() simulation that would converge in both ANIMEC and TERPSICHORE is treated. This implies that, especially for on-axis heating profiles, the $\langle \beta \rangle$
simulation that would converge in both ANIMEC and TERPSICHORE is treated. This implies that, especially for on-axis heating profiles, the $\langle \beta \rangle$![]() value shown can be significantly lower than the maximum of the $\langle \beta \rangle$
value shown can be significantly lower than the maximum of the $\langle \beta \rangle$![]() scan.
scan.
The plasma displacement sum over all modes will be used to compare the plasma displacement between different levels of anisotropy

where $K$![]() is the total number of computed modes, $\{n_k\}$
is the total number of computed modes, $\{n_k\}$![]() and $\{m_k\}$
and $\{m_k\}$![]() are sequences containing toroidal and poloidal mode numbers, respectively, sorted based on maximum amplitude and where
are sequences containing toroidal and poloidal mode numbers, respectively, sorted based on maximum amplitude and where
Note that the unit vector $\hat {\boldsymbol {\xi }}_{n,m}(s)$![]() is normal to the flux surface $s$
is normal to the flux surface $s$![]() and is pointing away from the magnetic axis. The sequences $\{n_k\}$
and is pointing away from the magnetic axis. The sequences $\{n_k\}$![]() and $\{m_k\}$
and $\{m_k\}$![]() are constructed such that
are constructed such that
Note also that the eigenvector $\boldsymbol {\xi }$![]() calculated by TERPSICHORE can be scaled arbitrarily. The figures containing $\varXi (s)$
calculated by TERPSICHORE can be scaled arbitrarily. The figures containing $\varXi (s)$![]() throughout this work illustrate the direct results from calculations performed by TERPSICHORE and have not been rescaled.
throughout this work illustrate the direct results from calculations performed by TERPSICHORE and have not been rescaled.
5.1. On-axis deposition profiles
Figure 5 shows the graph of $\varXi (s)$![]() for the parabolic, peaked and broad hot-particle pressure profiles, normalised per simulation result by the maximum value $\varXi _{\max } \equiv \max _{s\in [0,1]} \varXi (s)$
for the parabolic, peaked and broad hot-particle pressure profiles, normalised per simulation result by the maximum value $\varXi _{\max } \equiv \max _{s\in [0,1]} \varXi (s)$![]() . The mode width of the plasma displacement is observed to be significantly smaller for parallel dominant plasmas for all on-axis deposition profiles, while the differences between the isotropic and perpendicular dominant cases are negligible. In global mode analysis, this mode width directly relates to the growth rate (Sugama & Wakatani Reference Sugama and Wakatani1989; Gupta, Callen & Hegna Reference Gupta, Callen and Hegna2002). Moreover, the mode width pertaining to the plasma displacement is proportional to the volume of plasma displaced. Thus, following from (3.5), this difference in mode width indicates that the energy associated with the plasma displacement is smallest for parallel dominant plasmas for on-axis profiles, which is conducive to plasma stability. A shift in $s_{\mathrm {max}}$
. The mode width of the plasma displacement is observed to be significantly smaller for parallel dominant plasmas for all on-axis deposition profiles, while the differences between the isotropic and perpendicular dominant cases are negligible. In global mode analysis, this mode width directly relates to the growth rate (Sugama & Wakatani Reference Sugama and Wakatani1989; Gupta, Callen & Hegna Reference Gupta, Callen and Hegna2002). Moreover, the mode width pertaining to the plasma displacement is proportional to the volume of plasma displaced. Thus, following from (3.5), this difference in mode width indicates that the energy associated with the plasma displacement is smallest for parallel dominant plasmas for on-axis profiles, which is conducive to plasma stability. A shift in $s_{\mathrm {max}}$![]() , the flux surface coordinate $s$
, the flux surface coordinate $s$![]() for which the plasma displacement is largest, is also observed with $s_{\mathrm {max}}$
for which the plasma displacement is largest, is also observed with $s_{\mathrm {max}}$![]() decreasing for increasing $\langle \beta _{\perp / \|} \rangle$
decreasing for increasing $\langle \beta _{\perp / \|} \rangle$![]() . The change in $s_{\mathrm {max}}$
. The change in $s_{\mathrm {max}}$![]() is a direct consequence of the change in shape of the $\iota (s)$
is a direct consequence of the change in shape of the $\iota (s)$![]() profile for different hot-pressure profiles. The underlying mode structure of the displacement vector is shown in figure 6 for an example case that corresponds to a pressure isotropic simulation of the parabolic hot-particle pressure profile. This figure also shows the graph of the rotational transform $\iota (s)$
profile for different hot-pressure profiles. The underlying mode structure of the displacement vector is shown in figure 6 for an example case that corresponds to a pressure isotropic simulation of the parabolic hot-particle pressure profile. This figure also shows the graph of the rotational transform $\iota (s)$![]() , which allows us to conclude that the most dominant mode is the resonant $n=1,m=2$
, which allows us to conclude that the most dominant mode is the resonant $n=1,m=2$![]() mode at the $\iota = 0.5$
mode at the $\iota = 0.5$![]() surface. The mode structure for the parabolic, peaked and broad hot-particle profiles look very similar.
surface. The mode structure for the parabolic, peaked and broad hot-particle profiles look very similar.

Figure 5. The normalised plasma displacement sum over all modes as a function of the flux surface coordinate $s$![]() , $\varXi (s)/\varXi _{\max }$
, $\varXi (s)/\varXi _{\max }$![]() , for the parabolic, peaked and broad hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. The $\langle \beta \rangle$
, for the parabolic, peaked and broad hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. The $\langle \beta \rangle$![]() values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$
values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$![]() , $1.5\,\%$
, $1.5\,\%$![]() and $3\,\%$
and $3\,\%$![]() , respectively.
, respectively.

Figure 6. The five most dominant modes in line with ordering in (5.3) of the displacement vector and the $\iota$![]() profile for a parabolic hot-pressure profile. This figure shows a pressure isotropic simulation with $\langle \beta \rangle \approx 2.5\,\%$
profile for a parabolic hot-pressure profile. This figure shows a pressure isotropic simulation with $\langle \beta \rangle \approx 2.5\,\%$![]() . The red dotted lines indicate the location of the $\iota (s)=0.5$
. The red dotted lines indicate the location of the $\iota (s)=0.5$![]() surface.
surface.
The growth rates corresponding to the eigenvalues found in (3.1) are shown in figure 7. From the growth rates we conclude that the plasma becomes more unstable for increasing $\langle \beta _{\perp / \|} \rangle$![]() for all on-axis deposition profiles. Noticeably, for high $\langle \beta \rangle$
for all on-axis deposition profiles. Noticeably, for high $\langle \beta \rangle$![]() values, parallel dominant plasmas have significantly lower growth rates than isotropic or perpendicular dominant plasmas, which is in agreement with the plasma displacement results. Analysing the mode structure of the plasma displacement for the on-axis deposition profiles, it is concluded that the $n=1,m=2$
values, parallel dominant plasmas have significantly lower growth rates than isotropic or perpendicular dominant plasmas, which is in agreement with the plasma displacement results. Analysing the mode structure of the plasma displacement for the on-axis deposition profiles, it is concluded that the $n=1,m=2$![]() is present and dominant for all $\langle \beta \rangle$
is present and dominant for all $\langle \beta \rangle$![]() values. The Mercier criteria at $s=0.81$
values. The Mercier criteria at $s=0.81$![]() ($\rho =0.9$
($\rho =0.9$![]() ) corresponding to the on-axis deposition profiles are shown in figure 8.
) corresponding to the on-axis deposition profiles are shown in figure 8.

Figure 7. The growth rates corresponding to the parabolic, peaked and broad hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. The $\langle \beta \rangle$![]() values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$
values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$![]() , $1.5\,\%$
, $1.5\,\%$![]() and $3\,\%$
and $3\,\%$![]() , respectively. The value for $\langle \beta _{\perp / \|} \rangle$
, respectively. The value for $\langle \beta _{\perp / \|} \rangle$![]() represents the average value over all simulations in the $\langle \beta \rangle$
represents the average value over all simulations in the $\langle \beta \rangle$![]() -scan with the same ratio $T_\perp / T_{\|}$
-scan with the same ratio $T_\perp / T_{\|}$![]() .
.

Figure 8. The Mercier criteria corresponding to the parabolic, peaked and broad hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. The $\langle \beta \rangle$![]() values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$
values for the parabolic, peaked and broad profiles are approximately equal to $2.5\,\%$![]() , $1.5\,\%$
, $1.5\,\%$![]() and $3\,\%$
and $3\,\%$![]() , respectively. The value for $\langle \beta _{\perp / \|} \rangle$
, respectively. The value for $\langle \beta _{\perp / \|} \rangle$![]() represents the average value over all simulations in the $\langle \beta \rangle$
represents the average value over all simulations in the $\langle \beta \rangle$![]() -scan with the same ratio $T_\perp / T_{\|}$
-scan with the same ratio $T_\perp / T_{\|}$![]() . The black lines indicate the stability boundary where the Mercier criterion is zero.
. The black lines indicate the stability boundary where the Mercier criterion is zero.
5.2. Off-axis deposition profiles
The hollow and realistic hot-particle pressure profile simulations contain an additional parameter $B_C$![]() , which has been scanned over to vary the deposition location of the hot-particle species. Figure 9 shows $\varXi (s)$
, which has been scanned over to vary the deposition location of the hot-particle species. Figure 9 shows $\varXi (s)$![]() corresponding to the hollow and realistic off-axis deposition profiles for varying pressure anisotropy and critical magnetic field $B_C$
corresponding to the hollow and realistic off-axis deposition profiles for varying pressure anisotropy and critical magnetic field $B_C$![]() . It is found that, for parallel dominant plasmas, the value of $B_C$
. It is found that, for parallel dominant plasmas, the value of $B_C$![]() has a negligible effect on the plasma displacement $\varXi (s)$
has a negligible effect on the plasma displacement $\varXi (s)$![]() . This can be explained by the fact that the trapped particle fraction for parallel dominant plasmas is relatively low compared with perpendicular dominant plasmas. From this figure, we can also conclude that LF deposition of perpendicular dominant ions has a pronounced destabilising effect for both hot-pressure profiles. This is corroborated by figure 10, which shows the growth rates corresponding to the simulations of the off-axis deposition profiles. The growth rates pertaining to the perpendicular dominant plasmas for both hot-pressure profiles are observed to decrease substantially when transitioning from LF to HF deposition. The realistic profile shows the only case in all simulations carried out for which a perpendicular dominant plasma in the context of the same hot-pressure profile appears to be more stable than parallel dominant plasmas. It is observed in figure 10 that the growth rate is more sensitive to the plasma anisotropy ratio $\langle \beta _{\perp / \|} \rangle$
. This can be explained by the fact that the trapped particle fraction for parallel dominant plasmas is relatively low compared with perpendicular dominant plasmas. From this figure, we can also conclude that LF deposition of perpendicular dominant ions has a pronounced destabilising effect for both hot-pressure profiles. This is corroborated by figure 10, which shows the growth rates corresponding to the simulations of the off-axis deposition profiles. The growth rates pertaining to the perpendicular dominant plasmas for both hot-pressure profiles are observed to decrease substantially when transitioning from LF to HF deposition. The realistic profile shows the only case in all simulations carried out for which a perpendicular dominant plasma in the context of the same hot-pressure profile appears to be more stable than parallel dominant plasmas. It is observed in figure 10 that the growth rate is more sensitive to the plasma anisotropy ratio $\langle \beta _{\perp / \|} \rangle$![]() for LF deposition than for HF deposition for both the hollow and realistic hot-particle pressure profiles. This result is in agreement with the eigenvalue analysis performed for the mode family $n=2$
for LF deposition than for HF deposition for both the hollow and realistic hot-particle pressure profiles. This result is in agreement with the eigenvalue analysis performed for the mode family $n=2$![]() for the hollow profile in Cooper et al. (Reference Cooper, Graves, Jucker, Watanabe, Narushima and Yamaguchi2007).
for the hollow profile in Cooper et al. (Reference Cooper, Graves, Jucker, Watanabe, Narushima and Yamaguchi2007).

Figure 9. The function $\varXi (s)/\varXi _{\max }$![]() for the hollow and realistic hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. For both pressure profiles, $\langle \beta \rangle \approx 3\,\%$
for the hollow and realistic hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. For both pressure profiles, $\langle \beta \rangle \approx 3\,\%$![]() .
.

Figure 10. The growth rates corresponding to the hollow and realistic hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. For both pressure profiles, $\langle \beta \rangle \approx 3\,\%$![]() . The value for $\langle \beta _{\perp / \|} \rangle$
. The value for $\langle \beta _{\perp / \|} \rangle$![]() represents the average value over all simulations in the $\langle \beta \rangle$
represents the average value over all simulations in the $\langle \beta \rangle$![]() -scan with the same ratio $T_\perp / T_{\|}$
-scan with the same ratio $T_\perp / T_{\|}$![]() .
.
In the case of a hollow hot-pressure profile, the $n=1,m=1$![]() mode component is clearly visible, peaking at $s\approx 0.75$
mode component is clearly visible, peaking at $s\approx 0.75$![]() , and is most pronounced for the parallel dominant case. The Mercier criteria at $s=0.81$
, and is most pronounced for the parallel dominant case. The Mercier criteria at $s=0.81$![]() corresponding to the off-axis deposition profiles are shown in figure 11. As opposed to the Mercier criteria for on-axis profiles, figure 8, a large change in Mercier criterion value is observed in the case of perpendicular dominant plasmas. For perpendicular dominant plasmas, the Mercier criterion value crosses the stability boundary at a lower value of $\langle \beta \rangle$
corresponding to the off-axis deposition profiles are shown in figure 11. As opposed to the Mercier criteria for on-axis profiles, figure 8, a large change in Mercier criterion value is observed in the case of perpendicular dominant plasmas. For perpendicular dominant plasmas, the Mercier criterion value crosses the stability boundary at a lower value of $\langle \beta \rangle$![]() . The results shown in figure 11 are in agreement with the results corresponding to the plasma displacement and growth rate to some degree. The main discrepancy that exists for both hot-pressure profiles is the fact that the difference in Mercier criteria for the isotropic and parallel dominant cases is negligible, while the difference in growth rate is substantial, for high values of $\langle \beta \rangle$
. The results shown in figure 11 are in agreement with the results corresponding to the plasma displacement and growth rate to some degree. The main discrepancy that exists for both hot-pressure profiles is the fact that the difference in Mercier criteria for the isotropic and parallel dominant cases is negligible, while the difference in growth rate is substantial, for high values of $\langle \beta \rangle$![]() .
.

Figure 11. The Mercier criteria corresponding to the hollow and realistic hot-particle pressure profiles. For each profile, three levels of anisotropy were considered. For both pressure profiles, $\langle \beta \rangle \approx 3\,\%$![]() . The value for $\langle \beta _{\perp / \|} \rangle$
. The value for $\langle \beta _{\perp / \|} \rangle$![]() represents the average value over all simulations in the $\langle \beta \rangle$
represents the average value over all simulations in the $\langle \beta \rangle$![]() -scan with the same ratio $T_\perp / T_{\|}$
-scan with the same ratio $T_\perp / T_{\|}$![]() . The black lines indicate the stability boundary where the Mercier criterion is zero.
. The black lines indicate the stability boundary where the Mercier criterion is zero.
6. Conclusion
The 3-D magnetic equilibrium and linear MHD stability have been calculated for anisotropic plasmas in the case of the LHD stellarator for a low magnetic field configuration and have been compared with isotropic plasmas. The magnetic equilibrium has been calculated using the ANIMEC code, while TERPSICHORE has been used for the linear MHD stability calculations. A modified version of the bi-Maxwellian was used to model the effect of pressure anisotropy on the particle velocity distribution. In the simulations carried out, we chose a parabolic thermal-pressure profile in order to match experimental conditions. Five hot-particle pressure profiles were analysed, three of which correspond with on-axis particle deposition and two with off-axis deposition. The KO energy principle, which has been implemented in TERPSICHORE, has been used to calculate the following stability parameters: the growth rate, the mode structure of the plasma displacement and the Mercier criterion at $s=0.81$![]() . The $n=1$
. The $n=1$![]() mode family has been analysed in TERPSICHORE.
mode family has been analysed in TERPSICHORE.
The growth rates for the on-axis hot-particle pressure profiles reveal a clear dependence on the level of anisotropy $\langle \beta _{\perp / \|} \rangle$![]() . For all $\langle \beta \rangle > 0.5\,\%$
. For all $\langle \beta \rangle > 0.5\,\%$![]() , the growth rate is observed to increase for increasing $\langle \beta _{\perp / \|} \rangle$
, the growth rate is observed to increase for increasing $\langle \beta _{\perp / \|} \rangle$![]() , regardless of the specific profile shape. The plasma displacement for parallel dominant plasmas is observed to have a small mode width in comparison with the isotropic and perpendicular cases. These two facts combined allows us to conclude that the parallel dominant case represents the most stable plasma configuration and is noticeably more stable than the more common case of plasma isotropy. For the off-axis hot-particle pressure profiles, the plasma displacement, growth rate and Mercier criterion at $s=0.81$
, regardless of the specific profile shape. The plasma displacement for parallel dominant plasmas is observed to have a small mode width in comparison with the isotropic and perpendicular cases. These two facts combined allows us to conclude that the parallel dominant case represents the most stable plasma configuration and is noticeably more stable than the more common case of plasma isotropy. For the off-axis hot-particle pressure profiles, the plasma displacement, growth rate and Mercier criterion at $s=0.81$![]() show that perpendicular dominant plasmas with LF deposition are very unstable compared with all other plasma configurations. The Mercier criterion shows a clear discrepancy in stability between perpendicular dominant plasmas on the one hand and isotropic and parallel dominant plasmas on the other. For the realistic hot-pressure profile, perpendicular dominant plasmas with HF deposition are found to be most stable. For LF deposition, however, parallel dominant plasmas are found to be most stable for this profile. We can conclude that the fact that the theoretical threshold for isotropic plasmas is found to be crossed under a low magnetic field configuration for LHD can be attributed to anisotropy in plasmas. Specifically, tangential NBI heating, which is used as a main heating scheme in LHD, is found to stabilise such plasmas.
show that perpendicular dominant plasmas with LF deposition are very unstable compared with all other plasma configurations. The Mercier criterion shows a clear discrepancy in stability between perpendicular dominant plasmas on the one hand and isotropic and parallel dominant plasmas on the other. For the realistic hot-pressure profile, perpendicular dominant plasmas with HF deposition are found to be most stable. For LF deposition, however, parallel dominant plasmas are found to be most stable for this profile. We can conclude that the fact that the theoretical threshold for isotropic plasmas is found to be crossed under a low magnetic field configuration for LHD can be attributed to anisotropy in plasmas. Specifically, tangential NBI heating, which is used as a main heating scheme in LHD, is found to stabilise such plasmas.
Future research could concentrate on the treatment of higher-order modes such as the $n=2$![]() mode in TERPSICHORE. This could form a more comprehensive picture of the effect of pressure anisotropy on plasma stability. Another topic for future research is to expand on this work by calculating equilibria using the slowing-down distribution. This distribution is generally found to be more relevant and accurate in modelling NBI heating. Our work provides a theoretical treatment of the effect of pressure anisotropy on plasma stability. Further research, however, is needed to provide a connection between MHD stability theory and experiment, where experimental research such as that provided by Watanabe et al. (Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005) should be taken into account.
mode in TERPSICHORE. This could form a more comprehensive picture of the effect of pressure anisotropy on plasma stability. Another topic for future research is to expand on this work by calculating equilibria using the slowing-down distribution. This distribution is generally found to be more relevant and accurate in modelling NBI heating. Our work provides a theoretical treatment of the effect of pressure anisotropy on plasma stability. Further research, however, is needed to provide a connection between MHD stability theory and experiment, where experimental research such as that provided by Watanabe et al. (Reference Watanabe, Sakakibara, Narushima, Funaba, Narihara, Tanaka, Yamaguchi, Toi, Ohdachi and Kaneko2005) should be taken into account.
Acknowledgements
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. This work was also partially supported by ‘PLADyS’, JSPS (Japan Society of the Promotion of Science) Core-to-Core Program, A. Advanced Research Network.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are available from the corresponding author, T.E. Moen, upon reasonable request.