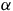1. The Choice-functional Approach to Population Ethics
In ‘Path independence and a persistent paradox of population ethics’, Rush Stewart (Reference Stewart2021) develops a choice-functional approach to population ethics.Footnote
1
The fundamental element of his argument is a choice function
![]() $C$
that assigns permissible alternatives (populations in the context of population ethics),
$C$
that assigns permissible alternatives (populations in the context of population ethics),
![]() $C\left( S \right)$
, to each menu (i.e. set of available options). If a population
$C\left( S \right)$
, to each menu (i.e. set of available options). If a population
![]() $A$
is an element of
$A$
is an element of
![]() $C\left( S \right)$
, then
$C\left( S \right)$
, then
![]() $A$
is said to be permissible (or chosen) under menu
$A$
is said to be permissible (or chosen) under menu
![]() $S$
. For each menu
$S$
. For each menu
![]() $S$
,
$S$
,
![]() $C\left( S \right) \subseteq S$
and
$C\left( S \right) \subseteq S$
and
![]() $C\left( S \right)$
is nonempty. An advantage of Stewart’s approach is that a wider range of concerns can be incorporated than in the standard approach with a better-than relation/preference. For example, menu-dependent relations can be captured using a choice-functional framework.Footnote
2
$C\left( S \right)$
is nonempty. An advantage of Stewart’s approach is that a wider range of concerns can be incorporated than in the standard approach with a better-than relation/preference. For example, menu-dependent relations can be captured using a choice-functional framework.Footnote
2
The paradox mentioned in the title of Stewart’s paper is an extension of the Mere Addition Paradox, which he obtains by using a choice function. This paradox is understood as a logical relation between the following three conditions.
Mere Addition. If
![]() $A$
and
$A$
and
![]() $B$
are populations that contain only positive utility levels, then
$B$
are populations that contain only positive utility levels, then
![]() $A \cup B \in C\left( {\left\{ {A \cup B,A} \right\}} \right)$
.
$A \cup B \in C\left( {\left\{ {A \cup B,A} \right\}} \right)$
.
Non-Anti-Egalitarianism. Let
![]() $A$
and
$A$
and
![]() $B$
be two populations of the same population size. If all individuals have the same utility level in
$B$
be two populations of the same population size. If all individuals have the same utility level in
![]() $B$
and the total sum of utility in
$B$
and the total sum of utility in
![]() $B$
is higher than that in
$B$
is higher than that in
![]() $A$
, then
$A$
, then
![]() $A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
.
$A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
.
Repugnant Conclusion. For any large population
![]() $A$
with blissful utility levels, there is another much larger population
$A$
with blissful utility levels, there is another much larger population
![]() $B$
such that all individuals are at a positive, but drab utility level, and
$B$
such that all individuals are at a positive, but drab utility level, and
![]() $B \in C\left( {\left\{ {A,B} \right\}} \right)$
.
$B \in C\left( {\left\{ {A,B} \right\}} \right)$
.
Stewart (Reference Stewart2021) shows that Mere Addition and Non-Anti-Egalitarianism imply the Repugnant Conclusion if the following choice axiom is satisfied:
According to this axiom, any large choice problem can be decomposed into a collection of smaller choice problems, which is called Path Independence (Plott Reference Plott1973). Stewart’s novel contribution is the introduction of this axiom into the formal analysis of population ethics. By using Path Independence as a necessary condition of plausible population ethics, Stewart establishes a paradox, which is a natural extension of Ng’s (1989) axiological impossibility result. Ng (1989) uses a transitive relation, but Stewart replaces transitivity with Path Independence, which implies that transitivity might be unnecessary. Notably, Stewart motivates his result by arguing that Path Independence is a minimally acceptable choice constraint on axiology.
In this paper, I will show that Path Independence can be replaced with logically weaker properties. Let us define
wherein
![]() ${R^{\rm{*}}}$
represents what is called the base relation in the literature (Sen Reference Sen1971; Suzumura Reference Suzumura1983).
${R^{\rm{*}}}$
represents what is called the base relation in the literature (Sen Reference Sen1971; Suzumura Reference Suzumura1983).
![]() $A$
is at least as good as
$A$
is at least as good as
![]() $B$
with regard to the base relation if and only if
$B$
with regard to the base relation if and only if
![]() $A$
is permissible in the choice between
$A$
is permissible in the choice between
![]() $A$
and
$A$
and
![]() $B$
. It can be proved that
$B$
. It can be proved that
![]() ${R^{\rm{*}}}$
is quasi-transitive (and complete) if Path Independence is satisfied (Suzumura Reference Suzumura1983: 95–96). Quasi-transitivity is defined as the transitivity of the asymmetric part (strict preference)
${R^{\rm{*}}}$
is quasi-transitive (and complete) if Path Independence is satisfied (Suzumura Reference Suzumura1983: 95–96). Quasi-transitivity is defined as the transitivity of the asymmetric part (strict preference)
![]() ${P^{\rm{*}}}$
of
${P^{\rm{*}}}$
of
![]() ${R^{\rm{*}}}$
(i.e.
${R^{\rm{*}}}$
(i.e.
![]() $A{P^{\rm{*}}}B$
if and only if
$A{P^{\rm{*}}}B$
if and only if
![]() $\left\{ A \right\} = C\left( {\left\{ {A,B} \right\}} \right)$
). Thus, if
$\left\{ A \right\} = C\left( {\left\{ {A,B} \right\}} \right)$
). Thus, if
![]() $A{P^{\rm{*}}}B$
and
$A{P^{\rm{*}}}B$
and
![]() $B{P^{\rm{*}}}C$
, then
$B{P^{\rm{*}}}C$
, then
![]() $A{P^{\rm{*}}}C$
for all
$A{P^{\rm{*}}}C$
for all
![]() $A,B,$
and
$A,B,$
and
![]() $C$
.Footnote
3
$C$
.Footnote
3
To see that the quasi-transitivity of the base relation is crucial to Stewart’s main observations, imagine some population
![]() $A$
with blissful utility levels and add a large number of individuals with positive but negligible utility levels resulting in a much larger population
$A$
with blissful utility levels and add a large number of individuals with positive but negligible utility levels resulting in a much larger population
![]() ${A^ + }$
. Then, consider an egalitarian population
${A^ + }$
. Then, consider an egalitarian population
![]() $E$
that has the same population size as
$E$
that has the same population size as
![]() ${A^ + }$
, but with a higher total utility level, while the utility of each individual is at a drab level.Footnote
4
By Mere Addition,
${A^ + }$
, but with a higher total utility level, while the utility of each individual is at a drab level.Footnote
4
By Mere Addition,
![]() ${A^ + } \in C\left( {\left\{ {{A^ + },A} \right\}} \right)$
, which implies that
${A^ + } \in C\left( {\left\{ {{A^ + },A} \right\}} \right)$
, which implies that
![]() ${A^ + }{R^{\rm{*}}}A$
. Non-Anti-Egalitarianism requires that
${A^ + }{R^{\rm{*}}}A$
. Non-Anti-Egalitarianism requires that
![]() ${A^ + } \;\notin\; C\left( {\left\{ {{A^ + },E} \right\}} \right)$
, implying that
${A^ + } \;\notin\; C\left( {\left\{ {{A^ + },E} \right\}} \right)$
, implying that
![]() $\left\{ E \right\} = C\left( {\left\{ {{A^ + },E} \right\}} \right)$
. Therefore,
$\left\{ E \right\} = C\left( {\left\{ {{A^ + },E} \right\}} \right)$
. Therefore,
![]() $E{P^{\rm{*}}}{A^ + }$
. If
$E{P^{\rm{*}}}{A^ + }$
. If
![]() $A{P^{\rm{*}}}E$
, then quasi-transitivity implies that
$A{P^{\rm{*}}}E$
, then quasi-transitivity implies that
![]() $A{P^{\rm{*}}}{A^ + }$
, which contradicts
$A{P^{\rm{*}}}{A^ + }$
, which contradicts
![]() ${A^ + }{R^{\rm{*}}}A$
. It follows that
${A^ + }{R^{\rm{*}}}A$
. It follows that
![]() $E{R^{\rm{*}}}A$
, and thus that the Repugnant Conclusion holds true. In short, the quasi-transitivity of the base relation leads to the Mere Addition Paradox.
$E{R^{\rm{*}}}A$
, and thus that the Repugnant Conclusion holds true. In short, the quasi-transitivity of the base relation leads to the Mere Addition Paradox.
Notice that this proof does not depend on Path Independence. However, the quasi-transitivity of the base relation logically follows from Path Independence (Suzumura Reference Suzumura1983: 95), which means that my proof entails Stewart’s observation as a corollary. For this reason, it can be argued that the quasi-transitivity of the base relation is more essential for the Mere Addition Paradox in the choice-functional framework than Path Independence, which suggests that Path Independence is not an indispensable property in Stewart’s observation.
To see this from another perspective, consider the following two alternative choice axioms:
and
According to Weak
![]() $\alpha $
, if
$\alpha $
, if
![]() $A$
is permissible under
$A$
is permissible under
![]() $\left\{ {A,B,D} \right\}$
and
$\left\{ {A,B,D} \right\}$
and
![]() $\left\{ {A,B} \right\}$
, then it is also permissible under
$\left\{ {A,B} \right\}$
, then it is also permissible under
![]() $\left\{ {A,D} \right\}$
. Property
$\left\{ {A,D} \right\}$
. Property
![]() $\delta $
requires that if both
$\delta $
requires that if both
![]() $A$
and
$A$
and
![]() $B$
are permissible under
$B$
are permissible under
![]() $S$
, which is a subset of
$S$
, which is a subset of
![]() $T$
, then
$T$
, then
![]() $A$
cannot be the only permissible population under
$A$
cannot be the only permissible population under
![]() $T$
. Both of these axioms are implied by Path Independence, and therefore, if Path Independence is considered to be plausible, then these axioms must be considered plausible as well because of this logical relation; see Appendix A. Together, Weak
$T$
. Both of these axioms are implied by Path Independence, and therefore, if Path Independence is considered to be plausible, then these axioms must be considered plausible as well because of this logical relation; see Appendix A. Together, Weak
![]() $\alpha $
and Property
$\alpha $
and Property
![]() $\delta $
imply that the base relation is quasi-transitive, and these two axioms are, therefore, sufficient to obtain the Mere Addition Paradox, which means that Path Independence can be replaced by weaker properties. The unfortunate fallout hereof is that the impossibility of finding an appropriate theory in population ethics is even more fundamental.
$\delta $
imply that the base relation is quasi-transitive, and these two axioms are, therefore, sufficient to obtain the Mere Addition Paradox, which means that Path Independence can be replaced by weaker properties. The unfortunate fallout hereof is that the impossibility of finding an appropriate theory in population ethics is even more fundamental.
Given the observation that Weak
![]() $\alpha $
and Property
$\alpha $
and Property
![]() $\delta $
are logically implied by Path Independence, that the conjunction of Weak
$\delta $
are logically implied by Path Independence, that the conjunction of Weak
![]() $\alpha $
and Property
$\alpha $
and Property
![]() $\delta $
is indeed weaker than Path Independence can be seen in the following example. Consider the following choice function:
$\delta $
is indeed weaker than Path Independence can be seen in the following example. Consider the following choice function:
This satisfies Weak
![]() $\alpha $
and Property
$\alpha $
and Property
![]() $\delta $
but violates Path Independence. Notice that the violation of Path Independence occurs when the choice of
$\delta $
but violates Path Independence. Notice that the violation of Path Independence occurs when the choice of
![]() $\left\{ {{A_1},{A_2},{A_3},{A_4}} \right\}$
is considered. This suggests that the requirement of Path Independence is imposed even when many options are included, and that when it comes to very complex paths with many options, Path Independence may be too demanding. For example, Path Independence requires that
$\left\{ {{A_1},{A_2},{A_3},{A_4}} \right\}$
is considered. This suggests that the requirement of Path Independence is imposed even when many options are included, and that when it comes to very complex paths with many options, Path Independence may be too demanding. For example, Path Independence requires that
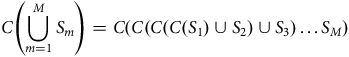 $$C\left( {\mathop \bigcup \limits_{m = 1}^M {S_m}} \right) = C\left( {C\left( {C\left( {C\left( {{S_1}} \right) \cup {S_2}} \right) \cup {S_3}} \right) \ldots {S_M}} \right)$$
$$C\left( {\mathop \bigcup \limits_{m = 1}^M {S_m}} \right) = C\left( {C\left( {C\left( {C\left( {{S_1}} \right) \cup {S_2}} \right) \cup {S_3}} \right) \ldots {S_M}} \right)$$
where each
![]() ${S_m}$
contains over 1,000,000 populations. (See Suzumura Reference Suzumura1983: Theorem 2.4.) In some issues in population ethics, such as Parfit’s Continuum Argument, a very large number of populations may be considered as options, but in the present context, it would be natural to restrict the requirement for consistency to cases with a limited number of options such as Weak
${S_m}$
contains over 1,000,000 populations. (See Suzumura Reference Suzumura1983: Theorem 2.4.) In some issues in population ethics, such as Parfit’s Continuum Argument, a very large number of populations may be considered as options, but in the present context, it would be natural to restrict the requirement for consistency to cases with a limited number of options such as Weak
![]() $\alpha $
.Footnote
5
Our result shows that the impossibility (of finding an appropriate theory in population ethics) holds true even with this restriction.
$\alpha $
.Footnote
5
Our result shows that the impossibility (of finding an appropriate theory in population ethics) holds true even with this restriction.
Before proceeding to the next topic and the main point of this paper, let me summarize the implications of the brief review of Stewart’s results described above. First, the choice-functional approach is useful for extending existing work in population ethics. Second, Path Independence is not the logically weakest requirement for obtaining the Mere Addition Paradox because the quasi-transitivity of the base relation is mathematically more essential than Path Independence, as shown above. Third, given this latter point, Stewart’s result can be substantially generalized.
2. Acyclic Population Ethics
In this section I will examine the Mere Addition Paradox in a choice-functional approach that uses an acyclic better-than relation. Since it is possible to infer a choice function by using the better-than relation, the relational approach can be connected with the choice-functional approach. Key to this connection is the acyclicity of the better-than relation, because a choice function inferred from the better-than relation is well-defined only when the relation is acyclic. Related to this, Stewart (Reference Stewart2021) notes that the ‘choice pattern’ that Frick (Reference Frick, McMahan, Campbell, Goodrich and Ramakrishnan2022) advocates is consistent with maximizing an acyclic binary relation and even offers an example of the relation in footnote 27. However, his binary relation is limited to the case of three options, and neither its applicability to the case with
![]() $m$
options for
$m$
options for
![]() $m \ge 4$
, nor the general idea behind it is entirely clear. Hence, by offering a general principle that can apply to any number of options, in some sense, I complement Stewart’s point.
$m \ge 4$
, nor the general idea behind it is entirely clear. Hence, by offering a general principle that can apply to any number of options, in some sense, I complement Stewart’s point.
Let us define a population principle called ‘Theory
![]() $\alpha $
’. I will show that Theory
$\alpha $
’. I will show that Theory
![]() $\alpha $
yields a choice function that satisfies Non-Anti-Egalitarianism, Mere Addition, Weak
$\alpha $
yields a choice function that satisfies Non-Anti-Egalitarianism, Mere Addition, Weak
![]() $\gamma $
(explained below) and Property
$\gamma $
(explained below) and Property
![]() $\alpha $
, and that, moreover, avoids the Repugnant Conclusion. As an auxiliary step, I introduce the concept of an extension. Given two populations
$\alpha $
, and that, moreover, avoids the Repugnant Conclusion. As an auxiliary step, I introduce the concept of an extension. Given two populations
![]() $F$
and
$F$
and
![]() $G$
, population
$G$
, population
![]() $F$
is an extension of population
$F$
is an extension of population
![]() $G$
if and only if there is a nonempty sub-population
$G$
if and only if there is a nonempty sub-population
![]() $F{\rm{'}}$
of
$F{\rm{'}}$
of
![]() $F$
such that
$F$
such that
![]() $F{\rm{'}}$
is distinct from
$F{\rm{'}}$
is distinct from
![]() $G$
and
$G$
and
![]() $F = F{\rm{'}} \cup G$
.Footnote
6
That is,
$F = F{\rm{'}} \cup G$
.Footnote
6
That is,
![]() $F$
is obtained by adding
$F$
is obtained by adding
![]() $F{\rm{'}}$
to
$F{\rm{'}}$
to
![]() $G$
. Notably,
$G$
. Notably,
![]() $F$
is an extension of
$F$
is an extension of
![]() $G$
when
$G$
when
![]() $G$
is a proper sub-population of
$G$
is a proper sub-population of
![]() $F$
(i.e.
$F$
(i.e.
![]() $F \varsupsetneq G$
);
$F \varsupsetneq G$
);
![]() $F \not\supsetneq G$
means that
$F \not\supsetneq G$
means that
![]() $F$
is not an extension of
$F$
is not an extension of
![]() $G$
.
$G$
.
Theory
![]() $\alpha $
is defined as follows: For all two populations
$\alpha $
is defined as follows: For all two populations
![]() $A$
and
$A$
and
![]() $B$
, population
$B$
, population
![]() $A$
is strictly better than population
$A$
is strictly better than population
![]() $B$
(formalized as ‘
$B$
(formalized as ‘
![]() $A{P_\alpha }B$
’) if and only if either of the following two conditions holds: (i) the population size of
$A{P_\alpha }B$
’) if and only if either of the following two conditions holds: (i) the population size of
![]() $A$
is the same as that of
$A$
is the same as that of
![]() $B$
, and the total sum of utility in
$B$
, and the total sum of utility in
![]() $A$
is greater than that in
$A$
is greater than that in
![]() $B$
, or (ii) the population size of
$B$
, or (ii) the population size of
![]() $A$
is smaller than that of
$A$
is smaller than that of
![]() $B$
,
$B$
,
![]() $B$
is not an extension of
$B$
is not an extension of
![]() $A$
, and the average utility in
$A$
, and the average utility in
![]() $A$
is greater than that in
$A$
is greater than that in
![]() $B$
.Footnote
7
Formally:
$B$
.Footnote
7
Formally:
where
![]() ${N_A}$
is the population size of
${N_A}$
is the population size of
![]() $A$
,
$A$
,
![]() $T{U_A}$
is the total sum of the utilities in
$T{U_A}$
is the total sum of the utilities in
![]() $A$
and
$A$
and
![]() $A{U_A}$
is the average utility level in
$A{U_A}$
is the average utility level in
![]() $A$
(where
$A$
(where
![]() ${N_B}$
,
${N_B}$
,
![]() $T{U_B}$
and
$T{U_B}$
and
![]() $A{U_B}$
are defined in parallel).Footnote
8
Notably,
$A{U_B}$
are defined in parallel).Footnote
8
Notably,
![]() $A$
is strictly better than
$A$
is strictly better than
![]() $B$
only when the population size of
$B$
only when the population size of
![]() $A$
is less than or equal to that of
$A$
is less than or equal to that of
![]() $B$
.
$B$
.
It is worth mentioning that Theory
![]() $\alpha $
is a hybrid of total utilitarian and average utilitarian methods of assessment. It conditionally uses total utilitarianism and average utilitarianism, switching between the two. It may be interesting to compare the proposed principle with the class of variable population principles (Hurka 1883; Ng 1986). For a variable population principle, there is a non-decreasing function
$\alpha $
is a hybrid of total utilitarian and average utilitarian methods of assessment. It conditionally uses total utilitarianism and average utilitarianism, switching between the two. It may be interesting to compare the proposed principle with the class of variable population principles (Hurka 1883; Ng 1986). For a variable population principle, there is a non-decreasing function
![]() $f$
such that
$f$
such that
![]() $A$
is better than
$A$
is better than
![]() $B$
if and only if
$B$
if and only if
When
![]() $f\left( n \right) = n$
for all natural numbers
$f\left( n \right) = n$
for all natural numbers
![]() $n$
, this principle corresponds to total utilitarianism, and when
$n$
, this principle corresponds to total utilitarianism, and when
![]() $f\left( n \right) = 1$
for all natural numbers
$f\left( n \right) = 1$
for all natural numbers
![]() $n$
, it corresponds to average utilitarianism. Hence, variable population principles take an intermediate position between the two. Theory
$n$
, it corresponds to average utilitarianism. Hence, variable population principles take an intermediate position between the two. Theory
![]() $\alpha $
is similar in nature to variable value principles in its reconciliation of the two extreme types of utilitarianism, but there is a significant difference. While in the traditional approach to variable principles a continuous function
$\alpha $
is similar in nature to variable value principles in its reconciliation of the two extreme types of utilitarianism, but there is a significant difference. While in the traditional approach to variable principles a continuous function
![]() $f$
is used to construct an intermediate principle that is neither total utilitarianism nor average utilitarianism, in Theory
$f$
is used to construct an intermediate principle that is neither total utilitarianism nor average utilitarianism, in Theory
![]() $\alpha $
a radical switch is made by combining the two directly. And more importantly, while a variable value principle cannot avoid the mere addition paradox (Bossert et al. Reference Bossert, Cato and Kamaga2023), Theory
$\alpha $
a radical switch is made by combining the two directly. And more importantly, while a variable value principle cannot avoid the mere addition paradox (Bossert et al. Reference Bossert, Cato and Kamaga2023), Theory
![]() $\alpha $
can. Hence, Theory
$\alpha $
can. Hence, Theory
![]() $\alpha $
can be seen as a new arrangement that avoids the mere addition paradox while embracing the spirit of traditional variable value principles, at least to some extent.
$\alpha $
can be seen as a new arrangement that avoids the mere addition paradox while embracing the spirit of traditional variable value principles, at least to some extent.
Significantly, theory
![]() $\alpha $
is acyclic.Footnote
9
Acyclicity is a necessary and sufficient condition for the non-emptiness of the set of maximal elements. In a sense, acyclicity guarantees that the decision-making over the populations is decisive (Sen Reference Sen1970: Lemma 1*1). The claim that Theory
$\alpha $
is acyclic.Footnote
9
Acyclicity is a necessary and sufficient condition for the non-emptiness of the set of maximal elements. In a sense, acyclicity guarantees that the decision-making over the populations is decisive (Sen Reference Sen1970: Lemma 1*1). The claim that Theory
![]() $\alpha $
is acyclic can be proved as follows. If this theory is cyclic, there is a chain of populations,
$\alpha $
is acyclic can be proved as follows. If this theory is cyclic, there is a chain of populations,
![]() ${A^1},{A^2}, \ldots, {A^K}$
, such that
${A^1},{A^2}, \ldots, {A^K}$
, such that
![]() ${A^1}{P_\alpha }{A^2}$
,
${A^1}{P_\alpha }{A^2}$
,
![]() ${A^2}{P_\alpha }{A^3}, \ldots, {A^{K - 1}}{P_\alpha }{A^K}$
, and
${A^2}{P_\alpha }{A^3}, \ldots, {A^{K - 1}}{P_\alpha }{A^K}$
, and
![]() ${A^K}{P_\alpha }{A^1}$
. As mentioned above,
${A^K}{P_\alpha }{A^1}$
. As mentioned above,
![]() ${A^1}$
is strictly better than
${A^1}$
is strictly better than
![]() ${A^2}$
only when
${A^2}$
only when
![]() ${N_{{A^1}}} \le {N_{{A^2}}}$
. Similarly,
${N_{{A^1}}} \le {N_{{A^2}}}$
. Similarly,
![]() ${A^2}$
is strictly better than
${A^2}$
is strictly better than
![]() ${A^3}$
only when
${A^3}$
only when
![]() ${N_{{A^2}}} \le {N_{{A^3}}}$
. This holds for all adjacent pairs in
${N_{{A^2}}} \le {N_{{A^3}}}$
. This holds for all adjacent pairs in
![]() ${A^1},{A^2}, \ldots, {A^K}$
. Therefore, it follows that
${A^1},{A^2}, \ldots, {A^K}$
. Therefore, it follows that
which immediately implies that
Therefore, all of
![]() ${A^1},{A^2}, \ldots, {A^K}$
have the same population size. This being the case, total utilitarianism applies, and because of the preference cycle, it follows that
${A^1},{A^2}, \ldots, {A^K}$
have the same population size. This being the case, total utilitarianism applies, and because of the preference cycle, it follows that
which is a contradiction, implying that Theory
![]() $\alpha $
is not cyclic and, thus, proving our claim.
$\alpha $
is not cyclic and, thus, proving our claim.
Next, consider the following choice function that is inferred from Theory
![]() $\alpha $
:
$\alpha $
:
![]() $A$
is permissible under menu
$A$
is permissible under menu
![]() $S$
if and only if there is no population
$S$
if and only if there is no population
![]() ${A^{\rm{*}}}$
in menu
${A^{\rm{*}}}$
in menu
![]() $S$
such that
$S$
such that
![]() ${A^{\rm{*}}}$
is strictly better than
${A^{\rm{*}}}$
is strictly better than
![]() $A$
with regard to Theory
$A$
with regard to Theory
![]() $\alpha $
. It is easy to see that this choice function coincides with the set of maximal elements under Theory
$\alpha $
. It is easy to see that this choice function coincides with the set of maximal elements under Theory
![]() $\alpha $
.Footnote
10
I will refer to this as the ‘Choice-Functional Theory
$\alpha $
.Footnote
10
I will refer to this as the ‘Choice-Functional Theory
![]() $\alpha $
’ hereafter. Because it is defined as the set of maximal elements, we can take advantage of the large body of literature on choice theory that has been developed since Arrow (Reference Arrow1959). It is well known that if a better-than relation is acyclic, the set of maximal elements inferred from it satisfies several noteworthy properties (Suzumura Reference Suzumura1983: Ch. 2):
$\alpha $
’ hereafter. Because it is defined as the set of maximal elements, we can take advantage of the large body of literature on choice theory that has been developed since Arrow (Reference Arrow1959). It is well known that if a better-than relation is acyclic, the set of maximal elements inferred from it satisfies several noteworthy properties (Suzumura Reference Suzumura1983: Ch. 2):
-
(i) Non-Emptiness:
 $C$
is well-defined (i.e.
$C$
is well-defined (i.e.
 $C\left( S \right)$
is non-empty for all menus
$C\left( S \right)$
is non-empty for all menus
 $S$
);
$S$
); -
(ii) Property
 $\alpha $
:
$\alpha $
:
 $C\left( T \right) \cap S \subseteq C\left( S \right)$
for all menus
$C\left( T \right) \cap S \subseteq C\left( S \right)$
for all menus
 $S,T$
such that
$S,T$
such that
 $S \subseteq T$
if
$S \subseteq T$
if
 $C\left( T \right) \cap S$
is nonempty;
$C\left( T \right) \cap S$
is nonempty; -
(iii) Weak Path-Independence:
 $C\left( {S \cup T} \right) \subseteq C\left( {C\left( S \right) \cup C\left( T \right)} \right)$
for all menus
$C\left( {S \cup T} \right) \subseteq C\left( {C\left( S \right) \cup C\left( T \right)} \right)$
for all menus
 $S,T$
;
$S,T$
; -
(iv) Generalized Condorcet Property:Footnote 11
 $\{ A \in S|A{R^{\rm{*}}}B\;{\rm{for\;all\;}}B \in S\} \subseteq C\left( S \right)$
.
$\{ A \in S|A{R^{\rm{*}}}B\;{\rm{for\;all\;}}B \in S\} \subseteq C\left( S \right)$
.
According to Property
![]() $\alpha $
, if
$\alpha $
, if
![]() $A$
is permissible under
$A$
is permissible under
![]() $T$
that includes all options in
$T$
that includes all options in
![]() $S$
, then
$S$
, then
![]() $A$
is permissible under
$A$
is permissible under
![]() $S$
. Property
$S$
. Property
![]() $\alpha $
is logically equivalent to Weak Path-Independence (Ferejohn and Grether Reference Ferejohn and Grether1977: 24).
$\alpha $
is logically equivalent to Weak Path-Independence (Ferejohn and Grether Reference Ferejohn and Grether1977: 24).
The choice axiom Weak
![]() $\gamma $
, which was introduced by Stewart in an earlier paper (Stewart Reference Stewart2020), follows from Generalized Condorcet Property and Property
$\gamma $
, which was introduced by Stewart in an earlier paper (Stewart Reference Stewart2020), follows from Generalized Condorcet Property and Property
![]() $\alpha $
. This choice axiom states that if
$\alpha $
. This choice axiom states that if
![]() $A$
is the only permissible population under
$A$
is the only permissible population under
![]() $S$
and is permissible under
$S$
and is permissible under
![]() $T$
, then it is also permissible under the union of the two menus,
$T$
, then it is also permissible under the union of the two menus,
![]() $S \cup T$
. Formally:
$S \cup T$
. Formally:
To see that Weak
![]() $\gamma $
follows from Generalized Condorcet Property and Property
$\gamma $
follows from Generalized Condorcet Property and Property
![]() $\alpha $
, assume that Generalized Condorcet Property and Property
$\alpha $
, assume that Generalized Condorcet Property and Property
![]() $\alpha $
are satisfied and that the antecedent of Weak
$\alpha $
are satisfied and that the antecedent of Weak
![]() $\gamma $
is true (i.e.
$\gamma $
is true (i.e.
![]() $A$
is uniquely permissible in menu
$A$
is uniquely permissible in menu
![]() $S$
and permissible in menu
$S$
and permissible in menu
![]() $T$
). That is, we have
$T$
). That is, we have
![]() $\left\{ A \right\} = C\left( S \right){\rm{\;and\;\;}}A \in C\left( T \right)$
. Then, by Property
$\left\{ A \right\} = C\left( S \right){\rm{\;and\;\;}}A \in C\left( T \right)$
. Then, by Property
![]() $\alpha $
,
$\alpha $
,
![]() $A$
is at least as good as all populations in
$A$
is at least as good as all populations in
![]() $S$
with regard to the base relation,Footnote
12
and
$S$
with regard to the base relation,Footnote
12
and
![]() $A$
is also at least as good as all populations in
$A$
is also at least as good as all populations in
![]() $T$
with regard to the base relation.Footnote
13
This implies that
$T$
with regard to the base relation.Footnote
13
This implies that
![]() $A$
is at least as good as all populations in
$A$
is at least as good as all populations in
![]() $S \cup T$
with regard to the base relation. Again, by Generalized Condorcet Property,
$S \cup T$
with regard to the base relation. Again, by Generalized Condorcet Property,
![]() $A$
is permissible in the menu
$A$
is permissible in the menu
![]() $S \cup T$
. Hence, Weak
$S \cup T$
. Hence, Weak
![]() $\gamma $
is satisfied.
$\gamma $
is satisfied.
The proof that Choice-Functional Theory
![]() $\alpha $
avoids the Mere Addition Paradox consists of three steps. First, it is shown that Mere Addition is satisfied. Take two populations,
$\alpha $
avoids the Mere Addition Paradox consists of three steps. First, it is shown that Mere Addition is satisfied. Take two populations,
![]() $A$
and
$A$
and
![]() $B$
, that contain only positive utility levels, and for which it is the case that
$B$
, that contain only positive utility levels, and for which it is the case that
![]() ${N_{A \cup B}} \gt {N_A}$
and that
${N_{A \cup B}} \gt {N_A}$
and that
![]() $A \cup B$
is an extension of
$A \cup B$
is an extension of
![]() $A$
. Notice that neither (i) nor (ii) in Theory
$A$
. Notice that neither (i) nor (ii) in Theory
![]() $\alpha $
applies to these populations, and therefore, that
$\alpha $
applies to these populations, and therefore, that
![]() $A$
is not preferred to
$A$
is not preferred to
![]() $A \cup B$
according to Theory
$A \cup B$
according to Theory
![]() $\alpha $
. This means that
$\alpha $
. This means that
![]() $A \cup B$
is permissible (in the choice between
$A \cup B$
is permissible (in the choice between
![]() $A \cup B$
and
$A \cup B$
and
![]() $A$
) under Choice-Functional Theory
$A$
) under Choice-Functional Theory
![]() $\alpha $
.
$\alpha $
.
Second, to show that Non-Anti-Egalitarianism is satisfied, assume that two populations
![]() $A$
and
$A$
and
![]() $B$
have the same population size, that all individuals in
$B$
have the same population size, that all individuals in
![]() $B$
have the same utility level, and that the sum total utility in
$B$
have the same utility level, and that the sum total utility in
![]() $B$
is greater than that in
$B$
is greater than that in
![]() $A$
. Since total utilitarianism applies to these populations,
$A$
. Since total utilitarianism applies to these populations,
![]() $B$
is strictly better than
$B$
is strictly better than
![]() $A$
according to Theory
$A$
according to Theory
![]() $\alpha $
. This implies that
$\alpha $
. This implies that
![]() $A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
under Choice-Functional Theory
$A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
under Choice-Functional Theory
![]() $\alpha $
, which satisfies Non-Anti-Egalitarianism.
$\alpha $
, which satisfies Non-Anti-Egalitarianism.
Third (and final), take any large population
![]() $A$
with blissful utility levels and another much larger population
$A$
with blissful utility levels and another much larger population
![]() $B$
such that all individuals are at a positive but drab utility level. It holds that
$B$
such that all individuals are at a positive but drab utility level. It holds that
![]() ${N_A} \lt {N_B}$
and
${N_A} \lt {N_B}$
and
![]() $A{U_A} \gt A{U_B}$
. Moreover,
$A{U_A} \gt A{U_B}$
. Moreover,
![]() $B$
is not an extension of
$B$
is not an extension of
![]() $A$
because the individuals in
$A$
because the individuals in
![]() $A$
enjoy blissful utility levels while those in
$A$
enjoy blissful utility levels while those in
![]() $B$
do not. Theory
$B$
do not. Theory
![]() $\alpha $
suggests that
$\alpha $
suggests that
![]() $A$
is strictly better than
$A$
is strictly better than
![]() $B$
, and therefore,
$B$
, and therefore,
![]() $B$
is not permissible (i.e.
$B$
is not permissible (i.e.
![]() $B \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
) implying that the Repugnant Conclusion is avoided.
$B \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
) implying that the Repugnant Conclusion is avoided.
Before proceeding, let me recapitulate the findings of this section. There is at least one choice-functional population theory that can avoid the Mere Addition Paradox.Footnote
14
The theory proposed in this section satisfies Property
![]() $\alpha $
and Generalized Condorcet Property, which means that Weak
$\alpha $
and Generalized Condorcet Property, which means that Weak
![]() $\gamma $
is satisfied. Moreover, a further implication is that the theory is rationalizable. That is, there is a relation under which the set of maximal elements coincides with the actual choice for each menu (Suzumura Reference Suzumura1983: 36). I showed this point by providing an example of such a relation in this section. While I mentioned only one possibility, there may be many other rationalizable theories that can avoid the paradox, and some of them might be considered plausible.Footnote
15
Our example is based on a single binary relation, but it is worth noting that the general choice-functional setting would allow a wide range of non-binary theories, or theories with menu-dependent preferences. In the next section, I will examine how the possibility pointed out in this section (i.e. Theory
$\gamma $
is satisfied. Moreover, a further implication is that the theory is rationalizable. That is, there is a relation under which the set of maximal elements coincides with the actual choice for each menu (Suzumura Reference Suzumura1983: 36). I showed this point by providing an example of such a relation in this section. While I mentioned only one possibility, there may be many other rationalizable theories that can avoid the paradox, and some of them might be considered plausible.Footnote
15
Our example is based on a single binary relation, but it is worth noting that the general choice-functional setting would allow a wide range of non-binary theories, or theories with menu-dependent preferences. In the next section, I will examine how the possibility pointed out in this section (i.e. Theory
![]() $\alpha $
) is related to menu-dependent relations.
$\alpha $
) is related to menu-dependent relations.
3. The Possibility of Menu Dependent Relations
After obtaining ‘the persistent paradox’, Stewart (Reference Stewart2021) discusses the possibility of relaxing Path Independence by means of an extension of the menu-dependent relations proposed by Frick (Reference Frick, McMahan, Campbell, Goodrich and Ramakrishnan2022).Footnote
16
In relation to this idea, Stewart mentions his choice axiom Weak
![]() $\gamma $
. Recall that this choice axiom states that if
$\gamma $
. Recall that this choice axiom states that if
![]() $A$
is the only permissible population under
$A$
is the only permissible population under
![]() $S$
and is permissible under
$S$
and is permissible under
![]() $T$
, then it is also permissible under the union of the two menus,
$T$
, then it is also permissible under the union of the two menus,
![]() $S \cup T$
. (A formal definition was given in the previous section.) This is indeed a natural way of relaxing Path Independence.
$S \cup T$
. (A formal definition was given in the previous section.) This is indeed a natural way of relaxing Path Independence.
Although Stewart (Reference Stewart2021) only mentions Weak
![]() $\gamma $
, the menu-dependent-relation approach has been previously established in the revealed preference theory. Indeed, Tyson (Reference Tyson2008) and Cato (Reference Cato2014) provide a set of results on rationalizability of menu-dependent relations. Consider a menu-dependent relation,
$\gamma $
, the menu-dependent-relation approach has been previously established in the revealed preference theory. Indeed, Tyson (Reference Tyson2008) and Cato (Reference Cato2014) provide a set of results on rationalizability of menu-dependent relations. Consider a menu-dependent relation,
![]() ${R_S}$
, on menu
${R_S}$
, on menu
![]() $S$
. A system
$S$
. A system
![]() $\langle {R_S}\rangle $
of menu-dependent relations is a collection of binary relations such that for each menu
$\langle {R_S}\rangle $
of menu-dependent relations is a collection of binary relations such that for each menu
![]() $S$
,
$S$
,
![]() ${R_S}$
is a transitive and complete relation over
${R_S}$
is a transitive and complete relation over
![]() $S$
.Footnote
17
As pointed out correctly by Stewart (Reference Stewart2021: sec. 5), representing menu-dependent relations becomes trivial if there is no restriction.Footnote
18
He also suggests that ‘at the very least, there is a constructive challenge here to complete a seriously incomplete case’, and asks: ‘What principles relate the various menu-relative relations such that rational choice theory is not entirely trivialized?’ (Stewart Reference Stewart2021: sec. 5).
$S$
.Footnote
17
As pointed out correctly by Stewart (Reference Stewart2021: sec. 5), representing menu-dependent relations becomes trivial if there is no restriction.Footnote
18
He also suggests that ‘at the very least, there is a constructive challenge here to complete a seriously incomplete case’, and asks: ‘What principles relate the various menu-relative relations such that rational choice theory is not entirely trivialized?’ (Stewart Reference Stewart2021: sec. 5).
In response to this ‘constructive challenge’, the present section considers the following restriction: a system
![]() $\langle {R_S}\rangle $
is said to be nested if and only if for all menus
$\langle {R_S}\rangle $
is said to be nested if and only if for all menus
![]() $S,T$
such that
$S,T$
such that
![]() $S \subseteq T$
,
$S \subseteq T$
,
According to nestedness, if
![]() $S$
is a subset of
$S$
is a subset of
![]() $T$
, then
$T$
, then
![]() $A$
is at least as good as
$A$
is at least as good as
![]() $B$
in menu
$B$
in menu
![]() $S$
whenever
$S$
whenever
![]() $A$
is at least as good as
$A$
is at least as good as
![]() $B$
in menu
$B$
in menu
![]() $T$
and both
$T$
and both
![]() $A$
and
$A$
and
![]() $B$
are elements of
$B$
are elements of
![]() $S$
.Footnote
19
Nestedness is a well-behaving restriction because a choice function satisfies Property
$S$
.Footnote
19
Nestedness is a well-behaving restriction because a choice function satisfies Property
![]() $\alpha $
if and only if there exists a nested system of menu-dependent transitive relations that rationalizes the choice function (Cato Reference Cato2014: Theorem 3).
$\alpha $
if and only if there exists a nested system of menu-dependent transitive relations that rationalizes the choice function (Cato Reference Cato2014: Theorem 3).
Three points are worth discussing here. First, Frick’s (Reference Frick, McMahan, Campbell, Goodrich and Ramakrishnan2022) proposal can be meaningfully understood in my theory, which suggests that representing menu-dependent relations is worthwhile. Stewart (Reference Stewart2021: sec. 5) writes:
Certain egalitarians, for example, may find considerations of equality compelling grounds to regard
![]() ${A^ + }$
as impermissible in the presence of
${A^ + }$
as impermissible in the presence of
![]() $E$
in the three-option menu
$E$
in the three-option menu
![]() $\left\{ {A,{A^ + },E} \right\}$
, yet think that such considerations are insufficient to exclude
$\left\{ {A,{A^ + },E} \right\}$
, yet think that such considerations are insufficient to exclude
![]() ${A^ + }$
from the choice set for the menu
${A^ + }$
from the choice set for the menu
![]() $\left\{ {A,{A^ + }} \right\}$
. In the latter menu, invoking egalitarian considerations to exclude
$\left\{ {A,{A^ + }} \right\}$
. In the latter menu, invoking egalitarian considerations to exclude
![]() ${A^ + }$
has the drastic effect of reducing the number of lives worth living … we have
${A^ + }$
has the drastic effect of reducing the number of lives worth living … we have
![]() $C\left( {\left\{ {A,{A^ + },E} \right\}} \right) = \left\{ A \right\}$
since
$C\left( {\left\{ {A,{A^ + },E} \right\}} \right) = \left\{ A \right\}$
since
![]() $E$
effectively blocks
$E$
effectively blocks
![]() ${A^ + }$
even though
${A^ + }$
even though
![]() $E$
is not itself permissible. Johann Frick advocates precisely this choice pattern in his paper (Reference Frick, McMahan, Campbell, Goodrich and Ramakrishnan2022).
$E$
is not itself permissible. Johann Frick advocates precisely this choice pattern in his paper (Reference Frick, McMahan, Campbell, Goodrich and Ramakrishnan2022).
It is easy to confirm that
![]() $C\left( {\left\{ {A,{A^ + },E} \right\}} \right) = \left\{ A \right\}$
and
$C\left( {\left\{ {A,{A^ + },E} \right\}} \right) = \left\{ A \right\}$
and
![]() $C\left( {\left\{ {A,{A^ + }} \right\}} \right) = \left\{ {A,{A^ + }} \right\}$
under Choice-Functional Theory
$C\left( {\left\{ {A,{A^ + }} \right\}} \right) = \left\{ {A,{A^ + }} \right\}$
under Choice-Functional Theory
![]() $\alpha $
, which was proposed in the previous section, and therefore, the proposed theory is compatible with what Johann Frick advocates. One may wonder, however, why the acyclic population theory can capture Frick’s attempt to consider menu-dependent relations. The answer is that any acyclic population theory is compatible with Property
$\alpha $
, which was proposed in the previous section, and therefore, the proposed theory is compatible with what Johann Frick advocates. One may wonder, however, why the acyclic population theory can capture Frick’s attempt to consider menu-dependent relations. The answer is that any acyclic population theory is compatible with Property
![]() $\alpha $
, which is (necessary and) sufficient for generating a nested system of menu-dependent transitive relations over the populations. Examining a choice function with Property
$\alpha $
, which is (necessary and) sufficient for generating a nested system of menu-dependent transitive relations over the populations. Examining a choice function with Property
![]() $\alpha $
is not a trivial issue, and therefore, Frick’s proposal is meaningful in the context of choice theory, regardless of whether it is based on sufficient strength of rationality.
$\alpha $
is not a trivial issue, and therefore, Frick’s proposal is meaningful in the context of choice theory, regardless of whether it is based on sufficient strength of rationality.
Second and related to the previous point, it seems important to examine population ethics with Property
![]() $\alpha $
because a system of transitive menu-dependent relations is associated with the choice function, as proved by Cato (Reference Cato2014: Theorem 4). As alluded to above, this is considered a plausible trial for the ‘constructive challenge’ suggested by Stewart (Reference Stewart2021: sec. 5). Of course, a potential problem is the acceptability of nestedness. However, even if nestedness is considered objectionable, this would open up the possibility of exploring a plausible restriction on the system of menu-dependent relations.Footnote
20
For such explorations, Theory
$\alpha $
because a system of transitive menu-dependent relations is associated with the choice function, as proved by Cato (Reference Cato2014: Theorem 4). As alluded to above, this is considered a plausible trial for the ‘constructive challenge’ suggested by Stewart (Reference Stewart2021: sec. 5). Of course, a potential problem is the acceptability of nestedness. However, even if nestedness is considered objectionable, this would open up the possibility of exploring a plausible restriction on the system of menu-dependent relations.Footnote
20
For such explorations, Theory
![]() $\alpha $
is a natural starting point because it satisfies various well-known properties of the choice theory, as proved in the previous section.
$\alpha $
is a natural starting point because it satisfies various well-known properties of the choice theory, as proved in the previous section.
Third, any path-independent choice function is rationalized by a system of menu-dependent relations because Path Independence implies Property
![]() $\alpha $
. Nevertheless, this observation does not mean that a path-independent choice function is necessarily rationalized by menu-dependent relations. Indeed, Moulin (Reference Moulin1985) established the equivalence between path-independence and pseudo-rationalizability. A choice function
$\alpha $
. Nevertheless, this observation does not mean that a path-independent choice function is necessarily rationalized by menu-dependent relations. Indeed, Moulin (Reference Moulin1985) established the equivalence between path-independence and pseudo-rationalizability. A choice function
![]() $C$
is said to be pseudo-rationalizable by
$C$
is said to be pseudo-rationalizable by
![]() ${\langle {R_i}\rangle _{i \in I}}$
if, for all menus
${\langle {R_i}\rangle _{i \in I}}$
if, for all menus
![]() $A$
,
$A$
,
Here,
![]() ${R_i}$
, which is a relation on
${R_i}$
, which is a relation on
![]() $X$
, applies across all menus. Moulin’s result states that any path-independent choice function can be pseudo-rationalizable by a set of transitive and complete relations (Moulin Reference Moulin1985: Theorem 5 and Lemma 6). This suggests that Property
$X$
, applies across all menus. Moulin’s result states that any path-independent choice function can be pseudo-rationalizable by a set of transitive and complete relations (Moulin Reference Moulin1985: Theorem 5 and Lemma 6). This suggests that Property
![]() $\alpha $
is also equivalent to a similar type of rationalizability somehow. That is, even Property
$\alpha $
is also equivalent to a similar type of rationalizability somehow. That is, even Property
![]() $\alpha $
might admit rationalization by means of a set of menu-independent relations with certain properties; see Duggan (Reference Duggan2019) who proposes proto-rationalizability, which is equivalent to Property
$\alpha $
might admit rationalization by means of a set of menu-independent relations with certain properties; see Duggan (Reference Duggan2019) who proposes proto-rationalizability, which is equivalent to Property
![]() $\alpha $
.Footnote
21
Indeed, related to this, Stewart (Reference Stewart2020: Theorem 4) shows that the conjunction of Property
$\alpha $
.Footnote
21
Indeed, related to this, Stewart (Reference Stewart2020: Theorem 4) shows that the conjunction of Property
![]() $\alpha $
and Weak
$\alpha $
and Weak
![]() $\gamma $
is equivalent to what is called weak pseudo-rationalizability, which is rationalizability by a set of acyclic relations.
$\gamma $
is equivalent to what is called weak pseudo-rationalizability, which is rationalizability by a set of acyclic relations.
4. Concluding Remarks
In closing I want to offer some remarks on the role of acyclicity or quasi-transitivity of betterness relations. As shown above, switching from quasi-transitivity to acyclicity gives a possibility result. A missing piece here is Suzumura consistency, which has been substantially developed by Bossert and Suzumura (Reference Bossert2010).Footnote 22
I also think that Stewart’s (Reference Stewart2021) choice-functional approach is quite significant for the development of population ethics, especially when taking account of the recent call for new directions for population ethics beyond the standardized Repugnant Conclusions by Zuber et al. (Reference Zuber, Venkatesh and Tännsjö2021). The current deadlock in population ethics is related to the well-trodden approach based on better-than binary relations. Stewart’s observations come down to the properties of the base relation for the same reason. That is, his three conditions are formulated over binary menus. There can be various ethical issues that cannot be captured by binary choices, however, and to explore such issues, it seems that the choice-functional framework is a plausible approach for theorists of population ethics.
Acknowledgements
I thank Akira Inoue, Lajos Brons and two anonymous reviewers for their helpful comments and suggestions.
Financial support
The author gratefully acknowledges financial support from KAKENHI under grants JP18H05204, JP20H01446, JP22K01387, JP22H05083, JP22H05086 and JP23K01316, as well as from the Mitsubishi Foundation (ID201920011).
Appendix A. Auxiliary Results
Proposition A.1. Path Independence implies Weak
![]() $\alpha $
.
$\alpha $
.
Proof. Path Independence implies Property
![]() $\alpha $
. It is obvious that Weak
$\alpha $
. It is obvious that Weak
![]() $\alpha $
follows from Property
$\alpha $
follows from Property
![]() $\alpha $
. Thus, the claim holds. ▪
$\alpha $
. Thus, the claim holds. ▪
Proposition A.2. Path Independence implies Property
![]() $\delta $
.
$\delta $
.
Proof. By way of contradiction, assume that
![]() $A,B \in C\left( S \right) \subseteq S \subseteq T$
, whereas
$A,B \in C\left( S \right) \subseteq S \subseteq T$
, whereas
![]() $\left\{ A \right\} = C\left( T \right)$
. By Path Independence,
$\left\{ A \right\} = C\left( T \right)$
. By Path Independence,
![]() $C\left( T \right) = C\left( {C\left( S \right) \cup C\left( T \right)} \right)$
. Therefore,
$C\left( T \right) = C\left( {C\left( S \right) \cup C\left( T \right)} \right)$
. Therefore,
![]() $\left\{ A \right\} = C\left( {C\left( S \right) \cup \left\{ A \right\}} \right)$
. Because
$\left\{ A \right\} = C\left( {C\left( S \right) \cup \left\{ A \right\}} \right)$
. Because
![]() $A \in C\left( S \right)$
, it follows that
$A \in C\left( S \right)$
, it follows that
![]() $\left\{ A \right\} = C\left( {C\left( S \right)} \right)$
. From Path Independence,
$\left\{ A \right\} = C\left( {C\left( S \right)} \right)$
. From Path Independence,
![]() $C\left( S \right) = C\left( {C\left( S \right)} \right)$
by considering the case in which
$C\left( S \right) = C\left( {C\left( S \right)} \right)$
by considering the case in which
![]() $S = T$
in its definition. We obtain
$S = T$
in its definition. We obtain
![]() $\left\{ A \right\} = C\left( S \right)$
, which is a contradiction because
$\left\{ A \right\} = C\left( S \right)$
, which is a contradiction because
![]() $B \in C\left( S \right)$
. The proposition is thus proved. ▪
$B \in C\left( S \right)$
. The proposition is thus proved. ▪
Proposition A.3. If Property
![]() $\delta $
and Weak
$\delta $
and Weak
![]() $\alpha $
are satisfied, then the base relation is quasi-transitive.
$\alpha $
are satisfied, then the base relation is quasi-transitive.
Proof. To the best of my knowledge, this has not been explicitly proved, and thus, I provide the proof here. By way of contradiction, assume that there exist
![]() $A^{\rm{\prime}},B^{\rm{\prime}},D{\rm{'}}$
such that
$A^{\rm{\prime}},B^{\rm{\prime}},D{\rm{'}}$
such that
![]() $A{\rm{'}}{P^{\rm{*}}}B{\rm{'}}$
,
$A{\rm{'}}{P^{\rm{*}}}B{\rm{'}}$
,
![]() $B{\rm{'}}{P^{\rm{*}}}D{\rm{'}}$
, and
$B{\rm{'}}{P^{\rm{*}}}D{\rm{'}}$
, and
![]() $D{\rm{'}}{R^{\rm{*}}}A{\rm{'}}$
. If
$D{\rm{'}}{R^{\rm{*}}}A{\rm{'}}$
. If
![]() $D{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, Weak
$D{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, Weak
![]() $\alpha $
implies that
$\alpha $
implies that
![]() $D{\rm{'}} \in C\left( {\left\{ {B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, which contradicts
$D{\rm{'}} \in C\left( {\left\{ {B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, which contradicts
![]() $B{\rm{'}}{P^{\rm{*}}}D{\rm{'}}$
. If
$B{\rm{'}}{P^{\rm{*}}}D{\rm{'}}$
. If
![]() $B{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, Weak
$B{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
, Weak
![]() $\alpha $
again implies
$\alpha $
again implies
![]() $B{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}}} \right\}} \right)$
, which contradicts
$B{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},B{\rm{'}}} \right\}} \right)$
, which contradicts
![]() $A{\rm{'}}{P^{\rm{*}}}B{\rm{'}}$
. Thus,
$A{\rm{'}}{P^{\rm{*}}}B{\rm{'}}$
. Thus,
![]() $\left\{ {A{\rm{'}}} \right\} = C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
. By Weak
$\left\{ {A{\rm{'}}} \right\} = C\left( {\left\{ {A{\rm{'}},B{\rm{'}},D{\rm{'}}} \right\}} \right)$
. By Weak
![]() $\alpha $
,
$\alpha $
,
![]() $A{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},D{\rm{'}}} \right\}} \right)$
, and thus,
$A{\rm{'}} \in C\left( {\left\{ {A{\rm{'}},D{\rm{'}}} \right\}} \right)$
, and thus,
![]() $\left\{ {A{\rm{'}},D{\rm{'}}} \right\} = C\left( {\left\{ {A{\rm{'}},D{\rm{'}}} \right\}} \right)$
. This contradicts Property
$\left\{ {A{\rm{'}},D{\rm{'}}} \right\} = C\left( {\left\{ {A{\rm{'}},D{\rm{'}}} \right\}} \right)$
. This contradicts Property
![]() $\delta $
. This proof follows the same strategy as that provided by Sen (Reference Sen, Arrow and Intriligator1986: 1099), who uses a similar but different definition of Weak
$\delta $
. This proof follows the same strategy as that provided by Sen (Reference Sen, Arrow and Intriligator1986: 1099), who uses a similar but different definition of Weak
![]() $\alpha $
. ▪
$\alpha $
. ▪
Appendix B. Sadistic Conclusions
Considering that Arrhenius (Reference Arrhenius2000) proved that if the Repugnant Conclusion is avoided, it is likely that the Sadistic Conclusion holds, an obvious question is whether Theory
![]() $\alpha $
(and/or the variants suggested in footnote Footnote 7) can avoid the Sadistic Conclusion. This appendix aims to answer that question.
$\alpha $
(and/or the variants suggested in footnote Footnote 7) can avoid the Sadistic Conclusion. This appendix aims to answer that question.
The Sadistic Conclusion is an impossibility result that is considered just as important as the Mere Addition Paradox in population ethics. If one accepts the view that a population with positive utilities must always be better than a population with negative utilities, then this conclusion is undesirable. Following Arrhenius (Reference Arrhenius2000), I define two variants of the Sadistic Conclusion:
Very Sadistic Conclusion. There are populations
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $A$
contains only positive utility levels,
$A$
contains only positive utility levels,
![]() $B$
contains only negative utility levels, and
$B$
contains only negative utility levels, and
![]() $A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
.
$A \;\notin\; C\left( {\left\{ {A,B} \right\}} \right)$
.
Sadistic Conclusion. There are three populations
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $G$
such that
$G$
such that
![]() $A$
contains only positive utility levels,
$A$
contains only positive utility levels,
![]() $B$
contains only negative utility levels, and
$B$
contains only negative utility levels, and
![]() $A \cup G \;\notin\; C\left( {\left\{ {A \cup G,B \cup G} \right\}} \right)$
, where
$A \cup G \;\notin\; C\left( {\left\{ {A \cup G,B \cup G} \right\}} \right)$
, where
![]() $G$
may be an empty population.
$G$
may be an empty population.
Although both variants have similar undesirable implications, avoiding the second variant tends to be more demanding than avoiding the first.
It is easy to see that Choice-Functional Theory
![]() $\alpha $
(or Theory
$\alpha $
(or Theory
![]() $\alpha $
) can avoid the Very Sadistic Conclusion. If it would not, then there would be
$\alpha $
) can avoid the Very Sadistic Conclusion. If it would not, then there would be
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $A$
contains only positive utility levels while
$A$
contains only positive utility levels while
![]() $B$
contains only negative utility levels and
$B$
contains only negative utility levels and
![]() $B{P_\alpha }A$
. This would imply that
$B{P_\alpha }A$
. This would imply that
![]() $T{U_B} \gt T{U_A}$
or
$T{U_B} \gt T{U_A}$
or
![]() $A{U_B} \gt A{U_A}$
by the definition of Theory
$A{U_B} \gt A{U_A}$
by the definition of Theory
![]() $\alpha $
, but this is impossible because both
$\alpha $
, but this is impossible because both
![]() $T{U_A}$
and
$T{U_A}$
and
![]() $A{U_A}$
are positive, while both
$A{U_A}$
are positive, while both
![]() $T{U_B}$
and
$T{U_B}$
and
![]() $A{U_B}$
are negative. Consequently, Choice-Functional Theory
$A{U_B}$
are negative. Consequently, Choice-Functional Theory
![]() $\alpha $
(or Theory
$\alpha $
(or Theory
![]() $\alpha $
) avoids the Very Sadistic Conclusion. On the other hand, Choice-Functional Theory
$\alpha $
) avoids the Very Sadistic Conclusion. On the other hand, Choice-Functional Theory
![]() $\alpha $
entails the Sadistic Conclusion. To see this, consider the following three populations:
$\alpha $
entails the Sadistic Conclusion. To see this, consider the following three populations:
Notice that both
![]() $G$
and
$G$
and
![]() $B$
have only one individual, and that
$B$
have only one individual, and that
![]() $A{U_{G \cup A}} = 100/4 = 25$
and
$A{U_{G \cup A}} = 100/4 = 25$
and
![]() $A{U_{G \cup B}} = 96/2 = 48$
. Furthermore,
$A{U_{G \cup B}} = 96/2 = 48$
. Furthermore,
![]() $2 = {N_{G \cup B}} \lt {N_{G \cup A}} = 4$
, and
$2 = {N_{G \cup B}} \lt {N_{G \cup A}} = 4$
, and
![]() $G \cup A$
is not an extension of
$G \cup A$
is not an extension of
![]() $G \cup B$
. Consequently, by the definition of Theory
$G \cup B$
. Consequently, by the definition of Theory
![]() $\alpha $
,
$\alpha $
,
![]() $G \cup B$
is strictly better than
$G \cup B$
is strictly better than
![]() $G \cup A$
, and therefore, Choice-Functional Theory
$G \cup A$
, and therefore, Choice-Functional Theory
![]() $\alpha $
implies that
$\alpha $
implies that
![]() $A \cup G \;\notin\; C\left( {\left\{ {A \cup G,B \cup G} \right\}} \right)$
, which means that the Sadistic Conclusion holds.
$A \cup G \;\notin\; C\left( {\left\{ {A \cup G,B \cup G} \right\}} \right)$
, which means that the Sadistic Conclusion holds.
However, a variant of Theory
![]() $\alpha $
proposed in footnote Footnote 7 can avoid the Sadistic Conclusion as well. In this variant, the average utility level is replaced by the worst-off as follows:
$\alpha $
proposed in footnote Footnote 7 can avoid the Sadistic Conclusion as well. In this variant, the average utility level is replaced by the worst-off as follows:
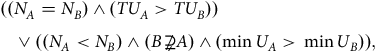 \[(\left( {{N_A} = {N_B}} \right) \wedge (T{U_A}{\text{ > }}T{U_B})) \vee (({N_A}{\text{ < }}{N_B}) \wedge \left( {B\not \supsetneq A} \right) \wedge (\min {U_A}{\text{ > }}\min {U_B})),\]
\[(\left( {{N_A} = {N_B}} \right) \wedge (T{U_A}{\text{ > }}T{U_B})) \vee (({N_A}{\text{ < }}{N_B}) \wedge \left( {B\not \supsetneq A} \right) \wedge (\min {U_A}{\text{ > }}\min {U_B})),\]
where
![]() ${\rm{min\;}}{U_A}$
(resp.
${\rm{min\;}}{U_A}$
(resp.
![]() ${\rm{min\;}}{U_B}$
) represents the worst-off in
${\rm{min\;}}{U_B}$
) represents the worst-off in
![]() $A$
(resp. B). According to this theory, population
$A$
(resp. B). According to this theory, population
![]() $A$
is strictly better than population
$A$
is strictly better than population
![]() $B$
if and only if either of the following two holds: (i) the population size of
$B$
if and only if either of the following two holds: (i) the population size of
![]() $A$
is the same as that of
$A$
is the same as that of
![]() $B$
, and the total sum of utility in
$B$
, and the total sum of utility in
![]() $A$
is greater than that in
$A$
is greater than that in
![]() $B$
, or (ii
$B$
, or (ii
![]() ${\rm{'}}$
) the population size of
${\rm{'}}$
) the population size of
![]() $A$
is smaller than that of
$A$
is smaller than that of
![]() $B$
,
$B$
,
![]() $B$
is not an extension of
$B$
is not an extension of
![]() $A$
, and the worst-off in
$A$
, and the worst-off in
![]() $A$
is better than that in
$A$
is better than that in
![]() $B$
.
$B$
.
To show that this principle can avoid the Very Sadistic Conclusion as well as the Sadistic Conclusion, I will focus on the Sadistic Conclusion because the argument for the Very Sadistic Conclusion is similar. Take three populations
![]() $G$
,
$G$
,
![]() $A$
and
$A$
and
![]() $B$
such that
$B$
such that
![]() $A$
contains only positive utility levels while
$A$
contains only positive utility levels while
![]() $B$
contains only negative utility levels. Then, it is the case that
$B$
contains only negative utility levels. Then, it is the case that
![]() $T{U_{G \cup A}} \gt T{U_{G \cup B}}$
and
$T{U_{G \cup A}} \gt T{U_{G \cup B}}$
and
![]() ${\rm{min}}\;{U_{G \cup A}} \ge {\rm{min\;}}{U_{G \cup B}}$
. Note that the Sadistic Conclusion holds only when
${\rm{min}}\;{U_{G \cup A}} \ge {\rm{min\;}}{U_{G \cup B}}$
. Note that the Sadistic Conclusion holds only when
![]() $T{U_{G \cup B}} \gt T{U_{G \cup A}}$
or
$T{U_{G \cup B}} \gt T{U_{G \cup A}}$
or
![]() ${\rm{min}}\;{U_{G \cup B}} \gt \min\;{U_{G \cup A}}$
. Hence, the Sadistic Conclusion is avoided.
${\rm{min}}\;{U_{G \cup B}} \gt \min\;{U_{G \cup A}}$
. Hence, the Sadistic Conclusion is avoided.
As in the case of the original Theory
![]() $\alpha $
, this worst-off-based variant is an acyclic population principle that can avoid the Mere Addition Paradox. Consequently, the corresponding choice function satisfies Non-Anti-Egalitarianism, Mere Addition, Generalized Condorcet Property, and Property
$\alpha $
, this worst-off-based variant is an acyclic population principle that can avoid the Mere Addition Paradox. Consequently, the corresponding choice function satisfies Non-Anti-Egalitarianism, Mere Addition, Generalized Condorcet Property, and Property
![]() $\alpha $
, and avoids the Repugnant Conclusion. Moreover the above argument shows that the Sadistic Conclusion can also be avoided. This suggests that in addition to the Mere Addition Paradox, the paradox associated with the Sadistic Conclusion can also be overcome if transitivity is relaxed to acyclicity or a rationalizable choice function.
$\alpha $
, and avoids the Repugnant Conclusion. Moreover the above argument shows that the Sadistic Conclusion can also be avoided. This suggests that in addition to the Mere Addition Paradox, the paradox associated with the Sadistic Conclusion can also be overcome if transitivity is relaxed to acyclicity or a rationalizable choice function.
Susumu Cato is Professor of Economics at the Institute of Social Science, University of Tokyo. His research interests include decision theory, social choice theory, axiology, political philosophy and organizational economics.