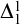Hostname: page-component-6bb9c88b65-9c7xm Total loading time: 0 Render date: 2025-07-23T23:33:35.295Z Has data issue: false hasContentIssue false
  • English
  • Français

$\Delta ^1_1$ EFFECTIVIZATION IN BOREL COMBINATORICS

Part of: Set theory

Published online by Cambridge University Press:  17 May 2024

RILEY THORNTON
RILEY THORNTON*
Affiliation:
DEPARTMENT OF MATHEMATICS CARNEGIE MELLON UNIVERSITY PITTSBURGH, PA USA
*
E-mail: rthornto@andrew.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a flexible method for showing that Borel witnesses to some combinatorial property of 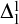$\Delta ^1_1$ objects yield 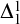$\Delta ^1_1$ witnesses. We use a modification the Gandy–Harrington forcing method of proving dichotomies, and we can recover the complexity consequences of many known dichotomies with short and simple proofs. Using our methods, we give a simplified proof that smooth 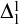$\Delta ^1_1$ equivalence relations are 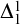$\Delta ^1_1$-reducible to equality; we prove effective versions of the Lusin–Novikov and Feldman–Moore theorems; we prove new effectivization results related to dichotomy theorems due to Hjorth and Miller (originally proven using “forceless, ineffective, and powerless” methods); and we prove a new upper bound on the complexity of the set of Schreier graphs for 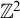$\mathbb {Z}^2$ actions. We also prove an equivariant version of the 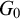$G_0$ dichotomy that implies some of these new results and a dichotomy for graphs induced by Borel actions of 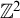$\mathbb {Z}^2$.

Keywords

effective descriptive set theorydichotomy theoremsSchreier graphs

MSC classification

Primary: 03E15: Descriptive set theory

Information

Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 25
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Carroy, R., Miller, B., Schrittesser, D., and Vidnyanszky, Z., Minimal definable graphs of definable chromatic number at least three, Forum of Math, Sigma, vol. 9 (2021), e7, pp. 1–16.Google Scholar
Harrintgon, L., Marker, D., and Shelah, S., Borel orders . Transactions of the American Mathematical Society, vol. 310 (1998), no. 1, pp. 293–302.Google Scholar
Hjorth, G. and Miller, B., Ends of graphed equivalence relations II . Israel Journal of Mathematics, vol. 169 (2009), pp. 393–415.Google Scholar
Kechris, A., Classical Descriptive Set Theory, Springer, New York, 1995.Google Scholar
Kechris, A. and Miller, B., Topics in Orbit Equivalence, Lecture Notes in Mathematics, 1852, Springer, New York, 1995.Google Scholar
Kechris, A., Solecki, S., and Todorcevic, S., Borel chromatic numbers . Advances in Mathematics, vol. 141 (1999), pp. 1–44.Google Scholar
Marks, A., Effective descriptive set theory, eprint, 2019. Available at https://www.math.ucla.edu/marks/notes/edst_notes.pdf.Google Scholar
Miller, B., Full groups, classification, and equivalence relations, Ph.D. thesis, University of California, Berkeley, 2004.Google Scholar
Miller, B., Lacunary sets for actions of tsi groups, preprint, 2020, arXiv:2002.10456.Google Scholar
Miller, B., Structural dichotomies in descriptive set theory, eprint, 2019. Available at https://homepage.univie.ac.at/benjamin.miller/lecturenotes/dichotomies.pdf.Google Scholar
Thornton, R., Orienting Borel graphs, Proceedings of the AMS, vol. 150 (2020), no. 4, pp. 1779–1793.Google Scholar
Todorcevic, S. and Vidnyánszky, Z., A complexity problem for Borel graphs, Inventiones Mathematicae, vol. 226 (2021), pp. 225–249.Google Scholar