INTRODUCTION
Dengue is a viral mosquito-borne infection, which in recent years has become a major international public health concern because it is a leading cause of illness and death in the tropics and subtropics [Reference Gubler1–Reference Wilder-Smith3]. It is estimated that there are 70–500 million dengue infections, 36 million cases of dengue fever (DF), 2·1 million cases of dengue haemorrhagic fever (DHF), and more than 20 000 dengue-related deaths every year [Reference Wilder-Smith3].
Due to increased epidemic activity and difficulties in controlling the insect vector, dengue has become a major public health problem in many parts of the tropics [Reference Heintzem, Velasco Garrido and Kroeger4]. Human behaviours, which are influenced by social, cultural, economic and political factors [Reference Heggenhougen, Hackethal and Vivek5], can increase or decrease the risk of dengue infection, depending on the relationship with the insect vector. Because no vaccine is currently available, the spread of dengue can be curtailed only by controlling vector populations (Aedes aegypti and others) and by protecting individuals. Aedes larvae are the main target for vector control efforts; their populations can be reduced by using biological agents, including larvivorous fish (e.g. Poecilia reticulata, Gambusia affinis) and copepods (e.g. Mesocyclops) [Reference Kay6], larvicides (e.g. Bacillus thuringiensis subsp. israelensis, methoprene, permethrin, and temephos) and by removing water containers. Environmental management is generally considered an important component of dengue prevention and control.
During the past few decades, efforts to promote community-oriented activities for dengue control have increased. These have included multi-component interventions to reduce larval, and ultimately adult, vector populations through chemical, biological and physical interventions, as well as promoting behavioural change at the community level.
The advent of several candidate tetravalent vaccines against the dengue viruses gives hope of controlling and eventually eliminating the disease [Reference Chao7]. The efficacy of the potential vaccines, however, is likely to be much less than 100% [Reference Amaku, Coudeville and Massad8]. This raises the concern that people might reduce their vector-control practices if they believe that the vaccine is affording them full protection. It should be expected that with a vaccine available, vector-control practices such as finding and destroying mosquito breeding sites, will be perceived as requiring too much effort. Hence, if a vaccine's efficacy is not sufficient, then its introduction may increase the spread of the disease. This apparent paradox has already been observed in the case of the introduction of antiretroviral therapies against HIV, which provided incomplete protection but led to a reduction of safe behaviour [Reference Perez, Domingo and Hartnoll9]. This situation was modelled by Massad et al. [Reference Massad10]. An earlier hepatitis B vaccine trial involving homosexual and bisexual men provided indirect evidence that men increased their participation in risky behaviours. Indeed, infection rates in the placebo group increased after participants received all of their injections. This finding suggests that the study participants actually waited for this point and then engaged in more risky behaviours, believing that they were protected, even though they knew that they were in a placebo-controlled trial [Reference Buchbinder11].
This study aimed to test the hypothesis that dengue-affected populations will reduce their vector-control practices if a potentially protective vaccine becomes available. The hypothesis was tested using two approaches: a mathematical model designed to describe dengue transmission and an empirical field test in which the local population of an endemic area was interviewed about their vector-control habits given the presence of a theoretical vaccine.
METHODS
The model
The model's dynamics were modified from a version of the model described previously [Reference Burattini12–Reference Lopez14]. The structure, including the number of compartments, transition rates, etc., is the same as the models presented previously [Reference Burattini12–Reference Lopez14].
The populations involved in transmission are human hosts, mosquitoes, and their eggs (including intermediate stages, such as larvae and pupae). The population densities, therefore, were divided into the following compartments: susceptible humans, S H; infected humans, I H; recovered (and immune) humans, R H; total humans, N H; susceptible mosquitoes, S M; infected and latent mosquitoes, L M; infected and infectious mosquitoes, I M; non-infected eggs, S E; and infected eggs, I E.
The model's equations are:
 $$\left. \eqalign{\displaystyle{{{\rm d}S_{\rm H}} \over {{\rm d}t}} = & abI_{\rm M} \displaystyle{{S_{\rm H}} \over {N_{\rm H}}} - \mu _{\rm H} S_{\rm H} + r_{\rm H} N_{\rm H} \left( {1 - \displaystyle{{N_{\rm H}} \over {\kappa _{\rm H}}}} \right) - \upsilon \varphi S_{\rm H} \cr \displaystyle{{{\rm d}I_{\rm H}} \over {{\rm d}t}} = & abI_{\rm M} \displaystyle{{S_{\rm H}} \over {N_{\rm H}}} - (\mu _{\rm H} + \alpha _{\rm H} + \gamma _{\rm H} )I_{\rm H} \cr \displaystyle{{{\rm d}R_{\rm H}} \over {{\rm d}t}} = & \gamma _{\rm H} I_H - \mu _{\rm H} R_{\rm H} + \upsilon \varphi S_{\rm H} \cr \displaystyle{{{\rm d}S_{\rm M}} \over {{\rm d}t}} = & p_{\rm s} c_{\rm s} (t)S_{\rm E} - \mu _{\rm M} S_{\rm M} - acS_{\rm M} \displaystyle{{I_{\rm H}} \over {N_{\rm H}}} \cr \displaystyle{{{\rm d}L_{\rm M}} \over {{\rm d}t}} = & acS_{\rm M} \displaystyle{{I_{\rm H}} \over {N_{\rm H}}} - {\rm e}^{ - \mu _{\rm M} \tau _{\rm I}} acS_{\rm M} (t - \tau _1 )\displaystyle{{I_{\rm H} (t - \tau _1 )} \over {N_{\rm H} (t - \tau _1 )}} \cr\tab- \mu _{\rm M} L_{\rm M} \cr \displaystyle{{{\rm d}I_{\rm M}} \over {{\rm d}t}} = & {\rm e}^{ - \mu _{\rm M} \tau _{\rm I}} acS_{\rm M} (t - \tau _1 )\displaystyle{{I_{\rm H} (t - \tau _1 )} \over {N_{\rm H} (t - \tau _1 )}} \cr\tab- \mu _{\rm M} I_{\rm M} + p_{\rm I} c_{\rm S} (t)I_{\rm E} \cr \displaystyle{{{\rm d}S_{\rm E}} \over {{\rm d}t}} = & [r_{\rm M} S_{\rm M} + (1 - g)r_{\rm M} I_{\rm M} ]\left( {1 - \displaystyle{{(S_{\rm E} + I_{\rm E} )} \over {\kappa _{\rm E}}}} \right) \cr\tab- \mu _{\rm E} S_{\rm E} - p_{\rm S} c_{\rm S} (t)S_{\rm E} \cr \displaystyle{{{\rm d}I_{\rm E}} \over {{\rm d}t}} = & [gr_{\rm M} I_{\rm M} ]\left( {1 - \displaystyle{{(S_{\rm E} + I_{\rm E} )} \over {\kappa _{\rm E}}}} \right) - \mu _{\rm E} I_{\rm E} - p_{\rm I} c_{\rm S} (t)I_{\rm E}} \right\}$$
$$\left. \eqalign{\displaystyle{{{\rm d}S_{\rm H}} \over {{\rm d}t}} = & abI_{\rm M} \displaystyle{{S_{\rm H}} \over {N_{\rm H}}} - \mu _{\rm H} S_{\rm H} + r_{\rm H} N_{\rm H} \left( {1 - \displaystyle{{N_{\rm H}} \over {\kappa _{\rm H}}}} \right) - \upsilon \varphi S_{\rm H} \cr \displaystyle{{{\rm d}I_{\rm H}} \over {{\rm d}t}} = & abI_{\rm M} \displaystyle{{S_{\rm H}} \over {N_{\rm H}}} - (\mu _{\rm H} + \alpha _{\rm H} + \gamma _{\rm H} )I_{\rm H} \cr \displaystyle{{{\rm d}R_{\rm H}} \over {{\rm d}t}} = & \gamma _{\rm H} I_H - \mu _{\rm H} R_{\rm H} + \upsilon \varphi S_{\rm H} \cr \displaystyle{{{\rm d}S_{\rm M}} \over {{\rm d}t}} = & p_{\rm s} c_{\rm s} (t)S_{\rm E} - \mu _{\rm M} S_{\rm M} - acS_{\rm M} \displaystyle{{I_{\rm H}} \over {N_{\rm H}}} \cr \displaystyle{{{\rm d}L_{\rm M}} \over {{\rm d}t}} = & acS_{\rm M} \displaystyle{{I_{\rm H}} \over {N_{\rm H}}} - {\rm e}^{ - \mu _{\rm M} \tau _{\rm I}} acS_{\rm M} (t - \tau _1 )\displaystyle{{I_{\rm H} (t - \tau _1 )} \over {N_{\rm H} (t - \tau _1 )}} \cr\tab- \mu _{\rm M} L_{\rm M} \cr \displaystyle{{{\rm d}I_{\rm M}} \over {{\rm d}t}} = & {\rm e}^{ - \mu _{\rm M} \tau _{\rm I}} acS_{\rm M} (t - \tau _1 )\displaystyle{{I_{\rm H} (t - \tau _1 )} \over {N_{\rm H} (t - \tau _1 )}} \cr\tab- \mu _{\rm M} I_{\rm M} + p_{\rm I} c_{\rm S} (t)I_{\rm E} \cr \displaystyle{{{\rm d}S_{\rm E}} \over {{\rm d}t}} = & [r_{\rm M} S_{\rm M} + (1 - g)r_{\rm M} I_{\rm M} ]\left( {1 - \displaystyle{{(S_{\rm E} + I_{\rm E} )} \over {\kappa _{\rm E}}}} \right) \cr\tab- \mu _{\rm E} S_{\rm E} - p_{\rm S} c_{\rm S} (t)S_{\rm E} \cr \displaystyle{{{\rm d}I_{\rm E}} \over {{\rm d}t}} = & [gr_{\rm M} I_{\rm M} ]\left( {1 - \displaystyle{{(S_{\rm E} + I_{\rm E} )} \over {\kappa _{\rm E}}}} \right) - \mu _{\rm E} I_{\rm E} - p_{\rm I} c_{\rm S} (t)I_{\rm E}} \right\}$$
where c S(t) = (d 1 – d 2 sin(2πft + φ)) is a climatic factor mimicking seasonal influences on the mosquito population (see below and references [Reference Burattini12–Reference Lopez14]). The parameters are defined in Table 1.
Table 1. The notation, biological meaning and values of parameters applied in the simulations. Values are derived from [Reference Burattini12]

* From [Reference Yasuno and Tonn15].
Note that the parameters υ and φ always occur together, therefore it would seem more correct to represent them as a single parameter. However, in order to provide generality for the model and flexibility to the simulations we decided to represent them separately. Hence, when we vary the vaccine efficacy in the simulations, we vary only the value of φ, keeping the vaccination rate υ constant.
An important assumption related to vector-control habits is that reducing the time-dependent intensity of breeding-site elimination will result in an improvement in the breeding conditions of Aedes mosquitoes, which can be simulated by a linear increase in the aquatic forms’ carrying capacity, κ E, such that:
that is, κ E increases linearly at a rate ε with time until t = t′. If the affected population has a given intensity of breeding-site elimination of Aedes mosquitoes until time t < t′ before the vaccine, and this is reduced after the vaccine, then the carrying capacity will increase by an additional constant Ω to the rate ε, and equation (2) reads as:
The term θ(t–t′) is the Heaviside step function that is zero for t < t′ and 1 for t ⩾ t′.
Empirical test of the hypothesis
Source population
The source population was comprised of patients and their relatives or acquaintances in the waiting room of the outpatient service of the Clinic's Hospital of the School of Medicine of the University of São Paulo, Brazil. This outpatient service receives more than one million patients per year from all parts of the country, and most of these patients are accompanied by a relative or an acquaintance. They can, therefore, be considered as a good representation of the general population.
Sampling method
The sample sizes of the two groups investigated (details below) were calculated using the method described by [Reference Bland16] for comparative studies. To calculate the sample size for a study that compares two groups, the following information is required:
-
• The expected population proportion in group 1, P 1,
-
• The expected population proportion in group 2, P 2,
-
• The significance level α.
-
• The power of the test (1−β).
The number of individuals in each group is:
where κ is a multiplier that depends on the significance level and power.
Assuming P 1 = 0·15 and P 2 = 0·05, with α = 5% and (1 – β) = 80%, κ is equal to 7·8 (see [Reference Bland16]), which results in 136 individuals in each group. This was corrected for the finite size of the population, resulting in 100 individuals for each group.
The dependent variable is the change in vector-control habits (decreasing the search for, and destroying of, intra-domiciliary breeding places). This variable has two levels: (a) change behaviour significantly in the presence of vaccine efficacy information; and (b) do not change vector-control habits.
The first group was informed about the existence of a dengue vaccine candidate with an attributed efficacy of >90%, and the second group was informed about a candidate vaccine with an efficacy of <50%. These two different pieces of information are the independent variables. The level of behavioural change was assessed using a structured questionnaire (see Appendix) that queried demographic information, education level, current knowledge about dengue transmission, and current vector-control behaviour (all potential confounders) and that also included items related to potential changes in vector-control behaviours, conditional upon the information provided by the interviewers about vaccine efficacy. A computer program randomized the order of the questions before each interview so that carry-over effect could be controlled. After being invited to participate, people who agreed and signed an informed consent form were assigned to one of the two groups randomly. The responses related to knowledge about dengue transmission, current vector-control behaviour, and potential changes in vector-control behaviours were re-coded to obtain a single score for each group of responses. This procedure was also applied to the independent variable, creating a single score that combined all of the answers, such that the higher the score the higher the behavioural change.
The questionnaire items related to vector-control habits in the presence of a vaccine are given in Table 2.
Table 2. Items related to changes in vector-control habits, which compose the total score


The scores for each response are shown in the cells. If, for example, an individual answered ‘I fully disagree’ with the affirmations he/she would receive a score of +2, whereas an answer of ‘I fully agree’ would receive a score of –2, and so on. The scores were summed for each individual questionnaire. As the distribution of scores was not known a priori we tested its normality through a Kolmogorov–Smirnov test of normality. This test result rejected the normality hypothesis and hence the variable ‘total score’ for items related to vector-control habits was compared between the two groups using a Mann–Whitney test for independent analysis.
RESULTS
Model simulation
Figure 1 shows the result of the numerical simulation of system (1) with six projected scenarios related to the probability of relaxing vector-control measures, from 10% to 50%. The figure shows the force of infection as a function of vaccine efficacy. It should be noted that at baseline, a vaccine with ∼40% efficacy is sufficient to eradicate the infection. When the probability of relaxing vector-control measures is 10%, the vaccine efficacy necessary to bring the force of infection down to zero is ∼50%, and so on. In the worst scenario simulated, the probability of relaxing vector-control measures is 50% and the eradication is >80%. Hence, for the latter scenario, unless the vaccine efficacy is >0·5%, the introduction of the vaccine worsens the epidemic (the force of infection is greater than the baseline situation, i.e. 0% probability of relaxing vector control measures).
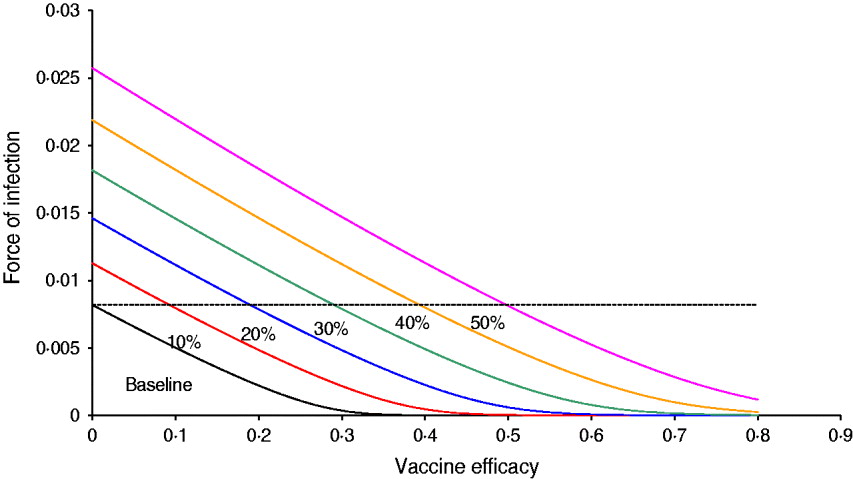
Fig. 1 [colour online]. Results of the numerical simulation of system (1) with six projected scenarios related to the probability of relaxing vector-control measures, from 10% to 50%. The figure shows the force of infection as a function of the vaccine efficacy. The dotted line represents the force of infection in the absence of vaccination.
Note that in the baseline scenario (i.e. 0% probability of relaxing vector control measures) any vaccine with efficacy >40% is enough to eradicate the disease (provided, of course that 100% of the target population is vaccinated). This is compatible with the relatively low value of R 0 (in this case, around 1·7).
Another way to see this phenomenon is shown in Figure 2, in which a simulation of system (1) is shown for the dengue situation in Singapore. The vaccine is introduced by week 180, and the population is assumed to reduce vector control by 45%. In this case, it can be observed that unless the vaccine efficacy is >75%, it is better not to introduce the vaccine because the number of cases with the less efficacious vaccine is greater than that in the absence of vaccination.
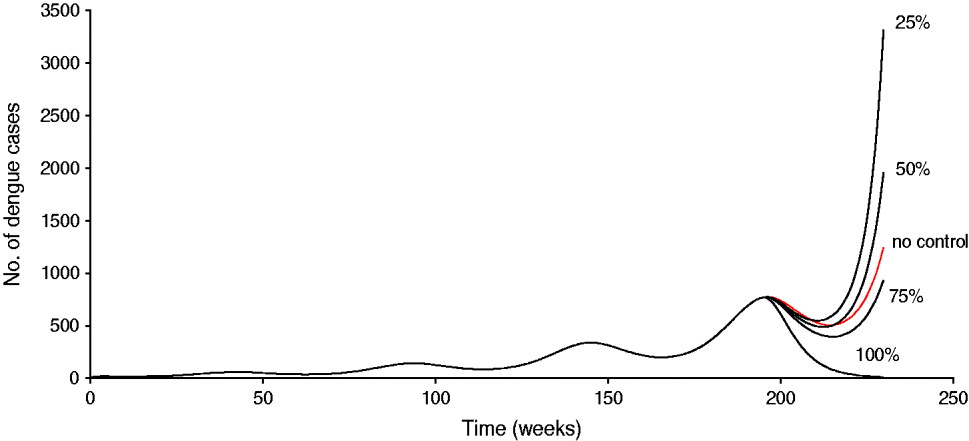
Fig. 2 [colour online]. Simulation of system (1) for the dengue situation in Singapore. The vaccine is introduced by week 180 and the population is assumed to reduce vector control by 45%. In the simulation, the carrying capacity for the aquatic phases increases according to equation (3). The situation labelled ‘no control’ means the natural course of the epidemic without vaccination.
Interviews
In both groups, the variable ‘total score’ showed a non-normal distribution by the Kolmogorov–Smirnov test. The average scores were 5·72 (s.e. = 0·16) for the group that was informed of a high-efficacy vaccine and 6·22 (s.e. = 0·12) for the group that was informed of a low-efficacy vaccine. This difference was statistically significant [Mann–Whitney U (n 1 = 100; n 2 = 100) = 3350·5, P = 3·2 × 10–6, one-tailed, d = 0·67), although the size effect (Cohen's d) was not too great. This finding suggests that there is a trend in the direction of vector-control habit relaxation, such that the more people feel protected by the vaccine the less the total score, i.e. the less people care about measures related to mosquito control.
DISCUSSION
No medical intervention has such an unambiguous record of preventing morbidity and mortality from infectious diseases than that of vaccines [Reference Massad, Burattini and Ortega17]. However, there is no vaccine that is absolutely safe with no side-effects. Some vaccines are relatively safe, with only minor side-effects, such as low fever and a discrete cutaneous rash. Other vaccines, such as the rubella vaccine, can cause grave and undesirable effects when the age of the target population or the minimum proportion vaccinated are not optimized [Reference Azevedo18]. In some cases, serious adverse effects, including death, can reach unacceptable levels, as occurred during the recent yellow fever outbreak in São Paulo, Brazil, in which there was 1 death/200 000 doses of live-attenuated yellow fever vaccine (described in [Reference Moreno19]).
The candidate dengue vaccines tested so far have been demonstrated to be safe [Reference Leo20] regarding adverse effects primarily caused by the vaccine itself, such as mild symptoms of headache, malaise, and eye pain. In some cases, those who received the vaccine noted more moderate symptoms with onset from study days 8–11 and developed maculopapular rashes distributed over the trunk and extremities. Transient neutropenia (white blood cells <4000 mm3), but not thrombocytopenia (platelets <100 000 mm3), were noted after vaccination [Reference Kanesa-thasan21]. Hence, live-attenuated dengue virus vaccines are safe and tolerable in humans and their mild-to-moderate side-effects should not cause too much concern. However, the efficacy demonstrated by the most advanced dengue vaccine candidate in a recent phase 2b trial in Thailand [Reference Sabchareon22] was 30·2% (95% confidence interval 13·4–56·6), and differed by serotype. Although still preliminary and very much dependent on larger trials, these results demonstrate that the likely dengue vaccine will not be (and should not be expected to be) 100% efficacious. The high expectations of the affected populations of a vaccine as the only hope to eliminate dengue, however, are worrisome. The false feeling of perfect protection may cause the population to reduce costly vector-control measures. Thus, depending on the intensity of behavioural change by the affected population, unless the vaccine has a minimum efficacy, its introduction may increase the intensity of transmission.
The results of the questionnaire strongly suggest that the population will relax vector-control measures, and this relaxation may result in a significant increase in dengue transmission, as shown by the model. These results support the proposed hypothesis.
The present study has some important limitations, such as the oversimplified structure of the proposed model and the small sample interviewed, but our approach was not intended to be comprehensive. Rather, this study aimed to raise the hypothesis about changing vector-control behaviour in the presence of a dengue vaccine and to test it in two different ways. In addition, the conclusions presented hold only when people's behavioural change (for worse) in the initial period after the introduction of the vaccine is not modified with time. However, it is likely that this ‘static’ behavioural scenario might not be observed. Indeed, it is expected that people's perception will rapidly change when it becomes clear that the vaccine is not working as expected during the course of an epidemic, and their behaviour will revert to their original practices. In a future work we will expand the questionnaire to accommodate the possibility of changing one's behaviour under such a dynamic scenario. We are planning a more extensive study in which a lager sample will be interviewed, to provide increased statistical power to verify the preliminary results we found in the current study.
ACKNOWLEDGEMENTS
This research received funding from the European Union's Seventh Framework Programme (FP7/2007–2013) under grant agreement no. 282 589 from LIM01 HCFMUSP and CNPq. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
DECLARATION OF INTEREST
None.
APPENDIX
Questionnaire used for estimating the sample's vector-control habits and knowledge about dengue transmission and prevention









