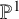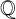1 Introduction
Let
![]() $\pi :X\to \mathbb {P}^1$
be a nonconstant elliptic surface (with section) defined over
$\pi :X\to \mathbb {P}^1$
be a nonconstant elliptic surface (with section) defined over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $\mathrm {MW}(X,\pi )$
be its group of sections defined over
$\mathrm {MW}(X,\pi )$
be its group of sections defined over
![]() $\mathbb {Q}$
. This group is finitely generated by the Lang–Néron theorem [Reference Lang and Néron7]. By a theorem of Silverman [Reference Silverman16], for all but finitely many
$\mathbb {Q}$
. This group is finitely generated by the Lang–Néron theorem [Reference Lang and Néron7]. By a theorem of Silverman [Reference Silverman16], for all but finitely many
![]() $b\in \mathbb {P}^1(\mathbb {Q})$
, the fibre
$b\in \mathbb {P}^1(\mathbb {Q})$
, the fibre
![]() $X_b$
is an elliptic curve with
$X_b$
is an elliptic curve with
![]() $\mathrm {rk}\, X_b(\mathbb {Q})\ge \mathrm {rk}\, \mathrm {MW}(X,\pi )$
and one can ask when is this inequality strict and when is it an equality. Thus, let us define
$\mathrm {rk}\, X_b(\mathbb {Q})\ge \mathrm {rk}\, \mathrm {MW}(X,\pi )$
and one can ask when is this inequality strict and when is it an equality. Thus, let us define
and
These are the sets of points
![]() $b\in \mathbb {P}^1(\mathbb {Q})$
where the rank jumps and where it does not jump, respectively. The question is whether these sets are infinite. There is a considerable body of work addressing this problem for
$b\in \mathbb {P}^1(\mathbb {Q})$
where the rank jumps and where it does not jump, respectively. The question is whether these sets are infinite. There is a considerable body of work addressing this problem for
![]() $\mathscr {J}(X,\pi )$
and we refer the reader to [Reference Salgado13] and the references therein.
$\mathscr {J}(X,\pi )$
and we refer the reader to [Reference Salgado13] and the references therein.
However, much less is known for
![]() $\mathscr {N}(X,\pi )$
. In [Reference Cassels and Schinzel2], Cassels and Schinzel produced an example where
$\mathscr {N}(X,\pi )$
. In [Reference Cassels and Schinzel2], Cassels and Schinzel produced an example where
![]() $\mathscr {N}(X,\pi )$
is empty, conditional on a conjecture of Selmer. Regarding the infinitude of
$\mathscr {N}(X,\pi )$
is empty, conditional on a conjecture of Selmer. Regarding the infinitude of
![]() $\mathscr {N}(X,\pi )$
, there are plenty of results where this set is infinite for quadratic twist families (see [Reference Li, Ji, Cheng, Yau and Zhu8] for a survey on recent results). The example of Cassels and Schinzel, as well as quadratic twist families, are isotrivial.
$\mathscr {N}(X,\pi )$
, there are plenty of results where this set is infinite for quadratic twist families (see [Reference Li, Ji, Cheng, Yau and Zhu8] for a survey on recent results). The example of Cassels and Schinzel, as well as quadratic twist families, are isotrivial.
In the nonisotrivial case, one expects the following result.
Conjecture 1.1. If
![]() $\pi :X\to \mathbb {P}^1$
is nonisotrivial, then both
$\pi :X\to \mathbb {P}^1$
is nonisotrivial, then both
![]() $\mathscr {J}(X,\pi )$
and
$\mathscr {J}(X,\pi )$
and
![]() $\mathscr {N}(X,\pi )$
are infinite.
$\mathscr {N}(X,\pi )$
are infinite.
A heuristic for this conjecture is implicit in Appendix A of [Reference Conrad, Conrad and Helfgott3]. We revisit this heuristic in Section 4.1 for the convenience of the reader.
Let us consider the case when
![]() $\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$
. Such elliptic surfaces over
$\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$
. Such elliptic surfaces over
![]() $\mathbb {Q}$
are abundant (see for instance [Reference Kloosterman6]). Regarding the infinitude of
$\mathbb {Q}$
are abundant (see for instance [Reference Kloosterman6]). Regarding the infinitude of
![]() $\mathscr {N}(X,\pi )$
, the following assertion is a very special case of Conjecture 1.1.
$\mathscr {N}(X,\pi )$
, the following assertion is a very special case of Conjecture 1.1.
Conjecture 1.2. Let
![]() $\pi :X\to \mathbb {P}^1$
be a nonisotrivial elliptic surface defined over
$\pi :X\to \mathbb {P}^1$
be a nonisotrivial elliptic surface defined over
![]() $\mathbb {Q}$
with the property that
$\mathbb {Q}$
with the property that
![]() $\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$
. Then there are infinitely many
$\mathrm {rk}\, \mathrm {MW}(X,\pi )=0$
. Then there are infinitely many
![]() $b\in \mathbb {P}^1(\mathbb {Q})$
with
$b\in \mathbb {P}^1(\mathbb {Q})$
with
![]() $\mathrm {rk}\, X_b(\mathbb {Q})=0$
. That is,
$\mathrm {rk}\, X_b(\mathbb {Q})=0$
. That is,
![]() $\mathscr {N}(X,\pi )$
is infinite.
$\mathscr {N}(X,\pi )$
is infinite.
This problem remains open and, to the best of our knowledge, not a single example of a nonisotrivial elliptic surface with an infinite
![]() $\mathscr {N}(X,\pi )$
is known. Nevertheless, let us consider the elliptic surface
$\mathscr {N}(X,\pi )$
is known. Nevertheless, let us consider the elliptic surface
![]() $\pi :S\to \mathbb {P}^1$
defined by the Weierstrass equation:
$\pi :S\to \mathbb {P}^1$
defined by the Weierstrass equation:
where t is an affine coordinate on
![]() $\mathbb {P}^1$
. This elliptic surface is nonisotrivial and it was first studied by Neumann [Reference Neumann10] and Setzer [Reference Setzer15] (see also [Reference Stein and Watkins18]). If p is a prime of the form
$\mathbb {P}^1$
. This elliptic surface is nonisotrivial and it was first studied by Neumann [Reference Neumann10] and Setzer [Reference Setzer15] (see also [Reference Stein and Watkins18]). If p is a prime of the form
![]() $p=b^2+64$
for an integer
$p=b^2+64$
for an integer
![]() $b\equiv 3\bmod 4$
, then
$b\equiv 3\bmod 4$
, then
![]() $S_b(\mathbb {Q})\simeq \mathbb {Z}/2\mathbb {Z}$
and in particular
$S_b(\mathbb {Q})\simeq \mathbb {Z}/2\mathbb {Z}$
and in particular
![]() $S_b$
has rank
$S_b$
has rank
![]() $0$
over
$0$
over
![]() $\mathbb {Q}$
. A well-known conjecture of Bunyakovsky predicts that there are infinitely many primes p of this form, so one gets a conditional example where Conjecture 1.2 holds.
$\mathbb {Q}$
. A well-known conjecture of Bunyakovsky predicts that there are infinitely many primes p of this form, so one gets a conditional example where Conjecture 1.2 holds.
In this note, we consider instead the Legendre elliptic surface
![]() $\pi :Y\to \mathbb {P}^1$
defined by the Weierstrass equation:
$\pi :Y\to \mathbb {P}^1$
defined by the Weierstrass equation:
This elliptic surface has
![]() $\mathrm {rk}\,\mathrm {MW}(Y,\pi )=0$
(see Lemma 2.2). To state our main result, let us recall that a Mersenne prime is a prime number p of the form
$\mathrm {rk}\,\mathrm {MW}(Y,\pi )=0$
(see Lemma 2.2). To state our main result, let us recall that a Mersenne prime is a prime number p of the form
![]() $p=2^q-1$
with q a prime. It is conjectured that there are infinitely many of them (see Section 4.2 for details). We prove the following result.
$p=2^q-1$
with q a prime. It is conjectured that there are infinitely many of them (see Section 4.2 for details). We prove the following result.
Theorem 1.3. Let
![]() $q\ge 5$
be a prime such that
$q\ge 5$
be a prime such that
![]() $p=2^q-1$
is a Mersenne prime. Then the elliptic curve
$p=2^q-1$
is a Mersenne prime. Then the elliptic curve
![]() $E_q$
defined by
$E_q$
defined by
![]() $y^2=x(x+1)(x+2^q)$
has
$y^2=x(x+1)(x+2^q)$
has
![]() $\mathrm {rk}\, E_q(\mathbb {Q})=0$
.
$\mathrm {rk}\, E_q(\mathbb {Q})=0$
.
In particular, if there are infinitely Mersenne primes, then the (nonisotrivial) Legendre elliptic surface
![]() $\pi :Y\to \mathbb {P}^1$
has the property that
$\pi :Y\to \mathbb {P}^1$
has the property that
![]() $\mathscr {N}(Y,\pi )$
is infinite.
$\mathscr {N}(Y,\pi )$
is infinite.
The proof of Theorem 1.3 has two main ingredients. First, using a descent bound, we show that
![]() $\mathrm {rk}\, E_q(\mathbb {Q})\le 1$
, which falls short of proving the result. However, using known cases of the parity conjecture due to Monsky [Reference Monsky9] as well as some control on Shafarevich–Tate groups, we deduce that
$\mathrm {rk}\, E_q(\mathbb {Q})\le 1$
, which falls short of proving the result. However, using known cases of the parity conjecture due to Monsky [Reference Monsky9] as well as some control on Shafarevich–Tate groups, we deduce that
![]() $\mathrm {rk}\, E_q(\mathbb {Q})=1$
is not possible. For this strategy to work, we need to carefully analyse the reduction type of
$\mathrm {rk}\, E_q(\mathbb {Q})=1$
is not possible. For this strategy to work, we need to carefully analyse the reduction type of
![]() $E_q$
at the primes
$E_q$
at the primes
![]() $2$
and p.
$2$
and p.
Finally, let us mention a somewhat unexpected motivation for Conjecture 1.2. Although we have only discussed elliptic surfaces over
![]() $\mathbb {Q}$
, Conjecture 1.2 can also be formulated over number fields. In [Reference Pasten12], it is shown that this conjecture over number fields implies that for every number field K, the analogue of Hilbert’s tenth problem for the ring of integers
$\mathbb {Q}$
, Conjecture 1.2 can also be formulated over number fields. In [Reference Pasten12], it is shown that this conjecture over number fields implies that for every number field K, the analogue of Hilbert’s tenth problem for the ring of integers
![]() $O_K$
is undecidable.
$O_K$
is undecidable.
2 Preliminaries
2.1 The Legendre elliptic surface
Let t be the affine coordinate on
![]() $\mathbb {P}^1$
. The Legendre elliptic surface is the (relatively minimal) elliptic surface
$\mathbb {P}^1$
. The Legendre elliptic surface is the (relatively minimal) elliptic surface
![]() $\pi :Y\to \mathbb {P}^1$
defined over
$\pi :Y\to \mathbb {P}^1$
defined over
![]() $\mathbb {Q}$
by the affine Weierstrass equation:
$\mathbb {Q}$
by the affine Weierstrass equation:
We refer the reader to [Reference Ulmer20] for a detailed study of this elliptic surface. The first lemma is a direct computation.
Lemma 2.1. The Legendre elliptic surface is nonisotrivial and rational. It has three singular fibres: at
![]() $t=0$
of Kodaira type
$t=0$
of Kodaira type
![]() $I_2$
, at
$I_2$
, at
![]() $t=-1$
of Kodaira type
$t=-1$
of Kodaira type
![]() $I_2$
and at
$I_2$
and at
![]() $t=\infty $
of Kodaira type
$t=\infty $
of Kodaira type
![]() $I_2^*$
.
$I_2^*$
.
Using this, we get the next lemma.
Lemma 2.2. We have
![]() $\mathrm {rk}\, \mathrm {MW}(Y,\pi )=0$
. In fact, the group of sections over
$\mathrm {rk}\, \mathrm {MW}(Y,\pi )=0$
. In fact, the group of sections over
![]() $\mathbb {C}$
is formed by the
$\mathbb {C}$
is formed by the
![]() $2$
-torsion sections.
$2$
-torsion sections.
Proof. Let us base change to
![]() $\mathbb {C}$
. Since
$\mathbb {C}$
. Since
![]() $\pi :Y_{\mathbb {C}}\to \mathbb {P}^1$
is a rational elliptic surface with singular fibres of types
$\pi :Y_{\mathbb {C}}\to \mathbb {P}^1$
is a rational elliptic surface with singular fibres of types
![]() $I_2$
,
$I_2$
,
![]() $I_2$
and
$I_2$
and
![]() $I_2^*$
, its group of sections is given in the entry 71 of the main theorem of [Reference Oguiso and Shioda11].
$I_2^*$
, its group of sections is given in the entry 71 of the main theorem of [Reference Oguiso and Shioda11].
2.2 Bounds for the rank
The following result is a more precise version of the bound provided by [Reference Caro and Pasten1, Proposition 1.3]; the argument is a variation of the proof of [Reference Caro and Pasten1, Lemma 3.1].
Theorem 2.3. Let E be an elliptic curve over
![]() $\mathbb {Q}$
admitting a
$\mathbb {Q}$
admitting a
![]() $2$
-isogeny
$2$
-isogeny
![]() $\theta :E\to E'$
over
$\theta :E\to E'$
over
![]() $\mathbb {Q}$
. Let
$\mathbb {Q}$
. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\mu $
be the number of places of additive and of multiplicative reduction of E, respectively. Then,
$\mu $
be the number of places of additive and of multiplicative reduction of E, respectively. Then,
If equality holds, then the
![]() $2$
-primary part of the Shafarevich–Tate group
$2$
-primary part of the Shafarevich–Tate group
![]() is trivial.
is trivial.
Proof. The claimed bound is precisely [Reference Caro and Pasten1, Proposition 1.3]. Suppose that equality holds. We will show that the
![]() $2$
-torsion part of
$2$
-torsion part of
![]() is trivial, which is sufficient.
is trivial, which is sufficient.
Let
![]() $S_2(E)$
be the
$S_2(E)$
be the
![]() $2$
-Selmer group of E. Then we have the exact sequence
$2$
-Selmer group of E. Then we have the exact sequence
and we see that it suffices to show
because
![]() $\dim _{\mathbb {F}_2}E(\mathbb {Q})/2E(\mathbb {Q}) = \mathrm {rk}\, E(\mathbb {Q}) + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]=2\alpha +\mu -1 + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]$
.
$\dim _{\mathbb {F}_2}E(\mathbb {Q})/2E(\mathbb {Q}) = \mathrm {rk}\, E(\mathbb {Q}) + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]=2\alpha +\mu -1 + \dim _{\mathbb {F}_2}E(\mathbb {Q})[2]$
.
Let
![]() $\theta :E\to E'$
be a rational
$\theta :E\to E'$
be a rational
![]() $2$
-isogeny and let
$2$
-isogeny and let
![]() $\theta ':E'\to E$
be its dual. For the corresponding Selmer groups
$\theta ':E'\to E$
be its dual. For the corresponding Selmer groups
![]() $S_\theta (E)$
and
$S_\theta (E)$
and
![]() $S_{\theta '}(E)$
,
$S_{\theta '}(E)$
,
(see [Reference Caro and Pasten1, Theorem 2.2]). These Selmer groups are related to
![]() $S_2(E)$
via the exact sequence
$S_2(E)$
via the exact sequence
(see [Reference Schaefer and Stoll14, Lemma 6.1]; note that although this is only claimed for odd primes p in [Reference Schaefer and Stoll14], the hypothesis
![]() $p>2$
is not really needed at this point).
$p>2$
is not really needed at this point).
Let us consider two cases. First, let us assume that
![]() $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. Then (2.2) and (2.3) give
$E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. Then (2.2) and (2.3) give
where
![]() $\theta (E(\mathbb {Q})[2])=(0)$
because
$\theta (E(\mathbb {Q})[2])=(0)$
because
![]() $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. This proves (2.1) when
$E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. This proves (2.1) when
![]() $E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. Now let us assume
$E(\mathbb {Q})[2]\simeq \mathbb {Z}/2\mathbb {Z}$
. Now let us assume
![]() $E(\mathbb {Q})[2]\simeq (\mathbb {Z}/2\mathbb {Z})^2$
. Then (2.2) and (2.3) directly give
$E(\mathbb {Q})[2]\simeq (\mathbb {Z}/2\mathbb {Z})^2$
. Then (2.2) and (2.3) directly give
which proves (2.1) in this case.
2.3 Root numbers
The root number
![]() $w(E)$
of an elliptic curve E over
$w(E)$
of an elliptic curve E over
![]() $\mathbb {Q}$
is the sign of the functional equation of E. Furthermore, one can define the local root number
$\mathbb {Q}$
is the sign of the functional equation of E. Furthermore, one can define the local root number
![]() $w_p(E)$
at a prime p, and these local root numbers are related to
$w_p(E)$
at a prime p, and these local root numbers are related to
![]() $w(E)$
by
$w(E)$
by
 $$ \begin{align*}w(E)=-\prod_{p}w_p(E).\end{align*} $$
$$ \begin{align*}w(E)=-\prod_{p}w_p(E).\end{align*} $$
When E is semi-stable, we have a complete characterisation for the local root numbers:
 $$ \begin{align*} w_p(E)= \begin{cases}1 & \mbox{if }E\mbox{ has good or nonsplit multiplicative reduction at }p,\\ -1 & \mbox{if }E\mbox{ has split multiplicative reduction at }p. \end{cases}\end{align*} $$
$$ \begin{align*} w_p(E)= \begin{cases}1 & \mbox{if }E\mbox{ has good or nonsplit multiplicative reduction at }p,\\ -1 & \mbox{if }E\mbox{ has split multiplicative reduction at }p. \end{cases}\end{align*} $$
2.4 The parity conjecture
The following conjecture is an immediate consequence of the Birch and Swinnerton-Dyer conjecture.
Conjecture 2.4 (Parity conjecture).
Let E be an elliptic curve over
![]() $\mathbb {Q}$
. Then we have
$\mathbb {Q}$
. Then we have
![]() $(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$
.
$(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$
.
The following result is a direct consequence of [Reference Monsky9, Theorem 1.5].
Lemma 2.5. Let E be an elliptic curve over
![]() $\mathbb {Q}$
. If the
$\mathbb {Q}$
. If the
![]() $2$
-primary part of
$2$
-primary part of
![]() is finite, then
is finite, then
![]() $(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$
.
$(-1)^{\mathrm {rk}\, E(\mathbb {Q})}=w(E)$
.
3 Proof of the main result
3.1 Reduction types
Lemma 3.1. Let
![]() $p=2^q-1$
be a Mersenne prime with
$p=2^q-1$
be a Mersenne prime with
![]() $q\ge 5$
, and let
$q\ge 5$
, and let
![]() $E_q$
be the elliptic curve defined by
$E_q$
be the elliptic curve defined by
![]() $y^2=x(x+1)(x+2^q)$
. Then,
$y^2=x(x+1)(x+2^q)$
. Then,
![]() $E_q$
has split multiplicative reduction at
$E_q$
has split multiplicative reduction at
![]() $2$
, nonsplit multiplicative reduction at p and good reduction at all other primes.
$2$
, nonsplit multiplicative reduction at p and good reduction at all other primes.
Proof. [Reference Diamond and Kramer4, Lemma 1] implies that
![]() $E_q$
has multiplicative reduction at
$E_q$
has multiplicative reduction at
![]() $2$
and p, and good reduction at every other prime. The reduction of
$2$
and p, and good reduction at every other prime. The reduction of
![]() $E_q$
modulo p is defined by
$E_q$
modulo p is defined by
Replacing x by
![]() $x-1$
, we get the model
$x-1$
, we get the model
![]() $y^2=x^3-x^2$
with the singular point at
$y^2=x^3-x^2$
with the singular point at
![]() $(x,y)=(0,0)$
. Thus,
$(x,y)=(0,0)$
. Thus,
![]() $E_q$
has split multiplicative reduction at p if and only if
$E_q$
has split multiplicative reduction at p if and only if
![]() $\sqrt {-1}\in \mathbb {F}_p$
. Since
$\sqrt {-1}\in \mathbb {F}_p$
. Since
we conclude that
![]() $E_q$
has nonsplit multiplicative reduction at p. However, the proof of [Reference Diamond and Kramer4, Lemma 2] yields the following minimal equation for
$E_q$
has nonsplit multiplicative reduction at p. However, the proof of [Reference Diamond and Kramer4, Lemma 2] yields the following minimal equation for
![]() $E_q$
over
$E_q$
over
![]() $\mathbb {Q}_2$
:
$\mathbb {Q}_2$
:
As
![]() $q\ge 5$
, the reduction modulo
$q\ge 5$
, the reduction modulo
![]() $2$
is given by the equation
$2$
is given by the equation
![]() $y^2+xy=x^3$
, with the singular point at
$y^2+xy=x^3$
, with the singular point at
![]() $(x,y)=(0,0)$
. This singular point is a nodal singularity with tangent slopes
$(x,y)=(0,0)$
. This singular point is a nodal singularity with tangent slopes
![]() $0$
and
$0$
and
![]() $1$
, both defined over
$1$
, both defined over
![]() $\mathbb {F}_2$
. As a consequence,
$\mathbb {F}_2$
. As a consequence,
![]() $E_q$
has split multiplicative reduction at
$E_q$
has split multiplicative reduction at
![]() $2$
.
$2$
.
3.2 Bounding the rank
Proof of Theorem 1.3.
By Lemma 3.1, the bad primes for
![]() $E_q$
are
$E_q$
are
![]() $2$
with split multiplicative reduction, and p with nonsplit multiplicative reduction. Therefore,
$2$
with split multiplicative reduction, and p with nonsplit multiplicative reduction. Therefore,
![]() $w(E)=1$
since
$w(E)=1$
since
![]() $w_2(E)=-1$
and
$w_2(E)=-1$
and
![]() $w_p(E)=1$
.
$w_p(E)=1$
.
Let us apply Theorem 2.3. We obtain
![]() $\mathrm {rk}\, E_q(\mathbb {Q})\leq 1$
and we claim that, in fact,
$\mathrm {rk}\, E_q(\mathbb {Q})\leq 1$
and we claim that, in fact,
![]() $\mathrm {rk}\, E_q(\mathbb {Q})=0$
. For the sake of contradiction, assume that
$\mathrm {rk}\, E_q(\mathbb {Q})=0$
. For the sake of contradiction, assume that
![]() $\mathrm {rk}\, E_q(\mathbb {Q})= 1$
. Then, Theorem 2.3 implies that the
$\mathrm {rk}\, E_q(\mathbb {Q})= 1$
. Then, Theorem 2.3 implies that the
![]() $2$
-primary part of
$2$
-primary part of
![]() is trivial, and hence, by Lemma 2.5, we would obtain
is trivial, and hence, by Lemma 2.5, we would obtain
![]() $w(E)=(-1)^{\mathrm {rk}\, E_q(\mathbb {Q})}=-1$
, which contradicts the fact that
$w(E)=(-1)^{\mathrm {rk}\, E_q(\mathbb {Q})}=-1$
, which contradicts the fact that
![]() $w(E)=1$
.
$w(E)=1$
.
4 Heuristics
4.1 On Conjecture 1.1
Let
![]() $\pi :X\to \mathbb {P}^1$
be a nonisotrivial elliptic surface defined over
$\pi :X\to \mathbb {P}^1$
be a nonisotrivial elliptic surface defined over
![]() $\mathbb {Q}$
and let
$\mathbb {Q}$
and let
![]() $R=\mathrm {rk}\, \mathrm {MW}(X,\pi )$
. Following the terminology in [Reference Conrad, Conrad and Helfgott3], the density conjecture of Silverman [Reference Silverman17] asserts that
$R=\mathrm {rk}\, \mathrm {MW}(X,\pi )$
. Following the terminology in [Reference Conrad, Conrad and Helfgott3], the density conjecture of Silverman [Reference Silverman17] asserts that
for all
![]() $b\in \mathbb {P}^1(\mathbb {Q})$
outside a set of density
$b\in \mathbb {P}^1(\mathbb {Q})$
outside a set of density
![]() $0$
in
$0$
in
![]() $\mathbb {P}^1(\mathbb {Q})$
.
$\mathbb {P}^1(\mathbb {Q})$
.
In [Reference Helfgott5], Helfgott proved that under some conjectures in analytic number theory, the average value of the root numbers
![]() $w(X_b)$
as b varies in
$w(X_b)$
as b varies in
![]() $\mathbb {P}^1(\mathbb {Q})$
(ordered by height) exists and it is expressed in terms of local densities. As pointed out in [Reference Conrad, Conrad and Helfgott3, Appendix A, page 728], the conjectural value for this average of root numbers lies strictly between
$\mathbb {P}^1(\mathbb {Q})$
(ordered by height) exists and it is expressed in terms of local densities. As pointed out in [Reference Conrad, Conrad and Helfgott3, Appendix A, page 728], the conjectural value for this average of root numbers lies strictly between
![]() $-1$
and
$-1$
and
![]() $1$
in the nonisotrivial case.
$1$
in the nonisotrivial case.
Therefore, under the previous conjectures, we deduce Conjecture 1.1 in a strong form: both sets
![]() $\mathscr {J}(X,\pi )$
and
$\mathscr {J}(X,\pi )$
and
![]() $\mathscr {N}(X,\pi )$
should have positive density in
$\mathscr {N}(X,\pi )$
should have positive density in
![]() $\mathbb {P}^1(\mathbb {Q})$
.
$\mathbb {P}^1(\mathbb {Q})$
.
4.2 On Mersenne primes
Let us recall the following folklore conjecture.
Conjecture 4.1. There are infinitely many Mersenne primes.
Mersenne primes provide a way to construct large prime numbers and considerable efforts are made to search for them, such as the Great Internet Mersenne Prime Search collaborative project [19].
Here we recall that the Lenstra–Pomerance–Wagstaff heuristic [Reference Wagstaff21] suggests that the number of Mersenne primes
![]() $p=2^q-1$
in the interval
$p=2^q-1$
in the interval
![]() $[1,x]$
is asymptotic to
$[1,x]$
is asymptotic to
 $$ \begin{align*} \frac{e^{\gamma}}{\log 2}\log \log x, \end{align*} $$
$$ \begin{align*} \frac{e^{\gamma}}{\log 2}\log \log x, \end{align*} $$
where
![]() $\gamma $
is Euler’s constant. This gives a more precise form of Conjecture 4.1.
$\gamma $
is Euler’s constant. This gives a more precise form of Conjecture 4.1.
Acknowledgements
We thank Cecília Salgado for answering some questions on the relevant literature. We also thank the referee for carefully reading this article and for the feedback provided.