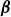At a few instances in our paper, we make the claim that $\boldsymbol{\nabla }Q_2 \perp \mathbf{U}$ is equivalent to the planetary, topographic and stretching PV gradients all being aligned with each other. This claim is incorrect. The lower layer PV gradient is given by

(0.1) \begin{align} \boldsymbol{\nabla }Q_2 = \big(F_2 V + B_x, -F_2 U + B_y + \beta \big), \\[-8pt] \nonumber \end{align}

and so

(0.2) \begin{align} \boldsymbol{\nabla }Q_2 \boldsymbol{\cdot }\mathbf{U} = U \boldsymbol{\cdot }B_x + V \big(B_y + \beta \big). \\[-8pt] \nonumber \end{align}

Hence, $\boldsymbol{\nabla }Q_2 \perp \mathbf{U}$ means that $(B_x, B_y + \beta )$ is perpendicular to the mean shear $\mathbf{U} = (U,V)$ , and hence aligned with the stretching PV gradient $(F_2 V, -F_2 U)$ . So rather, the sum of the topographic and planetary PV gradient is aligned with the stretching PV gradient. The three gradients can only be aligned when they are all meridional.

Thus we make a few changes to the article. In the abstract, the sentence ‘The system is stable across all wavenumbers only if friction is absent and if the planetary, topographic and stretching PV gradients are aligned.’ is replaced by ‘The system is stable across all wavenumbers only if friction is absent and if the lower layer PV gradient is perpendicular to the mean shear.’ On the second page of the Introduction, the last sentence of the first paragraph, ‘In other words, the topographic and stretching PV gradients are still aligned, though not with the planetary PV gradient.’ is replaced by ‘In other words, the topographic and stretching PV gradients are still aligned.’ Finally, in § 3.3, the sentence ‘Note that $\boldsymbol{\nabla }Q_2 \perp \mathbf{U}$ is equivalent to the planetary, topographic and stretching PV gradients all being aligned with each other.’ is removed.