1. Introduction
Land degradation is on the rise each year due to competing pressures for food, energy and shelter. At the same time, the carbon emissions associated with economic activity put additional pressure on the environmental impact of economic growth. The main objective of this study is to analyze the contribution of land capital to the growth of emissions and income per capita in the long run in a context where land productivity can directly be improved through investment. With this purpose, land capital – or natural capital excluding sub-soil assets – is introduced into the Green Solow model of Brock and Taylor (Reference Brock and Taylor2010). Using natural capital data from the World Bank and Enhanced Vegetation Index (EVI) data from the Earth Observatory, it is shown that the model is consistent with the cross-country variation in growth rates of carbon emissions and that initial EVI-adjusted land endowments play a statistically-significant role in the convergence analysis, which to the best of our knowledge, has not been studied previously. Our main finding is that the initial land capital endowment has a positive impact on the growth of emissions but that land capital investment contributes significantly to reducing the growth of emissions in the long run.
In this paper we treat land in a broad sense as a renewable resource. Economic growth and population growth entail economic pressure on natural resources that are essential for life, such as clean water and fertile soil. The expansion of modern agriculture and industrial production is often associated with unsustainable practices and harmful waste disposal that cause soil degradation and biodiversity loss, which in turn can contribute to an increased flow of carbon emissions. We consider the natural resources essential for life as a form of capital and assume that this land capital is as essential in aggregate production as manufactured capital.
As a first step in this direction, we explore empirically the relationship between natural capital excluding sub-soil assets and new quality-adjusted land endowments based on a normalization of the EVI. Based on the positive relationship found between these two indicators, we define land capital as a combination of embodied environmental knowledge and quality-adjusted land. We propose the Green Solow model of Brock and Taylor (Reference Brock and Taylor2010) as the reference framework for various reasons. First, it provides a simple, intuitive and well-known growth framework whose quantitative implications concerning long-run per capita income are consistent with the main stylized facts of developed economies. Second, the implied dynamics of air pollution (modelled as a pure production externality) along the transition to balanced growth are well in accord with some puzzling evidence regarding emissions such as the Environmental Kuznets Curve (EKC) or the convergence hypothesis. Thus it seems natural to extend (Brock and Taylor, Reference Brock and Taylor2010) empirical analysis of carbon emissions convergence by adding land capital into the growth equation.Footnote 1
The conditions under which economic growth and environmental preservation are compatible in the long run are the focus of a large body of endogenous growth studies starting in the early 1990s. Notable contributions are, for example, Bovenberg and Smulders (Reference Bovenberg and Smulders1995), Smulders and Gradus (Reference Smulders and Gradus1996), Bretschger (Reference Bretschger1998) and Bretschger and Smulders (Reference Bretschger and Smulders2012). In these models, a broad concept of capital including knowledge becomes the ultimate substitute for natural inputs and the existence of technological progress in abatement holds the pollution in check. Following this tradition of endogenous (AK) growth models, Braussman and Bretscheger (Reference Braussman and Bretscheger2018) consider soil as a natural accumulable input whose quantity depends on investment decisions and on the extent of human-induced damage effects. More recent Schumpeterian endogenous growth models, such as Peretto and Valente (Reference Peretto and Valente2015) and Lanz et al. (Reference Lanz, Dietz and Swanson2017a, Reference Lanz, Dietz and Swanson2017b, Reference Lanz, Dietz and Swanson2018), put the accent on the interactions between agricultural technological change, land (food) scarcity and endogenous population dynamics at the global level, but only Lanz et al. (Reference Lanz, Dietz and Swanson2018) explicitly treats the harmful influence of economic expansion on the environment, connecting agricultural productivity with biodiversity loss.
In this paper we abstract away from endogenous growth, technological progress is an exogenous process and accumulable factors present diminishing returns. Our setup of the natural factor is closer to Braussman and Bretscheger (Reference Braussman and Bretscheger2018) specification in the way it treats soil, combining quality and quantity of the natural input. In that model manufactured capital and soil display constant returns at the aggregate level and investment is on the unique combined integrated asset, whereas here we want to highlight the importance of land resources in a broad sense (not only soil) and the need to analyze land capital investment separately from manufactured capital investment. We conceive land capital investment as a country's effort to transfer the existing scientific knowledge towards a better environmental management, noting that this transfer of knowledge is costly. It involves, for example, learning and adapting basic science to spread good practices, which becomes especially important in developing economies.
We show that this extended model is consistent with the cross-country variation in growth rates of carbon emissions per capita. Moreover, we find that there exists convergence of per capita emissions at the global level, with the long-run contribution of land capital investment to the growth rate of emissions being negative and significant in all specifications. Furthermore, the estimated coefficients of initial emissions and EVI-adjusted land levels have significant opposite signs in all specifications, with the absolute values being of the same order of magnitude. In general, the empirical evidence shows convergence in per capita carbon dioxide emissions for countries grouped by institutional structure, income classification and geographic region, but also shows persistent gaps or divergence for large multi-country studies. Moreover, the role of initial conditions in this analysis is crucial, but to the best of our knowledge at the time of writing this article, the empirical literature lacks explicit reference to land quality endowments (see Acar et al., Reference Acar, Soderholm and Brannlund2018; Payne, Reference Payne2020 for a review). Despite the limitation of the data on land quality, our contribution to this strand of the literature introduces new variables into the debate and highlights the need to generate more and better land data.
The rest of the paper is organized as follows. Section 2 describes the data and shows the stylized facts regarding natural capital and EVI-adjusted land and carbon emissions. Section 3 describes the Green Solow model with land degradation and land capital investment. Section 4 undertakes the empirical analysis of emissions convergence. Section 5 concludes.
2. Data and stylized facts
2.1. Data description
The United Nations Convention to Combat Desertification in 2017 defined land as “the terrestrial bio-productive system that comprises soil, vegetation, other biota, and the ecological and hydrological processes that operate within the system.” Land degradation describes how one or more of the land resources has changed for the worse. In general, land degradation signifies the temporary or permanent decline in the productive capacity of land, including its major uses (rain-fed, arable, irrigated, rangeland, forest), its farming systems and its value as an economic resource (?).
To carry out the calibration and estimation implemented in this study, we use land data from different sources.Footnote 2 Bai et al. (Reference Bai, Dent, Olsson and Schaepman2008) quantify degradation over 1981–2003 by using the normalized difference vegetation index (NDVI) as a proxy for net primary productivity. They find a declining trend in net primary production across 2.7 bn ha (21 per cent) of global land area, but at the same time, they also find that 16 per cent of global land area is increasing in net primary production. We will use their estimates to calibrate some key parameters of the model, but for the empirical exploration we use our own estimates from the EVI. We collect Monthly Moderate resolution Imaging Spectroradiometer (MODIS) data at resolution 0.05 degree (5600 m), from the MODIS data we select the Global MOD13C2 version 6 product, which provides vegetation index values at a per pixel basis. This product provides two vegetation indices: the NDVI and the EVI. In this study we opt for the EVI because it has improved sensitivity over high biomass regions.Footnote 3 The EVI data are monthly data and are available from 2000. As data are at a per pixel basis, the computation of the country's average EVI is time consuming. Therefore, we only collect the MOD13C2 for one month (March) from 2000 to 2015. Afterwards, we import the MODIS data and the country boundaries shapefile into ArcGis and compute the average EVI for each country and year.
The EVI for a given pixel is always a number that ranges from $-1$![]() to $+1$
to $+1$![]() . Positive values generally indicate the presence of vegetation and negative values generally indicate a lack of vegetation (water, rock, etc.). However, no green leaves gives a value close to zero (a zero means no vegetation) and close to one indicates the highest possible density of green leaves. For instance, the USA's average EVI value over the period 2000–2011 is 0.135 while the average EVI values for the United Kingdom and Spain are 0.332 and 0.267, respectively. We will use a normalization of the EVI data to compute a land quality index as follows: $1-(\max EVI-EVI_{i})$
. Positive values generally indicate the presence of vegetation and negative values generally indicate a lack of vegetation (water, rock, etc.). However, no green leaves gives a value close to zero (a zero means no vegetation) and close to one indicates the highest possible density of green leaves. For instance, the USA's average EVI value over the period 2000–2011 is 0.135 while the average EVI values for the United Kingdom and Spain are 0.332 and 0.267, respectively. We will use a normalization of the EVI data to compute a land quality index as follows: $1-(\max EVI-EVI_{i})$![]() , where $\max EVI$
, where $\max EVI$![]() is the maximum value of EVI in our sample which is 0.69 (Samoa) and $EVI_{i}$
is the maximum value of EVI in our sample which is 0.69 (Samoa) and $EVI_{i}$![]() is the average value of EVI observed in each country $i$
is the average value of EVI observed in each country $i$![]() . The physical measure of land adjusted by quality will be the product of this normalized index by the land area. The data on land area are from FAO (land area excluding area under inland water bodies) measured in 1000 ha. We will call this measure of land the “EVI-adjusted land”.
. The physical measure of land adjusted by quality will be the product of this normalized index by the land area. The data on land area are from FAO (land area excluding area under inland water bodies) measured in 1000 ha. We will call this measure of land the “EVI-adjusted land”.
From the World Bank's Wealth of Nations data we obtain estimates of the land-to-output ratios. In this case the value of land is the value of natural capital excluding sub-soil assets. Unfortunately, these estimates are only available for the years 1995, 2000 and 2005, but we will try to get some insights to define our land capital input from the available evidence. The data on income come from the Penn World Table (PWT) in Feenstra et al. (Reference Feenstra, Inklaar and Timmer2015), which cover 182 countries between 1950 and 2014.
The data on pollution abatement efforts to be used in the empirical convergence analysis come from the OECD environmental protection expenditure and revenues dataset and are available for the period 2000-2011 for 35 countries. Finally, data on carbon dioxide emissions are from the World Development Indicators 2016 (World Bank, 2016), which cover 214 countries over the period 1960-2011. These data include gases from the burning of fossil fuels and cement manufacture, but unfortunately exclude emissions from land use and land cover change due to large uncertainties.Footnote 4
2.2. Stylized facts
In this section we provide new evidence regarding the EVI-adjusted land, the World Bank's natural capital estimates, and carbon dioxide (CO$_{2}$![]() ) emissions. First, we have found a positive significant relationship between the input output ratios of natural capital (excluding sub-soil assets) and the EVI-adjusted land for the available years, 2000 and 2005. Figure 1 shows the positive relationship between these two estimates after controlling for the urban land share effect. It is evident that figure 1 also tells us that there must be other important factors affecting the land capital intensity of economic activity, such as land demand forces stemming from different land uses.Footnote 5 We will use this positive relationship as a proxy of the efficiency of land in the production of final goods, meaning that healthier land in a given period is, on average, more valuable and productive. Specifically, we define the variable ‘land capital’ as the product $Z=Q\cdot N,$
) emissions. First, we have found a positive significant relationship between the input output ratios of natural capital (excluding sub-soil assets) and the EVI-adjusted land for the available years, 2000 and 2005. Figure 1 shows the positive relationship between these two estimates after controlling for the urban land share effect. It is evident that figure 1 also tells us that there must be other important factors affecting the land capital intensity of economic activity, such as land demand forces stemming from different land uses.Footnote 5 We will use this positive relationship as a proxy of the efficiency of land in the production of final goods, meaning that healthier land in a given period is, on average, more valuable and productive. Specifically, we define the variable ‘land capital’ as the product $Z=Q\cdot N,$![]() where $N$
where $N$![]() represents the EVI-adjusted land and $Q$
represents the EVI-adjusted land and $Q$![]() a technological efficiency factor. Thus, given output, the slopes of the lines in figure 1 can be interpreted as proxies of (proportional to) the average $Q$
a technological efficiency factor. Thus, given output, the slopes of the lines in figure 1 can be interpreted as proxies of (proportional to) the average $Q$![]() for the years 2000 and 2005, respectively. Then, according to this interpretation, the (average world) productivity of land might have decreased over this five-year period. For instance, Amundson et al. (Reference Amundson, Berhe, Hopmans, Olson, Sztein and Sparks2015) show that the ability of soil to support the growth of food supply is plateauing, pointing out that we have the knowledge to recycle soil nutrients but that stronger commitment to implement the solutions is needed.
for the years 2000 and 2005, respectively. Then, according to this interpretation, the (average world) productivity of land might have decreased over this five-year period. For instance, Amundson et al. (Reference Amundson, Berhe, Hopmans, Olson, Sztein and Sparks2015) show that the ability of soil to support the growth of food supply is plateauing, pointing out that we have the knowledge to recycle soil nutrients but that stronger commitment to implement the solutions is needed.

Figure 1. Conditional land capital per dollar and EVI-adjusted land per dollar. (a) 2000, (b) 2005. Notes: The land capital per dollar is the value of natural capital excluding sub-soil assets divided by the real GDP at constant 2005 national prices. The EVI-adjusted land per dollar is the product between the normalized vegetation index, $1-(\max EVI - EVI_{i})$![]() , which is between zero and one, and the land area (in 1000 ha) divided by the real GDP at constant 2005 national prices (in mil. 2005US). Figures 1(a) and 1(b) represent the relationship between land capital per dollar and EVI-adjusted land per dollar conditional on the urban land share in the 2000 and 2005, respectively. To remove some outliers, the studentized residuals were calculated and the observations with a residual larger than 3 were removed. The regression in panel (a) has a slope parameter of 0.709 with a standard error of 0.15 and $R^2$
, which is between zero and one, and the land area (in 1000 ha) divided by the real GDP at constant 2005 national prices (in mil. 2005US). Figures 1(a) and 1(b) represent the relationship between land capital per dollar and EVI-adjusted land per dollar conditional on the urban land share in the 2000 and 2005, respectively. To remove some outliers, the studentized residuals were calculated and the observations with a residual larger than 3 were removed. The regression in panel (a) has a slope parameter of 0.709 with a standard error of 0.15 and $R^2$![]() of 0.20. The regression in panel (b) has a slope parameter of 0.608 with a standard error of 0.13 and $R^2$
of 0.20. The regression in panel (b) has a slope parameter of 0.608 with a standard error of 0.13 and $R^2$![]() of 0.17.
of 0.17.
Figure 2 illustrates the relationship between the (log) natural capital output and the (log) CO$_{2}$![]() emissions output ratios for the years 2000 and 2005. It shows that countries with higher natural capital output ratios (higher propensities to save natural capital) are, on average, those with lower emissions per unit of output. Comparing the 2000 and 2005 slopes of this relation, we note that an additional unit of land capital output is associated with a drop in the emissions intensity from 2000 to 2005 of $-0.055$
emissions output ratios for the years 2000 and 2005. It shows that countries with higher natural capital output ratios (higher propensities to save natural capital) are, on average, those with lower emissions per unit of output. Comparing the 2000 and 2005 slopes of this relation, we note that an additional unit of land capital output is associated with a drop in the emissions intensity from 2000 to 2005 of $-0.055$![]() units. Although data on anthropogenic CO$_{2}$
units. Although data on anthropogenic CO$_{2}$![]() emissions do not include emissions from the land use and land cover change, we find that there is a statistically-significant relation between the growth of CO$_{2}$
emissions do not include emissions from the land use and land cover change, we find that there is a statistically-significant relation between the growth of CO$_{2}$![]() emissions per capita and the growth of EVI-adjusted land per capita. Figure 3 shows that, on average, an increase of one percentage point in the latter is associated with a decrease in the growth rate of emissions per capita of 0.33 percentage points, ceteris paribus.
emissions per capita and the growth of EVI-adjusted land per capita. Figure 3 shows that, on average, an increase of one percentage point in the latter is associated with a decrease in the growth rate of emissions per capita of 0.33 percentage points, ceteris paribus.

Figure 2. CO2 emissions per dollar and land capital per dollar (in logs). (a) 2000, (b) 2005. Notes: To compute the CO2 emissions per dollar, we divide CO2 emissions (in kilotons) by the real GDP at constant 2005 national prices (in mil. 2005US). The land capital per dollar is the value of natural capital excluding sub-soil assets divided by the real GDP at constant 2005 national prices (in mil. 2005US). The left-hand side regression has a slope parameter of -.131 with a standard error of .058 and $R^2$![]() of 0.05. The right-hand side regression has a slope parameter of -.186 with a standard error of .045 and $R^2$
of 0.05. The right-hand side regression has a slope parameter of -.186 with a standard error of .045 and $R^2$![]() of 0.13.
of 0.13.

Figure 3. Growth of emissions per capita and growth of EVI-adjusted land per capita. Notes: To compute the CO2 emissions per capita, we divide CO2 emissions (in kilotons) by the population (in millions). The EVI-adjusted land per capita is the product of the normalized vegetation index, which is between zero and one, and the land area (in 1000 ha) divided by the total population (in millions). The growth rates of these two variables are annual growth rates. The corresponding regression has a slope parameter of $-.3349$![]() with a standard error of $.1673$
with a standard error of $.1673$![]() and $R^2$
and $R^2$![]() of $0.022$
of $0.022$![]() .
.
Finally, we plot the evolution of CO$_{2}$![]() output ratios and CO$_{2}$
output ratios and CO$_{2}$![]() emissions per capita by income groups. Figure 4 illustrates the evolution of CO$_{2}$
emissions per capita by income groups. Figure 4 illustrates the evolution of CO$_{2}$![]() emissions per dollar (emissions per unit of gross domestic product or GDP) over time. The first observation is the declining trend on emissions per dollar for the high income countries in line with the evidence in Brock and Taylor (Reference Brock and Taylor2010). The second observation is that, unfortunately, this fact is not the rule. In a context of technological progress and resource scarcity, emissions per dollar should reflect a downward trend if cleaner and energy-saving technologies are being adopted. In middle income countries the emissions per dollar present a constant positive trend over time and both in low and low-middle income countries the emissions per dollar have in general increased over the last 50 years, which suggests high inefficiencies in production and/or weak growth processes.
emissions per dollar (emissions per unit of gross domestic product or GDP) over time. The first observation is the declining trend on emissions per dollar for the high income countries in line with the evidence in Brock and Taylor (Reference Brock and Taylor2010). The second observation is that, unfortunately, this fact is not the rule. In a context of technological progress and resource scarcity, emissions per dollar should reflect a downward trend if cleaner and energy-saving technologies are being adopted. In middle income countries the emissions per dollar present a constant positive trend over time and both in low and low-middle income countries the emissions per dollar have in general increased over the last 50 years, which suggests high inefficiencies in production and/or weak growth processes.

Figure 4. CO2 emissions per dollar by income level. (a) High income, (b) Upper-middle income, (c) Low-middle income, (d) Low income. Notes: To compute the CO2 emissions per dollar, we divide CO2 emissions (in kilotons) by the real GDP at constant 2005 national prices (in mil. 2005US). To classify countries by income group we use the Atlas method used by the World Bank.
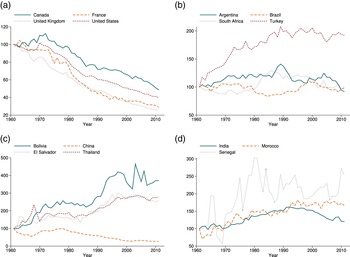
Figure 5 illustrates total CO$_{2}$![]() emissions for the same groups of countries. We can observe, however, that for the high income countries there is not always a tendency for total carbon emissions to fall. Except for the United Kingdom, showing a downward trend over the whole period, high income countries show something like an inverted-U relationship (an EKC) over time. France and the United States follow similar upward trends until the beginning of the eighties, but only France shows a clear downward trend afterwards. Total emissions in the United States and Canada show a very marked upward trend until 2008 and then start to decline, though Canada registers the highest growth in total emissions over the whole period.
emissions for the same groups of countries. We can observe, however, that for the high income countries there is not always a tendency for total carbon emissions to fall. Except for the United Kingdom, showing a downward trend over the whole period, high income countries show something like an inverted-U relationship (an EKC) over time. France and the United States follow similar upward trends until the beginning of the eighties, but only France shows a clear downward trend afterwards. Total emissions in the United States and Canada show a very marked upward trend until 2008 and then start to decline, though Canada registers the highest growth in total emissions over the whole period.

Figure 5. Total CO2 emissions by income level. (a) High income, (b) Upper-middle income, (c) Low-middle income, (d) Low income. Notes: Total CO2 emissions in kilotons. To classify countries by income group we use the Atlas method used by the World Bank.
3. The framework
This section proposes an extension of the Green Solow model of Brock and Taylor (Reference Brock and Taylor2010) by incorporating a renewable natural (land) capital input and a land degradation function.
3.1. Adding land capital to the Green Solow model
The level of economic activity is represented by an aggregate production function, $F( K,Z,BL)$![]() , satisfying the standard neoclassical properties. In this function, $K$
, satisfying the standard neoclassical properties. In this function, $K$![]() represents manufactured capital, $Z$
represents manufactured capital, $Z$![]() is land capital, $L$
is land capital, $L$![]() is labor, and $B$
is labor, and $B$![]() is a labor-augmenting technology parameter that grows exogenously at the rate $g_{B}$
is a labor-augmenting technology parameter that grows exogenously at the rate $g_{B}$![]() . We assume that the labor supply of the economy is equal to the population size and that population grows at the rate $g_{L}$
. We assume that the labor supply of the economy is equal to the population size and that population grows at the rate $g_{L}$![]() , which is also exogenous. For simplicity, and since we are interested in finding convenient closed-form solutions for the empirical analysis, we assume that $F$
, which is also exogenous. For simplicity, and since we are interested in finding convenient closed-form solutions for the empirical analysis, we assume that $F$![]() is a Cobb-Douglas production function,
is a Cobb-Douglas production function,
Land capital, $Z=Q\cdot N,$![]() is an environmental asset that results from the combination of environmental knowledge, $Q$
is an environmental asset that results from the combination of environmental knowledge, $Q$![]() , and a quality (EVI-adjusted) land area, $N.$
, and a quality (EVI-adjusted) land area, $N.$![]() Environmental knowledge is the result of learning and adapting the existing knowledge to land services, which is costly.Footnote 6 Thus, given a fixed land area, land productivity is captured by the product of the biological index (normalized EVI) and the knowledge factor, which is modelled just as a land-augmenting efficiency factor.Footnote 7 The definition of land capital is related to the soil input in Braussman and Bretscheger (Reference Braussman and Bretscheger2018), where the quality and quantity aspects of soil are important. In that model, soil investments include both investment effort to increase productivity and land clearing to increase quantity, but they only study aggregate investment in an integrated manufactured capital-soil asset. Here, we treat land in a broad sense, including all land resources (not only soil) and consider land capital investment and manufactured capital investment separately. Nevertheless, the mechanism by which the productivity of the natural input can be improved is the same as in Braussman and Bretscheger (Reference Braussman and Bretscheger2018); the rise in productivity is driven by the amount of environmental investment. We assume that the resulting environmental knowledge is proportional to the amount spent on environmental investment, $I_{z},$
Environmental knowledge is the result of learning and adapting the existing knowledge to land services, which is costly.Footnote 6 Thus, given a fixed land area, land productivity is captured by the product of the biological index (normalized EVI) and the knowledge factor, which is modelled just as a land-augmenting efficiency factor.Footnote 7 The definition of land capital is related to the soil input in Braussman and Bretscheger (Reference Braussman and Bretscheger2018), where the quality and quantity aspects of soil are important. In that model, soil investments include both investment effort to increase productivity and land clearing to increase quantity, but they only study aggregate investment in an integrated manufactured capital-soil asset. Here, we treat land in a broad sense, including all land resources (not only soil) and consider land capital investment and manufactured capital investment separately. Nevertheless, the mechanism by which the productivity of the natural input can be improved is the same as in Braussman and Bretscheger (Reference Braussman and Bretscheger2018); the rise in productivity is driven by the amount of environmental investment. We assume that the resulting environmental knowledge is proportional to the amount spent on environmental investment, $I_{z},$![]() per unit of land. Taking into account the depreciation of knowledge, which occurs at the rate $\delta _{Q}$
per unit of land. Taking into account the depreciation of knowledge, which occurs at the rate $\delta _{Q}$![]() , the net environmental productivity gains are
, the net environmental productivity gains are
In addition, the economic activity generates a negative production externality on land quality, which is assumed to be proportional to the land capital intensity of economic activity, $\Psi \frac {F}{Z}$![]() , where $\Psi$
, where $\Psi$![]() is a constant externality parameter. This externality includes, for example, land damage from industrial residuals, inadequate management of households’ residuals and harmful soil management practices. With this specification, given output and land endowment, larger stocks of environmental knowledge tend to alleviate the effect of production on land degradation. We follow Braussman and Bretscheger (Reference Braussman and Bretscheger2018) and assume that the economy's efforts in protection and abatement activities decrease the human-induced damage on land quality. We define the net damage as $( \Psi F-\Psi P) /Z$
is a constant externality parameter. This externality includes, for example, land damage from industrial residuals, inadequate management of households’ residuals and harmful soil management practices. With this specification, given output and land endowment, larger stocks of environmental knowledge tend to alleviate the effect of production on land degradation. We follow Braussman and Bretscheger (Reference Braussman and Bretscheger2018) and assume that the economy's efforts in protection and abatement activities decrease the human-induced damage on land quality. We define the net damage as $( \Psi F-\Psi P) /Z$![]() , where protection $P$
, where protection $P$![]() is a strictly concave constant returns to scale function of total output and the economy's protection efforts, $P( F,\theta F)$
is a strictly concave constant returns to scale function of total output and the economy's protection efforts, $P( F,\theta F)$![]() , with $\theta$
, with $\theta$![]() being the fraction of output spent on protection and abatement activities. Then, we can write the evolution of the quality (EVI)-land $N$
being the fraction of output spent on protection and abatement activities. Then, we can write the evolution of the quality (EVI)-land $N$![]() as
as
where the function $\mu$![]() represents the overall rate of land degradation; $\delta _{N}-\eta$
represents the overall rate of land degradation; $\delta _{N}-\eta$![]() is the exogenous rate of land depreciation upon use in production net of natural regeneration; $P( 1,\theta )$
is the exogenous rate of land depreciation upon use in production net of natural regeneration; $P( 1,\theta )$![]() represents total protection per unit of output; and so $\Psi p( \theta )$
represents total protection per unit of output; and so $\Psi p( \theta )$![]() is net damage per unit of output. Then, taking into account (2), (3) and (4), the evolution of $Z$
is net damage per unit of output. Then, taking into account (2), (3) and (4), the evolution of $Z$![]() can be written as
can be written as
In this framework, gross output net of protection and abatement expenditures, $( 1-\theta ) F$![]() , will be allocated to consumption, $C$
, will be allocated to consumption, $C$![]() , environmental investment, $I_{Z}$
, environmental investment, $I_{Z}$![]() , and manufactured capital investment, $I_{K}$
, and manufactured capital investment, $I_{K}$![]() . So, given a constant rate of depreciation of manufactured capital, $\delta _{K}$
. So, given a constant rate of depreciation of manufactured capital, $\delta _{K}$![]() , we can write the evolution of $K$
, we can write the evolution of $K$![]() as
as
Let $s_{K}$![]() and $s_{Z}$
and $s_{Z}$![]() be the exogenous investment rates of manufactured capital and land capital out of $( 1-\theta ) F$
be the exogenous investment rates of manufactured capital and land capital out of $( 1-\theta ) F$![]() , respectively. Then, transforming the measures of output, manufactured capital and land capital into intensive units, and defining the normalized variable of $X$
, respectively. Then, transforming the measures of output, manufactured capital and land capital into intensive units, and defining the normalized variable of $X$![]() as $x\equiv X/BL,$
as $x\equiv X/BL,$![]() capital accumulation in the extended Green Solow model with land degradation is given by
capital accumulation in the extended Green Solow model with land degradation is given by
3.1.1. Balanced growth in the extended Green Solow model
A Balanced Growth (BG) solution to manufactured capital and land capital accumulation is a stationary solution $( k^{\ast },z^{\ast })$![]() to the above system, where $K$
to the above system, where $K$![]() , $Z$
, $Z$![]() and $F$
and $F$![]() will grow at the rate $g_{B}+g_{L},$
will grow at the rate $g_{B}+g_{L},$![]() and the corresponding per capita variables at the rate $g_{B}.$
and the corresponding per capita variables at the rate $g_{B}.$![]() This solution exists and it is unique as long as $\upsilon s_{Z}( 1-\theta ) -\Psi p( \theta ) >0$
This solution exists and it is unique as long as $\upsilon s_{Z}( 1-\theta ) -\Psi p( \theta ) >0$![]() , that is, that the economy's efforts at investing and protecting land capital are sufficient to counter land degradation. Under this condition, the economy converges to $( k^{\ast },z^{\ast })$
, that is, that the economy's efforts at investing and protecting land capital are sufficient to counter land degradation. Under this condition, the economy converges to $( k^{\ast },z^{\ast })$![]() for any given $k( 0) >0,$
for any given $k( 0) >0,$![]() $z( 0) >0.$
$z( 0) >0.$![]() The corresponding capital output ratios and the BG solution are, respectively:
The corresponding capital output ratios and the BG solution are, respectively:


To close the Green Solow model, we have to add the emissions externality equation. As in Brock and Taylor (Reference Brock and Taylor2010), we assume that each unit of output generates $\Omega$![]() units of pollution that can be in part reduced by the economy's efforts at abatement. The emissions abatement function is a concave constant returns to scale function of output and the economy's abatement effort, $A( F,\theta ^{a}F)$
units of pollution that can be in part reduced by the economy's efforts at abatement. The emissions abatement function is a concave constant returns to scale function of output and the economy's abatement effort, $A( F,\theta ^{a}F)$![]() , where $\theta ^{a}$
, where $\theta ^{a}$![]() is the fraction of output spent specifically on air emissions abatement. So the level of emissions released into the atmosphere is $E=( 1-A( 1,\theta ^{a}) ) \Omega F( K,Z,BL) ,$
is the fraction of output spent specifically on air emissions abatement. So the level of emissions released into the atmosphere is $E=( 1-A( 1,\theta ^{a}) ) \Omega F( K,Z,BL) ,$![]() or in terms of the normalized variables:
or in terms of the normalized variables:
where it is assumed that each period technological progress in abatement makes the intensity of emissions, $\Omega$![]() , fall at the exogenous rate $g_{A}.$
, fall at the exogenous rate $g_{A}.$![]() To this setting we add a link between the growth rate of emissions and the change in land capital intensity of economic activity, trying to incorporate the facts illustrated in figures 2 and 3. Specifically, taking into account equation (4), we assume that
To this setting we add a link between the growth rate of emissions and the change in land capital intensity of economic activity, trying to incorporate the facts illustrated in figures 2 and 3. Specifically, taking into account equation (4), we assume that

where the parameter $\zeta$![]() captures the sensitivity of emissions intensity to the change in the land degradation rate. We call this parameter the environmental stress parameter. Since environmental stress appears when the demand or use of a natural factor grows faster than its natural supply, land degradation is a form of environmental stress. Assuming that the growth rate of demand for natural capital services is proportional to the growth rate of economic activity, the difference between the growth rate of output and the growth rate of natural capital supply will capture the extent of this environmental stress. However, note that along the BG solution, total output and total capital output will grow at the same rate, so
captures the sensitivity of emissions intensity to the change in the land degradation rate. We call this parameter the environmental stress parameter. Since environmental stress appears when the demand or use of a natural factor grows faster than its natural supply, land degradation is a form of environmental stress. Assuming that the growth rate of demand for natural capital services is proportional to the growth rate of economic activity, the difference between the growth rate of output and the growth rate of natural capital supply will capture the extent of this environmental stress. However, note that along the BG solution, total output and total capital output will grow at the same rate, so
Therefore, the long-run air quality condition, $g_{E}^{\ast }<0,$![]() and sustained output growth, $g_{B}>0$
and sustained output growth, $g_{B}>0$![]() , will imply the same sustainability restrictions as in Brock and Taylor (Reference Brock and Taylor2010):
, will imply the same sustainability restrictions as in Brock and Taylor (Reference Brock and Taylor2010):
3.2. Parameter values
In this subsection we discuss the numerical values that will be assigned to some technology and environmental parameters, which will be assumed to be the same across countries in the empirical analysis, and compute the investment rates implied by the model. We take the US economy as the reference for most of the parameters, assuming that it is on its balanced growth path.
The US average growth rates of population and income per capita over the last 30 years are $1$![]() per cent and $2$
per cent and $2$![]() per cent, respectively. So the estimated rate of technological progress is also $2$
per cent, respectively. So the estimated rate of technological progress is also $2$![]() per cent, $g_{B}=0.02$
per cent, $g_{B}=0.02$![]() . The factor shares of total output in the Cobb-Douglas technology can be calibrated using the respective factor income shares of total GDP. The problem we face here is that the natural factor comprises the value of services that do not always have a market value. We will rely on the World Bank's estimates provided in “Changing wealth of nations, measuring sustainable development in the new millennium” (World Bank, 2011, table 5.4), where the elasticities of output for all countries with respect to natural capital and produced capital are $0.068$
. The factor shares of total output in the Cobb-Douglas technology can be calibrated using the respective factor income shares of total GDP. The problem we face here is that the natural factor comprises the value of services that do not always have a market value. We will rely on the World Bank's estimates provided in “Changing wealth of nations, measuring sustainable development in the new millennium” (World Bank, 2011, table 5.4), where the elasticities of output for all countries with respect to natural capital and produced capital are $0.068$![]() and $0.32$
and $0.32$![]() , respectively. These values are similar to the land and capital income shares estimated by Valentinyi and Herrendof (Reference Valentinyi and Herrendof2008) from the USA input-output dataset, which are $0.05$
, respectively. These values are similar to the land and capital income shares estimated by Valentinyi and Herrendof (Reference Valentinyi and Herrendof2008) from the USA input-output dataset, which are $0.05$![]() and $0.33$
and $0.33$![]() , respectively. The ratios of land capital and manufactured capital to output can be calculated from the World Bank data available for the years 1995, 2000 and 2005. These data imply an average value of produced capital to gross national income equal to $2.27$
, respectively. The ratios of land capital and manufactured capital to output can be calculated from the World Bank data available for the years 1995, 2000 and 2005. These data imply an average value of produced capital to gross national income equal to $2.27$![]() , and an average value of natural capital excluding sub-soil assets (crop land, pasture land, forest land and protected areas) to gross output equal to $0.29.$
, and an average value of natural capital excluding sub-soil assets (crop land, pasture land, forest land and protected areas) to gross output equal to $0.29.$![]()
With respect to the depreciation rate of manufactured capital, we can set $\delta _{K}=0.1$![]() , a frequent value in global economy models (e.g., Lanz et al., Reference Lanz, Dietz and Swanson2017a; Hwang et al., Reference Hwang, Tol and Hofkes2019), or $\delta _{K}=0.05$
, a frequent value in global economy models (e.g., Lanz et al., Reference Lanz, Dietz and Swanson2017a; Hwang et al., Reference Hwang, Tol and Hofkes2019), or $\delta _{K}=0.05$![]() , a standard value in the growth literature.Footnote 8 However, we do not have standard values for the depreciation of land. To assign values to $( \delta _{N}-\eta )$
, a standard value in the growth literature.Footnote 8 However, we do not have standard values for the depreciation of land. To assign values to $( \delta _{N}-\eta )$![]() and $\mu$
and $\mu$![]() in equation (4), we will assume that the former corresponds to the part of land degradation that is directly due to agricultural activities. Based on the NDVI, Bai et al. (Reference Bai, Dent, Olsson and Schaepman2008) estimate that the degrading land for the USA over $1981-2003$
in equation (4), we will assume that the former corresponds to the part of land degradation that is directly due to agricultural activities. Based on the NDVI, Bai et al. (Reference Bai, Dent, Olsson and Schaepman2008) estimate that the degrading land for the USA over $1981-2003$![]() accounted for $20.6$
accounted for $20.6$![]() per cent of total land area, which would imply an annual average degrading rate of $1$
per cent of total land area, which would imply an annual average degrading rate of $1$![]() per cent over that period given that significant human-induced land degradation started 200 years ago. Assuming $\ 23$
per cent over that period given that significant human-induced land degradation started 200 years ago. Assuming $\ 23$![]() per cent of total degraded area is due to agricultural activities, this would imply an annual depreciation rate due to agriculture of around $0.18$
per cent of total degraded area is due to agricultural activities, this would imply an annual depreciation rate due to agriculture of around $0.18$![]() per cent.Footnote 9 In summary, we fix $\mu ^{\ast }=0.01$
per cent.Footnote 9 In summary, we fix $\mu ^{\ast }=0.01$![]() and $( \delta _{N}-\eta ) =0.0018$
and $( \delta _{N}-\eta ) =0.0018$![]() .Footnote 10 With these values, we can use equation (4) and the land capital output ratio set above, $z/f=0.29$
.Footnote 10 With these values, we can use equation (4) and the land capital output ratio set above, $z/f=0.29$![]() , to get an estimate for the net human-induced damage factor, $\Psi p( \theta ) =0.0024.$
, to get an estimate for the net human-induced damage factor, $\Psi p( \theta ) =0.0024.$![]() Under a situation of zero protection effort, this equation would imply a damage parameter of $\Psi =0.0024.$
Under a situation of zero protection effort, this equation would imply a damage parameter of $\Psi =0.0024.$![]() Finally, regarding land capital depreciation, we consider a depreciation rate of environmental research equal to $\delta _{Q}=0.1,$
Finally, regarding land capital depreciation, we consider a depreciation rate of environmental research equal to $\delta _{Q}=0.1,$![]() as in the active learning approach of Hwang et al. (Reference Hwang, Tol and Hofkes2019).
as in the active learning approach of Hwang et al. (Reference Hwang, Tol and Hofkes2019).
The enacted budgets of the Environmental Protection Agency (EPA) yield an average agency budget share of GDP around $0.058$![]() per cent per year over $1998-2018$
per cent per year over $1998-2018$![]() , with a maximum $0.08$
, with a maximum $0.08$![]() per cent share in $1998$
per cent share in $1998$![]() and around $0.04$
and around $0.04$![]() per cent since $2014$
per cent since $2014$![]() . Data from the US Department of Agriculture (USDA) budget outlays report spending shares of natural resources conservation service and wildland fire management that add up to $0.02$
. Data from the US Department of Agriculture (USDA) budget outlays report spending shares of natural resources conservation service and wildland fire management that add up to $0.02$![]() per cent every year over $2006-2015.$
per cent every year over $2006-2015.$![]() With respect to pollution abatement costs, Brock and Taylor (Reference Brock and Taylor2010) report a GDP share of $1.6$
With respect to pollution abatement costs, Brock and Taylor (Reference Brock and Taylor2010) report a GDP share of $1.6$![]() per cent, or $0.5$
per cent, or $0.5$![]() per cent if abatement costs refer specifically to air pollutants. Altogether, these estimates suggest an average protection and abatement expenditure share $\theta$
per cent if abatement costs refer specifically to air pollutants. Altogether, these estimates suggest an average protection and abatement expenditure share $\theta$![]() of GDP around $1.68$
of GDP around $1.68$![]() per cent.
per cent.
Taking into account these parameter values, we use equations (9 ) and (10) to compute the implied investment rates of the model. The investment rate for manufactured capital is $18$![]() or $30$
or $30$![]() per cent depending on whether the depreciation rate considered is $5$
per cent depending on whether the depreciation rate considered is $5$![]() or $10$
or $10$![]() per cent, respectively, which is consistent with average historical values of the USA economy of around 20 per cent. In contrast, the implied investment rate for land capital hinges on the conversion factor of environmental investment, $0.04/\upsilon,$
per cent, respectively, which is consistent with average historical values of the USA economy of around 20 per cent. In contrast, the implied investment rate for land capital hinges on the conversion factor of environmental investment, $0.04/\upsilon,$![]() and we do not have systematic historical data to compare with. The environmental research spending that we have found for the USA economy (which for other countries is even worse) refers to the USDA annual spending on Agricultural, Forest and Rangeland research services over $2006-2015$
and we do not have systematic historical data to compare with. The environmental research spending that we have found for the USA economy (which for other countries is even worse) refers to the USDA annual spending on Agricultural, Forest and Rangeland research services over $2006-2015$![]() and to the EPA annual spending in Science and Technology over $2010-2018.$
and to the EPA annual spending in Science and Technology over $2010-2018.$![]() They yield annual average GDP shares of $0.0098$
They yield annual average GDP shares of $0.0098$![]() and $0.004$
and $0.004$![]() per cent, respectively. Altogether these values would imply an environmental investment rate of $\ 0.014$
per cent, respectively. Altogether these values would imply an environmental investment rate of $\ 0.014$![]() per cent, which assuming a very optimistic conversion factor $\upsilon =1,$
per cent, which assuming a very optimistic conversion factor $\upsilon =1,$![]() would clearly be well below the $4$
would clearly be well below the $4$![]() per cent investment rate implied by the model. Note that this parameter captures the conversion of foregone consumption (or manufactured capital) to environmental knowledge, and so it is a key parameter, together with $\Psi$
per cent investment rate implied by the model. Note that this parameter captures the conversion of foregone consumption (or manufactured capital) to environmental knowledge, and so it is a key parameter, together with $\Psi$![]() in the tradeoff between land protection and land investment efforts.
in the tradeoff between land protection and land investment efforts.
Finally, we assign values to $\zeta$![]() (the environmental stress parameter of emissions) and $g_{A}$
(the environmental stress parameter of emissions) and $g_{A}$![]() (the rate of technological progress in air emissions abatement). Figure 2 implies that the estimated change in emissions intensity from $2000$
(the rate of technological progress in air emissions abatement). Figure 2 implies that the estimated change in emissions intensity from $2000$![]() to $2005$
to $2005$![]() due to an additional unit of land capital output ratio is, on average, $-0.055.$
due to an additional unit of land capital output ratio is, on average, $-0.055.$![]() So we fix the environmental stress parameter (partial effect of the change in the output land capital ratio on the change of emissions intensity in equation (14)) to $\zeta =0.055.$
So we fix the environmental stress parameter (partial effect of the change in the output land capital ratio on the change of emissions intensity in equation (14)) to $\zeta =0.055.$![]() With respect to the rate of technological progress in air emissions abatement, first we note that since emissions per capita have been falling at an average rate of $-0.6$
With respect to the rate of technological progress in air emissions abatement, first we note that since emissions per capita have been falling at an average rate of $-0.6$![]() per cent per year and population has been rising at an average rate of $1$
per cent per year and population has been rising at an average rate of $1$![]() per cent per year, the growth rate of total emissions is positive in the USA economy. In other words, these data do not satisfy the sustainability condition in emissions, $g_{E}^{\ast }<0.$
per cent per year, the growth rate of total emissions is positive in the USA economy. In other words, these data do not satisfy the sustainability condition in emissions, $g_{E}^{\ast }<0.$![]() Note that equation (15) would imply that $g_{A}=g_{B}+g_{L}-g_{E}^{\ast }=0.026,$
Note that equation (15) would imply that $g_{A}=g_{B}+g_{L}-g_{E}^{\ast }=0.026,$![]() thus, violating the condition that requires long-run sustainability, $g_{A}>0.03$
thus, violating the condition that requires long-run sustainability, $g_{A}>0.03$![]() .
.
Table 1 summarizes the calibrated parameters. The empirical tests in the regression analysis will confirm that most of these parameter values are reasonable.
Table 1. Calibrated parameters

4. Empirical analysis
4.1. Econometric specification
In this section we derive the estimating equation and estimate the model using the data described in section 2.1. Our purpose is to explore how the EVI-adjusted land input, economic activity and actual environmental policies affect the growth of emissions per capita. To do that, we rewrite equation ( 13) in per capita terms,
where $x^{c}$![]() is variable $x$
is variable $x$![]() in per capita terms. Differentiating with respect to time and taking into account expression (14), we obtain the growth rate of emissions per capita,
in per capita terms. Differentiating with respect to time and taking into account expression (14), we obtain the growth rate of emissions per capita,

As our data is discrete and we are interested in a time horizon of size T, we follow the approach in Mankiw et al. (Reference Mankiw, Romer and Weil1992) and Brock and Taylor (Reference Brock and Taylor2010), approximating the continuous growth rates of emissions per capita and income per capita by their log changes, and the growth rate over a given period by the average of log changes:
Next, following the standard approach we log-linearize the growth of income per capita and land capital per capita around the model's steady state:Footnote 11
where $\gamma _{y}$![]() and $\gamma _{z}$
and $\gamma _{z}$![]() denote the long-run convergence rates of $y$
denote the long-run convergence rates of $y$![]() and $z$
and $z$![]() , given by $\gamma _{y}\approx ( 1-\alpha -\beta ) (\delta +g_{B}+g_{L})$
, given by $\gamma _{y}\approx ( 1-\alpha -\beta ) (\delta +g_{B}+g_{L})$![]() and $\gamma _{z}\approx ( 1-\beta ) ( \delta +g_{B}+g_{L})$
and $\gamma _{z}\approx ( 1-\beta ) ( \delta +g_{B}+g_{L})$![]() , respectively. Substituting $y^{c\ast }=( 1-\theta ) Bk^{\ast ^{\alpha }}z^{\ast ^{\beta }}$
, respectively. Substituting $y^{c\ast }=( 1-\theta ) Bk^{\ast ^{\alpha }}z^{\ast ^{\beta }}$![]() into equation (19) and using equation (17) to get $y_{t-T}^{c}=\frac {( 1-\theta ) e_{t-T}^{c}}{a(\theta )\Omega _{t-T}}$
into equation (19) and using equation (17) to get $y_{t-T}^{c}=\frac {( 1-\theta ) e_{t-T}^{c}}{a(\theta )\Omega _{t-T}}$![]() , we can rewrite (18) and obtain the estimating equation:
, we can rewrite (18) and obtain the estimating equation:


Thus, the average change in emissions per capita over a period of length $T$![]() is determined by the initial value of emissions per capita, $e_{t-T}^{c}$
is determined by the initial value of emissions per capita, $e_{t-T}^{c}$![]() , the initial value of land capital per capita, $z_{t-T}^{c}$
, the initial value of land capital per capita, $z_{t-T}^{c}$![]() , and a set of variables that capture the effect of income per capita in the long run. These variables are the manufactured capital investment rate, $s_{k}$
, and a set of variables that capture the effect of income per capita in the long run. These variables are the manufactured capital investment rate, $s_{k}$![]() ; the land capital investment rate, $s_{z}$
; the land capital investment rate, $s_{z}$![]() ; the abatement effort, $\theta$
; the abatement effort, $\theta$![]() ; the human-induced damage, $\Psi$
; the human-induced damage, $\Psi$![]() ; and the depreciation term, $( \delta +g_{B}+g_{L})$
; and the depreciation term, $( \delta +g_{B}+g_{L})$![]() , which depends on the depreciation rate of capital ($\delta =\delta _{k}=\delta _{z}$
, which depends on the depreciation rate of capital ($\delta =\delta _{k}=\delta _{z}$![]() ), the rate of labor-augmenting technological progress, $g_{B}$
), the rate of labor-augmenting technological progress, $g_{B}$![]() , and the rate of population growth, $g_{L}$
, and the rate of population growth, $g_{L}$![]() .
.
4.2. Empirical results
Data used in the econometric analysis were described in sections 2 and 3.2. To summarize briefly, for emissions we consider data on CO$_{2}$![]() in kilotons (kt) from the World Development Indicators 2016. For data on population, GDP and GDP share of manufactured capital investment, we collect data from the Penn World Table. Data on abatement efforts come from the OECD, and data related to land capital come from different sources: natural capital excluding sub-soil assets from the World Bank, land area from FAO, and EVI data from the NASA Earth Observatory.
in kilotons (kt) from the World Development Indicators 2016. For data on population, GDP and GDP share of manufactured capital investment, we collect data from the Penn World Table. Data on abatement efforts come from the OECD, and data related to land capital come from different sources: natural capital excluding sub-soil assets from the World Bank, land area from FAO, and EVI data from the NASA Earth Observatory.
The time period under analysis is 2000–2011. Recall that land capital in the model is defined as $Z=Q\ast EVI\ast \overline {N}$![]() , and that data on this asset is only available from the World Bank for a few years. We proxy $Z$
, and that data on this asset is only available from the World Bank for a few years. We proxy $Z$![]() by the EVI-adjusted land variable and the land capital investment term by the World Bank capital output ratio estimates. By doing this, first note that the constant term in equation (21) will include an additional term proportional to $\ln Q_{t-T}$
by the EVI-adjusted land variable and the land capital investment term by the World Bank capital output ratio estimates. By doing this, first note that the constant term in equation (21) will include an additional term proportional to $\ln Q_{t-T}$![]() . Second, using the land capital output data and the calibrated values of $\delta _{Z}=0.1$
. Second, using the land capital output data and the calibrated values of $\delta _{Z}=0.1$![]() , $g_{B}=0.02$
, $g_{B}=0.02$![]() and $g_{L}=0.01$
and $g_{L}=0.01$![]() , we obtain from equation (9) the country values of the variable $\upsilon s_{Z}(1-\theta )-p( \theta ) \Psi$
, we obtain from equation (9) the country values of the variable $\upsilon s_{Z}(1-\theta )-p( \theta ) \Psi$![]() to be used in the estimation of (21). It is worth mentioning that $s_{z}{}_{i},$
to be used in the estimation of (21). It is worth mentioning that $s_{z}{}_{i},$![]() $s_{k}{}_{i}$
$s_{k}{}_{i}$![]() , $\theta _{i}$
, $\theta _{i}$![]() and $( \delta +g_{B}+g_{L}) _{i}$
and $( \delta +g_{B}+g_{L}) _{i}$![]() are time-average country specific. Moreover, we follow Brock and Taylor (Reference Brock and Taylor2010) and set the abatement technology factor as $a(\theta ^{a})=(1-\theta ^{a})^{\varepsilon }$
are time-average country specific. Moreover, we follow Brock and Taylor (Reference Brock and Taylor2010) and set the abatement technology factor as $a(\theta ^{a})=(1-\theta ^{a})^{\varepsilon }$![]() , with $\varepsilon >1$
, with $\varepsilon >1$![]() . As the abatement intensity for carbon is close to zero, we set $\theta ^{a}=0.005$
. As the abatement intensity for carbon is close to zero, we set $\theta ^{a}=0.005$![]() for every country.
for every country.
Finally, regarding the variable $(\delta +g_{B}+g_{L})$![]() , we use the population data to find the population growth over the period 2000–2011, and use the calibrated values of $\delta _{k}=0.1$
, we use the population data to find the population growth over the period 2000–2011, and use the calibrated values of $\delta _{k}=0.1$![]() and $g_{B}=0.02$
and $g_{B}=0.02$![]() . Thus, this term captures only the variation in population growth rates across countries. The study covers 146 countries; the country sample is limited by the availability of data in the Penn World Table.
. Thus, this term captures only the variation in population growth rates across countries. The study covers 146 countries; the country sample is limited by the availability of data in the Penn World Table.
To estimate the model, we follow Barro (Reference Barro1991), Durlauf and Johnson (Reference Durlauf and Johnson1995), Brock and Taylor (Reference Brock and Taylor2010), and others, and employ the heteroskedasticity-corrected standard error estimates. The estimation results are presented in table 2 and the empirical tests presented have to be interpreted as a test of the devised model.Footnote 12 Column A presents the unconditional convergence results, column B reports the results for the shorter specification of the model (controlling only for the initial value of land capital) and columns C-E report the results for the longer specification of the model. Columns A-C include all countries in our sample while columns D and E only include the upper-middle income and the low income countries, respectively.Footnote 13
Table 2. Estimated model results for CO2 emissions per capita growth rates

Notes: Standard errors are in parentheses. Columns (A) and (B) estimate the short version of our model described in (21) and the remaining columns estimate the longer version of the model. Columns (A)-(C) include all countries in the sample while Columns (D) and (E) only include the upper-middle income and the low income countries, respectively. Column (C) is the preferred model. The dependent variable is the average growth rate in log emissions per capita over the 2000–2011 period, $e_{t-T}^c$![]() is the emissions per capita in 2000, $z_{t-T}^c$
is the emissions per capita in 2000, $z_{t-T}^c$![]() is the land capital per capita in 2000 (proxied by the EVI-adjusted land per capita), the $s_{k}$
is the land capital per capita in 2000 (proxied by the EVI-adjusted land per capita), the $s_{k}$![]() is the average capital investment to GDP ratio over the 2000–2011 period, $(\delta +g_{B}+g_{L})$
is the average capital investment to GDP ratio over the 2000–2011 period, $(\delta +g_{B}+g_{L})$![]() is the average population growth over the period where $\delta$
is the average population growth over the period where $\delta$![]() is set equal to 0.1, $g_{B}$
is set equal to 0.1, $g_{B}$![]() is set equal to 0.02 and $s_{z}$
is set equal to 0.02 and $s_{z}$![]() represents the land capital investment rate net of land degradation (proxied by the average land capital output ratio).
represents the land capital investment rate net of land degradation (proxied by the average land capital output ratio).
The Green Solow model with land capital explains quite well the cross-country variation in the growth rates of CO$_{2}$![]() emissions per capita over the period 2000–2011. The short version of the empirical model (column B) shows that the negative coefficient of the initial emissions per capita, $\ln e_{t-T}^{c}$
emissions per capita over the period 2000–2011. The short version of the empirical model (column B) shows that the negative coefficient of the initial emissions per capita, $\ln e_{t-T}^{c}$![]() , and the positive coefficient of the initial quality-adjusted land per capita, $\ln z_{t-T}^{c}$
, and the positive coefficient of the initial quality-adjusted land per capita, $\ln z_{t-T}^{c}$![]() , are both statistically significant. These results are confirmed by the longer version of the model in column C, which is our preferred model, and by the subsequent restricted country samples (columns D and E). Not surprisingly, the explanatory power of the long version of the model is greater than that of the short version, explaining approximately $24$
, are both statistically significant. These results are confirmed by the longer version of the model in column C, which is our preferred model, and by the subsequent restricted country samples (columns D and E). Not surprisingly, the explanatory power of the long version of the model is greater than that of the short version, explaining approximately $24$![]() per cent of the variation of the per capita carbon emissions growth rates over the period.
per cent of the variation of the per capita carbon emissions growth rates over the period.
The empirical results imply that, given control variables, an equal proportional increase in initial emissions and land capital would reduce the growth rate of emissions per capita (columns B (short version) and C (long version)). That is, the net convergence effect (i.e., the combined impact from initial per capita values of emissions and land capital on the growth rate of emissions per capita) is negative and statistically significant. Moreover, the speed of convergence (i.e., the reaction of the growth rate of emissions to the initial emissions level) is greater in the long version of the model despite the higher influence of the initial EVI-adjusted land endowment. In the short version of the model (column B), the speed of convergence is slightly lower than in the unconditional convergence case (column A), implying that the omission of the natural endowment might be behind the convergence results in some empirical studies. In the long version of the model (column C), however, the speed of convergence more than doubles the unconditional rate of the shorter version (column B). Figure 6 plots the absolute and conditional convergence results for the whole country sample (columns A, B and C). In other words, if there were identical parameter values across countries (same steady states), the model would predict absolute convergence in emissions per capita but at a slower speed for countries with better initial endowments of EVI-adjusted land.

Figure 6. Unconditional and conditional convergence. (a) Unconditional convergence, (b) Conditional convergence, (c) Conditional convergence. Notes: Panel (a) plots the growth of emissions per capita against the initial emissions per capita. Panel (b) plots the growth of emissions per capita against the initial emissions per capita conditional on the initial adjusted land quality. Panel (c) plots the the growth of emissions per capita against the initial emissions per capita conditional on the initial EVI-adjusted land per capita, the average capital investment share $(s_{k})$![]() , the population growth rate, $(\delta +g_{B}+g_{L})$
, the population growth rate, $(\delta +g_{B}+g_{L})$![]() , and the land capital investment rate net of land degradation $(\upsilon s_{z}(1-\theta )-\Psi p( \theta ) )$
, and the land capital investment rate net of land degradation $(\upsilon s_{z}(1-\theta )-\Psi p( \theta ) )$![]() .
.
A positive and statistically-significant coefficient of the initial EVI-adjusted land means that the implied environmental stress parameter $\zeta$![]() is positive in all estimations (see definition of $\rho _{2}$
is positive in all estimations (see definition of $\rho _{2}$![]() in equation (22)), which is in accordance with the theoretical prediction of the model. Everything else constant, a lower initial value of land capital means a higher growth rate of $z$
in equation (22)), which is in accordance with the theoretical prediction of the model. Everything else constant, a lower initial value of land capital means a higher growth rate of $z$![]() and so a lower growth rate of emissions (see equation (14)). This is a direct negative effect of the growth rate of land capital on the growth rate of emissions. But the theoretical model also establishes an indirect positive effect that goes through the growth of final output; that is, lower initial levels of land capital are associated with lower initial levels of output and so higher growth rates of output and emissions along the transition path. What the empirical result tells us about the role of the initial EVI-adjusted land endowment is that the direct effect dominates. In contrast, the coefficient of the land capital investment rate is negative (statistically significant in all specifications of the model except for the low income country subsample, column D). This coefficient captures the overall long-run effect of land capital intensity on the growth rate of emissions per capita. A higher land capital output ratio means faster land capital growth relative to output growth and a lower emissions intensity. Note that this effect is driven by the effectiveness of technological progress in abatement (equation (11)); without this collateral effect, a higher land capital investment rate would just increase both long-run output and emissions. Thus, the model predicts that the overall effect of investment can slow down the growth rate of emissions per capita through higher investment rates in land capital. No doubt there are other plausible theoretical interpretations arising from alternative frameworks, but the estimates in table 2 have to be interpreted as a test of the extended Green Solow model with land capital.Footnote 14
and so a lower growth rate of emissions (see equation (14)). This is a direct negative effect of the growth rate of land capital on the growth rate of emissions. But the theoretical model also establishes an indirect positive effect that goes through the growth of final output; that is, lower initial levels of land capital are associated with lower initial levels of output and so higher growth rates of output and emissions along the transition path. What the empirical result tells us about the role of the initial EVI-adjusted land endowment is that the direct effect dominates. In contrast, the coefficient of the land capital investment rate is negative (statistically significant in all specifications of the model except for the low income country subsample, column D). This coefficient captures the overall long-run effect of land capital intensity on the growth rate of emissions per capita. A higher land capital output ratio means faster land capital growth relative to output growth and a lower emissions intensity. Note that this effect is driven by the effectiveness of technological progress in abatement (equation (11)); without this collateral effect, a higher land capital investment rate would just increase both long-run output and emissions. Thus, the model predicts that the overall effect of investment can slow down the growth rate of emissions per capita through higher investment rates in land capital. No doubt there are other plausible theoretical interpretations arising from alternative frameworks, but the estimates in table 2 have to be interpreted as a test of the extended Green Solow model with land capital.Footnote 14
Also in accordance with the predictions of the theoretical model, the manufactured capital investment rate has a positive and statistically-significant effect on the growth rate of CO$_{2}$![]() emissions per capita (not statistically significant in the upper-middle income subsample, column D). The population growth effect is not in accordance with Brock and Taylor (Reference Brock and Taylor2010) results (negative or not significant); here it is positive and statistically significant only for the restricted sample of upper-middle income countries. A possible interpretation of this result is that upper-middle income countries are those undergoing faster degradation due to structural changes and greater population pressure.
emissions per capita (not statistically significant in the upper-middle income subsample, column D). The population growth effect is not in accordance with Brock and Taylor (Reference Brock and Taylor2010) results (negative or not significant); here it is positive and statistically significant only for the restricted sample of upper-middle income countries. A possible interpretation of this result is that upper-middle income countries are those undergoing faster degradation due to structural changes and greater population pressure.
These convergence results should be interpreted with caution due to the limited time horizon considered. Nevertheless, they shed light on the mixed evidence about convergence of CO$_{2}$![]() emissions across countries, pointing to the need to account for specific structural characteristics such as climate or natural resources (see Pettersson et al., Reference Pettersson, Maddison, Acar and Soderholm2014 for a review of the literature). Therefore, better international data on environmental services is a prerequisite for more profound analysis of the emissions convergence issue. Another prerequisite, as already mentioned, is better data on emissions from land use and land cover change at the country or regional level.
emissions across countries, pointing to the need to account for specific structural characteristics such as climate or natural resources (see Pettersson et al., Reference Pettersson, Maddison, Acar and Soderholm2014 for a review of the literature). Therefore, better international data on environmental services is a prerequisite for more profound analysis of the emissions convergence issue. Another prerequisite, as already mentioned, is better data on emissions from land use and land cover change at the country or regional level.
Despite the data limitations, the implied values for the key parameters of the model, $\zeta$![]() and $\beta,$
and $\beta,$![]() are very close to the calibrated values reported in table 1. Specifically, using the estimated coefficients of the general case (column B) and equations in (22), the imputed values are $\zeta =0.065$
are very close to the calibrated values reported in table 1. Specifically, using the estimated coefficients of the general case (column B) and equations in (22), the imputed values are $\zeta =0.065$![]() and $\beta =0.051$
and $\beta =0.051$![]() . In contrast, the implied GDP share of manufactured capital, $\alpha =0.697$
. In contrast, the implied GDP share of manufactured capital, $\alpha =0.697$![]() , and the speed of convergence of income per capita, $\gamma _{y}=0.02$
, and the speed of convergence of income per capita, $\gamma _{y}=0.02$![]() , are too large and too low, respectively, compared to reasonable theoretical values, but similar to those reported in Brock and Taylor (Reference Brock and Taylor2010) and other related empirical work (see, for example, Barro and Sala-i-Martin (Reference Barro and Sala-i-Martin2004), chapter 12).
, are too large and too low, respectively, compared to reasonable theoretical values, but similar to those reported in Brock and Taylor (Reference Brock and Taylor2010) and other related empirical work (see, for example, Barro and Sala-i-Martin (Reference Barro and Sala-i-Martin2004), chapter 12).
5. Conclusion
In this paper we collected satellite vegetation data and obtained estimates of the EVI at the country level. We presented some stylized facts on this biological index, natural capital excluding sub-soil assets and carbon emissions. Based on these facts, we defined land capital and proposed an extension of the Green Solow model of Brock and Taylor (Reference Brock and Taylor2010) with land capital investment and land degradation. In our framework land capital is the product of a normalized measure of EVI-adjusted land and an environmental productivity factor that is directly linked to a country's efforts to implement better environmental practices, taking knowledge to practical users, which is costly.
We have shown that the model is consistent with the cross-country variation in growth rates of carbon emissions per capita and that there exists convergence at the global level, with the long-run contribution of land capital investment to the growth rate of emissions being negative and significant in all specifications. Furthermore, we have found a positive effect of initial EVI-adjusted land on the growth of emissions, suggesting that the environmental stress parameter (i.e., the sensitivity of the growth of emissions to the growth in the land capital intensity of economic activity) is positive and statistically significant, in accordance with the theoretical prediction of the model. Furthermore, the estimation results imply that the overall effect of investment in the extended Green Solow model can slow down the growth rate of emissions per capita through higher investment rates in land capital.
Although these empirical results should be interpreted with caution due to data limitations, they shed light on the mixed evidence about convergence of CO$_{2}$![]() emissions across countries, pointing to the need to account for specific structural characteristics such as climate or natural resources in the growth equation, but also to the need for more systematic data on environmental investment and land quality indicators.Footnote 15 To the best of our knowledge at the time of writing this article, previous empirical literature on emissions convergence has not included land quality in the growth equation.
emissions across countries, pointing to the need to account for specific structural characteristics such as climate or natural resources in the growth equation, but also to the need for more systematic data on environmental investment and land quality indicators.Footnote 15 To the best of our knowledge at the time of writing this article, previous empirical literature on emissions convergence has not included land quality in the growth equation.
One limitation of the framework is that emissions are just the reflection of the production externality and do not capture the possible effect of emissions on land degradation through changes in climate conditions, which is beyond the scope of this paper. Moreover, one natural extension of the theoretical model is the development of an optimal growth setup in which to perform a quantitative analysis of the welfare tradeoff between environmental protection and land capital investment efforts and their implications for policy. These are open questions for future research.
Acknowledgments
A previous version of this paper circulated under the title ”Long-run sustainability in the Green Solow model”.
We gratefully acknowledge partial financial support from the Spanish government and FEDER funds under projects PGC2018-093542-B-I00, PID2019-111208GB-I00, and PID2019-107161GB-C33, from the Generalitat Valenciana under AICO/2019/295, and from the Fundação para a Ciê ncia e Tecnologia under the Project UIDB/04007/2020. Open Access funding provided by the Public University of Navarre. We would like to also thank the two anonymous reviewers, the associate editor, the assistant editor (Ms. Dimi Xepapadeas), and the editor (Dr. Carlos Chávez), for their insightful comments on this article.
Competing interests
The authors declare none.