1. Introduction
Alfvén waves (AWs) were first theoretically predicted by Hannes Alfvén in 1942 and later verified experimentally by Bostick and Levine in [Reference Bostick and Levine1]. These are the low-frequency electromagnetic waves propagating along the background magnetic field in space and laboratory plasmas [Reference Alfvén2, Reference Gekelman3]. These waves are nondispersive in nature but can obtain dispersive properties due to finite frequency correction and finite electron inertia effects [Reference Shukla, Stenflo, Passot and Sulem4] in low-β plasmas with
![]() (whereme/mi is the ratio of the electron mass to the ion mass and β is the ratio of the thermal pressure to the magnetic pressure). When their perpendicular length scales become finite and comparable to the electron inertial length [Reference Goertz and Boswell5] or to the ion gyroradius/finite gyroradius, these waves become dispersive in nature and are known as dispersive Alfvén waves (DAWs). The most vital physical property of the DAWs is the presence of the finite parallel electric field [Reference Hollweg6]. Inertial Alfvén waves (IAWs) are known to play a vital role in the energization of the auroral plasma [Reference Chaston7, Reference Wygant, Keiling and Cattell8].
(whereme/mi is the ratio of the electron mass to the ion mass and β is the ratio of the thermal pressure to the magnetic pressure). When their perpendicular length scales become finite and comparable to the electron inertial length [Reference Goertz and Boswell5] or to the ion gyroradius/finite gyroradius, these waves become dispersive in nature and are known as dispersive Alfvén waves (DAWs). The most vital physical property of the DAWs is the presence of the finite parallel electric field [Reference Hollweg6]. Inertial Alfvén waves (IAWs) are known to play a vital role in the energization of the auroral plasma [Reference Chaston7, Reference Wygant, Keiling and Cattell8].
In the literature, several authors have studied the strong density depletion in the low-β plasma. Wu et al. [Reference Wu, Wang and Lu9] discussed the density depletion in the corona due to the presence of beams of energetic particles and magnetic compression.
Many researchers [Reference Wu and Chao10, Reference Wu, Huang and Wang11] have pointed out the role of solitary IAWs, which are accompanied by both density dips and humps in auroral particle heating. In the literature, it has been suggested that these cavities are associated with the ponderomotive nonlinearity of the inertial Alfvén wave [Reference Bellan and Stasiewicz12].
The nonlinear evolution of IAWs and magnetosonic waves (MSWs) taking nonadiabatic response of the magnetic field for the low-β plasmas is carried out by many researchers. These cavities are known to be associated with low-frequency electromagnetic perturbations and have perpendicular width of the order of the electron skin depth, i.e., c/ωpe [Reference Benson and Hilgers13–Reference Chaston, Carlson, McFadden and Strangeway15].
Observational signatures of the presence of AWs in auroral regions of Earth’s ionosphere are also reported in the literature [Reference Dubinin, Israelevich, Kutiev and NikolaevaNS16, Reference Stasiewicz, Holmgren and Zanetti17]. Several observed phenomena in the space plasmas are known to be associated with the nonlinear DAWs. Many authors have studied various mechanisms of electron acceleration and ion heating through DAWs. Hasegawa and Chen [Reference Hasegawa and Chen18] discussed the utilization of Alfvén waves in the heating of plasma particles. Stochastic ion heating by the decay of the DAW was reported by Stasiewicz et al. [Reference Stasiewicz, Bellan and Chaston19]. Besides Hasegawa and Stasiewicz, other researchers also studied different mechanisms of particle acceleration such as modulation instabilities [Reference Buti, Velli, Liewer, Goldstein and Hada20], turbulent dissipation [Reference Goldstein and Roberts21–Reference Zhao, Wu and Lu23], and field localization [Reference Sundkvist, Krasnoselskikh and Shukla24]. Zhao et al. [Reference Zhao, Wu, Yu and Lu25, Reference Zhao, Wu, LU, Yang and Yu26] also studied nonlinear interaction between kinetic Alfvén waves (KAWs) and the electrostatic and magnetostatic convective cells in plasmas. The formation of coherent structures in auroral plasmas is governed by the nonlinear dispersion relation and interaction of KAW and convective cells. The localized structures thus obtained offer a possible mechanism for the dissipation and offer a possible way of energy transportation from larger scales to the smaller scales.
The nonlinear coupling between IAWs and MSWs, taking ponderomotive force into account, has also been investigated in a great deal in the literature which plays a crucial role for the particle acceleration and plasma heating in the space plasma. Kumar and Singh [Reference Kumar and Singh27] examined the nonlinear interplay between the low-frequency IAW and magnetosonic wave for the auroral region. They found that the turbulence spectrum follows the power law (∼k −5/3) at a larger scale (in the inertial range) using numerical simulation techniques. Magnetic field turbulence and filamentary structure of density can also be explained by the interaction of the IAW with various other modes of waves present in the Earth’s auroral region such as fast magnetosonic, slow magnetosonic, low-frequency IAW, and ion acoustic waves. Frycz et al. [Reference Frycz, Rankin, Samson and Tikhonchuk28] investigated the nonlinear interaction of the dispersive shear Alfvén wave and ion acoustic wave in the Earth’s magnetosphere considering two limits in their model: low-β plasma (finite electron inertia) and high-β plasma (electron thermal effect). Their results suggest that the ponderomotive force steepens the SAW leading to rapid density and electric field fluctuations. Mottez [Reference Mottez29] also extended his investigation about the interaction of parallel propagating Alfven waves to explain the formation of deep plasma cavities in the Earth auroral zone.
In the present paper, we propose to study the nonlinear coupling between IAWs and MSWs taking the correction effect of finite frequency (ω 0 < ωci) of the pump IAW applicable to auroral plasma. This leads to a change in the dispersive properties of IAWs and also in the resulting localized structures, turbulence scaling, and density depletions (cavities). From the observation of Hawkeye 1, Kintner [Reference Kintner30] showed that the average turbulence scaling near the auroral region varies as 4.02 ± 0.59 at the smaller scales. A similar observation is recorded by Heos 2 spacecraft, as reported by D’Angelo et al. [Reference D'Angelo, Bahnsen and Rosenbauer31] for the polar cusp region. Gurnett et al. [Reference Gurnett, Huff, Menietti, Burch, Winningham and Shawhan32] also reported similar scaling from the observation of Dynamics Explorer 1. Small-scale Alfvénic structures are also observed in aurora and are considered to be associated with stochastic heating of the plasma particles in the auroral region [Reference Stasiewicz, Bellan and Chaston19, Reference Zhao, Wu and Lu33].
Although the localization of the IAW and density cavitations have been discussed in the literature, nonlinear interaction of the 3D-IAW including correction effect of finite frequency (ω 0 < ωci of the pump IAW with the perpendicularly propagating magnetosonic wave (PMSW) has not been studied in detail. The main aim of this work is to study the nonlinear coupling of finite-frequency IAW (when the frequency of the IAW is not much less than the ion gyrofrequency (ω 0 <ωci)) with the PMSW to study the formation of localized structures, turbulence, and density cavitations for the auroral region. It should be pointed out here that recently, observation of the magnetosonic wave has been reported by THEMIS [Reference Ma, Li, Thorne and Angelopoulos34] in the Earth’s magnetosphere. For this purpose, the coupled system of 3D-IAW and PMSW, in the presence of ponderomotive nonlinearity, has been developed using a two-fluid approach. Furthermore, numerical simulation has been pointed out to study the nonlinear stage of modulation instability. The content of the paper is organized as follows: dynamics of the 3D-IAW and PMSW has been presented in Sections 2 and 3, respectively. Numerical simulation and results are presented in Sections 4 and 5, respectively. Results are discussed in Section 5, and finally, Section 6 comprises the conclusion.
2. Dynamics of the Inertial Alfvén Wave
The nonlinear governing equation of the finite-frequency (ω 0 < ωci) IAW is assumed to be propagating in the x − y − z plane, i.e.,
![]() having background magnetic field B 0 along the z-direction, i.e.,
having background magnetic field B 0 along the z-direction, i.e.,
![]() , and the dynamical equation for the 3D-IAW can be obtained as follows:
, and the dynamical equation for the 3D-IAW can be obtained as follows:
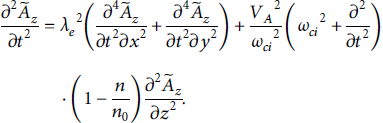
Here,
![]() and
and
![]() is the electron inertial length. Equation (1) gives the dispersion relation as follows:
is the electron inertial length. Equation (1) gives the dispersion relation as follows:
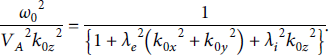
Here,
![]() is an ion inertial length. The term
is an ion inertial length. The term
![]() in equation (2) appears due to the finite frequency correction (ω0/ωci).
in equation (2) appears due to the finite frequency correction (ω0/ωci).
We seek the solution of equation (1) for vector potential Az as follows:
Using equation (3) in equation (1), the following equation has been obtained for the case when
![]()
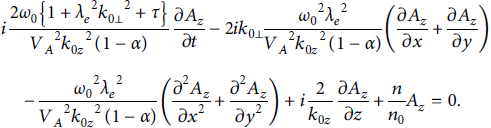
Here,
![]() , k0x, k0y (k0z) is the component of the wave vector perpendicular (parallel) to
, k0x, k0y (k0z) is the component of the wave vector perpendicular (parallel) to
![]() , and ω 0 is the frequency of the 3D-IAW.
, and ω 0 is the frequency of the 3D-IAW.
3. Dynamics of the Magnetosonic Wave
Let us assume that the low-frequency magnetosonic wave is propagating perpendicularly with respect to the background magnetic field along the x− axis, i.e.,
![]() . The dynamical equation for the PMSW can be obtained by the standard approach using the basic plasma equations mentioned in the following:
. The dynamical equation for the PMSW can be obtained by the standard approach using the basic plasma equations mentioned in the following:
-
(i) The equation of motion:
(5)
-
(ii) The continuity equation:
(6)
-
(iii) Faraday’s law:
(7)
Here, the index j = e or i accounts for the electrons and ions, respectively, q
i
= −q
e
= e is the charge,
![]() is the current density, vj is the velocity, n0 is the background number density, mj and Tj are the masses and temperature of jth species, and
is the current density, vj is the velocity, n0 is the background number density, mj and Tj are the masses and temperature of jth species, and
![]() is the ponderomotive force due to 3D-IAW. Putting the values of
is the ponderomotive force due to 3D-IAW. Putting the values of
![]() in the wave equation and taking the y component of that, one can have
in the wave equation and taking the y component of that, one can have
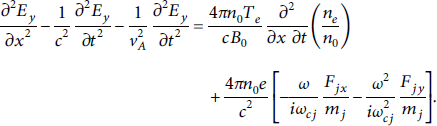
Here, ions are assumed to be cold and
![]() . The electron continuity equation yields
. The electron continuity equation yields
Components of ponderomotive force are given as
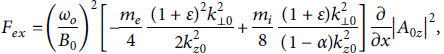
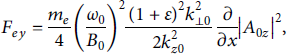
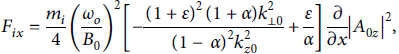
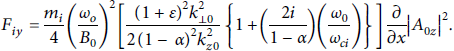
Substituting equations (9), (11), and (12) into equation (8), one obtains
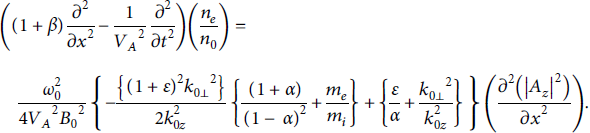
Here,
![]()
![]() ,
,
![]() , and
, and
![]() .
.
Equation (13) represents the dynamical equation of the PMSW, and its right-hand side represents the ponderomotive force due to 3D-IAW.
After normalization of equations (4) and (13), these can be written in the dimensionless form as
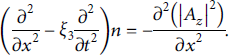
Here,
![]() ,
,
![]() , and
, and
![]() . The normalizing parameters are
. The normalizing parameters are
![]()
![]()
![]()
![]() , and
, and
![]()
4. Numerical Simulation
Numerical simulation has been performed using the pseudo-spectral method for equations (13) and (14). The wave numbers of perturbation are taken as αx = αy = αz = 0.2 which is normalized by
![]() ,
,
![]() , and
, and
![]() , respectively. Simulation has been carried out with (64)3 grid points, and a periodic spatial domain of
, respectively. Simulation has been carried out with (64)3 grid points, and a periodic spatial domain of
![]() with the initial conditions of simulation is as follows:
with the initial conditions of simulation is as follows:
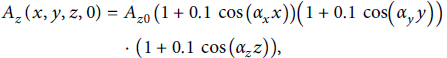
Here, |Az0| = 1 is the amplitude of the homogenous pump 3D-IAW. An algorithm for the nonlinear Schrödinger (NLS) equation has been studied and tested against its invariant in order to carry out the simulation of equations (13) and (14).
The accuracy was determined by consistency of the number
![]() in the case of cubic NLS equation. During computation, the conserved quantity was preserved to the order of 10−5. After testing algorithm of cubic NLS, it has been modified for solving dimensionless equations (13) and (14), which is used to study nonlinear coupling of 3D-IAW with PMSW and the resulting formation of localized structures, turbulent scaling, and density cavities.
in the case of cubic NLS equation. During computation, the conserved quantity was preserved to the order of 10−5. After testing algorithm of cubic NLS, it has been modified for solving dimensionless equations (13) and (14), which is used to study nonlinear coupling of 3D-IAW with PMSW and the resulting formation of localized structures, turbulent scaling, and density cavities.
The values of ξ 1 and ξ 2 can be evaluated from the low-β plasma parameters applicable to aurora. For the application purpose in low-β plasma, the typical parameters for the auroral altitude of 1700 km [Reference Wu, Huang and Wang11] are as follows:
![]()
![]() and
and
![]() Using these parameters, one can find
Using these parameters, one can find
![]()
![]()
![]() For
For
![]() and
and
![]() , one can calculate
, one can calculate
![]()
![]()
![]() , and
, and
![]() . The normalizing parameter values are
. The normalizing parameter values are
![]()
![]()
![]() , and
, and
![]() .
.
5. Results and Discussion
In Section 4, numerical simulation has been carried out for dimensionless equations (13) and (14) to study the formation of localized structures, turbulent scaling, and density cavitation phenomenon, applicable to the auroral region. In simulation, time history of nonlinear evolution is studied from state t = 0 to the state when the system reaches to the quasi-steady state. For the chosen parameters, the time required to set up the ponderomotive nonlinearity r 0/c s ∼ 0.2 sec. In order to study the effect of ponderomotive nonlinearity, simulation is carried out from t = 0 to the time t = 29 (∼3.22 sec), which is larger than the time required to set up the ponderomotive nonlinearity and to reach the system in the quasi-steady state. Results shown in Figures 1–3 are obtained at different time scales after the system achieves the quasi-steady state. Equation (12) represents the dynamical equation of the PMSW, and its right-hand side represents the ponderomotive force due to 3D-IAW, and in equation (15), the time-dependent density depends on magnitude of ponderomotive force as well as the interaction between 3D-IAW and PMSW. Figures 1(a)–1(c) show the magnetic field intensity profile of the IAW in the X-Y plane at time t = 18, 24, and 29, respectively, showing a nonlinear evolution of the coherent structure, while Figure 1(d) presents the evolution of Fourier transformation |A kz |2 of the IAW with K x − K y at time t = 22. One can observe from Figures 1(a)–1(d) that the magnetic field intensity gets localized and becomes more complex with time. The PMSW in the presence of the nonlinearity (ponderomotive force, which changes with time) starts getting localized and hence affects the dynamics of the 3D-IAW which leads to the localization of the 3D-IAWs through equations (13) and (14).
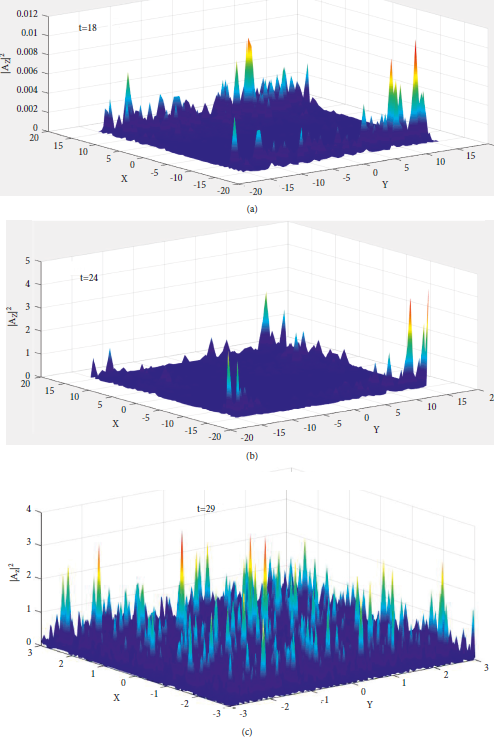
Figure 1: (a) The magnetic field intensity profile of the IAW for low-β plasma (auroral region) at time t = 18. (b) The magnetic field intensity profile of the IAW for low-β plasma (auroral region) at time t = 24. (c) The magnetic field intensity profile of the IAW for low-β plasma (auroral region) at time t = 29. (d) Evolution of |A kz |2 of the IAW with K x − K y at time t = 22.
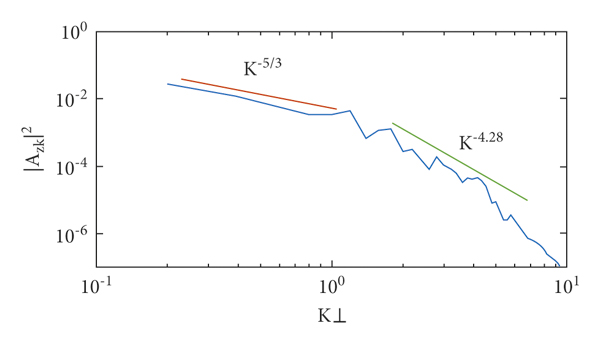
Figure 2: Variation of
![]() (power spectrum) against k for low-β plasma (auroral region) at time t = 29.
(power spectrum) against k for low-β plasma (auroral region) at time t = 29.
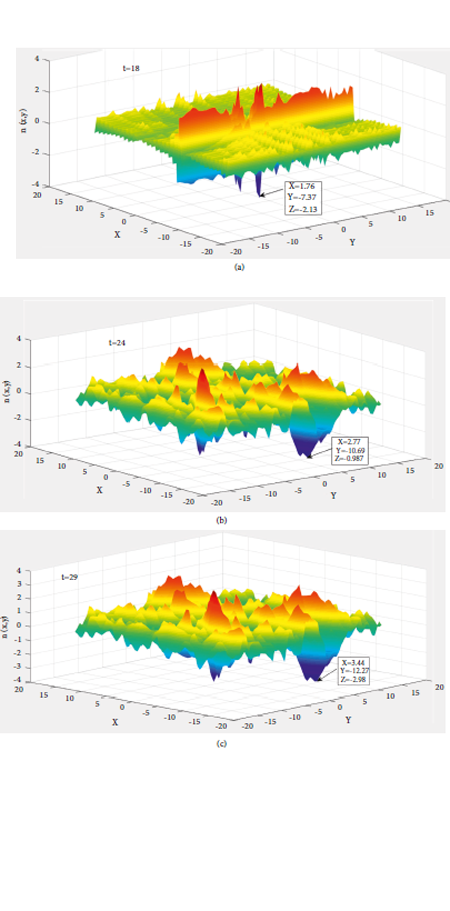
Figure 3: (a) 3D evolution of the density profile at time t = 18. (b) 3D evolution of the density profile at time t = 24. (c) 3D evolution of the density profile at time t = 29.
Next, the power spectral index has been illustrated in Figure 2. It reveals the variation of
![]() against k at time t = 29. It is evident from the wavenumber spectrum that, for kλe < 1, the spectral index follows nearly Kolmogorov ( ∼ k −5/3) scaling (a typical inertial range scaling). A spectral break appears at kλe ≈ 1, and for kλe > 1, the spectral index follows nearly ( ∼ k −4.28. From the steepening of the spectrum, it is clear that the nonlinear interaction of the 3D-IAW and PMSW might be helpful for the energy transfer from a small wavenumber to large wavenumber. These kinds of power spectra have also been reported (observation of Hoes 2, Hawkeye 1, and Dynamics Explorer 1 spacecrafts) in the auroral and other magnetosphere regions by D’Angelo et al. [Reference D'Angelo, Bahnsen and Rosenbauer31], Kintner [Reference Kintner30], and Gurnett et al. [Reference Gurnett, Huff, Menietti, Burch, Winningham and Shawhan32].
against k at time t = 29. It is evident from the wavenumber spectrum that, for kλe < 1, the spectral index follows nearly Kolmogorov ( ∼ k −5/3) scaling (a typical inertial range scaling). A spectral break appears at kλe ≈ 1, and for kλe > 1, the spectral index follows nearly ( ∼ k −4.28. From the steepening of the spectrum, it is clear that the nonlinear interaction of the 3D-IAW and PMSW might be helpful for the energy transfer from a small wavenumber to large wavenumber. These kinds of power spectra have also been reported (observation of Hoes 2, Hawkeye 1, and Dynamics Explorer 1 spacecrafts) in the auroral and other magnetosphere regions by D’Angelo et al. [Reference D'Angelo, Bahnsen and Rosenbauer31], Kintner [Reference Kintner30], and Gurnett et al. [Reference Gurnett, Huff, Menietti, Burch, Winningham and Shawhan32].
Figures 3(a)–3(c) represent the 3D evolution of the resulting density structures in the x-y plane. From Figure 3, one can observe that three-dimensional (3D) density dips are formed which changes with time. The formation of the coherent structure and turbulence in density profile can be explained with the help of equations (13) and (16). Equation (13) represents the dynamical equation of the PMSW, and its right-hand side represents the ponderomotive force due to 3D-IAW where the intensity of the IAW is X-Y dependent. At the same time, equation (15) represents that the density profile of the PMSW also depends on amplitude of the pump 3D-IAW. Although the PMSW is propagating along the X-direction, the ponderomotive force due to 3D-IAW and the interaction between the 3D-IAW and PMSW alter the density of the PMSW in X-, Y-, and Z-directions. Since the interaction of the IAW and PMSW is chaotic at later times, not only the location of density dips changes but also the depth of these dips changes with time (marked as x, y, and z in Figure 3). The nonlinear interaction between IAW and PMSW varies in space with time, and hence, the magnitude of ponderomotive force associated with them also changes in space with time accordingly. Eventually the density profile is affected by the ponderomotive force and creates the density cavity of different depth at different position with time. The magnetic field is trapped in the regions of low density due to the ponderomotive nonlinearity. Small-scale length density cavities have been observed in the auroral zone by Viking and Freja spacecrafts [Reference Chaston, CarlsonCW, Ergun and McFadden35, Reference Wahlund, Louarn and Chust36]. For the auroral region, we observed the density fluctuations of ∼0.12n 0, consistent with the FAST observation reported by Chaston et al. [Reference Chaston, Carlson, Ergun and McFadden14, Reference Chaston, Carlson, McFadden and Strangeway15]. Thus, in the present paper, efforts have been made to understand the phenomena of turbulence, localization, and density cavitations due to the nonlinear interplay of the finite-frequency IAW (ω 0 < ω ci) with the PMSW. The finite frequency correction effect is expected to change the dispersive property of the 3D-IAW and resulting ponderomotive force by the IAW.
6. Conclusion
To summarize, our primary aim of the present study is to understand the physical mechanism behind the processes of localization and density cavitations during the nonlinear interaction of the finite-frequency IAW (ω 0 < ωci) with the PMSW. Numerical simulation of equations (13) and (14), governing the dynamics of the 3D-IAW and PMSW, has been carried out, applicable to the auroral region. The background density of the PMSW gets altered due to the ponderomotive nonlinearity of the pump 3D-IAW, which results in the density cavitations and field localization. The field associated with the 3D-IAW gets trapped in the density cavities and breaks into a localized coherent structure. The result reveals that these localized structures and density cavity become progressively more complex and grow towards larger to smaller length scales.The depth of the density cavity and formation of the localized structure depend on the magnitude of the ponderomotive force and the nature of the interacting waves. From the obtained results, we have found that the depth of density cavities is of the order of ∼0.10 n 0, and these density-depleted regions are of the transverse scale size of the order of electron inertial length. These kinds of small-scale-sized density cavities have been observed in the auroral region and are consistent with the FAST satellite observation reported by Chaston et al. [Reference Chaston, Carlson, Ergun and McFadden14, Reference Chaston, Carlson, McFadden and Strangeway15].
Since the nature of the interacting waves discussed in the present paper is different at various locations, the magnitude of ponderomotive force associated with them is also different. This is the main reason that the depth of the density cavity in each location is not the same. Therefore, it becomes clear that the depth of the density cavities changes with the magnitude of the ponderomotive force and the nature of the waves associated with them. On the basis of obtained results, we can conclude that the nonlinear interaction of the 3D-IAW and PMSW is responsible for the localized coherent structure and density cavitations.
Data Availability
The main aim of this work is to study the nonlinear coupling of the finite-frequency IAW (when the frequency of the IAW is not much less than the ion gyrofrequency) with the PMSW to study the formation of localized structures, turbulence, and density cavitation for the auroral region. It should be pointed out here that recently, the observation of the magnetosonic wave has been reported by THEMIS [Reference Ma, Li, Thorne and Angelopoulos34] in the Earth’s magnetosphere.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Authors’ Contributions
Prof. R. P. Sharma proposed the problem, and under his guidance, Motilal Rinawa and Prashant Chauhan formulated the analytical part, while Sintu Kumar was responsible for numerical simulation and result preparation. Manoh Kumar Singh and Hari Kumar Singh were responsible to simulate the results in the revised manuscript, while Amit Sharma helped in the preparation of the revised manuscript.
Acknowledgments
This research was partially supported by the Indian Space Research Organisation (ISRO) under the RESPOND Programme and Department of Science and Technology (DST), India.







