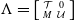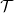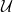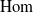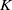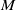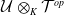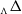1. Introduction
The notion of quasi-hereditary algebra and highest weight category were introduced and studied by E. Cline, B. Parshall, and L. Scott [Reference Cline, Parshall and Scott8, Reference Parshall and Scott24, Reference Scott27]. Highest weight categories arise in the representation theory of Lie algebras and algebraic groups. For the setting of finite dimensional algebras, quasi-hereditary algebras were amply studied by V. Dlab and C. M. Ringel in [Reference Dlab9, Reference Dlab and Ringel11, Reference Dlab and Ringel12, Reference Ringel25]. In addition, they introduced the set of standard modules
![]() ${}_\Lambda \Delta$
associated with an algebra
${}_\Lambda \Delta$
associated with an algebra
![]() $\Lambda .$
In [Reference Ringel25], C. M. Ringel studied the homological properties of the category
$\Lambda .$
In [Reference Ringel25], C. M. Ringel studied the homological properties of the category
![]() $\mathcal{F}({}_\Lambda \Delta )$
of
$\mathcal{F}({}_\Lambda \Delta )$
of
![]() ${}_\Lambda \Delta$
-filtered
${}_\Lambda \Delta$
-filtered
![]() $\Lambda$
-modules and constructed the characteristic tilting module
$\Lambda$
-modules and constructed the characteristic tilting module
![]() ${}_\Lambda T$
associated with
${}_\Lambda T$
associated with
![]() $\mathcal{F}(_\Lambda \Delta ).$
In [Reference Šťovíček29], B. Zhu studied the triangular matrix algebra
$\mathcal{F}(_\Lambda \Delta ).$
In [Reference Šťovíček29], B. Zhu studied the triangular matrix algebra
![]() $\Lambda =\left [ \begin{smallmatrix} T &0\\ M& U\end{smallmatrix} \right ]$
where
$\Lambda =\left [ \begin{smallmatrix} T &0\\ M& U\end{smallmatrix} \right ]$
where
![]() $T$
and
$T$
and
![]() $U$
are quasi-hereditary algebras, and he proved that under suitable conditions on
$U$
are quasi-hereditary algebras, and he proved that under suitable conditions on
![]() $M$
,
$M$
,
![]() $\Lambda$
is a quasi-hereditary algebra.
$\Lambda$
is a quasi-hereditary algebra.
On the other hand, B. Mitchell developed the idea that additive categories can be thought as rings with several objects and he showed that a substantial amount of non-commutative ring theory is still true in this generality [Reference Mitchell22]. Recently, R. Martínez-Villa and M. Ortíz studied tilting theory in arbitrary functor categories, in [Reference Martínez-Villa and Ortíz-Morales19, Reference Martínez-Villa and Ortíz-Morales20]. They proved that most of the properties that are satisfied by a tilting module over an artin algebra also hold for functor categories. Following the line of the above-mentioned works, M. Ortíz introduced in [Reference Ortiz23] the concept of quasi-hereditary category to study the Auslander–Reiten components of a finite dimensional algebra
![]() $\Lambda .$
Similarly, as the standard modules appear in the theory of quasi-hereditary algebras, the concept of standard functors appears in this context. We note that the notion of standard functor is a generalization of the notion of standard module. As a consequence, a connection is obtained between highest weight categories and quasi-hereditary categories as stated by H. Krause in [Reference Krause14].
$\Lambda .$
Similarly, as the standard modules appear in the theory of quasi-hereditary algebras, the concept of standard functors appears in this context. We note that the notion of standard functor is a generalization of the notion of standard module. As a consequence, a connection is obtained between highest weight categories and quasi-hereditary categories as stated by H. Krause in [Reference Krause14].
Finally, the concept of the triangular matrix category is introduced in [Reference Leszczyński15, Reference León-Galeana, Ortíz-Morales and Santiago16], as the analog of the triangular matrix algebra to the context of rings with several objects, and they obtain some applications to path categories given by infinite quivers, the construction of recollements, and the study of functorially finite subcategories in functor categories.
The aim of this paper is to show that the triangular matrix category
![]() $\Lambda =\left [ \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right ]$
, where
$\Lambda =\left [ \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right ]$
, where
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $\mathcal{U}$
are
$\mathcal{U}$
are
![]() $\textrm{Hom}$
-finite, Krull–Schmidt
$\textrm{Hom}$
-finite, Krull–Schmidt
![]() $K$
-quasi-hereditary categories and
$K$
-quasi-hereditary categories and
![]() $M$
is a
$M$
is a
![]() $\mathcal{U}\otimes _K \mathcal{T}^{op}$
-module that satisfies suitable conditions, is quasi-hereditary in the sense of [Reference Leszczyński15] and [Reference Ortiz23], generalizing some of the results obtained by B. Zhu in [Reference Šťovíček29].
$\mathcal{U}\otimes _K \mathcal{T}^{op}$
-module that satisfies suitable conditions, is quasi-hereditary in the sense of [Reference Leszczyński15] and [Reference Ortiz23], generalizing some of the results obtained by B. Zhu in [Reference Šťovíček29].
It is worth mentioning that recently in [Reference Marcos, Mendoza, Sáenz and Santiago18], similar results have been obtained in the context of standardly stratified lower triangular
![]() $\mathbb K$
-algebras with enough idempotents.
$\mathbb K$
-algebras with enough idempotents.
We outline the content of the paper section-by-section as follows.
In Section 1, we recall basic results about path categories, functor categories, quasi-hereditary categories, and triangular matrix categories.
In Section 2, we give the main result of this article (see Theorem 3.7), which is a generalization of a result given in [Reference Šťovíček29, Theorem 3.1] as stated above (see Remark 3.8). Moreover, we obtain a characterization of the category of the
![]() $_\Lambda \Delta$
-filtered
$_\Lambda \Delta$
-filtered
![]() $\Lambda$
-modules, and we give an example a triangular matrix category
$\Lambda$
-modules, and we give an example a triangular matrix category
![]() $\Lambda$
, which is quasi-hereditary with respect to certain filtration
$\Lambda$
, which is quasi-hereditary with respect to certain filtration
![]() $\{\Lambda _j\}_{j\ge 0 }$
.
$\{\Lambda _j\}_{j\ge 0 }$
.
2. Preliminaries
2.1.
 $K$
-categories, path categories, representations, and functor categories
$K$
-categories, path categories, representations, and functor categories
In this part, we recall some basic definitions to approach this work. The reader can consult [Reference Assem, Simson and Skowrónski1] and [Reference Barot6] for more details.
K-Categories. Let
![]() $K$
be a field. A category
$K$
be a field. A category
![]() $\mathcal{C}$
is a
$\mathcal{C}$
is a
![]() $K$
-category if for each pair of objects
$K$
-category if for each pair of objects
![]() $X$
and
$X$
and
![]() $Y$
in
$Y$
in
![]() $\mathcal{C}$
, the set of morphisms
$\mathcal{C}$
, the set of morphisms
![]() $\mathcal{C}(X,Y)$
is equipped with a
$\mathcal{C}(X,Y)$
is equipped with a
![]() $K$
-vector space structure such that the composition
$K$
-vector space structure such that the composition
![]() $\circ$
of morphisms in
$\circ$
of morphisms in
![]() $\mathcal{C}$
is a
$\mathcal{C}$
is a
![]() $K$
-bilinear map. A
$K$
-bilinear map. A
![]() $K$
-category
$K$
-category
![]() $\mathcal{C}$
is called Hom-finite if
$\mathcal{C}$
is called Hom-finite if
![]() $\textrm{dim}_K\mathcal{C}(X,Y)\lt \infty$
.
$\textrm{dim}_K\mathcal{C}(X,Y)\lt \infty$
.
A Krull–Schmidt category is an additive category such that each object decomposes into a finite direct sum of indecomposable objects with local endomorphism rings.
Ideals
. Let
![]() $\mathcal{C}$
be an additive
$\mathcal{C}$
be an additive
![]() $K$
-category. A class
$K$
-category. A class
![]() $I$
of morphisms of
$I$
of morphisms of
![]() $\mathcal{C}$
is a two-sided ideal in
$\mathcal{C}$
is a two-sided ideal in
![]() $\mathcal{C}$
if:
$\mathcal{C}$
if:
-
(a) the zero morphism
 $0_X\in \mathcal{C}(X,X)$
belongs to
$0_X\in \mathcal{C}(X,X)$
belongs to
 $I$
;
$I$
; -
(b) if
 $f,g\,:\,X\rightarrow Y$
are morphisms in
$f,g\,:\,X\rightarrow Y$
are morphisms in
 $I$
and
$I$
and
 $\lambda$
,
$\lambda$
,
 $\mu \in K$
, then
$\mu \in K$
, then
 $\lambda f+ \mu g\in I$
;
$\lambda f+ \mu g\in I$
; -
(c) if
 $f \in I$
and
$f \in I$
and
 $g$
is a morphism in
$g$
is a morphism in
 $\mathcal{C}$
that is left-composable with
$\mathcal{C}$
that is left-composable with
 $f$
, then
$f$
, then
 $g\circ f\in I$
and
$g\circ f\in I$
and -
(d) if
 $f \in I$
and
$f \in I$
and
 $h$
is a morphism in
$h$
is a morphism in
 $\mathcal{C}$
that is right-composable with
$\mathcal{C}$
that is right-composable with
 $f$
, then
$f$
, then
 $ f\circ h\in I$
.
$ f\circ h\in I$
.
Equivalently, a two-sided ideal
![]() $I$
of
$I$
of
![]() $\mathcal{C}$
can be considered as a subfunctor
$\mathcal{C}$
can be considered as a subfunctor
![]() $I (-,-) \subseteq \mathcal{C} (-,- ) \,:\, \mathcal{C}^{op} \times \mathcal{C}\rightarrow \textrm{Mod}\ K$
, defined by assigning to each pair
$I (-,-) \subseteq \mathcal{C} (-,- ) \,:\, \mathcal{C}^{op} \times \mathcal{C}\rightarrow \textrm{Mod}\ K$
, defined by assigning to each pair
![]() $(X,Y)$
of objects
$(X,Y)$
of objects
![]() $X$
,
$X$
,
![]() $Y$
of
$Y$
of
![]() $\mathcal{C}$
a
$\mathcal{C}$
a
![]() $K$
-subspace
$K$
-subspace
![]() $I(X,Y )$
of
$I(X,Y )$
of
![]() $\mathcal{C}(X,Y )$
such that if
$\mathcal{C}(X,Y )$
such that if
![]() $f \in I(X,Y )$
,
$f \in I(X,Y )$
,
![]() $g\in \mathcal{C}(Y,Z)$
and
$g\in \mathcal{C}(Y,Z)$
and
![]() $h\in \mathcal{C}(U,X)$
then
$h\in \mathcal{C}(U,X)$
then
![]() $gfh \in I(U,Z)$
.
$gfh \in I(U,Z)$
.
Given a two-sided ideal
![]() $I$
in an additive
$I$
in an additive
![]() $K$
-category
$K$
-category
![]() $\mathcal{C}$
, the quotient category
$\mathcal{C}$
, the quotient category
![]() $\mathcal{C}/I$
is the category whose objects are the same as the objects of
$\mathcal{C}/I$
is the category whose objects are the same as the objects of
![]() $\mathcal{C}$
and the space of morphisms from
$\mathcal{C}$
and the space of morphisms from
![]() $X$
to
$X$
to
![]() $Y$
in
$Y$
in
![]() $\mathcal{C}/I$
is the quotient space
$\mathcal{C}/I$
is the quotient space
![]() $(\mathcal{C}/I)(X,Y) = \mathcal{C}(X,Y)/I(X,Y)$
of
$(\mathcal{C}/I)(X,Y) = \mathcal{C}(X,Y)/I(X,Y)$
of
![]() $\mathcal{C}(X,Y)$
. It is easy to see that the quotient category
$\mathcal{C}(X,Y)$
. It is easy to see that the quotient category
![]() $ \mathcal{C}/I$
is an additive
$ \mathcal{C}/I$
is an additive
![]() $K$
-category, and the projection functor
$K$
-category, and the projection functor
![]() $ \pi \,:\, \mathcal{C}\rightarrow \mathcal{C}/I$
assigning to each
$ \pi \,:\, \mathcal{C}\rightarrow \mathcal{C}/I$
assigning to each
![]() $f \,:\, X \rightarrow Y$
in
$f \,:\, X \rightarrow Y$
in
![]() $\mathcal{C}$
the coset
$\mathcal{C}$
the coset
![]() $f + I \in (\mathcal{C}/I) (X, Y )$
is a
$f + I \in (\mathcal{C}/I) (X, Y )$
is a
![]() $K$
-linear functor. Moreover,
$K$
-linear functor. Moreover,
![]() $\pi$
is full and dense, and
$\pi$
is full and dense, and
![]() $\textrm{Ker} (\pi ) =I$
.
$\textrm{Ker} (\pi ) =I$
.
The (Jacobson) radical of an additive
![]() $K$
-category
$K$
-category
![]() $\mathcal{C}$
is the two-sided ideal
$\mathcal{C}$
is the two-sided ideal
![]() $\textrm{rad}_{\mathcal{C}}(-,-)$
in
$\textrm{rad}_{\mathcal{C}}(-,-)$
in
![]() $\mathcal{C}$
defined by the formula
$\mathcal{C}$
defined by the formula
for all objects
![]() $X$
and
$X$
and
![]() $Y$
of
$Y$
of
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Tensor Product of K-Categories
. Let
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
![]() $\mathcal{C}^{\prime}$
be
$\mathcal{C}^{\prime}$
be
![]() $K$
-categories. The tensor product
$K$
-categories. The tensor product
![]() $\mathcal{C}\otimes _K \mathcal{C}^{\prime}$
is the category whose class of objects is
$\mathcal{C}\otimes _K \mathcal{C}^{\prime}$
is the category whose class of objects is
![]() $\textrm{Obj } \ \mathcal{C}\times \textrm{Obj }\ \mathcal{C}^{\prime}$
, where the set of morphisms from
$\textrm{Obj } \ \mathcal{C}\times \textrm{Obj }\ \mathcal{C}^{\prime}$
, where the set of morphisms from
![]() $(p_1,q_1)$
to
$(p_1,q_1)$
to
![]() $(p_2,q_2)$
is the ordinary tensor product
$(p_2,q_2)$
is the ordinary tensor product
![]() $\mathcal{C}(p_1,p_2)\otimes \mathcal{C}^{\prime}(q_1,q_2)$
. The composition
$\mathcal{C}(p_1,p_2)\otimes \mathcal{C}^{\prime}(q_1,q_2)$
. The composition
is given by the rule
![]() $((f_1\otimes g_1),(f_2\otimes g_2))\mapsto (f_2f_1\otimes g_2 g_1)$
. This composition is bilinear; see [Reference Mitchell22].
$((f_1\otimes g_1),(f_2\otimes g_2))\mapsto (f_2f_1\otimes g_2 g_1)$
. This composition is bilinear; see [Reference Mitchell22].
Quivers, Path Algebras and Path Categories
. A quiver is an oriented graph, formally denoted by a quadruple
![]() $Q=(Q_0,Q_1,s,t)$
, with a set of vertices
$Q=(Q_0,Q_1,s,t)$
, with a set of vertices
![]() $Q_0$
and a set of arrows
$Q_0$
and a set of arrows
![]() $Q_1$
, and two maps
$Q_1$
, and two maps
![]() $s,t\,:\, Q_1\rightarrow Q_0$
, called source and target, defined by
$s,t\,:\, Q_1\rightarrow Q_0$
, called source and target, defined by
![]() $s(a\rightarrow b)=a$
and
$s(a\rightarrow b)=a$
and
![]() $t(a\rightarrow b)=b, b)=b$
, respectively, if
$t(a\rightarrow b)=b, b)=b$
, respectively, if
![]() $\alpha \,:\,a\rightarrow b$
is an arrow in
$\alpha \,:\,a\rightarrow b$
is an arrow in
![]() $Q_1$
.
$Q_1$
.
A path of length
![]() $l\ge 1$
from
$l\ge 1$
from
![]() $a$
to
$a$
to
![]() $b$
in a quiver
$b$
in a quiver
![]() $Q$
is of the form
$Q$
is of the form
![]() $(a|\alpha _1,\ldots,\alpha _l|b)$
with arrows
$(a|\alpha _1,\ldots,\alpha _l|b)$
with arrows
![]() $\alpha _i$
satisfying
$\alpha _i$
satisfying
![]() $t(\alpha _i)=s(\alpha _{i+1})$
for all
$t(\alpha _i)=s(\alpha _{i+1})$
for all
![]() $1\le i\le l$
and
$1\le i\le l$
and
![]() $a=s(\alpha _1)$
as well as
$a=s(\alpha _1)$
as well as
![]() $b=t(\alpha _l)$
. In addition, for any vertex
$b=t(\alpha _l)$
. In addition, for any vertex
![]() $a$
in
$a$
in
![]() $Q_0$
, a path of length 0 from
$Q_0$
, a path of length 0 from
![]() $a$
to itself is denoted by
$a$
to itself is denoted by
![]() $\epsilon _a$
.
$\epsilon _a$
.
Given a quiver
![]() $Q$
, its path category
$Q$
, its path category
![]() $K\mathcal{Q}$
is an additive category, with objects being direct sums of indecomposable objects. The indecomposable objects in the path category are given by the set
$K\mathcal{Q}$
is an additive category, with objects being direct sums of indecomposable objects. The indecomposable objects in the path category are given by the set
![]() $Q_0$
, and given
$Q_0$
, and given
![]() $a,b\in Q_0$
, the set of maps from
$a,b\in Q_0$
, the set of maps from
![]() $a$
to
$a$
to
![]() $b$
is given by the
$b$
is given by the
![]() $K$
-vector space with basis the set of all paths from
$K$
-vector space with basis the set of all paths from
![]() $a$
to
$a$
to
![]() $b$
. The composition of maps is induced from the usual composition of paths:
$b$
. The composition of maps is induced from the usual composition of paths:
where
![]() $(a|\alpha _1,\ldots,\alpha _l|b)$
is a path from
$(a|\alpha _1,\ldots,\alpha _l|b)$
is a path from
![]() $a$
to
$a$
to
![]() $b$
and
$b$
and
![]() $(b|\beta _1,\ldots,\beta _s|c)$
is a path from
$(b|\beta _1,\ldots,\beta _s|c)$
is a path from
![]() $b$
to
$b$
to
![]() $c$
.
$c$
.
Similarly, the path algebra of
![]() $Q$
denoted by
$Q$
denoted by
![]() $KQ$
, is the
$KQ$
, is the
![]() $K$
-vector space with basis the set of all paths in
$K$
-vector space with basis the set of all paths in
![]() $Q$
, and the product of two paths is defined by (2.1) if they are composable, and it is zero if they are non-composable. In
$Q$
, and the product of two paths is defined by (2.1) if they are composable, and it is zero if they are non-composable. In
![]() $KQ$
, any ideal
$KQ$
, any ideal
![]() $I$
is generated by a set of paths
$I$
is generated by a set of paths
![]() $\{\rho _i| i\}$
, that is
$\{\rho _i| i\}$
, that is
![]() $I=\langle \rho _i| i\ \rangle$
. Let
$I=\langle \rho _i| i\ \rangle$
. Let
![]() $I$
be an ideal in
$I$
be an ideal in
![]() $KQ$
, then given a pair of finite sets of vertices
$KQ$
, then given a pair of finite sets of vertices
![]() $\{X_i\}_{i=1}^n$
,
$\{X_i\}_{i=1}^n$
,
![]() $\{Y_j\}_{j=1}^m$
we set
$\{Y_j\}_{j=1}^m$
we set
![]() $\mathcal{I}(\oplus _{i=1}^n{X_i}, \oplus _{j=1}^m{Y_j})=\{(f_{ij})\in K\mathcal{Q}(\oplus _{i=1}^n{X_i}, \oplus _{j=1}^m{Y_j})|f_{ij}\in I\}$
. This allows us to define an ideal
$\mathcal{I}(\oplus _{i=1}^n{X_i}, \oplus _{j=1}^m{Y_j})=\{(f_{ij})\in K\mathcal{Q}(\oplus _{i=1}^n{X_i}, \oplus _{j=1}^m{Y_j})|f_{ij}\in I\}$
. This allows us to define an ideal
![]() $\mathcal{I}$
in
$\mathcal{I}$
in
![]() $K\mathcal{Q}$
, and we refer to it as the ideal generated by
$K\mathcal{Q}$
, and we refer to it as the ideal generated by
![]() $I$
. If
$I$
. If
![]() $I\subset KQ$
is generated by the set of paths
$I\subset KQ$
is generated by the set of paths
![]() $\{\rho _i| i\}$
, we say that
$\{\rho _i| i\}$
, we say that
![]() $\mathcal{I}$
is generated by the set
$\mathcal{I}$
is generated by the set
![]() $\{\rho _i| i\}$
.
$\{\rho _i| i\}$
.
The ideal generated by all arrows is denoted by
![]() $KQ^{+}$
. Note that
$KQ^{+}$
. Note that
![]() $(KQ^{+})^n$
is the ideal generated by all paths of length
$(KQ^{+})^n$
is the ideal generated by all paths of length
![]() $\ge n$
. Given vertices
$\ge n$
. Given vertices
![]() $a,b\in Q_0$
, a finite linear combination
$a,b\in Q_0$
, a finite linear combination
![]() $\sum _{w}c_w w$
with
$\sum _{w}c_w w$
with
![]() $c_w\in K$
where
$c_w\in K$
where
![]() $w$
are paths of lengths
$w$
are paths of lengths
![]() $\ge 2$
from
$\ge 2$
from
![]() $a$
to
$a$
to
![]() $b$
is called a relation on
$b$
is called a relation on
![]() $Q$
. Any ideal
$Q$
. Any ideal
![]() $I\subseteq (K Q^{+})^2$
can be generated, as an ideal, by relations. An ideal
$I\subseteq (K Q^{+})^2$
can be generated, as an ideal, by relations. An ideal
![]() $I\subset KQ$
is called admisible if it is generated by a set of relations. We then say that an ideal
$I\subset KQ$
is called admisible if it is generated by a set of relations. We then say that an ideal
![]() $\mathcal{I}$
in
$\mathcal{I}$
in
![]() $K\mathcal{Q}$
is admissible if it is generated by an admissible ideal in
$K\mathcal{Q}$
is admissible if it is generated by an admissible ideal in
![]() $KQ$
.
$KQ$
.
Representations of Quivers
. A representation of a quiver
![]() $Q$
is a pair
$Q$
is a pair
![]() $V=\left ( (V_i)_{i\in Q_0}, (V_\alpha )_{\alpha \in Q_1}\right )$
, where each element of the family
$V=\left ( (V_i)_{i\in Q_0}, (V_\alpha )_{\alpha \in Q_1}\right )$
, where each element of the family
![]() $\{V_i\}_{i\in Q_0}$
is a vector space and
$\{V_i\}_{i\in Q_0}$
is a vector space and
![]() $V_\alpha \,:\, V_{s(\alpha )}\rightarrow V_{t(\alpha )}$
is a
$V_\alpha \,:\, V_{s(\alpha )}\rightarrow V_{t(\alpha )}$
is a
![]() $K$
-linear map. Let
$K$
-linear map. Let
![]() $V$
and
$V$
and
![]() $ W$
be two representations of
$ W$
be two representations of
![]() $ Q$
. A morphism from
$ Q$
. A morphism from
![]() $V$
to
$V$
to
![]() $W$
is a family of linear maps
$W$
is a family of linear maps
![]() $f=(f_i\,:\,V_i\rightarrow W_i)_{i\in Q_0}$
such that for each arrow
$f=(f_i\,:\,V_i\rightarrow W_i)_{i\in Q_0}$
such that for each arrow
![]() $\alpha \,:\, i\rightarrow j$
we have
$\alpha \,:\, i\rightarrow j$
we have
![]() $f_jV_\alpha =W_\alpha f_i$
. We denote by
$f_jV_\alpha =W_\alpha f_i$
. We denote by
![]() $\textrm{rep}\ Q$
the abelian category that has as objects the representations of
$\textrm{rep}\ Q$
the abelian category that has as objects the representations of
![]() $Q$
and as morphisms just the morphisms of representations. Let
$Q$
and as morphisms just the morphisms of representations. Let
![]() $\rho =(a|\alpha _1,\ldots,\alpha _l|b)$
a path in
$\rho =(a|\alpha _1,\ldots,\alpha _l|b)$
a path in
![]() $Q$
, we set
$Q$
, we set
![]() $V_\rho =V_{\alpha _l}\circ \cdots \circ V_{\alpha _1}$
. Let
$V_\rho =V_{\alpha _l}\circ \cdots \circ V_{\alpha _1}$
. Let
![]() $I\subset KQ$
be an ideal, we then say the representation
$I\subset KQ$
be an ideal, we then say the representation
![]() $V$
is bounded by
$V$
is bounded by
![]() $I$
if
$I$
if
![]() $V_\rho =0$
for all
$V_\rho =0$
for all
![]() $\rho \in I$
. The full subcategory of
$\rho \in I$
. The full subcategory of
![]() $\textrm{rep}\ Q$
consisting of representations bounded by
$\textrm{rep}\ Q$
consisting of representations bounded by
![]() $I$
is denoted by
$I$
is denoted by
![]() $\textrm{rep} \ (Q,I)$
.
$\textrm{rep} \ (Q,I)$
.
Strongly Locally Finite Quivers
. Let
![]() $Q$
be a quiver. For
$Q$
be a quiver. For
![]() $x\in Q_0$
, we denote by
$x\in Q_0$
, we denote by
![]() $x^+$
and
$x^+$
and
![]() $x^{-}$
the set of arrows starting in
$x^{-}$
the set of arrows starting in
![]() $x$
and the set of arrows ending in
$x$
and the set of arrows ending in
![]() $x$
, respectively. Recall that
$x$
, respectively. Recall that
![]() $x$
is a sink vertex or a source vertex if
$x$
is a sink vertex or a source vertex if
![]() $x^{+}=\emptyset$
or
$x^{+}=\emptyset$
or
![]() $x^-=\emptyset$
. One says that
$x^-=\emptyset$
. One says that
![]() $Q$
is locally finite if
$Q$
is locally finite if
![]() $x^+$
and
$x^+$
and
![]() $x^{-}$
are finite sets and interval finite if the set of paths from
$x^{-}$
are finite sets and interval finite if the set of paths from
![]() $x$
to
$x$
to
![]() $y$
is finite for any
$y$
is finite for any
![]() $x, y \in Q_0$
. For short, we say that Q is strongly locally finite if it is locally finite and interval finite. In particular,
$x, y \in Q_0$
. For short, we say that Q is strongly locally finite if it is locally finite and interval finite. In particular,
![]() $Q$
contains no oriented cycle in case it is interval finite. Note that under these conditions, if
$Q$
contains no oriented cycle in case it is interval finite. Note that under these conditions, if
![]() $Q$
is a strongly locally finite quiver, the path category
$Q$
is a strongly locally finite quiver, the path category
![]() $K\mathcal{Q}$
is a
$K\mathcal{Q}$
is a
![]() $\textrm{Hom}$
-finite Krull–Schmidt
$\textrm{Hom}$
-finite Krull–Schmidt
![]() $K$
-category; see [Reference Bautista, Liu and Paquette7].
$K$
-category; see [Reference Bautista, Liu and Paquette7].
Functor Categories
. Recall that a category
![]() $\mathcal{C}$
is said to be skeletally small if it has a small dense subcategory
$\mathcal{C}$
is said to be skeletally small if it has a small dense subcategory
![]() $\mathcal{C}^{\prime}$
, see [Reference Auslander2]. Let
$\mathcal{C}^{\prime}$
, see [Reference Auslander2]. Let
![]() $\mathcal{C}$
be a
$\mathcal{C}$
be a
![]() $\textrm{Hom}$
-finite Krull–Schmidt and skeletally small
$\textrm{Hom}$
-finite Krull–Schmidt and skeletally small
![]() $K-$
category. The abelian category
$K-$
category. The abelian category
![]() $(\mathcal{C}, \textbf{Ab})$
is the category of all additive covariant functors from
$(\mathcal{C}, \textbf{Ab})$
is the category of all additive covariant functors from
![]() $\mathcal{C}$
to the category of abelian groups, which we will call
$\mathcal{C}$
to the category of abelian groups, which we will call
![]() $\mathcal{C}$
-modules. Given two
$\mathcal{C}$
-modules. Given two
![]() $\mathcal{C}$
-modules
$\mathcal{C}$
-modules
![]() $F$
and
$F$
and
![]() $G$
, the set of morphisms
$G$
, the set of morphisms
![]() $\textrm{Hom}_{(\mathcal{C}, \textbf{Ab})}(F,G)$
is denoted simply by
$\textrm{Hom}_{(\mathcal{C}, \textbf{Ab})}(F,G)$
is denoted simply by
![]() $\textrm{Hom}_{\mathcal{C}}(F,G)$
. Following [Reference Auslander2, Reference Auslander, Platzeck and Todorov3],
$\textrm{Hom}_{\mathcal{C}}(F,G)$
. Following [Reference Auslander2, Reference Auslander, Platzeck and Todorov3],
![]() $(\mathcal{C}, \textbf{Ab})$
is denoted by
$(\mathcal{C}, \textbf{Ab})$
is denoted by
![]() $\textrm{Mod}(\mathcal{C})$
. A
$\textrm{Mod}(\mathcal{C})$
. A
![]() $\mathcal{C}$
-module
$\mathcal{C}$
-module
![]() $M$
is finitely presented if an exact sequence
$M$
is finitely presented if an exact sequence
![]() $P_1\rightarrow P_0\rightarrow M\rightarrow 0$
of
$P_1\rightarrow P_0\rightarrow M\rightarrow 0$
of
![]() $\mathcal{C}$
-modules exist where
$\mathcal{C}$
-modules exist where
![]() $P_0$
and
$P_0$
and
![]() $P_1$
are finitely generated projective
$P_1$
are finitely generated projective
![]() $\mathcal{C}$
-modules. We recall that a
$\mathcal{C}$
-modules. We recall that a
![]() $\mathcal{C}$
-module
$\mathcal{C}$
-module
![]() $P$
is finitely generated projective if
$P$
is finitely generated projective if
![]() $P$
is a direct summand of a finite coproduct of representable functors. We denote by
$P$
is a direct summand of a finite coproduct of representable functors. We denote by
![]() $\textrm{mod}(\mathcal{C})$
the full subcategory of
$\textrm{mod}(\mathcal{C})$
the full subcategory of
![]() $\textrm{Mod}(\mathcal{C})$
consisting of finitely presented
$\textrm{Mod}(\mathcal{C})$
consisting of finitely presented
![]() $\mathcal{C}$
-modules. Let
$\mathcal{C}$
-modules. Let
![]() $M$
be a
$M$
be a
![]() $\mathcal{C}$
-module, so each
$\mathcal{C}$
-module, so each
![]() $C$
in
$C$
in
![]() $\mathcal{C}$
the abelian group
$\mathcal{C}$
the abelian group
![]() $M(C)$
has a structure as a
$M(C)$
has a structure as a
![]() $\textrm{End}_{\mathcal{C}}(C)$
-module and hence as a
$\textrm{End}_{\mathcal{C}}(C)$
-module and hence as a
![]() $K$
-module since
$K$
-module since
![]() $\textrm{End}_{\mathcal{C}}(C)$
is a
$\textrm{End}_{\mathcal{C}}(C)$
is a
![]() $K$
-algebra. We denote by
$K$
-algebra. We denote by
![]() $(\mathcal{C}, \textrm{mod} \ K)$
the full subcategory of
$(\mathcal{C}, \textrm{mod} \ K)$
the full subcategory of
![]() $\textrm{Mod}(\mathcal{C})$
of all
$\textrm{Mod}(\mathcal{C})$
of all
![]() $\mathcal{C}$
-modules such that
$\mathcal{C}$
-modules such that
![]() $M(C)$
is a finitely generated
$M(C)$
is a finitely generated
![]() $K$
-module. The category
$K$
-module. The category
![]() $(\mathcal{C}, \textrm{mod} \ K)$
is an abelian category with the property that the inclusion
$(\mathcal{C}, \textrm{mod} \ K)$
is an abelian category with the property that the inclusion
![]() $(\mathcal{C}, \textrm{mod} \ K)\rightarrow \textrm{Mod}(\mathcal{C})$
is exact and contains
$(\mathcal{C}, \textrm{mod} \ K)\rightarrow \textrm{Mod}(\mathcal{C})$
is exact and contains
![]() $\textrm{mod}(\mathcal{C})$
as a full subcategory. Let
$\textrm{mod}(\mathcal{C})$
as a full subcategory. Let
![]() $Q$
be a quiver and
$Q$
be a quiver and
![]() $I$
be an ideal
$I$
be an ideal
![]() $I\subset KQ$
. Set
$I\subset KQ$
. Set
![]() $\mathcal{C}=K\mathcal{Q}/\mathcal{I}$
. Then each representation
$\mathcal{C}=K\mathcal{Q}/\mathcal{I}$
. Then each representation
![]() $V=\left ( (V_i)_{i\in Q_0}, (V_\alpha )_{\alpha \in Q_1}\right )$
in
$V=\left ( (V_i)_{i\in Q_0}, (V_\alpha )_{\alpha \in Q_1}\right )$
in
![]() $\textrm{rep} \ (Q,I)$
defines a
$\textrm{rep} \ (Q,I)$
defines a
![]() $\mathcal{C}$
-module
$\mathcal{C}$
-module
![]() $\tilde V$
in
$\tilde V$
in
![]() $(\mathcal{C}, \textrm{mod} \ K)$
by setting
$(\mathcal{C}, \textrm{mod} \ K)$
by setting
![]() $\tilde V(i)=V_i$
and
$\tilde V(i)=V_i$
and
![]() $\tilde V(\alpha )=V_\alpha$
.
$\tilde V(\alpha )=V_\alpha$
.
In general, the functor
![]() $D\,:\, (\mathcal{C}, \textrm{mod} \ K)\rightarrow (\mathcal{C}^{op}, \textrm{mod} \ K)$
given by
$D\,:\, (\mathcal{C}, \textrm{mod} \ K)\rightarrow (\mathcal{C}^{op}, \textrm{mod} \ K)$
given by
for all
![]() $X$
in
$X$
in
![]() $\mathcal{C}$
defines a duality between
$\mathcal{C}$
defines a duality between
![]() $(\mathcal{C}, \textrm{mod} \ K)$
and
$(\mathcal{C}, \textrm{mod} \ K)$
and
![]() $(\mathcal{C}^{op}, \textrm{mod} \ K)$
, and we refer to it as the standard duality.
$(\mathcal{C}^{op}, \textrm{mod} \ K)$
, and we refer to it as the standard duality.
2.2. Quasi-hereditary categories and triangular matrix categories
Assume
![]() $\mathcal{C}$
is a
$\mathcal{C}$
is a
![]() $\textrm{Hom}$
-finite Krull–Schmidt
$\textrm{Hom}$
-finite Krull–Schmidt
![]() $K$
-category. In order to generalize the notion of quasi-hereditary algebra to
$K$
-category. In order to generalize the notion of quasi-hereditary algebra to
![]() $K$
-categories, the notion of heredity ideal and heredity chain is introduced in [Reference Ortiz23].
$K$
-categories, the notion of heredity ideal and heredity chain is introduced in [Reference Ortiz23].
Remark 2.1. We note that definition of quasi-hereditary category in [Reference Ortiz23, Definition 3.4] is given for contravariant functors; however, by considering the opposite category
![]() $\mathcal{C}^{op}$
we have that contravariant functors over
$\mathcal{C}^{op}$
we have that contravariant functors over
![]() $\mathcal{C}^{op}$
coincide with covariant functors over
$\mathcal{C}^{op}$
coincide with covariant functors over
![]() $\mathcal{C}$
. So, we can translate all the results in [Reference Ortiz23] to the setting of covariant functors.
$\mathcal{C}$
. So, we can translate all the results in [Reference Ortiz23] to the setting of covariant functors.
H Eredity Ideals. A two-sided ideal
![]() $I$
in
$I$
in
![]() $\mathcal{C}$
is called (left) heredity if the following conditions hold:
$\mathcal{C}$
is called (left) heredity if the following conditions hold:
-
(i)
 $I^2=I$
, i.e,
$I^2=I$
, i.e,
 $I$
is an idempotent ideal;
$I$
is an idempotent ideal; -
(ii)
 $I\textrm{rad}\ \mathcal{C}(-,?)I=0$
, and
$I\textrm{rad}\ \mathcal{C}(-,?)I=0$
, and -
(iii)
 $I(X,-)$
is a projective finitely generated
$I(X,-)$
is a projective finitely generated
 $\mathcal{C}-$
module for all
$\mathcal{C}-$
module for all
 $X\in \mathcal{C}$
.
$X\in \mathcal{C}$
.
A chain of two-sided ideals
is exhaustive if
![]() $\cup _{j\in J}I_j=\mathcal{C}(-,?)$
. The category
$\cup _{j\in J}I_j=\mathcal{C}(-,?)$
. The category
![]() $\mathcal{C}$
is called quasi-hereditary if there exists an exhaustive chain
$\mathcal{C}$
is called quasi-hereditary if there exists an exhaustive chain
![]() $\{I_j\}_{j\in J}$
, where
$\{I_j\}_{j\in J}$
, where
![]() $J$
is at most countable, of two-sided ideals
$J$
is at most countable, of two-sided ideals
such that
![]() $I_{j}/I_{j-1}$
is heredity in the quotient category
$I_{j}/I_{j-1}$
is heredity in the quotient category
![]() $\mathcal{C}/I_{j-1}$
. Such a chain is called a heredity chain.
$\mathcal{C}/I_{j-1}$
. Such a chain is called a heredity chain.
Remark 2.2.
-
(a) We note that we consider exhaustive chain of ideals because as in the classical case, we need to reach
 $\mathcal{C}(-,?)$
in some way and if the set
$\mathcal{C}(-,?)$
in some way and if the set
 $J$
is infinite we can do that by requiring the equality
$J$
is infinite we can do that by requiring the equality
 $\cup _{j\in J}I_j=\mathcal{C}(-,?)$
.
$\cup _{j\in J}I_j=\mathcal{C}(-,?)$
. -
(b) In the spirit of the Remark 2.1, we should have called left heredity ideal and left quasi-hereditary category to the notions given above for covariant functors and the notions given for contravarian functors in [Reference Ortiz23] should have been called right heredity ideal and right quasi-hereditary category. However, in order to avoid overloading the notation, we will not write the left adjective in all those notions.
-
(c) By Remark 2.1 we have that
 $\mathcal{C}$
is quasi-hereditary in the sense given above if and only if
$\mathcal{C}$
is quasi-hereditary in the sense given above if and only if
 $\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23].
$\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23].
Let
![]() $\mathcal{B}$
be a full additive subcategory of
$\mathcal{B}$
be a full additive subcategory of
![]() $\mathcal{C}$
. Given
$\mathcal{C}$
. Given
![]() $C,C^{\prime}\in \mathcal{C}$
, we denote by
$C,C^{\prime}\in \mathcal{C}$
, we denote by
![]() $I_{\mathcal{B}}(C,C^{\prime})$
the subset of
$I_{\mathcal{B}}(C,C^{\prime})$
the subset of
![]() $\mathcal{C}(C,C^{\prime})$
consisting of morphisms which factor through some object in
$\mathcal{C}(C,C^{\prime})$
consisting of morphisms which factor through some object in
![]() $\mathcal{B}$
. This allows us to define the two-sided ideal
$\mathcal{B}$
. This allows us to define the two-sided ideal
![]() $I_{\mathcal{B}}(-,?)$
which is an idempotent ideal in
$I_{\mathcal{B}}(-,?)$
which is an idempotent ideal in
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Moreover, we denote by
![]() $\textrm{Tr}_{\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}}} \mathcal{C}(X,-)$
with
$\textrm{Tr}_{\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}}} \mathcal{C}(X,-)$
with
![]() $X\in \mathcal{C}$
, the trace of
$X\in \mathcal{C}$
, the trace of
![]() $\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}}$
in
$\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}}$
in
![]() $\mathcal{C}(X,-)$
, that is,
$\mathcal{C}(X,-)$
, that is,
By the covariant version of [Reference Ortiz23, Lemma 3.1], we have that:
Lemma 2.3.
Let
![]() $\mathcal{B}$
be a full additive subcategory of
$\mathcal{B}$
be a full additive subcategory of
![]() $\mathcal{C}$
. Then for
$\mathcal{C}$
. Then for
![]() $X\in \mathcal{C}$
we have that:
$X\in \mathcal{C}$
we have that:
Quasi-Hereditary Categories
. In the previous section, we gave a definition of quasi-hereditary category respect to a chain
![]() $\{I_j\}_{j\in J}$
of two-sided ideals. Now, in order to produce a chain of two sided ideals of
$\{I_j\}_{j\in J}$
of two-sided ideals. Now, in order to produce a chain of two sided ideals of
![]() $\mathcal{C}$
, we will need a filtration of the category
$\mathcal{C}$
, we will need a filtration of the category
![]() $\mathcal{C}$
. So, assume we have an exhaustive filtration
$\mathcal{C}$
. So, assume we have an exhaustive filtration
of
![]() $\mathcal{C}$
into additive full subcategories (that is,
$\mathcal{C}$
into additive full subcategories (that is,
![]() $\cup _{j\ge 0} \mathcal{B}_j=\mathcal{C}$
). We then have an exhaustive chain of two-sided idempotent ideals:
$\cup _{j\ge 0} \mathcal{B}_j=\mathcal{C}$
). We then have an exhaustive chain of two-sided idempotent ideals:
Note that
![]() $\frac{I_{\mathcal{B}_j}}{I_{\mathcal{B}_{j-1}}}$
is an idempotent ideal in the quotient category
$\frac{I_{\mathcal{B}_j}}{I_{\mathcal{B}_{j-1}}}$
is an idempotent ideal in the quotient category
![]() $\frac{\mathcal{C}}{I_{\mathcal{B}_{j-1}}}$
since
$\frac{\mathcal{C}}{I_{\mathcal{B}_{j-1}}}$
since
![]() $I_{\mathcal{B}_{j}}$
and
$I_{\mathcal{B}_{j}}$
and
![]() $I_{\mathcal{B}_{j-1}}$
are idempotents in
$I_{\mathcal{B}_{j-1}}$
are idempotents in
![]() $\mathcal{C}$
and
$\mathcal{C}$
and
The above motivates us to introduce the definition of quasi-hereditary category respect to an exhaustive
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
filtration of
$\{\mathcal{B}_j\}_{j\geq 0}$
filtration of
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Definition 2.4. [Reference Ortiz23, Definition 3.4 (b)] Let
![]() $\mathcal{C}$
be a
$\mathcal{C}$
be a
![]() $\textrm{Hom}$
-finite Krull–Schmidt
$\textrm{Hom}$
-finite Krull–Schmidt
![]() $K$
-category. Assume that
$K$
-category. Assume that
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
is an exhaustive filtration of
$\{\mathcal{B}_j\}_{j\geq 0}$
is an exhaustive filtration of
![]() $\mathcal{C}$
into full additive subcategories. We say that
$\mathcal{C}$
into full additive subcategories. We say that
![]() $\mathcal{C}$
is quasi-hereditary with respect to
$\mathcal{C}$
is quasi-hereditary with respect to
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
if
$\{\mathcal{B}_j\}_{j\geq 0}$
if
is a heredity chain.
Remark 2.5.
-
(a) We note that the advantage of using the Definition 2.4 instead of the more general definition of quasi-hereditary category given previously, is that exhaustive filtrations are easier to compute than idempotent ideals in general, and exhaustive filtrations induce an exhaustive chain of idempotent ideals.
-
(b) Now, by [Reference Ortiz23, Lemma 3.9] we can see that if
 $\textrm{rad}^{\infty }(\mathcal{C})=0$
then all idempotent ideals of
$\textrm{rad}^{\infty }(\mathcal{C})=0$
then all idempotent ideals of
 $\mathcal{C}$
are of the form
$\mathcal{C}$
are of the form
 $I_{\mathcal{B}}$
for some additive subcategory of
$I_{\mathcal{B}}$
for some additive subcategory of
 $\mathcal{C}$
; and hence all the exhaustive chains
$\mathcal{C}$
; and hence all the exhaustive chains
 $\{I_{i}\}_{i\geq 0}$
of idempotent ideals are constructed in this way. Unfortunately, there are categories where all the idempotent ideals are not of the form
$\{I_{i}\}_{i\geq 0}$
of idempotent ideals are constructed in this way. Unfortunately, there are categories where all the idempotent ideals are not of the form
 $\mathcal{I}_{\mathcal{B}}$
for some
$\mathcal{I}_{\mathcal{B}}$
for some
 $\mathcal{B}$
. For example, if
$\mathcal{B}$
. For example, if
 $A$
is a wild algebra over an algebraically closed field, then the transfinite radical
$A$
is a wild algebra over an algebraically closed field, then the transfinite radical
 $\textrm{rad}^{\ast }$
is not zero (see [Reference Zhu28, Proposition 4]) and
$\textrm{rad}^{\ast }$
is not zero (see [Reference Zhu28, Proposition 4]) and
 $\textrm{rad}^{\ast }$
is an idempotent ideal of
$\textrm{rad}^{\ast }$
is an idempotent ideal of
 $\textrm{mod}(A)$
which does not contain any identity morphisms (see [Reference Zhu28, Lemma 1]); and hence it is not of the form
$\textrm{mod}(A)$
which does not contain any identity morphisms (see [Reference Zhu28, Lemma 1]); and hence it is not of the form
 $\mathcal{I}_{B}$
.
$\mathcal{I}_{B}$
.
Let
![]() $\mathcal{B}$
be an additive subcategory of
$\mathcal{B}$
be an additive subcategory of
![]() $\mathcal{C}$
, we denote by
$\mathcal{C}$
, we denote by
![]() $\textrm{add}(\mathcal{B})$
the full subcategory of
$\textrm{add}(\mathcal{B})$
the full subcategory of
![]() $\mathcal{C}$
whose objects are the direct summands of finite coproducts of objects in
$\mathcal{C}$
whose objects are the direct summands of finite coproducts of objects in
![]() $\mathcal{B}$
. A subcategory
$\mathcal{B}$
. A subcategory
![]() $\mathcal{B}$
of
$\mathcal{B}$
of
![]() $\mathcal{C}$
is closed under direct summands if
$\mathcal{C}$
is closed under direct summands if
![]() $\textrm{add}(\mathcal{B})=\mathcal{B}$
. Let
$\textrm{add}(\mathcal{B})=\mathcal{B}$
. Let
![]() $\mathcal{B}$
be an additive subcategory of
$\mathcal{B}$
be an additive subcategory of
![]() $\mathcal{C}$
, we denote by
$\mathcal{C}$
, we denote by
![]() ${\textbf{Ind}}(\mathcal{B})$
the class of all the indecomposable objects belonging to
${\textbf{Ind}}(\mathcal{B})$
the class of all the indecomposable objects belonging to
![]() $\mathcal{B}$
. The following result given in [Reference Ortiz23] will be useful in the remainder of this work.
$\mathcal{B}$
. The following result given in [Reference Ortiz23] will be useful in the remainder of this work.
Theorem 2.6. [Reference Ortiz23, Theorem 3.6] Let
![]() $\mathcal{C}$
be a
$\mathcal{C}$
be a
![]() $\textrm{Hom}$
-finite Krull–Schmidt
$\textrm{Hom}$
-finite Krull–Schmidt
![]() $K$
-category and let
$K$
-category and let
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
$\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
![]() $\mathcal{C}$
. Suppose that
$\mathcal{C}$
. Suppose that
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
is an exhaustive filtration of
$\{\mathcal{B}_j\}_{j\geq 0}$
is an exhaustive filtration of
![]() $\mathcal{C}$
. Then
$\mathcal{C}$
. Then
![]() $\mathcal{C}$
is quasi-hereditary with respect to
$\mathcal{C}$
is quasi-hereditary with respect to
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
if and only if the following conditions hold:
$\{\mathcal{B}_j\}_{j\geq 0}$
if and only if the following conditions hold:
-
(i)
 $\textrm{rad}_{\mathcal{C}}(E,E^{\prime})=I_{\mathcal{B}_{j-1}}(E,E^{\prime})$
, for all
$\textrm{rad}_{\mathcal{C}}(E,E^{\prime})=I_{\mathcal{B}_{j-1}}(E,E^{\prime})$
, for all
 $E,E^{\prime}\in \textrm{ Ind} \ \mathcal{B}_{j}-\textrm{ Ind} \ \mathcal{B}_{j-1}$
;
$E,E^{\prime}\in \textrm{ Ind} \ \mathcal{B}_{j}-\textrm{ Ind} \ \mathcal{B}_{j-1}$
; -
(ii) and for all
 $X \in \mathcal{C}$
and
$X \in \mathcal{C}$
and
 $j\geq 1$
, there exists an exact sequence
$j\geq 1$
, there exists an exact sequence

with
 $E_{j} \in \mathcal{B}_{j}$
and
$E_{j} \in \mathcal{B}_{j}$
and
 $E_{j-1} \in \mathcal{B}_{j-1}$
.
$E_{j-1} \in \mathcal{B}_{j-1}$
.
Remark 2.7. (a). Let us see why the Definition 2.4 is a generalization of the classical notion of quasi-hereditary algebra. Let
![]() $A$
be a finite dimensional
$A$
be a finite dimensional
![]() $K$
-algebra. In this case, we consider the
$K$
-algebra. In this case, we consider the
![]() $K$
-category
$K$
-category
![]() $\mathcal{C}\,:\!=\,\textrm{proj}(A)$
, that is, the full subcategory of
$\mathcal{C}\,:\!=\,\textrm{proj}(A)$
, that is, the full subcategory of
![]() $\textrm{mod}(A)$
whose objects are the finitely generated projective
$\textrm{mod}(A)$
whose objects are the finitely generated projective
![]() $A$
-modules. Since
$A$
-modules. Since
![]() $A$
is semiperfect we have that
$A$
is semiperfect we have that
![]() $\mathcal{C}=\textrm{proj}(A)$
is a Krull–Schmidt category (see [Reference Krause13, Proposition 4.1]).
$\mathcal{C}=\textrm{proj}(A)$
is a Krull–Schmidt category (see [Reference Krause13, Proposition 4.1]).
Suppose that
![]() $\textrm{proj}(A)$
is a quasi-hereditary category in the sense of Definition 2.4, with respect to the exhaustive filtration
$\textrm{proj}(A)$
is a quasi-hereditary category in the sense of Definition 2.4, with respect to the exhaustive filtration
of
![]() $\textrm{proj}(A)$
into additive full subcategories and closed under direct summands. Then we have an exhaustive chain of two-sided idempotent ideals of
$\textrm{proj}(A)$
into additive full subcategories and closed under direct summands. Then we have an exhaustive chain of two-sided idempotent ideals of
![]() $\mathcal{C}(-,?)$
:
$\mathcal{C}(-,?)$
:
By [Reference Krause14, Lemma 4.5], we have the corresponding chain of idempotent ideals of
![]() $A^{op}$
$A^{op}$
where
![]() $J_{i}\,:\!=\,I_{\mathcal{B}_{i}}(A,A)$
for all
$J_{i}\,:\!=\,I_{\mathcal{B}_{i}}(A,A)$
for all
![]() $i$
. In this case,
$i$
. In this case,
![]() $J_{i}=Ae_{i}A$
for some idempotent
$J_{i}=Ae_{i}A$
for some idempotent
![]() $e_{i}\in A$
and by [Reference Krause14, Lemma 4.5], we have that
$e_{i}\in A$
and by [Reference Krause14, Lemma 4.5], we have that
![]() $\mathcal{B}_{i}=\textrm{add}(Ae_{i})$
for all
$\mathcal{B}_{i}=\textrm{add}(Ae_{i})$
for all
![]() $i\geq 0$
.
$i\geq 0$
.
Now, let us see that
![]() $J_{1}$
is a heredity ideal of
$J_{1}$
is a heredity ideal of
![]() $A^{op}$
.
$A^{op}$
.
![]() $(i)$
. By Theorem 2.6(i), we have that
$(i)$
. By Theorem 2.6(i), we have that
![]() $\textrm{rad}_{\mathcal{C}}(E,E^{\prime})=I_{\mathcal{B}_{0}}(E,E^{\prime})=0,$
for all pair of objects
$\textrm{rad}_{\mathcal{C}}(E,E^{\prime})=I_{\mathcal{B}_{0}}(E,E^{\prime})=0,$
for all pair of objects
![]() $E,E^{\prime}\in \textrm{ Ind} \ \mathcal{B}_{1}$
, since
$E,E^{\prime}\in \textrm{ Ind} \ \mathcal{B}_{1}$
, since
![]() $\mathcal{B}_{0}=\{0\}$
. Hence,
$\mathcal{B}_{0}=\{0\}$
. Hence,
![]() $\textrm{rad}(\mathcal{B}_{1})=0$
and thus
$\textrm{rad}(\mathcal{B}_{1})=0$
and thus
![]() $e_{1}\textrm{rad}(A)e_{1}=0$
. We conclude that
$e_{1}\textrm{rad}(A)e_{1}=0$
. We conclude that
![]() $J_{1}A^{op}J_{1}=0$
.
$J_{1}A^{op}J_{1}=0$
.
![]() $(ii)$
By Theorem 2.6(ii) we have an exact sequence
$(ii)$
By Theorem 2.6(ii) we have an exact sequence
with
![]() $Y\in \mathcal{B}_{1}=\textrm{add}(Ae_{1})$
and
$Y\in \mathcal{B}_{1}=\textrm{add}(Ae_{1})$
and
![]() $Z\in \mathcal{B}_{0}=\{0\}$
.
$Z\in \mathcal{B}_{0}=\{0\}$
.
Hence,
![]() $J_{1}=I_{\mathcal{B}_{1}}(A,A)\simeq \mathcal{C}(Y,A)=\textrm{proj}(Y,A)=\textrm{Hom}_{A}(Y,A)$
which is projective over
$J_{1}=I_{\mathcal{B}_{1}}(A,A)\simeq \mathcal{C}(Y,A)=\textrm{proj}(Y,A)=\textrm{Hom}_{A}(Y,A)$
which is projective over
![]() $A^{op}\simeq \textrm{proj}(A,A)$
.
$A^{op}\simeq \textrm{proj}(A,A)$
.
Hence,
![]() $J_{1}$
is a heredity ideal of
$J_{1}$
is a heredity ideal of
![]() $A^{op}$
. We can proceed inductively and conclude that
$A^{op}$
. We can proceed inductively and conclude that
![]() $J_{i}/J_{i-1}$
is a heredity ideal of
$J_{i}/J_{i-1}$
is a heredity ideal of
![]() $A^{op}/J_{i-1}$
for all
$A^{op}/J_{i-1}$
for all
![]() $i\geq 1$
. Therefore,
$i\geq 1$
. Therefore,
![]() $A^{op}$
is quasi-hereditary and hence by [Reference Dlab and Ringel11, Statement 9] we conclude that
$A^{op}$
is quasi-hereditary and hence by [Reference Dlab and Ringel11, Statement 9] we conclude that
![]() $A$
is quasi-hereditary. Similarly, by using [Reference Krause14, Lemma 4.5], it can be proved that if
$A$
is quasi-hereditary. Similarly, by using [Reference Krause14, Lemma 4.5], it can be proved that if
![]() $A$
is a quasi-hereditary algebra then
$A$
is a quasi-hereditary algebra then
![]() $\textrm{proj}(A)$
is a quasi-hereditary category.
$\textrm{proj}(A)$
is a quasi-hereditary category.
(b). Suppose that
![]() $A$
is quasi-hereditary, then there exists a chain of idempotent ideals
$A$
is quasi-hereditary, then there exists a chain of idempotent ideals
such that
![]() $J_{t}/J_{t-1}$
is a heredity ideal of
$J_{t}/J_{t-1}$
is a heredity ideal of
![]() $A/J_{t-1}$
for all
$A/J_{t-1}$
for all
![]() $t$
.
$t$
.
By [Reference Auslander and Reiten4, Proposition 6.1], there exists projective
![]() $A$
-modules
$A$
-modules
![]() $P_{1},\cdots, P_{m}$
such that
$P_{1},\cdots, P_{m}$
such that
![]() $J_{i}=\textrm{Tr}_{P_{1}\oplus \cdots \oplus P_{i}}(A)$
for
$J_{i}=\textrm{Tr}_{P_{1}\oplus \cdots \oplus P_{i}}(A)$
for
![]() $i=1,\cdots, m$
. Moreover, if
$i=1,\cdots, m$
. Moreover, if
![]() $\mathcal{B}_{i}=\textrm{add}(P_{1}\oplus \cdots \oplus P_{i})$
, then for each
$\mathcal{B}_{i}=\textrm{add}(P_{1}\oplus \cdots \oplus P_{i})$
, then for each
![]() $i=1,\cdots, m$
there exists an exact sequence in
$i=1,\cdots, m$
there exists an exact sequence in
![]() $\textrm{mod}(A)$
$\textrm{mod}(A)$
such that
![]() $P_{i,0}\in \mathcal{B}_{i}$
and
$P_{i,0}\in \mathcal{B}_{i}$
and
![]() $P_{i,1}\in \mathcal{B}_{i-1}$
.
$P_{i,1}\in \mathcal{B}_{i-1}$
.
We note that these exact sequences are the analogous of the exact sequences given in the Theorem 2.6(ii):
with
![]() $P_{i,0} \in \mathcal{B}_{i}$
,
$P_{i,0} \in \mathcal{B}_{i}$
,
![]() $P_{i,1} \in \mathcal{B}_{i-1}$
, and
$P_{i,1} \in \mathcal{B}_{i-1}$
, and
![]() $X\in \mathcal{C}$
.
$X\in \mathcal{C}$
.
It is well known that a semiprimary ring
![]() $A$
is quasi-hereditary if and only if
$A$
is quasi-hereditary if and only if
![]() $A^{op}$
is quasi-hereditary (see [Reference Dlab and Ringel11, Statement 9] in p. 288). We have somehow a similar result for the context of quasi-hereditary categories.
$A^{op}$
is quasi-hereditary (see [Reference Dlab and Ringel11, Statement 9] in p. 288). We have somehow a similar result for the context of quasi-hereditary categories.
We recall the following notions. Let
![]() $\mathcal{A}$
be an arbitrary category and
$\mathcal{A}$
be an arbitrary category and
![]() $\mathcal{B}$
a full subcategory of
$\mathcal{B}$
a full subcategory of
![]() $\mathcal{A}$
. The full subcategory
$\mathcal{A}$
. The full subcategory
![]() $\mathcal{B}$
is contravariantly finite if for every
$\mathcal{B}$
is contravariantly finite if for every
![]() $A\in \mathcal{A}$
there exists a morphism
$A\in \mathcal{A}$
there exists a morphism
![]() $f_{A}\,:\,B\longrightarrow A$
with
$f_{A}\,:\,B\longrightarrow A$
with
![]() $B\in \mathcal{B}$
such that if
$B\in \mathcal{B}$
such that if
![]() $f^{\prime}\,:\,B^{\prime}\longrightarrow A$
is other morphism with
$f^{\prime}\,:\,B^{\prime}\longrightarrow A$
is other morphism with
![]() $B^{\prime}\in \mathcal{B}$
, then there exist a morphism
$B^{\prime}\in \mathcal{B}$
, then there exist a morphism
![]() $g\,:\,B^{\prime}\longrightarrow B$
such that
$g\,:\,B^{\prime}\longrightarrow B$
such that
![]() $f^{\prime}=f_{A} g$
. The morphism
$f^{\prime}=f_{A} g$
. The morphism
![]() $f_{A}$
is called a
$f_{A}$
is called a
![]() $\textbf{right}$
$\textbf{right}$
![]() $\boldsymbol{\mathcal{B}}$
$\boldsymbol{\mathcal{B}}$
![]() $\textbf{-approximation}$
of
$\textbf{-approximation}$
of
![]() $A$
. A right
$A$
. A right
![]() $\mathcal{B}$
-approximation
$\mathcal{B}$
-approximation
![]() $f_{A}\,:\,B\longrightarrow A$
of
$f_{A}\,:\,B\longrightarrow A$
of
![]() $A$
is
$A$
is
![]() $\text{minimal}$
if whenever
$\text{minimal}$
if whenever
![]() $g\,:\,B\longrightarrow B$
is a morphism such that
$g\,:\,B\longrightarrow B$
is a morphism such that
![]() $g f_{A}=f_{A}$
then
$g f_{A}=f_{A}$
then
![]() $g$
is an isomorphism. Dually, is defined the notion of
$g$
is an isomorphism. Dually, is defined the notion of
![]() $\textbf{covariantly finite}$
and
$\textbf{covariantly finite}$
and
![]() $\textbf{left minimal}$
$\textbf{left minimal}$
![]() $\boldsymbol{\mathcal{B}}$
$\boldsymbol{\mathcal{B}}$
![]() $\textbf{-approximation}$
. We say that
$\textbf{-approximation}$
. We say that
![]() $\mathcal{B}$
is
$\mathcal{B}$
is
![]() $\textbf{functorially finite}$
if
$\textbf{functorially finite}$
if
![]() $\mathcal{B}$
is contravariantly finite and covariantly finite.
$\mathcal{B}$
is contravariantly finite and covariantly finite.
Proposition 2.8. Let
![]() $\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
$\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
$\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
![]() $\mathcal{C}$
; and suppose that each
$\mathcal{C}$
; and suppose that each
![]() $\mathcal{B}_{j}$
is covariantly finite. If
$\mathcal{B}_{j}$
is covariantly finite. If
![]() $\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23, Definition 3.4], then
$\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23, Definition 3.4], then
![]() $\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23, Definition 3.4].
$\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23, Definition 3.4].
Proof. Suppose that
![]() $\mathcal{C}$
is quasi-hereditary with respect to
$\mathcal{C}$
is quasi-hereditary with respect to
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
. By [Reference Ortiz23, Theorem 3.6], there exist exact sequences for all
$\{\mathcal{B}_j\}_{j\geq 0}$
. By [Reference Ortiz23, Theorem 3.6], there exist exact sequences for all
![]() $X \in \mathcal{C}$
and
$X \in \mathcal{C}$
and
![]() $j\geq 1$
:
$j\geq 1$
:
with
![]() $E_{j} \in \mathcal{B}_{j}$
and
$E_{j} \in \mathcal{B}_{j}$
and
![]() $E_{j-1}\in \mathcal{B}_{j-1}$
. Now, since
$E_{j-1}\in \mathcal{B}_{j-1}$
. Now, since
![]() $B_{j}$
is covariantly finite, there exists an epimorphism
$B_{j}$
is covariantly finite, there exists an epimorphism
![]() $\mathcal{C}(X,-)\longrightarrow I_{\mathcal{B}_{j}}(C,-)$
for every
$\mathcal{C}(X,-)\longrightarrow I_{\mathcal{B}_{j}}(C,-)$
for every
![]() $C\in \mathcal{C}$
by using the proof of [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12]. Then, this implies that
$C\in \mathcal{C}$
by using the proof of [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12]. Then, this implies that
![]() $B_{j}$
is functorially finite by [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12].
$B_{j}$
is functorially finite by [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12].
We assert that for all
![]() $X\in \mathcal{C}$
there exists a monic right
$X\in \mathcal{C}$
there exists a monic right
![]() $\mathcal{B}_{1}$
-approximation of
$\mathcal{B}_{1}$
-approximation of
![]() $X$
. Indeed, by taking,
$X$
. Indeed, by taking,
![]() $j=1$
, from the above exact sequence we get that
$j=1$
, from the above exact sequence we get that
![]() $\mathcal{C}(-,E_{1})\simeq I_{\mathcal{B}_{1}}(-,X)$
. By Yoneda’s Lemma we get a morphism
$\mathcal{C}(-,E_{1})\simeq I_{\mathcal{B}_{1}}(-,X)$
. By Yoneda’s Lemma we get a morphism
![]() $\gamma \,:\,E_{1} \longrightarrow X$
and this morphism is a right
$\gamma \,:\,E_{1} \longrightarrow X$
and this morphism is a right
![]() $\mathcal{B}_{1}$
-approximation of
$\mathcal{B}_{1}$
-approximation of
![]() $X$
. Now, let
$X$
. Now, let
![]() $\alpha \,:\,Y \longrightarrow E_{1}$
such that
$\alpha \,:\,Y \longrightarrow E_{1}$
such that
![]() $\gamma \alpha =0$
. Since
$\gamma \alpha =0$
. Since
![]() $\mathcal{C}(-,\gamma )\,:\,\mathcal{C}(-,E_{1})\longrightarrow I_{\mathcal{B}_{1}}(-,X)$
is an isomorphism, we conclude that
$\mathcal{C}(-,\gamma )\,:\,\mathcal{C}(-,E_{1})\longrightarrow I_{\mathcal{B}_{1}}(-,X)$
is an isomorphism, we conclude that
![]() $\alpha =0$
, this implies that
$\alpha =0$
, this implies that
![]() $\gamma$
is a monomorphism.
$\gamma$
is a monomorphism.
Now, since
![]() $\mathcal{B}_{1}$
is covariantly finite,
$\mathcal{B}_{1}$
is covariantly finite,
![]() $\textrm{add}(\mathcal{B}_{1})=\mathcal{B}_{1}$
and
$\textrm{add}(\mathcal{B}_{1})=\mathcal{B}_{1}$
and
![]() $\mathcal{C}$
is a Krull–Schmidt category, every object of
$\mathcal{C}$
is a Krull–Schmidt category, every object of
![]() $\mathcal{C}$
has a left minimal
$\mathcal{C}$
has a left minimal
![]() $\mathcal{B}_{1}$
-approximation. So, let
$\mathcal{B}_{1}$
-approximation. So, let
![]() $\theta \,:\,X\longrightarrow E^{\prime}_{1}$
be a left minimal
$\theta \,:\,X\longrightarrow E^{\prime}_{1}$
be a left minimal
![]() $\mathcal{B}_{1}$
-approximation of
$\mathcal{B}_{1}$
-approximation of
![]() $X$
.
$X$
.
We assert that
![]() $\theta$
is an epimorphism. Indeed, consider
$\theta$
is an epimorphism. Indeed, consider
![]() $\beta \,:\,E^{\prime}_{1}\longrightarrow Y$
a morphism such that
$\beta \,:\,E^{\prime}_{1}\longrightarrow Y$
a morphism such that
![]() $\beta \theta =0$
. By the first assertion above, there exists
$\beta \theta =0$
. By the first assertion above, there exists
![]() $\lambda \,:\,E\longrightarrow Y$
a monic right
$\lambda \,:\,E\longrightarrow Y$
a monic right
![]() $\mathcal{B}_{1}$
-approximation of
$\mathcal{B}_{1}$
-approximation of
![]() $Y$
; and hence
$Y$
; and hence
![]() $\beta =\lambda \delta$
for some
$\beta =\lambda \delta$
for some
![]() $\delta \,:\,E^{\prime}_{1}\longrightarrow E$
. Since,
$\delta \,:\,E^{\prime}_{1}\longrightarrow E$
. Since,
![]() $0=\beta \theta =\lambda \delta \theta$
and
$0=\beta \theta =\lambda \delta \theta$
and
![]() $\lambda$
is a monomorphism we get that
$\lambda$
is a monomorphism we get that
![]() $\delta \theta =0$
.
$\delta \theta =0$
.
Now, for all
![]() $g\,:\,E \longrightarrow E^{\prime}_{1}$
we have that
$g\,:\,E \longrightarrow E^{\prime}_{1}$
we have that
![]() $(1_{E^{\prime}_{1}}-g \delta )\theta =\theta$
. Since
$(1_{E^{\prime}_{1}}-g \delta )\theta =\theta$
. Since
![]() $\theta$
is minimal we get that
$\theta$
is minimal we get that
![]() $(1_{E^{\prime}_{1}}-g\delta )$
is an isomorphism; and thus we conclude that
$(1_{E^{\prime}_{1}}-g\delta )$
is an isomorphism; and thus we conclude that
![]() $\delta \in \textrm{rad}_{\mathcal{C}}(E^{\prime}_{1},E)=\textrm{rad}_{\mathcal{B}_{1}}(E^{\prime}_{1},E)=0$
(see [Reference Ortiz23, Theorem 3.6(i)]). Hence,
$\delta \in \textrm{rad}_{\mathcal{C}}(E^{\prime}_{1},E)=\textrm{rad}_{\mathcal{B}_{1}}(E^{\prime}_{1},E)=0$
(see [Reference Ortiz23, Theorem 3.6(i)]). Hence,
![]() $\delta =0$
and we obtain that
$\delta =0$
and we obtain that
![]() $\beta =\lambda \delta =0$
. This proves that
$\beta =\lambda \delta =0$
. This proves that
![]() $\theta$
is an epimorphism. Now,
$\theta$
is an epimorphism. Now,
![]() $\mathcal{C}(\theta,-)$
is an epimorphism as established in the proof of [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12]. Therefore, we get an isomorphism
$\mathcal{C}(\theta,-)$
is an epimorphism as established in the proof of [Reference Rodríguez-Valdés, Sandoval-Miranda and Santiago-Vargas26, Proposition 4.12]. Therefore, we get an isomorphism
We note that
![]() $I_{\mathcal{B}_{j}}^{op}=I_{\mathcal{B}_{j}^{op}}$
is a bilateral ideal of
$I_{\mathcal{B}_{j}}^{op}=I_{\mathcal{B}_{j}^{op}}$
is a bilateral ideal of
![]() $\mathcal{C}^{op}$
for all
$\mathcal{C}^{op}$
for all
![]() $j$
. Thus, we get that
$j$
. Thus, we get that
![]() $I_{\mathcal{B}_{1}^{op}}(-,X)=I_{\mathcal{B}_{1}}(X,-)\simeq \mathcal{C}(E^{\prime}_{1},-)\simeq \mathcal{C}^{op}(-,E^{\prime}_{1})$
is a projective
$I_{\mathcal{B}_{1}^{op}}(-,X)=I_{\mathcal{B}_{1}}(X,-)\simeq \mathcal{C}(E^{\prime}_{1},-)\simeq \mathcal{C}^{op}(-,E^{\prime}_{1})$
is a projective
![]() $\mathcal{C}^{op}$
-module. Since
$\mathcal{C}^{op}$
-module. Since
![]() $\textrm{rad}\mathcal{C}(-,-)$
is a bilateral ideal we have that
$\textrm{rad}\mathcal{C}(-,-)$
is a bilateral ideal we have that
![]() $I_{\mathcal{B}_{1}}\textrm{rad}\ \mathcal{C}(-,?)I_{\mathcal{B}_{1}}=0$
implies that
$I_{\mathcal{B}_{1}}\textrm{rad}\ \mathcal{C}(-,?)I_{\mathcal{B}_{1}}=0$
implies that
![]() $I_{\mathcal{B}_{1}^{op}}\textrm{rad}\mathcal{C}^{op}(-,?)I_{\mathcal{B}_{1}^{op}}=0.$
Hence, we obtain that
$I_{\mathcal{B}_{1}^{op}}\textrm{rad}\mathcal{C}^{op}(-,?)I_{\mathcal{B}_{1}^{op}}=0.$
Hence, we obtain that
![]() $I_{\mathcal{B}_{1}^{op}}(-,X)$
is a heredity ideal of
$I_{\mathcal{B}_{1}^{op}}(-,X)$
is a heredity ideal of
![]() $\mathcal{C}^{op}$
. Proceeding inductively, we conclude that
$\mathcal{C}^{op}$
. Proceeding inductively, we conclude that
is a heredity chain. Hence,
![]() $\mathcal{C}^{op}$
is quasi-hereditary with respect to
$\mathcal{C}^{op}$
is quasi-hereditary with respect to
![]() $\{\mathcal{B}_j^{op}\}_{j\geq 0}$
in the sense of [Reference Ortiz23, Definition 3.4].
$\{\mathcal{B}_j^{op}\}_{j\geq 0}$
in the sense of [Reference Ortiz23, Definition 3.4].
Corollary 2.9.
Let
![]() $\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
$\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
$\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
![]() $\mathcal{C}$
and suppose that each
$\mathcal{C}$
and suppose that each
![]() $\mathcal{B}_{j}$
is functorially finite. Then
$\mathcal{B}_{j}$
is functorially finite. Then
![]() $\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4] if and only if
$\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4] if and only if
![]() $\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4].
$\mathcal{C}^{op}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4].
Proof. It follows from Proposition 2.8 and its dual.
By the Corollary above and Remark 2.2(c), we conclude the following.
Corollary 2.10.
Let
![]() $\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
$\mathcal{C}$
be a Hom-finite and Krull–Schmidt category and let
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
$\{\mathcal{B}_j\}_{j\geq 0}$
be a family of closed under direct summands additive subcategories of
![]() $\mathcal{C}$
and suppose that each
$\mathcal{C}$
and suppose that each
![]() $\mathcal{B}_{j}$
is functorially finite. Then
$\mathcal{B}_{j}$
is functorially finite. Then
![]() $\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4] if and only if
$\mathcal{C}$
is quasi-hereditary in the sense of [Reference Ortiz23
, Definition 3.4] if and only if
![]() $\mathcal{C}$
is quasi-hereditary in the sense of Definition 2.4
.
$\mathcal{C}$
is quasi-hereditary in the sense of Definition 2.4
.
Standard
![]() $\mathcal{C}$
-Modules
. Let
$\mathcal{C}$
-Modules
. Let
![]() $\mathcal{C}$
be a quasi-hereditary category with respect to a family of additively closed subcategories
$\mathcal{C}$
be a quasi-hereditary category with respect to a family of additively closed subcategories
![]() $\{\mathcal{B}_j\}$
. Each module
$\{\mathcal{B}_j\}$
. Each module
with
![]() $E\in \textrm{Ind} \mathcal{B}_j-\textrm{Ind} \mathcal{B}_{j-1}$
is called standard, and
$E\in \textrm{Ind} \mathcal{B}_j-\textrm{Ind} \mathcal{B}_{j-1}$
is called standard, and
![]() $_{\mathcal{C}}\Delta (j)$
denotes the category consisting of the standard
$_{\mathcal{C}}\Delta (j)$
denotes the category consisting of the standard
![]() $\mathcal{C}$
-modules
$\mathcal{C}$
-modules
![]() $_{\mathcal{C}}\Delta _E(j)$
. In addition,
$_{\mathcal{C}}\Delta _E(j)$
. In addition,
![]() $_{\mathcal{C}}\Delta$
denotes the full subcategory consisting of the standard
$_{\mathcal{C}}\Delta$
denotes the full subcategory consisting of the standard
![]() $\mathcal{C}$
-modules.
$\mathcal{C}$
-modules.
Filtered
![]() $\mathcal{C}$
-Modules. Let
$\mathcal{C}$
-Modules. Let
![]() $\mathcal{A}$
be an abelian category, and
$\mathcal{A}$
be an abelian category, and
![]() $\mathcal{X}\subseteq \mathcal{A}.$
We denote by
$\mathcal{X}\subseteq \mathcal{A}.$
We denote by
![]() $\mathcal{X}^{\amalg }$
the class of objects of
$\mathcal{X}^{\amalg }$
the class of objects of
![]() $\mathcal{A}$
, which are a finite direct sum of objects in
$\mathcal{A}$
, which are a finite direct sum of objects in
![]() $\mathcal{X}.$
We say that
$\mathcal{X}.$
We say that
![]() $M\in \mathcal{A}$
is
$M\in \mathcal{A}$
is
![]() $\mathcal{X}$
-
$\mathcal{X}$
-
![]() $\textbf{filtered}$
if there exists a chain
$\textbf{filtered}$
if there exists a chain
![]() $\{M_{j}\}_{j\ge 0}$
of subobjects of
$\{M_{j}\}_{j\ge 0}$
of subobjects of
![]() $M$
such that
$M$
such that
![]() $M_{j+1}/M_{j}\in \mathcal{X}^{\amalg }$
for
$M_{j+1}/M_{j}\in \mathcal{X}^{\amalg }$
for
![]() $j\ge 0.$
In case
$j\ge 0.$
In case
![]() $M=M_n$
for some
$M=M_n$
for some
![]() $n\in \mathbb N$
, we say that
$n\in \mathbb N$
, we say that
![]() $M$
has a finite
$M$
has a finite
![]() $\mathcal{X}$
-filtration of length
$\mathcal{X}$
-filtration of length
![]() $n$
. We denote by
$n$
. We denote by
![]() $\mathcal{F}(\mathcal{X})$
the class of objects that are
$\mathcal{F}(\mathcal{X})$
the class of objects that are
![]() $\mathcal{X}$
-filtered and by
$\mathcal{X}$
-filtered and by
![]() $\mathcal{F}_f(\mathcal{X})$
the class of objects that have a finite filtration. For
$\mathcal{F}_f(\mathcal{X})$
the class of objects that have a finite filtration. For
![]() $M \in \mathcal{F}_f(\mathcal{X})$
, the
$M \in \mathcal{F}_f(\mathcal{X})$
, the
![]() $\mathcal{X}$
-length of
$\mathcal{X}$
-length of
![]() $M$
can be defined as follows
$M$
can be defined as follows
![]() $l_{\mathcal{X}}(M)\,:\!=\,\textrm{min}\{ n\in \mathbb{N} \,:\, M \text{ has an $\mathcal{X}$-filtration of length $n$}\}$
.
$l_{\mathcal{X}}(M)\,:\!=\,\textrm{min}\{ n\in \mathbb{N} \,:\, M \text{ has an $\mathcal{X}$-filtration of length $n$}\}$
.
By using the notion of
![]() $\mathcal{X}$
-length and induction, the following useful remark can be proven.
$\mathcal{X}$
-length and induction, the following useful remark can be proven.
Remark 2.11. Let
![]() $\mathcal{X}$
be a class of objects in an abelian category
$\mathcal{X}$
be a class of objects in an abelian category
![]() $A$
. Then, the class
$A$
. Then, the class
![]() $\mathcal{F}_f (\mathcal{X})$
is closed under extensions.
$\mathcal{F}_f (\mathcal{X})$
is closed under extensions.
Given
![]() $F$
a
$F$
a
![]() $\mathcal{C}-$
module, its trace filtration with respect to
$\mathcal{C}-$
module, its trace filtration with respect to
![]() $\{\mathcal{B}_j\}_{j\geq 0}$
is given by
$\{\mathcal{B}_j\}_{j\geq 0}$
is given by
where
![]() $F^{[j]}\,:\!=\,\textrm{Tr}_{\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}_j}}F$
and
$F^{[j]}\,:\!=\,\textrm{Tr}_{\{\mathcal{C}(E,-)\}_{E\in \mathcal{B}_j}}F$
and
![]() $F= \bigcup \limits _{j\geq 0}F^{[j]}$
.
$F= \bigcup \limits _{j\geq 0}F^{[j]}$
.
It is of interest to study the
![]() $ \mathcal{C}$
-modules
$ \mathcal{C}$
-modules
![]() $F$
that possesses a trace filtration that satisfies
$F$
that possesses a trace filtration that satisfies
![]() $ \frac{F ^{[j]}}{F ^{[j-1]}} \in{}_{\mathcal{C}}\Delta (j) ^{\amalg }$
for all
$ \frac{F ^{[j]}}{F ^{[j-1]}} \in{}_{\mathcal{C}}\Delta (j) ^{\amalg }$
for all
![]() $ j \geq 1$
. It then follows that these
$ j \geq 1$
. It then follows that these
![]() $ \mathcal{C}$
-modules are
$ \mathcal{C}$
-modules are
![]() $ \Delta$
-filtered. We denote the full subcategory of the
$ \Delta$
-filtered. We denote the full subcategory of the
![]() $ \Delta$
-filtered modules by
$ \Delta$
-filtered modules by
![]() $ \mathcal{F} (_{\mathcal{C}}\Delta )$
.
$ \mathcal{F} (_{\mathcal{C}}\Delta )$
.
The following result will be very useful, the item
![]() $(b)$
is a generalization of a result of Dlab (see [Reference Dlab9, Proposition A.3.2]).
$(b)$
is a generalization of a result of Dlab (see [Reference Dlab9, Proposition A.3.2]).
Lemma 2.12. [Reference Ortiz23, Lemmas 3.17, 3.18] Let
![]() $F \in \mathcal{F}(\Delta )$
.
$F \in \mathcal{F}(\Delta )$
.
-
(a) For all
 $j\geq 0$
,
$j\geq 0$
,
 $F^{[j]}$
has a presentation
(2.2)
$F^{[j]}$
has a presentation
(2.2) \begin{equation} \mathcal{C}(E_{j-1},-) \rightarrow \mathcal{C}(E_{j},-) \rightarrow F^{[j]} \rightarrow 0,\ E_{j-1} \in \mathcal{B}_{j-1}, E_{j}\in \mathcal{B}_{j}. \end{equation}
\begin{equation} \mathcal{C}(E_{j-1},-) \rightarrow \mathcal{C}(E_{j},-) \rightarrow F^{[j]} \rightarrow 0,\ E_{j-1} \in \mathcal{B}_{j-1}, E_{j}\in \mathcal{B}_{j}. \end{equation}
-
(b)
 $F^{[j]}\cong \mathcal{C} \otimes _{\mathcal{B}_j}(F|_{\mathcal{B}_{j}})$
.
$F^{[j]}\cong \mathcal{C} \otimes _{\mathcal{B}_j}(F|_{\mathcal{B}_{j}})$
. -
(c) If the filtration
 $0=\mathcal{B}_{0}\subseteq \mathcal{B}_{1}\subseteq \cdots \subseteq \mathcal{B}_{n}=\mathcal{C}$
is finite, then
$0=\mathcal{B}_{0}\subseteq \mathcal{B}_{1}\subseteq \cdots \subseteq \mathcal{B}_{n}=\mathcal{C}$
is finite, then
 $\mathcal{F}(\Delta )$
consists of finitely presented functors.
$\mathcal{F}(\Delta )$
consists of finitely presented functors.
Triangular Matrix Categories. In this section, we recall some results from the article [Reference Leszczyński15]. The notion of triangular matrix categories is introduced in [Reference Leszczyński15, Reference León-Galeana, Ortíz-Morales and Santiago16] in order to define the analogous of the triangular matrix algebras to the context of rings with several objects.
Definition 2.13. [Reference Leszczyński15, Definition 3.5] Given
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $\mathcal{U}$
additive
$\mathcal{U}$
additive
![]() $K$
-categories and a functor
$K$
-categories and a functor
![]() $M\,:\,\mathcal{U}\otimes _K \mathcal{T}^{op}\rightarrow \textrm{Mod}(K)$
, the triangular matrix category
$M\,:\,\mathcal{U}\otimes _K \mathcal{T}^{op}\rightarrow \textrm{Mod}(K)$
, the triangular matrix category
![]() $\Lambda = \left (\begin{smallmatrix} \mathcal{T}& \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\right )$
is the additive
$\Lambda = \left (\begin{smallmatrix} \mathcal{T}& \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\right )$
is the additive
![]() $K$
-category whose collection of objects are the matrices
$K$
-category whose collection of objects are the matrices
![]() $\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
, where
$\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
, where
![]() $U$
and
$U$
and
![]() $T$
are objects in
$T$
are objects in
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
, respectively.
$\mathcal{T}$
, respectively.
Let
![]() $X=\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
,
$X=\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
,
![]() $X^{\prime}=\left (\begin{smallmatrix} T^{\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
, and
$X^{\prime}=\left (\begin{smallmatrix} T^{\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
, and
![]() $X^{\prime\prime}=\left (\begin{smallmatrix} T^{\prime\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right )$
be objects in
$X^{\prime\prime}=\left (\begin{smallmatrix} T^{\prime\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right )$
be objects in
![]() $\Lambda$
. The set of morphisms from
$\Lambda$
. The set of morphisms from
![]() $X$
to
$X$
to
![]() $X^{\prime}$
is
$X^{\prime}$
is
![]() $\Lambda (X,X^{\prime})=\left ( \begin{smallmatrix} \mathcal{T}(T,T^{\prime})& \quad\!\! 0 \\[2pt] M (U^{\prime},T)& \quad\!\! \mathcal{U}(U,U^{\prime}) \end{smallmatrix}\right )$
, where
$\Lambda (X,X^{\prime})=\left ( \begin{smallmatrix} \mathcal{T}(T,T^{\prime})& \quad\!\! 0 \\[2pt] M (U^{\prime},T)& \quad\!\! \mathcal{U}(U,U^{\prime}) \end{smallmatrix}\right )$
, where
![]() $\left ( \begin{smallmatrix} \mathcal{T}(T,T^{\prime})& \quad\!\! 0 \\[2pt] M (U^{\prime},T)& \quad\!\! \mathcal{U}(U,U^{\prime}) \end{smallmatrix}\right )\,:\!=\,\left \{\left ( \begin{smallmatrix} f& \quad\!\! 0 \\[2pt] m & \quad\!\! g\end{smallmatrix}\right )\,:\, f\in \mathcal{T}(T,T^{\prime}),\right.$
$\left ( \begin{smallmatrix} \mathcal{T}(T,T^{\prime})& \quad\!\! 0 \\[2pt] M (U^{\prime},T)& \quad\!\! \mathcal{U}(U,U^{\prime}) \end{smallmatrix}\right )\,:\!=\,\left \{\left ( \begin{smallmatrix} f& \quad\!\! 0 \\[2pt] m & \quad\!\! g\end{smallmatrix}\right )\,:\, f\in \mathcal{T}(T,T^{\prime}),\right.$
![]() $\left. g\in \mathcal{U}(U,U^{\prime}), m\in M(U^{\prime},T)\right \}$
, and the composition
$\left. g\in \mathcal{U}(U,U^{\prime}), m\in M(U^{\prime},T)\right \}$
, and the composition
![]() $\Lambda (X^{\prime},X^{\prime\prime})\times \Lambda (X,X^{\prime})\rightarrow \Lambda (X,X^{\prime\prime})$
is defined by
$\Lambda (X^{\prime},X^{\prime\prime})\times \Lambda (X,X^{\prime})\rightarrow \Lambda (X,X^{\prime\prime})$
is defined by
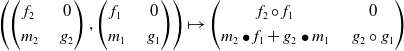 \begin{equation*} \hspace {1.2cm}\left (\left (\begin {matrix} f_2 & \quad 0 \\[3pt] m_2 & \quad g_2 \end {matrix}\right ), \left (\begin {matrix} f_1 & \quad 0 \\[3pt] m_1 & \quad g_1 \end {matrix}\right )\right ) \mapsto \left (\begin {matrix} f_2 \circ f_1 & \quad 0 \\[3pt] m_2 \bullet f_1+g_2 \bullet m_1 & \quad g_2 \circ g_1 \end {matrix}\right ) \end{equation*}
\begin{equation*} \hspace {1.2cm}\left (\left (\begin {matrix} f_2 & \quad 0 \\[3pt] m_2 & \quad g_2 \end {matrix}\right ), \left (\begin {matrix} f_1 & \quad 0 \\[3pt] m_1 & \quad g_1 \end {matrix}\right )\right ) \mapsto \left (\begin {matrix} f_2 \circ f_1 & \quad 0 \\[3pt] m_2 \bullet f_1+g_2 \bullet m_1 & \quad g_2 \circ g_1 \end {matrix}\right ) \end{equation*}
with
![]() $m_2 \bullet f_1\,:\!=\,M(1_{U^{\prime\prime}}\otimes f_1^{op})(m_2)$
and
$m_2 \bullet f_1\,:\!=\,M(1_{U^{\prime\prime}}\otimes f_1^{op})(m_2)$
and
![]() $g_2 \bullet m_1\,:\!=\,M(g_2\otimes 1_{T})(m_1)$
.
$g_2 \bullet m_1\,:\!=\,M(g_2\otimes 1_{T})(m_1)$
.
We note that
are morphisms in
![]() $\textrm{Mod}(K)$
.
$\textrm{Mod}(K)$
.
Let
![]() $ M\in \textrm{Mod}(\mathcal{U}\otimes _{K} \mathcal{T}^{op})$
. Then, there exists a covariant functor
$ M\in \textrm{Mod}(\mathcal{U}\otimes _{K} \mathcal{T}^{op})$
. Then, there exists a covariant functor
defined as follows:
![]() $(a)$
. For
$(a)$
. For
![]() $T\in \mathcal{T}$
, we have a covariant functor
$T\in \mathcal{T}$
, we have a covariant functor
![]() $E(T)\,:\!=\,M_{T}\,:\,\mathcal{U} \longrightarrow \textbf{Ab}$
given as:
$E(T)\,:\!=\,M_{T}\,:\,\mathcal{U} \longrightarrow \textbf{Ab}$
given as:
-
(i)
 $ M_{T}(U)\,:\!=\,M(U,T)$
, for all
$ M_{T}(U)\,:\!=\,M(U,T)$
, for all
 $ U\in \mathcal{U}$
.
$ U\in \mathcal{U}$
. -
(ii)
 $ M_{T}(u)\,:\!=\,M(u\otimes 1_{T})$
, for all
$ M_{T}(u)\,:\!=\,M(u\otimes 1_{T})$
, for all
 $ u\in \textrm{Hom}_{\mathcal{U}}(U,U^{\prime}).$
$ u\in \textrm{Hom}_{\mathcal{U}}(U,U^{\prime}).$
![]() $(b)$
. Now, given a morphism
$(b)$
. Now, given a morphism
![]() $t\,:\,T\longrightarrow T^{\prime}$
in
$t\,:\,T\longrightarrow T^{\prime}$
in
![]() $\mathcal{T}$
we define the natural transformation
$\mathcal{T}$
we define the natural transformation
![]() $E(t)\,:\!=\,\bar{t}\,:\,M_{T^{\prime}}\longrightarrow M_{T}$
where
$E(t)\,:\!=\,\bar{t}\,:\,M_{T^{\prime}}\longrightarrow M_{T}$
where
![]() $ \bar{t}=\lbrace [\bar{t}]_{U}\,:\,M_{T^{\prime}}(U)\longrightarrow M_{T}(U)\rbrace _{ U\in \mathcal{U}}$
with
$ \bar{t}=\lbrace [\bar{t}]_{U}\,:\,M_{T^{\prime}}(U)\longrightarrow M_{T}(U)\rbrace _{ U\in \mathcal{U}}$
with
![]() $ [\bar{t}]_{U}=M(1_{U}\otimes t^{op})\,:\,M(U,T^{\prime})\longrightarrow M(U,T)$
.
$ [\bar{t}]_{U}=M(1_{U}\otimes t^{op})\,:\,M(U,T^{\prime})\longrightarrow M(U,T)$
.
Now, let
![]() $Y\,:\,\textrm{Mod}(\mathcal{U})\longrightarrow \textrm{Mod}\Big (\textrm{Mod}(\mathcal{U})^{op}\Big )$
be the Yoneda functor given as follows
$Y\,:\,\textrm{Mod}(\mathcal{U})\longrightarrow \textrm{Mod}\Big (\textrm{Mod}(\mathcal{U})^{op}\Big )$
be the Yoneda functor given as follows
![]() $Y(B)\,:\!=\,\textrm{Hom}_{\textrm{Mod}(\mathcal{U})}(-,B)$
; and consider the following functor
$Y(B)\,:\!=\,\textrm{Hom}_{\textrm{Mod}(\mathcal{U})}(-,B)$
; and consider the following functor
![]() $I\,:\,\textrm{Mod}\Big (\textrm{Mod}(\mathcal{U})^{op}\Big )\longrightarrow \textrm{Mod}(\mathcal{T})$
, which is induced by composing with
$I\,:\,\textrm{Mod}\Big (\textrm{Mod}(\mathcal{U})^{op}\Big )\longrightarrow \textrm{Mod}(\mathcal{T})$
, which is induced by composing with
![]() $E\,:\,\mathcal{T}\longrightarrow \textrm{Mod}(\mathcal{U})^{op}$
. We set
$E\,:\,\mathcal{T}\longrightarrow \textrm{Mod}(\mathcal{U})^{op}$
. We set
Hence, we have the comma category
![]() $ \Big ( \textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\Big )$
whose objects are the triples
$ \Big ( \textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\Big )$
whose objects are the triples
![]() $ (A,f,B)$
with
$ (A,f,B)$
with
![]() $A\in \textrm{Mod}(\mathcal{T}), B\in \textrm{Mod}(\mathcal{U}),$
and
$A\in \textrm{Mod}(\mathcal{T}), B\in \textrm{Mod}(\mathcal{U}),$
and
![]() $ f\,:\,A\longrightarrow \mathbb{G}(B)$
is a morphism of
$ f\,:\,A\longrightarrow \mathbb{G}(B)$
is a morphism of
![]() $ \mathcal{T}$
-modules. A morphism between two objects
$ \mathcal{T}$
-modules. A morphism between two objects
![]() $ (A,f,B)$
and
$ (A,f,B)$
and
![]() $ (A^{\prime},f^{\prime},B^{\prime})$
is a pair of morphism
$ (A^{\prime},f^{\prime},B^{\prime})$
is a pair of morphism
![]() $(\alpha,\beta )$
where
$(\alpha,\beta )$
where
![]() $\alpha \,:\,A\longrightarrow A^{\prime}$
is a morphism of
$\alpha \,:\,A\longrightarrow A^{\prime}$
is a morphism of
![]() $\mathcal{T}$
-modules and
$\mathcal{T}$
-modules and
![]() $\beta \,:\,B\longrightarrow B^{\prime}$
is a morphism of
$\beta \,:\,B\longrightarrow B^{\prime}$
is a morphism of
![]() $\mathcal{U}$
-modules such that the diagram
$\mathcal{U}$
-modules such that the diagram
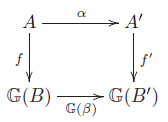
commutes. Now, given
![]() $(A,f,B) \in \Big (\textrm{Mod}(\mathcal{T}),\mathbb{G}\textrm{Mod}(\mathcal{U})\Big )$
, we can construct a functor
$(A,f,B) \in \Big (\textrm{Mod}(\mathcal{T}),\mathbb{G}\textrm{Mod}(\mathcal{U})\Big )$
, we can construct a functor
defined as follows:
-
(a) For
 $\left [\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right ]\in \boldsymbol{\Lambda }$
we set
$\left [\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right ]\in \boldsymbol{\Lambda }$
we set
 $\Big (A\amalg _f B\Big )\left(\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right )\right) \,:\!=\,A (T)\amalg B(U)\in \textbf{Ab}.$
$\Big (A\amalg _f B\Big )\left(\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right )\right) \,:\!=\,A (T)\amalg B(U)\in \textbf{Ab}.$
-
(b) If
 $\left (\begin{smallmatrix} t& \quad\!\! 0 \\[2pt] m& \quad\!\! u \\[2pt] \end{smallmatrix} \right )\in \textrm{Hom}_{\boldsymbol{\Lambda }}\left(\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right ), \left (\begin{smallmatrix} T^{\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \\[2pt] \end{smallmatrix} \right )\right)$
we define the mapgiven by
$\left (\begin{smallmatrix} t& \quad\!\! 0 \\[2pt] m& \quad\!\! u \\[2pt] \end{smallmatrix} \right )\in \textrm{Hom}_{\boldsymbol{\Lambda }}\left(\left (\begin{smallmatrix} T& \quad\!\! 0 \\[2pt] M & \quad\!\! U \\[2pt] \end{smallmatrix} \right ), \left (\begin{smallmatrix} T^{\prime}& \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \\[2pt] \end{smallmatrix} \right )\right)$
we define the mapgiven by \begin{equation*}\Big (A\amalg _f B\Big )\left(\left (\begin {matrix} t& \quad 0 \\[2pt] m& \quad u \\[2pt] \end {matrix} \right )\right)\,:\!=\,\left (\begin {matrix} A(t)& \quad 0 \\[2pt] m & \quad B(u) \\[2pt] \end {matrix} \right )\,:\, A(T)\amalg B(U)\rightarrow A(T^{\prime})\amalg B(U^{\prime})\end{equation*}
\begin{equation*}\Big (A\amalg _f B\Big )\left(\left (\begin {matrix} t& \quad 0 \\[2pt] m& \quad u \\[2pt] \end {matrix} \right )\right)\,:\!=\,\left (\begin {matrix} A(t)& \quad 0 \\[2pt] m & \quad B(u) \\[2pt] \end {matrix} \right )\,:\, A(T)\amalg B(U)\rightarrow A(T^{\prime})\amalg B(U^{\prime})\end{equation*}
 $\left (\begin{smallmatrix} A(t)& 0 \\[2pt] m& B(u) \\[2pt] \end{smallmatrix} \right )\left (\begin{smallmatrix} x \\[2pt] y \\[2pt] \end{smallmatrix} \right )=\left (\begin{smallmatrix} A(t)(x) \\[2pt] m\cdot x+ B(u)(y) \\[2pt] \end{smallmatrix} \right )$
for
$\left (\begin{smallmatrix} A(t)& 0 \\[2pt] m& B(u) \\[2pt] \end{smallmatrix} \right )\left (\begin{smallmatrix} x \\[2pt] y \\[2pt] \end{smallmatrix} \right )=\left (\begin{smallmatrix} A(t)(x) \\[2pt] m\cdot x+ B(u)(y) \\[2pt] \end{smallmatrix} \right )$
for
 $(x,y)\in A(T)\amalg B(U)$
, where
$(x,y)\in A(T)\amalg B(U)$
, where
 $m\cdot x\,:\!=\,[f_{T}(x)]_{U^{\prime}}(m)\in B(U^{\prime})$
.
$m\cdot x\,:\!=\,[f_{T}(x)]_{U^{\prime}}(m)\in B(U^{\prime})$
.
We define
![]() $\mathfrak{f}\,:\, \left (\textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\right ) \rightarrow \textrm{Mod}(\Lambda )$
as
$\mathfrak{f}\,:\, \left (\textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\right ) \rightarrow \textrm{Mod}(\Lambda )$
as
![]() $\mathfrak{f}((A,f,B))=A\amalg _f B$
and it is a covariant functor (see [Reference Leszczyński15, Proposition 3.12]). We have the following Theorem.
$\mathfrak{f}((A,f,B))=A\amalg _f B$
and it is a covariant functor (see [Reference Leszczyński15, Proposition 3.12]). We have the following Theorem.
Theorem 2.14. [Reference Leszczyński15, Theorem 3.17] There exists an equivalence of categories
Hence, given a
![]() $\Lambda$
-module
$\Lambda$
-module
![]() $C$
, there exists a pair of functors
$C$
, there exists a pair of functors
![]() $C^{(1)}\,:\, \mathcal{T} \rightarrow \textbf{Ab}$
,
$C^{(1)}\,:\, \mathcal{T} \rightarrow \textbf{Ab}$
,
![]() $C^{(2)}\,:\, \mathcal{U} \rightarrow \textbf{Ab}$
and
$C^{(2)}\,:\, \mathcal{U} \rightarrow \textbf{Ab}$
and
![]() $C^{(1)} \overset{f}{\longrightarrow } \mathbb{G}(C^{(2)})$
such that
$C^{(1)} \overset{f}{\longrightarrow } \mathbb{G}(C^{(2)})$
such that
![]() $\mathfrak{f}((C^{(1)},f,C^{(2)}))\cong C$
, where we have that
$\mathfrak{f}((C^{(1)},f,C^{(2)}))\cong C$
, where we have that
![]() $C^{(1)}(T^{\prime})\,:\!=\,C\left (\left( \begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix} \right)\right )$
and
$C^{(1)}(T^{\prime})\,:\!=\,C\left (\left( \begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix} \right)\right )$
and
![]() $C^{(2)}(U^{\prime})\,:\!=\,C\left ( \left(\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right) \right )$
.
$C^{(2)}(U^{\prime})\,:\!=\,C\left ( \left(\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right) \right )$
.
Now, we have the following Proposition.
Proposition 2.15.
Let
![]() $C\in \textrm{Mod}(\Lambda )$
and consider
$C\in \textrm{Mod}(\Lambda )$
and consider
![]() $C^{(1)}\,:\, \mathcal{T} \rightarrow \textbf{Ab}$
and
$C^{(1)}\,:\, \mathcal{T} \rightarrow \textbf{Ab}$
and
![]() $C^{(2)}\,:\, \mathcal{U} \rightarrow \textbf{Ab}$
and
$C^{(2)}\,:\, \mathcal{U} \rightarrow \textbf{Ab}$
and
![]() $C^{(1)} \overset{f}{\longrightarrow } \mathbb{G}(C^{(2)})$
such that
$C^{(1)} \overset{f}{\longrightarrow } \mathbb{G}(C^{(2)})$
such that
![]() $\mathfrak{f}((C^{(1)},f,C^{(2)}))\cong C$
. Suppose that there exists exact sequences
$\mathfrak{f}((C^{(1)},f,C^{(2)}))\cong C$
. Suppose that there exists exact sequences
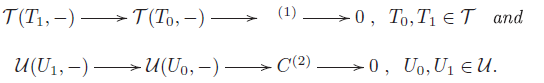
Then there exists an exact sequence in
![]() $\textrm{Mod}(\Lambda )$
$\textrm{Mod}(\Lambda )$
where
![]() $P_j\,:\!=\,\Lambda \left (\left ( \begin{smallmatrix} T_j & 0 \\ M & U_j \end{smallmatrix}\right ), - \right )$
is a projective
$P_j\,:\!=\,\Lambda \left (\left ( \begin{smallmatrix} T_j & 0 \\ M & U_j \end{smallmatrix}\right ), - \right )$
is a projective
![]() $\Lambda -$
module for
$\Lambda -$
module for
![]() $j=0,1$
.
$j=0,1$
.
Proof. It is similar to the proof of [Reference Leszczyński15, Proposition 6.3]).
Proposition 2.16 (Reference Leszczyński15, Proposition 5.5). The subcategory
![]() $\textrm{proj}(\textrm{Mod}(\Lambda ))$
of
$\textrm{proj}(\textrm{Mod}(\Lambda ))$
of
![]() $\textrm{Mod}(\Lambda )$
consisting of finitely generated projective
$\textrm{Mod}(\Lambda )$
consisting of finitely generated projective
![]() $\Lambda$
-modules is equivalent to the subcategory of
$\Lambda$
-modules is equivalent to the subcategory of
![]() $( \textrm{Mod}(\mathcal{T}), \mathbb{G}\textrm{Mod}(\mathcal{U}))$
consisting of morphism of
$( \textrm{Mod}(\mathcal{T}), \mathbb{G}\textrm{Mod}(\mathcal{U}))$
consisting of morphism of
![]() $\mathcal{T}$
-modules
$\mathcal{T}$
-modules
given by
![]() $g\,:\!=\,\big \{[g]_{T^{\prime}}\,:\, \mathcal{T}(T,T^{\prime})\longrightarrow \textrm{Hom}_{\textrm{Mod}(\mathcal{U})}\big (M_{T^{\prime}},M_{T}\amalg \mathcal{U}(U,-)\big )\big \}_{T^{\prime}\in \mathcal{T}}$
, with
$g\,:\!=\,\big \{[g]_{T^{\prime}}\,:\, \mathcal{T}(T,T^{\prime})\longrightarrow \textrm{Hom}_{\textrm{Mod}(\mathcal{U})}\big (M_{T^{\prime}},M_{T}\amalg \mathcal{U}(U,-)\big )\big \}_{T^{\prime}\in \mathcal{T}}$
, with
![]() $[g]_{T^{\prime}}(t)\,:\!=\,\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\,:\,M_{T^{\prime}}\rightarrow M_{T}\amalg \mathcal{U}(U,-)$
for all
$[g]_{T^{\prime}}(t)\,:\!=\,\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\,:\,M_{T^{\prime}}\rightarrow M_{T}\amalg \mathcal{U}(U,-)$
for all
![]() $t\in \mathcal{T}(T,T^{\prime})$
, where for
$t\in \mathcal{T}(T,T^{\prime})$
, where for
![]() $U^{\prime}\in \mathcal{U}$
, the map
$U^{\prime}\in \mathcal{U}$
, the map
![]() $\left[\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\right]_{U^{\prime}}\,:\,M(U^{\prime},T^{\prime})\rightarrow M(U^{\prime},T)\amalg \mathcal{U}(U,U^{\prime})$
is defined by
$\left[\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\right]_{U^{\prime}}\,:\,M(U^{\prime},T^{\prime})\rightarrow M(U^{\prime},T)\amalg \mathcal{U}(U,U^{\prime})$
is defined by
![]() $\left[\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\right]_{U^{\prime}}(m)\,:\!=\,(M(1_{U}\otimes t^{op})(m),0)=(m\bullet t,0), \forall m\in M(U^{\prime},T).$
$\left[\left [ \begin{smallmatrix} \overline{t} \\[2pt] 0 \end{smallmatrix} \right ]\right]_{U^{\prime}}(m)\,:\!=\,(M(1_{U}\otimes t^{op})(m),0)=(m\bullet t,0), \forall m\in M(U^{\prime},T).$
Proposition 2.17 (Reference Leszczyński15, Proposition 5.6). A sequence of maps
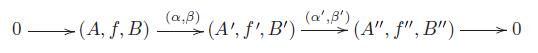
is exact in
![]() $\big ( \textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U}))\big )$
if and only if the following are exact sequences
$\big ( \textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U}))\big )$
if and only if the following are exact sequences
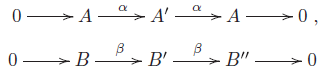
in
![]() $\textrm{Mod}(\mathcal{T})$
and
$\textrm{Mod}(\mathcal{T})$
and
![]() $\textrm{Mod}(\mathcal{U})$
, respectively.
$\textrm{Mod}(\mathcal{U})$
, respectively.
3. Triangular matrix categories over quasi-hereditary categories
In this section, we will prove the main result of this paper. First, we recall by [Reference Leszczyński15, Proposition 3.7], that if
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
have finite coproducts, then
$\mathcal{T}$
have finite coproducts, then
![]() $\Lambda = \left (\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\right )$
has finite coproducts. For the convenience of the reader, we will give an idea of how construct finite coproducts in
$\Lambda = \left (\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\right )$
has finite coproducts. For the convenience of the reader, we will give an idea of how construct finite coproducts in
![]() $\Lambda$
. Let
$\Lambda$
. Let
![]() $\left (\begin{smallmatrix}T_{1} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{1} \end{smallmatrix}\right )$
,
$\left (\begin{smallmatrix}T_{1} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{1} \end{smallmatrix}\right )$
,
![]() $\left (\begin{smallmatrix}T_{2} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{2} \end{smallmatrix}\right )$
two objects in
$\left (\begin{smallmatrix}T_{2} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{2} \end{smallmatrix}\right )$
two objects in
![]() $\Lambda$
. Consider the coproduct
$\Lambda$
. Consider the coproduct
![]() $\{u_{i}\,:\,U_{i}\longrightarrow U_{1}\oplus U_{2}\}_{i=1}^{2}$
of the family
$\{u_{i}\,:\,U_{i}\longrightarrow U_{1}\oplus U_{2}\}_{i=1}^{2}$
of the family
![]() $\{U_{i}\}_{i=1}^{2}$
in
$\{U_{i}\}_{i=1}^{2}$
in
![]() $\mathcal{U}$
and the coproduct
$\mathcal{U}$
and the coproduct
![]() $\{v_{i}\,:\,T_{i}\longrightarrow T_{1}\oplus T_{2}\}_{i=1}^{2}$
of the family
$\{v_{i}\,:\,T_{i}\longrightarrow T_{1}\oplus T_{2}\}_{i=1}^{2}$
of the family
![]() $\{T_{i}\}_{i=1}^{2}$
in
$\{T_{i}\}_{i=1}^{2}$
in
![]() $\mathcal{T}$
. Then we can construct the following morphisms in
$\mathcal{T}$
. Then we can construct the following morphisms in
![]() $\Lambda$
$\Lambda$
and it is straightforward to see that this family is a coproduct for the family of objects
![]() $\left\{\left (\begin{smallmatrix}T_{i} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{i} \end{smallmatrix}\right )\right\}_{i=1}^{2}$
. Now, let
$\left\{\left (\begin{smallmatrix}T_{i} & \quad\!\! 0 \\[2pt] M & \quad\!\! U_{i} \end{smallmatrix}\right )\right\}_{i=1}^{2}$
. Now, let
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
be
$\mathcal{T}$
be
![]() $\textrm{Hom}$
-finite Krull–Schmidt quasi-hereditary
$\textrm{Hom}$
-finite Krull–Schmidt quasi-hereditary
![]() $K$
-categories with respect to filtrations
$K$
-categories with respect to filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
, respectively, consisting of full additive subcategories which are closed under direct summands. Assume that the
$\{\mathcal{T}_j\}_{j\ge 0}$
, respectively, consisting of full additive subcategories which are closed under direct summands. Assume that the
![]() $\mathcal{U}$
-module
$\mathcal{U}$
-module
![]() $M_T=M(-,T)$
lies in
$M_T=M(-,T)$
lies in
![]() $\mathcal{F}(_{\mathcal{U}}\Delta )$
for all
$\mathcal{F}(_{\mathcal{U}}\Delta )$
for all
![]() $T\in \mathcal{T}$
; therefore,
$T\in \mathcal{T}$
; therefore,
![]() $M_T$
is finitely presented since the filtration of
$M_T$
is finitely presented since the filtration of
![]() $\mathcal{U}$
is finite (see Lemma 2.12 (c)). Thus,
$\mathcal{U}$
is finite (see Lemma 2.12 (c)). Thus,
![]() $\Lambda = \Big(\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\Big)$
is a
$\Lambda = \Big(\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\[2pt] M & \quad\!\! \mathcal{U} \end{smallmatrix}\Big)$
is a
![]() $\textrm{Hom}$
-finite Krull–Schmidt
$\textrm{Hom}$
-finite Krull–Schmidt
![]() $K$
-category (see [Reference Leszczyński15, Proposition 6.9]).
$K$
-category (see [Reference Leszczyński15, Proposition 6.9]).
Consider the filtration of
![]() $\Lambda$
into subcategories
$\Lambda$
into subcategories
![]() $\{\Lambda _j\}_{j\ge 0}$
given by
$\{\Lambda _j\}_{j\ge 0}$
given by
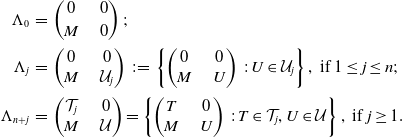 \begin{eqnarray} \Lambda _0&=&\left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad 0 \end{matrix}\right );\notag \\ \Lambda _j&=&\left (\begin{matrix} 0 & \quad 0 \\ M & \quad \mathcal{U}_j \end{matrix}\right )\,:\!=\,\left\{\left ( \begin{matrix} 0 & \quad 0 \\ M & \quad U \end{matrix} \right )\,:\, U \in \mathcal{U}_j \right\}, \text{ if $1\le j\le n$};\\[2pt] \Lambda _{n+j}&=&\left (\begin{matrix} \mathcal{T}_{j} & \quad 0 \\ M & \quad \mathcal{U} \end{matrix}\right )=\left\{ \left (\begin{matrix} T & \quad 0 \\ M & \quad U \end{matrix}\right ) \,:\,T\in \mathcal{T}_j, U \in \mathcal{U} \right\}, \text{ if $j\ge 1$}\notag . \end{eqnarray}
\begin{eqnarray} \Lambda _0&=&\left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad 0 \end{matrix}\right );\notag \\ \Lambda _j&=&\left (\begin{matrix} 0 & \quad 0 \\ M & \quad \mathcal{U}_j \end{matrix}\right )\,:\!=\,\left\{\left ( \begin{matrix} 0 & \quad 0 \\ M & \quad U \end{matrix} \right )\,:\, U \in \mathcal{U}_j \right\}, \text{ if $1\le j\le n$};\\[2pt] \Lambda _{n+j}&=&\left (\begin{matrix} \mathcal{T}_{j} & \quad 0 \\ M & \quad \mathcal{U} \end{matrix}\right )=\left\{ \left (\begin{matrix} T & \quad 0 \\ M & \quad U \end{matrix}\right ) \,:\,T\in \mathcal{T}_j, U \in \mathcal{U} \right\}, \text{ if $j\ge 1$}\notag . \end{eqnarray}
It is clear that
![]() $\Lambda _j\subseteq \Lambda$
is an additive full subcategory for all
$\Lambda _j\subseteq \Lambda$
is an additive full subcategory for all
![]() $j\ge 0$
. For and object
$j\ge 0$
. For and object
![]() $\left ( \begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix} \right )\in \Lambda$
with
$\left ( \begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix} \right )\in \Lambda$
with
![]() $U\in \textrm{Ind}\,\,\mathcal{U}_{j}$
we have that
$U\in \textrm{Ind}\,\,\mathcal{U}_{j}$
we have that
is local. Hence, we get that
![]() $\left ( \begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix} \right )$
is an indecomposable object in
$\left ( \begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix} \right )$
is an indecomposable object in
![]() $\Lambda _{j}$
. Similarly, for an object
$\Lambda _{j}$
. Similarly, for an object
![]() $\left ( \begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix} \right )\in \Lambda$
with
$\left ( \begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix} \right )\in \Lambda$
with
![]() $T \in \textrm{Ind}\,\,\mathcal{T}_{j}$
, we have that
$T \in \textrm{Ind}\,\,\mathcal{T}_{j}$
, we have that
![]() $\left ( \begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0\end{smallmatrix} \right )$
is an indecomposable object in
$\left ( \begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0\end{smallmatrix} \right )$
is an indecomposable object in
![]() $\Lambda _{n+j}$
. It follows that
$\Lambda _{n+j}$
. It follows that
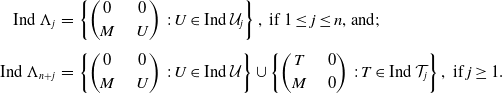 \begin{eqnarray*} \textrm{Ind}\ \Lambda _j& = & \left\{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U \end{matrix}\right ) \,:\, U \in \textrm{Ind} \ \mathcal{U}_j \right\}, \text{ if $1\le j\le n$, and};\\[2pt] \textrm{Ind} \ \Lambda _{n+j}& =& \left\{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U \end{matrix}\right ) \,:\, U \in \textrm{Ind} \ \mathcal{U} \right\}\cup \left\{ \left (\begin{matrix} T & \quad 0 \\[2pt] M & \quad 0 \end{matrix}\right ) \,:\,T\in \textrm{Ind} \ \mathcal{T}_j \right\}, \text{ if $j\ge 1$}. \end{eqnarray*}
\begin{eqnarray*} \textrm{Ind}\ \Lambda _j& = & \left\{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U \end{matrix}\right ) \,:\, U \in \textrm{Ind} \ \mathcal{U}_j \right\}, \text{ if $1\le j\le n$, and};\\[2pt] \textrm{Ind} \ \Lambda _{n+j}& =& \left\{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U \end{matrix}\right ) \,:\, U \in \textrm{Ind} \ \mathcal{U} \right\}\cup \left\{ \left (\begin{matrix} T & \quad 0 \\[2pt] M & \quad 0 \end{matrix}\right ) \,:\,T\in \textrm{Ind} \ \mathcal{T}_j \right\}, \text{ if $j\ge 1$}. \end{eqnarray*}
In this way, we have that
![]() $\Lambda _j$
, for
$\Lambda _j$
, for
![]() $j\ge 0$
, is closed under direct summands. Moreover,
$j\ge 0$
, is closed under direct summands. Moreover,
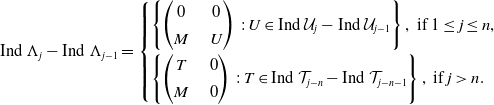 \begin{eqnarray*} \textrm{Ind}\ \Lambda _{j } - \textrm{Ind} \ \Lambda _{j-1}= \begin{cases} \left \{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U\end{matrix}\right ) \,:\, U\in \textrm{Ind} \ \mathcal{U}_j- \textrm{Ind}\ \mathcal{U}_{j-1}\right\}, \text{ if $1\le j\le n$}, \\[10pt] \left \{ \left (\begin{matrix} T & \quad 0 \\[2pt] M & \quad 0\end{matrix}\right ) \,:\, T\in \textrm{Ind} \ \mathcal{T}_{j-n}- \textrm{Ind}\ \mathcal{T}_{j-n-1}\right \}, \text{ if $j\gt n$}. \end{cases} \end{eqnarray*}
\begin{eqnarray*} \textrm{Ind}\ \Lambda _{j } - \textrm{Ind} \ \Lambda _{j-1}= \begin{cases} \left \{ \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U\end{matrix}\right ) \,:\, U\in \textrm{Ind} \ \mathcal{U}_j- \textrm{Ind}\ \mathcal{U}_{j-1}\right\}, \text{ if $1\le j\le n$}, \\[10pt] \left \{ \left (\begin{matrix} T & \quad 0 \\[2pt] M & \quad 0\end{matrix}\right ) \,:\, T\in \textrm{Ind} \ \mathcal{T}_{j-n}- \textrm{Ind}\ \mathcal{T}_{j-n-1}\right \}, \text{ if $j\gt n$}. \end{cases} \end{eqnarray*}
One of the main results of this section is a generalization of a Theorem due to B. Zhu (see [Reference Šťovíček29, Theorem 3.1]). The proof of such Theorem 3.7 will be a consequence of a series of results that are presented below.
Lemma 3.1.
Let
![]() $\mathcal{U}$
be a quasi-hereditary category with respect to a filtration
$\mathcal{U}$
be a quasi-hereditary category with respect to a filtration
![]() $\{\mathcal{U}_j\}_{j\ge 0}$
. Let
$\{\mathcal{U}_j\}_{j\ge 0}$
. Let
![]() $M$
be a
$M$
be a
![]() $\mathcal{U}$
-module, and set
$\mathcal{U}$
-module, and set
Assume that
![]() $M\in \mathcal{F}(_{\mathcal{U}}\Delta )$
. Then for all
$M\in \mathcal{F}(_{\mathcal{U}}\Delta )$
. Then for all
![]() $U^{\prime}\in \mathcal{U}$
we have that
$U^{\prime}\in \mathcal{U}$
we have that
Proof. (
![]() $\subseteq$
). By Yoneda’s isomorphism
$\subseteq$
). By Yoneda’s isomorphism
![]() $Y^{U^{\prime}}\,:\,\textrm{Nat}\left ((U^{\prime},-), M^{[j]}\right )\cong M^{[j]}(U^{\prime})$
,
$Y^{U^{\prime}}\,:\,\textrm{Nat}\left ((U^{\prime},-), M^{[j]}\right )\cong M^{[j]}(U^{\prime})$
,
![]() $\eta \mapsto \eta _{U^{\prime}}(1_{U^{\prime}})$
. Let
$\eta \mapsto \eta _{U^{\prime}}(1_{U^{\prime}})$
. Let
![]() $m\in M^{[j]}(U^{\prime})$
, then there exists
$m\in M^{[j]}(U^{\prime})$
, then there exists
![]() $\eta ^m\,:\,\mathcal{U}(U^{\prime},-)\rightarrow M^{[j]}$
such that
$\eta ^m\,:\,\mathcal{U}(U^{\prime},-)\rightarrow M^{[j]}$
such that
![]() $\eta ^m_{U^{\prime}}(1_{U^{\prime}})=m$
. On the other hand, by Lemma 2.12, there exists
$\eta ^m_{U^{\prime}}(1_{U^{\prime}})=m$
. On the other hand, by Lemma 2.12, there exists
![]() $p\,:\, \mathcal{U}(U^{\prime\prime},-) \rightarrow M^{[j]} \rightarrow 0$
, with
$p\,:\, \mathcal{U}(U^{\prime\prime},-) \rightarrow M^{[j]} \rightarrow 0$
, with
![]() $U^{\prime\prime}\in \mathcal{U}_j$
and since
$U^{\prime\prime}\in \mathcal{U}_j$
and since
![]() $\mathcal{U}(U^{\prime},-)$
is a projective
$\mathcal{U}(U^{\prime},-)$
is a projective
![]() $\mathcal{U}$
-module, there exists a morphism
$\mathcal{U}$
-module, there exists a morphism
![]() $s\,:\,U^{\prime\prime}\rightarrow U^{\prime}$
for which the following diagram is commutative:
$s\,:\,U^{\prime\prime}\rightarrow U^{\prime}$
for which the following diagram is commutative:
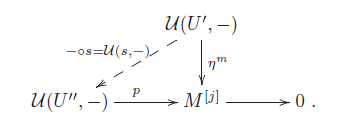
Again by Yoneda’s lemma we have the following commutative diagram:
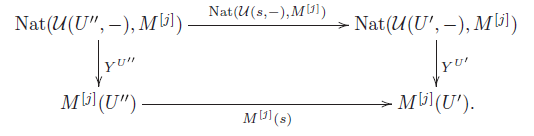
Let
![]() $m^{\prime}\,:\!=\,Y^{U^{\prime\prime}}(p)$
. Since
$m^{\prime}\,:\!=\,Y^{U^{\prime\prime}}(p)$
. Since
![]() $M^{[j]}$
is a subfunctor of
$M^{[j]}$
is a subfunctor of
![]() $M$
, we obtain the equality
$M$
, we obtain the equality
![]() $M^{[j]}(s)(m^{\prime})=M(s)(m^{\prime})$
and hence by the above commutative diagram we have that
$M^{[j]}(s)(m^{\prime})=M(s)(m^{\prime})$
and hence by the above commutative diagram we have that
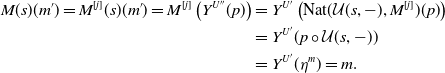 \begin{align*} M(s)(m^{\prime})=M^{[j]}(s)(m^{\prime})=M^{[j]}\left(Y^{U^{\prime\prime}}(p)\right) & =Y^{U^{\prime}}\left(\textrm{Nat}(\mathcal{U}(s,-),M^{[j]})(p)\right)\\ & =Y^{U^{\prime}}(p\circ \mathcal{U}(s,-))\\ & =Y^{U^{\prime}}(\eta ^{m})=m. \end{align*}
\begin{align*} M(s)(m^{\prime})=M^{[j]}(s)(m^{\prime})=M^{[j]}\left(Y^{U^{\prime\prime}}(p)\right) & =Y^{U^{\prime}}\left(\textrm{Nat}(\mathcal{U}(s,-),M^{[j]})(p)\right)\\ & =Y^{U^{\prime}}(p\circ \mathcal{U}(s,-))\\ & =Y^{U^{\prime}}(\eta ^{m})=m. \end{align*}
(
![]() $\supseteq$
). Let
$\supseteq$
). Let
![]() $m\in M(U^{\prime})$
and assume there exists
$m\in M(U^{\prime})$
and assume there exists
![]() $s\,:\,U^{\prime\prime}\rightarrow U^{\prime}$
, with
$s\,:\,U^{\prime\prime}\rightarrow U^{\prime}$
, with
![]() $U^{\prime\prime}\in \mathcal{U}_j$
, such that
$U^{\prime\prime}\in \mathcal{U}_j$
, such that
![]() $ m=M(s)(m^{\prime})$
for some
$ m=M(s)(m^{\prime})$
for some
![]() $ m^{\prime}\in M(U^{\prime\prime})$
. Then there exist two morphisms
$ m^{\prime}\in M(U^{\prime\prime})$
. Then there exist two morphisms
![]() $\eta ^m\,:\,\mathcal{U}(U^{\prime},-)\rightarrow M$
and
$\eta ^m\,:\,\mathcal{U}(U^{\prime},-)\rightarrow M$
and
![]() $p^{m^{\prime}}\,:\,\mathcal{U}(U^{\prime\prime},-) \rightarrow M$
satisfying the following:
$p^{m^{\prime}}\,:\,\mathcal{U}(U^{\prime\prime},-) \rightarrow M$
satisfying the following:
![]() $Y^{U^{\prime}}(\eta ^{m})=\eta ^m_{U^{\prime}}(1_{U^{\prime}})=m$
and
$Y^{U^{\prime}}(\eta ^{m})=\eta ^m_{U^{\prime}}(1_{U^{\prime}})=m$
and
![]() $Y^{U^{\prime\prime}}\left(p^{m^{\prime}}\right)=p^{m^{\prime}}_{U^{\prime\prime}}(1_{U^{\prime\prime}})=m^{\prime}$
. Thus, by using the diagram (3.2) (with
$Y^{U^{\prime\prime}}\left(p^{m^{\prime}}\right)=p^{m^{\prime}}_{U^{\prime\prime}}(1_{U^{\prime\prime}})=m^{\prime}$
. Thus, by using the diagram (3.2) (with
![]() $M$
instead of
$M$
instead of
![]() $M^{[j]}$
), we have that
$M^{[j]}$
), we have that
Since
![]() $Y^{U^{\prime}}$
is an isomorphism, we conclude that
$Y^{U^{\prime}}$
is an isomorphism, we conclude that
![]() $p^{m^{\prime}}\circ \mathcal{U}(s,-)=\eta ^m$
. Note that
$p^{m^{\prime}}\circ \mathcal{U}(s,-)=\eta ^m$
. Note that
![]() $\textrm{Im}\left(p^{m^{\prime}}\right)$
is a subfunctor of
$\textrm{Im}\left(p^{m^{\prime}}\right)$
is a subfunctor of
![]() $M$
and is generated by
$M$
and is generated by
![]() $\mathcal{U}(U^{\prime\prime},-)$
. Since
$\mathcal{U}(U^{\prime\prime},-)$
. Since
![]() $U^{\prime\prime}\in \mathcal{U}_j$
,
$U^{\prime\prime}\in \mathcal{U}_j$
,
![]() $\textrm{Im}\left(p^{m^{\prime}}\right)$
is contained in the largest
$\textrm{Im}\left(p^{m^{\prime}}\right)$
is contained in the largest
![]() $\mathcal{U}$
-submodule of
$\mathcal{U}$
-submodule of
![]() $M$
generated by
$M$
generated by
![]() $\{\mathcal{U}(U,-)\,:\,U\in \mathcal{U}_j\}$
, namely
$\{\mathcal{U}(U,-)\,:\,U\in \mathcal{U}_j\}$
, namely
![]() $M^{[j]}$
, we obtain that
$M^{[j]}$
, we obtain that
![]() $\textrm{Im}\left(p^{m^{\prime}}\right)\subset M^{[j]}$
. It follows that
$\textrm{Im}\left(p^{m^{\prime}}\right)\subset M^{[j]}$
. It follows that
that is,
![]() $m \in M^{[j]}(U^{\prime})$
.
$m \in M^{[j]}(U^{\prime})$
.
Let
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
be
$\mathcal{T}$
be
![]() $\textrm{Hom}$
-finite Krull–Schmidt categories and consider exhaustive filtrations
$\textrm{Hom}$
-finite Krull–Schmidt categories and consider exhaustive filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
of
$\{\mathcal{T}_j\}_{j\ge 0}$
of
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
, consisting of full additive subcategories which are closed under direct summands. In the remainder of this section, we will assume that the categories
$\mathcal{T}$
, consisting of full additive subcategories which are closed under direct summands. In the remainder of this section, we will assume that the categories
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
are quasi-hereditary categories with respect to the filtrations
$\mathcal{T}$
are quasi-hereditary categories with respect to the filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
, respectively, and
$\{\mathcal{T}_j\}_{j\ge 0}$
, respectively, and
![]() $M_T\in \mathcal{F}(_{\mathcal{U}}\Delta )$
for all
$M_T\in \mathcal{F}(_{\mathcal{U}}\Delta )$
for all
![]() $T\in \mathcal{T}$
.
$T\in \mathcal{T}$
.
Proposition 3.2.
Let
![]() $E=\left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
and
$E=\left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
and
![]() $E^{\prime}=\left (\begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
in
$E^{\prime}=\left (\begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
in
![]() $\Lambda$
. Then,
$\Lambda$
. Then,
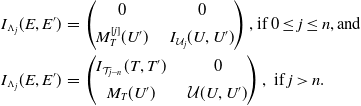 \begin{eqnarray*} I_{\Lambda _j}(E,E^{\prime})&=&\begin{pmatrix} 0 & \quad 0 \\[4pt] M^{[j]}_T(U^{\prime}) & \quad I_{\mathcal{U}_j}(U,U^{\prime}) \end{pmatrix}, \text{if } 0\leq j\leq n, \text{and }\\ I_{\Lambda _j}(E,E^{\prime})&=& \begin{pmatrix} I_{\mathcal{T}_{j-n}}(T,T^{\prime}) & \quad 0 \\[4pt] M_T(U^{\prime}) & \quad \mathcal{U}(U,U^{\prime}) \end{pmatrix}, \text{ if } j\gt n. \end{eqnarray*}
\begin{eqnarray*} I_{\Lambda _j}(E,E^{\prime})&=&\begin{pmatrix} 0 & \quad 0 \\[4pt] M^{[j]}_T(U^{\prime}) & \quad I_{\mathcal{U}_j}(U,U^{\prime}) \end{pmatrix}, \text{if } 0\leq j\leq n, \text{and }\\ I_{\Lambda _j}(E,E^{\prime})&=& \begin{pmatrix} I_{\mathcal{T}_{j-n}}(T,T^{\prime}) & \quad 0 \\[4pt] M_T(U^{\prime}) & \quad \mathcal{U}(U,U^{\prime}) \end{pmatrix}, \text{ if } j\gt n. \end{eqnarray*}
Proof. Let
![]() $\left (\begin{smallmatrix}f & 0 \\ m & h \end{smallmatrix}\right )\in \textrm{Hom}_{\Lambda }(E,E^{\prime})$
. Therefore,
$\left (\begin{smallmatrix}f & 0 \\ m & h \end{smallmatrix}\right )\in \textrm{Hom}_{\Lambda }(E,E^{\prime})$
. Therefore,
![]() $f\in \textrm{ Hom}_{\mathcal{T}}(T,T^{\prime})$
,
$f\in \textrm{ Hom}_{\mathcal{T}}(T,T^{\prime})$
,
![]() $m\in M(U^{\prime},T)$
, and
$m\in M(U^{\prime},T)$
, and
![]() $h\in \textrm{Hom}_{\mathcal{U}}(U,U^{\prime})$
.
$h\in \textrm{Hom}_{\mathcal{U}}(U,U^{\prime})$
.
Consider the case
![]() $0\leq j\leq n$
. The morphism
$0\leq j\leq n$
. The morphism
![]() $\left (\begin{smallmatrix}f & 0 \\ m & h \end{smallmatrix}\right )$
lies in
$\left (\begin{smallmatrix}f & 0 \\ m & h \end{smallmatrix}\right )$
lies in
![]() $I_{\Lambda _j}(E,E^{\prime})$
if and only if there is a commutative diagram
$I_{\Lambda _j}(E,E^{\prime})$
if and only if there is a commutative diagram
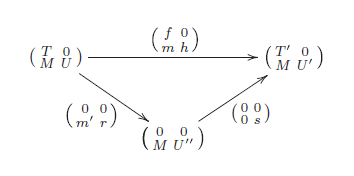
with
![]() $\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _j$
,
$\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _j$
,
![]() $1\leq j \leq n$
. Thus,
$1\leq j \leq n$
. Thus,
![]() $U^{\prime\prime} \in \mathcal{U}_j$
and
$U^{\prime\prime} \in \mathcal{U}_j$
and
![]() $\left (\begin{smallmatrix}0 & \quad\!\! 0 \\[2pt] 0 & \quad\!\! s \end{smallmatrix}\right )\left (\begin{smallmatrix}0 & \quad\!\! 0 \\[2pt] m^{\prime} & \quad\!\! r \end{smallmatrix}\right )$
=
$\left (\begin{smallmatrix}0 & \quad\!\! 0 \\[2pt] 0 & \quad\!\! s \end{smallmatrix}\right )\left (\begin{smallmatrix}0 & \quad\!\! 0 \\[2pt] m^{\prime} & \quad\!\! r \end{smallmatrix}\right )$
=
![]() $\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )$
; therefore,
$\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )$
; therefore,
![]() $f=0$
,
$f=0$
,
![]() $m=s\bullet m^{\prime}$
and
$m=s\bullet m^{\prime}$
and
![]() $h=s\circ r$
. It is clear that
$h=s\circ r$
. It is clear that
![]() $h \in I_{\mathcal{U}_j}(U,U^{\prime})$
because
$h \in I_{\mathcal{U}_j}(U,U^{\prime})$
because
![]() $U^{\prime\prime} \in \mathcal{U}_j$
. In this way, we conclude that
$U^{\prime\prime} \in \mathcal{U}_j$
. In this way, we conclude that
![]() $\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right ) \in I_{\Lambda _j}(E,E^{\prime})$
if and only if
$\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right ) \in I_{\Lambda _j}(E,E^{\prime})$
if and only if
![]() $h\in I_{\mathcal{U}_j}(U,U^{\prime})$
and
$h\in I_{\mathcal{U}_j}(U,U^{\prime})$
and
![]() $m=s\bullet m^{\prime}= M(s\otimes 1_{T})(m^{\prime})=M_T(s)(m^{\prime})$
(see Definition 2.13) and
$m=s\bullet m^{\prime}= M(s\otimes 1_{T})(m^{\prime})=M_T(s)(m^{\prime})$
(see Definition 2.13) and
![]() $f=0$
where
$f=0$
where
![]() $h\,:\, U\xrightarrow{r}U^{\prime\prime}\xrightarrow{s} U^{\prime}$
and
$h\,:\, U\xrightarrow{r}U^{\prime\prime}\xrightarrow{s} U^{\prime}$
and
![]() $U^{\prime\prime} \in \mathcal{U}_j$
. In other words,
$U^{\prime\prime} \in \mathcal{U}_j$
. In other words,
![]() $h\in I_{\mathcal{U}_j}(U,U^{\prime})$
and
$h\in I_{\mathcal{U}_j}(U,U^{\prime})$
and
![]() $m\in M_T^{[j]}(U^{\prime})$
, by Lemma 3.1. Thus,
$m\in M_T^{[j]}(U^{\prime})$
, by Lemma 3.1. Thus,
![]() $I_{\Lambda _j}(E,E^{\prime})=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M^{[j]}_T(U^{\prime}) & \quad\!\! I_{\mathcal{U}_j}(U,U^{\prime}) \end{smallmatrix}\right )$
.
$I_{\Lambda _j}(E,E^{\prime})=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M^{[j]}_T(U^{\prime}) & \quad\!\! I_{\mathcal{U}_j}(U,U^{\prime}) \end{smallmatrix}\right )$
.
Now, consider the case
![]() $j\gt n$
. We have that
$j\gt n$
. We have that
![]() $\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )\in I_{\Lambda _j}(E,E^{\prime})$
if and only if there is a commutative diagram
$\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )\in I_{\Lambda _j}(E,E^{\prime})$
if and only if there is a commutative diagram

with
![]() $\left (\begin{smallmatrix} T^{\prime\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _j$
, for
$\left (\begin{smallmatrix} T^{\prime\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _j$
, for
![]() $j=n+(j-n)\gt n$
, that is,
$j=n+(j-n)\gt n$
, that is,
![]() $T^{\prime\prime}\in \mathcal{T}_{j-n}$
and
$T^{\prime\prime}\in \mathcal{T}_{j-n}$
and
![]() $U^{\prime\prime} \in \mathcal{U}$
.
$U^{\prime\prime} \in \mathcal{U}$
.
Since
![]() $\left (\begin{smallmatrix}s & \quad\!\! 0 \\[2pt] m_2 & \quad\!\! h_2 \end{smallmatrix}\right )\left (\begin{smallmatrix}r & \quad\!\! 0 \\[2pt] m_1 & \quad\!\! h_1 \end{smallmatrix}\right )=\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )$
, we get that
$\left (\begin{smallmatrix}s & \quad\!\! 0 \\[2pt] m_2 & \quad\!\! h_2 \end{smallmatrix}\right )\left (\begin{smallmatrix}r & \quad\!\! 0 \\[2pt] m_1 & \quad\!\! h_1 \end{smallmatrix}\right )=\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )$
, we get that
![]() $f=s\circ r$
,
$f=s\circ r$
,
![]() $m=m_2\bullet r+h_2\bullet m_1$
and
$m=m_2\bullet r+h_2\bullet m_1$
and
![]() $h=h_2\circ h_1$
; moreover,
$h=h_2\circ h_1$
; moreover,
![]() $m\in M(U^{\prime},T)$
,
$m\in M(U^{\prime},T)$
,
![]() $h\in \mathcal{U}(U,U^{\prime})$
, and
$h\in \mathcal{U}(U,U^{\prime})$
, and
![]() $f\in I_{\mathcal{T}_{j-n}}(T,T^{\prime})$
since
$f\in I_{\mathcal{T}_{j-n}}(T,T^{\prime})$
since
![]() $T^{\prime\prime}\in \mathcal{T}_{j-n}$
. Therefore,
$T^{\prime\prime}\in \mathcal{T}_{j-n}$
. Therefore,
![]() $\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )\in I_{\Lambda _j}(E,E^{\prime})$
if and only if
$\left (\begin{smallmatrix}f & \quad\!\! 0 \\[2pt] m & \quad\!\! h \end{smallmatrix}\right )\in I_{\Lambda _j}(E,E^{\prime})$
if and only if
![]() $m\in M(U^{\prime},T)$
,
$m\in M(U^{\prime},T)$
,
![]() $h\in \mathcal{U}(U,U^{\prime})$
, and
$h\in \mathcal{U}(U,U^{\prime})$
, and
![]() $f\in I_{\mathcal{T}_{j-n}}(T,T^{\prime})$
.
$f\in I_{\mathcal{T}_{j-n}}(T,T^{\prime})$
.
Proposition 3.3.
For each pair
![]() $E,E^{\prime}\in \textrm{Ind} \hspace{.1cm} \Lambda _j- \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, we have
$E,E^{\prime}\in \textrm{Ind} \hspace{.1cm} \Lambda _j- \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, we have
Proof. The proof is divided in two cases.
Case
![]() $1\leq j \leq n$
. Let
$1\leq j \leq n$
. Let
![]() $E=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
and
$E=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
and
![]() $E^{\prime}=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
for which
$E^{\prime}=\left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
for which
![]() $U,U^{\prime}\in \textrm{Ind} \hspace{.1cm} \mathcal{U}_j- \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
. Therefore, by [Reference Leszczyński15, Proposition 3.8]
$U,U^{\prime}\in \textrm{Ind} \hspace{.1cm} \mathcal{U}_j- \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
. Therefore, by [Reference Leszczyński15, Proposition 3.8]
On the other hand, by Theorem 2.6, we have
![]() $\textrm{rad}_{\mathcal{U}}(U,U^{\prime})=I_{\mathcal{U}_{j-1}}(U,U^{\prime})$
. Therefore, by Proposition 3.2, we conclude that
$\textrm{rad}_{\mathcal{U}}(U,U^{\prime})=I_{\mathcal{U}_{j-1}}(U,U^{\prime})$
. Therefore, by Proposition 3.2, we conclude that
Case
![]() $j\gt n$
. Let
$j\gt n$
. Let
![]() $E=\left (\begin{smallmatrix} T & 0 \\[2pt] M & 0 \end{smallmatrix}\right )$
and
$E=\left (\begin{smallmatrix} T & 0 \\[2pt] M & 0 \end{smallmatrix}\right )$
and
![]() $E^{\prime}=\left (\begin{smallmatrix} T^{\prime} & 0 \\[2pt] M & 0 \end{smallmatrix}\right )$
such that the objects
$E^{\prime}=\left (\begin{smallmatrix} T^{\prime} & 0 \\[2pt] M & 0 \end{smallmatrix}\right )$
such that the objects
![]() $T,T^{\prime}\in \textrm{Ind}\hspace{.1cm} \mathcal{T}_{j-n}-\textrm{Ind}\hspace{.1cm} \mathcal{T}_{j-n-1}$
. By [Reference Leszczyński15, Proposition 3.8] we have
$T,T^{\prime}\in \textrm{Ind}\hspace{.1cm} \mathcal{T}_{j-n}-\textrm{Ind}\hspace{.1cm} \mathcal{T}_{j-n-1}$
. By [Reference Leszczyński15, Proposition 3.8] we have
Again by Theorem 2.6 we know that
![]() $\textrm{rad}_{\mathcal{T}}(T,T^{\prime})=I_{\mathcal{T}_{j-n-1}}(T,T^{\prime})$
. It follows from Proposition 3.2 that
$\textrm{rad}_{\mathcal{T}}(T,T^{\prime})=I_{\mathcal{T}_{j-n-1}}(T,T^{\prime})$
. It follows from Proposition 3.2 that
Remark 3.4. For
![]() $X= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )\in \Lambda$
, we consider
$X= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )\in \Lambda$
, we consider
![]() $I_{\Lambda _{j}}(X,-)\in \textrm{Mod}(\Lambda )$
. By Theorem 2.14, there exists
$I_{\Lambda _{j}}(X,-)\in \textrm{Mod}(\Lambda )$
. By Theorem 2.14, there exists
![]() $I_{\Lambda _{j}}^{(1)}(X,-)\in \textrm{Mod}(\mathcal{T})$
and
$I_{\Lambda _{j}}^{(1)}(X,-)\in \textrm{Mod}(\mathcal{T})$
and
![]() $I_{\Lambda _{j}}^{(2)}(X,-)\in \textrm{Mod}(\mathcal{U})$
and a morphism of
$I_{\Lambda _{j}}^{(2)}(X,-)\in \textrm{Mod}(\mathcal{U})$
and a morphism of
![]() $\mathcal{T}$
-modules
$\mathcal{T}$
-modules
![]() $f\,:\,I_{\Lambda _{j}}^{(1)}(X,-)\longrightarrow \mathbb{G}\left(I_{\Lambda _{j}}^{(2)}(X,-)\right)$
such that
$f\,:\,I_{\Lambda _{j}}^{(1)}(X,-)\longrightarrow \mathbb{G}\left(I_{\Lambda _{j}}^{(2)}(X,-)\right)$
such that
As a direct result of the above proposition, we have:
Lemma 3.5.
Let
![]() $X= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )\in \Lambda$
. Let us identify
$X= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )\in \Lambda$
. Let us identify
![]() $I_{\Lambda _j}(X,-)$
with its corresponding object
$I_{\Lambda _j}(X,-)$
with its corresponding object
![]() $\left (I_{\Lambda _j}^{(1)}(X,-), f, I_{\Lambda _j}^{(2)}(X,-)\right )$
in
$\left (I_{\Lambda _j}^{(1)}(X,-), f, I_{\Lambda _j}^{(2)}(X,-)\right )$
in
![]() $(\textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U})))$
. Then the following holds:
$(\textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U})))$
. Then the following holds:
-
(i)
 $ I_{\Lambda _j}^{(1)}(X,-)=0$
and
$ I_{\Lambda _j}^{(1)}(X,-)=0$
and
 $I_{\Lambda _j}^{(2)}(X,-)\cong M_T^{[j]} \coprod I_{\mathcal{U}_j}(U,-)$
, if
$I_{\Lambda _j}^{(2)}(X,-)\cong M_T^{[j]} \coprod I_{\mathcal{U}_j}(U,-)$
, if
 $0\le j\le n$
;
$0\le j\le n$
; -
(ii)
 $ I_{\Lambda _j}^{(1)}(X,-)\cong I_{\mathcal{T}_{j-n}}(T,-)$
and
$ I_{\Lambda _j}^{(1)}(X,-)\cong I_{\mathcal{T}_{j-n}}(T,-)$
and
 $I_{\Lambda _j}^{(2)}(X,-)\cong M_T \coprod \mathcal{U}(U,-)$
, if
$I_{\Lambda _j}^{(2)}(X,-)\cong M_T \coprod \mathcal{U}(U,-)$
, if
 $j\gt n$
.
$j\gt n$
.
Proof. Let
![]() $T^{\prime}\in \mathcal{T}$
and
$T^{\prime}\in \mathcal{T}$
and
![]() $U^{\prime}\in \mathcal{U}$
. The proof is divided into two cases.
$U^{\prime}\in \mathcal{U}$
. The proof is divided into two cases.
Case
![]() $1\leq j \leq n$
. By Proposition 3.2, we have that
$1\leq j \leq n$
. By Proposition 3.2, we have that
where the first equality is by Theorem 2.14, the and similarly by Proposition 3.2 and Theorem 2.14 we have that
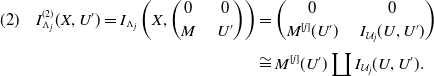 \begin{align*} (2)\quad I_{\Lambda _j}^{(2)}(X,U^{\prime}) = I_{\Lambda _j}\left ( X, \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end{matrix}\right ) \right ) & =\left (\begin{matrix} 0 & \quad 0 \\[2pt] M^{[j]}(U^{\prime}) & \quad I_{\mathcal{U}_j}(U,U^{\prime}) \end{matrix}\right ) \quad \quad \quad \quad \quad \\[2pt] & \cong M^{[j]}(U^{\prime}) \coprod I_{\mathcal{U}_j}(U,U^{\prime}). \end{align*}
\begin{align*} (2)\quad I_{\Lambda _j}^{(2)}(X,U^{\prime}) = I_{\Lambda _j}\left ( X, \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end{matrix}\right ) \right ) & =\left (\begin{matrix} 0 & \quad 0 \\[2pt] M^{[j]}(U^{\prime}) & \quad I_{\mathcal{U}_j}(U,U^{\prime}) \end{matrix}\right ) \quad \quad \quad \quad \quad \\[2pt] & \cong M^{[j]}(U^{\prime}) \coprod I_{\mathcal{U}_j}(U,U^{\prime}). \end{align*}
Case
![]() $j\gt n$
. By Theorem 2.14, and Proposition 3.2, we have that
$j\gt n$
. By Theorem 2.14, and Proposition 3.2, we have that
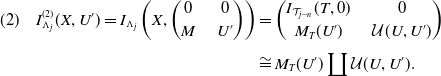 \begin{align*} (2)\quad I_{\Lambda _j}^{(2)}(X,U^{\prime})=I_{\Lambda _j}\left ( X, \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end{matrix}\right ) \right ) & = \left (\begin{matrix} I_{\mathcal{T}_{j-n}}(T,0) & \quad 0 \\[2pt] M_T(U^{\prime}) & \quad \mathcal{U}(U,U^{\prime}) \end{matrix}\right )\\[2pt] & \cong M_T(U^{\prime}) \coprod \mathcal{U}(U,U^{\prime}).\quad \quad \quad \quad \end{align*}
\begin{align*} (2)\quad I_{\Lambda _j}^{(2)}(X,U^{\prime})=I_{\Lambda _j}\left ( X, \left (\begin{matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end{matrix}\right ) \right ) & = \left (\begin{matrix} I_{\mathcal{T}_{j-n}}(T,0) & \quad 0 \\[2pt] M_T(U^{\prime}) & \quad \mathcal{U}(U,U^{\prime}) \end{matrix}\right )\\[2pt] & \cong M_T(U^{\prime}) \coprod \mathcal{U}(U,U^{\prime}).\quad \quad \quad \quad \end{align*}
Proposition 3.6.
Let
![]() $X= \left (\begin{smallmatrix} T & 0 \\ M & U \end{smallmatrix}\right )\in \Lambda$
, and assume
$X= \left (\begin{smallmatrix} T & 0 \\ M & U \end{smallmatrix}\right )\in \Lambda$
, and assume
![]() $M_T\in \mathcal{F}({}_{\mathcal{U}}\Delta )$
for all
$M_T\in \mathcal{F}({}_{\mathcal{U}}\Delta )$
for all
![]() $T\in \mathcal{T}$
. Then, for all
$T\in \mathcal{T}$
. Then, for all
![]() $j\geq 1$
the following exact sequence exists:
$j\geq 1$
the following exact sequence exists:
with
![]() $E_j\in \Lambda _j$
and
$E_j\in \Lambda _j$
and
![]() $E_{j-1}\in \Lambda _{j-1}$
.
$E_{j-1}\in \Lambda _{j-1}$
.
Proof. The proof is divided into two cases.
Case
![]() $1\leq j \leq n$
. By Lemma 2.12 and Theorem 2.6, there exist exact sequences
$1\leq j \leq n$
. By Lemma 2.12 and Theorem 2.6, there exist exact sequences
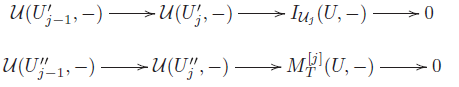
with
![]() $U^{\prime}_{j}, U^{\prime\prime}_{j}\in \mathcal{U}_j$
,
$U^{\prime}_{j}, U^{\prime\prime}_{j}\in \mathcal{U}_j$
,
![]() $U^{\prime}_{j-1}, U^{\prime\prime}_{j-1}\in \mathcal{U}_{j-1}$
. Since in functor categories limits and colimits are computed pointwise, we have an exact sequence
$U^{\prime}_{j-1}, U^{\prime\prime}_{j-1}\in \mathcal{U}_{j-1}$
. Since in functor categories limits and colimits are computed pointwise, we have an exact sequence
with
![]() $U_{j-1}=U^{\prime}_{j-1}\coprod U^{\prime\prime}_{j-1}\in \mathcal{U}_{j-1}$
and
$U_{j-1}=U^{\prime}_{j-1}\coprod U^{\prime\prime}_{j-1}\in \mathcal{U}_{j-1}$
and
![]() $U_{j}=U^{\prime}_{j}\coprod U^{\prime\prime}_{j}\in \mathcal{U}_{j}$
. By Remark 3.4, we get that
$U_{j}=U^{\prime}_{j}\coprod U^{\prime\prime}_{j}\in \mathcal{U}_{j}$
. By Remark 3.4, we get that
![]() $\mathfrak{f}\left ((I_{\Lambda _j}^{(1)}(X,-),f,I_{\Lambda _j}^{(2)}(X,-)\right )\simeq I_{\Lambda _j}(X,-)$
, and by Lemma 3.5 we have that
$\mathfrak{f}\left ((I_{\Lambda _j}^{(1)}(X,-),f,I_{\Lambda _j}^{(2)}(X,-)\right )\simeq I_{\Lambda _j}(X,-)$
, and by Lemma 3.5 we have that
![]() $ I_{\Lambda _j}^{(1)}(X,-)=0$
and hence
$ I_{\Lambda _j}^{(1)}(X,-)=0$
and hence
![]() $\mathfrak{f}\left ((I_{\Lambda _j}^{(1)}(X,-),0,I_{\Lambda _j}^{(2)}(X,-)\right )\simeq I_{\Lambda _j}(X,-)$
. It follows by Proposition 2.15, that there exists a exact sequence of
$\mathfrak{f}\left ((I_{\Lambda _j}^{(1)}(X,-),0,I_{\Lambda _j}^{(2)}(X,-)\right )\simeq I_{\Lambda _j}(X,-)$
. It follows by Proposition 2.15, that there exists a exact sequence of
![]() $\Lambda$
-modules
$\Lambda$
-modules
where
![]() $\left (\begin{smallmatrix} 0 & \quad 0 \\[2pt] M & \quad U_{j-1} \end{smallmatrix}\right ) \in \Lambda _{j-1}$
and
$\left (\begin{smallmatrix} 0 & \quad 0 \\[2pt] M & \quad U_{j-1} \end{smallmatrix}\right ) \in \Lambda _{j-1}$
and
![]() $\left (\begin{smallmatrix} 0 & 0 \\[2pt] M & \quad U_{j} \end{smallmatrix}\right ) \in \Lambda _j$
.
$\left (\begin{smallmatrix} 0 & 0 \\[2pt] M & \quad U_{j} \end{smallmatrix}\right ) \in \Lambda _j$
.
Case
![]() $j\gt n$
. Since
$j\gt n$
. Since
![]() $M_T\in \mathcal{F}({}_{\mathcal{U}}\Delta )$
,
$M_T\in \mathcal{F}({}_{\mathcal{U}}\Delta )$
,
![]() $M_T$
is a finitely presented
$M_T$
is a finitely presented
![]() $\mathcal{U}$
-module, then
$\mathcal{U}$
-module, then
![]() $M_T\coprod \mathcal{U}(U,-)\cong I_{\Lambda _j}^{(2)}(X,-)$
is finitely presented. Then, there exists an exact sequence of
$M_T\coprod \mathcal{U}(U,-)\cong I_{\Lambda _j}^{(2)}(X,-)$
is finitely presented. Then, there exists an exact sequence of
![]() $\mathcal{U}$
-modules
$\mathcal{U}$
-modules
On the other hand, by Theorem 2.6, there exists an exact sequence of
![]() $\mathcal{T}$
-modules
$\mathcal{T}$
-modules
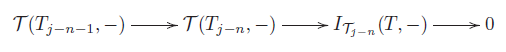
with
![]() $T_{j-n}\in \mathcal{T}_{j-n}$
and
$T_{j-n}\in \mathcal{T}_{j-n}$
and
![]() $T_{j-n-1}\in \mathcal{T}_{j-n-1}$
. Thus, we get an exact sequence
$T_{j-n-1}\in \mathcal{T}_{j-n-1}$
. Thus, we get an exact sequence
where
![]() $\mathfrak{f}\left(\left(I_{\Lambda _j}^{(1)},f,I_{\Lambda _j}^{(2)}\right)\right)\cong I_{\Lambda _j}(X,-)$
such that
$\mathfrak{f}\left(\left(I_{\Lambda _j}^{(1)},f,I_{\Lambda _j}^{(2)}\right)\right)\cong I_{\Lambda _j}(X,-)$
such that
![]() $\left (\begin{smallmatrix} T_{j-n-1} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _{j-1}$
and also
$\left (\begin{smallmatrix} T_{j-n-1} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime\prime} \end{smallmatrix}\right ) \in \Lambda _{j-1}$
and also
![]() $\left (\begin{smallmatrix} T_{j-n} & 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right ) \in \Lambda _j$
.
$\left (\begin{smallmatrix} T_{j-n} & 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right ) \in \Lambda _j$
.
Theorem 3.7.
Let
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
be
$\mathcal{T}$
be
![]() $\textrm{Hom}$
-finite Krull–Schmidt categories and consider exhaustive filtrations
$\textrm{Hom}$
-finite Krull–Schmidt categories and consider exhaustive filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
of
$\{\mathcal{T}_j\}_{j\ge 0}$
of
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
, consisting of full additive subcategories which are closed under direct summands. Suppose that
$\mathcal{T}$
, consisting of full additive subcategories which are closed under direct summands. Suppose that
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
are quasi-hereditary categories with respect to the filtrations
$\mathcal{T}$
are quasi-hereditary categories with respect to the filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
, respectively. Assume that
$\{\mathcal{T}_j\}_{j\ge 0}$
, respectively. Assume that
![]() $M_T\in \mathcal{F}(_{\mathcal{U}}\Delta )$
for all
$M_T\in \mathcal{F}(_{\mathcal{U}}\Delta )$
for all
![]() $T\in \mathcal{T}$
. Then
$T\in \mathcal{T}$
. Then
![]() $\Lambda = \left(\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\ M & \quad\!\! \mathcal{U} \end{smallmatrix}\right)$
is quasi-hereditary with respect to the filtration
$\Lambda = \left(\begin{smallmatrix} \mathcal{T} & \quad\!\! 0 \\ M & \quad\!\! \mathcal{U} \end{smallmatrix}\right)$
is quasi-hereditary with respect to the filtration
![]() $\{\Lambda _j\}_{j\ge 0 }$
given in equation (3.1).
$\{\Lambda _j\}_{j\ge 0 }$
given in equation (3.1).
Proof. It follows from Theorem 2.6; and Propositions 3.3 and 3.6.
Remark 3.8. Now, let us explain why Theorem 3.7 is a generalization of a Theorem given by B. Zhu in [Reference Šťovíček29]. Suppose that
![]() $U$
and
$U$
and
![]() $T$
are quasi-hereditary algebras and that
$T$
are quasi-hereditary algebras and that
![]() ${}_{U}M_{T}$
is a bimodule such that
${}_{U}M_{T}$
is a bimodule such that
![]() ${}_{U}M \in \mathcal{F}(_{U}\Delta )$
. Consider the triangular matrix algebra
${}_{U}M \in \mathcal{F}(_{U}\Delta )$
. Consider the triangular matrix algebra
![]() $A\,:\!=\,\begin{pmatrix} T & \quad\!\! 0 \\ M & \quad\!\! U \end{pmatrix}$
.
$A\,:\!=\,\begin{pmatrix} T & \quad\!\! 0 \\ M & \quad\!\! U \end{pmatrix}$
.
By Remark 2.7(a), we get that
![]() $\textrm{proj}(U)$
and
$\textrm{proj}(U)$
and
![]() $\textrm{proj}(T)$
are quasi-hereditary categories in the sense of the Definition 2.4. Since
$\textrm{proj}(T)$
are quasi-hereditary categories in the sense of the Definition 2.4. Since
![]() ${}_{U}M \in \mathcal{F}(_{U}\Delta )$
, we can see that
${}_{U}M \in \mathcal{F}(_{U}\Delta )$
, we can see that
![]() $M$
satisfies the hypothesis in Theorem 3.7. Thus, by Theorem 3.7, we get that
$M$
satisfies the hypothesis in Theorem 3.7. Thus, by Theorem 3.7, we get that
![]() $\begin{pmatrix} \textrm{proj}(T) & \quad\!\! 0 \\ M & \quad\!\! \textrm{proj}(U) \end{pmatrix}$
is a quasi-hereditary category. Now, by using [Reference Auslander, Reiten and Smalø5, Proposition 2.3] in p. 75, we have that
$\begin{pmatrix} \textrm{proj}(T) & \quad\!\! 0 \\ M & \quad\!\! \textrm{proj}(U) \end{pmatrix}$
is a quasi-hereditary category. Now, by using [Reference Auslander, Reiten and Smalø5, Proposition 2.3] in p. 75, we have that
![]() $\textrm{proj}(A)= \begin{pmatrix} \textrm{proj}(T) & \quad\!\! 0 \\ M & \quad\!\! \textrm{proj}(U)\end{pmatrix}$
. Therefore, by Remark 2.7(a), we obtain that
$\textrm{proj}(A)= \begin{pmatrix} \textrm{proj}(T) & \quad\!\! 0 \\ M & \quad\!\! \textrm{proj}(U)\end{pmatrix}$
. Therefore, by Remark 2.7(a), we obtain that
![]() $A$
is a quasi-hereditary algebra.
$A$
is a quasi-hereditary algebra.
3.1. The standard modules in
 $\textrm{Mod}(\Lambda )$
and
$\textrm{Mod}(\Lambda )$
and
 $\mathcal{F}(_\Lambda \Delta )$
$\mathcal{F}(_\Lambda \Delta )$
Assume that
![]() $\mathcal{U}$
and
$\mathcal{U}$
and
![]() $\mathcal{T}$
are
$\mathcal{T}$
are
![]() $\textrm{Hom}$
-finite Krull–Schmidt and quasi-hereditary
$\textrm{Hom}$
-finite Krull–Schmidt and quasi-hereditary
![]() $K-$
categories with respect to filtrations
$K-$
categories with respect to filtrations
![]() $\{\mathcal{U}_j\}_{0\le j\le n}$
and
$\{\mathcal{U}_j\}_{0\le j\le n}$
and
![]() $\{\mathcal{T}_j\}_{j\ge 0}$
. If
$\{\mathcal{T}_j\}_{j\ge 0}$
. If
![]() $M\,:\, \mathcal{U}\otimes _K\mathcal{T}^{op}\rightarrow \textrm{mod} (K)$
is a functor such that
$M\,:\, \mathcal{U}\otimes _K\mathcal{T}^{op}\rightarrow \textrm{mod} (K)$
is a functor such that
![]() $M_T=M(-,T)\,:\,\textrm{Mod}(\mathcal{U})\rightarrow \textrm{mod}(K)$
is finitely presented
$M_T=M(-,T)\,:\,\textrm{Mod}(\mathcal{U})\rightarrow \textrm{mod}(K)$
is finitely presented
![]() $\mathcal{U}$
-module, then by Theorem 3.7, the triangular matrix category
$\mathcal{U}$
-module, then by Theorem 3.7, the triangular matrix category
![]() $\Lambda =(\begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U}\end{smallmatrix})$
is a quasi-hereditary
$\Lambda =(\begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U}\end{smallmatrix})$
is a quasi-hereditary
![]() $K$
-category with respect to some filtration
$K$
-category with respect to some filtration
![]() $\{\Lambda _j\}_{j\ge 0}$
. In this part, we study the relation between the full standard subcategories
$\{\Lambda _j\}_{j\ge 0}$
. In this part, we study the relation between the full standard subcategories
![]() $_{\mathcal{U}}\Delta$
,
$_{\mathcal{U}}\Delta$
,
![]() $_{\mathcal{T}}\Delta$
, and
$_{\mathcal{T}}\Delta$
, and
![]() $_\Lambda \Delta$
of
$_\Lambda \Delta$
of
![]() $\textrm{Mod}(\mathcal{U})$
,
$\textrm{Mod}(\mathcal{U})$
,
![]() $\textrm{Mod}(\mathcal{T})$
, and
$\textrm{Mod}(\mathcal{T})$
, and
![]() $\textrm{Mod}(\Lambda )$
, respectively. More concretely, we will show in Theorem 3.10, by using the notation of Theorem 2.14, that
$\textrm{Mod}(\Lambda )$
, respectively. More concretely, we will show in Theorem 3.10, by using the notation of Theorem 2.14, that
see [Reference Šťovíček29, Theorem 3.1]. Recall that given an abelian category
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{X}\subseteq \mathcal{A}.$
We denote by
$\mathcal{X}\subseteq \mathcal{A}.$
We denote by
![]() $\mathcal{X}^{\amalg }$
the class of objects of
$\mathcal{X}^{\amalg }$
the class of objects of
![]() $\mathcal{A}$
, which are a finite direct sum of objects in
$\mathcal{A}$
, which are a finite direct sum of objects in
![]() $\mathcal{X}.$
We say that
$\mathcal{X}.$
We say that
![]() $M\in \mathcal{A}$
is
$M\in \mathcal{A}$
is
![]() $\mathcal{X}$
-
$\mathcal{X}$
-
![]() $\textbf{filtered}$
if there exists a chain
$\textbf{filtered}$
if there exists a chain
![]() $\{M_{j}\}_{j\ge 0}$
of subobjects of
$\{M_{j}\}_{j\ge 0}$
of subobjects of
![]() $M$
such that
$M$
such that
![]() $M_{j+1}/M_{j}\in \mathcal{X}^{\amalg }$
for
$M_{j+1}/M_{j}\in \mathcal{X}^{\amalg }$
for
![]() $j\ge 0.$
In case
$j\ge 0.$
In case
![]() $M=M_n$
for some
$M=M_n$
for some
![]() $n\in \mathbb N$
, we say that
$n\in \mathbb N$
, we say that
![]() $M$
has a finite
$M$
has a finite
![]() $\mathcal{X}$
-filtration. We denote by
$\mathcal{X}$
-filtration. We denote by
![]() $\mathcal{F}(\mathcal{X})$
the class of objects that are
$\mathcal{F}(\mathcal{X})$
the class of objects that are
![]() $\mathcal{X}$
-filtered and by
$\mathcal{X}$
-filtered and by
![]() $\mathcal{F}_f(\mathcal{X})$
the class of objects that have a finite filtration.
$\mathcal{F}_f(\mathcal{X})$
the class of objects that have a finite filtration.
Regardless, we need the following result.
Proposition 3.9.
The functor
![]() $\mathfrak{f}\,:\,(\textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U}))) \rightarrow \textrm{Mod}( \Lambda )$
induce equivalences of full subcategories:
$\mathfrak{f}\,:\,(\textrm{Mod}(\mathcal{T}), \mathbb{G}(\textrm{Mod}(\mathcal{U}))) \rightarrow \textrm{Mod}( \Lambda )$
induce equivalences of full subcategories:
Proof. First, for
![]() $E \in \textrm{Ind} \hspace{.1cm} \Lambda _j - \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, consider
$E \in \textrm{Ind} \hspace{.1cm} \Lambda _j - \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, consider
![]() $_{\Lambda }\Delta _E=\frac{\Lambda (E,-)}{I_{\Lambda _{j-1}}(E,-)}$
. Then there exists a triple
$_{\Lambda }\Delta _E=\frac{\Lambda (E,-)}{I_{\Lambda _{j-1}}(E,-)}$
. Then there exists a triple
![]() $\left( \Delta _E^{(1)}, g, \Delta _E^{(2)}\right)$
such that
$\left( \Delta _E^{(1)}, g, \Delta _E^{(2)}\right)$
such that
![]() $\mathfrak{f}\left(\left( \Delta _E^{(1)}, g, \Delta _E^{(2)}\right)\right)=\,_{\Lambda }\Delta _E$
where
$\mathfrak{f}\left(\left( \Delta _E^{(1)}, g, \Delta _E^{(2)}\right)\right)=\,_{\Lambda }\Delta _E$
where
![]() $\Delta _E^{(1)}\,:\,\mathcal{T}\rightarrow \textbf{Ab}$
and
$\Delta _E^{(1)}\,:\,\mathcal{T}\rightarrow \textbf{Ab}$
and
![]() $\Delta _E^{(2)}\,:\,\mathcal{U}\rightarrow \textbf{Ab}$
. Now, we consider two cases.
$\Delta _E^{(2)}\,:\,\mathcal{U}\rightarrow \textbf{Ab}$
. Now, we consider two cases.
Case
![]() $1\leq j \leq n$
. Let
$1\leq j \leq n$
. Let
![]() $T^{\prime}\in \mathcal{T}$
and
$T^{\prime}\in \mathcal{T}$
and
![]() $E= \left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right ) \in \textrm{Ind} \hspace{.1cm} \Lambda _j - \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, with
$E= \left (\begin{smallmatrix} 0 & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right ) \in \textrm{Ind} \hspace{.1cm} \Lambda _j - \textrm{Ind} \hspace{.1cm} \Lambda _{j-1}$
, with
![]() $U \in \textrm{Ind} \hspace{.1cm} \mathcal{U}_j - \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
. Then
$U \in \textrm{Ind} \hspace{.1cm} \mathcal{U}_j - \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
. Then
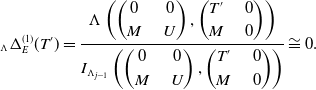 \begin{equation*} _{\Lambda }\Delta _E^{(1)}(T^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}\cong 0. \end{equation*}
\begin{equation*} _{\Lambda }\Delta _E^{(1)}(T^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}\cong 0. \end{equation*}
On the other hand, if
![]() $U^{\prime} \in \mathcal{U}$
, we get
$U^{\prime} \in \mathcal{U}$
, we get
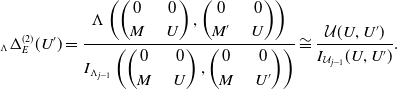 \begin{equation*} _{\Lambda }\Delta _E^{(2)}(U^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M^{\prime} & \quad U \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}\cong \frac {\mathcal {U}(U,U^{\prime})}{I_{\mathcal {U}_{j-1}}(U,U^{\prime})}. \end{equation*}
\begin{equation*} _{\Lambda }\Delta _E^{(2)}(U^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M^{\prime} & \quad U \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}\cong \frac {\mathcal {U}(U,U^{\prime})}{I_{\mathcal {U}_{j-1}}(U,U^{\prime})}. \end{equation*}
In this way,
![]() $_{\Lambda }\Delta _E^{(1)}\cong 0$
and
$_{\Lambda }\Delta _E^{(1)}\cong 0$
and
![]() $_{\Lambda }\Delta _E^{(2)}\cong \frac{\mathcal{U}(U,-)}{I_{\mathcal{U}_{j-1}}(U,-)}=\,{}_{\mathcal{U}}\Delta _U$
, where the object
$_{\Lambda }\Delta _E^{(2)}\cong \frac{\mathcal{U}(U,-)}{I_{\mathcal{U}_{j-1}}(U,-)}=\,{}_{\mathcal{U}}\Delta _U$
, where the object
![]() $U$
belongs to
$U$
belongs to
![]() $\textrm{Ind} \hspace{.1cm} \mathcal{U}_j - \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
.
$\textrm{Ind} \hspace{.1cm} \mathcal{U}_j - \textrm{Ind} \hspace{.1cm} \mathcal{U}_{j-1}$
.
Case
![]() $j\gt n$
. Let
$j\gt n$
. Let
![]() $T^{\prime} \in \mathcal{T}$
and
$T^{\prime} \in \mathcal{T}$
and
![]() $E= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix}\right )$
with
$E= \left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! 0 \end{smallmatrix}\right )$
with
![]() $T \in \textrm{Ind} \hspace{.1cm} \mathcal{T}_{j-n} - \textrm{Ind} \hspace{.1cm} \mathcal{T}_{j-n-1}$
. Thus, we obtain that:
$T \in \textrm{Ind} \hspace{.1cm} \mathcal{T}_{j-n} - \textrm{Ind} \hspace{.1cm} \mathcal{T}_{j-n-1}$
. Thus, we obtain that:
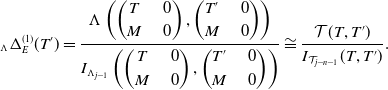 \begin{equation*} _{\Lambda }\Delta _E^{(1)}(T^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}\cong \frac {\mathcal {T}(T,T^{\prime})}{I_{\mathcal {T}_{j-n-1}}(T,T^{\prime})}. \end{equation*}
\begin{equation*} _{\Lambda }\Delta _E^{(1)}(T^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} T^{\prime} & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ) \right )}\cong \frac {\mathcal {T}(T,T^{\prime})}{I_{\mathcal {T}_{j-n-1}}(T,T^{\prime})}. \end{equation*}
If
![]() $U^{\prime} \in \mathcal{U}$
, we obtain
$U^{\prime} \in \mathcal{U}$
, we obtain
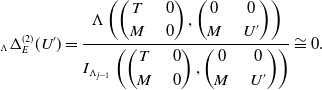 \begin{equation*} _{\Lambda }\Delta _E^{(2)}(U^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}\cong 0. \end{equation*}
\begin{equation*} _{\Lambda }\Delta _E^{(2)}(U^{\prime})=\frac {\Lambda \left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}{I_{\Lambda _{j-1}}\left ( \left (\begin {matrix} T & \quad 0 \\[2pt] M & \quad 0 \end {matrix}\right ), \left (\begin {matrix} 0 & \quad 0 \\[2pt] M & \quad U^{\prime} \end {matrix}\right ) \right )}\cong 0. \end{equation*}
Therefore,
![]() $_{\Lambda }\Delta _E^{(1)}\cong \frac{\mathcal{T}(T,-)}{I_{\mathcal{T}_{j-n-1}}(T,-)} \cong \,{} _{\mathcal{T}}\Delta _T$
, with
$_{\Lambda }\Delta _E^{(1)}\cong \frac{\mathcal{T}(T,-)}{I_{\mathcal{T}_{j-n-1}}(T,-)} \cong \,{} _{\mathcal{T}}\Delta _T$
, with
![]() $T \in \textrm{Ind} \hspace{.1cm} \mathcal{T}_{n-j} - \textrm{Ind} \hspace{.1cm} \mathcal{T}_{n-j-1}$
and
$T \in \textrm{Ind} \hspace{.1cm} \mathcal{T}_{n-j} - \textrm{Ind} \hspace{.1cm} \mathcal{T}_{n-j-1}$
and
![]() $_{\Lambda }\Delta _E^{(2)}\cong 0$
.
$_{\Lambda }\Delta _E^{(2)}\cong 0$
.
Theorem 3.10.
Let
![]() $F=\mathfrak{f}\big (F^{(1)}, g, F^{(2)}\big )\in \textrm{mod}(\Lambda )$
, and consider its trace filtration
$F=\mathfrak{f}\big (F^{(1)}, g, F^{(2)}\big )\in \textrm{mod}(\Lambda )$
, and consider its trace filtration
![]() $\{F^{[j]} \}_{j\ge 0}= \left\{\left(\left(F^{[j]}\right)^{(1)}, g^{[j]}, \left(F^{[j]}\right)^{(2)}\right)\right\} _{j\ge 0}$
with respect to
$\{F^{[j]} \}_{j\ge 0}= \left\{\left(\left(F^{[j]}\right)^{(1)}, g^{[j]}, \left(F^{[j]}\right)^{(2)}\right)\right\} _{j\ge 0}$
with respect to
![]() $\{\Lambda _j\}_{j\geq 0}$
. Then the following conditions hold.
$\{\Lambda _j\}_{j\geq 0}$
. Then the following conditions hold.
-
(i)
 $(F^{[j]})^{(1)}\cong 0$
if
$(F^{[j]})^{(1)}\cong 0$
if
 $0\le j\le n$
, and
$0\le j\le n$
, and
 $(F^{[j]})^{(2)}\cong F^{(2)}$
if
$(F^{[j]})^{(2)}\cong F^{(2)}$
if
 $j\gt n$
.
$j\gt n$
. -
(ii) If
 $F=\mathfrak{f}\left(\left(F^{(1)},g,F^{(2)}\right)\right)\in \mathcal{ F}(_{\Lambda }\Delta )$
, then we have that
$F=\mathfrak{f}\left(\left(F^{(1)},g,F^{(2)}\right)\right)\in \mathcal{ F}(_{\Lambda }\Delta )$
, then we have that
 $F^{(1)}\in \mathcal{F}(_{\mathcal{T}}\Delta )$
and
$F^{(1)}\in \mathcal{F}(_{\mathcal{T}}\Delta )$
and
 $F^{(2)}\in \mathcal{F}(_{\mathcal{U}}\Delta )$
.
$F^{(2)}\in \mathcal{F}(_{\mathcal{U}}\Delta )$
. -
(iii)
 $\mathcal{ F}_f(_{\Lambda }\Delta )=\left\{\mathfrak{f}\big (F^{(1)}, g, F^{(2)}\big )\,:\, F^{(1)}\in \mathcal{F}_f(_{\mathcal{T}}\Delta ) \text{ and } F^{(2)}\in \mathcal{F}_f(_{\mathcal{U}}\Delta )\right\}$
.
$\mathcal{ F}_f(_{\Lambda }\Delta )=\left\{\mathfrak{f}\big (F^{(1)}, g, F^{(2)}\big )\,:\, F^{(1)}\in \mathcal{F}_f(_{\mathcal{T}}\Delta ) \text{ and } F^{(2)}\in \mathcal{F}_f(_{\mathcal{U}}\Delta )\right\}$
.
Proof. (i) Since
![]() $F\in \textrm{mod}(\Lambda )$
, we have an exact sequence of
$F\in \textrm{mod}(\Lambda )$
, we have an exact sequence of
![]() $\Lambda$
-modules
$\Lambda$
-modules
with
![]() $X^{\prime}=\left (\begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
and
$X^{\prime}=\left (\begin{smallmatrix} T^{\prime} & \quad\!\! 0 \\[2pt] M & \quad\!\! U^{\prime} \end{smallmatrix}\right )$
and
![]() $X=\left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
. By applying
$X=\left (\begin{smallmatrix} T & \quad\!\! 0 \\[2pt] M & \quad\!\! U \end{smallmatrix}\right )$
. By applying
![]() $\textrm{Tr}_{\{\Lambda (E,-)\}_{E\in \Lambda _j}}(-)$
to the previous exact sequence and using that each
$\textrm{Tr}_{\{\Lambda (E,-)\}_{E\in \Lambda _j}}(-)$
to the previous exact sequence and using that each
![]() $\Lambda (E,-)$
is a projective
$\Lambda (E,-)$
is a projective
![]() $\Lambda$
-module and by Lemma 2.3, we get an exact sequence
$\Lambda$
-module and by Lemma 2.3, we get an exact sequence
By Proposition 2.16 and Theorem 2.14, we identify the exact sequence in (3.3) with the following exact sequence in the comma category
![]() $\left (\textrm{Mod}(\mathcal{T}),\mathbb{G}\left(\textrm{Mod}(\mathcal{U})\right)\right )$
:
$\left (\textrm{Mod}(\mathcal{T}),\mathbb{G}\left(\textrm{Mod}(\mathcal{U})\right)\right )$
:
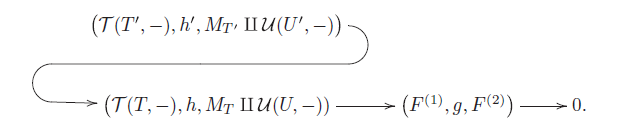
By Proposition 2.17, we have the exact sequence in
![]() $\textrm{Mod}(\mathcal{U})$
:
$\textrm{Mod}(\mathcal{U})$
:
Second, by Theorem 2.14, we identify the exact sequence in (3.4) with the exact sequence in the comma category
![]() $\left (\textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\right )$
:
$\left (\textrm{Mod}(\mathcal{T}),\mathbb{G}(\textrm{Mod}(\mathcal{U}))\right )$
:
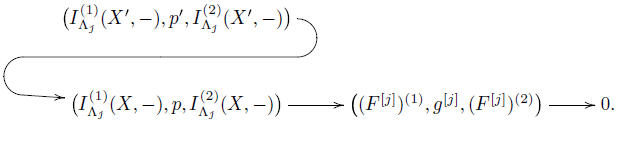
By Proposition 2.17, we get exact sequences
in
![]() $\textrm{Mod}(\mathcal{T})$
and
$\textrm{Mod}(\mathcal{T})$
and
![]() $\textrm{Mod}(\mathcal{U})$
. By Lemma 3.5(i), we have that
$\textrm{Mod}(\mathcal{U})$
. By Lemma 3.5(i), we have that
![]() $ I_{{ \Lambda }_j}^{(1)}(X^{\prime},-)$
$ I_{{ \Lambda }_j}^{(1)}(X^{\prime},-)$
![]() $\cong 0$
and
$\cong 0$
and
![]() $ I_{{ \Lambda }_j}^{(1)}(X,-) \cong 0$
if
$ I_{{ \Lambda }_j}^{(1)}(X,-) \cong 0$
if
![]() $0\le j\le n$
; therefore,
$0\le j\le n$
; therefore,
![]() $(F^{[j]})^{(1)}\cong 0$
for
$(F^{[j]})^{(1)}\cong 0$
for
![]() $0\le j\le n$
.
$0\le j\le n$
.
If
![]() $j\gt n$
, by Lemma 3.5(ii), we have
$j\gt n$
, by Lemma 3.5(ii), we have
![]() $ I_{{ \Lambda }_j}^{(2)}(X^{\prime},-)\cong M_{T^{\prime}}\amalg \mathcal{U}(U^{\prime},-)$
and
$ I_{{ \Lambda }_j}^{(2)}(X^{\prime},-)\cong M_{T^{\prime}}\amalg \mathcal{U}(U^{\prime},-)$
and
![]() $ I_{{ \Lambda }_j}^{(2)}(X,-)\cong M_{T}\amalg \,\,\mathcal{U}(U,-)$
. By the exact sequence (3.5), we get
$ I_{{ \Lambda }_j}^{(2)}(X,-)\cong M_{T}\amalg \,\,\mathcal{U}(U,-)$
. By the exact sequence (3.5), we get
![]() $ (F^{[j]})^{(2)}\cong F^{(2)}$
if
$ (F^{[j]})^{(2)}\cong F^{(2)}$
if
![]() $j\gt n$
.
$j\gt n$
.
(ii). If
![]() $F\in \mathcal{F}(\Delta )$
, we have that
$F\in \mathcal{F}(\Delta )$
, we have that
![]() $F^{[j]}/F^{[j-1]}$
is a sum of copies of elements in
$F^{[j]}/F^{[j-1]}$
is a sum of copies of elements in
![]() $_{\Lambda } \Delta (j)$
and hence by using item (i) we have that
$_{\Lambda } \Delta (j)$
and hence by using item (i) we have that
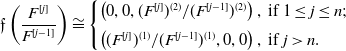 \begin{equation*} \mathfrak {f}\left(\frac {F^{[j]}}{F^{[j-1]}}\right)\cong \begin {cases} \left (0,0, (F^{[j]})^{(2)}/(F^{[j-1]})^{(2)}\right ), \text { if $1\le j\le n$};\\[3pt] \left ((F^{[j]})^{(1)}/(F^{[j-1]})^{(1)},0, 0\right ), \text { if $j\gt n$}. \end {cases} \end{equation*}
\begin{equation*} \mathfrak {f}\left(\frac {F^{[j]}}{F^{[j-1]}}\right)\cong \begin {cases} \left (0,0, (F^{[j]})^{(2)}/(F^{[j-1]})^{(2)}\right ), \text { if $1\le j\le n$};\\[3pt] \left ((F^{[j]})^{(1)}/(F^{[j-1]})^{(1)},0, 0\right ), \text { if $j\gt n$}. \end {cases} \end{equation*}
Then (ii) follows by Proposition 3.9.
(iii) Assume that
![]() $F=\mathfrak{f}\big (F^{(1)},g,F^{(2)}\big )\in \mathcal{F}_f(_\Lambda \Delta )$
. By (ii), it only remains to prove that if
$F=\mathfrak{f}\big (F^{(1)},g,F^{(2)}\big )\in \mathcal{F}_f(_\Lambda \Delta )$
. By (ii), it only remains to prove that if
![]() $F^{(1)}\in \mathcal{F}_f(_{\mathcal{T}}\Delta )$
and
$F^{(1)}\in \mathcal{F}_f(_{\mathcal{T}}\Delta )$
and
![]() $F^{(2)} \in \mathcal{F}_f(_{\mathcal{U}}\Delta )$
, then
$F^{(2)} \in \mathcal{F}_f(_{\mathcal{U}}\Delta )$
, then
![]() $F\in \mathcal{F}_f(_\Lambda \Delta )$
. In fact, the
$F\in \mathcal{F}_f(_\Lambda \Delta )$
. In fact, the
![]() $\Lambda$
-modules
$\Lambda$
-modules
![]() $\mathfrak{f}\big (F^{(1)},0,0\big )$
and
$\mathfrak{f}\big (F^{(1)},0,0\big )$
and
![]() $\mathfrak{f}\left(0,0,F^{(2)}\right)$
are in
$\mathfrak{f}\left(0,0,F^{(2)}\right)$
are in
![]() $\mathcal{F}_f(_{\Lambda }\Delta )$
by Proposition 3.9. It follows that we have a short exact sequence
$\mathcal{F}_f(_{\Lambda }\Delta )$
by Proposition 3.9. It follows that we have a short exact sequence
Thus,
![]() $ \mathfrak{f}\left(F^{(1)},g,F^{(2)}\right)$
is in
$ \mathfrak{f}\left(F^{(1)},g,F^{(2)}\right)$
is in
![]() $\mathcal{F}_f(_{\Lambda }\Delta )$
since
$\mathcal{F}_f(_{\Lambda }\Delta )$
since
![]() $\mathcal{F}_f(_{\Lambda }\Delta )$
is closed under extensions by Remark 2.11.
$\mathcal{F}_f(_{\Lambda }\Delta )$
is closed under extensions by Remark 2.11.
We end this section with an example.
Example 3.11. Consider the infinite quivers
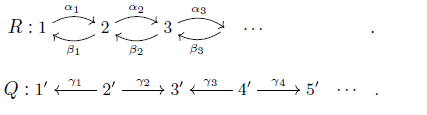
Let
![]() $\mathcal{U}=K\mathcal{Q}$
and
$\mathcal{U}=K\mathcal{Q}$
and
![]() $\mathcal{T}=K\mathcal{R}/\mathcal{J}$
be the path categories of the above quivers, where
$\mathcal{T}=K\mathcal{R}/\mathcal{J}$
be the path categories of the above quivers, where
![]() $\mathcal{J}$
is the ideal in
$\mathcal{J}$
is the ideal in
![]() $K\mathcal{R}$
generated by the set of relations
$K\mathcal{R}$
generated by the set of relations
First, we will see that
![]() $\mathcal{T}$
and
$\mathcal{T}$
and
![]() $\mathcal{U}$
are quasi-hereditary categories.
$\mathcal{U}$
are quasi-hereditary categories.
Set
![]() $\mathcal{T}_0=\{0\}$
, and let
$\mathcal{T}_0=\{0\}$
, and let
![]() $\mathcal{T}_j=\textrm{add} \{ t\,:\, 1\le t\le j\}$
, for
$\mathcal{T}_j=\textrm{add} \{ t\,:\, 1\le t\le j\}$
, for
![]() $j\ge 1$
. Therefore,
$j\ge 1$
. Therefore,
is a filtration of
![]() $\mathcal{T}$
into additively closed subcategories.
$\mathcal{T}$
into additively closed subcategories.
-
(i) It is clear that
 $\textrm{rad}_{\mathcal{T}}(1,1)=0$
because
$\textrm{rad}_{\mathcal{T}}(1,1)=0$
because
 $\beta _1\alpha _1=0$
. Since we have that
$\beta _1\alpha _1=0$
. Since we have that
 $\textrm{Ind} \mathcal{T}_j-\textrm{Ind} \mathcal{T}_{j-1}=\{j\}$
for all
$\textrm{Ind} \mathcal{T}_j-\textrm{Ind} \mathcal{T}_{j-1}=\{j\}$
for all
 $j\ge 1$
, we conclude the following:
$j\ge 1$
, we conclude the following:
 $\textrm{rad}_{\mathcal{T}}(j,j)=(\beta _j\alpha _j)= (\alpha _{j-1}\beta _{j-1})=I_{\mathcal{T}_{j-1}}(j,j)$
.
$\textrm{rad}_{\mathcal{T}}(j,j)=(\beta _j\alpha _j)= (\alpha _{j-1}\beta _{j-1})=I_{\mathcal{T}_{j-1}}(j,j)$
. -
(ii)
 $I_{\mathcal{T}_1}(1,-)\cong \mathcal{T}(1,-)$
,
$I_{\mathcal{T}_1}(1,-)\cong \mathcal{T}(1,-)$
,
 $I_{\mathcal{T}_1}(2,-)\cong \mathcal{T}(1,-)$
and
$I_{\mathcal{T}_1}(2,-)\cong \mathcal{T}(1,-)$
and
 $I_{\mathcal{T}_1}(j,-)=0$
, if
$I_{\mathcal{T}_1}(j,-)=0$
, if
 $j\ge 3$
.
$j\ge 3$
.
For
![]() $j\ge 2$
, we can readily check that there exists an exact sequence
$j\ge 2$
, we can readily check that there exists an exact sequence
and
![]() $I_{\mathcal{T}_j}(j+t,-)=0$
if
$I_{\mathcal{T}_j}(j+t,-)=0$
if
![]() $t\ge 2$
.
$t\ge 2$
.
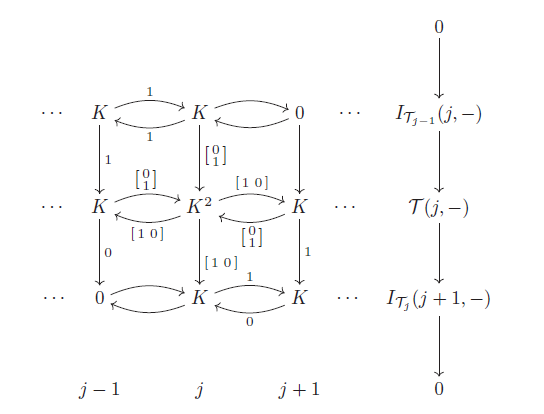
By Theorem
2.6
, we have that
![]() $\mathcal{T}$
is quasi-hereditary. Now, we define the following subcategories
$\mathcal{T}$
is quasi-hereditary. Now, we define the following subcategories
![]() $\mathcal{U}_0=\{0\}$
,
$\mathcal{U}_0=\{0\}$
,
![]() $\mathcal{U}_1=\textrm{add}\{ j^{\prime} \in \mathbb{N}\,:\, j\,\,\text{is odd }\}$
and consider
$\mathcal{U}_1=\textrm{add}\{ j^{\prime} \in \mathbb{N}\,:\, j\,\,\text{is odd }\}$
and consider
![]() $\mathcal{U}_2=\textrm{add}\{ j^{\prime}\,:\, j \in \mathbb{N}\}=K\mathcal{Q}$
. Thus,
$\mathcal{U}_2=\textrm{add}\{ j^{\prime}\,:\, j \in \mathbb{N}\}=K\mathcal{Q}$
. Thus,
![]() $K\mathcal{Q}$
is quasi-hereditary with respect to the finite filtration
$K\mathcal{Q}$
is quasi-hereditary with respect to the finite filtration
![]() $\{0\}=\mathcal{U}_0\subset \mathcal{U}_1\subset \mathcal{U}_2=K\mathcal{Q}$
. The condition (i) in Definition
2.6
, clearly holds since
$\{0\}=\mathcal{U}_0\subset \mathcal{U}_1\subset \mathcal{U}_2=K\mathcal{Q}$
. The condition (i) in Definition
2.6
, clearly holds since
![]() $\textrm{rad}_{\mathcal{U}}(E,E^{\prime})=I_{\mathcal{U}_{j-1}}(E,E^{\prime})=0$
for all pairs
$\textrm{rad}_{\mathcal{U}}(E,E^{\prime})=I_{\mathcal{U}_{j-1}}(E,E^{\prime})=0$
for all pairs
![]() $E,E^{\prime}\in \textrm{Ind}\ \mathcal{U}_j-\textrm{Ind}\ \mathcal{U}_{j-1}$
and
$E,E^{\prime}\in \textrm{Ind}\ \mathcal{U}_j-\textrm{Ind}\ \mathcal{U}_{j-1}$
and
![]() $j=1,2$
. On the other hand,
$j=1,2$
. On the other hand,
![]() $I_{\mathcal{U}_1}(j,-)=\mathcal{U}(j,-)$
if
$I_{\mathcal{U}_1}(j,-)=\mathcal{U}(j,-)$
if
![]() $j$
is odd and
$j$
is odd and
![]() $I_{\mathcal{U}_1}(j,-)\cong \mathcal{U}(j-1,-)\oplus \mathcal{U}(j+1,-)=\mathcal{U}((j-1)\oplus (j+1),-)$
if
$I_{\mathcal{U}_1}(j,-)\cong \mathcal{U}(j-1,-)\oplus \mathcal{U}(j+1,-)=\mathcal{U}((j-1)\oplus (j+1),-)$
if
![]() $j$
is even. Then in this case we have that condition (ii) in Theorem
2.6
also holds and hence
$j$
is even. Then in this case we have that condition (ii) in Theorem
2.6
also holds and hence
![]() $K\mathcal{Q}$
is quasi-hereditary.
$K\mathcal{Q}$
is quasi-hereditary.
Now, by a result of Z. Leszczyński given in [Reference León-Galeana, Ortíz-Morales and Santiago17
, Lemma 1.3], we have that
![]() $(K\mathcal{Q})\otimes _{K} (K\mathcal{R}/\mathcal{J})^{op}\simeq K(\mathcal{Q}\times \mathcal{R}^{op})/0\square \mathcal{J}$
where
$(K\mathcal{Q})\otimes _{K} (K\mathcal{R}/\mathcal{J})^{op}\simeq K(\mathcal{Q}\times \mathcal{R}^{op})/0\square \mathcal{J}$
where
![]() $K(\mathcal{Q}\times \mathcal{R}^{op})$
is the product quiver given in p. 145 in [Reference León-Galeana, Ortíz-Morales and Santiago17]; and
$K(\mathcal{Q}\times \mathcal{R}^{op})$
is the product quiver given in p. 145 in [Reference León-Galeana, Ortíz-Morales and Santiago17]; and
![]() $0\square \mathcal{J}$
is generated by the sets of relations
$0\square \mathcal{J}$
is generated by the sets of relations
![]() $Q_0\times \mathcal{J}$
and
$Q_0\times \mathcal{J}$
and
where
![]() $\gamma \in Q_1$
and
$\gamma \in Q_1$
and
![]() $\alpha, \beta \in R_1$
. A functor
$\alpha, \beta \in R_1$
. A functor
![]() $M\,:\, K\mathcal{Q}\otimes K(\mathcal{R}/\mathcal{J})^{op}\rightarrow \textrm{mod}\ K$
can be identified with a functor
$M\,:\, K\mathcal{Q}\otimes K(\mathcal{R}/\mathcal{J})^{op}\rightarrow \textrm{mod}\ K$
can be identified with a functor
![]() $M\,:\,K(\mathcal{Q}\times \mathcal{R}^{op})/0\square \mathcal{J}\rightarrow \textrm{mod}\ K$
. In this example, we consider
$M\,:\,K(\mathcal{Q}\times \mathcal{R}^{op})/0\square \mathcal{J}\rightarrow \textrm{mod}\ K$
. In this example, we consider
![]() $M$
as the following representation on the right below:
$M$
as the following representation on the right below:
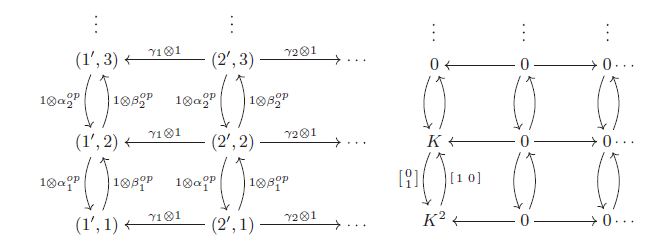
We see that
![]() $M(1^{\prime},1)=K^2$
,
$M(1^{\prime},1)=K^2$
,
![]() $M(1^{\prime},2)=K$
. Thus, the functor
$M(1^{\prime},2)=K$
. Thus, the functor
![]() $M$
satisfies that
$M$
satisfies that
![]() $M_T\,:\,K\mathcal{Q}\rightarrow \textrm{mod}\ K$
is projective for all
$M_T\,:\,K\mathcal{Q}\rightarrow \textrm{mod}\ K$
is projective for all
![]() $T$
since we have that
$T$
since we have that
![]() $M_{1}\cong \mathcal{U}(1,-)^2$
,
$M_{1}\cong \mathcal{U}(1,-)^2$
,
![]() $M_2\cong \mathcal{U}(1,-)$
, and
$M_2\cong \mathcal{U}(1,-)$
, and
![]() $M_t\cong 0$
, for all
$M_t\cong 0$
, for all
![]() $t\gt 2$
, which are all in
$t\gt 2$
, which are all in
![]() $\mathcal{F}(_{\mathcal{U}}\Delta )$
because
$\mathcal{F}(_{\mathcal{U}}\Delta )$
because
![]() $\mathcal{U}$
is quasi-hereditary.
$\mathcal{U}$
is quasi-hereditary.
In this way using results in [Reference León-Galeana, Ortíz-Morales and Santiago17], we can see that the matrix category
![]() $\left ( \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right )$
is equivalent to the path category of the quiver
$\left ( \begin{smallmatrix} \mathcal{T}&0\\ M&\mathcal{U} \end{smallmatrix} \right )$
is equivalent to the path category of the quiver
![]() $Q^{\prime\prime}$
given below, modulo the ideal generated by the set of relations (3.6) and is quasi-hereditary with respect to the filtration
$Q^{\prime\prime}$
given below, modulo the ideal generated by the set of relations (3.6) and is quasi-hereditary with respect to the filtration
where
![]() $\Lambda _1=\mathcal{U}_1$
,
$\Lambda _1=\mathcal{U}_1$
,
![]() $\Lambda _2=\mathcal{U}_2$
and
$\Lambda _2=\mathcal{U}_2$
and
![]() $\Lambda _{j+2}= \textrm{add}\left ( \{ j^{\prime}\,:\, j \in \mathbb{N}\}\cup \{ t\in \mathbb N\,:\, 1\le t\le j\} \right )$
and
$\Lambda _{j+2}= \textrm{add}\left ( \{ j^{\prime}\,:\, j \in \mathbb{N}\}\cup \{ t\in \mathbb N\,:\, 1\le t\le j\} \right )$
and
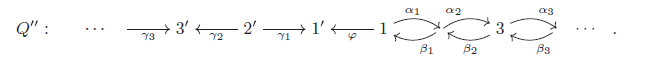
Acknowledgments
The authors thank for the referee’s valuable comments and suggestions, which improve the quality and readability of the paper.