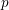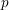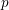Introduction
Consider a finite
![]() $p$
-group
$p$
-group
![]() $G$
acting on a smooth projective variety
$G$
acting on a smooth projective variety
![]() $X$
over an algebraically closed field. One of the first questions arising in this situation concerns the existence of fixed points, and finding effective methods to predict their existence is desirable. In this paper we exhibit invariants of the variety which may be used to detect fixed points. Each such invariant has the following key properties.
$X$
over an algebraically closed field. One of the first questions arising in this situation concerns the existence of fixed points, and finding effective methods to predict their existence is desirable. In this paper we exhibit invariants of the variety which may be used to detect fixed points. Each such invariant has the following key properties.
(a) It depends solely on the intrinsic geometry of the variety
 $X$
, and not on the particular group action.
$X$
, and not on the particular group action.(b) It takes values in
 $\mathbb{Z}$
and is accessible to computation.
$\mathbb{Z}$
and is accessible to computation.(c) If it is prime to
 $p$
, then the group
$p$
, then the group
 $G$
must fix a point of the variety
$G$
must fix a point of the variety
 $X$
.
$X$
.
It is instructive to start by looking at the case of finite sets, which are precisely zero-dimensional varieties (over a given algebraically closed field). They are classified by their cardinality, a numerical invariant which may be used to detect fixed points: a
![]() $p$
-group acting on a finite set of cardinality prime to
$p$
-group acting on a finite set of cardinality prime to
![]() $p$
must fix a point. A direct generalisation of the cardinality of a finite set to higher-dimensional (possibly singular and nonprojective) varieties is the so-called topological Euler characteristic, an integer
$p$
must fix a point. A direct generalisation of the cardinality of a finite set to higher-dimensional (possibly singular and nonprojective) varieties is the so-called topological Euler characteristic, an integer
![]() $\unicode[STIX]{x1D712}(X)$
defined as the alternating sum of the
$\unicode[STIX]{x1D712}(X)$
defined as the alternating sum of the
![]() $l$
-adic Betti numbers of
$l$
-adic Betti numbers of
![]() $X$
(with compact supports). Much like in the case of finite sets, this invariant satisfies the requirements (a)–(c), provided that the characteristic of the base field differs from
$X$
(with compact supports). Much like in the case of finite sets, this invariant satisfies the requirements (a)–(c), provided that the characteristic of the base field differs from
![]() $p$
.
$p$
.
In this paper, we restrict ourselves to the consideration of smooth projective varieties. This allows us to use intersection theory to produce more invariants satisfying (a)–(c), and also to include the case of base fields of characteristic
![]() $p$
. Perhaps the most natural way to construct a numerical invariant of a smooth projective variety using intersection theory is to take the degree of a product of Chern classes of its tangent bundle. Such invariants are called Chern numbers; they satisfy the requirements (a) and (b). Our first result asserts that they also detect fixed points in the sense of (c), under any of the following additional assumptions:
$p$
. Perhaps the most natural way to construct a numerical invariant of a smooth projective variety using intersection theory is to take the degree of a product of Chern classes of its tangent bundle. Such invariants are called Chern numbers; they satisfy the requirements (a) and (b). Our first result asserts that they also detect fixed points in the sense of (c), under any of the following additional assumptions:
(i)
 $G$
is abelian;
$G$
is abelian;(ii) the characteristic of the base field is
 $p$
;
$p$
;(iii)
 $\dim X<p$
.
$\dim X<p$
.
Another numerical invariant of a smooth projective variety
![]() $X$
is its arithmetic genus
$X$
is its arithmetic genus
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
. This is not quite a Chern number, but rather a
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
. This is not quite a Chern number, but rather a
![]() $\mathbb{Q}$
-linear combination of Chern numbers which happens to take integral values on any smooth projective variety (this assertion is a form of the Hirzebruch–Riemann–Roch theorem). The arithmetic genus
$\mathbb{Q}$
-linear combination of Chern numbers which happens to take integral values on any smooth projective variety (this assertion is a form of the Hirzebruch–Riemann–Roch theorem). The arithmetic genus
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
depends solely on the birational geometry of
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
depends solely on the birational geometry of
![]() $X$
. In fact it contains all the birational information obtainable using Chern numbers: any linear combination of Chern numbers which is a birational invariant must be a multiple of the arithmetic genus [Reference FultonFul98, Example 15.12.3(c)]. We prove that the invariant
$X$
. In fact it contains all the birational information obtainable using Chern numbers: any linear combination of Chern numbers which is a birational invariant must be a multiple of the arithmetic genus [Reference FultonFul98, Example 15.12.3(c)]. We prove that the invariant
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
detects fixed points (in the sense of (c) above), under any of the following additional assumptions:
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
detects fixed points (in the sense of (c) above), under any of the following additional assumptions:
- (i ′ )
 $G$
is cyclic;
$G$
is cyclic;- (ii ′ )
the characteristic of the base field is
 $p$
;
$p$
;- (iii ′ )
 $\dim X<p-1$
.
$\dim X<p-1$
.
Under any of the assumptions (i
′
), (ii
′
) and (iii
′
), we prove in fact that the cobordism class of the variety
![]() $X$
is divisible by
$X$
is divisible by
![]() $p$
in the Lazard ring as soon as the group
$p$
in the Lazard ring as soon as the group
![]() $G$
acts without fixed points on
$G$
acts without fixed points on
![]() $X$
. This essentially means that fixed points may be detected using any
$X$
. This essentially means that fixed points may be detected using any
![]() $\mathbb{Q}$
-linear combination of Chern numbers taking integral values on smooth projective varieties, and not just the arithmetic genus.
$\mathbb{Q}$
-linear combination of Chern numbers taking integral values on smooth projective varieties, and not just the arithmetic genus.
The results are stated in more details in § 1, where we also give an algebraic version of a theorem of Browder in topology [Reference BrowderBro87] concerning the pull-back of fixed points under maps of degree prime to
![]() $p$
. The rest of the paper is written using the language of algebraic groups. This allows us to prove more general statements (by including in particular infinitesimal groups in characteristic
$p$
. The rest of the paper is written using the language of algebraic groups. This allows us to prove more general statements (by including in particular infinitesimal groups in characteristic
![]() $p$
), but also makes some arguments more transparent. For instance the conditions (i) and (ii) appear as special cases of the condition that the
$p$
), but also makes some arguments more transparent. For instance the conditions (i) and (ii) appear as special cases of the condition that the
![]() $p$
-group
$p$
-group
![]() $G$
be trigonalisable.
$G$
be trigonalisable.
A notable tool introduced in § 3.4 is a cohomology theory that we denote by
![]() $K_{G}$
, which lies between the equivariant and usual
$K_{G}$
, which lies between the equivariant and usual
![]() $K_{0}$
-theory. It is built using a variant of Borel’s construction, where roughly speaking the space
$K_{0}$
-theory. It is built using a variant of Borel’s construction, where roughly speaking the space
![]() $EG$
is replaced by its generic point. The same construction may be applied to other cohomology theories (such as the Chow group), yielding a theory which keeps track of some of the equivariant information while being smaller than the Borel-type equivariant theory.
$EG$
is replaced by its generic point. The same construction may be applied to other cohomology theories (such as the Chow group), yielding a theory which keeps track of some of the equivariant information while being smaller than the Borel-type equivariant theory.
Even though these results are, in our view, principally of geometric nature, they also have an arithmetic component. Indeed our methods permit in some cases the detection of closed fixed points of degree prime to
![]() $p$
, when the base field is not algebraically closed. This is so for Chern numbers (assuming that the base field contains enough roots of unity in case (i)), or the arithmetic genus in case (iii
′
). Strikingly, this does not work for the arithmetic genus in case (i
′
), nor in case (ii
′
) over an imperfect base field (see Examples 5.1.6 and 5.1.7 for counterexamples). This suggests a difference of nature between these situations, and may provide a reason for the absence of a uniform proof for the cases (i
′
) and (iii
′
).
$p$
, when the base field is not algebraically closed. This is so for Chern numbers (assuming that the base field contains enough roots of unity in case (i)), or the arithmetic genus in case (iii
′
). Strikingly, this does not work for the arithmetic genus in case (i
′
), nor in case (ii
′
) over an imperfect base field (see Examples 5.1.6 and 5.1.7 for counterexamples). This suggests a difference of nature between these situations, and may provide a reason for the absence of a uniform proof for the cases (i
′
) and (iii
′
).
1 Statement of results
Here we summarise the main results of the paper. In order to make the statements as simple as possible, we assume in this section that
![]() $G$
is an ordinary finite
$G$
is an ordinary finite
![]() $p$
-group and that the base field
$p$
-group and that the base field
![]() $k$
is algebraically closed. A
$k$
is algebraically closed. A
![]() $G$
-action on a (
$G$
-action on a (
![]() $k$
-)variety
$k$
-)variety
![]() $X$
is a group morphism
$X$
is a group morphism
![]() $G\rightarrow \operatorname{Aut}_{k}(X)$
. A coherent
$G\rightarrow \operatorname{Aut}_{k}(X)$
. A coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is called
${\mathcal{F}}$
is called
![]() $G$
-equivariant if it is endowed with isomorphisms
$G$
-equivariant if it is endowed with isomorphisms
![]() $\unicode[STIX]{x1D70F}_{g}:g^{\ast }{\mathcal{F}}\rightarrow {\mathcal{F}}$
for
$\unicode[STIX]{x1D70F}_{g}:g^{\ast }{\mathcal{F}}\rightarrow {\mathcal{F}}$
for
![]() $g\in G$
, satisfying the cocycle condition
$g\in G$
, satisfying the cocycle condition
![]() $\unicode[STIX]{x1D70F}_{h}\circ h^{\ast }(\unicode[STIX]{x1D70F}_{g})=\unicode[STIX]{x1D70F}_{gh}$
for every
$\unicode[STIX]{x1D70F}_{h}\circ h^{\ast }(\unicode[STIX]{x1D70F}_{g})=\unicode[STIX]{x1D70F}_{gh}$
for every
![]() $g,h\in G$
.
$g,h\in G$
.
1.1 Equivariant cycles and Chern numbers
In the next statement
![]() $\operatorname{CH}_{G}$
denotes the equivariant Chow group of [Reference Edidin and GrahamEG98].
$\operatorname{CH}_{G}$
denotes the equivariant Chow group of [Reference Edidin and GrahamEG98].
Theorem 1.1.1. Let
![]() $X$
be a projective variety with an action of
$X$
be a projective variety with an action of
![]() $G$
. Assume that one of the following conditions holds:
$G$
. Assume that one of the following conditions holds:
(i)
 $G$
is abelian;
$G$
is abelian;(ii)
 $\operatorname{char}k=p$
;
$\operatorname{char}k=p$
;(iii)
 $\dim X<p-1$
.
$\dim X<p-1$
.
Then
![]() $X(k)^{G}=\varnothing$
if and only if every element of the image of the morphism
$X(k)^{G}=\varnothing$
if and only if every element of the image of the morphism
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
has degree divisible by
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
has degree divisible by
![]() $p$
.
$p$
.
Proof. The class of a fixed closed point belongs to
![]() $\operatorname{im}(\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X))$
and has degree one. The converse follows from Theorem 4.4 in cases (i) and (ii), since
$\operatorname{im}(\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X))$
and has degree one. The converse follows from Theorem 4.4 in cases (i) and (ii), since
![]() $G$
is trigonalisable (see § 2.1.5), and from Theorem 5.2.3(ii) in case (iii).◻
$G$
is trigonalisable (see § 2.1.5), and from Theorem 5.2.3(ii) in case (iii).◻
A Chern number of a smooth projective variety is the degree of a product of Chern classes (with values in the Chow group) of its tangent bundle.
Corollary 1.1.2. Let
![]() $X$
be a smooth projective variety with an action of
$X$
be a smooth projective variety with an action of
![]() $G$
. Assume that one of the following conditions holds:
$G$
. Assume that one of the following conditions holds:
(i)
 $G$
is abelian;
$G$
is abelian;(ii)
 $\operatorname{char}k=p$
;
$\operatorname{char}k=p$
;(iii)
 $\dim X<p$
.
$\dim X<p$
.
If
![]() $X(k)^{G}=\varnothing$
, then every Chern number of
$X(k)^{G}=\varnothing$
, then every Chern number of
![]() $X$
is divisible by
$X$
is divisible by
![]() $p$
.
$p$
.
Proof. By [Reference Edidin and GrahamEG98, §2.4] any
![]() $G$
-equivariant vector bundle over
$G$
-equivariant vector bundle over
![]() $X$
(i.e. a vector bundle whose
$X$
(i.e. a vector bundle whose
![]() ${\mathcal{O}}_{X}$
-module of sections is
${\mathcal{O}}_{X}$
-module of sections is
![]() $G$
-equivariant) admits Chern classes with values in
$G$
-equivariant) admits Chern classes with values in
![]() $\operatorname{CH}_{G}(X)$
mapping under the forgetful morphism
$\operatorname{CH}_{G}(X)$
mapping under the forgetful morphism
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
to its usual Chern classes. Since the tangent bundle of
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
to its usual Chern classes. Since the tangent bundle of
![]() $X$
is
$X$
is
![]() $G$
-equivariant (see Remark 2.4.8), the result follows from Theorem 1.1.1 in cases (i) and (ii) (or when
$G$
-equivariant (see Remark 2.4.8), the result follows from Theorem 1.1.1 in cases (i) and (ii) (or when
![]() $\dim X<p-1$
). In case (iii), the result may also be deduced from Theorem 1.1.1, albeit less directly, see Theorem 5.2.3(iii).◻
$\dim X<p-1$
). In case (iii), the result may also be deduced from Theorem 1.1.1, albeit less directly, see Theorem 5.2.3(iii).◻
Counterexamples show that the conditions of the theorem, and of the corollary in case
![]() $p\neq 2$
, are sharp, see Example 4.5 below. The dimensional bound (iii) in the corollary may however be improved when
$p\neq 2$
, are sharp, see Example 4.5 below. The dimensional bound (iii) in the corollary may however be improved when
![]() $p=2$
, see Remark 1.1.4.
$p=2$
, see Remark 1.1.4.
Remark 1.1.3. The following statement may be found in [Reference SerreSer09, §7.2]: assume that
![]() $\operatorname{char}k\neq p$
, and let
$\operatorname{char}k\neq p$
, and let
![]() $X$
be a variety with an action of
$X$
be a variety with an action of
![]() $G$
. If the topological Euler characteristic
$G$
. If the topological Euler characteristic
![]() $\unicode[STIX]{x1D712}(X)$
is prime to
$\unicode[STIX]{x1D712}(X)$
is prime to
![]() $p$
, then
$p$
, then
![]() $X(k)^{G}\neq \varnothing$
.
$X(k)^{G}\neq \varnothing$
.
The assumption on the characteristic of
![]() $k$
is necessary: the group
$k$
is necessary: the group
![]() $\mathbb{Z}/p$
acts without fixed points on
$\mathbb{Z}/p$
acts without fixed points on
![]() $\mathbb{A}^{1}$
by
$\mathbb{A}^{1}$
by
![]() $x\mapsto x+1$
in characteristic
$x\mapsto x+1$
in characteristic
![]() $p$
, and
$p$
, and
![]() $\unicode[STIX]{x1D712}(\mathbb{A}^{1})=1$
. Note that when
$\unicode[STIX]{x1D712}(\mathbb{A}^{1})=1$
. Note that when
![]() $X$
is smooth projective of pure dimension
$X$
is smooth projective of pure dimension
![]() $d$
, the integer
$d$
, the integer
![]() $\unicode[STIX]{x1D712}(X)=\deg c_{d}(T_{X})$
is a Chern number of
$\unicode[STIX]{x1D712}(X)=\deg c_{d}(T_{X})$
is a Chern number of
![]() $X$
. It thus follows from Corollary 1.1.2(ii) that the above statement is in fact valid in characteristic
$X$
. It thus follows from Corollary 1.1.2(ii) that the above statement is in fact valid in characteristic
![]() $p$
when
$p$
when
![]() $X$
is smooth and projective.
$X$
is smooth and projective.
Remark 1.1.4. Let us now comment on the situation in Corollary 1.1.2 when
![]() $p=2$
and
$p=2$
and
![]() $X$
has small pure dimension. We denote the Chern number
$X$
has small pure dimension. We denote the Chern number
![]() $\deg c_{i_{1}}(T_{X})\cdots c_{i_{n}}(T_{X})$
by
$\deg c_{i_{1}}(T_{X})\cdots c_{i_{n}}(T_{X})$
by
![]() $c_{i_{1}}\cdots c_{i_{n}}$
.
$c_{i_{1}}\cdots c_{i_{n}}$
.
—
![]() $\dim X=1$
: The only Chern number
$\dim X=1$
: The only Chern number
![]() $c_{1}=\unicode[STIX]{x1D712}(X)=2\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
is even. Thus Corollary 1.1.2 says nothing for curves when
$c_{1}=\unicode[STIX]{x1D712}(X)=2\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
is even. Thus Corollary 1.1.2 says nothing for curves when
![]() $p=2$
.
$p=2$
.
—
![]() $\dim X=2$
: The two Chern numbers
$\dim X=2$
: The two Chern numbers
![]() $c_{2}=\unicode[STIX]{x1D712}(X)$
and
$c_{2}=\unicode[STIX]{x1D712}(X)$
and
![]() $c_{1}^{2}$
have the same parity by Noether’s formula
$c_{1}^{2}$
have the same parity by Noether’s formula
![]() $\unicode[STIX]{x1D712}(X)+c_{1}^{2}=12\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
(see e.g. [Reference FultonFul98, Example 15.2]). Thus Corollary 1.1.2 reduces to the statement in Remark 1.1.3 for surfaces when
$\unicode[STIX]{x1D712}(X)+c_{1}^{2}=12\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
(see e.g. [Reference FultonFul98, Example 15.2]). Thus Corollary 1.1.2 reduces to the statement in Remark 1.1.3 for surfaces when
![]() $p=2$
.
$p=2$
.
—
![]() $\dim X=3$
: We have by the Hirzebruch–Riemann–Roch theorem (see e.g. [Reference FultonFul98, Example 15.2.5(a)])
$\dim X=3$
: We have by the Hirzebruch–Riemann–Roch theorem (see e.g. [Reference FultonFul98, Example 15.2.5(a)])
so that the two Chern numbers
![]() $c_{1}c_{2}$
and
$c_{1}c_{2}$
and
![]() $c_{1}^{3}$
are even. The other Chern number
$c_{1}^{3}$
are even. The other Chern number
![]() $c_{3}=\unicode[STIX]{x1D712}(X)$
is also even (for instance by Poincaré duality for
$c_{3}=\unicode[STIX]{x1D712}(X)$
is also even (for instance by Poincaré duality for
![]() $l$
-adic cohomology). Thus Corollary 1.1.2 says nothing for threefolds when
$l$
-adic cohomology). Thus Corollary 1.1.2 says nothing for threefolds when
![]() $p=2$
.
$p=2$
.
Summarising, we see that the condition (iii) of Corollary 1.1.2 may be weakened to the condition ‘
![]() $\dim X<4$
’ when
$\dim X<4$
’ when
![]() $p=2$
. This new dimensional bound is sharp, see Example 4.5.
$p=2$
. This new dimensional bound is sharp, see Example 4.5.
1.2 Equivariant modules and the cobordism ring
Theorem 1.2.1. Let
![]() $X$
be a projective variety with an action of
$X$
be a projective variety with an action of
![]() $G$
. Assume that one of the following conditions holds:
$G$
. Assume that one of the following conditions holds:
(i)
 $G$
is cyclic;
$G$
is cyclic;(ii)
 $\operatorname{char}k=p$
;
$\operatorname{char}k=p$
;(iii)
 $\dim X<p-1$
.
$\dim X<p-1$
.
Then
![]() $X(k)^{G}=\varnothing$
if and only if the Euler characteristic
$X(k)^{G}=\varnothing$
if and only if the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of every
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of every
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is divisible by
${\mathcal{F}}$
is divisible by
![]() $p$
.
$p$
.
Proof. If
![]() ${\mathcal{I}}$
is the ideal in
${\mathcal{I}}$
is the ideal in
![]() ${\mathcal{O}}_{X}$
of a fixed closed point, then the
${\mathcal{O}}_{X}$
of a fixed closed point, then the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{O}}_{X}/{\mathcal{I}}$
is
${\mathcal{O}}_{X}/{\mathcal{I}}$
is
![]() $G$
-equivariant and satisfies
$G$
-equivariant and satisfies
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}/{\mathcal{I}})=1$
. The converse is proved respectively in Theorems 5.1.1, 5.3.1 and 5.2.3(i).◻
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X}/{\mathcal{I}})=1$
. The converse is proved respectively in Theorems 5.1.1, 5.3.1 and 5.2.3(i).◻
The sharpness of the conditions of the theorem is illustrated by Example 5.1.5 below.
Let us declare two smooth projective varieties equivalent if their collections of Chern numbers (indexed by the monomials in the Chern classes) coincide. The disjoint union operation endows the set of equivalence classes with the structure of a cancellative abelian monoid. Its group completionFootnote
1
has a ring structure, where the product is induced by the cartesian product of varieties. This ring does not depend on the field
![]() $k$
, in fact Merkurjev proved that it coincides with the Lazard ring
$k$
, in fact Merkurjev proved that it coincides with the Lazard ring
![]() $\mathbb{L}$
, the coefficient ring of the universal commutative one-dimensional formal group law [Reference MerkurjevMer02, Theorem 8.2]. Thus to each smooth projective variety
$\mathbb{L}$
, the coefficient ring of the universal commutative one-dimensional formal group law [Reference MerkurjevMer02, Theorem 8.2]. Thus to each smooth projective variety
![]() $X$
corresponds a class
$X$
corresponds a class
![]() $[X]\in \mathbb{L}$
. When the characteristic of
$[X]\in \mathbb{L}$
. When the characteristic of
![]() $k$
is zero, the ring
$k$
is zero, the ring
![]() $\mathbb{L}$
may be identified with the coefficient ring
$\mathbb{L}$
may be identified with the coefficient ring
![]() $\unicode[STIX]{x1D6FA}(\operatorname{Spec}k)$
of the algebraic cobordism of Levine-Morel, and
$\unicode[STIX]{x1D6FA}(\operatorname{Spec}k)$
of the algebraic cobordism of Levine-Morel, and
![]() $[X]$
is the cobordism class of the morphism
$[X]$
is the cobordism class of the morphism
![]() $X\rightarrow \operatorname{Spec}k$
[Reference Levine and MorelLM07, Remark 4.3.4, Theorem 4.3.7].
$X\rightarrow \operatorname{Spec}k$
[Reference Levine and MorelLM07, Remark 4.3.4, Theorem 4.3.7].
Corollary 1.2.2. In the conditions of Theorem 1.2.1, assume additionally that
![]() $X$
is smooth. If
$X$
is smooth. If
![]() $X(k)^{G}=\varnothing$
, then
$X(k)^{G}=\varnothing$
, then
![]() $[X]\in p\mathbb{L}$
.
$[X]\in p\mathbb{L}$
.
Proof. The sheaf of sections of the tangent bundle
![]() $T_{X}$
is a
$T_{X}$
is a
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module (see Remark 2.4.8). The corollary thus follows from Theorem 1.2.1, in view of the Hattori–Stong theorem, see [Reference Esnault, Levine and WittenbergELW15, Lemma 5.4, Proposition 5.5]. In case (iii), this is also a consequence of Theorem 1.1.1: indeed one may see using [Reference AdamsAda74, II, Theorem 7.8, Lemma 7.9(iii)] that the class of a smooth projective variety of dimension
${\mathcal{O}}_{X}$
-module (see Remark 2.4.8). The corollary thus follows from Theorem 1.2.1, in view of the Hattori–Stong theorem, see [Reference Esnault, Levine and WittenbergELW15, Lemma 5.4, Proposition 5.5]. In case (iii), this is also a consequence of Theorem 1.1.1: indeed one may see using [Reference AdamsAda74, II, Theorem 7.8, Lemma 7.9(iii)] that the class of a smooth projective variety of dimension
![]() ${<}p-1$
is divisible by
${<}p-1$
is divisible by
![]() $p$
in
$p$
in
![]() $\mathbb{L}$
if and only if each of its Chern numbers is divisible by
$\mathbb{L}$
if and only if each of its Chern numbers is divisible by
![]() $p$
.◻
$p$
.◻
Remark 1.2.3 (Corollary 1.2.2 has a converse).
If the group
![]() $G$
is nontrivial, then
$G$
is nontrivial, then
![]() $p\mathbb{L}$
consists of classes of smooth projective varieties
$p\mathbb{L}$
consists of classes of smooth projective varieties
![]() $X$
admitting a
$X$
admitting a
![]() $G$
-action such that
$G$
-action such that
![]() $X(k)^{G}=\varnothing$
. Indeed, we may find a subgroup
$X(k)^{G}=\varnothing$
. Indeed, we may find a subgroup
![]() $H\subset G$
of index
$H\subset G$
of index
![]() $p$
. Then
$p$
. Then
![]() $G$
acts without fixed points on the set
$G$
acts without fixed points on the set
![]() $G/H$
, whose cardinality is
$G/H$
, whose cardinality is
![]() $p$
. Thus, given any smooth projective variety
$p$
. Thus, given any smooth projective variety
![]() $Y$
, we may make
$Y$
, we may make
![]() $G$
act without fixed point on
$G$
act without fixed point on
![]() $X=Y^{\sqcup p}$
by permuting the copies of
$X=Y^{\sqcup p}$
by permuting the copies of
![]() $Y$
.
$Y$
.
Remark 1.2.4. Fixed points were known to exist under the assumption that
![]() $X$
is connected and
$X$
is connected and
![]() $H^{i}(X,{\mathcal{O}}_{X})=0$
for
$H^{i}(X,{\mathcal{O}}_{X})=0$
for
![]() $i>0$
: in characteristic
$i>0$
: in characteristic
![]() $p$
this follows from Smith theory and the Artin–Schreier sequence [Reference SerreSer09, §7.4, Remark]; the cyclic case in characteristic
$p$
this follows from Smith theory and the Artin–Schreier sequence [Reference SerreSer09, §7.4, Remark]; the cyclic case in characteristic
![]() $\neq p$
follows from the Lefschetz fixed point formula [Reference Fulton and LangFL85, VI §9]. Let us also mention a fixed point theorem of Kollár for smooth projective separably rationally connected varieties [Reference StarrSta09, Corollary 3.36].
$\neq p$
follows from the Lefschetz fixed point formula [Reference Fulton and LangFL85, VI §9]. Let us also mention a fixed point theorem of Kollár for smooth projective separably rationally connected varieties [Reference StarrSta09, Corollary 3.36].
Since the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{O}}_{X}$
admits a natural
${\mathcal{O}}_{X}$
admits a natural
![]() $G$
-equivariant structure, Theorem 1.2.1 implies that a projective variety
$G$
-equivariant structure, Theorem 1.2.1 implies that a projective variety
![]() $X$
has a fixed point under the weaker assumption that the arithmetic genus
$X$
has a fixed point under the weaker assumption that the arithmetic genus
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
is prime to
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
is prime to
![]() $p$
. By contrast to the above-mentioned results, this applies to singular varieties, and also to some smooth projective varieties which are not ‘rational-like’, such as curves of genus two.
$p$
. By contrast to the above-mentioned results, this applies to singular varieties, and also to some smooth projective varieties which are not ‘rational-like’, such as curves of genus two.
1.3 Browder’s theorem
The next statement is an analog of a theorem of Browder in topology [Reference BrowderBro87].
Theorem 1.3.1. Let
![]() $f:Y\rightarrow X$
be a projective surjective
$f:Y\rightarrow X$
be a projective surjective
![]() $G$
-equivariant morphism, where
$G$
-equivariant morphism, where
![]() $X$
is smooth and connected, and
$X$
is smooth and connected, and
![]() $Y$
is integral. Assume that
$Y$
is integral. Assume that
![]() $[k(Y):k(X)]$
is finite and prime to
$[k(Y):k(X)]$
is finite and prime to
![]() $p$
, and that one of the following conditions holds:
$p$
, and that one of the following conditions holds:
(i)
 $G$
is abelian;
$G$
is abelian;(ii)
 $\operatorname{char}k=p$
;
$\operatorname{char}k=p$
;(iii)
 $\dim X<p$
.
$\dim X<p$
.
Then the induced morphism
![]() $f^{G}:Y^{G}\rightarrow X^{G}$
is surjective.
$f^{G}:Y^{G}\rightarrow X^{G}$
is surjective.
Proof. See Theorem 6.1 (and Remark 6.2(i) and § 2.1.5). Observe that the last condition implies that the fibers of
![]() $f$
all have dimension
$f$
all have dimension
![]() ${<}p-1$
, since
${<}p-1$
, since
![]() $f$
is a dominant morphism between integral varieties of the same dimension.◻
$f$
is a dominant morphism between integral varieties of the same dimension.◻
When
![]() $\operatorname{char}k\neq p$
, we prove in fact that the
$\operatorname{char}k\neq p$
, we prove in fact that the
![]() $\mathbb{Z}_{(p)}$
-module
$\mathbb{Z}_{(p)}$
-module
![]() $H(X^{G})$
is a direct summand of
$H(X^{G})$
is a direct summand of
![]() $H(Y^{G})$
, for any
$H(Y^{G})$
, for any
![]() $\mathbb{Z}_{(p)}$
-linear cohomology theory
$\mathbb{Z}_{(p)}$
-linear cohomology theory
![]() $H$
satisfying the projection formula, for instance
$H$
satisfying the projection formula, for instance
![]() $H=\operatorname{CH}(-)\,\otimes \,\mathbb{Z}_{(p)}$
(see Remark 6.2(iii)).
$H=\operatorname{CH}(-)\,\otimes \,\mathbb{Z}_{(p)}$
(see Remark 6.2(iii)).
Remark 1.3.2. A different method is used by Kollár and Szabó in [Reference Reichstein and YoussinRY00] to treat questions of similar nature. In particular, the fact that
![]() $X(k)^{G}\neq \varnothing$
implies that
$X(k)^{G}\neq \varnothing$
implies that
![]() $Y(k)^{G}\neq \varnothing$
under the condition Theorem 1.3.1(i) was already stated and proved in [Reference Reichstein and YoussinRY00, Proposition A4].
$Y(k)^{G}\neq \varnothing$
under the condition Theorem 1.3.1(i) was already stated and proved in [Reference Reichstein and YoussinRY00, Proposition A4].
2 Group actions on varieties
A variety will be a separated scheme of finite type over
![]() $k$
with the property that every finite family of points is contained in some affine open subscheme. In particular quasi-projective schemes over
$k$
with the property that every finite family of points is contained in some affine open subscheme. In particular quasi-projective schemes over
![]() $k$
will be considered varieties, and quotients of varieties by finite algebraic groups will remain varieties (see § 2.2.3). Products of varieties will be understood as cartesian products over
$k$
will be considered varieties, and quotients of varieties by finite algebraic groups will remain varieties (see § 2.2.3). Products of varieties will be understood as cartesian products over
![]() $k$
. Morphisms of varieties will be
$k$
. Morphisms of varieties will be
![]() $k$
-morphisms; unless otherwise stated a morphism will mean a morphism of varieties. If
$k$
-morphisms; unless otherwise stated a morphism will mean a morphism of varieties. If
![]() $X$
is a variety and
$X$
is a variety and
![]() $R$
a
$R$
a
![]() $k$
-algebra, the set of
$k$
-algebra, the set of
![]() $k$
-morphisms
$k$
-morphisms
![]() $\operatorname{Spec}R\rightarrow X$
will be denoted by
$\operatorname{Spec}R\rightarrow X$
will be denoted by
![]() $X(R)$
. The residue field at a point
$X(R)$
. The residue field at a point
![]() $x\in X$
will be denoted by
$x\in X$
will be denoted by
![]() $k(x)$
.
$k(x)$
.
2.1 Algebraic groups
We refer e.g. to [Reference Mumford, Fogarty and KirwanMFK94, ch. 0, §1] for the basic definitions concerning algebraic groups and their actions. An algebraic group will mean an affine group scheme of finite type over
![]() $k$
. When
$k$
. When
![]() $Y$
and
$Y$
and
![]() $X$
are two varieties with a
$X$
are two varieties with a
![]() $G$
-action, we always will endow the product
$G$
-action, we always will endow the product
![]() $X\times Y$
with the diagonal
$X\times Y$
with the diagonal
![]() $G$
-action.
$G$
-action.
2.1.1 The order of a group
The order of an algebraic group
![]() $G$
is the dimension of the
$G$
is the dimension of the
![]() $k$
-vector space
$k$
-vector space
![]() $H^{0}(G,{\mathcal{O}}_{G})$
. An algebraic group is called a
$H^{0}(G,{\mathcal{O}}_{G})$
. An algebraic group is called a
![]() $p$
-group if its order is (finite and) a power of the prime
$p$
-group if its order is (finite and) a power of the prime
![]() $p$
. When
$p$
. When
![]() $G$
is finite, the order of a subgroup
$G$
is finite, the order of a subgroup
![]() $H$
of
$H$
of
![]() $G$
divides the order of
$G$
divides the order of
![]() $G$
; this follows from the fact that the quotient morphism
$G$
; this follows from the fact that the quotient morphism
![]() $G\rightarrow G/H$
is flat and finite of degree equal to the order of
$G\rightarrow G/H$
is flat and finite of degree equal to the order of
![]() $H$
(see Proposition 2.3.2).
$H$
(see Proposition 2.3.2).
2.1.2 Constant finite groups
Let
![]() $\unicode[STIX]{x1D6E4}$
be an ordinary finite group. Then there exists an algebraic group
$\unicode[STIX]{x1D6E4}$
be an ordinary finite group. Then there exists an algebraic group
![]() $\unicode[STIX]{x1D6E4}_{k}$
such that
$\unicode[STIX]{x1D6E4}_{k}$
such that
![]() $\unicode[STIX]{x1D6E4}_{k}(R)=\unicode[STIX]{x1D6E4}$
for any connected commutative
$\unicode[STIX]{x1D6E4}_{k}(R)=\unicode[STIX]{x1D6E4}$
for any connected commutative
![]() $k$
-algebra
$k$
-algebra
![]() $R$
. The order of
$R$
. The order of
![]() $\unicode[STIX]{x1D6E4}_{k}$
coincides with the order of
$\unicode[STIX]{x1D6E4}_{k}$
coincides with the order of
![]() $\unicode[STIX]{x1D6E4}$
. If
$\unicode[STIX]{x1D6E4}$
. If
![]() $G$
is an algebraic group and
$G$
is an algebraic group and
![]() $\unicode[STIX]{x1D6E4}$
is a subgroup of
$\unicode[STIX]{x1D6E4}$
is a subgroup of
![]() $G(k)$
, then the constant group
$G(k)$
, then the constant group
![]() $\unicode[STIX]{x1D6E4}_{k}$
is a subgroup of
$\unicode[STIX]{x1D6E4}_{k}$
is a subgroup of
![]() $G$
.
$G$
.
2.1.3 Diagonalisable groups
(See [Reference Demazure and GrothendieckSGA31
, I, §4.4]) A diagonalisable group
![]() $G$
is entirely determined by its character group
$G$
is entirely determined by its character group
![]() $\widehat{G}$
, an ordinary abelian group. The order of
$\widehat{G}$
, an ordinary abelian group. The order of
![]() $G$
coincides with the order of
$G$
coincides with the order of
![]() $\widehat{G}$
.
$\widehat{G}$
.
When
![]() $n$
is a positive integer, the functor assigning to a commutative
$n$
is a positive integer, the functor assigning to a commutative
![]() $k$
-algebra
$k$
-algebra
![]() $R$
the multiplicative group consisting of those
$R$
the multiplicative group consisting of those
![]() $x\in R$
such that
$x\in R$
such that
![]() $x^{n}=1$
is represented by the diagonalisable group
$x^{n}=1$
is represented by the diagonalisable group
![]() $\unicode[STIX]{x1D707}_{n}$
satisfying
$\unicode[STIX]{x1D707}_{n}$
satisfying
![]() $\widehat{\unicode[STIX]{x1D707}_{n}}=\mathbb{Z}/n$
. When
$\widehat{\unicode[STIX]{x1D707}_{n}}=\mathbb{Z}/n$
. When
![]() $k$
contains a root of unity order
$k$
contains a root of unity order
![]() $n$
, the algebraic group
$n$
, the algebraic group
![]() $\unicode[STIX]{x1D707}_{n}$
is isomorphic to the constant group
$\unicode[STIX]{x1D707}_{n}$
is isomorphic to the constant group
![]() $(\mathbb{Z}/n)_{k}$
.
$(\mathbb{Z}/n)_{k}$
.
There is an anti-equivalence between the category of affine varieties with a
![]() $G$
-action and that of commutative
$G$
-action and that of commutative
![]() $\widehat{G}$
-graded
$\widehat{G}$
-graded
![]() $k$
-algebras of finite type [Reference Demazure and GrothendieckSGA31
, I, 4.7.3.1].
$k$
-algebras of finite type [Reference Demazure and GrothendieckSGA31
, I, 4.7.3.1].
2.1.4 Unipotent groups
An algebraic group
![]() $G$
is called unipotent if every nonzero
$G$
is called unipotent if every nonzero
![]() $G$
-representation over
$G$
-representation over
![]() $k$
admits a nonzero trivial subrepresentation. Constant finite
$k$
admits a nonzero trivial subrepresentation. Constant finite
![]() $p$
-groups over a field of characteristic
$p$
-groups over a field of characteristic
![]() $p$
are unipotent.
$p$
are unipotent.
When
![]() $k$
has positive characteristic
$k$
has positive characteristic
![]() $p$
, the functor assigning to a commutative
$p$
, the functor assigning to a commutative
![]() $k$
-algebra
$k$
-algebra
![]() $R$
the additive group consisting of those
$R$
the additive group consisting of those
![]() $x\in R$
such that
$x\in R$
such that
![]() $x^{p}=0$
is represented by a unipotent group
$x^{p}=0$
is represented by a unipotent group
![]() $\unicode[STIX]{x1D6FC}_{p}$
, whose order is
$\unicode[STIX]{x1D6FC}_{p}$
, whose order is
![]() $p$
.
$p$
.
2.1.5 Trigonalisable groups
An algebraic group
![]() $G$
is called trigonalisable if every nonzero
$G$
is called trigonalisable if every nonzero
![]() $G$
-representation over
$G$
-representation over
![]() $k$
admits a subrepresentation of codimension one. It is equivalent to require that
$k$
admits a subrepresentation of codimension one. It is equivalent to require that
![]() $G$
contain a normal unipotent subgroup
$G$
contain a normal unipotent subgroup
![]() $U$
such that
$U$
such that
![]() $G/U$
is diagonalisable [Reference Demazure and GabrielDG70, IV, §2, Proposition 3.4].
$G/U$
is diagonalisable [Reference Demazure and GabrielDG70, IV, §2, Proposition 3.4].
A finite constant group
![]() $G=\unicode[STIX]{x1D6E4}_{k}$
is trigonalisable in each of the following cases.
$G=\unicode[STIX]{x1D6E4}_{k}$
is trigonalisable in each of the following cases.
– The ordinary group
 $\unicode[STIX]{x1D6E4}$
is abelian, and
$\unicode[STIX]{x1D6E4}$
is abelian, and
 $k$
contains a root of unity of order equal to the exponent of
$k$
contains a root of unity of order equal to the exponent of
 $\unicode[STIX]{x1D6E4}$
(the group
$\unicode[STIX]{x1D6E4}$
(the group
 $G$
is diagonalisable, see [Reference HautionHau16, Lemma 3.6.1]).
$G$
is diagonalisable, see [Reference HautionHau16, Lemma 3.6.1]).– The field
 $k$
has characteristic
$k$
has characteristic
 $p>0$
, and
$p>0$
, and
 $G$
is a
$G$
is a
 $p$
-group (it is then unipotent).
$p$
-group (it is then unipotent).
2.2 Fixed locus and quotient
2.2.1 Invariant subschemes
Let
![]() $X$
be a variety with an action of an algebraic group
$X$
be a variety with an action of an algebraic group
![]() $G$
. A closed (respectively An open) subscheme
$G$
. A closed (respectively An open) subscheme
![]() $S$
of
$S$
of
![]() $X$
is called
$X$
is called
![]() $G$
-invariant if the composite morphism
$G$
-invariant if the composite morphism
![]() $G\times S\rightarrow G\times X\rightarrow X$
factors through
$G\times S\rightarrow G\times X\rightarrow X$
factors through
![]() $S\rightarrow X$
. Note that the scheme theoretic image of a
$S\rightarrow X$
. Note that the scheme theoretic image of a
![]() $G$
-equivariant morphism is a
$G$
-equivariant morphism is a
![]() $G$
-invariant closed subscheme.
$G$
-invariant closed subscheme.
2.2.2 Fixed locus
By [Reference Conrad, Gabber and PrasadCGP15, Proposition A.8.10(1)] there is a
![]() $G$
-invariant closed subscheme
$G$
-invariant closed subscheme
![]() $X^{G}$
of
$X^{G}$
of
![]() $X$
with trivial
$X$
with trivial
![]() $G$
-action, such that for any variety
$G$
-action, such that for any variety
![]() $T$
with trivial
$T$
with trivial
![]() $G$
-action, the set of
$G$
-action, the set of
![]() $G$
-equivariant morphisms
$G$
-equivariant morphisms
![]() $T\rightarrow X$
coincides with the set of morphisms
$T\rightarrow X$
coincides with the set of morphisms
![]() $T\rightarrow X^{G}$
(as subsets of
$T\rightarrow X^{G}$
(as subsets of
![]() $\operatorname{Hom}(T,X)$
). When
$\operatorname{Hom}(T,X)$
). When
![]() $G=\unicode[STIX]{x1D6E4}_{k}$
for an ordinary finite group
$G=\unicode[STIX]{x1D6E4}_{k}$
for an ordinary finite group
![]() $\unicode[STIX]{x1D6E4}$
, a
$\unicode[STIX]{x1D6E4}$
, a
![]() $G$
-action is precisely a group morphism
$G$
-action is precisely a group morphism
![]() $\unicode[STIX]{x1D6E4}\rightarrow \operatorname{Aut}_{k}(X)$
, and
$\unicode[STIX]{x1D6E4}\rightarrow \operatorname{Aut}_{k}(X)$
, and
![]() $X^{G}(k)=X(k)^{\unicode[STIX]{x1D6E4}}$
.
$X^{G}(k)=X(k)^{\unicode[STIX]{x1D6E4}}$
.
2.2.3 Quotient
When it exists, we denote by
![]() $X\rightarrow X/G$
the categorical quotient morphism, defined as the coequaliser of the two morphisms
$X\rightarrow X/G$
the categorical quotient morphism, defined as the coequaliser of the two morphisms
![]() $G\times X\rightarrow X$
(the action and the second projection). This morphism always exists in the category of varieties when
$G\times X\rightarrow X$
(the action and the second projection). This morphism always exists in the category of varieties when
![]() $G$
is a finite algebraic group (see [Reference Demazure and GrothendieckSGA31
, V, Théorème 4.1(i)]). A
$G$
is a finite algebraic group (see [Reference Demazure and GrothendieckSGA31
, V, Théorème 4.1(i)]). A
![]() $G$
-action on an affine scheme
$G$
-action on an affine scheme
![]() $X=\operatorname{Spec}A$
is given by a
$X=\operatorname{Spec}A$
is given by a
![]() $k$
-algebra morphism
$k$
-algebra morphism
![]() $\unicode[STIX]{x1D707}:A\rightarrow A\otimes _{k}R$
, where
$\unicode[STIX]{x1D707}:A\rightarrow A\otimes _{k}R$
, where
![]() $R=H^{0}(G,{\mathcal{O}}_{G})$
. The set
$R=H^{0}(G,{\mathcal{O}}_{G})$
. The set
is a
![]() $k$
-subalgebra of
$k$
-subalgebra of
![]() $A$
, and the morphism
$A$
, and the morphism
![]() $X\rightarrow X/G$
is given by the inclusion
$X\rightarrow X/G$
is given by the inclusion
![]() $A^{G}\rightarrow A$
.
$A^{G}\rightarrow A$
.
2.2.4
When
![]() $H$
is a finite normal subgroup of
$H$
is a finite normal subgroup of
![]() $G$
, the variety
$G$
, the variety
![]() $X/H$
inherits a
$X/H$
inherits a
![]() $G/H$
-action making the quotient morphism
$G/H$
-action making the quotient morphism
![]() $X\rightarrow X/H$
a
$X\rightarrow X/H$
a
![]() $G$
-equivariant morphism.
$G$
-equivariant morphism.
Lemma 2.2.5. Let
![]() $G$
be a finite algebraic group acting on a variety
$G$
be a finite algebraic group acting on a variety
![]() $X$
. Then the morphism
$X$
. Then the morphism
![]() $X^{G}\rightarrow X/G$
is radicial.
$X^{G}\rightarrow X/G$
is radicial.
Proof. We may assume that
![]() $X=\operatorname{Spec}A$
and that
$X=\operatorname{Spec}A$
and that
![]() $k$
is infinite. Let
$k$
is infinite. Let
![]() $R$
be the coordinate ring of
$R$
be the coordinate ring of
![]() $G$
. Denote by
$G$
. Denote by
![]() $m:R\rightarrow R\,\otimes \,R$
the co-multiplication morphism (tensor products are taken over
$m:R\rightarrow R\,\otimes \,R$
the co-multiplication morphism (tensor products are taken over
![]() $k$
) and by
$k$
) and by
![]() $\unicode[STIX]{x1D707}:A\rightarrow A\,\otimes \,R$
be the co-action morphism. Then we have
$\unicode[STIX]{x1D707}:A\rightarrow A\,\otimes \,R$
be the co-action morphism. Then we have
When
![]() $C$
is a
$C$
is a
![]() $k$
-algebra, we denote by
$k$
-algebra, we denote by
![]() $N_{C}:C\,\otimes \,R\rightarrow C$
the norm, which maps
$N_{C}:C\,\otimes \,R\rightarrow C$
the norm, which maps
![]() $x\in C\,\otimes \,R$
to the determinant of the
$x\in C\,\otimes \,R$
to the determinant of the
![]() $C$
-linear morphism
$C$
-linear morphism
![]() $\unicode[STIX]{x1D6FC}_{x}:C\,\otimes \,R\rightarrow C\,\otimes \,R$
given by multiplication with
$\unicode[STIX]{x1D6FC}_{x}:C\,\otimes \,R\rightarrow C\,\otimes \,R$
given by multiplication with
![]() $x$
. If
$x$
. If
![]() $h:C\rightarrow C^{\prime }$
is a
$h:C\rightarrow C^{\prime }$
is a
![]() $k$
-algebra morphism, then
$k$
-algebra morphism, then
The morphism
![]() $G\times G\rightarrow G\times G$
given by
$G\times G\rightarrow G\times G$
given by
![]() $(g,h)\mapsto (g,g^{-1}h)$
is an automorphism and is compatible with the first projection. Therefore the corresponding ring endomorphism
$(g,h)\mapsto (g,g^{-1}h)$
is an automorphism and is compatible with the first projection. Therefore the corresponding ring endomorphism
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $R\,\otimes \,R$
is an
$R\,\otimes \,R$
is an
![]() $R$
-algebra automorphism, for the algebra structure given by
$R$
-algebra automorphism, for the algebra structure given by
![]() $\operatorname{id}_{R}\,\otimes \,1:R\rightarrow R\,\otimes \,R$
. Thus for
$\operatorname{id}_{R}\,\otimes \,1:R\rightarrow R\,\otimes \,R$
. Thus for
![]() $x\in A\,\otimes \,R\,\otimes \,R$
, we have
$x\in A\,\otimes \,R\,\otimes \,R$
, we have
![]() $\unicode[STIX]{x1D6FC}_{(\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})(x)}=(\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})\circ \unicode[STIX]{x1D6FC}_{x}\circ (\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})^{-1}$
, and taking determinants we obtain
$\unicode[STIX]{x1D6FC}_{(\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})(x)}=(\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})\circ \unicode[STIX]{x1D6FC}_{x}\circ (\operatorname{id}_{A}\,\otimes \,\unicode[STIX]{x1D711})^{-1}$
, and taking determinants we obtain
In addition, the composite of the above automorphism
![]() $G\times G\rightarrow G\times G$
with the multiplication map of
$G\times G\rightarrow G\times G$
with the multiplication map of
![]() $G$
is the second projection, so that
$G$
is the second projection, so that
Since

the map
![]() $N_{A}\circ \unicode[STIX]{x1D707}:A\rightarrow A$
factors through a map
$N_{A}\circ \unicode[STIX]{x1D707}:A\rightarrow A$
factors through a map
![]() $N:A\rightarrow A^{G}$
(see (2.2a)).
$N:A\rightarrow A^{G}$
(see (2.2a)).
When
![]() $K$
is a field containing
$K$
is a field containing
![]() $k$
, any element of
$k$
, any element of
![]() $X^{G}(K)$
is given by a
$X^{G}(K)$
is given by a
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $\operatorname{Spec}K\rightarrow X$
for the trivial
$\operatorname{Spec}K\rightarrow X$
for the trivial
![]() $G$
-action on
$G$
-action on
![]() $K$
. Let
$K$
. Let
![]() $f:A\rightarrow K$
be the corresponding
$f:A\rightarrow K$
be the corresponding
![]() $k$
-algebra morphism. Then for any
$k$
-algebra morphism. Then for any
![]() $x\in A$
, by (2.2c) we have
$x\in A$
, by (2.2c) we have
where
![]() $n=\dim _{k}R$
is the order of
$n=\dim _{k}R$
is the order of
![]() $G$
.
$G$
.
Now let
![]() $f_{1},f_{2}:A\rightarrow K$
be the
$f_{1},f_{2}:A\rightarrow K$
be the
![]() $k$
-algebra morphisms corresponding to a pair of elements of
$k$
-algebra morphisms corresponding to a pair of elements of
![]() $X^{G}(K)$
mapping to the same element in
$X^{G}(K)$
mapping to the same element in
![]() $(X/G)(K)$
. Then the restriction of
$(X/G)(K)$
. Then the restriction of
![]() $f_{i}$
to
$f_{i}$
to
![]() $A^{G}$
does not depend on
$A^{G}$
does not depend on
![]() $i$
. It follows that the map
$i$
. It follows that the map
does not depend on
![]() $i$
. In view of (2.2f), we have in
$i$
. In view of (2.2f), we have in
![]() $K$
, for any
$K$
, for any
![]() $x\in A$
$x\in A$
Writing
![]() $n=p^{m}q$
, where
$n=p^{m}q$
, where
![]() $p$
is the characteristic exponent of
$p$
is the characteristic exponent of
![]() $k$
and
$k$
and
![]() $q$
is prime to
$q$
is prime to
![]() $p$
, we obtain in
$p$
, we obtain in
![]() $K$
, for any
$K$
, for any
![]() $x\in A$
,
$x\in A$
,
Now let
![]() $a\in A$
and
$a\in A$
and
![]() $\unicode[STIX]{x1D706}\in k$
. The above equality for
$\unicode[STIX]{x1D706}\in k$
. The above equality for
![]() $x=a+\unicode[STIX]{x1D706}$
yields
$x=a+\unicode[STIX]{x1D706}$
yields
so that any element of
![]() $k\subset K$
is a root of the polynomial
$k\subset K$
is a root of the polynomial
which must therefore vanish (as
![]() $k$
is infinite). Its coefficient at
$k$
is infinite). Its coefficient at
![]() $X^{q-1}$
is
$X^{q-1}$
is
Since
![]() $q$
is invertible in
$q$
is invertible in
![]() $k$
, we conclude that
$k$
, we conclude that
![]() $f_{1}=f_{2}$
.◻
$f_{1}=f_{2}$
.◻
2.3 Free actions
Definition 2.3.1. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
. The group
$X$
. The group
![]() $G$
acts freely on
$G$
acts freely on
![]() $X$
if the morphism
$X$
if the morphism
![]() $\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
given by
$\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
given by
![]() $(g,x)\mapsto (g\cdot x,x)$
is a monomorphism. It is equivalent to require that for every variety
$(g,x)\mapsto (g\cdot x,x)$
is a monomorphism. It is equivalent to require that for every variety
![]() $B$
and
$B$
and
![]() $x\in X(B)$
the set of those
$x\in X(B)$
the set of those
![]() $g\in G(B)$
such that
$g\in G(B)$
such that
![]() $g\cdot x=x$
be reduced to the unit element
$g\cdot x=x$
be reduced to the unit element
![]() $1\in G(B)$
.
$1\in G(B)$
.
Proposition 2.3.2. Let
![]() $G$
be a finite algebraic group acting freely on a variety
$G$
be a finite algebraic group acting freely on a variety
![]() $X$
. Then the quotient morphism
$X$
. Then the quotient morphism
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/G$
is flat and finite of degree equal to the order of
$\unicode[STIX]{x1D711}:X\rightarrow X/G$
is flat and finite of degree equal to the order of
![]() $G$
, and the following square is cartesian, where the unlabelled arrows denote respectively the second projection and the action morphism.
$G$
, and the following square is cartesian, where the unlabelled arrows denote respectively the second projection and the action morphism.

Proof. See [Reference MumfordMum08, §12, Theorem 1(B)], or [Reference Demazure and GrothendieckSGA31 , V, Théorème 4.1(iv)]. ◻
Lemma 2.3.3. Let
![]() $G$
be a finite algebraic group acting freely on a variety
$G$
be a finite algebraic group acting freely on a variety
![]() $X$
. Let
$X$
. Let
![]() $X^{\prime }\rightarrow X$
be a
$X^{\prime }\rightarrow X$
be a
![]() $G$
-equivariant morphism. Then
$G$
-equivariant morphism. Then
![]() $G$
acts freely on
$G$
acts freely on
![]() $X^{\prime }$
, and the following square is cartesian.
$X^{\prime }$
, and the following square is cartesian.

Proof. The first statement follows from the definition of a free action in terms of functors of points. To prove that the square is cartesian, by descent and Proposition 2.3.2 we may assume that
![]() $X=G\times S$
, where
$X=G\times S$
, where
![]() $G$
acts trivially on
$G$
acts trivially on
![]() $S$
. Let
$S$
. Let
![]() $S^{\prime }=X^{\prime }/G$
. We need to prove that the
$S^{\prime }=X^{\prime }/G$
. We need to prove that the
![]() $G$
-equivariant
$G$
-equivariant
![]() $S^{\prime }$
-morphism
$S^{\prime }$
-morphism
![]() $X^{\prime }\rightarrow G\times S^{\prime }$
is an isomorphism. To do so, by descent and Proposition 2.3.2 we may assume that
$X^{\prime }\rightarrow G\times S^{\prime }$
is an isomorphism. To do so, by descent and Proposition 2.3.2 we may assume that
![]() $X^{\prime }=G\times S^{\prime }$
. But any equivariant
$X^{\prime }=G\times S^{\prime }$
. But any equivariant
![]() $S^{\prime }$
-endomorphism of an
$S^{\prime }$
-endomorphism of an
![]() $S^{\prime }$
-group scheme coincides with multiplication by the image of the unit, hence must be an isomorphism.◻
$S^{\prime }$
-group scheme coincides with multiplication by the image of the unit, hence must be an isomorphism.◻
Lemma 2.3.4. Let
![]() $G$
be an algebraic group of prime order acting on a variety
$G$
be an algebraic group of prime order acting on a variety
![]() $X$
. If
$X$
. If
![]() $X^{G}=\varnothing$
, then the action is free.
$X^{G}=\varnothing$
, then the action is free.
Proof. For a
![]() $k$
-scheme
$k$
-scheme
![]() $F$
and
$F$
and
![]() $x,y\in X(F)$
, we denote by
$x,y\in X(F)$
, we denote by
![]() $S_{x,y}$
the fiber of the morphism
$S_{x,y}$
the fiber of the morphism
![]() $\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
over
$\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
over
![]() $(x,y):F\rightarrow X\times X$
. Let us write
$(x,y):F\rightarrow X\times X$
. Let us write
![]() $G_{F}=G\times F$
and
$G_{F}=G\times F$
and
![]() $X_{F}=X\times F$
. For any
$X_{F}=X\times F$
. For any
![]() $k$
-scheme
$k$
-scheme
![]() $E$
, the set
$E$
, the set
![]() $S_{x,y}(E)$
may be identified with the subset of
$S_{x,y}(E)$
may be identified with the subset of
![]() $G_{F}(E)$
consisting of those
$G_{F}(E)$
consisting of those
![]() $g$
such that
$g$
such that
![]() $g\cdot y=x\in X(E)$
. In particular
$g\cdot y=x\in X(E)$
. In particular
![]() $S_{x,x}$
is a subgroup of the
$S_{x,x}$
is a subgroup of the
![]() $F$
-group scheme
$F$
-group scheme
![]() $G_{F}$
(the stabiliser of
$G_{F}$
(the stabiliser of
![]() $x$
), and the
$x$
), and the
![]() $F$
-scheme
$F$
-scheme
![]() $S_{x,y}$
is isomorphic to
$S_{x,y}$
is isomorphic to
![]() $S_{x,x}$
as soon as
$S_{x,x}$
as soon as
![]() $S_{x,y}(F)\neq \varnothing$
.
$S_{x,y}(F)\neq \varnothing$
.
We now prove the statement. The morphism
![]() $\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
being proper, by [Reference GrothendieckEGAIV3
, (8.11.5)] it will suffice to prove that
$\unicode[STIX]{x1D6FE}:G\times X\rightarrow X\times X$
being proper, by [Reference GrothendieckEGAIV3
, (8.11.5)] it will suffice to prove that
![]() $S_{x,y}\rightarrow F$
is either empty or an isomorphism, when
$S_{x,y}\rightarrow F$
is either empty or an isomorphism, when
![]() $F=\operatorname{Spec}K$
for an algebraically closed field
$F=\operatorname{Spec}K$
for an algebraically closed field
![]() $K$
containing
$K$
containing
![]() $k$
, and
$k$
, and
![]() $x,y\in X(F)$
. Assume that
$x,y\in X(F)$
. Assume that
![]() $S_{x,y}$
is nonempty. Then the finite type
$S_{x,y}$
is nonempty. Then the finite type
![]() $K$
-scheme
$K$
-scheme
![]() $S_{x,y}$
possesses a rational point. It follows from the discussion above that the
$S_{x,y}$
possesses a rational point. It follows from the discussion above that the
![]() $F$
-scheme
$F$
-scheme
![]() $S_{x,y}$
is isomorphic to the subgroup
$S_{x,y}$
is isomorphic to the subgroup
![]() $S_{x,x}$
of
$S_{x,x}$
of
![]() $G_{F}$
. But the
$G_{F}$
. But the
![]() $K$
-group scheme
$K$
-group scheme
![]() $G_{F}$
has exactly two subgroups (the order of a subgroup must divide its order). If
$G_{F}$
has exactly two subgroups (the order of a subgroup must divide its order). If
![]() $S_{x,x}=G_{F}$
, then the morphism
$S_{x,x}=G_{F}$
, then the morphism
![]() $x:F\rightarrow X$
is
$x:F\rightarrow X$
is
![]() $G$
-equivariant for the trivial action on
$G$
-equivariant for the trivial action on
![]() $F$
, hence factors through
$F$
, hence factors through
![]() $X^{G}$
; this would contradict the assumption that
$X^{G}$
; this would contradict the assumption that
![]() $X^{G}=\varnothing$
. Thus the
$X^{G}=\varnothing$
. Thus the
![]() $K$
-group scheme
$K$
-group scheme
![]() $S_{x,x}$
is trivial, and
$S_{x,x}$
is trivial, and
![]() $S_{x,y}\rightarrow F$
is an isomorphism.◻
$S_{x,y}\rightarrow F$
is an isomorphism.◻
2.4 Equivariant modules
Definition 2.4.1. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
, and
$X$
, and
![]() ${\mathcal{F}}$
a quasi-coherent
${\mathcal{F}}$
a quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module. A
${\mathcal{O}}_{X}$
-module. A
![]() $G$
-equivariant structure on
$G$
-equivariant structure on
![]() ${\mathcal{F}}$
is an isomorphism
${\mathcal{F}}$
is an isomorphism
![]() $\unicode[STIX]{x1D707}:a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
, where
$\unicode[STIX]{x1D707}:a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
, where
![]() $a,p:G\times X\rightarrow X$
are respectively the action morphism and the second projection, making the following diagram commute
$a,p:G\times X\rightarrow X$
are respectively the action morphism and the second projection, making the following diagram commute

where
![]() $q:G\,\times \,G\,\times \,X\rightarrow G\,\times \,X$
is the projection on the last two factors, and
$q:G\,\times \,G\,\times \,X\rightarrow G\,\times \,X$
is the projection on the last two factors, and
![]() $m:G\,\times \,G\,\times \,X\rightarrow G\times X$
is the base-change of the multiplication map of
$m:G\,\times \,G\,\times \,X\rightarrow G\times X$
is the base-change of the multiplication map of
![]() $G$
. We will often omit to mention the isomorphism
$G$
. We will often omit to mention the isomorphism
![]() $\unicode[STIX]{x1D707}$
, and simply say that
$\unicode[STIX]{x1D707}$
, and simply say that
![]() ${\mathcal{F}}$
is a
${\mathcal{F}}$
is a
![]() $G$
-equivariant quasi-coherent
$G$
-equivariant quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module. This is the same definition as [Reference Demazure and GrothendieckSGA31
, I, §6.5], where the cocycle condition is instead expressed in terms of the inverse
${\mathcal{O}}_{X}$
-module. This is the same definition as [Reference Demazure and GrothendieckSGA31
, I, §6.5], where the cocycle condition is instead expressed in terms of the inverse
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
![]() $\unicode[STIX]{x1D707}$
. We will say that a vector bundle is
$\unicode[STIX]{x1D707}$
. We will say that a vector bundle is
![]() $G$
-equivariant when its sheaf of sections is a
$G$
-equivariant when its sheaf of sections is a
![]() $G$
-equivariant module.
$G$
-equivariant module.
Let
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{G}}$
be two
${\mathcal{G}}$
be two
![]() $G$
-equivariant quasi-coherent
$G$
-equivariant quasi-coherent
![]() ${\mathcal{O}}_{X}$
-modules. A morphism
${\mathcal{O}}_{X}$
-modules. A morphism
![]() $\unicode[STIX]{x1D719}:{\mathcal{F}}\rightarrow {\mathcal{G}}$
of
$\unicode[STIX]{x1D719}:{\mathcal{F}}\rightarrow {\mathcal{G}}$
of
![]() ${\mathcal{O}}_{X}$
-modules will be called
${\mathcal{O}}_{X}$
-modules will be called
![]() $G$
-equivariant if the following diagram commutes.
$G$
-equivariant if the following diagram commutes.

This defines a category
![]() ${\mathcal{M}}(X;G)$
. The category
${\mathcal{M}}(X;G)$
. The category
![]() ${\mathcal{M}}(\operatorname{Spec}k;G)$
(for the trivial
${\mathcal{M}}(\operatorname{Spec}k;G)$
(for the trivial
![]() $G$
-action on
$G$
-action on
![]() $\operatorname{Spec}k$
) is the category of
$\operatorname{Spec}k$
) is the category of
![]() $G$
-representations over
$G$
-representations over
![]() $k$
. A
$k$
. A
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $f:Y\rightarrow X$
induces functors
$f:Y\rightarrow X$
induces functors
![]() $f^{\ast }:{\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(Y;G)$
(see [Reference Demazure and GrothendieckSGA31
, I, Lemme 6.3.1]) and
$f^{\ast }:{\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(Y;G)$
(see [Reference Demazure and GrothendieckSGA31
, I, Lemme 6.3.1]) and
![]() $\operatorname{R}^{i}f_{\ast }:{\mathcal{M}}(Y;G)\rightarrow {\mathcal{M}}(X;G)$
for every
$\operatorname{R}^{i}f_{\ast }:{\mathcal{M}}(Y;G)\rightarrow {\mathcal{M}}(X;G)$
for every
![]() $i$
(the proof of [Reference Demazure and GrothendieckSGA31
, I, Lemme 6.6.1] also works for higher direct images).
$i$
(the proof of [Reference Demazure and GrothendieckSGA31
, I, Lemme 6.6.1] also works for higher direct images).
2.4.2
A morphism of algebraic groups
![]() $H\rightarrow G$
induces a functor
$H\rightarrow G$
induces a functor
![]() ${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;H)$
. The category
${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;H)$
. The category
![]() ${\mathcal{M}}(X;1)$
coincides with the category of quasi-coherent
${\mathcal{M}}(X;1)$
coincides with the category of quasi-coherent
![]() ${\mathcal{O}}_{X}$
-modules.
${\mathcal{O}}_{X}$
-modules.
2.4.3
If
![]() ${\mathcal{F}}$
is a quasi-coherent
${\mathcal{F}}$
is a quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module, any
${\mathcal{O}}_{X}$
-module, any
![]() $G$
-equivariant structure
$G$
-equivariant structure
![]() $a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
is a
$a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
is a
![]() $G$
-equivariant morphism. Thus we may define a morphism
$G$
-equivariant morphism. Thus we may define a morphism
![]() $a^{\ast }\rightarrow p^{\ast }$
of functors
$a^{\ast }\rightarrow p^{\ast }$
of functors
![]() ${\mathcal{M}}(G\times X;G)\rightarrow {\mathcal{M}}(G\times X;G)$
.
${\mathcal{M}}(G\times X;G)\rightarrow {\mathcal{M}}(G\times X;G)$
.
2.4.4
If a diagonalisable group
![]() $G$
acts trivially on a variety
$G$
acts trivially on a variety
![]() $X$
, and
$X$
, and
![]() ${\mathcal{F}}$
is a quasi-coherent
${\mathcal{F}}$
is a quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module, a
${\mathcal{O}}_{X}$
-module, a
![]() $G$
-equivariant structure on
$G$
-equivariant structure on
![]() ${\mathcal{F}}$
is the same thing as a
${\mathcal{F}}$
is the same thing as a
![]() $\widehat{G}$
-grading on the
$\widehat{G}$
-grading on the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
, i.e. a direct sum decomposition
${\mathcal{F}}$
, i.e. a direct sum decomposition
![]() ${\mathcal{F}}=\bigoplus _{g\in \widehat{G}}{\mathcal{F}}_{g}$
(see [Reference Demazure and GrothendieckSGA31
, I, 4.7.3]).
${\mathcal{F}}=\bigoplus _{g\in \widehat{G}}{\mathcal{F}}_{g}$
(see [Reference Demazure and GrothendieckSGA31
, I, 4.7.3]).
Lemma 2.4.5. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
, and
$X$
, and
![]() $D$
a central diagonalisable subgroup of
$D$
a central diagonalisable subgroup of
![]() $G$
acting trivially on
$G$
acting trivially on
![]() $X$
. Let
$X$
. Let
![]() ${\mathcal{F}}$
be a
${\mathcal{F}}$
be a
![]() $G$
-equivariant quasi-coherent
$G$
-equivariant quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module. Then the
${\mathcal{O}}_{X}$
-module. Then the
![]() $\widehat{D}$
-grading of the
$\widehat{D}$
-grading of the
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
lifts to the category
${\mathcal{F}}$
lifts to the category
![]() ${\mathcal{M}}(X;G)$
.
${\mathcal{M}}(X;G)$
.
Proof. We denote by
![]() $a,p:G\times X\rightarrow X$
the action and projection morphisms, and by
$a,p:G\times X\rightarrow X$
the action and projection morphisms, and by
![]() $d:D\times X\rightarrow X$
their common restriction. Let
$d:D\times X\rightarrow X$
their common restriction. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70B}:G\times D\times X\rightarrow D\times X$
the base-changes of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70B}:G\times D\times X\rightarrow D\times X$
the base-changes of
![]() $a,p$
, and
$a,p$
, and
![]() $\unicode[STIX]{x1D6FF}:G\times D\times X\rightarrow G\times X$
the base-change of
$\unicode[STIX]{x1D6FF}:G\times D\times X\rightarrow G\times X$
the base-change of
![]() $d$
. Let
$d$
. Let
![]() $m:G\times D\times X\rightarrow G\times X$
be the multiplication morphism. Let
$m:G\times D\times X\rightarrow G\times X$
be the multiplication morphism. Let
![]() $s:G\times D\times X\rightarrow D\times G\times X$
the exchange morphism, and write
$s:G\times D\times X\rightarrow D\times G\times X$
the exchange morphism, and write
![]() $\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FC}\circ s^{-1}$
and
$\unicode[STIX]{x1D6FC}^{\prime }=\unicode[STIX]{x1D6FC}\circ s^{-1}$
and
![]() $\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}\circ s^{-1}$
. Since
$\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}\circ s^{-1}$
. Since
![]() $D$
is central, the multiplication morphism
$D$
is central, the multiplication morphism
![]() $m^{\prime }:D\times G\times X\rightarrow G\times X$
coincides with
$m^{\prime }:D\times G\times X\rightarrow G\times X$
coincides with
![]() $m\circ s^{-1}$
.
$m\circ s^{-1}$
.
Denote by
![]() $\unicode[STIX]{x1D707}:a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
the
$\unicode[STIX]{x1D707}:a^{\ast }{\mathcal{F}}\rightarrow p^{\ast }{\mathcal{F}}$
the
![]() $G$
-equivariant structure, and by
$G$
-equivariant structure, and by
![]() $\unicode[STIX]{x1D70F}:d^{\ast }{\mathcal{F}}\rightarrow d^{\ast }{\mathcal{F}}$
the induced
$\unicode[STIX]{x1D70F}:d^{\ast }{\mathcal{F}}\rightarrow d^{\ast }{\mathcal{F}}$
the induced
![]() $D$
-equivariant structure. Using the commutativity of (2.4a) twice, we see that the following diagram commutes.
$D$
-equivariant structure. Using the commutativity of (2.4a) twice, we see that the following diagram commutes.

We let
![]() $D$
act on
$D$
act on
![]() $G\times X$
via the trivial action on
$G\times X$
via the trivial action on
![]() $G$
. Then the morphisms
$G$
. Then the morphisms
![]() $a,p:G\times X\rightarrow X$
are
$a,p:G\times X\rightarrow X$
are
![]() $D$
-equivariant (since
$D$
-equivariant (since
![]() $D$
is central). The commutativity of the exterior rectangle asserts that the morphism
$D$
is central). The commutativity of the exterior rectangle asserts that the morphism
![]() $\unicode[STIX]{x1D707}$
is
$\unicode[STIX]{x1D707}$
is
![]() $D$
-equivariant, and the lemma follows.◻
$D$
-equivariant, and the lemma follows.◻
Definition 2.4.6. Let
![]() $X$
be a variety with an action of
$X$
be a variety with an action of
![]() $G$
, and
$G$
, and
![]() $H$
a normal subgroup of
$H$
a normal subgroup of
![]() $G$
acting trivially on
$G$
acting trivially on
![]() $X$
. We let
$X$
. We let
![]() $G$
act on
$G$
act on
![]() $H$
by
$H$
by
![]() $(g,h)\mapsto ghg^{-1}$
. The second projection
$(g,h)\mapsto ghg^{-1}$
. The second projection
![]() $\unicode[STIX]{x1D70B}:H\times X\rightarrow X$
is
$\unicode[STIX]{x1D70B}:H\times X\rightarrow X$
is
![]() $G$
-equivariant, and coincides with the action morphism
$G$
-equivariant, and coincides with the action morphism
![]() $\unicode[STIX]{x1D6FC}:H\times X\rightarrow X$
. The category
$\unicode[STIX]{x1D6FC}:H\times X\rightarrow X$
. The category
![]() ${\mathcal{M}}(X;G/H)$
may be identified with the full subcategory of
${\mathcal{M}}(X;G/H)$
may be identified with the full subcategory of
![]() ${\mathcal{M}}(X;G)$
consisting of those objects
${\mathcal{M}}(X;G)$
consisting of those objects
![]() ${\mathcal{F}}$
on which
${\mathcal{F}}$
on which
![]() $H$
acts trivially, i.e. such that
$H$
acts trivially, i.e. such that
![]() $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}=\unicode[STIX]{x1D6FC}^{\ast }{\mathcal{F}}\rightarrow \unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}$
is the identity. Consider the two morphisms
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}=\unicode[STIX]{x1D6FC}^{\ast }{\mathcal{F}}\rightarrow \unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}$
is the identity. Consider the two morphisms
![]() $\operatorname{id}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }$
of functors
$\operatorname{id}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }$
of functors
![]() ${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;G)$
, respectively adjoint to the morphism
${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;G)$
, respectively adjoint to the morphism
![]() $\unicode[STIX]{x1D70B}^{\ast }=\unicode[STIX]{x1D6FC}^{\ast }\rightarrow \unicode[STIX]{x1D70B}^{\ast }$
(see § 2.4.3) and the identity of
$\unicode[STIX]{x1D70B}^{\ast }=\unicode[STIX]{x1D6FC}^{\ast }\rightarrow \unicode[STIX]{x1D70B}^{\ast }$
(see § 2.4.3) and the identity of
![]() $\unicode[STIX]{x1D70B}^{\ast }$
. Their equaliser defines a morphism
$\unicode[STIX]{x1D70B}^{\ast }$
. Their equaliser defines a morphism
2.4.7
In the conditions of Definition 2.4.6, let
![]() ${\mathcal{F}}\in {\mathcal{M}}(X;G)$
and let
${\mathcal{F}}\in {\mathcal{M}}(X;G)$
and let
![]() $U$
be an open subscheme of
$U$
be an open subscheme of
![]() $X$
. Since taking the sections over
$X$
. Since taking the sections over
![]() $U$
is a left exact functor
$U$
is a left exact functor
![]() ${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(\operatorname{Spec}k;G)$
, it follows that
${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(\operatorname{Spec}k;G)$
, it follows that
![]() ${\mathcal{F}}^{H}(U)={\mathcal{F}}(U)^{H}$
.
${\mathcal{F}}^{H}(U)={\mathcal{F}}(U)^{H}$
.
2.4.8
The ideal of a
![]() $G$
-invariant closed subscheme is naturally
$G$
-invariant closed subscheme is naturally
![]() $G$
-equivariant. Using this observation for the diagonal immersion
$G$
-equivariant. Using this observation for the diagonal immersion
![]() $X\rightarrow X\times X$
and pulling back to
$X\rightarrow X\times X$
and pulling back to
![]() $X$
, we deduce that the cotangent module of
$X$
, we deduce that the cotangent module of
![]() $X$
is
$X$
is
![]() $G$
-equivariant. Thus if
$G$
-equivariant. Thus if
![]() $X$
is smooth, its tangent bundle is
$X$
is smooth, its tangent bundle is
![]() $G$
-equivariant.
$G$
-equivariant.
Proposition 2.4.9. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
. Let
$X$
. Let
![]() $H$
be a finite normal subgroup of
$H$
be a finite normal subgroup of
![]() $G$
acting freely on
$G$
acting freely on
![]() $X$
, and denote by
$X$
, and denote by
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/H$
the quotient morphism. Then the composite
$\unicode[STIX]{x1D711}:X\rightarrow X/H$
the quotient morphism. Then the composite
is an equivalence of categories, with quasi-inverse
These equivalences preserve the full subcategories of coherent, respectively locally free coherent, equivariant modules.
Proof. Consider the morphism
![]() $\unicode[STIX]{x1D711}^{\ast }((\unicode[STIX]{x1D711}_{\ast }(-))^{H})\rightarrow \operatorname{id}$
of functors
$\unicode[STIX]{x1D711}^{\ast }((\unicode[STIX]{x1D711}_{\ast }(-))^{H})\rightarrow \operatorname{id}$
of functors
![]() ${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;G)$
which is adjoint to the natural morphism
${\mathcal{M}}(X;G)\rightarrow {\mathcal{M}}(X;G)$
which is adjoint to the natural morphism
![]() $(\unicode[STIX]{x1D711}_{\ast }(-))^{H}\rightarrow \unicode[STIX]{x1D711}_{\ast }(-)$
. It will suffice to prove that for every
$(\unicode[STIX]{x1D711}_{\ast }(-))^{H}\rightarrow \unicode[STIX]{x1D711}_{\ast }(-)$
. It will suffice to prove that for every
![]() $G$
-equivariant quasi-coherent
$G$
-equivariant quasi-coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
, the morphism
${\mathcal{F}}$
, the morphism
![]() $\unicode[STIX]{x1D711}^{\ast }((\unicode[STIX]{x1D711}_{\ast }({\mathcal{F}}))^{H})\rightarrow {\mathcal{F}}$
is an isomorphism of
$\unicode[STIX]{x1D711}^{\ast }((\unicode[STIX]{x1D711}_{\ast }({\mathcal{F}}))^{H})\rightarrow {\mathcal{F}}$
is an isomorphism of
![]() ${\mathcal{O}}_{X}$
-modules (its inverse is then automatically
${\mathcal{O}}_{X}$
-modules (its inverse is then automatically
![]() $G$
-equivariant). But this follows from descent theory: in view of Proposition 2.3.2, the
$G$
-equivariant). But this follows from descent theory: in view of Proposition 2.3.2, the
![]() $H$
-equivariant structure on
$H$
-equivariant structure on
![]() ${\mathcal{F}}$
is precisely a descent datum with respect to the faithfully flat morphism
${\mathcal{F}}$
is precisely a descent datum with respect to the faithfully flat morphism
![]() $\unicode[STIX]{x1D711}$
.◻
$\unicode[STIX]{x1D711}$
.◻
3 Algebraic cycles
3.1 Grothendieck groups
3.1.1
Let
![]() $X$
be a noetherian separated scheme. We denote by
$X$
be a noetherian separated scheme. We denote by
![]() $K_{0}^{\prime }(X)$
(respectively
$K_{0}^{\prime }(X)$
(respectively
![]() $K_{0}(X)$
) the Grothendieck group (respectively ring) of coherent (respectively locally free coherent)
$K_{0}(X)$
) the Grothendieck group (respectively ring) of coherent (respectively locally free coherent)
![]() ${\mathcal{O}}_{X}$
-modules. The class of an
${\mathcal{O}}_{X}$
-modules. The class of an
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
will be denoted by
${\mathcal{F}}$
will be denoted by
![]() $[{\mathcal{F}}]$
. The tensor product induces a
$[{\mathcal{F}}]$
. The tensor product induces a
![]() $K_{0}(X)$
-module structure on
$K_{0}(X)$
-module structure on
![]() $K_{0}^{\prime }(X)$
. A proper, respectively flat, morphism
$K_{0}^{\prime }(X)$
. A proper, respectively flat, morphism
![]() $f:Y\rightarrow X$
induces a push-forward morphism
$f:Y\rightarrow X$
induces a push-forward morphism
![]() $f_{\ast }:K_{0}^{\prime }(Y)\rightarrow K_{0}^{\prime }(X)$
, respectively pull-back morphism
$f_{\ast }:K_{0}^{\prime }(Y)\rightarrow K_{0}^{\prime }(X)$
, respectively pull-back morphism
![]() $f^{\ast }:K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(Y)$
.
$f^{\ast }:K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(Y)$
.
3.1.2
A filtration is defined by letting
![]() $K_{0}^{\prime }(X)_{(n)}$
be the subgroup of
$K_{0}^{\prime }(X)_{(n)}$
be the subgroup of
![]() $K_{0}^{\prime }(X)$
generated by images of the push-forward morphisms
$K_{0}^{\prime }(X)$
generated by images of the push-forward morphisms
![]() $K_{0}^{\prime }(Z)\rightarrow K_{0}^{\prime }(X)$
, where
$K_{0}^{\prime }(Z)\rightarrow K_{0}^{\prime }(X)$
, where
![]() $Z$
runs over the closed subschemes of
$Z$
runs over the closed subschemes of
![]() $X$
of dimension less than or equal to
$X$
of dimension less than or equal to
![]() $n$
. This filtration is compatible with push-forward morphisms [Reference Berthelot, Grothendieck and IllusieSGA6, X, Proposition 1.1.8]. If
$n$
. This filtration is compatible with push-forward morphisms [Reference Berthelot, Grothendieck and IllusieSGA6, X, Proposition 1.1.8]. If
![]() $f:Y\rightarrow X$
is a flat morphism of relative dimension
$f:Y\rightarrow X$
is a flat morphism of relative dimension
![]() $d$
, then
$d$
, then
![]() $f^{\ast }K_{0}^{\prime }(X)_{(n)}\subset K_{0}^{\prime }(Y)_{(n+d)}$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, §3.3]).
$f^{\ast }K_{0}^{\prime }(X)_{(n)}\subset K_{0}^{\prime }(Y)_{(n+d)}$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, §3.3]).
3.1.3
When
![]() $X$
is a complete variety, we denote by
$X$
is a complete variety, we denote by
![]() $\unicode[STIX]{x1D712}(X,-):K_{0}^{\prime }(X)\rightarrow \mathbb{Z}$
the push-forward morphism along the structural morphism
$\unicode[STIX]{x1D712}(X,-):K_{0}^{\prime }(X)\rightarrow \mathbb{Z}$
the push-forward morphism along the structural morphism
![]() $X\rightarrow \operatorname{Spec}k$
. This is the unique morphism sending the class of a coherent
$X\rightarrow \operatorname{Spec}k$
. This is the unique morphism sending the class of a coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
to its Euler characteristic
${\mathcal{F}}$
to its Euler characteristic
3.1.4
Now let
![]() $X$
be a variety with an action of an algebraic group
$X$
be a variety with an action of an algebraic group
![]() $G$
. We denote by
$G$
. We denote by
![]() $K_{0}^{\prime }(X;G)$
the Grothendieck group of
$K_{0}^{\prime }(X;G)$
the Grothendieck group of
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-modules [Reference ThomasonTho87, §1.4]. Forgetting the
${\mathcal{O}}_{X}$
-modules [Reference ThomasonTho87, §1.4]. Forgetting the
![]() $G$
-equivariant structure induces a morphism
$G$
-equivariant structure induces a morphism
![]() $K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
. A finite, respectively flat,
$K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
. A finite, respectively flat,
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $f:Y\rightarrow X$
induces a push-forward morphism
$f:Y\rightarrow X$
induces a push-forward morphism
![]() $f_{\ast }:K_{0}^{\prime }(Y;G)\rightarrow K_{0}^{\prime }(X;G)$
, respectively pull-back morphism
$f_{\ast }:K_{0}^{\prime }(Y;G)\rightarrow K_{0}^{\prime }(X;G)$
, respectively pull-back morphism
![]() $f^{\ast }:K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(Y;G)$
. The Grothendieck ring of
$f^{\ast }:K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(Y;G)$
. The Grothendieck ring of
![]() $G$
-equivariant locally free coherent
$G$
-equivariant locally free coherent
![]() ${\mathcal{O}}_{X}$
-modules will be denoted by
${\mathcal{O}}_{X}$
-modules will be denoted by
![]() $K_{0}(X;G)$
. Any
$K_{0}(X;G)$
. Any
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $f:Y\rightarrow X$
induces a pull-back morphism
$f:Y\rightarrow X$
induces a pull-back morphism
![]() $K_{0}(X;G)\rightarrow K_{0}(Y;G)$
, and
$K_{0}(X;G)\rightarrow K_{0}(Y;G)$
, and
![]() $K_{0}^{\prime }(X;G)$
is naturally a
$K_{0}^{\prime }(X;G)$
is naturally a
![]() $K_{0}(X;G)$
-module.
$K_{0}(X;G)$
-module.
Proposition 3.1.5. Let
![]() $G$
be an algebraic group acting on
$G$
be an algebraic group acting on
![]() $X$
, and
$X$
, and
![]() $H$
a finite normal subgroup of
$H$
a finite normal subgroup of
![]() $G$
acting freely on
$G$
acting freely on
![]() $X$
. Then the pull-back morphism
$X$
. Then the pull-back morphism
![]() $K_{0}^{\prime }(X/H;G)\rightarrow K_{0}^{\prime }(X;G)$
is surjective.
$K_{0}^{\prime }(X/H;G)\rightarrow K_{0}^{\prime }(X;G)$
is surjective.
Proof. This follows from Proposition 2.4.9. ◻
3.2 Chow groups
3.2.1
When
![]() $X$
is a variety, we denote by
$X$
is a variety, we denote by
![]() ${\mathcal{Z}}(X)$
the free abelian group generated by the integral closed subschemes of
${\mathcal{Z}}(X)$
the free abelian group generated by the integral closed subschemes of
![]() $X$
. Every closed subscheme
$X$
. Every closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
has a class
$X$
has a class
![]() $[Z]\in {\mathcal{Z}}(X)$
(defined as the sum of its irreducible components weighted by the lengths of the local rings of
$[Z]\in {\mathcal{Z}}(X)$
(defined as the sum of its irreducible components weighted by the lengths of the local rings of
![]() $Z$
at their generic points). The Chow group
$Z$
at their generic points). The Chow group
![]() $\operatorname{CH}(X)$
is the quotient of
$\operatorname{CH}(X)$
is the quotient of
![]() ${\mathcal{Z}}(X)$
by rational equivalence; we refer to [Reference FultonFul98] (where the notation
${\mathcal{Z}}(X)$
by rational equivalence; we refer to [Reference FultonFul98] (where the notation
![]() $A_{\ast }(X)$
is used) for its basic properties.
$A_{\ast }(X)$
is used) for its basic properties.
3.2.2
When
![]() $X$
is a variety with an action of an algebraic group
$X$
is a variety with an action of an algebraic group
![]() $G$
, we will write
$G$
, we will write
![]() $\operatorname{CH}_{G}(X)$
for the equivariant Chow group of
$\operatorname{CH}_{G}(X)$
for the equivariant Chow group of
![]() $X$
, denoted by
$X$
, denoted by
![]() $A_{\ast }^{G}(X)$
in [Reference Edidin and GrahamEG98]. This group is constructed using intersection theory on algebraic spaces. The consideration of algebraic spaces is not required when
$A_{\ast }^{G}(X)$
in [Reference Edidin and GrahamEG98]. This group is constructed using intersection theory on algebraic spaces. The consideration of algebraic spaces is not required when
![]() $G$
is a finite algebraic group (the main case of interest in this paper), since quotients of varieties always exist as varieties (see § 2.2.3).
$G$
is a finite algebraic group (the main case of interest in this paper), since quotients of varieties always exist as varieties (see § 2.2.3).
3.2.3
Let
![]() $i:Y\rightarrow X$
be the immersion of a
$i:Y\rightarrow X$
be the immersion of a
![]() $G$
-invariant closed subscheme, and
$G$
-invariant closed subscheme, and
![]() $u:U\rightarrow X$
its open complement. The localisation sequence [Reference FultonFul98, Proposition 1.8] induces an exact sequence
$u:U\rightarrow X$
its open complement. The localisation sequence [Reference FultonFul98, Proposition 1.8] induces an exact sequence
3.2.4
The forgetful morphism
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
is defined as follows. Any element of
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
is defined as follows. Any element of
![]() $\operatorname{CH}_{G}(X)$
is represented by an element of
$\operatorname{CH}_{G}(X)$
is represented by an element of
![]() $\operatorname{CH}((X\times W)/G)$
, where
$\operatorname{CH}((X\times W)/G)$
, where
![]() $W$
is a nonempty
$W$
is a nonempty
![]() $G$
-invariant open subscheme of a finite-dimensional
$G$
-invariant open subscheme of a finite-dimensional
![]() $G$
-representation where
$G$
-representation where
![]() $G$
acts freely (the quotient
$G$
acts freely (the quotient
![]() $(X\times \,W)/G$
exists as an algebraic space by [Reference ArtinArt74, Corollary 6.3]). Composing the flat pull-back
$(X\times \,W)/G$
exists as an algebraic space by [Reference ArtinArt74, Corollary 6.3]). Composing the flat pull-back
![]() $\operatorname{CH}((X\times \,W)/G)\rightarrow \operatorname{CH}(X\times \,W)$
with the isomorphism
$\operatorname{CH}((X\times \,W)/G)\rightarrow \operatorname{CH}(X\times \,W)$
with the isomorphism
![]() $\operatorname{CH}(X\times \,W)\simeq \operatorname{CH}(X)$
of Lemma 3.3.1 below, we obtain a morphism
$\operatorname{CH}(X\times \,W)\simeq \operatorname{CH}(X)$
of Lemma 3.3.1 below, we obtain a morphism
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
.
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
.
Lemma 3.2.5. Let
![]() $G$
be a finite algebraic group acting on
$G$
be a finite algebraic group acting on
![]() $X$
, and
$X$
, and
![]() $H$
a normal subgroup of
$H$
a normal subgroup of
![]() $G$
acting freely on
$G$
acting freely on
![]() $X$
. Then the morphism
$X$
. Then the morphism
![]() $\operatorname{CH}_{G}(X/H)\rightarrow \operatorname{CH}_{G}(X)$
is surjective.
$\operatorname{CH}_{G}(X/H)\rightarrow \operatorname{CH}_{G}(X)$
is surjective.
Proof. Let
![]() $Q=G/H$
and
$Q=G/H$
and
![]() $Y=X/H$
. Let
$Y=X/H$
. Let
![]() $W$
be a
$W$
be a
![]() $G$
-invariant open subscheme of a finite-dimensional
$G$
-invariant open subscheme of a finite-dimensional
![]() $G$
-representation where
$G$
-representation where
![]() $G$
acts freely, and
$G$
acts freely, and
![]() $U$
a
$U$
a
![]() $Q$
-invariant open subscheme of a finite-dimensional
$Q$
-invariant open subscheme of a finite-dimensional
![]() $Q$
-representation where
$Q$
-representation where
![]() $Q$
acts freely.
$Q$
acts freely.
The morphism
![]() $f:Y\times \,U\times (W/H)\rightarrow Y\times \,U$
is flat and
$f:Y\times \,U\times (W/H)\rightarrow Y\times \,U$
is flat and
![]() $Q$
-equivariant. Since
$Q$
-equivariant. Since
![]() $Q$
acts freely on its target, it follows by faithfully flat descent and Lemma 2.3.3 that the morphism
$Q$
acts freely on its target, it follows by faithfully flat descent and Lemma 2.3.3 that the morphism
![]() $f/Q$
, which may be identified with
$f/Q$
, which may be identified with
![]() $(Y\times \,U\times \,W)/G\rightarrow (Y\times \,U)/G$
, is flat.
$(Y\times \,U\times \,W)/G\rightarrow (Y\times \,U)/G$
, is flat.
The morphism
![]() $X\times \,U\times \,W\rightarrow Y\times \,U\times \,W$
is flat (by Proposition 2.3.2) and
$X\times \,U\times \,W\rightarrow Y\times \,U\times \,W$
is flat (by Proposition 2.3.2) and
![]() $G$
-equivariant. Since
$G$
-equivariant. Since
![]() $G$
acts freely on its target, it follows as above that the morphism
$G$
acts freely on its target, it follows as above that the morphism
![]() $(X\times \,U\times \,W)/G\times (Y\times \,U\times \,W)/G$
is flat.
$(X\times \,U\times \,W)/G\times (Y\times \,U\times \,W)/G$
is flat.
Since
![]() $W$
is a
$W$
is a
![]() $G$
-invariant open subscheme of a finite-dimensional
$G$
-invariant open subscheme of a finite-dimensional
![]() $G$
-representation, and
$G$
-representation, and
![]() $H$
acts freely on
$H$
acts freely on
![]() $X\times \,U$
, it follows by faithfully flat descent, Lemma 2.3.3 and Proposition 2.4.9 that
$X\times \,U$
, it follows by faithfully flat descent, Lemma 2.3.3 and Proposition 2.4.9 that
![]() $(X\times \,U\times \,W)/H$
is a
$(X\times \,U\times \,W)/H$
is a
![]() $Q$
-invariant open subscheme of a
$Q$
-invariant open subscheme of a
![]() $Q$
-equivariant vector bundle over
$Q$
-equivariant vector bundle over
![]() $(X\times \,U)/H=Y\times \,U$
. Since
$(X\times \,U)/H=Y\times \,U$
. Since
![]() $Q$
acts freely on
$Q$
acts freely on
![]() $Y\times \,U$
, by the same argument
$Y\times \,U$
, by the same argument
![]() $((X\times \,U\times \,W)/H)/Q=(X\times \,U\times W)/G$
is an open subscheme of a vector bundle over
$((X\times \,U\times \,W)/H)/Q=(X\times \,U\times W)/G$
is an open subscheme of a vector bundle over
![]() $(Y\times \,U)/Q=(X\times \,U)/G$
.
$(Y\times \,U)/Q=(X\times \,U)/G$
.
Finally, the morphism
![]() $(X\times \,U)/G\rightarrow (Y\times \,U)/G$
is an isomorphism, hence we have a commutative diagram of flat pull-backs
$(X\times \,U)/G\rightarrow (Y\times \,U)/G$
is an isomorphism, hence we have a commutative diagram of flat pull-backs

where the upper horizontal morphism is surjective by homotopy invariance and the localisation sequence [Reference FultonFul98, Propositions 1.9 and 1.8]. Therefore the right vertical morphism is surjective. Its component of degree
![]() $n$
coincides with that of
$n$
coincides with that of
![]() $\operatorname{CH}_{G}(Y)\rightarrow \operatorname{CH}_{G}(X)$
, as soon as
$\operatorname{CH}_{G}(Y)\rightarrow \operatorname{CH}_{G}(X)$
, as soon as
![]() $U$
and
$U$
and
![]() $W$
are chosen so that their closed complements both have codimension
$W$
are chosen so that their closed complements both have codimension
![]() ${>}\dim X-n$
.◻
${>}\dim X-n$
.◻
3.2.6
We now explain how to lift the construction of [Reference FultonFul98, Definition 8.1.1] to equivariant Chow groups, as this will be needed in § 6. Let
![]() $f:X\rightarrow Y$
be a
$f:X\rightarrow Y$
be a
![]() $G$
-equivariant morphism with
$G$
-equivariant morphism with
![]() $Y$
smooth. Let
$Y$
smooth. Let
![]() $Y^{\prime }\rightarrow Y$
and
$Y^{\prime }\rightarrow Y$
and
![]() $X^{\prime }\rightarrow X$
be
$X^{\prime }\rightarrow X$
be
![]() $G$
-equivariant morphisms. Associated with the cartesian square of
$G$
-equivariant morphisms. Associated with the cartesian square of
![]() $G$
-equivariant morphisms
$G$
-equivariant morphisms

is a morphism
![]() $(\unicode[STIX]{x1D6FE}_{f})^{!}:\operatorname{CH}_{G}(X^{\prime }\times \,Y^{\prime })\rightarrow \operatorname{CH}_{G}(X^{\prime }\times _{Y}Y^{\prime })$
such that the diagram
$(\unicode[STIX]{x1D6FE}_{f})^{!}:\operatorname{CH}_{G}(X^{\prime }\times \,Y^{\prime })\rightarrow \operatorname{CH}_{G}(X^{\prime }\times _{Y}Y^{\prime })$
such that the diagram

commutes (see [Reference BrosnanBro03, §3.1.1]). Given
![]() $x\in \operatorname{CH}_{G}(X^{\prime })$
and
$x\in \operatorname{CH}_{G}(X^{\prime })$
and
![]() $y\in \operatorname{CH}_{G}(Y^{\prime })$
, let
$y\in \operatorname{CH}_{G}(Y^{\prime })$
, let
![]() $x\,\times _{G}y\in \operatorname{CH}_{G}(X^{\prime }\times \,Y^{\prime })$
be their exterior product [Reference Edidin and GrahamEG98, Definition-Proposition 2], and define
$x\,\times _{G}y\in \operatorname{CH}_{G}(X^{\prime }\times \,Y^{\prime })$
be their exterior product [Reference Edidin and GrahamEG98, Definition-Proposition 2], and define
3.3 Purely transcendental extensions
Let us record here a couple of well-known observations.
Lemma 3.3.1. Let
![]() $W$
be a nonempty open subscheme of the affine space
$W$
be a nonempty open subscheme of the affine space
![]() $\mathbb{A}^{d}$
, and let
$\mathbb{A}^{d}$
, and let
![]() $X$
be a variety. Then the flat pull-backs
$X$
be a variety. Then the flat pull-backs
![]() $\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times W)$
and
$\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times W)$
and
![]() $K_{0}^{\prime }(X)_{(n)}\rightarrow K_{0}^{\prime }(X\times \,W)_{(n+d)}$
(for every integer
$K_{0}^{\prime }(X)_{(n)}\rightarrow K_{0}^{\prime }(X\times \,W)_{(n+d)}$
(for every integer
![]() $n$
) are bijective.
$n$
) are bijective.
Proof. We may find a nonconstant polynomial in
![]() $d$
variables with coefficients in
$d$
variables with coefficients in
![]() $k$
whose nonvanishing locus
$k$
whose nonvanishing locus
![]() $U$
is contained in
$U$
is contained in
![]() $W$
. Let
$W$
. Let
![]() $\unicode[STIX]{x1D6FF}$
be its degree. If the field
$\unicode[STIX]{x1D6FF}$
be its degree. If the field
![]() $k$
is finite, it possesses two finite field extensions
$k$
is finite, it possesses two finite field extensions
![]() $k_{0},k_{1}$
of coprime degree, each containing more than
$k_{0},k_{1}$
of coprime degree, each containing more than
![]() $\unicode[STIX]{x1D6FF}+1$
elements. By a restriction–corestriction argument, it will suffice to prove the statement after successively replacing
$\unicode[STIX]{x1D6FF}+1$
elements. By a restriction–corestriction argument, it will suffice to prove the statement after successively replacing
![]() $k$
with
$k$
with
![]() $k_{0}$
and
$k_{0}$
and
![]() $k_{1}$
. Thus we may assume that
$k_{1}$
. Thus we may assume that
![]() $k$
contains
$k$
contains
![]() $\unicode[STIX]{x1D6FF}+1$
distinct elements. Then one sees by induction on
$\unicode[STIX]{x1D6FF}+1$
distinct elements. Then one sees by induction on
![]() $m$
that any nonzero polynomial of degree less than or equal to
$m$
that any nonzero polynomial of degree less than or equal to
![]() $\unicode[STIX]{x1D6FF}$
in
$\unicode[STIX]{x1D6FF}$
in
![]() $m$
variables with coefficients in
$m$
variables with coefficients in
![]() $k$
induces a nonzero map
$k$
induces a nonzero map
![]() $k^{m}\rightarrow k$
. In particular
$k^{m}\rightarrow k$
. In particular
![]() $U$
, and thus also
$U$
, and thus also
![]() $W$
, possesses a rational point. Then by [Reference Elman, Karpenko and MerkurjevEKM08, Lemma 55.7], respectively [Reference QuillenQui73, §7.2.5], the pull-back along the corresponding regular closed immersion
$W$
, possesses a rational point. Then by [Reference Elman, Karpenko and MerkurjevEKM08, Lemma 55.7], respectively [Reference QuillenQui73, §7.2.5], the pull-back along the corresponding regular closed immersion
![]() $i:X\rightarrow X\times \,W$
is a retraction of the flat pull-back
$i:X\rightarrow X\times \,W$
is a retraction of the flat pull-back
![]() $\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,W)$
, respectively
$\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,W)$
, respectively
![]() $K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(X\times \,W)$
. Since the latter is surjective by homotopy invariance and the localisation sequence (see [Reference FultonFul98, Propositions 1.9 and 1.8], respectively [Reference QuillenQui73, Propositions 7.3.2 and 7.4.1]), it is bijective. In addition, we have
$K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(X\times \,W)$
. Since the latter is surjective by homotopy invariance and the localisation sequence (see [Reference FultonFul98, Propositions 1.9 and 1.8], respectively [Reference QuillenQui73, Propositions 7.3.2 and 7.4.1]), it is bijective. In addition, we have
![]() $i^{\ast }K_{0}^{\prime }(X\times \,W)_{(n+d)}\subset K_{0}^{\prime }(X)_{(n)}$
by [Reference GilletGil05, Theorem 83], concluding the proof.◻
$i^{\ast }K_{0}^{\prime }(X\times \,W)_{(n+d)}\subset K_{0}^{\prime }(X)_{(n)}$
by [Reference GilletGil05, Theorem 83], concluding the proof.◻
Lemma 3.3.2. Let
![]() $K$
be a finitely generated purely transcendental field extension of
$K$
be a finitely generated purely transcendental field extension of
![]() $k$
. Then for any variety
$k$
. Then for any variety
![]() $X$
, the pull-back
$X$
, the pull-back
![]() $K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(X\times \,\operatorname{Spec}K)$
is an isomorphism of filtered groups.
$K_{0}^{\prime }(X)\rightarrow K_{0}^{\prime }(X\times \,\operatorname{Spec}K)$
is an isomorphism of filtered groups.
Proof. Let
![]() $d=\operatorname{tr.deg.}(K/k)$
. Then
$d=\operatorname{tr.deg.}(K/k)$
. Then
![]() $E=\operatorname{Spec}K$
is the limit of a filtered family of nonempty open subschemes
$E=\operatorname{Spec}K$
is the limit of a filtered family of nonempty open subschemes
![]() $W_{\unicode[STIX]{x1D6FC}}$
of
$W_{\unicode[STIX]{x1D6FC}}$
of
![]() $\mathbb{A}^{d}$
with affine transition morphisms. Thus by [Reference QuillenQui73, Proposition 7.2.2] the morphism
$\mathbb{A}^{d}$
with affine transition morphisms. Thus by [Reference QuillenQui73, Proposition 7.2.2] the morphism
is bijective. Since each morphism
![]() $E\rightarrow W_{\unicode[STIX]{x1D6FC}}$
is flat of relative dimension
$E\rightarrow W_{\unicode[STIX]{x1D6FC}}$
is flat of relative dimension
![]() $-d$
, the above morphism restricts for every
$-d$
, the above morphism restricts for every
![]() $n$
to an injective morphism of subgroups
$n$
to an injective morphism of subgroups
It follows that
![]() $\dim Z_{\unicode[STIX]{x1D6FC}}\leqslant n+d$
. We have a commutative diagram.
$\dim Z_{\unicode[STIX]{x1D6FC}}\leqslant n+d$
. We have a commutative diagram.

Since the upper horizontal morphism is surjective, we deduce that (3.3a) is surjective, and thus bijective. Now the statement follows from Lemma 3.3.1. ◻
3.4 An equivariant theory
In this section, we introduce an equivariant theory
![]() $K_{G}$
, for
$K_{G}$
, for
![]() $G$
a finite algebraic group, which will be used exclusively in § 5.2. Its key properties may be summarised as follows (when
$G$
a finite algebraic group, which will be used exclusively in § 5.2. Its key properties may be summarised as follows (when
![]() $X$
is a variety with a
$X$
is a variety with a
![]() $G$
-action).
$G$
-action).
(i) The forgetful morphism factors as
 $K_{0}^{\prime }(X;G)\rightarrow K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
.
$K_{0}^{\prime }(X;G)\rightarrow K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
.(ii) The morphism
 $K_{0}^{\prime }(X;G)\rightarrow K_{G}(X)$
is surjective.
$K_{0}^{\prime }(X;G)\rightarrow K_{G}(X)$
is surjective.(iii) The morphism
 $K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
is bijective when
$K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
is bijective when
 $X=\operatorname{Spec}k$
.
$X=\operatorname{Spec}k$
.(iv) The group
 $K_{G}(X)$
is endowed with a filtration vanishing in negative degrees, which is compatible with the topological filtration of
$K_{G}(X)$
is endowed with a filtration vanishing in negative degrees, which is compatible with the topological filtration of
 $K_{0}^{\prime }(X)$
via the morphism
$K_{0}^{\prime }(X)$
via the morphism
 $K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
.
$K_{G}(X)\rightarrow K_{0}^{\prime }(X)$
.
Remark 3.4.1. The theory
![]() $K_{G}$
is constructed using the theory
$K_{G}$
is constructed using the theory
![]() $K_{0}^{\prime }$
. One could perform the same construction using other cohomology theories instead; taking the Chow group would yield a quotient of the equivariant Chow group
$K_{0}^{\prime }$
. One could perform the same construction using other cohomology theories instead; taking the Chow group would yield a quotient of the equivariant Chow group
![]() $\operatorname{CH}_{G}$
.
$\operatorname{CH}_{G}$
.
Let
![]() $G$
be a finite algebraic group. Let
$G$
be a finite algebraic group. Let
![]() $V=H^{0}(G,{\mathcal{O}}_{G})$
be the regular representation of
$V=H^{0}(G,{\mathcal{O}}_{G})$
be the regular representation of
![]() $G$
over
$G$
over
![]() $k$
. We view
$k$
. We view
![]() $E=\operatorname{End}(V)$
as a
$E=\operatorname{End}(V)$
as a
![]() $G$
-representation by letting
$G$
-representation by letting
![]() $G$
act by left composition. Then the group
$G$
act by left composition. Then the group
![]() $G$
acts freely on the nonempty
$G$
acts freely on the nonempty
![]() $G$
-invariant open subscheme
$G$
-invariant open subscheme
![]() $\operatorname{GL}(V)$
of
$\operatorname{GL}(V)$
of
![]() $E$
. The scheme
$E$
. The scheme
may be identified with the generic fiber of the morphism
![]() $E\rightarrow E/G$
. Therefore
$E\rightarrow E/G$
. Therefore
![]() $T$
is a variety over the field
$T$
is a variety over the field
![]() $F=k(E/G)=k(E)^{G}$
, and is equipped with a free
$F=k(E/G)=k(E)^{G}$
, and is equipped with a free
![]() $G$
-action.
$G$
-action.
Definition 3.4.2. When
![]() $X$
is a variety with a
$X$
is a variety with a
![]() $G$
-action, we may view the scheme
$G$
-action, we may view the scheme
![]() $X\times \,T$
as an
$X\times \,T$
as an
![]() $F$
-variety with a free
$F$
-variety with a free
![]() $G$
-action, and we define
$G$
-action, and we define
A filtration is defined by letting
![]() $K_{G}(X)_{(n)}=K_{0}^{\prime }((X\times T)/G)_{(n)}$
.
$K_{G}(X)_{(n)}=K_{0}^{\prime }((X\times T)/G)_{(n)}$
.
Remark 3.4.3. If
![]() $W$
is any generically free
$W$
is any generically free
![]() $G$
-representation of finite dimension over
$G$
-representation of finite dimension over
![]() $k$
, replacing
$k$
, replacing
![]() $T$
by
$T$
by
![]() $\operatorname{Spec}k(W)$
and
$\operatorname{Spec}k(W)$
and
![]() $F$
by
$F$
by
![]() $k(W)^{G}$
in the above definition yields a canonically isomorphic filtered group. This observation will play no role in this paper, but may be used to construct a change of group morphism, for instance.
$k(W)^{G}$
in the above definition yields a canonically isomorphic filtered group. This observation will play no role in this paper, but may be used to construct a change of group morphism, for instance.
We may use Lemma 3.3.2 to define a morphism of filtered groups
Using the isomorphism induced by Proposition 2.4.9, we construct a morphism
The composite of (3.4b) and (3.4a) is the canonical morphism
![]() $K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
.
$K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
.
Lemma 3.4.4. The morphism (3.4b) is surjective.
Proof. This morphism may be factored as
The first morphism is surjective by the equivariant versions of homotopy invariance and of the localisation sequence [Reference ThomasonTho87, Theorems 2.7 and 4.1], the middle isomorphism follows from Proposition 2.4.9. The scheme
![]() $\operatorname{Spec}F=T/G$
is a filtered limit of open subschemes of
$\operatorname{Spec}F=T/G$
is a filtered limit of open subschemes of
![]() $\operatorname{GL}(V)/G$
with affine transition morphisms, hence by base-change (in view of Lemma 2.3.3) the scheme
$\operatorname{GL}(V)/G$
with affine transition morphisms, hence by base-change (in view of Lemma 2.3.3) the scheme
![]() $(X\times \,T)/G$
is a filtered limit of open subschemes of
$(X\times \,T)/G$
is a filtered limit of open subschemes of
![]() $(X\times \,\operatorname{GL}(V))/G$
with affine transition morphisms. Thus the last morphism of (3.4c) is surjective by [Reference QuillenQui73, Propositions 7.2.2 and 7.3.2].◻
$(X\times \,\operatorname{GL}(V))/G$
with affine transition morphisms. Thus the last morphism of (3.4c) is surjective by [Reference QuillenQui73, Propositions 7.2.2 and 7.3.2].◻
A flat, respectively proper,
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $f:Y\rightarrow X$
induces a morphism
$f:Y\rightarrow X$
induces a morphism
![]() $f^{\ast }:K_{G}(X)\rightarrow K_{G}(Y)$
, respectively
$f^{\ast }:K_{G}(X)\rightarrow K_{G}(Y)$
, respectively
![]() $f_{\ast }:K_{G}(Y)\rightarrow K_{G}(X)$
. The Grothendieck ring
$f_{\ast }:K_{G}(Y)\rightarrow K_{G}(X)$
. The Grothendieck ring
![]() $K_{0}(X;G)$
naturally acts on
$K_{0}(X;G)$
naturally acts on
![]() $K_{G}(X)$
: any element
$K_{G}(X)$
: any element
![]() $\unicode[STIX]{x1D6FC}\in K_{0}(X;G)$
pulls back to an element of
$\unicode[STIX]{x1D6FC}\in K_{0}(X;G)$
pulls back to an element of
![]() $K_{0}(X\times \,T;G)$
, which acts on
$K_{0}(X\times \,T;G)$
, which acts on
![]() $K_{0}^{\prime }(X\times \,T;G)=K_{G}(X)$
. We denote this action by
$K_{0}^{\prime }(X\times \,T;G)=K_{G}(X)$
. We denote this action by
![]() $\unicode[STIX]{x1D6FC}\cap -:K_{G}(X)\rightarrow K_{G}(X)$
.
$\unicode[STIX]{x1D6FC}\cap -:K_{G}(X)\rightarrow K_{G}(X)$
.
Lemma 3.4.5. Let
![]() $i:Y\rightarrow X$
be the immersion of a
$i:Y\rightarrow X$
be the immersion of a
![]() $G$
-invariant closed subscheme, and
$G$
-invariant closed subscheme, and
![]() $u:U\rightarrow X$
its open complement. Then the following sequence is exact:
$u:U\rightarrow X$
its open complement. Then the following sequence is exact:
Proof. Since
![]() $(Y\times \,T)/G$
is a closed subscheme of
$(Y\times \,T)/G$
is a closed subscheme of
![]() $(X\times \,T)/G$
with open complement
$(X\times \,T)/G$
with open complement
![]() $(U\times \,T)/G$
by Lemma 2.3.3 and faithfully flat descent, the lemma follows from the localisation sequence for
$(U\times \,T)/G$
by Lemma 2.3.3 and faithfully flat descent, the lemma follows from the localisation sequence for
![]() $K_{0}^{\prime }$
(see [Reference QuillenQui73, Proposition 7.3.2]).◻
$K_{0}^{\prime }$
(see [Reference QuillenQui73, Proposition 7.3.2]).◻
4 The degree of equivariant cycles
Definition 4.1. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
. We denote by
$X$
. We denote by
![]() ${\mathcal{Z}}_{G}(X)$
the subgroup of
${\mathcal{Z}}_{G}(X)$
the subgroup of
![]() ${\mathcal{Z}}(X)$
generated by classes of equidimensional
${\mathcal{Z}}(X)$
generated by classes of equidimensional
![]() $G$
-invariant closed subschemes of
$G$
-invariant closed subschemes of
![]() $X$
.
$X$
.
If
![]() $U$
is a
$U$
is a
![]() $G$
-invariant open subscheme of
$G$
-invariant open subscheme of
![]() $X$
, then the restriction morphism
$X$
, then the restriction morphism
![]() ${\mathcal{Z}}(X)\rightarrow {\mathcal{Z}}(U)$
maps the subgroup
${\mathcal{Z}}(X)\rightarrow {\mathcal{Z}}(U)$
maps the subgroup
![]() ${\mathcal{Z}}_{G}(X)$
surjectively onto
${\mathcal{Z}}_{G}(X)$
surjectively onto
![]() ${\mathcal{Z}}_{G}(U)$
.
${\mathcal{Z}}_{G}(U)$
.
Lemma 4.2. Let
![]() $i:D\rightarrow X$
be a
$i:D\rightarrow X$
be a
![]() $G$
-equivariant principal effective Cartier divisor. Then the image of the composite
$G$
-equivariant principal effective Cartier divisor. Then the image of the composite
![]() ${\mathcal{Z}}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{i^{\ast }}\operatorname{CH}(D)$
is contained in the image of the morphism
${\mathcal{Z}}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{i^{\ast }}\operatorname{CH}(D)$
is contained in the image of the morphism
![]() ${\mathcal{Z}}_{G}(D)\rightarrow \operatorname{CH}(D)$
.
${\mathcal{Z}}_{G}(D)\rightarrow \operatorname{CH}(D)$
.
Proof. Let
![]() $Z$
be an equidimensional
$Z$
be an equidimensional
![]() $G$
-invariant closed subscheme of
$G$
-invariant closed subscheme of
![]() $X$
. Let
$X$
. Let
![]() $Z_{0}$
(respectively
$Z_{0}$
(respectively
![]() $Z_{1}$
) be the scheme theoretic closure of
$Z_{1}$
) be the scheme theoretic closure of
![]() $Z-(D\cap Z)$
(respectively of
$Z-(D\cap Z)$
(respectively of
![]() $Z-Z_{0}$
) in
$Z-Z_{0}$
) in
![]() $Z$
. Then
$Z$
. Then
![]() $Z_{0}$
is an equidimensional
$Z_{0}$
is an equidimensional
![]() $G$
-invariant closed subscheme of
$G$
-invariant closed subscheme of
![]() $X$
, and we have
$X$
, and we have
![]() $[Z]=[Z_{0}]+[Z_{1}]$
in
$[Z]=[Z_{0}]+[Z_{1}]$
in
![]() ${\mathcal{Z}}(X)$
. In addition the closed subscheme
${\mathcal{Z}}(X)$
. In addition the closed subscheme
![]() $Z_{1}$
is supported inside
$Z_{1}$
is supported inside
![]() $D$
, hence we may find
$D$
, hence we may find
![]() $y\in {\mathcal{Z}}(D)$
such
$y\in {\mathcal{Z}}(D)$
such
![]() $[Z_{1}]=i_{\ast }(y)$
in
$[Z_{1}]=i_{\ast }(y)$
in
![]() ${\mathcal{Z}}(X)$
. Since
${\mathcal{Z}}(X)$
. Since
![]() $i$
is a principal effective Cartier divisor, it follows from [Reference FultonFul98, Proposition 2.6(c)] that the composite
$i$
is a principal effective Cartier divisor, it follows from [Reference FultonFul98, Proposition 2.6(c)] that the composite
![]() $i^{\ast }\circ i_{\ast }$
is the zero endomorphism of
$i^{\ast }\circ i_{\ast }$
is the zero endomorphism of
![]() $\operatorname{CH}(D)$
, hence we have in
$\operatorname{CH}(D)$
, hence we have in
![]() $\operatorname{CH}(D)$
$\operatorname{CH}(D)$
By construction, no associated point of
![]() $Z_{0}$
lies in
$Z_{0}$
lies in
![]() $D$
, so that
$D$
, so that
![]() $D\cap Z_{0}\rightarrow Z_{0}$
is an effective Cartier divisor. Then by [Reference FultonFul98, Lemma 1.7.2] the cycle class
$D\cap Z_{0}\rightarrow Z_{0}$
is an effective Cartier divisor. Then by [Reference FultonFul98, Lemma 1.7.2] the cycle class
![]() $i^{\ast }[Z]=i^{\ast }[Z_{0}]\in \operatorname{CH}(D)$
is represented by the cycle
$i^{\ast }[Z]=i^{\ast }[Z_{0}]\in \operatorname{CH}(D)$
is represented by the cycle
![]() $[Z_{0}\cap D]\in {\mathcal{Z}}(D)$
, which belongs to
$[Z_{0}\cap D]\in {\mathcal{Z}}(D)$
, which belongs to
![]() ${\mathcal{Z}}_{G}(D)$
, since
${\mathcal{Z}}_{G}(D)$
, since
![]() $Z_{0}\cap D$
is an equidimensional
$Z_{0}\cap D$
is an equidimensional
![]() $G$
-invariant closed subscheme of
$G$
-invariant closed subscheme of
![]() $D$
.◻
$D$
.◻
We recall that
![]() $\operatorname{CH}_{G}$
denotes the equivariant Chow group, see § 3.2.2.
$\operatorname{CH}_{G}$
denotes the equivariant Chow group, see § 3.2.2.
Proposition 4.3. Let
![]() $G$
be a trigonalisable (§ 2.1.5) algebraic group acting on a variety
$G$
be a trigonalisable (§ 2.1.5) algebraic group acting on a variety
![]() $X$
. Then the two morphisms
$X$
. Then the two morphisms
have the same image.
Proof. Let
![]() $W$
be a nonempty
$W$
be a nonempty
![]() $G$
-invariant open subscheme of a finite-dimensional
$G$
-invariant open subscheme of a finite-dimensional
![]() $G$
-representation
$G$
-representation
![]() $V$
over
$V$
over
![]() $k$
, and assume that
$k$
, and assume that
![]() $G$
acts freely on
$G$
acts freely on
![]() $W$
. Consider the commutative diagram (see Lemma 3.3.1 for the indicated isomorphisms).
$W$
. Consider the commutative diagram (see Lemma 3.3.1 for the indicated isomorphisms).

(If
![]() $G$
is not finite, then
$G$
is not finite, then
![]() $(X\times \,W)/G$
may be only an algebraic space.) To prove the statement, it will suffice to prove that for every finite-dimensional
$(X\times \,W)/G$
may be only an algebraic space.) To prove the statement, it will suffice to prove that for every finite-dimensional
![]() $G$
-representation
$G$
-representation
![]() $V$
over
$V$
over
![]() $k$
, the two morphisms
$k$
, the two morphisms
have the same image. We proceed by induction on
![]() $\dim V$
, the case
$\dim V$
, the case
![]() $V=0$
being clear. Assume that
$V=0$
being clear. Assume that
![]() $V\neq 0$
. Since
$V\neq 0$
. Since
![]() $G$
is trigonalisable, we can find a subrepresentation
$G$
is trigonalisable, we can find a subrepresentation
![]() $V^{\prime }\subset V$
of codimension one. Let
$V^{\prime }\subset V$
of codimension one. Let
![]() $i:X\times \,V^{\prime }\rightarrow X\times \,V$
be the induced
$i:X\times \,V^{\prime }\rightarrow X\times \,V$
be the induced
![]() $G$
-equivariant closed immersion. By Lemma 4.2, for any
$G$
-equivariant closed immersion. By Lemma 4.2, for any
![]() $x\in {\mathcal{Z}}_{G}(X\times \,V)$
, the cycle class
$x\in {\mathcal{Z}}_{G}(X\times \,V)$
, the cycle class
![]() $i^{\ast }(x)\in \operatorname{CH}(X\times \,V^{\prime })$
is represented by a cycle in
$i^{\ast }(x)\in \operatorname{CH}(X\times \,V^{\prime })$
is represented by a cycle in
![]() ${\mathcal{Z}}_{G}(X\times \,V^{\prime })$
.
${\mathcal{Z}}_{G}(X\times \,V^{\prime })$
.
By induction, we may find a cycle
![]() $y\in {\mathcal{Z}}_{G}(X)$
such that
$y\in {\mathcal{Z}}_{G}(X)$
such that
![]() $i^{\ast }(x)=y\times \,[V^{\prime }]\in \operatorname{CH}(X\times \,V^{\prime })$
. Using the surjectivity of
$i^{\ast }(x)=y\times \,[V^{\prime }]\in \operatorname{CH}(X\times \,V^{\prime })$
. Using the surjectivity of
![]() $\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,V)$
, we find
$\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,V)$
, we find
![]() $z\in \operatorname{CH}(X)$
such that
$z\in \operatorname{CH}(X)$
such that
![]() $x=z\,\,\times [V]\in \operatorname{CH}(X\times \,V)$
. Then
$x=z\,\,\times [V]\in \operatorname{CH}(X\times \,V)$
. Then
![]() $z\times \,[V^{\prime }]=i^{\ast }(x)=y\,\times \,[V^{\prime }]\in \operatorname{CH}(X\times \,V^{\prime })$
(see [Reference Elman, Karpenko and MerkurjevEKM08, Lemma 55.7]), hence
$z\times \,[V^{\prime }]=i^{\ast }(x)=y\,\times \,[V^{\prime }]\in \operatorname{CH}(X\times \,V^{\prime })$
(see [Reference Elman, Karpenko and MerkurjevEKM08, Lemma 55.7]), hence
![]() $z=y\in \operatorname{CH}(X)$
by injectivity of
$z=y\in \operatorname{CH}(X)$
by injectivity of
![]() $\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,V^{\prime })$
, and finally
$\operatorname{CH}(X)\rightarrow \operatorname{CH}(X\times \,V^{\prime })$
, and finally
![]() $x=y\times \,[V]\in \operatorname{CH}(X\times \,V)$
, as required.◻
$x=y\times \,[V]\in \operatorname{CH}(X\times \,V)$
, as required.◻
Theorem 4.4. Let
![]() $G$
be a trigonalisable (§ 2.1.5) algebraic
$G$
be a trigonalisable (§ 2.1.5) algebraic
![]() $p$
-group acting on a projective variety
$p$
-group acting on a projective variety
![]() $X$
. Assume that the degree of every closed point of
$X$
. Assume that the degree of every closed point of
![]() $X^{G}$
is divisible by
$X^{G}$
is divisible by
![]() $p$
. Then the morphism
$p$
. Then the morphism
![]() $d_{X}:\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero.
$d_{X}:\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero.
Proof. By Proposition 4.3, it will suffice to prove that
![]() $\deg [T]=0\in \mathbb{F}_{p}$
for any equidimensional
$\deg [T]=0\in \mathbb{F}_{p}$
for any equidimensional
![]() $G$
-invariant closed subscheme
$G$
-invariant closed subscheme
![]() $T$
of
$T$
of
![]() $X$
. It will of course suffice to consider the case
$X$
. It will of course suffice to consider the case
![]() $\dim T=0$
. Replacing
$\dim T=0$
. Replacing
![]() $X$
with
$X$
with
![]() $T$
, we may assume that
$T$
, we may assume that
![]() $\dim X=0$
. Given a
$\dim X=0$
. Given a
![]() $G$
-invariant closed subscheme
$G$
-invariant closed subscheme
![]() $Z$
of
$Z$
of
![]() $X$
, consider the exact sequence of § 3.2.3
$X$
, consider the exact sequence of § 3.2.3
where
![]() $i:Z\rightarrow X$
, respectively
$i:Z\rightarrow X$
, respectively
![]() $u:X-Z\rightarrow X$
, is the closed, respectively open, immersion. Since
$u:X-Z\rightarrow X$
, is the closed, respectively open, immersion. Since
![]() $\dim X=0$
, the open immersion
$\dim X=0$
, the open immersion
![]() $u$
is also closed, and the push-forward morphism
$u$
is also closed, and the push-forward morphism
![]() $u_{\ast }$
is a section of
$u_{\ast }$
is a section of
![]() $u^{\ast }$
. In addition
$u^{\ast }$
. In addition
![]() $d_{X}\circ i_{\ast }=d_{Z}$
and
$d_{X}\circ i_{\ast }=d_{Z}$
and
![]() $d_{X}\circ u_{\ast }=d_{X-Z}$
, so that
$d_{X}\circ u_{\ast }=d_{X-Z}$
, so that
Taking
![]() $Z=X^{G}$
, we see that in order to prove the proposition, it will suffice to assume that
$Z=X^{G}$
, we see that in order to prove the proposition, it will suffice to assume that
![]() $X^{G}=\varnothing$
and prove that
$X^{G}=\varnothing$
and prove that
![]() $d_{X}=0$
. To do so, we may assume that
$d_{X}=0$
. To do so, we may assume that
![]() $k$
is algebraically closed. Using (4.1a) and noetherian induction, we may assume that
$k$
is algebraically closed. Using (4.1a) and noetherian induction, we may assume that
![]() $X$
possesses exactly two
$X$
possesses exactly two
![]() $G$
-invariant closed subschemes (
$G$
-invariant closed subschemes (
![]() $\varnothing$
and
$\varnothing$
and
![]() $X$
). It will thus suffice to prove that
$X$
). It will thus suffice to prove that
![]() $\deg [X]=0\in \mathbb{F}_{p}$
. The choice of a rational point of
$\deg [X]=0\in \mathbb{F}_{p}$
. The choice of a rational point of
![]() $X$
induces a
$X$
induces a
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $G\rightarrow X$
, which must be scheme theoretically dominant. By [Reference Demazure and GrothendieckSGA31
, V, Théorème 10.1.2], there is a subgroup
$G\rightarrow X$
, which must be scheme theoretically dominant. By [Reference Demazure and GrothendieckSGA31
, V, Théorème 10.1.2], there is a subgroup
![]() $H$
of
$H$
of
![]() $G$
such that
$G$
such that
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $G/H$
. The morphism
$G/H$
. The morphism
![]() $G\rightarrow G/H$
is flat and finite by Proposition 2.3.2, so that the integer
$G\rightarrow G/H$
is flat and finite by Proposition 2.3.2, so that the integer
![]() $n=\dim _{k}H^{0}(X,{\mathcal{O}}_{X})$
divides the order of
$n=\dim _{k}H^{0}(X,{\mathcal{O}}_{X})$
divides the order of
![]() $G$
, and is thus a
$G$
, and is thus a
![]() $p$
th power. Since
$p$
th power. Since
![]() $H\neq G$
(as
$H\neq G$
(as
![]() $X^{G}=\varnothing$
and
$X^{G}=\varnothing$
and
![]() $X\neq \varnothing$
), it follows that
$X\neq \varnothing$
), it follows that
![]() $\deg [X]=n~\text{mod}~p$
vanishes in
$\deg [X]=n~\text{mod}~p$
vanishes in
![]() $\mathbb{F}_{p}$
.◻
$\mathbb{F}_{p}$
.◻
Example 4.5. Assume that the field
![]() $k$
is algebraically closed of characteristic
$k$
is algebraically closed of characteristic
![]() $\neq p$
, and let
$\neq p$
, and let
![]() $G$
be a constant nonabelian finite
$G$
be a constant nonabelian finite
![]() $p$
-group. Then
$p$
-group. Then
![]() $G$
admits a simple representation
$G$
admits a simple representation
![]() $V$
of dimension
$V$
of dimension
![]() $d=p^{n}$
with
$d=p^{n}$
with
![]() $n>0$
. Observe that the case
$n>0$
. Observe that the case
![]() $n=1$
actually occurs, when
$n=1$
actually occurs, when
![]() $G$
has order
$G$
has order
![]() $p^{3}$
.
$p^{3}$
.
The group
![]() $G$
acts without fixed point on
$G$
acts without fixed point on
![]() $\mathbb{P}(V)$
, but the cycle class
$\mathbb{P}(V)$
, but the cycle class
![]() $c_{1}({\mathcal{O}}(1))^{d-1}$
is in the image of
$c_{1}({\mathcal{O}}(1))^{d-1}$
is in the image of
![]() $\operatorname{CH}_{G}(\mathbb{P}(V))\rightarrow \operatorname{CH}(\mathbb{P}(V))$
and has degree prime to
$\operatorname{CH}_{G}(\mathbb{P}(V))\rightarrow \operatorname{CH}(\mathbb{P}(V))$
and has degree prime to
![]() $p$
(equal to
$p$
(equal to
![]() $1$
). When
$1$
). When
![]() $n=1$
, we have
$n=1$
, we have
![]() $\dim \mathbb{P}(V)=p-1$
.
$\dim \mathbb{P}(V)=p-1$
.
The group
![]() $G$
also acts on
$G$
also acts on
![]() $\mathbb{P}(V\oplus 1)$
with a single fixed point
$\mathbb{P}(V\oplus 1)$
with a single fixed point
![]() $\mathbb{P}(1)$
. Let
$\mathbb{P}(1)$
. Let
![]() $f:X\rightarrow \mathbb{P}(V\oplus 1)$
be the blow-up at this point. There is a
$f:X\rightarrow \mathbb{P}(V\oplus 1)$
be the blow-up at this point. There is a
![]() $G$
-action on
$G$
-action on
![]() $X$
making
$X$
making
![]() $f$
a
$f$
a
![]() $G$
-equivariant morphism. Then any fixed point of
$G$
-equivariant morphism. Then any fixed point of
![]() $X$
must be contained in the exceptional divisor
$X$
must be contained in the exceptional divisor
![]() $E$
, which is
$E$
, which is
![]() $G$
-equivariantly isomorphic to
$G$
-equivariantly isomorphic to
![]() $\mathbb{P}(V)$
. Since the latter has no fixed point, it follows that
$\mathbb{P}(V)$
. Since the latter has no fixed point, it follows that
![]() $X(k)^{G}=\varnothing$
. The normal bundle of the effective Cartier divisor
$X(k)^{G}=\varnothing$
. The normal bundle of the effective Cartier divisor
![]() $j:\mathbb{P}(V)\simeq E\rightarrow X$
is
$j:\mathbb{P}(V)\simeq E\rightarrow X$
is
![]() ${\mathcal{O}}_{\mathbb{P}(V)}(-1)$
, hence the zero-cycle class
${\mathcal{O}}_{\mathbb{P}(V)}(-1)$
, hence the zero-cycle class
has degree
![]() $(-1)^{d-1}$
. The zero-cycle class on
$(-1)^{d-1}$
. The zero-cycle class on
![]() $\mathbb{P}(V\oplus 1)$
$\mathbb{P}(V\oplus 1)$
has degree
![]() $(d+1)^{d}$
. By [Reference FultonFul98, 15.4.3], we have
$(d+1)^{d}$
. By [Reference FultonFul98, 15.4.3], we have
so that
![]() $\deg (c_{1}(T_{X})^{d})=2~\text{mod}~p$
. Thus we have found a Chern number of
$\deg (c_{1}(T_{X})^{d})=2~\text{mod}~p$
. Thus we have found a Chern number of
![]() $X$
which is not divisible by
$X$
which is not divisible by
![]() $p$
, when
$p$
, when
![]() $p\neq 2$
. When
$p\neq 2$
. When
![]() $n=1$
, we have
$n=1$
, we have
![]() $\dim X=p$
.
$\dim X=p$
.
Now assume that
![]() $p=2$
. The group
$p=2$
. The group
![]() $G$
acts on
$G$
acts on
![]() $P=\mathbb{P}(V\oplus 1)\times \mathbb{P}(V\oplus 1)$
with a single fixed point
$P=\mathbb{P}(V\oplus 1)\times \mathbb{P}(V\oplus 1)$
with a single fixed point
![]() $\mathbb{P}(1)\times \,\mathbb{P}(1)$
. Let
$\mathbb{P}(1)\times \,\mathbb{P}(1)$
. Let
![]() $g:Y\rightarrow P$
be the blow-up at this point. As above, we have
$g:Y\rightarrow P$
be the blow-up at this point. As above, we have
![]() $Y(k)^{G}=\varnothing$
, and by [Reference FultonFul98, Example 15.4.2(c)]
$Y(k)^{G}=\varnothing$
, and by [Reference FultonFul98, Example 15.4.2(c)]
so that we have in
![]() $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
Therefore one of the Chern numbers of
![]() $Y$
is odd. When
$Y$
is odd. When
![]() $n=1$
, we have
$n=1$
, we have
![]() $\dim Y=4$
.
$\dim Y=4$
.
5 The Euler characteristic of equivariant modules
We now investigate divisibility properties of Euler characteristics of equivariant modules on a variety upon which a finite
![]() $p$
-group acts without fixed points. The next proposition shows that the case of a free action can be easily handled.
$p$
-group acts without fixed points. The next proposition shows that the case of a free action can be easily handled.
Proposition 5.0.1. Let
![]() $G$
be a finite algebraic group acting freely on a projective variety
$G$
be a finite algebraic group acting freely on a projective variety
![]() $X$
. Then the Euler characteristic
$X$
. Then the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is divisible by the order of
${\mathcal{F}}$
is divisible by the order of
![]() $G$
.
$G$
.
Proof. By Proposition 2.4.9 we may find a coherent
![]() ${\mathcal{O}}_{X/G}$
-module
${\mathcal{O}}_{X/G}$
-module
![]() ${\mathcal{G}}$
whose pull-back to
${\mathcal{G}}$
whose pull-back to
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() ${\mathcal{F}}$
. Then
${\mathcal{F}}$
. Then
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})=n\cdot \unicode[STIX]{x1D712}(X/G,{\mathcal{G}})$
, where
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})=n\cdot \unicode[STIX]{x1D712}(X/G,{\mathcal{G}})$
, where
![]() $n$
is the order of
$n$
is the order of
![]() $G$
, see [Reference MumfordMum08, §12, Theorem 2].◻
$G$
, see [Reference MumfordMum08, §12, Theorem 2].◻
5.1 Dual cyclic groups
Theorem 5.1.1. Let
![]() $p$
be a prime, and
$p$
be a prime, and
![]() $G=\unicode[STIX]{x1D707}_{p^{r}}$
for some integer
$G=\unicode[STIX]{x1D707}_{p^{r}}$
for some integer
![]() $r$
. Let
$r$
. Let
![]() $X$
be a projective variety with a
$X$
be a projective variety with a
![]() $G$
-action such that
$G$
-action such that
![]() $X^{G}=\varnothing$
. Then the Euler characteristic
$X^{G}=\varnothing$
. Then the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is divisible by
${\mathcal{F}}$
is divisible by
![]() $p$
.
$p$
.
Proof. We may assume that
![]() $X\neq \varnothing$
. Then
$X\neq \varnothing$
. Then
![]() $r\geqslant 1$
, and
$r\geqslant 1$
, and
![]() $G$
contains a subgroup
$G$
contains a subgroup
![]() $H$
isomorphic to
$H$
isomorphic to
![]() $\unicode[STIX]{x1D707}_{p^{r-1}}$
. It follows from Proposition 5.1.3 below that
$\unicode[STIX]{x1D707}_{p^{r-1}}$
. It follows from Proposition 5.1.3 below that
![]() $(X/H)^{G/H}=(X/H)^{G}=\varnothing$
. Let
$(X/H)^{G/H}=(X/H)^{G}=\varnothing$
. Let
![]() $\unicode[STIX]{x1D713}:X\rightarrow X/H$
be the quotient morphism. By Lemma 5.1.2 below, there is a
$\unicode[STIX]{x1D713}:X\rightarrow X/H$
be the quotient morphism. By Lemma 5.1.2 below, there is a
![]() $G/H$
-equivariant coherent
$G/H$
-equivariant coherent
![]() ${\mathcal{O}}_{X/H}$
-module
${\mathcal{O}}_{X/H}$
-module
![]() ${\mathcal{G}}$
such that
${\mathcal{G}}$
such that
![]() $\unicode[STIX]{x1D712}(X/H,{\mathcal{G}})$
is congruent modulo
$\unicode[STIX]{x1D712}(X/H,{\mathcal{G}})$
is congruent modulo
![]() $p$
to
$p$
to
![]() $\unicode[STIX]{x1D712}(X/H,\unicode[STIX]{x1D713}_{\ast }{\mathcal{F}})=\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
. Replacing the variety
$\unicode[STIX]{x1D712}(X/H,\unicode[STIX]{x1D713}_{\ast }{\mathcal{F}})=\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
. Replacing the variety
![]() $X$
with
$X$
with
![]() $X/H$
, the group
$X/H$
, the group
![]() $G$
with
$G$
with
![]() $G/H$
, and the module
$G/H$
, and the module
![]() ${\mathcal{F}}$
with
${\mathcal{F}}$
with
![]() ${\mathcal{G}}$
, we may assume that
${\mathcal{G}}$
, we may assume that
![]() $G=\unicode[STIX]{x1D707}_{p}$
. Then
$G=\unicode[STIX]{x1D707}_{p}$
. Then
![]() $G$
acts freely on
$G$
acts freely on
![]() $X$
by Lemma 2.3.4, and the theorem follows from Proposition 5.0.1.◻
$X$
by Lemma 2.3.4, and the theorem follows from Proposition 5.0.1.◻
Lemma 5.1.2. Let
![]() $G$
be an algebraic group acting on a projective variety
$G$
be an algebraic group acting on a projective variety
![]() $X$
. Let
$X$
. Let
![]() $D$
be a diagonalisable central subgroup of
$D$
be a diagonalisable central subgroup of
![]() $G$
acting trivially on
$G$
acting trivially on
![]() $X$
. Then for any prime
$X$
. Then for any prime
![]() $p$
and any
$p$
and any
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
, we may find a
${\mathcal{F}}$
, we may find a
![]() $G/D$
-equivariant coherent
$G/D$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{G}}$
such that
${\mathcal{G}}$
such that
Proof. By Lemma 2.4.5 we may assume that the
![]() $\widehat{D}$
-grading of
$\widehat{D}$
-grading of
![]() ${\mathcal{F}}$
is concentrated in a single degree
${\mathcal{F}}$
is concentrated in a single degree
![]() $d\in \widehat{D}$
. If
$d\in \widehat{D}$
. If
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
is divisible by
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
is divisible by
![]() $p$
, we may simply take
$p$
, we may simply take
![]() ${\mathcal{G}}=0$
. Otherwise by the definition (3.1a) there is an integer
${\mathcal{G}}=0$
. Otherwise by the definition (3.1a) there is an integer
![]() $i$
such that
$i$
such that
![]() $\dim _{k}H^{i}(X,{\mathcal{F}})$
is prime to
$\dim _{k}H^{i}(X,{\mathcal{F}})$
is prime to
![]() $p$
. Then
$p$
. Then
![]() $V=H^{i}(X,{\mathcal{F}})$
is a
$V=H^{i}(X,{\mathcal{F}})$
is a
![]() $G$
-representation whose induced
$G$
-representation whose induced
![]() $\widehat{D}$
-grading is concentrated in degree
$\widehat{D}$
-grading is concentrated in degree
![]() $d$
. The group
$d$
. The group
![]() $D$
acts trivially on the
$D$
acts trivially on the
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}\otimes _{k}V^{\vee }$
, and the integer
${\mathcal{F}}\otimes _{k}V^{\vee }$
, and the integer
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}}\otimes _{k}V^{\vee })=\unicode[STIX]{x1D712}(X,{\mathcal{F}})\cdot \dim _{k}V^{\vee }$
is prime to
$\unicode[STIX]{x1D712}(X,{\mathcal{F}}\otimes _{k}V^{\vee })=\unicode[STIX]{x1D712}(X,{\mathcal{F}})\cdot \dim _{k}V^{\vee }$
is prime to
![]() $p$
. We may thus construct
$p$
. We may thus construct
![]() ${\mathcal{G}}$
as a direct sum of copies of
${\mathcal{G}}$
as a direct sum of copies of
![]() ${\mathcal{F}}\otimes _{k}V^{\vee }$
.◻
${\mathcal{F}}\otimes _{k}V^{\vee }$
.◻
Proposition 5.1.3. Let
![]() $p$
be a prime, and
$p$
be a prime, and
![]() $G=\unicode[STIX]{x1D707}_{p^{r}}$
for some integer
$G=\unicode[STIX]{x1D707}_{p^{r}}$
for some integer
![]() $r$
. Let
$r$
. Let
![]() $X$
be a variety with a
$X$
be a variety with a
![]() $G$
-action and
$G$
-action and
![]() $H$
a subgroup of
$H$
a subgroup of
![]() $G$
such that
$G$
such that
![]() $H\neq G$
. Then the morphism
$H\neq G$
. Then the morphism
![]() $X^{G}\rightarrow (X/H)^{G}$
is surjective.
$X^{G}\rightarrow (X/H)^{G}$
is surjective.
Proof. Let us write
![]() $Y=X/H$
. Let
$Y=X/H$
. Let
![]() $y\in Y^{G}(K)$
for some algebraically closed field extension
$y\in Y^{G}(K)$
for some algebraically closed field extension
![]() $K$
of
$K$
of
![]() $k$
with trivial
$k$
with trivial
![]() $G$
-action. We may lift
$G$
-action. We may lift
![]() $y\in Y(K)$
to a point
$y\in Y(K)$
to a point
![]() $x\in X(K)$
, and it will suffice to prove that
$x\in X(K)$
, and it will suffice to prove that
![]() $x\in X^{G}(K)$
. To do so, we may assume that
$x\in X^{G}(K)$
. To do so, we may assume that
![]() $X=\operatorname{Spec}A$
. Then we have a
$X=\operatorname{Spec}A$
. Then we have a
![]() $k$
-algebra morphism
$k$
-algebra morphism
![]() $f:A\rightarrow K$
whose restriction
$f:A\rightarrow K$
whose restriction
![]() $A^{H}\rightarrow K$
(see (2.2a)) induces a
$A^{H}\rightarrow K$
(see (2.2a)) induces a
![]() $G$
-equivariant morphism (of schemes), and want prove that
$G$
-equivariant morphism (of schemes), and want prove that
![]() $f$
induces a
$f$
induces a
![]() $G$
-equivariant morphism.
$G$
-equivariant morphism.
A
![]() $G$
-action on
$G$
-action on
![]() $\operatorname{Spec}A$
is a
$\operatorname{Spec}A$
is a
![]() $k$
-vector space decomposition
$k$
-vector space decomposition
![]() $A=\bigoplus _{i\in \mathbb{Z}/p^{r}}A_{i}$
such that
$A=\bigoplus _{i\in \mathbb{Z}/p^{r}}A_{i}$
such that
![]() $A_{i}\cdot A_{j}\subset A_{i+j}$
(see § 2.1.3). The group
$A_{i}\cdot A_{j}\subset A_{i+j}$
(see § 2.1.3). The group
![]() $H^{\ast }=\ker (\mathbb{Z}/p^{r}\rightarrow \widehat{H})$
is nontrivial by the assumption
$H^{\ast }=\ker (\mathbb{Z}/p^{r}\rightarrow \widehat{H})$
is nontrivial by the assumption
![]() $H\neq G$
, and we have
$H\neq G$
, and we have
![]() $A^{H}=\bigoplus _{j\in H^{\ast }}A_{j}$
. The assumption that
$A^{H}=\bigoplus _{j\in H^{\ast }}A_{j}$
. The assumption that
![]() $f|_{A^{H}}$
induces a
$f|_{A^{H}}$
induces a
![]() $G$
-equivariant morphism means that
$G$
-equivariant morphism means that
![]() $f|_{A_{j}}=0$
whenever
$f|_{A_{j}}=0$
whenever
![]() $j\in H^{\ast }-\{0\}$
. Now let
$j\in H^{\ast }-\{0\}$
. Now let
![]() $i\in \mathbb{Z}/p^{r}-\{0\}$
and
$i\in \mathbb{Z}/p^{r}-\{0\}$
and
![]() $a\in A_{i}$
. Since any two nontrivial subgroups of a cyclic
$a\in A_{i}$
. Since any two nontrivial subgroups of a cyclic
![]() $p$
-group must have a nontrivial intersection, we may find an integer
$p$
-group must have a nontrivial intersection, we may find an integer
![]() $n$
such that
$n$
such that
![]() $ni\in H^{\ast }-\{0\}$
. Then
$ni\in H^{\ast }-\{0\}$
. Then
![]() $a^{n}\in A_{ni}$
with
$a^{n}\in A_{ni}$
with
![]() $ni\in H^{\ast }-\{0\}$
, hence
$ni\in H^{\ast }-\{0\}$
, hence
![]() $0=f(a^{n})=f(a)^{n}$
. Since
$0=f(a^{n})=f(a)^{n}$
. Since
![]() $K$
is a field, we conclude that
$K$
is a field, we conclude that
![]() $f(a)=0$
, proving that
$f(a)=0$
, proving that
![]() $f$
induces a
$f$
induces a
![]() $G$
-equivariant morphism.◻
$G$
-equivariant morphism.◻
Example 5.1.4. We define a group morphism
![]() $\unicode[STIX]{x1D707}_{p}\rightarrow \operatorname{GL}_{p}$
by mapping
$\unicode[STIX]{x1D707}_{p}\rightarrow \operatorname{GL}_{p}$
by mapping
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{p}(R)$
for a
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{p}(R)$
for a
![]() $k$
-algebra
$k$
-algebra
![]() $R$
to the diagonal matrix with coefficients
$R$
to the diagonal matrix with coefficients
![]() $1,\unicode[STIX]{x1D709},\ldots ,\unicode[STIX]{x1D709}^{p-1}$
. This induces an action of
$1,\unicode[STIX]{x1D709},\ldots ,\unicode[STIX]{x1D709}^{p-1}$
. This induces an action of
![]() $\unicode[STIX]{x1D707}_{p}$
on
$\unicode[STIX]{x1D707}_{p}$
on
![]() $X=\mathbb{P}^{p-1}$
. If
$X=\mathbb{P}^{p-1}$
. If
![]() $K$
is a field extension of
$K$
is a field extension of
![]() $k$
, then
$k$
, then
![]() $X^{\unicode[STIX]{x1D707}_{p}}(K)$
consists of the
$X^{\unicode[STIX]{x1D707}_{p}}(K)$
consists of the
![]() $p$
points
$p$
points
![]() $[1:0:\cdots :0],[0:1:0\cdots :0],\ldots ,[0:\cdots :0:1]$
.
$[1:0:\cdots :0],[0:1:0\cdots :0],\ldots ,[0:\cdots :0:1]$
.
We define a group morphism
![]() $(\mathbb{Z}/p)_{k}\rightarrow \operatorname{GL}_{p}$
by mapping the generator to the automorphism
$(\mathbb{Z}/p)_{k}\rightarrow \operatorname{GL}_{p}$
by mapping the generator to the automorphism
![]() $(x_{0},\ldots ,x_{p-1})\mapsto (x_{1},\ldots ,x_{p-1},x_{0})$
. This induces an action of
$(x_{0},\ldots ,x_{p-1})\mapsto (x_{1},\ldots ,x_{p-1},x_{0})$
. This induces an action of
![]() $(\mathbb{Z}/p)_{k}$
on
$(\mathbb{Z}/p)_{k}$
on
![]() $X$
. If
$X$
. If
![]() $K$
is a field extension of
$K$
is a field extension of
![]() $k$
, then
$k$
, then
![]() $X^{(\mathbb{Z}/p)_{k}}(K)=\{[1:\unicode[STIX]{x1D709}:\cdots :\unicode[STIX]{x1D709}^{p-1}]|\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{p}(K)\}$
.
$X^{(\mathbb{Z}/p)_{k}}(K)=\{[1:\unicode[STIX]{x1D709}:\cdots :\unicode[STIX]{x1D709}^{p-1}]|\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{p}(K)\}$
.
The two actions commute, inducing an action of
![]() $G=\unicode[STIX]{x1D707}_{p}\times (\mathbb{Z}/p)_{k}$
on
$G=\unicode[STIX]{x1D707}_{p}\times (\mathbb{Z}/p)_{k}$
on
![]() $X$
such that
$X$
such that
![]() $X^{G}=\varnothing$
, while
$X^{G}=\varnothing$
, while
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
is prime to
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
is prime to
![]() $p$
.
$p$
.
Example 5.1.5. Assume that the field
![]() $k$
is algebraically closed of characteristic
$k$
is algebraically closed of characteristic
![]() $\neq p$
. Let
$\neq p$
. Let
![]() $G$
be a constant abelian noncyclic
$G$
be a constant abelian noncyclic
![]() $p$
-group. Then
$p$
-group. Then
![]() $G$
admits a quotient isomorphic to
$G$
admits a quotient isomorphic to
![]() $(\mathbb{Z}/p)_{k}\times (\mathbb{Z}/p)_{k}$
and thus to
$(\mathbb{Z}/p)_{k}\times (\mathbb{Z}/p)_{k}$
and thus to
![]() $\unicode[STIX]{x1D707}_{p}\times (\mathbb{Z}/p)_{k}$
by our assumptions on
$\unicode[STIX]{x1D707}_{p}\times (\mathbb{Z}/p)_{k}$
by our assumptions on
![]() $k$
. Therefore by Example 5.1.4 the group
$k$
. Therefore by Example 5.1.4 the group
![]() $G$
acts without fixed point on
$G$
acts without fixed point on
![]() $\mathbb{P}^{p-1}$
, and
$\mathbb{P}^{p-1}$
, and
![]() $\unicode[STIX]{x1D712}(\mathbb{P}^{p-1},{\mathcal{O}}_{\mathbb{P}^{p-1}})$
is prime to
$\unicode[STIX]{x1D712}(\mathbb{P}^{p-1},{\mathcal{O}}_{\mathbb{P}^{p-1}})$
is prime to
![]() $p$
.
$p$
.
The next two examples show that in Theorem 5.1.1 the assumption ‘
![]() $X^{G}=\varnothing$
’ may not be weakened to the assumption ‘every closed point of
$X^{G}=\varnothing$
’ may not be weakened to the assumption ‘every closed point of
![]() $X^{G}$
has degree divisible by
$X^{G}$
has degree divisible by
![]() $p$
’.
$p$
’.
Example 5.1.6. Let
![]() $X$
be the Severi–Brauer variety of a finite-dimensional central division
$X$
be the Severi–Brauer variety of a finite-dimensional central division
![]() $k$
-algebra of degree
$k$
-algebra of degree
![]() $p$
. Let a
$p$
. Let a
![]() $p$
-group
$p$
-group
![]() $G$
act trivially on
$G$
act trivially on
![]() $X$
. Then
$X$
. Then
![]() $\dim X=p-1$
and the degree of every closed point of
$\dim X=p-1$
and the degree of every closed point of
![]() $X^{G}$
is divisible by
$X^{G}$
is divisible by
![]() $p$
, but
$p$
, but
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
.
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
.
Example 5.1.7. For a less degenerate example, assume that an element
![]() $a\in k-k^{p}$
exists. The automorphism
$a\in k-k^{p}$
exists. The automorphism
![]() $(x_{0},\ldots ,x_{p-1})\mapsto (x_{1},\ldots ,x_{p-1},ax_{0})$
in
$(x_{0},\ldots ,x_{p-1})\mapsto (x_{1},\ldots ,x_{p-1},ax_{0})$
in
![]() $\operatorname{GL}_{p}(k)$
maps to an element of order
$\operatorname{GL}_{p}(k)$
maps to an element of order
![]() $p$
in
$p$
in
![]() $\operatorname{PGL}_{p}(k)$
. This defines an action of
$\operatorname{PGL}_{p}(k)$
. This defines an action of
![]() $(\mathbb{Z}/p)_{k}$
on
$(\mathbb{Z}/p)_{k}$
on
![]() $X=\mathbb{P}^{p-1}$
. The fixed locus
$X=\mathbb{P}^{p-1}$
. The fixed locus
![]() $X^{(\mathbb{Z}/p)_{k}}$
is supported on the closed point
$X^{(\mathbb{Z}/p)_{k}}$
is supported on the closed point
![]() $\{[1:z:\cdots :z^{p-1}]|z^{p}=a\}$
of degree
$\{[1:z:\cdots :z^{p-1}]|z^{p}=a\}$
of degree
![]() $p$
. Thus
$p$
. Thus
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
is not the degree of a zero-cycle supported on
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=1$
is not the degree of a zero-cycle supported on
![]() $X^{(\mathbb{Z}/p)_{k}}$
.
$X^{(\mathbb{Z}/p)_{k}}$
.
5.2 Varieties of small dimension
Let us consider the morphism (see § 3.4)
Proposition 5.2.1. Let
![]() $G$
be a finite algebraic group acting on a projective variety
$G$
be a finite algebraic group acting on a projective variety
![]() $X$
. Assume that
$X$
. Assume that
![]() $G$
contains
$G$
contains
![]() $\unicode[STIX]{x1D707}_{p}$
as a central subgroup. If
$\unicode[STIX]{x1D707}_{p}$
as a central subgroup. If
![]() $\dim X<p-1$
, then
$\dim X<p-1$
, then
Proof. The action of
![]() $\unicode[STIX]{x1D707}_{p}$
on
$\unicode[STIX]{x1D707}_{p}$
on
![]() $U=X-X^{\unicode[STIX]{x1D707}_{p}}$
is free by Lemma 2.3.4. Let
$U=X-X^{\unicode[STIX]{x1D707}_{p}}$
is free by Lemma 2.3.4. Let
![]() $\unicode[STIX]{x1D719}:U\rightarrow U/\unicode[STIX]{x1D707}_{p}$
be the quotient morphism. The
$\unicode[STIX]{x1D719}:U\rightarrow U/\unicode[STIX]{x1D707}_{p}$
be the quotient morphism. The
![]() $\mathbb{Z}/p$
-grading
$\mathbb{Z}/p$
-grading
![]() $\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}=\bigoplus _{n\in \mathbb{Z}/p}(\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{n}$
is compatible with the
$\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}=\bigoplus _{n\in \mathbb{Z}/p}(\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{n}$
is compatible with the
![]() $G$
-equivariant structure of
$G$
-equivariant structure of
![]() $\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}$
by Lemma 2.4.5. By [Reference Demazure and GrothendieckSGA31
, VIII, Proposition 4.1] the
$\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}$
by Lemma 2.4.5. By [Reference Demazure and GrothendieckSGA31
, VIII, Proposition 4.1] the
![]() $G$
-equivariant
$G$
-equivariant
![]() ${\mathcal{O}}_{U/\unicode[STIX]{x1D707}_{p}}$
-module
${\mathcal{O}}_{U/\unicode[STIX]{x1D707}_{p}}$
-module
![]() ${\mathcal{L}}=(\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{1}$
is invertible, and for
${\mathcal{L}}=(\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{1}$
is invertible, and for
![]() $i\in \mathbb{Z}$
, the morphism
$i\in \mathbb{Z}$
, the morphism
![]() ${\mathcal{L}}^{\,\otimes \,i}\rightarrow (\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{i~\text{mod}~p}$
is an isomorphism; in addition it is
${\mathcal{L}}^{\,\otimes \,i}\rightarrow (\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U})_{i~\text{mod}~p}$
is an isomorphism; in addition it is
![]() $G$
-equivariant, since the product morphism of the ring
$G$
-equivariant, since the product morphism of the ring
![]() $\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}$
is
$\unicode[STIX]{x1D719}_{\ast }{\mathcal{O}}_{U}$
is
![]() $G$
-equivariant. We thus obtain a
$G$
-equivariant. We thus obtain a
![]() $G$
-equivariant decomposition
$G$
-equivariant decomposition
Let
![]() $\unicode[STIX]{x1D6FC}\in K_{G}(X)$
. Consider the following commutative diagram.
$\unicode[STIX]{x1D6FC}\in K_{G}(X)$
. Consider the following commutative diagram.

Since the upper horizontal and left vertical morphisms are surjective, respectively by Lemma 3.4.4 and Proposition 3.1.5, it follows that the right vertical morphism is surjective as well. Thus we may find
![]() $\unicode[STIX]{x1D6FD}\in K_{G}(U/\unicode[STIX]{x1D707}_{p})$
such that
$\unicode[STIX]{x1D6FD}\in K_{G}(U/\unicode[STIX]{x1D707}_{p})$
such that
![]() $\unicode[STIX]{x1D719}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}|_{U}\in K_{G}(U)$
. By the projection formula [Reference Berthelot, Grothendieck and IllusieSGA6, IV, (2.12.4)] and the decomposition (5.2a), we have in
$\unicode[STIX]{x1D719}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}|_{U}\in K_{G}(U)$
. By the projection formula [Reference Berthelot, Grothendieck and IllusieSGA6, IV, (2.12.4)] and the decomposition (5.2a), we have in
![]() $K_{G}(U/\unicode[STIX]{x1D707}_{p})$
$K_{G}(U/\unicode[STIX]{x1D707}_{p})$
There is a polynomial
![]() $Q$
with integral coefficients such that we have in
$Q$
with integral coefficients such that we have in
![]() $K_{0}(U/\unicode[STIX]{x1D707}_{p};G)$
$K_{0}(U/\unicode[STIX]{x1D707}_{p};G)$
Since
![]() $(1-[{\mathcal{L}}])\cap K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(n)}\subset K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(n-1)}$
for every
$(1-[{\mathcal{L}}])\cap K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(n)}\subset K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(n-1)}$
for every
![]() $n$
(see [Reference Fulton and LangFL85, VI, Proposition 5.2] or [Reference Berthelot, Grothendieck and IllusieSGA6, X, Théorème 1.3.2]), and
$n$
(see [Reference Fulton and LangFL85, VI, Proposition 5.2] or [Reference Berthelot, Grothendieck and IllusieSGA6, X, Théorème 1.3.2]), and
![]() $\dim U/\unicode[STIX]{x1D707}_{p}\leqslant p-2$
, we have
$\dim U/\unicode[STIX]{x1D707}_{p}\leqslant p-2$
, we have
![]() $(1-[{\mathcal{L}}])^{p-1}\,\cap \,\unicode[STIX]{x1D6FD}\in K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(-1)}=0$
, and the combination of (5.2b) and (5.2c) yields
$(1-[{\mathcal{L}}])^{p-1}\,\cap \,\unicode[STIX]{x1D6FD}\in K_{G}(U/\unicode[STIX]{x1D707}_{p})_{(-1)}=0$
, and the combination of (5.2b) and (5.2c) yields
By Lemma 3.4.5 we can find
![]() $y\in K_{G}(X/\unicode[STIX]{x1D707}_{p})$
such that
$y\in K_{G}(X/\unicode[STIX]{x1D707}_{p})$
such that
![]() $\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-py$
restricts to zero in
$\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-py$
restricts to zero in
![]() $K_{G}(U/\unicode[STIX]{x1D707}_{p})$
, where
$K_{G}(U/\unicode[STIX]{x1D707}_{p})$
, where
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/\unicode[STIX]{x1D707}_{p}$
denotes the quotient morphism. The morphism
$\unicode[STIX]{x1D711}:X\rightarrow X/\unicode[STIX]{x1D707}_{p}$
denotes the quotient morphism. The morphism
![]() $i:X^{\unicode[STIX]{x1D707}_{p}}\rightarrow X/\unicode[STIX]{x1D707}_{p}$
is a closed immersion by [Reference HautionHau16, (3.2.3(ii))], with open complement
$i:X^{\unicode[STIX]{x1D707}_{p}}\rightarrow X/\unicode[STIX]{x1D707}_{p}$
is a closed immersion by [Reference HautionHau16, (3.2.3(ii))], with open complement
![]() $U/\unicode[STIX]{x1D707}_{p}$
. By Lemma 3.4.5 we may find
$U/\unicode[STIX]{x1D707}_{p}$
. By Lemma 3.4.5 we may find
![]() $z\in K_{G}(X^{\unicode[STIX]{x1D707}_{p}})$
such that
$z\in K_{G}(X^{\unicode[STIX]{x1D707}_{p}})$
such that
![]() $i_{\ast }(z)=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-py$
. To finish, observe that
$i_{\ast }(z)=\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-py$
. To finish, observe that
Proposition 5.2.2. Let
![]() $X$
be a projective variety such that
$X$
be a projective variety such that
![]() $\dim X<p-1$
. Then the Euler characteristic
$\dim X<p-1$
. Then the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any coherent
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is congruent modulo
${\mathcal{F}}$
is congruent modulo
![]() $p$
to the degree of some zero-cycle supported on
$p$
to the degree of some zero-cycle supported on
![]() $X$
.
$X$
.
Proof. The group
![]() $K_{0}^{\prime }(X)$
is generated by classes
$K_{0}^{\prime }(X)$
is generated by classes
![]() $[{\mathcal{O}}_{Z}]$
for
$[{\mathcal{O}}_{Z}]$
for
![]() $Z$
a closed subscheme of
$Z$
a closed subscheme of
![]() $X$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, Corollaire 1.1.4]). By [Reference HautionHau12, Proposition 9.1], for such
$X$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, Corollaire 1.1.4]). By [Reference HautionHau12, Proposition 9.1], for such
![]() $Z$
the integer
$Z$
the integer
![]() $\unicode[STIX]{x1D712}(Z,{\mathcal{O}}_{Z})$
is congruent modulo
$\unicode[STIX]{x1D712}(Z,{\mathcal{O}}_{Z})$
is congruent modulo
![]() $p$
to the degree of some zero-cycle supported on
$p$
to the degree of some zero-cycle supported on
![]() $Z$
, and in particular on
$Z$
, and in particular on
![]() $X$
.◻
$X$
.◻
Theorem 5.2.3. Let
![]() $G$
be a finite algebraic
$G$
be a finite algebraic
![]() $p$
-group acting on a projective variety
$p$
-group acting on a projective variety
![]() $X$
. Assume that the degree of every closed point of
$X$
. Assume that the degree of every closed point of
![]() $X^{G}$
is divisible by
$X^{G}$
is divisible by
![]() $p$
. If
$p$
. If
![]() $\operatorname{char}k=p$
, assume that there are normal subgroups
$\operatorname{char}k=p$
, assume that there are normal subgroups
![]() $1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that the subgroup
$1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that the subgroup
![]() $G_{i}/G_{i-1}$
is central in
$G_{i}/G_{i-1}$
is central in
![]() $G/G_{i-1}$
and isomorphic to
$G/G_{i-1}$
and isomorphic to
![]() $\unicode[STIX]{x1D707}_{p}$
, for
$\unicode[STIX]{x1D707}_{p}$
, for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
(i) If
 $\dim X<p-1$
, then the Euler characteristic
$\dim X<p-1$
, then the Euler characteristic
 $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
 $G$
-equivariant coherent
$G$
-equivariant coherent
 ${\mathcal{O}}_{X}$
-module is divisible by
${\mathcal{O}}_{X}$
-module is divisible by
 $p$
.
$p$
.(ii) If
 $\dim X<p-1$
, then the morphism
$\dim X<p-1$
, then the morphism
 $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero.
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero.(iii) If
 $\dim X<p$
and
$\dim X<p$
and
 $X$
is smooth, then any Chern number (§ 1.1) of
$X$
is smooth, then any Chern number (§ 1.1) of
 $X$
is divisible by
$X$
is divisible by
 $p$
.
$p$
.
Proof. Let us first assume that
![]() $\operatorname{char}k\neq p$
. In order to prove the theorem, we may replace
$\operatorname{char}k\neq p$
. In order to prove the theorem, we may replace
![]() $k$
with an extension of degree prime to
$k$
with an extension of degree prime to
![]() $p$
. Applying Lemma 5.2.4 recursively and extending scalars, we obtain normal subgroups
$p$
. Applying Lemma 5.2.4 recursively and extending scalars, we obtain normal subgroups
![]() $1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that
$1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that
![]() $G_{i}/G_{i-1}$
is central in
$G_{i}/G_{i-1}$
is central in
![]() $G/G_{i-1}$
and isomorphic to
$G/G_{i-1}$
and isomorphic to
![]() $(\mathbb{Z}/p)_{k}$
. Enlarging once more the field
$(\mathbb{Z}/p)_{k}$
. Enlarging once more the field
![]() $k$
, we may assume that it contains a nontrivial
$k$
, we may assume that it contains a nontrivial
![]() $p$
th root of unity, so that
$p$
th root of unity, so that
![]() $(\mathbb{Z}/p)_{k}\simeq \unicode[STIX]{x1D707}_{p}$
.
$(\mathbb{Z}/p)_{k}\simeq \unicode[STIX]{x1D707}_{p}$
.
It will thus suffice to prove the theorem when the characteristic of
![]() $k$
is arbitrary, assuming that
$k$
is arbitrary, assuming that
![]() $G$
admits normal subgroups
$G$
admits normal subgroups
![]() $1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that the subgroup
$1=G_{0}\subset G_{1}\subset \cdots \subset G_{n}=G$
such that the subgroup
![]() $G_{i}/G_{i-1}$
is central in
$G_{i}/G_{i-1}$
is central in
![]() $G/G_{i-1}$
and isomorphic to
$G/G_{i-1}$
and isomorphic to
![]() $\unicode[STIX]{x1D707}_{p}$
.
$\unicode[STIX]{x1D707}_{p}$
.
Assume that
![]() $\dim X<p-1$
. We prove by descending induction on
$\dim X<p-1$
. We prove by descending induction on
![]() $i=n,\ldots ,0$
that
$i=n,\ldots ,0$
that
If
![]() $i=n$
, then
$i=n$
, then
![]() $G=G_{n}$
, and
$G=G_{n}$
, and
![]() $\unicode[STIX]{x1D6FF}(K_{G/G_{n}}(X^{G}))$
is contained in the image of
$\unicode[STIX]{x1D6FF}(K_{G/G_{n}}(X^{G}))$
is contained in the image of
![]() $K_{0}^{\prime }(X^{G})\xrightarrow[{}]{\unicode[STIX]{x1D712}(X,-)}\mathbb{Z}\rightarrow \mathbb{F}_{p}$
. The latter is zero by Proposition 5.2.2 and the assumption on
$K_{0}^{\prime }(X^{G})\xrightarrow[{}]{\unicode[STIX]{x1D712}(X,-)}\mathbb{Z}\rightarrow \mathbb{F}_{p}$
. The latter is zero by Proposition 5.2.2 and the assumption on
![]() $X^{G}$
, so that (5.2d) holds for
$X^{G}$
, so that (5.2d) holds for
![]() $i=n$
. Now (5.2d) follows by induction, since for
$i=n$
. Now (5.2d) follows by induction, since for
![]() $i\in \{1,\ldots ,n\}$
we have
$i\in \{1,\ldots ,n\}$
we have
Indeed, the first equality follows by applying Proposition 5.2.1 to the central subgroup
![]() $G_{i}/G_{i-1}\simeq \unicode[STIX]{x1D707}_{p}$
of
$G_{i}/G_{i-1}\simeq \unicode[STIX]{x1D707}_{p}$
of
![]() $G/G_{i-1}$
acting on the variety
$G/G_{i-1}$
acting on the variety
![]() $X^{G_{i-1}}$
. The second equality follows from Lemma 5.1.2, since the diagonalisable central subgroup
$X^{G_{i-1}}$
. The second equality follows from Lemma 5.1.2, since the diagonalisable central subgroup
![]() $G_{i}/G_{i-1}\simeq \unicode[STIX]{x1D707}_{p}$
of
$G_{i}/G_{i-1}\simeq \unicode[STIX]{x1D707}_{p}$
of
![]() $G/G_{i-1}$
acts trivially on the variety
$G/G_{i-1}$
acts trivially on the variety
![]() $X^{G_{i}}$
.
$X^{G_{i}}$
.
Taking
![]() $i=0$
in (5.2d), we obtain
$i=0$
in (5.2d), we obtain
![]() $\unicode[STIX]{x1D6FF}(K_{G}(X))=0$
. Since the morphism
$\unicode[STIX]{x1D6FF}(K_{G}(X))=0$
. Since the morphism
![]() $K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
factors through
$K_{0}^{\prime }(X;G)\rightarrow K_{0}^{\prime }(X)$
factors through
![]() $K_{G}(X)$
, we have proved (i).
$K_{G}(X)$
, we have proved (i).
Using the notation of § 3.4, the morphism
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
factors as
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
factors as
The last isomorphism follows from Lemma 3.3.1 (in view of [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 52.9]), and the first from [Reference Edidin and GrahamEG98, Proposition 8(a)] (since
![]() $G$
acts freely on
$G$
acts freely on
![]() $X\times \,T$
). Consider the composite
$X\times \,T$
). Consider the composite
Since
![]() $\dim T=0$
, we have
$\dim T=0$
, we have
![]() $\unicode[STIX]{x1D6E5}(\operatorname{CH}_{d}((X\times \,T)/G))=0$
unless
$\unicode[STIX]{x1D6E5}(\operatorname{CH}_{d}((X\times \,T)/G))=0$
unless
![]() $d=0$
. Thus in order to prove (ii), it will suffice to consider a zero-dimensional closed subscheme
$d=0$
. Thus in order to prove (ii), it will suffice to consider a zero-dimensional closed subscheme
![]() $Z$
of
$Z$
of
![]() $(X\times T)/G$
, and prove that
$(X\times T)/G$
, and prove that
![]() $\unicode[STIX]{x1D6E5}[Z]=0$
. But for such
$\unicode[STIX]{x1D6E5}[Z]=0$
. But for such
![]() $Z$
, we have
$Z$
, we have
![]() $\unicode[STIX]{x1D6E5}[Z]=\unicode[STIX]{x1D6FF}[{\mathcal{O}}_{Z}]$
, which vanishes by (i).
$\unicode[STIX]{x1D6E5}[Z]=\unicode[STIX]{x1D6FF}[{\mathcal{O}}_{Z}]$
, which vanishes by (i).
We now prove (iii) by induction on the length
![]() $n$
of the central series. The statement is true if
$n$
of the central series. The statement is true if
![]() $n=0$
. Assume that
$n=0$
. Assume that
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $\dim X<p$
. Let
$\dim X<p$
. Let
![]() $Y$
be the scheme theoretic closure of
$Y$
be the scheme theoretic closure of
![]() $U=X-X^{G_{1}}$
in
$U=X-X^{G_{1}}$
in
![]() $X$
, and
$X$
, and
![]() $Z$
the open complement of
$Z$
the open complement of
![]() $Y$
. Then
$Y$
. Then
![]() $Y$
is the union of the connected components of
$Y$
is the union of the connected components of
![]() $X$
meeting
$X$
meeting
![]() $U$
(as
$U$
(as
![]() $X$
is smooth), hence is open in
$X$
is smooth), hence is open in
![]() $X$
. Thus
$X$
. Thus
![]() $X$
decomposes
$X$
decomposes
![]() $G$
-equivariantly as the disjoint union of the open subschemes
$G$
-equivariantly as the disjoint union of the open subschemes
![]() $Y$
and
$Y$
and
![]() $Z$
. Every Chern number of
$Z$
. Every Chern number of
![]() $X$
is the sum of a Chern number of
$X$
is the sum of a Chern number of
![]() $Y$
and one of
$Y$
and one of
![]() $Z$
. Applying the induction hypothesis to the
$Z$
. Applying the induction hypothesis to the
![]() $G/G_{1}$
-action on the variety
$G/G_{1}$
-action on the variety
![]() $Z$
(which is a closed subscheme of
$Z$
(which is a closed subscheme of
![]() $X^{G_{1}}$
by construction), we may replace
$X^{G_{1}}$
by construction), we may replace
![]() $X$
with
$X$
with
![]() $Y$
, and thus assume that
$Y$
, and thus assume that
![]() $\dim X^{G_{1}}<p-1$
. Since the tangent bundle of
$\dim X^{G_{1}}<p-1$
. Since the tangent bundle of
![]() $X$
is
$X$
is
![]() $G$
-equivariant by Remark 2.4.8, its Chern classes lie in the image of
$G$
-equivariant by Remark 2.4.8, its Chern classes lie in the image of
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
, hence it will suffice to prove that the composite
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)$
, hence it will suffice to prove that the composite
![]() $\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero. To do so, we proceed as in the proof of Proposition 5.2.1. The group
$\operatorname{CH}_{G}(X)\rightarrow \operatorname{CH}(X)\xrightarrow[{}]{\deg }\mathbb{F}_{p}$
is zero. To do so, we proceed as in the proof of Proposition 5.2.1. The group
![]() $G_{1}\simeq \unicode[STIX]{x1D707}_{p}$
acts freely on
$G_{1}\simeq \unicode[STIX]{x1D707}_{p}$
acts freely on
![]() $U$
by Lemma 2.3.4. Denote by
$U$
by Lemma 2.3.4. Denote by
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/G_{1}$
and
$\unicode[STIX]{x1D711}:X\rightarrow X/G_{1}$
and
![]() $\unicode[STIX]{x1D719}:U\rightarrow U/G_{1}$
be the quotient morphisms, and let
$\unicode[STIX]{x1D719}:U\rightarrow U/G_{1}$
be the quotient morphisms, and let
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{CH}_{G}(X)$
. Then the pull-back morphism
$\unicode[STIX]{x1D6FC}\in \operatorname{CH}_{G}(X)$
. Then the pull-back morphism
![]() $\unicode[STIX]{x1D719}^{\ast }:\operatorname{CH}_{G}(U/G_{1})\rightarrow \operatorname{CH}_{G}(U)$
is surjective by Lemma 3.2.5, so that we may find
$\unicode[STIX]{x1D719}^{\ast }:\operatorname{CH}_{G}(U/G_{1})\rightarrow \operatorname{CH}_{G}(U)$
is surjective by Lemma 3.2.5, so that we may find
![]() $\unicode[STIX]{x1D6FD}\in \operatorname{CH}_{G}(U/G_{1})$
such that
$\unicode[STIX]{x1D6FD}\in \operatorname{CH}_{G}(U/G_{1})$
such that
![]() $\unicode[STIX]{x1D719}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}|_{U}$
. By the localisation sequence of § 3.2.3, we may find
$\unicode[STIX]{x1D719}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}|_{U}$
. By the localisation sequence of § 3.2.3, we may find
![]() $\unicode[STIX]{x1D6FD}^{\prime }\in \operatorname{CH}_{G}(X/G_{1})$
such that
$\unicode[STIX]{x1D6FD}^{\prime }\in \operatorname{CH}_{G}(X/G_{1})$
such that
![]() $\unicode[STIX]{x1D6FD}^{\prime }|_{U/G_{1}}=\unicode[STIX]{x1D6FD}$
. Since the morphism
$\unicode[STIX]{x1D6FD}^{\prime }|_{U/G_{1}}=\unicode[STIX]{x1D6FD}$
. Since the morphism
![]() $\unicode[STIX]{x1D719}$
is flat and finite of degree
$\unicode[STIX]{x1D719}$
is flat and finite of degree
![]() $p$
by Proposition 2.3.2, the endomorphism
$p$
by Proposition 2.3.2, the endomorphism
![]() $\unicode[STIX]{x1D719}_{\ast }\circ \unicode[STIX]{x1D719}^{\ast }$
of
$\unicode[STIX]{x1D719}_{\ast }\circ \unicode[STIX]{x1D719}^{\ast }$
of
![]() $\operatorname{CH}_{G}(U/G_{1})$
is multiplication by
$\operatorname{CH}_{G}(U/G_{1})$
is multiplication by
![]() $p$
, and it follows that
$p$
, and it follows that
![]() $\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-p\unicode[STIX]{x1D6FD}^{\prime }$
restricts to zero in
$\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})-p\unicode[STIX]{x1D6FD}^{\prime }$
restricts to zero in
![]() $\operatorname{CH}_{G}(U/G_{1})$
. The morphism
$\operatorname{CH}_{G}(U/G_{1})$
. The morphism
![]() $i:X^{G_{1}}\rightarrow X/G_{1}$
is a closed immersion by [Reference HautionHau16, (3.2.3(ii))], with open complement
$i:X^{G_{1}}\rightarrow X/G_{1}$
is a closed immersion by [Reference HautionHau16, (3.2.3(ii))], with open complement
![]() $U/G_{1}$
. Using the localisation sequence of § 3.2.3, we see that
$U/G_{1}$
. Using the localisation sequence of § 3.2.3, we see that
![]() $\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})=p\unicode[STIX]{x1D6FD}^{\prime }+i_{\ast }(\unicode[STIX]{x1D6FE})$
for some
$\unicode[STIX]{x1D711}_{\ast }(\unicode[STIX]{x1D6FC})=p\unicode[STIX]{x1D6FD}^{\prime }+i_{\ast }(\unicode[STIX]{x1D6FE})$
for some
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{CH}_{G}(X^{G_{1}})$
. Since
$\unicode[STIX]{x1D6FE}\in \operatorname{CH}_{G}(X^{G_{1}})$
. Since
![]() $\dim X^{G_{1}}<p-1$
, we may finish the proof using (ii).◻
$\dim X^{G_{1}}<p-1$
, we may finish the proof using (ii).◻
Lemma 5.2.4. Let
![]() $G$
be an étale
$G$
be an étale
![]() $p$
-group satisfying
$p$
-group satisfying
![]() $G\neq 1$
. Then, after an extension of degree prime to
$G\neq 1$
. Then, after an extension of degree prime to
![]() $p$
of the base field, the algebraic group
$p$
of the base field, the algebraic group
![]() $G$
possesses a central subgroup isomorphic to the constant algebraic group
$G$
possesses a central subgroup isomorphic to the constant algebraic group
![]() $(\mathbb{Z}/p)_{k}$
.
$(\mathbb{Z}/p)_{k}$
.
Proof. Let
![]() $C$
be the centre of
$C$
be the centre of
![]() $G$
and
$G$
and
![]() $\overline{k}$
an algebraic closure of
$\overline{k}$
an algebraic closure of
![]() $k$
. Then the ordinary group
$k$
. Then the ordinary group
![]() $C(\overline{k})$
is the centre of the nontrivial ordinary
$C(\overline{k})$
is the centre of the nontrivial ordinary
![]() $p$
-group
$p$
-group
![]() $G(\overline{k})$
, hence is nontrivial. Thus the algebraic group
$G(\overline{k})$
, hence is nontrivial. Thus the algebraic group
![]() $C$
is nontrivial (and is again an étale
$C$
is nontrivial (and is again an étale
![]() $p$
-group). The open complement of the unit in
$p$
-group). The open complement of the unit in
![]() $C$
is a variety which is reduced and finite of degree prime to
$C$
is a variety which is reduced and finite of degree prime to
![]() $p$
, hence possesses a closed point of degree prime to
$p$
, hence possesses a closed point of degree prime to
![]() $p$
. Extending scalars, we may assume that the ordinary
$p$
. Extending scalars, we may assume that the ordinary
![]() $p$
-group
$p$
-group
![]() $C(k)$
is nontrivial, hence contains a subgroup isomorphic to
$C(k)$
is nontrivial, hence contains a subgroup isomorphic to
![]() $\mathbb{Z}/p$
, which implies that the algebraic group
$\mathbb{Z}/p$
, which implies that the algebraic group
![]() $C$
contains a subgroup isomorphic to the constant algebraic group
$C$
contains a subgroup isomorphic to the constant algebraic group
![]() $(\mathbb{Z}/p)_{k}$
.◻
$(\mathbb{Z}/p)_{k}$
.◻
5.3 Characteristic
 $p$
$p$
In the next statement it is necessary to assume that
![]() $k$
is perfect, as shown by Examples 5.1.6 and 5.1.7.
$k$
is perfect, as shown by Examples 5.1.6 and 5.1.7.
Theorem 5.3.1. Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $G$
be either a constant algebraic
$G$
be either a constant algebraic
![]() $p$
-group, or an extension of one by
$p$
-group, or an extension of one by
![]() $\unicode[STIX]{x1D6FC}_{p}$
. Let
$\unicode[STIX]{x1D6FC}_{p}$
. Let
![]() $X$
be a projective variety with a
$X$
be a projective variety with a
![]() $G$
-action such that the degree of every closed point of
$G$
-action such that the degree of every closed point of
![]() $X^{G}$
is divisible by
$X^{G}$
is divisible by
![]() $p$
. Then the Euler characteristic
$p$
. Then the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
is divisible by
${\mathcal{F}}$
is divisible by
![]() $p$
.
$p$
.
Proof. We proceed by induction on the order of
![]() $G$
. When the group
$G$
. When the group
![]() $G$
is trivial, the statement follows from Lemma 5.3.2 below. Note that referring to that result is unnecessary when
$G$
is trivial, the statement follows from Lemma 5.3.2 below. Note that referring to that result is unnecessary when
![]() $k$
is algebraically closed (in particular while proving Theorem 1.1.1): since the variety
$k$
is algebraically closed (in particular while proving Theorem 1.1.1): since the variety
![]() $X$
possesses no closed point of degree prime to
$X$
possesses no closed point of degree prime to
![]() $p$
, it must be empty, so that
$p$
, it must be empty, so that
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})=0$
.
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})=0$
.
If the group
![]() $G$
is nontrivial, it admits a normal subgroup
$G$
is nontrivial, it admits a normal subgroup
![]() $C$
isomorphic to
$C$
isomorphic to
![]() $\unicode[STIX]{x1D6FC}_{p}$
or
$\unicode[STIX]{x1D6FC}_{p}$
or
![]() $(\mathbb{Z}/p)_{k}$
, and such that
$(\mathbb{Z}/p)_{k}$
, and such that
![]() $G/C$
is a constant
$G/C$
is a constant
![]() $p$
-group. Let
$p$
-group. Let
![]() $Y$
be the scheme theoretic image of the composite morphism
$Y$
be the scheme theoretic image of the composite morphism
![]() $X^{C}\rightarrow X\rightarrow X/C$
, and denote by
$X^{C}\rightarrow X\rightarrow X/C$
, and denote by
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/C$
the quotient morphism. Let
$\unicode[STIX]{x1D711}:X\rightarrow X/C$
the quotient morphism. Let
![]() $U=\unicode[STIX]{x1D711}^{-1}(X/C-Y)$
, and
$U=\unicode[STIX]{x1D711}^{-1}(X/C-Y)$
, and
![]() $\unicode[STIX]{x1D713}:U\rightarrow U/C=X/C-Y$
the restriction of
$\unicode[STIX]{x1D713}:U\rightarrow U/C=X/C-Y$
the restriction of
![]() $\unicode[STIX]{x1D711}$
. Since
$\unicode[STIX]{x1D711}$
. Since
![]() $U^{C}=\varnothing$
, it follows from Lemma 2.3.4 that the group
$U^{C}=\varnothing$
, it follows from Lemma 2.3.4 that the group
![]() $C$
acts freely on
$C$
acts freely on
![]() $U$
. Thus by Proposition 3.1.5, there is an element
$U$
. Thus by Proposition 3.1.5, there is an element
![]() $\unicode[STIX]{x1D6FD}\in K_{0}^{\prime }(U/C;G)$
such that
$\unicode[STIX]{x1D6FD}\in K_{0}^{\prime }(U/C;G)$
such that
![]() $[{\mathcal{F}}]|_{U}=\unicode[STIX]{x1D713}^{\ast }(\unicode[STIX]{x1D6FD})$
in
$[{\mathcal{F}}]|_{U}=\unicode[STIX]{x1D713}^{\ast }(\unicode[STIX]{x1D6FD})$
in
![]() $K_{0}^{\prime }(U;G)$
. By Lemma 5.3.4, we have
$K_{0}^{\prime }(U;G)$
. By Lemma 5.3.4, we have
![]() $\unicode[STIX]{x1D713}_{\ast }([{\mathcal{F}}]|_{U})=p\unicode[STIX]{x1D6FD}\in K_{0}^{\prime }(U/C;G)$
. By the localisation sequence [Reference ThomasonTho87, Theorem 2.7], it follows that
$\unicode[STIX]{x1D713}_{\ast }([{\mathcal{F}}]|_{U})=p\unicode[STIX]{x1D6FD}\in K_{0}^{\prime }(U/C;G)$
. By the localisation sequence [Reference ThomasonTho87, Theorem 2.7], it follows that
![]() $\unicode[STIX]{x1D711}_{\ast }[{\mathcal{F}}]\in K_{0}^{\prime }(X/C;G)$
is modulo
$\unicode[STIX]{x1D711}_{\ast }[{\mathcal{F}}]\in K_{0}^{\prime }(X/C;G)$
is modulo
![]() $p$
the image of an element of
$p$
the image of an element of
![]() $K_{0}^{\prime }(Y;G)$
, and thus by Lemma 5.3.3 of
$K_{0}^{\prime }(Y;G)$
, and thus by Lemma 5.3.3 of
![]() $K_{0}^{\prime }(Y;G/C)$
. Since
$K_{0}^{\prime }(Y;G/C)$
. Since
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})=\unicode[STIX]{x1D712}(X/C,\unicode[STIX]{x1D711}_{\ast }{\mathcal{F}})$
, it will suffice to prove that
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})=\unicode[STIX]{x1D712}(X/C,\unicode[STIX]{x1D711}_{\ast }{\mathcal{F}})$
, it will suffice to prove that
![]() $\unicode[STIX]{x1D712}(Y,{\mathcal{E}})$
is divisible by
$\unicode[STIX]{x1D712}(Y,{\mathcal{E}})$
is divisible by
![]() $p$
for any
$p$
for any
![]() $G/C$
-equivariant coherent
$G/C$
-equivariant coherent
![]() ${\mathcal{O}}_{Y}$
-module
${\mathcal{O}}_{Y}$
-module
![]() ${\mathcal{E}}$
. To do so, it will suffice by induction to prove that the degree of any closed point
${\mathcal{E}}$
. To do so, it will suffice by induction to prove that the degree of any closed point
![]() $y\in Y^{G/C}$
is divisible by
$y\in Y^{G/C}$
is divisible by
![]() $p$
. The field
$p$
. The field
![]() $k(y)$
is perfect, being a finite extension of the perfect field
$k(y)$
is perfect, being a finite extension of the perfect field
![]() $k$
. The
$k$
. The
![]() $G/C$
-equivariant morphism
$G/C$
-equivariant morphism
![]() $X^{C}\rightarrow Y$
is surjective, and radicial by Lemma 2.2.5. Therefore by Lemma 5.3.5 (applied to the smooth group
$X^{C}\rightarrow Y$
is surjective, and radicial by Lemma 2.2.5. Therefore by Lemma 5.3.5 (applied to the smooth group
![]() $G/C$
) we may find a closed point of
$G/C$
) we may find a closed point of
![]() $(X^{C})^{G/C}=X^{G}$
(mapping to
$(X^{C})^{G/C}=X^{G}$
(mapping to
![]() $y$
) with residue field isomorphic to
$y$
) with residue field isomorphic to
![]() $k(y)$
, so that the degree of
$k(y)$
, so that the degree of
![]() $y$
must be divisible by
$y$
must be divisible by
![]() $p$
, by our assumption on
$p$
, by our assumption on
![]() $X^{G}$
.◻
$X^{G}$
.◻
The next lemma is due to Rost [Reference RostRos08, Corollary 1].
Lemma 5.3.2. Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $X$
be a projective variety, and
$X$
be a projective variety, and
![]() $n$
a positive integer. If the degree of every closed point of
$n$
a positive integer. If the degree of every closed point of
![]() $X$
is divisible by
$X$
is divisible by
![]() $p^{n}$
, then so is the Euler characteristic
$p^{n}$
, then so is the Euler characteristic
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any coherent
$\unicode[STIX]{x1D712}(X,{\mathcal{F}})$
of any coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{F}}$
.
${\mathcal{F}}$
.
Proof. We proceed by induction on
![]() $d=\dim X$
. Since the group
$d=\dim X$
. Since the group
![]() $K_{0}^{\prime }(X)$
is generated by classes
$K_{0}^{\prime }(X)$
is generated by classes
![]() $[{\mathcal{O}}_{Z}]$
for
$[{\mathcal{O}}_{Z}]$
for
![]() $Z$
an integral closed subscheme of
$Z$
an integral closed subscheme of
![]() $X$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, Corollaire 1.1.4]), we may assume that
$X$
(see [Reference Berthelot, Grothendieck and IllusieSGA6, X, Corollaire 1.1.4]), we may assume that
![]() $X$
is integral and that
$X$
is integral and that
![]() ${\mathcal{F}}={\mathcal{O}}_{X}$
. The case
${\mathcal{F}}={\mathcal{O}}_{X}$
. The case
![]() $d=0$
is clear, since
$d=0$
is clear, since
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=[k(X):k]$
. Assume that
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})=[k(X):k]$
. Assume that
![]() $d>0$
. Denote by
$d>0$
. Denote by
![]() $X^{(p)}=X\times _{\operatorname{Spec}k}\operatorname{Spec}k$
the base-change of
$X^{(p)}=X\times _{\operatorname{Spec}k}\operatorname{Spec}k$
the base-change of
![]() $X$
under the absolute Frobenius morphism of
$X$
under the absolute Frobenius morphism of
![]() $\operatorname{Spec}k$
. Since
$\operatorname{Spec}k$
. Since
![]() $k$
is perfect, the first projection
$k$
is perfect, the first projection
![]() $\unicode[STIX]{x1D70B}:X^{(p)}\rightarrow X$
is an
$\unicode[STIX]{x1D70B}:X^{(p)}\rightarrow X$
is an
![]() $\mathbb{F}_{p}$
-isomorphism. In particular
$\mathbb{F}_{p}$
-isomorphism. In particular
![]() $X^{(p)}$
is integral; let
$X^{(p)}$
is integral; let
![]() $\unicode[STIX]{x1D702}$
be its generic point. The relative Frobenius
$\unicode[STIX]{x1D702}$
be its generic point. The relative Frobenius
![]() $F:X\rightarrow X^{(p)}$
is a finite
$F:X\rightarrow X^{(p)}$
is a finite
![]() $k$
-morphism. By [Reference LiuLiu02, Corollary 3.2.27] the
$k$
-morphism. By [Reference LiuLiu02, Corollary 3.2.27] the
![]() $k(X^{(p)})$
-vector space
$k(X^{(p)})$
-vector space
![]() $(F_{\ast }{\mathcal{O}}_{X})_{\unicode[STIX]{x1D702}}=k(X)$
has dimension
$(F_{\ast }{\mathcal{O}}_{X})_{\unicode[STIX]{x1D702}}=k(X)$
has dimension
![]() $p^{d}$
, hence there is a nonempty open subscheme
$p^{d}$
, hence there is a nonempty open subscheme
![]() $V$
of
$V$
of
![]() $X^{(p)}$
such that the
$X^{(p)}$
such that the
![]() ${\mathcal{O}}_{V}$
-module
${\mathcal{O}}_{V}$
-module
![]() $(F_{\ast }{\mathcal{O}}_{X})|_{V}$
is free of rank
$(F_{\ast }{\mathcal{O}}_{X})|_{V}$
is free of rank
![]() $p^{d}$
. By the localisation sequence for
$p^{d}$
. By the localisation sequence for
![]() $K_{0}^{\prime }$
(see [Reference QuillenQui73, Proposition 7.3.2]), this implies that
$K_{0}^{\prime }$
(see [Reference QuillenQui73, Proposition 7.3.2]), this implies that
![]() $[F_{\ast }{\mathcal{O}}_{X}]-p^{d}[{\mathcal{O}}_{X^{(p)}}]=i_{\ast }\unicode[STIX]{x1D700}\in K_{0}^{\prime }(X^{(p)})$
for some
$[F_{\ast }{\mathcal{O}}_{X}]-p^{d}[{\mathcal{O}}_{X^{(p)}}]=i_{\ast }\unicode[STIX]{x1D700}\in K_{0}^{\prime }(X^{(p)})$
for some
![]() $\unicode[STIX]{x1D700}\in K_{0}^{\prime }(Y)$
, where
$\unicode[STIX]{x1D700}\in K_{0}^{\prime }(Y)$
, where
![]() $i:Y\rightarrow X^{(p)}$
is the immersion of the reduced closed complement of
$i:Y\rightarrow X^{(p)}$
is the immersion of the reduced closed complement of
![]() $V$
. The composite
$V$
. The composite
![]() $\unicode[STIX]{x1D70B}\circ i:Y\rightarrow X^{(p)}\rightarrow X$
maps closed points to closed points (being a closed immersion), multiplying their degrees by
$\unicode[STIX]{x1D70B}\circ i:Y\rightarrow X^{(p)}\rightarrow X$
maps closed points to closed points (being a closed immersion), multiplying their degrees by
![]() $[k:k^{p}]=1$
. Thus the degree of every closed point of
$[k:k^{p}]=1$
. Thus the degree of every closed point of
![]() $Y$
is a multiple of
$Y$
is a multiple of
![]() $p^{n}$
, hence
$p^{n}$
, hence
![]() $p^{n}$
divides
$p^{n}$
divides
![]() $\unicode[STIX]{x1D712}(Y,\unicode[STIX]{x1D700})$
by induction. It follows from (3.1a) and [Reference LiuLiu02, Corollary 5.2.27] that
$\unicode[STIX]{x1D712}(Y,\unicode[STIX]{x1D700})$
by induction. It follows from (3.1a) and [Reference LiuLiu02, Corollary 5.2.27] that
![]() $\unicode[STIX]{x1D712}(X^{(p)},{\mathcal{O}}_{X^{(p)}})=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
. We have
$\unicode[STIX]{x1D712}(X^{(p)},{\mathcal{O}}_{X^{(p)}})=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
. We have
![]() $\unicode[STIX]{x1D712}(X^{(p)},F_{\ast }{\mathcal{O}}_{X})=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
, because
$\unicode[STIX]{x1D712}(X^{(p)},F_{\ast }{\mathcal{O}}_{X})=\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
, because
![]() $F$
is a finite
$F$
is a finite
![]() $k$
-morphism. Thus
$k$
-morphism. Thus
Since
![]() $d>0$
and
$d>0$
and
![]() $p^{n}$
divides
$p^{n}$
divides
![]() $\unicode[STIX]{x1D712}(Y,\unicode[STIX]{x1D700})$
, we conclude that
$\unicode[STIX]{x1D712}(Y,\unicode[STIX]{x1D700})$
, we conclude that
![]() $p^{n}$
must divide
$p^{n}$
must divide
![]() $\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
.◻
$\unicode[STIX]{x1D712}(X,{\mathcal{O}}_{X})$
.◻
Lemma 5.3.3. Let
![]() $G$
be an algebraic group acting on a variety
$G$
be an algebraic group acting on a variety
![]() $X$
. Let
$X$
. Let
![]() $H$
be a normal unipotent subgroup of
$H$
be a normal unipotent subgroup of
![]() $G$
acting trivially on
$G$
acting trivially on
![]() $X$
. Then the natural morphism
$X$
. Then the natural morphism
![]() $K_{0}^{\prime }(X;G/H)\rightarrow K_{0}^{\prime }(X;G)$
is surjective.
$K_{0}^{\prime }(X;G/H)\rightarrow K_{0}^{\prime }(X;G)$
is surjective.
Proof. Let
![]() ${\mathcal{F}}$
be a
${\mathcal{F}}$
be a
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-module. We construct inductively
${\mathcal{O}}_{X}$
-module. We construct inductively
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
![]() ${\mathcal{F}}_{i}$
for
${\mathcal{F}}_{i}$
for
![]() $i\in \mathbb{N}$
as follows. Let
$i\in \mathbb{N}$
as follows. Let
![]() ${\mathcal{F}}_{0}={\mathcal{F}}$
. Assuming
${\mathcal{F}}_{0}={\mathcal{F}}$
. Assuming
![]() ${\mathcal{F}}_{i}$
constructed, we consider its
${\mathcal{F}}_{i}$
constructed, we consider its
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X}$
-submodule
${\mathcal{O}}_{X}$
-submodule
![]() $({\mathcal{F}}_{i})^{H}$
(see Definition 2.4.6), and define
$({\mathcal{F}}_{i})^{H}$
(see Definition 2.4.6), and define
![]() ${\mathcal{F}}_{i+1}={\mathcal{F}}_{i}/({\mathcal{F}}_{i})^{H}$
. As
${\mathcal{F}}_{i+1}={\mathcal{F}}_{i}/({\mathcal{F}}_{i})^{H}$
. As
![]() ${\mathcal{F}}$
is coherent and
${\mathcal{F}}$
is coherent and
![]() $X$
noetherian, there is an integer
$X$
noetherian, there is an integer
![]() $n$
such that the morphism
$n$
such that the morphism
![]() ${\mathcal{F}}_{i}\rightarrow {\mathcal{F}}_{i+1}$
is an isomorphism for all
${\mathcal{F}}_{i}\rightarrow {\mathcal{F}}_{i+1}$
is an isomorphism for all
![]() $i\geqslant n$
. Thus we have
$i\geqslant n$
. Thus we have
![]() $({\mathcal{F}}_{i})^{H}=0$
for
$({\mathcal{F}}_{i})^{H}=0$
for
![]() $i\geqslant n$
. We claim that this implies that
$i\geqslant n$
. We claim that this implies that
![]() ${\mathcal{F}}_{i}=0$
for such
${\mathcal{F}}_{i}=0$
for such
![]() $i$
. Indeed, let
$i$
. Indeed, let
![]() $U$
be an open subscheme of
$U$
be an open subscheme of
![]() $X$
such that
$X$
such that
![]() ${\mathcal{F}}_{i}(U)\neq 0$
. Then
${\mathcal{F}}_{i}(U)\neq 0$
. Then
![]() ${\mathcal{F}}_{i}(U)$
is a nonzero
${\mathcal{F}}_{i}(U)$
is a nonzero
![]() $H$
-representation over
$H$
-representation over
![]() $k$
, and, since
$k$
, and, since
![]() $H$
is unipotent, it follows that
$H$
is unipotent, it follows that
![]() ${\mathcal{F}}_{i}(U)^{H}\neq 0$
. But
${\mathcal{F}}_{i}(U)^{H}\neq 0$
. But
![]() $({\mathcal{F}}_{i})^{H}(U)={\mathcal{F}}_{i}(U)^{H}$
by Remark 2.4.7, a contradiction.
$({\mathcal{F}}_{i})^{H}(U)={\mathcal{F}}_{i}(U)^{H}$
by Remark 2.4.7, a contradiction.
Using the relations
![]() $[{\mathcal{F}}_{i}]=[{\mathcal{F}}_{i+1}]+[({\mathcal{F}}_{i})^{H}]$
for
$[{\mathcal{F}}_{i}]=[{\mathcal{F}}_{i+1}]+[({\mathcal{F}}_{i})^{H}]$
for
![]() $i=0,\ldots ,n-1$
and
$i=0,\ldots ,n-1$
and
![]() $[{\mathcal{F}}_{n}]=0$
in
$[{\mathcal{F}}_{n}]=0$
in
![]() $K_{0}^{\prime }(X;G)$
, we see that
$K_{0}^{\prime }(X;G)$
, we see that
![]() $[{\mathcal{F}}]=[{\mathcal{F}}_{0}]\in K_{0}^{\prime }(X;G)$
is the image of an element of
$[{\mathcal{F}}]=[{\mathcal{F}}_{0}]\in K_{0}^{\prime }(X;G)$
is the image of an element of
![]() $K_{0}^{\prime }(X;G/H)$
, namely
$K_{0}^{\prime }(X;G/H)$
, namely
![]() $[({\mathcal{F}}_{0})^{H}]+\cdots +[({\mathcal{F}}_{n-1})^{H}]$
.◻
$[({\mathcal{F}}_{0})^{H}]+\cdots +[({\mathcal{F}}_{n-1})^{H}]$
.◻
Lemma 5.3.4. Let
![]() $G$
be a unipotent algebraic group acting on a variety
$G$
be a unipotent algebraic group acting on a variety
![]() $X$
. Let
$X$
. Let
![]() $H$
be a finite normal subgroup of
$H$
be a finite normal subgroup of
![]() $G$
acting freely on
$G$
acting freely on
![]() $X$
. Let
$X$
. Let
![]() $\unicode[STIX]{x1D711}:X\rightarrow X/H$
be the quotient morphism. Then the endomorphism
$\unicode[STIX]{x1D711}:X\rightarrow X/H$
be the quotient morphism. Then the endomorphism
![]() $\unicode[STIX]{x1D711}_{\ast }\circ \unicode[STIX]{x1D711}^{\ast }$
of
$\unicode[STIX]{x1D711}_{\ast }\circ \unicode[STIX]{x1D711}^{\ast }$
of
![]() $K_{0}^{\prime }(X/H;G)$
is multiplication by the order of
$K_{0}^{\prime }(X/H;G)$
is multiplication by the order of
![]() $H$
.
$H$
.
Proof. Let
![]() $R$
be the coordinate ring of
$R$
be the coordinate ring of
![]() $H$
, and
$H$
, and
![]() $d=\dim _{k}R$
the order of
$d=\dim _{k}R$
the order of
![]() $H$
. We let
$H$
. We let
![]() $G$
act on
$G$
act on
![]() $H$
by
$H$
by
![]() $(g,h)\mapsto ghg^{-1}$
. The commutative square of
$(g,h)\mapsto ghg^{-1}$
. The commutative square of
![]() $G$
-equivariant morphisms
$G$
-equivariant morphisms

where
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70B}$
denote respectively the action and projection, is cartesian by Proposition 2.3.2. For any
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70B}$
denote respectively the action and projection, is cartesian by Proposition 2.3.2. For any
![]() $G$
-equivariant coherent
$G$
-equivariant coherent
![]() ${\mathcal{O}}_{X/H}$
-module
${\mathcal{O}}_{X/H}$
-module
![]() ${\mathcal{F}}$
, the
${\mathcal{F}}$
, the
![]() $G$
-equivariant morphism of
$G$
-equivariant morphism of
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
is an isomorphism by [Reference GrothendieckEGAII, (1.5.2)]. The forgetful morphism
![]() $K_{0}^{\prime }(\operatorname{Spec}k;G)\rightarrow K_{0}^{\prime }(\operatorname{Spec}k)$
is injective, being a retraction of a surjective morphism by Lemma 5.3.3. It follows that
$K_{0}^{\prime }(\operatorname{Spec}k;G)\rightarrow K_{0}^{\prime }(\operatorname{Spec}k)$
is injective, being a retraction of a surjective morphism by Lemma 5.3.3. It follows that
![]() $[R]=d\in K_{0}^{\prime }(\operatorname{Spec}k;G)$
. Thus
$[R]=d\in K_{0}^{\prime }(\operatorname{Spec}k;G)$
. Thus
Lemma 5.3.5. Let
![]() $G$
be a smooth algebraic group and
$G$
be a smooth algebraic group and
![]() $Y\rightarrow X$
a
$Y\rightarrow X$
a
![]() $G$
-equivariant surjective radicial morphism. Then the map
$G$
-equivariant surjective radicial morphism. Then the map
![]() $Y^{G}(K)\rightarrow X^{G}(K)$
is bijective for any perfect field extension
$Y^{G}(K)\rightarrow X^{G}(K)$
is bijective for any perfect field extension
![]() $K/k$
with trivial
$K/k$
with trivial
![]() $G$
-action.
$G$
-action.
Proof. Let
![]() $F$
be the fiber of
$F$
be the fiber of
![]() $Y\rightarrow X$
over a point in
$Y\rightarrow X$
over a point in
![]() $X^{G}(K)$
, and
$X^{G}(K)$
, and
![]() $F_{\text{red}}$
the underlying reduced closed subscheme. The scheme
$F_{\text{red}}$
the underlying reduced closed subscheme. The scheme
![]() $F$
, and thus also
$F$
, and thus also
![]() $F_{\text{red}}$
, is nonempty and radicial over
$F_{\text{red}}$
, is nonempty and radicial over
![]() $\operatorname{Spec}K$
. Since
$\operatorname{Spec}K$
. Since
![]() $K$
is perfect, the morphism
$K$
is perfect, the morphism
![]() $F_{\text{red}}\rightarrow \operatorname{Spec}K$
is an isomorphism. As the group
$F_{\text{red}}\rightarrow \operatorname{Spec}K$
is an isomorphism. As the group
![]() $G$
is reduced, the closed subscheme
$G$
is reduced, the closed subscheme
![]() $F_{\text{red}}$
of
$F_{\text{red}}$
of
![]() $F$
is
$F$
is
![]() $G$
-invariant. It follows that the isomorphism
$G$
-invariant. It follows that the isomorphism
![]() $F_{\text{red}}\rightarrow \operatorname{Spec}K$
is
$F_{\text{red}}\rightarrow \operatorname{Spec}K$
is
![]() $G$
-equivariant. Its inverse provides a
$G$
-equivariant. Its inverse provides a
![]() $G$
-equivariant morphism
$G$
-equivariant morphism
![]() $\operatorname{Spec}K\rightarrow F_{\text{red}}\rightarrow F\rightarrow Y$
, and therefore the required
$\operatorname{Spec}K\rightarrow F_{\text{red}}\rightarrow F\rightarrow Y$
, and therefore the required
![]() $K$
-point of
$K$
-point of
![]() $Y^{G}$
.◻
$Y^{G}$
.◻
We now provide two examples showing that Theorem 5.3.1 does not generalise to arbitrary algebraic
![]() $p$
-groups.
$p$
-groups.
Example 5.3.6. Let
![]() $k$
be a field of characteristic two. The subgroups of
$k$
be a field of characteristic two. The subgroups of
![]() $\operatorname{GL}_{2}$
$\operatorname{GL}_{2}$
induce two actions of
![]() $\unicode[STIX]{x1D6FC}_{2}$
on
$\unicode[STIX]{x1D6FC}_{2}$
on
![]() $\mathbb{P}^{1}$
. For a field extension
$\mathbb{P}^{1}$
. For a field extension
![]() $K/k$
with trivial
$K/k$
with trivial
![]() $G$
-action, the sets
$G$
-action, the sets
![]() $(\mathbb{P}^{1})^{\unicode[STIX]{x1D6FC}_{2}}(K)$
are respectively
$(\mathbb{P}^{1})^{\unicode[STIX]{x1D6FC}_{2}}(K)$
are respectively
![]() $\{[1:0]\}$
and
$\{[1:0]\}$
and
![]() $\{[0:1]\}$
. Since the two actions commute with one another, this gives an action of
$\{[0:1]\}$
. Since the two actions commute with one another, this gives an action of
![]() $\unicode[STIX]{x1D6FC}_{2}\times \,\unicode[STIX]{x1D6FC}_{2}$
on
$\unicode[STIX]{x1D6FC}_{2}\times \,\unicode[STIX]{x1D6FC}_{2}$
on
![]() $\mathbb{P}^{1}$
without fixed point, and
$\mathbb{P}^{1}$
without fixed point, and
![]() $\unicode[STIX]{x1D712}(\mathbb{P}^{1},{\mathcal{O}}_{\mathbb{P}^{1}})=1$
is odd.
$\unicode[STIX]{x1D712}(\mathbb{P}^{1},{\mathcal{O}}_{\mathbb{P}^{1}})=1$
is odd.
Example 5.3.7. Let
![]() $k$
be a field of characteristic two. Sending
$k$
be a field of characteristic two. Sending
![]() $a\in \unicode[STIX]{x1D6FC}_{2}(R)$
, for a commutative
$a\in \unicode[STIX]{x1D6FC}_{2}(R)$
, for a commutative
![]() $k$
-algebra
$k$
-algebra
![]() $R$
, to the matrix
$R$
, to the matrix
defines a group morphism
![]() $\unicode[STIX]{x1D6FC}_{2}\rightarrow \operatorname{PGL}_{2}$
. If
$\unicode[STIX]{x1D6FC}_{2}\rightarrow \operatorname{PGL}_{2}$
. If
![]() $K/k$
is a field extension with trivial
$K/k$
is a field extension with trivial
![]() $G$
-action, the only fixed
$G$
-action, the only fixed
![]() $K$
-point for the induced action of
$K$
-point for the induced action of
![]() $\unicode[STIX]{x1D6FC}_{2}$
on
$\unicode[STIX]{x1D6FC}_{2}$
on
![]() $\mathbb{P}^{1}$
is
$\mathbb{P}^{1}$
is
![]() $[1:1]$
.
$[1:1]$
.
We define a group morphism
![]() $\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{GL}_{2}$
by sending
$\unicode[STIX]{x1D707}_{2}\rightarrow \operatorname{GL}_{2}$
by sending
![]() $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{2}(R)$
, for a commutative
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{2}(R)$
, for a commutative
![]() $k$
-algebra
$k$
-algebra
![]() $R$
, to the matrix
$R$
, to the matrix
If
![]() $K/k$
is a field extension with trivial
$K/k$
is a field extension with trivial
![]() $G$
-action, the only fixed
$G$
-action, the only fixed
![]() $K$
-points for the induced action of
$K$
-points for the induced action of
![]() $\unicode[STIX]{x1D707}_{2}$
on
$\unicode[STIX]{x1D707}_{2}$
on
![]() $\mathbb{P}^{1}$
are
$\mathbb{P}^{1}$
are
![]() $[0:1]$
and
$[0:1]$
and
![]() $[1:0]$
.
$[1:0]$
.
Letting
![]() $\unicode[STIX]{x1D707}_{2}$
act on
$\unicode[STIX]{x1D707}_{2}$
act on
![]() $\unicode[STIX]{x1D6FC}_{2}$
via the restriction of the natural action of
$\unicode[STIX]{x1D6FC}_{2}$
via the restriction of the natural action of
![]() $\mathbb{G}_{m}$
on
$\mathbb{G}_{m}$
on
![]() $\mathbb{G}_{a}$
, we obtain an action of
$\mathbb{G}_{a}$
, we obtain an action of
![]() $\unicode[STIX]{x1D6FC}_{2}\rtimes \unicode[STIX]{x1D707}_{2}$
on
$\unicode[STIX]{x1D6FC}_{2}\rtimes \unicode[STIX]{x1D707}_{2}$
on
![]() $\mathbb{P}^{1}$
without fixed point, and
$\mathbb{P}^{1}$
without fixed point, and
![]() $\unicode[STIX]{x1D712}(\mathbb{P}^{1},{\mathcal{O}}_{\mathbb{P}^{1}})=1$
is odd.
$\unicode[STIX]{x1D712}(\mathbb{P}^{1},{\mathcal{O}}_{\mathbb{P}^{1}})=1$
is odd.
Remark 5.3.8. It would be interesting to determine for which algebraic
![]() $p$
-groups
$p$
-groups
![]() $G$
in characteristic
$G$
in characteristic
![]() $p$
does the arithmetic genus detect fixed points (in the sense of (c) in the introduction). We have proved that it does when
$p$
does the arithmetic genus detect fixed points (in the sense of (c) in the introduction). We have proved that it does when
![]() $G\in \{\unicode[STIX]{x1D6FC}_{p}\times \,\mathbb{Z}/p,\mathbb{Z}/p\times \,\mathbb{Z}/p,\mathbb{Z}/p^{2},\unicode[STIX]{x1D707}_{p^{2}}\}$
(see Theorems 5.3.1 and 5.1.1), but not when
$G\in \{\unicode[STIX]{x1D6FC}_{p}\times \,\mathbb{Z}/p,\mathbb{Z}/p\times \,\mathbb{Z}/p,\mathbb{Z}/p^{2},\unicode[STIX]{x1D707}_{p^{2}}\}$
(see Theorems 5.3.1 and 5.1.1), but not when
![]() $G\in \{\unicode[STIX]{x1D6FC}_{p}\times \,\unicode[STIX]{x1D6FC}_{p},\unicode[STIX]{x1D707}_{p}\times \,\mathbb{Z}/p,\unicode[STIX]{x1D6FC}_{p}\rtimes \unicode[STIX]{x1D707}_{p}\}$
(see Examples 5.3.6, 5.1.4 and 5.3.7).
$G\in \{\unicode[STIX]{x1D6FC}_{p}\times \,\unicode[STIX]{x1D6FC}_{p},\unicode[STIX]{x1D707}_{p}\times \,\mathbb{Z}/p,\unicode[STIX]{x1D6FC}_{p}\rtimes \unicode[STIX]{x1D707}_{p}\}$
(see Examples 5.3.6, 5.1.4 and 5.3.7).
6 Browder’s theorem
The next statement may be thought of as a relative version of Theorems 4.4 and 5.2.3(ii). It implies an algebraic version of a theorem of Browder in topology (see § 1.3).
Theorem 6.1. Let
![]() $G$
be an algebraic
$G$
be an algebraic
![]() $p$
-group and
$p$
-group and
![]() $f:Y\rightarrow X$
a projective
$f:Y\rightarrow X$
a projective
![]() $G$
-equivariant morphism. Assume that
$G$
-equivariant morphism. Assume that
![]() $X$
is smooth, and that one of the following conditions holds.
$X$
is smooth, and that one of the following conditions holds.
(i) The group
 $G$
is trigonalisable.
$G$
is trigonalisable.(ii) Every fiber of
 $f$
has dimension
$f$
has dimension
 ${<}p-1$
, and
${<}p-1$
, and
 $\operatorname{char}k\neq p$
.
$\operatorname{char}k\neq p$
.
Assume the image of
![]() $f_{\ast }:\operatorname{CH}_{G}(Y)/p\rightarrow \operatorname{CH}_{G}(X)/p$
contains the class
$f_{\ast }:\operatorname{CH}_{G}(Y)/p\rightarrow \operatorname{CH}_{G}(X)/p$
contains the class
![]() $[X]$
. Then the morphism
$[X]$
. Then the morphism
![]() $(f^{G})_{\ast }:\operatorname{CH}(Y^{G})/p\rightarrow \operatorname{CH}(X^{G})/p$
is surjective.
$(f^{G})_{\ast }:\operatorname{CH}(Y^{G})/p\rightarrow \operatorname{CH}(X^{G})/p$
is surjective.
Proof. If
![]() $T\rightarrow X$
is a morphism, respectively
$T\rightarrow X$
is a morphism, respectively
![]() $x\in X$
is a point, we will denote by
$x\in X$
is a point, we will denote by
![]() $f_{T}:Y_{T}\rightarrow T$
, respectively
$f_{T}:Y_{T}\rightarrow T$
, respectively
![]() $f_{x}:Y_{x}\rightarrow \operatorname{Spec}k(x)$
, the base-change of
$f_{x}:Y_{x}\rightarrow \operatorname{Spec}k(x)$
, the base-change of
![]() $f$
.
$f$
.
We first prove that for any point
![]() $x\in X^{G}$
the morphism
$x\in X^{G}$
the morphism
is surjective. Let
![]() $\unicode[STIX]{x1D6FC}^{\prime }\in \operatorname{CH}_{G}(Y)$
be such that
$\unicode[STIX]{x1D6FC}^{\prime }\in \operatorname{CH}_{G}(Y)$
be such that
![]() $f_{\ast }(\unicode[STIX]{x1D6FC}^{\prime })=[X]\in \operatorname{CH}_{G}(X)/p$
, and let
$f_{\ast }(\unicode[STIX]{x1D6FC}^{\prime })=[X]\in \operatorname{CH}_{G}(X)/p$
, and let
![]() $\unicode[STIX]{x1D6FC}\in \operatorname{CH}(Y)$
be the image of
$\unicode[STIX]{x1D6FC}\in \operatorname{CH}(Y)$
be the image of
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
. Let
$\unicode[STIX]{x1D6FC}^{\prime }$
. Let
![]() $R$
be the reduced closure of
$R$
be the reduced closure of
![]() $x$
in
$x$
in
![]() $X$
. Since
$X$
. Since
![]() $f_{\ast }(\unicode[STIX]{x1D6FC})=[X]\in \operatorname{CH}(X)/p$
, for any
$f_{\ast }(\unicode[STIX]{x1D6FC})=[X]\in \operatorname{CH}(X)/p$
, for any
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{CH}(R)/p$
we have by the projection formula [Reference FultonFul98, 8.1.1.c]
$\unicode[STIX]{x1D6FE}\in \operatorname{CH}(R)/p$
we have by the projection formula [Reference FultonFul98, 8.1.1.c]
Let
![]() $\unicode[STIX]{x1D6FE}^{\prime }\in \operatorname{CH}_{G}(R)$
be a preimage of
$\unicode[STIX]{x1D6FE}^{\prime }\in \operatorname{CH}_{G}(R)$
be a preimage of
![]() $\unicode[STIX]{x1D6FE}$
(the morphism
$\unicode[STIX]{x1D6FE}$
(the morphism
![]() $\operatorname{CH}_{G}(R)\rightarrow \operatorname{CH}(R)$
is surjective because
$\operatorname{CH}_{G}(R)\rightarrow \operatorname{CH}(R)$
is surjective because
![]() $G$
acts trivially on
$G$
acts trivially on
![]() $R$
). Then the element
$R$
). Then the element
![]() $\unicode[STIX]{x1D6FC}^{\prime }\cdot _{f}\unicode[STIX]{x1D6FE}^{\prime }\in \operatorname{CH}_{G}(Y_{R})$
constructed in § 3.2.6 is a preimage of
$\unicode[STIX]{x1D6FC}^{\prime }\cdot _{f}\unicode[STIX]{x1D6FE}^{\prime }\in \operatorname{CH}_{G}(Y_{R})$
constructed in § 3.2.6 is a preimage of
![]() $\unicode[STIX]{x1D6FC}\cdot _{f}\unicode[STIX]{x1D6FE}\in \operatorname{CH}(Y_{R})$
. In view of (6b), this proves that the composite
$\unicode[STIX]{x1D6FC}\cdot _{f}\unicode[STIX]{x1D6FE}\in \operatorname{CH}(Y_{R})$
. In view of (6b), this proves that the composite
![]() $\operatorname{CH}_{G}(Y_{R})\rightarrow \operatorname{CH}(Y_{R})\rightarrow \operatorname{CH}(R)/p$
is surjective. Let
$\operatorname{CH}_{G}(Y_{R})\rightarrow \operatorname{CH}(Y_{R})\rightarrow \operatorname{CH}(R)/p$
is surjective. Let
![]() $r=\dim R$
. We may find a
$r=\dim R$
. We may find a
![]() $G$
-invariant open subscheme
$G$
-invariant open subscheme
![]() $W$
of a finite-dimensional
$W$
of a finite-dimensional
![]() $G$
-representation over
$G$
-representation over
![]() $k$
whose complement has codimension greater than
$k$
whose complement has codimension greater than
![]() $\dim Y_{x}=\dim Y_{R}-r$
, such that
$\dim Y_{x}=\dim Y_{R}-r$
, such that
![]() $G$
acts freely on
$G$
acts freely on
![]() $W$
. Let
$W$
. Let
![]() $w=\dim W$
. It follows from [Reference Elman, Karpenko and MerkurjevEKM08, Propositions 49.18 and 49.20] that we have a commutative diagram (where
$w=\dim W$
. It follows from [Reference Elman, Karpenko and MerkurjevEKM08, Propositions 49.18 and 49.20] that we have a commutative diagram (where
![]() $W_{k(x)}=W\times _{k}\operatorname{Spec}k(x)$
).
$W_{k(x)}=W\times _{k}\operatorname{Spec}k(x)$
).

The right vertical morphism is surjective by the localisation sequence [Reference FultonFul98, Proposition 1.8] and [Reference Elman, Karpenko and MerkurjevEKM08, Proposition 52.9]. The upper horizontal composite may be identified with the degree
![]() $r$
component of the composite
$r$
component of the composite
![]() $\operatorname{CH}_{G}(Y_{R})\rightarrow \operatorname{CH}(Y_{R})\rightarrow \operatorname{CH}(R)$
. The lower horizontal composite may be identified with the degree-zero component of the composite
$\operatorname{CH}_{G}(Y_{R})\rightarrow \operatorname{CH}(Y_{R})\rightarrow \operatorname{CH}(R)$
. The lower horizontal composite may be identified with the degree-zero component of the composite
![]() $\operatorname{CH}_{G}(Y_{x})\rightarrow \operatorname{CH}(Y_{x})\rightarrow \operatorname{CH}(\operatorname{Spec}k(x))$
. Since the former is surjective modulo
$\operatorname{CH}_{G}(Y_{x})\rightarrow \operatorname{CH}(Y_{x})\rightarrow \operatorname{CH}(\operatorname{Spec}k(x))$
. Since the former is surjective modulo
![]() $p$
, so is the latter, proving that (6a) is surjective.
$p$
, so is the latter, proving that (6a) is surjective.
We now prove that for any closed subscheme
![]() $S$
of
$S$
of
![]() $X^{G}$
, the morphism
$X^{G}$
, the morphism
![]() $\operatorname{CH}((Y_{S})^{G})/p\rightarrow \operatorname{CH}(S)/p$
is surjective. The theorem will then follow from the case
$\operatorname{CH}((Y_{S})^{G})/p\rightarrow \operatorname{CH}(S)/p$
is surjective. The theorem will then follow from the case
![]() $S=X^{G}$
. We proceed by noetherian induction, the case
$S=X^{G}$
. We proceed by noetherian induction, the case
![]() $S=\varnothing$
being clear. Let
$S=\varnothing$
being clear. Let
![]() $s$
be a generic point of
$s$
be a generic point of
![]() $S$
. For any closed subscheme
$S$
. For any closed subscheme
![]() $Z$
of
$Z$
of
![]() $S$
not containing
$S$
not containing
![]() $s$
, we have a commutative diagram with exact rows, where
$s$
, we have a commutative diagram with exact rows, where
![]() $U=S-Z$
(see [Reference FultonFul98, Propositions 1.7 and 1.8]).
$U=S-Z$
(see [Reference FultonFul98, Propositions 1.7 and 1.8]).

By induction the left vertical morphism is surjective, hence so is its colimit over the closed subschemes
![]() $Z$
not containing
$Z$
not containing
![]() $s$
. In view of Theorem 4.4 in case (i) and Theorem 5.2.3(ii) in case (ii), the surjectivity of (6a) for
$s$
. In view of Theorem 4.4 in case (i) and Theorem 5.2.3(ii) in case (ii), the surjectivity of (6a) for
![]() $x=s$
implies that
$x=s$
implies that
![]() $\operatorname{CH}((Y_{s})^{G})/p\rightarrow \operatorname{CH}(\operatorname{Spec}k(s))/p=\mathbb{F}_{p}$
is also surjective. The latter morphism may be identified with the colimit of the right vertical morphism in the above diagram. We conclude that the middle vertical morphism is surjective, as required.◻
$\operatorname{CH}((Y_{s})^{G})/p\rightarrow \operatorname{CH}(\operatorname{Spec}k(s))/p=\mathbb{F}_{p}$
is also surjective. The latter morphism may be identified with the colimit of the right vertical morphism in the above diagram. We conclude that the middle vertical morphism is surjective, as required.◻
Remark 6.2. The conclusion of the theorem implies the following.
(i) The morphism
 $f^{G}$
is surjective, and in particular
$f^{G}$
is surjective, and in particular
 $\dim Y^{G}\geqslant \dim X^{G}$
.
$\dim Y^{G}\geqslant \dim X^{G}$
.(ii) If
 $X^{G}$
is projective and possesses a closed point of degree
$X^{G}$
is projective and possesses a closed point of degree
 $n$
, then
$n$
, then
 $Y^{G}$
possesses a closed point of some degree
$Y^{G}$
possesses a closed point of some degree
 $m$
whose
$m$
whose
 $p$
-adic valuation satisfies
$p$
-adic valuation satisfies
 $v_{p}(m)\leqslant v_{p}(n)$
.
$v_{p}(m)\leqslant v_{p}(n)$
.(iii) If
 $X^{G}$
is smooth (for instance if
$X^{G}$
is smooth (for instance if
 $p\neq \operatorname{char}k$
by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.8.10(2)]), then the
$p\neq \operatorname{char}k$
by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.8.10(2)]), then the
 $\mathbb{Z}_{(p)}$
-module
$\mathbb{Z}_{(p)}$
-module
 $\operatorname{CH}(X^{G})\,\otimes \,\mathbb{Z}_{(p)}$
is a direct summand of
$\operatorname{CH}(X^{G})\,\otimes \,\mathbb{Z}_{(p)}$
is a direct summand of
 $\operatorname{CH}(Y^{G})\,\otimes \,\mathbb{Z}_{(p)}$
. More generally
$\operatorname{CH}(Y^{G})\,\otimes \,\mathbb{Z}_{(p)}$
. More generally
 $H(X^{G})\,\otimes \,\mathbb{Z}_{(p)}$
is a direct summand of
$H(X^{G})\,\otimes \,\mathbb{Z}_{(p)}$
is a direct summand of
 $H(Y^{G})\,\otimes \,\mathbb{Z}_{(p)}$
when
$H(Y^{G})\,\otimes \,\mathbb{Z}_{(p)}$
when
 $H$
is a cohomology theory such as motivic cohomology,
$H$
is a cohomology theory such as motivic cohomology,
 $K$
-theory or algebraic cobordism (see [Reference HautionHau13, Conditions 3.1, Lemma 4.1] for precise conditions).
$K$
-theory or algebraic cobordism (see [Reference HautionHau13, Conditions 3.1, Lemma 4.1] for precise conditions).
Acknowledgement
I thank the anonymous referee for his/her careful reading and constructive comments.