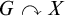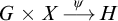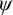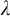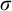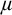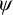1 Introduction
This article establishes some new instances of topological rigidity of cocycles in the context of Polish groups and their actions. For the setup, let us recall that by a Polish group action we understand a continuous action
$G\curvearrowright X$
by a Polish group G on a Polish space X, that is, such that the action map
$G\times X\to X$
is jointly continuous. Also, if
$G\curvearrowright X$
is any action by a group G on a set X, a group valued cocycle is a map
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
with values in another group H such that
$$ \begin{align*}\psi(gf,x)=\psi(g,fx)\cdot\psi(f,x) \end{align*} $$
for all
$g,f\in G$
and
$x\in X$
. For example, if
$X\mathop {\overset {\phi }\longrightarrow } H$
is any function, then the differential
$$ \begin{align*}d\phi(g,x)=\phi(gx)^{-1}\phi(x) \end{align*} $$
defines a so-called trivial cocycle, but general cocycles need not be that simple. The principal example of a nontrivial cocycle comes from calculus. Namely, if we let
$\mathsf {Diff}^1(\mathbb R)$
denote the group of
$C^1$
-diffeomorphisms of
$\mathbb R$
, then the chain rule simply expresses that the map
$$ \begin{align*}(f,x)\in \mathsf{Diff}^1(\mathbb R)\times \mathbb R\mapsto f'(x)\in \mathbb R^\times \end{align*} $$
is a cocycle for the tautological action of
$\mathsf {Diff}^1(\mathbb R)$
on
$\mathbb R$
. Nevertheless,
$f'(x)$
is not a function of
$(x,fx)$
, so the cocycle fails to be trivial.
A third example of cocycles arises when H acts freely on some set Y and
$X\mathop {\overset {\phi }\longrightarrow } Y$
is a map so that
$$ \begin{align*}x_1E_G^X x_2\;\Rightarrow\; \phi(x_1)E^Y_H\phi(x_2), \end{align*} $$
where
$E^X_G$
and
$E^Y_H$
are the orbit equivalence relations induced by the actions
$G\curvearrowright X$
and
$H\curvearrowright Y$
, respectively. Indeed, in that case, a cocycle
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is uniquely defined by the requirement that
$$ \begin{align*}\psi(g,x)\phi(x)=\phi(gx). \end{align*} $$
We note that this cocycle is trivial, although to write it as a differential requires us finding a transversal for the orbit equivalence relation
$E^Y_H$
.
There are several results in the literature on the continuity of cocycles under various notions of measurability (see, for example, [Reference Becker1]). Our main result, however, is most closely related to a recent result by T. Meyerovitch and O. N. Solan [Reference Meyerovitch and Solan5, Theorem 1.6].
To state this precisely, suppose
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle for a Polish group action
$G\curvearrowright X$
with values in a topological group H. Then, for fixed
$g\in G$
and
$x\in X$
, we may define the section maps
$X\mathop {\overset {\psi _g}\longrightarrow }H$
and
$G\mathop {\overset {\psi _x}\longrightarrow }H$
by
$\psi _g(z)=\psi (g,z)$
and
$\psi _x(f)=\psi (f,x),$
respectively. We say that
$\psi $
is continuous in the second variable if the maps
$X\mathop {\overset {\psi _g}\longrightarrow }H$
are continuous for all
$g\in G$
. Similarly for the other variable or for notions of measurability. Let us remark that the relationship between joint and separate measurability is in general more subtle than that of continuity. Indeed, if a map
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is continuous, then it is automatically continuous in each variable. However, if
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is only assumed to be Baire measurable, then it need not be Baire measurable in any of the two variables. Similarly, if
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is just assumed to be measurable with respect to a product
$\lambda \times \mu $
of
$\sigma $
-finite Borel measures on G and X, then it need not be measurable in any of the two variables.
In this language, [Reference Meyerovitch and Solan5, Theorem 1.6] states that, if G,
$H,$
and X are locally compact Polish,
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle for a continuous action
$G\curvearrowright X$
,
$\psi $
is assumed to be continuous in the second variable, and
$\psi _x$
is Haar measurable for every
$x\in X$
, then
$\psi $
is continuous. We extend this result in multiple directions.
Theorem 1.1. Let
$G\curvearrowright X$
be a Polish group action and suppose that
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle with values in a Polish group H. Assume also that
$\psi $
is continuous in the second variable. Then
$\psi $
is continuous in each of the following cases:
-
(1)
$\psi $
is Baire measurable; -
(2)
$\psi _x$
is Baire measurable for a dense set of
$x\in X$
; -
(3) G is locally compact and
$\psi _x$
is Haar measurable for a dense set of
$x\in X$
; -
(4) G is locally compact with Haar measure
$\lambda $
and there is a fully supported
$\sigma $
-finite Borel measure
$\mu $
on X such that
$\psi $
is
$\lambda \times \mu $
-measurable.
Observe, in particular, that case (3) is a direct extension of [Reference Meyerovitch and Solan5, Theorem 1.6] discarding the hypothesis of local compactness of H and X and weakening the measurability assumption on
$\psi $
. Note also that the measure
$\mu $
in (4) is not assumed to be invariant or even quasi-invariant under the G-action.
Remark 1.2. For completeness and later use, we mention that the assumption of continuity in the second variable can be slightly weakened. In fact, it suffices to assume that
$\psi _g$
is continuous for all g belonging to a set
$\Sigma $
that generates G. If
$\psi _g$
and
$\psi _f$
are continuous, then so are
$\psi _{gf}=\psi _g(f\,\cdot \,)\psi _f(\cdot )$
and
$\psi _{g^{-1}}=\big (\psi _g(g^{-1}\,\cdot \,)\big )^{-1}$
. Thus, for example, it is enough to assume that
$\psi _g$
is continuous for a comeagre set of
$g\in G$
or, in the case of locally compact groups, a conull set of
$g\in G$
.
Even in the case of trivial cocycles, Theorem 1.1 provides nontrivial information, assuming that we restrict ourselves to transitive Polish group actions
$G\mathop {\overset {}\curvearrowright }X$
. Observe first that, if
$X\mathop {\overset {\phi }\longrightarrow } H$
and
$g\in G$
, we may define the directional differential in the direction of g to be the section map
$d_g\phi =(d\phi )_g$
. Since
$d_g\phi $
is itself a function from X to H, this means that we can iterate this procedure to get higher order directional differentials. Thus, for example,
$$\begin{align*}\begin{aligned} d_g\phi(x)&=\phi(gx)^{-1}\phi(x),\\ d_fd_g\phi(x)&=\phi(fx)^{-1}\phi(gfx)\phi(gx)^{-1}\phi(x),\\ d_kd_fd_g\phi(x)&=\phi(kx)^{-1}\phi(gkx)\phi(gfkx)^{-1}\phi(fkx) \phi(fx)^{-1}\phi(gfx)\phi(gx)^{-1}\phi(x). \end{aligned}\end{align*}$$
Theorem 1.3. Suppose
$G\mathop {\overset {}\curvearrowright }X$
is a transitive Polish group action and that
$X\mathop {\overset {\phi }\longrightarrow } H$
is a Baire measurable function with values in a Polish group H. Then the following conditions are equivalent:
-
(1)
$\phi $
is continuous; -
(2)
$d\phi $
is continuous; -
(3) there is a comeagre set of
$g\in G$
such that
$d_g\phi $
is continuous; -
(4) for every proper subgroup
$F<G$
, there is some
$g\in G\setminus F$
so that
$d_g\phi $
is continuous; -
(5) for any infinite sequence
$g_1,g_2,\ldots \in G$
, there is some n so that is continuous.
$$ \begin{align*}d_{g_n}d_{g_{n-1}}\dots d_{g_1}\phi \end{align*} $$
Similarly to [Reference Meyerovitch and Solan5, Theorem 1.6], Theorem 1.3 has consequences for the notion of polynomial maps between groups, which is due to A. Leibman [Reference Leibman4] and is especially useful in the setting of nilpotent groups, but which applies to all groups in general.
Suppose
$G\mathop {\overset {\phi }\longrightarrow } H$
is a map between two groups. Viewing G as a G-space under the action
$G\curvearrowright G$
by left multiplication, we may define the differential
$G\times G \mathop {\overset {d\phi }\longrightarrow }H$
as before. For
$k\geqslant 0$
, a map
$G\mathop {\overset {\phi }\longrightarrow } H$
between two groups is said to be a polynomial of degree
$\leqslant k$
in case
$$ \begin{align*}d_{g_k}\dots d_{g_0}\phi\;\equiv\; 1_H \end{align*} $$
for all
$g_0,\ldots , g_k\in G$
. More generally, we may define
$G\mathop {\overset {\phi }\longrightarrow } H$
to be a polynomial of potentially transfinite degree provided that, for all
$g_0,g_1,g_2,\ldots \in G$
, there is a k such that
$$ \begin{align*}d_{g_k}\dots d_{g_0}\phi\;\equiv\; 1_H. \end{align*} $$
It follows immediately from the definition that
$\phi $
has degree
$\leqslant 0$
if and only if
$\phi $
is a constant map. Similarly,
$\phi $
has degree
$\leqslant 1$
if and only if
$\phi (1)\phi (\,\cdot \,)^{-1}$
is a group homomorphism.
Because constant maps
$G\to H$
are obviously continuous, the following is an immediate consequence of Theorem 1.3.
Corollary 1.4. Every Baire measurable polynomial
$G\mathop {\overset {\phi }\longrightarrow } H$
between Polish groups is continuous.
2 Measurable cocycles
In this section we prove Theorem 1.1. Observe first that, if
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle associated with a group action
$G\curvearrowright X$
, then by applying the cocycle equation to
$g=f=1$
we have that
$\psi (1,x)=1$
for all
$x\in X$
.
Lemma 2.1. Let
$(\Omega ,\mathcal S)$
be a measurable space and X, Y be separable metrisable topological spaces. Assume also that
$\Omega \times X\mathop {\overset {\psi }\longrightarrow } Y$
is a map such that
$\psi _\omega \colon X\to Y$
is continuous for all
$\omega \in \Omega $
, whereas
$\psi _x\colon \Omega \to Y$
is measurable for a dense set of
$x\in X$
. Then
$\psi _x\colon \Omega \to Y$
is measurable for all
$x\in X$
.
Proof. Let
$\mathcal X\subseteq X$
be a countable dense subset such that
$\psi _z$
is
$\mathcal S$
-measurable for all
$z\in \mathcal X$
. Suppose also
$W\subseteq Y$
is a given non-empty open set and find a countable collection
$\mathcal V$
of open subsets
$V\subseteq W$
so that
$W=\bigcup _{V\in \mathcal V}V=\bigcup _{V\in \mathcal V}\overline V$
. Also, for a given point
$x\in X$
, let
$\mathcal N$
be a countable neighbourhood basis for x.
Then, for any
$\omega \in \Omega $
, we have by the continuity in the second variable that
$$\begin{align*}\begin{aligned} \omega\in \psi_x^{-1}(W) &\Leftrightarrow \psi(\omega,x)\in W\\ &\Leftrightarrow \exists V\in \mathcal V\;\; \psi(\omega,x)\in V\\ &\Leftrightarrow \exists V\in \mathcal V\;\; \exists U\in \mathcal N\;\; \psi\big[\{\omega\}\times U\big]\subseteq V\\ &\Rightarrow \exists V\in \mathcal V\; \;\exists U\in \mathcal N\;\; \forall z\in U\cap \mathcal X\; \;\psi(\omega,z)\in V\\ &\Leftrightarrow \omega\in \bigcup_{V\in \mathcal V}\;\bigcup_{U\in \mathcal N}\;\bigcap_{z\in U\cap \mathcal X}\; \psi_z^{-1}(V) \\ &\Rightarrow \exists V\in \mathcal V\; \;\exists U\in \mathcal N\;\; \psi\big[\{\omega\}\times U\big]\subseteq \overline V\\ &\Rightarrow \exists V\in \mathcal V\; \;\psi(\omega,x)\in \overline V\\ &\Rightarrow \omega\in \psi_x^{-1}(W). \end{aligned}\end{align*}$$
It thus follows that
$$ \begin{align*}\psi_x^{-1}(W)= \bigcup_{V\in \mathcal V}\;\bigcup_{U\in \mathcal N}\;\bigcap_{z\in U\cap \mathcal X}\; \psi_z^{-1}(V) \end{align*} $$
is
$\mathcal S$
-measurable.
Lemma 2.2. Let
$G\curvearrowright X$
be a continuous action by a topological group G on a topological space X and suppose that
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle with values in a topological group H such that
$\psi $
is continuous in the second variable. Assume also that, for some
$x\in X$
, the map
$\psi _x$
is continuous at a single point in G. Then
$\psi _x$
is continuous at every point of G.
Proof. Suppose
$\psi _x$
is continuous at some point
$f\in G$
and let
$g\in G$
be any given point. To see that
$\psi _x$
is also continuous at
$gf$
, suppose that
$k_i\to gf$
is a convergent net. Then
$g^{-1} k_i\to f$
and hence
$$\begin{align*}\begin{aligned} {\psi}(gf,x) &={\psi}(g, fx)\cdot {\psi}(f ,x)\\ &=\lim_i{\psi}(g ,g^{-1} k_ix)\;\cdot\;\lim_i {\psi}(g^{-1} k_i, x)\\ &=\lim_i\Big({\psi}(g ,g^{-1} k_ix)\;\cdot\; {\psi}(g^{-1} k_i, x)\Big)\\ &=\lim_i{\psi}(gg^{-1} k_i,x)\\ &=\lim_i{\psi}(k_i,x), \end{aligned}\end{align*}$$
showing continuity of
$\psi _x$
at
$gf$
.
Lemma 2.3. Let
$G\curvearrowright X$
be a continuous action by a topological group G on a topological space X and suppose that
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is a cocycle with values in a Polish group H such that
$\psi $
is continuous in the second variable. Then, if
$\psi $
is continuous at some point
$(f,x)$
,
$\psi $
is in fact continuous at every point of
$G\times Gx$
.
Proof. We first show that, if the cocycle
$\psi $
is continuous at a point
$(f,x)$
, then it is also continuous at all points
$(gf,x)$
for
$g\in G$
. To see this, suppose that
$k_i\to gf$
and
$x_i\to x$
are convergent nets. Then
$g^{-1} k_i\to f$
and hence
$$\begin{align*}\begin{aligned} {\psi}(gf,x) &={\psi}(g, fx)\cdot {\psi}(f ,x)\\ &=\lim_i{\psi}(g ,g^{-1} k_ix_i)\;\cdot\;\lim_i {\psi}(g^{-1} k_i, x_i)\\ &=\lim_i\Big({\psi}(g ,g^{-1} k_ix_i)\;\cdot\; {\psi}(g^{-1} k_i, x_i)\Big)\\ &=\lim_i{\psi}(gg^{-1} k_i,x_i)\\ &=\lim_i{\psi}(k_i,x_i). \end{aligned}\end{align*}$$
We next show that, if the cocycle
$\psi $
is continuous at a point
$(f,x)$
, then it is also continuous at all points
$(f,gx)$
for
$g\in G$
. To see this, suppose that
$f_i\to f$
and
$y_i\to gx$
. Then
$f_ig\to fg$
and
$g^{-1} y_i\to x$
. Because
$\psi $
is continuous at
$(fg,x)$
, it follows that
$$\begin{align*}\begin{aligned} {\psi}(f,gx) &={\psi}(fgg^{-1} ,gx)\\ &={\psi}(fg, g^{-1} gx)\cdot {\psi}(g^{-1} ,gx)\\ &={\psi}(fg, x)\cdot {\psi}(g^{-1} ,gx)\\ &=\lim_i{\psi}(f_ig ,g^{-1} y_i)\;\cdot\; \lim_i{\psi}(g^{-1} , y_i)\\ &=\lim_i\Big({\psi}(f_ig ,g^{-1} y_i)\;\cdot\; {\psi}(g^{-1} , y_i)\Big)\\ &=\lim_i{\psi}(f_igg^{-1}, y_i)\\ &=\lim_i{\psi}(f_i,y_i). \end{aligned}\end{align*}$$
The lemma now follows from the conjunction of these two facts.
Proof of Theorem 1.1 (2).
Recall that we are given a Polish group action
$G\curvearrowright X$
and a cocycle
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
with values in a Polish group H such that
$\psi $
is continuous in the second variable. Furthermore,
$\psi _x$
is assumed to be Baire measurable for a dense set of
$x\in X$
. Thus, by Lemma 2.1,
$\psi _x$
will be Baire measurable for all
$x\in X$
.
We first show that, for any
$x\in X$
, the function
$\psi _x$
has a point of continuity in G. To see this, note that, for any fixed
$g\in G$
,
$\psi _x$
is continuous at g if and only if, for every open identity neighbourhood
$W\subseteq H$
, there is some
$h\in H$
such that
$$ \begin{align*}g\in \mathsf{int}\Big(\psi_x^{-1}(hW^2)\Big). \end{align*} $$
Indeed, the sets of the form
$hW^2$
, where
$W\subseteq H$
is an open identity neighbourhood and
$h\in H$
is such that
$\psi _x(g)\in hW^2$
, form a neighbourhood basis at the point
$\psi _x(g)$
.
Thus, by the Baire category theorem and first countability of H, it suffices to show that, for every open identity neighbourhood
$W\subseteq H$
, the open set
$$ \begin{align*}\bigcup_{h\in H}\mathsf{int}\Big(\psi_x^{-1}(hW^2)\Big) \end{align*} $$
is dense in G.
So let W be given and fix some countable dense subset
$\mathcal H\subseteq H$
. Assume also that
$O\subseteq G$
is a given non-empty open set and find non-empty open subsets
$U_1,U_2\subseteq G$
so that
$U_1U_2\subseteq O$
. Then,
$$ \begin{align*}U_2\subseteq \bigcup_{h\in \mathcal H}\psi_x^{-1}(hW) \end{align*} $$
and hence there must be some
$h_1\in \mathcal H$
such that
$U_2\cap \psi _x^{-1}(h_1W)$
is nonmeagre.
Choose now some open identity neighbourhood
$W'\subseteq H$
so that
$\overline {W'}h_1\subseteq h_1W$
and fix an element
$f\in U_2\cap \psi _x^{-1}(h_1W)$
so that
$U_2\cap \psi _x^{-1}(h_1W)$
is comeagre in a neighbourhood of f. As above, we may then find some
$h_2\in \mathcal H$
so that
$U_1\cap \psi _{fx}^{-1}(h_2W')$
is nonmeagre.
Fix a countable neighbourhood basis
$\mathcal V$
for f consisting of open sets. We claim that
$$\begin{align*}\begin{aligned} \psi_{fx}^{-1}(h_2W') &\;\subseteq\; \bigcup_{V\in \mathcal V}\big\{ {g\in G}\;\big|\; {\forall k\in V \; \psi(g,kx)\in h_2{W'}} \big\}. \end{aligned}\end{align*}$$
Indeed, suppose that
$g\in \psi _{fx}^{-1}(h_2W')$
is given. Then
$\psi (g,fx)\in h_2W'$
and so, because
$\psi $
is continuous in the second variable, there is some
$V\in \mathcal V$
such that
$\psi (g,kx)\in h_2W'$
for all
$k\in V$
, which proves the claim. Because
$U_1\cap \psi _{fx}^{-1}(h_2W')$
is nonmeagre, it follows that there is some
$V\in \mathcal V$
such that
$$ \begin{align*}U_1\cap \big\{ {g\in G}\;\big|\; { \forall k\in V \;\psi(g,kx)\in h_2W'} \big\} \end{align*} $$
is nonmeagre.
Let now
$\mathcal G$
be a countable dense subset of G and observe that
$$\begin{align*}\begin{aligned} \big\{ {g\in G}\;\big|\; {\forall k\in V \; \psi(g,kx)\in h_2{W'}} \big\} &\;\subseteq\; \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W')\\ &\;\subseteq\; \big\{ {g\in G}\;\big|\; {\forall k\in V \; \psi(g,kx)\in h_2\overline{W'}} \big\}. \end{aligned}\end{align*}$$
Indeed, the first inclusion is immediate and to verify the last inclusion assume
$\psi (g,kx)\in h_2W'$
for all
$k\in V\cap \mathcal G$
. Then every
$k\in V$
is the limit of some sequence
$(k_n)\subseteq V\cap \mathcal G$
and therefore
$$ \begin{align*}\psi(g,kx)=\lim_n\psi(g,k_nx)\in \overline{h_2W'}=h_2\overline {W'} \end{align*} $$
as claimed. We thus conclude that
$$ \begin{align*}U_1\cap \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W') \end{align*} $$
is nonmeagre.
Observe that the two factors in the product
$$ \begin{align*}A=\Big(U_1\cap \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W')\Big) \cdot \Big(U_2\cap V\cap \psi_x^{-1}(h_1W)\Big) \end{align*} $$
are both nonmeagre sets with the Baire property. By the Pettis theorem [Reference Pettis6] (see [Reference Rosendal7, Lemma 2.1] for the exact statement needed), the product A therefore has non-empty interior. Moreover, for
$$ \begin{align*}g\;\in\; U_1\cap \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W') \end{align*} $$
and
$$ \begin{align*}k\in U_2\cap V\cap \psi_x^{-1}(h_1W), \end{align*} $$
we have
$$\begin{align*}\begin{aligned} \psi(gk,x) &=\psi(g,kx)\cdot\psi(k,x)\\ &\in h_2\overline{W'} \cdot h_1W\\ &\subseteq h_2h_1W^2. \end{aligned}\end{align*}$$
In other words,
$A\subseteq \psi _x^{-1} \big (h_2h_1W^2\big )$
. As also
$\emptyset \neq \mathsf {int}\, A\subseteq A\subseteq U_1U_2\subseteq O$
, we see that
$\bigcup _{h\in H}\mathsf { int}\Big (\psi _x^{-1}(hW^2)\Big )$
is dense in G.
We have shown that, for every
$x\in X$
, the map
$\psi _x$
is continuous at some point of G. Therefore, by Lemma 2.2,
$\psi _x$
is continuous at every point of G. By the assumptions of the theorem,
$G\times X\mathop {\overset {\psi }\longrightarrow } H$
is separately continuous.
We may now apply [Reference Kechris3, Theorem 8.51] to conclude that there is a comeagre subset
$Z\subseteq G\times X$
such that the section
$$ \begin{align*}Z^x=\big\{ {g\in G}\;\big|\; { (g,x)\in Z} \big\} \end{align*} $$
is comeagre for every
$x\in X$
and so that
$\psi $
is continuous at every point of Z. In particular, this shows that, for all
$x\in X$
there is some
$g\in G$
such that
$\psi $
is continuous at
$(g,x)$
. By Lemma 2.3, it follows that
$\psi $
is continuous at all points of
$G\times X$
.
Proof of Theorem 1.1 (3).
The proof of this is very similar to that of Theorem 1.1 (2), so we will keep the same notation and just point out the small changes that are needed. We begin by fixing a left-invariant Haar measure
$\lambda $
on G.
As before, we must show that the open set
$\bigcup _{h\in H}\mathsf {int}\Big (\psi _x^{-1}(hW^2)\Big )$
intersects some given non-empty open set
$O\subseteq G$
. We choose
$U_1U_2\subseteq O$
as before and find
$h_1\in \mathcal H$
so that
$U_2\cap \psi _x^{-1}(h_1W)$
is non-null.
Again we find
$W'$
satisfying
$\overline {W'}h_1\subseteq h_1W$
. Define now
$$ \begin{align*}D=\bigcup\big\{ {U\subseteq X \text{ open }}\;\big|\; {\lambda\big(U\cap U_2\cap \psi_x^{-1}(h_1W)\big)=0} \big\}. \end{align*} $$
Then D is open and
$\lambda \big (D\cap U_2\cap \psi _x^{-1}(h_1W)\big )=0$
. Because
$U_2\cap \psi _x^{-1}(h_1W)$
is non-null, we may therefore find some
$f\in \big (U_2\cap \psi _x^{-1}(h_1W)\big )\setminus D$
, which means that
${U_2\cap \psi _x^{-1}(h_1W)}$
has non-null intersection with every neighbourhood of f.
Choose then
$h_2\in \mathcal H$
so that
$U_1\cap \psi _{fx}^{-1}(h_2W')$
is non-null and find an open neighbourhood V of f so that
$$ \begin{align*}U_1\cap \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W') \end{align*} $$
is non-null. Then the two factors in the product
$$ \begin{align*}\Big(U_1\cap \bigcap_{k\in V\cap \mathcal G} \psi_{kx}^{-1}(h_2W')\Big) \cdot \Big(U_2\cap \psi_x^{-1}(h_1W)\cap V\Big) \;\;\subseteq\;\; \psi_x^{-1} \big(h_2h_1W^2\big) \end{align*} $$
are both non-null Haar measurable sets. It follows therefore that the product has non-empty interior (see, e.g., [Reference Rosendal7, Theorem 2.3]). The rest of the proof remains unaltered.
Proof of Theorem 1.1(1).
Let
$\mathcal W$
be a countable basis for the topology on H. Then, for every
$W\in \mathcal W$
, the inverse image
$\psi ^{-1}(W)$
has the Baire property in
${G\times X}$
and therefore, by the Kuratowski–Ulam theorem [Reference Kechris3, Theorem 8.41], there is a comeagre subset
$Z_W\subseteq X$
such that
$$ \begin{align*}\psi^{-1}(W)_z=\big\{ {g\in G}\;\big|\; {(g,z)\in \psi^{-1}(W)} \big\} =\psi_z^{-1}(W) \end{align*} $$
has the Baire property in G for all
$z\in Z_W$
. Thus, for all z belonging to the comeagre set
$\bigcap _{W\in \mathcal W}Z_W$
and all
$W\in \mathcal W$
,
$\psi _z^{-1}(W)$
has the Baire property, whereby
$\psi _z$
is Baire measurable. The result now follows from Theorem 1.1(2).
Proof of Theorem 1.1(4).
Let
$\mathcal W$
be a countable basis for the topology on H. Then, for every
$W\in \mathcal W$
, the inverse image
$\psi ^{-1}(W)$
is a
$\lambda \times \mu $
-measurable subset of
$G\times X$
. Because both
$\lambda $
and
$\mu $
are
$\sigma $
-finite Borel measures, it follows from the Fubini–Tonelli theorem that there is a
$\mu $
-conull subset
$Z_W\subseteq X$
such that, for all
$z\in Z_W$
,
$$ \begin{align*}\psi^{-1}(W)_z=\big\{ {g\in G}\;\big|\; {(g,z)\in \psi^{-1}(W)} \big\} =\psi_z^{-1}(W) \end{align*} $$
is a
$\lambda $
-measurable subset of G. Thus, for all z belonging to the
$\mu $
-conull set
${Z=\bigcap _{W\in \mathcal W}Z_W}$
and all
$W\in \mathcal W$
,
$\psi _z^{-1}(W)$
is
$\lambda $
-measurable. So
$\psi _z$
is
$\lambda $
-measurable for all
$z\in Z$
. Because
$\mu $
is fully supported, we see that Z is dense in X and the conclusion now follows from Theorem 1.1(3).
3 Differentials and polynomial mappings
Proof of Theorem 1.3.
Assume
$G\mathop {\overset {}\curvearrowright }X$
is a transitive Polish group action and that
$X\mathop {\overset {\phi }\longrightarrow } H$
is a Baire measurable function with values in a Polish group H.
We first show that the differentials
$G\times X\mathop {\overset {d\phi }\longrightarrow }H$
and
$X\mathop {\overset {d_g\phi }\longrightarrow }H$
are Baire measurable for all
$g\in G$
. So let
$g\in G$
be fixed and let
$U\subseteq H$
be open. Because the group operation in H is continuous, we have that
$$ \begin{align*}\big\{ {(h,k)\in H\times H}\;\big|\; { h^{-1} k\in U} \big\} =\bigcup_nV_n\times W_n \end{align*} $$
for some sequence of open sets
$V_n,W_n\subseteq H$
. If
$G\times X\mathop {\overset {\mathsf {a}}\longrightarrow } X$
denotes the action map, it follows that
$$\begin{align*}\begin{aligned} \big(d_g\phi\big)^{-1}(U)&=\bigcup_{n}\big\{ {x\in X}\;\big|\; {\phi(gx)\in V_n \;\&\; \phi(x)\in W_n} \big\} \\&=\bigcup_n \Big( \phi^{-1}(W_n)\cap g^{-1}\!\cdot \!\phi^{-1}(V_n)\Big) \end{aligned}\end{align*}$$
and
$$\begin{align*}\begin{aligned} \big(d\phi\big)^{-1}(U) &=\bigcup_n\big\{(f,x)\in G\times X \; \big| \; fx\in \phi^{-1} (V_n)\;\&\;x\in \phi^{-1}(W_n)\big\}\\ &=\bigcup_n \Big(\mathsf{a}^{-1}\big(\phi^{-1} (V_n)\big)\cap \big( G\times \phi^{-1}(W_n)\big)\Big).\\ \end{aligned}\end{align*}$$
Because
$\phi $
is Baire measurable, the sets
$\phi ^{-1} (V_n)$
and
$\phi ^{-1} (W_n)$
have the Baire property. This shows that
$d_g\phi $
is Baire measurable. Furthermore, because the action map
$G\times X\mathop {\overset {\mathsf {a}}\longrightarrow } X$
is surjective, continuous, and open, the inverse image
$\mathsf {a}^{-1}\big (\phi ^{-1} (V_n)\big )$
will also have the Baire property, whereby
$d\phi $
is Baire measurable.
Secondly, it is immediate that (1) implies (2)–(5). Conversely, to see that (2) implies (1), suppose that
$d\phi $
is continuous and that
$x_n\to x$
. Since the action
$G\curvearrowright X$
is transitive, the orbit map
$g\in G\mapsto gx\in X$
is open by Effros’ theorem [Reference Effros2, Theorem 2.1] and so there is a sequence
$(g_n)$
in G converging to
$1$
with
$x_n=g_nx$
. So, by the continuity of
$d\phi $
, we have that
$$ \begin{align*}\lim_n \phi(x_n)^{-1}\phi(x) =\lim_n \phi(g_nx)^{-1}\phi(x) =\lim_nd\phi(g_n,x) =d\phi(1,x)=1, \end{align*} $$
whence
$\phi (x_n)\to \phi (x)$
, showing continuity of
$\phi $
.
Observe also that, because
$\big (d\phi \big )_g=d_g\phi $
, each of (3) and (4) imply that the set
$$ \begin{align*}\Sigma=\big\{ {g\in G}\;\big|\; {(d\phi)_g \text{ is continuous}} \big\} \end{align*} $$
must generate G and hence, by Remark 1.2 and Theorem 1.1(1), that
$d\phi $
is continuous. So (3) and (4) each imply (2).
To see that (5) implies (1), assume that (1) fails. Then, by the implication (4)
$\Rightarrow $
(1), there is some
$g_1\in G$
so that also
$d_{g_1}\phi $
is discontinuous and still is Baire measurable. Continuing like this, we may in fact choose an infinite sequence
$g_1,g_2,g_3,\ldots $
so that
$d_{g_k}\dots d_{g_1}\phi $
is discontinuous for all
$k\geqslant 0$
, whereby also (5) fails.
Acknowledgments
Thanks are also due to Uri Bader and Rémi Barritault for interesting comments and helpful conversations.
Funding
The author was partially supported by the U.S. National Science Foundation under Grant Number DMS-2246986.
Open access
