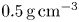1. Introduction
Controlled fusion is one of the most promising methods for solving the energy crisis in the future (Wesson & Campbell Reference Wesson and Campbell2011). The reaction can be divided into three categories according to the velocity distribution of reactants: thermonuclear reaction, beam–target reaction and beam–beam reaction (Dolan Reference Dolan2013). The thermonuclear reaction is caused by high-temperature plasmas with Maxwellian distributions, for which the reactivity can be calculated by (Atzeni & Meyer-ter Vehn Reference Atzeni and Meyer-ter Vehn2004)

where $v$![]() is the relative velocity, $\beta =(\beta _1+\beta _2)/(\beta _1\beta _2)$
is the relative velocity, $\beta =(\beta _1+\beta _2)/(\beta _1\beta _2)$![]() , with $\beta _i=m_i/(2kT_i)$
, with $\beta _i=m_i/(2kT_i)$![]() , and $\sigma (v)$
, and $\sigma (v)$![]() is the nuclear reaction cross-section depending on $v$
is the nuclear reaction cross-section depending on $v$![]() . The thermonuclear reactivity only depends on temperature.
. The thermonuclear reactivity only depends on temperature.
High-energy incident particles in plasmas can be slowed down by Coulomb scattering, nuclear scattering and other interactions. The particles would undergo fusion reaction with surrounding plasmas before they lose all of the kinetic energy and reach local thermodynamic equilibrium. The fusion reaction during the slowing-down process is called the beam–target reaction. The beam–target reaction is caused by incident particles with a monoenergetic distribution and target plasmas with a Maxwellian distribution. The reactivity can be expressed by (Dolan Reference Dolan2013)
where $v_b$![]() is the velocity of the particles with monoenergetic distribution. The beam–beam reaction is caused by two plasmas both with monoenergetic distributions, which is usually too small and can be ignored.
is the velocity of the particles with monoenergetic distribution. The beam–beam reaction is caused by two plasmas both with monoenergetic distributions, which is usually too small and can be ignored.
The thermonuclear reaction is the most important one in both magnetic confinement fusion (Ongena et al. Reference Ongena, Koch, Wolf and Zohm2016) and inertial confinement fusion (ICF) (Betti & Hurricane Reference Betti and Hurricane2016). The beam–target reaction is widely studied in tokamak neutral beam injection (Cordey, Keilhacker & Watkins Reference Cordey, Keilhacker and Watkins1987; Wilhelmsson Reference Wilhelmsson1987; Dawson, Furth & Tenney Reference Dawson, Furth and Tenney1971; Hendel et al. Reference Hendel, England, Jassby, Mirin and Nieschmidt1986). The most general scenario is the injection of deuterium and tritium beams into a DT plasma. It is found that the thermonuclear reaction is dominant in high-density ($>10^{20}\,{\rm m}^{-3}$![]() ) plasmas, such as conventional reactor operation; the beam–target reaction becomes dominant at moderate densities ($2$
) plasmas, such as conventional reactor operation; the beam–target reaction becomes dominant at moderate densities ($2$![]() –$4\times 10^{19}\,{\rm m}^{-3}$
–$4\times 10^{19}\,{\rm m}^{-3}$![]() ), this regime often being called the two-component torus (Wilhelmsson Reference Wilhelmsson1987). At low densities ($<2\times 10^{19}\,{\rm m}^{-3}$
), this regime often being called the two-component torus (Wilhelmsson Reference Wilhelmsson1987). At low densities ($<2\times 10^{19}\,{\rm m}^{-3}$![]() ), it is necessary to take the beam–beam reaction into account. When the neutral beams are both co- and counter-injected with roughly equal magnitude, this regime is often referred to as the colliding-beam torus (Cordey & Core Reference Cordey and Core1975; Jassby Reference Jassby1976). Experimental results in JET also show that the beam–target reaction is comparable with the thermonuclear reaction in neutral beam injection (Jarvis Reference Jarvis1999).
), it is necessary to take the beam–beam reaction into account. When the neutral beams are both co- and counter-injected with roughly equal magnitude, this regime is often referred to as the colliding-beam torus (Cordey & Core Reference Cordey and Core1975; Jassby Reference Jassby1976). Experimental results in JET also show that the beam–target reaction is comparable with the thermonuclear reaction in neutral beam injection (Jarvis Reference Jarvis1999).
The beam–target reaction also plays an important role in intense laser–plasma interactions. For example, a beam–target neutron source is widely studied to produce neutrons with high energy and low divergence angle (Zweiback et al. Reference Zweiback, Cowan, Smith, Hartley, Howell, Steinke, Hays, Wharton, Crane and Ditmire2000; Lu et al. Reference Lu, Liu, Wang, Wang, Zhou, Deng, Xia, Xu, Lu and Jiang2009; Willingale et al. Reference Willingale, Petrov, Maksimchuk, Davis, Freeman, Joglekar, Matsuoka, Murphy, Ovchinnikov and Thomas2011). Intense laser beams are focused onto a target and accelerate particles to high energy by various acceleration mechanisms such as target neutral sheath acceleration (Wilks et al. Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001) and breakout afterburner acceleration (Henig et al. Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin and Albright2009). Then the high-energy particles bombard the fuel target and produce neutrons by means of the beam–target reaction. Roth et al. (Reference Roth, Jung, Falk, Guler, Deppert, Devlin, Favalli, Fernandez, Gautier and Geissel2013) accelerated deuterium ions using breakout afterburner acceleration to bombard a Be target and obtained a neutron yield of $10^{10}\,{\rm sr}^{-1}$![]() . The energy of generated neutrons is up to 150 MeV, which is the highest energy obtained using a beam–target neutron source at present.
. The energy of generated neutrons is up to 150 MeV, which is the highest energy obtained using a beam–target neutron source at present.
As for fusion ignition schemes research, He et al. (Reference He, Cai, Zhang, Dong, Zhou, Wu, Sheng, Cao, Zheng and Wu2015) proposed a spherical shell target scheme where a CD$_2$![]() layer was set outside to react with high-energy ions travelling across the cavity centre through beam–target reaction to deposit more energy. Finally, the energy conversion efficiency from laser to target can reach as high as 71 %. The beam–target reaction and thermonuclear reaction dominate in different stages and the peak neutron yield is $10^3$
layer was set outside to react with high-energy ions travelling across the cavity centre through beam–target reaction to deposit more energy. Finally, the energy conversion efficiency from laser to target can reach as high as 71 %. The beam–target reaction and thermonuclear reaction dominate in different stages and the peak neutron yield is $10^3$![]() and $10^5\,{\rm J}^{-1}$
and $10^5\,{\rm J}^{-1}$![]() , respectively. Zhang et al. (Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017) observed anomalous neutron yield in indirect-drive ICF, and they attributed it to electrostatic shock wave collisions. Some of the deuterium particles are accelerated to high energy by the electrostatic shock wave and react with centre plasmas by means of the beam–target reaction (Zhang et al. Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017; Shan et al. Reference Shan, Cai, Zhang, Tang, Zhang, Song, Bi, Ge, Chen and Liu2018). Other research such as that concerning laser-driven plasma collider (Fu et al. Reference Fu, Bao, Chen, He, Hou, Li, Li, Li, Liao and Rhee2015) also takes the beam–target reaction into account.
, respectively. Zhang et al. (Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017) observed anomalous neutron yield in indirect-drive ICF, and they attributed it to electrostatic shock wave collisions. Some of the deuterium particles are accelerated to high energy by the electrostatic shock wave and react with centre plasmas by means of the beam–target reaction (Zhang et al. Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017; Shan et al. Reference Shan, Cai, Zhang, Tang, Zhang, Song, Bi, Ge, Chen and Liu2018). Other research such as that concerning laser-driven plasma collider (Fu et al. Reference Fu, Bao, Chen, He, Hou, Li, Li, Li, Liao and Rhee2015) also takes the beam–target reaction into account.
Generally speaking, the beam–target reaction is more likely to be encountered in magnetic confinement fusion because of the relatively high beam energy and low density. But in ICF research, when the implosion velocity is large enough, a large beam–target reaction may be induced. It is necessary to employ a precise calculation method in order to evaluate quantitatively the importance of the beam–target reaction rate in fusion. However, the traditional method (Yue et al. Reference Yue, Shen, Wang and Kuang1993; Perkins et al. Reference Perkins, Logan, Rosen, Perry, de la Rubia, Ghoniem, Ditmire, Springer and Wilks2000; He et al. Reference He, Cai, Zhang, Dong, Zhou, Wu, Sheng, Cao, Zheng and Wu2015; Zhang et al. Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017; Shan et al. Reference Shan, Cai, Zhang, Tang, Zhang, Song, Bi, Ge, Chen and Liu2018) ignores the transport process and may introduce large errors when the temperature and density along the transport path of incident plasmas vary obviously. An improved method is proposed in this paper, in which we take the transport process into account to eliminate the errors.
The paper is organized as follows. In § 2 the traditional method and its deficiencies are introduced. An improved method is proposed to ameliorate the deficiencies. In § 3 a high-speed plasma collisions model is established and the two methods are applied to the model at the same time to display the differences. In § 4 calculation results are described and some conclusions are drawn. Section 5 is a brief summary. The improved method will be beneficial to ICF schemes with large implosion velocity like double-cone ignition (Zhang et al. Reference Zhang, Wang, Yang, Wu, Ma, Jiao, Zhang, Wu, Yuan and Li2020) and impact ignition (Murakami et al. Reference Murakami, Nagatomo, Johzaki, Sakaiya, Velikovich, Karasik, Gus'kov and Zmitrenko2014, Reference Murakami, Nagatomo, Sakaiya, Azechi, Fujioka, Shiraga, Nakai, Shigemori, Saito and Obenschain2005), in which high-speed plasmas collide with each other and realize ignition.
2. Algorithm for beam–target reaction rate calculation
Here we will take the DD reaction as an example, and assume that: (1) the deuterium ion beam undergoes no angular scattering during its transport (Perkins et al. Reference Perkins, Logan, Rosen, Perry, de la Rubia, Ghoniem, Ditmire, Springer and Wilks2000) and (2) for the incident plasmas, the velocity distribution can be regarded as a monoenergetic distribution and for the target plasmas can be regarded as a Maxwellian distribution. As regards target plasmas, the velocity is always too low and can be ignored. In this work, the velocities are set to 300, 600 and 1000 km s$^{-1}$![]() . For deuterium particles, the corresponding kinetic energies are 0.94, 3.76 and 10.45 keV, respectively, which is around three times higher than the thermal energy (i.e. temperature) as displayed in table 2. As regards incident plasmas, the velocity is close to the initial setting value, which makes the kinetic energies much larger than the thermal energies. Thus, ignoring the thermal energy of incident plasmas would not lead to large errors.
. For deuterium particles, the corresponding kinetic energies are 0.94, 3.76 and 10.45 keV, respectively, which is around three times higher than the thermal energy (i.e. temperature) as displayed in table 2. As regards incident plasmas, the velocity is close to the initial setting value, which makes the kinetic energies much larger than the thermal energies. Thus, ignoring the thermal energy of incident plasmas would not lead to large errors.
According to (1.1) and (1.2), the thermonuclear reactivity only depends on target temperature, while the beam–target reactivity depends on both target temperature and beam energy. Figure 1 shows the thermonuclear reactivity and beam–target reactivity for the DD reaction with different beam energies and target temperatures. It is seen that the beam–target reactivity is comparable to the thermonuclear one for beam plasma energies from 0 to 10 keV and target plasma temperatures from 1 to 4 keV. The beam–target reactivity and thermonuclear reactivity both increase as the beam energy or the target temperature increase. However, the ratio of beam–target reactivity to thermonuclear reactivity increases as the beam plasma energy increases, while it decreases as the target plasma temperature increases. Other work has more detailed descriptions for conditions with larger beam energy and target temperature (Niikura, Nagami & Horiike Reference Niikura, Nagami and Horiike1988).

Figure 1. Comparison of beam–target reactivity and thermonuclear reactivity for the DD reaction with different target plasma temperatures and beam plasma energies.
High-speed beam ions occur in the beam–target reaction with surrounding plasmas while slowing down, and the neutrons produced during the whole slowing-down process have to be taken into account. When a deuterium ion with energy $E$![]() propagates in the plasma, the energy loss during a given time ${\rm d}t$
propagates in the plasma, the energy loss during a given time ${\rm d}t$![]() is
is
where $\varepsilon$![]() is the stopping power. It is a function of beam energy, target density and target temperature.
is the stopping power. It is a function of beam energy, target density and target temperature.
The number of beam–target reactions caused in this process can be expressed by
where $\langle \sigma v\rangle _b$![]() is the beam–target reactivity obtained by (1.2). According to (2.1) and (2.2), the total number of beam–target reactions caused by the beam ions is
is the beam–target reactivity obtained by (1.2). According to (2.1) and (2.2), the total number of beam–target reactions caused by the beam ions is
Assuming the incident ion velocity distribution is $f_i$![]() , then the total reaction caused by incident ions can be calculated (He et al. Reference He, Cai, Zhang, Dong, Zhou, Wu, Sheng, Cao, Zheng and Wu2015; Zhang et al. Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017; Shan et al. Reference Shan, Cai, Zhang, Tang, Zhang, Song, Bi, Ge, Chen and Liu2018; Perkins et al. Reference Perkins, Logan, Rosen, Perry, de la Rubia, Ghoniem, Ditmire, Springer and Wilks2000):
, then the total reaction caused by incident ions can be calculated (He et al. Reference He, Cai, Zhang, Dong, Zhou, Wu, Sheng, Cao, Zheng and Wu2015; Zhang et al. Reference Zhang, Cai, Shan, Zhang, Gu and Zhu2017; Shan et al. Reference Shan, Cai, Zhang, Tang, Zhang, Song, Bi, Ge, Chen and Liu2018; Perkins et al. Reference Perkins, Logan, Rosen, Perry, de la Rubia, Ghoniem, Ditmire, Springer and Wilks2000):
For the thermonuclear reaction,
Equation (2.4) provides a convenient method to calculate the total beam–target reaction rate during the slowing-down process. The beam–target reaction rate and thermonuclear reaction rate can be estimated according to (2.4) and (2.5). In addition, some authors write $\langle \sigma v\rangle _b/v_i$![]() as $\sigma$
as $\sigma$![]() in (2.4). That means the target plasma temperature is too low and can be ignored, i.e. cold target, and $\langle \sigma v\rangle _b$
in (2.4). That means the target plasma temperature is too low and can be ignored, i.e. cold target, and $\langle \sigma v\rangle _b$![]() is equal to $\sigma v_i$
is equal to $\sigma v_i$![]() in this case.
in this case.
However, there is an obvious defect in (2.4). The stopping power $\varepsilon$![]() is a function of beam plasma energy, target plasma temperature and density. The beam–target reactivity $\langle \sigma v\rangle _b$
is a function of beam plasma energy, target plasma temperature and density. The beam–target reactivity $\langle \sigma v\rangle _b$![]() is a function of beam energy and target temperature. Equation (2.4) only integrates the beam ion energy and considers the target plasma temperature and density as constant. But in reality, the temperature and density in the transport trace of incident particles may change much in inhomogeneous plasmas. If the range of incident particles is sufficiently smaller than the inhomogeneity length of the plasma, (2.4) is accurate. Otherwise, the equation may lead to large errors.
is a function of beam energy and target temperature. Equation (2.4) only integrates the beam ion energy and considers the target plasma temperature and density as constant. But in reality, the temperature and density in the transport trace of incident particles may change much in inhomogeneous plasmas. If the range of incident particles is sufficiently smaller than the inhomogeneity length of the plasma, (2.4) is accurate. Otherwise, the equation may lead to large errors.
An example with one-dimensional simulation is shown in figure 2. A deuterium ion travels in the CD plasma system with a velocity of 1000 km s$^{-1}$![]() (equal to the thermal velocity of a deuterium ion with 10 keV kinetic energy) from $x=0$
(equal to the thermal velocity of a deuterium ion with 10 keV kinetic energy) from $x=0$![]() . The grid size is set to $1.3 \,\mathrm {\mu }{\rm m}$
. The grid size is set to $1.3 \,\mathrm {\mu }{\rm m}$![]() . The density and temperature are different in the two grids and the specific values are shown in figure 2(a). The results without transport process are obtained directly if we set $T=T_1$
. The density and temperature are different in the two grids and the specific values are shown in figure 2(a). The results without transport process are obtained directly if we set $T=T_1$![]() , $\rho =\rho _1$
, $\rho =\rho _1$![]() during the entire integral path. While if we set $T=T_1$
during the entire integral path. While if we set $T=T_1$![]() , $\rho =\rho _1$
, $\rho =\rho _1$![]() when $x< l$
when $x< l$![]() and $T=T_2$
and $T=T_2$![]() , $\rho =\rho _2$
, $\rho =\rho _2$![]() when $x \geqslant l$
when $x \geqslant l$![]() , the results considering the transport process can be obtained, which are shown in figure 2(b). As shown in figure 2(b), the range of incident particles is around $2 \,\mathrm {\mu }{\rm m}$
, the results considering the transport process can be obtained, which are shown in figure 2(b). As shown in figure 2(b), the range of incident particles is around $2 \,\mathrm {\mu }{\rm m}$![]() in the initial grids, which is larger than the grid size. Thus, the temperature and density change obviously in the transport path and errors may appear. The results without transport are identical to those with transport when $x<1.3\,\mathrm {\mu }{\rm m}$
in the initial grids, which is larger than the grid size. Thus, the temperature and density change obviously in the transport path and errors may appear. The results without transport are identical to those with transport when $x<1.3\,\mathrm {\mu }{\rm m}$![]() , and the results with transport process deviate from the trend rapidly at $x=1.3\,\mathrm {\mu }{\rm m}$
, and the results with transport process deviate from the trend rapidly at $x=1.3\,\mathrm {\mu }{\rm m}$![]() due to the fact that the density and temperature vary much at this point. Finally, the total beam–target reactions for the cases without and with the influence of the transport process are ${\rm 8}.67\times {10}^{-4}$
due to the fact that the density and temperature vary much at this point. Finally, the total beam–target reactions for the cases without and with the influence of the transport process are ${\rm 8}.67\times {10}^{-4}$![]() and ${\rm 1}.17\times {10}^{-3}$
and ${\rm 1}.17\times {10}^{-3}$![]() , respectively.
, respectively.

Figure 2. Diagram of one-dimensional simulation to show discrepancies in the traditional method. (a) A deuterium ion with a velocity of 1000 km s$^{-1}$![]() travels in the CD plasma system. (b) The reaction rate for the cases with and without transport process.
travels in the CD plasma system. (b) The reaction rate for the cases with and without transport process.
The integral value of (2.4) depends on the transport path. However, the density and temperature in the transport path are much different in different physical models. As a result, more detailed simulations should be employed to calculate the beam–target reaction rate accurately. An improved method to calculate the beam–target reaction rate in a specific physical model is proposed, as shown in figure 3.

Figure 3. Flow chart of the improved beam–target reaction rate calculation algorithm.
Our proposed scheme is as follows:
Step 1. Using a radiation hydrodynamics program to simulate the physical process, and the density and ion temperature distribution in each grid could be obtained.
Step 2. For a time $t_i$![]() , searching for the target plasma area. The velocity inside the target plasma area is relatively low and the density and temperature are relatively high. The division criterion depends on the specific physical model.
, searching for the target plasma area. The velocity inside the target plasma area is relatively low and the density and temperature are relatively high. The division criterion depends on the specific physical model.
Step 3. According to the velocity, determining which grid can enter the target plasma area at a given time, i.e. incident plasma grid. For the time $t_i$![]() , assuming all the particles in the incident plasma grids could enter other grids with a monoenergetic velocity distribution.
, assuming all the particles in the incident plasma grids could enter other grids with a monoenergetic velocity distribution.
Step 4. Calculating the transport path for each incident grid. Then calculating the total reaction number. The incident plasma may pass through several grids. Since the temperature and density are quite different in different grids, the beam–target reaction rate in each target grid has to be calculated independently. Then they are added to get the total beam–target reaction number. The calculation method is similar to (2.4) which calculates the beam–target reaction rate independently in each grid.
3. Simulation model
In order to see the importance of the beam–target reaction in high-speed plasma collisions, we consider two cylindrical CD plasmas with high-speed collisions, as shown in figure 4. The CD plasmas move towards each other with high velocity and collide head-on. Because of the high temperature and density in the collision area, a large thermonuclear reaction may occur in this region.

Figure 4. Diagram of the high-speed plasma collisions model.
The radiation hydrodynamic program FLASH can meet the research needs (Fryxell et al. Reference Fryxell, Olson, Ricker, Timmes, Zingale, Lamb, MacNeice, Rosner, Truran and Tufo2000). FLASH is an open-source program developed by the University of Chicago for more than 20 years. The program is widely used in the areas of high-energy-density physics and ICF research. The equation of state data are generated from the FEOS code (Young & Corey Reference Young and Corey1995; Faik, Tauschwitz & Iosilevskiy Reference Faik, Tauschwitz and Iosilevskiy2018) and the opacity data are calculated using the SNOP code (Eidmann Reference Eidmann1994), which are both widely used data. In this paper, a two-dimensional cylindrical coordinate model is employed to simulate the collision process. Here we set $d=0$![]() and $h=0.3$
and $h=0.3$![]() mm. The initial density of the high-speed plasma is set to 0.5 g cm$^{-3}$
mm. The initial density of the high-speed plasma is set to 0.5 g cm$^{-3}$![]() and the initial temperature is set to 100 eV. For comparison, the velocities are set to 300, 600 and 1000 km s$^{-1}$
and the initial temperature is set to 100 eV. For comparison, the velocities are set to 300, 600 and 1000 km s$^{-1}$![]() , respectively. The radii of the CD plasma are set to 0.05, 0.10 and 0.15 mm, respectively. The grid size is set to 1.3 $\mathrm {\mu }{\rm m}$
, respectively. The radii of the CD plasma are set to 0.05, 0.10 and 0.15 mm, respectively. The grid size is set to 1.3 $\mathrm {\mu }{\rm m}$![]() .
.
Note that in laser-driven neutron source research, the PIC+MC code is widely used. But it is not suitable for our model. Because of numerical noise, the PIC method could only simulate cases of several hundred micrometres and several hundred femtoseconds. It is not suitable for investigating cases with large spatial scale and time scale. In these cases, a radiation hydrodynamic program should be applied.
The nuclear reaction cross-section data here are obtained from the ENDF database (Chadwick et al. Reference Chadwick, Herman, Obložinský, Dunn, Danon, Kahler, Smith, Pritychenko, Arbanas and Arcilla2011) and the stopping power data are from the classic model (Honrubia & Murakami Reference Honrubia and Murakami2015) given by

where $\ln (\varLambda _j)$![]() is the Coulomb logarithm. The subscript $j$
is the Coulomb logarithm. The subscript $j$![]() means different particles, including electron and deuterium particles. Also,
means different particles, including electron and deuterium particles. Also,
where ${\rm erf}(x)$![]() is an error function given by
is an error function given by
Parameters $m_j$![]() , $q_j$
, $q_j$![]() , $v_j$
, $v_j$![]() and $\theta _j$
and $\theta _j$![]() are the mass, charge, average particle velocity and average temperature of particles $j$
are the mass, charge, average particle velocity and average temperature of particles $j$![]() , respectively.
, respectively.
The temperature and density inside the collision area are relatively high and the velocity is relatively low. Thus, the collision area should be regarded as the target plasma area. The velocity outside the collision area is relatively large so that the velocity gradient is a good criterion for dividing the collision area.
4. Results and discussion
The density distribution and ion temperature distribution for the case of $v=300$![]() km s$^{-1}$
km s$^{-1}$![]() and $R=0.10$
and $R=0.10$![]() mm are shown in figure 5. The white dotted line in the density distribution in figure 5 is the collision area edge divided by velocity gradient. The division result shows that the collision area is of high density and relatively high ion temperature, so that it is an ideal place to induce the thermonuclear reaction.
mm are shown in figure 5. The white dotted line in the density distribution in figure 5 is the collision area edge divided by velocity gradient. The division result shows that the collision area is of high density and relatively high ion temperature, so that it is an ideal place to induce the thermonuclear reaction.

Figure 5. Density distribution and ion temperature distribution for the case of $v=300$![]() km s$^{-1}$
km s$^{-1}$![]() and $R=0.10$
and $R=0.10$![]() mm. The dotted line is the division result of the collision area described in Step 2 in § 2.
mm. The dotted line is the division result of the collision area described in Step 2 in § 2.
It is seen that the CD plasmas are compressed after they collide at the centre area. The collision area is small with a peak density of around 5 g cm$^{-3}$![]() at $t=0.25$
at $t=0.25$![]() ns, which is around 10 times larger than the initial density. At $t=0.50$
ns, which is around 10 times larger than the initial density. At $t=0.50$![]() ns, the collision area becomes larger and the peak density is almost the same as that at $t=0.25$
ns, the collision area becomes larger and the peak density is almost the same as that at $t=0.25$![]() ns. At $t=0.75$
ns. At $t=0.75$![]() ns, the cylindrical plasmas outside the collision area are almost completely incident to the collision area. The range of collision area along the $Z$
ns, the cylindrical plasmas outside the collision area are almost completely incident to the collision area. The range of collision area along the $Z$![]() direction is around 0.1 mm. And the peak density is still around 5 g cm$^{-3}$
direction is around 0.1 mm. And the peak density is still around 5 g cm$^{-3}$![]() . The ion temperature has a similar evolution trend. At the beginning of the collision process, temperature may be very large in the cylinder outside edge because of the diffusion effect. At $t=0.50$
. The ion temperature has a similar evolution trend. At the beginning of the collision process, temperature may be very large in the cylinder outside edge because of the diffusion effect. At $t=0.50$![]() ns, the high-temperature area becomes larger and the peak temperature in the collision area is around 0.3 keV, which is maintained to $t=0.75$
ns, the high-temperature area becomes larger and the peak temperature in the collision area is around 0.3 keV, which is maintained to $t=0.75$![]() ns.
ns.
As we can see in figure 6, at $t=0$![]() ns, the two cylindrical plasmas have not collided yet so that the temperature and density distributions are flat along the $Z$
ns, the two cylindrical plasmas have not collided yet so that the temperature and density distributions are flat along the $Z$![]() direction. At $t=0.4$
direction. At $t=0.4$![]() ns, the density and temperature in the collision area reach the peak values of 5 g cm$^{-3}$
ns, the density and temperature in the collision area reach the peak values of 5 g cm$^{-3}$![]() and 0.3 keV, respectively. At $t=0.8$
and 0.3 keV, respectively. At $t=0.8$![]() ns, the density and temperature decrease slightly and the collision region area becomes larger. It is seen that the temperature in the collision region edge is larger than that in the collision region. This can be attributed to the superposition effect of shock waves.
ns, the density and temperature decrease slightly and the collision region area becomes larger. It is seen that the temperature in the collision region edge is larger than that in the collision region. This can be attributed to the superposition effect of shock waves.

Figure 6. Density distribution (a) and ion temperature distribution (b) along the $Z$![]() direction.
direction.
The reaction rates of thermonuclear reaction and beam–target reaction obtained by the traditional method and the improved method are shown in figure 7. It is seen that the thermonuclear reaction rate is much larger than the beam–target one. When $v=300$![]() km s$^{-1}$
km s$^{-1}$![]() , the peak thermonuclear reaction rate is around 30 times larger than the peak beam–target reaction rate. The results of the traditional method are almost identical to those of the improved method. However, when the velocity reaches 1000 km s$^{-1}$
, the peak thermonuclear reaction rate is around 30 times larger than the peak beam–target reaction rate. The results of the traditional method are almost identical to those of the improved method. However, when the velocity reaches 1000 km s$^{-1}$![]() , the peak thermonuclear reaction rate is hundreds of times larger than the peak beam–target reaction rate. The results of the traditional method are around two times lower than those of the improved method, indicating that the traditional method is not suitable for large-collision-velocity cases.
, the peak thermonuclear reaction rate is hundreds of times larger than the peak beam–target reaction rate. The results of the traditional method are around two times lower than those of the improved method, indicating that the traditional method is not suitable for large-collision-velocity cases.

Figure 7. Reaction rate for the cases with (a) $v=300$![]() km s$^{-1}$
km s$^{-1}$![]() , $R=0.10$
, $R=0.10$![]() mm and (b) $v=1000$
mm and (b) $v=1000$![]() km s$^{-1}$
km s$^{-1}$![]() , $R=0.10$
, $R=0.10$![]() mm.
mm.
The total neutron yield of thermonuclear reaction and beam–target reaction in each case is presented in table 1, which is also shown in figure 8. It is seen that the beam–target reaction numbers by the traditional method $N_{b1}$![]() and by the improved method $N_{b2}$
and by the improved method $N_{b2}$![]() are almost the same at $v=300$
are almost the same at $v=300$![]() km s$^{-1}$
km s$^{-1}$![]() . When the velocity goes to 600 km s$^{-1}$
. When the velocity goes to 600 km s$^{-1}$![]() , slight differences appear. The two methods are different obviously at $v=1000$
, slight differences appear. The two methods are different obviously at $v=1000$![]() km s$^{-1}$
km s$^{-1}$![]() . The discrepancy between the two methods can reach 70 %.
. The discrepancy between the two methods can reach 70 %.

Figure 8. (a) Number of thermonuclear reactions and beam–target reactions by the traditional method and improved method. At the same velocity conditions, the three values of the same kind of reaction number from large to small correspond to $R=0.05$![]() , $R=0.10$
, $R=0.10$![]() and $R=0.15$
and $R=0.15$![]() mm, respectively. (b) Ratios of beam–target reaction to thermonuclear reaction by the traditional method and improved method. At the same velocity conditions, the three values of the same kind of ratios from large to small correspond to $R=0.05$
mm, respectively. (b) Ratios of beam–target reaction to thermonuclear reaction by the traditional method and improved method. At the same velocity conditions, the three values of the same kind of ratios from large to small correspond to $R=0.05$![]() , $R=0.10$
, $R=0.10$![]() and $R=0.15$
and $R=0.15$![]() mm respectively.
mm respectively.
Table 1. Simulation result of various neutron yields. Here $v$![]() is the velocity, $R$
is the velocity, $R$![]() is the radius of the cylinder, $N_t$
is the radius of the cylinder, $N_t$![]() is the number of thermonuclear reactions, $N_{b1}$
is the number of thermonuclear reactions, $N_{b1}$![]() is the number of beam–target reactions by the traditional method and $N_{b2}$
is the number of beam–target reactions by the traditional method and $N_{b2}$![]() is the number of beam–target reactions by the improved method.
is the number of beam–target reactions by the improved method.

In addition, the following points can be made from table 1 and figure 8:
(i) Both the thermonuclear reaction number and beam–target reaction number increase as the velocity increases. However, the ratio of beam–target reaction to thermonuclear reaction decreases with an increase of the velocity in general.
(ii) The ratio of beam–target reaction by the improved method to thermonuclear reaction shows an anomalous increase at $v=1000$
 km s$^{-1}$
km s$^{-1}$ . The reason is given below in terms of the results in table 2 and figure 9.
. The reason is given below in terms of the results in table 2 and figure 9.(iii) The beam–target reaction is more important (the ratio is larger) when the cylindrical radius is small. From the simulation result, because of the diffusion effect in the plasma cylinder outside surface, the collision region volume with high temperature increases faster than the volume of a cylinder as the cylindrical radius increases. Therefore, the thermonuclear reaction increases faster than the beam–target reaction as the cylindrical radius increases.

Figure 9. Range of incident particles for different beam velocity conditions in the collision area. Corresponding ion temperature for each velocity can be obtained from the simulation result as shown in table 2.
Table 2. Simulation result of temperature for different conditions. Here $T_{i,e}$![]() is the ion temperature in the edge, $T_{i,c}$
is the ion temperature in the edge, $T_{i,c}$![]() is the ion temperature in the collision area, where the temperature data are from the simulation result directly, $n_{b,e}$
is the ion temperature in the collision area, where the temperature data are from the simulation result directly, $n_{b,e}$![]() is the beam–target reaction rate in the collision area edge, $n_{b,c}$
is the beam–target reaction rate in the collision area edge, $n_{b,c}$![]() is the beam–target reaction rate in the collision centre according to (1.2) and $n_{t,e}$
is the beam–target reaction rate in the collision centre according to (1.2) and $n_{t,e}$![]() and $n_{t,c}$
and $n_{t,c}$![]() are thermonuclear reaction rate in the collision area edge and collision centre, respectively.
are thermonuclear reaction rate in the collision area edge and collision centre, respectively.

With the temperature in the collision area and the edge obtained from the simulation, according to (1.1) and (1.2), the reaction rate for different velocities and temperatures can be calculated, as shown in table 2. As seen in table 2, the ratio of beam–target reaction rate to thermonuclear reaction rate for 300 km s$^{-1}$![]() is much larger than that for other velocity conditions. In the edge of the collision area, the ratios are 27.8, 4.08 and 3.10, respectively, when the velocities are 300, 600 and 1000 km s$^{-1}$
is much larger than that for other velocity conditions. In the edge of the collision area, the ratios are 27.8, 4.08 and 3.10, respectively, when the velocities are 300, 600 and 1000 km s$^{-1}$![]() . The trend fits well the traditional method result in figure 8(b).
. The trend fits well the traditional method result in figure 8(b).
However, the improved method takes the transport process into consideration. When the velocity is high enough (e.g. $v=1000$![]() km s$^{-1}$
km s$^{-1}$![]() ), the incident particles from the collision area edge may reach the collision centre, so that the ratios should be modified to 27.8, 4.08 and 4.79, respectively. These ratios could explain why the ratio of the beam–target reaction by the improved method to the thermonuclear reaction shows an anomalous increase at $v=1000$
), the incident particles from the collision area edge may reach the collision centre, so that the ratios should be modified to 27.8, 4.08 and 4.79, respectively. These ratios could explain why the ratio of the beam–target reaction by the improved method to the thermonuclear reaction shows an anomalous increase at $v=1000$![]() km s$^{-1}$
km s$^{-1}$![]() .
.
To prove this statement, the range of incident particles is shown in figure 9. Figure 9 is a rough estimate to the range of incident particles. It is seen that it is hard for the incident particle to leave its initial grid when the velocity is low. When the velocity reaches 1000 km s$^{-1}$![]() , the range of the incident particles is close to the grid size (1.3 $\mathrm {\mu }{\rm m}$
, the range of the incident particles is close to the grid size (1.3 $\mathrm {\mu }{\rm m}$![]() ) at a density of near 4 g cm$^{-3}$
) at a density of near 4 g cm$^{-3}$![]() so that the particles may leave their initial grid and travel to neighbouring grids.
so that the particles may leave their initial grid and travel to neighbouring grids.
5. Summary
An improved method taking the incident particle transport process into account is proposed to calculate the beam–target reaction rate accurately. The method is applied to study high-speed plasma collisions. When the initial density and temperature are set to 0.5 g cm$^{-3}$![]() and 100 eV, it is found that the results of the traditional method are close to those of the improved method if the collision velocity is less than 600 km s$^{-1}$
and 100 eV, it is found that the results of the traditional method are close to those of the improved method if the collision velocity is less than 600 km s$^{-1}$![]() . However, large differences appear for the case with higher collision velocity. The differences between the two methods can reach 70 % at 1000 km s$^{-1}$
. However, large differences appear for the case with higher collision velocity. The differences between the two methods can reach 70 % at 1000 km s$^{-1}$![]() . That is, the improved method can lead to much more accurate results for high-velocity conditions.
. That is, the improved method can lead to much more accurate results for high-velocity conditions.
The thermonuclear reaction and beam–target reaction both increase much as the collision velocity increases. The ratio of beam–target reaction to thermonuclear reaction decreases with increasing collision velocity. When the collision velocity is high enough (e.g. 1000 km s$^{-1}$![]() ), because of plasma transport, the ratio of beam–target reaction to thermonuclear reaction may increase a little anomalously.
), because of plasma transport, the ratio of beam–target reaction to thermonuclear reaction may increase a little anomalously.
The improved method will make large corrections to evaluate the importance of the non-negligible beam–target reaction for ICF schemes with large implosion velocity, such as the double-cone ignition scheme and impact ignition scheme.
Acknowledgements
We would like to thank X. Jiang for beneficial discussions.
Editor Luís O. Silva thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Strategic Priority Research Program of Chinese Academy of Science (grant no. XDA25050200), the National Natural Science Foundation of China (grant nos. 12175309, 11775305, 11975308 and 12005297), the fund of Science Challenge Project (no. TZ2018001) and the State Key Laboratory of Laser Interaction with Matter (no. SKLLIM1908). X.H.Y. also acknowledges the financial support from Fund for NUDT Young Innovator Awards (no. 20180104).
Declaration of interests
The authors report no conflict of interest.
Author contributions
B.Z. and Z.Z. derived the theory and proposed the improved method. Results were prepared by S.Y. X.Y. and Y.M. contributed to data analysis. The article was written by B.Z.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.