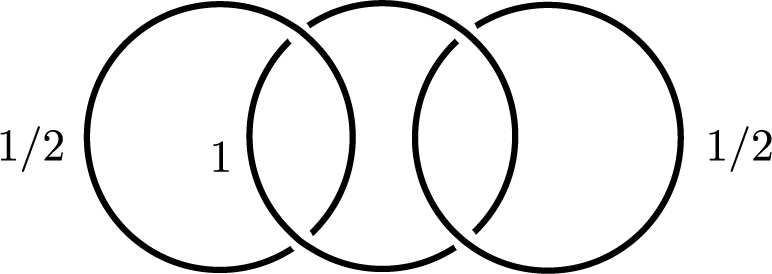1 Introduction
A knot K is said to be n-adjacent to a knot
![]() $K'$
if there exists a diagram of K containing a set of n crossings such that changing any nonempty subset of them yields a diagram of
$K'$
if there exists a diagram of K containing a set of n crossings such that changing any nonempty subset of them yields a diagram of
![]() $K'$
. Any knot that is adjacent to the unknot is, of course, unknotting number one, but the condition is much more restrictive. For example, nontrivial knots which are n-adjacent to the unknot for
$K'$
. Any knot that is adjacent to the unknot is, of course, unknotting number one, but the condition is much more restrictive. For example, nontrivial knots which are n-adjacent to the unknot for
![]() $n\geq 3$
have a trivial Alexander polynomial, are non-fibered, non-alternating, and have vanishing Vassiliev invariants of degree less than
$n\geq 3$
have a trivial Alexander polynomial, are non-fibered, non-alternating, and have vanishing Vassiliev invariants of degree less than
![]() $2n-1$
. These restrictions on their invariants are shown by Askitas–Kalfagianni [Reference Askitas and Kalfagianni1] to result from a diagrammatic characterization of n-adjacent knots,
$2n-1$
. These restrictions on their invariants are shown by Askitas–Kalfagianni [Reference Askitas and Kalfagianni1] to result from a diagrammatic characterization of n-adjacent knots,
![]() $n\geq 3$
, as those constructed from certain spatial chord diagrams called Brunnian–Suzuki graphs [Reference Askitas and Kalfagianni1, Theorem 4.4]. A Suzuki graph is given by a collection of weighted, embedded arcs along an unknotted circle in
$n\geq 3$
, as those constructed from certain spatial chord diagrams called Brunnian–Suzuki graphs [Reference Askitas and Kalfagianni1, Theorem 4.4]. A Suzuki graph is given by a collection of weighted, embedded arcs along an unknotted circle in
![]() $S^3$
, where the arcs describe a pattern along which a sequence of bandings and clasps converts the graph into a knot.
$S^3$
, where the arcs describe a pattern along which a sequence of bandings and clasps converts the graph into a knot.
In this article, we generalize the concept of n-adjacency from knots to three-manifolds. We say that a closed, oriented three-manifold Y is integrally n-adjacent to another three-manifold Z if there exists an n-component link L and an integral multi-slope p of the link such that performing Dehn surgery along any nonempty subset of L yields Z. The triple realizing the adjacency will be denoted
![]() $(Y,L,p)$
. Rational adjacency, denoted
$(Y,L,p)$
. Rational adjacency, denoted
![]() $(Y,L,\alpha )$
, is defined similarly where rational surgeries are permitted. In an analogy to Askitas–Kalfagianni, we characterize all n-adjacencies to the three-sphere as those arising from particular Dehn surgeries along Brunnian-like links. This recovers Askitas–Kalfagianni’s diagrammatic characterization of knots adjacent to the unknot, and we similarly obtain a statement on the finite-type invariants of three-manifolds.
$(Y,L,\alpha )$
, is defined similarly where rational surgeries are permitted. In an analogy to Askitas–Kalfagianni, we characterize all n-adjacencies to the three-sphere as those arising from particular Dehn surgeries along Brunnian-like links. This recovers Askitas–Kalfagianni’s diagrammatic characterization of knots adjacent to the unknot, and we similarly obtain a statement on the finite-type invariants of three-manifolds.
Given a link in a three-manifold, and a choice of surgery slopes, the core curves of the surgery solid tori produce a new link in the surgered manifold. We call this the core or dual of the surgery. Using dual links, it is in fact quite easy to construct examples of adjacent manifolds for all n: Let J be a Brunnian link in
![]() $S^3$
, and perform
$S^3$
, and perform
![]() $(\pm 1,\ldots , \pm 1)$
-surgery on J. This yields a homology sphere Y that is n-adjacent to the three-sphere via the dual link. The homology sphere will be distinct from
$(\pm 1,\ldots , \pm 1)$
-surgery on J. This yields a homology sphere Y that is n-adjacent to the three-sphere via the dual link. The homology sphere will be distinct from
![]() $S^3$
provided that J is a non-trivial link. For a concrete example,
$S^3$
provided that J is a non-trivial link. For a concrete example,
![]() $(1,1,1)$
-surgery on the Borromean rings produces the Poincaré homology sphere, which is
$(1,1,1)$
-surgery on the Borromean rings produces the Poincaré homology sphere, which is
![]() $3$
-adjacent to
$3$
-adjacent to
![]() $S^3$
, as shown in Figure 1. In fact, we will see shortly that all integral n-adjacencies for
$S^3$
, as shown in Figure 1. In fact, we will see shortly that all integral n-adjacencies for
![]() $n \geq 3$
arise from surgery on Brunnian links.
$n \geq 3$
arise from surgery on Brunnian links.

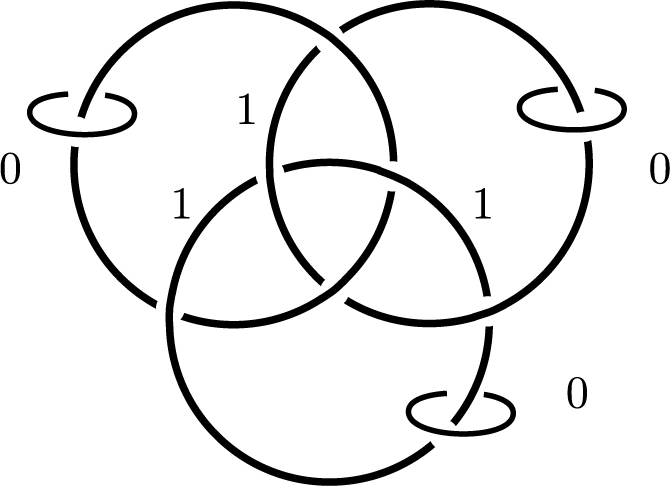
Figure 1 The Poincaré homology sphere results from
![]() $(1, 1, 1)$
-surgery on the Borromean rings. The meridians with surgery slopes
$(1, 1, 1)$
-surgery on the Borromean rings. The meridians with surgery slopes
![]() $(0, 0, 0)$
realize a
$(0, 0, 0)$
realize a
![]() $3$
-adjacency of the Poincaré homology sphere to
$3$
-adjacency of the Poincaré homology sphere to
![]() $S^3$
.
$S^3$
.
Next, consider the example in Figure 2. An exercise in Kirby calculus shows that
![]() $(1/2, 1, 1/2)$
-surgery yields
$(1/2, 1, 1/2)$
-surgery yields
![]() $-L(3, 1)$
and induced surgery on any proper sublink yields
$-L(3, 1)$
and induced surgery on any proper sublink yields
![]() $S^3$
. This surgery description will demonstrate that
$S^3$
. This surgery description will demonstrate that
![]() $-L(3,1)$
is 3-adjacent to
$-L(3,1)$
is 3-adjacent to
![]() $S^3$
. Thus, Hopf links can and do appear in the characterization of rational adjacencies. We define the family of Hopf–Brunnian links as follows. An n-component link is Hopf–Brunnian if all
$S^3$
. Thus, Hopf links can and do appear in the characterization of rational adjacencies. We define the family of Hopf–Brunnian links as follows. An n-component link is Hopf–Brunnian if all
![]() $n-1$
component sublinks are split unions of Hopf links and unknots. We prove the following theorem.
$n-1$
component sublinks are split unions of Hopf links and unknots. We prove the following theorem.

Figure 2 This three-component Hopf–Brunnian link J admits a
![]() $(1/2, 1, 1/2)$
-rational surgery to
$(1/2, 1, 1/2)$
-rational surgery to
![]() $-L(3, 1)$
. The core of J after surgery is a link L realizing the 3-adjacency of
$-L(3, 1)$
. The core of J after surgery is a link L realizing the 3-adjacency of
![]() $-L(3,1)$
to
$-L(3,1)$
to
![]() $S^3$
.
$S^3$
.
Theorem 1.1. The triple
![]() $(Y, L, \alpha )$
realizes an n-adjacency to
$(Y, L, \alpha )$
realizes an n-adjacency to
![]() $S^3$
with surgery core J if and only if J is Hopf–Brunnian, the dual surgery slopes of J are of the form
$S^3$
with surgery core J if and only if J is Hopf–Brunnian, the dual surgery slopes of J are of the form
![]() $1/k_i$
,
$1/k_i$
,
![]() $k_i\in \mathbb {Z}^*$
, and any proper Hopf sublink of J must have surgery slopes
$k_i\in \mathbb {Z}^*$
, and any proper Hopf sublink of J must have surgery slopes
![]() $\pm (1, 1/2)$
or
$\pm (1, 1/2)$
or
![]() $\pm (1/2, 1)$
.
$\pm (1/2, 1)$
.
Corollary 1.2. The triple
![]() $(Y, L, p)$
realizes an integral n-adjacency to
$(Y, L, p)$
realizes an integral n-adjacency to
![]() $S^3$
with surgery core J if and only if J is Brunnian and the dual surgery slopes of J are
$S^3$
with surgery core J if and only if J is Brunnian and the dual surgery slopes of J are
![]() $\pm 1$
(signs need not be consistent).
$\pm 1$
(signs need not be consistent).
With a little more work, we can obtain the following corollary.
Corollary 1.3. If Y is integrally n-adjacent to
![]() $S^3$
for
$S^3$
for
![]() $n\geq 3$
, or rationally n-adjacent to
$n\geq 3$
, or rationally n-adjacent to
![]() $S^3$
for
$S^3$
for
![]() $n\geq 4$
, then Y is an integer homology sphere.
$n\geq 4$
, then Y is an integer homology sphere.
Proof. Let J denote the dual link as discussed above. We first consider the case of an integral adjacency with
![]() $n \geq 3$
. By Corollary 1.2, since the dual surgery slopes are integral, all 2-component sublinks of J are unlinks, and hence the pairwise linking numbers are zero. Further, the surgery coefficients are all
$n \geq 3$
. By Corollary 1.2, since the dual surgery slopes are integral, all 2-component sublinks of J are unlinks, and hence the pairwise linking numbers are zero. Further, the surgery coefficients are all
![]() $\pm 1$
. Surgery on such a framed link (which is Y) gives an integer homology sphere. Now suppose that
$\pm 1$
. Surgery on such a framed link (which is Y) gives an integer homology sphere. Now suppose that
![]() $n \geq 4$
, but the adjacency may be rational. Theorem 1.1 implies that J is Hopf–Brunnian, and in particular, all 2-component sublinks of J are unlinks with surgery slopes of the form
$n \geq 4$
, but the adjacency may be rational. Theorem 1.1 implies that J is Hopf–Brunnian, and in particular, all 2-component sublinks of J are unlinks with surgery slopes of the form
![]() $\pm 1/k$
or Hopf links with surgery slope
$\pm 1/k$
or Hopf links with surgery slope
![]() $\pm (1, 1/2)$
. We claim that each pair of Hopf link components has zero linking number with all other components; note that this immediately implies that the surgery will result in an integral homology sphere. To see this, suppose that
$\pm (1, 1/2)$
. We claim that each pair of Hopf link components has zero linking number with all other components; note that this immediately implies that the surgery will result in an integral homology sphere. To see this, suppose that
![]() $H_1 \cup H_2$
is a Hopf sublink of J and Q is a third component of J. Since J is Hopf Brunnian, and this is a 3-component sublink of a link with at least four components, we see that Q must be split from
$H_1 \cup H_2$
is a Hopf sublink of J and Q is a third component of J. Since J is Hopf Brunnian, and this is a 3-component sublink of a link with at least four components, we see that Q must be split from
![]() $H_1 \cup H_2$
, and hence Q has linking number 0 with
$H_1 \cup H_2$
, and hence Q has linking number 0 with
![]() $H_1$
and
$H_1$
and
![]() $H_2$
. This completes the proof.
$H_2$
. This completes the proof.
Note that in the case
![]() $n=2$
, any
$n=2$
, any
![]() $(1/k_1, 1/k_2), k_i \in \mathbb {Z}^*$
, surgery along any link
$(1/k_1, 1/k_2), k_i \in \mathbb {Z}^*$
, surgery along any link
![]() $J_1\cup J_2$
of unknotted components in
$J_1\cup J_2$
of unknotted components in
![]() $S^3$
will yield a manifold adjacent to the three-sphere. In order to prove Theorem 1.1, we give a stronger characterization for self-adjacencies from the three-sphere to itself.
$S^3$
will yield a manifold adjacent to the three-sphere. In order to prove Theorem 1.1, we give a stronger characterization for self-adjacencies from the three-sphere to itself.
Proposition 3.2
The triple
![]() $(S^3, J, \alpha )$
realizes an n-adjacency to
$(S^3, J, \alpha )$
realizes an n-adjacency to
![]() $S^3$
if and only if J itself is a split union of Hopf links and unknots, all slopes
$S^3$
if and only if J itself is a split union of Hopf links and unknots, all slopes
![]() $\alpha _i = 1/k_i$
, where
$\alpha _i = 1/k_i$
, where
![]() $k_i\in \mathbb {Z}^*$
, and the surgery slopes of Hopf components are either
$k_i\in \mathbb {Z}^*$
, and the surgery slopes of Hopf components are either
![]() $\pm (1, 1/2)$
or
$\pm (1, 1/2)$
or
![]() $\pm (1/2, 1)$
.
$\pm (1/2, 1)$
.
Note that the requirement that J itself is a split union of Hopf links and unknots is stronger than requiring J be Hopf–Brunnian.
Using Proposition 3.2, we may now prove Theorem 1.1.
Proof of Theorem 1.1
In Proposition 2.2 below, we show that if
![]() $(Y,L, \alpha )$
realizes a rational n-adjacency to
$(Y,L, \alpha )$
realizes a rational n-adjacency to
![]() $S^3$
, then the core of the surgery is an n-component link J in
$S^3$
, then the core of the surgery is an n-component link J in
![]() $S^3$
and performing
$S^3$
and performing
![]() $\alpha $
-framed surgery on
$\alpha $
-framed surgery on
![]() $\cup _{i \in I } L_i$
, for any
$\cup _{i \in I } L_i$
, for any
![]() $I \subset \{1,\ldots ,n\}$
, yields the same result as performing surgery on
$I \subset \{1,\ldots ,n\}$
, yields the same result as performing surgery on
![]() $\cup _{i \in [n] - I} J_i$
with the corresponding dual slopes (see Section 2.1 for more details). In particular, surgery on every proper sublink of J in
$\cup _{i \in [n] - I} J_i$
with the corresponding dual slopes (see Section 2.1 for more details). In particular, surgery on every proper sublink of J in
![]() $S^3$
gives back
$S^3$
gives back
![]() $S^3$
. By Proposition 3.2, every proper sublink of J is a split union of Hopf links and an unlink. The Hopf pairs have surgery coefficients
$S^3$
. By Proposition 3.2, every proper sublink of J is a split union of Hopf links and an unlink. The Hopf pairs have surgery coefficients
![]() $\pm (1, 1/2)$
and split unknotted components have surgery coefficients
$\pm (1, 1/2)$
and split unknotted components have surgery coefficients
![]() $1/k$
,
$1/k$
,
![]() $k\neq 0$
.
$k\neq 0$
.
Let us return to n-adjacency in knots. Using Theorem 1.1, we are now able to recover Askitas–Kalfagianni’s characterization of knots which are n-adjacent to the unknot [Reference Askitas and Kalfagianni1, Theorem 4.4].
Theorem 1.4 (Askitas–Kalfagianni).
Let K be n-adjacent to the unknot for
![]() $n \geq 3$
. Then, K is the realization of a Brunnian–Suzuki n-graph.
$n \geq 3$
. Then, K is the realization of a Brunnian–Suzuki n-graph.
Proof. Let
![]() $n\geq 3$
, and let K be n-adjacent to the unknot U. This means that there is an associated diagram of K with n crossings, such that changing any non-empty subset of these produces the unknot. Each of these n crossings yields an unknotting arc in
$n\geq 3$
, and let K be n-adjacent to the unknot U. This means that there is an associated diagram of K with n crossings, such that changing any non-empty subset of these produces the unknot. Each of these n crossings yields an unknotting arc in
![]() $S^3$
with boundary on K; more precisely, given an unknotting crossing in the diagram, consider the preimage of the associated double point, which gives an arc in
$S^3$
with boundary on K; more precisely, given an unknotting crossing in the diagram, consider the preimage of the associated double point, which gives an arc in
![]() $S^3$
with boundary on K. The collection of unknotting arcs lifts to a strongly invertible link
$S^3$
with boundary on K. The collection of unknotting arcs lifts to a strongly invertible link
![]() $L=L_1\cup \cdots \cup L_n$
in the double cover of
$L=L_1\cup \cdots \cup L_n$
in the double cover of
![]() $S^3$
branched over K, which we will call Y. Likewise, there is a corresponding collection of “knotting” arcs
$S^3$
branched over K, which we will call Y. Likewise, there is a corresponding collection of “knotting” arcs
![]() $\gamma _1, \ldots , \gamma _n$
from U to K, which lifts to a strongly invertible link J in
$\gamma _1, \ldots , \gamma _n$
from U to K, which lifts to a strongly invertible link J in
![]() $S^3$
. The Montesinos trick [Reference Montesinos-Amilibia10] provides a half-integral multi-slope
$S^3$
. The Montesinos trick [Reference Montesinos-Amilibia10] provides a half-integral multi-slope
![]() $\beta $
on J such that
$\beta $
on J such that
![]() $\beta _i$
-surgery on
$\beta _i$
-surgery on
![]() $J_i$
corresponds to the associated crossing change downstairs on
$J_i$
corresponds to the associated crossing change downstairs on
![]() $\gamma _i$
.
$\gamma _i$
.
Applying crossing changes associated with any subset of crossing arcs
![]() $\cup _{i\in I}\gamma _i$
along U yields the same result as applying the complementary
$\cup _{i\in I}\gamma _i$
along U yields the same result as applying the complementary
![]() $[n]-I$
crossing changes in K. By the n-adjacency of K, this produces the unknot for any proper subset
$[n]-I$
crossing changes in K. By the n-adjacency of K, this produces the unknot for any proper subset
![]() $I\subset \{1,\ldots , n\}$
. At the level of the branched double cover, we see that surgery on every proper sublink of J produces
$I\subset \{1,\ldots , n\}$
. At the level of the branched double cover, we see that surgery on every proper sublink of J produces
![]() $S^3$
(see Proposition 2.2 below). We now apply Proposition 3.2 to the
$S^3$
(see Proposition 2.2 below). We now apply Proposition 3.2 to the
![]() $(n-1)$
-component sublinks of J. Since
$(n-1)$
-component sublinks of J. Since
![]() $n\geq 3$
and none of the surgery slopes are
$n\geq 3$
and none of the surgery slopes are
![]() $\pm 1$
(because they are all half-integral), all of the pairwise linking numbers of J must be zero and the proper sublinks are unlinks, that is, J is Brunnian, and each
$\pm 1$
(because they are all half-integral), all of the pairwise linking numbers of J must be zero and the proper sublinks are unlinks, that is, J is Brunnian, and each
![]() $\beta _i$
is
$\beta _i$
is
![]() $\pm 1/2$
.
$\pm 1/2$
.
Consider now the union of the arcs
![]() $\gamma _1,\ldots , \gamma _n$
together with the unknot U. Again by the Montesinos trick [Reference Montesinos-Amilibia10], an arc with weight
$\gamma _1,\ldots , \gamma _n$
together with the unknot U. Again by the Montesinos trick [Reference Montesinos-Amilibia10], an arc with weight
![]() $(w, z)$
in the terminology of [Reference Askitas and Kalfagianni1, Section 3] realizes a surgery in the branched double cover with slope
$(w, z)$
in the terminology of [Reference Askitas and Kalfagianni1, Section 3] realizes a surgery in the branched double cover with slope
![]() $w+\frac {z}{2}$
. The theorem will follow from the following claim.
$w+\frac {z}{2}$
. The theorem will follow from the following claim.
Claim 1.5. The graph
![]() $G = U\cup \bigcup _{i=1}^n\gamma _i$
is a Brunnian–Suzuki n-graph.
$G = U\cup \bigcup _{i=1}^n\gamma _i$
is a Brunnian–Suzuki n-graph.
Proof of claim
Notice that no pair of arcs
![]() $\gamma _i$
and
$\gamma _i$
and
![]() $\gamma _j$
have endpoints interleaved along the unknot because they would lift to a link
$\gamma _j$
have endpoints interleaved along the unknot because they would lift to a link
![]() $J_i\cup J_j$
of nonzero linking number, a contradiction. This means that G is admissible, in the terminology of [Reference Askitas and Kalfagianni1, Definition 3.2]. For any proper subset
$J_i\cup J_j$
of nonzero linking number, a contradiction. This means that G is admissible, in the terminology of [Reference Askitas and Kalfagianni1, Definition 3.2]. For any proper subset
![]() $I\subset \{1, \ldots , n\}$
of components of
$I\subset \{1, \ldots , n\}$
of components of
![]() $J_1\cup \cdots \cup J_n$
, the quotient under
$J_1\cup \cdots \cup J_n$
, the quotient under
![]() $\tau $
is a proper subset of the
$\tau $
is a proper subset of the
![]() $\gamma $
arcs. Because each subset of J is an unlink, and there is a unique strong inversion
$\gamma $
arcs. Because each subset of J is an unlink, and there is a unique strong inversion
![]() $\tau $
on the unlink [Reference Kim and Tollefson7], these descend to arcs embedded disjointly in the spanning disk for the unknot. Moreover, because the surgery slopes on each
$\tau $
on the unlink [Reference Kim and Tollefson7], these descend to arcs embedded disjointly in the spanning disk for the unknot. Moreover, because the surgery slopes on each
![]() $J_i$
are
$J_i$
are
![]() $\pm 1/2$
, these descend to weighted arcs of the form
$\pm 1/2$
, these descend to weighted arcs of the form
![]() $(0, \pm 1)$
. Thus, subgraphs of G with
$(0, \pm 1)$
. Thus, subgraphs of G with
![]() $n-1$
arcs are standard. The graph G is therefore a Brunnian–Suzuki n-graph, as in [Reference Askitas and Kalfagianni1, Definition 3.4].
$n-1$
arcs are standard. The graph G is therefore a Brunnian–Suzuki n-graph, as in [Reference Askitas and Kalfagianni1, Definition 3.4].
Note that Theorem 1.4 is the key ingredient in the claimed vanishing of the Vassiliev invariants of a knot n-adjacent to the unknot, as mentioned above.
In analogy with the work of Askitas–Kalfagianni, we are also able to apply Theorem 1.1 more generally to prove a vanishing result for finite-type invariants of homology spheres. (For a quick survey on finite-type invariants, see [Reference Lin8].)
Corollary 1.6. Let Y be a homology sphere which is integrally n-adjacent to
![]() $S^3$
. Then, all finite-type invariants of order less than
$S^3$
. Then, all finite-type invariants of order less than
![]() $2n-4$
vanish.
$2n-4$
vanish.
Proof. By Corollary 1.2, Y is obtained by surgery on an n-component Brunnian link. The required vanishing result is given by [Reference Meilhan9, Theorem 1.1].
2 Dehn surgery
2.1. The dual perspective
Let Y be a closed, oriented three-manifold, and let
![]() $L=L_1\cup \cdots \cup L_n$
denote a link in Y. Let
$L=L_1\cup \cdots \cup L_n$
denote a link in Y. Let
![]() $\alpha =(\alpha _1, \ldots , \alpha _n)$
denote a multi-slope on L. The notation
$\alpha =(\alpha _1, \ldots , \alpha _n)$
denote a multi-slope on L. The notation
![]() $Y_{\alpha }(L)$
denotes the three-manifold obtained by performing
$Y_{\alpha }(L)$
denotes the three-manifold obtained by performing
![]() $\alpha _i$
Dehn surgery along
$\alpha _i$
Dehn surgery along
![]() $L_i$
for all
$L_i$
for all
![]() $i=1, \ldots , n$
.
$i=1, \ldots , n$
.
Definition 2.1. Consider the triple
![]() $(Y, L, \alpha )$
, where Y is a closed, oriented 3-manifold,
$(Y, L, \alpha )$
, where Y is a closed, oriented 3-manifold,
![]() $L=L_1\cup \cdots \cup L_n$
is a link in Y, and
$L=L_1\cup \cdots \cup L_n$
is a link in Y, and
![]() $\alpha =(\alpha _1, \ldots , \alpha _n)$
is a multi-slope on L. Let Z be a closed, oriented three-manifold. If
$\alpha =(\alpha _1, \ldots , \alpha _n)$
is a multi-slope on L. Let Z be a closed, oriented three-manifold. If
![]() $Y_{\alpha _I}(L_I) = Z$
for any nonempty subset I of
$Y_{\alpha _I}(L_I) = Z$
for any nonempty subset I of
![]() $\{1, \ldots , n\}$
, then
$\{1, \ldots , n\}$
, then
![]() $(Y, L, \alpha )$
realizes an n-adjacency to Z. We say that Y is integrally n-adjacent to Z if the multi-slopes are integral and rationally adjacent to Z otherwise.
$(Y, L, \alpha )$
realizes an n-adjacency to Z. We say that Y is integrally n-adjacent to Z if the multi-slopes are integral and rationally adjacent to Z otherwise.
Notice that n-adjacency is not a symmetric relation.
In order to circumvent the difficulty in describing surgeries in arbitrary three-manifolds, we take the following perspective.
Suppose that L is an n-component link in a three-manifold Y with a surgery to
![]() $S^3$
along the multi-slope
$S^3$
along the multi-slope
![]() $\alpha $
. Let J be the core of the surgery in
$\alpha $
. Let J be the core of the surgery in
![]() $S^3$
, and write
$S^3$
, and write
![]() $J = J_1 \cup \cdots \cup J_n$
. Note that we can identify the exterior of J and the exterior of L, so a slope on the boundary of the exterior of J naturally determines one on the exterior of L and vice versa. Now, we will associate to J rational numbers
$J = J_1 \cup \cdots \cup J_n$
. Note that we can identify the exterior of J and the exterior of L, so a slope on the boundary of the exterior of J naturally determines one on the exterior of L and vice versa. Now, we will associate to J rational numbers
![]() $r=(r_1,\ldots , r_n)$
which describe how to “undo” the surgery performed on each
$r=(r_1,\ldots , r_n)$
which describe how to “undo” the surgery performed on each
![]() $J_i$
. To be more precise, in the exterior of L, we have two slopes
$J_i$
. To be more precise, in the exterior of L, we have two slopes
![]() $\eta _i$
and
$\eta _i$
and
![]() $\alpha _i$
on the boundary torus coming from
$\alpha _i$
on the boundary torus coming from
![]() $L_i$
:
$L_i$
:
![]() $\eta _i$
is the meridian of
$\eta _i$
is the meridian of
![]() $L_i$
and Dehn filling along
$L_i$
and Dehn filling along
![]() $\alpha _i$
corresponds to the non-trivial surgery we are going to do to get to
$\alpha _i$
corresponds to the non-trivial surgery we are going to do to get to
![]() $S^3$
. Viewing J as a link in
$S^3$
. Viewing J as a link in
![]() $S^3$
, we can still view these slopes in the boundary of a neighborhood of
$S^3$
, we can still view these slopes in the boundary of a neighborhood of
![]() $J_i$
. Express
$J_i$
. Express
![]() $\eta _i = p_i \mu _i + q_i \lambda _i$
, where
$\eta _i = p_i \mu _i + q_i \lambda _i$
, where
![]() $\mu _i$
and
$\mu _i$
and
![]() $\lambda _i$
are the meridian and longitudes for
$\lambda _i$
are the meridian and longitudes for
![]() $J_i$
as a knot in
$J_i$
as a knot in
![]() $S^3$
. (Note that
$S^3$
. (Note that
![]() $\mu _i = \alpha _i$
.) We say that the slopes
$\mu _i = \alpha _i$
.) We say that the slopes
![]() $\eta _i$
and
$\eta _i$
and
![]() $\alpha _i$
are dual to each other. We calculate these in the following order:
$\alpha _i$
are dual to each other. We calculate these in the following order:
-
1. First, perform surgery on all components of L to get J in
 $S^3$
, not just some of the components (which still produces
$S^3$
, not just some of the components (which still produces
 $S^3$
if L is realizing an n-adjacency).
$S^3$
if L is realizing an n-adjacency). -
2. Then, identify the slopes
 $\eta _i$
with
$\eta _i$
with
 $r_i=p_i/q_i$
.
$r_i=p_i/q_i$
.
Note that the adjacency is integral if and only if all
![]() $p_i/q_i$
are integral. This is because
$p_i/q_i$
are integral. This is because
![]() $\Delta (\eta _i,\alpha _i) = \Delta (\mu _i, p_i \mu _i + q_i \lambda _i) = |q_i|$
. In general, when discussing the dual link of a surgery to
$\Delta (\eta _i,\alpha _i) = \Delta (\mu _i, p_i \mu _i + q_i \lambda _i) = |q_i|$
. In general, when discussing the dual link of a surgery to
![]() $S^3$
, we will assume that it naturally inherits these rational surgery slopes in
$S^3$
, we will assume that it naturally inherits these rational surgery slopes in
![]() $S^3$
as above.
$S^3$
as above.
Now, the data
![]() $(S^3, J, r)$
in
$(S^3, J, r)$
in
![]() $S^3$
actually recover
$S^3$
actually recover
![]() $(Y,L,\alpha )$
. Performing surgery on all components of J gives
$(Y,L,\alpha )$
. Performing surgery on all components of J gives
![]() $Y,$
and by construction, L is the core of the surgery on J while the meridian of each
$Y,$
and by construction, L is the core of the surgery on J while the meridian of each
![]() $J_i$
becomes the slope
$J_i$
becomes the slope
![]() $\alpha _i$
. But we can also recover sublinks in the following way. If we look at a sublink
$\alpha _i$
. But we can also recover sublinks in the following way. If we look at a sublink
![]() $J'$
of J, without loss of generality,
$J'$
of J, without loss of generality,
![]() $J_1 \cup \cdots \cup J_k$
, then surgery on
$J_1 \cup \cdots \cup J_k$
, then surgery on
![]() $J'$
produces the same manifold as surgery in Y on
$J'$
produces the same manifold as surgery in Y on
![]() $L_{k+1} \cup \cdots \cup L_n$
. And further, the core of surgery on
$L_{k+1} \cup \cdots \cup L_n$
. And further, the core of surgery on
![]() $J'$
, a k-component link, is exactly the image of
$J'$
, a k-component link, is exactly the image of
![]() $L_1 \cup \cdots \cup L_k$
in the surgery on
$L_1 \cup \cdots \cup L_k$
in the surgery on
![]() $L_{k+1} \cup \cdots \cup L_n$
.
$L_{k+1} \cup \cdots \cup L_n$
.
We also use the fact that
![]() $|H_1(Y; \mathbb {Z})| =|H_1(S^3_r(J); \mathbb {Z})|$
may be obtained from the determinant of the linking matrix defined by
$|H_1(Y; \mathbb {Z})| =|H_1(S^3_r(J); \mathbb {Z})|$
may be obtained from the determinant of the linking matrix defined by
 $$ \begin{align} B_{ij}:= \left\{ \begin{array}{ll} p_i & \text{if } i=j,\\ q_j \ell k(L_i, L_j) & \text{if } i\neq j. \end{array} \right. \end{align} $$
$$ \begin{align} B_{ij}:= \left\{ \begin{array}{ll} p_i & \text{if } i=j,\\ q_j \ell k(L_i, L_j) & \text{if } i\neq j. \end{array} \right. \end{align} $$
Now, we return to the case that a rational surgery on L is realizing an n-adjacency from Y to
![]() $S^3$
. Build
$S^3$
. Build
![]() $(S^3, J,r)$
as discussed. The above paragraph can be reinterpreted as saying that doing the corresponding surgery on every proper sublink of J gives
$(S^3, J,r)$
as discussed. The above paragraph can be reinterpreted as saying that doing the corresponding surgery on every proper sublink of J gives
![]() $S^3$
. For the benefit of the reader, we summarize this discussion with the following proposition.
$S^3$
. For the benefit of the reader, we summarize this discussion with the following proposition.
Proposition 2.2. Let
![]() $\alpha $
be a multi-slope on an n-component link L in Y. Then,
$\alpha $
be a multi-slope on an n-component link L in Y. Then,
![]() $(Y,L,\alpha )$
realizes an n-adjacency to
$(Y,L,\alpha )$
realizes an n-adjacency to
![]() $S^3$
if and only if there exists a multi-slope
$S^3$
if and only if there exists a multi-slope
![]() $\beta $
on a link J in
$\beta $
on a link J in
![]() $S^3$
such that:
$S^3$
such that:
-
1.
 $S^3_\beta (J) = Y$
;
$S^3_\beta (J) = Y$
; -
2. L is the core of the surgery on J;
-
3. each
 $\alpha _i$
is the dual slope to
$\alpha _i$
is the dual slope to
 $\beta _i$
;
$\beta _i$
; -
4. surgery on every proper sublink of J yields
 $S^3$
.
$S^3$
.
Furthermore, the adjacency is integral if and only if
![]() $\beta $
is integral.
$\beta $
is integral.
2.2. The linking of the dual curves
In light of the dual perspective from Proposition 2.2, we want to understand the effects of surgery on links in
![]() $S^3$
whose sublinks also surger to
$S^3$
whose sublinks also surger to
![]() $S^3$
. The next lemma allows us to constrain the linking numbers and surgery coefficients for the dual link in
$S^3$
. The next lemma allows us to constrain the linking numbers and surgery coefficients for the dual link in
![]() $S^3$
arising from an n-adjacency.
$S^3$
arising from an n-adjacency.
Lemma 2.3. Suppose that
![]() $(S^3, J,\alpha )$
realizes a 2-adjacency to
$(S^3, J,\alpha )$
realizes a 2-adjacency to
![]() $S^3$
. Then, either the linking number of J is zero or the linking number is
$S^3$
. Then, either the linking number of J is zero or the linking number is
![]() $\pm 1$
and the surgery coefficients
$\pm 1$
and the surgery coefficients
![]() $\alpha _i$
are
$\alpha _i$
are
![]() $\pm (1,1/2)$
or
$\pm (1,1/2)$
or
![]() $\pm (1/2, 1)$
.
$\pm (1/2, 1)$
.
Proof. Since surgery on each individual component of
![]() $J = J_1 \cup J_2$
produces
$J = J_1 \cup J_2$
produces
![]() $S^3$
, an integer homology sphere, the surgery coefficient for
$S^3$
, an integer homology sphere, the surgery coefficient for
![]() $J_i$
is of the form
$J_i$
is of the form
![]() $1/q_i$
. The linking matrix B from (2.1) for the surgery presentation on J then gives
$1/q_i$
. The linking matrix B from (2.1) for the surgery presentation on J then gives
 $$\begin{align*}1 = \left |det \begin{pmatrix} 1 & q_2 \ell \\ q_1 \ell & 1 \end{pmatrix} \right | = |q_1 q_2 \ell^2 - 1|, \end{align*}$$
$$\begin{align*}1 = \left |det \begin{pmatrix} 1 & q_2 \ell \\ q_1 \ell & 1 \end{pmatrix} \right | = |q_1 q_2 \ell^2 - 1|, \end{align*}$$
where
![]() $\ell $
is the linking number of
$\ell $
is the linking number of
![]() $J_1$
and
$J_1$
and
![]() $J_2$
(say after choosing orientations of each component). Since
$J_2$
(say after choosing orientations of each component). Since
![]() $q_1, q_2 \neq 0$
, we see that
$q_1, q_2 \neq 0$
, we see that
![]() $|\ell | = 0$
or
$|\ell | = 0$
or
![]() $1$
. If
$1$
. If
![]() $|\ell | = 1$
, then we must have that
$|\ell | = 1$
, then we must have that
![]() $(q_1,q_2) = \pm (1,2)$
or
$(q_1,q_2) = \pm (1,2)$
or
![]() $\pm (2, 1)$
, as desired.
$\pm (2, 1)$
, as desired.
Proposition 2.4. Suppose that J is an n-component link in
![]() $S^3$
, with
$S^3$
, with
![]() $n \geq 3$
, and
$n \geq 3$
, and
![]() $\alpha $
is a multi-slope on J. If surgery on every proper sublink of J produces
$\alpha $
is a multi-slope on J. If surgery on every proper sublink of J produces
![]() $S^3$
, then all pairwise linking numbers are 0 or
$S^3$
, then all pairwise linking numbers are 0 or
![]() $\pm 1$
. If
$\pm 1$
. If
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are a pair of components with
$J_2$
are a pair of components with
![]() $|\ell k(J_1,J_2)| = 1$
, then the slopes are
$|\ell k(J_1,J_2)| = 1$
, then the slopes are
![]() $\pm (1,1/2)$
or
$\pm (1,1/2)$
or
![]() $\pm (1/2, 1)$
. If
$\pm (1/2, 1)$
. If
![]() $n = 3$
and
$n = 3$
and
![]() $S^3_\alpha (J)$
is an integer homology sphere or
$S^3_\alpha (J)$
is an integer homology sphere or
![]() $n \geq 4$
, then each of
$n \geq 4$
, then each of
![]() $J_1$
and
$J_1$
and
![]() $J_2$
has linking number zero with all other components.
$J_2$
has linking number zero with all other components.
Proof. Since
![]() $n \geq 3$
, every two-component sublink of J with induced multi-slope from
$n \geq 3$
, every two-component sublink of J with induced multi-slope from
![]() $\alpha $
provides a 2-adjacency from
$\alpha $
provides a 2-adjacency from
![]() $S^3$
to itself. Therefore, by Lemma 2.3, the pairwise linking numbers are 0 or
$S^3$
to itself. Therefore, by Lemma 2.3, the pairwise linking numbers are 0 or
![]() $\pm 1$
and for the 2-component sublinks with linking number having absolute value 1, the surgery coefficients are
$\pm 1$
and for the 2-component sublinks with linking number having absolute value 1, the surgery coefficients are
![]() $\pm (1,1/2)$
or
$\pm (1,1/2)$
or
![]() $\pm (1/2,1)$
.
$\pm (1/2,1)$
.
Now suppose that
![]() $S^3_\alpha (J)$
is an integer homology sphere. It remains to consider the pairwise linking of
$S^3_\alpha (J)$
is an integer homology sphere. It remains to consider the pairwise linking of
![]() $J_1, J_2$
with the other components. Let
$J_1, J_2$
with the other components. Let
![]() $J_3$
be another component. Then, we know that the associated surgery on
$J_3$
be another component. Then, we know that the associated surgery on
![]() $J_1 \cup J_2 \cup J_3$
produces
$J_1 \cup J_2 \cup J_3$
produces
![]() $S^3_\alpha (J)$
if
$S^3_\alpha (J)$
if
![]() $n = 3$
and
$n = 3$
and
![]() $S^3$
if
$S^3$
if
![]() $n> 3$
. Either way, the result is an integer homology sphere. Orient
$n> 3$
. Either way, the result is an integer homology sphere. Orient
![]() $J_1, J_2$
such that the pairwise linking is 1, fix an orientation on
$J_1, J_2$
such that the pairwise linking is 1, fix an orientation on
![]() $J_3$
and let
$J_3$
and let
![]() $\ell _1, \ell _2$
be the linking numbers of
$\ell _1, \ell _2$
be the linking numbers of
![]() $J_3$
with
$J_3$
with
![]() $J_1, J_2$
, respectively. Without loss of generality, the surgery coefficients on
$J_1, J_2$
, respectively. Without loss of generality, the surgery coefficients on
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are 1 and
$J_2$
are 1 and
![]() $1/2,$
respectively. (Otherwise, rearrange the order of the components and/or mirror J and reverse the signs of
$1/2,$
respectively. (Otherwise, rearrange the order of the components and/or mirror J and reverse the signs of
![]() $\alpha $
.) Suppose for contradiction that
$\alpha $
.) Suppose for contradiction that
![]() $\ell _1, \ell _2$
are not both zero.
$\ell _1, \ell _2$
are not both zero.
The first case is that
![]() $\ell _1 \neq 0$
. In this case, by applying the first part of the proposition to the pair
$\ell _1 \neq 0$
. In this case, by applying the first part of the proposition to the pair
![]() $(J_1, J_3)$
, we see that
$(J_1, J_3)$
, we see that
![]() $\ell _1 =1$
and the surgery coefficient for
$\ell _1 =1$
and the surgery coefficient for
![]() $J_3$
must be
$J_3$
must be
![]() $1/2$
. Applying the first part of the proposition to the pair
$1/2$
. Applying the first part of the proposition to the pair
![]() $(J_2, J_3)$
, we see that
$(J_2, J_3)$
, we see that
![]() $J_2$
and
$J_2$
and
![]() $J_3$
have linking number zero, since the pair of surgery coefficients is not
$J_3$
have linking number zero, since the pair of surgery coefficients is not
![]() $\pm (1/2,1)$
or
$\pm (1/2,1)$
or
![]() $\pm (1,1/2)$
. In this case, the linking matrix for the 3-component surgery description computes the order of
$\pm (1,1/2)$
. In this case, the linking matrix for the 3-component surgery description computes the order of
![]() $H_1$
of the surgery on
$H_1$
of the surgery on
![]() $J_1 \cup J_2 \cup J_3$
to be:
$J_1 \cup J_2 \cup J_3$
to be:
 $$\begin{align*}1 = \left |det \begin{pmatrix} 1 & 2 & 2 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} \right | = 3, \end{align*}$$
$$\begin{align*}1 = \left |det \begin{pmatrix} 1 & 2 & 2 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} \right | = 3, \end{align*}$$
a contradiction.
The other case is that
![]() $\ell _1=0$
, and so
$\ell _1=0$
, and so
![]() $\ell _2 = 1$
. Now, we see the surgery coefficients are
$\ell _2 = 1$
. Now, we see the surgery coefficients are
![]() $1$
for
$1$
for
![]() $J_1$
and
$J_1$
and
![]() $J_3$
, and
$J_3$
, and
![]() $1/2$
for
$1/2$
for
![]() $J_2$
. Then, we compute again
$J_2$
. Then, we compute again
 $$\begin{align*}1 = \left | det \begin{pmatrix} 1 & 2 & 0 \\ 1 & 1 & 1 \\ 0 & 2 & 1 \end{pmatrix} \right | = 3, \end{align*}$$
$$\begin{align*}1 = \left | det \begin{pmatrix} 1 & 2 & 0 \\ 1 & 1 & 1 \\ 0 & 2 & 1 \end{pmatrix} \right | = 3, \end{align*}$$
another contradiction. This completes the proof.
3 Self-adjacencies from
 $S^3$
$S^3$
In this section, we constrain the self-adjacencies from
![]() $S^3$
to itself. As a warm-up, we begin with a special case.
$S^3$
to itself. As a warm-up, we begin with a special case.
Proposition 3.1. Suppose
![]() $(S^3,J,\alpha )$
realizes an n-adjacency to
$(S^3,J,\alpha )$
realizes an n-adjacency to
![]() $S^3$
and the pairwise linking numbers of J vanish. Then, J is the unlink and
$S^3$
and the pairwise linking numbers of J vanish. Then, J is the unlink and
![]() $\alpha _i = 1/k_i$
for
$\alpha _i = 1/k_i$
for
![]() $k_i \in \mathbb {Z}^*$
for all i.
$k_i \in \mathbb {Z}^*$
for all i.
Proof. First, it is clear that
![]() $\alpha _i = 1/k_i$
for each i by a homological computation. We proceed by induction to show that J is the unlink. The case of
$\alpha _i = 1/k_i$
for each i by a homological computation. We proceed by induction to show that J is the unlink. The case of
![]() $n = 1$
is handled by the knot complement theorem [Reference Gordon and Luecke5]. Next, we do the case of a 2-component link,
$n = 1$
is handled by the knot complement theorem [Reference Gordon and Luecke5]. Next, we do the case of a 2-component link,
![]() $J_1 \cup J_2$
. From the
$J_1 \cup J_2$
. From the
![]() $n = 1$
case, each component is unknotted. Since
$n = 1$
case, each component is unknotted. Since
![]() $1/k_2$
-surgery on
$1/k_2$
-surgery on
![]() $J_2$
is
$J_2$
is
![]() $S^3$
, the image of
$S^3$
, the image of
![]() $J_1$
in
$J_1$
in
![]() $1/k_2$
-surgery on
$1/k_2$
-surgery on
![]() $J_2$
has a surgery to
$J_2$
has a surgery to
![]() $S^3$
. Hence, the image of
$S^3$
. Hence, the image of
![]() $J_1$
is also unknotted. In particular, the component
$J_1$
is also unknotted. In particular, the component
![]() $J_2$
in the complement of
$J_2$
in the complement of
![]() $J_1$
in
$J_1$
in
![]() $S^3$
is a knot in a solid torus which has a non-trivial solid torus surgery. By [Reference Gabai3],
$S^3$
is a knot in a solid torus which has a non-trivial solid torus surgery. By [Reference Gabai3],
![]() $J_1$
is contained in a ball or is a braid in the solid torus, so has non-zero winding number. However, because
$J_1$
is contained in a ball or is a braid in the solid torus, so has non-zero winding number. However, because
![]() $\ell k(J_1,J_2)=0$
, it must be the case that
$\ell k(J_1,J_2)=0$
, it must be the case that
![]() $J_1$
is contained in a ball in the complement of
$J_1$
is contained in a ball in the complement of
![]() $J_2$
in
$J_2$
in
![]() $S^3$
, meaning
$S^3$
, meaning
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are unlinked. This completes the proof for
$J_2$
are unlinked. This completes the proof for
![]() $n = 2$
components.
$n = 2$
components.
For the inductive step, our hypothesis is that J is a Brunnian link and then we will deduce that J is in fact an unlink. This can be found in [Reference Gorsky, Lidman, Liu and Moore6, Proposition 4.1], but for self-containedness, we present an elementary proof that does not rely on Heegaard Floer homology. Suppose the result is true for
![]() $(n-1)$
-component links and that
$(n-1)$
-component links and that
![]() $(S^3,J,\alpha )$
realizes an n-adjacency to
$(S^3,J,\alpha )$
realizes an n-adjacency to
![]() $S^3$
. Then, J is Brunnian,
$S^3$
. Then, J is Brunnian,
![]() $J_1 \cup \cdots \cup J_{n-1}$
is an unlink, and so
$J_1 \cup \cdots \cup J_{n-1}$
is an unlink, and so
![]() $(1/k_1,\ldots , 1/k_{n-1})$
-surgery on
$(1/k_1,\ldots , 1/k_{n-1})$
-surgery on
![]() $J_1 \cup \cdots \cup J_{n-1}$
gives
$J_1 \cup \cdots \cup J_{n-1}$
gives
![]() $S^3$
. Thus, the image of
$S^3$
. Thus, the image of
![]() $J_{n}$
must be unknotted after this surgery. Hence, we see that
$J_{n}$
must be unknotted after this surgery. Hence, we see that
![]() $(1/k_1, \ldots , 1/k_{n-1}, 1/m)$
-surgery on J gives
$(1/k_1, \ldots , 1/k_{n-1}, 1/m)$
-surgery on J gives
![]() $S^3$
for arbitrary m. For the sake of concreteness, fix
$S^3$
for arbitrary m. For the sake of concreteness, fix
![]() $m=5$
.
$m=5$
.
We claim that the image of
![]() $J_1 \cup \cdots \cup J_{n-1}$
after performing
$J_1 \cup \cdots \cup J_{n-1}$
after performing
![]() $1/5$
-surgery on
$1/5$
-surgery on
![]() $J_n$
, denoted
$J_n$
, denoted
![]() $K_1 \cup \cdots \cup K_{n-1}$
, yields an
$K_1 \cup \cdots \cup K_{n-1}$
, yields an
![]() $(n-1)$
-component Brunnian link. To see that the
$(n-1)$
-component Brunnian link. To see that the
![]() $(n-1)$
-component image link is Brunnian, note that all
$(n-1)$
-component image link is Brunnian, note that all
![]() $(n-1)$
-component sublinks of J are unlinks by our inductive hypothesis. In particular,
$(n-1)$
-component sublinks of J are unlinks by our inductive hypothesis. In particular,
![]() $J_1\cup \cdots \cup J_{n-2}\cup J_n$
is an unlink, hence
$J_1\cup \cdots \cup J_{n-2}\cup J_n$
is an unlink, hence
![]() $1/5$
-surgery along
$1/5$
-surgery along
![]() $J_n$
shows that
$J_n$
shows that
![]() $K_1 \cup \cdots \cup K_{n-2}$
is an unlink. A similar argument applies to the other
$K_1 \cup \cdots \cup K_{n-2}$
is an unlink. A similar argument applies to the other
![]() $n-2$
-component sublinks of
$n-2$
-component sublinks of
![]() $K_1\cup \cdots \cup K_{n-1}$
.
$K_1\cup \cdots \cup K_{n-1}$
.
Thus, the link
![]() $K_1 \cup \cdots \cup K_{n-1}$
is a Brunnian link with a surgery to
$K_1 \cup \cdots \cup K_{n-1}$
is a Brunnian link with a surgery to
![]() $S^3$
, and so is an unlink by induction. In other words,
$S^3$
, and so is an unlink by induction. In other words,
![]() $1/5$
-surgery on
$1/5$
-surgery on
![]() $J_n$
in the exterior of
$J_n$
in the exterior of
![]() $J_1 \cup \cdots \cup J_{n-1}$
produces a reducible 3-manifold (the exterior of an
$J_1 \cup \cdots \cup J_{n-1}$
produces a reducible 3-manifold (the exterior of an
![]() $(n-1)$
-component unlink). Yet, the distance between the trivial slope
$(n-1)$
-component unlink). Yet, the distance between the trivial slope
![]() $\infty $
and
$\infty $
and
![]() $1/5$
is
$1/5$
is
![]() $5$
. A theorem of Gordon and Litherland [Reference Gordon and Litherland4, Theorem 1.1] implies that for any pair of reducible Dehn fillings on an irreducible manifold, the slopes have distance at most four. This is a contradiction. This implies that the exterior of J must be reducible. Hence, J is split. However, a split Brunnian link is an unlink.
$5$
. A theorem of Gordon and Litherland [Reference Gordon and Litherland4, Theorem 1.1] implies that for any pair of reducible Dehn fillings on an irreducible manifold, the slopes have distance at most four. This is a contradiction. This implies that the exterior of J must be reducible. Hence, J is split. However, a split Brunnian link is an unlink.
We now build on the previous proposition to complete our characterization of the self-adjacencies of
![]() $S^3$
promised in the introduction.
$S^3$
promised in the introduction.
Proposition 3.2. The triple
![]() $(S^3, J, \alpha )$
realizes an n-adjacency to
$(S^3, J, \alpha )$
realizes an n-adjacency to
![]() $S^3$
if and only if J itself is a split union of Hopf links and unknots, all slopes
$S^3$
if and only if J itself is a split union of Hopf links and unknots, all slopes
![]() $\alpha _i = 1/k_i$
, where
$\alpha _i = 1/k_i$
, where
![]() $k_i\in \mathbb {Z}^*$
, and the surgery slopes of Hopf components are either
$k_i\in \mathbb {Z}^*$
, and the surgery slopes of Hopf components are either
![]() $\pm (1, 1/2)$
or
$\pm (1, 1/2)$
or
![]() $\pm (1/2, 1)$
.
$\pm (1/2, 1)$
.
Proof. As in the proof of Proposition 3.1, the knot complement theorem implies that the components are unknotted and of course the surgery coefficients are of the form
![]() $1/k_i$
.
$1/k_i$
.
We begin with the case of
![]() $n = 2$
. Consider
$n = 2$
. Consider
![]() $J_1\cup J_2$
. The case that
$J_1\cup J_2$
. The case that
![]() $\ell k(J_1, J_2)=0$
follows from Proposition 3.1. By Lemma 2.3, we assume
$\ell k(J_1, J_2)=0$
follows from Proposition 3.1. By Lemma 2.3, we assume
![]() $\ell k(J_1, J_2)=1$
and the surgery coefficients are
$\ell k(J_1, J_2)=1$
and the surgery coefficients are
![]() $\pm (1,1/2)$
. Note that
$\pm (1,1/2)$
. Note that
![]() $J_1$
is unknotted in
$J_1$
is unknotted in
![]() $1/2$
-surgery on
$1/2$
-surgery on
![]() $J_2$
, so
$J_2$
, so
![]() $J_2$
can again be viewed as a knot in the solid torus with a solid torus surgery. Therefore, by [Reference Gabai3],
$J_2$
can again be viewed as a knot in the solid torus with a solid torus surgery. Therefore, by [Reference Gabai3],
![]() $J_2$
is a braid in the complement of
$J_2$
is a braid in the complement of
![]() $J_1$
and the winding number is the linking number of
$J_1$
and the winding number is the linking number of
![]() $J_1$
and
$J_1$
and
![]() $J_2$
. The only winding number 1 braid in the solid torus is the core. We see that
$J_2$
. The only winding number 1 braid in the solid torus is the core. We see that
![]() $J_1 \cup J_2$
is a Hopf link.
$J_1 \cup J_2$
is a Hopf link.
Next, we handle the case of
![]() $n = 3$
. If the pairwise linking numbers are zero, we appeal to Proposition 3.1. So, assume some pair of components
$n = 3$
. If the pairwise linking numbers are zero, we appeal to Proposition 3.1. So, assume some pair of components
![]() $J_1, J_2$
have nonzero linking number. By Proposition 2.4,
$J_1, J_2$
have nonzero linking number. By Proposition 2.4,
![]() $J_1, J_2$
have surgery coefficients
$J_1, J_2$
have surgery coefficients
![]() $\pm (1,1/2)$
and linking number 1. Further, by Proposition 2.4, we have that
$\pm (1,1/2)$
and linking number 1. Further, by Proposition 2.4, we have that
![]() $J_3$
is algebraically split from
$J_3$
is algebraically split from
![]() $J_1$
and
$J_1$
and
![]() $J_2$
. By the
$J_2$
. By the
![]() $n = 2$
case of the proof,
$n = 2$
case of the proof,
![]() $J_1 \cup J_2$
must form a Hopf link. We also have that
$J_1 \cup J_2$
must form a Hopf link. We also have that
![]() $J_3$
is an unknot that is geometrically split from
$J_3$
is an unknot that is geometrically split from
![]() $J_1$
and
$J_1$
and
![]() $J_2$
individually, but possibly not split from the link
$J_2$
individually, but possibly not split from the link
![]() $J_1 \cup J_2$
.
$J_1 \cup J_2$
.
It remains to show that
![]() $J_3$
is in fact split from
$J_3$
is in fact split from
![]() $J_1 \cup J_2$
. Since
$J_1 \cup J_2$
. Since
![]() $J_1 \cup J_3$
is an unlink, trivial surgery on
$J_1 \cup J_3$
is an unlink, trivial surgery on
![]() $J_2$
produces the 2-component unlink
$J_2$
produces the 2-component unlink
![]() $J_1 \cup J_3$
. Also, the image of
$J_1 \cup J_3$
. Also, the image of
![]() $J_1 \cup J_3$
under
$J_1 \cup J_3$
under
![]() $1/2$
-surgery on
$1/2$
-surgery on
![]() $J_2$
is a 2-component unlink because this image is a 2-component link, all of whose induced surgeries give
$J_2$
is a 2-component unlink because this image is a 2-component link, all of whose induced surgeries give
![]() $S^3$
. We now appeal to [Reference Culler, Gordon, Luecke and Shalen2, Corollary 2.4.7]. This states that if an irreducible three-manifold admits two reducible Dehn fillings along slopes of distance at least two on a torus boundary component, one of the filled manifolds contains a lens space summand. However, a link complement in
$S^3$
. We now appeal to [Reference Culler, Gordon, Luecke and Shalen2, Corollary 2.4.7]. This states that if an irreducible three-manifold admits two reducible Dehn fillings along slopes of distance at least two on a torus boundary component, one of the filled manifolds contains a lens space summand. However, a link complement in
![]() $S^3$
cannot contain a lens space summand. As the surgered manifolds are link complements in
$S^3$
cannot contain a lens space summand. As the surgered manifolds are link complements in
![]() $S^3$
, the exterior of J is reducible, and so J is a split link.
$S^3$
, the exterior of J is reducible, and so J is a split link.
Now, we complete the induction using a similar strategy. Suppose that J has n-components. By assumption, all proper sublinks are split unions of unlinks and Hopf links. If J has pairwise linking numbers all zero, we can again apply Proposition 3.1. Therefore, up to reordering of the components, we have at least one two-component sublink
![]() $J_1 \cup J_2$
which is a Hopf link. Up to mirroring and reordering
$J_1 \cup J_2$
which is a Hopf link. Up to mirroring and reordering
![]() $J_1$
and
$J_1$
and
![]() $J_2$
, the surgery coefficient on
$J_2$
, the surgery coefficient on
![]() $J_1$
is
$J_1$
is
![]() $1/2$
. Trivial surgery on
$1/2$
. Trivial surgery on
![]() $J_2$
produces a split link as does
$J_2$
produces a split link as does
![]() $1/2$
-surgery, since the resulting link is an
$1/2$
-surgery, since the resulting link is an
![]() $(n-1)$
-component link satisfying the same hypotheses of the theorem. Therefore, by appealing again to [Reference Culler, Gordon, Luecke and Shalen2, Corollary 2.4.7], we get that the complement of J is reducible, so J is split. Since all
$(n-1)$
-component link satisfying the same hypotheses of the theorem. Therefore, by appealing again to [Reference Culler, Gordon, Luecke and Shalen2, Corollary 2.4.7], we get that the complement of J is reducible, so J is split. Since all
![]() $(n-1)$
-component sublinks are split unions of Hopf links and unknots, and because J itself is split, we now have that J is a split union of Hopf links and unknots.
$(n-1)$
-component sublinks are split unions of Hopf links and unknots, and because J itself is split, we now have that J is a split union of Hopf links and unknots.
Acknowledgements
T.L. was supported by NSF DMS–2105469. A.H.M. was supported by NSF Grant DMS–2204148 and The Thomas F. and Kate Miller Jeffress Memorial Trust, Bank of America, Trustee.