Article contents
On non-separated zero sequences of solutions of a linear differential equation
Published online by Cambridge University Press: 30 April 2021
Abstract
Let $(z_k)$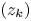 be a sequence of distinct points in the unit disc $\mathbb {D}$
be a sequence of distinct points in the unit disc $\mathbb {D}$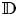 without limit points there. We are looking for a function $a(z)$
without limit points there. We are looking for a function $a(z)$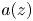 analytic in $\mathbb {D}$
analytic in $\mathbb {D}$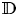 and such that possesses a solution having zeros precisely at the points $z_k$
and such that possesses a solution having zeros precisely at the points $z_k$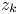 , and the resulting function $a(z)$
, and the resulting function $a(z)$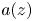 has ‘minimal’ growth. We focus on the case of non-separated sequences $(z_k)$
has ‘minimal’ growth. We focus on the case of non-separated sequences $(z_k)$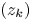 in terms of the pseudohyperbolic distance when the coefficient $a(z)$
in terms of the pseudohyperbolic distance when the coefficient $a(z)$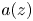 is of zero order, but $\sup _{z\in {\mathbb D}}(1-|z|)^p|a(z)| = + \infty$
is of zero order, but $\sup _{z\in {\mathbb D}}(1-|z|)^p|a(z)| = + \infty$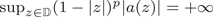 for any $p > 0$
for any $p > 0$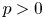 . We established a new estimate for the maximum modulus of $a(z)$
. We established a new estimate for the maximum modulus of $a(z)$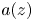 in terms of the functions $n_z(t)=\sum \nolimits _{|z_k-z|\le t} 1$
in terms of the functions $n_z(t)=\sum \nolimits _{|z_k-z|\le t} 1$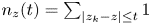 and $N_z(r) = \int_0^r {{(n_z(t)-1)}^ + } /t{\rm d}t.$
and $N_z(r) = \int_0^r {{(n_z(t)-1)}^ + } /t{\rm d}t.$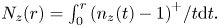 The estimate is sharp in some sense. The main result relies on a new interpolation theorem.
The estimate is sharp in some sense. The main result relies on a new interpolation theorem.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society
References
A correction has been issued for this article:
- 1
- Cited by
Linked content
Please note a has been issued for this article.


