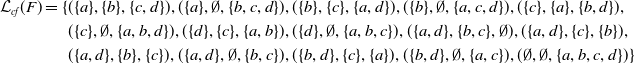1. Introduction
In the last two decades, the research field of formal argumentation has gained an important role in Artificial Intelligence and especially in Knowledge Representation Atkinson et al. (Reference Atkinson, Baroni, Giacomin, Hunter, Prakken, Reed, Simari, Thimm and Villata2017). There are several reasons for this success story, in particular its wide range of applications such as non-monotonic reasoning, multi-agent systems and as an analysis tool for debates or dialogues (cf. Bench-Capon & Dunne Reference Bench-Capon and Dunne2007; Baroni et al. Reference Baroni, Gabbay, Giacomin and van der Torre2018b for more information). One can distinguish two major lines of research in the field, namely logic-based and abstract approaches. The former takes the underlying structure of arguments into account and defines notions like attack, undercut or defensibility in terms of logical properties of the chosen argument structures (Besnard et al. Reference Besnard, Garcia, Hunter, Modgil, Prakken, Simari and Toni2014). In contrast, abstract approaches abstract away from the internal structure of arguments and focus entirely on the relations between them. In the latter field, there is one leading formalism, namely abstract argumentation frameworks (AFs) introduced by Phan Minh Dung in 1995 (Dung Reference Dung1995). Dung-style AFs represent arguments as nodes and attacks as directed arcs. They are thus just directed graphs. The major focus is on resolving conflicts, or more precisely, on the question of how to determine acceptable positions. To this end a variety of semantics have been introduced, each of them specifying different criteria for being acceptable. One can distinguish three different families, namely semantics based on naivety, admissibility as well as weak admissibility (van der Torre & Vesic Reference van der Torre and Vesic2017; Baumann et al. Reference Baumann, Brewka and Ulbricht2022).
From the 2010s onward dynamic aspects of abstract argumentation have become an important focus of research—which is hardly surprising, given that argumentation is an inherently dynamic process. One extensively studied problem in this context is the so-called enforcing problem. Enforcement is concerned with (minimal) syntactic manipulations of argumentation frameworks in such a way that a desired set of arguments becomes an extension (Baumann & Brewka Reference Baumann and Brewka2010; Baumann Reference Baumann2012; Wallner et al. Reference Wallner, Niskanen and Järvisalo2017; Baumann et al. Reference Baumann, Doutre, Mailly and Wallner2021). Another important issue regarding dynamics is the topic of forgetting. Roughly speaking, forgetting deals with removing irrelevant arguments or hiding sensitive ones, while preserving as much as possible of the initial semantics. Several syntactical and semantical criteria have been proposed and analysed with respect to their combined satisfiability and possible implementations (Bisquert et al. Reference Bisquert, Cayrol, de Saint-Cyr and Lagasquie-Schiex2011; Eiter & Kern-Isberner Reference Eiter and Kern-Isberner2019; Baumann et al. Reference Baumann, Gabbay and Rodrigues2020; Baumann et al. Reference Baumann, Berthold, Gabbay and Rodrigues2025). In general, much of this work has been influenced by the famous AGM theory (Alchourrón et al. Reference Alchourrón, Gärdenfors and Makinson1985), the leading formal account of revision in the context of propositional logic. In general, belief revision deals with the problem of integrating new pieces of information to a current knowledge base. To this end—given a certain logical formalism
${{\mathcal{L}}}$
together with its semantics
$\sigma_{{{\mathcal{L}}}}$
—one is typically faced with the problem of modifying an
${{\mathcal{L}}}$
-theory T in such a way that the revised version S satisfies
$\sigma_{{{\mathcal{L}}}}(S) = M$
for some model set M. Now, before trying to do this revision in a certain minimal way it is essential to know whether M is realizable at all.
Realizability is a central task in knowledge representation and has been studied for many different formalisms. For instance, in case of propositional logic any finite set of two-valued interpretations is realizable. This means, for any finite set of interpretations
$\mathcal{I}$
, we find a formula
$\phi$
, s.t.
$Mod(\phi) = {{\mathcal{I}}}$
. Differently, in case of normal logic programs under stable model semantics (Gelfond & Lifschitz Reference Gelfond and Lifschitz1988) we have that any finite candidate set is realizable if and only if it forms a
$\subseteq$
-antichain, that is any two sets of the candidate set have to be incomparable w.r.t. subset relation (Eiter et al. Reference Eiter, Fink, Pührer, Tompits and Woltran2013; Strass Reference Strass2015). Such characterizing properties may rule out a logic/semantics or make it perfectly appropriate for a certain application. The first formal treatment of realizability in abstract argumentation was given by Dunne et al. (Reference Dunne, Dvorák, Linsbichler, Woltran, Baral, Giacomo and Eiter2014, Reference Dunne, Dvorák, Linsbichler and Woltran2015). They coined the term signature for the set of all realizable sets of extensions. The authors provided simple criteria for several mature semantics deciding whether a set of extensions is contained in the corresponding signature. For instance, forming a
$\subseteq$
-antichain is necessary for many mature semantics but not sufficient as in case of logic programming.
In this article we convey the topic of realizability to the more informative labelling-based versions of argumenation semantics. It is important to note that existing characterization theorems for extension-based semantics are of little help in characterizing the corresponding labelling-based versions. This is due to the fact that the latter are more restrictive as they assign a status to any argument implying that the possible number of realizing frameworks is limited from the start. Moreover, they are more fine-grained as they explicitly distinguish two non-acceptance cases, namely rejected and undecided.
We mention that the presented article summarizes and combines recent results on the expressivness of conflict-free labellings (Baumann & Heine Reference Baumann and Heine2023) and naive labellings (Baumann & Heine Reference Baumann and Heine2024). In addition we provide full proofs and some first reflections on the realizability of stable labellings.
The article is organized as follows: Section 2 reviews the relevant background in argumentation theory. In Section 3, we present our results regarding conflict-free realizability. To that end, we introduce three new criteria, namely L-tightness, reject-witnessing and reject-compositionality. Moreover, we present a witnessing construction as well as our findings on equivalence and redundancy. Section 4 introduces the corresponding results for the naive labelling semantics. By establishing the construction of a labellings-downward-closure we attain a characterization through the connection to the conflict-free labellings. Section 5 provides an outlook on the realizability of stable labellings. Lastly, Section 6 concludes the paper and discusses future work.
2. Formal preliminaries
2.1. Argumentation frameworks and semantics
We start with the necessary background on abstract argumentation. An argumentation framework (AF) is a pair
${F} = (A,R)$
where A, the set of arguments, is a finite subset of a fixed infinite background set
${{\mathcal{U}}}$
, and
$R \subseteq A \times A$
. The set of all finite AFs is denoted by
${{\mathcal{F}}}$
(cf. Baumann & Spanring Reference Baumann and Spanring2015, Reference Baumann and Spanring2017 for a treatment of infinite AFs). We say a attacks b, or b is defeated by a in
${F}$
whenever
$(a,b)\in R$
. For a set
${E}\subseteq A$
we use
$R^+_{{F}}({E})$
or simply,
${E}^+$
for
$\{b\mid (a,b)\in R, a\in {E}\}$
. Moreover,
$E^\oplus_{F}$
or just
$E^\oplus$
, is called the range of E and stands for
$E\cup E^+$
. If
${G} = (B,S)$
, we use
$A({G})$
as well as
$R({G})$
to refer to the first or second component of
${G}$
, that is B or S, respectively.
An extension-based semantics
${{\mathcal{E}}}_{\sigma}\;:\;{{\mathcal{F}}}\rightarrow 2^{2^{{\mathcal{U}}}}$
is a function which assigns to any AF
${F}=(A,R)$
a set of sets of arguments denoted by
${{\mathcal{E}}}_{\sigma}({F})\subseteq 2^A$
. Each one of them, a so-called
$\sigma$
-extension, is considered to be acceptable with respect to
${F}$
. The most basic criteria is conflict-freeness (
${cf}$
) which guarantees no internal conflicts. Furthermore, we consider a
$\subseteq$
-maximal version of conflict-freeness, so-called naive semantics (
${na}$
) which can be seen as an upper bound for the widely known stable semantics (
${{stb}}$
).
Definition 1 Let
${F} = (A,R)$
be an AF and
${E}\subseteq A$
.
-
1.
${E}\in{{\mathcal{E}}}_{{cf}}({F})$
iff there are no
$a,b\in A$
, s.t.
$(a,b)\in R$
, -
2.
${E}\in{{\mathcal{E}}}_{{na}}({F})$
iff E is
$\subseteq$
-maximal in
${{\mathcal{E}}}_{{cf}}({F})$
, -
3.
${E}\in{{\mathcal{E}}}_{{{stb}}}({F})$
iff
${E}\in{{\mathcal{E}}}_{{cf}}({F})$
and
$E^+ = A\setminus E$
.
A labelling-based semantics
${{\mathcal{L}}}_{\sigma}\;:\;{{\mathcal{F}}}\rightarrow 2^{\left(2^{{\mathcal{U}}}\right)^3}$
is a function which assigns to any AF
${F}=(A,R)$
a set of triples of sets of arguments denoted by
${{\mathcal{L}}}_{\sigma}({F})\subseteq \left(2^A\right)^3$
. Each one of them, a so-called
$\sigma$
-labelling of
${F}$
, is a triple
${L} = (I,O,U)$
indicating that arguments in I, O or U are considered to be accepted (in), rejected (out) or undecided with respect to
${F}$
. We further assume pairwise disjointness and covering, that is
$I\cap O = I\cap U = O \cap U = \emptyset$
and
$I \cup O \cup U = A$
. We use
${L}^{\text{I}}$
(or
${L}^{\text{I}}(a)$
) to refer to (a is an element of) the first component of the labelling
${L}$
. Analogously for
${L}^{\text{O}}$
and
${L}^{\text{U}}$
. We proceed with the central notions of conflict-free labellings (Caminada Reference Caminada2011; Arieli Reference Arieli2012).
Definition 2 A labelling
${L}$
of
${F}=(A,R)$
is called conflict-free if we have:
-
1. If
$a,b\in {L}^{\text{I}}$
, then
$(a,b)\notin R$
, and (no internal conflicts) -
2. If
$a\in {L}^{\text{O}}$
, then there is a
$b\in{L}^{\text{I}}$
with
$(b,a)\in R$
. (reason for rejecting)
We now introduce the labelling-based counterparts to the extension-based semantics.
Definition 3 Let
${F} = (A,R)$
be an AF and
${L}\in\left(2^A\right)^3$
a labelling of
${F}$
.
-
1.
${L}\in{{\mathcal{L}}}_{{cf}}({F})$
iff
${L}$
is a conflict-free labelling of
${F}$
, -
2.
${L}\in{{\mathcal{L}}}_{{na}}({F})$
iff
${L}\in{{\mathcal{L}}}_{{cf}}({F})$
and
${L}^{\text{I}}$
is
$\subseteq$
-maximal in
$\{{M}^{\text{I}}\mid M\in{{\mathcal{L}}}_{{cf}}({F})\}$
, -
3.
${L}\in{{\mathcal{L}}}_{{{stb}}}({F})$
iff
${L}\in{{\mathcal{L}}}_{{cf}}({F})$
and
${L}^{\text{U}} = \emptyset$
.
We mention that conflict-free sets and naive semantics are universally defined, that is they always provide one with acceptable sets or labellings, respectively. This assertion does not hold for stable semantics.
Let us proceed with an illustrating example.
Example 1 Consider the following AF
${F}$
. The introduced extension-based semantics together with its labelling-based counterparts are given below.
-
•
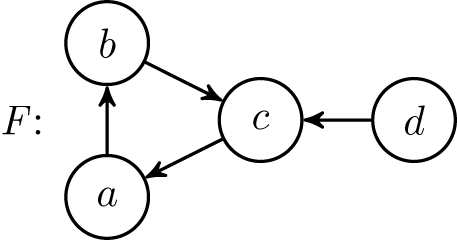
${{\mathcal{E}}}_{{cf}}({F}) =\{\{ a\}, \{b\}, \{c\}, \{d\},\{a,d\}, \{b,d\}, \emptyset \} $
-
•
$\begin{aligned}[t] {{\mathcal{L}}}_{{cf}}({F}) = \{ &(\{ a\}, \{b \}, \{ c,d\}), (\{ a\}, \emptyset, \{ b,c,d\}), (\{ b\}, \{c \}, \{ a,d\}), (\{ b\}, \emptyset, \{a,c,d\}), ( \{c\} , \{a\}, \{b,d\}), \\ &( \{c\} ,\emptyset , \{a,b,d\}), ( \{d\} , \{c\}, \{a,b\}),( \{d\} , \emptyset, \{a,b,c\}), ( \{a,d\} , \{b,c\}, \emptyset) , ( \{a,d\} , \{c\}, \{b\}), \\ &( \{a,d\} , \{b\}, \{c\}), ( \{a,d\} , \emptyset, \{b,c\}), ( \{b,d\} , \{c\},\{a\}), ( \{b,d\} , \emptyset, \{a,c\}) , ( \emptyset , \emptyset, \{a,b,c,d\})\} \end{aligned}$
-
•
${{\mathcal{E}}}_{{na}}({F}) =\{\{c\},\{a,d\}, \{b,d\} \} $
-
•
$\begin{aligned}[t] {{\mathcal{L}}}_{{na}}({F}) = \{ &( \{c\} , \{a\}, \{b,d\}),(\{c\} ,\emptyset , \{a,b,d\}), ( \{a,d\} , \{b,c\}, \emptyset) , ( \{a,d\} , \{c\}, \{b\}), ( \{a,d\} , \{b\}, \{c\}),\\ &( \{a,d\} , \emptyset, \{b,c\}), ( \{b,d\} , \{c\},\{a\}), ( \{b,d\} , \emptyset, \{a,c\}) \} \end{aligned}$
-
•
${{\mathcal{E}}}_{{{stb}}}({F}) = \{\{a,d\}\}$
-
•
${{\mathcal{L}}}_{{{stb}}}({F}) = \{(\{a,d\},\{b,c\},\emptyset)\}$
Please observe that apart from stable semantics we do not have a match between the numbers of conflict-free/naive extensions and conflict-free/naive labellings. This observation is essential and one reason why realizability results for extension-based semantics do not directly carry over to their labelling-based counterparts.
In the following we list some well-known properties and relations between semantics which will be frequently used throughout the whole paper. For more details and explanations please confer (Baumann Reference Baumann2016; Baroni et al. Reference Baroni, Caminada, Giacomin, Baroni, Gabbay, Giacomin and van der Torre2018a).
Proposition 1 Given an AF
${F} = (A,R)$
, a set
$E\subseteq A$
and a semantics
$\sigma\in\{{cf},{na},{{stb}}\}$
. In the following we use
$E^{{{\mathcal{L}}}}$
as shorthand for
$(E,E^+,A\setminus(E\cup E^+))$
.
-
1.
${{\mathcal{E}}}_{{{stb}}}({F})\subseteq{{\mathcal{E}}}_{{na}}({F})\subseteq{{\mathcal{E}}}_{{cf}}({F})$
, -
2.
${{\mathcal{L}}}_{{{stb}}}({F})\subseteq{{\mathcal{L}}}_{{na}}({F})\subseteq{{\mathcal{L}}}_{{cf}}({F})$
, -
3. If
${E}\in{{\mathcal{E}}}_{\sigma}({F})$
, then
${E}^{{{\mathcal{L}}}}\in{{\mathcal{L}}}_{\sigma}({F})$
, -
4. If
${L}\in{{\mathcal{L}}}_{\sigma}({F})$
, then
${L}^{\text{I}}\in{{\mathcal{E}}}_{\sigma}({F})$
, and -
5. Obviously,
$(E^{{{\mathcal{L}}}})^I = E$
.
In case of stable semantics we even have the following additional relations:
-
1. For any
${L},{M}\in{{\mathcal{L}}}_{{{stb}}}({F}), {L}^{\text{I}} = {M}^{\text{I}}$
iff
${L} = {M}$
, -
2. Given
${L}\in{{\mathcal{L}}}_{{{stb}}}({F})$
, then
$({L}^{\text{I}})^{{{\mathcal{L}}}} = {L}$
, and -
3.
$\left\lvert{{\mathcal{L}}}_{{{stb}}}({F})\right\rvert = \left\lvert{{\mathcal{E}}}_{{{stb}}}({F})\right\rvert$
.
We encourage the reader to verify the presented relations using Example 1.
2.2. Equivalence notions
Representational freedom is highly connected with patterns of redundancy. In particular, we want to study whether and to which extent it is possible to syntactically change a given AF without changing its current semantics, so-called ordinary equivalence as well as changes which do not affect any future expansion, so-called strong equivalence (Oikarinen & Woltran Reference Oikarinen and Woltran2011; Baumann Reference Baumann2016, Reference Baumann2018).
Consider the following formal definition of the weaker version of equivalence.
Definition 4 Given a semantics
$X\in\{{{\mathcal{E}}}_\sigma,{{\mathcal{L}}}_\sigma\}$
and two AFs
${F}$
and
${G}$
.
${F}$
and
${G}$
are called ordinarily equivalent if
$X({F}) = X({G})$
. We use
${F}\equiv^X\!{G}$
to indicate this relation.
We mention one decisive difference between the two versions of semantics. In contrast to extension-based semantics, being ordinarily equivalent in the realm of labellings requires to share the same arguments. This is due to the fact that each labelling assigns a label to any argument of the considered AF implying that labellings are necessarily different if the frameworks in question possess different arguments. The following example illustrate this observation.
Example 2 Compare the following basic AFs F, G and H:
For all three frameworks we get the same conflict-free extension, namely the set
$\{a\}$
. However the conflict-free labelling differs for each AF. While the in-sets still concide, they comverge in terms of the out-, and undec-set:
$\mathcal L(cf)(F)=\{(\{a\}, \{\}, \{\})\}$
,
$\mathcal L(cf)(G)=\{(\{a\}, \{\}, \{b\})\}$
,
$\mathcal L(cf)(H)=\{(\{a\}, \{b\}, \{\})\}$
.
We now introduce the formal definition of strong equivalence. To this end we use the notation
$F\sqcup G$
to represent the union AF
$(A_1 \cup A_2 , R_1\cup R_2)$
of the AFs
$F=(A_1, R_1)$
and
$G=(A_2, R_2)$
.
Definition 5 Given a semantics
$X\in\{{{\mathcal{E}}}_\sigma,{{\mathcal{L}}}_\sigma\}$
and two AFs
${F}$
and
${G}$
.
${F}$
and
${G}$
are called strongly equivalent if for each AF
${H}$
,
$X({F}\sqcup{H}) = X({G}\sqcup{H})$
. We use
${F}\equiv^X_s\!{G}$
to indicate this relation.
It was shown that in order to decide strong equivalence for extension-based semantics one may use a syntactical concept called kernels (Oikarinen & Woltran Reference Oikarinen and Woltran2011). A kernel is again a directed graph obtained from the initial AF via adding or deleting attacks. It represents a distinguished object in the associated strong equivalence class (cf. Baumann Reference Baumann2018 for more details) In the following we introduce two well-known versions of kernels, namely the stable kernel as well as naive kernel.
Definition 6 Let
$F = (A,R)$
be an AF. The stable and naive kernels of F are defined as:
-
1.
${F}^{sk} = (A^{sk},R^{sk}) = (A,R\setminus \{(a,b)\in R\mid a\neq b, (a,a)\in R\})$
and -
2.
${F}^{nk} = (A^{nk},R^{nk}) = (A,R\cup \{(a,b)\in R\mid a\neq b, \{(a,a), (b,a), (b,b)\} \cap R \neq \emptyset\})$
Example 3 Consider a slight modification of the AF from Example 1.
Using Definition 6 we built the stable and naive kernel of F.
The following properties are well-known and will be used to simplify proofs.
Proposition 2 Given an AF
$F = (A,R)$
, we have
-
1.
$A = A^{sk} = A^{nk}$
-
2.
$R^{sk} \subseteq R \subseteq R^{nk}$
-
3.
$R, R^{sk}, R^{nk}$
share the same self-loops -
4. If F is selfloop-free, then
$F = {F}^{sk}$
. -
5.
${{\mathcal{E}}}_{{stb}}({F}) = {{\mathcal{E}}}_{{stb}}({F}^{sk})$
and
${{\mathcal{E}}}_{na}({F}) = {{\mathcal{E}}}_{{stb}}({F}^{nk})$
Finally, for two AFs
${F}$
and
${G}$
and kernel
${k}\in\{sk,nk\}$
we have:
6. If
${F}^{{k}} = {G}^{{k}}$
, then
$\left({F}\sqcup {H}\right)^{{k}} = \left({G}\sqcup {H}\right)^{{k}}$
for any AF H.
Now the central characterization theorems for the extension-based versions.
Proposition 3 Given two AFs F and G we have:
-
1.
$F\equiv^{\mathcal E_{stb}}_s G$
$\Leftrightarrow$
$F^{sk}=G^{sk}$
-
2.
$F\equiv^{\mathcal E_{na}}_s G$
$\Leftrightarrow$
$F^{nk}=G^{nk}$
Please remember that we deal with finite AFs. A consideration of unrestricted AFs can be found in Baumann and Spanring (Reference Baumann and Spanring2017).
2.3. Realizability in abstract argumentation
The first formal treatment of expressibility issues in abstract argumentation was given by Dunne et al. (Reference Dunne, Dvorák, Linsbichler, Woltran, Baral, Giacomo and Eiter2014, Reference Dunne, Dvorák, Linsbichler and Woltran2015). They considered extension-based semantics and provided simple criteria for several mature semantics deciding whether a certain set of sets of arguments can be the semantical outcome of a framework.
Let us start with the two central concepts, namely realizability as well as signature. In a nutshell, we say that a certain set
$\mathbb{S}$
is realizable under the semantics
$\sigma$
, if there is an AF
${F}$
such that its set of
$\sigma$
-extensions/
$\sigma$
-labellings coincides with
$\mathbb{S}$
. Collecting all realizable sets defines the concept of a signature. Consider the following formal definition of realizability in the context of abstract argumentation. Note that only
$n=1$
(extension-case) and
$n=3$
(labelling-case) will be relevant for this paper.
Definition 7 Given a semantics
$\sigma\;:\; {{\mathcal{F}}}\rightarrow 2^{\left(2^{{\mathcal{U}}}\right)^n}$
. A set
$\mathbb{S}\subseteq \left(2^{{\mathcal{U}}}\right)^n$
is
$\sigma$
-realizable if there is an AF
${F}\in{{\mathcal{F}}}$
, s.t.
$\sigma({F})=\mathbb{S}$
. Moreover, the
$\sigma$
-signature is defined as
$\Sigma_{\sigma} = \left\{\sigma({F}) \mid {F}\in{{\mathcal{F}}} \right\}$
.
2.3.1. Extension-based semantics
We proceed with further notation as well as the central notions of downward-closedness and tightness (Dunne et al. Reference Dunne, Dvorák, Linsbichler and Woltran2015).
Definition 8 A finite
$\mathbb{S} \subseteq 2^{{\mathcal{U}}}$
is called extension-set. We use
-
•
${Args}_\mathbb{S}$
to denote
$\bigcup_{S\in\mathbb{S}} S$
and
$\left\lvert\mathbb{S}\right\rvert$
for
$\left\lvert{Args}_\mathbb{S}\right\rvert$
, -
•
$\textit{Pairs}_\mathbb{S}$
to denote
$\{ (a,b) \mid \exists S\in \mathbb{S}\;:\; \{a,b\}\subseteq S\}$
and -
•
$\textit{dcl}(\mathbb{S})$
to denote (the so-called downward-closure)
$\{S' \subseteq S \mid S \in \mathbb{S}\}$
In order to familiarize the reader with the introduced definitions we give the following example.
Example 4 Let
$\mathbb{S} = \{\{a,d\},\{b,d\},\{c\}\}$
. Then
-
•
${Args}_\mathbb{S} = \{a,b,c,d\}$
and
$\left\lvert\mathbb{S}\right\rvert = 4$
, -
•
$\textit{Pairs}_\mathbb{S} = \{(a,a),(b,b),(c,c),(d,d),(a,d),(b,d)\} \cup \{(d,a),(d,b)\}$
, and -
•
$\textit{dcl}(\mathbb{S}) = \{\emptyset,\{a\},\{b\},\{c\},\{d\},\{a,d\},\{b,d\}\}$
.
Definition 9 Given an extension-set
$\mathbb{S} \subseteq 2^{{\mathcal{U}}}$
. We call
$\mathbb{S}$
-
• downward-closed if
$\mathbb{S}=\textit{dcl}(\mathbb{S})$
, -
• incomparable if
$\mathbb{S}$
is a
$\subseteq$
-antichain that is for any
$E_1,E_2\in \mathbb{S}$
we have: If
$E_1\subseteq E_2$
, then
$E_1 = E_2$
, -
• tight if for all
$S \in \mathbb{S}$
and
$a \in {Args}_\mathbb{S}$
it holds that if
$S \cup \{a\} \notin \mathbb{S}$
then there exists an
$s \in S$
such that
$(a,s) \notin \textit{Pairs}_\mathbb{S}$
.
Example 5 Consider again the extension-set
$\mathbb{S}$
given in Example 4.
-
• Obviously,
$\textit{dcl}(\mathbb{S})\neq \mathbb{S}$
. Hence,
$\mathbb{S}$
is not downward-closed, -
•
$\mathbb{S}$
is incomparable as there are no proper subset relations. -
•
$\mathbb{S}$
is tight. To exemplify we consider
$S = \{b,d\}$
and
$S\cup\{a\}$
. We have
$S\cup\{a\}\notin\mathbb{S}$
and moreover, for the argument
$b\in\mathbb{S}$
we deduce
$(a,b)\notin \textit{Pairs}_\mathbb{S}$
.
Now, we present the central characterization theorems in case of extension-based semantics (Dunne et al. Reference Dunne, Dvorák, Linsbichler and Woltran2015).
Theorem 1 Given a finite extension-set
$\mathbb{S} \subseteq 2^{{\mathcal{U}}}$
, then
-
1.
$\mathbb{S}\in \Sigma_{{{\mathcal{E}}}_{{cf}}} \Leftrightarrow \mathbb{S} \text{ is a non-empty, downward-closed, and tight extension-set,}$
-
2.
$\mathbb{S}\in \Sigma_{{{\mathcal{E}}}_{{na}}} \Leftrightarrow \mathbb{S} \text{ is a non-empty, incomparable extension-set and } \textit{dcl}{(\mathbb{S})} \text{ is tight},$
-
3.
$\mathbb{S}\in \Sigma_{{{\mathcal{E}}}_{{{stb}}}} \Leftrightarrow \mathbb{S} \text{ is an incomparable and tight extension-set.}$
2.3.2. Labelling-based semantics
Now let us turn to labelling-based semantics. Again, we start with some relevant notations and shorthands. Moreover, we introduce the central concept of a labelling-set.
Definition 10 Given a finite set
$\mathbb{L} \subseteq \left(2^{{\mathcal{U}}}\right)^3$
. We use
-
•
$\mathbb{L}^I$
,
$\mathbb{L}^O$
and
$\mathbb{L}^U$
to denote
$\{L^{I} \mid L\in\mathbb{L}\}$
,
$\{L^{O} \mid L\in\mathbb{L}\}$
or
$\{L^{U} \mid L\in\mathbb{L}\}$
, respectively.
Moreover, we say that
$\mathbb{L}$
is a labelling-set if
-
1.
$ L_1^{I}\cup L_1^{O} \cup L_1^{U}=L_2^{I}\cup L_2^{O} \cup L_2^{U}$
for any
$L_1,L_2\in \mathbb{L}$
and, (same arguments) -
2.
$L_1^{I}\cap L_1^{O} = L_1^{I}\cap L_1^{U} = L_1^{O}\cap L_1^{U} = \emptyset$
for each
$L_1\in\mathbb{L}$
. (disjointness)
Finally, for a fixed set of arguments
$E\subseteq{{\mathcal{U}}}$
we use
-
•
$\mathbb{L}_{I=E} = \{L \mid L\in \mathbb{L} , L^{I} = E\}$
, and (corresponding labellings) -
•
$\mathbb{L}^{O}_{I=E} = \{L^{O} \mid L\in \mathbb{L} , L^{I}=E\}$
. (corresponding out-labels)
Let us illustrate the introduced concepts with the following example.
Example 6 Consider
$\mathbb{L} = \{ (\{a,d\}, \{b\}, \{c\}),(\{b,d\}, \{a,c\}, \emptyset ), (\{b,d\}, \{a\}, \{c\} ) \}$
. First of all, we observe that
$\mathbb{L}$
is indeed a labelling-set as all triples refer to the same arguments, namely a,b,c,d and moreover, for any triple we have that each argument occurs in one of the three sets only. We obtain the following sets:
-
•
$\mathbb{L}^I= \{ \{a,d\}, \{b,d\} \}$
,
$\mathbb{L}^O=\{ \{b\}, \{a,c\}, \{a\} \}$
and
$\mathbb{L}^U=\{\{c\}, \emptyset \} $
, -
•
$\mathbb{L}^{O}_{I=\{a,d\}}= \{ \{b\}\}$
and
$\mathbb{L}^{O}_{I=\{b,d\}}= \{ \{a,c\}, \{a\}\}$
, and -
•
$\mathbb{L}_{I=\{a,d\}}=\{(\{a,d\}, \{b\}, \{c\})\}$
and
$\mathbb{L}_{I=\{b,d\}}=\{ (\{b,d\}, \{a,c\}, \emptyset ), (\{b,d\}, \{a\}, \{c\}) \}$
.
3. Conflict-free labellings
3.1. L-tightness and rejection properties
The presence of characterization theorems for extension-based semantics is of little help in characterizing the corresponding labelling-based version. This is due to the fact that the latter provides one with strictly more information. First of all, they are more restrictive as they assign a status to any argument. Consequently, the possible number of realizing frameworks is limited from the start. Secondly, they are more fine-grained as they explicitly distinguish two non-acceptance cases, namely rejected and undecided (compare Example 2).
In this section we introduce three new properties relevant for characterizing conflict-free labellings. We start with so-called L-tightness. A labelling-set
$\mathbb{L}$
is L-tight if: First, greatest out-labels exist and secondly, the union of two in-labels
$I_1, I_2$
is an in-label too if and only if the greatest out-label regarding
$I_1$
does not share elements with
$I_2$
and vice versa. Intuitively, L-tightness fulfills a similar purpose for labelling-sets as tightness for extensions since it gives a reason why certain sets are not in-labels.
Definition 11 A labelling-set
$\mathbb{L}$
is called L-tight, if
-
1. for each
$E \in\mathbb{L}^I$
we have:
$\mathbb{L}^{O}_{I=E}$
possesses a
$\subseteq$
-greatest element.(Notation: We use
$\overline{\mathbb{L}}^{O}_{I=E}$
for the
$\subseteq$
-greatest element and
$\overline{\mathbb{L}}_{I=E}$
for the associated labelling.) -
2. for all
$I_1,I_2 \in\mathbb{L}^I$
we have:
$ I_1 \cup I_2 \in \mathbb{L}^I \Leftrightarrow (\overline{\mathbb{L}}^{O}_{I=I_1} \cap I_2) \cup (\overline{\mathbb{L}}^{O}_{I=I_2} \cap I_1) = \emptyset.$
Example 7 First note, that
$\subseteq$
-greatest elements do not exist in general as witnessed by the two-element set
$\{(\{a\},\{b\},\{c\}),(\{a\},\{c\},\{b\})\}$
. Let us verify that the labelling-set
$\mathbb{L} = {{\mathcal{L}}}_{{cf}}({F})$
from the running AF
${F}$
presented in Example 1 satisfy L-tightness. We have:
-
•
$\mathbb{L}^I = {{\mathcal{E}}}_{{cf}}({F}) =\{\{ a\}, \{b\}, \{c\}, \{d\},\{a,d\}, \{b,d\}, \emptyset \}$
. -
• For each
$E \in\mathbb{L}^I$
we have a
$\subseteq$
-greatest element in
$\mathbb{L}^{O}_{I=E}$
. More precisely,
$\overline{\mathbb{L}}^{O}_{I=\{a\}} = \{b\}$
,
$\overline{\mathbb{L}}^{O}_{I=\{b\}} = \{c\}$
,
$\overline{\mathbb{L}}^{O}_{I=\{c\}} = \{a\}$
,
$\overline{\mathbb{L}}^{O}_{I=\{d\}} = \{c\}$
,
$\overline{\mathbb{L}}^{O}_{I=\{a,d\}} = \{b,c\}$
,
$\overline{\mathbb{L}}^{O}_{I=\{b,d\}} = \{c\}$
,
$\overline{\mathbb{L}}^{O}_{I=\emptyset} = \emptyset$
. -
• Now, for the second item of L-tightness we have to consider each possible pairing of in-labels. For space reasons we will consider only two pairings and left the remaining combinations for the reader.
-
1. Consider
$I_1 = \{a\}$
and
$I_2 = \{d\}$
. We have
$I_1 \cup I_2 = \{a,d\} \in \mathbb{L}^I$
and moreover,
$\overline{\mathbb{L}}^{O}_{I=I_1} \cap I_2 = \{b\} \cap \{d\} = \emptyset = \{c\}\cap \{a\} = \overline{\mathbb{L}}^{O}_{I=I_2} \cap I_1$
. -
2. Consider
$I_1 = \{a\}$
and
$I_2 = \{b\}$
.We have
$I_1 \cup I_2 = \{a,b\} \notin \mathbb{L}^I$
and the corresponding non-emptiness of the union witnessed by
$\overline{\mathbb{L}}^{O}_{I=I_1} \cap I_2 = \{b\} \cap \{b\} = \{b\}\neq \emptyset.$
The second newly introduced property is called reject-compositionality. In a nutshell, a labelling-set
$\mathbb{L}$
is reject-compositional, if the out-labelled arguments for a given in-labelled set E can be found in the union of out-labels of single arguments in E.
Definition 12 A labelling-set
$\mathbb{L}$
is called reject-compositional, if for each
$E\in\mathbb{L}^I$
, we have:
\begin{align*}\displaystyle{\bigcup\mathbb{L}^{O}_{I = E} = \bigcup_{a\in E} \bigcup\mathbb{L}^{O}_{I=\{a\}}}\end{align*}
We mention that in case of L-tight labelling-sets the equation transforms to
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} = \bigcup_{a\in E} \overline{\mathbb{L}}^{O}_{I=\{a\}}}$
.
Before turning to an example we introduce the third new concept. A labelling-set
$\mathbb{L}$
is reject-witnessing if each out-labelled argument o for a fixed in-labelled set E possesses a witnessing ‘basic’ labelling. That is, we find an element
$i\in E$
with
$\left(\{i\},\{o\},Args_{\mathbb{L}}\setminus\{i,o\}\right)\in \mathbb{L}$
.
Definition 13 A labelling-set
$\mathbb{L}$
is called reject-witnessing, if for each
$L \in\mathbb{L}$
we have:
\begin{align*}\forall o\in L^O\ \exists i\in L^I,\; \text{ s.t. } \left(\{i\},\{o\},Args_{\mathbb{L}}\setminus\{i,o\}\right)\in \mathbb{L}\end{align*}
Example 8 (Example 1 cont.) Consider again the labelling-set
$\mathbb{L} = {{\mathcal{L}}}_{{cf}}({F})$
from the running AF
${F}$
presented in Example 1. We will show that
$\mathbb{L}$
is reject-witnessing as well as reject-compositional.
For reject-witnessing it suffices to consider
${L}_1 = ( \{a,d\} , \{b,c\}, \emptyset)\in {{\mathcal{L}}}_{{cf}}({F})$
as well as
${L}_2 = (\{b,d\} , \{c\},\{a\}))\in {{\mathcal{L}}}_{{cf}}({F})$
. For the first labelling the rejections are witnessed by
$(\{ a\}, \{b \}, \{ c,d\})\in {{\mathcal{L}}}_{{cf}}({F})$
and
$( \{d\} , \{c\}, \{a,b\})\in{{\mathcal{L}}}_{{cf}}({F})$
. The latter basic labelling also serves as a witness for
${L}_2$
.
Now, for reject-compositionality. We have already seen that
$\mathbb{L}$
is L-tight (Example 7). This means, it suffices to show
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} = \bigcup_{a\in E} \overline{\mathbb{L}}^{O}_{I=\{a\}}}$
. We only have to consider both two-element sets. Let us start with
$E = \{a,d\}$
. We have,
$\overline{\mathbb{L}}^{O}_{I = \{a,d\}}= \{b,c\}$
and the matching sets,
$\overline{\mathbb{L}}^{O}_{I = \{a\}}= \{b\}$
and
$\overline{\mathbb{L}}^{O}_{I = \{d\}} = \{c\}$
. Finally, for
$E = \{b,d\}$
we get
$\overline{\mathbb{L}}^{O}_{I = \{b,d\}} = \{c\}$
and,
$\overline{\mathbb{L}}^{O}_{I = \{b\}}= \{c\}$
and
$\overline{\mathbb{L}}^{O}_{I = \{d\}} = \{c\}$
as required.
Finally, we mention that none of the properties can be derived from the remaining two. This means, for example, that there are labelling-sets satisfying both rejection properties without being L-tight.
3.2. Standard construction
As a matter of fact, knowing that a certain set is realizable or not is a valuable feature. However, for many applications it is not only of interest whether a certain set is realizable, but also how to realize it. In the following we introduce a standard construction witnessing the realizability of a considered labelling-set. This construction is not only generally of interest but is a vital step towards a characterization of conflict-free realizability.
First, with respect to arguments, we simply collect any that occur in a labelling. Secondly, for the attack relation, a self-loop is added to an argument a if
$\{a\}$
is not present as an in-labelled set. Moreover, a attacks an other argument b, if
$\{a\}$
can be found as an in-labelled set and b is contained in at least one corresponding out-labelled set.
Definition 14 Given a labelling-set
$\mathbb{L}$
. We define
${F}_{\mathbb{L}}^{{cf}} = (A_{\mathbb{L}},R_{\mathbb{L}})$
with
$A_{\mathbb{L}}={Args}(\mathbb{L})$
and
-
1.
$\forall a\in A_{\mathbb{L}}$
:
$(a,a)\in R_{\mathbb{L}}$
if and only if
$\{a\}\notin\mathbb{L}^I$
, and -
2.
$\forall a,b\in A_{\mathbb{L}}$
: If
$a\neq b$
, then
$(a,b)\in R_{\mathbb{L}}$
iff
$\{a\}\in\mathbb{L}^I$
and
$b\in \bigcup\mathbb{L}^{O}_{I = \{a\}}$
.
First we want to emphasize an important point: the construction is well-defined. This means, the AF
${F}_{\mathbb{L}}^{{cf}}$
can be built for any labelling-set
$\mathbb{L}$
, even if the considered set is not
${cf}$
-realizable. We proceed with an illustrating example.
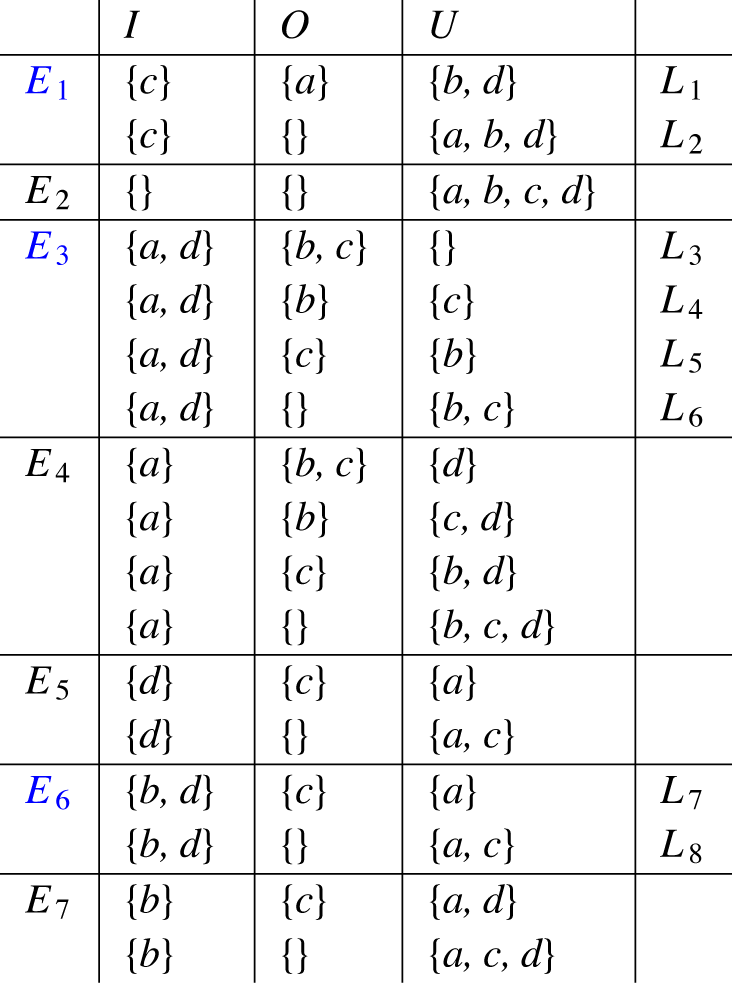
Example 9 Consider the following labelling-set
$\mathbb{L}$
presented in form of a table.
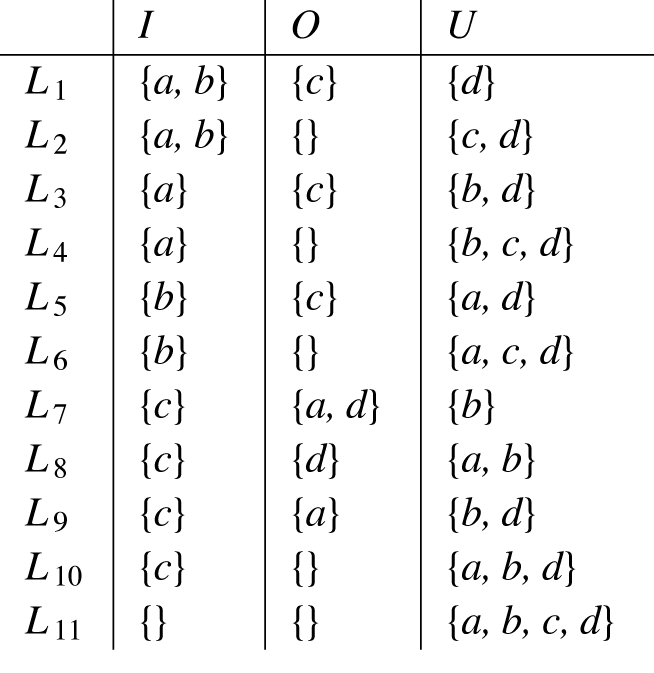
We obtain
$A_{\mathbb{L}} = {Args}(\mathbb{L}) = \{a, b, c, d\}$
. Regarding
$R_{\mathbb{L}}$
we have to consider the singletons
$\{a\},\{b\},\{c\}$
and
$\{d\}$
.
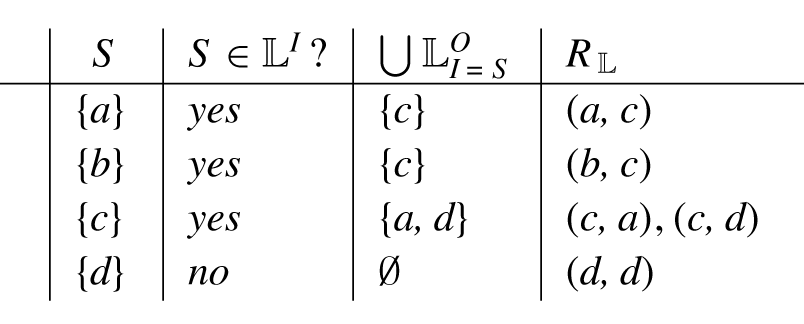
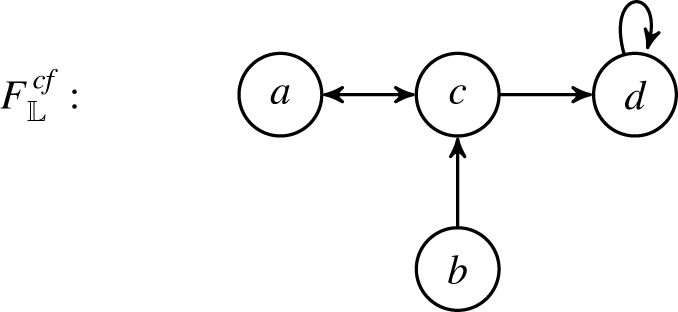
The obtained construction is depicted below.
3.3. Characterization theorem
In the following we present the central characterization theorem for conflict-free labellings. It can be seen that the newly introduced properties play a central role here. Please note that any of the five properties can be decided by looking at the labelling-set in question only.
Theorem 2 Given a labelling-set
$\mathbb{L} \subseteq \left(2^{{\mathcal{U}}}\right)^3$
we have
$\mathbb{L}\in\Sigma_{\mathcal{L}_{cf}}\; \Leftrightarrow$
-
1.
$\mathbb{L}^I$
is downward-closed and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for all
$E\in \mathbb{L}^I$
, -
3.
$\mathbb{L}$
is L-tight, and -
4.
$\mathbb{L}$
is reject-witnessing, and -
5.
$\mathbb{L}$
is reject-compositional.
Proof. If-direction. This means:
Given a labelling-set
$\mathbb{L}$
.If
$\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
, then:
-
1.
$\mathbb{L}^I$
is downward-closed and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for all
$E\in \mathbb{L}^I$
, -
3.
$\mathbb{L}$
is L-tight, and -
4.
$\mathbb{L}$
is reject-witnessing, and -
5.
$\mathbb{L}$
is reject-compositional.
Given
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}}$
. Hence, there is an AF
${F} = (A,R)$
with
${{\mathcal{L}}}_{{cf}}({F}) = \mathbb{L}$
and
${Args}_{\mathbb{L}} = A$
. We further deduce
$\mathbb{L}^{I} = {{\mathcal{E}}}_{{cf}}({F})$
(Items 1,2 of Proposition 1). According to Theorem 1 we obtain
$\mathbb{L}^{I}$
is downward-closed and non-empty.
Consider now
$\mathbb{L}^{O}_{I=E}$
for a certain
$E\in \mathbb{L}^I$
. Due to Item 1 of Definition 2 we deduce
$\left(E\times E\right) \cap R = \emptyset$
. Let us consider now the associated range given as
${E}^+ =\{b\mid (a,b)\in R, a\in {E}\}$
. In light of Item 2 of Definition 2 we obtain
$\mathbb{L}_{I=E}=\{(E,E', A\setminus (E\cup E') ) | E'\subseteq E^+\}$
. Consequently,
$\mathbb{L}^{O}_{I=E} = \left\{E'\mid E'\subseteq E^+\right\}$
which is obviously downward-closed. (Item 2)
We now turn to L-tightness. According to Definition 11 we have to show two properties. First, the existence of a greatest element. Consider therefore a fixed set
$E \in\mathbb{L}^I$
. The associated range
${E}^+ =\{b\mid (a,b)\in R, a\in {E}\}$
together with Item 2 of Definition 2 yields
$\mathbb{L}_{I=E}=\{(E,E', A\setminus (E\cup E') ) | E'\subseteq E^+\}$
. Consequently,
$\mathbb{L}^{O}_{I=E}$
possesses a
$\subseteq$
-greatest element, namely
$E^+ = \overline{\mathbb{L}}^{O}_{I=E}$
.
Secondly, the compatibility criteria. Let
$I_1,I_2 \in\mathbb{L}^I$
and assume
$I_1 \cup I_2 \in \mathbb{L}^I$
. Note that
$\overline{\mathbb{L}}^{O}_{I=I_1} = I_1^+$
and
$\overline{\mathbb{L}}^{O}_{I=I_2} = I_2^+$
. The assumption
$I_1 \cup I_2 \in \mathbb{L}^I$
yields
$\left((I_1 \cup I_2)\times(I_1 \cup I_2)\right) \cap R = \emptyset$
as Item 1 of Definition 2 holds true. Thus,
$(I_1^+ \cap I_2) = (I_2^+ \cap I_1) = \emptyset.$
Consequently,
$(\overline{\mathbb{L}}^{O}_{I=I_1} \cap I_2) \cup (\overline{\mathbb{L}}^{O}_{I=I_2} \cap I_1) = \emptyset.$
Now, for the reverse direction. We assume
$(\overline{\mathbb{L}}^{O}_{I=I_1} \cap I_2) \cup (\overline{\mathbb{L}}^{O}_{I=I_2} \cap I_1)=\emptyset.$
This means,
$(I_1^+ \cap I_2) = (I_2^+ \cap I_1) = \emptyset.$
Moreover, since
$I_1,I_2 \in\mathbb{L}^I$
is assumed we further have
$(I_1^+ \cap I_1) = (I_2^+ \cap I_2) = \emptyset.$
From these two equations we deduce
$\left((I_1 \cup I_2)\times(I_1 \cup I_2)\right) \cap R = \emptyset$
justifying
$L = \left(I_1 \cup I_2,(I_1 \cup I_2)^+,{Args}(\mathbb{L})\setminus \left((I_1 \cup I_2) \cup (I_1 \cup I_2)^+\right)\right) \in\mathbb{L}$
. Hence,
$I_1 \cup I_2 \in \mathbb{L}^I$
is shown concluding L-tightness. (Item 3)
We further have to show that
$\mathbb{L}$
is reject-witnessing. This can be seen as follows: Consider a labelling
$L = \left(L^I,L^O,L^U\right)\in\mathbb{L}$
. Due to Item 1 of Definition 2 we deduce
$\left(L^I\times L^I\right) \cap R = \emptyset$
. Hence, each singleton
$\{i\}\subseteq L^I$
is conflict-free too. Moreover, due to Item 2 of Definition 2 we infer
$L^O \subseteq \left(L^I\right)^+ =\left\{o\mid (i,o)\in R, i\in L^I\right\}$
. Consequently, for each
$o\in L^O\ \exists i\in L^I$
with
$(i,o)\in R$
. Hence,
$\left(\{i\},\{o\},A\setminus\{i,o\}\right)\in \mathbb{L}$
as there are no conditions for undec-labels. (Item 4)
Finally, we show that
$\mathbb{L}$
is reject-compositional. Let us fix a set
$E\in \mathbb{L}^{I}$
. Since
$\mathbb{L}^{I} = {{\mathcal{E}}}_{{cf}}({F})$
we deduce
$\{a\}\in\mathbb{L}^{I}$
for all
$a\in E$
. Let now
$b\in \overline{\mathbb{L}}^{O}_{I=\{a\}}$
for a fixed
$a\in E$
. Due to Definition 2, Item 2 we obtain
$(a,b)\in R({F})$
. Hence,
$b\in E^+ = \overline{\mathbb{L}}^{O}_{I=\{E\}}$
showing
$\displaystyle{\bigcup_{a\in E} \overline{\mathbb{L}}^{O}_{I=\{a\}}\subseteq \overline{\mathbb{L}}^{O}_{I=\{E\}}}$
. Consider now
$b\in \overline{\mathbb{L}}^{O}_{I=E} = E^+$
. Consequently, there is an
$a\in E$
with
$(a,b)\in R({F})$
. We already know that
$\{a\}\in \mathbb{L}^{I}$
yielding
$b\in \overline{\mathbb{L}}^{O}_{I=\{a\}}$
. Thus,
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} \subseteq \bigcup_{a\in E} \overline{\mathbb{L}}^{O}_{I=\{a\}}}$
concluding the proof. (Item 5)
Only-if-direction. This means:
Given a labelling-set
$\mathbb{L}$
, we have:
$\mathbb{L} = {{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
(and thus,
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}}$
), if
-
1.
$\mathbb{L}^I$
is downward-closed and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for all
$E\in \mathbb{L}^I$
, -
3.
$\mathbb{L}$
is L-tight, -
4.
$\mathbb{L}$
is reject-witnessing, and -
5.
$\mathbb{L}$
is reject-compositional.
We split the proof into two subset relations.
-
• We start with
$\mathbb{L} \subseteq {{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
. Consider
${L}\in\mathbb{L}$
. We have to show
${L}\in{{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
.-
1. No internal conflicts. This means, for each two
$a,b\in {L}^{\text{I}}$
, we have
$(a,b)\notin R_{\mathbb{L}}$
.Let
$a = b$
. According to Definition 14, Item 2 we have:
$(a,a)\in R_{\mathbb{L}}$
iff
$\{a\}\notin\mathbb{L}^I$
. Since downward-closedness of
$\mathbb{L}^I$
is assumed, we deduce for any
$E \subseteq {L}^{\text{I}}$
,
$E\in\mathbb{L}^I$
. Hence,
$\{a\}\in\mathbb{L}^I$
and thus
$(a,a)\notin R_{\mathbb{L}}$
.Let
$a\neq b$
. According to Definition 14, Item 3 we have:
$(a,b)\in R_{\mathbb{L}}$
iff
$\{a\}\in\mathbb{L}^I$
and
$b\in \bigcup\mathbb{L}^{O}_{I = \{a\}}$
. The latter union can be replaced with
$\overline{\mathbb{L}}^{O}_{I = \{a\}}$
as L-tightness of
$\mathbb{L}$
is given. Since
$a,b\in {L}^{\text{I}}$
is assumed, we obtain
$\{a\}\in\mathbb{L}^I$
due to the downward-closedness of
$\mathbb{L}^I$
. Thus, we have to show
$b\notin \overline{\mathbb{L}}^{O}_{I = \{a\}}$
. Suppose, towards a contradiction that
$b\in \overline{\mathbb{L}}^{O}_{I = \{a\}}$
. This means, there is label
${M}\in\mathbb{L}$
with
${M}^I = \{a\}$
and
$b\in {M}^O$
. Since
$\mathbb{L}$
is reject-witnessing we deduce the existence of
$N=(\{a\},\{b\},A_{\mathbb{L}}\setminus\{a,b\})\in\mathbb{L}$
. Moreover, since
$\mathbb{L}$
is assumed to be L-tight and
$ {L}^{\text{I}} \cup N^I = {L}^{\text{I}} \cup \{a\} = {L}^{\text{I}} \in \mathbb{L}^I$
we deduce:
$(\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}} \cap \{a\}) \cup (\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap {L}^{\text{I}}) = \emptyset.$
However, the second set is non-empty as
$b\in(\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap {L}^{\text{I}}) \neq \emptyset$
. Thus,
$b\notin \overline{\mathbb{L}}^{O}_{I = \{a\}}$
and finally,
$(a,b)\notin R_{\mathbb{L}}$
. -
2. Reason for rejecting. This means, if
$a\in {L}^{\text{O}}$
, then there is a
$b\in{L}^{\text{I}}$
with
$(b,a)\in R_{\mathbb{L}}$
.Let
$a\in {L}^{\text{O}}$
. As
$\mathbb{L}$
is reject-witnessing, we deduce for some
$b\in{L}^{\text{I}}$
the existence of a labelling
$N = \left(\{b\},\{a\},{Args}_{\mathbb{L}}\setminus\{a,b\}\right)\in \mathbb{L}$
. This means,
$\{b\}\in\mathbb{L}^I$
and
$a\in \overline{\mathbb{L}}^{O}_{I=\{b\}}$
. Thus, according to Definition 14, Item 3 we obtain
$(b,a)\in R_{\mathbb{L}}$
.
-
-
• It remains to show
$\mathbb{L} \supseteq {{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
. Let
${L}\in{{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
. Towards a contradiction we suppose
${L}\notin\mathbb{L}$
. Case distinction:-
1. Assume
${L}^{\text{I}}\notin\mathbb{L}^{I}$
.As
${L}$
is a conflict-free labelling we deduce
$\left({L}^{\text{I}}\times {L}^{\text{I}}\right) \cap R_{\mathbb{L}} = \emptyset$
(Definition 2, Item 1). Now, according to Definition 14, Item 2 we obtain
$\{a\}\in\mathbb{L}^I$
for each
$a\in{L}^{\text{I}}$
. Moreover, applying Item 3 of Definition 14 yields
$b\notin \overline{\mathbb{L}}^{O}_{I = \{a\}}$
for any
$b\in{L}^{\text{I}}$
. Due to finiteness we may assume that
${L}^{\text{I}} = \{a_1,\ldots,a_n\}$
for some
$n\in\mathbb{N}$
. Let us consider two elements
$a_1$
and
$a_2$
. The observations above ensure that
$\overline{\mathbb{L}}^{O}_{I = \{a_1\}} \cap \{a_2\} = \overline{\mathbb{L}}^{O}_{I = \{a_2\}} \cap \{a_1\} = \emptyset$
. Hence, given the L-tightness of
$\mathbb{L}$
we obtain
$\{a_1,a_2\}\in\mathbb{L}^I$
. Now, as
$\mathbb{L}$
is assumed to be reject-compositional we infer
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=\{a_1,a_2\}} = \overline{\mathbb{L}}^{O}_{I=\{a_1\}} \cup \overline{\mathbb{L}}^{O}_{I=\{a_2\}}}$
. Hence, again, for each
$b\in{L}^{\text{I}}$
we get
$b\notin \overline{\mathbb{L}}^{O}_{I = \{a_1,a_2\}}$
. Consequently,
$\overline{\mathbb{L}}^{O}_{I = \{a_1,a_2\}} \cap \{a_3\} = \overline{\mathbb{L}}^{O}_{I = \{a_3\}} \cap \{a_1,a_2\} = \emptyset$
justifying
$\{a_1,a_2,a_3\}\in\mathbb{L}^I$
. This procedure is repeated until
$\{a_1,\ldots,a_n\} = {L}^{\text{I}} \in \mathbb{L}^I$
is reached. Contradiction. -
2. Assume
$({L}^{\text{I}},{L}^{\text{O}},{L}^{\text{U}})\notin\mathbb{L}$
.By Definition 2, Item 2 we have: for each
$b\in {L}^{\text{O}}$
, exists an
$a\in{L}^{\text{I}}$
with
$(a,b)\in R_\mathbb{L}$
. Applying Item 3 of Definition 14 yields for each
$b\in {L}^{\text{O}}$
, exists an
$a\in{L}^{\text{I}}$
with
$\{a\}\in\mathbb{L}^I$
and
$b\in \overline{\mathbb{L}}^{O}_{I = \{a\}}$
. From the upper part of the proof we know that
${L}^{\text{I}}\in\mathbb{L}^{I}$
has to hold. Thus, we may consider the
$\subseteq$
-greatest out-label set
$\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}}$
which exists due to tightness. Moreover, applying that
$\mathbb{L}$
is reject-compositional yields
$\displaystyle{\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}} = \bigcup_{a\in {L}^{\text{I}}} \overline{\mathbb{L}}^{O}_{I=\{a\}}}$
. This means,
$\displaystyle{({L}^{\text{I}},\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}},{Args}_{\mathbb{L}}\setminus({L}^{\text{I}}\cup\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}}))\in\mathbb{L}}$
and by construction
$b\in \displaystyle{\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}}}$
, whenever
$b\in {L}^{\text{O}}$
. In other words,
${L}^{\text{O}}\subseteq\displaystyle{\overline{\mathbb{L}}^{O}_{I={L}^{\text{I}}}}$
. Finally, we take advantage of the downward-closedness of
$\mathbb{L}^{O}_{I={L}^{\text{I}}}$
and obtain
$({L}^{\text{I}},{L}^{\text{O}},{L}^{\text{U}})\in\mathbb{L}$
. Contradiction.
-
In a sense we could also formulate a characterization theorem using only the introduced standard construction. However, in contrast to Theorem 2, it requires the construction of an AF and the computation of semantics.
Theorem 3 For any labelling-set
$\mathbb{L}$
, we have:
\begin{align*}\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}} \Leftrightarrow \mathbb{L} = {{\mathcal{L}}}_{cf}\left({F}_{\mathbb{L}}^{{cf}}\right).\end{align*}
Proof. Given a labelling-set
$\mathbb{L}$
.
-
(⇐) Since
$\mathbb{L} = {{\mathcal{L}}}_{cf}\left({F}_{\mathbb{L}}^{{cf}}\right)$
is given, we immediately have found a
${cf}$
-realizing AF, namely
${F}_{\mathbb{L}}^{{cf}}$
. Consequently,
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}}$
. -
(⇒) Given
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}}$
. Consider the proof of Theorem 2. Via the if-direction we obtain:
-
1.
$\mathbb{L}^I$
is downward-closed and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for all
$E\in \mathbb{L}^I$
, -
3.
$\mathbb{L}$
is L-tight, and -
4.
$\mathbb{L}$
is reject-witnessing, and -
5.
$\mathbb{L}$
is reject-compositional.
Now, we can apply the only-if direction and obtain
$\mathbb{L} = {{\mathcal{L}}}_{{cf}}\left(F_{\mathbb{L}}^{{cf}}\right)$
concluding the proof.
Lastly we mention that the characterization Theorem 2 can be presented in a more compact way since the presented set of properties is not independent. More precisely, reject-witness is redundant as it is implied by reject-compositionality (Theorem 2 property 4.) and requiring downward-closedness for each in-associated out-label set (Theorem 2 property 2.). Confer the subsequent proposition.
Proposition 4 Given a labelling-set
$\mathbb{L}$
. If
$\mathbb{L}$
is reject-compositional and for each
$E\in \mathbb{L}^I$
,
$\mathbb{L}^{O}_{I=E}$
is downward-closed, then
$\mathbb{L}$
is reject-witnessing.
Proof. Let
$L\in\mathbb{L}$
and
$o\in L^{O}$
. For proving reject-witness of
$\mathbb{L}$
we have to deduce the existence of an
$i\in L^I$
, s.t.
$\displaystyle{\left(\{i\},\{o\},Args_{\mathbb{L}}\setminus\{i,o\}\right)\in \mathbb{L}}$
. The assumption
$o\in L^{O}$
yields
$o\in \bigcup\mathbb{L}^{O}_{I = L^{I}}$
. Since reject-compositionality is given we have
$\displaystyle{\bigcup\mathbb{L}^{O}_{I = E} = \bigcup_{a\in E} \bigcup\mathbb{L}^{O}_{I=\{a\}}}$
for each
$E\subseteq{Args}_\mathbb{L}$
. Consequently,
$\displaystyle{o\in\bigcup_{a\in L^I} \bigcup\mathbb{L}^{O}_{I=\{a\}}}$
. Hence, there is a certain
$i\in L^I$
, s.t.
$o\in\mathbb{L}^{O}_{I=\{i\}}$
. This means, there is a labelling
$M\in\mathbb{L}$
, s.t.
${M}^I = \{i\}$
and
$o\in{M}^O$
. Now, as
${M}^O\in\mathbb{L}^{O}_{I=\{i\}}$
is known we may finally apply the required downward-closedness of
$\mathbb{L}^{O}_{I=\{i\}}$
and infer
$\{o\}\in\mathbb{L}^{O}_{I=\{i\}}$
. This entails
$\displaystyle{\left(\{i\},\{o\},Args_{\mathbb{L}}\setminus\{i,o\}\right)\in \mathbb{L}}$
concluding the proof.
Let us briefly compare the achieved characterization theorem with the already existing one regarding conflict-free sets (Theorem 1). In light of Proposition 1 one can see that labelling-based
${cf}$
-realizability of
$\mathbb{L}$
requires extension-based
${cf}$
-realizability of the corresponding set of in-labelled arguments.Footnote
1
This means,
$\mathbb{L}^I$
has to be tight, non-empty and downward-closed. The last two (Theorem 2 poperty 1.) are explicitly given in Theorem 2 and one may wonder about the ‘missing’ tightness property. This property of
$\mathbb{L}^I$
is implicit as shown next.
Proposition 5 Let
$\mathbb{L}$
be a labelling-set
$\mathbb{L}$
. Given L-tightness and reject-compositionality of
$\mathbb{L}$
and downward-closedness of
$\mathbb{L}^{I}$
, then
$\mathbb{L}^{I}$
is tight.
Proof. Let
$E\in \mathbb{L}^{I}$
and
$a\in {Args}_{\mathbb{L}^{I}}$
s.t.
$E\cup \{a\}\notin \mathbb{L}^{I}$
. For tightness of
$\mathbb{L}^{I}$
we have to show the existence of some
$s\in E$
with
$(a,s)\notin\textit{Pairs}_{\mathbb{L}^{I}}$
. Towards a contradiction, we assume
$(a,s)\in\textit{Pairs}_{\mathbb{L}^{I}}$
for each single
$s\in E$
. Consequently, for each
$s\in E$
exists a set
$E_s\in \mathbb{L}^{I}$
, s.t.
$\{a,s\}\subseteq E_s$
. Due to downward-closedness of
$\mathbb{L}^{I}$
we infer
$\{a\}\in\mathbb{L}^{I}$
as well as
$\{s\}\in\mathbb{L}^{I}$
for each
$s\in E$
. The L-tightness of
$\mathbb{L}$
entails
$E\cup \{a\}\in \mathbb{L}^{I} \Leftrightarrow (\overline{\mathbb{L}}^{O}_{I=E} \cap \{a\}) \cup (\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap E) = \emptyset$
. Since
$E\cup \{a\}\notin \mathbb{L}^{I}$
is given, we deduce
$(\overline{\mathbb{L}}^{O}_{I=E} \cap \{a\}) \cup (\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap E) \neq \emptyset$
. Case distinction:
-
1.
$\overline{\mathbb{L}}^{O}_{I=E} \cap \{a\} \neq \emptyset$
. Applying
$\mathbb{L}$
-tightness and reject-compositionality we infer
$\overline{\mathbb{L}}^{O}_{I=\{s\}} \cap \{a\} \neq\emptyset$
for some
$s\in E$
. Consequently, by using the same arguments, we obtain
$\overline{\mathbb{L}}^{O}_{I=E_s} \cap \{a\} \neq\emptyset$
. This means, we have found a labelling
$\overline{\mathbb{L}}_{I=E_s} = (E_s,\overline{\mathbb{L}}^{O}_{I=E_s},U)$
with
$a\in E_s$
and
$a\in\overline{\mathbb{L}}^{O}_{I=E_s}$
. Contradiction! -
2.
$\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap E \neq \emptyset$
. Hence there is some
$s\in E$
s.t.
$\overline{\mathbb{L}}^{O}_{I=\{a\}} \cap \{s\} \neq\emptyset$
. By assumption we infer the existence of a set
$E_s$
with
$\{a,s\}\subseteq E_s$
. Moreover, by
$\mathbb{L}$
-tightness and reject-compositionality we obtain
$\overline{\mathbb{L}}^{O}_{I=E_s} \cap \{s\} \neq\emptyset$
. This means, again we have found a labelling
$\overline{\mathbb{L}}_{I=E_s} = (E_s,\overline{\mathbb{L}}^{O}_{I=E_s},U)$
with
$s\in E_s$
and
$s\in\overline{\mathbb{L}}^{O}_{I=E_s}$
. Contradiction!
3.4. Representational freedom: Ordinary and strong equivalence
In the former sections we studied whether and how a set
$\mathbb{L}$
is realizable. Now, we go a step further. We want to formally describe any possible witnessing AF for
$\mathbb{L}$
. Are there regularities, similarities and is it possible to easily navigate through the space of options? This question is strongly related to patterns of redundancy and requires no more and no less than a non-semantical characterization of ordinary equivalence (Baumann Reference Baumann2018; Dvorák et al. Reference Dvorák, Järvisalo, Linsbichler, Niskanen and Woltran2019).
Example 10
(Example 9 cont.) Consider the following AF
${G}$
. One may easily verify that
${{\mathcal{L}}}_{{cf}}({G}) = \mathbb{L}$
. Thus,
${F}^{cf}_{\mathbb{L}}\equiv^{{{\mathcal{L}}}_{{cf}}}\! {G}$
.
In case of the above example we observe that the representational freedom is linked to outgoing attacks from self-defeating arguments. The following theorem proves that this observation holds in general. Moreover, there are no other patterns of redundancy. We use the stable kernel (see Definition 6) to formulate the central result in a compact way.
Theorem 4 Given two AFs
${F}$
and
${G}$
. We have:
\begin{align*}{F}\equiv^{{{\mathcal{L}}}_{{cf}}} {G} \Leftrightarrow {F}^{sk} = {G}^{sk}.\end{align*}
Proof. Let
${F} = (A,R)$
and
${G} = (B,S)$
. The associated stable kernels are
${F}^{sk} = (A,R^{sk})$
and
${G}^{sk} = (B,S^{sk})$
. We split the proof into two directions.
-
(⇒) We show the contrapositive:
${F}^{sk} \neq {G}^{sk} \Rightarrow {F}\not\equiv^{{{\mathcal{L}}}_{{cf}}}\! {G}.$
Case Distinction:-
1. Assume
$A\neq B$
. W.l.o.g. let
$a\in A\setminus B$
. Remember that conflict-free labellings always exist. Hence,
$a\in{Args}_{{{\mathcal{L}}}_{{cf}}({F})} = A$
as each labelling covers the underlying set A. Since
$a\notin B$
and
${{\mathcal{L}}}_{{cf}}({G})\subseteq \left(2^B\right)^3$
we obtain
${{\mathcal{L}}}_{{cf}}({F})\neq{{\mathcal{L}}}_{{cf}}({G})$
. -
2. Assume
$(a,a)\in R^{sk}\setminus S^{sk}$
. By definition of the stable kernel we get
$(a,a)\in R\setminus S$
. Due to the first case we further assume
$A = B$
. The labelling
${L}$
with
${L}^I = \{a\}$
,
${L}^O = \emptyset$
,
${L}^U = A\setminus\{a\}$
is a conflict-free one for
${G}$
but not for
${F}$
. Consider Definition 2. We do not have any condition for undecided arguments. Hence
${L}^U = A\setminus\{a\}$
is justified in
${G}$
. Moreover,
$a\in{L}^I$
is eligible since
$(a,a)\notin S$
is assumed. In contrast,
${L}\notin{{\mathcal{L}}}_{{cf}}({F})$
since
$(a,a)\in R$
. Thus,
${{\mathcal{L}}}_{{cf}}({F})\neq{{\mathcal{L}}}_{{cf}}({G})$
. -
3. Assume
$(a,b)\in R^{sk}\setminus S^{sk}$
with
$a\neq b$
. Due to the previous two cases we may further assume sharing the same arguments as well as sharing the same self-loops. Since
$(a,b)\in R^{sk} \subseteq R$
we derive
$(a,a)\notin R,S$
. Consequently,
$(a,b)\in S$
is impossible and we have to distinguish the main cases regarding the presence or absence of (b,b). Moreover, the attack (b,a) may independently be in R or S. We depict the restrictions to
$\{a,b\}$
only.We have to consider 8 pairings, namely
$(F_i,G_j)$
with
$i,j\in\{1,2\}$
or
$i,j\in\{3,4\}$
. However, for each pairing we may use one and the same distinguishing labelling
${L}$
, namely
$L^U = A\setminus \{a,b\}$
,
$L^I = \{a\}$
and
$L^O = \{b\}$
. One may easily check that
$L\in{{\mathcal{L}}}_{{cf}}({F}_i)$
and
$L\notin{{\mathcal{L}}}_{{cf}}({G}_j)$
for each
$i,j\in\{1,2,3,4\}$
. Thus,
${{\mathcal{L}}}_{{cf}}({F})\neq{{\mathcal{L}}}_{{cf}}({G})$
concluding the if-direction.
-
-
(⇐) It suffices to show that
${{\mathcal{L}}}_{{cf}}({F}) = {{\mathcal{L}}}_{{cf}}({F}^{sk})$
for each AF
${F}$
. We show both subset relations.-
(⊆) Given
$L\in{{\mathcal{L}}}_{{cf}}({F})$
. Regarding
$L^I$
we obtain
$(L^I\times L^I)\cap R = \emptyset$
. Since
$R^{sk}\subseteq R$
we deduce
$(L^I\times L^I)\cap R^{sk} = \emptyset$
. Hence,
$L^I$
is justified in
${F}^{sk}$
too. Secondly, regarding
$L^O$
. For each
$o\in L^O$
we have an
$i\in L^I$
with
$(i,o)\in R$
. Since
$(i,i)\notin R$
we obtain
$(i,i)\notin R^{sk}$
and thus,
$(i,o)\in R^{sk}$
too, justifying
$L^O$
w.r.t.
${F}^{sk}$
. Regarding
$L^U$
we do not have to check any condition. Consequently,
$L\in{{\mathcal{L}}}_{{cf}}({F}^{sk})$
. -
(⊇) Assume now
$L\in{{\mathcal{L}}}_{{cf}}({F}^{sk})$
. We deduce
$(L^I\times L^I)\cap R^{sk} = \emptyset$
. In particular, we do not have any self-defeating arguments in
$L^I$
implying that
$(L^I\times L^I)\cap R^{sk} = (L^I\times L^I)\cap R$
. This means,
$L^I$
is also justified in
${F}$
. Consider now
$L^O$
. For each
$o\in L^O$
, we have an
$i\in L^I$
with
$(i,o)\in R^{sk}$
. Since
$L^I$
is justified in
${F}$
and
$R^{sk}\subseteq R$
we deduce that even
$L^O$
is justified in
${F}$
. Regarding
$L^U$
we have nothing to show which concludes
$L\in{{\mathcal{L}}}_{{cf}}({F})$
as well as the whole proof.
-
We continue with an astonishing result which does not have any counterpart in the realm of extension-based semantics. If starting with a self-loop free AF, then there are no syntactic manipulations preserving ordinary equivalence.
Proposition 6 Given two AFs
${F}$
and
${G}$
. If
${G}$
is self-loop free, then:
${F}\equiv^{{{\mathcal{L}}}_{{cf}}}\! {G} \Leftrightarrow {F} ={G}$
.
Proof. For self-loop free AFs
${F}$
we know:
${F} = {F}^{sk}$
(Proposition 2). Consequently, applying Theorem 4 yields the assertion.
This means, if the standard AF
${F}_{\mathbb{L}}^{{cf}}$
does not possess any self-loop, then
${F}_{\mathbb{L}}^{{cf}}$
is the only option to
${cf}$
-realize
$\mathbb{L}$
. In other words, in this class the realizing framework is uniquely determined.
We have already shown that the stable kernels characterize ordinary equivalence and are thus necessary for the more restrictive notion of strong equivalence. The following theorem shows that they are also sufficient:
Theorem 5 Given two AFs
${F}$
and
${G}$
. We have:
\begin{align*}{F}\equiv^{{{\mathcal{L}}}_{{cf}}}_s\! {G} \Leftrightarrow {F}^{sk} = {G}^{sk}.\end{align*}
Proof. Given AFs
${F}$
and
${G}$
. The associated stable kernels are
${F}^{sk} = (A,R^{sk})$
and
${G}^{sk} = (B,S^{sk})$
. We split the proof into two directions.
-
(⇒) If
${F}\equiv^{{{\mathcal{L}}}_{{cf}}}_s\! {G}$
is given, then it follows directly from the definition of strong equivalence (Definition 5) that F and G are ordinarily equivalent also, meaning
${F}\equiv^{{{\mathcal{L}}}_{{cf}}}\! {G}$
. Thus Theorem 4 applies and
${F}^{sk} = {G}^{sk}$
. -
(⇐) If
${F}^{sk} = {G}^{sk}$
is given, using Proposition 2 we get
$\left({F}\sqcup {H}\right)^{sk} = \left({G}\sqcup {H}\right)^{sk}$
. Thus Theorem 4 is again applicable and
${F}\sqcup {H} \equiv^{{{\mathcal{L}}}_{{cf}}}\! {G}\sqcup {H}$
.
4. Naive labellings
Conflict-free sets and naive extensions have a close relationship to each other. They are connected via the so-called downward-closure, that is for any given AF F we have,
$\textit{dcl}\left({{\mathcal{E}}}_{{na}}(F)\right) = {{\mathcal{E}}}_{{cf}}(F)$
. The underlying idea in this paper is to transfer this connection to the realm of labellings. We will see that this works to a certain extent. However, further conditions are needed.
4.1. The downward-closure of a labelling-set
In the following we transfer the concept of a downward-closed set to the realm of labellings. Given a labelling-set
$\mathbb{L}$
we first downward-close
$\mathbb{L}^{I}$
and obtain any new in-label. In the next step we construct the corresponding out-labels for a given in-label E. This is done as follows: For each
$a\in E$
we obtain a building block
$O_{\{a\}}$
. Such an
$O_{\{a\}}$
contains an argument b if each former in-set I containing a possesses a witnessing out-label containing b. For a given in-label E the
$\subseteq$
-greatest out-label
$O_E$
is then defined as the union of all such
$O_{\{a\}}$
’s.
Definition 15 For a given labelling-set
$\mathbb{L}$
we define a new labelling-set
${}^\downarrow\mathbb{L}$
, the so-called downward-closure of
$\mathbb{L} $
, as follows:
\begin{equation*}{}^\downarrow\mathbb{L}\;:\!=\;\{(E,O, {Args}_{\mathbb{L}}\setminus (E \cup O)) | E \subseteq L^{I}, L^{I}\in\mathbb{L}^I, O\subseteq O_E\}\end{equation*}
where
\begin{equation*}O_E = \bigcup_{a\in E} O_{\{a\}}\quad\text{ with } O_{\{a\}} = \bigcap_{I'\in\mathbb{L}^I, \{a\}\subseteq I'} \bigcup\mathbb{L}^{O}_{I = I'}.\end{equation*}
Please note that
$\bigcup\mathbb{L}^{O}_{I = I'}$
can be replaced with
$\overline{\mathbb{L}}^{O}_{I = I'}$
in case of L-tight labelling-sets.
Example 11 Consider now
$\mathbb{L}\;:\!=\;\mathcal L_{na}(F)$
from Example 1 given by the following table.
We want to determine the associated downward-closure
${}^\downarrow\mathbb{L}$
. In order to obtain the resulting labellings we first have to compute the set
$O_{\{a\}}$
for each single
$a\in {Args}_{\mathbb{L}^I}$
. Note that the considered labelling-set
$\mathbb{L}$
is L-tight. Consequently, we may compute
$O_{\{a\}}$
with the more convenient
$\displaystyle{\bigcap_{I'\in\mathbb{L}^I, \{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
.
-
1. We obtain:
-
•
$\displaystyle{O_{\{a\}}=\bigcap_{I'\in\mathbb{L}^I, \{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\overline{\mathbb{L}}^{O}_{I = \{a,d\}} = L_3^O = \{b,c\}}.$
-
•
$\displaystyle{O_{\{b\}}=\bigcap_{I'\in\mathbb{L}^I, \{b\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\overline{\mathbb{L}}^{O}_{I = \{b,d\}} = L_7^O = \{c\}}.$
-
•
$\displaystyle{O_{\{c\}}=\bigcap_{I'\in\mathbb{L}^I, \{c\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\overline{\mathbb{L}}^{O}_{I = \{c\}} = L_1^O = \{a\}}.$
-
•
$\displaystyle{O_{\{d\}}=\bigcap_{I'\in\mathbb{L}^I, \{d\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\overline{\mathbb{L}}^{O}_{I = \{a,d\}} \cap \overline{\mathbb{L}}^{O}_{I = \{b,d\}}= L_3^O \cap L_7^O = \{b,c\} \cap \{c \} =\{c\}}.$
-
-
2. The next step is to built
$O_E$
for each set
$E\subseteq I\in\mathbb{L}^{I}$
. This set is build via the union of any
$O_{\{a\}}$
with
$a\in E$
. As
$\mathbb{L}^I = \{\{c\},\{a,d\},\{b,d\}\}$
we have to consider three main cases:-
•
$\{c\}\in\mathbb{L}^I$
. We have to consider
$E_1 = \{c\}$
and
$E_2 = \emptyset$
and obtain:
$O_{E_1} = \bigcup_{x\in E_1} O_{\{x\}} = O_{\{c\}} = \{a\}$
and
$O_{E_2} = \bigcup_{x\in E_2} O_{\{x\}} = \emptyset$
. -
•
$\{a,d\}\in \mathbb{L}^{I}$
. We have to consider
$E_3 = \{a,d\}$
,
$E_4 = \{a\}$
and
$E_5 = \{d\}$
. Note that the empty set was already considered in the case above. We obtain:
$O_{E_3} = \bigcup_{x\in E_3} O_{\{x\}} = O_{\{a\}}\cup O_{\{d\}} = \{b,c\} \cup \{c\} = \{b,c\}$
,
$O_{E_4} = O_{\{a\}}=\{b,c\}$
and
$O_{E_5} = O_{\{d\}}=\{c\}$
. -
•
$\{b,d\}\in\mathbb{L}^{I}$
. We have to consider
$E_6 = \{b,d\}$
and
$E_7 = \{b\}$
. Please note that
$E_5 = \{d\}$
and
$E_2 = \emptyset$
were already considered. We obtain:
$O_{E_6} = O_{\{b\}}\cup O_{\{d\}} = \{c\} \cup \{c\} = \{c\}$
and
$O_{E_7} = O_{\{b\}}=\{c\}$
.
-
-
3. Finally, we may construct the resulting labellings. Each single
$E_i$
(in-sets) corresponds to several labellings induced by the subsets
$O\subseteq O_{E_i}$
(out-sets). Consider the following table representing
${}^\downarrow\mathbb{L}$
in a compact way.Observing the above table reveals that for each
$E\in \mathbb{L}^{I}$
we have:
$O_{E} =\overline{\mathbb{L}}^{O}_{I = E}$
. For better visibility these are marked in blue above. This means, the set of the constructed blue marked labellings coincides with original set
$\mathbb{L}$
. This is no coincidence as we will see (Proposition 12).
We now prove the well-definedness of the construction.
Proposition 7 If
$\mathbb{L}$
is a labelling-set, then
${}^\downarrow\mathbb{L}$
is a labelling-set.
Proof. We first have to show that any labelling
$M\in {}^\downarrow\mathbb{L}$
considers the same arguments. Let
$M = (E,O,U)$
. Thus, by definition
$M^{I}\cup M^{O} \cup M^{U} = E \cup O \cup ({Args}_{\mathbb{L}}\setminus ( E\cup O)) = {Args}_{\mathbb{L}}$
. The latter equals
${Args}_{\mathbb{L}}$
as
$E,O\subseteq {Args}_{\mathbb{L}}$
.
Secondly, we have to show disjointness, that is
$M^{I}\cap M^{O} = M^{I}\cap M^{U} = M^{O}\cap M^{U} = \emptyset$
.
-
•
$M^{I}\cap M^{O} = \emptyset$
.Towards a contradiction assume
$E\cap O \neq \emptyset$
, that is there is an element
$a\in E\cap O$
. Since
$a\in E$
we deduce the existence of a labelling
$L\in\mathbb{L}$
with
$a(\in E) \subseteq {L}^I$
. Moreover, since by assumption
$a\in O$
and by definition
$O\subseteq O_E=\bigcup_{c\in E} O_{\{c\}}$
we obtain the existence of an element
$b\in E$
with
$a\in O_{\{b\}}$
. Since
$O_{\{b\}} = \bigcap_{I'\in\mathbb{L}^I, \{b\}\subseteq I'} \bigcup\mathbb{L}^{O}_{I = I'}$
we infer
$a\in\bigcup\mathbb{L}^{O}_{I = {L}^I}$
. Thus, there has to be a labelling
${L}'\in\mathbb{L}$
with
$a\in({L}')^I = {L}^I$
and
$a\in ({L}')^O$
contradicting disjointness and thus, the labelling-set property of
$\mathbb{L}$
. -
• The cases
$M^{I}\cap M^{U} = \emptyset$
and
$M^{O}\cap M^{U} = \emptyset$
follow immediately by construction as
$U = {Args}_{\mathbb{L}}\setminus (E \cup O)$
concluding the proof.
We list some simple properties which are frequently used throughout the article.
Proposition 8 Let
$\mathbb{L}$
be a set of labellings. Then
-
1. For
$E\in \left({}^\downarrow\mathbb{L}\right)^I$
we have:
$\left({}^\downarrow\mathbb{L}\right)^{O}_{I=E} = \{S\mid S\subseteq O_E\}$
, -
2. For
$E\in \left({}^\downarrow\mathbb{L}\right)^I$
we have:
$\overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=E} = O_E$
, -
3.
$\mathbb{L} = \emptyset\ \Leftrightarrow\ {}^\downarrow\mathbb{L} = \emptyset$
, -
4.
$\mathbb{L}^{I}\subseteq \left({}^\downarrow\mathbb{L}\right)^I$
, -
5.
$dcl(\mathbb{L}^I)=\left({}^\downarrow\mathbb{L}\right)^I$
.
Proof. Items 1–4 follow immediately by construction of
${}^\downarrow\mathbb{L}$
. Let us prove the last assertion in more detail.
-
(⊆) Let
$E \in \textit{dcl}(\mathbb{L}^{I})$
. Thus, by definition of the downward-closure of a set we obtain the existence of an
$I'\in \mathbb{L}^{I}$
s.t.
$E \subseteq I'$
. Consequently, by definition of
$\mathbb{L}^{I}$
there exists a labelling
${L}\in\mathbb{L}$
with
${L}^I = I'$
. Hence, due to the construction of the downward-closure of a labelling-set we infer the existence of a labelling
$M\in {}^\downarrow\mathbb{L}$
with
$M^{I} = E$
implying
$E \in \left({}^\downarrow\mathbb{L}\right)^I$
. -
(⊇) Let
$E \in ({}^\downarrow\mathbb{L})^I$
. Thus, by definition of
$(^\downarrow\mathbb{L})^{I}$
we obtain the existence of an
$I'\in \mathbb{L}^{I}$
s.t.
$E \subseteq I'$
. Hence,
$E\in \textit{dcl}(\mathbb{L}^{I})$
by definition of the downward-closure of a set.
4.2. Inheritance of L-tightness
The underlying idea in our approach is to reproduce (as far as possible) the relationship between conflict-free sets and naive extension sets in the realm of labellings. One important step towards a characterization is to show that naive realizability of a labelling-set implies conflict-free realizability of the associated downward-closure, that is the downward-closure satisfies any criteria listed in Theorem 2. While most of them can be shown quite easily, L-tightness requires a closer examination. The goal of this section is to show that L-tightness of a labelling-set carries over to the downward-closure under certain conditions. Before proving this important ingredient we have to show a few technical results first. To this end, we now introduce in-maximal labellings of a given labelling-set. Applying this concept to a set of conflict-free labellings yields the naive ones of the AF in question.
Definition 16 For any labelling-set
$\mathbb{L}$
we define the set of in-maximal labellings as
$\{{L}\in\mathbb{L}\mid {L}^I \subseteq \,\mbox{--}\textrm{maximal in } \mathbb{L}^{I}\}$
.
Next, we show that L-tightness is inherited from the initial set to its in-maximal labellings.
Proposition 9 Let
$\mathbb{L}$
be an L-tight labelling-set and
$\mathbb{M}$
the associated set of its in-maximal labellings. Then:
-
1.
$\overline{\mathbb{M}}_{I=E}^{O}$
exists and
$\overline{\mathbb{M}}_{I=E}^{O} = \overline{\mathbb{L}}^{O}_{I = E}$
for all
$E\in \mathbb{M}^{I}$
. -
2.
$\mathbb{M}$
is L-tight.
Proof.
-
1. We first prove the existence of
$\subseteq$
-greatest elements regarding out-labels w.r.t. fixed in-sets. Consider
$E\in\mathbb{M}^I$
. By construction
$\mathbb{M}$
and
$\mathbb{L}$
share the same labellings with E as in-sets, that is
$\mathbb{M}_{I=E} = \mathbb{L}_{I=E}$
. Consequently,
$\mathbb{M}^{O}_{I=E} = \mathbb{L}^{O}_{I=E}$
. Now, due to L-tightness of
$\mathbb{L}$
we deduce the existence of
$\overline{\mathbb{L}}^{O}_{I=E}$
, the
$\subseteq$
-greatest labelling regarding out-labels w.r.t. to the in-set E. Hence,
$\overline{\mathbb{M}}^{O}_{I=E}$
is guarenteed and given as
$\overline{\mathbb{L}}^{O}_{I=E}$
. -
2. Now, for the second property, consider
$E_1, E_2\in \mathbb{M}^I$
. We immediately observe that
$E_1\cup E_2\notin\mathbb{M}^I$
as
$\mathbb{M}$
contains in-maximal labellings only. Hence, by definition of L-tightness we have to show
$(\overline{\mathbb{M}}^{O}_{I=E_1} \cap E_2) \cup (\overline{\mathbb{M}}^{O}_{I=E_2} \cap E_1) \neq \emptyset$
. Since
$\mathbb{M}\subseteq \mathbb{L}$
we know that
$E_1, E_2\in \mathbb{L}^{I}$
. Moreover,
$E_1\cup E_2\notin\mathbb{L}^{I}$
as
$E_1, E_2\in \mathbb{M}^I$
is assumed. We may now apply L-tightness of
$\mathbb{L}$
and derive
$(\overline{\mathbb{L}}^{O}_{I=E_1} \cap E_2) \cup (\overline{\mathbb{L}}^{O}_{I=E_2} \cap E_1) \neq \emptyset$
. Thus, using the equality
$\overline{\mathbb{M}}^{O}_{I=E} = \overline{\mathbb{L}}^{O}_{I=E}$
for
$E\in\mathbb{M}^I$
from above we obtain
$(\overline{\mathbb{M}}^{O}_{I=E_1} \cap E_2) \cup (\overline{\mathbb{M}}^{O}_{I=E_2} \cap E_1) \neq \emptyset$
as required.
Now we are prepared to extend L-tightness to naive labelling-sets.
Proposition 10 Given a labelling-set
$\mathbb{L}$
. If
$\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{na}}}}$
, then
$\mathbb{L}$
is L-tight.
Proof. Since
$\mathbb{L}$
is naive-realizable we conclude the existence of an AF F with
$\mathcal L_{{na}}(F)=\mathbb{L}$
. By Definition 3 we have that
$\mathbb{L}$
contains exactly the in-maximal labellings of
$\mathcal L_{cf}(F)$
. By Theorem 2 we know that
$\mathcal L_{cf}(F)$
is L-tight. Thus, applying Proposition 9 yields L-tightness of
$\mathbb{L}$
.
Next we want to show that L-tightness also carries over to the downward-closure (see Proposition 14). However, in order to do so, we have to show the following three non-trivial properties first.
Proposition 11 Given a labelling-set
$\mathbb{L}$
. If
$\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{na}}}}$
, then for any
$E\in\mathbb{L}^I$
we have:
$\overline{\mathbb{L}}^{O}_{I=E} = O_E$
.
Proof. First of all, due to Proposition 10 we know that
$\mathbb{L}$
is L-tight and thus, the existence of
$\overline{\mathbb{L}}^{O}_{I=E}$
is guarenteed. Moreover,
$\displaystyle{O_E = \bigcup_{a\in E} O_{\{a\}}\text{ with } O_{\{a\}} = \bigcap_{I'\in\mathbb{L}^I, \{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
.
-
(⊆) Let
$x\in O_E$
. Thus, there is an
$a\in E$
with
$x\in O_{\{a\}}$
. Since
$E\in\mathbb{L}^I$
and
$\{a\}\subseteq E$
we obtain
$x\in \overline{\mathbb{L}}^{O}_{I=E}$
. -
(⊇) Let
$x\in\overline{\mathbb{L}}^{O}_{I=E}$
. Hence, there is an
${L}\in\mathbb{L}$
with
${L}^I= E$
and
$x\in{L}^O$
. Due to naive realizability we have the existence of an
${F} = (A,R)$
, s.t.
${{\mathcal{L}}}_{{na}}({F}) = \mathbb{L}$
. Consequently, since
${L}$
is a conflict-free labelling too, there has to be an
$e\in{L}^I$
with
$(e,x)\in R$
(Definition 2). Thus, due to reject-witness of
${{\mathcal{L}}}_{{cf}}({F})$
(Theorem 2), we have
$\left(\{e\},\{x\},Args_{\mathbb{L}}\setminus\{e,x\}\right)\in{{\mathcal{L}}}_{{cf}}({F})$
. Consequently,
$x\in\overline{{{\mathcal{L}}}_{{cf}}({F})}^{O}_{I=\{e\}}$
. Now, for each naive set
$I'\in\mathbb{L}^I = \left({{\mathcal{L}}}_{{na}}({F})\right)^I = {{\mathcal{E}}}_{{na}}({F})$
with
$\{e\}\subseteq I'$
we have:
$x\in\overline{\mathbb{L}}^{O}_{I = I'}$
. This is due to fact that
$\overline{\mathbb{L}}^{O}_{I = I'} = \overline{{{\mathcal{L}}}_{{na}}({F})}^{O}_{I=I'} = \overline{{{\mathcal{L}}}_{{cf}}({F})}^{O}_{I=I'} = \bigcup_{a\in I'} \overline{{{\mathcal{L}}}_{{cf}}({F})}^{O}_{I=\{a\}}$
. The latter equation is justified by reject-compositionality and L-tightness of
${{\mathcal{L}}}_{{cf}}({F})$
(Theorem 2). This means, we have shown that
$x\in O_{\{e\}}\subseteq O_E$
concluding the proof.
Proposition 12 Given an AF
${F}=(A,R)$
, then
$\overline{(\mathcal L_{{cf}}(F))}_{I=E}^{O}\subseteq \overline{\left({}^\downarrow \mathcal L_{{na}}(F) \right)}^{O}_{I=E}$
for all
$E\in( \mathcal L_{{cf}}(F))^{I}$
.
Proof. For the proof we set
$\mathcal L_{{na}}(F)=\mathbb{L}$
and
$\mathcal L_{{cf}}(F) = \mathbb{M}$
.
Via the L-tightness of
$\mathbb{M}$
(Theorem 2) the existence of the
$\subseteq$
-greatest element
$\overline{\mathbb{M}}_{I=E}^{O}$
is ensured as well as the existence of
$\overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=E} = O_E$
due to the construction of the downward-closure. This means, the desired subset relation coincides with
$\overline{\mathbb{M}}_{I=E}^{O}\subseteq O_E$
. Let
$b\in \overline{\mathbb{M}}_{I=E}^{O}$
. Due to reject-compositionality and L-tightness of
$\mathbb{M}$
(Theorem 2) the existence of an
$a\in E$
, s.t.
$b\in \overline{\mathbb{M}}_{I=\{a\}}^{O}$
is guaranteed. Consequently, for each
$I'\in \mathbb{M}^{I}$
with
$a\in I'$
we have
$b\in \overline{\mathbb{M}}_{I=I'}^{O}$
. This applies in particular to the in-maximal labellings of
$\mathbb{M}$
, that is to the labellings in
$\mathbb{L}$
. Moreover, in Proposition 9 we have shown that for such labellings
$\overline{\mathbb{M}}_{I=I'}^{O} = \overline{\mathbb{L}}^{O}_{I = I'}$
. Consequently,
$\displaystyle{b\in \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=O_{\{a\}}}$
. Hence,
$\displaystyle{b\in \bigcup_{a\in E} O_{\{a\}}=O_{E}}$
is shown concluding the proof.
Proposition 13 Given an AF
${F}$
, we have:
$\mathcal L_{cf}(F)^{I} =\left({}^\downarrow\mathcal L_{na}(F)\right)^{I}$
as well as
$\mathcal L_{cf}(F)\subseteq {}^\downarrow\mathcal L_{na}(F)$
.
Proof. For the proof we set
$\mathcal L_{{na}}(F)=\mathbb{L}$
and
$\mathcal L_{{cf}}(F) = \mathbb{M}$
.
We first show
$\mathbb{M}^{I}={}^\downarrow\mathbb{L}^I$
. By Item 5 of Proposition 8 we have
$\textit{dcl}(\mathbb{L}^I)={}^\downarrow\mathbb{L}^I$
for any labelling-set
$\mathbb{L}$
. Furthermore, due to Definition 1 we have
$\textit{dcl}(\mathbb{L}^{I})=\mathbb{M}^{I}$
which guarentees
$\mathbb{M}^{I}={}^\downarrow\mathbb{L}^I$
as required.
In order to show
$\mathbb{M} \subseteq {}^\downarrow\mathbb{L}$
it suffices to prove that for each single
$E\in \mathbb{M}^{I}$
,
$\mathbb{M}_{I=E}^{O}\subseteq \left({}^\downarrow\mathbb{L}\right)_{I=E}^{O}$
as
$\mathbb{M}^{I}={}^\downarrow\mathbb{L}^I$
is already known. Let us fix a certain
$E\in \mathbb{M}^{I}$
. According to Proposition 8, Items 1 and 2 we have downward-closedness of
$\left({}^\downarrow\mathbb{L}\right)^{O}_{I=E}$
and the existence of a
$\subseteq$
-greatest element, namely
$\overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=E} = O_E$
. Furthermore, due to Definition 3 we have downward-closedness of
$\mathbb{M}_{I=E}^{O}$
and via L-tightness of
$\mathbb{M}$
(Theorem 2) we derive the existence of a
$\subseteq$
-greatest element
$\overline{\mathbb{M}}_{I=E}^{O}$
. Consequently, instead of showing
$\mathbb{M}_{I=E}^{O}\subseteq \left({}^\downarrow\mathbb{L}\right)_{I=E}^{O}$
it suffices to prove
$\overline{\mathbb{M}}_{I=E}^{O}\subseteq O_E$
, which was already shown in Proposition 12.
Proposition 14 Given a labelling-set
$\mathbb{L}$
. If
$\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{na}}}}$
, then
${}^\downarrow\mathbb{L}$
is L-tight.
Proof. First, the existence of a
$\subseteq$
-greatest element in
$\left({}^\downarrow\mathbb{L}\right)^{O}_{I=E}$
for a fixed
$E\in \left({}^\downarrow\mathbb{L}\right)^I$
was already shown (Item 2, Proposition 8). In particular,
$\overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=E} = O_E$
.
For the second property let
$E_1, E_2\in ({}^\downarrow\mathbb{L})^I$
. We will show the following equivalence:
$E_1\cup E_2\in({}^\downarrow\mathbb{L})^I \Leftrightarrow (\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_1} \cap E_2) \cup (\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_2} \cap E_1) = \emptyset$
.
-
(⇒) Given
$E_1\cup E_2\in({}^\downarrow\mathbb{L})^I$
. According to Definition 15 we deduce the existence of an
$E\in \mathbb{L}^{I}$
with
$E_{1}\cup E_{2}\subseteq E$
. Note that
$E\in({}^\downarrow\mathbb{L})^I$
(Item 4, Proposition 8). Due to L-tightness of
$\mathbb{L}$
(Proposition 10) the existence of
$\overline{\mathbb{L}}^{O}_{I = E}$
is guaranteed. Please note that
$E \cap \overline{\mathbb{L}}^{O}_{I = E} = \emptyset$
as
$\mathbb{L}$
is a labelling-set.Thus, showing
$\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_i}\subseteq \overline{\mathbb{L}}^{O}_{I = E}$
for
$i\in\{1,2\}$
would yield
$(\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_1} \cap E_2) \cup (\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_2} \cap E_1) = \emptyset$
as required. This can be seen as follows:The last equality is due to Proposition 11.
\begin{equation*} \overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_i} = O_{E_i} = \bigcup_{a\in E_i} O_{\{a\}} \subseteq \bigcup_{a\in E} O_{\{a\}}= O_{E} =\overline{\mathbb{L}}^{O}_{I = E} \end{equation*}
-
(⇐) Given
$(\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_1} \cap E_2) \cup (\overline{({}^\downarrow\mathbb{L})}^{O}_{I=E_2} \cap E_1) = \emptyset$
. Hence,
$(O_{E_{1}} \cap E_{2}) \cup (O_{E_{2}} \cap E_{1}) = \emptyset.$
Since
$\mathbb{L}$
is
${na}$
-realizable there is an AF
$F=(A,R)$
with
$\mathcal L_{{na}}(F)=\mathbb{L}$
. We set
$\mathcal L_{cf}(F) = \mathbb{M}$
. As
$E_1, E_2 \in {}^\downarrow\mathbb{L}^I$
we derive the existence of
$I_1, I_2\in \mathbb{L}^{I}$
with
$E_1 \subseteq I_1$
and
$E_2 \subseteq I_2$
. Moreover,
$E_1, E_2\in \mathbb{M}^{I}$
since
$\mathbb{M}^{I} = {}^\downarrow\mathbb{L}^I$
by Proposition 13. Applying Proposition 12 we obtain
$\overline{\mathbb{M}}^{O}_{I = E_{1}} \subseteq O_{E_{1}}$
as well as
$\overline{\mathbb{M}}^{O}_{I = E_{2}}\subseteq O_{E_{2}}$
. Consequently,
$(E_{1}\cap \overline{\mathbb{M}}^{O}_{I = E_{2}})\cup (E_{2}\cap \overline{\mathbb{M}}^{O}_{I = E_{1}}) = \emptyset$
. Since
$\mathbb{M}$
is itself L-tight (Theorem 2) we deduce
$E_1\cup E_2 \in \mathbb{M}^{I}$
and finally, applying Proposition 13
$E_1\cup E_2\in({}^\downarrow\mathbb{L})^I$
concluding the proof.
4.3. Characterization theorem
Now, the central realizability result for naive labellings Theorem 6. Beside properties induced by extension-based realizability (1) and further technical properties (2–4), the decisive point is the conflict-free realizability of the associated downward-closure (5). To mention a subtle difference: in contrast to naive extensions and conflict-free sets, where each precisely determines the other, naive labellings may be induced by different conflict-free labelling sets (cf. Example 13). This means, the introduced downward-closure of labelling-sets is only one possibility. However, the characterization theorem shows that it can be used to decide naive realizability. Please note that each property can be verified by examining the given labelling-set only.
Theorem 6 Given a labelling-set
$\mathbb{L}$
, we have
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}}\mbox{ }\Leftrightarrow\mbox{ }$
-
1.
$\mathbb{L}^I$
is incomparable and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for each
$E\in \mathbb{L}^I$
, -
3.
$\overline{\mathbb{L}}_{I=E}^{O}$
exists for each
$E\in \mathbb{L}^I$
, -
4.
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} \subseteq \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
for each
$E\in \mathbb{L}^I$
, -
5.
${}^\downarrow\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
.
Proof. We will split the prove in if- and only-if-direction as usual.
-
(⇒) Let
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}}$
be given. Hence, there is an AF
${F} = (A,R)$
with
${{\mathcal{L}}}_{{na}}({F}) = \mathbb{L}$
. Applying Items 3 and 4 of Proposition 1 we deduce
$\mathbb{L}^{I} = {{\mathcal{E}}}_{{na}}({F})$
. Moreover, Theorem 1 yields the incomparability and non-emptiness of
$\mathbb{L}^{I}$
.Let
$\mathbb{M} = {{\mathcal{L}}}_{{cf}}({F})$
. We have
$\mathbb{M}^{O}_{I=E}$
is downward-closed for all
$E\in \mathbb{M}^I$
(Item 2, Theorem 2). In light of Definition 3 we obtain:
$\mathbb{L} = {{\mathcal{L}}}_{{na}}({F}) = \left\{ {L}\in\mathbb{M}\mid {L}^{\text{I}} \text{ is }\subseteq-\text{maximal in } \{{M}^{\text{I}}\mid M\in\mathbb{M}\}\right\}$
. Thus,
$\mathbb{L}^{O}_{I=E}$
is downward-closed for each
$E\in \mathbb{L}^I$
.The existence of a
$\subseteq$
-greatest element
$\overline{\mathbb{L}}^{O}_{I=E}$
for each single
$E\in \mathbb{L}^I$
follows by the L-tightness (Item 1, Definition 11) of any naive realizable labelling-set (Proposition 10).By Proposition 11 we have
$\overline{\mathbb{L}}^{O}_{I=E} = O_E$
. Moreover,
$O_E = \displaystyle{\bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
(Definition 15). Consequently,
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} \subseteq \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
for each
$E\in \mathbb{L}^I$
as required.Finally, in order to show the fifth item, that is
${}^\downarrow\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
it suffices to prove the following four properties (Theorem 2).-
(i)
$\left({}^\downarrow\mathbb{L}\right)^I$
is downward-closed and non-empty.Downward-closedness is due to Item 5 of Proposition 8. Since naive semantics is universally defined we have
${{\mathcal{L}}}_{{na}}({F}) = \mathbb{L} \neq \emptyset$
. Thus,
${}^\downarrow\mathbb{L} \neq \emptyset$
and therefore
$\left({}^\downarrow\mathbb{L}\right)^I\neq\emptyset$
(Item 3, Proposition 8). -
(ii)
$\left({}^\downarrow\mathbb{L}\right)^{O}_{I=E}$
is downward-closed for all
$E\in \left({}^\downarrow\mathbb{L}\right)^I$
(Item 1, Proposition 8). -
(iii)
${}^\downarrow\mathbb{L}$
is L-tight (Proposition 14). -
(iv)
${}^\downarrow\mathbb{L}$
is reject-compositional.Since L-tightness of
${}^\downarrow\mathbb{L}$
is already shown we have to prove: for any
$E\in \left({}^\downarrow \mathbb{L}\right)^{I}$
we have,
$\displaystyle{\overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=E} = \bigcup_{a\in E} \overline{\left({}^\downarrow\mathbb{L}\right)}^{O}_{I=\{a\}}}$
. As
$\left({}^\downarrow\mathbb{L}\right)^I$
is shown to be downward-closed we infer that
$E\in \left({}^\downarrow \mathbb{L}\right)^{I}$
implies
$\{a\}\in \left({}^\downarrow \mathbb{L}\right)^{I}$
for each
$a\in E$
. Consequently, the equality transforms to
$\displaystyle{O_E = \bigcup_{a\in E} O_{\{a\}}}$
(Item 2, Proposition 8). There is nothing further to show as this equality holds by construction (Definition 15).
-
-
(⇐) By assumption
${}^\downarrow\mathbb{L}$
is
${cf}$
-realizable (Item 5). Hence, by applying Theorem 3 we immediately obtain
${}^\downarrow\mathbb{L} = {{\mathcal{L}}}_{{cf}}\left(F_{{}^\downarrow\mathbb{L}}^{{cf}}\right)$
. Given incomparability and non-emptiness of
$\mathbb{L}^{I}$
(Item 1) as well as the way of constructing
${}^\downarrow\mathbb{L}$
(Definition 15) we may conclude that
$\mathbb{L}^{I}$
represents the
$\subseteq$
-maximal sets of
$({}^\downarrow\mathbb{L} )^{I}$
being the naive sets of
$F_{{}^\downarrow\mathbb{L}}^{{cf}}$
. Now consider a certain set
$E\in\mathbb{L}^{I}$
and an argument
$b\in O_E$
. By Definition 15 we may replace
$O_E$
with
$\displaystyle{b\in \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
. Note that the existence of
$\overline{\mathbb{L}}_{I=E}^{O}$
is assured by assumption (Item 3). By
$\displaystyle{b\in \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
we derive the existence of an
$a\in E$
s.t.
$b\in \overline{\mathbb{L}}^{O}_{I = I'}$
for all
$I'\in\mathbb{L}^{I}$
where
$a\in I'$
. In particular,
$b\in \overline{\mathbb{L}}^{O}_{I = E}$
. Consequently,
$O_E\subseteq \overline{\mathbb{L}}^{O}_{I = E}$
. Combining this subset relation with the assumed superset relation (Item 4) yields
$\overline{\mathbb{L}}^{O}_{I = E}=O_E$
for each
$E\in \mathbb{L}^{I}$
. Finally, since
$\mathbb{L}^{O}_{I=E}$
is downward-closed for each
$E\in \mathbb{L}^I$
(Item 2) we deduce that
$\mathbb{L}$
represents the in-maximal labellings of
${}^\downarrow\mathbb{L}$
. Thus,
$\mathbb{L} = {{\mathcal{L}}}_{{na}}\left(F_{{}^\downarrow\mathbb{L}}^{{cf}}\right)$
concluding the proof.
The proof of Theorem 6 additionally provides us with a construction of a witnessing AF in case of naive realizability. We simply apply the conflict-free construction (Theorem 3) to the downward-closure of the labelling-set in question.
Theorem 7 For any labelling-set
$\mathbb{L}$
, we have:
\begin{align*}\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}} \Leftrightarrow \mathbb{L} = {{\mathcal{L}}}_{na}\left({F}_{{}^\downarrow\mathbb{L}}^{{cf}}\right).\end{align*}
Proof. Given a labelling-set
$\mathbb{L}$
.
-
(⇐) Since
${{\mathcal{L}}}_{na}\left({F}_{{}^\downarrow\mathbb{L}}^{{cf}}\right)$
is given, we immediately have found a
${na}$
-realizing AF, namely
${F}_{^\downarrow\mathbb{L}}^{{cf}}$
. Consequently,
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}}$
. -
(⇒) Given
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}}$
. Consider Theorem 6. Via the if-direction we obtain
${}^\downarrow\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
. Now, we can apply Theorem 3 and obtain
${}^\downarrow\mathbb{L} = {{\mathcal{L}}}_{cf}\left({F}_{{}^\downarrow\mathbb{L}}^{{cf}}\right)$
. Through only-if direction of the proof of Theorem 6 we arrive at
$\mathbb{L} = {{\mathcal{L}}}_{na}\left({F}_{{}^\downarrow\mathbb{L}}^{{cf}}\right)$
concluding the proof.
The properties 1–3 of the characterization Theorem 6 ensure the basic properties necessary for naive realizability. Property
$5.$
connects the conflict-free with the naive labelling-realizability via the newly introduced labelling-downward-closure as planned. Intuitively, it is clear why these properties are necessary. However, this is less straightforward for property 4. To make the necessity more apparent the following example shows a case where the
$4.$
property is not satisfied.
Example 12 Consider labelling-set
$\mathbb{L}$
given by the following table:
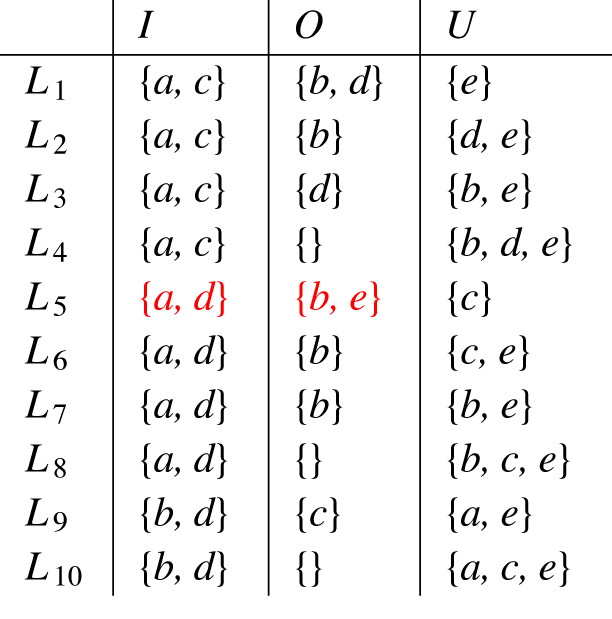
It is easily verified that
$\mathbb{L}$
satisfies all properties given in Theorem 6 except the fourth since
\begin{equation*}\overline{\mathbb{L}}^{O}_{I=\{a,d\}}=\{b,e\} \nsubseteq \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\{b\}\end{equation*}
(colored red in the table above). We encourage the reader to verify this for themselves. Believing Theorem 6 the set
$\mathbb{L}$
should not be naive realizable. To identify the reason we have a look at
${}^\downarrow\mathbb{L}$
and compare it with
$\mathbb{L}$
(for the sake of clarity we will only list the labellings
$\overline{{}^\downarrow\mathbb{L}}_{I=E}$
for each
$E\in {}^\downarrow\mathbb{L}^{I}$
and
$E\in \mathbb{L}^{I}$
respectively)
In
$L_5$
in
$\mathbb{L}$
, we get the information that a or d has to attack e and at the same time from
$L_1, L_9$
that neither a nor d attack e. So
$\mathbb{L}$
contains a contradiction. Please keep in mind all these statements are made in terms of naive realizability of
$\mathbb{L}$
. This contradiction is easily seen in
${}^\downarrow\mathbb{L}$
. The attack to e is ‘lost’ here meaning neither
$\overline{({}^\downarrow\mathbb{L})}^{O}_{I=\{a\}}$
not
$\overline{({}^\downarrow\mathbb{L})}^{O}_{I=\{d\}}$
contains e and so
\begin{equation*}\overline{\mathbb{L}}^{O}_{I=\{a,d\}}=\{b,e\} \nsubseteq L'^{O}_{5}=\overline{({}^\downarrow\mathbb{L})}^{O}_{I=\{a,d\}}= \bigcup_{a\in {\{a,d\}}} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}=\{b\}\end{equation*}
does not either. This is exacly what we already checked with Theorem 6 item 4 in the beginning of the example.
As in the previous chapter the characterization Theorem 6 can be presented in a more compact way since the presented set of properties is not independent. In place of demanding the cf-realizability of the downward-closure (Theorem 6 property 5.), demanding only L-tightness and reject-compositionality of
${}^\downarrow\mathbb{L}$
suffices. The remaining properties of cf-realizability (compare Theorem 2) are implied, as shown in the subsequent proposition. Hence, we can state a version of the characterization with a weaker version of the
$5.$
property of Theorem 6:
Proposition 15 Given a labelling-set
$\mathbb{L}$
we have
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{na}}}\mbox{ }\Leftrightarrow\mbox{ }$
-
1.
$\mathbb{L}^I$
is incomparable and non-empty, -
2.
$\mathbb{L}^{O}_{I=E}$
is downward-closed for each
$E\in \mathbb{L}^I$
, -
3.
$\overline{\mathbb{L}}_{I=E}^{O}$
exists for each
$E\in \mathbb{L}^I$
, -
4.
$\displaystyle{\overline{\mathbb{L}}^{O}_{I=E} \subseteq \bigcup_{a\in E} \bigcap_{I'\in\mathbb{L}^I,\{a\}\subseteq I'} \overline{\mathbb{L}}^{O}_{I = I'}}$
for each
$E\in \mathbb{L}^I$
, -
5.
${}^\downarrow\mathbb{L}$
is L-tight und reject-compositional.
Proof. It suffices to show, that
${}^\downarrow\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
can be deduced from 1–4 and 5′. To that end, we show that
${}^\downarrow\mathbb{L}$
satisfies all remaining properties given in Theorem 2. Then, the realizability of
$\mathbb{L}$
follows from Theorem 6.
-
(i)
$\left({}^\downarrow\mathbb{L}\right)^I$
is downward-closed and non-empty.Proposition 8 item 4 shows
$\mathbb{L}^{I}\subseteq ({}^\downarrow\mathbb{L})^{I}$
.
$\mathbb{L}^I$
is non-empty, thus
$({}^\downarrow\mathbb{L})^{I}$
. Furthermore,
$dcl(\mathbb{L}^{I})= ({}^\downarrow\mathbb{L})^{I}$
according to Proposition 8 item 5. Hence
$({}^\downarrow\mathbb{L})^{I}$
is downward-closed. -
(ii)
$\left({}^\downarrow\mathbb{L}\right)^{O}_{I=E}$
is downward-closed for all
$E\in \left({}^\downarrow\mathbb{L}\right)^I$
.Follows immediately from the construction of the labelling-downward-closure Definition 15.
-
(iii)
${}^\downarrow\mathbb{L}$
is reject-witnessing.The redundancy was already shown in the previous chapter in Proposition 15.
Finally, we compare the achieved characterization theorem with the already existing one regarding naive extensions (Theorem 1). Due to Proposition 1 we know that labelling-based
${na}$
-realizability of
$\mathbb{L}$
requires extension-based
${na}$
-realizability of
$\mathbb{L}^I$
. This means,
$\mathbb{L}^I$
has to be non-empty and incomparable, and
$\textit{dcl}(\mathbb{L}^{I})$
has to be tight. The first two properties are explicitly given in Theorem 6. The tightness of the downward-closure of
$\mathbb{L}^I$
is implicit as shown next.
Proposition 16 Given a labelling-set
$\mathbb{L}$
. If
${}^\downarrow\mathbb{L}\in\Sigma_{{{{\mathcal{L}}}_{{cf}}}}$
, then
$\textit{dcl}(\mathbb{L}^{I})$
is tight.
Proof. It suffices to show that
$({}^\downarrow\mathbb{L})^{I}$
is tight as
$\textit{dcl}(\mathbb{L}^{I}) = ({}^\downarrow\mathbb{L})^{I}$
(Proposition 8, Item 5). Moreover, the equality implies that
$({}^\downarrow\mathbb{L})^{I}$
is downward-closed. The assumption
${}^\downarrow\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{cf}}}$
gives us L-tightness and reject-compositionality of
${}^\downarrow\mathbb{L}$
(Theorem 2). Thus, applying Proposition 5 yields tightness of
$({}^\downarrow\mathbb{L})^{I}$
concluding the proof.
Figure 1. Tables Example 13.
4.4. Representational freedom and patterns of redundancy
4.4.1. Standard construction and maximality
In case of conflict-free labellings it has been discovered that surprisingly the standard construction (cf. Definition 14) represents the uniquely determined witnessing AF in case of selfloop-free AFs (Proposition 6). This means, for selfloop-free AFs, we do not have any representational freedom. The following example shows that this property does not carry over to naive labellings.
Example 13 Consider the following two selfloop-free AFs
${F}$
and
${G}$
.
The tables in Figure 1 show conflict-free labellings of the selfloop-free AFs
${F}$
and
${G}$
. Although
${F}$
and
${G}$
are syntactically different, they possess matching naive labellings which can be found above the separating line (
${L}_1,\ldots,{L}_{10}$
). According to Proposition 6 they have to disagree on their conflict-free labellings illustrated, for example, by
${L}_{13}\in\mathcal L_{{cf}}({F})\setminus\mathcal L_{{cf}}({G})$
.
However, instead of a uniqueness result as in case of conflict-free labellings, we may show a maximality result. More precisely, in the realm of selfloop-free AFs, the standard construction (applied to the downward closure) contains any possible attack, that is it represents the greatest witness w.r.t. subgraph relation.
Proposition 17 Given a labelling-set
$\mathbb{L}$
and the AF
${F}_{{}^\downarrow\mathbb{L}}^{{cf}}=(A_{{}^\downarrow\mathbb{L}}, R_{{}^\downarrow\mathbb{L}})$
. For any selfloop-free AF
${F} = (A,R)$
with
$\mathcal L_{{na}}(F) = \mathbb{L}$
we have:
\begin{equation*} A = A_{{}^\downarrow\mathbb{L}}\quad \text{and}\quad R\subseteq R_{{}^\downarrow\mathbb{L}}. \end{equation*}
Proof. Given a selfloop-free
$F=(A,R)$
with
$\mathcal L_{na}(F)=\mathbb{L}$
and let
$\mathcal L_{cf}(F) = \mathbb{M}$
.
-
1. Arguments: Since
$\mathcal L_{na}(F)=\mathbb{L}$
we have
$A = {Args}_\mathbb{L}$
. Moreover, by Definition 15, we deduce
${Args}_\mathbb{L} = {Args}_{{}^\downarrow \mathbb{L}}$
. Finally, in light of the standard construction (Definition 14) we get
${Args}_{{}^\downarrow \mathbb{L}} = A_{{}^\downarrow\mathbb{L}}$
proving
$A = A_{{}^\downarrow\mathbb{L}}$
. -
2. Attacks: Let
$(a,b)\in R$
. As
${F}$
is assumed to be selfloop-free we deduce
$a\neq b$
. In order to prove
$(a,b)\in R_{{}^\downarrow\mathbb{L}}$
we have to show (1)
$\{a\}\in\left({}^\downarrow\mathbb{L}\right)^I$
and (2)
$b\in \bigcup\left({}^\downarrow\mathbb{L}\right)^{O}_{I = \{a\}}$
(Item 2, Definition 14). The latter can be replaced by
$b\in\overline{{}^\downarrow\mathbb{L}}^{O}_{I = \{a\}}$
as L-tightness of
${}^\downarrow\mathbb{L}$
(and thus, the existence of a
$\subseteq$
-greatest element) is given via
${na}$
-realizability of
$\mathbb{L}$
(Proposition 14). Regarding the first requirement. Since
${F}$
is selfloop-free we obtain
$\{a\}\in\mathbb{M}^I$
. Consequently,
$\{a\}\in\left({}^\downarrow\mathbb{L}\right)^I$
as
$\mathbb{M}^I = \left({}^\downarrow\mathbb{L}\right)^I$
(Proposition 13). Regarding the second condition. Since
$\{a\}\in\mathbb{M}^I$
and
$(a,b)\in R$
we deduce
$b\in \overline{\mathbb{M}}_{I=\{a\}}^{O}$
. By Proposition 12, we know
$\overline{\mathbb{M}}_{I=\{a\}}^{O}\subseteq \overline{{}^\downarrow\mathbb{L}}_{I=\{a\}}^{O}$
for any
$\{a\}\in \mathbb{M}^{I}$
. Thus,
$b\in\overline{{}^\downarrow\mathbb{L}}_{I=\{a\}}^{O}$
concluding the proof.
Example 14 Consider the labelling set
$\mathbb{L}=\{(\{a,d\}, \{b,c\}, \{\})\}$
. Using Theorem 6 we can verify that this set is naive realizable. We leave it to the reader to check this.
We obtain the following downward-closure
${}^\downarrow\mathbb{L}$
(to keep it concise we only give the maximal labellings) and corresponding witnessing AF
${F}_{{}^\downarrow\mathbb{L}}^{{cf}}$
:
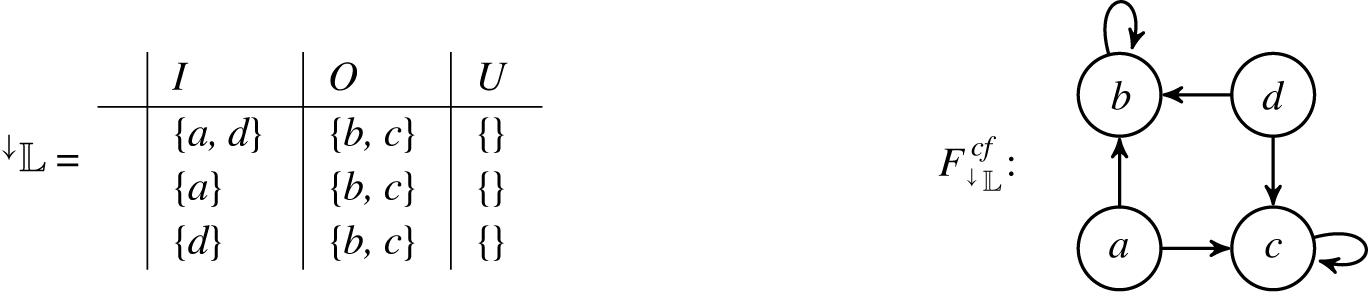
As expected
$\mathcal L_{na}({F}_{{}^\downarrow\mathbb{L}}^{{cf}})= \mathbb{L}$
. Consider now the following AF G:
$\mathcal L_{na}(G)= \mathbb{L}$
also holds true. However, evidently G is not a subgraph of
${F}_{{}^\downarrow\mathbb{L}}^{{cf}}$
. Hence Proposition 17 is not valid in the presence of self-loops.
4.5. Strong equivalence
Now let us turn to strong equivalence. In case of naive extensions, the so-called naive kernel characterizes strong equivalence (Baumann et al. Reference Baumann, Linsbichler, Woltran, Baroni, Gordon, Scheffler and Stede2016). The following example shows that this property does not carry over to naive labelling.
Example 15 Consider the two AFs F and G
and their associated naive kernels:
Obviously
$F^{nk}=G^{nk}$
. However, F and G are not strongly equivalent w.r.t their naive labellings, since they are not even ordinary equivalent:
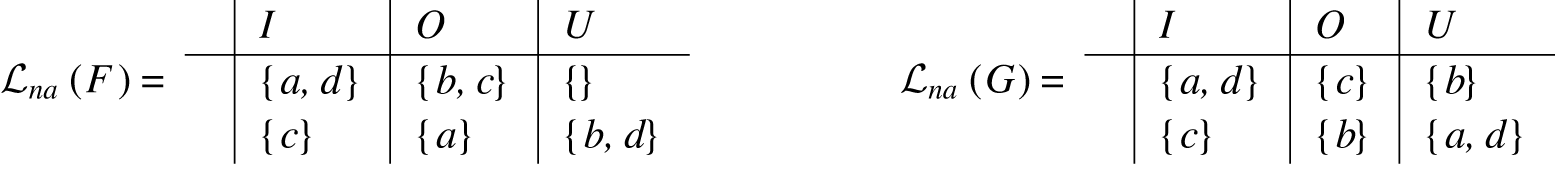
The following result shows that for naive labellings the classical stable kernel has to be used.
Theorem 8 Given two AFs
${F}$
and
${G}$
. We have:
\begin{align*}{F}\equiv^{{{\mathcal{L}}}_{{na}}}_s\! {G} \Leftrightarrow {F}^{sk} = {G}^{sk}.\end{align*}
Proof. Given AFs
${F}$
and
${G}$
. The associated stable kernels are
${F}^{sk} = (A,R^{sk})$
and
${G}^{sk} = (B,S^{sk})$
. We split the proof into two directions.
-
(⇒) We show the contrapositive. Let
${F}^{sk} \neq {G}^{sk}$
. We first show that
$A({F})\neq A({G})$
immediately yields
${F}\not\equiv^{{{\mathcal{L}}}_{{na}}}_s\! {G}$
. W.l.o.g. let
$a\in A({F})\setminus A({G})$
. Case distinction. If
$(a,a)\notin R({F})$
, we have nothing to show as there has to be a naive extension
$E\in{{\mathcal{E}}}_{{na}}({F})$
with
$a\in E$
. Consequently,
${E}^{{{\mathcal{L}}}}\in{{\mathcal{L}}}_{{na}}({F})$
(Proposition 1) and obviously,
${E}^{{{\mathcal{L}}}}\notin{{\mathcal{L}}}_{{na}}({G})$
as
$a\notin A({G})$
. In case of
$(a,a)\in R({F})$
, we consider
${H} = (\{a\},\emptyset)$
. In the same fashion as above we conclude there has to be an E with
$a\in E$
and
${E}^{{{\mathcal{L}}}}\in{{\mathcal{L}}}_{{na}}({G}\sqcup{H})$
. Moreover,
${E}^{{{\mathcal{L}}}}\notin{{\mathcal{L}}}_{{na}}({F}\sqcup{H})$
as
$(a,a)\in R({F}\sqcup{H})$
. Let us now assume that
$A({F}) = A({G})$
. As
${F}^{sk} \neq {G}^{sk}$
is given, we deduce
${F}\not\equiv^{{{\mathcal{L}}}_{{cf}}}\! {G}$
(Theorem 4). Consequently, w.l.o.g. there is a labelling
$L\in {{\mathcal{L}}}_{{cf}}({F})\setminus {{\mathcal{L}}}_{{cf}}({G})$
. Consider the AF
${H} = (A({F}),\{(a,a)\mid a\in A({F})\setminus {L}^I\})$
. Obviously,
${L}\in{{\mathcal{L}}}_{{cf}}({F}\sqcup {H})$
as regarding
${L}^I$
, no internal conflicts are added and secondly, regarding
${L}^O$
, the reason for rejection still holds in
${F}\sqcup {H}$
(cf. Definition 3). Moreover, by construction,
${L}\in{{\mathcal{L}}}_{{na}}({F}\sqcup {H})$
as
${L}^I$
is even the
$\subseteq$
-greatest conflict-free in-label. On the other hand, the assumption
$L\notin {{\mathcal{L}}}_{{cf}}({G})$
implies two possible reasons: (1)
$L^I$
is conflicting in
${G}$
or (2) there is an element in
${L}^O$
not attacked by an element in
${L}^I$
. Please observe that both reasons still hold in
${G}\sqcup{H}$
. Consequently,
${L}\notin{{\mathcal{L}}}_{{cf}}({G}\sqcup {H})$
and thus,
${L}\notin{{\mathcal{L}}}_{{na}}({G}\sqcup {H})$
. -
(⇐) Given
${F}^{sk} = {G}^{sk}$
. Consequently, for any AF
${H}$
,
$\left({F} \sqcup H\right)^{sk} = \left({G} \sqcup H\right)^{sk}$
Oikarinen & Woltran (Reference Oikarinen and Woltran2011), Lemma 2 and thus,
${{\mathcal{L}}}_{cf}\left({F}\sqcup H\right) = {{\mathcal{L}}}_{cf}\left({G}\sqcup H\right)$
(Theorem 4). Hence,
${{\mathcal{L}}}_{cf}\left({F}\sqcup H\right) = {{\mathcal{L}}}_{cf}\left({G}\sqcup H\right)$
implying
${F}\equiv^{{{\mathcal{L}}}_{{na}}}_s\! {G}$
concluding the proof.
5. First reflections on stable labellings and compact realizability
Finally, let us consider stable labellings. The following proposition strengthens a former result regarding realizability Baumann (Reference Baumann2018), Theorem 3.70. If a set of labellings is stable realizable, then the set of in-labels is incomparable and tight. Moreover, no argument is labelled undecided.
Proposition 18 Given a labelling-set
$\mathbb{L} \subseteq \left(2^{{\mathcal{U}}}\right)^3$
. We have,
\begin{align*}\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{{stb}}}}\mbox{ }\Rightarrow\mbox{ } \bigcup\mathbb{L}^U = \emptyset \text{ and, } \mathbb{L}^{I} \text{ is incomparable and tight.}\end{align*}
Proof. (
$\Rightarrow$
) Given
$\mathbb{L}\in \Sigma_{{{\mathcal{L}}}_{{{stb}}}}$
. Hence, there is an AF
${F}$
with
${{\mathcal{L}}}_{{{stb}}}({F}) = \mathbb{L}$
. We further deduce
$\mathbb{L}^{I} = {{\mathcal{E}}}_{{{stb}}}({F})$
(Items 3,4 of Proposition 1). According to Theorem 1 we obtain
$\mathbb{L}^{I}$
is incomparable and tight. Moreover,
$\bigcup\mathbb{L}^U = \emptyset$
is fulfilled since Definition 3 requires
${L}^U = \emptyset$
for each
$L\in{{\mathcal{L}}}_{{{stb}}}({F})$
.
We would like to mention that we initially thought that the given necessary condition is even sufficient for realizing stable labellings. The following example shows that this was a misconception. We will see that the notion of compactness plays a central role (Baumann et al. Reference Baumann, Dvorák, Linsbichler, Strass and Woltran2014; Dunne et al. Reference Dunne, Dvorák, Linsbichler and Woltran2015). In the extension-based case we say that an AF
$F = (A,R)$
is compact w.r.t. a certain semantics
$\sigma$
if
$\bigcup {{\mathcal{E}}}_{\sigma}({F}) = A$
. This means, each argument occurs at least once in a
$\sigma$
-extension of
${F}$
.
Example 16 Consider the following AF
${F} = (A,R)$
.
We have
${{\mathcal{E}}}_{{{stb}}} = \left\{\{a,b,c\}, \{a,b',c'\}, \{a',b,c'\}, \{a',b',c\}, \{a,b,c'\}, \{a',b,c\}, \{a,b',c\}\right\}$
. It was shown that there is no compact AF
${F}'$
realizing this extension-set (Baumann et al. Reference Baumann, Dvorák, Linsbichler, Strass and Woltran2014; Dunne et al. Reference Dunne, Dvorák, Linsbichler and Woltran2015). This means, the additional argument x is essential for realizing under stable semantics.
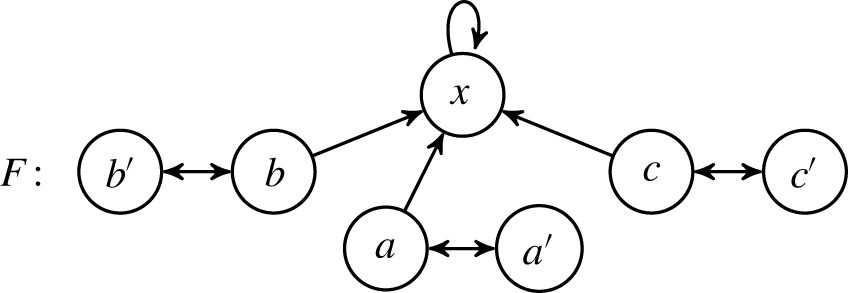
Consider now the corresponding labelling-set (see the table below)
$\mathbb{L} = \left({{\mathcal{E}}}_{{{stb}}}\right)^{{{\mathcal{L}}}} = \left\{(E,A\setminus E,\emptyset)\mid E\in {{\mathcal{E}}}_{{{stb}}}({F}) \right\}$
. We obviously have
$\bigcup\mathbb{L}^U = \emptyset$
and moreover, due to Theorem 1, we deduce
$\mathbb{L}^{I} = {{\mathcal{E}}}_{{{stb}}}({F})$
is incomparable and tight. We now modify
$\mathbb{L}$
, s.t. the argument x is deleted from any out-label. More precisely, we define
$\mathbb{M} = \left\{(E,A\setminus (E\cup \{x\}),\emptyset)\mid E\in {{\mathcal{E}}}_{{{stb}}}({F}) \right\}$
. Please note that
$\mathbb{L}^U = \mathbb{M}^U$
and
$\mathbb{L}^{I} = \mathbb{M}^{I}$
. However,
$\mathbb{M}\notin\Sigma_{{{\mathcal{L}}}_{{{stb}}}}$
whereas an affirmative answer would imply the compact realizability of
${{\mathcal{E}}}_{{{stb}}}({F})$
.
To clarify we give a more intuitive explanation. Let us have a closer look at the set
$X:=\{a', b', c'\}$
. While the set is conflict-free in F, it does not attack x and thus
$X\notin \mathbb{L}^{I}$
. Now we modify
$\mathbb{L}$
, by ‘deleting’ the argument x (as described above). Looking only at the extension, nothing changed:
$\mathbb{M}^{I}=\mathbb{L}^{I}$
is still incomparable and tight, since x only appears in the out-sets. However, to stable realize the labelling-set
$\mathbb{L}$
, the argument x is essential. By ‘deleting’ x, we lose the reason, why the set X is not stable.
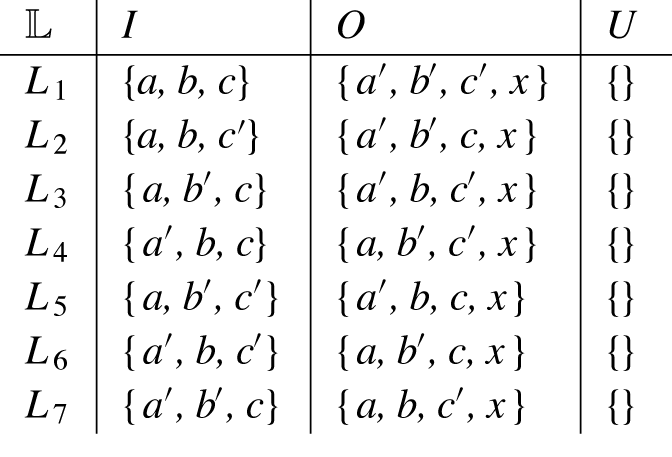
The stable labelling semantics indeed reduces the situation again to a case of only acceptance and rejection, like in the extension-based case. However, as the example above shows, the explicit knowledge of the rejected arguments adds an underlying layer of structure, that cannot be captured by the extension-based characterization.
6. Conclusion and related work
Expressibility is one central issue for knowledge representation formalisms (Linsbichler et al. Reference Linsbichler, Pührer, Strass, Kaminka, Fox, Bouquet, Hüllermeier, Dignum, Dignum and van Harmelen2016). Dung AFs are well-studied if considered under extension-based semantics (Dunne et al. Reference Dunne, Dvorák, Linsbichler and Woltran2015; Baumann Reference Baumann2018). In this paper, we summarized the first results of our investigation into labelling-based semantics. More precisely, we considered the most basic criteria underlying each mature semantics, namely conflict-freeness and the semantics acting as a gateway to the characterization of more mature semantics, the naive semantics. We provided simple criteria for deciding whether a certain set of labels can be the conflict-free or naive outcome of a framework. Among the conditions are the newly introduced notions of L-tightness, reject-witnessing and reject-compositional. For the characterization of the naive semantics we introduced the construction of a downward-closure for labellings. This enables us to connect the naive and conflict-free semantics much in the same way as in the expansion based-case and connect the naive to the conflict-free realizability characterization. Moreover, we clarified the question of representational freedom and patterns of redundancy.
Finally, we shared the first findings about the stable realizability of labellings, which revealed the semantic to be surprisingly rich in underlying structure. In our future work, we plan to analyse the stable semantics extensively and establish characterization theorems for stable and stage semantics (Dung Reference Dung1995; Baroni et al. Reference Baroni, Caminada, Giacomin, Baroni, Gabbay, Giacomin and van der Torre2018a). It will be interesting to see to which extent, if any at all, characterizing properties for extension-based semantics carry over to their labelling-based version.
There is only few related work. One important one is realizibility under projection (Dyrkolbotn Reference Dyrkolbotn, Baral, Giacomo and Eiter2014). In this setup, it suffices to come up with an AF
${F}$
, s.t. its set of labellings restricted to the desired arguments coincide with
$\mathbb{L}$
. A second related work deals with the standard notion of realizability and presents a propagate-and-guess algorithm which returns either ‘No’ in case of non-realizability or a witnessing AF (Linsbichler et al. Reference Linsbichler, Pührer, Strass, Kaminka, Fox, Bouquet, Hüllermeier, Dignum, Dignum and van Harmelen2016). The mentioned papers do not consider naive or conflict-free labellings, nor do they provide simple criteria for realizability.
Moreover, regarding dynamic scenarios the so-called synthesis problem seems to be highly significant (Niskanen et al. Reference Niskanen, Wallner and Järvisalo2019). Rather than demanding precise realizability, we are faced with a set of positive labels that need to be realized, and simultaneously, a set of negative labels that must be avoided.
Acknowledgements
This work was supported by the German Research Foundation (DFG, BA 6170/3-1) and by the German Federal Ministry of Education and Research (BMBF, 01/S18026A-F) by funding the competence center for Big Data and AI ‘ScaDS.AI’ Dresden/Leipzig.
Competing interests
The author(s) declare none.
Open access
