Introduction
Biological surfaces are rarely flat. Surface patterning has long been found to occur concurrently with growth, development, and aging of biological systems. These surface patterns not only manifest the beauty of nature,Reference Thompson1,Reference Stevens2 they can also be critical to the survival and well-being of living organisms (Figure 1a). For example, surface patterns help organs grow extended surface areas to facilitate mass exchange in blood cellsReference Wang, Castro and Boyce3 and intestinal villi,Reference Shyer, Tallinen, Nerurkar, Wei, Gil, Kaplan, Tabin and Mahadevan4–Reference Hannezo, Prost and Joanny7 and to enhance intellectual capacity of the brain.Reference Hohlfeld and Mahadevan8,Reference Tallinen, Biggins and Mahadevan9 Furrows form on animal skinsReference Cerda and Mahadevan10–Reference Kücken and Newell12 or plant surfacesReference Yin, Cao, Li, Sheinman and Chen13–Reference Li, Jia, Cao, Feng and Gao15 to adapt to the aging process; biofilms form channels within structures to aid the transport of nutrients and water critical for biofilm growth;Reference Trejo, Douarche, Bailleux, Poulard, Mariot, Regeard and Raspaud16,Reference Wilking, Zaburdaev, De Volder, Losick, Brenner and Weitz17 and epithelial cells delaminate to avoid tissue overcrowding.Reference Marinari, Mehonic, Curran, Gale, Duke and Baum18,Reference Eisenhoffer, Loftus, Yoshigi, Otsuna, Chien, Morcos and Rosenblatt19 Although these surface patterns are believed to be the result of complex interactions between genetic, biochemical, and biological processes, accumulating evidence has shown that mechanical forces play a critical role in controlling their formation.Reference Wang and Zhao20–Reference Budday, Kuhl and Hutchinson24

Figure 1. Surface instabilities in (a) nature and (b) engineering across multiple length scales. The scale indicates the dimensions of typical surface features. Reproduced with permission from References Reference Wang, Castro and Boyce3 and Reference Wang, Niu, Pei, Dickey and Zhao98. © 2011, 2010 Royal Society of Chemistry. References Reference Shyer, Tallinen, Nerurkar, Wei, Gil, Kaplan, Tabin and Mahadevan4 and Reference Khang, Jiang, Huang and Rogers61. © 2013, 2006 AAAS. References Reference Yin, Cao, Li, Sheinman and Chen13 and Reference Wilking, Zaburdaev, De Volder, Losick, Brenner and Weitz17. © 2010, 2012 National Academy of Sciences. References Reference Efimenko, Rackaitis, Manias, Vaziri, Mahadevan and Genzer58, Reference Stafford, Harrison, Beers, Karim, Amis, Vanlandingham, Kim, Volksen, Miller and Simonyi60, Reference Kim, Yoon and Hayward72, and Reference Zang, Ryu, Pugno, Wang, Tu, Buehler and Zhao80. © 2005, 2004, 2010, 2013 Nature Publishing Group. Reference Reference Moon, Jensen, Hutchinson, Oh and Evans28. © 2002 Elsevier. Reference Reference Wang, Zhang and Zhao45. © 2011 APS.
In engineering systems, surface instability patterns have been traditionally regarded as indicators of failure. For example, buckling of stiff skins on soft cores is regarded to be a failure mechanism of core–shell composites.Reference Allen25–Reference Shield, Kim and Shield27 Similarly, the delamination of thermal barrier coatings has been found to compromise the overall barrier performance and may further lead to exfoliation.Reference Moon, Jensen, Hutchinson, Oh and Evans28–Reference Gioia and Ortiz31 Conversely, researchers have recently begun to realize that surface instabilities, rather than being viewed only as a detrimental failure, can also be harnessed to give tunable topographic features that are useful in many technological applications (Figure 1b). For example, wrinkling instabilities on stressed layered structures, manifested as sinusoidally undulating surfaces, have been used in tunable adhesion, optics, hydrophobicity, microfluidics, property metrology, and flexible electronics.Reference Chen and Yin32–Reference Li, Cao, Feng and Gao37
Beyond wrinkling, a number of new modes of surface instabilities that yield topographic characteristics distinctly different from sinusoidal undulation have been recently observed in experiments and simulations, including creasing, delaminated buckling, folding, period doubling, and ridging. These new modes of instabilities not only require new physical and mechanical explanations, they also open new avenues to exploit diverse surface patterns across multiple length scales for new applications.Reference Wang and Zhao20,Reference Bowden, Brittain, Evans, Hutchinson and Whitesides38 Despite intensive research, prior studies have mostly focused on theory, experiments, or applications of individual modes of instability such as wrinkling. A systematic understanding of various instability patterns and quantitative prediction of their topographic characteristics will not only significantly contribute to the knowledge of fundamental physics of surface instabilities, but also provide rational guidance to design new patterns for novel applications.
Given the complexity and importance of this emerging field, this article is aimed at providing a systematic summary of the fundamental mechanisms and functions of various types of surface instability patterns. By adopting the Maxwell stability criterion, we categorize various surface instabilities into a quantitatively defined thermodynamic phase diagram. We then discuss the unique features of different surface instability patterns and their emerging applications in various fields. We conclude by offering our perspective on future directions of this rapidly evolving field.
Phase diagram of surface instabilities
Generically, surface instabilities on layered structures are caused by compressive strains in one or more of the component layers. For simplicity, in this article, we focus on bilayer structures of thin films bonded on thick substrates, as these structures have been widely used in surface instability studies and applications. The compressive strains in film–substrate structures are usually induced by two mechanisms. First, compression is applied to an initially stress-free structure with a significant stiffness difference between film and substrate. The different deformation reactions in response to the applied compression trigger the film to undulate into a certain topographic pattern.Reference Allen25,Reference Shield, Kim and Shield27 Second, the films and substrates undergo different dimension changes, which can lead to compressive mismatch strains in the films (Figure 2a). Mismatch deformation can be induced by thermal expansion in microelectronic systems,Reference Gioia and Ortiz31,Reference Bowden, Brittain, Evans, Hutchinson and Whitesides38–Reference Cai, Breid, Crosby, Suo and Hutchinson41 ion irradiation treatment,Reference Moon, Lee, Sun, Oh, Vaziri and Hutchinson42,Reference Kim, Abkarian and Stone43 electromagnetic fields,Reference Wang, Tahir, Zhang and Zhao44–Reference Xu and Hayward48 mass growth or cell death,Reference Shyer, Tallinen, Nerurkar, Wei, Gil, Kaplan, Tabin and Mahadevan4,Reference Amar and Jia6,Reference Yin, Cao, Li, Sheinman and Chen13,Reference Tallinen, Chung, Biggins and Mahadevan22 and diffusion-induced swelling.Reference Chan, Smith, Hayward and Crosby49–Reference Tanaka, Sun, Hirokawa, Katayama, Kucera, Hirose and Amiya51 While these two ways of applying compressive strains are related, we primarily focus on the second one.

Figure 2. (a) A process to induce mismatch strain in film–substrate structures. At a detached stress-free state, the film thickness, H f, has a longer lateral length (L f) than that of the substrate (L s). Compressing and bonding the film to substrate induces a mismatch compressive strain (εM). (b) Schematics of various modes of surface instability. (c) A 3D phase diagram of surface instabilities in film–substrate structures. Three axes represent mismatch strain, εM, normalized adhesion energy, Γ/(µsH f), and modulus ratio, µf/µs. Reproduced with permission from Reference Reference Wang and Zhao20. © 2015 Nature Publishing Group.
To capture the key physics, we assume that the film–substrate structure undergoes a two-dimensional (2D) deformation, and the surface-pattern formation follows the following process (Figure 2a). Imagine that the film and substrate are initially detached from each other and are stress-free. In this imaginary stress-free state, the film features a longer lateral length (L f) than that of the substrate (L s). Thereafter, we laterally compress the film (keeping it flat) to the same length as that of the substrate (L s) and then bond it to the substrate. During this process, a compressive mismatch strain develops in the film, denoted as εM = (L f – L s)/L f. If this mismatch strain is high enough, the film ceases to be flat and bifurcates into various corrugated topographic patterns on the substrate (as shown in Figure 2b).
Based on their topographic characteristics, these patterns can be classified into several types. For example, with increasing mismatch strain, the initially flat film can form wrinkles by sinusoidally undulating and remaining locally smooth (Figure 2b(i)). The film can also pinch into self-contacting regions to form creases (Figure 2b(ii)). If the adhesion between the film and the substrate is weak, the film can delaminate from the substrate to form buckled regions, called delaminated buckling (Figure 2b(iii)). As the mismatch strain is further increased, these patterns change their topographic character and transform into more complex patterns or combinations of these phenomena. For instance, with excessive mismatch strains, the wrinkles can transform into three different pattern types: folds—some valleys of the wrinkles fold into self-contacts (Figure 2b(iv)), period doubles—the sinusoidal wrinkles transit into a pattern with twice the wavelength and variable valley depth (Figure 2b(v)), and ridges—the wrinkles drastically increase their amplitude, forming a high-aspect-ratio pattern without following a sinusoidal shape (Figure 2b(vi)). In addition, each type of surface instability pattern can have different feature sizes, including amplitude and wavelength.
A systematic understanding of various instability patterns will significantly contribute to the knowledge of fundamental physics of surface instabilities. Quantitative models of pattern characteristics and feature sizes can further provide a rational foundation to guide the design of surface instability patterns for novel applications. However, the development of such a systematic understanding and of predictive models has been complicated by the various types of instability patterns, multiple physical parameters that affect the instabilities, and geometrical and material nonlinearity.
To address the previously mentioned issues, a phase-diagram approach to categorize various surface instabilities into a quantitatively defined thermodynamic phase diagram was reported.Reference Wang and Zhao20,Reference Wang and Zhao52 Within the time scale of determining instability patterns, we take the film–substrate structure as a thermodynamic system, and assume that the current surface-instability pattern always seeks the lowest potential energy among all possible configurations (Figure 2b) (i.e., following the Maxwell stability criterion).Reference Thompson and Hunt26,Reference Wang and Zhao52–Reference Abeyaratne54 The potential energy per unit width of the film–substrate system under plane-strain deformation can be expressed as:Reference Wang and Zhao52
where U f and U s are strain energies per unit width of the film and substrate, respectively, D is the current delaminated length of the substrate measured in the stress-free state, and Γ is the adhesion energy per unit area between the film and the substrate. To describe the strain energies due to the large deformation, both the film and the substrate are taken as incompressible rubber-like materials with shear modulus µf and µs, respectively. The film thickness, H f, was further assumed to be much smaller than all the other dimensions (i.e., film length, L f, substrate length, L s, and substrate thickness, H s) in the system, thus becoming the only relevant length scale for analyzing the instability patterns.Reference Wang and Zhao20,Reference Wang and Zhao52
Therefore, this simplified model (Figure 2a–b) involves five physical parameters that determine the instability patterns: µf, µs, H f, Γ, and εM, where εM is the strain mismatch between the film and substrate. By dimensional argument, they can be normalized into three dimensionless parameters: modulus ratio µf/µs, normalized adhesion energy Γ/(µsH f) , and mismatch strain εM. The types of instability patterns will be solely determined by the three dimensionless parameters, and therefore governed by a three-dimensional (3D) phase diagram, as shown in Figure 2c.Reference Wang and Zhao20,Reference Wang and Zhao52
To quantitatively calculate the phase boundaries between different surface instability patterns, both analytical and computational methods can be employed.Reference Wang and Zhao20,Reference Wang and Zhao52 Along the phase boundaries, the adjacent patterns can coexist within a system as follows:
where i and j denote two adjacent phases of surface instabilities.
Following this criterion, we can categorize all modes of surface instabilities previously discussed into a 3D phase diagram with quantitatively determined phase boundaries (Figure 2c). As shown in Figure 2c, if the normalized adhesion energies between the films and substrates are sufficiently high, the preferable patterns are creasing and folding for structures with relatively compliant films, but wrinkling, period doubling, and ridging for structures with relatively stiff films. As the normalized adhesion energy decreases to critical values, the undelaminated patterns transit into the delaminated-buckle patterns.Reference Wang and Zhao20
Features and emerging applications of surface instability patterns
The instabilities on film–substrate structures provide a library of self-organized surface patterns across multiple length scales that introduce various opportunities in engineering and biological applications. Guided by quantitative models such as the phase diagram (Figure 2c), surface patterns can be flexibly and reversibly switched between different phases with a large range of freedom by simple elastic deformation of the structures. This tunability, in both topographic patterns and their feature sizes, can also offer dynamic and switchable functionalities for fruitful applications. In this section, for each surface instability pattern, we review the topographic features, including amplitude, and wavelength, and highlight their applications. A list of detailed applications of various surface instability patterns is included in Table I.
Table I. Emerging applications of surface instability patterns.

The mechanical parameters mismatch strain, εM, normalized adhesion energy, Γ/(µsH f), and modulus ratio, µf/µs, are estimated from the references.
Wrinkles
If the modulus ratio of the system µf/µs is above 1.3, the initially flat surface first bifurcates into the wrinkle phase (Figure 2b(i)). The wavelength of wrinkles at initiation (just transited from the flat state) can be calculated by linear stability analysis and expressed as a function of µf/µs.Reference Cao and Hutchinson85 For large modulus ratios (µf/µs > 103), the wavelength of wrinkles at initiation λCwrinkle can be explicitly written as:Reference Chen and Hutchinson39
Further increasing the mismatch strain will decrease the wavelengths of the wrinkles. An accordion model assumes that the number of undulations in the wrinkles does not change as the mismatch strain increases above the critical mismatch strain and can be used to calculate the wavelength of developed wrinkles, λwrinkle:Reference Khang, Jiang, Huang and Rogers61,Reference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86,Reference Jiang, Khang, Song, Sun, Huang and Rogers87
where ![]() $\varepsilon _{wrinkle}^C$ is the critical mismatch strain for wrinkle initiation. Subsequently, the amplitude of the wrinkles, A wrinkle, can be calculated by approximating the arc-length of the wrinkles at various mismatch strains to be equal to the wavelength of wrinkles at initiation,Reference Khang, Jiang, Huang and Rogers61,Reference Jiang, Khang, Song, Sun, Huang and Rogers87 for example:
$\varepsilon _{wrinkle}^C$ is the critical mismatch strain for wrinkle initiation. Subsequently, the amplitude of the wrinkles, A wrinkle, can be calculated by approximating the arc-length of the wrinkles at various mismatch strains to be equal to the wavelength of wrinkles at initiation,Reference Khang, Jiang, Huang and Rogers61,Reference Jiang, Khang, Song, Sun, Huang and Rogers87 for example:
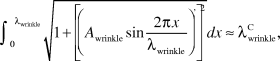 $$\int_0^{{\lambda _{wrinkle}}} {\sqrt {1 + {{\left[ {{{\left( {{A_{wrinkle}}\sin {{2\pi x} \over {{\lambda _{wrinkle}}}}} \right)}^'}} \right]}^2}} } dx \approx \lambda _{wrinkle}^C$$ ,
$$\int_0^{{\lambda _{wrinkle}}} {\sqrt {1 + {{\left[ {{{\left( {{A_{wrinkle}}\sin {{2\pi x} \over {{\lambda _{wrinkle}}}}} \right)}^'}} \right]}^2}} } dx \approx \lambda _{wrinkle}^C$$ ,where ![]() ${\left( {} \right)^'}$ is the differential operation with respect to x.
${\left( {} \right)^'}$ is the differential operation with respect to x.
As sinusoidal undulations with wavelengths and amplitudes given by Equations 3–5, wrinkles have found a number of engineering applications, where well-defined and smooth surface undulations are needed. For example, the sinusoidal structure can be used as an optical grating when the wavelength of the wrinkle is controlled in a range similar to that of visible light (430–770 nm).Reference Chandra, Yang and Lin56,Reference Harrison, Stafford, Zhang and Karim88,Reference Kim, Hu, Alvarenga, Kolle, Suo and Aizenberg89 The colors of the grating can in turn be used to predict the mechanical properties of the thin film or substrate.Reference Chung, Nolte and Stafford35,Reference Stafford, Harrison, Beers, Karim, Amis, Vanlandingham, Kim, Volksen, Miller and Simonyi60
As another example, periodic wrinkle valleys provide template arrays to guide the placement, alignment, or transport of engineering objects that are smaller than the wavelength of the wrinkle, such as nanoparticles,Reference Genzer and Groenewold34,Reference Efimenko, Rackaitis, Manias, Vaziri, Mahadevan and Genzer58 nanowires,Reference Kim, Choi, Kim, Shin, Kim, Son, Kim and Kim90 and cells.Reference Lam, Clem and Takayama66 The wrinkled surfaces can also be harnessed to control surface-wetting properties,Reference Yang, Khare and Lin36,Reference Chung, Youngblood and Stafford57,Reference Khare, Zhou and Yang59,Reference Lin and Yang91 adhesion,Reference Chan, Smith, Hayward and Crosby49,Reference Lin, Vajpayee, Jagota, Hui and Yang92 and friction.Reference Terwagne, Brojan and Reis67 Due to elastic deformation of the bilayer, the wrinkle wavelength and amplitude can be tuned over a large range according to Equations 4 and 5. Therefore, the aforementioned applications of wrinkles can also be dynamically modulated to achieve high flexibility with external stimuli. In addition, reversible wrinkling of thin films on substrates allows for large deformation of film–substrate structures by inducing only small strains in rigid films such as Si and SiO2—a mechanism that enables flexible electronic devices to undergo reversible large stretching, bending, and twisting.Reference Song, Jiang, Huang and Rogers33,Reference Khang, Jiang, Huang and Rogers61,Reference Yu, Masarapu, Rong, Wei and Jiang65 The dynamic switching of wavy topographic patterns can also help shake off fouling sediments to maintain clean surfaces in biomedical devices and engineering tools submerged in water.Reference Efimenko, Finlay, Callow, Callow and Genzer68,Reference Epstein, Hong, Kim and Aizenberg69
Creases
When the modulus of the film is smaller or similar to that of the substrate (e.g., µf/µs < 1.3), nucleation of scattered creases on the surface of the film occurs once mismatch strain reaches a critical value, for example:
This phase boundary can be calculated using Equation 2, where i represents the flat phase and j the crease phase.Reference Hohlfeld and Mahadevan8,Reference Hohlfeld and Mahadevan93,Reference Hong, Zhao and Suo94 Further, increasing ![]() ${\varepsilon _M}$ leads to a pattern of creases with a wavelength λcrease. The wavelength of the crease pattern approximately follows a linear relation with εM as:Reference Wang and Zhao20,Reference Cai, Chen, Suo and Hayward95
${\varepsilon _M}$ leads to a pattern of creases with a wavelength λcrease. The wavelength of the crease pattern approximately follows a linear relation with εM as:Reference Wang and Zhao20,Reference Cai, Chen, Suo and Hayward95
Increasing with the mismatch strains, the folded regions of the creases become deeper. The depths of the creases, δcrease, have been calculated by finite element models and can be approximately expressed as:
This has been validated by experimental observations of creases on elastomer surfaces using confocal microscopy.Reference Cai, Chen, Suo and Hayward95
The creases feature self-contacting regions on the surface that form along parallelReference Wang, Tahir, Zang and Zhao46,Reference Cai, Chen, Suo and Hayward95 or randomly distributed lines.Reference Tallinen, Biggins and Mahadevan9,Reference Wang, Zhang and Zhao45,Reference Tanaka, Sun, Hirokawa, Katayama, Kucera, Hirose and Amiya51,Reference Cai, Bertoldi, Wang and Suo96 These patterns can also be formed on curved surfaces, thanks to the deformability of elastomer films and substrates.Reference Wang, Tahir, Zang and Zhao46 Along with tunability, a library of crease patterns not only offers new options for fabricating reversible surface textures,Reference Wang, Tahir, Zhang and Zhao44,Reference Wang, Tahir, Zang and Zhao46,Reference Xu and Hayward48,Reference Wang, Robinson and Zhao70,Reference Wang and Zhao97,Reference Wang, Niu, Pei, Dickey and Zhao98 it also introduces new topographic cues to grow cells and tissues.Reference Saha, Kim, Irwin, Yoon, Momin, Trujillo, Schaffer, Healy and Hayward73 In addition, stimuli-triggered reversibly folded regions of creases enable localized self-contacts of small surfaces hidden within the film (Figure 2b(ii)). This has two consequences. First, two initially separated material points can physically contact and communicate with each other through the contact spot. Such a contact may enable on-off electronic conduction by forming and flattening a crease. Reversible electronic contact has been used to make gated electrical switches.Reference Xu, Chen and Hayward71 Second, the initially flat regions fold against themselves to be intentionally hidden within the bulk—this can be used to sequestrate particles, cells, and chemical groups attached to specific regions on the surface (Figure 3a).Reference Kim, Yoon and Hayward72 As shown in Figure 3a, nanoparticles and cells can be reversibly sequestrated and shown up by triggering creasing instability.Reference Kim, Yoon and Hayward72

Figure 3. Examples of potential applications of surface instabilities in (a) biology: biomolecules and cells reversibly sequestrated by dynamic creases, (b) energy: the efficiency of a photovoltaic enhanced by folding surfaces, (c) manufacturing: 3D structures manufactured through delaminated-buckling, and (d) mechanochemistry: an electrically triggered crater pattern in an electro-mechano-chemically responsive (EMCR) polymer. (a,b,d) Reproduced with permission from References Reference Kim, Yoon and Hayward72, Reference Kim, Kim, Pégard, Oh, Kagan, Fleischer, Stone and Loo76, and Reference Wang, Gossweiler, Craig and Zhao47. © 2010, 2012, and 2014 Nature Publishing Group. (c) Reproduced with permission from Reference Reference Xu, Yan, Jang, Huang, Fu, Kim, Wei, Flavin, McCracken and Wang82. © 2015 AAAS.
Other modes of instabilities
For a well-bonded film–substrate system with excessive mismatch strains (εM > ∼0.33), the wrinkles and creases can transit into advanced modes of instabilities, including folds, period doubles, and ridges, depending on the modulus ratio µf/µs (Figure 2c). For example, the wrinkles on film–substrate structures with 1 < µf/µs < 10 can transform to folds by forming self-contacting tips in the valleys of the wrinkles (Figure 2b(iv)).Reference Wang and Zhao20,Reference Jin, Auguste, Hayward and Suo99 Wrinkles with 10 < µf/µs < 103 vary the adjacent valley heights to form period doubles with twice the wavelength of the corresponding wrinkles (Figure 2b(v)). For µf/µs > 103, however, the wrinkles dramatically increase their crest heights to a pattern of ridges (Figure 2b(vi)). If the mismatch strain increases beyond 0.6, more complicated patterns develop, such as period triples,Reference Budday, Kuhl and Hutchinson24,Reference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86,Reference Sun, Xia, Moon, Oh and Kim100 period quadruples,Reference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86 and coexisting folds, period doubles, and ridges.
An accordion model can also be used to predict the wavelengths of folds, period doubles, and ridges by assuming that the number of undulations in the patterns remain unchanged when the wrinkles transit into advanced modes. We can calculate the wavelengths of folds, period doubles, and ridges under various mismatch strains, respectively, as:
It should be noted that the period double has a wavelength twice that of the corresponding wrinkles, as given in Equation 10.
Although the wavelength behaviors of folds, period doubles, and ridges follow similar laws, their vertical amplitudes differ dramatically. On a wrinkled film–substrate structure with 1 < µf/µs < 10, folds can snap to a finite depth at the critical mismatch strain.Reference Jin, Auguste, Hayward and Suo99 After the onset, the folds penetrate into the substrate with depth increasing in an approximately linear fashion with the mismatch strain.Reference Jin, Auguste, Hayward and Suo99 For example, the depth of the folds on a film–substrate structure with H s/H f ∼ 20 can be calculated as:Reference Jin, Auguste, Hayward and Suo99
where ![]() ${A_{wrinkle}}\left( {\varepsilon _{fold}^C} \right)$ is the wrinkle amplitude predicted in Equation 5, and
${A_{wrinkle}}\left( {\varepsilon _{fold}^C} \right)$ is the wrinkle amplitude predicted in Equation 5, and ![]() $\varepsilon _{fold}^C$ is the mismatch strain for the onset of folds.
$\varepsilon _{fold}^C$ is the mismatch strain for the onset of folds.
The vertical amplitude of period doubles is different from that of folds. At the onset of period doubles, the initially equal amplitudes of adjacent wrinkle valleys begin to bifurcate into two branches.Reference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86,Reference Sun, Xia, Moon, Oh and Kim100–Reference Zhao, Cao, Hong, Wadee and Feng102 While the wavelength of period doubles can be approximately expressed by Equation 10, the amplitude of period doubles can also be calculated theoreticallyReference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86,Reference Brau, Damman, Diamant and Witten101 and by finite element models.Reference Wang and Zhao20,Reference Zhao, Cao, Hong, Wadee and Feng102
A major feature of ridges is their high-aspect ratios (i.e., high values of height over wavelength). During the transition from wrinkles (Figure 2b(i)) to ridges (Figure 2b(vi)), the crest height increases drastically to values much higher than the amplitude of the corresponding wrinkle.Reference Wang and Zhao20,Reference Takei, Jin, Hutchinson and Fujita103,Reference Jin, Takei and Hutchinson104 Thereafter, the amplitude of ridges increases linearly with the mismatch strain. This relation can be approximately expressed as:Reference Wang and Zhao20
where A ridge is the amplitude of the ridge.
These advanced modes of instabilities, manifested as surface characteristics beyond wrinkles, provide a number of topographic options that greatly broaden the functional horizon of surface instability patterns. For example, the complex surface structures can help trap more incident solar light for more efficient photovoltaic devices. Loo, Stone, and co-workers demonstrated that, compared to wrinkles, the folded surface patterns can increase internal light-scattering more significantly, thus enabling higher light-harvesting efficiency in solar cells (Figure 3b).Reference Kim, Kim, Pégard, Oh, Kagan, Fleischer, Stone and Loo76 As another example, with excessive mismatch strains, the lower valleys of period doubles can close into pocket channels. These closed channels within the substrate have been used as precise microfluidic channels to hold and deliver nanoparticles or cells.Reference Nagashima, Ebrahimi, Lee, Vaziri and Moon77 As a third example, ridge arrays, with much higher-aspect ratios (A ridge/λridge) than wrinkles, can be used to make hydrophobic surfaces to achieve higher-contact angles than surfaces with wrinkles.Reference Cao, Chan, Zang, Leong and Zhao78 In addition, these ridge-covered surfaces can also be used as a cell–culture substrate to induce better cell alignment than surfaces with wrinkles.Reference Cao, Chan, Zang, Leong and Zhao78 Ridges formed on graphene surfaces have been shown to provide microstructures that can be harnessed to design reversibly stretchable capacitors with high energy density.Reference Zang, Cao, Feng, Liu and Zhao79
Delaminated buckle
When the adhesion between a film and substrate is relatively weak (i.e., relatively low Г/(µsHf)), the film can de-bond from the substrate to form delaminated buckles. To calculate the geometrical characteristics of delaminated buckles, including wavelength and delaminated length, we minimize the potential energy of the structure by considering:Reference Wang and Zhao20,Reference Vella, Bico, Boudaoud, Roman and Reis105
where Πbuckle (see Equation 1) is the potential energy of the delaminated-buckle state with delaminated length D and delaminated-buckle wavelength λbuckle. By solving Equations 14 and 15, we can obtain a set of D and λbuckle for the film–substrate structure.
Delaminated buckles have been used in diverse engineering applications (Table I). For example, the delaminated regions offer enclosed channels whose size can be precisely tuned by controlling the film thickness, mismatch strain, and mechanical properties of film and substrate. These channels, if carefully connected, can be used to deliver microfluidics and microengineered objects.Reference Moon, Chung, Lee, Oh, Stone and Hutchinson84 In addition, the delaminated regions can significantly increase the surface roughness of the structures to change their light transmittance.Reference Zang, Ryu, Pugno, Wang, Tu, Buehler and Zhao80,Reference Thomas, Andow, Suresh, Eksik, Yin, Dyson and Koratkar83 The delaminated buckles, featuring extended lengths of films compared to the substrates while maintaining the films within small strains, can also accommodate reversible and large deformation of film–substrate structures composed of rigid films (e.g., Si and SiO2) and compliant substrates (e.g., elastomers). This mechanism has enabled highly stretchable electronic devices.Reference Sun, Choi, Jiang, Huang and Rogers81 Furthermore, the formation of delaminated buckles involves a 3D pop-up process from the initial planar layout which has been utilized to manufacture 3D architectures based on 2D planar film–substrate structures (Figure 3c).Reference Xu, Yan, Jang, Huang, Fu, Kim, Wei, Flavin, McCracken and Wang82
Future directions
Although surface-instability-based pattern formation has been intensively studied in physics and mechanics and widely exploited for innovative applications in engineering and biology, many unanswered questions and unexplored opportunities still exist. In terms of fundamental aspects, a systematic understanding of the conditions and topographic characteristics of complex modes of instabilities in layered structures remains a core theme. For example, a number of surface instability patterns have been observed, such as hierarchical wrinkles,Reference Efimenko, Rackaitis, Manias, Vaziri, Mahadevan and Genzer58 period triples,Reference Budday, Kuhl and Hutchinson24 and period quadruples,Reference Brau, Vandeparre, Sabbah, Poulard, Boudaoud and Damman86 but these are not well understood. Understanding and predicting these instabilities require new experiments and models to give quantitative phase boundaries at regions of large mismatch strains on the phase diagram. While current studies have been focused on flat, isotropic, and homogeneous structures, pattern formation with instabilities of layered structures with intrinsic curvatures,Reference Yin, Cao, Li, Sheinman and Chen13,Reference Tallinen, Chung, Biggins and Mahadevan22 anisotropy, and inhomogeneityReference Shyer, Tallinen, Nerurkar, Wei, Gil, Kaplan, Tabin and Mahadevan4,Reference Amar and Jia6,Reference Yin, Cao, Li, Sheinman and Chen13,Reference Li, Jia, Cao, Feng and Gao15,Reference Grason and Davidovitch106,Reference Wu, Bouklas and Huang107 offers many intriguing problems and exciting opportunities.
In terms of application, we envision that more tangible functions of surface instability patterns will be achieved in various fields, owing to their intrinsic merits such as low cost, easy fabrication, flexibility, diversity, and tunability. For example, in biomedical applications, studies of surface instabilities may help uncover pathological mechanisms and inspire better treatments for diseases with abnormal tissue patterns.Reference Tallinen, Chung, Biggins and Mahadevan22 Surface instabilities in biomaterials such as hydrogels can offer smart platforms to detect biological signals, intervene in biological procedures, and guide biological behaviors (example as Figure 3a).Reference Kim, Yoon and Hayward72 In energy-related applications, structures with tunable surface instability patterns can dynamically interact with the incident energy flow (e.g., solar energy, acoustic energy, elastic wave energy, or electromagnetic energy), thus helping acquire, absorb (example as Figure 3b),Reference Kim, Kim, Pégard, Oh, Kagan, Fleischer, Stone and Loo76 store, or transfer more energy. In manufacturing applications, tunable surface structures can be used to design tunable origami structures that in turn offer a large number of potential applications in flexible electronics, wearable devices, and biomedical implants (example in Figure 3c).Reference Xu, Yan, Jang, Huang, Fu, Kim, Wei, Flavin, McCracken and Wang82 In mechanochemical applications, mechanical cues, including topographic structures and related deformation, can be used to trigger chemical reactions that are usually accompanied by change of color or fluorescence and release of molecules (Figure 3d).Reference Wang, Gossweiler, Craig and Zhao47 Dynamic changes in color and fluorescence controlled by tunable surface instability patterns may be particularly useful in displays and camouflage applications,Reference Wang, Gossweiler, Craig and Zhao47 and the controlled release of molecules may be harnessed for drug-delivery applications.
Acknowledgments
Q.W. is thankful for the start-up grant from the University of Southern California. X.Z. thanks support from ONR (No. N00014–14–1-0528), NSF (Nos. CMMI-1253495, CMMI-1200515), and NIH (UH3TR000505).



