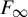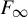1 Introduction
A group G is left orderable if it admits a total order which is invariant under left multiplication by any group element. This concept has a remarkable connection with dynamics of group actions on the line: a countable group G is left orderable if and only if it admits a faithful action by orientation-preserving homeomorphisms on the real line.
One of the fundamental questions in the field is to understand the following. Given a left orderable group, what are the possible actions on the line by orientation-preserving homeomorphisms? It is folklore that up to semiconjugacy, every action of a finitely generated left orderable group on the line by orientation-preserving homeomorphisms and without global fixed points is of one of three types [Reference Deroin, Navas and Rivas13, Theorem 3.5.19]:
-
(1) cyclic or type 1 if there exists an invariant Radon measure on
 $\mathbb {R}$
, in which case the group surjects onto the integers;
$\mathbb {R}$
, in which case the group surjects onto the integers; -
(2) locally proximal or type 2 if it does not preserve a Radon measure on
 $\mathbb {R}$
, yet it is semiconjugate to a minimal action that commutes with integer translations. Equivalently, such an action descends to a minimal and proximal action on the circle (see Proposition 2.5);
$\mathbb {R}$
, yet it is semiconjugate to a minimal action that commutes with integer translations. Equivalently, such an action descends to a minimal and proximal action on the circle (see Proposition 2.5); -
(3) proximal or type 3 if for every bounded interval I and open interval J, there is a group element f such that
 $I\cdot f\subset J$
.
$I\cdot f\subset J$
.
The above framework has shed light on various algebraic and dynamical properties of left orderable groups, and on the question of when certain groups are left orderable. For example, it was unknown until very recently whether lattices in higher-rank semisimple Lie groups admit actions on the line or not; it turns out that outside some exceptional cases, they do not [Reference Deroin and Hurtado12]. Before this breakthrough solution, given that lattices do not admit actions of type 1 [Reference Kazhdan24] or 2 [Reference Burger and Monod4, Reference Burger and Monod5, Reference Ghys17], it was thought that a promising approach could be to leverage finite generation to also rule out type-3 actions. More succinctly, [Reference Navas32, Question 4] (see also [Reference Deroin, Navas and Rivas13, Question 3.5.11]) asks the following question.
Question 1.1. (Navas ICM
 $2018$
)
$2018$
)
Do there exist finitely generated left orderable groups all of whose fixed point-free actions by homeomorphisms on the line are of type 3?
Definition 1.2. (Navas)
A finitely generated left orderable group G is a left orderable monster if all of its fixed point-free actions by homeomorphisms on the line are of type 3.
Given the negative solution in [Reference Deroin and Hurtado12] to the question concerning higher-rank lattices, it is intriguing that in fact left orderable monsters do exist. This fact was proved independently by Matte Bon and Triestino [Reference Matte Bon and Triestino30], and by Hyde, the second author, Navas, and Rivas [Reference Hyde and Lodha22, Reference Hyde, Lodha, Navas and Rivas23]. In both cases, the examples are families of groups whose construction is non-trivial, and that have a number of stronger properties. First, both families of groups are simple: a property much stronger than the absence of type-1 actions. Second, these groups are uniformly perfect, and even have vanishing second bounded cohomology [Reference Fournier-Facio and Lodha14]; in fact, they admit no fixed point-free action on the circle whatsoever [Reference Fournier-Facio and Lodha14, Reference Matte Bon and Triestino30]—these properties are much stronger than the absence of type-2 actions.
However, the groups in [Reference Hyde and Lodha22, Reference Hyde, Lodha, Navas and Rivas23, Reference Matte Bon and Triestino30] are not finitely presentable since each is a non-trivial limit of markings of a finitely presented group in the space of marked groups. Therefore, one might hope that the above still yields an alternative approach to disprove left orderability of lattices, namely leveraging finite presentability to rule out type-3 actions. In particular, one may hope that this approach works for lattices in products of trees [Reference Burger and Mozes6], whose left orderability is still an open question. Indeed, it follows from their simplicity and from [Reference Burger and Monod5, Corollary 26] that if they are left orderable, then they must be left orderable monsters. One of the key motivations of this article is to show that this modified approach cannot work, that is, there do in fact exist finitely presentable left orderable monsters.
Our examples are very different in nature from those in [Reference Hyde and Lodha22, Reference Matte Bon and Triestino30]. First, as we already mentioned, they are finitely presentable, and even of type
![]() $F_\infty $
(finite presentability is equivalent to admitting a classifying space with a finite
$F_\infty $
(finite presentability is equivalent to admitting a classifying space with a finite
![]() $2$
-skeleton, and type
$2$
-skeleton, and type
![]() $F_\infty $
means there is a classifying space with a finite n-skeleton for all n). Second, the absence of type-1 or type-2 actions is shown via a direct dynamical argument, and not via some much stronger property such as simplicity, uniform perfection, or vanishing of second bounded cohomology. Indeed, each of these properties is shown to fail. Lastly, in our construction, the group itself is much more straightforward than in previous examples.
$F_\infty $
means there is a classifying space with a finite n-skeleton for all n). Second, the absence of type-1 or type-2 actions is shown via a direct dynamical argument, and not via some much stronger property such as simplicity, uniform perfection, or vanishing of second bounded cohomology. Indeed, each of these properties is shown to fail. Lastly, in our construction, the group itself is much more straightforward than in previous examples.
We now describe a concrete instance of our general construction. Let
![]() $\overline {T}$
denote the lift of Thompson’s group T to the real line. Let z denote the generator of the center of
$\overline {T}$
denote the lift of Thompson’s group T to the real line. Let z denote the generator of the center of
![]() $\overline {T}$
. Let
$\overline {T}$
. Let
![]() $\overline {T}_{2,3}$
denote the lift of the Stein–Thompson group
$\overline {T}_{2,3}$
denote the lift of the Stein–Thompson group
![]() $T_{2,3}$
, and let
$T_{2,3}$
, and let
![]() $g\in \overline {T}_{2,3}$
denote a lift of an element with an irrational rotation number in
$g\in \overline {T}_{2,3}$
denote a lift of an element with an irrational rotation number in
![]() $T_{2,3}$
. Such elements exist, e.g., it was proved in [Reference Liousse25] that
$T_{2,3}$
. Such elements exist, e.g., it was proved in [Reference Liousse25] that
![]() $T_{2,3}$
contains elements whose rotation number equals
$T_{2,3}$
contains elements whose rotation number equals
![]() ${\log 2}/{\log 3}$
. We now take the amalgamated product and define
${\log 2}/{\log 3}$
. We now take the amalgamated product and define
Now we can state our main result.
Theorem 1.3. The group M is a left orderable monster.
A number of notable properties can be quickly established for this group. First, the space of homogeneous quasimorphisms of M is infinite-dimensional. In particular, M is not uniformly perfect, and the second bounded cohomology of M is infinite-dimensional. Moreover, M surjects onto Thompson’s group T. In particular, there exists a minimal action of M on the circle, and M is not simple. This showcases the difference with previous examples, which not only do not share these properties, but also were all more complicated to construct and harder to analyze.
To state our more general construction, we define
![]() $\mathcal {G}$
to be the class of infinite groups G of orientation-preserving homeomorphisms of the circle that satisfy:
$\mathcal {G}$
to be the class of infinite groups G of orientation-preserving homeomorphisms of the circle that satisfy:
-
(1) the lift
 $\overline {G}$
of G to the real line is perfect;
$\overline {G}$
of G to the real line is perfect; -
(2) G is simple;
-
(3) G has a unique proximal action on the circle, up to conjugacy;
-
(4) G has torsion.
Groups in
![]() $\mathcal {G}$
include: Thompson’s group T [Reference Cannon, Floyd and Parry10], the Stein–Thompson groups
$\mathcal {G}$
include: Thompson’s group T [Reference Cannon, Floyd and Parry10], the Stein–Thompson groups
![]() $T_{2, 3, n_3, \ldots, n_k}$
[Reference Guelman, Liousse and Arnoux21, Reference Stein33] (for example
$T_{2, 3, n_3, \ldots, n_k}$
[Reference Guelman, Liousse and Arnoux21, Reference Stein33] (for example
![]() $T_{2, 3}$
), the commutator subgroup of the golden ratio Thompson group
$T_{2, 3}$
), the commutator subgroup of the golden ratio Thompson group
![]() $T_{\tau }$
[Reference Burillo, Nucinkis and Reeves8], and the piecewise projective group S constructed by the second author [Reference Lodha26]. Some of these groups are known to have irrational rotation numbers, e.g.,
$T_{\tau }$
[Reference Burillo, Nucinkis and Reeves8], and the piecewise projective group S constructed by the second author [Reference Lodha26]. Some of these groups are known to have irrational rotation numbers, e.g.,
![]() $T_\tau^{\prime}$
[Reference Fournier-Facio and Lodha14], and
$T_\tau^{\prime}$
[Reference Fournier-Facio and Lodha14], and
![]() $T_{n_1,\dots ,n_k}$
if some
$T_{n_1,\dots ,n_k}$
if some
![]() $n_i$
and
$n_i$
and
![]() $n_j$
are coprime [Reference Liousse25]. A peculiarity of T is that the rotation numbers of all of its elements are rational [Reference Ghys and Sergiescu19]. We do not know whether S contains an element with irrational rotation number.
$n_j$
are coprime [Reference Liousse25]. A peculiarity of T is that the rotation numbers of all of its elements are rational [Reference Ghys and Sergiescu19]. We do not know whether S contains an element with irrational rotation number.
The following is our main result (with Theorem 1.3 as a special case).
Theorem 1.4. Let
![]() $G_1,G_2\in \mathcal {G}$
be groups such that
$G_1,G_2\in \mathcal {G}$
be groups such that
![]() $G_2$
contains an element with an irrational rotation number. Let
$G_2$
contains an element with an irrational rotation number. Let
![]() $\overline {G}_i$
denote the lift of the standard action of
$\overline {G}_i$
denote the lift of the standard action of
![]() $G_i$
, let z denote the generator of the center of
$G_i$
, let z denote the generator of the center of
![]() $\overline {G}_1$
, and let
$\overline {G}_1$
, and let
![]() $g \in \overline {G}_2$
denote the lift of an element with irrational rotation number. Then the following hold.
$g \in \overline {G}_2$
denote the lift of an element with irrational rotation number. Then the following hold.
-
(1) The group
 $M := \overline {G}_1*_{z = g}\overline {G}_2$
is a left orderable monster.
$M := \overline {G}_1*_{z = g}\overline {G}_2$
is a left orderable monster. -
(2) If
 $G_1,G_2$
are finitely presented (respectively of type
$G_1,G_2$
are finitely presented (respectively of type
 $F_{\infty }$
), then M is also finitely presented (respectively of type
$F_{\infty }$
), then M is also finitely presented (respectively of type
 $F_{\infty }$
.)
$F_{\infty }$
.) -
(3) The space of homogeneous quasimorphisms of M is infinite-dimensional. In particular, M is not uniformly perfect, and the second bounded cohomology of M is infinite-dimensional.
-
(4) M admits a unique proximal action on the circle (up to conjugacy), and this coincides with the unique proximal action of the quotient
 $G_1$
. In particular,
$G_1$
. In particular,
 $G_1$
is an isomorphism invariant of M.
$G_1$
is an isomorphism invariant of M.
Using the above, we will conclude the following.
Corollary 1.5. There exist infinitely many isomorphism classes of finitely presentable (and type
![]() $F_{\infty }$
) left orderable monsters.
$F_{\infty }$
) left orderable monsters.
2 Actions on the line and on the circle
We denote by
![]() ${\operatorname {Homeo}}^+(\mathbb {R})$
and
${\operatorname {Homeo}}^+(\mathbb {R})$
and
![]() ${\operatorname {Homeo}}^+(\mathbb {S}^1)$
the groups of orientation-preserving homeomorphisms of the real line and the circle, respectively. Given
${\operatorname {Homeo}}^+(\mathbb {S}^1)$
the groups of orientation-preserving homeomorphisms of the real line and the circle, respectively. Given
![]() $f\in {\operatorname {Homeo}}^+(\mathbb {R})$
, the support of f, denoted
$f\in {\operatorname {Homeo}}^+(\mathbb {R})$
, the support of f, denoted
![]() $\mathrm{supp}(f)$
, is the set of points that are moved by f. Note that the support of a homeomorphism is always an open set. Given
$\mathrm{supp}(f)$
, is the set of points that are moved by f. Note that the support of a homeomorphism is always an open set. Given
![]() $G \leq {\operatorname {Homeo}}^+(\mathbb {R})$
or
$G \leq {\operatorname {Homeo}}^+(\mathbb {R})$
or
![]() ${\operatorname {Homeo}}^+(\mathbb {S}^1)$
, we denote by
${\operatorname {Homeo}}^+(\mathbb {S}^1)$
, we denote by
![]() $\mathrm{Fix}(G)$
the set of global fixed points of G, which is closed. We say that an action
$\mathrm{Fix}(G)$
the set of global fixed points of G, which is closed. We say that an action
![]() $\rho $
of a group G is fixed point-free if
$\rho $
of a group G is fixed point-free if
![]() $\mathrm{Fix}(\rho (G)) = \varnothing $
.
$\mathrm{Fix}(\rho (G)) = \varnothing $
.
Recall that a group action on a topological space by homeomorphisms is minimal if each orbit is dense. We say that
![]() $\Lambda \subset \mathbb {R}$
(or
$\Lambda \subset \mathbb {R}$
(or
![]() $\Lambda \subset \mathbb {S}^1$
) is exceptional if
$\Lambda \subset \mathbb {S}^1$
) is exceptional if
![]() $\Lambda $
is perfect and totally disconnected. Let
$\Lambda $
is perfect and totally disconnected. Let
![]() $G\leq {\operatorname {Homeo}}^+(\mathbb {M})$
, where
$G\leq {\operatorname {Homeo}}^+(\mathbb {M})$
, where
![]() $\mathbb {M}\in \{\mathbb {R},\mathbb {S}^1\}$
, and let
$\mathbb {M}\in \{\mathbb {R},\mathbb {S}^1\}$
, and let
![]() $\Lambda \subset \mathbb {M}$
be an exceptional set. We say that
$\Lambda \subset \mathbb {M}$
be an exceptional set. We say that
![]() $\Lambda $
is minimal if it is G-invariant and the action of G on
$\Lambda $
is minimal if it is G-invariant and the action of G on
![]() $\Lambda $
is minimal.
$\Lambda $
is minimal.
The following are some fundamental results concerning actions of groups on the circle and the real line.
Theorem 2.1. [Reference Navas31, Theorem 2.1.1]
If
![]() $\Gamma \leq {\operatorname {Homeo}}^+(\mathbb {S}^1)$
is a countable group, then precisely one of the following holds.
$\Gamma \leq {\operatorname {Homeo}}^+(\mathbb {S}^1)$
is a countable group, then precisely one of the following holds.
-
(1) The action admits a finite orbit.
-
(2) The action is minimal.
-
(3) There exists a unique, minimal, exceptional subset
 $\Lambda \subset \mathbb {S}^1$
which is homeomorphic to the Cantor set.
$\Lambda \subset \mathbb {S}^1$
which is homeomorphic to the Cantor set.
For the case of the line, a similar result holds under the additional assumption of finite generation.
Proposition 2.2. [Reference Navas31, Proposition 2.1.12]
Every fixed point-free action of a finitely generated group G on
![]() $\mathbb {R}$
by orientation-preserving homeomorphisms admits a non-empty minimal invariant closed set. This closed set is one of the following.
$\mathbb {R}$
by orientation-preserving homeomorphisms admits a non-empty minimal invariant closed set. This closed set is one of the following.
-
(1) Discrete, in which case the group surjects onto the integers.
-
(2) The whole real line, in which case the group action is minimal.
-
(3) A unique minimal, exceptional set
 $\Lambda \subset \mathbb {R}$
.
$\Lambda \subset \mathbb {R}$
.
We are particularly interested in the third case of the previous proposition. The following is a fact concerning this case.
Proposition 2.3. [Reference Navas31, §§2.1.1 and 2.1.2]
Let
![]() $\mathbb {M}\in \{\mathbb {R},\mathbb {S}^1\}$
. Let
$\mathbb {M}\in \{\mathbb {R},\mathbb {S}^1\}$
. Let
![]() $G\leq {\operatorname {Homeo}}^+(\mathbb {M})$
be such that G admits a unique, exceptional, minimal set
$G\leq {\operatorname {Homeo}}^+(\mathbb {M})$
be such that G admits a unique, exceptional, minimal set
![]() $\Lambda \subset \mathbb {M}$
. Then there is a continuous surjective map
$\Lambda \subset \mathbb {M}$
. Then there is a continuous surjective map
![]() $\phi :\mathbb {M}\to \mathbb {M}$
, a group
$\phi :\mathbb {M}\to \mathbb {M}$
, a group
![]() $H\leq {\operatorname {Homeo}}^+(\mathbb {M})$
, and a surjective homomorphism
$H\leq {\operatorname {Homeo}}^+(\mathbb {M})$
, and a surjective homomorphism
![]() $\psi :G\to H$
, such that:
$\psi :G\to H$
, such that:
-
(1) the restriction of
 $\phi $
to
$\phi $
to
 $\Lambda $
is surjective, and every fiber has size at most
$\Lambda $
is surjective, and every fiber has size at most
 $2$
;
$2$
; -
(2) for each
 $g\in G$
,
$g\in G$
,
 $\phi \circ g=\psi (g)\circ \phi $
;
$\phi \circ g=\psi (g)\circ \phi $
; -
(3) the action of H on
 $\mathbb {M}$
is minimal.
$\mathbb {M}$
is minimal.
Using the above, we define the following process, which we call the minimalization of an action. We start with the action of a finitely generated group G on
![]() $\mathbb {R}$
(or
$\mathbb {R}$
(or
![]() $\mathbb {S}^1$
) by orientation-preserving homeomorphisms. We assume that this action is not minimal; in the case of
$\mathbb {S}^1$
) by orientation-preserving homeomorphisms. We assume that this action is not minimal; in the case of
![]() $\mathbb {R}$
, we assume that there is no discrete orbit, and in the case of
$\mathbb {R}$
, we assume that there is no discrete orbit, and in the case of
![]() $\mathbb {S}^1$
, we assume that there is no finite orbit. Using the above, we obtain the (possibly non-faithful) action of G on
$\mathbb {S}^1$
, we assume that there is no finite orbit. Using the above, we obtain the (possibly non-faithful) action of G on
![]() $\mathbb {R}$
(or
$\mathbb {R}$
(or
![]() $\mathbb {S}^1$
) which is minimal. This new action is called the minimalization of the original action, and is semiconjugate to the original. If the original action was minimal to begin with, then this is the same as the original action.
$\mathbb {S}^1$
) which is minimal. This new action is called the minimalization of the original action, and is semiconjugate to the original. If the original action was minimal to begin with, then this is the same as the original action.
For actions on the circle, a further property will be relevant for us. An action of a group G on
![]() $\mathbb {S}^1$
is said to be proximal if for every non-empty open arc
$\mathbb {S}^1$
is said to be proximal if for every non-empty open arc
![]() $J \subset \mathbb {S}^1$
and every proper arc
$J \subset \mathbb {S}^1$
and every proper arc
![]() $I \subset \mathbb {S}^1$
, there exists
$I \subset \mathbb {S}^1$
, there exists
![]() $f \in G$
such that
$f \in G$
such that
![]() $I \cdot f \subset J$
. We warn the reader that in the literature, this property is referred to by various other names, such as strongly proximal, extremely proximal, strongly expansive, or compact-open transitive (some of these properties have well-established and distinct meanings in topological dynamics that happen to coincide for the case of actions on the circle). In this article, we refer to it as proximal.
$I \cdot f \subset J$
. We warn the reader that in the literature, this property is referred to by various other names, such as strongly proximal, extremely proximal, strongly expansive, or compact-open transitive (some of these properties have well-established and distinct meanings in topological dynamics that happen to coincide for the case of actions on the circle). In this article, we refer to it as proximal.
Theorem 2.4. (Margulis [Reference Margulis29], see also [Reference Ghys18, §5.2])
Let G act faithfully and minimally on the circle. Suppose that G is non-abelian. Then:
-
(1) if the action is proximal, the centralizer of G in
 ${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is trivial;
${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is trivial; -
(2) otherwise, the centralizer of G in
 ${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is a finite cyclic group
${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is a finite cyclic group
 $\langle \theta \rangle $
, and the induced action of G on
$\langle \theta \rangle $
, and the induced action of G on
 $\mathbb {S}^1 / \langle \theta \rangle \cong \mathbb {S}^1$
is proximal.
$\mathbb {S}^1 / \langle \theta \rangle \cong \mathbb {S}^1$
is proximal.
Now we can push our minimalization process one step further. Given a minimal action of G on the circle such that the image of G in
![]() ${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is non-abelian, we obtain a proximal action of G on the circle, which we call the proximalization of the original action. If the original action was proximal to begin with, then this is the same as the original action.
${\operatorname {Homeo}}^+(\mathbb {S}^1)$
is non-abelian, we obtain a proximal action of G on the circle, which we call the proximalization of the original action. If the original action was proximal to begin with, then this is the same as the original action.
Proximal actions on the circle are especially relevant for type-
![]() $2$
actions on the line.
$2$
actions on the line.
Proposition 2.5. [Reference Malyutin28, Theorem 1]
Let G be a group, and let
![]() $\rho $
be a minimal type-
$\rho $
be a minimal type-
![]() $2$
action on
$2$
action on
![]() $\mathbb {R}$
by orientation-preserving homeomorphisms. Then there exists a fixed point-free homeomorphism
$\mathbb {R}$
by orientation-preserving homeomorphisms. Then there exists a fixed point-free homeomorphism
![]() $t \in {\operatorname {Homeo}}^+(\mathbb {R})$
which commutes with
$t \in {\operatorname {Homeo}}^+(\mathbb {R})$
which commutes with
![]() $\rho (G)$
, such that the induced action of G on
$\rho (G)$
, such that the induced action of G on
![]() $\mathbb {R}/\langle t \rangle \cong \mathbb {S}^1$
is proximal.
$\mathbb {R}/\langle t \rangle \cong \mathbb {S}^1$
is proximal.
Finally, we prove a basic fact about rotation numbers of homeomorphisms of the circle, which will be the crucial tool for our proof of Theorem 1.4. Let
![]() $g \in {\operatorname {Homeo}}^+(\mathbb {S}^1)$
, and let
$g \in {\operatorname {Homeo}}^+(\mathbb {S}^1)$
, and let
![]() $\overline {g}$
be a lift of g to the real line. Then the quantity
$\overline {g}$
be a lift of g to the real line. Then the quantity
is independent of the choice of
![]() $x \in \mathbb {R}$
, and moreover depends on the choice of lift only up to integers. In particular, the rotation number
$x \in \mathbb {R}$
, and moreover depends on the choice of lift only up to integers. In particular, the rotation number
![]() ${\operatorname {rot}}(g) \in \mathbb {R}/\mathbb {Z}$
is well defined.
${\operatorname {rot}}(g) \in \mathbb {R}/\mathbb {Z}$
is well defined.
Proposition 2.6. Let
![]() $\rho : G \to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
be a group action on the circle. Let
$\rho : G \to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
be a group action on the circle. Let
![]() $\rho _m$
be the minimalization of
$\rho _m$
be the minimalization of
![]() $\rho $
, and suppose that
$\rho $
, and suppose that
![]() $\rho _m(G)$
is non-abelian, so that there exists a proximalization
$\rho _m(G)$
is non-abelian, so that there exists a proximalization
![]() $\rho _p$
. Then there exists an integer
$\rho _p$
. Then there exists an integer
![]() $n \geq 1$
such that for all
$n \geq 1$
such that for all
![]() $g \in G$
, we have
$g \in G$
, we have
![]() ${\operatorname {rot}}(\rho _p(g)) = n {\operatorname {rot}}(\rho (g))$
. In particular, the rationality or irrationality of
${\operatorname {rot}}(\rho _p(g)) = n {\operatorname {rot}}(\rho (g))$
. In particular, the rationality or irrationality of
![]() ${\operatorname {rot}}(\rho (g))$
is preserved under proximalization.
${\operatorname {rot}}(\rho (g))$
is preserved under proximalization.
Proof. The rotation number of a circle homeomorphism is a semiconjugacy invariant [Reference Ghys18, §5.1]. In particular, if
![]() $\rho _m$
is the minimalization of
$\rho _m$
is the minimalization of
![]() $\rho $
, then for all
$\rho $
, then for all
![]() $g \in G$
, it holds that
$g \in G$
, it holds that
![]() ${\operatorname {rot}}(\rho _m(g)) = {\operatorname {rot}}(\rho (g))$
.
${\operatorname {rot}}(\rho _m(g)) = {\operatorname {rot}}(\rho (g))$
.
Now by Proposition 2.4, since
![]() $\rho _m(G)$
is non-abelian, there exists a (possibly trivial) finite-order homeomorphism
$\rho _m(G)$
is non-abelian, there exists a (possibly trivial) finite-order homeomorphism
![]() $\theta $
that centralizes
$\theta $
that centralizes
![]() $\rho _m(G)$
and such that the proximalization
$\rho _m(G)$
and such that the proximalization
![]() $\rho _p$
is the induced action on the quotient
$\rho _p$
is the induced action on the quotient
![]() $\mathbb {S}^1 / \langle \theta \rangle $
. Let
$\mathbb {S}^1 / \langle \theta \rangle $
. Let
![]() $n \geq 1$
be the order of
$n \geq 1$
be the order of
![]() $\theta $
. By [Reference Ghys18, Proposition 4.1], up to conjugacy and changing the generator of
$\theta $
. By [Reference Ghys18, Proposition 4.1], up to conjugacy and changing the generator of
![]() $\langle \theta \rangle $
, we may assume that
$\langle \theta \rangle $
, we may assume that
![]() $\theta $
is rotation by
$\theta $
is rotation by
![]() $1/n$
. It then follows from the definition of rotation numbers that
$1/n$
. It then follows from the definition of rotation numbers that
![]() ${\operatorname {rot}}(\rho_p(g)) = n {\operatorname {rot}}(\rho_m(g))$
, and we conclude.
${\operatorname {rot}}(\rho_p(g)) = n {\operatorname {rot}}(\rho_m(g))$
, and we conclude.
3 Groups in
 $\mathcal {G}$
and their lifts
$\mathcal {G}$
and their lifts
In this section, we state and prove various results about the groups
![]() $G\in \mathcal {G}$
that play a crucial role in our general construction. Given a group
$G\in \mathcal {G}$
that play a crucial role in our general construction. Given a group
![]() $G \in \mathcal {G}$
, recall that
$G \in \mathcal {G}$
, recall that
![]() $\overline {G}$
denotes the lift of G to the real line, that is, the group of all homeomorphisms of
$\overline {G}$
denotes the lift of G to the real line, that is, the group of all homeomorphisms of
![]() $\mathbb {R}$
that commute with integer translations and induce elements of G on the quotient
$\mathbb {R}$
that commute with integer translations and induce elements of G on the quotient
![]() $\mathbb {R}/\mathbb {Z}=\mathbb {S}^1$
. We have a central extension
$\mathbb {R}/\mathbb {Z}=\mathbb {S}^1$
. We have a central extension
Lemma 3.1. Let
![]() $G\in \mathcal {G}$
and let
$G\in \mathcal {G}$
and let
![]() $f\in \overline {G}$
be an element that does not lie in the center. Then f normally generates
$f\in \overline {G}$
be an element that does not lie in the center. Then f normally generates
![]() $\overline {G}$
.
$\overline {G}$
.
Proof. Let
![]() $N=\langle \!\langle f\rangle \!\rangle $
and let
$N=\langle \!\langle f\rangle \!\rangle $
and let
![]() $Z=Z(\overline {G})\cong \mathbb {Z}$
. The image of N under the quotient
$Z=Z(\overline {G})\cong \mathbb {Z}$
. The image of N under the quotient
![]() $\overline {G}\to G$
is a normal subgroup of G, and is non-trivial since N is not contained in Z. Since G is simple, this image must equal G. This implies
$\overline {G}\to G$
is a normal subgroup of G, and is non-trivial since N is not contained in Z. Since G is simple, this image must equal G. This implies
![]() $\overline {G}=NZ$
, so
$\overline {G}=NZ$
, so
![]() $\overline {G}/N\cong Z/(N\cap Z)$
is abelian. Now the fact that
$\overline {G}/N\cong Z/(N\cap Z)$
is abelian. Now the fact that
![]() $\overline {G}$
is perfect implies
$\overline {G}$
is perfect implies
![]() $N=\overline {G}$
.
$N=\overline {G}$
.
Lemma 3.2. For
![]() $G\in \mathcal {G}$
, every proper normal subgroup of
$G\in \mathcal {G}$
, every proper normal subgroup of
![]() $\overline {G}$
is central. Hence,
$\overline {G}$
is central. Hence,
![]() $\overline {G}$
has no proper non-trivial torsion-free quotients, and no non-trivial finite quotients.
$\overline {G}$
has no proper non-trivial torsion-free quotients, and no non-trivial finite quotients.
Proof. That every proper normal subgroup is central follows from Lemma 3.1. The center itself corresponds to the quotient G, which has torsion. For any other non-trivial proper normal subgroup, the generator of the center will map to a non-trivial torsion element in the quotient. All non-trivial quotients surject onto G, and thus are infinite.
Next, we want to study the possible dynamics of
![]() $\overline {G}$
(
$\overline {G}$
(
![]() $G\in \mathcal {G}$
) on the line (see [Reference Matte Bon and Triestino30, Theorem 8.7] for the case of Thompson’s group T).
$G\in \mathcal {G}$
) on the line (see [Reference Matte Bon and Triestino30, Theorem 8.7] for the case of Thompson’s group T).
Lemma 3.3. For
![]() $G\in \mathcal {G}$
, every fixed point-free action of
$G\in \mathcal {G}$
, every fixed point-free action of
![]() $\overline {G}$
by homeomorphisms on the line is semiconjugate to the standard action.
$\overline {G}$
by homeomorphisms on the line is semiconjugate to the standard action.
Proof. Let
![]() $\rho $
be a fixed point-free action of
$\rho $
be a fixed point-free action of
![]() $\overline {G}$
by orientation-preserving homeomorphisms on the line. Note that
$\overline {G}$
by orientation-preserving homeomorphisms on the line. Note that
![]() $\rho $
cannot fix a Radon measure because
$\rho $
cannot fix a Radon measure because
![]() $\overline {G}$
is perfect, and hence non-indicable. Therefore, via a semiconjugacy, we pass to a minimal action (Proposition 2.3), which we denote as
$\overline {G}$
is perfect, and hence non-indicable. Therefore, via a semiconjugacy, we pass to a minimal action (Proposition 2.3), which we denote as
![]() $\rho^{\prime} $
. We also know from Lemma 3.2 that
$\rho^{\prime} $
. We also know from Lemma 3.2 that
![]() $\rho^{\prime} $
must be a faithful action of
$\rho^{\prime} $
must be a faithful action of
![]() $\overline {G}$
. Since
$\overline {G}$
. Since
![]() $\overline {G}$
has a cofinal central element, it cannot admit a minimal faithful type-
$\overline {G}$
has a cofinal central element, it cannot admit a minimal faithful type-
![]() $3$
action [Reference Deroin, Navas and Rivas13, Proposition 3.5.12]. Therefore,
$3$
action [Reference Deroin, Navas and Rivas13, Proposition 3.5.12]. Therefore,
![]() $\rho^{\prime}$
is a type-
$\rho^{\prime}$
is a type-
![]() $2$
action. By Proposition 2.5, there exists a fixed point-free homeomorphism t that commutes with
$2$
action. By Proposition 2.5, there exists a fixed point-free homeomorphism t that commutes with
![]() $\rho^{\prime}(\overline{G})$
and such that the induced action of
$\rho^{\prime}(\overline{G})$
and such that the induced action of
![]() $\overline{G}$
on
$\overline{G}$
on
![]() $\mathbb {R}/ \langle t \rangle \cong \mathbb {S}^1$
is proximal.
$\mathbb {R}/ \langle t \rangle \cong \mathbb {S}^1$
is proximal.
Now, using our rigidity assumption on proximal actions of groups in
![]() $\mathcal {G}$
—together with the fact that the center must act trivially, by Theorem 2.4—this action is even topologically conjugate to the standard action of G. Lifting this conjugacy, we obtain that
$\mathcal {G}$
—together with the fact that the center must act trivially, by Theorem 2.4—this action is even topologically conjugate to the standard action of G. Lifting this conjugacy, we obtain that
![]() $\rho^{\prime}$
is conjugate to an action
$\rho^{\prime}$
is conjugate to an action
![]() $\rho^{\prime\prime}$
of
$\rho^{\prime\prime}$
of
![]() $\overline {G}$
on the line that sends the center to itself and induces the standard representation on the quotient G. In other words, we can write
$\overline {G}$
on the line that sends the center to itself and induces the standard representation on the quotient G. In other words, we can write
![]() $\rho^{\prime\prime} (g) = \rho _{st}(g) z^{i_g}$
, where z is the generator of the center and
$\rho^{\prime\prime} (g) = \rho _{st}(g) z^{i_g}$
, where z is the generator of the center and
![]() $i_g \in \mathbb {Z}$
. Since z is central, the map
$i_g \in \mathbb {Z}$
. Since z is central, the map
![]() $g \mapsto i_g$
is a homomorphism, which must be trivial because
$g \mapsto i_g$
is a homomorphism, which must be trivial because
![]() $\overline {G}$
is perfect. Therefore,
$\overline {G}$
is perfect. Therefore,
![]() $\rho^{\prime\prime} = \rho _{st}$
and we conclude.
$\rho^{\prime\prime} = \rho _{st}$
and we conclude.
Finally, we consider actions of
![]() $\overline {G}$
on the circle.
$\overline {G}$
on the circle.
Proposition 3.4. Let
![]() $G \in \mathcal {G}$
. Let
$G \in \mathcal {G}$
. Let
![]() $\rho $
be an action of
$\rho $
be an action of
![]() $\overline {G}$
on the circle without global fixed points, and let
$\overline {G}$
on the circle without global fixed points, and let
![]() $\rho _{st}$
be the standard action, that is, the one induced by the unique (up to conjugacy) proximal action of the quotient G. Then, for all
$\rho _{st}$
be the standard action, that is, the one induced by the unique (up to conjugacy) proximal action of the quotient G. Then, for all
![]() $g \in \overline {G}$
, it holds that
$g \in \overline {G}$
, it holds that
Proof. Let
![]() $\rho _m$
be the minimalization of
$\rho _m$
be the minimalization of
![]() $\rho $
. Since every non-trivial quotient of
$\rho $
. Since every non-trivial quotient of
![]() $\overline {G}$
surjects onto G,
$\overline {G}$
surjects onto G,
![]() $\rho _m(\overline {G})$
is not abelian, so we can produce a proximalization
$\rho _m(\overline {G})$
is not abelian, so we can produce a proximalization
![]() $\rho _p$
. By Theorem 2.4, the centralizer of
$\rho _p$
. By Theorem 2.4, the centralizer of
![]() $\rho _p(\overline {G})$
is trivial, therefore, the whole center of
$\rho _p(\overline {G})$
is trivial, therefore, the whole center of
![]() $\overline {G}$
lies in the kernel of
$\overline {G}$
lies in the kernel of
![]() $\rho _p$
. It follows that
$\rho _p$
. It follows that
![]() $\rho _p$
induces a proximal action of G, and so by the definition of
$\rho _p$
induces a proximal action of G, and so by the definition of
![]() $\mathcal {G}$
, we deduce that
$\mathcal {G}$
, we deduce that
![]() $\rho _p$
is conjugate to
$\rho _p$
is conjugate to
![]() $\rho _{st}$
. We conclude by Proposition 2.6 and the fact that rotation numbers are conjugacy-invariant [Reference Ghys18, §5.1].
$\rho _{st}$
. We conclude by Proposition 2.6 and the fact that rotation numbers are conjugacy-invariant [Reference Ghys18, §5.1].
3.1 Examples
Here we provide some examples of groups in
![]() $\mathcal {G}$
. We start with the most well-known example.
$\mathcal {G}$
. We start with the most well-known example.
Example 3.5. (Thompson)
Our first example is Thompson’s group T, which is the group of orientation-preserving piecewise linear homeomorphisms of the circle
![]() $\mathbb {R}/\mathbb {Z}$
stabilizing
$\mathbb {R}/\mathbb {Z}$
stabilizing
![]() $\mathbb {Z}[\tfrac 12]$
, with slopes in
$\mathbb {Z}[\tfrac 12]$
, with slopes in
![]() $2^{\mathbb {Z}}$
and breakpoints in
$2^{\mathbb {Z}}$
and breakpoints in
![]() $\mathbb {Z}[\tfrac 12]$
. It is well known that T lies in
$\mathbb {Z}[\tfrac 12]$
. It is well known that T lies in
![]() $\mathcal {G}$
and that it is of type
$\mathcal {G}$
and that it is of type
![]() $F_\infty $
; all necessary facts can be found in [Reference Brown3, Reference Cannon, Floyd and Parry10, Reference Ghys and Sergiescu19]. For the uniqueness of the action on the circle, this is only stated explicitly in [Reference Ghys and Sergiescu19] in a weaker form (uniqueness among
$F_\infty $
; all necessary facts can be found in [Reference Brown3, Reference Cannon, Floyd and Parry10, Reference Ghys and Sergiescu19]. For the uniqueness of the action on the circle, this is only stated explicitly in [Reference Ghys and Sergiescu19] in a weaker form (uniqueness among
![]() $C^2$
actions), however, it can be deduced from their cohomological computations or from the rest of the discussion in this section.
$C^2$
actions), however, it can be deduced from their cohomological computations or from the rest of the discussion in this section.
For the remainder of the examples, simplicity and torsion can be found in the literature, and perfection of the lift is easy to check and can sometimes be reduced to the case of T. The uniqueness of the proximal action is less well studied, but can be established via the following general criterion.
Theorem 3.6. [Reference Fournier-Facio, Löh and Moraschini15, Proposition 6.9], [Reference Fournier-Facio and Lodha14, Corollary 4.2]
Let
![]() $G \le {\operatorname {Homeo}}^+(\mathbb {S}^1)$
be either piecewise linear or piecewise projective. Suppose that there exists a dense orbit
$G \le {\operatorname {Homeo}}^+(\mathbb {S}^1)$
be either piecewise linear or piecewise projective. Suppose that there exists a dense orbit
![]() $Y \subset \mathbb {S}^1$
such that the action of G on positively oriented triples in Y is transitive. Then the given action of G on
$Y \subset \mathbb {S}^1$
such that the action of G on positively oriented triples in Y is transitive. Then the given action of G on
![]() $\mathbb {S}^1$
is proximal, and it is the unique proximal action of G on the circle, up to conjugacy.
$\mathbb {S}^1$
is proximal, and it is the unique proximal action of G on the circle, up to conjugacy.
This next example provides an infinite family of groups in
![]() $\mathcal {G}$
, which will be used in the proof of Corollary 1.5.
$\mathcal {G}$
, which will be used in the proof of Corollary 1.5.
Example 3.7. (Stein–Thompson)
For
![]() $n_1,\dots ,n_k\in \mathbb {N}$
(
$n_1,\dots ,n_k\in \mathbb {N}$
(
![]() $n_i\ge 2$
), let
$n_i\ge 2$
), let
![]() $\unicode{x3bb} := n_1\ldots n_k$
, let
$\unicode{x3bb} := n_1\ldots n_k$
, let
![]() $Y := \mathbb {Z}[{1}/{\unicode{x3bb} }]/\mathbb {Z}$
, and let
$Y := \mathbb {Z}[{1}/{\unicode{x3bb} }]/\mathbb {Z}$
, and let
![]() $P := \langle n_1, \ldots , n_k \rangle \leq \mathbb {R}^{\times }$
. The Stein–Thompson group
$P := \langle n_1, \ldots , n_k \rangle \leq \mathbb {R}^{\times }$
. The Stein–Thompson group
![]() $T_{n_1,\dots ,n_k}$
is the group of orientation-preserving piecewise linear homeomorphisms of the circle
$T_{n_1,\dots ,n_k}$
is the group of orientation-preserving piecewise linear homeomorphisms of the circle
![]() $\mathbb {R}/\mathbb {Z}$
, stabilizing Y, with slopes in P and breakpoints in Y; see [Reference Stein33]. When
$\mathbb {R}/\mathbb {Z}$
, stabilizing Y, with slopes in P and breakpoints in Y; see [Reference Stein33]. When
![]() $k=1$
and
$k=1$
and
![]() $n_1=2$
, we recover the classical Thompson’s group T.
$n_1=2$
, we recover the classical Thompson’s group T.
We claim that any Stein–Thompson group of the form
![]() $G := T_{2,3,n_3,\dots ,n_k}$
is in
$G := T_{2,3,n_3,\dots ,n_k}$
is in
![]() $\mathcal {G}$
, for example
$\mathcal {G}$
, for example
![]() $T_{2,3}$
. All Stein–Thompson groups clearly have torsion, and these particular Stein–Thompson groups are all simple [Reference Guelman, Liousse and Arnoux21]. Since
$T_{2,3}$
. All Stein–Thompson groups clearly have torsion, and these particular Stein–Thompson groups are all simple [Reference Guelman, Liousse and Arnoux21]. Since
![]() $\overline {T} \leq \overline {G}$
, we deduce that the group of translations is contained in the commutator subgroup of
$\overline {T} \leq \overline {G}$
, we deduce that the group of translations is contained in the commutator subgroup of
![]() $\overline {G}$
. Together with simplicity of G, this shows that
$\overline {G}$
. Together with simplicity of G, this shows that
![]() $\overline {G}$
is perfect.
$\overline {G}$
is perfect.
Finally, we claim that Theorem 3.6 applies, with Y as above; in fact, we claim that the action is transitive on positively ordered p-tuples for all
![]() $p \geq 1$
. Let
$p \geq 1$
. Let
![]() $x_1, \ldots , x_p$
and
$x_1, \ldots , x_p$
and
![]() $y_1, \ldots , y_p$
be two positively ordered p-tuples in Y. Then there exists some
$y_1, \ldots , y_p$
be two positively ordered p-tuples in Y. Then there exists some
![]() $q \geq 1$
such that the representatives of all
$q \geq 1$
such that the representatives of all
![]() $x_i$
and
$x_i$
and
![]() $y_i$
in
$y_i$
in
![]() $[0, 1)$
are integer multiples of
$[0, 1)$
are integer multiples of
![]() $\unicode{x3bb} ^{-q}$
. Setting
$\unicode{x3bb} ^{-q}$
. Setting
![]() $\mathbf {x} = \mathbf {y} = \{ 0, \ldots , 1 - \unicode{x3bb} ^{-q} \}\; \mod \mathbb {Z}$
includes both p-tuples inside larger tuples
$\mathbf {x} = \mathbf {y} = \{ 0, \ldots , 1 - \unicode{x3bb} ^{-q} \}\; \mod \mathbb {Z}$
includes both p-tuples inside larger tuples
![]() $\mathbf {x}, \mathbf {y}$
with the additional property that the difference between two consecutive points lies in P. Now, adding the midpoint of two consecutive points to
$\mathbf {x}, \mathbf {y}$
with the additional property that the difference between two consecutive points lies in P. Now, adding the midpoint of two consecutive points to
![]() $\mathbf {x}$
or
$\mathbf {x}$
or
![]() $\mathbf {y}$
keeps the elements of the tuple inside Y, and does not change the property that the difference between two consecutive points in
$\mathbf {y}$
keeps the elements of the tuple inside Y, and does not change the property that the difference between two consecutive points in
![]() $\mathbf {x}$
or
$\mathbf {x}$
or
![]() $\mathbf {y}$
lies in P. Therefore, we can add midpoints inductively to
$\mathbf {y}$
lies in P. Therefore, we can add midpoints inductively to
![]() $\mathbf {x}$
or
$\mathbf {x}$
or
![]() $\mathbf {y}$
to ensure that for each
$\mathbf {y}$
to ensure that for each
![]() $i = 1, \ldots , p$
, the number of points in the arc
$i = 1, \ldots , p$
, the number of points in the arc
![]() $\mathbf {x} \cap (x_{i-1}, x_i)$
is the same as the number of points in the arc
$\mathbf {x} \cap (x_{i-1}, x_i)$
is the same as the number of points in the arc
![]() $\mathbf {y} \cap (y_{i-1}, y_i)$
(where we abuse the notation and interpret
$\mathbf {y} \cap (y_{i-1}, y_i)$
(where we abuse the notation and interpret
![]() $x_0, y_0$
as
$x_0, y_0$
as
![]() $x_p, y_p$
). This ensures that the piecewise linear homeomorphism of
$x_p, y_p$
). This ensures that the piecewise linear homeomorphism of
![]() $\mathbb {S}^1$
sending
$\mathbb {S}^1$
sending
![]() $\mathbf {x}$
to
$\mathbf {x}$
to
![]() $\mathbf {y}$
and interpolating linearly also sends
$\mathbf {y}$
and interpolating linearly also sends
![]() $x_i$
to
$x_i$
to
![]() $y_i$
for each i. Since
$y_i$
for each i. Since
![]() $\mathbf {x}$
and
$\mathbf {x}$
and
![]() $\mathbf {y}$
are contained in Y, and the difference between two consecutive points is in the multiplicative group P, the corresponding homeomorphism of the circle is an element of G that sends
$\mathbf {y}$
are contained in Y, and the difference between two consecutive points is in the multiplicative group P, the corresponding homeomorphism of the circle is an element of G that sends
![]() $x_i$
to
$x_i$
to
![]() $y_i$
for each i, as desired.
$y_i$
for each i, as desired.
This shows that
![]() $T_{2,3,n_3,\dots ,n_k}$
is in
$T_{2,3,n_3,\dots ,n_k}$
is in
![]() $\mathcal {G}$
. Also note that all Stein–Thompson groups are of type
$\mathcal {G}$
. Also note that all Stein–Thompson groups are of type
![]() $F_\infty $
[Reference Stein33], and that any
$F_\infty $
[Reference Stein33], and that any
![]() $T_{2,3,n_3,\dots ,n_k}$
has elements with irrational rotation number [Reference Liousse25].
$T_{2,3,n_3,\dots ,n_k}$
has elements with irrational rotation number [Reference Liousse25].
We end with two more exotic examples.
Example 3.8. (Golden ratio Thompson)
Let
![]() $\tau := {(\sqrt {5} - 1)}/{2}$
be the small golden ratio. The golden ratio Thompson’s group
$\tau := {(\sqrt {5} - 1)}/{2}$
be the small golden ratio. The golden ratio Thompson’s group
![]() $T_{\tau }$
is a circle version of Cleary’s golden ratio Thompson’s group
$T_{\tau }$
is a circle version of Cleary’s golden ratio Thompson’s group
![]() $F_{\tau }$
[Reference Burillo, Nucinkis and Reeves7, Reference Cleary11], introduced in [Reference Burillo, Nucinkis and Reeves8]. The commutator subgroup
$F_{\tau }$
[Reference Burillo, Nucinkis and Reeves7, Reference Cleary11], introduced in [Reference Burillo, Nucinkis and Reeves8]. The commutator subgroup
![]() $T_\tau^{\prime}$
has index
$T_\tau^{\prime}$
has index
![]() $2$
and is simple [Reference Burillo, Nucinkis and Reeves8, Theorem 3.2]. Moreover, the action of
$2$
and is simple [Reference Burillo, Nucinkis and Reeves8, Theorem 3.2]. Moreover, the action of
![]() $T_\tau^{\prime}$
on
$T_\tau^{\prime}$
on
![]() $\mathbb {Z}[\tau ]$
is transitive on positively oriented n-tuples for all n [Reference Fournier-Facio and Lodha14, Lemmas 5.5 and 5.7], so Theorem 3.6 applies to
$\mathbb {Z}[\tau ]$
is transitive on positively oriented n-tuples for all n [Reference Fournier-Facio and Lodha14, Lemmas 5.5 and 5.7], so Theorem 3.6 applies to
![]() $T_\tau^{\prime}$
. Moreover,
$T_\tau^{\prime}$
. Moreover,
![]() $T_\tau^{\prime}$
is of type
$T_\tau^{\prime}$
is of type
![]() $F_\infty $
[Reference Fournier-Facio and Lodha14, Proposition 5.8], and the lift
$F_\infty $
[Reference Fournier-Facio and Lodha14, Proposition 5.8], and the lift
![]() $\overline {T_\tau^{\prime}}$
is perfect [Reference Fournier-Facio and Lodha14, Lemma 5.13]. Thus,
$\overline {T_\tau^{\prime}}$
is perfect [Reference Fournier-Facio and Lodha14, Lemma 5.13]. Thus,
![]() $T_\tau^{\prime}\in \mathcal {G}$
. Finally,
$T_\tau^{\prime}\in \mathcal {G}$
. Finally,
![]() $T_\tau^{\prime}$
clearly has elements with irrational rotation number, for instance, the rotation by
$T_\tau^{\prime}$
clearly has elements with irrational rotation number, for instance, the rotation by
![]() $2 \tau $
(see [Reference Fournier-Facio and Lodha14] for more detail).
$2 \tau $
(see [Reference Fournier-Facio and Lodha14] for more detail).
Example 3.9. (Piecewise projective)
The group S introduced in [Reference Lodha26] is simple, has torsion, and is of type
![]() $F_\infty $
[Reference Lodha and Zaremsky27]. It is a group of piecewise projective homeomorphisms of the circle
$F_\infty $
[Reference Lodha and Zaremsky27]. It is a group of piecewise projective homeomorphisms of the circle
![]() $\mathbb {R}\cup \{\infty \}$
, which is the real projective line. The action of S preserves
$\mathbb {R}\cup \{\infty \}$
, which is the real projective line. The action of S preserves
![]() $\mathbb {Q}\cup \{\infty \}$
, and it acts transitively on positively oriented triples of this set. (Indeed, the copy of T in S already acts transitively on such triples). Thus, Theorem 3.6 applies to S. Moreover,
$\mathbb {Q}\cup \{\infty \}$
, and it acts transitively on positively oriented triples of this set. (Indeed, the copy of T in S already acts transitively on such triples). Thus, Theorem 3.6 applies to S. Moreover,
![]() $\overline {S}$
is perfect with a similar argument as above: its derived subgroup contains
$\overline {S}$
is perfect with a similar argument as above: its derived subgroup contains
![]() $\overline {T}$
, and therefore all of the integer translations. Thus,
$\overline {T}$
, and therefore all of the integer translations. Thus,
![]() $S\in \mathcal {G}$
. We do not know whether S has elements with irrational rotation number.
$S\in \mathcal {G}$
. We do not know whether S has elements with irrational rotation number.
4 Monstrousness and the proof of Theorem 1.4
Now we can prove our main result.
Proof of Theorem 1.4
We recall our hypothesis:
![]() $G_1,G_2\in \mathcal {G}$
are groups such that
$G_1,G_2\in \mathcal {G}$
are groups such that
![]() $G_2$
contains an element with an irrational rotation number. For example, for the special case in Theorem 1.3, one can use
$G_2$
contains an element with an irrational rotation number. For example, for the special case in Theorem 1.3, one can use
![]() $G_1=T$
(Example 3.5) and
$G_1=T$
(Example 3.5) and
![]() $G_2=T_{2,3}$
(Example 3.7). We denote as usual by
$G_2=T_{2,3}$
(Example 3.7). We denote as usual by
![]() $\overline {G}_i$
the lift of the standard action of
$\overline {G}_i$
the lift of the standard action of
![]() $G_i$
, we let z denote the generator of the center of
$G_i$
, we let z denote the generator of the center of
![]() $\overline {G}_1$
, and let
$\overline {G}_1$
, and let
![]() $g\in \overline {G}_2$
denote a lift of an element of
$g\in \overline {G}_2$
denote a lift of an element of
![]() $G_2$
with irrational rotation number.
$G_2$
with irrational rotation number.
(1) The left orderability of M follows from the fact that an amalgamated product of two left orderable groups along a cyclic subgroup is left orderable [Reference Bludov and Glass1] (see [Reference Bludov and Glass2] for a more general result).
Being an amalgamated product of two perfect groups, M is perfect, therefore, it has no type-1 action. Now suppose by contradiction that M admits a fixed point-free type-
![]() $2$
action
$2$
action
![]() $\rho : M \to {\operatorname {Homeo}}^+(\mathbb {R})$
, which we may assume to be minimal by Proposition 2.3. This implies the existence of a fixed point-free element
$\rho : M \to {\operatorname {Homeo}}^+(\mathbb {R})$
, which we may assume to be minimal by Proposition 2.3. This implies the existence of a fixed point-free element
![]() $t \in {\operatorname {Homeo}}^+(\mathbb {R})$
that commutes with
$t \in {\operatorname {Homeo}}^+(\mathbb {R})$
that commutes with
![]() $\rho (M)$
. Up to conjugating our action by a suitable homeomorphism, we may assume for the rest of the proof that
$\rho (M)$
. Up to conjugating our action by a suitable homeomorphism, we may assume for the rest of the proof that
![]() $x\cdot t=x+1$
for each
$x\cdot t=x+1$
for each
![]() $x\in \mathbb {R}$
(this follows, for example, from Hölder’s theorem [Reference Deroin, Navas and Rivas13, Theorem 3.1.2]). Also, we declare
$x\in \mathbb {R}$
(this follows, for example, from Hölder’s theorem [Reference Deroin, Navas and Rivas13, Theorem 3.1.2]). Also, we declare
![]() $ H_1=\rho (\overline {G}_1)$
and
$ H_1=\rho (\overline {G}_1)$
and
![]() $H_2=\rho (\overline {G}_2)$
.
$H_2=\rho (\overline {G}_2)$
.
We first claim that neither
![]() $H_1$
nor
$H_1$
nor
![]() $H_2$
have global fixed points in
$H_2$
have global fixed points in
![]() $\mathbb {R}$
. Indeed, suppose by contradiction that
$\mathbb {R}$
. Indeed, suppose by contradiction that
![]() $H_1$
fixes a point x (the proof for
$H_1$
fixes a point x (the proof for
![]() $H_2$
is identical). Since
$H_2$
is identical). Since
![]() $\rho (M)$
has no global fixed points,
$\rho (M)$
has no global fixed points,
![]() $H_2$
does not fix x. Thus, there is an
$H_2$
does not fix x. Thus, there is an
![]() $H_2$
-invariant open interval J containing x on which the restriction of the action of
$H_2$
-invariant open interval J containing x on which the restriction of the action of
![]() $H_2$
is fixed point-free. Since
$H_2$
is fixed point-free. Since
![]() $\overline {G}_2$
does not have proper non-trivial torsion-free quotients by Lemma 3.2, this action on J is faithful.
$\overline {G}_2$
does not have proper non-trivial torsion-free quotients by Lemma 3.2, this action on J is faithful.
By Lemma 3.3, the action of
![]() $H_2$
on
$H_2$
on
![]() $J\cong \mathbb {R}$
is semiconjugate to the standard action. In particular,
$J\cong \mathbb {R}$
is semiconjugate to the standard action. In particular,
![]() $\rho (g)$
does not fix a point in J: otherwise the rotation number of the image of g in
$\rho (g)$
does not fix a point in J: otherwise the rotation number of the image of g in
![]() $G_2$
would be
$G_2$
would be
![]() $0$
. However, looking at the action of all of M, this contradicts the fact that
$0$
. However, looking at the action of all of M, this contradicts the fact that
![]() $\rho (g) = \rho (z) \in H_1$
fixes x. This proves our claim. Moreover, it follows from Lemma 3.3 that
$\rho (g) = \rho (z) \in H_1$
fixes x. This proves our claim. Moreover, it follows from Lemma 3.3 that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are semiconjugate to their standard actions on the real line.
$H_2$
are semiconjugate to their standard actions on the real line.
Now the quotient
![]() $\mathbb {R} \to \mathbb {R}/\langle t \rangle \cong \mathbb {S}^1$
induces a homomorphism
$\mathbb {R} \to \mathbb {R}/\langle t \rangle \cong \mathbb {S}^1$
induces a homomorphism
![]() $\phi :M\to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
with kernel
$\phi :M\to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
with kernel
![]() $\langle t\rangle \cap M$
. The restriction of
$\langle t\rangle \cap M$
. The restriction of
![]() $\phi $
to each
$\phi $
to each
![]() $\overline {G}_i$
is fixed point-free on
$\overline {G}_i$
is fixed point-free on
![]() $\mathbb {S}^1$
. Indeed, if it fixed a point, then this fixed point would lift to a discrete orbit, which would have to be fixed pointwise because
$\mathbb {S}^1$
. Indeed, if it fixed a point, then this fixed point would lift to a discrete orbit, which would have to be fixed pointwise because
![]() $\overline {G}_i$
is perfect (and hence non-indicable). However, we have already shown that the restriction of
$\overline {G}_i$
is perfect (and hence non-indicable). However, we have already shown that the restriction of
![]() $\rho $
to
$\rho $
to
![]() $\overline {G}_i$
has no global fixed points.
$\overline {G}_i$
has no global fixed points.
We can therefore use Proposition 3.4 on
![]() $\overline {G}_1$
to obtain
$\overline {G}_1$
to obtain
![]() ${\operatorname {rot}}(\phi (z)) \in \mathbb {Q}/\mathbb {Z}$
, and then on
${\operatorname {rot}}(\phi (z)) \in \mathbb {Q}/\mathbb {Z}$
, and then on
![]() $\overline {G}_2$
to obtain
$\overline {G}_2$
to obtain
![]() ${\operatorname {rot}}(\phi (g)) \notin \mathbb {Q}/\mathbb {Z}$
. However,
${\operatorname {rot}}(\phi (g)) \notin \mathbb {Q}/\mathbb {Z}$
. However,
![]() $\phi $
is an action of M, so
$\phi $
is an action of M, so
![]() $\phi (g) = \phi (z)$
, which is a contradiction.
$\phi (g) = \phi (z)$
, which is a contradiction.
(2) It is a standard fact that an amalgamation of two type
![]() $F_\infty $
groups along a type
$F_\infty $
groups along a type
![]() $F_\infty $
subgroup is of type
$F_\infty $
subgroup is of type
![]() $F_\infty $
; indeed, the amalgamation acts cocompactly on a tree with type
$F_\infty $
; indeed, the amalgamation acts cocompactly on a tree with type
![]() $F_{\infty }$
vertex and edge stabilizers, and hence is itself
$F_{\infty }$
vertex and edge stabilizers, and hence is itself
![]() $F_\infty $
, for example, by [Reference Brown3, Propositions 1.1 and 3.1]. The same holds for other finiteness properties, such as finite presentability. Therefore, part (
$F_\infty $
, for example, by [Reference Brown3, Propositions 1.1 and 3.1]. The same holds for other finiteness properties, such as finite presentability. Therefore, part (
![]() $2$
) of the theorem follows.
$2$
) of the theorem follows.
(3) We use the following fact [Reference Grigorchuk20] (see also [Reference Fujiwara16]): an amalgamated product
![]() $A *_C B$
has an infinite-dimensional space of homogeneous quasimorphisms whenever
$A *_C B$
has an infinite-dimensional space of homogeneous quasimorphisms whenever
![]() $C \neq B$
and C has at least
$C \neq B$
and C has at least
![]() $3$
double cosets in A. This automatically holds if C is not maximal in A, in particular, it applies to M, which therefore has an infinite-dimensional space of homogeneous quasimorphisms. Being moreover perfect, all such quasimorphisms represent non-trivial classes in bounded cohomology, and witness that M is not uniformly perfect [Reference Calegari9].
$3$
double cosets in A. This automatically holds if C is not maximal in A, in particular, it applies to M, which therefore has an infinite-dimensional space of homogeneous quasimorphisms. Being moreover perfect, all such quasimorphisms represent non-trivial classes in bounded cohomology, and witness that M is not uniformly perfect [Reference Calegari9].
(4) The fact that M admits a proximal action follows from the fact that the quotient of M by the normal closure of
![]() $\overline {G}_2$
is
$\overline {G}_2$
is
![]() $G_1$
, which acts proximally on the circle. We now show that this action of M is unique (up to conjugacy).
$G_1$
, which acts proximally on the circle. We now show that this action of M is unique (up to conjugacy).
Let
![]() $\rho $
be a proximal action of M on the circle. First, we claim that
$\rho $
be a proximal action of M on the circle. First, we claim that
![]() $\rho (g)$
fixes a point. Assume otherwise. In this case, we obtain that both actions
$\rho (g)$
fixes a point. Assume otherwise. In this case, we obtain that both actions
![]() $\rho (\overline {G}_1),\rho (\overline {G}_2)$
are fixed point-free, since the element
$\rho (\overline {G}_1),\rho (\overline {G}_2)$
are fixed point-free, since the element
![]() $\rho (g)=\rho (z)$
acts without fixed points on the circle and is contained in both actions. Since
$\rho (g)=\rho (z)$
acts without fixed points on the circle and is contained in both actions. Since
![]() $\overline {G}_1,\overline {G}_2$
do not admit non-trivial finite quotients by Lemma 3.2, it further follows that
$\overline {G}_1,\overline {G}_2$
do not admit non-trivial finite quotients by Lemma 3.2, it further follows that
![]() $\rho (\overline {G}_1),\rho (\overline {G}_2)$
do not admit a finite orbit. This means that they both admit proximalizations, using Theorems 2.1 and 2.4. Now, using the same argument as in the proof of part (
$\rho (\overline {G}_1),\rho (\overline {G}_2)$
do not admit a finite orbit. This means that they both admit proximalizations, using Theorems 2.1 and 2.4. Now, using the same argument as in the proof of part (
![]() $1$
), we obtain the contradiction that
$1$
), we obtain the contradiction that
![]() $\rho (g)=\rho (z)$
has both a rational and an irrational rotation number. This proves our claim that
$\rho (g)=\rho (z)$
has both a rational and an irrational rotation number. This proves our claim that
![]() $\rho (g)$
fixes a point in the circle.
$\rho (g)$
fixes a point in the circle.
Next, we claim that
![]() $\rho (\overline {G}_2)$
fixes a point in the circle. If not, again it also cannot admit a finite orbit, so by Theorems 2.1 and 2.4, it must admit a proximalization
$\rho (\overline {G}_2)$
fixes a point in the circle. If not, again it also cannot admit a finite orbit, so by Theorems 2.1 and 2.4, it must admit a proximalization
![]() $\rho^{\prime}$
. Since this is conjugate to the standard action (by our assumption on groups in
$\rho^{\prime}$
. Since this is conjugate to the standard action (by our assumption on groups in
![]() $\mathcal {G}$
), this means that
$\mathcal {G}$
), this means that
![]() $\rho^{\prime}(g)$
has an irrational rotation number. However, this is impossible, since
$\rho^{\prime}(g)$
has an irrational rotation number. However, this is impossible, since
![]() $\rho (g),\rho^{\prime}(g)$
are semiconjugate, and
$\rho (g),\rho^{\prime}(g)$
are semiconjugate, and
![]() $\rho (g)$
admits a fixed point, so it has rotation number
$\rho (g)$
admits a fixed point, so it has rotation number
![]() $0$
. This proves that
$0$
. This proves that
![]() $\rho (\overline {G}_2)$
fixes a point in the circle.
$\rho (\overline {G}_2)$
fixes a point in the circle.
The complement of
![]() $\mathrm{Fix}(\rho (\overline {G}_2))$
is a union of open intervals, each of which are individually
$\mathrm{Fix}(\rho (\overline {G}_2))$
is a union of open intervals, each of which are individually
![]() $\rho (\overline {G}_2)$
-invariant. Since
$\rho (\overline {G}_2)$
-invariant. Since
![]() $\overline {G}_2$
does not admit a non-trivial left orderable quotient by Lemma 3.2, the action of
$\overline {G}_2$
does not admit a non-trivial left orderable quotient by Lemma 3.2, the action of
![]() $\rho (\overline {G}_2)$
on each these intervals is faithful. Thanks to Lemma 3.3, each of these is semiconjugate to the standard action of
$\rho (\overline {G}_2)$
on each these intervals is faithful. Thanks to Lemma 3.3, each of these is semiconjugate to the standard action of
![]() $\overline {G}_2$
on
$\overline {G}_2$
on
![]() $\mathbb {R}$
. Since in the standard action, g does not fix a point, this implies that
$\mathbb {R}$
. Since in the standard action, g does not fix a point, this implies that
![]() $\mathrm{Fix}(\rho (\overline {G}_2))=\mathrm{Fix}(\rho (g))$
.
$\mathrm{Fix}(\rho (\overline {G}_2))=\mathrm{Fix}(\rho (g))$
.
Now let
![]() $X=\mathrm{Fix}(\rho (\overline {G}_2))=\mathrm{Fix}(\rho (g)) \subset \mathbb {S}^1$
. Clearly, X is a closed subset of the circle, and X is
$X=\mathrm{Fix}(\rho (\overline {G}_2))=\mathrm{Fix}(\rho (g)) \subset \mathbb {S}^1$
. Clearly, X is a closed subset of the circle, and X is
![]() $\rho (\overline {G}_1)$
-invariant, since
$\rho (\overline {G}_1)$
-invariant, since
![]() $\mathrm{Fix}(\rho (g))=\mathrm{Fix}(\rho (z))$
and
$\mathrm{Fix}(\rho (g))=\mathrm{Fix}(\rho (z))$
and
![]() $\rho (z)$
is central in
$\rho (z)$
is central in
![]() $\rho (\overline {G}_1)$
. Hence, X is a closed non-empty
$\rho (\overline {G}_1)$
. Hence, X is a closed non-empty
![]() $\rho (M)$
-invariant set. By the minimality of
$\rho (M)$
-invariant set. By the minimality of
![]() $\rho (M)$
, we conclude that
$\rho (M)$
, we conclude that
![]() $X=\mathbb {S}^1$
. It follows that the element
$X=\mathbb {S}^1$
. It follows that the element
![]() $\rho (g)=\rho (z)$
fixes the circle pointwise, and hence lies in the kernel
$\rho (g)=\rho (z)$
fixes the circle pointwise, and hence lies in the kernel
![]() $\rho :M\to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
. Therefore,
$\rho :M\to {\operatorname {Homeo}}^+(\mathbb {S}^1)$
. Therefore,
![]() $\rho (M)$
descends to a proximal action of
$\rho (M)$
descends to a proximal action of
![]() $G_1$
, which is unique by our assumption.
$G_1$
, which is unique by our assumption.
We conclude with the main corollary.
Proof of Corollary 1.5
Let
![]() $G_1,G_2,M$
be as in the statement of Theorem 1.4, and moreover assume that they are finitely presented (or type
$G_1,G_2,M$
be as in the statement of Theorem 1.4, and moreover assume that they are finitely presented (or type
![]() $F_\infty $
). Part (
$F_\infty $
). Part (
![]() $4$
) of Theorem 1.4 tells us that
$4$
) of Theorem 1.4 tells us that
![]() $G_1$
is an invariant for the isomorphism type of M. The class
$G_1$
is an invariant for the isomorphism type of M. The class
![]() $\mathcal {G}$
contains the finitely presented (even type
$\mathcal {G}$
contains the finitely presented (even type
![]() $F_\infty $
) groups
$F_\infty $
) groups
![]() $T_{2,3,n_3,\dots ,n_k}$
(Example 3.7), which are pairwise non-isomorphic [Reference Liousse25]. We conclude that finitely presented (even type
$T_{2,3,n_3,\dots ,n_k}$
(Example 3.7), which are pairwise non-isomorphic [Reference Liousse25]. We conclude that finitely presented (even type
![]() $F_\infty $
) M can also take on infinitely many isomorphism types.
$F_\infty $
) M can also take on infinitely many isomorphism types.
Acknowledgements
The first author was supported by an ETH Zürich Doc. Mobility Fellowship. The third author was supported by grant no. 635763 from the Simons Foundation.