Article contents
The inertial orientation dynamics of anisotropic particles in planar linear flows
Published online by Cambridge University Press: 04 April 2018
Abstract
In the Stokes limit, the trajectories of neutrally buoyant torque-free non-Brownian spheroids in ambient planar linear flows are well known. These flows form a one-parameter family, with the velocity gradient tensor given by 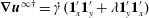 $\unicode[STIX]{x1D735}\boldsymbol{u}^{\infty \dagger }=\dot{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\unicode[STIX]{x1D706}\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })$. The parameter
$\unicode[STIX]{x1D735}\boldsymbol{u}^{\infty \dagger }=\dot{\unicode[STIX]{x1D6FE}}(\mathbf{1}_{x}^{\prime }\mathbf{1}_{y}^{\prime }+\unicode[STIX]{x1D706}\mathbf{1}_{y}^{\prime }\mathbf{1}_{x}^{\prime })$. The parameter 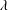 $\unicode[STIX]{x1D706}$ is related to the ratio of the vorticity to the extension (given by
$\unicode[STIX]{x1D706}$ is related to the ratio of the vorticity to the extension (given by 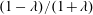 $(1-\unicode[STIX]{x1D706})/(1+\unicode[STIX]{x1D706})$), and ranges from
$(1-\unicode[STIX]{x1D706})/(1+\unicode[STIX]{x1D706})$), and ranges from 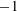 $-1$ to 1, with
$-1$ to 1, with 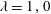 $\unicode[STIX]{x1D706}=1\,,0$ and
$\unicode[STIX]{x1D706}=1\,,0$ and 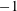 $-1$ being planar extensional flow, simple shear flow and solid-body rotation respectively. The unit vectors
$-1$ being planar extensional flow, simple shear flow and solid-body rotation respectively. The unit vectors 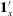 $\mathbf{1}_{x}^{\prime }$ and
$\mathbf{1}_{x}^{\prime }$ and 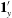 $\mathbf{1}_{y}^{\prime }$ are unit vectors along the flow and gradient axes of the simple shear flow (
$\mathbf{1}_{y}^{\prime }$ are unit vectors along the flow and gradient axes of the simple shear flow ( $\unicode[STIX]{x1D706}=0$). The trajectories, as described by a unit vector along the spheroid symmetry axis, are closed orbits for
$\unicode[STIX]{x1D706}=0$). The trajectories, as described by a unit vector along the spheroid symmetry axis, are closed orbits for 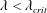 $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$, where
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$, where 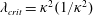 $\unicode[STIX]{x1D706}_{crit}=\unicode[STIX]{x1D705}^{2}(1/\unicode[STIX]{x1D705}^{2})$ for an oblate (a prolate) spheroid of aspect ratio
$\unicode[STIX]{x1D706}_{crit}=\unicode[STIX]{x1D705}^{2}(1/\unicode[STIX]{x1D705}^{2})$ for an oblate (a prolate) spheroid of aspect ratio  $\unicode[STIX]{x1D705}$. We investigate analytically the orientation dynamics of such a spheroid in the presence of weak inertial effects. The inertial corrections to the angular velocities at
$\unicode[STIX]{x1D705}$. We investigate analytically the orientation dynamics of such a spheroid in the presence of weak inertial effects. The inertial corrections to the angular velocities at 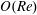 $O(Re)$ and
$O(Re)$ and 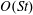 $O(St)$, where
$O(St)$, where 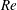 $Re$ and
$Re$ and 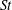 $St$ are the Reynolds (
$St$ are the Reynolds (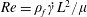 $Re=\unicode[STIX]{x1D70C}_{f}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$) and Stokes numbers (
$Re=\unicode[STIX]{x1D70C}_{f}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$) and Stokes numbers (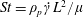 $St=\unicode[STIX]{x1D70C}_{p}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$) respectively, are derived using a reciprocal theorem formulation. Here,
$St=\unicode[STIX]{x1D70C}_{p}\dot{\unicode[STIX]{x1D6FE}}L^{2}/\unicode[STIX]{x1D707}$) respectively, are derived using a reciprocal theorem formulation. Here, 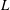 $L$ is the semimajor axis of the spheroid,
$L$ is the semimajor axis of the spheroid, 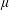 $\unicode[STIX]{x1D707}$ is the viscosity of the suspending fluid,
$\unicode[STIX]{x1D707}$ is the viscosity of the suspending fluid, 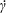 $\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate, and
$\dot{\unicode[STIX]{x1D6FE}}$ is the shear rate, and 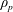 $\unicode[STIX]{x1D70C}_{p}$ and
$\unicode[STIX]{x1D70C}_{p}$ and 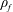 $\unicode[STIX]{x1D70C}_{f}$ are the particle and fluid densities respectively. A spheroidal harmonics formalism is then used to evaluate the reciprocal theorem integrals and obtain closed-form expressions for the inertial corrections. The detailed examination of these corrections is restricted to the aforementioned Stokesian closed-orbit regime (
$\unicode[STIX]{x1D70C}_{f}$ are the particle and fluid densities respectively. A spheroidal harmonics formalism is then used to evaluate the reciprocal theorem integrals and obtain closed-form expressions for the inertial corrections. The detailed examination of these corrections is restricted to the aforementioned Stokesian closed-orbit regime (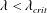 $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$). Here, even weak inertia, for asymptotically long times, of
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$). Here, even weak inertia, for asymptotically long times, of 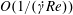 $O(1/(\dot{\unicode[STIX]{x1D6FE}}Re))$ or
$O(1/(\dot{\unicode[STIX]{x1D6FE}}Re))$ or 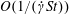 $O(1/(\dot{\unicode[STIX]{x1D6FE}}St))$, will affect the leading-order orientation distribution on account of the indeterminate nature of the distribution across orbits in the Stokes limit. For
$O(1/(\dot{\unicode[STIX]{x1D6FE}}St))$, will affect the leading-order orientation distribution on account of the indeterminate nature of the distribution across orbits in the Stokes limit. For 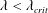 $\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$, inertia results in a drift across the closed orbits in Stokes flow, and this orbital drift is characterized using a multiple time scale analysis. The orbits stabilized by the inertial drift, at
$\unicode[STIX]{x1D706}<\unicode[STIX]{x1D706}_{crit}$, inertia results in a drift across the closed orbits in Stokes flow, and this orbital drift is characterized using a multiple time scale analysis. The orbits stabilized by the inertial drift, at 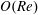 $O(Re)$ and
$O(Re)$ and 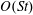 $O(St)$, are identified in the
$O(St)$, are identified in the 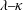 $\unicode[STIX]{x1D706}{-}\unicode[STIX]{x1D705}$ plane. For the majority of (
$\unicode[STIX]{x1D706}{-}\unicode[STIX]{x1D705}$ plane. For the majority of (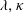 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$) combinations, the stabilized orbit is either one confined to the plane of symmetry (the flow-gradient plane) of the ambient flow (the tumbling orbit) or one where the spheroid is aligned with the ambient vorticity vector (the spinning orbit). However, for some (
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$) combinations, the stabilized orbit is either one confined to the plane of symmetry (the flow-gradient plane) of the ambient flow (the tumbling orbit) or one where the spheroid is aligned with the ambient vorticity vector (the spinning orbit). However, for some (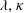 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$) combinations, depending on the initial orientation, the orbit stabilized can be either the spinning or the tumbling orbit, since both orbits have non-trivial basins of attraction, separated by a pair of unstable (repelling) limit cycles, on the unit sphere of orientations. A stochastic orientation decorrelation mechanism in the form of rotary Brownian motion, characterized by a Péclet number,
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D705}$) combinations, depending on the initial orientation, the orbit stabilized can be either the spinning or the tumbling orbit, since both orbits have non-trivial basins of attraction, separated by a pair of unstable (repelling) limit cycles, on the unit sphere of orientations. A stochastic orientation decorrelation mechanism in the form of rotary Brownian motion, characterized by a Péclet number, 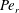 $Pe_{r}$ (
$Pe_{r}$ (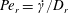 $Pe_{r}=\dot{\unicode[STIX]{x1D6FE}}/D_{r}$, where
$Pe_{r}=\dot{\unicode[STIX]{x1D6FE}}/D_{r}$, where 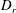 $D_{r}$ is the rotary Brownian diffusivity), is included to eliminate the aforementioned dependence on the initial orientation distribution for certain (
$D_{r}$ is the rotary Brownian diffusivity), is included to eliminate the aforementioned dependence on the initial orientation distribution for certain (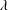 $\unicode[STIX]{x1D706}$,
$\unicode[STIX]{x1D706}$,  $\unicode[STIX]{x1D705}$) combinations. The unique steady-state orientation distribution determined by the combined effect of Brownian motion and inertia is obtained by solving a closed-orbit-averaged drift–diffusion equation. The steady-state orientation dynamics of an inertial spheroid in a planar linear flow, in the presence of weak thermal orientation fluctuations, has similarities to the thermodynamic description of a one-component system. Thus, we identify a tumbling–spinning transition in a
$\unicode[STIX]{x1D705}$) combinations. The unique steady-state orientation distribution determined by the combined effect of Brownian motion and inertia is obtained by solving a closed-orbit-averaged drift–diffusion equation. The steady-state orientation dynamics of an inertial spheroid in a planar linear flow, in the presence of weak thermal orientation fluctuations, has similarities to the thermodynamic description of a one-component system. Thus, we identify a tumbling–spinning transition in a 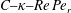 $C{-}\unicode[STIX]{x1D705}{-}Re\,Pe_{r}$ space. Here,
$C{-}\unicode[STIX]{x1D705}{-}Re\,Pe_{r}$ space. Here, 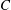 $C$ is the orbital coordinate that acts as a label for the closed orbits in the Stokes limit. This transition implies hysteretic orientation dynamics in certain regions in the
$C$ is the orbital coordinate that acts as a label for the closed orbits in the Stokes limit. This transition implies hysteretic orientation dynamics in certain regions in the 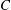 $C$–
$C$– $\unicode[STIX]{x1D705}$–
$\unicode[STIX]{x1D705}$–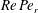 $Re\,Pe_{r}$ space, although the hysteretic volume shrinks rapidly on either side of simple shear flow. In the hysteretic region, one requires exceedingly large times to achieve the unique steady-state distribution (underlying the thermodynamic interpretation), and for durations relevant to experiments, the system may instead attain an initial-condition-dependent metastable distribution.
$Re\,Pe_{r}$ space, although the hysteretic volume shrinks rapidly on either side of simple shear flow. In the hysteretic region, one requires exceedingly large times to achieve the unique steady-state distribution (underlying the thermodynamic interpretation), and for durations relevant to experiments, the system may instead attain an initial-condition-dependent metastable distribution.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
A correction has been issued for this article:
- 23
- Cited by
Linked content
Please note a has been issued for this article.

