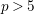1 Introduction
All varieties are assumed to be over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
.
$p>5$
.
The log minimal model program (LMMP) for klt threefold pairs in characteristic
![]() $p>5$
has recently been completed [Reference Birkar5, Reference Birkar and Waldron6, Reference Hacon and Xu11, Reference Keel13]. Here we prove some results on the LMMP for log canonical threefold pairs in characteristic
$p>5$
has recently been completed [Reference Birkar5, Reference Birkar and Waldron6, Reference Hacon and Xu11, Reference Keel13]. Here we prove some results on the LMMP for log canonical threefold pairs in characteristic
![]() $p>5$
. Our proofs rely on the LMMP for klt pairs in a crucial way.
$p>5$
. Our proofs rely on the LMMP for klt pairs in a crucial way.
Our main results are the following:
Theorem 1.1. (Good log minimal models 1)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
with
$p>5$
with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
, together with a projective contraction
$B$
, together with a projective contraction
![]() $X\rightarrow Z$
. Suppose that
$X\rightarrow Z$
. Suppose that
![]() $K_{X}+B$
is nef
$K_{X}+B$
is nef
![]() $/Z$
and big
$/Z$
and big
![]() $/Z$
. Then
$/Z$
. Then
![]() $K_{X}+B$
is semi-ample
$K_{X}+B$
is semi-ample
![]() $/Z$
.
$/Z$
.
Theorem 1.2. (Good log minimal models 2)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
with
$p>5$
with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
, together with a projective contraction
$B$
, together with a projective contraction
![]() $X\rightarrow Z$
. Suppose that
$X\rightarrow Z$
. Suppose that
![]() $A$
is a big and semi-ample
$A$
is a big and semi-ample
![]() $/Z$
$/Z$
![]() $\mathbb{R}$
-divisor such that
$\mathbb{R}$
-divisor such that
![]() $K_{X}+B+A$
is nef
$K_{X}+B+A$
is nef
![]() $/Z$
. Then
$/Z$
. Then
![]() $K_{X}+B+A$
is semi-ample
$K_{X}+B+A$
is semi-ample
![]() $/Z$
.
$/Z$
.
Similar results in characteristic zero were proven in [Reference Birkar4], and also in great generality in [Reference Fujino8] using vanishing theorems. In place of vanishing theorems we use Keel’s theorem [Reference Keel13], which says that a line bundle in positive characteristic is semi-ample if and only if it is semi-ample when restricted to its exceptional locus. We use the LMMP to replace
![]() $(X,B)$
with a dlt pair
$(X,B)$
with a dlt pair
![]() $(Y,B_{Y})$
such that the exceptional locus of
$(Y,B_{Y})$
such that the exceptional locus of
![]() $K_{Y}+B_{Y}$
is contained in the reduced part
$K_{Y}+B_{Y}$
is contained in the reduced part
![]() $\left\lfloor B_{Y}\right\rfloor$
of
$\left\lfloor B_{Y}\right\rfloor$
of
![]() $B_{Y}$
. We can then obtain semi-ampleness of the restriction to the exceptional locus by using adjunction to a partial normalization of
$B_{Y}$
. We can then obtain semi-ampleness of the restriction to the exceptional locus by using adjunction to a partial normalization of
![]() $\left\lfloor B_{Y}\right\rfloor$
and applying abundance for semi-log canonical surfaces [Reference Tanaka21].
$\left\lfloor B_{Y}\right\rfloor$
and applying abundance for semi-log canonical surfaces [Reference Tanaka21].
Thus one of the main technical results used in the proof is the following:
Theorem 1.3. Let
![]() $(Y,B_{Y})$
be a projective
$(Y,B_{Y})$
be a projective
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
with
$p>5$
with
![]() $\mathbb{Q}$
-boundary
$\mathbb{Q}$
-boundary
![]() $B_{Y}$
, such that
$B_{Y}$
, such that
![]() $K_{Y}+B_{Y}$
is nef. Then
$K_{Y}+B_{Y}$
is nef. Then
![]() $(K_{Y}+B_{Y})|_{\left\lfloor B_{Y}\right\rfloor }$
is semi-ample.
$(K_{Y}+B_{Y})|_{\left\lfloor B_{Y}\right\rfloor }$
is semi-ample.
Theorems 1.1 and 1.2 can be used to contract an extremal ray via a projective morphism.
Corollary 1.4. (Contraction theorem)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Suppose
$B$
. Suppose
![]() $R$
is a
$R$
is a
![]() $K_{X}+B$
-negative extremal ray. Then there exists a projective contraction
$K_{X}+B$
-negative extremal ray. Then there exists a projective contraction
![]() $X\rightarrow Z$
contracting precisely the curves in
$X\rightarrow Z$
contracting precisely the curves in
![]() $R$
.
$R$
.
In particular, this gives projective flipping contractions, and we can also apply Theorem 1.1 to construct flips.
Corollary 1.5. (Existence of flips)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Suppose there is an extremal
$B$
. Suppose there is an extremal
![]() $K_{X}+B$
-flipping contraction
$K_{X}+B$
-flipping contraction
![]() $f:X\rightarrow Z$
. Then the flip of
$f:X\rightarrow Z$
. Then the flip of
![]() $f$
exists.
$f$
exists.
We also use the ascending chain condition (ACC) for log canonical thresholds to show that any LMMP which begins from an effective pair terminates, as in characteristic zero [Reference Birkar2].
Theorem 1.6. (Termination for effective pairs)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Then any sequence of
$B$
. Then any sequence of
![]() $K_{X}+B$
-flips which are also
$K_{X}+B$
-flips which are also
![]() $M$
-flips for some
$M$
-flips for some
![]() $\mathbb{R}$
-Cartier
$\mathbb{R}$
-Cartier
![]() $M\geqslant 0$
terminates.
$M\geqslant 0$
terminates.
In Section 3, we extend the cone theorem to log canonical
![]() $3$
-folds in characteristic
$3$
-folds in characteristic
![]() $p>5$
. Note that this gives new information even in the klt case if the variety is not
$p>5$
. Note that this gives new information even in the klt case if the variety is not
![]() $\mathbb{Q}$
-factorial.
$\mathbb{Q}$
-factorial.
Theorem 1.7. (Cone theorem)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Then there exists a countable collection of rational curves
$B$
. Then there exists a countable collection of rational curves
![]() $\{C_{i}\}$
on
$\{C_{i}\}$
on
![]() $X$
such that:
$X$
such that:
(1)
 $\overline{NE}_{1}(X)=\overline{NE}_{1}(X)\cap (K_{X}+B)_{{\geqslant}0}+\sum _{i}\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]$
.
$\overline{NE}_{1}(X)=\overline{NE}_{1}(X)\cap (K_{X}+B)_{{\geqslant}0}+\sum _{i}\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]$
.(2)
 $-6\leqslant (K_{X}+B)\cdot C_{i}<0$
.
$-6\leqslant (K_{X}+B)\cdot C_{i}<0$
.(3) For any ample
 $\mathbb{R}$
-divisor
$\mathbb{R}$
-divisor
 $A$
,
$A$
,
 $(K_{X}+B+A)\cdot C_{i}\geqslant 0$
for all but finitely many
$(K_{X}+B+A)\cdot C_{i}\geqslant 0$
for all but finitely many
 $i$
.
$i$
.(4) The rays
 $\{\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]\}$
do not accumulate in
$\{\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]\}$
do not accumulate in
 $(K_{X}+B)_{{<}0}$
.
$(K_{X}+B)_{{<}0}$
.
Putting all of our results together allows us to deduce the following:
Corollary 1.8. (Log minimal models)
Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Suppose there is a projective contraction
$B$
. Suppose there is a projective contraction
![]() $X\rightarrow Z$
, such that there exists
$X\rightarrow Z$
, such that there exists
![]() $M\geqslant 0$
with
$M\geqslant 0$
with
![]() $K_{X}+B\equiv M/Z$
. Then there exists a log minimal model
$K_{X}+B\equiv M/Z$
. Then there exists a log minimal model
![]() $(Y/Z,B_{Y})$
for
$(Y/Z,B_{Y})$
for
![]() $(X/Z,B)$
, such that
$(X/Z,B)$
, such that
![]() $Y{\dashrightarrow}X$
does not contract divisors.
$Y{\dashrightarrow}X$
does not contract divisors.
In fact this log minimal model can be produced by running a terminating LMMP
![]() $/Z$
starting from
$/Z$
starting from
![]() $(X/Z,B)$
.
$(X/Z,B)$
.
If in addition
![]() $K_{X}+B$
is big
$K_{X}+B$
is big
![]() $/Z$
then this log minimal model is good.
$/Z$
then this log minimal model is good.
A stronger version of Theorem 1.1 over
![]() $\overline{\mathbb{F}}_{p}$
was proven by Martinelli et al. in [Reference Martinelli, Nakamura and Witaszek18], using different methods. A version of our Theorem 1.2 over
$\overline{\mathbb{F}}_{p}$
was proven by Martinelli et al. in [Reference Martinelli, Nakamura and Witaszek18], using different methods. A version of our Theorem 1.2 over
![]() $\overline{\mathbb{F}}_{p}$
has been obtained independently in [Reference Nakamura and Witaszek19] by Nakamura and Witaszek using methods similar to our own proof of Theorem 1.2 in Section 6. A similar method was also used for
$\overline{\mathbb{F}}_{p}$
has been obtained independently in [Reference Nakamura and Witaszek19] by Nakamura and Witaszek using methods similar to our own proof of Theorem 1.2 in Section 6. A similar method was also used for
![]() $4$
-folds in characteristic zero in [Reference Hashizume12].
$4$
-folds in characteristic zero in [Reference Hashizume12].
The layout of our paper is as follows. We first prove the cone theorem (Theorem 1.7) in Section 3. We then prove the termination result (Theorem 1.6) in Section 4. Next we come to our main results, proving Theorem 1.3 in Section 5 on the way to Theorem 1.1 and Theorem 1.2 in Section 6. Finally we prove the remaining results, Corollaries 1.5, 1.4 and 1.8, in Section 7.
2 Preliminaries
2.1 Semi-ampleness results in positive characteristic
This section summarizes some special features of positive characteristic which we use later. The first is a criterion for semi-ampleness due to Keel.
Definition 2.1. [Reference Keel13, 0.1]
Let
![]() $X$
be a scheme proper over a field, with nef line bundle
$X$
be a scheme proper over a field, with nef line bundle
![]() $L$
. The exceptional locus
$L$
. The exceptional locus
![]() $\mathbb{E}(L)$
of
$\mathbb{E}(L)$
of
![]() $L$
is defined to be the Zariski closure of the union of all subvarieties
$L$
is defined to be the Zariski closure of the union of all subvarieties
![]() $V$
of
$V$
of
![]() $X$
such that
$X$
such that
![]() $L|_{V}$
is not big, given the reduced scheme structure.
$L|_{V}$
is not big, given the reduced scheme structure.
Proposition 2.2. [Reference Keel13, 1.9]
Let
![]() $X$
be a scheme projective over a field of positive characteristic, with a nef line bundle
$X$
be a scheme projective over a field of positive characteristic, with a nef line bundle
![]() $L$
. Then
$L$
. Then
![]() $L$
is semi-ample if and only if
$L$
is semi-ample if and only if
![]() $L|_{\mathbb{E}(L)}$
is semi-ample.
$L|_{\mathbb{E}(L)}$
is semi-ample.
A universal homeomorphism is a morphism of varieties which remains a homeomorphism after arbitrary base change. For finite morphisms, this is equivalent to a simple condition:
Proposition 2.3. [Reference Grothendieck and Dieudonné9, I.3.7-8],[Reference Kollár16, 49]
For a finite morphism
![]() $f:Y\rightarrow X$
, the following are equivalent:
$f:Y\rightarrow X$
, the following are equivalent:
(1)
 $f$
is a universal homeomorphism.
$f$
is a universal homeomorphism.(2)
 $f$
is surjective and injective on geometric points.
$f$
is surjective and injective on geometric points.
Any finite universal homeomorphism can be composed with some other finite universal homeomorphism to give a power of the Frobenius morphism. This allows us to move information on line bundles in the reverse direction to usual:
Proposition 2.4. [Reference Keel13, 1.4]
Let
![]() $f:X\rightarrow Y$
be a finite universal homeomorphism between schemes of finite type over a field of positive characteristic. Let
$f:X\rightarrow Y$
be a finite universal homeomorphism between schemes of finite type over a field of positive characteristic. Let
![]() $L$
be a line bundle on
$L$
be a line bundle on
![]() $Y$
. Then
$Y$
. Then
![]() $L$
is semi-ample if and only if
$L$
is semi-ample if and only if
![]() $f^{\ast }L$
is semi-ample.
$f^{\ast }L$
is semi-ample.
2.2 Demi-normality
We describe a generalization of normality particularly suited to use in the LMMP.
Definition 2.5. A scheme satisfies Serre’s
![]() $S_{2}$
condition at
$S_{2}$
condition at
![]() $x\in X$
if
$x\in X$
if
Proposition 2.6. [Reference Grothendieck and Dieudonné10, 5.10–11], [Reference Alexeev1, Section 2]
If
![]() $X$
is a quasiprojective, reduced, equidimensional variety, then the set
$X$
is a quasiprojective, reduced, equidimensional variety, then the set
![]() $U$
where
$U$
where
![]() $X$
satisfies
$X$
satisfies
![]() $S_{2}$
is open and
$S_{2}$
is open and
![]() $\text{codim}(X-U,X)\geqslant 2$
. There exists a birational morphism
$\text{codim}(X-U,X)\geqslant 2$
. There exists a birational morphism
![]() $\unicode[STIX]{x1D719}:Y\rightarrow X$
, called the
$\unicode[STIX]{x1D719}:Y\rightarrow X$
, called the
![]() $S_{2}$
-fication, such that the following hold:
$S_{2}$
-fication, such that the following hold:
(i) For
 $x\in X$
,
$x\in X$
,
 $X$
satisfies
$X$
satisfies
 $S_{2}$
at
$S_{2}$
at
 $x$
if and only if
$x$
if and only if
 $\unicode[STIX]{x1D719}$
is an isomorphism at
$\unicode[STIX]{x1D719}$
is an isomorphism at
 $x$
.
$x$
.(ii)
 $Y$
satisfies
$Y$
satisfies
 $S_{2}$
at all points.
$S_{2}$
at all points.(iii)
 $\unicode[STIX]{x1D719}$
is finite and the normalization of
$\unicode[STIX]{x1D719}$
is finite and the normalization of
 $X$
factors through
$X$
factors through
 $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Remark 2.7. This partial normalization is also called by various other names in the literature, for example the
![]() $S_{2}$
-ization,
$S_{2}$
-ization,
![]() $Z^{[2]}$
-closure and saturation in codimension
$Z^{[2]}$
-closure and saturation in codimension
![]() $2$
.
$2$
.
The best generalization of normality for the purposes of the LMMP is demi-normality:
Definition 2.8. [Reference Kollár15]
A scheme is demi-normal if it is
![]() $S_{2}$
and has at worst nodes in codimension
$S_{2}$
and has at worst nodes in codimension
![]() $1$
.
$1$
.
For example, in characteristic zero, the reduced part of the boundary of a dlt pair is demi-normal [Reference Kollár14, 17.5].
2.3 Singularities of the LMMP
Here we define the singularity classes most commonly encountered in the LMMP. For more information, see [Reference Kollár15]. This work is concerned with extending results known for klt
![]() $3$
-fold pairs to log canonical
$3$
-fold pairs to log canonical
![]() $3$
-fold pairs.
$3$
-fold pairs.
Definition 2.9. Let
![]() $k$
be an algebraically closed field. A pair
$k$
be an algebraically closed field. A pair
![]() $(X,B)$
over
$(X,B)$
over
![]() $k$
consists of a normal variety
$k$
consists of a normal variety
![]() $X$
over
$X$
over
![]() $k$
and an effective
$k$
and an effective
![]() $\mathbb{R}$
-divisor
$\mathbb{R}$
-divisor
![]() $B$
, called the boundary, such that
$B$
, called the boundary, such that
![]() $K_{X}+B$
is
$K_{X}+B$
is
![]() $\mathbb{R}$
-Cartier. Given a birational morphism
$\mathbb{R}$
-Cartier. Given a birational morphism
![]() $\unicode[STIX]{x1D719}:Y\rightarrow X$
from another normal variety, we can define
$\unicode[STIX]{x1D719}:Y\rightarrow X$
from another normal variety, we can define
![]() $B_{Y}$
to be the unique
$B_{Y}$
to be the unique
![]() $\mathbb{R}$
-divisor satisfying
$\mathbb{R}$
-divisor satisfying
![]() $\unicode[STIX]{x1D719}_{\ast }B_{Y}=B$
and
$\unicode[STIX]{x1D719}_{\ast }B_{Y}=B$
and
For a prime Weil divisor
![]() $D$
on such a birational model
$D$
on such a birational model
![]() $Y$
, we define the log discrepancy of
$Y$
, we define the log discrepancy of
![]() $D$
with respect to
$D$
with respect to
![]() $(X,B)$
to be
$(X,B)$
to be
![]() $a(D,X,B):=1-b$
where
$a(D,X,B):=1-b$
where
![]() $b$
is the coefficient of
$b$
is the coefficient of
![]() $D$
in
$D$
in
![]() $B_{Y}$
.
$B_{Y}$
.
We say the pair
![]() $(X,B)$
is:
$(X,B)$
is:
∙ Kawamata log terminal (klt) if all
 $D$
on all birational models of
$D$
on all birational models of
 $X$
have
$X$
have
 $a(D,X,B)>0$
.
$a(D,X,B)>0$
.∙ Log canonical if all
 $D$
on all birational models of
$D$
on all birational models of
 $X$
have
$X$
have
 $a(D,X,B)\geqslant 0$
.
$a(D,X,B)\geqslant 0$
.
A log canonical center of
![]() $(X,B)$
is the image on
$(X,B)$
is the image on
![]() $X$
of a divisor of log discrepancy zero with respect to
$X$
of a divisor of log discrepancy zero with respect to
![]() $(X,B)$
. We denote the union of all log canonical centers of a log canonical pair
$(X,B)$
. We denote the union of all log canonical centers of a log canonical pair
![]() $(X,B)$
by
$(X,B)$
by
![]() $\text{LCS}(X,B)$
.
$\text{LCS}(X,B)$
.
∙ We say
 $(X,B)$
is divisorially log terminal (dlt) if it is log canonical and there exists a closed subvariety
$(X,B)$
is divisorially log terminal (dlt) if it is log canonical and there exists a closed subvariety
 $V\subset X$
such that
$V\subset X$
such that
 $(X,B)$
is log smooth outside
$(X,B)$
is log smooth outside
 $V$
and no log canonical center is contained in
$V$
and no log canonical center is contained in
 $V$
.
$V$
.
If we are in a situation where log resolutions exist, such as for
![]() $3$
-folds in positive characteristic, to determine if a pair is log canonical or klt it is enough to check discrepancies of just the irreducible Weil divisors on a fixed log resolution of
$3$
-folds in positive characteristic, to determine if a pair is log canonical or klt it is enough to check discrepancies of just the irreducible Weil divisors on a fixed log resolution of
![]() $(X,B)$
.
$(X,B)$
.
We need to work with pairs on nonnormal surfaces after adjunction, so we need to be able to talk about singularities in the nonnormal case.
Definition 2.10. [Reference Kollár15, 5.10]
We say a pair
![]() $(X,B)$
consisting of a (possibly nonnormal) variety
$(X,B)$
consisting of a (possibly nonnormal) variety
![]() $X$
and effective
$X$
and effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $B$
is semi-log canonical (slc) if:
$B$
is semi-log canonical (slc) if:
∙
 $X$
is a demi-normal scheme with normalization
$X$
is a demi-normal scheme with normalization
 $\unicode[STIX]{x1D70B}:\tilde{X}\rightarrow X$
.
$\unicode[STIX]{x1D70B}:\tilde{X}\rightarrow X$
.∙ The support of
 $B$
does not contain any component of the conductor
$B$
does not contain any component of the conductor
 $D$
.
$D$
.∙
 $K_{X}+B$
is
$K_{X}+B$
is
 $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.∙
 $(\tilde{X},\tilde{D}+\tilde{B})$
is log canonical, where
$(\tilde{X},\tilde{D}+\tilde{B})$
is log canonical, where
 $\tilde{D}$
is the conductor on
$\tilde{D}$
is the conductor on
 $\tilde{X}$
and
$\tilde{X}$
and
 $\tilde{B}$
is the birational transform of
$\tilde{B}$
is the birational transform of
 $B$
.
$B$
.
The following result was largely proven in [Reference Hacon and Xu11] and [Reference Kollár15], and stated in this form as [Reference Das and Hacon7, 2.2].
Proposition 2.11. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair over an algebraically closed field of characteristic
$3$
-fold pair over an algebraically closed field of characteristic
![]() $p>5$
, with
$p>5$
, with
![]() $B=\sum _{i}D_{i}+B^{\prime }$
where
$B=\sum _{i}D_{i}+B^{\prime }$
where
![]() $\left\lfloor B\right\rfloor =\sum _{i}D_{i}$
. Then the following hold:
$\left\lfloor B\right\rfloor =\sum _{i}D_{i}$
. Then the following hold:
∙ The
 $s$
-codimensional log canonical centers of
$s$
-codimensional log canonical centers of
 $(X,B)$
are exactly the irreducible components of the various intersections
$(X,B)$
are exactly the irreducible components of the various intersections
 $D_{i_{1}}\cap \cdots \cap D_{i_{s}}$
.
$D_{i_{1}}\cap \cdots \cap D_{i_{s}}$
.∙ If
 $i_{1},\ldots ,i_{s}$
are distinct, each irreducible component of
$i_{1},\ldots ,i_{s}$
are distinct, each irreducible component of
 $D_{i_{1}}\cap \cdots \cap D_{i_{s}}$
is normal and of pure codimension
$D_{i_{1}}\cap \cdots \cap D_{i_{s}}$
is normal and of pure codimension
 $s$
.
$s$
.
2.4 3-fold LMMP
Given a
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair
$3$
-fold pair
![]() $(X,B)$
over an algebraically closed field
$(X,B)$
over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
and a projective contraction
$p>5$
and a projective contraction
![]() $X\rightarrow Z$
we may run a
$X\rightarrow Z$
we may run a
![]() $K_{X}+B$
-MMP
$K_{X}+B$
-MMP
![]() $/Z$
using the results of [Reference Birkar5] and [Reference Birkar and Waldron6]. In particular, we can locate extremal rays using the cone theorem [Reference Birkar and Waldron6, 1.1], contract extremal rays using [Reference Birkar and Waldron6, 1.3] and construct flips using [Reference Birkar5, 1.1]. We also use the following results:
$/Z$
using the results of [Reference Birkar5] and [Reference Birkar and Waldron6]. In particular, we can locate extremal rays using the cone theorem [Reference Birkar and Waldron6, 1.1], contract extremal rays using [Reference Birkar and Waldron6, 1.3] and construct flips using [Reference Birkar5, 1.1]. We also use the following results:
Proposition 2.12. [Reference Birkar5, 5.5]
Let
![]() $(X,B)$
be a projective
$(X,B)$
be a projective
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
with
$p>5$
with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Suppose we are given a sequence of
$B$
. Suppose we are given a sequence of
![]() $K_{X}+B$
-flips. Then after finitely many flips, each remaining flip is an isomorphism near
$K_{X}+B$
-flips. Then after finitely many flips, each remaining flip is an isomorphism near
![]() $\left\lfloor B\right\rfloor$
.
$\left\lfloor B\right\rfloor$
.
Proposition 2.13. [Reference Birkar5, 1.6]
Let
![]() $(X,B)$
be a log canonical
$(X,B)$
be a log canonical
![]() $3$
-fold pair over an algebraically closed field
$3$
-fold pair over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>5$
with
$p>5$
with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. Then
$B$
. Then
![]() $(X,B)$
has a crepant
$(X,B)$
has a crepant
![]() $\mathbb{Q}$
-factorial dlt model. In particular, this morphism is small over the klt locus of
$\mathbb{Q}$
-factorial dlt model. In particular, this morphism is small over the klt locus of
![]() $(X,B)$
.
$(X,B)$
.
We follow the convention that, by definition, if
![]() $(Y,B_{Y})$
is a log minimal model of
$(Y,B_{Y})$
is a log minimal model of
![]() $(X,B)$
then
$(X,B)$
then
![]() $Y{\dashrightarrow}X$
does not contract divisors. Note that this is stronger than the definition used in [Reference Birkar5], but the difference only occurs when working on non-klt pairs.
$Y{\dashrightarrow}X$
does not contract divisors. Note that this is stronger than the definition used in [Reference Birkar5], but the difference only occurs when working on non-klt pairs.
2.5 Polytopes of boundary divisors
We use the following result from [Reference Birkar and Waldron6], proven in characteristic zero in [Reference Birkar3].
Proposition 2.14. [Reference Birkar and Waldron6, 3.8], [Reference Birkar3, 3.2]
Let
![]() $X$
be a projective
$X$
be a projective
![]() $\mathbb{Q}$
-factorial klt variety over
$\mathbb{Q}$
-factorial klt variety over
![]() $k$
and
$k$
and
![]() $V$
be a finite-dimensional rational affine subspace of the space of
$V$
be a finite-dimensional rational affine subspace of the space of
![]() $\mathbb{R}$
-divisors on
$\mathbb{R}$
-divisors on
![]() $X$
. For an
$X$
. For an
![]() $\mathbb{R}$
-divisor
$\mathbb{R}$
-divisor
![]() $D$
, if
$D$
, if
![]() $D=\sum _{i}d_{i}D_{i}$
with
$D=\sum _{i}d_{i}D_{i}$
with
![]() $D_{i}$
distinct and prime, define
$D_{i}$
distinct and prime, define
![]() $||D||=\max \{|d_{i}|\}$
. Finally define
$||D||=\max \{|d_{i}|\}$
. Finally define
![]() ${\mathcal{L}}\subset V$
by
${\mathcal{L}}\subset V$
by
![]() ${\mathcal{L}}$
is a polytope with rational vertices. Fix
${\mathcal{L}}$
is a polytope with rational vertices. Fix
![]() $B\in {\mathcal{L}}$
. Then there are real numbers
$B\in {\mathcal{L}}$
. Then there are real numbers
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FF}>0$
, depending only on
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FF}>0$
, depending only on
![]() $(X,B)$
and
$(X,B)$
and
![]() $V$
, such that:
$V$
, such that:
(1) If
 $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
,
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
,
 $||\unicode[STIX]{x1D6E5}-B||<\unicode[STIX]{x1D6FF}$
and
$||\unicode[STIX]{x1D6E5}-B||<\unicode[STIX]{x1D6FF}$
and
 $(K_{X}+\unicode[STIX]{x1D6E5})\cdot R\leqslant 0$
for an extremal ray
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot R\leqslant 0$
for an extremal ray
 $R$
, then
$R$
, then
 $(K_{X}+B)\cdot R\leqslant 0$
.
$(K_{X}+B)\cdot R\leqslant 0$
.(2) Let
 $\{R_{t}\}_{t\in T}$
be a family of extremal rays of
$\{R_{t}\}_{t\in T}$
be a family of extremal rays of
 $\overline{NE}(X)$
. Then the set is a rational polytope.
$\overline{NE}(X)$
. Then the set is a rational polytope. $$\begin{eqnarray}{\mathcal{N}}_{T}=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}\mid (K_{X}+\unicode[STIX]{x1D6E5})\cdot R_{t}\geqslant 0\text{ for any }t\in T\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{N}}_{T}=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}\mid (K_{X}+\unicode[STIX]{x1D6E5})\cdot R_{t}\geqslant 0\text{ for any }t\in T\}\end{eqnarray}$$
(3) Assume
 $K_{X}+B$
is nef,
$K_{X}+B$
is nef,
 $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
satisfies
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
satisfies
 $||\unicode[STIX]{x1D6E5}-B||<\unicode[STIX]{x1D6FF}$
, and that
$||\unicode[STIX]{x1D6E5}-B||<\unicode[STIX]{x1D6FF}$
, and that
 $X_{i}{\dashrightarrow}X_{i+1}/Z_{i}$
is a sequence of
$X_{i}{\dashrightarrow}X_{i+1}/Z_{i}$
is a sequence of
 $K_{X}+\unicode[STIX]{x1D6E5}$
-flips which are
$K_{X}+\unicode[STIX]{x1D6E5}$
-flips which are
 $K_{X}+B$
-trivial (where
$K_{X}+B$
-trivial (where
 $X=X_{1}$
). Let
$X=X_{1}$
). Let
 $B_{i}$
(resp.
$B_{i}$
(resp.
 $\unicode[STIX]{x1D6E5}_{i}$
) be the birational transform of
$\unicode[STIX]{x1D6E5}_{i}$
) be the birational transform of
 $B$
(resp.
$B$
(resp.
 $\unicode[STIX]{x1D6E5}$
) on
$\unicode[STIX]{x1D6E5}$
) on
 $X_{i}$
. Then if
$X_{i}$
. Then if
 $(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot R\leqslant 0$
for an extremal ray
$(K_{X_{i}}+\unicode[STIX]{x1D6E5}_{i})\cdot R\leqslant 0$
for an extremal ray
 $R$
on some
$R$
on some
 $X_{i}$
, then
$X_{i}$
, then
 $(K_{X_{i}}+B_{i})\cdot R=0$
.
$(K_{X_{i}}+B_{i})\cdot R=0$
.
2.6 The LMMP with scaling
In this subsection we describe a special LMMP, called the LMMP with scaling. For the purpose of describing the process we assume that all necessary ingredients exist.
Definition 2.15. Let
![]() $(X,B)$
be a log canonical pair and
$(X,B)$
be a log canonical pair and
![]() $A\geqslant 0$
an
$A\geqslant 0$
an
![]() $\mathbb{R}$
-Cartier divisor on
$\mathbb{R}$
-Cartier divisor on
![]() $X$
. Suppose also that there is
$X$
. Suppose also that there is
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
![]() $(X,B+t_{0}A)$
is log canonical and
$(X,B+t_{0}A)$
is log canonical and
![]() $K_{X}+B+t_{0}A$
is nef. We describe how to run a
$K_{X}+B+t_{0}A$
is nef. We describe how to run a
![]() $K_{X}+B$
-MMP with scaling of
$K_{X}+B$
-MMP with scaling of
![]() $A$
.
$A$
.
Let
![]() $\unicode[STIX]{x1D706}_{0}=\inf \{t:K_{X}+B+tA\text{ is nef}\}$
, so that
$\unicode[STIX]{x1D706}_{0}=\inf \{t:K_{X}+B+tA\text{ is nef}\}$
, so that
![]() $\unicode[STIX]{x1D706}_{0}\leqslant t_{0}$
. Suppose we can find a
$\unicode[STIX]{x1D706}_{0}\leqslant t_{0}$
. Suppose we can find a
![]() $K_{X}+B$
-negative extremal ray
$K_{X}+B$
-negative extremal ray
![]() $R_{0}$
which satisfies
$R_{0}$
which satisfies
![]() $(K_{X}+B+\unicode[STIX]{x1D706}_{0}A)\cdot R_{0}=0$
. This is the first ray we contract in our LMMP. If the contraction is a Mori fiber contraction we stop, otherwise let
$(K_{X}+B+\unicode[STIX]{x1D706}_{0}A)\cdot R_{0}=0$
. This is the first ray we contract in our LMMP. If the contraction is a Mori fiber contraction we stop, otherwise let
![]() $X_{1}$
be the result of the divisorial contraction or flip.
$X_{1}$
be the result of the divisorial contraction or flip.
![]() $K_{X_{1}}+B_{X_{1}}+\unicode[STIX]{x1D706}_{0}A_{X_{1}}$
is also nef, where
$K_{X_{1}}+B_{X_{1}}+\unicode[STIX]{x1D706}_{0}A_{X_{1}}$
is also nef, where
![]() $B_{X_{1}}$
and
$B_{X_{1}}$
and
![]() $A_{X_{1}}$
denote the birational transforms on
$A_{X_{1}}$
denote the birational transforms on
![]() $X_{1}$
of
$X_{1}$
of
![]() $B$
and
$B$
and
![]() $A$
, respectively. We define
$A$
, respectively. We define
![]() $\unicode[STIX]{x1D706}_{1}=\inf \{t:K_{X_{1}}+B_{X_{1}}+tA_{X_{1}}\text{ is nef}\}$
. The next step in our LMMP is chosen to be a
$\unicode[STIX]{x1D706}_{1}=\inf \{t:K_{X_{1}}+B_{X_{1}}+tA_{X_{1}}\text{ is nef}\}$
. The next step in our LMMP is chosen to be a
![]() $K_{X_{1}}+B_{X_{1}}$
-negative extremal ray
$K_{X_{1}}+B_{X_{1}}$
-negative extremal ray
![]() $R_{1}$
which is
$R_{1}$
which is
![]() $K_{X_{1}}+B_{X_{1}}+\unicode[STIX]{x1D706}_{1}A_{X_{1}}$
-trivial. So long as we can always find the appropriate extremal rays, contractions and flips, we can continue this process indefinitely or until the LMMP terminates.
$K_{X_{1}}+B_{X_{1}}+\unicode[STIX]{x1D706}_{1}A_{X_{1}}$
-trivial. So long as we can always find the appropriate extremal rays, contractions and flips, we can continue this process indefinitely or until the LMMP terminates.
Lemma 2.16. Let
![]() $(X,B)$
be a projective
$(X,B)$
be a projective
![]() $\mathbb{Q}$
-factorial log canonical pair with
$\mathbb{Q}$
-factorial log canonical pair with
![]() $K_{X}+B$
nef, and let
$K_{X}+B$
nef, and let
![]() $E$
be an effective
$E$
be an effective
![]() $\mathbb{R}$
-Cartier divisor satisfying
$\mathbb{R}$
-Cartier divisor satisfying
![]() $E\leqslant B$
and such that
$E\leqslant B$
and such that
![]() $(X,B-\unicode[STIX]{x1D716}E)$
is klt for
$(X,B-\unicode[STIX]{x1D716}E)$
is klt for
![]() $\unicode[STIX]{x1D716}\leqslant 1$
. Assume Theorem 1.7, and that all contractions and flips that we need exist.
$\unicode[STIX]{x1D716}\leqslant 1$
. Assume Theorem 1.7, and that all contractions and flips that we need exist.
Suppose that we wish to obtain a log minimal model or Mori fiber space for
![]() $(X,B-\unicode[STIX]{x1D716}E)$
for some sufficiently small
$(X,B-\unicode[STIX]{x1D716}E)$
for some sufficiently small
![]() $\unicode[STIX]{x1D716}$
, where we are free to shrink
$\unicode[STIX]{x1D716}$
, where we are free to shrink
![]() $\unicode[STIX]{x1D716}$
. Then if we attempt to do so by running a
$\unicode[STIX]{x1D716}$
. Then if we attempt to do so by running a
![]() $K_{X}+B-\unicode[STIX]{x1D716}E$
-MMP with scaling of
$K_{X}+B-\unicode[STIX]{x1D716}E$
-MMP with scaling of
![]() $E$
we may assume that every extremal ray contracted is
$E$
we may assume that every extremal ray contracted is
![]() $K_{X}+B$
-trivial.
$K_{X}+B$
-trivial.
In addition, such an LMMP is also a
![]() $K_{X}+B-\unicode[STIX]{x1D716}^{\prime }E$
-MMP with scaling of
$K_{X}+B-\unicode[STIX]{x1D716}^{\prime }E$
-MMP with scaling of
![]() $E$
for all
$E$
for all
![]() $\unicode[STIX]{x1D716}^{\prime }<\unicode[STIX]{x1D716}$
, so if the LMMP terminates it produces a log minimal model or Mori fiber space for
$\unicode[STIX]{x1D716}^{\prime }<\unicode[STIX]{x1D716}$
, so if the LMMP terminates it produces a log minimal model or Mori fiber space for
![]() $(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
for any
$(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
for any
![]() $0<\unicode[STIX]{x1D716}^{\prime }\leqslant \unicode[STIX]{x1D716}$
.
$0<\unicode[STIX]{x1D716}^{\prime }\leqslant \unicode[STIX]{x1D716}$
.
Proof. Choose some
![]() $\unicode[STIX]{x1D716}<1$
to start the process with. As we know that
$\unicode[STIX]{x1D716}<1$
to start the process with. As we know that
![]() $K_{X}+B$
is nef,
$K_{X}+B$
is nef,
![]() $\unicode[STIX]{x1D706}_{0}\leqslant \unicode[STIX]{x1D716}$
, where
$\unicode[STIX]{x1D706}_{0}\leqslant \unicode[STIX]{x1D716}$
, where
![]() $\unicode[STIX]{x1D706}_{0}$
is defined as in Definition 2.15. Suppose first that
$\unicode[STIX]{x1D706}_{0}$
is defined as in Definition 2.15. Suppose first that
![]() $\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D716}$
. Then
$\unicode[STIX]{x1D706}_{0}<\unicode[STIX]{x1D716}$
. Then
![]() $K_{X}+B-(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0})E$
is nef. As
$K_{X}+B-(\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0})E$
is nef. As
![]() $K_{X}+B$
is also nef, then
$K_{X}+B$
is also nef, then
![]() $(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
is its own log minimal model for all
$(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
is its own log minimal model for all
![]() $\unicode[STIX]{x1D716}^{\prime }\in [0,\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0}]$
. This means we can terminate the process by replacing
$\unicode[STIX]{x1D716}^{\prime }\in [0,\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0}]$
. This means we can terminate the process by replacing
![]() $\unicode[STIX]{x1D716}$
with
$\unicode[STIX]{x1D716}$
with
![]() $\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0}$
.
$\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{0}$
.
Suppose instead that
![]() $\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D716}$
. We claim that there is a
$\unicode[STIX]{x1D706}_{0}=\unicode[STIX]{x1D716}$
. We claim that there is a
![]() $K_{X}+B-\unicode[STIX]{x1D716}E$
-negative extremal ray
$K_{X}+B-\unicode[STIX]{x1D716}E$
-negative extremal ray
![]() $R_{0}$
which satisfies
$R_{0}$
which satisfies
![]() $(K_{X}+B)\cdot R_{0}=0$
. For if not, by definition of
$(K_{X}+B)\cdot R_{0}=0$
. For if not, by definition of
![]() $\unicode[STIX]{x1D706}_{0}$
and Theorem 1.7, there exists a sequence of extremal rays
$\unicode[STIX]{x1D706}_{0}$
and Theorem 1.7, there exists a sequence of extremal rays
![]() $R_{i}$
and a decreasing sequence of rational numbers
$R_{i}$
and a decreasing sequence of rational numbers
![]() $\unicode[STIX]{x1D6FF}_{i}\rightarrow 0$
which satisfy
$\unicode[STIX]{x1D6FF}_{i}\rightarrow 0$
which satisfy
![]() $(K_{X}+B-\unicode[STIX]{x1D6FF}_{i}E)\cdot R_{i}<0$
but
$(K_{X}+B-\unicode[STIX]{x1D6FF}_{i}E)\cdot R_{i}<0$
but
![]() $(K_{X}+B)\cdot R_{i}>0$
. This is impossible by Proposition 2.14(1). So there is a
$(K_{X}+B)\cdot R_{i}>0$
. This is impossible by Proposition 2.14(1). So there is a
![]() $K_{X}+B$
-trivial extremal ray
$K_{X}+B$
-trivial extremal ray
![]() $R_{0}$
which we contract as the first step of our LMMP. By linearity this is also
$R_{0}$
which we contract as the first step of our LMMP. By linearity this is also
![]() $K_{X}+B-\unicode[STIX]{x1D716}^{\prime }E$
-negative for all
$K_{X}+B-\unicode[STIX]{x1D716}^{\prime }E$
-negative for all
![]() $\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}]$
.
$\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}]$
.
If we have not obtained a Mori fiber space then let the result of the flip or divisorial contraction be
![]() $X_{1}$
. Define
$X_{1}$
. Define
![]() $\unicode[STIX]{x1D706}_{1}$
as in Definition 2.15. Again
$\unicode[STIX]{x1D706}_{1}$
as in Definition 2.15. Again
![]() $\unicode[STIX]{x1D706}_{1}\leqslant \unicode[STIX]{x1D716}$
. If
$\unicode[STIX]{x1D706}_{1}\leqslant \unicode[STIX]{x1D716}$
. If
![]() $\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D716}$
then
$\unicode[STIX]{x1D706}_{1}<\unicode[STIX]{x1D716}$
then
![]() $(X_{1},B_{X_{1}}-\unicode[STIX]{x1D716}^{\prime }E_{X_{1}})$
is a log minimal model for
$(X_{1},B_{X_{1}}-\unicode[STIX]{x1D716}^{\prime }E_{X_{1}})$
is a log minimal model for
![]() $(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
for all
$(X,B-\unicode[STIX]{x1D716}^{\prime }E)$
for all
![]() $\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{1})$
, so we may terminate the process by replacing
$\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{1})$
, so we may terminate the process by replacing
![]() $\unicode[STIX]{x1D716}$
with
$\unicode[STIX]{x1D716}$
with
![]() $\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{1}$
. On the other hand if
$\unicode[STIX]{x1D716}-\unicode[STIX]{x1D706}_{1}$
. On the other hand if
![]() $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D716}$
, we get a
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D716}$
, we get a
![]() $K_{X_{1}}+B_{X_{1}}$
-trivial contraction. Continuing this process produces the LMMP described in the statement (even if it does not terminate). Note that we only needed to replace
$K_{X_{1}}+B_{X_{1}}$
-trivial contraction. Continuing this process produces the LMMP described in the statement (even if it does not terminate). Note that we only needed to replace
![]() $\unicode[STIX]{x1D716}$
at the end, when we had obtained the model which will give the result.◻
$\unicode[STIX]{x1D716}$
at the end, when we had obtained the model which will give the result.◻
3 Cone theorem
We prove the cone theorem for log canonical pairs by passing to a crepant
![]() $\mathbb{Q}$
-factorial dlt model and using the
$\mathbb{Q}$
-factorial dlt model and using the
![]() $\mathbb{Q}$
-factorial dlt cone theorem [Reference Birkar and Waldron6, Theorem 1.1].
$\mathbb{Q}$
-factorial dlt cone theorem [Reference Birkar and Waldron6, Theorem 1.1].
Lemma 3.1. Let
![]() $f:V\rightarrow W$
be a surjective linear map of finite-dimensional vector spaces. Suppose
$f:V\rightarrow W$
be a surjective linear map of finite-dimensional vector spaces. Suppose
![]() $C_{V}\subset V$
and
$C_{V}\subset V$
and
![]() $C_{W}\subset W$
are closed convex cones of maximal dimension and
$C_{W}\subset W$
are closed convex cones of maximal dimension and
![]() $H\subset W$
is a linear subspace of codimension
$H\subset W$
is a linear subspace of codimension
![]() $1$
. Assume:
$1$
. Assume:
∙
 $f(C_{V})=C_{W}$
;
$f(C_{V})=C_{W}$
;∙
 $C_{W}\cap H\subset \unicode[STIX]{x2202}C_{W}$
.
$C_{W}\cap H\subset \unicode[STIX]{x2202}C_{W}$
.
Then
![]() $f^{-1}H\cap C_{V}\subset \unicode[STIX]{x2202}C_{V}$
and also
$f^{-1}H\cap C_{V}\subset \unicode[STIX]{x2202}C_{V}$
and also
![]() $f^{-1}H\cap C_{V}=f^{-1}(H\cap C_{W})\cap C_{V}$
.
$f^{-1}H\cap C_{V}=f^{-1}(H\cap C_{W})\cap C_{V}$
.
Proof. First we claim that
Take
![]() $v\in f^{-1}(\unicode[STIX]{x2202}C_{W})\cap C_{V}$
. Let
$v\in f^{-1}(\unicode[STIX]{x2202}C_{W})\cap C_{V}$
. Let
![]() $w=f(v)$
. As
$w=f(v)$
. As
![]() $w\in \unicode[STIX]{x2202}C_{W}$
there is a convergent sequence
$w\in \unicode[STIX]{x2202}C_{W}$
there is a convergent sequence
![]() $w_{i}\rightarrow w$
such that
$w_{i}\rightarrow w$
such that
![]() $w_{i}\not \in C_{W}$
for all
$w_{i}\not \in C_{W}$
for all
![]() $i$
.
$i$
.
![]() $f^{-1}(w_{i})$
is an affine space in
$f^{-1}(w_{i})$
is an affine space in
![]() $V$
which does not intersect
$V$
which does not intersect
![]() $C_{V}$
(else
$C_{V}$
(else
![]() $w_{i}\in C_{W}$
), and these affine spaces converge to the affine space
$w_{i}\in C_{W}$
), and these affine spaces converge to the affine space
![]() $f^{-1}(w)$
. Therefore, we can choose
$f^{-1}(w)$
. Therefore, we can choose
![]() $v_{i}\in f^{-1}(w_{i})$
such that
$v_{i}\in f^{-1}(w_{i})$
such that
![]() $v_{i}$
converge to
$v_{i}$
converge to
![]() $v$
. Thus we have sequence
$v$
. Thus we have sequence
![]() $v_{i}$
not in
$v_{i}$
not in
![]() $C_{V}$
converging to
$C_{V}$
converging to
![]() $v$
and so
$v$
and so
![]() $v\in \unicode[STIX]{x2202}C_{V}$
.
$v\in \unicode[STIX]{x2202}C_{V}$
.
We prove the first claim of the Lemma. Suppose
![]() $v\in f^{-1}H\cap C_{V}$
. Then
$v\in f^{-1}H\cap C_{V}$
. Then
![]() $f(v)\in C_{W}\cap H\subset \unicode[STIX]{x2202}C_{W}$
. So
$f(v)\in C_{W}\cap H\subset \unicode[STIX]{x2202}C_{W}$
. So
![]() $v\in f^{-1}(\unicode[STIX]{x2202}C_{W})$
and also in
$v\in f^{-1}(\unicode[STIX]{x2202}C_{W})$
and also in
![]() $C_{V}$
so it is in
$C_{V}$
so it is in
![]() $\unicode[STIX]{x2202}C_{V}$
by the initial claim.
$\unicode[STIX]{x2202}C_{V}$
by the initial claim.
We prove the second claim. Suppose
![]() $v\in f^{-1}H\cap C_{V}$
. Let
$v\in f^{-1}H\cap C_{V}$
. Let
![]() $w=f(v)$
. Then
$w=f(v)$
. Then
![]() $w\in H$
, but also
$w\in H$
, but also
![]() $w\in C_{W}$
as
$w\in C_{W}$
as
![]() $f(C_{V})=C_{W}$
. The other inclusion is even more obvious.◻
$f(C_{V})=C_{W}$
. The other inclusion is even more obvious.◻
Proof of Theorem 1.7.
![]() $(X,B)$
has a crepant
$(X,B)$
has a crepant
![]() $\mathbb{Q}$
-factorial dlt model
$\mathbb{Q}$
-factorial dlt model
![]() $(Y,B_{Y})$
by Proposition 2.13. This comes with birational morphism
$(Y,B_{Y})$
by Proposition 2.13. This comes with birational morphism
![]() $f:Y\rightarrow X$
, and
$f:Y\rightarrow X$
, and
![]() $B_{Y}$
is defined to be the dlt boundary satisfying
$B_{Y}$
is defined to be the dlt boundary satisfying
![]() $K_{Y}+B_{Y}{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. There is a surjective linear map of vector spaces
$K_{Y}+B_{Y}{\sim}_{\mathbb{Q}}\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. There is a surjective linear map of vector spaces
which induces a surjection on the pseudo-effective cones
By the
![]() $\mathbb{Q}$
-factorial dlt cone theorem, there is a countable collection of rational curves
$\mathbb{Q}$
-factorial dlt cone theorem, there is a countable collection of rational curves
![]() $C_{i}^{Y}$
on
$C_{i}^{Y}$
on
![]() $Y$
satisfying the requirements of the cone theorem. In particular,
$Y$
satisfying the requirements of the cone theorem. In particular,
Let
![]() $C_{i}$
be the countable collection of rational curves on
$C_{i}$
be the countable collection of rational curves on
![]() $X$
given by letting
$X$
given by letting
![]() $C_{i}$
be
$C_{i}$
be
![]() $f_{\ast }C_{i}^{Y}$
with reduced structure. We claim that these curves satisfy (1). Suppose instead
$f_{\ast }C_{i}^{Y}$
with reduced structure. We claim that these curves satisfy (1). Suppose instead
Then there is some
![]() $\mathbb{R}$
-Cartier divisor
$\mathbb{R}$
-Cartier divisor
![]() $D$
which is positive on the right hand side, but nonpositive somewhere on
$D$
which is positive on the right hand side, but nonpositive somewhere on
![]() $\overline{NE}_{1}(X)$
. Let
$\overline{NE}_{1}(X)$
. Let
![]() $A$
be an ample divisor and
$A$
be an ample divisor and
![]() $\unicode[STIX]{x1D706}=\inf \{t:D+tA\text{ is nef}\}$
. Then
$\unicode[STIX]{x1D706}=\inf \{t:D+tA\text{ is nef}\}$
. Then
![]() $D+\unicode[STIX]{x1D706}A$
is nef but not ample so by Kleiman’s criterion it takes value zero somewhere on
$D+\unicode[STIX]{x1D706}A$
is nef but not ample so by Kleiman’s criterion it takes value zero somewhere on
![]() $\overline{NE}_{1}(X)\backslash \{0\}$
. By replacing
$\overline{NE}_{1}(X)\backslash \{0\}$
. By replacing
![]() $D$
by
$D$
by
![]() $D+\unicode[STIX]{x1D706}A$
we may assume
$D+\unicode[STIX]{x1D706}A$
we may assume
![]() $D$
is nonnegative on
$D$
is nonnegative on
![]() $\overline{NE}_{1}(X)\backslash \{0\}$
but
$\overline{NE}_{1}(X)\backslash \{0\}$
but
![]() $D_{=0}$
intersects
$D_{=0}$
intersects
![]() $\overline{NE}_{1}(X)$
nontrivially. So
$\overline{NE}_{1}(X)$
nontrivially. So
![]() $D_{=0}$
cuts out some extremal face
$D_{=0}$
cuts out some extremal face
![]() $F$
of
$F$
of
![]() $\overline{NE}_{1}(X)$
. By Lemma 3.1,
$\overline{NE}_{1}(X)$
. By Lemma 3.1,
is some nonempty extremal face of
![]() $\overline{NE}_{1}(Y)$
, which is
$\overline{NE}_{1}(Y)$
, which is
![]() $K_{Y}+B_{Y}$
-negative away from the lower dimensional
$K_{Y}+B_{Y}$
-negative away from the lower dimensional
![]() $f_{\ast }^{-1}(0)$
. But any such extremal face contains a
$f_{\ast }^{-1}(0)$
. But any such extremal face contains a
![]() $K_{Y}+B_{Y}$
-negative extremal ray
$K_{Y}+B_{Y}$
-negative extremal ray
![]() $R$
by the cone theorem [Reference Birkar and Waldron6, 1.1] on
$R$
by the cone theorem [Reference Birkar and Waldron6, 1.1] on
![]() $Y$
, and
$Y$
, and
![]() $R$
contains one of the
$R$
contains one of the
![]() $C_{i}^{Y}$
. But then
$C_{i}^{Y}$
. But then
![]() $D_{=0}$
contains one of the
$D_{=0}$
contains one of the
![]() $C_{i}$
, which contradicts our assumption of inequality.
$C_{i}$
, which contradicts our assumption of inequality.
The inequality
follows directly from the definition of the
![]() $C_{i}$
, the
$C_{i}$
, the
![]() $\mathbb{Q}$
-factorial dlt cone theorem, the projection formula and the observation
$\mathbb{Q}$
-factorial dlt cone theorem, the projection formula and the observation
Next we show that the rays
![]() $R_{i}=\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]$
do not accumulate in
$R_{i}=\mathbb{R}_{{\geqslant}0}\cdot [C_{i}]$
do not accumulate in
![]() $(K_{X}+B)_{{<}0}$
. Suppose otherwise, so there is some sequence
$(K_{X}+B)_{{<}0}$
. Suppose otherwise, so there is some sequence
![]() $R_{i}$
converging to a
$R_{i}$
converging to a
![]() $K_{X}+B$
-negative ray
$K_{X}+B$
-negative ray
![]() $R$
. Let
$R$
. Let
![]() $R_{i}^{Y}$
be an extremal ray in
$R_{i}^{Y}$
be an extremal ray in
![]() $\overline{NE}_{1}(Y)$
satisfying
$\overline{NE}_{1}(Y)$
satisfying
![]() $f_{\ast }R_{i}^{Y}=R_{i}$
. Such a ray exists by definition of the
$f_{\ast }R_{i}^{Y}=R_{i}$
. Such a ray exists by definition of the
![]() $R_{i}$
. By compactness of the unit ball in
$R_{i}$
. By compactness of the unit ball in
![]() $\overline{NE}_{1}(Y)$
, some subsequence of the
$\overline{NE}_{1}(Y)$
, some subsequence of the
![]() $R_{i}^{Y}$
must converge to a ray
$R_{i}^{Y}$
must converge to a ray
![]() $R^{Y}$
. This must satisfy
$R^{Y}$
. This must satisfy
![]() $f_{\ast }R^{Y}=R$
, and so by the projection formula it is
$f_{\ast }R^{Y}=R$
, and so by the projection formula it is
![]() $K_{Y}+B_{Y}$
-negative. This contradicts the cone theorem for dlt
$K_{Y}+B_{Y}$
-negative. This contradicts the cone theorem for dlt
![]() $\mathbb{Q}$
-factorial pairs [Reference Birkar and Waldron6, 1.1].
$\mathbb{Q}$
-factorial pairs [Reference Birkar and Waldron6, 1.1].
Finally, let
![]() $A$
be an ample
$A$
be an ample
![]() $\mathbb{R}$
-divisor on
$\mathbb{R}$
-divisor on
![]() $X$
. Suppose there are infinitely many
$X$
. Suppose there are infinitely many
![]() $C_{i}$
with
$C_{i}$
with
![]() $(K_{X}+B+A)\cdot C_{i}<0$
. By compactness, some subsequence of the corresponding
$(K_{X}+B+A)\cdot C_{i}<0$
. By compactness, some subsequence of the corresponding
![]() $R_{i}$
converge to a ray
$R_{i}$
converge to a ray
![]() $R$
. This must satisfy
$R$
. This must satisfy
![]() $(K_{X}+B+A)\cdot R\leqslant 0$
, but
$(K_{X}+B+A)\cdot R\leqslant 0$
, but
![]() $R\subset \overline{NE}_{1}(X)$
so this implies
$R\subset \overline{NE}_{1}(X)$
so this implies
![]() $(K_{X}+B)\cdot R<0$
, which contradicts (4).◻
$(K_{X}+B)\cdot R<0$
, which contradicts (4).◻
4 Termination
In this section we prove Theorem 1.6, using the ideas of the characteristic zero proof in [Reference Birkar2, 3.2]. The next remark is important for the proof.
Remark 4.1. [Reference Birkar2, 3.1]
Given a log canonical
![]() $3$
-fold pair
$3$
-fold pair
![]() $(X,B)$
we may take a crepant
$(X,B)$
we may take a crepant
![]() $\mathbb{Q}$
-factorial dlt model
$\mathbb{Q}$
-factorial dlt model
![]() $\unicode[STIX]{x1D719}:Y\rightarrow X$
using Proposition 2.13. Let
$\unicode[STIX]{x1D719}:Y\rightarrow X$
using Proposition 2.13. Let
![]() $B_{Y}$
be the dlt boundary such that
$B_{Y}$
be the dlt boundary such that
![]() $K_{Y}+B_{Y}{\sim}_{\mathbb{R}}\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. Suppose we have a
$K_{Y}+B_{Y}{\sim}_{\mathbb{R}}\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. Suppose we have a
![]() $K_{X}+B$
-flip
$K_{X}+B$
-flip
![]() $X{\dashrightarrow}X^{+}/Z$
. Then
$X{\dashrightarrow}X^{+}/Z$
. Then
![]() $(X^{+},B_{X^{+}})$
is the unique log canonical model of
$(X^{+},B_{X^{+}})$
is the unique log canonical model of
![]() $(X,B)$
over
$(X,B)$
over
![]() $Z$
. As remarked in Subsection 2.4 we may run a
$Z$
. As remarked in Subsection 2.4 we may run a
![]() $K_{Y}+B_{Y}$
-MMP over
$K_{Y}+B_{Y}$
-MMP over
![]() $Z$
. If this LMMP terminates (which will follow from Theorem 1.6), say with
$Z$
. If this LMMP terminates (which will follow from Theorem 1.6), say with
![]() $Y{\dashrightarrow}Y^{+}$
,
$Y{\dashrightarrow}Y^{+}$
,
![]() $(X^{+},B_{X^{+}})$
is also the unique log canonical model for
$(X^{+},B_{X^{+}})$
is also the unique log canonical model for
![]() $(Y^{+},B_{Y^{+}})$
over
$(Y^{+},B_{Y^{+}})$
over
![]() $Z$
, so we get a morphism
$Z$
, so we get a morphism
![]() $Y^{+}\rightarrow X^{+}$
and
$Y^{+}\rightarrow X^{+}$
and
![]() $(Y^{+},B_{Y^{+}})$
is a crepant
$(Y^{+},B_{Y^{+}})$
is a crepant
![]() $\mathbb{Q}$
-factorial dlt model of
$\mathbb{Q}$
-factorial dlt model of
![]() $(X^{+},B_{X^{+}})$
.
$(X^{+},B_{X^{+}})$
.
Proof of Theorem 1.6.
Suppose we have a log canonical pair
![]() $(X,B)$
, and an infinite sequence of
$(X,B)$
, and an infinite sequence of
![]() $K_{X}+B$
-flips which are also
$K_{X}+B$
-flips which are also
![]() $M$
-flips for
$M$
-flips for
![]() $M\geqslant 0$
.
$M\geqslant 0$
.

Let
![]() $t^{1}=\text{lct}(X,B,M)$
and
$t^{1}=\text{lct}(X,B,M)$
and
![]() $(X^{1},B^{1},M^{1})=(X,B,M)$
.
$(X^{1},B^{1},M^{1})=(X,B,M)$
.
Let
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
be a crepant
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
be a crepant
![]() $\mathbb{Q}$
-factorial dlt model of
$\mathbb{Q}$
-factorial dlt model of
![]() $(X,B+t^{1}M)$
, with birational morphism
$(X,B+t^{1}M)$
, with birational morphism
![]() $f:Y\rightarrow X$
. Let
$f:Y\rightarrow X$
. Let
![]() $B_{Y}$
(resp.
$B_{Y}$
(resp.
![]() $M_{Y}$
) be the birational transform of
$M_{Y}$
) be the birational transform of
![]() $B$
(resp.
$B$
(resp.
![]() $M$
) on
$M$
) on
![]() $Y$
, so that
$Y$
, so that
![]() $\unicode[STIX]{x1D6E5}_{Y}=B_{Y}+t^{1}M_{Y}+E$
where
$\unicode[STIX]{x1D6E5}_{Y}=B_{Y}+t^{1}M_{Y}+E$
where
![]() $E$
is the reduced exceptional divisor of
$E$
is the reduced exceptional divisor of
![]() $f$
. In addition, let
$f$
. In addition, let
![]() $0\leqslant B_{Y}^{\prime }\leqslant B_{Y}$
(resp.
$0\leqslant B_{Y}^{\prime }\leqslant B_{Y}$
(resp.
![]() $0\leqslant M_{Y}^{\prime }\leqslant M_{Y}$
) be the divisors formed as follows:
$0\leqslant M_{Y}^{\prime }\leqslant M_{Y}$
) be the divisors formed as follows:
∙ If a component of
 $B_{Y}$
(resp.
$B_{Y}$
(resp.
 $M_{Y}$
) has coefficient
$M_{Y}$
) has coefficient
 $1$
in
$1$
in
 $B_{Y}+t^{1}M_{Y}$
, give it coefficient
$B_{Y}+t^{1}M_{Y}$
, give it coefficient
 $0$
in
$0$
in
 $B_{Y}^{\prime }$
(resp.
$B_{Y}^{\prime }$
(resp.
 $M_{Y}^{\prime }$
).
$M_{Y}^{\prime }$
).∙ If a component of
 $B_{Y}$
(resp.
$B_{Y}$
(resp.
 $M_{Y}$
) has coefficient less than
$M_{Y}$
) has coefficient less than
 $1$
in
$1$
in
 $B_{Y}+t^{1}M_{Y}$
, give it coefficient in
$B_{Y}+t^{1}M_{Y}$
, give it coefficient in
 $B_{Y}^{\prime }$
(resp.
$B_{Y}^{\prime }$
(resp.
 $M_{Y}^{\prime }$
) equal to its coefficient in
$M_{Y}^{\prime }$
) equal to its coefficient in
 $B_{Y}$
(resp.
$B_{Y}$
(resp.
 $M_{Y}$
).
$M_{Y}$
).
Thus we have
![]() $\unicode[STIX]{x1D6E5}_{Y}=B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }+\left\lfloor B_{Y}+t^{1}M_{Y}\right\rfloor +E$
. Run a
$\unicode[STIX]{x1D6E5}_{Y}=B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }+\left\lfloor B_{Y}+t^{1}M_{Y}\right\rfloor +E$
. Run a
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-MMP
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-MMP
![]() $/Z_{1}$
. If this terminates it gives us
$/Z_{1}$
. If this terminates it gives us
![]() $(Y_{2},\unicode[STIX]{x1D6E5}_{Y_{2}})$
which is a crepant
$(Y_{2},\unicode[STIX]{x1D6E5}_{Y_{2}})$
which is a crepant
![]() $\mathbb{Q}$
-factorial dlt model for
$\mathbb{Q}$
-factorial dlt model for
![]() $(X_{2},B_{2}+t^{1}M_{2})$
by Remark 4.1. In particular, this cannot be isomorphic to
$(X_{2},B_{2}+t^{1}M_{2})$
by Remark 4.1. In particular, this cannot be isomorphic to
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
. Now repeat the process from
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
. Now repeat the process from
![]() $(Y_{2},\unicode[STIX]{x1D6E5}_{Y_{2}})$
. Either way we get an infinite sequence of
$(Y_{2},\unicode[STIX]{x1D6E5}_{Y_{2}})$
. Either way we get an infinite sequence of
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-flips.
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-flips.
By Proposition 2.12, these flips are eventually isomorphisms near
![]() $\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor$
, so we may replace
$\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor$
, so we may replace
![]() $Y$
and the sequence of flips with a truncated version to assume that each flipping locus is disjoint from
$Y$
and the sequence of flips with a truncated version to assume that each flipping locus is disjoint from
![]() $\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
and also to ensure there are no divisorial contractions. Each of the
$\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
and also to ensure there are no divisorial contractions. Each of the
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-flips is now also a
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
-flips is now also a
![]() $K_{Y}+B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }$
-flip and an
$K_{Y}+B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }$
-flip and an
![]() $M_{Y}^{\prime }$
-flip. This is because
$M_{Y}^{\prime }$
-flip. This is because
![]() $K_{Y}+B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }$
(resp.
$K_{Y}+B_{Y}^{\prime }+t^{1}M_{Y}^{\prime }$
(resp.
![]() $M_{Y}^{\prime }$
) only differs from
$M_{Y}^{\prime }$
) only differs from
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
(resp.
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
(resp.
![]() $M_{Y}$
) on the components of
$M_{Y}$
) on the components of
![]() $\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
. By assumption the flipping loci are all disjoint from the birational transforms of
$\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
. By assumption the flipping loci are all disjoint from the birational transforms of
![]() $\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
, and so the intersections with the flipping curves are unchanged by changing coefficients of components of
$\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
, and so the intersections with the flipping curves are unchanged by changing coefficients of components of
![]() $\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
.
$\text{Supp}(\left\lfloor \unicode[STIX]{x1D6E5}_{Y}\right\rfloor )$
.
Let
![]() $t^{2}=\text{lct}(Y,B_{Y}^{\prime },M_{Y}^{\prime })$
.
$t^{2}=\text{lct}(Y,B_{Y}^{\prime },M_{Y}^{\prime })$
.
![]() $t^{2}>t^{1}$
because
$t^{2}>t^{1}$
because
![]() $(Y,B_{Y}^{\prime }+t^{1}M_{Y}^{\prime })$
is klt by construction. Let
$(Y,B_{Y}^{\prime }+t^{1}M_{Y}^{\prime })$
is klt by construction. Let
![]() $(X^{2},B^{2},M^{2},t^{2})=(Y,B_{Y}^{\prime },M_{Y}^{\prime },t^{2})$
. We are in the same situation with
$(X^{2},B^{2},M^{2},t^{2})=(Y,B_{Y}^{\prime },M_{Y}^{\prime },t^{2})$
. We are in the same situation with
![]() $X^{2}$
as we began in with
$X^{2}$
as we began in with
![]() $X$
. Therefore, we can inductively create a sequence
$X$
. Therefore, we can inductively create a sequence
![]() $t^{1}<t^{2}<t^{3}<\cdots \,$
of log canonical thresholds for pairs and divisors with coefficients in a finite set. This contradicts ACC [Reference Birkar5, 1.10], so there cannot have been such an infinite sequence of flips.◻
$t^{1}<t^{2}<t^{3}<\cdots \,$
of log canonical thresholds for pairs and divisors with coefficients in a finite set. This contradicts ACC [Reference Birkar5, 1.10], so there cannot have been such an infinite sequence of flips.◻
We now use this to extend special termination for
![]() $\mathbb{Q}$
-factorial dlt pairs (Proposition 2.12) to general log canonical pairs.
$\mathbb{Q}$
-factorial dlt pairs (Proposition 2.12) to general log canonical pairs.
Proposition 4.2. Let
![]() $(X,B)$
be a projective log canonical
$(X,B)$
be a projective log canonical
![]() $3$
-fold pair over
$3$
-fold pair over
![]() $k$
. Suppose we are given a sequence of
$k$
. Suppose we are given a sequence of
![]() $K_{X}+B$
-flips,
$K_{X}+B$
-flips,
Then the flipping locus is eventually disjoint from
![]() $\text{LCS}(X,B)$
.
$\text{LCS}(X,B)$
.
Proof. Suppose the flipping contractions are
![]() $f_{i}:X_{i}\rightarrow Z_{i}$
with
$f_{i}:X_{i}\rightarrow Z_{i}$
with
![]() $X=X_{1}$
. Let
$X=X_{1}$
. Let
![]() $(Y_{1},B_{Y_{1}})$
be a crepant
$(Y_{1},B_{Y_{1}})$
be a crepant
![]() $\mathbb{Q}$
-factorial dlt model of
$\mathbb{Q}$
-factorial dlt model of
![]() $(X,B)$
, which exists by Proposition 2.13. Run the
$(X,B)$
, which exists by Proposition 2.13. Run the
![]() $K_{Y_{1}}+B_{Y_{1}}$
-MMP
$K_{Y_{1}}+B_{Y_{1}}$
-MMP
![]() $/Z_{1}$
as in Remark 4.1 . This LMMP is also a
$/Z_{1}$
as in Remark 4.1 . This LMMP is also a
![]() $K_{Y_{1}}+B_{Y_{1}}+f_{1}^{\ast }A$
-MMP for
$K_{Y_{1}}+B_{Y_{1}}+f_{1}^{\ast }A$
-MMP for
![]() $A$
ample on
$A$
ample on
![]() $Z_{1}$
. In particular, we may choose
$Z_{1}$
. In particular, we may choose
![]() $A$
sufficiently ample that
$A$
sufficiently ample that
![]() $K_{Y_{1}}+B_{Y_{1}}+f_{1}^{\ast }A$
is big, and so the LMMP terminates by Theorem 1.6. By Remark 4.1 it terminates on
$K_{Y_{1}}+B_{Y_{1}}+f_{1}^{\ast }A$
is big, and so the LMMP terminates by Theorem 1.6. By Remark 4.1 it terminates on
![]() $(Y_{2},B_{Y_{2}})$
, a crepant
$(Y_{2},B_{Y_{2}})$
, a crepant
![]() $\mathbb{Q}$
-factorial dlt model for
$\mathbb{Q}$
-factorial dlt model for
![]() $(X_{2},B_{X_{2}})$
. Continuing to run these LMMPs we get a diagram:
$(X_{2},B_{X_{2}})$
. Continuing to run these LMMPs we get a diagram:

where
![]() $(Y_{i},B_{Y_{i}})$
is a
$(Y_{i},B_{Y_{i}})$
is a
![]() $\mathbb{Q}$
-factorial dlt model of
$\mathbb{Q}$
-factorial dlt model of
![]() $(X_{i},B_{X_{i}})$
with birational morphism
$(X_{i},B_{X_{i}})$
with birational morphism
![]() $g_{i}:Y_{i}\rightarrow X_{i}$
. The top row is a
$g_{i}:Y_{i}\rightarrow X_{i}$
. The top row is a
![]() $K_{Y_{1}}+B_{Y_{1}}$
-MMP, so by special termination for
$K_{Y_{1}}+B_{Y_{1}}$
-MMP, so by special termination for
![]() $\mathbb{Q}$
-factorial dlt pairs the birational maps
$\mathbb{Q}$
-factorial dlt pairs the birational maps
![]() $Y_{i}{\dashrightarrow}Y_{i+1}$
are isomorphisms near
$Y_{i}{\dashrightarrow}Y_{i+1}$
are isomorphisms near
![]() $\left\lfloor B_{Y_{i}}\right\rfloor$
for
$\left\lfloor B_{Y_{i}}\right\rfloor$
for
![]() $i\gg 0$
. Replace the sequences to assume that this holds for all
$i\gg 0$
. Replace the sequences to assume that this holds for all
![]() $i$
. We may also assume that there are no divisorial contractions in
$i$
. We may also assume that there are no divisorial contractions in
![]() $Y_{i}{\dashrightarrow}Y_{i-1}$
for each
$Y_{i}{\dashrightarrow}Y_{i-1}$
for each
![]() $i$
.
$i$
.
Suppose
![]() $X_{i}{\dashrightarrow}X_{i+1}$
is not an isomorphism near
$X_{i}{\dashrightarrow}X_{i+1}$
is not an isomorphism near
![]() $\text{LCS}(X_{i},B_{X_{i}})$
. Let
$\text{LCS}(X_{i},B_{X_{i}})$
. Let
![]() $\unicode[STIX]{x1D719}_{i}:W\rightarrow Y_{i}$
and
$\unicode[STIX]{x1D719}_{i}:W\rightarrow Y_{i}$
and
![]() $\unicode[STIX]{x1D719}_{i+1}:W\rightarrow Y_{i+1}$
be birational morphisms resolving the rational map
$\unicode[STIX]{x1D719}_{i+1}:W\rightarrow Y_{i+1}$
be birational morphisms resolving the rational map
![]() $Y_{i}{\dashrightarrow}Y_{i+1}$
. We can assume that
$Y_{i}{\dashrightarrow}Y_{i+1}$
. We can assume that
![]() $\unicode[STIX]{x1D719}_{i}$
and
$\unicode[STIX]{x1D719}_{i}$
and
![]() $\unicode[STIX]{x1D719}_{i+1}$
are isomorphisms over the locus where
$\unicode[STIX]{x1D719}_{i+1}$
are isomorphisms over the locus where
![]() $Y_{i}{\dashrightarrow}Y_{i+1}$
is an isomorphism. In particular, they are isomorphisms near
$Y_{i}{\dashrightarrow}Y_{i+1}$
is an isomorphism. In particular, they are isomorphisms near
![]() $\left\lfloor B_{Y_{i}}\right\rfloor$
and
$\left\lfloor B_{Y_{i}}\right\rfloor$
and
![]() $\left\lfloor B_{Y_{i+1}}\right\rfloor$
.
$\left\lfloor B_{Y_{i+1}}\right\rfloor$
.
is exceptional over
![]() $Y_{i}$
and anti-nef
$Y_{i}$
and anti-nef
![]() $/Z_{i}$
, so is effective.
$/Z_{i}$
, so is effective.
![]() $Y_{i}{\dashrightarrow}Y_{i+1}$
being an isomorphism near
$Y_{i}{\dashrightarrow}Y_{i+1}$
being an isomorphism near
![]() $\left\lfloor B_{Y_{i}}\right\rfloor$
implies that
$\left\lfloor B_{Y_{i}}\right\rfloor$
implies that
![]() $D$
does not intersect
$D$
does not intersect
![]() $\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
. Note that
$\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
. Note that
Let
![]() $\unicode[STIX]{x1D6E4}_{X_{i}}$
be a curve in the flipping locus which is not disjoint from
$\unicode[STIX]{x1D6E4}_{X_{i}}$
be a curve in the flipping locus which is not disjoint from
![]() $\text{LCS}(X_{i},B_{X_{i}})$
. Let
$\text{LCS}(X_{i},B_{X_{i}})$
. Let
![]() $\unicode[STIX]{x1D6E4}_{Y_{i}}$
be a curve on
$\unicode[STIX]{x1D6E4}_{Y_{i}}$
be a curve on
![]() $Y_{i}$
surjective to
$Y_{i}$
surjective to
![]() $\unicode[STIX]{x1D6E4}_{X_{i}}$
and
$\unicode[STIX]{x1D6E4}_{X_{i}}$
and
![]() $\unicode[STIX]{x1D6E4}_{W}$
a curve on
$\unicode[STIX]{x1D6E4}_{W}$
a curve on
![]() $W$
surjective to
$W$
surjective to
![]() $\unicode[STIX]{x1D6E4}_{Y_{i}}$
. As
$\unicode[STIX]{x1D6E4}_{Y_{i}}$
. As
![]() $\unicode[STIX]{x1D6E4}_{X_{i}}$
is a flipping curve,
$\unicode[STIX]{x1D6E4}_{X_{i}}$
is a flipping curve,
![]() $(K_{X_{i}}+B_{X_{i}})\cdot \unicode[STIX]{x1D6E4}_{X_{i}}<0$
. By the projection formula, we see that
$(K_{X_{i}}+B_{X_{i}})\cdot \unicode[STIX]{x1D6E4}_{X_{i}}<0$
. By the projection formula, we see that
![]() $D\cdot \unicode[STIX]{x1D6E4}_{W}<0$
, and so
$D\cdot \unicode[STIX]{x1D6E4}_{W}<0$
, and so
![]() $\unicode[STIX]{x1D6E4}_{W}$
is contained in
$\unicode[STIX]{x1D6E4}_{W}$
is contained in
![]() $\text{Supp}(D)$
.
$\text{Supp}(D)$
.
By assumption,
![]() $\unicode[STIX]{x1D6E4}_{X_{i}}$
intersects
$\unicode[STIX]{x1D6E4}_{X_{i}}$
intersects
![]() $\text{LCS}(X_{i},B_{X_{i}})$
and so
$\text{LCS}(X_{i},B_{X_{i}})$
and so
![]() $\unicode[STIX]{x1D6E4}_{W}$
intersects
$\unicode[STIX]{x1D6E4}_{W}$
intersects
![]() $\unicode[STIX]{x1D719}_{i}^{-1}g_{i}^{-1}(\text{LCS}(X_{i},B_{X_{i}}))$
.
$\unicode[STIX]{x1D719}_{i}^{-1}g_{i}^{-1}(\text{LCS}(X_{i},B_{X_{i}}))$
.
![]() $g_{i}^{-1}(\text{LCS}(X_{i},B_{X_{i}}))$
consists of
$g_{i}^{-1}(\text{LCS}(X_{i},B_{X_{i}}))$
consists of
![]() $\left\lfloor B_{Y_{i}}\right\rfloor$
and possibly finitely many curves which are contracted over
$\left\lfloor B_{Y_{i}}\right\rfloor$
and possibly finitely many curves which are contracted over
![]() $X_{i}$
. We know that
$X_{i}$
. We know that
![]() $D$
cannot intersect
$D$
cannot intersect
![]() $\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
, so
$\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
, so
![]() $D$
must be connected to
$D$
must be connected to
![]() $\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
by a chain of curves, each of which is contracted over
$\unicode[STIX]{x1D719}_{i}^{-1}(\left\lfloor B_{Y_{i}}\right\rfloor )$
by a chain of curves, each of which is contracted over
![]() $Z_{i}$
. Suppose for contradiction that some of these curves are not contained in
$Z_{i}$
. Suppose for contradiction that some of these curves are not contained in
![]() $\text{Supp}(D)$
. There must be one such curve,
$\text{Supp}(D)$
. There must be one such curve,
![]() $C$
say, which satisfies
$C$
say, which satisfies
![]() $D\cdot C>0$
, because at least one must intersect
$D\cdot C>0$
, because at least one must intersect
![]() $D$
but not be contained in
$D$
but not be contained in
![]() $\text{Supp}(D)$
. But
$\text{Supp}(D)$
. But
![]() $C$
is contracted over
$C$
is contracted over
![]() $Z_{i}$
, which gives a contradiction, for
$Z_{i}$
, which gives a contradiction, for
![]() $D$
is anti-nef
$D$
is anti-nef
![]() $/Z_{i}$
.◻
$/Z_{i}$
.◻
5 Restriction
In characteristic zero, the reduced boundary
![]() $\left\lfloor B_{Y}\right\rfloor$
of a dlt pair
$\left\lfloor B_{Y}\right\rfloor$
of a dlt pair
![]() $(Y,B_{Y})$
is
$(Y,B_{Y})$
is
![]() $S_{2}$
and consequently demi-normal. The proof [Reference Kollár14, 17.5] uses vanishing theorems and may fail in positive characteristic. Instead we exploit the Frobenius morphism to work on a partial normalization in place of
$S_{2}$
and consequently demi-normal. The proof [Reference Kollár14, 17.5] uses vanishing theorems and may fail in positive characteristic. Instead we exploit the Frobenius morphism to work on a partial normalization in place of
![]() $\left\lfloor B_{Y}\right\rfloor$
.
$\left\lfloor B_{Y}\right\rfloor$
.
Proposition 5.1. Let
![]() $(Y,B_{Y})$
be a
$(Y,B_{Y})$
be a
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair over
$3$
-fold pair over
![]() $k$
. Let
$k$
. Let
![]() $\unicode[STIX]{x1D70B}:S\rightarrow \left\lfloor B_{Y}\right\rfloor$
be the
$\unicode[STIX]{x1D70B}:S\rightarrow \left\lfloor B_{Y}\right\rfloor$
be the
![]() $S_{2}$
-fication of
$S_{2}$
-fication of
![]() $\left\lfloor B_{Y}\right\rfloor$
. Then
$\left\lfloor B_{Y}\right\rfloor$
. Then
![]() $\unicode[STIX]{x1D70B}:S\rightarrow \left\lfloor B_{Y}\right\rfloor$
is a finite universal homeomorphism from a demi-normal scheme.
$\unicode[STIX]{x1D70B}:S\rightarrow \left\lfloor B_{Y}\right\rfloor$
is a finite universal homeomorphism from a demi-normal scheme.
Proof.
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism in codimension
$\unicode[STIX]{x1D70B}$
is an isomorphism in codimension
![]() $1$
because
$1$
because
![]() $\left\lfloor B_{Y}\right\rfloor$
is reduced and equidimensional. We show that
$\left\lfloor B_{Y}\right\rfloor$
is reduced and equidimensional. We show that
![]() $\unicode[STIX]{x1D70B}$
is injective and surjective on geometric points in order to apply Proposition 2.3. It is surjective because the normalization is surjective and
$\unicode[STIX]{x1D70B}$
is injective and surjective on geometric points in order to apply Proposition 2.3. It is surjective because the normalization is surjective and
![]() $\unicode[STIX]{x1D70B}$
factors into the normalization by Proposition 2.6.
$\unicode[STIX]{x1D70B}$
factors into the normalization by Proposition 2.6.
Suppose
![]() $P$
is a geometric point on
$P$
is a geometric point on
![]() $\left\lfloor B_{Y}\right\rfloor$
with more than one pre-image. We use what we know of
$\left\lfloor B_{Y}\right\rfloor$
with more than one pre-image. We use what we know of
![]() $\left\lfloor B_{Y}\right\rfloor$
from Proposition 2.11 to reach a contradiction. First note that each component of
$\left\lfloor B_{Y}\right\rfloor$
from Proposition 2.11 to reach a contradiction. First note that each component of
![]() $\left\lfloor B_{Y}\right\rfloor$
is normal. This means that we can identify the normalization of
$\left\lfloor B_{Y}\right\rfloor$
is normal. This means that we can identify the normalization of
![]() $\left\lfloor B_{Y}\right\rfloor$
with the disjoint union of its components. Now observe that
$\left\lfloor B_{Y}\right\rfloor$
with the disjoint union of its components. Now observe that
![]() $P$
cannot have more than one pre-image in any irreducible component of
$P$
cannot have more than one pre-image in any irreducible component of
![]() $S$
, because
$S$
, because
![]() $\unicode[STIX]{x1D70B}$
factors into the normalization of
$\unicode[STIX]{x1D70B}$
factors into the normalization of
![]() $\left\lfloor B_{Y}\right\rfloor$
, which is just projection from the disjoint union of the components.
$\left\lfloor B_{Y}\right\rfloor$
, which is just projection from the disjoint union of the components.
Therefore, we may assume
![]() $P$
is contained in at least two components
$P$
is contained in at least two components
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
of
$E_{2}$
of
![]() $\left\lfloor B_{Y}\right\rfloor$
and has distinct pre-images
$\left\lfloor B_{Y}\right\rfloor$
and has distinct pre-images
![]() $Q_{i}$
for
$Q_{i}$
for
![]() $i=1,2$
, each contained in the component of
$i=1,2$
, each contained in the component of
![]() $S$
corresponding to
$S$
corresponding to
![]() $E_{i}$
.
$E_{i}$
.
![]() $C:=E_{1}\cap E_{2}$
is of pure dimension
$C:=E_{1}\cap E_{2}$
is of pure dimension
![]() $1$
and its irreducible components are smooth curves by Proposition 2.11. Let
$1$
and its irreducible components are smooth curves by Proposition 2.11. Let
![]() $R_{i}$
be the unique geometric point in the pre-image of
$R_{i}$
be the unique geometric point in the pre-image of
![]() $P$
in
$P$
in
![]() $E_{i}\subset E_{1}\sqcup E_{2}$
. As
$E_{i}\subset E_{1}\sqcup E_{2}$
. As
![]() $\unicode[STIX]{x1D70B}$
factors through the normalization
$\unicode[STIX]{x1D70B}$
factors through the normalization
![]() $E_{1}\sqcup E_{2}\rightarrow \left\lfloor B_{Y}\right\rfloor$
, the image of
$E_{1}\sqcup E_{2}\rightarrow \left\lfloor B_{Y}\right\rfloor$
, the image of
![]() $R_{i}$
in
$R_{i}$
in
![]() $S$
is
$S$
is
![]() $Q_{i}$
. The pre-image of
$Q_{i}$
. The pre-image of
![]() $C$
in
$C$
in
![]() $E_{1}\sqcup E_{2}$
is supported in pure dimension
$E_{1}\sqcup E_{2}$
is supported in pure dimension
![]() $1$
. Therefore, the pre-image of
$1$
. Therefore, the pre-image of
![]() $C$
on
$C$
on
![]() $S$
,
$S$
,
![]() $C_{S}$
is also supported in pure dimension
$C_{S}$
is also supported in pure dimension
![]() $1$
. If
$1$
. If
![]() $\unicode[STIX]{x1D6E4}$
is an irreducible component of
$\unicode[STIX]{x1D6E4}$
is an irreducible component of
![]() $C$
which contains
$C$
which contains
![]() $P$
, the pre-image
$P$
, the pre-image
![]() $\unicode[STIX]{x1D6E4}_{i}$
of
$\unicode[STIX]{x1D6E4}_{i}$
of
![]() $\unicode[STIX]{x1D6E4}$
in
$\unicode[STIX]{x1D6E4}$
in
![]() $E_{i}\subset E_{1}\sqcup E_{2}$
is an irreducible curve passing through
$E_{i}\subset E_{1}\sqcup E_{2}$
is an irreducible curve passing through
![]() $R_{i}$
. There is a unique irreducible curve
$R_{i}$
. There is a unique irreducible curve
![]() $\unicode[STIX]{x1D6E4}_{S}$
which is the pre-image of
$\unicode[STIX]{x1D6E4}_{S}$
which is the pre-image of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $S$
because
$S$
because
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism away from a finite set of points. So
$\unicode[STIX]{x1D70B}$
is an isomorphism away from a finite set of points. So
![]() $\unicode[STIX]{x1D6E4}_{S}$
is the image of both
$\unicode[STIX]{x1D6E4}_{S}$
is the image of both
![]() $\unicode[STIX]{x1D6E4}_{i}$
and it follows that
$\unicode[STIX]{x1D6E4}_{i}$
and it follows that
![]() $\unicode[STIX]{x1D6E4}_{S}$
must contain both
$\unicode[STIX]{x1D6E4}_{S}$
must contain both
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
. Now let
$Q_{2}$
. Now let
![]() $\unicode[STIX]{x1D6E4}^{\unicode[STIX]{x1D708}}$
be the normalization of
$\unicode[STIX]{x1D6E4}^{\unicode[STIX]{x1D708}}$
be the normalization of
![]() $\unicode[STIX]{x1D6E4}_{S}$
. The composition
$\unicode[STIX]{x1D6E4}_{S}$
. The composition
![]() $\unicode[STIX]{x1D6E4}^{\unicode[STIX]{x1D708}}\rightarrow \unicode[STIX]{x1D6E4}$
is an isomorphism of smooth curves, but some point has two geometric pre-images. We have a contradiction, and so
$\unicode[STIX]{x1D6E4}^{\unicode[STIX]{x1D708}}\rightarrow \unicode[STIX]{x1D6E4}$
is an isomorphism of smooth curves, but some point has two geometric pre-images. We have a contradiction, and so
![]() $\unicode[STIX]{x1D70B}$
must be a universal homeomorphism.
$\unicode[STIX]{x1D70B}$
must be a universal homeomorphism.
![]() $S$
is nodal in codimension
$S$
is nodal in codimension
![]() $1$
because
$1$
because
![]() $\left\lfloor B_{Y}\right\rfloor$
is nodal in codimension
$\left\lfloor B_{Y}\right\rfloor$
is nodal in codimension
![]() $1$
by [Reference Kollár15, 2.32] and
$1$
by [Reference Kollár15, 2.32] and
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism in codimension
$\unicode[STIX]{x1D70B}$
is an isomorphism in codimension
![]() $1$
.
$1$
.
![]() $S$
is
$S$
is
![]() $S_{2}$
by definition, so we conclude that
$S_{2}$
by definition, so we conclude that
![]() $S$
is demi-normal.◻
$S$
is demi-normal.◻
Proof of Theorem 1.3.
The conditions (1)–(6) of [Reference Kollár15, 4.2] for adjunction to
![]() $S$
are satisfied. The only condition which is not obvious is (5), which holds because
$S$
are satisfied. The only condition which is not obvious is (5), which holds because
![]() $S$
is demi-normal [Reference Kollár15, 5.1]. Thus there is a different,
$S$
is demi-normal [Reference Kollár15, 5.1]. Thus there is a different,
![]() $B_{S}$
, satisfying
$B_{S}$
, satisfying
We can check discrepancies to ensure this pair is slc by pulling back to the normalization, and applying adjunction to the individual normal components of
![]() $\left\lfloor B_{Y}\right\rfloor$
. By Tanaka’s abundance for slc surfaces [Reference Tanaka21],
$\left\lfloor B_{Y}\right\rfloor$
. By Tanaka’s abundance for slc surfaces [Reference Tanaka21],
![]() $K_{S}+B_{S}$
is semi-ample. Now because
$K_{S}+B_{S}$
is semi-ample. Now because
![]() $S\rightarrow \left\lfloor B_{Y}\right\rfloor$
is a finite universal homeomorphism, by Proposition 2.4,
$S\rightarrow \left\lfloor B_{Y}\right\rfloor$
is a finite universal homeomorphism, by Proposition 2.4,
![]() $(K_{Y}+B_{Y})|_{\left\lfloor B_{Y}\right\rfloor }$
is semi-ample.◻
$(K_{Y}+B_{Y})|_{\left\lfloor B_{Y}\right\rfloor }$
is semi-ample.◻
6 Good log minimal models
6.1 Big log divisors
In this subsection we prove Theorem 1.1, which will allow us to contract birational extremal rays.
Proof of Theorem 1.1 when
 $Z$
is a point.
$Z$
is a point.
Step 1: Set-up.
We first prove that if
![]() $(Y,B_{Y})$
is a projective
$(Y,B_{Y})$
is a projective
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold pair over
$3$
-fold pair over
![]() $k$
with
$k$
with
![]() $\mathbb{Q}$
-boundary
$\mathbb{Q}$
-boundary
![]() $B_{Y}$
, such that
$B_{Y}$
, such that
![]() $K_{Y}+B_{Y}$
is big and nef, then
$K_{Y}+B_{Y}$
is big and nef, then
![]() $K_{Y}+B_{Y}$
is semi-ample. We spend most of the proof on this case, and then extend to general log canonical pairs with
$K_{Y}+B_{Y}$
is semi-ample. We spend most of the proof on this case, and then extend to general log canonical pairs with
![]() $\mathbb{R}$
-boundaries in the final step. We may assume
$\mathbb{R}$
-boundaries in the final step. We may assume
![]() $\left\lfloor B_{Y}\right\rfloor \neq 0$
as otherwise
$\left\lfloor B_{Y}\right\rfloor \neq 0$
as otherwise
![]() $(Y,B_{Y})$
is klt and we can apply the base-point free theorem [Reference Birkar5, 1.4]. If it were the case that
$(Y,B_{Y})$
is klt and we can apply the base-point free theorem [Reference Birkar5, 1.4]. If it were the case that
![]() $\mathbb{E}(K_{Y}+B_{Y})\subseteq \left\lfloor B_{Y}\right\rfloor$
, we would be able to apply Theorem 2.2 together with Theorem 1.3 to conclude the statement. However, this need not be true, so we proceed by modifying
$\mathbb{E}(K_{Y}+B_{Y})\subseteq \left\lfloor B_{Y}\right\rfloor$
, we would be able to apply Theorem 2.2 together with Theorem 1.3 to conclude the statement. However, this need not be true, so we proceed by modifying
![]() $Y$
to reach a situation where it holds. For this reason, we would like to remove
$Y$
to reach a situation where it holds. For this reason, we would like to remove
![]() $K_{Y}+B_{Y}$
-trivial curves which are not contained in
$K_{Y}+B_{Y}$
-trivial curves which are not contained in
![]() $\left\lfloor B_{Y}\right\rfloor$
.
$\left\lfloor B_{Y}\right\rfloor$
.
Step 2: Contract
![]() $K_{Y}+B_{Y}$
-trivial curves which intersect
$K_{Y}+B_{Y}$
-trivial curves which intersect
![]() $\left\lfloor B_{Y}\right\rfloor$
positively.
$\left\lfloor B_{Y}\right\rfloor$
positively.
![]() $K_{Y}+B_{Y}$
is big by assumption, so let
$K_{Y}+B_{Y}$
is big by assumption, so let
![]() $\unicode[STIX]{x1D716}$
be sufficiently small that
$\unicode[STIX]{x1D716}$
be sufficiently small that
![]() $K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
is also big, and so any
$K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
is also big, and so any
![]() $K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP terminates by Theorem 1.6. If we run a
$K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP terminates by Theorem 1.6. If we run a
![]() $K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
$K_{Y}+B_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
![]() $\left\lfloor B_{Y}\right\rfloor$
, by Lemma 2.16, we can replace
$\left\lfloor B_{Y}\right\rfloor$
, by Lemma 2.16, we can replace
![]() $\unicode[STIX]{x1D716}$
by a smaller number to assume that the LMMP contracts only
$\unicode[STIX]{x1D716}$
by a smaller number to assume that the LMMP contracts only
![]() $K_{Y}+B_{Y}$
-trivial extremal rays.
$K_{Y}+B_{Y}$
-trivial extremal rays.
As any contraction
![]() $Y_{i}\rightarrow Z_{i}$
in this LMMP is
$Y_{i}\rightarrow Z_{i}$
in this LMMP is
![]() $K_{Y_{i}}+B_{Y_{i}}$
-trivial, we claim that at each step
$K_{Y_{i}}+B_{Y_{i}}$
-trivial, we claim that at each step
![]() $K_{Y_{i}}+B_{Y_{i}}$
pulls back from some
$K_{Y_{i}}+B_{Y_{i}}$
pulls back from some
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() $Z_{i}$
. This follows from the klt cone and base-point free theorems (see [Reference Kollár and Mori17, 3.7(4)]).
$Z_{i}$
. This follows from the klt cone and base-point free theorems (see [Reference Kollár and Mori17, 3.7(4)]).
Therefore, this LMMP results in a model
![]() $Y^{\prime }$
on which the birational transform
$Y^{\prime }$
on which the birational transform
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
is semi-ample if and only if
$K_{Y^{\prime }}+B_{Y^{\prime }}$
is semi-ample if and only if
![]() $K_{Y}+B_{Y}$
is semi-ample.
$K_{Y}+B_{Y}$
is semi-ample.
![]() $(Y^{\prime },B_{Y^{\prime }})$
is
$(Y^{\prime },B_{Y^{\prime }})$
is
![]() $\mathbb{Q}$
-factorial and log canonical but may no longer be dlt. By our application of Lemma 2.16, we have that
$\mathbb{Q}$
-factorial and log canonical but may no longer be dlt. By our application of Lemma 2.16, we have that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
is nef for all
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
is nef for all
![]() $\unicode[STIX]{x1D716}^{\prime }\in [0,\unicode[STIX]{x1D716}]$
. Thus any
$\unicode[STIX]{x1D716}^{\prime }\in [0,\unicode[STIX]{x1D716}]$
. Thus any
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial curve cannot intersect
$K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial curve cannot intersect
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
positively: it is therefore forced to either be disjoint from
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
positively: it is therefore forced to either be disjoint from
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
or completely contained in
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
or completely contained in
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
.
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
.
Step 3: Contract
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial curves not contained in
$K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial curves not contained in
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
.
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
.
The underlying variety
![]() $Y^{\prime }$
is klt and
$Y^{\prime }$
is klt and
![]() $\mathbb{Q}$
-factorial because it was formed by running the LMMP from a klt
$\mathbb{Q}$
-factorial because it was formed by running the LMMP from a klt
![]() $\mathbb{Q}$
-factorial pair, so by Proposition 2.14(1), we may replace
$\mathbb{Q}$
-factorial pair, so by Proposition 2.14(1), we may replace
![]() $\unicode[STIX]{x1D716}$
to be sufficiently small that any
$\unicode[STIX]{x1D716}$
to be sufficiently small that any
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
-trivial curve is also
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
-trivial curve is also
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial. Apply the base-point free theorem [Reference Birkar5, 1.4] on the klt
$K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial. Apply the base-point free theorem [Reference Birkar5, 1.4] on the klt
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
to produce another birational
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
to produce another birational
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial contraction
$K_{Y^{\prime }}+B_{Y^{\prime }}$
-trivial contraction
![]() $f:Y^{\prime }\rightarrow Y^{\prime \prime }$
such that
$f:Y^{\prime }\rightarrow Y^{\prime \prime }$
such that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor {\sim}_{\mathbb{Q}}f^{\ast }A$
for some ample
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor {\sim}_{\mathbb{Q}}f^{\ast }A$
for some ample
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $A$
. Notice that if
$A$
. Notice that if
![]() $0<\unicode[STIX]{x1D716}^{\prime }<\unicode[STIX]{x1D716}$
,
$0<\unicode[STIX]{x1D716}^{\prime }<\unicode[STIX]{x1D716}$
,
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
is also semi-ample and its associated morphism contracts the same curves as
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
is also semi-ample and its associated morphism contracts the same curves as
![]() $f$
. Therefore,
$f$
. Therefore,
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
also pulls back from
$K_{Y^{\prime }}+B_{Y^{\prime }}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y^{\prime }}\right\rfloor$
also pulls back from
![]() $Y^{\prime \prime }$
.
$Y^{\prime \prime }$
.
This implies
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
pulls back from a
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
pulls back from a
![]() $\mathbb{Q}$
-Cartier divisor
$\mathbb{Q}$
-Cartier divisor
![]() $D$
on
$D$
on
![]() $Y^{\prime \prime }$
, and so does
$Y^{\prime \prime }$
, and so does
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
. Let
$K_{Y^{\prime }}+B_{Y^{\prime }}$
. Let
![]() $B_{Y^{\prime \prime }}$
be the birational transform of
$B_{Y^{\prime \prime }}$
be the birational transform of
![]() $B_{Y^{\prime }}$
on
$B_{Y^{\prime }}$
on
![]() $Y^{\prime \prime }$
, so that
$Y^{\prime \prime }$
, so that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}=f^{\ast }(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})$
and
$K_{Y^{\prime }}+B_{Y^{\prime }}=f^{\ast }(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})$
and
![]() $D=f_{\ast }\left\lfloor B_{Y^{\prime }}\right\rfloor =\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
.
$D=f_{\ast }\left\lfloor B_{Y^{\prime }}\right\rfloor =\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
.
We get a new log canonical pair
![]() $(Y^{\prime \prime },B_{Y^{\prime \prime }})$
such that
$(Y^{\prime \prime },B_{Y^{\prime \prime }})$
such that
![]() $K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }}{\sim}_{\mathbb{Q}}A+\unicode[STIX]{x1D716}D$
for ample
$K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }}{\sim}_{\mathbb{Q}}A+\unicode[STIX]{x1D716}D$
for ample
![]() $A$
and effective
$A$
and effective
![]() $D$
as above. This implies that
$D$
as above. This implies that
![]() $\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})\subset D=\left\lfloor B_{Y}^{\prime \prime }\right\rfloor$
, and we also know that
$\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})\subset D=\left\lfloor B_{Y}^{\prime \prime }\right\rfloor$
, and we also know that
![]() $K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }}$
is semi-ample if and only if
$K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }}$
is semi-ample if and only if
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}$
is. However,
$K_{Y^{\prime }}+B_{Y^{\prime }}$
is. However,
![]() $(Y^{\prime \prime },B_{Y^{\prime \prime }})$
need not be either dlt or
$(Y^{\prime \prime },B_{Y^{\prime \prime }})$
need not be either dlt or
![]() $\mathbb{Q}$
-factorial in general, so we still cannot apply Theorem 1.3.
$\mathbb{Q}$
-factorial in general, so we still cannot apply Theorem 1.3.
Step 4: Construct a model where Keel’s theorem applies.
Let
![]() $(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }})$
be a
$(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }})$
be a
![]() $\mathbb{Q}$
-factorial dlt model of
$\mathbb{Q}$
-factorial dlt model of
![]() $(Y^{\prime \prime },B_{Y^{\prime \prime }})$
with morphism
$(Y^{\prime \prime },B_{Y^{\prime \prime }})$
with morphism
![]() $g:Y^{\prime \prime \prime }\rightarrow Y^{\prime \prime }$
. We claim that every irreducible component of
$g:Y^{\prime \prime \prime }\rightarrow Y^{\prime \prime }$
. We claim that every irreducible component of
![]() $\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
is either contained within
$\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
is either contained within
![]() $\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or is completely disjoint from it. First note that
$\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or is completely disjoint from it. First note that
![]() $\text{LCS}(Y^{\prime \prime },B_{Y^{\prime \prime }})=\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
, because
$\text{LCS}(Y^{\prime \prime },B_{Y^{\prime \prime }})=\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
, because
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
pulls back from
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
pulls back from
![]() $\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
, and
$\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
, and
![]() $\text{LCS}(Y^{\prime },B_{Y^{\prime }})=\left\lfloor B_{Y^{\prime }}\right\rfloor$
because
$\text{LCS}(Y^{\prime },B_{Y^{\prime }})=\left\lfloor B_{Y^{\prime }}\right\rfloor$
because
![]() $(Y^{\prime },B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is klt.
$(Y^{\prime },B_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is klt.
To complete the proof of the claim, suppose
![]() $V$
is an irreducible component of
$V$
is an irreducible component of
![]() $\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
and first assume that it is
$\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
and first assume that it is
![]() $2$
-dimensional. If
$2$
-dimensional. If
![]() $V$
is contracted over
$V$
is contracted over
![]() $Y^{\prime \prime }$
then it is in
$Y^{\prime \prime }$
then it is in
![]() $\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
by definition of the crepant dlt
$\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
by definition of the crepant dlt
![]() $\mathbb{Q}$
-factorial modification. If it is not contracted over
$\mathbb{Q}$
-factorial modification. If it is not contracted over
![]() $Y^{\prime \prime }$
then its birational transform on
$Y^{\prime \prime }$
then its birational transform on
![]() $Y$
is in
$Y$
is in
![]() $\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})\subset \left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
. So we may assume
$\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})\subset \left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
. So we may assume
![]() $V$
is
$V$
is
![]() $1$
-dimensional.
$1$
-dimensional.
![]() $g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
is an effective
$g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
is an effective
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() $Y^{\prime \prime \prime }$
with support equal to
$Y^{\prime \prime \prime }$
with support equal to
![]() $\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
(because
$\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
(because
![]() $\text{LCS}(Y^{\prime \prime },B_{Y^{\prime \prime }})=\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
). If
$\text{LCS}(Y^{\prime \prime },B_{Y^{\prime \prime }})=\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
). If
![]() $V$
is contracted over
$V$
is contracted over
![]() $Y^{\prime \prime }$
then by the projection formula
$Y^{\prime \prime }$
then by the projection formula
![]() $V\cdot g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor =0$
. If it is not contracted over
$V\cdot g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor =0$
. If it is not contracted over
![]() $Y^{\prime \prime }$
then its birational transform is again contained within
$Y^{\prime \prime }$
then its birational transform is again contained within
![]() $\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})$
and hence within
$\mathbb{E}(K_{Y^{\prime \prime }}+B_{Y^{\prime \prime }})$
and hence within
![]() $\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
. Either way this implies that either
$\left\lfloor B_{Y^{\prime \prime }}\right\rfloor$
. Either way this implies that either
![]() $V$
is contained within
$V$
is contained within
![]() $\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or it is completely disjoint from it. This completes the proof of the claim.
$\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or it is completely disjoint from it. This completes the proof of the claim.
We may now apply Keel’s theorem (Proposition 2.2) to
![]() $(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }})$
. Any connected component of
$(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }})$
. Any connected component of
![]() $\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
is either contained within
$\mathbb{E}(K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }})$
is either contained within
![]() $\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or is completely disjoint from it. In this first case
$\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
or is completely disjoint from it. In this first case
![]() $K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }}$
is semi-ample when restricted to this connected component by Theorem 1.3. In the second it is semi-ample because in a neighborhood of the component,
$K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }}$
is semi-ample when restricted to this connected component by Theorem 1.3. In the second it is semi-ample because in a neighborhood of the component,
![]() $K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }}$
is equal to
$K_{Y^{\prime \prime \prime }}+B_{Y^{\prime \prime \prime }}$
is equal to
which is nef and big, and the pair
![]() $(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }}-\unicode[STIX]{x1D716}g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor )$
is klt because
$(Y^{\prime \prime \prime },B_{Y^{\prime \prime \prime }}-\unicode[STIX]{x1D716}g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor )$
is klt because
![]() $\text{Supp}\,g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor =\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
, so we may apply base-point freeness in the klt case [Reference Birkar5, 1.4].
$\text{Supp}\,g^{\ast }\left\lfloor B_{Y^{\prime \prime }}\right\rfloor =\left\lfloor B_{Y^{\prime \prime \prime }}\right\rfloor$
, so we may apply base-point freeness in the klt case [Reference Birkar5, 1.4].
Step 5: Log canonical pairs with
![]() $\mathbb{R}$
-boundaries.
$\mathbb{R}$
-boundaries.
So far we have proved Theorem 1.1 for
![]() $\mathbb{Q}$
-factorial dlt pairs with
$\mathbb{Q}$
-factorial dlt pairs with
![]() $\mathbb{Q}$
-boundaries. Suppose now that
$\mathbb{Q}$
-boundaries. Suppose now that
![]() $(X,B)$
is as in the statement, that is, log canonical with
$(X,B)$
is as in the statement, that is, log canonical with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
. A crepant
$B$
. A crepant
![]() $\mathbb{Q}$
-factorial dlt model
$\mathbb{Q}$
-factorial dlt model
![]() $\unicode[STIX]{x1D719}:Y\rightarrow X$
exists by Proposition 2.13, and let
$\unicode[STIX]{x1D719}:Y\rightarrow X$
exists by Proposition 2.13, and let
![]() $B_{Y}$
be the dlt
$B_{Y}$
be the dlt
![]() $\mathbb{R}$
-boundary defined by
$\mathbb{R}$
-boundary defined by
![]() $K_{Y}+B_{Y}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. Let
$K_{Y}+B_{Y}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
. Let
![]() $V$
be the
$V$
be the
![]() $\mathbb{R}$
-vector space of Weil divisors spanned by the components of
$\mathbb{R}$
-vector space of Weil divisors spanned by the components of
![]() $B_{Y}$
, and define
$B_{Y}$
, and define
![]() ${\mathcal{L}}$
to be the rational polytope from Proposition 2.14. Apply Proposition 2.14(2) with the family of extremal rays equal to all extremal rays of
${\mathcal{L}}$
to be the rational polytope from Proposition 2.14. Apply Proposition 2.14(2) with the family of extremal rays equal to all extremal rays of
![]() $\overline{NE}(X)$
. We get a smaller rational polytope
$\overline{NE}(X)$
. We get a smaller rational polytope
![]() ${\mathcal{P}}$
containing
${\mathcal{P}}$
containing
![]() $B_{Y}$
such that
$B_{Y}$
such that
![]() $K_{Y}+\unicode[STIX]{x1D6E5}$
is nef for all
$K_{Y}+\unicode[STIX]{x1D6E5}$
is nef for all
![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{P}}$
. Let the vertices of
$\unicode[STIX]{x1D6E5}\in {\mathcal{P}}$
. Let the vertices of
![]() ${\mathcal{P}}$
be
${\mathcal{P}}$
be
![]() $B_{1},\ldots ,B_{n}$
. We may shrink
$B_{1},\ldots ,B_{n}$
. We may shrink
![]() ${\mathcal{P}}$
around
${\mathcal{P}}$
around
![]() $B_{Y}$
to assume that
$B_{Y}$
to assume that
![]() $K_{Y}+B_{i}$
is big for all
$K_{Y}+B_{i}$
is big for all
![]() $i$
. By the case we have already proved,
$i$
. By the case we have already proved,
![]() $K_{Y}+B_{i}$
is semi-ample for each
$K_{Y}+B_{i}$
is semi-ample for each
![]() $i$
. But we can write
$i$
. But we can write
![]() $B_{Y}$
as some
$B_{Y}$
as some
![]() $\mathbb{R}$
-linear combination of the
$\mathbb{R}$
-linear combination of the
![]() $B_{i}$
with positive coefficients, and so this implies that
$B_{i}$
with positive coefficients, and so this implies that
![]() $K_{Y}+B_{Y}$
is also semi-ample. This in turn implies that
$K_{Y}+B_{Y}$
is also semi-ample. This in turn implies that
![]() $K_{X}+B$
is semi-ample.◻
$K_{X}+B$
is semi-ample.◻
Proof of Theorem 1.1 in relative case.
We now have a projective contraction
![]() $f:X\rightarrow Z$
. Let
$f:X\rightarrow Z$
. Let
![]() $A$
be an ample divisor on
$A$
be an ample divisor on
![]() $Z$
. Because
$Z$
. Because
![]() $K_{X}+B$
is big
$K_{X}+B$
is big
![]() $/Z$
, there exits
$/Z$
, there exits
![]() $n\gg 0$
such that
$n\gg 0$
such that
![]() $K_{X}+B+nf^{\ast }A$
is big. Now using Theorem 1.7(2), perhaps after increasing
$K_{X}+B+nf^{\ast }A$
is big. Now using Theorem 1.7(2), perhaps after increasing
![]() $n$
,
$n$
,
![]() $K_{X}+B+nf^{\ast }A$
is also globally nef and positive on every curve not contracted
$K_{X}+B+nf^{\ast }A$
is also globally nef and positive on every curve not contracted
![]() $/Z$
. Our ground field is algebraically closed, so it is
$/Z$
. Our ground field is algebraically closed, so it is
![]() $F$
-finite, infinite and perfect. By the results of [Reference Tanaka20] we can find
$F$
-finite, infinite and perfect. By the results of [Reference Tanaka20] we can find
![]() $A^{\prime }{\sim}_{\mathbb{R}}nf^{\ast }A$
such that
$A^{\prime }{\sim}_{\mathbb{R}}nf^{\ast }A$
such that
![]() $(X,B+A^{\prime })$
is log canonical. We may now apply the global case.◻
$(X,B+A^{\prime })$
is log canonical. We may now apply the global case.◻
6.2 Big boundary divisors
Now we move on to Theorem 1.2. The proof follows that of Theorem 1.1 in outline, but differs in detail as we must deal with nonbirational morphisms and non- pseudo-effective log divisors.
Proof of Theorem 1.2 when
 $Z$
is a point.
$Z$
is a point.
Step 1: Set-up.
As before, we first prove the theorem in the
![]() $\mathbb{Q}$
-boundary,
$\mathbb{Q}$
-boundary,
![]() $\mathbb{Q}$
-factorial dlt case. To this end, assume that
$\mathbb{Q}$
-factorial dlt case. To this end, assume that
![]() $(Y,B_{Y})$
is a projective
$(Y,B_{Y})$
is a projective
![]() $\mathbb{Q}$
-factorial dlt
$\mathbb{Q}$
-factorial dlt
![]() $3$
-fold over
$3$
-fold over
![]() $k$
with
$k$
with
![]() $\mathbb{Q}$
-boundary
$\mathbb{Q}$
-boundary
![]() $B_{Y}$
. Assume also that
$B_{Y}$
. Assume also that
![]() $A_{Y}$
is a big and semi-ample
$A_{Y}$
is a big and semi-ample
![]() $\mathbb{Q}$
-divisor, such that
$\mathbb{Q}$
-divisor, such that
![]() $K_{Y}+B_{Y}+A_{Y}$
is nef. We prove that
$K_{Y}+B_{Y}+A_{Y}$
is nef. We prove that
![]() $K_{Y}+B_{Y}+A_{Y}$
is semi-ample. By [Reference Tanaka20], we may replace
$K_{Y}+B_{Y}+A_{Y}$
is semi-ample. By [Reference Tanaka20], we may replace
![]() $A_{Y}$
to assume that
$A_{Y}$
to assume that
![]() $(Y,B_{Y}+A_{Y})$
is log canonical. We may also assume that
$(Y,B_{Y}+A_{Y})$
is log canonical. We may also assume that
![]() $\left\lfloor B_{Y}\right\rfloor \neq 0$
by the base-point free theorem.
$\left\lfloor B_{Y}\right\rfloor \neq 0$
by the base-point free theorem.
Step 2: Run a
![]() $K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
$K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
![]() $\left\lfloor B_{Y}\right\rfloor$
.
$\left\lfloor B_{Y}\right\rfloor$
.
In fact, this step consists of showing that there is a way to choose such an LMMP which terminates, and that by taking
![]() $\unicode[STIX]{x1D716}$
sufficiently small we may assume that each contraction is
$\unicode[STIX]{x1D716}$
sufficiently small we may assume that each contraction is
![]() $K_{Y}+B_{Y}+A_{Y}$
-trivial.
$K_{Y}+B_{Y}+A_{Y}$
-trivial.
First note that by Lemma 2.16, whenever the LMMP with scaling attempts to contract an extremal ray which is not
![]() $K_{Y}+B_{Y}+A_{Y}$
-trivial, we may replace
$K_{Y}+B_{Y}+A_{Y}$
-trivial, we may replace
![]() $\unicode[STIX]{x1D716}$
with a smaller number so that we terminate instead. Lemma 2.16 also tells us that our LMMP is also a
$\unicode[STIX]{x1D716}$
with a smaller number so that we terminate instead. Lemma 2.16 also tells us that our LMMP is also a
![]() $K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y}\right\rfloor$
-MMP for any
$K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}^{\prime }\left\lfloor B_{Y}\right\rfloor$
-MMP for any
![]() $\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}]$
. This means that we are free to replace
$\unicode[STIX]{x1D716}^{\prime }\in (0,\unicode[STIX]{x1D716}]$
. This means that we are free to replace
![]() $\unicode[STIX]{x1D716}$
by a smaller number at any point during the LMMP without affecting the validity of the previous steps.
$\unicode[STIX]{x1D716}$
by a smaller number at any point during the LMMP without affecting the validity of the previous steps.
We now show that we can choose such an LMMP which terminates. As a first step we claim that there is some choice of
![]() $K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
$K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP with scaling of
![]() $\left\lfloor B_{Y}\right\rfloor$
with the following properties:
$\left\lfloor B_{Y}\right\rfloor$
with the following properties:
∙ Every step is
 $K_{Y}+B_{Y}+A_{Y}$
-trivial.
$K_{Y}+B_{Y}+A_{Y}$
-trivial.∙ It reaches (but may not terminate on) a model
 ${\tilde{Y}}$
such that:
${\tilde{Y}}$
such that:∙ No
 $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
 $\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
which contracts only
$\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
which contracts only
 $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
-trivial rays will ever contain a divisorial contraction.
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
-trivial rays will ever contain a divisorial contraction.
Suppose otherwise. Then given any model reachable via a
![]() $K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP which contracts only
$K_{Y}+B_{Y}+A_{Y}-\unicode[STIX]{x1D716}\left\lfloor B_{Y}\right\rfloor$
-MMP which contracts only
![]() $K_{Y}+B_{Y}+A_{Y}$
-trivial extremal rays, it is possible to find a way to continue contracting only
$K_{Y}+B_{Y}+A_{Y}$
-trivial extremal rays, it is possible to find a way to continue contracting only
![]() $K_{Y}+B_{Y}+A_{Y}$
-trivial rays and reach a divisorial contraction. By induction this produces an infinite sequence of divisorial contractions, which is impossible. Therefore, there must exist a model
$K_{Y}+B_{Y}+A_{Y}$
-trivial rays and reach a divisorial contraction. By induction this produces an infinite sequence of divisorial contractions, which is impossible. Therefore, there must exist a model
![]() ${\tilde{Y}}$
as described. Thus, however we continue to run our LMMP with scaling from
${\tilde{Y}}$
as described. Thus, however we continue to run our LMMP with scaling from
![]() ${\tilde{Y}}$
then we may assume that every step is a flip.
${\tilde{Y}}$
then we may assume that every step is a flip.
Let
![]() $H_{{\tilde{Y}}}$
be an ample
$H_{{\tilde{Y}}}$
be an ample
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() ${\tilde{Y}}$
such that
${\tilde{Y}}$
such that
![]() $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor +H_{{\tilde{Y}}}$
is nef. We may apply [Reference Tanaka20] to assume that
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor +H_{{\tilde{Y}}}$
is nef. We may apply [Reference Tanaka20] to assume that
![]() $({\tilde{Y}},B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}})$
is log canonical. Apply Proposition 2.14 to
$({\tilde{Y}},B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}})$
is log canonical. Apply Proposition 2.14 to
![]() ${\tilde{Y}}$
and the rational vector space of Weil divisors spanned by
${\tilde{Y}}$
and the rational vector space of Weil divisors spanned by
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
. Let
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
. Let
![]() ${\mathcal{L}}$
be the polytope and
${\mathcal{L}}$
be the polytope and
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FF}$
be the real numbers obtained in Proposition 2.14. Note that by definition, each of
$\unicode[STIX]{x1D6FF}$
be the real numbers obtained in Proposition 2.14. Note that by definition, each of
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
lie within the polytope
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
lie within the polytope
![]() ${\mathcal{L}}$
. Choose
${\mathcal{L}}$
. Choose
![]() $0<\unicode[STIX]{x1D706}\ll 1$
and let
$0<\unicode[STIX]{x1D706}\ll 1$
and let
![]() ${\mathcal{P}}$
be the subpolytope with vertices given by
${\mathcal{P}}$
be the subpolytope with vertices given by
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
,
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
and
![]() $B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+\unicode[STIX]{x1D706}(H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
. By taking
$B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+\unicode[STIX]{x1D706}(H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
. By taking
![]() $\unicode[STIX]{x1D706}$
sufficiently small we may assume that
$\unicode[STIX]{x1D706}$
sufficiently small we may assume that
![]() $||\unicode[STIX]{x1D6E5}-(B_{{\tilde{Y}}}+A_{{\tilde{Y}}})||<\unicode[STIX]{x1D6FF}$
for any
$||\unicode[STIX]{x1D6E5}-(B_{{\tilde{Y}}}+A_{{\tilde{Y}}})||<\unicode[STIX]{x1D6FF}$
for any
![]() $\unicode[STIX]{x1D6E5}$
in
$\unicode[STIX]{x1D6E5}$
in
![]() ${\mathcal{P}}$
where
${\mathcal{P}}$
where
![]() $||\cdot ||$
is as in Proposition 2.14. Note that
$||\cdot ||$
is as in Proposition 2.14. Note that
![]() $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+\unicode[STIX]{x1D706}(H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
is nef, as it is a linear combination of two nef divisors, and we are happy to replace
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}+\unicode[STIX]{x1D706}(H_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
is nef, as it is a linear combination of two nef divisors, and we are happy to replace
![]() $\unicode[STIX]{x1D716}$
by
$\unicode[STIX]{x1D716}$
by
![]() $\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}$
for the purposes of our LMMP.
$\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}$
for the purposes of our LMMP.
Now run a
![]() $({\tilde{Y}},B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
-MMP with scaling of
$({\tilde{Y}},B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor )$
-MMP with scaling of
![]() $\unicode[STIX]{x1D706}H_{{\tilde{Y}}}$
. At every stage, so long as we contract no divisor, Proposition 2.14 ensures that every extremal ray contracted is also
$\unicode[STIX]{x1D706}H_{{\tilde{Y}}}$
. At every stage, so long as we contract no divisor, Proposition 2.14 ensures that every extremal ray contracted is also
![]() $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
-trivial. This means that this LMMP is also a
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}$
-trivial. This means that this LMMP is also a
![]() $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D706}\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
![]() $\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
, and hence also a
$\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
, and hence also a
![]() $K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
$K_{{\tilde{Y}}}+B_{{\tilde{Y}}}+A_{{\tilde{Y}}}-\unicode[STIX]{x1D716}\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
-MMP with scaling of
![]() $\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
and so by the construction of
$\left\lfloor B_{{\tilde{Y}}}\right\rfloor$
and so by the construction of
![]() ${\tilde{Y}}$
we indeed never contract a divisor. This LMMP terminates by klt termination with scaling [Reference Birkar and Waldron6, 1.5] on some model
${\tilde{Y}}$
we indeed never contract a divisor. This LMMP terminates by klt termination with scaling [Reference Birkar and Waldron6, 1.5] on some model
![]() $Y^{\prime }$
, which is either a log minimal model or a Mori fiber space.
$Y^{\prime }$
, which is either a log minimal model or a Mori fiber space.
Step 3: Case where
![]() $(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is a Mori fiber space.
$(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is a Mori fiber space.
Suppose
![]() $Y^{\prime }$
has
$Y^{\prime }$
has
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
-Mori fiber space structure
$K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
-Mori fiber space structure
![]() $g:Y^{\prime }\rightarrow V$
, where
$g:Y^{\prime }\rightarrow V$
, where
![]() $V$
is normal. By construction,
$V$
is normal. By construction,
![]() $g$
is
$g$
is
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}$
-trivial, so the fibers of
$K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}$
-trivial, so the fibers of
![]() $g$
intersect
$g$
intersect
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
positively and there is some component
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
positively and there is some component
![]() $V^{\prime }$
of
$V^{\prime }$
of
![]() $\left\lfloor B_{Y^{\prime }}\right\rfloor$
which is surjective to
$\left\lfloor B_{Y^{\prime }}\right\rfloor$
which is surjective to
![]() $V$
. By [Reference Kollár and Mori17, 3.7(4)],
$V$
. By [Reference Kollár and Mori17, 3.7(4)],
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}$
pulls back from some
$K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}$
pulls back from some
![]() $\mathbb{Q}$
-Cartier divisor
$\mathbb{Q}$
-Cartier divisor
![]() $D$
on
$D$
on
![]() $V$
. Using Proposition 2.13, let
$V$
. Using Proposition 2.13, let
![]() $\unicode[STIX]{x1D713}:Y^{\prime \prime }\rightarrow Y^{\prime }$
be a crepant
$\unicode[STIX]{x1D713}:Y^{\prime \prime }\rightarrow Y^{\prime }$
be a crepant
![]() $\mathbb{Q}$
-factorial dlt model for
$\mathbb{Q}$
-factorial dlt model for
![]() $(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})$
, with
$(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})$
, with
![]() $V^{\prime \prime }$
the birational transform of
$V^{\prime \prime }$
the birational transform of
![]() $V^{\prime }$
on
$V^{\prime }$
on
![]() $Y^{\prime \prime }$
.
$Y^{\prime \prime }$
.
![]() $\unicode[STIX]{x1D713}^{\ast }(K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }})|_{V^{\prime \prime }}=((g\circ \unicode[STIX]{x1D713})|_{V^{\prime \prime }})^{\ast }D$
, and by Theorem 1.3 the left hand side is semi-ample. Thus
$\unicode[STIX]{x1D713}^{\ast }(K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }})|_{V^{\prime \prime }}=((g\circ \unicode[STIX]{x1D713})|_{V^{\prime \prime }})^{\ast }D$
, and by Theorem 1.3 the left hand side is semi-ample. Thus
![]() $D$
is semi-ample because
$D$
is semi-ample because
![]() $g|_{V^{\prime }}:V^{\prime }\rightarrow V$
is a surjective projective morphism to a normal variety (see [Reference Keel13, 2.10]). Thus we are done in this case.
$g|_{V^{\prime }}:V^{\prime }\rightarrow V$
is a surjective projective morphism to a normal variety (see [Reference Keel13, 2.10]). Thus we are done in this case.
Step 4: Case where
![]() $(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is a log minimal model.
$(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor )$
is a log minimal model.
For a given
![]() $\unicode[STIX]{x1D716}$
, we may assume that
$\unicode[STIX]{x1D716}$
, we may assume that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
is not big by Theorem 1.1. We may write
$K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
is not big by Theorem 1.1. We may write
![]() $A_{Y^{\prime }}{\sim}_{\mathbb{Q}}C+E$
for some ample
$A_{Y^{\prime }}{\sim}_{\mathbb{Q}}C+E$
for some ample
![]() $C$
and effective
$C$
and effective
![]() $E$
. Choosing
$E$
. Choosing
![]() $\unicode[STIX]{x1D6FF}$
sufficiently small we may ensure that
$\unicode[STIX]{x1D6FF}$
sufficiently small we may ensure that
is klt. The base-point free theorem for klt pairs [Reference Birkar and Waldron6, 1.2] now implies that
![]() $K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
is semi-ample. As in the proof of Theorem 1.1, by applying this for various values of
$K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }}-\unicode[STIX]{x1D716}\left\lfloor B_{Y^{\prime }}\right\rfloor$
is semi-ample. As in the proof of Theorem 1.1, by applying this for various values of
![]() $\unicode[STIX]{x1D716}$
we obtain a contraction
$\unicode[STIX]{x1D716}$
we obtain a contraction
![]() $f:Y^{\prime }\rightarrow V$
satisfying.
$f:Y^{\prime }\rightarrow V$
satisfying.
for some
![]() $H$
ample on
$H$
ample on
![]() $V$
and
$V$
and
![]() $D\geqslant 0$
. We show that
$D\geqslant 0$
. We show that
![]() $H+\unicode[STIX]{x1D716}D$
is semi-ample. If
$H+\unicode[STIX]{x1D716}D$
is semi-ample. If
![]() $V$
has dimension less than
$V$
has dimension less than
![]() $2$
this is obvious, so we may assume it has dimension
$2$
this is obvious, so we may assume it has dimension
![]() $2$
.
$2$
.
![]() $\mathbb{E}(H+\unicode[STIX]{x1D716}D)\subset \text{Supp}(D)$
, and
$\mathbb{E}(H+\unicode[STIX]{x1D716}D)\subset \text{Supp}(D)$
, and
![]() $f^{-1}(\text{Supp}(D))=\left\lfloor B_{Y^{\prime }}\right\rfloor$
because
$f^{-1}(\text{Supp}(D))=\left\lfloor B_{Y^{\prime }}\right\rfloor$
because
![]() $D$
is
$D$
is
![]() $\mathbb{Q}$
-Cartier and so
$\mathbb{Q}$
-Cartier and so
![]() $f^{-1}(\text{Supp}(D))$
is equidimensional. Let
$f^{-1}(\text{Supp}(D))$
is equidimensional. Let
![]() $g:Y^{\prime \prime }\rightarrow Y^{\prime }$
be a crepant
$g:Y^{\prime \prime }\rightarrow Y^{\prime }$
be a crepant
![]() $\mathbb{Q}$
-factorial dlt modification of
$\mathbb{Q}$
-factorial dlt modification of
![]() $(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})$
with
$(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})$
with
![]() $K_{Y^{\prime \prime }}+\unicode[STIX]{x1D6E5}=g^{\ast }(K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }})$
. As
$K_{Y^{\prime \prime }}+\unicode[STIX]{x1D6E5}=g^{\ast }(K_{Y^{\prime }}+B_{Y^{\prime }}+A_{Y^{\prime }})$
. As
![]() $Y^{\prime }$
is
$Y^{\prime }$
is
![]() $\mathbb{Q}$
-factorial and
$\mathbb{Q}$
-factorial and
![]() $\text{LCS}(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})=\left\lfloor B_{Y^{\prime }}\right\rfloor$
,
$\text{LCS}(Y^{\prime },B_{Y^{\prime }}+A_{Y^{\prime }})=\left\lfloor B_{Y^{\prime }}\right\rfloor$
,
![]() $g^{-1}(\left\lfloor B_{Y^{\prime }}\right\rfloor )=\left\lfloor \unicode[STIX]{x1D6E5}\right\rfloor$
. Theorem 1.3 implies that
$g^{-1}(\left\lfloor B_{Y^{\prime }}\right\rfloor )=\left\lfloor \unicode[STIX]{x1D6E5}\right\rfloor$
. Theorem 1.3 implies that
![]() $(K_{Y^{\prime \prime }}+\unicode[STIX]{x1D6E5})|_{(f\circ g)^{-1}D}$
is semi-ample. We may now apply the semi-ampleness criterion [Reference Birkar and Waldron6, 7.1], derived from Keel’s theorem to deduce that
$(K_{Y^{\prime \prime }}+\unicode[STIX]{x1D6E5})|_{(f\circ g)^{-1}D}$
is semi-ample. We may now apply the semi-ampleness criterion [Reference Birkar and Waldron6, 7.1], derived from Keel’s theorem to deduce that
![]() $H+\unicode[STIX]{x1D716}D$
is semi-ample.
$H+\unicode[STIX]{x1D716}D$
is semi-ample.
Step 5: Log canonical pairs with
![]() $\mathbb{R}$
-boundaries and
$\mathbb{R}$
-boundaries and
![]() $\mathbb{R}$
-Cartier
$\mathbb{R}$
-Cartier
![]() $A$
.
$A$
.
We now work with the log canonical pair
![]() $(X,B)$
with
$(X,B)$
with
![]() $\mathbb{R}$
-boundary
$\mathbb{R}$
-boundary
![]() $B$
and
$B$
and
![]() $\mathbb{R}$
-Cartier
$\mathbb{R}$
-Cartier
![]() $A$
from the statement. Let
$A$
from the statement. Let
![]() $\unicode[STIX]{x1D719}:Y\rightarrow X$
be a crepant
$\unicode[STIX]{x1D719}:Y\rightarrow X$
be a crepant
![]() $\mathbb{Q}$
-factorial dlt modification of
$\mathbb{Q}$
-factorial dlt modification of
![]() $(X,B)$
which exists by Proposition 2.13. We claim that we may replace
$(X,B)$
which exists by Proposition 2.13. We claim that we may replace
![]() $A$
by some
$A$
by some
![]() $A^{\prime }{\sim}_{\mathbb{R}}A$
to assume that
$A^{\prime }{\sim}_{\mathbb{R}}A$
to assume that
![]() $(X,B+A)$
is also log canonical and that
$(X,B+A)$
is also log canonical and that
![]() $\unicode[STIX]{x1D719}$
is a crepant
$\unicode[STIX]{x1D719}$
is a crepant
![]() $\mathbb{Q}$
-factorial dlt modification of
$\mathbb{Q}$
-factorial dlt modification of
![]() $(X,B+A)$
. To see this, note that by [Reference Tanaka20] there is some
$(X,B+A)$
. To see this, note that by [Reference Tanaka20] there is some
![]() $A^{\prime \prime }{\sim}_{\mathbb{R}}2A$
such that
$A^{\prime \prime }{\sim}_{\mathbb{R}}2A$
such that
![]() $(X,B+A^{\prime \prime })$
is log canonical. Set
$(X,B+A^{\prime \prime })$
is log canonical. Set
![]() $A^{\prime }=\frac{1}{2}A^{\prime \prime }$
. Any log canonical place of
$A^{\prime }=\frac{1}{2}A^{\prime \prime }$
. Any log canonical place of
![]() $(X,B+A^{\prime })$
is then also a log canonical place of
$(X,B+A^{\prime })$
is then also a log canonical place of
![]() $(X,B)$
.
$(X,B)$
.
We also wish to assume that
![]() $A$
is a
$A$
is a
![]() $\mathbb{Q}$
-divisor. To this end, write
$\mathbb{Q}$
-divisor. To this end, write
![]() $A=\sum a_{i}A_{i}$
where
$A=\sum a_{i}A_{i}$
where
![]() $0<a_{i}\in \mathbb{R}$
and
$0<a_{i}\in \mathbb{R}$
and
![]() $A_{i}$
are semi-ample
$A_{i}$
are semi-ample
![]() $\mathbb{Q}$
-divisors. Let
$\mathbb{Q}$
-divisors. Let
![]() $a_{i}=a_{i}^{1}+a_{i}^{2}$
for each
$a_{i}=a_{i}^{1}+a_{i}^{2}$
for each
![]() $i$
, where we freely choose
$i$
, where we freely choose
![]() $0<a_{i}^{1}\in \mathbb{R}$
and
$0<a_{i}^{1}\in \mathbb{R}$
and
![]() $0<a_{i}^{2}\in \mathbb{Q}$
. Define
$0<a_{i}^{2}\in \mathbb{Q}$
. Define
![]() $A_{\mathbb{R}}=\sum a_{i}^{1}A_{i}$
and
$A_{\mathbb{R}}=\sum a_{i}^{1}A_{i}$
and
![]() $A_{\mathbb{Q}}=\sum a_{i}^{2}A_{i}$
. By choosing
$A_{\mathbb{Q}}=\sum a_{i}^{2}A_{i}$
. By choosing
![]() $a_{i}^{1}$
sufficiently small, we may assume that
$a_{i}^{1}$
sufficiently small, we may assume that
![]() $A_{\mathbb{Q}}$
is big. Now we may replace
$A_{\mathbb{Q}}$
is big. Now we may replace
![]() $B$
with
$B$
with
![]() $B+A_{\mathbb{R}}$
and
$B+A_{\mathbb{R}}$
and
![]() $A$
with
$A$
with
![]() $A_{\mathbb{Q}}$
to assume
$A_{\mathbb{Q}}$
to assume
![]() $A$
is
$A$
is
![]() $\mathbb{Q}$
-Cartier.
$\mathbb{Q}$
-Cartier.
Define
![]() $B_{Y}$
to be the dlt
$B_{Y}$
to be the dlt
![]() $\mathbb{R}$
-boundary satisfying
$\mathbb{R}$
-boundary satisfying
![]() $K_{Y}+B_{Y}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
, and let
$K_{Y}+B_{Y}=\unicode[STIX]{x1D719}^{\ast }(K_{X}+B)$
, and let
![]() $A_{Y}=\unicode[STIX]{x1D719}^{\ast }A$
(which is also big and semi-ample). It is now enough to show that
$A_{Y}=\unicode[STIX]{x1D719}^{\ast }A$
(which is also big and semi-ample). It is now enough to show that
![]() $K_{Y}+B_{Y}+A_{Y}$
is semi-ample when
$K_{Y}+B_{Y}+A_{Y}$
is semi-ample when
![]() $(Y,B_{Y})$
is
$(Y,B_{Y})$
is
![]() $\mathbb{Q}$
-factorial dlt but
$\mathbb{Q}$
-factorial dlt but
![]() $B_{Y}$
may be an
$B_{Y}$
may be an
![]() $\mathbb{R}$
-boundary.
$\mathbb{R}$
-boundary.
Let
![]() $V^{\prime }$
be the
$V^{\prime }$
be the
![]() $\mathbb{R}$
-vector space of
$\mathbb{R}$
-vector space of
![]() $\mathbb{R}$
-Weil divisors generated by the components of
$\mathbb{R}$
-Weil divisors generated by the components of
![]() $B_{Y}$
. Now let
$B_{Y}$
. Now let
![]() $V=V^{\prime }+A_{Y}$
. This is an affine space of Weil divisors, so let
$V=V^{\prime }+A_{Y}$
. This is an affine space of Weil divisors, so let
![]() ${\mathcal{L}}$
be as defined in Proposition 2.14. Let
${\mathcal{L}}$
be as defined in Proposition 2.14. Let
![]() ${\mathcal{P}}\subset {\mathcal{L}}$
be those
${\mathcal{P}}\subset {\mathcal{L}}$
be those
![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
such that
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}$
such that
![]() $(K_{Y}+\unicode[STIX]{x1D6E5})\cdot R\geqslant 0$
for all extremal rays
$(K_{Y}+\unicode[STIX]{x1D6E5})\cdot R\geqslant 0$
for all extremal rays
![]() $R$
of
$R$
of
![]() $\overline{NE}(X)$
. This is a rational polytope by Proposition 2.14(2). Label the vertices
$\overline{NE}(X)$
. This is a rational polytope by Proposition 2.14(2). Label the vertices
![]() $B_{1}+A_{Y},\ldots ,B_{n}+A_{Y}$
. For each
$B_{1}+A_{Y},\ldots ,B_{n}+A_{Y}$
. For each
![]() $i$
,
$i$
,
![]() $K_{Y}+B_{i}+A_{Y}$
is nef and so we may apply the version of Theorem 1.2 for
$K_{Y}+B_{i}+A_{Y}$
is nef and so we may apply the version of Theorem 1.2 for
![]() $\mathbb{Q}$
-boundaries to deduce that
$\mathbb{Q}$
-boundaries to deduce that
![]() $K_{Y}+B_{i}+A_{Y}$
is semi-ample. But as
$K_{Y}+B_{i}+A_{Y}$
is semi-ample. But as
![]() $K_{Y}+B_{Y}+A_{Y}$
can be written as a linear combination of
$K_{Y}+B_{Y}+A_{Y}$
can be written as a linear combination of
![]() $K_{Y}+B_{i}+A_{Y}$
with positive coefficients, this is also semi-ample.◻
$K_{Y}+B_{i}+A_{Y}$
with positive coefficients, this is also semi-ample.◻
Proof of Theorem 1.2 in relative case.
As in the relative case of Theorem 1.1, if we let
![]() $H$
be the pullback to
$H$
be the pullback to
![]() $X$
of a sufficiently ample divisor on
$X$
of a sufficiently ample divisor on
![]() $Z$
,
$Z$
,
![]() $A+H$
is big and semi-ample and by Theorem 1.7
$A+H$
is big and semi-ample and by Theorem 1.7
![]() $K_{X}+B+A+H$
is globally nef. By [Reference Tanaka20] we may replace
$K_{X}+B+A+H$
is globally nef. By [Reference Tanaka20] we may replace
![]() $H$
up to
$H$
up to
![]() $\mathbb{Q}$
-linear equivalence so that
$\mathbb{Q}$
-linear equivalence so that
![]() $(X,B+A+H)$
is log canonical. Now we may apply the global case.◻
$(X,B+A+H)$
is log canonical. Now we may apply the global case.◻
7 The LMMP
Next we apply Theorem 1.1 to construct flips for log canonical pairs.
Proof of Corollary 1.5.
Let
![]() $(X,B)$
be a projective log canonical 3-fold pair with flipping contraction
$(X,B)$
be a projective log canonical 3-fold pair with flipping contraction
![]() $f:X\rightarrow Z$
.
$f:X\rightarrow Z$
.
![]() $(X,B)$
has a
$(X,B)$
has a
![]() $\mathbb{Q}$
-factorial dlt model
$\mathbb{Q}$
-factorial dlt model
![]() $g:Y\rightarrow X$
where
$g:Y\rightarrow X$
where
![]() $K_{Y}+B_{Y}=g^{\ast }(K_{X}+B)$
by Proposition 2.13. Run an LMMP
$K_{Y}+B_{Y}=g^{\ast }(K_{X}+B)$
by Proposition 2.13. Run an LMMP
![]() $/Z$
for
$/Z$
for
![]() $(Y,B_{Y})$
. If
$(Y,B_{Y})$
. If
![]() $A$
is an ample divisor on
$A$
is an ample divisor on
![]() $Z$
,
$Z$
,
![]() $K_{Y}+B_{Y}+ng^{\ast }f^{\ast }A$
is big for
$K_{Y}+B_{Y}+ng^{\ast }f^{\ast }A$
is big for
![]() $n\gg 0$
and so the LMMP terminates on a log minimal model
$n\gg 0$
and so the LMMP terminates on a log minimal model
![]() $(Y^{+},B_{Y^{+}})$
by Theorem 1.6. By Theorem 1.1,
$(Y^{+},B_{Y^{+}})$
by Theorem 1.6. By Theorem 1.1,
![]() $K_{Y^{+}}+B_{Y^{+}}$
is semi-ample
$K_{Y^{+}}+B_{Y^{+}}$
is semi-ample
![]() $/Z$
. It therefore has a log canonical model
$/Z$
. It therefore has a log canonical model
![]() $(X^{+},B^{+})/Z$
, which we show is the flip of
$(X^{+},B^{+})/Z$
, which we show is the flip of
![]() $(X,B)/Z$
. It suffices to show that no divisors are contracted by
$(X,B)/Z$
. It suffices to show that no divisors are contracted by
![]() $X^{+}{\dashrightarrow}X$
as
$X^{+}{\dashrightarrow}X$
as
![]() $K_{X^{+}}+B_{X^{+}}$
is ample
$K_{X^{+}}+B_{X^{+}}$
is ample
![]() $/Z$
.
$/Z$
.
Let
![]() $\unicode[STIX]{x1D719}:W\rightarrow X$
and
$\unicode[STIX]{x1D719}:W\rightarrow X$
and
![]() $\unicode[STIX]{x1D719}^{+}:W\rightarrow X^{+}$
be a common resolution.
$\unicode[STIX]{x1D719}^{+}:W\rightarrow X^{+}$
be a common resolution.
is anti-nef
![]() $/Z$
and so by the negativity lemma is effective. Suppose there is a divisor
$/Z$
and so by the negativity lemma is effective. Suppose there is a divisor
![]() $E_{+}$
which is contracted by
$E_{+}$
which is contracted by
![]() $X^{+}{\dashrightarrow}X$
, and let
$X^{+}{\dashrightarrow}X$
, and let
![]() $E_{W}$
be its birational transform on
$E_{W}$
be its birational transform on
![]() $W$
.
$W$
.
![]() $L$
must have coefficient zero in
$L$
must have coefficient zero in
![]() $E_{W}$
, for any Weil divisor extracted by
$E_{W}$
, for any Weil divisor extracted by
![]() $Y\rightarrow X$
has log discrepancy
$Y\rightarrow X$
has log discrepancy
![]() $0$
with respect to
$0$
with respect to
![]() $(X,B)$
, and hence
$(X,B)$
, and hence
![]() $E_{+}$
appears with coefficient
$E_{+}$
appears with coefficient
![]() $1$
in
$1$
in
![]() $B_{X^{+}}$
. Note that
$B_{X^{+}}$
. Note that
![]() $\unicode[STIX]{x1D719}^{+\ast }(K_{X^{+}}+B_{X^{+}})|_{E_{W}}$
is big and nef over
$\unicode[STIX]{x1D719}^{+\ast }(K_{X^{+}}+B_{X^{+}})|_{E_{W}}$
is big and nef over
![]() $Z$
, so
$Z$
, so
![]() $L$
intersects negatively with a general curve on
$L$
intersects negatively with a general curve on
![]() $E_{W}$
which is contracted over
$E_{W}$
which is contracted over
![]() $Z$
. There is a family of such curves, because
$Z$
. There is a family of such curves, because
![]() $E_{W}$
is contracted over
$E_{W}$
is contracted over
![]() $X$
and hence over
$X$
and hence over
![]() $Z$
. But this negative intersection is impossible if
$Z$
. But this negative intersection is impossible if
![]() $L$
has coefficient zero in
$L$
has coefficient zero in
![]() $E_{W}$
, because
$E_{W}$
, because
![]() $L$
is effective.◻
$L$
is effective.◻
Next we prove the contraction theorem:
Proof of Corollary 1.4.
Let
![]() $A$
be an ample
$A$
be an ample
![]() $\mathbb{R}$
-divisor on
$\mathbb{R}$
-divisor on
![]() $X$
. For a sufficiently small rational
$X$
. For a sufficiently small rational
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
![]() $R$
is also
$R$
is also
![]() $K_{X}+B+\unicode[STIX]{x1D716}A$
negative. By Theorem 1.7, there are only finitely many
$K_{X}+B+\unicode[STIX]{x1D716}A$
negative. By Theorem 1.7, there are only finitely many
![]() $K_{X}+B+\unicode[STIX]{x1D716}A$
-negative extremal rays. Therefore, we may find an
$K_{X}+B+\unicode[STIX]{x1D716}A$
-negative extremal rays. Therefore, we may find an
![]() $\mathbb{R}$
-divisor
$\mathbb{R}$
-divisor
![]() $H$
such that
$H$
such that
![]() $R$
is the only
$R$
is the only
![]() $H$
-negative extremal ray of
$H$
-negative extremal ray of
![]() $\overline{NE}_{1}(X)$
. We may also assume that
$\overline{NE}_{1}(X)$
. We may also assume that
![]() $A^{\prime }=H-(K_{X}+B+\unicode[STIX]{x1D716}A)$
is ample (i.e., positive on all of
$A^{\prime }=H-(K_{X}+B+\unicode[STIX]{x1D716}A)$
is ample (i.e., positive on all of
![]() $\overline{NE}_{1}(X)$
). So we may replace
$\overline{NE}_{1}(X)$
). So we may replace
![]() $A$
by
$A$
by
![]() $A^{\prime }+\unicode[STIX]{x1D716}A$
such that
$A^{\prime }+\unicode[STIX]{x1D716}A$
such that
![]() $R$
is the only
$R$
is the only
![]() $K_{X}+B+A$
-negative extremal ray.
$K_{X}+B+A$
-negative extremal ray.
Let
![]() $\unicode[STIX]{x1D706}=\inf \{t:K_{X}+B+tA\text{ is nef}\}$
(so
$\unicode[STIX]{x1D706}=\inf \{t:K_{X}+B+tA\text{ is nef}\}$
(so
![]() $\unicode[STIX]{x1D706}>1$
).
$\unicode[STIX]{x1D706}>1$
).
![]() $K_{X}+B+\unicode[STIX]{x1D706}A$
is positive wherever
$K_{X}+B+\unicode[STIX]{x1D706}A$
is positive wherever
![]() $K_{X}+B$
is nonnegative, and also positive on every extremal
$K_{X}+B$
is nonnegative, and also positive on every extremal
![]() $K_{X}+B$
-negative extremal ray except
$K_{X}+B$
-negative extremal ray except
![]() $R$
. This means the extremal face
$R$
. This means the extremal face
![]() $(K_{X}+B+\unicode[STIX]{x1D706}A)_{=0}\cap \overline{NE}(X)$
must be
$(K_{X}+B+\unicode[STIX]{x1D706}A)_{=0}\cap \overline{NE}(X)$
must be
![]() $R$
itself. By Theorem 1.7
$R$
itself. By Theorem 1.7
![]() $R$
contains a curve.
$R$
contains a curve.
By Theorem 1.2,
![]() $K_{X}+B+\unicode[STIX]{x1D706}A$
is semi-ample, and so induces the contraction of
$K_{X}+B+\unicode[STIX]{x1D706}A$
is semi-ample, and so induces the contraction of
![]() $R$
.◻
$R$
.◻
Proof of Corollary 1.8.
This is a consequence of all our other results. Given a log canonical pair
![]() $(X,B)$
such that
$(X,B)$
such that
![]() $K_{X}+B$
is not nef, we may find a
$K_{X}+B$
is not nef, we may find a
![]() $K_{X}+B$
-negative extremal ray using Theorem 1.7. There is a projective contraction contracting the curves in this ray by Corollary 1.4. If it is a flipping contraction, the flip exists by Corollary 1.5. Finally, if
$K_{X}+B$
-negative extremal ray using Theorem 1.7. There is a projective contraction contracting the curves in this ray by Corollary 1.4. If it is a flipping contraction, the flip exists by Corollary 1.5. Finally, if
![]() $K_{X}+B\equiv M\geqslant 0$
the program terminates by Theorem 1.6. Under the additional assumption the log minimal model is good by Theorem 1.1.◻
$K_{X}+B\equiv M\geqslant 0$
the program terminates by Theorem 1.6. Under the additional assumption the log minimal model is good by Theorem 1.1.◻
Acknowledgments
The author wishes to thank his advisor Caucher Birkar for his support and advice. He would also like to thank the referee, whose comments have greatly improved the article. This research was funded by the Engineering and Physical Sciences Research Council.