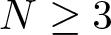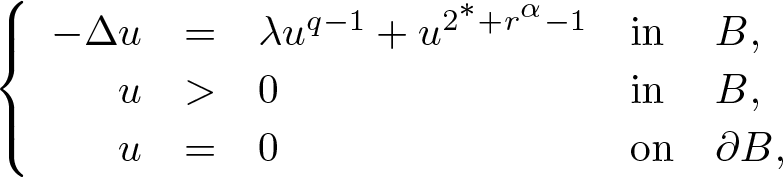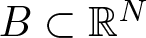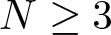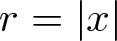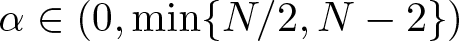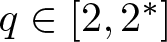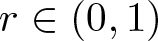1. Introduction and main results
In 1983, Brézis and Nirenberg in [1.1] studied the following problem:
 \begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^*-1} & \mbox{in} & \Omega, \\
u & \gt & 0 & \mbox{in} & \Omega, \\
u&=&0 & \mbox{on} & \partial \Omega,\\
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^*-1} & \mbox{in} & \Omega, \\
u & \gt & 0 & \mbox{in} & \Omega, \\
u&=&0 & \mbox{on} & \partial \Omega,\\
\end{array}
\right.
\end{equation} where ![]() $\Omega \subset \mathbb{R}^N$ is a bounded domain,
$\Omega \subset \mathbb{R}^N$ is a bounded domain, ![]() $N \geq 3$, λ is a fixed real parameter,
$N \geq 3$, λ is a fixed real parameter, ![]() $q \in [2,2^{*})$ and
$q \in [2,2^{*})$ and ![]() $2^*=2N/(N-2)$ is the critical exponent in the sense of Sobolev’s embedding.
$2^*=2N/(N-2)$ is the critical exponent in the sense of Sobolev’s embedding.
Brézis and Nirenberg proved the following results:
(a) For q = 2 and
 $ N \geq 4 $, problem (1.1) has a solution for every
$ N \geq 4 $, problem (1.1) has a solution for every  $ \lambda \in (0, \lambda_1) $, where λ 1 denotes the first eigenvalue of
$ \lambda \in (0, \lambda_1) $, where λ 1 denotes the first eigenvalue of  $ -\Delta $. Moreover, it has no solution if
$ -\Delta $. Moreover, it has no solution if  $ \lambda \not\in (0, \lambda_1) $ and Ω is star-shaped.
$ \lambda \not\in (0, \lambda_1) $ and Ω is star-shaped.(b) When q = 2, N = 3, and Ω is a ball, problem (1.1) has a solution if and only if
 $ \lambda \in \left(\frac{\lambda_1}{4}, \lambda_1\right) $.
$ \lambda \in \left(\frac{\lambda_1}{4}, \lambda_1\right) $.(c) For
 $ q \in (2, 2^*) $ and
$ q \in (2, 2^*) $ and  $ N \geq 4 $, problem (1.1) has a solution for every λ > 0.
$ N \geq 4 $, problem (1.1) has a solution for every λ > 0.(d) When N = 3 and
 $ 4 \lt q \lt 6 $, problem (1.1) has a solution for every λ > 0.
$ 4 \lt q \lt 6 $, problem (1.1) has a solution for every λ > 0.(e) When N = 3 and
 $ 2 \lt q \leq 4 $, problem (1.1) has a solution only for sufficiently large values of λ.
$ 2 \lt q \leq 4 $, problem (1.1) has a solution only for sufficiently large values of λ.
Recently, do Ó, Ruf, and Ubilla in [Reference do Ó, Ruf and Ubilla5] studied the following problem:
 \begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & u^{2^* + r^{\alpha}-1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & u^{2^* + r^{\alpha}-1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation} where ![]() $ B \subset \mathbb{R}^N $ is the unit ball centred at the origin,
$ B \subset \mathbb{R}^N $ is the unit ball centred at the origin, ![]() $N\geq 3$,
$N\geq 3$, ![]() $r=|x|$, and
$r=|x|$, and ![]() $\alpha \in (0,\min\{N/2,N-2\})$.
$\alpha \in (0,\min\{N/2,N-2\})$.
The authors demonstrated that problem (1.2) has a radial solution, which is surprising because it corresponds to a supercritical perturbation of the equation ![]() $-\Delta u = u^{2^* - 1}$, which has no solution due to the known Pohozaev identity. In this same line of reasoning, in the context of the situation of item (b), we studied the effect of a supercritical perturbation for the case of non-existence
$-\Delta u = u^{2^* - 1}$, which has no solution due to the known Pohozaev identity. In this same line of reasoning, in the context of the situation of item (b), we studied the effect of a supercritical perturbation for the case of non-existence  $\lambda \in (0,\frac{\lambda_1}{4 }]$, which also generated the existence of a positive solution. We will also have the same conclusion for situation (e), in which, due to the supercritical perturbation, we will obtain a solution for all positive λ and not just for sufficiently large λ. Motivated by the results of [1.1] and [Reference do Ó, Ruf and Ubilla5], we studied this problem in a more general context, more precisely, let us consider the following problem:
$\lambda \in (0,\frac{\lambda_1}{4 }]$, which also generated the existence of a positive solution. We will also have the same conclusion for situation (e), in which, due to the supercritical perturbation, we will obtain a solution for all positive λ and not just for sufficiently large λ. Motivated by the results of [1.1] and [Reference do Ó, Ruf and Ubilla5], we studied this problem in a more general context, more precisely, let us consider the following problem:
 \begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^*+ r^\alpha -1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^*+ r^\alpha -1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation} where ![]() $B \subset \mathbb{R}^N$ is a unit ball centred at the origin,
$B \subset \mathbb{R}^N$ is a unit ball centred at the origin, ![]() $N\geq 3$,
$N\geq 3$, ![]() $r=\vert x \vert$, and
$r=\vert x \vert$, and ![]() $\alpha \in (0,\min\{N/2,N-2\})$ and λ is a fixed real parameter and
$\alpha \in (0,\min\{N/2,N-2\})$ and λ is a fixed real parameter and ![]() $q\in [2,2^*]$.
$q\in [2,2^*]$.
We will now present the main result of this article.
Theorem 1.1 If q = 2, ![]() $\lambda \in [0, \lambda_1)$ and
$\lambda \in [0, \lambda_1)$ and ![]() $N\geq 3$, then the problem (1.3) has a radial weak solution. If
$N\geq 3$, then the problem (1.3) has a radial weak solution. If ![]() $q\in (2,2^*]$, problem (1.3) has a radial weak solution for every
$q\in (2,2^*]$, problem (1.3) has a radial weak solution for every ![]() $\lambda \geq 0$ and
$\lambda \geq 0$ and ![]() $N\geq 3$.
$N\geq 3$.
We would like to highlight that in the case N = 3 we obtain a solution for the perturbed problem for each ![]() $\lambda \in [0,\lambda_1)$, that is, the perturbation solves the non-existence interval
$\lambda \in [0,\lambda_1)$, that is, the perturbation solves the non-existence interval ![]() $[0,\lambda_1/4]$.
$[0,\lambda_1/4]$.
Let ![]() $H_0^1(B) := \{u \in L^{2}(B) \colon \nabla u \in L^2(B) \colon u=0 \, \text{on} \, \partial B \} $ be the usual Sobolev space equipped with the gradient norm, or let
$H_0^1(B) := \{u \in L^{2}(B) \colon \nabla u \in L^2(B) \colon u=0 \, \text{on} \, \partial B \} $ be the usual Sobolev space equipped with the gradient norm, or let  $\| u \|_{H^1_0(B)} = \|\nabla u \|_{L^2(B)}$. We say that
$\| u \|_{H^1_0(B)} = \|\nabla u \|_{L^2(B)}$. We say that ![]() $u\in H_0^1(B)$ is a weak solution to problem (1.3) if u > 0 in B and it holds:
$u\in H_0^1(B)$ is a weak solution to problem (1.3) if u > 0 in B and it holds:
 \begin{align}
\int_B \nabla u \nabla\varphi \, \text{d}x = \lambda \int_B u^{q-1}\varphi \, \text{d}x + \int_B u^{2^*-1+r^{\alpha}}\varphi \, \text{d}x, \, \forall\, \varphi \in H_0^1(B).
\end{align}
\begin{align}
\int_B \nabla u \nabla\varphi \, \text{d}x = \lambda \int_B u^{q-1}\varphi \, \text{d}x + \int_B u^{2^*-1+r^{\alpha}}\varphi \, \text{d}x, \, \forall\, \varphi \in H_0^1(B).
\end{align}Remark 1.2. It is important to emphasize that the Eq. (1.4) is well defined due to the results obtained in proposition 2.2 and corollary 2.3. Note that (1.4) is not well-defined for ![]() $ q \gt 2^* $.
$ q \gt 2^* $.
Theorem 1.1 shows (see (b) and (e)) that there are critical equations without solutions that have a solution when a non-negative term is added to them, converting them into supercritical equations. Note that this phenomenon was already observed in [Reference do Ó, Ruf and Ubilla5].
We also consider some perturbations of problem (1.1) that become superlinear on the ball and subcritical for ![]() $ r \in (0, \delta) $, for some small δ. However, it can be supercritical away from
$ r \in (0, \delta) $, for some small δ. However, it can be supercritical away from ![]() $r= 0,$ as in the following equation:
$r= 0,$ as in the following equation:
 \begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^* + f(r)-1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation}
\begin{equation}
\left\{
\begin{array}{rllll}
-\Delta u & = & \lambda u^{q-1} + u^{2^* + f(r)-1} & \mbox{in} & B, \\
u & \gt & 0 & \mbox{in} & B, \\
u&=&0 & \mbox{on} & \partial B,\\
\end{array}
\right.
\end{equation} where ![]() $B \subset \mathbb{R}^N$ is a unit ball centred at the origin,
$B \subset \mathbb{R}^N$ is a unit ball centred at the origin, ![]() $N\geq 3$,
$N\geq 3$, ![]() $r=\vert x \vert$, λ is a fixed real parameter,
$r=\vert x \vert$, λ is a fixed real parameter, ![]() $q\in [2,2^*)$ and
$q\in [2,2^*)$ and ![]() $f\colon [0,1) \rightarrow \mathbb{R}$ is a continuous function satisfying:
$f\colon [0,1) \rightarrow \mathbb{R}$ is a continuous function satisfying:
(f)
 $ f(0) \lt 0$ and
$ f(0) \lt 0$ and  $\displaystyle\inf_{r\in [0,1)}(2^* + f(r)) \gt 2$.
$\displaystyle\inf_{r\in [0,1)}(2^* + f(r)) \gt 2$.
The next result involves the assumption (f):
Theorem 1.3 Let ![]() $q \in [2,2^*)$,
$q \in [2,2^*)$, ![]() $N\geq 3$, and
$N\geq 3$, and ![]() $f\colon [0,1) \rightarrow \mathbb{R}$ a continuous function satisfying condition (f). Then the problem (1.5) has a radial weak solution in the following cases:
$f\colon [0,1) \rightarrow \mathbb{R}$ a continuous function satisfying condition (f). Then the problem (1.5) has a radial weak solution in the following cases:
(i) q = 2 and
 $\lambda \in [0,\lambda_1)$.
$\lambda \in [0,\lambda_1)$.(ii)
 $q \in (2,2^*)$ and
$q \in (2,2^*)$ and  $\lambda \geq 0$.
$\lambda \geq 0$.
Remark 1.4. In theorem 1.3, due to the generality of the growth condition considered for the function f, it was not possible to reach the case ![]() $ q = 2^* $.
$ q = 2^* $.
The definition of a weak solution for problem (1.5) is analogous to the one we defined in Eq. (1.4). The case ![]() $0 \lt q \lt 2$, which corresponds to a concave-convex problem, was studied in [Reference Clemente, Marcos do Ó and Ubilla3] under a subcritical assumption. Therefore, theorem 1.3 complements the result in [Reference Clemente, Marcos do Ó and Ubilla3].
$0 \lt q \lt 2$, which corresponds to a concave-convex problem, was studied in [Reference Clemente, Marcos do Ó and Ubilla3] under a subcritical assumption. Therefore, theorem 1.3 complements the result in [Reference Clemente, Marcos do Ó and Ubilla3].
The article is organized as follows: In §2, we present preliminary results, in §3, we prove theorem 1.1, and in §4, we prove theorem 1.3.
2. Preliminaries
First, we define the Sobolev space of radial functions  $H_{0,\mathrm{rad}}^1(B) := \{u \in H_0^1(B) \colon u(x) = u(|x|) \}$ equipped with the usual standard
$H_{0,\mathrm{rad}}^1(B) := \{u \in H_0^1(B) \colon u(x) = u(|x|) \}$ equipped with the usual standard ![]() $\|u\|=\|\nabla u \|_2$. We will now present the ‘radial lemma’, which can be found in [Reference do Ó, Ruf and Ubilla5, Reference Strauss8].
$\|u\|=\|\nabla u \|_2$. We will now present the ‘radial lemma’, which can be found in [Reference do Ó, Ruf and Ubilla5, Reference Strauss8].
Lemma 2.1. Let  $u \in H_{0,\mathrm{rad}}^1(B)$. Then
$u \in H_{0,\mathrm{rad}}^1(B)$. Then
 \begin{equation}
|u(r)| \leq \frac{1}{(N-2)^{1/2}}\frac{\|\nabla u\|_2}{r^{(N-2)/2}}
\end{equation}
\begin{equation}
|u(r)| \leq \frac{1}{(N-2)^{1/2}}\frac{\|\nabla u\|_2}{r^{(N-2)/2}}
\end{equation}and
 \begin{equation}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\|\nabla u\|_2 .
\end{equation}
\begin{equation}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\|\nabla u\|_2 .
\end{equation}For the next result, we refer [Reference do Ó, Ruf and Ubilla5]
Proposition 2.2. Let α > 0; then
 \begin{equation}
\sup \Big\{\int_{B} |u(x)|^{2^* + r^\alpha} \, \text{d} x \colon u \in H^1_{0, \mathrm{rad}}(B), \, \Vert \nabla u \Vert_2 = 1 \Big\} \lt +\infty.
\end{equation}
\begin{equation}
\sup \Big\{\int_{B} |u(x)|^{2^* + r^\alpha} \, \text{d} x \colon u \in H^1_{0, \mathrm{rad}}(B), \, \Vert \nabla u \Vert_2 = 1 \Big\} \lt +\infty.
\end{equation}Corollary 2.3. The following embedding is continuous:
 \begin{equation}
H^1_{0,\mathrm{rad}}(B)\hookrightarrow L^{2^*+r^{\alpha}}(B) \ ,
\end{equation}
\begin{equation}
H^1_{0,\mathrm{rad}}(B)\hookrightarrow L^{2^*+r^{\alpha}}(B) \ ,
\end{equation} where  $L^{2^*+r^{\alpha}}(B)$ is defined as follows (see, e.g., [Reference Diening, Harjulehto, Hästö and Rocircuvzivcka4])
$L^{2^*+r^{\alpha}}(B)$ is defined as follows (see, e.g., [Reference Diening, Harjulehto, Hästö and Rocircuvzivcka4])
 \begin{equation*}
L^{2^*+r^{\alpha}} (B) := \Big\{u\colon B \to \mathbb R\ \mathrm{measurable} \colon \int_B|u(x)|^{2^*+r^{\alpha}} \; \mathrm{d} x \lt \infty \Big\}
\end{equation*}
\begin{equation*}
L^{2^*+r^{\alpha}} (B) := \Big\{u\colon B \to \mathbb R\ \mathrm{measurable} \colon \int_B|u(x)|^{2^*+r^{\alpha}} \; \mathrm{d} x \lt \infty \Big\}
\end{equation*}with norm
 \begin{equation*}\ \|u\|_{2^*+r^{\alpha}} = \inf \Big\{\lambda \gt 0 \ , \ \int_B\Big|\frac {u(x)}{\lambda}\Big|^{2^*+r^{\alpha}} \mathrm{d} x \le 1 \Big\}.
\end{equation*}
\begin{equation*}\ \|u\|_{2^*+r^{\alpha}} = \inf \Big\{\lambda \gt 0 \ , \ \int_B\Big|\frac {u(x)}{\lambda}\Big|^{2^*+r^{\alpha}} \mathrm{d} x \le 1 \Big\}.
\end{equation*}The following proposition follows directly from the definition:
Proposition 2.4. Let ![]() $p:[0,1) \rightarrow \mathbb{R}$ be a bounded continuous function and
$p:[0,1) \rightarrow \mathbb{R}$ be a bounded continuous function and ![]() $u\in L^{p(r)}(B)$. Consider
$u\in L^{p(r)}(B)$. Consider ![]() $\|u\|_{p(r)}=\mu$. Then we have:
$\|u\|_{p(r)}=\mu$. Then we have:
(i) If
 $\mu\geq 1$, then
$\mu\geq 1$, then  $\mu^{p_-}\leq\displaystyle \int_{B} |u(x)|^{p(r)}\mathrm{d}x\leq \mu^{p_+}$,
$\mu^{p_-}\leq\displaystyle \int_{B} |u(x)|^{p(r)}\mathrm{d}x\leq \mu^{p_+}$,(ii) If
 $\mu\leq 1$, then
$\mu\leq 1$, then  $\mu^{p_+}\leq\displaystyle\int_{B} |u(x)|^{p(r)}\mathrm{d}x\leq \mu^{p_-}$,
$\mu^{p_+}\leq\displaystyle\int_{B} |u(x)|^{p(r)}\mathrm{d}x\leq \mu^{p_-}$,
where  $p_+= \sup_{r \in [0,1)}p(r)$ and
$p_+= \sup_{r \in [0,1)}p(r)$ and ![]() $p_-=\inf_{r \in [0,1)}p(r)$.
$p_-=\inf_{r \in [0,1)}p(r)$.
3. Proof of theorem 1.1
To establish a weak solution of problem (1.3), we define the functional  $J \colon H^{1}_{0, \text{rad}}(B) \to \mathbb{R}$ given by
$J \colon H^{1}_{0, \text{rad}}(B) \to \mathbb{R}$ given by
 \begin{equation}
J(u) = \frac 1 2 \Vert \nabla u \Vert^2_2 -\frac{\lambda}{q}\Vert u^+ \Vert_q^q - \int_B \frac 1{2^* + r^\alpha}\, (u^+)^{2^* + r^{\alpha}} \text{d} x,
\end{equation}
\begin{equation}
J(u) = \frac 1 2 \Vert \nabla u \Vert^2_2 -\frac{\lambda}{q}\Vert u^+ \Vert_q^q - \int_B \frac 1{2^* + r^\alpha}\, (u^+)^{2^* + r^{\alpha}} \text{d} x,
\end{equation} where ![]() $u^+(x)=\operatorname{max}\{u(x),0\}$. By proposition 2.2 and by corollary 2.3, it follows that the functional J is well defined. We also note that J is a functional of class C 1. If u > 0 is a critical point of the functional then u is a weak solution to problem (1.3) thanks to the symmetric criticality principle (see [Reference Palais7, Reference Willem10]). The strategy then consists of obtaining positive critical points of the functional J. For this, we will use the Mountain Pass Lemma, due to Ambrosetti and Rabinowitz [Reference Ambrosetti and Rabinowitz1].
$u^+(x)=\operatorname{max}\{u(x),0\}$. By proposition 2.2 and by corollary 2.3, it follows that the functional J is well defined. We also note that J is a functional of class C 1. If u > 0 is a critical point of the functional then u is a weak solution to problem (1.3) thanks to the symmetric criticality principle (see [Reference Palais7, Reference Willem10]). The strategy then consists of obtaining positive critical points of the functional J. For this, we will use the Mountain Pass Lemma, due to Ambrosetti and Rabinowitz [Reference Ambrosetti and Rabinowitz1].
In the next lemmas, we will demonstrate that the functional J has the geometry of the Mountain Pass Theorem.
Lemma 3.1. There exist ρ > 0 and θ > 0 such that
Proof. Note that
 \begin{align*}
J(u) & = \frac{1}{2} \Vert \nabla u \Vert_{2}^2 - \frac{\lambda}{q}\Vert u^+ \Vert_q^{q} - \int_{B} \dfrac{( u^+ )^{2^* + r^\alpha}}{2^*+r^\alpha}\, \mathrm{d} x \\
& \geq \frac{1}{2} \Vert \nabla u \Vert_{2}^2 - \frac{\lambda}{q}\Vert u \Vert_q^{q} - \frac{1}{2^*}\int_{B}\vert u \vert^{2^* + r^\alpha}\, \mathrm{d} x.
\end{align*}
\begin{align*}
J(u) & = \frac{1}{2} \Vert \nabla u \Vert_{2}^2 - \frac{\lambda}{q}\Vert u^+ \Vert_q^{q} - \int_{B} \dfrac{( u^+ )^{2^* + r^\alpha}}{2^*+r^\alpha}\, \mathrm{d} x \\
& \geq \frac{1}{2} \Vert \nabla u \Vert_{2}^2 - \frac{\lambda}{q}\Vert u \Vert_q^{q} - \frac{1}{2^*}\int_{B}\vert u \vert^{2^* + r^\alpha}\, \mathrm{d} x.
\end{align*} Let  $u \in H_{0, \mathrm{rad}}^1(B)$ be such that
$u \in H_{0, \mathrm{rad}}^1(B)$ be such that ![]() $\Vert \nabla u \Vert_2 = \theta$ where
$\Vert \nabla u \Vert_2 = \theta$ where ![]() $\theta \in (0,1)$ will be chosen. By proposition 2.4 and corollary 2.3 follow that
$\theta \in (0,1)$ will be chosen. By proposition 2.4 and corollary 2.3 follow that
 \begin{align*}
\int_{B}\vert u \vert^{2^* + r^\alpha}\, \mathrm{d} x \leq \Vert u \Vert^{2^*}_{2^* + r^\alpha} \leq C \Vert \nabla u \Vert^{2^*}_2.
\end{align*}
\begin{align*}
\int_{B}\vert u \vert^{2^* + r^\alpha}\, \mathrm{d} x \leq \Vert u \Vert^{2^*}_{2^* + r^\alpha} \leq C \Vert \nabla u \Vert^{2^*}_2.
\end{align*}Therefore,
 \begin{align}
J(u) \geq \frac{1}{2} \Vert \nabla u\Vert^2_2 - \frac{\lambda}{q}\Vert u \Vert_q^q - \frac{C}{2^*} \Vert \nabla u\Vert^{2^*}_2.
\end{align}
\begin{align}
J(u) \geq \frac{1}{2} \Vert \nabla u\Vert^2_2 - \frac{\lambda}{q}\Vert u \Vert_q^q - \frac{C}{2^*} \Vert \nabla u\Vert^{2^*}_2.
\end{align} We observe that when q = 2, we consider ![]() $\lambda \in [0, \lambda_1)$, then the expression
$\lambda \in [0, \lambda_1)$, then the expression ![]() $ \sqrt{\Vert \nabla u \Vert^2 - \lambda \Vert u \Vert^2}$ defines a norm in
$ \sqrt{\Vert \nabla u \Vert^2 - \lambda \Vert u \Vert^2}$ defines a norm in ![]() $H_{0}^1(B)$ equivalent to norm
$H_{0}^1(B)$ equivalent to norm ![]() $\|\nabla u \|_2$. Since
$\|\nabla u \|_2$. Since ![]() $\| \nabla u \|_2 = \theta$, we have
$\| \nabla u \|_2 = \theta$, we have
 \begin{align*}
J(u) \geq \frac{C}{2} \theta^2 - \frac{C}{2^*} \theta^{2^*}.
\end{align*}
\begin{align*}
J(u) \geq \frac{C}{2} \theta^2 - \frac{C}{2^*} \theta^{2^*}.
\end{align*} So, choosing ![]() $\theta_1 \in (0,1)$ small enough we have that for
$\theta_1 \in (0,1)$ small enough we have that for ![]() $\theta \in (0,\theta_1)$ fixed there is
$\theta \in (0,\theta_1)$ fixed there is ![]() $\rho_1 \gt 0$ such that
$\rho_1 \gt 0$ such that ![]() $J(u) \geq \rho_1 \gt 0$.
$J(u) \geq \rho_1 \gt 0$.
If ![]() $q \in (2, 2^*]$, by using (3.2) and Sobolev inequality, we get
$q \in (2, 2^*]$, by using (3.2) and Sobolev inequality, we get
 \begin{align*}
J(u) &\geq \frac{1}{2} \Vert \nabla u\Vert^2_2 - \frac{C_1\lambda}{q}\Vert\nabla u \Vert_q^q - \frac{C}{2^*} \Vert \nabla u\Vert^{2^*}_2 \\
&= \frac{1}{2} \theta^2 - \frac{\lambda C_1}{q} \theta^q - \frac{C}{2^*} \theta^{2^*}.
\end{align*}
\begin{align*}
J(u) &\geq \frac{1}{2} \Vert \nabla u\Vert^2_2 - \frac{C_1\lambda}{q}\Vert\nabla u \Vert_q^q - \frac{C}{2^*} \Vert \nabla u\Vert^{2^*}_2 \\
&= \frac{1}{2} \theta^2 - \frac{\lambda C_1}{q} \theta^q - \frac{C}{2^*} \theta^{2^*}.
\end{align*} Since ![]() $2^* \geq q \gt 2$, we can choose
$2^* \geq q \gt 2$, we can choose ![]() $\theta_2 \in (0,1)$ small enough such that for any fixed
$\theta_2 \in (0,1)$ small enough such that for any fixed ![]() $\theta \in (0, \theta_2)$, there exists
$\theta \in (0, \theta_2)$, there exists ![]() $\rho_2 \gt 0$ such that
$\rho_2 \gt 0$ such that ![]() $J(u) \geq \rho_2 \gt 0$.
$J(u) \geq \rho_2 \gt 0$.
Now, we will state the second condition of the mountain pass geometry.
Lemma 3.2. Exist  $u \in H_{0, \mathrm{rad}}^1(B)$ such that
$u \in H_{0, \mathrm{rad}}^1(B)$ such that ![]() $\Vert \nabla u\Vert_2 \gt \theta $ and
$\Vert \nabla u\Vert_2 \gt \theta $ and ![]() $J(u) \lt 0$.
$J(u) \lt 0$.
Proof. Let  $u \in H_{0, \mathrm{rad}}^1(B) \setminus \{0 \}$ such that u > 0 in B. We have for t > 1 that
$u \in H_{0, \mathrm{rad}}^1(B) \setminus \{0 \}$ such that u > 0 in B. We have for t > 1 that
 \begin{align*}
J(tu) &= \frac{t^2}{2} \Vert \nabla u^+ \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \int_{B} \dfrac{t^{2^* + r^\alpha }( u^+)^{2^* + r^\alpha}}{2^* + r^\alpha}\, \mathrm{d} x \\
& \leq \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u^+ \Vert^q_q - \frac{t^{2^*}}{{2^* + 1}}\int_{B} (u^+)^{2^* + r^\alpha}\, \mathrm{d} x.
\end{align*}
\begin{align*}
J(tu) &= \frac{t^2}{2} \Vert \nabla u^+ \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \int_{B} \dfrac{t^{2^* + r^\alpha }( u^+)^{2^* + r^\alpha}}{2^* + r^\alpha}\, \mathrm{d} x \\
& \leq \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u^+ \Vert^q_q - \frac{t^{2^*}}{{2^* + 1}}\int_{B} (u^+)^{2^* + r^\alpha}\, \mathrm{d} x.
\end{align*} Therefore, since ![]() $2 \leq q \leq 2^*$ we get
$2 \leq q \leq 2^*$ we get
 \begin{align*}
\lim_{t \to + \infty} J(tu) = - \infty,
\end{align*}
\begin{align*}
\lim_{t \to + \infty} J(tu) = - \infty,
\end{align*}which proves the lemma.
We now define SN as the best constant in the Sobolev embedding  $H^1(\mathbb{R}^N) \hookrightarrow L^{2^*}(\mathbb{R}^N)$, that is,
$H^1(\mathbb{R}^N) \hookrightarrow L^{2^*}(\mathbb{R}^N)$, that is,
 \begin{align}
S_N := \inf \left\{\frac{\Vert \nabla u \Vert^2_{L^2(\mathbb{R}^N)}}{\Vert u \Vert_{L^{2^*}(\mathbb{R}^N)}^2} \, \colon u\in L^{2^*}(\mathbb{R}^N)\setminus\{0\}; \,\, \nabla u \in L^2(\mathbb{R}^N) \right\}.
\end{align}
\begin{align}
S_N := \inf \left\{\frac{\Vert \nabla u \Vert^2_{L^2(\mathbb{R}^N)}}{\Vert u \Vert_{L^{2^*}(\mathbb{R}^N)}^2} \, \colon u\in L^{2^*}(\mathbb{R}^N)\setminus\{0\}; \,\, \nabla u \in L^2(\mathbb{R}^N) \right\}.
\end{align}We consider
 \begin{align*}
\bar{u}(x) = C\left( 1+ \vert x \vert^{2}\right)^{-\frac{(N-2)}{2}}
\end{align*}
\begin{align*}
\bar{u}(x) = C\left( 1+ \vert x \vert^{2}\right)^{-\frac{(N-2)}{2}}
\end{align*}the standard Sobolev instantons, which satisfy the equation (see [Reference Talenti9])
 \begin{equation*}
-\Delta u = u^{2^*-1} \ , \ \hbox{on } \ \mathbb R^N.
\end{equation*}
\begin{equation*}
-\Delta u = u^{2^*-1} \ , \ \hbox{on } \ \mathbb R^N.
\end{equation*} We also consider  $u^*(x)=\bar{u}(x/S_N^{1/2})$ and
$u^*(x)=\bar{u}(x/S_N^{1/2})$ and  $U_\varepsilon (x) = \varepsilon^{-\frac{(N-2)}{2}}u^*(x/\varepsilon)$. As in [Reference Talenti9] and also [Reference Willem10], we know that,
$U_\varepsilon (x) = \varepsilon^{-\frac{(N-2)}{2}}u^*(x/\varepsilon)$. As in [Reference Talenti9] and also [Reference Willem10], we know that,
 \begin{equation*}
\int_{\mathbb{R}^N} \vert \nabla U_\varepsilon \vert^2 \,\text{d}x = S_N^{N/2} \ \hbox{and } \ \int_{\mathbb R^N} |U_\varepsilon|^{2^*} \text{d}x = S_N^{N/2}.
\end{equation*}
\begin{equation*}
\int_{\mathbb{R}^N} \vert \nabla U_\varepsilon \vert^2 \,\text{d}x = S_N^{N/2} \ \hbox{and } \ \int_{\mathbb R^N} |U_\varepsilon|^{2^*} \text{d}x = S_N^{N/2}.
\end{equation*} Taking a suitable cut-off function η and setting ![]() $u_\varepsilon = \eta\, U_\varepsilon$, it is known that
$u_\varepsilon = \eta\, U_\varepsilon$, it is known that
 \begin{align}
\int_B \vert \nabla u_{\varepsilon} \vert^2 \,\text{d}x = S_N^{N/2} + O(\varepsilon^{N-2})\ \ , \ \int_B|u_\varepsilon(x)|^{2^*}\; \mathrm{d} x = S_N^{N/2} + O(\varepsilon^N).
\end{align}
\begin{align}
\int_B \vert \nabla u_{\varepsilon} \vert^2 \,\text{d}x = S_N^{N/2} + O(\varepsilon^{N-2})\ \ , \ \int_B|u_\varepsilon(x)|^{2^*}\; \mathrm{d} x = S_N^{N/2} + O(\varepsilon^N).
\end{align}Do Ó, Ruf, and Ubilla, in [Reference do Ó, Ruf and Ubilla5], demonstrated the following lemma:
Lemma 3.3. There exists a constant C > 0 such that for all ɛ > 0 small
 \begin{equation*}
\int_{B} |u_{\varepsilon}(x)|^{2^*+r^\alpha} \; \mathrm{d} x \ge \int_B|u_\varepsilon (x)|^{2^*}\; \mathrm{d} x + C\, |\log \varepsilon |
\varepsilon^{\alpha} + O(\varepsilon^{N/2}) + O(\varepsilon^{N-2}) . \
\end{equation*}
\begin{equation*}
\int_{B} |u_{\varepsilon}(x)|^{2^*+r^\alpha} \; \mathrm{d} x \ge \int_B|u_\varepsilon (x)|^{2^*}\; \mathrm{d} x + C\, |\log \varepsilon |
\varepsilon^{\alpha} + O(\varepsilon^{N/2}) + O(\varepsilon^{N-2}) . \
\end{equation*}Now let’s control the min-max level of the mountain pass theorem.
Lemma 3.4. The level c of the mountain pass of the functional J satisfies  $0 \lt c \lt \frac 1N S_N^{N/2}$.
$0 \lt c \lt \frac 1N S_N^{N/2}$.
Proof. By lemmas 3.1 and 3.2, J has the geometry of the Mountain Pass lemma. We consider uɛ as before and set
 \begin{equation*}
c = \inf_{\gamma \in \Gamma} \max_{u \in \gamma} J(u)
\end{equation*}
\begin{equation*}
c = \inf_{\gamma \in \Gamma} \max_{u \in \gamma} J(u)
\end{equation*}where
 \begin{equation*}\Gamma := \Big\{\gamma : [0,R] \to H_0^1(B) \hbox{continuous }, \gamma(0) = 0, \gamma(1) = R\, u_\varepsilon \Big\},
\end{equation*}
\begin{equation*}\Gamma := \Big\{\gamma : [0,R] \to H_0^1(B) \hbox{continuous }, \gamma(0) = 0, \gamma(1) = R\, u_\varepsilon \Big\},
\end{equation*} with R > 0 sufficiently large such that ![]() $J(R\, u_\varepsilon) \le 0$. By (3.4) and lemma 3.3, we note that R can be chosen independent of ɛ. The path
$J(R\, u_\varepsilon) \le 0$. By (3.4) and lemma 3.3, we note that R can be chosen independent of ɛ. The path ![]() $\gamma_\varepsilon(t) = t u_\varepsilon, \, t \in [0,R]$, belongs to Γ, and
$\gamma_\varepsilon(t) = t u_\varepsilon, \, t \in [0,R]$, belongs to Γ, and
 \begin{equation}
c \le \max_{t \in [0,R]} J(t\,u_\varepsilon) := J(t_\varepsilon u_\varepsilon) .
\end{equation}
\begin{equation}
c \le \max_{t \in [0,R]} J(t\,u_\varepsilon) := J(t_\varepsilon u_\varepsilon) .
\end{equation} We have also that  $\frac d{dt} J(t\, u_\varepsilon)\Big|_{t = t_\varepsilon} = 0$ and by J satisfying the geometric conditions of the Mountain Pass lemma, we can assume that
$\frac d{dt} J(t\, u_\varepsilon)\Big|_{t = t_\varepsilon} = 0$ and by J satisfying the geometric conditions of the Mountain Pass lemma, we can assume that ![]() $ t_\varepsilon \in (\delta, R]$ with δ > 0 because if
$ t_\varepsilon \in (\delta, R]$ with δ > 0 because if ![]() $t_\varepsilon \rightarrow 0$ by (3.4) and lemma 3.3 we obtain that
$t_\varepsilon \rightarrow 0$ by (3.4) and lemma 3.3 we obtain that ![]() $J(t_\varepsilon u_\varepsilon) \rightarrow 0$. So, for ɛ > 0 small enough, we have
$J(t_\varepsilon u_\varepsilon) \rightarrow 0$. So, for ɛ > 0 small enough, we have  $J(t_\varepsilon u_\varepsilon) \lt S_N^{N/2}/N$.
$J(t_\varepsilon u_\varepsilon) \lt S_N^{N/2}/N$.
Now, let’s consider the following auxiliary functional:
 \begin{align*}
J_A(u) = \frac{1}{2}\Vert \nabla u \Vert_2^2 - \int_B \frac{(u^+)^{2^*+r^\alpha}}{2^*+r^\alpha}\,\mathrm{d}x, \,\, u \in H_{0,\mathrm{rad}}^1(B).
\end{align*}
\begin{align*}
J_A(u) = \frac{1}{2}\Vert \nabla u \Vert_2^2 - \int_B \frac{(u^+)^{2^*+r^\alpha}}{2^*+r^\alpha}\,\mathrm{d}x, \,\, u \in H_{0,\mathrm{rad}}^1(B).
\end{align*} So, for ![]() $ t_\varepsilon \in (\delta, R]$ we have the estimate
$ t_\varepsilon \in (\delta, R]$ we have the estimate
 \begin{align}
J(t_\varepsilon u_\varepsilon) & = \frac{t_\varepsilon^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 -\frac{\lambda t_\varepsilon^q}{q}\Vert u_\varepsilon \Vert_q^q - \int_B \frac {t_\varepsilon^{2^*+r^{\alpha}}}{2^* + r^\alpha} (u_\varepsilon)^{2^* + r^\alpha} \, \mathrm{d} x \nonumber
\\
& \leq J_A(t_\varepsilon u_\varepsilon) \nonumber \\
& = \frac{t_\varepsilon^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 - \frac{t_\varepsilon^{2^{*}}}{2^*}\int_B u_\varepsilon^{2^*} \, \mathrm{d} x \nonumber \\
&\quad + t_\varepsilon^{2^*}\int_B \left(\frac 1{2^*} - \frac 1{2^* + r^\alpha}\right) u_\varepsilon^{2^*} \, \mathrm{d} x \nonumber \\
&\quad+ \int_B \frac 1{2^* + r^\alpha}\left( (t_\varepsilon u_\varepsilon)^{2^*} - (t_\varepsilon u_\varepsilon)^{2^* + r^\alpha}\right) \, \mathrm{d} x \nonumber \\
& \leq \max_{t \in [0,R]}\left( \frac{t^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 - \frac{t^{2^{*}}}{2^*}\Vert u_{\varepsilon}\Vert^{2^*}_{2^*} \right) + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert \nonumber \\
&\quad + O(\varepsilon^{N/2}) + O(\varepsilon^{N-2})\nonumber \\
& = \frac{1}{2} \bigg( \frac{\Vert \nabla u_\varepsilon \Vert^2_2}{\Vert u_{\varepsilon} \Vert^{2^*}_{2^*}} \bigg)^{2/(2^*-2)} \Vert\nabla u_\varepsilon \Vert^{2}_2 - \frac{1}{2^*}\bigg( \frac{\Vert \nabla u_\varepsilon \Vert^2_2}{\Vert u_{\varepsilon}\Vert_{2^*}^{2^*}} \bigg)^{2^*/(2^*-2)}\Vert u_{\varepsilon}\Vert_{2^*}^{2^*} \nonumber \\
& \quad + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert \nonumber \\
& = \frac{1}{N} \frac{\big( \Vert \nabla u_\varepsilon \Vert^2_2\big)^{2^*/(2^*-2)}}{\big( \Vert u_{\varepsilon}\Vert^{2^*}_{2^*} \big)^{2/(2^*-2)}} + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert,
\end{align}
\begin{align}
J(t_\varepsilon u_\varepsilon) & = \frac{t_\varepsilon^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 -\frac{\lambda t_\varepsilon^q}{q}\Vert u_\varepsilon \Vert_q^q - \int_B \frac {t_\varepsilon^{2^*+r^{\alpha}}}{2^* + r^\alpha} (u_\varepsilon)^{2^* + r^\alpha} \, \mathrm{d} x \nonumber
\\
& \leq J_A(t_\varepsilon u_\varepsilon) \nonumber \\
& = \frac{t_\varepsilon^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 - \frac{t_\varepsilon^{2^{*}}}{2^*}\int_B u_\varepsilon^{2^*} \, \mathrm{d} x \nonumber \\
&\quad + t_\varepsilon^{2^*}\int_B \left(\frac 1{2^*} - \frac 1{2^* + r^\alpha}\right) u_\varepsilon^{2^*} \, \mathrm{d} x \nonumber \\
&\quad+ \int_B \frac 1{2^* + r^\alpha}\left( (t_\varepsilon u_\varepsilon)^{2^*} - (t_\varepsilon u_\varepsilon)^{2^* + r^\alpha}\right) \, \mathrm{d} x \nonumber \\
& \leq \max_{t \in [0,R]}\left( \frac{t^2}{2} \Vert \nabla u_\varepsilon \Vert^2_2 - \frac{t^{2^{*}}}{2^*}\Vert u_{\varepsilon}\Vert^{2^*}_{2^*} \right) + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert \nonumber \\
&\quad + O(\varepsilon^{N/2}) + O(\varepsilon^{N-2})\nonumber \\
& = \frac{1}{2} \bigg( \frac{\Vert \nabla u_\varepsilon \Vert^2_2}{\Vert u_{\varepsilon} \Vert^{2^*}_{2^*}} \bigg)^{2/(2^*-2)} \Vert\nabla u_\varepsilon \Vert^{2}_2 - \frac{1}{2^*}\bigg( \frac{\Vert \nabla u_\varepsilon \Vert^2_2}{\Vert u_{\varepsilon}\Vert_{2^*}^{2^*}} \bigg)^{2^*/(2^*-2)}\Vert u_{\varepsilon}\Vert_{2^*}^{2^*} \nonumber \\
& \quad + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert \nonumber \\
& = \frac{1}{N} \frac{\big( \Vert \nabla u_\varepsilon \Vert^2_2\big)^{2^*/(2^*-2)}}{\big( \Vert u_{\varepsilon}\Vert^{2^*}_{2^*} \big)^{2/(2^*-2)}} + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert,
\end{align} where we use that ![]() $\alpha \in (0,\min \{N/2,N-2\})$, the lemma 3.3, and the estimate
$\alpha \in (0,\min \{N/2,N-2\})$, the lemma 3.3, and the estimate
 \begin{equation}
\begin{aligned}
\int_B\Big( \frac 1{2^*}- \frac{1}{2^* + r^\alpha}\Big) |u_\varepsilon|^{2^*} \mathrm{d} x & = \int_B \dfrac{r^\alpha}{2^*(2^* + r^\alpha)} |u_\varepsilon|^{2^*}r^{N-1} \; \mathrm{d} x \\
& \leq c \int_0^\varepsilon r^\alpha \varepsilon^{-N}r^{N-1}\; \mathrm{d} r + c \int_\varepsilon^1 r^\alpha \frac {\varepsilon^N}{r^{2N}}r^{N-1}\; \mathrm{d} r \\
& \leq c\, \varepsilon^\alpha + c\, (\varepsilon^\alpha - \varepsilon^N) = c\, \varepsilon^\alpha.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\int_B\Big( \frac 1{2^*}- \frac{1}{2^* + r^\alpha}\Big) |u_\varepsilon|^{2^*} \mathrm{d} x & = \int_B \dfrac{r^\alpha}{2^*(2^* + r^\alpha)} |u_\varepsilon|^{2^*}r^{N-1} \; \mathrm{d} x \\
& \leq c \int_0^\varepsilon r^\alpha \varepsilon^{-N}r^{N-1}\; \mathrm{d} r + c \int_\varepsilon^1 r^\alpha \frac {\varepsilon^N}{r^{2N}}r^{N-1}\; \mathrm{d} r \\
& \leq c\, \varepsilon^\alpha + c\, (\varepsilon^\alpha - \varepsilon^N) = c\, \varepsilon^\alpha.
\end{aligned}
\end{equation}Therefore, by using (3.4) and (3.6), we obtain
 \begin{align*}
J(t_\varepsilon u_\varepsilon) \leq J_A(t_\varepsilon u_\varepsilon) & \leq
\frac{1}{N} \frac{\big( S_N^{N/2} + O(\varepsilon^{N-2})\big)^{2^*/(2^*-2)}}{\big( S_N^{N/2} + O(\varepsilon^{N})\big)^{2/(2^*-2)}} + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert, \\
&=\frac{1}{N}S_N^{N/2} + O(\varepsilon^{N-2}) + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert, \\
& \lt \frac{1}{N}S_N^{N/2}, \; \text{for}\; \varepsilon \gt 0 \; \text{small enough and for all}\, N \geq 3.
\end{align*}
\begin{align*}
J(t_\varepsilon u_\varepsilon) \leq J_A(t_\varepsilon u_\varepsilon) & \leq
\frac{1}{N} \frac{\big( S_N^{N/2} + O(\varepsilon^{N-2})\big)^{2^*/(2^*-2)}}{\big( S_N^{N/2} + O(\varepsilon^{N})\big)^{2/(2^*-2)}} + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert, \\
&=\frac{1}{N}S_N^{N/2} + O(\varepsilon^{N-2}) + c\varepsilon^{\alpha} - c\varepsilon^{\alpha}\vert \log \varepsilon \vert, \\
& \lt \frac{1}{N}S_N^{N/2}, \; \text{for}\; \varepsilon \gt 0 \; \text{small enough and for all}\, N \geq 3.
\end{align*}3.1. Proof of theorem 1.1
By lemmas 3.1 and 3.2, we know that the functional J satisfies the geometric conditions of the Mountain Pass lemma; by lemma 3.4, it follows that there is a sequence of Palais-Smale  $\{u_n\}\subset H_{0,\text{rad}}^1(B)$ such that:
$\{u_n\}\subset H_{0,\text{rad}}^1(B)$ such that:
 \begin{align*}
J(u_n) \rightarrow c \lt \frac 1N S_N^{N/2}, \, \text{and}\, J'(u_n) \rightarrow 0.
\end{align*}
\begin{align*}
J(u_n) \rightarrow c \lt \frac 1N S_N^{N/2}, \, \text{and}\, J'(u_n) \rightarrow 0.
\end{align*} Let’s show that the sequence ![]() $\{u_n\}$ is bounded in
$\{u_n\}$ is bounded in  $H_{0,\text{rad}}^1(B)$. Indeed, for n sufficiently large and
$H_{0,\text{rad}}^1(B)$. Indeed, for n sufficiently large and ![]() $q \in (2,2^*] $, we have:
$q \in (2,2^*] $, we have:
 \begin{align*}
c + 1 + \Vert \nabla u_n \Vert_2 & \geq J(u_n) - \frac{1}{q} J'(u_n)u_n \\
& = \left( \frac{1}{2} - \frac{1}{q}\right)\Vert \nabla u_n \Vert_2^2 + \int_B \left( \frac{1}{q}-\frac{1}{2^*+r^\alpha}\right)(u_n^+)^{2^*+r^\alpha}\,\mathrm{d}x \\
& \geq \left( \frac{1}{2} - \frac{1}{q}\right)\Vert \nabla u_n \Vert_2^2.
\end{align*}
\begin{align*}
c + 1 + \Vert \nabla u_n \Vert_2 & \geq J(u_n) - \frac{1}{q} J'(u_n)u_n \\
& = \left( \frac{1}{2} - \frac{1}{q}\right)\Vert \nabla u_n \Vert_2^2 + \int_B \left( \frac{1}{q}-\frac{1}{2^*+r^\alpha}\right)(u_n^+)^{2^*+r^\alpha}\,\mathrm{d}x \\
& \geq \left( \frac{1}{2} - \frac{1}{q}\right)\Vert \nabla u_n \Vert_2^2.
\end{align*} It follows that ![]() $\{u_n\}$ is bounded in
$\{u_n\}$ is bounded in  $H_{0,\mathrm{rad}}^1(B)$. If q = 2, we recall that
$H_{0,\mathrm{rad}}^1(B)$. If q = 2, we recall that ![]() $\lambda \in [0, \lambda_1)$ and in this case the expression
$\lambda \in [0, \lambda_1)$ and in this case the expression ![]() $(\Vert \nabla u \Vert^2_2 - \lambda \Vert u \Vert^2_2)^{1/2}$ defines a norm in
$(\Vert \nabla u \Vert^2_2 - \lambda \Vert u \Vert^2_2)^{1/2}$ defines a norm in  $H^1_{0,\mathrm{rad}}(B)$ equivalent to the usual norm
$H^1_{0,\mathrm{rad}}(B)$ equivalent to the usual norm ![]() $\Vert \nabla u \Vert_2$. Thus, we will also have for n sufficiently large that:
$\Vert \nabla u \Vert_2$. Thus, we will also have for n sufficiently large that:
 \begin{align*}
c + 1 + \Vert \nabla u_n \Vert_2 & \geq J(u_n) - \frac{1}{2^*} J'(u_n)u_n \\
& \geq \left( \frac{1}{2} - \frac{1}{2^*}\right)\left( \Vert \nabla u_n \Vert_2^2 - \lambda \Vert u \Vert_2^2\right) \\
& \quad + \int_B \left( \frac{1}{2^*}-\frac{1}{2^*+r^\alpha}\right)(u_n^+)^{2^*+r^\alpha}\,\mathrm{d}x \\
& \geq c_1 \Vert \nabla u_n \Vert_2^2.
\end{align*}
\begin{align*}
c + 1 + \Vert \nabla u_n \Vert_2 & \geq J(u_n) - \frac{1}{2^*} J'(u_n)u_n \\
& \geq \left( \frac{1}{2} - \frac{1}{2^*}\right)\left( \Vert \nabla u_n \Vert_2^2 - \lambda \Vert u \Vert_2^2\right) \\
& \quad + \int_B \left( \frac{1}{2^*}-\frac{1}{2^*+r^\alpha}\right)(u_n^+)^{2^*+r^\alpha}\,\mathrm{d}x \\
& \geq c_1 \Vert \nabla u_n \Vert_2^2.
\end{align*} It follows that ![]() $\{u_n\}$ is bounded in
$\{u_n\}$ is bounded in  $H_{0,\mathrm{rad}}^1(B)$. So there exists
$H_{0,\mathrm{rad}}^1(B)$. So there exists  $ u \in H_{0,\text{rad}}^1(B) $ such that
$ u \in H_{0,\text{rad}}^1(B) $ such that ![]() $ u_n \rightharpoonup u $ in
$ u_n \rightharpoonup u $ in  $ H_{0,\text{rad}}^1(B) $. We have two possibilities:
$ H_{0,\text{rad}}^1(B) $. We have two possibilities:
If ![]() $ u \not\equiv 0 $, then u is a non-trivial non-negative solution to problem (1.3). By the maximum principle, we guarantee that u is positive, thus proving the theorem.
$ u \not\equiv 0 $, then u is a non-trivial non-negative solution to problem (1.3). By the maximum principle, we guarantee that u is positive, thus proving the theorem.
If u = 0, we have ![]() $ u_n \rightharpoonup 0 $, and for every ɛ > 0 and n sufficiently large, the following inequality holds:
$ u_n \rightharpoonup 0 $, and for every ɛ > 0 and n sufficiently large, the following inequality holds:
 \begin{align}
\int_B |u_n|^{2^* + r^{\alpha}} \, \text{d}x - \int_B |u_n|^{2^*} \, \text{d}x \leq \varepsilon.
\end{align}
\begin{align}
\int_B |u_n|^{2^* + r^{\alpha}} \, \text{d}x - \int_B |u_n|^{2^*} \, \text{d}x \leq \varepsilon.
\end{align} Indeed, note that for all η > 0, we have  $H^1_{0,\mathrm{rad}}(B \setminus B_\eta) \subset\subset L^s(B \setminus B_\eta)$ for all
$H^1_{0,\mathrm{rad}}(B \setminus B_\eta) \subset\subset L^s(B \setminus B_\eta)$ for all ![]() $s \geq 1$. Therefore,
$s \geq 1$. Therefore,
and consequently,
 \begin{align}
\int_{B \setminus B_\eta} |u_n|^{2^*+r^{\alpha}} \, \text{d} x \rightarrow 0 \text{and } \int_{B \setminus B_\eta} |u_n|^{2^*} \, \text{d} x \rightarrow 0 \text{as } n \rightarrow \infty.
\end{align}
\begin{align}
\int_{B \setminus B_\eta} |u_n|^{2^*+r^{\alpha}} \, \text{d} x \rightarrow 0 \text{and } \int_{B \setminus B_\eta} |u_n|^{2^*} \, \text{d} x \rightarrow 0 \text{as } n \rightarrow \infty.
\end{align}By (3.9), we can write
 \begin{align}
\int_{B_\eta} |u_n|^{2^*+r^{\alpha}} \, \text{d} x &= \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*+r^{\alpha}} \; r^{N-1} \text{d} r \\
&= \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \tag{(3.11)} \\
&\quad + \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \; r^{N-1} \text{d} r \nonumber \\
& = \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \tag{(3.12)}\\
&\quad + \int_B |u_n(x)|^{2^*} \, \text{d}x + o(1).\tag{(3.13)}
\end{align}
\begin{align}
\int_{B_\eta} |u_n|^{2^*+r^{\alpha}} \, \text{d} x &= \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*+r^{\alpha}} \; r^{N-1} \text{d} r \\
&= \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \tag{(3.11)} \\
&\quad + \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \; r^{N-1} \text{d} r \nonumber \\
& = \omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \tag{(3.12)}\\
&\quad + \int_B |u_n(x)|^{2^*} \, \text{d}x + o(1).\tag{(3.13)}
\end{align}Using lemma 2.1 (Radial Lemma), we can estimate
 \begin{align*}
& \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r\\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} \left[ \left( \frac{1}{r^{(N-2)/2}} \right)^{r^{\alpha}} - 1 \right] \; r^{N-1} \text{d} r \\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} \left[ \exp\left( r^{\alpha} \log \left( \frac{1}{r^{(N-2)/2}} \right) \right) - 1 \right] \; r^{N-1} \text{d} r \\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} r^{\alpha} \left| \log r^{(N-2)/2} \right| \; r^{N-1} \text{d} r \\
& \quad \leq C_1 \eta^{\alpha} \left| \log \eta \right| \int_0^1 |u_n(r)|^{2^*} \; r^{N-1} \text{d} r \\
& \quad \leq C_2 \eta^\alpha \left| \log \eta \right|,
\end{align*}
\begin{align*}
& \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r\\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} \left[ \left( \frac{1}{r^{(N-2)/2}} \right)^{r^{\alpha}} - 1 \right] \; r^{N-1} \text{d} r \\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} \left[ \exp\left( r^{\alpha} \log \left( \frac{1}{r^{(N-2)/2}} \right) \right) - 1 \right] \; r^{N-1} \text{d} r \\
& \quad \leq \int_0^{\eta} |u_n(r)|^{2^*} r^{\alpha} \left| \log r^{(N-2)/2} \right| \; r^{N-1} \text{d} r \\
& \quad \leq C_1 \eta^{\alpha} \left| \log \eta \right| \int_0^1 |u_n(r)|^{2^*} \; r^{N-1} \text{d} r \\
& \quad \leq C_2 \eta^\alpha \left| \log \eta \right|,
\end{align*}where C 1 and C 2 are constants.
Therefore, for all ɛ > 0, we can choose ![]() $\eta = \eta(\varepsilon) \gt 0$ sufficiently small such that
$\eta = \eta(\varepsilon) \gt 0$ sufficiently small such that
 \begin{equation*}
C_2 \eta^{\alpha} \left| \log \eta \right| \leq \frac{\varepsilon}{2},
\end{equation*}
\begin{equation*}
C_2 \eta^{\alpha} \left| \log \eta \right| \leq \frac{\varepsilon}{2},
\end{equation*}which implies
 \begin{equation}
\omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \leq \frac{\varepsilon}{2}.
\end{equation}
\begin{equation}
\omega_{N-1} \int_0^{\eta} |u_n(r)|^{2^*} \left( |u_n(r)|^{r^{\alpha}} - 1 \right) \; r^{N-1} \text{d} r \leq \frac{\varepsilon}{2}.
\end{equation}From (3.9), (3.10), and (3.14), we obtain that for sufficiently large n and for all ɛ > 0,
 \begin{align*}
\int_B |u_n|^{2^*+r^{\alpha}} \, \text{d} x - \int_B |u_n|^{2^*} \, \text{d}x \leq \varepsilon.
\end{align*}
\begin{align*}
\int_B |u_n|^{2^*+r^{\alpha}} \, \text{d} x - \int_B |u_n|^{2^*} \, \text{d}x \leq \varepsilon.
\end{align*}Therefore, we have proven (3.8).
Now, for sufficiently large n, we obtain the inequality
 \begin{align*}
-\frac{1}{2^*} \int_B |u_n|^{2^*} \, \text{d}x \leq - \int_B \frac{|u_n|^{2^* + r^\alpha}}{2^* + r^\alpha} \, \text{d}x.
\end{align*}
\begin{align*}
-\frac{1}{2^*} \int_B |u_n|^{2^*} \, \text{d}x \leq - \int_B \frac{|u_n|^{2^* + r^\alpha}}{2^* + r^\alpha} \, \text{d}x.
\end{align*}Thus, for sufficiently large n, we get
where
 \begin{align*}
J_0(u) &= \frac{1}{2} \| \nabla u \|_2^2 - \frac{\lambda}{q} \| u^+ \|_q^q - \frac{1}{2^*} \int_B (u^+)^{2^*} \, \text{d}x, \quad u \in H_{0,\mathrm{rad}}^1(B).
\end{align*}
\begin{align*}
J_0(u) &= \frac{1}{2} \| \nabla u \|_2^2 - \frac{\lambda}{q} \| u^+ \|_q^q - \frac{1}{2^*} \int_B (u^+)^{2^*} \, \text{d}x, \quad u \in H_{0,\mathrm{rad}}^1(B).
\end{align*}Then, we have
 \begin{align*}
J_0(u_n) \rightarrow d \leq c \lt \frac{1}{N}S^{N/2}.
\end{align*}
\begin{align*}
J_0(u_n) \rightarrow d \leq c \lt \frac{1}{N}S^{N/2}.
\end{align*} Since ![]() $ u_n \rightharpoonup 0 $ also in
$ u_n \rightharpoonup 0 $ also in  $ L^{2^*}(B) $, it follows that
$ L^{2^*}(B) $, it follows that ![]() $ \langle J_0'(u_n), \varphi \rangle \rightarrow 0 $ for all
$ \langle J_0'(u_n), \varphi \rangle \rightarrow 0 $ for all  $ \varphi \in H_{0,\text{rad}}^1(B) $. Indeed, by the embedding
$ \varphi \in H_{0,\text{rad}}^1(B) $. Indeed, by the embedding  $ H_{0,\mathrm{rad}}^1(B) \hookrightarrow L^s(B) $ for all
$ H_{0,\mathrm{rad}}^1(B) \hookrightarrow L^s(B) $ for all ![]() $ s \in [1,2^*] $, we have
$ s \in [1,2^*] $, we have
 \begin{align*}
& \int_B \nabla u_n \cdot \nabla \varphi \, \text{d}x \rightarrow 0, \quad \int_B (u_n^+)^{q-1} \varphi \, \text{d}x \rightarrow 0, \quad \text{and} \\
& \int_B (u_n^+)^{2^*-1} \varphi \, \text{d}x \rightarrow 0 \text{as } n \rightarrow \infty.
\end{align*}
\begin{align*}
& \int_B \nabla u_n \cdot \nabla \varphi \, \text{d}x \rightarrow 0, \quad \int_B (u_n^+)^{q-1} \varphi \, \text{d}x \rightarrow 0, \quad \text{and} \\
& \int_B (u_n^+)^{2^*-1} \varphi \, \text{d}x \rightarrow 0 \text{as } n \rightarrow \infty.
\end{align*} Therefore, ![]() $\{u_n\}$ is a Palais-Smale sequence for the functional J 0 at the level
$\{u_n\}$ is a Palais-Smale sequence for the functional J 0 at the level  $d \lt \frac{1}{N} S^{N/2}$. According to [1.1, Reference Willem10], the functional J 0 satisfies the Palais–Smale condition for levels
$d \lt \frac{1}{N} S^{N/2}$. According to [1.1, Reference Willem10], the functional J 0 satisfies the Palais–Smale condition for levels  $d \lt \frac{1}{N} S^{N/2}$. Thus, we have
$d \lt \frac{1}{N} S^{N/2}$. Thus, we have ![]() $u_n \rightarrow 0$ strongly in
$u_n \rightarrow 0$ strongly in  $H_{0,\text{rad}}^1(B)$, and by the continuity of the functional J, it follows that
$H_{0,\text{rad}}^1(B)$, and by the continuity of the functional J, it follows that ![]() $J(u_n) \rightarrow 0$, which leads to a contradiction.
$J(u_n) \rightarrow 0$, which leads to a contradiction.
Therefore, we have ![]() $u \not\equiv 0$. Choosing
$u \not\equiv 0$. Choosing ![]() $\varphi = u^-$ as the test function in the equation
$\varphi = u^-$ as the test function in the equation ![]() $\langle J'(u), \varphi \rangle = 0$, we get that
$\langle J'(u), \varphi \rangle = 0$, we get that ![]() $u = u^+ \geq 0$. By the strong maximum principle (see [Reference Evans6, theorem 4, pp. 333]), it follows that u > 0 in B. Therefore, u is a weak solution of the problem (1.3), and this completes the proof of theorem 1.1.
$u = u^+ \geq 0$. By the strong maximum principle (see [Reference Evans6, theorem 4, pp. 333]), it follows that u > 0 in B. Therefore, u is a weak solution of the problem (1.3), and this completes the proof of theorem 1.1.
4. Proof of theorem 1.3
For problem (1.5), we will follow a similar strategy to the one we used in the proof of theorem 1.1. We define the functional  $J\colon H_{0, \text{rad}}^1(B) \rightarrow \mathbb{R}$ given by
$J\colon H_{0, \text{rad}}^1(B) \rightarrow \mathbb{R}$ given by
 \begin{align}
J(u) = \frac 12 \Vert \nabla u \Vert^2_2 - \frac{\lambda}{q}\Vert u^+ \Vert_{q}^q - \int_B \frac{(u^+)^{2^* + f(r)}}{2^*+f(r)}\, \text{d}x,
\end{align}
\begin{align}
J(u) = \frac 12 \Vert \nabla u \Vert^2_2 - \frac{\lambda}{q}\Vert u^+ \Vert_{q}^q - \int_B \frac{(u^+)^{2^* + f(r)}}{2^*+f(r)}\, \text{d}x,
\end{align} where ![]() $u^{+}(x) = \max \{u(x),0 \}$,
$u^{+}(x) = \max \{u(x),0 \}$, ![]() $f\colon [0,1) \rightarrow \mathbb{R}$ is a continuous function satisfying condition (f) and
$f\colon [0,1) \rightarrow \mathbb{R}$ is a continuous function satisfying condition (f) and ![]() $q \in [2,2^*)$. The parameter λ is considered in two cases: if q = 2 then
$q \in [2,2^*)$. The parameter λ is considered in two cases: if q = 2 then ![]() $\lambda \in [0,\lambda_1)$, if
$\lambda \in [0,\lambda_1)$, if ![]() $q \in (2,2^*)$ then
$q \in (2,2^*)$ then ![]() $\lambda \geq 0$. We will show in the following lemma that the functional J is well defined and by standard arguments, we will obtain that J is of class C 1. We also know that positive critical points of J are weak solutions to the problem (1.5).
$\lambda \geq 0$. We will show in the following lemma that the functional J is well defined and by standard arguments, we will obtain that J is of class C 1. We also know that positive critical points of J are weak solutions to the problem (1.5).
Lemma 4.1. Let J be the functional given in (4.1). Then J is well-defined.
Proof. We only have to demonstrate that the variable integral is finite. Let  $u \in H^{1}_{0, \mathrm{rad}}(B)$, then we write
$u \in H^{1}_{0, \mathrm{rad}}(B)$, then we write
 \begin{align}
\int_B |u|^{2^* + f(r)}\, \text{d}x & = \int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x + \int_{B_{\rho_2}\setminus B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \nonumber\\
& \quad + \int_{B \setminus B_{\rho_2}} |u|^{2^* + f(r)}\, \text{d}x
\end{align}
\begin{align}
\int_B |u|^{2^* + f(r)}\, \text{d}x & = \int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x + \int_{B_{\rho_2}\setminus B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \nonumber\\
& \quad + \int_{B \setminus B_{\rho_2}} |u|^{2^* + f(r)}\, \text{d}x
\end{align} where ρ 1 and ρ 2 will be chosen later. By hypothesis (f), it follows that there exists ![]() $\rho_1 \gt 0$ such that
$\rho_1 \gt 0$ such that ![]() $2 \lt 2^* + f(r) \lt 2^*, \forall r \in [0, \rho_1]$. From Hölder’s inequality and proposition 2.4, it follows that
$2 \lt 2^* + f(r) \lt 2^*, \forall r \in [0, \rho_1]$. From Hölder’s inequality and proposition 2.4, it follows that
 \begin{align}
\int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \leq C( \| u \|_{2^*}^{F_+} + \| u \|_{2^*}^{F_-}) \lt + \infty
\end{align}
\begin{align}
\int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \leq C( \| u \|_{2^*}^{F_+} + \| u \|_{2^*}^{F_-}) \lt + \infty
\end{align} where ![]() $F_+ = \sup_{r \in [0,\rho_1]}( 2^* +f(r))$ and
$F_+ = \sup_{r \in [0,\rho_1]}( 2^* +f(r))$ and ![]() $F_-= \inf_{r\in [0,\rho_1]}(2^*+f(r))$. Now, we consider
$F_-= \inf_{r\in [0,\rho_1]}(2^*+f(r))$. Now, we consider ![]() $\rho_2 \gt 0$ sufficiently close to 1. By lemma 2.1, we know that, for
$\rho_2 \gt 0$ sufficiently close to 1. By lemma 2.1, we know that, for ![]() $r \in [\rho_1 , \rho_2]$
$r \in [\rho_1 , \rho_2]$
 \begin{align}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\| \nabla u \|_2 \leq \frac{(1-\rho_1)^{1/2}}{\rho_1^{(N-2)/2}}\| \nabla u\|_2 := C_{\rho_1}\|\nabla u\|_2.
\end{align}
\begin{align}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\| \nabla u \|_2 \leq \frac{(1-\rho_1)^{1/2}}{\rho_1^{(N-2)/2}}\| \nabla u\|_2 := C_{\rho_1}\|\nabla u\|_2.
\end{align} Since f is continuous in ![]() $[\rho_1,\rho_2]$ it follows that
$[\rho_1,\rho_2]$ it follows that ![]() $f\in L^\infty[\rho_1,\rho_2]$ and therefore the second integral in (4.2) is finite. For
$f\in L^\infty[\rho_1,\rho_2]$ and therefore the second integral in (4.2) is finite. For ![]() $r \in [\rho_2 , 1)$, again by lemma 2.1, we get
$r \in [\rho_2 , 1)$, again by lemma 2.1, we get
 \begin{align}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\| \nabla u \|_2 \leq \frac{(1-\rho_2)^{1/2}}{\rho_2^{(N-2)/2}}\| \nabla u\|_2 := C_{\rho_2}\|\nabla u \|_2 \leq 1
\end{align}
\begin{align}
|u(r)| \leq \frac{(1-r)^{1/2}}{r^{(N-2)/2}}\| \nabla u \|_2 \leq \frac{(1-\rho_2)^{1/2}}{\rho_2^{(N-2)/2}}\| \nabla u\|_2 := C_{\rho_2}\|\nabla u \|_2 \leq 1
\end{align}since ρ 2 was chosen sufficiently close to 1. Therefore, we obtain that the third integral in (4.2) is also finite. Therefore, we conclude that the J functional is well-defined.
As previously mentioned, we must ensure that the functional J has a positive critical point, for this, we will use the Mountain Pass Theorem, due to Ambrosetti and Rabinowitz [Reference Ambrosetti and Rabinowitz1]. We will show now that the functional J has the geometry of the Mountain Pass Theorem.
Lemma 4.2. There exist ρ > 0 and θ > 0 such that
Proof. Let ![]() $u \in H^1_{0 \mathrm{rad}}(B)$ be such that
$u \in H^1_{0 \mathrm{rad}}(B)$ be such that ![]() $\| \nabla u \|_2 = \theta \lt 1$. By (4.3) and Sobolev’s inequality, we have for ρ 1 small enough that
$\| \nabla u \|_2 = \theta \lt 1$. By (4.3) and Sobolev’s inequality, we have for ρ 1 small enough that
 \begin{align}
\int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \leq C( \| u \|_{2^*}^{F_+} + \| u \|_{2^*}^{F_-}) \leq C_1 (\| \nabla u \|_2^{F_+} + \| \nabla u \|_2^{F_-}) \leq C_2 \| \nabla u \|_2^{F_-},
\end{align}
\begin{align}
\int_{B_{\rho_1}} |u|^{2^* + f(r)}\, \text{d}x \leq C( \| u \|_{2^*}^{F_+} + \| u \|_{2^*}^{F_-}) \leq C_1 (\| \nabla u \|_2^{F_+} + \| \nabla u \|_2^{F_-}) \leq C_2 \| \nabla u \|_2^{F_-},
\end{align} where ![]() $F_+ = \sup_{r \in [0,\rho_1]}( 2^* +f(r))$ and
$F_+ = \sup_{r \in [0,\rho_1]}( 2^* +f(r))$ and ![]() $F_-= \inf_{r\in [0,\rho_1]}(2^*+f(r))$. Let
$F_-= \inf_{r\in [0,\rho_1]}(2^*+f(r))$. Let ![]() $\rho_2 \gt 0$ be sufficiently close to 1 as in lemma 4.1. By (4.4) and (4.5), and choosing θ > 0 small enough such that
$\rho_2 \gt 0$ be sufficiently close to 1 as in lemma 4.1. By (4.4) and (4.5), and choosing θ > 0 small enough such that ![]() $\operatorname{Max}\{C_{\rho_1},C_{\rho_2}\} \| \nabla u \|_2 \lt 1$, we obtain
$\operatorname{Max}\{C_{\rho_1},C_{\rho_2}\} \| \nabla u \|_2 \lt 1$, we obtain
 \begin{align}
\int_{B\setminus B_{\rho_1}} |u|^{2^*+f(r)}\,\text{d}x \leq \int_{B} \left( \operatorname{Max}\{C_{\rho_1},C_{\rho_2}\} \| \nabla u \|_2\right)^{2^* + f(r)} \, \text{d}x \leq C_3 \|\nabla u \|_2^{F_-}
\end{align}
\begin{align}
\int_{B\setminus B_{\rho_1}} |u|^{2^*+f(r)}\,\text{d}x \leq \int_{B} \left( \operatorname{Max}\{C_{\rho_1},C_{\rho_2}\} \| \nabla u \|_2\right)^{2^* + f(r)} \, \text{d}x \leq C_3 \|\nabla u \|_2^{F_-}
\end{align} where  $C_3 =|B| \left( \operatorname{Max}\{C_{\rho_1},C_{\rho_2}\}\right)^{F_-} $. Then, by (4.6) and (4.7), we get
$C_3 =|B| \left( \operatorname{Max}\{C_{\rho_1},C_{\rho_2}\}\right)^{F_-} $. Then, by (4.6) and (4.7), we get
 \begin{align}
\int_B |u|^{2^* + f(r)}\, \text{d}x \leq C \| \nabla u \|_2^{F_-},
\end{align}
\begin{align}
\int_B |u|^{2^* + f(r)}\, \text{d}x \leq C \| \nabla u \|_2^{F_-},
\end{align} where ![]() $C= \operatorname{Max}\{C_2,C_3\}$. Therefore, we have
$C= \operatorname{Max}\{C_2,C_3\}$. Therefore, we have
 \begin{align*}
J(u) & = \frac{1}{2}\|\nabla u \|_2^2 - \frac{\lambda}{q}\|u\|_q^q - \int_B \frac{|u|^{2^*+f(r)}}{2^*+f(r)}\mathrm{d}x\\
& \geq \frac{1}{2}\|\nabla u \|_2^2 - \frac{\lambda}{q}\|u\|_q^q - C \| \nabla u \|_2^{F_-}.
\end{align*}
\begin{align*}
J(u) & = \frac{1}{2}\|\nabla u \|_2^2 - \frac{\lambda}{q}\|u\|_q^q - \int_B \frac{|u|^{2^*+f(r)}}{2^*+f(r)}\mathrm{d}x\\
& \geq \frac{1}{2}\|\nabla u \|_2^2 - \frac{\lambda}{q}\|u\|_q^q - C \| \nabla u \|_2^{F_-}.
\end{align*} When q = 2, we consider ![]() $\lambda \in [0,\lambda_1)$ and then the expression
$\lambda \in [0,\lambda_1)$ and then the expression ![]() $ \sqrt{\Vert \nabla u \Vert^2 - \lambda \Vert u \Vert^2}$ define a norm in
$ \sqrt{\Vert \nabla u \Vert^2 - \lambda \Vert u \Vert^2}$ define a norm in ![]() $H_{0}^1(B)$ equivalent to usual norm. Since
$H_{0}^1(B)$ equivalent to usual norm. Since ![]() $2^* \gt q \geq 2$ and
$2^* \gt q \geq 2$ and ![]() $F_- \gt 2$ due to the above inequality and by Sobolev inequality follows that for
$F_- \gt 2$ due to the above inequality and by Sobolev inequality follows that for ![]() $\|\nabla u \|_2 = \theta$ with θ sufficiently small, that there exists ρ > 0 such that
$\|\nabla u \|_2 = \theta$ with θ sufficiently small, that there exists ρ > 0 such that ![]() $J(u) \geq \rho \gt 0$.
$J(u) \geq \rho \gt 0$.
Lemma 4.3. Exist  $u \in H_{0, \mathrm{rad}}^1(B)$ such that
$u \in H_{0, \mathrm{rad}}^1(B)$ such that ![]() $\Vert \nabla u\Vert_2 \gt \theta $ and
$\Vert \nabla u\Vert_2 \gt \theta $ and ![]() $J(u) \lt 0$.
$J(u) \lt 0$.
Proof. Let  $u \in H_{0, \mathrm{rad}}^1(B) \setminus \{0 \}$ such that u > 0 in B. We have for t > 1 that
$u \in H_{0, \mathrm{rad}}^1(B) \setminus \{0 \}$ such that u > 0 in B. We have for t > 1 that
 \begin{align*}
J(tu) &= \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \int_{B} \dfrac{t^{2^* + f(r) }\vert u \vert^{2^* + f(r)}}{2^* + r^\alpha}\, \text{d} x \\
& \leq \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \frac{t^{F_-}}{{2^* + F_+}}\int_{B}\vert u \vert^{2^* + f(r)}\, \text{d} x.
\end{align*}
\begin{align*}
J(tu) &= \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \int_{B} \dfrac{t^{2^* + f(r) }\vert u \vert^{2^* + f(r)}}{2^* + r^\alpha}\, \text{d} x \\
& \leq \frac{t^2}{2} \Vert \nabla u \Vert^2_2 - \frac{\lambda t^q}{q}\Vert u \Vert^q_q - \frac{t^{F_-}}{{2^* + F_+}}\int_{B}\vert u \vert^{2^* + f(r)}\, \text{d} x.
\end{align*} Therefore, since ![]() $F_- \gt 2$ and
$F_- \gt 2$ and ![]() $q\in [2,2^*)$, we get
$q\in [2,2^*)$, we get
 \begin{align*}
\lim_{t \to + \infty} J(tu) = - \infty,
\end{align*}
\begin{align*}
\lim_{t \to + \infty} J(tu) = - \infty,
\end{align*}which proves the lemma.
Now we will show that the functional J satisfies the (PS) condition.
Lemma 4.4. Palais–Smale condition
Let ![]() $q \in [2, 2^*)$,
$q \in [2, 2^*)$, ![]() $\lambda \geq 0$, and
$\lambda \geq 0$, and ![]() $f\colon [0,1) \rightarrow \mathbb{R}$ a continuous function satisfying condition (f). Then the functional J given in (4.1) satisfies the Palais–Smale condition.
$f\colon [0,1) \rightarrow \mathbb{R}$ a continuous function satisfying condition (f). Then the functional J given in (4.1) satisfies the Palais–Smale condition.
Proof. Let  $\{u_n\} \subset H^1_{0,\text{rad}}(B)$ be a Palais–Smale sequence. So, we get
$\{u_n\} \subset H^1_{0,\text{rad}}(B)$ be a Palais–Smale sequence. So, we get
Since ![]() $2^* + f(r) \gt 1$ for
$2^* + f(r) \gt 1$ for ![]() $r \in [0,1)$ by standard calculations we know that the sequence
$r \in [0,1)$ by standard calculations we know that the sequence ![]() $\{u_n\}$ is bounded in
$\{u_n\}$ is bounded in  $H^1_{0, \text{rad}}(B)$, So, up to a subsequence, there exists
$H^1_{0, \text{rad}}(B)$, So, up to a subsequence, there exists  $u \in H_{0,\text{rad}}^1(B)$ such that
$u \in H_{0,\text{rad}}^1(B)$ such that
 \begin{equation}
\begin{aligned}
& u_n \rightharpoonup u \,\, \text{in} \,\, H_{0,\text{rad}}^1(B), \\
& u_n \rightarrow u \,\, \text{in} \,\, L^s(B) \,\, \forall \,\, s \in [1,2^*).
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& u_n \rightharpoonup u \,\, \text{in} \,\, H_{0,\text{rad}}^1(B), \\
& u_n \rightarrow u \,\, \text{in} \,\, L^s(B) \,\, \forall \,\, s \in [1,2^*).
\end{aligned}
\end{equation} From ![]() $J'(u_n) \rightarrow 0$, we can choose
$J'(u_n) \rightarrow 0$, we can choose ![]() $\varphi = u_n -u$ as the test function and obtain the following inequality:
$\varphi = u_n -u$ as the test function and obtain the following inequality:
 \begin{equation}
\begin{aligned}
\bigg|\int_B \nabla u_n \nabla (u_n-u) \, \text{d}x - &\lambda \int_B (u_n^+)^{q-1}(u_n-u)\,\text{d}x - \int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x \bigg|\\
& \leq \varepsilon_n \Vert \nabla(u_n-u)\Vert_2 \leq C \varepsilon_n,
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\bigg|\int_B \nabla u_n \nabla (u_n-u) \, \text{d}x - &\lambda \int_B (u_n^+)^{q-1}(u_n-u)\,\text{d}x - \int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x \bigg|\\
& \leq \varepsilon_n \Vert \nabla(u_n-u)\Vert_2 \leq C \varepsilon_n,
\end{aligned}
\end{equation} where ![]() $\varepsilon_n \rightarrow 0$. As
$\varepsilon_n \rightarrow 0$. As ![]() $q \in [2,2^*)$, by Hölder inequality and (4.10), we obtain
$q \in [2,2^*)$, by Hölder inequality and (4.10), we obtain
 \begin{align*}
\int_B (u_n^+)^{q-1}(u_n-u)\,\text{d}x & \leq \left(\int_B \vert (u_n^+)^q\,\text{d}x\right)^{(q-1)/q}\left( \int_B \vert u_n - u \vert^q\, \text{d}x\right)^{1/q} \\
& \leq C \Vert u_n -u \Vert_{q} \rightarrow 0.
\end{align*}
\begin{align*}
\int_B (u_n^+)^{q-1}(u_n-u)\,\text{d}x & \leq \left(\int_B \vert (u_n^+)^q\,\text{d}x\right)^{(q-1)/q}\left( \int_B \vert u_n - u \vert^q\, \text{d}x\right)^{1/q} \\
& \leq C \Vert u_n -u \Vert_{q} \rightarrow 0.
\end{align*}Therefore, by (4.11), the lemma will be proved if we check that
 \begin{align}
\int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x \rightarrow 0.
\end{align}
\begin{align}
\int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x \rightarrow 0.
\end{align}Indeed,
 \begin{align*}
\frac {1}{\omega_{N-1}} \int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x & = \int_0^{\rho_1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r \\
&\quad + \int_{\rho_1}^{\rho_2}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}x \\
& \quad + \int_{\rho_2}^{1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r,
\end{align*}
\begin{align*}
\frac {1}{\omega_{N-1}} \int_B(u_n^+)^{2^*-1+f(r)}(u_n-u)\, \text{d}x & = \int_0^{\rho_1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r \\
&\quad + \int_{\rho_1}^{\rho_2}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}x \\
& \quad + \int_{\rho_2}^{1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r,
\end{align*} where ρ 1 and ρ 2 will be chosen later. We will estimate each integral above separately. First, for r > 0 small enough, we know that ![]() $2-2^* \lt f(r) \lt 0$ because f is continuous at r = 0 and
$2-2^* \lt f(r) \lt 0$ because f is continuous at r = 0 and ![]() $f(0) \lt 0$. Therefore, for r small enough, we have that
$f(0) \lt 0$. Therefore, for r small enough, we have that ![]() $2 \lt 2^*+f(r) \lt 2^*$. So, we can choose
$2 \lt 2^*+f(r) \lt 2^*$. So, we can choose ![]() $\rho_1 \gt 0$ small enough such that
$\rho_1 \gt 0$ small enough such that ![]() $2 \lt 2^*+f_+(\rho^1) \lt 2^*$, where
$2 \lt 2^*+f_+(\rho^1) \lt 2^*$, where  $f_+(\rho^1) = \displaystyle\sup_{r \in [0,\rho_1]}f(r)$. Then, we get
$f_+(\rho^1) = \displaystyle\sup_{r \in [0,\rho_1]}f(r)$. Then, we get
 \begin{align*}
& \omega_{N-1}\int_0^{\rho_1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r \\
& \quad \leq 2 \Vert (u_n^+)^{2^*-1+f(r)}\Vert_{\frac{2^*+f(r)}{2^*-1+f(r)}}\Vert u_n-u \Vert_{2^*+f(r)}\\
& \quad \leq C \Vert u_n-u \Vert_{2^*+f_+(\rho^1)} \rightarrow 0.
\end{align*}
\begin{align*}
& \omega_{N-1}\int_0^{\rho_1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r \\
& \quad \leq 2 \Vert (u_n^+)^{2^*-1+f(r)}\Vert_{\frac{2^*+f(r)}{2^*-1+f(r)}}\Vert u_n-u \Vert_{2^*+f(r)}\\
& \quad \leq C \Vert u_n-u \Vert_{2^*+f_+(\rho^1)} \rightarrow 0.
\end{align*} To estimate the second integral, we need to choose ![]() $\rho_2 = 1-\rho^{N-2}_1$ sufficiently close to 1. So, by inequality (2.1) of the lemma 2.1, we get
$\rho_2 = 1-\rho^{N-2}_1$ sufficiently close to 1. So, by inequality (2.1) of the lemma 2.1, we get
 \begin{align*}
\int_{\rho_1}^{\rho_2}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}x &\leq \left( \frac{1}{\rho_1^{(N-2)/2}}\right)^{2^*-1+f_+(\rho)}\int_{\rho_1}^{\rho_2}(u_n-u)r^{N-1}\,\text{d}r \\
&\leq C \Vert u_n-u \Vert_{L^1(B)} \rightarrow 0,
\end{align*}
\begin{align*}
\int_{\rho_1}^{\rho_2}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}x &\leq \left( \frac{1}{\rho_1^{(N-2)/2}}\right)^{2^*-1+f_+(\rho)}\int_{\rho_1}^{\rho_2}(u_n-u)r^{N-1}\,\text{d}r \\
&\leq C \Vert u_n-u \Vert_{L^1(B)} \rightarrow 0,
\end{align*} where  $f_{+}(\rho)= \displaystyle\sup_{r\in [\rho_1,\rho_2]}f(r)$.
$f_{+}(\rho)= \displaystyle\sup_{r\in [\rho_1,\rho_2]}f(r)$.
To estimate the last integral. Note that for ![]() $\rho_2 = 1-\rho^{N-2}_1$ and
$\rho_2 = 1-\rho^{N-2}_1$ and ![]() $\rho_2 \lt r \lt 1$, we have
$\rho_2 \lt r \lt 1$, we have
 \begin{align*}
\frac{(1-r)^{1/2}}{\rho_1^{(N-2)/2}} \leq 1.
\end{align*}
\begin{align*}
\frac{(1-r)^{1/2}}{\rho_1^{(N-2)/2}} \leq 1.
\end{align*}By inequality (2.2) from lemma 2.1, we get
 \begin{align*}
\int_{\rho_2}^{1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r &\leq \int_{\rho_1}^1\left( \frac{(1-r)^{1/2}}{\rho_1^{(N-2)/2}}\right)^{2^*-1+f(r)}(u_n-u)r^{N-1}\,\text{d}r\\
&\leq \Vert u_n-u \Vert_{L^1(B)} \rightarrow 0.
\end{align*}
\begin{align*}
\int_{\rho_2}^{1}(u_n^+)^{2^*-1+f(r)}(u_n-u)r^{N-1}\, \text{d}r &\leq \int_{\rho_1}^1\left( \frac{(1-r)^{1/2}}{\rho_1^{(N-2)/2}}\right)^{2^*-1+f(r)}(u_n-u)r^{N-1}\,\text{d}r\\
&\leq \Vert u_n-u \Vert_{L^1(B)} \rightarrow 0.
\end{align*}Therefore, (4.12) is verified and the proof of the lemma is concluded.
From lemmas 4.2, 4.3, and 4.4, we conclude that the functional J has a non-trivial critical point u. Using ![]() $\varphi = u_-$ as a test function in equation
$\varphi = u_-$ as a test function in equation ![]() $\langle J'(u),\varphi \rangle =0$, we obtain that
$\langle J'(u),\varphi \rangle =0$, we obtain that ![]() $u = u_+\geq 0$ and by the strong maximum principle (see [Reference Evans6, theorem 4, pp. 333]) it follows that u is positive, thus finishing the proof of the theorem 1.3.
$u = u_+\geq 0$ and by the strong maximum principle (see [Reference Evans6, theorem 4, pp. 333]) it follows that u is positive, thus finishing the proof of the theorem 1.3.
Acknowledgements
The authors would like to express their sincere gratitude to the anonymous referee for their valuable comments and suggestions, which have significantly improved the quality of this article.
Funding
Luiz Faria was partially financed by FAPEMIG APQ-02146-23, APQ 04528/22 and CNPq. Jeferson Camilo was partially financed by FAPEMIG BPD-00347-22 and CNPq. Pedro Ubilla was partially financed by FONDECYT 1220675.