Published online by Cambridge University Press: 09 November 2018
We consider compact Kählerian manifolds 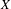 $X$ of even dimension 4 or more, endowed with a log-symplectic holomorphic Poisson structure
$X$ of even dimension 4 or more, endowed with a log-symplectic holomorphic Poisson structure 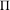 $\unicode[STIX]{x1D6F1}$ which is sufficiently general, in a precise linear sense, with respect to its (normal-crossing) degeneracy divisor
$\unicode[STIX]{x1D6F1}$ which is sufficiently general, in a precise linear sense, with respect to its (normal-crossing) degeneracy divisor 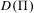 $D(\unicode[STIX]{x1D6F1})$. We prove that
$D(\unicode[STIX]{x1D6F1})$. We prove that  $(X,\unicode[STIX]{x1D6F1})$ has unobstructed deformations, that the tangent space to its deformation space can be identified in terms of the mixed Hodge structure on
$(X,\unicode[STIX]{x1D6F1})$ has unobstructed deformations, that the tangent space to its deformation space can be identified in terms of the mixed Hodge structure on 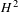 $H^{2}$ of the open symplectic manifold
$H^{2}$ of the open symplectic manifold 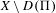 $X\setminus D(\unicode[STIX]{x1D6F1})$, and in fact coincides with this
$X\setminus D(\unicode[STIX]{x1D6F1})$, and in fact coincides with this 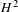 $H^{2}$ provided the Hodge number
$H^{2}$ provided the Hodge number 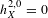 $h_{X}^{2,0}=0$, and finally that the degeneracy locus
$h_{X}^{2,0}=0$, and finally that the degeneracy locus 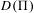 $D(\unicode[STIX]{x1D6F1})$ deforms locally trivially under deformations of
$D(\unicode[STIX]{x1D6F1})$ deforms locally trivially under deformations of 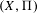 $(X,\unicode[STIX]{x1D6F1})$.
$(X,\unicode[STIX]{x1D6F1})$.
Please note a has been issued for this article.