1. Introduction
Short-pulse lasers offer new experimental approaches to create and study fusion plasmas. In contrast to long-pulse lasers which have been a primary tool in inertial-confinement fusion (ICF), short-pulse lasers have pulse durations < 1 ps and use small focal spots to obtain peak intensities upto 1023 W/cm2 in a single pulse. Short-pulse lasers deliver their energy to the plasma in a time much shorter than the typical expansion timescale, and both electrons and ions achieve much higher momenta. These plasma conditions are far from the quasi-thermal equilibrium of ICF, where burn has recently been achieved [Reference Zylstra, Hurricane and Callahan1], and the question is open whether or not the dynamics admit a pathway to net energy gain [Reference Mehlhorn, Labun, Hegelich, Margarone and Gu2]. Short-pulse lasers have successfully driven high-yield beam-fusion experiments [Reference Labaune, Baccou and Depierreux3, Reference Baccou, Depierreux and Yahia4], which can in turn be translated into novel high-flux, ultrashort-pulse ions [Reference Giuffrida, Belloni and Margarone5–Reference Bonvalet, Nicolaï and Raffestin7], and neutron sources [Reference Norreys, Fews and Beg8–Reference Jiao, Shaw and Wang11].
Short-pulse lasers can drive fusion in two ways: direct irradiation of a target containing the fusion reactants or laser-ion acceleration creating an ion beam that is dumped into a catcher/target. To our knowledge, no experiment can claim to have optimized the fusion yield, and the efficiencies of these two methods for different candidate fusion reactions remain a topic of research. Naively, one expects direct irradiation to convert laser energy more efficiently into fusion yield, in part because fusion can occur both in the neighbourhood of the focus where all ion species are heated and in the colder bulk of the target by ions accelerated out of the focal region. Anecdotally, recent experiments support this hypothesis [Reference Mehlhorn, Labun, Hegelich, Margarone and Gu2].
Proper optimization will require greatly improved understanding and control of experimental outcomes compared to current capabilities. However, the same laser properties, namely, ultrashort-pulse and typically small
![]() focal volume make the plasma difficult to diagnose. Most interpretation is based on inference from the measured particle yields and spectra, sometimes supported by Monte Carlo or numerically-expensive kinetic laser-plasma simulations. Improving experimental diagnostics of laser-driven nuclear reactions has, thus, become a significant topic of discussion [12]. Our goal in this work is to identify new diagnostics providing information on the plasma conditions and nuclear reaction dynamics.
focal volume make the plasma difficult to diagnose. Most interpretation is based on inference from the measured particle yields and spectra, sometimes supported by Monte Carlo or numerically-expensive kinetic laser-plasma simulations. Improving experimental diagnostics of laser-driven nuclear reactions has, thus, become a significant topic of discussion [12]. Our goal in this work is to identify new diagnostics providing information on the plasma conditions and nuclear reaction dynamics.
Out of the reactions studied with short-pulse lasers, we focus on the proton-boron-11 fusion reaction
![]() , which is of particular interest because it releases ≃8 MeV into kinetic energy of the 3 α particles and no neutrons. The α particles themselves provide the most direct measure of the fusion yield, but because they deposit their kinetic energy into the surrounding medium very efficiently, only a small fraction of those produced escape the target. This problem is especially acute in direct-irradiation experiments [Reference Giuffrida, Belloni and Margarone5, Reference Belyaev, Vinogradov and Kurilov13–Reference Margarone, Bonvalet and Giuffrida18], where the mean kinetic energy and density of the medium vary by orders of magnitude in different regions of the target, precluding a systematic analytic correction for α stopping.
, which is of particular interest because it releases ≃8 MeV into kinetic energy of the 3 α particles and no neutrons. The α particles themselves provide the most direct measure of the fusion yield, but because they deposit their kinetic energy into the surrounding medium very efficiently, only a small fraction of those produced escape the target. This problem is especially acute in direct-irradiation experiments [Reference Giuffrida, Belloni and Margarone5, Reference Belyaev, Vinogradov and Kurilov13–Reference Margarone, Bonvalet and Giuffrida18], where the mean kinetic energy and density of the medium vary by orders of magnitude in different regions of the target, precluding a systematic analytic correction for α stopping.
Since direct diagnostics of plasma conditions, such as probe laser pulses or atomic spectroscopy, remains an enormous technical challenge, we investigate other nuclear reactions for products whose yield or spectrum can be measured more reliably. Photons and neutrons are the best candidates, but not all reactions will yield enough photons or neutrons that can be identified as coming from a specific reaction. We introduce the yield ratio as a phenomenological tool to relate an easily-measured yield to the yield of interest. Yield ratios have an established history in diagnosing the ICF plasma, where they can determine several of the important
![]() parameters [Reference Frenje19]. We have previously used the ratio between α and 11C yields to determine the
parameters [Reference Frenje19]. We have previously used the ratio between α and 11C yields to determine the
![]() reaction yield more accurately in beam-target experiments [Reference McCary, Labun, Labun and Hegelich20], and here, we demonstrate its utility in direct-irradiation experiments as well. The yield ratio eliminates normalization unknowns such as the local density of reactants, effective reaction volume, and time and takes as input a few model parameters, such as the mean ion kinetic energy, that can be determined from particle diagnostics. We conclude by identifying the two best candidate reactions for proxy measurements of the
reaction yield more accurately in beam-target experiments [Reference McCary, Labun, Labun and Hegelich20], and here, we demonstrate its utility in direct-irradiation experiments as well. The yield ratio eliminates normalization unknowns such as the local density of reactants, effective reaction volume, and time and takes as input a few model parameters, such as the mean ion kinetic energy, that can be determined from particle diagnostics. We conclude by identifying the two best candidate reactions for proxy measurements of the
![]() yield in direct-irradiation experiments and confirm 11C as the best proxy in beam-target experiments.
yield in direct-irradiation experiments and confirm 11C as the best proxy in beam-target experiments.
2. Accessible Reactions
The goal is to predict the outcomes and analyse the data from experiments on the aneutronic proton-boron fusion reaction
![]() . The
. The
![]() cross-section reaches ∼ 1 b around 650 keV center-of-mass (CM) energy, significantly higher than DD or DT fusion reactions because of the higher charge of boron. In fact, most other proton-boron reactions require even higher CM energy before the cross-section approaches 100 mb, and the high cross-section of
cross-section reaches ∼ 1 b around 650 keV center-of-mass (CM) energy, significantly higher than DD or DT fusion reactions because of the higher charge of boron. In fact, most other proton-boron reactions require even higher CM energy before the cross-section approaches 100 mb, and the high cross-section of
![]() in the E < 1 MeV range is due to two identified resonances, related to above-threshold excited states of 12C [Reference Ajzenberg-Selove21]. Recent work has resolved apparent normalization discrepancies in the measured cross-section [Reference Sikora and Weller22], resulting in reevaluation of the process as a candidate for fusion energy.
in the E < 1 MeV range is due to two identified resonances, related to above-threshold excited states of 12C [Reference Ajzenberg-Selove21]. Recent work has resolved apparent normalization discrepancies in the measured cross-section [Reference Sikora and Weller22], resulting in reevaluation of the process as a candidate for fusion energy.
With its cross-section reaching ∼ 1 b already at 650 keV CM energy, lower than the thresholds of many other proton-initiated reactions on boron,
![]() is expected to have the highest yield in the laser-driven beam-fusion experiments. With higher laser intensities
is expected to have the highest yield in the laser-driven beam-fusion experiments. With higher laser intensities
![]() W/cm 2 though, the proton beam in the experiment can provide energies upto ∼ 50 MeV [Reference McCary, Labun, Labun and Hegelich20], allowing many additional reactions that are naturally grouped as “primary” or “secondary.” Primary reactions are initiated by the protons scattering on 11B, 10B, or 14N as present in typical boron or boron-nitride solid targets. These are listed in Table 1 with peak cross-section, the corresponding CM energy at which the peak cross-section is found, and the range of CM energy over which data is available. Secondary reactions are rescattering of the α particles on the boron and nitrogen nuclei most prevalent in the environment. These are listed in Table 2, similarly to the primary reactions. The databases contain additional processes, such as
W/cm 2 though, the proton beam in the experiment can provide energies upto ∼ 50 MeV [Reference McCary, Labun, Labun and Hegelich20], allowing many additional reactions that are naturally grouped as “primary” or “secondary.” Primary reactions are initiated by the protons scattering on 11B, 10B, or 14N as present in typical boron or boron-nitride solid targets. These are listed in Table 1 with peak cross-section, the corresponding CM energy at which the peak cross-section is found, and the range of CM energy over which data is available. Secondary reactions are rescattering of the α particles on the boron and nitrogen nuclei most prevalent in the environment. These are listed in Table 2, similarly to the primary reactions. The databases contain additional processes, such as
![]() and
and
![]() , but the data are too sparse, and the larger number of fragments generally makes the Q values for such reactions negative and large in magnitude. Consequently, their cross-sections should have somewhat higher thresholds suppressing their contributions to the yields.
, but the data are too sparse, and the larger number of fragments generally makes the Q values for such reactions negative and large in magnitude. Consequently, their cross-sections should have somewhat higher thresholds suppressing their contributions to the yields.
Table 1: Primary reactions in the range of proton energies. The range of CoM energy for which data are available as well as the maximum cross-section and its CoM energy are given for numerical comparison. All data retried from sources in the EXFOR and JANIS databases, with the exception of
 for which we use the concordant normalization of Reference [Reference Sikora and Weller22].
for which we use the concordant normalization of Reference [Reference Sikora and Weller22].

* Q values marked with an * are computed from the mass difference of the initial and final states. Others are from the literature. a A recent measurement [Reference Alves, Jensen, Jensen, Nickles and Holm23] finds
![]() larger cross-section than several previous measurements. To be conservative, we quote the older but more consistent results here. b There appear two distinct groups of cross-sections measurements: two experiments find the cross-section roughly
larger cross-section than several previous measurements. To be conservative, we quote the older but more consistent results here. b There appear two distinct groups of cross-sections measurements: two experiments find the cross-section roughly
![]() larger than the majority of others.
larger than the majority of others.
Table 2: Secondary reactions in the range of α particle energies. The range of CoM energy for which data are available as well as the maximum cross-section and its CoM energy are given for numerical comparison.

* Q values marked with an * are computed from the mass difference of the initial and final states. Others are from the literature.
The corresponding cross-sections are plotted in Figure 1. The global sets from EXFOR [Reference Zerkin and Pritychenko24] frequently include inconsistent measurements, as, for example, the recently resolved normalization in the
![]() cross-section [Reference Sikora and Weller22]. Cross-section data are one significant source of uncertainty in our yield predictions. We have plotted the global data sets for each cross-section without distinguishing their sources and in our calculations, and we will use fits to these global data with a few exceptions described in the captions of Tables 1 and 2. We do not attempt to model the cross-sections outside the range of available data. Instead, for numerical integrations, we implement best fit curves that are forced rapidly to zero outside the range of experimental data. This choice almost certainly underestimates the yield for several processes. Notably, the cross-sections of
cross-section [Reference Sikora and Weller22]. Cross-section data are one significant source of uncertainty in our yield predictions. We have plotted the global data sets for each cross-section without distinguishing their sources and in our calculations, and we will use fits to these global data with a few exceptions described in the captions of Tables 1 and 2. We do not attempt to model the cross-sections outside the range of available data. Instead, for numerical integrations, we implement best fit curves that are forced rapidly to zero outside the range of experimental data. This choice almost certainly underestimates the yield for several processes. Notably, the cross-sections of
![]() ,
,
![]() , and all secondary reactions for which data are available and seem likely to continue to increase with CM energy. However, the lack of information precludes quantifying the uncertainty in any attempted modeling of the cross-section.
, and all secondary reactions for which data are available and seem likely to continue to increase with CM energy. However, the lack of information precludes quantifying the uncertainty in any attempted modeling of the cross-section.
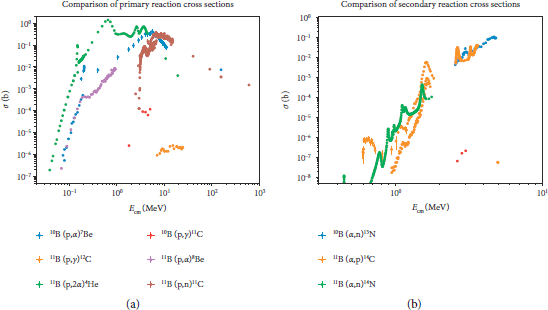
Figure 1: Cross-sections of primary reactions (a) and secondary reactions (b) Data from EXFOR with all sources combined. The scales are logarithmic, and the extent of the energy range is different on each.
Among these primary and secondary reactions, we identify promising candidates to be diagnostics. As mentioned above, the difficulty in verifying the
![]() yield is greater in direct-irradiation type of experiments. For these, we need a reaction occurring in parallel with a product that escapes the plasma unperturbed, such as neutrons and photons.
yield is greater in direct-irradiation type of experiments. For these, we need a reaction occurring in parallel with a product that escapes the plasma unperturbed, such as neutrons and photons.
To strengthen the identification of the originating reaction, a neutron or photon produced with definite energy is preferable. Exothermic reactions (Q>0 are, therefore, better candidates, since we can expect the neutron or photon spectrum to peak at nonzero kinetic energy. Of the primary reactions Table 1, only two satisfy these conditions,
![]() and
and
![]() , both emitting photons. The cross-section data for both reactions are very limited. For the
, both emitting photons. The cross-section data for both reactions are very limited. For the
![]() reaction especially, the trend in the available data suggests our calculations here may significantly underestimate the photon yield. Of the secondary reactions, three satisfy these conditions,
reaction especially, the trend in the available data suggests our calculations here may significantly underestimate the photon yield. Of the secondary reactions, three satisfy these conditions,
![]() ,
,
![]() , and
, and
![]() .
.
As several of the candidate reactions have limited cross-section data available and even more limited data on the spectrum of the outgoing neutron or photon, it would be a reasonable first step to verify yields with beam-target type of experiments. Since the target remains intact, we can measure a wider variety of reaction products, in particular unstable nuclides with half-lives much greater than the experiment duration. Several of the reactions selected by the previous approach also yield unstable nuclei, specifically 11C, 13N, and 18F with half-lives on the order of 103 s. Other unstable nuclides produced are listed in Table 3. The significantly differing half-lives make identification by reactivity straightforward with a Geiger counter placed near the target, though 14C probably has too long a half-life and 10C too has short a half-life for reliable identification.
![]() is undetectable by this means but arises from a reaction without particular interest in this study.
is undetectable by this means but arises from a reaction without particular interest in this study.
Now, synthesizing and narrowing the list of promising reactions, two of the photon- and neutron-producing reactions stand out in utility. First,
![]() is promising to directly correlate with the reaction
is promising to directly correlate with the reaction
![]() , because it has the same initial state and produces a photon with energy significantly above most other products. The
, because it has the same initial state and produces a photon with energy significantly above most other products. The
![]() larger cross-section for
larger cross-section for
![]() makes it a practical proxy in the near term, though it has a different initial state, which introduces additional uncertainty. Ultimately, the yields of these two reactions will determine which is more useful in the experiment.
makes it a practical proxy in the near term, though it has a different initial state, which introduces additional uncertainty. Ultimately, the yields of these two reactions will determine which is more useful in the experiment.
The second
![]() could help verify the α yield. Since this reaction is the isospin partner of
could help verify the α yield. Since this reaction is the isospin partner of
![]() , the cross-sections are very similar in magnitude and energy dependence, and its measurement would verify the role of proton-recycling from secondary reactions and propose as an important mechanism in enhancing
, the cross-sections are very similar in magnitude and energy dependence, and its measurement would verify the role of proton-recycling from secondary reactions and propose as an important mechanism in enhancing
![]() yields in some experiments [Reference Labaune, Baccou, Yahia, Neuville and Rafelski25]. Moreover, 13N is unstable, and its yield can be measured independently in beam-target experiments. A small drawback to this reaction is that the cross-section decreases sharply below CM energy of 3 MeV. The majority of αs produced by
yields in some experiments [Reference Labaune, Baccou, Yahia, Neuville and Rafelski25]. Moreover, 13N is unstable, and its yield can be measured independently in beam-target experiments. A small drawback to this reaction is that the cross-section decreases sharply below CM energy of 3 MeV. The majority of αs produced by
![]() should have energy above this threshold, but αs also lose energy quickly in a cold medium, and the yield is expected to be small.
should have energy above this threshold, but αs also lose energy quickly in a cold medium, and the yield is expected to be small.
Of the remaining two, (a) there is unfortunately no cross-section data for
![]() , though it should produce a peak in the photon spectrum, and (b) the neutron produced in
, though it should produce a peak in the photon spectrum, and (b) the neutron produced in
![]() is likely have very little kinetic energy, making detection difficult.
is likely have very little kinetic energy, making detection difficult.
Of the radioactive nuclides, 11C has already proven its utility in beam-target experiments providing a significantly higher-confidence estimate of the α yield than a direct measurement of the αs by CR-39 [Reference McCary, Labun, Labun and Hegelich20]. 18F has been detected [Reference McCary, Labun, Labun and Hegelich20, Reference Labaune, Baccou, Yahia, Neuville and Rafelski25] but the absence of a cross-section for its production limits the information gained. More surprisingly, 13N has not been detected, probably due to a combination of shorter half-life and low yield making it difficult to distinguish from the 11C signal. Since better data exist for the 13N production cross-section and it is generated almost entirely by α scattering, we consider it the most important candidate for future experiments as a means to help verify the α yield. 14O and 17F are of little interest in both production processes, Q<0 so the neutron released is not a potential diagnostic in direct-irradiation experiments.
3. Yield Equations
Having winnowed the set of interesting reactions based on general criteria for good diagnostics of the fusion dynamics, we now evaluate the yields of the various products.
The challenge in deriving analytic expressions for the yield expression is two-fold. First, the ion momentum distribution function generally varies from shot to shot due to variations in the laser. Therefore, the ion distribution should be measured on each shot as well as possible and used in predictions. We address modeling related to incomplete measurement in Section 4
Second, the ion momentum distribution is heterogeneous, with two or more distinguishable populations. Short-pulse, high-intensity lasers deposit energy into a region of 10–100 μm in radius from the focal spot, which we call the directly-irradiated (DI) volume. In this volume, electrons gain many MeV of energy, and ions are likely to have more isotropic momentum distributions. Fast electrons pushed through and out of this volume, largely in the laser beam direction, can create large magnitude electrostatic fields that accelerate ions out of the DI volume. The precise ion acceleration mechanism and shape of the resulting ion spectrum depend on the thickness of the target. To maximize fusion yields, we assume the target is thick, that is, greater than the stopping range of these high-energy ions, so that the probability of undergoing fusion is saturated. The fast ions are more likely to collide with at-rest ions much deeper in the bulk of the target, and the reaction kinematics are essentially those of beam fusion. We model the yield from each of these regions and ion populations separately, addressing reactions in the DI volume first and the beam-fusion reactions second.
The dichotomy between the DI volume and the beam-fusion region is artificial, and the plasma will certainly contain some transitional regions. Given the dynamics described so far, these transitional regions are likely to contain electrons of intermediate kinetic energy
![]() , both low energy ions and some beam ions and particle number densities similar to the initial state. In this region, ion stopping is reduced compared to the cold limit, and the fusion probability is similar to the beam-fusion limit. Thus, the contribution to the yield can be thought of as a correction to the beam-fusion yield since the length of such transitional regions is much less than the stopping range of the fast ions passing through.
, both low energy ions and some beam ions and particle number densities similar to the initial state. In this region, ion stopping is reduced compared to the cold limit, and the fusion probability is similar to the beam-fusion limit. Thus, the contribution to the yield can be thought of as a correction to the beam-fusion yield since the length of such transitional regions is much less than the stopping range of the fast ions passing through.
The starting point to derive the yield is a classical expression for the total number of particles of type A produced in a 2-body collision:
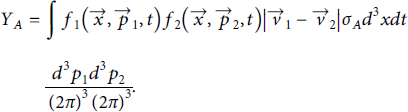
Here,
![]() is the distribution function describing the probability of finding particle i = 1, 2 with momentum
is the distribution function describing the probability of finding particle i = 1, 2 with momentum
![]() in the volume element
in the volume element
![]() at time t, σ is the cross-section, and
at time t, σ is the cross-section, and
![]() is the relative speed of the incident particles. We integrate over all initial particle momenta, all final states, and all space and time for the reaction to occur. For the reactions of interest here, sufficiently complete cross-sections differential in a solid angle are generally not available, and cross-sections for the process exhibit resonances of nuclei with different quantum numbers, suggesting that the angular dependence will have a strong energy dependence, which we will not attempt to model here. We can focus on the total yield as the most relevant observable for both applications and practically available measurements from recent experiments.
is the relative speed of the incident particles. We integrate over all initial particle momenta, all final states, and all space and time for the reaction to occur. For the reactions of interest here, sufficiently complete cross-sections differential in a solid angle are generally not available, and cross-sections for the process exhibit resonances of nuclei with different quantum numbers, suggesting that the angular dependence will have a strong energy dependence, which we will not attempt to model here. We can focus on the total yield as the most relevant observable for both applications and practically available measurements from recent experiments.
We consider two models for our yield calculations, corresponding to the direct-irradiation and beam-target experiments.
3.1. Direct Irradiation
The laser deposits a large amount of energy in the fusion target, and reactions occur within the 10 s of picosecond timescale that the ions are heated but before the target expands and its density drops. Although neither the electron nor the ion population can equilibrate in this short time, experimental ion spectra are frequently fit by the Maxwellian distribution,
![]() . The parameter β is an inverse energy scale that characterizes the mean kinetic energy per particle of the distribution
. The parameter β is an inverse energy scale that characterizes the mean kinetic energy per particle of the distribution
![]() . We stress that local thermal equilibrium is certainly not achieved, and we do not assume equilibrium distributions. The Maxwellian fit to experimental spectra is a phenomenological choice, enabling simple quantitative comparison between shots and facilities.
. We stress that local thermal equilibrium is certainly not achieved, and we do not assume equilibrium distributions. The Maxwellian fit to experimental spectra is a phenomenological choice, enabling simple quantitative comparison between shots and facilities.
Maxwellian ion distributions are a strong simplifying approximation: kinetic simulations of short-pulse laser-target interaction have found that the ion distributions can have significantly higher numbers of high-energy ions
![]() than expected from the Maxwellian distribution. To account for the excess of high-energy
than expected from the Maxwellian distribution. To account for the excess of high-energy
![]() ions, the single Maxwellian model can be improved by introducing a second Maxwellian distribution of smaller β. This second population often corresponds to the beam population that has significant directionality and is less likely to react with the larger β population, being accelerated out of the DI region by plasma fields on its boundary. Even so, the contribution is computed easily since the yield is linear in the distribution function, and the yield in the double Maxwellian case can be derived by summing four yields corresponding to the four combinations of the two ion species’ two β values. Therefore, for simplicity and clarity here, we use the single Maxwellian.
ions, the single Maxwellian model can be improved by introducing a second Maxwellian distribution of smaller β. This second population often corresponds to the beam population that has significant directionality and is less likely to react with the larger β population, being accelerated out of the DI region by plasma fields on its boundary. Even so, the contribution is computed easily since the yield is linear in the distribution function, and the yield in the double Maxwellian case can be derived by summing four yields corresponding to the four combinations of the two ion species’ two β values. Therefore, for simplicity and clarity here, we use the single Maxwellian.
Since the electrons have MeV-scale kinetic energy in the DI region, their stopping power is significantly reduced. While the high-intensity laser can drive large, short-lived, local increases in the electron density, the ion density varies from the initial value by a factor much less than 1, at least until the target expands significantly on the 10 s of picosecond timescale. Consequently, the proton and α stopping ranges (> 100μm) are certainly larger than the radius of the DI region (≲ 100μm), and we consider that the ion energy losses are negligible for the duration in the DI region.
Given these conditions, the yield of a given process is straightforwardly derived from equation (1). The reaction volume is a few times larger than the focal volume but is generally not known precisely. Reactions will continue as long as the plasma remains relatively dense upto several picoseconds, though this plasma “confinement time” as it is sometimes known is not well-determined either. We, therefore, consider the yield per unit volume per unit time for a
![]() reaction for nonrelativistic ions with Maxwellian distributions:
reaction for nonrelativistic ions with Maxwellian distributions:
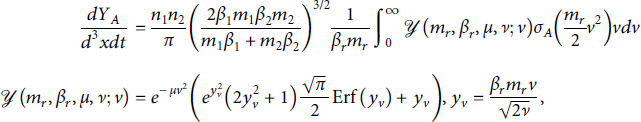
where the parameters
![]() for i = 1, 2 are the number densities, masses, and inverse mean kinetic energy of the two ion species. The remaining parameters are the reduced mass mr, difference of inverse mean kinetic energy, and combinations thereof:
for i = 1, 2 are the number densities, masses, and inverse mean kinetic energy of the two ion species. The remaining parameters are the reduced mass mr, difference of inverse mean kinetic energy, and combinations thereof:
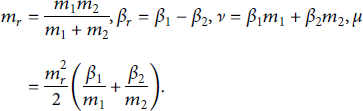
The result is even in βr as it must be since the choice of labels is arbitrary and the yield should always be positive. The integration variable corresponds to the magnitude of the relative velocity of the two ions. The integration will be performed numerically to use experimental data for the cross-section
![]() , which is a function of the CM energy. Erf (z) is the usual error function with the normalization defined by
, which is a function of the CM energy. Erf (z) is the usual error function with the normalization defined by
The limit of equal mean kinetic energies simplifies the result considerably to
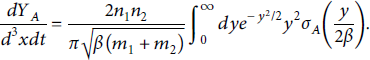
Considering our interest in particular reactions as in situ diagnostics of the
![]() reaction, we introduce ratios of yields to eliminate experimental unknowns. For reactions with the same initial state, e.g., p-11B scattering, all the prefactors in equation (2) cancel. For example, to use the
reaction, we introduce ratios of yields to eliminate experimental unknowns. For reactions with the same initial state, e.g., p-11B scattering, all the prefactors in equation (2) cancel. For example, to use the
![]() reaction as a diagnostic on
reaction as a diagnostic on
![]() , we might consider the ratio
, we might consider the ratio
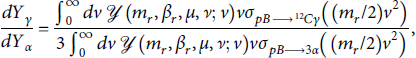
in which all the mass- and β-dependent parameters are identical in the numerator and denominator. Only the cross-sections differ. For 2⟶2 reactions such as considered here, the spectra of produced neutrons and photons have been computed semianalytically showing that their widths and small shifts in the peak depend on the momentum distribution of scattering ions [Reference Appelbe and Chittenden26]. This allows the (approximate) β parameters of the ions to be retrieved by fitting spectra of the measured neutron or photon. Since the reactions have exactly the same initial state, potentially large scaling factors such as volume and time must be the same. Thus, this yield ratio depends only on the mean kinetic energies of the two ion species. Considered as a function of these two energy scales, the ratio manifests the difference in the energy dependence of the cross-sections, though less so than the beam-target experiments described below. In equation (6), the factor 3 has been included in the numerator to count the total number of αs produced for each
![]() reaction. With this yield ratio, the number of
reaction. With this yield ratio, the number of
![]() reactions is recovered by multiplying by the measured yield of photons identified as arising from this reaction.
reactions is recovered by multiplying by the measured yield of photons identified as arising from this reaction.
Another reaction of interest for diagnostics is
![]() , which differs from
, which differs from
![]() in the isotope of boron in the initial state. As a consequence, some prefactors remain in the yield ratio:
in the isotope of boron in the initial state. As a consequence, some prefactors remain in the yield ratio:
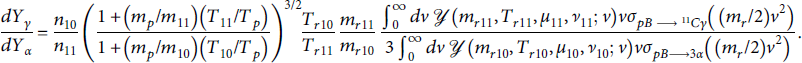
The subscripts for boron parameters have been shortened to the isotope number for clarity. The measured constants in the prefactor, such as masses, are no trouble, but for this ratio to be useful we must argue that the ratio of densities remains nearly constant during the relevant period of plasma evolution. Since the charge is the same and the masses differ only by 10%, we suppose significant separation of isotopes from the initially uniform mixture can only develop slowly, on the same time scale (or longer) that the plasma expands and diffuses into free space. Note that dynamically, we expect the mean kinetic energy of the boron ions and protons to be similar, making the prefactor in parentheses close to 1. The remaining ratio of reduced kinetic energies is expected to be near unity for the same reason.
Another useful yield ratio could be
![]() relative to
relative to
![]() . The ratio would cancel dynamical unknowns such as the density of αs. The other proton-producing secondary reaction
. The ratio would cancel dynamical unknowns such as the density of αs. The other proton-producing secondary reaction
![]() could be added to the ratio to completely determine the secondary proton production, though the same remarks as above would apply to the prefactor. A measurement of the neutrons produced from
could be added to the ratio to completely determine the secondary proton production, though the same remarks as above would apply to the prefactor. A measurement of the neutrons produced from
![]() constrains the number of protons able to be recycled into the
constrains the number of protons able to be recycled into the
![]() reaction. In this case, the input is the α spectrum derived from all primary reactions, is a complicated function of energy, and is expected to vary significantly as a function of mean ion kinetic energy. We consider its derivation beyond the scope of this study.
reaction. In this case, the input is the α spectrum derived from all primary reactions, is a complicated function of energy, and is expected to vary significantly as a function of mean ion kinetic energy. We consider its derivation beyond the scope of this study.
3.2. Beam-Target
The beam-target experiment involves simpler kinematics. In the frame with the target material at rest, the center-of-mass energy is
with the reduced mass given above by equation (3). The b subscript indicates a particle from the beam, and the t subscript indicates a particle in the target. For pB scattering,
![]() . The momentum integral then only runs over the proton distribution. The target particle distribution function is nonzero only in the spatial region of the target material, and integrating over the beam axis and time convolves the projectile beam with the target distribution.
. The momentum integral then only runs over the proton distribution. The target particle distribution function is nonzero only in the spatial region of the target material, and integrating over the beam axis and time convolves the projectile beam with the target distribution.
In standard beam-target experiments in order to maximize exposure, the target is placed on or adjacent to the anticipated axis of the ion beam. In the TPW experiment of particular interest, we were able to verify that the target material contained the cone of the highest ion flux, which subtended an opening angle θ≲0.3. We, therefore, assume that the transverse momentum of the beam is small relative to longitudinal momentum. These together imply that we can reduce the beam momentum integral to the longitudinal momentum only and integrate the transverse position dependence into a 1-dimensional beam distribution function:
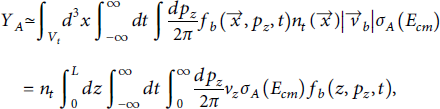
where Vt signifies the volume of the target. In this expression, the longitudinal coordinate can also be considered as parameterizing the distance along the on-average straight-line trajectory; trajectories diverging from the beam axis would make a small geometric correction due to exiting through the side of the target rather than the opposite end. The constant density of the target has been taken outside the integral and the target length defined as L.
Due to energy loss in the target, the beam distribution evolves as it propagates through the target. First, as a limiting model, we compute the yield neglecting the beam energy loss. This case also clarifies the dynamics in the subsequent derivation that includes stopping. The beam distribution function remains constant in the absence of stopping, so the convolution yields the length of the target times the spatial length scale of the beam divided by the longitudinal velocity, i.e., the length of the beam multiplying the traverse time and a numerical factor depending on the longitudinal profile of the beam. Then, the yield can be written simply
The beam distribution function fb has been reduced to its energy dependence
![]() .
.
The importance of stopping is seen by comparing the stopping range to the target dimensions. The stopping range is defined as
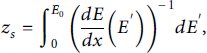
where E 0 is the initial energy of the ion before interacting with the target, dE/ dx from data is conventionally positive, and the expected minus sign is compensated by the flipping the limits on the integral. Note that dE/ dx is frequently given in units of energy/(mass density) or energy/(number density) so that one multiplies by the density of the medium to obtain the energy loss in units of energy/length.
The target temperature is more difficult to estimate in direct-irradiation experiments. As the laser energy is absorbed within the first few 10 s of microns of the target (at most), the bulk is only heated by ions and electrons accelerated out of the laser-heated region. Ions dominate the energy transfer to the bulk; electrons have very low (a few-MeV cm2/g) stopping power in the few-MeV energy range compared to ions. With similar estimates for the total energy of laser-accelerated ions as in the preceding paragraph, the average energy transferred is 10–100 eV per electron, orders of magnitude higher because the volume into which it is deposited is orders of magnitude smaller ∼ (0.1mm)3. The temperature-dependent correction to ion stopping would be non-negligible in this case. For this reason, in yield calculations below, we compare zero-temperature stopping to finite-temperature stopping.
For a zero-temperature boron target and ion energies representative of the higher end of the expected distributions, SRIM predicts the stopping range of a 20 MeV proton as 2 mm and 8 MeV α as 38 micron. However, target can be heated by both the ion beam and the even higher energy electrons that are accelerated out of the ion source by the laser driver. Using the fact that the stopping range is less than the target length even for the highest energy ions, the total energy deposited is just the total energy of the beam that enters the target. Even for the relatively high-energy ions obtained from the Texas Petawatt, the total ion beam energy transferred to the target is at most ∼ 10% of the laser energy. For the upper limit on the Texas Petawatt, 10 J deposited into a hemisphere of radius equal to the 2 mm stopping range, the specific heats of boron and boron-nitride imply a temperature change
![]() K
K
![]() –
–
![]() eV. Without direct measurements of the electron spectrum emitted by the ion source, we resort to an estimate. While experiments and simulations of ion acceleration suggest that electrons absorb a similar amount of energy from the laser-plasma interaction as the ions, the electrons are less efficient at depositing energy in the target. Therefore, an estimated upper bound on the deposition of energy in the target by electrons is 10 J. Carbon and other heavy ions that may come from the ion sources carry equal or less energy than the protons and in any case arrive later. Thus, our best estimate for the temperature of the target remains
eV. Without direct measurements of the electron spectrum emitted by the ion source, we resort to an estimate. While experiments and simulations of ion acceleration suggest that electrons absorb a similar amount of energy from the laser-plasma interaction as the ions, the electrons are less efficient at depositing energy in the target. Therefore, an estimated upper bound on the deposition of energy in the target by electrons is 10 J. Carbon and other heavy ions that may come from the ion sources carry equal or less energy than the protons and in any case arrive later. Thus, our best estimate for the temperature of the target remains
![]() eV. This estimate, much less than the work function (
eV. This estimate, much less than the work function (
![]() ) of the target material, is consistent with the target’s survival of the interaction.
) of the target material, is consistent with the target’s survival of the interaction.
Nevertheless, for reference and comparison, Figure 2 shows the stopping power and stopping range equation (11) for both cold and high-temperature (T = 1 keV) boron and boron-nitride. This unphysically high target temperature is chosen to exhibit its negligible impact on the yields for the processes of interest. The stopping power data are obtained from calculations using the enhanced RPA-LDA (eRPA-LDA) model of Mehlhorn [Reference Mehlhorn27, Reference Gu, Mehlhorn and Golovkin28]. Stopping ranges for lower energy ions are shorter, and ranges are generally less than the typical length (≲cm) of the targets. The highest energy protons (
![]() MeV) have stopping ranges equal to or greater than the target length, but their number and hence contribution are smaller by an order of magnitude or more. Neglecting this not-quite-stopped component, therefore, amounts to an error of ∼ 10% or less, smaller than the error propagated from the cross-section and certainly smaller than the error due to the limited energy range of the cross-section data. Therefore, to our working accuracy, the target can be considered “thick” in that almost all particles in the beam will be stopped.
MeV) have stopping ranges equal to or greater than the target length, but their number and hence contribution are smaller by an order of magnitude or more. Neglecting this not-quite-stopped component, therefore, amounts to an error of ∼ 10% or less, smaller than the error propagated from the cross-section and certainly smaller than the error due to the limited energy range of the cross-section data. Therefore, to our working accuracy, the target can be considered “thick” in that almost all particles in the beam will be stopped.

Figure 2: (a) Stopping power, dE/ dx, for protons in pure boron and boron-nitride, cold and warm T = 1 keV thick targets. (b) Resulting range zs equation (11).
The conventional definition of the “thick-target yield” for a monoenergetic input is
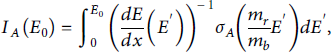
where dE/ dx from data is conventionally positive, and the expected minus sign is compensated by the flipping the limits on the integral. The density factor in converting tabulated dE/ dx data into energy loss per unit length cancels with the density of target nuclei in the yield. Note that the integration can effectively be restricted to the energy range where the cross-section is non-negligible. Since most of the cross-sections have thresholds of order 1 MeV, Figure 2 shows that finite-temperature corrections to stopping matter only for T ≳ 1 keV. Raising the target temperature increases the projectile energy at which dE/ dx achieves its maximum, but 1 keV is a much higher temperature than can be dynamically achieved in a typical beam-target experiment without external heating.
Thick target yields for all of the primary reactions in Figure 3 show these properties.
![]() and
and
![]() display the greatest sensitivity to the target temperature because
display the greatest sensitivity to the target temperature because
![]() cross-section is largest, and the cross-section for
cross-section is largest, and the cross-section for
![]() is only available for CM energy ≲1MeV, where the dE/ dx curves differ the most.
is only available for CM energy ≲1MeV, where the dE/ dx curves differ the most.
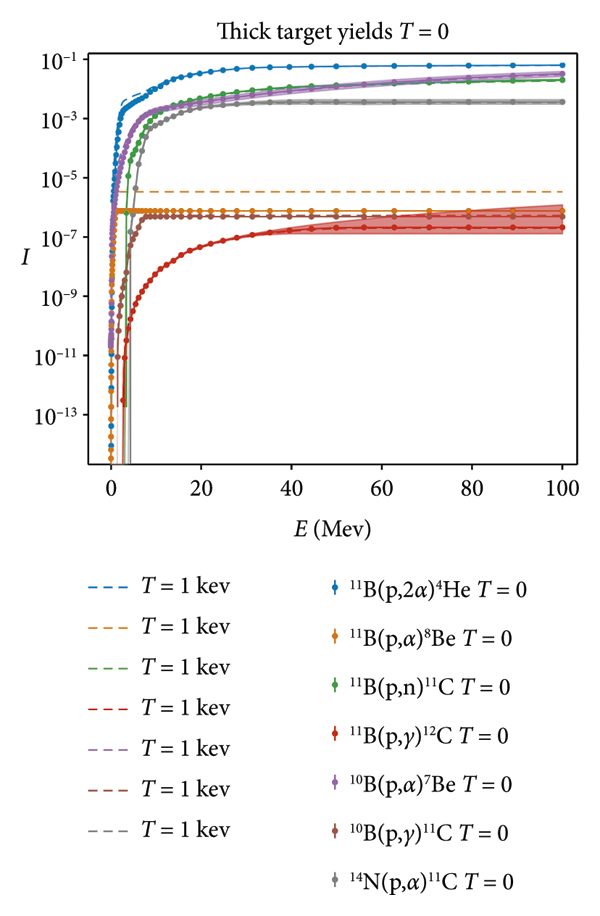
Figure 3: Thick target yields for the reactions in Table 1. Solid bands show the error propagated from the cross-section. Error bars, where visible, present the numerical error.
The total yield of the product nucleus A is obtained by integrating the thick target yield over the beam, weighted by the beam energy distribution dN/dEb:
Yield ratios in the beam-fusion geometry, as in direct-irradiation experiments, analytically eliminate dependence on geometric factors in the yield, such as target length and density. Less obviously, the overall normalization of the beam energy distribution also cancels in the ratio, since one could easily write
![]() where Nb is the total number of particles (that interact with the target) and f(E) is a normalized probability distribution for the ion energy. For example, the ratio of γs from
where Nb is the total number of particles (that interact with the target) and f(E) is a normalized probability distribution for the ion energy. For example, the ratio of γs from
![]() to αs from
to αs from
![]() is
is
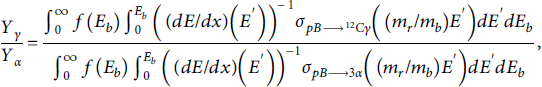
with the same stopping power
![]() and normalized proton spectrum. Removing this dependence on the total number in the beam significantly reduces uncertainty in practice given the available on-shot beam measurements.
and normalized proton spectrum. Removing this dependence on the total number in the beam significantly reduces uncertainty in practice given the available on-shot beam measurements.
The yield ratio retains important information of the beam energy distribution. As seen in Figure 1, different reactions have different thresholds and collision energies where the cross-section approaches its maximum usually in the 0.1–1 b range. The yield ratio is greatly enhanced in case the beam energy distribution reaches the threshold of one reaction but not the other. Since laser-driven ion beams generally have a broad and decreasing energy distribution at low energy, the typical case is that a beam may contain ions of sufficient energy for a reaction with a low threshold but not for a reaction with a higher threshold. Thus, for example, the
![]() has a peak cross-section around 650 keV whereas the
has a peak cross-section around 650 keV whereas the
![]() has a peak around 7 MeV, so that the Maxwellian distribution with
has a peak around 7 MeV, so that the Maxwellian distribution with
![]() –5 MeV would yield significant α particles but not 11C. This effect is demonstrated in Figure 4.
–5 MeV would yield significant α particles but not 11C. This effect is demonstrated in Figure 4.
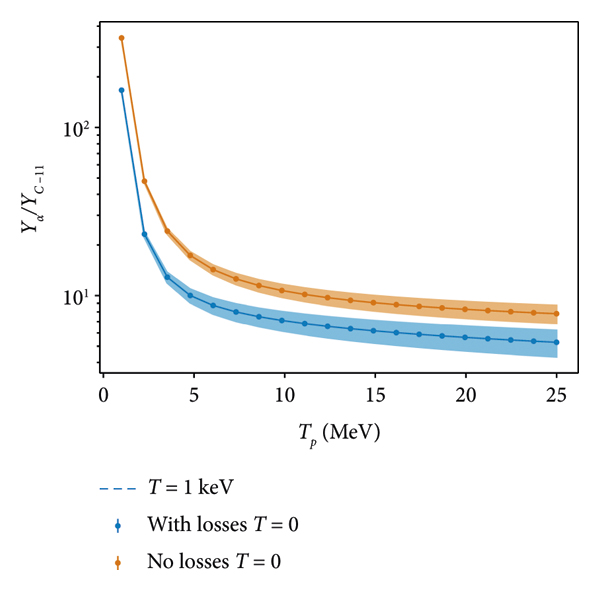
Figure 4: Yield ratio of α to 11C for a normalized Maxwellian input proton spectrum in boron, comparing the yield with and without beam energy losses in the target. Target temperature makes a negligible difference to the energy loss for proton energies in this regime, and the T = 1 keV curve lies on top of the T = 0. Solid bands show the error propagated from the cross-section. Error bars, where visible, present the numerical error.
4. Modeling and Results
Some modeling and assumptions have already been established in setting up expressions for the yield. We, now, discuss the details and quantitative inputs to the models.
As seen in Tables 1 and 2 and Figure 1, data for the cross-sections of interest are available only for limited ranges of CM energy. The available data and comparison with analogous reactions suggest that the cross-sections may have similar values across a wider range of CM energies. However, to avoid undue speculation and modeling, we assume the cross-section vanishes quickly outside the available data range. Considering also the ion mean kinetic energy not likely exceeding ∼10 MeV, the numerical results for the yields are likely under estimates by a factor of a few, but not more than ten.
4.1. Direct Irradiation
The yield ratio eliminates dependence on local, dynamic quantities, including effective reaction volume, confinement time, and the densities. We need both the absolute kinetic energy scale and the relative kinetic energies of the two ion species. The absolute energy scale is determined by how efficiently laser energy is transferred the plasma, which in turn generally depends on laser properties, such as total pulse energy, pulse length (if it is greater than ps-scale), and contrast. For comparison between facilities, we scan the absolute kinetic energy scale, using the proton mean kinetic energy as the reference. For intensities upto 1022 W/cm2, we expect ion kinetic energies inside the target to be MeV-scale as the typical momentum obtained from a cycle of the laser field and so also from plasma-generated electrostatic fields.
The relative kinetic energy can be estimated from kinematics. For the same field strength and duration of interaction, the relative work done on ions of charge Z 1,Z 2 and mass m 1,m 2 is
![]() . This suggests the typical energy of protons should be smaller than that of (fully-ionized) boron by factor of 2.5 (i.e.,
. This suggests the typical energy of protons should be smaller than that of (fully-ionized) boron by factor of 2.5 (i.e.,
![]() ). Good experimental measurements of ion kinetic energy distributions inside the laser-heated target are difficult to come by. Fortunately, we find that the yield is mostly sensitive to the absolute kinetic energy scale, controlling how much of the ion distribution is above the threshold CM energy determined by the cross-section. Once the threshold CM energy is achieved by a majority of the distribution, the yield becomes less sensitive to further increases in kinetic energy. At next order, the yield equation (2) is more sensitive to the kinetic energy of the heavier ion, due to the residual exponential dependence on ν. Note, however, that these yields are likely to increase somewhat for higher kinetic energy range if cross-section data across a wider range of CM energy were available. These results are exhibited in Figure 5.
). Good experimental measurements of ion kinetic energy distributions inside the laser-heated target are difficult to come by. Fortunately, we find that the yield is mostly sensitive to the absolute kinetic energy scale, controlling how much of the ion distribution is above the threshold CM energy determined by the cross-section. Once the threshold CM energy is achieved by a majority of the distribution, the yield becomes less sensitive to further increases in kinetic energy. At next order, the yield equation (2) is more sensitive to the kinetic energy of the heavier ion, due to the residual exponential dependence on ν. Note, however, that these yields are likely to increase somewhat for higher kinetic energy range if cross-section data across a wider range of CM energy were available. These results are exhibited in Figure 5.
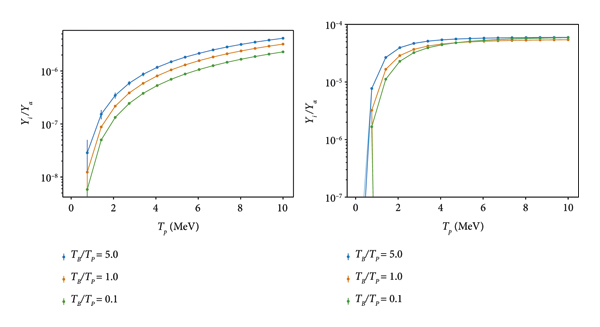
Figure 5: Ratio of photon (γ) yield to α yield in a quasi-thermal plasma as a function of proton mean kinetic energy. At left for the
![]() reaction and at right for the
reaction and at right for the
![]() reaction. The yield increases rapidly as the mean kinetic energy nears the CM energy corresponding to the threshold for the cross-section (of Figure 1) and then plateaus. Different curves correspond to different boron to proton kinetic energy, showing that the yield is only sensitive to the relative kinetic energy if the boron mean kinetic energy is much less than the proton mean kinetic energy. Error bars, where visible, present the numerical error.
reaction. The yield increases rapidly as the mean kinetic energy nears the CM energy corresponding to the threshold for the cross-section (of Figure 1) and then plateaus. Different curves correspond to different boron to proton kinetic energy, showing that the yield is only sensitive to the relative kinetic energy if the boron mean kinetic energy is much less than the proton mean kinetic energy. Error bars, where visible, present the numerical error.
The relative insensitivity of
![]() to ion mean kinetic energy is probably an artifact of the limited data range available for the cross-section, which causes the thick target yield to plateau rapidly above ∼ 8 MeV. The greater sensitivity of
to ion mean kinetic energy is probably an artifact of the limited data range available for the cross-section, which causes the thick target yield to plateau rapidly above ∼ 8 MeV. The greater sensitivity of
![]() to the mean kinetic energy could allow the yield ratio to be used in a more conventional manner: measuring both yields in the ratio determines the mean ion kinetic energy in the target to high accuracy. This method is in fact how yield ratios are commonly used in heavy-ion collisions [Reference Letessier and Rafelski29]. In particular, if photons from both processes
to the mean kinetic energy could allow the yield ratio to be used in a more conventional manner: measuring both yields in the ratio determines the mean ion kinetic energy in the target to high accuracy. This method is in fact how yield ratios are commonly used in heavy-ion collisions [Reference Letessier and Rafelski29]. In particular, if photons from both processes
![]() and
and
![]() can be detected, the ratio of these photon yields alone could probe the mean kinetic energy of ions in the target. We expect the sensitivity of the photon ratio can only be established with more cross-section data.
can be detected, the ratio of these photon yields alone could probe the mean kinetic energy of ions in the target. We expect the sensitivity of the photon ratio can only be established with more cross-section data.
4.2. Beam Target
More experimental information is available on the inputs for the beam-target setup. With a ∼ 1/2 reduction to the total yield, experiments can measure the laser-produced ion beam on-shot. For example, the target can cover roughly half the solid angle of the beam, so that the other half the beam propagates unperturbed into a diagnostic. Since ion acceleration mechanisms are azimuthally symmetric or at most display a dipole azimuthal mode (for example, in BOA [Reference Yin, Albright, Bowers, Jung, Fernández and Hegelich30]), we can infer the distribution in the unmeasured half by mirroring the measured half. Experiments on the TPW and else frequently show single or double Maxwellian ion spectra. For simplicity and clarity, we consider a single Maxwellian distribution describing the beam, though with much smaller β parameter than in the DI-region ion distributions. The yield for a double Maxwellian is a suitably weighted superposition of the yield for single Maxwellians, and the effect on the yield ratios can be naturally deduced from this.
We first compare the total α yield to the 11C yield in boron and boron-nitride targets. As shown in Figure 4, for the cross-sections and expected temperature of the target, beam energy losses are well-approximated by the cold limit, which we use here. In boron targets,
![]() is the dominant source of α particles, while in boron-nitride targets, the
is the dominant source of α particles, while in boron-nitride targets, the
![]() process can contribute a similar number. Therefore, for BN targets, we show both the total α to 11C ratio and the
process can contribute a similar number. Therefore, for BN targets, we show both the total α to 11C ratio and the
![]() yield relative to the (total) 11C yield, so that the measured 11C number can be both compared to the measured α yield (e.g., in CR-39) and used to estimate the number of
yield relative to the (total) 11C yield, so that the measured 11C number can be both compared to the measured α yield (e.g., in CR-39) and used to estimate the number of
![]() reactions occuring.
reactions occuring.
Photons are also produced by
![]() and
and
![]() processes in the beam-target geometry. Detection of the photons in the beam-target experiment is a natural proof-of-principle/validation step before using the photon measurement to diagnose the direct-irradiation experiments. As shown in Figure 6, the photon yields are 5 to 6 orders of magnitude smaller than the α yield and display different dependence on the beam β parameter in beam-target experiments compared to the quasi-thermal plasma of direct irradiation. The yield of
processes in the beam-target geometry. Detection of the photons in the beam-target experiment is a natural proof-of-principle/validation step before using the photon measurement to diagnose the direct-irradiation experiments. As shown in Figure 6, the photon yields are 5 to 6 orders of magnitude smaller than the α yield and display different dependence on the beam β parameter in beam-target experiments compared to the quasi-thermal plasma of direct irradiation. The yield of
![]() peaks around 3 MeV due to the narrow range of energies for which cross-section data are available; this peak may disappear with more complete cross-section data.
peaks around 3 MeV due to the narrow range of energies for which cross-section data are available; this peak may disappear with more complete cross-section data.

Figure 6: Yield ratios: number of photons per
![]() reaction for
reaction for
![]() and
and
![]() processes.
processes.
5. Conclusion
We have, thus, arrived at a list of reactions and their products with diagnostic potential:
-
(1) 11C is produced by three reactions in Table 1 with cross-sections of several hundred millibarns in 5–20 MeV center-of-mass energy range. The third channel,
 , generally contributes less than 10−4 to the total yield. Although it requires higher proton energy, in experiments on an ultrahigh-intensity laser, 1 11C is produced for every 10–100 α particles from the
, generally contributes less than 10−4 to the total yield. Although it requires higher proton energy, in experiments on an ultrahigh-intensity laser, 1 11C is produced for every 10–100 α particles from the
 reaction (see Figure 7). Modulo some uncertainty in modeling the proton beam, the 11C yield thus offers a strong, easily-measured signal to corroborate or substitute more direct measurements of the α yield [Reference McCary, Labun, Labun and Hegelich20].
reaction (see Figure 7). Modulo some uncertainty in modeling the proton beam, the 11C yield thus offers a strong, easily-measured signal to corroborate or substitute more direct measurements of the α yield [Reference McCary, Labun, Labun and Hegelich20]. -
(2)
 has the same initial state as the
has the same initial state as the
 , so that in both direct-irradiation and beam-target experiments, macroscopic factors such as density, volume, and time as well as physical constant prefactors cancel in the yield ratio. The drawback to this process is its low cross-section and higher threshold: only 1 photon per million
, so that in both direct-irradiation and beam-target experiments, macroscopic factors such as density, volume, and time as well as physical constant prefactors cancel in the yield ratio. The drawback to this process is its low cross-section and higher threshold: only 1 photon per million
 reactions is expected, according to Figure 5. That suggests ∼ 103 − 104 such photons were produced in recent experiments such as References [Reference Giuffrida, Belloni and Margarone5, Reference Bonvalet, Nicolaï and Raffestin7, Reference McCary, Labun, Labun and Hegelich20]. Pending a direct measurement though the photon should be easily distinguishable at an energy ≳ 10 MeV.
reactions is expected, according to Figure 5. That suggests ∼ 103 − 104 such photons were produced in recent experiments such as References [Reference Giuffrida, Belloni and Margarone5, Reference Bonvalet, Nicolaï and Raffestin7, Reference McCary, Labun, Labun and Hegelich20]. Pending a direct measurement though the photon should be easily distinguishable at an energy ≳ 10 MeV. -
(3)
 involves boron-10, generally leaving nontrivial prefactors in the yield ratio. While these prefactors are expected to be order 1, due to the similar dynamics of boron-10 versus boron-11 in a laser-heated target, they introduce additional uncertainty, which also grows with the duration of the fusion. The yield ratio Figure 5 predicts 1 photon per 100,000
involves boron-10, generally leaving nontrivial prefactors in the yield ratio. While these prefactors are expected to be order 1, due to the similar dynamics of boron-10 versus boron-11 in a laser-heated target, they introduce additional uncertainty, which also grows with the duration of the fusion. The yield ratio Figure 5 predicts 1 photon per 100,000
 , implying roughly 105 such photons in recent experiments. The photon energy is lower, but still likely high enough in the several MeV range to be distinguishable from other plasma sources.
, implying roughly 105 such photons in recent experiments. The photon energy is lower, but still likely high enough in the several MeV range to be distinguishable from other plasma sources. -
(4)
 has not been evaluated here but is an excellent candidate for corroborating the α yield if the neutron number can be measured. This reaction could also determine the importance of p recycling by virtue of its probably near-unity yield ratio to the isospin partner reaction
has not been evaluated here but is an excellent candidate for corroborating the α yield if the neutron number can be measured. This reaction could also determine the importance of p recycling by virtue of its probably near-unity yield ratio to the isospin partner reaction
 . A rough estimate of the thick target yield for a 4 MeV α suggests that ∼ 10−5 of the αs produced may be converted to neutrons by this process. The neutron is slow enough to be easily identified by time-of-flight spectrometers.
. A rough estimate of the thick target yield for a 4 MeV α suggests that ∼ 10−5 of the αs produced may be converted to neutrons by this process. The neutron is slow enough to be easily identified by time-of-flight spectrometers.
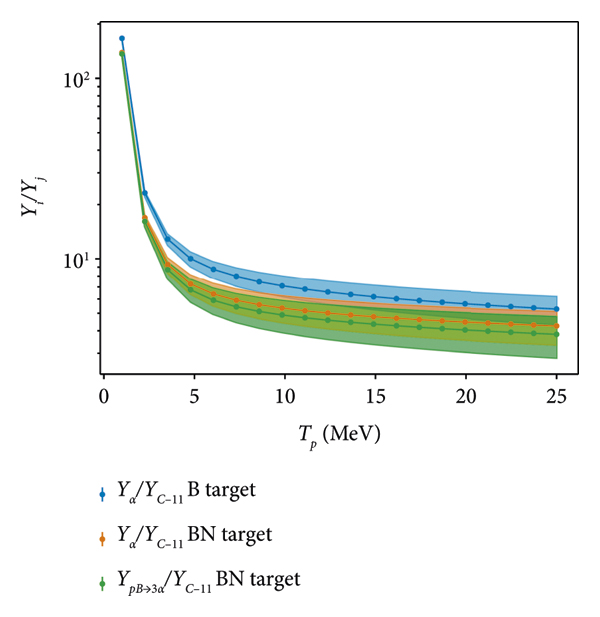
Figure 7: Yield ratios: measured total α and
![]() yield relative to measured 11C for boron and boron-nitride targets. Beam energy losses are included with a cold target.
yield relative to measured 11C for boron and boron-nitride targets. Beam energy losses are included with a cold target.
One other reaction could be a good proxy for α yield if its cross-section was independently measured in conventional nuclear scattering experiments:
![]() . This reaction has the benefit of producing an unstable nuclide so that its yield can be first checked in beam-target experiments. We have also noted that the ratio between the two photon-producing processes,
. This reaction has the benefit of producing an unstable nuclide so that its yield can be first checked in beam-target experiments. We have also noted that the ratio between the two photon-producing processes,
![]() and
and
![]() , could provide a measurement sensitive to the mean kinetic energy of the ions in the plasma. However, its accuracy is currently severely limited by the little cross-section data available for
, could provide a measurement sensitive to the mean kinetic energy of the ions in the plasma. However, its accuracy is currently severely limited by the little cross-section data available for
![]() .
.
Considering the experimental interest and potential applications of the
![]() reaction and other laser-driven fusion reactions, we strongly recommend increasing engagement with the accelerator-nuclear physics community to improve cross-section measurements and add photon and neutron diagnostics. Particle yields and yield ratios can become a powerful tool to determine laser-driven fusion plasma conditions in the same way, they have been thoroughly developed for probing nuclear-matter plasmas.
reaction and other laser-driven fusion reactions, we strongly recommend increasing engagement with the accelerator-nuclear physics community to improve cross-section measurements and add photon and neutron diagnostics. Particle yields and yield ratios can become a powerful tool to determine laser-driven fusion plasma conditions in the same way, they have been thoroughly developed for probing nuclear-matter plasmas.
Data Availability
Nuclear cross-sections are freely available from the EXFOR database. Energy loss predictions and tabulated results of numerical integrations are available from the authors upon request.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Acknowledgments
The work performed under the auspices of the University of Texas at Austin was supported in part by the National Science Foundation under grant no. 2108921 and the Air Force Office of Scientific Research under grant nos. FA9550-14-1-0045. This work and a related experiment at the University of Texas, Austin were also supported in part by HB11 Energy PTY, LTD. Experiment time at Texas Petawatt was supplied by LaserNetUS.




















