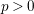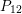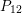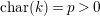Introduction
The main technical result of the present article, expressed in modern language, is the following one:
Main Theorem.
Let
![]() $S$
be a projective surface of Kodaira dimension 1 defined over an algebraically closed field
$S$
be a projective surface of Kodaira dimension 1 defined over an algebraically closed field
![]() $k$
, and let
$k$
, and let
![]() $K_{S}$
be a canonical divisor on
$K_{S}$
be a canonical divisor on
![]() $S$
, so that
$S$
, so that
![]() $\unicode[STIX]{x1D6FA}_{S}^{2}\cong {\mathcal{O}}_{S}(K_{S})$
.
$\unicode[STIX]{x1D6FA}_{S}^{2}\cong {\mathcal{O}}_{S}(K_{S})$
.
Then the growth of the
![]() $\text{plurigenera}~P_{n}(S)=\dim H^{0}({\mathcal{O}}_{S}(nK_{S}))=\dim H^{0}((\unicode[STIX]{x1D6FA}_{S}^{2})^{\otimes n})$
satisfies:
$\text{plurigenera}~P_{n}(S)=\dim H^{0}({\mathcal{O}}_{S}(nK_{S}))=\dim H^{0}((\unicode[STIX]{x1D6FA}_{S}^{2})^{\otimes n})$
satisfies:
(1)
 $P_{12}(S)\geqslant 2$
;
$P_{12}(S)\geqslant 2$
;(2) there exists
 $n\leqslant 4$
such that
$n\leqslant 4$
such that
 $P_{n}(S)\geqslant 1$
;
$P_{n}(S)\geqslant 1$
;(3) there exists
 $n\leqslant 8$
such that
$n\leqslant 8$
such that
 $P_{n}(S)\geqslant 2$
;
$P_{n}(S)\geqslant 2$
;(4)
 $\forall n\geqslant 14$
$\forall n\geqslant 14$
 $P_{n}(S)\geqslant 2$
.
$P_{n}(S)\geqslant 2$
.
While (2)–(3) of the above theorem are new also in the classical case where
![]() $k$
is a field of characteristic zero, (1) is due to Enriques [Reference Enriques15] in characteristic 0 and (4) was shown by Katsura and Ueno [Reference Katsura and Ueno23] for elliptic surfaces in all characteristics (but we reprove their result here as a part of the above more general statement). Needless to say, we use in the proof of our theorem many results, lemmas and propositions previously established by many authors, especially Bombieri–Mumford, Raynaud, and Katsura–Ueno [Reference Mumford27], [Reference Bombieri and Mumford5], [Reference Bombieri and Mumford6], [Reference Raynaud31], [Reference Katsura and Ueno23].
$k$
is a field of characteristic zero, (1) is due to Enriques [Reference Enriques15] in characteristic 0 and (4) was shown by Katsura and Ueno [Reference Katsura and Ueno23] for elliptic surfaces in all characteristics (but we reprove their result here as a part of the above more general statement). Needless to say, we use in the proof of our theorem many results, lemmas and propositions previously established by many authors, especially Bombieri–Mumford, Raynaud, and Katsura–Ueno [Reference Mumford27], [Reference Bombieri and Mumford5], [Reference Bombieri and Mumford6], [Reference Raynaud31], [Reference Katsura and Ueno23].
Statement (1) is most important, which allows us to extend to the positive characteristic case the main classification theorem of Castelnuovo and Enriques. In modern language (see the next section for more details, and a more precise and informative statement), the classification theorem implies the following:
 $P_{12}$
-Theorem.
$P_{12}$
-Theorem.
Let
![]() $S$
be a projective surface defined over an algebraically closed field
$S$
be a projective surface defined over an algebraically closed field
![]() $k$
.
$k$
.
Then for the Kodaira dimension
![]() $\text{Kod}(S)$
we have:
$\text{Kod}(S)$
we have:
∙
 $\text{(I) Kod}(S)=-\infty \;\Longleftrightarrow \;P_{12}(S)=0$
;
$\text{(I) Kod}(S)=-\infty \;\Longleftrightarrow \;P_{12}(S)=0$
;∙
 $\text{(II) Kod}(S)=0\;\Longleftrightarrow \;P_{12}(S)=1$
;
$\text{(II) Kod}(S)=0\;\Longleftrightarrow \;P_{12}(S)=1$
;∙
 $\text{(III) Kod}(S)=1\;\Longleftrightarrow \;P_{12}(S)\geqslant 2$
and, for
$\text{(III) Kod}(S)=1\;\Longleftrightarrow \;P_{12}(S)\geqslant 2$
and, for
 $S$
minimal,
$S$
minimal,
 $K_{S}^{2}=0$
;
$K_{S}^{2}=0$
;∙
 $\text{(IV) Kod}(S)=2\;\Longleftrightarrow \;P_{12}(S)\geqslant 2$
and, for
$\text{(IV) Kod}(S)=2\;\Longleftrightarrow \;P_{12}(S)\geqslant 2$
and, for
 $S$
minimal,
$S$
minimal,
 $K_{S}^{2}>0$
.
$K_{S}^{2}>0$
.
It should be observed that the estimates for the growth of the plurigenera are much weaker if one considers properly elliptic nonalgebraic surfaces, see [Reference Iitaka.21], where the analogue of (4) of the main theorem for nonalgebraic surfaces is proved. Iitaka showed that, for
![]() $n\geqslant 86$
,
$n\geqslant 86$
,
![]() $H^{0}({\mathcal{O}}_{S}(nK_{S}))$
yields the canonical elliptic fibration. One of the reasons why the estimate is much weaker depends on the failure of the Poincaré reducibility theorem, implying in the algebraic case that a certain monodromy group
$H^{0}({\mathcal{O}}_{S}(nK_{S}))$
yields the canonical elliptic fibration. One of the reasons why the estimate is much weaker depends on the failure of the Poincaré reducibility theorem, implying in the algebraic case that a certain monodromy group
![]() $G$
is Abelian. Hence, for instance, if
$G$
is Abelian. Hence, for instance, if
![]() $G$
is Abelian, it cannot be a Hurwitz group, i.e.,
$G$
is Abelian, it cannot be a Hurwitz group, i.e.,
![]() $G$
cannot have generators
$G$
cannot have generators
![]() $a,b,c$
of respective orders
$a,b,c$
of respective orders
![]() $(2,3,7)$
satisfying
$(2,3,7)$
satisfying
![]() $abc=1$
.
$abc=1$
.
Indeed (we omit here the simple proof), the analogue of statement (1) for nonalgebraic surfaces is that
![]() $P_{42}\geqslant 2$
.
$P_{42}\geqslant 2$
.
Concerning higher dimensional algebraic varieties, a natural question emerges:
Question 0.1. Given a projective manifold of
![]() $X$
dimension
$X$
dimension
![]() $N$
, is there a sharp number
$N$
, is there a sharp number
![]() $d=d(N)$
such that:
$d=d(N)$
such that:
(1)
 $\text{Kod}(X)=-\infty \;\Longleftrightarrow \;P_{d}(X)=0$
;
$\text{Kod}(X)=-\infty \;\Longleftrightarrow \;P_{d}(X)=0$
;(2)
 $\text{Kod}(X)=0\;\Longleftrightarrow \;P_{d}(X)=1$
;
$\text{Kod}(X)=0\;\Longleftrightarrow \;P_{d}(X)=1$
;(3)
 $\text{Kod}(X)\geqslant 1\;\Longleftrightarrow \;P_{d}(X)\geqslant 2$
?
$\text{Kod}(X)\geqslant 1\;\Longleftrightarrow \;P_{d}(X)\geqslant 2$
?
Progress on a related question, about effectivity of the Iitaka fibration, was made, among others, by Fujino and Mori [Reference Fujino and Mori.18] and Birkar and Zhang [Reference Birkar and Zhang9].
1 The classification theorem of Castelnuovo and Enriques
Let
![]() $S$
be a nonsingular projective surface defined over an algebraically closed field
$S$
be a nonsingular projective surface defined over an algebraically closed field
![]() $k$
, and let
$k$
, and let
![]() $K_{S}$
be a canonical divisor on
$K_{S}$
be a canonical divisor on
![]() $S$
, so that
$S$
, so that
![]() $\unicode[STIX]{x1D6FA}_{S}^{2}\cong {\mathcal{O}}_{S}(K_{S})$
. We assume that
$\unicode[STIX]{x1D6FA}_{S}^{2}\cong {\mathcal{O}}_{S}(K_{S})$
. We assume that
![]() $S$
is minimal: this means that there does not exist an irreducible exceptional curve
$S$
is minimal: this means that there does not exist an irreducible exceptional curve
![]() $C$
of the first kind, i.e., an integral curve
$C$
of the first kind, i.e., an integral curve
![]() $C$
with
$C$
with
![]() $C^{2}=K_{S}\cdot C=-1$
. Let us recall the definition of the basic numerical invariants associated with
$C^{2}=K_{S}\cdot C=-1$
. Let us recall the definition of the basic numerical invariants associated with
![]() $S$
, which allow its birational classification.
$S$
, which allow its birational classification.
For each integer
![]() $m\in \mathbb{N}$
, we denote as usual, following Castelnuovo and Enriques, by
$m\in \mathbb{N}$
, we denote as usual, following Castelnuovo and Enriques, by
the mth plurigenus of
![]() $S$
.
$S$
.
In particular, the geometric genus is
![]() $p_{g}(S):=P_{1}(S)$
, while the arithmetic irregularity is defined as
$p_{g}(S):=P_{1}(S)$
, while the arithmetic irregularity is defined as
![]() $h(S):=h^{1}({\mathcal{O}}_{S})$
, and the arithmetic genus is defined as
$h(S):=h^{1}({\mathcal{O}}_{S})$
, and the arithmetic genus is defined as
To finish our comparison of classical and modern notation, recall that the geometric irregularity is defined as
![]() $q(S):=1/2b_{1}(S)$
, where
$q(S):=1/2b_{1}(S)$
, where
![]() $b_{1}(S)$
is the first
$b_{1}(S)$
is the first
![]() $l$
-adic Betti number of
$l$
-adic Betti number of
![]() $S$
,
$S$
,
![]() $b_{1}(S):=\dim _{\mathbb{Q}_{l}}H_{et}^{1}(S,\mathbb{Q}_{l}).$
$b_{1}(S):=\dim _{\mathbb{Q}_{l}}H_{et}^{1}(S,\mathbb{Q}_{l}).$
![]() $q(S)$
is equal to the dimension of the Picard scheme
$q(S)$
is equal to the dimension of the Picard scheme
![]() $\operatorname{Pic}^{0}(S)$
, and also (cf. [Reference Mumford28, Chapter III. 13]) of the dual scheme
$\operatorname{Pic}^{0}(S)$
, and also (cf. [Reference Mumford28, Chapter III. 13]) of the dual scheme
![]() $\operatorname{Pic}^{0}(\operatorname{Pic}^{0}(S))$
, and of the Albanese variety
$\operatorname{Pic}^{0}(\operatorname{Pic}^{0}(S))$
, and of the Albanese variety
![]() $Alb(S):=\operatorname{Pic}^{0}(\operatorname{Pic}^{0}(S)_{\text{red}})$
.
$Alb(S):=\operatorname{Pic}^{0}(\operatorname{Pic}^{0}(S)_{\text{red}})$
.
The above numbers are all equal in characteristic zero:
![]() $q(S)=h(S)=h^{0}(\unicode[STIX]{x1D6FA}_{S}^{1})$
, but not in characteristic
$q(S)=h(S)=h^{0}(\unicode[STIX]{x1D6FA}_{S}^{1})$
, but not in characteristic
![]() $p>0$
, where one just has some inequalities.
$p>0$
, where one just has some inequalities.
Since
![]() $H^{1}({\mathcal{O}}_{S})$
is the Zariski tangent space to the Picard scheme at the origin [Reference Mumford26, Lecture 24. 2
$H^{1}({\mathcal{O}}_{S})$
is the Zariski tangent space to the Picard scheme at the origin [Reference Mumford26, Lecture 24. 2
![]() $^{\circ }$
], one has the inequalities (cf. [Reference Bombieri and Mumford5, pp. 34–35])
$^{\circ }$
], one has the inequalities (cf. [Reference Bombieri and Mumford5, pp. 34–35])
The inequality
![]() $h^{0}(\unicode[STIX]{x1D6FA}_{S}^{1})\geqslant q$
was shown by Igusa [Reference Igusa19], and there are examples where the equality does not hold, cf. [Reference Igusa20, p. 964, The Example], [Reference Mumford25, p. 341, Corollary]Footnote
1
.
$h^{0}(\unicode[STIX]{x1D6FA}_{S}^{1})\geqslant q$
was shown by Igusa [Reference Igusa19], and there are examples where the equality does not hold, cf. [Reference Igusa20, p. 964, The Example], [Reference Mumford25, p. 341, Corollary]Footnote
1
.
Moreover, the linear genus
![]() $p^{(1)}(S):=K_{S}^{2}+1$
is the arithmetic genus of any canonical divisor on the minimal surface. It is a birational invariant for every nonruled algebraic surface.
$p^{(1)}(S):=K_{S}^{2}+1$
is the arithmetic genus of any canonical divisor on the minimal surface. It is a birational invariant for every nonruled algebraic surface.
The classification of smooth projective integral curves
![]() $C$
is given in terms of the genus
$C$
is given in terms of the genus
![]() $g(C):=h^{0}({\mathcal{O}}_{C}(K_{C}))$
:
$g(C):=h^{0}({\mathcal{O}}_{C}(K_{C}))$
:
(I)
 $g(C)=0\;\Longleftrightarrow \;C\cong \mathbb{P}^{1}$
;
$g(C)=0\;\Longleftrightarrow \;C\cong \mathbb{P}^{1}$
;(II)
 $g(C)=1\;\Longleftrightarrow \;{\mathcal{O}}_{C}\cong {\mathcal{O}}_{C}(K_{C})\;\Longleftrightarrow \;C$
is an elliptic curve (it is isomorphic to a plane cubic curve);
$g(C)=1\;\Longleftrightarrow \;{\mathcal{O}}_{C}\cong {\mathcal{O}}_{C}(K_{C})\;\Longleftrightarrow \;C$
is an elliptic curve (it is isomorphic to a plane cubic curve);(III)
 $g(C)\geqslant 2\;\Longleftrightarrow \;C$
is of general type, i.e.,
$g(C)\geqslant 2\;\Longleftrightarrow \;C$
is of general type, i.e.,
 $H^{0}(C,{\mathcal{O}}_{C}(mK_{C}))$
yields an embedding of
$H^{0}(C,{\mathcal{O}}_{C}(mK_{C}))$
yields an embedding of
 $C$
for all
$C$
for all
 $m\geqslant 3$
.
$m\geqslant 3$
.
Enriques and Castelnuovo ([Reference Enriques15] and [Reference Castelnuovo and Enriques10]) were able to classify surfaces essentially in terms of
![]() $P_{12}(S)$
, as follows:
$P_{12}(S)$
, as follows:
Theorem 1.1. (
 $P_{12}$
-theorem of Castelnuovo–Enriques)
$P_{12}$
-theorem of Castelnuovo–Enriques)
Let
![]() $S$
be a smooth projective surface defined over an algebraically closed field
$S$
be a smooth projective surface defined over an algebraically closed field
![]() $k$
of characteristic zero, and let
$k$
of characteristic zero, and let
![]() $p^{(1)}(S):=K_{S}^{2}+1$
be the linear genus of a minimal model in the birational equivalence class of
$p^{(1)}(S):=K_{S}^{2}+1$
be the linear genus of a minimal model in the birational equivalence class of
![]() $S$
where
$S$
where
![]() $P_{12}>0$
. Then
$P_{12}>0$
. Then
(I)
 $P_{12}(S)=0\;\Longleftrightarrow \;S$
is ruled
$P_{12}(S)=0\;\Longleftrightarrow \;S$
is ruled
 $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
 $S$
is birational to a product
$S$
is birational to a product
 $C\times \mathbb{P}^{1}$
,
$C\times \mathbb{P}^{1}$
,
 $g(C)=q(S)=h(S)$
.
$g(C)=q(S)=h(S)$
.(II)
 $P_{12}=1\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(12K_{S})$
.
$P_{12}=1\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(12K_{S})$
.(III)
 $P_{12}\geqslant 2$
and
$P_{12}\geqslant 2$
and
 $p^{(1)}(S)=1\;\Longleftrightarrow \;S$
is properly elliptic, i.e.,
$p^{(1)}(S)=1\;\Longleftrightarrow \;S$
is properly elliptic, i.e.,
 $H^{0}(S,{\mathcal{O}}_{S}(12K_{S}))$
yields a fibration over a curve with general fibers elliptic curves
$H^{0}(S,{\mathcal{O}}_{S}(12K_{S}))$
yields a fibration over a curve with general fibers elliptic curves(IV)
 $P_{12}\geqslant 2$
and
$P_{12}\geqslant 2$
and
 $p^{(1)}(S)>1\;\Longleftrightarrow \;S$
is of general type, i.e.,
$p^{(1)}(S)>1\;\Longleftrightarrow \;S$
is of general type, i.e.,
 $H^{0}(S,{\mathcal{O}}_{S}(mK_{S}))$
yields a birational embedding of
$H^{0}(S,{\mathcal{O}}_{S}(mK_{S}))$
yields a birational embedding of
 $S$
for
$S$
for
 $m$
large (
$m$
large (
 $m\geqslant 5$
indeed suffices, as conjectured by Enriques in [Reference Enriques17] and proven by Bombieri [Reference Bombieri3, Main Theorem]).
$m\geqslant 5$
indeed suffices, as conjectured by Enriques in [Reference Enriques17] and proven by Bombieri [Reference Bombieri3, Main Theorem]).
Moreover, if
![]() $S$
is minimal, then in modern terminology:
$S$
is minimal, then in modern terminology:
∙
 $\text{Case (I)}~S\cong \mathbb{P}^{2}$
or
$\text{Case (I)}~S\cong \mathbb{P}^{2}$
or
 $S$
is a
$S$
is a
 $\mathbb{P}^{1}$
-bundle over a curve
$\mathbb{P}^{1}$
-bundle over a curve
 $C$
.
$C$
.∙
 $\text{Case (II)}~p_{g}(S)=1,q(S)=2\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(K_{S})$
,
$\text{Case (II)}~p_{g}(S)=1,q(S)=2\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(K_{S})$
,
 $q(S)=2\;\Longleftrightarrow \;S$
is an Abelian surface.
$q(S)=2\;\Longleftrightarrow \;S$
is an Abelian surface.∙
 $\text{Case (II)}~p_{g}(S)=1,q(S)=0\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(K_{S})$
,
$\text{Case (II)}~p_{g}(S)=1,q(S)=0\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(K_{S})$
,
 $q(S)=0\;\Longleftrightarrow \;S$
is a K3 surface.
$q(S)=0\;\Longleftrightarrow \;S$
is a K3 surface.∙
 $\text{Case (II)}~p_{g}(S)=0,q(S)=0\;\Longleftrightarrow \;{\mathcal{O}}_{S}\ncong {\mathcal{O}}_{S}(K_{S})$
,
$\text{Case (II)}~p_{g}(S)=0,q(S)=0\;\Longleftrightarrow \;{\mathcal{O}}_{S}\ncong {\mathcal{O}}_{S}(K_{S})$
,
 ${\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(2K_{S})$
,
${\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(2K_{S})$
,
 $q(S)=0\;\Longleftrightarrow \;S$
is an Enriques surface.
$q(S)=0\;\Longleftrightarrow \;S$
is an Enriques surface.∙
 $\text{Case (II)}~q(S)=1(\Rightarrow p_{g}(S)=0)\;\Longleftrightarrow \;{\mathcal{O}}_{S}\ncong {\mathcal{O}}_{S}(K_{S}),{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(mK_{S})$
, for some
$\text{Case (II)}~q(S)=1(\Rightarrow p_{g}(S)=0)\;\Longleftrightarrow \;{\mathcal{O}}_{S}\ncong {\mathcal{O}}_{S}(K_{S}),{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(mK_{S})$
, for some
 $m\in \{2,3,4,6\},q(S)=1\;\Longleftrightarrow \;S$
is a hyperelliptic surface.
$m\in \{2,3,4,6\},q(S)=1\;\Longleftrightarrow \;S$
is a hyperelliptic surface.∙
 $\text{Case (III)}~p_{a}(S)=-1\;\Longleftrightarrow \;S\cong C\times E,g(E)=1,g(C)=q(S)-1$
.
$\text{Case (III)}~p_{a}(S)=-1\;\Longleftrightarrow \;S\cong C\times E,g(E)=1,g(C)=q(S)-1$
.
A modern account of the Castelnuovo–Enriques classification of surfaces was first given in [Reference S̆afarevic̆, Averbuh, Vaĭnberg, Z̆iz̆c̆enko, Manin, Moĭs̆ezon, Tjurina and Tjurin32], [Reference Kodaira24], then it appeared also in [Reference Bombieri and Husemoller4], [Reference Beauville2] ([Reference Beauville2] is the only text which mentions the
![]() $P_{12}$
-theorem, in the historical note on p. 118), later also in [Reference Bădescu1] and [Reference Barth, Peters and Van de Ven7].
$P_{12}$
-theorem, in the historical note on p. 118), later also in [Reference Bădescu1] and [Reference Barth, Peters and Van de Ven7].
Remark 1.2. (i) Nowadays, cases (I)-(IV) are distinguished according to the Kodaira dimension, which is defined to be
![]() $-\infty$
if all the plurigenera vanish (
$-\infty$
if all the plurigenera vanish (
![]() $P_{n}=0~\forall n\geqslant 1$
), otherwise it is defined as the maximal dimension of the image of some
$P_{n}=0~\forall n\geqslant 1$
), otherwise it is defined as the maximal dimension of the image of some
![]() $n$
-pluricanonical map (the map associated with
$n$
-pluricanonical map (the map associated with
![]() $H^{0}({\mathcal{O}}_{X}(nK_{X}))$
).
$H^{0}({\mathcal{O}}_{X}(nK_{X}))$
).
(ii) The occurrence of the number
![]() $12$
is rather miraculous: it first appears since, by the canonical divisor formula 1.6, in case (II) the equation
$12$
is rather miraculous: it first appears since, by the canonical divisor formula 1.6, in case (II) the equation
admits only the following (positive) integer solutions:
and then we get a set of integers
![]() $m_{j}$
whose least common multiple is precisely
$m_{j}$
whose least common multiple is precisely
![]() $12$
.
$12$
.
Respectively, we have
![]() $2K_{S}\equiv 0,3K_{S}\equiv 0,4K_{S}\equiv 0,6K_{S}\equiv 0,$
where
$2K_{S}\equiv 0,3K_{S}\equiv 0,4K_{S}\equiv 0,6K_{S}\equiv 0,$
where
![]() $D\equiv 0$
means that
$D\equiv 0$
means that
![]() $D$
is linearly equivalent to zero, i.e.,
$D$
is linearly equivalent to zero, i.e.,
![]() ${\mathcal{O}}_{S}(D)\cong {\mathcal{O}}_{S}$
. It follows that in case (II) we have
${\mathcal{O}}_{S}(D)\cong {\mathcal{O}}_{S}$
. It follows that in case (II) we have
![]() $12K_{S}\equiv 0$
, hence
$12K_{S}\equiv 0$
, hence
![]() $P_{12}=1$
.
$P_{12}=1$
.
The second occurrence is more subtle, and is the heart of the theorem: in case (III) one has
![]() $P_{12}\geqslant 2$
.
$P_{12}\geqslant 2$
.
It is now customary (the name “key theorem” is due to [Reference Beauville2]) to see the two major steps of surface classification as follows:
Theorem 1.3. (Key theorem)
If
![]() $S$
is minimal, then
$S$
is minimal, then
![]() $K_{S}$
is
$K_{S}$
is
![]() $\text{nef}$
(i.e.,
$\text{nef}$
(i.e.,
![]() $K_{S}\cdot C\geqslant 0$
for all curves
$K_{S}\cdot C\geqslant 0$
for all curves
![]() $C\subset S$
)
$C\subset S$
)
![]() $\;\Longleftrightarrow \;S$
is nonruled.
$\;\Longleftrightarrow \;S$
is nonruled.
Theorem 1.4. (Crucial theorem)
![]() $S$
is minimal, with
$S$
is minimal, with
![]() $p_{g}(S)=0,q(S)=1$
$p_{g}(S)=0,q(S)=1$
![]() $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
![]() $S$
is
$S$
is
![]() $\text{isogenous}$
to a product, i.e.,
$\text{isogenous}$
to a product, i.e.,
![]() $S$
is the quotient
$S$
is the quotient
![]() $(C_{1}\times C_{2})/G$
of a product of curves of genera
$(C_{1}\times C_{2})/G$
of a product of curves of genera
by a free action of a finite group of product type (
![]() $G$
acts faithfully on
$G$
acts faithfully on
![]() $C_{1},C_{2}$
and we take the diagonal action
$C_{1},C_{2}$
and we take the diagonal action
![]() $g(x,y):=(gx,gy)$
), and such that moreover if we denote by
$g(x,y):=(gx,gy)$
), and such that moreover if we denote by
![]() $g_{j}^{\prime }=g(C_{j}/G)$
, then
$g_{j}^{\prime }=g(C_{j}/G)$
, then
![]() $g_{1}^{\prime }+g_{2}^{\prime }=1$
.
$g_{1}^{\prime }+g_{2}^{\prime }=1$
.
More precisely, let
![]() $A$
be the Albanese variety of
$A$
be the Albanese variety of
![]() $S$
, which is an elliptic curve and let
$S$
, which is an elliptic curve and let
be the Albanese map.
Then either:
(1)
 $S$
is a hyperelliptic surface,
$S$
is a hyperelliptic surface,
 $g_{2}=1$
,
$g_{2}=1$
,
 $G$
is a subgroup of translations of
$G$
is a subgroup of translations of
 $C_{1}$
,
$C_{1}$
,
 $A=C_{1}/G$
, while
$A=C_{1}/G$
, while
 $C_{2}/G\cong \mathbb{P}^{1}$
.
$C_{2}/G\cong \mathbb{P}^{1}$
.In this case all the fibers of the Albanese map are isomorphic to
 $C_{2}$
,
$C_{2}$
,
 $P_{12}(S)=1$
and
$P_{12}(S)=1$
and
 $S$
admits also an elliptic fibration
$S$
admits also an elliptic fibration
 $\unicode[STIX]{x1D713}:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
.
$\unicode[STIX]{x1D713}:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
.(2)
 $S$
is properly elliptic (
$S$
is properly elliptic (
 $P_{12}(S)\geqslant 2$
) and the genus
$P_{12}(S)\geqslant 2$
) and the genus
 $g=g_{2}$
of the Albanese fibers satisfies
$g=g_{2}$
of the Albanese fibers satisfies
 $g_{2}\geqslant 2$
: again
$g_{2}\geqslant 2$
: again
 $G$
is a subgroup of translations of
$G$
is a subgroup of translations of
 $C_{1}$
,
$C_{1}$
,
 $A=C_{1}/G$
,
$A=C_{1}/G$
,
 $C_{2}/G\cong \mathbb{P}^{1}$
, all the fibers of the Albanese map are isomorphic to
$C_{2}/G\cong \mathbb{P}^{1}$
, all the fibers of the Albanese map are isomorphic to
 $C_{2}$
.
$C_{2}$
.(3)
 $S$
is properly elliptic (
$S$
is properly elliptic (
 $P_{12}(S)\geqslant 2$
) and the genus
$P_{12}(S)\geqslant 2$
) and the genus
 $g=g_{1}$
of an Albanese fiber satisfies
$g=g_{1}$
of an Albanese fiber satisfies
 $g_{1}=1$
:
$g_{1}=1$
:
 $A=C_{2}/G$
,
$A=C_{2}/G$
,
 $C_{1}/G\cong \mathbb{P}^{1}$
, and the fibers of the Albanese map are either isomorphic to the elliptic curve
$C_{1}/G\cong \mathbb{P}^{1}$
, and the fibers of the Albanese map are either isomorphic to the elliptic curve $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:S=(C_{1}\times C_{2})/G\rightarrow A=C_{2}/G\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:S=(C_{1}\times C_{2})/G\rightarrow A=C_{2}/G\end{eqnarray}$$
 $C_{1}$
or are multiples of smooth elliptic curves isogenous to
$C_{1}$
or are multiples of smooth elliptic curves isogenous to
 $C_{1}$
.
$C_{1}$
.
Remark 1.5. A crucial observation, used by Enriques in [Reference Enriques15] for the
![]() $P_{12}$
-theorem is that in the first two cases the group
$P_{12}$
-theorem is that in the first two cases the group
![]() $G$
is Abelian. The crucial ingredient is the canonical divisor (canonical bundle) formula, established by Enriques and Kodaira, and then extended to positive characteristic by Bombieri and Mumford.
$G$
is Abelian. The crucial ingredient is the canonical divisor (canonical bundle) formula, established by Enriques and Kodaira, and then extended to positive characteristic by Bombieri and Mumford.
Theorem 1.6. [Reference Bombieri and Mumford5, p. 27, Theorem 2]
Let
![]() $f:S\rightarrow C$
be a relatively minimal fibration such that the arithmetic genus of a fiber equals
$f:S\rightarrow C$
be a relatively minimal fibration such that the arithmetic genus of a fiber equals
![]() $1$
(the general fiber is necessarily smooth elliptic in characteristic zero, but it can be rational with one cusp in characteristic
$1$
(the general fiber is necessarily smooth elliptic in characteristic zero, but it can be rational with one cusp in characteristic
![]() $2$
or
$2$
or
![]() $3$
: the latter is called the quasielliptic case).
$3$
: the latter is called the quasielliptic case).
Let
![]() $\{q_{1},\ldots ,q_{r}\}\subset C$
be the set of points over which the fiber
$\{q_{1},\ldots ,q_{r}\}\subset C$
be the set of points over which the fiber
![]() $f^{-1}(q_{i})=m_{i}F_{i}^{\prime }$
is a multiple fiber (i.e.,
$f^{-1}(q_{i})=m_{i}F_{i}^{\prime }$
is a multiple fiber (i.e.,
![]() $m_{i}\geqslant 2$
and
$m_{i}\geqslant 2$
and
![]() $F_{i}^{\prime }$
is not a multiple of any proper subdivisor), and consider the coherent sheaf
$F_{i}^{\prime }$
is not a multiple of any proper subdivisor), and consider the coherent sheaf
![]() $R^{1}f_{\ast }({\mathcal{O}}_{{\mathcal{S}}})$
on the smooth curve
$R^{1}f_{\ast }({\mathcal{O}}_{{\mathcal{S}}})$
on the smooth curve
![]() $C$
, which decomposes as
$C$
, which decomposes as
where
![]() ${\mathcal{O}}_{C}(L)$
is an invertible sheaf and
${\mathcal{O}}_{C}(L)$
is an invertible sheaf and
![]() $T$
is a torsion subsheaf with
$T$
is a torsion subsheaf with
![]() $\text{supp}(T)\subset \{q_{1},\ldots ,q_{r}\}$
. The fibers over the points of
$\text{supp}(T)\subset \{q_{1},\ldots ,q_{r}\}$
. The fibers over the points of
![]() $\text{supp}(T)$
are called
$\text{supp}(T)$
are called
![]() $\text{wild fibers}$
, moreover
$\text{wild fibers}$
, moreover
![]() $T=0$
if
$T=0$
if
![]() $\text{char}(k)=0$
.
$\text{char}(k)=0$
.
Then
where
(i)
 $0\leqslant a_{i}<m_{i}$
;
$0\leqslant a_{i}<m_{i}$
;(ii)
 $a_{i}=m_{i}-1$
if
$a_{i}=m_{i}-1$
if
 $m_{i}F_{i}^{\prime }$
is not wild (i.e.,
$m_{i}F_{i}^{\prime }$
is not wild (i.e.,
 $q_{i}\notin \text{supp}(T)$
);
$q_{i}\notin \text{supp}(T)$
);(iii)
 $d:=\deg (\unicode[STIX]{x1D6FF})=\deg (-L+K_{C})=2g(C)-2+\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+length(T)$
, where
$d:=\deg (\unicode[STIX]{x1D6FF})=\deg (-L+K_{C})=2g(C)-2+\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+length(T)$
, where
 $g(C)$
is the genus of
$g(C)$
is the genus of
 $C$
.
$C$
.
Let us see how the above applies in characteristic zero and in the special subcase:
![]() $p_{g}=0,q=1$
, the genus of the Albanese fibers equals
$p_{g}=0,q=1$
, the genus of the Albanese fibers equals
![]() $1$
, and there exists a multiple fiber.
$1$
, and there exists a multiple fiber.
Then, for
![]() $n=2$
, since we have
$n=2$
, since we have
![]() $\deg (\unicode[STIX]{x1D6FF})=0$
, it follows that
$\deg (\unicode[STIX]{x1D6FF})=0$
, it follows that
The divisor
![]() $2\unicode[STIX]{x1D6FF}+\sum _{i=1}^{r}q_{i}$
is effective by the Riemann–Roch theorem on the elliptic curve
$2\unicode[STIX]{x1D6FF}+\sum _{i=1}^{r}q_{i}$
is effective by the Riemann–Roch theorem on the elliptic curve
![]() $A$
, so we have written
$A$
, so we have written
![]() $2K_{S}$
as the sum of two effective divisors.
$2K_{S}$
as the sum of two effective divisors.
Hence we obtain that
![]() $P_{2}\geqslant 1$
, and similarly one gets that
$P_{2}\geqslant 1$
, and similarly one gets that
![]() $P_{12}\geqslant 6$
.
$P_{12}\geqslant 6$
.
2 The
 $P_{12}$
-theorem in positive characteristic
$P_{12}$
-theorem in positive characteristic
The extension of the Castelnuovo–Enriques classification of surfaces to the case of positive characteristic was achieved by Mumford and Bombieri (cf. [Reference Bombieri and Mumford6, Section 3], [Reference Bombieri and Mumford5, Theorem 1]).
In a remarkable series of three papers they got most of the following full result.
Theorem 2.1. (
 $P_{12}$
-theorem in positive characteristic)
$P_{12}$
-theorem in positive characteristic)
Let
![]() $S$
be a projective smooth surface defined over an algebraically closed field
$S$
be a projective smooth surface defined over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $p^{(1)}(S):=K_{S}^{2}+1$
be the linear genus of a minimal model in the birational equivalence class of
$p^{(1)}(S):=K_{S}^{2}+1$
be the linear genus of a minimal model in the birational equivalence class of
![]() $S$
where
$S$
where
![]() $P_{12}>0$
. Then
$P_{12}>0$
. Then
(I)
 $P_{12}(S)=0\;\Longleftrightarrow \;S$
is ruled
$P_{12}(S)=0\;\Longleftrightarrow \;S$
is ruled
 $\;\Longleftrightarrow \;S$
is birational to a product
$\;\Longleftrightarrow \;S$
is birational to a product
 $C\times \mathbb{P}^{1}$
,
$C\times \mathbb{P}^{1}$
,
 $g(C)=q(S)=h(S)$
.
$g(C)=q(S)=h(S)$
.(II)
 $P_{12}=1\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(12K_{S})$
.
$P_{12}=1\;\Longleftrightarrow \;{\mathcal{O}}_{S}\cong {\mathcal{O}}_{S}(12K_{S})$
.(III)
 $P_{12}\geqslant 2$
and
$P_{12}\geqslant 2$
and
 $p^{(1)}(S)=1\;\Longleftrightarrow \;S$
is properly elliptic or properly quasielliptic, i.e.,
$p^{(1)}(S)=1\;\Longleftrightarrow \;S$
is properly elliptic or properly quasielliptic, i.e.,
 $H^{0}(S,{\mathcal{O}}_{S}(12K_{S}))$
yields a fibration over a curve with general fibers either elliptic curves or rational curves with one cusp.
$H^{0}(S,{\mathcal{O}}_{S}(12K_{S}))$
yields a fibration over a curve with general fibers either elliptic curves or rational curves with one cusp.(IV)
 $P_{12}\geqslant 2$
and
$P_{12}\geqslant 2$
and
 $p^{(1)}(S)>1\;\Longleftrightarrow \;S$
is of general type, i.e.,
$p^{(1)}(S)>1\;\Longleftrightarrow \;S$
is of general type, i.e.,
 $H^{0}(S,{\mathcal{O}}_{S}(mK_{S}))$
yields a birational embedding of
$H^{0}(S,{\mathcal{O}}_{S}(mK_{S}))$
yields a birational embedding of
 $S$
for
$S$
for
 $m$
large (indeed,
$m$
large (indeed,
 $m\geqslant 5$
suffices).
$m\geqslant 5$
suffices).
Moreover, Bombieri and Mumford in [Reference Bombieri and Mumford5] and [Reference Bombieri and Mumford6] gave a full description of the surfaces in the classes (I) and (II) (with new nonclassical surfaces), but classes (II) and (III) were not distinguished by the behavior of the 12th plurigenus, but only by the Kodaira dimension, i.e., by the growth of
![]() $P_{n}(S)$
as
$P_{n}(S)$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
The sharp statement (
![]() $\forall m\geqslant 5$
) in case (IV), established by Bombieri [Reference Bombieri3, Main Theorem] in characteristic zero, was extended by Ekedahl’s to the case of positive characteristic (cf. [Reference Ekedahl14, Main Theorem], see also [Reference Catanese and Franciosi11] and [Reference Catanese, Franciosi, Hulek and Reid12] for a somewhat simpler proof).
$\forall m\geqslant 5$
) in case (IV), established by Bombieri [Reference Bombieri3, Main Theorem] in characteristic zero, was extended by Ekedahl’s to the case of positive characteristic (cf. [Reference Ekedahl14, Main Theorem], see also [Reference Catanese and Franciosi11] and [Reference Catanese, Franciosi, Hulek and Reid12] for a somewhat simpler proof).
3 Auxiliary results and proof of the
 $P_{12}$
-theorem
$P_{12}$
-theorem
Case (III) can be divided into two subcases: properly elliptic fibrations and properly quasielliptic fibrations.
Recall the definition of quasielliptic surfaces:
Definition 3.1. A quasielliptic surface
![]() $S$
is a nonsingular projective surface admitting a fibration
$S$
is a nonsingular projective surface admitting a fibration
![]() $f:S\rightarrow C$
over a nonsingular projective curve
$f:S\rightarrow C$
over a nonsingular projective curve
![]() $C$
such that
$C$
such that
![]() $f_{\ast }{\mathcal{O}}_{S}={\mathcal{O}}_{C}$
and such that the general fibers of
$f_{\ast }{\mathcal{O}}_{S}={\mathcal{O}}_{C}$
and such that the general fibers of
![]() $f$
are rational curves with one cusp.
$f$
are rational curves with one cusp.
If the fibration
![]() $f$
is induced by
$f$
is induced by
![]() $H^{0}(S,{\mathcal{O}}_{S}(nK_{S}))$
for some
$H^{0}(S,{\mathcal{O}}_{S}(nK_{S}))$
for some
![]() $n>0$
, we call
$n>0$
, we call
![]() $S$
a properly quasielliptic surface.
$S$
a properly quasielliptic surface.
Remark 3.2. (1) By a result of Tate (cf. [Reference Tate34, Corollary 1]), quasielliptic fibrations only appear in characteristic 2 and 3.
(2) In case (III), where
![]() $P_{n}(S):=\dim H^{0}(S,{\mathcal{O}}_{S}(nK_{S}))$
grows linearly with
$P_{n}(S):=\dim H^{0}(S,{\mathcal{O}}_{S}(nK_{S}))$
grows linearly with
![]() $n$
,
$n$
,
![]() $S$
is necessarily properly elliptic or properly quasielliptic.
$S$
is necessarily properly elliptic or properly quasielliptic.
The case where
![]() $S$
admits a properly elliptic fibration was treated by T. Katsura and K. Ueno who proved in [Reference Katsura and Ueno23, Theorem 5.2] that for any properly elliptic surface
$S$
admits a properly elliptic fibration was treated by T. Katsura and K. Ueno who proved in [Reference Katsura and Ueno23, Theorem 5.2] that for any properly elliptic surface
![]() $S$
,
$S$
,
![]() $\forall m\geqslant 14$
,
$\forall m\geqslant 14$
,
![]() $P_{m}(S)\geqslant 2$
and showed the existence of an example where
$P_{m}(S)\geqslant 2$
and showed the existence of an example where
![]() $P_{13}=1$
. They show that the situation is essentially the same as in characteristic zero. The fact that
$P_{13}=1$
. They show that the situation is essentially the same as in characteristic zero. The fact that
![]() $P_{12}(S)\geqslant 2$
follows from our more general theorem, which uses several auxiliary results developed by Raynaud and Katsura–Ueno (they will be recalled in the sequel).
$P_{12}(S)\geqslant 2$
follows from our more general theorem, which uses several auxiliary results developed by Raynaud and Katsura–Ueno (they will be recalled in the sequel).
Theorem 3.3. (Main Theorem)
Let
![]() $f:S\rightarrow C$
be a properly elliptic or quasielliptic fibration. Then:
$f:S\rightarrow C$
be a properly elliptic or quasielliptic fibration. Then:
(1)
 $P_{12}(S)\geqslant 2$
;
$P_{12}(S)\geqslant 2$
;(2) there exists
 $n\leqslant 4$
such that
$n\leqslant 4$
such that
 $P_{n}(S)\neq 0$
;
$P_{n}(S)\neq 0$
;(3) there exists
 $n\leqslant 8$
such that
$n\leqslant 8$
such that
 $P_{n}(S)\geqslant 2$
;
$P_{n}(S)\geqslant 2$
;(4)
 $\forall n\geqslant 14$
$\forall n\geqslant 14$
 $P_{n}(S)\geqslant 2$
.
$P_{n}(S)\geqslant 2$
.
Remark 3.4. Let us indicate the examples (see Remark 4.3) which show that in Theorem 3.3 the inequalities in our assumptions are best possible.
(2) and (4): in the notation of (2) of Theorem 1.4 we let
![]() $G=\mathbb{Z}/2\oplus \mathbb{Z}/6$
; in characteristic
$G=\mathbb{Z}/2\oplus \mathbb{Z}/6$
; in characteristic
![]() $\neq 2,3$
,
$\neq 2,3$
,
![]() $G$
is isomorphic to a subgroup of any elliptic curve. In order to obtain a curve
$G$
is isomorphic to a subgroup of any elliptic curve. In order to obtain a curve
![]() $C_{2}$
with an action of
$C_{2}$
with an action of
![]() $G$
such that
$G$
such that
![]() $C_{2}/G\cong \mathbb{P}^{1}$
we consider a
$C_{2}/G\cong \mathbb{P}^{1}$
we consider a
![]() $G$
-Galois covering
$G$
-Galois covering
![]() $C_{2}$
of
$C_{2}$
of
![]() $\mathbb{P}^{1}$
branched in
$\mathbb{P}^{1}$
branched in
![]() $3$
points, and with local monodromies
$3$
points, and with local monodromies
In the characteristic zero case this exists by Riemann’s existence theorem (since the sum of the three local monodromies equals zero). Indeed the resulting curve has affine equation
![]() $y^{2}=x^{6}-1$
, which is smooth in characteristic
$y^{2}=x^{6}-1$
, which is smooth in characteristic
![]() $\neq 2,3$
. Hence we get such a curve for any characteristic
$\neq 2,3$
. Hence we get such a curve for any characteristic
![]() $\neq 2,3$
(see [Reference Katsura and Ueno23, Example 4.6]).
$\neq 2,3$
(see [Reference Katsura and Ueno23, Example 4.6]).
The fibration
![]() $f:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
is elliptic and has exactly three singular fibers, with multiplicities
$f:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
is elliptic and has exactly three singular fibers, with multiplicities
![]() $2,6,6$
. It follows that
$2,6,6$
. It follows that
where
![]() $[a]$
denotes the integral part of
$[a]$
denotes the integral part of
![]() $a$
.
$a$
.
It follows that
![]() $P_{1}=P_{2}=P_{3}=0$
,
$P_{1}=P_{2}=P_{3}=0$
,
![]() $P_{4}=P_{5}=1$
,
$P_{4}=P_{5}=1$
,
![]() $P_{6}=2$
,
$P_{6}=2$
,
![]() $P_{13}=1$
.
$P_{13}=1$
.
(2) and (3): in the notation of (2) of Theorem 1.4 we let
![]() $G=\mathbb{Z}/10$
; in characteristic
$G=\mathbb{Z}/10$
; in characteristic
![]() $\neq 2,5$
,
$\neq 2,5$
,
![]() $G$
is isomorphic to a subgroup of any elliptic curve. In order to obtain a curve
$G$
is isomorphic to a subgroup of any elliptic curve. In order to obtain a curve
![]() $C_{2}$
with an action of
$C_{2}$
with an action of
![]() $G$
such that
$G$
such that
![]() $C_{2}/G\cong \mathbb{P}^{1}$
we consider a
$C_{2}/G\cong \mathbb{P}^{1}$
we consider a
![]() $G$
-Galois covering
$G$
-Galois covering
![]() $C_{2}$
of
$C_{2}$
of
![]() $\mathbb{P}^{1}$
branched in
$\mathbb{P}^{1}$
branched in
![]() $3$
points, and with local monodromies
$3$
points, and with local monodromies
This exists in characteristic zero by Riemann’s existence theorem, since the sum of the three local monodromies is
![]() $10$
, which equals zero in
$10$
, which equals zero in
![]() $G$
. Indeed, the resulting curve is defined by the affine equation
$G$
. Indeed, the resulting curve is defined by the affine equation
![]() $y^{2}=x^{5}-1$
and we obtain therefore such a smooth curve for each characteristic
$y^{2}=x^{5}-1$
and we obtain therefore such a smooth curve for each characteristic
![]() $\neq 2,5$
.
$\neq 2,5$
.
The fibration
![]() $f:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
is elliptic and has exactly three singular fibers, with multiplicities
$f:S\rightarrow C_{2}/G\cong \mathbb{P}^{1}$
is elliptic and has exactly three singular fibers, with multiplicities
![]() $2,5,10$
. It follows that
$2,5,10$
. It follows that
Follows that
![]() $P_{1}=P_{2}=P_{3}=0$
,
$P_{1}=P_{2}=P_{3}=0$
,
![]() $P_{4}=P_{5}=P_{6}=P_{7}=1$
,
$P_{4}=P_{5}=P_{6}=P_{7}=1$
,
![]() $P_{8}=P_{9}=2$
,
$P_{8}=P_{9}=2$
,
![]() $P_{10}=3,P_{11}=1,P_{12}=P_{13}=2$
.
$P_{10}=3,P_{11}=1,P_{12}=P_{13}=2$
.
In the case of properly quasielliptic fibrations, we shall use some result of Raynaud, [Reference Raynaud31], and a corollary developed by Katsura and Ueno [Reference Katsura and Ueno23, Lemmas 2.3 and 2.4].
Given a multiple fiber
![]() $mF^{\prime }$
we denote by
$mF^{\prime }$
we denote by
![]() $\unicode[STIX]{x1D714}_{n}:={\mathcal{O}}_{nF^{\prime }}(K_{S}+nF^{\prime })$
the dualizing sheaf of
$\unicode[STIX]{x1D714}_{n}:={\mathcal{O}}_{nF^{\prime }}(K_{S}+nF^{\prime })$
the dualizing sheaf of
![]() $nF^{\prime }$
.
$nF^{\prime }$
.
Observe that
![]() $F^{\prime }$
is an indecomposable divisor of elliptic type (see [Reference Mumford27, p. 330]Footnote
2
for the definition), hence (see [Reference Mumford27, p. 332] [Reference Catanese, Franciosi, Hulek and Reid12, Theorem 3.3]) for any degree-zero divisor
$F^{\prime }$
is an indecomposable divisor of elliptic type (see [Reference Mumford27, p. 330]Footnote
2
for the definition), hence (see [Reference Mumford27, p. 332] [Reference Catanese, Franciosi, Hulek and Reid12, Theorem 3.3]) for any degree-zero divisor
![]() $L$
on
$L$
on
![]() $F^{\prime }$
, we have
$F^{\prime }$
, we have
![]() $h^{0}({\mathcal{O}}_{F^{\prime }}(L))=h^{1}({\mathcal{O}}_{F^{\prime }}(L))$
, and these dimensions are either
$h^{0}({\mathcal{O}}_{F^{\prime }}(L))=h^{1}({\mathcal{O}}_{F^{\prime }}(L))$
, and these dimensions are either
![]() $=0$
, or
$=0$
, or
![]() $=1$
, the latter case occurring if and only if
$=1$
, the latter case occurring if and only if
![]() ${\mathcal{O}}_{F^{\prime }}(L)\cong {\mathcal{O}}_{F^{\prime }}$
.
${\mathcal{O}}_{F^{\prime }}(L)\cong {\mathcal{O}}_{F^{\prime }}$
.
Consider now the exact sequence
and apply the previous remark for
![]() $L=-(n-1)F^{\prime }$
to deduce that
$L=-(n-1)F^{\prime }$
to deduce that
The second equality holds only if
Conversely, if (∗) holds, either
![]() $h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})$
and
$h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})$
and
![]() $h^{1}({\mathcal{O}}_{nF^{\prime }})=h^{1}({\mathcal{O}}_{(n-1)F^{\prime }})$
, or both
$h^{1}({\mathcal{O}}_{nF^{\prime }})=h^{1}({\mathcal{O}}_{(n-1)F^{\prime }})$
, or both
![]() $h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})+1$
and
$h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})+1$
and
![]() $h^{1}({\mathcal{O}}_{nF^{\prime }})=h^{1}({\mathcal{O}}_{(n-1)F^{\prime }})+1$
.
$h^{1}({\mathcal{O}}_{nF^{\prime }})=h^{1}({\mathcal{O}}_{(n-1)F^{\prime }})+1$
.
This in any case shows that the function
![]() $h^{0}({\mathcal{O}}_{nF^{\prime }})$
is monotonously nondecreasing. One says that
$h^{0}({\mathcal{O}}_{nF^{\prime }})$
is monotonously nondecreasing. One says that
![]() $n$
is a jumping value if
$n$
is a jumping value if
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})+1.$
Considering all the
$h^{0}({\mathcal{O}}_{nF^{\prime }})=h^{0}({\mathcal{O}}_{(n-1)F^{\prime }})+1.$
Considering all the
![]() $n\geqslant 1$
, we can then define the first jumping value, the second, and so on (they are then clearly
$n\geqslant 1$
, we can then define the first jumping value, the second, and so on (they are then clearly
![]() ${\geqslant}2$
).
${\geqslant}2$
).
Recall now:
Proposition 3.5. [Reference Bombieri and Mumford5, Proposition 4]
Since
![]() $({\mathcal{O}}_{F_{i}^{\prime }}(F_{i}^{\prime }))$
is a torsion element in the Picard group of
$({\mathcal{O}}_{F_{i}^{\prime }}(F_{i}^{\prime }))$
is a torsion element in the Picard group of
![]() $F_{i}^{\prime }$
, we consider its torsion order:
$F_{i}^{\prime }$
, we consider its torsion order:
We have then
(1)
 $\unicode[STIX]{x1D708}_{i}$
divides both
$\unicode[STIX]{x1D708}_{i}$
divides both
 $m_{i}$
and
$m_{i}$
and
 $a_{i}+1$
;
$a_{i}+1$
;(2) letting
 $p=\text{char}(k)$
, there exists an integer
$p=\text{char}(k)$
, there exists an integer
 $e_{i}\geqslant 0$
such that
$e_{i}\geqslant 0$
such that
 $m_{i}=\unicode[STIX]{x1D708}_{i}\cdot p^{e_{i}};$
$m_{i}=\unicode[STIX]{x1D708}_{i}\cdot p^{e_{i}};$
(3)
 $h^{0}(F_{i}^{\prime },{\mathcal{O}}_{(\unicode[STIX]{x1D708}_{i}+1)F_{i}^{\prime }})=2$
,
$h^{0}(F_{i}^{\prime },{\mathcal{O}}_{(\unicode[STIX]{x1D708}_{i}+1)F_{i}^{\prime }})=2$
,
 $h^{0}(F_{i},{\mathcal{O}}_{\unicode[STIX]{x1D708}_{i}F_{i}^{\prime }})=1$
, so that
$h^{0}(F_{i},{\mathcal{O}}_{\unicode[STIX]{x1D708}_{i}F_{i}^{\prime }})=1$
, so that
 $\unicode[STIX]{x1D708}_{i}+1$
is a jumping value;
$\unicode[STIX]{x1D708}_{i}+1$
is a jumping value;(4)
 $h^{0}(F_{i}^{\prime },{\mathcal{O}}_{rF_{i}^{\prime }})$
is a nondecreasing function of
$h^{0}(F_{i}^{\prime },{\mathcal{O}}_{rF_{i}^{\prime }})$
is a nondecreasing function of
 $r$
.
$r$
.
Proof. In the proof we suppress the subscripts.
(4) follows from the above discussion.
(3) consider the exact sequence:
Passing to the exact cohomology sequence we get
By our previous argument, we see that
![]() $H^{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}F^{\prime }})\simeq k$
. Since
$H^{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}F^{\prime }})\simeq k$
. Since
![]() $H^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F^{\prime }}(-\unicode[STIX]{x1D708}F^{\prime }))$
is a space of functions which have value zero on
$H^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F^{\prime }}(-\unicode[STIX]{x1D708}F^{\prime }))$
is a space of functions which have value zero on
![]() $F^{\prime }$
, and the constants in
$F^{\prime }$
, and the constants in
![]() $H^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F})$
are mapped to constants in
$H^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F})$
are mapped to constants in
![]() $H^{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}F^{\prime }})$
, we see that
$H^{0}({\mathcal{O}}_{\unicode[STIX]{x1D708}F^{\prime }})$
, we see that
![]() $h^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F^{\prime }})=2$
.
$h^{0}({\mathcal{O}}_{(\unicode[STIX]{x1D708}+1)F^{\prime }})=2$
.
(1)
![]() $\unicode[STIX]{x1D708}$
divides
$\unicode[STIX]{x1D708}$
divides
![]() $m$
since
$m$
since
![]() $mF^{\prime }$
is trivial in a neighborhood of
$mF^{\prime }$
is trivial in a neighborhood of
![]() $F^{\prime }$
.
$F^{\prime }$
.
Note that
![]() ${\mathcal{O}}_{F^{\prime }}((a+1)F)\simeq \unicode[STIX]{x1D714}_{F^{\prime }}$
,
${\mathcal{O}}_{F^{\prime }}((a+1)F)\simeq \unicode[STIX]{x1D714}_{F^{\prime }}$
,
![]() $\unicode[STIX]{x1D714}_{F^{\prime }}$
is nef and has degree zero and
$\unicode[STIX]{x1D714}_{F^{\prime }}$
is nef and has degree zero and
![]() $h^{0}(\unicode[STIX]{x1D714}_{F^{\prime }})=h^{1}({\mathcal{O}}_{F^{\prime }})=h^{0}({\mathcal{O}}_{F^{\prime }})=1$
. Since
$h^{0}(\unicode[STIX]{x1D714}_{F^{\prime }})=h^{1}({\mathcal{O}}_{F^{\prime }})=h^{0}({\mathcal{O}}_{F^{\prime }})=1$
. Since
![]() $F^{\prime }$
is indecomposable of elliptic type, from the previous discussion, we have
$F^{\prime }$
is indecomposable of elliptic type, from the previous discussion, we have
![]() $\unicode[STIX]{x1D714}_{F^{\prime }}\simeq {\mathcal{O}}_{F^{\prime }}$
, hence
$\unicode[STIX]{x1D714}_{F^{\prime }}\simeq {\mathcal{O}}_{F^{\prime }}$
, hence
![]() $\unicode[STIX]{x1D708}|(a+1)$
.
$\unicode[STIX]{x1D708}|(a+1)$
.
(2) Set
![]() $o_{n}:=\text{Ord}({\mathcal{O}}_{nF^{\prime }}(F^{\prime }))$
. Since
$o_{n}:=\text{Ord}({\mathcal{O}}_{nF^{\prime }}(F^{\prime }))$
. Since
![]() ${\mathcal{O}}_{nF^{\prime }}(mF^{\prime })$
is trivial for any
${\mathcal{O}}_{nF^{\prime }}(mF^{\prime })$
is trivial for any
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
![]() $o_{n}|m$
. Using Lemma 3.8 (ii) we see that
$o_{n}|m$
. Using Lemma 3.8 (ii) we see that
![]() $o_{n-1}$
divides
$o_{n-1}$
divides
![]() $o_{n}$
and
$o_{n}$
and
![]() $o_{n}=p^{e_{n}}\unicode[STIX]{x1D708}$
for some nonnegative integer
$o_{n}=p^{e_{n}}\unicode[STIX]{x1D708}$
for some nonnegative integer
![]() $e_{n}$
. Noting that
$e_{n}$
. Noting that
![]() $m$
is the order of
$m$
is the order of
![]() $F^{\prime }$
in the formal neighborhood of
$F^{\prime }$
in the formal neighborhood of
![]() $F^{\prime }$
(cf. [Reference Raynaud30, Proposition 6.1.11 (3)]) it follows that
$F^{\prime }$
(cf. [Reference Raynaud30, Proposition 6.1.11 (3)]) it follows that
![]() $m|o_{n}$
for large
$m|o_{n}$
for large
![]() $n$
(cf. [Reference Raynaud30, Lemme 6.4.4]), hence
$n$
(cf. [Reference Raynaud30, Lemme 6.4.4]), hence
![]() $m=o_{n}$
for some large
$m=o_{n}$
for some large
![]() $n$
, therefore
$n$
, therefore
![]() $m=p^{e}\unicode[STIX]{x1D708}$
for some
$m=p^{e}\unicode[STIX]{x1D708}$
for some
![]() $e\geqslant 0$
.◻
$e\geqslant 0$
.◻
Using Proposition 3.5, we get the following corollary:
Corollary 3.6. [Reference Bombieri and Mumford5, p. 30, Corollary]
If
![]() $h^{1}(S,{\mathcal{O}}_{S})\leqslant 1$
, we have either
$h^{1}(S,{\mathcal{O}}_{S})\leqslant 1$
, we have either
or
More precise results are the following two lemmas of Raynaud (cf. [Reference Raynaud31], [Reference Bertapelle and Tong8, Section 2]).
Lemma 3.7. [Reference Raynaud31, Corollaire 3.7.6], [Reference Bertapelle and Tong8, Lemma 2.1.8]
Let
![]() $f:S\rightarrow C$
be an elliptic or quasielliptic fibration with
$f:S\rightarrow C$
be an elliptic or quasielliptic fibration with
![]() $f^{-1}(q)=mF^{\prime }$
a multiple fiber over
$f^{-1}(q)=mF^{\prime }$
a multiple fiber over
![]() $q\in C$
. Then for any integer
$q\in C$
. Then for any integer
![]() $n\geqslant 2$
:
$n\geqslant 2$
:
(i) The dualizing sheaf
 $\unicode[STIX]{x1D714}_{n}:={\mathcal{O}}_{nF^{\prime }}(K_{S}+nF^{\prime })$
of
$\unicode[STIX]{x1D714}_{n}:={\mathcal{O}}_{nF^{\prime }}(K_{S}+nF^{\prime })$
of
 $nF^{\prime }$
is nontrivial iff
$nF^{\prime }$
is nontrivial iff
 $h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})$
.
$h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})$
.(ii)
 $\unicode[STIX]{x1D714}_{n}$
is trivial iff
$\unicode[STIX]{x1D714}_{n}$
is trivial iff
 $h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})+1$
.
$h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})+1$
.
Lemma 3.8. [Reference Raynaud31, Lemma 3.7.7]
Notation being as in Lemma 3.7, observe that the invertible sheaves
![]() ${\mathcal{O}}_{nF^{\prime }}(F^{\prime })$
are torsion elements in the Picard group of
${\mathcal{O}}_{nF^{\prime }}(F^{\prime })$
are torsion elements in the Picard group of
![]() $nF^{\prime }$
. There are only two possibilities for their torsion orders. Setting
$nF^{\prime }$
. There are only two possibilities for their torsion orders. Setting
![]() $o_{n}:=\text{Ord}({\mathcal{O}}_{nF^{\prime }}(F^{\prime }))$
(hence
$o_{n}:=\text{Ord}({\mathcal{O}}_{nF^{\prime }}(F^{\prime }))$
(hence
![]() $o_{1}=\unicode[STIX]{x1D708}$
), we have
$o_{1}=\unicode[STIX]{x1D708}$
), we have
(i)
 $o_{n}=o_{n-1}$
;
$o_{n}=o_{n-1}$
;(ii)
 $o_{n}=p~o_{n-1}$
.
$o_{n}=p~o_{n-1}$
.
Moreover, case
![]() $(ii)$
occurs only if
$(ii)$
occurs only if
![]() $\unicode[STIX]{x1D714}_{n}$
is trivial.
$\unicode[STIX]{x1D714}_{n}$
is trivial.
Proof. Setting
![]() $\mathfrak{N}:={\mathcal{O}}_{F^{\prime }}(-(n-1)F^{\prime })$
, we consider the following two exact sequences:
$\mathfrak{N}:={\mathcal{O}}_{F^{\prime }}(-(n-1)F^{\prime })$
, we consider the following two exact sequences:
Since
![]() $\mathfrak{N}^{2}=0$
, the map
$\mathfrak{N}^{2}=0$
, the map
![]() $x\mapsto 1+x$
defines an isomorphism of abelian sheaves:
$x\mapsto 1+x$
defines an isomorphism of abelian sheaves:
Taking the induced long exact sequences of (2) and (3) and observing that
![]() $H^{2}(F^{\prime },\mathfrak{N})\simeq H^{2}(F^{\prime },1+\mathfrak{N})=0$
, we get
$H^{2}(F^{\prime },\mathfrak{N})\simeq H^{2}(F^{\prime },1+\mathfrak{N})=0$
, we get
and
By a result of Oort (cf. [Reference Oort.29, §6]), we have that
![]() $H^{1}(\unicode[STIX]{x1D6FD})(\text{Im}(\unicode[STIX]{x2202}))=\text{Im}(\unicode[STIX]{x2202}^{\ast })$
.
$H^{1}(\unicode[STIX]{x1D6FD})(\text{Im}(\unicode[STIX]{x2202}))=\text{Im}(\unicode[STIX]{x2202}^{\ast })$
.
Since
![]() $H^{1}(\mathfrak{N})$
is a
$H^{1}(\mathfrak{N})$
is a
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space, we see that any element in
$\mathbb{Z}/p\mathbb{Z}$
-vector space, we see that any element in
![]() $\ker (\unicode[STIX]{x1D6FC}^{\ast })$
has
$\ker (\unicode[STIX]{x1D6FC}^{\ast })$
has
![]() $p$
th power equal to
$p$
th power equal to
![]() $1$
, hence we have
$1$
, hence we have
![]() $o_{n}=o_{n-1}$
or
$o_{n}=o_{n-1}$
or
![]() $o_{n}=po_{n-1}$
.
$o_{n}=po_{n-1}$
.
If
![]() $o_{n}=po_{n-1}$
, then
$o_{n}=po_{n-1}$
, then
![]() $\ker (\unicode[STIX]{x1D6FC}^{\ast })\neq \{1\}$
and hence
$\ker (\unicode[STIX]{x1D6FC}^{\ast })\neq \{1\}$
and hence
![]() $\ker (\unicode[STIX]{x1D6FC})\neq \{0\}$
. Since
$\ker (\unicode[STIX]{x1D6FC})\neq \{0\}$
. Since
![]() $h^{1}(nF^{\prime },{\mathcal{O}}_{nF^{\prime }})=h^{0}(\unicode[STIX]{x1D714}_{n})$
, by Lemma 3.7 we have that
$h^{1}(nF^{\prime },{\mathcal{O}}_{nF^{\prime }})=h^{0}(\unicode[STIX]{x1D714}_{n})$
, by Lemma 3.7 we have that
![]() $h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})+1$
and
$h^{0}(\unicode[STIX]{x1D714}_{n})=h^{0}(\unicode[STIX]{x1D714}_{n-1})+1$
and
![]() $\unicode[STIX]{x1D714}_{n}$
is trivial.◻
$\unicode[STIX]{x1D714}_{n}$
is trivial.◻
Assume that we have a multiple fiber over the point
![]() $q_{j}$
, and denote by
$q_{j}$
, and denote by
![]() $t_{j}$
the length of the skyscraper sheaf
$t_{j}$
the length of the skyscraper sheaf
![]() $T$
at
$T$
at
![]() $q_{j}$
.
$q_{j}$
.
Then, by the base change theorem we have
The two lemmas by Raynaud imply the following useful corollary.
Corollary 3.9. [Reference Raynaud31, Lemma 3.7.9], [Reference Bertapelle and Tong8, Lemma 2.1.11], [Reference Katsura and Ueno23, Lemmas 2.3–2.4]
(1) Let
 $n_{j}^{(i)}$
be the
$n_{j}^{(i)}$
be the
 $i$
th jumping value of a wild fiber
$i$
th jumping value of a wild fiber
 $mF_{j}^{\prime }$
(recall that
$mF_{j}^{\prime }$
(recall that
 $n_{j}^{(i)}\geqslant 2$
).
$n_{j}^{(i)}\geqslant 2$
).Setting
 $\unicode[STIX]{x1D708}_{j}:=\text{Ord}({\mathcal{O}}_{F_{j}^{\prime }}(F_{j}^{\prime }))$
, we have and
$\unicode[STIX]{x1D708}_{j}:=\text{Ord}({\mathcal{O}}_{F_{j}^{\prime }}(F_{j}^{\prime }))$
, we have and $$\begin{eqnarray}n_{j}^{(1)}=\unicode[STIX]{x1D708}_{j}+1,\end{eqnarray}$$
$$\begin{eqnarray}n_{j}^{(1)}=\unicode[STIX]{x1D708}_{j}+1,\end{eqnarray}$$
 $$\begin{eqnarray}n_{j}^{(2)}=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D708}_{j}+1\quad & if~\text{Ord}({\mathcal{O}}_{(\unicode[STIX]{x1D708}_{j}+1)F_{j}^{\prime }})=\unicode[STIX]{x1D708}_{j},\\ (p+1)\unicode[STIX]{x1D708}_{j}+1\quad & if~\text{Ord}({\mathcal{O}}_{(\unicode[STIX]{x1D708}_{j}+1)F_{j}^{\prime }})=p\unicode[STIX]{x1D708}_{j}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}n_{j}^{(2)}=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D708}_{j}+1\quad & if~\text{Ord}({\mathcal{O}}_{(\unicode[STIX]{x1D708}_{j}+1)F_{j}^{\prime }})=\unicode[STIX]{x1D708}_{j},\\ (p+1)\unicode[STIX]{x1D708}_{j}+1\quad & if~\text{Ord}({\mathcal{O}}_{(\unicode[STIX]{x1D708}_{j}+1)F_{j}^{\prime }})=p\unicode[STIX]{x1D708}_{j}.\end{array}\right.\end{eqnarray}$$
(2) If
 $h^{0}({\mathcal{O}}_{mF_{j}^{\prime }})=2\Leftrightarrow t_{j}=1$
, then
$h^{0}({\mathcal{O}}_{mF_{j}^{\prime }})=2\Leftrightarrow t_{j}=1$
, then
 $a_{j}=m_{j}-1$
or
$a_{j}=m_{j}-1$
or
 $a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
.
$a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
.(3) If
 $h^{0}({\mathcal{O}}_{mF_{j}^{\prime }})=3\Leftrightarrow t_{j}=2$
, then
$h^{0}({\mathcal{O}}_{mF_{j}^{\prime }})=3\Leftrightarrow t_{j}=2$
, then
 $a_{j}=m_{j}-1$
,
$a_{j}=m_{j}-1$
,
 $a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
,
$a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
,
 $a_{j}=m_{j}-1-2\unicode[STIX]{x1D708}_{j}$
, or
$a_{j}=m_{j}-1-2\unicode[STIX]{x1D708}_{j}$
, or
 $a_{j}=m_{j}-1-(p+1)\unicode[STIX]{x1D708}_{j}$
.
$a_{j}=m_{j}-1-(p+1)\unicode[STIX]{x1D708}_{j}$
.
Finally, Katsura and Ueno proved for elliptic fibrations in characteristic
![]() $p$
the analogue of a result which in characteristic zero follows from the description of the fundamental group of the complement of a finite set of points on
$p$
the analogue of a result which in characteristic zero follows from the description of the fundamental group of the complement of a finite set of points on
![]() $\mathbb{P}^{1}$
.
$\mathbb{P}^{1}$
.
Definition 3.10. [Reference Katsura and Ueno23, Definition 3.1]
Let
![]() $f:S\rightarrow \mathbb{P}^{1}$
be an elliptic fibration with
$f:S\rightarrow \mathbb{P}^{1}$
be an elliptic fibration with
![]() $\unicode[STIX]{x1D712}(S,{\mathcal{O}}_{S})=0$
, let
$\unicode[STIX]{x1D712}(S,{\mathcal{O}}_{S})=0$
, let
![]() $m_{i}F_{i}^{\prime }$
,
$m_{i}F_{i}^{\prime }$
,
![]() $i=1,\ldots ,k$
, be the multiple fibers, and let as usual
$i=1,\ldots ,k$
, be the multiple fibers, and let as usual
![]() $\unicode[STIX]{x1D708}_{i}$
be the order of
$\unicode[STIX]{x1D708}_{i}$
be the order of
![]() ${\mathcal{O}}_{F_{i}^{\prime }}(F_{i}^{\prime })$
.
${\mathcal{O}}_{F_{i}^{\prime }}(F_{i}^{\prime })$
.
Then
![]() $S$
is said to be of type
$S$
is said to be of type
![]() $(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
.
$(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
.
Definition 3.11. [Reference Katsura and Ueno23, Definition 3.2]
Given
![]() $1\leqslant i\leqslant r$
, we say that two sequences
$1\leqslant i\leqslant r$
, we say that two sequences
![]() $(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
satisfy condition
$(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
satisfy condition
![]() $U_{i}$
, if there exist integers
$U_{i}$
, if there exist integers
![]() $n_{1},\ldots ,n_{r}$
(depending on
$n_{1},\ldots ,n_{r}$
(depending on
![]() $i$
) such that
$i$
) such that
∙
 $n_{i}\equiv 1\,\text{mod}\,\unicode[STIX]{x1D708}_{i}$
and
$n_{i}\equiv 1\,\text{mod}\,\unicode[STIX]{x1D708}_{i}$
and∙
 $\sum _{j=1}^{r}n_{j}/m_{j}\in \mathbb{Z}$
.
$\sum _{j=1}^{r}n_{j}/m_{j}\in \mathbb{Z}$
.
Theorem 3.12. [Reference Katsura and Ueno23, Theorem 3.3]
In the situation of Definition 3.10, the sequences
![]() $(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
satisfy condition
$(m_{1},\ldots ,m_{r}|\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{r})$
satisfy condition
![]() $U_{i}$
$U_{i}$
![]() $\forall i=1,2,\ldots ,r$
.
$\forall i=1,2,\ldots ,r$
.
4 Proof of the main theorem 3.3
Let
![]() $f:S\rightarrow C$
be a relatively minimal properly elliptic or properly quasielliptic fibration. Set here
$f:S\rightarrow C$
be a relatively minimal properly elliptic or properly quasielliptic fibration. Set here
![]() $g:=g(C)$
and set
$g:=g(C)$
and set
![]() $t:=length(T)$
, where
$t:=length(T)$
, where
![]() $T$
is the torsion sheaf appearing in the canonical bundle formula.
$T$
is the torsion sheaf appearing in the canonical bundle formula.
The first important observation is that in the canonical bundle formula the term
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})$
is
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})$
is
![]() ${\geqslant}0$
, by Mumford’s extension of Castelnuovo’s theorem [Reference Mumford27, p. 330].
${\geqslant}0$
, by Mumford’s extension of Castelnuovo’s theorem [Reference Mumford27, p. 330].
The case
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+t\geqslant 1$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+t\geqslant 1$
and
![]() $g\geqslant 1$
follows from the inequality
$g\geqslant 1$
follows from the inequality
If
![]() $g\geqslant 2$
, and
$g\geqslant 2$
, and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
, then we are done, since
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
, then we are done, since
![]() $P_{n}\geqslant (2n-1)(g-1)$
.
$P_{n}\geqslant (2n-1)(g-1)$
.
If instead
![]() $g=1$
and
$g=1$
and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
, then there are no wild fibers, hence
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
, then there are no wild fibers, hence
where
![]() $D:=\sum _{j}[n(m_{j}-1)/m_{j}]F_{j}$
.
$D:=\sum _{j}[n(m_{j}-1)/m_{j}]F_{j}$
.
Since the canonical divisor is nef and not numerically trivial, we have
![]() $\sum _{j}(1-1/m_{j})>0$
, therefore
$\sum _{j}(1-1/m_{j})>0$
, therefore
![]() $D$
is an effective divisor (with integral coefficients).
$D$
is an effective divisor (with integral coefficients).
Hence
We may therefore assume that
![]() $g=0$
.
$g=0$
.
If
![]() $g=0$
, and
$g=0$
, and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+t\geqslant 3$
, then
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})+t\geqslant 3$
, then
![]() $P_{n}(S)\geqslant n+1$
.
$P_{n}(S)\geqslant n+1$
.
If
![]() $g=t=0$
, and
$g=t=0$
, and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=2$
, then again there are no wild fibers and the same argument as in
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=2$
, then again there are no wild fibers and the same argument as in
![]() $(\ast \ast )$
yields
$(\ast \ast )$
yields
We are left with the following possibilities:
- Case (1)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=1$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=1$
and
 $g=0$
;
$g=0$
;- Case (2)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,~t=2$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,~t=2$
and
 $g=0$
;
$g=0$
;- Case (3)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=0$
and
 $g=0$
;
$g=0$
;- Case (4)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,~t=1$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,~t=1$
and
 $g=0$
;
$g=0$
;- Case (5)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0$
and
 $g=0$
.
$g=0$
.
The next lemma shows that, except possibly in cases (1) and (3), we have only to consider the properly elliptic case.
Lemma 4.1. There exists no quasielliptic fibration
![]() $f:S\rightarrow \mathbb{P}^{1}$
with
$f:S\rightarrow \mathbb{P}^{1}$
with
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0$
.
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0$
.
Proof. Assume we have such a fibration.
Let
![]() $\unicode[STIX]{x1D6FC}:S\rightarrow A$
be the Albanese map of
$\unicode[STIX]{x1D6FC}:S\rightarrow A$
be the Albanese map of
![]() $S$
and assume that
$S$
and assume that
![]() $q:=\dim (A)\geqslant 1$
. Since a general fiber of
$q:=\dim (A)\geqslant 1$
. Since a general fiber of
![]() $f$
is a cuspidal rational curve, whose image in
$f$
is a cuspidal rational curve, whose image in
![]() $A$
must be a single point, we see that
$A$
must be a single point, we see that
![]() $\unicode[STIX]{x1D6FC}$
factors through
$\unicode[STIX]{x1D6FC}$
factors through
![]() $f$
. Hence the image of
$f$
. Hence the image of
![]() $\unicode[STIX]{x1D6FC}$
is a point: since the image generates
$\unicode[STIX]{x1D6FC}$
is a point: since the image generates
![]() $A$
,
$A$
,
![]() $A$
is a point, and
$A$
is a point, and
![]() $q=0$
, a contradiction.
$q=0$
, a contradiction.
We conclude that
![]() $q=0$
, hence
$q=0$
, hence
![]() $p_{g}\geqslant h$
and
$p_{g}\geqslant h$
and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})\geqslant 1$
, a contradiction.◻
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})\geqslant 1$
, a contradiction.◻
Let us now proceed with the proof.
Lemma 4.2. We write
where
![]() $F$
is a fiber of
$F$
is a fiber of
![]() $f$
. Then we have
$f$
. Then we have
![]() $p_{g}(S)=\max (0,d+1)$
.
$p_{g}(S)=\max (0,d+1)$
.
Proof. Indeed, if
![]() $p_{g}\geqslant 1$
, we can write
$p_{g}\geqslant 1$
, we can write
![]() $|K_{S}|=|M|+\unicode[STIX]{x1D6F7}$
, where
$|K_{S}|=|M|+\unicode[STIX]{x1D6F7}$
, where
![]() $\unicode[STIX]{x1D6F7}$
is the fixed part, and where the movable part is of the form
$\unicode[STIX]{x1D6F7}$
is the fixed part, and where the movable part is of the form
![]() $(p_{g}-1)F$
.
$(p_{g}-1)F$
.
Hence
![]() $K_{S}$
is linearly equivalent to an effective divisor
$K_{S}$
is linearly equivalent to an effective divisor
![]() $D$
of the form
$D$
of the form
![]() $(p_{g}-1)F+\sum _{i}b_{i}F_{i}^{\prime },$
with
$(p_{g}-1)F+\sum _{i}b_{i}F_{i}^{\prime },$
with
![]() $0\leqslant b_{i}<m_{i}$
.
$0\leqslant b_{i}<m_{i}$
.
If
![]() $d\geqslant 0$
, then
$d\geqslant 0$
, then
![]() $p_{g}=d+1$
and the fixed part
$p_{g}=d+1$
and the fixed part
![]() $\unicode[STIX]{x1D6F7}=\sum _{i}a_{i}F_{i}^{\prime }$
.
$\unicode[STIX]{x1D6F7}=\sum _{i}a_{i}F_{i}^{\prime }$
.
Otherwise, if
![]() $d<0$
, and we assume
$d<0$
, and we assume
![]() $p_{g}\geqslant 1$
we have a linear equivalence of effective divisors:
$p_{g}\geqslant 1$
we have a linear equivalence of effective divisors:
![]() $(|d|+p_{g}-1)F+\sum _{i}b_{i}F_{i}^{\prime }\equiv \sum _{i}a_{i}F_{i}^{\prime }$
, which shows that
$(|d|+p_{g}-1)F+\sum _{i}b_{i}F_{i}^{\prime }\equiv \sum _{i}a_{i}F_{i}^{\prime }$
, which shows that
![]() $|d|+p_{g}-1=0$
, a contradiction.◻
$|d|+p_{g}-1=0$
, a contradiction.◻
Hence in our cases we have respectively:
- Case (1)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=1,h=1,p_{g}=1$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,~t=1,h=1,p_{g}=1$
and
 $g=0$
;
$g=0$
;- Case (2)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,t=2,h=2,p_{g}=1$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,t=2,h=2,p_{g}=1$
and
 $g=0$
;
$g=0$
;- Case (3)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,t=0,h=1,p_{g}=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=1,t=0,h=1,p_{g}=0$
and
 $g=0$
;
$g=0$
;- Case (4)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,t=1,h=1,p_{g}=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=0,t=1,h=1,p_{g}=0$
and
 $g=0$
;
$g=0$
;- Case (5)
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0,h=1,p_{g}=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{S})=t=0,h=1,p_{g}=0$
and
 $g=0$
.
$g=0$
.
Observe therefore that Corollary 3.6 applies in all cases except (2).
Case (1):
![]() $K_{S}\equiv \sum _{i}a_{i}F_{i}^{\prime },$
and if there exists a multiple fiber for which
$K_{S}\equiv \sum _{i}a_{i}F_{i}^{\prime },$
and if there exists a multiple fiber for which
![]() $a_{j}=m_{j}-1$
, we are done, since
$a_{j}=m_{j}-1$
, we are done, since
![]() $P_{n}\geqslant [n/2]+1$
.
$P_{n}\geqslant [n/2]+1$
.
Otherwise, there is exactly one multiple fiber, wild, with
![]() $t_{j}=1$
, and by Corollary 3.6 and Proposition 3.5
$t_{j}=1$
, and by Corollary 3.6 and Proposition 3.5
![]() $a:=a_{j}$
satisfies
$a:=a_{j}$
satisfies
If
![]() $\unicode[STIX]{x1D708}=1$
, we obtain
$\unicode[STIX]{x1D708}=1$
, we obtain
![]() $a/m=m-2/m\geqslant 1/3$
. If
$a/m=m-2/m\geqslant 1/3$
. If
![]() $\unicode[STIX]{x1D708}\geqslant 2$
, then we get
$\unicode[STIX]{x1D708}\geqslant 2$
, then we get
Thus the inequality
 $$\begin{eqnarray}P_{n}\geqslant \left\{\begin{array}{@{}ll@{}}\bigg[{\displaystyle \frac{n}{3}}\bigg]+1\quad & \text{if }\unicode[STIX]{x1D708}=1,\\ \bigg[{\displaystyle \frac{n}{4}}\bigg]+1\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 2,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant \left\{\begin{array}{@{}ll@{}}\bigg[{\displaystyle \frac{n}{3}}\bigg]+1\quad & \text{if }\unicode[STIX]{x1D708}=1,\\ \bigg[{\displaystyle \frac{n}{4}}\bigg]+1\quad & \text{if }\unicode[STIX]{x1D708}\geqslant 2,\end{array}\right.\end{eqnarray}$$
holds.◻
Case (2): Again
![]() $K_{S}\equiv \sum _{i}a_{i}F_{i}^{\prime },$
and if there exists a multiple fiber for which
$K_{S}\equiv \sum _{i}a_{i}F_{i}^{\prime },$
and if there exists a multiple fiber for which
![]() $a_{j}=m_{j}-1$
, we are done, since then
$a_{j}=m_{j}-1$
, we are done, since then
![]() $P_{n}\geqslant [n/2]+1$
.
$P_{n}\geqslant [n/2]+1$
.
Otherwise there are only wild fibers, either one with
![]() $t_{1}=2$
, or two with
$t_{1}=2$
, or two with
![]() $t_{1}=t_{2}=1$
. In the latter case by Corollary 3.9 we have
$t_{1}=t_{2}=1$
. In the latter case by Corollary 3.9 we have
![]() $a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
, and we argue as in Case (1).
$a_{j}=m_{j}-1-\unicode[STIX]{x1D708}_{j}$
, and we argue as in Case (1).
In the former case, we are left (set
![]() $m:=m_{1},a:=a_{1}$
, and
$m:=m_{1},a:=a_{1}$
, and
![]() $\unicode[STIX]{x1D708}:=\unicode[STIX]{x1D708}_{1}$
) with the case
$\unicode[STIX]{x1D708}:=\unicode[STIX]{x1D708}_{1}$
) with the case
![]() $a=m-1-2\unicode[STIX]{x1D708}$
or
$a=m-1-2\unicode[STIX]{x1D708}$
or
![]() $a=m-1-(p+1)\unicode[STIX]{x1D708}$
. It is clear that the first case will give a better estimate than the second. Thus, we have only to consider the second case.
$a=m-1-(p+1)\unicode[STIX]{x1D708}$
. It is clear that the first case will give a better estimate than the second. Thus, we have only to consider the second case.
Here
which is a monotonously increasing function of
![]() $e,\unicode[STIX]{x1D708}$
, and
$e,\unicode[STIX]{x1D708}$
, and
![]() $p$
.
$p$
.
We must have
![]() $e\geqslant 2$
. For
$e\geqslant 2$
. For
![]() $e=2$
and
$e=2$
and
![]() $\unicode[STIX]{x1D708}=1$
, we must have
$\unicode[STIX]{x1D708}=1$
, we must have
![]() $p\geqslant 3$
.
$p\geqslant 3$
.
In conclusion, for
![]() $\unicode[STIX]{x1D708}=1$
,
$\unicode[STIX]{x1D708}=1$
,
![]() $a/m\geqslant \min (4/9,4/8)=4/9\Rightarrow P_{n}\geqslant [4n/9]+1$
.
$a/m\geqslant \min (4/9,4/8)=4/9\Rightarrow P_{n}\geqslant [4n/9]+1$
.
Instead, for
![]() $\unicode[STIX]{x1D708}\geqslant 2$
, the minimum is given in the case
$\unicode[STIX]{x1D708}\geqslant 2$
, the minimum is given in the case
![]() $p=2,e=2$
and
$p=2,e=2$
and
![]() $\unicode[STIX]{x1D708}=2$
, and we obtain
$\unicode[STIX]{x1D708}=2$
, and we obtain
![]() $a/m\geqslant 1/8$
.
$a/m\geqslant 1/8$
.
In this case, we get
![]() $P_{n}=[n/8]+1$
, which would be a limit case.Footnote
3
◻
$P_{n}=[n/8]+1$
, which would be a limit case.Footnote
3
◻
Case (3): Here
![]() $K_{S}\equiv -F+\sum _{i}^{r}a_{i}F_{i}^{\prime }$
, where
$K_{S}\equiv -F+\sum _{i}^{r}a_{i}F_{i}^{\prime }$
, where
![]() $F$
is a fiber of
$F$
is a fiber of
![]() $f$
. Since
$f$
. Since
![]() $K_{S}$
is
$K_{S}$
is
![]() $\mathbb{Q}$
-linearly equivalent to an effective divisor, for any ample divisor
$\mathbb{Q}$
-linearly equivalent to an effective divisor, for any ample divisor
![]() $H$
on
$H$
on
![]() $S$
, we have
$S$
, we have
which is equivalent to
It follows that
![]() $r\geqslant 2$
. The condition
$r\geqslant 2$
. The condition
![]() $t=0$
implies that there is no wild fiber, hence
$t=0$
implies that there is no wild fiber, hence
![]() $a_{i}=m_{i}-1$
for all
$a_{i}=m_{i}-1$
for all
![]() $i$
.
$i$
.
If
![]() $r\geqslant 3$
, one sees easily that
$r\geqslant 3$
, one sees easily that
![]() $P_{n}\geqslant [n/2]+1$
and we are done.
$P_{n}\geqslant [n/2]+1$
and we are done.
If
![]() $r=2$
, we have at least one
$r=2$
, we have at least one
![]() $m_{i}\geqslant 3$
, therefore we get
$m_{i}\geqslant 3$
, therefore we get
We have
![]() $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
![]() $n\geqslant 3$
and
$n\geqslant 3$
and
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 8$
.◻
$n\geqslant 8$
.◻
Case (4): Here
![]() $K_{S}\equiv -F+\sum _{i}^{r}a_{i}F_{i}^{\prime }$
, where
$K_{S}\equiv -F+\sum _{i}^{r}a_{i}F_{i}^{\prime }$
, where
![]() $F$
is a fiber of
$F$
is a fiber of
![]() $f$
. For the same reason as in Case (3), we have
$f$
. For the same reason as in Case (3), we have
![]() $r\geqslant 2$
. Since
$r\geqslant 2$
. Since
![]() $t=1$
, there exists exactly one wild fiber, say
$t=1$
, there exists exactly one wild fiber, say
![]() $m_{1}F_{1}^{\prime }$
, with
$m_{1}F_{1}^{\prime }$
, with
![]() $t_{1}=1$
: by Corollary 3.6 and Proposition 3.5
$t_{1}=1$
: by Corollary 3.6 and Proposition 3.5
![]() $a_{1}=m_{1}-1$
, or
$a_{1}=m_{1}-1$
, or
![]() $a_{1}=m_{1}-1-\unicode[STIX]{x1D708}_{1}$
. Hence we can rewrite
$a_{1}=m_{1}-1-\unicode[STIX]{x1D708}_{1}$
. Hence we can rewrite
![]() $K_{S}$
as follows:
$K_{S}$
as follows:
so that
If
![]() $r\geqslant 4$
, or if
$r\geqslant 4$
, or if
![]() $r=3$
and
$r=3$
and
![]() $a_{1}=m_{1}-1$
, we have
$a_{1}=m_{1}-1$
, we have
![]() $P_{n}\geqslant 1-n+3[n/2]$
, and writing
$P_{n}\geqslant 1-n+3[n/2]$
, and writing
![]() $n=2k+s,~s\in \{0,1\}$
, we get
$n=2k+s,~s\in \{0,1\}$
, we get
![]() $P_{n}\geqslant 1-2k-s+3k=1+k-s$
, which is
$P_{n}\geqslant 1-2k-s+3k=1+k-s$
, which is
![]() ${\geqslant}1$
for
${\geqslant}1$
for
![]() $n\geqslant 2$
, and
$n\geqslant 2$
, and
![]() ${\geqslant}2$
for
${\geqslant}2$
for
![]() $n\geqslant 4$
.
$n\geqslant 4$
.
In the case where
![]() $r=3$
and
$r=3$
and
![]() $a_{1}=m_{1}-\,1-\unicode[STIX]{x1D708}_{1}$
, consider first the case
$a_{1}=m_{1}-\,1-\unicode[STIX]{x1D708}_{1}$
, consider first the case
![]() $a_{1}=\,0$
.
$a_{1}=\,0$
.
Then (⋇) implies that
![]() $m_{2}$
or
$m_{2}$
or
![]() $m_{3}$
$m_{3}$
![]() ${\geqslant}3$
, and we get
${\geqslant}3$
, and we get
Writing
![]() $n=2k+s$
with
$n=2k+s$
with
![]() $s\in \{0,1\}$
, we get
$s\in \{0,1\}$
, we get
which is
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}1+\bigg[{\displaystyle \frac{k}{3}}\bigg]\quad & \text{if }s=0,\\ \bigg[{\displaystyle \frac{k+2}{3}}\bigg]\quad & \text{if }s=1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}1+\bigg[{\displaystyle \frac{k}{3}}\bigg]\quad & \text{if }s=0,\\ \bigg[{\displaystyle \frac{k+2}{3}}\bigg]\quad & \text{if }s=1.\end{array}\right.\end{eqnarray}$$
Hence we get
![]() $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
![]() $P_{6}\geqslant 2$
and
$P_{6}\geqslant 2$
and
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 8$
.
$n\geqslant 8$
.
If
![]() $a_{1}>0$
, we are done if
$a_{1}>0$
, we are done if
![]() $m_{2}$
or
$m_{2}$
or
![]() $m_{3}$
is
$m_{3}$
is
![]() ${\geqslant}3$
. The remaining case is
${\geqslant}3$
. The remaining case is
![]() $m_{2}=m_{3}=2$
, and Condition
$m_{2}=m_{3}=2$
, and Condition
![]() $U_{1}$
implies that there exists an integer
$U_{1}$
implies that there exists an integer
![]() $l$
such that
$l$
such that
![]() $(l\unicode[STIX]{x1D708}_{1}+1)/(p^{e_{1}}\unicode[STIX]{x1D708}_{1})\in \mathbb{Z}$
, which implies
$(l\unicode[STIX]{x1D708}_{1}+1)/(p^{e_{1}}\unicode[STIX]{x1D708}_{1})\in \mathbb{Z}$
, which implies
![]() $\unicode[STIX]{x1D708}_{1}=1$
. Therefore we conclude that
$\unicode[STIX]{x1D708}_{1}=1$
. Therefore we conclude that
whence
![]() $m_{1}\geqslant 3$
and
$m_{1}\geqslant 3$
and
![]() $a_{1}/m_{1}\geqslant 1/3$
. Hence we have
$a_{1}/m_{1}\geqslant 1/3$
. Hence we have
We get
 $$\begin{eqnarray}P_{n}\geqslant \left\{\begin{array}{@{}ll@{}}1+\biggl[{\displaystyle \frac{2k}{3}}\biggr]\quad & n=2k\\ \biggl[{\displaystyle \frac{2k+1}{3}}\biggr]\quad & n=2k+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant \left\{\begin{array}{@{}ll@{}}1+\biggl[{\displaystyle \frac{2k}{3}}\biggr]\quad & n=2k\\ \biggl[{\displaystyle \frac{2k+1}{3}}\biggr]\quad & n=2k+1.\end{array}\right.\end{eqnarray}$$
Hence we have
![]() $P_{2}\geqslant 1$
,
$P_{2}\geqslant 1$
,
![]() $P_{4}\geqslant 2$
, and
$P_{4}\geqslant 2$
, and
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 6$
.
$n\geqslant 6$
.
We are left with the case
![]() $r=2$
.
$r=2$
.
Assume first that
![]() $a_{1}=m_{1}-1$
: the situation is then identical to the case
$a_{1}=m_{1}-1$
: the situation is then identical to the case
![]() $r=3$
and
$r=3$
and
![]() $a_{1}=0$
, and we are done.
$a_{1}=0$
, and we are done.
We may therefore assume that
![]() $a_{1}=m_{1}-1-\unicode[STIX]{x1D708}_{1}>0$
, and Inequality (⋇) becomes now
$a_{1}=m_{1}-1-\unicode[STIX]{x1D708}_{1}>0$
, and Inequality (⋇) becomes now
and we have
Conditions
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
imply that
$U_{2}$
imply that
![]() $\unicode[STIX]{x1D708}_{1}|m_{2}$
and
$\unicode[STIX]{x1D708}_{1}|m_{2}$
and
![]() $m_{2}|m_{1}=p^{e_{1}}\unicode[STIX]{x1D708}_{1}$
, hence
$m_{2}|m_{1}=p^{e_{1}}\unicode[STIX]{x1D708}_{1}$
, hence
![]() $m_{2}=\unicode[STIX]{x1D708}_{1}p^{\unicode[STIX]{x1D716}}$
and
$m_{2}=\unicode[STIX]{x1D708}_{1}p^{\unicode[STIX]{x1D716}}$
and
![]() $\unicode[STIX]{x1D716}\leqslant e_{1}$
.
$\unicode[STIX]{x1D716}\leqslant e_{1}$
.
If
![]() $\unicode[STIX]{x1D708}_{1}=1$
, then an immediate consequence is that
$\unicode[STIX]{x1D708}_{1}=1$
, then an immediate consequence is that
![]() $m_{2}\geqslant p$
. Moreover, combining with (⋇⋇), we get
$m_{2}\geqslant p$
. Moreover, combining with (⋇⋇), we get
![]() $p^{e_{1}}\geqslant 5$
or
$p^{e_{1}}\geqslant 5$
or
![]() $p^{e_{1}}=p^{\unicode[STIX]{x1D716}}=4$
; however, in the latter case, we have
$p^{e_{1}}=p^{\unicode[STIX]{x1D716}}=4$
; however, in the latter case, we have
Let us consider the former case:
∙ If
 $p\geqslant 5$
, then
$p\geqslant 5$
, then
 $m_{2}\geqslant 5$
, hence
$m_{2}\geqslant 5$
, hence
 $P_{n}\geqslant f_{n}:=1-n+[3n/5]+[4n/5]$
. Writing
$P_{n}\geqslant f_{n}:=1-n+[3n/5]+[4n/5]$
. Writing
 $n=5k+s$
with
$n=5k+s$
with
 $0\leqslant s\leqslant 4$
, we get Therefore we have
$0\leqslant s\leqslant 4$
, we get Therefore we have $$\begin{eqnarray}P_{n}\geqslant f_{n}=2k+f_{s},\quad f_{s}=1,0,1,1,2,\quad s=0,1,2,3,4.\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant f_{n}=2k+f_{s},\quad f_{s}=1,0,1,1,2,\quad s=0,1,2,3,4.\end{eqnarray}$$
 $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
 $n\geqslant 2$
, and
$n\geqslant 2$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 4$
.
$n\geqslant 4$
.∙ If
 $p=3$
, then
$p=3$
, then
 $e_{1}\geqslant 2$
and
$e_{1}\geqslant 2$
and
 $m_{2}\geqslant 3$
. It follows that
$m_{2}\geqslant 3$
. It follows that
 $P_{n}\geqslant f_{n}:=1-n+[7n/9]+[2n/3]$
. Writing
$P_{n}\geqslant f_{n}:=1-n+[7n/9]+[2n/3]$
. Writing
 $n=3k+s$
with
$n=3k+s$
with
 $0\leqslant s\leqslant 2$
, we get Hence
$0\leqslant s\leqslant 2$
, we get Hence $$\begin{eqnarray}\displaystyle P_{n} & {\geqslant} & \displaystyle 1-3k-s+2k+\bigg[{\displaystyle \frac{3k+7s}{9}}\bigg]+2k+\bigg[{\displaystyle \frac{2s}{3}}\bigg]\nonumber\\ \displaystyle & = & \displaystyle 1+k+\bigg[{\displaystyle \frac{3k+7s}{9}}\bigg]+\bigg[{\displaystyle \frac{2s}{3}}\bigg]-s.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{n} & {\geqslant} & \displaystyle 1-3k-s+2k+\bigg[{\displaystyle \frac{3k+7s}{9}}\bigg]+2k+\bigg[{\displaystyle \frac{2s}{3}}\bigg]\nonumber\\ \displaystyle & = & \displaystyle 1+k+\bigg[{\displaystyle \frac{3k+7s}{9}}\bigg]+\bigg[{\displaystyle \frac{2s}{3}}\bigg]-s.\nonumber\end{eqnarray}$$
 $P_{n}\geqslant 1+k$
except for the case
$P_{n}\geqslant 1+k$
except for the case
 $k=0$
and
$k=0$
and
 $s=1$
, which implies that
$s=1$
, which implies that
 $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
 $n\geqslant 2$
, and
$n\geqslant 2$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 3$
.
$n\geqslant 3$
.∙ If finally
 $p=2$
, observe that
$p=2$
, observe that
 $e_{1}\geqslant 3$
and
$e_{1}\geqslant 3$
and
 $m_{2}\geqslant 2$
, hence we have
$m_{2}\geqslant 2$
, hence we have
 $P_{n}\geqslant f_{n}:=1-n+[3n/4]+[n/2]$
. This case which was already treated in (∗∗∗).
$P_{n}\geqslant f_{n}:=1-n+[3n/4]+[n/2]$
. This case which was already treated in (∗∗∗).
In the following, we assume
![]() $\unicode[STIX]{x1D708}_{1}\geqslant 2$
.
$\unicode[STIX]{x1D708}_{1}\geqslant 2$
.
∙ If
 $p^{e_{1}}\geqslant 4$
, we have that
$p^{e_{1}}\geqslant 4$
, we have that
 $P_{n}\geqslant 1-n+[5n/8]+[n/2]$
. Writing
$P_{n}\geqslant 1-n+[5n/8]+[n/2]$
. Writing
 $n=2k+s$
with
$n=2k+s$
with
 $s\in \{0,1\}$
, we get It follows that
$s\in \{0,1\}$
, we get It follows that $$\begin{eqnarray}\displaystyle P_{n} & {\geqslant} & \displaystyle 1-2k-s+k+\bigg[{\displaystyle \frac{2k+5s}{8}}\bigg]+k\nonumber\\ \displaystyle & = & \displaystyle 1+\bigg[{\displaystyle \frac{2k+5s}{8}}\bigg]-s.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{n} & {\geqslant} & \displaystyle 1-2k-s+k+\bigg[{\displaystyle \frac{2k+5s}{8}}\bigg]+k\nonumber\\ \displaystyle & = & \displaystyle 1+\bigg[{\displaystyle \frac{2k+5s}{8}}\bigg]-s.\nonumber\end{eqnarray}$$
 $P_{n}\geqslant 1+[k/4]$
for
$P_{n}\geqslant 1+[k/4]$
for
 $s=0$
and
$s=0$
and
 $P_{n}\geqslant [(2k+5)/8]$
for
$P_{n}\geqslant [(2k+5)/8]$
for
 $s=1$
. In the worst case where
$s=1$
. In the worst case where
 $p^{e_{1}}=4$
and
$p^{e_{1}}=4$
and
 $\unicode[STIX]{x1D708}_{1}=m_{2}=2$
(this case does not actually occur by Condition
$\unicode[STIX]{x1D708}_{1}=m_{2}=2$
(this case does not actually occur by Condition
 $U_{1}$
), we have that
$U_{1}$
), we have that
 $P_{1}=P_{3}=0$
,
$P_{1}=P_{3}=0$
,
 $P_{2}=P_{4}=P_{5}=P_{6}=P_{7}=1$
,
$P_{2}=P_{4}=P_{5}=P_{6}=P_{7}=1$
,
 $P_{8}=2$
and
$P_{8}=2$
and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 12$
.
$n\geqslant 12$
.∙ If
 $p^{e_{1}}=3$
, we cannot have
$p^{e_{1}}=3$
, we cannot have
 $m_{2}=\unicode[STIX]{x1D708}_{1}=2$
, since this would contradict inequality (⋇⋇). Hence we have either
$m_{2}=\unicode[STIX]{x1D708}_{1}=2$
, since this would contradict inequality (⋇⋇). Hence we have either
 $m_{2},~\unicode[STIX]{x1D708}_{1}\geqslant 3$
or
$m_{2},~\unicode[STIX]{x1D708}_{1}\geqslant 3$
or
 $\unicode[STIX]{x1D708}_{1}=2$
,
$\unicode[STIX]{x1D708}_{1}=2$
,
 $m_{2}=6$
. We obtain (∗1)respectively
$m_{2}=6$
. We obtain (∗1)respectively $$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{5n}{9}}\bigg]+\bigg[{\displaystyle \frac{2n}{3}}\bigg]\end{eqnarray}$$
(∗2)For (∗1), writing
$$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{5n}{9}}\bigg]+\bigg[{\displaystyle \frac{2n}{3}}\bigg]\end{eqnarray}$$
(∗2)For (∗1), writing $$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{n}{2}}\bigg]+\bigg[{\displaystyle \frac{5n}{6}}\bigg].\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{n}{2}}\bigg]+\bigg[{\displaystyle \frac{5n}{6}}\bigg].\end{eqnarray}$$
 $n=3k+s$
with
$n=3k+s$
with
 $0\leqslant s\leqslant 2$
, we get which implies that
$0\leqslant s\leqslant 2$
, we get which implies that $$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{6k+5s}{9}}\bigg]+\bigg[{\displaystyle \frac{2s}{3}}\bigg]-s,\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{6k+5s}{9}}\bigg]+\bigg[{\displaystyle \frac{2s}{3}}\bigg]-s,\end{eqnarray}$$
 $P_{n}\geqslant 1+[2k/3]$
for
$P_{n}\geqslant 1+[2k/3]$
for
 $s=0$
,
$s=0$
,
 $P_{n}\geqslant [(6k+5)/9]$
for
$P_{n}\geqslant [(6k+5)/9]$
for
 $s=1$
and
$s=1$
and
 $P_{n}\geqslant 1+[(6k+1)/9]$
for
$P_{n}\geqslant 1+[(6k+1)/9]$
for
 $s=2$
. Hence
$s=2$
. Hence
 $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
 $n\geqslant 2$
,
$n\geqslant 2$
,
 $P_{6}\geqslant 2$
, and
$P_{6}\geqslant 2$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 8$
. For (∗2), writing
$n\geqslant 8$
. For (∗2), writing
 $n=2k+s$
with
$n=2k+s$
with
 $s\in \{0,1\}$
, we get it follows that
$s\in \{0,1\}$
, we get it follows that $$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{4k+5s}{6}}\bigg]-s,\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{4k+5s}{6}}\bigg]-s,\end{eqnarray}$$
 $P_{n}\geqslant 1+[2k/3]$
for
$P_{n}\geqslant 1+[2k/3]$
for
 $s=0$
and
$s=0$
and
 $P_{n}\geqslant [(4k+5)/6]$
for
$P_{n}\geqslant [(4k+5)/6]$
for
 $s=1$
. We see that
$s=1$
. We see that
 $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
 $n\geqslant 2$
, and
$n\geqslant 2$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 4$
.
$n\geqslant 4$
.∙ If
 $p^{e_{1}}=2$
, we have either
$p^{e_{1}}=2$
, we have either
 $m_{2}=\unicode[STIX]{x1D708}_{1},~\unicode[STIX]{x1D708}_{1}\geqslant 4$
or
$m_{2}=\unicode[STIX]{x1D708}_{1},~\unicode[STIX]{x1D708}_{1}\geqslant 4$
or
 $m_{2}=2\unicode[STIX]{x1D708}_{1},~\unicode[STIX]{x1D708}_{1}\geqslant 3$
. It follows that (∗3)respectively
$m_{2}=2\unicode[STIX]{x1D708}_{1},~\unicode[STIX]{x1D708}_{1}\geqslant 3$
. It follows that (∗3)respectively $$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{3n}{8}}\bigg]+\bigg[{\displaystyle \frac{3n}{4}}\bigg]\end{eqnarray}$$
(∗4)For (∗3), writing
$$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{3n}{8}}\bigg]+\bigg[{\displaystyle \frac{3n}{4}}\bigg]\end{eqnarray}$$
(∗4)For (∗3), writing $$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{n}{3}}\bigg]+\bigg[{\displaystyle \frac{5n}{6}}\bigg].\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1-n+\bigg[{\displaystyle \frac{n}{3}}\bigg]+\bigg[{\displaystyle \frac{5n}{6}}\bigg].\end{eqnarray}$$
 $n=4k+s$
with
$n=4k+s$
with
 $0\leqslant s\leqslant 3$
, we get which equals
$0\leqslant s\leqslant 3$
, we get which equals $$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{4k+3s}{8}}\bigg]+\bigg[{\displaystyle \frac{3s}{4}}\bigg]-s,\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{4k+3s}{8}}\bigg]+\bigg[{\displaystyle \frac{3s}{4}}\bigg]-s,\end{eqnarray}$$
 $1+[k/2]$
for
$1+[k/2]$
for
 $s=0$
,
$s=0$
,
 $[(4k+3)/8]$
for
$[(4k+3)/8]$
for
 $s=1$
,
$s=1$
,
 $[(4k+6)/8]$
for
$[(4k+6)/8]$
for
 $s=2$
, and
$s=2$
, and
 $1+[(4k+1)/8]$
for
$1+[(4k+1)/8]$
for
 $s=3$
. In the worst numerical case
$s=3$
. In the worst numerical case
 $\unicode[STIX]{x1D708}_{1}=m_{2}=4$
(this case does not actually occur by Condition
$\unicode[STIX]{x1D708}_{1}=m_{2}=4$
(this case does not actually occur by Condition
 $U_{1}$
), we have
$U_{1}$
), we have
 $P_{3}=P_{4}=P_{6}=P_{7}=1$
,
$P_{3}=P_{4}=P_{6}=P_{7}=1$
,
 $P_{2}=P_{5}=0$
,
$P_{2}=P_{5}=0$
,
 $P_{8}=2$
,
$P_{8}=2$
,
 $P_{12}=2$
,
$P_{12}=2$
,
 $P_{13}=1$
, and
$P_{13}=1$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 14$
. For (∗4), writing
$n\geqslant 14$
. For (∗4), writing
 $n=3k+s$
with
$n=3k+s$
with
 $0\leqslant s\leqslant 2$
, we get hence
$0\leqslant s\leqslant 2$
, we get hence $$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{3k+5s}{6}}\bigg]-s,\end{eqnarray}$$
$$\begin{eqnarray}P_{n}\geqslant 1+\bigg[{\displaystyle \frac{3k+5s}{6}}\bigg]-s,\end{eqnarray}$$
 $P_{n}\geqslant 1+[k/2]$
for
$P_{n}\geqslant 1+[k/2]$
for
 $s=0$
,
$s=0$
,
 ${\geqslant}[(3k+5)/6]$
for
${\geqslant}[(3k+5)/6]$
for
 $s=1$
, and
$s=1$
, and
 ${\geqslant}[(3k+4)/6]$
for
${\geqslant}[(3k+4)/6]$
for
 $s=2$
. We conclude that
$s=2$
. We conclude that
 $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
 $n\geqslant 3$
,
$n\geqslant 3$
,
 $P_{6}\geqslant 2$
, and
$P_{6}\geqslant 2$
, and
 $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
 $n\geqslant 9$
.◻
$n\geqslant 9$
.◻
Case (5): Here
![]() $K_{S}\equiv -2F+\sum _{i=1}^{r}(m_{i}-1)F_{i}^{\prime },$
since
$K_{S}\equiv -2F+\sum _{i=1}^{r}(m_{i}-1)F_{i}^{\prime },$
since
![]() $t=0$
implies that there is no wild fiber.
$t=0$
implies that there is no wild fiber.
In view of Theorem 3.12 this situation is exactly as in the classical case (of characteristic
![]() $0$
). However, our main theorem is new also in the classical case, so we proceed to treat case (4).
$0$
). However, our main theorem is new also in the classical case, so we proceed to treat case (4).
We may assume that
and we recall that
For
![]() $r\geqslant 5$
we have
$r\geqslant 5$
we have
![]() $P_{n}\geqslant 1-2n+5[n/2]$
, and writing
$P_{n}\geqslant 1-2n+5[n/2]$
, and writing
![]() $n=2k+s,s\in \{0,1\}$
, we get
$n=2k+s,s\in \{0,1\}$
, we get
![]() $P_{n}\geqslant 1-4k-2s+5k=1+k-2s$
, which is at least
$P_{n}\geqslant 1-4k-2s+5k=1+k-2s$
, which is at least
![]() $1$
for
$1$
for
![]() $n\geqslant 4$
, and
$n\geqslant 4$
, and
![]() ${\geqslant}2$
for
${\geqslant}2$
for
![]() $n\geqslant 6$
.
$n\geqslant 6$
.
Assume
![]() $r=4$
and observe once more that the right hand side of (⋆) is an increasing function of the multiplicities
$r=4$
and observe once more that the right hand side of (⋆) is an increasing function of the multiplicities
![]() $m_{j}$
, hence the worst case is
$m_{j}$
, hence the worst case is
![]() $(2,2,3,3)$
. However, the worst case would be
$(2,2,3,3)$
. However, the worst case would be
![]() $(2,2,2,3)$
, this case does not occur, since Condition
$(2,2,2,3)$
, this case does not occur, since Condition
![]() $U_{4}$
is not fulfilled.
$U_{4}$
is not fulfilled.
Hence we obtain
For even numbers
![]() $n=2k$
, we get
$n=2k$
, we get
![]() $P_{n}=1+2[k/3]$
, which is
$P_{n}=1+2[k/3]$
, which is
![]() ${\geqslant}1$
, and
${\geqslant}1$
, and
![]() ${\geqslant}3$
whenever
${\geqslant}3$
whenever
![]() $n\geqslant 6$
. For odd numbers
$n\geqslant 6$
. For odd numbers
![]() $n=2k+1$
we get
$n=2k+1$
we get
which is
![]() ${\geqslant}1$
for
${\geqslant}1$
for
![]() $n\geqslant 3$
,
$n\geqslant 3$
,
![]() ${\geqslant}3$
whenever
${\geqslant}3$
whenever
![]() $n\geqslant 9$
.
$n\geqslant 9$
.
In the case
![]() $r=3$
, note that Conditions
$r=3$
, note that Conditions
![]() $U_{1},U_{2},U_{3}$
are equivalent to the condition that
$U_{1},U_{2},U_{3}$
are equivalent to the condition that
![]() $m_{k}$
divides
$m_{k}$
divides
![]() $\text{LCM}(m_{i},m_{j})$
for each choice of
$\text{LCM}(m_{i},m_{j})$
for each choice of
![]() $\{i,j,k\}=\{1,2,3\}$
.
$\{i,j,k\}=\{1,2,3\}$
.
Assume that
![]() $m_{1}\geqslant 4$
: by monotonicity, the worst case is
$m_{1}\geqslant 4$
: by monotonicity, the worst case is
![]() $(4,4,4)$
, where, setting
$(4,4,4)$
, where, setting
![]() $n=4k+s,0\leqslant s\leqslant 3$
,
$n=4k+s,0\leqslant s\leqslant 3$
,
We get
∙
 $k+1$
for
$k+1$
for
 $s=0,3$
;
$s=0,3$
;∙
 $k$
for
$k$
for
 $s=2$
;
$s=2$
;∙
 $k-1$
for
$k-1$
for
 $s=1$
.
$s=1$
.
Hence
![]() $P_{3}=1,P_{4}=2$
,
$P_{3}=1,P_{4}=2$
,
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 10$
.
$n\geqslant 10$
.
Assume that
![]() $m_{1}=3$
. Then
$m_{1}=3$
. Then
![]() $3$
divides
$3$
divides
![]() $\text{LCM}(m_{2},m_{3})$
. Hence either
$\text{LCM}(m_{2},m_{3})$
. Hence either
![]() $3$
divides both
$3$
divides both
![]() $m_{2}$
and
$m_{2}$
and
![]() $m_{3}$
or
$m_{3}$
or
![]() $3$
does not divide
$3$
does not divide
![]() $m_{2}$
or
$m_{2}$
or
![]() $m_{3}$
.
$m_{3}$
.
Keeping in mind the positivity of
![]() $K_{S}$
, equivalent here to
$K_{S}$
, equivalent here to
![]() $\sum _{j}(1/m_{j})<1$
, each case leads to the worst possible case, i.e., one maximizing
$\sum _{j}(1/m_{j})<1$
, each case leads to the worst possible case, i.e., one maximizing
![]() $\sum _{j}(1/m_{j})<1$
.
$\sum _{j}(1/m_{j})<1$
.
(1)
 $(3,3a,3b)$
,
$(3,3a,3b)$
,
 $a|b$
,
$a|b$
,
 $b|a\Rightarrow a=b\Rightarrow (3,3a,3a)$
: the worst case
$b|a\Rightarrow a=b\Rightarrow (3,3a,3a)$
: the worst case
 $(3,6,6)$
;
$(3,6,6)$
;(2)
 $(3,c,3b)$
$(3,c,3b)$
 $c$
not divisible by
$c$
not divisible by
 $3$
,
$3$
,
 $3b|3c,~c|b\Rightarrow b=c\Rightarrow (3,c,3c)$
: worst case
$3b|3c,~c|b\Rightarrow b=c\Rightarrow (3,c,3c)$
: worst case
 $(3,4,12)$
;
$(3,4,12)$
;(3)
 $(3,3a,c)$
$(3,3a,c)$
 $c$
not divisible by
$c$
not divisible by
 $3$
,
$3$
,
 $3a|3c,~c|a\Rightarrow a=c\Rightarrow (3,3a,a)$
: same as in the previous case.
$3a|3c,~c|a\Rightarrow a=c\Rightarrow (3,3a,a)$
: same as in the previous case.
Recall the plurigenus formula, here it gives respectively
 $$\begin{eqnarray}\displaystyle & \displaystyle (3,6,6):\quad P_{n}=\max (0,F(n)),\quad F(n):=1-2n+\bigg[{\displaystyle \frac{2n}{3}}\bigg]+2\bigg[{\displaystyle \frac{5n}{6}}\bigg]. & \displaystyle \nonumber\\ \displaystyle & \displaystyle (3,4,12):\quad P_{n}=\max (0,F(n)),\quad F(n):=1-2n+\bigg[{\displaystyle \frac{2n}{3}}\bigg]+\bigg[{\displaystyle \frac{3n}{4}}\bigg]+\bigg[{\displaystyle \frac{11n}{12}}\bigg]. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (3,6,6):\quad P_{n}=\max (0,F(n)),\quad F(n):=1-2n+\bigg[{\displaystyle \frac{2n}{3}}\bigg]+2\bigg[{\displaystyle \frac{5n}{6}}\bigg]. & \displaystyle \nonumber\\ \displaystyle & \displaystyle (3,4,12):\quad P_{n}=\max (0,F(n)),\quad F(n):=1-2n+\bigg[{\displaystyle \frac{2n}{3}}\bigg]+\bigg[{\displaystyle \frac{3n}{4}}\bigg]+\bigg[{\displaystyle \frac{11n}{12}}\bigg]. & \displaystyle \nonumber\end{eqnarray}$$
In the former case, writing
![]() $n=6k+s$
,
$n=6k+s$
,
![]() $0\leqslant s\leqslant 5$
, we get
$0\leqslant s\leqslant 5$
, we get
hence
![]() $P_{3}\geqslant 1,P_{5}\geqslant 2$
, and
$P_{3}\geqslant 1,P_{5}\geqslant 2$
, and
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 8$
.
$n\geqslant 8$
.
In the latter case, writing
![]() $n=12k+s$
,
$n=12k+s$
,
![]() $0\leqslant s\leqslant 11$
, we get
$0\leqslant s\leqslant 11$
, we get
 $$\begin{eqnarray}\displaystyle & \displaystyle F(n)=4k+F(s),~F(0)=1\Rightarrow F(s)=-s+\bigg[{\displaystyle \frac{2s}{3}}\bigg]+\bigg[{\displaystyle \frac{3s}{4}}\bigg]\quad \text{for }s\geqslant 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle F(s)=1,-1,0,1,1,1,2,2,3,3,3,4,\quad 0\leqslant s\leqslant 11, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F(n)=4k+F(s),~F(0)=1\Rightarrow F(s)=-s+\bigg[{\displaystyle \frac{2s}{3}}\bigg]+\bigg[{\displaystyle \frac{3s}{4}}\bigg]\quad \text{for }s\geqslant 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle F(s)=1,-1,0,1,1,1,2,2,3,3,3,4,\quad 0\leqslant s\leqslant 11, & \displaystyle \nonumber\end{eqnarray}$$
hence
![]() $P_{n}\geqslant 1$
for
$P_{n}\geqslant 1$
for
![]() $n\geqslant 3$
,
$n\geqslant 3$
,
![]() $P_{n}\geqslant 2$
for
$P_{n}\geqslant 2$
for
![]() $n\geqslant 6$
.
$n\geqslant 6$
.
Assume finally
![]() $m_{1}=2$
. Then one of
$m_{1}=2$
. Then one of
![]() $m_{2}$
and
$m_{2}$
and
![]() $m_{3}$
is even. If
$m_{3}$
is even. If
![]() $m_{j}=c$
is odd and
$m_{j}=c$
is odd and
![]() $m_{i}=2b$
, then
$m_{i}=2b$
, then
![]() $c|b$
and
$c|b$
and
![]() $2b|2c\Rightarrow b=c$
, hence we get
$2b|2c\Rightarrow b=c$
, hence we get
![]() $(2,b,2b)$
and the worst case is
$(2,b,2b)$
and the worst case is
![]() $(2,5,10)$
, which was already considered in Remark 3.4.
$(2,5,10)$
, which was already considered in Remark 3.4.
Similarly, in case
![]() $(2,2a,2b)$
again
$(2,2a,2b)$
again
![]() $a=b$
, hence we get a triple
$a=b$
, hence we get a triple
![]() $(2,2a,2a)$
and the worst case is the case
$(2,2a,2a)$
and the worst case is the case
![]() $(2,6,6)$
, which was already considered in Remark 3.4.
$(2,6,6)$
, which was already considered in Remark 3.4.
Remark 4.3. Our analysis allows us also to see (cf. Remark 3.4) which the possible cases are where the estimates are sharp in the main theorem.
∙ (2):
 $P_{1}=P_{2}=P_{3}=0$
in Case (4) for triples
$P_{1}=P_{2}=P_{3}=0$
in Case (4) for triples
 $(2,b,2b),~b\geqslant 5,2\nmid b,$
or
$(2,b,2b),~b\geqslant 5,2\nmid b,$
or
 $(2,2a,2a),~a\geqslant 3$
.
$(2,2a,2a),~a\geqslant 3$
.∙ (3):
 $P_{n}\leqslant 1$
for
$P_{n}\leqslant 1$
for
 $n\leqslant 7$
in Case (4) for the triple
$n\leqslant 7$
in Case (4) for the triple
 $(2,5,10)$
and possibly in Case (2) with one wild fiber and
$(2,5,10)$
and possibly in Case (2) with one wild fiber and
 $p=\unicode[STIX]{x1D708}=e=2$
.
$p=\unicode[STIX]{x1D708}=e=2$
.∙ (4):
 $P_{13}=1$
in Case (4) for the triple
$P_{13}=1$
in Case (4) for the triple
 $(2,6,6)$
.
$(2,6,6)$
.
Acknowledgments
Both authors gratefully acknowledge the support of the ERC Advanced Grant no. 340258, “TADMICAMT.” The first author would like to thank Ciro Ciliberto, Mirella Manaresi and Sandro Verra for organizing a Conference in memory of Federigo Enriques 70 years after his death: their invitation provided stimulus to extend Enriques’
![]() $P_{12}$
-theorem to positive characteristic; and Igor Dolgachev for his question about item (3) of the main theorem. The second author would like to thank Michel Raynaud for helpful communications.
$P_{12}$
-theorem to positive characteristic; and Igor Dolgachev for his question about item (3) of the main theorem. The second author would like to thank Michel Raynaud for helpful communications.