1 INTRODUCTION
The period over which the first sources ionised the hydrogen in the intergalactic medium (IGM) and ended the preceding cosmic ‘dark ages’ is the Epoch of Reionisation (EoR), and determining exactly when and how reionisation happened is a key goal for observational and theoretical cosmology (Loeb & Furlanetto Reference Loeb and Furlanetto2013). Understanding reionisation is important for several reasons. First, it is a major event in our cosmic history that impacted on almost every baryon in the Universe; a better understanding of the EoR is thus vital for developing a complete picture of the Universe’s history. Second, detailed measurements of IGM properties during reionisation will strongly inform models of the first luminous sources and high-redshift structure formation, addressing a broad range of open questions regarding the nature of the early Universe. Third, these early generations of ionising sources influenced the formation of subsequent galaxy populations. Finally, uncertainties in reionisation physics lead to ‘nuisance parameters’ that may limit our ability to extract cosmological parameters from cosmic microwave background (CMB) and Ly α forest data sets, amongst others.
Although some aspects of reionisation may be understood by studying high-redshift galaxy populations directly, IGM measurements play an important complementary role. After all, it is fundamentally the interplay between the ionising sources and the surrounding intergalactic gas that determines the nature of reionisation; the properties of the intergalactic gas, including its ionisation state, temperature, and metallicity, generally depend on the collective impact of all of the luminous sources while galaxy surveys typically detect only bright sources that lie above survey flux detection limits.
In this context, it has been half a century since Gunn & Peterson (Reference Gunn and Peterson1965) drew attention to the lack of prominent Ly α absorption troughs in the spectra of the—then newly discovered—quasars. The absence of strong absorption revealed that there was very little intervening neutral hydrogen in intergalactic space, all the way out to the highest-redshift object observed at the time, quasar 3C 9 at z = 2.01 (Schmidt Reference Schmidt1965). In the intervening 50 years, there has been tremendous progress in the study of the IGM using quasar absorption lines, and we now have detailed constraints on many of properties of the IGM and the EoR which extend to the current highest-redshift quasar, ULAS J1120 + 0641 at z = 7.085 (Mortlock et al. Reference Mortlock2011). The aim of the present article is to review these constraints, examine their implications, and consider the prospects for improving them in the future.
In Section 2, we review the properties of the ultraviolet background (UVB) inferred from the post-reionisation Ly α forest at z ⩽ 6. We compare these measurements to the number of ionising photons expected from star-forming galaxies and quasars, and assess what these data imply for the sources likely responsible for reionising the IGM. In Section 3, we review current observations of IGM metal line abundances at z > 5, address whether the known galaxy population approaching and during the EoR can account for the observed metal enrichment, and consider the implications of metal line populations for high-redshift galaxy formation. Direct constraints on the reionisation history using quasar absorption line data are then described in Section 4. We also briefly compare these data with other, complementary probes of reionisation. Finally, in Section 5 we conclude with a discussion of future prospects for exploring the EoR with quasar absorption lines.
For further orientation, Figure 1 provides an example of a z ≳ 6 quasar spectrum in the observed-frame; this illustrates key spectral features used to infer IGM properties approaching the EoR. Redward of the Ly α emission from the quasar (red-dashed line), one can identify a series of metal absorption lines (Section 3). Close to the quasar redshift lies the Ly α proximity or near-zone, where the quasar contributes significantly to ionising the hydrogen in its vicinity (Section 4.5). Next, moving to shorter wavelengths, is the Ly α absorption forest from intervening neutral hydrogen in the cosmic web (Section 2). This z ≳ 6 spectrum also shows a complete Gunn–Peterson absorption trough (Section 2.1) above 8 400 Å (from hydrogen at z ≳ 5.9 absorbing in the Ly α line) that continues until the near-zone region. Between the green- and orange-dashed lines, which mark the wavelengths of the Ly β and Ly γ transitions at the quasar systemic redshift, lies the Ly β forest. In this region of the spectrum, high-redshift gas absorbs in the Ly β line and at lower redshift, foreground gas absorbs in Ly α (Section 4.3). At even shorter wavelengths, overlapping higher-order Lyman series transitions occur. Finally, below the line marked ‘LyC’ there is continuum absorption from neutral hydrogen: photons at these wavelengths—with rest frame wavelength λ ⩽ 912 Å—are energetic enough to photoionise hydrogen atoms. In lower-redshift quasar spectra where there is less overall absorption, Lyman-limit systems (LLSs)—absorbers that have an optical depth of unity to photons at the hydrogen photoionisation edge—can be identified here. LLSs, along with cumulative absorption from lower-column density absorbers, set the mean free path to ionising photons in the IGM (Section 2.4).

Figure 1. A high signal-to-noise spectrum of the quasar ULAS J1319+0959 at z = 6.13 from Becker et al. (Reference Becker, Bolton, Madau, Pettini, Ryan-Weber and Venemans2015), obtained with the X-Shooter spectrograph on the Very Large Telescope (VLT). The spectrum has been rebinned to 1.5 Å per pixel for presentation purposes. This illustrates many of the features reviewed here—see the text in Section 1 for a description.
2 THE UV BACKGROUND
The UVB is a key probe of the sources of hydrogen ionising photons (E ⩾ 13.6 eV) in the post-reionisation era at z < 6; its intensity and spectral shape provides a complete census of ionising photon production and its evolution with redshift (Haardt & Madau Reference Haardt and Madau1996, Reference Haardt and Madau2012; Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Zaldarriaga and Hernquist2009). One of the primary observational techniques used to probe the UVB is quasar absorption line spectroscopy. The Ly α forest—the observable manifestation of the intergalactic neutral hydrogen that traces the cosmic web of large-scale structure (see e.g. Rauch Reference Rauch1998; Meiksin Reference Meiksin2009)—is particularly important in this regard. In this section, we discuss the theoretical and observational framework on which UVB measurements using the Ly α forest are based, and examine the implications of these data for the properties of high-redshift galaxies during the reionisation era.
2.1 The Gunn–Peterson effect
It is instructive to first review the relationship between the neutral hydrogen fraction of the IGM and the intergalactic Ly α opacity. Gunn & Peterson (Reference Gunn and Peterson1965) demonstrated that quasar spectra are a useful probe of the intergalactic neutral hydrogen density. If the intervening IGM along a quasar line of sight contains sufficient neutral hydrogen, the transmitted flux blueward of a quasar’s Ly α emission line (at rest-frame wavelength λα = 1215.67Å) will be completely attenuated, producing a saturated absorption trough.
The Gunn & Peterson (Reference Gunn and Peterson1965) argument is as follows. Consider light emitted by a quasar at redshift z q passing through a uniform IGM with proper neutral hydrogen number density n HI(z). This light is observed at redshift z < z q with frequency ν = να/(1 + z), such that the emitted photons have redshifted into Ly α resonance with the local IGM. The total optical depth along the line of sight is then
where dl/dz = −c/[H(z)(1 + z)] is the proper line element. Ignoring line-broadening effects, the effective scattering cross-section, σs, may be approximated by a Dirac delta function peaked at να
where σα = 4.48 × 10−18 cm2 is the Ly α cross-section. Changing the variable of integration to ν, where dl/dν = λα(1 + z)/H(z) and noting that ταGP = 0 when ν ⩽ να/(1 + z) then yields
using the high-redshift (z ⩾ 2) approximation for the Hubble parameter, H(z) ≃ H 0Ω1/2m(1 + z)3/2. Identifying ![]() $\langle x_{\rm HI} \rangle =n_{\rm HI}/{\bar{n}}_{\rm H}$ as the average neutral hydrogen fraction, the Gunn–Peterson optical depth at the background density,
$\langle x_{\rm HI} \rangle =n_{\rm HI}/{\bar{n}}_{\rm H}$ as the average neutral hydrogen fraction, the Gunn–Peterson optical depth at the background density, ![]() ${\bar{n}}_{\rm H}=\rho _{\rm crit}\Omega _{\rm b}(1-Y)(1+z)^{3}/m_{\rm H}$, is then
${\bar{n}}_{\rm H}=\rho _{\rm crit}\Omega _{\rm b}(1-Y)(1+z)^{3}/m_{\rm H}$, is then
 $$\begin{eqnarray}
\tau _{\rm GP}^{\alpha } &\simeq 2.3 \times 10^{5} \, \langle x_{\rm HI} \rangle \left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right)\left(\frac{\Omega _{\rm m}h^{2}}{0.142}\right)^{-1/2} \nonumber \\
&\times \left(\frac{1-Y}{0.76}\right)\left(\frac{1+z}{5}\right)^{3/2},
\end{eqnarray}$$
$$\begin{eqnarray}
\tau _{\rm GP}^{\alpha } &\simeq 2.3 \times 10^{5} \, \langle x_{\rm HI} \rangle \left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right)\left(\frac{\Omega _{\rm m}h^{2}}{0.142}\right)^{-1/2} \nonumber \\
&\times \left(\frac{1-Y}{0.76}\right)\left(\frac{1+z}{5}\right)^{3/2},
\end{eqnarray}$$
where Y is the primordial helium fraction by mass.
The transmittance shortward of a quasar’s Ly α emission line is just e−ταGP. Consequently, even for a modest neutral fraction of ⟨x HI⟩ ~ 10−4.5 the Gunn–Peterson optical depth is fully saturated (i.e. e−ταGP ≈ 0). Observationally, the decline in the observed Ly α opacity and especially the absence of Ly α troughs in quasar spectra at z < 5.5 indicates the volume-weighted neutral hydrogen fraction in the IGM is very small by this redshift (Becker et al. Reference Becker2001; Djorgovski et al. Reference Djorgovski, Castro, Stern and Mahabal2001; Songaila Reference Songaila2004; Fan et al. Reference Fan2006, see also McGreer et al. Reference McGreer, Mesinger and D’Odorico2015)—we shall return to this point in Section 4.2.
2.2 The Ly α forest opacity and the metagalactic hydrogen ionisation rate
The Gunn & Peterson (Reference Gunn and Peterson1965) argument implies the IGM is highly ionised along observed quasar sight-lines at z < 5.5. However, it does not directly relate the observed Ly α opacity to the quantity of interest here—the intensity of the UVB. To progress further, we must recognise that intergalactic Ly α absorption arises not from a uniform medium, but the continuous, fluctuating distribution of baryons which forms through hierarchical structure formation within cold dark matter models. Estimates of the ionising photon production by sources in the early Universe rely on the resultant relationship between the opacity of the Ly α ‘forest’ of absorption lines and the intensity of the UVB.
We may consider the relationship between the Ly α forest opacity and the UVB as follows. The UVB-specific intensity at redshift z 0 and frequency ν0, is given by (e.g. Haardt & Madau Reference Haardt and Madau1996; Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Hernquist and Zaldarriaga2008b; Becker & Bolton Reference Becker and Bolton2013)
This expression is obtained by solving the cosmological radiative transfer equation, where ε(ν, z) is the proper specific emissivity, ν = ν0(1 + z)/(1 + z 0) and ![]() ${\bar{\tau }}(\nu _{0},z_{0},z)$ is the intervening effective optical depth for photons with frequency ν0 at redshift z 0 that were emitted at redshift z (see Equation (10) later). The number of hydrogen atoms photoionised per unit time, ΓHI, is then related to the specific intensity of the UVB by
${\bar{\tau }}(\nu _{0},z_{0},z)$ is the intervening effective optical depth for photons with frequency ν0 at redshift z 0 that were emitted at redshift z (see Equation (10) later). The number of hydrogen atoms photoionised per unit time, ΓHI, is then related to the specific intensity of the UVB by
where σHI is the H Iphotoionisation cross-section (see e.g. Verner et al. Reference Verner, Ferland, Korista and Yakovlev1996), h P is Planck’s constant and νLL is the photon frequency at the Lyman limit. The final step makes the simplifying assumption of a power-law UVB spectrum, J(ν) = J LL(ν/νLL)−αbg, and approximatesFootnote 1the photoionisation cross-section as σHI ≃ σLL(ν/νLL)−3, where σLL = 6.35 × 10−18 cm2.
The photoionisation rate can be related to the neutral hydrogen fraction in the IGM. Following reionisation, hydrogen in the low-density IGM is in ionisation equilibrium with the UVB. If ignoring collisional ionisations (appropriate for the low temperatures, T < 105 K associated with gas in the Ly α forest),
Here, n HI, n HII, and n e are the number densities of neutral hydrogen, ionised hydrogen, and free electrons, and αHII(T) is the temperature-dependent radiative recombination coefficient. We adopt the case-A recombination rate αHII(T) = 4.063 × 10−13(T/104 K)−0.72 cm3 s−1 in what follows, although more accurate fits are available (e.g. Verner & Ferland Reference Verner and Ferland1996). If the hydrogen is highly ionised, then n HII ≃ n H, n e ≃ n H(1 + n He/n H), and Equation (6) may be rewritten as
 $$\begin{eqnarray}
x_{\rm HI} &\simeq 9.6\times 10^{-6}\, \Delta \frac{(1+\chi _{\rm He})}{\Gamma _{-12}}\left(\frac{T}{10^{4}\,\rm K}\right)^{-0.72}\left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right) \nonumber \\
&\times \left(\frac{1-Y}{0.76}\right)\left(\frac{1+z}{5}\right)^{3},
\end{eqnarray}$$
$$\begin{eqnarray}
x_{\rm HI} &\simeq 9.6\times 10^{-6}\, \Delta \frac{(1+\chi _{\rm He})}{\Gamma _{-12}}\left(\frac{T}{10^{4}\,\rm K}\right)^{-0.72}\left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right) \nonumber \\
&\times \left(\frac{1-Y}{0.76}\right)\left(\frac{1+z}{5}\right)^{3},
\end{eqnarray}$$
where x HI = n HI/n H is the H Ifraction, ![]() $\Delta = \rho /\bar{\rho }$ is the fractional overdensity,
$\Delta = \rho /\bar{\rho }$ is the fractional overdensity, ![]() $\chi _{\rm He}=\frac{\eta Y}{4(1-Y)}$ accounts for electrons released by singly (η = 1) and doubly (η = 2) ionised heliumFootnote 2, and Γ−12 = ΓHI/10−12 s−1.
$\chi _{\rm He}=\frac{\eta Y}{4(1-Y)}$ accounts for electrons released by singly (η = 1) and doubly (η = 2) ionised heliumFootnote 2, and Γ−12 = ΓHI/10−12 s−1.
Finally, note that photoionisation by the UVB also heats the low-density IGM (Miralda-Escudé & Rees Reference Miralda-Escudé and Rees1994). Well after reionisation, photoheating and cooling due to the adiabatic expansion of the Universe produces a well-defined temperature–density relationFootnote 3 for gas overdensities Δ ≲ 10, where T = T 0Δγ − 1 (Hui & Gnedin Reference Hui and Gnedin1997; McQuinn & Upton Sanderbeck Reference McQuinn and Upton Sanderbeck2015). Typically, the temperature at mean density is 103.7 ⩽ T 0 ⩽ 104.3 K, while the slope of the relation is 1 ⩽ γ ⩽ 1.6 (Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000; Ricotti, Gnedin, & Shull Reference Ricotti, Gnedin and Shull2000; McDonald et al. Reference McDonald, Miralda-Escudé, Rauch, Sargent, Barlow and Cen2001; Lidz et al. Reference Lidz, Faucher-Giguère, Dall’Aglio, McQuinn, Fechner, Zaldarriaga, Hernquist and Dutta2010; Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011a; Garzilli et al. Reference Garzilli, Bolton, Kim, Leach and Viel2012; Rudie, Steidel, & Pettini Reference Rudie, Steidel and Pettini2012; Bolton et al. Reference Bolton, Becker, Haehnelt and Viel2014; Boera et al. Reference Boera, Murphy, Becker and Bolton2014). Combining this temperature–density relation with Equations (2) and (6) gives
 $$\begin{eqnarray}
\tau _{\rm FGPA}^{\alpha } &\simeq 2.2 \,\Delta ^{\beta } \frac{(1+\chi _{\rm He})}{\Gamma _{-12}} \left(\frac{T_{0}}{10^{4}\,\rm K}\right)^{-0.72}\left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right)^{2} \nonumber \\
&\times \left(\frac{\Omega _{\rm m}h^{2}}{0.141}\right)^{-1/2}\left(\frac{1-Y}{0.76}\right)^{2}\left(\frac{1+z}{5}\right)^{9/2},
\end{eqnarray}$$
$$\begin{eqnarray}
\tau _{\rm FGPA}^{\alpha } &\simeq 2.2 \,\Delta ^{\beta } \frac{(1+\chi _{\rm He})}{\Gamma _{-12}} \left(\frac{T_{0}}{10^{4}\,\rm K}\right)^{-0.72}\left(\frac{\Omega _{\rm b}h^{2}}{0.022}\right)^{2} \nonumber \\
&\times \left(\frac{\Omega _{\rm m}h^{2}}{0.141}\right)^{-1/2}\left(\frac{1-Y}{0.76}\right)^{2}\left(\frac{1+z}{5}\right)^{9/2},
\end{eqnarray}$$
where β = 2 − 0.72(γ − 1). This is the Fluctuating Gunn–Peterson Approximation (FGPA, e.g. Rauch et al. Reference Rauch1997; Weinberg et al. Reference Weinberg, Banday, Sheth and da Costa1999). It neglects redshift space distortions and spatial fluctuations in the UVB, but elucidates the dependence of the Ly α forest optical depth on underlying physical quantities. Importantly, this includes the photoionisation rate ΓHI (and hence specific intensity J(ν, z)) of the UVB.
2.3 Measurements of the photoionisation rate
With the relationship between the Ly α forest opacity and the UVB intensity established, we now consider how measurements are made in practice. There are two main techniques employed in the literature to measure the metagalactic photoionisation rate, ΓHI: modelling the mean transmitted flux in the Ly α forest (Rauch et al. Reference Rauch1997) and the quasar proximity effect (Murdoch et al. Reference Murdoch, Hunstead, Pettini and Blades1986; Bajtlik, Duncan, & Ostriker Reference Bajtlik, Duncan and Ostriker1988).
The first approach typically relies on using numerical simulations of structure formation to reproduce the observed mean transmission in the Ly α forest, ⟨F⟩ = ⟨e−τα⟩. Mock Ly α forest spectra are extracted from simulations performed using a spatially uniform, time-dependent UVB model (e.g. Haardt & Madau Reference Haardt and Madau1996, Reference Haardt and Madau2012; Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Zaldarriaga and Hernquist2009). The amplitude of the UVB model is then treated as an adjustable parameter; since in photoionisation equilibrium τα∝Γ−1HI (e.g. Equation (8)), rescaling the simulated Ly α optical depths is straightforward. The photoionisation rate ΓHI (and hence J(ν), if the UVB spectral shape is known) may then be obtained by matching the mean transmission in the simulated spectra to observational measurements at 2 < z < 6 (e.g. Kim et al. Reference Kim, Carswell, Cristiani, D’Odorico and Giallongo2002; Schaye et al. Reference Schaye, Aguirre, Kim, Theuns, Rauch and Sargent2003; Kirkman et al. Reference Kirkman2005; Fan et al. Reference Fan2006; Faucher-Giguère et al. Reference Faucher-Giguère, Prochaska, Lidz, Hernquist and Zaldarriaga2008a; Pâris et al. Reference Pâris2011; Becker et al. Reference Becker, Hewett, Worseck and Prochaska2013, Reference Becker, Bolton, Madau, Pettini, Ryan-Weber and Venemans2015).
This method has been widely applied to Ly α forest data at z > 2 (McDonald & Miralda-Escudé Reference McDonald and Miralda-Escudé2001; Meiksin & White Reference Meiksin and White2003; Tytler et al. Reference Tytler2004; Bolton et al. Reference Bolton, Haehnelt, Viel and Springel2005; Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Hernquist and Zaldarriaga2008b; Wyithe & Bolton Reference Wyithe and Bolton2011; Rollinde et al. Reference Rollinde, Theuns, Schaye, Pâris and Petitjean2013; Becker & Bolton Reference Becker and Bolton2013). However, this approach will start to break down approaching z = 6, when the assumption of a spatially uniform UVB no longer holds (see also Section 2.7). Corrections for the effect of spatial fluctuations in the UVB are therefore applied to the measurements (Meiksin & White Reference Meiksin and White2003; Bolton & Haehnelt Reference Bolton and Haehnelt2007c). The mean transmitted flux furthermore depends on the IGM temperature and cosmology (e.g. Equation (8)). Independent constraints on these quantities are therefore required, and the historical range of estimates for ΓHI in literature are in part attributable to differing assumptions for these parameters.
The second widely used approach, the line-of-sight proximity effect, estimates ΓHI by quantifying the reduction in the average Ly α opacity approaching the systemic redshift of a quasar (Weymann, Carswell, & Smith Reference Weymann, Carswell and Smith1981; Carswell et al. Reference Carswell, Whelan, Smith, Boksenberg and Tytler1982). The ionising radiation from a quasar will locally ionise the hydrogen in the IGM to a higher degree than the UVB. Ignoring peculiar velocities and spatial variations in gas temperature, since τα∝Γ−1HI it follows that the Ly α optical depth as a function of proper distance r from a quasar is
where τUVBα is the typical optical depth in the Ly α forest, ΓQHI(r) is the ionisation rate of the quasar, and ΓUVBHI is the UVB ionisation rate. If the absolute magnitude, redshift and spectral energy distribution of the quasar are known, ΓQHI(r) may be computed with Equation (5). Estimates for τUVB + Qα and τUVBα then lead to ΓUVBHI.
The optical depth, however, is not a directly observable quantity; early proximity effect analyses therefore focussed on measuring the number density of Ly α absorption lines blueward of a quasar’s Ly α emission line (e.g. Murdoch et al. Reference Murdoch, Hunstead, Pettini and Blades1986; Bajtlik et al. Reference Bajtlik, Duncan and Ostriker1988; Giallongo et al. Reference Giallongo, Cristiani, D’Odorico, Fontana and Savaglio1996; Scott et al. Reference Scott, Bechtold, Dobrzycki and Kulkarni2000). More recent approaches have instead analysed the transmitted flux, F = e−τα, often combined with numerical simulations of the IGM which model the density, temperature, and velocity field around quasar host haloes in detail (Faucher-Giguère et al. Reference Faucher-Giguère, Prochaska, Lidz, Hernquist and Zaldarriaga2008a; Dall’Aglio et al. Reference Dall’Aglio, Wisotzki and Worseck2008; Calverley et al. Reference Calverley, Becker, Haehnelt and Bolton2011). In addition to modelling the atypical environment of quasars, care must be taken to avoid further potential biases in the measurements arising from line-of-sight variations in the IGM density distribution (e.g Loeb & Eisenstein Reference Loeb and Eisenstein1995; Rollinde et al. Reference Rollinde, Srianand, Theuns, Petitjean and Chand2005; Guimarães et al. Reference Guimarães, Petitjean, Rollinde, de Carvalho, Djorgovski, Srianand, Aghaee and Castro2007; Partl et al. Reference Partl, Müller, Yepes and Gottlöber2011).
The typical values obtained using both these techniques are ΓHI ~ 10−12 s−1 at 2 ⩽ z ⩽ 4, declining by approximately a factor of 2 and 4 approaching reionisation at z = 5 and z = 6, respectively. Some recent measurements are summarised in Figure 2. Inferences about the underlying ionising source population can be made by comparing these measurements to estimates of the emissivity from known ionising sources at 2 < z < 6, obtained by integrating observed quasar and Lyman break galaxy (LBG) luminosity functions. We discuss this comparison in more detail in Section 2.6. However, this first requires converting ΓHI into an emissivity, which itself relies on estimates for the typical mean free path for ionising photons and its evolution with redshift.

Figure 2. Summary of recent ΓHI measurements obtained from the mean Ly α forest transmission (Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Hernquist and Zaldarriaga2008b; Wyithe & Bolton Reference Wyithe and Bolton2011; Becker & Bolton Reference Becker and Bolton2013) and the proximity effect (Dall’Aglio, Wisotzki, & Worseck Reference Dall’Aglio, Wisotzki and Worseck2008; Calverley et al. Reference Calverley, Becker, Haehnelt and Bolton2011). Note that some of the data points have been offset by Δz = 0.05 for clarity, and the Dall’Aglio et al. (Reference Dall’Aglio, Wisotzki and Worseck2008) data have been rebinned and converted from a specific intensity assuming αbg = 1.5. These data are furthermore quoted directly from the literature. However, caution must be exercised with any direct comparison here as differing assumptions for systematic uncertainties in these studies such as e.g. the IGM temperature, can increase the scatter in the measurements. For further discussion of this point, see Becker & Bolton (Reference Becker and Bolton2013). For comparison, the dashed and dotted curves display the empirically calibrated UVB models constructed by Haardt & Madau (Reference Haardt and Madau2012) and Faucher-Gigu et al. (Reference Faucher-Giguère, Lidz, Zaldarriaga and Hernquist2009), respectively. These are based on the expected contribution to the UVB from star-forming galaxies and quasars, and an empirical model for the ionising opacity of the IGM.
2.4 The mean free path at the Lyman limit
Consider the mean free path for ionising photons in an IGM populated by Poisson distributed H Iabsorbers, with column densities N HI described by the column density distribution function (CDDF), f(N HI, z) = ∂2n/∂N HI∂z. The intervening effective optical depth (see also Equation (4)) for photons with frequency ν0 at redshift z 0 that were emitted at redshift z is then (Paresce, McKee, & Bowyer Reference Paresce, McKee and Bowyer1980)
where τν = σHI(ν)N HI. Parameterising the CDDF as f(N HI, z) = N 0N −βNHI(1 + z)βz and evaluating the integral yields (e.g. Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Hernquist and Zaldarriaga2008b)
 $$\begin{eqnarray*}
{\bar{\tau }} &=N_{0} \frac{\Gamma (2-\beta _{\rm N}) (1+z_{0})^{3(\beta _{\rm N}-1)}}{(\beta _{\rm N}-1)(\beta _{\rm z}-3\beta _{\rm N} + 4)}\left(\frac{\nu _{0}}{\nu _{\rm LL}}\right)^{-3(\beta _{\rm N}-1)} \nonumber \\
&\times \sigma _{\rm LL}^{\beta _{\rm N}-1} \left[(1+z)^{\beta _{\rm z}-3\beta _{\rm N}+4}-(1+z_{0})^{\beta _{\rm z}-3\beta _{\rm N}+4}\right], \nonumber
\end{eqnarray*}$$
$$\begin{eqnarray*}
{\bar{\tau }} &=N_{0} \frac{\Gamma (2-\beta _{\rm N}) (1+z_{0})^{3(\beta _{\rm N}-1)}}{(\beta _{\rm N}-1)(\beta _{\rm z}-3\beta _{\rm N} + 4)}\left(\frac{\nu _{0}}{\nu _{\rm LL}}\right)^{-3(\beta _{\rm N}-1)} \nonumber \\
&\times \sigma _{\rm LL}^{\beta _{\rm N}-1} \left[(1+z)^{\beta _{\rm z}-3\beta _{\rm N}+4}-(1+z_{0})^{\beta _{\rm z}-3\beta _{\rm N}+4}\right], \nonumber
\end{eqnarray*}$$
where Γ is the Gamma function. The mean free path is then the distance a photon can travel before encountering an optical depth of unity. Noting that ![]() ${\rm d}l/{\rm d}{\bar{\tau }}=({\rm d}l/{\rm d}z)/({\rm d}{\bar{\tau }}/{\rm d}z)\simeq \lambda _{\rm mfp}$ when
${\rm d}l/{\rm d}{\bar{\tau }}=({\rm d}l/{\rm d}z)/({\rm d}{\bar{\tau }}/{\rm d}z)\simeq \lambda _{\rm mfp}$ when ![]() $\Delta {\bar{\tau }}=1$ thus leads to
$\Delta {\bar{\tau }}=1$ thus leads to
 $$\begin{eqnarray}
\lambda _{\rm mfp}(\nu ) &\simeq \frac{c(\beta _{\rm N}-1)}{N_{0}\sigma _{\rm LL}^{\beta _{\rm N}-1}\Gamma (2-\beta _{\rm N})}\left(\frac{\nu }{\nu _{\rm LL}}\right)^{3(\beta _{\rm N}-1)} \nonumber \\
&\times \frac{1}{H_{0}\Omega _{\rm m}^{1/2}(1+z)^{\beta _{\rm z}+5/2}},
\end{eqnarray}$$
$$\begin{eqnarray}
\lambda _{\rm mfp}(\nu ) &\simeq \frac{c(\beta _{\rm N}-1)}{N_{0}\sigma _{\rm LL}^{\beta _{\rm N}-1}\Gamma (2-\beta _{\rm N})}\left(\frac{\nu }{\nu _{\rm LL}}\right)^{3(\beta _{\rm N}-1)} \nonumber \\
&\times \frac{1}{H_{0}\Omega _{\rm m}^{1/2}(1+z)^{\beta _{\rm z}+5/2}},
\end{eqnarray}$$
which gives an analytical approximation for the mean free path for ionising photons at z ≳ 2. This may be written more compactly as λmfp = λLL(z)(ν/νLL)3(βN − 1), where λLL(z) is the mean free path at the Lyman limit. In general, therefore, higher frequency photons have a larger mean free path and λLL(z) decreases with increasing redshift, but the precise normalisation, frequency, and redshift dependence of Equation (11) relies on an accurate observational determination of the CDDF or a related quantity.
Many surveys have attempted to infer λLL(z) by measuring f(N HI, z) and using Equation (11). Critically, however, the absorption systems which dominate the opacity, the so-called LLSs (![]() $10^{17.2}\rm \,cm^{-2}\le N_{\rm HI}\le 10^{19}\rm \,cm^{-2}$) and saturated Ly α forest absorbers (
$10^{17.2}\rm \,cm^{-2}\le N_{\rm HI}\le 10^{19}\rm \,cm^{-2}$) and saturated Ly α forest absorbers (![]() $ 10^{14.5} \rm \,cm^{-2}\le N_{\rm HI}\le 10^{17.2}\rm \,cm^{-2}$), are those for which N HI is most difficult to determine observationally. Extrapolations over this N HI range are therefore often employed. Previous studies have generally found βz ≃ 1–3 (note this is dependent on N HI) and βN ≃ 1.3–1.7 at z > 2 (Tytler Reference Tytler1987; Petitjean et al. Reference Petitjean, Webb, Rauch, Carswell and Lanzetta1993; Storrie-Lombardi et al. Reference Storrie-Lombardi, McMahon, Irwin and Hazard1994; Kim et al. Reference Kim, Hu, Cowie and Songaila1997; Songaila & Cowie Reference Songaila and Cowie2010; Rudie et al. Reference Rudie, Steidel, Shapley and Pettini2013).
$ 10^{14.5} \rm \,cm^{-2}\le N_{\rm HI}\le 10^{17.2}\rm \,cm^{-2}$), are those for which N HI is most difficult to determine observationally. Extrapolations over this N HI range are therefore often employed. Previous studies have generally found βz ≃ 1–3 (note this is dependent on N HI) and βN ≃ 1.3–1.7 at z > 2 (Tytler Reference Tytler1987; Petitjean et al. Reference Petitjean, Webb, Rauch, Carswell and Lanzetta1993; Storrie-Lombardi et al. Reference Storrie-Lombardi, McMahon, Irwin and Hazard1994; Kim et al. Reference Kim, Hu, Cowie and Songaila1997; Songaila & Cowie Reference Songaila and Cowie2010; Rudie et al. Reference Rudie, Steidel, Shapley and Pettini2013).
However, recent work has demonstrated that the CDDF is not well described by a single power-law index βN, and may be better represented by a series of broken power laws (Prochaska, O’Meara, & Worseck Reference Prochaska, O’Meara and Worseck2010; Kim et al. Reference Kim, Partl, Carswell and Müller2013; O’Meara et al. Reference O’Meara, Prochaska, Worseck, Chen and Madau2013). The expected clustering of LLS will also impact on λmfp estimated from Equation (11), as this expression assumes the absorbers are Poisson distributed (Prochaska et al. Reference Prochaska, Madau, O’Meara and Fumagalli2014). This has led to the development of alternative approaches based on directly measuring the optical depth at the Lyman limit, τLL, using stacked spectra (Prochaska, Worseck, & O’Meara Reference Prochaska, Worseck and O’Meara2009; O’Meara et al. Reference O’Meara, Prochaska, Worseck, Chen and Madau2013; Fumagalli et al. Reference Fumagalli, O’Meara, Prochaska and Worseck2013; Worseck et al. Reference Worseck2014). Another approach used for estimating λmfp is to use hydrodynamical simulations which explicitly model the distribution of gas in the IGM, coupled with radiative transfer or analytical treatments for self-shielding (Miralda-Escudé, Haehnelt, & Rees Reference Miralda-Escudé, Haehnelt and Rees2000; Meiksin & White Reference Meiksin and White2004; Gnedin & Fan Reference Gnedin and Fan2006; Bolton & Haehnelt Reference Bolton and Haehnelt2007c; McQuinn, Oh, & Faucher-Giguère Reference McQuinn, Oh and Faucher-Giguère2011; Emberson, Thomas, & Alvarez Reference Emberson, Thomas and Alvarez2013; Sobacchi & Mesinger Reference Sobacchi and Mesinger2014; Muñoz et al. Reference Muñoz, Oh, Davies and Furlanetto2016).
A selection of recent measurements and simulation predictions are shown in Figure 3, from Worseck et al. (Reference Worseck2014). A recent analysis of τLL in stacked quasar spectra by Worseck et al. (Reference Worseck2014) provides a best-fitting evolution of λLL = 37[(1 + z)/5]−5.4 proper Mpc at 2 < z < 5. Using an alternative approach based on the observed incidence of LLSs, Songaila & Cowie (Reference Songaila and Cowie2010) instead find a slightly shallower evolution with redshift, λLL = 32[(1 + z)/5]−4.4 proper Mpc. Regardless of the precise normalisation and slope, however, these results indicate λmfp evolves more quickly than expected for a population of absorbers with no intrinsic evolution.Footnote 4

Figure 3. Summary of estimates for the proper mean free path at the Lyman limit, λLL(z). The results are based on stacked quasar spectra (Worseck et al. Reference Worseck2014), observations of discrete H Iabsorption systems (Faucher-Gigu et al. Reference Faucher-Giguère, Lidz, Hernquist and Zaldarriaga2008b; Songaila & Cowie Reference Songaila and Cowie2010; Haardt & Madau Reference Haardt and Madau2012; Rudie et al. Reference Rudie, Steidel, Shapley and Pettini2013), optically thin IGM simulations using either semi-analytical (Miralda-Escudé et al. Reference Miralda-Escudé, Haehnelt and Rees2000; Bolton & Haehnelt Reference Bolton and Haehnelt2007c) or empirical (Meiksin & White Reference Meiksin and White2004) corrections for the abundance of self-shielded absorbers, and full radiative transfer models (Gnedin & Fan Reference Gnedin and Fan2006; McQuinn et al. Reference McQuinn, Oh and Faucher-Giguère2011; Haardt & Madau Reference Haardt and Madau2012; Emberson et al. Reference Emberson, Thomas and Alvarez2013). Note that the estimates at z ≳ 6 are either extrapolations from data at z < 6 or predictions from simulations. Reproduced from Figure 11 of Worseck et al. (Reference Worseck2014) by permission of the authors.
Consequently, there is significant evolution in the comoving number density and typical cross-section of Lyman limit absorbers toward higher redshift. This is directly related to the decline in the photoionisation rate at z > 5; as the overall level of ionisation in the IGM drops, the typical density of LLS decreases, extending these optically thick systems out from the central regions of dark matter haloes to the surrounding filaments in the IGM. It has been suggested this coupling between λmfp and ΓHI (or equivalently, the sinks and sources of ionising photons in the IGM) naturally explains the flat evolution in ΓHI from 2 < z < 5 and its sudden decline approaching z = 6 (McQuinn et al. Reference McQuinn, Oh and Faucher-Giguère2011; Muñoz et al. Reference Muñoz, Oh, Davies and Furlanetto2016) when in contrast, the comoving ionising emissivity evolves slowly.
2.5 The ionising emissivity
Armed with observational determinations of ΓHI(z) and λLL(z) at z < 6, constraints on the integrated emissivity from ionising sources may now be obtained. If the typical mean free path for Lyman-limit photons is much smaller than the horizon scale, λmfp(ν) ≪ c/H(z), photon redshifting effects are minimal and Equation (4) may be written as
This is referred to as the local source approximation (Madau et al. Reference Madau, Haardt and Rees1999; Schirber & Bullock Reference Schirber and Bullock2003). The proper specific emissivity, ε(ν), is related to the comoving emissivity of ionising photons by
where the simplifying assumption of a power-law source spectrum, ε(ν) = εLL(ν/νLL)−αs is adopted. Substituting Equations (5), (12) and (11) into this expression gives
where we may also identify αbg = αs − 3(βN − 1) if the CDDF is described by a single power-law index (but see Section 2.4).
Equation (14) may be used to estimate the total ionising emissivity in the IGM, given observational determinations of ΓHI(z) and λLL(z). Values for αs will depend on the sources which dominate the UVB. For AGN, αs = 1.5–1.8 (Telfer et al. Reference Telfer, Zheng, Kriss and Davidsen2002; Stevans et al. Reference Stevans, Shull, Danforth and Tilton2014), whereas for star-forming galaxies αs = 1–3 (e.g. Leitherer et al. Reference Leitherer1999; Eldridge & Stanway Reference Eldridge and Stanway2012). Note, however, the local source approximation ignores the cosmological redshifting of ionising photons to frequencies ν < νLL, and thus underestimates ![]() $\dot{N}_{\rm ion}$ for a given ΓHI by ~ 50% (~ 10%) at z = 2 (z = 5) (Becker & Bolton Reference Becker and Bolton2013). Modelling λLL with Equation (11) and adopting a single power-law source spectrum are further simplifications; these enable analytical forms for the integrals, but more detailed treatments often require these equations to be solved numerically.
$\dot{N}_{\rm ion}$ for a given ΓHI by ~ 50% (~ 10%) at z = 2 (z = 5) (Becker & Bolton Reference Becker and Bolton2013). Modelling λLL with Equation (11) and adopting a single power-law source spectrum are further simplifications; these enable analytical forms for the integrals, but more detailed treatments often require these equations to be solved numerically.
Recent inferences are consistent with ![]() ${\dot{N}_{\rm ion}}\sim 10^{51}\rm \,s^{-1}\,Mpc^{-3}$ at 2 < z < 6 (Becker & Bolton Reference Becker and Bolton2013). These are around a factor of 2 higher than earlier estimates (Bolton & Haehnelt Reference Bolton and Haehnelt2007c; Kuhlen & Faucher-Giguère Reference Kuhlen and Faucher-Giguère2012), largely due to improved constraints for the mean free path at z > 4 and the temperature of the IGM at 2 < z < 5. The emissivity is also often expressed as the number of ionising photons emitted per hydrogen atom over a Hubble time,
${\dot{N}_{\rm ion}}\sim 10^{51}\rm \,s^{-1}\,Mpc^{-3}$ at 2 < z < 6 (Becker & Bolton Reference Becker and Bolton2013). These are around a factor of 2 higher than earlier estimates (Bolton & Haehnelt Reference Bolton and Haehnelt2007c; Kuhlen & Faucher-Giguère Reference Kuhlen and Faucher-Giguère2012), largely due to improved constraints for the mean free path at z > 4 and the temperature of the IGM at 2 < z < 5. The emissivity is also often expressed as the number of ionising photons emitted per hydrogen atom over a Hubble time, ![]() ${\dot{n}}_{\rm ion}={\dot{N}}_{\rm ion}(1+z)^{3}/{\bar{n}}_{\rm H}H(z)$, where t age ≃ 2/3H(z) is the age of the Universe at z ⩾ 2. Miralda-Escudé (Reference Miralda-Escudé2003) first pointed out that the emissivity at z = 4 corresponds to
${\dot{n}}_{\rm ion}={\dot{N}}_{\rm ion}(1+z)^{3}/{\bar{n}}_{\rm H}H(z)$, where t age ≃ 2/3H(z) is the age of the Universe at z ⩾ 2. Miralda-Escudé (Reference Miralda-Escudé2003) first pointed out that the emissivity at z = 4 corresponds to ![]() $\dot{n}_{\rm ion}\le 7$, which strictly limits the amount by which it may decline at z > 4 if reionisation is to complete by z = 6. Similar conclusions were reached by Meiksin (Reference Meiksin2005), and later Bolton & Haehnelt (Reference Bolton and Haehnelt2007c), who extended the analysis to z = 6, finding
$\dot{n}_{\rm ion}\le 7$, which strictly limits the amount by which it may decline at z > 4 if reionisation is to complete by z = 6. Similar conclusions were reached by Meiksin (Reference Meiksin2005), and later Bolton & Haehnelt (Reference Bolton and Haehnelt2007c), who extended the analysis to z = 6, finding ![]() ${\dot{n}}_{\rm ion} \le 2$–5.
${\dot{n}}_{\rm ion} \le 2$–5.
In comparison, recent cosmological radiative transfer simulations indicate the reionisation of the IGM requires ≳ 2–3 ionising photons per atom to counterbalance radiative recombinations (Finlator et al. Reference Finlator, Oh, Özel and Davé2012; So et al. Reference So, Norman, Reynolds and Wise2014). The close correspondence between this number and ![]() ${\dot{n}}_{\rm ion}$ indicates reionisation may be a ‘photon-starved’ process; there are only just enough photons present to reionise the IGM at z ≃ 6. Consequently, the metagalactic ionising emissivity at z ⩽ 6 is an important observational constraint which viable reionisation models at z > 6 must anchor to Pritchard, Loeb, & Wyithe (Reference Pritchard, Loeb and Wyithe2010), Alvarez, Finlator, & Trenti (Reference Alvarez, Finlator and Trenti2012), Finlator et al. (Reference Finlator, Oh, Özel and Davé2012), Mitra, Ferrara, & Choudhury (Reference Mitra, Ferrara and Choudhury2013), and Fontanot et al. (Reference Fontanot, Cristiani, Pfrommer, Cupani and Vanzella2014).
${\dot{n}}_{\rm ion}$ indicates reionisation may be a ‘photon-starved’ process; there are only just enough photons present to reionise the IGM at z ≃ 6. Consequently, the metagalactic ionising emissivity at z ⩽ 6 is an important observational constraint which viable reionisation models at z > 6 must anchor to Pritchard, Loeb, & Wyithe (Reference Pritchard, Loeb and Wyithe2010), Alvarez, Finlator, & Trenti (Reference Alvarez, Finlator and Trenti2012), Finlator et al. (Reference Finlator, Oh, Özel and Davé2012), Mitra, Ferrara, & Choudhury (Reference Mitra, Ferrara and Choudhury2013), and Fontanot et al. (Reference Fontanot, Cristiani, Pfrommer, Cupani and Vanzella2014).
2.6 The contribution from galaxies and AGN
The ionising emissivity inferred from the Ly α forest may be directly compared to estimates based on the observed population of sources at high redshift. The power of this approach is that the metagalactic emissivity represents the combined photon output from all ionising sources, irrespective of uncertain physics at galactic scales. If the UV luminosity function, ϕ(L UV, z), for a given source population is known, the proper UV specific emissivityFootnote 5 is given by
The luminosity function for LBGs is typically parameterised as a Schechter (Reference Schechter1976) function, whereas AGN are often described by a double power law (e.g. Ueda et al. Reference Ueda, Akiyama, Ohta and Miyaji2003; Richards et al. Reference Richards2006; Croom et al. Reference Croom2009). The proper emissivity at the Lyman limit is then εLL = f escf LLεUV, where f LL = εLL, int/εUV is the ratio of the intrinsic Lyman limit and UV emissivities, and f esc is the (average) fraction of ionising photons which escape the local interstellar medium. For AGN, a broken power-law approximation is often used to estimate f LL and f esc = 1 is typically assumed (e.g. Madau et al. Reference Madau, Haardt and Rees1999), while for high-redshift galaxies stellar population synthesis models are employed to obtain f LL and f esc is a free parameter. The spectral properties of galaxies may also be constrained further with observed UV spectral slopes (Finkelstein et al. Reference Finkelstein2012; Dunlop et al. Reference Dunlop2013; Robertson et al. Reference Robertson2013; Bouwens et al. Reference Bouwens2014; Duncan & Conselice Reference Duncan and Conselice2015). The comoving emissivity of ionising photons is then obtained using Equation (13).
Figure 4 displays ![]() ${\dot{N}}_{\rm ion}$ inferred from the UV luminosity densities reported by Oesch et al. (Reference Oesch2013), Bouwens et al. (Reference Bouwens2015), and Finkelstein et al. (Reference Finkelstein2015), assumingFootnote 6f LL = 0.25 ± 0.10, f esc = 0.3 ± 0.2 and a power-law spectral index below the Lyman limit, αs = 2 ± 1 (e.g Becker & Bolton Reference Becker and Bolton2013). These data are based on recent measurements of the LBG luminosity function to a limiting absolute magnitude of M UV ≃ −17 at 4 < z < 10.5, and are compared to independent measurements of
${\dot{N}}_{\rm ion}$ inferred from the UV luminosity densities reported by Oesch et al. (Reference Oesch2013), Bouwens et al. (Reference Bouwens2015), and Finkelstein et al. (Reference Finkelstein2015), assumingFootnote 6f LL = 0.25 ± 0.10, f esc = 0.3 ± 0.2 and a power-law spectral index below the Lyman limit, αs = 2 ± 1 (e.g Becker & Bolton Reference Becker and Bolton2013). These data are based on recent measurements of the LBG luminosity function to a limiting absolute magnitude of M UV ≃ −17 at 4 < z < 10.5, and are compared to independent measurements of ![]() ${\dot{N}}_{\rm ion}$ from the Ly α forest at 2 < z < 5, along with models for the expected emissivity from AGN (blue curves) and star-forming galaxies (red curves). The dotted curves display the comoving emissivity required to balance radiative recombinations in the IGM (Madau et al. Reference Madau, Haardt and Rees1999), where
${\dot{N}}_{\rm ion}$ from the Ly α forest at 2 < z < 5, along with models for the expected emissivity from AGN (blue curves) and star-forming galaxies (red curves). The dotted curves display the comoving emissivity required to balance radiative recombinations in the IGM (Madau et al. Reference Madau, Haardt and Rees1999), where
Here, ![]() $C_{\rm HII}=\langle n_{\rm HII}^{2} \rangle /{\bar{n}}_{\rm HII}^{2}$ is the clumping factor. This takes into account the enhancement in the volume averaged recombination rate due to small scale, dense structures. Typical values for the ionised, low-density IGM obtained from numerical simulations are C HII ≃ 1–5 (Pawlik, Schaye, & van Scherpenzeel Reference Pawlik, Schaye and van Scherpenzeel2009; Finlator et al. Reference Finlator, Oh, Özel and Davé2012; Shull et al. Reference Shull, Harness, Trenti and Smith2012; Jeeson-Daniel et al. Reference Jeeson-Daniel, Ciardi and Graziani2014; So et al. Reference So, Norman, Reynolds and Wise2014; Kaurov & Gnedin Reference Kaurov and Gnedin2014). Alternatively, assuming the IGM is in ionisation equilibrium (cf. Equation 6), then Equation (14) and (16) may be equated and rearranged for C HII. Inserting observational estimates for ΓHI and λLL yields C HII ≃ 2–3 (Bolton & Haehnelt Reference Bolton and Haehnelt2007c; McQuinn et al. Reference McQuinn, Oh and Faucher-Giguère2011).
$C_{\rm HII}=\langle n_{\rm HII}^{2} \rangle /{\bar{n}}_{\rm HII}^{2}$ is the clumping factor. This takes into account the enhancement in the volume averaged recombination rate due to small scale, dense structures. Typical values for the ionised, low-density IGM obtained from numerical simulations are C HII ≃ 1–5 (Pawlik, Schaye, & van Scherpenzeel Reference Pawlik, Schaye and van Scherpenzeel2009; Finlator et al. Reference Finlator, Oh, Özel and Davé2012; Shull et al. Reference Shull, Harness, Trenti and Smith2012; Jeeson-Daniel et al. Reference Jeeson-Daniel, Ciardi and Graziani2014; So et al. Reference So, Norman, Reynolds and Wise2014; Kaurov & Gnedin Reference Kaurov and Gnedin2014). Alternatively, assuming the IGM is in ionisation equilibrium (cf. Equation 6), then Equation (14) and (16) may be equated and rearranged for C HII. Inserting observational estimates for ΓHI and λLL yields C HII ≃ 2–3 (Bolton & Haehnelt Reference Bolton and Haehnelt2007c; McQuinn et al. Reference McQuinn, Oh and Faucher-Giguère2011).

Figure 4. The comoving emissivity of ionising photons with redshift. The filled circles correspond to estimates from the Ly α forest opacity (Becker & Bolton Reference Becker and Bolton2013) (see their Table 3 for a full breakdown of the systematic uncertainties), and the grey symbols show results derived here from the comoving UV luminosity density, ρUV, of Lyman break galaxies (Oesch et al. Reference Oesch2013; Finkelstein et al. Reference Finkelstein2015; Bouwens et al. Reference Bouwens2015). The error bars on these data are computed by adding the published uncertainties on ρUV in quadrature with the systematic uncertainties f LL = 0.25 ± 0.10, f esc = 0.3 ± 0.2 and αs = 2 ± 1 (see the text and Equations (13) and (15) for details). The red curves display a model for the emissivity from star-forming galaxies, where the ionising efficiency is fixed at ζ = 25 independent of redshift. Here, ![]() ${\dot{N}}_{\rm ion}$ is proportional to the rate of change of the collapsed fraction of matter in haloes with M min ⩾ 108M ⊙ (solid curve) and M min ⩾ 1010M ⊙ (long-dashed curve). The blue short-dashed and dot–dashed curves show the AGN emissivity models from Haardt & Madau (Reference Haardt and Madau2012) and Giallongo et al. (Reference Giallongo, Menci, Fiore, Castellano, Fontana, Grazian and Pentericci2012), respectively. The dotted curves correspond to the ionising emissivity required to balance recombinations for three different hydrogen clumping factors, C HII = 1, 2 and 5; these are truncated where the recombination timescale exceeds the age of the Universe.
${\dot{N}}_{\rm ion}$ is proportional to the rate of change of the collapsed fraction of matter in haloes with M min ⩾ 108M ⊙ (solid curve) and M min ⩾ 1010M ⊙ (long-dashed curve). The blue short-dashed and dot–dashed curves show the AGN emissivity models from Haardt & Madau (Reference Haardt and Madau2012) and Giallongo et al. (Reference Giallongo, Menci, Fiore, Castellano, Fontana, Grazian and Pentericci2012), respectively. The dotted curves correspond to the ionising emissivity required to balance recombinations for three different hydrogen clumping factors, C HII = 1, 2 and 5; these are truncated where the recombination timescale exceeds the age of the Universe.
Figure 4 demonstrates that the observed population of LBGs at z < 6 is consistent with the emissivity inferred from the Ly α forest, although the lack of evolution in the latter from z = 4–5 implies that the escape fraction of ionising photons, f esc, may be increasing toward higher redshift (e.g. Alvarez et al. Reference Alvarez, Finlator and Trenti2012; Ciardi et al. Reference Ciardi, Bolton, Maselli and Graziani2012; Kuhlen & Faucher-Giguère Reference Kuhlen and Faucher-Giguère2012; Shull et al. Reference Shull, Harness, Trenti and Smith2012; Ferrara & Loeb Reference Ferrara and Loeb2013). However, the emissivity from these galaxies rapidly drops below the critical rate required to balance recombinations at z ≳ 6, indicating the observed sources are insufficient to drive reionisation to completion. There are three ways to resolve this dilemma: (i) there are many more faint galaxies below the detection limit which contribute to the total photon budget; (ii) the ionising efficiency (the product of f LL and f esc) of these galaxies increases significantly toward higher redshift, or (iii) there is another population of sources which produce ionising photons. A combination of all three may also be plausible.
To illustrate this further, the red curves in Figure 4 display a simple model for the expected emissivity from star-forming galaxies, where
(e.g Pritchard et al. Reference Pritchard, Loeb and Wyithe2010; Wyithe et al. Reference Wyithe, Hopkins, Kistler, Yüksel and Beacom2010; Sobacchi & Mesinger Reference Sobacchi and Mesinger2014). Here, f coll is the collapsed fraction of matter in haloes above a minimum mass threshold M min (Sheth & Tormen Reference Sheth and Tormen2002), and ζ(z) = f ⋆f escN γ is the ionising efficiency of star-forming galaxies (assumed to be constant, ζ = 25, in Figure 4). This ionising efficiency is itself a function of three uncertain parameters, the star formation efficiency f ⋆, the number of ionising photons produced per baryon within stars, N γ, and the escape fraction.Footnote 7
Considering all haloes above the mass threshold at which atomic cooling ceases to be efficient, M min ≃ 108 M⊙, produces an emissivity in excess of that observed from galaxies with M UV ≲ −17 at z ≳ 6.5. Better agreement may be obtained by extrapolating the observed faint end of the luminosity function to M UV ≃ −10 with Equation (15); faint, high-redshift dwarf galaxies are therefore widely postulated as likely candidates for making up the observed ionising photon shortfall at z > 6 (Trenti et al. Reference Trenti, Stiavelli, Bouwens, Oesch, Shull, Illingworth, Bradley and Carollo2010; Robertson et al. Reference Robertson2013, Reference Robertson, Ellis, Furlanetto and Dunlop2015; Fontanot et al. Reference Fontanot, Cristiani, Pfrommer, Cupani and Vanzella2014; Bouwens et al. Reference Bouwens2015). This illustrates the important role of IGM studies in providing a complete census of early galaxy populations; many of the ionising sources are too faint to detect individually, but we can nevertheless observe their combined impact on the surrounding intergalactic gas. Alternatively, as discussed above the ionising efficiency may increase with redshift, if e.g. f esc evolves with redshift. However, direct measurements of f esc approaching reionisation are prohibited by the high opacity of the intervening IGM, and searches for analogues at lower redshift indicate the amount of Lyman continuum radiation escaping from galaxies is modest (e.g. Vanzella et al. Reference Vanzella2010; Boutsia et al. Reference Boutsia2011; Nestor et al. Reference Nestor, Shapley, Kornei, Steidel and Siana2013; Mostardi et al. Reference Mostardi, Shapley, Nestor, Steidel, Reddy and Trainor2013).
Lastly, it remains possible that other sources contribute to the total ionising emissivity. The most natural candidate are AGN, with hard, non-thermal spectra which produce an abundance of ionising photons. The blue curves in Figure 4 display two very different models for the predicted contribution of AGN to ![]() $\dot{N}_{\rm ion}$. The lower estimate is from the UVB model of Haardt & Madau (Reference Haardt and Madau2012), which is based on the bolometric luminosity functions presented by Hopkins et al. (Reference Hopkins, Richards and Hernquist2007) at 0 < z < 6. There is a sharp drop in
$\dot{N}_{\rm ion}$. The lower estimate is from the UVB model of Haardt & Madau (Reference Haardt and Madau2012), which is based on the bolometric luminosity functions presented by Hopkins et al. (Reference Hopkins, Richards and Hernquist2007) at 0 < z < 6. There is a sharp drop in ![]() ${\dot{N}}_{\rm ion}$ at z > 4 as the number density of sources falls, implying that AGN are unlikely to be the dominant sources powering reionisation (see also Cowie, Barger, & Trouille Reference Cowie, Barger and Trouille2009). On the other hand, semi-analytical modelling by Giallongo et al. (Reference Giallongo, Menci, Fiore, Castellano, Fontana, Grazian and Pentericci2012), incorporating faint (M UV ≃ −18.5) AGN, produces
${\dot{N}}_{\rm ion}$ at z > 4 as the number density of sources falls, implying that AGN are unlikely to be the dominant sources powering reionisation (see also Cowie, Barger, & Trouille Reference Cowie, Barger and Trouille2009). On the other hand, semi-analytical modelling by Giallongo et al. (Reference Giallongo, Menci, Fiore, Castellano, Fontana, Grazian and Pentericci2012), incorporating faint (M UV ≃ −18.5) AGN, produces ![]() $\dot{N}_{\rm ion}$ estimates up to two orders of magnitude larger. If such faint AGN are widespread, these could provide almost all the ionising photons required to complete reionisation. However, uncertainties associated with the number of faint AGN at z > 4 remain considerable, leaving their precise contribution to the ionising photon budget a matter of debate (e.g. Glikman et al. Reference Glikman, Djorgovski, Stern, Dey, Jannuzi and Lee2011; Masters et al. Reference Masters2012; Giallongo et al. Reference Giallongo2015). The number and relative contribution of AGN to the UVB must furthermore remain consistent with upper limits on the unresolved X-ray background (Dijkstra, Haiman, & Loeb Reference Dijkstra, Haiman and Loeb2004a; Haardt & Salvaterra Reference Haardt and Salvaterra2015) and the spectral shape of the UVB inferred from metal ion absorption lines (Section 3) at 2 < z < 4 (Agafonova et al. Reference Agafonova, Levshakov, Reimers, Fechner, Tytler, Simcoe and Songaila2007; Fechner Reference Fechner2011; Boksenberg & Sargent Reference Boksenberg and Sargent2015). Lastly, the double reionisation of helium is expected to compete around z ≃ 2–3, based on observations of the intergalactic He IIopacity (Shull et al. Reference Shull, France, Danforth, Smith and Tumlinson2010; Worseck et al. Reference Worseck2011) and the IGM temperature (Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000; Lidz et al. Reference Lidz, Faucher-Giguère, Dall’Aglio, McQuinn, Fechner, Zaldarriaga, Hernquist and Dutta2010; Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011a). This is thought to be driven by the hard photons emitted by AGN (Furlanetto & Oh Reference Furlanetto and Oh2008; McQuinn et al. Reference McQuinn, Lidz, Zaldarriaga, Hernquist, Hopkins, Dutta and Faucher-Giguère2009). Consequently, their contribution at z > 4 must avoid a premature end to He IIreionisation (McQuinn Reference McQuinn2012).
$\dot{N}_{\rm ion}$ estimates up to two orders of magnitude larger. If such faint AGN are widespread, these could provide almost all the ionising photons required to complete reionisation. However, uncertainties associated with the number of faint AGN at z > 4 remain considerable, leaving their precise contribution to the ionising photon budget a matter of debate (e.g. Glikman et al. Reference Glikman, Djorgovski, Stern, Dey, Jannuzi and Lee2011; Masters et al. Reference Masters2012; Giallongo et al. Reference Giallongo2015). The number and relative contribution of AGN to the UVB must furthermore remain consistent with upper limits on the unresolved X-ray background (Dijkstra, Haiman, & Loeb Reference Dijkstra, Haiman and Loeb2004a; Haardt & Salvaterra Reference Haardt and Salvaterra2015) and the spectral shape of the UVB inferred from metal ion absorption lines (Section 3) at 2 < z < 4 (Agafonova et al. Reference Agafonova, Levshakov, Reimers, Fechner, Tytler, Simcoe and Songaila2007; Fechner Reference Fechner2011; Boksenberg & Sargent Reference Boksenberg and Sargent2015). Lastly, the double reionisation of helium is expected to compete around z ≃ 2–3, based on observations of the intergalactic He IIopacity (Shull et al. Reference Shull, France, Danforth, Smith and Tumlinson2010; Worseck et al. Reference Worseck2011) and the IGM temperature (Schaye et al. Reference Schaye, Theuns, Rauch, Efstathiou and Sargent2000; Lidz et al. Reference Lidz, Faucher-Giguère, Dall’Aglio, McQuinn, Fechner, Zaldarriaga, Hernquist and Dutta2010; Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011a). This is thought to be driven by the hard photons emitted by AGN (Furlanetto & Oh Reference Furlanetto and Oh2008; McQuinn et al. Reference McQuinn, Lidz, Zaldarriaga, Hernquist, Hopkins, Dutta and Faucher-Giguère2009). Consequently, their contribution at z > 4 must avoid a premature end to He IIreionisation (McQuinn Reference McQuinn2012).
2.7 Spatial fluctuations in the UVB
Finally in this section, we turn to consider spatial inhomogeneities in the UVB. In addition to the average photoionisation rate determined from the mean transmission of the Ly α forest, one can also examine spatial fluctuations in ΓHI using the line-of-sight variation in the transmission as a function of redshift (Fan et al. Reference Fan2006). If reionisation is incomplete, this may boost the amplitude of spatial variations in the transmission, with some lines-of-sight crossing mostly through ionised bubbles, and others intersecting multiple neutral regions in the IGM (Wyithe & Loeb Reference Wyithe and Loeb2006). Note, however, the scatter in the average transmission may also be large shortly after reionisation completes, when the local mean free path to ionising photons is similar to the typical separation between (clustered) sources. In this scenario, the mean free path itself may vary spatially; even though the IGM is highly ionised, the UVB will exhibit significant spatial fluctuations (e.g. Zuo Reference Zuo1992; Meiksin & White Reference Meiksin and White2004; Mesinger & Furlanetto Reference Mesinger and Furlanetto2009).
Importantly, these fluctuations potentially yield information on the timing of patchy reionisation and the distribution of the ionising sources; the scatter in the average transmission may be an interesting diagnostic in this respect. However, fluctuations owing to spatial variations in the underlying density field may also contribute significantly to the observed scatter (Lidz et al. Reference Lidz, Oh and Furlanetto2006). The aliasing of transverse, small-scale density fluctuations in three dimensions to larger scales along the one-dimensional quasar sightlines can further obscure effects from incomplete reionisation (cf. Kaiser & Peacock Reference Kaiser and Peacock1991).
Nevertheless, recent work indicates that the observed scatter is indeed larger than expected in uniform UVB models, especially at z ≳ 5.5 (Becker et al. Reference Becker, Bolton, Madau, Pettini, Ryan-Weber and Venemans2015). This finding is driven in part by the discovery of a contiguous 110h −1 comoving Mpc dark region in the z ~ 5.7 Ly α forest. Such a large scatter in the mean transmission is seen at z < 6 in radiative transfer simulations where reionisation competes between z = 6 and 7 (Gnedin Reference Gnedin2014), and may be a natural consequence of spatial variations in the mean free path at the tail-end of reionisation (Furlanetto & Oh Reference Furlanetto and Oh2005). It has also been recently suggested the fluctuations may instead be indicative of photoionisation by rare, bright quasars (Chardin et al. Reference Chardin, Haehnelt, Aubert and Puchwein2015). Alternatively, reionisation may be incomplete at z ~ 5.5–6 (Lidz et al. Reference Lidz, McQuinn, Zaldarriaga, Hernquist and Dutta2007; Mesinger Reference Mesinger2010, and see Section 4.2). Consequently, while these observations are highly suggestive, we have yet to determine their full implications for the reionisation history of the Universe.
3 METAL ABSORPTION LINES
Metal absorption lines complement the Ly α forest as probes of the high-redshift Universe in that they reflect the chemical enrichment and ionisation state in the regions in and around galaxies. The overall abundance of metals reflects the integrated global star formation history, while the number densities, ionic ratios, and kinematic profiles of absorbers contain information on the mechanisms by which galaxies produce and expel metals (i.e., feedback mechanisms), the stellar populations that produced the metals, and the ionisation state of the metal-enriched gas. Metal absorbers are particularly valuable tracers of galaxies during reionisation, as they can arise from faint galaxies that are below the detection thresholds of direct galaxy surveys. In this section, we give an overview of recent results on metal lines over z ~ 5–6. We first describe the observations, then examine what metal absorbers tell us about galaxies and their environments at these redshifts.
3.1 Observations of metal lines near z ~ 6
Studies of metal lines near reionisation have tended to focus on three types of absorbers: highly ionised systems traced by C iv and/or Si iv (which we will generally refer to as C iv systems); low-ionisation systems traced by O i, C ii, Si ii, and Fe ii (which we will refer to as O i systems); and Mg ii systems, which can trace a range of ionisation statesFootnote 8. Studies of C iv (rest-frame λ = 1 548, 1 551 \AA) and Mg ii (λ = 2 796, 2 804 \AA), which are observed in the infrared at z > 5.5 and 2.6, respectively, have particularly benefited from the substantial increase in infrared spectroscopic sensitivity recently provided by the X-Shooter spectrograph on the Very Large Telescope (D’Odorico et al. Reference D’Odorico2006), and the Folded-port Infrared Echellette (FIRE) spectrograph on Magellan (Simcoe et al. Reference Simcoe2013). We will begin by describing the observations of C iv, O i, and Mg ii absorbers separately, although the reader should bear in mind that these often trace different components of the same system. To date, quasars have been used for systematic surveys of metals at z > 5; however, gamma ray burst (GRB) afterglows have also started to yield samples of metal lines at these redshifts (e.g. Chornock et al. Reference Chornock, Berger, Fox, Lunnan, Drout, fai Fong, Laskar and Roth2013; Castro-Tirado et al. Reference Castro-Tirado2013; Hartoog et al. Reference Hartoog2015).
3.1.1 Metrics
Before describing the observations, we first introduce some of the metrics used to quantify metal absorption line samples. An absorber population can be characterised by its column density distribution, f(N) = ∂2n/∂N∂X, which gives the number of systems per unit column density, N, and absorption path length interval X (see also Section 2.4). The absorption path length interval is related to the redshift interval by
Bahcall & Peebles (Reference Bahcall and Peebles1969), and has the useful property that a population of sources with a fixed physical cross-section will have a constant number density per unit X.
Two quantities related to f(N) that are often quoted for metal absorbers are the line-of-sight number density, dn/dX (or dn/dz), and the comoving mass density. The total mass density of an ion can be expressed as a fraction of ρcrit, the critical density at z = 0,
which can be approximated as
Here, N ion is the column density of an absorber and ΔX is the total survey path length.
3.1.2 C iv
The C iv doublet is perhaps the most commonly used absorption line tracer of metals due to its sensitivity to enriched, highly ionised gas. The first C iv measurements at z ~ 6 were made by Simcoe (Reference Simcoe2006) and Ryan-Weber, Pettini, & Madau (Reference Ryan-Weber, Pettini and Madau2006), with larger samples and improved sensitivity provided by Becker, Rauch, & Sargent (Reference Becker, Rauch and Sargent2009), Ryan-Weber et al. (Reference Ryan-Weber, Pettini, Madau and Zych2009), Simcoe et al. (Reference Simcoe2011), and D’Odorico et al. (Reference D’Odorico2013). At present, 13 z ~ 6 quasars have been surveyed for C iv along their line of sight. An example system at z = 5.9 is shown in Figure 5, which in this case displays both C iv and Si iv absorption.

Figure 5. Examples of C iv (left) and low-ionisation (right) metal absorption line systems observed with VLT/X-Shooter, at z = 5.92 and 5.79, respectively. The transitions for a given absorber have been shifted onto a common velocity scale. Histograms show the continuum-normalised flux, while the dashed lines are the flux uncertainty. Solid lines are Voigt profile fits. Reproduced from Figures 5 and 17 of D’Odorico et al. (Reference D’Odorico2013) with permission of the authors.
While precise fits to f(N C IV) at z ~ 6 remain difficult due to the small number of absorbers, D’Odorico et al. (Reference D’Odorico2013) find that the z > 5.3 data can be fit with a power law in N C IV with a slope similar to that for C iv populations at lower redshifts, but with a normalisation that is a factor of 2 to 4 lower (see also Becker et al. Reference Becker, Rauch and Sargent2009).
Figure 6 shows the evolution for ΩC IV over 0 < z < 6. In general, the mass density of C iv increases towards lower redshifts, which is consistent with the buildup of highly ionised metals in the circumgalactic medium of galaxies due to processes such as outflows (e.g. Oppenheimer & Davé Reference Oppenheimer and Davé2006). Changes in the ionisation state of the metal-enriched gas will also affect the C iv statistics, however. The ionisation state of C iv-selected gas will tend to evolve due to changes in density and/or the UVB, such that the fraction of carbon in these systems traced by C iv will change with redshift. The evolution of ΩC IV is therefore the product of increasing metal enrichment and changes in the ionisation state of the metal-enriched gas. Generally speaking, C iv becomes a preferred ionisation state at lower overdensities towards higher redshifts (e.g. Oppenheimer & Davé Reference Oppenheimer and Davé2006; Oppenheimer, Davé, & Finlator Reference Oppenheimer, Davé and Finlator2009). It is noteworthy that ΩC IV appears to increase by a factor of 2 to 4 from z ~ 6 to 5. This suggests a substantial buildup of metal-enriched regions around galaxies over this interval, although the rate of increase may depend partly on the range of column densities being considered (D’Odorico et al. Reference D’Odorico2013).

Figure 6. Evolution of the comoving mass density of C iv, expressed as a fraction of the critical density. Results from the literature are plotted with symbols indicated in the figure legend (Pettini et al. Reference Pettini, Madau, Bolte, Prochaska, Ellison and Fan2003; Danforth & Shull Reference Danforth and Shull2008; Becker et al. Reference Becker, Rauch and Sargent2009; Ryan-Weber et al. Reference Ryan-Weber, Pettini, Madau and Zych2009; Cooksey et al. Reference Cooksey, Thom, Prochaska and Chen2010, Reference Cooksey, Kao, Simcoe, O’Meara and Prochaska2013; D’Odorico et al. Reference D’Odorico, Calura, Cristiani and Viel2010, Reference D’Odorico2013; Simcoe et al. Reference Simcoe2011; Tilton et al. Reference Tilton, Danforth, Shull and Ross2012; Danforth et al. Reference Danforth2014; Boksenberg & Sargent Reference Boksenberg and Sargent2015, where ‘Bok+Sar 14’ in the caption refers to Boksenberg & Sargent Reference Boksenberg and Sargent2015). Note that some of the variation in these results is due to differences in the column density range over which ΩC IV is integrated. Reproduced from Figure 1 of Shull, Danforth, & Tilton (Reference Shull, Danforth and Tilton2014) by permission of the authors and the AAS.
3.1.3 O i
Low-ionisation metal lines are potentially powerful probes of the high-redshift Universe in multiple ways. First, they trace the dense gas in and around galaxies, offering insights into the interstellar media of these objects analogous to the ways in which damped Ly α systems (DLAs) trace the kinematics and composition of lower-redshift galaxies (e.g. Wolfe, Gawiser, & Prochaska Reference Wolfe, Gawiser and Prochaska2005). Second, because the metals in these systems are often dominated by a single ionisation state, determining abundances is relatively straightforward. Finally, if the last regions of the IGM to be reionised are metal enriched, then they may give rise to a ‘forest’ of absorption lines such as O i and C ii that can be detected in quasar spectra (e.g. Oh Reference Oh2002; Furlanetto & Loeb Reference Furlanetto and Loeb2003).
Metal-enriched gas where the hydrogen is largely neutral is traced by lines such as O i, C ii, Si ii, and Fe ii. O i is particularly useful for studying neutral gas since the first ionisation potential of oxygen and hydrogen are very similar, and due to charge exchange, n(O+)/n(O) ≃ n(H+)/n(H) over a wide range of physical conditions (e.g. Osterbrock & Ferland Reference Osterbrock and Ferland2006). Elements where the first ionisation potential is significantly less than 13.6 eV, such as carbon, silicon, and iron, are not shielded by atomic hydrogen, and therefore appear as singly ionised species in otherwise ‘neutral’ gas. At z < 5, low-ionisation systems are typically found by their strong, often damped, hydrogen Ly α lines. At higher redshifts, however, the growing saturation of the Ly α forest makes identifying individual Ly α absorbers difficult, and metal systems must be identified using ‘pseudo multiplets’ of lines redward of Ly α, such as O i λ1302; C ii λ1334; and Si ii λ1260, λ1304, and λ1526.
Becker et al. (Reference Becker, Sargent, Rauch and Simcoe2006, Reference Becker, Sargent, Rauch and Calverley2011b) searched for low-ionisation systems over 5.3 < z abs < 6.4. In 17 lines of sight, they find 10 systems with C ii and Si ii, nine of which also contain O i. Infrared spectra have been used to obtain Fe ii for many of these systems (Becker et al. Reference Becker, Sargent, Rauch and Carswell2012; D’Odorico et al. Reference D’Odorico2013). Among the nine O i systems, the ratios of O i, C ii, Si ii, and Fe ii column densities are reasonably constant, which suggests that neither ionisation corrections nor dust depletion are large factors, as these would tend to introduce scatter. This supports the expectation that O i systems trace predominantly neutral gas, and are therefore the analogues of lower-redshift DLAs (N H I ⩾ 1020.3 cm−2) (e.g. Wolfe et al. Reference Wolfe, Gawiser and Prochaska2005) and sub-DLAs (1019 cm−2 < N H I < 1020.3 cm−2) (e.g. Dessauges-Zavads et al. Reference Dessauges-Zavadsky, Péroux, Kim, D’Odorico and McMahon2003).Footnote 9 It is therefore reasonable to compare O i systems at z > 5 to these systems, although it should be emphasised that H i-selected systems with N H I > 1019 cm−2 may not represent a complete census of O i systems at lower redshifts.
In terms of number density, Becker et al. (Reference Becker, Sargent, Rauch and Calverley2011b) find dn/dX = 0.25+ 0.21−0.13, which is similar to the combined number density of DLAs and sub-DLAs over 3 < z < 5 (Péroux et al. Reference Péroux, Dessauges-Zavadsky, D’Odorico, Kim and McMahon2005; O’Meara et al. Reference O’Meara, Prochaska, Burles, Prochter, Bernstein and BurgessO’Meara et al.; Prochaska & Wolfe Reference Prochaska and Wolfe2009; Noterdaeme et al. Reference Noterdaeme, Petitjean, Ledoux and Srianand2009; Guimarães et al. Reference Guimarães, Petitjean, de Carvalho, Djorgovski, Noterdaeme, Castro, Poppe and Aghaee2009; Crighton et al. Reference Crighton2015). At least one of the O i systems lies close to the detection limit of the existing data, however (Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b), so it is possible that the number density of weak low-ionisation systems (N O I ≲ 1013.5 cm−2, N C II ≲ 1013.0 cm−2) may be larger. The observed mass density of O i in systems at z ~ 6 can be directly computed using Equation (20) because the lines are typically unsaturated, and so have measurable column densities. At lower redshifts, O i is generally saturated; however, the total mass density can be estimated by combining measurements of ΩH I in DLAs, which dominate the neutral gas budget (e.g. Noterdaeme et al. Reference Noterdaeme, Petitjean, Ledoux and Srianand2009; Crighton et al. Reference Crighton2015) with the column density-weighted mean DLA metallicity (e.g. Rafelski et al. Reference Rafelski, Neeleman, Fumagalli, Wolfe and Prochaska2014). Figure 7 shows ΩO I at z ~ 6 computed from the Becker et al. (Reference Becker, Sargent, Rauch and Calverley2011b) measurements, along with an estimates over 2 < z < 4.5 based on the fit to ΩH I(z) in Crighton et al. (Reference Crighton2015) and a fit to the mean metallicity evolution at z < 4.7 from Rafelski et al. (Reference Rafelski, Neeleman, Fumagalli, Wolfe and Prochaska2014). A separate estimate at z = 4.85 is also given based on discrete ΩH I and mean DLA metallicity measurements by these authors near z ~ 5.

Figure 7. Evolution of the comoving mass density of O i, expressed as a fraction of the critical density. The open square is derived from measurements of individual absorbers in Becker et al. (Reference Becker, Sargent, Rauch and Calverley2011b). The shaded region is an estimate based on fits to ΩH I(z) for DLAs from Crighton et al. (Reference Crighton2015) and the mean DLA metallicity from Rafelski et al. (Reference Rafelski, Neeleman, Fumagalli, Wolfe and Prochaska2014). The open triangle at z = 4.85 is calculated from discrete ΩH I and mean DLA metallicity values from these works near z ~ 5.
While these mass density estimates should be treated with caution, they broadly suggest a substantial buildup of metals in the low-ionisation phase over 4.5 ≲ z ≲ 6, followed by a more gradual buildup down to z ~ 2. Given that ΩH I decreases with time (Prochaska & Wolfe Reference Prochaska and Wolfe2009; Noterdaeme et al. Reference Noterdaeme, Petitjean, Ledoux and Srianand2009; Crighton et al. Reference Crighton2015), and that the number density of low-ionisation absorbers does not change rapidly (see above), the increase in the mass density of low-ionisation metals may be largely driven by an increase in the (low-ionisation phase) metal content of the absorbers.
3.1.4 Mg ii
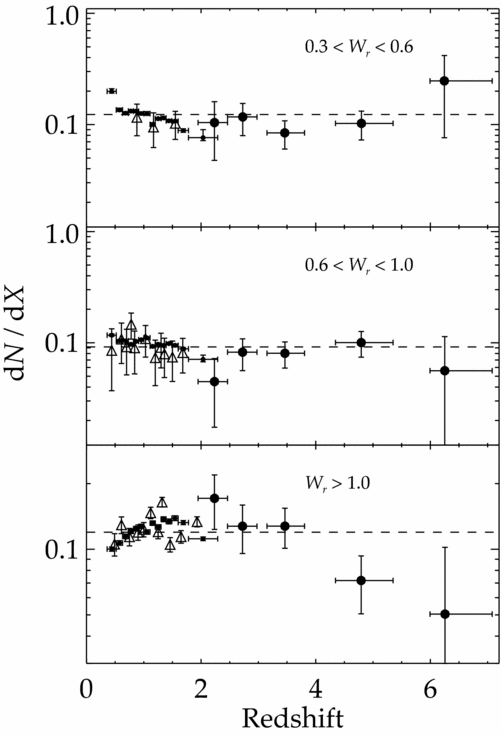
The final absorption-line probe of metals at z > 5 is the Mg ii doublet, which can trace both neutral and ionised gas phases. The first survey for Mg ii over 2.5 < z < 6 was conducted by Matejek & Simcoe (Reference Matejek and Simcoe2012), followed by an expanded sample from Chen et al. (in preparation), both using FIRE data. Column densities of strong Mg ii systems are often difficult to measure due to saturation effects, and it is therefore common to quantify these systems in terms of the rest-frame equivalent width, W r, of the 2796 \AA line. Incidence rates of Mg ii systems in different ranges in W r are shown in Figure 8. The z > 2 data are compared to lower-redshift measurements using Sloan Digital Sky Survey (SDSS) data from Nestor et al. (Reference Nestor, Turnshek and Rao2005) and Seyffert et al. (Reference Seyffert, Cooksey, Simcoe, O’Meara, Kao and Prochaska2013). For weak systems, the higher-resolution FIRE spectra tend to be more sensitive than the larger SDSS samples. Incompleteness corrections are therefore important in comparing these samples, particularly for W r < 1 \AA. At face value, however, the incidence rate of weak (W r < 1 \AA) systems appears to relatively flat with redshift, while stronger systems appear to become more numerous from z ~ 6 to z ~ 2–3, before declining towards lower redshifts.

Figure 8. Evolution of the line-of-sight number density of Mg ii absorbers. The three panels give dn/dX for three ranges of λ2796 rest-frame equivalent width. Triangles are from Nestor, Turnshek, & Rao (Reference Nestor, Turnshek and Rao2005). Small circles are from Seyffert et al. (Reference Seyffert, Cooksey, Simcoe, O’Meara, Kao and Prochaska2013). Large circles are from Chen et al. (in preparation). Dashed lines shows the mean dn/dX for the Nestor et al. (Reference Nestor, Turnshek and Rao2005) and Seyffert et al. (Reference Seyffert, Cooksey, Simcoe, O’Meara, Kao and Prochaska2013) data. For more details, see Chen et al. (in preparation). Figure provided courtesy of R. Simcoe.
The fact that the evolution in dn/dX for strong Mg ii systems shows the same shape as the cosmic star formation rate density has been cited as evidence that these systems are closely linked to star-forming galaxies (Prochter, Prochaska, & Burles Reference Prochter, Prochaska and Burles2006; Ménard et al. Reference Ménard, Wild, Nestor, Quider, Zibetti and Turnshek2011; Matejek & Simcoe Reference Matejek and Simcoe2012). Ménard et al. (Reference Ménard, Wild, Nestor, Quider, Zibetti and Turnshek2011) also note a correlation between W r and the [O ii] luminosity, a tracer of star formation, enclosed in an SDSS fibre. By comparison, the relatively constant incidence of weak Mg ii systems suggests that these absorbers are a feature of metal-enriched haloes that are established early in the process of galaxy formation, and change as a population relatively little, even as other galaxy properties evolve (see discussion in Matejek & Simcoe Reference Matejek and Simcoe2012).
3.1.5 Summary of observations: enrichment versus ionisation
Although observations of metals near the reionisation epoch are still in an early phase, the results generally indicate substantial metal enrichment in the interstellar and circumgalactic environments of galaxies between z ~ 6 and 5. The buildup of metals is expected to correlate with the increase in stellar mass density; however, changes in the ionisation state of the metals must also play a role. For example, the ratio of ![]() $N({\mbox{Si\ {\sc iv}}})/N({\mbox{C\ {\sc iv}}})$ in C iv-selected systems tends to increase with redshift, an indication that higher-redshift systems are tracing denser gas and/or a weaker ionising background (D’Odorico et al. Reference D’Odorico2013; Boksenberg & Sargent Reference Boksenberg and Sargent2015). The fact that the incidence of low-ionisation systems remains roughly constant out to z ~ 6, even while the number density of galaxies is declining with redshift also suggests that the cross-sections of metal-enriched haloes that are largely neutral may be increasing with redshift due to a declining UVB (Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b; Keating et al. Reference Keating, Haehnelt, Becker and Bolton2014). Matejek et al. (Reference Matejek, Simcoe, Cooksey and Seyffert2013) also find evidence that Mg ii systems tend to trace DLAs, which are predominantly neutral, with increasing frequency towards higher redshifts. For high-ionisation systems, shock heating may play a role in setting the ionisation state (Cen & Chisari Reference Cen and Chisari2011), along with the UVB.
$N({\mbox{Si\ {\sc iv}}})/N({\mbox{C\ {\sc iv}}})$ in C iv-selected systems tends to increase with redshift, an indication that higher-redshift systems are tracing denser gas and/or a weaker ionising background (D’Odorico et al. Reference D’Odorico2013; Boksenberg & Sargent Reference Boksenberg and Sargent2015). The fact that the incidence of low-ionisation systems remains roughly constant out to z ~ 6, even while the number density of galaxies is declining with redshift also suggests that the cross-sections of metal-enriched haloes that are largely neutral may be increasing with redshift due to a declining UVB (Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b; Keating et al. Reference Keating, Haehnelt, Becker and Bolton2014). Matejek et al. (Reference Matejek, Simcoe, Cooksey and Seyffert2013) also find evidence that Mg ii systems tend to trace DLAs, which are predominantly neutral, with increasing frequency towards higher redshifts. For high-ionisation systems, shock heating may play a role in setting the ionisation state (Cen & Chisari Reference Cen and Chisari2011), along with the UVB.
3.2 The metal mass budget
We now examine in more detail what these observations tell us about high-redshift galaxies and reionisation. First, we ask whether the observed mass density of metals at z ~ 6 is consistent with expectations from the star-formation history at higher redshifts. Following Pettini (Reference Pettini, Walsh and Rosa1999), we can estimate the global mass density of metals by multiplying the stellar mass density by a nucleosynthetic yield derived from stellar models (for similar calculations at lower redshifts, see Peeples et al. Reference Peeples, Werk, Tumlinson, Oppenheimer, Prochaska, Katz and Weinberg2014; Shull et al. Reference Shull, Danforth and Tilton2014). We emphasise that there are considerable uncertainties in the stellar mass density at these redshifts, the theoretical yields, and, as described above, the measured metal mass densities. This exercise is therefore intended only to give a rough insight into whether the observed metals constitute a reasonable fraction of the metals expected to be produced at z > 6.
The stellar mass density at z ~ 6 for galaxies more massive than 108 M⊙ is ρ* ~ 6 × 106 M⊙ Mpc−3 (González et al. Reference González, Labbé, Bouwens, Illingworth, Franx and Kriek2011), taking into account the correction factor of 1.6 suggested by Stark et al. (Reference Stark, Schenker, Ellis, Robertson, McLure and Dunlop2013) for contamination due to nebular lines. Following Peeples et al. (Reference Peeples, Werk, Tumlinson, Oppenheimer, Prochaska, Katz and Weinberg2014), we adopt a total metal yield of y = 0.030 for Type II supernovae, which should dominate the metal production at these early times. The yields of oxygen and carbon are taken as y O = 0.015 and y C = 0.0083, respectively. Using these values, we would expect ρO ~ 9 × 104 M⊙ Mpc−3 and ρC ~ 5 × 104 M⊙ Mpc−3, or ΩO ~ 6 × 10−7 and ΩC ~ 4 × 10−7. By comparison, the observed mass densities are ΩO I ~ 4 × 10−8 (Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b) and ΩC II + ΩC IV ~ 2 × 10−8 (Ryan-Weber et al. Reference Ryan-Weber, Pettini, Madau and Zych2009; Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b; Simcoe et al. Reference Simcoe2011; D’Odorico et al. Reference D’Odorico2013). The mass density sampled via metal absorption lines is therefore only ~ 5% of the expected total. This indicates that the observed metals can easily be produced by the known galaxies at these redshifts. Furthermore, it suggests that a large fraction of the metals reside in phases not easily probed by absorption lines. This includes the metals re-accreted onto stars, in dense pockets of the interstellar medium with small cross-sections, and in ionisation states not directly measured by the available lines. These scenarios are seen in numerical simulations of metal enrichment (e.g. Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009; Cen & Chisari Reference Cen and Chisari2011; Finlator et al. Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015) Similar conclusions have also been reached at lower redshifts (for a recent, more detailed accounting at z ~ 0 see Peeples et al. Reference Peeples, Werk, Tumlinson, Oppenheimer, Prochaska, Katz and Weinberg2014).
3.3 Constraints on stellar populations
Although metal absorption lines provide only a tracer of the total metal budget, their composition can nevertheless provide constraints on the nature of the stars that formed during the reionisation epoch. At z ≳ 5.5, the Ly α forest becomes too thick to measure H i column densities of individual absorbers (Section 2.1), which hinders direct metallicity measurements. Relative abundances can still be inferred, however, particularly for low-ionisation systems where ionisation corrections should be minimal (e.g. Wolfe et al. Reference Wolfe, Gawiser and Prochaska2005; Becker et al. Reference Becker, Sargent, Rauch and Calverley2011b). The relative abundances of O, C, Si, and Fe were measured for nine low-ionisation systems at z ~ 5 to 6 by Becker et al. (Reference Becker, Sargent, Rauch and Carswell2012). Results for [C/O] and [O/Fe] are shown in Figure 9, where [X/Y] gives the logarithmic abundances with respect to solar, [X/Y] = log (X/Y) − log (X/Y)⊙. The results at z ~ 5–6 are generally consistent with relative abundances measured in DLAs and sub-DLAs over 2 < z < 4 (e.g. Dessauges-Zavads et al. Reference Dessauges-Zavadsky, Péroux, Kim, D’Odorico and McMahon2003; Wolfe et al. Reference Wolfe, Gawiser and Prochaska2005; Péroux et al. Reference Péroux, Dessauges-Zavadsky, D’Odorico, Kim and McMahon2007; Cooke et al. Reference Cooke, Pettini, Steidel, Rudie and Nissen2011). Moreover, the absorption line measurements at high redshift are broadly consistent with the abundances in (non carbon-enhanced) metal-poor halo stars (e.g. Cayrel et al. Reference Cayrel2004), particularly those with [O/H] ≲ −2 (Fabbian et al. Reference Fabbian, Nissen, Asplund, Pettini and Akerman2009) (see discussions in Cooke et al. Reference Cooke, Pettini, Steidel, Rudie and Nissen2011; Becker et al. Reference Becker, Sargent, Rauch and Carswell2012). The [O/Fe] values are consistent with enrichment from Type II supernovae (e.g. Chieffi & Limongi Reference Chieffi and Limongi2004), as expected given there has been little time at z ~ 5–6 for a contribution from Type Ia supernovae. The lack of strong variations in the absorption-line ratios suggests that these systems are enriched by broadly similar stellar populations. There is no clear evidence of unusual abundance patterns that would indicate enrichment from exotic sources such as Population III stars, although trends in [C/O] among metal-poor DLAs and halo stars may indicate a Population III contribution at the very low-metallicity end ([O/H] < −2; Cooke et al. Reference Cooke, Pettini, Steidel, Rudie and Nissen2011). In semi-analytic models of galaxy formation including metal enrichment, Kulkarni et al. (Reference Kulkarni, Hennawi, Rollinde and Vangioni2014) also conclude that measured ionic ratios at z ≲ 6, particularly [O/Si], preclude a large contribution from Population III stars to the metal or ionising photon budget during reionisation.

Figure 9. Relative abundances of carbon and oxygen (top panel), and oxygen and iron (bottom panel), expressed logarithmically as a fraction of the solar value. Triangles and arrows at z < 4.5 are for metal-poor DLAs from Cooke et al. (Reference Cooke, Pettini, Steidel, Rudie and Nissen2011). Open circles are for sub-DLAs from Dessauges-Zavads et al. (Reference Dessauges-Zavadsky, Péroux, Kim, D’Odorico and McMahon2003) and Péroux et al. (Reference Péroux, Dessauges-Zavadsky, D’Odorico, Kim and McMahon2007). Filled circles and arrows at z > 4.7 are for low-ionisation absorbers from Becker et al. (Reference Becker, Sargent, Rauch and Carswell2012). The mean value given in each panel has been calculated from all measurements. The nominal intrinsic rms scatter (accounting for measurement uncertainties), σ0, and the 95% upper limit on σ0 (in parentheses) are shown as dark and light shaded bands, respectively. Reproduced from Figure 11 of Becker et al. (Reference Becker, Sargent, Rauch and Carswell2012) by permission of the authors and the AAS.
3.4 The connection to galaxies and reionisation
Numerous studies over 0 < z < 5 have demonstrated that the gas traced by metal lines reflects a cycle of inflows and outflows that help to regulate galaxy growth (e.g. Davé & Oppenheimer Reference Davé and Oppenheimer2007; Steidel et al. Reference Steidel, Erb, Shapley, Pettini, Reddy, Bogosavljević, Rudie and Rakic2010; Tumlinson et al.Tumlinson et al. Reference Tumlinson2011; Turner et al. Reference Turner, Schaye, Steidel, Rudie and Strom2014; Crighton et al. Reference Crighton2015). The lower-redshift studies have shown that galaxies over a wide range of luminosities and star formation rates are surrounded by an enriched circumgalactic medium out to typical distances of at least ~ 100 proper kpc (e.g. Simcoe et al. Reference Simcoe, Sargent, Rauch and Becker2006; Bordoloi et al. Reference Bordoloi2014), indicative of the volume filled by outflows or other enrichment mechanisms. Metal lines at z ~ 5–6 should therefore trace the early stages of the enrichment process, helping to elucidate the mechanisms that shape the earliest galaxies. In addition, if metal absorption lines tend to be associated with low-mass galaxies, then these lines may help to identify vital sources of ionising photons that are beyond the reach of current direct galaxy surveys.
We can use lower-redshift observations to gain some insight into the type of galaxies associated with metal absorbers near z ~ 6. The line-of-sight number density of C iv absorbers at z ~ 6 with N C IV > 1013 cm−2 is dn/dX ~ 1 (D’Odorico et al. Reference D’Odorico2013). For a population with a fixed physical cross-section, σ, the comoving number density can be computed as
If we take the lower-redshift value of 100 kpc (proper) as an upper limit on the radius to which haloes are enriched at z ~ 6, then the number density of such haloes would be ϕ ~ 7 × 10−3 Mpc−3. This corresponds to the number density of galaxies with absolute UV magnitudes M UV ≲ −17 to − 18 (Finkelstein et al. Reference Finkelstein2015; Bouwens et al. Reference Bouwens2015), which is near the limit of direct galaxy surveys. In terms of dark matter haloes, this number density corresponds to haloes with masses M h ≳ 2 × 1010 M⊙ (Murray, Power, & Robotham Reference Murray, Power and Robotham2013). These figures already suggest that metal absorbers at z ~ 6 are likely to be associated with relatively modest galaxies, particularly given that an enrichment radius of 100 kpc is probably a conservative upper limit due to the limited time available for metal-enriched outflows to travel by z ~ 6 (e.g. Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009). Further insights can be gained by directly searching for galaxies associated with absorbers, and through more sophisticated modelling.
Directly identifying the galaxies associated with metal absorbers at these redshifts is challenging due to the faintness of the sources and the corresponding difficulty in obtaining spectroscopic redshifts. Díaz et al. (Reference Díaz, Ryan-Weber, Cooke, Pettini and Madau2011, Reference Díaz, Koyama, Ryan-Weber, Cooke, Ouchi, Shimasaku and Nakata2014, Reference Díaz, Ryan-Weber, Cooke, Koyama and Ouchi2015) have searched for galaxies associated with C iv systems at z ≃ 5.7. In at least one case, on ~ 10 h −1 Mpc scales the C iv absorber appears to be more closely associated with narrow-band-selected Ly α emitting galaxies (LAEs), rather than broad-band-selected LBGs. This suggests that C iv systems may trace lower-density environments dominated by low-mass galaxies (Díaz et al. Reference Díaz, Koyama, Ryan-Weber, Cooke, Ouchi, Shimasaku and Nakata2014). Further efforts at identifying galaxies associated with C iv and other types of metal absorbers will help to clarify this picture.
On the theoretical side, considerable efforts have been made to model the production and distribution of metals near reionisation using hydrodynamical simulations (Oppenheimer & Davé Reference Oppenheimer and Davé2006, Reference Oppenheimer and Davé2008; Davé & Oppenheimer Reference Davé and Oppenheimer2007; Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009; Cen & Chisari Reference Cen and Chisari2011; Keating et al. Reference Keating, Haehnelt, Becker and Bolton2014; Pallottini et al. Reference Pallottini, Ferrara, Gallerani, Salvadori and D’Odorico2014; Finlator et al. Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015) and analytical methods (Bagla, Kulkarni, & Padmanabhan Reference Bagla, Kulkarni and Padmanabhan2009). The simulations generally support a picture where metals reside in overdense regions, and that only a few percent of the IGM needs to be enriched in order to reproduce the observed line statistics (Figure 10). Metal lines should therefore closely trace the environments of galaxies, and be sensitive to the details of feedback mechanisms (e.g. Oppenheimer & Davé Reference Oppenheimer and Davé2006, Reference Oppenheimer and Davé2008; Cen & Chisari Reference Cen and Chisari2011). Finlator et al. (Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015) further showed that ion ratios are sensitive to the local variations in the UVB induced by these galaxies (see also Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009).

Figure 10. A slice through a hydrodynamical simulation at z = 6.0 showing the location of galaxies with stellar masses greater than 106 M⊙ (upper left), the metallicity as a fraction of solar (upper right), and the integrated C ii (lower left) and C iv (lower right) column densities. The grey scale in the upper panels shows the total mass density as a fraction of the mean density. The slice is 16 h −1 Mpc on a side and 25 km s−1 thick. In this simulation, metal absorbers closely trace the galaxies, with only a small fraction of the volume enriched above 1/10, 000th of solar metallicity. The cross-section of C iv, which favours lower densities, is more extended than that of C ii. Reproduced from Figure 5 of Oppenheimer et al. (Reference Oppenheimer, Davé and Finlator2009) by permission of the authors.
A further conclusion of simulations is that, while absorbers arise from galaxies over a wide range in mass, low-ionisation lines tend to trace lower-mass galaxies than C iv (e.g. Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009; Finlator et al. Reference Finlator, Muñoz, Oppenheimer, Oh, Özel and Davé2013). This occurs because strong outflows are required to transport enriched material out to the low densities where C iv becomes a favoured ionisation state. Oppenheimer et al. (Reference Oppenheimer, Davé and Finlator2009) find that C iv absorbers with N C IV ⩾ 1013 cm−2 should largely be found around galaxies with stellar masses M * = 106.5 − 8.5 M⊙ (UV magnitudes M UV ≃ −14.5 to − 19), whereas C ii absorbers should trace galaxies that are roughly a factor of 10 less massive. In both cases, the absorber strength is found to anti-correlate with projected distance from the galaxy, and for C iv it is found to correlate with galaxy stellar mass. The likelihood that metal lines, and in particular low-ionisation lines, trace low-mass galaxies underlines the importance of these lines as probes of the faint galaxies that may be largely responsible for reionisation.
The hydrodynamical simulations discussed above demonstrate that the redshift evolution of essentially all ions is sensitive to (i) the increase in the total mass density of metals towards lower redshifts due to ongoing star formation, (ii) the propagation of enrichment towards lower densities with declining redshift, and (iii) the decline in the mean UV background with redshift at z > 5 (see also Section 2.3). The last two factors mean that systems traced by C iv (C ii) should constitute a decreasing (increasing) fraction of the metals towards higher redshifts (Figure 11). This helps to explain the substantial decline in C iv from z ~ 5 to 6, even while the number density of low-ionisation absorbers remains relatively constant (Oppenheimer et al. Reference Oppenheimer, Davé and Finlator2009; Keating et al. Reference Keating, Haehnelt, Becker and Bolton2014; Finlator et al. Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015). If these trends continue, then low-ionisation lines may become numerous at z ≳ 7 (Finlator et al. Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015). Some authors have suggested that a ‘forest’ of low-ionisation lines such as O i and C ii may appear during reionisation if significant amounts of the IGM are enriched at earlier times (Oh Reference Oh2002; Furlanetto & Loeb Reference Furlanetto and Loeb2003). At present, there is little evidence for an O i forest in the z ~ 6 data; however, higher-redshift lines of sight may yet reveal substantial quantities of enriched, neutral gas in the reionisation epoch. The prospects for this depend partly on whether early metal enrichment extends to truly intergalactic regions, or if it is mainly confined to the circumgalactic environments around galaxies.

Figure 11. Evolution of the carbon (top panel) and hydrogen (bottom panel) in a radiation hydrodynamical simulation by Finlator et al. (Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015). The solid line in the upper panel shows the total metal mass fraction, normalised to its value at z = 5. The red-dashed and blue-dotted lines show the volume-weighted fractions of carbon that are in C iv and C ii, respectively. The thick and thin lines give the results for the UV background predicted by the simulation and for a uniform Haardt & Madau (Reference Haardt and Madau2012) background. The solid line in the bottom panel shows the volume-weighted fraction of neutral hydrogen. Simulations similar to this one predict that low-ionisation metal lines should become more prominent relative to high-ionisation lines in the reionisation epoch. Reproduced from Figure 6 of Finlator et al. (Reference Finlator, Thompson, Huang, Davé, Zackrisson and Oppenheimer2015) by permission of the authors.
4 THE REIONISATION HISTORY
Thus far, we have examined how quasar absorption line observations elucidate the properties of high-redshift galaxies by probing the post-reionisation UVB and heavy element production in the early Universe. In this section, we now turn to focus on how quasar absorption line studies directly constrain the reionisation history at z ≳ 6. We begin by briefly describing the basic properties of the EoR relevant for current and future observations of the IGM, and then proceed to examine the current quasar absorption line data.
4.1 The IGM during reionisation
The IGM is expected to resemble a two-phase medium during reionisation, with part of the IGM in highly ionised ‘bubbles’ that form around collections of galaxies and accreting black holes, while the rest remains mostly neutral (e.g. Figure 12). This two-phase medium can be broadly characterised by two quantities: the volume filling factor of ionised hydrogen and the size distribution of the ionised regions (see e.g Madau et al. Reference Madau, Haardt and Rees1999; Miralda-Escudé et al. Reference Miralda-Escudé, Haehnelt and Rees2000; Gnedin Reference Gnedin2000; Furlanetto et al. Reference Furlanetto, Zaldarriaga and Hernquist2004). A primary goal of reionisation studies is to constrain these properties from observations, and to then use them to inform models of galaxy formation and the high-redshift IGM.

Figure 12. Models illustrating the size and distribution of ionised regions at different stages of reionisation. Each panel shows a slice (0.25h −1 comoving Mpc thick) through a numerical simulation of reionisation, spanning 65.6h −1 comoving Mpc on a side. The white regions show highly ionised hydrogen while the dark regions are neutral. The columns, from left to right, show different models for the ionising sources which reside in progressively more massive and highly clustered host haloes. The rows, from top to bottom, show different stages of the reionisation process: in each model the efficiency of the ionising sources is normalised so that the mean ionised fraction is ⟨xi⟩ = 0.2, 0.5, and 0.7, respectively. Reproduced from Figure 3 of McQuinn et al. (Reference McQuinn, Lidz, Zahn, Dutta, Hernquist and Zaldarriaga2007a) by permission of the authors.
However, this two-phase description does not completely describe the ionisation state of the IGM. Firstly, there is also some residual neutral hydrogen within the bubble interiors; this neutral fraction will shrink during and after reionisation as the mean free path of the ionising photons grows; this is eventually observed as the Ly α forest at z < 6. Secondly, in addition to this highly ionised diffuse gas, there will be some mostly neutral, self-shielded dense clumps (LLSs) that remain, both in the bubble interiors and in the post-reionisation IGM (Furlanetto & Oh Reference Furlanetto and Oh2005; Gnedin & Fan Reference Gnedin and Fan2006; Choudhury, Haehnelt, & Regan Reference Choudhury, Haehnelt and Regan2009; Alvarez & Abel Reference Alvarez and Abel2012; Sobacchi & Mesinger Reference Sobacchi and Mesinger2014). These systems play an important role in setting the mean free path for ionising photons. Consequently, at the tail-end of reionisation the IGM can be almost completely filled by ionised gas once bubbles have overlapped, yet the mean free path of ionising photons nevertheless has significant spatial fluctuations (Section 2.7). This intermediate period is what Furlanetto & Oh (Reference Furlanetto and Oh2005) refer to as the transition between the ‘bubble-dominated and cosmic-web dominated’ eras in the reionisation history of the Universe. Capturing this transition era is challenging for modellers, in part because of the large dynamic range in spatial scale involved: this requires fully resolving the dense sinks of ionising photons that (mostly) regulate the mean free path of the ionising photons at the end of reionisation, while simultaneously capturing representative samples of the ionised bubbles and the large-scale spatial variations in the source abundance.
Quasar absorption line measurements play an important role within this context. First, these observations presently provide our most detailed probe of the properties of the high-redshift IGM, with current studies extending out to z ~ 7 (Fan et al. Reference Fan2006; Mortlock et al. Reference Mortlock2011). In terms of constraining the redshift evolution of the filling factor of ionised regions, these observations may then address whether reionisation completes at z ⩽ 7 or at some earlier time. As we discuss below, there are some interesting hints that reionisation may be incomplete at z ⩽ 7, and there are good prospects for placing more definitive constraints in the future.
4.2 Mean Ly α forest transmission
The first measurement to consider is the redshift evolution of the average Ly α forest transmission as a function of redshift, ⟨F⟩. As is evident from the Gunn & Peterson (Reference Gunn and Peterson1965) argument presented in Section 2.1, at the redshifts of interest even gas with neutral fractions of ⟨x HI⟩ ≳ 10−4–10−5 should produce highly saturated absorption in the Ly α line. Although this large opacity makes direct inferences about reionisation from the Ly α forest challenging, progress can still be made. Figure 13 displays the observed redshift evolution of the effective optical depth, ταeff = −ln ⟨F⟩, in the Ly α forest at z > 3.8. Each point shows an estimate from an individual stretch of spectrum of width either Δz ~ 0.15 or 50h −1 comoving Mpc, which are similar at the redshifts of interest. The upward pointing arrows show 1σ lower bounds on the effective optical depth in regions where the average transmitted flux is consistent with zero.

Figure 13. The evolution of the Ly α forest effective optical depth with redshift. The measurements are from Fan et al. (Reference Fan2006) (black circles and arrows, Δz = 0.15 bins) and Becker et al. (Reference Becker, Bolton, Madau, Pettini, Ryan-Weber and Venemans2015) (blue circles, error bars and arrows, Δl = 50h −1 Mpc bins). The lower limits at z > 5.5 are obtained where the Ly α absorption saturates in the presence of a Gunn–Peterson trough. Reproduced from Figure 6 of Becker et al. (Reference Becker, Bolton, Madau, Pettini, Ryan-Weber and Venemans2015) by permission of the authors.
Figure 13 reveals several striking features. First, the presence of any transmission at z ⩽ 6 might seem to require that reionisation completed by z = 6. However, this is not completely secure (Lidz et al. Reference Lidz, McQuinn, Zaldarriaga, Hernquist and Dutta2007; Mesinger Reference Mesinger2010). The transmission only demands that some regions in the IGM are highly ionised: since the forest shows a mixture of completely opaque and partly transmissive regions at z = 5–6 (Fan et al. Reference Fan2006), it may be that some of the opaque regions are actually significantly neutral, with order unity neutral fractions. It appears feasible that some so-called ‘neutral islands’ remain as late as z ~ 5.5 (Malloy & Lidz Reference Malloy and Lidz2015); this possibility is constrained by the dark pixel fraction tests described in Section 4.4.
Additionally, the redshift evolution of ταeff near z ~ 6 may be interpreted as being extremely rapid, requiring reionisation to complete near z ~ 6 (e.g. Fan et al. Reference Fan2006; Gnedin & Fan Reference Gnedin and Fan2006). However, it remains unclear whether the mean transmission should evolve rapidly as reionisation completes. This behaviour is predicted in numerical simulations if the mean free path, and hence photoionisation rate incident on a typical region, grows rapidly as reionisation finishes (Gnedin Reference Gnedin2000; Bauer et al. Reference Bauer, Springel, Vogelsberger, Genel, Torrey, Sijacki, Nelson and Hernquist2015; Chardin et al. Reference Chardin, Haehnelt, Aubert and Puchwein2015). This may not happen, however, if the mean free path to ionising photons at the end of reionisation is limited by dense photon sinks, and not the size of the ionised regions themselves (Furlanetto & Mesinger Reference Furlanetto and Mesinger2009; Alvarez & Abel Reference Alvarez and Abel2012).
Finally, the small levels of remaining transmission through the Ly α forest near z ~ 5–6 trace only rare, underdense regions of the IGM (Bolton & Becker Reference Bolton and Becker2009). This is the case even if reionisation is complete at these redshifts, and the IGM gas is highly ionised. Extrapolating from the behaviour in low-density voids to make inferences about the overall ionisation state in more typical regions of the IGM can therefore be uncertain and model dependent (Oh & Furlanetto Reference Oh and Furlanetto2005). In summary, while the mean Ly α forest transmission clearly indicates the IGM neutral fraction is increasing toward z = 6, on its own it is unable to unambiguously determine the duration and end point of the reionisation process.
4.3 Higher-order Lyman series lines
Further progress can be made by considering the transmission through higher-order Lyman-series lines. These transitions have smaller cross-sectionsFootnote 10 relative to Lyα, and so become fully saturated at larger neutral hydrogen fractions. The analogue of the Gunn–Peterson formula (Equation (2)) for Ly β is then simply:
It is important to keep in mind, however, that it is the effective optical depths, τeff = ⟨F⟩, which are observable, and these do not scale in the same way as the true optical depths (e.g. Songaila & Cowie Reference Songaila and Cowie2002; Oh & Furlanetto Reference Oh and Furlanetto2005). The ratio of τeff, α/τeff, β depends on the gas density distribution, the relation between temperature and density (Furlanetto & Oh Reference Furlanetto and Oh2009), and other aspects of the IGM model. In typical models considered in the literature, τeff, α/τeff, β ~ 3 (e.g. Fan et al. Reference Fan2006), which is around a factor of 2 smaller than the ratio of the Ly α and Ly β cross-sections. The corresponding factors for higher-order lines, such as Ly γ, are still larger.
One complication here is that the higher-order transitions land in regions of the spectrum that also contain absorption from lower-order lines, sourced by gas at lower redshift (e.g. Figure 1). For example, a wavelength that contains Ly β absorption at z β = 6 also contains Ly α absorption from gas at z α = λβ(1 + z β)/λα − 1 = 4.9. However, since these two sources of absorption are widely separated in physical space, they are to a very good approximation uncorrelated (Dijkstra, Lidz, & Hui Reference Dijkstra, Lidz and Hui2004b), and so
The average transmission through the Ly α line at z α can be easily measured using lower-redshift quasar spectra. This expression further generalises to the Ly γ region of the quasar spectrum—which contains overlapping absorption from Ly γ and lower-redshift absorption in Ly β and Ly α—and to still higher-order lines.
In practice, measurements of the mean transmission in the Ly β and Ly γ forest—after dividing out estimates of the foreground absorption in the lower-order lines as described above—are also mostly consistent with saturated absorption above z ≳ 6 (Fan et al. Reference Fan2006). This strengthens the case that the opacity is evolving near z ~ 6, and allows a slightly stronger limit on the possibility that the absorption arises from highly ionised gas after reionisation. Nevertheless, even the current upper limits on the transmission through the Ly γ forest imply fairly modest lower limits on the neutral fraction of ⟨x HI⟩ ≳ 10−4–10−3, depending on the precise model. Hence, even high effective optical depth absorption in Ly γ does not, by itself, imply that reionisation is incomplete at z ≳ 6. However, higher-order Lyman series lines are also useful for constraining the possibility that there are neutral islands left over at z ⩽ 6, since these lines help in placing upper limits on the dark pixel fraction, as described next.
4.4 Dark pixel fraction and dark gaps
Recent work has demonstrated that a conservative, almost model-independent lower bound on the filling factor of ionised regions can be placed by counting the fraction of spectral pixels that are completely absorbed (McGreer et al. Reference McGreer, Mesinger and Fan2011, Reference McGreer, Mesinger and D’Odorico2015). This is because regions with transmission through the Ly α line are certain to contain highly ionised gas. One can place a stronger limit by including the Ly β region of the quasar spectrum and potentially other higher series lines. In this sense, the dark pixel fraction analysis directly targets one of the main properties of the EoR, the filling factor of ionised bubbles. However, the trade-off is that the limit obtained is conservative and highly ionised regions may be responsible for some (or all) of the dark pixels.
In the first analysis of this sort, McGreer et al. (Reference McGreer, Mesinger and Fan2011) found that the volume-averaged neutral fraction needs to be smaller than ⟨x HI⟩ < 0.2 at 5 ⩽ z ⩽ 5.5, and smaller than ⟨x HI⟩ < 0.5 at z = 6, each at 1σ confidence. A subsequent study incorporating new, higher signal to noise spectra has improved these limits to ⟨x HI⟩ < 0.11 at z = 5.6, ⟨x HI⟩ < 0.09 at z = 5.9 at 1σ confidence (McGreer et al. Reference McGreer, Mesinger and D’Odorico2015). At z = 6.1, there are significantly more dark pixels and the limit is weaker with ⟨x HI⟩ < 0.58, again at 1σ confidence. These results suggest that if significantly neutral diffuse gas remains at z ⩽ 6, it fills a rather small fraction of the IGM volume.
An approach to search for direct signatures of any remaining neutral islands is to stack spectra around long, highly absorbed regions in the Ly α and Ly β forests (Malloy & Lidz Reference Malloy and Lidz2015). If significantly neutral gas remains in some of the fully absorbed regions, the stacked spectra should recover slowly as one moves from absorbed to transmitted regions, owing to the damping wing of the Ly α line from diffuse neutral gas in the IGM (Miralda-Escudé Reference Miralda-Escudé1998; Malloy & Lidz Reference Malloy and Lidz2015). However, one can only apply this test at redshifts where the spectra show both completely absorbed regions and regions with some transmission. In typical regions of the IGM, this means this test can only be applied at z ≲ 6.
Finally, a related diagnostic is the size distribution of contiguous saturated regions in the Ly α forest, and the redshift evolution of these so-called ‘dark gaps’ (e.g. Songaila & Cowie Reference Songaila and Cowie2002; Paschos & Norman Reference Paschos and Norman2005; Fan et al. Reference Fan2006; Gallerani et al. Reference Gallerani, Choudhury and Ferrara2006, Reference Gallerani, Ferrara, Fan and Choudhury2008; Mesinger Reference Mesinger2010). Some measurements of dark gap sizes and their redshift evolution are shown in Figure 14. As with many of the other observed properties of the z ~ 6 Ly α forest, the abundance of large dark gaps grows steeply near z ~ 6. On the other hand, even by z ~ 5.3, there are some ≳ 30 Mpc contiguous regions that appear entirely absorbed, with τα ⩾ 3.5 across the entire stretch of spectrum. This evolution might result in part from the presence of remaining neutral islands in the IGM, or may instead reflect the thickening of the Ly α forest owing to the increasing mean density of the Universe and the dropping intensity of the UVB, along with fluctuations in the mean free path and the IGM temperature. As with many of the other z ~ 6 measurements, improved models of the transition era—in which the IGM is filled with ionised gas, yet the mean free path still has sizable spatial fluctuations—will help with unravelling the precise implications of the dark gap distributions and their redshift evolution.

Figure 14. The size of dark gaps as a function of redshift measured from 12 quasar spectra obtained with Keck/Echellete Spectrograph and Imager. The gaps are defined as contiguous regions in the observed Ly α forest where the optical depth never goes beneath the threshold of τα < 3.5. The upward pointing arrows show lower limits on the dark gap size for observed gaps that are close to the quasar near-zone (see Section 4.5). The spectra at z ≳ 5.2 show fully absorbed regions that are tens of comoving Mpc in size, and the dark gap sizes grow steeply in length at z ≳ 5.7. Reproduced from Figure 10 of Fan et al. (Reference Fan2006) by permission of the authors and the AAS.
4.5 Quasar near-zones
As already discussed, at z ≳ 6 the Ly α forest is almost completely saturated. Inferring the ionisation state (and other properties) of the z ≳ 6 IGM from typical regions of the Ly α forest is therefore challenging. However, gas in spectral regions close to the background quasar itself, in the proximity or ‘near-zone’, are exposed to ionising radiation from the nearby quasar as well as the UVB. These regions show some transmission through the Ly α forest, and can hence be used to study the z ≳ 6 IGM.
The simplest measurable property is the size of these zones. Observationally, this is usually defined as the distance over which the continuum normalised transmission first drops below some threshold; in Fan et al. (Reference Fan2006) the threshold was chosen to be F = 0.1, after smoothing each spectrum to 20 Å spectral resolution. Early work interpreted the sizes of these zones as indicating the radii of ionised bubbles expanding around the quasars into a largely neutral IGM (Wyithe & Loeb Reference Wyithe and Loeb2004; Wyithe, Loeb, & Carilli Reference Wyithe, Loeb and Carilli2005). However, subsequent work showed that the transmission profile may instead reflect only the classical proximity effect: the transmission will fall below the chosen threshold in a highly ionised IGM when the combined photoionisation rate from the quasar and background galaxies is small enough (Bolton & Haehnelt Reference Bolton and Haehnelt2007a, Reference Bolton and Haehnelt2007b; Maselli et al. Reference Maselli, Gallerani, Ferrara and Choudhury2007, Reference Maselli, Ferrara and Gallerani2009; Lidz et al. Reference Lidz, McQuinn, Zaldarriaga, Hernquist and Dutta2007). This means that the observed size is an unreliable indicator of the position of the ionisation front around the quasar; this is essentially the usual problem that the Ly α optical depth is large even for highly ionised gas at z ~ 6 (see Equation 3).
Nevertheless, the size of the near-zones does evolve with redshift near z ~ 6 (Fan et al. Reference Fan2006). Carilli et al. (Reference Carilli2010) fit a linear function to the near-zone size as a function of redshift from z = 5.7 to z = 6.4, and find that the proper size—after correcting for differences in quasar luminosities—drops by over a factor of 2 across this narrow redshift interval. This evolution may be driven by rapid evolution in the ionising photon mean free path just after reionisation completes (Wyithe, Bolton, & Haehnelt Reference Wyithe, Bolton and Haehnelt2008). However, the size evolution may also partly reflect the presence of remaining diffuse neutral gas in the IGM, and so the interpretation of the observed evolution is still unclear.
In another approach, Mesinger & Haiman (Reference Mesinger and Haiman2004), Mesinger & Haiman (Reference Mesinger and Haiman2007), and Schroeder, Mesinger, & Haiman (Reference Schroeder, Mesinger and Haiman2013) have compared the near-zone transmission in both Ly α and Ly β to mock spectra. The latter study compares mock spectra with three quasar spectra at z = 6.2, 6.3, and 6.4 and argues that each spectrum prefers the presence of damping wing absorption blueward of the Ly α line, arising from the natural broadening of the transition. Crucially, this damping wing is prominent only if the gas is significantly neutral (Miralda-Escudé Reference Miralda-Escudé1998). A potential source of confusion, however, is from high column density absorbers—DLAs—which also have prominent damping wings. However, the damping wing from a DLA has a different shape compared to extended, diffuse neutral gas in the IGM, so these two possibilities may be distinguished, at least in principle (Miralda-Escudé Reference Miralda-Escudé1998).
In practice, however, it can be difficult to distinguish damping wings from possible diffuse neutral gas and DLAs over a limited stretch of spectrum. In addition, multiple neutral regions may each contribute through their damping wings to the absorption in a given pixel and impact the form of the damping wing profile from the diffuse IGM (Mesinger & Furlanetto Reference Mesinger and Furlanetto2008a; McQuinn et al. Reference McQuinn, Lidz, Zaldarriaga, Hernquist and Dutta2008; Malloy & Lidz Reference Malloy and Lidz2015). Based on the spectra alone, Schroeder et al. (Reference Schroeder, Mesinger and Haiman2013) cannot rule out the possibility that the putative damping wing comes from a DLA. However, DLAs of the required column density should be rare and these authors find that the data prefer incomplete reionisation at z ~ 6 and a neutral fraction of ⟨x HI⟩ ⩾ 0.1 at 95% confidence.
Perhaps, the most intriguing near-zone result comes from the spectrum of the highest-redshift quasar presently known, at z = 7.1, which shows possible evidence for damping wing absorption on the red side of its Ly α line (Mortlock et al. Reference Mortlock2011). The spectrum close to the Ly α emission line, along with toy damping wing models for a partly neutral IGM and a DLA, are shown in Figure 15. This comparison suggests that the damping wing could be sourced by significantly neutral material, although the fully neutral model produces too strong a wing. Bolton et al. (Reference Bolton, Haehnelt, Warren, Hewett, Mortlock, Venemans, McMahon and Simpson2011) performed a detailed comparison of the transmission profile with simulated spectra, and find that either a neutral fraction of ⟨x HI⟩ ≳ 0.1 is required, or a highly ionised IGM can be reconciled with the data if a DLA lies within ~ 5 proper Mpc of the quasar (see also Keating et al. Reference Keating, Haehnelt, Cantalupo and Puchwein2015). There are two challenges for the DLA scenario however. First, a DLA of the required column density should be rare: in their model, Bolton et al. (Reference Bolton, Haehnelt, Warren, Hewett, Mortlock, Venemans, McMahon and Simpson2011) find a 5% probability for a DLA of the requisite properties. A second argument against a DLA is that there is no detectable metal line absorption at the same redshift as the damping wing feature (Simcoe et al. Reference Simcoe, Sullivan, Cooksey, Kao, Matejek and Burgasser2012). Quantitatively, this study derives an upper limit on the metal abundance of ⩽ 10−4 times the solar abundance for a dense absorber, although the feature could nevertheless be due to a very low-metallicity proto-galaxy.

Figure 15. Possible damping wing feature in the spectrum of a z = 7.1 quasar. The black binned data shows an estimate of the transmission near the systemic redshift (dashed line) of the quasar ULAS J1120+0641. The blue lines show damping wing absorption models (assuming a fully transparent ionised zone around the quasar for simplicity), and uniform neutral fractions of ⟨x HI⟩ = 0.1, 0.5, and 1.0, with the more neutral models giving more absorption. The ionised zone is assumed to end abruptly, 2.2 Mpc in front of the quasar. The green solid line shows an alternate fit in which the IGM is highly ionised and the damping wing is instead sourced by a DLA of column density N HI = 4 × 1020 cm−2, situated 2.6 Mpc in front of the quasar. Reproduced from Figure 4 of Mortlock et al. (Reference Mortlock2011) by permission of the authors and Macmillan Publishers Ltd.
An alternative use of these proximity or near-zones is measuring the temperature of the IGM at z ≃ 6 (Bolton et al. Reference Bolton, Becker, Wyithe, Haehnelt and Sargent2010, Reference Bolton, Becker, Raskutti, Wyithe, Haehnelt and Sargent2012; Padmanabhan, Choudhury, & Srianand Reference Padmanabhan, Choudhury and Srianand2014); the long cooling time for the low-density gas in the IGM allows the gas temperature to be used as a probe of the timing of reionisation (Miralda-Escudé & Rees Reference Miralda-Escudé and Rees1994; Theuns et al. Reference Theuns, Schaye, Zaroubi, Kim, Tzanavaris and Carswell2002; Hui & Haiman Reference Hui and Haiman2003). High-redshift temperature measurements close to the EoR are therefore desirable; this limits the time available for gas to cool following reionisation and also bypasses the expected heating from He IIreionisation at z < 4. In an analysis of gas temperatures inferred from the line widths in near-zones observed in seven high-resolution (R ~ 40 000) quasar spectra at 5.8 < z < 6.4, Raskutti et al. (Reference Raskutti, Bolton, Wyithe and Becker2012) concluded these data were consistent with reionisation completing at z > 6.5 at 95% confidence. However, this inference is model dependent, and relies on assumptions for the typical spectrum of ionising sources during reionisation as well as the amount of photoheating by the quasar itself.
Finally, note that an important systematic concern in all these analyses is fitting the unabsorbed quasar continuum close to the Ly α line. Simcoe et al. (Reference Simcoe, Sullivan, Cooksey, Kao, Matejek and Burgasser2012) investigate this issue, considering four different composite spectra derived from various lower-redshift observations, and also perform a principle component analysis in an effort to extrapolate the continuum estimate from the red side of Lyα. They find that the damping wing fits are fairly stable across the range of continuum fits considered. Nevertheless, it may be helpful to further explore the range of possible continuum shapes close to Ly α in lower-redshift spectra; these spectra can serve as a control sample from an epoch when the IGM is certainly ionised (Kramer & Haiman Reference Kramer and Haiman2009; Bosman & Becker Reference Bosman and Becker2015).
4.6 Consistency with other probes of reionisation
Having summarised the implications of current quasar absorption line observations for our understanding of the EoR, we now consider these studies in the context of a wide range of complementary multi-wavelength EoR observations. We start with a brief description of existing reionisation probes, and then turn to consider current constraints from these observations.
• CMB: As CMB photons propagate from the surface of last scattering, they may scatter off the free electrons that are (again) prevalent during and after reionisation. This has the effect of damping the primary temperature anisotropies and generating large-scale polarisation anisotropies (Zaldarriaga Reference Zaldarriaga1997; Hu & White Reference Hu and White1997), while also producing secondary anisotropies through the kinetic Sunyaev–Zel’dovich (kSZ) effect (Gruzinov & Hu Reference Gruzinov and Hu1998; Zahn et al. Reference Zahn, Zaldarriaga, Hernquist and McQuinn2005; McQuinn et al. Reference McQuinn, Furlanetto, Hernquist, Zahn and Zaldarriaga2005). The distinctive large-scale polarisation signal depends on the total probability that a CMB photon Thomson scatters off a free electron along the line of sight. This is quantified by the electron scattering optical depth, τe; this measurement therefore constrains an integral over the entire reionisation history. The patchy kSZ effect results when CMB photons scatter off free electrons in ionised regions during the EoR and receive a redshift or blueshift owing to the peculiar velocity of these regions. The small-scale CMB fluctuations that are induced arise in part because of spatial variations in the ionisation field (Aghanim et al. Reference Aghanim, Desert, Puget and Gispert1996; Gruzinov & Hu Reference Gruzinov and Hu1998).
• UV luminosity functions: Measurements using the Wide Field Camera 3 (WFC3) on board the Hubble Space Telescope (HST) have found large populations of high-redshift galaxy candidates—some of which are spectroscopically confirmed—using the Lyman break technique (see also Section 2.6). Ground-based surveys have also played an important role at the bright end of the luminosity function (Bowler et al. Reference Bowler2014). These observations have allowed measurements of the UV luminosity function of LBGs at rest-frame wavelength of 1500 Å out to z ~ 8 (Oesch et al. Reference Oesch2013; McLure et al. Reference McLure2013; Finkelstein et al. Reference Finkelstein2015; Ishigaki et al. Reference Ishigaki, Kawamata, Ouchi, Oguri, Shimasaku and Ono2015). There are also now a handful of candidates out to z ~ 9–10 (Bouwens et al. Reference Bouwens2015; McLeod et al. Reference McLeod, McLure, Dunlop, Robertson, Ellis and Targett2015). These measurements allow the contribution of observed galaxies to the overall ionising photon budget to be assessed (Duncan & Conselice Reference Duncan and Conselice2015; Robertson et al. Reference Robertson, Ellis, Furlanetto and Dunlop2015; Bouwens et al. Reference Bouwens2015), modulo uncertainties in the escape fraction, the galaxy UV spectral energy distributions, and the contribution from faint, unobserved sources (see discussion in Section 2.6).
• Lyman α emitter surveys: Another highly successful approach for finding high-redshift galaxies uses a narrow-band selection technique to target objects with prominent Ly α emission lines (see Dijkstra Reference Dijkstra2014 and references therein). The visibility of these Ly α emitters (LAEs) is impacted by the damping wing arising from neutral gas in the IGM (Miralda-Escudé Reference Miralda-Escudé1998), and so these surveys are sensitive to the reionisation history. Consequently, the abundance of observable LAEs will drop and their clustering will increase as one probes deeper into the EoR (Furlanetto et al. Reference Furlanetto, Zaldarriaga and Hernquist2006b; McQuinn et al. Reference McQuinn, Hernquist, Zaldarriaga and Dutta2007b; Mesinger & Furlanetto Reference Mesinger and Furlanetto2008b).
• GRB optical afterglows: The optical afterglow spectra of GRBs are potentially useful in searching for the damping wing redward of the Ly α emission line (Totani et al. Reference Totani, Kawai, Kosugi, Aoki, Yamada, Iye, Ohta and Hattori2006; Totani et al. Reference Totani2014; Chornock et al. Reference Chornock, Berger, Fox, Lunnan, Drout, fai Fong, Laskar and Roth2013). These sources are extremely luminous (for a short time) and so can be detected at high redshift. Compared to quasars, GRB optical afterglows also have a simpler unabsorbed continuum spectrum and are more likely to occur in typical ionised regions (which are smaller than the ionised bubbles around quasars). On the other hand, GRB afterglow spectra typically show high-column density DLA absorption from neutral hydrogen in the host galaxy. The absorption from the GRB host can overwhelm any damping wing signature from diffuse neutral gas in the IGM. However, an afterglow spectrum without prominent host absorption will allow a detection of—or sharper upper limits on the presence of—diffuse neutral gas in the IGM (McQuinn et al. Reference McQuinn, Lidz, Zaldarriaga, Hernquist and Dutta2008).
• Redshifted 21-cm line: Perhaps, the most promising way of studying reionisation is to detect redshifted 21-cm emission from neutral gas in the IGM during reionisation (Madau et al. Reference Madau, Meiksin and Rees1997; Furlanetto et al. Reference Furlanetto, Oh and Briggs2006a). First-generation surveys aiming to detect this signal have started to place upper limits on the amplitude of redshifted 21-cm fluctuations (Paciga et al. Reference Paciga2013; Parsons et al. Reference Parsons2014; Dillon et al. Reference Dillon2014). These limits do not yet place interesting constraints on the ionisation history, however, and are therefore not discussed further here. We nevertheless mention this probe in passing, since it may ultimately provide the most powerful approach for studying reionisation.
A selection of current constraints on reionisation are summarised in Figure 16, from Robertson et al. (Reference Robertson, Ellis, Furlanetto and Dunlop2015). We first consider constraints on τe from the large-scale polarisation CMB power spectrum measurements. Wilkinson Microwave Anisostropy Probe (WMAP) nine-year E-mode polarisation data, combined with Planck temperature anisotropy data, give τe = 0.089+ 0.012−0.014 (1σ error bars, Planck Collaboration et al. 2014; Bennett et al. Reference Bennett2013); this optical depth corresponds to an (instantaneous) reionisation redshift of z r = 11.1 ± 1.1. Recent large-scale polarisation data from the 2015 Planck data release, however, suggest a smaller optical depth of τe = 0.066 ± 0.016, when Planck polarisation data are combined with temperature anisotropy and CMB lensing measurements from Planck (Planck Collaboration et al. 2015). The optical depthFootnote 11 preferred by Planck corresponds to an instantaneous reionisation redshift of z r = 8.8+ 1.7−1.4. In practice, this measurement translates into an end point for reionisation which may be close to z ≃ 6.

Figure 16. A summary of current multi-probe reionisation constraints. The filling factor of neutral hydrogen is displayed as a function of redshift. The constraints shown in the legend are from the Ly α forest transmission (Fan et al. Reference Fan2006), dark Ly α forest pixels (McGreer et al. Reference McGreer, Mesinger and D’Odorico2015), quasar near-zones (Mortlock et al. Reference Mortlock2011; Bolton et al. Reference Bolton, Haehnelt, Warren, Hewett, Mortlock, Venemans, McMahon and Simpson2011; Schroeder et al. Reference Schroeder, Mesinger and Haiman2013), GRB damping wing absorption (Chornock et al. Reference Chornock, Berger, Fox, Lunnan, Drout, fai Fong, Laskar and Roth2013), Ly α emitters (Ota et al. Reference Ota2008; Ouchi et al. Reference Ouchi2010), Ly α galaxy clustering (McQuinn et al. Reference McQuinn, Hernquist, Zaldarriaga and Dutta2007b; Ouchi et al. Reference Ouchi2010) and the Ly α emission fraction (Schenker et al. Reference Schenker, Ellis, Konidaris and Stark2014; Pentericci et al. Reference Pentericci2014). The white line and red band show a reionisation history consistent with the observed star formation rate density and the Planck electron scattering optical depth (Planck Collaboration et al. 2015). The orange band shows a model consistent with the earlier WMAP-9 constraint. Reproduced from Figure 3 of Robertson et al. (Reference Robertson, Ellis, Furlanetto and Dunlop2015) by permission of the authors and the AAS.
Second, we consider the patchy kSZ effect. Studies using the South Pole Telescope (SPT) placed upper limits on the amplitude of CMB fluctuations induced by the patchy kSZ effect at multi-pole moments of ℓ ~ 3, 000 (Zahn et al. Reference Zahn2012; George et al. Reference George2015, see also Mesinger et al. Reference Mesinger, McQuinn and Spergel2012). A grid of patchy ksZ effect models have been used to place an upper limit on the duration of reionisation of Δz ⩽ 7.9 at 95% confidence (Zahn et al. Reference Zahn2012). The duration here is defined as the redshift interval over which the ionisation fraction transitions from ⟨xi⟩ = 0.20 to ⟨xi⟩ = 0.99. Note, however, this limit is dependent on separation from other contributions to the anisotropies, such as the thermal SZ (tSZ) effect and the Cosmic Infrared Background (CIB), using their differing frequency and angular scale dependence. Here, we have quoted the most conservative constraints that allow a large (anti-)correlation between the tSZ and CIB: in the absence of any correlation, the 95% confidence limit shrinks to Δz ⩽ 4.4. A more recent analysis by George et al. (Reference George2015) finds a similar value of Δz ⩽ 5.4 at 95% confidence.
The implications of the UV luminosity functions of LBGs for reionisation are discussed in Section 2.6. Here, we simply remark that although the details depend on the assumed escape fraction, ionising spectrum, and faint-end extrapolation, these observations are compatible with reionisation completing late, at z ⩽ 6 or so. The red band in Figure 16 displays a reionisation model consistent with UV luminosity functions extrapolated to absolute magnitudes of M UV ≃ −13 and a constant escape fraction f esc = 0.2 (Robertson et al. Reference Robertson, Ellis, Furlanetto and Dunlop2015). This is also in accord with the recent Planck optical depth measurements (Planck Collaboration et al. 2015).
Results from a selection of LAE surveys are also shown in Figure 16. Recent studies of the abundance of LAEs detect a relatively small drop from z = 5.7 to z = 6.6, while these surveys are thus far finding very few galaxies at z = 7.3.Footnote 12 Based on the lack of LAE candidates in the Subaru Deep Field at z = 7.3, Konno et al. (Reference Konno2014) argue that the neutral filling factor is ⟨x HI⟩ = 0.3 − 0.8 at z = 7.3. From the z = 6.6 LAE abundance, Ouchi et al. (Reference Ouchi2010) place an upper limit of ⟨x HI⟩ ⩽ 0.4, and from the lack of strong LAE clustering these authors conclude that ⟨x HI⟩ ⩽ 0.5. Finally, from measuring the redshift evolution of the Ly-α fraction—the fraction of LBGs that emit appreciably in Ly α —Schenker et al. (Reference Schenker, Ellis, Konidaris and Stark2014) find ⟨x HI⟩ = 0.34+ 0.09−0.12 at z = 7 and ⟨x HI⟩ > 0.65 at z = 8 (1σ). Note, however, these inferences are model dependent; see e.g. Bolton & Haehnelt (Reference Bolton and Haehnelt2013), Dijkstra et al. (Reference Dijkstra, Wyithe, Haiman, Mesinger and Pentericci2014), Taylor & Lidz (Reference Taylor and Lidz2014), Pentericci et al. (Reference Pentericci2014), Choudhury et al. (Reference Choudhury, Puchwein, Haehnelt and Bolton2015), and Mesinger et al. (Reference Mesinger, Aykutalp, Vanzella, Pentericci, Ferrara and Dijkstra2015) for further discussion regarding these results.
Finally, current high-redshift GRB optical afterglow spectra have mostly been limited by the presence of strong host DLA absorption, as we alluded to previously. Nevertheless, some limits are possible. For example, Totani et al. (Reference Totani, Kawai, Kosugi, Aoki, Yamada, Iye, Ohta and Hattori2006) find ⟨x HI⟩ < 0.60 at 95% confidence at z = 6.3, while Chornock et al. (Reference Chornock, Berger, Fox, Lunnan, Drout, fai Fong, Laskar and Roth2013) find a 2σ upper limit of ⟨x HI⟩ < 0.11 at z = 5.91.
In summary, when compared to the constraints from quasar absorption lines discussed earlier in this section and displayed in Figure 16 (Fan et al. Reference Fan2006; Bolton et al. Reference Bolton, Haehnelt, Warren, Hewett, Mortlock, Venemans, McMahon and Simpson2011; Mortlock et al. Reference Mortlock2011; Schroeder et al. Reference Schroeder, Mesinger and Haiman2013; McGreer et al. Reference McGreer, Mesinger and D’Odorico2015), at present the various probes appear broadly consistent with each other. The current data point to a scenario where the completion redshift (when the filling factor of ionised hydrogen reaches unity) is relatively late, between 5.5 ⩽ z ⩽ 7. However, as discussed there remain many significant uncertainties associated with all these measurements—the challenge is therefore to make a more precise and definitive statement. As we now briefly discuss, in the next decade the prospects for further progress toward this goal are promising.
5 CONCLUSIONS AND FUTURE PROSPECTS
Quasar absorption line studies yield a rich body of information describing the ionisation, thermal, and chemical enrichment history of the intergalactic gas, allowing us to study the evolution of most of the baryons in the Universe all the way out to—and perhaps into—the EoR. The properties of the intergalactic gas are in turn determined by the underlying cosmic web of structure formation—as specified, for example, according to the currently favoured inflationary, cold dark matter cosmological model with dark energy—along with the properties of galaxies and AGN, which strongly influence the gas in their surroundings. The combination of IGM measurements with direct censuses of galaxies and AGN then provide a powerful probe of early galaxy and structure formation.
In the next 5–10 years, there are excellent prospects for improving our understanding of the EoR using quasar absorption lines. First, we emphasise that several independent observations, summarised in Figure 16, are now converging towards reionisation histories that complete sometime between 5.5 ⩽ z ⩽ 7; these are redshifts at which significant amounts of quasar absorption line data already exist. This further motivates studies aimed at understanding reionisation’s precise signatures—and that of reionisation’s immediate aftermath—in absorption line spectra. Renewed efforts to model the challenging end phases of the EoR, in conjunction with novel data analysis techniques, may therefore lead to breakthroughs in our understanding of the EoR using only currently available data.
Still more compelling, though, will be the advances enabled by future data sets. Current optical and near-infrared wide-area photometric surveys such as those from Panoramic Survey Telescope and Rapid Response System (Pan-STARRS), the Dark Energy Survey (DES), and the Visible and Infrared Survey Telescope for Astronomy (VISTA) are already increasing the number of known quasars at z ~ 6–7 (e.g. Venemans et al. Reference Venemans2013, Reference Venemans2015; Bañados et al. Reference Bañados2014; Reed et al. Reference Reed2015). Over the next several years, these surveys should roughly double the number of known quasars at z ~ 6 and provide the first significant samples at z ⩾ 7. These quasars will provide greatly improved statistics for metal line, Ly α forest, and quasar near-zones studies at z ⩾ 6. For example, they should reveal whether the possible red damping wing feature observed by Mortlock et al. (Reference Mortlock2011) at z ~ 7 is ubiquitous amongst quasars near this redshift, and may uncover evidence of chemical enrichment from metal-free stars. Further dramatic increases in the number of known high-redshift quasars will come from deep surveys conducted by the Large Synoptic Survey Telescope (LSST), Euclid, and the Wide-Field Infrared Survey Telescope (WFIRST).
In the next decade, there will be further progress from high-resolution spectrographs on 30 metre class telescopes, such as the Thirty Meter Telescope (TMT), the Giant Magellan Telescope (GMT), and the European Extremely Large Telescope (E-ELT). The enhanced collecting area of these telescopes will allow significant improvements in the spectroscopy of high-redshift quasars. First, it will enable spectroscopic follow-up of much fainter quasars than is currently feasible in reasonable integration times. Since the quasar luminosity function is quite steep, this translates into a significant boost in the density of quasar sightlines that may be probed spectroscopically, as illustrated in Figure 17. This will improve statistics, and especially provide large samples of close quasar pairs at high spectral resolution; this can be used to measure, among other quantities, the pressure or Jeans smoothing scale, which is sensitive to the timing of reionisation (e.g. Rorai, Hennawi, & White Reference Rorai, Hennawi and White2013).

Figure 17. Illustration of the increased density of quasar targets for spectroscopic follow-up made accessible by 30 metre class telescopes. The left-hand panel shows the quasars in a 100 deg2 patch of the sky surveyed by the Baryon Oscillation Spectroscopic Survey (BOSS) out to m r < 18. These represent targets for which high-quality data can be obtained in ~ 1 h of observing using high-resolution spectrographs on current 8-m telescopes. For contrast, the right-hand panel shows the quasars—in the same patch of sky—that may be readily observed using a high-resolution spectrograph on a 30-m telescope (mr < 21).
In addition to the higher density of observable sightlines, it will be practical to obtain higher resolution and signal-to-noise ratio spectra in relatively short exposure times. This is illustrated in Figure 18, which shows mock spectra of the Ly α forest at z = 6.1, comparing what is presently achievable (at a spectral resolution of R ~ 5 000, e.g. White et al. Reference White, Becker, Fan and Strauss2003; Fan et al. Reference Fan2006) with what will be accessible to a high-resolution (R ~ 50 000) spectrograph on a 30 metre class telescope. This improved spectroscopy will make it easier to discern whether ‘fully absorbed’ regions in the forest are truly saturated, facilitate the detection of weak metal absorption lines, and will help resolve Ly α line-widths, facilitating measurements of the temperature of the IGM at z ⩾ 5 (e.g. Becker et al. Reference Becker, Bolton, Haehnelt and Sargent2011a; Trac et al. Reference Trac, Cen and Loeb2008; Furlanetto & Oh Reference Furlanetto and Oh2009; Lidz & Malloy Reference Lidz and Malloy2014), including temperature measurements in the quasar near-zones at z ⩾ 6 (Bolton et al. Reference Bolton, Becker, Raskutti, Wyithe, Haehnelt and Sargent2012; Raskutti et al. Reference Raskutti, Bolton, Wyithe and Becker2012).

Figure 18. An example of the sensitivity gains enabled by future 30–40 metre class telescopes. The top panel shows a simulated region of Ly α forest at z ≃ 6.1 in the spectrum of a moderate luminosity quasar with magnitude z AB = 20.5 as it would be observed in roughly a one-hour exposure with the 10 metre Keck/Echellete Spectrograph and Imager (ESI). The bottom panels shows the same spectrum obtained with a high-resolution spectrograph on a 39 metre telescope. Note the narrow transmission peaks from ionised regions which are now clearly detected and resolved.
In conjunction with improved quasar absorption line studies, we expect an enhanced interplay with other reionisation probes in the near-future. The James Webb Space Telescope (JWST) is scheduled to launch in 2018, and will allow detailed studies of early galaxy populations in the infrared, while the Atacama Large Millimeter Array (ALMA) may detect the same galaxies at sub-millimeter wavelengths through dust emission, and molecular and atomic fine-structure emission lines (e.g. Maiolino et al. Reference Maiolino2015; Capak et al. Reference Capak2015; Willott et al. Reference Willott, Carilli, Wagg and Wang2015; Watson et al. Reference Watson, Christensen, Knudsen, Richard, Gallazzi and Michałowski2015). The Subaru Hyper Suprime-Cam will map-out the positions of sizable populations of LAEs out to z = 7.3 over wide regions of the sky, enabling improved measurements of the abundance and clustering of these galaxies; these observations will in turn inform our understanding of the ionisation state of the surrounding IGM. Finally, redshifted 21-cm surveys will provide a direct probe of the neutral hydrogen in the IGM during the EoR, and potentially earlier phases of cosmic structure formation (Furlanetto et al. Reference Furlanetto, Oh and Briggs2006a; Paciga et al. Reference Paciga2013; Yatawatta et al. Reference Yatawatta2013; Parsons et al. Reference Parsons2014; Dillon et al. Reference Dillon2014). Insights gained from quasar absorption lines can help plan and optimise the observing strategy for many of the other future surveys. In addition, absorption line studies will continue to play an important role in piecing together a consistent picture of the EoR in conjunction with the full suite of upcoming observations. For example, quasar near-zone measurements, LAE abundance and clustering observations, GRB optical afterglow spectra, and redshifted 21-cm surveys may all provide independent measurements of the volume-averaged neutral fraction over overlapping redshift ranges. Metal absorption lines, combined with direct galaxy observations with JWST and ALMA will further help to reveal the nature of the galaxies responsible for reionisation. In summary, the prospects for greatly expanding our understanding of the reionisation epoch are excellent over the next several years.
ACKNOWLEDGEMENTS
We thank Kristian Finlator, Emma Ryan-Weber, Rob Simcoe, and the anonymous referee for helpful comments. JSB acknowledges the support of a Royal Society University Research Fellowship. AL acknowledges support from NASA grant NNX12AC97G and from the NSF through grant AST-1109156.