Introduction
The St Elias Mountains of Yukon and Alaska, North America, are rich in surge-type glaciers (Reference Meier and PostMeier and Post, 1969). Some of these glaciers, including Variegated Glacier (e.g. Reference KambKamb and others, 1985) and Trapridge Glacier (e.g. Reference Clarke, Collins and ThompsonClarke and others, 1984; Reference Frappé and ClarkeFrapp’e and Clarke, 2007), have been the subject of comprehensive study. Many surge-type glaciers in this region are thought to be of the ‘Alaskan type’ (Reference Murray, Strozzi, Luckman, Jiskoot and ChristakosMurray and others, 2003) with: (1) surges lasting 2–3 years; (2) characteristically rapid surge onset and termination; (3) surge velocities ∼10–100 times faster than quiescent velocities; and (4) quiescent periods of 20–40 years (Reference Meier and PostMeier and Post, 1969). Reference Frappé and ClarkeFrapp’e and Clarke (2007) recently reported on an unusual surge of Trapridge Glacier, which was characterized by an active phase of ∼20 years and a surge velocity only four times that of the quiescent velocity. They suggested that the lack of vigour in the surge may be linked to low accumulation rates in recent years.
Here we examine the dynamics of a small surge-type glacier in the Donjek Range of the St Elias Mountains (Fig. 1), in order to distinguish between internal and external factors influencing the glacier flow regime. The work forms part of a broader study, one of whose aims is to evaluate the modulating role of glacier dynamics on the regional glacier response to climate. For this exercise to be carried out in the St Elias Mountains, glacier surges must be taken into account. We use inverse methods to examine the contribution of basal motion to overall ice-surface motion, as a means of characterizing the glacier dynamic regime. Geophysical inverse theory is widely used in seismology and mineral exploration, and has been gaining popularity among hydrologists and glaciologists. Inverse methods have recently been used by Reference Waddington, Neumann, Koutnik, Marshall and MorseWaddington and others (2007) to infer accumulation rates from deep internal layers, by Reference EisenEisen (2008) to determine the velocity field from isochrones in the firn and by Reference TrufferTruffer (2004), whose inverse approach to estimate the basal speed of valley glaciers is the basis for the work described here.

Fig. 1. Donjek Range study area (a) and study glacier outline with velocity stake locations labelled (b).
Study site
The study glacier is ∼5 km long and ∼1 km wide, and occupies a tributary valley of Kaskawulsh Glacier, southwest Yukon, Canada. Reference KasperKasper (1989), Reference Johnson and KasperJohnson and Kasper (1992) and Reference JohnsonJohnson (1997) identified this glacier as surge-type, with a frontal margin chronology that differs from that of two adjacent glaciers feeding into a common valley that terminates in an ice-dammed lake. Reference Johnson and KasperJohnson and Kasper (1992) identify deltas formed during surges of the study glacier and find evidence for disruption of drainage routes by these surges. Aerial photographs from 1951 and 1977 (Fig. 2) show the glacier during a surge and during quiescence, respectively. In the 1951 photograph, the glacier terminus was >1 km further down-valley than at present. Another surge was photographed by P.G. Johnson in 1986/87. These photographs show a vertical ice cliff at the glacier terminus, extensive crevassing over the lower two-thirds of the glacier and at the glacier margin, water-filled crevasses and a surface that is clearly inflated relative to the present in the lower ablation area.

Fig. 2. Study glacier during a surge (1951 (a)) and during quiescence (1977 (b)). Note the difference in glacier front position between the two images, particularly compared to the front position of the adjacent glacier near the bottom left of the images. (Photographs: National Air Photo Library, Ottawa, Ontario: Department of Energy, Mines and Resources.)
Data and Derived Model Inputs
Data were collected on the study glacier during the 2006–08 summer field seasons from which several model inputs are derived. The primary data requirements of the model relate to glacier geometry and surface velocity. We obtained ice-surface elevations over most of the main trunk of the glacier by real-time kinematic (RTK) global positioning system (GPS) surveying using Trimble R7 receivers with Zephyr geodetic antennas and a base station ∼200 m from the glacier margin. Dense spatial coverage of the glacier was achieved in all but a few inaccessible areas during surveys in 2006/07. Two steep tributaries of the trunk glacier, one of which is effectively disconnected, were not surveyed. Reference De PaoliDe Paoli (2009) constructed a digital elevation model (DEM) of the glacier surface from the GPS data using kriging. From the DEM, an approximate flowline was determined and flowline profiles of local surface slope and shape factor were computed (Fig. 3).

Fig. 3. Study glacier flowline profiles. (a) Surface and bed elevation, (b) ice thickness, (c) surface slope and (d) shape factor.
We obtained ground-based ice-penetrating radar data in 2007/08 using a Reference Narod and ClarkeNarod and Clarke (1994) high-power impulse transmitter (pulse rate 512 Hz), along with resistively loaded transmitting and receiving antennas, fabricated by Icefield Instruments Inc., to produce a centre frequency of 8 MHz. We used a National Instruments USB-5133 2CH 100 MS s−1 digitizer in place of an oscilloscope to capture the receiver signal, which was displayed on a miniature laptop computer. Data acquisition and analysis software were custom-designed by Blue System Integration Ltd, and include GPS capability (Rikaline SiRF III USB GPS receiver). We acquired data at ∼10 s intervals while travelling on skis. Each saved trace comprised a stack of 50–100 individual traces. Antennas were oriented parallel to the direction of motion for ease of travel. Transverse line spacing was ∼200 m over the lower two-thirds of the glacier, and we obtained clear bed reflections over much of this area. Adverse travelling conditions and frequent clutter in the radar returns resulted in patchy coverage over the upper third of the glacier. Several highly crevassed areas were avoided altogether. We assume a planar geometry and a velocity in ice of 1.68 × 10° m s−1 to compute ice thickness from the picked radar returns. We generate an ice-thickness map from these data by kriging (Reference De PaoliDe Paoli, 2009), with data quality being taken into account following Reference Flowers and ClarkeFlowers and Clarke (1999). A flowline profile of ice thickness is then extracted from this map.
Flowline profiles of glacier geometry, surface slope and shape factor (Fig. 3) are used as input to the inverse model. Glacier surface elevation ranges from 2000 to 2800 m a.s.l., with a mean surface slope of 10°. The lower 1500 m of the glacier is characterized by ice less than ∼60 m thick. The ice thickens up-glacier to ∼100 m, on average, over the upper 2000 m of the flowline. This leads to creep velocities calculated according to Reference NyeNye (1965) of <10 m a−1 over much of the flowline, with one prominent peak corresponding to a steep section located ∼3500 m from the terminus.
We established a network of velocity stakes (10 ft (∼3 m) lengths of metal or PVC conduit) in 2006, including 12 stakes along the flowline (Fig. 1). These stakes, or a subset thereof, were surveyed on the dates listed in Table 1 using the GPS equipment described above. All 12 stakes were within a range of ∼400–3000 m from the base station. RTK GPS measurements were carried out by placing a roving antenna, mounted on a backpack or survey pole, adjacent to the stake on its upstream side. In this way we surveyed the position of the base of the stake rather than its top, in order to avoid errors associated with stakes leaning as they melted out. Uncertainties in the horizontal-position measurements due to our methodology were estimated empirically to be ±5 cm, by having different team members measure the same stake in succession. Standard error propagation (e.g. Reference TaylorTaylor, 1982) is used to assign errors to the velocities computed from measured stake positions. An additional set of four velocity stakes (G1–G4 in Fig. 1) was installed between 2006 and 2008. These stakes differ from those described above in that a GPS antenna was attached to the stake for the duration of the measurement period (up to ∼50 days). The displacements of these stakes were determined using post-processing kinematic (PPK) GPS. In these cases, we only include an instrumental uncertainty of ±1 cm on the measured positions. This gives rise to errors on the velocity calculations that are much lower than those for stakes S1–S12.
Table 1. Velocity stake measurement dates and resulting datasets. Most stakes were measured within 2 days for each survey period. Stakes G1 and G4 are used instead of S6 and S10 for summer 2006 and stakes G1, G2 and G3 are used instead of S6, S7 and S9 for summer 2007

Velocities derived from stakes G1 and G4 were used to replace measurements missing from stakes S6 and S10, respectively, for the summer 2006 dataset, and velocities derived from stakes G1, G2 and G3 were used to replace measurements from stakes S6, S7 and S9, respectively, for the summer 2007 dataset. The measurement dates in Table 1 permit us to define four datasets; two of these we refer to as ‘summer’ datasets for convenience, though they cover only 1–2 weeks of the melt season. Although the ‘summer’ velocities we report are measured over short and slightly variable time periods, we have verified they are consistent with mean velocities measured over an extended time period (up to ∼50 days) at stakes G1–G4.
Flowline velocities derived from each of the four datasets comprise the primary input to the inversion model. The flowline velocity structure (Fig. 4) is similar for the four datasets, with velocities <10 m a−1 over the lowermost 1500 m of the flowline, and velocities >10 m a−1 above. Velocities are highest (up to ∼30 m a−1 for the annual datasets and >35 m a−1 for the summer datasets) in a zone ∼1700–3300 m from the glacier terminus. Velocities above 3300 m are slightly lower than this peak. Figure 4 also reveals a distinct difference between the summer and annual velocities above 1500 m from the terminus, with an offset of ∼10 m a−1 above 2000 m from the terminus. We might expect the true seasonality to be stronger than these data indicate, as our ‘summer’ measurements do not include the late spring and early summer.

Fig. 4. Measured ice-surface velocities with associated uncertainties. Uncertainties on the annual data are very small, compared to those on the summer data, due to the longer period over which displacements were measured.
Methods
We use geophysical inverse methods to recover the basal velocity profiles from the measured surface velocities. The forward model used here is identical to that developed by Reference TrufferTruffer (2004), which itself uses the model of Reference Kamb and EchelmeyerKamb and Echelmeyer (1986).
Forward model
The forward model requires an expression for the deformational or creep velocity of ice flowing down an inclined channel. Ice is treated as a non-linear viscous fluid whose rheology is described by Glen’s flow law (Reference GlenGlen, 1955) with an exponent n = 3. We consider an idealized slab glacier of uniform thickness, h, and uniform bed inclination, α. Using this glacier geometry and the assumption of laminar flow, Reference PatersonPaterson (1994, p. 251) showed that the deformational velocity at the surface of the glacier can be expressed analytically as
where A is the flow-law coefficient, ρ is ice density, g is gravitational acceleration and f is the shape factor. The shape factor accounts for the reduction in ice-flow speed along the glacier centre line due to drag exerted by the valley walls (Reference NyeNye, 1965). The values of f, α and h are determined from the data described above. Examination of the bed DEM leads to the choice of shape factors appropriate to a semi-elliptical idealized bed shape. The value of A is estimated as described in the Appendix.
A model is needed to link the glacier surface velocity to the contributions from creep and basal flow (sliding and substrate deformation). Longitudinal variations in slope and thickness cause longitudinal compression or extension that varies over the length of the glacier (Reference NyeNye, 1952), giving rise to non-zero longitudinal stress gradients. The coupling introduced by the longitudinal stress gradients can considerably modify the velocity from that calculated using local slope and thickness (Equation (1)). Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) parameterize the longitudinal stress-gradient coupling in terms of longitudinal averages of local slope and thickness. They write the creep velocity, u, at any position, x, along the length of the glacier as
where u obs(x0) is the velocity at a point of observation along the flowline and T is defined as

The relative coordinate, x′ − x, is the distance between a point x on the flowline and a point x′ of measurement. Wl is a weighting function, and l, the longitudinal coupling length, depends on rheological parameters and is generally about one to three times the ice thickness (Reference Kamb and EchelmeyerKamb and Echelmeyer, 1986). Equations (2) and (3) correspond to Kamb and Echelmeyer’s equations (35a and 35b).
Reference TrufferTruffer (2004) combined and adapted these equations into the following form:
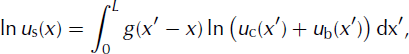
where u s is the observed surface velocity, u b is the basal velocity along the centre line of the glacier, L is the total length of the glacier and x is the longitudinal flowline coordinate. The weighting function, g, corresponds to the function Wl of Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) and is defined as
A value of three times the local ice thickness is used for l (the longitudinal coupling length) in the following. The length 4l is called the ‘averaging length’ and provides a measure of the distance over which the effects of varying slope and thickness are averaged. C is a normalizing factor whose purpose is to ensure that

Equation (4) constitutes the foundation of the forward model and can be used to estimate glacier surface velocities, given an appropriate boundary condition at the glacier bed.
Linear inverse problem
The forward model can be written mathematically as an inner product:
where dj are the data, m is the model and gj are continuous kernel functions calculated using the weighting function, g. Using this notation, the forward model can be formulated as
(Reference TrufferTruffer, 2004). In Equation (8), the data dj = ln u s are N discrete real numbers, while the model m = ln(u c + u b) is a function of a Hilbert space, H. Following the approach of Reference TrufferTruffer (2004), we rewrite Equation (8) as
With this notation, the data become dj = In u s − [g, In u c] and the model m = In(1 + u b/u c). Using the surface velocity measurements, as well as measurements of local slope and ice thickness, the data, dj , can be evaluated at each of the N longitudinal coordinate positions, xj , for which measurements of surface velocity exist.
Numerical treatment of the inverse problem requires that the model be evaluated at a finite number of locations. Both the model and kernel function are discretized into M components, with M > N, so the inverse problem is underdetermined. The kernel functions depend on the relative coordinate, x′ − x, such that there is one kernel function, gj , associated with each of the N data. Computation of the N kernel functions at each of the M discrete spatial locations results in the N × M Gram matrix, usually denoted G (Reference ParkerParker, 1994, p. 36). The Gram matrix relates the data to the model such that Equation (9) becomes
Finding an accurate model m involves inverting G. In most underdetermined problems, G is singular and a special technique is needed to perform the inversion.
Model norm and misfit function
The inverse problem is underdetermined, so the solution is non-unique and an infinite number of models satisfy the data. The process of selecting the best model is called ‘optimization’ and is usually carried out by minimizing a model norm (Reference ParkerParker, 1994, p.34). Following the method of Occam’s inversion (Reference Constable, Parker and ConstableConstable and others, 1987), we choose a norm that favours the smoothest model by minimizing the second derivative. The model norm is expressed in terms of a weighting matrix, W m, containing coefficients of a second-order finite-difference stencil:

where Δx is the grid spacing of the model. The first and last rows of the matrix contain coefficients reflecting boundary conditions adapted to the problem to ensure that W m is invertible. The weighting matrix, W m, is applied to the model, m, to form a quantity known as the model objective function, φ m, which can be expressed as a norm or in matrix form as
where ![]() is the transpose of the weighting matrix. The optimization process finds smooth models that fit the data by minimizing the model objective function, φ
m, subject to the condition d = Gm.
is the transpose of the weighting matrix. The optimization process finds smooth models that fit the data by minimizing the model objective function, φ
m, subject to the condition d = Gm.
Because the data contain errors, we construct a misfit function that is used to control how precisely the data are predicted. Like the model objective function, the misfit function is expressed as a norm and is parameterized using a weighting matrix:

where σj are the standard deviations of the errors. The standard rules of error propagation are used to assign errors to the data, based on errors in the measured surface velocities. The misfit function, φ d, can then be written
where the product Gm is the predicted data, that is to say, the data that are obtained when the model resulting from the inversion is used as input to the forward model. It has been shown that, in most cases, the criterion ϕ d = N yields models that fit the data within the error (Reference ParkerParker, 1994, p.192). As a final step, we introduce a reference model equal to the local difference between the measured surface velocity and the calculated velocity due to deformation. We find that using a reference model results in better recovery of basal velocity profiles in control tests (Reference De PaoliDe Paoli, 2009), but has little impact on computational performance. The inverse problem now becomes:

Singular-value decomposition
We solve the inverse problem using two methods: a straight minimization with a Lagrange multiplier, and a singular-value decomposition (SVD). Reference De PaoliDe Paoli (2009) investigated both methods, and found SVD simpler to implement in this case, as direct minimization occasionally led to poorly conditioned problems that would require special treatment. This study therefore employs SVD. The misfit and model norm are transformed by first defining x such that
The misfit criterion can then be written
where A is an N × M matrix such that ![]() , and b is an N × 1 vector such that b = W
d
d
obs − W
d
G m
ref. The inverse problem then becomes:
, and b is an N × 1 vector such that b = W
d
d
obs − W
d
G m
ref. The inverse problem then becomes:
The matrix A is rectangular and can be written in the form of a spectral factorization (Reference ParkerParker, 1994, p.145), also called singular-value decomposition:
where U and V are matrices containing the eigenvectors of AA T and Λ is the matrix containing the eigenvalues of AA T (eigenvalues of AA T are singular values of A). The matrices U and V are square and have N and M components, respectively, but the eigenvalue matrix Λ is not square (N × M) and is therefore singular. Because the purpose of the inversion process is to recover the model m from Equation (17), x must be computed. Λ must therefore be rendered square. This is done by recognizing that many of the eigenvalues are zero, and by truncating Λ to keep only the first p non-zero eigenvalues (Reference ParkerParker, 1994, p.148). Eigenvectors are truncated accordingly. Expressed as a singular-value decomposition (Equation (21)), matrix A is now invertible. The variable x becomes
with F the identity matrix, which will become important during the regularization process. The model m can then be recovered from x using Equation (17). The model norm, φ m, and misfit, φ d, are computed as
where Ip and IN are p × p and N × N identity matrices, respectively.
The inversion is carried out by minimizing a model norm, subject to a misfit criterion. To optimize the result, a balance is sought between the two in the form of regularization. This is done by truncating the SVD a second time. The appropriate number of eigenvalues, J, that should be retained is determined by identifying the point at which the misfit attains the value of N. Smaller eigenvalues are then ignored. While F = I when computing the full SVD, F is now altered so that its first J values are ones and the rest of its values are zeros. This sets all eigenvalues λi >J to zero when computing x (Equation (22)). The regularized model, m, is then computed using Equations (17) and (22), and the basal velocity profile, u b, is recovered from the model m using Equation (9).
Results
Control tests of the algorithm were performed to test the validity of the inversion scheme described above. We then invert the measured surface velocities and examine the sensitivity of inversion results to three key parameters.
Control tests
In a successful control test, a synthetic basal velocity profile is accurately recovered by the inversion algorithm. The control tests proceed as follows:
-
1. a synthetic basal velocity profile (or synthetic model) is chosen;
-
2. the synthetic basal velocity profile is used as input to the forward model to generate a synthetic surface velocity profile;
-
3. the synthetic surface velocities are perturbed by adding a small random component of noise (1% of the mean surface velocity);
-
4. the perturbed synthetic data are computed from the perturbed synthetic surface velocities using Equation (10);
-
5. the perturbed dataset is run through the inversion algorithm to recover a basal velocity profile;
-
6. this basal velocity profile is input to the forward model to generate a set of predicted surface velocities.
Comparing the synthetic and recovered models, as well as the synthetic and predicted data, allows us to assess the performance of the algorithm and the inversion method. In the six control tests presented here, we use sinusoidal and step-like synthetic basal velocity profiles, and slab-like, wedge-shaped and real glacier geometries (Table 2). Other control tests were performed without a reference model and with alternative solution methods (Reference De PaoliDe Paoli, 2009) but are not presented here.
Table 2. Glacier geometry and prescribed model parameters for the inversion control tests. Values in parentheses are averages. The thickness and slope profiles used for the real glacier geometry are presented in Figure 3. All shape factors are calculated for semi-elliptical beds

In all six tests, the synthetic data are predicted closely and the synthetic model is recovered fairly well (Fig. 5). The rectangular basal velocity profile (tests 2, 4, 6) is less well reproduced than the sinusoidal basal velocity profile (tests 1, 3, 5), as expected for a method constructed to select the smoothest model. The quality of the results also depends on glacier geometry, with the recovered model deteriorating from the simple slab glacier (tests 1 and 2), to the more complex wedge-shaped glacier (tests 3 and 4), to the glacier with real geometry (tests 5 and 6). This effect is also linked to an increase in the amplitude of the synthetic basal velocity profile, as the synthetic surface velocity depends on both the synthetic basal velocity profile and the glacier geometry. Large amplitudes of the synthetic basal velocity model were chosen for the control tests on real geometry to make the contributions from deformation and basal motion of similar magnitude.

Fig. 5. Control test results shown as flowline profiles of synthetic and recovered basal velocity (bold dashed and solid curves, respectively), synthetic surface velocity with noise added (crosses), predicted surface velocity (fine solid curve) and deformational velocity (fine dashed curve). (a) Test 1: slab geometry/sinusoidal basal velocity. (b) Test 2: slab geometry/step basal velocity. (c) Test 3: wedge geometry/sinusoidal basal velocity. (d) Test 4: wedge geometry/step basal velocity. (e) Test 5: real geometry/sinusoidal basal velocity. (f) Test 6: real geometry/step basal velocity.
An additional test is performed to examine the influence of variable amounts of noise on the data. This test is conducted with a slab-like glacier geometry and a sinusoidal basal velocity profile (test 1). Synthetic surface velocity data generated from this model are first perturbed with noise amounts of 2%, 5%, 10% and 20% of the mean synthetic surface velocity and then inverted. Figure 6 shows the reduction in accuracy of the recovered model with increasing noise, and can be compared to Figure 5 where noise is 1%. The uncertainty in the measured annual surface velocity is <1% over the upper 3500 m of the glacier and <5% over the lower 1500 m for both the 2006/07 and 2007/08 annual datasets. For the summer 2006 and 2007 datasets, the error amounts to <5% over the upper 3500 m but far exceeds 20% over the lower 1500 m. These high relative errors are a product of low measured velocities (<10 m a−1).

Fig. 6. Control test results with variable amounts of noise for a slab-like glacier with a sinusoidal basal velocity profile (test 1). Noise amounts: (a) 2%, (b) 5%, (c) 10% and (d) 20% of the mean synthetic surface velocity. Profiles shown are: synthetic and recovered basal velocity (bold dashed and solid curves, respectively), synthetic surface velocity with noise added (crosses), predicted surface velocity (fine solid curve) and deformational velocity (fine dashed curve).
Inversion of real data
We invert each of the four datasets presented in Table 1. The resulting basal velocity and predicted surface velocity profiles are shown in Figure 7. It is important to note that calculated errors have been multiplied by a factor of 17, as explained below, to obtain the results shown in Figure 7a and b for the annual datasets. Inversion of the annual datasets using the original calculated errors produces basal velocity profiles that exhibit unrealistic oscillations between 2000 and 3000 m along the flowline (Fig. 8). Similar oscillations have been reported by Reference TrufferTruffer (2004) for inversions that do not take uncertainties into account. The errors associated with the annual data are, indeed, so small that the inversion effectively attempts to fit the data exactly. This interpretation of the cause of the oscillations is substantiated by tests performed using a range of data errors (not shown). A factor of 17 was experimentally found to suppress oscillations in the basal velocity model for the annual datasets. The increased errors used to generate the annual basal velocity profiles are of the same order of magnitude as the uncertainty in the summer datasets. Increasing the magnitude of the errors can be justified by the fact that the original calculated errors do not account for uncertainties in the position of the flowline itself, nor the fact that some poles are slightly off the flowline and may have velocities that are not tangential to it. More importantly, the forward model itself is only an approximation of reality and therefore introduces an additional source of unquantified error.

Fig. 7. Inversion of real data: (a) summer 2006; (b) summer 2007; (c) annual 2006/07; (d) annual 2007/08. The predicted surface velocity is plotted as a continuous curve to avoid confusion with the measured surface velocity but should not be interpreted as a continuous profile. The errors associated with the annual datasets (c, d) have been increased from their original estimates.

Fig. 8. Inversion of the 2007/08 annual velocity data with original errors.
The percentage contribution of basal motion, defined as
is similar for all four datasets (Fig. 9). Basal motion accounts for ∼60–100% of the total surface motion over the lower ∼3400 m of the glacier and ranges between 0 and 80% above. The only substantial difference between summer and annual datasets occurs over the lowermost 1500 m of the glacier, where basal motion accounts for a higher fraction of summer velocities.

Fig. 9. Contribution of basal motion along the flowline for inversion results shown in Figure 7.
Sensitivity tests
Several parameters used in the inversion are subject to uncertainty that cannot be eliminated with the available field measurements. In these cases, we adopt values that are qualitatively consistent with the study glacier environment or values prescribed in the literature. This is the case for the shape factor, used to parameterize the effect of drag from the valley walls, and for the longitudinal coupling length, taken as three times the local ice thickness. Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) suggest that the coupling length is itself a function of basal motion. This parameter could thus be better constrained using an iterative approach. Englacial temperature was modelled (see Appendix) in order to select an appropriate flow-law coefficient. We conduct three tests to outline the impact of the shape factor, f, longitudinal coupling length, l, and flow-law coefficient, A, on modelled basal motion. We present results only for the annual 2007/08 dataset, as they are broadly representative of results from all the datasets.
In the control tests and the inversion of real data, the bed was assumed to have a semi-elliptical shape. This choice was motivated by the geometry of the valley and the bed DEM. Here we experiment with rectangular and parabolic beds with shape factors given by Reference PatersonPaterson (1994, p.269). Figure 10 presents the shape-factor profiles, along with the contribution of basal motion computed from the inversion of the data generated using these shape factors. Profiles of the contribution of basal motion computed with the three bed shapes are identical over most of the length of the glacier and differ only slightly between 3000 and 4500 m.

Fig. 10. Sensitivity test with a variable shape factor for the 2007/08 annual dataset. (a) Shape-factor profiles. (b) Contribution of basal motion for each shape factor. In both (a) and (b) the thick solid curve represents the shape factor used in the control tests and inversion of real data.
Figure 11 shows the result of varying the longitudinal coupling length from the default value of three ice thicknesses (l = 3h) to one, two, four and five ice thicknesses. The effect of the value of l on the contribution of basal motion is only significant when l is increased to four or five ice thicknesses. Significant deviations are restricted to short sections of the flowline in each case.

Fig. 11. Sensitivity test for variable longitudinal coupling lengths, l, for the 2007/08 annual dataset. A value of l = 3h was used in the control tests and inversion of real data.
The procedure we used to select an appropriate value of the flow-law coefficient is described in the Appendix. The default value corresponds to an effective ice temperature of −2°C. The contribution of basal motion is recomputed for flow-law coefficients corresponding to effective ice temperatures of 0, −1 and −3°C (see Table 3). Figure 12 shows that there is little change in the contribution of basal motion for an effective temperature of −3°C, but that the contribution of basal motion decreases significantly for effective temperatures of −1°C and 0°C. The temperature modelling detailed by Reference De PaoliDe Paoli (2009), summarized in the Appendix, suggests that effective temperatures less than −3°C are not realistic for the study glacier. An effective temperature between 0 and −2°C is more plausible; thus the contribution of basal motion may be lower than shown in Figure 9, but still accounts for >50% of the total glacier motion over most of the length of the flowline. Note that the actual glacier flow velocities are very low over the lower 1500 m of the glacier where the largest percentage variations in basal motion occur (Fig. 12).

Fig. 12. Sensitivity test with a variable flow-law coefficient, A, for the 2007/08 annual dataset. The flow-law coefficient is expressed in terms of effective ice temperature. A value of −2°C was used in the control tests and inversion of real data.
Table 3. Values of effective ice temperatures and associated flow-law coefficients (Reference PatersonPaterson, 1994, p.97) used in the sensitivity test. A = 2.4 × 10 − 24 Pa − 3 s − 1 was used in the control tests and inversion of real data

Interpretation and Discussion
The study glacier exhibits three distinct zones, both dynamically and morphologically, based on observations made in 2006–08. The lower ∼1700 m of the glacier length is free of crevasses and presents a less variable surface slope than the rest of the glacier. The zone between ∼1700 and 3300 m along the flowline exhibits surface undulations and extensive crevassing in many areas. The zone above 3300 m is also crevassed, with surface slopes that vary in association with two prominent icefalls. This pattern is reflected in the surface velocity measurements, with the lowest velocities over the lowermost ∼1700 m of the flowline, velocities from ∼20 to 35 m a−1 in the central region (1700–3300 m), and from ∼10 to 30 m a−1 above this. We interpret the nearly stagnant ice over the lower glacier to be a remnant of the 1986/87 surge based on: (1) photographic evidence of the ice in this area during the surge being much thicker and clearly involved in the surge itself; (2) the glacier terminus currently being ∼1 km further down-valley than it was in 1977 (prior to the last surge); and (3) the marked denudation (erosional stripping) of the valley walls adjacent to and downstream of the lower reaches of the glacier. The relatively high flow velocities above ∼1700 m are consistent with the observation of ongoing crevasse formation in this area. In the accumulation area, fresh crevasses are recognized as narrow fractures at the surface where the small-scale geometry is mirrored in detail on both sides of the fracture. In the ablation area, fresh crevasses have been encountered near stakes where the local crevasse geometry is well known from repeat visits to the sites.
Our inverse modelling reveals that basal motion is responsible for 50–100% of the total glacier motion for both summer and annual velocity datasets. The contribution of basal motion is highest in the central region of the glacier (∼1700–3300 m), over 80% across a significant fraction of this zone for most model parameters. The surface undulations observed between ∼1700 and 3300 m from the terminus (Fig. 13) are consistent with the high contribution of basal motion modelled over this area for all datasets. Such a flow regime is expected to enhance the transmission of basal topography to the glacier surface, as demonstrated by Reference Gudmundsson, Aðalgeirsdóttir and BjörnssonGudmundsson and others (2003). The contribution of basal motion is lowest in the upper region (above 3300 m), though it still reaches a maximum of ∼80%. The dynamics of the lower glacier (below ∼1700 m) are the most difficult to interpret, because of the low velocities in this area. However, the contribution of basal motion below ∼1700 m appears to be lower than that of the central region and is the most sensitive to uncertain model parameters.

Fig. 13. Photograph of the study glacier in July 2007, showing the transition between the faster-flowing ice above (characterized by surface undulations ∼20–30 m high) and the slowly flowing ice below (C.G. Schoof). This transition marks what we interpret as the active ice front or surge ‘bulge’.
The measured surface velocities between 1700 and 3300 m are higher than expected for a surge-type glacier of this size in its quiescent phase. For example, Reference Frappé and ClarkeFrappé and Clarke (2007) report surface velocities of ∼8 ma−1 in 2005 for Trapridge Glacier, which is similar in areal extent and thickness to the study glacier and located in the same region. High measured flow speeds in the central zone of the study glacier are accomplished primarily by basal motion, as determined by the inverse model and visually substantiated by the glacier surface morphology. Although the surface velocities appear to exhibit a seasonal cycle, the high contribution of basal motion over the central region of the glacier applies equally to annual and summer datasets.
Balance velocity calculations made with the current glacier geometry and a net surface mass-balance profile based on 2006/07 measurements show that the current flow regime is in a state of disequilibrium (Reference De PaoliDe Paoli, 2009) and requires glacier thinning in order to be maintained. We do not have long-term mass-balance records for this glacier, but there is little evidence that mass balance has recently been close to zero or positive in this region, as would be required to sustain the current flow rates. Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others (2002) calculate high rates of thinning (>1.5 m a−1) for nearby Kaskawulsh Glacier for the period ∼1950–1995, and somewhat lower rates of thinning (∼0.5 m a−1) for the period ∼1995–2001 from repeat airborne laser altimetry. Our 2007 net mass-balance estimates for the study glacier and another glacier in the Donjek Range (Reference WhelerWheler, 2009) are very similar to the negative 2003–07 net mass-balance estimates for the St Elias region derived from Gravity Recovery and Climate Experiment (GRACE) data (Reference Luthcke, Arendt, Rowlands, McCarthy and LarsenLuthcke and others, 2008) and from aircraft laser altimetry (Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008). This leads us to conclude that the current dynamic regime is unlikely to be a remnant of some recent period of higher mass balance. Furthermore, calculation of ice flux along the flowline shows a distinct gradient across the transition at ∼1700 m with higher flux above and lower flux below (not shown) that cannot be explained by the surface mass balance. This is suggestive of a dynamically driven propagation of mass. Preliminary force-balance calculations, including longitudinal stresses, give no indication of the elevated flow speeds observed over the central region of the glacier flowline (personal communication from N. Roux, 2009), which argues against the current flow regime being simply a product of glacier geometry.
Based on the evidence above, we suggest that the glacier is undergoing a ‘slow surge’, as described for Trapridge Glacier by Reference Frappé and ClarkeFrappé and Clarke (2007). The active phase of the Trapridge Glacier surge lasted 20 years and was characterized by peak velocities of ∼40 m a−1 in the central region of the glacier; these velocities were attributed primarily to basal motion (Reference Frappé and ClarkeFrappé and Clarke, 2007). The active ice was not particularly heavily crevassed but did form a bulge that was ultimately coincident with the glacier margin. Although Trapridge Glacier had undergone a dramatic surge some time before 1951, its most recent surge was too slow to be attended by many of the obvious surge diagnostics, such as lateral shear margins and extensive chaotic crevassing. The description of Reference Frappé and ClarkeFrappé and Clarke (2007) bears a striking similarity to our observations on the study glacier, with the dynamic and morphological transition at ∼1700 m marking the active ice front or surge ‘bulge’ (Fig. 13). It is unclear whether the region above ∼3300 m is actively involved in the surge. Photographs of the two previous surges make it difficult to determine the extent to which the upper basin has participated in these surges. If the comparison with Trapridge Glacier holds, we might expect the upper basin to undergo a subdued flow acceleration compared to the central glacier (Reference Frappé and ClarkeFrappé and Clarke, 2007).
The study glacier surged around 1951 (Fig. 2) and again in 1986–87. Other available imagery, from the early 1970s to the early 1980s, shows no signs of surge behaviour or recent recovery from a surge. Unless the glacier surged again after 1951 but well before the early 1970s, the observations above suggest a surge period of 30–40 years, a value within the range established by Reference Meier and PostMeier and Post (1969) for surge-type glaciers in the St Elias Mountains. If, as Reference Frappé and ClarkeFrappé and Clarke (2007) suggest, the long slow phase of a surge may simply be a preamble to the shorter faster phase, perhaps the current behaviour of the study glacier is part of the natural surge cycle. If the natural surge cycle does not include these two phases, then the current surge is much weaker than the previous two and may have occurred prematurely. If this is the case, it seems plausible that the glacier has been unable to accumulate sufficient mass to support a vigorous surge. If changes in glacier mass balance are having a significant effect on the nature of glacier surges, this challenges the traditional notion of surges being independent of climate and may lead us to reconsider this relationship (e.g. Reference HewittHewitt, 2007).
Conclusion
We measured surface velocities along an approximate flowline of a small surge-type glacier in Yukon from 2006 to 2008. Three zones are identified along the flowline, based on the velocity structure and observed surface morphology of the glacier: (1) lower 1700 m: slowly flowing crevasse-free ice; (2) 1700–3300 m: ice with the highest velocities (20–35 m a−1), pronounced surface undulations and significant crevassing; and (3) distances greater than 3300 m: ice with moderate velocities, surface topography and crevassing. While these velocities are much lower than typical surge velocities reported for small surge-type glaciers in the St Elias Mountains, the velocities in the central zone of the glacier are comparable to those measured on Trapridge Glacier during its recently reported ‘slow surge’ (Reference Frappé and ClarkeFrappé and Clarke, 2007).
We used geophysical inversion methods to infer basal velocity profiles from the surface velocities described above. Sliding or bed deformation is responsible for ∼50–100% of the total glacier motion over much of the flowline, with the contribution of basal motion being particularly high over the central region of the glacier. This flow regime characterizes both the ‘summer’ and annual mean datasets, demonstrating a significant role for basal motion year-round. Calculations of ice flux reveal a strong gradient at ∼1700 m, indicative of dynamically driven propagation of mass from the fast-flowing central region to the nearly stagnant lower region of the glacier. Balance velocity calculations show the glacier to be out of equilibrium with recent mass balance, with glacier thinning required to sustain the current flow regime.
Based on what we know of its surge history, and what this study has revealed about its current dynamics, we suggest that the study glacier may currently be undergoing a ‘slow surge’ as described by Reference Frappé and ClarkeFrappé and Clarke (2007). Whether this behaviour represents a climatically driven departure from the glacier’s previous surge behaviour is unknown at this time. In either case, the dynamics of this glacier are driving changes in glacier morphology that may have implications for its future mass balance. This study provides a starting point for investigating the mutual influence of surge-type glacier dynamics and mass balance at a wider scale.
Acknowledgements
We are grateful to the Natural Sciences and Engineering Research Council of Canada (NSERC), the Canada Foundation for Innovation (CFI), the Canada Research Chairs (CRC) Program and Simon Fraser University for funding. Permission to conduct this research was granted by the Kluane First Nation, Parks Canada, and the Yukon Territorial Government. Support from the Kluane Lake Research Station (KLRS) and Kluane National Park and Reserve is greatly appreciated. We are indebted to A. Williams, S. Williams, L. Goodwin (KLRS) and D. Makkonen (Trans North Helicopters) for logistical support, and to B. Wheler, J. Logher, C. Doughty, P. Belliveau and A. Jarosch for field assistance. We thank Whistler–Blackcomb for facilitating the testing of our radar system. Finally, we are grateful to M. Truffer, H. Pritchard and C. Martin for their thoughtful comments on the manuscript, and to H.A. Fricker, our Scientific Editor.
Appendix: Determination of the Flow-Law Coefficient, A
In order to constrain the flow-law coefficient, we use a simple one-dimensional model to calculate plausible vertical temperature profiles within the ice. These temperatures are weighted according to a hypothetical strain-rate profile, to calculate an effective ice temperature that can be used to guide our choice of A according to Reference PatersonPaterson (1994, p.97). A detailed methodology and description of the results are given by Reference De PaoliDe Paoli (2009). The temperature distribution with depth, z, and time, t, can be described by the following partial differential equation:

where ρ is the ice density, c(T) = 7.7929T − 13.331 J kg−1 K−1 is the heat capacity, K(T) = 9.085 × 10−5 T 2 −0.053T + 10.4204 W m − 1 K−1 is the thermal conductivity and Φ = 2A 0 exp (−Q/RT) [ρg (h − z) sin θ] n +1 is the strain heating with the temperature-independent component of the flow-law coefficient, A 0 = 8.75 × 10−13 Pa−3 s−1 (Reference PatersonPaterson, 1994, p. 97), the creep activation energy for ice Q = 6.07 × 104 J mol−1, the ideal gas constant R = 8.314 J mol−1 K−1, the acceleration due to gravity g = 9.81 m s−2 and Glen’s flow-law exponent n = 3. We solve this equation numerically at Δz = 1 m intervals for a slab of thickness h = 78 m and slope of θ = 10.1°, the respective means of ice thickness and surface slope for the study glacier. The boundary condition at the surface is derived from year-round measurements of 2 m air temperature near stake S6 (Fig. 1). We experiment with both constant and varying surface temperatures, as well as with Neumann (fixed heat flux) and Dirichlet (fixed temperature) boundary conditions at the glacier bed. Values for both surface and bed boundary conditions are presented in Table 4. Simulations are initialized with a linear temperature profile and run to steady state before a varying surface boundary condition is imposed. In the simulations with a Dirichlet boundary condition at the bed, ice temperatures reach a minimum between −6 and −8°C below the surface layer affected by the annual temperature wave. Neumann boundary conditions at the bed result in basal temperatures between −6 and −7°C.
Table 4. Boundary conditions used in the temperature model

To calculate an effective ice temperature from these hypothetical temperature profiles, we vertically integrate the temperature weighted by a normalized strain rate. The strain rate is calculated for a slab glacier as

The result is an effective ice temperature of −1.7 to −1.9°C for a temperate glacier bed, and −6.4 to −7.0°C for a frozen bed. From preliminary measurements of ice temperature in 2008, and the glacier behaviour inferred from our measurements and modelling, we posit that the glacier bed is at the melting point over most of the flowline. We have therefore adopted a reference value for the effective temperature of −2°C, and a flow-law coefficient of A = 2.4 × 10−24 Pa−3 s−1 according to Reference PatersonPaterson (1994, p. 97). This simple modelling exercise does not include the effect of glacier dynamics on temperature, beyond the strain-rate weighting. It is only performed for one glacier geometry and surface temperature forcing, and at one location along the glacier flowline.


















