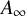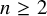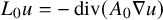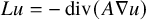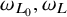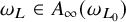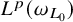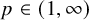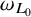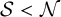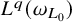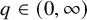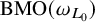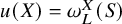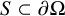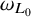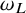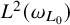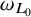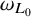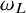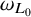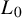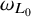1 Introduction
The solvability of the Dirichlet problem (1.1) on rough domains has been of great interest in the last 50 years. Given a domain
![]() $\Omega \subset \mathbb {R}^{n+1}$
and a uniformly elliptic operator L on
$\Omega \subset \mathbb {R}^{n+1}$
and a uniformly elliptic operator L on
![]() $\Omega $
, it consists on finding a solution u (satisfying natural conditions in accordance to what is known for the boundary data f) to the boundary value problem
$\Omega $
, it consists on finding a solution u (satisfying natural conditions in accordance to what is known for the boundary data f) to the boundary value problem
 $$ \begin{align} \begin{cases} L u =0 & \quad\text{in}\quad\Omega,\\ u =f & \quad\text{on}\quad\partial \Omega. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} L u =0 & \quad\text{in}\quad\Omega,\\ u =f & \quad\text{on}\quad\partial \Omega. \end{cases} \end{align} $$
To address this question, one typically investigates the properties of the corresponding elliptic measure since it is the fundamental tool that enables us to construct solutions of equation (1.1). The techniques from harmonic analysis and geometric measure theory have allowed us to study the regularity of elliptic measures and hence understand this subject well. Conversely, the good properties of elliptic measures allow us to effectively use the machinery from these fields to obtain information about the topology and the regularity of the domains. These ideas have led to a quite active research at the intersection of harmonic analysis, partial differential equations and geometric measure theory.
The connection between the geometry of a domain and the absolute continuity properties of its harmonic measure goes back to the classical result of F. and M. Riesz [Reference Riesz and Riesz50], which showed that, for a simply connected domain in the plane, the rectifiability of its boundary implies that harmonic measure is mutually absolutely continuous with respect to the surface measure. After that, considerable attention has focused on establishing higher-dimensional analogues and the converse of the F. and M. Riesz theorem. For a planar domain, Bishop and Jones [Reference Bishop and Jones6] proved that, if only a portion of the boundary is rectifiable, harmonic measure is absolutely continuous with respect to arclength on that portion. A counterexample was also constructed to show that the result of [Reference Riesz and Riesz50] may fail in the absence of some strong connectivity property (like simple connectivity). In dimensions greater than
![]() $2$
, Dahlberg [Reference Dahlberg13] established a quantitative version of the absolute continuity of harmonic measures with respect to surface measure on the boundary of a Lipschitz domain. This result was extended to
$2$
, Dahlberg [Reference Dahlberg13] established a quantitative version of the absolute continuity of harmonic measures with respect to surface measure on the boundary of a Lipschitz domain. This result was extended to
![]() $\mathrm {BMO}_1$
domains by Jerison and Kenig [Reference Jerison and Kenig41] and to chord-arc domains by David and Jerison [Reference David and Jerison17] (see also [Reference Azzam, Hofmann, Martell, Nyström and Toro5, Reference Hofmann and Martell31, Reference Hofmann, Martell and Uriarte-Tuero36] for the case of
$\mathrm {BMO}_1$
domains by Jerison and Kenig [Reference Jerison and Kenig41] and to chord-arc domains by David and Jerison [Reference David and Jerison17] (see also [Reference Azzam, Hofmann, Martell, Nyström and Toro5, Reference Hofmann and Martell31, Reference Hofmann, Martell and Uriarte-Tuero36] for the case of
![]() $1$
-sided chord-arc domains). In this direction, this was culminated in the recent results of [Reference Azzam, Hofmann, Martell, Mourgoglou and Tolsa4] under some optimal background hypothesis (an open set in
$1$
-sided chord-arc domains). In this direction, this was culminated in the recent results of [Reference Azzam, Hofmann, Martell, Mourgoglou and Tolsa4] under some optimal background hypothesis (an open set in
![]() $\mathbb {R}^{n+1}$
satisfying an interior corkscrew condition with an n-dimensional Ahlfors–David regular boundary). Indeed, [Reference Azzam, Hofmann, Martell, Mourgoglou and Tolsa4] gives a complete picture of the relationship between the quantitative absolute continuity of harmonic measure with respect to surface measure (or, equivalently, the solvability of equation (1.1) for singular data; see [Reference Hofmann and Le29]) and the rectifiability of the boundary plus some weak local John condition (that is, local accessibility by nontangential paths to some pieces of the boundary). Another significant extension of the F. and M. Riesz theorem was obtained in [Reference Azzam, Hofmann, Martell, Mayboroda, Mourgoglou, Tolsa and Volberg3], where it was proved that, in any dimension and in the absence of any connectivity condition, every piece of the boundary with finite surface measure is rectifiable, provided surface measure is absolutely continuous with respect to harmonic measure on that piece. It is worth pointing out that all the aforementioned results are restricted to the n-dimensional boundaries of domains in
$\mathbb {R}^{n+1}$
satisfying an interior corkscrew condition with an n-dimensional Ahlfors–David regular boundary). Indeed, [Reference Azzam, Hofmann, Martell, Mourgoglou and Tolsa4] gives a complete picture of the relationship between the quantitative absolute continuity of harmonic measure with respect to surface measure (or, equivalently, the solvability of equation (1.1) for singular data; see [Reference Hofmann and Le29]) and the rectifiability of the boundary plus some weak local John condition (that is, local accessibility by nontangential paths to some pieces of the boundary). Another significant extension of the F. and M. Riesz theorem was obtained in [Reference Azzam, Hofmann, Martell, Mayboroda, Mourgoglou, Tolsa and Volberg3], where it was proved that, in any dimension and in the absence of any connectivity condition, every piece of the boundary with finite surface measure is rectifiable, provided surface measure is absolutely continuous with respect to harmonic measure on that piece. It is worth pointing out that all the aforementioned results are restricted to the n-dimensional boundaries of domains in
![]() $\mathbb {R}^{n+1}$
. Some analogues have been obtained in [Reference David, Engelstein and Mayboroda15, Reference David, Feneuil and Mayboroda16, Reference David and Mayboroda18, Reference Mayboroda and Zhao47] on lower-dimensional sets.
$\mathbb {R}^{n+1}$
. Some analogues have been obtained in [Reference David, Engelstein and Mayboroda15, Reference David, Feneuil and Mayboroda16, Reference David and Mayboroda18, Reference Mayboroda and Zhao47] on lower-dimensional sets.
On the other hand, the solvability of the Dirichlet problem (1.1) is closely linked with the absolute continuity properties of elliptic measures. The importance of the quantitative absolute continuity of the elliptic measure with respect to the surface measure comes from the fact that
![]() $\omega _L \in RH_q(\sigma )$
(short for the reverse Hölder class with respect to
$\omega _L \in RH_q(\sigma )$
(short for the reverse Hölder class with respect to
![]() $\sigma $
, being
$\sigma $
, being
![]() $\sigma $
the surface measure) is equivalent to the
$\sigma $
the surface measure) is equivalent to the
![]() $L^{q'}(\sigma )$
-solvability of the Dirichlet problem (see, e.g., [Reference Hofmann and Le29]). In 1984, Dahlberg formulated a conjecture concerning the optimal conditions on a matrix of coefficients guaranteeing that the Dirichlet problem (1.1) with
$L^{q'}(\sigma )$
-solvability of the Dirichlet problem (see, e.g., [Reference Hofmann and Le29]). In 1984, Dahlberg formulated a conjecture concerning the optimal conditions on a matrix of coefficients guaranteeing that the Dirichlet problem (1.1) with
![]() $L^p$
data for some
$L^p$
data for some
![]() $p \in (1, \infty )$
is solvable. Kenig and Pipher [Reference Kenig and Pipher44] made the first attempt on bounded Lipschitz domains and gave an affirmative answer to Dahlberg’s conjecture. More precisely, they showed that elliptic measure is quantitatively absolutely continuous with respect to surface measure whenever the gradient of the coefficients satisfies a Carleson measure condition. This was done in Lipschitz domains but can be naturally extended to chord-arc domains. In some sense, some recent results have shown that this class of domains is optimal. First, [Reference Hofmann and Martell31, Reference Hofmann, Martell and Uriarte-Tuero36, Reference Azzam, Hofmann, Martell, Nyström and Toro5] show that, in the case of the Laplacian and for 1-sided chord-arc domains, the fact that the harmonic measure is quantitatively absolutely continuous with respect to surface measure (equivalently, the
$p \in (1, \infty )$
is solvable. Kenig and Pipher [Reference Kenig and Pipher44] made the first attempt on bounded Lipschitz domains and gave an affirmative answer to Dahlberg’s conjecture. More precisely, they showed that elliptic measure is quantitatively absolutely continuous with respect to surface measure whenever the gradient of the coefficients satisfies a Carleson measure condition. This was done in Lipschitz domains but can be naturally extended to chord-arc domains. In some sense, some recent results have shown that this class of domains is optimal. First, [Reference Hofmann and Martell31, Reference Hofmann, Martell and Uriarte-Tuero36, Reference Azzam, Hofmann, Martell, Nyström and Toro5] show that, in the case of the Laplacian and for 1-sided chord-arc domains, the fact that the harmonic measure is quantitatively absolutely continuous with respect to surface measure (equivalently, the
![]() $L^{p}(\sigma )$
-Dirichlet problem is solvable for some finite p) implies that the domains must have exterior corkscrews; hence, they are chord-arc domains. Indeed, in a first attempt to generalize this to the class of Kenig–Pipher operators, Hofmann, the third author of the present paper and Toro [Reference Hofmann, Martell and Toro34] were able to consider variable coefficients whose gradient satisfies some
$L^{p}(\sigma )$
-Dirichlet problem is solvable for some finite p) implies that the domains must have exterior corkscrews; hence, they are chord-arc domains. Indeed, in a first attempt to generalize this to the class of Kenig–Pipher operators, Hofmann, the third author of the present paper and Toro [Reference Hofmann, Martell and Toro34] were able to consider variable coefficients whose gradient satisfies some
![]() $L^1$
-Carleson condition (in turn, stronger than the one in [Reference Kenig and Pipher44]). The general case, on which the operators are in the optimal Kenig–Pipher-class (that is, the gradient of the coefficients satisfies an
$L^1$
-Carleson condition (in turn, stronger than the one in [Reference Kenig and Pipher44]). The general case, on which the operators are in the optimal Kenig–Pipher-class (that is, the gradient of the coefficients satisfies an
![]() $L^2$
-Carleson condition) has been recently solved by Hofmann et al. [Reference Hofmann, Martell, Mayboroda, Toro and Zhao33].
$L^2$
-Carleson condition) has been recently solved by Hofmann et al. [Reference Hofmann, Martell, Mayboroda, Toro and Zhao33].
One can also relate the solvability of the Dirichlet problem (1.1), with data in
![]() $\mathrm {BMO}$
, with the fact that the elliptic measure belongs to
$\mathrm {BMO}$
, with the fact that the elliptic measure belongs to
![]() $A_{\infty }$
. This was first shown by Fefferman and Stein [Reference Fefferman and Stein23] for the Laplacian in
$A_{\infty }$
. This was first shown by Fefferman and Stein [Reference Fefferman and Stein23] for the Laplacian in
![]() $\mathbb {R}^{n+1}_+$
and extended to uniformly elliptic operators in [Reference Dindos, Kenig and Pipher19] and [Reference Zhao51] in the contexts of Lipschitz and
$\mathbb {R}^{n+1}_+$
and extended to uniformly elliptic operators in [Reference Dindos, Kenig and Pipher19] and [Reference Zhao51] in the contexts of Lipschitz and
![]() $1$
-sided chord-arc domains, respectively. In the nonconnected case, Hofmann and Le [Reference Hofmann and Le29] showed that
$1$
-sided chord-arc domains, respectively. In the nonconnected case, Hofmann and Le [Reference Hofmann and Le29] showed that
![]() $\mathrm {BMO}$
-solvability implies that the elliptic measure belongs to the class weak-
$\mathrm {BMO}$
-solvability implies that the elliptic measure belongs to the class weak-
![]() $A_{\infty }$
with respect to surface measure. Kenig et al. [Reference Kenig, Kirchheim, Pipher and Toro42], extending [Reference Kenig, Koch, Pipher and Toro43], proved in the context of bounded Lipschitz domains that if all bounded solutions satisfy Carleson measure estimates (CME), then the elliptic measure belongs to the class
$A_{\infty }$
with respect to surface measure. Kenig et al. [Reference Kenig, Kirchheim, Pipher and Toro42], extending [Reference Kenig, Koch, Pipher and Toro43], proved in the context of bounded Lipschitz domains that if all bounded solutions satisfy Carleson measure estimates (CME), then the elliptic measure belongs to the class
![]() $A_{\infty }$
(see also [Reference Cavero, Hofmann, Martell and Toro9] for
$A_{\infty }$
(see also [Reference Cavero, Hofmann, Martell and Toro9] for
![]() $1$
-sided chord-arc domains). An examination of the proofs of [Reference Kenig, Kirchheim, Pipher and Toro42, Reference Cavero, Hofmann, Martell and Toro9] reveals that the Carleson measure conditions are only used for solutions of the form
$1$
-sided chord-arc domains). An examination of the proofs of [Reference Kenig, Kirchheim, Pipher and Toro42, Reference Cavero, Hofmann, Martell and Toro9] reveals that the Carleson measure conditions are only used for solutions of the form
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
, with
$X\in \Omega $
, with
![]() $S\subset \partial \Omega $
being a Borel set. Hence, in those contexts, to show that the elliptic measure is a Muckenhoupt weight, it suffices to see that all elliptic measure solutions with bounded data satisfy CME, and this may be simpler than establishing the
$S\subset \partial \Omega $
being a Borel set. Hence, in those contexts, to show that the elliptic measure is a Muckenhoupt weight, it suffices to see that all elliptic measure solutions with bounded data satisfy CME, and this may be simpler than establishing the
![]() $\mathrm {BMO}$
-solvability as in [Reference Dindos, Kenig and Pipher19, Reference Zhao51, Reference Hofmann and Le29].
$\mathrm {BMO}$
-solvability as in [Reference Dindos, Kenig and Pipher19, Reference Zhao51, Reference Hofmann and Le29].
In another direction, one can consider perturbations of elliptic operators in rough domains. That is, one seeks for conditions on the disagreement of two coefficient matrices so that the solvability of the Dirichlet problem or the quantitative absolute continuity with respect to the surface measure of the elliptic measure for one elliptic operator could be transferred to the other operator. This problem was initiated by Fabes, Jerison and Kenig [Reference Fabes, Jerison and Kenig20] in the case of continuous and symmetric coefficients and extended by Dahlberg [Reference Dahlberg14] to a more general setting under a vanishing Carleson measure condition. Soon after, working again in the domain
![]() $\Omega =B(0, 1)$
and with symmetric operators, Fefferman [Reference Fefferman21] improved Dahlberg’s result by formulating the boundedness of a conical square function, which allows one to preserve the
$\Omega =B(0, 1)$
and with symmetric operators, Fefferman [Reference Fefferman21] improved Dahlberg’s result by formulating the boundedness of a conical square function, which allows one to preserve the
![]() $A_{\infty }$
property of elliptic measures but without preserving the reverse Hölder exponent (see [Reference Fefferman, Kenig and Pipher22, Theorem 2.24]). A major step forward was made by Fefferman, Kenig and Pipher [Reference Fefferman, Kenig and Pipher22] by giving an optimal Carleson measure perturbation on Lipschitz domains. Additionally, they established another kind of perturbation to study the quantitative absolute continuity between two elliptic measures. Beyond the Lipschitz setting, these results were extended to chord-arc domains [Reference Milakis, Pipher and Toro48, Reference Milakis, Pipher and Toro49], 1-sided chord-arc domains [Reference Cavero, Hofmann and Martell8, Reference Cavero, Hofmann, Martell and Toro9] and 1-sided nontangentially accessible (NTA) domains satisfying the capacity density condition (CDC) [Reference Akman, Hofmann, Martell and Toro2]. It is worth mentioning that the so-called extrapolation of Carleson measure was utilized in [Reference Akman, Hofmann, Martell and Toro2, Reference Cavero, Hofmann and Martell8]. Nevertheless, a simpler and novel argument was presented in [Reference Cavero, Hofmann, Martell and Toro9] to get the large constant perturbation. More specifically, the authors use that the
$A_{\infty }$
property of elliptic measures but without preserving the reverse Hölder exponent (see [Reference Fefferman, Kenig and Pipher22, Theorem 2.24]). A major step forward was made by Fefferman, Kenig and Pipher [Reference Fefferman, Kenig and Pipher22] by giving an optimal Carleson measure perturbation on Lipschitz domains. Additionally, they established another kind of perturbation to study the quantitative absolute continuity between two elliptic measures. Beyond the Lipschitz setting, these results were extended to chord-arc domains [Reference Milakis, Pipher and Toro48, Reference Milakis, Pipher and Toro49], 1-sided chord-arc domains [Reference Cavero, Hofmann and Martell8, Reference Cavero, Hofmann, Martell and Toro9] and 1-sided nontangentially accessible (NTA) domains satisfying the capacity density condition (CDC) [Reference Akman, Hofmann, Martell and Toro2]. It is worth mentioning that the so-called extrapolation of Carleson measure was utilized in [Reference Akman, Hofmann, Martell and Toro2, Reference Cavero, Hofmann and Martell8]. Nevertheless, a simpler and novel argument was presented in [Reference Cavero, Hofmann, Martell and Toro9] to get the large constant perturbation. More specifically, the authors use that the
![]() $A_{\infty }$
property of elliptic measures can be characterized by the fact bounded solutions satisfy CME; see [Reference Cavero, Hofmann, Martell and Toro9, Theorem 1.4], extending the main result of [Reference Kenig, Kirchheim, Pipher and Toro42] to the 1-sided chord-arc setting. Also, it is worth mentioning that [Reference Akman, Hofmann, Martell and Toro2] considers for the first time perturbation results on sets with bad surface measures.
$A_{\infty }$
property of elliptic measures can be characterized by the fact bounded solutions satisfy CME; see [Reference Cavero, Hofmann, Martell and Toro9, Theorem 1.4], extending the main result of [Reference Kenig, Kirchheim, Pipher and Toro42] to the 1-sided chord-arc setting. Also, it is worth mentioning that [Reference Akman, Hofmann, Martell and Toro2] considers for the first time perturbation results on sets with bad surface measures.
The goal of this paper is to continue with the line of research initiated in [Reference Akman, Hofmann, Martell and Toro1, Reference Akman, Hofmann, Martell and Toro2]. We work with
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, a
$n\ge 2$
, a
![]() $1$
-sided NTA domain satisfying the CDC. We consider two real (not necessarily symmetric) uniformly elliptic operators
$1$
-sided NTA domain satisfying the CDC. We consider two real (not necessarily symmetric) uniformly elliptic operators
![]() $L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
$L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
in
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
in
![]() $\Omega $
and denote by
$\Omega $
and denote by
![]() $\omega _{L_0}, \omega _L$
the respective associated elliptic measures. The paper [Reference Akman, Hofmann, Martell and Toro2] considered the perturbation theory in this context providing natural conditions on the disagreement of the coefficients so that
$\omega _{L_0}, \omega _L$
the respective associated elliptic measures. The paper [Reference Akman, Hofmann, Martell and Toro2] considered the perturbation theory in this context providing natural conditions on the disagreement of the coefficients so that
![]() $\omega _L$
is quantitatively absolutely continuous with respect to
$\omega _L$
is quantitatively absolutely continuous with respect to
![]() $\omega _{L_0}$
(see also [Reference Fefferman, Kenig and Pipher22]). In our first main result, we single out the latter property and characterize it in terms of the solvability of the Dirichlet problem or some other properties that certain solutions satisfy. In a nutshell, we show that such condition is equivalent to the fact that null solutions of L have a good behavior with respect to
$\omega _{L_0}$
(see also [Reference Fefferman, Kenig and Pipher22]). In our first main result, we single out the latter property and characterize it in terms of the solvability of the Dirichlet problem or some other properties that certain solutions satisfy. In a nutshell, we show that such condition is equivalent to the fact that null solutions of L have a good behavior with respect to
![]() $\omega _{L_0}$
. The precise statement is as follows:
$\omega _{L_0}$
. The precise statement is as follows:
Theorem 1.1. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. Bearing in mind the notions introduced in Definition 3.3, the following statements are equivalent:
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. Bearing in mind the notions introduced in Definition 3.3, the following statements are equivalent:
-
(a)
 $\omega _L \in A_{\infty }(\partial \Omega , \omega _{L_0})$
(cf. Definition 3.1).
$\omega _L \in A_{\infty }(\partial \Omega , \omega _{L_0})$
(cf. Definition 3.1). -
(b) L is
 $L^{p}(\omega _{L_0})$
-solvable for some
$L^{p}(\omega _{L_0})$
-solvable for some
 $p\in (1,\infty )$
.
$p\in (1,\infty )$
. -
(b)′ L is
 $L^{p}(\omega _{L_0})$
-solvable for characteristic functions for some
$L^{p}(\omega _{L_0})$
-solvable for characteristic functions for some
 $p\in (1,\infty )$
.
$p\in (1,\infty )$
. -
(c) L satisfies
 $\mathrm {CME}(\omega _{L_0})$
.
$\mathrm {CME}(\omega _{L_0})$
. -
(c)′ L satisfies
 $\mathrm {CME}(\omega _{L_0})$
for characteristic functions.
$\mathrm {CME}(\omega _{L_0})$
for characteristic functions. -
(d) L satisfies
 $\mathcal {S}<\mathcal {N}$
in
$\mathcal {S}<\mathcal {N}$
in
 $L^q(\omega _{L_0})$
for some (or all)
$L^q(\omega _{L_0})$
for some (or all)
 $q\in (0,\infty )$
.
$q\in (0,\infty )$
. -
(d)′ L satisfies
 $\mathcal {S}<\mathcal {N}$
in
$\mathcal {S}<\mathcal {N}$
in
 $L^q(\omega _{L_0})$
for characteristic functions for some (or all)
$L^q(\omega _{L_0})$
for characteristic functions for some (or all)
 $q\in (0,\infty )$
.
$q\in (0,\infty )$
. -
(e) L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable.
$\mathrm {BMO}(\omega _{L_0})$
-solvable. -
(e)′ L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable for characteristic functions.
$\mathrm {BMO}(\omega _{L_0})$
-solvable for characteristic functions. -
(f) L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense.
$\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense. -
(f)′ L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense for characteristic functions.
$\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense for characteristic functions.
Furthermore, for any
![]() $p\in (1,\infty )$
there hold
$p\in (1,\infty )$
there hold
and
Remark 1.2. Note that in Definition 3.3 the
![]() $L^{p}(\omega _{L_0})$
-solvability depends on some fixed
$L^{p}(\omega _{L_0})$
-solvability depends on some fixed
![]() $\alpha $
and N. However, in the previous result what we prove is that if
$\alpha $
and N. However, in the previous result what we prove is that if
![]() $\mathrm {(a)}$
holds, then
$\mathrm {(a)}$
holds, then
![]() $\mathrm {(b)}$
is valid for all
$\mathrm {(b)}$
is valid for all
![]() $\alpha $
and N. For the converse, we see that if
$\alpha $
and N. For the converse, we see that if
![]() $\mathrm {(b)}$
holds for some
$\mathrm {(b)}$
holds for some
![]() $\alpha $
and N, then we get
$\alpha $
and N, then we get
![]() $\mathrm {(a)}$
. This eventually says that if
$\mathrm {(a)}$
. This eventually says that if
![]() $\mathrm {(b)}$
holds for some
$\mathrm {(b)}$
holds for some
![]() $\alpha $
and N, then it also holds for every
$\alpha $
and N, then it also holds for every
![]() $\alpha $
and N. The same occurs with
$\alpha $
and N. The same occurs with
![]() $\mathrm {(d)}$
where now there is only
$\mathrm {(d)}$
where now there is only
![]() $\alpha $
.
$\alpha $
.
As an immediate consequence of Theorem 1.1, if we take
![]() $L_0=L$
, in which case we clearly have
$L_0=L$
, in which case we clearly have
![]() $\omega _L \in A_{\infty }(\partial \Omega , \omega _{L_0})$
(indeed,
$\omega _L \in A_{\infty }(\partial \Omega , \omega _{L_0})$
(indeed,
![]() $\omega _L \in RH_p(\partial \Omega , \omega _{L_0})$
for any
$\omega _L \in RH_p(\partial \Omega , \omega _{L_0})$
for any
![]() $1<p<\infty $
), then we obtain the following estimates for the null solutions of L (note that (ii) and (iii) coincide with [Reference Akman, Hofmann, Martell and Toro1, Theorems 1.3 and 1.5], respectively):
$1<p<\infty $
), then we obtain the following estimates for the null solutions of L (note that (ii) and (iii) coincide with [Reference Akman, Hofmann, Martell and Toro1, Theorems 1.3 and 1.5], respectively):
Corollary 1.3. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. Bearing in mind the notions introduced in Definition 3.3, the following statements hold:
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. Bearing in mind the notions introduced in Definition 3.3, the following statements hold:
-
(i) L is
 $L^{p}(\omega _{L})$
-solvable and also
$L^{p}(\omega _{L})$
-solvable and also
 $L^{p}(\omega _{L})$
-solvable for characteristic functions, for all
$L^{p}(\omega _{L})$
-solvable for characteristic functions, for all
 $p\in (1,\infty )$
.
$p\in (1,\infty )$
. -
(ii) L satisfies
 $\mathrm {CME}(\omega _{L})$
.
$\mathrm {CME}(\omega _{L})$
. -
(iii) L satisfies
 $\mathcal {S}<\mathcal {N}$
in
$\mathcal {S}<\mathcal {N}$
in
 $L^q(\omega _{L})$
for all
$L^q(\omega _{L})$
for all
 $q\in (0,\infty )$
.
$q\in (0,\infty )$
. -
(iv) L is
 $\mathrm {BMO}(\omega _{L})$
-solvable and also
$\mathrm {BMO}(\omega _{L})$
-solvable and also
 $\mathrm {BMO}(\omega _{L})$
-solvable for characteristic functions.
$\mathrm {BMO}(\omega _{L})$
-solvable for characteristic functions. -
(v) L is
 $\mathrm {BMO}(\omega _{L})$
-solvable and also
$\mathrm {BMO}(\omega _{L})$
-solvable and also
 $\mathrm {BMO}(\omega _{L})$
-solvable for characteristic functions, in the generalized sense.
$\mathrm {BMO}(\omega _{L})$
-solvable for characteristic functions, in the generalized sense.
Remark 1.4. We would like to emphasize that in
![]() $\mathrm {(i)}$
the
$\mathrm {(i)}$
the
![]() $L^{p}(\omega _{L_0})$
-solvability holds for all
$L^{p}(\omega _{L_0})$
-solvability holds for all
![]() $\alpha $
and N, the same occurs with
$\alpha $
and N, the same occurs with
![]() $\mathrm {(iii)}$
which holds for all
$\mathrm {(iii)}$
which holds for all
![]() $\alpha $
; see Definition 3.3.
$\alpha $
; see Definition 3.3.
Our second application is a direct consequence of [Reference Akman, Hofmann, Martell and Toro2, Theorems 1.5, 1.10] and Theorem 1.1:
Corollary 1.5. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. Define
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. Define
and
 $$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \varrho(A, A_0) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} := \sup_{B} \sup_{B'} \frac{1}{\omega^{X_{\Delta}}_{L_0}(\Delta')} \iint_{B' \cap \Omega} \varrho(A, A_0)(X)^2 \frac{G_{L_0}(X_{\Delta}, X)}{\delta(X)^2} dX, \end{align*} $$
$$ \begin{align*} {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert \varrho(A, A_0) \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert} := \sup_{B} \sup_{B'} \frac{1}{\omega^{X_{\Delta}}_{L_0}(\Delta')} \iint_{B' \cap \Omega} \varrho(A, A_0)(X)^2 \frac{G_{L_0}(X_{\Delta}, X)}{\delta(X)^2} dX, \end{align*} $$
where
![]() $\Delta =B \cap \Omega $
,
$\Delta =B \cap \Omega $
,
![]() $\Delta '=B' \cap \Omega $
, and the sup is taken, respectively, over all balls
$\Delta '=B' \cap \Omega $
, and the sup is taken, respectively, over all balls
![]() $B=B(x, r)$
with
$B=B(x, r)$
with
![]() $x \in \partial \Omega $
and
$x \in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x', r)$
with
$B'=B(x', r)$
with
![]() $x' \in 2 \Delta $
and
$x' \in 2 \Delta $
and
![]() $0<r'<c_0r/4$
, and
$0<r'<c_0r/4$
, and
![]() $c_0$
is the corkscrew constant. We also define
$c_0$
is the corkscrew constant. We also define
 $$ \begin{align*} \mathscr{A}_{\alpha}(\varrho(A, A_0))(x) := \left(\iint_{\Gamma^{\alpha}(x)} \frac{\varrho(A, A_0)(X)^2}{\delta(X)^{n+1}} dX \right)^{\frac12}, \qquad x \in \partial \Omega, \end{align*} $$
$$ \begin{align*} \mathscr{A}_{\alpha}(\varrho(A, A_0))(x) := \left(\iint_{\Gamma^{\alpha}(x)} \frac{\varrho(A, A_0)(X)^2}{\delta(X)^{n+1}} dX \right)^{\frac12}, \qquad x \in \partial \Omega, \end{align*} $$
where
![]() $\Gamma ^{\alpha }(x) := \{X \in \Omega : |X-x|\leq (1+\alpha ) \delta (X) \}$
.
$\Gamma ^{\alpha }(x) := \{X \in \Omega : |X-x|\leq (1+\alpha ) \delta (X) \}$
.
If
then all the properties
![]() $\mathrm {(a)}$
–
$\mathrm {(a)}$
–
![]() $\mathrm {(f)'}$
in Theorem 1.1 are satisfied.
$\mathrm {(f)'}$
in Theorem 1.1 are satisfied.
Moreover, given
![]() $1<p<\infty $
, there exists
$1<p<\infty $
, there exists
![]() $\varepsilon _p>0$
(depending only on dimension, the 1-sided NTA and CDC constants, the ellipticity constants of
$\varepsilon _p>0$
(depending only on dimension, the 1-sided NTA and CDC constants, the ellipticity constants of
![]() $L_0$
and L and p) such that if
$L_0$
and L and p) such that if
then
![]() $\omega _L\in RH_{p'}(\partial \Omega ,\omega _{L_0})$
, and hence, L is
$\omega _L\in RH_{p'}(\partial \Omega ,\omega _{L_0})$
, and hence, L is
![]() $L^{q}(\omega _{L_0})$
-solvable for
$L^{q}(\omega _{L_0})$
-solvable for
![]() $q\ge p$
.
$q\ge p$
.
Our next goal is to state a qualitative version of Theorem 1.1 in line with [Reference Cao, Martell and Olivo7]. The
![]() $A_{\infty }$
condition will turn into absolute continuity. The qualitative analog of
$A_{\infty }$
condition will turn into absolute continuity. The qualitative analog of
![]() $\mathcal {S}<\mathcal {N}$
is going to be that the conical square function satisfies
$\mathcal {S}<\mathcal {N}$
is going to be that the conical square function satisfies
![]() $L^q$
estimates in some pieces of the boundary. On the other hand, as seen from the proof of Theorem 1.1 (see Lemma 4.3 and equation (4.30)), the CME condition, more precisely, the left-hand side term of equation (3.8) is connected with the local
$L^q$
estimates in some pieces of the boundary. On the other hand, as seen from the proof of Theorem 1.1 (see Lemma 4.3 and equation (4.30)), the CME condition, more precisely, the left-hand side term of equation (3.8) is connected with the local
![]() $L^2$
-norm of the conical square function. Thus, the
$L^2$
-norm of the conical square function. Thus, the
![]() $L^2$
-estimates for the conical square function are the qualitative version of CME. In turn, all these are equivalent to the simple fact that the truncated conical square function is finite almost everywhere with respect to the elliptic measure
$L^2$
-estimates for the conical square function are the qualitative version of CME. In turn, all these are equivalent to the simple fact that the truncated conical square function is finite almost everywhere with respect to the elliptic measure
![]() $\omega _{L_0}$
.
$\omega _{L_0}$
.
Theorem 1.6. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
![]() $\alpha _0>0$
(depending only on the
$\alpha _0>0$
(depending only on the
![]() $1$
-sided NTA and CDC constants) such that for each fixed
$1$
-sided NTA and CDC constants) such that for each fixed
![]() $\alpha \geq \alpha _0$
and for every real (not necessarily symmetric) elliptic operators
$\alpha \geq \alpha _0$
and for every real (not necessarily symmetric) elliptic operators
![]() $L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
$L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
the following statements are equivalent:
$Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
the following statements are equivalent:
-
(a)
 $\omega _{L_0} \ll \omega _L$
on
$\omega _{L_0} \ll \omega _L$
on
 $\partial \Omega $
.
$\partial \Omega $
. -
(b)
 $\partial \Omega =\bigcup _{N \geq 0} F_N$
, where
$\partial \Omega =\bigcup _{N \geq 0} F_N$
, where
 $\omega _{L_0}(F_0)=0$
, for each
$\omega _{L_0}(F_0)=0$
, for each
 $N \geq 1$
,
$N \geq 1$
,
 $F_N=\partial \Omega \cap \partial \Omega _N$
for some bounded
$F_N=\partial \Omega \cap \partial \Omega _N$
for some bounded
 $1$
-sided NTA domain
$1$
-sided NTA domain
 $\Omega _N \subset \Omega $
satisfying the CDC, and
$\Omega _N \subset \Omega $
satisfying the CDC, and
 $\mathcal {S}^{\alpha }_r u \in L^q(F_N, \omega _{L_0})$
for every weak solution
$\mathcal {S}^{\alpha }_r u \in L^q(F_N, \omega _{L_0})$
for every weak solution
 $u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
of
$u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
of
 $Lu=0$
in
$Lu=0$
in
 $\Omega $
, for all (or for some)
$\Omega $
, for all (or for some)
 $r>0$
, and for all (or for some)
$r>0$
, and for all (or for some)
 $q\in (0,\infty )$
.
$q\in (0,\infty )$
. -
(b)′
 $\partial \Omega =\bigcup _{N \geq 0} F_N$
, where
$\partial \Omega =\bigcup _{N \geq 0} F_N$
, where
 $\omega _{L_0}(F_0)=0$
, for each
$\omega _{L_0}(F_0)=0$
, for each
 $N \geq 1$
,
$N \geq 1$
,
 $F_N=\partial \Omega \cap \partial \Omega _N$
for some bounded
$F_N=\partial \Omega \cap \partial \Omega _N$
for some bounded
 $1$
-sided NTA domain
$1$
-sided NTA domain
 $\Omega _N \subset \Omega $
satisfying the CDC, and
$\Omega _N \subset \Omega $
satisfying the CDC, and
 $\mathcal {S}^{\alpha }_r u \in L^q(F_N, \omega _{L_0})$
, where
$\mathcal {S}^{\alpha }_r u \in L^q(F_N, \omega _{L_0})$
, where
 $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
 $X\in \Omega $
, for any arbitrary Borel set
$X\in \Omega $
, for any arbitrary Borel set
 $S\subset \partial \Omega $
, for all (or for some)
$S\subset \partial \Omega $
, for all (or for some)
 $r>0$
and for all (or for some)
$r>0$
and for all (or for some)
 $q\in (0,\infty )$
.
$q\in (0,\infty )$
. -
(c)
 $\mathcal {S}^{\alpha }_r u(x)<\infty $
for
$\mathcal {S}^{\alpha }_r u(x)<\infty $
for
 $\omega _{L_0}$
-a.e.
$\omega _{L_0}$
-a.e.
 $x \in \partial \Omega $
, for every weak solution
$x \in \partial \Omega $
, for every weak solution
 $u \in W_{\mathrm {loc}}^{1,2}(\Omega )\cap L^{\infty }(\Omega )$
of
$u \in W_{\mathrm {loc}}^{1,2}(\Omega )\cap L^{\infty }(\Omega )$
of
 $Lu=0$
in
$Lu=0$
in
 $\Omega $
and for all (or for some)
$\Omega $
and for all (or for some)
 $r>0$
.
$r>0$
. -
(c)′
 $\mathcal {S}^{\alpha }_r u(x)<\infty $
for
$\mathcal {S}^{\alpha }_r u(x)<\infty $
for
 $\omega _{L_0}$
-a.e.
$\omega _{L_0}$
-a.e.
 $x \in \partial \Omega $
, where
$x \in \partial \Omega $
, where
 $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
 $X\in \Omega $
, for any arbitrary Borel set
$X\in \Omega $
, for any arbitrary Borel set
 $S\subset \partial \Omega $
and for all (or for some)
$S\subset \partial \Omega $
and for all (or for some)
 $r>0$
.
$r>0$
. -
(d) For every weak solution
 $u \in W_{\mathrm {loc}}^{1,2}(\Omega )\cap L^{\infty }(\Omega )$
of
$u \in W_{\mathrm {loc}}^{1,2}(\Omega )\cap L^{\infty }(\Omega )$
of
 $Lu=0$
in
$Lu=0$
in
 $\Omega $
and for
$\Omega $
and for
 $\omega _{L_0}$
-a.e.
$\omega _{L_0}$
-a.e.
 $x \in \partial \Omega $
, there exists
$x \in \partial \Omega $
, there exists
 $r_x>0$
such that
$r_x>0$
such that
 $\mathcal {S}^{\alpha }_{r_x} u(x)<\infty $
.
$\mathcal {S}^{\alpha }_{r_x} u(x)<\infty $
. -
(d)′ For every Borel set
 $S\subset \partial \Omega $
and for
$S\subset \partial \Omega $
and for
 $\omega _{L_0}$
-a.e.
$\omega _{L_0}$
-a.e.
 $x \in \partial \Omega $
, there exists
$x \in \partial \Omega $
, there exists
 $r_x>0$
such that
$r_x>0$
such that
 $\mathcal {S}^{\alpha }_{r_x} u(x)<\infty $
, where
$\mathcal {S}^{\alpha }_{r_x} u(x)<\infty $
, where
 $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
 $X\in \Omega $
.
$X\in \Omega $
.
Our first application of the previous result is a qualitative version of [Reference Akman, Hofmann, Martell and Toro2, Theorem 1.10]:
Theorem 1.7. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
![]() $\alpha _0>0$
(depending only on the
$\alpha _0>0$
(depending only on the
![]() $1$
-sided NTA and CDC constants) such that, if the real (not necessarily symmetric) elliptic operators
$1$
-sided NTA and CDC constants) such that, if the real (not necessarily symmetric) elliptic operators
![]() $L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
$L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
![]() $L u = -\mathop {\operatorname {div}}\nolimits (A \nabla u)$
satisfy for some
$L u = -\mathop {\operatorname {div}}\nolimits (A \nabla u)$
satisfy for some
![]() $\alpha \ge \alpha _0$
and for some
$\alpha \ge \alpha _0$
and for some
![]() $r>0$
$r>0$
 $$ \begin{align} \iint_{\Gamma^{\alpha}_{r}(x)} \frac{\varrho(A, A_0)(X)^2}{\delta(X)^{n+1}} dX < \infty, \qquad \text{for } \omega_{L_0}\text{-a.e.}~ x \in \partial \Omega, \end{align} $$
$$ \begin{align} \iint_{\Gamma^{\alpha}_{r}(x)} \frac{\varrho(A, A_0)(X)^2}{\delta(X)^{n+1}} dX < \infty, \qquad \text{for } \omega_{L_0}\text{-a.e.}~ x \in \partial \Omega, \end{align} $$
where
![]() $\varrho (A, A_0)$
is as in equation (1.2), then
$\varrho (A, A_0)$
is as in equation (1.2), then
![]() $\omega _{L_0} \ll \omega _L$
.
$\omega _{L_0} \ll \omega _L$
.
To present another application of Theorem 1.6, we introduce some notation. For any real (not necessarily symmetric) elliptic operator
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
, we let
$Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
, we let
![]() $L^{\top }$
denote the transpose of L, and let
$L^{\top }$
denote the transpose of L, and let
![]() $L^{\mathrm {sym}}=\frac {L+L^{\top }}{2}$
be the symmetric part of L. These are, respectively, the divergence form elliptic operators with associated matrices
$L^{\mathrm {sym}}=\frac {L+L^{\top }}{2}$
be the symmetric part of L. These are, respectively, the divergence form elliptic operators with associated matrices
![]() $A^{\top }$
(the transpose of A) and
$A^{\top }$
(the transpose of A) and
![]() $A^{\mathrm {sym}}=\frac {A+A^{\top }}{2}$
.
$A^{\mathrm {sym}}=\frac {A+A^{\top }}{2}$
.
Theorem 1.8. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
![]() $\alpha _0>0$
(depending only on the
$\alpha _0>0$
(depending only on the
![]() $1$
-sided NTA and CDC constants) such that, if
$1$
-sided NTA and CDC constants) such that, if
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
is a real (not necessarily symmetric) elliptic operator and we assume that
$Lu=-\mathop {\operatorname {div}}\nolimits (A \nabla u)$
is a real (not necessarily symmetric) elliptic operator and we assume that
![]() $(A-A^{\top }) \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
and that for some
$(A-A^{\top }) \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
and that for some
![]() $\alpha \ge \alpha _0$
and for some
$\alpha \ge \alpha _0$
and for some
![]() $r>0$
one has
$r>0$
one has
where
 $$ \begin{align*} \mathop{\operatorname{div}}\nolimits_C(A-A^{\top})(X):=\bigg(\sum_{i=1}^{n+1} \partial_i(a_{i,j}-a_{j,i})(X) \bigg)_{1 \leq j \leq n+1}, \qquad X \in \Omega, \end{align*} $$
$$ \begin{align*} \mathop{\operatorname{div}}\nolimits_C(A-A^{\top})(X):=\bigg(\sum_{i=1}^{n+1} \partial_i(a_{i,j}-a_{j,i})(X) \bigg)_{1 \leq j \leq n+1}, \qquad X \in \Omega, \end{align*} $$
then
![]() $\omega _L \ll \omega _{L^{\top }}$
and
$\omega _L \ll \omega _{L^{\top }}$
and
![]() $\omega _L \ll \omega _{L^{\mathrm {sym}}}$
.
$\omega _L \ll \omega _{L^{\mathrm {sym}}}$
.
Moreover, if
then
![]() $\omega _L \ll \omega _{L^{\top }} \ll \omega _L \ll \omega _{L^{\mathrm {sym}}}$
.
$\omega _L \ll \omega _{L^{\top }} \ll \omega _L \ll \omega _{L^{\mathrm {sym}}}$
.
The structure of this paper is as follows. Section 2 contains some preliminaries, definitions and tools that will be used throughout. Also, for convenience of the reader, we gather in Section 3 several facts concerning elliptic measures and Green functions which can be found in the upcoming [Reference Hofmann, Martell and Toro35]. The proof of Theorem 1.1 is in Section 4. Section 5 is devoted to proving Theorem 1.6. In Section 6, we will present the proofs of Theorems 1.7 and 1.8 which follow easily from a more general perturbation result which is interesting in its own right.
We note that some interesting related work has been carried out while this manuscript was in preparation due to Feneuil and Poggi [Reference Feneuil and Poggi24]. This work can be particularized to our setting and contains some results which overlap with ours. First, [Reference Feneuil and Poggi24, Theorem 1.22] corresponds to
![]() $\mathrm {(c)'}\ \Longrightarrow \ \mathrm {(a)}$
in Theorem 1.1. It should be mentioned that both arguments use the ideas originated in [Reference Kenig, Kirchheim, Pipher and Toro42] (see also [Reference Kenig, Koch, Pipher and Toro43]) which present some problems when extended to the 1-sided NTA setting. Namely, elliptic measure may not always be a probability, and also it could happen that for a uniformly bounded number of generations the dyadic children of a given cube may agree with that cube. These two issues have been carefully addressed in [Reference Cavero, Hofmann, Martell and Toro9, Lemma 3.10] (see Lemma 4.2 with
$\mathrm {(c)'}\ \Longrightarrow \ \mathrm {(a)}$
in Theorem 1.1. It should be mentioned that both arguments use the ideas originated in [Reference Kenig, Kirchheim, Pipher and Toro42] (see also [Reference Kenig, Koch, Pipher and Toro43]) which present some problems when extended to the 1-sided NTA setting. Namely, elliptic measure may not always be a probability, and also it could happen that for a uniformly bounded number of generations the dyadic children of a given cube may agree with that cube. These two issues have been carefully addressed in [Reference Cavero, Hofmann, Martell and Toro9, Lemma 3.10] (see Lemma 4.2 with
![]() $\beta>0$
) and although such a result is stated in the setting of 1-sided CAD it is straightforward to see that it readily adapts to our case. Our proof of
$\beta>0$
) and although such a result is stated in the setting of 1-sided CAD it is straightforward to see that it readily adapts to our case. Our proof of
![]() $\mathrm {(c)'}\ \Longrightarrow \ \mathrm {(a)}$
in Theorem 1.1 follows easily from that lemma. Second, [Reference Feneuil and Poggi24, Theorem 1.27] (see also [Reference Feneuil and Poggi24, Corollary 1.33]) shows
$\mathrm {(c)'}\ \Longrightarrow \ \mathrm {(a)}$
in Theorem 1.1 follows easily from that lemma. Second, [Reference Feneuil and Poggi24, Theorem 1.27] (see also [Reference Feneuil and Poggi24, Corollary 1.33]) shows
![]() $\mathrm {(d)}$
in Theorem 1.1 with
$\mathrm {(d)}$
in Theorem 1.1 with
![]() $q=2$
for a class of perturbations of L. In our setting, we are showing that
$q=2$
for a class of perturbations of L. In our setting, we are showing that
![]() $\mathrm {(d)}$
follows if
$\mathrm {(d)}$
follows if
![]() $\mathrm {(a)}$
holds for any given operator L (whether or not it is a generalized perturbation of
$\mathrm {(a)}$
holds for any given operator L (whether or not it is a generalized perturbation of
![]() $L_0$
).
$L_0$
).
2 Preliminaries
2.1 Notation and conventions
-
○ We use the letters
 $c,C$
to denote harmless positive constants, not necessarily the same at each occurrence, which depend only on dimension and the constants appearing in the hypotheses of the theorems (which we refer to as the ‘allowable parameters’). We shall also sometimes write
$c,C$
to denote harmless positive constants, not necessarily the same at each occurrence, which depend only on dimension and the constants appearing in the hypotheses of the theorems (which we refer to as the ‘allowable parameters’). We shall also sometimes write
 $a\lesssim b$
and
$a\lesssim b$
and
 $a \approx b$
to mean, respectively, that
$a \approx b$
to mean, respectively, that
 $a \leq C b$
and
$a \leq C b$
and
 $0< c \leq a/b\leq C$
, where the constants c and C are as above unless explicitly noted to the contrary. Unless otherwise specified, uppercase constants are greater than
$0< c \leq a/b\leq C$
, where the constants c and C are as above unless explicitly noted to the contrary. Unless otherwise specified, uppercase constants are greater than
 $1$
, and lowercase constants are smaller than
$1$
, and lowercase constants are smaller than
 $1$
. In some occasions, it is important to keep track of the dependence on a given parameter
$1$
. In some occasions, it is important to keep track of the dependence on a given parameter
 $\gamma $
; in that case, we write
$\gamma $
; in that case, we write
 $a\lesssim _{\gamma } b$
or
$a\lesssim _{\gamma } b$
or
 $a\approx _{\gamma } b$
to emphasize that the implicit constants in the inequalities depend on
$a\approx _{\gamma } b$
to emphasize that the implicit constants in the inequalities depend on
 $\gamma $
.
$\gamma $
. -
○ Our ambient space is
 $\mathbb {R}^{n+1}$
,
$\mathbb {R}^{n+1}$
,
 $n\ge 2$
.
$n\ge 2$
. -
○ Given
 $E\subset \mathbb {R}^{n+1}$
, we write
$E\subset \mathbb {R}^{n+1}$
, we write
 $\operatorname {\mathrm {diam}}(E)=\sup _{x,y\in E}|x-y|$
to denote its diameter.
$\operatorname {\mathrm {diam}}(E)=\sup _{x,y\in E}|x-y|$
to denote its diameter. -
○ Given an open set
 $\Omega \subset \mathbb {R}^{n+1}$
, we shall use lowercase letters
$\Omega \subset \mathbb {R}^{n+1}$
, we shall use lowercase letters
 $x,y,z$
, etc., to denote points on
$x,y,z$
, etc., to denote points on
 $\partial \Omega $
, and capital letters
$\partial \Omega $
, and capital letters
 $X,Y,Z$
, etc., to denote generic points in
$X,Y,Z$
, etc., to denote generic points in
 $\mathbb {R}^{n+1}$
(especially those in
$\mathbb {R}^{n+1}$
(especially those in
 $\mathbb {R}^{n+1}\setminus \partial \Omega $
).
$\mathbb {R}^{n+1}\setminus \partial \Omega $
). -
○ The open
 $(n+1)$
-dimensional Euclidean ball of radius r will be denoted
$(n+1)$
-dimensional Euclidean ball of radius r will be denoted
 $B(x,r)$
when the center x lies on
$B(x,r)$
when the center x lies on
 $\partial \Omega $
or
$\partial \Omega $
or
 $B(X,r)$
when the center
$B(X,r)$
when the center
 $X \in \mathbb {R}^{n+1}\setminus \partial \Omega $
. A surface ball is denoted
$X \in \mathbb {R}^{n+1}\setminus \partial \Omega $
. A surface ball is denoted
 $\Delta (x,r):= B(x,r) \cap \partial \Omega $
, and unless otherwise specified, it is implicitly assumed that
$\Delta (x,r):= B(x,r) \cap \partial \Omega $
, and unless otherwise specified, it is implicitly assumed that
 $x\in \partial \Omega $
.
$x\in \partial \Omega $
. -
○ If
 $\partial \Omega $
is bounded, it is always understood (unless otherwise specified) that all surface balls have radii controlled by the diameter of
$\partial \Omega $
is bounded, it is always understood (unless otherwise specified) that all surface balls have radii controlled by the diameter of
 $\partial \Omega $
, that is, if
$\partial \Omega $
, that is, if
 $\Delta =\Delta (x,r)$
, then
$\Delta =\Delta (x,r)$
, then
 $r\lesssim \operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that in this way
$r\lesssim \operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that in this way
 $\Delta =\partial \Omega $
if
$\Delta =\partial \Omega $
if
 $\operatorname {\mathrm {diam}}(\partial \Omega )<r\lesssim \operatorname {\mathrm {diam}}(\partial \Omega )$
.
$\operatorname {\mathrm {diam}}(\partial \Omega )<r\lesssim \operatorname {\mathrm {diam}}(\partial \Omega )$
. -
○ For
 $X \in \mathbb {R}^{n+1}$
, we set
$X \in \mathbb {R}^{n+1}$
, we set
 $\delta (X):= \operatorname {dist}(X,\partial \Omega )$
.
$\delta (X):= \operatorname {dist}(X,\partial \Omega )$
. -
○ We let
 $\mathcal {H}^n$
denote the n-dimensional Hausdorff measure.
$\mathcal {H}^n$
denote the n-dimensional Hausdorff measure. -
○ For a Borel set
 $A\subset \mathbb {R}^{n+1}$
, we let
$A\subset \mathbb {R}^{n+1}$
, we let
 $\mathbf {1}_A$
denote the usual indicator function of A, i.e.,
$\mathbf {1}_A$
denote the usual indicator function of A, i.e.,
 $\mathbf {1}_A(X) = 1$
if
$\mathbf {1}_A(X) = 1$
if
 $X\in A$
, and
$X\in A$
, and
 $\mathbf {1}_A(X)= 0$
if
$\mathbf {1}_A(X)= 0$
if
 $X\notin A$
.
$X\notin A$
. -
○ We shall use the letter I (and sometimes J) to denote a closed
 $(n+1)$
-dimensional Euclidean cube with sides parallel to the coordinate axes, and we let
$(n+1)$
-dimensional Euclidean cube with sides parallel to the coordinate axes, and we let
 $\ell (I)$
denote the side length of I. We use Q to denote dyadic ‘cubes’ on E or
$\ell (I)$
denote the side length of I. We use Q to denote dyadic ‘cubes’ on E or
 $\partial \Omega $
. The latter exist as a consequence of Lemma 2.8 below.
$\partial \Omega $
. The latter exist as a consequence of Lemma 2.8 below.
2.2 Some definitions
Definition 2.1 (Corkscrew condition)
Following [Reference Jerison and Kenig41], we say that a domain
![]() $\Omega \subset \mathbb {R}^{n+1}$
satisfies the Corkscrew condition if for some uniform constant
$\Omega \subset \mathbb {R}^{n+1}$
satisfies the Corkscrew condition if for some uniform constant
![]() $0<c_0<1$
, and for every
$0<c_0<1$
, and for every
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, if we write
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, if we write
![]() $\Delta :=\Delta (x,r)$
, there is a ball
$\Delta :=\Delta (x,r)$
, there is a ball
![]() $B(X_{\Delta },c_0r)\subset B(x,r)\cap \Omega $
. The point
$B(X_{\Delta },c_0r)\subset B(x,r)\cap \Omega $
. The point
![]() $X_{\Delta }\subset \Omega $
is called a Corkscrew point relative to
$X_{\Delta }\subset \Omega $
is called a Corkscrew point relative to
![]() $\Delta $
(or, relative to B). We note that we may allow
$\Delta $
(or, relative to B). We note that we may allow
![]() $r<C\operatorname {\mathrm {diam}}(\partial \Omega )$
for any fixed C simply by adjusting the constant
$r<C\operatorname {\mathrm {diam}}(\partial \Omega )$
for any fixed C simply by adjusting the constant
![]() $c_0$
.
$c_0$
.
Definition 2.2 (Harnack chain condition)
Again following [Reference Jerison and Kenig41], we say that
![]() $\Omega $
satisfies the Harnack chain condition if there are uniform constants
$\Omega $
satisfies the Harnack chain condition if there are uniform constants
![]() $C_1,C_2>1$
such that for every pair of points
$C_1,C_2>1$
such that for every pair of points
![]() $X, X'\in \Omega $
there is a chain of balls
$X, X'\in \Omega $
there is a chain of balls
![]() $B_1, B_2, \dots , B_N\subset \Omega $
with
$B_1, B_2, \dots , B_N\subset \Omega $
with
![]() $N \leq C_1(2+\log _2^+ \Pi )$
, where
$N \leq C_1(2+\log _2^+ \Pi )$
, where
such that
![]() $X\in B_1$
,
$X\in B_1$
,
![]() $X'\in B_N$
,
$X'\in B_N$
,
![]() $B_k\cap B_{k+1}\neq \emptyset $
and for every
$B_k\cap B_{k+1}\neq \emptyset $
and for every
![]() $1\le k\le N$
$1\le k\le N$
The chain of balls is called a Harnack chain.
We note that in the context of the previous definition if
![]() $\Pi \le 1$
we can trivially form the Harnack chain
$\Pi \le 1$
we can trivially form the Harnack chain
![]() $B_1=B(X,3\delta (X)/5)$
and
$B_1=B(X,3\delta (X)/5)$
and
![]() $B_2=B(X', 3\delta (X')/5)$
, where equation (2.2) holds with
$B_2=B(X', 3\delta (X')/5)$
, where equation (2.2) holds with
![]() $C_2=3$
. Hence, the Harnack chain condition is nontrivial only when
$C_2=3$
. Hence, the Harnack chain condition is nontrivial only when
![]() $\Pi> 1$
.
$\Pi> 1$
.
Definition 2.3 (1-sided NTA and NTA)
We say that a domain
![]() $\Omega $
is a 1-sided NTA domain (1-sided NTA) if it satisfies both the corkscrew and Harnack chain conditions. Furthermore, we say that
$\Omega $
is a 1-sided NTA domain (1-sided NTA) if it satisfies both the corkscrew and Harnack chain conditions. Furthermore, we say that
![]() $\Omega $
is a NTA domain if it is a 1-sided NTA domain and if, in addition,
$\Omega $
is a NTA domain if it is a 1-sided NTA domain and if, in addition,
![]() $\Omega _{\mathrm {ext}}:= \mathbb {R}^{n+1}\setminus \overline {\Omega }$
also satisfies the corkscrew condition.
$\Omega _{\mathrm {ext}}:= \mathbb {R}^{n+1}\setminus \overline {\Omega }$
also satisfies the corkscrew condition.
Remark 2.4. In the literature, 1-sided NTA domains are also called uniform domains. We remark that the 1-sided NTA condition is a quantitative form of openness and path connectedness.
Definition 2.5 (Ahlfors regular)
We say that a closed set
![]() $E \subset \mathbb {R}^{n+1}$
is n-dimensional Ahlfors regular (AR for short) if there is some uniform constant
$E \subset \mathbb {R}^{n+1}$
is n-dimensional Ahlfors regular (AR for short) if there is some uniform constant
![]() $C_1>1$
such that
$C_1>1$
such that
Definition 2.6 (1-sided CAD and CAD)
A 1-sided chord-arc domain (1-sided CAD) is a 1-sided NTA domain with AR boundary. A chord-arc domain (CAD) is an NTA domain with AR boundary.
We next recall the definition of the capacity of a set. Given an open set
![]() $D\subset \mathbb {R}^{n+1}$
(where we recall that we always assume that
$D\subset \mathbb {R}^{n+1}$
(where we recall that we always assume that
![]() $n\ge 2$
) and a compact set
$n\ge 2$
) and a compact set
![]() $K\subset D$
, we define the capacity of K relative to D as
$K\subset D$
, we define the capacity of K relative to D as
 $$\begin{align*}\mathop{\operatorname{Cap}_2}\nolimits(K, D)=\inf\left\{\iint_{D} |\nabla v(X)|^2 dX:\, \, v\in \mathscr{C}^{\infty}_{c}(D),\, v(x)\geq 1 \mbox{ in }K\right\}. \end{align*}$$
$$\begin{align*}\mathop{\operatorname{Cap}_2}\nolimits(K, D)=\inf\left\{\iint_{D} |\nabla v(X)|^2 dX:\, \, v\in \mathscr{C}^{\infty}_{c}(D),\, v(x)\geq 1 \mbox{ in }K\right\}. \end{align*}$$
Definition 2.7 (CDC)
An open set
![]() $\Omega $
is said to satisfy the CDC if there exists a uniform constant
$\Omega $
is said to satisfy the CDC if there exists a uniform constant
![]() $c_1>0$
such that
$c_1>0$
such that
 $$ \begin{align} \frac{\mathop{\operatorname{Cap}_2}\nolimits(\overline{B(x,r)}\setminus \Omega, B(x,2r))}{\mathop{\operatorname{Cap}_2}\nolimits(\overline{B(x,r)}, B(x,2r))} \geq c_1 \end{align} $$
$$ \begin{align} \frac{\mathop{\operatorname{Cap}_2}\nolimits(\overline{B(x,r)}\setminus \Omega, B(x,2r))}{\mathop{\operatorname{Cap}_2}\nolimits(\overline{B(x,r)}, B(x,2r))} \geq c_1 \end{align} $$
for all
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
The CDC is also known as the uniform 2-fatness as studied by Lewis in [Reference Lewis45]. Using [Reference Heinonen, Kilpeläinen and Martio28, Example 2.12], one has that
and hence, the CDC is a quantitative version of the Wiener regularity, in particular every
![]() $x\in \partial \Omega $
is Wiener regular. It is easy to see that the exterior corkscrew condition implies CDC. Also, it was proved in [Reference Zhao51, Section 3] and [Reference Hofmann, Le, Martell and Nyström30, Lemma 3.27] that a set with Ahlfors regular boundary satisfies the CDC with constant
$x\in \partial \Omega $
is Wiener regular. It is easy to see that the exterior corkscrew condition implies CDC. Also, it was proved in [Reference Zhao51, Section 3] and [Reference Hofmann, Le, Martell and Nyström30, Lemma 3.27] that a set with Ahlfors regular boundary satisfies the CDC with constant
![]() $c_1$
depending only on n and the Ahlfors regular constant.
$c_1$
depending only on n and the Ahlfors regular constant.
2.3 Dyadic grids and sawtooths
In this section, we introduce a dyadic grid from [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.13] along the lines of that obtained in [Reference Christ10] but using the dyadic structure from [Reference Hytönen and Kairema39, Reference Hytönen and Kairema40, Reference Hofmann, Mitrea, Mitrea and Morris37]:
Lemma 2.8 (Existence and properties of the ‘dyadic grid’, [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.13])
Let
![]() $E\subset \mathbb {R}^{n+1}$
be a closed set. Then there exists a constant
$E\subset \mathbb {R}^{n+1}$
be a closed set. Then there exists a constant
![]() $C\ge 1$
depending just on n such that for each
$C\ge 1$
depending just on n such that for each
![]() $k\in \mathbb {Z}$
there is a collection of Borel sets (called ‘cubes’)
$k\in \mathbb {Z}$
there is a collection of Borel sets (called ‘cubes’)
where
![]() $\mathfrak {J}_k$
denotes some (possibly finite) index set depending on k satisfying:
$\mathfrak {J}_k$
denotes some (possibly finite) index set depending on k satisfying:
-
(a)
 $E=\bigcup _{j\in \mathfrak {J}_k}Q_j^k$
for each
$E=\bigcup _{j\in \mathfrak {J}_k}Q_j^k$
for each
 $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
. -
(b) If
 $m\le k$
, then either
$m\le k$
, then either
 $Q_j^k \subset Q_i^m$
or
$Q_j^k \subset Q_i^m$
or
 $Q_i^m\cap Q_j^k= \emptyset $
.
$Q_i^m\cap Q_j^k= \emptyset $
. -
(c) For each
 $k\in \mathbb {Z}$
,
$k\in \mathbb {Z}$
,
 $j\in \mathfrak {J}_k$
and
$j\in \mathfrak {J}_k$
and
 $m<k$
, there is a unique
$m<k$
, there is a unique
 $i\in \mathfrak {J}_m $
such that
$i\in \mathfrak {J}_m $
such that
 $Q_j^k\subset Q_i^m$
.
$Q_j^k\subset Q_i^m$
. -
(d) For each
 $k\in \mathbb {Z}$
,
$k\in \mathbb {Z}$
,
 $j\in \mathfrak {J}_k$
there is
$j\in \mathfrak {J}_k$
there is
 $x_j^k\in E$
such that
$x_j^k\in E$
such that  $$\begin{align*}B(x_j^k, C^{-1}2^{-k})\cap E\subset Q_j^k \subset B(x_j^k, C 2^{-k})\cap E. \end{align*}$$
$$\begin{align*}B(x_j^k, C^{-1}2^{-k})\cap E\subset Q_j^k \subset B(x_j^k, C 2^{-k})\cap E. \end{align*}$$
In what follows given
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in E$
, we will denote
$x\in E$
, we will denote
![]() $\Delta =\Delta (x,r)=B\cap E$
. A few remarks are in order concerning this lemma. Note that within the same generation (that is, within each
$\Delta =\Delta (x,r)=B\cap E$
. A few remarks are in order concerning this lemma. Note that within the same generation (that is, within each
![]() $\mathbb {D}_k$
) the cubes are pairwise disjoint (hence, there are no repetitions). On the other hand, we allow repetitions in the different generations, that is, we could have that
$\mathbb {D}_k$
) the cubes are pairwise disjoint (hence, there are no repetitions). On the other hand, we allow repetitions in the different generations, that is, we could have that
![]() $Q\in \mathbb {D}_k$
and
$Q\in \mathbb {D}_k$
and
![]() $Q'\in \mathbb {D}_{k-1}$
agree. Then, although Q and
$Q'\in \mathbb {D}_{k-1}$
agree. Then, although Q and
![]() $Q'$
are the same set, as cubes we understand that they are different. In short, it is then understood that
$Q'$
are the same set, as cubes we understand that they are different. In short, it is then understood that
![]() $\mathbb {D}$
is an indexed collection of sets, where repetitions of sets are allowed in the different generations but not within the same generation. With this in mind, we can give a proper definition of the ‘length’ of a cube (this concept has no geometric meaning in this context). For every
$\mathbb {D}$
is an indexed collection of sets, where repetitions of sets are allowed in the different generations but not within the same generation. With this in mind, we can give a proper definition of the ‘length’ of a cube (this concept has no geometric meaning in this context). For every
![]() $Q\in \mathbb {D}_k$
, we set
$Q\in \mathbb {D}_k$
, we set
![]() $\ell (Q)=2^{-k}$
, which is called the ‘length’ of Q. Note that the ‘length’ is well defined when considered on
$\ell (Q)=2^{-k}$
, which is called the ‘length’ of Q. Note that the ‘length’ is well defined when considered on
![]() $\mathbb {D}$
, but it is not well-defined on the family of sets induced by
$\mathbb {D}$
, but it is not well-defined on the family of sets induced by
![]() $\mathbb {D}$
. It is important to observe that the ‘length’ refers to the way the cubes are organized in the dyadic grid. It is clear from
$\mathbb {D}$
. It is important to observe that the ‘length’ refers to the way the cubes are organized in the dyadic grid. It is clear from
![]() $(d)$
that
$(d)$
that
![]() $\operatorname {\mathrm {diam}}(Q)\lesssim \ell (Q)$
. When
$\operatorname {\mathrm {diam}}(Q)\lesssim \ell (Q)$
. When
![]() $E=\partial \Omega $
, with
$E=\partial \Omega $
, with
![]() $\Omega $
being a 1-sided NTA domain satisfying the CDC condition, the converse holds, hence
$\Omega $
being a 1-sided NTA domain satisfying the CDC condition, the converse holds, hence
![]() $\operatorname {\mathrm {diam}}(Q)\approx \ell (Q)$
; see [Reference Akman, Hofmann, Martell and Toro1, Remark 2.56]. This means that the ‘length’ is related to the diameter of the cube.
$\operatorname {\mathrm {diam}}(Q)\approx \ell (Q)$
; see [Reference Akman, Hofmann, Martell and Toro1, Remark 2.56]. This means that the ‘length’ is related to the diameter of the cube.
Let us observe that if E is bounded and
![]() $k\in {\mathbb {Z}}$
is such that
$k\in {\mathbb {Z}}$
is such that
![]() $\operatorname {\mathrm {diam}}(E)<C^{-1}2^{-k}$
, then there cannot be two distinct cubes in
$\operatorname {\mathrm {diam}}(E)<C^{-1}2^{-k}$
, then there cannot be two distinct cubes in
![]() $\mathbb {D}_k$
. Thus,
$\mathbb {D}_k$
. Thus,
![]() $\mathbb {D}_k=\{Q^k\}$
with
$\mathbb {D}_k=\{Q^k\}$
with
![]() $Q^k=E$
. Therefore, we are going to ignore those
$Q^k=E$
. Therefore, we are going to ignore those
![]() $k\in \mathbb {Z}$
such that
$k\in \mathbb {Z}$
such that
![]() $2^{-k}\gtrsim \operatorname {\mathrm {diam}}(E)$
. Hence, we shall denote by
$2^{-k}\gtrsim \operatorname {\mathrm {diam}}(E)$
. Hence, we shall denote by
![]() $\mathbb {D}(E)$
the collection of all relevant
$\mathbb {D}(E)$
the collection of all relevant
![]() $Q_j^k$
, i.e.,
$Q_j^k$
, i.e.,
where, if
![]() $\operatorname {\mathrm {diam}}(E)$
is finite, the union runs over those
$\operatorname {\mathrm {diam}}(E)$
is finite, the union runs over those
![]() $k\in \mathbb {Z}$
such that
$k\in \mathbb {Z}$
such that
![]() $2^{-k}\lesssim \operatorname {\mathrm {diam}}(E)$
. We write
$2^{-k}\lesssim \operatorname {\mathrm {diam}}(E)$
. We write
![]() $\Xi =2C^2$
, with C being the constant in Lemma 2.8, which is purely dimensional. For
$\Xi =2C^2$
, with C being the constant in Lemma 2.8, which is purely dimensional. For
![]() $Q\in \mathbb {D}(E)$
, we will set
$Q\in \mathbb {D}(E)$
, we will set
![]() $k(Q)=k$
if
$k(Q)=k$
if
![]() $Q\in \mathbb {D}_k$
. Property
$Q\in \mathbb {D}_k$
. Property
![]() $(d)$
implies that for each cube
$(d)$
implies that for each cube
![]() $Q\in \mathbb {D}(E)$
, there exist
$Q\in \mathbb {D}(E)$
, there exist
![]() $x_Q\in E$
and
$x_Q\in E$
and
![]() $r_Q$
, with
$r_Q$
, with
![]() $\Xi ^{-1}\ell (Q)\leq r_Q\leq \ell (Q)$
(indeed
$\Xi ^{-1}\ell (Q)\leq r_Q\leq \ell (Q)$
(indeed
![]() $r_Q= (2C)^{-1}\ell (Q)$
), such that
$r_Q= (2C)^{-1}\ell (Q)$
), such that
We shall denote these balls and surface balls by
and we shall refer to the point
![]() $x_Q$
as the ‘center’ of Q.
$x_Q$
as the ‘center’ of Q.
Let
![]() $Q\in \mathbb {D}_k$
, and consider the family of its dyadic children
$Q\in \mathbb {D}_k$
, and consider the family of its dyadic children
![]() $\{Q'\in \mathbb {D}_{k+1}: Q'\subset Q\}$
. Note that for any two distinct children
$\{Q'\in \mathbb {D}_{k+1}: Q'\subset Q\}$
. Note that for any two distinct children
![]() $Q', Q"$
, one has
$Q', Q"$
, one has
![]() $|x_{Q'}-x_{Q"}|\ge r_{Q'}=r_{Q"}=r_Q/2$
, otherwise
$|x_{Q'}-x_{Q"}|\ge r_{Q'}=r_{Q"}=r_Q/2$
, otherwise
![]() $x_{Q"}\in Q"\cap \Delta _{Q'}\subset Q"\cap Q'$
, contradicting the fact that
$x_{Q"}\in Q"\cap \Delta _{Q'}\subset Q"\cap Q'$
, contradicting the fact that
![]() $Q'$
and
$Q'$
and
![]() $Q"$
are disjoint. Also,
$Q"$
are disjoint. Also,
![]() $x_{Q'}, x_{Q"}\in Q\subset \Delta (x_Q,\Xi r_Q)$
, hence by the geometric doubling property we have a purely dimensional bound for the number of such
$x_{Q'}, x_{Q"}\in Q\subset \Delta (x_Q,\Xi r_Q)$
, hence by the geometric doubling property we have a purely dimensional bound for the number of such
![]() $x_{Q'}$
, and hence, the number of dyadic children of a given dyadic cube is uniformly bounded.
$x_{Q'}$
, and hence, the number of dyadic children of a given dyadic cube is uniformly bounded.
We next introduce the ‘discretized Carleson region’ relative to
![]() $Q\in \mathbb {D}(E)$
,
$Q\in \mathbb {D}(E)$
,
![]() $\mathbb {D}_{Q}=\{Q'\in \mathbb {D}:Q'\subset Q\}$
. Let
$\mathbb {D}_{Q}=\{Q'\in \mathbb {D}:Q'\subset Q\}$
. Let
![]() $\mathcal {F}=\{Q_i\}\subset \mathbb {D}(E)$
be a family of pairwise disjoint cubes. The ‘global discretized sawtooth’ relative to
$\mathcal {F}=\{Q_i\}\subset \mathbb {D}(E)$
be a family of pairwise disjoint cubes. The ‘global discretized sawtooth’ relative to
![]() $\mathcal {F}$
is the collection of cubes
$\mathcal {F}$
is the collection of cubes
![]() $Q\in \mathbb {D}(E)$
that are not contained in any
$Q\in \mathbb {D}(E)$
that are not contained in any
![]() $Q_i\in \mathcal {F}$
, that is,
$Q_i\in \mathcal {F}$
, that is,
For a given
![]() $Q\in \mathbb {D}(E)$
, the ‘local discretized sawtooth’ relative to
$Q\in \mathbb {D}(E)$
, the ‘local discretized sawtooth’ relative to
![]() $\mathcal {F}$
is the collection of cubes in
$\mathcal {F}$
is the collection of cubes in
![]() $\mathbb {D}_Q$
that are not contained in any
$\mathbb {D}_Q$
that are not contained in any
![]() $Q_i\in \mathcal {F}$
or, equivalently,
$Q_i\in \mathcal {F}$
or, equivalently,
We also allow
![]() $\mathcal {F}$
to be the empty set in which case
$\mathcal {F}$
to be the empty set in which case
![]() $\mathbb {D}_{\tiny {\emptyset}}=\mathbb {D}(E)$
and
$\mathbb {D}_{\tiny {\emptyset}}=\mathbb {D}(E)$
and
![]() $\mathbb {D}_{{\tiny {\emptyset}},Q}=\mathbb {D}_Q$
.
$\mathbb {D}_{{\tiny {\emptyset}},Q}=\mathbb {D}_Q$
.
In the sequel,
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\geq 2$
, will be a 1-sided NTA domain satisfying the CDC. Write
$n\geq 2$
, will be a 1-sided NTA domain satisfying the CDC. Write
![]() $\mathbb {D}=\mathbb {D}(\partial \Omega )$
for the dyadic grid obtained from Lemma 2.8 with
$\mathbb {D}=\mathbb {D}(\partial \Omega )$
for the dyadic grid obtained from Lemma 2.8 with
![]() $E=\partial \Omega $
. In [Reference Akman, Hofmann, Martell and Toro1, Remark 2.56], it is shown that under the present assumptions one has that
$E=\partial \Omega $
. In [Reference Akman, Hofmann, Martell and Toro1, Remark 2.56], it is shown that under the present assumptions one has that
![]() $\operatorname {\mathrm {diam}}(\Delta )\approx r_{\Delta }$
for every surface ball
$\operatorname {\mathrm {diam}}(\Delta )\approx r_{\Delta }$
for every surface ball
![]() $\Delta $
and
$\Delta $
and
![]() $\operatorname {\mathrm {diam}}(Q)\approx \ell (Q)$
for every
$\operatorname {\mathrm {diam}}(Q)\approx \ell (Q)$
for every
![]() $Q\in \mathbb {D}$
. Given
$Q\in \mathbb {D}$
. Given
![]() $Q\in \mathbb {D}$
, we define the ‘corkscrew point relative to Q’ as
$Q\in \mathbb {D}$
, we define the ‘corkscrew point relative to Q’ as
![]() $X_Q:=X_{\Delta _Q}$
. We note that
$X_Q:=X_{\Delta _Q}$
. We note that
We also introduce the ‘geometric’ Carleson regions and sawtooths. Given
![]() $Q\in \mathbb {D}$
, we want to define some associated regions which inherit the good properties of
$Q\in \mathbb {D}$
, we want to define some associated regions which inherit the good properties of
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $\mathcal {W}=\mathcal {W}(\Omega )$
denote a collection of (closed) dyadic Whitney cubes of
$\mathcal {W}=\mathcal {W}(\Omega )$
denote a collection of (closed) dyadic Whitney cubes of
![]() $\Omega \subset \mathbb {R}^{n+1}$
so that the cubes in
$\Omega \subset \mathbb {R}^{n+1}$
so that the cubes in
![]() $\mathcal {W}$
form a covering of
$\mathcal {W}$
form a covering of
![]() $\Omega $
with nonoverlapping interiors and satisfy
$\Omega $
with nonoverlapping interiors and satisfy
and
Let
![]() $X(I)$
denote the center of I, let
$X(I)$
denote the center of I, let
![]() $\ell (I)$
denote the side length of I and write
$\ell (I)$
denote the side length of I and write
![]() $k=k_I$
if
$k=k_I$
if
![]() $\ell (I)=2^{-k}$
.
$\ell (I)=2^{-k}$
.
Given
![]() $0<\lambda <1$
and
$0<\lambda <1$
and
![]() $I\in \mathcal {W}$
, we write
$I\in \mathcal {W}$
, we write
![]() $I^*=(1+\lambda )I$
for the ‘fattening’ of I. By taking
$I^*=(1+\lambda )I$
for the ‘fattening’ of I. By taking
![]() $\lambda $
small enough, we can arrange matters so that, first,
$\lambda $
small enough, we can arrange matters so that, first,
![]() $\operatorname {dist}(I^*,J^*)\approx \operatorname {dist}(I,J)$
for every
$\operatorname {dist}(I^*,J^*)\approx \operatorname {dist}(I,J)$
for every
![]() $I,J\in \mathcal {W}$
. Secondly,
$I,J\in \mathcal {W}$
. Secondly,
![]() $I^*$
meets
$I^*$
meets
![]() $J^*$
if and only if
$J^*$
if and only if
![]() $\partial I$
meets
$\partial I$
meets
![]() $\partial J$
(the fattening thus ensures overlap of
$\partial J$
(the fattening thus ensures overlap of
![]() $I^*$
and
$I^*$
and
![]() $J^*$
for any pair
$J^*$
for any pair
![]() $I,J\in \mathcal {W}$
whose boundaries touch so that the Harnack chain property then holds locally in
$I,J\in \mathcal {W}$
whose boundaries touch so that the Harnack chain property then holds locally in
![]() $I^*\cup J^*$
, with constants depending upon
$I^*\cup J^*$
, with constants depending upon
![]() $\lambda $
.) By picking
$\lambda $
.) By picking
![]() $\lambda $
sufficiently small, say
$\lambda $
sufficiently small, say
![]() $0<\lambda <\lambda _0$
, we may also suppose that there is
$0<\lambda <\lambda _0$
, we may also suppose that there is
![]() $\tau \in (\frac 12,1)$
such that for distinct
$\tau \in (\frac 12,1)$
such that for distinct
![]() $I,J\in \mathcal {W}$
, we have that
$I,J\in \mathcal {W}$
, we have that
![]() $\tau J\cap I^*= {\emptyset }$
. In what follows, we will need to work with dilations
$\tau J\cap I^*= {\emptyset }$
. In what follows, we will need to work with dilations
![]() $I^{**}=(1+2\lambda )I$
or
$I^{**}=(1+2\lambda )I$
or
![]() $I^{***}=(1+4\lambda )I$
, and in order to ensure that the same properties hold, we further assume that
$I^{***}=(1+4\lambda )I$
, and in order to ensure that the same properties hold, we further assume that
![]() $0<\lambda <\lambda _0/4$
.
$0<\lambda <\lambda _0/4$
.
Given
![]() $\vartheta \in \mathbb {N}$
, for every cube
$\vartheta \in \mathbb {N}$
, for every cube
![]() $Q \in \mathbb {D}$
, we set
$Q \in \mathbb {D}$
, we set
We will choose
![]() $\vartheta \ge \vartheta _0$
, with
$\vartheta \ge \vartheta _0$
, with
![]() $\vartheta _0$
large enough depending on the constants of the corkscrew condition (cf. Definition 2.1) and in the dyadic cube construction (cf. Lemma 2.8) so that
$\vartheta _0$
large enough depending on the constants of the corkscrew condition (cf. Definition 2.1) and in the dyadic cube construction (cf. Lemma 2.8) so that
![]() $X_Q \in I$
for some
$X_Q \in I$
for some
![]() $I \in \mathcal {W}_Q^{\vartheta }$
, and for each dyadic child
$I \in \mathcal {W}_Q^{\vartheta }$
, and for each dyadic child
![]() $Q^j$
of Q, the respective corkscrew points
$Q^j$
of Q, the respective corkscrew points
![]() $X_{Q^j} \in I^j$
for some
$X_{Q^j} \in I^j$
for some
![]() $I^j \in \mathcal {W}_Q^{\vartheta }$
. Moreover, we may always find an
$I^j \in \mathcal {W}_Q^{\vartheta }$
. Moreover, we may always find an
![]() $I \in \mathcal {W}_Q^{\vartheta }$
with the slightly more precise property that
$I \in \mathcal {W}_Q^{\vartheta }$
with the slightly more precise property that
![]() $\ell (Q)/2 \leq \ell (I) \leq \ell (Q)$
and
$\ell (Q)/2 \leq \ell (I) \leq \ell (Q)$
and
For each
![]() $I \in \mathcal {W}_Q^{\vartheta }$
, we form a Harnack chain from the center
$I \in \mathcal {W}_Q^{\vartheta }$
, we form a Harnack chain from the center
![]() $X(I)$
to the corkscrew point
$X(I)$
to the corkscrew point
![]() $X_Q$
and call it
$X_Q$
and call it
![]() $H(I)$
. We now let
$H(I)$
. We now let
![]() $\mathcal {W}_{Q}^{\vartheta , *}$
denote the collection of all Whitney cubes which meet at least one ball in the Harnack chain
$\mathcal {W}_{Q}^{\vartheta , *}$
denote the collection of all Whitney cubes which meet at least one ball in the Harnack chain
![]() $H(I)$
with
$H(I)$
with
![]() $I \in \mathcal {W}_Q^{\vartheta }$
, that is,
$I \in \mathcal {W}_Q^{\vartheta }$
, that is,
We also define
 $$ \begin{align*} U_{Q}^{\vartheta} :=\bigcup_{I \in \mathcal{W}_{Q}^{\vartheta, *}}(1+\lambda) I=: \bigcup_{I \in \mathcal{W}_{Q}^{\vartheta, *}} I^{*}. \end{align*} $$
$$ \begin{align*} U_{Q}^{\vartheta} :=\bigcup_{I \in \mathcal{W}_{Q}^{\vartheta, *}}(1+\lambda) I=: \bigcup_{I \in \mathcal{W}_{Q}^{\vartheta, *}} I^{*}. \end{align*} $$
By construction, we then have that
for each child
![]() $Q^j$
of Q. It is also clear that there is a uniform constant
$Q^j$
of Q. It is also clear that there is a uniform constant
![]() $k^*$
(depending only on the
$k^*$
(depending only on the
![]() $1$
-sided CAD constants and
$1$
-sided CAD constants and
![]() $\vartheta $
) such that
$\vartheta $
) such that
 $$ \begin{align*} 2^{-k^*} \ell(Q) \leq \ell(I) \leq 2^{k^*}\ell(Q), &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}, \\ X(I) \rightarrow_{U_Q^{\vartheta}} X_Q, &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}, \\ \operatorname{dist}(I, Q) \leq 2^{k^*} \ell(Q), &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}. \end{align*} $$
$$ \begin{align*} 2^{-k^*} \ell(Q) \leq \ell(I) \leq 2^{k^*}\ell(Q), &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}, \\ X(I) \rightarrow_{U_Q^{\vartheta}} X_Q, &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}, \\ \operatorname{dist}(I, Q) \leq 2^{k^*} \ell(Q), &\quad \forall\,I \in \mathcal{W}_{Q}^{\vartheta, *}. \end{align*} $$
Here,
![]() $X(I) \to _{U_Q^{\vartheta }} X_Q$
means that the interior of
$X(I) \to _{U_Q^{\vartheta }} X_Q$
means that the interior of
![]() $U_Q^{\vartheta }$
contains all balls in a Harnack chain (in
$U_Q^{\vartheta }$
contains all balls in a Harnack chain (in
![]() $\Omega $
) connecting
$\Omega $
) connecting
![]() $X(I)$
to
$X(I)$
to
![]() $X_Q$
, and moreover, for any point Z contained in any ball in the Harnack chain, we have
$X_Q$
, and moreover, for any point Z contained in any ball in the Harnack chain, we have
![]() $\operatorname {dist}(Z, \partial \Omega ) \approx \operatorname {dist}(Z, \Omega \setminus U_Q^{\vartheta })$
with uniform control of implicit constants. The constant
$\operatorname {dist}(Z, \partial \Omega ) \approx \operatorname {dist}(Z, \Omega \setminus U_Q^{\vartheta })$
with uniform control of implicit constants. The constant
![]() $k^*$
and the implicit constants in the condition
$k^*$
and the implicit constants in the condition
![]() $X(I) \to _{U_Q^{\vartheta }} X_Q$
depend at most on the allowable parameters on
$X(I) \to _{U_Q^{\vartheta }} X_Q$
depend at most on the allowable parameters on
![]() $\lambda $
and on
$\lambda $
and on
![]() $\vartheta $
. Moreover, given
$\vartheta $
. Moreover, given
![]() $I \in \mathcal {W}$
, we have that
$I \in \mathcal {W}$
, we have that
![]() $I \in \mathcal {W}^{\vartheta ,*}_{Q_I}$
, where
$I \in \mathcal {W}^{\vartheta ,*}_{Q_I}$
, where
![]() $Q_I \in \mathbb {D}$
satisfies
$Q_I \in \mathbb {D}$
satisfies
![]() $\ell (Q_I)=\ell (I)$
and contains any fixed
$\ell (Q_I)=\ell (I)$
and contains any fixed
![]() $\widehat {y} \in \partial \Omega $
such that
$\widehat {y} \in \partial \Omega $
such that
![]() $\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(I, \widehat {y})$
. The reader is referred to [Reference Hofmann and Martell31, Reference Hofmann, Martell and Toro35] for full details. We note, however, that in [Reference Hofmann and Martell31] the parameter
$\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(I, \widehat {y})$
. The reader is referred to [Reference Hofmann and Martell31, Reference Hofmann, Martell and Toro35] for full details. We note, however, that in [Reference Hofmann and Martell31] the parameter
![]() $\vartheta $
is fixed. Here, we need to allow
$\vartheta $
is fixed. Here, we need to allow
![]() $\vartheta $
to depend on the aperture of the cones, and hence, it is convenient to include the superindex
$\vartheta $
to depend on the aperture of the cones, and hence, it is convenient to include the superindex
![]() $\vartheta $
.
$\vartheta $
.
For a given
![]() $Q\in \mathbb {D}$
, the ‘Carleson box’ relative to Q is defined by
$Q\in \mathbb {D}$
, the ‘Carleson box’ relative to Q is defined by
 $$ \begin{align*}T_Q^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_Q}U_{Q'}^{\vartheta}\bigg). \end{align*} $$
$$ \begin{align*}T_Q^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_Q}U_{Q'}^{\vartheta}\bigg). \end{align*} $$
For a given family
![]() $\mathcal {F}=\{Q_i\}\subset \mathbb {D}$
of pairwise disjoint cubes and a given
$\mathcal {F}=\{Q_i\}\subset \mathbb {D}$
of pairwise disjoint cubes and a given
![]() $Q\in \mathbb {D}$
, we define the ‘local sawtooth region’ relative to
$Q\in \mathbb {D}$
, we define the ‘local sawtooth region’ relative to
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
 $$ \begin{align} \Omega_{\mathcal{F},Q}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F},Q}}U_{Q'}^{\vartheta}\bigg)=\operatorname{\mathrm{int}} \bigg(\bigcup_{I\in\mathcal{W}_{\mathcal{F},Q}^{\vartheta}} I^*\bigg), \end{align} $$
$$ \begin{align} \Omega_{\mathcal{F},Q}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F},Q}}U_{Q'}^{\vartheta}\bigg)=\operatorname{\mathrm{int}} \bigg(\bigcup_{I\in\mathcal{W}_{\mathcal{F},Q}^{\vartheta}} I^*\bigg), \end{align} $$
where
![]() $\mathcal {W}_{\mathcal {F},Q}^{\vartheta }:=\bigcup _{Q'\in \mathbb {D}_{\mathcal {F},Q}}\mathcal {W}_{Q'}^{\vartheta ,*}$
. Note that in the previous definition we may allow
$\mathcal {W}_{\mathcal {F},Q}^{\vartheta }:=\bigcup _{Q'\in \mathbb {D}_{\mathcal {F},Q}}\mathcal {W}_{Q'}^{\vartheta ,*}$
. Note that in the previous definition we may allow
![]() $\mathcal {F}$
to be empty in which case clearly
$\mathcal {F}$
to be empty in which case clearly
![]() $\Omega ^{\vartheta }_{{\tiny {\emptyset}} ,Q}=T_Q^{\vartheta }$
. Similarly, the ‘global sawtooth region’ relative to
$\Omega ^{\vartheta }_{{\tiny {\emptyset}} ,Q}=T_Q^{\vartheta }$
. Similarly, the ‘global sawtooth region’ relative to
![]() $\mathcal {F}$
is defined as
$\mathcal {F}$
is defined as
 $$ \begin{align} \Omega_{\mathcal{F}}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F}}}U_{Q'}^{\vartheta}\bigg) = \operatorname{\mathrm{int}}\bigg(\bigcup_{I\in\mathcal{W}_{\mathcal{F}}^{\vartheta}}I^*\bigg), \end{align} $$
$$ \begin{align} \Omega_{\mathcal{F}}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F}}}U_{Q'}^{\vartheta}\bigg) = \operatorname{\mathrm{int}}\bigg(\bigcup_{I\in\mathcal{W}_{\mathcal{F}}^{\vartheta}}I^*\bigg), \end{align} $$
where
![]() $\mathcal {W}_{\mathcal {F}}^{\vartheta }:=\bigcup _{Q'\in \mathbb {D}_{\mathcal {F}}}\mathcal {W}_{Q'}^{\vartheta ,*}$
. If
$\mathcal {W}_{\mathcal {F}}^{\vartheta }:=\bigcup _{Q'\in \mathbb {D}_{\mathcal {F}}}\mathcal {W}_{Q'}^{\vartheta ,*}$
. If
![]() $\mathcal {F}$
is the empty set clearly
$\mathcal {F}$
is the empty set clearly
![]() $\Omega _{{\tiny {\emptyset}}}^{\vartheta }=\Omega $
. For a given
$\Omega _{{\tiny {\emptyset}}}^{\vartheta }=\Omega $
. For a given
![]() $Q\in \mathbb {D}$
and
$Q\in \mathbb {D}$
and
![]() $x\in \partial \Omega $
, let us introduce the ‘truncated dyadic cone’
$x\in \partial \Omega $
, let us introduce the ‘truncated dyadic cone’
 $$\begin{align*}\Gamma_{Q}^{\vartheta}(x) := \bigcup_{x\in Q'\in\mathbb{D}_{Q}} U_{Q'}^{\vartheta}, \end{align*}$$
$$\begin{align*}\Gamma_{Q}^{\vartheta}(x) := \bigcup_{x\in Q'\in\mathbb{D}_{Q}} U_{Q'}^{\vartheta}, \end{align*}$$
where it is understood that
![]() $\Gamma _{Q}^{\vartheta }(x)= \emptyset $
if
$\Gamma _{Q}^{\vartheta }(x)= \emptyset $
if
![]() $x\notin Q$
. Analogously, we can slightly fatten the Whitney boxes and use
$x\notin Q$
. Analogously, we can slightly fatten the Whitney boxes and use
![]() $I^{**}$
to define new fattened Whitney regions and sawtooth domains. More precisely, for every
$I^{**}$
to define new fattened Whitney regions and sawtooth domains. More precisely, for every
![]() $Q\in \mathbb {D}$
,
$Q\in \mathbb {D}$
,
 $$\begin{align*}T_Q^{\vartheta,*}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_Q}U_{Q'}^{\vartheta,*}\bigg),\quad\Omega^{\vartheta,*}_{\mathcal{F},Q}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F},Q}}U_{Q'}^{\vartheta,*}\bigg), \quad \Gamma^{\vartheta,*}_{Q}(x) := \bigcup_{x\in Q'\in\mathbb{D}_{Q_0}} U_{Q'}^{\vartheta,*}, \end{align*}$$
$$\begin{align*}T_Q^{\vartheta,*}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_Q}U_{Q'}^{\vartheta,*}\bigg),\quad\Omega^{\vartheta,*}_{\mathcal{F},Q}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q'\in\mathbb{D}_{\mathcal{F},Q}}U_{Q'}^{\vartheta,*}\bigg), \quad \Gamma^{\vartheta,*}_{Q}(x) := \bigcup_{x\in Q'\in\mathbb{D}_{Q_0}} U_{Q'}^{\vartheta,*}, \end{align*}$$
where
![]() $U_{Q}^{\vartheta ,*}:=\bigcup _{I\in \mathcal {W}_Q^{\vartheta ,*}}I^{**}$
. Similarly, we can define
$U_{Q}^{\vartheta ,*}:=\bigcup _{I\in \mathcal {W}_Q^{\vartheta ,*}}I^{**}$
. Similarly, we can define
![]() $T_Q^{\vartheta ,**}$
,
$T_Q^{\vartheta ,**}$
,
![]() $\Omega ^{\vartheta ,**}_{\mathcal {F},Q}$
,
$\Omega ^{\vartheta ,**}_{\mathcal {F},Q}$
,
![]() $\Gamma _Q^{\vartheta ,**}(x)$
, and
$\Gamma _Q^{\vartheta ,**}(x)$
, and
![]() $U^{\vartheta ,**}_{Q}$
by using
$U^{\vartheta ,**}_{Q}$
by using
![]() $I^{***}$
in place of
$I^{***}$
in place of
![]() $I^{**}$
.
$I^{**}$
.
To define the ‘Carleson box’,
![]() $T_{\Delta }^{\vartheta }$
associated with a surface ball
$T_{\Delta }^{\vartheta }$
associated with a surface ball
![]() $\Delta =\Delta (x,r)$
, let
$\Delta =\Delta (x,r)$
, let
![]() $k(\Delta )$
denote the unique
$k(\Delta )$
denote the unique
![]() $k\in \mathbb {Z}$
such that
$k\in \mathbb {Z}$
such that
![]() $2^{-k-1}<200r\leq 2^{-k}$
and set
$2^{-k-1}<200r\leq 2^{-k}$
and set
We then define
 $$ \begin{align} T_{\Delta}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta}}\bigg). \end{align} $$
$$ \begin{align} T_{\Delta}^{\vartheta}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta}}\bigg). \end{align} $$
We can also consider fattened versions of
![]() $T_{\Delta }^{\vartheta }$
given by
$T_{\Delta }^{\vartheta }$
given by
 $$ \begin{align*} T_{\Delta}^{\vartheta,*}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta,*}}\bigg),\qquad T_{\Delta}^{\vartheta,**}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta,**}}\bigg). \end{align*} $$
$$ \begin{align*} T_{\Delta}^{\vartheta,*}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta,*}}\bigg),\qquad T_{\Delta}^{\vartheta,**}:=\operatorname{\mathrm{int}}\bigg(\bigcup_{Q\in\mathbb{D}^{\Delta}}\overline{T_Q^{\vartheta,**}}\bigg). \end{align*} $$
Following [Reference Hofmann and Martell31, Reference Hofmann, Martell and Toro35], one can easily see that there exist constants
![]() $0<\kappa _1<1$
and
$0<\kappa _1<1$
and
![]() $\kappa _0\geq 16\Xi $
(with
$\kappa _0\geq 16\Xi $
(with
![]() $\Xi $
the constant in equation (2.6)), depending only on the allowable parameters and on
$\Xi $
the constant in equation (2.6)), depending only on the allowable parameters and on
![]() $\vartheta $
, so that
$\vartheta $
, so that
and also
where
![]() $B_Q$
is defined as in equation (2.7),
$B_Q$
is defined as in equation (2.7),
![]() $\Delta =\Delta (x,r)$
with
$\Delta =\Delta (x,r)$
with
![]() $x\in \partial \Omega $
,
$x\in \partial \Omega $
,
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
![]() $B_{\Delta }=B(x,r)$
is so that
$B_{\Delta }=B(x,r)$
is so that
![]() $\Delta =B_{\Delta }\cap \partial \Omega $
. From our choice of the parameters, one also has that
$\Delta =B_{\Delta }\cap \partial \Omega $
. From our choice of the parameters, one also has that
![]() $B_Q^*\subset B_{Q'}^*$
whenever
$B_Q^*\subset B_{Q'}^*$
whenever
![]() $Q\subset Q'$
.
$Q\subset Q'$
.
Lemma 2.9 [Reference Akman, Hofmann, Martell and Toro1, Proposition 2.37] and [Reference Hofmann and Martell31, Appendices A.1-A.2]
Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain satisfying the CDC. For every
$n\ge 2$
, be a 1-sided NTA domain satisfying the CDC. For every
![]() $\vartheta \ge \vartheta _0$
, all of its Carleson boxes
$\vartheta \ge \vartheta _0$
, all of its Carleson boxes
![]() $T_Q^{\vartheta }, T_Q^{\vartheta ,*}, T_Q^{\vartheta ,**}$
and
$T_Q^{\vartheta }, T_Q^{\vartheta ,*}, T_Q^{\vartheta ,**}$
and
![]() $T_{\Delta }^{\vartheta }, T_{\Delta }^{\vartheta ,*}, T_{\Delta }^{\vartheta ,**}$
and sawtooth regions
$T_{\Delta }^{\vartheta }, T_{\Delta }^{\vartheta ,*}, T_{\Delta }^{\vartheta ,**}$
and sawtooth regions
![]() $\Omega _{\mathcal {F}}^{\vartheta },\Omega _{\mathcal {F}}^{\vartheta ,*}, \Omega _{\mathcal {F}}^{\vartheta ,**}$
and
$\Omega _{\mathcal {F}}^{\vartheta },\Omega _{\mathcal {F}}^{\vartheta ,*}, \Omega _{\mathcal {F}}^{\vartheta ,**}$
and
![]() $\Omega _{\mathcal {F},Q}^{\vartheta }, \Omega _{\mathcal {F},Q}^{\vartheta , *}, \Omega _{\mathcal {F},Q}^{\vartheta , **}$
are 1-sided NTA domains and satisfy the CDC with uniform implicit constants depending only on dimension, the corresponding constants for
$\Omega _{\mathcal {F},Q}^{\vartheta }, \Omega _{\mathcal {F},Q}^{\vartheta , *}, \Omega _{\mathcal {F},Q}^{\vartheta , **}$
are 1-sided NTA domains and satisfy the CDC with uniform implicit constants depending only on dimension, the corresponding constants for
![]() $\Omega $
, and
$\Omega $
, and
![]() $\vartheta $
.
$\vartheta $
.
Given Q we define the ‘localized dyadic conical square function’
 $$ \begin{align} \mathcal{S}_{Q}^{\vartheta} u(x):=\bigg(\iint_{\Gamma_{Q}^{\vartheta} (x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \qquad x\in \partial\Omega, \end{align} $$
$$ \begin{align} \mathcal{S}_{Q}^{\vartheta} u(x):=\bigg(\iint_{\Gamma_{Q}^{\vartheta} (x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \qquad x\in \partial\Omega, \end{align} $$
for every
![]() $u\in W^{1,2}_{\mathrm {loc}} (T_{Q}^{\vartheta })$
. Note that
$u\in W^{1,2}_{\mathrm {loc}} (T_{Q}^{\vartheta })$
. Note that
![]() $\mathcal {S}_{Q}^{\vartheta } u(x)=0$
for every
$\mathcal {S}_{Q}^{\vartheta } u(x)=0$
for every
![]() $x\in \partial \Omega \setminus Q$
since
$x\in \partial \Omega \setminus Q$
since
![]() $\Gamma _Q^{\vartheta } (x)= \emptyset $
in such case. The ‘localized dyadic nontangential maximal function’ is given by
$\Gamma _Q^{\vartheta } (x)= \emptyset $
in such case. The ‘localized dyadic nontangential maximal function’ is given by
 $$ \begin{align} \mathcal{N}_{Q}^{\vartheta} u(x) : = \sup_{Y\in \Gamma^{\vartheta,*}_{Q}(x)} |u(Y)|, \qquad x\in \partial\Omega, \end{align} $$
$$ \begin{align} \mathcal{N}_{Q}^{\vartheta} u(x) : = \sup_{Y\in \Gamma^{\vartheta,*}_{Q}(x)} |u(Y)|, \qquad x\in \partial\Omega, \end{align} $$
for every
![]() $u\in \mathscr {C}(T_{Q}^{\vartheta ,*})$
, where it is understood that
$u\in \mathscr {C}(T_{Q}^{\vartheta ,*})$
, where it is understood that
![]() $\mathcal {N}_{Q}^{\vartheta } u(x)= 0$
for every
$\mathcal {N}_{Q}^{\vartheta } u(x)= 0$
for every
![]() $x\in \partial \Omega \setminus Q$
.
$x\in \partial \Omega \setminus Q$
.
Given
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $x\in \partial \Omega $
, we introduce the ‘cone with vertex at x and aperture
$x\in \partial \Omega $
, we introduce the ‘cone with vertex at x and aperture
![]() $\alpha $
’ defined as
$\alpha $
’ defined as
![]() $\Gamma ^{\alpha }(x) = \{X \in \Omega : |X - x| \leq (1+\alpha ) \delta (X)\}$
. One can also introduce the ‘truncated cone’ for every
$\Gamma ^{\alpha }(x) = \{X \in \Omega : |X - x| \leq (1+\alpha ) \delta (X)\}$
. One can also introduce the ‘truncated cone’ for every
![]() $x\in \partial \Omega $
, and
$x\in \partial \Omega $
, and
![]() $0<r<\infty $
we set
$0<r<\infty $
we set
![]() $\Gamma _{r}^{\alpha }(x) = B(x,r)\cap \Gamma ^{\alpha }(x)$
.
$\Gamma _{r}^{\alpha }(x) = B(x,r)\cap \Gamma ^{\alpha }(x)$
.
The ‘conical square function’ and the ‘nontangential maximal function’ are defined, respectively, as
 $$ \begin{align} \mathcal{S}^{\alpha} u(x):=\bigg(\iint_{\Gamma^{\alpha}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \qquad \mathcal{N}^{\alpha} u (x) := \sup_{X \in \Gamma^{\alpha} (x)} |u(X)|,\qquad x\in\partial\Omega \end{align} $$
$$ \begin{align} \mathcal{S}^{\alpha} u(x):=\bigg(\iint_{\Gamma^{\alpha}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \qquad \mathcal{N}^{\alpha} u (x) := \sup_{X \in \Gamma^{\alpha} (x)} |u(X)|,\qquad x\in\partial\Omega \end{align} $$
for every
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
and
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
and
![]() $u\in \mathscr {C}(\Omega )$
, respectively. Analogously, the ‘truncated conical square function’ and the ‘truncated nontangential maximal function’ are defined, respectively, as
$u\in \mathscr {C}(\Omega )$
, respectively. Analogously, the ‘truncated conical square function’ and the ‘truncated nontangential maximal function’ are defined, respectively, as
 $$ \begin{align} \mathcal{S}_{r}^{\alpha} u(x):=\bigg(\iint_{\Gamma_{r}^{\alpha}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \quad \mathcal{N}^{\alpha}_{r} u (x) := \sup_{X \in \Gamma^{\alpha}_{r} (x)} |u(X)|, \quad \end{align} $$
$$ \begin{align} \mathcal{S}_{r}^{\alpha} u(x):=\bigg(\iint_{\Gamma_{r}^{\alpha}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12}, \quad \mathcal{N}^{\alpha}_{r} u (x) := \sup_{X \in \Gamma^{\alpha}_{r} (x)} |u(X)|, \quad \end{align} $$
where
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\infty $
, for every
$0<r<\infty $
, for every
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega \cap B(x,r))$
and
$u\in W^{1,2}_{\mathrm {loc}}(\Omega \cap B(x,r))$
and
![]() $u\in \mathscr {C}(\Omega \cap B(x,r))$
, respectively.
$u\in \mathscr {C}(\Omega \cap B(x,r))$
, respectively.
We would like to note that truncated dyadic cones are never empty. Indeed, in our construction, we have made sure that
![]() $X_Q\in U_Q^{\vartheta }$
for every
$X_Q\in U_Q^{\vartheta }$
for every
![]() $Q\in \mathbb {D}$
; hence, for any
$Q\in \mathbb {D}$
; hence, for any
![]() $Q\in \mathbb {D}$
and
$Q\in \mathbb {D}$
and
![]() $x\in Q$
one has
$x\in Q$
one has
![]() $X_Q\in \Gamma _Q^{\vartheta }(x)$
. Moreover,
$X_Q\in \Gamma _Q^{\vartheta }(x)$
. Moreover,
![]() $X_{Q'}\in \Gamma _Q^{\vartheta }(x)$
for every
$X_{Q'}\in \Gamma _Q^{\vartheta }(x)$
for every
![]() $Q'\in \mathbb {D}_Q$
with
$Q'\in \mathbb {D}_Q$
with
![]() $Q'\ni x$
. For the regular truncated cones, it could happen that
$Q'\ni x$
. For the regular truncated cones, it could happen that
![]() $\Gamma ^{\alpha }_r(x)= \emptyset $
unless
$\Gamma ^{\alpha }_r(x)= \emptyset $
unless
![]() $\alpha $
is sufficiently large. Suppose for instance that
$\alpha $
is sufficiently large. Suppose for instance that
![]() $\Omega =\{X=(x_1,\dots ,x_{n+1})\in \mathbb {R}^{n+1}: x_{1},\dots , x_{n+1}>0\}$
is the first orthant, then
$\Omega =\{X=(x_1,\dots ,x_{n+1})\in \mathbb {R}^{n+1}: x_{1},\dots , x_{n+1}>0\}$
is the first orthant, then
![]() $\Gamma _{r}^{\alpha }(0)= \emptyset $
for any
$\Gamma _{r}^{\alpha }(0)= \emptyset $
for any
![]() $0<r<\infty $
if
$0<r<\infty $
if
![]() $\alpha <\sqrt {n+1}-1$
. On the other hand, if
$\alpha <\sqrt {n+1}-1$
. On the other hand, if
![]() $\alpha $
is sufficiently large, more precisely, if
$\alpha $
is sufficiently large, more precisely, if
![]() $\alpha \ge c_0^{-1}-1$
, where
$\alpha \ge c_0^{-1}-1$
, where
![]() $c_0$
is the corkscrew constant (cf. Definition 2.1), then
$c_0$
is the corkscrew constant (cf. Definition 2.1), then
3 Uniformly elliptic operators, elliptic measure and the Green function
Next, we recall several facts concerning elliptic measures and Green functions. To set the stage, let
![]() $\Omega \subset \mathbb {R}^{n+1}$
be an open set. Throughout, we consider elliptic operators L of the form
$\Omega \subset \mathbb {R}^{n+1}$
be an open set. Throughout, we consider elliptic operators L of the form
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
with
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
with
![]() $A(X)=(a_{i,j}(X))_{i,j=1}^{n+1}$
being a real (nonnecessarily symmetric) matrix such that
$A(X)=(a_{i,j}(X))_{i,j=1}^{n+1}$
being a real (nonnecessarily symmetric) matrix such that
![]() $a_{i,j}\in L^{\infty }(\Omega )$
, and there exists
$a_{i,j}\in L^{\infty }(\Omega )$
, and there exists
![]() $\Lambda \geq 1$
such that the following uniform ellipticity condition holds
$\Lambda \geq 1$
such that the following uniform ellipticity condition holds
for all
![]() $\xi ,\eta \in \mathbb {R}^{n+1}$
and for almost every
$\xi ,\eta \in \mathbb {R}^{n+1}$
and for almost every
![]() $X\in \Omega $
. We write
$X\in \Omega $
. We write
![]() $L^{\top }$
to denote the transpose of L, or, in other words,
$L^{\top }$
to denote the transpose of L, or, in other words,
![]() $L^{\top } u = -\mathop {\operatorname {div}}\nolimits (A^{\top } \nabla u)$
with
$L^{\top } u = -\mathop {\operatorname {div}}\nolimits (A^{\top } \nabla u)$
with
![]() $A^{\top }$
being the transpose matrix of A.
$A^{\top }$
being the transpose matrix of A.
We say that u is a weak solution to
![]() $Lu=0$
in
$Lu=0$
in
![]() $\Omega $
provided that
$\Omega $
provided that
![]() $u\in W_{\mathrm {loc}}^{1,2}(\Omega )$
satisfies
$u\in W_{\mathrm {loc}}^{1,2}(\Omega )$
satisfies
Associated with L, one can construct the elliptic measure
![]() $\{\omega _L^X\}_{X\in \Omega }$
and the Green function
$\{\omega _L^X\}_{X\in \Omega }$
and the Green function
![]() $G_L$
. For the latter, the reader is referred to the work of Grüter and Widman [Reference Grüter and Widman27] in the bounded case, while the existence of the corresponding elliptic measure is an application of the Riesz representation theorem. The behavior of
$G_L$
. For the latter, the reader is referred to the work of Grüter and Widman [Reference Grüter and Widman27] in the bounded case, while the existence of the corresponding elliptic measure is an application of the Riesz representation theorem. The behavior of
![]() $\omega _L$
and
$\omega _L$
and
![]() $G_L$
, as well as the relationship between them, depends crucially on the properties of
$G_L$
, as well as the relationship between them, depends crucially on the properties of
![]() $\Omega $
, and assuming that
$\Omega $
, and assuming that
![]() $\Omega $
is a 1-sided NTA domain satisfying CDC, one can follow the program carried out in [Reference Jerison and Kenig41]. For a comprehensive treatment of the subject and the proofs, we refer the reader to the forthcoming monograph [Reference Hofmann, Martell and Toro35].
$\Omega $
is a 1-sided NTA domain satisfying CDC, one can follow the program carried out in [Reference Jerison and Kenig41]. For a comprehensive treatment of the subject and the proofs, we refer the reader to the forthcoming monograph [Reference Hofmann, Martell and Toro35].
If
![]() $\Omega $
satisfies the CDC, then it follows that all boundary points are Wiener regular, and hence, for a given
$\Omega $
satisfies the CDC, then it follows that all boundary points are Wiener regular, and hence, for a given
![]() $f\in \mathscr {C}_c(\partial \Omega )$
we can define
$f\in \mathscr {C}_c(\partial \Omega )$
we can define
and
![]() $u:=f$
on
$u:=f$
on
![]() $\partial \Omega $
, and obtain that
$\partial \Omega $
, and obtain that
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap \mathscr {C}(\overline {\Omega })$
and
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap \mathscr {C}(\overline {\Omega })$
and
![]() $Lu=0$
in the weak sense in
$Lu=0$
in the weak sense in
![]() $\Omega $
. Moreover, if
$\Omega $
. Moreover, if
![]() $f\in \operatorname *{\mathrm {Lip}}(\partial \Omega )$
, then
$f\in \operatorname *{\mathrm {Lip}}(\partial \Omega )$
, then
![]() $u\in W^{1,2}(\Omega )$
.
$u\in W^{1,2}(\Omega )$
.
We first define the reverse Hölder class and the
![]() $A_{\infty }$
classes with respect to a fixed elliptic measure in
$A_{\infty }$
classes with respect to a fixed elliptic measure in
![]() $\Omega $
. One reason we take this approach is that we do not know whether
$\Omega $
. One reason we take this approach is that we do not know whether
![]() $\mathcal {H}^{n}|_{\partial \Omega }$
is well-defined since we do not assume any Ahlfors regularity in Theorem 1.1. Hence, we have to develop these notions in terms of elliptic measures. To this end, let
$\mathcal {H}^{n}|_{\partial \Omega }$
is well-defined since we do not assume any Ahlfors regularity in Theorem 1.1. Hence, we have to develop these notions in terms of elliptic measures. To this end, let
![]() $\Omega $
satisfy the CDC, and let
$\Omega $
satisfy the CDC, and let
![]() $L_0$
and L be two real (nonnecessarily symmetric) elliptic operators associated with
$L_0$
and L be two real (nonnecessarily symmetric) elliptic operators associated with
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
and
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
and
![]() $L u=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
, where A and
$L u=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
, where A and
![]() $A_0$
satisfy equation (3.1). Let
$A_0$
satisfy equation (3.1). Let
![]() $\omega ^{X}_{L_0}$
and
$\omega ^{X}_{L_0}$
and
![]() $\omega _{L}^{X}$
be the elliptic measures of
$\omega _{L}^{X}$
be the elliptic measures of
![]() $\Omega $
associated with the operators
$\Omega $
associated with the operators
![]() $L_0$
and L, respectively, with pole at
$L_0$
and L, respectively, with pole at
![]() $X\in \Omega $
. Note that if we further assume that
$X\in \Omega $
. Note that if we further assume that
![]() $\Omega $
is connected, then Harnack’s inequality readily implies that
$\Omega $
is connected, then Harnack’s inequality readily implies that
![]() $\omega _{L}^{X}\ll \omega _L^{Y}$
on
$\omega _{L}^{X}\ll \omega _L^{Y}$
on
![]() $\partial \Omega $
for every
$\partial \Omega $
for every
![]() $X,Y\in \Omega $
. Hence, if
$X,Y\in \Omega $
. Hence, if
![]() $\omega _L^{X_0}\ll \omega _{L_0}^{Y_0}$
on
$\omega _L^{X_0}\ll \omega _{L_0}^{Y_0}$
on
![]() $\partial \Omega $
for some
$\partial \Omega $
for some
![]() $X_0,Y_0\in \Omega $
, then
$X_0,Y_0\in \Omega $
, then
![]() $\omega _L^{X}\ll \omega _{L_0}^{Y}$
on
$\omega _L^{X}\ll \omega _{L_0}^{Y}$
on
![]() $\partial \Omega $
for every
$\partial \Omega $
for every
![]() $X,Y\in \Omega $
, and thus we can simply write
$X,Y\in \Omega $
, and thus we can simply write
![]() $\omega _{L}\ll \omega _{L_0}$
on
$\omega _{L}\ll \omega _{L_0}$
on
![]() $\partial \Omega $
. In the latter case, we will use the notation
$\partial \Omega $
. In the latter case, we will use the notation
 $$ \begin{align} h(\cdot\,;L, L_0, X)=\frac{d\omega_L^{X}}{d\omega_{L_0}^{X}} \end{align} $$
$$ \begin{align} h(\cdot\,;L, L_0, X)=\frac{d\omega_L^{X}}{d\omega_{L_0}^{X}} \end{align} $$
to denote the Radon–Nikodym derivative of
![]() $\omega _{L}^{X}$
with respect to
$\omega _{L}^{X}$
with respect to
![]() $\omega _{L_0}^{X}$
, which is a well-defined function
$\omega _{L_0}^{X}$
, which is a well-defined function
![]() $\omega _{L_0}^{X}$
-almost everywhere on
$\omega _{L_0}^{X}$
-almost everywhere on
![]() $\partial \Omega $
.
$\partial \Omega $
.
Definition 3.1 (Reverse Hölder and
 $A_{\infty }$
classes)
$A_{\infty }$
classes)
Fix
![]() $\Delta _0=B_0\cap \partial \Omega $
, where
$\Delta _0=B_0\cap \partial \Omega $
, where
![]() $B_0=B(x_0,r_0)$
with
$B_0=B(x_0,r_0)$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Given
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Given
![]() $1<p<\infty $
, we say that
$1<p<\infty $
, we say that
![]() $\omega _L\in RH_p(\Delta _0,\omega _{L_0})$
, provided that
$\omega _L\in RH_p(\Delta _0,\omega _{L_0})$
, provided that
![]() $\omega _L\ll \omega _{L_0}$
on
$\omega _L\ll \omega _{L_0}$
on
![]() $\Delta _0$
, and there exists
$\Delta _0$
, and there exists
![]() $C\geq 1$
such that
$C\geq 1$
such that

for every
![]() $\Delta =B\cap \partial \Omega $
, where
$\Delta =B\cap \partial \Omega $
, where
![]() $B\subset B(x_0,r_0)$
,
$B\subset B(x_0,r_0)$
,
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
,
$x\in \partial \Omega $
,
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. The infimum of the constants C as above is denoted by
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. The infimum of the constants C as above is denoted by
![]() $[\omega _{L}]_{RH_p(\Delta _0,\omega _{L_0})}$
.
$[\omega _{L}]_{RH_p(\Delta _0,\omega _{L_0})}$
.
Similarly, we say that
![]() $\omega _L\in RH_p(\partial \Omega ,\omega _{L_0})$
provided that for every
$\omega _L\in RH_p(\partial \Omega ,\omega _{L_0})$
provided that for every
![]() $\Delta _0=\Delta (x_0,r_0)$
with
$\Delta _0=\Delta (x_0,r_0)$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
one has
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
one has
![]() $\omega _L\in RH_p(\Delta _0,\omega _{L_0})$
uniformly on
$\omega _L\in RH_p(\Delta _0,\omega _{L_0})$
uniformly on
![]() $\Delta _0$
, that is,
$\Delta _0$
, that is,
Finally,
Definition 3.2 (
 $\mathrm {BMO}$
)
$\mathrm {BMO}$
)
Fix
![]() $\Delta _0=B_0\cap \partial \Omega $
, where
$\Delta _0=B_0\cap \partial \Omega $
, where
![]() $B_0=B(x_0,r_0)$
with
$B_0=B(x_0,r_0)$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. We say that
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. We say that
![]() $f\in \mathrm {BMO}(\Delta _0, \omega _L)$
provided
$f\in \mathrm {BMO}(\Delta _0, \omega _L)$
provided
![]() $f \in L^1_{\mathrm {loc}}(\Delta _0, \omega _L^{X_{\Delta _0}})$
and
$f \in L^1_{\mathrm {loc}}(\Delta _0, \omega _L^{X_{\Delta _0}})$
and
where the sup is taken over all surface balls
![]() $\Delta =B\cap \partial \Omega $
, where
$\Delta =B\cap \partial \Omega $
, where
![]() $B\subset B(x_0,r_0)$
,
$B\subset B(x_0,r_0)$
,
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
,
$x\in \partial \Omega $
,
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
Similarly, we say that
![]() $f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
provided that for every
$f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
provided that for every
![]() $\Delta _0=\Delta (x_0,r_0)$
with
$\Delta _0=\Delta (x_0,r_0)$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
one has
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
one has
![]() $f\in \mathrm {BMO}(\Delta _0, \omega _L)$
uniformly on
$f\in \mathrm {BMO}(\Delta _0, \omega _L)$
uniformly on
![]() $\Delta _0$
, that is,
$\Delta _0$
, that is,
![]() $f \in L^1_{\mathrm {loc}}(\partial \Omega , \omega _L)$
(that is,
$f \in L^1_{\mathrm {loc}}(\partial \Omega , \omega _L)$
(that is,
![]() $\|f\,\mathbf {1}_{\Delta }\|_{L^1(\partial \Omega ,\omega _L^X)}<\infty $
for every surface ball
$\|f\,\mathbf {1}_{\Delta }\|_{L^1(\partial \Omega ,\omega _L^X)}<\infty $
for every surface ball
![]() $\Delta \subset \partial \Omega $
and for every
$\Delta \subset \partial \Omega $
and for every
![]() $X\in \Omega $
—albeit with a constant that may depend on
$X\in \Omega $
—albeit with a constant that may depend on
![]() $\Delta $
and X) and satisfies
$\Delta $
and X) and satisfies

where the sups are taken, respectively, over all surface balls
![]() $\Delta _0=B(x_0,r_0)\cap \partial \Omega $
with
$\Delta _0=B(x_0,r_0)\cap \partial \Omega $
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $B=B(x,r)\subset B_0$
with
$B=B(x,r)\subset B_0$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
.
Definition 3.3 (Solvability, CME,
 $\mathcal {S}<\mathcal {N}$
)
$\mathcal {S}<\mathcal {N}$
)
Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators.
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators.
-
○ Given
 $1<p<\infty $
, we say that L is
$1<p<\infty $
, we say that L is
 $L^{p}(\omega _{L_0})$
-solvable if for a given
$L^{p}(\omega _{L_0})$
-solvable if for a given
 $\alpha>0$
and
$\alpha>0$
and
 $N\ge 1$
there exists
$N\ge 1$
there exists
 $C_{\alpha , N}\ge 1$
(depending only on n, the
$C_{\alpha , N}\ge 1$
(depending only on n, the
 $1$
-sided NTA constants, the CDC constant, the ellipticity of
$1$
-sided NTA constants, the CDC constant, the ellipticity of
 $L_0$
and L,
$L_0$
and L,
 $\alpha $
, N and p) such that for every
$\alpha $
, N and p) such that for every
 $\Delta _0 = \Delta (x_0, r_0)$
with
$\Delta _0 = \Delta (x_0, r_0)$
with
 $x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
, and for every
$x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
, and for every
 $f \in \mathscr {C}(\partial \Omega )$
with
$f \in \mathscr {C}(\partial \Omega )$
with
 $\operatorname {\mathrm {supp}} f \subset N\Delta _0$
if one sets (3.4)then
$\operatorname {\mathrm {supp}} f \subset N\Delta _0$
if one sets (3.4)then $$ \begin{align} u(X):=\int_{\partial\Omega} f(y)\,d\omega_{L}^X(y),\qquad X\in\Omega, \end{align} $$
(3.5)
$$ \begin{align} u(X):=\int_{\partial\Omega} f(y)\,d\omega_{L}^X(y),\qquad X\in\Omega, \end{align} $$
(3.5) $$ \begin{align} \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_{\alpha,N} \|f\|_{L^p(N\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
$$ \begin{align} \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_{\alpha,N} \|f\|_{L^p(N\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
-
○ We say that L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable if there exists
$\mathrm {BMO}(\omega _{L_0})$
-solvable if there exists
 $C\ge 1$
(depending only on n, the
$C\ge 1$
(depending only on n, the
 $1$
-sided NTA constants, the CDC constant and the ellipticity of
$1$
-sided NTA constants, the CDC constant and the ellipticity of
 $L_0$
and L) such that for every
$L_0$
and L) such that for every
 $f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega , \omega _{L_0})$
if one takes u as in equation (3.4) and we set
$f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega , \omega _{L_0})$
if one takes u as in equation (3.4) and we set
 $u_{L,\Omega }(X):=\omega _{L}^X(\partial \Omega )$
,
$u_{L,\Omega }(X):=\omega _{L}^X(\partial \Omega )$
,
 $X\in \Omega $
, then (3.6)where
$X\in \Omega $
, then (3.6)where $$ \begin{align} \sup_B \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla (u-f_{\Delta, L_0}u_{L,\Omega})(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \le C \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}, \end{align} $$
$$ \begin{align} \sup_B \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla (u-f_{\Delta, L_0}u_{L,\Omega})(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \le C \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}, \end{align} $$
 $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
 $\Delta '=B'\cap \partial \Omega $
,
$\Delta '=B'\cap \partial \Omega $
,
 , and the sups are taken, respectively, over all balls
, and the sups are taken, respectively, over all balls
 $B=B(x,r)$
with
$B=B(x,r)$
with
 $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
 $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
 $B'=B(x',r')$
with
$B'=B(x',r')$
with
 $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
 $0<r'<r c_0/4$
, and
$0<r'<r c_0/4$
, and
 $c_0$
is the corkscrew constant.
$c_0$
is the corkscrew constant.
-
○ We say that L is
 $\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense (see [Reference Hofmann and Le29, Section 5]) if there exists
$\mathrm {BMO}(\omega _{L_0})$
-solvable in the generalized sense (see [Reference Hofmann and Le29, Section 5]) if there exists
 $C\ge 1$
(depending only on n, the
$C\ge 1$
(depending only on n, the
 $1$
-sided NTA constants, the CDC constant, and the ellipticity of
$1$
-sided NTA constants, the CDC constant, and the ellipticity of
 $L_0$
and L) such that for every
$L_0$
and L) such that for every
 $\varepsilon \in (0,1]$
there exists
$\varepsilon \in (0,1]$
there exists
 $\varrho (\varepsilon )\ge 0$
such that
$\varrho (\varepsilon )\ge 0$
such that
 $\varrho (\varepsilon )\longrightarrow 0$
as
$\varrho (\varepsilon )\longrightarrow 0$
as
 $\varepsilon \to 0^+$
in such a way that for every
$\varepsilon \to 0^+$
in such a way that for every
 $f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega , \omega _{L_0})$
if one takes u as in equation (3.4), then (3.7)where
$f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega , \omega _{L_0})$
if one takes u as in equation (3.4), then (3.7)where $$ \begin{align} \sup_{B_{\varepsilon}} \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \le C \big(\|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} + \varrho(\varepsilon)\|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2\big), \end{align} $$
$$ \begin{align} \sup_{B_{\varepsilon}} \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \le C \big(\|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} + \varrho(\varepsilon)\|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2\big), \end{align} $$
 $\Delta _{\varepsilon }=B_{\varepsilon }\cap \partial \Omega $
,
$\Delta _{\varepsilon }=B_{\varepsilon }\cap \partial \Omega $
,
 $\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
$\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
 $B_{\varepsilon }=B(x,\varepsilon r)$
with
$B_{\varepsilon }=B(x,\varepsilon r)$
with
 $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
 $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
 $B'=B(x',r')$
with
$B'=B(x',r')$
with
 $x'\in 2\Delta _{\varepsilon }$
and
$x'\in 2\Delta _{\varepsilon }$
and
 $0<r'<\varepsilon r c_0/4$
, and
$0<r'<\varepsilon r c_0/4$
, and
 $c_0$
is the corkscrew constant.
$c_0$
is the corkscrew constant.
-
○ We say that L satisfies
 $\mathrm {CME}(\omega _{L_0})$
if there exists
$\mathrm {CME}(\omega _{L_0})$
if there exists
 $C\ge 1$
(depending only on n, the
$C\ge 1$
(depending only on n, the
 $1$
-sided NTA constants, the CDC constant and the ellipticity of
$1$
-sided NTA constants, the CDC constant and the ellipticity of
 $L_0$
and L) such that for every
$L_0$
and L) such that for every
 $u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
 $Lu=0$
in the weak sense in
$Lu=0$
in the weak sense in
 $\Omega $
the following estimate holds (3.8)where
$\Omega $
the following estimate holds (3.8)where $$ \begin{align} \sup_B \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \leq C \|u\|_{L^{\infty}(\Omega)}^2, \end{align} $$
$$ \begin{align} \sup_B \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \leq C \|u\|_{L^{\infty}(\Omega)}^2, \end{align} $$
 $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
 $\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
$\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
 $B=B(x,r)$
with
$B=B(x,r)$
with
 $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
 $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
 $B'=B(x',r')$
with
$B'=B(x',r')$
with
 $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
 $0<r'<r c_0/4$
, and
$0<r'<r c_0/4$
, and
 $c_0$
is the corkscrew constant.
$c_0$
is the corkscrew constant.
-
○ Given
 $0<q<\infty $
, we say that L satisfies
$0<q<\infty $
, we say that L satisfies
 $\mathcal {S}<\mathcal {N}$
in
$\mathcal {S}<\mathcal {N}$
in
 $L^q(\omega _{L_0})$
if, for some given
$L^q(\omega _{L_0})$
if, for some given
 $\alpha>0$
, there exists
$\alpha>0$
, there exists
 $C_{\alpha }\ge 1$
(depending only on n, the
$C_{\alpha }\ge 1$
(depending only on n, the
 $1$
-sided NTA constants, the CDC constant, the ellipticity of
$1$
-sided NTA constants, the CDC constant, the ellipticity of
 $L_0$
and L,
$L_0$
and L,
 $\alpha $
and q) such that for every
$\alpha $
and q) such that for every
 $\Delta _0 = \Delta (x_0, r_0)$
with
$\Delta _0 = \Delta (x_0, r_0)$
with
 $x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
, and for every
$x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
, and for every
 $u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
satisfying
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
satisfying
 $Lu=0$
in the weak sense in
$Lu=0$
in the weak sense in
 $\Omega $
the following estimate holds (3.9)
$\Omega $
the following estimate holds (3.9) $$ \begin{align} \|\mathcal{S}^{\alpha}_{r_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_{\alpha} \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^q(5\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
$$ \begin{align} \|\mathcal{S}^{\alpha}_{r_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_{\alpha} \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^q(5\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
-
○ We say that any of the previous properties holds for characteristic functions if the corresponding estimate is valid for all solutions of the form
 $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
 $X\in \Omega $
, with
$X\in \Omega $
, with
 $S\subset \partial \Omega $
being an arbitrary Borel set (with
$S\subset \partial \Omega $
being an arbitrary Borel set (with
 $S\subset N\Delta _0$
in the case of
$S\subset N\Delta _0$
in the case of
 $L^{p}(\omega _{L_0})$
-solvability.)
$L^{p}(\omega _{L_0})$
-solvability.)
Remark 3.4. We would like to observe that, when either
![]() $\Omega $
and
$\Omega $
and
![]() $\partial \Omega $
are both bounded or
$\partial \Omega $
are both bounded or
![]() $\partial \Omega $
is unbounded, the elliptic measure is a probability (that is,
$\partial \Omega $
is unbounded, the elliptic measure is a probability (that is,
![]() $u_{L,\Omega }(X)=\omega _L^X(\partial \Omega )\equiv 1$
for every
$u_{L,\Omega }(X)=\omega _L^X(\partial \Omega )\equiv 1$
for every
![]() $X\in \Omega $
.) Hence, it has vanishing gradient and one can then remove the term
$X\in \Omega $
.) Hence, it has vanishing gradient and one can then remove the term
![]() $f_{\Delta , L_0}u_{L,\Omega }$
in equation (3.6). This means that the only case on which subtracting
$f_{\Delta , L_0}u_{L,\Omega }$
in equation (3.6). This means that the only case on which subtracting
![]() $f_{\Delta , L_0}u_{L,\Omega }$
is relevant is that where
$f_{\Delta , L_0}u_{L,\Omega }$
is relevant is that where
![]() $\Omega $
is unbounded and
$\Omega $
is unbounded and
![]() $\partial \Omega $
is bounded (e.g., the complementary of a ball.) As a matter of fact, one must subtract that term or a similar one for equation (3.6) to hold. To see this, take
$\partial \Omega $
is bounded (e.g., the complementary of a ball.) As a matter of fact, one must subtract that term or a similar one for equation (3.6) to hold. To see this, take
![]() $f\equiv 1\in \mathrm {BMO}(\partial \Omega , \omega _{L_0})$
so that
$f\equiv 1\in \mathrm {BMO}(\partial \Omega , \omega _{L_0})$
so that
![]() $\|f\|_{\mathrm {BMO}(\partial \Omega , \omega _{L_0})}=0$
and let
$\|f\|_{\mathrm {BMO}(\partial \Omega , \omega _{L_0})}=0$
and let
![]() $u=u_{L,\Omega }$
be the associated elliptic measure solution. One can see (cf. [Reference Hofmann, Martell and Toro35]) that the function
$u=u_{L,\Omega }$
be the associated elliptic measure solution. One can see (cf. [Reference Hofmann, Martell and Toro35]) that the function
![]() $u_{L,\Omega }$
is nonconstant (it decays at infinity), hence
$u_{L,\Omega }$
is nonconstant (it decays at infinity), hence
![]() $0<u_{L,\Omega }(X)< 1$
for every
$0<u_{L,\Omega }(X)< 1$
for every
![]() $X\in \Omega $
and
$X\in \Omega $
and
![]() $|\nabla u_{L,\Omega }|\not \equiv 0$
. This means that the version of equation (3.6) without the term
$|\nabla u_{L,\Omega }|\not \equiv 0$
. This means that the version of equation (3.6) without the term
![]() $f_{\Delta , L_0}u_{L,\Omega }$
cannot hold. Moreover, note that in this case equation (3.6) is trivial:
$f_{\Delta , L_0}u_{L,\Omega }$
cannot hold. Moreover, note that in this case equation (3.6) is trivial:
![]() $f_{\Delta , L_0}u_{L,\Omega }=u_{L,\Omega }$
and the left-hand side of equation (3.6) vanishes.
$f_{\Delta , L_0}u_{L,\Omega }=u_{L,\Omega }$
and the left-hand side of equation (3.6) vanishes.
Remark 3.5. As just explained in the previous remark, when either
![]() $\Omega $
and
$\Omega $
and
![]() $\partial \Omega $
are both bounded or
$\partial \Omega $
are both bounded or
![]() $\partial \Omega $
is unbounded, the left-hand sides of equations (3.6) and (3.7) are the same. As a result, (e) clearly implies (f)—and (e)
$\partial \Omega $
is unbounded, the left-hand sides of equations (3.6) and (3.7) are the same. As a result, (e) clearly implies (f)—and (e)
![]() $'$
implies (f)
$'$
implies (f)
![]() $'$
—upon taking
$'$
—upon taking
![]() $\varrho (\varepsilon )\equiv 0$
(we will see in the course of the proof that these two implications always hold). Much as before, when
$\varrho (\varepsilon )\equiv 0$
(we will see in the course of the proof that these two implications always hold). Much as before, when
![]() $\Omega $
is unbounded and
$\Omega $
is unbounded and
![]() $\partial \Omega $
is bounded, equation (3.7) needs to incorporate the term
$\partial \Omega $
is bounded, equation (3.7) needs to incorporate the term
![]() $\varrho (\varepsilon )\|f\|_{L^{\infty }(\partial \Omega , \omega _{L_0})}^2$
, otherwise it would fail for
$\varrho (\varepsilon )\|f\|_{L^{\infty }(\partial \Omega , \omega _{L_0})}^2$
, otherwise it would fail for
![]() $u=u_{L,\Omega }$
.
$u=u_{L,\Omega }$
.
Remark 3.6. In equation (3.6), one can replace
![]() $f_{\Delta , L_0}$
by
$f_{\Delta , L_0}$
by
![]() $f_{\Delta ', L_0}$
(see Remark 4.5 below). Also, when
$f_{\Delta ', L_0}$
(see Remark 4.5 below). Also, when
![]() $\Omega $
is unbounded and
$\Omega $
is unbounded and
![]() $\partial \Omega $
bounded, one can subtract a constant that does not depend on
$\partial \Omega $
bounded, one can subtract a constant that does not depend on
![]() $\Delta $
nor
$\Delta $
nor
![]() $\Delta '$
. Namely, let
$\Delta '$
. Namely, let
![]() $X_{\Omega }\in \Omega $
satisfy
$X_{\Omega }\in \Omega $
satisfy
![]() $\delta (X_{\Omega })\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
(say,
$\delta (X_{\Omega })\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
(say,
![]() $X_{\Omega }=X_{\Delta (x_0, r_0)}$
with
$X_{\Omega }=X_{\Delta (x_0, r_0)}$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
.) Then in equation (3.6) one can replace
$r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
.) Then in equation (3.6) one can replace
![]() $f_{\Delta , L_0}$
by
$f_{\Delta , L_0}$
by
![]() ; see Remark 4.5.
; see Remark 4.5.
The following lemmas state some properties of Green functions and elliptic measures. Proofs may be found in the forthcoming monograph [Reference Hofmann, Martell and Toro35]. See also [Reference Grüter and Widman27] for the properties of the Green function in bounded domains.
Lemma 3.7. Suppose that
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, is an open set satisfying the CDC. Given a real (nonnecessarily symmetric) elliptic operator
$n\ge 2$
, is an open set satisfying the CDC. Given a real (nonnecessarily symmetric) elliptic operator
![]() $L=-\mathop {\operatorname {div}}\nolimits (A\nabla )$
, there exist
$L=-\mathop {\operatorname {div}}\nolimits (A\nabla )$
, there exist
![]() $C>1$
(depending only on dimension and on the ellipticity constant of L) and
$C>1$
(depending only on dimension and on the ellipticity constant of L) and
![]() $c_{\theta }>0$
(depending on the above parameters and on
$c_{\theta }>0$
(depending on the above parameters and on
![]() $\theta \in (0,1)$
) such that
$\theta \in (0,1)$
) such that
![]() $G_L$
, the Green function associated with L, satisfies
$G_L$
, the Green function associated with L, satisfies
Moreover,
![]() $G_L(\cdot ,Y)\in W_{\mathrm {loc}}^{1,2}(\Omega \setminus \{Y\})$
for any
$G_L(\cdot ,Y)\in W_{\mathrm {loc}}^{1,2}(\Omega \setminus \{Y\})$
for any
![]() $Y\in \Omega $
and satisfies
$Y\in \Omega $
and satisfies
![]() $L G_L(\cdot ,Y)=\delta _Y$
in the sense of distributions, that is,
$L G_L(\cdot ,Y)=\delta _Y$
in the sense of distributions, that is,
In particular,
![]() $G_L(\cdot ,Y)$
is a weak solution to
$G_L(\cdot ,Y)$
is a weak solution to
![]() $L G_L(\cdot ,Y)=0$
in the open set
$L G_L(\cdot ,Y)=0$
in the open set
![]() $\Omega \setminus \{Y\}$
.
$\Omega \setminus \{Y\}$
.
Finally, the following Riesz formula holds:
for every
![]() $\varphi \in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
.
$\varphi \in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
.
Remark 3.8. If we also assume that
![]() $\Omega $
is bounded, following [Reference Hofmann, Martell and Toro35] we know that the Green function
$\Omega $
is bounded, following [Reference Hofmann, Martell and Toro35] we know that the Green function
![]() $G_L$
coincides with the one constructed in [Reference Grüter and Widman27]. Consequently, for each
$G_L$
coincides with the one constructed in [Reference Grüter and Widman27]. Consequently, for each
![]() $Y\in \Omega $
and
$Y\in \Omega $
and
![]() $0<r<\delta (Y)$
, there holds
$0<r<\delta (Y)$
, there holds
Moreover, for every
![]() $\varphi \in \mathscr {C}_c^{\infty }(\Omega )$
such that
$\varphi \in \mathscr {C}_c^{\infty }(\Omega )$
such that
![]() $0\le \varphi \le 1 $
and
$0\le \varphi \le 1 $
and
![]() $\varphi \equiv 1$
in
$\varphi \equiv 1$
in
![]() $B(Y,r)$
with
$B(Y,r)$
with
![]() $0<r<\delta (Y)$
, we have that
$0<r<\delta (Y)$
, we have that
The following result lists a number of properties which will be used throughout the paper:
Lemma 3.9. Suppose that
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, is a 1-sided NTA domain satisfying the CDC. Let
$n\ge 2$
, is a 1-sided NTA domain satisfying the CDC. Let
![]() $L_0=-\mathop {\operatorname {div}}\nolimits (A_0\nabla )$
and
$L_0=-\mathop {\operatorname {div}}\nolimits (A_0\nabla )$
and
![]() $L=-\mathop {\operatorname {div}}\nolimits (A\nabla )$
be two real (nonnecessarily symmetric) elliptic operators. There exist
$L=-\mathop {\operatorname {div}}\nolimits (A\nabla )$
be two real (nonnecessarily symmetric) elliptic operators. There exist
![]() $C_1\ge 1$
,
$C_1\ge 1$
,
![]() $\rho \in (0,1)$
(depending only on dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L) and
$\rho \in (0,1)$
(depending only on dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L) and
![]() $C_2\ge 1$
(depending on the same parameters and on the ellipticity of
$C_2\ge 1$
(depending on the same parameters and on the ellipticity of
![]() $L_0$
) such that for every
$L_0$
) such that for every
![]() $B_0=B(x_0,r_0)$
with
$B_0=B(x_0,r_0)$
with
![]() $x_0\in \partial \Omega $
,
$x_0\in \partial \Omega $
,
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
![]() $\Delta _0=B_0\cap \partial \Omega $
we have the following properties:
$\Delta _0=B_0\cap \partial \Omega $
we have the following properties:
-
(a)
 $\omega _L^Y(\Delta _0)\geq C_1^{-1}$
for every
$\omega _L^Y(\Delta _0)\geq C_1^{-1}$
for every
 $Y\in C_1^{-1}B_0\cap \Omega $
and
$Y\in C_1^{-1}B_0\cap \Omega $
and
 $\omega _L^{X_{\Delta _0}}(\Delta _0)\ge C_1^{-1}$
.
$\omega _L^{X_{\Delta _0}}(\Delta _0)\ge C_1^{-1}$
. -
(b) If
 $B=B(x,r)$
with
$B=B(x,r)$
with
 $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
 $\Delta =B\cap \partial \Omega $
is such that
$\Delta =B\cap \partial \Omega $
is such that
 $2B\subset B_0$
, then for all
$2B\subset B_0$
, then for all
 $X\in \Omega \setminus B_0$
we have that
$X\in \Omega \setminus B_0$
we have that  $$\begin{align*}\frac{1}{C_1}\omega_L^X(\Delta)\leq r^{n-1} G_L(X,X_{\Delta})\leq C_1\omega_L^X(\Delta). \end{align*}$$
$$\begin{align*}\frac{1}{C_1}\omega_L^X(\Delta)\leq r^{n-1} G_L(X,X_{\Delta})\leq C_1\omega_L^X(\Delta). \end{align*}$$
-
(c) If
 $X\in \Omega \setminus 4B_0$
, then
$X\in \Omega \setminus 4B_0$
, then  $$ \begin{align*} \omega_{L}^X(2\Delta_0)\leq C_1\omega_{L}^X(\Delta_0). \end{align*} $$
$$ \begin{align*} \omega_{L}^X(2\Delta_0)\leq C_1\omega_{L}^X(\Delta_0). \end{align*} $$
-
(d) If
 $B=B(x,r)$
with
$B=B(x,r)$
with
 $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
 $\Delta :=B\cap \partial \Omega $
is such that
$\Delta :=B\cap \partial \Omega $
is such that
 $B\subset B_0$
, then for every
$B\subset B_0$
, then for every
 $X\in \Omega \setminus 2\kappa _0B_0$
with
$X\in \Omega \setminus 2\kappa _0B_0$
with
 $\kappa _0$
as in equation (2.16), we have that As a consequence,
$\kappa _0$
as in equation (2.16), we have that As a consequence, $$ \begin{align*} \frac{1}{C_1}\omega_L^{X_{\Delta_0}}(\Delta)\leq \frac{\omega_L^X(\Delta)}{\omega_L^X(\Delta_0)}\leq C_1\omega_L^{X_{\Delta_0}}(\Delta). \end{align*} $$
$$ \begin{align*} \frac{1}{C_1}\omega_L^{X_{\Delta_0}}(\Delta)\leq \frac{\omega_L^X(\Delta)}{\omega_L^X(\Delta_0)}\leq C_1\omega_L^{X_{\Delta_0}}(\Delta). \end{align*} $$
 $$\begin{align*}\frac1C_1 \frac1{\omega_L^X(\Delta_0)}\le \frac{d\omega_L^{{X_{\Delta_0}}}}{d\omega_L^X}(y)\le C_1 \frac1{\omega_L^X(\Delta_0)}, \qquad\mbox{for} \ \omega_L^X\mbox{-a.e.} \ y\in\Delta_0. \end{align*}$$
$$\begin{align*}\frac1C_1 \frac1{\omega_L^X(\Delta_0)}\le \frac{d\omega_L^{{X_{\Delta_0}}}}{d\omega_L^X}(y)\le C_1 \frac1{\omega_L^X(\Delta_0)}, \qquad\mbox{for} \ \omega_L^X\mbox{-a.e.} \ y\in\Delta_0. \end{align*}$$
-
(e) For every
 $X\in B_0\cap \Omega $
and for any
$X\in B_0\cap \Omega $
and for any
 $j\ge 1$
$j\ge 1$
 $$\begin{align*}\frac{d\omega_L^X}{d\omega_L^{X_{2^j\Delta_0}}}(y)\le C_1\,\bigg(\frac{\delta(X)}{2^j\,r_0}\bigg)^{\rho}, \qquad\mbox{for} \ \omega_L^X\mbox{-a.e.} \ y\in\partial\Omega\setminus 2^j\,\Delta_0. \end{align*}$$
$$\begin{align*}\frac{d\omega_L^X}{d\omega_L^{X_{2^j\Delta_0}}}(y)\le C_1\,\bigg(\frac{\delta(X)}{2^j\,r_0}\bigg)^{\rho}, \qquad\mbox{for} \ \omega_L^X\mbox{-a.e.} \ y\in\partial\Omega\setminus 2^j\,\Delta_0. \end{align*}$$
-
(f) If
 $0\le u\in W^{1,2}_{\mathrm {loc}}(B_0\cap \Omega )\cap \mathscr {C}(\overline {B_0\cap \Omega })$
satisfies
$0\le u\in W^{1,2}_{\mathrm {loc}}(B_0\cap \Omega )\cap \mathscr {C}(\overline {B_0\cap \Omega })$
satisfies
 $Lu=0$
in the weak-sense in
$Lu=0$
in the weak-sense in
 $B_0\cap \Omega $
and
$B_0\cap \Omega $
and
 $u\equiv 0$
in
$u\equiv 0$
in
 $\Delta _0$
then
$\Delta _0$
then  $$\begin{align*}u(X) \le C_1\, \Big(\frac{\delta(X)}{r_0}\Big)^{\rho} u(X_{\Delta_0}), \qquad \text{for } X\in\tfrac12 B_0\cap\Omega. \end{align*}$$
$$\begin{align*}u(X) \le C_1\, \Big(\frac{\delta(X)}{r_0}\Big)^{\rho} u(X_{\Delta_0}), \qquad \text{for } X\in\tfrac12 B_0\cap\Omega. \end{align*}$$
Remark 3.10. We note that from
![]() $(d)$
in the previous result and Harnack’s inequality one can easily see that given
$(d)$
in the previous result and Harnack’s inequality one can easily see that given
![]() $Q, Q', Q"\in \mathbb {D}(\partial \Omega )$
$Q, Q', Q"\in \mathbb {D}(\partial \Omega )$
 $$ \begin{align} \frac{\omega_L^{X_{Q"}}(Q)}{\omega_L^{X_{Q"}}(Q')}\approx \omega_L^{X_{Q'}}(Q), \qquad\mbox{whenever } Q\subset Q'\subset Q". \end{align} $$
$$ \begin{align} \frac{\omega_L^{X_{Q"}}(Q)}{\omega_L^{X_{Q"}}(Q')}\approx \omega_L^{X_{Q'}}(Q), \qquad\mbox{whenever } Q\subset Q'\subset Q". \end{align} $$
Also,
![]() $(d)$
, Harnack’s inequality and equation (2.6) give
$(d)$
, Harnack’s inequality and equation (2.6) give
 $$ \begin{align} \frac{d\omega_L^{X_{Q'}}}{d\omega_L^{X_{Q"}}}(y) \approx \frac1{\omega_L^{X_{Q"}}(Q')}, \qquad \mbox{ for} \ \omega_L^{X_{Q"}}\mbox{-a.e.} \ y\in Q', \mbox{whenever }Q'\subset Q". \end{align} $$
$$ \begin{align} \frac{d\omega_L^{X_{Q'}}}{d\omega_L^{X_{Q"}}}(y) \approx \frac1{\omega_L^{X_{Q"}}(Q')}, \qquad \mbox{ for} \ \omega_L^{X_{Q"}}\mbox{-a.e.} \ y\in Q', \mbox{whenever }Q'\subset Q". \end{align} $$
Observe that since
![]() $\omega _L^{X_{Q"}}\ll \omega _L^{X_{Q'}}$
we can easily get an analogous inequality for the reciprocal of the Radon–Nikodym derivative.
$\omega _L^{X_{Q"}}\ll \omega _L^{X_{Q'}}$
we can easily get an analogous inequality for the reciprocal of the Radon–Nikodym derivative.
Remark 3.11. It is not hard to see that if
![]() $\omega _L\ll \omega _{L_0}$
, then Lemma 3.9 gives the following:
$\omega _L\ll \omega _{L_0}$
, then Lemma 3.9 gives the following:
The left-to-right implication follows at once from equation (3.3) by taking
![]() $B=B_0$
(hence,
$B=B_0$
(hence,
![]() $\Delta =\Delta _0$
) and Lemma 3.9 part
$\Delta =\Delta _0$
) and Lemma 3.9 part
![]() $(a)$
. For the converse, fix
$(a)$
. For the converse, fix
![]() $B_0=B(x_0,r_0)$
and
$B_0=B(x_0,r_0)$
and
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $B\subset B_0$
,
$B\subset B_0$
,
![]() $x_0,x \in \partial \Omega $
and
$x_0,x \in \partial \Omega $
and
![]() $0 < r_0,r < \operatorname {\mathrm {diam}}(\partial \Omega )$
. Write
$0 < r_0,r < \operatorname {\mathrm {diam}}(\partial \Omega )$
. Write
![]() $\Delta _0=B_0\cap \partial \Omega $
and
$\Delta _0=B_0\cap \partial \Omega $
and
![]() $\Delta =B\cap \partial \Omega $
. If
$\Delta =B\cap \partial \Omega $
. If
![]() $r\approx r_0$
, we have by Lemma 3.9 part
$r\approx r_0$
, we have by Lemma 3.9 part
![]() $(a)$
,
$(a)$
,

On the other hand, if
![]() $r\ll r_0$
, we have by Lemma 3.9 part
$r\ll r_0$
, we have by Lemma 3.9 part
![]() $(d)$
and the fact that
$(d)$
and the fact that
![]() $\omega _L\ll \omega _{L_0}$
that
$\omega _L\ll \omega _{L_0}$
that
 $$\begin{align*}h(\cdot\,;L,L_0,X_{\Delta_0}) = \frac{d\omega_L^{X_{\Delta_0}}}{d\omega_{L_0}^{X_{\Delta_0}}} = \frac{d\omega_L^{X_{\Delta_0}}}{d\omega_{L}^{X_{\Delta}}} \frac{d\omega_L^{X_{\Delta}}}{d\omega_{L_0}^{X_{\Delta}}} \frac{d\omega_{L_0}^{X_{\Delta}}}{d\omega_{L_0}^{X_{\Delta_0}}} \approx h(\cdot\,;L,L_0,X_{\Delta})\frac{\omega_{L}^{X_{\Delta_0}}(\Delta)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}, \quad\omega_{L_0}\text{-a.e. in } \Delta. \end{align*}$$
$$\begin{align*}h(\cdot\,;L,L_0,X_{\Delta_0}) = \frac{d\omega_L^{X_{\Delta_0}}}{d\omega_{L_0}^{X_{\Delta_0}}} = \frac{d\omega_L^{X_{\Delta_0}}}{d\omega_{L}^{X_{\Delta}}} \frac{d\omega_L^{X_{\Delta}}}{d\omega_{L_0}^{X_{\Delta}}} \frac{d\omega_{L_0}^{X_{\Delta}}}{d\omega_{L_0}^{X_{\Delta_0}}} \approx h(\cdot\,;L,L_0,X_{\Delta})\frac{\omega_{L}^{X_{\Delta_0}}(\Delta)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}, \quad\omega_{L_0}\text{-a.e. in } \Delta. \end{align*}$$
This and Lemma 3.9 part
![]() $(d)$
give
$(d)$
give

Thus, equation (3.3) holds and the right-to-left implication holds.
Remark 3.12. It is not difficult to see that under the assumptions of Lemma 3.9 one has
where the sup is taken over all surface balls
![]() $\Delta =B(x,r)\cap \partial \Omega $
with
$\Delta =B(x,r)\cap \partial \Omega $
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Thus, we could have taken this as the definition of
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Thus, we could have taken this as the definition of
![]() $f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
.
$f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
.
Remark 3.13. Under the assumptions of Lemma 3.9, for every
![]() $\Delta _0$
as above if
$\Delta _0$
as above if
![]() $f\in \mathrm {BMO}(\Delta _0, \omega _L)$
, then John–Nirenberg’s inequality holds locally in
$f\in \mathrm {BMO}(\Delta _0, \omega _L)$
, then John–Nirenberg’s inequality holds locally in
![]() $\Delta _0$
and the implicit constants depend on the doubling property of
$\Delta _0$
and the implicit constants depend on the doubling property of
![]() $\omega _L^{X_{\Delta _0}}$
in
$\omega _L^{X_{\Delta _0}}$
in
![]() $2\Delta _0$
. Thus, if one further assumes that
$2\Delta _0$
. Thus, if one further assumes that
![]() $f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
, then for every
$f\in \mathrm {BMO}(\partial \Omega , \omega _L)$
, then for every
![]() $1<q<\infty $
there holds
$1<q<\infty $
there holds

where the sups are taken, respectively, over all surface balls
![]() $\Delta _0=B(x_0,r_0)\cap \partial \Omega $
with
$\Delta _0=B(x_0,r_0)\cap \partial \Omega $
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $B=B(x,r)\subset B_0$
with
$B=B(x,r)\subset B_0$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that the implicit constants depend only on dimension, the 1-sided NTA constants, the CDC constant, the ellipticity of L and q.
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that the implicit constants depend only on dimension, the 1-sided NTA constants, the CDC constant, the ellipticity of L and q.
4 Proof of Theorem 1.1
We first observe that if the equivalence
![]() $\mathrm {(a)}{}_{p'}\Longleftrightarrow \mathrm {(b)}{}_p$
holds for each
$\mathrm {(a)}{}_{p'}\Longleftrightarrow \mathrm {(b)}{}_p$
holds for each
![]() $p\in (1,\infty )$
, then
$p\in (1,\infty )$
, then
![]() $\mathrm {(a)} \Longleftrightarrow \mathrm {(b)}$
. Also, since Jensen’s inequality readily gives that
$\mathrm {(a)} \Longleftrightarrow \mathrm {(b)}$
. Also, since Jensen’s inequality readily gives that
![]() $ \omega _L \in RH_{p'}(\partial \Omega , \omega _{L_0})$
implies
$ \omega _L \in RH_{p'}(\partial \Omega , \omega _{L_0})$
implies
![]() $\omega _L \in RH_{q'}(\partial \Omega , \omega _{L_0})$
for all
$\omega _L \in RH_{q'}(\partial \Omega , \omega _{L_0})$
for all
![]() $q\ge p$
, the equivalence
$q\ge p$
, the equivalence
![]() $\mathrm {(a)}{}_{p'}\Longleftrightarrow \mathrm {(b)}{}_p$
yields
$\mathrm {(a)}{}_{p'}\Longleftrightarrow \mathrm {(b)}{}_p$
yields
![]() $\mathrm {(b)}_p\Longrightarrow \mathrm {(b)}_q$
for all
$\mathrm {(b)}_p\Longrightarrow \mathrm {(b)}_q$
for all
![]() $q\ge p$
. Finally,
$q\ge p$
. Finally,
![]() $\mathrm {(b)}_p\Longrightarrow \mathrm {(b)}_p'$
clearly implies
$\mathrm {(b)}_p\Longrightarrow \mathrm {(b)}_p'$
clearly implies
![]() $\mathrm {(b)}\Longrightarrow \mathrm {(b)'}$
. With all these in mind, we will follow the scheme
$\mathrm {(b)}\Longrightarrow \mathrm {(b)'}$
. With all these in mind, we will follow the scheme
Before proving all these implications we present some auxiliary results:
Lemma 4.1. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. There exists
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. There exists
![]() $\rho \in (0,1)$
(depending only on dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L) and
$\rho \in (0,1)$
(depending only on dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L) and
![]() $C_1\ge 1$
(depending on the same parameters and on the ellipticity of
$C_1\ge 1$
(depending on the same parameters and on the ellipticity of
![]() $L_0$
) such that the following holds: If
$L_0$
) such that the following holds: If
![]() $\Delta =B\cap \partial \Omega $
and
$\Delta =B\cap \partial \Omega $
and
![]() $\Delta '=B'\cap \partial \Omega $
, where
$\Delta '=B'\cap \partial \Omega $
, where
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
, where
$0<r'<r c_0/4$
, where
![]() $c_0$
is the corkscrew constant, and
$c_0$
is the corkscrew constant, and
![]() $u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
$u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
![]() $X\in \Omega $
, then
$X\in \Omega $
, then
 $$ \begin{align} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u_{L,\Omega}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \leq C_1 \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}. \end{align} $$
$$ \begin{align} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u_{L,\Omega}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \leq C_1 \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}. \end{align} $$
Proof. Fix
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
. Let
$0<r'<r c_0/4$
. Let
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
.
$\Delta '=B'\cap \partial \Omega $
.
We note that when either
![]() $\partial \Omega $
is unbounded or
$\partial \Omega $
is unbounded or
![]() $\partial \Omega $
and
$\partial \Omega $
and
![]() $\Omega $
are both bounded then the elliptic measure is a probability; hence,
$\Omega $
are both bounded then the elliptic measure is a probability; hence,
![]() $u_{L,\Omega }\equiv 1$
and the desired estimate is trivial. This means that we may assume that
$u_{L,\Omega }\equiv 1$
and the desired estimate is trivial. This means that we may assume that
![]() $\partial \Omega $
is bounded and
$\partial \Omega $
is bounded and
![]() $\Omega $
is unbounded (e.g., the complement of a closed ball). In that scenario,
$\Omega $
is unbounded (e.g., the complement of a closed ball). In that scenario,
![]() $u_{L,\Omega }$
decays at
$u_{L,\Omega }$
decays at
![]() $\infty $
,
$\infty $
,
![]() $0<u_{L, \Omega }<1$
in
$0<u_{L, \Omega }<1$
in
![]() $\Omega $
, and
$\Omega $
, and
![]() $u_{L,\Omega }|_{\partial \Omega }\equiv 1$
. Define
$u_{L,\Omega }|_{\partial \Omega }\equiv 1$
. Define
![]() $v:=1-u_{L,\Omega }$
, and note that our assumptions guarantee that
$v:=1-u_{L,\Omega }$
, and note that our assumptions guarantee that
![]() $v\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap \mathscr {C}(\overline {\Omega })$
with
$v\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap \mathscr {C}(\overline {\Omega })$
with
![]() $0\le v\le 1$
and
$0\le v\le 1$
and
![]() $v|_{\partial \Omega }\equiv 0$
. By Lemma 3.9 part
$v|_{\partial \Omega }\equiv 0$
. By Lemma 3.9 part
![]() $(f)$
applied in
$(f)$
applied in
![]() $B(x',\operatorname {\mathrm {diam}}(\partial \Omega )/2)$
we have
$B(x',\operatorname {\mathrm {diam}}(\partial \Omega )/2)$
we have
Set
![]() $\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
, and pick
$\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
, and pick
![]() $Z_{I, B'}\in I\cap B'$
for
$Z_{I, B'}\in I\cap B'$
for
![]() $I \in \mathcal {W}_{B'}$
. Caccioppoli’s and Harnack’s inequalities and the previous estimate yield
$I \in \mathcal {W}_{B'}$
. Caccioppoli’s and Harnack’s inequalities and the previous estimate yield
Thus, Lemma 3.9 gives
 $$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\ell(I)^{1-n} \iint_{I} |\nabla v(X)|^2 \, d X \\ &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I) \Big(\frac{\ell(I)}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\\ &\lesssim \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\sum_{I\in \mathcal{W}_{B'}: \ell(I)=2^{-k}} \omega_{L_0}^{X_{\Delta}}(Q_I), \end{align*} $$
$$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\ell(I)^{1-n} \iint_{I} |\nabla v(X)|^2 \, d X \\ &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I) \Big(\frac{\ell(I)}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\\ &\lesssim \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\sum_{I\in \mathcal{W}_{B'}: \ell(I)=2^{-k}} \omega_{L_0}^{X_{\Delta}}(Q_I), \end{align*} $$
where
![]() $Q_I\in \mathbb {D}(\partial \Omega )$
is so that
$Q_I\in \mathbb {D}(\partial \Omega )$
is so that
![]() $\ell (Q_I)=\ell (I)$
and contains
$\ell (Q_I)=\ell (I)$
and contains
![]() $\widehat {y}_I \in \partial \Omega $
such that
$\widehat {y}_I \in \partial \Omega $
such that
![]() $\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. It is easy to see that if
$\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. It is easy to see that if
![]() $2^{-k}\lesssim r$
, then the family
$2^{-k}\lesssim r$
, then the family
![]() $\{Q_I\}_{I\in \mathcal {W}_{B'}, \ell (I)=2^{-k}}$
has bounded overlap uniformly on k and also that
$\{Q_I\}_{I\in \mathcal {W}_{B'}, \ell (I)=2^{-k}}$
has bounded overlap uniformly on k and also that
![]() $Q_I\subset C\Delta '$
for every
$Q_I\subset C\Delta '$
for every
![]() $I\in \mathcal {W}_{B'}$
, where C is some harmless dimensional constant. Hence,
$I\in \mathcal {W}_{B'}$
, where C is some harmless dimensional constant. Hence,
 $$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\omega_{L_0}^{X_{\Delta}}(C\,\Delta') \lesssim \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align*} $$
$$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\omega_{L_0}^{X_{\Delta}}(C\,\Delta') \lesssim \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align*} $$
This gives the desired estimate.
Given
![]() $Q_0\in \mathbb {D}(\partial \Omega ), \vartheta \in \mathbb {N}$
, for every
$Q_0\in \mathbb {D}(\partial \Omega ), \vartheta \in \mathbb {N}$
, for every
![]() $\eta \in (0,1)$
, we define the modified nontangential cone
$\eta \in (0,1)$
, we define the modified nontangential cone

It is not hard to see that the sets
![]() $\{U_{Q,\eta ^3}^{\vartheta }\}_{Q\in \mathbb {D}_{Q_0}}$
have bounded overlap with constant depending on
$\{U_{Q,\eta ^3}^{\vartheta }\}_{Q\in \mathbb {D}_{Q_0}}$
have bounded overlap with constant depending on
![]() $\eta $
.
$\eta $
.
The following result was obtained in [Reference Cavero, Hofmann, Martell and Toro9, Lemma 3.10] (for
![]() $\beta>0$
) and in [Reference Cao, Martell and Olivo7, Lemma 3.30] (for
$\beta>0$
) and in [Reference Cao, Martell and Olivo7, Lemma 3.30] (for
![]() $\beta =0$
), both in the context of 1-sided CAD, extending [Reference Kenig, Koch, Pipher and Toro43, Lemma 2.6] and [Reference Kenig, Kirchheim, Pipher and Toro42, Lemma 2.3]. It is not hard to see that the proof works with no changes in our setting:
$\beta =0$
), both in the context of 1-sided CAD, extending [Reference Kenig, Koch, Pipher and Toro43, Lemma 2.6] and [Reference Kenig, Kirchheim, Pipher and Toro42, Lemma 2.3]. It is not hard to see that the proof works with no changes in our setting:
Lemma 4.2. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. There exist
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. There exist
![]() $0<\eta \ll 1$
(depending only on the dimension, the 1-sided NTA constants, the CDC constant, and the ellipticity of L), and
$0<\eta \ll 1$
(depending only on the dimension, the 1-sided NTA constants, the CDC constant, and the ellipticity of L), and
![]() $\beta _0\in (0,1)$
,
$\beta _0\in (0,1)$
,
![]() $C_{\eta }\ge 1$
both depending on the same parameters and additionally on
$C_{\eta }\ge 1$
both depending on the same parameters and additionally on
![]() $\eta $
such that, for every
$\eta $
such that, for every
![]() $Q_0\in \mathbb {D}(\partial \Omega )$
, for every
$Q_0\in \mathbb {D}(\partial \Omega )$
, for every
![]() $0<\beta <\beta _0$
and for every Borel set
$0<\beta <\beta _0$
and for every Borel set
![]() $F\subset Q_0$
satisfying
$F\subset Q_0$
satisfying
![]() $\omega _L^{X_{Q_0}}(F)\le \beta \omega _L^{X_{Q_0}}(Q_0)$
, there exists a Borel set
$\omega _L^{X_{Q_0}}(F)\le \beta \omega _L^{X_{Q_0}}(Q_0)$
, there exists a Borel set
![]() $S\subset Q_0$
such that the bounded weak solution
$S\subset Q_0$
such that the bounded weak solution
![]() $u(X)=\omega ^X_L(S)$
,
$u(X)=\omega ^X_L(S)$
,
![]() $X\in \Omega $
, satisfies
$X\in \Omega $
, satisfies
 $$ \begin{align} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x):=\bigg(\iint_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12} \ge C_{\eta}^{-1} \big(\log(\beta^{-1})\big)^{\frac12} ,\qquad \forall\,x\in F. \end{align} $$
$$ \begin{align} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x):=\bigg(\iint_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)^{\frac12} \ge C_{\eta}^{-1} \big(\log(\beta^{-1})\big)^{\frac12} ,\qquad \forall\,x\in F. \end{align} $$
Furthermore, in the case
![]() $\beta =0$
, that is, when
$\beta =0$
, that is, when
![]() $\omega _L^{X_{Q_0}}(F)=0$
, there exists a Borel set
$\omega _L^{X_{Q_0}}(F)=0$
, there exists a Borel set
![]() $S\subset Q_0$
such that the bounded weak solution
$S\subset Q_0$
such that the bounded weak solution
![]() $u(X)=\omega ^X_L(S)$
,
$u(X)=\omega ^X_L(S)$
,
![]() $X\in \Omega $
, satisfies
$X\in \Omega $
, satisfies
Lemma 4.3. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$
and
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. There exists
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be real (nonnecessarily symmetric) elliptic operators. There exists
![]() $C\ge 1$
(depending only on the dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L and
$C\ge 1$
(depending only on the dimension, the 1-sided NTA constants, the CDC constant and the ellipticity of L and
![]() $L_0$
) such that the following holds. Given
$L_0$
) such that the following holds. Given
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
, let
$0<r'<r c_0/4$
, let
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
, for every
$\Delta '=B'\cap \partial \Omega $
, for every
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
![]() $Lu=0$
in the weak sense in
$Lu=0$
in the weak sense in
![]() $\Omega $
, we have
$\Omega $
, we have
 $$ \begin{align*} \frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} & |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X\\ &\qquad\le C\,\int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ C\,\sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2. \end{align*} $$
$$ \begin{align*} \frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} & |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X\\ &\qquad\le C\,\int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ C\,\sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2. \end{align*} $$
Proof. Fix B,
![]() $B'$
,
$B'$
,
![]() $\Delta $
,
$\Delta $
,
![]() $\Delta '$
and u as in the statement. Define
$\Delta '$
and u as in the statement. Define
![]() $\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
and
$\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
and
![]() $\mathcal {W}_{B'}^M:=\{I\in \mathcal {W}_{B'}: \ell (I)<r'/M\}$
for
$\mathcal {W}_{B'}^M:=\{I\in \mathcal {W}_{B'}: \ell (I)<r'/M\}$
for
![]() $M\ge 1$
large enough to be taken. For each
$M\ge 1$
large enough to be taken. For each
![]() $I\in \mathcal {W}_{B'}$
, pick
$I\in \mathcal {W}_{B'}$
, pick
![]() $Z_I\in I\cap B'$
and
$Z_I\in I\cap B'$
and
![]() $Q_I\in \mathbb {D}(\partial \Omega )$
so that
$Q_I\in \mathbb {D}(\partial \Omega )$
so that
![]() $\ell (Q_I)=\ell (I)$
and contains
$\ell (Q_I)=\ell (I)$
and contains
![]() $\widehat {y}_I \in \partial \Omega $
such that
$\widehat {y}_I \in \partial \Omega $
such that
![]() $\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. If
$\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. If
![]() $z\in Q_I$
and
$z\in Q_I$
and
![]() $I\in \mathcal {W}_{B'}^M$
, then
$I\in \mathcal {W}_{B'}^M$
, then
provided
![]() $M>C_n$
. Hence,
$M>C_n$
. Hence,
![]() $Q_I\subset 2\Delta '$
for every
$Q_I\subset 2\Delta '$
for every
![]() $I\in \mathcal {W}_{B'}^M$
. Write
$I\in \mathcal {W}_{B'}^M$
. Write
![]() $\mathcal {F}$
for the collection of maximal cubes in
$\mathcal {F}$
for the collection of maximal cubes in
![]() $\{Q_I\}_{I\in \mathcal {W}_{B'}^M}$
, with respect to the inclusion (maximal cubes exist since
$\{Q_I\}_{I\in \mathcal {W}_{B'}^M}$
, with respect to the inclusion (maximal cubes exist since
![]() $Q_I\subset 2\Delta '$
for every
$Q_I\subset 2\Delta '$
for every
![]() $I\in \mathcal {W}_{B'}^M$
.) Hence,
$I\in \mathcal {W}_{B'}^M$
.) Hence,
![]() $Q_I\subset Q$
for some
$Q_I\subset Q$
for some
![]() $Q\in \mathcal {F}$
. Let
$Q\in \mathcal {F}$
. Let
![]() $\vartheta =\vartheta _0$
and by construction
$\vartheta =\vartheta _0$
and by construction
![]() $I\in \mathcal {W}_{Q_I}^{\vartheta }\subset \mathcal {W}_{Q_I}^{\vartheta ,*}$
(see Section 2.3.) Hence, for every
$I\in \mathcal {W}_{Q_I}^{\vartheta }\subset \mathcal {W}_{Q_I}^{\vartheta ,*}$
(see Section 2.3.) Hence, for every
![]() $y\in Q\in \mathcal {F}$
$y\in Q\in \mathcal {F}$
 $$\begin{align*}\bigcup_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} I \subset \bigcup_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} U_{Q_I}^{\vartheta} \subset \bigcup_{y\in Q'\in\mathbb{D}_Q} U_{Q'}^{\vartheta} = \Gamma_{Q}^{\vartheta}(y). \end{align*}$$
$$\begin{align*}\bigcup_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} I \subset \bigcup_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} U_{Q_I}^{\vartheta} \subset \bigcup_{y\in Q'\in\mathbb{D}_Q} U_{Q'}^{\vartheta} = \Gamma_{Q}^{\vartheta}(y). \end{align*}$$
This gives
 $$ \begin{align*} \Sigma_1: &= \sum_{I\in \mathcal{W}_{B'}^M} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &= \sum_{Q\in\mathcal{F}} \sum_{I\in \mathcal{W}_{B'}^M:Q_I\in\mathbb{D}_Q} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &= \sum_{Q\in\mathcal{F}} \int_{Q} \sum_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} \iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X\, d\omega_{L_0}^{X_{\Delta}}(y) \\ &\le \sum_{Q\in\mathcal{F}} \int_{Q} \iint_{\Gamma_{Q}^{\vartheta}(y) } |\nabla u(X)|^2 \, \delta(X)^{1-n} d X d\omega_{L_0}^{X_{\Delta}}(y) \\ &= \sum_{Q\in\mathcal{F}} \int_{Q} \mathcal{S}_Q^{\vartheta} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y). \end{align*} $$
$$ \begin{align*} \Sigma_1: &= \sum_{I\in \mathcal{W}_{B'}^M} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &= \sum_{Q\in\mathcal{F}} \sum_{I\in \mathcal{W}_{B'}^M:Q_I\in\mathbb{D}_Q} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &= \sum_{Q\in\mathcal{F}} \int_{Q} \sum_{I\in \mathcal{W}_{B'}^M: y\in Q_I\in\mathbb{D}_Q} \iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X\, d\omega_{L_0}^{X_{\Delta}}(y) \\ &\le \sum_{Q\in\mathcal{F}} \int_{Q} \iint_{\Gamma_{Q}^{\vartheta}(y) } |\nabla u(X)|^2 \, \delta(X)^{1-n} d X d\omega_{L_0}^{X_{\Delta}}(y) \\ &= \sum_{Q\in\mathcal{F}} \int_{Q} \mathcal{S}_Q^{\vartheta} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y). \end{align*} $$
To continue, let
![]() $y\in Q\in \mathcal {F}$
and
$y\in Q\in \mathcal {F}$
and
![]() $X\in \Gamma _Q^{\vartheta }(y)$
. Then
$X\in \Gamma _Q^{\vartheta }(y)$
. Then
![]() $X\in I^*$
with
$X\in I^*$
with
![]() $I\in \mathcal {W}_{Q'}^{\vartheta ,*}$
and
$I\in \mathcal {W}_{Q'}^{\vartheta ,*}$
and
![]() $y\in Q'\in \mathbb {D}_{Q}$
. Thus,
$y\in Q'\in \mathbb {D}_{Q}$
. Thus,
where we have used equation (2.15), and the last estimate holds since
![]() $\ell (I)<r'/M$
for every
$\ell (I)<r'/M$
for every
![]() $I\in \mathcal {W}_{B'}^M$
. This shows that taking M large enough
$I\in \mathcal {W}_{B'}^M$
. This shows that taking M large enough
![]() $X\in \Gamma ^{\alpha '}_{2 r'}(y)$
for some
$X\in \Gamma ^{\alpha '}_{2 r'}(y)$
for some
![]() $\alpha '=\alpha '(\vartheta )$
. Note also that
$\alpha '=\alpha '(\vartheta )$
. Note also that
![]() $2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now conclude that
$2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now conclude that
 $$ \begin{align*} \Sigma_1 \lesssim \sum_{Q\in\mathcal{F}} \int_{Q} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y) \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y) \approx \omega_{L_0}^{X_{\Delta}}(\Delta') \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y), \end{align*} $$
$$ \begin{align*} \Sigma_1 \lesssim \sum_{Q\in\mathcal{F}} \int_{Q} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y) \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{\Delta}}(y) \approx \omega_{L_0}^{X_{\Delta}}(\Delta') \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y), \end{align*} $$
where we have used Lemma 3.9.
Now, we note that for each
![]() $I\in \mathcal {W}_{B'}\setminus \mathcal {W}_{B'}^M$
we have
$I\in \mathcal {W}_{B'}\setminus \mathcal {W}_{B'}^M$
we have
![]() $\ell (Q_I)=\ell (I)\approx _M r'$
; hence, for every
$\ell (Q_I)=\ell (I)\approx _M r'$
; hence, for every
![]() $Y\in I^*$
we have
$Y\in I^*$
we have
Also,
Thus, Lemma 3.9 implies that
![]() $\omega _{L_0}^{X_{\Delta }}(Q_I)\approx _M \omega _{L_0}^{X_{\Delta }}(\Delta ')$
. As a consequence of this, we get
$\omega _{L_0}^{X_{\Delta }}(Q_I)\approx _M \omega _{L_0}^{X_{\Delta }}(\Delta ')$
. As a consequence of this, we get
 $$ \begin{align*} \Sigma_2: &= \sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \ell(I)^{1-n} \iint_{I} |\nabla u(X)|^2 d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta') \sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \ell(I)^{-n-1}\iint_{I^*} |u(X)|^2 \, d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\,\#(\mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M) \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ &\lesssim_M \omega_{L_0}^{X_{\Delta}}(\Delta') \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2, \end{align*} $$
$$ \begin{align*} \Sigma_2: &= \sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \ell(I)^{1-n} \iint_{I} |\nabla u(X)|^2 d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta') \sum_{I\in \mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M} \ell(I)^{-n-1}\iint_{I^*} |u(X)|^2 \, d X \\ &\lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\,\#(\mathcal{W}_{B'}\setminus \mathcal{W}_{B'}^M) \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ &\lesssim_M \omega_{L_0}^{X_{\Delta}}(\Delta') \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2, \end{align*} $$
where we have used that
![]() $\mathcal {W}_{B'}\setminus \mathcal {W}_{B'}^M$
has bounded cardinality depending on n and M.
$\mathcal {W}_{B'}\setminus \mathcal {W}_{B'}^M$
has bounded cardinality depending on n and M.
To complete the proof, we use Lemma 3.9 and the estimates proved for
![]() $\Sigma _1$
and
$\Sigma _1$
and
![]() $\Sigma _2$
:
$\Sigma _2$
:
 $$ \begin{align*} &\iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \le \sum_{I\in \mathcal{W}_{B'}} \iint_{I} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\qquad \approx \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &\qquad = \Sigma_1+\Sigma_2 \\ &\qquad \lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\Big( \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2\Big). \end{align*} $$
$$ \begin{align*} &\iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \le \sum_{I\in \mathcal{W}_{B'}} \iint_{I} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\qquad \approx \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\iint_{I} |\nabla u(X)|^2 \, \delta(X)^{1-n} d X \\ &\qquad = \Sigma_1+\Sigma_2 \\ &\qquad \lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\Big( \int_{2\Delta'} \mathcal{S}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2\Big). \end{align*} $$
This completes the proof.
For the following result, we need to introduce some notation:
 $$ \begin{align*} \mathcal{A}_{r}^{\alpha} F(x):=\bigg(\iint_{\Gamma_{r}^{\alpha}(x)}|F(Y)|^2\,dY\bigg)^{\frac12}, \qquad x\in\partial\Omega,\ 0<r<\infty, \alpha>0, \end{align*} $$
$$ \begin{align*} \mathcal{A}_{r}^{\alpha} F(x):=\bigg(\iint_{\Gamma_{r}^{\alpha}(x)}|F(Y)|^2\,dY\bigg)^{\frac12}, \qquad x\in\partial\Omega,\ 0<r<\infty, \alpha>0, \end{align*} $$
for any
![]() $F\in L^2_{\mathrm {loc}}(\Omega \cap B(x,r))$
.
$F\in L^2_{\mathrm {loc}}(\Omega \cap B(x,r))$
.
Lemma 4.4. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
$n\ge 2$
, be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7), and let
![]() $L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. Given
$L_0u=-\mathop {\operatorname {div}}\nolimits (A_0\nabla u)$
be a real (nonnecessarily symmetric) elliptic operator. Given
![]() $0<q<\infty $
,
$0<q<\infty $
,
![]() $0<\alpha ,\alpha '<\infty $
, there exists
$0<\alpha ,\alpha '<\infty $
, there exists
![]() $C\ge 1$
(depending only on dimension, the 1-sided NTA constants, the CDC constant, the ellipticity of
$C\ge 1$
(depending only on dimension, the 1-sided NTA constants, the CDC constant, the ellipticity of
![]() $L_0$
, q,
$L_0$
, q,
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
) such that the following holds. Given
$\alpha '$
) such that the following holds. Given
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, let
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, let
![]() $\Delta =B\cap \partial \Omega $
, for every
$\Delta =B\cap \partial \Omega $
, for every
![]() $F\in L^2_{\mathrm {loc}}(\Omega )$
there holds
$F\in L^2_{\mathrm {loc}}(\Omega )$
there holds
and
Proof. We start with equation (4.5) and borrow some ideas from [Reference Martell and Prisuelos-Arribas46, Proposition 3.2]. We may assume that
![]() $\alpha>\alpha '$
, otherwise the desired estimate follows trivially. Let
$\alpha>\alpha '$
, otherwise the desired estimate follows trivially. Let
![]() $v\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. By the classical theory of weights (cf. [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]), we can find
$v\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. By the classical theory of weights (cf. [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]), we can find
![]() $p\in (1,\infty )$
such for every
$p\in (1,\infty )$
such for every
![]() $\Delta $
as in the statement we have
$\Delta $
as in the statement we have
where the sups are taken over all
![]() $\Delta '=B'\cap \partial \Omega $
with
$\Delta '=B'\cap \partial \Omega $
with
![]() $B'\subset 5B$
,
$B'\subset 5B$
,
![]() $B'=B(x',r')$
,
$B'=B(x',r')$
,
![]() $x'\in \partial \Omega $
,
$x'\in \partial \Omega $
,
![]() $0<r'<\operatorname {\mathrm {diam}}(\partial \Omega )$
and where
$0<r'<\operatorname {\mathrm {diam}}(\partial \Omega )$
and where
![]() $C_0$
depends on
$C_0$
depends on
![]() $[v]_{A_{\infty }(\partial \Omega , \omega _{L_0})}$
. Note that for any such
$[v]_{A_{\infty }(\partial \Omega , \omega _{L_0})}$
. Note that for any such
![]() $\Delta '$
and for any Borel set
$\Delta '$
and for any Borel set
![]() $F\subset \Delta '$
we have, by Hölder’s inequality,
$F\subset \Delta '$
we have, by Hölder’s inequality,

Let
![]() $y\in \Delta $
and
$y\in \Delta $
and
![]() $X\in \Gamma _{r}^{\alpha }(y)$
, and pick
$X\in \Gamma _{r}^{\alpha }(y)$
, and pick
![]() $\widehat {x}$
so that
$\widehat {x}$
so that
![]() $|X-\widehat {x}|=\delta (X)$
. Then one can easily see that
$|X-\widehat {x}|=\delta (X)$
. Then one can easily see that
Then, by equation (4.7) and Lemma 3.9, we get
 $$ \begin{align*} \int_{\widetilde{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}} \le C_0 \Big( \frac{\omega_{L_0}^{X_{\Delta}}(\widetilde{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\widehat{\Delta})}\Big)^{p} \int_{\widehat{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}} \lesssim_{\alpha,\alpha',p} C_0 \int_{\widehat{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}}, \end{align*} $$
$$ \begin{align*} \int_{\widetilde{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}} \le C_0 \Big( \frac{\omega_{L_0}^{X_{\Delta}}(\widetilde{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\widehat{\Delta})}\Big)^{p} \int_{\widehat{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}} \lesssim_{\alpha,\alpha',p} C_0 \int_{\widehat{\Delta}} v\,d\omega_{L_0}^{X_{\Delta}}, \end{align*} $$
where
![]() $\widehat {\Delta }:=\Delta (\widehat {x}, \min \{\alpha ',1\}\delta (X))$
. Moreover, if
$\widehat {\Delta }:=\Delta (\widehat {x}, \min \{\alpha ',1\}\delta (X))$
. Moreover, if
![]() $X\in 2B$
with
$X\in 2B$
with
![]() $\delta (X)<r$
and
$\delta (X)<r$
and
![]() $y\in \widehat {\Delta }$
, one can easily show that
$y\in \widehat {\Delta }$
, one can easily show that
If we now combine the previous estimates, then we conclude that
 $$ \begin{align*} \|\mathcal{A}_{r}^{\alpha} F\|_{L^2(\Delta, v\,d\omega_{L_0}^{X_{\Delta}})} ^2 &=\int_{\Delta} \iint_{\Gamma_{r}^{\alpha}(y)}|F(X)|^2\,dX\,v(y)\,d\omega_{L_0}^{X_{\Delta}}(y) \\ &\le \iint_{2B\cap\{\delta(X)<r\}} |F(X)|^2\, \Big(\int_{\widetilde{\Delta}} v(y)\,d\omega_{L_0}^{X_{\Delta}}(y)\Big) dX\\ & \lesssim_{\alpha,\alpha',p} C_0 \iint_{2B\cap\{\delta(X)<r\}} |F(X)|^2\, \Big(\int_{\widehat{\Delta}} v(y)\,d\omega_{L_0}^{X_{\Delta}}(y)\Big) dX \\ & \le C_0 \int_{3\Delta} \iint_{\Gamma_{3r}^{\alpha'}(y)}|F(X)|^2\,dX\,v(y)\,d\omega_{L_0}^{X_{\Delta}}(y) \\ & = C_0 \|\mathcal{A}_{3r}^{\alpha'} F\|_{L^2(3\Delta, v\,d\omega_{L_0}^{X_{\Delta}})}^2. \end{align*} $$
$$ \begin{align*} \|\mathcal{A}_{r}^{\alpha} F\|_{L^2(\Delta, v\,d\omega_{L_0}^{X_{\Delta}})} ^2 &=\int_{\Delta} \iint_{\Gamma_{r}^{\alpha}(y)}|F(X)|^2\,dX\,v(y)\,d\omega_{L_0}^{X_{\Delta}}(y) \\ &\le \iint_{2B\cap\{\delta(X)<r\}} |F(X)|^2\, \Big(\int_{\widetilde{\Delta}} v(y)\,d\omega_{L_0}^{X_{\Delta}}(y)\Big) dX\\ & \lesssim_{\alpha,\alpha',p} C_0 \iint_{2B\cap\{\delta(X)<r\}} |F(X)|^2\, \Big(\int_{\widehat{\Delta}} v(y)\,d\omega_{L_0}^{X_{\Delta}}(y)\Big) dX \\ & \le C_0 \int_{3\Delta} \iint_{\Gamma_{3r}^{\alpha'}(y)}|F(X)|^2\,dX\,v(y)\,d\omega_{L_0}^{X_{\Delta}}(y) \\ & = C_0 \|\mathcal{A}_{3r}^{\alpha'} F\|_{L^2(3\Delta, v\,d\omega_{L_0}^{X_{\Delta}})}^2. \end{align*} $$
We can now extrapolate (locally in
![]() $3\Delta $
) as in [Reference Cruz-Uribe, Martell and Pérez12, Corollary 3.15] to conclude that
$3\Delta $
) as in [Reference Cruz-Uribe, Martell and Pérez12, Corollary 3.15] to conclude that
The desired estimate follows at once by taking
![]() $v\equiv 1$
which clearly belongs to
$v\equiv 1$
which clearly belongs to
![]() $A_{\infty }(\partial \Omega , \omega _{L_0})$
.
$A_{\infty }(\partial \Omega , \omega _{L_0})$
.
Let us next consider equation (4.6). First, introduce
We proceed as in [Reference Hofmann, Mitrea and Taylor38, Proposition 2.2] and write for any
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $\beta>0$
$\beta>0$
Let
![]() $y\in E(\alpha ,r,\lambda )\cap \Delta $
. Hence, there is
$y\in E(\alpha ,r,\lambda )\cap \Delta $
. Hence, there is
![]() $X\in \Gamma _{r}^{\alpha }(y)$
with
$X\in \Gamma _{r}^{\alpha }(y)$
with
![]() $|F(X)|>\lambda $
. Pick
$|F(X)|>\lambda $
. Pick
![]() $\widehat {x}\in \partial \Omega $
so that
$\widehat {x}\in \partial \Omega $
so that
![]() $|X-\widehat {x}|=\delta (X)$
. Note that
$|X-\widehat {x}|=\delta (X)$
. Note that
One can easily see that if
![]() $z\in \widehat {\Delta }$
, then
$z\in \widehat {\Delta }$
, then
![]() $X\in \Gamma _{3r}^{\alpha '}(z)$
. Hence,
$X\in \Gamma _{3r}^{\alpha '}(z)$
. Hence,
and
 $$\begin{align*}\mathcal{M}^{\Delta}_{\omega_{L_0}} \mathbf{1}_{ E(\alpha',3r,\lambda)}(y) \ge \frac{\omega_{L_0}^{X_{\Delta}}( E(\alpha',3r,\lambda)\cap \check{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\check{\Delta})} \ge \frac{\omega_{L_0}^{X_{\Delta}}(\widehat{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\check{\Delta})}> \gamma=\gamma_{\alpha,\alpha'}, \end{align*}$$
$$\begin{align*}\mathcal{M}^{\Delta}_{\omega_{L_0}} \mathbf{1}_{ E(\alpha',3r,\lambda)}(y) \ge \frac{\omega_{L_0}^{X_{\Delta}}( E(\alpha',3r,\lambda)\cap \check{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\check{\Delta})} \ge \frac{\omega_{L_0}^{X_{\Delta}}(\widehat{\Delta})}{\omega_{L_0}^{X_{\Delta}}(\check{\Delta})}> \gamma=\gamma_{\alpha,\alpha'}, \end{align*}$$
where in the last estimate we have used that
We have then shown that
and by the Hardy–Littlewood maximal inequality, we get
 $$ \begin{align*} \omega_{L_0}^{X_{\Delta}}( E(\alpha,r,\lambda)\cap\Delta) \le \omega_{L_0}^{X_{\Delta}} &(\{y\in\Delta:\mathcal{M}^{\Delta}_{\omega_{L_0}} \mathbf{1}_{ E(\alpha',3r,\lambda)}(y)>\gamma \})\\ &\qquad\qquad\quad\lesssim \omega_{L_0}^{X_{\Delta}}( E(\alpha',3r,\lambda)\cap4 \Delta) \lesssim \omega_{L_0}^{X_{4\Delta}}( E(\alpha',4r,\lambda)\cap4 \Delta). \end{align*} $$
$$ \begin{align*} \omega_{L_0}^{X_{\Delta}}( E(\alpha,r,\lambda)\cap\Delta) \le \omega_{L_0}^{X_{\Delta}} &(\{y\in\Delta:\mathcal{M}^{\Delta}_{\omega_{L_0}} \mathbf{1}_{ E(\alpha',3r,\lambda)}(y)>\gamma \})\\ &\qquad\qquad\quad\lesssim \omega_{L_0}^{X_{\Delta}}( E(\alpha',3r,\lambda)\cap4 \Delta) \lesssim \omega_{L_0}^{X_{4\Delta}}( E(\alpha',4r,\lambda)\cap4 \Delta). \end{align*} $$
This readily implies equation (4.6).
4.1 Proof of
 $\mathrm {(a)}_{p'}\ \Longrightarrow \ \mathrm {(b)}_p$
$\mathrm {(a)}_{p'}\ \Longrightarrow \ \mathrm {(b)}_p$
Fix
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $N\ge 1$
. Take
$N\ge 1$
. Take
![]() $\Delta _0 = \Delta (x_0, r_0)$
with
$\Delta _0 = \Delta (x_0, r_0)$
with
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 <\operatorname {\mathrm {diam}}(\partial \Omega )$
, and fix
$0 < r_0 <\operatorname {\mathrm {diam}}(\partial \Omega )$
, and fix
![]() $f \in \mathscr {C}(\partial \Omega )$
with
$f \in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f \subset N\Delta _0$
. We may assume that
$\operatorname {\mathrm {supp}} f \subset N\Delta _0$
. We may assume that
![]() $N r_0<4\,\operatorname {\mathrm {diam}}(\partial \Omega )$
; otherwise,
$N r_0<4\,\operatorname {\mathrm {diam}}(\partial \Omega )$
; otherwise,
![]() $\partial \Omega $
is bounded and
$\partial \Omega $
is bounded and
![]() $4\operatorname {\mathrm {diam}}(\partial \Omega )/N\le r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
and we can work with
$4\operatorname {\mathrm {diam}}(\partial \Omega )/N\le r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
and we can work with
![]() $N'= 2\operatorname {\mathrm {diam}}(\partial \Omega )/r_0\in (2, N/2]$
and
$N'= 2\operatorname {\mathrm {diam}}(\partial \Omega )/r_0\in (2, N/2]$
and
![]() $N'\Delta _0=\partial \Omega $
.
$N'\Delta _0=\partial \Omega $
.
Let u be the associated elliptic measure L-solution as in equation (3.4). Assume
![]() $\omega _L \in RH_{p'}(\partial \Omega , \omega _{L_0})$
, and our goal is to obtain that equation (3.5) holds. By Gehring’s lemma [Reference Gehring26] (see also [Reference Coifman and Fefferman11]), there exists
$\omega _L \in RH_{p'}(\partial \Omega , \omega _{L_0})$
, and our goal is to obtain that equation (3.5) holds. By Gehring’s lemma [Reference Gehring26] (see also [Reference Coifman and Fefferman11]), there exists
![]() $s>1$
such that
$s>1$
such that
![]() $\omega _{L}\in RH_{p's} (\partial \Omega ,\omega _{L_0})$
.
$\omega _{L}\in RH_{p's} (\partial \Omega ,\omega _{L_0})$
.
Introduce the family of pairwise disjoint cubes
Take
![]() $x \in \Delta _0$
and
$x \in \Delta _0$
and
![]() $X \in \Gamma _{r_0}^{\alpha }(x)$
. Let
$X \in \Gamma _{r_0}^{\alpha }(x)$
. Let
![]() $I_X \in \mathcal {W}$
be such that
$I_X \in \mathcal {W}$
be such that
![]() $X \in I_X$
. Take
$X \in I_X$
. Take
![]() $y_X \in \partial \Omega $
such that
$y_X \in \partial \Omega $
such that
![]() $\operatorname {dist}(I_X, \partial \Omega ) = \operatorname {dist}(I_X, y_X)$
, and let
$\operatorname {dist}(I_X, \partial \Omega ) = \operatorname {dist}(I_X, y_X)$
, and let
![]() $Q_X \in \mathbb {D}$
be the unique dyadic cube satisfying
$Q_X \in \mathbb {D}$
be the unique dyadic cube satisfying
![]() $\ell (Q_X) = \ell (I_X)$
and
$\ell (Q_X) = \ell (I_X)$
and
![]() $y_X \in Q_X$
. By construction (see Section 2.3),
$y_X \in Q_X$
. By construction (see Section 2.3),
![]() $I_X \in \mathcal {W}_{Q_X}^{\vartheta ,*}$
and thus
$I_X \in \mathcal {W}_{Q_X}^{\vartheta ,*}$
and thus
![]() $I^* \subset \Gamma _{Q_X}(y_X)$
. Thus, by the properties of the Whitney cubes
$I^* \subset \Gamma _{Q_X}(y_X)$
. Thus, by the properties of the Whitney cubes
and
These and the fact that
![]() $X \in \Gamma _{r_0}^{\alpha }(x)$
give
$X \in \Gamma _{r_0}^{\alpha }(x)$
give
Also, for every
![]() $z\in Q_X$
$z\in Q_X$
since
![]() $\Xi \ge 2$
, and
$\Xi \ge 2$
, and
since
![]() $X \in \Gamma _{r_0}^{\alpha }(x)$
. Thus,
$X \in \Gamma _{r_0}^{\alpha }(x)$
. Thus,
![]() $Q_X\subset 3\Xi \Delta _0\cap \Delta (x, C_{\alpha }\delta (X))$
and there exists a unique
$Q_X\subset 3\Xi \Delta _0\cap \Delta (x, C_{\alpha }\delta (X))$
and there exists a unique
![]() $\widetilde {Q}_X\in \mathcal {F}_{\Delta _0}$
such that
$\widetilde {Q}_X\in \mathcal {F}_{\Delta _0}$
such that
![]() $Q_X\subsetneq \widetilde {Q}_X$
. In particular,
$Q_X\subsetneq \widetilde {Q}_X$
. In particular,
![]() $X\in I_X\subset U_{Q_X}\subset \Gamma _{\widetilde {Q}_X}(y)$
for all
$X\in I_X\subset U_{Q_X}\subset \Gamma _{\widetilde {Q}_X}(y)$
for all
![]() $y \in Q_X$
and
$y \in Q_X$
and
Taking the average over
![]() $Q_X$
with respect to
$Q_X$
with respect to
![]() $\omega _{L_0}^{X_{\Delta _0}}$
, we arrive at
$\omega _{L_0}^{X_{\Delta _0}}$
, we arrive at

where in the last inequality we have used that
![]() $\delta (X)\le |X-x|< r_0$
since
$\delta (X)\le |X-x|< r_0$
since
![]() $\Gamma _{r_0}^{\alpha }(x)\subset B(x,r_0)$
. Taking now the supremum over all
$\Gamma _{r_0}^{\alpha }(x)\subset B(x,r_0)$
. Taking now the supremum over all
![]() $X \in \Gamma _{r_0}^{\alpha }(x)$
, we arrive at
$X \in \Gamma _{r_0}^{\alpha }(x)$
, we arrive at

Applying the Hardy–Littlewood maximal inequality and the fact that the set
![]() $\mathcal {F}_{\Delta _0}$
has bounded cardinality, we have
$\mathcal {F}_{\Delta _0}$
has bounded cardinality, we have

where we have used that for every
![]() $Q \in \mathcal {F}_{\Delta _0}$
we have
$Q \in \mathcal {F}_{\Delta _0}$
we have
![]() $\operatorname {\mathrm {supp}} (\mathcal {N}_Q u)\subset Q$
.
$\operatorname {\mathrm {supp}} (\mathcal {N}_Q u)\subset Q$
.
Let us also observe that for every
![]() $Q\in \mathcal {F}_{\Delta _0}$
we can pick
$Q\in \mathcal {F}_{\Delta _0}$
we can pick
![]() $y_Q\in Q\cap 3\Xi \Delta _0$
so that if
$y_Q\in Q\cap 3\Xi \Delta _0$
so that if
![]() $z\in N\Delta _0$
there holds
$z\in N\Delta _0$
there holds
That is,
![]() $N\Delta _0\subset 2\widetilde {\Delta }_{Q}$
, and we are now ready to invoke [Reference Akman, Hofmann, Martell and Toro1, Proposition 2.57] to see that
$N\Delta _0\subset 2\widetilde {\Delta }_{Q}$
, and we are now ready to invoke [Reference Akman, Hofmann, Martell and Toro1, Proposition 2.57] to see that

To continue let
![]() $x\in Q\in \mathcal {F}_{\Delta _0}$
, and let
$x\in Q\in \mathcal {F}_{\Delta _0}$
, and let
![]() $\Delta $
be a surface ball such that
$\Delta $
be a surface ball such that
![]() $x \in \Delta $
and
$x \in \Delta $
and
![]() $0 < r_{\Delta } < 4\Xi r_Q$
. In particular,
$0 < r_{\Delta } < 4\Xi r_Q$
. In particular,
![]() $\Delta \subset C_N\Delta _0=\widetilde {\Delta }_0$
and
$\Delta \subset C_N\Delta _0=\widetilde {\Delta }_0$
and
![]() $Q\subset \widetilde {\Delta }_0$
. Note that
$Q\subset \widetilde {\Delta }_0$
. Note that
![]() $\omega _{L_0}^{X_{\Delta _0}}\approx _N \omega _{L_0}^{X_{\widetilde {\Delta }_0}}$
by Harnack’s inequality and the fact that
$\omega _{L_0}^{X_{\Delta _0}}\approx _N \omega _{L_0}^{X_{\widetilde {\Delta }_0}}$
by Harnack’s inequality and the fact that
![]() $\delta (X_{\Delta _0})\approx r_0$
,
$\delta (X_{\Delta _0})\approx r_0$
,
![]() $\delta (X_{\widetilde {\Delta }_0})\approx _N r_0$
and
$\delta (X_{\widetilde {\Delta }_0})\approx _N r_0$
and
![]() $|X_{\Delta _0}-X_{\widetilde {\Delta }_0}|\lesssim _N r_0$
.
$|X_{\Delta _0}-X_{\widetilde {\Delta }_0}|\lesssim _N r_0$
.
Recall that
![]() $\omega _L \in RH_{p' s}(\partial \Omega , \omega _{L_0})$
implies
$\omega _L \in RH_{p' s}(\partial \Omega , \omega _{L_0})$
implies
![]() $\omega _L \in RH_{p' s}(\widetilde {\Delta }_0, \omega ^{X_{\widetilde {\Delta }_0}}_{L_0})$
(uniformly). Therefore, using Hölder’s inequality and recalling that
$\omega _L \in RH_{p' s}(\widetilde {\Delta }_0, \omega ^{X_{\widetilde {\Delta }_0}}_{L_0})$
(uniformly). Therefore, using Hölder’s inequality and recalling that
![]() $h(\cdot; L, L_0, X)$
denotes the Radon–Nikodym derivative of
$h(\cdot; L, L_0, X)$
denotes the Radon–Nikodym derivative of
![]() $\omega _L^X$
with respect to
$\omega _L^X$
with respect to
![]() $\omega _{L_0}^X$
, we get
$\omega _{L_0}^X$
, we get

This, equation (4.9) and equation (4.8) yield

where we have used the boundedness of the local Hardy–Littlewood maximal function in the second term on
![]() $L^{\frac {p}{(p's)'}}(\widetilde {\Delta }_0,\omega _{L_0}^{X_{\widetilde {\Delta }_0}})$
, which follows from
$L^{\frac {p}{(p's)'}}(\widetilde {\Delta }_0,\omega _{L_0}^{X_{\widetilde {\Delta }_0}})$
, which follows from
![]() $p>(p's)'$
and the fact that
$p>(p's)'$
and the fact that
![]() $\omega _{L_0}^{X_{\widetilde {\Delta }_0}}$
is doubling in
$\omega _{L_0}^{X_{\widetilde {\Delta }_0}}$
is doubling in
![]() $10\widetilde {\Delta }_0$
. This completes the proof of
$10\widetilde {\Delta }_0$
. This completes the proof of
![]() $\mathrm {(b)}_p$
.
$\mathrm {(b)}_p$
.
![]() $\Box $
$\Box $
4.2 Proof of
 $\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(a)}_{p'}$
$\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(a)}_{p'}$
Fix
![]() $p\in (1,\infty )$
, and assume that L is
$p\in (1,\infty )$
, and assume that L is
![]() $L^{p}(\omega _{L_0})$
-solvable. That is, for some fixed
$L^{p}(\omega _{L_0})$
-solvable. That is, for some fixed
![]() $\alpha _0$
and some
$\alpha _0$
and some
![]() $N\ge 1$
, there exists
$N\ge 1$
, there exists
![]() $C_{\alpha _0, N}\ge 1$
(depending only on n, the
$C_{\alpha _0, N}\ge 1$
(depending only on n, the
![]() $1$
-sided NTA constants, the CDC constant, the ellipticity of
$1$
-sided NTA constants, the CDC constant, the ellipticity of
![]() $L_0$
and L,
$L_0$
and L,
![]() $\alpha _0$
, N and p) such that equation (3.5) holds for u as in equation (3.4) for any
$\alpha _0$
, N and p) such that equation (3.5) holds for u as in equation (3.4) for any
![]() $f\in \mathscr {C}(\partial \Omega )$
with
$f\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f\subset N\Delta _0$
. From this and equation (4.6), we conclude that we can assume that
$\operatorname {\mathrm {supp}} f\subset N\Delta _0$
. From this and equation (4.6), we conclude that we can assume that
![]() $\alpha \ge c_0^{-1}-1$
, where
$\alpha \ge c_0^{-1}-1$
, where
![]() $c_0$
is the corkscrew constant (cf. Definition 2.1), and we have
$c_0$
is the corkscrew constant (cf. Definition 2.1), and we have
for u as in equation (3.4) with
![]() $f\in \mathscr {C}(\partial \Omega )$
with
$f\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f\subset N\Delta _0$
and for any
$\operatorname {\mathrm {supp}} f\subset N\Delta _0$
and for any
![]() $\Delta _0 = \Delta (x_0,r_0)$
,
$\Delta _0 = \Delta (x_0,r_0)$
,
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/4$
. It is routine to see this estimate also holds with
$0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/4$
. It is routine to see this estimate also holds with
![]() $r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
. Indeed, by splitting f into its positive and negative parts we may assume that
$r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
. Indeed, by splitting f into its positive and negative parts we may assume that
![]() $f\ge 0$
. In that case, if
$f\ge 0$
. In that case, if
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $X\in \Gamma ^{\alpha }_{r_0}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5}(x)$
, we have that
$X\in \Gamma ^{\alpha }_{r_0}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5}(x)$
, we have that
![]() $\delta (X)\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
, and by equation (2.22), one has that
$\delta (X)\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
, and by equation (2.22), one has that
![]() $X':=X_{\Delta (x,\operatorname {\mathrm {diam}}(\partial \Omega )/5)}\in \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5}(x)$
. Harnack’s inequality implies then that
$X':=X_{\Delta (x,\operatorname {\mathrm {diam}}(\partial \Omega )/5)}\in \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5}(x)$
. Harnack’s inequality implies then that
![]() $u(X)\approx u(X')$
, and this shows that
$u(X)\approx u(X')$
, and this shows that
![]() $\mathcal {N}^{\alpha }_{r_0} u(x)\lesssim \mathcal {N}^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5} u(x)$
. Further details are left to the interested reader.
$\mathcal {N}^{\alpha }_{r_0} u(x)\lesssim \mathcal {N}^{\alpha }_{\operatorname {\mathrm {diam}}(\partial \Omega )/5} u(x)$
. Further details are left to the interested reader.
We claim that, for every
![]() $\Delta _0 = \Delta (x_0,r_0)$
,
$\Delta _0 = \Delta (x_0,r_0)$
,
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )$
, and for every
$0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )$
, and for every
![]() $ f\in \mathscr {C}(\partial \Omega )$
with
$ f\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f\subset N\Delta _0$
$\operatorname {\mathrm {supp}} f\subset N\Delta _0$
 $$ \begin{align} \Big|\int_{\Delta_0} f(y)\,d\omega_L^{X_{\Delta_0}}(y)\Big| \lesssim_{\alpha, N}\|f\|_{L^{p}(N \Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
$$ \begin{align} \Big|\int_{\Delta_0} f(y)\,d\omega_L^{X_{\Delta_0}}(y)\Big| \lesssim_{\alpha, N}\|f\|_{L^{p}(N \Delta_0, \omega_{L_0}^{X_{\Delta_0}})}. \end{align} $$
To see this, let u be the L-solution with datum
![]() $|f|$
(see equation (3.4)). Write
$|f|$
(see equation (3.4)). Write
![]() $X_0:=X_{\Delta _0}$
and
$X_0:=X_{\Delta _0}$
and
![]() $\widetilde {X}_0:=X_{(2+\alpha )^{-1}\Delta _0}$
. Note that
$\widetilde {X}_0:=X_{(2+\alpha )^{-1}\Delta _0}$
. Note that
![]() $\delta (X_0)\approx r_0$
,
$\delta (X_0)\approx r_0$
,
![]() $\delta (\widetilde {X}_0)\approx _{\alpha } r_0$
, and
$\delta (\widetilde {X}_0)\approx _{\alpha } r_0$
, and
![]() $|X_0-\widetilde {X}_0|<2\,r_0$
. Hence, Harnack’s inequality yields
$|X_0-\widetilde {X}_0|<2\,r_0$
. Hence, Harnack’s inequality yields
![]() $u(\widetilde {X}_0)\approx _{\alpha } u(X_0)$
. The choice of
$u(\widetilde {X}_0)\approx _{\alpha } u(X_0)$
. The choice of
![]() $\alpha $
guarantees that
$\alpha $
guarantees that
![]() $\widetilde {X}_0\in \Gamma _{(2+\alpha )^{-1}r_0}^{\alpha }(x_0)\subset \Gamma _{r_0}^{\alpha }(x_0)$
; see equation (2.22). Let
$\widetilde {X}_0\in \Gamma _{(2+\alpha )^{-1}r_0}^{\alpha }(x_0)\subset \Gamma _{r_0}^{\alpha }(x_0)$
; see equation (2.22). Let
![]() $\widetilde {x}_0\in \partial \Omega $
so that
$\widetilde {x}_0\in \partial \Omega $
so that
![]() $\delta (\widetilde {X}_0)=|\widetilde {X}_0-\widetilde {x}_0|$
. Clearly, for every
$\delta (\widetilde {X}_0)=|\widetilde {X}_0-\widetilde {x}_0|$
. Clearly, for every
![]() $z\in \Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))$
,
$z\in \Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))$
,
thus
![]() $\widetilde {X}_0\in \Gamma _{r_0}^{\alpha }(z) $
and
$\widetilde {X}_0\in \Gamma _{r_0}^{\alpha }(z) $
and
Note also that if
![]() $z\in \Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))$
, then
$z\in \Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))$
, then
hence
![]() $\Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))\subset \Delta _0$
. Additionally, if
$\Delta (\widetilde {x}_0,\alpha \delta (\widetilde {X}_0))\subset \Delta _0$
. Additionally, if
![]() $z\in \Delta _0$
, then
$z\in \Delta _0$
, then
and this shows that
![]() $\Delta _0\subset \Delta (\widetilde {x}_0, 2r_0)$
. This together with Lemma 3.9 gives
$\Delta _0\subset \Delta (\widetilde {x}_0, 2r_0)$
. This together with Lemma 3.9 gives
and the previous estimates readily give equation (4.11):
 $$ \begin{align*} \Big|\int_{\Delta_0} f(y)\,d\omega_L^{X_{\Delta_0}}(y)\Big| \le u(X_0) \lesssim_{\alpha} u(\widetilde{X}_0)\omega_{L_0}^{X_0}&(\Delta(\widetilde{x}_0,\alpha\delta(\widetilde{X}_0)))^{\frac1p} \\ &\quad\qquad\le \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{0}})} \lesssim_{\alpha, N} \|f\|_{L^{p}(N \Delta_0, \omega_{L_0}^{X_{0}})}. \end{align*} $$
$$ \begin{align*} \Big|\int_{\Delta_0} f(y)\,d\omega_L^{X_{\Delta_0}}(y)\Big| \le u(X_0) \lesssim_{\alpha} u(\widetilde{X}_0)\omega_{L_0}^{X_0}&(\Delta(\widetilde{x}_0,\alpha\delta(\widetilde{X}_0)))^{\frac1p} \\ &\quad\qquad\le \|\mathcal{N}^{\alpha}_{r_0} u\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{0}})} \lesssim_{\alpha, N} \|f\|_{L^{p}(N \Delta_0, \omega_{L_0}^{X_{0}})}. \end{align*} $$
To proceed, we fix
![]() $\Delta _0 = \Delta (x_0,r_0)$
,
$\Delta _0 = \Delta (x_0,r_0)$
,
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/2$
. Let
$0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/2$
. Let
![]() $F \subset \Delta _0$
be a Borel set. Since
$F \subset \Delta _0$
be a Borel set. Since
![]() $\omega _{L_0}^{X_{2\,\Delta _0}}$
and
$\omega _{L_0}^{X_{2\,\Delta _0}}$
and
![]() $\omega _L^{X_{2\,\Delta _0}}$
are Borel regular, for each
$\omega _L^{X_{2\,\Delta _0}}$
are Borel regular, for each
![]() $\varepsilon> 0$
, there exist a compact set K and an open set U such that
$\varepsilon> 0$
, there exist a compact set K and an open set U such that
![]() $K \subset F \subset U \subset 2\,\Delta _0$
and
$K \subset F \subset U \subset 2\,\Delta _0$
and
Using Urysohn’s lemma, we can construct
![]() $f_F \in \mathscr {C}_c(\partial \Omega )$
such that
$f_F \in \mathscr {C}_c(\partial \Omega )$
such that
![]() $\mathbf {1}_K \leq f_F \leq \mathbf {1}_U$
. Then, by equation (4.11) (applied with
$\mathbf {1}_K \leq f_F \leq \mathbf {1}_U$
. Then, by equation (4.11) (applied with
![]() $2\Delta _0$
) and equation (4.12) yield
$2\Delta _0$
) and equation (4.12) yield
 $$ \begin{align*} \omega_L^{X_{2\,\Delta_0}}(F) &< \varepsilon + \omega_L^{X_{2\,\Delta_0}}(K) \leq \varepsilon + \int_{\partial \Omega} f_F(z) \, d \omega_L^{X_{2\,\Delta_0}}(z) \\ &\quad\le \varepsilon + C_{\alpha, N}\|f_F\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{2\,\Delta_0}})} \lesssim \varepsilon + C_{\alpha, N}\omega_{L_0}^{X_{2 \Delta_0}} (U)^{\frac1p} < \varepsilon + C_{\alpha, N}(\omega_{L_0}^{X_{2 \Delta_0}} (F) + \varepsilon)^{\frac1p}. \end{align*} $$
$$ \begin{align*} \omega_L^{X_{2\,\Delta_0}}(F) &< \varepsilon + \omega_L^{X_{2\,\Delta_0}}(K) \leq \varepsilon + \int_{\partial \Omega} f_F(z) \, d \omega_L^{X_{2\,\Delta_0}}(z) \\ &\quad\le \varepsilon + C_{\alpha, N}\|f_F\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{2\,\Delta_0}})} \lesssim \varepsilon + C_{\alpha, N}\omega_{L_0}^{X_{2 \Delta_0}} (U)^{\frac1p} < \varepsilon + C_{\alpha, N}(\omega_{L_0}^{X_{2 \Delta_0}} (F) + \varepsilon)^{\frac1p}. \end{align*} $$
Letting
![]() $\varepsilon \to 0+$
, we obtain that
$\varepsilon \to 0+$
, we obtain that
![]() $\omega _L^{X_{2\,\Delta _0}}(F) \lesssim _{\alpha , N}\omega _{L_0}^{X_{2 \Delta _0}} (F)^{\frac 1p}$
. Hence,
$\omega _L^{X_{2\,\Delta _0}}(F) \lesssim _{\alpha , N}\omega _{L_0}^{X_{2 \Delta _0}} (F)^{\frac 1p}$
. Hence,
![]() $\omega _L^{X_{2\,\Delta _0}}\ll \omega _{L_0}^{X_{2 \Delta _0}}$
in
$\omega _L^{X_{2\,\Delta _0}}\ll \omega _{L_0}^{X_{2 \Delta _0}}$
in
![]() $\Delta _0$
. By Harnack’s inequality and the fact that we can cover
$\Delta _0$
. By Harnack’s inequality and the fact that we can cover
![]() $\partial \Omega $
with surface balls like
$\partial \Omega $
with surface balls like
![]() $\Delta _0$
we conclude that
$\Delta _0$
we conclude that
![]() $\omega _L \ll \omega _{L_0}$
in
$\omega _L \ll \omega _{L_0}$
in
![]() $\partial \Omega $
. We can write
$\partial \Omega $
. We can write
![]() $h(\cdot; L, L_0, X) = \frac {d \omega _L^{X}}{d \omega _{L_0}^{X}} \in L_{\mathrm {loc}}^1(\partial \Omega , \omega _{L_0}^{X})$
which is well-defined
$h(\cdot; L, L_0, X) = \frac {d \omega _L^{X}}{d \omega _{L_0}^{X}} \in L_{\mathrm {loc}}^1(\partial \Omega , \omega _{L_0}^{X})$
which is well-defined
![]() $\omega _{L_0}^{X}$
-a.e. in
$\omega _{L_0}^{X}$
-a.e. in
![]() $\partial \Omega $
. Thus, for every
$\partial \Omega $
. Thus, for every
![]() $ f\in \mathscr {C}(\partial \Omega )$
with
$ f\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f\subset 2\Delta _0$
, we obtain from equation (4.11)
$\operatorname {\mathrm {supp}} f\subset 2\Delta _0$
, we obtain from equation (4.11)
 $$\begin{align*}\Big|\int_{2\Delta_0} f(y)\,h(y; L, L_0, X_{2\Delta_0})\,d\omega_{L_0}^{X_{2\Delta_0}}(y)\Big| = \Big|\int_{2\Delta_0} f(y)\,d\omega_L^{X_{2\Delta_0}}(y)\Big| \lesssim_{\alpha, N}\|f\|_{L^{p}(2\Delta_0, \omega_{L_0}^{X_{2\Delta_0}})}. \end{align*}$$
$$\begin{align*}\Big|\int_{2\Delta_0} f(y)\,h(y; L, L_0, X_{2\Delta_0})\,d\omega_{L_0}^{X_{2\Delta_0}}(y)\Big| = \Big|\int_{2\Delta_0} f(y)\,d\omega_L^{X_{2\Delta_0}}(y)\Big| \lesssim_{\alpha, N}\|f\|_{L^{p}(2\Delta_0, \omega_{L_0}^{X_{2\Delta_0}})}. \end{align*}$$
Using the ideas in [Reference Akman, Hofmann, Martell and Toro2, Lemma 3.23] and with the help of [Reference Akman, Hofmann, Martell and Toro2, Lemma 3.14], we can then conclude that
This, Harnack’s inequality and the fact that
![]() $\Delta _0 = \Delta (x_0,r_0)$
with
$\Delta _0 = \Delta (x_0,r_0)$
with
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/2$
arbitrary easily yield that
$0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )/2$
arbitrary easily yield that
This and Remark 3.11 readily imply that
![]() $\omega _L\in RH_{p'}(\partial \Omega ,\omega _{L_0})$
, and the proof is complete.
$\omega _L\in RH_{p'}(\partial \Omega ,\omega _{L_0})$
, and the proof is complete.
![]() $\Box $
$\Box $
4.3 Proof of
 $\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(b)}_p'$
$\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(b)}_p'$
Assume that L is
![]() $L^{p}(\omega _{L_0})$
-solvable with
$L^{p}(\omega _{L_0})$
-solvable with
![]() $p\in (1,\infty )$
. Fix
$p\in (1,\infty )$
. Fix
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $N\ge 1$
, a surface ball
$N\ge 1$
, a surface ball
![]() $\Delta _0$
and a Borel set
$\Delta _0$
and a Borel set
![]() $S\subset N\Delta _0$
. Take an arbitrary
$S\subset N\Delta _0$
. Take an arbitrary
![]() $\varepsilon>0$
, and since
$\varepsilon>0$
, and since
![]() $\omega _{L_0}^{X_{\Delta _0}}$
and
$\omega _{L_0}^{X_{\Delta _0}}$
and
![]() $\omega _L^{X_{\Delta _0}}$
are Borel regular, we can find a closed set F and an open set U such that
$\omega _L^{X_{\Delta _0}}$
are Borel regular, we can find a closed set F and an open set U such that
![]() $F\subset S\subset U\subset (N+1)\Delta _0$
and
$F\subset S\subset U\subset (N+1)\Delta _0$
and
Using Urysohn’s lemma, we can then construct
![]() $f \in \mathscr {C}_c(\partial \Omega )$
such that
$f \in \mathscr {C}_c(\partial \Omega )$
such that
![]() $\mathbf {1}_S \leq f \leq \mathbf {1}_U$
. Set
$\mathbf {1}_S \leq f \leq \mathbf {1}_U$
. Set
For every
![]() $M\ge c_0^{-1}$
, define the truncated cone and truncated nontangential maximal function
$M\ge c_0^{-1}$
, define the truncated cone and truncated nontangential maximal function
Note that if
![]() $x\in \Delta _0$
and
$x\in \Delta _0$
and
![]() $X\in \Gamma _{r_0, M}^{\alpha }(x)$
, then
$X\in \Gamma _{r_0, M}^{\alpha }(x)$
, then
![]() $r_0/M\le \delta (X)\le r_0$
,
$r_0/M\le \delta (X)\le r_0$
,
![]() $c_0\,r_0\le \delta (X_{\Delta _0})\le r_0$
and
$c_0\,r_0\le \delta (X_{\Delta _0})\le r_0$
and
![]() $|X-X_{\Delta _0}|<2r_0$
. Hence, by the Harnack chain condition and Harnack’s inequality, there is a constant
$|X-X_{\Delta _0}|<2r_0$
. Hence, by the Harnack chain condition and Harnack’s inequality, there is a constant
![]() $C_M$
depending on M such that
$C_M$
depending on M such that
and
Thus
Note that our assumption is that
![]() $L^{p}(\omega _{L_0})$
-solvability holds with the fixed parameters
$L^{p}(\omega _{L_0})$
-solvability holds with the fixed parameters
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $N\ge 1$
, but since we already know that
$N\ge 1$
, but since we already know that
![]() $\mathrm {(a)} \Longleftrightarrow \ \mathrm {(b)}$
, it follows that the
$\mathrm {(a)} \Longleftrightarrow \ \mathrm {(b)}$
, it follows that the
![]() $L^{p}(\omega _{L_0})$
-solvability holds with
$L^{p}(\omega _{L_0})$
-solvability holds with
![]() $\alpha>0$
and
$\alpha>0$
and
![]() $N+1$
. Thus, the fact that
$N+1$
. Thus, the fact that
![]() $f \in \mathscr {C}_c(\partial \Omega )$
with
$f \in \mathscr {C}_c(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} f\subset U\subset (N+1)\Delta _0$
gives
$\operatorname {\mathrm {supp}} f\subset U\subset (N+1)\Delta _0$
gives
 $$ \begin{align*} &\|\mathcal{N}^{\alpha}_{r_0,M} u\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_M\,\varepsilon\, \omega_{L_0}^{X_{\Delta_0}}(\Delta_0)^{\frac1p} + \|\mathcal{N}^{\alpha}_{r_0} v\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_M\,\varepsilon+ C_{\alpha,N} \|f\|_{L^p((N+1)\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \\[6pt] \le & C_M\,\varepsilon+ C_{\alpha,N} \omega_{L_0}^{X_{\Delta_0}}(U)^{\frac1{p}} < C_M\,\varepsilon+ C_{\alpha,N} (\omega_{L_0}^{X_{\Delta_0}}(S)+\varepsilon)^{\frac1{p}} = C_M\,\varepsilon+ C_{\alpha,N} \big(\|\mathbf{1}_S\|^p_{L^p(N\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} +\varepsilon)^{\frac1{p}}. \end{align*} $$
$$ \begin{align*} &\|\mathcal{N}^{\alpha}_{r_0,M} u\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_M\,\varepsilon\, \omega_{L_0}^{X_{\Delta_0}}(\Delta_0)^{\frac1p} + \|\mathcal{N}^{\alpha}_{r_0} v\|_{L^p(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \leq C_M\,\varepsilon+ C_{\alpha,N} \|f\|_{L^p((N+1)\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \\[6pt] \le & C_M\,\varepsilon+ C_{\alpha,N} \omega_{L_0}^{X_{\Delta_0}}(U)^{\frac1{p}} < C_M\,\varepsilon+ C_{\alpha,N} (\omega_{L_0}^{X_{\Delta_0}}(S)+\varepsilon)^{\frac1{p}} = C_M\,\varepsilon+ C_{\alpha,N} \big(\|\mathbf{1}_S\|^p_{L^p(N\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} +\varepsilon)^{\frac1{p}}. \end{align*} $$
We let
![]() $\varepsilon \to 0^+$
and obtain
$\varepsilon \to 0^+$
and obtain
![]() $\|\mathcal {N}^{\alpha }_{r_0,M} u\|_{L^p(\Delta _0, \omega _{L_0}^{X_{\Delta _0}})} \le C_{\alpha ,N} \|\mathbf {1}_S\|_{L^p(N\Delta _0, \omega _{L_0}^{X_{\Delta _0}})}$
. Since
$\|\mathcal {N}^{\alpha }_{r_0,M} u\|_{L^p(\Delta _0, \omega _{L_0}^{X_{\Delta _0}})} \le C_{\alpha ,N} \|\mathbf {1}_S\|_{L^p(N\Delta _0, \omega _{L_0}^{X_{\Delta _0}})}$
. Since
![]() $\mathcal {N}^{\alpha }_{r_0,M} u(x)\nearrow \mathcal {N}^{\alpha }_{r_0} u(x)$
for every
$\mathcal {N}^{\alpha }_{r_0,M} u(x)\nearrow \mathcal {N}^{\alpha }_{r_0} u(x)$
for every
![]() $x\in \partial \Omega $
as
$x\in \partial \Omega $
as
![]() $M\to \infty $
, we conclude the desired estimate by simply applying the monotone convergence theorem.
$M\to \infty $
, we conclude the desired estimate by simply applying the monotone convergence theorem.
![]() $\Box $
$\Box $
4.4 Proof of
 $\mathrm {(b)}'\ \Longrightarrow \ \mathrm {(a)}$
$\mathrm {(b)}'\ \Longrightarrow \ \mathrm {(a)}$
Fix
![]() $p\in (1,\infty )$
, and assume that L is
$p\in (1,\infty )$
, and assume that L is
![]() $L^{p}(\omega _{L_0})$
-solvable for characteristic functions. That is for some
$L^{p}(\omega _{L_0})$
-solvable for characteristic functions. That is for some
![]() $\alpha>0$
and some
$\alpha>0$
and some
![]() $N\ge 1$
there exists
$N\ge 1$
there exists
![]() $C_{\alpha , N}\ge 1$
(depending only on n, the
$C_{\alpha , N}\ge 1$
(depending only on n, the
![]() $1$
-sided NTA constants, the CDC constant, the ellipticity of
$1$
-sided NTA constants, the CDC constant, the ellipticity of
![]() $L_0$
and L,
$L_0$
and L,
![]() $\alpha $
, N and p) such that equation (3.5) holds for u as in equation (3.4) for any
$\alpha $
, N and p) such that equation (3.5) holds for u as in equation (3.4) for any
![]() $f=\mathbf {1}_S$
with S being a Borel set
$f=\mathbf {1}_S$
with S being a Borel set
![]() $S\subset N\Delta _0$
.
$S\subset N\Delta _0$
.
Take an arbitrary
![]() $\Delta _0 = \Delta (x_0,r_0)$
,
$\Delta _0 = \Delta (x_0,r_0)$
,
![]() $x_0 \in \partial \Omega $
and
$x_0 \in \partial \Omega $
and
![]() $0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )$
. We follow the proof of
$0 < r_0 < \operatorname {\mathrm {diam}}(\partial \Omega )$
. We follow the proof of
![]() $\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(a)}_{p'}$
and observe that the same argument we used to obtain equation (4.11) easily gives, taking
$\mathrm {(b)}_p\ \Longrightarrow \ \mathrm {(a)}_{p'}$
and observe that the same argument we used to obtain equation (4.11) easily gives, taking
![]() $f=\mathbf {1}_S$
with S being a Borel set
$f=\mathbf {1}_S$
with S being a Borel set
![]() $S\subset N \Delta _0$
, that
$S\subset N \Delta _0$
, that
 $$ \begin{align} \omega_L^{X_{\Delta_0}}(S)= \int_{\Delta_0} \mathbf{1}_S(y)\,d\omega_L^{X_{\Delta_0}}(y) \lesssim_{\alpha, N} \|\mathbf{1}_S\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} = \omega_{L_0}^{X_{\Delta_0}}(S)^{\frac1p}. \end{align} $$
$$ \begin{align} \omega_L^{X_{\Delta_0}}(S)= \int_{\Delta_0} \mathbf{1}_S(y)\,d\omega_L^{X_{\Delta_0}}(y) \lesssim_{\alpha, N} \|\mathbf{1}_S\|_{L^{p}(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} = \omega_{L_0}^{X_{\Delta_0}}(S)^{\frac1p}. \end{align} $$
This readily implies that
![]() $\omega _L^{X_{\Delta _0}}\ll \omega _{L_0}^{X_{\Delta _0}}$
in
$\omega _L^{X_{\Delta _0}}\ll \omega _{L_0}^{X_{\Delta _0}}$
in
![]() $\Delta _0$
, and since
$\Delta _0$
, and since
![]() $\Delta _0$
is arbitrary, we conclude that
$\Delta _0$
is arbitrary, we conclude that
![]() $\omega _L\ll \omega _{L_0}$
in
$\omega _L\ll \omega _{L_0}$
in
![]() $\partial \Omega $
. To proceed, fix
$\partial \Omega $
. To proceed, fix
![]() $B_0=B(x_0,r_0)$
and
$B_0=B(x_0,r_0)$
and
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $B\subset B_0$
,
$B\subset B_0$
,
![]() $x_0,x \in \partial \Omega $
and
$x_0,x \in \partial \Omega $
and
![]() $0 < r_0,r < \operatorname {\mathrm {diam}}(\partial \Omega )$
. Write
$0 < r_0,r < \operatorname {\mathrm {diam}}(\partial \Omega )$
. Write
![]() $\Delta _0=B_0\cap \partial \Omega $
and
$\Delta _0=B_0\cap \partial \Omega $
and
![]() $\Delta =B\cap \partial \Omega $
. Let
$\Delta =B\cap \partial \Omega $
. Let
![]() $S\subset \Delta $
be an arbitrary Borel set. If
$S\subset \Delta $
be an arbitrary Borel set. If
![]() $r\approx r_0$
, we have by Harnack’s inequality and Lemma 3.9 part
$r\approx r_0$
, we have by Harnack’s inequality and Lemma 3.9 part
![]() $(a)$
$(a)$
 $$ \begin{align*} \frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \frac{\omega_L^{X_{\Delta}}(S)}{\omega_L^{X_{\Delta}}(\Delta)} \approx \omega_L^{X_{\Delta}}(S) \lesssim_{\alpha, N} \omega_{L_0}^{X_{\Delta}}(S)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta}}(S)}{\omega_{L_0}^{X_{\Delta}}(\Delta)}\Big)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \end{align*} $$
$$ \begin{align*} \frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \frac{\omega_L^{X_{\Delta}}(S)}{\omega_L^{X_{\Delta}}(\Delta)} \approx \omega_L^{X_{\Delta}}(S) \lesssim_{\alpha, N} \omega_{L_0}^{X_{\Delta}}(S)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta}}(S)}{\omega_{L_0}^{X_{\Delta}}(\Delta)}\Big)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \end{align*} $$
where in the third estimate we have used equation (4.13) with
![]() $\Delta $
in place of
$\Delta $
in place of
![]() $\Delta _0$
. On the other hand, if
$\Delta _0$
. On the other hand, if
![]() $r\ll r_0$
we have by Lemma 3.9 part
$r\ll r_0$
we have by Lemma 3.9 part
![]() $(d)$
that
$(d)$
that
![]() $\omega _L\ll \omega _{L_0}$
with
$\omega _L\ll \omega _{L_0}$
with
 $$ \begin{align*} \frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \omega_L^{X_{\Delta}}(S) \lesssim_{\alpha, N} \omega_{L_0}^{X_{\Delta}}(S)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \end{align*} $$
$$ \begin{align*} \frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \omega_L^{X_{\Delta}}(S) \lesssim_{\alpha, N} \omega_{L_0}^{X_{\Delta}}(S)^{\frac1p} \approx \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \end{align*} $$
where again we have used equation (4.13) with
![]() $\Delta $
in place of
$\Delta $
in place of
![]() $\Delta _0$
in the middle estimate. In short, we have proved that
$\Delta _0$
in the middle estimate. In short, we have proved that
 $$\begin{align*}\frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \lesssim_{\alpha, N} \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \qquad \text{for any Borel set } S\subset\Delta. \end{align*}$$
$$\begin{align*}\frac{\omega_L^{X_{\Delta_0}}(S)}{\omega_L^{X_{\Delta_0}}(\Delta)} \lesssim_{\alpha, N} \Big(\frac{\omega_{L_0}^{X_{\Delta_0}}(S)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}\Big)^{\frac1p}, \qquad \text{for any Borel set } S\subset\Delta. \end{align*}$$
Using the fact that the implicit constants do not depend on
![]() $\Delta $
(nor on
$\Delta $
(nor on
![]() $\Delta _0$
) and Lemma 3.9 part
$\Delta _0$
) and Lemma 3.9 part
![]() $(c)$
, this readily implies that
$(c)$
, this readily implies that
![]() $\omega _L^{X_{\Delta _0}}\in RH_q(\Delta _0, \omega _{L_0}^{X_{\Delta _0}})$
for some
$\omega _L^{X_{\Delta _0}}\in RH_q(\Delta _0, \omega _{L_0}^{X_{\Delta _0}})$
for some
![]() $q\in (1,\infty )$
, where q and the implicit constants do not depend on
$q\in (1,\infty )$
, where q and the implicit constants do not depend on
![]() $\Delta _0$
, see [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]. Hence, we readily conclude that
$\Delta _0$
, see [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]. Hence, we readily conclude that
![]() $\omega _L\in RH_q(\partial \Omega , \omega _{L_0})$
(see Definition 3.1). This completes the proof of the present implication.
$\omega _L\in RH_q(\partial \Omega , \omega _{L_0})$
(see Definition 3.1). This completes the proof of the present implication.
![]() $\Box $
$\Box $
4.5 Proof of
 $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(d)}$
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(d)}$
Assume that
![]() $\omega _L\in A_{\infty }(\partial \Omega ,\omega _{L_0})$
. By the classical theory of weights (cf. [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]) and Lemma 3.9 part
$\omega _L\in A_{\infty }(\partial \Omega ,\omega _{L_0})$
. By the classical theory of weights (cf. [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]) and Lemma 3.9 part
![]() $(c)$
, it is not hard to see that
$(c)$
, it is not hard to see that
![]() $\omega _{L_0}\in A_{\infty }(\partial \Omega ,\omega _{L})$
, hence
$\omega _{L_0}\in A_{\infty }(\partial \Omega ,\omega _{L})$
, hence
![]() $\omega _{L_0}\in RH_{p}(\partial \Omega ,\omega _{L})$
for some
$\omega _{L_0}\in RH_{p}(\partial \Omega ,\omega _{L})$
for some
![]() $1<p<\infty $
. In particular for every
$1<p<\infty $
. In particular for every
![]() $Q_0\in \mathbb {D}(\partial \Omega )$
and
$Q_0\in \mathbb {D}(\partial \Omega )$
and
![]() $Q\in \mathbb {D}_{Q_0}$
, by Lemma 3.9 part
$Q\in \mathbb {D}_{Q_0}$
, by Lemma 3.9 part
![]() $(c)$
we have
$(c)$
we have

Thus, for
![]() $F\subset Q$
we obtain, by Hölder’s inequality,
$F\subset Q$
we obtain, by Hölder’s inequality,

To continue, we need a dyadic version of equation (3.9): for every
![]() $Q_0\in \mathbb {D}(\partial \Omega )$
, and for every
$Q_0\in \mathbb {D}(\partial \Omega )$
, and for every
![]() $\vartheta \ge \vartheta _0$
, we claim that
$\vartheta \ge \vartheta _0$
, we claim that
This estimate can be proved following the argument in [Reference Akman, Hofmann, Martell and Toro1, Section 4.2] with the following changes. Recall [Reference Akman, Hofmann, Martell and Toro1, (4.5)] (here we note that in [Reference Akman, Hofmann, Martell and Toro1, Section 4.2] our parameter
![]() $\vartheta $
is implicit)
$\vartheta $
is implicit)
where
![]() $\lambda $
,
$\lambda $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
,
$\gamma $
,
![]() $\theta> 0$
,
$\theta> 0$
,
![]() $Q_j$
is some dyadic cube (see [Reference Akman, Hofmann, Martell and Toro1, Section 4.2]),
$Q_j$
is some dyadic cube (see [Reference Akman, Hofmann, Martell and Toro1, Section 4.2]),
![]() $\mathcal {S}_{Q_j}^{\vartheta , k_0}u$
is a truncated localized dyadic conical square function with respect to the cones
$\mathcal {S}_{Q_j}^{\vartheta , k_0}u$
is a truncated localized dyadic conical square function with respect to the cones
 $$\begin{align*}\Gamma_{Q_j}^{\vartheta, k_0}(x) := \bigcup_{\substack{x\in Q'\in\mathbb{D}_{Q} \\ \ell(Q')\ge 2^{-k_0}\,\ell(Q_0)}} U_{Q'}^{\vartheta} \end{align*}$$
$$\begin{align*}\Gamma_{Q_j}^{\vartheta, k_0}(x) := \bigcup_{\substack{x\in Q'\in\mathbb{D}_{Q} \\ \ell(Q')\ge 2^{-k_0}\,\ell(Q_0)}} U_{Q'}^{\vartheta} \end{align*}$$
and
![]() $k_0$
is large enough (eventually
$k_0$
is large enough (eventually
![]() $k_0\to \infty $
). It should be noted that the implicit constant in the inequality equation (4.16) does not depend on
$k_0\to \infty $
). It should be noted that the implicit constant in the inequality equation (4.16) does not depend on
![]() $k_0$
. Combining equation (4.16) with equation (4.14), we easily arrive at
$k_0$
. Combining equation (4.16) with equation (4.14), we easily arrive at
 $$ \begin{align} \omega_{L_0}^{X_{Q_0}}\big(\big\{x\in Q_j: \mathcal{S}_{Q_j}^{\vartheta, k_0}u(x)>\beta\,\lambda,\ \mathcal{N}_{Q_0}^{\vartheta} u(x)\le \gamma\,\lambda \big\}\big) \lesssim \Big(\frac{\gamma}{\beta}\Big)^{\frac{\theta}{p'}}\, \omega_{L_0}^{X_{Q_0}}(Q_j). \end{align} $$
$$ \begin{align} \omega_{L_0}^{X_{Q_0}}\big(\big\{x\in Q_j: \mathcal{S}_{Q_j}^{\vartheta, k_0}u(x)>\beta\,\lambda,\ \mathcal{N}_{Q_0}^{\vartheta} u(x)\le \gamma\,\lambda \big\}\big) \lesssim \Big(\frac{\gamma}{\beta}\Big)^{\frac{\theta}{p'}}\, \omega_{L_0}^{X_{Q_0}}(Q_j). \end{align} $$
From this, we can derive [Reference Akman, Hofmann, Martell and Toro1, (4.3)] with
![]() $\omega _{L_0}^{X_{Q_0}}$
in place of
$\omega _{L_0}^{X_{Q_0}}$
in place of
![]() $\omega _{L}^{X_{Q_0}}$
and a typical good-
$\omega _{L}^{X_{Q_0}}$
and a typical good-
![]() $\lambda $
argument much as in [Reference Akman, Hofmann, Martell and Toro1, Section 4.2] readily leads to equation (4.15).
$\lambda $
argument much as in [Reference Akman, Hofmann, Martell and Toro1, Section 4.2] readily leads to equation (4.15).
With equation (4.15) at our disposal, we can then proceed to obtain equation (3.9). Fix
![]() $\Delta _0 = \Delta (x_0, r_0)$
with
$\Delta _0 = \Delta (x_0, r_0)$
with
![]() $x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
. Let
$x_0 \in \partial \Omega , 0 < r_0 < \operatorname {\mathrm {diam}} (\partial \Omega )$
. Let
![]() $M\ge 1$
be large enough to be chosen, and set
$M\ge 1$
be large enough to be chosen, and set
One has that
![]() $\mathcal {F}_{\Delta _0}$
is a pairwise disjoint family and
$\mathcal {F}_{\Delta _0}$
is a pairwise disjoint family and
 $$\begin{align*}\Delta_0 \subset \bigcup_{Q\in \mathcal{F}_{\Delta_0}} Q \subset \tfrac54\Delta_0, \end{align*}$$
$$\begin{align*}\Delta_0 \subset \bigcup_{Q\in \mathcal{F}_{\Delta_0}} Q \subset \tfrac54\Delta_0, \end{align*}$$
provided M is large enough.
Write
![]() $\widetilde {r}_0:=r_0/2M$
. Let
$\widetilde {r}_0:=r_0/2M$
. Let
![]() $x\in Q_0\in \mathcal {F}_{\Delta _0}$
and
$x\in Q_0\in \mathcal {F}_{\Delta _0}$
and
![]() $X\in \Gamma _{\widetilde {r}_0}^{\alpha }(x)$
. Let
$X\in \Gamma _{\widetilde {r}_0}^{\alpha }(x)$
. Let
![]() $I_X\in \mathcal {W}$
be so that
$I_X\in \mathcal {W}$
be so that
![]() $I_X\ni X$
, and pick
$I_X\ni X$
, and pick
![]() $Q_X\in \mathbb {D}(\partial \Omega )$
with
$Q_X\in \mathbb {D}(\partial \Omega )$
with
![]() $x\in Q_X$
and
$x\in Q_X$
and
![]() $\ell (Q_X)=\ell (I_X)$
. Note that
$\ell (Q_X)=\ell (I_X)$
. Note that
This and the fact that
![]() $x\in Q_0\cap Q_X$
give
$x\in Q_0\cap Q_X$
give
![]() $Q_X\subset Q_0$
. On the other hand,
$Q_X\subset Q_0$
. On the other hand,
 $$ \begin{align*} \operatorname{dist}(I_X,Q_X) \le |X-x| \le (1+\alpha)\delta(X) &\le (1+\alpha)(\operatorname{\mathrm{diam}}(I_X)+\operatorname{dist}(I_X,\partial\Omega)) \\ &\qquad\le 41\sqrt{n+1}(1+\alpha)\ell(I_X) = 41\sqrt{n+1}(1+\alpha)\ell(Q_X). \end{align*} $$
$$ \begin{align*} \operatorname{dist}(I_X,Q_X) \le |X-x| \le (1+\alpha)\delta(X) &\le (1+\alpha)(\operatorname{\mathrm{diam}}(I_X)+\operatorname{dist}(I_X,\partial\Omega)) \\ &\qquad\le 41\sqrt{n+1}(1+\alpha)\ell(I_X) = 41\sqrt{n+1}(1+\alpha)\ell(Q_X). \end{align*} $$
This shows that if we fix
![]() $\vartheta =\vartheta (\alpha )$
so that
$\vartheta =\vartheta (\alpha )$
so that
![]() $2^{\vartheta }\ge 41\sqrt {n+1}(1+\alpha )$
, then
$2^{\vartheta }\ge 41\sqrt {n+1}(1+\alpha )$
, then
![]() $I_X\in \mathcal {W}^{\vartheta }_{Q_X}\subset \mathcal {W}^{\vartheta ,*}_{Q_X}$
. As a result,
$I_X\in \mathcal {W}^{\vartheta }_{Q_X}\subset \mathcal {W}^{\vartheta ,*}_{Q_X}$
. As a result,
![]() $X\in I_X\subset U_{Q_X}^{\vartheta }$
and
$X\in I_X\subset U_{Q_X}^{\vartheta }$
and
![]() $X\in \Gamma _{Q_0}^{\vartheta }(x)$
. All these show that for every
$X\in \Gamma _{Q_0}^{\vartheta }(x)$
. All these show that for every
![]() $Q_0\in \mathcal {F}_{\Delta _0}$
and
$Q_0\in \mathcal {F}_{\Delta _0}$
and
![]() $x\in Q_0\in \mathcal {F}_{\Delta _0}$
we have
$x\in Q_0\in \mathcal {F}_{\Delta _0}$
we have
![]() $\Gamma _{\widetilde {r}_0}^{\alpha }(x)\subset \Gamma _{Q_0}^{\vartheta }(x)$
. Thus, equation (4.15) yields
$\Gamma _{\widetilde {r}_0}^{\alpha }(x)\subset \Gamma _{Q_0}^{\vartheta }(x)$
. Thus, equation (4.15) yields
 $$ \begin{align*} \|\mathcal{S}^{\alpha}_{\widetilde{r}_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}^q &\le \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{S}^{\alpha}_{\widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \\ &\qquad \le \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{S}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \lesssim_{\alpha} \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{N}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x). \end{align*} $$
$$ \begin{align*} \|\mathcal{S}^{\alpha}_{\widetilde{r}_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})}^q &\le \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{S}^{\alpha}_{\widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \\ &\qquad \le \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{S}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \lesssim_{\alpha} \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{N}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x). \end{align*} $$
To continue, let
![]() $Q_0\in \mathcal {F}_{\Delta _0}$
,
$Q_0\in \mathcal {F}_{\Delta _0}$
,
![]() $x\in Q_0$
and
$x\in Q_0$
and
![]() $X\in \Gamma _{Q_0}^{\vartheta , *}(x)$
. Then
$X\in \Gamma _{Q_0}^{\vartheta , *}(x)$
. Then
![]() $X\in I^{**}$
with
$X\in I^{**}$
with
![]() $I\in \mathcal {W}_{Q}^{\vartheta ,*}$
and
$I\in \mathcal {W}_{Q}^{\vartheta ,*}$
and
![]() $x\in Q\subset Q_0$
. As a consequence,
$x\in Q\subset Q_0$
. As a consequence,
where we have used equation (2.15), and the last estimate holds provided M is large enough. This shows that
![]() $X\in \Gamma ^{\alpha '}_{2\kappa _0 \widetilde {r}_0}(x)$
for some
$X\in \Gamma ^{\alpha '}_{2\kappa _0 \widetilde {r}_0}(x)$
for some
![]() $\alpha '=\alpha '(\vartheta )$
(hence, depending on
$\alpha '=\alpha '(\vartheta )$
(hence, depending on
![]() $\alpha $
). As a consequence of these, we obtain
$\alpha $
). As a consequence of these, we obtain
 $$ \begin{align*} \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{N}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) &\le \int_{\frac54\Delta_0} \mathcal{N}^{\alpha'}_{2\kappa_0 \widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \\ &\qquad \lesssim_{\alpha} \int_{5\Delta_0} \mathcal{N}^{\alpha}_{8\kappa_0 \widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \le \int_{5\Delta_0} \mathcal{N}^{\alpha}_{r_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x), \end{align*} $$
$$ \begin{align*} \sum_{Q_0\in \mathcal{F}_{\Delta_0}} \int_{Q_0} \mathcal{N}^{\vartheta}_{Q_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) &\le \int_{\frac54\Delta_0} \mathcal{N}^{\alpha'}_{2\kappa_0 \widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \\ &\qquad \lesssim_{\alpha} \int_{5\Delta_0} \mathcal{N}^{\alpha}_{8\kappa_0 \widetilde{r}_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x) \le \int_{5\Delta_0} \mathcal{N}^{\alpha}_{r_0} u(x)^q\,d\omega_{L_0}^{X_{\Delta_0}}(x), \end{align*} $$
where we have used equation (4.6) and the last estimate follows provided M is large enough.
![]() $\Box $
$\Box $
4.6 Proof of
 $\mathrm {(d)}\ \Longrightarrow \ \mathrm {(d)}'$
$\mathrm {(d)}\ \Longrightarrow \ \mathrm {(d)}'$
This is trivial since, for any arbitrary Borel set
![]() $S\subset \partial \Omega $
, the solution
$S\subset \partial \Omega $
, the solution
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
belongs to
$X\in \Omega $
belongs to
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
.
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )$
.
![]() $\Box $
$\Box $
4.7 Proof of
 $\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(a)}$
$\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(a)}$
Assume that equation (3.9) holds for some fixed
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $q\in (0,\infty )$
and for
$q\in (0,\infty )$
and for
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
, for any arbitrary Borel set
$X\in \Omega $
, for any arbitrary Borel set
![]() $S\subset \partial \Omega $
. By Lemma 4.4 (applied to
$S\subset \partial \Omega $
. By Lemma 4.4 (applied to
![]() $F(X)=|\nabla u(X)|\delta (X)^{(1-n)/2}$
), for any
$F(X)=|\nabla u(X)|\delta (X)^{(1-n)/2}$
), for any
![]() $\alpha $
large enough to be chosen we have
$\alpha $
large enough to be chosen we have
for every
![]() $\Delta _0 = \Delta (x_0, r_0)$
with
$\Delta _0 = \Delta (x_0, r_0)$
with
![]() $x_0 \in \partial \Omega , 0 < r_0< \operatorname {\mathrm {diam}} (\partial \Omega )/3$
and where we have used that
$x_0 \in \partial \Omega , 0 < r_0< \operatorname {\mathrm {diam}} (\partial \Omega )/3$
and where we have used that
![]() $0\le u\le 1$
. Let us see how to extend the previous estimate, in the case
$0\le u\le 1$
. Let us see how to extend the previous estimate, in the case
![]() $\partial \Omega $
is bounded, to any
$\partial \Omega $
is bounded, to any
![]() $\operatorname {\mathrm {diam}}(\partial \Omega )/3\le r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that if
$\operatorname {\mathrm {diam}}(\partial \Omega )/3\le r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Note that if
![]() $x\in \Delta _0$
and
$x\in \Delta _0$
and
![]() $X\in \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )/4}(x)$
, then
$X\in \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )/4}(x)$
, then
Set
![]() $\mathcal {W}_{x}=\{I\in \mathcal {W}: I\cap (\Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )/4}(x))\neq \emptyset \}$
, whose cardinality is uniformly bounded (depending in dimension and
$\mathcal {W}_{x}=\{I\in \mathcal {W}: I\cap (\Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )}(x)\setminus \Gamma ^{\alpha }_{\operatorname {\mathrm {diam}} (\partial \Omega )/4}(x))\neq \emptyset \}$
, whose cardinality is uniformly bounded (depending in dimension and
![]() $\alpha $
). Thus, since
$\alpha $
). Thus, since
![]() $\|u\|_{L^{\infty }(\Omega )}\le 1$
, Caccioppoli’s inequality gives
$\|u\|_{L^{\infty }(\Omega )}\le 1$
, Caccioppoli’s inequality gives
 $$ \begin{align*} \iint_{\Gamma^{\alpha}_{\operatorname{\mathrm{diam}} (\partial \Omega)}(x)\setminus \Gamma^{\alpha}_{\operatorname{\mathrm{diam}} (\partial \Omega)/4}(x)} |\nabla u(X)|^2 \delta(X)^{1-n}\,dX &\lesssim \sum_{I\in \mathcal{W}_{x}} \ell(I)^{1-n} \iint_I |\nabla u(X)|^2\,dX \\ &\quad\lesssim \sum_{I\in \mathcal{W}_{x}} \ell(I)^{-1-n} \iint_{I^*} |u(X)|^2\,dX \lesssim \# \mathcal{W}_{x} \lesssim_{\alpha} 1. \end{align*} $$
$$ \begin{align*} \iint_{\Gamma^{\alpha}_{\operatorname{\mathrm{diam}} (\partial \Omega)}(x)\setminus \Gamma^{\alpha}_{\operatorname{\mathrm{diam}} (\partial \Omega)/4}(x)} |\nabla u(X)|^2 \delta(X)^{1-n}\,dX &\lesssim \sum_{I\in \mathcal{W}_{x}} \ell(I)^{1-n} \iint_I |\nabla u(X)|^2\,dX \\ &\quad\lesssim \sum_{I\in \mathcal{W}_{x}} \ell(I)^{-1-n} \iint_{I^*} |u(X)|^2\,dX \lesssim \# \mathcal{W}_{x} \lesssim_{\alpha} 1. \end{align*} $$
With this in hand and equation (4.18) applied with
![]() $r_0=\operatorname {\mathrm {diam}}(\partial \Omega )/4<\operatorname {\mathrm {diam}}(\partial \Omega )/3$
, we readily obtain
$r_0=\operatorname {\mathrm {diam}}(\partial \Omega )/4<\operatorname {\mathrm {diam}}(\partial \Omega )/3$
, we readily obtain
 $$ \begin{align*} &\|\mathcal{S}^{\alpha}_{r_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \le \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \\ &\qquad\qquad \le \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)} u-\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)/4} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} + \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)/4} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \lesssim \omega_{L_0}^{X_{\Delta_0}}(\Delta_0)^{\frac1q}. \end{align*} $$
$$ \begin{align*} &\|\mathcal{S}^{\alpha}_{r_0} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \le \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \\ &\qquad\qquad \le \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)} u-\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)/4} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} + \|\mathcal{S}^{\alpha}_{\operatorname{\mathrm{diam}}(\partial\Omega)/4} u\|_{L^q(\Delta_0, \omega_{L_0}^{X_{\Delta_0}})} \lesssim \omega_{L_0}^{X_{\Delta_0}}(\Delta_0)^{\frac1q}. \end{align*} $$
We next see that given
![]() $\gamma \in (0,1)$
there exists
$\gamma \in (0,1)$
there exists
![]() $\beta \in (0,1)$
so that for every
$\beta \in (0,1)$
so that for every
![]() $Q_0\in \mathbb {D}(\partial \Omega )$
and for every Borel set
$Q_0\in \mathbb {D}(\partial \Omega )$
and for every Borel set
![]() $F\subset Q_0$
we have
$F\subset Q_0$
we have
 $$ \begin{align} \frac{\omega_{L}^{X_{Q_0}}(F)}{\omega_{L}^{X_{Q_0}}(Q_0)}\le \beta \quad\Longrightarrow\quad \frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)}\le \gamma. \end{align} $$
$$ \begin{align} \frac{\omega_{L}^{X_{Q_0}}(F)}{\omega_{L}^{X_{Q_0}}(Q_0)}\le \beta \quad\Longrightarrow\quad \frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)}\le \gamma. \end{align} $$
Indeed, fix
![]() $\gamma \in (0,1)$
and
$\gamma \in (0,1)$
and
![]() $Q_0\in \mathbb {D}(\partial \Omega )$
, and take a Borel set
$Q_0\in \mathbb {D}(\partial \Omega )$
, and take a Borel set
![]() $F\subset Q_0$
so that
$F\subset Q_0$
so that
![]() ${\omega _L^{X_{Q_0}}(F)}\le \beta \omega _L^{X_{Q_0}}(Q_0) $
, where
${\omega _L^{X_{Q_0}}(F)}\le \beta \omega _L^{X_{Q_0}}(Q_0) $
, where
![]() $\beta \in (0,1)$
is small enough to be chosen. Applying Lemma 4.2, if we assume that
$\beta \in (0,1)$
is small enough to be chosen. Applying Lemma 4.2, if we assume that
![]() $0<\beta <\beta _0$
, then
$0<\beta <\beta _0$
, then
![]() $u(X)=\omega ^X_L(S)$
satisfies equation (4.3) and therefore
$u(X)=\omega ^X_L(S)$
satisfies equation (4.3) and therefore
 $$ \begin{align} C_{\eta}^{-q} \log{(\beta^{-1})}^{\frac{q}{2}}\omega_{L_0}^{X_{Q_0}}(F) \leq \int_F \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x) \leq \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x). \end{align} $$
$$ \begin{align} C_{\eta}^{-q} \log{(\beta^{-1})}^{\frac{q}{2}}\omega_{L_0}^{X_{Q_0}}(F) \leq \int_F \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x) \leq \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x). \end{align} $$
We claim that there exists
![]() $\alpha _0=\alpha _0(\vartheta _0, \eta )$
(hence, depending on the allowable parameters) such that
$\alpha _0=\alpha _0(\vartheta _0, \eta )$
(hence, depending on the allowable parameters) such that
with
![]() $r_{Q_0}^*=2 \kappa _0 r_{Q_0}$
(cf. equation (2.15)). To see this, let
$r_{Q_0}^*=2 \kappa _0 r_{Q_0}$
(cf. equation (2.15)). To see this, let
![]() $x\in Q_0$
and
$x\in Q_0$
and
![]() $X\in \Gamma _{Q_0,\eta }^{\vartheta _0}(x)$
. Then
$X\in \Gamma _{Q_0,\eta }^{\vartheta _0}(x)$
. Then
![]() $X\in I^*$
for some
$X\in I^*$
for some
![]() $I\in \mathcal {W}_{Q'}^{\vartheta _0,*}$
, where
$I\in \mathcal {W}_{Q'}^{\vartheta _0,*}$
, where
![]() $Q'\subset Q\in \mathbb {D}_{Q_0}$
with
$Q'\subset Q\in \mathbb {D}_{Q_0}$
with
![]() $Q\ni x$
and
$Q\ni x$
and
![]() $\ell (Q')>\eta ^3\ell (Q)$
. Then
$\ell (Q')>\eta ^3\ell (Q)$
. Then
![]() $X\in T_{Q_0}^{\vartheta _0,*}\subset B_{Q_0}^*\cap \Omega $
(see equation (2.15)) and
$X\in T_{Q_0}^{\vartheta _0,*}\subset B_{Q_0}^*\cap \Omega $
(see equation (2.15)) and
and also
Hence, there exists
![]() $\alpha _0=\alpha _0(\vartheta _0, \eta )$
such that
$\alpha _0=\alpha _0(\vartheta _0, \eta )$
such that
![]() $X\in \Gamma ^{\alpha _0}_{r_{Q_0}^*}(x)$
, that is, equation (4.21) holds.
$X\in \Gamma ^{\alpha _0}_{r_{Q_0}^*}(x)$
, that is, equation (4.21) holds.
To continue, observe first that by equation (2.6) and the fact that
![]() $\kappa _0\ge 16 \Xi $
(cf. equation (2.15)), we have
$\kappa _0\ge 16 \Xi $
(cf. equation (2.15)), we have
![]() $Q_0\subset \Delta _{Q_0}^*$
. This, equation (4.21), Harnack’s inequality, equation (4.18) and Lemma 3.9 imply
$Q_0\subset \Delta _{Q_0}^*$
. This, equation (4.21), Harnack’s inequality, equation (4.18) and Lemma 3.9 imply
 $$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x) &\lesssim \int_{\Delta_{Q_0}^*} \mathcal{S}_{r_{Q_0}^*}^{\alpha}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x)\notag \\ & \quad \approx \int_{\Delta_{Q_0}^*} \mathcal{S}_{r_{Q_0}^*}^{\alpha}u(x)^q\,d \omega_{L_0}^{X_{\Delta_{Q_0}^*}} (x) \lesssim_{\alpha} \omega_{L_0}^{X_{\Delta_{Q_0}^*}} (2\Delta_{Q_0}^*) \approx \omega_{L_0}^{X_{Q_0}}(Q_0). \end{align} $$
$$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta_0}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x) &\lesssim \int_{\Delta_{Q_0}^*} \mathcal{S}_{r_{Q_0}^*}^{\alpha}u(x)^q\,d \omega_{L_0}^{X_{Q_0}} (x)\notag \\ & \quad \approx \int_{\Delta_{Q_0}^*} \mathcal{S}_{r_{Q_0}^*}^{\alpha}u(x)^q\,d \omega_{L_0}^{X_{\Delta_{Q_0}^*}} (x) \lesssim_{\alpha} \omega_{L_0}^{X_{\Delta_{Q_0}^*}} (2\Delta_{Q_0}^*) \approx \omega_{L_0}^{X_{Q_0}}(Q_0). \end{align} $$
Combining equations (4.20) and (4.22), we conclude that
 $$\begin{align*}\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \le C_{\eta,\vartheta_0,q} \, \log{(\beta^{-1})}^{-\frac{q}{2}}. \end{align*}$$
$$\begin{align*}\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \le C_{\eta,\vartheta_0,q} \, \log{(\beta^{-1})}^{-\frac{q}{2}}. \end{align*}$$
This readily gives equation (4.19) by choosing
![]() $\beta $
small enough so that
$\beta $
small enough so that
![]() $C_{\eta ,\vartheta _0,q} \, \log {(\beta ^{-1})}^{-\frac {q}{2}}<\gamma $
.
$C_{\eta ,\vartheta _0,q} \, \log {(\beta ^{-1})}^{-\frac {q}{2}}<\gamma $
.
Next, we show that equation (4.19) implies
![]() $\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. To see this, we first obtain a dyadic-
$\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. To see this, we first obtain a dyadic-
![]() $A_{\infty }$
condition. Fix
$A_{\infty }$
condition. Fix
![]() $Q^0, Q_0\in \mathbb {D}$
with
$Q^0, Q_0\in \mathbb {D}$
with
![]() $Q_0\subset Q^0$
. Remark 3.10 gives for every
$Q_0\subset Q^0$
. Remark 3.10 gives for every
![]() $F\subset Q_0$
$F\subset Q_0$
 $$ \begin{align} \frac{1}{C_1}\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \leq \frac{\omega_{L_0}^{X_{Q^0}}(F)}{\omega_{L_0}^{X_{Q^0}}(Q_0)} \leq C_1\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \ \ \ \text{and}\ \ \ \frac{1}{C_1}\frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)} \leq \frac{\omega_L^{X_{Q^0}}(F)}{\omega_L^{X_{Q^0}}(Q_0)} \leq C_1\frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)}, \end{align} $$
$$ \begin{align} \frac{1}{C_1}\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \leq \frac{\omega_{L_0}^{X_{Q^0}}(F)}{\omega_{L_0}^{X_{Q^0}}(Q_0)} \leq C_1\frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)} \ \ \ \text{and}\ \ \ \frac{1}{C_1}\frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)} \leq \frac{\omega_L^{X_{Q^0}}(F)}{\omega_L^{X_{Q^0}}(Q_0)} \leq C_1\frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)}, \end{align} $$
for some
![]() $C_1>1$
. Thus, given
$C_1>1$
. Thus, given
![]() $\gamma \in (0,1)$
, take the corresponding
$\gamma \in (0,1)$
, take the corresponding
![]() $\beta \in (0,1)$
so that equation (4.19) holds with
$\beta \in (0,1)$
so that equation (4.19) holds with
![]() $\gamma /C_1$
in place of
$\gamma /C_1$
in place of
![]() $\gamma $
. Then,
$\gamma $
. Then,
 $$ \begin{align} \frac{\omega_L^{X_{Q^0}}(F)}{\omega_L^{X_{Q^0}}(Q_0)}\le \frac{\beta}{C_1} \implies \frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)}\le \beta \implies \frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)}\le \frac{\gamma}{C_1} \implies \frac{\omega_{L_0}^{X_{Q^0}}(F)}{\omega_{L_0}^{X_{Q^0}}(Q_0)}\le \gamma. \end{align} $$
$$ \begin{align} \frac{\omega_L^{X_{Q^0}}(F)}{\omega_L^{X_{Q^0}}(Q_0)}\le \frac{\beta}{C_1} \implies \frac{\omega_L^{X_{Q_0}}(F)}{\omega_L^{X_{Q_0}}(Q_0)}\le \beta \implies \frac{\omega_{L_0}^{X_{Q_0}}(F)}{\omega_{L_0}^{X_{Q_0}}(Q_0)}\le \frac{\gamma}{C_1} \implies \frac{\omega_{L_0}^{X_{Q^0}}(F)}{\omega_{L_0}^{X_{Q^0}}(Q_0)}\le \gamma. \end{align} $$
To complete the proof, we need to see that equation (4.24) gives
![]() $\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. Fix
$\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
. Fix
![]() $\gamma \in (0,1)$
and a surface ball
$\gamma \in (0,1)$
and a surface ball
![]() $\Delta _0=B_0\cap \partial \Omega $
, with
$\Delta _0=B_0\cap \partial \Omega $
, with
![]() $B_0=B(x_0,r_0)$
,
$B_0=B(x_0,r_0)$
,
![]() $x_0\in \partial \Omega $
, and
$x_0\in \partial \Omega $
, and
![]() $0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Take an arbitrary surface ball
$0<r_0<\operatorname {\mathrm {diam}}(\partial \Omega )$
. Take an arbitrary surface ball
![]() $\Delta =B\cap \partial \Omega $
centered at
$\Delta =B\cap \partial \Omega $
centered at
![]() $\partial \Omega $
with
$\partial \Omega $
with
![]() $B=B(x,r)\subset B_0$
, and let
$B=B(x,r)\subset B_0$
, and let
![]() $F\subset \Delta $
be a Borel set such that
$F\subset \Delta $
be a Borel set such that
![]() $\omega _{L_0}^{X_{\Delta _0}}(F)>\gamma \omega _{L_0}^{X_{\Delta _0}}(\Delta )$
. Consider the pairwise disjoint family
$\omega _{L_0}^{X_{\Delta _0}}(F)>\gamma \omega _{L_0}^{X_{\Delta _0}}(\Delta )$
. Consider the pairwise disjoint family
![]() $\mathcal {F}=\{Q\in \mathbb {D}: Q\cap \Delta \neq \emptyset , \frac {r}{4\,\Xi }<\ell (Q)\le \frac {r}{2\,\Xi }\}$
, where
$\mathcal {F}=\{Q\in \mathbb {D}: Q\cap \Delta \neq \emptyset , \frac {r}{4\,\Xi }<\ell (Q)\le \frac {r}{2\,\Xi }\}$
, where
![]() $\Xi $
is the constant in equation (2.6). In particular,
$\Xi $
is the constant in equation (2.6). In particular,
![]() $\Delta \subset \bigcup _{Q\in \mathcal {F}} Q\subset 2\Delta $
. The pigeon-hole principle yields that there is a constant
$\Delta \subset \bigcup _{Q\in \mathcal {F}} Q\subset 2\Delta $
. The pigeon-hole principle yields that there is a constant
![]() $C'>1$
depending just on the doubling constant of
$C'>1$
depending just on the doubling constant of
![]() $\omega _{L_0}^{X_{\Delta _0}}$
so that
$\omega _{L_0}^{X_{\Delta _0}}$
so that
![]() ${\omega _{L_0}^{X_{\Delta _0}}(F\cap Q_0)}/{\omega _{L_0}^{X_{\Delta _0}}(Q_0)}>{\gamma }/{C'}$
for some
${\omega _{L_0}^{X_{\Delta _0}}(F\cap Q_0)}/{\omega _{L_0}^{X_{\Delta _0}}(Q_0)}>{\gamma }/{C'}$
for some
![]() $Q_0\in \mathcal {F}$
. Let
$Q_0\in \mathcal {F}$
. Let
![]() $Q^0\in \mathbb {D}$
be the unique dyadic cube such that
$Q^0\in \mathbb {D}$
be the unique dyadic cube such that
![]() $Q_0\subset Q^0$
and
$Q_0\subset Q^0$
and
![]() $\frac {r_0}{2}<\ell (Q^0)\le r_0$
. We can then invoke the contrapositive of equation (4.24) with
$\frac {r_0}{2}<\ell (Q^0)\le r_0$
. We can then invoke the contrapositive of equation (4.24) with
![]() ${\gamma }/{C'}$
in place of
${\gamma }/{C'}$
in place of
![]() $\gamma $
to find
$\gamma $
to find
![]() $\beta \in (0,1)$
such that by Lemma 3.9 and Harnack’s inequality we arrive at
$\beta \in (0,1)$
such that by Lemma 3.9 and Harnack’s inequality we arrive at
 $$\begin{align*}\frac{\omega_L^{X_{\Delta_0}}(F)}{\omega_L^{X_{\Delta_0}}(\Delta)} \ge \frac{\omega_L^{X_{\Delta_0}}(F\cap Q_0)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \frac{\omega_L^{X_{\Delta_0}}(F\cap Q_0)}{\omega_L^{X_{\Delta_0}}(Q_0)} \approx \frac{\omega_L^{X_{Q^0}}(F\cap Q_0)}{\omega_L^{X_{Q^0}}(Q_0)}>\frac{\beta}{C_1}. \end{align*}$$
$$\begin{align*}\frac{\omega_L^{X_{\Delta_0}}(F)}{\omega_L^{X_{\Delta_0}}(\Delta)} \ge \frac{\omega_L^{X_{\Delta_0}}(F\cap Q_0)}{\omega_L^{X_{\Delta_0}}(\Delta)} \approx \frac{\omega_L^{X_{\Delta_0}}(F\cap Q_0)}{\omega_L^{X_{\Delta_0}}(Q_0)} \approx \frac{\omega_L^{X_{Q^0}}(F\cap Q_0)}{\omega_L^{X_{Q^0}}(Q_0)}>\frac{\beta}{C_1}. \end{align*}$$
In short, we have obtained that for every
![]() $\gamma \in (0,1)$
there exists
$\gamma \in (0,1)$
there exists
![]() $\widetilde {\beta }\in (0,1)$
such that
$\widetilde {\beta }\in (0,1)$
such that
 $$\begin{align*}\frac{\omega_{L_0}^{X_{\Delta_0}}(F)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}>\gamma \implies \frac{\omega_L^{X_{\Delta_0}}(F)}{\omega_L^{X_{\Delta_0}}(\Delta)}>\widetilde{\beta}. \end{align*}$$
$$\begin{align*}\frac{\omega_{L_0}^{X_{\Delta_0}}(F)}{\omega_{L_0}^{X_{\Delta_0}}(\Delta)}>\gamma \implies \frac{\omega_L^{X_{\Delta_0}}(F)}{\omega_L^{X_{\Delta_0}}(\Delta)}>\widetilde{\beta}. \end{align*}$$
This and the classical theory of weights (cf. [Reference Coifman and Fefferman11, Reference García-Cuerva and Rubio de Francia25]) show that
![]() $\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
, and the proof is complete.
$\omega _{L}\in A_{\infty }(\partial \Omega , \omega _{L_0})$
, and the proof is complete.
![]() $\Box $
$\Box $
4.8 Proof of
 $\mathrm {(c)}\ \Longrightarrow \ \mathrm {(c)}'$
$\mathrm {(c)}\ \Longrightarrow \ \mathrm {(c)}'$
This is trivial since for any arbitrary Borel set
![]() $S\subset \partial \Omega $
, the solution
$S\subset \partial \Omega $
, the solution
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
, belongs to
$X\in \Omega $
, belongs to
![]() $W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
.
$W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
.
![]() $\Box $
$\Box $
4.9 Proof of
 $\mathrm {(e)} \ \Longrightarrow \ \mathrm {(f)}$
$\mathrm {(e)} \ \Longrightarrow \ \mathrm {(f)}$
Let
![]() $\Delta _{\varepsilon }=B_{\varepsilon }\cap \partial \Omega $
,
$\Delta _{\varepsilon }=B_{\varepsilon }\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
, where
$\Delta '=B'\cap \partial \Omega $
, where
![]() $B_{\varepsilon }=B(x,\varepsilon r)$
with
$B_{\varepsilon }=B(x,\varepsilon r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta _{\varepsilon }$
and
$x'\in 2\Delta _{\varepsilon }$
and
![]() $0<r'<\varepsilon r c_0/4$
and
$0<r'<\varepsilon r c_0/4$
and
![]() $c_0$
is the corkscrew constant. Using equation (3.6) and Lemma 4.1, we easily obtain
$c_0$
is the corkscrew constant. Using equation (3.6) and Lemma 4.1, we easily obtain
 $$ \begin{align*} & \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \\ &\qquad\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} +|f_{\Delta, L_0}|^2 \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u_{L,\Omega}(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \\ &\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}+\|f\|^2_{L^{\infty}(\partial \Omega, \omega_{L_0})} \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\\ &\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}+\|f\|^2_{L^{\infty}(\partial \Omega, \omega_{L_0})} \varepsilon^{2\rho}. \end{align*} $$
$$ \begin{align*} & \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \\ &\qquad\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} +|f_{\Delta, L_0}|^2 \frac{1}{\omega_{L_0}^{X_{\Delta_{\varepsilon}}} (\Delta')} \iint_{B'\cap \Omega} |\nabla u_{L,\Omega}(X)|^2 G_{L_0}(X_{\Delta_{\varepsilon}},X) \, d X \\ &\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}+\|f\|^2_{L^{\infty}(\partial \Omega, \omega_{L_0})} \Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho}\\ &\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}+\|f\|^2_{L^{\infty}(\partial \Omega, \omega_{L_0})} \varepsilon^{2\rho}. \end{align*} $$
Taking the sup over
![]() $B_{\varepsilon }$
and
$B_{\varepsilon }$
and
![]() $B'$
, we readily arrive at equation (3.7).
$B'$
, we readily arrive at equation (3.7).
![]() $\Box $
$\Box $
4.10 Proof of
 $\mathrm {(f)} \ \Longrightarrow \ \mathrm {(c)}'$
$\mathrm {(f)} \ \Longrightarrow \ \mathrm {(c)}'$
We first observe that (f) applied with
![]() $\varepsilon =1$
gives
$\varepsilon =1$
gives
 $$ \begin{align} \sup_{B} \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &|\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \notag \\ &\quad \le C \big(\|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} + \varrho(1)\|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2\big) \lesssim \|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2 , \end{align} $$
$$ \begin{align} \sup_{B} \sup_{B'} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &|\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \notag \\ &\quad \le C \big(\|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} + \varrho(1)\|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2\big) \lesssim \|f\|_{L^{\infty}(\partial\Omega, \omega_{L_0})}^2 , \end{align} $$
where
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
$\Delta '=B'\cap \partial \Omega $
, and the sups are taken, respectively, over all balls
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
and
$0<r'<r c_0/4$
and
![]() $c_0$
is the corkscrew constant.
$c_0$
is the corkscrew constant.
With this in place, we are now ready to establish (c)
![]() $'$
. Take an arbitrary Borel set
$'$
. Take an arbitrary Borel set
![]() $S\subset \partial \Omega $
, and let
$S\subset \partial \Omega $
, and let
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
. Fix
$X\in \Omega $
. Fix
![]() $X_0\in \Omega $
, and use that
$X_0\in \Omega $
, and use that
![]() $\omega _L^{X_0}$
is Borel regular to see that for every
$\omega _L^{X_0}$
is Borel regular to see that for every
![]() $j\ge 1$
there exist a closed set
$j\ge 1$
there exist a closed set
![]() $F_j$
and an open set
$F_j$
and an open set
![]() $U_j$
so that
$U_j$
so that
![]() $F_j\subset S\subset U_j$
and
$F_j\subset S\subset U_j$
and
![]() $\omega _L^{X_0}(U_j\setminus F_j)<j^{-1}$
. Using Urysohn’s lemma, we can construct
$\omega _L^{X_0}(U_j\setminus F_j)<j^{-1}$
. Using Urysohn’s lemma, we can construct
![]() $f_j \in \mathscr {C}(\partial \Omega )$
such that
$f_j \in \mathscr {C}(\partial \Omega )$
such that
![]() $\mathbf {1}_{F_j} \leq f_j \leq \mathbf {1}_{U_j}$
and for
$\mathbf {1}_{F_j} \leq f_j \leq \mathbf {1}_{U_j}$
and for
![]() $X\in \Omega $
set
$X\in \Omega $
set
It is straightforward to see that
![]() $|\mathbf {1}_S(x)-f_j(x)|\le \mathbf {1}_{U_j\setminus F_j}(x)$
for every
$|\mathbf {1}_S(x)-f_j(x)|\le \mathbf {1}_{U_j\setminus F_j}(x)$
for every
![]() $x\in \partial \Omega $
; hence, for every compact set
$x\in \partial \Omega $
; hence, for every compact set
![]() $K\subset \Omega $
and for every
$K\subset \Omega $
and for every
![]() $X\in K$
, we have by Harnack’s inequality
$X\in K$
, we have by Harnack’s inequality
Thus,
![]() $v_j\longrightarrow u$
uniformly on compacta in
$v_j\longrightarrow u$
uniformly on compacta in
![]() $\Omega $
. This together with Caccioppoli’s inequality readily imply that
$\Omega $
. This together with Caccioppoli’s inequality readily imply that
![]() $\nabla v_j \longrightarrow \nabla u$
in
$\nabla v_j \longrightarrow \nabla u$
in
![]() $L^2_{\mathrm {loc} }(\Omega )$
. In particular,
$L^2_{\mathrm {loc} }(\Omega )$
. In particular,
![]() $\nabla v_j \longrightarrow \nabla u$
in
$\nabla v_j \longrightarrow \nabla u$
in
![]() $L^2(K)$
for every compact set
$L^2(K)$
for every compact set
![]() $K\subset \Omega $
.
$K\subset \Omega $
.
Fix
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
, with
$\Delta '=B'\cap \partial \Omega $
, with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
and
$0<r'<r c_0/4$
and
![]() $c_0$
is the corkscrew constant. Let
$c_0$
is the corkscrew constant. Let
![]() and
and
![]() $u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
$u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
![]() $X\in \Omega $
. For every compact set
$X\in \Omega $
. For every compact set
![]() $K\subset \Omega $
, we then have by equation (4.25) applied to each
$K\subset \Omega $
, we then have by equation (4.25) applied to each
![]() $f_j$
$f_j$
 $$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{K\cap B'\cap \Omega} |\nabla u(X)|^2 G_{L_0} &(X_{\Delta},X) \, d X\\ &\qquad = \lim_{j\to\infty} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{K\cap B'\cap \Omega} |\nabla v_j(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim 1. \end{align*} $$
$$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{K\cap B'\cap \Omega} |\nabla u(X)|^2 G_{L_0} &(X_{\Delta},X) \, d X\\ &\qquad = \lim_{j\to\infty} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{K\cap B'\cap \Omega} |\nabla v_j(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim 1. \end{align*} $$
Taking the sup over B and
![]() $B'$
, we then conclude that
$B'$
, we then conclude that
![]() $(c)'$
holds since by the maximum principle one has
$(c)'$
holds since by the maximum principle one has
![]() $\|u\|_{L^{\infty }(\Omega )}=1$
.
$\|u\|_{L^{\infty }(\Omega )}=1$
.
![]() $\Box $
$\Box $
4.11 Proof of
 $\mathrm {(e)}' \ \Longrightarrow \ \mathrm {(f)}'$
$\mathrm {(e)}' \ \Longrightarrow \ \mathrm {(f)}'$
The argument used to see that
![]() $\mathrm {(e)} \ \Longrightarrow \ \mathrm {(f)}$
can be carried out in the present scenario with no changes.
$\mathrm {(e)} \ \Longrightarrow \ \mathrm {(f)}$
can be carried out in the present scenario with no changes.
![]() $\Box $
$\Box $
4.12 Proof of
 $\mathrm {(f)}'\ \Longrightarrow \ \mathrm {(c)}'$
$\mathrm {(f)}'\ \Longrightarrow \ \mathrm {(c)}'$
Let
![]() $f=\mathbf {1}_S$
with
$f=\mathbf {1}_S$
with
![]() $S\subset \partial \Omega $
a Borel set such that
$S\subset \partial \Omega $
a Borel set such that
![]() $\omega _{L_0}^X(S)\not = 0$
for some (or all)
$\omega _{L_0}^X(S)\not = 0$
for some (or all)
![]() $X\in \Omega $
. Note that
$X\in \Omega $
. Note that
![]() $\|f\|_{\mathrm {BMO}(\partial \Omega , \omega _{L_0})}\le \|f\|_{L^{\infty }(\partial \Omega , \omega _{L_0})}=1$
. From this and the fact that
$\|f\|_{\mathrm {BMO}(\partial \Omega , \omega _{L_0})}\le \|f\|_{L^{\infty }(\partial \Omega , \omega _{L_0})}=1$
. From this and the fact that
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
, satisfies
$X\in \Omega $
, satisfies
![]() $\|u\|_{L^{\infty }(\Omega )}=1$
, we readily see that equation (3.7) with
$\|u\|_{L^{\infty }(\Omega )}=1$
, we readily see that equation (3.7) with
![]() $\varepsilon =1$
implies equation (3.8).
$\varepsilon =1$
implies equation (3.8).
![]() $\Box $
$\Box $
4.13 Proof of
 $\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
$\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
Let
![]() $u(X)=\omega _L^X(S)$
,
$u(X)=\omega _L^X(S)$
,
![]() $X\in \Omega $
, for an arbitrary Borel set
$X\in \Omega $
, for an arbitrary Borel set
![]() $S\subset \partial \Omega $
. Let
$S\subset \partial \Omega $
. Let
![]() $\vartheta \ge \vartheta _0$
and
$\vartheta \ge \vartheta _0$
and
![]() $\eta \in (0,1)$
. Then
$\eta \in (0,1)$
. Then
 $$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x)^2\,d \omega_{L_0}^{X_{Q_0}} (x) &= \int_{Q_0}\bigg(\iint_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)\,d\omega_{L_0}^{X_{Q_0}}(x)\notag \\ &\quad =\iint_{B_{Q_0}^*\cap \Omega}|\nabla u(Y)|^2\delta(Y)^{1-n} \bigg(\int_{Q_0}\mathbf{1}_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}(Y)\,d\omega_{L_0}^{X_{Q_0}}(x)\bigg)\,dY, \end{align} $$
$$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x)^2\,d \omega_{L_0}^{X_{Q_0}} (x) &= \int_{Q_0}\bigg(\iint_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}|\nabla u(Y)|^2\delta(Y)^{1-n}\,dY\bigg)\,d\omega_{L_0}^{X_{Q_0}}(x)\notag \\ &\quad =\iint_{B_{Q_0}^*\cap \Omega}|\nabla u(Y)|^2\delta(Y)^{1-n} \bigg(\int_{Q_0}\mathbf{1}_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}(Y)\,d\omega_{L_0}^{X_{Q_0}}(x)\bigg)\,dY, \end{align} $$
where we have used that
![]() $\Gamma _{Q_0,\eta }^{\vartheta }(x)\subset T_{Q_0}^{\vartheta ,*}\subset B_{Q_0}^*\cap \overline {\Omega }$
(see equation (2.15)) and Fubini’s theorem. To estimate the inner integral, we fix
$\Gamma _{Q_0,\eta }^{\vartheta }(x)\subset T_{Q_0}^{\vartheta ,*}\subset B_{Q_0}^*\cap \overline {\Omega }$
(see equation (2.15)) and Fubini’s theorem. To estimate the inner integral, we fix
![]() $Y\in B_{Q_0}^*\cap \Omega $
and
$Y\in B_{Q_0}^*\cap \Omega $
and
![]() $\widehat {y}\in \partial \Omega $
such that
$\widehat {y}\in \partial \Omega $
such that
![]() $|Y-\widehat {y}|=\delta (Y)$
. We claim that
$|Y-\widehat {y}|=\delta (Y)$
. We claim that
To show this, let
![]() $x\in Q_0$
be such that
$x\in Q_0$
be such that
![]() $Y\in \Gamma _{Q_0,\eta }^{\vartheta }(x)$
. This means that there exists
$Y\in \Gamma _{Q_0,\eta }^{\vartheta }(x)$
. This means that there exists
![]() $Q\in \mathbb {D}_{Q_0}$
such that
$Q\in \mathbb {D}_{Q_0}$
such that
![]() $x\in Q$
and
$x\in Q$
and
![]() $Y\in U^{\vartheta }_{Q,\eta ^3}$
. Hence, there is
$Y\in U^{\vartheta }_{Q,\eta ^3}$
. Hence, there is
![]() $Q'\in \mathbb {D}_Q$
with
$Q'\in \mathbb {D}_Q$
with
![]() $\ell (Q')>\eta ^3\ell (Q)$
such that
$\ell (Q')>\eta ^3\ell (Q)$
such that
![]() $Y\in U^{\vartheta }_{Q'}$
and consequently
$Y\in U^{\vartheta }_{Q'}$
and consequently
![]() $\delta (Y)\approx _{\vartheta } \operatorname {dist}(Y,Q')\approx _{\vartheta } \ell (Q')$
. As a result,
$\delta (Y)\approx _{\vartheta } \operatorname {dist}(Y,Q')\approx _{\vartheta } \ell (Q')$
. As a result,
thus
![]() $x\in \Delta (\widehat {y},C_{\vartheta }\eta ^{-3}\delta (Y))$
as desired. If we now use equation (4.27), we conclude that for every
$x\in \Delta (\widehat {y},C_{\vartheta }\eta ^{-3}\delta (Y))$
as desired. If we now use equation (4.27), we conclude that for every
![]() $Y\in B_{Q_0}^*\cap \Omega $
$Y\in B_{Q_0}^*\cap \Omega $
 $$ \begin{align} \int_{Q_0}\mathbf{1}_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}(Y)\,d\omega_{L_0}^{X_{Q_0}}(x) \le \omega_{L_0}^{X_{Q_0}}\big(\Delta(\widehat{y},C_{\vartheta} \eta^{-3}\delta(Y))\big) \lesssim_{\vartheta,\eta} \omega_{L_0}^{X_{Q_0}}\big(\Delta(\widehat{y},\delta(Y))\big). \end{align} $$
$$ \begin{align} \int_{Q_0}\mathbf{1}_{\Gamma_{Q_0,\eta}^{\vartheta}(x)}(Y)\,d\omega_{L_0}^{X_{Q_0}}(x) \le \omega_{L_0}^{X_{Q_0}}\big(\Delta(\widehat{y},C_{\vartheta} \eta^{-3}\delta(Y))\big) \lesssim_{\vartheta,\eta} \omega_{L_0}^{X_{Q_0}}\big(\Delta(\widehat{y},\delta(Y))\big). \end{align} $$
Write
![]() $B=8c_0^{-1} B_{Q_0}^*$
,
$B=8c_0^{-1} B_{Q_0}^*$
,
![]() $B'=B_{Q_0}^*$
,
$B'=B_{Q_0}^*$
,
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
. Assuming that
$\Delta '=B'\cap \partial \Omega $
. Assuming that
![]() $r_B=16c_0^{-1} \kappa _0 r_{Q_0}<\operatorname {\mathrm {diam}}(\partial \Omega )$
, we have by Lemma 3.9 part (b) and Harnack’s inequality
$r_B=16c_0^{-1} \kappa _0 r_{Q_0}<\operatorname {\mathrm {diam}}(\partial \Omega )$
, we have by Lemma 3.9 part (b) and Harnack’s inequality
If we then combine equations (4.26), (4.28) and (4.29), we conclude that (c)
![]() $'$
and Lemma 3.9 yield
$'$
and Lemma 3.9 yield
 $$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x)^2\,d \omega_{L_0}^{X_{Q_0}} (x) \lesssim_{\vartheta,\eta} \iint_{B' \cap\Omega}|\nabla u(Y)|^2 G_{L_0}(X_{\Delta}, Y)\,dY \lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\,\|u\|^2_{L^{\infty}(\Omega)} \lesssim \omega_{L_0}^{X_{Q_0}}(Q_0). \end{align} $$
$$ \begin{align} \int_{Q_0} \mathcal{S}_{Q_0,\eta}^{\vartheta}u(x)^2\,d \omega_{L_0}^{X_{Q_0}} (x) \lesssim_{\vartheta,\eta} \iint_{B' \cap\Omega}|\nabla u(Y)|^2 G_{L_0}(X_{\Delta}, Y)\,dY \lesssim \omega_{L_0}^{X_{\Delta}}(\Delta')\,\|u\|^2_{L^{\infty}(\Omega)} \lesssim \omega_{L_0}^{X_{Q_0}}(Q_0). \end{align} $$
Note that this estimate corresponds to equation (4.22) for
![]() $q=2$
. Hence, the same argument we used in
$q=2$
. Hence, the same argument we used in
![]() $\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(a)}$
applies in this scenario. Note, however, that we have assumed that
$\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(a)}$
applies in this scenario. Note, however, that we have assumed that
![]() $16c_0^{-1} \kappa _0 r_{Q_0}<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and this causes that equation (4.24) is valid under this restriction. If
$16c_0^{-1} \kappa _0 r_{Q_0}<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and this causes that equation (4.24) is valid under this restriction. If
![]() $\partial \Omega $
is unbounded, then the same argument applies. When
$\partial \Omega $
is unbounded, then the same argument applies. When
![]() $\partial \Omega $
is bounded, we can replace the family
$\partial \Omega $
is bounded, we can replace the family
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
![]() $\mathcal {F}'$
consisting of all
$\mathcal {F}'$
consisting of all
![]() $Q'\in \mathbb {D}$
with
$Q'\in \mathbb {D}$
with
![]() $Q'\subset Q$
for some
$Q'\subset Q$
for some
![]() $Q\in \mathcal {F}$
and
$Q\in \mathcal {F}$
and
![]() $\ell (Q')=2^{-M}\ell (Q)$
, where M is large enough so that
$\ell (Q')=2^{-M}\ell (Q)$
, where M is large enough so that
![]() $2^{-M}<\Xi c_0/(8\kappa _0)$
. This guarantees that
$2^{-M}<\Xi c_0/(8\kappa _0)$
. This guarantees that
![]() $16c_0^{-1} \kappa _0 r_{Q'}<\operatorname {\mathrm {diam}}(\partial \Omega )$
for every
$16c_0^{-1} \kappa _0 r_{Q'}<\operatorname {\mathrm {diam}}(\partial \Omega )$
for every
![]() $Q'\in \mathcal {F}'$
, and thus, equation (4.24) holds for every
$Q'\in \mathcal {F}'$
, and thus, equation (4.24) holds for every
![]() $Q'\in \mathcal {F}'$
. At this point, the rest of the argument can be carried out mutatis mutandis; details are left to the reader.
$Q'\in \mathcal {F}'$
. At this point, the rest of the argument can be carried out mutatis mutandis; details are left to the reader.
![]() $\Box $
$\Box $
4.14 Proof of
 $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(c)}$
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(c)}$
Note that we have already proved that (a) implies (d). In particular, we know that equation (3.9) holds with
![]() $q=2$
and for any
$q=2$
and for any
![]() $\alpha \ge c_0^{-1}$
. Our goal is to see that the latter estimate implies (c). With this goal in mind, consider
$\alpha \ge c_0^{-1}$
. Our goal is to see that the latter estimate implies (c). With this goal in mind, consider
![]() $u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
$u\in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
satisfying
![]() $Lu=0$
in the weak sense in
$Lu=0$
in the weak sense in
![]() $\Omega $
. Fix
$\Omega $
. Fix
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
. Let
$0<r'<r c_0/4$
. Let
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
. Note that
$\Delta '=B'\cap \partial \Omega $
. Note that
![]() $2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now invoke Lemma 4.3 and equation (3.9) with
$2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now invoke Lemma 4.3 and equation (3.9) with
![]() $q=2$
to conclude that
$q=2$
to conclude that
 $$ \begin{align*} &\frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\qquad \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ &\qquad \lesssim \int_{10\Delta'} \mathcal{N}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y) + \|u\|_{L^{\infty}(\Omega)}^2 \\ &\qquad \lesssim \|u\|_{L^{\infty}(\Omega)}^2. \end{align*} $$
$$ \begin{align*} &\frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} |\nabla u(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\qquad \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|u(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ &\qquad \lesssim \int_{10\Delta'} \mathcal{N}_{2r'}^{\alpha'} u(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y) + \|u\|_{L^{\infty}(\Omega)}^2 \\ &\qquad \lesssim \|u\|_{L^{\infty}(\Omega)}^2. \end{align*} $$
Taking the sup over B and
![]() $B'$
we have then shown equation (3.8).
$B'$
we have then shown equation (3.8).
![]() $\Box $
$\Box $
4.15 Proof of
 $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(e)}$
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(e)}$
Fix
![]() $f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega )$
, and let u be its associated solution as in equation (3.4). Let
$f \in \mathscr {C}(\partial \Omega )\cap L^{\infty }(\partial \Omega )$
, and let u be its associated solution as in equation (3.4). Let
![]() $u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
$u_{L,\Omega }(X):=\omega _L^X(\partial \Omega )$
,
![]() $X\in \Omega $
. Fix
$X\in \Omega $
. Fix
![]() $B=B(x,r)$
with
$B=B(x,r)$
with
![]() $x\in \partial \Omega $
and
$x\in \partial \Omega $
and
![]() $0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
$0<r<\operatorname {\mathrm {diam}}(\partial \Omega )$
and
![]() $B'=B(x',r')$
with
$B'=B(x',r')$
with
![]() $x'\in 2\Delta $
and
$x'\in 2\Delta $
and
![]() $0<r'<r c_0/4$
. Let
$0<r'<r c_0/4$
. Let
![]() $\Delta =B\cap \partial \Omega $
,
$\Delta =B\cap \partial \Omega $
,
![]() $\Delta '=B'\cap \partial \Omega $
. Let
$\Delta '=B'\cap \partial \Omega $
. Let
![]() $\varphi \in \mathscr {C}(\mathbb {R})$
with
$\varphi \in \mathscr {C}(\mathbb {R})$
with
![]() $\mathbf {1}_{[0,4)}\le \varphi \le \mathbf {1}_{[0,8)}$
and
$\mathbf {1}_{[0,4)}\le \varphi \le \mathbf {1}_{[0,8)}$
and
![]() $\varphi _{\Delta '}:=\varphi (|\cdot -x'|/r')$
so that
$\varphi _{\Delta '}:=\varphi (|\cdot -x'|/r')$
so that
![]() $\mathbf {1}_{4\Delta '}\le \varphi _{\Delta '} \le \mathbf {1}_{8\Delta '}$
. Recall that for every surface ball
$\mathbf {1}_{4\Delta '}\le \varphi _{\Delta '} \le \mathbf {1}_{8\Delta '}$
. Recall that for every surface ball
![]() $\widetilde {\Delta }$
we write
$\widetilde {\Delta }$
we write
![]() . Then,
. Then,
 $$ \begin{align*} f-f_{\Delta, L_0} = (f-f_{8\Delta', L_0})+ (f_{8\Delta', L_0}-f_{\Delta, L_0}) = (f-f_{8\Delta', L_0})\varphi_{\Delta'} &+ (f-f_{8\Delta', L_0})(1-\varphi_{\Delta'})+(f_{8\Delta', L_0}-f_{\Delta, L_0}) \\ &\qquad =: h_{\mathrm{loc}}+h_{\mathrm{glob}}+ (f_{8\Delta', L_0}-f_{\Delta, L_0}). \end{align*} $$
$$ \begin{align*} f-f_{\Delta, L_0} = (f-f_{8\Delta', L_0})+ (f_{8\Delta', L_0}-f_{\Delta, L_0}) = (f-f_{8\Delta', L_0})\varphi_{\Delta'} &+ (f-f_{8\Delta', L_0})(1-\varphi_{\Delta'})+(f_{8\Delta', L_0}-f_{\Delta, L_0}) \\ &\qquad =: h_{\mathrm{loc}}+h_{\mathrm{glob}}+ (f_{8\Delta', L_0}-f_{\Delta, L_0}). \end{align*} $$
Hence,
 $$ \begin{align} v(X) &:= u(X)-f_{\Delta, L_0}u_{L,\Omega}(X) = \int_{\partial\Omega} (f(y)-f_{\Delta, L_0})\,d\omega_{L}^{X}(y)\notag \\ &\qquad = \int_{\partial\Omega} h_{\mathrm{loc}}(y)\,d\omega_{L}^{X}(y) + \int_{\partial\Omega} h_{\mathrm{glob}}(y)\,d\omega_{L}^{X}(y) +(f_{8\Delta', L_0}-f_{\Delta, L_0})u_{L,\Omega}(X) \notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad =: v_{\mathrm{loc}}(X)+v_{\mathrm{glob}}(X)+(f_{8\Delta', L_0}-f_{\Delta, L_0})u_{L,\Omega}(X). \end{align} $$
$$ \begin{align} v(X) &:= u(X)-f_{\Delta, L_0}u_{L,\Omega}(X) = \int_{\partial\Omega} (f(y)-f_{\Delta, L_0})\,d\omega_{L}^{X}(y)\notag \\ &\qquad = \int_{\partial\Omega} h_{\mathrm{loc}}(y)\,d\omega_{L}^{X}(y) + \int_{\partial\Omega} h_{\mathrm{glob}}(y)\,d\omega_{L}^{X}(y) +(f_{8\Delta', L_0}-f_{\Delta, L_0})u_{L,\Omega}(X) \notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad =: v_{\mathrm{loc}}(X)+v_{\mathrm{glob}}(X)+(f_{8\Delta', L_0}-f_{\Delta, L_0})u_{L,\Omega}(X). \end{align} $$
Note that
![]() $h_{\mathrm {loc}}, h_{\mathrm {glob}} \in \mathscr {C}(\partial \Omega ) \cap L^{\infty }(\partial \Omega )$
.
$h_{\mathrm {loc}}, h_{\mathrm {glob}} \in \mathscr {C}(\partial \Omega ) \cap L^{\infty }(\partial \Omega )$
.
Let us observe that we have already proved that (a) implies (d). In particular, we know that equation (3.9) holds with
![]() $q=2$
and for any
$q=2$
and for any
![]() $\alpha \ge c_0^{-1}$
. Hence, since
$\alpha \ge c_0^{-1}$
. Hence, since
![]() $2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now invoke Lemma 4.3 and equation (3.9) with
$2r'<r c_0/2<\operatorname {\mathrm {diam}}(\partial \Omega )$
, and we can now invoke Lemma 4.3 and equation (3.9) with
![]() $q=2$
to conclude that
$q=2$
to conclude that
 $$ \begin{align} \nonumber &\frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} |\nabla v_{\mathrm{loc}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ \nonumber &\qquad \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|v_{\mathrm{loc}}(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ \nonumber &\qquad \lesssim \int_{4\Delta'} \mathcal{N}_{2r'}^{\alpha'} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y) + \Big(\int_{\partial\Omega} |h_{\mathrm{loc}}(y)|\,d\omega_{L_0}^{X_{\Delta'}}(y)\Big)^2 \\ \nonumber &\qquad \lesssim \int_{4\Delta'} \mathcal{N}_{4r'}^{\alpha'} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{4\Delta'}}(y) + \Big(\int_{\partial\Omega} |h_{\mathrm{loc}}(y)|\,d\omega_{L_0}^{X_{8\Delta'}}(y)\Big)^2 \\ &\qquad =: \mathcal{I}_1+\mathcal{I}_2. \end{align} $$
$$ \begin{align} \nonumber &\frac1{\omega_{L_0}^{X_{\Delta}}(\Delta')}\iint_{B'\cap \Omega} |\nabla v_{\mathrm{loc}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \\ \nonumber &\qquad \lesssim \int_{2\Delta'} \mathcal{S}_{2r'}^{C\alpha} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y)+ \sup \{|v_{\mathrm{loc}}(Y)|: Y\in 2\,B', \delta(Y)\ge r'/C\}^2 \\ \nonumber &\qquad \lesssim \int_{4\Delta'} \mathcal{N}_{2r'}^{\alpha'} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{2\Delta'}}(y) + \Big(\int_{\partial\Omega} |h_{\mathrm{loc}}(y)|\,d\omega_{L_0}^{X_{\Delta'}}(y)\Big)^2 \\ \nonumber &\qquad \lesssim \int_{4\Delta'} \mathcal{N}_{4r'}^{\alpha'} v_{\mathrm{loc}}(y)^2\,d\omega_{L_0}^{X_{4\Delta'}}(y) + \Big(\int_{\partial\Omega} |h_{\mathrm{loc}}(y)|\,d\omega_{L_0}^{X_{8\Delta'}}(y)\Big)^2 \\ &\qquad =: \mathcal{I}_1+\mathcal{I}_2. \end{align} $$
Regarding
![]() $\mathcal {I}_2$
, we note that by Lemma 3.9 part
$\mathcal {I}_2$
, we note that by Lemma 3.9 part
![]() $(a)$
there holds
$(a)$
there holds
To estimate
![]() $\mathcal {I}_1$
, we first observe that, since
$\mathcal {I}_1$
, we first observe that, since
![]() $\omega _L\in A_{\infty }(\partial \Omega , \omega _{L_0})$
, there is
$\omega _L\in A_{\infty }(\partial \Omega , \omega _{L_0})$
, there is
![]() $q\in (1,\infty )$
so that
$q\in (1,\infty )$
so that
![]() $\omega _L\in RH_q(\partial \Omega , \omega _{L_0})$
. Note that, by Jensen’s inequality, we may assume that
$\omega _L\in RH_q(\partial \Omega , \omega _{L_0})$
. Note that, by Jensen’s inequality, we may assume that
![]() $q<2$
(since
$q<2$
(since
![]() $RH_{q_1}(\partial \Omega , \omega _{L_0})\subset RH_{q_2}(\partial \Omega , \omega _{L_0})$
if
$RH_{q_1}(\partial \Omega , \omega _{L_0})\subset RH_{q_2}(\partial \Omega , \omega _{L_0})$
if
![]() $q_2\le q_1$
). Note that we have already proved that (a)
$q_2\le q_1$
). Note that we have already proved that (a)
![]() ${}_{q}$
implies (b)
${}_{q}$
implies (b)
![]() ${}_{q'}$
; hence, equation (3.5) holds with
${}_{q'}$
; hence, equation (3.5) holds with
![]() $p=q'> 2$
. This, Hölder’s inequality and the fact that
$p=q'> 2$
. This, Hölder’s inequality and the fact that
![]() $h_{\mathrm {loc}}\in \mathscr {C}(\partial \Omega )$
with
$h_{\mathrm {loc}}\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} h_{\mathrm {loc}}\subset 8\Delta '$
readily lead to
$\operatorname {\mathrm {supp}} h_{\mathrm {loc}}\subset 8\Delta '$
readily lead to
 $$ \begin{align} \mathcal{I}_1 \le \|\mathcal{N}_{4r'}^{\alpha'} v_{\mathrm{loc}}\|_{L^{q'}(4\Delta',\omega_{L_0}^{X_{4\Delta'}})}^2 &\omega_{L_0}^{X_{4\Delta'}}(4\Delta')^{\frac1{(q'/2)'}} \lesssim \|h_{\mathrm{loc}}\|_{L^{q'}(8\Delta',\omega_{L_0}^{X_{4\Delta'}})}^2 \notag \\ &\quad \lesssim \Big(\int_{8\Delta'} |f(y)-f_{8\Delta', L_0}|^{q'}d\omega_{L_0}^{X_{4\Delta'}}(y) \Big)^{\frac{2}{q'}} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}, \end{align} $$
$$ \begin{align} \mathcal{I}_1 \le \|\mathcal{N}_{4r'}^{\alpha'} v_{\mathrm{loc}}\|_{L^{q'}(4\Delta',\omega_{L_0}^{X_{4\Delta'}})}^2 &\omega_{L_0}^{X_{4\Delta'}}(4\Delta')^{\frac1{(q'/2)'}} \lesssim \|h_{\mathrm{loc}}\|_{L^{q'}(8\Delta',\omega_{L_0}^{X_{4\Delta'}})}^2 \notag \\ &\quad \lesssim \Big(\int_{8\Delta'} |f(y)-f_{8\Delta', L_0}|^{q'}d\omega_{L_0}^{X_{4\Delta'}}(y) \Big)^{\frac{2}{q'}} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}, \end{align} $$
where the last estimate uses Lemma 3.9 part
![]() $(a)$
and John–Nirenberg’s inequality (cf. equation (3.21)).
$(a)$
and John–Nirenberg’s inequality (cf. equation (3.21)).
We next turn our attention to the estimate involving
![]() $v_{\mathrm {glob}}$
. Note that
$v_{\mathrm {glob}}$
. Note that
 $$ \begin{align*} |h_{\mathrm{glob}}| \le |f-f_{8\Delta', L_0}|\mathbf{1}_{\partial\Omega\setminus 4\Delta'} &= \sum_{k=2}^{\infty} |f-f_{8\Delta', L_0}|\mathbf{1}_{2^{k+1}\Delta'\setminus 2^k\Delta'} \\ &\qquad \le \sum_{k=2}^{\infty} |f-f_{8\Delta', L_0}|(\varphi_{2^{k-1}\Delta'}-\varphi_{2^{k-3}\Delta'}) =: \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)}h_{\mathrm{glob,k}}, \end{align*} $$
$$ \begin{align*} |h_{\mathrm{glob}}| \le |f-f_{8\Delta', L_0}|\mathbf{1}_{\partial\Omega\setminus 4\Delta'} &= \sum_{k=2}^{\infty} |f-f_{8\Delta', L_0}|\mathbf{1}_{2^{k+1}\Delta'\setminus 2^k\Delta'} \\ &\qquad \le \sum_{k=2}^{\infty} |f-f_{8\Delta', L_0}|(\varphi_{2^{k-1}\Delta'}-\varphi_{2^{k-3}\Delta'}) =: \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)}h_{\mathrm{glob,k}}, \end{align*} $$
with the understanding that the sum runs from
![]() $k=2$
to infinity when
$k=2$
to infinity when
![]() $\partial \Omega $
is unbounded.
$\partial \Omega $
is unbounded.
Fix
![]() $k\ge 2$
with
$k\ge 2$
with
![]() $2^kr' \leq \operatorname {\mathrm {diam}}(\partial \Omega )$
, and note that
$2^kr' \leq \operatorname {\mathrm {diam}}(\partial \Omega )$
, and note that
![]() $h_{\mathrm {glob, k}}\in \mathscr {C}(\partial \Omega )$
with
$h_{\mathrm {glob, k}}\in \mathscr {C}(\partial \Omega )$
with
![]() $\operatorname {\mathrm {supp}} h_{\mathrm {glob, k}}\subset 2^{k+2}\Delta '\setminus 2^{k-1}\Delta '$
. Thus, for every
$\operatorname {\mathrm {supp}} h_{\mathrm {glob, k}}\subset 2^{k+2}\Delta '\setminus 2^{k-1}\Delta '$
. Thus, for every
![]() $X\in B'\cap \Omega $
, by Lemma 3.9 part
$X\in B'\cap \Omega $
, by Lemma 3.9 part
![]() $(f)$
, we have
$(f)$
, we have
Next, we estimate
![]() $v_{\mathrm {glob,k}}(X_{2^{k-1} \Delta '}), k \geq 2,$
via a telescopic argument. Indeed applying Harnack’s inequality, that
$v_{\mathrm {glob,k}}(X_{2^{k-1} \Delta '}), k \geq 2,$
via a telescopic argument. Indeed applying Harnack’s inequality, that
![]() $\omega _L \in RH_q(\partial \Omega , \omega _{L_0})$
, Lemma 3.9, and John–Nirenberg’s inequality (cf. equation (3.21)) we arrive at
$\omega _L \in RH_q(\partial \Omega , \omega _{L_0})$
, Lemma 3.9, and John–Nirenberg’s inequality (cf. equation (3.21)) we arrive at

This and equation (4.35) give for every
![]() $X\in B' \cap \Omega $
$X\in B' \cap \Omega $
 $$ \begin{align*} \int_{\partial\Omega} |h_{\mathrm{glob}}(y)|\,d\omega_{L}^{X}(y) \le \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)} \int_{\partial\Omega} h_{\mathrm{glob,k}}(y) \,d\omega_{L}^{X}(y) = \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)} v_{\mathrm{glob,k}}(X) \\ \lesssim \sum_{k\ge 2} k\,\Big(\frac{\delta(X)}{2^{k-1}r'}\Big)^{\rho} \|f\|_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \approx \Big(\frac{\delta(X)}{r'}\Big)^{\rho} \|f\|_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
$$ \begin{align*} \int_{\partial\Omega} |h_{\mathrm{glob}}(y)|\,d\omega_{L}^{X}(y) \le \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)} \int_{\partial\Omega} h_{\mathrm{glob,k}}(y) \,d\omega_{L}^{X}(y) = \sum_{k\ge 2: 2^kr' \leq \operatorname{\mathrm{diam}}(\partial\Omega)} v_{\mathrm{glob,k}}(X) \\ \lesssim \sum_{k\ge 2} k\,\Big(\frac{\delta(X)}{2^{k-1}r'}\Big)^{\rho} \|f\|_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \approx \Big(\frac{\delta(X)}{r'}\Big)^{\rho} \|f\|_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
If we next write
![]() $\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
and pick
$\mathcal {W}_{B'}:=\{I\in \mathcal {W}: I\cap B'\neq \emptyset \}$
and pick
![]() $Z_{I, B'}\in I\cap B'$
, the previous estimate gives for every
$Z_{I, B'}\in I\cap B'$
, the previous estimate gives for every
![]() $I\in \mathcal {W}_{B'}$
$I\in \mathcal {W}_{B'}$
 $$ \begin{align*} \iint_I |\nabla v_{\mathrm{glob}}(X)|^2 dX &\lesssim \ell(I)^{-2} \iint_{I^*} v_{\mathrm{glob}}(X)^2 dX \le \ell(I)^{-2} \iint_{I^*} \Big(\int_{\partial\Omega} |h_{\mathrm{glob}}(y)|\,d\omega_{L}^{X}(y)\Big)^2\,dX \\ &\quad \approx \ell(I)^{n-1} \Big(\int_{\partial\Omega} h_{\mathrm{glob}}(y)\,d\omega_{L}^{Z_{I, B'}}(y)\Big)^2 \lesssim \ell(I)^{n-1} \Big(\frac{\ell(I)}{r'}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
$$ \begin{align*} \iint_I |\nabla v_{\mathrm{glob}}(X)|^2 dX &\lesssim \ell(I)^{-2} \iint_{I^*} v_{\mathrm{glob}}(X)^2 dX \le \ell(I)^{-2} \iint_{I^*} \Big(\int_{\partial\Omega} |h_{\mathrm{glob}}(y)|\,d\omega_{L}^{X}(y)\Big)^2\,dX \\ &\quad \approx \ell(I)^{n-1} \Big(\int_{\partial\Omega} h_{\mathrm{glob}}(y)\,d\omega_{L}^{Z_{I, B'}}(y)\Big)^2 \lesssim \ell(I)^{n-1} \Big(\frac{\ell(I)}{r'}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
Thus, Lemma 3.9 gives
 $$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\ell(I)^{1-n} \iint_{I} |\nabla v_{\mathrm{glob}}(X)|^2 \, d X \\ &\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I) \Big(\frac{\ell(I)}{r'}\Big)^{2\rho} \\ &\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{r'}\Big)^{2\rho} \sum_{I\in \mathcal{W}_{B'}: \ell(I)=2^{-k}} \omega_{L_0}^{X_{\Delta}}(Q_I), \end{align*} $$
$$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I)\ell(I)^{1-n} \iint_{I} |\nabla v_{\mathrm{glob}}(X)|^2 \, d X \\ &\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \sum_{I\in \mathcal{W}_{B'}} \omega_{L_0}^{X_{\Delta}}(Q_I) \Big(\frac{\ell(I)}{r'}\Big)^{2\rho} \\ &\lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{r'}\Big)^{2\rho} \sum_{I\in \mathcal{W}_{B'}: \ell(I)=2^{-k}} \omega_{L_0}^{X_{\Delta}}(Q_I), \end{align*} $$
where
![]() $Q_I\in \mathbb {D}(\partial \Omega )$
is so that
$Q_I\in \mathbb {D}(\partial \Omega )$
is so that
![]() $\ell (Q_I)=\ell (I)$
and contains
$\ell (Q_I)=\ell (I)$
and contains
![]() $\widehat {y}_I \in \partial \Omega $
such that
$\widehat {y}_I \in \partial \Omega $
such that
![]() $\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. It is easy to see that, for every k with
$\operatorname {dist}(I, \partial \Omega )=\operatorname {dist}(\widehat {y}_I, I)$
. It is easy to see that, for every k with
![]() $2^{-k}\lesssim r'$
, the family
$2^{-k}\lesssim r'$
, the family
![]() $\{Q_I\}_{I\in \mathcal {W}_{B'}, \ell (I)=2^{-k}}$
has bounded overlap and also that
$\{Q_I\}_{I\in \mathcal {W}_{B'}, \ell (I)=2^{-k}}$
has bounded overlap and also that
![]() $Q_I\subset C\Delta '$
for every
$Q_I\subset C\Delta '$
for every
![]() $I\in \mathcal {W}_{B'}$
, where C is some harmless dimensional constant. Hence,
$I\in \mathcal {W}_{B'}$
, where C is some harmless dimensional constant. Hence,
 $$ \begin{align} \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} &\sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{r'}\Big)^{2\rho} \omega_{L_0}^{X_{\Delta}}(C\,\Delta') \notag \\ &\qquad\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}\omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align} $$
$$ \begin{align} \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} &\sum_{k: 2^{-k}\lesssim r'} \Big(\frac{2^{-k}}{r'}\Big)^{2\rho} \omega_{L_0}^{X_{\Delta}}(C\,\Delta') \notag \\ &\qquad\qquad \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}\omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align} $$
To continue, we pick
![]() $k_0\ge 3$
such that
$k_0\ge 3$
such that
![]() $r<2^{k_0}r'\le 2\,r$
. Note that
$r<2^{k_0}r'\le 2\,r$
. Note that
![]() $2^{k_0+1} \Delta '$
and
$2^{k_0+1} \Delta '$
and
![]() $\Delta $
have comparable radius and
$\Delta $
have comparable radius and
![]() $x'\in 2\Delta \cap 2^{k_0+1} \Delta '$
. Hence, Lemma 3.9 and Harnack’s inequality yield
$x'\in 2\Delta \cap 2^{k_0+1} \Delta '$
. Hence, Lemma 3.9 and Harnack’s inequality yield

This and Lemma 4.1 imply
 $$ \begin{align} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &\big| (f_{8\Delta', L_0}-f_{\Delta, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \notag \\ &\qquad\lesssim (1+\log(r/r'))^2\,\Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \notag \\ &\qquad\qquad\le (1+\log(r/r'))^2\,\Big(\frac{r'}{r}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align} $$
$$ \begin{align} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &\big| (f_{8\Delta', L_0}-f_{\Delta, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \notag \\ &\qquad\lesssim (1+\log(r/r'))^2\,\Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \notag \\ &\qquad\qquad\le (1+\log(r/r'))^2\,\Big(\frac{r'}{r}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align} $$
Here, we note in passing that if
![]() $\operatorname {\mathrm {diam}}(\partial \Omega )=\infty $
(or if both
$\operatorname {\mathrm {diam}}(\partial \Omega )=\infty $
(or if both
![]() $\partial \Omega $
and
$\partial \Omega $
and
![]() $\Omega $
are bounded), then the left-hand side of the previous estimate vanishes as we know that
$\Omega $
are bounded), then the left-hand side of the previous estimate vanishes as we know that
![]() $u_{L,\Omega }\equiv 1$
.
$u_{L,\Omega }\equiv 1$
.
To complete the proof, we just collect equations (4.31)–(4.34), (4.36) and (4.38):
 $$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \iint_{B'\cap \Omega} |\nabla v_{\mathrm{loc}}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \qquad\qquad+ \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \qquad\qquad+ \iint_{B'\cap \Omega} \big| (f_{8\Delta', L_0}-f_{\Delta, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}\omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align*} $$
$$ \begin{align*} \iint_{B'\cap \Omega} |\nabla v(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X &\lesssim \iint_{B'\cap \Omega} |\nabla v_{\mathrm{loc}}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \qquad\qquad+ \iint_{B'\cap \Omega} |\nabla v_{\mathrm{glob}}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \qquad\qquad+ \iint_{B'\cap \Omega} \big| (f_{8\Delta', L_0}-f_{\Delta, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ & \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}\omega_{L_0}^{X_{\Delta}}(\Delta'). \end{align*} $$
This completes the proof.
![]() $\Box $
$\Box $
Remark 4.5. It is not difficult to see that in equation (3.6) one can replace
![]() $f_{\Delta , L_0}$
by
$f_{\Delta , L_0}$
by
![]() $f_{\Delta ', L_0}$
. Indeed, this is what we have essentially done in the proof: Much as in equation (4.37), one has that
$f_{\Delta ', L_0}$
. Indeed, this is what we have essentially done in the proof: Much as in equation (4.37), one has that
With this, we can proceed as in equation (4.38) to see that
 $$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} \big| (f_{\Delta, L_0}-f_{\Delta', L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
$$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} \big| (f_{\Delta, L_0}-f_{\Delta', L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
Hence, equation (3.6) with
![]() $f_{\Delta , L_0}$
is equivalent to equation (3.6) with
$f_{\Delta , L_0}$
is equivalent to equation (3.6) with
![]() $f_{\Delta ', L_0}$
.
$f_{\Delta ', L_0}$
.
On the other hand, when
![]() $\Omega $
is unbounded and
$\Omega $
is unbounded and
![]() $\partial \Omega $
bounded, in equation (3.6), one can replace
$\partial \Omega $
bounded, in equation (3.6), one can replace
![]() $f_{\Delta , L_0}$
by
$f_{\Delta , L_0}$
by
![]() , where
, where
![]() $X_{\Omega }\in \Omega $
satisfy
$X_{\Omega }\in \Omega $
satisfy
![]() $\delta (X_{\Omega })\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
(say,
$\delta (X_{\Omega })\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
(say,
![]() $X_{\Omega }=X_{\Delta (x_0, r_0)}$
with
$X_{\Omega }=X_{\Delta (x_0, r_0)}$
with
![]() $x_0\in \partial \Omega $
and
$x_0\in \partial \Omega $
and
![]() $r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
). To see this, one proceeds as in equation (4.37) to see that
$r_0\approx \operatorname {\mathrm {diam}}(\partial \Omega )$
). To see this, one proceeds as in equation (4.37) to see that
This and Lemma 4.1 readily give
 $$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &\big| (f_{\Delta, L_0}-f_{\partial\Omega, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\quad\lesssim (1+\log(\operatorname{\mathrm{diam}}(\partial\Omega)/r))^2\,\Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \\ & \le (1+\log(\operatorname{\mathrm{diam}}(\partial\Omega)/r))^2\,\Big(\frac{r}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
$$ \begin{align*} \frac{1}{\omega_{L_0}^{X_{\Delta}} (\Delta')} \iint_{B'\cap \Omega} &\big| (f_{\Delta, L_0}-f_{\partial\Omega, L_0}) \nabla u_{L,\Omega}(X)\big|^2 G_{L_0}(X_{\Delta},X) \, d X \\ &\quad\lesssim (1+\log(\operatorname{\mathrm{diam}}(\partial\Omega)/r))^2\,\Big(\frac{r'}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \\ & \le (1+\log(\operatorname{\mathrm{diam}}(\partial\Omega)/r))^2\,\Big(\frac{r}{\operatorname{\mathrm{diam}}(\partial\Omega)}\Big)^{2\rho} \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})} \lesssim \|f\|^2_{\mathrm{BMO}(\partial \Omega, \omega_{L_0})}. \end{align*} $$
Hence, equation (3.6) with
![]() $f_{\Delta , L_0}$
is equivalent to equation (3.6) with
$f_{\Delta , L_0}$
is equivalent to equation (3.6) with
![]() $f_{\partial \Omega , L_0}$
.
$f_{\partial \Omega , L_0}$
.
4.16 Proof of
 $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(e)}'$
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(e)}'$
The proof is almost the same as the previous one with the following modifications. We work with
![]() $f=\mathbf {1}_S$
with
$f=\mathbf {1}_S$
with
![]() $S\subset \partial \Omega $
an arbitrary Borel set. We replace
$S\subset \partial \Omega $
an arbitrary Borel set. We replace
![]() $\varphi $
by
$\varphi $
by
![]() $\mathbf {1}_{[0,4)}$
and use in equation (4.32) that Lemma 4.3 is also valid for the associated
$\mathbf {1}_{[0,4)}$
and use in equation (4.32) that Lemma 4.3 is also valid for the associated
![]() $v_{\mathrm {loc}}$
since it belongs to
$v_{\mathrm {loc}}$
since it belongs to
![]() $W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
. Also, in equation (4.33) we need to invoke that
$W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
. Also, in equation (4.33) we need to invoke that
![]() $\mathrm {(a)}{}_{q}\ \Longrightarrow \ \mathrm {(b)}_{q'}\ \Longrightarrow \ \mathrm {(b)}^{\prime }_{q'}$
. The rest of the proof remains the same, details are left to the interested reader.
$\mathrm {(a)}{}_{q}\ \Longrightarrow \ \mathrm {(b)}_{q'}\ \Longrightarrow \ \mathrm {(b)}^{\prime }_{q'}$
. The rest of the proof remains the same, details are left to the interested reader.
![]() $\Box $
$\Box $
5 Proof of Theorem 1.6
The implications
![]() $\mathrm {(b)}\ \Longrightarrow \ \mathrm {(c)}\ \Longrightarrow \ \mathrm {(d)}$
,
$\mathrm {(b)}\ \Longrightarrow \ \mathrm {(c)}\ \Longrightarrow \ \mathrm {(d)}$
,
![]() $\mathrm {(b)}'\ \Longrightarrow \ \mathrm {(c)}'\ \Longrightarrow \ \mathrm {(d)'}$
are trivial. Also, since for any Borel set
$\mathrm {(b)}'\ \Longrightarrow \ \mathrm {(c)}'\ \Longrightarrow \ \mathrm {(d)'}$
are trivial. Also, since for any Borel set
![]() $S\subset \partial \Omega $
the solution
$S\subset \partial \Omega $
the solution
![]() $u(X)=\omega _L^X(S)$
belongs to
$u(X)=\omega _L^X(S)$
belongs to
![]() $W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
, it is also straightforward that
$W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
, it is also straightforward that
![]() $\mathrm {(b)}\ \Longrightarrow \ \mathrm {(b)}'$
,
$\mathrm {(b)}\ \Longrightarrow \ \mathrm {(b)}'$
,
![]() $\mathrm {(c)}\ \Longrightarrow \ \mathrm {(c)}'$
, and
$\mathrm {(c)}\ \Longrightarrow \ \mathrm {(c)}'$
, and
![]() $\mathrm {(d)}\ \Longrightarrow \ \mathrm {(d)}'$
.
$\mathrm {(d)}\ \Longrightarrow \ \mathrm {(d)}'$
.
We next observe that for every
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $0<r<r'$
and
$0<r<r'$
and
![]() $\varpi \in \mathbb {R}$
, if
$\varpi \in \mathbb {R}$
, if
![]() $F \subset \partial \Omega $
is a bounded set and
$F \subset \partial \Omega $
is a bounded set and
![]() $v\in L^2_{\mathrm {loc}}(\Omega )$
, then
$v\in L^2_{\mathrm {loc}}(\Omega )$
, then
 $$ \begin{align} \sup_{x\in F}\iint_{\Gamma^{\alpha}_{r'}(x) \setminus \Gamma^{\alpha}_{r}(x)} |v(Y)|^2 \delta(Y)^{\varpi} dY <\infty. \end{align} $$
$$ \begin{align} \sup_{x\in F}\iint_{\Gamma^{\alpha}_{r'}(x) \setminus \Gamma^{\alpha}_{r}(x)} |v(Y)|^2 \delta(Y)^{\varpi} dY <\infty. \end{align} $$
To see this, we first note that since F is bounded we can find R large enough so that
![]() $F\subset B(0,R)$
. Then, if
$F\subset B(0,R)$
. Then, if
![]() $x\in F$
, one readily sees that
$x\in F$
, one readily sees that
Note that
![]() $K \subset \Omega $
is a compact set. Then, since
$K \subset \Omega $
is a compact set. Then, since
![]() $v \in L^2_{\mathrm {loc}}(\Omega )$
, we conclude that
$v \in L^2_{\mathrm {loc}}(\Omega )$
, we conclude that
 $$ \begin{align} \sup_{x\in F}\iint_{\Gamma^{\alpha}_{r'}(x) \setminus \Gamma^{\alpha}_{r}(x)} |v(Y)|^2 \delta(Y)^{\varpi} dY \leq \max\left\{r',\frac{1+\alpha}{r}\right\}^{|\varpi|} \iint_{K} |v(Y)|^2 dY<\infty. \end{align} $$
$$ \begin{align} \sup_{x\in F}\iint_{\Gamma^{\alpha}_{r'}(x) \setminus \Gamma^{\alpha}_{r}(x)} |v(Y)|^2 \delta(Y)^{\varpi} dY \leq \max\left\{r',\frac{1+\alpha}{r}\right\}^{|\varpi|} \iint_{K} |v(Y)|^2 dY<\infty. \end{align} $$
Using, then, equation (5.1), it is also trivial to see that
![]() $\mathrm {(d)}\ \Longrightarrow \ \mathrm {(c)}$
and
$\mathrm {(d)}\ \Longrightarrow \ \mathrm {(c)}$
and
![]() $\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(c)}'$
. Hence, we are left with showing
$\mathrm {(d)}'\ \Longrightarrow \ \mathrm {(c)}'$
. Hence, we are left with showing
5.1 Proof of
 $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(b)}$
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(b)}$
Assume that
![]() $\omega _{L_0} \ll \omega _L$
. Let
$\omega _{L_0} \ll \omega _L$
. Let
![]() $\vartheta \ge \vartheta _0$
large enough to be chosen (this choice will depend on
$\vartheta \ge \vartheta _0$
large enough to be chosen (this choice will depend on
![]() $\alpha $
). Fix an arbitrary
$\alpha $
). Fix an arbitrary
![]() $Q_0 \in \mathbb {D}_{k_0}$
, where
$Q_0 \in \mathbb {D}_{k_0}$
, where
![]() $k_0 \in \mathbb {Z}$
is taken so that
$k_0 \in \mathbb {Z}$
is taken so that
![]() $2^{-k_0}=\ell (Q_0) < \operatorname {\mathrm {diam}}(\partial \Omega )/M_0$
, where
$2^{-k_0}=\ell (Q_0) < \operatorname {\mathrm {diam}}(\partial \Omega )/M_0$
, where
![]() $M_0>8\kappa _0 c_0^{-1}$
,
$M_0>8\kappa _0 c_0^{-1}$
,
![]() $\kappa _0$
is taken from equation (2.15) and
$\kappa _0$
is taken from equation (2.15) and
![]() $c_0$
is the corkscrew constant. Let
$c_0$
is the corkscrew constant. Let
![]() $X_0:=X_{M_0 \Delta _{Q_0}}$
be a corkscrew point relative to
$X_0:=X_{M_0 \Delta _{Q_0}}$
be a corkscrew point relative to
![]() $M_0 \Delta _{Q_0}$
so that
$M_0 \Delta _{Q_0}$
so that
![]() $X_0 \notin 4B_{Q_0}^*$
by the choice of
$X_0 \notin 4B_{Q_0}^*$
by the choice of
![]() $M_0$
. By Lemma 3.9 part
$M_0$
. By Lemma 3.9 part
![]() $(a)$
and Harnack’s inequality, there exists
$(a)$
and Harnack’s inequality, there exists
![]() $C_0>1$
such that
$C_0>1$
such that
Set
By assumption, we have
![]() $\omega _0 \ll \omega $
. Also, equation (5.3) gives
$\omega _0 \ll \omega $
. Also, equation (5.3) gives
For
![]() $N> C_0$
, we let
$N> C_0$
, we let
![]() $\mathcal {F}_N^+ :=\{Q_j\} \subset \mathbb {D}_{Q_0} \backslash \{Q_0\}$
, respectively,
$\mathcal {F}_N^+ :=\{Q_j\} \subset \mathbb {D}_{Q_0} \backslash \{Q_0\}$
, respectively,
![]() $\mathcal {F}_N^- :=\{Q_j\} \subset \mathbb {D}_{Q_0} \backslash \{Q_0\}$
, be the collection of descendants of
$\mathcal {F}_N^- :=\{Q_j\} \subset \mathbb {D}_{Q_0} \backslash \{Q_0\}$
, be the collection of descendants of
![]() $Q_0$
which are maximal (and therefore pairwise disjoint) with respect to the property that
$Q_0$
which are maximal (and therefore pairwise disjoint) with respect to the property that
 $$ \begin{align} \frac{\omega(Q_j)}{\omega_0(Q_j)} < \frac{1}{N}, \qquad\text{ respectively}\quad \frac{\omega(Q_j)}{\omega_0(Q_j)}>N. \end{align} $$
$$ \begin{align} \frac{\omega(Q_j)}{\omega_0(Q_j)} < \frac{1}{N}, \qquad\text{ respectively}\quad \frac{\omega(Q_j)}{\omega_0(Q_j)}>N. \end{align} $$
Write
![]() $\mathcal {F}_N:=\mathcal {F}_N^+\cup \mathcal {F}_N^-$
, and note that
$\mathcal {F}_N:=\mathcal {F}_N^+\cup \mathcal {F}_N^-$
, and note that
![]() $\mathcal {F}_N^+\cap \mathcal {F}_N^-= \emptyset $
. By maximality, there holds
$\mathcal {F}_N^+\cap \mathcal {F}_N^-= \emptyset $
. By maximality, there holds
Denote, for every
![]() $N>C_0$
,
$N>C_0$
,
 $$ \begin{align} E_N^{\pm} := \bigcup_{Q \in \mathcal{F}_N^{\pm}} Q, \qquad E_N^0:=E_N^+\cup E_N^-, \qquad E_N := Q_0\setminus E_N^0, \end{align} $$
$$ \begin{align} E_N^{\pm} := \bigcup_{Q \in \mathcal{F}_N^{\pm}} Q, \qquad E_N^0:=E_N^+\cup E_N^-, \qquad E_N := Q_0\setminus E_N^0, \end{align} $$
and
 $$ \begin{align} Q_0 = \bigg(\bigcap_{N>C_0} E_N^0\bigg)\cup \bigg(\bigcup_{N>C_0} E_N \bigg) =: E_0\cup \bigg(\bigcup_{N>C_0} E_N \bigg). \end{align} $$
$$ \begin{align} Q_0 = \bigg(\bigcap_{N>C_0} E_N^0\bigg)\cup \bigg(\bigcup_{N>C_0} E_N \bigg) =: E_0\cup \bigg(\bigcup_{N>C_0} E_N \bigg). \end{align} $$
By Lemma 2.9,
![]() $\Omega _{\mathcal {F}_N, Q_0}^{\vartheta }$
is a bounded
$\Omega _{\mathcal {F}_N, Q_0}^{\vartheta }$
is a bounded
![]() $1$
-sided NTA satisfying the CDC for any
$1$
-sided NTA satisfying the CDC for any
![]() $\vartheta \ge \vartheta _0$
. As in [Reference Hofmann and Martell31, Proposition 6.1]
$\vartheta \ge \vartheta _0$
. As in [Reference Hofmann and Martell31, Proposition 6.1]
 $$ \begin{align*} E_N \subset F_N:=\partial \Omega \cap \partial \Omega_{\mathcal{F}_N, Q_0}^{\vartheta} \subset \overline{Q}_0 \setminus \bigcup_{Q_j \in \mathcal{F}_N} \operatorname{int}(Q_j). \end{align*} $$
$$ \begin{align*} E_N \subset F_N:=\partial \Omega \cap \partial \Omega_{\mathcal{F}_N, Q_0}^{\vartheta} \subset \overline{Q}_0 \setminus \bigcup_{Q_j \in \mathcal{F}_N} \operatorname{int}(Q_j). \end{align*} $$
Hence,
 $$ \begin{align*} F_N \backslash E_N \subset \bigg(\overline{Q}_0 \backslash \bigcup_{Q_j \in \mathcal{F}_N} \operatorname{int}(Q_j) \bigg) \backslash \bigg(Q_0 \backslash \bigcup_{Q_j \in \mathcal{F}_N} Q_j \bigg) \subset \partial Q_0 \cup \bigg(\bigcup_{Q_j \in \mathcal{F}_N} \partial Q_j\bigg). \end{align*} $$
$$ \begin{align*} F_N \backslash E_N \subset \bigg(\overline{Q}_0 \backslash \bigcup_{Q_j \in \mathcal{F}_N} \operatorname{int}(Q_j) \bigg) \backslash \bigg(Q_0 \backslash \bigcup_{Q_j \in \mathcal{F}_N} Q_j \bigg) \subset \partial Q_0 \cup \bigg(\bigcup_{Q_j \in \mathcal{F}_N} \partial Q_j\bigg). \end{align*} $$
This, [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.17] and Lemma 3.9 imply
Next, we are going to show
Let
![]() $x \in E_{N+1}^{ \pm }$
. Then there exists
$x \in E_{N+1}^{ \pm }$
. Then there exists
![]() $Q_x \in \mathcal {F}_{N+1}^{\pm }$
such that
$Q_x \in \mathcal {F}_{N+1}^{\pm }$
such that
![]() $x \in Q_x$
. By equation (5.6), we have
$x \in Q_x$
. By equation (5.6), we have
By the maximality of the cubes in
![]() $\mathcal {F}_N^{\pm }$
, one has
$\mathcal {F}_N^{\pm }$
, one has
![]() $Q_x \subset Q^{\prime }_x$
for some
$Q_x \subset Q^{\prime }_x$
for some
![]() $Q^{\prime }_x \in \mathcal {F}_N^{\pm }$
with
$Q^{\prime }_x \in \mathcal {F}_N^{\pm }$
with
![]() $x \in Q^{\prime }_x \subset E_N^{\pm }$
. Thus,
$x \in Q^{\prime }_x \subset E_N^{\pm }$
. Thus,
![]() $\{E_N^+\}_N$
,
$\{E_N^+\}_N$
,
![]() $\{E_N^-\}_N$
and
$\{E_N^-\}_N$
and
![]() $\{E_N^0\}_N$
are decreasing sequences of sets. This, together with the fact that
$\{E_N^0\}_N$
are decreasing sequences of sets. This, together with the fact that
![]() $\omega (E_N^{\pm })\le \omega (Q_0)\le C_0\omega _0(Q_0) \le C_0$
and
$\omega (E_N^{\pm })\le \omega (Q_0)\le C_0\omega _0(Q_0) \le C_0$
and
![]() $\omega _0(E_N^{\pm })\le \omega _0(Q_0) \le 1$
, imply that
$\omega _0(E_N^{\pm })\le \omega _0(Q_0) \le 1$
, imply that
 $$ \begin{align} \omega\bigg(\bigcap_{N>C_0} E_N^{\pm}\bigg)=\lim_{N\to\infty} \omega(E_N^{\pm}) \qquad\text{and}\qquad \omega_0\bigg(\bigcap_{N>C_0} E_N^{\pm}\bigg)=\lim_{N\to\infty} \omega_0(E_N^{\pm}). \end{align} $$
$$ \begin{align} \omega\bigg(\bigcap_{N>C_0} E_N^{\pm}\bigg)=\lim_{N\to\infty} \omega(E_N^{\pm}) \qquad\text{and}\qquad \omega_0\bigg(\bigcap_{N>C_0} E_N^{\pm}\bigg)=\lim_{N\to\infty} \omega_0(E_N^{\pm}). \end{align} $$
 $$\begin{align*}\omega(E_N^+) = \sum_{Q\in \mathcal{F}_N^+} \omega(Q) <\frac1N\sum_{Q\in \mathcal{F}_N^+} \omega_0(Q) =\frac1N\omega_0(E_N^+) \le \frac1N, \end{align*}$$
$$\begin{align*}\omega(E_N^+) = \sum_{Q\in \mathcal{F}_N^+} \omega(Q) <\frac1N\sum_{Q\in \mathcal{F}_N^+} \omega_0(Q) =\frac1N\omega_0(E_N^+) \le \frac1N, \end{align*}$$
which together with equation (5.12) yield
 $$\begin{align*}\omega\bigg(\bigcap_{N>C_0} E_N^+\bigg)=\lim_{N\to\infty} \omega(E_N^+)=0. \end{align*}$$
$$\begin{align*}\omega\bigg(\bigcap_{N>C_0} E_N^+\bigg)=\lim_{N\to\infty} \omega(E_N^+)=0. \end{align*}$$
In view of the fact that by assumption
![]() $\omega _0 \ll \omega $
, we then conclude that
$\omega _0 \ll \omega $
, we then conclude that
 $$ \begin{align} 0=\omega_0\bigg(\bigcap_{N>C_0} E_N^+\bigg)=\lim_{N\to\infty} \omega_0(E_N^+). \end{align} $$
$$ \begin{align} 0=\omega_0\bigg(\bigcap_{N>C_0} E_N^+\bigg)=\lim_{N\to\infty} \omega_0(E_N^+). \end{align} $$
On the other hand, equation (5.6) yields
 $$\begin{align*}\omega_0(E_N^-) = \sum_{Q\in \mathcal{F}_N^-} \omega_0(Q) <\frac1N\sum_{Q\in \mathcal{F}_N^-} \omega(Q) =\frac1N\omega(E_N^-) \le \frac{C_0}N, \end{align*}$$
$$\begin{align*}\omega_0(E_N^-) = \sum_{Q\in \mathcal{F}_N^-} \omega_0(Q) <\frac1N\sum_{Q\in \mathcal{F}_N^-} \omega(Q) =\frac1N\omega(E_N^-) \le \frac{C_0}N, \end{align*}$$
and hence,
 $$ \begin{align} \omega_0\bigg(\bigcap_{N>C_0} E_N^-\bigg)=\lim_{N\to\infty} \omega_0(E_N^-)=0. \end{align} $$
$$ \begin{align} \omega_0\bigg(\bigcap_{N>C_0} E_N^-\bigg)=\lim_{N\to\infty} \omega_0(E_N^-)=0. \end{align} $$
Since
![]() $\{E_N^0\}_N$
is a decreasing sequence of sets with
$\{E_N^0\}_N$
is a decreasing sequence of sets with
![]() $\omega _0(E_N^0) \le \omega _0(Q_0) \le 1$
, equations (5.13) and (5.14) readily imply equation (5.11):
$\omega _0(E_N^0) \le \omega _0(Q_0) \le 1$
, equations (5.13) and (5.14) readily imply equation (5.11):
Now, we turn our attention to the square function estimates in
![]() $L^q(F_N, \omega _0)$
for
$L^q(F_N, \omega _0)$
for
![]() $q\in (0,\infty )$
. Let
$q\in (0,\infty )$
. Let
![]() $u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
be a weak solution of
$u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
be a weak solution of
![]() $Lu=0$
in
$Lu=0$
in
![]() $\Omega $
. To continue, we observe that if
$\Omega $
. To continue, we observe that if
![]() $Q \in \mathbb {D}_{Q_0}$
is so that
$Q \in \mathbb {D}_{Q_0}$
is so that
![]() $Q \cap E_N \neq \emptyset $
, then necessarily
$Q \cap E_N \neq \emptyset $
, then necessarily
![]() $Q \in \mathbb {D}_{\mathcal {F}_N, Q_0}$
, otherwise,
$Q \in \mathbb {D}_{\mathcal {F}_N, Q_0}$
, otherwise,
![]() $Q \subset Q' \in \mathcal {F}_N$
, hence
$Q \subset Q' \in \mathcal {F}_N$
, hence
![]() $Q \subset Q_0 \backslash E_N$
which is a contradiction. As a result, equation (5.7) yields
$Q \subset Q_0 \backslash E_N$
which is a contradiction. As a result, equation (5.7) yields
By the (dyadic) Lebesgue differentiation theorem with respect to
![]() $\omega $
, along with the fact that
$\omega $
, along with the fact that
![]() $\omega _0\ll \omega $
(cf. equation (5.4)), we conclude that
$\omega _0\ll \omega $
(cf. equation (5.4)), we conclude that
![]() $d\omega _0/d\omega (x)\approx _N 1$
for
$d\omega _0/d\omega (x)\approx _N 1$
for
![]() $\omega $
-a.e.
$\omega $
-a.e.
![]() $x\in E_N$
, hence also for
$x\in E_N$
, hence also for
![]() $\omega _0$
-a.e.
$\omega _0$
-a.e.
![]() $x\in E_N$
. Thus,
$x\in E_N$
. Thus,
 $$ \begin{align*} &\int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q d\omega_0(x) = \int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \frac{d\omega_0}{d\omega}(x) \,d\omega(x) \approx_N \int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \\ &\qquad\qquad\qquad \lesssim \int_{Q_0} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \lesssim \int_{Q_0} \mathcal{N}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \lesssim \|u\|_{L^{\infty}(\Omega)}^q \omega(Q_0) \lesssim \|u\|_{L^{\infty}(\Omega)}^q , \end{align*} $$
$$ \begin{align*} &\int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q d\omega_0(x) = \int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \frac{d\omega_0}{d\omega}(x) \,d\omega(x) \approx_N \int_{E_N} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \\ &\qquad\qquad\qquad \lesssim \int_{Q_0} \mathcal{S}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \lesssim \int_{Q_0} \mathcal{N}_{Q_0}^{\vartheta} u(x)^q \,d\omega(x) \lesssim \|u\|_{L^{\infty}(\Omega)}^q \omega(Q_0) \lesssim \|u\|_{L^{\infty}(\Omega)}^q , \end{align*} $$
where in the third estimate we have used equation (4.15) with
![]() $\omega _{L_0}=\omega _L$
(see also [Reference Akman, Hofmann, Martell and Toro1, Theorem 1.5]) which holds since
$\omega _{L_0}=\omega _L$
(see also [Reference Akman, Hofmann, Martell and Toro1, Theorem 1.5]) which holds since
![]() $\omega _L\in A_{\infty }(\partial \Omega ,\omega _L)$
. This and equation (5.10) imply
$\omega _L\in A_{\infty }(\partial \Omega ,\omega _L)$
. This and equation (5.10) imply
Now, note that for fixed
![]() $\alpha>0$
, we can find
$\alpha>0$
, we can find
![]() $\vartheta $
sufficiently large depending on
$\vartheta $
sufficiently large depending on
![]() $\alpha $
such that, for any
$\alpha $
such that, for any
![]() $r_0 \ll 2^{-k_0}$
,
$r_0 \ll 2^{-k_0}$
,
Indeed, let
![]() $Y \in \Gamma ^{\alpha }_{r_0}(x)$
. Pick
$Y \in \Gamma ^{\alpha }_{r_0}(x)$
. Pick
![]() $I \in \mathcal {W}$
so that
$I \in \mathcal {W}$
so that
![]() $I\ni Y$
, hence
$I\ni Y$
, hence
![]() $\ell (I) \approx \delta (Y) \leq |Y-x|<r_0 \ll 2^{-k_0} = \ell (Q_0)$
. Pick
$\ell (I) \approx \delta (Y) \leq |Y-x|<r_0 \ll 2^{-k_0} = \ell (Q_0)$
. Pick
![]() $Q_I \in \mathbb {D}_{Q_0}$
such that
$Q_I \in \mathbb {D}_{Q_0}$
such that
![]() $x \in Q_I$
and
$x \in Q_I$
and
![]() $\ell (Q_I)=\ell (I) \ll \ell (Q_0)$
. Thus,
$\ell (Q_I)=\ell (I) \ll \ell (Q_0)$
. Thus,
Recalling equation (2.10), if we take
![]() $\vartheta \ge \vartheta _0$
large enough so that
$\vartheta \ge \vartheta _0$
large enough so that
![]() $ 2^{\vartheta } \geq C(1+\alpha )$
, then
$ 2^{\vartheta } \geq C(1+\alpha )$
, then
![]() $Y \in I \in \mathcal {W}_{Q_I}^{\vartheta } \subset \mathcal {W}^{\vartheta ,*}_{Q_I}$
. The latter gives that
$Y \in I \in \mathcal {W}_{Q_I}^{\vartheta } \subset \mathcal {W}^{\vartheta ,*}_{Q_I}$
. The latter gives that
![]() $Y \in U_{Q_I}^{\vartheta } \subset \Gamma _{Q_0}^{\vartheta }(x)$
, and consequently, equation (5.16) holds. We would like to mention that the dependence of
$Y \in U_{Q_I}^{\vartheta } \subset \Gamma _{Q_0}^{\vartheta }(x)$
, and consequently, equation (5.16) holds. We would like to mention that the dependence of
![]() $\vartheta $
on
$\vartheta $
on
![]() $\alpha $
implies that all the sawtooth regions
$\alpha $
implies that all the sawtooth regions
![]() $\Omega _{\mathcal {F}_N, Q_0}^{\vartheta }$
above as well as all the implicit constants depend on
$\Omega _{\mathcal {F}_N, Q_0}^{\vartheta }$
above as well as all the implicit constants depend on
![]() $\alpha $
.
$\alpha $
.
Next, equation (5.16) readily yields that
![]() $\mathcal {S}^{\alpha }_{r_0}u(x) \leq \mathcal {S}_{Q_0}^{\vartheta } u(x)$
for every
$\mathcal {S}^{\alpha }_{r_0}u(x) \leq \mathcal {S}_{Q_0}^{\vartheta } u(x)$
for every
![]() $x \in Q_0$
. This, together with equation (5.15), implies that
$x \in Q_0$
. This, together with equation (5.15), implies that
![]() $\mathcal {S}^{\alpha }_{r_0} u \in L^q(F_N, \omega _0)$
. If we next take an arbitrary
$\mathcal {S}^{\alpha }_{r_0} u \in L^q(F_N, \omega _0)$
. If we next take an arbitrary
![]() $X\in \Omega $
, by Harnack’s inequality (albeit with constants depending on X) and by equation (5.1), then we have
$X\in \Omega $
, by Harnack’s inequality (albeit with constants depending on X) and by equation (5.1), then we have
Note also that by equation (5.11) and Harnack’s inequality
To complete the proof, we perform the preceding operation for an arbitrary
![]() $Q_0\in \mathbb {D}_{k_0}$
. Therefore, invoking equations (5.8), (5.9) and (5.10) with
$Q_0\in \mathbb {D}_{k_0}$
. Therefore, invoking equations (5.8), (5.9) and (5.10) with
![]() $Q_k\in \mathbb {D}_{k_0}$
, we conclude, with the induced notation, that
$Q_k\in \mathbb {D}_{k_0}$
, we conclude, with the induced notation, that
 $$ \begin{align} \partial \Omega = \bigcup_{Q_k \in \mathbb{D}_{k_0}} Q_k =\bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} E^k_0\bigg) &\bigcup \bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} \bigcup_{N>C_0} E^k_N \bigg) \notag \\ &=\bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} E^k_0\bigg) \bigcup \bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} \bigcup_{N>C_0} F^k_N \bigg) =: F_0 \cup \bigg(\bigcup_{k, N} F^k_N \bigg), \end{align} $$
$$ \begin{align} \partial \Omega = \bigcup_{Q_k \in \mathbb{D}_{k_0}} Q_k =\bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} E^k_0\bigg) &\bigcup \bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} \bigcup_{N>C_0} E^k_N \bigg) \notag \\ &=\bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} E^k_0\bigg) \bigcup \bigg(\bigcup_{Q_k \in \mathbb{D}_{k_0}} \bigcup_{N>C_0} F^k_N \bigg) =: F_0 \cup \bigg(\bigcup_{k, N} F^k_N \bigg), \end{align} $$
where
![]() $\omega _{L_0}^{X}(F_0)=0$
(by equation (5.18)) and
$\omega _{L_0}^{X}(F_0)=0$
(by equation (5.18)) and
![]() $F^k_N=\partial \Omega \cap \partial \Omega _{\mathcal {F}^k_N, Q_k}^{\vartheta }$
, where each
$F^k_N=\partial \Omega \cap \partial \Omega _{\mathcal {F}^k_N, Q_k}^{\vartheta }$
, where each
![]() $\Omega _{\mathcal {F}^k_N, Q_k}^{\vartheta } \subset \Omega $
is a bounded 1-sided NTA domain satisfying the CDC. Combining equations (5.19) and (5.17) with
$\Omega _{\mathcal {F}^k_N, Q_k}^{\vartheta } \subset \Omega $
is a bounded 1-sided NTA domain satisfying the CDC. Combining equations (5.19) and (5.17) with
![]() $F_N^k$
in place of
$F_N^k$
in place of
![]() $F_N$
, the proof of
$F_N$
, the proof of
![]() $\mathrm {(a)}\ \Longrightarrow \ \mathrm {(b)}$
is complete.
$\mathrm {(a)}\ \Longrightarrow \ \mathrm {(b)}$
is complete.
![]() $\Box $
$\Box $
5.2 Proof of
 $\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
$\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
Let
![]() $\alpha _0$
be so that equation (4.21) holds. Suppose that
$\alpha _0$
be so that equation (4.21) holds. Suppose that
![]() $\mathrm {(c)}'$
holds where throughout it is assumed that
$\mathrm {(c)}'$
holds where throughout it is assumed that
![]() $\alpha \ge \alpha _0$
. In order to prove that
$\alpha \ge \alpha _0$
. In order to prove that
![]() $\omega _{L_0} \ll \omega _L$
on
$\omega _{L_0} \ll \omega _L$
on
![]() $\partial \Omega $
, by Lemma 2.8 and the fact that by Harnack’s inequality
$\partial \Omega $
, by Lemma 2.8 and the fact that by Harnack’s inequality
![]() $\omega _L^X\ll \omega _L^Y$
and
$\omega _L^X\ll \omega _L^Y$
and
![]() $\omega _{L_0}^X\ll \omega _{L_0}^Y$
for any
$\omega _{L_0}^X\ll \omega _{L_0}^Y$
for any
![]() $X,Y\in \Omega $
, it suffices to show that for any given
$X,Y\in \Omega $
, it suffices to show that for any given
![]() $Q_0 \in \mathbb {D}$
,
$Q_0 \in \mathbb {D}$
,
Consider then
![]() $F \subset Q_0$
with
$F \subset Q_0$
with
![]() $\omega _L^{X_{Q_0}}(F)=0$
. Lemma 4.2 applied to F gives a Borel set
$\omega _L^{X_{Q_0}}(F)=0$
. Lemma 4.2 applied to F gives a Borel set
![]() $S\subset Q_0$
such that
$S\subset Q_0$
such that
![]() $u(X):=\omega _L^{X}(S)$
,
$u(X):=\omega _L^{X}(S)$
,
![]() $X\in \Omega $
, satisfies
$X\in \Omega $
, satisfies
where the first inequality follows from equation (4.21) and the fact that
![]() $\alpha \ge \alpha _0$
, and
$\alpha \ge \alpha _0$
, and
![]() $r_{Q_0}^*=2\kappa _0 r_{Q_0}$
. By assumption and equation (5.1), we have that
$r_{Q_0}^*=2\kappa _0 r_{Q_0}$
. By assumption and equation (5.1), we have that
![]() $\mathcal {S}^{\alpha }_{r_{Q_0}^*} u(x)<\infty $
for
$\mathcal {S}^{\alpha }_{r_{Q_0}^*} u(x)<\infty $
for
![]() $\omega _{L_0}^{X_{Q_0}}$
-a.e.
$\omega _{L_0}^{X_{Q_0}}$
-a.e.
![]() $x\in \partial \Omega $
. Hence,
$x\in \partial \Omega $
. Hence,
![]() $\omega _{L_0}^{X_{Q_0}}(F)=0$
as desired and the proof of
$\omega _{L_0}^{X_{Q_0}}(F)=0$
as desired and the proof of
![]() $\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
is complete.
$\mathrm {(c)}'\ \Longrightarrow \ \mathrm {(a)}$
is complete.
![]() $\Box $
$\Box $
6 Proof of Theorems 1.7 and 1.8
We will obtain Theorems 1.7 and 1.8 as a consequence of the following qualitative version of [Reference Cavero, Hofmann, Martell and Toro9, Theorem 4.13]:
Theorem 6.1. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
,
$\Omega \subset \mathbb {R}^{n+1}$
,
![]() $n \ge 2$
, be a
$n \ge 2$
, be a
![]() $1$
-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
$1$
-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). There exists
![]() $\widetilde {\alpha }_0>0$
(depending only on the
$\widetilde {\alpha }_0>0$
(depending only on the
![]() $1$
-sided NTA and CDC constants) such that the following holds. Assume that
$1$
-sided NTA and CDC constants) such that the following holds. Assume that
![]() $L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
$L_0 u = -\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$
and
![]() $L_1 u = -\mathop {\operatorname {div}}\nolimits (A_1 \nabla u)$
are real (not necessarily symmetric) elliptic operators such that
$L_1 u = -\mathop {\operatorname {div}}\nolimits (A_1 \nabla u)$
are real (not necessarily symmetric) elliptic operators such that
![]() $A_0-A_1=A+D$
, where
$A_0-A_1=A+D$
, where
![]() $A, D \in L^{\infty }(\Omega )$
are real matrices satisfying the following conditions:
$A, D \in L^{\infty }(\Omega )$
are real matrices satisfying the following conditions:
-
(i) There exist
 $\alpha _1 \geq \widetilde {\alpha }_0$
and
$\alpha _1 \geq \widetilde {\alpha }_0$
and
 $r_1>0$
such that (6.1)where
$r_1>0$
such that (6.1)where $$ \begin{align} \iint_{\Gamma^{\alpha_1}_{r_1}(x)} a(X)^2 \delta(X)^{-n-1} dX < \infty, \qquad \text{for } \omega_{L_0}\text{-a.e.~} x \in \partial \Omega, \end{align} $$
$$ \begin{align} \iint_{\Gamma^{\alpha_1}_{r_1}(x)} a(X)^2 \delta(X)^{-n-1} dX < \infty, \qquad \text{for } \omega_{L_0}\text{-a.e.~} x \in \partial \Omega, \end{align} $$
 $a(X):=\sup \limits _{Y \in B(X, \delta (X)/2)}|A(Y)|$
,
$a(X):=\sup \limits _{Y \in B(X, \delta (X)/2)}|A(Y)|$
,
 $X \in \Omega $
.
$X \in \Omega $
.
-
(ii)
 $D \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
is antisymmetric and there exist
$D \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
is antisymmetric and there exist
 $\alpha _2 \geq \widetilde {\alpha }_0$
and
$\alpha _2 \geq \widetilde {\alpha }_0$
and
 $r_2>0$
such that (6.2)
$r_2>0$
such that (6.2) $$ \begin{align} \iint_{\Gamma^{\alpha_2}_{r_2}(x)} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX < \infty, \quad \text{for } \omega_{L_0}\text{-a.e.~} x \in \partial \Omega. \end{align} $$
$$ \begin{align} \iint_{\Gamma^{\alpha_2}_{r_2}(x)} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX < \infty, \quad \text{for } \omega_{L_0}\text{-a.e.~} x \in \partial \Omega. \end{align} $$
Then
![]() $\omega _{L_0} \ll \omega _{L_1}$
.
$\omega _{L_0} \ll \omega _{L_1}$
.
Assuming this result momentarily, we deduce Theorems 1.7 and 1.8:
Proof of Theorem 1.7
For
![]() $L_0$
and L as in the statement set
$L_0$
and L as in the statement set
![]() $\widetilde {A}_0=A_0$
,
$\widetilde {A}_0=A_0$
,
![]() $\widetilde {A}_1=A$
,
$\widetilde {A}_1=A$
,
![]() $\widetilde {A}=A_0-A$
and
$\widetilde {A}=A_0-A$
and
![]() $D=0$
so that
$D=0$
so that
![]() $\widetilde {A}_0-\widetilde {A}_1= \widetilde {A}+D$
. Note that equation (6.1) follows at once from equation (1.4) and also that equation (6.2) holds automatically. With all these in hand, Theorem 6.1 gives
$\widetilde {A}_0-\widetilde {A}_1= \widetilde {A}+D$
. Note that equation (6.1) follows at once from equation (1.4) and also that equation (6.2) holds automatically. With all these in hand, Theorem 6.1 gives
![]() $\omega _{L_0}= \omega _{\widetilde {L}_0}\ll \omega _{\widetilde {L}_1}= \omega _{L}$
.
$\omega _{L_0}= \omega _{\widetilde {L}_0}\ll \omega _{\widetilde {L}_1}= \omega _{L}$
.
Proof of Theorem 1.8
Set
![]() $A_0=A$
,
$A_0=A$
,
![]() $A_1=A^{\top }$
,
$A_1=A^{\top }$
,
![]() $\widetilde {A}=0$
and
$\widetilde {A}=0$
and
![]() $D=A-A^{\top }$
so that
$D=A-A^{\top }$
so that
![]() $A_0-A_1=\widetilde {A}+D$
. Observe that
$A_0-A_1=\widetilde {A}+D$
. Observe that
![]() $D \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
is antisymmetric, equation (6.1) holds trivially and equation (6.2) agrees with equation (1.5). Thus, Theorem 6.1 implies that
$D \in \operatorname *{\mathrm {Lip}}_{\mathrm {loc}}(\Omega )$
is antisymmetric, equation (6.1) holds trivially and equation (6.2) agrees with equation (1.5). Thus, Theorem 6.1 implies that
![]() $\omega _L \ll \omega _{L^{\top }}$
.
$\omega _L \ll \omega _{L^{\top }}$
.
On the other hand,
![]() $\omega _L \ll \omega _{L^{\mathrm {sym}}}$
follows similarly if we set
$\omega _L \ll \omega _{L^{\mathrm {sym}}}$
follows similarly if we set
![]() $A_0=A$
,
$A_0=A$
,
![]() $A_1=(A+A^{\top })/2$
,
$A_1=(A+A^{\top })/2$
,
![]() $\widetilde {A}=0$
and
$\widetilde {A}=0$
and
![]() $D=(A-A^{\top })/2$
.
$D=(A-A^{\top })/2$
.
Finally,
![]() $\omega _{L^{\top }} \ll \omega _L$
follows from what has been proved by switching the roles of L and
$\omega _{L^{\top }} \ll \omega _L$
follows from what has been proved by switching the roles of L and
![]() $L^{\top }$
and the fact that
$L^{\top }$
and the fact that
![]() $\mathscr {F}^{\alpha }_r(x; A)<\infty $
for
$\mathscr {F}^{\alpha }_r(x; A)<\infty $
for
![]() $\omega _{L^{\top }}$
-a.e.
$\omega _{L^{\top }}$
-a.e.
![]() $x\in \partial \Omega $
.
$x\in \partial \Omega $
.
Before proving Theorem 6.1, we need the following auxiliary result which adapts [Reference Hofmann, Martell and Toro34, Lemma 4.44] and [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.39] to our current setting. We would like to mention that [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.39] corresponds to the case
![]() $\mathcal {F}= \emptyset $
in the following statement.
$\mathcal {F}= \emptyset $
in the following statement.
Lemma 6.2. Let
![]() $\Omega \subset \mathbb {R}^{n+1}$
be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). Given
$\Omega \subset \mathbb {R}^{n+1}$
be a 1-sided NTA domain (cf. Definition 2.3) satisfying the CDC (cf. Definition 2.7). Given
![]() $Q_0\in \mathbb {D}$
, a pairwise disjoint collection
$Q_0\in \mathbb {D}$
, a pairwise disjoint collection
![]() $\mathcal {F}\subset \mathbb {D}_{Q_0}$
, and
$\mathcal {F}\subset \mathbb {D}_{Q_0}$
, and
![]() $N\ge 4$
, let
$N\ge 4$
, let
![]() $\mathcal {F}_N$
be the family of maximal cubes of the collection
$\mathcal {F}_N$
be the family of maximal cubes of the collection
![]() ${\mathcal {F}}$
augmented by adding all the cubes
${\mathcal {F}}$
augmented by adding all the cubes
![]() $Q \in \mathbb {D}_{Q_0}$
such that
$Q \in \mathbb {D}_{Q_0}$
such that
![]() $\ell (Q) \leq 2^{-N} \ell (Q_0)$
. There exist
$\ell (Q) \leq 2^{-N} \ell (Q_0)$
. There exist
![]() $\Psi _N^{\vartheta }\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
and a constant
$\Psi _N^{\vartheta }\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
and a constant
![]() $C\ge 1$
depending only on dimension n, the 1-sided NTA constants, the CDC constant and
$C\ge 1$
depending only on dimension n, the 1-sided NTA constants, the CDC constant and
![]() $\vartheta $
, but independent of N,
$\vartheta $
, but independent of N,
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $Q_0$
such that the following hold:
$Q_0$
such that the following hold:
-
(i)
 $C^{-1}\,\mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{\vartheta }}\le \Psi _N^{\vartheta } \le \mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{\vartheta ,*}}$
.
$C^{-1}\,\mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{\vartheta }}\le \Psi _N^{\vartheta } \le \mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{\vartheta ,*}}$
. -
(ii)
 $\sup _{X\in \Omega } |\nabla \Psi _N^{\vartheta }(X)|\,\delta (X)\le C$
.
$\sup _{X\in \Omega } |\nabla \Psi _N^{\vartheta }(X)|\,\delta (X)\le C$
. -
(iii) Setting
(6.3) $$ \begin{align} \mathcal{W}_N^{\vartheta}:=\bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},Q_0}} \mathcal{W}_Q^{\vartheta,*}, \quad \mathcal{W}_N^{\vartheta,\Sigma}:= \big\{I\in \mathcal{W}_{N}^{\vartheta}:\, \exists\,J\in \mathcal{W}\setminus \mathcal{W}_N^{\vartheta}\ \mbox{with}\ \partial I\cap\partial J\neq\emptyset \big\}, \end{align} $$
$$ \begin{align} \mathcal{W}_N^{\vartheta}:=\bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},Q_0}} \mathcal{W}_Q^{\vartheta,*}, \quad \mathcal{W}_N^{\vartheta,\Sigma}:= \big\{I\in \mathcal{W}_{N}^{\vartheta}:\, \exists\,J\in \mathcal{W}\setminus \mathcal{W}_N^{\vartheta}\ \mbox{with}\ \partial I\cap\partial J\neq\emptyset \big\}, \end{align} $$
one has
 $$ \begin{align} \nabla \Psi_N^{\vartheta}\equiv 0 \quad \mbox{in} \quad \bigcup_{I\in \mathcal{W}_N^{\vartheta} \setminus \mathcal{W}_N^{\vartheta,\Sigma} }I^{**}, \end{align} $$
$$ \begin{align} \nabla \Psi_N^{\vartheta}\equiv 0 \quad \mbox{in} \quad \bigcup_{I\in \mathcal{W}_N^{\vartheta} \setminus \mathcal{W}_N^{\vartheta,\Sigma} }I^{**}, \end{align} $$
and there exists a family
![]() $\{\widehat {Q}_I\}_{I\in \mathcal {W}_N^{\vartheta ,\Sigma }}$
so that
$\{\widehat {Q}_I\}_{I\in \mathcal {W}_N^{\vartheta ,\Sigma }}$
so that
 $$ \begin{align} C^{-1}\,\ell(I)\le \ell(\widehat{Q}_I)\le C\,\ell(I), \qquad \operatorname{dist}(I, \widehat{Q}_I)\le C\,\ell(I), \qquad \sum_{I\in \mathcal{W}_N^{\vartheta,\Sigma}} \mathbf{1}_{\widehat{Q}_I} \le C. \end{align} $$
$$ \begin{align} C^{-1}\,\ell(I)\le \ell(\widehat{Q}_I)\le C\,\ell(I), \qquad \operatorname{dist}(I, \widehat{Q}_I)\le C\,\ell(I), \qquad \sum_{I\in \mathcal{W}_N^{\vartheta,\Sigma}} \mathbf{1}_{\widehat{Q}_I} \le C. \end{align} $$
Proof. The proof combines ideas from [Reference Hofmann, Martell and Toro34, Lemma 4.44], [Reference Akman, Hofmann, Martell and Toro1, Lemma 2.39], and [Reference Hofmann, Martell and Mayboroda32, Appendix A.2]. The parameter
![]() $\vartheta \ge \vartheta _0$
will remain fixed in the proof, and then constants are allowed to depend on it. To ease the notation, we will omit the superscript
$\vartheta \ge \vartheta _0$
will remain fixed in the proof, and then constants are allowed to depend on it. To ease the notation, we will omit the superscript
![]() $\vartheta $
everywhere in the proof. Recall that given I, any closed dyadic cube in
$\vartheta $
everywhere in the proof. Recall that given I, any closed dyadic cube in
![]() $\mathbb {R}^{n+1}$
, we set
$\mathbb {R}^{n+1}$
, we set
![]() $I^{*}=(1+\lambda )I$
and
$I^{*}=(1+\lambda )I$
and
![]() $I^{**}=(1+2\,\lambda )I$
. Let us introduce
$I^{**}=(1+2\,\lambda )I$
. Let us introduce
![]() $\widetilde {I^{*}}=(1+\frac 32\,\lambda )I$
so that
$\widetilde {I^{*}}=(1+\frac 32\,\lambda )I$
so that
Given
![]() $I_0:=[-\frac 12,\frac 12]^{n+1}\subset \mathbb {R}^{n+1}$
, fix
$I_0:=[-\frac 12,\frac 12]^{n+1}\subset \mathbb {R}^{n+1}$
, fix
![]() $\phi _0\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
such that
$\phi _0\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
such that
![]() $1_{I_0^{*}}\le \phi _0\le 1_{\widetilde {I_0^{*}}}$
and
$1_{I_0^{*}}\le \phi _0\le 1_{\widetilde {I_0^{*}}}$
and
![]() $|\nabla \phi _0|\lesssim 1$
(the implicit constant depends on the parameter
$|\nabla \phi _0|\lesssim 1$
(the implicit constant depends on the parameter
![]() $\lambda $
). For every
$\lambda $
). For every
![]() $I\in \mathcal {W}=\mathcal {W}(\Omega )$
, we set
$I\in \mathcal {W}=\mathcal {W}(\Omega )$
, we set
![]() $\phi _I(\cdot )=\phi _0\big (\frac {\,\cdot \,-X(I)}{\ell (I)}\big )$
so that
$\phi _I(\cdot )=\phi _0\big (\frac {\,\cdot \,-X(I)}{\ell (I)}\big )$
so that
![]() $\phi _I\in \mathscr {C}^{\infty }(\mathbb {R}^{n+1})$
,
$\phi _I\in \mathscr {C}^{\infty }(\mathbb {R}^{n+1})$
,
![]() $1_{I^{*}}\le \phi _I\le 1_{\widetilde {I^{*}}}$
and
$1_{I^{*}}\le \phi _I\le 1_{\widetilde {I^{*}}}$
and
![]() $ |\nabla \phi _I|\lesssim \ell (I)^{-1}$
(with implicit constant depending only on n and
$ |\nabla \phi _I|\lesssim \ell (I)^{-1}$
(with implicit constant depending only on n and
![]() $\lambda $
).
$\lambda $
).
For every
![]() $X\in \Omega $
, we let
$X\in \Omega $
, we let
![]() $\Phi (X):=\sum _{I\in \mathcal {W}} \phi _I(X)$
. It then follows that
$\Phi (X):=\sum _{I\in \mathcal {W}} \phi _I(X)$
. It then follows that
![]() $\Phi \in \mathscr {C}^{\infty }(\Omega )$
since, for every compact subset of
$\Phi \in \mathscr {C}^{\infty }(\Omega )$
since, for every compact subset of
![]() $\Omega $
, the previous sum has finitely many nonvanishing terms. Also,
$\Omega $
, the previous sum has finitely many nonvanishing terms. Also,
![]() $1\le \Phi (X)\le C_{\lambda }$
for every
$1\le \Phi (X)\le C_{\lambda }$
for every
![]() $X\in \Omega $
since the family
$X\in \Omega $
since the family
![]() $\{\widetilde {I^{*}}\}_{I\in \mathcal {W}}$
has bounded overlap by our choice of
$\{\widetilde {I^{*}}\}_{I\in \mathcal {W}}$
has bounded overlap by our choice of
![]() $\lambda $
. Hence, we can set
$\lambda $
. Hence, we can set
![]() $\Phi _I=\phi _I/\Phi $
, and one can easily see that
$\Phi _I=\phi _I/\Phi $
, and one can easily see that
![]() $\Phi _I\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
,
$\Phi _I\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
,
![]() $C_{\lambda }^{-1}1_{I^{*}}\le \Phi _I\le 1_{\widetilde {I^{*}}}$
and
$C_{\lambda }^{-1}1_{I^{*}}\le \Phi _I\le 1_{\widetilde {I^{*}}}$
and
![]() $ |\nabla \Phi _I|\lesssim \ell (I)^{-1}$
. With this at hand, set
$ |\nabla \Phi _I|\lesssim \ell (I)^{-1}$
. With this at hand, set
 $$\begin{align*}\Psi_N(X) := \sum_{I\in \mathcal{W}_N} \Phi_I(X) = \frac{\sum\limits_{I\in \mathcal{W}_N} \phi_I(X)}{\sum\limits_{I\in \mathcal{W}} \phi_I(X)}, \qquad X\in\Omega. \end{align*}$$
$$\begin{align*}\Psi_N(X) := \sum_{I\in \mathcal{W}_N} \Phi_I(X) = \frac{\sum\limits_{I\in \mathcal{W}_N} \phi_I(X)}{\sum\limits_{I\in \mathcal{W}} \phi_I(X)}, \qquad X\in\Omega. \end{align*}$$
We first note that the number of terms in the sum defining
![]() $\Psi _N$
is bounded depending on N. Indeed, if
$\Psi _N$
is bounded depending on N. Indeed, if
![]() $Q\in \mathbb {D}_{\mathcal {F}_N, Q_0}$
, then
$Q\in \mathbb {D}_{\mathcal {F}_N, Q_0}$
, then
![]() $Q\in \mathbb {D}_{Q_0}$
and
$Q\in \mathbb {D}_{Q_0}$
and
![]() $2^{-N}\ell (Q_0)<\ell (Q)\le \ell (Q_0)$
, which implies that
$2^{-N}\ell (Q_0)<\ell (Q)\le \ell (Q_0)$
, which implies that
![]() $\mathbb {D}_{\mathcal {F}_N, Q_0}$
has finite cardinality with bounds depending on dimension and N (here, we recall that the number of dyadic children of a given cube is uniformly controlled). Also, by construction
$\mathbb {D}_{\mathcal {F}_N, Q_0}$
has finite cardinality with bounds depending on dimension and N (here, we recall that the number of dyadic children of a given cube is uniformly controlled). Also, by construction
![]() $\mathcal {W}_Q^*$
has cardinality depending only on the allowable parameters. Hence,
$\mathcal {W}_Q^*$
has cardinality depending only on the allowable parameters. Hence,
![]() $\# \mathcal {W}_N\lesssim C_N<\infty $
. This and the fact that each
$\# \mathcal {W}_N\lesssim C_N<\infty $
. This and the fact that each
![]() $\Phi _I\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
yield that
$\Phi _I\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
yield that
![]() $\Psi _N\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
. Note also that equation (6.6) and the definition of
$\Psi _N\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
. Note also that equation (6.6) and the definition of
![]() $\mathcal {W}_N$
give
$\mathcal {W}_N$
give
 $$ \begin{align*} \operatorname{\mathrm{supp}} \Psi_N \subset \bigcup_{I\in \mathcal{W}_N} \widetilde{I^{*}} = \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} \bigcup_{I\in \mathcal{W}_Q^*} \widetilde{I^{*}} \subset \operatorname{int}\Big( \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} \bigcup_{I\in \mathcal{W}_Q^*} I^{**} \Big) = \operatorname{int}\Big( \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} U_Q^{*} \Big) = \Omega_{\mathcal{F}_N,Q_0}^{*}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{supp}} \Psi_N \subset \bigcup_{I\in \mathcal{W}_N} \widetilde{I^{*}} = \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} \bigcup_{I\in \mathcal{W}_Q^*} \widetilde{I^{*}} \subset \operatorname{int}\Big( \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} \bigcup_{I\in \mathcal{W}_Q^*} I^{**} \Big) = \operatorname{int}\Big( \bigcup_{Q\in\mathbb{D}_{\mathcal{F}_{N},{Q}_0}} U_Q^{*} \Big) = \Omega_{\mathcal{F}_N,Q_0}^{*}. \end{align*} $$
This, the fact that
![]() $\mathcal {W}_N\subset \mathcal {W}$
and the definition of
$\mathcal {W}_N\subset \mathcal {W}$
and the definition of
![]() $\Psi _N$
immediately give that
$\Psi _N$
immediately give that
![]() $\Psi _N\le \mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{*}}$
. On the other hand, if
$\Psi _N\le \mathbf {1}_{\Omega _{\mathcal {F}_N,Q_0}^{*}}$
. On the other hand, if
![]() $X\in \Omega _N=\Omega _{\mathcal {F}_{N},Q_0}$
, then there exists
$X\in \Omega _N=\Omega _{\mathcal {F}_{N},Q_0}$
, then there exists
![]() $I\in \mathcal {W}_N$
such that
$I\in \mathcal {W}_N$
such that
![]() $X\in I^{*}$
, in which case
$X\in I^{*}$
, in which case
![]() $\Psi _N(X)\ge \Phi _I(X)\ge C_{\lambda }^{-1}$
. All these imply
$\Psi _N(X)\ge \Phi _I(X)\ge C_{\lambda }^{-1}$
. All these imply
![]() $(i)$
. Note that
$(i)$
. Note that
![]() $(ii)$
follows by observing that for every
$(ii)$
follows by observing that for every
![]() $X\in \Omega $
we have
$X\in \Omega $
we have
where we have used that if
![]() $X\in \widetilde {I^{*}}$
, then
$X\in \widetilde {I^{*}}$
, then
![]() $\delta (X)\approx \ell (I)$
and also that the family
$\delta (X)\approx \ell (I)$
and also that the family
![]() $\{\widetilde {I^{*}}\}_{I\in \mathcal {W}}$
has bounded overlap.
$\{\widetilde {I^{*}}\}_{I\in \mathcal {W}}$
has bounded overlap.
To see
![]() $(iii)$
, fix
$(iii)$
, fix
![]() $I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
and
$I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
and
![]() $X\in I^{**}$
, and set
$X\in I^{**}$
, and set
![]() $\mathcal {W}_X:=\{J\in \mathcal {W}: \phi _J(X)\neq 0\}$
. We first note that
$\mathcal {W}_X:=\{J\in \mathcal {W}: \phi _J(X)\neq 0\}$
. We first note that
![]() $\mathcal {W}_X\subset \mathcal {W}_N$
. Indeed, if
$\mathcal {W}_X\subset \mathcal {W}_N$
. Indeed, if
![]() $\phi _J(X)\neq 0$
, then
$\phi _J(X)\neq 0$
, then
![]() $X\in \widetilde {J^{*}}$
. Hence,
$X\in \widetilde {J^{*}}$
. Hence,
![]() $X\in I^{**}\cap J^{**}$
, and our choice of
$X\in I^{**}\cap J^{**}$
, and our choice of
![]() $\lambda $
gives that
$\lambda $
gives that
![]() $\partial I$
meets
$\partial I$
meets
![]() $\partial J$
, this in turn implies that
$\partial J$
, this in turn implies that
![]() $J\in \mathcal {W}_N$
since
$J\in \mathcal {W}_N$
since
![]() $I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
. All these yield
$I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
. All these yield
 $$ \begin{align*}\Psi_N(X) = \frac{\sum\limits_{J\in \mathcal{W}_N} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}} \phi_J(X)} = \frac{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}_X} \phi_J(X)} = \frac{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)} = 1. \end{align*} $$
$$ \begin{align*}\Psi_N(X) = \frac{\sum\limits_{J\in \mathcal{W}_N} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}} \phi_J(X)} = \frac{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}_X} \phi_J(X)} = \frac{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)}{\sum\limits_{J\in \mathcal{W}_N\cap \mathcal{W}_X} \phi_J(X)} = 1. \end{align*} $$
Hence,
![]() $\Psi _N\big |_{I^{**}}\equiv 1$
for every
$\Psi _N\big |_{I^{**}}\equiv 1$
for every
![]() $I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
. This and the fact that
$I\in \mathcal {W}_N\setminus \mathcal {W}^{\Sigma }_N$
. This and the fact that
![]() $\Psi _N\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
immediately give that
$\Psi _N\in \mathscr {C}_c^{\infty }(\mathbb {R}^{n+1})$
immediately give that
![]() $\nabla \Psi _N\equiv 0$
in
$\nabla \Psi _N\equiv 0$
in
![]() $\bigcup _{I\in \mathcal {W}_N \setminus \mathcal {W}_N^{\Sigma } }I^{**}$
.
$\bigcup _{I\in \mathcal {W}_N \setminus \mathcal {W}_N^{\Sigma } }I^{**}$
.
We are left with showing the last part of
![]() $(iii)$
, and for that we borrow some ideas from [Reference Hofmann, Martell and Mayboroda32, Appendix A.2]. Fix
$(iii)$
, and for that we borrow some ideas from [Reference Hofmann, Martell and Mayboroda32, Appendix A.2]. Fix
![]() $I\in \mathcal {W}_N^{\Sigma }$
, and let J be so that
$I\in \mathcal {W}_N^{\Sigma }$
, and let J be so that
![]() $J\in \mathcal {W}\setminus \mathcal {W}_N$
with
$J\in \mathcal {W}\setminus \mathcal {W}_N$
with
![]() $\partial I\cap \partial J\neq \emptyset $
, in particular
$\partial I\cap \partial J\neq \emptyset $
, in particular
![]() $\ell (I)\approx \ell (J)$
. Since
$\ell (I)\approx \ell (J)$
. Since
![]() $I\in \mathcal {W}_N^{\Sigma }$
, there exists
$I\in \mathcal {W}_N^{\Sigma }$
, there exists
![]() $Q_I\in \mathbb {D}_{\mathcal {F}_N,Q_0}$
. Pick
$Q_I\in \mathbb {D}_{\mathcal {F}_N,Q_0}$
. Pick
![]() $Q_J\in \mathbb {D}$
so that
$Q_J\in \mathbb {D}$
so that
![]() $\ell (Q_J)=\ell (J)$
and it contains any fixed
$\ell (Q_J)=\ell (J)$
and it contains any fixed
![]() $\widehat {y}\in \partial \Omega $
such that
$\widehat {y}\in \partial \Omega $
such that
![]() $\operatorname {dist}(J,\partial \Omega )=\operatorname {dist}(J,\widehat {y})$
. Then, as observed in Section 2.3, one has
$\operatorname {dist}(J,\partial \Omega )=\operatorname {dist}(J,\widehat {y})$
. Then, as observed in Section 2.3, one has
![]() $J\in \mathcal {W}_{Q_J}^*$
. But, since
$J\in \mathcal {W}_{Q_J}^*$
. But, since
![]() $J\in \mathcal {W}\setminus \mathcal {W}_N$
, we necessarily have
$J\in \mathcal {W}\setminus \mathcal {W}_N$
, we necessarily have
![]() $Q_J\notin \mathbb {D}_{\mathcal {F}_N,Q_0}=\mathbb {D}_{\mathcal {F}_N}\cap \mathbb {D}_{Q_0}$
. Hence,
$Q_J\notin \mathbb {D}_{\mathcal {F}_N,Q_0}=\mathbb {D}_{\mathcal {F}_N}\cap \mathbb {D}_{Q_0}$
. Hence,
![]() $\mathcal {W}_N^{\Sigma }=\mathcal {W}_N^{\Sigma ,1}\cup \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
where
$\mathcal {W}_N^{\Sigma }=\mathcal {W}_N^{\Sigma ,1}\cup \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
where
 $$ \begin{align*} \mathcal{W}_N^{\Sigma,1}:&=\{I\in \mathcal{W}_N^{\Sigma}: Q_0\subset Q_J\}, \\[3pt] \mathcal{W}_N^{\Sigma,2}:&=\{I\in \mathcal{W}_N^{\Sigma}: \ Q_J\subset Q\in\mathcal{F}_N\}, \\[3pt] \mathcal{W}_N^{\Sigma,3}:&=\{I\in \mathcal{W}_N^{\Sigma}: Q_J\cap Q_0=\emptyset\}. \end{align*} $$
$$ \begin{align*} \mathcal{W}_N^{\Sigma,1}:&=\{I\in \mathcal{W}_N^{\Sigma}: Q_0\subset Q_J\}, \\[3pt] \mathcal{W}_N^{\Sigma,2}:&=\{I\in \mathcal{W}_N^{\Sigma}: \ Q_J\subset Q\in\mathcal{F}_N\}, \\[3pt] \mathcal{W}_N^{\Sigma,3}:&=\{I\in \mathcal{W}_N^{\Sigma}: Q_J\cap Q_0=\emptyset\}. \end{align*} $$
For later use, it is convenient to observe that
Let us first consider
![]() $\mathcal {W}_N^{\Sigma ,1}$
. If
$\mathcal {W}_N^{\Sigma ,1}$
. If
![]() $I\in \mathcal {W}_N^{\Sigma ,1}$
, we clearly have
$I\in \mathcal {W}_N^{\Sigma ,1}$
, we clearly have
and since
![]() $Q_I\in \mathbb {D}_{Q_0}$
$Q_I\in \mathbb {D}_{Q_0}$
In particular,
![]() $\# \mathcal {W}_N^{\Sigma ,1}\lesssim 1$
. Thus, if we set
$\# \mathcal {W}_N^{\Sigma ,1}\lesssim 1$
. Thus, if we set
![]() $\widehat {Q}_I:=Q_J$
, it follows from equation (6.7) that the two first conditions in equation (6.5) hold and also
$\widehat {Q}_I:=Q_J$
, it follows from equation (6.7) that the two first conditions in equation (6.5) hold and also
![]() $\sum _{I\in \mathcal {W}_N^{\Sigma ,1}} \mathbf {1}_{\widehat {Q}_I} \le \# \mathcal {W}_N^{\Sigma ,1}\lesssim 1$
.
$\sum _{I\in \mathcal {W}_N^{\Sigma ,1}} \mathbf {1}_{\widehat {Q}_I} \le \# \mathcal {W}_N^{\Sigma ,1}\lesssim 1$
.
To see that equation (6.5) holds for
![]() $\mathcal {W}_N^{\Sigma ,2}$
and
$\mathcal {W}_N^{\Sigma ,2}$
and
![]() $\mathcal {W}_N^{\Sigma ,3}$
, we proceed as follows. For any
$\mathcal {W}_N^{\Sigma ,3}$
, we proceed as follows. For any
![]() $I\in \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
, we pick
$I\in \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
, we pick
![]() $\widehat {Q}_I\in \mathbb {D}$
so that
$\widehat {Q}_I\in \mathbb {D}$
so that
![]() $ \widehat {Q}_I\ni x_{Q_J}$
and
$ \widehat {Q}_I\ni x_{Q_J}$
and
![]() $\ell (\widehat {Q}_I)=2^{-M'}\,\ell (Q_J)$
with
$\ell (\widehat {Q}_I)=2^{-M'}\,\ell (Q_J)$
with
![]() $M'\ge 3$
large enough so that
$M'\ge 3$
large enough so that
![]() $2^{M'}\ge 2 \Xi ^2$
(cf. equation (2.6)). Note that
$2^{M'}\ge 2 \Xi ^2$
(cf. equation (2.6)). Note that
![]() $\widehat {Q}_I\subset \Delta _{Q_J}\subset Q_J$
which, together with equation (6.7), imply
$\widehat {Q}_I\subset \Delta _{Q_J}\subset Q_J$
which, together with equation (6.7), imply
and
Hence, the first two conditions in equation (6.5) hold for
![]() $I\in \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
.
$I\in \mathcal {W}_N^{\Sigma ,2}\cup \mathcal {W}_N^{\Sigma ,3}$
.
To see that the last condition in equation (6.5) holds, we start with the family
![]() $\mathcal {W}_N^{\Sigma ,2}$
. For any
$\mathcal {W}_N^{\Sigma ,2}$
. For any
![]() $I\in \mathcal {W}_N^{\Sigma ,2}$
there is a unique
$I\in \mathcal {W}_N^{\Sigma ,2}$
there is a unique
![]() $Q_j\in \mathcal {F}_N$
such that
$Q_j\in \mathcal {F}_N$
such that
![]() $Q_J\subset Q_j$
. But, since
$Q_J\subset Q_j$
. But, since
![]() $Q_I\in \mathbb {D}_{\mathcal {F}_N,Q_0}$
, then necessarily
$Q_I\in \mathbb {D}_{\mathcal {F}_N,Q_0}$
, then necessarily
![]() $Q_I\not \subset Q_j$
and
$Q_I\not \subset Q_j$
and
![]() $Q_I\setminus Q_j\neq \emptyset $
. This and the fact that
$Q_I\setminus Q_j\neq \emptyset $
. This and the fact that
![]() $2\Delta _{Q_J}\subset Q_J\subset Q_j$
imply
$2\Delta _{Q_J}\subset Q_J\subset Q_j$
imply
 $$ \begin{align*} &2\Xi^{-1}\,\ell(Q_J) \le \operatorname{dist}(x_{Q_J}, \partial\Omega\setminus Q_j) \le \operatorname{dist}(x_{Q_J}, Q_I\setminus Q_j) \\[3pt] &\qquad \quad \le \operatorname{\mathrm{diam}}(Q_J)+\operatorname{dist}(Q_J, J)+\operatorname{\mathrm{diam}}(J) +\operatorname{\mathrm{diam}}(I)+\operatorname{dist}(I,Q_I)+\operatorname{\mathrm{diam}}(Q_I) \approx \ell(J)\approx\ell(I). \end{align*} $$
$$ \begin{align*} &2\Xi^{-1}\,\ell(Q_J) \le \operatorname{dist}(x_{Q_J}, \partial\Omega\setminus Q_j) \le \operatorname{dist}(x_{Q_J}, Q_I\setminus Q_j) \\[3pt] &\qquad \quad \le \operatorname{\mathrm{diam}}(Q_J)+\operatorname{dist}(Q_J, J)+\operatorname{\mathrm{diam}}(J) +\operatorname{\mathrm{diam}}(I)+\operatorname{dist}(I,Q_I)+\operatorname{\mathrm{diam}}(Q_I) \approx \ell(J)\approx\ell(I). \end{align*} $$
Thus,
![]() $2\,\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, \partial \Omega \setminus Q_j) \le C\,\ell (J)$
. Suppose next that
$2\,\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, \partial \Omega \setminus Q_j) \le C\,\ell (J)$
. Suppose next that
![]() $I, I'\in \mathcal {W}_N^{\Sigma ,2}$
are so that
$I, I'\in \mathcal {W}_N^{\Sigma ,2}$
are so that
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
(it could even happen that they are indeed the same cube), and assume without loss of generality that
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
(it could even happen that they are indeed the same cube), and assume without loss of generality that
![]() $\widehat {Q}_{I'}\subset \widehat {Q}_{I}$
, hence
$\widehat {Q}_{I'}\subset \widehat {Q}_{I}$
, hence
![]() $\ell (I')\le \ell (I)$
. Let
$\ell (I')\le \ell (I)$
. Let
![]() $Q_j, Q_{j'}\in \mathcal {F}_N$
be so that
$Q_j, Q_{j'}\in \mathcal {F}_N$
be so that
![]() $Q_J\subset Q_j$
and
$Q_J\subset Q_j$
and
![]() $Q_{J'}\subset Q_{j'}$
. Then,
$Q_{J'}\subset Q_{j'}$
. Then,
![]() $x_{Q_J}\in \widehat {Q}_I$
and
$x_{Q_J}\in \widehat {Q}_I$
and
![]() $x_{Q_{J'}}\in \widehat {Q}_{I'} \subset \widehat {Q}_I\subset Q_J$
. As a consequence,
$x_{Q_{J'}}\in \widehat {Q}_{I'} \subset \widehat {Q}_I\subset Q_J$
. As a consequence,
![]() $x_{Q_{J'}}\in Q_{J'}\cap Q_J\subset Q_{j}\cap Q_j'$
, and this forces
$x_{Q_{J'}}\in Q_{J'}\cap Q_J\subset Q_{j}\cap Q_j'$
, and this forces
![]() $Q_j=Q_{j'}$
(since
$Q_j=Q_{j'}$
(since
![]() $\mathcal {F}_N$
is a pairwise disjoint family). This and equation (6.9) readily imply
$\mathcal {F}_N$
is a pairwise disjoint family). This and equation (6.9) readily imply
 $$ \begin{align*} 2\,\Xi^{-1}\,\ell(Q_{J}) &\le \operatorname{dist}(x_{Q_J}, \partial\Omega\setminus Q_j) \le |x_{Q_{J}}- x_{Q_{J'}}|+ \operatorname{dist}(x_{Q_{J'}}, \partial\Omega\setminus Q_j) \\[3pt] &\quad \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+\operatorname{dist}(x_{Q_{J'}}, \partial\Omega\setminus Q_{j'}) \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+C\ell(J') \le \Xi^{-1}\,\ell(Q_J)+C\ell(J') \end{align*} $$
$$ \begin{align*} 2\,\Xi^{-1}\,\ell(Q_{J}) &\le \operatorname{dist}(x_{Q_J}, \partial\Omega\setminus Q_j) \le |x_{Q_{J}}- x_{Q_{J'}}|+ \operatorname{dist}(x_{Q_{J'}}, \partial\Omega\setminus Q_j) \\[3pt] &\quad \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+\operatorname{dist}(x_{Q_{J'}}, \partial\Omega\setminus Q_{j'}) \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+C\ell(J') \le \Xi^{-1}\,\ell(Q_J)+C\ell(J') \end{align*} $$
and therefore
![]() $\Xi ^{-1}\,\ell (Q_{J})\le C\,\ell (J')$
. This in turn gives
$\Xi ^{-1}\,\ell (Q_{J})\le C\,\ell (J')$
. This in turn gives
![]() $\ell (I)\approx \ell (J)\approx \ell (J')\approx \ell (I')$
. Note also that since I touches J,
$\ell (I)\approx \ell (J)\approx \ell (J')\approx \ell (I')$
. Note also that since I touches J,
![]() $I'$
touches
$I'$
touches
![]() $J'$
and
$J'$
and
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, we obtain
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, we obtain
 $$ \begin{align*} \operatorname{dist}(I,I') \le \operatorname{\mathrm{diam}}(J)+\operatorname{dist}(J, Q_J)+\operatorname{\mathrm{diam}}(Q_J)&+\operatorname{\mathrm{diam}}(Q_{J'}) \\ &+\operatorname{dist}(Q_{J'}, J')+\operatorname{\mathrm{diam}}(J') \approx \ell(J)+\ell(J')\approx\ell(I). \end{align*} $$
$$ \begin{align*} \operatorname{dist}(I,I') \le \operatorname{\mathrm{diam}}(J)+\operatorname{dist}(J, Q_J)+\operatorname{\mathrm{diam}}(Q_J)&+\operatorname{\mathrm{diam}}(Q_{J'}) \\ &+\operatorname{dist}(Q_{J'}, J')+\operatorname{\mathrm{diam}}(J') \approx \ell(J)+\ell(J')\approx\ell(I). \end{align*} $$
As a result, for fixed
![]() $I\in \mathcal {W}_N^{\Sigma ,2}$
there is a uniformly bounded number of
$I\in \mathcal {W}_N^{\Sigma ,2}$
there is a uniformly bounded number of
![]() $I'\in \mathcal {W}_N^{\Sigma ,2}$
with
$I'\in \mathcal {W}_N^{\Sigma ,2}$
with
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, thus
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, thus
![]() $\sum _{I\in \mathcal {W}_N^{\Sigma ,2}} \mathbf {1}_{\widehat {Q}_I} \lesssim 1$
.
$\sum _{I\in \mathcal {W}_N^{\Sigma ,2}} \mathbf {1}_{\widehat {Q}_I} \lesssim 1$
.
We finally take into consideration
![]() $\mathcal {W}_N^{\Sigma ,3}$
. Let
$\mathcal {W}_N^{\Sigma ,3}$
. Let
![]() $I\in \mathcal {W}_N^{\Sigma ,3}$
. Then,
$I\in \mathcal {W}_N^{\Sigma ,3}$
. Then,
![]() $Q_0\cap 2\Delta _{Q_J}\subset Q_0\cap Q_J= \emptyset $
and therefore
$Q_0\cap 2\Delta _{Q_J}\subset Q_0\cap Q_J= \emptyset $
and therefore
![]() $2\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, Q_0)$
. Besides, since
$2\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, Q_0)$
. Besides, since
![]() $Q_I\subset Q_0$
, we have
$Q_I\subset Q_0$
, we have
 $$ \begin{align*} \operatorname{dist}(x_{Q_J}, Q_0)\le\operatorname{\mathrm{diam}}(Q_J)+\operatorname{dist}(Q_J, J)+\operatorname{\mathrm{diam}}(J) +\operatorname{\mathrm{diam}}(I)+\operatorname{dist}(I,Q_I)&+\operatorname{\mathrm{diam}}(Q_I) \\ &\qquad \approx \ell(J)\approx\ell(I). \end{align*} $$
$$ \begin{align*} \operatorname{dist}(x_{Q_J}, Q_0)\le\operatorname{\mathrm{diam}}(Q_J)+\operatorname{dist}(Q_J, J)+\operatorname{\mathrm{diam}}(J) +\operatorname{\mathrm{diam}}(I)+\operatorname{dist}(I,Q_I)&+\operatorname{\mathrm{diam}}(Q_I) \\ &\qquad \approx \ell(J)\approx\ell(I). \end{align*} $$
Thus,
![]() $2\,\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, Q_0) \le C\,\ell (J)$
. Suppose next that
$2\,\Xi ^{-1}\,\ell (Q_J)\le \operatorname {dist}(x_{Q_J}, Q_0) \le C\,\ell (J)$
. Suppose next that
![]() $I, I'\in \mathcal {W}_N^{\Sigma ,3}$
are so that
$I, I'\in \mathcal {W}_N^{\Sigma ,3}$
are so that
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
(it could even happen that they are indeed the same cube), and assume without loss of generality that
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
(it could even happen that they are indeed the same cube), and assume without loss of generality that
![]() $\widehat {Q}_{I'}\subset \widehat {Q}_{I}$
, hence
$\widehat {Q}_{I'}\subset \widehat {Q}_{I}$
, hence
![]() $\ell (J')\le \ell (J)$
. Then, since
$\ell (J')\le \ell (J)$
. Then, since
![]() $x_{Q_J}\in \widehat {Q}_I$
and
$x_{Q_J}\in \widehat {Q}_I$
and
![]() $x_{Q_{J'}}\in \widehat {Q}_{I'} \subset \widehat {Q}_I$
, we get from equation (6.9) that
$x_{Q_{J'}}\in \widehat {Q}_{I'} \subset \widehat {Q}_I$
, we get from equation (6.9) that
 $$ \begin{align*} 2\,\Xi^{-1}\,\ell(Q_{J})\le \operatorname{dist}(x_{Q_{J}}, Q_0) \le |x_{Q_{J}}- x_{Q_{J'}}| &+\operatorname{dist}(x_{Q_{J'}}, Q_0)\\ &\qquad \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+C\ell(J') \le \Xi^{-1}\,\ell(Q_J)+C\ell(J'), \end{align*} $$
$$ \begin{align*} 2\,\Xi^{-1}\,\ell(Q_{J})\le \operatorname{dist}(x_{Q_{J}}, Q_0) \le |x_{Q_{J}}- x_{Q_{J'}}| &+\operatorname{dist}(x_{Q_{J'}}, Q_0)\\ &\qquad \le \operatorname{\mathrm{diam}}(\widehat{Q}_{I})+C\ell(J') \le \Xi^{-1}\,\ell(Q_J)+C\ell(J'), \end{align*} $$
and therefore
![]() $\Xi ^{-1}\,\ell (Q_{J})\le C\,\ell (J')$
. This yields
$\Xi ^{-1}\,\ell (Q_{J})\le C\,\ell (J')$
. This yields
![]() $\ell (I)\approx \ell (J)\approx \ell (J')\approx \ell (I')$
. Note also that since I touches J,
$\ell (I)\approx \ell (J)\approx \ell (J')\approx \ell (I')$
. Note also that since I touches J,
![]() $I'$
touches
$I'$
touches
![]() $J'$
and
$J'$
and
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, we obtain
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
, we obtain
 $$ \begin{align*} \operatorname{dist}(I,I')\le\operatorname{\mathrm{diam}}(J)+\operatorname{dist}(J, Q_J)+\operatorname{\mathrm{diam}}(Q_J)&+\operatorname{\mathrm{diam}}(Q_{J'}) \\ &+\operatorname{dist}(Q_{J'}, J')+\operatorname{\mathrm{diam}}(J') \approx \ell(J)+\ell(J')\approx\ell(I). \end{align*} $$
$$ \begin{align*} \operatorname{dist}(I,I')\le\operatorname{\mathrm{diam}}(J)+\operatorname{dist}(J, Q_J)+\operatorname{\mathrm{diam}}(Q_J)&+\operatorname{\mathrm{diam}}(Q_{J'}) \\ &+\operatorname{dist}(Q_{J'}, J')+\operatorname{\mathrm{diam}}(J') \approx \ell(J)+\ell(J')\approx\ell(I). \end{align*} $$
Consequently, for fixed
![]() $I\in \mathcal {W}_N^{\Sigma ,3}$
, there is a uniformly bounded number of
$I\in \mathcal {W}_N^{\Sigma ,3}$
, there is a uniformly bounded number of
![]() $I'\in \mathcal {W}_N^{\Sigma ,3}$
with
$I'\in \mathcal {W}_N^{\Sigma ,3}$
with
![]() $\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
. As a result,
$\widehat {Q}_I\cap \widehat {Q}_{I'}\neq \emptyset $
. As a result,
![]() $\sum _{I\in \mathcal {W}_N^{\Sigma ,3}} \mathbf {1}_{\widehat {Q}_I} \lesssim 1$
. This completes the proof of
$\sum _{I\in \mathcal {W}_N^{\Sigma ,3}} \mathbf {1}_{\widehat {Q}_I} \lesssim 1$
. This completes the proof of
![]() $(iii)$
and hence that of Lemma 6.2.
$(iii)$
and hence that of Lemma 6.2.
We are now ready to prove Theorem 6.1.
Proof of Theorem 6.1
We use some ideas from [Reference Cavero, Hofmann, Martell and Toro9, Section 4] and [Reference Cao, Martell and Olivo7, Section 4]. Let
![]() $u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
be a weak solution of
$u \in W_{\mathrm {loc}}^{1,2}(\Omega ) \cap L^{\infty }(\Omega )$
be a weak solution of
![]() $L_1u=0$
in
$L_1u=0$
in
![]() $\Omega $
and assume that
$\Omega $
and assume that
![]() $\|u\|_{L^{\infty }(\Omega )}=1$
. Applying Theorem 1.6
$\|u\|_{L^{\infty }(\Omega )}=1$
. Applying Theorem 1.6
![]() $\mathrm {(c)} \Longrightarrow \mathrm {(a)}$
to u, we are reduced to showing that for some
$\mathrm {(c)} \Longrightarrow \mathrm {(a)}$
to u, we are reduced to showing that for some
![]() $r>0$
,
$r>0$
,
where
![]() $\alpha _0$
is given in Theorem 1.6. By equation (5.16) and Lemma 2.8, it suffices to see that for every fixed
$\alpha _0$
is given in Theorem 1.6. By equation (5.16) and Lemma 2.8, it suffices to see that for every fixed
![]() $Q_0 \in \mathbb {D}_{k_0}$
and for some fixed large
$Q_0 \in \mathbb {D}_{k_0}$
and for some fixed large
![]() $\vartheta $
(which depends on
$\vartheta $
(which depends on
![]() $\alpha _0$
and hence solely on the 1-sided NTA and CDC constants) one has
$\alpha _0$
and hence solely on the 1-sided NTA and CDC constants) one has
where
![]() $X_0$
is given at the beginning of Section 5.1. Fix then
$X_0$
is given at the beginning of Section 5.1. Fix then
![]() $Q_0 \in \mathbb {D}_{k_0}$
, and write
$Q_0 \in \mathbb {D}_{k_0}$
, and write
Much as in equation (4.21) (with
![]() $\eta =2^{-1/3}$
so that
$\eta =2^{-1/3}$
so that
![]() $\Gamma ^{\vartheta ,*}_{Q_0}=\Gamma ^{\vartheta ,*}_{Q_0,\eta }$
), there exist
$\Gamma ^{\vartheta ,*}_{Q_0}=\Gamma ^{\vartheta ,*}_{Q_0,\eta }$
), there exist
![]() $\widetilde {\alpha }_0>0$
and C (depending on the 1-sided NTA and CDC constants) such that if we set
$\widetilde {\alpha }_0>0$
and C (depending on the 1-sided NTA and CDC constants) such that if we set
![]() $\widetilde {r}:=C\,r_{Q_0}>0$
, then
$\widetilde {r}:=C\,r_{Q_0}>0$
, then
 $$ \begin{align} \Gamma^{\vartheta,*}_{Q_0}(x) :=\bigcup_{x \in Q \in \mathbb{D}_{Q_0}} U^{\vartheta, *}_{Q} \subset \Gamma^{\widetilde{\alpha}_0}_{\widetilde{r}}(x),\qquad x \in Q_0. \end{align} $$
$$ \begin{align} \Gamma^{\vartheta,*}_{Q_0}(x) :=\bigcup_{x \in Q \in \mathbb{D}_{Q_0}} U^{\vartheta, *}_{Q} \subset \Gamma^{\widetilde{\alpha}_0}_{\widetilde{r}}(x),\qquad x \in Q_0. \end{align} $$
As a result,
 $$ \begin{align} \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)^2 :&= \sum_{x \in Q \in \mathbb{D}_{Q_0}} \gamma_{Q} ^{\vartheta} := \sum_{x \in Q \in \mathbb{D}_{Q_0}} \iint_{U^{\vartheta, *}_Q} a(X)^2 \delta(X)^{-n-1} dX \nonumber\\ & \qquad\qquad +\iint_{U^{\vartheta, *}_Q} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX \nonumber\\ &\lesssim \iint_{\Gamma^{\vartheta,*}_{Q_0}(x) } a(X)^2 \delta(X)^{-n-1} dX + \iint_{\Gamma^{\vartheta,*}_{Q_0}(x) } |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX \nonumber\\ &\le \iint_{\Gamma^{{\alpha}_1}_{\max\{\widetilde{r}, r_1\}}(x)} a(X)^2 \delta^{-n-1} dX + \iint_{\Gamma^{{\alpha}_2}_{\max\{\widetilde{r},r_2\}}(x)} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta^{1-n} dX < \infty, \end{align} $$
$$ \begin{align} \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)^2 :&= \sum_{x \in Q \in \mathbb{D}_{Q_0}} \gamma_{Q} ^{\vartheta} := \sum_{x \in Q \in \mathbb{D}_{Q_0}} \iint_{U^{\vartheta, *}_Q} a(X)^2 \delta(X)^{-n-1} dX \nonumber\\ & \qquad\qquad +\iint_{U^{\vartheta, *}_Q} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX \nonumber\\ &\lesssim \iint_{\Gamma^{\vartheta,*}_{Q_0}(x) } a(X)^2 \delta(X)^{-n-1} dX + \iint_{\Gamma^{\vartheta,*}_{Q_0}(x) } |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta(X)^{1-n} dX \nonumber\\ &\le \iint_{\Gamma^{{\alpha}_1}_{\max\{\widetilde{r}, r_1\}}(x)} a(X)^2 \delta^{-n-1} dX + \iint_{\Gamma^{{\alpha}_2}_{\max\{\widetilde{r},r_2\}}(x)} |\mathop{\operatorname{div}}\nolimits_{C} D(X)|^2 \delta^{1-n} dX < \infty, \end{align} $$
for
![]() $\omega _{L_0} $
-a.e.
$\omega _{L_0} $
-a.e.
![]() $x \in Q_0$
, where we have used the fact that the family
$x \in Q_0$
, where we have used the fact that the family
![]() $\{U^{\vartheta ,*}_Q\}_{Q \in \mathbb {D}}$
has bounded overlap, that
$\{U^{\vartheta ,*}_Q\}_{Q \in \mathbb {D}}$
has bounded overlap, that
![]() $\alpha _1, \alpha _2\ge \widetilde {\alpha }_0$
, and the last estimate follows from equations (6.1), (6.2) and (5.1).
$\alpha _1, \alpha _2\ge \widetilde {\alpha }_0$
, and the last estimate follows from equations (6.1), (6.2) and (5.1).
Given
![]() $N>C_0$
(
$N>C_0$
(
![]() $C_0$
is the constant that appeared in Section 5.1), let
$C_0$
is the constant that appeared in Section 5.1), let
![]() $\mathcal {F}_N\subset \mathbb {D}_{Q_0}$
be the collection of maximal cubes (with respect to the inclusion)
$\mathcal {F}_N\subset \mathbb {D}_{Q_0}$
be the collection of maximal cubes (with respect to the inclusion)
![]() $Q_j \in \mathbb {D}_{Q_0}$
such that
$Q_j \in \mathbb {D}_{Q_0}$
such that
 $$ \begin{align} \sum_{Q_j \subset Q \in \mathbb{D}_{Q_0}} \gamma_{Q}^{\vartheta}> N^2. \end{align} $$
$$ \begin{align} \sum_{Q_j \subset Q \in \mathbb{D}_{Q_0}} \gamma_{Q}^{\vartheta}> N^2. \end{align} $$
Write
 $$ \begin{align} {E}_0 :=\bigcap_{N>C_0} (Q_0\setminus E_N), \quad E_N:= Q_0 \backslash \bigcup_{Q_j \in {\mathcal{F}}_N}Q_j, \quad Q_0={E}_0\cup (Q_0\setminus E_0) = {E}_0\cup \Big(\bigcup_{N>C_0} {E}_N \Big). \end{align} $$
$$ \begin{align} {E}_0 :=\bigcap_{N>C_0} (Q_0\setminus E_N), \quad E_N:= Q_0 \backslash \bigcup_{Q_j \in {\mathcal{F}}_N}Q_j, \quad Q_0={E}_0\cup (Q_0\setminus E_0) = {E}_0\cup \Big(\bigcup_{N>C_0} {E}_N \Big). \end{align} $$
Let us observe that
Otherwise, there exists a cube
![]() $Q_x\ni x$
such that
$Q_x\ni x$
such that
![]() $\sum _{Q_x \subset Q \in \mathbb {D}_{Q_0}} \gamma _Q^{\vartheta }> N^2$
, hence
$\sum _{Q_x \subset Q \in \mathbb {D}_{Q_0}} \gamma _Q^{\vartheta }> N^2$
, hence
![]() $x \in Q_x \subset Q_j$
for some
$x \in Q_x \subset Q_j$
for some
![]() $Q_j \in {\mathcal {F}}_N$
, which is a contradiction.
$Q_j \in {\mathcal {F}}_N$
, which is a contradiction.
Note that if
![]() $x \in {E}_0$
, then for every
$x \in {E}_0$
, then for every
![]() $N>C_0$
there exists
$N>C_0$
there exists
![]() $Q_x^{N} \in {\mathcal {F}}_N$
such that
$Q_x^{N} \in {\mathcal {F}}_N$
such that
![]() $Q_x^N \ni x$
. By the definition of
$Q_x^N \ni x$
. By the definition of
![]() ${\mathcal {F}}_N$
, we then have
${\mathcal {F}}_N$
, we then have
 $$ \begin{align*} \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)^2 = \sum_{x \in Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} \geq \sum_{Q_x^N \subset Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta}> N^2. \end{align*} $$
$$ \begin{align*} \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)^2 = \sum_{x \in Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} \geq \sum_{Q_x^N \subset Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta}> N^2. \end{align*} $$
On the other hand, if
![]() $x \in Q_0\setminus {E}_{N+1}$
, there exists
$x \in Q_0\setminus {E}_{N+1}$
, there exists
![]() $Q_x \in {\mathcal {F}}_{N+1}$
such that
$Q_x \in {\mathcal {F}}_{N+1}$
such that
![]() $x \in Q_x$
. By equation (6.14), one has
$x \in Q_x$
. By equation (6.14), one has
 $$ \begin{align*} \sum_{Q_x \subset Q \in \mathbb{D}_{Q_0}} \gamma_{Q}^{\vartheta}> (N+1)^2>N^2, \end{align*} $$
$$ \begin{align*} \sum_{Q_x \subset Q \in \mathbb{D}_{Q_0}} \gamma_{Q}^{\vartheta}> (N+1)^2>N^2, \end{align*} $$
and the maximality of the cubes in
![]() ${\mathcal {F}}_N$
gives that
${\mathcal {F}}_N$
gives that
![]() $Q_x \subset Q^{\prime }_x$
for some
$Q_x \subset Q^{\prime }_x$
for some
![]() $Q^{\prime }_x \in {\mathcal {F}}_N$
with
$Q^{\prime }_x \in {\mathcal {F}}_N$
with
![]() $x \in Q^{\prime }_x \subset Q_0\setminus {E}_{N}$
. This shows that
$x \in Q^{\prime }_x \subset Q_0\setminus {E}_{N}$
. This shows that
![]() $\{Q_0\setminus {E}_{N}\}_N$
is a decreasing sequence of sets, and since
$\{Q_0\setminus {E}_{N}\}_N$
is a decreasing sequence of sets, and since
![]() $Q_0\setminus {E}_{N}\subset Q_0$
for every N we conclude that
$Q_0\setminus {E}_{N}\subset Q_0$
for every N we conclude that
 $$ \begin{align} \omega_0({E}_0 ) =\lim_{N\to\infty} \omega_0(Q_0\setminus {E}_{N}) \le \lim_{N\to\infty} \omega_0 &(\{x \in Q_0: \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)>N\}) \notag \\ &\qquad\qquad=\omega_0(\{x \in Q_0: \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)=\infty\})=0, \end{align} $$
$$ \begin{align} \omega_0({E}_0 ) =\lim_{N\to\infty} \omega_0(Q_0\setminus {E}_{N}) \le \lim_{N\to\infty} \omega_0 &(\{x \in Q_0: \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)>N\}) \notag \\ &\qquad\qquad=\omega_0(\{x \in Q_0: \mathcal{S}_{Q_0}\gamma^{\vartheta}(x)=\infty\})=0, \end{align} $$
where the last equality uses equation (6.13). This and equation (6.15) imply that to get equation (6.10) we are left with proving
With this goal in mind, note that if
![]() $Q \in \mathbb {D}_{Q_0}$
is so that
$Q \in \mathbb {D}_{Q_0}$
is so that
![]() $Q \cap {E}_N \neq \emptyset $
, then necessarily
$Q \cap {E}_N \neq \emptyset $
, then necessarily
![]() $Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
, otherwise,
$Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
, otherwise,
![]() $Q \subset Q' \in {\mathcal {F}}_N$
, hence
$Q \subset Q' \in {\mathcal {F}}_N$
, hence
![]() $Q \subset Q_0 \backslash {E}_N$
. Recalling equation (6.11) and the fact
$Q \subset Q_0 \backslash {E}_N$
. Recalling equation (6.11) and the fact
![]() $X_0 \not \in 4B_{Q_0}^*$
, we use Lemma 3.9 and Harnack’s inequality to conclude that
$X_0 \not \in 4B_{Q_0}^*$
, we use Lemma 3.9 and Harnack’s inequality to conclude that
 $$ \begin{align}\nonumber \int_{E_N}\mathcal{S}_{Q_0}^{\vartheta} u(x)^2 d\omega_0(x) &=\int_{E_N} \iint_{\bigcup\limits_{x \in Q \in \mathbb{D}_{Q_0}} U_Q^{\vartheta}} |\nabla u(Y)|^2 \delta(Y)^{1-n} dY d\omega_0(x) \\ &\lesssim \sum_{Q \in \mathbb{D}_{Q_0}} \ell(Q)^{1-n} \omega_0(Q \cap E_N) \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 dY \nonumber \\ & \le \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \ell(Q)^{1-n} \omega_0(Q) \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 dY \nonumber \\ &\lesssim \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) dY \nonumber \\ &\lesssim \iint_{\Omega_{\mathcal{F}_N, Q_0}^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) dY, \end{align} $$
$$ \begin{align}\nonumber \int_{E_N}\mathcal{S}_{Q_0}^{\vartheta} u(x)^2 d\omega_0(x) &=\int_{E_N} \iint_{\bigcup\limits_{x \in Q \in \mathbb{D}_{Q_0}} U_Q^{\vartheta}} |\nabla u(Y)|^2 \delta(Y)^{1-n} dY d\omega_0(x) \\ &\lesssim \sum_{Q \in \mathbb{D}_{Q_0}} \ell(Q)^{1-n} \omega_0(Q \cap E_N) \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 dY \nonumber \\ & \le \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \ell(Q)^{1-n} \omega_0(Q) \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 dY \nonumber \\ &\lesssim \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \iint_{U_Q^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) dY \nonumber \\ &\lesssim \iint_{\Omega_{\mathcal{F}_N, Q_0}^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) dY, \end{align} $$
where we have used that the family
![]() $\{U_Q^{\vartheta }\}_{Q\in \mathbb {D}}$
has bounded overlap. To estimate the last term, we make the following claim
$\{U_Q^{\vartheta }\}_{Q\in \mathbb {D}}$
has bounded overlap. To estimate the last term, we make the following claim
 $$ \begin{align} \iint_{\Omega_{\mathcal{F}_N, Q_0}^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) \, dY \lesssim \omega_0(Q_0) + \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q), \end{align} $$
$$ \begin{align} \iint_{\Omega_{\mathcal{F}_N, Q_0}^{\vartheta}} |\nabla u(Y)|^2 \mathcal{G}_0(Y) \, dY \lesssim \omega_0(Q_0) + \sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q), \end{align} $$
where the implicit constant is independent of N.
Assuming this momentarily, we note that
 $$ \begin{align} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} & \gamma_Q^{\vartheta} \, \omega_0(Q) =\int_{Q_0} \sum_{x \in Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta} \, d\omega_0(x) \notag \\ &\qquad\qquad\leq \int_{{E}_N} \mathcal{S}_{Q_0} \gamma^{\vartheta}(x)^2 \, d\omega_0(x) + \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta}\,\omega_0(Q\cap Q_j)\notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le N^2 \omega_0(Q_0)+ \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta}\,\omega_0(Q\cap Q_j), \end{align} $$
$$ \begin{align} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} & \gamma_Q^{\vartheta} \, \omega_0(Q) =\int_{Q_0} \sum_{x \in Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta} \, d\omega_0(x) \notag \\ &\qquad\qquad\leq \int_{{E}_N} \mathcal{S}_{Q_0} \gamma^{\vartheta}(x)^2 \, d\omega_0(x) + \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta}\,\omega_0(Q\cap Q_j)\notag \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\le N^2 \omega_0(Q_0)+ \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta}\,\omega_0(Q\cap Q_j), \end{align} $$
where the last estimate follows from equation (6.16). In order to control the last term, we fix
![]() $Q_j \in {\mathcal {F}}_N$
. Note that if
$Q_j \in {\mathcal {F}}_N$
. Note that if
![]() $Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
is so that
$Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
is so that
![]() $Q \cap Q_j \neq \emptyset $
, then necessarily
$Q \cap Q_j \neq \emptyset $
, then necessarily
![]() $Q_j \subsetneq Q\subset Q_0$
. Write
$Q_j \subsetneq Q\subset Q_0$
. Write
![]() $\widehat {Q}_j$
for the dyadic parent of
$\widehat {Q}_j$
for the dyadic parent of
![]() $Q_j$
, that is,
$Q_j$
, that is,
![]() $\widehat {Q}_j$
is the unique dyadic cube containing
$\widehat {Q}_j$
is the unique dyadic cube containing
![]() $Q_j$
with
$Q_j$
with
![]() $\ell (\widehat {Q}_j)=2\ell (Q_j)$
. By the fact that
$\ell (\widehat {Q}_j)=2\ell (Q_j)$
. By the fact that
![]() $Q_j$
is the maximal cube so that equation (6.14) holds one obtains
$Q_j$
is the maximal cube so that equation (6.14) holds one obtains
 $$ \begin{align*} \sum_{\widehat{Q}_j \subset Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} =\sum_{Q_j \subsetneq Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} \leq N^2. \end{align*} $$
$$ \begin{align*} \sum_{\widehat{Q}_j \subset Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} =\sum_{Q_j \subsetneq Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta} \leq N^2. \end{align*} $$
As a result,
 $$ \begin{align} \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q \cap Q_j) &=\sum_{Q_j \in {\mathcal{F}}_N} \omega_0(Q_j) \sum_{Q_j \subsetneq Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta}\notag \\ & \ \leq N^2 \sum_{Q_j \in {\mathcal{F}}_N} \omega_0(Q_j) \leq N^2 \omega_0 \bigg(\bigcup_{Q_j \in {\mathcal{F}}_N} Q_j \bigg)\leq N^2 \omega_0(Q_0). \end{align} $$
$$ \begin{align} \sum_{Q_j \in {\mathcal{F}}_N} \sum_{Q \in \mathbb{D}_{{\mathcal{F}}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q \cap Q_j) &=\sum_{Q_j \in {\mathcal{F}}_N} \omega_0(Q_j) \sum_{Q_j \subsetneq Q \in \mathbb{D}_{Q_0}} \gamma_Q^{\vartheta}\notag \\ & \ \leq N^2 \sum_{Q_j \in {\mathcal{F}}_N} \omega_0(Q_j) \leq N^2 \omega_0 \bigg(\bigcup_{Q_j \in {\mathcal{F}}_N} Q_j \bigg)\leq N^2 \omega_0(Q_0). \end{align} $$
Collecting equations (6.19), (6.20), (6.21) and (6.22), we deduce that
 $$ \begin{align*} \int_{E_N} (\mathcal{S}_{Q_0}^{\vartheta} u(x))^2 \, d\omega_0(x) \le C_N \, \omega_0(Q_0) \le C_N. \end{align*} $$
$$ \begin{align*} \int_{E_N} (\mathcal{S}_{Q_0}^{\vartheta} u(x))^2 \, d\omega_0(x) \le C_N \, \omega_0(Q_0) \le C_N. \end{align*} $$
This shows equations (6.18) and completes the proof of Theorem 6.1 modulo proving equation (6.20).
Let us then establish equation (6.20). For every
![]() $M \geq 4$
, we consider the pairwise disjoint collection
$M \geq 4$
, we consider the pairwise disjoint collection
![]() ${\mathcal {F}}_{N,M}$
given by the family of maximal cubes of the collection
${\mathcal {F}}_{N,M}$
given by the family of maximal cubes of the collection
![]() ${\mathcal {F}}_N$
augmented by adding all the cubes
${\mathcal {F}}_N$
augmented by adding all the cubes
![]() $Q \in \mathbb {D}_{Q_0}$
such that
$Q \in \mathbb {D}_{Q_0}$
such that
![]() $\ell (Q) \leq 2^{-M} \ell (Q_0)$
. In particular,
$\ell (Q) \leq 2^{-M} \ell (Q_0)$
. In particular,
![]() $Q \in \mathbb {D}_{{\mathcal {F}}_{N,M}, Q_0}$
if and only if
$Q \in \mathbb {D}_{{\mathcal {F}}_{N,M}, Q_0}$
if and only if
![]() $Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
and
$Q \in \mathbb {D}_{{\mathcal {F}}_N, Q_0}$
and
![]() $\ell (Q)>2^{-M}\ell (Q_0)$
. Moreover,
$\ell (Q)>2^{-M}\ell (Q_0)$
. Moreover,
![]() $\mathbb {D}_{{\mathcal {F}}_{N,M}, Q_0} \subset \mathbb {D}_{{\mathcal {F}}_{N,M'}, Q_0}$
for all
$\mathbb {D}_{{\mathcal {F}}_{N,M}, Q_0} \subset \mathbb {D}_{{\mathcal {F}}_{N,M'}, Q_0}$
for all
![]() $M \leq M'$
, and hence
$M \leq M'$
, and hence
![]() $\Omega _{{\mathcal {F}}_{N,M}, Q_0}^{\vartheta } \subset \Omega _{{\mathcal {F}}_{N,M'}, Q_0}^{\vartheta } \subset \Omega _{{\mathcal {F}}_N, Q_0}^{\vartheta }$
. Then the monotone convergence theorem implies
$\Omega _{{\mathcal {F}}_{N,M}, Q_0}^{\vartheta } \subset \Omega _{{\mathcal {F}}_{N,M'}, Q_0}^{\vartheta } \subset \Omega _{{\mathcal {F}}_N, Q_0}^{\vartheta }$
. Then the monotone convergence theorem implies
 $$ \begin{align} \iint_{\Omega_{{\mathcal{F}}_{N}, Q_0}^{\vartheta}} |\nabla u|^2 \mathcal{G}_0 \ dX =\lim_{M \to \infty}\iint_{\Omega_{{\mathcal{F}}_{N,M}, Q_0}^{\vartheta}} |\nabla u|^2 \mathcal{G}_0 \, dX =: \lim_{M \to \infty} \mathcal{K}_{N, M}. \end{align} $$
$$ \begin{align} \iint_{\Omega_{{\mathcal{F}}_{N}, Q_0}^{\vartheta}} |\nabla u|^2 \mathcal{G}_0 \ dX =\lim_{M \to \infty}\iint_{\Omega_{{\mathcal{F}}_{N,M}, Q_0}^{\vartheta}} |\nabla u|^2 \mathcal{G}_0 \, dX =: \lim_{M \to \infty} \mathcal{K}_{N, M}. \end{align} $$
Write
![]() $\mathcal {E}(X):=A_1(X)-A_0(X)$
, and pick
$\mathcal {E}(X):=A_1(X)-A_0(X)$
, and pick
![]() $\Psi _{N,M}$
from Lemma 6.2. By Leibniz’s rule,
$\Psi _{N,M}$
from Lemma 6.2. By Leibniz’s rule,
 $$ \begin{align} A_1 \nabla u &\cdot \nabla u \ \mathcal{G}_0 \Psi_{N,M}^2 =A_1 \nabla u \cdot \nabla (u \mathcal{G}_0 \Psi_{N,M}^2) - \frac12 A_0 \nabla (u^2 \Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \notag \\[3pt] &\quad + \frac12 A_0 \nabla(\Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \ u^2 -\frac12 A_0 \nabla (u^2) \cdot \nabla(\Psi_{N,M}^2) \mathcal{G}_0 - \frac12 \mathcal{E} \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2). \end{align} $$
$$ \begin{align} A_1 \nabla u &\cdot \nabla u \ \mathcal{G}_0 \Psi_{N,M}^2 =A_1 \nabla u \cdot \nabla (u \mathcal{G}_0 \Psi_{N,M}^2) - \frac12 A_0 \nabla (u^2 \Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \notag \\[3pt] &\quad + \frac12 A_0 \nabla(\Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \ u^2 -\frac12 A_0 \nabla (u^2) \cdot \nabla(\Psi_{N,M}^2) \mathcal{G}_0 - \frac12 \mathcal{E} \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2). \end{align} $$
Note that
![]() $u \in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
,
$u \in W^{1,2}_{\mathrm {loc}}(\Omega )\cap L^{\infty }(\Omega )$
,
![]() $\mathcal {G}_0 \in W^{1,2}_{\mathrm {loc}}(\Omega \setminus \{X_0\})$
and that
$\mathcal {G}_0 \in W^{1,2}_{\mathrm {loc}}(\Omega \setminus \{X_0\})$
and that
![]() $\overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**}}$
is a compact subset of
$\overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**}}$
is a compact subset of
![]() $\Omega $
away from
$\Omega $
away from
![]() $X_0$
since
$X_0$
since
![]() $X_0 \notin 4B_{Q_0}^*$
and equation (2.15). Hence,
$X_0 \notin 4B_{Q_0}^*$
and equation (2.15). Hence,
![]() $u \in W^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
and
$u \in W^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
and
![]() $u \mathcal {G}_0 \Psi _{N,M}^2 \in W_0^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
. These together with the fact that
$u \mathcal {G}_0 \Psi _{N,M}^2 \in W_0^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
. These together with the fact that
![]() $L_1u=0$
in the weak sense in
$L_1u=0$
in the weak sense in
![]() $\Omega $
give
$\Omega $
give
 $$ \begin{align} \iint_{\Omega} A_1 \nabla u \cdot \nabla(u \mathcal{G}_0 \Psi_{N,M}^2) dX =\iint_{\Omega_{\mathcal{F}_{N,M}, Q_0}^{\vartheta,**}} A_1 \nabla u \cdot \nabla(u \mathcal{G}_0 \Psi_{N,M}^2) dX=0. \end{align} $$
$$ \begin{align} \iint_{\Omega} A_1 \nabla u \cdot \nabla(u \mathcal{G}_0 \Psi_{N,M}^2) dX =\iint_{\Omega_{\mathcal{F}_{N,M}, Q_0}^{\vartheta,**}} A_1 \nabla u \cdot \nabla(u \mathcal{G}_0 \Psi_{N,M}^2) dX=0. \end{align} $$
On the other hand, Lemma 3.7 (see in particular equation (3.15)) implies that
![]() $\mathcal {G}_0 \in W^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
and
$\mathcal {G}_0 \in W^{1,2}(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
and
![]() $L_0^{\top }\mathcal {G}_0=0$
in the weak sense in
$L_0^{\top }\mathcal {G}_0=0$
in the weak sense in
![]() $\Omega \setminus \{X_0\}$
. Thanks to the fact that
$\Omega \setminus \{X_0\}$
. Thanks to the fact that
![]() $u^2 \Psi _{N,M}^2 \in W^{1,2}_0(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
, we then obtain
$u^2 \Psi _{N,M}^2 \in W^{1,2}_0(\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,**})$
, we then obtain
 $$ \begin{align} \iint_{\Omega} A_0 \nabla (u^2 \Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \, dX =\iint_{\Omega_{\mathcal{F}_{N,M}, Q_0}^{\vartheta,*}} A_0^{\top} \nabla \mathcal{G}_0 \cdot \nabla(u^2 \Psi_{N,M}^2)\, dX=0. \end{align} $$
$$ \begin{align} \iint_{\Omega} A_0 \nabla (u^2 \Psi_{N,M}^2) \cdot \nabla \mathcal{G}_0 \, dX =\iint_{\Omega_{\mathcal{F}_{N,M}, Q_0}^{\vartheta,*}} A_0^{\top} \nabla \mathcal{G}_0 \cdot \nabla(u^2 \Psi_{N,M}^2)\, dX=0. \end{align} $$
By Lemma 6.2, the ellipticity of
![]() $A_1$
and
$A_1$
and
![]() $A_0$
, and equations (6.24)–(6.26), the fact that
$A_0$
, and equations (6.24)–(6.26), the fact that
![]() $\|u\|_{L^{\infty }(\Omega )}=1$
and our assumption
$\|u\|_{L^{\infty }(\Omega )}=1$
and our assumption
![]() $\mathcal {E}=A_1-A_0=-(A+D)$
we then arrive at
$\mathcal {E}=A_1-A_0=-(A+D)$
we then arrive at
 $$ \begin{align}\nonumber \widetilde{\mathcal{K}}_{N,M} &:= \iint_{\Omega} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2 \, dX \lesssim \iint_{\Omega} A_1 \nabla u \cdot \nabla u \ \mathcal{G}_0 \Psi_{N,M}^2\, dX \\[3pt] \nonumber &\lesssim \iint_{\Omega} |\nabla\Psi_{N,M}|\,|\nabla \mathcal{G}_0|\, dX + \iint_{\Omega} |\nabla u|\, |\nabla \Psi_{N,M}|\,\mathcal{G}_0 \, dX \\[3pt] \nonumber &\qquad\qquad+ \bigg|\iint_{\Omega} A \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2)\,dX \bigg| + \bigg|\iint_{\Omega} D \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2)\,dX \bigg| \\[3pt] &=: \mathcal{I}_1+\mathcal{I}_2+\mathcal{I}_3+\mathcal{I}_4. \end{align} $$
$$ \begin{align}\nonumber \widetilde{\mathcal{K}}_{N,M} &:= \iint_{\Omega} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2 \, dX \lesssim \iint_{\Omega} A_1 \nabla u \cdot \nabla u \ \mathcal{G}_0 \Psi_{N,M}^2\, dX \\[3pt] \nonumber &\lesssim \iint_{\Omega} |\nabla\Psi_{N,M}|\,|\nabla \mathcal{G}_0|\, dX + \iint_{\Omega} |\nabla u|\, |\nabla \Psi_{N,M}|\,\mathcal{G}_0 \, dX \\[3pt] \nonumber &\qquad\qquad+ \bigg|\iint_{\Omega} A \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2)\,dX \bigg| + \bigg|\iint_{\Omega} D \nabla(u^2) \cdot \nabla(\mathcal{G}_0 \Psi_{N,M}^2)\,dX \bigg| \\[3pt] &=: \mathcal{I}_1+\mathcal{I}_2+\mathcal{I}_3+\mathcal{I}_4. \end{align} $$
We estimate each term in turn. Regarding
![]() $\mathcal {I}_1$
we use Lemma 6.2, Caccioppoli’s and Harnack’s inequalities, and Lemma 3.9:
$\mathcal {I}_1$
we use Lemma 6.2, Caccioppoli’s and Harnack’s inequalities, and Lemma 3.9:
 $$ \begin{align} \mathcal{I}_1 &\lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta, \Sigma}} \iint_{I^*} |\nabla \Psi_{N,M}|\, |\nabla \mathcal{G}_0|\, dX \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{-1} |I|^{\frac12} \bigg(\iint_{I^*} |\nabla \mathcal{G}_0|^2 dX \bigg)^{\frac12}\notag \\[3pt] &\qquad\qquad\qquad\qquad\qquad\ \ \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1} \mathcal{G}_0(X(I)) \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \omega_0(\widehat{Q}_I) \notag \\[3pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \lesssim \omega_0\bigg(\bigcup_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \widehat{Q}_I \bigg) \leq \omega_0(C \Delta_{Q_0}) \lesssim \omega_0(Q_0), \end{align} $$
$$ \begin{align} \mathcal{I}_1 &\lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta, \Sigma}} \iint_{I^*} |\nabla \Psi_{N,M}|\, |\nabla \mathcal{G}_0|\, dX \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{-1} |I|^{\frac12} \bigg(\iint_{I^*} |\nabla \mathcal{G}_0|^2 dX \bigg)^{\frac12}\notag \\[3pt] &\qquad\qquad\qquad\qquad\qquad\ \ \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1} \mathcal{G}_0(X(I)) \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \omega_0(\widehat{Q}_I) \notag \\[3pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \ \lesssim \omega_0\bigg(\bigcup_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \widehat{Q}_I \bigg) \leq \omega_0(C \Delta_{Q_0}) \lesssim \omega_0(Q_0), \end{align} $$
where the implicit constants do not depend on N nor M. We estimate
![]() $\mathcal {I}_2$
similarly:
$\mathcal {I}_2$
similarly:
 $$ \begin{align} \mathcal{I}_2 \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \iint_{I^*} |\nabla \Psi_{N,M}|\, |\nabla u|\, \mathcal{G}_0\, dX &\lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{-1} |I|^{\frac12} \mathcal{G}_0(X(I)) \bigg(\iint_{I^*} |\nabla u|^2 dX \bigg)^{\frac12}\notag \\ &\qquad\qquad \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1} \mathcal{G}_0(X(I)) \lesssim \omega_0(Q_0). \end{align} $$
$$ \begin{align} \mathcal{I}_2 \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \iint_{I^*} |\nabla \Psi_{N,M}|\, |\nabla u|\, \mathcal{G}_0\, dX &\lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{-1} |I|^{\frac12} \mathcal{G}_0(X(I)) \bigg(\iint_{I^*} |\nabla u|^2 dX \bigg)^{\frac12}\notag \\ &\qquad\qquad \lesssim \sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1} \mathcal{G}_0(X(I)) \lesssim \omega_0(Q_0). \end{align} $$
Concerning
![]() $\mathcal {I}_3$
, we use that
$\mathcal {I}_3$
, we use that
![]() $A \in L^{\infty }(\Omega )$
and
$A \in L^{\infty }(\Omega )$
and
![]() $\|u\|_{L^{\infty }(\Omega )}=1$
:
$\|u\|_{L^{\infty }(\Omega )}=1$
:
Observe that
![]() $I^{**} \subset \{Y\in \Omega : |Y-X|<\delta (X)/2\}$
for every
$I^{**} \subset \{Y\in \Omega : |Y-X|<\delta (X)/2\}$
for every
![]() $X \in I^*$
, and hence
$X \in I^*$
, and hence
![]() $\sup _{I^{**}} |A| \le \inf _{I^*} a$
. By Cauchy–Schwarz inequality, Caccioppoli’s and Harnack’s inequalities and Lemma 3.9, we have
$\sup _{I^{**}} |A| \le \inf _{I^*} a$
. By Cauchy–Schwarz inequality, Caccioppoli’s and Harnack’s inequalities and Lemma 3.9, we have
 $$ \begin{align}\nonumber \mathcal{I}_3' & \lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \sup_{I^{**}} |A| \bigg(\iint_{I^{**}} |\nabla u|^2 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\iint_{I^{**}} |\nabla \mathcal{G}_0|^2 dX\bigg)^{\frac12} \\ \nonumber &\lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \bigg(\iint_{I^{**}} |\nabla u|^2 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \Big(\sup_{I^{**}} |A|^2 \mathcal{G}_0(X(I))^2 \ell(I)^{n-1}\Big)^{\frac12} \\ \nonumber &\lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \bigg(\iint_{I^{**}} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\omega_0(Q) \iint_{I^*} a(X)^2 \delta(X)^{-n-1} dX \bigg)^{\frac12} \\ \nonumber &\lesssim \bigg(\iint_{\Omega} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \omega_0(Q) \iint_{U_Q^{\vartheta,*}} a(X)^2 \delta(X)^{-n-1}\, dX \bigg)^{\frac12} \\ & \le \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12}, \end{align} $$
$$ \begin{align}\nonumber \mathcal{I}_3' & \lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \sup_{I^{**}} |A| \bigg(\iint_{I^{**}} |\nabla u|^2 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\iint_{I^{**}} |\nabla \mathcal{G}_0|^2 dX\bigg)^{\frac12} \\ \nonumber &\lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \bigg(\iint_{I^{**}} |\nabla u|^2 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \Big(\sup_{I^{**}} |A|^2 \mathcal{G}_0(X(I))^2 \ell(I)^{n-1}\Big)^{\frac12} \\ \nonumber &\lesssim \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \bigg(\iint_{I^{**}} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\omega_0(Q) \iint_{I^*} a(X)^2 \delta(X)^{-n-1} dX \bigg)^{\frac12} \\ \nonumber &\lesssim \bigg(\iint_{\Omega} |\nabla u|^2 \mathcal{G}_0 \Psi_{N,M}^2\, dX \bigg)^{\frac12} \bigg(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \omega_0(Q) \iint_{U_Q^{\vartheta,*}} a(X)^2 \delta(X)^{-n-1}\, dX \bigg)^{\frac12} \\ & \le \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12}, \end{align} $$
where we used the fact that the family
![]() $\{I^{**}\}_{I \in \mathcal {W}}$
has bounded overlap. Additionally, as in equation (6.28)
$\{I^{**}\}_{I \in \mathcal {W}}$
has bounded overlap. Additionally, as in equation (6.28)
 $$ \begin{align} \mathcal{I}_3" \lesssim \bigg(\iint_{\Omega} |\nabla u|^2 \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} &\bigg(\iint_{\Omega} |\nabla \Psi_{N,M}|^2 \mathcal{G}_0 \, dX\bigg)^{\frac12} \notag \\ &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1}\, \mathcal{G}_0(X(I)) \bigg)^{\frac12} \lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \omega_0(Q_0)^{\frac12}. \end{align} $$
$$ \begin{align} \mathcal{I}_3" \lesssim \bigg(\iint_{\Omega} |\nabla u|^2 \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} &\bigg(\iint_{\Omega} |\nabla \Psi_{N,M}|^2 \mathcal{G}_0 \, dX\bigg)^{\frac12} \notag \\ &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{I \in \mathcal{W}_{N,M}^{\vartheta,\Sigma}} \ell(I)^{n-1}\, \mathcal{G}_0(X(I)) \bigg)^{\frac12} \lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \omega_0(Q_0)^{\frac12}. \end{align} $$
Finally, to bound
![]() $\mathcal {I}_4$
, we note that
$\mathcal {I}_4$
, we note that
![]() $u^2 \in W_{\mathrm {loc}}^{1,2}(\Omega )$
,
$u^2 \in W_{\mathrm {loc}}^{1,2}(\Omega )$
,
![]() $\mathcal {G}_0 \Psi _{N,M}^2 \in W^{1,2}(\Omega )$
and
$\mathcal {G}_0 \Psi _{N,M}^2 \in W^{1,2}(\Omega )$
and
![]() $\operatorname {\mathrm {supp}}(\mathcal {G}_0 \Psi _{N,M}^2) \subset \overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,*}}$
is compactly contained in
$\operatorname {\mathrm {supp}}(\mathcal {G}_0 \Psi _{N,M}^2) \subset \overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,*}}$
is compactly contained in
![]() $\Omega $
. Then [Reference Cavero, Hofmann, Martell and Toro9, Lemma 4.1] and Lemma 3.9 imply that
$\Omega $
. Then [Reference Cavero, Hofmann, Martell and Toro9, Lemma 4.1] and Lemma 3.9 imply that
 $$ \begin{align}\nonumber \mathcal{I}_4 & = \bigg|\iint_{\Omega} \mathop{\operatorname{div}}\nolimits_C D \cdot \nabla(u^2)\, \mathcal{G}_0\, \Psi_{N,M}^2\, dX \bigg| \\ \nonumber &\lesssim \bigg(\iint_{\Omega} |\nabla u|^2\, \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} \bigg(\iint_{\Omega} |\mathop{\operatorname{div}}\nolimits_C D|^2\, \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg( \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \mathcal{G}_0(X(I)) \iint_{I^{**}} |\mathop{\operatorname{div}}\nolimits_C D|^2\, dX \bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \omega_0(Q) \iint_{I^{**}} |\mathop{\operatorname{div}}\nolimits_C D(X)|^2\, \delta(X)^{1-n}\, dX \bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \omega_0(Q) \iint_{U_Q^{\vartheta,*}} |\mathop{\operatorname{div}}\nolimits_C D(X)|^2\, \delta(X)^{1-n}\, dX \bigg)^{\frac12} \\ & \le \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12}. \end{align} $$
$$ \begin{align}\nonumber \mathcal{I}_4 & = \bigg|\iint_{\Omega} \mathop{\operatorname{div}}\nolimits_C D \cdot \nabla(u^2)\, \mathcal{G}_0\, \Psi_{N,M}^2\, dX \bigg| \\ \nonumber &\lesssim \bigg(\iint_{\Omega} |\nabla u|^2\, \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} \bigg(\iint_{\Omega} |\mathop{\operatorname{div}}\nolimits_C D|^2\, \mathcal{G}_0\, \Psi_{N,M}^2 \, dX\bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg( \sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \mathcal{G}_0(X(I)) \iint_{I^{**}} |\mathop{\operatorname{div}}\nolimits_C D|^2\, dX \bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{Q\in\mathbb{D}_{\mathcal{F}_{N}, Q_0}}\sum_{I \in \mathcal{W}_{Q}^{\vartheta,*}} \omega_0(Q) \iint_{I^{**}} |\mathop{\operatorname{div}}\nolimits_C D(X)|^2\, \delta(X)^{1-n}\, dX \bigg)^{\frac12} \\ \nonumber &\lesssim \widetilde{\mathcal{K}}_{N,M}^{\frac12} \bigg(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \omega_0(Q) \iint_{U_Q^{\vartheta,*}} |\mathop{\operatorname{div}}\nolimits_C D(X)|^2\, \delta(X)^{1-n}\, dX \bigg)^{\frac12} \\ & \le \widetilde{\mathcal{K}}_{N,M}^{\frac12} \, \Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12}. \end{align} $$
Gathering equations (6.27)–(6.33) and using Young’s inequality, we obtain
 $$ \begin{align*} \widetilde{\mathcal{K}}_{N,M} \lesssim \omega_0(Q_0)+\widetilde{\mathcal{K}}_{N,M}^{\frac12}\,\omega_0(Q_0)^{\frac12} + \widetilde{\mathcal{K}}_{N,M}^{\frac12}\, &\Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12} \\ &\quad\le C\,\omega_0(Q_0)+C\,\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)+\frac12\,\widetilde{\mathcal{K}}_{N,M}, \end{align*} $$
$$ \begin{align*} \widetilde{\mathcal{K}}_{N,M} \lesssim \omega_0(Q_0)+\widetilde{\mathcal{K}}_{N,M}^{\frac12}\,\omega_0(Q_0)^{\frac12} + \widetilde{\mathcal{K}}_{N,M}^{\frac12}\, &\Big(\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)\Big)^{\frac12} \\ &\quad\le C\,\omega_0(Q_0)+C\,\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q)+\frac12\,\widetilde{\mathcal{K}}_{N,M}, \end{align*} $$
where the implicit constants are independent of N and M. Note that
![]() $\widetilde {\mathcal {K}}_{N,M}<\infty $
because
$\widetilde {\mathcal {K}}_{N,M}<\infty $
because
![]() $\operatorname {\mathrm {supp}} \Psi _{N,M} \subset \overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,*}}$
, which is a compact subset of
$\operatorname {\mathrm {supp}} \Psi _{N,M} \subset \overline {\Omega _{\mathcal {F}_{N,M}, Q_0}^{\vartheta ,*}}$
, which is a compact subset of
![]() $\Omega $
and
$\Omega $
and
![]() $u \in W^{1,2}_{\mathrm {loc}}(\Omega )$
. Thus, the last term can be hidden, and we eventually obtain
$u \in W^{1,2}_{\mathrm {loc}}(\Omega )$
. Thus, the last term can be hidden, and we eventually obtain
 $$ \begin{align*} \mathcal{K}_{N, M} \le\widetilde{\mathcal{K}}_{N,M} \lesssim \omega_0(Q_0) +\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q). \end{align*} $$
$$ \begin{align*} \mathcal{K}_{N, M} \le\widetilde{\mathcal{K}}_{N,M} \lesssim \omega_0(Q_0) +\sum_{Q \in \mathbb{D}_{\mathcal{F}_N, Q_0}} \gamma_Q^{\vartheta} \, \omega_0(Q). \end{align*} $$
This estimate (whose implicit constant is independent of N and M) and equation (6.23) readily yield equation (6.20), and the proof is complete.
Acknowledgments
The authors would like to thank the anonymous referees for their comments to improve the presentation of the paper.
All the authors acknowledge financial support from MCIN/AEI/ 10.13039/501100011033 grants FJC2018-038526-I (first authors), CEX2019-000904-S (first, third and last authors), PID2019-107914GB-I00 (first and third authors), MTM2017-84058-P (second author) and PID2020-116398GB-I00 (last author). The third author also acknowledges that the research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ ERC agreement no. 615112 HAPDEGMT.
Conflict of Interest
None.