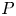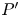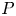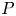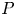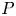1. Introduction
It is a classical result of Clebsch [Reference ClebschCle71] that every planar pentagon ![]() $P$ is projectively equivalent to the pentagon
$P$ is projectively equivalent to the pentagon ![]() $P'$ formed by intersections of diagonals of
$P'$ formed by intersections of diagonals of ![]() $P$. More precisely, if we label the vertices of
$P$. More precisely, if we label the vertices of ![]() $P$ and
$P$ and ![]() $P'$ in such way that the
$P'$ in such way that the ![]() $k$th vertex of
$k$th vertex of ![]() $P'$ is opposite to the
$P'$ is opposite to the ![]() $k$th vertex of
$k$th vertex of ![]() $P$ (see Figure 1), then there is a projective transformation that takes
$P$ (see Figure 1), then there is a projective transformation that takes ![]() $P$ to
$P$ to ![]() $P'$ and respects the labelings.
$P'$ and respects the labelings.

Figure 1. Pentagons ![]() $P = v_1v_2v_3v_4v_5$ and
$P = v_1v_2v_3v_4v_5$ and ![]() $P' = v_1'v_2'v_3'v_4'v_5'$ are projectively equivalent.
$P' = v_1'v_2'v_3'v_4'v_5'$ are projectively equivalent.
Furthermore, as was proved by Schwartz [Reference SchwartzSch07], Clebsch's theorem is true for all Poncelet polygons with an odd number of vertices. Recall that a Poncelet polygon is a polygon which is inscribed in a conic and circumscribed about another conic. In particular, any pentagon is Poncelet, whereas for ![]() $n$-gons with
$n$-gons with ![]() $n\geq 6$ being Poncelet is a non-trivial restriction. Poncelet polygons owe their name to Poncelet and his famous ‘porism’ which states that if there exists an
$n\geq 6$ being Poncelet is a non-trivial restriction. Poncelet polygons owe their name to Poncelet and his famous ‘porism’ which states that if there exists an ![]() $n$-gon inscribed in a conic
$n$-gon inscribed in a conic ![]() $C_1$ and circumscribed about a conic
$C_1$ and circumscribed about a conic ![]() $C_2$, then any point of
$C_2$, then any point of ![]() $C_1$ is a vertex of such an
$C_1$ is a vertex of such an ![]() $n$-gon (see Figure 2).
$n$-gon (see Figure 2).

Figure 2. Every point of ![]() $C_1$ is a vertex of a pentagon inscribed in
$C_1$ is a vertex of a pentagon inscribed in ![]() $C_1$ and circumscribed about
$C_1$ and circumscribed about ![]() $C_2$.
$C_2$.
Schwartz's generalization of Clebsch's theorem is as follows. Let ![]() $P$ be an
$P$ be an ![]() $n$-gon with odd
$n$-gon with odd ![]() $n$, and let
$n$, and let ![]() $P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of
$P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of ![]() $P$, that is, diagonals connecting second-nearest vertices. Label the vertices of
$P$, that is, diagonals connecting second-nearest vertices. Label the vertices of ![]() $P'$ as in Clebsch's theorem: the
$P'$ as in Clebsch's theorem: the ![]() $k$th vertex of
$k$th vertex of ![]() $P'$ is opposite to the
$P'$ is opposite to the ![]() $k$th vertex of
$k$th vertex of ![]() $P$ (see Figure 3). Assume that
$P$ (see Figure 3). Assume that ![]() $P$ is Poncelet. Then there is a projective transformation that carries
$P$ is Poncelet. Then there is a projective transformation that carries ![]() $P$ to
$P$ to ![]() $P'$ and respects the labelings (a weaker result saying that if
$P'$ and respects the labelings (a weaker result saying that if ![]() $P$ is Poncelet, then
$P$ is Poncelet, then ![]() $P'$ is circumscribed about a conic was known to Darboux, see [Reference Dragović and RadnovićDR14, Theorem 2.1]). The goal of the present paper is to show that in the convex setting the converse is also true. More precisely, we prove the converse of Schwartz's theorem for a broader class of weakly convex polygons. Weak convexity is a technical condition (see Definition 3.1) which, in particular, holds for truly convex polygons.
$P'$ is circumscribed about a conic was known to Darboux, see [Reference Dragović and RadnovićDR14, Theorem 2.1]). The goal of the present paper is to show that in the convex setting the converse is also true. More precisely, we prove the converse of Schwartz's theorem for a broader class of weakly convex polygons. Weak convexity is a technical condition (see Definition 3.1) which, in particular, holds for truly convex polygons.
Theorem A Let ![]() $P$ be a weakly convex closed polygon with an odd number of vertices. Let also
$P$ be a weakly convex closed polygon with an odd number of vertices. Let also ![]() $P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of
$P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of ![]() $P$, labeled as in Figure 3. Assume that there is a projective transformation that carries
$P$, labeled as in Figure 3. Assume that there is a projective transformation that carries ![]() $P$ to
$P$ to ![]() $P'$ and respects the labelings. Then
$P'$ and respects the labelings. Then ![]() $P$ (and, hence,
$P$ (and, hence, ![]() $P'$) is a Poncelet polygon.
$P'$) is a Poncelet polygon.

Figure 3. A convex polygon ![]() $P$ is Poncelet if and only if it is projectively equivalent to
$P$ is Poncelet if and only if it is projectively equivalent to ![]() $P'$.
$P'$.
Combining Theorem A with Schwartz's theorem, we obtain the following characterization of weakly convex Poncelet polygons.
Corollary 1.1 Let ![]() $P$ be a weakly convex closed polygon with an odd number of vertices. Let also
$P$ be a weakly convex closed polygon with an odd number of vertices. Let also ![]() $P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of
$P'$ be the polygon whose vertices are the intersections of consecutive shortest diagonals of ![]() $P$, labeled as in Figure 3. Then
$P$, labeled as in Figure 3. Then ![]() $P$ is Poncelet if and only if it is projectively equivalent to
$P$ is Poncelet if and only if it is projectively equivalent to ![]() $P'$.
$P'$.
The map taking the polygon ![]() $P$ in Figure 3 to
$P$ in Figure 3 to ![]() $P'$ is known as the pentagram map. It was defined by Schwartz in 1992 [Reference SchwartzSch92] but became especially popular in the last decade thanks to the discovery that it is a discrete integrable system [Reference Ovsienko, Schwartz and TabachnikovOST10, Reference Ovsienko, Schwartz and TabachnikovOST13, Reference SolovievSol13], and also because of its connections with cluster algebras [Reference GlickGli11, Reference Gekhtman, Shapiro, Tabachnikov and VainshteinGSTV16, Reference Glick and PylyavskyyGP16, Reference Kedem and VichitkunakornKV15, Reference Fock and MarshakovFM16]. As the pentagram map commutes with projective transformations, it is usually considered as a dynamical system on the space of polygons modulo projective equivalence. Our result can thus be viewed as a description of fixed points of the pentagram map, which has been an open question since Schwartz's first paper [Reference SchwartzSch92].
$P'$ is known as the pentagram map. It was defined by Schwartz in 1992 [Reference SchwartzSch92] but became especially popular in the last decade thanks to the discovery that it is a discrete integrable system [Reference Ovsienko, Schwartz and TabachnikovOST10, Reference Ovsienko, Schwartz and TabachnikovOST13, Reference SolovievSol13], and also because of its connections with cluster algebras [Reference GlickGli11, Reference Gekhtman, Shapiro, Tabachnikov and VainshteinGSTV16, Reference Glick and PylyavskyyGP16, Reference Kedem and VichitkunakornKV15, Reference Fock and MarshakovFM16]. As the pentagram map commutes with projective transformations, it is usually considered as a dynamical system on the space of polygons modulo projective equivalence. Our result can thus be viewed as a description of fixed points of the pentagram map, which has been an open question since Schwartz's first paper [Reference SchwartzSch92].
Remark 1.2 Note that the pentagram map can be considered either on labeled polygons (i.e. polygons with labeled vertices) or on unlabeled polygons. Theorem A describes fixed points of the pentagram map on the space of projective equivalence classes of labeled polygons, where the labeling rule is depicted in Figure 3. Although this is not the only possible labeling, it is the only one for which the pentagram map commutes with the action of the dihedral group and, hence, the most symmetric of all labelings. A more common, non-symmetric labeling is given by the rule ![]() $v_k' := (v_{k-1}, v_{k+1}) \cap (v_k, v_{k+2})$. One can easily see that the only fixed points of the pentagram map with this non-symmetric labeling are regular polygons (again, assuming that the number of vertices is odd). The problem of describing the fixed points of the pentagram map for an arbitrary labeling can also be approached using the techniques of the present paper, but due to the break of symmetry, one should not expect an answer as nice as for the symmetric labeling.
$v_k' := (v_{k-1}, v_{k+1}) \cap (v_k, v_{k+2})$. One can easily see that the only fixed points of the pentagram map with this non-symmetric labeling are regular polygons (again, assuming that the number of vertices is odd). The problem of describing the fixed points of the pentagram map for an arbitrary labeling can also be approached using the techniques of the present paper, but due to the break of symmetry, one should not expect an answer as nice as for the symmetric labeling.
Theorem A also has an interpretation in terms of billiards. Indeed, if the conic ![]() $C_1$ circumscribed about a Poncelet polygon
$C_1$ circumscribed about a Poncelet polygon ![]() $P$ is confocal to the inscribed conic
$P$ is confocal to the inscribed conic ![]() $C_2$ (which can always be arranged by applying a suitable projective transformation), then
$C_2$ (which can always be arranged by applying a suitable projective transformation), then ![]() $P$ can be viewed as a closed trajectory of a billiard ball in the domain bounded by
$P$ can be viewed as a closed trajectory of a billiard ball in the domain bounded by ![]() $C_1$. Conversely, any closed billiard trajectory in a conic is a Poncelet polygon. Thus, Corollary 1.1 establishes a correspondence between fixed points of the pentagram map and periodic billiard trajectories in conics. Also note that, as shown in [Reference Levi and TabachnikovLT07], the fact that a closed billiard trajectory in a conic is projectively equivalent to its pentagram image is essentially a corollary of integrability of the corresponding billiard system. At the same time, we show that if
$C_1$. Conversely, any closed billiard trajectory in a conic is a Poncelet polygon. Thus, Corollary 1.1 establishes a correspondence between fixed points of the pentagram map and periodic billiard trajectories in conics. Also note that, as shown in [Reference Levi and TabachnikovLT07], the fact that a closed billiard trajectory in a conic is projectively equivalent to its pentagram image is essentially a corollary of integrability of the corresponding billiard system. At the same time, we show that if ![]() $P$ is projectively equivalent to its pentagram image then the vertices of
$P$ is projectively equivalent to its pentagram image then the vertices of ![]() $P$ are contained in a conic. Thus, one may hope to combine our results with the approach of [Reference Levi and TabachnikovLT07] to show that for any integrable billiard the impact points of a periodic trajectory are contained in a conic and, hence, shed some light on the Birkhoff conjecture which says that the only integrable billiards are those in conics.
$P$ are contained in a conic. Thus, one may hope to combine our results with the approach of [Reference Levi and TabachnikovLT07] to show that for any integrable billiard the impact points of a periodic trajectory are contained in a conic and, hence, shed some light on the Birkhoff conjecture which says that the only integrable billiards are those in conics.
It is also an interesting question whether this correspondence between periodic billiard trajectories in conics and fixed points of the pentagram map extends to higher dimensions. There exists numerous generalizations of the pentagram map to higher-dimensional spaces [Reference Gekhtman, Shapiro, Tabachnikov and VainshteinGSTV16, Reference Khesin and SolovievKS13, Reference Khesin and SolovievKS16, Reference Felipe and BeffaFB19] and one may wonder if their fixed points are related to periodic trajectories of billiards in multidimensional quadrics.
Remark 1.3 We do not know whether Theorem A is true with no convexity-type assumptions, but it is certainly not true over complex numbers, as demonstrated by the following example. Let ![]() $\lambda := \exp ({{2\pi {i}}/{7}})$, where
$\lambda := \exp ({{2\pi {i}}/{7}})$, where ![]() ${i} = \sqrt {-1}$, and let
${i} = \sqrt {-1}$, and let ![]() $P$ be a heptagon in
$P$ be a heptagon in ![]() $\mathbb {C}^2$ with vertices
$\mathbb {C}^2$ with vertices ![]() $v_k := (\lambda ^{2k}, \lambda ^{3k})$. Then a direct computation shows that there exists a projective (in fact, even affine) transformation
$v_k := (\lambda ^{2k}, \lambda ^{3k})$. Then a direct computation shows that there exists a projective (in fact, even affine) transformation ![]() $\phi$ taking
$\phi$ taking ![]() $P$ to
$P$ to ![]() $P'$ (see also Remark 4.3 for a conceptual proof). Moreover, for any vertex
$P'$ (see also Remark 4.3 for a conceptual proof). Moreover, for any vertex ![]() $v$ of
$v$ of ![]() $P$ and
$P$ and ![]() $v'$ of
$v'$ of ![]() $P'$, the map
$P'$, the map ![]() $\phi$ can be chosen to take
$\phi$ can be chosen to take ![]() $v$ to
$v$ to ![]() $v'$. This means that the projective equivalence class of
$v'$. This means that the projective equivalence class of ![]() $P$ is fixed by the pentagram map, regardless of the labeling convention used to define the map. However,
$P$ is fixed by the pentagram map, regardless of the labeling convention used to define the map. However, ![]() $P$ is not Poncelet. Moreover, it is not even inscribed in a conic. Indeed, the vertices of
$P$ is not Poncelet. Moreover, it is not even inscribed in a conic. Indeed, the vertices of ![]() $P$ lie on a semi-cubical parabola
$P$ lie on a semi-cubical parabola ![]() $y^2 = x^3$, which has at most six intersection points with any conic. Thus, there exists no conic which contains all seven vertices of
$y^2 = x^3$, which has at most six intersection points with any conic. Thus, there exists no conic which contains all seven vertices of ![]() $P$.
$P$.
Theorem A being not true over ![]() $\mathbb {C}$ is one of the reasons one should not expect it to have any kind of ‘elementary’ proof, as such a proof would be valid over any field. Another reason is that the theorem is not true for non-closed polygons (see Remark 1.4). Again, if there was a local (i.e. involving only a few adjacent vertices) geometric construction producing inscribed and circumscribed conics for
$\mathbb {C}$ is one of the reasons one should not expect it to have any kind of ‘elementary’ proof, as such a proof would be valid over any field. Another reason is that the theorem is not true for non-closed polygons (see Remark 1.4). Again, if there was a local (i.e. involving only a few adjacent vertices) geometric construction producing inscribed and circumscribed conics for ![]() $P$ based on the projective equivalence between
$P$ based on the projective equivalence between ![]() $P$ and
$P$ and ![]() $P'$, such a construction would work whether
$P'$, such a construction would work whether ![]() $P$ is closed or not.
$P$ is closed or not.
We now outline the scheme of the proof of Theorem A. As a first step, we prove the theorem under an additional assumption that the polygon ![]() $P$ is self-dual. Recall that the dual of a polygon is the polygon in the dual projective plane whose vertices are the sides of the initial one. We label the vertices of the dual polygon as shown in Figure 4. A polygon is self-dual if it is projectively equivalent to its dual.
$P$ is self-dual. Recall that the dual of a polygon is the polygon in the dual projective plane whose vertices are the sides of the initial one. We label the vertices of the dual polygon as shown in Figure 4. A polygon is self-dual if it is projectively equivalent to its dual.

Figure 4. The ![]() $k$th vertex of the dual polygon is opposite to the
$k$th vertex of the dual polygon is opposite to the ![]() $k$th vertex of the initial one.
$k$th vertex of the initial one.
Under this additional assumption of self-duality, Theorem A is true in a more general setting of twisted polygons, that is, polygons that are closed only up to a projective transformation. More precisely, a twisted ![]() $n$-gon is a sequence
$n$-gon is a sequence ![]() $v_k \in \mathbb {P}^2$ such that
$v_k \in \mathbb {P}^2$ such that ![]() $v_{k+n} = \psi (v_k)$ for a certain projective transformation
$v_{k+n} = \psi (v_k)$ for a certain projective transformation ![]() $\psi$, called the monodromy.
$\psi$, called the monodromy.
Theorem B Let ![]() $P$ be a weakly convex twisted
$P$ be a weakly convex twisted ![]() $n$-gon with odd
$n$-gon with odd ![]() $n$, and let
$n$, and let ![]() $P'$ be as in Theorem A. Assume that
$P'$ be as in Theorem A. Assume that ![]() $P$ is self-dual and projectively equivalent to
$P$ is self-dual and projectively equivalent to ![]() $P'$. Then
$P'$. Then ![]() $P$ is a Poncelet polygon.
$P$ is a Poncelet polygon.
Remark 1.4 Theorem B is not true without the self-duality assumption (in other words, Theorem A is not true for non-closed polygons). As an example, consider a polygon ![]() $P$ in
$P$ in ![]() $\mathbb {R}^2$ whose vertices are given by
$\mathbb {R}^2$ whose vertices are given by ![]() $v_k := (4^k, 8^k)$. This is a twisted
$v_k := (4^k, 8^k)$. This is a twisted ![]() $n$-gon for any
$n$-gon for any ![]() $n$, weakly convex and projectively equivalent to its pentagram image
$n$, weakly convex and projectively equivalent to its pentagram image ![]() $P'$. However,
$P'$. However, ![]() $P$ is not Poncelet (cf. Remark 1.3).
$P$ is not Poncelet (cf. Remark 1.3).
The proof of Theorem B is based on the theory of commuting difference operators, elliptic curves, and theta functions. Given the result of the theorem, the appearance of elliptic curves is not surprising, as their connection to Poncelet polygons is well-known. However, we are not given a priori that ![]() $P$ is Poncelet, so there should be some other source where the elliptic curve is coming from. In our approach, that source is the theory of commuting difference operators. Namely, we show that a twisted polygon
$P$ is Poncelet, so there should be some other source where the elliptic curve is coming from. In our approach, that source is the theory of commuting difference operators. Namely, we show that a twisted polygon ![]() $P$ is projectively equivalent to its pentagram image
$P$ is projectively equivalent to its pentagram image ![]() $P'$ if and only if certain associated difference operators commute (see § 4). The general theory then states that the joint spectrum of those operators is a Riemann surface
$P'$ if and only if certain associated difference operators commute (see § 4). The general theory then states that the joint spectrum of those operators is a Riemann surface ![]() $\Gamma$, called the spectral curve (see, e.g., [Reference Krichever and NovikovKN03]). Using further that the operators in question are of special form and, in particular, dual to each other (which is a reflection of self-duality of
$\Gamma$, called the spectral curve (see, e.g., [Reference Krichever and NovikovKN03]). Using further that the operators in question are of special form and, in particular, dual to each other (which is a reflection of self-duality of ![]() $P$), we show that the genus of
$P$), we show that the genus of ![]() $\Gamma$ is at most one, that is,
$\Gamma$ is at most one, that is, ![]() $\Gamma$ is rational or elliptic (see § 5.1). This is one of the few places in the proof where we use weak convexity in an essential way. Without that assumption, one only seems to be able to conclude that the genus is at most two. In particular, it seems possible to construct non-weakly-convex counterexamples to Theorems A and B using genus-
$\Gamma$ is rational or elliptic (see § 5.1). This is one of the few places in the proof where we use weak convexity in an essential way. Without that assumption, one only seems to be able to conclude that the genus is at most two. In particular, it seems possible to construct non-weakly-convex counterexamples to Theorems A and B using genus-![]() $2$ theta functions.
$2$ theta functions.
The next step is to show that our upper bound on the genus of ![]() $\Gamma$ implies that
$\Gamma$ implies that ![]() $P$ is Poncelet (as a priori there is no connection between the elliptic curve
$P$ is Poncelet (as a priori there is no connection between the elliptic curve ![]() $\Gamma$ and that which is classically associated with a Poncelet polygon). More precisely, we show that elliptic spectral curves correspond to generic Poncelet polygons, whereas rational curves correspond to their degenerations (such as the regular polygon). To that end, we express coordinates of vertices of
$\Gamma$ and that which is classically associated with a Poncelet polygon). More precisely, we show that elliptic spectral curves correspond to generic Poncelet polygons, whereas rational curves correspond to their degenerations (such as the regular polygon). To that end, we express coordinates of vertices of ![]() $P$ in terms of certain meromorphic functions on the spectral curve
$P$ in terms of certain meromorphic functions on the spectral curve ![]() $\Gamma$. One ends up with elementary functions or theta functions, depending on whether the curve
$\Gamma$. One ends up with elementary functions or theta functions, depending on whether the curve ![]() $\Gamma$ is rational or elliptic. In both cases, using relations between those functions (e.g. Riemann's relation in the elliptic case), one shows that
$\Gamma$ is rational or elliptic. In both cases, using relations between those functions (e.g. Riemann's relation in the elliptic case), one shows that ![]() $P$ is a Poncelet polygon, so Theorem B holds (see § 6.1 for the rational case and § 6.2 for the elliptic case). Furthermore, in the elliptic case the spectral curve
$P$ is a Poncelet polygon, so Theorem B holds (see § 6.1 for the rational case and § 6.2 for the elliptic case). Furthermore, in the elliptic case the spectral curve ![]() $\Gamma$ turns out to be isogenous to the elliptic curve attached to
$\Gamma$ turns out to be isogenous to the elliptic curve attached to ![]() $P$ due to its Poncelet property.
$P$ due to its Poncelet property.
After that, we proceed to prove Theorem A. To that end, we first show that the self-duality assumption of Theorem B is not too restrictive. Namely, given a polygon that is projectively equivalent to its pentagram image, it can be what is called rescaled so that it becomes self-dual. This rescaling (closely related to the notion of spectral parameter) is a one-parametric group of transformations of the moduli space of twisted polygons which preserves weak convexity but not closedness. Thus, starting with a closed polygon as in Theorem A, we rescale it to a non-necessarily closed, but self-dual, weakly convex polygon, which is the setting of Theorem B. In this way, we conclude that a weakly convex closed polygon projectively equivalent to its pentagram image is Poncelet up to rescaling. The last step is to show that this rescaling must actually be trivial. To that end, we show that no non-trivial rescaling of a weakly convex Poncelet polygon is closed. In the rational case, this is proved by an elementary argument (see § 7.2), whereas the elliptic case requires careful analysis of the real part of the spectral curve (see § 7.3). In the latter case, the proof once again essentially relies on weak convexity.
In addition to proofs of Theorems A and B, the paper contains an appendix (Appendix A) where we establish an auxiliary result on correspondence between dual difference operators and dual polygons. Although that result seems to be well-known, we could not find a proof in the literature that does not rely on a computation. Thus, we provide a proof here.
We tried to make the exposition self-contained. In particular, we do not assume that the reader is familiar with the general theory of integrable systems or commuting difference operators. Only basic knowledge of Riemann surfaces is assumed.
2. Background results: polygons, difference operators, and corner invariants
This section is an overview of mostly well-known results on the relation between difference operators and polygons. Namely, we give an introduction to difference operators in § 2.1, after which we connect them to polygons in § 2.2. Note that although the description of the moduli space of polygons in terms of difference operators is well-known, our point of view is slightly different from the standard one. In particular, we identify the space of polygons with a certain quotient of the space of third-order difference operators, as opposed to the standard approach in which one identifies polygons with a certain subspace of that space. In that respect, our approach is close to that of [Reference Conley and OvsienkoCO19]. In addition, we provide, in § 2.3, another description of the polygon space, in terms of so-called corner invariants. Note that although corner invariants per se are not used heavily in the paper, they are needed to define weakly convex polygons and rescaling. Rescaling is also defined in § 2.3, whereas weakly convex polygons are discussed in § 3.
2.1 A primer on difference operators
This section is a brief introduction to the elementary theory of difference operators. Our terminology mainly follows that of [Reference Van Moerbeke and MumfordVM79]. Let ![]() $\mathbb {R}^\infty$ be the vector space of bi-infinite sequences of real numbers. For
$\mathbb {R}^\infty$ be the vector space of bi-infinite sequences of real numbers. For ![]() $\xi \in \mathbb {R}^\infty$ and any
$\xi \in \mathbb {R}^\infty$ and any ![]() $k \in \mathbb {Z}$, let
$k \in \mathbb {Z}$, let ![]() $\xi _k \in \mathbb {R}$ be the
$\xi _k \in \mathbb {R}$ be the ![]() $k$th entry of the sequence
$k$th entry of the sequence ![]() $\xi$, so that
$\xi$, so that ![]() $\xi = (\xi _k)_{k \in \mathbb {Z}}$. Let also
$\xi = (\xi _k)_{k \in \mathbb {Z}}$. Let also ![]() $m_- \leq m_+$ be integers. A linear operator
$m_- \leq m_+$ be integers. A linear operator ![]() $\mathcal {D} \colon \mathbb {R}^\infty \to \mathbb {R}^\infty$ is called a difference operator supported in
$\mathcal {D} \colon \mathbb {R}^\infty \to \mathbb {R}^\infty$ is called a difference operator supported in ![]() $[m_-,m_+]:=\{m_-, \ldots, m_+\}$ if it can be written as
$[m_-,m_+]:=\{m_-, \ldots, m_+\}$ if it can be written as
 \begin{equation} (\mathcal{D}\xi)_k = \sum_{j = m_-}^{m_+} a_k^j \xi_{k+j}, \end{equation}
\begin{equation} (\mathcal{D}\xi)_k = \sum_{j = m_-}^{m_+} a_k^j \xi_{k+j}, \end{equation}
where ![]() $a_k^j \in \mathbb {R}$ for every
$a_k^j \in \mathbb {R}$ for every ![]() $k \in \mathbb {Z}$ and every
$k \in \mathbb {Z}$ and every ![]() $j \in [m_-,m_+]$. In matrix terms, this can be rewritten as
$j \in [m_-,m_+]$. In matrix terms, this can be rewritten as
 \begin{equation} \mathcal{D}\xi = \left(\begin{array}{@{}ccccccccc@{}} \ddots & & \ddots & & \\ & a_{k-1}^{m_-} & \ldots & a_{k-1}^{m_+} & \\ & & a_k^{m_-} & \ldots & a_k^{m_+} & & \\ & & & a_{k+1}^{m_-} & \ldots & a_{k+1}^{m_+} & \\ & & & & \ddots & & \ddots \end{array}\right)\xi, \end{equation}
\begin{equation} \mathcal{D}\xi = \left(\begin{array}{@{}ccccccccc@{}} \ddots & & \ddots & & \\ & a_{k-1}^{m_-} & \ldots & a_{k-1}^{m_+} & \\ & & a_k^{m_-} & \ldots & a_k^{m_+} & & \\ & & & a_{k+1}^{m_-} & \ldots & a_{k+1}^{m_+} & \\ & & & & \ddots & & \ddots \end{array}\right)\xi, \end{equation}
so difference operators can be equivalently described as those whose matrices are finite band (i.e. have only finitely many non-zero diagonals). Furthermore, denoting, for every ![]() $j$, the sequence of
$j$, the sequence of ![]() $a_k^j$ by
$a_k^j$ by ![]() $a^j$, formula (1) can be rewritten as
$a^j$, formula (1) can be rewritten as
 \begin{equation} \mathcal{D} =\sum_{j = m_-}^{m_+} a^j T^j, \end{equation}
\begin{equation} \mathcal{D} =\sum_{j = m_-}^{m_+} a^j T^j, \end{equation}
where ![]() $T \colon \mathbb {R}^\infty \to \mathbb {R}^\infty$ is the left shift operator
$T \colon \mathbb {R}^\infty \to \mathbb {R}^\infty$ is the left shift operator ![]() $(T\xi )_k = \xi _{k+1}$, and each
$(T\xi )_k = \xi _{k+1}$, and each ![]() $a^j \in \mathbb {R}^\infty$ acts on
$a^j \in \mathbb {R}^\infty$ acts on ![]() $\mathbb {R}^\infty$ by term-wise multiplication.
$\mathbb {R}^\infty$ by term-wise multiplication.
The order of difference operator (1) is the number ![]() $\mathrm {ord}\, \mathcal {D} := m_+ - m_-$. Difference operator (1) is called properly bounded if
$\mathrm {ord}\, \mathcal {D} := m_+ - m_-$. Difference operator (1) is called properly bounded if ![]() $a_k^{m_-} \neq 0$ and
$a_k^{m_-} \neq 0$ and ![]() $a_k^{m_+} \neq 0$ for every
$a_k^{m_+} \neq 0$ for every ![]() $k \in \mathbb {Z}$. Clearly, for a properly bounded difference operator
$k \in \mathbb {Z}$. Clearly, for a properly bounded difference operator ![]() $\mathcal {D}$ one has
$\mathcal {D}$ one has ![]() $\dim \mathrm {Ker}\, \mathcal {D} = \mathrm {ord}\, \mathcal {D}.$ Sequences
$\dim \mathrm {Ker}\, \mathcal {D} = \mathrm {ord}\, \mathcal {D}.$ Sequences ![]() $\xi ^{1}, \ldots, \xi ^{d} \in \mathrm {Ker}\, \mathcal {D}$, where
$\xi ^{1}, \ldots, \xi ^{d} \in \mathrm {Ker}\, \mathcal {D}$, where ![]() $d:=\mathrm {ord}\, \mathcal {D}$, form a basis in
$d:=\mathrm {ord}\, \mathcal {D}$, form a basis in ![]() $\mathrm {Ker}\, \mathcal {D}$ if and only if the associated difference Wronskian
$\mathrm {Ker}\, \mathcal {D}$ if and only if the associated difference Wronskian
 \[ W_k := \left|\begin{array}{@{}ccc@{}}\xi^{1}_{k} & \ldots & \xi^{d}_{k} \\ & \ldots \\ \xi^{1}_{k+d-1} & \ldots & \xi^{d}_{k+d-1} \end{array}\right|, \]
\[ W_k := \left|\begin{array}{@{}ccc@{}}\xi^{1}_{k} & \ldots & \xi^{d}_{k} \\ & \ldots \\ \xi^{1}_{k+d-1} & \ldots & \xi^{d}_{k+d-1} \end{array}\right|, \]
(where ![]() $|M|$ denotes the determinant of the matrix
$|M|$ denotes the determinant of the matrix ![]() $M$) is non-vanishing for some
$M$) is non-vanishing for some ![]() $k \in \mathbb {Z}$. This is equivalent to non-vanishing of
$k \in \mathbb {Z}$. This is equivalent to non-vanishing of ![]() $W_k$ for any
$W_k$ for any ![]() $k$ due to the relation
$k$ due to the relation
 \begin{equation} W_{k+1} = (-1)^d \frac{a_{k-m_-}^{m_-}}{a_{k-m_-}^{m_+}} W_k. \end{equation}
\begin{equation} W_{k+1} = (-1)^d \frac{a_{k-m_-}^{m_-}}{a_{k-m_-}^{m_+}} W_k. \end{equation} Along with ![]() $\mathbb {R}^\infty$, difference operators naturally act on the space
$\mathbb {R}^\infty$, difference operators naturally act on the space ![]() $(\mathbb {R}^d)^\infty$ of bi-infinite sequences of vectors in
$(\mathbb {R}^d)^\infty$ of bi-infinite sequences of vectors in ![]() $\mathbb {R}^d$. The case
$\mathbb {R}^d$. The case ![]() $d = \mathrm {ord}\, \mathcal {D}$ is of particular interest. Let
$d = \mathrm {ord}\, \mathcal {D}$ is of particular interest. Let ![]() $V \in (\mathbb {R}^d)^\infty$, where
$V \in (\mathbb {R}^d)^\infty$, where ![]() $d = \mathrm {ord}\, \mathcal {D}$, be a solution of the difference equation
$d = \mathrm {ord}\, \mathcal {D}$, be a solution of the difference equation ![]() $\mathcal {D} V = 0$. Define scalar sequences
$\mathcal {D} V = 0$. Define scalar sequences ![]() $\xi ^{1}, \ldots, \xi ^{d} \in \mathbb {R}^\infty$ by setting
$\xi ^{1}, \ldots, \xi ^{d} \in \mathbb {R}^\infty$ by setting ![]() $\xi _k^j$ to be equal to the
$\xi _k^j$ to be equal to the ![]() $j$th coordinate of
$j$th coordinate of ![]() $V_k$. We say that
$V_k$. We say that ![]() $V$ is a fundamental solution if the sequences
$V$ is a fundamental solution if the sequences ![]() $\xi ^{1}, \ldots, \xi ^{d} \in \mathbb {R}^\infty$ form a basis in
$\xi ^{1}, \ldots, \xi ^{d} \in \mathbb {R}^\infty$ form a basis in ![]() $\mathrm {Ker}\, \mathcal {D}$. As follows from the Wronskian criterion, a solution of
$\mathrm {Ker}\, \mathcal {D}$. As follows from the Wronskian criterion, a solution of ![]() $\mathcal {D} V = 0$ is fundamental if and only if the vectors
$\mathcal {D} V = 0$ is fundamental if and only if the vectors ![]() $V_k, \ldots, V_{k + d -1}$ are linearly independent for some (equivalently, for all)
$V_k, \ldots, V_{k + d -1}$ are linearly independent for some (equivalently, for all) ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
A difference operator ![]() $\mathcal {D}$ is
$\mathcal {D}$ is ![]() $n$-periodic if its coefficients
$n$-periodic if its coefficients ![]() $a_k^j$ are
$a_k^j$ are ![]() $n$-periodic in the index
$n$-periodic in the index ![]() $k$. This is equivalent to saying that
$k$. This is equivalent to saying that ![]() $\mathcal {D}$ commutes with the
$\mathcal {D}$ commutes with the ![]() $n$th power of the shift operator:
$n$th power of the shift operator: ![]() $\mathcal {D} T^n = T^n\mathcal {D}$, so the kernel of an
$\mathcal {D} T^n = T^n\mathcal {D}$, so the kernel of an ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {D}$ is invariant under the action of
$\mathcal {D}$ is invariant under the action of ![]() $T^n$. The finite-dimensional operator
$T^n$. The finite-dimensional operator ![]() $T^n\vert _{\mathrm {Ker}\, \mathcal {D}}$ is called the monodromy of
$T^n\vert _{\mathrm {Ker}\, \mathcal {D}}$ is called the monodromy of ![]() $\mathcal {D}$. Note that the eigenvectors of the monodromy are exactly scalar quasi-periodic solutions of the equation
$\mathcal {D}$. Note that the eigenvectors of the monodromy are exactly scalar quasi-periodic solutions of the equation ![]() $\mathcal {D}\xi = 0$, that is, solutions which belong to the space
$\mathcal {D}\xi = 0$, that is, solutions which belong to the space
for some ![]() $z \in \mathbb {R}^*$.
$z \in \mathbb {R}^*$.
The monodromy can also be understood in terms of fundamental solutions. Namely, note that any two fundamental solutions ![]() $V, V' \in (\mathbb {R}^d)^\infty$ of
$V, V' \in (\mathbb {R}^d)^\infty$ of ![]() $\mathcal {D}$ are related by
$\mathcal {D}$ are related by ![]() $V' = AV$, where
$V' = AV$, where ![]() $A \in \mathrm {GL}_d(\mathbb {R})$ acts on
$A \in \mathrm {GL}_d(\mathbb {R})$ acts on ![]() $(\mathbb {R}^d)^\infty$ by term-wise multiplication. Furthermore, if
$(\mathbb {R}^d)^\infty$ by term-wise multiplication. Furthermore, if ![]() $V$ is a fundamental solution of an
$V$ is a fundamental solution of an ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {D}$, then so is
$\mathcal {D}$, then so is ![]() $T^nV$, which means that
$T^nV$, which means that ![]() $T^n V = AV$ for some
$T^n V = AV$ for some ![]() $A \in \mathrm {GL}_d(\mathbb {R})$. In other words, we have
$A \in \mathrm {GL}_d(\mathbb {R})$. In other words, we have ![]() $V_{k+n} = AV_k$ for every
$V_{k+n} = AV_k$ for every ![]() $k \in \mathbb {Z}$, which means that the fundamental solution of a periodic difference operator is always quasi-periodic. Furthermore, the matrix
$k \in \mathbb {Z}$, which means that the fundamental solution of a periodic difference operator is always quasi-periodic. Furthermore, the matrix ![]() $A$ can be easily seen to be the transpose of the monodromy matrix
$A$ can be easily seen to be the transpose of the monodromy matrix ![]() $M$ of
$M$ of ![]() $\mathcal {D}$, written in the basis of
$\mathcal {D}$, written in the basis of ![]() $\mathrm {Ker}\, \mathcal {D}$ associated with the fundamental solution
$\mathrm {Ker}\, \mathcal {D}$ associated with the fundamental solution ![]() $V$. In particular, this implies that the Wronskian of an
$V$. In particular, this implies that the Wronskian of an ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {D}$ satisfies
$\mathcal {D}$ satisfies ![]() $W_{k+n} = (\det M)W_k$. Combined with (4), the latter formula gives the following expression for the determinant of the monodromy, which is used several times throughout the paper:
$W_{k+n} = (\det M)W_k$. Combined with (4), the latter formula gives the following expression for the determinant of the monodromy, which is used several times throughout the paper:
 \begin{equation} \det M = (-1)^{nd} \prod_{k=1}^n \frac{ a_k^{m_-}}{a_k^{m_+}}. \end{equation}
\begin{equation} \det M = (-1)^{nd} \prod_{k=1}^n \frac{ a_k^{m_-}}{a_k^{m_+}}. \end{equation}The dual of the operator (3) is defined by
 \[ \mathcal{D}^* := \sum_{j = l}^{m} T^{-j} a^j = \sum_{j = l}^{m} \tilde a^jT^{-j}, \]
\[ \mathcal{D}^* := \sum_{j = l}^{m} T^{-j} a^j = \sum_{j = l}^{m} \tilde a^jT^{-j}, \]
where ![]() $\tilde a^j_k = a_{k-j}^j$. In other words,
$\tilde a^j_k = a_{k-j}^j$. In other words, ![]() $\mathcal {D}^*$ is the formal adjoint of
$\mathcal {D}^*$ is the formal adjoint of ![]() $\mathcal {D}$ with respect to the
$\mathcal {D}$ with respect to the ![]() $l^2$ inner product on
$l^2$ inner product on ![]() $\mathbb {R}^\infty$, that is,
$\mathbb {R}^\infty$, that is, ![]() $\langle \xi, \mathcal {D} \eta \rangle = \langle \mathcal {D}^*\xi, \eta \rangle$ whenever at least one of these inner products is well-defined. In the periodic case, the duality between
$\langle \xi, \mathcal {D} \eta \rangle = \langle \mathcal {D}^*\xi, \eta \rangle$ whenever at least one of these inner products is well-defined. In the periodic case, the duality between ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {D}^*$ can also be understood as follows. If
$\mathcal {D}^*$ can also be understood as follows. If ![]() $\mathcal {D}$ is an
$\mathcal {D}$ is an ![]() $n$-periodic operator, then
$n$-periodic operator, then ![]() $\mathcal {D}^*$ is
$\mathcal {D}^*$ is ![]() $n$-periodic as well. Furthermore, the formula
$n$-periodic as well. Furthermore, the formula
 \begin{equation} \langle \xi, \eta \rangle := \sum_{k=1}^n \xi_k\eta_k \end{equation}
\begin{equation} \langle \xi, \eta \rangle := \sum_{k=1}^n \xi_k\eta_k \end{equation}
defines an inner product on the space ![]() $Q^n({1})$ of
$Q^n({1})$ of ![]() $n$-periodic sequences, and the restrictions of
$n$-periodic sequences, and the restrictions of ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {D}^*$ to
$\mathcal {D}^*$ to ![]() $Q^n({1})$ are dual to each other with respect to this inner product. More generally, for every
$Q^n({1})$ are dual to each other with respect to this inner product. More generally, for every ![]() $z \in \mathbb {R}^*$, the restriction of
$z \in \mathbb {R}^*$, the restriction of ![]() $\mathcal {D}$ to
$\mathcal {D}$ to ![]() $Q^n({z})$ is dual to the restriction of
$Q^n({z})$ is dual to the restriction of ![]() $\mathcal {D}^*$ to
$\mathcal {D}^*$ to ![]() $Q^n({z^{-1}})$ with respect to the pairing between
$Q^n({z^{-1}})$ with respect to the pairing between ![]() $Q^n({z})$ and
$Q^n({z})$ and ![]() $Q^n({z^{-1}})$ given by the same formula (7). As a corollary, we have
$Q^n({z^{-1}})$ given by the same formula (7). As a corollary, we have
In particular, a non-zero number ![]() $z \in \mathbb {R}^*$ is an eigenvalue of the monodromy of
$z \in \mathbb {R}^*$ is an eigenvalue of the monodromy of ![]() $\mathcal {D}$ if and only if
$\mathcal {D}$ if and only if ![]() $z^{-1}$ is an eigenvalue of the monodromy of
$z^{-1}$ is an eigenvalue of the monodromy of ![]() $\mathcal {D}^*$.
$\mathcal {D}^*$.
2.2 Difference operators and polygons
In this section we describe the space of projective equivalence classes of planar polygons as a certain quotient of third-order difference operators.
Definition 2.1 A polygon in ![]() $\mathbb {R}\mathbb {P}^2$ is a bi-infinite sequence of points
$\mathbb {R}\mathbb {P}^2$ is a bi-infinite sequence of points ![]() $v_k \in \mathbb {R}\mathbb {P}^2$ satisfying the following
$v_k \in \mathbb {R}\mathbb {P}^2$ satisfying the following ![]() $3$-in-a-row condition: for every
$3$-in-a-row condition: for every ![]() $k \in \mathbb {Z}$ the points
$k \in \mathbb {Z}$ the points ![]() $v_{k-1}, v_k, v_{k+1}$ are in general position.
$v_{k-1}, v_k, v_{k+1}$ are in general position.
Polygons modulo projective transformations can be encoded by means of properly bounded third-order difference operators, that is, operators of the form
where ![]() $a,b,c,d \in \mathbb {R}^\infty$ are such that
$a,b,c,d \in \mathbb {R}^\infty$ are such that ![]() $a_k \neq 0$,
$a_k \neq 0$, ![]() $d_k \neq 0$ for any
$d_k \neq 0$ for any ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
Proposition 2.2 (Cf. [Reference Ovsienko, Schwartz and TabachnikovOST10, Proposition 4.1])
For any ![]() $j \in \mathbb {Z}$, there is a one-to-one correspondence between projective equivalence classes of planar polygons and properly bounded difference operators
$j \in \mathbb {Z}$, there is a one-to-one correspondence between projective equivalence classes of planar polygons and properly bounded difference operators ![]() $\mathcal {D}$ supported in
$\mathcal {D}$ supported in ![]() $[j,j+3]$, considered up to the action
$[j,j+3]$, considered up to the action ![]() $\mathcal {D} \mapsto \lambda \circ \mathcal {D}\circ \mu ^{-1}$, where
$\mathcal {D} \mapsto \lambda \circ \mathcal {D}\circ \mu ^{-1}$, where ![]() $\lambda, \mu \in (\mathbb {R}^*)^\infty$ are sequences of non-zero real numbers, acting on
$\lambda, \mu \in (\mathbb {R}^*)^\infty$ are sequences of non-zero real numbers, acting on ![]() $\mathbb {R}^\infty$ by term-wise multiplication.
$\mathbb {R}^\infty$ by term-wise multiplication.
Proof. Given a properly bounded difference operator ![]() $\mathcal {D}$ supported in
$\mathcal {D}$ supported in ![]() $[j,j+3]$, consider its fundamental solution
$[j,j+3]$, consider its fundamental solution ![]() $V$, which is a sequence of non-zero vectors in
$V$, which is a sequence of non-zero vectors in ![]() $\mathbb {R}^3$ (see § 2.1). Each term
$\mathbb {R}^3$ (see § 2.1). Each term ![]() $V_k$ of that sequence determines a point
$V_k$ of that sequence determines a point ![]() $v_k \in \mathbb {R}\mathbb {P}^2$ with homogeneous coordinates given by
$v_k \in \mathbb {R}\mathbb {P}^2$ with homogeneous coordinates given by ![]() $V_k$. Furthermore, because
$V_k$. Furthermore, because ![]() $V$ is a fundamental solution, the vectors
$V$ is a fundamental solution, the vectors ![]() $V_k$,
$V_k$, ![]() $V_{k+1}$,
$V_{k+1}$, ![]() $V_{k+2}$ are linearly independent, and, thus, the sequence
$V_{k+2}$ are linearly independent, and, thus, the sequence ![]() $v_k \in \mathbb {R}\mathbb {P}^2$ satisfies the
$v_k \in \mathbb {R}\mathbb {P}^2$ satisfies the ![]() $3$-in-a-row condition. Note also that because the fundamental solution
$3$-in-a-row condition. Note also that because the fundamental solution ![]() $V$ is unique up to a linear transformation
$V$ is unique up to a linear transformation ![]() $V \mapsto AV$, it follows that the polygon
$V \mapsto AV$, it follows that the polygon ![]() $\{v_k\}$ is well-defined up to projective equivalence. Thus, with each properly bounded difference operator
$\{v_k\}$ is well-defined up to projective equivalence. Thus, with each properly bounded difference operator ![]() $\mathcal {D}$ supported in
$\mathcal {D}$ supported in ![]() $[j,j+3]$ one can associate a polygon
$[j,j+3]$ one can associate a polygon ![]() $\{v_k\}$, defined up to a projective transformation. Conversely, given a polygon
$\{v_k\}$, defined up to a projective transformation. Conversely, given a polygon ![]() $\{v_k\}$, one can revert this construction to obtain a properly bounded difference operator
$\{v_k\}$, one can revert this construction to obtain a properly bounded difference operator ![]() $\mathcal {D}$ supported in
$\mathcal {D}$ supported in ![]() $[j,j+3]$. To that end, one first lifts every point
$[j,j+3]$. To that end, one first lifts every point ![]() $v_k \in \mathbb {P}^2$ to a vector
$v_k \in \mathbb {P}^2$ to a vector ![]() $V_k \in \mathbb {R}^3$, and then finds an operator
$V_k \in \mathbb {R}^3$, and then finds an operator ![]() $\mathcal {D}$ whose fundamental solution is given by
$\mathcal {D}$ whose fundamental solution is given by ![]() $V$. Since the lifts
$V$. Since the lifts ![]() $V_k$ of the points
$V_k$ of the points ![]() $v_k$ are unique up to a transformation
$v_k$ are unique up to a transformation ![]() $V_k \mapsto \mu _k V_k$, whereas the choice of an operator
$V_k \mapsto \mu _k V_k$, whereas the choice of an operator ![]() $\mathcal {D}$ with a given fundamental solution
$\mathcal {D}$ with a given fundamental solution ![]() $V$ is unique up to
$V$ is unique up to ![]() $\mathcal {D} \mapsto \lambda \circ \mathcal {D}$, where
$\mathcal {D} \mapsto \lambda \circ \mathcal {D}$, where ![]() $\lambda \in (\mathbb {R}^*)^\infty$, it follows that the operator
$\lambda \in (\mathbb {R}^*)^\infty$, it follows that the operator ![]() $\mathcal {D}$ corresponding to a given polygon is defined up to the action
$\mathcal {D}$ corresponding to a given polygon is defined up to the action ![]() $\mathcal {D} \mapsto \lambda \circ \mathcal {D} \circ \mu ^{-1}$, as desired.
$\mathcal {D} \mapsto \lambda \circ \mathcal {D} \circ \mu ^{-1}$, as desired.
In what follows, we are interested in closed and, more generally, twisted polygons. A closed ![]() $n$-gon is a polygon satisfying
$n$-gon is a polygon satisfying ![]() $v_{k+n} = v_k$ for every
$v_{k+n} = v_k$ for every ![]() $k \in \mathbb {Z}$. For such a polygon, the corresponding difference operator
$k \in \mathbb {Z}$. For such a polygon, the corresponding difference operator ![]() $\mathcal {D}$ can be chosen to be
$\mathcal {D}$ can be chosen to be ![]() $n$-periodic. The converse is, however, not true: polygons corresponding to periodic operators are, in general, not closed but twisted. Indeed, if
$n$-periodic. The converse is, however, not true: polygons corresponding to periodic operators are, in general, not closed but twisted. Indeed, if ![]() $\mathcal {D}$ is a periodic operator, then its fundamental solution
$\mathcal {D}$ is a periodic operator, then its fundamental solution ![]() $V \in (\mathbb {R}^3)^\infty$ is, in general, not periodic, but satisfies
$V \in (\mathbb {R}^3)^\infty$ is, in general, not periodic, but satisfies ![]() $V_{k+n} = AV_k$, where
$V_{k+n} = AV_k$, where ![]() $A \in \mathrm {GL}_3(\mathbb {R})$ is the transposed monodromy of
$A \in \mathrm {GL}_3(\mathbb {R})$ is the transposed monodromy of ![]() $\mathcal {D}$. Therefore, the corresponding polygon satisfies
$\mathcal {D}$. Therefore, the corresponding polygon satisfies ![]() $v_{k+n} = \psi (v_k)$, where
$v_{k+n} = \psi (v_k)$, where ![]() $\psi \in \mathbb {P} \mathrm {GL}_3(\mathbb {R})$ is the projective transformation determined by the linear operator
$\psi \in \mathbb {P} \mathrm {GL}_3(\mathbb {R})$ is the projective transformation determined by the linear operator ![]() $A$.
$A$.
Definition 2.3 A twisted ![]() $n$-gon in
$n$-gon in ![]() $\mathbb {R}\mathbb {P}^2$ is a polygon
$\mathbb {R}\mathbb {P}^2$ is a polygon ![]() $\{v_k\}$ which satisfies
$\{v_k\}$ which satisfies ![]() $v_{k+n} = \psi (v_k)$ for some projective transformation
$v_{k+n} = \psi (v_k)$ for some projective transformation ![]() $\psi \in \mathbb {P} \mathrm {GL}_3$, called the monodromy of the polygon.
$\psi \in \mathbb {P} \mathrm {GL}_3$, called the monodromy of the polygon.
The above construction (see the proof of Proposition 2.2) allows one to identify the space of projective equivalence classes of twisted ![]() $n$-gons with an appropriate quotient of the space of
$n$-gons with an appropriate quotient of the space of ![]() $n$-periodic properly bounded difference operators supported in
$n$-periodic properly bounded difference operators supported in ![]() $[j, j+3]$. Under this identification, closed polygons correspond to those operators whose monodromy is a scalar multiple of the identity (furthermore, one can arrange that the monodromy of an operator corresponding to a closed polygon is exactly the identity).
$[j, j+3]$. Under this identification, closed polygons correspond to those operators whose monodromy is a scalar multiple of the identity (furthermore, one can arrange that the monodromy of an operator corresponding to a closed polygon is exactly the identity).
Remark 2.4 One can adapt the proof of Proposition 2.2 to show that for every ![]() $j \in \mathbb {Z}$ there is a one-to-one correspondence between projective equivalence classes of twisted planar
$j \in \mathbb {Z}$ there is a one-to-one correspondence between projective equivalence classes of twisted planar ![]() $n$-gons and properly bounded
$n$-gons and properly bounded ![]() $n$-periodic difference operators
$n$-periodic difference operators ![]() $\mathcal {D}$ supported in
$\mathcal {D}$ supported in ![]() $[j,j+3]$, considered up to the action
$[j,j+3]$, considered up to the action ![]() $\mathcal {D} \mapsto \lambda \circ \mathcal {D}\circ \mu ^{-1}$, where
$\mathcal {D} \mapsto \lambda \circ \mathcal {D}\circ \mu ^{-1}$, where ![]() $\lambda, \mu \in (\mathbb {R}^*)^\infty$ are sequences of non-zero real numbers which are
$\lambda, \mu \in (\mathbb {R}^*)^\infty$ are sequences of non-zero real numbers which are ![]() $n$-quasi-periodic and have the same monodromy. In other words, one has
$n$-quasi-periodic and have the same monodromy. In other words, one has ![]() $\lambda, \mu \in (\mathbb {R}^*)^\infty \cap Q^n({z})$ for some
$\lambda, \mu \in (\mathbb {R}^*)^\infty \cap Q^n({z})$ for some ![]() $z \in \mathbb {R}^*$ where the space
$z \in \mathbb {R}^*$ where the space ![]() $Q^n({z})$ is defined by (5). We do not use the result in this form in the paper, so we omit the proof.
$Q^n({z})$ is defined by (5). We do not use the result in this form in the paper, so we omit the proof.
We also mention that when ![]() $n$ is not divisible by three, the above-described action of quasi-periodic sequences on difference operators admits a section given by
$n$ is not divisible by three, the above-described action of quasi-periodic sequences on difference operators admits a section given by ![]() $n$-periodic operators of the form
$n$-periodic operators of the form ![]() $T^j + b T^{j+1} + aT^{j+2} - T^{j+3}.$ This is essentially the content of [Reference Ovsienko, Schwartz and TabachnikovOST10, Proposition 4.1]. As a result, the entries of periodic sequences
$T^j + b T^{j+1} + aT^{j+2} - T^{j+3}.$ This is essentially the content of [Reference Ovsienko, Schwartz and TabachnikovOST10, Proposition 4.1]. As a result, the entries of periodic sequences ![]() $a$,
$a$, ![]() $b$ constitute a global coordinate system on the space of projective equivalence classes of twisted planar
$b$ constitute a global coordinate system on the space of projective equivalence classes of twisted planar ![]() $n$-gons. Such a coordinate system is no longer available when
$n$-gons. Such a coordinate system is no longer available when ![]() $n$ is divisible by three, however our description of the twisted
$n$ is divisible by three, however our description of the twisted ![]() $n$-gons space as a quotient remains valid.
$n$-gons space as a quotient remains valid.
Dual difference operators correspond to projectively dual polygons. Recall that the dual of a polygon is the polygon in the dual projective plane whose vertices are the sides of the initial one. Note that although there is, in general, no canonical way to label the vertices of the dual polygon, polygons with odd number of vertices admit one particular labeling which is more symmetric than the others. This labeling is depicted in Figure 4. For closed polygons, such labeling makes projective duality an involution. For twisted polygons, it is only an involution up to the action of the monodromy, but still an actual involution on projective equivalence classes.
Definition 2.5 Let ![]() $P$ be a closed or twisted
$P$ be a closed or twisted ![]() $n$-gon with odd
$n$-gon with odd ![]() $n$. Then the
$n$. Then the ![]() $k$th vertex of its dual polygon
$k$th vertex of its dual polygon ![]() $P^*$ is the side of
$P^*$ is the side of ![]() $P$ which joins the vertices with indices
$P$ which joins the vertices with indices ![]() ${k+(n-1)/2}$,
${k+(n-1)/2}$, ![]() ${k+(n+1)/2}$. A polygon
${k+(n+1)/2}$. A polygon ![]() $P$ is called self-dual if it is projectively equivalent to its dual polygon
$P$ is called self-dual if it is projectively equivalent to its dual polygon ![]() $P^*$.
$P^*$.
Remark 2.6 Closed self-dual polygons are studied in [Reference Fuchs and TabachnikovFT09]. In that paper, polygons which are self-dual in the sense of Definition 2.5 are called ![]() $n$-self-dual (where
$n$-self-dual (where ![]() $n$ is the number of vertices).
$n$ is the number of vertices).
With our definition of duality, we have the following result.
Proposition 2.7 Let ![]() $n$ be odd. Consider a
$n$ be odd. Consider a ![]() $n$-periodic properly bounded difference operator supported in
$n$-periodic properly bounded difference operator supported in ![]() $[(n-3)/2, (n+3)/2]$ and its dual operator
$[(n-3)/2, (n+3)/2]$ and its dual operator ![]() $\mathcal {D}^*.$ Then the polygons corresponding to
$\mathcal {D}^*.$ Then the polygons corresponding to ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {D}^*$ are dual to each other in the sense of Definition 2.5.
$\mathcal {D}^*$ are dual to each other in the sense of Definition 2.5.
Proof. This follows from more general Proposition A.1 in Appendix A.
2.3 Corner invariants and rescaling
Another description of the space of polygons modulo projective transformations is by means of so-called corner invariants [Reference SchwartzSch08, Reference Ovsienko, Schwartz and TabachnikovOST10]. To every vertex ![]() $v_k$ of a polygon, one associates two cross-ratios
$v_k$ of a polygon, one associates two cross-ratios ![]() $x_k, y_k$, as shown in Figure 5. The definition of the cross-ratio that we use is
$x_k, y_k$, as shown in Figure 5. The definition of the cross-ratio that we use is
Remark 2.8 Note that the definition of ![]() $x_k, y_k$ requires somewhat more than the
$x_k, y_k$ requires somewhat more than the ![]() $3$-in-a-row condition. However, we do not need to care about this, because in this paper we only deal with weakly convex polygons (see Definition 3.1 below) for which the numbers
$3$-in-a-row condition. However, we do not need to care about this, because in this paper we only deal with weakly convex polygons (see Definition 3.1 below) for which the numbers ![]() $x_k, y_k$ are well-defined by definition.
$x_k, y_k$ are well-defined by definition.

Figure 5. The definition of corner invariants.
Clearly, the sequences ![]() $x_k$,
$x_k$, ![]() $y_k$ only depend on the projective equivalence class of the polygon. Furthermore, in the twisted case these sequences are
$y_k$ only depend on the projective equivalence class of the polygon. Furthermore, in the twisted case these sequences are ![]() $n$-periodic, and
$n$-periodic, and ![]() $\{ x_1, y_1, \ldots, x_n, y_n\}$ is a coordinate chart on an open dense subset of twisted
$\{ x_1, y_1, \ldots, x_n, y_n\}$ is a coordinate chart on an open dense subset of twisted ![]() $n$-gons modulo projective transformations. Therefore, because the pentagram map preserves the space of twisted polygons and commutes with projective transformations, it can be written in terms of the
$n$-gons modulo projective transformations. Therefore, because the pentagram map preserves the space of twisted polygons and commutes with projective transformations, it can be written in terms of the ![]() $(x,y)$ coordinates. The following formulas were obtained in [Reference Ovsienko, Schwartz and TabachnikovOST10].
$(x,y)$ coordinates. The following formulas were obtained in [Reference Ovsienko, Schwartz and TabachnikovOST10].
Proposition 2.9 One has
where ![]() $x_k,y_k$ are the corner invariants of the polygon
$x_k,y_k$ are the corner invariants of the polygon ![]() $P$, and
$P$, and ![]() $x_k', y_k'$ are corner invariants of its pentagram image
$x_k', y_k'$ are corner invariants of its pentagram image ![]() $P'$.
$P'$.
Here we label ![]() $P'$ as in [Reference Ovsienko, Schwartz and TabachnikovOST10]. The labeling used in Figure 3 leads to the same formulas with a certain shift of indices. Although we never use these explicit formulas, we use the following corollary: the pentagram map, with any labeling of vertices, commutes with the
$P'$ as in [Reference Ovsienko, Schwartz and TabachnikovOST10]. The labeling used in Figure 3 leads to the same formulas with a certain shift of indices. Although we never use these explicit formulas, we use the following corollary: the pentagram map, with any labeling of vertices, commutes with the ![]() $1$-parametric group of transformations
$1$-parametric group of transformations ![]() $R_s$ given by
$R_s$ given by
These transformations are known as rescaling. They were introduced in [Reference Ovsienko, Schwartz and TabachnikovOST10] to prove that the pentagram map is a completely integrable system.
We now discuss the relation between two representations of the space of polygons: in terms of difference operators, and in terms of corner invariants.
Proposition 2.10 Assume we are given a polygon ![]() $P$ defined by a difference operator (8) supported in
$P$ defined by a difference operator (8) supported in ![]() $[j,j+3]$. Then the corner invariants of
$[j,j+3]$. Then the corner invariants of ![]() $P$ are given by
$P$ are given by
Proof. The proof is a computation following the lines of the proof of Lemma 4.5 in [Reference Ovsienko, Schwartz and TabachnikovOST10].
Formulas (10) allow one to describe rescaling operation (9) in terms of difference operators as follows.
Corollary 2.11 In terms of difference operators, rescaling (9) can be defined as
Proof. Formulas (10) show that multiplying ![]() $c$ and
$c$ and ![]() $d$ coefficients by
$d$ coefficients by ![]() $s$ is equivalent to multiplying
$s$ is equivalent to multiplying ![]() $x$ variables by
$x$ variables by ![]() $s$ and
$s$ and ![]() $y$ variables by
$y$ variables by ![]() $s^{-1}$, which is exactly rescaling (9).
$s^{-1}$, which is exactly rescaling (9).
Remark 2.12 Note that because there are many operators corresponding to a given polygon, there are also many different ways to define the rescaling on operators. For example, the following formula defines the same operation on polygons as the formula provided above:
3. Weakly convex polygons
In this section we define weakly convex polygons and describe their properties needed to prove Theorems B and A.
Definition 3.1 A polygon is weakly convex if its corner invariants are well-defined and satisfy
Proposition 3.2 Convex polygons are weakly convex.
Proof. For convex polygons, the collinear points ![]() $v_{k-2}$,
$v_{k-2}$, ![]() $v_{k-1}$,
$v_{k-1}$, ![]() $\tilde v_k$,
$\tilde v_k$, ![]() $\bar v_k$ in Figure 5 are distinct and their cyclic order is exactly as shown. Thus,
$\bar v_k$ in Figure 5 are distinct and their cyclic order is exactly as shown. Thus, ![]() $x_k$ is well-defined and
$x_k$ is well-defined and ![]() $0 < x_k< 1$. Likewise, we have
$0 < x_k< 1$. Likewise, we have ![]() $y_k \in (0,1)$. The result follows.
$y_k \in (0,1)$. The result follows.
Remark 3.3 More generally, all corner invariants of a polygon satisfy ![]() $x_k, y_k \in (0,1)$ if and only if any five consecutive vertices of that polygon form a convex pentagon (where by a convex pentagon in
$x_k, y_k \in (0,1)$ if and only if any five consecutive vertices of that polygon form a convex pentagon (where by a convex pentagon in ![]() $\mathbb {R}\mathbb {P}^2$ we mean a pentagon which is convex in a suitable affine chart). Thus, all polygons satisfying this ‘5-in-a-row’ condition are weakly convex. The geometric meaning of the general weak convexity condition is not that clear. However, it turns out to be really convenient for the purposes of the present paper.
$\mathbb {R}\mathbb {P}^2$ we mean a pentagon which is convex in a suitable affine chart). Thus, all polygons satisfying this ‘5-in-a-row’ condition are weakly convex. The geometric meaning of the general weak convexity condition is not that clear. However, it turns out to be really convenient for the purposes of the present paper.
The following is an exhaustive list of properties of weakly convex polygons needed for our purposes.
Proposition 3.4 Assume that ![]() $P$ is a closed or twisted weakly convex
$P$ is a closed or twisted weakly convex ![]() $n$-gon, where
$n$-gon, where ![]() $n \geq 3$ is odd.
$n \geq 3$ is odd.
1. The corresponding third-order
 $n$-periodic difference operator (8) can be chosen in such a way that for all
$n$-periodic difference operator (8) can be chosen in such a way that for all  $k \in \mathbb {Z}$ we have
(11)
$k \in \mathbb {Z}$ we have
(11) \begin{equation} a_k, c_k > 0, \quad b_k, d_k < 0. \end{equation}
\begin{equation} a_k, c_k > 0, \quad b_k, d_k < 0. \end{equation}2. For any difference operator (8) corresponding to
 $P$ and satisfying (11), consider the operators
$P$ and satisfying (11), consider the operators  $\mathcal {D}_l := a T^j + bT^{j+1}, \mathcal {D}_r := cT^{j+2} + dT^{j+3}$. Then the monodromies
$\mathcal {D}_l := a T^j + bT^{j+1}, \mathcal {D}_r := cT^{j+2} + dT^{j+3}$. Then the monodromies  $z_l, z_r$ of these operators (which are real numbers because the operators are of first order) satisfy
$z_l, z_r$ of these operators (which are real numbers because the operators are of first order) satisfy  $0 < z_l < z_r$. In particular, we have
$0 < z_l < z_r$. In particular, we have  $\mathrm {Ker}\, \mathcal {D}_l \cap \mathrm {Ker}\, \mathcal {D}_r = 0$.
$\mathrm {Ker}\, \mathcal {D}_l \cap \mathrm {Ker}\, \mathcal {D}_r = 0$.3. Any polygon obtained from
 $P$ by means of rescaling (9) with
$P$ by means of rescaling (9) with  $s > 0$ is weakly convex.
$s > 0$ is weakly convex.4. Any polygon obtained from
 $P$ by means of rescaling (9) with
$P$ by means of rescaling (9) with  $s < 0$ has monodromy with distinct eigenvalues.
$s < 0$ has monodromy with distinct eigenvalues.
Proof. To prove the first statement, consider the corner invariants ![]() $x_k, y_k > 0$ of
$x_k, y_k > 0$ of ![]() $P$, and let
$P$, and let
Then, by Proposition 2.10, the polygon associated with ![]() $\mathcal {D}$ is
$\mathcal {D}$ is ![]() $P$. Furthermore, the signs of coefficients of
$P$. Furthermore, the signs of coefficients of ![]() $\mathcal {D}$ satisfy (11), as needed.
$\mathcal {D}$ satisfy (11), as needed.
To prove the second statement, consider an arbitrary operator (8) representing ![]() $P$ and satisfying (11), along with the associated operators
$P$ and satisfying (11), along with the associated operators ![]() $\mathcal {D}_r, \mathcal {D}_l$. Then, by formula (6), the monodromies of those operators are given by
$\mathcal {D}_r, \mathcal {D}_l$. Then, by formula (6), the monodromies of those operators are given by
 \[ z_l = -\prod_{k=1}^n \frac{ a_k}{ b_k}, \quad z_r = -\prod_{k=1}^n\frac{ c_k}{ d_k}, \]
\[ z_l = -\prod_{k=1}^n \frac{ a_k}{ b_k}, \quad z_r = -\prod_{k=1}^n\frac{ c_k}{ d_k}, \]
so ![]() $z_l, z_r > 0$ due to (11) and
$z_l, z_r > 0$ due to (11) and ![]() $n$ being odd. Further, using formulas (10), we obtain
$n$ being odd. Further, using formulas (10), we obtain
 \[ \frac{z_l}{z_r} = \prod_{k=1}^n \frac{ a _k d_{k}}{b_{k} c_{k}} = \prod_{k=1}^n x_{k} y_k, \]
\[ \frac{z_l}{z_r} = \prod_{k=1}^n \frac{ a _k d_{k}}{b_{k} c_{k}} = \prod_{k=1}^n x_{k} y_k, \]
where ![]() $x_k, y_k$ are the corner invariants of
$x_k, y_k$ are the corner invariants of ![]() $P$. However, because
$P$. However, because ![]() $P$ is weakly convex, we have
$P$ is weakly convex, we have ![]() $x_ky_k < 1$ and, thus,
$x_ky_k < 1$ and, thus, ![]() $z_l < z_r$. This, in turn, implies
$z_l < z_r$. This, in turn, implies ![]() $\mathrm {Ker}\, \mathcal {D}_l \cap \mathrm {Ker}\, \mathcal {D}_r = 0$, because non-zero elements of the kernel of
$\mathrm {Ker}\, \mathcal {D}_l \cap \mathrm {Ker}\, \mathcal {D}_r = 0$, because non-zero elements of the kernel of ![]() $\mathcal {D}_l$ are sequences with monodromy
$\mathcal {D}_l$ are sequences with monodromy ![]() $z_l$, whereas non-zero elements of the kernel of
$z_l$, whereas non-zero elements of the kernel of ![]() $\mathcal {D}_r$ are sequences with monodromy
$\mathcal {D}_r$ are sequences with monodromy ![]() $z_r \neq z_l$. Thus, the second statement is proved.
$z_r \neq z_l$. Thus, the second statement is proved.
The third statement is obvious from the definitions of weak convexity and rescaling, so we proceed to the fourth statement. Let ![]() $P_{\rm sd}$ be a polygon obtained from
$P_{\rm sd}$ be a polygon obtained from ![]() $P$ by means of rescaling with
$P$ by means of rescaling with ![]() $s < 0$. Then the corner invariants
$s < 0$. Then the corner invariants ![]() $\hat x_k, \hat y_k$ of
$\hat x_k, \hat y_k$ of ![]() $P_{\rm sd}$ satisfy
$P_{\rm sd}$ satisfy ![]() $\hat x_k, \hat y_k < 0$,
$\hat x_k, \hat y_k < 0$, ![]() $\hat x_k\hat y_k < 1$. To show that the monodromy of such a polygon has distinct eigenvalues, we use a result from [Reference IzosimovIzo16, Appendix A] which states that the monodromy of a twisted
$\hat x_k\hat y_k < 1$. To show that the monodromy of such a polygon has distinct eigenvalues, we use a result from [Reference IzosimovIzo16, Appendix A] which states that the monodromy of a twisted ![]() $n$-gon with corner invariants
$n$-gon with corner invariants ![]() $\hat x_k, \hat y_k$ is conjugate to the product
$\hat x_k, \hat y_k$ is conjugate to the product ![]() $L_1\cdot \cdots \cdot L_n$, where
$L_1\cdot \cdots \cdot L_n$, where
 \[ L_k := \left(\begin{array}{@{}ccc@{}} 1 & 0 & 1 \\ 1-\hat x_k\hat y_k & 0 & 1 \\ 0 & -\hat y_k & 0\end{array}\right).\]
\[ L_k := \left(\begin{array}{@{}ccc@{}} 1 & 0 & 1 \\ 1-\hat x_k\hat y_k & 0 & 1 \\ 0 & -\hat y_k & 0\end{array}\right).\]
Note that because ![]() $\hat y_k < 0$ and
$\hat y_k < 0$ and ![]() $\hat x_k \hat y_k < 1$, the matrices
$\hat x_k \hat y_k < 1$, the matrices ![]() $L_k$ are non-negative. Furthermore, the product of at least three such matrices is positive, so the matrix
$L_k$ are non-negative. Furthermore, the product of at least three such matrices is positive, so the matrix ![]() $M := L_1\cdot \cdots \cdot L_n$ is positive. Therefore, by the Perron–Frobenius theorem,
$M := L_1\cdot \cdots \cdot L_n$ is positive. Therefore, by the Perron–Frobenius theorem, ![]() $M$ has a real positive eigenvalue
$M$ has a real positive eigenvalue ![]() $z_1$ such that its any other eigenvalue
$z_1$ such that its any other eigenvalue ![]() $z$ satisfies
$z$ satisfies ![]() $|z| < z_1$. Furthermore, because
$|z| < z_1$. Furthermore, because ![]() $\hat x_k < 0$ and
$\hat x_k < 0$ and ![]() $n$ is odd, we have
$n$ is odd, we have ![]() $\det M= \hat x_1 \cdot \cdots \cdot \hat x_n(\hat y_1 \cdot \cdots \cdot \hat y_n)^2 < 0$, so the product of two other eigenvalues
$\det M= \hat x_1 \cdot \cdots \cdot \hat x_n(\hat y_1 \cdot \cdots \cdot \hat y_n)^2 < 0$, so the product of two other eigenvalues ![]() $z_2, z_3$ of
$z_2, z_3$ of ![]() $M$ is negative, which means that they are real and distinct. The result follows.
$M$ is negative, which means that they are real and distinct. The result follows.
4. Polygons fixed by the pentagram map and commuting difference operators
In this section we show that a closed or twisted polygon ![]() $P$ projectively equivalent to its pentagram image
$P$ projectively equivalent to its pentagram image ![]() $P'$ gives rise to commuting difference operators. This is the first step in the proof of both Theorems A and B. In addition, in the self-dual case (i.e. in the setting of Theorem B) we show that those commuting operators are negative duals of each other.
$P'$ gives rise to commuting difference operators. This is the first step in the proof of both Theorems A and B. In addition, in the self-dual case (i.e. in the setting of Theorem B) we show that those commuting operators are negative duals of each other.
Let ![]() $P = \{v_k\}$ be a closed or twisted
$P = \{v_k\}$ be a closed or twisted ![]() $n$-gon with odd
$n$-gon with odd ![]() $n$, and let
$n$, and let ![]() $P' = \{v_k'\}$ be the image of
$P' = \{v_k'\}$ be the image of ![]() $P$ under the pentagram map, labeled as in Figure 3. Then, as explained in § 2.2, one can encode
$P$ under the pentagram map, labeled as in Figure 3. Then, as explained in § 2.2, one can encode ![]() $P'$ by means of a difference operator
$P'$ by means of a difference operator ![]() $\mathcal {D}$ of the form
$\mathcal {D}$ of the form
The coefficients of this operator are related to the polygon ![]() $P'$ by means of the equation
$P'$ by means of the equation
where ![]() $V'_k$ are lifts of the vertices
$V'_k$ are lifts of the vertices ![]() $v_k'$ of
$v_k'$ of ![]() $P'$.
$P'$.
Proposition 4.1 The vector
is the lift of the vertex ![]() $v_k$ of
$v_k$ of ![]() $P$.
$P$.
Proof. Indeed, we have
which means that the projection of ![]() $V_k$ to
$V_k$ to ![]() $\mathbb {P}^2$ is the intersection point of the lines
$\mathbb {P}^2$ is the intersection point of the lines ![]() $(v'_{k + (n-3)/2},v'_{k+(n-1)/2})$ and
$(v'_{k + (n-3)/2},v'_{k+(n-1)/2})$ and ![]() $(v'_{k + (n+1)/2}, v'_{k+(n+3)/2})$. By the definition of the pentagram map with our labeling convention, this is exactly the vertex
$(v'_{k + (n+1)/2}, v'_{k+(n+3)/2})$. By the definition of the pentagram map with our labeling convention, this is exactly the vertex ![]() $v_k$ of
$v_k$ of ![]() $P$, as desired.
$P$, as desired.
Now, as in Proposition 3.4, consider the operators
By Proposition 4.1, these operators take the lifts ![]() $V_k'$ of the vertices of
$V_k'$ of the vertices of ![]() $P'$ to the lifts
$P'$ to the lifts ![]() $\pm V_k$ of the vertices of
$\pm V_k$ of the vertices of ![]() $P$.
$P$.
Proposition 4.2 Assume that a closed or twisted ![]() $n$-gon (where
$n$-gon (where ![]() $n \geq 5$ is arbitrary)
$n \geq 5$ is arbitrary) ![]() $P$ is projectively equivalent to its pentagram image
$P$ is projectively equivalent to its pentagram image ![]() $P'$.
$P'$.
1. One can choose the
 $n$-periodic operator
$n$-periodic operator  $\mathcal {D}$ of the form (12) associated with
$\mathcal {D}$ of the form (12) associated with  $P$ in such a way that the corresponding operators
$P$ in such a way that the corresponding operators  $\mathcal {D}_l , \mathcal {D}_r$ given by (13) commute:
(14)
$\mathcal {D}_l , \mathcal {D}_r$ given by (13) commute:
(14) \begin{equation} \mathcal{D}_l \mathcal{D}_r = \mathcal{D}_r \mathcal{D}_l . \end{equation}
\begin{equation} \mathcal{D}_l \mathcal{D}_r = \mathcal{D}_r \mathcal{D}_l . \end{equation}2. Furthermore, if
 $P$ is weakly convex and
$P$ is weakly convex and  $n$ is odd, then
$n$ is odd, then  $\mathcal {D}$ can be chosen to satisfy the alternating signs condition (11).
$\mathcal {D}$ can be chosen to satisfy the alternating signs condition (11).3. If, on top of that,
 $P$ is self-dual, then
$P$ is self-dual, then  $\mathcal {D}_l$,
$\mathcal {D}_l$,  $\mathcal {D}_r$ may be chosen to be negative duals of each other (up to multiplication by
$\mathcal {D}_r$ may be chosen to be negative duals of each other (up to multiplication by  $T^{-n}$):
Equivalently, the operator
$T^{-n}$):
Equivalently, the operator \[ \mathcal{D}_l^* = -T^{-n}\mathcal{D}_r. \]
\[ \mathcal{D}_l^* = -T^{-n}\mathcal{D}_r. \] $\mathcal {D} = \mathcal {D}_l + \mathcal {D}_r$ can be chosen to be anti-self-dual (again, up to multiplication by
$\mathcal {D} = \mathcal {D}_l + \mathcal {D}_r$ can be chosen to be anti-self-dual (again, up to multiplication by  $T^{-n}$):
$T^{-n}$):
 \[ \mathcal{D}^* = -T^{-n}\mathcal{D}. \]
\[ \mathcal{D}^* = -T^{-n}\mathcal{D}. \]
Proof of Proposition 4.2 We begin with the first statement. Take an arbitrary ![]() $n$-periodic operator
$n$-periodic operator ![]() $\tilde{\mathcal {D}}$ of the form (12) representing the polygon
$\tilde{\mathcal {D}}$ of the form (12) representing the polygon ![]() $P$. Then, because
$P$. Then, because ![]() $P'$ is projectively equivalent to
$P'$ is projectively equivalent to ![]() $P$, there is a fundamental solution
$P$, there is a fundamental solution ![]() $V'$ of
$V'$ of ![]() $\tilde{\mathcal {D}}$ such that the projection of
$\tilde{\mathcal {D}}$ such that the projection of ![]() $V'_k$ to
$V'_k$ to ![]() $\mathbb {P}^2$ is the
$\mathbb {P}^2$ is the ![]() $k$th vertex of
$k$th vertex of ![]() $P'$. Consider the projective transformation taking
$P'$. Consider the projective transformation taking ![]() $P'$ to
$P'$ to ![]() $P$. Any lift
$P$. Any lift ![]() $A \in \mathrm {GL}_3(\mathbb {R})$ of this projective transformation will then take the sequence
$A \in \mathrm {GL}_3(\mathbb {R})$ of this projective transformation will then take the sequence ![]() $V'$ to a sequence of lifts of vertices of
$V'$ to a sequence of lifts of vertices of ![]() $P$. On the other hand, by Proposition 4.1, lifts of vertices of
$P$. On the other hand, by Proposition 4.1, lifts of vertices of ![]() $P$ are given by the sequence
$P$ are given by the sequence ![]() $\tilde{\mathcal {D}}_l V'$. Thus, there is an
$\tilde{\mathcal {D}}_l V'$. Thus, there is an ![]() $n$-periodic sequence
$n$-periodic sequence ![]() $\mu$ of non-zero real numbers such that
$\mu$ of non-zero real numbers such that ![]() $AV' = \mu \tilde{\mathcal {D}}_l V',$ where
$AV' = \mu \tilde{\mathcal {D}}_l V',$ where ![]() $A$ acts on sequences of vectors by term-wise multiplication. Let
$A$ acts on sequences of vectors by term-wise multiplication. Let ![]() $\mathcal {D}:=\mu \tilde{\mathcal {D}}$. Then the operator
$\mathcal {D}:=\mu \tilde{\mathcal {D}}$. Then the operator ![]() $\mathcal {D}$ still satisfies
$\mathcal {D}$ still satisfies ![]() $\mathcal {D} V'=0$ and, hence, represents the same polygons
$\mathcal {D} V'=0$ and, hence, represents the same polygons ![]() $P$ and
$P$ and ![]() $P'$. Furthermore, the corresponding operator
$P'$. Furthermore, the corresponding operator ![]() $\mathcal {D}_l$ satisfies
$\mathcal {D}_l$ satisfies ![]() $AV' = \mathcal {D}_l V'.$ Applying the operator
$AV' = \mathcal {D}_l V'.$ Applying the operator ![]() $\mathcal {D}$ to both sides, we obtain
$\mathcal {D}$ to both sides, we obtain ![]() $\mathcal {D} \mathcal {D}_l V' = 0.$ Also taking into account that
$\mathcal {D} \mathcal {D}_l V' = 0.$ Also taking into account that ![]() $\mathcal {D} V' = 0$, this can be rewritten as
$\mathcal {D} V' = 0$, this can be rewritten as
At the same time, we have
so (15) gives
Now it remains to note that the commutator ![]() $[\mathcal {D}_r , \mathcal {D}_l ]$ is of the form
$[\mathcal {D}_r , \mathcal {D}_l ]$ is of the form ![]() $\alpha T^{n-1} + \beta T^n + \gamma T^{n+1},$ so (16) is equivalent to
$\alpha T^{n-1} + \beta T^n + \gamma T^{n+1},$ so (16) is equivalent to ![]() $\alpha _k V'_{k + n -1} + \beta _k V'_{k+n} + \gamma _k V'_{k+n+1} = 0,$ which, in view of the
$\alpha _k V'_{k + n -1} + \beta _k V'_{k+n} + \gamma _k V'_{k+n+1} = 0,$ which, in view of the ![]() $3$-in-a-row condition for
$3$-in-a-row condition for ![]() $P'$ (which holds because it holds for
$P'$ (which holds because it holds for ![]() $P$), gives
$P$), gives ![]() $\alpha _k = \beta _k = \gamma _k = 0$ and, thus,
$\alpha _k = \beta _k = \gamma _k = 0$ and, thus, ![]() $[\mathcal {D}_r , \mathcal {D}_l ] = 0,$ as desired.
$[\mathcal {D}_r , \mathcal {D}_l ] = 0,$ as desired.
To prove the second statement, one repeats the same argument, with the only modification that the initial operator ![]() $\tilde{\mathcal {D}}$ should be chosen to satisfy (11), which can be done by the first statement of Proposition 3.4. Then the coefficients
$\tilde{\mathcal {D}}$ should be chosen to satisfy (11), which can be done by the first statement of Proposition 3.4. Then the coefficients ![]() $a,b,c,d$ of the operator
$a,b,c,d$ of the operator ![]() $\mathcal {D} = \mu \tilde{\mathcal {D}}$ satisfy
$\mathcal {D} = \mu \tilde{\mathcal {D}}$ satisfy ![]() $\mathrm {sgn}\,(a_k) = -\mathrm {sgn}\,(b_k) = \mathrm {sgn}\,( c_k) = -\mathrm {sgn}\,(d_k)$. Furthermore, we claim that
$\mathrm {sgn}\,(a_k) = -\mathrm {sgn}\,(b_k) = \mathrm {sgn}\,( c_k) = -\mathrm {sgn}\,(d_k)$. Furthermore, we claim that ![]() $a_k$ are all of the same sign. Indeed, using explicit formulas (13) for
$a_k$ are all of the same sign. Indeed, using explicit formulas (13) for ![]() $\mathcal {D}_l$ and
$\mathcal {D}_l$ and ![]() $\mathcal {D}_r$ and equating the coefficients of
$\mathcal {D}_r$ and equating the coefficients of ![]() $T^{n-1}$ in (14), we obtain
$T^{n-1}$ in (14), we obtain
Furthermore, we have ![]() $\mathrm {sgn} c_j = \mathrm {sgn} a_j$ for any
$\mathrm {sgn} c_j = \mathrm {sgn} a_j$ for any ![]() $j$, so taking the signs of both sides of (17) we obtain
$j$, so taking the signs of both sides of (17) we obtain
which means that the sequence ![]() $\mathrm {sgn} a_k$ is
$\mathrm {sgn} a_k$ is ![]() $2$-periodic. However, because the period
$2$-periodic. However, because the period ![]() $n$ of the sequence
$n$ of the sequence ![]() $a_k$ is an odd number, it follows that
$a_k$ is an odd number, it follows that ![]() $\mathrm {sgn} a_k = \mathrm {const}$. Now, multiplying
$\mathrm {sgn} a_k = \mathrm {const}$. Now, multiplying ![]() $\mathcal {D}$ by
$\mathcal {D}$ by ![]() $-1$ is necessary, we can arrange that
$-1$ is necessary, we can arrange that ![]() $a_k > 0$ for all
$a_k > 0$ for all ![]() $k$, so that
$k$, so that ![]() $\mathcal {D}$ has satisfies (11), as needed.
$\mathcal {D}$ has satisfies (11), as needed.
To prove the third statement, we consider the operator ![]() $\mathcal {D}$ constructed above and show that if
$\mathcal {D}$ constructed above and show that if ![]() $P$ is self-dual, then
$P$ is self-dual, then ![]() $\mathcal {D}$ can be replaced with another operator, which has all the properties of
$\mathcal {D}$ can be replaced with another operator, which has all the properties of ![]() $\mathcal {D}$ and is, in addition, anti-self-dual. To that end, observe that if
$\mathcal {D}$ and is, in addition, anti-self-dual. To that end, observe that if ![]() $P$ is self-dual, then the operators
$P$ is self-dual, then the operators ![]() $\mathcal {D}$ and
$\mathcal {D}$ and ![]() $\mathcal {D}^*$ represent the same polygon, so
$\mathcal {D}^*$ represent the same polygon, so
for certain sequences ![]() $\alpha, \beta$ of non-zero real numbers. Taking the duals, we obtain
$\alpha, \beta$ of non-zero real numbers. Taking the duals, we obtain
which implies ![]() $\beta = \pm \alpha$. Further, because
$\beta = \pm \alpha$. Further, because ![]() $\mathcal {D}$ satisfies (11), the corresponding coefficients of
$\mathcal {D}$ satisfies (11), the corresponding coefficients of ![]() $\mathcal {D}^*$ and
$\mathcal {D}^*$ and ![]() $T^{-n } \mathcal {D}$ are of opposite sign, so (18) implies
$T^{-n } \mathcal {D}$ are of opposite sign, so (18) implies ![]() $\mathrm {sgn}\,(\alpha _k) = -\mathrm {sgn}\,(\beta _k) = \mathrm {const}$, and we must have
$\mathrm {sgn}\,(\alpha _k) = -\mathrm {sgn}\,(\beta _k) = \mathrm {const}$, and we must have ![]() $\beta = -\alpha$. Therefore,
$\beta = -\alpha$. Therefore,
where ![]() $\mathrm {sgn}\,(\alpha _k) = \mathrm {const}$ and without loss of generality we can assume
$\mathrm {sgn}\,(\alpha _k) = \mathrm {const}$ and without loss of generality we can assume ![]() $\alpha _k > 0$. Furthermore, because both operators
$\alpha _k > 0$. Furthermore, because both operators ![]() $\mathcal {D}^*$,
$\mathcal {D}^*$, ![]() $T^{-n } \mathcal {D}$ are
$T^{-n } \mathcal {D}$ are ![]() $n$-periodic, the sequence
$n$-periodic, the sequence ![]() $\alpha$ is quasi-periodic, that is,
$\alpha$ is quasi-periodic, that is, ![]() $\alpha _{k+n} = z\alpha _k$ for some
$\alpha _{k+n} = z\alpha _k$ for some ![]() $z \in \mathbb {R}^*$ (actually,
$z \in \mathbb {R}^*$ (actually, ![]() $z \in \mathbb {R}_+$). Now, let
$z \in \mathbb {R}_+$). Now, let ![]() $\gamma _k := \sqrt {\alpha _k}$. Then the sequence
$\gamma _k := \sqrt {\alpha _k}$. Then the sequence ![]() $\gamma$ is also quasi-periodic, so the operator
$\gamma$ is also quasi-periodic, so the operator ![]() $\mathcal {D}': = \gamma \mathcal {D} \gamma ^{-1}$ is
$\mathcal {D}': = \gamma \mathcal {D} \gamma ^{-1}$ is ![]() $n$-periodic. Moreover, it has all the properties of
$n$-periodic. Moreover, it has all the properties of ![]() $\mathcal {D}$ and is anti-self-dual. Thus, the proposition is proved.
$\mathcal {D}$ and is anti-self-dual. Thus, the proposition is proved.
Remark 4.3 It is easy to see from the proof that the converse of the first statement is also true: if ![]() $\mathcal {D}_r$ and
$\mathcal {D}_r$ and ![]() $\mathcal {D}_l$ commute, then
$\mathcal {D}_l$ commute, then ![]() $P$ is projectively equivalent to
$P$ is projectively equivalent to ![]() $P'$. For instance, consider the polygon
$P'$. For instance, consider the polygon ![]() $P$ from Remark 1.3. The vertices of that polygon can be lifted to vectors
$P$ from Remark 1.3. The vertices of that polygon can be lifted to vectors ![]() $V_k := (\lambda ^{2k}, \lambda ^{3k}, 1)$, where
$V_k := (\lambda ^{2k}, \lambda ^{3k}, 1)$, where ![]() $\lambda := \exp ({{2\pi {i}}/{7}})$. The sequence
$\lambda := \exp ({{2\pi {i}}/{7}})$. The sequence ![]() $V_k$ is annihilated by a difference operator with constant coefficients, namely by
$V_k$ is annihilated by a difference operator with constant coefficients, namely by ![]() $\mathcal {D} := a T^{{(n-3)}/{2}}+ bT^{{(n-1)}/{2}} + cT^{{(n+1)}/{2}} + dT^{{(n+3)}/{2}}$, where
$\mathcal {D} := a T^{{(n-3)}/{2}}+ bT^{{(n-1)}/{2}} + cT^{{(n+1)}/{2}} + dT^{{(n+3)}/{2}}$, where ![]() $a,b,c,d \in \mathbb {C}$ are such that the roots of the corresponding characteristic equation
$a,b,c,d \in \mathbb {C}$ are such that the roots of the corresponding characteristic equation ![]() $a + bx + cx^2 + {{d} x}^3 = 0$ are
$a + bx + cx^2 + {{d} x}^3 = 0$ are ![]() $\lambda ^2$,
$\lambda ^2$, ![]() $\lambda ^3$, and
$\lambda ^3$, and ![]() $1$. Therefore, the associated operators
$1$. Therefore, the associated operators ![]() $\mathcal {D}_r$ and
$\mathcal {D}_r$ and ![]() $\mathcal {D}_l$ also have constant coefficients and hence commute. Thus, the polygon
$\mathcal {D}_l$ also have constant coefficients and hence commute. Thus, the polygon ![]() $P$ is indeed projectively equivalent to its pentagram image
$P$ is indeed projectively equivalent to its pentagram image ![]() $P'$.
$P'$.
5. The spectral curve
The results of this section are central to the proof of Theorem B (and are also used to derive Theorem A from Theorem B). Namely, in § 5.1 we consider the joint spectrum of the commuting difference operators ![]() $\mathcal {D}_l$,
$\mathcal {D}_l$, ![]() $\mathcal {D}_r$ constructed above (see § 4), the so-called spectral curve, and show that the genus
$\mathcal {D}_r$ constructed above (see § 4), the so-called spectral curve, and show that the genus ![]() $g$ of that curve is at most one. We note that this estimate on the genus is not predicted by the general theory of commuting difference operators. It seems that the best bound one can get from the general theory is
$g$ of that curve is at most one. We note that this estimate on the genus is not predicted by the general theory of commuting difference operators. It seems that the best bound one can get from the general theory is ![]() $g \leq 2$. Proving the
$g \leq 2$. Proving the ![]() $g \leq 1$ estimate requires somewhat more careful analysis of the field of meromorphic functions. Also note that even the
$g \leq 1$ estimate requires somewhat more careful analysis of the field of meromorphic functions. Also note that even the ![]() $g \leq 1$ result is still insufficient to prove Theorem B. Another important ingredient of the proof is the so-called eigenvector function, which encodes the joint eigenvectors of the commuting operators
$g \leq 1$ result is still insufficient to prove Theorem B. Another important ingredient of the proof is the so-called eigenvector function, which encodes the joint eigenvectors of the commuting operators ![]() $\mathcal {D}_l$,
$\mathcal {D}_l$, ![]() $\mathcal {D}_r$. We study that function in § 5.2 and, in particular, prove that it has very few poles.
$\mathcal {D}_r$. We study that function in § 5.2 and, in particular, prove that it has very few poles.
5.1 The spectral curve and a bound on its genus
In this section, we construct the spectral curve associated with commuting difference operators ![]() $\mathcal {D}_l$,
$\mathcal {D}_l$, ![]() $\mathcal {D}_r$ given by Proposition 7.1 and discuss its properties, in particular prove that its genus is at most one.
$\mathcal {D}_r$ given by Proposition 7.1 and discuss its properties, in particular prove that its genus is at most one.
Remark 5.1 Note that instead of defining the spectral curve using commuting difference operators, we could have done this using the Lax representation, as in [Reference SolovievSol13]. However, at the end of the day these two definitions turn out to be equivalent to each other (see Remark 5.14). Furthermore, even if we defined the spectral curve using the Lax representation, we would still need commuting difference operators to establish the properties of the curve that we need. Thus, all in all, these two approaches are equivalent, and our choice is just a matter of convenience.
Remark 5.2 A different notion of a spectral curve corresponding to a difference operator (and, hence, a polygon) is defined in [Reference KricheverKri15]. In our terminology, it is the spectral curve corresponding to commuting difference operators ![]() $\hat{\mathcal {D}}$,
$\hat{\mathcal {D}}$, ![]() $T^n$ where
$T^n$ where ![]() $\hat{\mathcal {D}}$ is a difference operator supported in
$\hat{\mathcal {D}}$ is a difference operator supported in ![]() $[0,3]$ associated with a given polygon. As the operator
$[0,3]$ associated with a given polygon. As the operator ![]() $\hat{\mathcal {D}}$ does not, generally speaking, commute with
$\hat{\mathcal {D}}$ does not, generally speaking, commute with ![]() $\mathcal {D}_l$ and
$\mathcal {D}_l$ and ![]() $\mathcal {D}_r$, the corresponding spectral curve seems to have no relation to ours.
$\mathcal {D}_r$, the corresponding spectral curve seems to have no relation to ours.
Assume that ![]() $P$ is a weakly convex twisted
$P$ is a weakly convex twisted ![]() $n$-gon, self-dual, and projectively equivalent to its pentagram image. Then, by Proposition 4.2, we have an
$n$-gon, self-dual, and projectively equivalent to its pentagram image. Then, by Proposition 4.2, we have an ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {D}_l = a T^{{(n-3)}/{2}}+ bT^{{(n-1)}/{2}}$ which commutes with its dual. For notational convenience, we define
$\mathcal {D}_l = a T^{{(n-3)}/{2}}+ bT^{{(n-1)}/{2}}$ which commutes with its dual. For notational convenience, we define
Periodicity of these operators means that they also commute with ![]() $T^n$. Therefore, we have a whole algebra
$T^n$. Therefore, we have a whole algebra ![]() $\mathcal {A}$ of commuting operators, generated by
$\mathcal {A}$ of commuting operators, generated by ![]() $\mathcal {D}_+$,
$\mathcal {D}_+$, ![]() $\mathcal {D}_-$, and
$\mathcal {D}_-$, and ![]() $T^n$ (to preserve the left–right symmetry, it is natural to include
$T^n$ (to preserve the left–right symmetry, it is natural to include ![]() $T^{-n}$ in
$T^{-n}$ in ![]() $\mathcal {A}$ too, so that
$\mathcal {A}$ too, so that ![]() $\mathcal {A}= \mathbb {C}[ \mathcal {D}_+, \mathcal {D}_-, T^{\pm n}]$). To such an algebra
$\mathcal {A}= \mathbb {C}[ \mathcal {D}_+, \mathcal {D}_-, T^{\pm n}]$). To such an algebra ![]() $\mathcal {A}$, one can always associate an algebraic curve. This curve may be constructed using any two generic elements of
$\mathcal {A}$, one can always associate an algebraic curve. This curve may be constructed using any two generic elements of ![]() $\mathcal {A}$. As such elements, we pick the operators
$\mathcal {A}$. As such elements, we pick the operators ![]() $T^n$ and the product
$T^n$ and the product ![]() $\mathcal {D}_+\mathcal {D}_- = \mathcal {D}_-\mathcal {D}_+$. This choice is motivated by a particularly simple form of the operator
$\mathcal {D}_+\mathcal {D}_- = \mathcal {D}_-\mathcal {D}_+$. This choice is motivated by a particularly simple form of the operator ![]() $\mathcal {D}_+\mathcal {D}_-$. Namely, that operator is self-dual and supported in
$\mathcal {D}_+\mathcal {D}_-$. Namely, that operator is self-dual and supported in ![]() $[-1,1]$:
$[-1,1]$:
where ![]() $\alpha, \beta$ are
$\alpha, \beta$ are ![]() $n$-periodic sequences, and
$n$-periodic sequences, and ![]() $\alpha _k \neq 0$ for any
$\alpha _k \neq 0$ for any ![]() $k$.
$k$.
Definition 5.3 The affine spectral curve ![]() $\Gamma _a$ is the joint spectrum of
$\Gamma _a$ is the joint spectrum of ![]() $T^n$ and
$T^n$ and ![]() $\mathcal {D}_+\mathcal {D}_-$:
$\mathcal {D}_+\mathcal {D}_-$:
In other words, a point ![]() $(z,w) \in \mathbb {C}^* \times \mathbb {C}$ is in
$(z,w) \in \mathbb {C}^* \times \mathbb {C}$ is in ![]() $\Gamma _a$ if and only if
$\Gamma _a$ if and only if ![]() $w$ is an eigenvalue of the restriction of
$w$ is an eigenvalue of the restriction of ![]() $\mathcal {D}_+\mathcal {D}_-$ to the space
$\mathcal {D}_+\mathcal {D}_-$ to the space ![]() $Q^n({z})$ defined by (5).
$Q^n({z})$ defined by (5).
To obtain an explicit equation of the affine spectral curve ![]() $\Gamma _a$, take a basis
$\Gamma _a$, take a basis ![]() $e^{1}, \ldots, e^{n}$ in
$e^{1}, \ldots, e^{n}$ in ![]() $Q^n({z})$ determined by the condition
$Q^n({z})$ determined by the condition ![]() $e^{j}_k = \delta _k^j$ for
$e^{j}_k = \delta _k^j$ for ![]() $k = 1,\ldots, n$. In this basis, the matrix of the operator
$k = 1,\ldots, n$. In this basis, the matrix of the operator ![]() $\mathcal {D}_+\mathcal {D}_-$ is almost tridiagonal, with two additional elements in the upper-right and bottom-left corners:
$\mathcal {D}_+\mathcal {D}_-$ is almost tridiagonal, with two additional elements in the upper-right and bottom-left corners:
 \begin{equation} \left(\begin{array}{@{}cccccc@{}}\beta_1 & \alpha_1 & & & \alpha_n z^{-1} \\ \alpha_1 & \beta_2 & \alpha_2 & \\ & \ddots & \ddots & \ddots \\ & & \alpha_{n-2} & \beta_{n-1} & \alpha_{n-1} \\ \alpha_n z & & & \alpha_{n-1} & \beta_n\end{array}\right). \end{equation}
\begin{equation} \left(\begin{array}{@{}cccccc@{}}\beta_1 & \alpha_1 & & & \alpha_n z^{-1} \\ \alpha_1 & \beta_2 & \alpha_2 & \\ & \ddots & \ddots & \ddots \\ & & \alpha_{n-2} & \beta_{n-1} & \alpha_{n-1} \\ \alpha_n z & & & \alpha_{n-1} & \beta_n\end{array}\right). \end{equation} The affine spectral curve ![]() $\Gamma _a$ is the zero locus of the characteristic polynomial of (20), which, up to the factor
$\Gamma _a$ is the zero locus of the characteristic polynomial of (20), which, up to the factor ![]() $\alpha _1\ldots \alpha _n$, reads
$\alpha _1\ldots \alpha _n$, reads
for a certain polynomial ![]() $q(w)$ of degree
$q(w)$ of degree ![]() $n$. In particular, the spectral curve is algebraic, as predicted by the general theory of commuting difference operators.
$n$. In particular, the spectral curve is algebraic, as predicted by the general theory of commuting difference operators.
Proposition 5.4 The affine spectral curve ![]() $\Gamma _a$ is irreducible.
$\Gamma _a$ is irreducible.
Proof. This curve is the zero locus of the polynomial (21), which is irreducible whenever ![]() $q(w)$ is non-constant.
$q(w)$ is non-constant.
We now define the spectral curve ![]() $\Gamma$ as the Riemann surface corresponding to the affine curve
$\Gamma$ as the Riemann surface corresponding to the affine curve ![]() $\Gamma _a$. In other words,
$\Gamma _a$. In other words, ![]() $\Gamma$ is the unique Riemann surface biholomorphic to
$\Gamma$ is the unique Riemann surface biholomorphic to ![]() $\Gamma _a$ away from a finite number of points. The existence of such a Riemann surface is guaranteed by Riemann's theorem. It can be obtained from
$\Gamma _a$ away from a finite number of points. The existence of such a Riemann surface is guaranteed by Riemann's theorem. It can be obtained from ![]() $\Gamma _a$ by means of normalization (which we actually explicitly construct in Remark 5.23), followed by compactification. As
$\Gamma _a$ by means of normalization (which we actually explicitly construct in Remark 5.23), followed by compactification. As ![]() $\Gamma _a$ is irreducible (Proposition 5.4), it follows that
$\Gamma _a$ is irreducible (Proposition 5.4), it follows that ![]() $\Gamma$ is connected. Furthermore, the Riemann surface
$\Gamma$ is connected. Furthermore, the Riemann surface ![]() $\Gamma$ comes equipped with:
$\Gamma$ comes equipped with:
• two meromorphic functions
 $z$ and
$z$ and  $w$, obtained from coordinate functions on
$w$, obtained from coordinate functions on  $\Gamma _a$, and satisfying the equation
$\Gamma _a$, and satisfying the equation  $p(z,w) = 0$, with
$p(z,w) = 0$, with  $p$ given by (21);
$p$ given by (21);• a holomorphic involution
 $\sigma \colon \Gamma \to \Gamma$, coming from the involution
$\sigma \colon \Gamma \to \Gamma$, coming from the involution  $(z,w) \mapsto (z^{-1},w)$ on
$(z,w) \mapsto (z^{-1},w)$ on  $\Gamma _a$, and satisfying
$\Gamma _a$, and satisfying  $\sigma ^*w = w$ and
$\sigma ^*w = w$ and  $\sigma ^*z = z^{-1}$.
$\sigma ^*z = z^{-1}$.
Proposition 5.5 The degrees of the functions ![]() $w$ and
$w$ and ![]() $z$ on
$z$ on ![]() $\Gamma$ are equal to
$\Gamma$ are equal to ![]() $2$ and
$2$ and ![]() $n$, respectively.
$n$, respectively.
Proof. As the polynomial ![]() $q(w)$ in (21) has degree
$q(w)$ in (21) has degree ![]() $n$, the equation
$n$, the equation ![]() $p(z,w) = 0$ has
$p(z,w) = 0$ has ![]() $n$ solutions in terms of
$n$ solutions in terms of ![]() $w$ for generic
$w$ for generic ![]() $z$. Thus, the degree of
$z$. Thus, the degree of ![]() $z$ on
$z$ on ![]() $\Gamma$ is
$\Gamma$ is ![]() $n$. Likewise, the number of solutions of
$n$. Likewise, the number of solutions of ![]() $p(z,w) = 0$ in terms of
$p(z,w) = 0$ in terms of ![]() $z$ is
$z$ is ![]() $2$ for generic
$2$ for generic ![]() $w$, so the degree of
$w$, so the degree of ![]() $w$ is
$w$ is ![]() $2$.
$2$.
As ![]() $w$ is a function of degree
$w$ is a function of degree ![]() $2$, and
$2$, and ![]() $\sigma$ is a non-trivial involution preserving
$\sigma$ is a non-trivial involution preserving ![]() $w$, it follows that
$w$, it follows that ![]() $\sigma$ interchanges the two points in any level set of
$\sigma$ interchanges the two points in any level set of ![]() $w$. In particular, the fixed points set of
$w$. In particular, the fixed points set of ![]() $\sigma$ coincides with the set of branch points of
$\sigma$ coincides with the set of branch points of ![]() $w$, that is, points where
$w$, that is, points where ![]() $dw = 0$. At the end of this section we show that the number of such branch points is at most four, which implies, by the Riemann–Hurwitz formula, that the genus of
$dw = 0$. At the end of this section we show that the number of such branch points is at most four, which implies, by the Riemann–Hurwitz formula, that the genus of ![]() $\Gamma$ is at most one. However, first we need to discuss in detail the analytic properties of the functions
$\Gamma$ is at most one. However, first we need to discuss in detail the analytic properties of the functions ![]() $z$ and
$z$ and ![]() $w$, as well as of some other functions on
$w$, as well as of some other functions on ![]() $\Gamma$ which we introduce in the following.
$\Gamma$ which we introduce in the following.
Proposition 5.6 The Riemann surface ![]() $\Gamma$ is obtained from the normalization of
$\Gamma$ is obtained from the normalization of ![]() $\Gamma _a$ by adding two points
$\Gamma _a$ by adding two points ![]() $Z_\pm$, interchanged by the involution
$Z_\pm$, interchanged by the involution ![]() $\sigma$. The point
$\sigma$. The point ![]() $Z_+$ is a zero of order
$Z_+$ is a zero of order ![]() $n$ for the function
$n$ for the function ![]() $z$, whereas
$z$, whereas ![]() $Z_-$ is its pole of order
$Z_-$ is its pole of order ![]() $n$. Both points are simple poles of the function
$n$. Both points are simple poles of the function ![]() $w$.
$w$.
Proof. Let ![]() $\Gamma _n \subset \Gamma$ be the normalization of
$\Gamma _n \subset \Gamma$ be the normalization of ![]() $\Gamma _a$. This set can be described as the preimage of
$\Gamma _a$. This set can be described as the preimage of ![]() $\Gamma _a$ under the map
$\Gamma _a$ under the map ![]() $(z,w) \colon \Gamma \to \mathbb {P}^1 \times \mathbb {P}^1$. Also note that the image of
$(z,w) \colon \Gamma \to \mathbb {P}^1 \times \mathbb {P}^1$. Also note that the image of ![]() $\Gamma$ under the latter map is precisely the closure of
$\Gamma$ under the latter map is precisely the closure of ![]() $\Gamma _a$ in
$\Gamma _a$ in ![]() $\mathbb {P}^1 \times \mathbb {P}^1$, which consists of
$\mathbb {P}^1 \times \mathbb {P}^1$, which consists of ![]() $\Gamma _a$ and the points
$\Gamma _a$ and the points ![]() $(0, \infty )$ and
$(0, \infty )$ and ![]() $(\infty, \infty )$. Thus, the image of
$(\infty, \infty )$. Thus, the image of ![]() $\Gamma {\setminus} \Gamma _n$ under the map
$\Gamma {\setminus} \Gamma _n$ under the map ![]() $(z,w)$ is two points
$(z,w)$ is two points ![]() $(0, \infty )$ and
$(0, \infty )$ and ![]() $(\infty, \infty )$. This means, first, that any point in
$(\infty, \infty )$. This means, first, that any point in ![]() $\Gamma {\setminus} \Gamma _n$ is a pole of
$\Gamma {\setminus} \Gamma _n$ is a pole of ![]() $w$, and second, that there are at least two such points. However, because
$w$, and second, that there are at least two such points. However, because ![]() $w$ has degree
$w$ has degree ![]() $2$ (Proposition 5.5), it follows that
$2$ (Proposition 5.5), it follows that ![]() $\Gamma {\setminus} \Gamma _n$ consists of exactly two points, and that these points are simple poles of
$\Gamma {\setminus} \Gamma _n$ consists of exactly two points, and that these points are simple poles of ![]() $w$. Furthermore, at one of these points, which we denote by
$w$. Furthermore, at one of these points, which we denote by ![]() $Z_+$, we have
$Z_+$, we have ![]() $z = 0$, whereas at the other, which we call
$z = 0$, whereas at the other, which we call ![]() $Z_-$, we have
$Z_-$, we have ![]() $z = \infty$. Finally, note that because all points of
$z = \infty$. Finally, note that because all points of ![]() $\Gamma$ except
$\Gamma$ except ![]() $Z_\pm$ belong to
$Z_\pm$ belong to ![]() $\Gamma _n$, it follows that
$\Gamma _n$, it follows that ![]() $z$ does not have zeros or poles except for
$z$ does not have zeros or poles except for ![]() $Z_\pm$. Thus,
$Z_\pm$. Thus, ![]() $Z_+$ is a zero of
$Z_+$ is a zero of ![]() $z$ of order
$z$ of order ![]() $n$, whereas
$n$, whereas ![]() $Z_-$ is a pole of order
$Z_-$ is a pole of order ![]() $n$, as desired.
$n$, as desired.
Denote also by ![]() $S_\pm$ the two zeros of the function
$S_\pm$ the two zeros of the function ![]() $w$ on
$w$ on ![]() $\Gamma$. A priori, these two points may coincide, but later we show that they are distinct (see the proof of Proposition 5.18). Table 1 summarizes information about the orders of the functions
$\Gamma$. A priori, these two points may coincide, but later we show that they are distinct (see the proof of Proposition 5.18). Table 1 summarizes information about the orders of the functions ![]() $z$ and
$z$ and ![]() $w$ at the points
$w$ at the points ![]() $Z_\pm$,
$Z_\pm$, ![]() $S_\pm$ (recall that the order of a meromorphic function
$S_\pm$ (recall that the order of a meromorphic function ![]() $f$ at a point
$f$ at a point ![]() $X$ is equal to
$X$ is equal to ![]() $m$ if
$m$ if ![]() $f$ has a zero of order
$f$ has a zero of order ![]() $m$ at
$m$ at ![]() $X$,
$X$, ![]() $-m$ if
$-m$ if ![]() $f$ has a pole of order
$f$ has a pole of order ![]() $m$ at
$m$ at ![]() $X$, and zero otherwise). Also note that the order of
$X$, and zero otherwise). Also note that the order of ![]() $z$ and
$z$ and ![]() $w$ at any other point of
$w$ at any other point of ![]() $\Gamma$ is equal to zero. The table also contains information about functions
$\Gamma$ is equal to zero. The table also contains information about functions ![]() $s$ and
$s$ and ![]() $\mu _\pm$, which we introduce in the following.
$\mu _\pm$, which we introduce in the following.
Proposition 5.7 The pair ![]() $\mathcal {D}_+\mathcal {D}_-$,
$\mathcal {D}_+\mathcal {D}_-$, ![]() $T^n$ of commuting difference operators is of rank one, which means that the generic common eigenspace of these operators is one-dimensional.
$T^n$ of commuting difference operators is of rank one, which means that the generic common eigenspace of these operators is one-dimensional.
Table 1. The orders of the functions ![]() $z,w,s, \mu _\pm$ at the points
$z,w,s, \mu _\pm$ at the points ![]() $Z_\pm, S_\pm \in \Gamma$. The order of these functions at any other point of
$Z_\pm, S_\pm \in \Gamma$. The order of these functions at any other point of ![]() $\Gamma$ is zero.
$\Gamma$ is zero.

Proof. As follows from the explicit form (21) for the characteristic polynomial of the matrix (20), for generic ![]() $z$ that matrix has distinct eigenvalues and, hence, one-dimensional eigenspaces.
$z$ that matrix has distinct eigenvalues and, hence, one-dimensional eigenspaces.
For a generic point ![]() $(z,w) \in \Gamma _a$, let
$(z,w) \in \Gamma _a$, let ![]() $\xi \in \mathbb {R}^\infty$ be the corresponding common eigenvector of
$\xi \in \mathbb {R}^\infty$ be the corresponding common eigenvector of ![]() $\mathcal {D}_+\mathcal {D}_-$ and
$\mathcal {D}_+\mathcal {D}_-$ and ![]() $T^n$, normalized by the condition
$T^n$, normalized by the condition ![]() $\xi _0 = 1$.
$\xi _0 = 1$.
Proposition 5.8 The components ![]() $\xi _k$ of
$\xi _k$ of ![]() $\xi$ extend to meromorphic functions on
$\xi$ extend to meromorphic functions on ![]() $\Gamma$. The corresponding vector-function
$\Gamma$. The corresponding vector-function ![]() $\xi$ on
$\xi$ on ![]() $\Gamma$ satisfies the equations
$\Gamma$ satisfies the equations
Proof. For ![]() $(z,w) \in \Gamma _a$, let
$(z,w) \in \Gamma _a$, let ![]() $\eta = (\eta _1, \ldots, \eta _n)$ be the first row of the comatrix of
$\eta = (\eta _1, \ldots, \eta _n)$ be the first row of the comatrix of ![]() $L - w\mathrm {Id}$, where
$L - w\mathrm {Id}$, where ![]() $L$ is given by (20). Extend
$L$ is given by (20). Extend ![]() $\eta$ to a bi-infinite sequence by the rule
$\eta$ to a bi-infinite sequence by the rule ![]() $\eta _{k+n} = z \eta _k$. Then
$\eta _{k+n} = z \eta _k$. Then ![]() $\eta$ is a common eigenvector of
$\eta$ is a common eigenvector of ![]() $T^n$ and
$T^n$ and ![]() $\mathcal {D}_+\mathcal {D}_-$:
$\mathcal {D}_+\mathcal {D}_-$: ![]() $T^n\eta = z \eta$,
$T^n\eta = z \eta$, ![]() $\mathcal {D}_+\mathcal {D}_- \eta = w \eta$. Furthermore, the components of
$\mathcal {D}_+\mathcal {D}_- \eta = w \eta$. Furthermore, the components of ![]() $\eta$ are, by construction, rational functions of
$\eta$ are, by construction, rational functions of ![]() $z$ and
$z$ and ![]() $w$. Thus, to obtain the desired function
$w$. Thus, to obtain the desired function ![]() $\xi$, it remains to normalize
$\xi$, it remains to normalize ![]() $\eta$:
$\eta$: ![]() $\xi _k = {\eta _k}/{\eta _0}$. Note that
$\xi _k = {\eta _k}/{\eta _0}$. Note that ![]() $\eta _0 = z^{-1}\eta _n$ does not vanish identically on
$\eta _0 = z^{-1}\eta _n$ does not vanish identically on ![]() $\Gamma _a$, because
$\Gamma _a$, because ![]() $\eta _n$ is a polynomial in
$\eta _n$ is a polynomial in ![]() $z,w$ which is linear in
$z,w$ which is linear in ![]() $z$ and, hence, cannot be divisible by the defining polynomial of
$z$ and, hence, cannot be divisible by the defining polynomial of ![]() $\Gamma _a$. Thus,
$\Gamma _a$. Thus, ![]() $\xi$ is a well-defined rational vector-function of
$\xi$ is a well-defined rational vector-function of ![]() $z,w$ and, hence, a meromorphic function on
$z,w$ and, hence, a meromorphic function on ![]() $\Gamma$.
$\Gamma$.
We call the vector-function ![]() $\xi$ the eigenvector function. Its analytic properties are studied in detail in § 5.2.
$\xi$ the eigenvector function. Its analytic properties are studied in detail in § 5.2.
Remark 5.9 Note that at every point ![]() $X \in \Gamma {\setminus} \{Z_\pm \}$, the vector-function
$X \in \Gamma {\setminus} \{Z_\pm \}$, the vector-function ![]() $\xi$ is meromorphic in the following strong sense: there exists a local holomorphic function
$\xi$ is meromorphic in the following strong sense: there exists a local holomorphic function ![]() $f$ such that
$f$ such that ![]() $f\xi$ is holomorphic at
$f\xi$ is holomorphic at ![]() $X$. Moreover, the function
$X$. Moreover, the function ![]() $f$ can chosen in such a way that
$f$ can chosen in such a way that ![]() $(f\xi )(X)$ does not vanish. Therefore, the value of the function
$(f\xi )(X)$ does not vanish. Therefore, the value of the function ![]() $\xi$ at any point
$\xi$ at any point ![]() $X \in \Gamma {\setminus} \{Z_\pm \}$ determines a direction in the infinite-dimensional projective space
$X \in \Gamma {\setminus} \{Z_\pm \}$ determines a direction in the infinite-dimensional projective space ![]() $\mathbb {P}^\infty$, regardless of whether the components of
$\mathbb {P}^\infty$, regardless of whether the components of ![]() $\xi$ are finite or infinite (note also that this direction does not change if we replace our particular normalization
$\xi$ are finite or infinite (note also that this direction does not change if we replace our particular normalization ![]() $\xi _0 = 1$ by any other normalization). This is not true, however, at the points
$\xi _0 = 1$ by any other normalization). This is not true, however, at the points ![]() $Z_\pm$. At those points, the components
$Z_\pm$. At those points, the components ![]() $\xi _k$ of
$\xi _k$ of ![]() $\xi$ are still meromorphic, but the order of the pole of
$\xi$ are still meromorphic, but the order of the pole of ![]() $\xi _k$ is an unbounded function of
$\xi _k$ is an unbounded function of ![]() $k$ (see Proposition 5.21), so there exists no
$k$ (see Proposition 5.21), so there exists no ![]() $f$ such that
$f$ such that ![]() $f\xi$ is holomorphic. In particular, the value of
$f\xi$ is holomorphic. In particular, the value of ![]() $\xi$ at
$\xi$ at ![]() $Z_\pm$ does not determine any direction.
$Z_\pm$ does not determine any direction.
We now show that every operator ![]() $\mathcal {L}$ from the commutative algebra
$\mathcal {L}$ from the commutative algebra ![]() $\mathcal {A}=\langle \mathcal {D}_+ , \mathcal {D}_-,T^{\pm n} \rangle$ gives rise to a meromorphic function
$\mathcal {A}=\langle \mathcal {D}_+ , \mathcal {D}_-,T^{\pm n} \rangle$ gives rise to a meromorphic function ![]() $f_{\mathcal {L}}$ on
$f_{\mathcal {L}}$ on ![]() $\Gamma$, which is holomorphic everywhere except possibly the points
$\Gamma$, which is holomorphic everywhere except possibly the points ![]() $Z_\pm$ and satisfies
$Z_\pm$ and satisfies ![]() $\mathcal {L} \xi = f_{\mathcal {L}} \xi$. In particular, the assignment
$\mathcal {L} \xi = f_{\mathcal {L}} \xi$. In particular, the assignment ![]() $\mathcal {L} \mapsto f_{\mathcal {L}}$ is a homomorphism from
$\mathcal {L} \mapsto f_{\mathcal {L}}$ is a homomorphism from ![]() $\mathcal {A}$ to the algebra of meromorphic functions on
$\mathcal {A}$ to the algebra of meromorphic functions on ![]() $\Gamma$ which are holomorphic in
$\Gamma$ which are holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$. We already have
$\Gamma {\setminus} \{Z_\pm \}$. We already have ![]() $f_{T^{\pm n}}= z^{\pm 1}$ and
$f_{T^{\pm n}}= z^{\pm 1}$ and ![]() $f_{\mathcal {D}_+\mathcal {D}_-} = w$, so it remains to construct the functions
$f_{\mathcal {D}_+\mathcal {D}_-} = w$, so it remains to construct the functions ![]() $f_{\mathcal {D}_+}$ and
$f_{\mathcal {D}_+}$ and ![]() $f_{\mathcal {D}_-}$ (of course, one of them determines the other, because their product must be equal to
$f_{\mathcal {D}_-}$ (of course, one of them determines the other, because their product must be equal to ![]() $w$). We denote these functions by
$w$). We denote these functions by ![]() $\mu _+$ and
$\mu _+$ and ![]() $\mu _-$.
$\mu _-$.
Proposition 5.10 There exist meromorphic functions ![]() $\mu _+, \mu _-$ on
$\mu _+, \mu _-$ on ![]() $\Gamma$ which are holomorphic in
$\Gamma$ which are holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$ and satisfy
$\Gamma {\setminus} \{Z_\pm \}$ and satisfy ![]() $\mathcal {D}_\pm \xi = \mu _\pm \xi.$ Furthermore, we have
$\mathcal {D}_\pm \xi = \mu _\pm \xi.$ Furthermore, we have ![]() $\mu _+\mu _- = w$.
$\mu _+\mu _- = w$.
Proof. By Proposition 5.7, a generic common eigenspace of ![]() $\mathcal {D}_+\mathcal {D}_-$ and
$\mathcal {D}_+\mathcal {D}_-$ and ![]() $T^n$ is one-dimensional, and is therefore generated by the vector
$T^n$ is one-dimensional, and is therefore generated by the vector ![]() $\xi$, evaluated at the corresponding point of the Riemann surface
$\xi$, evaluated at the corresponding point of the Riemann surface ![]() $\Gamma$. For this reason, because the operator
$\Gamma$. For this reason, because the operator ![]() $\mathcal {D}_+$ commutes with
$\mathcal {D}_+$ commutes with ![]() $\mathcal {D}_+\mathcal {D}_-$ and
$\mathcal {D}_+\mathcal {D}_-$ and ![]() $T^n$, at generic points of
$T^n$, at generic points of ![]() $\Gamma$ we must have
$\Gamma$ we must have
for certain numbers ![]() $\mu _\pm \in \mathbb {C}$ depending on the point of
$\mu _\pm \in \mathbb {C}$ depending on the point of ![]() $\Gamma$. Furthermore, because the left-hand side of (23) is a meromorphic vector-function on
$\Gamma$. Furthermore, because the left-hand side of (23) is a meromorphic vector-function on ![]() $\Gamma$, and so is
$\Gamma$, and so is ![]() $\xi$, it follows that the functions
$\xi$, it follows that the functions ![]() $\mu _\pm$ also extend to meromorphic functions on the whole of
$\mu _\pm$ also extend to meromorphic functions on the whole of ![]() $\Gamma$. Moreover, given a point
$\Gamma$. Moreover, given a point ![]() $X \in \Gamma {\setminus} \{Z_\pm \}$, renormalizing
$X \in \Gamma {\setminus} \{Z_\pm \}$, renormalizing ![]() $\xi$ if necessary, we can assume that
$\xi$ if necessary, we can assume that ![]() $\xi (X)$ is finite and non-zero (see Remark 5.9). However, then (23) implies that the functions
$\xi (X)$ is finite and non-zero (see Remark 5.9). However, then (23) implies that the functions ![]() $\mu _\pm$ are holomorphic at
$\mu _\pm$ are holomorphic at ![]() $X$. Finally, the equation
$X$. Finally, the equation ![]() $\mu _+\mu _- = w$ follows directly from (23) and the second of (22).
$\mu _+\mu _- = w$ follows directly from (23) and the second of (22).
Proposition 5.11 We have ![]() $\sigma ^* \mu _+ = \mu _-$.
$\sigma ^* \mu _+ = \mu _-$.
Remark 5.12 The existence of the involution ![]() $\sigma$ on
$\sigma$ on ![]() $\Gamma$ is due to the invariance of the algebra
$\Gamma$ is due to the invariance of the algebra ![]() $\mathcal {A}=\langle \mathcal {D}_+ , \mathcal {D}_-,T^{\pm n} \rangle$ under operator duality:
$\mathcal {A}=\langle \mathcal {D}_+ , \mathcal {D}_-,T^{\pm n} \rangle$ under operator duality: ![]() $\mathcal {A} = \mathcal {A}^* := \{ \mathcal {L}^* \mid \mathcal {L} \in \mathcal {A}\}$. Thus, because
$\mathcal {A} = \mathcal {A}^* := \{ \mathcal {L}^* \mid \mathcal {L} \in \mathcal {A}\}$. Thus, because ![]() $\mathcal {D}_+^* = \mathcal {D}_-$, it is only natural that
$\mathcal {D}_+^* = \mathcal {D}_-$, it is only natural that ![]() $\sigma ^*\mu _+ = \mu _-$.
$\sigma ^*\mu _+ = \mu _-$.
Proof of Proposition 5.11 It suffices to show that ![]() $\mu _+(X_+) = \mu _-(X_-)$, where
$\mu _+(X_+) = \mu _-(X_-)$, where ![]() $X_\pm$ is a generic pair of points interchanged by
$X_\pm$ is a generic pair of points interchanged by ![]() $\sigma$. As the points
$\sigma$. As the points ![]() $X_\pm$ are generic, one can assume that the vectors
$X_\pm$ are generic, one can assume that the vectors ![]() $\xi (X_\pm )$ are finite. Under this assumption, we have
$\xi (X_\pm )$ are finite. Under this assumption, we have ![]() $\mathcal {D}_\pm \xi (X_\pm ) = \mu _\pm (X_\pm ) \xi (X_\pm ).$ Furthermore, we have
$\mathcal {D}_\pm \xi (X_\pm ) = \mu _\pm (X_\pm ) \xi (X_\pm ).$ Furthermore, we have ![]() $\xi (X_\pm ) \in Q^n({z_+^{\pm 1}})$, where
$\xi (X_\pm ) \in Q^n({z_+^{\pm 1}})$, where ![]() $z_+ := z(X_+) = z(X_-)^{-1}$. Thus, using the pairing (7) between
$z_+ := z(X_+) = z(X_-)^{-1}$. Thus, using the pairing (7) between ![]() $Q^n({z_+})$ and
$Q^n({z_+})$ and ![]() $Q^n({z_+^{-1}})$, we obtain
$Q^n({z_+^{-1}})$, we obtain
Thus, to complete the proof, it suffices to show that ![]() $\left \langle \xi (X_+), \xi (X_-) \right \rangle \neq 0$. To that end, observe that
$\left \langle \xi (X_+), \xi (X_-) \right \rangle \neq 0$. To that end, observe that ![]() $\xi (X_+)$ belongs to the kernel of the operator
$\xi (X_+)$ belongs to the kernel of the operator ![]() $(\mathcal {D}_+\mathcal {D}_- - w_0)\vert _{Q^n({z_+})}$, where
$(\mathcal {D}_+\mathcal {D}_- - w_0)\vert _{Q^n({z_+})}$, where ![]() $w_0 := w(X_\pm )$, and, in the generic case, spans that kernel. Thus, the orthogonal complement to
$w_0 := w(X_\pm )$, and, in the generic case, spans that kernel. Thus, the orthogonal complement to ![]() $\xi (X_+)$ with respect to the pairing (7) is the image of the dual operator
$\xi (X_+)$ with respect to the pairing (7) is the image of the dual operator
However, for generic ![]() $z_+$ the operator
$z_+$ the operator ![]() $\mathcal {D}_+\mathcal {D}_-$ has simple spectrum on
$\mathcal {D}_+\mathcal {D}_-$ has simple spectrum on ![]() $Q^n({z_+^{-1}})$ and is, therefore, diagonalizable, which in particular implies
$Q^n({z_+^{-1}})$ and is, therefore, diagonalizable, which in particular implies
Therefore, we have ![]() $\left \langle \xi (X_+), \xi (X_-) \right \rangle \neq 0$, as desired.
$\left \langle \xi (X_+), \xi (X_-) \right \rangle \neq 0$, as desired.
Now, define a meromorphic function ![]() $s$ on
$s$ on ![]() $\Gamma$ by the formula
$\Gamma$ by the formula
This function does not correspond to any difference operator ![]() $\mathcal {L} \in \mathcal {A} = \mathbb {C}[ \mathcal {D}_+, \mathcal {D}_-, T^{\pm n}]$ but can be thought of as corresponding to a pseudo-difference operator
$\mathcal {L} \in \mathcal {A} = \mathbb {C}[ \mathcal {D}_+, \mathcal {D}_-, T^{\pm n}]$ but can be thought of as corresponding to a pseudo-difference operator ![]() $T^{-n}\mathcal {D}_+\mathcal {D}_-^{-1}$. Accordingly, the function
$T^{-n}\mathcal {D}_+\mathcal {D}_-^{-1}$. Accordingly, the function ![]() $s$ satisfies the equation
$s$ satisfies the equation
Recall that the operator on the left-hand side encodes the family of polygons obtained from ![]() $P$ by means of rescaling (9).
$P$ by means of rescaling (9).
Proposition 5.13 The function ![]() $s$ has degree
$s$ has degree ![]() $3$. There exist three distinct points on
$3$. There exist three distinct points on ![]() $\Gamma$ at which
$\Gamma$ at which ![]() $s = -1$. The function
$s = -1$. The function ![]() $z$ takes three distinct values at those points.
$z$ takes three distinct values at those points.
Proof. We first show that ![]() $\deg s \leq 3$. Let
$\deg s \leq 3$. Let ![]() $X_1, \ldots, X_m \in \Gamma$ belong to the level set
$X_1, \ldots, X_m \in \Gamma$ belong to the level set ![]() $s = s_0$. Then, for generic
$s = s_0$. Then, for generic ![]() $s_0 \in \mathbb {C}$, these points correspond to distinct points on the affine spectral curve
$s_0 \in \mathbb {C}$, these points correspond to distinct points on the affine spectral curve ![]() $\Gamma _a$. This, in particular, means that the vectors
$\Gamma _a$. This, in particular, means that the vectors ![]() $\xi (X_1), \ldots, \xi (X_m) \in \mathrm {Ker}\,(\mathcal {D}_+ - s_0T^n \mathcal {D}_-)$ are linearly independent (as joint eigenvectors of
$\xi (X_1), \ldots, \xi (X_m) \in \mathrm {Ker}\,(\mathcal {D}_+ - s_0T^n \mathcal {D}_-)$ are linearly independent (as joint eigenvectors of ![]() $T^n$ and
$T^n$ and ![]() $\mathcal {D}_+\mathcal {D}_-$ corresponding to distinct eigenvalues). However,
$\mathcal {D}_+\mathcal {D}_-$ corresponding to distinct eigenvalues). However,
so ![]() $m \leq 3$, and the degree of
$m \leq 3$, and the degree of ![]() $s$ is at most
$s$ is at most ![]() $3$, as desired.
$3$, as desired.
We now show that there exist three distinct points on ![]() $\Gamma$ at which
$\Gamma$ at which ![]() $s = -1$, which, in turn, implies that the degree of
$s = -1$, which, in turn, implies that the degree of ![]() $s$ is exactly
$s$ is exactly ![]() $3$. As the polygon
$3$. As the polygon ![]() $P$, given by the operator
$P$, given by the operator ![]() $\mathcal {D}_+ - T^n \mathcal {D}_-$, is weakly convex, it follows from the fourth statement of Proposition 3.4 that the monodromy of
$\mathcal {D}_+ - T^n \mathcal {D}_-$, is weakly convex, it follows from the fourth statement of Proposition 3.4 that the monodromy of ![]() $\mathcal {D}_+ + T^n \mathcal {D}_-$ has simple spectrum. This means that there exist three distinct numbers
$\mathcal {D}_+ + T^n \mathcal {D}_-$ has simple spectrum. This means that there exist three distinct numbers ![]() $z_1, z_2, z_3$ such that the operator
$z_1, z_2, z_3$ such that the operator ![]() $\mathcal {D}_+ +T^n \mathcal {D}_-$ has non-trivial (and, hence, one-dimensional) kernel on
$\mathcal {D}_+ +T^n \mathcal {D}_-$ has non-trivial (and, hence, one-dimensional) kernel on ![]() $Q^n({z_k})$. Let
$Q^n({z_k})$. Let ![]() $\xi ^{k}$ be the generator of that kernel. Then, because the operator
$\xi ^{k}$ be the generator of that kernel. Then, because the operator ![]() $\mathcal {D}_+ \mathcal {D}_-$ commutes with
$\mathcal {D}_+ \mathcal {D}_-$ commutes with ![]() $\mathcal {D}_+ +T^n \mathcal {D}_-$ and
$\mathcal {D}_+ +T^n \mathcal {D}_-$ and ![]() $T^n$, it follows that
$T^n$, it follows that ![]() $\xi ^{k}$ is also an eigenvector of
$\xi ^{k}$ is also an eigenvector of ![]() $\mathcal {D}_+ \mathcal {D}_-$, corresponding to some eigenvalue
$\mathcal {D}_+ \mathcal {D}_-$, corresponding to some eigenvalue ![]() $w_k$. Then the three points
$w_k$. Then the three points ![]() $(z_k,w_k)$ belong to the affine spectral curve
$(z_k,w_k)$ belong to the affine spectral curve ![]() $\Gamma _a$ and, thus, give rise to at least three points
$\Gamma _a$ and, thus, give rise to at least three points ![]() $X_1, X_2, X_3 \in \Gamma {\setminus} \{Z_\pm \}$ with
$X_1, X_2, X_3 \in \Gamma {\setminus} \{Z_\pm \}$ with ![]() $z(X_k) = z_k$,
$z(X_k) = z_k$, ![]() $w(X_k) = w_k$. We now claim that
$w(X_k) = w_k$. We now claim that ![]() $s(X_1) = s(X_2) = s(X_3) = -1$. Indeed, the vector
$s(X_1) = s(X_2) = s(X_3) = -1$. Indeed, the vector ![]() $\xi _k$ spans the
$\xi _k$ spans the ![]() $(z_k,w_k)$ joint eigenspace of
$(z_k,w_k)$ joint eigenspace of ![]() $T^n$ and
$T^n$ and ![]() $\mathcal {D}_+ \mathcal {D}_-$. Therefore, at each of the points
$\mathcal {D}_+ \mathcal {D}_-$. Therefore, at each of the points ![]() $X_k$, we have
$X_k$, we have ![]() $\xi (X_k) = c_k\xi ^{k}$, where
$\xi (X_k) = c_k\xi ^{k}$, where ![]() $c_k \in \mathbb {C}$ (here we assume here that the vectors
$c_k \in \mathbb {C}$ (here we assume here that the vectors ![]() $\xi (X_k)$ are finite, which can be always arranged by multiplying
$\xi (X_k)$ are finite, which can be always arranged by multiplying ![]() $\xi$ by an appropriate meromorphic function, see Remark 5.9). Thus, by construction of the vectors
$\xi$ by an appropriate meromorphic function, see Remark 5.9). Thus, by construction of the vectors ![]() $\xi ^{k}$, we have
$\xi ^{k}$, we have
On the other hand,
so
Note also that ![]() $X_k$ cannot be a common zero of
$X_k$ cannot be a common zero of ![]() $\mu _+$ and
$\mu _+$ and ![]() $\mu _-$, because that would imply
$\mu _-$, because that would imply ![]() $\xi (X_k) \in \mathrm {Ker}\, \mathcal {D}_+ \cap \mathrm {Ker}\, \mathcal {D}_-$, which is not possible by the second statement of Proposition 3.4 (the latter applies to
$\xi (X_k) \in \mathrm {Ker}\, \mathcal {D}_+ \cap \mathrm {Ker}\, \mathcal {D}_-$, which is not possible by the second statement of Proposition 3.4 (the latter applies to ![]() $\mathcal {D}_\pm$ because
$\mathcal {D}_\pm$ because ![]() $\mathcal {D}_+ = \mathcal {D}_l$,
$\mathcal {D}_+ = \mathcal {D}_l$, ![]() $\mathcal {D}_- = -T^{-n} \mathcal {D}_r$). Furthermore,
$\mathcal {D}_- = -T^{-n} \mathcal {D}_r$). Furthermore, ![]() $\mu _\pm$ cannot have a pole at
$\mu _\pm$ cannot have a pole at ![]() $X_k$ by Proposition 5.10. However, then (26) implies
$X_k$ by Proposition 5.10. However, then (26) implies ![]() $s(X_k) = -1$, as desired.
$s(X_k) = -1$, as desired.
Remark 5.14 It follows from Proposition 5.13 that the function ![]() $s$ has the following meaning. Fix some generic
$s$ has the following meaning. Fix some generic ![]() $s_0 \in \mathbb {C}$. Then there are three points
$s_0 \in \mathbb {C}$. Then there are three points ![]() $X_1, X_2, X_3$ in
$X_1, X_2, X_3$ in ![]() $\Gamma$ with
$\Gamma$ with ![]() $s = s_0$. Furthermore, the vectors
$s = s_0$. Furthermore, the vectors ![]() $\xi (X_k) \in Q^n({z(X_k)})$ belong to
$\xi (X_k) \in Q^n({z(X_k)})$ belong to ![]() $\mathrm {Ker}\,(\mathcal {D}_+ - s_0 T^n \mathcal {D}_-)$. Thus,
$\mathrm {Ker}\,(\mathcal {D}_+ - s_0 T^n \mathcal {D}_-)$. Thus, ![]() $z(X_1), z(X_2), z(X_3)$ is the spectrum of the monodromy of
$z(X_1), z(X_2), z(X_3)$ is the spectrum of the monodromy of ![]() $\mathcal {D}_+ - s_0T^n \mathcal {D}_-$. In other words, if we consider a meromorphic mapping
$\mathcal {D}_+ - s_0T^n \mathcal {D}_-$. In other words, if we consider a meromorphic mapping ![]() $\Gamma \to \mathbb {C}^2$ given by the functions
$\Gamma \to \mathbb {C}^2$ given by the functions ![]() $(z,s)$, then its image belongs to the algebraic curve
$(z,s)$, then its image belongs to the algebraic curve
Using also that ![]() $\deg z = n$ and
$\deg z = n$ and ![]() $\deg s = 3$, it is easy to show that the mapping
$\deg s = 3$, it is easy to show that the mapping ![]() $\Gamma \to \Gamma _a'$ is generically biholomorphic. Thus,
$\Gamma \to \Gamma _a'$ is generically biholomorphic. Thus, ![]() $\Gamma _a'$ is just another affine model of the spectral curve
$\Gamma _a'$ is just another affine model of the spectral curve ![]() $\Gamma$. This model can be thought of as the joint spectrum of the operators
$\Gamma$. This model can be thought of as the joint spectrum of the operators ![]() $T^n$ and
$T^n$ and ![]() $T^{-n} \mathcal {D}_+\mathcal {D}_-^{-1}$ (the latter is well-defined on a generic eigenspace of
$T^{-n} \mathcal {D}_+\mathcal {D}_-^{-1}$ (the latter is well-defined on a generic eigenspace of ![]() $T^n$). Furthermore, because the operator
$T^n$). Furthermore, because the operator ![]() $\mathcal {D}_+ - sT^n \mathcal {D}_-$ corresponds to the polygon
$\mathcal {D}_+ - sT^n \mathcal {D}_-$ corresponds to the polygon ![]() $R_s( P_{})$, where
$R_s( P_{})$, where ![]() $R_s$ is the rescaling action (9), it follows that
$R_s$ is the rescaling action (9), it follows that ![]() $\Gamma _a'$ can be regarded as the graph of the spectrum for the monodromy of
$\Gamma _a'$ can be regarded as the graph of the spectrum for the monodromy of ![]() $R_s( P_{})$. As explained in [Reference IzosimovIzo16], this definition of the spectral curve coincides with the one used in [Reference SolovievSol13] to prove algebraic integrability of the pentagram map. Thus, as a Riemann surface, our spectral curve is isomorphic to that of [Reference SolovievSol13].
$R_s( P_{})$. As explained in [Reference IzosimovIzo16], this definition of the spectral curve coincides with the one used in [Reference SolovievSol13] to prove algebraic integrability of the pentagram map. Thus, as a Riemann surface, our spectral curve is isomorphic to that of [Reference SolovievSol13].
We are now in a position to prove the main result of this section.
Proposition 5.15 The genus ![]() $g$ of
$g$ of ![]() $\Gamma$ satisfies
$\Gamma$ satisfies ![]() $g \leq 1$.
$g \leq 1$.
Proof. The function ![]() $w$ on
$w$ on ![]() $\Gamma$ is a
$\Gamma$ is a ![]() $2$-fold ramified covering of the Riemann sphere whose branch points coincide with fixed points of the involution
$2$-fold ramified covering of the Riemann sphere whose branch points coincide with fixed points of the involution ![]() $\sigma$. To estimate the number of such fixed points, note that from Proposition 5.11 and formula (24) it follows that
$\sigma$. To estimate the number of such fixed points, note that from Proposition 5.11 and formula (24) it follows that ![]() $\sigma ^*s = s^{-1}$. Thus, at each fixed point of
$\sigma ^*s = s^{-1}$. Thus, at each fixed point of ![]() $\sigma$ we must have
$\sigma$ we must have ![]() $s = \pm 1$. Furthermore, by Proposition 5.13, the function
$s = \pm 1$. Furthermore, by Proposition 5.13, the function ![]() $z$ takes three distinct values at points of
$z$ takes three distinct values at points of ![]() $\Gamma$ where
$\Gamma$ where ![]() $s = -1$, and because the set
$s = -1$, and because the set ![]() $s = -1$ is invariant under the involution
$s = -1$ is invariant under the involution ![]() $\sigma$ which takes
$\sigma$ which takes ![]() $z$ to
$z$ to ![]() $z^{-1}$, it follows that those values must be of the form
$z^{-1}$, it follows that those values must be of the form ![]() $\pm 1, z_0, {z_0}^{-1}$, where
$\pm 1, z_0, {z_0}^{-1}$, where ![]() $z_0 \neq \pm 1$. Thus,
$z_0 \neq \pm 1$. Thus, ![]() $\sigma$ must have exactly one fixed point at the level set
$\sigma$ must have exactly one fixed point at the level set ![]() $s = -1$. In addition, it may have up to three fixed points at the level set
$s = -1$. In addition, it may have up to three fixed points at the level set ![]() $s = 1$, which is up to four fixed points in total. Now, the desired inequality for the genus follows from the Riemann–Hurwitz formula.
$s = 1$, which is up to four fixed points in total. Now, the desired inequality for the genus follows from the Riemann–Hurwitz formula.
Remark 5.16 In fact, because the values of ![]() $z$ at points where
$z$ at points where ![]() $s = -1$ are the eigenvalues of the monodromy of
$s = -1$ are the eigenvalues of the monodromy of ![]() $\mathcal {D}_+ +T^n \mathcal {D}_-$, it follows from formula (6) that they are of the form
$\mathcal {D}_+ +T^n \mathcal {D}_-$, it follows from formula (6) that they are of the form ![]() $-1, z_0,z_0^{-1}$. Another way to see this is to notice that by Proposition 5.11 at fixed points of
$-1, z_0,z_0^{-1}$. Another way to see this is to notice that by Proposition 5.11 at fixed points of ![]() $\sigma$ we must have
$\sigma$ we must have ![]() $\mu _+ = \mu _-$ and thus
$\mu _+ = \mu _-$ and thus ![]() $z = s^{-1}$ (here we use that the functions
$z = s^{-1}$ (here we use that the functions ![]() $\mu _\pm$ do not have common zeros and also do not have poles in
$\mu _\pm$ do not have common zeros and also do not have poles in ![]() $\Gamma {\setminus} \{Z_\pm \}$). This also implies that if
$\Gamma {\setminus} \{Z_\pm \}$). This also implies that if ![]() $\Gamma$ has genus
$\Gamma$ has genus ![]() $1$, then
$1$, then ![]() $z = 1$ at points where
$z = 1$ at points where ![]() $s = 1$. In other words, all eigenvalues of the monodromy of the polygon
$s = 1$. In other words, all eigenvalues of the monodromy of the polygon ![]() $P$ are equal to one. Later on, we show that this monodromy is, in fact, the identity. In other words, if the spectral curve is elliptic, then in the setting of Theorem B the polygon
$P$ are equal to one. Later on, we show that this monodromy is, in fact, the identity. In other words, if the spectral curve is elliptic, then in the setting of Theorem B the polygon ![]() $P$ must be closed (see Remark 6.9).
$P$ must be closed (see Remark 6.9).
Remark 5.17 Note that without weak convexity (used to prove Proposition 5.13) we would not be able to say that there is just one fixed point of the involution ![]() $\sigma$ at the level
$\sigma$ at the level ![]() $s = -1$. In that case, nothing seems to prevent
$s = -1$. In that case, nothing seems to prevent ![]() $\sigma$ from having six fixed points, which means that
$\sigma$ from having six fixed points, which means that ![]() $\Gamma$ may be a genus-
$\Gamma$ may be a genus-![]() $2$ curve. Thus, it should be possible to construct a counterexample to Theorems A and B in the non-weakly-convex case using genus-
$2$ curve. Thus, it should be possible to construct a counterexample to Theorems A and B in the non-weakly-convex case using genus-![]() $2$ curves and their associated genus-
$2$ curves and their associated genus-![]() $2$ theta functions.
$2$ theta functions.
Another way to obtain the estimate ![]() $g \leq 2$ is to use the existence on
$g \leq 2$ is to use the existence on ![]() $\Gamma$ of meromorphic functions of degree
$\Gamma$ of meromorphic functions of degree ![]() $2$ and
$2$ and ![]() $3$ (namely,
$3$ (namely, ![]() $w$ and
$w$ and ![]() $s$). However, this does not guarantee the
$s$). However, this does not guarantee the ![]() $g \leq 1$ estimate obtained above.
$g \leq 1$ estimate obtained above.
We finish this section with two additional results on the spectral curve which are useful later on.
Proposition 5.18 The degrees of the functions ![]() $\mu _\pm, s$ and their orders at points
$\mu _\pm, s$ and their orders at points ![]() $Z_\pm, S_\pm$ are as listed in Table 1.
$Z_\pm, S_\pm$ are as listed in Table 1.
Proof. As for any ![]() $\lambda \in \mathbb {C}^*$ the degree of operators
$\lambda \in \mathbb {C}^*$ the degree of operators ![]() $\mathcal {D}_\pm - \lambda$ is
$\mathcal {D}_\pm - \lambda$ is ![]() $(n-1)/2$, an argument analogous to that we used to show that
$(n-1)/2$, an argument analogous to that we used to show that ![]() $\deg s \leq 3$ (see the proof of Proposition 5.13) gives
$\deg s \leq 3$ (see the proof of Proposition 5.13) gives ![]() ${\deg \mu _\pm \leq (n-1)/2}$. Further, let
${\deg \mu _\pm \leq (n-1)/2}$. Further, let ![]() $d_\pm := \mathrm {ord}\,_{Z_+}\mu _\pm$. Then, because
$d_\pm := \mathrm {ord}\,_{Z_+}\mu _\pm$. Then, because ![]() $\mathrm {ord}\,_{Z_+}w=-1$ (see Table 1), the equation
$\mathrm {ord}\,_{Z_+}w=-1$ (see Table 1), the equation ![]() $\mu _+\mu _- = w$ implies
$\mu _+\mu _- = w$ implies
Furthermore, using that ![]() $\mathrm {ord}\,_{Z_+}z=n$ and (24), we obtain
$\mathrm {ord}\,_{Z_+}z=n$ and (24), we obtain
so
and because ![]() $\deg \mu _- \leq (n-1)/2$, we must have
$\deg \mu _- \leq (n-1)/2$, we must have ![]() $d_- \geq - (n-1)/2$, which implies
$d_- \geq - (n-1)/2$, which implies ![]() $\mathrm {ord}\,_{Z_+}s \leq - 2$. On the other hand, we know that
$\mathrm {ord}\,_{Z_+}s \leq - 2$. On the other hand, we know that ![]() $\deg s = 3$, and from (29) it follows that
$\deg s = 3$, and from (29) it follows that ![]() $\mathrm {ord}\,_{Z_+}s$ is even. Thus, we must have
$\mathrm {ord}\,_{Z_+}s$ is even. Thus, we must have ![]() $\mathrm {ord}\,_{Z_+}s =- 2$, which, along with (29) implies
$\mathrm {ord}\,_{Z_+}s =- 2$, which, along with (29) implies ![]() $\mathrm {ord}\,_{Z_+}\mu _- = d_- = - (n-1)/2$ and thus
$\mathrm {ord}\,_{Z_+}\mu _- = d_- = - (n-1)/2$ and thus ![]() $\deg \mu _- = (n-1)/2$. Similarly, adding up (27) and (28), we get
$\deg \mu _- = (n-1)/2$. Similarly, adding up (27) and (28), we get ![]() $\mathrm {ord}\,_{Z_+}\mu _+ = d_+ = (n-3)/2$. Analogously, replacing the point
$\mathrm {ord}\,_{Z_+}\mu _+ = d_+ = (n-3)/2$. Analogously, replacing the point ![]() $Z_+$ with
$Z_+$ with ![]() $Z_-$, we find the orders of
$Z_-$, we find the orders of ![]() $\mu _\pm$ and
$\mu _\pm$ and ![]() $s$ at
$s$ at ![]() $Z_-$, as well as the degree of
$Z_-$, as well as the degree of ![]() $\mu _+$ (one can also use that
$\mu _+$ (one can also use that ![]() $\sigma ^*\mu _+ = \mu _-$ and
$\sigma ^*\mu _+ = \mu _-$ and ![]() $\sigma (Z_+) = Z_-$).
$\sigma (Z_+) = Z_-$).
It now remains to find the orders of the functions ![]() $\mu _\pm$ and
$\mu _\pm$ and ![]() $s$ at the points
$s$ at the points ![]() $S_\pm$. To that end, we first show that
$S_\pm$. To that end, we first show that ![]() $S_+ \neq S_-$. Assume, for the sake of contradiction, that
$S_+ \neq S_-$. Assume, for the sake of contradiction, that ![]() $S_+ = S_- = S$. Then
$S_+ = S_- = S$. Then ![]() $S$ is a double zero of the function
$S$ is a double zero of the function ![]() $w$. Furthermore, we have
$w$. Furthermore, we have ![]() $\mu _+\mu _- = w$, and both
$\mu _+\mu _- = w$, and both ![]() $\mu _+$ and
$\mu _+$ and ![]() $\mu _-$ are holomorphic and have at worst a simple zero at
$\mu _-$ are holomorphic and have at worst a simple zero at ![]() $S$ (indeed, these functions have degree
$S$ (indeed, these functions have degree ![]() $(n-1)/2$ and zeros of order
$(n-1)/2$ and zeros of order ![]() $(n-3)/2$ at the points
$(n-3)/2$ at the points ![]() $Z_+$ and
$Z_+$ and ![]() $Z_-$, respectively). Thus, both
$Z_-$, respectively). Thus, both ![]() $\mu _+$ and
$\mu _+$ and ![]() $\mu _-$ must have a simple zero at
$\mu _-$ must have a simple zero at ![]() $S$. However, then, from the definition (24) of the function
$S$. However, then, from the definition (24) of the function ![]() $s$, it follows that it does not have a zero at
$s$, it follows that it does not have a zero at ![]() $S$. Furthermore,
$S$. Furthermore, ![]() $s$ cannot have zeros at other points of
$s$ cannot have zeros at other points of ![]() $\Gamma {\setminus} \{Z_\pm \}$, because the only zero of
$\Gamma {\setminus} \{Z_\pm \}$, because the only zero of ![]() $\mu _+$ in that domain is the point
$\mu _+$ in that domain is the point ![]() $S$, but this means that
$S$, but this means that ![]() $s$ has just two zeros counting with multiplicities, which is impossible because
$s$ has just two zeros counting with multiplicities, which is impossible because ![]() $\deg s = 3$. Therefore, we must have that
$\deg s = 3$. Therefore, we must have that ![]() $S_+ \neq S_-$.
$S_+ \neq S_-$.
Now, the relation ![]() $\mu _+\mu _- = w$ implies that at both points
$\mu _+\mu _- = w$ implies that at both points ![]() $S_\pm$ one of the functions
$S_\pm$ one of the functions ![]() $\mu _\pm$ has a simple zero, whereas the second does not have a zero or a pole. Without loss of generality, assume that
$\mu _\pm$ has a simple zero, whereas the second does not have a zero or a pole. Without loss of generality, assume that ![]() $\mu _+(S_+) = 0$ and, thus,
$\mu _+(S_+) = 0$ and, thus, ![]() $\mathrm {ord}\,_{S_+}\mu _+ = 1$. Then
$\mathrm {ord}\,_{S_+}\mu _+ = 1$. Then ![]() $\mathrm {ord}\,_{S_+}\mu _- = 0$, and by formula (24) we obtain
$\mathrm {ord}\,_{S_+}\mu _- = 0$, and by formula (24) we obtain ![]() $\mathrm {ord}\,_{S_+}s = 1$. Furthermore, from
$\mathrm {ord}\,_{S_+}s = 1$. Furthermore, from ![]() $\sigma ^*\mu _+ = \mu _-$ and
$\sigma ^*\mu _+ = \mu _-$ and ![]() $\sigma (S_+) = S_-$ it follows that
$\sigma (S_+) = S_-$ it follows that ![]() $\mathrm {ord}\,_{S_-}\mu _+ = 0$,
$\mathrm {ord}\,_{S_-}\mu _+ = 0$, ![]() $\mathrm {ord}\,_{S_-}\mu _- = 1$, and
$\mathrm {ord}\,_{S_-}\mu _- = 1$, and ![]() $\mathrm {ord}\,_{S_+}s = -1$. Finally, note that the functions
$\mathrm {ord}\,_{S_+}s = -1$. Finally, note that the functions ![]() $\mu _\pm$ and
$\mu _\pm$ and ![]() $s$ do not have zeros or poles other than the points
$s$ do not have zeros or poles other than the points ![]() $Z_\pm, S_\pm$, because for each of them the total number of zeros and poles at those points (counting with multiplicities) coincides with the degree. Thus, the proposition is proved.
$Z_\pm, S_\pm$, because for each of them the total number of zeros and poles at those points (counting with multiplicities) coincides with the degree. Thus, the proposition is proved.
Proposition 5.19 The affine spectral curve ![]() $\Gamma _a$ is a nodal curve (i.e. all its singularities are double points).
$\Gamma _a$ is a nodal curve (i.e. all its singularities are double points).
Proof. The affine spectral curve ![]() $\Gamma _a$ is the zero locus of the characteristic polynomial
$\Gamma _a$ is the zero locus of the characteristic polynomial ![]() $p(z,w) = z + z^{-1} + q(w)$ of the matrix (20). Computing the differential of that polynomial, we get that
$p(z,w) = z + z^{-1} + q(w)$ of the matrix (20). Computing the differential of that polynomial, we get that ![]() $(z_0,w_0) \in \Gamma _a$ is singular if and only if
$(z_0,w_0) \in \Gamma _a$ is singular if and only if ![]() $z_0 = \pm 1$ and
$z_0 = \pm 1$ and ![]() $w_0$ is a multiple root of
$w_0$ is a multiple root of ![]() $p(z_0,w)$. Furthermore, computing the Hessian, we get that a singular point
$p(z_0,w)$. Furthermore, computing the Hessian, we get that a singular point ![]() $(z_0,w_0) \in \Gamma _a$ is a double point if and only if
$(z_0,w_0) \in \Gamma _a$ is a double point if and only if ![]() $w_0$ is a double root of
$w_0$ is a double root of ![]() $p(z_0,w)$. However, for
$p(z_0,w)$. However, for ![]() $z_0 = \pm 1$ the matrix (20) is symmetric (equivalently, the restriction of the operator
$z_0 = \pm 1$ the matrix (20) is symmetric (equivalently, the restriction of the operator ![]() $\mathcal {D}_+\mathcal {D}_-$ to
$\mathcal {D}_+\mathcal {D}_-$ to ![]() $Q^n({\pm 1})$ is self-adjoint), so the multiplicity of the root
$Q^n({\pm 1})$ is self-adjoint), so the multiplicity of the root ![]() $w_0$ of its characteristic polynomial is equal to the dimension of the corresponding eigenspace, which is
$w_0$ of its characteristic polynomial is equal to the dimension of the corresponding eigenspace, which is
Thus, indeed all singular points of ![]() $\Gamma _a$ are double points.
$\Gamma _a$ are double points.
Remark 5.20 It is easy to see that the genus of the normalization ![]() $\Gamma$ of
$\Gamma$ of ![]() $\Gamma _a$ is equal to
$\Gamma _a$ is equal to ![]() $n - d - 1$ where
$n - d - 1$ where ![]() $d$ is the number of double points of
$d$ is the number of double points of ![]() $\Gamma _a$. Furthermore, as can be seen from the proof of Proposition 5.19, double points of
$\Gamma _a$. Furthermore, as can be seen from the proof of Proposition 5.19, double points of ![]() $\Gamma _a$ correspond to double roots of the polynomials
$\Gamma _a$ correspond to double roots of the polynomials ![]() $q(w) \pm 2$. The polynomial
$q(w) \pm 2$. The polynomial ![]() $q$ is of degree
$q$ is of degree ![]() $n$, so each of those polynomials may have at most
$n$, so each of those polynomials may have at most ![]() $(n-1) / 2$ double roots. Therefore,
$(n-1) / 2$ double roots. Therefore, ![]() $\Gamma$ is rational when each of the polynomials
$\Gamma$ is rational when each of the polynomials ![]() $q(w) \pm 2$ has precisely
$q(w) \pm 2$ has precisely ![]() $(n-1) / 2$ double roots (and, in addition, one simple root). Likewise,
$(n-1) / 2$ double roots (and, in addition, one simple root). Likewise, ![]() $\Gamma$ is elliptic when one of the polynomial
$\Gamma$ is elliptic when one of the polynomial ![]() $q(w) \pm 2$ has
$q(w) \pm 2$ has ![]() $(n-1)/2$ double roots, whereas the second has
$(n-1)/2$ double roots, whereas the second has ![]() $(n-3)/2$ double roots. Using Remark 5.16 one can show that it is the polynomial
$(n-3)/2$ double roots. Using Remark 5.16 one can show that it is the polynomial ![]() $q(w) +2$ that has
$q(w) +2$ that has ![]() $(n-3)/2$ double roots.
$(n-3)/2$ double roots.
5.2 The eigenvector function
In this section, we study in detail the analytic properties of the meromorphic vector-function ![]() $\xi$ constructed in Proposition 5.8. This will allow us to obtain analytic formulas for coordinates of vertices of the polygon
$\xi$ constructed in Proposition 5.8. This will allow us to obtain analytic formulas for coordinates of vertices of the polygon ![]() $P$ (see § 6.1 for the rational case and § 6.2 for the elliptic case). We keep all the notation of § 5.1.
$P$ (see § 6.1 for the rational case and § 6.2 for the elliptic case). We keep all the notation of § 5.1.
Proposition 5.21 We have ![]() $\mathrm {ord}_{Z_\pm }\xi _k = \pm k$.
$\mathrm {ord}_{Z_\pm }\xi _k = \pm k$.
Proof. Let ![]() $d_k := \mathrm {ord}_{Z_+}\xi _k - k$. We need to show that
$d_k := \mathrm {ord}_{Z_+}\xi _k - k$. We need to show that ![]() $d_k = 0$ for every
$d_k = 0$ for every ![]() $k \in \mathbb {Z}$. Note that
$k \in \mathbb {Z}$. Note that ![]() $d_0 = 0$ because
$d_0 = 0$ because ![]() $\xi _0 = 1$. Thus, it suffices to show that
$\xi _0 = 1$. Thus, it suffices to show that ![]() $d_k$ is a constant sequence. Also note that because
$d_k$ is a constant sequence. Also note that because ![]() $\xi _{k+n} = z\xi _k$ and
$\xi _{k+n} = z\xi _k$ and ![]() $z$ has a zero of order
$z$ has a zero of order ![]() $n$ at
$n$ at ![]() $Z_+$ (see Table 1), the sequence
$Z_+$ (see Table 1), the sequence ![]() $d_k$ is
$d_k$ is ![]() $n$-periodic. Thus, if it is not constant, then there must exist
$n$-periodic. Thus, if it is not constant, then there must exist ![]() $k \in \mathbb {Z}$ such that
$k \in \mathbb {Z}$ such that ![]() $d_{k-1} > d_k \leq d_{k+1}$. However, because
$d_{k-1} > d_k \leq d_{k+1}$. However, because ![]() $\xi$ is the eigenvector of the operator (19) with eigenvalue
$\xi$ is the eigenvector of the operator (19) with eigenvalue ![]() $w$, we have
$w$, we have
As ![]() $\alpha$ is a non-vanishing sequence, the order of the left-hand side at
$\alpha$ is a non-vanishing sequence, the order of the left-hand side at ![]() $Z_+$ can be bounded as
$Z_+$ can be bounded as
On the other hand, because ![]() $\mathrm {ord}_{Z_+}w = -1$, the order of the right-hand side of (30) is
$\mathrm {ord}_{Z_+}w = -1$, the order of the right-hand side of (30) is ![]() $d_k + k - 1$. Thus,
$d_k + k - 1$. Thus, ![]() $d_k$ must be a constant sequence, as desired.
$d_k$ must be a constant sequence, as desired.
We now proceed to describe the behavior of ![]() $\xi$ away from the points
$\xi$ away from the points ![]() $Z_\pm$. We begin with the following preliminary lemma.
$Z_\pm$. We begin with the following preliminary lemma.
Lemma 5.22 Assume that ![]() $X_\pm \in \Gamma {\setminus} \{Z_\pm \}$ are distinct points such that
$X_\pm \in \Gamma {\setminus} \{Z_\pm \}$ are distinct points such that ![]() $w(X_+) = w(X_-)$ (equivalently,
$w(X_+) = w(X_-)$ (equivalently, ![]() $\sigma (X_+) = X_-$). Then the directions (i.e. points in
$\sigma (X_+) = X_-$). Then the directions (i.e. points in ![]() $\mathbb {P}^\infty$, see Remark 5.9) determined by the values of
$\mathbb {P}^\infty$, see Remark 5.9) determined by the values of ![]() $\xi$ at
$\xi$ at ![]() $X_\pm$ are distinct from each other.
$X_\pm$ are distinct from each other.
Proof. Without loss of generality, assume that the vectors ![]() $\xi (X_\pm )$ are finite and non-zero (if not, we multiply
$\xi (X_\pm )$ are finite and non-zero (if not, we multiply ![]() $\xi$ by an appropriate meromorphic function, see Remark 5.9). One then needs to show that these vectors are linearly independent. To that end, recall that
$\xi$ by an appropriate meromorphic function, see Remark 5.9). One then needs to show that these vectors are linearly independent. To that end, recall that ![]() $T^n\xi (X_\pm ) = z(X_\pm )\xi (X_\pm )$. Thus, if
$T^n\xi (X_\pm ) = z(X_\pm )\xi (X_\pm )$. Thus, if ![]() $z(X_+) \neq z(X_-)$, then the vectors
$z(X_+) \neq z(X_-)$, then the vectors ![]() $\xi (X_\pm )$ are independent as eigenvectors of
$\xi (X_\pm )$ are independent as eigenvectors of ![]() $T^n$ corresponding to distinct eigenvalues. Therefore, it suffices to consider the case
$T^n$ corresponding to distinct eigenvalues. Therefore, it suffices to consider the case ![]() $z(X_+) = z(X_-)$. In that case, we have
$z(X_+) = z(X_-)$. In that case, we have
so ![]() $z(X_\pm ) = \pm 1$. Suppose for the sake of contradiction that the corresponding vectors
$z(X_\pm ) = \pm 1$. Suppose for the sake of contradiction that the corresponding vectors ![]() $\xi (X_\pm )$ are linearly dependent. Then, without loss of generality, we can assume that
$\xi (X_\pm )$ are linearly dependent. Then, without loss of generality, we can assume that ![]() $\xi (X_+) = \xi (X_-)$ (this can be always arranged by multiplying
$\xi (X_+) = \xi (X_-)$ (this can be always arranged by multiplying ![]() $\xi$ by an appropriate meromorphic function). We use the notation
$\xi$ by an appropriate meromorphic function). We use the notation ![]() $\xi _0:=\xi (X_\pm )$,
$\xi _0:=\xi (X_\pm )$, ![]() $z_0 := z(X_\pm ) = \pm 1$,
$z_0 := z(X_\pm ) = \pm 1$, ![]() $w_0 := w(X_\pm )$. Note that because
$w_0 := w(X_\pm )$. Note that because ![]() $w(X_+) = w(X_-)$, the differential of
$w(X_+) = w(X_-)$, the differential of ![]() $w$ does not vanish at
$w$ does not vanish at ![]() $X_\pm$, so
$X_\pm$, so ![]() $w$ can be taken as a local parameter near those points. Then, differentiating the relation
$w$ can be taken as a local parameter near those points. Then, differentiating the relation ![]() $(T^n- z)\xi = 0$ with respect to
$(T^n- z)\xi = 0$ with respect to ![]() $w$ at
$w$ at ![]() $X_\pm$, we obtain
$X_\pm$, we obtain
Taking a linear combination of these equations, we obtain ![]() $(T^n - z_0)\hat \xi = 0,$ where
$(T^n - z_0)\hat \xi = 0,$ where ![]() $\hat \xi := z'(X_+)\xi '(X_-) - z'(X_-)\xi '(X_+).$ In other words, we have
$\hat \xi := z'(X_+)\xi '(X_-) - z'(X_-)\xi '(X_+).$ In other words, we have ![]() $\hat \xi \in Q^n({z_0}).$ Similarly, using the equation
$\hat \xi \in Q^n({z_0}).$ Similarly, using the equation ![]() $(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$, we obtain
$(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$, we obtain
where ![]() $\lambda :=z'(X_+) -z'(X_-).$ Note also that
$\lambda :=z'(X_+) -z'(X_-).$ Note also that ![]() $\lambda \neq 0$. Indeed,
$\lambda \neq 0$. Indeed, ![]() $\lambda = 0$ would mean that the two branches of the curve
$\lambda = 0$ would mean that the two branches of the curve ![]() $\Gamma _a$ given by the functions
$\Gamma _a$ given by the functions ![]() $z(w)$ near
$z(w)$ near ![]() $X_\pm$ are tangent to each other. This is, however, not possible, because
$X_\pm$ are tangent to each other. This is, however, not possible, because ![]() $\Gamma _a$ is a nodal curve (Proposition 5.19). Thus, because
$\Gamma _a$ is a nodal curve (Proposition 5.19). Thus, because ![]() $\lambda \neq 0$ and
$\lambda \neq 0$ and ![]() $\hat \xi \in Q^n({z_0})$, it follows from (31) that the operator
$\hat \xi \in Q^n({z_0})$, it follows from (31) that the operator ![]() $(\mathcal {D}_+\mathcal {D}_-)\vert _{Q^n({z_0})}$ has a non-trivial Jordan block. This is, however, not possible, because
$(\mathcal {D}_+\mathcal {D}_-)\vert _{Q^n({z_0})}$ has a non-trivial Jordan block. This is, however, not possible, because ![]() $z_0 = \pm 1$, and thus
$z_0 = \pm 1$, and thus ![]() $\mathcal {D}_+\mathcal {D}_-$ is self-adjoint on
$\mathcal {D}_+\mathcal {D}_-$ is self-adjoint on ![]() $Q^n({z_0})$. Thus, it must be that the vectors
$Q^n({z_0})$. Thus, it must be that the vectors ![]() $\xi (X_\pm )$ are linearly independent, as desired.
$\xi (X_\pm )$ are linearly independent, as desired.
Remark 5.23 In the elliptic case (i.e. when the genus of ![]() $\Gamma$ is
$\Gamma$ is ![]() $1$), one can also prove Lemma 5.22 as follows. The vectors
$1$), one can also prove Lemma 5.22 as follows. The vectors ![]() $\xi (X_\pm )$ are common eigenvectors of the operators
$\xi (X_\pm )$ are common eigenvectors of the operators ![]() $\mathcal {D}_+$,
$\mathcal {D}_+$, ![]() $\mathcal {D}_-$,
$\mathcal {D}_-$, ![]() $T^n$, with the corresponding eigenvalues given by the values of the function
$T^n$, with the corresponding eigenvalues given by the values of the function ![]() $\mu _+$,
$\mu _+$, ![]() $\mu _-$,
$\mu _-$, ![]() $z$ at the points
$z$ at the points ![]() $X_\pm$. Thus, it follows that
$X_\pm$. Thus, it follows that ![]() $\xi (X_\pm )$ are independent as long as at least one of the functions
$\xi (X_\pm )$ are independent as long as at least one of the functions ![]() $\mu _+, \mu _-, z$ separates
$\mu _+, \mu _-, z$ separates ![]() $X_+$ from
$X_+$ from ![]() $X_-$. Assume that this is not the case, which means that
$X_-$. Assume that this is not the case, which means that ![]() $\mu _\pm (X_+) = \mu _\pm (X_-)$ and
$\mu _\pm (X_+) = \mu _\pm (X_-)$ and ![]() $z(X_+) = z(X_-)$. Then we have
$z(X_+) = z(X_-)$. Then we have
Along with ![]() $z(X_\pm ) = \pm 1$, this gives
$z(X_\pm ) = \pm 1$, this gives ![]() $s(X_\pm ) = \pm 1$. However, in the elliptic case four of the six points where
$s(X_\pm ) = \pm 1$. However, in the elliptic case four of the six points where ![]() $s = \pm 1$ are fixed by
$s = \pm 1$ are fixed by ![]() $\sigma$ (which would force
$\sigma$ (which would force ![]() $X_+ = X_-$), whereas the remaining two points are separated by the function
$X_+ = X_-$), whereas the remaining two points are separated by the function ![]() $z$ (by Proposition 5.15). Thus, the functions
$z$ (by Proposition 5.15). Thus, the functions ![]() $\mu _\pm, z$ indeed separate any pair of points on
$\mu _\pm, z$ indeed separate any pair of points on ![]() $\Gamma$, which proves Lemma 5.22. As a byproduct, we also obtain the following result: the functions
$\Gamma$, which proves Lemma 5.22. As a byproduct, we also obtain the following result: the functions ![]() $\mu _\pm, z$ define an embedding
$\mu _\pm, z$ define an embedding ![]() $\Gamma {\setminus} \{Z_\pm \} \hookrightarrow \mathbb {C}^3$. In other words, if we view
$\Gamma {\setminus} \{Z_\pm \} \hookrightarrow \mathbb {C}^3$. In other words, if we view ![]() $\mu _\pm$ and
$\mu _\pm$ and ![]() $z$ as rational functions on
$z$ as rational functions on ![]() $\Gamma _a$, then these functions provide a resolution of singularities.
$\Gamma _a$, then these functions provide a resolution of singularities.
Lemma 5.22 also admits an infinitesimal version, corresponding to the case when ![]() $X_+ = X_- = X$ is a branch point of
$X_+ = X_- = X$ is a branch point of ![]() $w$ (equivalently, a fixed point of
$w$ (equivalently, a fixed point of ![]() $\sigma$). In this case, the role of
$\sigma$). In this case, the role of ![]() $\xi (X_\pm )$ is played by the vectors
$\xi (X_\pm )$ is played by the vectors ![]() $\xi (X)$,
$\xi (X)$, ![]() $\xi '(X)$, where the derivative is taken with respect to a local parameter near
$\xi '(X)$, where the derivative is taken with respect to a local parameter near ![]() $X$. Note that upon renormalization of
$X$. Note that upon renormalization of ![]() $\xi$, its derivative changes as
$\xi$, its derivative changes as ![]() $\xi ' \mapsto f\xi ' + f'\xi$, so the direction of
$\xi ' \mapsto f\xi ' + f'\xi$, so the direction of ![]() $\xi '$ is well-defined modulo the direction of
$\xi '$ is well-defined modulo the direction of ![]() $\xi$. In particular, linear independence of
$\xi$. In particular, linear independence of ![]() $\xi$ and
$\xi$ and ![]() $\xi '$ is well-defined.
$\xi '$ is well-defined.
Lemma 5.24 Assume that ![]() $X \in \Gamma$ is a branch point of
$X \in \Gamma$ is a branch point of ![]() $w$ (equivalently, a fixed point of
$w$ (equivalently, a fixed point of ![]() $\sigma$). Then the directions determined by the values of
$\sigma$). Then the directions determined by the values of ![]() $\xi$ and
$\xi$ and ![]() $\xi '$ at
$\xi '$ at ![]() $X$ are distinct from each other.
$X$ are distinct from each other.
Proof. Renormalizing ![]() $\xi$ if necessary, we can assume that its value at
$\xi$ if necessary, we can assume that its value at ![]() $X$ is finite and non-zero. Then, differentiating the equation
$X$ is finite and non-zero. Then, differentiating the equation ![]() $(T^n - z)\xi = 0$ with respect to a local parameter near
$(T^n - z)\xi = 0$ with respect to a local parameter near ![]() $X$, we obtain
$X$, we obtain
Also note that because ![]() $\Gamma _a$ is a nodal curve, it follows that the mapping
$\Gamma _a$ is a nodal curve, it follows that the mapping ![]() $(z,w) \colon \Gamma {\setminus} \{Z_\pm \} \to \mathbb {C}^2$ is an immersion, so at a branch point of
$(z,w) \colon \Gamma {\setminus} \{Z_\pm \} \to \mathbb {C}^2$ is an immersion, so at a branch point of ![]() $w$ me must have
$w$ me must have ![]() $z' \neq 0$. However, then (32) implies that the vectors
$z' \neq 0$. However, then (32) implies that the vectors ![]() $\xi (X)$ and
$\xi (X)$ and ![]() $\xi '(X)$ are linearly independent, as desired.
$\xi '(X)$ are linearly independent, as desired.
Remark 5.25 Differentiating ![]() $(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$ at
$(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$ at ![]() $X$ and using that
$X$ and using that ![]() $w'(X) = 0$, we obtain
$w'(X) = 0$, we obtain ![]() $(\mathcal {D}_+\mathcal {D}_- - w(X))\xi '(X) = 0$. Thus, Lemma 5.24 means that
$(\mathcal {D}_+\mathcal {D}_- - w(X))\xi '(X) = 0$. Thus, Lemma 5.24 means that ![]() $\xi (X)$ and
$\xi (X)$ and ![]() $\xi '(X)$ form a basis of solutions for the equation
$\xi '(X)$ form a basis of solutions for the equation ![]() $(\mathcal {D}_+\mathcal {D}_- - w(X))\xi = 0$.
$(\mathcal {D}_+\mathcal {D}_- - w(X))\xi = 0$.
Proposition 5.26 The function ![]() $\xi _1$ has
$\xi _1$ has ![]() $g$ poles in
$g$ poles in ![]() $\Gamma {\setminus} \{Z_\pm \}$, where
$\Gamma {\setminus} \{Z_\pm \}$, where ![]() $g \in \{0,1\}$ is the genus of
$g \in \{0,1\}$ is the genus of ![]() $\Gamma$.
$\Gamma$.
Proof. Let ![]() $u \in \bar{\mathbb{C}}$, and let
$u \in \bar{\mathbb{C}}$, and let ![]() $X_\pm$ be the two preimages of
$X_\pm$ be the two preimages of ![]() $u$ under the function
$u$ under the function ![]() $w \colon \Gamma \to \bar{\mathbb{C}}$. Recall that the trace of a meromorphic function
$w \colon \Gamma \to \bar{\mathbb{C}}$. Recall that the trace of a meromorphic function ![]() $f$ on
$f$ on ![]() $\Gamma$ under
$\Gamma$ under ![]() $w$ is a meromorphic function on
$w$ is a meromorphic function on ![]() $\bar{\mathbb{C}}$ is defined by
$\bar{\mathbb{C}}$ is defined by ![]() $(\mathrm {tr}_wf)(u) := f(X_+) + f(X_-)$. Let
$(\mathrm {tr}_wf)(u) := f(X_+) + f(X_-)$. Let
Note that ![]() $\xi _0 \equiv 1$ by the definition of the eigenvector function
$\xi _0 \equiv 1$ by the definition of the eigenvector function ![]() $\xi$, so
$\xi$, so ![]() $\zeta (u) = (\xi _1(X_+) - \xi _1(X_-))^2$. This means that
$\zeta (u) = (\xi _1(X_+) - \xi _1(X_-))^2$. This means that ![]() $\zeta := 2 \mathrm {tr}_w (\xi _1^2) - (\mathrm {tr}_w \xi _1)^2$, so in particular
$\zeta := 2 \mathrm {tr}_w (\xi _1^2) - (\mathrm {tr}_w \xi _1)^2$, so in particular ![]() $\zeta$ is meromorphic (i.e. rational). To understand the behavior of that function, fix a point
$\zeta$ is meromorphic (i.e. rational). To understand the behavior of that function, fix a point ![]() $u_0 \in \bar{\mathbb{C}}$. Let
$u_0 \in \bar{\mathbb{C}}$. Let ![]() $\Sigma := w(\{X \in \Gamma \mid dw(X) = 0\})\subset \bar{\mathbb{C}}$ be the set of critical values of
$\Sigma := w(\{X \in \Gamma \mid dw(X) = 0\})\subset \bar{\mathbb{C}}$ be the set of critical values of ![]() $w$ (this set contains two or four points depending on the genus of
$w$ (this set contains two or four points depending on the genus of ![]() $\Gamma$). Then the following cases are possible.
$\Gamma$). Then the following cases are possible.
Case 1: ![]() $u_0 \notin \Sigma$ is finite, and
$u_0 \notin \Sigma$ is finite, and ![]() $\xi _1$ is finite at both preimages
$\xi _1$ is finite at both preimages ![]() $X_\pm$ of
$X_\pm$ of ![]() $u_0$ under
$u_0$ under ![]() $w$. In this case,
$w$. In this case, ![]() $\zeta (u_0)$ is the squared Wronskian of the solutions
$\zeta (u_0)$ is the squared Wronskian of the solutions ![]() $\xi (X_\pm )$ of equation
$\xi (X_\pm )$ of equation ![]() $\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$. By Lemma 5.22, these solutions are independent, so
$\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$. By Lemma 5.22, these solutions are independent, so ![]() $\zeta (u_0)$ is finite and non-zero.
$\zeta (u_0)$ is finite and non-zero.
Case 2: ![]() $u_0 \notin \Sigma$ is finite,
$u_0 \notin \Sigma$ is finite, ![]() $\xi _1$ has a pole of order
$\xi _1$ has a pole of order ![]() $d$ at one of the preimages
$d$ at one of the preimages ![]() $X_\pm$ of
$X_\pm$ of ![]() $u_0$ (say,
$u_0$ (say, ![]() $X_+$), and is finite at the other preimage. In this case, the function
$X_+$), and is finite at the other preimage. In this case, the function ![]() $(u-u_0)^{2d}\zeta (u)$ is finite at
$(u-u_0)^{2d}\zeta (u)$ is finite at ![]() $u_0$ and is equal to the squared Wronskian of linearly independent solutions
$u_0$ and is equal to the squared Wronskian of linearly independent solutions ![]() $((w - u_0)^d\xi )({X_+})$,
$((w - u_0)^d\xi )({X_+})$, ![]() $\xi (X_-)$ of
$\xi (X_-)$ of ![]() $\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$. Thus,
$\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$. Thus, ![]() $\zeta$ has a pole of order
$\zeta$ has a pole of order ![]() $2d$ at
$2d$ at ![]() $u_0$.
$u_0$.
Case 3: ![]() $u_0 \notin \Sigma$ is finite, and
$u_0 \notin \Sigma$ is finite, and ![]() $\xi _1$ has poles at both preimages
$\xi _1$ has poles at both preimages ![]() $X_\pm$ of
$X_\pm$ of ![]() $u_0$. This is not possible, since after renormalizing
$u_0$. This is not possible, since after renormalizing ![]() $\xi$ we would obtain
$\xi$ we would obtain
which would mean that the Wronskian of ![]() $\xi (X_\pm )$ vanishes.
$\xi (X_\pm )$ vanishes.
Case 4: ![]() $u_0 = \infty$ (in which case we also have
$u_0 = \infty$ (in which case we also have ![]() $u \notin \Sigma$). In this case
$u \notin \Sigma$). In this case ![]() $X_\pm = Z_\pm$, so
$X_\pm = Z_\pm$, so ![]() $\zeta$ has a pole of order
$\zeta$ has a pole of order ![]() $2$ at
$2$ at ![]() $u_0$ by Proposition 5.21.
$u_0$ by Proposition 5.21.
All in all, the function ![]() $\zeta$ does not vanish in
$\zeta$ does not vanish in ![]() $\bar{\mathbb{C}} {\setminus} \Sigma$, whereas the number of its poles in that domain is twice the number of poles of
$\bar{\mathbb{C}} {\setminus} \Sigma$, whereas the number of its poles in that domain is twice the number of poles of ![]() $\xi _1$ in
$\xi _1$ in ![]() $\{X \in \Gamma \mid \,dw(X) \neq 0\}$ (counting with multiplicities). Now, consider
$\{X \in \Gamma \mid \,dw(X) \neq 0\}$ (counting with multiplicities). Now, consider ![]() $u_0 \in \Sigma$, and let
$u_0 \in \Sigma$, and let ![]() $X \in \Gamma$ be the unique point such that
$X \in \Gamma$ be the unique point such that ![]() $w(X) = u_0$. Then there exists a parameter
$w(X) = u_0$. Then there exists a parameter ![]() $t$ near
$t$ near ![]() $X$ such that the function
$X$ such that the function ![]() $w$ can be locally written as
$w$ can be locally written as ![]() $t \mapsto u_0 + t^2$. So
$t \mapsto u_0 + t^2$. So ![]() $\zeta (u)$ near
$\zeta (u)$ near ![]() $u_0$ can be written as
$u_0$ can be written as
where ![]() $t = \sqrt {u - u_0}$. Then at
$t = \sqrt {u - u_0}$. Then at ![]() $t = 0$ we have
$t = 0$ we have
up to a constant factor and higher-order terms. Thus, when ![]() $u_0 \in \Sigma$, we have the following two cases.
$u_0 \in \Sigma$, we have the following two cases.
Case 5: ![]() $u_0 \in \Sigma$, and
$u_0 \in \Sigma$, and ![]() $\xi _1$ is finite at the preimage
$\xi _1$ is finite at the preimage ![]() $X$ of
$X$ of ![]() $u_0$. In this case, in view of Remark 5.25, the determinant in (33) is the Wronskian of two independent solutions of
$u_0$. In this case, in view of Remark 5.25, the determinant in (33) is the Wronskian of two independent solutions of ![]() $\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$, so
$\mathcal {D}_+\mathcal {D}_-\eta = u_0\eta$, so ![]() $\zeta (u) \sim t^2 = u - u_0$ and, thus, has a simple zero at
$\zeta (u) \sim t^2 = u - u_0$ and, thus, has a simple zero at ![]() $u_0$.
$u_0$.
Case 6: ![]() $u_0 \in \Sigma$, and
$u_0 \in \Sigma$, and ![]() $\xi _1$ has a pole of order
$\xi _1$ has a pole of order ![]() $d$ at the preimage
$d$ at the preimage ![]() $X$ of
$X$ of ![]() $u_0$. In this case, renormalizing
$u_0$. In this case, renormalizing ![]() $\xi$ as in Case 2, we obtain that
$\xi$ as in Case 2, we obtain that ![]() $\zeta$ has a pole of order
$\zeta$ has a pole of order ![]() $2d - 1$ at
$2d - 1$ at ![]() $u_0$.
$u_0$.
In the latter case, one can regard a pole of order ![]() $2d - 1$ as a pole of order
$2d - 1$ as a pole of order ![]() $2d$ that collided with a simple zero. With this understanding, the number of zeros of
$2d$ that collided with a simple zero. With this understanding, the number of zeros of ![]() $\zeta$ is equal to the number of branch points of
$\zeta$ is equal to the number of branch points of ![]() $w$, whereas the number of poles of
$w$, whereas the number of poles of ![]() $\zeta$ is twice the number of poles of
$\zeta$ is twice the number of poles of ![]() $\xi _1$ (with some zeros and poles possibly cancelling each other out). In addition, because the number of zeros of
$\xi _1$ (with some zeros and poles possibly cancelling each other out). In addition, because the number of zeros of ![]() $\zeta$ is equal to the number of its poles, it follows that the number of poles of
$\zeta$ is equal to the number of its poles, it follows that the number of poles of ![]() $\xi _1$ is half the number of branch points of
$\xi _1$ is half the number of branch points of ![]() $w$, which is
$w$, which is ![]() $2g + 2$. Furthermore, because
$2g + 2$. Furthermore, because ![]() $Z_+$ is not a pole of
$Z_+$ is not a pole of ![]() $\xi _1$, whereas
$\xi _1$, whereas ![]() $Z_-$ is its pole of order
$Z_-$ is its pole of order ![]() $1$ (see Proposition 5.21), it follows that the number of poles of
$1$ (see Proposition 5.21), it follows that the number of poles of ![]() $\xi _1$ in
$\xi _1$ in ![]() $\Gamma {\setminus} \{Z_\pm \}$ is exactly
$\Gamma {\setminus} \{Z_\pm \}$ is exactly ![]() $g$, as desired.
$g$, as desired.
Corollary 5.27 In the rational case, all functions ![]() $\xi _k$ are holomorphic in
$\xi _k$ are holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$, whereas in the elliptic case all of them have at worst a simple pole at one and the same point
$\Gamma {\setminus} \{Z_\pm \}$, whereas in the elliptic case all of them have at worst a simple pole at one and the same point ![]() $X_p$, and no other poles.
$X_p$, and no other poles.
Proof. First note that ![]() $\xi _0 \equiv 1$ by construction. Furthermore, in the rational case
$\xi _0 \equiv 1$ by construction. Furthermore, in the rational case ![]() $\xi _1$ is holomorphic in
$\xi _1$ is holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$ by Proposition 5.26. Thus, both
$\Gamma {\setminus} \{Z_\pm \}$ by Proposition 5.26. Thus, both ![]() $\xi _0$ and
$\xi _0$ and ![]() $\xi _1$ are holomorphic in that domain. At the same time, by (30) we have
$\xi _1$ are holomorphic in that domain. At the same time, by (30) we have
and because ![]() $w$ is holomorphic in
$w$ is holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$ (Table 1), it follows by induction that so are all
$\Gamma {\setminus} \{Z_\pm \}$ (Table 1), it follows by induction that so are all ![]() $\xi _k$ with
$\xi _k$ with ![]() $k \geq 0$. Analogously, using (30) to express
$k \geq 0$. Analogously, using (30) to express ![]() $\xi _{k-1}$, we get that
$\xi _{k-1}$, we get that ![]() $\xi _k$ with
$\xi _k$ with ![]() $k < 0$ are holomorphic in
$k < 0$ are holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$ too. This proves the corollary in the rational case.
$\Gamma {\setminus} \{Z_\pm \}$ too. This proves the corollary in the rational case.
In the elliptic case, the argument is similar, but now Proposition 5.26 implies that ![]() $\xi _1$ has a single pole in
$\xi _1$ has a single pole in ![]() $\Gamma {\setminus} \{Z_\pm \}$. Denoting that pole by
$\Gamma {\setminus} \{Z_\pm \}$. Denoting that pole by ![]() $X_p$, we obtain by induction that all
$X_p$, we obtain by induction that all ![]() $\xi _k$ are holomorphic in
$\xi _k$ are holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm, X_p\}$, as desired.
$\Gamma {\setminus} \{Z_\pm, X_p\}$, as desired.
6. Proof of Theorem B: a self-dual polygon fixed by the pentagram map is Poncelet
In this section, we prove Theorem B: any weakly convex self-dual twisted odd-gon ![]() $P$ projectively equivalent to its pentagram image
$P$ projectively equivalent to its pentagram image ![]() $P'$ is Poncelet. To that end, we use the results of § 5 to obtain explicit formulas for coordinates of vertices of
$P'$ is Poncelet. To that end, we use the results of § 5 to obtain explicit formulas for coordinates of vertices of ![]() $P$ (see § 6.1 for the case
$P$ (see § 6.1 for the case ![]() $g = 0$ and § 6.2 for the case
$g = 0$ and § 6.2 for the case ![]() $g = 1$) and, hence, show that
$g = 1$) and, hence, show that ![]() $P$ is a Poncelet polygon.
$P$ is a Poncelet polygon.
6.1 The rational case: degenerate Poncelet polygons
In this section, we prove Theorem B in the case when the genus of ![]() $\Gamma$ is zero, that is, when
$\Gamma$ is zero, that is, when ![]() $\Gamma$ is a rational curve. In that case, we show that
$\Gamma$ is a rational curve. In that case, we show that ![]() $P$ is a degenerate Poncelet polygon in the sense that the corresponding inscribed and circumscribed conics are not in general position. We keep the notation of the previous two sections.
$P$ is a degenerate Poncelet polygon in the sense that the corresponding inscribed and circumscribed conics are not in general position. We keep the notation of the previous two sections.
Proposition 6.1 The set ![]() $s^{-1}(1) := \{X \in \Gamma \mid s(X) = 1\}$ consists of either one or three points.
$s^{-1}(1) := \{X \in \Gamma \mid s(X) = 1\}$ consists of either one or three points.
Proof. This set is invariant under the involution ![]() $\sigma$ and contains exactly one fixed point of that involution (see the proof of Proposition 5.15). Thus, it must contain odd number of points, and because
$\sigma$ and contains exactly one fixed point of that involution (see the proof of Proposition 5.15). Thus, it must contain odd number of points, and because ![]() $\deg s = 3$, it follows that
$\deg s = 3$, it follows that ![]() $|s^{-1}(1)| = 1$ or
$|s^{-1}(1)| = 1$ or ![]() $|s^{-1}(1)| = 3$.
$|s^{-1}(1)| = 3$.
We consider the cases ![]() $|s^{-1}(1)| = 1$ and
$|s^{-1}(1)| = 1$ and ![]() $|s^{-1}(1)| = 3$ separately. First, assume that
$|s^{-1}(1)| = 3$ separately. First, assume that ![]() $|s^{-1}(1)| = 3$. Denote points in
$|s^{-1}(1)| = 3$. Denote points in ![]() $s^{-1}(1)$ by
$s^{-1}(1)$ by ![]() $A,B,C$, where
$A,B,C$, where ![]() $A$ and
$A$ and ![]() $B$ are switched by
$B$ are switched by ![]() $\sigma$, whereas
$\sigma$, whereas ![]() $C$ is fixed by
$C$ is fixed by ![]() $\sigma$.
$\sigma$.
Proposition 6.2 The vectors ![]() $\xi (A)$,
$\xi (A)$, ![]() $\xi (B)$,
$\xi (B)$, ![]() $\xi (C)$ form a basis of
$\xi (C)$ form a basis of ![]() $\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$.
$\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$.
Remark 6.3 Note that the vectors ![]() $\xi (A)$,
$\xi (A)$, ![]() $\xi (B)$,
$\xi (B)$, ![]() $\xi (C)$ are finite because, by Corollary 5.27, the vector-function
$\xi (C)$ are finite because, by Corollary 5.27, the vector-function ![]() $\xi$ is holomorphic in
$\xi$ is holomorphic in ![]() $\Gamma {\setminus} \{Z_\pm \}$, and
$\Gamma {\setminus} \{Z_\pm \}$, and ![]() $A,B,C \neq Z_\pm$ because
$A,B,C \neq Z_\pm$ because ![]() $s(Z_+) = \infty$ and
$s(Z_+) = \infty$ and ![]() $s(Z_-) \!=\! 0$ (Table 1).
$s(Z_-) \!=\! 0$ (Table 1).
Proof of Proposition 6.2 We have ![]() $\xi (A), \xi (B), \xi (C) \in \mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$ by (25), so it suffices to show that these vectors are linearly independent. To that end, recall that they are eigenvectors of the operator
$\xi (A), \xi (B), \xi (C) \in \mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$ by (25), so it suffices to show that these vectors are linearly independent. To that end, recall that they are eigenvectors of the operator ![]() $\mathcal {D}_+\mathcal {D}_-$. Furthermore, the eigenvalue
$\mathcal {D}_+\mathcal {D}_-$. Furthermore, the eigenvalue ![]() $w(C)$ corresponding to
$w(C)$ corresponding to ![]() $\xi (C)$ is distinct from the eigenvalue
$\xi (C)$ is distinct from the eigenvalue ![]() $w(A) = w(B)$ corresponding to the other two vectors. Thus, it suffices to prove the independence of
$w(A) = w(B)$ corresponding to the other two vectors. Thus, it suffices to prove the independence of ![]() $\xi (A)$ and
$\xi (A)$ and ![]() $\xi (B)$. However, that follows from Lemma 5.22.
$\xi (B)$. However, that follows from Lemma 5.22.
Now recall that the polygon corresponding to the operator ![]() $\mathcal {D}_+ -T^n \mathcal {D}_-$ is
$\mathcal {D}_+ -T^n \mathcal {D}_-$ is ![]() $P$. Thus, by Proposition 6.2, the vertices of
$P$. Thus, by Proposition 6.2, the vertices of ![]() $P$ (defined up to a projective transformation) are given by
$P$ (defined up to a projective transformation) are given by ![]() $(\xi _k(A):\xi _k(B): \xi _k(C)) \in \mathbb {P}^2$. To explicitly compute the coordinates of vertices, we identify
$(\xi _k(A):\xi _k(B): \xi _k(C)) \in \mathbb {P}^2$. To explicitly compute the coordinates of vertices, we identify ![]() $\Gamma$ with
$\Gamma$ with ![]() $\bar{\mathbb{C}}$. Note that because automorphisms of
$\bar{\mathbb{C}}$. Note that because automorphisms of ![]() $\bar{\mathbb{C}}$ act transitively on triples of points, the map
$\bar{\mathbb{C}}$ act transitively on triples of points, the map ![]() $u \colon \Gamma \to \bar{\mathbb{C}}$ may be chosen in such a way that
$u \colon \Gamma \to \bar{\mathbb{C}}$ may be chosen in such a way that ![]() $u(Z_+ ) = 0$,
$u(Z_+ ) = 0$, ![]() $u(Z_-) = \infty$, and
$u(Z_-) = \infty$, and ![]() $u(C) = 1$. Then the involution
$u(C) = 1$. Then the involution ![]() $\sigma$, written in terms of
$\sigma$, written in terms of ![]() $u$, is
$u$, is ![]() $u \mapsto u^{-1}$, whereas the points
$u \mapsto u^{-1}$, whereas the points ![]() $A,B$ are identified with
$A,B$ are identified with ![]() $r$ and
$r$ and ![]() $r^{-1}$, where
$r^{-1}$, where ![]() $r \in \mathbb {C}^*{\setminus} \{\pm 1\}$. Furthermore, from Proposition 5.21 and Corollary 5.27 we obtain
$r \in \mathbb {C}^*{\setminus} \{\pm 1\}$. Furthermore, from Proposition 5.21 and Corollary 5.27 we obtain ![]() $\xi _k(u) = c_k u^k,$ where
$\xi _k(u) = c_k u^k,$ where ![]() $c_k \neq 0$ is a constant. Therefore, the vertices of
$c_k \neq 0$ is a constant. Therefore, the vertices of ![]() $P$ are given by
$P$ are given by
Thus, the polygon ![]() $P$ is inscribed in a conic with homogeneous equation
$P$ is inscribed in a conic with homogeneous equation
Furthermore, because ![]() $P$ is self-dual, it is also circumscribed and, hence, Poncelet. Thus, the proof of Theorem B in the case when the spectral curve is rational and
$P$ is self-dual, it is also circumscribed and, hence, Poncelet. Thus, the proof of Theorem B in the case when the spectral curve is rational and ![]() $|s^{-1}(1)| = 3$ is complete.
$|s^{-1}(1)| = 3$ is complete.
Remark 6.4 A direct calculation shows that the conic inscribed in the polygon (34) is
The conics (35) and (36) are tangent to each other at two points ![]() $(1:0:0)$ and
$(1:0:0)$ and ![]() $(0:1:0)$. In particular, they are not in general position (instead of four intersections we have two intersections of multiplicity
$(0:1:0)$. In particular, they are not in general position (instead of four intersections we have two intersections of multiplicity ![]() $2$).
$2$).
We now consider the case ![]() $|s^{-1}(1)| = 1$. To begin with, notice that this case can be thought of as a limit of the case
$|s^{-1}(1)| = 1$. To begin with, notice that this case can be thought of as a limit of the case ![]() $|s^{-1}(1)| = 3$, with the points
$|s^{-1}(1)| = 3$, with the points ![]() $A$,
$A$, ![]() $B$,
$B$, ![]() $C$ colliding and forming a single point
$C$ colliding and forming a single point ![]() $D \in s^{-1}(1)$. This observation leads to the following version of Proposition 6.2.
$D \in s^{-1}(1)$. This observation leads to the following version of Proposition 6.2.
Proposition 6.5 The vectors ![]() $\xi (D)$,
$\xi (D)$, ![]() $\xi '(D)$,
$\xi '(D)$, ![]() $\xi ''(D)$ form a basis of
$\xi ''(D)$ form a basis of ![]() $\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$, where the derivatives are taken with respect to any local parameter near
$\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$, where the derivatives are taken with respect to any local parameter near ![]() $D$.
$D$.
Proof. First, note that because the set ![]() $s^{-1}(1)$ consists of a single point
$s^{-1}(1)$ consists of a single point ![]() $D$, the latter must be an order
$D$, the latter must be an order ![]() $2$ branch point of the function
$2$ branch point of the function ![]() $s$. In other words, we have
$s$. In other words, we have ![]() $s'(D) = s''(D) = 0$. Thus, differentiating the equation
$s'(D) = s''(D) = 0$. Thus, differentiating the equation ![]() $(\mathcal {D}_+ -sT^n \mathcal {D}_-)\xi = 0$ at the point
$(\mathcal {D}_+ -sT^n \mathcal {D}_-)\xi = 0$ at the point ![]() $D$ twice, we obtain
$D$ twice, we obtain
Thus, we have ![]() $\xi (D), \xi '(D), \xi ''(D) \in \mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$, and it suffices to show that these vectors are linearly independent. To that end, we differentiate the equation
$\xi (D), \xi '(D), \xi ''(D) \in \mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$, and it suffices to show that these vectors are linearly independent. To that end, we differentiate the equation ![]() $(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$ twice at
$(\mathcal {D}_+\mathcal {D}_- - w)\xi = 0$ twice at ![]() $D$. Using that
$D$. Using that ![]() $D$ is a branch point of
$D$ is a branch point of ![]() $w$ and, thus,
$w$ and, thus, ![]() $w'(D) = 0$, we obtain
$w'(D) = 0$, we obtain
Furthermore, because the degree of the function ![]() $w$ is
$w$ is ![]() $2$,
$2$, ![]() $D$ is an order
$D$ is an order ![]() $1$ branch point for
$1$ branch point for ![]() $w$, so
$w$, so ![]() $w''(D) \neq 0$, which means that
$w''(D) \neq 0$, which means that ![]() $\xi (D)$,
$\xi (D)$, ![]() $\xi '(D)$ are eigenvectors of
$\xi '(D)$ are eigenvectors of ![]() $\mathcal {D}_+\mathcal {D}_-$, whereas
$\mathcal {D}_+\mathcal {D}_-$, whereas ![]() $\xi ''(D)$ is not. Furthermore, the vectors
$\xi ''(D)$ is not. Furthermore, the vectors ![]() $\xi (D)$ and
$\xi (D)$ and ![]() $\xi '(D)$ are linearly independent by Lemma 5.24. Thus,
$\xi '(D)$ are linearly independent by Lemma 5.24. Thus, ![]() $\xi (D)$,
$\xi (D)$, ![]() $\xi '(D)$,
$\xi '(D)$, ![]() $\xi ''(D)$ are indeed independent, as desired.
$\xi ''(D)$ are indeed independent, as desired.
We now find the vertices of the polygon ![]() $P$ in the same fashion as in the case
$P$ in the same fashion as in the case ![]() $|s^{-1}(1)| = 3$. Namely, choose an identification
$|s^{-1}(1)| = 3$. Namely, choose an identification ![]() $u \colon \Gamma \to \mathbb {P}^1$ in such a way that
$u \colon \Gamma \to \mathbb {P}^1$ in such a way that ![]() $u(Z_+ ) = 0$,
$u(Z_+ ) = 0$, ![]() $u(Z_-) = \infty$, and
$u(Z_-) = \infty$, and ![]() $u(D) = 1$. Then, as in the case
$u(D) = 1$. Then, as in the case ![]() $|s^{-1}(1)| = 3$, we obtain
$|s^{-1}(1)| = 3$, we obtain ![]() $\xi _k(u) = c_k u^k,$ where
$\xi _k(u) = c_k u^k,$ where ![]() $c_k \neq 0$ is a constant. In particular, at the point
$c_k \neq 0$ is a constant. In particular, at the point ![]() $D$ we obtain
$D$ we obtain ![]() $\xi _k = c_k$,
$\xi _k = c_k$, ![]() $\xi _k' = k c_k$,
$\xi _k' = k c_k$, ![]() $\xi _k'' = k(k-1) c_k$, so up to a projective transformation the vertices of
$\xi _k'' = k(k-1) c_k$, so up to a projective transformation the vertices of ![]() $P$ are given by
$P$ are given by
These points belong to a conic
so ![]() $P$ is inscribed and, hence, Poncelet. Thus, the proof of Theorem B in the rational case is complete.
$P$ is inscribed and, hence, Poncelet. Thus, the proof of Theorem B in the rational case is complete.
Remark 6.6 A direct calculation shows that the conic inscribed in the polygon (37) is
This is an even more degenerate case: the conics (38) and (39) intersect each other at one single point ![]() $(0:1:0)$, of multiplicity
$(0:1:0)$, of multiplicity ![]() $4$.
$4$.
Remark 6.7 Degenerate Poncelet polygons (34) and (37) correspond to degenerations of an elliptic curve to Abelian groups ![]() $\mathbb {C}^*$ and
$\mathbb {C}^*$ and ![]() $\mathbb {C}$, respectively. Indeed, removing the tangency points with the inscribed conic (36) from the circumscribed conic (35) we obtain an affine curve (a hyperbola) which is naturally isomorphic to
$\mathbb {C}$, respectively. Indeed, removing the tangency points with the inscribed conic (36) from the circumscribed conic (35) we obtain an affine curve (a hyperbola) which is naturally isomorphic to ![]() $\mathbb {C}^*$. The vertices of the Poncelet polygon (34) are uniformly spaced on that hyperbola with respect to the
$\mathbb {C}^*$. The vertices of the Poncelet polygon (34) are uniformly spaced on that hyperbola with respect to the ![]() $\mathbb {C}^*$ group structure. This should be compared with the case of genuine Poncelet polygons which are images of uniformly spaced points on an elliptic curve under a double covering map from the elliptic curve to the circumscribed conic. Thus, degenerate Poncelet polygons (34) correspond to degenerations of an elliptic curve to
$\mathbb {C}^*$ group structure. This should be compared with the case of genuine Poncelet polygons which are images of uniformly spaced points on an elliptic curve under a double covering map from the elliptic curve to the circumscribed conic. Thus, degenerate Poncelet polygons (34) correspond to degenerations of an elliptic curve to ![]() $\mathbb {C}^*$. Likewise, removing from (38) the tangency point with (39) we obtain a parabola which identifies with
$\mathbb {C}^*$. Likewise, removing from (38) the tangency point with (39) we obtain a parabola which identifies with ![]() $\mathbb {C}$, and points (37) are again uniformly spaced. Thus, degenerate Poncelet polygons (37) correspond to degenerations of an elliptic curve to
$\mathbb {C}$, and points (37) are again uniformly spaced. Thus, degenerate Poncelet polygons (37) correspond to degenerations of an elliptic curve to ![]() $\mathbb {C}$.
$\mathbb {C}$.
6.2 The elliptic case: genuine Poncelet polygons
In this section, we complete the proof of Theorem B in the case when the spectral curve ![]() $\Gamma$ has genus one, that is, is elliptic. The argument is similar to the rational case, but instead of elementary expressions (34) and (37), we obtain formulas for vertices of
$\Gamma$ has genus one, that is, is elliptic. The argument is similar to the rational case, but instead of elementary expressions (34) and (37), we obtain formulas for vertices of ![]() $P$ in terms of theta functions.
$P$ in terms of theta functions.
Recall that in the elliptic case the involution ![]() $\sigma$ on
$\sigma$ on ![]() $\Gamma$ has four fixed points, at three of which we have
$\Gamma$ has four fixed points, at three of which we have ![]() $s = 1$, whereas at the fourth we have
$s = 1$, whereas at the fourth we have ![]() $s = -1$ (see the proof of Proposition 5.15). Denote those points by
$s = -1$ (see the proof of Proposition 5.15). Denote those points by ![]() $A,B,C, D$, where
$A,B,C, D$, where ![]() $s(D) = -1$, and
$s(D) = -1$, and ![]() $s(A) = s(B) = s(C) = 1$.
$s(A) = s(B) = s(C) = 1$.
Proposition 6.8 The directions in ![]() $\mathbb {P}^\infty$ determined by the values of the vector-function
$\mathbb {P}^\infty$ determined by the values of the vector-function ![]() $\xi$ at the points
$\xi$ at the points ![]() $A$,
$A$, ![]() $B$,
$B$, ![]() $C$ (see Remark 5.9) are linearly independent.
$C$ (see Remark 5.9) are linearly independent.
Proof. They are eigendirections of the operator ![]() $\mathcal {D}_+\mathcal {D}_-$ corresponding to distinct eigenvalues
$\mathcal {D}_+\mathcal {D}_-$ corresponding to distinct eigenvalues ![]() $w(A)$,
$w(A)$, ![]() $w(B)$,
$w(B)$, ![]() $w(C)$.
$w(C)$.
As in the rational case, it follows that the vectors ![]() $\xi (A)$,
$\xi (A)$, ![]() $\xi (B)$,
$\xi (B)$, ![]() $\xi (C)$ form a basis of
$\xi (C)$ form a basis of ![]() $\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$ (as usual, one may need to renormalize these vectors to ensure that they are finite, see Remark 5.9). Therefore, the vertices of the corresponding polygon
$\mathrm {Ker}\,(\mathcal {D}_+ -T^n \mathcal {D}_-)$ (as usual, one may need to renormalize these vectors to ensure that they are finite, see Remark 5.9). Therefore, the vertices of the corresponding polygon ![]() $P$ (defined up to projective transformation) are given by
$P$ (defined up to projective transformation) are given by ![]() $(\xi _k(A):\xi _k(B): \xi _k(C)) \in \mathbb {P}^2.$
$(\xi _k(A):\xi _k(B): \xi _k(C)) \in \mathbb {P}^2.$
Remark 6.9 As ![]() $z(A) = z(B) = z(C) = 1$ (see Remark 5.16), it follows that the infinite vectors
$z(A) = z(B) = z(C) = 1$ (see Remark 5.16), it follows that the infinite vectors ![]() $\xi (A)$,
$\xi (A)$, ![]() $\xi (B)$,
$\xi (B)$, ![]() $\xi (C)$ are
$\xi (C)$ are ![]() $n$-periodic, so the polygon
$n$-periodic, so the polygon ![]() $P$ is closed.
$P$ is closed.
To explicitly compute the coordinates of vertices of ![]() $P$, we identify
$P$, we identify ![]() $\Gamma$ with
$\Gamma$ with ![]() $\mathbb {C}\!/\!\Lambda$, where
$\mathbb {C}\!/\!\Lambda$, where ![]() $\Lambda \subset \mathbb {C}$ is a lattice. Without loss of generality, assume that
$\Lambda \subset \mathbb {C}$ is a lattice. Without loss of generality, assume that ![]() $\Lambda$ is spanned by
$\Lambda$ is spanned by ![]() $1$ and
$1$ and ![]() $\tau$, where
$\tau$, where ![]() $\tau$ is in the upper half-plane. Furthermore, one can choose an identification between
$\tau$ is in the upper half-plane. Furthermore, one can choose an identification between ![]() $\Gamma$ and
$\Gamma$ and ![]() $\mathbb {C}\!/\!\Lambda$ in such a way that the point
$\mathbb {C}\!/\!\Lambda$ in such a way that the point ![]() $D \in \Gamma$ is identified with
$D \in \Gamma$ is identified with ![]() $d: = (1 + \tau )/2$. Then
$d: = (1 + \tau )/2$. Then ![]() $\sigma$, understood as an involution in
$\sigma$, understood as an involution in ![]() $\mathbb {C}\!/\!\Lambda$, is simply
$\mathbb {C}\!/\!\Lambda$, is simply ![]() $u \mapsto -u$. Thus,
$u \mapsto -u$. Thus, ![]() $A,B,C$ must coincide with the remaining order
$A,B,C$ must coincide with the remaining order ![]() $2$ points in
$2$ points in ![]() $\mathbb {C}\!/\!\Lambda$, namely
$\mathbb {C}\!/\!\Lambda$, namely ![]() $0$,
$0$, ![]() ${1}/{2}$,
${1}/{2}$, ![]() ${\tau }/{2}$. Without loss of generality, assume that
${\tau }/{2}$. Without loss of generality, assume that ![]() $A = 0$,
$A = 0$, ![]() $B = {1}/{2}$,
$B = {1}/{2}$, ![]() $C = {\tau }/{2}$.
$C = {\tau }/{2}$.
We express the vertices of ![]() $P$ using theta functions. Recall (see, e.g., [Reference MumfordMum83]) that the theta function corresponding to the lattice
$P$ using theta functions. Recall (see, e.g., [Reference MumfordMum83]) that the theta function corresponding to the lattice ![]() $\Lambda = \langle 1, \tau \rangle$ is defined by
$\Lambda = \langle 1, \tau \rangle$ is defined by
where ![]() ${i} = \sqrt {-1}$, and the dependence of
${i} = \sqrt {-1}$, and the dependence of ![]() $\theta$ on
$\theta$ on ![]() $\tau$ is suppressed for notational convenience. We also need theta functions with (half-integer) characteristics, defined by
$\tau$ is suppressed for notational convenience. We also need theta functions with (half-integer) characteristics, defined by
Choose complex numbers ![]() $x_p, z_\pm \in \mathbb {C}$ whose images in
$x_p, z_\pm \in \mathbb {C}$ whose images in ![]() $\mathbb {C}\, /\, \Lambda$ are the points
$\mathbb {C}\, /\, \Lambda$ are the points ![]() $X_p, Z_\pm \in \Gamma$ (see Corollary 5.27 for the definition of
$X_p, Z_\pm \in \Gamma$ (see Corollary 5.27 for the definition of ![]() $X_p$). Note that the points
$X_p$). Note that the points ![]() $Z_\pm$ are interchanged by the involution
$Z_\pm$ are interchanged by the involution ![]() $\sigma$, so
$\sigma$, so ![]() $z_+ + z_- = 0$ modulo
$z_+ + z_- = 0$ modulo ![]() $\Lambda$. Therefore, without loss of generality one can assume that
$\Lambda$. Therefore, without loss of generality one can assume that ![]() $z_+ + z_- = 1 + \tau$. Fix
$z_+ + z_- = 1 + \tau$. Fix ![]() $z_\pm$ satisfying the latter condition, and let
$z_\pm$ satisfying the latter condition, and let ![]() $\delta := z_+ - z_-$.
$\delta := z_+ - z_-$.
Proposition 6.10 Up to a projective transformation, the vertices of the polygon ![]() $P_{}$ are given by
$P_{}$ are given by
Before proving this proposition, we recall standard properties of the theta function ![]() $\theta (u)$. It is easily seen from its definition that the theta function is holomorphic in
$\theta (u)$. It is easily seen from its definition that the theta function is holomorphic in ![]() $\mathbb {C}$, even, periodic with period one, and quasi-periodic with period
$\mathbb {C}$, even, periodic with period one, and quasi-periodic with period ![]() $\tau$:
$\tau$:
In addition, one can show using the argument principle that the theta function has a unique simple zero at the point ![]() $d = (1 + \tau )/2$, and no other zeros in the fundamental parallelogram spanned by
$d = (1 + \tau )/2$, and no other zeros in the fundamental parallelogram spanned by ![]() $1$ and
$1$ and ![]() $\tau$. These properties allow one to express any meromorphic function on
$\tau$. These properties allow one to express any meromorphic function on ![]() $\mathbb {C}\!/\!\Lambda$ in terms of the theta function. The construction is based on the following well-known result: there exists a meromorphic function with zeros at
$\mathbb {C}\!/\!\Lambda$ in terms of the theta function. The construction is based on the following well-known result: there exists a meromorphic function with zeros at ![]() $p_1, \ldots, p_m \in \mathbb {C}\!/\!\Lambda$ and poles at
$p_1, \ldots, p_m \in \mathbb {C}\!/\!\Lambda$ and poles at ![]() $q_1, \ldots, q_m \in \mathbb {C} \,/\, \Lambda$ if and only if
$q_1, \ldots, q_m \in \mathbb {C} \,/\, \Lambda$ if and only if ![]() $\sum p_k = \sum q_k$. Thus, assume that we are given a collection of points with this property. Then the expression
$\sum p_k = \sum q_k$. Thus, assume that we are given a collection of points with this property. Then the expression
defines a meromorphic function on ![]() $\mathbb {C}$ which can be easily seen to be periodic with respect to both
$\mathbb {C}$ which can be easily seen to be periodic with respect to both ![]() $1$ and
$1$ and ![]() $\tau$ (here we regard
$\tau$ (here we regard ![]() $p_k$ and
$p_k$ and ![]() $q_k$ as points in
$q_k$ as points in ![]() $\mathbb {C}$ and assume that they are chosen in such a way that
$\mathbb {C}$ and assume that they are chosen in such a way that ![]() $\sum p_k = \sum q_k$ exactly, and not just modulo
$\sum p_k = \sum q_k$ exactly, and not just modulo ![]() $\Lambda$). Therefore, this function can be viewed as a meromorphic function on
$\Lambda$). Therefore, this function can be viewed as a meromorphic function on ![]() $\mathbb {C}\!/\!\Lambda$. Furthermore, the only zeros of
$\mathbb {C}\!/\!\Lambda$. Furthermore, the only zeros of ![]() $f(u)$ in
$f(u)$ in ![]() $\mathbb {C}\!/\!\Lambda$ are
$\mathbb {C}\!/\!\Lambda$ are ![]() $p_k$, whereas its only poles are
$p_k$, whereas its only poles are ![]() $q_k$. As zeros and poles determine a meromorphic function up to a constant factor, it follows that any meromorphic function on
$q_k$. As zeros and poles determine a meromorphic function up to a constant factor, it follows that any meromorphic function on ![]() $\mathbb {C}\!/\!\Lambda$ with zeros at
$\mathbb {C}\!/\!\Lambda$ with zeros at ![]() $p_1, \ldots, p_m$ and poles
$p_1, \ldots, p_m$ and poles ![]() $q_1, \ldots, q_m$ can be written as (41) times a constant.
$q_1, \ldots, q_m$ can be written as (41) times a constant.
Proof of Proposition 6.10 Using Proposition 5.21 and Corollary 5.27, we obtain
 \begin{equation} \xi_k(u) = c_k\frac{ \left(\theta(u - z_+ + d )\right)^k\theta(u - x_p + k\delta + d)}{\left(\theta(u - z_- + d)\right)^k\theta(u - x_p + d)}, \end{equation}
\begin{equation} \xi_k(u) = c_k\frac{ \left(\theta(u - z_+ + d )\right)^k\theta(u - x_p + k\delta + d)}{\left(\theta(u - z_- + d)\right)^k\theta(u - x_p + d)}, \end{equation}
where ![]() $c_k$ is a non-zero constant, and the term containing
$c_k$ is a non-zero constant, and the term containing ![]() $\delta$ is found by equating the sum of zeros with the sum of poles. Note that because we are only interested in the direction of the vector
$\delta$ is found by equating the sum of zeros with the sum of poles. Note that because we are only interested in the direction of the vector ![]() $\xi$, we may multiply all
$\xi$, we may multiply all ![]() $\xi _k$ by
$\xi _k$ by ![]() $\theta (u - x_p + d)$, which results in
$\theta (u - x_p + d)$, which results in
 \[ \tilde \xi_k(u) = c_k\frac{ \left(\theta(u - z_+ + d )\right)^k}{\left(\theta(u - z_- + d)\right)^k}{}{}\theta(u - x_p + k\delta + d). \]
\[ \tilde \xi_k(u) = c_k\frac{ \left(\theta(u - z_+ + d )\right)^k}{\left(\theta(u - z_- + d)\right)^k}{}{}\theta(u - x_p + k\delta + d). \]
These are no longer meromorphic functions on ![]() $\mathbb {C}\!/\!\Lambda$, but still meromorphic functions on
$\mathbb {C}\!/\!\Lambda$, but still meromorphic functions on ![]() $\mathbb {C}$. Furthermore, in contrast to
$\mathbb {C}$. Furthermore, in contrast to ![]() $\xi _k$, the functions
$\xi _k$, the functions ![]() $\tilde \xi _k$ are always finite at the points
$\tilde \xi _k$ are always finite at the points ![]() $0, {1}/{2}, {\tau }/{2} \in \mathbb {C}$ corresponding to
$0, {1}/{2}, {\tau }/{2} \in \mathbb {C}$ corresponding to ![]() $A,B,C \in \Gamma$, so the vertices of
$A,B,C \in \Gamma$, so the vertices of ![]() $P$ are given by
$P$ are given by ![]() $(\tilde \xi _k(0):\tilde \xi _k({{1}/{2}}): \tilde \xi _k({{\tau }/{2}}))$. Also note that the values of the constants
$(\tilde \xi _k(0):\tilde \xi _k({{1}/{2}}): \tilde \xi _k({{\tau }/{2}}))$. Also note that the values of the constants ![]() $c_k$ do not affect the latter expression, so one can assume that
$c_k$ do not affect the latter expression, so one can assume that ![]() $c_k=1$. Under this assumption, we obtain
$c_k=1$. Under this assumption, we obtain
 \[ \tilde \xi_k(0) =\frac{ \left(\theta( d - z_+ )\right)^k}{ \left(\theta( d - z_-)\right)^k}\theta( k\delta + d - x_p) = \theta( k\delta + d - x_p), \]
\[ \tilde \xi_k(0) =\frac{ \left(\theta( d - z_+ )\right)^k}{ \left(\theta( d - z_-)\right)^k}\theta( k\delta + d - x_p) = \theta( k\delta + d - x_p), \]
where the last equality follows from ![]() $d - z_- = -(d -z _+)$ and
$d - z_- = -(d -z _+)$ and ![]() $\theta (-u) = \theta (u)$. Similarly, we have
$\theta (-u) = \theta (u)$. Similarly, we have
 \begin{align*} \tilde \xi_k\left({{1}/{2}}\right) &=\frac{ \left(\theta({{1}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + d - z_-)\right)^k}\theta( {{1}/{2}} + k\delta + d - x_p) \\ &= \frac{ \left(\theta(-{{1}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + d - z_-)\right)^k}\theta( {{1}/{2}} + k\delta + d - x_p) = \theta( \textstyle{{1}/{2}} + k\delta + d - x_p), \end{align*}
\begin{align*} \tilde \xi_k\left({{1}/{2}}\right) &=\frac{ \left(\theta({{1}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + d - z_-)\right)^k}\theta( {{1}/{2}} + k\delta + d - x_p) \\ &= \frac{ \left(\theta(-{{1}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + d - z_-)\right)^k}\theta( {{1}/{2}} + k\delta + d - x_p) = \theta( \textstyle{{1}/{2}} + k\delta + d - x_p), \end{align*}
where the second last equality follows from ![]() $1$-periodicity of
$1$-periodicity of ![]() $\theta$, and the last equality follows from
$\theta$, and the last equality follows from ![]() $d - z_- = -(d -z _+)$ and
$d - z_- = -(d -z _+)$ and ![]() $\theta (-u) = \theta (u)$. Finally,
$\theta (-u) = \theta (u)$. Finally,
 \begin{align*} \tilde \xi_k\left(\textstyle{{\tau}/{2}}\right) &= \frac{ \left(\theta({{\tau}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{\tau}/{2}} + d - z_-)\right)^k} \theta( {{\tau}/{2}} + k\delta + d - x_p) = \frac{ \left(\theta({{1}/{2}} + \tau - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + \tau - z_-)\right)^k}\theta( {{\tau}/{2}} + k\delta + d - x_p)\\ &= \exp( \pi k{i} ( 2z_+ - 1- \tau)) \frac{ \left(\theta({{1}/{2}} - z_+ )\right)^k}{\left(\theta( {{1}/{2}} + \tau - z_-)\right)^k}\theta( {{\tau}/{2}} + k\delta + d - x_p) \\ & = \exp( \pi k {i} \delta)\theta( \textstyle{{\tau}/{2}} + k\delta + d - x_p), \end{align*}
\begin{align*} \tilde \xi_k\left(\textstyle{{\tau}/{2}}\right) &= \frac{ \left(\theta({{\tau}/{2}} + d - z_+ )\right)^k}{ \left(\theta( {{\tau}/{2}} + d - z_-)\right)^k} \theta( {{\tau}/{2}} + k\delta + d - x_p) = \frac{ \left(\theta({{1}/{2}} + \tau - z_+ )\right)^k}{ \left(\theta( {{1}/{2}} + \tau - z_-)\right)^k}\theta( {{\tau}/{2}} + k\delta + d - x_p)\\ &= \exp( \pi k{i} ( 2z_+ - 1- \tau)) \frac{ \left(\theta({{1}/{2}} - z_+ )\right)^k}{\left(\theta( {{1}/{2}} + \tau - z_-)\right)^k}\theta( {{\tau}/{2}} + k\delta + d - x_p) \\ & = \exp( \pi k {i} \delta)\theta( \textstyle{{\tau}/{2}} + k\delta + d - x_p), \end{align*}
where the second equality uses the definition ![]() $d = (1 + \tau )/2$, the third uses the formula for
$d = (1 + \tau )/2$, the third uses the formula for ![]() $\theta (u + \tau )$, whereas the last uses that
$\theta (u + \tau )$, whereas the last uses that ![]() $\theta$ is even along with the relation
$\theta$ is even along with the relation ![]() $\delta = 2z_+ - 1- \tau$.
$\delta = 2z_+ - 1- \tau$.
Now, to complete the proof it remains to rewrite the obtained formulas using theta functions with characteristics. We have ![]() $\tilde \xi _k(0)= \theta _{00}( k\delta + d - x_p)$,
$\tilde \xi _k(0)= \theta _{00}( k\delta + d - x_p)$, ![]() $\tilde \xi _k(\textstyle {{1}/{2}}) = \theta _{01}( k\delta + d - x_p),$ whereas
$\tilde \xi _k(\textstyle {{1}/{2}}) = \theta _{01}( k\delta + d - x_p),$ whereas ![]() $\tilde \xi _k(\textstyle {{\tau }/{2}}) = \theta _{10}( k\delta + d - x_p)$ up to a factor not depending on
$\tilde \xi _k(\textstyle {{\tau }/{2}}) = \theta _{10}( k\delta + d - x_p)$ up to a factor not depending on ![]() $k$. As the latter factor does not affect the projective equivalence class of
$k$. As the latter factor does not affect the projective equivalence class of ![]() $P_{}$, one obtains the desired formulas for vertices.
$P_{}$, one obtains the desired formulas for vertices.
Remark 6.11 Note that the functions ![]() $\xi _k$ may, but not necessarily do, have poles at
$\xi _k$ may, but not necessarily do, have poles at ![]() $X_p$ (see Corollary 5.27). However, formula (42) is valid anyway. Indeed, if
$X_p$ (see Corollary 5.27). However, formula (42) is valid anyway. Indeed, if ![]() $\xi _k$ does not have a pole at
$\xi _k$ does not have a pole at ![]() $X_p$, then its only pole is the point
$X_p$, then its only pole is the point ![]() $Z_-$ (which is of order
$Z_-$ (which is of order ![]() $k$), whereas its only zero is the point
$k$), whereas its only zero is the point ![]() $Z_+$ (which is also of order
$Z_+$ (which is also of order ![]() $k$). Thus, we must have
$k$). Thus, we must have ![]() $kz_+ = kz_-$ modulo
$kz_+ = kz_-$ modulo ![]() $\Lambda$, that is,
$\Lambda$, that is, ![]() $k \delta \in \Lambda$. However, then the factor
$k \delta \in \Lambda$. However, then the factor ![]() ${\theta (u - x_p + k\delta + d)}/{\theta (u - x_p + d)}$ in (42) is a non-vanishing holomorphic function, so the analytic properties (i.e. zeros and poles) of the right-hand side of (42) are the same as for the left-hand side, which means that these functions coincide for a suitable value of
${\theta (u - x_p + k\delta + d)}/{\theta (u - x_p + d)}$ in (42) is a non-vanishing holomorphic function, so the analytic properties (i.e. zeros and poles) of the right-hand side of (42) are the same as for the left-hand side, which means that these functions coincide for a suitable value of ![]() $c_k$.
$c_k$.
Now, to prove that ![]() $P_{}$ is Poncelet it suffices to establish the following.
$P_{}$ is Poncelet it suffices to establish the following.
Proposition 6.12 The image of the map ![]() $\Phi \colon \mathbb {C} \to \mathbb {C}\mathbb {P}^2$ given by
$\Phi \colon \mathbb {C} \to \mathbb {C}\mathbb {P}^2$ given by
is a conic.
Proof. First, note that the functions ![]() $\theta _{00}$,
$\theta _{00}$, ![]() $\theta _{01}$,
$\theta _{01}$, ![]() $\theta _{10}$ have no common zeros, so the mapping
$\theta _{10}$ have no common zeros, so the mapping ![]() $\Phi$ is well-defined. Further, following [Reference MumfordMum83], define the following operators
$\Phi$ is well-defined. Further, following [Reference MumfordMum83], define the following operators ![]() $\mathcal {S}, \mathcal {T}$ on holomorphic functions on
$\mathcal {S}, \mathcal {T}$ on holomorphic functions on ![]() $\mathbb {C}$:
$\mathbb {C}$:
Then
In particular, we have ![]() $\mathcal {S}^2\theta _{jk} = \theta _{jk}$,
$\mathcal {S}^2\theta _{jk} = \theta _{jk}$, ![]() $\mathcal {T}^2\theta _{jk} = \theta _{jk}$, which means that
$\mathcal {T}^2\theta _{jk} = \theta _{jk}$, which means that
From the latter it follows that ![]() $\Phi$ descends to a holomorphic mapping
$\Phi$ descends to a holomorphic mapping ![]() $\mathbb {C}{/}2\Lambda \to \mathbb {C}\mathbb {P}^2$, so the image of
$\mathbb {C}{/}2\Lambda \to \mathbb {C}\mathbb {P}^2$, so the image of ![]() $\Phi$ is an algebraic curve. To find the degree of that curve, one needs to find the number of its intersections with a generic line. Clearly, that number can be found as
$\Phi$ is an algebraic curve. To find the degree of that curve, one needs to find the number of its intersections with a generic line. Clearly, that number can be found as ![]() ${m}/{\deg \Phi }$, where
${m}/{\deg \Phi }$, where ![]() $m$ is the number of zeros of a generic linear combination of
$m$ is the number of zeros of a generic linear combination of ![]() $\theta _{00}$,
$\theta _{00}$, ![]() $\theta _{01}$,
$\theta _{01}$, ![]() $\theta _{10}$ in the fundamental parallelogram of the lattice
$\theta _{10}$ in the fundamental parallelogram of the lattice ![]() $2L$, whereas
$2L$, whereas ![]() $\deg \Phi$ is the degree of
$\deg \Phi$ is the degree of ![]() $\Phi$, when the latter is regarded as a mapping
$\Phi$, when the latter is regarded as a mapping ![]() $\mathbb {C} / 2\Lambda \to \mathbb {C}\mathbb {P}^2$. The number
$\mathbb {C} / 2\Lambda \to \mathbb {C}\mathbb {P}^2$. The number ![]() $m$ can be easily computed using quasi-periodicity relations (45) and the argument principle. That number is equal to four. Further, note that the functions
$m$ can be easily computed using quasi-periodicity relations (45) and the argument principle. That number is equal to four. Further, note that the functions ![]() $\theta _{00}$,
$\theta _{00}$, ![]() $\theta _{01}$,
$\theta _{01}$, ![]() $\theta _{10}$ are even, so
$\theta _{10}$ are even, so ![]() $\Phi (-x) = \Phi (x)$, which means that
$\Phi (-x) = \Phi (x)$, which means that ![]() $\deg \Phi \geq 2$. Therefore, the degree of the image of
$\deg \Phi \geq 2$. Therefore, the degree of the image of ![]() $\Phi$ is either two or one, that is, the image of
$\Phi$ is either two or one, that is, the image of ![]() $\Phi$ is a conic or a straight line. However, it cannot be a straight line, because the functions
$\Phi$ is a conic or a straight line. However, it cannot be a straight line, because the functions ![]() $\theta _{k,j}$ are linearly independent by (44). This, the image of
$\theta _{k,j}$ are linearly independent by (44). This, the image of ![]() $\Phi$ is a conic.
$\Phi$ is a conic.
Thus, we conclude that the vertices (40) of the polygon ![]() $P_{}$ lie on a conic. As
$P_{}$ lie on a conic. As ![]() $P_{}$ is self-dual, it is also circumscribed about a conic and, hence, Poncelet. Thus, Theorem B is proved.
$P_{}$ is self-dual, it is also circumscribed about a conic and, hence, Poncelet. Thus, Theorem B is proved.
Remark 6.13 One can also explicitly describe the image of the mapping (43) and, hence, the conic circumscribed about ![]() $P$ using Riemann's relation
$P$ using Riemann's relation
where ![]() $\beta _1 := (\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4)/2$,
$\beta _1 := (\alpha _1 + \alpha _2 + \alpha _3 + \alpha _4)/2$, ![]() $\beta _2 := (\alpha _1 + \alpha _2 - \alpha _3 - \alpha _4)/2$,
$\beta _2 := (\alpha _1 + \alpha _2 - \alpha _3 - \alpha _4)/2$, ![]() $\beta _3 := (\alpha _1 - \alpha _2 + \alpha _3 - \alpha _4)/2$,
$\beta _3 := (\alpha _1 - \alpha _2 + \alpha _3 - \alpha _4)/2$, ![]() $\beta _4 := (\alpha _1 - \alpha _2 - \alpha _3 + \alpha _4)/2$. Taking
$\beta _4 := (\alpha _1 - \alpha _2 - \alpha _3 + \alpha _4)/2$. Taking ![]() $\alpha _1 = 0$,
$\alpha _1 = 0$, ![]() $\alpha _2 = u$,
$\alpha _2 = u$, ![]() $\alpha _3 = v$,
$\alpha _3 = v$, ![]() $\alpha _4 = u + v$, we obtain the identity
$\alpha _4 = u + v$, we obtain the identity
which, after a further substitution ![]() $v = 0$, becomes
$v = 0$, becomes
Thus, the conic circumscribed about ![]() $P$ is given by
$P$ is given by
Similarly, the conic inscribed in ![]() $P$ is
$P$ is
Indeed, let ![]() $t_k: = k\delta + d - x_p$,
$t_k: = k\delta + d - x_p$, ![]() $m:= k+ 1/2$, and
$m:= k+ 1/2$, and ![]() $t'_{m}:= (t_k + t_{k+1})/2$. Then, as follows from (47), the point
$t'_{m}:= (t_k + t_{k+1})/2$. Then, as follows from (47), the point
belongs to the conic (49). Furthermore, the tangent line to (49) at ![]() $v'_{m}$ passes through the vertices
$v'_{m}$ passes through the vertices ![]() $v_k$ and
$v_k$ and ![]() $v_{k+1}$ of
$v_{k+1}$ of ![]() $P$. Indeed, that is equivalent to the relation
$P$. Indeed, that is equivalent to the relation
 \begin{align*} &- \theta_{00}(0)\theta_{00}(\delta/2)\theta_{00}(t'_m) \theta_{00}(t_{m \pm 1/2}) + \theta_{01}(0)\theta_{01}(\delta/2)\theta_{01}(t'_m)\theta_{01}(t_{m\pm 1/2}) \\ &\qquad + \theta_{10}(0)\theta_{10}(\delta/2)\theta_{10}(t'_m)\theta_{10}(t_{m \pm 1/2}) = 0, \end{align*}
\begin{align*} &- \theta_{00}(0)\theta_{00}(\delta/2)\theta_{00}(t'_m) \theta_{00}(t_{m \pm 1/2}) + \theta_{01}(0)\theta_{01}(\delta/2)\theta_{01}(t'_m)\theta_{01}(t_{m\pm 1/2}) \\ &\qquad + \theta_{10}(0)\theta_{10}(\delta/2)\theta_{10}(t'_m)\theta_{10}(t_{m \pm 1/2}) = 0, \end{align*}
which is a particular case of (46) corresponding to ![]() $u = t_{m \pm 1/2}$,
$u = t_{m \pm 1/2}$, ![]() $v = \mp \delta /2$. Thus, indeed, the polygon
$v = \mp \delta /2$. Thus, indeed, the polygon ![]() $P$ is circumscribed about the conic (49).
$P$ is circumscribed about the conic (49).
Remark 6.14 Note that formula (40) describes a family of polygons, parametrized by ![]() $x_p$. Our argument shows that all these polygons are inscribed in one and the same conic (48) and circumscribed about one and the same conic (49). Thus, polygons (40) form what is called a Poncelet family, that is, a family of polygons inscribed in the same conic and circumscribed about the same conic (recall that every Poncelet polygon is a member of such a family by Poncelet's porism). Also note that the expression (40) is periodic in
$x_p$. Our argument shows that all these polygons are inscribed in one and the same conic (48) and circumscribed about one and the same conic (49). Thus, polygons (40) form what is called a Poncelet family, that is, a family of polygons inscribed in the same conic and circumscribed about the same conic (recall that every Poncelet polygon is a member of such a family by Poncelet's porism). Also note that the expression (40) is periodic in ![]() $x_p$ with the periods given by the lattice
$x_p$ with the periods given by the lattice ![]() $2\Lambda$. Thus, the Poncelet family containing our polygon
$2\Lambda$. Thus, the Poncelet family containing our polygon ![]() $P$ is parametrized by the elliptic curve
$P$ is parametrized by the elliptic curve ![]() $\mathbb {C} / 2\Lambda$, which is a four-to-one covering of the spectral curve
$\mathbb {C} / 2\Lambda$, which is a four-to-one covering of the spectral curve ![]() $\Gamma = \mathbb {C}\!/\!\Lambda$. As a corollary, the Poncelet family containing
$\Gamma = \mathbb {C}\!/\!\Lambda$. As a corollary, the Poncelet family containing ![]() $P$ contains four polygons projectively equivalent to
$P$ contains four polygons projectively equivalent to ![]() $P$: one of those polygons is
$P$: one of those polygons is ![]() $P$, whereas the other three can be obtained from
$P$, whereas the other three can be obtained from ![]() $P$ by replacing
$P$ by replacing ![]() $x_p$ in formula (40) with
$x_p$ in formula (40) with ![]() $x_p + 1$,
$x_p + 1$, ![]() $x_p + \tau$, and
$x_p + \tau$, and ![]() $x_p + 1 + \tau$. This quadruple of polygons admits a geometric description when the circumscribed conic
$x_p + 1 + \tau$. This quadruple of polygons admits a geometric description when the circumscribed conic ![]() $C_1$ and inscribed one
$C_1$ and inscribed one ![]() $C_2$ are confocal. In this case, these polygons can be obtained from
$C_2$ are confocal. In this case, these polygons can be obtained from ![]() $P$ by means of reflection with respect to the common symmetry axes of
$P$ by means of reflection with respect to the common symmetry axes of ![]() $C_1$,
$C_1$, ![]() $C_2$.
$C_2$.
This argument also shows that the spectral curve is the same for all polygons in a Poncelet family. Using a different approach, this was earlier proved in [Reference SchwartzSch15]. Formulas for Poncelet families similar to (40) are given in [Reference VeselovVes88].
Remark 6.15 Note that because the polygon ![]() $P_{}$ is closed (Remark 6.9), the expression (40) must be
$P_{}$ is closed (Remark 6.9), the expression (40) must be ![]() $n$-periodic in
$n$-periodic in ![]() $k$. Therefore, we must have
$k$. Therefore, we must have ![]() $n\delta \in 2\Lambda$. Another way to see this is to consider the function
$n\delta \in 2\Lambda$. Another way to see this is to consider the function ![]() $(s-1)\mu _-$ on
$(s-1)\mu _-$ on ![]() $\Gamma$. Using Table 1 and the fact that
$\Gamma$. Using Table 1 and the fact that ![]() $s(A) = s(B) = s(C) = 1$, we conclude that this function has simple zeros at
$s(A) = s(B) = s(C) = 1$, we conclude that this function has simple zeros at ![]() $A$,
$A$, ![]() $B$,
$B$, ![]() $C$, a zero of order
$C$, a zero of order ![]() $(n-3)/2$ at
$(n-3)/2$ at ![]() $Z_-$, and a pole of order
$Z_-$, and a pole of order ![]() $(n+3)/2$ at
$(n+3)/2$ at ![]() $Z_+$. Thus, we have
$Z_+$. Thus, we have ![]() $0 + {1}/{2} + {\tau }/{2}+ {(n-3)}/{2} \cdot z_- = {(n+3)/}{2} \cdot z_+ \ (\mathrm {mod}\,\Lambda ),$ which implies
$0 + {1}/{2} + {\tau }/{2}+ {(n-3)}/{2} \cdot z_- = {(n+3)/}{2} \cdot z_+ \ (\mathrm {mod}\,\Lambda ),$ which implies ![]() ${n}/{2} \cdot \delta = {n}/{2} \cdot (z_+ - z_-) = {1}/{2} + {\tau }/{2} - {3}/{2} \cdot (z_+ + z_-) = -2d = 0 \ (\mathrm {mod}\,\Lambda ),$ and thus
${n}/{2} \cdot \delta = {n}/{2} \cdot (z_+ - z_-) = {1}/{2} + {\tau }/{2} - {3}/{2} \cdot (z_+ + z_-) = -2d = 0 \ (\mathrm {mod}\,\Lambda ),$ and thus ![]() $n\delta \in 2\Lambda$, as desired.
$n\delta \in 2\Lambda$, as desired.
Also note that formula (40) still defines a Poncelet polygon if ![]() $n\delta \in \Lambda {\setminus} 2\Lambda$. It is then a twisted
$n\delta \in \Lambda {\setminus} 2\Lambda$. It is then a twisted ![]() $n$-gon, which can also be viewed as a closed
$n$-gon, which can also be viewed as a closed ![]() $2n$-gon. Such twisted Poncelet polygons do not arise in our setting, because they are not fixed points of the pentagram map.
$2n$-gon. Such twisted Poncelet polygons do not arise in our setting, because they are not fixed points of the pentagram map.
7. Proof of Theorem A: a closed polygon fixed by the pentagram map is Poncelet
In this section, we derive Theorem A from Theorem B. To that end, we first show, in § 7.1, that the self-duality assumption of Theorem B is not very restrictive. Namely, any polygon satisfying all the assumptions of the theorem except for possibly self-duality, can be transformed, by means of rescaling (9) with ![]() $s > 0$, into a self-dual polygon. From that we conclude that a polygon as in Theorem A (i.e. weakly convex, closed, and projectively equivalent to its pentagram image) must be Poncelet up to rescaling (9) with
$s > 0$, into a self-dual polygon. From that we conclude that a polygon as in Theorem A (i.e. weakly convex, closed, and projectively equivalent to its pentagram image) must be Poncelet up to rescaling (9) with ![]() $s > 0$. Thus, to show that the polygon is actually Poncelet, we need to prove that the rescaling is trivial, that is, corresponds to
$s > 0$. Thus, to show that the polygon is actually Poncelet, we need to prove that the rescaling is trivial, that is, corresponds to ![]() $s = 1$. To that end, we show that if a weakly convex Poncelet polygon is rescaled in a non-trivial way, then the resulting polygon cannot be closed. This is done separately in the rational (see § 7.2) and elliptic (see § 7.3) cases. In the rational case we have a very simple explicit description of the corresponding degenerate Poncelet polygons (see § 6.1), so in that case the proof is completely elementary. As for the elliptic situation, in that case the proof relies on the study of the real part of the corresponding elliptic curve and location of various special points within that real part.
$s = 1$. To that end, we show that if a weakly convex Poncelet polygon is rescaled in a non-trivial way, then the resulting polygon cannot be closed. This is done separately in the rational (see § 7.2) and elliptic (see § 7.3) cases. In the rational case we have a very simple explicit description of the corresponding degenerate Poncelet polygons (see § 6.1), so in that case the proof is completely elementary. As for the elliptic situation, in that case the proof relies on the study of the real part of the corresponding elliptic curve and location of various special points within that real part.
7.1 Self-duality up to rescaling
Proposition 7.1 Assume that a closed or twisted weakly convex polygon ![]() $P$ is projectively equivalent to its pentagram image
$P$ is projectively equivalent to its pentagram image ![]() $P'$. Then one can choose the
$P'$. Then one can choose the ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {D}$ of the form (12) associated with
$\mathcal {D}$ of the form (12) associated with ![]() $P$ in such a way that the corresponding commuting operators
$P$ in such a way that the corresponding commuting operators ![]() $\mathcal {D}_l , \mathcal {D}_r$ given by (13) satisfy
$\mathcal {D}_l , \mathcal {D}_r$ given by (13) satisfy
for certain ![]() $s_0 \in \mathbb {R}_+$.
$s_0 \in \mathbb {R}_+$.
Proof. Let ![]() $\mathcal {D}$ be an
$\mathcal {D}$ be an ![]() $n$-periodic operator corresponding to
$n$-periodic operator corresponding to ![]() $P$ such that the corresponding operators
$P$ such that the corresponding operators ![]() $\mathcal {D}_l , \mathcal {D}_r$ commute, and, moreover, the coefficients of
$\mathcal {D}_l , \mathcal {D}_r$ commute, and, moreover, the coefficients of ![]() $\mathcal {D}$ satisfy the alternating signs condition (11) (such
$\mathcal {D}$ satisfy the alternating signs condition (11) (such ![]() $\mathcal {D}$ exists by Proposition 4.2). Then the operator
$\mathcal {D}$ exists by Proposition 4.2). Then the operator ![]() $T^{-n} \mathcal {D}_l \mathcal {D}_r$ has the form
$T^{-n} \mathcal {D}_l \mathcal {D}_r$ has the form
Moreover, from the alternating signs condition we have ![]() $\alpha _k, \gamma _k > 0$ for all
$\alpha _k, \gamma _k > 0$ for all ![]() $k \in \mathbb {Z}$. Therefore, the operator (51) can be symmetrized. Namely, there exists a positive quasi-periodic sequence
$k \in \mathbb {Z}$. Therefore, the operator (51) can be symmetrized. Namely, there exists a positive quasi-periodic sequence ![]() $\lambda$ such that the operator
$\lambda$ such that the operator ![]() $\lambda T^{-n} \mathcal {D}_l \mathcal {D}_r \lambda ^{-1}$ is self-dual. That sequence can be found from the equation
$\lambda T^{-n} \mathcal {D}_l \mathcal {D}_r \lambda ^{-1}$ is self-dual. That sequence can be found from the equation ![]() ${\lambda _{k+1}}/{\lambda _k} = \sqrt {{\gamma _k}/{\alpha _{k+1}}}$. Thus, conjugating
${\lambda _{k+1}}/{\lambda _k} = \sqrt {{\gamma _k}/{\alpha _{k+1}}}$. Thus, conjugating ![]() $\mathcal {D}$ by
$\mathcal {D}$ by ![]() $\lambda$ if needed, we may assume that the operator (51) is self-dual, meaning that
$\lambda$ if needed, we may assume that the operator (51) is self-dual, meaning that
We now show that under that assumption we must have (50). Let ![]() $z_l$,
$z_l$, ![]() $z_r$ be the monodromies of
$z_r$ be the monodromies of ![]() $\mathcal {D}_l$,
$\mathcal {D}_l$, ![]() $\mathcal {D}_r$ respectively. Then, by the second statement of Proposition 3.4, we have
$\mathcal {D}_r$ respectively. Then, by the second statement of Proposition 3.4, we have ![]() $0 < z_l < z_r$. Furthermore, because
$0 < z_l < z_r$. Furthermore, because ![]() $\mathcal {D}_l$ and
$\mathcal {D}_l$ and ![]() $\mathcal {D}_r$ commute, it follows that the kernels of both of them are contained in
$\mathcal {D}_r$ commute, it follows that the kernels of both of them are contained in ![]() $\mathrm {Ker}\, \mathcal {D}_l\mathcal {D}_r$. Thus, the spectrum of the monodromy of
$\mathrm {Ker}\, \mathcal {D}_l\mathcal {D}_r$. Thus, the spectrum of the monodromy of ![]() $\mathcal {D}_l\mathcal {D}_r$ is
$\mathcal {D}_l\mathcal {D}_r$ is ![]() $\{z_l, z_r\}$. Moreover, we have
$\{z_l, z_r\}$. Moreover, we have
Similarly, using that the monodromy of ![]() $\mathcal {D}_l^*$ and
$\mathcal {D}_l^*$ and ![]() $\mathcal {D}_r^*$ is given by
$\mathcal {D}_r^*$ is given by ![]() $z_l^{-1}$ and
$z_l^{-1}$ and ![]() $z_r^{-1}$, respectively, we conclude that the monodromy of
$z_r^{-1}$, respectively, we conclude that the monodromy of ![]() $\mathcal {D}_r ^* \mathcal {D}_l ^*$ is
$\mathcal {D}_r ^* \mathcal {D}_l ^*$ is ![]() $\{z_l^{-1}, z_r^{-1}\}$, which, in view of (52) and the inequality
$\{z_l^{-1}, z_r^{-1}\}$, which, in view of (52) and the inequality ![]() $0 < z_l < z_r$ implies
$0 < z_l < z_r$ implies ![]() $z_l = z_r^{-1}$. Furthermore, we have
$z_l = z_r^{-1}$. Furthermore, we have
thus,
for a certain ![]() $n$-periodic sequence
$n$-periodic sequence ![]() $\mu$ of non-zero real numbers. Taking the dual of both sides, we also obtain
$\mu$ of non-zero real numbers. Taking the dual of both sides, we also obtain ![]() $\mathcal {D}_r ^* = T^{-n}\mathcal {D}_l \mu ^{-1},$ so
$\mathcal {D}_r ^* = T^{-n}\mathcal {D}_l \mu ^{-1},$ so
At the same time, we have
so ![]() $\mu$ commutes with
$\mu$ commutes with ![]() $\mathcal {D}_l \mathcal {D}_r$. However, that is only possible if
$\mathcal {D}_l \mathcal {D}_r$. However, that is only possible if ![]() $\mu$ is a constant sequence
$\mu$ is a constant sequence ![]() $\mu _k = c$. Thus, (53) implies (50), with
$\mu _k = c$. Thus, (53) implies (50), with ![]() $s_0 = -c^{-1}$. Furthermore, because the coefficient of the highest degree term in
$s_0 = -c^{-1}$. Furthermore, because the coefficient of the highest degree term in ![]() $\mathcal {D}_r$ is a sequence of negative numbers, whereas the coefficient of the coefficient of the highest degree term in
$\mathcal {D}_r$ is a sequence of negative numbers, whereas the coefficient of the coefficient of the highest degree term in ![]() $\mathcal {D}_l^*$ is a sequence of positive numbers, (50) can only be satisfied for
$\mathcal {D}_l^*$ is a sequence of positive numbers, (50) can only be satisfied for ![]() $s_0 > 0$, as desired.
$s_0 > 0$, as desired.
Corollary 7.2 Assume that a closed or twisted weakly convex polygon ![]() $P$ is projectively equivalent to its pentagram image
$P$ is projectively equivalent to its pentagram image ![]() $P'$. Then there exists a polygon
$P'$. Then there exists a polygon ![]() $P_{\rm sd}$ with the same properties which is, in addition, self-dual (and, hence, Poncelet by Theorem B), such that
$P_{\rm sd}$ with the same properties which is, in addition, self-dual (and, hence, Poncelet by Theorem B), such that ![]() $P = R_{s_0} (P_{\rm sd})$ where
$P = R_{s_0} (P_{\rm sd})$ where ![]() $R_{s_0}$ is the rescaling (9) with
$R_{s_0}$ is the rescaling (9) with ![]() $s = s_0 > 0$.
$s = s_0 > 0$.
Proof. Take the operator ![]() $\mathcal {D}$ provided by Proposition 7.1. It has the form
$\mathcal {D}$ provided by Proposition 7.1. It has the form ![]() $\mathcal {D} = \mathcal {D}_l - s_0 T^n \mathcal {D}_l ^*,$ where
$\mathcal {D} = \mathcal {D}_l - s_0 T^n \mathcal {D}_l ^*,$ where ![]() $s_0 \in \mathbb {R}_+$. Consider also the operator
$s_0 \in \mathbb {R}_+$. Consider also the operator ![]() $\mathcal {D}_{\rm sd} = \mathcal {D}_l - T^n \mathcal {D}_l ^*,$ and the associated polygon
$\mathcal {D}_{\rm sd} = \mathcal {D}_l - T^n \mathcal {D}_l ^*,$ and the associated polygon ![]() $P_{\rm sd}$. Then, by Corollary 2.11, we have
$P_{\rm sd}$. Then, by Corollary 2.11, we have ![]() $P = R_{s_0} (P_{\rm sd})$. In particular,
$P = R_{s_0} (P_{\rm sd})$. In particular, ![]() $P_{\rm sd}$ is projectively equivalent to its pentagram image (because the pentagram map commutes with rescaling) and weakly convex (by the third statement of Proposition 3.4). Furthermore, we have
$P_{\rm sd}$ is projectively equivalent to its pentagram image (because the pentagram map commutes with rescaling) and weakly convex (by the third statement of Proposition 3.4). Furthermore, we have ![]() $\mathcal {D}_{\rm sd}^* = -T^{-n} \mathcal {D}_{\rm sd},$ so
$\mathcal {D}_{\rm sd}^* = -T^{-n} \mathcal {D}_{\rm sd},$ so ![]() $P_{\rm sd}$ is self-dual, as desired.
$P_{\rm sd}$ is self-dual, as desired.
7.2 End of proof in the rational case
Let ![]() $P$ be a weakly convex closed polygon projectively equivalent to its pentagram image
$P$ be a weakly convex closed polygon projectively equivalent to its pentagram image ![]() $P'$, as in Theorem A. Then, by Corollary 7.2, there exists a generally speaking twisted polygon
$P'$, as in Theorem A. Then, by Corollary 7.2, there exists a generally speaking twisted polygon ![]() $P_{\rm sd}$ such that
$P_{\rm sd}$ such that ![]() $P = R_{s_0} (P_{\rm sd})$ for some
$P = R_{s_0} (P_{\rm sd})$ for some ![]() $s_0 > 0$, and
$s_0 > 0$, and ![]() $P_{\rm sd}$ is self-dual. Consider the spectral curve associated with
$P_{\rm sd}$ is self-dual. Consider the spectral curve associated with ![]() $P_{\rm sd}$, constructed in the proof of Theorem B. In this section, we prove Theorem A in the case when the genus of
$P_{\rm sd}$, constructed in the proof of Theorem B. In this section, we prove Theorem A in the case when the genus of ![]() $\Gamma$ is zero, that is, when
$\Gamma$ is zero, that is, when ![]() $\Gamma$ is rational. To that end, we show that
$\Gamma$ is rational. To that end, we show that ![]() $s_0 = 1$, so
$s_0 = 1$, so ![]() $P = P_{\rm sd}$ and, hence, Poncelet.
$P = P_{\rm sd}$ and, hence, Poncelet.
As we know from § 6.1, in the rational case the vertices of ![]() $P_{\rm sd}$ are given by (34) or (37). In the case (34), the associated difference operator reads
$P_{\rm sd}$ are given by (34) or (37). In the case (34), the associated difference operator reads
where ![]() $a$ is such that the roots of the corresponding characteristic polynomial
$a$ is such that the roots of the corresponding characteristic polynomial ![]() $1 - ax + ax^2 - x^3$ are
$1 - ax + ax^2 - x^3$ are ![]() $r, r^{-1}$, and
$r, r^{-1}$, and ![]() $1$ (note that since the polygon
$1$ (note that since the polygon ![]() $P_{\rm sd}$ is real,
$P_{\rm sd}$ is real, ![]() $a$ must be real too, so we must have
$a$ must be real too, so we must have ![]() $|r| = 1$). Indeed, the kernel of such an operator is spanned by the sequences
$|r| = 1$). Indeed, the kernel of such an operator is spanned by the sequences ![]() $r^k$,
$r^k$, ![]() $r^{-k}$, and a constant sequence, so the associated polygon is precisely (34). Likewise, in the case (37), the associated difference operator is also of the form (54), with
$r^{-k}$, and a constant sequence, so the associated polygon is precisely (34). Likewise, in the case (37), the associated difference operator is also of the form (54), with ![]() $a = 3$. Thus, because the polygon
$a = 3$. Thus, because the polygon ![]() $P_{\rm sd}$ is defined by the operator (54), the polygon
$P_{\rm sd}$ is defined by the operator (54), the polygon ![]() $P = R_{s_0}(P_{\rm sd})$ is defined by
$P = R_{s_0}(P_{\rm sd})$ is defined by
The kernel of this operator is spanned by the sequences ![]() $x_1^k$,
$x_1^k$, ![]() $x_2^k$,
$x_2^k$, ![]() $x_3^k$, where
$x_3^k$, where ![]() $x_1$,
$x_1$, ![]() $x_2$,
$x_2$, ![]() $x_3$ are the roots of the characteristic polynomial
$x_3$ are the roots of the characteristic polynomial ![]() $h(x) := 1 - ax + s_0(ax^2 - x^3)$ (note that we do not need to consider the case of multiple roots, because in that case the monodromy of
$h(x) := 1 - ax + s_0(ax^2 - x^3)$ (note that we do not need to consider the case of multiple roots, because in that case the monodromy of ![]() $\mathcal {D}$ is not diagonalizable, and the polygon
$\mathcal {D}$ is not diagonalizable, and the polygon ![]() $P$ cannot be closed). Moreover, because
$P$ cannot be closed). Moreover, because ![]() $P$ is closed, we must have
$P$ is closed, we must have ![]() $x_1^n = x_2 ^n = x_3^n$, so
$x_1^n = x_2 ^n = x_3^n$, so ![]() $|x_1| = |x_2| = |x_3| = \lambda$, where
$|x_1| = |x_2| = |x_3| = \lambda$, where ![]() $\lambda > 0$ is a real number. Thus, the roots of the polynomial
$\lambda > 0$ is a real number. Thus, the roots of the polynomial ![]() $h(\lambda x) = 1 - a\lambda x + s_0(a\lambda ^2x^2 - \lambda ^3x^3)$ must all have absolute value
$h(\lambda x) = 1 - a\lambda x + s_0(a\lambda ^2x^2 - \lambda ^3x^3)$ must all have absolute value ![]() $1$. Also taking into account that this polynomial is real, and that
$1$. Also taking into account that this polynomial is real, and that ![]() $s_0 \lambda ^3 > 0$, we conclude that the roots of
$s_0 \lambda ^3 > 0$, we conclude that the roots of ![]() $h(\lambda x)$ are of the form
$h(\lambda x)$ are of the form ![]() $1, \alpha, \bar \alpha$, where
$1, \alpha, \bar \alpha$, where ![]() $|\alpha | = 1$. However, this yields
$|\alpha | = 1$. However, this yields ![]() $s_0 \lambda ^3 = 1$ and
$s_0 \lambda ^3 = 1$ and ![]() $s_0 \lambda ^2 = \lambda$, so
$s_0 \lambda ^2 = \lambda$, so ![]() $s_0 = 1$. Therefore, the polygon
$s_0 = 1$. Therefore, the polygon ![]() $P$ coincides with
$P$ coincides with ![]() $P_{\rm sd}$ and, hence, Poncelet. Thus, the proof of Theorem A in the rational case is complete.
$P_{\rm sd}$ and, hence, Poncelet. Thus, the proof of Theorem A in the rational case is complete.
Remark 7.3 One can also give a more concrete description of ![]() $P$, as follows. As the vertices of
$P$, as follows. As the vertices of ![]() $P$ are given by (34) (with (37) being impossible due to closedness of
$P$ are given by (34) (with (37) being impossible due to closedness of ![]() $P$), and
$P$), and ![]() $P$ is a closed
$P$ is a closed ![]() $n$-gon, it follows that
$n$-gon, it follows that ![]() $r^n = 1$. Thus, applying a linear transformation to (34), we obtain a polygon whose vertices have affine coordinates
$r^n = 1$. Thus, applying a linear transformation to (34), we obtain a polygon whose vertices have affine coordinates ![]() $\cos ({2\pi mk}/{n})$,
$\cos ({2\pi mk}/{n})$, ![]() $\sin ({2\pi mk}/{n}),$ where
$\sin ({2\pi mk}/{n}),$ where ![]() ${2\pi m}/{n} = \arg r$. In particular, if
${2\pi m}/{n} = \arg r$. In particular, if ![]() $m = 1$, then
$m = 1$, then ![]() $P$ is a regular
$P$ is a regular ![]() $n$-gon.
$n$-gon.
7.3 End of proof in the elliptic case
In this section, we prove Theorem A in the case when the genus of ![]() $\Gamma$ is one, that is, when
$\Gamma$ is one, that is, when ![]() $\Gamma$ is elliptic. As in the rational case, we show that
$\Gamma$ is elliptic. As in the rational case, we show that ![]() $s_0 = 1$, so
$s_0 = 1$, so ![]() $P = P_{\rm sd}$ and, hence, Poncelet. We keep the notation of §§ 5.1 and 6.2.
$P = P_{\rm sd}$ and, hence, Poncelet. We keep the notation of §§ 5.1 and 6.2.
Recall that a real structure on a Riemann surface ![]() $\Gamma$ is an anti-holomorphic involution
$\Gamma$ is an anti-holomorphic involution ![]() $\rho \colon \Gamma \to \Gamma$. The real part
$\rho \colon \Gamma \to \Gamma$. The real part ![]() $\Gamma _\mathbb {R}$ of
$\Gamma _\mathbb {R}$ of ![]() $\Gamma$ (with respect to the real structure
$\Gamma$ (with respect to the real structure ![]() $\rho$) is then defined as the set of fixed points of
$\rho$) is then defined as the set of fixed points of ![]() $\rho$:
$\rho$: ![]() $\Gamma _\mathbb {R} := \{ X \in \Gamma \mid \rho (X) = X\}$. A meromorphic function
$\Gamma _\mathbb {R} := \{ X \in \Gamma \mid \rho (X) = X\}$. A meromorphic function ![]() $f$ on
$f$ on ![]() $\Gamma$ is called a real function if
$\Gamma$ is called a real function if ![]() $\rho ^*f = \bar f$. Real functions take real values at real points (i.e. points in
$\rho ^*f = \bar f$. Real functions take real values at real points (i.e. points in ![]() $\Gamma _\mathbb {R}$).
$\Gamma _\mathbb {R}$).
In our case, the spectral curve ![]() $\Gamma$ is endowed with a real structure
$\Gamma$ is endowed with a real structure ![]() $\rho \colon \Gamma \to \Gamma$ induced by the involution
$\rho \colon \Gamma \to \Gamma$ induced by the involution ![]() $(z,w) \mapsto (\bar z, \bar w)$ on the affine spectral curve
$(z,w) \mapsto (\bar z, \bar w)$ on the affine spectral curve ![]() $\Gamma _a$.
$\Gamma _a$.
Proposition 7.4 The functions ![]() $z$,
$z$, ![]() $w$,
$w$, ![]() $\mu _\pm$,
$\mu _\pm$, ![]() $s$, and
$s$, and ![]() $\xi$ on
$\xi$ on ![]() $\Gamma$ are real (see § 5.1 for the definition of those functions).
$\Gamma$ are real (see § 5.1 for the definition of those functions).
Proof. The functions ![]() $z,w$ are real by construction of the real structure
$z,w$ are real by construction of the real structure ![]() $\rho$. To prove that the vector-function
$\rho$. To prove that the vector-function ![]() $\xi$ is real, note that it is defined by (22) up to a scalar factor. Taking the complex conjugate of those equations and then applying
$\xi$ is real, note that it is defined by (22) up to a scalar factor. Taking the complex conjugate of those equations and then applying ![]() $\rho ^*$, we get that
$\rho ^*$, we get that ![]() $\rho ^* \bar \xi = f\xi$ for a certain meromorphic function
$\rho ^* \bar \xi = f\xi$ for a certain meromorphic function ![]() $f$. However, then the normalization condition
$f$. However, then the normalization condition ![]() $\xi _1 = 1$ implies
$\xi _1 = 1$ implies ![]() $f = 1$, as desired. Now, the reality of the functions
$f = 1$, as desired. Now, the reality of the functions ![]() $\mu _\pm$ follows from (23), whereas the reality of
$\mu _\pm$ follows from (23), whereas the reality of ![]() $s$ follows from its definition (24).
$s$ follows from its definition (24).
Corollary 7.5 The points ![]() $Z_\pm,S_\pm,A,B,C,D \in \Gamma$ are real (see § 5.1 for the definition of
$Z_\pm,S_\pm,A,B,C,D \in \Gamma$ are real (see § 5.1 for the definition of ![]() $Z_\pm, S_\pm$ and § 6.2 for the definition of
$Z_\pm, S_\pm$ and § 6.2 for the definition of ![]() $A,B,C,D$).
$A,B,C,D$).
Proof. As ![]() $z$ is a real function (Proposition 7.4), the involution
$z$ is a real function (Proposition 7.4), the involution ![]() $\rho$ takes zeros of
$\rho$ takes zeros of ![]() $z$ to zeros of
$z$ to zeros of ![]() $z$. However, the only zero of
$z$. However, the only zero of ![]() $z$ is
$z$ is ![]() $Z_+$ (Table 1), so the latter must be real. Analogously,
$Z_+$ (Table 1), so the latter must be real. Analogously, ![]() $Z_-$ is real as the only pole of
$Z_-$ is real as the only pole of ![]() $z$,
$z$, ![]() $S_+$ is real as the only simple zero of
$S_+$ is real as the only simple zero of ![]() $s$,
$s$, ![]() $S_-$ is real as the only simple pole of
$S_-$ is real as the only simple pole of ![]() $s$, whereas
$s$, whereas ![]() $D$ is real as the only point where both
$D$ is real as the only point where both ![]() $s$ and
$s$ and ![]() $z$ are equal to
$z$ are equal to ![]() $-1$ (see Remark 5.16). To show that
$-1$ (see Remark 5.16). To show that ![]() $A, B, C$ are real, observe that they constitute the set of points where
$A, B, C$ are real, observe that they constitute the set of points where ![]() $s = 1$, so
$s = 1$, so ![]() $\rho$ takes the set
$\rho$ takes the set ![]() $\{A, B, C\}$ to itself. Further, note that the values of the function
$\{A, B, C\}$ to itself. Further, note that the values of the function ![]() $w$ at
$w$ at ![]() $A, B, C$ are eigenvalues of a self-adjoint operator
$A, B, C$ are eigenvalues of a self-adjoint operator ![]() $(\mathcal {D}_+\mathcal {D}_-)\vert _{Q^n({1})}$ and, hence, real. Furthermore, those values are distinct, because
$(\mathcal {D}_+\mathcal {D}_-)\vert _{Q^n({1})}$ and, hence, real. Furthermore, those values are distinct, because ![]() $A,B,C$ are branch points of
$A,B,C$ are branch points of ![]() $w$, whereas
$w$, whereas ![]() $\deg w = 2$. However, if, say,
$\deg w = 2$. However, if, say, ![]() $\rho (A) = B$, then we must have
$\rho (A) = B$, then we must have ![]() $w(B) = \bar w(A)$, which is not possible because
$w(B) = \bar w(A)$, which is not possible because ![]() $w(A), w(B)$ are real and distinct. Thus,
$w(A), w(B)$ are real and distinct. Thus, ![]() $\rho$ cannot permute
$\rho$ cannot permute ![]() $\{A, B, C\}$ and, thus, preserves each of them.
$\{A, B, C\}$ and, thus, preserves each of them.
Corollary 7.6 The real part ![]() $\Gamma _\mathbb {R}$ of
$\Gamma _\mathbb {R}$ of ![]() $\Gamma$ consists of two disjoint circles.
$\Gamma$ consists of two disjoint circles.
Proof. The real part of any Riemann surface consists a finite number of disjoint circles (ovals). Furthermore, because the genus of ![]() $\Gamma$ is one, the number of connected components of
$\Gamma$ is one, the number of connected components of ![]() $\Gamma _\mathbb {R}$ is at most two by Harnack's theorem. At the same time, the number of connected components is non-zero because the real part
$\Gamma _\mathbb {R}$ is at most two by Harnack's theorem. At the same time, the number of connected components is non-zero because the real part ![]() $\Gamma _\mathbb {R}$ of
$\Gamma _\mathbb {R}$ of ![]() $\Gamma$ is not empty (by Corollary 7.5). Thus, it remains to determine whether the number of connected components is one or two. These cases can be distinguished by counting the number of real points of order
$\Gamma$ is not empty (by Corollary 7.5). Thus, it remains to determine whether the number of connected components is one or two. These cases can be distinguished by counting the number of real points of order ![]() $2$ on
$2$ on ![]() $\Gamma$. Namely, if
$\Gamma$. Namely, if ![]() $\Gamma$ is identified with
$\Gamma$ is identified with ![]() $\mathbb {C}\!/\!\Lambda$ in such a way that
$\mathbb {C}\!/\!\Lambda$ in such a way that ![]() $0$ is a real point, then
$0$ is a real point, then ![]() $\Gamma _\mathbb {R}$ is a subgroup of
$\Gamma _\mathbb {R}$ is a subgroup of ![]() $\Gamma$ isomorphic to
$\Gamma$ isomorphic to ![]() $S^1$ if
$S^1$ if ![]() $\Gamma _\mathbb {R}$ is connected, and
$\Gamma _\mathbb {R}$ is connected, and ![]() $S^1 \times \mathbb {Z}_2$ if
$S^1 \times \mathbb {Z}_2$ if ![]() $\Gamma _\mathbb {R}$ has two components. Thus, the number of real order
$\Gamma _\mathbb {R}$ has two components. Thus, the number of real order ![]() $2$ points in
$2$ points in ![]() $\Gamma _\mathbb {R}$ is
$\Gamma _\mathbb {R}$ is ![]() $2^{m}$, where
$2^{m}$, where ![]() $m$ is the number of components of
$m$ is the number of components of ![]() $\Gamma$. Identifying
$\Gamma$. Identifying ![]() $\Gamma$ with
$\Gamma$ with ![]() $\mathbb {C} / L$ as in § 6.2, we see that the order
$\mathbb {C} / L$ as in § 6.2, we see that the order ![]() $2$ points are
$2$ points are ![]() $A,B,C,D$, which are all real. Thus,
$A,B,C,D$, which are all real. Thus, ![]() $m=2$.
$m=2$.
This argument also shows that one of the components of ![]() $\Gamma _\mathbb {R}$ contains the point
$\Gamma _\mathbb {R}$ contains the point ![]() $D$ and one of the points
$D$ and one of the points ![]() $\{A, B, C\}$, whereas the second component of
$\{A, B, C\}$, whereas the second component of ![]() $\Gamma _\mathbb {R}$ contains the remaining two points. Without loss of generality, assume that
$\Gamma _\mathbb {R}$ contains the remaining two points. Without loss of generality, assume that ![]() $C$ and
$C$ and ![]() $D$ are located in the same component. Denote that component by
$D$ are located in the same component. Denote that component by ![]() $\Gamma _\mathbb {R}^0$.
$\Gamma _\mathbb {R}^0$.
Proposition 7.7 We have ![]() $Z_\pm, S_\pm \in \Gamma _\mathbb {R}^0$.
$Z_\pm, S_\pm \in \Gamma _\mathbb {R}^0$.
Proof. The function ![]() $z$ is real-valued on
$z$ is real-valued on ![]() $\Gamma _\mathbb {R}^0$ and satisfies
$\Gamma _\mathbb {R}^0$ and satisfies ![]() $z(C) = 1$,
$z(C) = 1$, ![]() $z(D) = -1$. Thus, there must be at least two points on
$z(D) = -1$. Thus, there must be at least two points on ![]() $\Gamma _\mathbb {R}^0$ where
$\Gamma _\mathbb {R}^0$ where ![]() $z$ changes sign. But the only points which have this property are
$z$ changes sign. But the only points which have this property are ![]() $Z_\pm$ (Table 1). Similarly,
$Z_\pm$ (Table 1). Similarly, ![]() $s(C) = 1$,
$s(C) = 1$, ![]() $s(D) = -1$, so the function
$s(D) = -1$, so the function ![]() $s$ should also change sign at two points. Moreover, these cannot be the points
$s$ should also change sign at two points. Moreover, these cannot be the points ![]() $Z_\pm$, because at those points
$Z_\pm$, because at those points ![]() $s$ has a zero and a pole of order
$s$ has a zero and a pole of order ![]() $2$. Thus, we must have
$2$. Thus, we must have ![]() $S_\pm \in \Gamma _\mathbb {R}^0$, as desired.
$S_\pm \in \Gamma _\mathbb {R}^0$, as desired.
Proposition 7.8 The cyclic order of the points ![]() $C,D,Z_\pm,S_\pm$ on
$C,D,Z_\pm,S_\pm$ on ![]() $\Gamma _\mathbb {R}^0$ is as shown in Figure 6.
$\Gamma _\mathbb {R}^0$ is as shown in Figure 6.

Figure 6. Location of the points ![]() $C,D,Z_\pm,S_\pm$ in the component
$C,D,Z_\pm,S_\pm$ in the component ![]() $\Gamma _\mathbb {R}^0$ of the real part of the spectral curve.
$\Gamma _\mathbb {R}^0$ of the real part of the spectral curve.
The proof is based on the following two lemmas.
Lemma 7.9 We have ![]() $z(S_+) \in (0,1)$.
$z(S_+) \in (0,1)$.
Proof. Without loss of generality, assume that the vector ![]() $\xi (S_+)$ is finite and non-zero (see Remark 5.9). Then, using the definition of the function
$\xi (S_+)$ is finite and non-zero (see Remark 5.9). Then, using the definition of the function ![]() $\mu _+$ and the fact that
$\mu _+$ and the fact that ![]() $\mu _+(S_+) = 0$ (Table 1), we obtain
$\mu _+(S_+) = 0$ (Table 1), we obtain ![]() $\mathcal {D}_+ \xi (S_+) =\mu _+(S_+) \xi (S_+) = 0$. Therefore,
$\mathcal {D}_+ \xi (S_+) =\mu _+(S_+) \xi (S_+) = 0$. Therefore, ![]() $\xi (S_+)$ spans the kernel of the operator
$\xi (S_+)$ spans the kernel of the operator ![]() $\mathcal {D}_+$, whereas
$\mathcal {D}_+$, whereas ![]() $z(S_+)$ is the monodromy of that operator. Thus, by the second statement of Proposition 3.4, the number
$z(S_+)$ is the monodromy of that operator. Thus, by the second statement of Proposition 3.4, the number ![]() $z(S_+)$ is positive and is less than the monodromy of
$z(S_+)$ is positive and is less than the monodromy of ![]() $\mathcal {D}_r = -T^n\mathcal {D}_+^*$, but the monodromy of the latter operator is the same as the monodromy of
$\mathcal {D}_r = -T^n\mathcal {D}_+^*$, but the monodromy of the latter operator is the same as the monodromy of ![]() $\mathcal {D}_+^*$, which is
$\mathcal {D}_+^*$, which is ![]() $z(S_+)^{-1}$. Thus, we obtain
$z(S_+)^{-1}$. Thus, we obtain ![]() $0 < z(S_+) < z(S_+)^{-1},$ and the result follows.
$0 < z(S_+) < z(S_+)^{-1},$ and the result follows.
Lemma 7.10 The only point in ![]() $\Gamma _\mathbb {R}^0$ where
$\Gamma _\mathbb {R}^0$ where ![]() $z = 1$ is the point
$z = 1$ is the point ![]() $C$.
$C$.
Proof. Assume that ![]() $X \in \Gamma _\mathbb {R}^0$ and
$X \in \Gamma _\mathbb {R}^0$ and ![]() $z(X) = 1$. Then the latter condition, in particular, implies
$z(X) = 1$. Then the latter condition, in particular, implies ![]() $X \neq Z_\pm$. Therefore, without loss of generality, we may assume that the vector
$X \neq Z_\pm$. Therefore, without loss of generality, we may assume that the vector ![]() $\xi (X)$ is finite and non-zero (if not, we renormalize
$\xi (X)$ is finite and non-zero (if not, we renormalize ![]() $\xi$, see Remark 5.9). Under this assumption, using the inner product (7) on
$\xi$, see Remark 5.9). Under this assumption, using the inner product (7) on ![]() $Q^n({\pm 1})$, we obtain
$Q^n({\pm 1})$, we obtain
Furthermore, because the vector ![]() $\xi (X)$ is real, it follows that
$\xi (X)$ is real, it follows that ![]() $\left \langle \xi (X), \xi (X) \right \rangle > 0$ and, thus,
$\left \langle \xi (X), \xi (X) \right \rangle > 0$ and, thus, ![]() $\mu _+(X) = \mu _-(X)$. Thus, using formula (24) for the function
$\mu _+(X) = \mu _-(X)$. Thus, using formula (24) for the function ![]() $s$, we obtain
$s$, we obtain ![]() $s(X) = z(X)^{-1} = 1$ (here we use that the value
$s(X) = z(X)^{-1} = 1$ (here we use that the value ![]() $\mu _+(X) = \mu _-(X)$ is finite and non-zero, which is true because the functions
$\mu _+(X) = \mu _-(X)$ is finite and non-zero, which is true because the functions ![]() $\mu _\pm$ do not have common zeros or poles; Table 1). Furthermore, recall that the set of points where
$\mu _\pm$ do not have common zeros or poles; Table 1). Furthermore, recall that the set of points where ![]() $s = 1$ consists of the point
$s = 1$ consists of the point ![]() $C$, plus points
$C$, plus points ![]() $A$ and
$A$ and ![]() $B$ which do not belong to
$B$ which do not belong to ![]() $\Gamma _\mathbb {R}^0$. The result follows.
$\Gamma _\mathbb {R}^0$. The result follows.
Proof of Proposition 7.8 The restriction of the involution ![]() $\sigma$ to
$\sigma$ to ![]() $\Gamma _\mathbb {R}^0$ preserves the points
$\Gamma _\mathbb {R}^0$ preserves the points ![]() $C,D$, interchanges
$C,D$, interchanges ![]() $Z_+$ with
$Z_+$ with ![]() $Z_-$, and interchanges
$Z_-$, and interchanges ![]() $S_+$ with
$S_+$ with ![]() $S_-$. For this reason, the only possible locations of those points on
$S_-$. For this reason, the only possible locations of those points on ![]() $\Gamma _\mathbb {R}^0$ are those depicted in Figure 6, as well as those depicted in Figure 7. Assume that
$\Gamma _\mathbb {R}^0$ are those depicted in Figure 6, as well as those depicted in Figure 7. Assume that ![]() $C,D,Z_\pm,S_\pm$ are located as in Figure 7(a). Then, because
$C,D,Z_\pm,S_\pm$ are located as in Figure 7(a). Then, because ![]() $z(S_+) \in (0,1)$ by Lemma 7.9, whereas
$z(S_+) \in (0,1)$ by Lemma 7.9, whereas ![]() $Z_-$ is a pole of
$Z_-$ is a pole of ![]() $z$, there must be a point
$z$, there must be a point ![]() $X$ in the open arc
$X$ in the open arc ![]() $(S_+, Z_-)$ such that
$(S_+, Z_-)$ such that ![]() $z(X) = 1$ or
$z(X) = 1$ or ![]() $z(X) = 0$ (here and in the following
$z(X) = 0$ (here and in the following ![]() $(X,Y)$ denotes an open arc going from
$(X,Y)$ denotes an open arc going from ![]() $X$ to
$X$ to ![]() $Y$ in counter-clockwise direction). However, the former is impossible by Lemma 7.10, whereas the latter is impossible because the only zero of
$Y$ in counter-clockwise direction). However, the former is impossible by Lemma 7.10, whereas the latter is impossible because the only zero of ![]() $z$ is the point
$z$ is the point ![]() $Z_+$. Thus, the points cannot be located as in Figure 7(a). Further, because
$Z_+$. Thus, the points cannot be located as in Figure 7(a). Further, because ![]() $z(D) = -1$, whereas the only points where
$z(D) = -1$, whereas the only points where ![]() $z$ changes sign are
$z$ changes sign are ![]() $Z_\pm$, in Figures 7(b) and 7(c) we must have
$Z_\pm$, in Figures 7(b) and 7(c) we must have ![]() $z(S_+) < 0$, which is impossible by Lemma 7.9. Thus, the points
$z(S_+) < 0$, which is impossible by Lemma 7.9. Thus, the points ![]() $C,D,Z_\pm,S_\pm$ are located as in Figure 6.
$C,D,Z_\pm,S_\pm$ are located as in Figure 6.

Figure 7. Impossible locations of the points ![]() $C,D,Z_\pm,S_\pm$ on
$C,D,Z_\pm,S_\pm$ on ![]() $\Gamma _\mathbb {R}^0$.
$\Gamma _\mathbb {R}^0$.
Now recall that the elliptic curve ![]() $\Gamma$ is associated with a Poncelet
$\Gamma$ is associated with a Poncelet ![]() $n$-gon
$n$-gon ![]() $P_{\rm sd}$ and we have a closed
$P_{\rm sd}$ and we have a closed ![]() $n$-gon
$n$-gon ![]() $P = R_{s_0}(P_{\rm sd})$, where
$P = R_{s_0}(P_{\rm sd})$, where ![]() $s_0 > 0$. Our aim is to show that
$s_0 > 0$. Our aim is to show that ![]() $s_0 = 1$.
$s_0 = 1$.
Proposition 7.11 There is a point ![]() $X_0 \in \Gamma _\mathbb {R}^0$ such that
$X_0 \in \Gamma _\mathbb {R}^0$ such that ![]() $s(X_0) = s_0$ and
$s(X_0) = s_0$ and ![]() $z(X_0) = s_0^{-n/3}$.
$z(X_0) = s_0^{-n/3}$.
Proof. The function ![]() $s$ has one simple pole and one double pole in
$s$ has one simple pole and one double pole in ![]() $\Gamma _\mathbb {R}^0$ (Table 1). Therefore, the degree of the mapping
$\Gamma _\mathbb {R}^0$ (Table 1). Therefore, the degree of the mapping ![]() $s \colon \Gamma _\mathbb {R}^0 \to \mathbb {R}\mathbb {P}^1$ is equal to
$s \colon \Gamma _\mathbb {R}^0 \to \mathbb {R}\mathbb {P}^1$ is equal to ![]() $\pm 1$ (depending on the orientations). In particular, this mapping is surjective, so there exists
$\pm 1$ (depending on the orientations). In particular, this mapping is surjective, so there exists ![]() $X_0 \in \Gamma _\mathbb {R}^0$ such that
$X_0 \in \Gamma _\mathbb {R}^0$ such that ![]() $s(X_0) = s_0$. To show that
$s(X_0) = s_0$. To show that ![]() $z(X_0) = s_0^{-n/3}$, recall that the polygon
$z(X_0) = s_0^{-n/3}$, recall that the polygon ![]() $P$ associated with the operator
$P$ associated with the operator ![]() $\mathcal {D}_+ -s_0T^n \mathcal {D}_-$ is closed. Therefore, the monodromy of that operator has the form
$\mathcal {D}_+ -s_0T^n \mathcal {D}_-$ is closed. Therefore, the monodromy of that operator has the form ![]() $\lambda \mathrm {Id}$. At the same time, because
$\lambda \mathrm {Id}$. At the same time, because ![]() $\mathcal {D}_- = \mathcal {D}_+^*$, the explicit form of that operator is
$\mathcal {D}_- = \mathcal {D}_+^*$, the explicit form of that operator is
where the sequences ![]() $\tilde a$,
$\tilde a$, ![]() $\tilde b$ coincide with
$\tilde b$ coincide with ![]() $a$,
$a$, ![]() $b$ up to a shift of indices. Thus, by formula (6), the determinant of the monodromy of this operator is
$b$ up to a shift of indices. Thus, by formula (6), the determinant of the monodromy of this operator is ![]() $s_0^{-n}$. Thus, we have
$s_0^{-n}$. Thus, we have ![]() $\lambda = s_0^{-n/3}$, and the result follows.
$\lambda = s_0^{-n/3}$, and the result follows.
We now show that ![]() $X_0 = C$, which implies
$X_0 = C$, which implies ![]() $s_0 = 1$ and, thus, proves Theorem A. To that end, note that because
$s_0 = 1$ and, thus, proves Theorem A. To that end, note that because ![]() $s(X_0) = s_0$ is finite and positive,
$s(X_0) = s_0$ is finite and positive, ![]() $X_0$ must be located in the open arc
$X_0$ must be located in the open arc ![]() $(S_-, S_+)$ (see Figure 6). At the same time, because the function
$(S_-, S_+)$ (see Figure 6). At the same time, because the function ![]() $s$ is equal to one at
$s$ is equal to one at ![]() $C$, has a pole at
$C$, has a pole at ![]() $S_-$, and does not take values
$S_-$, and does not take values ![]() $0,1, \infty$ in
$0,1, \infty$ in ![]() $(S_-, C)$, it follows that
$(S_-, C)$, it follows that ![]() $s > 1$ in
$s > 1$ in ![]() $(S_-, C)$. Furthermore, the same argument applied to the function
$(S_-, C)$. Furthermore, the same argument applied to the function ![]() $z$ shows that
$z$ shows that ![]() $z > 1$ in
$z > 1$ in ![]() $(Z_-, C)$ and, in particular, in
$(Z_-, C)$ and, in particular, in ![]() $(S_-, C)$. However, then
$(S_-, C)$. However, then ![]() $X_0$ cannot belong to
$X_0$ cannot belong to ![]() $(S_-, C)$, because it is not possible that both
$(S_-, C)$, because it is not possible that both ![]() $s(X_0) = s_0$ and
$s(X_0) = s_0$ and ![]() $z(X_0) = s_0^{-n/3}$ are greater than
$z(X_0) = s_0^{-n/3}$ are greater than ![]() $1$. Analogously,
$1$. Analogously, ![]() $s$ and
$s$ and ![]() $z$ are both less than
$z$ are both less than ![]() $1$ in
$1$ in ![]() $(C, S_+)$, so
$(C, S_+)$, so ![]() $X_0$ cannot belong there either. Therefore, we must have
$X_0$ cannot belong there either. Therefore, we must have ![]() $X_0 = C$, which implies
$X_0 = C$, which implies ![]() $s_0 = 1$, but this means that the polygon
$s_0 = 1$, but this means that the polygon ![]() $P$ is the same as the polygon
$P$ is the same as the polygon ![]() $P_{\rm sd}$ and, hence, Poncelet. Thus, Theorem A is proved.
$P_{\rm sd}$ and, hence, Poncelet. Thus, Theorem A is proved.
Acknowledgements
The author is grateful to B. Khesin, V. Ovsienko, R. Schwartz, and S. Tabachnikov for fruitful discussions. Some of the figures were created with help of software package Cinderella. This work was supported by NSF grant DMS-2008021.
Appendix A. Duality of difference operators and polygons
The goal of this appendix is to prove that polygons corresponding to dual difference operators are dual to each other. This seems to be a well-known result, and it explicitly appears as Proposition 4.4.3 in [Reference Morier-Genoud, Ovsienko, Schwartz and TabachnikovMOST14]. Here we give a different proof, based on interpretation of difference operators as infinite matrices.
Proposition A.1 Let ![]() $\mathcal {D}$ be a properly bounded difference operator supported in
$\mathcal {D}$ be a properly bounded difference operator supported in ![]() $[m_-,m_+]$, and let
$[m_-,m_+]$, and let ![]() $P = \{v_k\}$ be the corresponding polygon in
$P = \{v_k\}$ be the corresponding polygon in ![]() $\mathbb {P}^{d-1}$, where
$\mathbb {P}^{d-1}$, where ![]() $d = m_+ - m_-$ is the order of
$d = m_+ - m_-$ is the order of ![]() $\mathcal {D}$. Then the dual operator
$\mathcal {D}$. Then the dual operator ![]() $\mathcal {D}^*$ corresponds to a polygon
$\mathcal {D}^*$ corresponds to a polygon ![]() $P^* = \{v_k^*\}$ in the dual space
$P^* = \{v_k^*\}$ in the dual space ![]() $(\mathbb {P}^{d-1})^*$ whose
$(\mathbb {P}^{d-1})^*$ whose ![]() $k$th vertex
$k$th vertex ![]() $v_k^*$ is the hyperplane in
$v_k^*$ is the hyperplane in ![]() $\mathbb {P}^{d-1}$ spanned by the vertices
$\mathbb {P}^{d-1}$ spanned by the vertices ![]() $v_{k + m_-+1}, \ldots, v_{k + m_+-1}$ of
$v_{k + m_-+1}, \ldots, v_{k + m_+-1}$ of ![]() $P$.
$P$.
Proof. Let ![]() $\mathcal {D} = \sum _{j = m_-}^{m_+} a^j T^j$. Then one can interpret
$\mathcal {D} = \sum _{j = m_-}^{m_+} a^j T^j$. Then one can interpret ![]() $\mathcal {D}$ as a finite-band matrix (2) whose non-zero diagonals have labels
$\mathcal {D}$ as a finite-band matrix (2) whose non-zero diagonals have labels ![]() $m_-, \ldots, m_+$. (Here and in what follows, the
$m_-, \ldots, m_+$. (Here and in what follows, the ![]() $k$th diagonal of an infinite matrix is the collection of its entries
$k$th diagonal of an infinite matrix is the collection of its entries ![]() $a_{ij}$ such that
$a_{ij}$ such that ![]() $j - i = k$. In other words, the diagonals are labeled from southwest to northeast, with the main diagonal labeled by
$j - i = k$. In other words, the diagonals are labeled from southwest to northeast, with the main diagonal labeled by ![]() $0$.) Note that even though infinite matrices do not form an algebra, any infinite matrix can be multiplied by a finite band matrix.
$0$.) Note that even though infinite matrices do not form an algebra, any infinite matrix can be multiplied by a finite band matrix.
Lemma A.2 There exists an infinite matrix ![]() $\mathcal {L}$ such that:
$\mathcal {L}$ such that:
1.
 $\mathcal {D}\mathcal {L} = \mathcal {L}\mathcal {D} = 0$;
$\mathcal {D}\mathcal {L} = \mathcal {L}\mathcal {D} = 0$;2. the diagonals of
 $\mathcal {L}$ with labels
$\mathcal {L}$ with labels  $-m_++1, \ldots, -m_- - 1$ vanish;
$-m_++1, \ldots, -m_- - 1$ vanish;3. none of the entries of
 $\mathcal {L}$ on the diagonals with labels
$\mathcal {L}$ on the diagonals with labels  $-m_+$ and
$-m_+$ and  $-m_-$ vanish.
$-m_-$ vanish.
Remark A.3 One can think of infinite matrices as formal Laurent series in terms of the shift operator ![]() $T$, with coefficients given by sequences. In this language, Lemma A.2 states the existence of
$T$, with coefficients given by sequences. In this language, Lemma A.2 states the existence of ![]() $\mathcal {L}$ of the form
$\mathcal {L}$ of the form ![]() $\sum _{j = -\infty }^{-m_+} b^j T^j + \sum _{j = -m_-}^{+\infty } b^j T^j,$ where
$\sum _{j = -\infty }^{-m_+} b^j T^j + \sum _{j = -m_-}^{+\infty } b^j T^j,$ where ![]() $b_k^{-m_+} \neq 0$,
$b_k^{-m_+} \neq 0$, ![]() $b_k^{-m_-} \neq 0$ for any
$b_k^{-m_-} \neq 0$ for any ![]() $k \in \mathbb {Z}$.
$k \in \mathbb {Z}$.
Proof of Lemma A.2 The infinite matrix ![]() $\mathcal {D}$ can be regarded as an element of two groups: the group
$\mathcal {D}$ can be regarded as an element of two groups: the group ![]() $\mathrm {GL}_{\infty }^+$ of invertible infinite matrices with finitely many non-zero diagonals below the main diagonal, and the group
$\mathrm {GL}_{\infty }^+$ of invertible infinite matrices with finitely many non-zero diagonals below the main diagonal, and the group ![]() $\mathrm {GL}_{\infty }^-$ of invertible infinite matrices with finitely many non-zero diagonals above the main diagonal. Denote by
$\mathrm {GL}_{\infty }^-$ of invertible infinite matrices with finitely many non-zero diagonals above the main diagonal. Denote by ![]() $\hat{\mathcal {D}}^{-1}, \check{\mathcal {D}}^{-1}$ the inverses of
$\hat{\mathcal {D}}^{-1}, \check{\mathcal {D}}^{-1}$ the inverses of ![]() $\mathcal {D}$ in these two groups, and set
$\mathcal {D}$ in these two groups, and set ![]() $\mathcal {L} := \hat{\mathcal {D}}^{-1} - \check{\mathcal {D}}^{-1}$. Then we clearly have
$\mathcal {L} := \hat{\mathcal {D}}^{-1} - \check{\mathcal {D}}^{-1}$. Then we clearly have ![]() $\mathcal {D}\mathcal {L} = \mathcal {L}\mathcal {D} = 0$. To see that
$\mathcal {D}\mathcal {L} = \mathcal {L}\mathcal {D} = 0$. To see that ![]() $\mathcal {L}$ is of desired form, write
$\mathcal {L}$ is of desired form, write ![]() $\mathcal {D}$ as
$\mathcal {D}$ as ![]() $a^{m_-}T^{m_-}(1 + \cdots ),$ where the dots denote terms of higher order in
$a^{m_-}T^{m_-}(1 + \cdots ),$ where the dots denote terms of higher order in ![]() $T$. Then the inverse of
$T$. Then the inverse of ![]() $(1 + \cdots )$ in
$(1 + \cdots )$ in ![]() $\mathrm {GL}^+_{\infty }$ can be computed using the Taylor series
$\mathrm {GL}^+_{\infty }$ can be computed using the Taylor series ![]() $(1+x)^{-1} = 1 - x + \cdots$. Thus, the inverse of
$(1+x)^{-1} = 1 - x + \cdots$. Thus, the inverse of ![]() $\mathcal {D}$ in
$\mathcal {D}$ in ![]() $\mathrm {GL}^+_{\infty }$ reads
$\mathrm {GL}^+_{\infty }$ reads ![]() $\hat{\mathcal {D}}^{-1} = (1 + \cdots )^{-1}T^{-m_-}(a^{m_-})^{-1}$ and, hence, is of the form
$\hat{\mathcal {D}}^{-1} = (1 + \cdots )^{-1}T^{-m_-}(a^{m_-})^{-1}$ and, hence, is of the form ![]() $\sum _{j = -m_-}^{+\infty } b^j T^j$ with
$\sum _{j = -m_-}^{+\infty } b^j T^j$ with ![]() $b_k^{-m_-} \neq 0$. Likewise,
$b_k^{-m_-} \neq 0$. Likewise, ![]() $\check{\mathcal {D}}^{-1}$ is of the form
$\check{\mathcal {D}}^{-1}$ is of the form ![]() $\sum _{j = -\infty }^{-m_+} b^j T^j$ with
$\sum _{j = -\infty }^{-m_+} b^j T^j$ with ![]() $b_k^{-m_+} \neq 0$. The result follows.
$b_k^{-m_+} \neq 0$. The result follows.
We now finish the proof of Proposition A.1. Let ![]() $V=\{V_k \in \mathbb {R}^d\}$ be a sequence of lifts of vertices
$V=\{V_k \in \mathbb {R}^d\}$ be a sequence of lifts of vertices ![]() $v_k$ of
$v_k$ of ![]() $P$ such that
$P$ such that ![]() $\mathcal {D} V = 0$. Then any scalar sequence
$\mathcal {D} V = 0$. Then any scalar sequence ![]() $\xi \in \mathrm {Ker}\, \mathcal {D}$ can be obtained from
$\xi \in \mathrm {Ker}\, \mathcal {D}$ can be obtained from ![]() $V$ by means of term-wise application of a linear functional. In particular, because
$V$ by means of term-wise application of a linear functional. In particular, because ![]() $\mathcal {D} \mathcal {L} = 0$, this applies to columns of the matrix
$\mathcal {D} \mathcal {L} = 0$, this applies to columns of the matrix ![]() $\mathcal {L}$. Thus, the
$\mathcal {L}$. Thus, the ![]() $j$th column of
$j$th column of ![]() $\mathcal {L}$ is of the form
$\mathcal {L}$ is of the form ![]() $W_j(V_k)$ for a certain linear functional
$W_j(V_k)$ for a certain linear functional ![]() $W_j \in (\mathbb {R}^d)^*$. Furthermore, because the diagonals of
$W_j \in (\mathbb {R}^d)^*$. Furthermore, because the diagonals of ![]() $\mathcal {L}$ with labels
$\mathcal {L}$ with labels ![]() $-m_++1, \ldots, -m_- - 1$ vanish, it follows that
$-m_++1, \ldots, -m_- - 1$ vanish, it follows that ![]() $W_j$ annihilates
$W_j$ annihilates ![]() $V_{j+m_-+1}, \ldots, V_{j + m_+ -1}$. Moreover, because
$V_{j+m_-+1}, \ldots, V_{j + m_+ -1}$. Moreover, because ![]() $\mathcal {L}$ has a non-vanishing diagonal, we have
$\mathcal {L}$ has a non-vanishing diagonal, we have ![]() $W_j \neq 0$. Therefore, the projection of
$W_j \neq 0$. Therefore, the projection of ![]() $W_j$ to
$W_j$ to ![]() $(\mathbb {P}^{d-1})^* = \mathbb {P}(\mathbb {R}^d)^*$ is exactly the hyperplane spanned by the vertices
$(\mathbb {P}^{d-1})^* = \mathbb {P}(\mathbb {R}^d)^*$ is exactly the hyperplane spanned by the vertices ![]() $v_{j + m_-+1}, \ldots, v_{j + m_+-1}$ of
$v_{j + m_-+1}, \ldots, v_{j + m_+-1}$ of ![]() $P$. Thus, to complete the proof, it suffices to show that the sequence of
$P$. Thus, to complete the proof, it suffices to show that the sequence of ![]() $W_j$ is annihilated by
$W_j$ is annihilated by ![]() $\mathcal {D}^*$. To that end, note that because
$\mathcal {D}^*$. To that end, note that because ![]() $\mathcal {L}\mathcal {D} = 0$, the rows of
$\mathcal {L}\mathcal {D} = 0$, the rows of ![]() $\mathcal {L}$ are annihilated by
$\mathcal {L}$ are annihilated by ![]() $\mathcal {D}^*$. However, those rows are of the form
$\mathcal {D}^*$. However, those rows are of the form ![]() $W_j(V_k)$, and because
$W_j(V_k)$, and because ![]() $V_k$ span
$V_k$ span ![]() $\mathbb {R}^d$, it follows that the sequence
$\mathbb {R}^d$, it follows that the sequence ![]() $W_j$ is annihilated by
$W_j$ is annihilated by ![]() $\mathcal {D}^*$, as desired.
$\mathcal {D}^*$, as desired.
Remark A.4 It is also easy to see that the matrix ![]() $\mathcal {L}$ provided by Lemma A.2 is unique up to a constant factor. It takes a particularly simple form when the polygon
$\mathcal {L}$ provided by Lemma A.2 is unique up to a constant factor. It takes a particularly simple form when the polygon ![]() $P$ is closed. To show that, assume for simplicity that
$P$ is closed. To show that, assume for simplicity that ![]() $m_- = 0$, so that the operator
$m_- = 0$, so that the operator ![]() $\mathcal {D}$ is supported in
$\mathcal {D}$ is supported in ![]() $[0,d]$. Furthermore, assume that
$[0,d]$. Furthermore, assume that ![]() $\mathcal {D}$ is
$\mathcal {D}$ is ![]() $n$-periodic and has trivial monodromy (in particular, the polygon
$n$-periodic and has trivial monodromy (in particular, the polygon ![]() $P$ corresponding to
$P$ corresponding to ![]() $\mathcal {D}$ is closed). Then, as shown in [Reference KricheverKri15], there exists an
$\mathcal {D}$ is closed). Then, as shown in [Reference KricheverKri15], there exists an ![]() $n$-periodic operator
$n$-periodic operator ![]() $\mathcal {R}$ supported in
$\mathcal {R}$ supported in ![]() $[0,n-d]$ such that
$[0,n-d]$ such that ![]() $\mathcal {R} \mathcal {D} = \mathcal {D} \mathcal {R} = 1 - T^n$ (the operator
$\mathcal {R} \mathcal {D} = \mathcal {D} \mathcal {R} = 1 - T^n$ (the operator ![]() $\mathcal {R}$ is closely related to the so-called Gale dual of
$\mathcal {R}$ is closely related to the so-called Gale dual of ![]() $\mathcal {D}$). Using that, one can find the inverses of
$\mathcal {D}$). Using that, one can find the inverses of ![]() $\mathcal {D}$ in
$\mathcal {D}$ in ![]() $\mathrm {GL}^\pm _{ \infty }$ as
$\mathrm {GL}^\pm _{ \infty }$ as

As a result, one obtains
 \[ \mathcal{L} = \hat{\mathcal{D}}^{-1} - \check{\mathcal{D}}^{-1} = \mathcal{R}\sum_{j = -\infty}^{+\infty} T^{jn}. \]
\[ \mathcal{L} = \hat{\mathcal{D}}^{-1} - \check{\mathcal{D}}^{-1} = \mathcal{R}\sum_{j = -\infty}^{+\infty} T^{jn}. \]