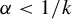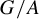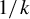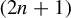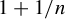1. Introduction
Given an integer
![]() $n\geq 0$
and a real number
$n\geq 0$
and a real number
![]() $\alpha \in [0,1)$
, we denote by
$\alpha \in [0,1)$
, we denote by
![]() $\mathrm {Diff}_+^{\, n+\alpha } ([0,1])$
the group of all orientation-preserving
$\mathrm {Diff}_+^{\, n+\alpha } ([0,1])$
the group of all orientation-preserving
![]() $C^n$
-diffeomorphisms of the closed interval
$C^n$
-diffeomorphisms of the closed interval
![]() $[0,1]$
whose nth derivative is
$[0,1]$
whose nth derivative is
![]() $\alpha $
-Hölder continuous (
$\alpha $
-Hölder continuous (
![]() $C^{n+\alpha }$
-diffeomorphisms for short). Observe that, with this notation, the group
$C^{n+\alpha }$
-diffeomorphisms for short). Observe that, with this notation, the group
![]() $\mathrm {Diff}_+^{\, 0}([0,1])$
is the group of all homeomorphisms of
$\mathrm {Diff}_+^{\, 0}([0,1])$
is the group of all homeomorphisms of
![]() $[0,1]$
isotopic to the identity. Finally, observe that the family of groups
$[0,1]$
isotopic to the identity. Finally, observe that the family of groups
![]() $\mathrm {Diff}_+^{\,n+\alpha }([0,1])$
is totally ordered by inclusion because
$\mathrm {Diff}_+^{\,n+\alpha }([0,1])$
is totally ordered by inclusion because
![]() $\mathrm {Diff}_+^{\,n+\alpha }([0,1]) \supseteq \mathrm {Diff}_+^{\,n'+\alpha '}([0,1]) $
if and only if
$\mathrm {Diff}_+^{\,n+\alpha }([0,1]) \supseteq \mathrm {Diff}_+^{\,n'+\alpha '}([0,1]) $
if and only if
![]() $n<n'$
, or
$n<n'$
, or
![]() $n=n'$
and
$n=n'$
and
![]() $\alpha \leq \alpha '$
.
$\alpha \leq \alpha '$
.
We are interested in computing the critical regularity of an abstract group G acting on the interval
![]() $[0,1]$
. Recall that, given a group G, the critical regularity of G on
$[0,1]$
. Recall that, given a group G, the critical regularity of G on
![]() $[0,1]$
is, by definition,
$[0,1]$
is, by definition,
where we set
![]() $\mathrm {Crit}_{[0,1]}(G)=-\infty $
if G does not embed into
$\mathrm {Crit}_{[0,1]}(G)=-\infty $
if G does not embed into
![]() $\mathrm {Diff}_+^{\, 0}([0,1])$
. The problem of computing the critical regularity of a group G is quite natural and turns out to be very interesting in the case when G is finitely generated (the reader may wish to consult [Reference Kim and Koberda15] for an introduction). For example, we know from a theorem of Deroin, Kleptsyn and Navas [Reference Deroin, Kleptsyn and Navas8] (see also [Reference Deroin, Klepstyn, Navas and Parwani7]) that every countable subgroup of
$\mathrm {Diff}_+^{\, 0}([0,1])$
. The problem of computing the critical regularity of a group G is quite natural and turns out to be very interesting in the case when G is finitely generated (the reader may wish to consult [Reference Kim and Koberda15] for an introduction). For example, we know from a theorem of Deroin, Kleptsyn and Navas [Reference Deroin, Kleptsyn and Navas8] (see also [Reference Deroin, Klepstyn, Navas and Parwani7]) that every countable subgroup of
![]() $\mathrm {Diff}^{\, 0}_+([0,1])$
is conjugated to a group of bi-Lipschitz transformations, and hence
$\mathrm {Diff}^{\, 0}_+([0,1])$
is conjugated to a group of bi-Lipschitz transformations, and hence
![]() $1\leq \mathrm {Crit}_{[0,1]}(G)$
for every countable subgroup of
$1\leq \mathrm {Crit}_{[0,1]}(G)$
for every countable subgroup of
![]() $\mathrm {Diff}^{\, 0}_+([0,1])$
(for uncountable subgroups of
$\mathrm {Diff}^{\, 0}_+([0,1])$
(for uncountable subgroups of
![]() $\mathrm {Diff}^{\, 0}_+([0,1])$
this is no longer true; see [Reference Calegari5]). However, the celebrated stability theorem of Thurston [Reference Thurston26] implies that every finitely generated subgroup of
$\mathrm {Diff}^{\, 0}_+([0,1])$
this is no longer true; see [Reference Calegari5]). However, the celebrated stability theorem of Thurston [Reference Thurston26] implies that every finitely generated subgroup of
![]() $\mathrm {Diff}^1_+([0,1])$
admits a surjective homomorphism onto the integers, and so not every group of homeomorphisms of the interval can be realized as a group of diffeomorphisms. (Concrete examples of finitely generated subgroups of
$\mathrm {Diff}^1_+([0,1])$
admits a surjective homomorphism onto the integers, and so not every group of homeomorphisms of the interval can be realized as a group of diffeomorphisms. (Concrete examples of finitely generated subgroups of
![]() $\mathrm {Diff}_+^{\,0}([0,1])$
having trivial abelianization can be found in [Reference Bergman2, Reference Rivas and Triestino24, Reference Thurston26]. However, Thurston’s obstruction is not the only obstruction for
$\mathrm {Diff}_+^{\,0}([0,1])$
having trivial abelianization can be found in [Reference Bergman2, Reference Rivas and Triestino24, Reference Thurston26]. However, Thurston’s obstruction is not the only obstruction for
![]() $C^1$
smoothability, as there are also known examples of finitely generated and locally indicable groups having no faithful
$C^1$
smoothability, as there are also known examples of finitely generated and locally indicable groups having no faithful
![]() $C^1$
action on the interval; see [Reference Bonatti, Monteverde, Navas and Rivas3, Reference Calegari5, Reference Kim, Koberda and Rivas16, Reference Navas19].) Further obstructions appear in higher regularity: for
$C^1$
action on the interval; see [Reference Bonatti, Monteverde, Navas and Rivas3, Reference Calegari5, Reference Kim, Koberda and Rivas16, Reference Navas19].) Further obstructions appear in higher regularity: for
![]() $C^2$
there is the important Kopell obstruction [Reference Kopell, Chern and Smale17], and between
$C^2$
there is the important Kopell obstruction [Reference Kopell, Chern and Smale17], and between
![]() $C^1$
and
$C^1$
and
![]() $C^2$
there is the generalized Kopell obstruction from [Reference Deroin, Kleptsyn and Navas8]. In a related spirit, Kim and Koberda [Reference Kim and Koberda14], and later Mann and Wolff [Reference Mann and Wolff18], have shown that, for every
$C^2$
there is the generalized Kopell obstruction from [Reference Deroin, Kleptsyn and Navas8]. In a related spirit, Kim and Koberda [Reference Kim and Koberda14], and later Mann and Wolff [Reference Mann and Wolff18], have shown that, for every
![]() $n\geq 1$
and every
$n\geq 1$
and every
![]() $\alpha $
in
$\alpha $
in
![]() $[0,1)$
, there is a finitely generated group whose critical regularity on
$[0,1)$
, there is a finitely generated group whose critical regularity on
![]() $[0,1]$
is exactly
$[0,1]$
is exactly
![]() $n+\alpha $
.
$n+\alpha $
.
In this work, we focus on actions on the interval of finitely generated and torsion-free nilpotent groups (basic definitions will be recalled in §2). Let G be one such group. It follows from the work of Mal’cev that G embeds into
![]() $\mathrm {Diff}^{\, 0}_+([0,1])$
(see, for example, [Reference Robinson25, §5.2] and [Reference Deroin, Navas and Rivas9, §1.2]), and we know from the work of Farb and Franks [Reference Farb and Franks10] that every action of G on
$\mathrm {Diff}^{\, 0}_+([0,1])$
(see, for example, [Reference Robinson25, §5.2] and [Reference Deroin, Navas and Rivas9, §1.2]), and we know from the work of Farb and Franks [Reference Farb and Franks10] that every action of G on
![]() $[0, 1]$
by homeomorphisms can be conjugated inside
$[0, 1]$
by homeomorphisms can be conjugated inside
![]() $\mathrm {Diff}^1_+([0, 1])$
(see also the universal construction from Jorquera [Reference Jorquera12]). This was further refined by Parkhe [Reference Parkhe21] who showed that actually any
$\mathrm {Diff}^1_+([0, 1])$
(see also the universal construction from Jorquera [Reference Jorquera12]). This was further refined by Parkhe [Reference Parkhe21] who showed that actually any
![]() $C^0$
-action of G on
$C^0$
-action of G on
![]() $[0,1]$
can be conjugated inside
$[0,1]$
can be conjugated inside
![]() $\mathrm {Diff}^{1+\alpha }_+([0, 1])$
as long as
$\mathrm {Diff}^{1+\alpha }_+([0, 1])$
as long as
![]() $\alpha < 1/\tau $
, where
$\alpha < 1/\tau $
, where
![]() $\tau $
is the degree of the polynomial growth of the nilpotent group G. On the other hand, Plante and Thurston [Reference Plante and Thurston23] have shown that every nilpotent subgroup of
$\tau $
is the degree of the polynomial growth of the nilpotent group G. On the other hand, Plante and Thurston [Reference Plante and Thurston23] have shown that every nilpotent subgroup of
![]() $\mathrm {Diff}^2_+([0, 1])$
must be abelian. So, if G is a torsion-free, finitely generated and nilpotent group that is non-abelian, then
$\mathrm {Diff}^2_+([0, 1])$
must be abelian. So, if G is a torsion-free, finitely generated and nilpotent group that is non-abelian, then
The exact critical regularity of concrete nilpotent groups has been computed in only few cases and one important goal of this work is to provide new explicit computations of critical regularity for certain groups. Castro, Jorquera and Navas [Reference Castro, Jorquera and Navas6] build a family of nilpotent abelian-by-cyclic groups whose critical regularity is two. These examples can be made of arbitrarily large nilpotency degree, yet they are all metabelian (that is their commutator subgroup is abelian). Jorquera, Navas and the second author showed in [Reference Jorquera, Navas and Rivas13] that the critical regularity of
![]() $N_4$
(the group of
$N_4$
(the group of
![]() $4$
-by-
$4$
-by-
![]() $4$
upper triangular matrices with
$4$
upper triangular matrices with
![]() $1$
on the diagonal) is
$1$
on the diagonal) is
![]() $1+1/2$
. We point out that, at the time of writing this article,
$1+1/2$
. We point out that, at the time of writing this article,
![]() $N_4$
is the only torsion-free nilpotent group whose critical regularity is known and turns out not to be an integer. Note that
$N_4$
is the only torsion-free nilpotent group whose critical regularity is known and turns out not to be an integer. Note that
![]() $N_4$
is also a metabelian group.
$N_4$
is also a metabelian group.
The main purpose of this article is to exhibit many other nilpotent groups whose critical regularity is strictly between one and two. Our main technical result is an improvement of Parkhe’s lower bound for the critical regularity in the class of finitely generated, torsion-free nilpotent groups that are metabelian (see Remark 1.1). For the statement, recall that the torsion-free rank of an abelian group H is the dimension of the
![]() $\mathbb Q$
-vector space
$\mathbb Q$
-vector space
![]() $H\otimes \mathbb Q$
. We denote this rank by
$H\otimes \mathbb Q$
. We denote this rank by
![]() $\mathrm {rank}(H)$
.
$\mathrm {rank}(H)$
.
Theorem A. Let G be a non-abelian, torsion-free, finitely generated nilpotent group that is metabelian, and let A be a maximal abelian subgroup containing
![]() $[G,G]$
. If
$[G,G]$
. If
![]() $k=\mathrm {rank}(G/A)$
, then
$k=\mathrm {rank}(G/A)$
, then
In particular,
![]() $1+ 1/k\leq \mathrm {Crit}_{[0,1]}(G)$
.
$1+ 1/k\leq \mathrm {Crit}_{[0,1]}(G)$
.
Remark 1.1. By the Bass–Guivarc’h formula [Reference Bass1, Reference Guivarc’h11], the degree of the polynomial growth of a nilpotent group G is
![]() $\tau = \sum _{i\geq 1} i \mathrm {rank}(\gamma _i/\gamma _{i+1}) $
, where
$\tau = \sum _{i\geq 1} i \mathrm {rank}(\gamma _i/\gamma _{i+1}) $
, where
![]() $G=\gamma _1\geqslant \gamma _2\geqslant \cdots $
is the lower central series of G. In particular, for a nilpotent group G as in Theorem A with maximal abelian subgroup A, we have that
$G=\gamma _1\geqslant \gamma _2\geqslant \cdots $
is the lower central series of G. In particular, for a nilpotent group G as in Theorem A with maximal abelian subgroup A, we have that
![]() $\mathrm {rank}(G/A)< \tau $
. Hence, the lower bound for
$\mathrm {rank}(G/A)< \tau $
. Hence, the lower bound for
![]() $\mathrm {Crit}_{[0,1]}(G)$
in Theorem A is (strictly) greater than Parkhe’s lower bound.
$\mathrm {Crit}_{[0,1]}(G)$
in Theorem A is (strictly) greater than Parkhe’s lower bound.
The proof of Theorem A is given in §3. Taking inspiration from the abelian-by-cyclic action from [Reference Castro, Jorquera and Navas6, §4], in §3.1, we build, for a metabelian and finitely generated torsion-free nilpotent group G, a family of actions of G on the interval
![]() $[0,1]$
by orientation-preserving homeomorphisms. This is done by first building actions of G on
$[0,1]$
by orientation-preserving homeomorphisms. This is done by first building actions of G on
![]() $\mathbb Z^{k+1}$
that preserve a lexicographic order and then ‘projecting’ them into the interval. In §3.2, we use the Pixton–Tsuboi technique [Reference Pixton22, Reference Tsuboi27] to show that these actions can be smoothed to actions by
$\mathbb Z^{k+1}$
that preserve a lexicographic order and then ‘projecting’ them into the interval. In §3.2, we use the Pixton–Tsuboi technique [Reference Pixton22, Reference Tsuboi27] to show that these actions can be smoothed to actions by
![]() $C^{1+\alpha }$
-diffeomorphisms for any
$C^{1+\alpha }$
-diffeomorphisms for any
![]() $\alpha < 1/k$
. This section closely follows the work in [Reference Castro, Jorquera and Navas6], the main difference being that we do not have explicit polynomials in the construction of the actions, but only bounds on them (see Proposition 3.1). Although these actions may not be faithful, in §3.3, we explain how to glue some of these actions to obtain an embedding of G into
$\alpha < 1/k$
. This section closely follows the work in [Reference Castro, Jorquera and Navas6], the main difference being that we do not have explicit polynomials in the construction of the actions, but only bounds on them (see Proposition 3.1). Although these actions may not be faithful, in §3.3, we explain how to glue some of these actions to obtain an embedding of G into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for any
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for any
![]() $\alpha <1/k$
.
$\alpha <1/k$
.
In some situations, even the lower bound in Theorem A is not sharp in the sense that there are groups for which the theorem applies yet their critical regularity is strictly greater than the predicted lower bound. This is related to the possibility of splitting the group as a product of two groups that each allow an embedding with higher regularity. We provide an easy example of this phenomenon in §4.3. However, in many cases, we can ensure that the inequality in Theorem A is indeed optimal and, in §§4.1 and 4.2, we provide two families of examples where we can obtain upper bounds for the regularity and hence compute the critical regularity.
The first family of examples are the
![]() $(2n+1)$
-dimensional discrete Heisenberg groups, which we denote by
$(2n+1)$
-dimensional discrete Heisenberg groups, which we denote by
![]() $\mathscr {H}_{n}$
. Recall that, by definition,
$\mathscr {H}_{n}$
. Recall that, by definition,
 $$ \begin{align*}\mathscr{H}_n:=\left\lbrace \begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^{\;t} & I_n & \vec{y}^{\; t}\\ 0 & \vec{0} & 1 \end{pmatrix}\;: \vec{x},\vec{y}\in \mathbb{Z}^n\quad\mathrm{and}\quad c\in\mathbb{Z} \right\rbrace\!, \end{align*} $$
$$ \begin{align*}\mathscr{H}_n:=\left\lbrace \begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^{\;t} & I_n & \vec{y}^{\; t}\\ 0 & \vec{0} & 1 \end{pmatrix}\;: \vec{x},\vec{y}\in \mathbb{Z}^n\quad\mathrm{and}\quad c\in\mathbb{Z} \right\rbrace\!, \end{align*} $$
where
![]() $I_n$
is the identity matrix of size n and
$I_n$
is the identity matrix of size n and
![]() $\vec {0}^{\;t}$
,
$\vec {0}^{\;t}$
,
![]() $\vec {y}^{\; t}$
are the transposes of
$\vec {y}^{\; t}$
are the transposes of
![]() $\vec {0}$
,
$\vec {0}$
,
![]() $\vec {y}$
, respectively. It is easy to see that these groups are nilpotent of degree two and hence they are metabelian. Moreover, a maximal abelian subgroup A of
$\vec {y}$
, respectively. It is easy to see that these groups are nilpotent of degree two and hence they are metabelian. Moreover, a maximal abelian subgroup A of
![]() $\mathscr H_n$
is given by the set of matrices whose corresponding vector
$\mathscr H_n$
is given by the set of matrices whose corresponding vector
![]() $\vec {x}=0$
. In particular,
$\vec {x}=0$
. In particular,
![]() $\mathscr H_n/A$
has torsion-free rank equal to n. For this family, we show in §4.1 that there is no embedding of
$\mathscr H_n/A$
has torsion-free rank equal to n. For this family, we show in §4.1 that there is no embedding of
![]() $\mathscr H_n$
into
$\mathscr H_n$
into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for
![]() $\alpha>1/n$
. In particular, we obtain the following theorem.
$\alpha>1/n$
. In particular, we obtain the following theorem.
Theorem B. Let
![]() $\mathscr H_n$
be the
$\mathscr H_n$
be the
![]() $(2n+1)$
-dimensional discrete Heisenberg group. Then
$(2n+1)$
-dimensional discrete Heisenberg group. Then
Finally, in §4.2, we produce examples of metabelian and torsion-free nilpotent groups for which we can compute the critical regularity but whose nilpotency degree can be chosen to be arbitrarily large. More precisely, we show the following theorem.
Theorem C. For any integers k and d with
![]() $d>k$
, there is a nilpotent group G and a maximal abelian subgroup A containing
$d>k$
, there is a nilpotent group G and a maximal abelian subgroup A containing
![]() $[G,G]$
such that d is the nilpotency degree of G, k is the torsion-free rank of
$[G,G]$
such that d is the nilpotency degree of G, k is the torsion-free rank of
![]() $G/A$
and
$G/A$
and
In both cases, the key to obtaining an upper bound for the regularity is to use the internal algebraic structure of the groups to be able to apply the generalized Kopell lemma from [Reference Deroin, Kleptsyn and Navas8].
Remark 1.2. We know from the results of Kim and Koberda [Reference Kim and Koberda14] that, for any real number
![]() $\alpha \geq 1$
, there is a finitely generated group whose critical regularity is exactly
$\alpha \geq 1$
, there is a finitely generated group whose critical regularity is exactly
![]() $\alpha $
. However, in all known cases where the critical regularity of a torsion-free nilpotent group has been computed, it is of the form
$\alpha $
. However, in all known cases where the critical regularity of a torsion-free nilpotent group has been computed, it is of the form
![]() $1+1/n$
for some integer n. See Theorems B, C and [Reference Castro, Jorquera and Navas6, Reference Jorquera, Navas and Rivas13]. So, we wonder whether this is always the case for torsion-free and finitely generated nilpotent groups (not necessarily metabelian).
$1+1/n$
for some integer n. See Theorems B, C and [Reference Castro, Jorquera and Navas6, Reference Jorquera, Navas and Rivas13]. So, we wonder whether this is always the case for torsion-free and finitely generated nilpotent groups (not necessarily metabelian).
2. Preliminaries on nilpotent groups and invariant orders
Given a group G and two elements
![]() $f,g\in G$
, we let
$f,g\in G$
, we let
![]() $[f,g]=fgf^{-1}g^{-1}$
denote the commutator of f and g. Further, if G is finitely generated and S is a finite generating set, an element of the form
$[f,g]=fgf^{-1}g^{-1}$
denote the commutator of f and g. Further, if G is finitely generated and S is a finite generating set, an element of the form
![]() $[s_1,s_2]$
with
$[s_1,s_2]$
with
![]() $s_1,s_2\in S$
is called a simple commutator of weight two. Inductively, a simple commutator of weight n is defined as an element of the form
$s_1,s_2\in S$
is called a simple commutator of weight two. Inductively, a simple commutator of weight n is defined as an element of the form
Note that, given n, there exists only a finite number of simple commutators of weight n.
Let H and K be subgroups of G.
![]() $[K,H]$
denotes the subgroup of G generated by commutators
$[K,H]$
denotes the subgroup of G generated by commutators
![]() $[g,h]$
with
$[g,h]$
with
![]() $g\in K$
and
$g\in K$
and
![]() $h\in H$
. The subgroup
$h\in H$
. The subgroup
![]() $[G,G]$
is called the commutator subgroup and we say that G is metabelian if
$[G,G]$
is called the commutator subgroup and we say that G is metabelian if
![]() $[G,G]$
is abelian.
$[G,G]$
is abelian.
Remember that the lower central series of G is
where
![]() $\gamma _1=[G,G]$
and
$\gamma _1=[G,G]$
and
![]() $\gamma _i=[G,\gamma _{i-1}]$
; and the upper central series of G is
$\gamma _i=[G,\gamma _{i-1}]$
; and the upper central series of G is
where
![]() $\zeta _{i}/\zeta _{i-1}=Z(G/\zeta _{i-1})$
, and
$\zeta _{i}/\zeta _{i-1}=Z(G/\zeta _{i-1})$
, and
![]() $Z(G)$
denotes the center of G.
$Z(G)$
denotes the center of G.
We recall some classic results about nilpotent groups. See [Reference Robinson25] for an in-depth exposition of them. The group G is nilpotent of degree n if
![]() $\zeta _n=G$
but
$\zeta _n=G$
but
![]() $\zeta _{n-1}\neq G$
. In this case, it also happens that
$\zeta _{n-1}\neq G$
. In this case, it also happens that
![]() $\gamma _n=\{e\}$
but
$\gamma _n=\{e\}$
but
![]() $\gamma _{n-1}\neq \{e\}$
. Therefore, in a finitely generated nilpotent group of degree n, we only have a finite number of simple commutators (for a fixed generating set). This is because all simple commutators of weight n are trivial.
$\gamma _{n-1}\neq \{e\}$
. Therefore, in a finitely generated nilpotent group of degree n, we only have a finite number of simple commutators (for a fixed generating set). This is because all simple commutators of weight n are trivial.
It is a result of Mal’cev that, if G is a torsion-free nilpotent group, then the factors
![]() $\zeta _i/\zeta _{i-1}$
are also torsion free for all
$\zeta _i/\zeta _{i-1}$
are also torsion free for all
![]() $ i \in \{1,\ldots ,n\}$
(see [Reference Robinson25, Proposition 5.2.19]). Recall also that finitely generated nilpotent groups are polycyclic, and hence every subgroup of a finitely generated nilpotent group is finitely generated as well (see [Reference Robinson25, Proposition 5.4.12]). In addition, nilpotent groups also satisfy that their non-trivial normal subgroups always intersect non-trivially the center of the group (see [Reference Robinson25, Proposition 5.2.1]). An immediate consequence of this is the following useful result.
$ i \in \{1,\ldots ,n\}$
(see [Reference Robinson25, Proposition 5.2.19]). Recall also that finitely generated nilpotent groups are polycyclic, and hence every subgroup of a finitely generated nilpotent group is finitely generated as well (see [Reference Robinson25, Proposition 5.4.12]). In addition, nilpotent groups also satisfy that their non-trivial normal subgroups always intersect non-trivially the center of the group (see [Reference Robinson25, Proposition 5.2.1]). An immediate consequence of this is the following useful result.
Proposition 2.1. Let G be a nilpotent group, let H be a group and let
![]() $\varphi : G \rightarrow H$
be a group homomorphism. Then
$\varphi : G \rightarrow H$
be a group homomorphism. Then
![]() $\varphi $
is injective if and only if
$\varphi $
is injective if and only if
![]() $\varphi \mid _{Z(G)}$
(the restriction of
$\varphi \mid _{Z(G)}$
(the restriction of
![]() $\varphi $
to
$\varphi $
to
![]() $Z(G)$
) is injective.
$Z(G)$
) is injective.
For
![]() $g\in G$
, Centr
$g\in G$
, Centr
![]() $(g)=\{h\in G\mid gh=hg\}$
denotes the centralizer of g. The following proposition, although elementary, will be very important for building actions of G on
$(g)=\{h\in G\mid gh=hg\}$
denotes the centralizer of g. The following proposition, although elementary, will be very important for building actions of G on
![]() $\mathbb Z^{k+1}$
in §3.1.
$\mathbb Z^{k+1}$
in §3.1.
Proposition 2.2. Let G be a torsion-free and finitely generated nilpotent group that is metabelian.
-
• Given
 $g\in G$
and
$g\in G$
and
 $0\neq m\in \mathbb {Z}$
, we have that
$0\neq m\in \mathbb {Z}$
, we have that
 $\mathrm {Centr}(g^m)=\mathrm {Centr}(g).$
$\mathrm {Centr}(g^m)=\mathrm {Centr}(g).$
-
• Let
 $A\leqslant G$
be a maximal abelian subgroup. If
$A\leqslant G$
be a maximal abelian subgroup. If
 $ A$
is normal in G, then
$ A$
is normal in G, then
 $G/A$
is torsion free.
$G/A$
is torsion free.
Proof. Assume that
![]() $f,g\in G$
and
$f,g\in G$
and
![]() $m\in \mathbb {Z}$
are such that
$m\in \mathbb {Z}$
are such that
![]() $[f,g^m]=e$
. Define
$[f,g^m]=e$
. Define
![]() $H:=\langle f,g\rangle $
, the subgroup generated by f and g. Since
$H:=\langle f,g\rangle $
, the subgroup generated by f and g. Since
![]() $[g,g^m]=[f,g^m]=e$
, we have that
$[g,g^m]=[f,g^m]=e$
, we have that
![]() $g^m\in Z(H)$
, and, since
$g^m\in Z(H)$
, and, since
![]() $H/Z(H)$
is torsion free (see [Reference Robinson25, Proposition 5.2.19]), we have that
$H/Z(H)$
is torsion free (see [Reference Robinson25, Proposition 5.2.19]), we have that
![]() $g\in Z(H)$
. Therefore,
$g\in Z(H)$
. Therefore,
![]() $\mathrm {Centr}(g^m)\subseteq \mathrm {Centr}(g)$
(the other inclusion is obvious).
$\mathrm {Centr}(g^m)\subseteq \mathrm {Centr}(g)$
(the other inclusion is obvious).
The second point follows from the first. Let A be a maximal abelian subgroup that is also normal and assume that
![]() $G/A$
is not torsion free. Suppose
$G/A$
is not torsion free. Suppose
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $g\notin A$
but
$g\notin A$
but
![]() $g^m\in A$
for some
$g^m\in A$
for some
![]() $m\neq 0$
. Then, since A is abelian, we have that
$m\neq 0$
. Then, since A is abelian, we have that
![]() $A\subseteq \mathrm {Centr}(g^m)=\mathrm {Centr}(g)$
. In particular,
$A\subseteq \mathrm {Centr}(g^m)=\mathrm {Centr}(g)$
. In particular,
![]() $\langle A, g\rangle $
, the group generated by A and g, is an abelian subgroup larger than A, which contradicts our assumption.
$\langle A, g\rangle $
, the group generated by A and g, is an abelian subgroup larger than A, which contradicts our assumption.
2.1. On the action of
 $G/A$
on A
$G/A$
on A
Let G be a torsion-free and finitely generated nilpotent group of degree n that is also metabelian. Let A be a maximal abelian subgroup containing
![]() $[G,G]$
(in particular, it is normal). In view of Proposition 2.2, we have that G is an extension of
$[G,G]$
(in particular, it is normal). In view of Proposition 2.2, we have that G is an extension of
![]() $\mathbb {Z}^k$
by
$\mathbb {Z}^k$
by
![]() $\mathbb {Z}^d$
,
$\mathbb {Z}^d$
,
where
![]() $A\simeq \mathbb {Z}^d$
and
$A\simeq \mathbb {Z}^d$
and
![]() $G/A\simeq \mathbb {Z}^k$
. In this section, we study the natural action of
$G/A\simeq \mathbb {Z}^k$
. In this section, we study the natural action of
![]() $G/A$
on A coming from the conjugacy action of G on A.
$G/A$
on A coming from the conjugacy action of G on A.
Let
![]() $\{ g_1,\ldots ,g_d\}$
and
$\{ g_1,\ldots ,g_d\}$
and
![]() $\{ f_1A,\ldots ,f_kA\}$
be generating sets of A and
$\{ f_1A,\ldots ,f_kA\}$
be generating sets of A and
![]() $G/A$
, respectively. Since A is normal, the subgroup of G generated by
$G/A$
, respectively. Since A is normal, the subgroup of G generated by
![]() $f_1,\ldots ,f_k$
acts on A by automorphisms yielding a homomorphism
$f_1,\ldots ,f_k$
acts on A by automorphisms yielding a homomorphism
Therefore, the action of each
![]() $f\in \langle f_1,\ldots ,f_k\rangle $
is given by a matrix
$f\in \langle f_1,\ldots ,f_k\rangle $
is given by a matrix
![]() ${A}_f\in GL_d(\mathbb {Z})$
, which depends on the set
${A}_f\in GL_d(\mathbb {Z})$
, which depends on the set
![]() $\{ g_1,\ldots ,g_d\}$
. We call
$\{ g_1,\ldots ,g_d\}$
. We call
![]() $A_f$
the conjugacy matrix of f. In the special case of the generators
$A_f$
the conjugacy matrix of f. In the special case of the generators
![]() $f_1,\ldots , f_k$
, we denote the conjugacy matrix of
$f_1,\ldots , f_k$
, we denote the conjugacy matrix of
![]() $f_i$
simply by
$f_i$
simply by
![]() $A_i$
.
$A_i$
.
In the next lemma, we will see that we can always choose a generating set of A such that the conjugacy matrices of the elements
![]() $f_1,\ldots ,f_k$
belong to
$f_1,\ldots ,f_k$
belong to
![]() $U_d(\mathbb {Z})$
, the group of upper triangular matrices with 1 in the diagonal. This is due to Mal’cev in the case where the matrix coefficients belong to a field. We write a direct proof in our special case. For the proof, we say that a generating set of a group is minimal if it has least possible cardinality.
$U_d(\mathbb {Z})$
, the group of upper triangular matrices with 1 in the diagonal. This is due to Mal’cev in the case where the matrix coefficients belong to a field. We write a direct proof in our special case. For the proof, we say that a generating set of a group is minimal if it has least possible cardinality.
Lemma 2.3. Let
![]() $A\leqslant G$
be a maximal abelian subgroup satisfying that
$A\leqslant G$
be a maximal abelian subgroup satisfying that
![]() $[G,G]\subseteq A$
. Suppose that
$[G,G]\subseteq A$
. Suppose that
![]() $\mathbb {Z}^d\simeq A$
and
$\mathbb {Z}^d\simeq A$
and
![]() $\mathbb {Z}^k\simeq G/A=\langle f_1A,\ldots ,f_kA\rangle $
. Then there exists a generating set
$\mathbb {Z}^k\simeq G/A=\langle f_1A,\ldots ,f_kA\rangle $
. Then there exists a generating set
![]() $\{g_1,\ldots ,g_d\}$
of A such that the conjugacy matrices of the elements
$\{g_1,\ldots ,g_d\}$
of A such that the conjugacy matrices of the elements
![]() $f_1,\ldots ,f_k$
belong to
$f_1,\ldots ,f_k$
belong to
![]() $U_d(\mathbb {Z})$
. In particular, the nilpotency degree of G is bounded by
$U_d(\mathbb {Z})$
. In particular, the nilpotency degree of G is bounded by
![]() $d+1$
.
$d+1$
.
Proof. Since G is nilpotent of degree n, the upper central series
is finite. Remember that all the factors
![]() $\zeta _i/\zeta _{i-1}$
are torsion free. Combining this with the fact that
$\zeta _i/\zeta _{i-1}$
are torsion free. Combining this with the fact that
![]() $G/A$
is also torsion free (see Proposition 2.2), we have, for
$G/A$
is also torsion free (see Proposition 2.2), we have, for
![]() $g\in G$
, that
$g\in G$
, that
Define
![]() $\Gamma _i:=\zeta _i\cap A$
and let m be the smallest element in
$\Gamma _i:=\zeta _i\cap A$
and let m be the smallest element in
![]() $\{1,\ldots ,n\}$
such that
$\{1,\ldots ,n\}$
such that
![]() $\Gamma _m=A$
. This yields the filtration
$\Gamma _m=A$
. This yields the filtration
such that
and, by (2.1), it also has the property that each factor
![]() $\Gamma _{i+1}/\Gamma _i$
is torsion-free abelian.
$\Gamma _{i+1}/\Gamma _i$
is torsion-free abelian.
Note that, if
![]() $\Gamma _{m-1}\simeq \mathbb Z^{n_{m-1}}$
and
$\Gamma _{m-1}\simeq \mathbb Z^{n_{m-1}}$
and
![]() $\Gamma _m/\Gamma _{m-1}\simeq \mathbb Z^{n_m}$
, then, since
$\Gamma _m/\Gamma _{m-1}\simeq \mathbb Z^{n_m}$
, then, since
![]() $\Gamma _m=A\simeq \mathbb Z^d$
is abelian, we have that
$\Gamma _m=A\simeq \mathbb Z^d$
is abelian, we have that
![]() $d=n_{m-1}+n_m$
. Therefore, if
$d=n_{m-1}+n_m$
. Therefore, if
![]() $\{g_1,\ldots ,g_{n_{m-1}}\}$
and
$\{g_1,\ldots ,g_{n_{m-1}}\}$
and
![]() $\{g_{n_{m-1}+1} \Gamma _{m-1},\ldots , g_{n_{m-1}+n_m}\Gamma _{m-1}\}$
are minimal generating sets of
$\{g_{n_{m-1}+1} \Gamma _{m-1},\ldots , g_{n_{m-1}+n_m}\Gamma _{m-1}\}$
are minimal generating sets of
![]() $\Gamma _{m-1}$
and
$\Gamma _{m-1}$
and
![]() $\Gamma _m/\Gamma _{m-1}$
, respectively, then
$\Gamma _m/\Gamma _{m-1}$
, respectively, then
![]() $\{g_1,\ldots ,g_{n_{m-1}}, g_{n_{m-1}+1},\ldots , g_d\}$
is a minimal generating set of
$\{g_1,\ldots ,g_{n_{m-1}}, g_{n_{m-1}+1},\ldots , g_d\}$
is a minimal generating set of
![]() $\Gamma _m=A$
.
$\Gamma _m=A$
.
Recursively, we obtain a minimal generating set
![]() $\{g_1,\ldots , g_d\}$
of A which, by (2.2), has the property that, for
$\{g_1,\ldots , g_d\}$
of A which, by (2.2), has the property that, for
![]() $g_s\in \{g_1,\ldots ,g_d\}\cap \Gamma _i$
, it holds that
$g_s\in \{g_1,\ldots ,g_d\}\cap \Gamma _i$
, it holds that
![]() $[f_j,g_s]\in \Gamma _{i-1}\subseteq \langle g_1,\ldots ,g_{s-1}\rangle $
for all
$[f_j,g_s]\in \Gamma _{i-1}\subseteq \langle g_1,\ldots ,g_{s-1}\rangle $
for all
![]() $ j \in \{1,\ldots ,k\}.$
In other words, the conjugacy matrices of each
$ j \in \{1,\ldots ,k\}.$
In other words, the conjugacy matrices of each
![]() $f\in \{f_1,\ldots ,f_k\}$
belong to
$f\in \{f_1,\ldots ,f_k\}$
belong to
![]() $U_d(\mathbb Z)$
.
$U_d(\mathbb Z)$
.
The fact that G has nilpotency degree bounded by
![]() $d+1$
follows from the fact that
$d+1$
follows from the fact that
![]() $U_d(\mathbb Z)$
has nilpotency degree
$U_d(\mathbb Z)$
has nilpotency degree
![]() $d+1$
.
$d+1$
.
2.2. Invariant orders and their dynamical versions
We close these preliminaries with the concepts of order and dynamical realization. A group G is left-orderable if it admits a total order relationship, say,
![]() $\preceq $
, which is invariant under multiplication from the left: that is,
$\preceq $
, which is invariant under multiplication from the left: that is,
![]() $\mathrm {if}\ f\preceq g,\ \mathrm {then}\ hf\preceq hg\ \mathrm {for\ all}\ h\in G.$
An important family of left-orderable groups is that of finitely generated and torsion-free abelian groups. Indeed, we will repetitively use the lexicographic order of
$\mathrm {if}\ f\preceq g,\ \mathrm {then}\ hf\preceq hg\ \mathrm {for\ all}\ h\in G.$
An important family of left-orderable groups is that of finitely generated and torsion-free abelian groups. Indeed, we will repetitively use the lexicographic order of
![]() $\mathbb Z^n$
defined by
$\mathbb Z^n$
defined by
 $$ \begin{align} (i_1,\ldots,i_n)\prec (i_1^\prime,\ldots,i_n^\prime) &\Leftrightarrow \mathrm{there\ exists}\ \: k\in \{1,\ldots,n\}\quad\mathrm{such\ that}\notag\\ &\qquad i_k< i_k^\prime\quad \mathrm{and}\quad i_s=i_s^\prime\quad\mathrm{for}\ s<k. \end{align} $$
$$ \begin{align} (i_1,\ldots,i_n)\prec (i_1^\prime,\ldots,i_n^\prime) &\Leftrightarrow \mathrm{there\ exists}\ \: k\in \{1,\ldots,n\}\quad\mathrm{such\ that}\notag\\ &\qquad i_k< i_k^\prime\quad \mathrm{and}\quad i_s=i_s^\prime\quad\mathrm{for}\ s<k. \end{align} $$
What is important for this work is that a countable group is left-orderable if and only if it embeds into
![]() $\mathrm {Diff}_+^{\, 0}({\mathbb R})$
(see [Reference Navas20, §2] or [Reference Deroin, Navas and Rivas9, §1.1.3] for details). Since
$\mathrm {Diff}_+^{\, 0}({\mathbb R})$
(see [Reference Navas20, §2] or [Reference Deroin, Navas and Rivas9, §1.1.3] for details). Since
![]() $\mathrm {Diff}_+^{\, 0}({\mathbb R})$
is isomorphic to
$\mathrm {Diff}_+^{\, 0}({\mathbb R})$
is isomorphic to
![]() $\mathrm {Diff}_+^{\, 0}([0,1])$
, left-orderability of a countable group is equivalent to being isomorphic to a subgroup of
$\mathrm {Diff}_+^{\, 0}([0,1])$
, left-orderability of a countable group is equivalent to being isomorphic to a subgroup of
![]() $\mathrm {Diff}_+^{\, 0}([0,1])$
. More generally, given a group G that acts on a countable and totally ordered set
$\mathrm {Diff}_+^{\, 0}([0,1])$
. More generally, given a group G that acts on a countable and totally ordered set
![]() $(\Omega ,\preceq )$
by order-preserving bijections, say,
$(\Omega ,\preceq )$
by order-preserving bijections, say,
![]() $\omega \mapsto g(\omega )$
, for
$\omega \mapsto g(\omega )$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $\omega \in \Omega $
, then there is a dynamical realization of this action. This means that there is an order-preserving map
$\omega \in \Omega $
, then there is a dynamical realization of this action. This means that there is an order-preserving map
![]() $i:(\Omega ,\preceq )\to ([0,1],\leq )$
and a homomorphism
$i:(\Omega ,\preceq )\to ([0,1],\leq )$
and a homomorphism
![]() $\psi :G\to \mathrm {Diff}_+^{\, 0}([0,1])$
satisfying that
$\psi :G\to \mathrm {Diff}_+^{\, 0}([0,1])$
satisfying that
![]() $\psi (g)(i(\omega ))=i(g(\omega ))$
for every
$\psi (g)(i(\omega ))=i(g(\omega ))$
for every
![]() $\omega \in \Omega $
and every
$\omega \in \Omega $
and every
![]() $g\in G$
. See [Reference Brum, Matte Bon, Rivas and Triestino4, Lemma 2.40] for a proof. Clearly,
$g\in G$
. See [Reference Brum, Matte Bon, Rivas and Triestino4, Lemma 2.40] for a proof. Clearly,
![]() $\psi $
is an embedding whenever the G action on
$\psi $
is an embedding whenever the G action on
![]() $\Omega $
is faithful.
$\Omega $
is faithful.
3. Proof of Theorem A
Throughout this section, G will denote a non-abelian, torsion-free, finitely generated nilpotent group that is metabelian, and A will denote a maximal abelian subgroup containing
![]() $[G,G]$
(in particular, it is normal). Recall that then G is an extension of
$[G,G]$
(in particular, it is normal). Recall that then G is an extension of
![]() $G/A\simeq \mathbb Z^k$
by
$G/A\simeq \mathbb Z^k$
by
![]() $A\simeq \mathbb Z^d$
(see §2.1). In particular, the nilpotency degree of G is bounded by
$A\simeq \mathbb Z^d$
(see §2.1). In particular, the nilpotency degree of G is bounded by
![]() $d+1$
(see Lemma 2.3).
$d+1$
(see Lemma 2.3).
3.1. An action of G on a totally ordered set
Proposition 3.1. Fix a generating set
![]() $\{g_1,\ldots ,g_d,f_1,\ldots ,f_k\}$
of G such that
$\{g_1,\ldots ,g_d,f_1,\ldots ,f_k\}$
of G such that
![]() $\{ g_1,\ldots ,g_d\}$
is a generating set of A given by Lemma 2.3 and
$\{ g_1,\ldots ,g_d\}$
is a generating set of A given by Lemma 2.3 and
![]() $\langle f_1A,\ldots ,f_kA\rangle = G/A\simeq \mathbb {Z}^k$
. Then, for a fixed
$\langle f_1A,\ldots ,f_kA\rangle = G/A\simeq \mathbb {Z}^k$
. Then, for a fixed
![]() $s\in \{1,\ldots ,d\}$
, there is an action of G on
$s\in \{1,\ldots ,d\}$
, there is an action of G on
![]() $\mathbb {Z}^{k+1}$
that satisfies the following.
$\mathbb {Z}^{k+1}$
that satisfies the following.
-
(1) For all
 $m\in \{1,\ldots ,d\}$
and all
$m\in \{1,\ldots ,d\}$
and all
 $t\in \{1,\ldots ,k\}$
, there exist functions
$t\in \{1,\ldots ,k\}$
, there exist functions
 $\ell _t,r_m:\mathbb {Z}^k\rightarrow \mathbb {Z}$
, such that In particular, the action of G on
$\ell _t,r_m:\mathbb {Z}^k\rightarrow \mathbb {Z}$
, such that In particular, the action of G on $$ \begin{align*}f_t\cdot(i_1,..,i_t,..,i_k,j)&=(i_1,..,i_t+1,..,i_k,j+\ell_t(i_1,\ldots,i_k)),\\g_m\cdot(i_1,\ldots,i_k,j)&=(i_1,\ldots,i_k,j+r_m(i_1,\ldots,i_k)). \end{align*} $$
$$ \begin{align*}f_t\cdot(i_1,..,i_t,..,i_k,j)&=(i_1,..,i_t+1,..,i_k,j+\ell_t(i_1,\ldots,i_k)),\\g_m\cdot(i_1,\ldots,i_k,j)&=(i_1,\ldots,i_k,j+r_m(i_1,\ldots,i_k)). \end{align*} $$
 $\mathbb {Z}^{k+1}$
preserves the lexicographic order. In addition,
$\mathbb {Z}^{k+1}$
preserves the lexicographic order. In addition,
 $r_s\equiv 1$
and
$r_s\equiv 1$
and
 $r_1=r_2=\cdots =r_{s-1}\equiv 0$
.
$r_1=r_2=\cdots =r_{s-1}\equiv 0$
.
-
(2) There exists a positive constant M such that, for all
 $t\in \{1,\ldots ,k\}$
,
$t\in \{1,\ldots ,k\}$
,
 $m\in \{1,\ldots ,d\}$
and
$m\in \{1,\ldots ,d\}$
and
 $(i_1,\ldots ,i_k)\neq (0,\ldots ,0)$
,
$(i_1,\ldots ,i_k)\neq (0,\ldots ,0)$
,  $$ \begin{align*}\lvert\ell_t(i_1,\ldots,i_k)\rvert\leq M(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d,\quad \lvert r_m(i_1,\ldots,i_k)\rvert\leq M(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d.\end{align*} $$
$$ \begin{align*}\lvert\ell_t(i_1,\ldots,i_k)\rvert\leq M(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d,\quad \lvert r_m(i_1,\ldots,i_k)\rvert\leq M(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d.\end{align*} $$
Proof. We start by showing item 1. To this end, fix
![]() $s\in \{1,\ldots ,d\}$
and consider the subgroup
$s\in \{1,\ldots ,d\}$
and consider the subgroup
![]() $H_s=\langle \{g_1,\ldots ,g_d\}\smallsetminus \{g_s\} \rangle $
. Since the sets
$H_s=\langle \{g_1,\ldots ,g_d\}\smallsetminus \{g_s\} \rangle $
. Since the sets
![]() $\{f_1^{i_1}\cdots f_k^{i_k} A:\;i_1,\ldots ,i_k\in \mathbb {Z}\}$
and
$\{f_1^{i_1}\cdots f_k^{i_k} A:\;i_1,\ldots ,i_k\in \mathbb {Z}\}$
and
![]() $\{g_s^jH_s:j\in \mathbb {Z}\}$
are partitions of G and A, respectively, the coset space can be described by the normal forms
$\{g_s^jH_s:j\in \mathbb {Z}\}$
are partitions of G and A, respectively, the coset space can be described by the normal forms
Hence, we can identify
![]() $G/H_s$
with
$G/H_s$
with
![]() $\mathbb {Z}^{k+1}$
(as sets) by identifying
$\mathbb {Z}^{k+1}$
(as sets) by identifying
![]() $f_1^{i_1}\cdots f_k^{i_k}g_s^jH_s$
with
$f_1^{i_1}\cdots f_k^{i_k}g_s^jH_s$
with
![]() $({i_1},\ldots ,{i_k},j)$
. In particular, the left-multiplication action of G on
$({i_1},\ldots ,{i_k},j)$
. In particular, the left-multiplication action of G on
![]() $G/H_s$
provides an action of G on
$G/H_s$
provides an action of G on
![]() $\mathbb Z^{k+1}$
. This is the action that we want to consider.
$\mathbb Z^{k+1}$
. This is the action that we want to consider.
Now, by Lemma 2.3, we have that, for all
![]() $i,j\in \{1,\ldots ,k\}$
and
$i,j\in \{1,\ldots ,k\}$
and
![]() $l\in \{1,\ldots ,d\}$
, it holds that
$l\in \{1,\ldots ,d\}$
, it holds that
Therefore, for
![]() $t\in \{1,\ldots , k\}$
, the action of
$t\in \{1,\ldots , k\}$
, the action of
![]() $f_t$
is addition by 1 on the t coordinate and the action on the
$f_t$
is addition by 1 on the t coordinate and the action on the
![]() $k+1$
coordinate depends on previous k coordinates, and hence the function
$k+1$
coordinate depends on previous k coordinates, and hence the function
![]() $\ell _t$
. The function
$\ell _t$
. The function
![]() $r_m$
, for
$r_m$
, for
![]() $m\in \{1,\ldots ,d\}$
, can be found analogously. Finally, as the maps
$m\in \{1,\ldots ,d\}$
, can be found analogously. Finally, as the maps
![]() $\ell _t$
and
$\ell _t$
and
![]() $r_m$
depend only on the coordinates
$r_m$
depend only on the coordinates
![]() $(i_1,\ldots , i_k)$
, the reader can easily verify that the G action on
$(i_1,\ldots , i_k)$
, the reader can easily verify that the G action on
![]() $\mathbb Z^{k+1}$
preserves the lexicographic order.
$\mathbb Z^{k+1}$
preserves the lexicographic order.
Now we check item 2. Let
![]() $t\in \{1,\ldots ,k\}$
. Recall that the action of
$t\in \{1,\ldots ,k\}$
. Recall that the action of
![]() $f_t$
on
$f_t$
on
![]() $\mathbb Z^{k+1}$
is nothing but the left-multiplication action of
$\mathbb Z^{k+1}$
is nothing but the left-multiplication action of
![]() $f_t $
on
$f_t $
on
![]() $G/H_s$
. Hence, in order to compute the image of
$G/H_s$
. Hence, in order to compute the image of
![]() $f_1^{i_1}\cdots f_t^{i_t}\cdots f_k^{i_k}g_s^jH_s$
under
$f_1^{i_1}\cdots f_t^{i_t}\cdots f_k^{i_k}g_s^jH_s$
under
![]() $f_t$
, we need to multiply and find the representative in normal form (3.1). To do this, observe that
$f_t$
, we need to multiply and find the representative in normal form (3.1). To do this, observe that
![]() $f_tf_j=[f_t,f_j]f_jf_t$
. Hence, bringing
$f_tf_j=[f_t,f_j]f_jf_t$
. Hence, bringing
![]() $f_t$
to the tth position generates at most
$f_t$
to the tth position generates at most
![]() $\lvert i_1\rvert +\cdots +\lvert i_k\rvert $
simple commutators of weight two, which we now need to move to the rightmost place (i.e. after the
$\lvert i_1\rvert +\cdots +\lvert i_k\rvert $
simple commutators of weight two, which we now need to move to the rightmost place (i.e. after the
![]() $f_k^{i_k}$
but before
$f_k^{i_k}$
but before
![]() $g_s^j$
). Since G is metabelian, the commutators commute with each other. So, moving them all to the rightmost place generates at most
$g_s^j$
). Since G is metabelian, the commutators commute with each other. So, moving them all to the rightmost place generates at most
![]() $(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^2$
simple commutators of weight three. Analogously, moving them all to the rightmost place, we have at most
$(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^2$
simple commutators of weight three. Analogously, moving them all to the rightmost place, we have at most
![]() $(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^3$
simple commutators of weight four, and so on. Since G has nilpotency degree bounded by
$(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^3$
simple commutators of weight four, and so on. Since G has nilpotency degree bounded by
![]() $d+1$
, all simple commutators of this weight are trivial (see Lemma 2.3). Therefore, repeating the previous argument
$d+1$
, all simple commutators of this weight are trivial (see Lemma 2.3). Therefore, repeating the previous argument
![]() $d+1$
times gives
$d+1$
times gives
where
![]() $g\in A$
is the product of at most
$g\in A$
is the product of at most
 $$ \begin{align*}\sum_{i=1}^d(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^i \leq d(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\end{align*} $$
$$ \begin{align*}\sum_{i=1}^d(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^i \leq d(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\end{align*} $$
simple commutators. Now note that
since
![]() $\ell _t(i_1,\ldots ,i_k)$
agrees with the exponent of
$\ell _t(i_1,\ldots ,i_k)$
agrees with the exponent of
![]() $g_s$
in the expression of g over the generators
$g_s$
in the expression of g over the generators
![]() $g_1,\ldots ,g_d$
. Therefore, letting
$g_1,\ldots ,g_d$
. Therefore, letting
![]() $\mathcal {S}\subseteq A$
be the set of all simple commutators of G (which is finite), and defining
$\mathcal {S}\subseteq A$
be the set of all simple commutators of G (which is finite), and defining
we see that
![]() $\ell _t(i_1,\ldots ,i_k)$
is bounded by
$\ell _t(i_1,\ldots ,i_k)$
is bounded by
![]() $\unicode{x3bb} $
times the number of simple commutators that were used to write g. Hence,
$\unicode{x3bb} $
times the number of simple commutators that were used to write g. Hence,
Analogous computations give the inequality for the functions
![]() $r_m$
.
$r_m$
.
3.2. Action by diffeomorphisms of
 $[0,1]$
$[0,1]$
For a fixed
![]() $s\in \{1,\ldots ,d\}$
, Proposition 3.1 builds an action of G on
$s\in \{1,\ldots ,d\}$
, Proposition 3.1 builds an action of G on
![]() $\mathbb {Z}^{k+1}$
that preserves the lexicographic order. Hence, we can consider the dynamical realization of this action (see the beginning of §2.2) to get a G-action by orientation-preserving homeomorphisms of
$\mathbb {Z}^{k+1}$
that preserves the lexicographic order. Hence, we can consider the dynamical realization of this action (see the beginning of §2.2) to get a G-action by orientation-preserving homeomorphisms of
![]() $[0,1]$
.
$[0,1]$
.
Now, since the group is nilpotent and we have good control from the polynomials appearing in Proposition 3.1, we will see that this action can actually be smoothed to an action by diffeomorphisms of
![]() $[0,1]$
. For this, we need the following result from Pixton and Tsuboi [Reference Pixton22, Reference Tsuboi27]. See the proof of Proposition 1.2 in [Reference Tsuboi27] for details.
$[0,1]$
. For this, we need the following result from Pixton and Tsuboi [Reference Pixton22, Reference Tsuboi27]. See the proof of Proposition 1.2 in [Reference Tsuboi27] for details.
Lemma 3.3. There exists a family of
![]() $C^{\infty }$
-diffeomorphisms
$C^{\infty }$
-diffeomorphisms
![]() $\varphi _{I^\prime ,I}^{J^\prime ,J}:I\rightarrow J$
, ranging over all bounded intervals I,
$\varphi _{I^\prime ,I}^{J^\prime ,J}:I\rightarrow J$
, ranging over all bounded intervals I,
![]() $I'$
, J,
$I'$
, J,
![]() $J'$
of
$J'$
of
![]() ${\mathbb R}$
, where
${\mathbb R}$
, where
![]() $I^\prime $
(respectively,
$I^\prime $
(respectively,
![]() $J^\prime $
) is adjacent to I (respectively, J) by the left, such that:
$J^\prime $
) is adjacent to I (respectively, J) by the left, such that:
-
(1) for all
 $I,I'$
,
$I,I'$
,
 $J,J', K,K'$
as above,
$J,J', K,K'$
as above,  $$ \begin{align*} \varphi_{J^\prime,J}^{K^\prime,K}\circ\varphi_{I^\prime,I}^{J^\prime,J}=\varphi_{I^\prime,I}^{K^\prime,K}; \end{align*} $$
$$ \begin{align*} \varphi_{J^\prime,J}^{K^\prime,K}\circ\varphi_{I^\prime,I}^{J^\prime,J}=\varphi_{I^\prime,I}^{K^\prime,K}; \end{align*} $$
-
(2) for all
 $I,I'$
,
$I,I'$
,
 $J,J'$
, where
$J,J'$
, where $$ \begin{align*}D\varphi^{J^\prime,J}_{I^\prime,I}(x_{-})=\frac{\lvert J^\prime\rvert}{\lvert I^\prime\rvert}\quad \mathrm{and}\quad D\varphi^{J^\prime,J}_{I^\prime,I}(x_{+})=\frac{\lvert J\rvert}{\lvert I\rvert},\end{align*} $$
$$ \begin{align*}D\varphi^{J^\prime,J}_{I^\prime,I}(x_{-})=\frac{\lvert J^\prime\rvert}{\lvert I^\prime\rvert}\quad \mathrm{and}\quad D\varphi^{J^\prime,J}_{I^\prime,I}(x_{+})=\frac{\lvert J\rvert}{\lvert I\rvert},\end{align*} $$
 $x_-$
(respectively,
$x_-$
(respectively,
 $x_+$
) is the left (respectively, right) endpoint of I;
$x_+$
) is the left (respectively, right) endpoint of I;
-
(3) there is a constant M such that, for all
 $I,I',J,J'$
as above, and all
$I,I',J,J'$
as above, and all
 $x\in I$
, provided that
$x\in I$
, provided that $$ \begin{align*} D\log(D\varphi_{I^\prime,I}^{J^\prime,J})(x)\leq \frac{M}{\lvert I\rvert}\bigg\lvert\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}-1\bigg\rvert,\end{align*} $$
$$ \begin{align*} D\log(D\varphi_{I^\prime,I}^{J^\prime,J})(x)\leq \frac{M}{\lvert I\rvert}\bigg\lvert\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}-1\bigg\rvert,\end{align*} $$
 $\max \{|I|, |I'|, |J|, |J'|\}\leq 2 \min \{|I|, |I'|, |J|, |J'|\};$
and
$\max \{|I|, |I'|, |J|, |J'|\}\leq 2 \min \{|I|, |I'|, |J|, |J'|\};$
and
-
(4) given
 $I, I', \;J,J', \;K,K',\: L,L'$
, as above, then for all
$I, I', \;J,J', \;K,K',\: L,L'$
, as above, then for all $$ \begin{align*}\lvert \log(D\varphi_{I^\prime,I}^{K^\prime,K})(x)-\log(D\varphi_{J^\prime,J}^{L^\prime,L})(y)\rvert\leq \bigg\lvert{\log}\ \frac{\lvert K\rvert\lvert J\rvert}{\lvert I\rvert\lvert L\rvert}\bigg\rvert+ \bigg\lvert{\log}\ \frac{\lvert K^\prime\rvert\lvert I\rvert}{\lvert I^\prime\rvert\lvert K\rvert}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert L^\prime\rvert\lvert J\rvert}{\lvert J^\prime\rvert\lvert L\rvert}\bigg\rvert, \end{align*} $$
$$ \begin{align*}\lvert \log(D\varphi_{I^\prime,I}^{K^\prime,K})(x)-\log(D\varphi_{J^\prime,J}^{L^\prime,L})(y)\rvert\leq \bigg\lvert{\log}\ \frac{\lvert K\rvert\lvert J\rvert}{\lvert I\rvert\lvert L\rvert}\bigg\rvert+ \bigg\lvert{\log}\ \frac{\lvert K^\prime\rvert\lvert I\rvert}{\lvert I^\prime\rvert\lvert K\rvert}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert L^\prime\rvert\lvert J\rvert}{\lvert J^\prime\rvert\lvert L\rvert}\bigg\rvert, \end{align*} $$
 $x\in I$
,
$x\in I$
,
 $y\in J$
.
$y\in J$
.
Now, let
![]() $\{I_{i_1,\ldots ,i_k,j}: (i_1,\ldots ,i_k,j)\in \mathbb {Z}^{k+1}\}$
be a family of intervals whose disjoint union is dense in
$\{I_{i_1,\ldots ,i_k,j}: (i_1,\ldots ,i_k,j)\in \mathbb {Z}^{k+1}\}$
be a family of intervals whose disjoint union is dense in
![]() $[0, 1]$
and that are disposed preserving the lexicographic order of
$[0, 1]$
and that are disposed preserving the lexicographic order of
![]() $\mathbb Z^{k+1}$
. We identify the generators
$\mathbb Z^{k+1}$
. We identify the generators
![]() $g_1,\ldots ,g_d,f_1,\ldots ,f_k$
from Lemma 2.3 with elements in
$g_1,\ldots ,g_d,f_1,\ldots ,f_k$
from Lemma 2.3 with elements in
![]() $\mathrm {Diff}^{\, 0}_+([0,1])$
as follows:
$\mathrm {Diff}^{\, 0}_+([0,1])$
as follows:
![]() $f_t$
and
$f_t$
and
![]() $g_s$
will be homeomorphisms of
$g_s$
will be homeomorphisms of
![]() $[0,1]$
whose restriction to
$[0,1]$
whose restriction to
![]() $I_{i_1,\ldots ,i_k,j}$
coincides, respectively, with
$I_{i_1,\ldots ,i_k,j}$
coincides, respectively, with
for
![]() $t\in \{1,\ldots ,k\}$
and
$t\in \{1,\ldots ,k\}$
and
![]() $s\in \{1,\ldots ,d\}$
. Thus, by (1) in Lemma 3.3, we have a group homomorphism
$s\in \{1,\ldots ,d\}$
. Thus, by (1) in Lemma 3.3, we have a group homomorphism
![]() $G\rightarrow \mathrm {Diff}^{\, 0}_+([0,1]).$
The main technical step for proving Theorem A is the following proposition.
$G\rightarrow \mathrm {Diff}^{\, 0}_+([0,1]).$
The main technical step for proving Theorem A is the following proposition.
Proposition 3.4. Given
![]() $\alpha <1/k$
, there is a choice of lengths of the intervals
$\alpha <1/k$
, there is a choice of lengths of the intervals
![]() $|I_{i_1,\ldots ,i_k,j}|$
such that the homeomorphisms
$|I_{i_1,\ldots ,i_k,j}|$
such that the homeomorphisms
![]() $f_1,\ldots ,f_k,g_1,\ldots ,g_d$
are diffeomorphisms of class
$f_1,\ldots ,f_k,g_1,\ldots ,g_d$
are diffeomorphisms of class
![]() $C^{1+\alpha }$
.
$C^{1+\alpha }$
.
The rest of §3.2 is devoted to the proof of Proposition 3.4. We assume that
![]() $k\geq 2$
since, after Condition (3) in Proposition 3.1, we can use the estimates from [Reference Castro, Jorquera and Navas6, §4] to ensure that, when
$k\geq 2$
since, after Condition (3) in Proposition 3.1, we can use the estimates from [Reference Castro, Jorquera and Navas6, §4] to ensure that, when
![]() $k=1$
, the action is by
$k=1$
, the action is by
![]() $C^{1+\alpha }$
diffeomorphisms for any
$C^{1+\alpha }$
diffeomorphisms for any
![]() $\alpha <1$
.
$\alpha <1$
.
So let
![]() $k\geq 2$
and consider
$k\geq 2$
and consider
![]() $\alpha <1/k$
. Choose positive real numbers
$\alpha <1/k$
. Choose positive real numbers
![]() $p_1,\ldots ,p_k,r$
such that, for all
$p_1,\ldots ,p_k,r$
such that, for all
![]() $n\in \{1,\ldots ,k\}$
:
$n\in \{1,\ldots ,k\}$
:
-
(I)
 $\alpha + r\leq 2$
;
$\alpha + r\leq 2$
; -
(II)
 $d(r-1)\leq (1-\alpha )$
;
$d(r-1)\leq (1-\alpha )$
; -
(III)
 $2dr\leq p_n$
;
$2dr\leq p_n$
; -
(IV)
 $2d\leq p_n(1-\alpha )$
;
$2d\leq p_n(1-\alpha )$
; -
(V)
 ${1}/{p_1} +\cdots + {1}/{p_k} + {1}/{r} < 1$
; and
${1}/{p_1} +\cdots + {1}/{p_k} + {1}/{r} < 1$
; and -
(VI)
 $\alpha \leq {1}/{p_n} + {1}/{r}$
and
$\alpha \leq {1}/{p_n} + {1}/{r}$
and
 $\alpha \leq {r}/{p_n(r-1)}$
.
$\alpha \leq {r}/{p_n(r-1)}$
.
For example, one can take
![]() $p_1=\cdots =p_k=3d/\alpha $
and
$p_1=\cdots =p_k=3d/\alpha $
and
![]() $r=3d/(3d-1)$
.
$r=3d/(3d-1)$
.
Now define the lengths of the intervals
![]() $I_{i_1,\ldots ,i_k,j}$
as
$I_{i_1,\ldots ,i_k,j}$
as
From condition (V,) it follows that
![]() $\sum \lvert I_{i_1,\ldots ,i_k,j}\rvert <\infty $
, and hence this family of intervals can be disposed on a finite interval respecting the lexicographic order. After renormalization, we can assume that this interval is
$\sum \lvert I_{i_1,\ldots ,i_k,j}\rvert <\infty $
, and hence this family of intervals can be disposed on a finite interval respecting the lexicographic order. After renormalization, we can assume that this interval is
![]() $[0,1]$
.
$[0,1]$
.
Following [Reference Jorquera, Navas and Rivas13], we say that two real-valued functions f and g satisfy
![]() $f\prec g$
if there is a constant
$f\prec g$
if there is a constant
![]() $M>0$
such that
$M>0$
such that
![]() $\lvert f(x)\rvert \leqslant Mg(x)$
for all x. We also write
$\lvert f(x)\rvert \leqslant Mg(x)$
for all x. We also write
![]() $f\asymp g$
if
$f\asymp g$
if
![]() $f\prec g$
and
$f\prec g$
and
![]() $g\prec f$
.
$g\prec f$
.
Let
![]() $\theta $
be a non-negative
$\theta $
be a non-negative
![]() $C^2$
real-valued function satisfying
$C^2$
real-valued function satisfying
![]() $\theta (\xi )=\lvert \xi \rvert ^r$
for
$\theta (\xi )=\lvert \xi \rvert ^r$
for
![]() $\lvert \xi \rvert \geqslant 1$
and
$\lvert \xi \rvert \geqslant 1$
and
![]() $\theta (0)=0$
. Consider the auxiliary functions (
$\theta (0)=0$
. Consider the auxiliary functions (
![]() $C^2$
with respect to
$C^2$
with respect to
![]() $\xi $
):
$\xi $
):
-
•
 $\psi (i_1,\ldots ,i_k,\xi ):=1+\lvert i_1\rvert ^{p_1}+\cdots +\lvert i_k\rvert ^{p_k}+\theta (\xi );$
and
$\psi (i_1,\ldots ,i_k,\xi ):=1+\lvert i_1\rvert ^{p_1}+\cdots +\lvert i_k\rvert ^{p_k}+\theta (\xi );$
and -
•
 $\Psi _{i_1,\ldots ,i_k}(\xi ):=\log (\psi (i_1,\ldots ,i_k,\xi )).$
$\Psi _{i_1,\ldots ,i_k}(\xi ):=\log (\psi (i_1,\ldots ,i_k,\xi )).$
Lemma 3.5. Let
![]() $S=1+\lvert i_1\rvert ^{p_1}+\cdots +\lvert i_k\rvert ^{p_k}$
. Given
$S=1+\lvert i_1\rvert ^{p_1}+\cdots +\lvert i_k\rvert ^{p_k}$
. Given
![]() $C>0$
, there exists a positive constant M such that the inequality
$C>0$
, there exists a positive constant M such that the inequality
holds for any
![]() $\xi $
satisfying
$\xi $
satisfying
![]() $\lvert \xi -j\rvert \leq C(S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
.
$\lvert \xi -j\rvert \leq C(S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
.
We remark that, in the situation of Lemma 3.5, we will still use the notation
![]() $\psi (i_1,\ldots ,i_k,j)\asymp \psi (i_1,\ldots ,i_k,\xi )$
. Even if this is a slight abuse of notation, it is justified by comparing the functions
$\psi (i_1,\ldots ,i_k,j)\asymp \psi (i_1,\ldots ,i_k,\xi )$
. Even if this is a slight abuse of notation, it is justified by comparing the functions
![]() $\psi _j$
and
$\psi _j$
and
![]() $\psi _\xi $
defined by
$\psi _\xi $
defined by
![]() $\psi _\xi (i_1,\ldots ,i_k)=\psi (i_1,\ldots ,i_k,\xi )$
and
$\psi _\xi (i_1,\ldots ,i_k)=\psi (i_1,\ldots ,i_k,\xi )$
and
![]() $\psi _j (i_1,\ldots ,i_k)=\psi (i_1,\ldots ,i_k,j)$
whenever the inequality
$\psi _j (i_1,\ldots ,i_k)=\psi (i_1,\ldots ,i_k,j)$
whenever the inequality
![]() $\lvert \xi -j\rvert \leq C(S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
holds.
$\lvert \xi -j\rvert \leq C(S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
holds.
Proof of Lemma 3.5
By symmetry, it is enough to show that
![]() $ {\psi (i_1,\ldots ,i_k,\xi )}/ {\psi (i_1,\ldots ,i_k,j)}$
is bounded above. For this we note that
$ {\psi (i_1,\ldots ,i_k,\xi )}/ {\psi (i_1,\ldots ,i_k,j)}$
is bounded above. For this we note that
 $$ \begin{align*} \frac{\psi(i_1,\ldots,i_k,\xi)}{\psi(i_1,\ldots,i_k,j)}&\prec \frac{1+\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k}+\lvert j\rvert^r+\lvert\xi-j\rvert^r} {\psi(i_1,\ldots,i_k,j)}\\ & \prec 1+ \frac{S+(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{dr}}{\psi(i_1,\ldots,i_k,j)}\\&\prec 2+\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{dr}}{\psi(i_1,\ldots,i_k,j)}, \end{align*} $$
$$ \begin{align*} \frac{\psi(i_1,\ldots,i_k,\xi)}{\psi(i_1,\ldots,i_k,j)}&\prec \frac{1+\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k}+\lvert j\rvert^r+\lvert\xi-j\rvert^r} {\psi(i_1,\ldots,i_k,j)}\\ & \prec 1+ \frac{S+(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{dr}}{\psi(i_1,\ldots,i_k,j)}\\&\prec 2+\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{dr}}{\psi(i_1,\ldots,i_k,j)}, \end{align*} $$
where we repeatedly use the inequality
![]() $\lvert x+y\rvert ^a\prec \lvert x\rvert ^a+\lvert y\rvert ^a$
, which holds for any
$\lvert x+y\rvert ^a\prec \lvert x\rvert ^a+\lvert y\rvert ^a$
, which holds for any
![]() $a>~0$
. Now, notice that the last expression is bounded. Indeed, since
$a>~0$
. Now, notice that the last expression is bounded. Indeed, since
![]() $(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^{dr} \prec \lvert i_1\rvert ^{dr}+\cdots +\lvert i_k\rvert ^{dr}$
, it is enough to observe that, for each
$(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^{dr} \prec \lvert i_1\rvert ^{dr}+\cdots +\lvert i_k\rvert ^{dr}$
, it is enough to observe that, for each
![]() $n\in \{1,\ldots ,k\}$
,
$n\in \{1,\ldots ,k\}$
,
which holds due to condition (III).
3.2.1. The maps
 $g_s$
are
$g_s$
are
 $C^{1+\alpha }$
-diffeomorphisms
$C^{1+\alpha }$
-diffeomorphisms
We start the proof of Proposition 3.4 by showing that the maps
![]() $g_s$
, for
$g_s$
, for
![]() $s\in \{1,\ldots ,d\}$
, are of class
$s\in \{1,\ldots ,d\}$
, are of class
![]() $C^{1+\alpha }$
. That is, we want to show that
$C^{1+\alpha }$
. That is, we want to show that
![]() $g_s$
is a
$g_s$
is a
![]() $C^1$
-diffeomorphism and that there is a constant
$C^1$
-diffeomorphism and that there is a constant
![]() $C>0$
such that
$C>0$
such that
To check this, it is enough to find a uniform C, as above, for points
![]() $x,y$
in
$x,y$
in
![]() $\bigcup _j I_{i_1,\ldots ,i_k,j}$
(independent of
$\bigcup _j I_{i_1,\ldots ,i_k,j}$
(independent of
![]() $i_1,\ldots ,i_k$
). Indeed, after condition (2) in Lemma 3.3 and the definition of
$i_1,\ldots ,i_k$
). Indeed, after condition (2) in Lemma 3.3 and the definition of
![]() $g_s$
, it follows that
$g_s$
, it follows that
![]() $g_s$
has derivative 1 at the end points of the intervals
$g_s$
has derivative 1 at the end points of the intervals
![]() $\bigcup _j I_{i_1,\ldots ,i_k,j}$
. Hence the conditions from [Reference Navas20, Lemma 4.1.22] are satisfied, and therefore we obtain that the
$\bigcup _j I_{i_1,\ldots ,i_k,j}$
. Hence the conditions from [Reference Navas20, Lemma 4.1.22] are satisfied, and therefore we obtain that the
![]() $g_s$
are of class
$g_s$
are of class
![]() $C^{1+\alpha }$
.
$C^{1+\alpha }$
.
Case 1: The points
![]() $x,y$
belong to the same
$x,y$
belong to the same
![]() $ I:=I_{i_1,\ldots ,i_k,j}.$
Condition (3) in Lemma 3.3 provides a Lipschitz constant for
$ I:=I_{i_1,\ldots ,i_k,j}.$
Condition (3) in Lemma 3.3 provides a Lipschitz constant for
![]() $\log (Dg_s)$
. So it is enough to bound
$\log (Dg_s)$
. So it is enough to bound
 $$ \begin{align*} \frac{1}{\lvert I\rvert^\alpha} \bigg| \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert} -1\bigg|, \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert I\rvert^\alpha} \bigg| \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert} -1\bigg|, \end{align*} $$
where
![]() $I^\prime =I_{i_1,\ldots ,i_k,j-1}$
,
$I^\prime =I_{i_1,\ldots ,i_k,j-1}$
,
![]() $J=I_{i_1,\ldots ,i_k,j+r_s(i_1,\ldots ,i_k)}$
and
$J=I_{i_1,\ldots ,i_k,j+r_s(i_1,\ldots ,i_k)}$
and
![]() $J^\prime =I_{i_1,\ldots ,i_k,j+r_s(i_1,\ldots ,i_k)-1}$
.
$J^\prime =I_{i_1,\ldots ,i_k,j+r_s(i_1,\ldots ,i_k)-1}$
.
We will, in fact, bound the following (a posteriori) asymptotically equivalent expression
 $$ \begin{align*}\frac{1}{\lvert I\rvert^\alpha}\log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}.\end{align*} $$
$$ \begin{align*}\frac{1}{\lvert I\rvert^\alpha}\log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}.\end{align*} $$
For this, notice that
![]() $\log {\lvert I\rvert \lvert J^\prime \rvert }/{\lvert J\rvert \lvert I^\prime \rvert }$
is equal to
$\log {\lvert I\rvert \lvert J^\prime \rvert }/{\lvert J\rvert \lvert I^\prime \rvert }$
is equal to
 $$ \begin{align*} &\Psi_{i_1,\ldots,i_k}(j+r_s(i_1,\ldots,i_k))-\Psi_{i_1,\ldots,i_k}(j+r_s(i_1,\ldots,i_k)-1)-(\Psi_{i_1,\ldots,i_k}(j)\\ &\qquad -\Psi_{i_1,\ldots,i_k}(j-1)). \end{align*} $$
$$ \begin{align*} &\Psi_{i_1,\ldots,i_k}(j+r_s(i_1,\ldots,i_k))-\Psi_{i_1,\ldots,i_k}(j+r_s(i_1,\ldots,i_k)-1)-(\Psi_{i_1,\ldots,i_k}(j)\\ &\qquad -\Psi_{i_1,\ldots,i_k}(j-1)). \end{align*} $$
So, applying the mean value theorem first to the function
![]() $x\mapsto \Psi _{i_1,\ldots ,i_k}(j+1+x)-\Psi _{i_1,\ldots ,i_k}(j+x)$
and then to the function
$x\mapsto \Psi _{i_1,\ldots ,i_k}(j+1+x)-\Psi _{i_1,\ldots ,i_k}(j+x)$
and then to the function
![]() $x\mapsto D\Psi _{i_1,\ldots ,i_k}(x)$
gives
$x\mapsto D\Psi _{i_1,\ldots ,i_k}(x)$
gives
 $$ \begin{align} \bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\bigg\rvert=\lvert r_s(i_1,\ldots,i_k)\rvert\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert, \end{align} $$
$$ \begin{align} \bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\bigg\rvert=\lvert r_s(i_1,\ldots,i_k)\rvert\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert, \end{align} $$
where
![]() $\xi $
is a point in the convex hull of
$\xi $
is a point in the convex hull of
![]() $\{j-1,j,j-1+r_s,j+r_s\}$
. We find an upper bound for
$\{j-1,j,j-1+r_s,j+r_s\}$
. We find an upper bound for
![]() $\lvert D^2(\Psi _{i_1,\ldots ,i_k})(\xi )\rvert $
. Since
$\lvert D^2(\Psi _{i_1,\ldots ,i_k})(\xi )\rvert $
. Since
![]() $D\theta $
and
$D\theta $
and
![]() $D^2\theta $
are bounded on
$D^2\theta $
are bounded on
![]() $[-1,1]$
, and
$[-1,1]$
, and
 $$ \begin{align*}D^2(\Psi_{i_1,\ldots,i_k})(\xi)=\frac{D^2\theta(\xi)}{\psi(i_1,\ldots,i_k,\xi)}-\frac{(D\theta(\xi))^2}{(\psi(i_1,\ldots,i_k,\xi))^2},\end{align*} $$
$$ \begin{align*}D^2(\Psi_{i_1,\ldots,i_k})(\xi)=\frac{D^2\theta(\xi)}{\psi(i_1,\ldots,i_k,\xi)}-\frac{(D\theta(\xi))^2}{(\psi(i_1,\ldots,i_k,\xi))^2},\end{align*} $$
we have that
for all
![]() $\xi \in [-1,1]$
. On the other hand, for
$\xi \in [-1,1]$
. On the other hand, for
![]() $\xi \notin [-1,1]$
, we have that
$\xi \notin [-1,1]$
, we have that
![]() $\theta (\xi )=\lvert \xi \rvert ^r$
. So, since
$\theta (\xi )=\lvert \xi \rvert ^r$
. So, since
![]() $\lvert \xi \rvert ^{r-2}<1$
and
$\lvert \xi \rvert ^{r-2}<1$
and
![]() $\lvert \xi \rvert ^r/\psi (i_1,\ldots ,i_k,\xi )<1$
, it follows that
$\lvert \xi \rvert ^r/\psi (i_1,\ldots ,i_k,\xi )<1$
, it follows that
 $$ \begin{align} D^2(\Psi_{i_1,\ldots,i_k})(\xi)\prec \frac{\lvert\xi\rvert^{r-2}}{\psi(i_1,\ldots,i_k,\xi)}\prec \frac{1}{\psi(i_1,\ldots,i_k,\xi)}. \end{align} $$
$$ \begin{align} D^2(\Psi_{i_1,\ldots,i_k})(\xi)\prec \frac{\lvert\xi\rvert^{r-2}}{\psi(i_1,\ldots,i_k,\xi)}\prec \frac{1}{\psi(i_1,\ldots,i_k,\xi)}. \end{align} $$
Now, going back to equation (3.2) and using (3) of Proposition 3.1,
 $$ \begin{align*}\log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\prec \frac{\lvert i_1\rvert^d+\cdots+\lvert i_k\rvert^d}{\psi(i_1,\ldots,i_k,\xi)}.\end{align*} $$
$$ \begin{align*}\log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\prec \frac{\lvert i_1\rvert^d+\cdots+\lvert i_k\rvert^d}{\psi(i_1,\ldots,i_k,\xi)}.\end{align*} $$
Note that, for all
![]() $n\in \{1,\ldots ,k\}$
, condition (IV) yields
$n\in \{1,\ldots ,k\}$
, condition (IV) yields
Finally, thanks to the fact that
![]() $\xi $
belongs to the convex hull of
$\xi $
belongs to the convex hull of
![]() $\{j-1,j,j-1+r_s,j+r_s\}$
, we use the bounds of
$\{j-1,j,j-1+r_s,j+r_s\}$
, we use the bounds of
![]() $r_s$
from Proposition 3.1 to apply Lemma 3.5 and conclude that
$r_s$
from Proposition 3.1 to apply Lemma 3.5 and conclude that
 $$ \begin{align*} \frac{1}{\lvert I\rvert^{\alpha}} \log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\prec\frac{ (\psi(i_1,\ldots,i_k,\xi))^{-\alpha}}{\lvert I\rvert^{\alpha}}\prec\frac{ (\psi(i_1,\ldots,i_k,j))^{-\alpha}}{\lvert I\rvert^{\alpha}}=1,\end{align*} $$
$$ \begin{align*} \frac{1}{\lvert I\rvert^{\alpha}} \log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert J\rvert\lvert I^\prime\rvert}\prec\frac{ (\psi(i_1,\ldots,i_k,\xi))^{-\alpha}}{\lvert I\rvert^{\alpha}}\prec\frac{ (\psi(i_1,\ldots,i_k,j))^{-\alpha}}{\lvert I\rvert^{\alpha}}=1,\end{align*} $$
as desired.
Case 2: The point x belongs to
![]() $I_{i_1,\ldots ,i_k,j}$
and y belongs to
$I_{i_1,\ldots ,i_k,j}$
and y belongs to
![]() $I_{i_1,\ldots ,i_k,j'}.$
We assume, without loss of generality, that
$I_{i_1,\ldots ,i_k,j'}.$
We assume, without loss of generality, that
![]() $j< j^\prime $
. Condition (4) of Lemma 3.3 tells us that
$j< j^\prime $
. Condition (4) of Lemma 3.3 tells us that
![]() $\lvert \log Dg_s(x)-\log Dg_s(y)\rvert $
is bounded above by
$\lvert \log Dg_s(x)-\log Dg_s(y)\rvert $
is bounded above by
 $$ \begin{align*} &\bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j+r_s}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert \lvert I_{i_1,\ldots,i_k,j^{\prime}+r_s}\rvert}}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j+r_s-1}\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}{{\lvert I_{i_1,\ldots,i_k,j-1}\rvert \lvert I_{i_1,\ldots,i_k,j+r_s}\rvert}}\bigg\rvert \\ &\qquad + \bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j^\prime+r_s-1}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j^\prime-1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime+r_s}\rvert}}\bigg\rvert. \end{align*} $$
$$ \begin{align*} &\bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j+r_s}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert \lvert I_{i_1,\ldots,i_k,j^{\prime}+r_s}\rvert}}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j+r_s-1}\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}{{\lvert I_{i_1,\ldots,i_k,j-1}\rvert \lvert I_{i_1,\ldots,i_k,j+r_s}\rvert}}\bigg\rvert \\ &\qquad + \bigg\lvert{\log}\ \frac{\lvert I_{i_1,\ldots,i_k,j^\prime+r_s-1}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j^\prime-1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime+r_s}\rvert}}\bigg\rvert. \end{align*} $$
The estimates in Case 1 allow us to control the last two terms (divided by
![]() $ |x-y|^\alpha $
), and thus we only need to bound the first term. So we look for a uniform bound for
$ |x-y|^\alpha $
), and thus we only need to bound the first term. So we look for a uniform bound for
 $$ \begin{align} \frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert, \end{align} $$
$$ \begin{align} \frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert, \end{align} $$
where
![]() $I=I_{i_1,\ldots ,i_k,j}$
,
$I=I_{i_1,\ldots ,i_k,j}$
,
![]() $I^\prime =I_{i_1,\ldots ,i_k,j^\prime }$
,
$I^\prime =I_{i_1,\ldots ,i_k,j^\prime }$
,
![]() $J=I_{i_1,\ldots ,i_k,j+r_s}$
and
$J=I_{i_1,\ldots ,i_k,j+r_s}$
and
![]() $J^\prime =I_{i_1,\ldots ,i_k,j^\prime +r_s}$
. Assume that j,
$J^\prime =I_{i_1,\ldots ,i_k,j^\prime +r_s}$
. Assume that j,
![]() $j^\prime $
are positive (the case where both are negative follows by symmetry, and if they have different sign, it suffices to consider an intermediate comparison with the term corresponding to
$j^\prime $
are positive (the case where both are negative follows by symmetry, and if they have different sign, it suffices to consider an intermediate comparison with the term corresponding to
![]() $j^{\prime \prime }=0$
). Assume, further, that
$j^{\prime \prime }=0$
). Assume, further, that
![]() $j^\prime -j\geq 2$
(the case where
$j^\prime -j\geq 2$
(the case where
![]() $j^\prime -j= 1$
follows from Case 1, passing through the point that separates the intervals and using the triangle inequality). Again, applying the mean value theorem first to the function
$j^\prime -j= 1$
follows from Case 1, passing through the point that separates the intervals and using the triangle inequality). Again, applying the mean value theorem first to the function
![]() $x\mapsto \Psi _{i_1,\ldots ,i_k}(j+1+x)-\Psi _{i_1,\ldots ,i_k}(j+x)$
and then to the function
$x\mapsto \Psi _{i_1,\ldots ,i_k}(j+1+x)-\Psi _{i_1,\ldots ,i_k}(j+x)$
and then to the function
![]() $x \mapsto D\Psi _{i_1,\ldots ,i_k}(x)$
gives
$x \mapsto D\Psi _{i_1,\ldots ,i_k}(x)$
gives
 $$ \begin{align} \bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert=\lvert j-j^\prime\rvert\cdot\lvert r_s(i_1,\ldots,i_k)\rvert \cdot\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert,\end{align} $$
$$ \begin{align} \bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert=\lvert j-j^\prime\rvert\cdot\lvert r_s(i_1,\ldots,i_k)\rvert \cdot\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert,\end{align} $$
for a certain
![]() $\xi $
in the convex hull of
$\xi $
in the convex hull of
![]() $\{j,j^\prime ,j+r_s,j^\prime +r_s\}$
.
$\{j,j^\prime ,j+r_s,j^\prime +r_s\}$
.
We start by bounding
![]() $|x-y|^{-\alpha }$
. For this, note that, by Case 1 and the triangle inequality, we can (and will) assume that x is the left endpoint of I and y is the right endpoint of
$|x-y|^{-\alpha }$
. For this, note that, by Case 1 and the triangle inequality, we can (and will) assume that x is the left endpoint of I and y is the right endpoint of
![]() $I^\prime $
. This yields
$I^\prime $
. This yields
 $$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}=\bigg(\frac{1}{\sum_{\ell=j}^{j^\prime}\lvert I_{i_1,\ldots,i_k,\ell}\rvert}\bigg)^\alpha\leq \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}\bigg)^\alpha, \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}=\bigg(\frac{1}{\sum_{\ell=j}^{j^\prime}\lvert I_{i_1,\ldots,i_k,\ell}\rvert}\bigg)^\alpha\leq \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}\bigg)^\alpha, \end{align*} $$
where the last inequality holds because
![]() $\lvert I_{i_1,\ldots ,i_k,j^\prime }\rvert <\lvert I_{i_1,\ldots ,i_k,\ell }\rvert $
for
$\lvert I_{i_1,\ldots ,i_k,j^\prime }\rvert <\lvert I_{i_1,\ldots ,i_k,\ell }\rvert $
for
![]() $\ell <j^\prime $
. Note that if, in addition,
$\ell <j^\prime $
. Note that if, in addition,
![]() $\lvert j^\prime -j\rvert \leq C( S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
, for some
$\lvert j^\prime -j\rvert \leq C( S^{1/r}+(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d)$
, for some
![]() $C>0$
, we can use Lemma 3.5 to compare
$C>0$
, we can use Lemma 3.5 to compare
![]() $\lvert I\rvert $
with
$\lvert I\rvert $
with
![]() $\lvert I^\prime \rvert $
, and we eventually obtain the inequality
$\lvert I^\prime \rvert $
, and we eventually obtain the inequality
 $$ \begin{align} \frac{1}{\lvert x-y\rvert^\alpha}\prec \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}\bigg)^\alpha. \end{align} $$
$$ \begin{align} \frac{1}{\lvert x-y\rvert^\alpha}\prec \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}\bigg)^\alpha. \end{align} $$
We now exhibit a bound for (3.4). We consider three separate cases. Let M be the constant in Proposition 3.1.
-
(i) The integers
 $j,j^\prime $
belong to
$j,j^\prime $
belong to
 $[0,2M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d]$
. Since
$[0,2M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d]$
. Since
 $\xi \in \mathrm {conv}\{j,j^\prime , j+r_s,j^\prime +r_s\}$
, it follows from (3.3) and Lemma 3.5 that Furthermore, we have that
$\xi \in \mathrm {conv}\{j,j^\prime , j+r_s,j^\prime +r_s\}$
, it follows from (3.3) and Lemma 3.5 that Furthermore, we have that $$ \begin{align*}\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert\prec\frac{1}{\psi(i_1,\ldots,i_k,\xi)}\asymp \frac{1}{\psi(i_1,\ldots,i_k,j)}.\end{align*} $$
where the last inequality holds by condition (IV). If we combine this with (3.5), (3.6), we conclude that
$$ \begin{align*}\lvert D^2(\Psi_{i_1,\ldots,i_k})(\xi)\rvert\prec\frac{1}{\psi(i_1,\ldots,i_k,\xi)}\asymp \frac{1}{\psi(i_1,\ldots,i_k,j)}.\end{align*} $$
where the last inequality holds by condition (IV). If we combine this with (3.5), (3.6), we conclude that $$ \begin{align*}\lvert j-j^\prime\rvert\lvert r_s(i_1,\ldots,i_k)\rvert \prec (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{2d}\prec (\psi(i_1,\ldots,i_k,j))^{1-\alpha},\end{align*} $$
$$ \begin{align*}\lvert j-j^\prime\rvert\lvert r_s(i_1,\ldots,i_k)\rvert \prec (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{2d}\prec (\psi(i_1,\ldots,i_k,j))^{1-\alpha},\end{align*} $$
 $$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert \prec \frac{1}{\lvert I\rvert^\alpha}\frac{(\psi(i_1,\ldots,i_k,j))^{1-\alpha}}{\psi(i_1,\ldots,i_k,j)}= 1.\end{align*} $$
$$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert \prec \frac{1}{\lvert I\rvert^\alpha}\frac{(\psi(i_1,\ldots,i_k,j))^{1-\alpha}}{\psi(i_1,\ldots,i_k,j)}= 1.\end{align*} $$
-
(ii) The integers
 $j,j'$
belong to (the constant
$j,j'$
belong to (the constant
 $k^d$
is just to ensure that the interval is non-empty)
$k^d$
is just to ensure that the interval is non-empty)
 $ [2M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d, 2M k^d S^{1/r}]$
. Similarly to
$ [2M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d, 2M k^d S^{1/r}]$
. Similarly to
 $i)$
, the reader can check that we are in the hypotheses of Lemma 3.5 and that
$i)$
, the reader can check that we are in the hypotheses of Lemma 3.5 and that
 $\lvert \xi \rvert \geq M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d$
. Therefore, by (3.3), (3.5) and (3.6), we get To prove that this last expression is bounded, it is enough to show that
$\lvert \xi \rvert \geq M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d$
. Therefore, by (3.3), (3.5) and (3.6), we get To prove that this last expression is bounded, it is enough to show that $$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert &\prec \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}\bigg)^\alpha \lvert j^\prime-j\rvert\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\lvert\xi\rvert^{r-2}}{\psi(i_1,\ldots,i_k,\xi)} \\& \prec \lvert j^\prime-j\rvert^{1-\alpha}\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}}{\psi(i_1,\ldots,i_k,j)^{1-\alpha}}. \end{align*} $$
Since
$$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{{\lvert I^\prime\rvert\lvert J\rvert}}\bigg\rvert &\prec \bigg(\frac{1}{\lvert j-j^\prime\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}\bigg)^\alpha \lvert j^\prime-j\rvert\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\lvert\xi\rvert^{r-2}}{\psi(i_1,\ldots,i_k,\xi)} \\& \prec \lvert j^\prime-j\rvert^{1-\alpha}\frac{(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}}{\psi(i_1,\ldots,i_k,j)^{1-\alpha}}. \end{align*} $$
Since $$ \begin{align*}\lvert j^\prime-j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}\prec \psi(i_1,\ldots,i_k,j)^{1-\alpha}.\end{align*} $$
$$ \begin{align*}\lvert j^\prime-j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}\prec \psi(i_1,\ldots,i_k,j)^{1-\alpha}.\end{align*} $$
 $j^\prime -j\leq 2M k^d S^{1/r}$
, it follows that so it suffices to prove that, given
$j^\prime -j\leq 2M k^d S^{1/r}$
, it follows that so it suffices to prove that, given $$ \begin{align*} & \lvert j^\prime-j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}\prec (1+\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k})^{{(1-\alpha)}/{r}}\\ &\qquad\times (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}, \end{align*} $$
$$ \begin{align*} & \lvert j^\prime-j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}\prec (1+\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k})^{{(1-\alpha)}/{r}}\\ &\qquad\times (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}, \end{align*} $$
 $n,m\in \{1,\ldots ,k\}$
, (3.7)However, note that
$n,m\in \{1,\ldots ,k\}$
, (3.7)However, note that $$ \begin{align} \lvert i_n\rvert^{{p_n(1-\alpha)}/{r}}\lvert i_m\rvert^{d(r-1)}\prec (\psi(i_1,\ldots ,i_k,j))^{1-\alpha}. \end{align} $$
and that conditions (II) and (V) guarantee that
$$ \begin{align} \lvert i_n\rvert^{{p_n(1-\alpha)}/{r}}\lvert i_m\rvert^{d(r-1)}\prec (\psi(i_1,\ldots ,i_k,j))^{1-\alpha}. \end{align} $$
and that conditions (II) and (V) guarantee that $$ \begin{align*}\lvert i_n\rvert^{{p_n(1-\alpha)}/{r}}\lvert i_m\rvert^{d(r-1)}\leq (\psi(i_1,\ldots,i_k,j))^{{(1-\alpha)}/{r} + {d(r-1)}/{p_m}},\end{align*} $$
$$ \begin{align*}\lvert i_n\rvert^{{p_n(1-\alpha)}/{r}}\lvert i_m\rvert^{d(r-1)}\leq (\psi(i_1,\ldots,i_k,j))^{{(1-\alpha)}/{r} + {d(r-1)}/{p_m}},\end{align*} $$
 ${(1-\alpha )}/{r} + {d(r-1)}/{p_m}\leq (1-~\alpha )$
, which implies (3.7).
${(1-\alpha )}/{r} + {d(r-1)}/{p_m}\leq (1-~\alpha )$
, which implies (3.7).
-
(iii) Finally suppose that the integers
 $j,j^\prime $
belong to
$j,j^\prime $
belong to
 $ [2M k^d S^{1/r},\infty )$
.
$ [2M k^d S^{1/r},\infty )$
.If
 $j^\prime \leq 2j$
, then (3.8)In particular, the intervals
$j^\prime \leq 2j$
, then (3.8)In particular, the intervals $$ \begin{align} \frac{\psi(i_1,\ldots,i_k,j^\prime)}{\psi(i_1,\ldots,i_k,j)}\prec 1+\frac{\lvert j-j^\prime\rvert^r}{\psi(i_1,\ldots,i_k,j)}\prec 1+ \frac{\lvert j\rvert^r}{\psi(i_1,\ldots,i_k,j)}\leq 2. \end{align} $$
$$ \begin{align} \frac{\psi(i_1,\ldots,i_k,j^\prime)}{\psi(i_1,\ldots,i_k,j)}\prec 1+\frac{\lvert j-j^\prime\rvert^r}{\psi(i_1,\ldots,i_k,j)}\prec 1+ \frac{\lvert j\rvert^r}{\psi(i_1,\ldots,i_k,j)}\leq 2. \end{align} $$
 $\lvert I^\prime \rvert $
and
$\lvert I^\prime \rvert $
and
 $\lvert I\rvert $
have comparable size and hence we conclude that (3.6) still holds. Also note that
$\lvert I\rvert $
have comparable size and hence we conclude that (3.6) still holds. Also note that
 $j^\prime \leq 2j$
implies that
$j^\prime \leq 2j$
implies that
 $\lvert \xi -j\rvert \leq \lvert j\rvert +M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d$
. Then, proceeding as in
$\lvert \xi -j\rvert \leq \lvert j\rvert +M(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d$
. Then, proceeding as in
 $ii)$
, we have that The reader can check, again as in
$ii)$
, we have that The reader can check, again as in $$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}\bigg\rvert\prec \frac{\lvert j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}}{\psi(i_1,\ldots,i_k,j)^{1-\alpha}}.\end{align*} $$
$$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}\bigg\rvert\prec \frac{\lvert j\rvert^{1-\alpha}(\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^{d(r-1)}}{\psi(i_1,\ldots,i_k,j)^{1-\alpha}}.\end{align*} $$
 $ii)$
, that this last expression is bounded.
$ii)$
, that this last expression is bounded.
For the case
 $j^\prime> 2j$
, we have where the last inequality holds because
$j^\prime> 2j$
, we have where the last inequality holds because $$ \begin{align*} \lvert x-y\rvert&=\sum_{\ell=j}^{j^\prime}\lvert I_{i_1,\ldots,i_k,\ell}\rvert=\sum_{\ell=j}^{j^\prime}\frac{1}{\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k}+\lvert\ell\rvert^r}\\& \succ \sum_{\ell=j}^{j^\prime} \frac{1}{\lvert\ell\rvert^r}\succ \int_{\ell=j}^{j^\prime} \frac{1}{x^r}\,dx\succ \frac{1}{\lvert j\rvert^{r-1}}, \end{align*} $$
$$ \begin{align*} \lvert x-y\rvert&=\sum_{\ell=j}^{j^\prime}\lvert I_{i_1,\ldots,i_k,\ell}\rvert=\sum_{\ell=j}^{j^\prime}\frac{1}{\lvert i_1\rvert^{p_1}+\cdots+\lvert i_k\rvert^{p_k}+\lvert\ell\rvert^r}\\& \succ \sum_{\ell=j}^{j^\prime} \frac{1}{\lvert\ell\rvert^r}\succ \int_{\ell=j}^{j^\prime} \frac{1}{x^r}\,dx\succ \frac{1}{\lvert j\rvert^{r-1}}, \end{align*} $$
 $j'>2j$
. On the other hand, applying the mean value theorem, it follows that where
$j'>2j$
. On the other hand, applying the mean value theorem, it follows that where $$ \begin{align*} \log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}&=\lvert r_s(i_1,\ldots,i_k)\rvert\lvert D(\Psi_{i_1,\ldots,i_k})(\xi)-D(\Psi_{i_1,\ldots,i_k})(\tilde{\xi})\rvert, \end{align*} $$
$$ \begin{align*} \log\frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}&=\lvert r_s(i_1,\ldots,i_k)\rvert\lvert D(\Psi_{i_1,\ldots,i_k})(\xi)-D(\Psi_{i_1,\ldots,i_k})(\tilde{\xi})\rvert, \end{align*} $$
 $\xi \in \mathrm {conv}\{j,j+r_s\}$
and
$\xi \in \mathrm {conv}\{j,j+r_s\}$
and
 $\tilde {\xi }\in \mathrm {conv}\{j^\prime ,j^\prime +r_s\}$
. Therefore, observing that the function
$\tilde {\xi }\in \mathrm {conv}\{j^\prime ,j^\prime +r_s\}$
. Therefore, observing that the function
 $\xi \mapsto D(\Psi _{i_1,\ldots ,i_k})(\xi )=r\lvert \xi \rvert ^{r-1}/\psi (i_1,\ldots ,i_k,\xi )$
is decreasing, Now we want to see that this last expression is bounded, in other words, that the inequality
$\xi \mapsto D(\Psi _{i_1,\ldots ,i_k})(\xi )=r\lvert \xi \rvert ^{r-1}/\psi (i_1,\ldots ,i_k,\xi )$
is decreasing, Now we want to see that this last expression is bounded, in other words, that the inequality $$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}\bigg\rvert\prec (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\frac{\lvert j\rvert^{(\alpha+1)(r-1)}}{\psi(i_1,\ldots,i_k,j)}.\end{align*} $$
$$ \begin{align*}\frac{1}{\lvert x-y\rvert^\alpha}\bigg\lvert{\log}\ \frac{\lvert I\rvert\lvert J^\prime\rvert}{\lvert I^\prime\rvert\lvert J\rvert}\bigg\rvert\prec (\lvert i_1\rvert+\cdots+\lvert i_k\rvert)^d\frac{\lvert j\rvert^{(\alpha+1)(r-1)}}{\psi(i_1,\ldots,i_k,j)}.\end{align*} $$
 $\lvert j\rvert ^{(\alpha +1)(r-1)}(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d\prec \psi (i_1,\ldots ,i_k,j)$
holds. For this, arguing as in (3.7), it is enough to check that, for all
$\lvert j\rvert ^{(\alpha +1)(r-1)}(\lvert i_1\rvert +\cdots +\lvert i_k\rvert )^d\prec \psi (i_1,\ldots ,i_k,j)$
holds. For this, arguing as in (3.7), it is enough to check that, for all
 $ n\in \{1,\ldots ,k\}$
, the inequality holds. To see this, note that, from IV) it follows that
$ n\in \{1,\ldots ,k\}$
, the inequality holds. To see this, note that, from IV) it follows that $$ \begin{align*}\frac{(\alpha +1)(r-1)}{r}+\frac{d}{p_n}\leq 1\end{align*} $$
$$ \begin{align*}\frac{(\alpha +1)(r-1)}{r}+\frac{d}{p_n}\leq 1\end{align*} $$
 ${d}/{p_n}\leq ({1-\alpha })/{2}$
. Finally notice that
${d}/{p_n}\leq ({1-\alpha })/{2}$
. Finally notice that
 ${(\alpha +1)(r-1)}/{r} + ({1-\alpha })/{2}\leq 1\Leftrightarrow r \leq 2$
, which is ensured by condition (I).
${(\alpha +1)(r-1)}/{r} + ({1-\alpha })/{2}\leq 1\Leftrightarrow r \leq 2$
, which is ensured by condition (I).
3.2.2. The maps
 $f_t$
are
$f_t$
are
 $C^{1+\alpha }$
-diffeomorphisms
$C^{1+\alpha }$
-diffeomorphisms
In the same way as for the maps
![]() $g_s$
, we want to see that there is a constant
$g_s$
, we want to see that there is a constant
![]() $C> 0$
such that
$C> 0$
such that
To simplify notation, we only work with
![]() $t=1$
, as the other cases are analogous. As for the case of the maps
$t=1$
, as the other cases are analogous. As for the case of the maps
![]() $g_s$
, we only have two cases to analyze.
$g_s$
, we only have two cases to analyze.
Case 1: The points
![]() $x,y$
belongs to the same interval
$x,y$
belongs to the same interval
![]() $I_{i_1,\ldots ,i_k,j}$
. By Lemma 3.3, it is enough to show that the expression
$I_{i_1,\ldots ,i_k,j}$
. By Lemma 3.3, it is enough to show that the expression
 $$ \begin{align*}\frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha}\log\frac{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert\lvert I_{i_1,\ldots,i_k,j-1}\rvert}\end{align*} $$
$$ \begin{align*}\frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha}\log\frac{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert\lvert I_{i_1,\ldots,i_k,j-1}\rvert}\end{align*} $$
is uniformly bounded. To see this, simply note that the above expression is equal to
 $$ \begin{align*} &\frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha}\log\frac{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1,\ldots,i_k,j-1}\rvert}\\ &\qquad + \frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha} \log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j-1}\rvert}. \end{align*} $$
$$ \begin{align*} &\frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha}\log\frac{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1,\ldots,i_k,j-1}\rvert}\\ &\qquad + \frac{1}{\lvert I_{i_1,\ldots,i_k,j}\rvert^\alpha} \log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1-1}\rvert}{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j-1}\rvert}. \end{align*} $$
By condition (VI), we know from [Reference Castro, Jorquera and Navas6, §3.3] that the first term is uniformly bounded. The second term is bounded as well since it is the same as we bounded when dealing with
![]() $g_s$
(changing
$g_s$
(changing
![]() $i_1$
to
$i_1$
to
![]() $i_1+1$
).
$i_1+1$
).
Case 2: The point
![]() $x\in I=I_{i_1,\ldots ,i_k,j}$
and
$x\in I=I_{i_1,\ldots ,i_k,j}$
and
![]() $y\in J=I_{i_1,\ldots ,i_k,j^\prime }$
, with
$y\in J=I_{i_1,\ldots ,i_k,j^\prime }$
, with
![]() $j< j^\prime $
. Here we can use (4) from Lemma 3.3 to bound
$j< j^\prime $
. Here we can use (4) from Lemma 3.3 to bound
![]() $\lvert \log Df_1(x)-\log Df_1(y)\rvert $
by
$\lvert \log Df_1(x)-\log Df_1(y)\rvert $
by
 $$ \begin{align*} &\bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,\ldots,i_k,j^{\prime}+\ell_1}\rvert}}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j+\ell_1-1}\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}{{\lvert I_{i_1,\ldots,i_k,j-1}\rvert \lvert I_{i_1+1,\ldots,i_k,j+\ell_1}\rvert}}\bigg\rvert \\ &\qquad + \bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j^\prime+\ell_1-1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j^\prime-1}\rvert\lvert I_{i_1+1,\ldots,i_k,j^\prime+\ell_1}\rvert}}\bigg\rvert, \end{align*} $$
$$ \begin{align*} &\bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,\ldots,i_k,j^{\prime}+\ell_1}\rvert}}\bigg\rvert + \bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j+\ell_1-1}\rvert\lvert I_{i_1,\ldots,i_k,j}\rvert}{{\lvert I_{i_1,\ldots,i_k,j-1}\rvert \lvert I_{i_1+1,\ldots,i_k,j+\ell_1}\rvert}}\bigg\rvert \\ &\qquad + \bigg\lvert{\log}\ \frac{\lvert I_{i_1+1,\ldots,i_k,j^\prime+\ell_1-1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j^\prime-1}\rvert\lvert I_{i_1+1,\ldots,i_k,j^\prime+\ell_1}\rvert}}\bigg\rvert, \end{align*} $$
and then work in the same way as for the functions
![]() $g_s$
. For example, we express the term
$g_s$
. For example, we express the term
 $$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j^{\prime}+\ell_1}\rvert}} \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1,\ldots,i_k,j}\rvert\lvert I_{i_1+1,i_2,\ldots,i_k,j^{\prime}+\ell_1}\rvert}} \end{align*} $$
as
 $$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1+1,i_2,\ldots,i_k,j^\prime}\rvert \lvert I_{i_1,\ldots,i_k,j}\rvert}}+\frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1+1,i_2,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert \lvert I_{i_1+1,i_2,\ldots,i_k,j^{\prime}+\ell_1}\rvert}}. \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert\lvert I_{i_1,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1+1,i_2,\ldots,i_k,j^\prime}\rvert \lvert I_{i_1,\ldots,i_k,j}\rvert}}+\frac{1}{\lvert x-y\rvert^\alpha}\log\frac{\lvert I_{i_1+1,i_2,\ldots,i_k,j+\ell_1}\rvert \lvert I_{i_1+1,i_2,\ldots,i_k,j^\prime}\rvert}{{\lvert I_{i_1+1,i_2,\ldots,i_k,j}\rvert \lvert I_{i_1+1,i_2,\ldots,i_k,j^{\prime}+\ell_1}\rvert}}. \end{align*} $$
The first term is bounded by [Reference Castro, Jorquera and Navas6, §3.3] and the second is also bounded by the same argument as used for the functions
![]() $g_s$
.
$g_s$
.
3.3. Faithful actions
Given
![]() $s\in \{1,\ldots ,d\}$
and a compact interval
$s\in \{1,\ldots ,d\}$
and a compact interval
![]() $I_s$
, we have seen in Proposition 3.4 how to produce an action
$I_s$
, we have seen in Proposition 3.4 how to produce an action
Recall that the action from Proposition 3.4 is a smoothing of the dynamical realization of the action given in Proposition 3.1. In particular, the subgroup
![]() $\langle g_1,\ldots ,g_{s-1}\rangle $
acts trivially, whereas
$\langle g_1,\ldots ,g_{s-1}\rangle $
acts trivially, whereas
![]() $\langle g_s\rangle $
acts faithfully.
$\langle g_s\rangle $
acts faithfully.
To obtain a faithful action of G, we do the following. Consider compact intervals
![]() $I_1,\ldots ,I_d$
such that, for all
$I_1,\ldots ,I_d$
such that, for all
![]() $s\in \{1,\ldots ,d-1\}$
,
$s\in \{1,\ldots ,d-1\}$
,
![]() $I_{s+1}$
is contiguous to
$I_{s+1}$
is contiguous to
![]() $I_s$
by the right. Then define on
$I_s$
by the right. Then define on
![]() $I:=I_1\cup \cdots \cup I_d$
the action
$I:=I_1\cup \cdots \cup I_d$
the action
![]() $\phi : G \rightarrow \mathrm {Diff}_+^{1+\alpha }(I)$
as
$\phi : G \rightarrow \mathrm {Diff}_+^{1+\alpha }(I)$
as
We claim that
![]() $\phi $
is injective. Indeed, since
$\phi $
is injective. Indeed, since
![]() $Z(G)\leqslant A=\langle g_1,\ldots , g_d\rangle $
, by Proposition 2.1 we only need to check that
$Z(G)\leqslant A=\langle g_1,\ldots , g_d\rangle $
, by Proposition 2.1 we only need to check that
![]() $\phi \mid _A$
is injective. Let
$\phi \mid _A$
is injective. Let
![]() $g\in A$
be an element that acts trivially on I. Then, there exist
$g\in A$
be an element that acts trivially on I. Then, there exist
![]() $j_1,\ldots ,j_d\in \mathbb {Z}$
such that
$j_1,\ldots ,j_d\in \mathbb {Z}$
such that
![]() $g=g_1^{j_1}\cdots g_d^{j_d}$
. Now, since
$g=g_1^{j_1}\cdots g_d^{j_d}$
. Now, since
![]() $\phi (g)=\mathrm{id}$
, it follows that
$\phi (g)=\mathrm{id}$
, it follows that
This yields that
![]() $j_d=\cdots =j_1=0$
and hence g is the trivial element. This finishes the proof of Theorem A.
$j_d=\cdots =j_1=0$
and hence g is the trivial element. This finishes the proof of Theorem A.
4. Examples
In this section, we give examples of nilpotent groups for which we can compute the critical regularity. In each case, we use Theorem A to obtain a lower bound for the critical regularity, and we argue that, in our examples, this is also an upper bound for the regularity.
We begin by recalling that if G is a finitely generated nilpotent group of homeomorphisms of
![]() $(0,1)$
that has no global fixed points, then there is a well-defined group homomorphism
$(0,1)$
that has no global fixed points, then there is a well-defined group homomorphism
![]() $\rho :G \rightarrow \mathbb {R},$
which is usually called the translation number of the action. This map characterizes the elements of G that have fixed points, in the sense that
$\rho :G \rightarrow \mathbb {R},$
which is usually called the translation number of the action. This map characterizes the elements of G that have fixed points, in the sense that
![]() $\rho (g)=0$
if and only if g has a fixed point in
$\rho (g)=0$
if and only if g has a fixed point in
![]() $(0,1)$
. Further, the action of G on the interval has no crossings. By this, we mean that if an element
$(0,1)$
. Further, the action of G on the interval has no crossings. By this, we mean that if an element
![]() $f\in G$
fixes an open subinterval I of
$f\in G$
fixes an open subinterval I of
![]() $(0,1)$
and satisfies that
$(0,1)$
and satisfies that
![]() $f(x)\neq x\ \mathrm {for\ all}\ x\ \mathrm {in}\ I$
, then, for any other
$f(x)\neq x\ \mathrm {for\ all}\ x\ \mathrm {in}\ I$
, then, for any other
![]() $g\in G$
, we have that
$g\in G$
, we have that
![]() $g(I)=I$
or
$g(I)=I$
or
![]() $g(I)\cap I=\emptyset $
. See [Reference Navas20, §2.2.5] for details. With this, it is easy to prove the following result that we will repeatedly use.
$g(I)\cap I=\emptyset $
. See [Reference Navas20, §2.2.5] for details. With this, it is easy to prove the following result that we will repeatedly use.
Lemma 4.1. Let
![]() $G\leqslant \mathrm{Diff}_+^{\ 0}(0,1)$
be a nilpotent group and let
$G\leqslant \mathrm{Diff}_+^{\ 0}(0,1)$
be a nilpotent group and let
![]() $c\in G$
be a non-trivial element such that
$c\in G$
be a non-trivial element such that
![]() $c=[a,b]$
for some elements
$c=[a,b]$
for some elements
![]() $a,b\in G$
. If c fixes an open interval I and has no fixed point inside, then either a or b moves I (disjointly).
$a,b\in G$
. If c fixes an open interval I and has no fixed point inside, then either a or b moves I (disjointly).
Proof. Looking for a contradiction, assume that a and b fix I. Then we have the translation number homomorphism for the group
![]() $\langle a, b, c\rangle \leqslant \mathrm {Diff}_+^{\, 0}(I)$
. Since c is a commutator, it is in the kernel of this homomorphism. Hence, we conclude that c has a fixed point inside I, which is contrary to our assumptions.
$\langle a, b, c\rangle \leqslant \mathrm {Diff}_+^{\, 0}(I)$
. Since c is a commutator, it is in the kernel of this homomorphism. Hence, we conclude that c has a fixed point inside I, which is contrary to our assumptions.
To obtain upper bounds for the regularity of our groups we will use a result from Deroin, Kleptsyn and Navas [Reference Deroin, Kleptsyn and Navas8]. We use the version from [Reference Castro, Jorquera and Navas6, Proposition 2.1].
Theorem 4.2. Let
![]() $f_1,\ldots ,f_k$
be
$f_1,\ldots ,f_k$
be
![]() $C^1$
-diffeomorphisms of the interval
$C^1$
-diffeomorphisms of the interval
![]() $[0, 1]$
that commute with a
$[0, 1]$
that commute with a
![]() $C^1$
-diffeomorphism g. Assume that g fixes a subinterval I of
$C^1$
-diffeomorphism g. Assume that g fixes a subinterval I of
![]() $[0, 1]$
and that its restriction to I is non-trivial. Moreover, assume that, for a certain
$[0, 1]$
and that its restriction to I is non-trivial. Moreover, assume that, for a certain
![]() $0 < \alpha < 1$
and a sequence of indexes
$0 < \alpha < 1$
and a sequence of indexes
![]() $i_j\in \{1,\ldots ,k\}$
, the sum
$i_j\in \{1,\ldots ,k\}$
, the sum
 $$ \begin{align*}\sum_{j\geq 0}\lvert f_{i_j}\cdots f_{i_1}(I)\rvert^\alpha <\infty. \end{align*} $$
$$ \begin{align*}\sum_{j\geq 0}\lvert f_{i_j}\cdots f_{i_1}(I)\rvert^\alpha <\infty. \end{align*} $$
Then,
![]() $f_1,\ldots , f_k $
cannot be all of class
$f_1,\ldots , f_k $
cannot be all of class
![]() $C^{1+\alpha }$
.
$C^{1+\alpha }$
.
The following lemma is useful to get into the hypotheses of Theorem 4.2. Although it is stated in a slightly different way, the reader can check that the proof is exactly the same as that of [Reference Deroin, Kleptsyn and Navas8, Lemma 3.3].
Lemma 4.3. Let
![]() $f_1,\ldots ,f_k$
be
$f_1,\ldots ,f_k$
be
![]() $C^1$
-diffeomorphisms of
$C^1$
-diffeomorphisms of
![]() $[0,1]$
and let I be a subinterval of
$[0,1]$
and let I be a subinterval of
![]() $[0,1]$
such that
$[0,1]$
such that
![]() $\mathbb {Z}^k\simeq \langle f_1,\ldots ,f_k\rangle /\mathrm {Stab}(I)$
, where
$\mathbb {Z}^k\simeq \langle f_1,\ldots ,f_k\rangle /\mathrm {Stab}(I)$
, where
![]() $\mathrm {Stab}(I)$
is the stabilizer of I (which is assumed to be a normal subgroup). Then, if
$\mathrm {Stab}(I)$
is the stabilizer of I (which is assumed to be a normal subgroup). Then, if
![]() $\alpha> 1/k$
, there exists a sequence
$\alpha> 1/k$
, there exists a sequence
![]() $(f_{i_j})_{j\in \mathbb {N}}$
of elements in
$(f_{i_j})_{j\in \mathbb {N}}$
of elements in
![]() $\{f_1,\ldots ,f_k\}$
such that
$\{f_1,\ldots ,f_k\}$
such that
 $$ \begin{align*}\sum_{j\geq 0}\lvert f_{i_j}\cdots f_{i_1}(I)\rvert^\alpha< \infty .\end{align*} $$
$$ \begin{align*}\sum_{j\geq 0}\lvert f_{i_j}\cdots f_{i_1}(I)\rvert^\alpha< \infty .\end{align*} $$
4.1. Heisenberg groups
For a natural number
![]() $n\geq 1$
, the discrete
$n\geq 1$
, the discrete
![]() $(2n+1)$
-dimensional Heisenberg group, is defined as the set of matrices
$(2n+1)$
-dimensional Heisenberg group, is defined as the set of matrices
 $$ \begin{align*}\mathscr{H}_n:=\left\lbrace\begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^t & I_n & \vec{y}^{\, t}\\ 0 & \vec{0} & 1 \end{pmatrix}: \vec{x},\vec{y}\in \mathbb{Z}^n, c\in \mathbb{Z}\ \mathrm{and}\ I_n\ \mathrm{is\ the\ identity\ matrix\ of\ size}\ n\right\rbrace\!,\end{align*} $$
$$ \begin{align*}\mathscr{H}_n:=\left\lbrace\begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^t & I_n & \vec{y}^{\, t}\\ 0 & \vec{0} & 1 \end{pmatrix}: \vec{x},\vec{y}\in \mathbb{Z}^n, c\in \mathbb{Z}\ \mathrm{and}\ I_n\ \mathrm{is\ the\ identity\ matrix\ of\ size}\ n\right\rbrace\!,\end{align*} $$
with the usual matrix product. Note that the center of
![]() $\mathscr H_n$
coincides with the commutator subgroup and is generated by the matrix
$\mathscr H_n$
coincides with the commutator subgroup and is generated by the matrix
 $$ \begin{align*}\mathbf{C}:= \begin{pmatrix} 1 & \vec{0} & 1\\ \vec{0}^t & I_n & \vec{0}^{\, t}\\ 0 & \vec{0} & 1 \end{pmatrix}\!.\end{align*} $$
$$ \begin{align*}\mathbf{C}:= \begin{pmatrix} 1 & \vec{0} & 1\\ \vec{0}^t & I_n & \vec{0}^{\, t}\\ 0 & \vec{0} & 1 \end{pmatrix}\!.\end{align*} $$
We want to prove Theorem B, but before this, it will be useful for us to bound the rank of maximal abelian subgroups. Assume that there exists a maximal abelian subgroup of
![]() $ \mathscr {H}_n$
of rank m. Then we can choose elements
$ \mathscr {H}_n$
of rank m. Then we can choose elements
 $$ \begin{align*}\mathbf{A}_i:=\begin{pmatrix} 1 & \vec{a_i} & c_i\\ \vec{0}^t & I_n & \vec{b_i}^t\\ 0 & \vec{0} & 1 \end{pmatrix}\in \mathscr{H}_n \quad \mathrm{for}\ i\in \{1,\ldots,m-1\},\end{align*} $$
$$ \begin{align*}\mathbf{A}_i:=\begin{pmatrix} 1 & \vec{a_i} & c_i\\ \vec{0}^t & I_n & \vec{b_i}^t\\ 0 & \vec{0} & 1 \end{pmatrix}\in \mathscr{H}_n \quad \mathrm{for}\ i\in \{1,\ldots,m-1\},\end{align*} $$
such that
![]() $\langle \mathbf {A}_1,\ldots \mathbf {A}_{m-1},\mathbf {C}\rangle \simeq \mathbb {Z}^{m}.$
Note that the commutativity of these matrices is equivalent to the equations
$\langle \mathbf {A}_1,\ldots \mathbf {A}_{m-1},\mathbf {C}\rangle \simeq \mathbb {Z}^{m}.$
Note that the commutativity of these matrices is equivalent to the equations
Note also that if
![]() $\{\mathbf {A}_1,\ldots , \mathbf {A}_{m-1},\mathbf {C}\}$
generates a free abelian group of rank m, then the set of vectors
$\{\mathbf {A}_1,\ldots , \mathbf {A}_{m-1},\mathbf {C}\}$
generates a free abelian group of rank m, then the set of vectors
![]() $\mathscr {B}:=\{(\vec {b}_i,\vec {a}_i)\in \mathbb {Z}^{n}\times \mathbb {Z}^{n}:1\leq i\leq m-1\}$
generates a free abelian group of rank
$\mathscr {B}:=\{(\vec {b}_i,\vec {a}_i)\in \mathbb {Z}^{n}\times \mathbb {Z}^{n}:1\leq i\leq m-1\}$
generates a free abelian group of rank
![]() $m-1$
. Indeed, if we have a dependency relationship, say,
$m-1$
. Indeed, if we have a dependency relationship, say,
![]() $r(\vec {b}_1,\vec {a}_1)\in \langle (\vec {b}_2,\vec {a}_2),\ldots ,(\vec {b}_{m-1},\vec {a}_{m-1})\rangle $
for some
$r(\vec {b}_1,\vec {a}_1)\in \langle (\vec {b}_2,\vec {a}_2),\ldots ,(\vec {b}_{m-1},\vec {a}_{m-1})\rangle $
for some
![]() $0\neq r\in \mathbb {Z},$
then
$0\neq r\in \mathbb {Z},$
then
![]() $\mathbf {A}_1^{r}\in \langle \mathbf {A}_2,\ldots ,\mathbf {A}_{m-1},\mathbf {C}\rangle ,$
which contradicts that the abelian group has rank m.
$\mathbf {A}_1^{r}\in \langle \mathbf {A}_2,\ldots ,\mathbf {A}_{m-1},\mathbf {C}\rangle ,$
which contradicts that the abelian group has rank m.
Having said this, we claim that
![]() $m\leq n+1$
. To see the latter, note that, by equations (4.1), any vector of the form
$m\leq n+1$
. To see the latter, note that, by equations (4.1), any vector of the form
![]() $(\vec a_i,-\vec b_i)$
, with
$(\vec a_i,-\vec b_i)$
, with
![]() $1\leq i\leq m -1$
, is perpendicular to
$1\leq i\leq m -1$
, is perpendicular to
![]() $\langle \mathscr B\rangle $
. Hence, we have two orthogonal subgroups of
$\langle \mathscr B\rangle $
. Hence, we have two orthogonal subgroups of
![]() $\mathbb Z^n\times \mathbb Z^n$
that both have rank
$\mathbb Z^n\times \mathbb Z^n$
that both have rank
![]() $m-1$
, and thus
$m-1$
, and thus
![]() $m-1\leq~n$
, which proves our claim.
$m-1\leq~n$
, which proves our claim.
Realization
Consider the abelian subgroup
 $$ \begin{align*}A:=\left\lbrace \begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^{\,t} & I_n & \vec{0}^{\,t}\\ 0 & \vec{0} & 1 \end{pmatrix}\;: \vec{x}\in \mathbb{Z}^n\quad\mathrm{and}\quad c\in\mathbb{Z} \right\rbrace\!.\end{align*} $$
$$ \begin{align*}A:=\left\lbrace \begin{pmatrix} 1 & \vec{x} & c\\ \vec{0}^{\,t} & I_n & \vec{0}^{\,t}\\ 0 & \vec{0} & 1 \end{pmatrix}\;: \vec{x}\in \mathbb{Z}^n\quad\mathrm{and}\quad c\in\mathbb{Z} \right\rbrace\!.\end{align*} $$
Notice that A has rank equal to
![]() $n+1$
, which is the largest we can expect. Since the rank of
$n+1$
, which is the largest we can expect. Since the rank of
![]() $\mathscr {H}_n/A$
is n, we have that Theorem A provides an injective group homomorphism
$\mathscr {H}_n/A$
is n, we have that Theorem A provides an injective group homomorphism
Bounding the regularity
Now we consider a faithful action
![]() $\phi :\mathscr {H}_n\hookrightarrow \mathrm {Diff}_+^1([0,1])$
. Abusing notation, we can think that
$\phi :\mathscr {H}_n\hookrightarrow \mathrm {Diff}_+^1([0,1])$
. Abusing notation, we can think that
![]() $\mathscr {H}_n\leqslant \mathrm {Diff}_+^1([0,1])$
.
$\mathscr {H}_n\leqslant \mathrm {Diff}_+^1([0,1])$
.
Since the commutator subgroup of
![]() $\mathscr {H}_n$
is generated by
$\mathscr {H}_n$
is generated by
![]() ${\mathbf C}$
, we deduce from Lemma 4.1 that C has fixed points inside
${\mathbf C}$
, we deduce from Lemma 4.1 that C has fixed points inside
![]() $(0,1)$
. Therefore, we can find an interval
$(0,1)$
. Therefore, we can find an interval
![]() $I\subsetneq [0,1]$
such that
$I\subsetneq [0,1]$
such that
![]() $\mathbf {C}(I)=I\ \mathrm {and}\ \mathbf {C}(x)\neq x$
for all x in the interior of I. Let
$\mathbf {C}(I)=I\ \mathrm {and}\ \mathbf {C}(x)\neq x$
for all x in the interior of I. Let
![]() $\mathrm {Stab}(I)$
be the stabilizer of I. It is easy to see that this is an abelian subgroup. Indeed, if we take
$\mathrm {Stab}(I)$
be the stabilizer of I. It is easy to see that this is an abelian subgroup. Indeed, if we take
![]() $\mathbf {A},\mathbf {B}\in \mathrm {Stab}(I)$
and assume that they do not commute, then there must exist
$\mathbf {A},\mathbf {B}\in \mathrm {Stab}(I)$
and assume that they do not commute, then there must exist
![]() $m\in \mathbb {Z}$
such that
$m\in \mathbb {Z}$
such that
![]() $[\mathbf {A},\mathbf {B}]=\mathbf {C}^m$
. Since
$[\mathbf {A},\mathbf {B}]=\mathbf {C}^m$
. Since
![]() $\mathbf {C}$
has no fixed points inside I, Lemma 4.1 tells us that either
$\mathbf {C}$
has no fixed points inside I, Lemma 4.1 tells us that either
![]() $\mathbf {A}$
or
$\mathbf {A}$
or
![]() $\mathbf {B}$
moves I, which is a contradiction. Note that Stab(I) is a normal subgroup as it contains the commutator subgroup. Further, we know that there is a natural number k and elements
$\mathbf {B}$
moves I, which is a contradiction. Note that Stab(I) is a normal subgroup as it contains the commutator subgroup. Further, we know that there is a natural number k and elements
![]() $\mathbf {B}_1,\ldots ,\mathbf {B}_k\in \mathscr {H}_n$
such that
$\mathbf {B}_1,\ldots ,\mathbf {B}_k\in \mathscr {H}_n$
such that
So, given
![]() $\alpha> 1/k$
, we can find by Lemma 4.3 a sequence
$\alpha> 1/k$
, we can find by Lemma 4.3 a sequence
![]() $(\mathbf {B}_{i_j})_{j\in \mathbb {N}}$
of elements in
$(\mathbf {B}_{i_j})_{j\in \mathbb {N}}$
of elements in
![]() $\{\mathbf {B}_1,\ldots ,\mathbf {B}_k\}$
such that
$\{\mathbf {B}_1,\ldots ,\mathbf {B}_k\}$
such that
 $$ \begin{align*}\sum_{j\geq 0}\lvert\mathbf{B}_{i_j}\cdots \mathbf{B}_{i_1}(I)\rvert^\alpha<\infty,\end{align*} $$
$$ \begin{align*}\sum_{j\geq 0}\lvert\mathbf{B}_{i_j}\cdots \mathbf{B}_{i_1}(I)\rvert^\alpha<\infty,\end{align*} $$
and hence Theorem 4.2 yields that
![]() $\phi $
is not an action by
$\phi $
is not an action by
![]() $C^{1+\alpha }$
-diffeomorphisms.
$C^{1+\alpha }$
-diffeomorphisms.
Now, since the rank of
![]() $\mathrm {Stab}(I)$
is bounded above by
$\mathrm {Stab}(I)$
is bounded above by
![]() $n-1=\mathrm {rank}(A)$
,
$n-1=\mathrm {rank}(A)$
,
 $$ \begin{align*} k=\mathrm{rank}\bigg(\frac{\mathscr{H}_n}{\mathrm{Stab}(I)}\bigg)\geq \mathrm{rank} \bigg(\frac{\mathscr{H}_n}{A}\bigg) = n, \end{align*} $$
$$ \begin{align*} k=\mathrm{rank}\bigg(\frac{\mathscr{H}_n}{\mathrm{Stab}(I)}\bigg)\geq \mathrm{rank} \bigg(\frac{\mathscr{H}_n}{A}\bigg) = n, \end{align*} $$
which implies that the regularity of the action
![]() $\phi $
is bounded above by
$\phi $
is bounded above by
![]() $1+1/n$
. So we conclude that
$1+1/n$
. So we conclude that
4.2. Examples with large nilpotency degree
Theorem B gives us the critical regularity for the Heisenberg groups, which are groups having nilpotency degree two. In this section, we provide more examples of nilpotent groups for which we can compute the critical regularity, but whose nilpotency degree can be arbitrarily large. As for the Heisenberg groups, in these examples, we show that the lower bound provided by Theorem A is also an upper bound.
Fix
![]() $d,k \in \mathbb {N}$
, assume that
$d,k \in \mathbb {N}$
, assume that
![]() $d\geq k$
and consider a matrix
$d\geq k$
and consider a matrix
![]() $(m_{i,s})\in M_{k}(\mathbb {Z})$
with non-zero determinant and positive entries. We let G be the group generated by the set
$(m_{i,s})\in M_{k}(\mathbb {Z})$
with non-zero determinant and positive entries. We let G be the group generated by the set
subject to the relationships:
-
•
 $[g_0,g_{i,j}]=[g_0,f_i]=[f_s,f_i]=[g_{i,j},g_{l,m}]=e,\ \mathrm {for\ all}\ s,i,l \in \{1,\ldots ,k\},\;j,m \in \{1,\ldots ,d\}$
;
$[g_0,g_{i,j}]=[g_0,f_i]=[f_s,f_i]=[g_{i,j},g_{l,m}]=e,\ \mathrm {for\ all}\ s,i,l \in \{1,\ldots ,k\},\;j,m \in \{1,\ldots ,d\}$
; -
•
 $[f_s,g_{i,j}]=g_{i,j-1}^{m_{i,s}}\ \mathrm {for\ all}\ s,i\in \{1,\ldots ,k\}$
and
$[f_s,g_{i,j}]=g_{i,j-1}^{m_{i,s}}\ \mathrm {for\ all}\ s,i\in \{1,\ldots ,k\}$
and
 $j\in \{2,\ldots ,d\}$
; and
$j\in \{2,\ldots ,d\}$
; and -
•
 $[f_s,g_{i,1}]=g_0^{m_{i,s}}\ \mathrm {for\ all}\ s,i\in \{1,\ldots ,k\}.$
$[f_s,g_{i,1}]=g_0^{m_{i,s}}\ \mathrm {for\ all}\ s,i\in \{1,\ldots ,k\}.$
Note that, from the identities
![]() $[ab,c]=a[b,c]a^{-1}[a,c]$
and
$[ab,c]=a[b,c]a^{-1}[a,c]$
and
![]() $[a,bc]=[a,b]b[a,c]b^{-1}$
, we immediately have the following additional relationships:
$[a,bc]=[a,b]b[a,c]b^{-1}$
, we immediately have the following additional relationships:
-
•
 $[f_s^{-1},g_{i,j}]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{-m_{i,s}}$
for all
$[f_s^{-1},g_{i,j}]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{-m_{i,s}}$
for all
 $s,i \in \{1,\ldots ,k\}, j\in \{2,\ldots ,d\}$
; and
$s,i \in \{1,\ldots ,k\}, j\in \{2,\ldots ,d\}$
; and -
•
 $[f_s^{-1},g_{i,1}]=g_0^{-m_{i,s}}\ \mathrm {for\ all}\ s,i \in \{1,\ldots ,k\}$
.
$[f_s^{-1},g_{i,1}]=g_0^{-m_{i,s}}\ \mathrm {for\ all}\ s,i \in \{1,\ldots ,k\}$
.
It is easy to see that G is a nilpotent group of degree
![]() $d+1$
, and that
$d+1$
, and that
![]() $A=\langle \{g_0\}\cup \{g_{i,j}: (i,j)\in \{1,\ldots ,k\}\times \{1,\ldots ,d\}\}\rangle $
is a maximal abelian subgroup containing the commutator of G (see Lemma 4.5 below). Moreover, k is the torsion-free rank of
$A=\langle \{g_0\}\cup \{g_{i,j}: (i,j)\in \{1,\ldots ,k\}\times \{1,\ldots ,d\}\}\rangle $
is a maximal abelian subgroup containing the commutator of G (see Lemma 4.5 below). Moreover, k is the torsion-free rank of
![]() $G/A$
. Therefore, in view of Theorem A, we know that G embeds in
$G/A$
. Therefore, in view of Theorem A, we know that G embeds in
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for
![]() $\alpha < 1/k$
. To show that
$\alpha < 1/k$
. To show that
![]() $1+1/k$
is actually an upper bound for the regularity, we need the following elementary lemma.
$1+1/k$
is actually an upper bound for the regularity, we need the following elementary lemma.
Lemma 4.5. For all
![]() $(i,j)\in \{1,\ldots ,k\}\times \{2,\ldots ,d\}$
and
$(i,j)\in \{1,\ldots ,k\}\times \{2,\ldots ,d\}$
and
![]() $n_1,\ldots ,n_k\in \mathbb {Z}$
:
$n_1,\ldots ,n_k\in \mathbb {Z}$
:
-
(1)
 $[f_1^{n_1}\cdots f_k^{n_k},g_{i,j}]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{\unicode{x3bb} _i};$
and
$[f_1^{n_1}\cdots f_k^{n_k},g_{i,j}]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{\unicode{x3bb} _i};$
and -
(2)
 $[f_1^{n_1}\cdots f_k^{n_k},g_{i,1}]= g_0^{\unicode{x3bb} _i},$
$[f_1^{n_1}\cdots f_k^{n_k},g_{i,1}]= g_0^{\unicode{x3bb} _i},$
where
![]() $\unicode{x3bb} _i=\sum _{s=1}^k n_s m_{i,s}$
. In particular, the subgroup A is a maximal abelian subgroup.
$\unicode{x3bb} _i=\sum _{s=1}^k n_s m_{i,s}$
. In particular, the subgroup A is a maximal abelian subgroup.
Proof. We show (1) by induction on
![]() $n=\sum _{s=1}^k \lvert n_s\rvert $
.
$n=\sum _{s=1}^k \lvert n_s\rvert $
.
Note that, when
![]() $n=1$
, we have the result by the relationships of G. So, consider an arbitrary natural number
$n=1$
, we have the result by the relationships of G. So, consider an arbitrary natural number
![]() $n=\sum _{j=1}^k \lvert n_j\rvert $
and assume that
$n=\sum _{j=1}^k \lvert n_j\rvert $
and assume that
![]() $n_k<0$
(the other case is similar). For all
$n_k<0$
(the other case is similar). For all
![]() $i \in \{1,\ldots ,k\}$
and
$i \in \{1,\ldots ,k\}$
and
![]() $j\in \{2,\ldots ,d\}$
,
$j\in \{2,\ldots ,d\}$
,
and since
![]() $[f_k^{-1},g_{i,j}]$
belongs to
$[f_k^{-1},g_{i,j}]$
belongs to
![]() $\langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{-m_{i,k}}$
, it follows that
$\langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle g_{i,j-1}^{-m_{i,k}}$
, it follows that
![]() $[f_1^{n_1}\cdots f_k^{n_k+1},[f_k^{-1},g_{i,j}]]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle $
. Also, by induction,
$[f_1^{n_1}\cdots f_k^{n_k+1},[f_k^{-1},g_{i,j}]]\in \langle g_0,g_{i,1},\ldots ,g_{i,j-2}\rangle $
. Also, by induction,
Plugging these into the previous equation yields assertion (1). The proof of assertion (2) is analogous.
Remark 4.6. The most useful part of Lemma 4.5 is the explicit expression for the integers
![]() $\unicode{x3bb} _i$
appearing. These will be used in the proof of Theorem C.
$\unicode{x3bb} _i$
appearing. These will be used in the proof of Theorem C.
Proof of Theorem C
Suppose that G embeds into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for some
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for some
![]() $\alpha>1/k$
. Let
$\alpha>1/k$
. Let
![]() $x_0$
be a point in
$x_0$
be a point in
![]() $(0,1)$
such that
$(0,1)$
such that
![]() $g_{0}(x_0)\neq x_0$
and define the intervals
$g_{0}(x_0)\neq x_0$
and define the intervals
Case 1:
![]() $f(I_0)\cap I_0=\emptyset $
for all
$f(I_0)\cap I_0=\emptyset $
for all
![]() $f\in \langle f_1,\ldots ,f_k\rangle \simeq \mathbb {Z}^k$
. In this case,
$f\in \langle f_1,\ldots ,f_k\rangle \simeq \mathbb {Z}^k$
. In this case,
![]() $I_0$
is a wandering interval for the dynamics of
$I_0$
is a wandering interval for the dynamics of
![]() $\langle f_1,\ldots ,f_k\rangle $
. A contradiction is provided by Lemma 4.3 followed by Theorem 4.2, because the central element
$\langle f_1,\ldots ,f_k\rangle $
. A contradiction is provided by Lemma 4.3 followed by Theorem 4.2, because the central element
![]() $g_0$
acts non-trivially on
$g_0$
acts non-trivially on
![]() $I_0$
.
$I_0$
.
Case 2: There is a non-trivial element
![]() $f\in \langle f_1,\ldots ,f_k\rangle $
such that
$f\in \langle f_1,\ldots ,f_k\rangle $
such that
![]() $f(I_0)= I_0$
. We put
$f(I_0)= I_0$
. We put
![]() $f=f_1^{n_1}\cdots f_k^{n_k}$
. Given
$f=f_1^{n_1}\cdots f_k^{n_k}$
. Given
![]() $i\in \{1,\ldots ,k\}$
, by Lemma 4.5,
$i\in \{1,\ldots ,k\}$
, by Lemma 4.5,
where
![]() $\unicode{x3bb} _i=\sum _{j=1}^k n_jm_{i,j}$
. Since the vectors
$\unicode{x3bb} _i=\sum _{j=1}^k n_jm_{i,j}$
. Since the vectors
![]() $(m_{i,1},\ldots ,m_{i,k})$
are linearly independent in
$(m_{i,1},\ldots ,m_{i,k})$
are linearly independent in
![]() $\mathbb {R}^k$
, we can choose i to obtain
$\mathbb {R}^k$
, we can choose i to obtain
![]() $\unicode{x3bb} _i\neq 0$
. Then, the relationships (4.2) and Lemma 4.1 imply that
$\unicode{x3bb} _i\neq 0$
. Then, the relationships (4.2) and Lemma 4.1 imply that
![]() $g_{i,1}(I_0)\cap I_0=\emptyset $
. Since the action has no crossings, the element f also fixes the intervals
$g_{i,1}(I_0)\cap I_0=\emptyset $
. Since the action has no crossings, the element f also fixes the intervals
![]() $I_{i,j}$
and hence the same argument also yields that
$I_{i,j}$
and hence the same argument also yields that
![]() $g_{i,j}(I_{i,j-1})\cap I_{i,j-1}=\emptyset $
for all
$g_{i,j}(I_{i,j-1})\cap I_{i,j-1}=\emptyset $
for all
![]() $j>2$
. Therefore,
$j>2$
. Therefore,
![]() $I_0$
is a wandering interval for the action of
$I_0$
is a wandering interval for the action of
![]() $\langle g_{i,1},\ldots , g_{i,k}\rangle \simeq \mathbb {Z}^k$
. So, a contradiction is reached using Lemma 4.3 and Theorem 4.2, as before.
$\langle g_{i,1},\ldots , g_{i,k}\rangle \simeq \mathbb {Z}^k$
. So, a contradiction is reached using Lemma 4.3 and Theorem 4.2, as before.
4.3. An example with even higher regularity
It is easy to see that, in some situations, the regularity given by Theorem A is not critical. In the examples that we know of, this is related to the fact that the group can be split as a direct product of groups, each of which allows an embedding with better regularity. Take, for example, the groups of [Reference Castro, Jorquera and Navas6, §4]. These are given by the presentation
Note that
![]() $G_d$
is isomorphic to a non-trivial semidirect product of the form
$G_d$
is isomorphic to a non-trivial semidirect product of the form
![]() $\mathbb {Z}^d\rtimes \mathbb {Z}$
. Now define the group
$\mathbb {Z}^d\rtimes \mathbb {Z}$
. Now define the group
![]() $G:=G_d\times G_d.$
On one hand, it is easy to see that
$G:=G_d\times G_d.$
On one hand, it is easy to see that
and
![]() $\mathbb {Z}^{2d}\times \{0\}$
is a maximal abelian subgroup of G. Therefore, if we apply Theorem A, we obtain an embedding of G into
$\mathbb {Z}^{2d}\times \{0\}$
is a maximal abelian subgroup of G. Therefore, if we apply Theorem A, we obtain an embedding of G into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
![]() $\alpha < 1/2$
. However, on the other hand, the critical regularity of G is two. Indeed, we can apply Theorem A to each factor of G to obtain an embedding of the factor into
$\alpha < 1/2$
. However, on the other hand, the critical regularity of G is two. Indeed, we can apply Theorem A to each factor of G to obtain an embedding of the factor into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
![]() $\alpha < 1$
. If we put these two actions together acting on disjoint intervals (as we did in §3.3), we end up with an embedding of G into
$\alpha < 1$
. If we put these two actions together acting on disjoint intervals (as we did in §3.3), we end up with an embedding of G into
![]() $\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
$\mathrm {Diff}_+^{1+\alpha }([0,1])$
for all
![]() $\alpha < 1$
.
$\alpha < 1$
.
Acknowledgements
The first author acknowledges the hospitality of the Institut de Mathématique de Bourgogne, where part of this project was carried out. In particular, he is grateful to Michele Triestino for fruitful discussion around this and other topics of mathematics. He is also grateful to Nicolás Matte Bon for discussions around the algebraic structure and actions of nilpotent groups. The first author acknowledges the partial support of Project Gromeov ANR-19-CE40-0007 and Mathamsud 210020 ‘Dynamical Groups Theory’. Both authors are grateful to Andrés Navas for reading a preliminary version of this work. Both authors acknowledge the support of FONDECYT 1210155. Finally, both authors acknowledge the careful reading of the referees.