1. Introduction
Spontaneous or forced imbibition in porous media and fractures (i.e. invasion of the pore space by a wetting fluid replacing a non-wetting one) is encountered in many engineering processes (Morrow & Mason Reference Morrow and Mason2001; Cheng et al. Reference Cheng, Perfect, Donnelly, Bilheux, Tremsin, McKay, DiStefano, Cai and Santodonato2015) and have concentrated thorough analyses during the past recent years, particularly in porous media (Gilman Reference Gilman1996; Gu, Liu & Wu Reference Gu, Liu and Wu2021) for which experimental, theoretical and numerical investigations have been reported (Lenormand, Touboul & Zarcone Reference Lenormand, Touboul and Zarcone1988; Zhang et al. Reference Zhang, Oostrom, Wietsma, Grate and Warner2011; Zheng, Rongy & Stone Reference Zheng, Rongy and Stone2015; Gu et al. Reference Gu, Liu and Wu2021). Following the seminal works of Lucas (Reference Lucas1918) and Washburn (Reference Washburn1921), many studies of imbibition in porous media or fractures have been carried out employing their approach, relying on a cylindrical tube of circular cross-section as an analog of the channel geometry at the pore scale. However, given the complex shapes of the interconnected pathways, and due to the expected capillary effects, it is of interest to consider the mechanism in channels of irregular shapes, as explored, for instance, in Cai et al. (Reference Cai, Chen, Liu, Li and Sun2022). Indeed, in the context of imbibition, the presence of liquid films that can develop in corners may significantly modify the overall flow dynamics and may explain, for instance, capillary instabilities leading to gas trapping (Rossen Reference Rossen2000). In this context, the case of a capillary of square cross-section initially saturated by gas was considered in Dong & Chatzis (Reference Dong and Chatzis1995) where the solution for the liquid film imbibition in a corner was proposed, without considering the invasion of the channel core by the liquid bulk. By making use of similarity solutions, it was shown that for a rectilinear channel, the triple point position and the film volume in the corner are proportional to the square root of time when flow is governed by capillary effects. Here, as in the rest of this work, the triple point refers to the three-phase (liquid–gas–solid) contact point, corresponding to the terminal point of the wetting phase in the corner. A similar simplified study in a rectilinear channel of triangular cross-section with flow rate or pressure imposed at the inlet of the channel was made in Amyot (Reference Amyot2004). In accordance with experimental observations, it was shown that the dynamics of the bulk meniscus is perturbed by that of the liquid film in the corner. This corroborates observations reported in Lenormand & Zarcone (Reference Lenormand and Zarcone1984) where flow visualisation in an etched square network of channels of roughly rectangular cross-section was carried out. The imbibition pattern was shown to depend on the capillary number (i.e. the ratio of viscous to capillary forces), the presence of surface roughness and edges. Flow solutions in a model roughness pattern and in the corner films were approximated by Poiseuille's law in an equivalent circular channel having the same local hydraulic diameter. Using a self-similar solution, the flow rate in the corner film was shown to depend on the square root of time.
More recently, imbibition triggered by capillarity counterbalanced by gravity and viscosity in a sharp corner formed by two intersecting vertical plates was investigated numerically on the basis of the lubrication approximation (Higuera, Medina & Liñán Reference Higuera, Medina and Liñán2008). The analysis showed that, at the early stage of the wedge imbibition, the wetting fluid rise in the vicinity of the triple point is proportional to time and gravity has a negligible effect. At later times, the height of the triple point was found to increase proportionally to the cubic root of time, ![]() $t$, whereas the thickness is self-similar when scaled as
$t$, whereas the thickness is self-similar when scaled as ![]() $t^{-1/3}$. These predictions were found in good agreement with experimental observations. A modified version of the later configuration was envisaged in Zhou & Doi (Reference Zhou and Doi2020), with the two walls having a curvature in the horizontal direction such that the gap between them is a power law of the distance from their intersection. The results derived from this work confirm that the interface height depends on
$t^{-1/3}$. These predictions were found in good agreement with experimental observations. A modified version of the later configuration was envisaged in Zhou & Doi (Reference Zhou and Doi2020), with the two walls having a curvature in the horizontal direction such that the gap between them is a power law of the distance from their intersection. The results derived from this work confirm that the interface height depends on ![]() $t^{1/3}$ with a rising dynamics that is quite universal, further justifying the observations reported in Ponomarenko, Quéré & Clanet (Reference Ponomarenko, Quéré and Clanet2011). This universality was recently revisited in Wu, Duprat & Stone (Reference Wu, Duprat and Stone2024). In Weislogel (Reference Weislogel2012) the classical Washburn approach, combined with the corner flow model developed in Weislogel & Lichter (Reference Weislogel and Lichter1998), together with scaling arguments, were employed to predict the capillary rise in a channel. An approximate solution for the position of the liquid column was obtained in terms of a third-order polynomial involving the ratio between the cross-section characteristic sizes in the corner film and in the bulk region, respectively, a parameter that needs to be identified a priori. It was outlined that corner films contribute to an increase in the flow rate.
$t^{1/3}$ with a rising dynamics that is quite universal, further justifying the observations reported in Ponomarenko, Quéré & Clanet (Reference Ponomarenko, Quéré and Clanet2011). This universality was recently revisited in Wu, Duprat & Stone (Reference Wu, Duprat and Stone2024). In Weislogel (Reference Weislogel2012) the classical Washburn approach, combined with the corner flow model developed in Weislogel & Lichter (Reference Weislogel and Lichter1998), together with scaling arguments, were employed to predict the capillary rise in a channel. An approximate solution for the position of the liquid column was obtained in terms of a third-order polynomial involving the ratio between the cross-section characteristic sizes in the corner film and in the bulk region, respectively, a parameter that needs to be identified a priori. It was outlined that corner films contribute to an increase in the flow rate.
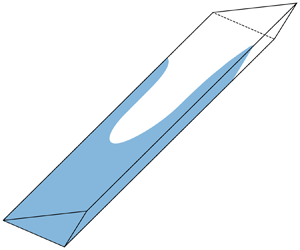
Among the diverse situations of disordered structures in which imbibition is of interest, the special case where the microstructure is made of channels characterised by a small aspect ratio (i.e. a width to height ratio much smaller than unity) is of particular relevance. The case of a fracture resulting from the contact between rough surfaces obtained by a manufacturing process pertains to this class of situations encountered in sealing for example (see the work by Marie & Lasseux Reference Marie and Lasseux2007). The prediction of the wetting fluid invasion in such a configuration still requires an in-depth analysis, which is the focus of the present study. In particular, it is of interest to investigate whether the contrast between the breakthrough of the triple point and the bulk meniscus is significant or not and how the bulk meniscus dynamics is affected by the corner film flow. As an archetypal geometry, representative of a machined surface resulting from turning, a straight channel of triangular cross-section with sharp side corners is considered (see figure 1). The purpose of the present analysis is the derivation of quasi-analytical solutions for the dynamics of the bulk meniscus, including that of the wetting liquid film in the corners that are further compared with experimental data from Amyot (Reference Amyot2004). To this aim, the paper is organised as follows.

Figure 1. Sketch of the imbibition problem in a narrow channel of triangular cross-section of small aspect ratio ![]() $\epsilon =h_0/\ell \ll 1$. (a) Three-dimensional view. For clarity in presentation, the aspect ratio has been expanded. (b) Cross-sectional illustration of the area occupied by the liquid film corners. (c) Top view illustration of the pure film regime, prior to the entrance of the bulk meniscus. (d) Top view of the bulk and corner film flow regime after entrance of the bulk meniscus.
$\epsilon =h_0/\ell \ll 1$. (a) Three-dimensional view. For clarity in presentation, the aspect ratio has been expanded. (b) Cross-sectional illustration of the area occupied by the liquid film corners. (c) Top view illustration of the pure film regime, prior to the entrance of the bulk meniscus. (d) Top view of the bulk and corner film flow regime after entrance of the bulk meniscus.
The flow formulation, relying on the lubrication approximation supported by the channel aspect ratio, together with the assumption of small capillary and Reynolds numbers (i.e. creeping flow), is provided in § 2. In § 3, flow in the liquid films developing in the corners of the channel is analysed. The criterion on the film width at the channel inlet that permits the bulk meniscus entrance is derived. These features are further used in the following sections to carry out the complete description of the imbibition process. Section 4 is dedicated to the case where a constant flow rate is imposed at the channel inlet. First, the regime corresponding to liquid wicking in the corner only is described in § 4.1 where it is shown that the triple point position varies with ![]() $t^{3/5}$. The threshold value of the film width allowing the bulk meniscus entrance is derived in § 4.2. Second, the imbibition dynamics, considering bulk and corner film flow in the whole channel, is described in § 4.3 on the basis of a quasi-static fluid–fluid interface approximation for the bulk meniscus, in accordance with the small capillary number assumption. Matching of the solution in the bulk region with that in the film (Lasseux & Quintard Reference Lasseux and Quintard1991; Lasseux Reference Lasseux1995) is employed. The dynamics of the bulk meniscus and triple point positions are shown to combine a linear and square root dependence on time. Results in the case of an imposed flow rate are discussed in § 4.4 and are further compared with experimental results. The case where imbibition results from a constant pressure imposed at the channel inlet is explored in § 5, following an approach similar to that developed in § 4. The triple point position in the pure liquid film regime (§ 5.1) and in the regime of bulk and film coupled flow (§ 5.2) is found to vary as
$t^{3/5}$. The threshold value of the film width allowing the bulk meniscus entrance is derived in § 4.2. Second, the imbibition dynamics, considering bulk and corner film flow in the whole channel, is described in § 4.3 on the basis of a quasi-static fluid–fluid interface approximation for the bulk meniscus, in accordance with the small capillary number assumption. Matching of the solution in the bulk region with that in the film (Lasseux & Quintard Reference Lasseux and Quintard1991; Lasseux Reference Lasseux1995) is employed. The dynamics of the bulk meniscus and triple point positions are shown to combine a linear and square root dependence on time. Results in the case of an imposed flow rate are discussed in § 4.4 and are further compared with experimental results. The case where imbibition results from a constant pressure imposed at the channel inlet is explored in § 5, following an approach similar to that developed in § 4. The triple point position in the pure liquid film regime (§ 5.1) and in the regime of bulk and film coupled flow (§ 5.2) is found to vary as ![]() $t^{1/2}$. The bulk meniscus dynamics is shown to scale as the square root of time as well and the contrast with the classical Washburn's result (Washburn Reference Washburn1921) is highlighted. Results from the models derived in the case of an imposed pressure are discussed and compared with experimental data in § 5.3. Finally, conclusions are presented in § 6.
$t^{1/2}$. The bulk meniscus dynamics is shown to scale as the square root of time as well and the contrast with the classical Washburn's result (Washburn Reference Washburn1921) is highlighted. Results from the models derived in the case of an imposed pressure are discussed and compared with experimental data in § 5.3. Finally, conclusions are presented in § 6.
2. Imbibition flow model: the lubrication approximation
The focus is laid on imbibition by a wetting liquid (the ![]() $\beta$ phase) of a channel initially saturated by a gas (the
$\beta$ phase) of a channel initially saturated by a gas (the ![]() $\gamma$ phase), as illustrated in figure 1. Two situations are envisaged, namely a constant flow rate (§ 4) or a constant pressure (§ 5) imposed at the inlet of the channel. Due to the viscosity contrast between the two phases
$\gamma$ phase), as illustrated in figure 1. Two situations are envisaged, namely a constant flow rate (§ 4) or a constant pressure (§ 5) imposed at the inlet of the channel. Due to the viscosity contrast between the two phases ![]() $\beta$ and
$\beta$ and ![]() $\gamma$, the latter is supposed to remain at constant pressure. The liquid flow is considered as isothermal, Newtonian, incompressible and in the creeping regime, i.e. for a Reynolds number much smaller than unity. No slip effects are considered at the solid–liquid interface and no body force is supposed to apply. The channel under consideration is of triangular cross-section, of height
$\gamma$, the latter is supposed to remain at constant pressure. The liquid flow is considered as isothermal, Newtonian, incompressible and in the creeping regime, i.e. for a Reynolds number much smaller than unity. No slip effects are considered at the solid–liquid interface and no body force is supposed to apply. The channel under consideration is of triangular cross-section, of height ![]() $h_0$ and width
$h_0$ and width ![]() $2\ell$, as depicted in figure 1, and is
$2\ell$, as depicted in figure 1, and is ![]() $y$ symmetric. It is assumed to have a small aspect ratio characterised by a slope given by
$y$ symmetric. It is assumed to have a small aspect ratio characterised by a slope given by
On the basis of the above listed assumptions, it is reasonable to make use of the lubrication approximation (Reynolds Reference Reynolds1886). This approach allows a simplification of the three-dimensional continuity and momentum (Stokes) equations for the ![]() $\beta$ phase resulting from their pre-integration in the
$\beta$ phase resulting from their pre-integration in the ![]() $z$ direction as detailed in Vallet et al. (Reference Vallet, Lasseux, Sainsot and Zahouani2009) and Zaouter, Lasseux & Prat (Reference Zaouter, Lasseux and Prat2018), which reduces the flow model to two dimensions in the region
$z$ direction as detailed in Vallet et al. (Reference Vallet, Lasseux, Sainsot and Zahouani2009) and Zaouter, Lasseux & Prat (Reference Zaouter, Lasseux and Prat2018), which reduces the flow model to two dimensions in the region ![]() $\mathcal {A}_\beta$ occupied by the
$\mathcal {A}_\beta$ occupied by the ![]() $\beta$ phase in the
$\beta$ phase in the ![]() $(x,y)$ plane (see figures 1a–d). The ensuing mass and momentum conservation equations, that are accurate at
$(x,y)$ plane (see figures 1a–d). The ensuing mass and momentum conservation equations, that are accurate at ![]() $O(\epsilon ^2)$, are given by
$O(\epsilon ^2)$, are given by
Here, ![]() $\boldsymbol {q}_{\beta }$ is the vector of the local volume flow rate per unit width of the
$\boldsymbol {q}_{\beta }$ is the vector of the local volume flow rate per unit width of the ![]() $\beta$ phase,
$\beta$ phase, ![]() $\mu _\beta$ is the (constant) liquid dynamic viscosity,
$\mu _\beta$ is the (constant) liquid dynamic viscosity, ![]() $p_\beta$ the pressure and
$p_\beta$ the pressure and ![]() $h(y)$ the aperture, that is, the distance along
$h(y)$ the aperture, that is, the distance along ![]() $z$ between two opposite walls of the channel. Furthermore, since
$z$ between two opposite walls of the channel. Furthermore, since ![]() $\beta$ and
$\beta$ and ![]() $\gamma$ are immiscible phases, there is no mass transport nor phase change at the liquid–gas interface,
$\gamma$ are immiscible phases, there is no mass transport nor phase change at the liquid–gas interface, ![]() $\mathcal {A}_{\beta \gamma }$, located at
$\mathcal {A}_{\beta \gamma }$, located at ![]() $y=e(x,t)\equiv e$ (see figure 1c,d). Consequently, the following boundary condition is deduced from the mass-jump condition at
$y=e(x,t)\equiv e$ (see figure 1c,d). Consequently, the following boundary condition is deduced from the mass-jump condition at ![]() $\mathcal {A}_{\beta \gamma }$ (Slattery Reference Slattery1999):
$\mathcal {A}_{\beta \gamma }$ (Slattery Reference Slattery1999):
Here ![]() $\boldsymbol {v}_{\beta \gamma }$ is the velocity of
$\boldsymbol {v}_{\beta \gamma }$ is the velocity of ![]() $\mathcal {A}_{\beta \gamma }$ in the
$\mathcal {A}_{\beta \gamma }$ in the ![]() $(x,y)$ plane.
$(x,y)$ plane.
Special attention may be dedicated to the momentum jump boundary condition at ![]() $\mathcal {A}_{\beta \gamma }$. In the original three-dimensional configuration, this condition writes
$\mathcal {A}_{\beta \gamma }$. In the original three-dimensional configuration, this condition writes ![]() $[(p_\gamma -p_\beta )\boldsymbol{\mathsf{I}}+\mu _\beta (\boldsymbol {\nabla } \boldsymbol {v}_{\beta \gamma }+\boldsymbol {\nabla } \boldsymbol {v}_{\beta \gamma }^{\rm T})]\boldsymbol {\cdot }\boldsymbol {n}_{\beta \gamma }=\sigma \kappa \boldsymbol {n}_{\beta \gamma }$,
$[(p_\gamma -p_\beta )\boldsymbol{\mathsf{I}}+\mu _\beta (\boldsymbol {\nabla } \boldsymbol {v}_{\beta \gamma }+\boldsymbol {\nabla } \boldsymbol {v}_{\beta \gamma }^{\rm T})]\boldsymbol {\cdot }\boldsymbol {n}_{\beta \gamma }=\sigma \kappa \boldsymbol {n}_{\beta \gamma }$, ![]() $\boldsymbol{\mathsf{I}}$ being the identity tensor,
$\boldsymbol{\mathsf{I}}$ being the identity tensor, ![]() $p_\gamma$ the (constant) gas pressure,
$p_\gamma$ the (constant) gas pressure, ![]() $\sigma$ the surface tension and
$\sigma$ the surface tension and ![]() $\kappa$ the double mean curvature of
$\kappa$ the double mean curvature of ![]() $\mathcal {A}_{\beta \gamma }$ whereas
$\mathcal {A}_{\beta \gamma }$ whereas ![]() $\boldsymbol{n}_{\beta\gamma}$ is the unit normal vector at the fluid-fluid interface, directed from the
$\boldsymbol{n}_{\beta\gamma}$ is the unit normal vector at the fluid-fluid interface, directed from the ![]() $\beta$ phase towards the
$\beta$ phase towards the ![]() $\gamma$ phase. In this expression, the scale of the pressure jump term on the left-hand side and the capillary term on the right-hand side can be taken as
$\gamma$ phase. In this expression, the scale of the pressure jump term on the left-hand side and the capillary term on the right-hand side can be taken as ![]() $\sigma /h$, whereas the order of magnitude of the viscous stress term is expected to be
$\sigma /h$, whereas the order of magnitude of the viscous stress term is expected to be ![]() $\mu _\beta u/h$,
$\mu _\beta u/h$, ![]() $u$ being the characteristic velocity in the
$u$ being the characteristic velocity in the ![]() $\beta$ phase. If the capillary number,
$\beta$ phase. If the capillary number, ![]() ${Ca} = \mu _{\beta } u / \sigma$, remains smaller than
${Ca} = \mu _{\beta } u / \sigma$, remains smaller than ![]() $\epsilon$, this boundary condition at
$\epsilon$, this boundary condition at ![]() $O(\epsilon )$ reduces to the Young–Laplace relationship
$O(\epsilon )$ reduces to the Young–Laplace relationship
Here, ![]() $p_c$ is the capillary pressure and
$p_c$ is the capillary pressure and ![]() $\kappa$ can be expressed as
$\kappa$ can be expressed as
 \begin{equation} \kappa = \frac{\dfrac{\partial^2 e}{\partial x^2} }{\left(1 + \left(\dfrac{\partial e}{\partial x}\right)^2 \right)^{3/2}}+\kappa_1. \end{equation}
\begin{equation} \kappa = \frac{\dfrac{\partial^2 e}{\partial x^2} }{\left(1 + \left(\dfrac{\partial e}{\partial x}\right)^2 \right)^{3/2}}+\kappa_1. \end{equation}
The two terms in (2.2e) represent the principal curvatures. In accordance with an approximation at ![]() $O(\epsilon )$, the first one is taken as the curvature in the
$O(\epsilon )$, the first one is taken as the curvature in the ![]() $(x,y)$ plane whereas the second one is that in the plane defined by
$(x,y)$ plane whereas the second one is that in the plane defined by ![]() $\boldsymbol {e}_z$ and the normal at
$\boldsymbol {e}_z$ and the normal at ![]() $\mathcal {A}_{\beta \gamma }$. The model given in (2.2) has an overall accuracy at
$\mathcal {A}_{\beta \gamma }$. The model given in (2.2) has an overall accuracy at ![]() $O(\epsilon )$.
$O(\epsilon )$.
The imbibition process in the channel under concern may typically comprise two distinct stages after liquid is in contact with the channel inlet. First, due to the strong capillary effect induced by the corner, a film settles in this region of the channel, a step that is referred to as the ‘liquid film regime’, as schematically depicted in figure 1(c). Second, once a sufficiently large area of the channel inlet is invaded by the ![]() $\beta$ phase so that the threshold capillary pressure compatible with the formation of a bulk meniscus is reached, the bulk meniscus may take place and the imbibition process can continue, including flow both in the corner films and in the liquid bulk behind the bulk meniscus. This second stage, schematised in figure 1(d), is called the ‘bulk and corner film flow regime’ in the following. The flow modelling developed in the next sections aims at the description of both regimes. Moreover, two different situations are envisaged, depending on the condition imposed at the channel inlet, namely, either a constant (volume) flow rate or a constant pressure. It should be noted that the bulk and corner film flow regime, that is conditioned by the penetration of the meniscus in the channel, may not be possible in the case of an imposed constant pressure at the channel inlet, as will be made clear in § 5. Note also that the initial stage of the process, when the liquid is brought in contact with the channel inlet, is subject to the existence of inertial effects (Quéré Reference Quéré1997). However, these effects are prone to rapidly decrease and are supposed to not influence the dynamics after they vanish. Therefore, they are ignored in the overall flow description that follows.
$\beta$ phase so that the threshold capillary pressure compatible with the formation of a bulk meniscus is reached, the bulk meniscus may take place and the imbibition process can continue, including flow both in the corner films and in the liquid bulk behind the bulk meniscus. This second stage, schematised in figure 1(d), is called the ‘bulk and corner film flow regime’ in the following. The flow modelling developed in the next sections aims at the description of both regimes. Moreover, two different situations are envisaged, depending on the condition imposed at the channel inlet, namely, either a constant (volume) flow rate or a constant pressure. It should be noted that the bulk and corner film flow regime, that is conditioned by the penetration of the meniscus in the channel, may not be possible in the case of an imposed constant pressure at the channel inlet, as will be made clear in § 5. Note also that the initial stage of the process, when the liquid is brought in contact with the channel inlet, is subject to the existence of inertial effects (Quéré Reference Quéré1997). However, these effects are prone to rapidly decrease and are supposed to not influence the dynamics after they vanish. Therefore, they are ignored in the overall flow description that follows.
In the sequel of this work, dimensionless quantities shall be used that are defined from their dimensional counterpart with a superscript ![]() $^*$ according to
$^*$ according to
where ![]() $\lambda$ denotes any variable having units of a length and
$\lambda$ denotes any variable having units of a length and ![]() $v_{\beta r}$ is a reference velocity given by
$v_{\beta r}$ is a reference velocity given by
Moreover, dimensionless pressures are defined as
3. Corner liquid film
To begin with, the liquid film regime is explored (cf. figure 1b,c). To do so, it is necessary to derive the governing equation for the evolution of the film profile between the inlet of the channel and the triple point as schematically depicted in figure 1(c). This description will be further used to determine the condition of entrance of the meniscus in the channel and the dynamics in the two regimes in both cases of an imposed flow rate and imposed pressure at the channel inlet.
3.1. Liquid film width
The liquid–gas interface, ![]() $\mathcal{A}_{\beta \gamma}$, is parameterised by denoting
$\mathcal{A}_{\beta \gamma}$, is parameterised by denoting ![]() $\phi (x, y, t) = y - e(x, t)$. Calling upon the kinematic condition, which expresses the fact that a fluid particle present at
$\phi (x, y, t) = y - e(x, t)$. Calling upon the kinematic condition, which expresses the fact that a fluid particle present at ![]() $\mathcal {A}_{\beta \gamma }$ remains at this interface during the flow, allows one to write
$\mathcal {A}_{\beta \gamma }$ remains at this interface during the flow, allows one to write
By making use of the mass condition given in (2.2c), this can be equivalently expressed as
Since the above equation is valid at the interface, the components ![]() $q_{\beta x}$,
$q_{\beta x}$, ![]() $q_{\beta y}$ of
$q_{\beta y}$ of ![]() $\boldsymbol {q}_\beta$, as well as
$\boldsymbol {q}_\beta$, as well as ![]() $h$, must be taken at
$h$, must be taken at ![]() $y=e$ and are respectively denoted as
$y=e$ and are respectively denoted as ![]() $q_{\beta x}(e)$,
$q_{\beta x}(e)$, ![]() $q_{\beta y}(e)$ and
$q_{\beta y}(e)$ and ![]() $h(e)$.
$h(e)$.
Integrating the mass conservation equation given in (2.2a) between ![]() $y=0$ and
$y=0$ and ![]() $y=e(x, t)$, and employing the Leibniz integral rule, yields the following expression of
$y=e(x, t)$, and employing the Leibniz integral rule, yields the following expression of ![]() $q_{\beta y}(e)$:
$q_{\beta y}(e)$:
Upon substitution of this result into (3.1b) and making use of the expression of the ![]() $x$ component of the momentum conservation equation (2.2b), yields
$x$ component of the momentum conservation equation (2.2b), yields
 \begin{equation} h{(e)}\frac{\partial e}{\partial t} -\frac{1}{12\mu_{\beta}} \frac{\partial }{\partial x} \left(\int_0^{e(x, t)} h^3(y) \frac{\partial p_\beta}{\partial x}\mathrm{d}y\right) = 0. \end{equation}
\begin{equation} h{(e)}\frac{\partial e}{\partial t} -\frac{1}{12\mu_{\beta}} \frac{\partial }{\partial x} \left(\int_0^{e(x, t)} h^3(y) \frac{\partial p_\beta}{\partial x}\mathrm{d}y\right) = 0. \end{equation}
For symmetry reasons, the flow description can be restricted to the part of the channel defined by ![]() $0\le y\le \ell$ and taking into account its triangular shape, the local aperture,
$0\le y\le \ell$ and taking into account its triangular shape, the local aperture, ![]() $h$, can be expressed as
$h$, can be expressed as
Consequently, the cross-sectional area, ![]() $S(x,t)$, of the liquid film in the corner can be calculated as proposed in Kantzas, Chatzis & Dullien (Reference Kantzas, Chatzis and Dullien1988) with the expression
$S(x,t)$, of the liquid film in the corner can be calculated as proposed in Kantzas, Chatzis & Dullien (Reference Kantzas, Chatzis and Dullien1988) with the expression
where the constant ![]() $A$ and radius
$A$ and radius ![]() $r(x, t)$ are respectively defined as (see figure 1b)
$r(x, t)$ are respectively defined as (see figure 1b)
with ![]() $B$ given by
$B$ given by
In these expressions, ![]() $\theta _e$ is the contact angle of the liquid onto the solid wall in the presence of the gas phase (
$\theta _e$ is the contact angle of the liquid onto the solid wall in the presence of the gas phase (![]() $\theta _e\le {\rm \pi}/2$). Since
$\theta _e\le {\rm \pi}/2$). Since ![]() ${Ca}\le \epsilon \ll 1$, the interface near the triple point can reasonably be considered as being unperturbed by the viscous effects, and therefore, the contact angle can be taken as that at equilibrium. Moreover, a condition is required for the liquid to spontaneously wick into the corner, that writes (Concus & Finn Reference Concus and Finn1969, Reference Concus and Finn1974)
${Ca}\le \epsilon \ll 1$, the interface near the triple point can reasonably be considered as being unperturbed by the viscous effects, and therefore, the contact angle can be taken as that at equilibrium. Moreover, a condition is required for the liquid to spontaneously wick into the corner, that writes (Concus & Finn Reference Concus and Finn1969, Reference Concus and Finn1974)
In the film region of interest here, the curvature in the ![]() $(x,y)$ plane is expected to be much smaller than
$(x,y)$ plane is expected to be much smaller than ![]() $\kappa _1$, and, to within an approximation at
$\kappa _1$, and, to within an approximation at ![]() $O(\epsilon )$, this motivates taking
$O(\epsilon )$, this motivates taking ![]() $\kappa _1$ as the curvature in the
$\kappa _1$ as the curvature in the ![]() $(y, z)$ plane that is given by
$(y, z)$ plane that is given by
and hence,
Upon making use of the definition of the capillary pressure, together with (3.3c) and the fact that ![]() $p_\gamma$ is constant, this allows one to write
$p_\gamma$ is constant, this allows one to write
Once this last relationship is substituted back into (3.1d), this yields
or, after rearranging,
where
Equation (3.8) has the same form as that obtained in the case of a liquid film invading a corner reported in Langbein (Reference Langbein2002) where it was shown that a similarity solution can be employed by using the change of variable
with
The boundary condition associated to (3.8) is such that ![]() $e(x,t)=0$ at
$e(x,t)=0$ at ![]() $x=L_{f}(t)$, where
$x=L_{f}(t)$, where ![]() $L_{f}(t)$ is the position of the triple point in the corner (see figure 1). To satisfy this condition, the constant
$L_{f}(t)$ is the position of the triple point in the corner (see figure 1). To satisfy this condition, the constant ![]() $n$ in (3.10) must be equal to zero as shown in Mayer, McGrath & Steele (Reference Mayer, McGrath and Steele1983) and this allows one to rewrite (3.8) as
$n$ in (3.10) must be equal to zero as shown in Mayer, McGrath & Steele (Reference Mayer, McGrath and Steele1983) and this allows one to rewrite (3.8) as
The associated boundary condition follows from ![]() $e(L_f,t)=0$ and is given by
$e(L_f,t)=0$ and is given by
The solution of this nonlinear differential equation requires an additional boundary condition that can be obtained from close attention to the differential equation itself. Indeed, at the triple point where ![]() $f=0$, it follows from (3.11) that either
$f=0$, it follows from (3.11) that either ![]() ${\mathrm {d}f}/{\mathrm {d}\zeta }=0$ or
${\mathrm {d}f}/{\mathrm {d}\zeta }=0$ or ![]() ${\mathrm {d}f}/{\mathrm {d}\zeta }=-({\alpha }/{3})L_f$. Since the former is not physically acceptable, the latter is retained:
${\mathrm {d}f}/{\mathrm {d}\zeta }=-({\alpha }/{3})L_f$. Since the former is not physically acceptable, the latter is retained:
A strategy to solve (3.11) was reported by Mayer et al. (Reference Mayer, McGrath and Steele1983) that consists in proposing an a priori form of the solution with a free parameter that is further identified by minimising the residue after the guessed solution is substituted into the differential equation. An alternative is to consider a simplified version of the above differential equation by neglecting the harmonic term. This is briefly reported in Appendix A where it is shown, however, that a simpler and more accurate approach can be used since a universal solution to (3.11) subject to the boundary conditions given in (3.12a) and (3.12b) can be found. An excellent approximation to this solution, written in terms of the variables ![]() $x$ and
$x$ and ![]() $t$, can be expressed as
$t$, can be expressed as
 \begin{equation} e(x,t) = \frac{\alpha L_f^2}{t}\left(a\left(\frac{x}{L_f}\right)^2+b\frac{x}{L_f}+c\right), \end{equation}
\begin{equation} e(x,t) = \frac{\alpha L_f^2}{t}\left(a\left(\frac{x}{L_f}\right)^2+b\frac{x}{L_f}+c\right), \end{equation}which, in dimensionless form, writes (see (2.3))
 \begin{equation} e^*(x^*,t^*)=\frac{36L_f^{*2}}{\epsilon B t^*}\left(a\left(\frac{x^*}{L_f^*}\right)^2+b \frac{x^*}{L_f^*}+c\right). \end{equation}
\begin{equation} e^*(x^*,t^*)=\frac{36L_f^{*2}}{\epsilon B t^*}\left(a\left(\frac{x^*}{L_f^*}\right)^2+b \frac{x^*}{L_f^*}+c\right). \end{equation}The coefficients in these two equations are given by
The film regime persists until the bulk meniscus can enter the channel, which is possible when the capillary pressure in the film present at the channel inlet is compatible with that of a bulk meniscus at this location. This threshold value corresponds to a maximum film width at ![]() $x=0$ that is referred to as
$x=0$ that is referred to as ![]() $e_{max}$ in the rest of the development. The methodology to determine
$e_{max}$ in the rest of the development. The methodology to determine ![]() $e_{max}$ is detailed in the following section.
$e_{max}$ is detailed in the following section.
3.2. Bulk meniscus entrance: the maximum film width
Entrance of the bulk meniscus in the channel can occur when ![]() $e(x=0)=e_{max}$. Following the assumption used in Weislogel, Baker & Jenson (Reference Weislogel, Baker and Jenson2011) and supported by observations in Amyot (Reference Amyot2004), the bulk meniscus, once entered in the channel, is considered to adopt a constant shape over time corresponding to that in a static configuration. This is a valid approximation provided
$e(x=0)=e_{max}$. Following the assumption used in Weislogel, Baker & Jenson (Reference Weislogel, Baker and Jenson2011) and supported by observations in Amyot (Reference Amyot2004), the bulk meniscus, once entered in the channel, is considered to adopt a constant shape over time corresponding to that in a static configuration. This is a valid approximation provided ![]() ${Ca} < \epsilon$ and allows one to consider
${Ca} < \epsilon$ and allows one to consider ![]() $e_{max}$ as the value of the film width at which the matching between the film region and the bulk meniscus region can be performed in order to describe the coupled flow dynamics in the bulk and corner film flow regime. It is therefore necessary to determine
$e_{max}$ as the value of the film width at which the matching between the film region and the bulk meniscus region can be performed in order to describe the coupled flow dynamics in the bulk and corner film flow regime. It is therefore necessary to determine ![]() $e_{max}$ prior to the flow description in both the film and behind the bulk meniscus.
$e_{max}$ prior to the flow description in both the film and behind the bulk meniscus.
The determination of ![]() $e_{max}$ can be carried out by matching the capillary pressure (i.e. the curvatures) of the bulk meniscus to that of the film at
$e_{max}$ can be carried out by matching the capillary pressure (i.e. the curvatures) of the bulk meniscus to that of the film at ![]() $e=e_{max}$. Since the bulk meniscus can be considered as the static one, its double mean curvature is a constant in the absence of body force so that the matching writes
$e=e_{max}$. Since the bulk meniscus can be considered as the static one, its double mean curvature is a constant in the absence of body force so that the matching writes
 \begin{equation} \frac{\dfrac{\partial ^2 e}{\partial x^2} }{\left(1 + \left(\dfrac{\partial e}{\partial x}\right)^2\right)^{3/2}}+ \frac{2B}{\epsilon e} =\frac{2B}{\epsilon e_{max}},\quad e_{max}\le e\le \ell. \end{equation}
\begin{equation} \frac{\dfrac{\partial ^2 e}{\partial x^2} }{\left(1 + \left(\dfrac{\partial e}{\partial x}\right)^2\right)^{3/2}}+ \frac{2B}{\epsilon e} =\frac{2B}{\epsilon e_{max}},\quad e_{max}\le e\le \ell. \end{equation}
The left-hand side of the above equation represents the double mean curvature in the bulk meniscus region, in accordance with (2.2e) in which the expression of ![]() $\kappa _1$ was kept as in the film region (see (3.4)) with the idea that it remains an approximation at
$\kappa _1$ was kept as in the film region (see (3.4)) with the idea that it remains an approximation at ![]() $O(\epsilon )$. Similarly, the right-hand side is the double mean curvature of the film at
$O(\epsilon )$. Similarly, the right-hand side is the double mean curvature of the film at ![]() $e=e_{max}$, approximated by (3.4). Equation (3.14a) describes the profile of the meniscus,
$e=e_{max}$, approximated by (3.4). Equation (3.14a) describes the profile of the meniscus, ![]() $e(x)$, from the matching point with the film at
$e(x)$, from the matching point with the film at ![]() $e=e_{max}$ to the centreline of the channel where
$e=e_{max}$ to the centreline of the channel where ![]() $e=\ell$. Multiplying this equation by
$e=\ell$. Multiplying this equation by ![]() ${\partial e}/{\partial x}$ leads to
${\partial e}/{\partial x}$ leads to
 \begin{equation} -\frac{\partial}{\partial x} \left(1 + \left(\frac{\partial e}{\partial x}\right)^2\right)^{{-}1/2}+ \frac{2B}{\epsilon}\left(\frac{1}{e}-\frac{1}{e_{max}}\right) \frac{\partial e}{\partial x} = 0,\quad e_{max}\le e\le \ell. \end{equation}
\begin{equation} -\frac{\partial}{\partial x} \left(1 + \left(\frac{\partial e}{\partial x}\right)^2\right)^{{-}1/2}+ \frac{2B}{\epsilon}\left(\frac{1}{e}-\frac{1}{e_{max}}\right) \frac{\partial e}{\partial x} = 0,\quad e_{max}\le e\le \ell. \end{equation}
The above relationship can now be integrated between ![]() $e=e_{max}$ and
$e=e_{max}$ and ![]() $e=\ell$, and, due to symmetry that implies
$e=\ell$, and, due to symmetry that implies ![]() ${\partial e}/{\partial x}\rightarrow \infty$ when
${\partial e}/{\partial x}\rightarrow \infty$ when ![]() $e\rightarrow \ell$, this yields the dimensionless relationship (cf. (2.3))
$e\rightarrow \ell$, this yields the dimensionless relationship (cf. (2.3))
 \begin{equation} \left( 1 + \left(\frac{\partial e^*}{\partial x^*}\right)^2_{e_{max}^*} \right)^{{-}1/2} - \frac{2B}{\epsilon}\left(\ln\left(e_{max}^*\right)+\frac{1-e_{max}^*}{e_{max}^*}\right)=0. \end{equation}
\begin{equation} \left( 1 + \left(\frac{\partial e^*}{\partial x^*}\right)^2_{e_{max}^*} \right)^{{-}1/2} - \frac{2B}{\epsilon}\left(\ln\left(e_{max}^*\right)+\frac{1-e_{max}^*}{e_{max}^*}\right)=0. \end{equation}
The value of ![]() ${\partial e}/{\partial x}|_{e_{max}}$ needs more careful attention and is further explored in § 4.2.
${\partial e}/{\partial x}|_{e_{max}}$ needs more careful attention and is further explored in § 4.2.
It should be noted that, since the meniscus shape is considered as in static conditions while moving in the channel after its entrance, ![]() $e_{max}$ is a characteristic of the fluid and channel and is independent of time. In other words, once the film thickness has grown to
$e_{max}$ is a characteristic of the fluid and channel and is independent of time. In other words, once the film thickness has grown to ![]() $e_{max}$ at the entrance of the channel, the meniscus enters and the section
$e_{max}$ at the entrance of the channel, the meniscus enters and the section ![]() $e=e_{max}$ is displaced at the same speed as the meniscus in the ensuing bulk and corner film flow regime, as sketched in figure 1(d).
$e=e_{max}$ is displaced at the same speed as the meniscus in the ensuing bulk and corner film flow regime, as sketched in figure 1(d).
With the above material at hand, the analysis is now focused on two different cases of imbibition: first when a constant flow rate, ![]() $Q_0$, is imposed at the channel inlet, which corresponds to forced imbibition (§ 4); and second, when, instead, a constant pressure is imposed at
$Q_0$, is imposed at the channel inlet, which corresponds to forced imbibition (§ 4); and second, when, instead, a constant pressure is imposed at ![]() $x=0$ (§ 5).
$x=0$ (§ 5).
4. Imbibition dynamics at imposed flow rate
This forced imbibition process is characterised by two distinct stages. First, the liquid wicks into the corners from ![]() $t=0$ until the film width reaches the value
$t=0$ until the film width reaches the value ![]() $e_{max}$ at
$e_{max}$ at ![]() $x=0$ at a time referred to as
$x=0$ at a time referred to as ![]() $t=t_{max}$ in the following. This corresponds to the ‘liquid film regime’ detailed in § 4.1. At
$t=t_{max}$ in the following. This corresponds to the ‘liquid film regime’ detailed in § 4.1. At ![]() $t=t_{max}$, the meniscus enters the channel and flow takes place in the so-called ‘bulk and corner film flow regime’ analysed in § 4.3.
$t=t_{max}$, the meniscus enters the channel and flow takes place in the so-called ‘bulk and corner film flow regime’ analysed in § 4.3.
4.1. Liquid film regime: triple point position
When a constant (volume) flow rate, ![]() $Q_0$, is imposed at the inlet of the channel, volume conservation for the
$Q_0$, is imposed at the inlet of the channel, volume conservation for the ![]() $\beta$ phase at time
$\beta$ phase at time ![]() $t$ can be written as
$t$ can be written as
Substituting the expressions of ![]() $S(x,t)$ and
$S(x,t)$ and ![]() $e(x,t)$ given in (3.3) and (3.13a) in the above equation provides the expression of the position of the triple point when imbibition occurs in the liquid film regime, which is given by
$e(x,t)$ given in (3.3) and (3.13a) in the above equation provides the expression of the position of the triple point when imbibition occurs in the liquid film regime, which is given by
 \begin{align} L_{f}(t) &= \left(\frac{125}{3(82+27\sqrt{6})} \frac{B^4}{A} Q_0 \left(\frac{\sigma}{\mu_{\beta}}\right)^2 \right)^{1/5} t^{3/5} \nonumber\\ &\simeq 0.7759\left(\frac{B^4}{A} Q_0 \left( \frac{\sigma}{\mu_{\beta}}\right)^2 \right)^{1/5} t^{3/5}, \end{align}
\begin{align} L_{f}(t) &= \left(\frac{125}{3(82+27\sqrt{6})} \frac{B^4}{A} Q_0 \left(\frac{\sigma}{\mu_{\beta}}\right)^2 \right)^{1/5} t^{3/5} \nonumber\\ &\simeq 0.7759\left(\frac{B^4}{A} Q_0 \left( \frac{\sigma}{\mu_{\beta}}\right)^2 \right)^{1/5} t^{3/5}, \end{align}
where ![]() $A$ and
$A$ and ![]() $B$ are respectively given in (3.3b) and (3.3d). In dimensionless form, it can be expressed as (see (2.3))
$B$ are respectively given in (3.3b) and (3.3d). In dimensionless form, it can be expressed as (see (2.3))
 \begin{equation} L_f^*(t^*)=\frac{L_f(t)}{\ell}=0.7759\left(\frac{\epsilon B^4}{A}\overline{Ca}\right)^{1/5}t^{*3/5}, \end{equation}
\begin{equation} L_f^*(t^*)=\frac{L_f(t)}{\ell}=0.7759\left(\frac{\epsilon B^4}{A}\overline{Ca}\right)^{1/5}t^{*3/5}, \end{equation}
in which ![]() $\overline {Ca}$ is a global capillary number defined as
$\overline {Ca}$ is a global capillary number defined as
![]() $S_t$ being the total cross-sectional area of the channel given by
$S_t$ being the total cross-sectional area of the channel given by
and ![]() $v_{\beta r}$ given in (2.3c). The result in (4.2) slightly differs from that reported in Amyot (Reference Amyot2004) due to a more detailed expression of the liquid film cross-sectional area,
$v_{\beta r}$ given in (2.3c). The result in (4.2) slightly differs from that reported in Amyot (Reference Amyot2004) due to a more detailed expression of the liquid film cross-sectional area, ![]() $S(x,t)$, and a more accurate solution for
$S(x,t)$, and a more accurate solution for ![]() $e(x,t)$.
$e(x,t)$.
Prior to the determination of ![]() $e_{max}$, the time referred to as
$e_{max}$, the time referred to as ![]() $t_{max}$, at which
$t_{max}$, at which ![]() $e=e_{max}$ at
$e=e_{max}$ at ![]() $x=0$, can be anticipated. This time corresponds to the end of the liquid film regime, at which the corresponding triple point position is denoted
$x=0$, can be anticipated. This time corresponds to the end of the liquid film regime, at which the corresponding triple point position is denoted ![]() $L_{f{max}}$. Indeed, upon substitution of (4.2a) into (3.13a), the expression of
$L_{f{max}}$. Indeed, upon substitution of (4.2a) into (3.13a), the expression of ![]() $t_{max}$ is obtained, that is, given by
$t_{max}$ is obtained, that is, given by
 \begin{align} t_{max} &= \frac{(82+27\sqrt{6})^2}{4320(1+\sqrt{6})^5} \frac{\epsilon^5 A^2}{B^3}\frac{\sigma}{\mu_\beta}\frac{e_{max}^5}{Q_0^2}\nonumber\\ &\simeq 0.0104\frac{\epsilon^5 A^2}{B^3}\frac{\sigma}{\mu_\beta} \frac{e_{max}^5}{Q_0^2}, \end{align}
\begin{align} t_{max} &= \frac{(82+27\sqrt{6})^2}{4320(1+\sqrt{6})^5} \frac{\epsilon^5 A^2}{B^3}\frac{\sigma}{\mu_\beta}\frac{e_{max}^5}{Q_0^2}\nonumber\\ &\simeq 0.0104\frac{\epsilon^5 A^2}{B^3}\frac{\sigma}{\mu_\beta} \frac{e_{max}^5}{Q_0^2}, \end{align}or in dimensionless form
Correspondingly, ![]() $L_{f{max}}$ can be expressed as
$L_{f{max}}$ can be expressed as
 \begin{align} L_{f{max}} &= L_f(t_{max})=\frac{82+27\sqrt{6}}{72(1+\sqrt{6})^3} \frac{\epsilon^3 A}{B}\frac{\sigma}{\mu_\beta}\frac{e_{max}^3}{Q_0} \nonumber\\ &\simeq 0.0501\frac{\epsilon^3 A}{B}\frac{\sigma}{\mu_\beta}\frac{e_{max}^3}{Q_0}, \end{align}
\begin{align} L_{f{max}} &= L_f(t_{max})=\frac{82+27\sqrt{6}}{72(1+\sqrt{6})^3} \frac{\epsilon^3 A}{B}\frac{\sigma}{\mu_\beta}\frac{e_{max}^3}{Q_0} \nonumber\\ &\simeq 0.0501\frac{\epsilon^3 A}{B}\frac{\sigma}{\mu_\beta}\frac{e_{max}^3}{Q_0}, \end{align}which, in dimensionless form, writes
These expressions require the evaluation of ![]() $e_{max}$ and this is carried out in the following section where different strategies are explored, including the complete solution from (3.14c) along with simplified versions of this equation providing quasi-analytical solutions for
$e_{max}$ and this is carried out in the following section where different strategies are explored, including the complete solution from (3.14c) along with simplified versions of this equation providing quasi-analytical solutions for ![]() $e_{max}^*$.
$e_{max}^*$.
4.2. Maximum film width
From (3.13a), and the fact that ![]() $e(x=0,t_{max})=e_{max}$ when the bulk meniscus enters the channel, it is deduced that
$e(x=0,t_{max})=e_{max}$ when the bulk meniscus enters the channel, it is deduced that
Using the expressions of ![]() $\alpha$,
$\alpha$, ![]() $t_{max}$,
$t_{max}$, ![]() $L_{f{max}}$ and the value of
$L_{f{max}}$ and the value of ![]() $b$ (see (3.9), (4.4a), (4.5a) and (3.13d)), the above equation yields
$b$ (see (3.9), (4.4a), (4.5a) and (3.13d)), the above equation yields
 \begin{equation} \left.\frac{\partial e}{\partial x}\right|_{e=e_{max}} ={-}\frac{36\left(23\sqrt{6}-42\right)}{47}\frac{B}{\epsilon^3 A} \frac{\mu_\beta}{\sigma}\frac{Q_0}{e_{max}^2}, \end{equation}
\begin{equation} \left.\frac{\partial e}{\partial x}\right|_{e=e_{max}} ={-}\frac{36\left(23\sqrt{6}-42\right)}{47}\frac{B}{\epsilon^3 A} \frac{\mu_\beta}{\sigma}\frac{Q_0}{e_{max}^2}, \end{equation}which, in dimensionless form, is given by
 \begin{equation} \left.\frac{\partial e^*}{\partial x^*}\right|_{e^*=e^*_{max}} \simeq{-}10.9825\frac{B}{\epsilon^2 A}\frac{\overline{Ca}}{e_{max}^{*2}}. \end{equation}
\begin{equation} \left.\frac{\partial e^*}{\partial x^*}\right|_{e^*=e^*_{max}} \simeq{-}10.9825\frac{B}{\epsilon^2 A}\frac{\overline{Ca}}{e_{max}^{*2}}. \end{equation}
The solution for ![]() $e_{max}$ can then be carried out by solving (3.14c) in which the above expression of
$e_{max}$ can then be carried out by solving (3.14c) in which the above expression of ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$ is substituted.
${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$ is substituted.
An analytical estimate of ![]() $e_{max}$ can nevertheless be obtained by noting that, when the constraint
$e_{max}$ can nevertheless be obtained by noting that, when the constraint ![]() $|{\partial e}/{\partial x}|_{e=e_{max}}|\ll 1$ is satisfied, that is,
$|{\partial e}/{\partial x}|_{e=e_{max}}|\ll 1$ is satisfied, that is,
(3.14c) reduces to
The solution to this equation can be expressed as
 \begin{equation} e_{max}^* =\frac{-1}{{W_{{-}1}}\left(-\exp{\left( - 1 - \dfrac{\epsilon}{2B}\right)}\right)}. \end{equation}
\begin{equation} e_{max}^* =\frac{-1}{{W_{{-}1}}\left(-\exp{\left( - 1 - \dfrac{\epsilon}{2B}\right)}\right)}. \end{equation}
In this expression, ![]() ${W}$ is the Lambert function and
${W}$ is the Lambert function and ![]() ${W_{-1}}$ its
${W_{-1}}$ its ![]() $-1$ branch (Corless et al. Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996). Furthermore, note that when
$-1$ branch (Corless et al. Reference Corless, Gonnet, Hare, Jeffrey and Knuth1996). Furthermore, note that when
(4.9) yields the following approximation of ![]() $e_{max}^*$:
$e_{max}^*$:
A similar expression was proposed by Amyot (Reference Amyot2004) (see also Geoffroy et al. Reference Geoffroy, Plouraboué, Prat and Amyot2006).
To better appreciate the relevance of the estimates of ![]() $e_{max}^*$ from (4.9) and (4.11) compared with the solution of (3.14c) (once (4.6c) is employed), illustrative results of
$e_{max}^*$ from (4.9) and (4.11) compared with the solution of (3.14c) (once (4.6c) is employed), illustrative results of ![]() $e_{max}^*$ are reported versus
$e_{max}^*$ are reported versus ![]() $\epsilon /B$ in figure 2. These results were obtained from the three above-mentioned equations, considering different values of the remaining parameter
$\epsilon /B$ in figure 2. These results were obtained from the three above-mentioned equations, considering different values of the remaining parameter ![]() ${\overline {Ca}}/{\epsilon A}$. In figure 2(a), for which
${\overline {Ca}}/{\epsilon A}$. In figure 2(a), for which ![]() ${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$, the estimate from (4.11) is shown to be inappropriate over the whole range of
${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$, the estimate from (4.11) is shown to be inappropriate over the whole range of ![]() ${\epsilon }/{B}$ for this value of the parameter
${\epsilon }/{B}$ for this value of the parameter ![]() ${\overline {Ca}}/{\epsilon A}$, indicating that the constraint (4.10) is extremely severe. Conversely, the approximation from (4.9) (open symbols) reveals to be in good agreement with the solution from (3.14c) (dashed line) when
${\overline {Ca}}/{\epsilon A}$, indicating that the constraint (4.10) is extremely severe. Conversely, the approximation from (4.9) (open symbols) reveals to be in good agreement with the solution from (3.14c) (dashed line) when ![]() ${\epsilon }/{B}$ is sufficiently large compared with
${\epsilon }/{B}$ is sufficiently large compared with ![]() ${10\overline {Ca}}/{\epsilon A e_{max}^{*2}}$, in accordance with the constraint expressed in (4.7). This last observation is further analysed with the results in figure 2(b) obtained from (4.9) (open symbols) and (3.14c) (dashed lines) for three values of
${10\overline {Ca}}/{\epsilon A e_{max}^{*2}}$, in accordance with the constraint expressed in (4.7). This last observation is further analysed with the results in figure 2(b) obtained from (4.9) (open symbols) and (3.14c) (dashed lines) for three values of ![]() ${\overline {Ca}}/{\epsilon A}$, namely,
${\overline {Ca}}/{\epsilon A}$, namely, ![]() ${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$,
${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$, ![]() ${\overline {Ca}}/{\epsilon A}=3\times 10^{-3}$ and
${\overline {Ca}}/{\epsilon A}=3\times 10^{-3}$ and ![]() ${\overline {Ca}}/{\epsilon A}=6\times 10^{-3}$. From this figure, it clearly appears that the constraint becomes more severe as
${\overline {Ca}}/{\epsilon A}=6\times 10^{-3}$. From this figure, it clearly appears that the constraint becomes more severe as ![]() ${\overline {Ca}}/{\epsilon A}$ increases, making difficult a practical use of (4.9). Therefore, the determination of
${\overline {Ca}}/{\epsilon A}$ increases, making difficult a practical use of (4.9). Therefore, the determination of ![]() $e_{max}$ from (3.14c) (with (4.6c)) is highly recommended, and this will be further confirmed with the analysis of the bulk meniscus size (see the end of § 4.3.2 and Appendix C).
$e_{max}$ from (3.14c) (with (4.6c)) is highly recommended, and this will be further confirmed with the analysis of the bulk meniscus size (see the end of § 4.3.2 and Appendix C).

Figure 2. Comparison of the dependence of ![]() $e_{max}^{*}=e_{max}/\ell$ estimated from (3.14c) (together with (4.6c)) (dashed lines), (4.9) (open symbols) or (4.11) (solid line in (a)) with the parameter
$e_{max}^{*}=e_{max}/\ell$ estimated from (3.14c) (together with (4.6c)) (dashed lines), (4.9) (open symbols) or (4.11) (solid line in (a)) with the parameter ![]() $\epsilon /B$. Results are shown for (a)
$\epsilon /B$. Results are shown for (a) ![]() ${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$ and (b)
${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$ and (b) ![]() ${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$,
${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$, ![]() ${\overline {Ca}}/{\epsilon A}=3\times 10^{-3}$ and
${\overline {Ca}}/{\epsilon A}=3\times 10^{-3}$ and ![]() ${\overline {Ca}}/{\epsilon A}=6\times 10^{-3}$. Vertical dotted lines indicate the critical values,
${\overline {Ca}}/{\epsilon A}=6\times 10^{-3}$. Vertical dotted lines indicate the critical values, ![]() $({\epsilon }/{B})_c$, of
$({\epsilon }/{B})_c$, of ![]() $\epsilon /B$ extracted from (4.7), i.e.
$\epsilon /B$ extracted from (4.7), i.e. ![]() $({\epsilon }/{B})_c={10\overline {Ca}}/{\epsilon A e_{max}^{*2}}\simeq 0.0108$,
$({\epsilon }/{B})_c={10\overline {Ca}}/{\epsilon A e_{max}^{*2}}\simeq 0.0108$, ![]() $0.0416$ and
$0.0416$ and ![]() $0.0984$ for the three above-mentioned values of
$0.0984$ for the three above-mentioned values of ![]() ${\overline {Ca}}/{\epsilon A}$, respectively.
${\overline {Ca}}/{\epsilon A}$, respectively.
As an additional remark, it should be noted that (4.6c) derives from (3.14c), which represents an approximation of the film profile, and may therefore be a source of inaccuracy in the subsequent solution of (3.14c). However, if the value of ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$ is extracted from the numerical solution of (3.11) reported in Appendix A, the relative error on
${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$ is extracted from the numerical solution of (3.11) reported in Appendix A, the relative error on ![]() $e^*_{max}$ proves to be insignificant. It is therefore preferable to keep (4.6c) that has the advantage of providing an analytical expression of
$e^*_{max}$ proves to be insignificant. It is therefore preferable to keep (4.6c) that has the advantage of providing an analytical expression of ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$.
${\partial e^*}/{\partial x^*}|_{e^*=e^*_{max}}$.
At this point, flow in the whole channel in the bulk and corner film flow regime can be further analysed, both in the film (§ 4.3.1) and liquid bulk including the bulk meniscus (§ 4.3.2), the latter closing the entire description.
4.3. Bulk and corner film flow regime
4.3.1. Dynamics in the liquid film
For the subsequent flow analysis, it is of interest to define a moving system of coordinates ![]() $(O',x',y)$, as schematised in figure 1(d), whose origin,
$(O',x',y)$, as schematised in figure 1(d), whose origin, ![]() $O'$, with respect to the fixed system of coordinates
$O'$, with respect to the fixed system of coordinates ![]() $(O,x,y)$, is defined by
$(O,x,y)$, is defined by ![]() $e(x=x_{O'},t)=e(x'=0,t)=e_{max}$. In the following the
$e(x=x_{O'},t)=e(x'=0,t)=e_{max}$. In the following the ![]() $x$ coordinate,
$x$ coordinate, ![]() $x_{O'}$, of
$x_{O'}$, of ![]() $O'$, which corresponds to the matching point between the film and bulk meniscus, is denoted
$O'$, which corresponds to the matching point between the film and bulk meniscus, is denoted ![]() $L_b(t)$ (see figures 1(d) and 12).
$L_b(t)$ (see figures 1(d) and 12).
Since flow is considered as a quasi-static process, the same description of the film as that developed in § 3.1 can be employed in the system of coordinates ![]() $(O',x',y))$ that is hence supposed to move at a constant velocity with respect to
$(O',x',y))$ that is hence supposed to move at a constant velocity with respect to ![]() $(O,x,y)$. This allows one to readily write
$(O,x,y)$. This allows one to readily write
 \begin{equation} e(x',t) = \frac{\alpha L_f^{'2}}{t}\left(a\left(\frac{x'}{L_f^{'}}\right)^2 +b\frac{x'}{L_f^{'}}+c\right), \end{equation}
\begin{equation} e(x',t) = \frac{\alpha L_f^{'2}}{t}\left(a\left(\frac{x'}{L_f^{'}}\right)^2 +b\frac{x'}{L_f^{'}}+c\right), \end{equation}or in dimensionless form (see (2.3))
 \begin{equation} e^*(x'^*,t^*)=\frac{36L_f^{'*2}}{\epsilon B t^*}\left(a\left(\frac{x'^*}{L_f^{'*}}\right)^2+b \frac{x'^*}{L_f^{'*}}+c\right). \end{equation}
\begin{equation} e^*(x'^*,t^*)=\frac{36L_f^{'*2}}{\epsilon B t^*}\left(a\left(\frac{x'^*}{L_f^{'*}}\right)^2+b \frac{x'^*}{L_f^{'*}}+c\right). \end{equation} Here, ![]() $L^{'}_f(t)$ denotes the triple point position in
$L^{'}_f(t)$ denotes the triple point position in ![]() $(O',x',y)$. Upon making use of the condition
$(O',x',y)$. Upon making use of the condition ![]() $e(x'=0,t)=e_{max}$,
$e(x'=0,t)=e_{max}$, ![]() $L^{'}_f(t)$ is given by
$L^{'}_f(t)$ is given by
 \begin{align} L_f^{'}(t) &= \frac{1}{6}\left(\frac{\epsilon B}{c}\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} =\left(\frac{5}{6(1+\sqrt{6})}\right)^{1/2}\left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} \nonumber\\ &\simeq 0.4915\left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2}, \quad t\ge t_{max}, \end{align}
\begin{align} L_f^{'}(t) &= \frac{1}{6}\left(\frac{\epsilon B}{c}\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} =\left(\frac{5}{6(1+\sqrt{6})}\right)^{1/2}\left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} \nonumber\\ &\simeq 0.4915\left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2}, \quad t\ge t_{max}, \end{align}or in dimensionless form (see(2.3))
In ![]() $(O,x,y)$, the triple point position is denoted
$(O,x,y)$, the triple point position is denoted ![]() $\mathcal {L}_f(t)$ with
$\mathcal {L}_f(t)$ with
with the straightforward equivalent relationship in dimensionless form.
The purpose is now to determine ![]() $L_b(t)$ and, subsequently,
$L_b(t)$ and, subsequently, ![]() $\mathcal {L}_f$.
$\mathcal {L}_f$.
4.3.2. Dynamics of the bulk meniscus and triple point
Since the bulk meniscus is assumed to remain in its static shape, all the interfacial points in this region move with the same velocity, which is simply equal to ![]() ${\mathrm {d}L_b(t)}/{\mathrm {d}t}$. To determine this last quantity, it is convenient to write the total volume conservation in the
${\mathrm {d}L_b(t)}/{\mathrm {d}t}$. To determine this last quantity, it is convenient to write the total volume conservation in the ![]() $\beta$ phase under the form (see details on how to reach this result in Appendix B)
$\beta$ phase under the form (see details on how to reach this result in Appendix B)
with ![]() $S_t$ the total cross-sectional area of the channel given by (4.3b). Here,
$S_t$ the total cross-sectional area of the channel given by (4.3b). Here, ![]() $Q'_{f}(t)$ is the volume flow rate in the corner film that can be expressed as
$Q'_{f}(t)$ is the volume flow rate in the corner film that can be expressed as
 \begin{equation} Q'_{f}(t) =\frac{\mathrm{d}}{\mathrm{d} t}\int_0 ^{L_f^{'}(t)} S(x{'},t) \,\mathrm{d}\kern 0.06em x', \end{equation}
\begin{equation} Q'_{f}(t) =\frac{\mathrm{d}}{\mathrm{d} t}\int_0 ^{L_f^{'}(t)} S(x{'},t) \,\mathrm{d}\kern 0.06em x', \end{equation}
with ![]() $S(x',t)$ the corner film cross-sectional area reported in (3.3a). Making use of the expression of the film width in the moving frame of reference given in (4.12a), noting that
$S(x',t)$ the corner film cross-sectional area reported in (3.3a). Making use of the expression of the film width in the moving frame of reference given in (4.12a), noting that ![]() ${\alpha ^2 c^2 L_f^{'4}}/{t^2}=e_{max}^2$ and employing the change of variable
${\alpha ^2 c^2 L_f^{'4}}/{t^2}=e_{max}^2$ and employing the change of variable ![]() $X'={x'}/{L^{'}_f}$, leads to
$X'={x'}/{L^{'}_f}$, leads to
 \begin{align} Q'_{f}(t) &=\frac{\epsilon ^2 A e_{max}^2}{4B^2} \frac{\mathrm{d}}{\mathrm{d}t} \left( L^{'}_f\int_0 ^1 \left(\frac{a}{c}X'^2+\frac{b}{c}X'+1\right)^2 \,\mathrm{d}\kern 0.06em X' \right) \nonumber\\ &= \frac{10+\sqrt{6}}{120}\frac{\epsilon ^2 A e_{max}^2}{B^2} \frac{\mathrm{d} L_f^{'} }{\mathrm{d}t}\simeq 0.1037\frac{\epsilon ^2 A e_{max}^2}{B^2} \frac{\mathrm{d} L_f^{'} }{\mathrm{d}t}. \end{align}
\begin{align} Q'_{f}(t) &=\frac{\epsilon ^2 A e_{max}^2}{4B^2} \frac{\mathrm{d}}{\mathrm{d}t} \left( L^{'}_f\int_0 ^1 \left(\frac{a}{c}X'^2+\frac{b}{c}X'+1\right)^2 \,\mathrm{d}\kern 0.06em X' \right) \nonumber\\ &= \frac{10+\sqrt{6}}{120}\frac{\epsilon ^2 A e_{max}^2}{B^2} \frac{\mathrm{d} L_f^{'} }{\mathrm{d}t}\simeq 0.1037\frac{\epsilon ^2 A e_{max}^2}{B^2} \frac{\mathrm{d} L_f^{'} }{\mathrm{d}t}. \end{align}Substituting the above relationship into (4.15) yields
 \begin{equation} \frac{\mathrm{d} L_b(t)}{\mathrm{d} t} =\frac{1}{S_{t}}\left({Q_0}-\frac{10+\sqrt{6}}{60} \frac{\epsilon ^2 A e_{max}^2}{B^2}\frac{\mathrm{d}L^{'}_f}{\mathrm{d}t}\right), \quad t\ge t_{max}, \end{equation}
\begin{equation} \frac{\mathrm{d} L_b(t)}{\mathrm{d} t} =\frac{1}{S_{t}}\left({Q_0}-\frac{10+\sqrt{6}}{60} \frac{\epsilon ^2 A e_{max}^2}{B^2}\frac{\mathrm{d}L^{'}_f}{\mathrm{d}t}\right), \quad t\ge t_{max}, \end{equation}or in dimensionless form (see (2.3) and (4.3a))
 \begin{equation} v_b^*= \frac{\mathrm{d}L_b^*}{\mathrm{d}t^*}=\left(\overline{Ca}- \frac{10+\sqrt{6}}{60}\frac{\epsilon A}{B^2}e_{max}^{*2}\frac{\mathrm{d}L_f^{'*}}{\mathrm{d}t^*}\right) . \end{equation}
\begin{equation} v_b^*= \frac{\mathrm{d}L_b^*}{\mathrm{d}t^*}=\left(\overline{Ca}- \frac{10+\sqrt{6}}{60}\frac{\epsilon A}{B^2}e_{max}^{*2}\frac{\mathrm{d}L_f^{'*}}{\mathrm{d}t^*}\right) . \end{equation}This expression is the speed of displacement of the interfacial matching point between the corner film and the bulk meniscus, which is also the speed of displacement of the bulk meniscus itself, since this part of the interface is assumed to move without deforming.
The above equation can now be integrated over time (between ![]() $t_{max}$ and
$t_{max}$ and ![]() $t$), and keeping in mind that
$t$), and keeping in mind that ![]() $L_b(t_{max})=0$, this leads to the expression of the position over time of the film to bulk meniscus matching point that is given by
$L_b(t_{max})=0$, this leads to the expression of the position over time of the film to bulk meniscus matching point that is given by
 \begin{align} L_b(t) &=\frac{1}{S_t}\left(Q_0(t-t_{max})-\frac{10+\sqrt{6}}{60} \frac{\epsilon ^2 A e_{max}^2}{B^2}\left(L^{'}_f(t)-L_{f{max}}\right)\right) \nonumber\\ &=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{60}\frac{\epsilon ^2 A e_{max}^2}{B^2}L^{'}_f(t)\right) \nonumber\\ &=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{12(30(1+\sqrt{6}))^{1/2}}A \left(\frac{\epsilon^5e^5_{max}}{B^3}\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right)\nonumber\\ &\simeq\frac{1}{S_t}\left(Q_0t-0.1020A\left(\frac{\epsilon^5e^5_{max}}{B^3} \frac{\sigma}{\mu_\beta}t\right)^{1/2}\right),\quad t\ge t_{max}, \end{align}
\begin{align} L_b(t) &=\frac{1}{S_t}\left(Q_0(t-t_{max})-\frac{10+\sqrt{6}}{60} \frac{\epsilon ^2 A e_{max}^2}{B^2}\left(L^{'}_f(t)-L_{f{max}}\right)\right) \nonumber\\ &=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{60}\frac{\epsilon ^2 A e_{max}^2}{B^2}L^{'}_f(t)\right) \nonumber\\ &=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{12(30(1+\sqrt{6}))^{1/2}}A \left(\frac{\epsilon^5e^5_{max}}{B^3}\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right)\nonumber\\ &\simeq\frac{1}{S_t}\left(Q_0t-0.1020A\left(\frac{\epsilon^5e^5_{max}}{B^3} \frac{\sigma}{\mu_\beta}t\right)^{1/2}\right),\quad t\ge t_{max}, \end{align}
where ![]() $A$,
$A$, ![]() $B$ and
$B$ and ![]() $S_t$ are respectively given by (3.3b), (3.3d) and (4.3b). In dimensionless form, it reads (cf. (2.3) and (4.3a))
$S_t$ are respectively given by (3.3b), (3.3d) and (4.3b). In dimensionless form, it reads (cf. (2.3) and (4.3a))
 \begin{equation} L_b^*(t^*)\simeq\overline{Ca}t^*-0.1020 A \left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}t^*\right)^{1/2}, \quad t^*\ge t^*_{max}. \end{equation}
\begin{equation} L_b^*(t^*)\simeq\overline{Ca}t^*-0.1020 A \left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}t^*\right)^{1/2}, \quad t^*\ge t^*_{max}. \end{equation} Finally, the position of the triple point with respect to the channel inlet (i.e. in the system of coordinates ![]() $(O,x,y)$) can be expressed upon substitution of (4.18a) into (4.14), which, along with (4.13a), gives
$(O,x,y)$) can be expressed upon substitution of (4.18a) into (4.14), which, along with (4.13a), gives
 \begin{align} \mathcal{L}_f(t)&=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{12(30(1+\sqrt{6}))^{1/2}}A \left(\frac{\epsilon^5e^5_{max}}{B^3}\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right) \nonumber\\ &\quad +\left(\frac{5}{6(1+\sqrt{6})}\right)^{1/2} \left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} \nonumber\\ &\simeq \frac{1}{S_t}\left[Q_0t+\left(0.4915(\epsilon^3B\ell^4e_{max})^{1/2} \vphantom{\left(\frac{\epsilon^5e^5_{max}}{B^3}\right)^{1/2}}\right.\right. \nonumber\\ &\quad \left.\left. -\,0.1020A\left(\frac{\epsilon^5e^5_{max}}{B^3}\right)^{1/2}\right) \left(\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right],\quad t\ge t_{max}, \end{align}
\begin{align} \mathcal{L}_f(t)&=\frac{1}{S_t}\left(Q_0t-\frac{10+\sqrt{6}}{12(30(1+\sqrt{6}))^{1/2}}A \left(\frac{\epsilon^5e^5_{max}}{B^3}\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right) \nonumber\\ &\quad +\left(\frac{5}{6(1+\sqrt{6})}\right)^{1/2} \left(\epsilon B\frac{\sigma}{\mu_\beta}e_{max}t\right)^{1/2} \nonumber\\ &\simeq \frac{1}{S_t}\left[Q_0t+\left(0.4915(\epsilon^3B\ell^4e_{max})^{1/2} \vphantom{\left(\frac{\epsilon^5e^5_{max}}{B^3}\right)^{1/2}}\right.\right. \nonumber\\ &\quad \left.\left. -\,0.1020A\left(\frac{\epsilon^5e^5_{max}}{B^3}\right)^{1/2}\right) \left(\frac{\sigma}{\mu_\beta}t\right)^{1/2}\right],\quad t\ge t_{max}, \end{align}
with ![]() $S_t$ given by (4.3b). In terms of dimensionless variables, this writes
$S_t$ given by (4.3b). In terms of dimensionless variables, this writes
 \begin{align} \mathcal{L}_f^*\simeq\overline{Ca}t^*+\left(0.4915(\epsilon Be_{max}^*)^{1/2} -0.1020 A\left(\left(\frac{\epsilon}{B}\right)^{3}e_{max}^{*5}\right)^{1/2}\right)t^{*1/2},\quad t^*\ge t^{*}_{max}. \end{align}
\begin{align} \mathcal{L}_f^*\simeq\overline{Ca}t^*+\left(0.4915(\epsilon Be_{max}^*)^{1/2} -0.1020 A\left(\left(\frac{\epsilon}{B}\right)^{3}e_{max}^{*5}\right)^{1/2}\right)t^{*1/2},\quad t^*\ge t^{*}_{max}. \end{align}
Note that the time scaling of ![]() $\mathcal {L}_f$ in the bulk and corner film flow regime analysed here contrasts with the dependence of
$\mathcal {L}_f$ in the bulk and corner film flow regime analysed here contrasts with the dependence of ![]() $L_f$ on
$L_f$ on ![]() $t^{3/5}$ in the liquid film regime (cf. (4.2)).
$t^{3/5}$ in the liquid film regime (cf. (4.2)).
Instead of ![]() $L_b(t)$, interest shall rather be on the position of the apex (or central point) of the bulk meniscus, denoted
$L_b(t)$, interest shall rather be on the position of the apex (or central point) of the bulk meniscus, denoted ![]() $L_a(t)$ (see figures 1(d) and 12). This position is given by
$L_a(t)$ (see figures 1(d) and 12). This position is given by
and a similar dimensionless form. Here, ![]() $\ell _m$ represents the (constant) size of the bulk meniscus in the
$\ell _m$ represents the (constant) size of the bulk meniscus in the ![]() $x$ direction, i.e. its extension from the apex to its ending point (the connection to the corner film) at
$x$ direction, i.e. its extension from the apex to its ending point (the connection to the corner film) at ![]() $e=e_{max}$. The value of
$e=e_{max}$. The value of ![]() $\ell _m$ can be obtained from a procedure detailed in Appendix C. However, since
$\ell _m$ can be obtained from a procedure detailed in Appendix C. However, since ![]() $\ell _m$ is expected to be
$\ell _m$ is expected to be ![]() $O(\ell )$,
$O(\ell )$, ![]() $L_a(t)$ does not significantly differ from
$L_a(t)$ does not significantly differ from ![]() $L_b(t)$ provided
$L_b(t)$ provided ![]() $L_b(t)\gg \ell$, which, from (4.18a), imposes
$L_b(t)\gg \ell$, which, from (4.18a), imposes
 \begin{equation} t-0.1020\frac{A}{Q_0}\left(\frac{\epsilon^5e^5_{max}}{B^3} \frac{\sigma}{\mu_\beta}\right)^{1/2} t^{1/2}\gg \frac{S_t \ell}{Q_0}, \end{equation}
\begin{equation} t-0.1020\frac{A}{Q_0}\left(\frac{\epsilon^5e^5_{max}}{B^3} \frac{\sigma}{\mu_\beta}\right)^{1/2} t^{1/2}\gg \frac{S_t \ell}{Q_0}, \end{equation}with the dimensionless equivalent form given by
 \begin{equation} t^*-0.1020 \frac{A}{\overline{Ca}}\left(\left(\frac{\epsilon}{B}\right)^3 e_{max}^{*5}\right)^{1/2}t^{*1/2}\gg \overline{Ca}. \end{equation}
\begin{equation} t^*-0.1020 \frac{A}{\overline{Ca}}\left(\left(\frac{\epsilon}{B}\right)^3 e_{max}^{*5}\right)^{1/2}t^{*1/2}\gg \overline{Ca}. \end{equation}
In other words, ![]() $\ell _m$ can be disregarded in this limit of time. For instance, for a channel with
$\ell _m$ can be disregarded in this limit of time. For instance, for a channel with ![]() $\ell = 100\,\mathrm {\mu }$m and
$\ell = 100\,\mathrm {\mu }$m and ![]() $h_0 = 1\,\mathrm {\mu }$m invaded by water (
$h_0 = 1\,\mathrm {\mu }$m invaded by water (![]() $\mu _\beta = 1$ mPa s,
$\mu _\beta = 1$ mPa s, ![]() $\sigma = 72\,{\rm mN}\,{\rm m}^{-1}$) or an oil (
$\sigma = 72\,{\rm mN}\,{\rm m}^{-1}$) or an oil (![]() $\mu _\beta = 100$ mPa s,
$\mu _\beta = 100$ mPa s, ![]() $\sigma = 20\,{\rm mN}\,{\rm m}^{-1}$) at
$\sigma = 20\,{\rm mN}\,{\rm m}^{-1}$) at ![]() $Q_0 = 10^{-4}$ ml min
$Q_0 = 10^{-4}$ ml min![]() $^{-1}$ with
$^{-1}$ with ![]() $\theta _e=0^\circ$, the left-hand side of (4.21a) is a hundred times larger than the right-hand side at a critical time
$\theta _e=0^\circ$, the left-hand side of (4.21a) is a hundred times larger than the right-hand side at a critical time ![]() $t \simeq 0.66$ s for water and
$t \simeq 0.66$ s for water and ![]() $t \simeq 0.60$ s for oil. This critical time is expected to decrease as the flow rate is further increased.
$t \simeq 0.60$ s for oil. This critical time is expected to decrease as the flow rate is further increased.
Should the corner film flow be omitted in the description of the imbibition dynamics, the position of the bulk meniscus at constant volume flow rate, ![]() $Q_0$, denoted
$Q_0$, denoted ![]() $L_w(t)$ in this case, would be linear in time, given by
$L_w(t)$ in this case, would be linear in time, given by
with ![]() $S_t$ defined in (4.3b). In dimensionless form (see (2.3) and (4.3a)), this writes
$S_t$ defined in (4.3b). In dimensionless form (see (2.3) and (4.3a)), this writes
At this point, the assumption of the moving frame of reference ![]() $(O', x', y')$ free of acceleration with respect to
$(O', x', y')$ free of acceleration with respect to ![]() $(O,x,y)$ shall be reinspected. Indeed, the expression of the speed of displacement of
$(O,x,y)$ shall be reinspected. Indeed, the expression of the speed of displacement of ![]() $O'$, given by
$O'$, given by ![]() ${\mathrm {d}L_b}/{\mathrm {d}t}$ in (4.17a), may appear in contradiction with this assumption. Nevertheless, the hypothesis can be considered as a valid one under the constraint extracted from this equation and given by
${\mathrm {d}L_b}/{\mathrm {d}t}$ in (4.17a), may appear in contradiction with this assumption. Nevertheless, the hypothesis can be considered as a valid one under the constraint extracted from this equation and given by
Upon substitution of the expressions of ![]() $L^{'}_f$, this leads to
$L^{'}_f$, this leads to
that is easily satisfied, keeping in mind that this constraint is of importance after the bulk meniscus entrance in the channel, which occurs at ![]() $t=t_{max}$.
$t=t_{max}$.
4.4. Results and discussion
4.4.1. Validation of the model
In this section a comparison of the predictions from the model derived above with experimental data reported by Amyot (Reference Amyot2004) is carried out for validation purposes in the bulk and corner film flow regime.
Details on the experimental set-up used in the above mentioned reference can be found in Geoffroy et al. (Reference Geoffroy, Plouraboué, Prat and Amyot2006). The triangular channel (![]() $2\ell =50\,{\rm mm}$,
$2\ell =50\,{\rm mm}$, ![]() $h_0=1\,{\rm mm}$) was obtained from a machining process on a resin slab and was closed with a Plexiglas plate clamped at the top of it. The channel was placed horizontally and, for the experiments at constant flow rate under interest here, two silicone oils were employed as wetting liquids, the characteristics of which are
$h_0=1\,{\rm mm}$) was obtained from a machining process on a resin slab and was closed with a Plexiglas plate clamped at the top of it. The channel was placed horizontally and, for the experiments at constant flow rate under interest here, two silicone oils were employed as wetting liquids, the characteristics of which are ![]() $\sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$,
$\sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$, ![]() $\mu _\beta =0.068\,{\rm Pa}\,{\rm s}$ (
$\mu _\beta =0.068\,{\rm Pa}\,{\rm s}$ (![]() $v_{\beta r}\simeq 0.3191\,{\rm m}\,{\rm s}^{-1}$, see (2.3c)) for fluid 1, and
$v_{\beta r}\simeq 0.3191\,{\rm m}\,{\rm s}^{-1}$, see (2.3c)) for fluid 1, and ![]() $\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$,
$\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$, ![]() $\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$ (
$\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$ (![]() $v_{\beta r}\simeq 0.1059\,{\rm m}\,{\rm s}^{-1}$) for fluid 2. They were injected with a screw-driven pump. Images of the imbibition front taken from the top of the channel were recorded every second during the experiments.
$v_{\beta r}\simeq 0.1059\,{\rm m}\,{\rm s}^{-1}$) for fluid 2. They were injected with a screw-driven pump. Images of the imbibition front taken from the top of the channel were recorded every second during the experiments.
Three examples of recorded images (at ![]() $t=100\,{\rm s}$,
$t=100\,{\rm s}$, ![]() $t=500\,{\rm s}$ and
$t=500\,{\rm s}$ and ![]() $t=1000\,{\rm s}$) are depicted in figure 3, illustrating the liquid film regime for the first one and the bulk and corner film flow regime for the last two ones. From image binarisation in the latter regime, the apex of the bulk meniscus can be located relative to the channel inlet so that
$t=1000\,{\rm s}$) are depicted in figure 3, illustrating the liquid film regime for the first one and the bulk and corner film flow regime for the last two ones. From image binarisation in the latter regime, the apex of the bulk meniscus can be located relative to the channel inlet so that ![]() $L_a(t)$ can be obtained. The corresponding experimental data are reported in a dimensionless form (
$L_a(t)$ can be obtained. The corresponding experimental data are reported in a dimensionless form (![]() $L_a^*=L_a/\ell$), versus the dimensionless time (
$L_a^*=L_a/\ell$), versus the dimensionless time (![]() $t^*=v_{\beta r} t/\ell$, see (2.3)) as open symbols in figure 4(a,b) for fluid 1 with
$t^*=v_{\beta r} t/\ell$, see (2.3)) as open symbols in figure 4(a,b) for fluid 1 with ![]() $Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$ (
$Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$ (![]() $\overline {Ca}\simeq 6.6851\times 10^{-4}$) and fluid 2 with
$\overline {Ca}\simeq 6.6851\times 10^{-4}$) and fluid 2 with ![]() $Q_0=0.1\,{\rm ml}\,{\rm min}^{-1}$ (
$Q_0=0.1\,{\rm ml}\,{\rm min}^{-1}$ (![]() $\overline {Ca}\simeq 6.2947\times 10^{-4}$), respectively. The predictions of
$\overline {Ca}\simeq 6.2947\times 10^{-4}$), respectively. The predictions of ![]() $L_a^*$ (see (4.20), (4.18b) and Appendix C) are also reported in these figures as continuous lines. Comparison between the two confirms the validity of the model, the relative difference between experimental data and the predictions remaining smaller than 10 %. The observations confirm the time laps before the bulk meniscus entrance in the channel, i.e. the existence of the liquid film regime up to
$L_a^*$ (see (4.20), (4.18b) and Appendix C) are also reported in these figures as continuous lines. Comparison between the two confirms the validity of the model, the relative difference between experimental data and the predictions remaining smaller than 10 %. The observations confirm the time laps before the bulk meniscus entrance in the channel, i.e. the existence of the liquid film regime up to ![]() $t^*=t^*_{max}$ (see (4.4b)), followed by the bulk and corner film flow regime.
$t^*=t^*_{max}$ (see (4.4b)), followed by the bulk and corner film flow regime.

Figure 3. Invasion of a wetting liquid in a channel with a triangular cross-section at a constant flow rate observed in Amyot (Reference Amyot2004). Top view of the channel at times ![]() $t=100\,{\rm s}$,
$t=100\,{\rm s}$, ![]() $t=500\,{\rm s}$ and
$t=500\,{\rm s}$ and ![]() $t=1000\,{\rm s}$. Here
$t=1000\,{\rm s}$. Here ![]() $2\ell =50\,{\rm mm}$,
$2\ell =50\,{\rm mm}$, ![]() $h_0=1\,{\rm mm}$,
$h_0=1\,{\rm mm}$, ![]() $\mu _\beta =0.068\,{\rm Pa}\,{\rm s},\ \sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$ (fluid 1),
$\mu _\beta =0.068\,{\rm Pa}\,{\rm s},\ \sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$ (fluid 1), ![]() $Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$.
$Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$.

Figure 4. Comparison of the dimensionless positions of the apex of the bulk meniscus, ![]() $L_a^*=L_a/\ell$ (see (4.20), (4.18b) and Appendix C), versus the dimensionless time,
$L_a^*=L_a/\ell$ (see (4.20), (4.18b) and Appendix C), versus the dimensionless time, ![]() $t^*=v_{\beta r}t/ \ell$, predicted from the model (see (4.20)) and obtained experimentally by Amyot (Reference Amyot2004). The evolution of the triple point position
$t^*=v_{\beta r}t/ \ell$, predicted from the model (see (4.20)) and obtained experimentally by Amyot (Reference Amyot2004). The evolution of the triple point position ![]() $\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (4.19b)) is also reported. The channel characteristics are
$\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (4.19b)) is also reported. The channel characteristics are ![]() $2\ell =50\,{\rm mm}$ and
$2\ell =50\,{\rm mm}$ and ![]() $h_0=1\,{\rm mm}$, assuming perfect wetting (
$h_0=1\,{\rm mm}$, assuming perfect wetting (![]() $\theta _e=0^\circ$) of the injected fluid. (a) Fluid 1:
$\theta _e=0^\circ$) of the injected fluid. (a) Fluid 1: ![]() $\sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$,
$\sigma =21.7\,{\rm mN}\,{\rm m}^{-1}$, ![]() $\mu _\beta =0.068\,{\rm Pa}\,{\rm s}$ (
$\mu _\beta =0.068\,{\rm Pa}\,{\rm s}$ (![]() $v_{\beta r}\simeq 0.3191\,{\rm m}\,{\rm s}^{-1}$) with
$v_{\beta r}\simeq 0.3191\,{\rm m}\,{\rm s}^{-1}$) with ![]() $Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$ (
$Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$ (![]() $\overline {Ca}\simeq 6.6851\times 10^{-4}$) (cf. (2.3) and (4.3a)); (b) fluid 2:
$\overline {Ca}\simeq 6.6851\times 10^{-4}$) (cf. (2.3) and (4.3a)); (b) fluid 2: ![]() $\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$
$\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$ ![]() $\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$ (
$\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$ (![]() $v_{\beta r}\simeq 0.1059\,{\rm m}\,{\rm s}^{-1}$) with
$v_{\beta r}\simeq 0.1059\,{\rm m}\,{\rm s}^{-1}$) with ![]() $Q_0=0.1\,{\rm ml}\,{\rm min}^{-1}$ (
$Q_0=0.1\,{\rm ml}\,{\rm min}^{-1}$ (![]() $\overline {Ca} \simeq 6.2947\times 10^{-4}$). Here
$\overline {Ca} \simeq 6.2947\times 10^{-4}$). Here ![]() $t^*_{max}$ (see (4.4b)) indicates the dimensionless time at which the bulk meniscus enters the channel. The dashed line represents the prediction of the dimensionless position of the bulk meniscus while neglecting the film ahead of it,
$t^*_{max}$ (see (4.4b)) indicates the dimensionless time at which the bulk meniscus enters the channel. The dashed line represents the prediction of the dimensionless position of the bulk meniscus while neglecting the film ahead of it, ![]() $L_w^*=L_w/\ell$ (see (4.22b)).
$L_w^*=L_w/\ell$ (see (4.22b)).
In figure 4(a,b) the dynamics of the bulk meniscus, ![]() $L_w^*(t^*)$ (see (4.22b)), when the liquid films ahead of it are neglected is also represented as dashed lines, showing that, this approximation overestimates the position of the bulk meniscus, as expected. Indeed, the flow fraction supplying the corner films contributes to slow down the bulk meniscus displacement. In these figures, the triple point dynamics,
$L_w^*(t^*)$ (see (4.22b)), when the liquid films ahead of it are neglected is also represented as dashed lines, showing that, this approximation overestimates the position of the bulk meniscus, as expected. Indeed, the flow fraction supplying the corner films contributes to slow down the bulk meniscus displacement. In these figures, the triple point dynamics, ![]() $\mathcal {L}^*_f(t^*)$ (see (4.19b)), is reported as dotted lines, showing that this point is ahead of the bulk meniscus with a distance that increases with time. In particular, this means that the wetting liquid is expected to be in contact with the outlet of a channel having a given finite length much before the bulk meniscus arrival.
$\mathcal {L}^*_f(t^*)$ (see (4.19b)), is reported as dotted lines, showing that this point is ahead of the bulk meniscus with a distance that increases with time. In particular, this means that the wetting liquid is expected to be in contact with the outlet of a channel having a given finite length much before the bulk meniscus arrival.
To further verify the validity of the theoretical development proposed above, the hypothesis that the bulk meniscus shape remains constant, identical to its static configuration, during the imbibition process is checked. The value of ![]() $e_{max}$ predicted from (3.14c) (after substitution of (4.6c)) was positioned at the corresponding location at the interface on recorded images and, from this point, the size of the bulk meniscus,
$e_{max}$ predicted from (3.14c) (after substitution of (4.6c)) was positioned at the corresponding location at the interface on recorded images and, from this point, the size of the bulk meniscus, ![]() $\ell _m$, was evaluated. This was performed in the case of the experiment with fluid 1 and a flow rate
$\ell _m$, was evaluated. This was performed in the case of the experiment with fluid 1 and a flow rate ![]() $Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$, yielding
$Q_0=0.32\,{\rm ml}\,{\rm min}^{-1}$, yielding ![]() $\ell _m^*\simeq 0.37, 0.31, 0.35, 0.33, 0.31$ at
$\ell _m^*\simeq 0.37, 0.31, 0.35, 0.33, 0.31$ at ![]() $t=400, 500, 600, 700, 800\,{\rm s}$, respectively, i.e. an average value
$t=400, 500, 600, 700, 800\,{\rm s}$, respectively, i.e. an average value ![]() $\ell _m^*\simeq 0.334$. The value predicted from the solution of (C2) (or (C3)) is
$\ell _m^*\simeq 0.334$. The value predicted from the solution of (C2) (or (C3)) is ![]() $\ell _m^*=0.3104$, which is in satisfactory agreement since the relative difference is
$\ell _m^*=0.3104$, which is in satisfactory agreement since the relative difference is ![]() ${\sim }7\,\%$.
${\sim }7\,\%$.
4.4.2. Analysis of the model
The impact of some of the parameters involved in the model is now shortly addressed, namely ![]() $\overline {Ca}$ and the contact angle,
$\overline {Ca}$ and the contact angle, ![]() $\theta _e$.
$\theta _e$.
The dependence of the dimensionless positions of the apex of the bulk meniscus, ![]() $L_a^{*}=L_a/\ell$ (cf. (4.20), (4.18b) and Appendix C), and of the triple point,
$L_a^{*}=L_a/\ell$ (cf. (4.20), (4.18b) and Appendix C), and of the triple point, ![]() $\mathcal {L}_f^{*}=\mathcal {L}_f/\ell$ (see (4.19b)), is illustrated versus
$\mathcal {L}_f^{*}=\mathcal {L}_f/\ell$ (see (4.19b)), is illustrated versus ![]() $t^*$ (see (2.3)) in figure 5(a) for two values of the capillary number,
$t^*$ (see (2.3)) in figure 5(a) for two values of the capillary number, ![]() $\overline {Ca}$, namely
$\overline {Ca}$, namely ![]() $\overline {Ca}_1\simeq 1.8519\times 10^{-5}$ and
$\overline {Ca}_1\simeq 1.8519\times 10^{-5}$ and ![]() $\overline {Ca}_2\simeq 0.0042$, taking
$\overline {Ca}_2\simeq 0.0042$, taking ![]() $\epsilon =0.08$. The time evolution of the position of the bulk meniscus,
$\epsilon =0.08$. The time evolution of the position of the bulk meniscus, ![]() $L_w^*=L_w/\ell$ (see (4.22b)), when the corner films are neglected is also reported as a dashed line in this figure. These results show that the dynamics of the triple point is significantly faster when
$L_w^*=L_w/\ell$ (see (4.22b)), when the corner films are neglected is also reported as a dashed line in this figure. These results show that the dynamics of the triple point is significantly faster when ![]() $\overline {Ca}$ decreases and, simultaneously, that the dynamics of the bulk meniscus is slowed down. This is explained by the fact that, when the capillary number decreases, capillary effects become more dominant compared with viscous effects, favouring the development of the corner films that contribute to deplete flow in the bulk behind the bulk meniscus, thus contributing to its slow down. This also explains the concomitant increase of the time,
$\overline {Ca}$ decreases and, simultaneously, that the dynamics of the bulk meniscus is slowed down. This is explained by the fact that, when the capillary number decreases, capillary effects become more dominant compared with viscous effects, favouring the development of the corner films that contribute to deplete flow in the bulk behind the bulk meniscus, thus contributing to its slow down. This also explains the concomitant increase of the time, ![]() $t_{max}^*$, at which the bulk meniscus enters the channel, depicted as
$t_{max}^*$, at which the bulk meniscus enters the channel, depicted as ![]() $t_{{max},1}^*$ and
$t_{{max},1}^*$ and ![]() $t_{{max},2}^*$ in figure 5(a) for the two capillary numbers under consideration. When viscous effects become more significant compared with capillary effects (see results for
$t_{{max},2}^*$ in figure 5(a) for the two capillary numbers under consideration. When viscous effects become more significant compared with capillary effects (see results for ![]() $\overline {Ca}_2$), the corner films are so short that
$\overline {Ca}_2$), the corner films are so short that ![]() $L_a^*\simeq L_w^*$.
$L_a^*\simeq L_w^*$.

Figure 5. Dimensionless positions versus ![]() $t^*$ (see (2.3)) of the triple point,
$t^*$ (see (2.3)) of the triple point, ![]() $\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (4.19b)), and of the apex of the bulk meniscus with the film ahead of it,
$\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (4.19b)), and of the apex of the bulk meniscus with the film ahead of it, ![]() $L_a^*=L_a/\ell$ (see (4.20), (4.18b) and Appendix C), and without the film,
$L_a^*=L_a/\ell$ (see (4.20), (4.18b) and Appendix C), and without the film, ![]() $L_w^*=L_w/\ell$ (see (4.22b)), for (a) two values of the global capillary number,
$L_w^*=L_w/\ell$ (see (4.22b)), for (a) two values of the global capillary number, ![]() $\overline {Ca}_1\simeq 1.8519\times 10^{-5}$ and
$\overline {Ca}_1\simeq 1.8519\times 10^{-5}$ and ![]() $\overline {Ca}_2\simeq 0.0042$, and (b) two values of the contact angle,
$\overline {Ca}_2\simeq 0.0042$, and (b) two values of the contact angle, ![]() $\theta _e=0^\circ$ and
$\theta _e=0^\circ$ and ![]() $\theta _e=30^\circ$, taking
$\theta _e=30^\circ$, taking ![]() $\overline {Ca}\simeq 1.8519\times 10^{-5}$. Here
$\overline {Ca}\simeq 1.8519\times 10^{-5}$. Here ![]() $\epsilon =0.08$. In (a),
$\epsilon =0.08$. In (a), ![]() $t_{{max},1}^*\simeq 2.2316\times 10^{6}$ and
$t_{{max},1}^*\simeq 2.2316\times 10^{6}$ and ![]() $t_{{max},2}^*\simeq 46.6631$ indicate the values of
$t_{{max},2}^*\simeq 46.6631$ indicate the values of ![]() $t_{max}^*$ (see (4.4b)) at which the bulk meniscus enters the channel for the above two values of
$t_{max}^*$ (see (4.4b)) at which the bulk meniscus enters the channel for the above two values of ![]() $\overline {Ca}$, respectively.
$\overline {Ca}$, respectively.
In figure 5(b) the impact of the contact angle, ![]() $\theta _e$, on the dynamics of the bulk meniscus and the triple point is explored in the range
$\theta _e$, on the dynamics of the bulk meniscus and the triple point is explored in the range ![]() $0^\circ \le \theta _e\le 30^\circ$, keeping
$0^\circ \le \theta _e\le 30^\circ$, keeping ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $\overline {Ca}\simeq 1.8519\times 10^{-5}$. As expected, when
$\overline {Ca}\simeq 1.8519\times 10^{-5}$. As expected, when ![]() $\theta _e$ increases, the triple point is slowed down, again due to the fact that capillary effects are weakened with respect to viscous effects and, consequently, the bulk meniscus dynamics is favoured, while
$\theta _e$ increases, the triple point is slowed down, again due to the fact that capillary effects are weakened with respect to viscous effects and, consequently, the bulk meniscus dynamics is favoured, while ![]() $t_{max}^*$ is shortened. Nevertheless, as indicated by this figure, the contrast remains weak in the range of
$t_{max}^*$ is shortened. Nevertheless, as indicated by this figure, the contrast remains weak in the range of ![]() $\theta _e$ investigated here, in particular regarding the bulk meniscus dynamics.
$\theta _e$ investigated here, in particular regarding the bulk meniscus dynamics.
In order to better illustrate the contrast in the dynamics of the bulk meniscus and the triple point induced by the corner film flow, the ratio between the times for the apex of the bulk meniscus and the triple point to reach a given distance from the channel inlet, namely ![]() $50\ell$, and denoted
$50\ell$, and denoted ![]() $t_p^*(L_a^*)/t_p^*(\mathcal {L}_f^*)$, is represented versus
$t_p^*(L_a^*)/t_p^*(\mathcal {L}_f^*)$, is represented versus ![]() $\overline {Ca}$ in figure 6 for
$\overline {Ca}$ in figure 6 for ![]() $\epsilon =0.04$,
$\epsilon =0.04$, ![]() $0.06$ and
$0.06$ and ![]() $0.08$, keeping
$0.08$, keeping ![]() $\theta _e=0^\circ$. As expected, the time contrast strongly increases when capillary forces increase as a result of a combined effect of the triple point dynamics enhancement and bulk meniscus slow down; it also increases with
$\theta _e=0^\circ$. As expected, the time contrast strongly increases when capillary forces increase as a result of a combined effect of the triple point dynamics enhancement and bulk meniscus slow down; it also increases with ![]() $\epsilon$. This indicates that the wetting liquid can reach the channel outlet with the corner film far before the bulk meniscus arrival, which can be of central importance in some applications.
$\epsilon$. This indicates that the wetting liquid can reach the channel outlet with the corner film far before the bulk meniscus arrival, which can be of central importance in some applications.

Figure 6. Ratio between the times, ![]() $t_{p}^*(L_a^*)$ and
$t_{p}^*(L_a^*)$ and ![]() $t_{p}^*(\mathcal {L}_f^*)$, necessary for, respectively, the apex of the bulk meniscus and the triple point to reach a position located at
$t_{p}^*(\mathcal {L}_f^*)$, necessary for, respectively, the apex of the bulk meniscus and the triple point to reach a position located at ![]() $50\ell$ from the channel inlet versus
$50\ell$ from the channel inlet versus ![]() ${\overline {Ca}}$ for
${\overline {Ca}}$ for ![]() $\epsilon =0.04$,
$\epsilon =0.04$, ![]() $0.06$ and
$0.06$ and ![]() $0.08$. Here
$0.08$. Here ![]() $\theta _e=0^\circ$.
$\theta _e=0^\circ$.
As a final analysis, the dimensionless speeds of displacement of the bulk meniscus, ![]() ${v_b^*}={\mathrm {d} L_b^*}/{\mathrm {d} t^*}$, in the fixed system of coordinates,
${v_b^*}={\mathrm {d} L_b^*}/{\mathrm {d} t^*}$, in the fixed system of coordinates, ![]() $(O,x,y)$ (see (4.17b)), and of the triple point both in
$(O,x,y)$ (see (4.17b)), and of the triple point both in ![]() $(O,x,y)$ (i.e.
$(O,x,y)$ (i.e. ![]() ${v_f^{*}}={\mathrm {d} \mathcal {L}_f^*}/{\mathrm {d} t^*}$) and relative to the bulk meniscus (namely,
${v_f^{*}}={\mathrm {d} \mathcal {L}_f^*}/{\mathrm {d} t^*}$) and relative to the bulk meniscus (namely, ![]() ${v_f^{'*}}={\mathrm {d} L^{'*}_f}/{\mathrm {d} t^*}$) extracted from (4.19b) and (4.13b), are represented versus the dimensionless time
${v_f^{'*}}={\mathrm {d} L^{'*}_f}/{\mathrm {d} t^*}$) extracted from (4.19b) and (4.13b), are represented versus the dimensionless time ![]() $t^*$ in figure 7(a,b), respectively. This is performed considering
$t^*$ in figure 7(a,b), respectively. This is performed considering ![]() $\overline {Ca}\simeq 1.8519\times 10^{-5}$,
$\overline {Ca}\simeq 1.8519\times 10^{-5}$, ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $\theta _e =0^\circ$. As can be inferred from (4.18b), which indicates that
$\theta _e =0^\circ$. As can be inferred from (4.18b), which indicates that ![]() $v_b^*$ scales as
$v_b^*$ scales as ![]() $t^{*-1/2}$, figure 7(a) shows that the bulk meniscus displacement strongly accelerates at the very early times and slows down to reach an asymptotic value at large times that corresponds to the dimensionless speed of displacement of the bulk meniscus if there were no attached corner films, which is exactly
$t^{*-1/2}$, figure 7(a) shows that the bulk meniscus displacement strongly accelerates at the very early times and slows down to reach an asymptotic value at large times that corresponds to the dimensionless speed of displacement of the bulk meniscus if there were no attached corner films, which is exactly ![]() ${\mathrm {d}L_w^*}/{\mathrm {d}t^*}=\overline {Ca}$ (see (4.22b)). It should be noted, that in the case under concern, the convergence towards this asymptotic value is quite slow. Conversely, the speed of displacement of the triple point decreases with time (see figure 7b), both in the fixed frame of reference and relative to the bulk meniscus, in accordance with (4.13b) and (4.19b). As shown by the inset of this figure, the triple point asymptotically moves at the same speed as the bulk meniscus at exceedingly large times (i.e. its velocity relative to the bulk meniscus tends to zero in this time limit).
${\mathrm {d}L_w^*}/{\mathrm {d}t^*}=\overline {Ca}$ (see (4.22b)). It should be noted, that in the case under concern, the convergence towards this asymptotic value is quite slow. Conversely, the speed of displacement of the triple point decreases with time (see figure 7b), both in the fixed frame of reference and relative to the bulk meniscus, in accordance with (4.13b) and (4.19b). As shown by the inset of this figure, the triple point asymptotically moves at the same speed as the bulk meniscus at exceedingly large times (i.e. its velocity relative to the bulk meniscus tends to zero in this time limit).

Figure 7. Dimensionless time evolution of the speed of displacement of (a) the bulk meniscus in the fixed system of coordinates ![]() $(O,x,y)$,
$(O,x,y)$, ![]() ${v_b^*}={\mathrm {d} L_b^*}/{\mathrm {d} t^*}$ (see (4.17b)), and (b) of the triple point in the moving frame of reference
${v_b^*}={\mathrm {d} L_b^*}/{\mathrm {d} t^*}$ (see (4.17b)), and (b) of the triple point in the moving frame of reference ![]() $(O',x',y)$ (see figure 1(d) and 12),
$(O',x',y)$ (see figure 1(d) and 12), ![]() ${v_f^{'*}}={\mathrm {d} L^{'*}_f}/{\mathrm {d} t^*}$ and in the fixed frame of reference
${v_f^{'*}}={\mathrm {d} L^{'*}_f}/{\mathrm {d} t^*}$ and in the fixed frame of reference ![]() $(O,x,y)$,
$(O,x,y)$, ![]() ${v_f^{*}}={\mathrm {d}\mathcal {L}_f^*}/{\mathrm {d}t^*}=v_f^{'*}+v_b^*$ (see (4.19b) and (4.13b)). The inset represents the evolution of
${v_f^{*}}={\mathrm {d}\mathcal {L}_f^*}/{\mathrm {d}t^*}=v_f^{'*}+v_b^*$ (see (4.19b) and (4.13b)). The inset represents the evolution of ![]() $v_f^*$ and
$v_f^*$ and ![]() $v_f^{'*}$ at large dimensionless times. The dimensionless speed of displacement of the bulk meniscus in the absence of corner films,
$v_f^{'*}$ at large dimensionless times. The dimensionless speed of displacement of the bulk meniscus in the absence of corner films, ![]() ${\mathrm {d}L_w^*}/{\mathrm {d}t^*}=\overline {Ca}$ (see (4.22b)), is represented as a dashed line. Here
${\mathrm {d}L_w^*}/{\mathrm {d}t^*}=\overline {Ca}$ (see (4.22b)), is represented as a dashed line. Here ![]() $\epsilon =0.08$,
$\epsilon =0.08$, ![]() ${\overline {Ca}}\simeq 1.8519\times 10^{-5}$ and
${\overline {Ca}}\simeq 1.8519\times 10^{-5}$ and ![]() $\theta _e =0^\circ$.
$\theta _e =0^\circ$.
5. Imbibition dynamics at imposed pressure
The analysis is now carried out in the case of a pressure, ![]() $P_0$, imposed in the
$P_0$, imposed in the ![]() $\beta$ phase at the inlet of the channel. As in the case of an imposed flow rate, the imbibition process under concern in this section starts with the liquid film regime explored in § 5.1. However, as will be understood in the development presented below, the regime of the bulk and corner film flow (§ 5.2) does not necessarily exist, depending on the value of
$\beta$ phase at the inlet of the channel. As in the case of an imposed flow rate, the imbibition process under concern in this section starts with the liquid film regime explored in § 5.1. However, as will be understood in the development presented below, the regime of the bulk and corner film flow (§ 5.2) does not necessarily exist, depending on the value of ![]() $P_0$ that does or does not allow entrance of the meniscus.
$P_0$ that does or does not allow entrance of the meniscus.
5.1. Liquid film regime
Imbibition may be first analysed when the wetting phase only flows through the channel corners. The condition for flow to remain in the liquid film regime and the determination of the triple point position starts with Laplace's law reported in (2.2d), considered at ![]() $x = 0$, which leads to
$x = 0$, which leads to
This relationship is nothing else than the definition of the inlet capillary pressure ![]() $p_\gamma -P_0$. With the same approximations as those made in the case of an imposed flow rate, the capillary pressure,
$p_\gamma -P_0$. With the same approximations as those made in the case of an imposed flow rate, the capillary pressure, ![]() $p_c$, expressed in (3.5) can be employed to obtain the film width at the inlet of the channel, that is given by
$p_c$, expressed in (3.5) can be employed to obtain the film width at the inlet of the channel, that is given by
which, from the definition of dimensionless variables given in (2.3), equivalently writes
with ![]() $B$ defined in (3.3d). Note that the film width at the inlet of the channel is independent of time. Moreover, this expression obviously provides a necessary constraint (although not a sufficient one as discussed below) for imbibition to take place in the film regime, that is,
$B$ defined in (3.3d). Note that the film width at the inlet of the channel is independent of time. Moreover, this expression obviously provides a necessary constraint (although not a sufficient one as discussed below) for imbibition to take place in the film regime, that is,
Noting that the development that leads to the film profile given in (3.13a) remains valid in the present case, the compatibility of the latter taken at ![]() $x=0$ with (5.2a) provides the evolution of the triple point position,
$x=0$ with (5.2a) provides the evolution of the triple point position, ![]() $L_f(t)$, which takes the expression
$L_f(t)$, which takes the expression
 \begin{align} L_{f}(t) &= \left(\frac{5}{3(1+\sqrt{6})}\right)^{1/2} \frac{B\sigma}{(\mu_\beta (p_\gamma-P_0))^{1/2}}t^{1/2} \nonumber\\ &\simeq 0.6951\frac{B \sigma}{(\mu_\beta (p_\gamma-P_0))^{1/2}}t^{1/2}, \end{align}
\begin{align} L_{f}(t) &= \left(\frac{5}{3(1+\sqrt{6})}\right)^{1/2} \frac{B\sigma}{(\mu_\beta (p_\gamma-P_0))^{1/2}}t^{1/2} \nonumber\\ &\simeq 0.6951\frac{B \sigma}{(\mu_\beta (p_\gamma-P_0))^{1/2}}t^{1/2}, \end{align}or in dimensionless form
 \begin{equation} L_f^*(t^*)\simeq 0.4915 B\left(\frac{\epsilon}{p_\gamma^*-P_0^*}\right)^{1/2}t^{*1/2}. \end{equation}
\begin{equation} L_f^*(t^*)\simeq 0.4915 B\left(\frac{\epsilon}{p_\gamma^*-P_0^*}\right)^{1/2}t^{*1/2}. \end{equation}This result is reminiscent of Washburn's relationship (Lucas Reference Lucas1918; Washburn Reference Washburn1921).
Attention shall now be focused on the situation where the liquid film regime no longer exists. This occurs as soon as the bulk meniscus penetrates in the channel. This is conditioned by a threshold value of ![]() $P_0$, denoted
$P_0$, denoted ![]() $P_{0{max}}$, which induces a film width at
$P_{0{max}}$, which induces a film width at ![]() $x=0$ that corresponds to
$x=0$ that corresponds to ![]() $e_{max}^*$ satisfying (3.14c). The occurrence of the bulk and corner film flow regime can therefore be deduced from (5.2a) with
$e_{max}^*$ satisfying (3.14c). The occurrence of the bulk and corner film flow regime can therefore be deduced from (5.2a) with ![]() $e=e_{max}$ when
$e=e_{max}$ when ![]() $P_0=P_{0{max}}$, yielding
$P_0=P_{0{max}}$, yielding
and its dimensionless expression
This relationship allows clarification of the pure film regime that is restricted to values of ![]() $P_0$ such that
$P_0$ such that
In other words, the condition for the bulk meniscus to enter the channel is that the inlet capillary pressure is smaller than the threshold capillary pressure, which means
i.e.
In the above relationship, ![]() $e_{max}^*$ remains to be determined. As in the case of an imposed flow rate, it would be necessary to estimate this quantity from (3.14c). However, as will be shown below (see end of § 5.2 and Appendix C regarding the size of the bulk meniscus), no estimate of
$e_{max}^*$ remains to be determined. As in the case of an imposed flow rate, it would be necessary to estimate this quantity from (3.14c). However, as will be shown below (see end of § 5.2 and Appendix C regarding the size of the bulk meniscus), no estimate of ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$, compatible with the hypothesis of a bulk meniscus that remains identical to its configuration without any forcing, is available for a pressure imposed at the inlet of the channel. Therefore,
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$, compatible with the hypothesis of a bulk meniscus that remains identical to its configuration without any forcing, is available for a pressure imposed at the inlet of the channel. Therefore, ![]() $e_{max}^*$ shall be estimated from (4.9), assuming that the constraint
$e_{max}^*$ shall be estimated from (4.9), assuming that the constraint ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}\ll 1$ remains satisfied. This hypothesis is retained in the remainder of the analysis when a pressure is imposed at the channel inlet.
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}\ll 1$ remains satisfied. This hypothesis is retained in the remainder of the analysis when a pressure is imposed at the channel inlet.
5.2. Bulk and corner film flow regime
When ![]() $P_0\ge P_{0{max}}$, the film width at the channel inlet takes the value
$P_0\ge P_{0{max}}$, the film width at the channel inlet takes the value ![]() $e_{max}$ and the bulk meniscus enters the channel. A detailed modelling of the bulk meniscus settling cannot be achieved in that case within the strict framework of the quasi-static assumption that forms the basis of the present analysis. An alternative approach would be to call upon the balance between inertia and viscous and capillary effects as proposed in Clanet & Quéré (Reference Clanet and Quéré2002), providing an estimate of the time scale over which the bulk meniscus enters the channel. However, for consistency of the whole description proposed in the present work, the bulk and corner film flow regime may be described by assuming that the bulk meniscus instantaneously enters the channel. Therefore, the same methodology as that developed in § 4.3.2 can be followed but with
$e_{max}$ and the bulk meniscus enters the channel. A detailed modelling of the bulk meniscus settling cannot be achieved in that case within the strict framework of the quasi-static assumption that forms the basis of the present analysis. An alternative approach would be to call upon the balance between inertia and viscous and capillary effects as proposed in Clanet & Quéré (Reference Clanet and Quéré2002), providing an estimate of the time scale over which the bulk meniscus enters the channel. However, for consistency of the whole description proposed in the present work, the bulk and corner film flow regime may be described by assuming that the bulk meniscus instantaneously enters the channel. Therefore, the same methodology as that developed in § 4.3.2 can be followed but with ![]() $t_{max}=0$ and, correspondingly,
$t_{max}=0$ and, correspondingly, ![]() $L_{f{max}}=0$.
$L_{f{max}}=0$.
The volume conservation given in (4.15) remains formally unchanged, although ![]() $Q_0$ is now the time-dependent flow rate (denoted
$Q_0$ is now the time-dependent flow rate (denoted ![]() $Q_0(t)$) at the channel inlet resulting from the uniform pressure
$Q_0(t)$) at the channel inlet resulting from the uniform pressure ![]() $P_0$ at this location. To make progress, an expression of
$P_0$ at this location. To make progress, an expression of ![]() $Q_0(t)$ can be obtained by integration of the
$Q_0(t)$ can be obtained by integration of the ![]() $x$ component of the Reynolds equation (2.2b) with respect to
$x$ component of the Reynolds equation (2.2b) with respect to ![]() $y$ downstream of the bulk meniscus, i.e. for
$y$ downstream of the bulk meniscus, i.e. for ![]() $0\le x\le L_a(t)$ (see figures 1(d) and 12). Assuming that the pressure remains uniform in each cross-section of the channel in this region of the
$0\le x\le L_a(t)$ (see figures 1(d) and 12). Assuming that the pressure remains uniform in each cross-section of the channel in this region of the ![]() $\beta$ phase allows one to write
$\beta$ phase allows one to write
Further integrating this last relationship between ![]() $x=0$ and
$x=0$ and ![]() $x=L_a(t)$ yields
$x=L_a(t)$ yields
Making use of (4.15), and noting that ![]() ${\mathrm {d}L_a(t)}/{{\rm d} t}={\mathrm {d}L_b(t)}/{\mathrm {d}t}$ since the bulk meniscus is not deforming, provides the differential equation for
${\mathrm {d}L_a(t)}/{{\rm d} t}={\mathrm {d}L_b(t)}/{\mathrm {d}t}$ since the bulk meniscus is not deforming, provides the differential equation for ![]() $L_a(t)$ that writes
$L_a(t)$ that writes
where ![]() $P_{0{max}}$,
$P_{0{max}}$, ![]() $S_t$ and
$S_t$ and ![]() $Q'_f$ are respectively given by (5.5a), (4.3b) and (4.16b) in which
$Q'_f$ are respectively given by (5.5a), (4.3b) and (4.16b) in which ![]() $L^{'}_f(t)$ is still given by (4.13a) but now for
$L^{'}_f(t)$ is still given by (4.13a) but now for ![]() $t\ge 0$.
$t\ge 0$.
Keeping in mind that ![]() $Q'_f$ is proportional to
$Q'_f$ is proportional to ![]() $t^{-1/2}$, the solution to this differential equation that satisfies the condition
$t^{-1/2}$, the solution to this differential equation that satisfies the condition ![]() $L_a(t)=0$ at
$L_a(t)=0$ at ![]() $t=0$ (the bulk meniscus is instantaneously present at the channel entrance) is given by
$t=0$ (the bulk meniscus is instantaneously present at the channel entrance) is given by
 \begin{equation} L_a(t)=((a_1^2+a_2)^{1/2}-a_1)\left(\frac{\sigma \ell}{\mu_\beta}\right)^{1/2} t^{1/2}, \end{equation}
\begin{equation} L_a(t)=((a_1^2+a_2)^{1/2}-a_1)\left(\frac{\sigma \ell}{\mu_\beta}\right)^{1/2} t^{1/2}, \end{equation}or in dimensionless form (see (2.3))
In these two equations, ![]() $a_1$ and
$a_1$ and ![]() $a_2$ take the following expressions:
$a_2$ take the following expressions:
 \begin{align} a_1 &= \frac{10+\sqrt{6}}{24 (30 (1+\sqrt{6}))^{1/2}}A \left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}\right)^{1/2} \nonumber\\ &\simeq 0.0510A\left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}\right)^{1/2}, \end{align}
\begin{align} a_1 &= \frac{10+\sqrt{6}}{24 (30 (1+\sqrt{6}))^{1/2}}A \left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}\right)^{1/2} \nonumber\\ &\simeq 0.0510A\left(\left(\frac{\epsilon}{B}\right)^3e_{max}^{*5}\right)^{1/2}, \end{align} Finally, the triple point position is obtained from (4.14) in which (4.13a) (valid here for ![]() $t\ge 0$) is substituted to give
$t\ge 0$) is substituted to give
 \begin{align} \mathcal{L}_f(t) &= L_a(t)+\ell_m+L^{'}_f(t) \nonumber\\ &\simeq ((a_1^2+a_2)^{1/2}-a_1+0.4915(\epsilon B e^*_{max})^{1/2}) \left(\frac{\sigma \ell}{\mu_\beta}\right)^{1/2}t^{1/2}+\ell_m,\quad t\ge 0. \end{align}
\begin{align} \mathcal{L}_f(t) &= L_a(t)+\ell_m+L^{'}_f(t) \nonumber\\ &\simeq ((a_1^2+a_2)^{1/2}-a_1+0.4915(\epsilon B e^*_{max})^{1/2}) \left(\frac{\sigma \ell}{\mu_\beta}\right)^{1/2}t^{1/2}+\ell_m,\quad t\ge 0. \end{align}In dimensionless form, this writes
As explained in Appendix C, ![]() $\ell _m$ remains difficult to estimate within the framework of the quasi-static hypothesis and an imposed pressure at the channel inlet. However, since
$\ell _m$ remains difficult to estimate within the framework of the quasi-static hypothesis and an imposed pressure at the channel inlet. However, since ![]() $\ell _m = O(\ell )$, it must be noted that
$\ell _m = O(\ell )$, it must be noted that
as soon as the constraint expressed as
is satisfied, i.e.
or in dimensionless form
To illustrate this constraint, the case of a channel with ![]() $\ell =100\,\mathrm {\mu }$m and
$\ell =100\,\mathrm {\mu }$m and ![]() $h_0=1\,\mathrm {\mu }$m invaded by water (
$h_0=1\,\mathrm {\mu }$m invaded by water (![]() $\mu _\beta =0.001$ Pa s,
$\mu _\beta =0.001$ Pa s, ![]() $\sigma =72$ mN m
$\sigma =72$ mN m![]() $^{-1}$) or an oil (
$^{-1}$) or an oil (![]() $\mu _\beta =0.1$ Pa s,
$\mu _\beta =0.1$ Pa s, ![]() $\sigma =20$ mN m
$\sigma =20$ mN m![]() $^{-1}$) at
$^{-1}$) at ![]() $P_0-P_{0{max}}=10$ Pa with
$P_0-P_{0{max}}=10$ Pa with ![]() $\theta _e=0^\circ$, leads to
$\theta _e=0^\circ$, leads to ![]() $t\gg 6\times 10^{-4}\,\mathrm {s}$ for water and
$t\gg 6\times 10^{-4}\,\mathrm {s}$ for water and ![]() $t\gg 0.2\,\mathrm {s}$ for oil.
$t\gg 0.2\,\mathrm {s}$ for oil.
Both the meniscus and triple point positions given by (5.11a) and (5.12a) scale as ![]() $t^{1/2}$. This is in agreement with the results obtained by Yu, Zhou & Doi (Reference Yu, Zhou and Doi2018) for spontaneous imbibition in a tube of square cross-section and recalls the dependence predicted by the classical Washburn solution.
$t^{1/2}$. This is in agreement with the results obtained by Yu, Zhou & Doi (Reference Yu, Zhou and Doi2018) for spontaneous imbibition in a tube of square cross-section and recalls the dependence predicted by the classical Washburn solution.
If the corner film flow is not taken into account in the imbibition process, the dynamics of the bulk meniscus is readily obtained from (5.10) in which ![]() $Q'_f=0$ and this leads to
$Q'_f=0$ and this leads to
 \begin{equation} L_w(t)=\left(\frac{\sigma\ell}{\mu_\beta}a_2\right)^{1/2}t^{1/2}, \end{equation}
\begin{equation} L_w(t)=\left(\frac{\sigma\ell}{\mu_\beta}a_2\right)^{1/2}t^{1/2}, \end{equation}or in dimensionless form
It must be noted that the imbibition dynamics in the bulk and corner film flow regime depends on ![]() $P_0-P_{0{max}}$, i.e. the difference between the threshold and inlet capillary pressures.
$P_0-P_{0{max}}$, i.e. the difference between the threshold and inlet capillary pressures.
Comparison between the dynamics of the apex of the bulk meniscus predicted with and without flow from the corner films from (5.11a) and (5.14a), respectively, shows important features. First the existence of the film does not impact the time scaling of the bulk meniscus position that remains ![]() $t^{1/2}$, a behaviour that coincides with the classical result of Lucas (Reference Lucas1918) and Washburn (Reference Washburn1921). Moreover, the constant
$t^{1/2}$, a behaviour that coincides with the classical result of Lucas (Reference Lucas1918) and Washburn (Reference Washburn1921). Moreover, the constant ![]() $a_1$ in (5.11a) is a direct signature of the film flow effect ahead of the bulk meniscus that contributes to slow down the advancement of the latter. Indeed, (5.14a) predicts larger values of the bulk meniscus position than (5.11a) at any time. Nevertheless, the difference between the two becomes vanishingly small when
$a_1$ in (5.11a) is a direct signature of the film flow effect ahead of the bulk meniscus that contributes to slow down the advancement of the latter. Indeed, (5.14a) predicts larger values of the bulk meniscus position than (5.11a) at any time. Nevertheless, the difference between the two becomes vanishingly small when ![]() $a_1^2\ll a_2$. In particular, the slowing effect of the corner film is expected to increase when
$a_1^2\ll a_2$. In particular, the slowing effect of the corner film is expected to increase when ![]() $P_0$ approaches
$P_0$ approaches ![]() $P_{0{max}}$.
$P_{0{max}}$.
5.3. Results and discussion
5.3.1. Comparison of the model predictions with experimental data
In this section the predictive model derived above is compared with experimental data reported in (Amyot Reference Amyot2004) in the liquid film regime, i.e. for ![]() $P_0< P_{0{max}}$. Experiments were carried out with the same channel as in the case of an imposed flow rate (
$P_0< P_{0{max}}$. Experiments were carried out with the same channel as in the case of an imposed flow rate (![]() $2\ell =50\,{\rm mm}$,
$2\ell =50\,{\rm mm}$, ![]() $h_0=1\,{\rm mm}$, see § 4.4.1), using fluid 2 (
$h_0=1\,{\rm mm}$, see § 4.4.1), using fluid 2 (![]() $\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$,
$\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$, ![]() $\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$) and a constant capillary pressure imposed at the inlet of the channel
$\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$) and a constant capillary pressure imposed at the inlet of the channel ![]() $p_\gamma -P_0=100\,{\rm Pa}$. The comparison of the dimensionless position of the triple point,
$p_\gamma -P_0=100\,{\rm Pa}$. The comparison of the dimensionless position of the triple point, ![]() $L_f^*=L_f/\ell$, obtained experimentally (open symbols) and from (5.4b) (dotted line) is reported versus
$L_f^*=L_f/\ell$, obtained experimentally (open symbols) and from (5.4b) (dotted line) is reported versus ![]() $\sqrt {t^*}=(v_{\beta r} t/\ell )^{1/2}$ (see (2.3) for the definition of
$\sqrt {t^*}=(v_{\beta r} t/\ell )^{1/2}$ (see (2.3) for the definition of ![]() $t^*$) in figure 8, assuming perfect wetting (
$t^*$) in figure 8, assuming perfect wetting (![]() $\theta _e=0^\circ$). As shown in this figure, the experimental evolution of
$\theta _e=0^\circ$). As shown in this figure, the experimental evolution of ![]() $L_f^*$ follows well a
$L_f^*$ follows well a ![]() $\sqrt {t^*}$ scaling. The agreement with the prediction from the model is satisfactory for
$\sqrt {t^*}$ scaling. The agreement with the prediction from the model is satisfactory for ![]() $\sqrt {t^*}\gtrsim 70$. For smaller times, fluctuations of the pressure at the channel inlet observed experimentally and inducing variations of the film thickness predicted by (5.2b) at
$\sqrt {t^*}\gtrsim 70$. For smaller times, fluctuations of the pressure at the channel inlet observed experimentally and inducing variations of the film thickness predicted by (5.2b) at ![]() $x=0$, may explain the discrepancy that is more noticeable in this time range. A linear regression on the experimental data yields a slope of 0.0719 whereas the slope from the predictive model is 0.0671, which represents a relative difference of
$x=0$, may explain the discrepancy that is more noticeable in this time range. A linear regression on the experimental data yields a slope of 0.0719 whereas the slope from the predictive model is 0.0671, which represents a relative difference of ![]() ${\sim }6.7\,\%$. The dashed line represented in figure 8 corresponds to the model proposed in Amyot (Reference Amyot2004), for which the slope is 0.0788, leading to a relative difference with the linear regression on the experimental data of
${\sim }6.7\,\%$. The dashed line represented in figure 8 corresponds to the model proposed in Amyot (Reference Amyot2004), for which the slope is 0.0788, leading to a relative difference with the linear regression on the experimental data of ![]() ${\sim }9.6\,\%$. The slight underperformance of the latter model may be explained by a less accurate solution of the film width compared with the solution developed in the present work, as discussed in Appendix A. The conclusions reached here confirm the relevance of the model proposed in this work.
${\sim }9.6\,\%$. The slight underperformance of the latter model may be explained by a less accurate solution of the film width compared with the solution developed in the present work, as discussed in Appendix A. The conclusions reached here confirm the relevance of the model proposed in this work.

Figure 8. Comparison of the dimensionless triple point position, ![]() ${L}_f^*={{L}_f }/{\ell }$, in the film regime, predicted from (5.4b) with experimental data from Amyot (Reference Amyot2004), versus
${L}_f^*={{L}_f }/{\ell }$, in the film regime, predicted from (5.4b) with experimental data from Amyot (Reference Amyot2004), versus ![]() $\sqrt {t^*}$ (see (2.3) for the definition of
$\sqrt {t^*}$ (see (2.3) for the definition of ![]() $t^*$). The channel characteristics are
$t^*$). The channel characteristics are ![]() $2\ell =50\,{\rm mm}$,
$2\ell =50\,{\rm mm}$, ![]() $h_0=1\,{\rm mm}$. The constant capillary pressure imposed at the inlet of the channel is
$h_0=1\,{\rm mm}$. The constant capillary pressure imposed at the inlet of the channel is ![]() $p_\gamma -P_0=100\,{\rm Pa}$. Here
$p_\gamma -P_0=100\,{\rm Pa}$. Here ![]() $\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$,
$\sigma =23.3\,{\rm mN}\,{\rm m}^{-1}$, ![]() $\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$,
$\mu _\beta =0.22\,{\rm Pa}\,{\rm s}$, ![]() $\theta _e=0^\circ$. The linear regression on the experimental data yields a slope of 0.0719, whereas the slopes corresponding to the present model and that from Amyot (Reference Amyot2004) are respectively 0.0671 and 0.0788.
$\theta _e=0^\circ$. The linear regression on the experimental data yields a slope of 0.0719, whereas the slopes corresponding to the present model and that from Amyot (Reference Amyot2004) are respectively 0.0671 and 0.0788.
5.3.2. Analysis of the model
When ![]() $P_0\ge P_{0{max}}$, leading to an imbibition process in the bulk and corner film flow regime, it is of interest to investigate the contrast between the dynamics of the apex of the bulk meniscus and the triple point. In figure 9(a) the dimensionless positions of these two points, respectively
$P_0\ge P_{0{max}}$, leading to an imbibition process in the bulk and corner film flow regime, it is of interest to investigate the contrast between the dynamics of the apex of the bulk meniscus and the triple point. In figure 9(a) the dimensionless positions of these two points, respectively ![]() $L_a^*=L_a/\ell$ and
$L_a^*=L_a/\ell$ and ![]() $\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (5.11b) and (5.12b)), are represented versus
$\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (5.11b) and (5.12b)), are represented versus ![]() $\sqrt {t^*}$ for two values of
$\sqrt {t^*}$ for two values of ![]() $P_0^*-P_{0{max}}^*$, namely,
$P_0^*-P_{0{max}}^*$, namely, ![]() $(P_0^*-P_{0{max}}^*)_1\simeq 1.3056$ and
$(P_0^*-P_{0{max}}^*)_1\simeq 1.3056$ and ![]() $(P_0^*-P_{0{max}}^*)_2\simeq 4.3318$, taking
$(P_0^*-P_{0{max}}^*)_2\simeq 4.3318$, taking ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $\theta _e=0^\circ$. As in the case of an imposed flow rate at the channel inlet, the contrast between the two positions is more pronounced when capillary effects are dominant (i.e. for the smallest value of
$\theta _e=0^\circ$. As in the case of an imposed flow rate at the channel inlet, the contrast between the two positions is more pronounced when capillary effects are dominant (i.e. for the smallest value of ![]() $P_0^*-P_{0{max}}^*\equiv (P_0^*-P_{0{max}}^*)_1$). Again, this results from the fact that capillarity is the driving force for the development of the corner films, whose liquid uptake from the bulk behind contributes to slow down the bulk meniscus.
$P_0^*-P_{0{max}}^*\equiv (P_0^*-P_{0{max}}^*)_1$). Again, this results from the fact that capillarity is the driving force for the development of the corner films, whose liquid uptake from the bulk behind contributes to slow down the bulk meniscus.

Figure 9. Dimensionless positions of the apex of the bulk meniscus, ![]() $L_a^*=L_a/\ell$, and triple point,
$L_a^*=L_a/\ell$, and triple point, ![]() $\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (5.11b) and (5.12b)), versus
$\mathcal {L}_f^*=\mathcal {L}_f/\ell$ (see (5.11b) and (5.12b)), versus ![]() $\sqrt {t^*}$ (see (2.3)) during imbibition in a channel for which
$\sqrt {t^*}$ (see (2.3)) during imbibition in a channel for which ![]() $\epsilon =0.08$ and (a)
$\epsilon =0.08$ and (a) ![]() $\theta _e=0^\circ$,
$\theta _e=0^\circ$, ![]() $(P_0^*-P_{0{max}}^*)_1\simeq 1.3056$ and
$(P_0^*-P_{0{max}}^*)_1\simeq 1.3056$ and ![]() $(P_{0}^*-P_{0{max}}^*)_2\simeq 4.3318$; (b)
$(P_{0}^*-P_{0{max}}^*)_2\simeq 4.3318$; (b) ![]() $P_{0}^*-P_{0{max}}^*\simeq 1.3056$ and
$P_{0}^*-P_{0{max}}^*\simeq 1.3056$ and ![]() $\theta _e=0^\circ$,
$\theta _e=0^\circ$, ![]() $30^\circ$. Dashed lines represent the dimensionless position of the apex of the bulk meniscus when corner films are disregarded,
$30^\circ$. Dashed lines represent the dimensionless position of the apex of the bulk meniscus when corner films are disregarded, ![]() $L_w^*=L_w/\ell$ (see (5.14b)).
$L_w^*=L_w/\ell$ (see (5.14b)).
The dependence of the contrast between the positions of the apex of the bulk meniscus and the triple point upon the contact angle is illustrated in figure 9(b), for ![]() $\theta _e=0^\circ$ and
$\theta _e=0^\circ$ and ![]() $\theta _e=30^\circ$, keeping
$\theta _e=30^\circ$, keeping ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $P_0^*-P_{0{max}}^*\simeq 1.3056$. In this range of the contact angle, the impact remains weak on both dynamics. Consistently, the smaller the contact angle, the faster the dynamics of the triple point, and simultaneously, the slower the dynamics of the bulk meniscus in accordance with the fact that capillary effects increase when
$P_0^*-P_{0{max}}^*\simeq 1.3056$. In this range of the contact angle, the impact remains weak on both dynamics. Consistently, the smaller the contact angle, the faster the dynamics of the triple point, and simultaneously, the slower the dynamics of the bulk meniscus in accordance with the fact that capillary effects increase when ![]() $\theta _e$ decreases.
$\theta _e$ decreases.
As can be observed from figure 9(a,b), the difference between the positions of the apex of the bulk meniscus predicted from the model including the corner films and from (5.14b) that disregards them (dashed lines), although noticeable, is not extremely large. The last feature is further illustrated in figure 10(a,b), respectively showing the dependence of the ratio ![]() $\mathcal {L}_f^*/L_a^*$ and
$\mathcal {L}_f^*/L_a^*$ and ![]() $L_a^*/L_w^*$ upon the dimensionless imbibition driving term
$L_a^*/L_w^*$ upon the dimensionless imbibition driving term ![]() $P_0^*-P_{0{max}}^*$, considering
$P_0^*-P_{0{max}}^*$, considering ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $\theta _e=0^\circ$. For figure 10(a), the constraint expressed in (5.13d) is assumed to be satisfied so that
$\theta _e=0^\circ$. For figure 10(a), the constraint expressed in (5.13d) is assumed to be satisfied so that ![]() $\ell _m^*$ can be omitted in the expression of
$\ell _m^*$ can be omitted in the expression of ![]() $\mathcal {L}_f^*$ in (5.12b), thus resulting in a ratio
$\mathcal {L}_f^*$ in (5.12b), thus resulting in a ratio ![]() $\mathcal {L}_f^*/L_a^*$ that is indeed independent of time. This ratio strongly decreases when
$\mathcal {L}_f^*/L_a^*$ that is indeed independent of time. This ratio strongly decreases when ![]() $P_0^*-P_{0{max}}^*$ increases and this simply results from the fact that increasing the forcing counterbalances the liquid suction from the bulk into the corner films that otherwise favours the triple point displacement ahead of the bulk meniscus. The same effects are reflected in figure 10(b) that shows that the corner films are shortened when
$P_0^*-P_{0{max}}^*$ increases and this simply results from the fact that increasing the forcing counterbalances the liquid suction from the bulk into the corner films that otherwise favours the triple point displacement ahead of the bulk meniscus. The same effects are reflected in figure 10(b) that shows that the corner films are shortened when ![]() $P_0^*-P_{0{max}}^*$ increases, yielding a ratio
$P_0^*-P_{0{max}}^*$ increases, yielding a ratio ![]() $L_a^*/L_w^*$ that asymptotically approaches unity. This is in agreement with the discussion provided at the end of § 5.2.
$L_a^*/L_w^*$ that asymptotically approaches unity. This is in agreement with the discussion provided at the end of § 5.2.

Figure 10. Influence of the dimensionless pressure difference ![]() $P_{0}^*-P_{0{max}}^*$ on the ratio between (a) the dimensionless positions of the triple point and the apex of the bulk meniscus,
$P_{0}^*-P_{0{max}}^*$ on the ratio between (a) the dimensionless positions of the triple point and the apex of the bulk meniscus, ![]() $\mathcal {L}_f^*/L_a^*$, and (b) the dimensionless positions of the apex of the bulk meniscus with and without the corner films ahead of it,
$\mathcal {L}_f^*/L_a^*$, and (b) the dimensionless positions of the apex of the bulk meniscus with and without the corner films ahead of it, ![]() $L_a^*/L_w^*$ (see (5.11b), (5.12b) and (5.14b) for
$L_a^*/L_w^*$ (see (5.11b), (5.12b) and (5.14b) for ![]() $L_a^*$,
$L_a^*$, ![]() $\mathcal {L}_f^*$ and
$\mathcal {L}_f^*$ and ![]() $L_w^*$, respectively). Here
$L_w^*$, respectively). Here ![]() $\epsilon =0.08$ and
$\epsilon =0.08$ and ![]() $\theta _e=0^\circ$.
$\theta _e=0^\circ$.
6. Conclusion
Approximated quasi-analytical solutions to the imbibition dynamics in a triangular channel is provided in this work, based on the lubrication approximation (relevant when the aspect ratio of the channel is small enough compared with unity), negligible inertial effects and the quasi-steady flow assumption, together with a capillary number characteristic of the flow that remains small enough compared with unity. The non-wetting fluid (gas) is assumed to remain at constant pressure due to the viscosity contrast with the wetting fluid (liquid). Two scenarios of imbibition have been explored, namely a constant flow rate or a constant pressure in the wetting fluid at the inlet of the channel. Several important features have been highlighted.
Imbibition at constant flow rate, ![]() $Q_0$, starts with wetting films developing in the corners of the channel. This liquid film regime, during which the film thickness at the channel inlet increases as
$Q_0$, starts with wetting films developing in the corners of the channel. This liquid film regime, during which the film thickness at the channel inlet increases as ![]() $t^{1/5}$, persists until this thickness reaches a threshold value compatible with the capillary pressure that allows the formation of a meniscus. During this period, the triple point displacement in each corner scales as
$t^{1/5}$, persists until this thickness reaches a threshold value compatible with the capillary pressure that allows the formation of a meniscus. During this period, the triple point displacement in each corner scales as ![]() $t^{3/5}$ and depends on
$t^{3/5}$ and depends on ![]() $Q_0^{1/5}$ as well on a reference velocity,
$Q_0^{1/5}$ as well on a reference velocity, ![]() $v_{\beta r}$, ratio of the interfacial tension to the dynamic viscosity of the wetting fluid, as
$v_{\beta r}$, ratio of the interfacial tension to the dynamic viscosity of the wetting fluid, as ![]() $v_{\beta r}^{2/5}$. After the bulk meniscus entrance in the channel, the imbibition process goes on in a bulk and corner film flow regime. During this regime, the bulk meniscus position in the channel evolves according to two antagonist mechanisms: (i) the forcing at the channel entrance pushing the bulk meniscus ahead and yielding a contribution to the position of the bulk meniscus proportional to
$v_{\beta r}^{2/5}$. After the bulk meniscus entrance in the channel, the imbibition process goes on in a bulk and corner film flow regime. During this regime, the bulk meniscus position in the channel evolves according to two antagonist mechanisms: (i) the forcing at the channel entrance pushing the bulk meniscus ahead and yielding a contribution to the position of the bulk meniscus proportional to ![]() $Q_0$; (ii) a slowing down effect resulting from the wetting fluid uptake by the films attached to the bulk meniscus and flowing in the corners that contribute as a term that scales as
$Q_0$; (ii) a slowing down effect resulting from the wetting fluid uptake by the films attached to the bulk meniscus and flowing in the corners that contribute as a term that scales as ![]() $t^{1/2}$. Meanwhile, the triple point position in each corner of the channel evolves faster than the bulk meniscus as a result of two co-driving effects: (i) the forcing at the channel inlet contributing with a term that scales as
$t^{1/2}$. Meanwhile, the triple point position in each corner of the channel evolves faster than the bulk meniscus as a result of two co-driving effects: (i) the forcing at the channel inlet contributing with a term that scales as ![]() $t$, and (ii) a term resulting from the competition of capillary and viscous effects that scales as
$t$, and (ii) a term resulting from the competition of capillary and viscous effects that scales as ![]() $t^{1/2}$. An important feature lies in the contrast between the position of the triple point and the apex of the bulk meniscus, the former being possibly far ahead of the later, indicating that the wetting fluid breakthrough can occur much earlier than the expected arrival of the bulk meniscus at the end of a channel of finite length. As expected, the contrast between the positions of the triple point and the apex of the bulk meniscus is weakened when capillary forces are less dominant. The classical Washburn type of approach (Washburn Reference Washburn1921), which omits the existence of the corner films, leads to overpredict the evolution of the bulk meniscus with an error that increases when capillary effects increase. Comparison of the predictions from the model derived in that case with experimental data available in the literature confirm the validity of the approach.
$t^{1/2}$. An important feature lies in the contrast between the position of the triple point and the apex of the bulk meniscus, the former being possibly far ahead of the later, indicating that the wetting fluid breakthrough can occur much earlier than the expected arrival of the bulk meniscus at the end of a channel of finite length. As expected, the contrast between the positions of the triple point and the apex of the bulk meniscus is weakened when capillary forces are less dominant. The classical Washburn type of approach (Washburn Reference Washburn1921), which omits the existence of the corner films, leads to overpredict the evolution of the bulk meniscus with an error that increases when capillary effects increase. Comparison of the predictions from the model derived in that case with experimental data available in the literature confirm the validity of the approach.
When imbibition is controlled by a constant pressure imposed at the inlet of the channel, two distinct situations may occur. If the pressure difference between the non-wetting phase and the wetting phase imposed at the channel inlet (i.e. the inlet capillary pressure) is larger than the threshold capillary pressure allowing the bulk meniscus to enter the channel, the imbibition process remains in the liquid film regime. The triple point position in this regime scales as ![]() $t^{1/2}$ and depends on the inverse square root of the inlet capillary pressure.
$t^{1/2}$ and depends on the inverse square root of the inlet capillary pressure.
If the inlet capillary pressure is smaller than the threshold capillary pressure, a bulk meniscus settles at the entrance and imbibition takes place in a bulk and corner film flow regime. Although the approach followed in this work does not allow a detailed description of the transition period corresponding to the bulk meniscus settlement due to the steady flow assumption, the description of the ensuing flow process shows that the forcing is the difference between the threshold and inlet capillary pressures. Both positions of the apex of the bulk meniscus and triple point scale as ![]() $t^{1/2}$, that is reminiscent of a Washburn approach. Nevertheless, the slowing down effect of the bulk meniscus due to the flow rate fraction that supplies flow in the corner ahead of it is prone to a significant overprediction of the bulk meniscus dynamics if the corner films are disregarded. This overprediction decreases when the forcing increases. Well-controlled imbibition experiments with a constant pressure imposed at the channel inlet are difficult to carry out, making experimental data scarce. Although the model derived in this work would require more thorough comparisons with direct observations, a comparison with experimental data in the liquid film regime confirm the relevance of the model developed in the present work.
$t^{1/2}$, that is reminiscent of a Washburn approach. Nevertheless, the slowing down effect of the bulk meniscus due to the flow rate fraction that supplies flow in the corner ahead of it is prone to a significant overprediction of the bulk meniscus dynamics if the corner films are disregarded. This overprediction decreases when the forcing increases. Well-controlled imbibition experiments with a constant pressure imposed at the channel inlet are difficult to carry out, making experimental data scarce. Although the model derived in this work would require more thorough comparisons with direct observations, a comparison with experimental data in the liquid film regime confirm the relevance of the model developed in the present work.
This work raises important conclusions, in particular regarding the role of corner films during imbibition in triangular-shaped channels that may be of central importance in some applications due to the early wetting fluid breakthrough, much before that of the bulk meniscus itself. Further work is required to better describe the bulk meniscus settlement in the channel. This problem may be addressed by taking into account inertial effects that play a significant role at this stage of the process (Clanet & Quéré Reference Clanet and Quéré2002). Another prospect lies in the description of the process once the triple point has reached the outlet of the channel in a finite-size system.
Acknowledgements
The authors gratefully acknowledge the support from the joint CEA – TECHNETICS Group France maestral sealing laboratory. All data and details on the numerical procedures reported in this work are available upon request to the authors.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Solution for the film width profile
In this appendix the solution for ![]() $e(x, t)$ to (3.8) (or, equivalently, for
$e(x, t)$ to (3.8) (or, equivalently, for ![]() $f(\zeta )$ to (3.11)) is explored. An appealing strategy, inspired from Weislogel & Lichter (Reference Weislogel and Lichter1998) and Amyot (Reference Amyot2004), is to assume that
$f(\zeta )$ to (3.11)) is explored. An appealing strategy, inspired from Weislogel & Lichter (Reference Weislogel and Lichter1998) and Amyot (Reference Amyot2004), is to assume that
Under these circumstances, (3.11) can be simplified to
This simplified version of the differential equation governing the film profile has the nice feature of only requiring the boundary condition given in (3.12a) and has an analytical solution that yields the following approximate expression for the width of the liquid film:
 \begin{equation} e(x, t) =\frac{\alpha }{12 }\frac{L_{f}^2}{t}\left(1 - \left( \frac{x}{L_{f}} \right)^2 \right). \end{equation}
\begin{equation} e(x, t) =\frac{\alpha }{12 }\frac{L_{f}^2}{t}\left(1 - \left( \frac{x}{L_{f}} \right)^2 \right). \end{equation}
With this solution at hand, the constraint expressed in (A1) can be made explicit, indicating that it remains a priori valid provided ![]() $x \gg L_f / \sqrt {5}$. In other words, the above simplified solution is expected to be acceptable in roughly half the extension of the film behind the triple point. For this reason, a more accurate solution is desirable.
$x \gg L_f / \sqrt {5}$. In other words, the above simplified solution is expected to be acceptable in roughly half the extension of the film behind the triple point. For this reason, a more accurate solution is desirable.
To this purpose, an alternative approach can be proposed as follows. First, a rescaling on ![]() $f$ and
$f$ and ![]() $\zeta$ given by
$\zeta$ given by
 \begin{equation} \zeta^* = \frac{\sqrt{2t}}{L_f}\zeta,\quad f^* = \frac{t}{\alpha L_f^2}f \end{equation}
\begin{equation} \zeta^* = \frac{\sqrt{2t}}{L_f}\zeta,\quad f^* = \frac{t}{\alpha L_f^2}f \end{equation}can be employed so that the differential equation (3.11) and associated boundary conditions (3.12a) and (3.12b) respectively take the form
The solution to this boundary value problem was carried out numerically with an implicit Euler method, starting from ![]() $\zeta ^*=1$ down to
$\zeta ^*=1$ down to ![]() $\zeta ^*=0$. The result is represented in figure 11, together with
$\zeta ^*=0$. The result is represented in figure 11, together with ![]() $f^*$ corresponding to the approximate solution given in (A3). This figure confirms that the latter remains accurate sufficiently close to the tip of the film as anticipated above, but is about 50 % in error for
$f^*$ corresponding to the approximate solution given in (A3). This figure confirms that the latter remains accurate sufficiently close to the tip of the film as anticipated above, but is about 50 % in error for ![]() $\zeta ^*\simeq 0$. In addition, the numerical solution indicates that a reasonable representation of
$\zeta ^*\simeq 0$. In addition, the numerical solution indicates that a reasonable representation of ![]() $f^*(\zeta ^*)$ may be sought under the form
$f^*(\zeta ^*)$ may be sought under the form
![]() $a$,
$a$, ![]() $b$ and
$b$ and ![]() $c$ being constants to be determined. The two boundary conditions
$c$ being constants to be determined. The two boundary conditions ![]() $f^*=0$ and
$f^*=0$ and ![]() ${\mathrm {d} f^*}/{\mathrm {d} \zeta ^*}=-\frac {1}{6}$ at
${\mathrm {d} f^*}/{\mathrm {d} \zeta ^*}=-\frac {1}{6}$ at ![]() $\zeta ^*=1$ yield
$\zeta ^*=1$ yield ![]() $a = c - \frac {1}{6}$ and
$a = c - \frac {1}{6}$ and ![]() $b = -(a + c) = \frac {1}{6} - 2c$, whereas substitution of the quadratic form of
$b = -(a + c) = \frac {1}{6} - 2c$, whereas substitution of the quadratic form of ![]() $f^*(\zeta ^*)$ into the differential equation (A5a) provides the residual function
$f^*(\zeta ^*)$ into the differential equation (A5a) provides the residual function ![]() $R = (2a\zeta ^* + b)(\zeta ^* + 6(2a\zeta ^* + b)) + 6a(a\zeta ^{*2} + b\zeta ^* + c)$. Following Boyd (Reference Boyd2000, chapter 1, p. 14), an accurate solution can be obtained by imposing
$R = (2a\zeta ^* + b)(\zeta ^* + 6(2a\zeta ^* + b)) + 6a(a\zeta ^{*2} + b\zeta ^* + c)$. Following Boyd (Reference Boyd2000, chapter 1, p. 14), an accurate solution can be obtained by imposing ![]() $R = 0$ at
$R = 0$ at ![]() $\zeta ^*=1/2$, and this yields
$\zeta ^*=1/2$, and this yields
The resulting quadratic prediction of ![]() $f^*$ is reported in figure 11, which shows an excellent agreement with the numerical solution, the maximum relative error on the whole interval of
$f^*$ is reported in figure 11, which shows an excellent agreement with the numerical solution, the maximum relative error on the whole interval of ![]() $\zeta ^*$ being 0.8 %, taking the numerical solution as the reference.
$\zeta ^*$ being 0.8 %, taking the numerical solution as the reference.
Switching back to the variables ![]() $x$ and
$x$ and ![]() $t$, (A6) provides an estimate for the width of the film that takes the following form:
$t$, (A6) provides an estimate for the width of the film that takes the following form:
 \begin{equation} e(x,t) = \frac{\alpha L_f^2}{t}\left(a\left(\frac{x}{L_f}\right)^2+b\frac{x}{L_f}+c\right). \end{equation}
\begin{equation} e(x,t) = \frac{\alpha L_f^2}{t}\left(a\left(\frac{x}{L_f}\right)^2+b\frac{x}{L_f}+c\right). \end{equation}This result is in full agreement with the derivation proposed by Dong & Chatzis (Reference Dong and Chatzis1995) in a slightly different manner for imbibition in a tube having a square cross-section.
Appendix B. Volume conservation
This appendix presents an expression for the distribution of the flow rate in the channel when flow occurs in the bulk and corner film regime, while a flow rate ![]() $Q_0$ is imposed at the entrance of the channel. The results are employed in § 4.3.2.
$Q_0$ is imposed at the entrance of the channel. The results are employed in § 4.3.2.
Following the notations proposed in figure 12, the volume conservation of the ![]() $\beta$ phase that is present in the channel at a given time after the entrance of the bulk meniscus can be written as
$\beta$ phase that is present in the channel at a given time after the entrance of the bulk meniscus can be written as

Figure 12. Notations used in the film and in the bulk behind the bulk meniscus. The different regions are identified with contrasted shaded blue areas.
The volume, ![]() $\varOmega _b(t)$, downstream of the bulk meniscus can be expressed as
$\varOmega _b(t)$, downstream of the bulk meniscus can be expressed as
 \begin{equation} \varOmega_{b}(t) = \int_{e_{max}}^{\ell} h(y) \left(\int_0^{x_m(y, t)}\,\mathrm{d}\kern 0.06em x\right) \,\mathrm{d}y = \epsilon\int_{e_{max}}^{\ell} y x_m(y, t) \,\mathrm{d}y, \end{equation}
\begin{equation} \varOmega_{b}(t) = \int_{e_{max}}^{\ell} h(y) \left(\int_0^{x_m(y, t)}\,\mathrm{d}\kern 0.06em x\right) \,\mathrm{d}y = \epsilon\int_{e_{max}}^{\ell} y x_m(y, t) \,\mathrm{d}y, \end{equation}
where ![]() $x_m(y,t)$ denotes the
$x_m(y,t)$ denotes the ![]() $x$ coordinate of a point at the interface in the bulk meniscus region (
$x$ coordinate of a point at the interface in the bulk meniscus region (![]() $L_a(t)\le x_m\le L_b(t)=L_a(t)+\ell _m$). The time derivative of the above expression yields
$L_a(t)\le x_m\le L_b(t)=L_a(t)+\ell _m$). The time derivative of the above expression yields
Since the bulk meniscus moves as a rigid entity (it keeps the shape corresponding to a static configuration), the term ![]() ${\partial {x_m}(y,t)}/{\partial t}$ is independent of
${\partial {x_m}(y,t)}/{\partial t}$ is independent of ![]() $y$ and is equal to
$y$ and is equal to ![]() ${\mathrm {d}L_b(t)}/{\mathrm {d}t}$, with
${\mathrm {d}L_b(t)}/{\mathrm {d}t}$, with ![]() $L_b(t)$ defined as in (4.14), whence
$L_b(t)$ defined as in (4.14), whence
In the liquid film region, ![]() $\varOmega _f(t)$ and
$\varOmega _f(t)$ and ![]() $\varOmega '_f(t)$ can be respectively expressed as
$\varOmega '_f(t)$ can be respectively expressed as
 $$\begin{gather} \varOmega_{f}(t) = \int_0^{e_{max}} h(y) \left( \int_0^{L_b(t)}\mathrm{d}\kern 0.06em x\right)\mathrm{d}y =\frac{\epsilon}{2} L_b(t) e^2_{max}, \end{gather}$$
$$\begin{gather} \varOmega_{f}(t) = \int_0^{e_{max}} h(y) \left( \int_0^{L_b(t)}\mathrm{d}\kern 0.06em x\right)\mathrm{d}y =\frac{\epsilon}{2} L_b(t) e^2_{max}, \end{gather}$$ $$\begin{gather}\varOmega'_{f}(t) = \int_0^{L^{'}_f(t)} S(x',t)\,\mathrm{d}\kern 0.06em x'. \end{gather}$$
$$\begin{gather}\varOmega'_{f}(t) = \int_0^{L^{'}_f(t)} S(x',t)\,\mathrm{d}\kern 0.06em x'. \end{gather}$$
In the latter expression, ![]() $S(x',t)$ is the corner film cross-sectional area that is given by (3.3a) with
$S(x',t)$ is the corner film cross-sectional area that is given by (3.3a) with ![]() $x'$ the coordinate along the channel axis in the moving frame of reference
$x'$ the coordinate along the channel axis in the moving frame of reference ![]() $(O',x',y')$. Taking the time derivative of expressions (B5) and (B6), using (B4) and combining the result into (B1) leads to
$(O',x',y')$. Taking the time derivative of expressions (B5) and (B6), using (B4) and combining the result into (B1) leads to
with ![]() $Q'_f(t)={\mathrm {d} \varOmega '_f}/{\mathrm {d}t}$. Equivalently, this result can be written as
$Q'_f(t)={\mathrm {d} \varOmega '_f}/{\mathrm {d}t}$. Equivalently, this result can be written as
![]() $S_t = \ell h_0 =\epsilon \ell ^2$ being the total cross-sectional area of the channel.
$S_t = \ell h_0 =\epsilon \ell ^2$ being the total cross-sectional area of the channel.
Appendix C. Size of the bulk meniscus
The extension of the bulk meniscus, ![]() $\ell _m$, in the main flow direction (
$\ell _m$, in the main flow direction (![]() $x$) is required to obtain its central point (or apex) position given in (4.20). A numerical procedure to identify
$x$) is required to obtain its central point (or apex) position given in (4.20). A numerical procedure to identify ![]() $\ell _m$ is proposed in this appendix.
$\ell _m$ is proposed in this appendix.
The starting point is to integrate (3.14b) with respect to ![]() $x$ between
$x$ between ![]() $e$ and
$e$ and ![]() $\ell$ yielding, in dimensionless form,
$\ell$ yielding, in dimensionless form,
 \begin{equation} \left(1 + \left(\frac{\partial e^*}{\partial x^*}\right)^2 \right)^{{-}1/2} - \frac{2B}{\epsilon}\left(\ln(e^*)+\frac{1-e^*}{e_{max}^*}\right)=0. \end{equation}
\begin{equation} \left(1 + \left(\frac{\partial e^*}{\partial x^*}\right)^2 \right)^{{-}1/2} - \frac{2B}{\epsilon}\left(\ln(e^*)+\frac{1-e^*}{e_{max}^*}\right)=0. \end{equation}
Noting that ![]() ${\partial e^*}/{\partial x^*} \le 0$, the above equation provides the expression of the slope at any interfacial point of the bulk meniscus given by
${\partial e^*}/{\partial x^*} \le 0$, the above equation provides the expression of the slope at any interfacial point of the bulk meniscus given by
 \begin{equation} \frac{\partial e^*}{\partial x^*}={-}\left[\left(\frac{2B}{\epsilon} \left(\ln(e^*)+\frac{1-e^*}{e_{max}^*}\right)\right)^{{-}2} - 1\right]^{1/2}. \end{equation}
\begin{equation} \frac{\partial e^*}{\partial x^*}={-}\left[\left(\frac{2B}{\epsilon} \left(\ln(e^*)+\frac{1-e^*}{e_{max}^*}\right)\right)^{{-}2} - 1\right]^{1/2}. \end{equation}This equation can be integrated numerically starting from the conditions
Integration is carried out increasing ![]() $x^*$ from 0 until reaching
$x^*$ from 0 until reaching ![]() $e^*=e_{max}^*$ at which the value of
$e^*=e_{max}^*$ at which the value of ![]() $x^*$ is
$x^*$ is ![]() $\ell _m^*$. Alternatively,
$\ell _m^*$. Alternatively, ![]() $\ell _m^*$ can be obtained upon numerical evaluation of the following expression that results from integration of (C2a) between
$\ell _m^*$ can be obtained upon numerical evaluation of the following expression that results from integration of (C2a) between ![]() $e_{max}^*$ and
$e_{max}^*$ and ![]() $1$, i.e.
$1$, i.e.
 \begin{equation} \ell_m^*= \int_{e_{max}^*}^1 \left[\left(\frac{2B}{\epsilon} \left(\ln(u)+\frac{1-u}{e_{max}^*}\right)\right)^{{-}2}-1\right]^{{-}1/2}\mathrm{d}u. \end{equation}
\begin{equation} \ell_m^*= \int_{e_{max}^*}^1 \left[\left(\frac{2B}{\epsilon} \left(\ln(u)+\frac{1-u}{e_{max}^*}\right)\right)^{{-}2}-1\right]^{{-}1/2}\mathrm{d}u. \end{equation}C.1. Imposed flow rate
Although the approximate value of ![]() $e_{max}^*$ provided in (4.9) may be acceptable in the subsequent calculations involving this quantity and developed in the body of the text, computation of (C2a) or (C3) with this approximate value that results from the hypothesis
$e_{max}^*$ provided in (4.9) may be acceptable in the subsequent calculations involving this quantity and developed in the body of the text, computation of (C2a) or (C3) with this approximate value that results from the hypothesis ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}= 0$ is impossible. This is due to the fact that integration diverges when
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}= 0$ is impossible. This is due to the fact that integration diverges when ![]() $e^*$ reaches
$e^*$ reaches ![]() $e_{max}^*$ (
$e_{max}^*$ (![]() $\ell _m^*$ has a logarithmic dependence on
$\ell _m^*$ has a logarithmic dependence on ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$ and, therefore, diverges when the latter approaches zero). Consequently, the evaluation of
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$ and, therefore, diverges when the latter approaches zero). Consequently, the evaluation of ![]() $e_{max}^*$ from the solution of (3.14c), after substitution of (4.6c), is required prior to the numerical solution of (C2a) or (C3).
$e_{max}^*$ from the solution of (3.14c), after substitution of (4.6c), is required prior to the numerical solution of (C2a) or (C3).
An illustration of the dependence of the dimensionless size of the bulk meniscus, ![]() $\ell _m^*$, on the parameter
$\ell _m^*$, on the parameter ![]() $\epsilon /B$ is reported in figure 13, considering three values of
$\epsilon /B$ is reported in figure 13, considering three values of ![]() ${\overline {Ca}}/{\epsilon A}$. This figure shows that
${\overline {Ca}}/{\epsilon A}$. This figure shows that ![]() $\ell _m^*$ increases with
$\ell _m^*$ increases with ![]() $\epsilon /B$ and becomes exceedingly small when this parameter approaches zero. Moreover,
$\epsilon /B$ and becomes exceedingly small when this parameter approaches zero. Moreover, ![]() $\ell _m^*$ increases when
$\ell _m^*$ increases when ![]() ${\overline {Ca}}/{\epsilon A}$ decreases.
${\overline {Ca}}/{\epsilon A}$ decreases.

Figure 13. Dependence of the dimensionless size of the bulk meniscus, ![]() $\ell _m^*=\ell _m/\ell$, upon the parameter
$\ell _m^*=\ell _m/\ell$, upon the parameter ![]() $\epsilon /B$ for
$\epsilon /B$ for ![]() ${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$,
${\overline {Ca}}/{\epsilon A}=9\times 10^{-4}$, ![]() $3\times 10^{-3}$ and
$3\times 10^{-3}$ and ![]() $6\times 10^{-3}$ (case of a constant flow rate imposed at the inlet of the channel).
$6\times 10^{-3}$ (case of a constant flow rate imposed at the inlet of the channel).
C.2. Imposed pressure
In the case of an imposed pressure at the channel inlet, the estimate of ![]() $e_{max}^*$ resulting from (4.9) remains a reasonable one (provided
$e_{max}^*$ resulting from (4.9) remains a reasonable one (provided ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}\ll 1$ is satisfied). However, since the bulk meniscus is supposed to instantaneously penetrate the channel and keep its static shape when
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}\ll 1$ is satisfied). However, since the bulk meniscus is supposed to instantaneously penetrate the channel and keep its static shape when ![]() $P_0\ge P_{0{max}}$, no estimate of the slope
$P_0\ge P_{0{max}}$, no estimate of the slope ![]() ${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$ is available that is compatible with this hypothesis.
${\partial e^*}/{\partial x^*}|_{e^*=e_{max}^*}$ is available that is compatible with this hypothesis.