1. INTRODUCTION
Disease cases, of either infectious or non-infectious cause, are usually clustered within groups (i.e. litters, pens, herds) due to their contagious nature [Reference Carpenter1] and/or the effect of managerial, environmental or nutritional factors. In the presence of disease clustering, individual sample size formulae should be inflated to adjust for the correlation of disease cases within the clusters. Traditionally, measures like the variance inflation factor (VIF) or comparable quantities [Reference Campbell, Mollison and Grimshaw2–Reference McDermott, Schukken and Shoukri4], which are based on the intra-cluster correlation coefficient (ICC), have been used to modify sample size formulae. The ICC is an average measure of clustering in the population under study. However, it would normally be expected that subgroups of individuals exposed to different risk factors have different heterogeneity patterns. Therefore, sample size estimates based on the ICC may not be adequate for such subgroups of individuals who have a heterogeneity pattern largely deviating from the overall heterogeneity of the population under study. For instance, a larger sample size may be required for subgroups with excessive heterogeneity and ICC-based sample sizes may in this case lead to an increased risk of type-I error. Contrarily, higher than needed sample size estimates and, hence, unnecessary allocation of resources, occurs for subgroups of individuals with markedly less heterogeneity. Measures of clustering, which are specific to subgroups with a common heterogeneity pattern should, therefore, be preferred to the ICC. Additionally, the overall heterogeneity – as measured by the ICC – may be due to the mix of distinct risk profiles present in the population. In these instances identifying these profiles leads to the formulation of more homogeneous subgroups with a significant impact/reduction in the required sample sizes.
The variance partition coefficient (VPC), which has been recently introduced [Reference Goldstein, Browne and Rasbash5], quantifies the percentage of variability explained by clustering for individuals that share a combination of characteristics/covariates, i.e. the same covariate pattern/risk profile. Marked differences in VPCs identify groups of individuals that exhibit markedly greater or lesser heterogeneity when compared to the average heterogeneity of the data. Furthermore, the VPC estimate from a model without fitted covariates (an intercept-only model) is a measure of the heterogeneity in the whole population [Reference Browne6]. This is equal to the ICC estimate in the case of standard random intercept models. The VPC of the intercept-only model can be compared to the VPCs from models that contain covariates to measure the amount of heterogeneity in the whole population that is explained by the fitted covariates [Reference Browne6, Reference Kostoulas7]. A larger reduction of the unexplained heterogeneity between clusters leads to more homogeneous subgroups of clusters. Differences in the heterogeneity profiles are attenuated if VPC estimation methods ignore the imperfect sensitivity (Se) and specificity (Sp) of the diagnostic process used to classify the disease outcome [Reference Kostoulas7].
In this paper we propose a stratified approach to sample size estimation in the presence of clustering. Our approach is based on VPCs because they quantify the unexplained heterogeneity for identified subgroups of individuals, while, at the same time, reveal the amount of heterogeneity that was explained by the fitted covariates. We present methods for the incorporation of VPCs in the estimation of sample size for substantiation of freedom-from-disease surveys. All methods adjust for the non-differential or – whenever present – differential Se and Sp of the diagnostic process. Two examples are given using data from a risk factor study on Mycobacterium avium subsp. paratuberculosis (MAP) infection, in Danish dairy cattle and on critical control points for Salmonella cross-contamination of pork, in Greek slaughterhouses. These examples illustrate the application of VPC-based sample size estimation in two extreme cases, where the fitted covariates explain little or most of the heterogeneity in the whole population.
2. MATERIALS AND METHODS
2.1. VPC estimation in binary data
We have recently presented predictive simulation methods for VPC estimation through random-effects logistic regression models that adjusted for the imperfect Se and Sp of the diagnostic process for the outcome variable, i.e. the disease/infection status of the ith individual in the jth population/herd [Reference Kostoulas7]. Here these models are modified to allow for adjustments in the presence of differential misclassification: Se and Sp of the diagnostic process that varies depending on the exposure to a k-level factor (e.g. diagnostic test usually have different Se and Sp for different age groups). Briefly, for a binary (0/1) response, the observed test outcome of the ith individual, in the kth factor level (e.g. the age-specific category) in the jth population/herd, y ikj, can be assumed to follow a Bernoulli distribution:
where p ikj denotes the probability that the ikjth individual is diseased/infected, and Sek and Spk are the Se and Sp of the diagnostic process for individuals falling in the kth category [Reference Rogan and Gladen8]. We fit a random effects logistic regression model for the probability of infection for the ikjth individual as follows:
where X ikjT is a vector of known predictor variables and the expression X ikjTβ is referred to as the linear predictor [Reference McCullagh and Nelder9]. To account for clustering within populations/herds we include normally distributed random effects u j.
where tau is the precision parameter, tau=1/σ2u. A standard non-informative gamma prior is given on tau ∼ gamma(0·001, 0·001). In a fully Bayesian framework, a previously proposed method [Reference Bedrick, Christensen and Johnson10] can be used to impose priors on the regression coefficients (β) of the covariate vector, while prior information on the Se and Sp can be incorporated in the form of beta distributions, beta(a, b).
Subsequently, from the fitted model VPCs are estimated using a predictive simulation approach [Reference Browne6, Reference Kostoulas7]. Briefly, at every Markov Chain Monte Carlo (MCMC) iteration, we draw simulated values from the posterior predictive distribution of replicated data y ikjrep.
with
where X ikjT(rep)β is the linear predictor for a selected covariate pattern (combination of covariates), p ikjrep and y ikjrep the predicted probability of disease/infection and the predicted disease/infection status of the ikjth individual under X ikjT(rep)β, respectively.
For each considered X ikjT(rep)β, the covariate-pattern-specific ![]() ${\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ is calculated as the fraction of the total variation that can be ascribed to the higher level of organization. We have previously given detailed description and extensively explained WinBUGS codes for the abovementioned process [Reference Kostoulas7].
${\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ is calculated as the fraction of the total variation that can be ascribed to the higher level of organization. We have previously given detailed description and extensively explained WinBUGS codes for the abovementioned process [Reference Kostoulas7].
2.2. Use of VPCs and predicted risks to formulate prevalence priors
Sample size estimation for either prevalence or freedom-from-disease surveys requires an a priori estimate on the mean expected prevalence and its heterogeneity. We advocate that, for subgroups of individuals with a common covariate pattern, the information conveyed in the predicted risk of disease/infection p ikjrep and the corresponding ![]() ${\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$, under the fitted model (section 2.1) should be used for prior derivation about the prevalence of disease/infection and its heterogeneity.
${\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$, under the fitted model (section 2.1) should be used for prior derivation about the prevalence of disease/infection and its heterogeneity.
For individuals that possess a specific covariate pattern X ikjT(rep)β a prior on the probability of being infected can be modelled using a beta distribution:
with E(p ikjrep) the mean predicted risk of disease/infection for the considered covariate pattern and ![]() $\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ related to the variability of this risk with larger values corresponding to less variability. The covariate-pattern-specific VPC can be utilized to derive a prior on
$\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ related to the variability of this risk with larger values corresponding to less variability. The covariate-pattern-specific VPC can be utilized to derive a prior on ![]() $\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ by the use of formulae that describe the relationship between measures of clustering (ICC or, here, VPC) and the within- and between-herd prevalence of infection [Reference Branscum11]:
$\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ by the use of formulae that describe the relationship between measures of clustering (ICC or, here, VPC) and the within- and between-herd prevalence of infection [Reference Branscum11]:
 $$\eqalign {\tab \psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \equals \cr \tab{{\left( {1 \minus {\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)\left( {E\lpar p_{ikj}^{{\rm rep}} \rpar \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \minus 1} \right)} \over {{\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \left( {E\lpar p_{ikj}^{{\rm rep}} \rpar \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \minus 1} \right) \plus E\lpar p_{ikj}^{{\rm rep}} \rpar \left( {1 \minus \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)}}$$
$$\eqalign {\tab \psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \equals \cr \tab{{\left( {1 \minus {\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)\left( {E\lpar p_{ikj}^{{\rm rep}} \rpar \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \minus 1} \right)} \over {{\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \left( {E\lpar p_{ikj}^{{\rm rep}} \rpar \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \minus 1} \right) \plus E\lpar p_{ikj}^{{\rm rep}} \rpar \left( {1 \minus \tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)}}$$where E(p ikjrep) is as previously defined and ![]() $\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ is the probability that the subgroups of individuals under consideration are free of infection. When disease/infection is known to be present, i.e.
$\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$ is the probability that the subgroups of individuals under consideration are free of infection. When disease/infection is known to be present, i.e. ![]() $\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 1, equation (9) simplifies to:
$\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 1, equation (9) simplifies to:
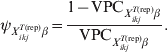 $$\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \equals {{1 \minus {\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \over {{\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } }}.\hfill$$
$$\psi _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } \equals {{1 \minus {\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \over {{\rm VPC}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } }}.\hfill$$Subsequently, we can simulate (m times) the expected outcome y.predikj for each of the sampled animals within each of the j herds that possess the covariate pattern under consideration:
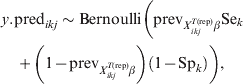 $$\eqalign {\tab y.{\rm pred}_{ikj} \sim {\rm Bernoulli}\left( {{\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } {\rm Se}_{k}}\right\cr \tab\quad \plus {\left( {1 \minus {\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)\left( {1 \minus {\rm Sp}_{k} } \right)} \bigg)\comma} \hfill$$
$$\eqalign {\tab y.{\rm pred}_{ikj} \sim {\rm Bernoulli}\left( {{\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } {\rm Se}_{k}}\right\cr \tab\quad \plus {\left( {1 \minus {\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta } } \right)\left( {1 \minus {\rm Sp}_{k} } \right)} \bigg)\comma} \hfill$$2.3. Sample size calculations for surveys to substantiate freedom from disease
Following equation (11), the possibility of herds being entirely free of disease can be modelled as previously suggested by Branscum and colleagues [Reference Branscum, Johnson and Gardner12]:
Those authors [Reference Branscum, Johnson and Gardner12] also allowed for the possibility (γ) that the entire region is free of infection:
If disease is known to be present in the region, this step can be excluded or γ can be simply set equal to 1.
To estimate the required sample size to substantiate freedom from disease we adopt the Bayesian predictive simulation approach described by these authors [Reference Branscum, Johnson and Gardner12]. Here, we modify this approach in order to apply for subgroups of clusters/herds with a common covariate pattern. Implicitly, this simulation approach assesses the required sample combination of i in j herds to substantiate freedom from disease when testing against the hypothesis that, if disease/infection is present, it would have a distribution pattern defined by the priors set on the ![]() $\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$, E(p ikjrep) and ψikj (through
$\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$, E(p ikjrep) and ψikj (through ![]() ${\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$). Initially, future survey data are generated under equation (11), assuming freedom from disease/infection (i.e.
${\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$). Initially, future survey data are generated under equation (11), assuming freedom from disease/infection (i.e. ![]() $\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 0). That is:
$\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 0). That is:
Generated data are then analysed under the model described in equations (11–13), which incorporates covariate-pattern-specific prior information on the ![]() ${\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$. Subsequently, the predictive probability of
${\rm prev}_{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$. Subsequently, the predictive probability of ![]() $\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 0 at a pre-specified level of confidence (usually 95%) is calculated. This procedure is repeated for different combinations of j and n, to determine the required herd and within-herd sample size to effectively substantiate freedom from disease at the specified confidence level. The computational details of this approach have been extensively described elsewhere [Reference Branscum, Johnson and Gardner12].
$\tau _{X_{{ikj}}^{{T\lpar {\rm rep}\rpar }} \beta }$= 0 at a pre-specified level of confidence (usually 95%) is calculated. This procedure is repeated for different combinations of j and n, to determine the required herd and within-herd sample size to effectively substantiate freedom from disease at the specified confidence level. The computational details of this approach have been extensively described elsewhere [Reference Branscum, Johnson and Gardner12].
The series of the modelling steps taken to calculate the minimum sample size requirements to substantiate freedom from disease are given in Figure 1.

Fig. 1. Flow diagram illustrating the proposed modelling approach for sample size estimation to substantiate freedom from disease. VPC, Variance partition coefficient.
2.4. Goodness-of-fit tests and convergence diagnostics
Goodness of fit for the VPC estimation model (section 2.1) is assessed through posterior predictive checking. Breifly, if the model fits the data well, then replicated data under the fitted model should be similar to the observed data. Simulated values under the fitted model are drawn from the posterior predictive distribution of replicated data and compared to the observed data. Subsequently, the replicated values are plotted against the observed data in a scatter plot. The scatter plot must be symmetric about the 45o line [Reference Gelman13]. This was true in the following applications (see sections 3.1 and 3.2).
2.5. Assessment of model convergence
Convergence diagnostics for MCMC sampling are not foolproof. Therefore, a combination of diagnostics plus visual inspection of the trace plots and summary statistics is recommended [Reference Best, Cowles and Vines14]. Use of standard diagnostic procedures [Reference Heidelberger and Welch15–Reference Gelman and Rubin17] in the following applications (sections 3.1 and 3.2) did not reveal any convergence problems. We also checked the autocorrelation plots and visually inspected the posterior distributions of the parameters. Parameter estimates and 95% credible intervals (CrIs) were based on the analytical summaries of 10 000 iterations of three parallel MCMC chains, with a thinning interval of 1 and a burn-in phase of 5000 iterations.
2.6. Statistical software
Models were run in WinBUGS [Reference Spiegelhalter18] through R [19]. The code with detailed step-by-step explanation for sections 2.2 and 2.3 is provided as Supplementary material. The code for section 2.1 has been given previously [Reference Kostoulas7]. BetaBuster software [20] was used to derive priors on Se and Sp.
3. EXAMPLES
The presented sample size estimation is of greater practical importance when considering subgroups of clusters that differ at higher levels of organization, such as the herd level, due to the infectious nature of most infections/diseases and/or the effect of management, nutritional and environmental factors that vary at this level. In the case of freedom from disease, definition of subgroups of clusters within the herd would not be applicable or biologically plausible. Thus, the following examples, which demonstrate the usefulness of these models, consider the inclusion of higher-level covariates. That is, the linear predictor is X ..jTβ rather than X ikjTβ and, hence, VPCs and predicted risks of disease/infection are the same for individuals within the same higher-level unit.
3.1. Sample size estimation for Danish dairy herds with different risk profiles of MAP infection
Individual animal records on the MAP antibody milk ELISA status and age were retrieved from the Danish Cattle database for 64 945 animals in 633 herds. Subsequently, details on the corresponding management practices regarding colostrum and milk feeding were recorded. Detailed information and a thorough descriptive analysis of the test responses and the distribution of these by feeding practice are given elsewhere [Reference Nielsen, Bjerre and Toft21].
A random-effects logistic regression model was used to assess the association between milk and colostrum feeding practices and the risk of MAP infection, adjusting for the differential (i.e. depending on the age) Se and Sp of the diagnostic process. Specifically, the Se and Sp of the milk ELISA for paratuberculosis is age dependent. Hence, herds with varying age distribution are expected to have different overall Se and Sp. Based on previously published estimates [Reference Nielsen and Toft22], we chose to split each herd into two groups: animals aged ⩽3 and >3 years. Thus, our model and subsequent VPC estimation adjusted for the age-specific Se and Sp of the milk ELISA.
For cattle aged ⩽3 years we were certain that the most probable value for Se was 0·15 and that the 5th percentile could not be less than 0·06; this translates to a beta(4·32, 19·84) prior. For Sp the most probable value was set to 0·99 and we were certain that the 5th percentile was not less than 0·98, which translates to a beta(560·72, 6·65) prior. Corresponding values for cattle aged >3 years were, for Se, an expectation of around 0·50 and a 5th percentile of 0·35, resulting in a beta(14·59, 14·59) prior and for Sp an expectation of around 0·98 and a 5th percentile of 0·95, resulting in a beta(151·77, 4·08) prior.
From the fitted model, VPCs and corresponding predicted risks of MAP infection were obtained for all possible covariate patterns. For the covariate patterns that exhibited the highest and lowest heterogeneity, as dictated by the VPC, we estimated the required i and j for substantiation of freedom from disease, via the predictive simulation approach described in section 2.3. The prior on ψ was derived according to Bedrick and colleagues [Reference Bedrick, Christensen and Johnson10] because the region was known to be infected with MAP, thus, τ=1. Due to the different priors set for the age-specific Se and Sp, the y.predijk is affected by the age distribution within the herd. Based on the available data, we assumed a 2:3 ratio between younger (⩽3 years) and older (>3 years) animals in all simulations. For each covariate pattern the VPC and the corresponding mean predicted risk of MAP infection were used to formulate our prevalence priors according to equation (8). Simulations to determine the required sample size for freedom from disease allowed j to vary but used a constant number of 50 animals sampled within each of the j herds to save simulation time.
Herds feeding colostrum to calves only from their own dam and/or using milk replacer exhibited the lowest risk of MAP infection and were of the least heterogeneous (i.e. had the lowest VPCs). The highest risk of MAP infection was in herds feeding colostrum from multiple cows and/or allowing suckling from foster cows. These herds were the most heterogeneous and hence had the highest VPCs. The VPC from the intercept-only model was comparable to the ones under the fitted model (Table 1). Estimated sample sizes are given in Table 3. Sampling requirements for the whole population, which were estimated from an intercept-only model, are also given for comparisons.
Table 1. Estimated VPCs (medians and 95% credible intervals) and predicted risk of Mycobacterium avium subsp. paratuberculosis (MAP) infection for subgroups of herds that share common characteristics – common covariate pattern. Estimations were based on models that adjusted for the age-specific diagnostic accuracy of the milk ELISA for MAP. Estimates from an intercept-only model are also given

VPC, Variance partition coefficient.
3.2. Critical control points for Salmonella cross-contamination on pork
We have re-analysed data from a study aimed at identifying critical control points for pork carcass contamination during the slaughter process. Samples were collected from two slaughterhouses located in Northern Greece, which were visited bi-monthly for 22 consecutive visits.
A random-effects logistic model was used to model the association between the Salmonella status of the individual pig carcass with the Salmonella daily status of the eviscerator and the excessive extra-muscular-fat trimmer. Sampling day was included as a higher-level random effect [Reference Kostoulas7]. Priors for Se and Sp were elicited from previously published relevant estimates [Reference Enøe23]. A priori, the most probable value for Se of the Salmonella culture was thought to be 30% and we were 95% certain that it was not more than 50%, resulting in a beta(6·28, 13·32) prior. For Sp, we allowed for about one false positive in 1000 tests, to acknowledge the fact that false positive results can occasionally occur due to the unlikely yet existent possibility of cross-contamination/mix-up during sample processing, i.e. a beta(999, 1) prior.
VPCs and predicted risks of carcass cross-contamination are given in Table 2. The highest risk of carcass cross-contamination was predicted when both the trimmer and the eviscerator had Salmonella on their hands/knives, while the risk was the lowest when neither of the sites was Salmonella positive. The VPC from the intercept-only model was high, suggesting that carcass cross-contamination varied daily. Inclusion of the day-level status of the trimmer and the eviscerator in the fitted model led to VPC estimates with median values that were practically zero. Required sample sizes to substantiate freedom from disease are given in Table 3 (as previously, the number of pork carcasses sampled in each of j sampling days was set to a constant – in this case 30 – to save simulation time). Sample size requirements are also given under an intercept-only model.
Table 2. Medians (95% credible intervals) of VPCs and predicted risk of carcass cross-contamination with Salmonella. Significant fitted covariates are the daily Salmonella status of the eviscerator and the trimmer. Estimates from an intercept-only model are also given

VPC, Variance partition coefficient.
Table 3. Estimated number of herds (j) required for sampling to substantiate freedom from (i) MAP infection (assuming a within-herd sample of i=50 animals) and (ii) Salmonella cross-contamination (assuming a within-day sample of i=30 pork carcasses), for selected covariate patterns that exhibit markedly greater or less heterogeneity. Estimates are based on the analysis of 100 simulated datasets for each considered combination of i and j. For each selected covariate pattern, priors on the minimum expected prevalence (μ) were based on the mean predicted risk of MAP infection and carcass cross-contamination for (i) and (ii), respectively. Priors on the variability of the within-herd prevalence (ψ) were based on the corresponding VPC estimates. Estimates from an intercept-only model that ignored the covariate-pattern-specific heterogeneity and correspond to the whole population are also given for comparisons

MAP, Mycobacterium avium subsp. paratuberculosis; VPC, variance partition coefficient.
4. DISCUSSION
We suggest that estimation of required sample sizes should be specific to subgroups of data/clusters with a common risk profile, which may possess a different heterogeneity pattern than that of the overall population. In such instances, sample size estimates based on average measures of heterogeneity, like the ICC, will lead to under- or over-estimation of the required sample sizes. Our examples suggest that different sample sizes are required depending on the attained risk as described by the different covariate patterns. Furthermore, a significant reduction in the total sample size requirements is achieved when a portion of the heterogeneity in the whole population is explained by the subgrouping characteristics, i.e. the fitted covariates. We give examples of two extreme cases where, under the fitted model, the unexplained heterogeneity either remains approximately equal to the estimate under the intercept-only model (section 3.1) or is markedly reduced (section 3.2). Most of the heterogeneity in the risk of MAP infection, in Danish dairy cattle, remained unexplained despite the inclusion of significant herd-level predictors in the fitted model (Table 1). This indicates that additional, unmeasured or immeasurable factors exist, which operate at the herd level and were not accounted for, thus, contributing to the between-herd heterogeneity of MAP infection [Reference Browne6, Reference Kostoulas7]. Contrarily, the inclusion of higher-level covariate information about the day-level Salmonella status of the eviscerators' and trimmers' hands/knives led to VPCs that were practically zero (Table 2). Practically, the observed heterogeneity of carcass cross-contamination among sampling days can be totally ascribed to the daily status of the trimmer and the eviscerator. The latter case is an ideal paradigm where the fitted covariates practically accounted for the whole heterogeneity in the risk of carcass cross-contamination between sampling days. Hence, covariate-pattern specific subgrouping led to the formulation of homogeneous groups and a significant reduction in the required sample sizes (Table 3). To put it simply, these results indicate that daily pig-carcass contamination levels depend on the status of the trimmer and/or the eviscerator; the delivered message is that daily samples at these points of the slaughter line are sufficient to provide information on the status of the daily contamination levels of the individual pig carcasses. The reduction to the required sample size is an additional advantage of the proposed approach to sample size estimation. Evidently, the benefits are higher when a larger part of the higher level heterogeneity is explained under the fitted model.
We have integrated methods of measuring the heterogeneity for subgroups of individuals with a common risk profile/covariate pattern [Reference Browne6, Reference Kostoulas7] in the predictive simulation approach to sample size estimation for substantiation of freedom from disease [Reference Branscum, Johnson and Gardner12]. Central to our approach is the formulation of a prevalence prior [equation (8)] to quantify our belief on the expected mean within-cluster/-herd prevalence of disease/infection (μ) and its variability (ψ) among disease/infected clusters/herds, which is specific to subgroups with a common risk profile; i.e. the same covariate pattern. The mean predicted risk of disease/infection and the corresponding VPCs, under the fitted models, were used to derive the corresponding priors on μ and ψ. Alternatively, more conservative estimates, such as the 5th percentile of the posterior distribution for the risk of disease/infection, can be used to generate the latter priors. The presented predictive simulation approach for freedom from disease simulates data points (animals sampled from herds) under the assumed distribution of disease/infection and subsequently assesses whether the specified j and i are sufficient to prove disease/infection freedom – at the required precision – when testing vs. a disease/infection pattern described by the abovementioned prior specifications. Essentially, under this predictive simulation approach [Reference Branscum, Johnson and Gardner12], the specified priors on γ, τ, μ and ψ, implicitly express our perceived risk of disease/infection for the whole area, the proportion of the infected herds and the between and within infected herds dispersion of infection, had the infection been present. These explicitly fall within the concept of specifying a minimum expected prevalence: disease is either present at the specified minimum level or not present at all. Specification of the minimum expected prevalence is normally based on biological grounds and quantifies the expected spread of disease due to its contagiousness and/or the presence of a specific mixture of risk factors, as was in our case. In other case specification of the minimum expected prevalence can be on the grounds that below a threshold value it will move towards extinction without intervention due to non-sustainable transmission rates. Finally, from a managerial/economical point of view the minimum expected prevalence, refers to a threshold value under which disease/infection is small enough to be considered negligible or not of major concern [Reference Cameron and Baldock24].
Several simulations – not shown here – have been performed to explore how various combinations of j and i affect our confidence in freedom from disease. In accordance with previous work [Reference Branscum, Johnson and Gardner12] our confidence increased with increasing j and/or i, with increasing j being the more efficient approach in reducing the total (i*j) sample size. In the presence of clustering, increasing the number of clusters to be sampled is the more efficient method of achieving the required precision with a smaller sample size [Reference Campbell, Mollison and Grimshaw2]. The total sample size is minimized if just one animal is sampled from every cluster. In practice, however, the optimum i and j is an informed decision that takes into account the relative costs of sampling different clusters (e.g. herds) to sampling units (e.g. animals) within the same cluster. Furthermore, we have assessed the impact of different scenarios on the distribution of disease/infection within herds. Increasing μ and ψ (which is equivalent to assuming a higher risk and more diversified distribution of within-herd prevalence) resulted in achieving the required confidence with a smaller sample size. The latter demonstrated the plausible idea that when the within-herd prevalence is expected to be high a smaller sample size is needed to differentiate a disease-free from a diseased/infected population.
We have extended our previous work [Reference Browne6, Reference Kostoulas7] to adjust for differential test errors on a specific exposure (section 3.1). Taking into account the presence of differential misclassification is crucial because a certain trend does not exist for differential errors. This can result in either over- or underestimation of measures of association such as the odds ratio. Contrarily, non-differential misclassification (i.e. Se and Sp invariant to exposure status) always leads to the underestimation of such measures [Reference McInturff25]. Hence, it is wrong, to use an average Se and Sp estimate for the whole data and falsely treat differential misclassification rates as invariant to exposure status because a difference from the true trend may be observed. We have recently demonstrated the severe impact on VPC underestimation that occurs when disregarding misclassification rates [Reference Kostoulas7] while previous work has revealed an analogous effect on the ICC [Reference Branscum11]. Ignoring differential or non-differential test errors would have a severe impact on the covariate-pattern-specific (i) VPCs and (ii) predicted risk of disease/infection and the corresponding sample size estimates.
We have integrated and developed methods for a simulation-based approach to sample size estimation to prove freedom from disease, which is specific to subgroups with a common risk profile. Clearly, the utility of the proposed model depends heavily on the availability of relevant data, which have to be specific to subgroups of clusters, in order to generate appropriate priors and correctly estimate the corresponding sample sizes. Such data may be difficult to obtain in a real life situation. Yet, the application of automated monitoring systems at the farm, clinic and national level, such as the Danish control scheme on MAP does and will increasingly provide such data in the future. We advocate that this approach betters resource allocation and, thus, falls within the context of a risk-based approach to surveillance, which is of great importance due to the currently increasing limits of human and financial resources available for disease surveillance, control and preventive measures. For greatly heterogeneous populations, sample size estimations specific to clusters with a common disease/infection risk profile would improve resource allocation and could, in several instances, significantly reduce sample size requirements.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0950268812001938.
ACKNOWLEDGEMENTS
The authors thank Dr A. J. Branscum, for his assistance with the implementation of our models in WinBUGS/R.
DECLARATION OF INTEREST
None.





