Article contents
Excitation and stability of nonlinear compressible Görtler vortices and streaks induced by free-stream vortical disturbances
Published online by Cambridge University Press: 04 December 2024
Abstract
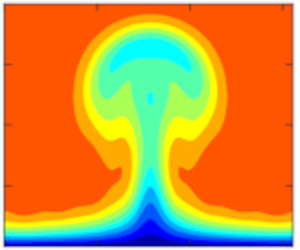
We study the generation, nonlinear development and secondary instability of unsteady Görtler vortices and streaks in compressible boundary layers exposed to free-stream vortical disturbances and evolving over concave, flat and convex walls. The formation and evolution of the disturbances are governed by the compressible nonlinear boundary-region equations, supplemented by initial and boundary conditions that characterise the impact of the free-stream disturbances on the boundary layer. Computations are performed for parameters typical of flows over high-pressure turbine blades, where the Görtler number, a measure of the curvature effects, and the disturbance Reynolds number, a measure of the nonlinear effects, are order-one quantities. At moderate intensities of the free-stream disturbances, increasing the Görtler number renders the boundary layer more unstable, while increasing the Mach number or the frequency stabilises the flow. As the free-stream disturbances become more intense, vortices over concave surfaces no longer develop into the characteristic mushroom-shaped structures, while the flow over convex surfaces is destabilised. An occurrence map identifies Görtler vortices or streaks for different levels of free-stream disturbances and Görtler numbers. Our calculations capture well the experimental measurements of the enhanced skin friction and wall-heat transfer over turbine-blade pressure surfaces. The time-averaged wall-heat transfer modulations, termed hot fingers, are elongated in the streamwise direction and their spanwise wavelength is half of the characteristic wavelength of the free-stream disturbances. Nonlinearly saturated disturbances are unstable to secondary high-frequency modes, whose growth rate increases with the Görtler number. A new varicose even mode is reported, which may promote transition to turbulence at the stem of nonlinear streaks.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by


