I. INTRODUCTION
Machine intelligence is all around us. Our financial institutions sift through our purchasing data to define patterns of usual – and by their complement unusual – activity in order to minimize fraud. Most likely words and queries show up in typed, spoken, and gestured applications and services. Self-driving cars are part of the everyday conversation. It is clear that a growing percentage of the intelligent decisions made in our world are performed by the machines, and not the minds, of humans.
This “additional level of indirection” for decision-making comes at a price. There is the risk that reliance on machine algorithms may make humans less capable in some intellectual capacities; however, this issue will not be addressed here. What is more germane – and potentially more frightening – is that machines will make critical mistakes which go unnoticed. This argument is not based on an apocalyptic or Luddite fear of computers. Computers have arguably improved human lives more than any other invention (water purification and agriculture notwithstanding). Instead, it is because machine intelligence is so very different from human intelligence that the reliability of machine intelligence output must be questioned.
Computers and their associated algorithms, systems and intelligence engines outperform humans on many mathematical and analytical tasks. To date, however, humans significantly outperform computers on more distributed, Gestalt, intuitive and unstructured tasks. As computers are tasked more and more in this purported “Big Data” era to discern information from ever-growing amounts of unstructured data, how can we be sure that the machine intelligence is consistent with human intelligence? One approach is to design machine intelligence systems that share the precepts of human intelligence. Paramount among these are the following precepts:
• The ability to incorporate new rules of discernment and models for analysis into an existing model or set of models;
• The ability to selectively apply different learned content based on the context;
• The ability to correctly solve problems in the absence of sufficient input;
• The ability to perform “real time ground truthing”; that is, the ability to assess a situation after a particular output is assumed and efficiently perform a minimal set of validation experiments to prove or disprove the correctness of the output.
These precepts will be re-considered (Section VII) after the stage for meta-algorithm-based architectures is given. The ensemble and meta-algorithmic approaches and their application to signal and image processing are outlined in Sections II and III. In Section IV, a new model for intelligent system architecture based on meta-algorithmics is supported. This model is then applied to Biological Signal Processing (Section V) and to general Image Processing, Object Segmentation and Classification (Section VI). Section VII provides the Discussion, Conclusions, and the Future of this approach to system design and deployment.
II. ENSEMBLE ARCHITECTURES
This section elaborates on Chapter 1, Section 6 of my earlier work [Reference Simske1]. As noted there, ensemble learning focuses on the handling of the output of two or more intelligent systems in parallel. The reviews provided by [Reference Berk2,Reference Sewell3] are recommended for their particular value in understanding ensemble methods.
In [Reference Berk2], ensemble methods are described as “bundled fits produced by a stochastic algorithm, the output of which is some combination of a large number of passes through the data”. This, then, constitutes an algorithm in which bundling or combining of the fitted values from a number of fitting attempts is used iteratively to converge on an intelligent output [Reference Hothorn4]. Classification and Regression Trees as introduced in [Reference Breiman, Friedman, Olshen and Stone5] provide the means to move from traditional modeling (e.g. manifold-based systems and mixture models) to algorithmic approaches. Partitioning of the input domain is used to create subclasses of the input space which correlate well with one class among a set of classes. However, partitioning often leads to overfitting of the data and the associated degradation of performance on test data relative to the training data.
To avoid overfitting, ensemble methods are used. Bagging, boosting and random forests are the three primary ensemble methods described in [Reference Berk2]. Bagging, or “bootstrap aggregation”, is an algorithm: random samples are drawn N times with replacement and non-pruned classification (decision) trees are created. This process is repeated many times, after which the classification for each case in the overall data set is decided by majority voting. Overfitting is avoided by this averaging and by the proper selection of a margin for the majority voting. This means some cases will go unclassified, but since multiple trees are created these samples will likely be classified through another case. Should any samples be unassigned, they can be assigned by nearest neighbor or other decisioning approaches.
Boosting [Reference Schapire6] is, generally speaking, a process in which the misclassified cases are more highly weighted after each iteration. This is conceptually – though not mathematically – analogous to the definition of a support vector wherein the samples most likely to be mis-classified are emphasized. In a support vector, the samples defining the boundary (or “manifold”) between classes are emphasized. Regardless, this approach often prevents overfitting, and as the AdaBoost [Reference Schapire6,Reference Freund and Schapire7] algorithm has certainly proven accurate in a number of machine-learning problems. The approach is not without problems, however. The stopping criterion – usually the error value during training – is not always effective, and convergence is not guaranteed.
Random forests [Reference Breiman8] are another important ensemble approach. These further the randomness introduced by bagging by selecting a random subset of predictors to create the node splits during tree creation. They are designed to allow trade-off between bias and variance in the fitted value [Reference Berk2]. They are often useful for defining structure in an otherwise unstructured data set.
The ensemble methods bagging, boosting, voting, and class set reduction are among the 18 classifier combination schemes overviewed in [Reference Jain, Duin and Mao9]. This broad and valuable paper mentions the possibility of having individual classifiers use in different feature sets. It also mentions different classifiers operating on different subsets of the input; for example, the random subspace method. This approach lays some of the groundworks for meta-algorithmics; in particular, the Predictive Selection approach. Systemization of that approach, however, does not occur until [Reference Simske1], and is covered in the next section of this paper.
In [Reference Sewell3], ensemble learning is defined as an approach to combine multiple learners. Sewell introduces bootstrap aggregating, or bagging, as a “meta-algorithm” which is a special case of model averaging. The bagging approach can be viewed as an incipient form of the Voting meta-algorithmic pattern described in [Reference Simske1], Chapter 6, Section 3.3. It is useful for both classification and regression machine-learning problems. Different from meta-algorithmic patterns, however, bagging operates on multiple related algorithms, such as decision stumps, and not on independently-derived algorithms. Boosting is also described in [Reference Sewell3] as a “meta-algorithm” that provides a model averaging approach. It, too, can be used for regression or classification. Boosting's value is in generating strong classifiers from a set of weak learners.
Another ensemble method is stacked generalization, described in [Reference Wolpert10]. Stacked generalization extends the combined training and validation approach to a plurality of base learners. This is a multiple model approach in that rather than implementing the base learner with the highest accuracy during validation, the base learners are combined, often non-linearly, to create the “meta-learner”. This paves, but does not systematize, the path for meta-algorithmic patterns such as Weighted Voting. However, stacked generalization is focused on combining weak learners, as opposed to meta-algorithmics which are focused on combining strong learners, engines or intelligent systems.
The final ensemble method that introduces some of the conceptual framework for meta-algorithmics is the random subspace method [Reference Ho11], in which the original training set input space is partitioned into random subspaces. Separate learning machines are then trained on the subspaces and the meta-model combines the output of the models, usually through majority voting. This shares much in common with the mixture of experts approach [Reference Jacobs, Jordan, Nowlan and Hinton12], which differs in that it has different components model the distribution in different regions of the input space and the gating function decides how to use these experts. The random subspace method leads to a single model – capable of classification or regression analysis – that can provide high accuracy even in the face of a highly non-linear input space. Both the random subspace and mixture of experts’ approaches are analogous in some ways to the Predictive Selection meta-algorithmic approach and related meta-algorithmic patterns. However, like other ensemble approaches, these models stop at providing an improved single model for data analysis. Meta-algorithmics, on the other hand – as seen in the next section – use the output of ensemble methods, other classifiers, and other intelligent systems as their starting points. Meta-algorithmics combine multiple models to make better decisions, meaning that, for example, bagging, boosting, stacked generalization, and random subspace methods could all be used together to create a more accurate, more robust and/or more cost-effective system.
III. META-ALGORITHMIC ARCHITECTURES
In [Reference Simske1], 20 specific meta-algorithmic patterns and one generalized meta-algorithmic pattern are presented. The patterns are arranged as first-, second-, and third-order patterns based on their relative complexity and for ease of instruction. Regardless of arrangement, the reader should appreciate that knowing how to apply the patterns is more important that their “structural clustering”. Each of the patterns will be overviewed briefly, and one or more examples of each given in the following sections. In this section, each pattern is summarized for its overall value to the owner of multiple machine intelligence generators (algorithms, systems, engines, etc.). The patterns are described in more detail in [Reference Simske1] and the meta-algorithmic system diagrams can be downloaded from [13].
A) First-order meta-algorithmics
The easiest meta-algorithmic pattern is named Sequential Try – and this consists of no more than trying one machine-learning approach after another until a task is completed with sufficient quality. Evaluation is performed manually or automatically. This pattern is very useful when the system architect can arrange her machine intelligence generators in order of cost, expected time to completion, licensing availability, etc.
Another relatively simple meta-algorithmic pattern is the Constrained Substitute pattern. This pattern allows one algorithm or machine intelligence system to substitute for another when it is certain (with a given statistical probability) that the substitute system (which saves licensing costs, processing time, storage, etc.) will perform acceptably well in comparison with the substituted system. This pattern is extremely useful for distributed systems with limited licensed versions of the software or when processing power is not a limiting factor in the system design.
Voting and Weighted Voting are simple means of using multiple machine intelligence approaches simultaneously. In using the Voting patterns, the outputs are simply summed. For classification problems this means that the class accumulating the highest total sum from the plurality of classifiers is the labeled class. For Weighted Voting, each algorithm or system is weighted based on its relative value to the overall solution. The weighting is usually inversely proportional to the error rate in some way. This pattern is probably the easiest choice for a system architect, as all systems contribute to the outcome for every case. However, it typically requires more processing time, has maximum cost, and is typically less robust than most other meta-algorithmic system architecture choices.
Predictive Selection is a powerful – and widely applicable – meta-algorithmic pattern that provides a very adaptive means of assigning input to one of several subclasses, each of which is best processed by a specific algorithmic or meta-algorithmic approach. The system architect thus assigns different analysis approaches to each of two or more different parallel pathways based on a – preferably highly accurate – prediction of which machine intelligence approach will perform best on each of the paths. This approach is valuable in many different intelligent systems, and is often a “first good guess” for the system architecture when the input domain is broad.
The final first-order meta-algorithmic approach is that of Tessellation and Recombination. This pattern requires some domain expertise, since the tessellation must logically break up larger data units into their atomic units prior to their recombination. This approach, however, has high likelihood to produce emergent results and behavior than the aforementioned first-order meta-algorithmic approaches. This pattern is valuable when the input to an intelligent system already represents, at some level, processed data. In other words, it is valuable when the input data is already “intelligent”. This pattern “reconsiders” the intelligence added at the previous level to create an additional level of intelligence. This pattern is particularly relevant to human learning, since the means in which to recombine information is, ideally, driven by domain expertise.
B) Second-order meta-algorithmics
The second-order meta-algorithmics feature two or more stages to perform the meta-algorithmic task. Several of these patterns rely on the confusion, which is a matrix showing all classification assignments. Those on the matrix diagonal are correctly assigned, whereas those off-diagonal provide the mis-classifications of the actual class (row) to the mis-assigned class (column). This matrix is very helpful for illuminating where subsets of classes may benefit from a less general intelligence engine that simplifies the overall classification problem.
The Confusion Matrix Pattern, as defined in [Reference Simske1], actually relies on an Output Probabilities Matrix (OPM) that effectively summarizes the relative classification confidence in each classification output. An illustrative example is shown in Table 1. Here, there are four Classifiers, each of which assigns a normalized (sum of 1.0) probability of output to each of the classes (here, there are three classes A, B, and C). Thus, each column sums to 1.0. The sum of each row is used to choose the overall assigned class. In the example below, Class C has the highest overall confidence even though Class B was chosen by three of the four classifiers.
Table 1. Example OPM. Each of four classifiers has a total (summed) confidence of 1.0, which shows up in the columns under “1”, “2”, etc.
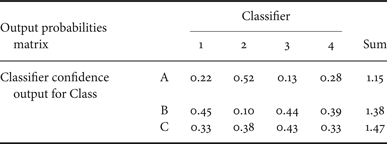
The sum of all Classifier confidence in each row can be used to select the “Class” assignment. In this case, the sum is greatest for Class “C”. See the text for more details.
The manner in which the confusion matrix is used determines the output classification. If the greatest sum is chosen, then the classification for Table 1 is “Class A”. Other possible classifications are possible, however. The OPM could be used, for example, as a mechanism for arranging votes by each of the classifiers. In this case, “Class B” would be chosen, with three votes. The OPM can also be weighted by the relative accuracy of the classifiers. An example of this is shown in Table 2, for which the Class “B” is chosen.
Table 2. Example OPM of Table 1 with Classifiers additionally weighted by their relative accuracy. The Weight of Classifier 1 is 2.0 times that of Classifier 2, with the other two Classifiers being intermediate to these two.

*The sum of all Classifier confidence in each row can be used to select the “Class” assignment. In this case, the sum is greatest for Class “B”.
The output of an OPM as shown in Tables 1 and 2 is used to generate the Confusion Matrix, an example of which is given in Table 3. Suppose that in the example of Tables 1 and 2 Class “C” is the correct classification. The result of Table 1 would be incorrect and would result in an off-diagonal entry in the Confusion Matrix (Classifier Output = “B”, True Class = “C”). The result of Table 2 would be correct and result in an on-diagonal entry in the Confusion Matrix (Classifier Output = “C”, True Class = “C”).
Table 3. Example confusion matrix.

Once a large enough set of samples has been classified, the confusion matrix can be normalized such that each class is equally represented and the sum of each row is 1.0. Such a normalized confusion matrix is shown in Table 3.
Table 2 provides the input for the meta-algorithmic pattern of Weighted Confusion Matrix. Here, the OPM of Table 1 is multiplied by the relative contribution of each classifier to the final decision. More accurate, robust, or otherwise valued classifiers are given higher OPM values in proportion to their overall confidence weighting. The impact of this is that differences in classifier confidence are exaggerated for the more trusted classifiers, allowing them to “outweigh” the other classifiers. In Table 2, the much higher confidence classifier “2” has for Class “C” instead of the correct Class “B” is thus overcome by the higher relative weights assigned to the OPM cells for the other classifiers. This results in a (column, row) assignment of (B,B) to the confusion matrix in Table 3, which is along the diagonal (and thus not confused).
The remainder of meta-algorithmic patterns will be described more briefly here. The main goal of overviewing the meta-algorithmic patterns is to support the argument for an architectural, or structural, change in how intelligent systems are designed and built. The plurality of meta-algorithmic approaches equates with many architectural choices for the intelligent system builder.
The second-order meta-algorithmic approaches are concerned with making the individual intelligent systems work better together. One mechanism is output space transformation, which allows us to use the same generators and the same meta-algorithmic pattern to optimize the system for different factors; for example, accuracy or robustness or cost. The goal is to coordinate the behavior of the probability differences between consecutively ranked classes among the multiple engines [Reference Simske, Wright and Sturgill14]. Depending on the transformation used, a significantly improved classification accuracy can be garnered.
Other second-order patterns internalize domain expertise (Tessellation and Recombination with Expert Decisioner), particularly in the recombination step of the algorithm which dictates how aggregates of the data will be reconstructed from the primitives resulting from the tessellation step. This is a formal pattern-based means of ingesting domain expertise into the recombination phase. Other approaches use one architecture when a particular grading criterion is achieved; and a different architecture if it is not.
C) Third-order meta-algorithmics
Third-order meta-algorithmics add even tighter coupling between the multiple steps in the algorithm. The primary analysis tools of these meta-algorithmics – feedback, sensitivity analysis, regional optimization, and hybridization – tightly connect not only one step to the next, but also connect the downstream steps back to the earlier steps.
Using the Feedback pattern, errors in the reconstructed information are immediately fed back to change the gain – e.g. weights – on the individual system architecture settings. This is related to the Proof by Task Completion pattern, which dynamically changes the weighting of the individual systems after tasks have successfully completed (effectively feeding back the successes rather than the errors). This approach affords limitless scalability, since new data do not change the complexity or storage needs of the meta-algorithmic pattern. Also, there is a wide range of choice in how to weight old and new data.
With the third-order meta-algorithmics, intelligent signal and image processing system architecting moves from science to art. The basic patterns provide a structural framework for the application of meta-algorithmics, which comprises the science of meta-algorithmics. However, there is a lot of art in the domain expertise needed to relatively weight old and new data, to know how strongly to incorporate feedback, and to know which other meta-algorithmic patterns to use in parallel. The crux is that for third-order meta-algorithmics, expert experience (incarnated as rules suitable to provide “expert system” guidance) is useful to determine the settings of not just the individual algorithms/systems, but also the settings of how the algorithms/systems combine.
For example, the Confusion Matrix for Feedback pattern incorporates the relationship between the errors in the intelligence algorithms/systems (as elucidated by the confusion matrix). The feedback is used here to identify the biggest source(s) of error to direct the creation of the most likely impactful binary decisions in the problem. The Expert Feedback pattern incorporates expert-learned rules which guide what elements of the output (and their relative weighting) is fed back to the input.
Another third-order meta-algorithmic approach, Sensitivity Analysis, is often used to optimize the weighting for expert feedback and other weighting-driven meta-algorithmic patterns. Sensitivity analysis can be used to:
a) determine stable areas within the confusion matrix
b) determine stable areas within the relative weighting of feedback parameters
c) determine stable areas within correlation matrices to provide dimensionality reduction
Sensitivity analysis can also be used to cluster expert feedback for subclass-based analysis. This enables the Regional Optimization pattern, which extends the highly adaptable and powerful Predictive Selection pattern by selecting by subclass first- or second-order meta-algorithmic patterns rather than just selecting individual algorithms, systems, or engines. As with Predictive Selection, the highest expected precision for the specific subclass is chosen. This pattern, obviously, takes the concept of meta-algorithm and makes it recursive. Algorithms, meta-algorithms, even meta-meta-algorithms can be combined to create new algorithms, affording multiple levels of learning. This concept is incarnated in the so-named Generalized Hybridization pattern. As expected, this pattern is for optimization of the combination and sequencing of first- and second-order meta-algorithmic patterns for a given – generally large – problem space. These final two patterns enable, at least in theory, a limitless number of meta-algorithmic approaches to machine learning.
IV. A NEW MODEL FOR ARCHITECTURE
The previous section illustrated the breadth of patterns available for the intelligent system architect. Here, their part in a new model for intelligent system architecture is presented in terms of adaptability, ease of rollout, robustness, accuracy, and cost.
There are, first and perhaps foremost, significant advantages for collaboration and cooperation. An architecture designed from the ground up to support additional machine intelligence algorithms and systems is not “threatened” by the creation of individually superior technologies. The design is innately superior in that is provides an ingestion mechanism for any new technology in the salient area of machine intelligence – including of course image and signal processing. The ingestion mechanism comprises:
(1) Generating statistics about the ingested machine intelligence algorithm/system;
(2) Internalizing these statistics;
(3) Assessing the new set of meta-algorithmic, combinatorial, and ensemble systems created by the ingestion of the new intelligence-generating algorithm or system;
(4) Re-deploying the system with the preferred architecture as determined by (3).
These steps are described in some detail here.
(1) Generating statistics about the ingested machine intelligence algorithm/system
The ground-truth data for this stage will typically be comprised: (a) existing tagged (training) sets used to determine the system's prior architecture; (b) specific new tagged (training) data used to develop the intelligent algorithm or system that is being ingested; and (c) successfully completed tasks associated with the machine intelligence task. The first of these, (a), is easy to use, as this is tagged for all the previous machine intelligence-generating algorithms or systems – the ingestion engine will naturally be able to use these since its interfaces must be made compatible with the existing architecture as part of the ingestion process. Likewise, (b) must be re-interfaced as necessary to be compatible as part of the ingestion process. For (c), the system designer may wish to weight the successfully completed tasks differently than the ground-truth based on her confidence that the tasks have been completed correctly (and not for example manually corrected later), on the relevancy of the completed tasks to the desired intelligence generation goals, on the recentness of the task completed, or upon other considerations.
(2) Internalizing these statistics
Once all applicable training data are properly gathered and weighted, the task of scoring each individual algorithm/system and every germane meta-algorithmic, combinatorial, and ensemble approach to using multiple algorithms/systems is scored. These statistics include how each possible architecture performs on specific subsets and tessellations of the ground truthing data (which is useful for Predictive Selection and related patterns).
(3) Assessing the new set of meta-algorithmic, combinatorial and ensemble systems created by the ingestion of the new intelligence-generating algorithm or system
As described above, the meta-algorithmic approach is recursive, and so in theory there are an infinite number of possible intelligent system architectures. In practice, the recursion rarely merits a single level of recursion (e.g., deploying the Predictive Selection pattern where each pathway selects a different meta-algorithmic approach, rather than a single algorithm or system), let alone multiple levels of recursion. The system architect will have enough domain knowledge to know how far to reach with the recursion. Moreover, depending on the nature of the task, a potentially large number of meta-algorithmic/combinatorial/ensemble approaches will be eliminated at the start. Regardless, all applicable system architectures are considered and measured against the salient training/tagged data to decide on the appropriate system architecture as an output of this step.
(4) Re-deploying the system with this newly determined preferred architecture
Assuming all or a portion of the preferred system deployment is altered by the addition of the new machine intelligence algorithm/system, the last step involves updating the needed portion(s). If the input is assigned to a sub-category as in Regional Optimization or Predictive Selection, then only one or more sub-classes may require an updated architecture that involves at least in part the ingested machine intelligence algorithm/system. It is worth noting here that the entry of new training sets into the system may result in new sub-category definitions, meaning any/all previous choices for algorithms or meta-algorithms may need to be refreshed – if the sub-category boundaries have changed, the best pattern to apply to each sub-category may also need to change.
As these brief overviews make clear, the advantages of adding new algorithms to a pool of algorithms is clear. As the new algorithms are added, the system architecture can be reconsidered and optimized for the most salient cost function – which includes overall system cost, system adaptability (meaning supporting a wide plurality of meta-algorithmic, combinatorial and ensemble approaches, and easy to update), system accuracy, and robustness to new input. This continual consideration of multiple meta-algorithmic patterns adds a built-in adaptability and robustness to the architecture. Real-time changes in the nature of the data can be assessed by considering successfully completed tasks as part of the augmented ground truth set, and over time alternative meta-algorithmic architectures may be (automatically) substituted for the current architecture to provide better performance. While this architecture is guided by domain expertise, particularly in amending the meta-algorithmic patterns to the specific machine intelligence task, the final decision on architectural deployment is data-driven and unambiguous.
In summary, then, the primary principles of this architectural approach, are:
(1) The system is architected by design to use a plurality of intelligent systems – or meta-algorithmic intelligent systems – purpose-built for the overall intelligence-generating task;
(2) The system architect need not have deep knowledge about the individual machine intelligence algorithms/systems;
(3) Domain knowledge is relevant – and useful – for some of the more in-depth meta-algorithmic patterns (such as tessellation and recombination).
This leads to a set of eight basic principles, originally outlined in [Reference Simske1], which are used to guide the machine intelligence system:
Principle 1
No single generator – algorithm, system, or engine – encapsulates the complexity of the most challenging problems in artificial intelligence, such as advanced machine learning, machine vision and intelligence, and dynamic biometric tasks. In image and signal analysis, multiple algorithms can be used to provide enhanced image segmentation, analysis, and recognition.
Principle 2
It makes sense for a system designer to optimize an algorithm for a portion of the input range and then leave the rest of the range to another algorithm. The Predictive Selection and Regional Optimization patterns, described above, are broadly applicable to many image and signal-processing tasks.
Principle 3
The patterns of usage are often more accurate, more robust, more trainable, more re-usable, and/or more cost-sensitive than a single, highly trained algorithm, system, or engine.
Principle 4
Ground truthing, or the tagging of training data, is generally inefficient and expensive – in practice, it is reasonable to assume that there will be a relative sparseness of training data.
Principle 5
First-, second-, and third-order meta-algorithmics are used to create a highly trainable system with relative ease of implementation. Any combinational of commercial-off-the-shelf, open source, and task-specific (“targeted”) algorithms and systems can be deployed together in these patterns. The targeted systems are designed to provide good results for partitions of the input space on which the existing systems do not perform acceptably.
Principle 6
The simultaneous use of bottom-up and top-down algorithms, and the combination of targeted and broad algorithms can be used to generate systems that are highly resilient to changes in the input data, and highly adaptable to subsystem deployment.
Principle 7
Weighting and confidence values must be built throughout the system in order to enable the use of meta-algorithmics on multiple classifiers at a time. This allows hybridizing the multiple classifiers in a plurality of ways and provides the means for simultaneously combining, learning, and parallel processing.
Principle 8
The goals of modern algorithm designers will be, increasingly, indistinguishable from the goals of modern system designers. Architecting for intelligence is becoming a primary need for architecting any system, with the increasing pervasiveness of Big Data, analytics, voice search, and other machine-to-machine intelligent systems.
V. BIOLOGICAL SIGNAL PROCESSING AND META-ALGORITHMS
The Constrained Substitute meta-algorithmic pattern can be used to replace a higher accuracy ECG analysis routine with a lower accuracy, but faster, routine when for example all one needs to know is that the heart is beating (when the patient is on her way to the hospital, for example).
Voting and Weighted Voting can be used when a plurality of electrocardiogram (ECG) algorithms are used simultaneously. Two of the algorithms may decide that the ECG shows signs of ventricular escape, while the third classifies the ECG pathology as atrial flutter. The direct Voting method classifies the anomaly as ventricular escape. However, if the third classifier has a weight greater than the sum of the other two classifiers, then the anomaly is classified as atrial flutter.
ECG analysis routines will perform with different accuracies in the presence of noise. The Predictive Selection algorithm can be helpful here. The subclasses to which input can be assigned might be, for example, “Low Noise”, “Medium Noise”, and “High Noise”. As shown in Table 4, each of these noise conditions has its own analysis approach (which provides the highest accuracy output).
Table 4. Predictive Selection approach to ECG analysis.

ECG can also be used in combination with other algorithms for real-time biometrics. The Regional Optimization approach is used here, since the biometric task involves a different meta-algorithmic approach based on which biometric measurements are available at the moment, and on the relative expected accuracy of each algorithm.
VI. IMAGE PROCESSING, OBJECT SEGMENTATION AND CLASSIFICATION, AND META-ALGORITHMS
Perhaps the simplest example of meta-algorithmics applied to image processing is employing the Sequential Try algorithm for compressing an image – or a large set of images – to a constrained amount of storage space. For example, a compression quality of 100% may be initially chosen. Suppose the images take up 50% more storage than allowed. They are then re-compressed at, for example, 67% quality, expecting them to “fit” in the allotted storage. However, the images may still take up too much room, and need to be re-compressed at 65% in order to fit. Here, the sequence of tries is for 100, 67, and 65% quality compression.
The Tessellation and Recombination algorithm can be very valuable for image segmentation. Individual segmentation algorithms can break an image up into different logical regions. When all the regions of all segmentation algorithms are logically overlaid, they are broken up into different smaller regions based on logical assignment in the segmentation algorithms. For example, suppose one segmentation algorithm breaks up a region comprised of subregions {A,B,C} into two segments {A+B} and {C}. Suppose that a second segmentation algorithm breaks the region {A+B+C} into two subregions {A} and {B+C}. The collective set of subregions is thus {A+B}, {C}, {A}, and {B+C}. Through alignment, it is observed that {A+B} and {B+C} overlap for subregion {B}, so that they are tessellated to {A}, {B} and {C}. Region {B} is an emergent subregion not output by either of the two segmentation systems. These subregions are then recombined based on how well they match the specific desired shapes or objects. A large possible set of recombinations is possible even for just these three subregions:
• {A}, {B}, and {C}
• {A+B} and {C}
• {A+C} and {B}
• {A} and {B+C}
• {A+B+C}.
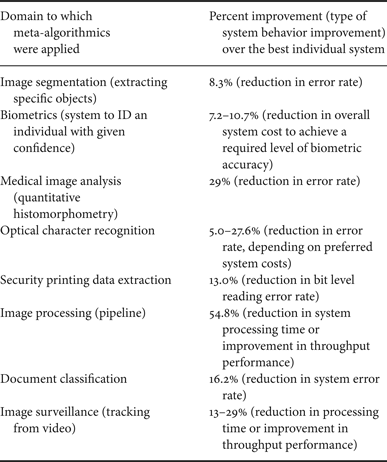
Meta-algorithmics are clearly broadly applicable to image and signal-processing machine intelligence tasks. Significant improvement in system output was obtained in a wide range of image and signal-processing experiments [Reference Simske1]. As shown in Table 5, (1) image segmentation error rate was reduced by 8.3%; (2) biometric system cost was reduced by 7.2–10.7%; (3) medical image analysis error rate was reduced 29%; (4) optical character recognition (OCR) error rate was reduced 5.0–27.6%; (5) error rate in the extraction of security printing data was reduced 13.0%; (6) image-processing time was reduced by 54.8%; (7) document classification error rate was reduced by 16.2%; and (8) image surveillance processing time was decreased by 13–29%.
Table 5. Signal and image processing tasks to which meta-algorithmics were applied, along with the percent improvement and type of system behavior improvement measured in parenthesis. Summarized from [Reference Simske1].

In each case (Table 5), multiple meta-algorithmic approaches provided improvement over the best individual algorithm/system. However, not every meta-algorithmic approach provided improvement. In general, the meta-algorithmic pattern(s) that will improve on the best individual algorithm/system are not known a priori, but can be identified after the assessment process described above.
VII. DISCUSSION, CONCLUSIONS, AND THE FUTURE
Here the four precepts for making machine learning more compatible with human learning are reviewed:
• The ability to incorporate new rules of discernment and models for analysis into an existing model or set of models;
• The ability to selectively apply different learned content based on context;
• The ability to correctly solve problems in the absence of sufficient input;
• The ability to perform “real time ground truthing”; that is, the ability to assess a situation after a particular output is assumed and efficiently perform a minimal set of validation experiments to prove or disprove the correctness of the output.
For each of these, the architectural approach outlined in this paper is enabling. New rules of discernment and models for analysis are ingested by design into a meta-algorithmic/ensemble method based architecture. The existing model for machine intelligence is crafted by design for incorporating new algorithms or systems. The ability to selectively apply content based on context was illustrated above particularly for the Predictive Selection, Regional Optimization, and Sensitivity Analysis methods. The ability to solve problems in the absence of sufficient input is also aided by the “rules based” methods for sub-categorization in some cases, and by the Central Limit Theorem in others (e.g., Voting, Weighted Voting, and Confusion Matrix-based approaches). Finally, Expert Decisioner, Tessellation and Recombination, and various Feedback patterns, among others, provide the means to perform an applicable set of validation experiments to prove or disprove the correctness of the output (by subtracting it from the expected value and feeding back this difference to the system).
As noted earlier, the adoption of a meta-algorithmic model for intelligent system architecture empowers the continual (re-)consideration of multiple meta-algorithmic patterns as the system is used over time. This provides adaptability and robustness by design. Real-time changes in the nature of the data, which is more or less inevitable due to changes in sensors, transducers, data collection, and data representation approaches – not to mention changes in the measured environment itself – can be continually reassessed by adding successfully completed tasks to the training set. The optimal meta-algorithmic pattern from those designed for the specific intelligent task will therein be automatically substituted for the current pattern as indicated by the measured function(s) of interest – cost, accuracy, performance, etc. Domain expertise is thus married nicely to automated system optimization.
Taken as a whole, the approach outlined in this paper leads to a methodology for machine learning – particularly in image and signal analysis – that thrives on the expertise provided by alternative approaches to the same machine-learning task. The meta-algorithmic approach does not focus on perfecting the machine learning per se, but rather perfecting the way that a multiplicity of machine-learning algorithms or systems work together to provide meaningful output.
The analogy to human learning is not inappropriate. A hard-earned set of rules govern the triaging, or sub-categorization of the input space, which increases the “surface area” of the machine-learning task, allowing multiple systems of expertise to contribute to the output. Humans learn the same way. When the scenario is familiar – for example, walking down a straight, uncrowded lane – a single, simple algorithm is applied for ambulation. When the path meanders, the ground becomes uneven, and the hiker competes for her part of the trail, however, a large number of algorithms can be brought to bear in a short period of time, including for example side-stepping, hopping, jumping, stopping, and turning the upper body sideways to avoid collisions and delays. The algorithms used suit the complexity of the task. No one approach will suffice. The same can certainly be said for the increasingly complex, hybridized tasks expected of machine intelligence systems.
ACKNOWLEDGEMENTS
The author thanks HP for support in performing the research summarized herein. The author thanks Wiley & Sons, and in particular Alex Jackson, for soliciting the book “Meta-Algorithms”, from which this paper borrows liberally.
Steven J. Simske is an HP Fellow and Director in HP Labs. His degrees are in Biomedical, Electrical and Aerospace Engineering. He is the holder of roughly 120 US Patents and 400 published articles, chapters and books. His LinkedIn profile is at StevenSimske.