1 Introduction
Canonical correlation analysis (CCA; Hotelling, Reference Hotelling1935, Reference Hotelling1936) and redundancy analysis (RA; Van Den Wollenberg, Reference Van Den Wollenberg1977) are two classic multivariate statistical methods that can be used to study the relationship between two sets of variables. In CCA, the first pair of canonical variates (i.e., linear combinations of original variables) is created from both sets to maximize the first canonical correlation (i.e., the correlation between the paired canonical variates), and subsequent pairs of canonical variates are created to maximize the following canonical correlations while obeying certain within-set and between-set orthogonality restrictions. One potential disadvantage of CCA is that the canonical variates may not be representative of the original variables in the sense of the explained variance within the same set. For instance, if all the canonical variates created from the first set can only explain 5% (or even less) of the variance of the original variables in the first set and all the canonical variates created from the second set can only explain 5% (or even less) of the variance of the original variables in the second set, no matter how large the canonical correlations are, it is impossible to have a big overlap in variance between the two sets of original variables (Fornell, Reference Fornell1979; Van Den Wollenberg, Reference Van Den Wollenberg1977). As a remedy, RA was proposed to create the redundancy variates (i.e., linear combinations of original variables) from only one set of original variables (say, the predictor variables) with the goal of maximizing the explained variance of the other set of original variables (say, the criterion variables). Mathematically, the redundancy variates can also be created from the criterion variables to maximize the explained variance of the predictor variables, but it is often not necessary to do so for theoretical reasons.
Despite the differences in mathematical goals, the two methods are similar in the sense that the interpretations of the linear combinations of original variables are often the focus of practical applications of the two methods. To interpret the canonical variates in CCA, researchers should select the original variables with prominent canonical loadings (i.e., the correlations between the canonical variates and the original variables within the same set) to assign meaningful interpretation to each canonical variate. In a similar way, a redundancy variate should be interpreted in terms of the predictor variables with prominent redundancy loadings (i.e., the correlations between the redundancy variates and the predictor variables). Nonetheless, there is no guarantee that meaningful interpretations can always be found for the canonical/redundancy variates.
To facilitate the interpretations, the idea of rotation that was originally developed to rotate the common factors in the context of exploratory factor analysis (EFA) has been adapted to rotate the canonical/redundancy variates. In the CCA context, Cliff and Krus (Reference Cliff and Krus1976) and Perreault and Spiro (Reference Perreault and Spiro1978) advocated the rotation of canonical variates, whereas, in the RA context, Israels (Reference Israels1986) discussed the rotation of redundancy variates. These authors showed that the rotated canonical/redundancy loading matrix often has a simple structure in the sense of Thurstone (Reference Thurstone1947), which makes it easier to interpret the rotated canonical/redundancy variates. Additionally, Cudeck and O’Dell (Reference Cudeck and O’Dell1994) suggested the use of standard error estimates to account for the sampling variability of rotated factor loadings when the rotated common factors are interpreted. Following this suggestion, Gu et al. (Reference Gu, Wu, Yung and Wilkins2021) developed the standard error estimates for rotated canonical loadings and other rotated CCA estimates. However, no work has been done to obtain the standard error estimates for rotated redundancy loadings or other rotated RA estimates. Therefore, the purpose of this paper is to develop the standard error estimates for rotated RA estimates. With the availability of standard error estimates, the researcher can better interpret the rotated redundancy variates by selecting the rotated redundancy loadings that are not only prominent but also statistically significant.
Because the technical details in this paper are closely related to Gu et al. (Reference Gu, Wu, Yung and Wilkins2021), it is useful to review the related work that leads to the standard error estimates for rotated CCA estimates. It is well known that CCA is almost always used in exploratory data analysis, because the traditional development of CCA does not provide the inferential information to test the CCA parameters, except the canonical correlations, of which the significance can be tested under the multivariate normality assumption of the data. Recently, Gu et al. (Reference Gu, Yung and Cheung2019) provided a model-based approach to CCA that can produce the standard error estimates for CCA estimates. Particularly, their model-based approach includes four covariance structure modelsFootnote 1 specifically designed for CCA, and one of the models (i.e., the CORR-L model) can produce the standard error estimates for canonical loadings. Based on the original CORR-L model, Gu et al. (Reference Gu, Wu, Yung and Wilkins2021) provided the specification of the modified CORR-L model that can accommodate the rotated canonical loadings and other rotated CCA estimates; and they further showed that the infinitesimal jackknife (IJ) methodFootnote 2 (Jennrich & Clarkson, Reference Jennrich and Clarkson1980; Jennrich, Reference Jennrich2008; Zhang et al., Reference Zhang, Preacher and Jennrich2012) can be applied with the modified CORR-L model to compute the standard error estimates for rotated canonical loadings and other rotated CCA estimates. The advantage of the IJ method is that it can handle non-normal data and produce robust standard error estimates. Thus, we also focus on the IJ method in this paper. In sum, it is the modified CORR-L model that serves as the basis for applying the IJ method.
Based on the work of Gu et al. (Reference Gu, Wu, Yung and Wilkins2021) in the CCA context, we can easily outline the work required to produce the standard error estimates for rotated redundancy loadings and other rotated RA estimates. First, we need a model that can accommodate the rotated RA estimates. Then, we can apply the IJ method with the specified model to compute the standard error estimates for rotated RA estimates. Recently, Gu et al. (Reference Gu, Yung, Cheung, Joo and Nimon2023) developed a model-based approach to RA that can produce the standard error estimates for RA estimates. Particularly, their model-based approach includes two covariance structure modelsFootnote 3 specifically designed for RA, and one of the models (i.e., the RA-L model) can produce the standard error estimates for redundancy loadings. Thus, a feasible way to develop a model that can accommodate the rotated redundancy loadings and other rotated RA estimates is to modify the original RA-L model. Then, the IJ method can be applied with the modified RA-L model. Hence, the required work is to specify the modified RA-L model, because the modified RA-L model serves as the basis to apply the IJ method to compute the standard error estimates for rotated RA estimates.
The organization of this paper is as follows. In Section 2, we first review the original RA-L model; then, we specify two modified RA-L models to accommodate the rotated RA estimates from orthogonal and oblique rotations, separately. In Section 3, we describe the IJ method with the two modified RA-L models estimated by the unweighted least squares (ULS) fitting function. In Section 4, we use a simulation study to validate the standard error estimates from the IJ method. In Section 5, we use two real examples to demonstrate the interpretation of rotated redundancy variates. Finally, in Section 6, we summarize the paper and provide additional remarks regarding the rotation methods and the use of numeric partial derivatives when applying the IJ method.
2 The original RA-L model and two modified RA-L models
In this section, we first review the original RA-L model and then specify two modified RA-L models for orthogonal and oblique rotations, separately.
2.1 The original RA-L model
Let x be a p × 1 vector for p predictor variables and y be a q × 1 vector for q criterion variables. With p predictor variables, one can construct up to p redundancy variates. Let
![]() $\boldsymbol{\xi} ={\left({\xi}_1\kern0.5em {\xi}_2\kern0.5em \cdots \kern0.5em {\xi}_p\right)}^{\prime }$
be the vector that includes all p redundancy variates. According to Van Den Wollenberg (Reference Van Den Wollenberg1977), ξi
(i = 1, 2, …, p) must satisfy two restrictions. First, ξi
is uncorrelated with ξj
(i ≠ j). Second, ξi
has unit variance (i = 1, 2, …, p). With these restrictions, Gu et al. (Reference Gu, Yung, Cheung, Joo and Nimon2023) specified the covariance structure of the original RA-L model as
$\boldsymbol{\xi} ={\left({\xi}_1\kern0.5em {\xi}_2\kern0.5em \cdots \kern0.5em {\xi}_p\right)}^{\prime }$
be the vector that includes all p redundancy variates. According to Van Den Wollenberg (Reference Van Den Wollenberg1977), ξi
(i = 1, 2, …, p) must satisfy two restrictions. First, ξi
is uncorrelated with ξj
(i ≠ j). Second, ξi
has unit variance (i = 1, 2, …, p). With these restrictions, Gu et al. (Reference Gu, Yung, Cheung, Joo and Nimon2023) specified the covariance structure of the original RA-L model as
 $$\begin{align}\boldsymbol{\Sigma} &=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi},{\mathbf{L}}_{y\xi},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\right)\left(\begin{array}{cc}{\mathbf{L}}_{x\xi}& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\right)\left(\begin{array}{cc}{\mathbf{I}}_p& {\mathbf{L}}_{y\xi}^{\prime}\\ {}{\mathbf{L}}_{y\xi}& {\mathbf{R}}_{y y}\end{array}\right)\left(\begin{array}{cc}{\mathbf{L}}_{x\xi}^{\prime }& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\right)\left(\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\right),\end{align}$$
$$\begin{align}\boldsymbol{\Sigma} &=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi},{\mathbf{L}}_{y\xi},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\right)\left(\begin{array}{cc}{\mathbf{L}}_{x\xi}& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\right)\left(\begin{array}{cc}{\mathbf{I}}_p& {\mathbf{L}}_{y\xi}^{\prime}\\ {}{\mathbf{L}}_{y\xi}& {\mathbf{R}}_{y y}\end{array}\right)\left(\begin{array}{cc}{\mathbf{L}}_{x\xi}^{\prime }& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\right)\left(\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\right),\end{align}$$
where I p and I q are identity matrices of orders p and q, separately, D x is a p × p diagonal matrix whose diagonal elements are the standard deviations of p predictor variables, D y is a q × q diagonal matrix whose diagonal elements are the standard deviations of q criterion variables, L xξ is a p × p square matrix that includes the redundancy loadings (i.e., the correlations between p predictor variables and p redundancy variates), L yξ is a q × p matrix that includes the cross-loadings (i.e., the correlations between q criterion variables and p redundancy variates), and R yy is a q × q correlation matrix whose off-diagonal elements are the correlations of q criterion variables.
To identify the original RA-L model, three types of constraints must be imposed. The first type of constraints is applicable only when the number of predictor variables exceeds that of criterion variables by two or more (i.e., p - q ≥ 2). Specifically, let d = p − q be a positive integer. When d ≥ 2, the first type of constraints requires one to arbitrarily fix d(d − 1)/2 elements in the last d columns of L xξ . When d = 1 or p ≤ q, the first type of constraints is not applicable. The second type of constraints is
where vecdiag(M) denotes a column vector created with the diagonal elements of M, and 1 p denotes a unit vector of order p, and 0 p denotes a null vector of order p. Finally, the third type of constraints is
where vecb(M) denotes a column vector created with the off-diagonal elements below the main diagonal of M, and 0 denotes a null vector of appropriate orderFootnote 4. The third type of constraints indicate that
![]() ${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
must be a diagonal matrix, but the number of constraints required by equation (3) depends on the relative magnitude of p and q. When p ≤ q, all p columns of L
yξ
include non-zero cross-loadings. In this situation,
${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
must be a diagonal matrix, but the number of constraints required by equation (3) depends on the relative magnitude of p and q. When p ≤ q, all p columns of L
yξ
include non-zero cross-loadings. In this situation,
![]() ${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
has p(p − 1)/2 unique off-diagonal elements that must be 0. When p > q, only the first q columns of L
yξ
include non-zero cross-loadings, while the last d = p - q columns of L
yξ
are null vectors (see Appendix A of Gu et al. Reference Gu, Yung, Cheung, Joo and Nimon2023). In this situation, the first q × q submatrix of
${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
has p(p − 1)/2 unique off-diagonal elements that must be 0. When p > q, only the first q columns of L
yξ
include non-zero cross-loadings, while the last d = p - q columns of L
yξ
are null vectors (see Appendix A of Gu et al. Reference Gu, Yung, Cheung, Joo and Nimon2023). In this situation, the first q × q submatrix of
![]() ${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
has q(q − 1)/2 unique off-diagonal elements that must be 0. This completes the three types of constraints for the original RA-L model.
${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
has q(q − 1)/2 unique off-diagonal elements that must be 0. This completes the three types of constraints for the original RA-L model.
To count the number of parameters of the RA-L model, it is obvious that D x has p standard deviations, D y has q standard deviations, and R yy has q(q − 1)/2 correlations. For L xξ and L yξ , however, the number of parameters in these two matrices also depends on the relative magnitude of p and q. For p ≤ q, L xξ has p 2 redundancy loadings, and L yξ has pq cross-loadings. For p > q, L xξ has p 2 − d(d − 1)/2 = (p 2 + 2pq − q 2 + p − q)/2 redundancy loadings, and L yξ has q 2 cross-loadings in the first q columns because the last d columns of L yξ are null vectors. Finally, given the number of constraints for identification and the number of parameters, we can verify that the RA-L model is a saturated model regardless of the relative magnitude of p and q (see Appendix B of Gu et al. Reference Gu, Yung, Cheung, Joo and Nimon2023).
2.2 Matrix partitions
To specify the two modified RA-L models in the next two subsections, it is necessary to partition some matrices of the original RA-L model. Let m be a positive integer that indicates the number of redundancy variates to be rotated. When p ≤ q, m must be equal to or less than p. When p > q, m must be equal to or less than q, because there is no need to rotate the last d = p − q redundancy variates.
With these settings, we first partition L xξ as
where
![]() ${\mathbf{L}}_{x\xi \mid m}$
is a p × m matrix,
${\mathbf{L}}_{x\xi \mid m}$
is a p × m matrix,
![]() ${\mathbf{L}}_{x\xi \mid u}$
is a p × u matrix, and u = p - m. Correspondingly, the submatrices I
p
and L
yξ
in
${\mathbf{L}}_{x\xi \mid u}$
is a p × u matrix, and u = p - m. Correspondingly, the submatrices I
p
and L
yξ
in
 $\left(\!\begin{array}{cc}{\mathbf{I}}_p& {\mathbf{L}}_{y\xi}^{\prime}\\ {}{\mathbf{L}}_{y\xi}& {\mathbf{R}}_{y y}\end{array}\!\right)$
of equation (1) should be partitioned as
$\left(\!\begin{array}{cc}{\mathbf{I}}_p& {\mathbf{L}}_{y\xi}^{\prime}\\ {}{\mathbf{L}}_{y\xi}& {\mathbf{R}}_{y y}\end{array}\!\right)$
of equation (1) should be partitioned as
 $$\begin{align}{\mathbf{I}}_p=\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)\kern0.36em \mathrm{and}\kern0.36em {\mathbf{L}}_{y\xi}=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right),\end{align}$$
$$\begin{align}{\mathbf{I}}_p=\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)\kern0.36em \mathrm{and}\kern0.36em {\mathbf{L}}_{y\xi}=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right),\end{align}$$
where
![]() ${\mathbf{L}}_{y\xi \mid m}$
is a q × m matrix and
${\mathbf{L}}_{y\xi \mid m}$
is a q × m matrix and
![]() ${\mathbf{L}}_{y\xi \mid u}$
is a q × u matrix.
${\mathbf{L}}_{y\xi \mid u}$
is a q × u matrix.
Based on the partitions in equations (4) and (5), the covariance structure of the original RA-L model can be re-written as
 $$\begin{align}\boldsymbol{\Sigma}&=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\mathbf{L}}_{y\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\mathbf{L}}_{x\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
$$\begin{align}\boldsymbol{\Sigma}&=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\mathbf{L}}_{y\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\mathbf{L}}_{x\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
In the next two subsections, we will show the effect of orthogonal and oblique rotations on
![]() ${\mathbf{L}}_{x\xi \mid m}$
, I
m
, and
${\mathbf{L}}_{x\xi \mid m}$
, I
m
, and
![]() ${\mathbf{L}}_{y\xi \mid m}$
in equation (6) and define the two modified RA-L models for orthogonal and oblique rotations, separately.
${\mathbf{L}}_{y\xi \mid m}$
in equation (6) and define the two modified RA-L models for orthogonal and oblique rotations, separately.
2.3 The modified RA-L model for orthogonal rotations
When the first m redundancy variates are rotated with an orthogonal rotation method,
![]() ${\mathbf{L}}_{x\xi \mid m}$
is transformed by an m × m orthogonal matrix Torth to produce
${\mathbf{L}}_{x\xi \mid m}$
is transformed by an m × m orthogonal matrix Torth to produce
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
, which is a p × m matrix that includes the rotated redundancy loadings. That is,
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
, which is a p × m matrix that includes the rotated redundancy loadings. That is,
At the same time, I
m
and
![]() ${\mathbf{L}}_{y\xi \mid m}$
are also transformed by Torth. For I
m
, the transformation is
${\mathbf{L}}_{y\xi \mid m}$
are also transformed by Torth. For I
m
, the transformation is
For
![]() ${\mathbf{L}}_{y\xi \mid m}$
, the transformation is
${\mathbf{L}}_{y\xi \mid m}$
, the transformation is
Obviously,
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
is a q × m matrix that includes the rotated cross-loadings. Given equations (7)–(9), the covariance structure of the modified RA-L model for orthogonal rotations is defined as
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
is a q × m matrix that includes the rotated cross-loadings. Given equations (7)–(9), the covariance structure of the modified RA-L model for orthogonal rotations is defined as
 $$\begin{align}\boldsymbol{\Sigma} &=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
$$\begin{align}\boldsymbol{\Sigma} &=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{I}}_m& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
To identify the modified RA-L model for orthogonal rotations, we must impose four types of constraints. The first three types of constraints are inherited with or without changes from the three types of constraints for the original RA-L model, whereas the fourth type of constraints is introduced to remove rotational indeterminacy. The first type of constraints is identical to that for the original RA-L model. That is, when x has 2 or more variables than y, one should arbitrarily fix d(d − 1)/2 elements in the last d columns of
![]() ${\mathbf{L}}_{x\xi \mid u}$
.
${\mathbf{L}}_{x\xi \mid u}$
.
The second type of constraints involves both rotated and unrotated redundancy loadings. That is,
 $$\begin{align}\mathrm{vecdiag}\left[\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)\right]-{\mathbf{1}}_p={\mathbf{0}}_p.\end{align}$$
$$\begin{align}\mathrm{vecdiag}\left[\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)\right]-{\mathbf{1}}_p={\mathbf{0}}_p.\end{align}$$
Compared to the p constraints in equation (2), the first m constraints in equation (11) are different, because these constraints are imposed on the rotated redundancy loadings in
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
.
To derive the third type of constraints, we must express
![]() ${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
in equation (3) with the partitioned matrix
${\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}$
in equation (3) with the partitioned matrix
![]() ${\mathbf{L}}_{y\xi}=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)$
. That is,
${\mathbf{L}}_{y\xi}=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)$
. That is,
 $$\begin{align*}{\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}&=\left(\!\begin{array}{c}{\mathbf{L}}_{y\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)\\ &=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid u}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\end{array}\!\right).\end{align*}$$
$$\begin{align*}{\mathbf{L}}_{y\xi}^{\prime }{\mathbf{L}}_{y\xi}&=\left(\!\begin{array}{c}{\mathbf{L}}_{y\xi \mid m}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)\\ &=\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid u}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}& {\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\end{array}\!\right).\end{align*}$$
Given the constraints required by equation (3), we can see that
![]() ${\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}$
and
${\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}$
and
![]() ${\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}$
must be diagonal matrices and
${\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}$
must be diagonal matrices and
![]() ${\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}$
must be a null matrix. Thus, we can re-write equation (3) as
${\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}$
must be a null matrix. Thus, we can re-write equation (3) as
 $$\begin{align*}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\end{array}\right]=\mathbf{0},\end{align*}$$
$$\begin{align*}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\end{array}\right]=\mathbf{0},\end{align*}$$
where vec(M) denotes a column vector created with all elements of M. With orthogonal rotations,
![]() ${\mathbf{L}}_{y\xi \mid m}$
should be substituted with
${\mathbf{L}}_{y\xi \mid m}$
should be substituted with
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}={\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}$
so that the first and last components in the above expression must be changed as follows:
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}={\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}$
so that the first and last components in the above expression must be changed as follows:
 $$\begin{align*}\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)\end{array}\right\}=\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right)\end{array}\right\}.\end{align*}$$
$$\begin{align*}\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)\end{array}\right\}=\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right)\end{array}\right\}.\end{align*}$$
It is easy to verify that
![]() $\mathrm{vecb}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)$
and
$\mathrm{vecb}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)$
and
![]() $\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right)$
remain to be null vectors after orthogonal rotations, but
$\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right)$
remain to be null vectors after orthogonal rotations, but
![]() $\mathrm{vecb}\left[{\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right]$
may not be a null vector, because
$\mathrm{vecb}\left[{\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}\right]$
may not be a null vector, because
![]() ${\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}$
in general is an m × m symmetric matrix. It means that rotation violates the first m(m − 1)/2 constraints required by equation (3). Therefore, the third type of constraints for the modified RA-L model for orthogonal rotations is
${\left({\mathbf{T}}^{\mathrm{orth}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{orth}}$
in general is an m × m symmetric matrix. It means that rotation violates the first m(m − 1)/2 constraints required by equation (3). Therefore, the third type of constraints for the modified RA-L model for orthogonal rotations is
 $$\begin{align}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)\end{array}\right]=\mathbf{0}.\end{align}$$
$$\begin{align}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}\right)\end{array}\right]=\mathbf{0}.\end{align}$$
In the fourth type of constraints, the results derived by Archer and Jennrich (Reference Archer and Jennrich1973) are adapted to remove rotational indeterminacy for orthogonal rotations. That is, the fourth type of constraints requires
![]() ${\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{orth}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}}$
to be a symmetric matrix, where
${\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{orth}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}}$
to be a symmetric matrix, where
![]() ${h}^{\mathrm{orth}}={h}^{\mathrm{orth}}\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)$
denotes the simplicity function of
${h}^{\mathrm{orth}}={h}^{\mathrm{orth}}\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)$
denotes the simplicity function of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
for a particular orthogonal rotation criterion, and this type of constraints includes m(m − 1)/2 constraints. Formally, we can write the fourth type of constraints as
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
for a particular orthogonal rotation criterion, and this type of constraints includes m(m − 1)/2 constraints. Formally, we can write the fourth type of constraints as
 $$\begin{align}\mathrm{vecb}\left[{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{orth}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}}-\frac{\partial {h}^{\mathrm{orth}}}{\partial {\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime }}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right]={\mathbf{0}}_{m\left(m-1\right)/2}.\end{align}$$
$$\begin{align}\mathrm{vecb}\left[{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{orth}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}}-\frac{\partial {h}^{\mathrm{orth}}}{\partial {\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right)}^{\prime }}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}\right]={\mathbf{0}}_{m\left(m-1\right)/2}.\end{align}$$
This completes the four types of constraints for the modified RA-L model for orthogonal rotations.
It can be seen that the number of parameters of the modified RA-L model for orthogonal rotations is the same as that of the original RA-L model, because orthogonal rotations do not increase the number of parameters. As for the number of constraints, equation (12) has m(m − 1)/2 fewer constraints than equation (3), while equation (13) introduces m(m − 1)/2 new constraints. Therefore, the modified RA-L model for orthogonal rotations is still a saturated model.
2.4 The modified RA-L model for oblique rotations
When the first m redundancy variates are rotated with an oblique rotation method,
![]() ${\mathbf{L}}_{x\xi \mid m}$
is transformed by an m × m nonsingular matrix Tobli that must satisfy the restriction
${\mathbf{L}}_{x\xi \mid m}$
is transformed by an m × m nonsingular matrix Tobli that must satisfy the restriction
![]() $\operatorname{diag}{\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{T}}^{\mathrm{obli}}\right]}^{-1}={\mathbf{I}}_m$
to produce
$\operatorname{diag}{\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{T}}^{\mathrm{obli}}\right]}^{-1}={\mathbf{I}}_m$
to produce
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, which is a p × m matrix that includes the rotated redundancy loadings. That is,
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, which is a p × m matrix that includes the rotated redundancy loadings. That is,
At the same time, I
m
and
![]() ${\mathbf{L}}_{y\xi \mid m}$
are also transformed by Tobli. For I
m
, the transformation is
${\mathbf{L}}_{y\xi \mid m}$
are also transformed by Tobli. For I
m
, the transformation is
where is Φ a m × m correlation matrixFootnote 5 of the rotated redundancy variates. For
![]() ${\mathbf{L}}_{y\xi \mid m}$
, the transformation is
${\mathbf{L}}_{y\xi \mid m}$
, the transformation is
where
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
is a q × m matrix that includes the rotated cross-loadings. Based on equations (14)–(16), the covariance structure of the modified RA-L model for oblique rotations is defined as
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
is a q × m matrix that includes the rotated cross-loadings. Based on equations (14)–(16), the covariance structure of the modified RA-L model for oblique rotations is defined as
 $$\begin{align}\boldsymbol{\Sigma}&=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{x\xi \mid u},\boldsymbol{\Phi}, {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}\boldsymbol{\Phi} & \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
$$\begin{align}\boldsymbol{\Sigma}&=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{x\xi \mid u},\boldsymbol{\Phi}, {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)\nonumber\\ &=\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{cc}\boldsymbol{\Phi} & \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)& \left(\!\begin{array}{c}{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{y\xi \mid u}^{\prime}\end{array}\!\right)\\ {}\left(\!\begin{array}{cc}{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{y\xi \mid u}\end{array}\!\right)& {\mathbf{R}}_{y y}\end{array}\!\right)\left(\!\begin{array}{cc}\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_q\end{array}\!\right)\left(\!\begin{array}{cc}{\mathbf{D}}_x& \mathbf{0}\\ {}\mathbf{0}& {\mathbf{D}}_y\end{array}\!\right).\end{align}$$
Note that equation (17) has m(m − 1)/2 more parameters than equations (6) due to the off-diagonal elements of Φ.
To identify the modified RA-L model for oblique rotations, we also need to impose four types of constraints. The first type of constraints is that when x has 2 or more variables than y, one should arbitrarily fix d(d − 1)/2 elements in the last d columns of
![]() ${\mathbf{L}}_{x\xi \mid u}$
in equation (17).
${\mathbf{L}}_{x\xi \mid u}$
in equation (17).
The second type of constraints involves not only the rotated and unrotated redundancy loadings but also the correlations of the rotated redundancy variates. That is,
 $$\begin{align}\mathrm{vecdiag}\left[\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)\left(\!\begin{array}{cc}\boldsymbol{\Phi} & \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)\right]-{\mathbf{1}}_p={\mathbf{0}}_p.\end{align}$$
$$\begin{align}\mathrm{vecdiag}\left[\left(\!\begin{array}{cc}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}& {\mathbf{L}}_{x\xi \mid u}\end{array}\!\right)\left(\!\begin{array}{cc}\boldsymbol{\Phi} & \mathbf{0}\\ {}\mathbf{0}& {\mathbf{I}}_u\end{array}\!\right)\left(\!\begin{array}{c}{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\\ {}{\mathbf{L}}_{x\xi \mid u}^{\prime}\end{array}\!\right)\right]-{\mathbf{1}}_p={\mathbf{0}}_p.\end{align}$$
Compared to the p constraints in equation (2), the first m constraints in equation (18) are different, because these m constraints involve the rotated redundancy loadings in
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
and the correlations in Φ.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
and the correlations in Φ.
The derivation of the third type of constraints for the modified RA-L model for oblique rotations is similar to that for the orthogonal rotations. Recall that equation (3) requires
 $$\begin{align*}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\end{array}\right]=\mathbf{0}.\end{align*}$$
$$\begin{align*}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}\right)\end{array}\right]=\mathbf{0}.\end{align*}$$
With oblique rotations,
![]() ${\mathbf{L}}_{y\xi \mid m}$
should be substituted with
${\mathbf{L}}_{y\xi \mid m}$
should be substituted with
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}={\mathbf{L}}_{y\xi \mid m}{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime -1}$
so that the first and last components in the above expression must be changed as follows:
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}={\mathbf{L}}_{y\xi \mid m}{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime -1}$
so that the first and last components in the above expression must be changed as follows:
 $$\begin{align*}\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)\end{array}\right\}=\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right)\end{array}\right\}.\end{align*}$$
$$\begin{align*}\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)\end{array}\right\}=\left\{\begin{array}{c}\mathrm{vec}\mathrm{b}\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right]\\ {}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right)\end{array}\right\}.\end{align*}$$
It is easy to verify that
![]() $\mathrm{vecb}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)$
and
$\mathrm{vecb}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)$
and
![]() $\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right)$
remain to be null vectors after oblique rotations, but
$\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right)$
remain to be null vectors after oblique rotations, but
![]() $\mathrm{vecb}\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right]$
may not be a null vector, because
$\mathrm{vecb}\left[{\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}\right]$
may not be a null vector, because
![]() ${\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}$
in general is an m × m symmetric matrix. Therefore, the third type of constraints for the modified RA-L model for oblique rotations is
${\left({\mathbf{T}}^{\mathrm{obli}}\right)}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\prime }{\mathbf{L}}_{y\xi \mid m}{\mathbf{T}}^{\mathrm{obli}}$
in general is an m × m symmetric matrix. Therefore, the third type of constraints for the modified RA-L model for oblique rotations is
 $$\begin{align}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)\end{array}\right]=\mathbf{0}.\end{align}$$
$$\begin{align}\left[\begin{array}{c}\mathrm{vec}\mathrm{b}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid u}\right)\\ {}\mathrm{vec}\left({\mathbf{L}}_{y\xi \mid u}^{\prime }{\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}\right)\end{array}\right]=\mathbf{0}.\end{align}$$
In the fourth type of constraints, the results derived by Jennrich (Reference Jennrich1973) are adapted to remove rotational indeterminacy for oblique rotations. That is, the fourth type of constraints requires
![]() ${\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{obli}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}}{\boldsymbol{\Phi}}^{-1}$
to be a diagonal matrix, where
${\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{obli}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}}{\boldsymbol{\Phi}}^{-1}$
to be a diagonal matrix, where
![]() ${h}^{\mathrm{obli}}={h}^{\mathrm{obli}}\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)$
denotes the simplicity function of
${h}^{\mathrm{obli}}={h}^{\mathrm{obli}}\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)$
denotes the simplicity function of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
for a particular oblique rotation criterion, and this type of constraints includes m(m − 1) constraints. Formally, we can write the fourth type of constraints as
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
for a particular oblique rotation criterion, and this type of constraints includes m(m − 1) constraints. Formally, we can write the fourth type of constraints as
 $$\begin{align}\mathrm{veco}\left[{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{obli}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}}{\boldsymbol{\Phi}}^{-1}\right]={\mathbf{0}}_{m\left(m-1\right)},\end{align}$$
$$\begin{align}\mathrm{veco}\left[{\left({\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}\right)}^{\prime}\frac{\partial {h}^{\mathrm{obli}}}{\partial {\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}}{\boldsymbol{\Phi}}^{-1}\right]={\mathbf{0}}_{m\left(m-1\right)},\end{align}$$
where veco(M) denotes a column vector created with all off-diagonal elements of M. This completes the four types of constraints for the modified RA-L model for oblique rotations.
It can be seen that the modified RA-L model for oblique rotations has m(m − 1)/2 more parameters (i.e., the off-diagonal elements of Φ) than the original RA-L model, equation (19) has m(m − 1)/2 fewer constraints than equation (3), and equation (20) introduces m(m − 1) new constraints. Therefore, the modified RA-L model for oblique rotations is still a saturated model.
3 The infinitesimal jackknife method
In this section, we describe the IJ method with the modified RA-L models estimated by the ULS fitting function. Computationally, the IJ method requires the pseudo values, which are obtained from two quantities: 1) the Jacobian matrix of the estimating equations with respect to the estimates and 2) the partial differentials of the estimating equations with respect to the sample covariance matrix S. The Jacobian matrix and the partial differentials are described first, followed by the descriptions of the pseudo values and the IJ estimate of the asymptotic covariance matrix.
3.1 Notations of the parameter vectors
Strictly speaking, we should use θorth and θobli to denote the parameter vectors for the two modified RA-L models, separately. With these notations, we have
![]() $\boldsymbol{\Sigma} \left({\boldsymbol{\unicode{x3b8}}}^{\mathrm{orth}}\right)=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)$
and
$\boldsymbol{\Sigma} \left({\boldsymbol{\unicode{x3b8}}}^{\mathrm{orth}}\right)=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{x\xi \mid u},{\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)$
and
![]() $\boldsymbol{\Sigma} \left({\boldsymbol{\unicode{x3b8}}}^{\mathrm{obli}}\right)=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{x\xi \mid u},\boldsymbol{\Phi}, {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)$
. However, to avoid repetitive descriptions in this section, we use θ as a generic symbol to denote the parameter vector for both modified RA-L models. As such,
$\boldsymbol{\Sigma} \left({\boldsymbol{\unicode{x3b8}}}^{\mathrm{obli}}\right)=\boldsymbol{\Sigma} \left({\mathbf{D}}_x,{\mathbf{D}}_y,{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{x\xi \mid u},\boldsymbol{\Phi}, {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}},{\mathbf{L}}_{y\xi \mid u},{\mathbf{R}}_{y y}\right)$
. However, to avoid repetitive descriptions in this section, we use θ as a generic symbol to denote the parameter vector for both modified RA-L models. As such,
![]() $\boldsymbol{\Sigma} \left(\boldsymbol{\theta} \right)$
is used to refer to either
$\boldsymbol{\Sigma} \left(\boldsymbol{\theta} \right)$
is used to refer to either
![]() $\boldsymbol{\Sigma} \left({\boldsymbol{\theta}}^{\mathrm{orth}}\right)$
or
$\boldsymbol{\Sigma} \left({\boldsymbol{\theta}}^{\mathrm{orth}}\right)$
or
![]() $\boldsymbol{\Sigma} \left({\boldsymbol{\theta}}^{\mathrm{obli}}\right)$
.
$\boldsymbol{\Sigma} \left({\boldsymbol{\theta}}^{\mathrm{obli}}\right)$
.
3.2 Jacobian matrix and partial differentials
For both modified RA-L models, the ULS fitting function is defined as
Then, the estimating equations have the following form
 $$\begin{align}\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)=\left[\begin{array}{c}\frac{\partial F}{\partial \boldsymbol{\theta}}\\ {}{\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)\\ {}{\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)\\ {}{\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)\end{array}\right]=\mathbf{0},\end{align}$$
$$\begin{align}\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)=\left[\begin{array}{c}\frac{\partial F}{\partial \boldsymbol{\theta}}\\ {}{\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)\\ {}{\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)\\ {}{\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)\end{array}\right]=\mathbf{0},\end{align}$$
where
![]() ${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
,
${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
,
![]() ${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
, and
${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
, and
![]() ${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
represent the second, third, and fourth type of constraints for either modified RA-L model. Specifically,
${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
represent the second, third, and fourth type of constraints for either modified RA-L model. Specifically,
![]() ${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
includes p constraints from either equation (11) for orthogonal rotations or equation (18) for oblique rotations,
${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
includes p constraints from either equation (11) for orthogonal rotations or equation (18) for oblique rotations,
![]() ${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
includes p(p − 1)/2 − m(m − 1)/2 or q(q − 1)/2 − m(m − 1)/2 constraints, depending on the relative magnitude of p and q, from either equation (12) for orthogonal rotations or equation (19) for oblique rotations, and
${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
includes p(p − 1)/2 − m(m − 1)/2 or q(q − 1)/2 − m(m − 1)/2 constraints, depending on the relative magnitude of p and q, from either equation (12) for orthogonal rotations or equation (19) for oblique rotations, and
![]() ${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
includes either m(m − 1)/2 constraints from equation (13) for orthogonal rotations or m(m − 1) constraints from equation (20) for oblique rotations.
${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
includes either m(m − 1)/2 constraints from equation (13) for orthogonal rotations or m(m − 1) constraints from equation (20) for oblique rotations.
Given equation (22), the Jacobian matrix of
![]() $\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
with respect to θ is
$\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
with respect to θ is
 $$\begin{align}\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)=\frac{\partial \mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)}{\partial {\boldsymbol{\theta}}^{\prime }}=\left[\begin{array}{c}\frac{\partial^2F}{\partial \boldsymbol{\theta} \partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\end{array}\right],\end{align}$$
$$\begin{align}\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)=\frac{\partial \mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)}{\partial {\boldsymbol{\theta}}^{\prime }}=\left[\begin{array}{c}\frac{\partial^2F}{\partial \boldsymbol{\theta} \partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\\[1pt] {}\frac{\partial {\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}\end{array}\right],\end{align}$$
where
![]() $\frac{\partial^2F}{\partial \boldsymbol{\theta} \partial {\boldsymbol{\theta}}^{\prime }}$
is the Hessian matrix of the ULS fitting function, and the remaining components are the partial derivatives of the constraints with respect to θ.
$\frac{\partial^2F}{\partial \boldsymbol{\theta} \partial {\boldsymbol{\theta}}^{\prime }}$
is the Hessian matrix of the ULS fitting function, and the remaining components are the partial derivatives of the constraints with respect to θ.
Let
![]() ${\partial}_2{\mathbf{g}}_{\left(\boldsymbol{\theta}, \mathbf{S}\right)}\left(d\mathbf{S}\right)$
be the partial differential of
${\partial}_2{\mathbf{g}}_{\left(\boldsymbol{\theta}, \mathbf{S}\right)}\left(d\mathbf{S}\right)$
be the partial differential of
![]() $\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
with respect to S evaluated at
$\mathbf{g}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
with respect to S evaluated at
![]() $\left(\boldsymbol{\theta}, \mathbf{S}\right)$
, and we define k
n
as
$\left(\boldsymbol{\theta}, \mathbf{S}\right)$
, and we define k
n
as
 $$\begin{align}{\mathbf{k}}_n&={\partial}_2{\mathbf{g}}_{\left(\boldsymbol{\theta}, \mathbf{S}\right)}\left[\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right){\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right)}^{\prime}\right]\nonumber\\ &=\left(\!\begin{array}{c}-{\frac{\partial \left\{\mathrm{vec}\left[\boldsymbol{\Sigma} \left(\boldsymbol{\theta} \right)\right]\right\}}{\partial \boldsymbol{\theta}}}^{\prime}\mathrm{vec}\left[\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right){\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right)}^{\prime}\right]\\ {}\mathbf{0}\\ {}\mathbf{0}\\ {}\mathbf{0}\end{array}\!\right),\end{align}$$
$$\begin{align}{\mathbf{k}}_n&={\partial}_2{\mathbf{g}}_{\left(\boldsymbol{\theta}, \mathbf{S}\right)}\left[\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right){\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right)}^{\prime}\right]\nonumber\\ &=\left(\!\begin{array}{c}-{\frac{\partial \left\{\mathrm{vec}\left[\boldsymbol{\Sigma} \left(\boldsymbol{\theta} \right)\right]\right\}}{\partial \boldsymbol{\theta}}}^{\prime}\mathrm{vec}\left[\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right){\left({\mathbf{z}}_n-\overline{\mathbf{z}}\right)}^{\prime}\right]\\ {}\mathbf{0}\\ {}\mathbf{0}\\ {}\mathbf{0}\end{array}\!\right),\end{align}$$
where n = 1, 2, …, N, N is the sample size, z
n
is a column vector for the nth observation of all predictor and criterion variables, and
![]() $\overline{\mathbf{z}}$
is a column vector of the sample means of all predictor and criterion variables. The last three components in equation (24) are null vectors, because
$\overline{\mathbf{z}}$
is a column vector of the sample means of all predictor and criterion variables. The last three components in equation (24) are null vectors, because
![]() ${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
,
${\boldsymbol{\varphi}}_1\left(\boldsymbol{\theta} \right)$
,
![]() ${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
, and
${\boldsymbol{\varphi}}_2\left(\boldsymbol{\theta} \right)$
, and
![]() ${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
are not functions of S.
${\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)$
are not functions of S.
3.3 Pseudo values and asymptotic covariance matrix of parameter estimates
Given the Jacobian matrix and the partial differentials, the pseudo values for each observation can be computed. Let λ n (n = 1, …, N) be a column vector collecting the pseudo values for the nth observation, and it can be solved from
Note that
![]() $\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
defined in equation (23) has more rows than columns so that the system of equations in equation (25) appears to be over-determined. Thus, we apply the QR decomposition to
$\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
defined in equation (23) has more rows than columns so that the system of equations in equation (25) appears to be over-determined. Thus, we apply the QR decomposition to
![]() $\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
to solve for λ
n
.
$\mathbf{J}\left(\boldsymbol{\theta}, \mathbf{S}\right)$
to solve for λ
n
.
After λ
n
is obtained for all observations, the IJ estimate of the asymptotic covariance matrix of
![]() $\hat{\boldsymbol{\theta}}$
is
$\hat{\boldsymbol{\theta}}$
is
where
![]() $\mathrm{scov}\left({\boldsymbol{\lambda}}_n\right)$
is the sample covariance matrix of all λ
n
. Finally, the standard error estimates for
$\mathrm{scov}\left({\boldsymbol{\lambda}}_n\right)$
is the sample covariance matrix of all λ
n
. Finally, the standard error estimates for
![]() $\hat{\boldsymbol{\theta}}$
are obtained from dividing the square roots of the diagonal elements of
$\hat{\boldsymbol{\theta}}$
are obtained from dividing the square roots of the diagonal elements of
![]() ${\mathrm{acov}}^{\mathrm{IJ}}\left(\hat{\boldsymbol{\theta}}\right)$
by
${\mathrm{acov}}^{\mathrm{IJ}}\left(\hat{\boldsymbol{\theta}}\right)$
by
![]() $\sqrt{N}$
.
$\sqrt{N}$
.
4 A simulation study
In this section, we use a simulation study to validate the standard error estimates from the IJ method under both multivariate normality and multivariate nonnormality and at different sample sizes.
4.1 Data generation
Two factors are manipulated in this simulation study. The first factor is the data distribution, including 1) multivariate normality and 2) multivariate nonnormality. The second factor is the sample size, including 1) 200, 2) 400, and 3) 600. In total, there are 6 combinations of data distribution and sample size. At each combination, we use the following population covariance matrix to generate 1000 random data sets:
 $$\begin{align*}{\boldsymbol{\Sigma}}_0=\left(\!\begin{array}{cc}{\boldsymbol{\Sigma}}_{xx}& {\boldsymbol{\Sigma}}_{yx}^{\prime}\\ {}{\boldsymbol{\Sigma}}_{yx}& {\boldsymbol{\Sigma}}_{yy}\end{array}\!\right),\end{align*}$$
$$\begin{align*}{\boldsymbol{\Sigma}}_0=\left(\!\begin{array}{cc}{\boldsymbol{\Sigma}}_{xx}& {\boldsymbol{\Sigma}}_{yx}^{\prime}\\ {}{\boldsymbol{\Sigma}}_{yx}& {\boldsymbol{\Sigma}}_{yy}\end{array}\!\right),\end{align*}$$
where the first eight variables are the predictor variables and the last eight variables are the criterion variablesFootnote 6. The submatrices of Σ 0 are
 $$\begin{align*}&{\boldsymbol{\Sigma}}_{xx}=\left(\begin{array}{rrrrrrrr}1.00& & & & & & & \\ {}.71& 1.00& & & & & & \\ {}.72& .72& 1.00& & & & & \\ {}.73& .73& .73& 1.00& & & & \\ {}.74& .74& .74& .74& 1.00& & & \\ {}.20& .10& .10& .10& .20& 1.00& & \\ {}.10& .20& .20& .20& .10& .52& 1.00& \\ {}.20& .10& .10& .10& .20& .53& .53& 1.00\end{array}\right),\\&{\boldsymbol{\Sigma}}_{yx}=\left(\begin{array}{cccccccc}.40& .50& .35& .50& .40& .05& .04& .03\\ {}.35& .35& .40& .40& .35& .04& .02& .01\\ {}.50& .40& .50& .35& .50& .03& .01& .04\\ {}.35& .35& .40& .40& .35& .02& .03& .02\\ {}.40& .50& .35& .50& .40& .01& .05& .05\\ {}.01& .01& .02& .02& .03& .40& .30& .35\\ {}.02& .03& .01& .03& .02& .35& .40& .30\\ {}.03& .02& .03& .01& .01& .30& .35& .40\end{array}\right),\\&{\boldsymbol{\Sigma}}_{yy}=\left(\begin{array}{rrrrrrrr}1.00& & & & & & & \\ {}.51& 1.00& & & & & & \\ {}.52& .52& 1.00& & & & & \\ {}.53& .53& .53& 1.00& & & & \\ {}.54& .54& .54& .54& 1.00& & & \\ {}.20& .00& .20& .00& .20& 1.00& & \\ {}.00& .20& .00& .20& .00& .52& 1.00& \\ {}.20& .00& .20& .00& .20& .53& .53& 1.00\end{array}\right).\end{align*}$$
$$\begin{align*}&{\boldsymbol{\Sigma}}_{xx}=\left(\begin{array}{rrrrrrrr}1.00& & & & & & & \\ {}.71& 1.00& & & & & & \\ {}.72& .72& 1.00& & & & & \\ {}.73& .73& .73& 1.00& & & & \\ {}.74& .74& .74& .74& 1.00& & & \\ {}.20& .10& .10& .10& .20& 1.00& & \\ {}.10& .20& .20& .20& .10& .52& 1.00& \\ {}.20& .10& .10& .10& .20& .53& .53& 1.00\end{array}\right),\\&{\boldsymbol{\Sigma}}_{yx}=\left(\begin{array}{cccccccc}.40& .50& .35& .50& .40& .05& .04& .03\\ {}.35& .35& .40& .40& .35& .04& .02& .01\\ {}.50& .40& .50& .35& .50& .03& .01& .04\\ {}.35& .35& .40& .40& .35& .02& .03& .02\\ {}.40& .50& .35& .50& .40& .01& .05& .05\\ {}.01& .01& .02& .02& .03& .40& .30& .35\\ {}.02& .03& .01& .03& .02& .35& .40& .30\\ {}.03& .02& .03& .01& .01& .30& .35& .40\end{array}\right),\\&{\boldsymbol{\Sigma}}_{yy}=\left(\begin{array}{rrrrrrrr}1.00& & & & & & & \\ {}.51& 1.00& & & & & & \\ {}.52& .52& 1.00& & & & & \\ {}.53& .53& .53& 1.00& & & & \\ {}.54& .54& .54& .54& 1.00& & & \\ {}.20& .00& .20& .00& .20& 1.00& & \\ {}.00& .20& .00& .20& .00& .52& 1.00& \\ {}.20& .00& .20& .00& .20& .53& .53& 1.00\end{array}\right).\end{align*}$$
To generate the multivariate normal data, the RANDNORMAL function in SAS PROC IML is used. To generate the multivariate non-normal data, we use the procedure developed by Qu et al. (Reference Qu, Liu and Zhang2020). This procedure is implemented by the MNONR package in R, which requires the user to specify the population values of multivariate skewness and multivariate kurtosis. In this simulation study, we set the values of multivariate skewness and multivariate kurtosis to 10 and 400, respectivelyFootnote 7.
4.2 Data analysis and evaluation criteria
By applying RA to Σ 0, we obtain the population values of the unrotated redundancy loadings and unrotated cross-loadings:
 $$\begin{align*}{\boldsymbol{L}}_{x\xi}=\left(\!\begin{array}{rrrrrrrr}.8401& .1341& -.2650& -.1836& .0465& .0428& .2225& .3447\\ {}.8901& .1721& .0814& -.2285& .0159& -.0920& .1257& -.3077\\ {}.8316& .1220& -.3780& .2809& -.0830& .1485& .0850& -.1886\\ {}.9066& .1797& .1418& .2203& -.1025& -.0981& -.1493& .1872\\ {}.8402& .1346& -.2597& -.1343& .2253& .0643& -.3674& -.0258\\ {}.0103& .8084& -.1790& .1924& .5022& .0500& .1456& .0374\\ {}.0121& .8119& -.1419& -.0416& -.2345& -.5073& -.0606& -.0527\\ {}.0123& .8081& -.1880& -.1739& -.2621& .4449& -.1104& .0502\end{array}\!\right),\end{align*}$$
$$\begin{align*}{\boldsymbol{L}}_{x\xi}=\left(\!\begin{array}{rrrrrrrr}.8401& .1341& -.2650& -.1836& .0465& .0428& .2225& .3447\\ {}.8901& .1721& .0814& -.2285& .0159& -.0920& .1257& -.3077\\ {}.8316& .1220& -.3780& .2809& -.0830& .1485& .0850& -.1886\\ {}.9066& .1797& .1418& .2203& -.1025& -.0981& -.1493& .1872\\ {}.8402& .1346& -.2597& -.1343& .2253& .0643& -.3674& -.0258\\ {}.0103& .8084& -.1790& .1924& .5022& .0500& .1456& .0374\\ {}.0121& .8119& -.1419& -.0416& -.2345& -.5073& -.0606& -.0527\\ {}.0123& .8081& -.1880& -.1739& -.2621& .4449& -.1104& .0502\end{array}\!\right),\end{align*}$$
 $$\begin{align*}{\mathbf{L}}_{y\xi}=\left(\!\begin{array}{rrrrrrrr}.5159& .0848& .2053& -.0324& .0356& -.0033& .0099& -.0000\\ {}.4209& .0139& -.0475& .1029& -.0095& .0014& .0053& .0001\\ {}.4729& -.0492& -.3565& -.0723& .0294& .0048& -.0001& .0000\\ {}.4203& .0119& -.0564& .0895& -.0406& -.0023& -.0053& -.0001\\ {}.5159& .0779& .1938& -.0580& -.0221& .0004& -.0098& .0000\\ {}-.0568& .4327& -.0045& .0378& .0801& .0614& -.0040& -.0000\\ {}-.0536& .4222& -.0495& .0030& .0102& -.1050& -.0006& .0000\\ {}-.0577& .4204& -.0616& -.0390& -.0908& .0434& .0045& -.0000\end{array}\!\right),\end{align*}$$
$$\begin{align*}{\mathbf{L}}_{y\xi}=\left(\!\begin{array}{rrrrrrrr}.5159& .0848& .2053& -.0324& .0356& -.0033& .0099& -.0000\\ {}.4209& .0139& -.0475& .1029& -.0095& .0014& .0053& .0001\\ {}.4729& -.0492& -.3565& -.0723& .0294& .0048& -.0001& .0000\\ {}.4203& .0119& -.0564& .0895& -.0406& -.0023& -.0053& -.0001\\ {}.5159& .0779& .1938& -.0580& -.0221& .0004& -.0098& .0000\\ {}-.0568& .4327& -.0045& .0378& .0801& .0614& -.0040& -.0000\\ {}-.0536& .4222& -.0495& .0030& .0102& -.1050& -.0006& .0000\\ {}-.0577& .4204& -.0616& -.0390& -.0908& .0434& .0045& -.0000\end{array}\!\right),\end{align*}$$
and the first two population redundancy indices are .1399 and .0698, while the subsequent population redundancy indices are less than .03. Thus, for each random data set, we only rotate the first two columns of redundancy loadings. In terms of the rotation method, we use a widely accepted oblique rotation method: QUARTIMIN (Browne, Reference Browne2001; Carroll, Reference Carroll1953) with Kaiser’s normalization (Reference Kaiser1958). In general, oblique rotations are more flexible than orthogonal rotations in the sense that oblique rotations can accommodate correlations among rotated factors/variates. If the rotated factors/variates are indeed uncorrelated, the resulting correlations from oblique rotations would be small and negligible. By applying QUARTIMIN to the first two columns of unrotated redundancy loadings, we obtain the population values of rotated redundancy loadings, rotated cross-loadings, and correlation of rotated redundancy variates:
 $$\begin{align*}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}=\left(\!\begin{array}{rr}.8525& -.0097\\ {}.9028& .0199\\ {}.8440& -.0203\\ {}.9194& .0240\\ {}.8525& -.0092\\ {}-.0011& .8087\\ {}.0006& .8119\\ {}.0008& 8080\end{array}\!\right),\kern0.36em \boldsymbol{\Phi} =\left(\!\begin{array}{cc}1.0000& \\ {}.1826& 1.0000\end{array}\!\right),\kern0.36em {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}=\left(\!\begin{array}{rr}.5228& .0921\\ {}.4172& .0199\\ {}4578& -.0425\\ {}.4162& .0178\\ {}.5216& .0852\\ {}.0170& .4318\\ {}.0184& .4214\\ {}.0140& .4195\end{array}\!\right).\end{align*}$$
$$\begin{align*}{\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}=\left(\!\begin{array}{rr}.8525& -.0097\\ {}.9028& .0199\\ {}.8440& -.0203\\ {}.9194& .0240\\ {}.8525& -.0092\\ {}-.0011& .8087\\ {}.0006& .8119\\ {}.0008& 8080\end{array}\!\right),\kern0.36em \boldsymbol{\Phi} =\left(\!\begin{array}{cc}1.0000& \\ {}.1826& 1.0000\end{array}\!\right),\kern0.36em {\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}=\left(\!\begin{array}{rr}.5228& .0921\\ {}.4172& .0199\\ {}4578& -.0425\\ {}.4162& .0178\\ {}.5216& .0852\\ {}.0170& .4318\\ {}.0184& .4214\\ {}.0140& .4195\end{array}\!\right).\end{align*}$$
The normalized QUARTIMIN rotation is implemented by SAS PROC FACTOR, and the IJ method is implemented by customized code written in SAS PROC IML.
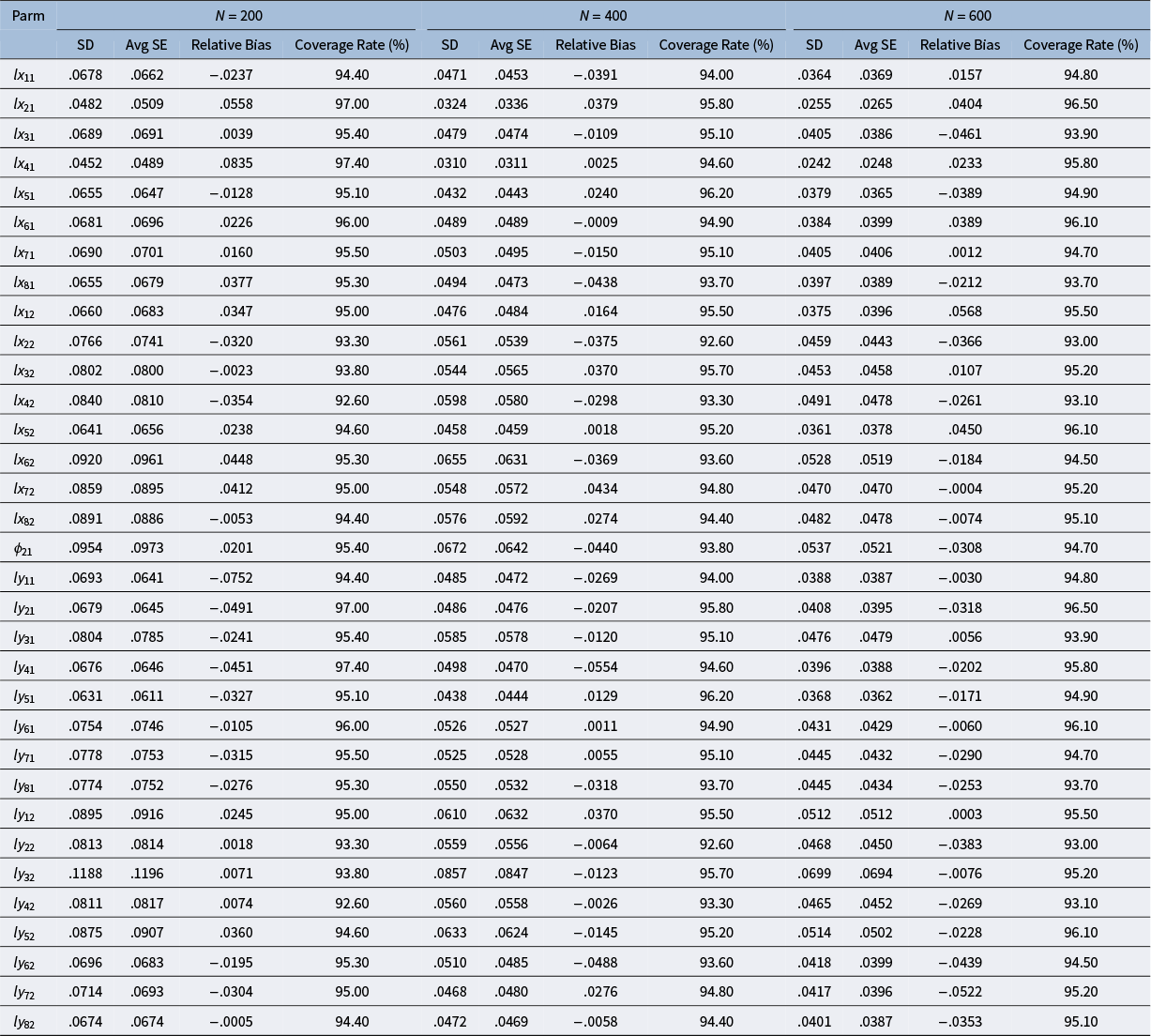
After the analyses are completed, we compute the means, standard deviations, and average standard error estimates across 1000 replications at each combination of data distribution and sample size. The standard deviations are used as the true standard errors to evaluate the performance of the IJ method. The first evaluation criterion we use is the relative bias of the average standard error estimate, which is calculated as
According to Hoogland and Boomsma (Reference Hoogland and Boomsma1998), the standard error estimate is acceptable when the absolute value of relative bias is less than .1. Additionally, we use the estimate and the associated standard error estimate to construct a symmetric 95% confidence interval (CI) and evaluate if the population value is included in the symmetric 95% CI. Thus, the second evaluation criterion is the coverage rate for each parameter across 1000 replications.
Table 1 Results from simulations under multivariate normality

Note: Parm = parameter, SD = standard deviation, Avg SE = average standard error, lx denotes the element of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, ϕ denotes the element of Φ, ly denotes the element of
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, ϕ denotes the element of Φ, ly denotes the element of
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and the subscript after lx, ϕ, and ly refers to the location of the element in the corresponding matrix.
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and the subscript after lx, ϕ, and ly refers to the location of the element in the corresponding matrix.
Table 2 Results from simulations under multivariate nonnormality
Note: Parm = parameter, SD = standard deviation, SE = standard error, lx denotes the element of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, ϕ denotes the element of Φ, ly denotes the element of
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
, ϕ denotes the element of Φ, ly denotes the element of
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and the subscript after lx, ϕ, and ly refers to the location of the element in the corresponding matrix.
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and the subscript after lx, ϕ, and ly refers to the location of the element in the corresponding matrix.
4.3 Results
Because our purpose is to validate the standard error estimates from the IJ method, the means of rotated estimates are omitted in this section but can be found from the Supplementary Materials. Instead, we show the standard deviations, average standard errors, relative biases, and coverage rates in Tables 1 and 2 under multivariate normality and multivariate nonnormality, separately. It is observed that 1) the means are getting closer to their population values as the sample size increases, 2) all the absolute values of relative biases are less than 0.1, and 3) all the coverage rates are close to 95%. Therefore, we conclude that the IJ method performs well under both multivariate normality and multivariate nonnormality.
5 Two real examples
In this section, we use two real examples to demonstrate the interpretation of rotated redundancy variates. In the first example, the dimensionality was determined by a previous study, and we apply the normalized VARIMAX (Kaiser, Reference Kaiser1958) for rotation. In the second example, we use the new criterion proposed by Gu et al. (Reference Gu, Yung, Cheung, Joo and Nimon2023) to determine the dimensionality and apply the normalized QUARTIMIN (Browne, Reference Browne2001; Carroll, Reference Carroll1953) for rotation. The data and code for Example 1 can be found from the Supplementary Materials, and those for Example 2 can be requested from the first author.
5.1 Example 1
In the first example, we use the data from van Dam and van Trijp (Reference Van Dam and Van Trijp2011), who collected 851 survey responses from the light users of sustainable products and applied RA to predict 10 variables measuring the motivational structure of sustainability by 15 variables that include psychographic variables and purchase behavior. The 10 motivational structure variables are healthiness (y 1), price (y 2), convenience (y 3), naturalness (y 4), taste (y 5), local production (y 6), environment friendliness (y 7), fair trade (y 8), animal friendliness (y 9), and waste (y 10). The 15 predictor variables are concern for future consequences (x 1), prevention focus (x 2), promotion focus (x 3), altruistic value (x 4), biospheric value (x 5), egoistic value (x 6), NEP Footnote 8 scale (x 7), connectedness to nature (x 8), environment affect (x 9), ethical orientation (x 10), health prevention (x 11), health promotion (x 12), social SVO Footnote 9 (x 13), individual SVO (x 14), and competitive SVO (x 15). More details of these variables can be found from van Dam and van Trijp (Reference Van Dam and Van Trijp2011).
By applying RA, we find that the first three redundancy indices are .2503, .0357, and .0074, which are exactly the same as those reported by van Dam and van Trijp (Reference Van Dam and Van Trijp2011, p. 736), and all subsequent redundancy indices are smaller than .005. According to van Dam and van Trijp (Reference Van Dam and Van Trijp2011), the first two redundancy indices are meaningful, and the third and subsequent redundancy indices can be ignored. Thus, we focus on the first two columns of the redundancy loadings and the cross-loadings.
To obtain the standard error estimates for unrotated RA estimates, we fit the original RA-L model. The estimation method we use include maximum likelihood (ML), which requires the multivariate normality assumption of the data, and ML with the Satorra–Bentler correction (referred to as MLSB hereafter), which does not require any distribution assumptions of the data. Table 3 shows the first two columns of L xξ and L yξ and the associated standard error estimates from ML and MLSB, separately.
Table 3 The first two columns of unrotated redundancy loadings and unrotated cross-loadings and the associated standard error estimates from ML and MLSB

Note: SE = standard error estimate, ML = maximum likelihood, MLSB = maximum likelihood with the Satorra–Bentler correction.
By applying the normalized VARIMAX, we obtain
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
and
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
and
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
. To obtain the standard error estimates for rotated RA estimates, we fit the modified RA-L model for orthogonal rotations estimated by ULS, and apply the IJ method described in this paper. Table 4 shows
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
. To obtain the standard error estimates for rotated RA estimates, we fit the modified RA-L model for orthogonal rotations estimated by ULS, and apply the IJ method described in this paper. Table 4 shows
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
,
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
,
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
, and the associated standard error estimates from the IJ method.
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{orth}}$
, and the associated standard error estimates from the IJ method.
Table 4 Rotated redundancy loadings, rotated cross-loadings, and the associated standard error estimates from the IJ method

Note: SE = standard error estimate, IJ = infinitesimal jackknife. The rotated redundancy loadings whose absolute values are significantly larger than .3 are in boldface.
Using the standard error estimates, we can test if the absolute value of a rotated redundancy loading in
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
is larger than some cutoff value. Because the rotated redundancy loadings are correlations, we take .3 as the cutoff value, which means that at least 9% of the variance of a predictor variable must be shared with a rotated redundancy variate. Because we need to test the statistical significance of 30 rotated redundancy loadings simultaneously, it is necessary to adjust the typical significance level of .05. For convenience, we use the Bonferroni adjustment so that the adjusted significance level is .00167. It means that we will select a rotated redundancy loading if the associated p-value is smaller than .00167.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
is larger than some cutoff value. Because the rotated redundancy loadings are correlations, we take .3 as the cutoff value, which means that at least 9% of the variance of a predictor variable must be shared with a rotated redundancy variate. Because we need to test the statistical significance of 30 rotated redundancy loadings simultaneously, it is necessary to adjust the typical significance level of .05. For convenience, we use the Bonferroni adjustment so that the adjusted significance level is .00167. It means that we will select a rotated redundancy loading if the associated p-value is smaller than .00167.
Based on the selected rotated redundancy loadings, we use the corresponding predictor variables to interpret the rotated redundancy variates. Specifically, the first rotated redundancy variate should be interpreted in terms of biospheric value (x
5), NEP scale (x
7), connectedness to nature (x
8), environment affect (x
9), and ethical orientation (x
10); however, all the rotated redundancy loadings are smaller than .3 in the second column of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
. Accordingly, the first rotated redundancy variate can be interpreted as people’s concern for environmental sustainability.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
. Accordingly, the first rotated redundancy variate can be interpreted as people’s concern for environmental sustainability.
It is worth noting that if we only compared the absolute values of rotated redundancy variates against .3 but did not consider the sampling variability, we would select two more rotated redundancy loadings in the first column of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
(i.e., .5698 and .5495) that correspond with altruistic value (x
4) and health prevention (x
11). Nevertheless, the significance tests indicate that the rotated redundancy loadings on these two variables are not really larger than .3, and their magnitude observed in this example just appears to be larger than .3 due to randomness. If these two variables would be used to interpret the first rotated redundancy variate, it would totally change the current interpretation of the first rotated redundancy variate. This reflects the advantage of the use of standard error estimates in selecting the rotated redundancy loadings.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{orth}}$
(i.e., .5698 and .5495) that correspond with altruistic value (x
4) and health prevention (x
11). Nevertheless, the significance tests indicate that the rotated redundancy loadings on these two variables are not really larger than .3, and their magnitude observed in this example just appears to be larger than .3 due to randomness. If these two variables would be used to interpret the first rotated redundancy variate, it would totally change the current interpretation of the first rotated redundancy variate. This reflects the advantage of the use of standard error estimates in selecting the rotated redundancy loadings.
Table 5 Results of the individual redundancy indices and cumulative redundancy for the real example

Note: CI = confidence interval, ML = maximum likelihood, MLSB = maximum likelihood with the Satorra–Bentler correction.
5.2 Example 2
In the second example, we use the data from Jurukasemthawee et al. (Reference Jurukasemthawee, Pisitsungkagarn, Taephant and Sittiwong2021) that collected responses from 424 young adults (mean age = 19.97, standard deviation of age = 1.64) on 9 psychological variables, serving as the predictor variables, and 7 spiritual well-being variables, serving as the outcome variables. The 9 predictor variables are family and environment background (x 1), crisis in life that contributed to self-development (x 2), positive personal predisposition (x 3), good role models (x 4), faith activities (x 5), mindfulness and self-regulation (x 6), voluntary activities (x 7), self-reflection (x 8), and listening to positive experience (x 9). The 7 spiritual well-being variables are: inner peace (y 1), acceptance in diversity (y 2), compassion (y 3), self-transcendence (y 4), value in self (y 5), meaning in life (y 6), and insight in learnings (y 7). Each of the predictor and outcome variables is computed from the sum of item scores that are measured on a Likert scale ranging from 0 to 6. The number of items used for each of the predictor and outcome variables is from 5 to 12 items. More details of these items can be found from Jurukasemthawee et al. (Reference Jurukasemthawee, Pisitsungkagarn, Taephant and Sittiwong2021).
To determine the dimensionality in this example, we apply a new criterion proposed by Gu et al. (Reference Gu, Yung, Cheung, Joo and Nimon2023), which relies on the inferential information of redundancy indices. Specifically, we need to compare the lower limit of the 95% confidence interval (CI) for cumulative redundancy with some cutoff value. As a result, the smallest cumulative redundancy, of which the lower limit is larger than the specified cutoff value, can be identified. The identified cumulative redundancy determines the dimensionality in RA. In other words, we should retain the individual redundancy indices that constitute the identified cumulative redundancy. As for the cutoff value, we choose .3, meaning that at least 30% of the variance of criterion variables must be explained. To apply this new criterion, we need to fit the original RA-L model. As for the estimation method, we still use ML and MLSB.
Table 5 shows the results of the individual redundancy indices and cumulative redundancy for this example. By examining the lower limit of the 95% CI of cumulative redundancy, we find that the second cumulative redundancy is the smallest cumulative redundancy whose lower limit is larger than .3. It means that we should retain the first two individual redundancy indices. In addition, we notice that the second and third redundancy indices have comparable magnitude and both of them are distinctively larger than the fourth and subsequent redundancy indices, all of which are smaller than .01. Thus, we further study the difference between the second and third redundancy indices and their sumFootnote 10. The results in Table 6 show that the 95% CI for the difference includes 0, indicating that the second and third redundancy indices are not significantly different; simultaneously, the lower limit of the 95% CI for their sum is larger than .06 and the upper limit is nearly .10, indicating that the second and third redundancy indices can explain about 6–10% of the variance of criterion variables. Based on these results, we decide to retain the first three redundancy variates. The unrotated redundancy loadings and unrotated cross-loadings of the first three redundancy variates are shown in Table 7.
Table 6 Difference between the 2nd and 3rd individual redundancy indices and sum of the 2nd and 3rd individual redundancy indices

Note: Difference = the 2nd individual redundancy index − the 3rd individual redundancy index, Sum = the 2nd individual redundancy index + the 3rd individual redundancy index, CI = confidence interval, ML = maximum likelihood, MLSB = maximum likelihood with the Satorra–Bentler correction.
Table 7 The unrotated redundancy loadings and unrotated cross-loadings for the first three redundancy variates

Note: SE = standard error estimate, ML = maximum likelihood, MLSB = maximum likelihood with the Satorra–Bentler correction.
By applying the normalized QUARTIMIN, we obtain
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
,
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
,
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and Φ. To obtain the standard error estimates for rotated RA estimates, we fit the modified RA-L model for oblique rotations estimated by ULS, and apply the IJ method described in this paper. Table 8 shows
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and Φ. To obtain the standard error estimates for rotated RA estimates, we fit the modified RA-L model for oblique rotations estimated by ULS, and apply the IJ method described in this paper. Table 8 shows
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
,
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
,
![]() ${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and Φ, and the associated standard error estimates from the IJ method.
${\mathbf{L}}_{y\xi \mid m}^{\mathrm{obli}}$
, and Φ, and the associated standard error estimates from the IJ method.
Table 8 Results of the rotated redundancy loadings, the rotated cross-loadings, and the correlations of the three rotated redundancy variates

Note: SE = standard error estimate, IJ = infinitesimal jackknife. The rotated redundancy loadings whose absolute values are significantly larger than .3 are in boldface.
Using the standard error estimates, we can test if the absolute value of a rotated redundancy loading in
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
is larger than some cutoff value. Again, we take .3 as the cutoff value. Because we need to test the statistical significance of 27 rotated redundancy loadings simultaneously, it is necessary to adjust the typical significance level of .05. We use the Bonferroni adjustment again so that the adjusted significance level is .00185. It means that we will select a rotated redundancy loading if the associated p-value is smaller than .00185.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
is larger than some cutoff value. Again, we take .3 as the cutoff value. Because we need to test the statistical significance of 27 rotated redundancy loadings simultaneously, it is necessary to adjust the typical significance level of .05. We use the Bonferroni adjustment again so that the adjusted significance level is .00185. It means that we will select a rotated redundancy loading if the associated p-value is smaller than .00185.
Based on the selected rotated redundancy loadings, we use the corresponding predictor variables to interpret the three rotated redundancy variates. Specifically, the first rotated redundancy variate should be interpreted in terms of positive personal predisposition (x 3), voluntary activities (x 7), self-reflection (x 8), and listening to positive experience (x 9); the second rotated redundancy variate should be interpreted in terms of family and environment background (x 1), crisis in life that contributed to self-development (x 2), and Mindfulness and Self-Regulation (x 6); and the third rotated redundancy variate should be interpreted in terms of faith activities (x 5). Accordingly, the first rotated redundancy variate can be interpreted as positive personal predispositions that facilitated attention to positive experiences, self-reflection, and voluntary activities; the second rotated redundancy variate can be interpreted as safe family and environmental backgrounds that facilitated the use of mindfulness and self-regulation in transforming crisis into self-development; and the third rotated redundancy variate can be interpreted as engagement in activities that were related to own faiths. Also, we found that the correlation between the first and second rotated redundancy variates is .7029 (with standard error estimate = .0265), suggesting that the first and second rotated redundancy variates share almost 50% of their variance. It implies that positive personal predispositions and safe family and environmental backgrounds are closely and significantly related. It should be noted that only oblique rotations can produce correlated rotated redundancy variates and the resulting correlations may bring more meaningful interpretations and insights to the study than the orthogonal rotations.
It is worth noting that if we only compared the absolute values of rotated redundancy variates against .3 but did not consider the sampling variability, we would select one more rotated redundancy loading in the third column of
![]() ${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
(i.e., .3102) that corresponds with voluntary activities (x
7). Nevertheless, the significance test indicates that the rotated redundancy loading on this variable is not really larger than .3. If this variable would be used to interpret both the first and third rotated redundancy variates, it would cause some inconvenience in the interpretation, which in turn reflects the advantage of the use of standard error estimates in selecting the rotated redundancy loadings.
${\mathbf{L}}_{x\xi \mid m}^{\mathrm{obli}}$
(i.e., .3102) that corresponds with voluntary activities (x
7). Nevertheless, the significance test indicates that the rotated redundancy loading on this variable is not really larger than .3. If this variable would be used to interpret both the first and third rotated redundancy variates, it would cause some inconvenience in the interpretation, which in turn reflects the advantage of the use of standard error estimates in selecting the rotated redundancy loadings.
6 Discussions
In this paper, we specify two modified RA-L models for orthogonal and oblique rotations, separately, and describe the IJ method with the ULS fitting function to produce the standard error estimates for rotated RA estimates. Then, a simulation study is conducted to validate the performance of the IJ method. Additionally, two real examples are used to demonstrate the use of standard error estimates for rotated redundancy loadings when the rotated redundancy variates are interpreted. It was observed that the use of standard error estimates refines the selection of the rotated redundancy loadings and provides meaningful interpretations of the rotated redundancy variates in both examples.
Regarding the rotation method, one can use any of the rotation methods from the Crawford–Ferguson family (Crawford & Ferguson, Reference Crawford and Ferguson1970), while the choice of rotation method only changes one thing in the implementation of the IJ method. Specifically, the choice of rotation method determines the simplicity function (i.e., h orth in equation 13 or h obli in equation 14) used in the fourth type of constraints of the modified RA-L model, and the fourth type of constraints determines the last component of the Jacobian matrix (i.e.,
![]() $\frac{\partial {\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}$
) in equation (23). In other words, if a different rotation method is used, it is only the partial derivatives of the constraints in equation (13) or (14) that must be changed in the implementation of the IJ method.
$\frac{\partial {\boldsymbol{\varphi}}_3\left(\boldsymbol{\theta} \right)}{\partial {\boldsymbol{\theta}}^{\prime }}$
) in equation (23). In other words, if a different rotation method is used, it is only the partial derivatives of the constraints in equation (13) or (14) that must be changed in the implementation of the IJ method.
Regarding the computation of partial derivatives, Lord (Reference Lord1975) and Browne and Du Toit (Reference Browne and Du Toit1992) recommended the use of numeric derivatives for nonstandard problems and models. Also, Jennrich (Reference Jennrich2008) reported good performance of numeric derivatives in the implementation of the IJ method. In our simulation study, we used numeric derivatives and obtained satisfactory results from the IJ method. Admittedly, one can argue that, in equations (23) and (24), the use of numeric derivatives is not as efficient/fast as the use of analytic derivatives. But this is a minor limitation in practical data analysis, because the difference in speed is trivial if there are only a few data sets to be analyzed. If there are a large number of data sets to be analyzed such as in simulation studies, then the difference would become noticeable. However, it is quite challenging to derive the necessary formulas for partial derivatives of different kinds of simplicity functions if the analytic derivatives must be used.
Finally, we would like to point out that the IJ method is a very general method for standard error estimation, but it is under-utilized in psychometrics. Historically, Jennrich and Clarkson (Reference Jennrich and Clarkson1980) first developed this method in the context of EFA. Later, Jennrich (Reference Jennrich2008) extended this method to the general framework of covariance structure analysis and referred to this method as the IJ method. Nonetheless, there are only two studies that applied the IJ method: Zhang et al. (Reference Zhang, Preacher and Jennrich2012) and Gu et al. (Reference Gu, Wu, Yung and Wilkins2021). We hope that our work would draw the attentions of not only the researchers but also the software developers who can develop accessible software programs to better promote the use of the IJ method.
Supplementary material
To view supplementary material for this article, please visit http://doi.org/10.1017/psy.2024.8.
Acknowledgements
This research project is supported by the New Faculty grant, Ratchadaphiseksombot Fund, Chulalongkorn University. The data collection of Example 1 was made possible by GfK Netherlands and Stichting Duurteelt. The data collection of Example 2 was supported by JitArsaBank Fund, Thai Health Promotion Foundation.
Competing interests
On behalf of all authors, the corresponding author states that there is no conflict of interest.










