2.1. The N–S problem and the operators $\mathcal {Z}$ , $\mathcal {G}$

In order to solve the inverse problem (2.3) using (2.5)–(2.7), we need to define $\mathcal {Z}$ and $\mathcal {G}$ . We start from the N–S boundary value problem in $\Omega \subset \mathbb {R}^3$ :

(2.9) \begin{gather} \boldsymbol {u}\boldsymbol {\cdot }\nabla \boldsymbol {u}-\nabla \boldsymbol {\cdot }\big (2\nu _e\nabla ^s\boldsymbol {u}\big ) + \nabla p = \boldsymbol {0} \quad \text {and}\quad \nabla \boldsymbol {\cdot } \boldsymbol {u} = 0 \quad \textrm {in}\quad \Omega,\nonumber \\ \boldsymbol {u} = \boldsymbol {0} \quad \textrm {on}\quad \Gamma,\quad \boldsymbol {u} = \boldsymbol {g}_i \quad \textrm {on}\quad \Gamma _i,\quad -2\nu _e\nabla ^s\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nu }+p\boldsymbol {\nu } = \boldsymbol {g}_o \quad \textrm {on} \quad \Gamma _o, \end{gather}

where $\boldsymbol {u}$ is the velocity, $p\leftarrow \!| p/\rho$ is the reduced pressure, $\rho$ is the density, $\nu _e$ is the effective kinematic viscosity, $(\nabla ^s \boldsymbol {u})_{ij} := ({1}/{2})(\partial _j u_i + \partial _i u_j)$ is the strain-rate tensor, $\boldsymbol {g}_i$ is the Dirichlet boundary condition (b.c.) at the inlet $\Gamma _i$ , $\boldsymbol {g}_o$ is the natural b.c. at the outlet $\Gamma _o$ , and $\boldsymbol {\nu }$ is the unit normal vector on the boundary $\partial \Omega = \Gamma \cup \Gamma _i\cup \Gamma _o$ , where $\Gamma$ is the no-slip boundary (wall). The construction of the operators $\mathcal {Z}, \mathcal {G}$ of the generalised inverse N–S problem, whose unknown parameters are the shape of the domain $\Omega$ , the boundary conditions $\boldsymbol {g}_i, \boldsymbol {g}_o$ , and the viscosity field $\nu _e$ , is treated in Kontogiannis et al. (Reference Kontogiannis, Elgersma, Sederman and Juniper2022); Kontogiannis & Juniper (Reference Kontogiannis and Juniper2023); Kontogiannis et al. (Reference Kontogiannis, Elgersma, Sederman and Juniper2024a ). Here, we fix the geometry, $\Omega$ , and the outlet b.c., $\boldsymbol {g}_o$ , and infer only the inlet b.c., $\boldsymbol {g}_i$ , and the effective viscosity field, $\nu _e$ . We further introduce the Carreau model for the effective viscosity field, which is given by

(2.10) \begin{align} \mu _e(\dot {\gamma };\boldsymbol {p}_\mu ) &:= \mu _\infty + \delta \mu \big (1 +(\lambda \dot {\gamma })^2\big )^{({n}-1)/{2}}, \end{align}

where $\mu _e := \nu _e\rho$ , $\dot {\gamma }(\boldsymbol {u}) := \sqrt {2\nabla ^s\boldsymbol {u}\boldsymbol {:}\nabla ^s\boldsymbol {u}}$ is the magnitude of the strain-rate tensor, and $\boldsymbol {p}_\mu := (\mu _\infty ,\delta \mu ,\lambda ,n )$ are the Carreau fluid parameters. In order to infer the most likely viscosity field, $\mu ^\circ _e$ , we therefore need to infer the most likely Carreau fluid parameters, $\boldsymbol {p}^\circ _\mu$ .

After linearising problem (2.9) around $\boldsymbol {u}_k$ , we obtain $\boldsymbol {u}(\boldsymbol {x}) \simeq \boldsymbol {u}_k + \mathcal {A}_k (\boldsymbol {x}-\boldsymbol {x}_k)$ , where $\mathcal {A}_k \equiv ((D^{\mathscr {M}}_{\boldsymbol {u}})^{-1}D^{\mathscr {M}}_{\boldsymbol {x}} )_k$ , with $\mathcal {A}_k$ being a linear, invertible operator, which encapsulates the inverse Jacobian of the N–S problem, $(D^{\mathscr {M}}_{\boldsymbol {u}})^{-1}$ , and the generalised gradient of the velocity field with respect to the parameters $\boldsymbol {x}$ , $D^{\mathscr {M}}_{\boldsymbol {x}}$ . Observing that $\mathcal {Z}, \mathcal {G}$ map from the N–S parameter space to the (velocimetry) data space, we define $\mathcal {Z} := \mathcal {S}\mathcal {Q}$ and $\mathcal {G}_k := \mathcal {S}\mathcal {A}_k$ , where $\mathcal {S}:\boldsymbol {M}\to \boldsymbol {D}$ is a projection from the model space, $\boldsymbol {M}$ , to the data space, $\boldsymbol {D}$ , and $\mathcal {Q}$ is the operator that maps $\boldsymbol {x}$ to $\boldsymbol {u}$ , i.e. that solves the N–S problem. (The operators $\mathcal {S},\mathcal {Q},\mathcal {A}$ are derived in Kontogiannis et al. (Reference Kontogiannis, Elgersma, Sederman and Juniper2024a) from the weak form of the N–S problem (2.9), $\mathscr {M}$ .)

Based on the above definitions, and due to (2.6), we observe that the model contribution to the objective’s steepest descent direction, for the Carreau parameters, $\boldsymbol {p}_\mu$ , is

(2.11) \begin{gather} \big (\delta \boldsymbol {p}_{\mu }\big )_k := \mathcal {G}_k^*\,\mathcal {C}_{\boldsymbol {u}^\star }^{-1}\big (\boldsymbol {u}^\star -\mathcal {Z}\boldsymbol {x}_k\big ) = \underbrace {\big (D^{\mathscr {M}}_{\boldsymbol {p}_{\mu }}\big )^*_k\, \big ((D^{\mathscr {M}}_{\boldsymbol {u}})^{*}\big )^{-1}_k}_{D^{\boldsymbol {p}_{\mu }}_{\boldsymbol {u}}}\,\underbrace {\mathcal {S}^*\,\mathcal {C}_{\boldsymbol {u}^\star }^{-1}\big (\boldsymbol {u}^\star -\mathcal {S}\boldsymbol {u}_k\big )}_{\text {data-model discrepancy } \delta \boldsymbol {u} \in \boldsymbol {M}}. \end{gather}

Even though $D^{\mathscr {M}}_{\boldsymbol {u}}$ is invertible, for large-scale problems (such as those in fluid dynamics) its inverse, $(D^{\mathscr {M}}_{\boldsymbol {u}})^{-1}$ , cannot be stored in computer memory because its discrete form produces a dense matrix. The discrete form of $D^{\mathscr {M}}_{\boldsymbol {u}}$ , however, produces a sparse matrix. Consequently, instead of using the explicit formula (2.11), the steepest descent directions are given by

(2.12) \begin{gather} \big (\delta \boldsymbol {p}_{\mu }\big )_k := \big (D^{\mathscr {M}}_{\boldsymbol {p}_{\mu }}\big )^*_k\,\boldsymbol {v}_k = 2\int _\Omega \big (D_{\boldsymbol {p}_\mu }\mu _e\big )_k\big (\nabla ^s\boldsymbol {u}_k\boldsymbol {:}\nabla ^s\boldsymbol {v}_k\big ), \end{gather}

where ${ (D_{\boldsymbol {p}_\mu }\mu _e )}_k \equiv D_{\boldsymbol {p}_\mu }\mu _e (\dot {\gamma }(\boldsymbol {u}_k);(\boldsymbol {p}_{\mu })_k )$ consists of the derivatives of the Carreau model with respect to its parameters, and $\boldsymbol {v}_k$ is the adjoint velocity field, which is obtained by solving the following linear operator equation:

(2.13) \begin{gather} A\boldsymbol {v}_k = b,\quad \text {where}\quad A \equiv \big (D^{\mathscr {M}}_{\boldsymbol {u}}\big )_k^*\quad \text {and}\quad b \equiv \mathcal {S}^*\mathcal {C}_{\boldsymbol {u}^\star }^{-1}\big (\boldsymbol {u}^\star -\mathcal {S}\boldsymbol {u}_k\big ). \end{gather}

The steepest descent directions for the inlet b.c., $\boldsymbol {g}_i$ , are derived in Kontogiannis et al. (Reference Kontogiannis, Elgersma, Sederman and Juniper2024a ).

Instead of explicitly computing $\mathcal {C}_{\boldsymbol {x}_k}$ at every iteration using (2.7), we approximate $\mathcal {C}_{\boldsymbol {x}_k}$ using the damped Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method (Goldfarb et al. Reference Goldfarb, Ren, Bahamou, Larochelle, Ranzato, Hadsell, Balcan and Lin2020), which ensures that $\mathcal {C}_{\boldsymbol {x}_k}$ remains positive definite, and its approximation remains numerically stable.

Algorithm 1. Learning rheological parameters from velocimetry data.

2.1.1. Note on effective viscosity model selection

In this study, although we fix the effective viscosity model to the Carreau fluid model, which is given by (2.10), the present Bayesian inversion framework is already set up for model selection (Yoko & Juniper Reference Yoko and Juniper2024a , § 4.3). The velocimetry data, $\boldsymbol {u}^\star$ , can be assimilated into the N–S boundary value problem with as many different viscosity models as the user likes. The model parameter uncertainties are then estimated, and the marginal likelihood of each model is calculated. The marginal likelihood is the likelihood of each model, given the experimental data, which is also known as the evidence for each model. The models are then ranked by their evidence, and the most accurate model is chosen. Bayesian rheological model ranking using rheometry data has been addressed in Freund & Ewoldt (Reference Freund and Ewoldt2015). Note that, here we infer the rheology of the fluid from velocimetry data (instead of rheometry data), which is a more difficult problem. Bayesian rheological model ranking from velocimetry data are a natural extension of the present Bayesian inversion framework, and provides scope for future work. (Another extension that follows naturally is optimal experiment design (Yoko & Juniper Reference Yoko and Juniper2024b , § 4.3, § 4.1), i.e. strategically planning experiments to maximise information gain in parameter estimation.)

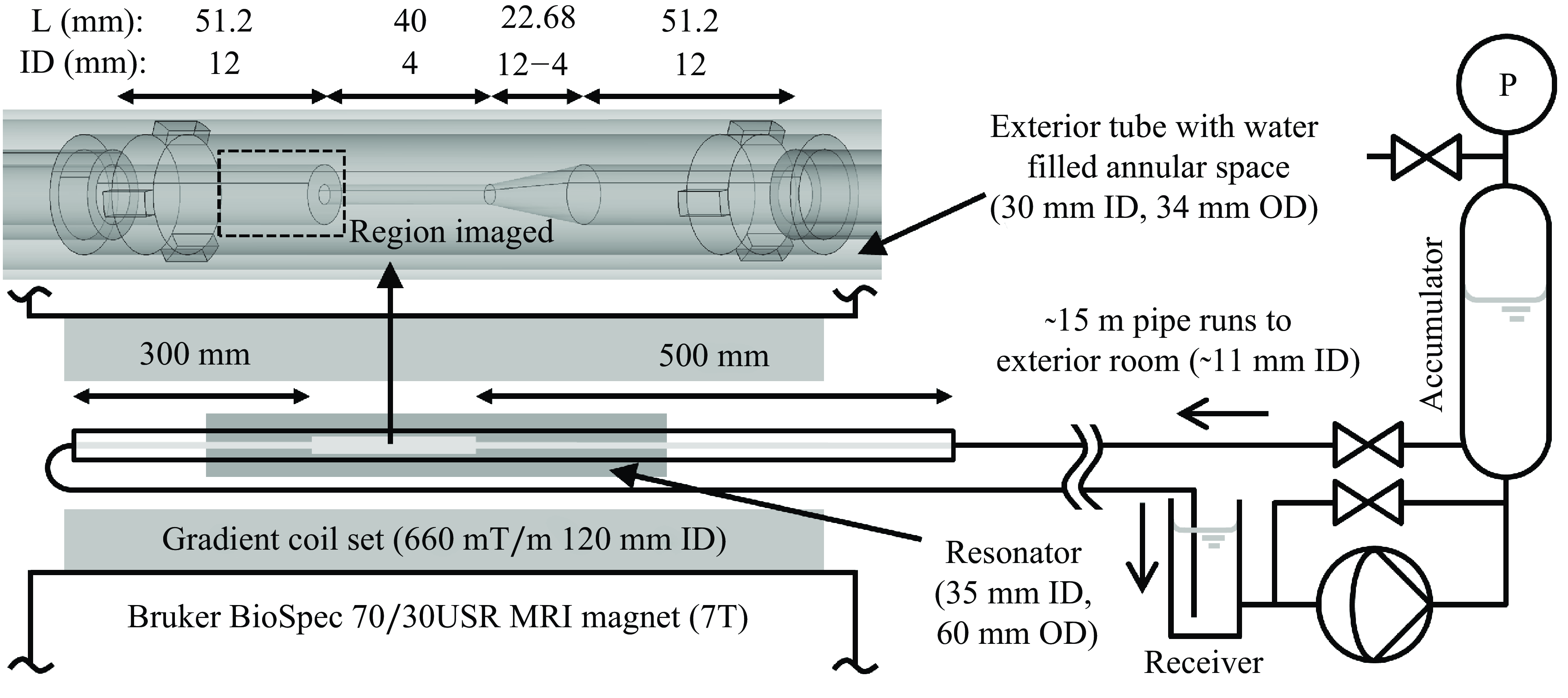
Figure 1. Overall flow system and set-up around the MRI scanner with detail of the FDA flow nozzle geometry implemented: ID, inner diameter; OD, outer diameter.

3.1. Flow-MRI data preprocessing

We use phase-contrast MRI and Hadamard encoding to measure all three components of a 3-D velocity field using a single set of four, fully sampled $\boldsymbol {k}$ -space scans, $\{{s}\}_{j=1}^4$ . For each scan we compute its respective complex image, $w_j$ , which is given by

(3.1) \begin{gather} w_j := \rho _j e^{i\varphi _j} = \mathcal {F}^{-1}s_j, \end{gather}

where $\rho _j$ is the nuclear spin density image, $\varphi _j$ is the phase image and $\mathcal {F}$ is the Fourier transform. The velocity components $u_i$ , for $i=1,\dots, 3$ , are then given by

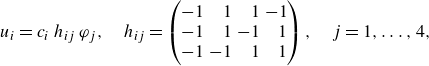(3.2) \begin{gather} u_i = c_i\,h_{ij}\,\varphi _j,\quad h_{ij}= \begin{pmatrix} -1 & \hphantom {-}1 & \hphantom {-}1 & -1\\ -1 & \hphantom {-}1 & -1 & \hphantom {-}1\\ -1 & -1 & \hphantom {-}1 & \hphantom {-}1 \end{pmatrix},\quad j=1,\ldots, 4, \end{gather}

where repeated indices imply summation, and $c_i$ is a known constant that depends on the gyromagnetic ratio of hydrogen and the gradient pulse properties. In order to remove any phase shift contributions that are not caused by the flow, we conduct an additional no-flow experiment. That is, we acquire a set of four $\boldsymbol {k}$ -space scans, $\{\bar {s}\}_{j=1}^4$ , for the same geometry and field-of-view, but with zero flow (stagnant fluid). We then obtain the no-flow complex images, $\bar {w}_j$ , using (3.1), and compute the corresponding no-flow velocity images using (3.2), such that $\bar {u}_i = \bar {c}_i h_{ij} \bar {\varphi }_j$ , where $\bar {c}_i$ is the no-flow constant, which is known. The corrected velocity is then given by $u_i = c_i\theta (h_{ij}\varphi _j) - \bar {c}_i\theta (h_{ij}\bar {\varphi }_j)$ , where $\theta (x) := x - 2\pi (\lfloor (\lfloor {x}/\pi \rfloor -1)/2\rfloor + 1)$ is the phase difference unwrapping function, and $\lfloor {\cdot }/\cdot \rfloor$ denotes integer division. To increase the signal-to-noise ratio (SNR) of steady flow images we acquire $n$ sets (in this study $n=4$ ) of $\boldsymbol {k}$ -space scans, generate their respective velocity images $\{u_i\}_{k=1}^{n}$ , and compute the average velocity image $\sum _{k=1}^{n} (u_i)_k/n$ . The noise variance in the averaged velocity images then reduces to $\sigma ^2/n$ , where $\sigma ^2$ is the noise variance of each individual velocity image. We straighten and centre the averaged flow-MRI images, and, since the flow is axisymmetric, we mirror-average the images to further increase SNR and enforce mirror-symmetry. We generate a mask for the region of interest by segmenting the mirror-averaged nuclear spin density image, and apply this mask to the velocity images. Because we solve an inverse N–S problem in a 3-D discrete space comprising trilinear finite elements (voxels), the final preprocessing step is to $L^2$ -project the two-dimensional (2-D) axisymmetric flow-MRI images, $(u_r,u_z)$ , to their corresponding 3-D flow field, $\boldsymbol {u}^\star =(u^\star _x,u^\star _y,u^\star _z)$ . Note that the 3-D data that we generate (Kontogiannis et al. Reference Kontogiannis, Hodgkinson, Reynolds and Manchester2024b ) have the same (2-D) spatial resolution as the 2-D images.

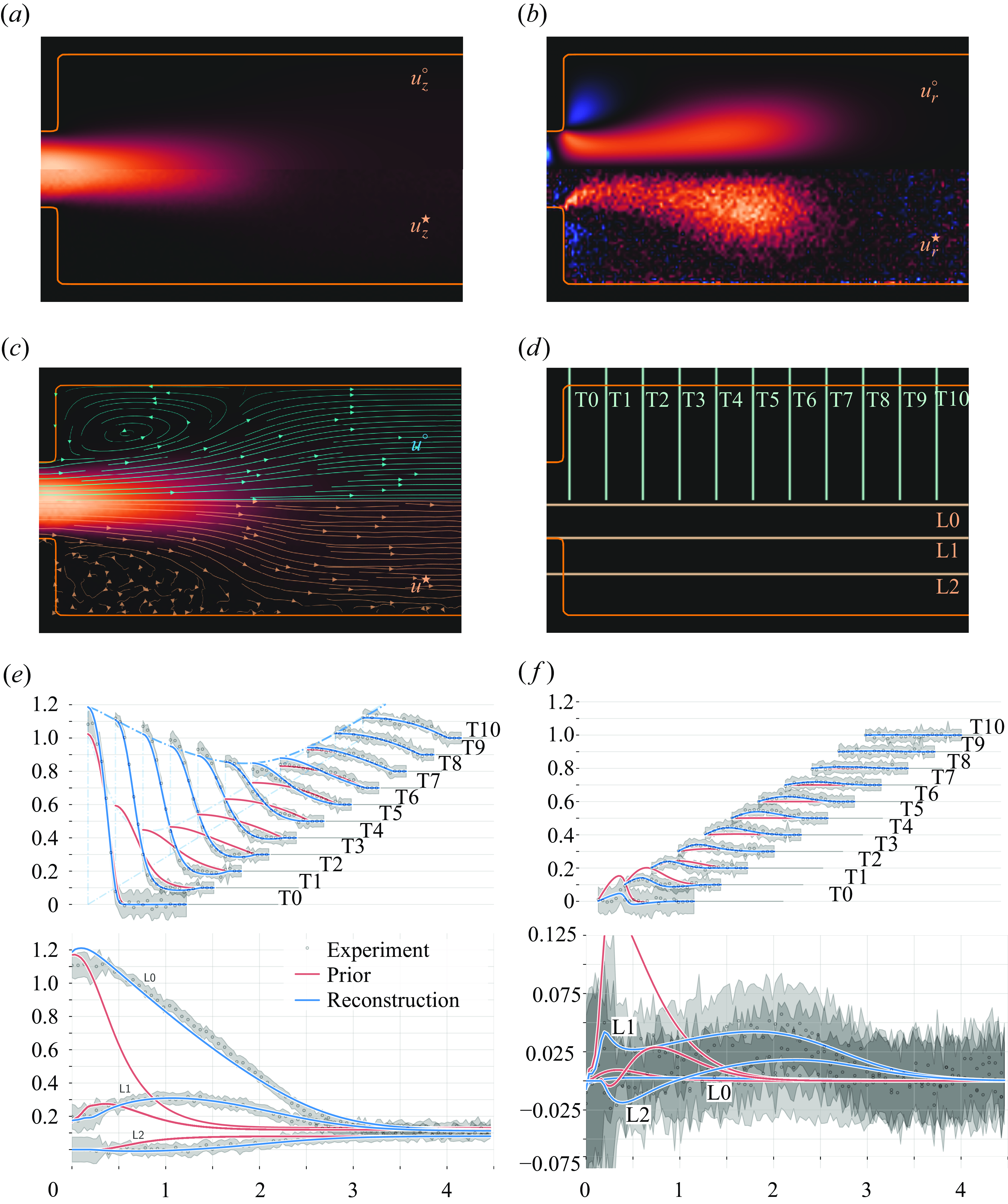
Figure 2. Images, streamlines and slices of reconstructed (MAP) flow, $\boldsymbol{u}^\circ$ , versus velocimetry data, $\boldsymbol{u}^\star$ . Panels (a) and (e) show the axial velocity, $u_z$ , and panels (b) and (f) show the radial velocity component, $u_r$ . In panels (e) and (f), velocity is normalised by U = 20 cm s⁻¹, and length is normalised by L = 5 mm. We separate the transverse slices in the plot by applying a vertical offset of 0.1 $n$ to the $n$ th slice (the horizontal offset value is immaterial).

4.1. Flow field reconstruction

The reconstructed flow field, $\boldsymbol {u}^\circ$ , which is generated using algorithm1, is shown in figure 2 versus the velocimetry data, $\boldsymbol {u}^\star$ . We define the average data-model distance by $\mathcal {E}(u_\square ) := \lvert \Omega \rvert ^{-1}\lVert u^\star _\square -\mathcal {S}u_\square \rVert _{L^2(\Omega )}$ , where $\lvert \Omega \rvert$ is the volume of $\Omega$ , and $\square$ is a symbol placeholder. For the reconstructed velocity field, $\boldsymbol {u}^\circ$ , we then find $\mathcal {E}(u^\circ _x) = \mathcal {E}(u^\circ _y)= 0.71\sigma$ , $\mathcal {E}(u^\circ _z) = 1.40\sigma$ , and compare this to the distance between the initial guess, $\boldsymbol {u}^{(0)}$ , and the data $\mathcal {E}(u^{(0)}_x) = \mathcal {E}(u^{(0)}_y) = 1.39\sigma$ , $\mathcal {E}(u^{(0)}_z) = 5.87\sigma$ . The inferred (MAP) versus prior strain-rate magnitude, $\dot {\gamma }$ , and effective viscosity field, $\mu _e(\dot {\gamma })$ , are shown in figure 3. Note that we initialise algorithm1 using the prior means, and thus $\mu _e^{(0)} = \mu _e (\dot {\gamma }(\boldsymbol {u}_0);\bar {\boldsymbol {p}}_{\mu } ) \simeq 0.1$ Pa $\cdot$ s. Using the reconstructed flow field, $\boldsymbol {u}^\circ$ , and the inferred effective viscosity field, $\mu _e^\circ$ , we find that the generalised Reynolds number of this flow is ${\textit {Re}}_g = 37.5$ , where ${\textit {Re}}_g := \rho U_cL_c/\mu _c$ , $U_c:= Q/A = 11.1$ cm s^–1, $Q$ is the volumetric flow rate, $A$ is the cross-section area before the expansion, $L_c = 4$ mm, and $\mu _c=13$ mPa is the value of the effective viscosity on the wall, before the expansion.

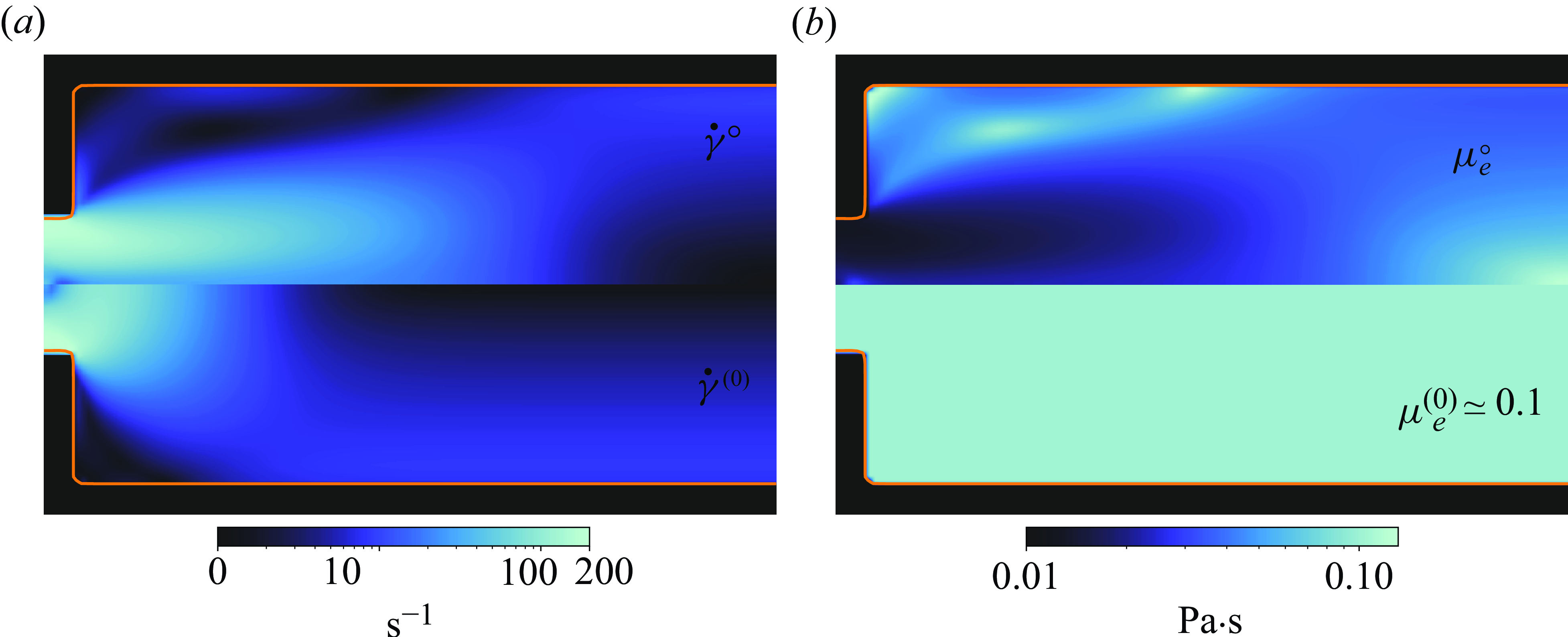
Figure 3. Inferred (MAP) versus prior strain-rate magnitude (a), $\dot{\gamma} (\textrm{s}^{-1})$ , and effective viscosity (b), $\mu_e ({\textrm{Pa}{\cdot}\textrm{s}})$ .

4.2. Carreau parameter learning

According to the optimisation log (figure 4 a), the algorithm learns the unknown N–S parameters (i.e. the Carreau parameters and the inlet b.c.) in $\sim$ 20 iterations, but most of the work is done in $\sim$ 10 iterations. Using the Carreau parameters learned at every step, $k$ , of the optimisation process, we plot the evolution of the posterior p.d.f. of $\mu _e$ (mean, $\mu _e^{(k)}$ , and covariance, $\mathcal {C}^{(k)}_{\mu _e}$ ) in figure 4(b). The posterior covariance of $\mu _e^{(k)}$ is given by

(4.1) \begin{align} \mathcal {C}^{(k)}_{\mu _e} := \mathcal {G}^{(k)}_{\mu _e}\,\widetilde {\mathcal {C}}^{(k)}_{\boldsymbol {p}_{\mu }}\,\big (\mathcal {G}^{(k)}_{\mu _e}\big )^*, \end{align}

where $\mathcal {G}^{(k)}_{\mu _e}$ is the Jacobian of the Carreau fluid model (2.10) with respect to its parameters, $\boldsymbol {p}_{\mu }$ , and $\widetilde {\mathcal {C}}^{(k)}_{\boldsymbol {p}_{\mu }}$ is the BFGS approximation of the posterior covariance of the Carreau parameters, ${\mathcal {C}}^{(k)}_{\boldsymbol {p}_{\mu }}$ . The prior uncertainty, shown in figure 4(b) as a $\pm 3\sigma$ red shaded region, is sufficiently high and extends beyond the $\mu _e -\dot {\gamma }$ plotting range. (To ensure that the inversion is stable with respect to prior perturbations, we performed inversions with different priors and found that the inferred posterior parameter distributions were practically the same. A sensitivity analysis with respect to the priors is, however, beyond the scope of the present study.) We observe that the posterior uncertainty of $\mu _e$ reduces significantly after assimilating the data in the model, and that the highest uncertainty reduction is for $10 \lessapprox \dot {\gamma } \lessapprox 200$ s⁻¹, which is the $\dot {\gamma }$ -range of the laminar jet (see figure 3 a). It is worth mentioning that, even though we observe a flow for which $\dot {\gamma }\in [0,200]$ s⁻¹, the region that provided the most information is that around the jet because (i) inertial effects balance viscous effects, and (ii) the local velocity-to-noise ratio is high, hence the uncertainty collapse in the jet-operating $\dot {\gamma }$ -range.

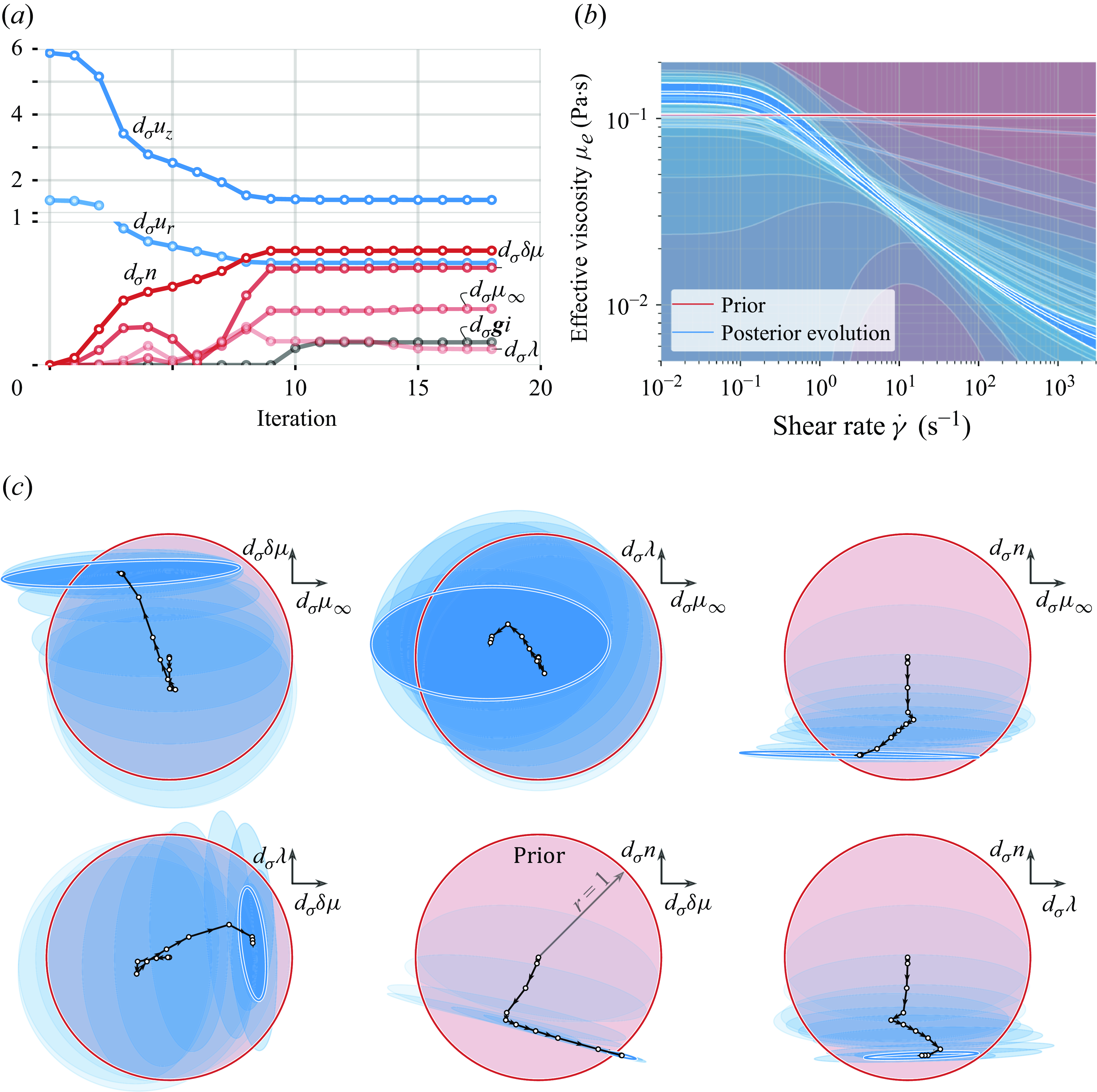
Figure 4. Optimisation log (a), and posterior p.d.f. evolution of the effective viscosity (b) and the Carreau parameters (c). In panel (c), the axes are such that $d_\sigma x := (x-\bar {x})/\sigma _{\bar {x}}$ , where $\bar {x}$ is the prior mean and $\sigma _{\bar {x}}$ is the prior standard deviation.

The posterior p.d.f. evolution of the Carreau parameters is shown in figure 4(c). In this case, the prior uncertainty isocontours can be visualised using hyperellipsoids in $\mathbb {R}^4$ whose centres are $\bar {\boldsymbol {p}}_{\mu }$ , and axis lengths are proportional to (the columns of) $\mathcal {C}_{\bar {\boldsymbol {p}_\mu }}$ . To highlight the parameter uncertainty reduction after assimilating the data, we set the origin to $\bar {\boldsymbol {p}}_{\mu }$ , and scale each dimension of $\mathbb {R}^4$ using (the columns of) $\mathcal {C}_{\bar {\boldsymbol {p}}_\mu }$ . In this transformed space, the prior uncertainty isocontours are hyperspheres, and the posterior uncertainty isocontours are hyperellipsoids, whose slices are shown in figure 4(c). It is interesting to note that, after assimilating the velocimetry data, the posterior uncertainty collapses along the axes $n$ , $\delta \mu$ , whilst it slightly decreases along the axes $\mu _\infty$ , $\lambda$ . This indicates that there is insufficient information in the data to further collapse the prior uncertainties of $\lambda$ and $\mu _\infty$ .

It is known that for models with univariate design (e.g. shear rate, $\dot {\gamma }$ ) and observable variables (e.g. effective viscosity, $\mu _e$ ) in order to learn the most about the unknown parameters (e.g. $\boldsymbol {p}_{\mu }$ ) we need to perform experiments with the design parameters at which the model is most uncertain (Yoko & Juniper Reference Yoko and Juniper2024b , § 4.1). Here, figure 4(b) shows that the model is most uncertain for $\dot {\gamma } \ll 10$ s⁻¹ and $\dot {\gamma } \gg 200$ s⁻¹. Consequently, in order to further collapse the uncertainty of $\lambda$ and $\mu _\infty$ , we require more (or higher SNR) flow-MRI data for $\dot {\gamma } \ll 10$ s⁻¹ and $\dot {\gamma } \gg 200$ s⁻¹. In particular, since we have used flow-MRI data of a jet for which $\dot {\gamma }\in [0,200]$ s⁻¹, we would require new experiments with (i) higher SNR, since information at low velocity magnitudes, i.e. $\dot {\gamma } \ll 10$ s⁻¹, is corrupted by noise, and (ii) higher velocity magnitudes (for the same geometry), since information at $\dot {\gamma } \gg 200$ s⁻¹ is missing from the current experiment.

4.3. Validation via an independent rheometry experiment

Steady-shear rheometry of the test solution was conducted using a Netzsch Kinexus rheometer with a $\varnothing$ 27.5 mm cup and a $\varnothing$ 25 mm bob geometry, at the same temperature as the flow-MRI experiment. The experiment was conducted to validate the Carreau parameters learned from the flow-MRI data (§ 4.2) against rheometry data. To find the most likely Carreau parameters that fit the rheometry data, we use Bayesian inversion (see § 2). In this case, operator $\mathcal {Z}$ corresponds to the Carreau model, given by the explicit relation (2.10), and operator $\mathcal {G}$ corresponds to the Jacobian of the Carreau model with respect to its parameters. We use the same prior as in § 4. Because the prior uncertainty is sufficiently high relative to the noise variance, the bias it introduces to the model fit is negligible. The Carreau parameters learned from flow-MRI versus rheometry are shown in figure 5. We observe that the parameters learned from flow-MRI agree well with rheometry data, considering uncertainties (figure 5 b), and that the learned effective viscosity field fits the rheometry data (figure 5 a). As in the case of learning from flow-MRI, it is not possible to infer $\lambda$ and $\mu _\infty$ with high certainty when data, $\mu _e(\dot {\gamma })$ , for $\dot {\gamma } \ll 10$ s⁻¹ and $\dot {\gamma } \gg 200$ s⁻¹ are missing (or the measurement uncertainty is high).

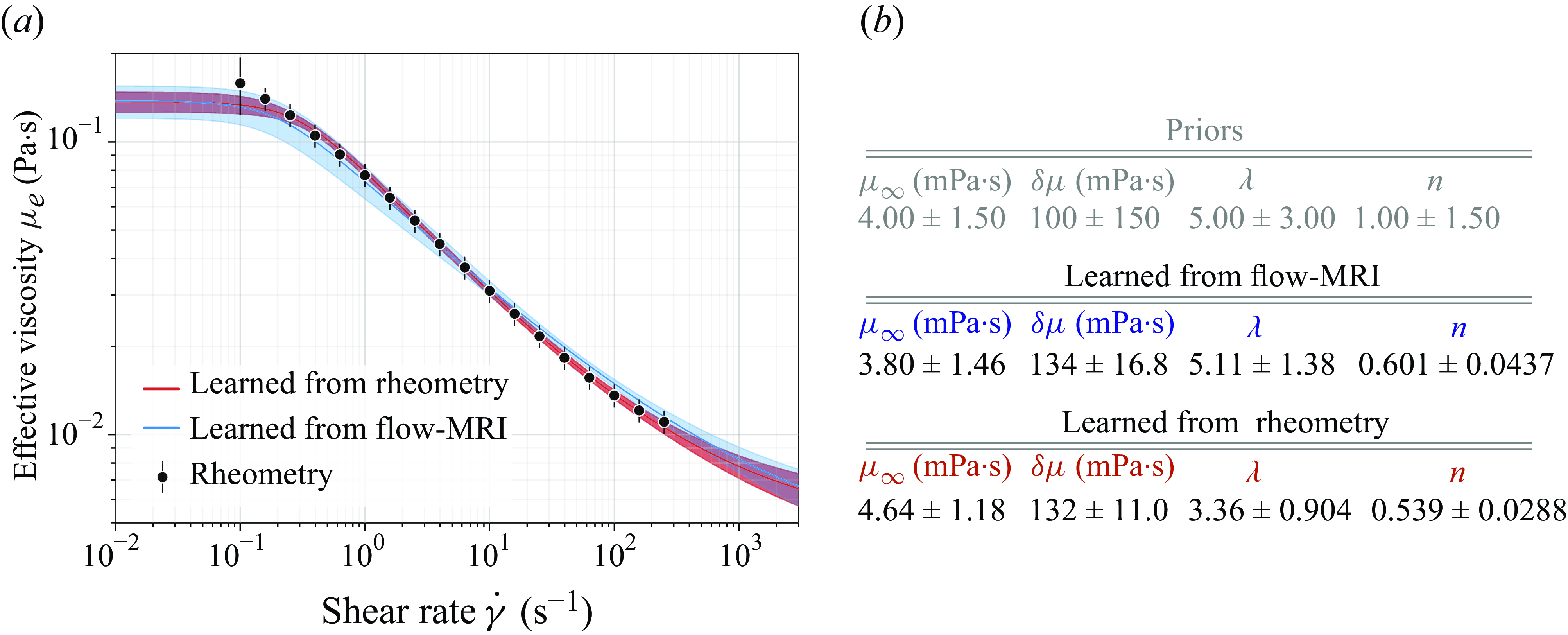
Figure 5. Learned Carreau fit to rheometry data, learned model parameters (MAP estimates), and assumed priors. Uncertainties in the figures correspond to $3\sigma$ intervals.