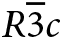Introduction
Pezzottaite is a Cs-rich mineral, ideal formula Cs(Be2Li)Al2Si6O18, that was discovered about 20 years ago (Hawthorne et al., Reference Hawthorne, Cooper, Simmons, Falster, Laurs, Armbruster, Rossman, Peretti, Günter and Grobéty2004) at the Sakavalana pegmatite 25 km south of the village of Mandosonoro, SW of the town of Antsirabe, 140 km SW of Ambatofinandrahana, central Madagascar. Interest in this mineral was enhanced by it being a significant gemstone (Laurs et al., Reference Laurs, Simmons, Rossman, Quinn, McClure, Peretti, Armbruster, Hawthorne, Falster, Günther, Cooper and Grobéty2003; Simmons et al., Reference Simmons, Falster, McClure, Quinn, Rossman and Hawthorne2003; Warin and Jacques, Reference Warin and Jacques2003; Peretti et al., Reference Peretti, Armbruster, Günther, Grobéty, Hawthorne, Cooper, Simmons, Falster, Rossman and Laurs2004) with prices up to US$10,000 per carat. The crystal structure proved to be an ordered superstructure of beryl, ideally Be3Al2Si6O18. For many years, there has been interest in the incorporation of Cs+ and/or Li+ into the beryl structure (Belov, Reference Belov1958; Beus, Reference Beus1960; Evans and Mrose, Reference H.T. and M.E1966; Bakakin et al., Reference Bakakin, Rvlov and Belov1969; Černý and Hawthorne, Reference Černý and Hawthorne1976; Hawthorne and Černý, Reference Hawthorne and P.C1977; Aurisicchio et al., Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988; Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991; Abduriyim et al., Reference Abduriyim and Kitawaki2003; Andersson, Reference Andersson2006) and some discussion about how much Cs+ can substitute into the structure of beryl. Nevertheless, the discovery of pezzottaite came as a surprise as the occurrence of such an ordered superstructure was completely unexpected. Here, I report on the crystal structures of a series of samples of Cs-bearing beryl and pezzottaite and examine the detailed crystal-chemistry of the beryl–pezzottaite series. Crystallographic sites are indicated by italicised symbols (e.g. Be, Si), atoms and ions are indicated by Roman symbols (e.g. Be, Be2+); polyhedra are labelled by the central site (e.g. Be tetrahedron), or BeLi+ where the Be tetrahedron is occupied by Li+. When discussing the refinement of site occupancies, atoms are written as neutral as neutral scattering factors were used in the refinements.
Previous work
There is some confusion in the literature, sometimes within individual papers, concerning the occupancy of the various sites in the beryl structure. Table 1 lists the Wykoff positions, point symmetries and general coordinates of sites in the beryl and pezzottaite structures.
Table 1. Wykoff positions, point symmetries and general coordinates for the beryl and pezzottaite structures
Li+ and Cs+ in the beryl structure
The details of the incorporation of Li+ into the beryl structure have been contentious since the early work of Belov (Reference Belov1958) and Beus (Reference Beus1960). Belov (Reference Belov1958) and Bakakin and Belov (Reference Bakakin and Belov1962) proposed that Li+ replaces Be2+ directly in the structure via the substitution BeLi+ → BeBe2+ with alkalis entering the channel site(s) to maintain electroneutrality. Beus (Reference Beus1960) proposed that Li+ enters beryl via the coupled substitution AlLi+ + BeAl3+ → AlAl3+ + BeBe2+ with alkalis entering the channel site(s) to maintain electroneutrality. On the basis of preliminary structure-refinement results, Evans and Mrose (Reference H.T. and M.E1966) supported the mechanism of Beus (Reference Beus1960) whereas Bakakin et al. (Reference Bakakin, Rvlov and Belov1969) reported structural results on a (Cs,Li)-rich beryl which supported the mechanism of Belov (Reference Belov1958). Hawthorne and Černý (Reference Hawthorne and P.C1977) refined the crystal structure of a beryl with Cs+ + Rb+ = 0.14, Na+ = 0.31 and H2O = 0.66 apfu (atoms per formula unit) and found that Cs+ occupies the 2a site at 0 0 ¼, Na+ occupies the 2b site at 0 0 0, and (H2O) occupies the 2a site. In this beryl, the <Be–O> distance is significantly larger than that in synthetic Be3Al2Si6O18, whereas the <Al–O> distance is the same as that in synthetic Be3Al2Si6O18, compatible with the model of Belov (Reference Belov1958) and not with the model of Beus (Reference Beus1960). Brown and Mills (Reference G.E. and Mills1986) and Aurisicchio et al. (Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988) reported similar results. Sherriff et al. (Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991) examined four beryls of different Cs+ and Li+ contents, showing that the <Be–O> distance increases linearly with increasing Li+ content in beryl, and that 7Li MAS NMR spectra show the presence of two signals that they attributed to Li+ at the Be site and Li+ at a channel site adjacent to the Be site. Andersson (Reference Andersson2006) also found two sites by EPR for Li+ in the beryl structure, one associated with the framework and another within the channel. Structure-refinement studies have not located any Li+ site in the channel, but this may be due to the low occupancy of such a site. Andersson (Reference Andersson2006) also proposed that Li+ does not replace Be2+ at the Be site but is located in a tetrahedron to one side of the (locally empty) Be tetrahedron. However, this mechanism does not account for the expansion of the Be tetrahedron with increasing [4]Li in the structure (Hawthorne and Černý, Reference Hawthorne and P.C1977; Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991) and does not provide a mechanism for satisfying the valence-sum rule at every O2– anion locally coordinating an empty Be site.
Li+ and Cs+ in the pezzottaite structure
In the formal description of pezzottaite (Hawthorne et al., Reference Hawthorne, Cooper, Simmons, Falster, Laurs, Armbruster, Rossman, Peretti, Günter and Grobéty2004; page 377), it was stated that “In beryl, Cs is incorporated into the channel at the 2a position…Cs occupies the analogous position in the pezzottaite structure, complete details of which will be presented in a future publication.” The structure of the intergrowths described here delayed publication of the structure details of pezzottaite. Meanwhile, several descriptions of the structure have appeared: Gi et al. (Reference Gi, Guowu and Peng2008); Yakubovich et al. (Reference Yakubovich, Pekov, Steele, Massa and Chukanov2009); and Gatta et al. (Reference Gatta, Adamo and Lambruschi2012). The structure is rhombohedral 
$R\bar 3c$, the bond topology is the same as that of (Cs,Na,Li)-bearing beryl; Cs+ occupies the 6a and 12c sites, Na+ occupies the 6b and 12c sites, and Be2+ and Li+ alternately dominate at two distinct tetrahedrally coordinated sites, although some disorder is proposed by Yakubovich et al. (Reference Yakubovich, Pekov, Steele, Massa and Chukanov2009) and Gatta et al. (Reference Gatta, Adamo and Lambruschi2012). Ende et al. (Reference Ende, Gatta, Lotti, Grandtner and Miletich2021) refined the structure at different temperatures and pressures, showed that there is a transition from 
$R\bar 3c$ to R3c at ~4 GPa, and noted the occurrence of diffuse scattering that they suggest is due to ordering of the channel constituents along c.
(H2O) in beryl and pezzottaite
Quantitative chemical analysis of structural (H2O) is not practical because of the ubiquitous presence of fluid inclusions in these minerals, and our knowledge of structural (H2O) has come from an enormous amount of vibrational spectroscopy for beryl and some for pezzottaite.
In an extensive study of the polarised infrared spectra of both natural and synthetic beryl, Wood and Nassau (Reference Wood and Nassau1968) showed that there are two types of (H2O) groups in beryl: Type-I and Type-II. According to Wood and Nassau (Reference Wood and Nassau1968, page 777): “The Type I molecule is oriented in the channels with its C2 symmetry axis perpendicular to the crystal C6-axis, while the Type II molecule is rotated 90° by the action of a nearby alkali ion on the molecular electric dipole”. A major amount of spectroscopic work on beryl has basically confirmed their suggestions while adding much quantitative information about the spectroscopic details. One expects the situation in pezzottaite to be similar, and in the formal description of this mineral (Hawthorne et al., Reference Hawthorne, Cooper, Simmons, Falster, Laurs, Armbruster, Rossman, Peretti, Günter and Grobéty2004), an infrared spectrum showed the presence in the principal OH-stretching region of type-II (H2O) bands at 3595 and 3547 cm–1 and an H–O–H bending mode at 1636 cm–1 (see also Gatta et al., Reference Gatta, Adamo and Lambruschi2012). Lambruschi et al. (Reference Lambruschi, Gatta, Adamo, Bersani, Salvioli-Mariani and Lottici2014) and Ende et al. (Reference Ende, Gatta, Lotti, Grandtner and Miletich2021) obtained similar results by Raman spectroscopy.
Samples
Samples were obtained from our initial work on the description of pezzottaite as a distinct mineral species (Hawthorne et al., Reference Hawthorne, Cooper, Simmons, Falster, Laurs, Armbruster, Rossman, Peretti, Günter and Grobéty2004). At the same time, Hänni and Krzemnicki (Reference Hänni and M.S2003) reported Cs-rich morganite from the Dara-i-Pech pegmatite field, Chapa Dara District, Konar Province, and the Deva Mine, Paroon pegmatite field, Vama District, Nuristan Province, Afghanistan. Samples of this material were generously supplied by the well-known mineral dealer Herb Obodda. Fourteen samples were characterised here by a combination of single-crystal X-ray diffraction and electron microprobe analysis.
Following collection of the X-ray intensity data, electron-microprobe analysis showed that all individual crystals are reasonably chemically homogeneous at the micrometre scale. However, the structure refinement revealed that these small crystal volumes are structurally complex: all rhombohedral crystals are twinned (~1 to 41% twin fraction), and also contain variable amounts of a hexagonal phase.
Single-crystal selection and data acquisition
Crystal fragments were mounted in epoxy, polished and first examined by electron-microprobe analysis for their Cs+ and Na+ content and spatial homogeneity. Complex chemical zoning at various scales is prevalent throughout the material examined. Small reasonably homogeneous regions (of different Cs+ and Na+ contents) were then identified and removed for single-crystal diffraction study. The crystal fragments were ground to spheres (or ellipsoids) and fixed to tapered glass fibres prior to collection of X-ray intensity data, and later set in epoxy and polished for quantitative chemical characterisation by electron-microprobe analysis.
Single-crystal X-ray diffraction
Single crystals (~150 m in size, Table 2) were mounted on a Bruker four-circle diffractometer equipped with a 4K CCD detector at a crystal-to-detector distance of 5 cm. In excess of a hemisphere of intensity data was collected to 60°2θ using a frame width of 0.2° and an exposure time per frame of 20 s. Additional scans were used to increase data redundancy to improve X-ray absorption correction for the non-spherical crystals. Careful examination of the raw-data frames ‘on-screen’ showed simple sharp uniform diffraction spots for all crystals. However, correct indexing and subsequent integration of the intensity data was not straightforward. Three different types of diffraction patterns were encountered (Table 2):
(1) Hexagonal (P6/mcc) [Cs-rich beryl: 5 samples: P3, P8, P10, P11, P14]: All reflections fit a P hexagonal cell with a ≈ 9.22 and c ≈ 9.26 Å.
(2) Hexagonal–rhombohedral (
$R\overline 3 c$) [pezzottaite: 7 samples: P1, P2, P4, P5, P6, P7, P12]: All reflections fit a hexagonal R cell with a ≈ 15.93 and c ≈ 27.83 Å. This rhombohedral cell has a volume nine times greater than that of the hexagonal P cell, giving rise to reflections with hkl indices 1/3 and 2/3 relative to the hexagonal P cell. Careful inspection of the data showed that all rhombohedral crystals have reflections that violate the general rhombohedral lattice restriction. So how can one be sure that the basic structure is rhombohedral? Two crystals, P2 and P7, have reasonably prominent superlattice reflections (relative to the small hexagonal beryl cell) and contain very minor (<1%) twin components; thus the entire diffraction patterns are consistent with a large R(obv) cell. Integrating the data on the R(obv) cell (ignoring the twin fraction) gave the following merge results for the data: Sample, number of reflections, number of unique reflections, R(merge) in
$R\overline 3 c$: P2, 19381, 2002, 1.9%; P7, 15520, 2002, 1.9%; these results confirm
$R\bar 3c$ as the symmetry of the structure. Some reflections are present (with l ≠ 3n) that violate the obverse condition (–h+k+l = 3n) and other reflections are present that violate the reverse condition (h–k+l = 3n). This observation is consistent with twinning by reticular merohedry through the introduction of a 2-fold twin axis along [001] (Herbst-lrmer and Sheldrick, Reference Herbst-Irmer and G.M1998).(3) Incommensurate (trigonal–hexagonal) [beryl-like: 2 samples: P9, P13]: All reflections fit a P cell with a ≈ 9.22 and c ≈ 18.52 Å. Relative to the hexagonal P cell (1) above, there are additional reflections that support an approximate doubling of the c-axis; however, these additional spots are not quite commensurate and their l-indices deviate from ideal integer values by ±0.05–0.10. Attempts to refine these structures were not successful.
Table 2. Miscellaneous data for beryl–pezzottaite pertaining to data collection and structure refinement
* R = rhombohedral, R(w) = weak rhombohedral, H = hexagonal, I = incommensurate;
** ignoring h k l/2 reflections;
† F.P. = Federico Pezzotta, B.L. = Brendan Laurs, P.F.D. = purchased from dealer, H.O. = Herbert Obodda
Processing of the X-ray intensity data
Due to the complex nature of the diffraction patterns, processing of the X-ray intensity data was quite complicated. For each crystal, numerous raw-frame sequences were carefully inspected on the computer screen with optimised signal:noise settings, such that additional diffraction spots (i.e. not fitting the smaller hexagonal P cell) could be identified visually. After all sets of data had been examined visually, it was apparent that reflections supporting the large rhombohedral R cell [a ≈ 15.97 and c ≈ 27.83 Å] are quite variable in their expression from one crystal to the next. For crystals that show evidence of either the smaller hexagonal P cell or the larger rhombohedral R cell, these data sets were integrated initially on the large rhombohedral cell using a primitive lattice constraint (data for the apparent hexagonal crystals were forcibly re-indexed by applying the transformation 1 2 0/ 2 
$\bar 1$ 0/ 0 0 3). After integration, all reflections with l = 3n were removed, and the remaining reflections were carefully examined; observed reflections with l ≠ 3n establishes the presence of some component of the rhombohedral superstructure within the crystal. For those crystals having observed reflections with l ≠ 3n, the relative ratio of reflections violating the obverse or reverse settings served to establish the dominant twin-component in the absence of any possible hexagonal P component (i.e. mutual overlap occurs on layers where l = 3n).
Standard (final) integration (with Bruker software SAINT) was then done on the simple hexagonal P datasets, followed by processing with Bruker SADABS and final merging of identical reflections in XPREP to produce a normal HKLF 4 file for structure refinement. For the rhombohedral crystals, the dominant twin-component was first set as the primary obverse component (the transformation reverse → obverse via 1 1 0/
$\bar 1$ 0 0/0 0 1 was used if necessary), and the secondary component was then defined by the twin law [
$\bar 1$ 0 0/0 
$\bar 1$ 0/0 0 1]; the two orientation matrices were used in the twin-integration procedure. Absorption corrections and merging of data were then done with the Bruker TWINABS program, and an HKLF 5 data file [that distinguishes the data of the primary component (l ≠ 3n) from the data overlapping with the twin component (l = 3n)] was written for refinement of the twinned structure.
For one of the incommensurate crystals (P9), attempts to integrate the data and refine the structure on the a ≈ 9.22, c ≈ 18.52 Å cell gave poor results that are not presented here. As a comparative index for all the crystals refined here, all the hexagonal and rhombohedral crystals and one of the incommensurate crystals were processed in a standard manner on the small hexagonal P cell, ignoring any superlattice reflections; all refinements gave R 1 values between 2.3 and 2.7%, suggesting that all crystals studied are of similar high quality.
Space-group assignment for the hexagonal P and rhombohedral crystals
Crystals with the smaller hexagonal P unit-cell have Laue merging results and systematically absent reflections consistent with the space group P6/mcc. In order to correctly assign a space group to the rhombohedral crystals, data that is unaffected by twinning and the possible presence of a hexagonal component was treated in the following manner. Special subsets of data were generated in the following way: the data were integrated using the orientation matrix of the dominant twin-component; data were then processed using SADABS; reflections affected by twinning or possible overlap with a hexagonal P contribution (i.e. reflections with l = 3n) were removed. The remaining reflections are in accord with Laue-group symmetry 
$\bar 3$m1 and the presence of a c-glide plane, suggesting that the correct space group is 
$R\bar 3c$ for the rhombohedral crystals. Note that the final twin refinements (HKLF 5 data from TWINABS) for the rhombohedral crystals commonly list several reflections h, k, l (with l = 3n) that significantly violate (F o2 > 5–10 σ) the c-glide reflection condition. However, if the twinning is ignored (HKLF 4 data from SADABS), the refinements list no such c-glide violations above 5σ, suggesting that the apparent violations result from twin integration and TWINABS data-processing.
Refinement of the simple hexagonal structure
The structure of each sample was refined in the space group P6/mcc using F2 in the SHELXTL PLUS (Bruker PC version) software package with neutral scattering factors. Full occupancy was assumed for all sites except those occupying the channel. According to previous crystal-structure refinements of Li-bearing beryl (Hawthorne and Černý, Reference Hawthorne and P.C1977; Aurisicchio et al., Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988; Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991), the Be site is occupied by Be and Li. However, attempts to refine the relative amounts of Be and Li were not always successful; this is not surprising as complete replacement of Be2+ by Li+ as indicated by the chemical analyses will affect the total scattering from the crystal by ≪0.3%. Thus, Be site-occupancies were assigned from the analysed chemical formulae. The structures converged to R 1 indices of 2.36 to 2.91%; details of the data collection and structure refinement are listed in Table 3. Final atom coordinates and anisotropic-displacement parameters are given in Table 4, selected interatomic distances and angles are given in Table 5, refined site-populations are given in Table 6, and Table 7 shows a bond-valence table for beryl P10 calculated with the parameters of Gagné and Hawthorne (Reference Hawthorne2015).
Table 3. Details of data collection and refinement for beryl structures
Table 4. Atom positions and displacement parameters (A2) for crystals of the beryl–pezzottaite series with space-group symmetry P6/mcc
Table 5. Selected interatomic distances (Å) for crystals of the beryl–pezzottaite series with space-group symmetry P6/mcc
Equivalent positions: a: y, –x+z, –z.
Table 6. Refined site-populations (apfu) for beryl structures
Table 7. Bond-valence* table for beryl P10
* Bond-valence parameters from Gagné and Hawthorne (Reference Hawthorne2015); note that the bond valences are long range and are weighted by the site populations;
** omitting bonds to (H2O).
Refinement of the rhombohedral structure
The intensity data (HKLF 5 format from TWINABS) for the rhombohedral crystals consist of reflections merged with Laue symmetry 
$\overline 3 $m1, that is with I ≠ 3n, belonging only to the dominant obverse domain (batch 1), and with l = 3n, belonging to both the dominant domain and the subordinate twin-domain (batch 2). Refinement of this data gave R 1 values from 3.3 to 6.0%, and in all cases, the worst-fit reflections are those with l = 3n for which |F o| > |F c|. The twin fraction (i.e. the BASF value) ranges from 0.159 to 0.524 for the seven rhombohedral crystals, indicating that in all cases, a significant twin component is present. If the correct intensity contributions for both domains were simply related by the BASF value from the refinement, then one would expect an even distribution of |F o| and |F c| values for the worst-fit reflections, but this is not the case. Normally, obverse–reverse twins are refined in this manner, without reflections that belong only to the minor component as they are weaker and unlikely to improve the model (Herbst-lrmer and Sheldrick Reference Herbst-Irmer and G.M1998). For comparison, new HKLF 5 data files were generated (using TWINABS) that contained the full reflection set, i.e. all reflections with I ≠ 3n were present in either batch 1 or batch 2, in addition to the overlapped reflections with l = 3n (batch 2). As expected, refinements from these full datasets did indeed result in higher R 1 values (4.5 to 9.7%); however, the BASF values in all cases refined to significantly lower values than for the previous set of refinements. The new BASF values ranged from 0.009 to 0.415 and indicate that the twinned fractions vary from <1 to 41% for the seven rhombohedral crystals. For two of the rhombohedral crystals (P2 and P7), there was no on-screen evidence for the presence of a twin component, and the initial test for the relative ratio of obverse:reverse components (see section above on Processing of X-ray intensity data) indicated less than 1% twin component. The refined BASF values derived using both individual-component contributions on I ≠ 3n layers result in more realistic contributions from the minor twin-component for crystals P2 and P7 (and presumably also for the other twinned rhombohedral crystals). Furthermore, it seems that, in the absence of the twin-component data on I ≠ 3n layers, the twin fraction is significantly overestimated for these seven rhombohedral crystals as a result of an unaccounted additional hexagonal component that only overlaps with the l = 3n reflections of the rhombohedral structure.
It is not feasible to refine the simple hexagonal and twinned rhombohedral structures simultaneously, and one must accept the results of refinement of the twinned rhombohedral structure without accounting for the presence of a simple hexagonal component. Details of the data collection and structure refinement for the twinned rhombohedral structures are listed in Table 8. Attempts to refine the amounts of Be and Li at both the Be and Li sites were not successful (as expected). The Be site was assigned initially as completely occupied by Be and the Li site as occupied by the amounts of Li from the chemical formulae plus the Be in excess of 2 apfu, and these occupancies were fixed in the refinement. Local stereochemistry will be a more reliable way to assign Be,Li site-occupancies a posteriori than direct refinement that will rely on differences of ≪0.3% in the total scattering of the crystal.
Table 8. Details of data collection and refinement for pezzottaite structures
Atom coordinates and displacement parameters are given in Table 9, selected interatomic distances and angles in Table 10, and refined site-populations are listed in Table 11. A bond-valence table for pezzottaite P6 is given in Table 12. All Crystallographic Information Files (CIFs) for the refined structures have been deposited with the Principal Editor of Mineralogical Magazine and are available as Supplementary Material (see below)..
Table 9. Atom positions and displacement parameters (Å2) for crystals of the beryl–pezzottaite series with space-group symmetry 
$R\bar 3c$
Table 10. Selected interatomic distances (Å) for crystals of the beryl–pezzottaite series with space-group symmetry 
$R\overline 3 c$
Equivalent positions: a: x–y, x, –z; b: x, y, z–1; c: y, –x+y, –z; d: –y+1, x–y, z–1; e: y+⅓, x–⅓, –z+1/6; f: x–y+1, x, –z; g: –x+⅔, –y+⅓, –z+⅓; h: y+⅔, –x+y+⅓, –z+⅓; i: x+⅓, x–y+⅔, z+1/6; j: –y+⅓, –x+⅔, z–5/6; k: –x, –y, –z.
Table 11. Refined site-populations (apfu) for pezzottaite structures
Table 12. Bond-valence * table for pezzottaite P6
* Bond-valence parameters from Gagné and Hawthorne (Reference Hawthorne2015).
Electron-microprobe analysis
The single crystals used for collection of the X-ray-diffraction intensity data were subsequently set in epoxy, ground, polished and coated with carbon prior to being mounted in a Cameca SX100 electron microprobe They were analysed in wavelength-dispersion mode with an accelerating voltage of 15 kV, a specimen current of 15 nA, and a beam diameter of 7 µm. The following standards were used: TAP: Ca, diopside; Al, andradite; Na, albite; PET: Si, albite; K, orthoclase; LiF: Fe, fayalite, Cs, pollucite; Rb: Rb-leucite. The data were reduced and corrected by the PAP method of Pouchou and Pichoir (Reference Pouchou, Pichoir and Armstrong1985). Unit formulae were normalised on the basis of 18 anions with Li+ = [Na++ Cs+ + K+ + Rb+ + (Ca2+ x 2)] – Fe2+ and Be2+ = 3 – [Na+ + Cs+ + K+ + Rb+ + (Ca2+ × 2)] – Fe2+ apfu. Chemical compositions (mean of 10 determinations) and unit formulae are given in Table 13. Beryl P3 contains a small amount of Fe (Table 13) that substitutes for Al3+ at the Al site. Aurisicchio et al. (Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988) note that the main ions substituting for Al3+ at the Al site are Fe2+ and Mg2+, and hence the formula for P3 was calculated accordingly. <Al–O> for P3 is 1.909 Å, whereas the ≪Al–O≫ distance for the other beryls is 1.903 A; this difference of 0.006 Å is in accord with the weighted difference in ionic radii between Al3+ and Fe2+: (0.78 – 0.535) × 0.054/2 = 0.007 Å.
Table 13. Chemical composition (wt.%) and unit formulae (apfu) of beryl–pezzottaite crystals
* Calculated by stoichiometry; ** includes FeO 0.67 wt.%; † includes FeO 0.054 apfu.
The beryl and pezzottaite structures
The beryl structure (Fig. 1) consists of a series of six-membered rings of (SiO4) tetrahedra that are linked into a framework by (BeO4) tetrahedra and (AlO6) octahedra (Fig. 1a). The beryl structure is very strongly compositionally layered (Fig. 1b) with layers of (SiO4) tetrahedra interleaved with layers of (BeO4) tetrahedra and (AlO6) octahedra. Li+ substitutes for Be2+ in the (BeO4) tetrahedra (shown in blue in Fig. 1) and the interstitial species Na+, Cs+ and (H2O) occur in the channels formed by columns of [Si 6O18] rings extending along the c-axis (Fig. 1a).
Figure 1. The crystal structure of beryl (a) projected down the c-axis, and (b) viewed orthogonal to the c-axis; Si tetrahedra are mauve, Be tetrahedra are pale blue, Al octahedra are bright green, Cs atoms are red circles, Na atoms are concealed beneath the Cs atoms.
Pezzottaite (Fig. 2) is a superstructure of the beryl structure, as suggested by the relation between the cell dimensions (Table 1, Figs 1 and 2). There are prominent six-membered rings of (SiO4) tetrahedra arranged at the vertices of a simple hexagonal plane net. These rings are linked into a framework by (BeO4) and (LiO4) tetrahedra (Fig. 2), and Cs+ and Na+ are incorporated into the prominent channels that extend through the structure along the c-axis (Fig. 2a). As with beryl, the pezzottaite structure is very strongly compositionally layered (Fig. 2b) with layers of (SiO4) tetrahedra interleaved with layers of (BeO4) and (LiO4) tetrahedra and (AlO6) octahedra, with alkalis (Cs+, Na+) and (H2O) occurring in the channels. The structure differs from that of beryl (Gibbs et al., Reference Gibbs, Breck and Meagher1968; Morosin, Reference Morosin1972; Aurisicchio et al., Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988) and Li-bearing beryl (Bakakin et al., Reference Bakakin, Rvlov and Belov1969; Hawthorne and Černý, Reference Hawthorne and P.C1977; Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991) by having two distinct tetrahedrally coordinated sites, here labelled Be (shown in blue in Fig. 2) and Li (shown in yellow in Fig. 2) that cross-link the [Si 6O18] units.
Figure 2. The crystal structure of pezzottaite (a) projected down the c-axis, and (b) viewed orthogonal to the c-axis; colour scheme as in Figure 1 plus Li tetrahedra are yellow and Na atoms are yellow.
Site populations
The assignment of site populations is far from straightforward in these two structures. I assigned scattering factors to the specific sites in each structure, indicating the scattering factors by the italicised labels of the sites. For the reasons discussed by Hawthorne et al. (Reference Hawthorne, Ungaretti and Oberti1995), I will express the results of the site-scattering refinement (Tables 6 and 11) in a chemically independent form as effective epfu (electrons per formula unit) such that there is direct correspondence between the refined site-scattering values, site populations, the structural formula and the formula unit of the mineral.
Na+, Cs+, Li+ and (H2O) in beryl
The behaviour of these species is reasonably well-understood in beryl. As discussed above, Na+ occupies the 2b site at 0 0 0, Cs+ occupies the 2a site at 0 0 ¼, and (H2O) occupies the 2a site. Na+ occurs in the plane of the closest ring of Si tetrahedra (Fig. 3a) and has 6 bonds of equal length to the bridging O1 atoms. Cs+ occurs halfway between two six-membered rings of Si tetrahedra (Fig. 3b) and has 12 bonds of equal length to the bridging O1 atoms of the two adjacent rings of Si tetrahedra (Figs 3b,c), occupying a hexagonal antiprism.
Figure 3. The local environments of the channel cations in beryl: (a) Na+, (b), (c) Cs+; Na: yellow circle, other colours as in Figure 1.
Na+ occurs at the channel Na site where it is coordinated by a planar hexagon of anions at a distance of 2.54 Å (Fig. 3c) which leads to an incident bond-valence of 0.134 × 6 = 0.804 vu (valence units) where the Na site is occupied by Na+, insufficient to satisfy the valence-sum rule (Brown, Reference Brown2016; Hawthorne, Reference Hawthorne2012, Reference Hawthorne2015) at Na+. An (H2O) group at a locally adjacent 2a site (at a distance of 2.25 Å) will contribute a bond valence of 0.267 vu to the bonded Na+, and to satisfy the valence-sum rule, channel Na+ will have to bond to one (H2O) group at an adjacent 2a site for a local incident bond-valence sum of 1.071 vu. Kolesnikov et al. (Reference Kolesnikov, Reiter, Prisk, Krzystyniak, Romanelli, Wesolowski and Anovitz2018, Reference Kolesnikov, Anovitz, Hawthorne, Podlesnyak and Schenter2019) showed that in beryl, (H2O) is particularly sensitive to very small differences in the size and local structure of the channel which can cause drastic changes in the confined (H2O) dynamics.
In beryl, (H2O) is commonly described as having two types of occurrence: (1) with the H–H vector of the (H2O) group parallel to the c-axis, and (2) with the H–H vector of the (H2O) group perpendicular to the c-axis. However, this is not exactly what Wood and Nassau (Reference Wood and Nassau1968) stated (see above). They defined type-I and type-II (H2O) in terms of the orientation of their 2-fold rotation axis: perpendicular and parallel to the c-axis of the crystal. Fig. 4a shows type-II (H2O) bonded to a single Na+ ion and the 2-fold rotation axis of the (H2O) group parallel to the c-axis. Fig. 4b shows (H2O) bonded to two Na+ ions; the 2-fold rotation axis of the (H2O) group is perpendicular to the c-axis but the H–H vector is also perpendicular to the c-axis, although the arrangement shown in Fig. 4b does not conform well to the valence-sum rule (see above).
Figure 4. Geometrically possible arrangements of the coordination of channel (H2O) by Na+ ions; (a) bonded to one Na+ ions with the 2-fold symmetry axis of the (H2O) group parallel to the c-axis; (b) bonded to two Na+ ion with the 2-fold symmetry axis of the (H2O) group perpendicular to the c-axis; yellow circle: Na+; green circle: O2– ion of the (H2O) group; red circle: H+ ion.
One aspect that needs to be considered is the coordination of (H2O). Type-I (H2O) is coordinated by zero Na+ ions, and type-II (H2O) is coordinated by one Na+ ion. However, the Na–(H2O) bond-valence is ~0.267 vu (see above) which would result in an incident bond-valence of 0.267 × 2 = 0.534 vu at (H2O). This is not possible as it would require very strong H···O hydrogen bonds to the anions coordinating Si4+ and suggests a frequency of absorption in the infrared or Raman spectra lower than that observed (3450 cm–1) by Lambruschi et al. (Reference Lambruschi, Gatta, Adamo, Bersani, Salvioli-Mariani and Lottici2014). On balance, the evidence points to Na+ being incorporated into beryl as Na+–(H2O) and not as Na+–(H2O)2.
Cs+ occurs at the channel Cs site where it is coordinated by a hexagonal antiprism of anions at a distance of 3.43 Å (Figs 3b,c) which leads to a local incident bond-valence of 0.0633 × 12 = 0.760 vu where Cs is occupied by Cs+. This seems somewhat low compared with the valence-sum rule but is well within the variation of 3.21–3.54 Å given by Gagné and Hawthorne (Reference Gagné and F.C2016) for ninety (CsO12) polyhedra. The separation between the 2a and 2b sites along the channel in beryl is ~2.31–2.32 Å which places significant constraints on what species can occupy locally adjacent 2a and 2b sites. This issue was examined by Hawthorne and Černý (Reference Hawthorne and P.C1977) who noted that neither Cs+ and Na+ nor Cs+ and (H2O) can occupy locally adjacent 2a and 2b sites. This conclusion is in accord with the observed ranges of [12]Cs+–O2– and [6]Na+–O2– distances in inorganic structures: 2.910–4.072 and 2.019–3.055 Å, respectively (Gagné and Hawthorne, Reference Gagné and F.C2016). Hence Cs+ and (H2O) cannot occupy locally adjacent 2a and 2b sites whereas Na+ and (H2O) can occupy locally adjacent 2a and 2b sites (Hawthorne and Černý, Reference Hawthorne and P.C1977).
Li+ substitutes for Be2+ at the Be site and there is a reasonably well-developed relation between the variation in the <Be–O> distance and the amount of Li+ in the structure (Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991). We may write the incorporation of Li+ into the ideal beryl structure as follows: (Cs+,Na+) + Li+ → □ + Be2+ [we will look at the effect of (H2O) later]. This is a long-range description that specifies how overall electroneutrality in the structure is maintained. However, what about short-range issues; how is the valence-sum rule (Brown, Reference Brown2016; Hawthorne, Reference Hawthorne2012, Reference Hawthorne2015) maintained where this incorporation occurs? Inspection of Table 5 shows that the ions at the Be, Al, Cs and Na sites are each coordinated by only one crystallographically distinct O2– ion whereas Si4+ is coordinated by two crystallographically distinct O2– ions: O1 and O2. Inspection of Figs 1a and 3 show that Cs+ and Na+ do not bond to anions that coordinate the Be site in beryl: Cs+ and Na+ bond only to O1 whereas Be2+ (and Li+) bond only to O2 (Table 5). Where Li+ is incorporated at the Be site, the bond valence incident at O2 from the ions at the Be site must decrease. This decrease in bond valence must be compensated by bond valence contributed to the structure by Cs+ and Na+ at the channel site. However, the ions at the channel site do not bond to the O2 anion and hence cannot contribute directly to O2; Cs+ and Na+ bond to O1 and the influence of their additional bond valence is transferred to O2 by cooperative change in bond lengths within the (SiO4) tetrahedron. This mechanism is shown in Fig. 5. Where Li+ occupies the Be site, the bond valence of the BeLi+–O2 bond decreases (shown by yellow bonds in Fig. 5a). Bond valence from the incorporated Cs+ and Na+ is transferred to O1 to Si4+ to O2 as indicated by the path of red-yellow-red bonds in Fig. 5a. The long-range consequences of this mechanism will be to shorten the two Si–O2 distances as Li+ and (Cs+,Na+) increase. In turn, the mean of the two Si–O1 distances will increase in order to maintain the valence-sum rule at Si4+. Figs 5b,c show that the variation in Si–O bond-lengths is in accord with this mechanism.
Figure 5. (a) The local atom arrangement around the BeLi and channel Na in beryl; the yellow bonds between BeLi and O2 have a lower bond-valence than when the Be site is occupied by Be; Na in the channel bonds to O1, increasing the strength of the O1–Si bonds (red lines) and decreasing the strength of the Si–O2 bonds (yellow lines), allowing the O2 anion to accord with the valence-sum rule; other chemical bonds are shown by thin black lines; (b),(c) variation in the length of the Si–O1 bonds (red circles) and Si–O2 bonds (green circles) as a function of the amounts of channel alkalis in beryl.
This mechanism is apparent in the bond-valence table for beryl (Table 7). Cations at Cs and Na bond to O1 and the Si–O1 bond-valences are correspondingly less than the Si1–O2 bond-valence which compensates somewhat for the reduced Be–O2 bond-valence due to the presence of Li+ at the Be site.
Na+, Cs+, Li+, K+ and (H2O) in pezzottaite
The pezzottaite structure is bond-topologically analogous to the beryl structure but differs in having a larger unit-cell and lower space-group symmetry, giving rise to a greater number of crystallographically distinct sites and different point symmetries of those sites (Figs 1, 2; Table 1).
Occupancy of the Na1 and Na2 sites
There are two crystallographically distinct Na sites, Na1 and Na2, and two crystallographically distinct Cs sites, Cs1 and Cs2, all of which occur in the channels bounded by [Si6O18] rings (Fig. 2a). The lower symmetry and larger unit cell of pezzottaite (relative to those of beryl) complicate the assignment of site populations, particularly as both the different Na sites and different Cs sites have different point symmetry (Table 1).
Figure 6a shows the variation in the refined total scattering at the (Na1 + Na2) sites (red circles) as a function of the Na+ content determined by EMPA and expressed in epfu. The data lie above the 1:1 line, indicating that another scattering species also occurs at the Na1 and/or Na2 sites. Crystals P1 and P2 depart from the 1:1 line far more than the other crystals and inspection of Table 13 shows that these two crystals contain significantly more Ca2+ than the other crystals in the figure. In Fig. 6b, the refined scattering from the Na sites has been corrected for the presence of Ca2+ at these sites and now accords with the 1:1 line, indicating that Ca2+ also occupies one or more of the Na sites.
Figure 6. (a) Scattering (in epfu) from the Na1 + Na2 sites (red circles) versus the effective scattering from Na+ content determined by EMPA; (b) scattering (in epfu) from the Na1 + Na2 sites corrected for the Ca2+ content of the crystal occupying the Na sites (yellow circles) versus the effective scattering from Na+ content determined by EMPA; the red line is the 1:1 relation.
Occupancy of the Cs1 and Cs2 sites
Figure 7a shows the variation in the refined total scattering at the (Cs1 + Cs2) sites (red circles) and at the Cs1 site (green circles) in pezzottaite as a function of the (Cs+ + Rb+) content from EMPA and expressed in epfu. It is immediately apparent that the total scattering at the Cs1 + Cs2 sites exceeds that of the Cs+ and Rb+ from EMPA, and the scattering at Cs1 is less than that of the Cs+ and Rb+ from EMPA. Hence both Cs1 and Cs2 must be occupied by Cs+, and each site must also be occupied by another scattering species. Figure 7b shows the effect of assigning type-II (H2O) to Cs1 and Cs2 and subtracting the amounts of scattering due to this (H2O) for Na bonding to one (H2O) (yellow circles). This brings the data significantly closer to the 1:1 line in Fig. 7b. Moreover, infrared and Raman spectroscopy (Hawthorne et al., Reference Hawthorne, Cooper, Simmons, Falster, Laurs, Armbruster, Rossman, Peretti, Günter and Grobéty2004; Gatta et al., Reference Gatta, Adamo and Lambruschi2012; Lambruschi et al., Reference Lambruschi, Gatta, Adamo, Bersani, Salvioli-Mariani and Lottici2014) indicate the presence of both type-I and type-II (H2O) in pezzottaite, and hence we may attribute the displacement of the data from the 1:1 line in Fig. 7b to the presence of type-I (H2O) at the Cs1 and Cs2 sites. Thus, Cs1 and Cs2 are occupied by Cs+, type-I (H2O) and type-II (H2O) in pezzottaite.
Figure 7. (a) Scattering (in epfu) from the Cs1 + Cs2 sites (red circles) and from the Cs1 site (green circles) determined by SREF (Site-REFinement) versus effective scattering from the (Cs+ + Rb+) content determined by EMPA; (b) red circles: scattering (in epfu) from the Cs1 + Cs2 sites determined by SREF; yellow circles: scattering (in epfu) from the Cs1 + Cs2 sites minus the scattering from (H2O) groups assuming Na+–O2– arrangements for Na+ determined by EMPA; the black lines are fit ‘by eye’ to emphasise the linear correlation of the data and the red lines are the 1:1 relation.
Differences between the Cs1 and Cs2 sites and between the Na1 and Na2 sites
Details of the coordinations of these sites are shown in Fig. 8. Cs1 and Cs2 are both [12]-coordinated but there are significant differences in the arrangements of next-next-nearest polyhedra. Inspection of Fig. 8a shows that the two [Si6O18] rings that surround the Cs1 site are linked by a single 12-membered ring of edge-sharing polyhedra that contains three (BeO4) tetrahedra, three (LiO4) tetrahedra and six Al octahedra that girdle the channel at the height of the Cs1 site. In contrast, the two [Si6O18] rings that surround the Cs2 site are linked by a single 12-membered ring of six (BeO4) tetrahedra and six Al octahedra. Figure 8b shows the same arrangement as Fig. 8a except viewed in the opposite direction. Figure 8c shows the next-next-nearest arrangements of polyhedra surrounding the Na1 and Na2 sites in which the single [Si6O18] ring that surrounds each of the Na sites is girdled by two 12-membered rings of edge-sharing polyhedra. The rings surrounding both the Na1 and Na2 sites consist of three (BeO4) tetrahedra, three (LiO4) tetrahedra and six Al octahedra (Fig. 8c). When viewed from the opposite direction as in Fig. 8d, the top ring girdling Na1 consists of three (BeO4) tetrahedra, three (LiO4) tetrahedra and six Al octahedra whereas the top ring girdling Na2 consists of six (BeO4) tetrahedra and six Al octahedra. Thus (1) the Cs1 and Na1 sites are locally associated with six (LiO4) tetrahedra; (2) the Na2 site is locally associated with three (LiO4) tetrahedra; and (3) the Cs2 site is not locally associated with any (LiO4) tetrahedra.
Figure 8. The local environments of the channel cations in pezzottaite: (a,b) Cs+; (c,d) Na+; colours as indicated on figure, other colours as in Figure 1. Note the difference in axis orientation between (a) and (b) and between (c) and (d); each pair of diagrams gives views of each arrangement along +c and along –c.
Occupancies of the Be and Li sites
It was not possible to reliably refine the Be2+ and Li+ occupancies at the Be and Li sites and it was necessary to make an initial assignment on little evidence. I will now examine the validity of these initial assignments. I will deal with site populations directly as apfu as these were not refined for the Be and Li sites but were assigned and fixed during structure refinement.
The variation in <Be–O> distance as a function of the assigned site-population at the Be site for both beryl (red circles) and pezzottaite (green circles) is shown in Fig. 9a. The lack of a (expected) linear relation indicates that the initial assigned site-populations are not correct. In particular, there is a wide dispersion of the <Be–O> distance in pezzottaite for which the site population was assigned as 2 Be2+ apfu. Gagné and Hawthorne (Reference Gagné and F.C2016) listed the grand <Be2+–O2–> distance in 161 tetrahedra in inorganic structures as 1.637 Å, close to the values of the three lowest data for pezzottaite in Fig. 9a. The pezzottaite crystals with the aberrantly large <Be–O> distances are P4 and P12 which are the only pezzottaite crystals identified in Table 2 as ‘weakly rhombohedral’. The data for beryl in Fig. 9a correspond to the curve of Sherriff et al. (Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991), shown as the red line in Fig. 9b, which runs through the grand <Be–O> distance of Morosin (Reference Morosin1972) and Gibbs et al. (Reference Gibbs, Breck and Meagher1968) for Li-free beryl indicated by the pink square. It seems reasonable to suggest that the weakly rhombohedral refinements of pezzottaite P4 and P12 have significant Li+ at their Be sites, and these amounts may be calculated as indicated by the dotted lines in Fig. 9b.
Figure 9. (a) <Be–O> distance as a function of assigned occupancies in beryl (red circles) and pezzottaite (green circles); (b) as in (a) with addition of (1) the relation of Sherriff et al. (Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991) between <Be–O> distance in beryl crystals as a function of the Be2+ content of the Be site in apfu, (2) the grand <Be–O> distance in Li-free beryl crystals (pink square) from Gibbs et al. (Reference Gibbs, Breck and Meagher1968) and Morosin (Reference Morosin1972). The red line is drawn through the data for beryl and the dotted lines enable calculation of the Li content of the Be site in the weakly rhombohedral crystals P4 and P12.
The variation in <Li–O> distance as a function of the assigned site-population at the Li site for pezzottaite is shown in Fig. 10a. The data for four pezzottaite structures show a linear relation but crystals P4 and P12 deviate strongly from this relation. However, in Fig. 9b, some Li+ was reassigned to the Be site in P4 and P12, decreasing the amount of Li+ at the Li site in these crystals. This change in assigned Li+ at the Li site is shown in Fig. 10b where it is seen that this reassignment brings linearity to both relations in Figs 9 and 10. Thus in compositions approximately halfway between beryl and pezzottaite, there is significant disorder of Be2+ and Li+ at the two distinct tetrahedrally coordinated Be and Li sites.
Figure 10. (a) <Li–O> distance as a function of assigned occupancies in pezzottaite (green circles); (b) as in (a) with the addition of (1) the Li content of the Li site in the weakly rhombohedral crystals P4 and P12 corrected for the Li occupying the Be site (indicated by yellow circles) as calculated from Figure 5b, and (2) a red line indicating the resulting linear relation between the <Li–O> distance and the reassigned Li site-populations.
Replacement of LiBe2+ by LiLi+ and the valence-sum rule
The lower symmetry in pezzottaite when compared with beryl (Table 1) allows a slightly different style of structural adjustment to accommodate the replacement of Be2+ by Li+ in the Li tetrahedron and to conform with the valence-sum rule.
The mechanism is shown in Fig. 11: the yellow bonds LiLi–O5 and LiLi–O8 have lower bond-valences than where the Li site is occupied by Be2+. In the channel, Cs+ at Cs1 (Fig. 11a) and Na+ at Na1 (Fig. 11b) bond to O2– anions coordinating Si4+. Thus in Fig. 11a, Cs1–O3 bonds provide additional bond valence to the O3 anions, causing the O3–Si1 bonds to weaken as required by the valence-sum rule at O3 (indicated by the grey bonds), and in turn the valence-sum rule at Si1 requires a stronger (red) bond to O8 which compensates for the weaker bond (yellow) from LiLi+ compared to where Li was occupied by Be2+. However, the lower symmetry of pezzottaite compared to that of beryl also allows Al3+ at Al1 and Al2 to participate in the bond-valence-transfer mechanism. Four of the bonds coordinating each Al octahedron are weakened by this mechanism and bonds Al1–O5 and Al2–O8 are strengthened (this is apparent in Table 9), also compensating for the weaker LiLi–O5 and LiLi–O8 bonds.
Figure 11. The local atom arrangements around the LiLi+ and channel Cs+ and Na+ in pezzottaite; the yellow bonds LiLi–O5 and LiLi–O8 have lower bond-valences than where the Li site is occupied by Be2+. (a) Cs+ in the channel at Cs1 bonds to the O1, O2 and O3 anions coordinating Si4+ via the Cs1–O bonds shown in red. The O1, O2 and O3 anions therefore require less bond-valence from Si4+ and these bonds (Si1–O3, Si1–O6, Si2–O1, Si2–O2, Si3–O1 and Si3–O2, shown in grey) weaken (lengthen). To maintain the valence-sum rule at the Si4+ ions, Si1–O8 and Si2–O5 (shown in red) increase their bond valence (shorten) which compensates for the occurrence of Li+ at the Li site which is occupied by Be2+ in Cs-free beryl. (b) Na+ in the channel at Na1 bonds to O3 and the valence-sum rule causes O3–Si1 bonds (shown in grey) to decrease in bond valence (lengthen). In turn, Si1–O8 increases its bond valence. A similar mechanism increases the bond valence of the Si2–O5 bond in an adjacent channel (not shown) to compensate for the occurrence of Li+ at the Li site which is occupied by Be2+ in Cs-free beryl. For the Al octahedra, Al–O5 and Al–O8 bonds are stronger (shorter and shown in red) and other Al–O bonds are weaker (slightly longer and shown in grey) where the local Li site is occupied by Li+.
Figure 11b shows the analogous mechanism for channel Na+ at Na1; note that Fig. 11b has a different orientation to Fig. 11a in order that the arrangement of Be and Li tetrahedra are the same in both figures. Channel Na+ at Na1 bonds to O3, weakening the O3–Si1 bonds (and the bond to O6 that coordinates Be2+ at the Be site), with the result that the Si1–O8 bond is strengthened and compensates for the weaker LiLi–O8 bond. The O5 anion receives additional bond-valence from a bond out of the plane of Fig. 11b. Thus far, the effect of Be–Li order on the distribution of channel (H2O) has not been considered. The latter must occur at the 2a site in beryl (Figs 3a,b) and by analogy at the 6a and 12c sites in pezzottaite (Figs 8a,b). These mechanisms are apparent in the bond-valence table for pezzottaite (Table 12). Cations at Cs1, Cs2 and Na2 bond to O1 and O2 and Si2–O1 and Si2–O2 bond-valences reduce accordingly. The bond valence for Si2–O5 increases together with that of Al1–O5 to compensate for Li+ bonding to O5. Cations at Cs1 and Na1 bond to O3 and Si1–O3 bond-valences reduce accordingly. The bond valence for Si1–O8 increases together with that of Al2–O8 to compensate for Li+ bonding to O8.
Order of Cs+ over Cs1 and Cs2
It is important to note that because the Cs sites are occupied by (Cs+ + Rb+) and (H2O), we cannot assign real site occupancies because we have four scattering species (Cs, Rb, (H2O) and □) distributed over two sites. The case is similar for the Na sites which contain the scattering species Na, Ca and □. Thus we may examine only the total scattering (expressed as Cs+ and Na+) ordered over the pairs of Cs and Na sites.
Figure 12a shows the relative order of Cs+ over the Cs1 and Cs2 sites and Fig. 12b shows the relative order of Na+ over the Na1 and Na2 sites. Cs+ is strongly ordered at the Cs1 site with a well-developed linear correlation except for crystals P4 and P12. Na+ is disordered over the Na1 and Na2 sites, again with a well-developed linear correlation except for crystals P4 and P12. Inspection of Figs 9 and 10 shows that crystals P4 and P12 differ from the other pezzottaites by having Li+ partly disordered between the Be and Li sites whereas the other pezzottaite crystals have the Be site completely occupied by Be2+ and the Li site occupied by Be2+ and Li+. This means that crystals P4 and P12 have a beryl-like component in their structure in which Li+ occupies the Be site and there is only one Cs site and one Na site. The mechanism of local satisfaction of the valence-sum rule pictured in Fig. 11 indicates that Cs+ should preferentially occupy the Cs sites that are most locally associated with the (LiO4) tetrahedra, i.e. Cs1 (Fig. 8a,b), and (H2O) should preferentially occupy the Cs2 site that is locally associated with the (BeBeO4) tetrahedra.
Figure 12. Order of channel cations in pezzottaite; (a) (Cs+ + Rb+) over Cs1 and Cs2; (b) (Na+ + Ca2+) over Na1 and Na2. Note that P4 and P12 deviate from the linear relations shown by the dashed lines as Li+ is disordered over the Li and Be sites (unlike the other crystals).
Order of Na+ over Na1 and Na2
Similarly, Na+ should occupy the Na sites that are most locally associated with the (LiO4) tetrahedra, i.e. Na1 (Fig. 8c,d). The ordering of Cs+ is stronger that the ordering of Na+ as the contrast between the numbers of next-nearest (LiO4) is greater for the Cs sites than for the Na sites (Fig. 8). The mixing of a beryl-like component into the ordering of Li+ and Be2+ (as in crystals P4 and P12) will decrease the drive for ordering of Cs+ and Na+ over the Cs and Na sites and lead to the deviations from linearity shown in Fig. 12.
Crystal-chemical constraints on channel constituents
Schematics of the sequence of the Cs and Na sites in a single channel in the beryl and pezzottaite structures are shown in Fig. 13 and the distances between sites in the refined pezzottaite structures are shown in Table 14. The distances listed in Table 14 are too short to allow ions to occur locally at both constituent sites, and this effect propagates along the channel to generate complicated constraints on the overall chemical variation in channel constituents.
Figure 13. Possible arrangements of channel cations and (H2O) groups in (a) beryl, and (b) pezzottaite; red circle: Cs+, yellow circle: Na+, blue circle: (H2O), □: vacancy.
Table 14. Alkali–alkali distances in the channel of the pezzottaite structures
Possible channel arrangements in beryl
These are shown in Fig. 13a: (a) Cs+ at 2a forces vacancies at the two adjacent 2b sites; (b) type-I (H2O) at 2a forces vacancies at the two adjacent 2b sites; (c) Na+ at 2b forces type-II (H2O) at one adjacent 2a site and a vacancy at the other adjacent 2a site, and the type-II (H2O) at the adjacent 2a site forces a vacancy at the adjacent 2b site; (d) as (c) except oriented in the opposite direction along the c-axis.
Arrangements (c) and (d) strongly limit the amount of Na+ that can be incorporated in beryl: each Na+–(H2O) bonded pair also forces two vacancies at the adjacent 2a and 2b sites, and hence the maximum amount of Na+ that can be incorporated in beryl is 0.50 apfu with an associated 0.50 (H2O) pfu. Arrangement (a) provides a limit on the aggregate amount of Na and Cs: each Cs+ ion blocks two 2b (Na+) sites and hence the maximum amount of Cs and Na obeys the constraint Cs+ + 2Na+ = 1 apfu. Although arrangement (b) blocks two adjacent 2b sites, 2b is occupied only by Na+, and occupancy of one of the blocked sites would change the type-I (H2O) to type-II (H2O) and generate arrangement (c) and (d).
Possible channel arrangements in pezzottaite
These are shown in Fig. 13b: although the lower symmetry and larger unit-cell in pezzottaite relative to beryl gives more distinct crystallographic arrangements, the number of crystal-chemical arrangements and the site separations are the same (Table 14). Both minerals have alternating Cs and Na sites along the c-axis and hence the constraints are the same: (e) Cs+ at 12c (Cs1, Table 1) forces vacancies at the two adjacent Na1(6b) and Na2 (12c) sites, and (f) Cs+ at 6a (Cs2, Table 1) forces vacancies at the two adjacent Na2 (12c) sites; (g) type-I (H2O) at 12c (Cs1, Table 1) forces vacancies at the adjacent Na1(6b) and Na2 (12c) sites, and (h) type-I (H2O) at 6a (Cs2) forces vacancies at the two adjacent Na2 (12c) sites; (i,j) Na+ at 6b (Na1, Table 1) forces type-II (H2O) at the adjacent Cs1 (12c) and vacancies at the adjacent Cs1 (6a) and Na2 (12c) sites along both +c and –c; (k,l) Na+ at 12c (Na2, Table 1) forces type-II (H2O) at the adjacent Cs1 site and vacancies at the adjacent Cs2 (6a) and Na1 (6b) sites along both +c and –c.
Although the details of the stereochemistry are more complicated in pezzottaite than in beryl, the compositional constraints are basically the same: (1) each Cs+ (or Rb+) ion blocks two Na sites irrespective of whether Cs+ (or Rb+) occupies Cs1 or Cs2 and hence the maximum amount of Cs+ and Na+ obeys the constraint Cs+ + Rb+ + 2Na+ = 1 apfu; (2) at full occupancy of the Cs1 and Cs2 sites by Cs+ + Rb+, there is no room for (H2O) in the channel and hence there cannot be any Na+, which is also in accord with the requirement of electroneutrality of the structure. Incidentally, if the Cs1 and Cs2 sites are completely occupied by Cs+, there is no reason why this composition should not have the beryl structure sensu stricto. Unlike beryl, pezzottaite seems to incorporate small amounts of Ca2+ in the channels. This substitution adds an additional electroneutrality constraint to compositional variation in pezzottaite.
Inspection of Table 13 shows the presence of minor amounts of K+ (0.005–0.019 apfu) in the channel of the pezzottaite structure: where exactly does K+ occur? We may use the bond-valence parameters for K+–O2– (Gagné and Hawthorne, Reference Hawthorne2015) to consider this issue. If K+ were to occur at the Na1 or Na2 sites, the incident bond-valence at K+ would be ~1.8 vu; if K+ were to occur at the Cs1 or Cs2 sites, the incident bond-valence at K+ would be ~0.4 vu; neither of these possibilities satisfy the valence-sum rule and hence they may be ruled out. The valence-sum rule is satisfied for [5]K+ by a K+–O2– distance of 2.688 Å which requires that K+ occur at approximately 0 0 ±0.0326 and/or 0 0 0.1307/0.1959. There are various other possibilities if K+ bonds to type-II (H2O) within the channel.
The join beryl–pezzottaite
Figure 14 shows the variation in (Cs+ + Rb+) and (Na+ + Ca2+) along the beryl–pezzottaite join for the structures reported here and for selected compositions from the literature. As discussed above, compositions lie below the line (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu (except for the incommensurate structures around (Cs+ + Rb+) ≈ 0.50 apfu which will be discussed later), supporting the constraint that Na+ and Ca2+ bond to only one channel (H2O) group. The constraint (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu needs to be modified slightly to maintain electroneutrality: (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 – 2Ca2+ apfu. This is apparent from Fig. 14, which shows that the pezzottaite compositions tend to lie slightly below the line (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu due to the presence of small amounts of Ca2+ (Table 13). Taking a value of Ca2+ = 0.03 apfu (Table 13), the heavy black line in Fig. 14 indicates the maximum amount of Na+ + Ca2+ allowed by a combination of channel-cation and (H2O) interactions and the constraint of electroneutrality, and this line passes through the data for pezzottaite.
Figure 14. Variation in Na+ + Ca2+ and Cs+ + Rb+ (determined by EMPA) across the beryl–pezzottaite join. Data reported here are shown as circles: red circles: beryl; green circles: pezzottaite; yellow circles: incommensurate structures. Literature data are shown as crosses (Hawthorne and Černý, Reference Hawthorne and P.C1977; Sherriff et al., Reference Sherriff, Grundy, Hartman, Hawthorne and Černý1991), stars (Aurisicchio et al., Reference Aurisicchio, Fioravanti, Grubessi and Zanazzi1988), plus signs (Pieczka et al., Reference Pieczka, Szełęg, Szuszkiewicz, Gołębiowska, Zelek, Ilnicki, Nejbert and Turniak2016). The upper black diagonal line denotes the equation (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu; the lower black diagonal line denotes the maximum amount of Na+ + Ca2+ allowed by a combination of channel-cation and (H2O) interactions and the constraint of electroneutrality. The coloured areas denote the presumed stability of the various phases. The curved dashed red line denotes the lower limit of observed chemical compositions.
The distribution of compositions across the beryl–pezzottaite join is very non-uniform. The maximum (Na+ + Ca2+) content occurs for (Cs+ + Rb+) contents close to zero and (Na+ + Ca2+) contents are fairly uniform from 0.0–0.50 apfu typical of NYF (Niobium, Yttrium and Fluorine enriched) pegmatites (sensu lato) and other parageneses. Significant incorporation of Cs+ is typical of LCT (Lithium, Caesium and Tantalum enriched) pegmatites, but is also accompanied by the incorporation of significant Na+. The result is a large area across the beryl–pezzottaite join in which beryl and pezzottaite compositions do not occur (or have not yet been found); this area is delimited by the dashed red line in Fig. 14. Is this blank area (1) the result of restricted source-rock compositions; (2) due to the fact that extreme fractionation enriches both Cs+ and Na+; or (3) the result of crystal-chemical factors: the aggregate (Cs+ + Rb+) and (Na+ + Ca2+) contents are restricted by the relation (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu that arises because of the requirement of channel Na+ to bond to one channel (H2O) group? A combination of all three factors is probably involved.
Incommensurate structures
What gives rise to the incommensurate structures at intermediate compositions? Figure 5a shows how the channel constituents in beryl satisfy the local bond-valence requirements of the anions coordinating the Be site where it is occupied by Li+. However, this mechanism addresses the local bond-valence requirements of only two of the four anions coordinating BeLi+. The other two anions of the (BeO4) tetrahedron containing Li+ face an adjacent channel: their bond-valence requirements must be satisfied by alkali cations in that adjacent channel. In this way, adjacent channels in the beryl structure affect each other. Inspection of Fig. 8a,b shows that where adjacent channels contain Cs+ at the same level along c, the local bond-valence requirements of the anions coordinating BeLi+ are satisfied by the Cs+ in these adjacent channels, i.e. by □···Cs+···□ arrangements. The situation where Na+ is involved in satisfying the local bond-valence requirements of the anions coordinating BeLi+ is completely different. Inspection of Fig. 8c,d shows that the bond path from Na+ to (BeLiO4) links only to one anion of the tetrahedron, unlike the case where Cs+ is the local channel constituent and has two bond paths to a specific Li-containing (BeO4) tetrahedron. In order for the two anions of the (BeLiO4) tetrahedron in a specific channel to have their bond-valence requirements satisfied by channel Na+, Na sites locally adjacent along c must be occupied (Fig. 15a,b). Where this is the case, the constraints outlined in Fig. 13a extend the channel arrangements involving Na+ beyond the length of the c-dimension. This effect is shown in Figs 15 and 16: (1) Na+ occurs at the Na (2b) site both above and below the level of the (BeLiO4) tetrahedron; (2) each Na+ must bond to a type-II (H2O) group each of which occupies a Cs (2a) site; (3) each type-II (H2O) group must have a vacancy on the side not bonded to Na+. This gives the channel sequence □···(H2O)–Na+–□–Na+–(H2O)···□ which is ~14 Å long (Fig. 16), much longer than the c-dimension. The unoccupied 2a and 2b sites that complete an ordered string of cations + vacancies can be occupied by □···□, Cs+···□, (H2O)···□ or (H2O)···Na+ and these arrangements can point both ways along the c-axis. These arrangements break the translational symmetry of ~9.22 Å along c and the resultant arrangements will have a pseudo-repeat of approximately double this value, the exact value of the repeat depending on the occupancies of the pair of 2a and 2b sites that dominate in a particular channel (i.e. the structure is incommensurate along c). This will result in an approximate repeat of 18.52 Å along c. Adjacent channels will be disordered relative to each other and thus the a-dimensions remain ~9.22 Å and the space group is still P6/mcc.
Figure 15. Adjacent channel arrangements in beryl that satisfy the local bond-valence requirements of Li+ replacing Be2+ at the Be site, showing how the alkali cations Na+ and Cs+ give additional bond-valence to the anions of the (BeLiO4) tetrahedra required by the replacement of Be2+ by Li+; four of the six girdling (BeO4) tetrahedra and several of the O2– ions linked to Si4+ are omitted to avoid obscuring the view of the important features of these diagrams; (a) view down c showing how the channel cation in one channel provides additional bond-valence to two anions of the (BeLiO4) tetrahedron via the bonds of the (SiO4) tetrahedra (as shown in Figure 5), and what arrangements are required in adjacent channels to complete the mechanism for the entire (BeLiO4) tetrahedron; (b) view orthogonal to c showing how Na+ is required both above and below the level of the (SiO4) tetrahedron to satisfy the bond-valence requirements for two of the anions of the (BeLiO4) tetrahedron, and how the arrangement in the adjacent channel may be the same (i.e. two Na+ cations) or may be a single Cs+ cation. Legend as in Figure 13.
Of course, this effect will not be apparent in compositions with negligible Li+ (e.g. the bulk of the compositions marked by stars in Fig. 14) in which the incorporation of channel Na+ is balanced by replacement of [6]Al3+ by [6](Mg,Fe2+).
X-ray topography
Nanoscale variations in crystal texture may be characterised by X-ray topography. Liu et al. (Reference Liu, Peng and Meng2006) examined gem-quality pezzottaite from Madagascar using monochromatic synchrotron radiation to measure the variation in diffracted intensity for a specific reflection as a function of variation of angle away from its ideal diffraction angle; the variation in intensity as a function of angular displacement is known as a rocking curve. For a perfect crystal, the rocking curve will consist of a single peak centred on the ideal diffraction angle. Deviations from ideal crystallinity will result in an asymmetric peak or several closely spaced peaks depending on the character of the microtexture. Liu et al. (Reference Liu, Peng and Meng2006) collected rocking curves for the reflections (006), (0012) and (0018) for seven pezzottaite crystals. The rocking curves showed significant variation from sample to sample: some showed a single distorted peak indicating ‘fairly good crystallinity’ and others showed a broad intensity with several maxima (Fig. 17). The presence of several maxima in Fig. 17 is consistent with our finding that pezzottaite grains commonly consist of heterogeneous intergrowths of twinned pezzottaite and Cs-rich beryl.
Figure 17. X-ray rocking curve for the gem-quality pezzottaite showing complex microstructure. Modified from Liu et al. (Reference Liu, Peng and Meng2006).
Occurrence
The extreme enrichment of Cs in pezzottaite suggests that pezzottaite should occur in highly fractionated LCT pegmatites. Simmons et al. (Reference Simmons, Falster, Laurs, Pezzotta and Hawthorne2004, page 116) stated that “in Madagascar, pezzottaite occurs in a pegmatite that has characteristics of both the LCT (Lithium-Cesium-Tantalum) and NYF (Niobium-Yttrium-Fluorine) families of the Rare-Element and Miarolitic pegmatite classes”. The Afghanistan occurrences are associated with large-scale LCT pegmatite fields. The most intensely investigated occurrence is in the Julianna pegmatitic system at Piława G´orna, Sudetes, SW Poland (Pieczka et al., Reference Pieczka, Szełęg, Szuszkiewicz, Gołębiowska, Zelek, Ilnicki, Nejbert and Turniak2016), where similar to the Madagascar occurrence, the host pegmatite is of hybrid NYF–LCT character and pezzottaite occurs in rare highly fractionated LCT pods in more extensive NYF phases. Review of the development of pegmatite classifications over the past ~100 years (Müller et al., Reference Müller, Simmons, Beurlen, Thomas, Ihlen, Wise, Roda-Robles, Neiva and Zagorsky2022) has noted that pegmatites described as having a ‘mixed’ or ‘hybrid’ character have been particularly problematic due to their combined NYF and LCT mineralogical and chemical features. Their genetic interpretation is often ambiguous, at times leading to misidentification, and the classification of Wise et al. (Reference Wise, Müller and Simmons2022) uses a much broader array of criteria while maintaining the useful aspects of previous classifications. The occurrences of pezzottaite highlight the complexity of the ‘hybrid-character’ pegmatites and emphasise the need for detailed careful study such as that of the Julianna pegmatite (Pieczka et al., Reference Pieczka, Szełęg, Szuszkiewicz, Gołębiowska, Zelek, Ilnicki, Nejbert and Turniak2016).
Coda
[1]All crystals with (Cs+ + Rb+) ≥ ~0.5 apfu are microscale mixtures of more than one structure although all crystals showed diffraction spots that appeared sharp and uniform to the eye.
[2]Three distinct phases were identified with different diffraction characteristics: (1) hexagonal (P6/mcc) Cs-rich beryl; (2) hexagonal-rhombohedral (
$R\bar 3c$) twinned pezzottaite; (3) two crystals showed an approximate doubling of the beryl c-axis but the additional spots are incommensurate, and indexing gave l indices deviating from integer values by ±0.05–0.10.
[3]Note that the rhombohedral refinements do not explicitly account for the presence of an intergrown hexagonal component.
[4]Two pezzottaite crystals with compositions close to 50% (with weak rhombohedral reflections) show some disorder of Li+ over the Li and Be sites whereas pezzottaite crystals with higher Cs+ (and Li+) content and strong rhombohedral reflections show the Be site occupied only by Be2+ and the Li site occupied by both Li+ and Be2+.
[5]The ordering of (Cs+ + Rb+) and (Na+ + Ca2+) in pezzottaite is driven by the incident bond-valence requirements of the anions coordinating the (LiO4) tetrahedron.
[6]The occurrence of an incommensurate phase at intermediate compositions is due to the interaction of the species in adjacent columns of the P6/mcc beryl structure.
[7]The valence-sum rule requires both Na+ and Ca2+ to bond to one channel (type-II) (H2O) group.
[8]As a result of [7], the compositions along the beryl–pezzottaite join must lie below the line (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 apfu. This relation is modified by the requirement of electroneutrality to become (Cs+ + Rb+) + 2(Na+ + Ca2+) = 1 – 2Ca2+ apfu.
[9]There is a large area of the (ideally possible) beryl–pezzottaite compositional field that is (currently) unoccupied by analysed compositions; the reason(s) for this are not well-understood.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1180/mgm.2024.74.
Acknowledgements
FCH thanks two anonymous referees for their very careful reviews of this manuscript; Mark Cooper for collecting the X-ray data and data reduction; and Herb Obodda for donating samples for this work. FCH was supported by a Canada Research Chair in Crystallography and Mineralogy and Natural Sciences and Engineering Research Council of Canada Discovery, Research Tools and Equipment, Major Installation and Major Facilities Access Grants, and by the Canada Foundation for Innovation.
Competing interests
The author declares none.
Open access
