Precise indispensable amino acid (AA) requirement values are necessary for elaborating balanced aquafeeds that ensure both cost-effectiveness and minimal environmental impact. This necessity has been heightened by the increasing use of plant protein sources to replace fishmeal in aquafeeds. Large variations in relative indispensable AA requirement estimates for different salmonid species and within species alike still subsist in the literature(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1). Even for lysine (Lys), which is often the first limiting AA in plant proteins, the published relative requirement estimates vary greatly, from 1·3 to 2·9 % of the diet(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1). Plausible causes of the variation are the units used to express the requirement(Reference Hauler and Carter2–Reference Encarnação, De Lange and Rodehutscord4), diet composition(Reference Encarnação, De Lange and Rodehutscord4), laboratory variance(Reference Cowey5), overfeeding(Reference Hauler and Carter2, Reference Hauler and Carter3), response criterion(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1) and experimental design, statistical analysis and model choice(Reference Shearer6). Basal diet composition(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1) and, more specifically, the influence of dietary protein level on the requirement of the first limiting indispensable AA has not yet been examined for fish. The implications are far-reaching, especially when one considers that diet formulators may choose to increase or decrease the dietary protein level for a wide variety of reasons. They may wish to achieve maximum growth performance, decrease environmental impact, increase cost-effectiveness, or to adapt the diet to the life stage of the fish. Also, the protein level in the diet may be affected by the use of large amounts of plant protein sources which may contain lower protein concentrations than fishmeal.
In warm-blooded terrestrial animals, it has been reported for a long time that relative AA requirements are related to dietary protein concentration(Reference Grau7–Reference Mendonca and Jensen17). In general, the requirement for an AA expressed as a percentage of the diet increased as dietary protein concentration increased up to the level of protein required for maximum growth(Reference Almquist18). For instance, Brinegar et al. (Reference Brinegar, Williams and Ferris9) showed that the mimimum level of Lys which produced the maximum weight gain, considered as the Lys requirement, in swine, was 6 g/kg in a 10·6 % protein diet and 12 g/kg in a 22 % protein diet. This difference in the requirements almost disappeared when the requirements were expressed in terms of their proportion to the protein in the diets. However, the AA requirement expressed as a percentage of the diet has also been reported to remain constant or even to decrease slightly when expressed as a percentage of dietary protein(Reference Becker, Jensen and Terrill11–Reference Baker, Katz and Easter14, Reference Forbes, Baughan and Norton19–Reference Sowers and Meade21). This situation is usually observed under conditions of optimal and supra-optimal protein intakes or concentrations in the diets(Reference Baker, Katz and Easter14). For example, Bressani & Mertz(Reference Bressani and Mertz12) demonstrated that the Lys requirement expressed as a percentage of the diet remained essentially constant in the range of 16–40 % protein, i.e. above optimal protein level for rats(22).
The main objective of the present study was to determine the effect of the dietary protein level on the relative and absolute Lys requirements of rainbow trout fry. Two secondary objectives were to examine the influence of the model choice and the response criterion on the Lys requirement estimate. Both a linear model and a non-linear model were fitted to the data to estimate the Lys requirements. The broken-line model (BLM) of Robbins et al. (Reference Robbins, Norton and Baker23) was chosen because it is the most widely used method of evaluating dose–response data in nutrient requirement studies in fish(Reference Shearer6) including Lys(Reference Hauler and Carter2). On the other hand, the saturation kinetics model(Reference Morgan, Mercer and Flodin24) with four parameters (SKM-4) was also selected in the present study because we used a wide range(Reference Rodehutscord, Borchert and Gregus25) of Lys concentrations of about three times the requirement without observing any inhibition in the response of trout fry(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1, Reference Shearer6, Reference Rodehutscord and Pack26). The main response criteria studied were gains in body weight, protein and Lys. The total Lys requirement was expressed in both absolute (g Lys/kg metabolic body weight (MBW) per d) and in relative (g Lys/kg dry diet (DM) or g/100 g protein) terms.
Materials and methods
Two experiments were undertaken. The first was designed to establish the response of protein and Lys gains to Lys intake for a wide range of Lys intakes at two different protein levels. The second experiment was a digestibility trial performed with two diets obtained by blending diets of experiment one. The two diets differed in their protein level and contained the optimal Lys level found with the first experiment. The second experiment was necessary to evaluate the digestibility of proteins and energy in the two basal diets and the relative and absolute Lys requirements on a digestible basis.
Experimental diets
Thirty-two isoenergetic experimental diets were formulated to contain sixteen Lys levels and two protein levels, giving a 16 × 2 factorial design. For the low-protein (LP) and high-protein (HP) diets the targeted crude protein levels were of 300 and 450 g crude protein/kg DM, respectively. For diets LP0 to LP15, the targeted Lys levels in g/kg diet DM were of 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 33, 40, 47 and for diets HP0 to HP15, the total targeted Lys levels in g/kg diet DM were of 2, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 50, 60, 70. The AA diet profile followed the National Research Council recommendations(27), except for Lys. Wheat gluten provided the main protein source. A mixture of non-essential crystalline AA was added in order to compensate for the reduction in Lys and to maintain the same digestible N and total crystalline AA levels for all diets. The experimental diets were produced as previously reported(Reference Abboudi, Mambrini and Ooghe28). In particular, the crystalline AA mixtures were coated with 1 % agar, as described by Mambrini & Kaushik(Reference Mambrini and Kaushik29), to hinder leakage, delay its digestive absorption and optimise its use for protein accretion. After extrusion, the experimental diets were stored at − 20°C. The ingredients and proximate compositions of the diets are shown in Tables 1 and 2. The AA composition was analysed once for the following eight diets: LP0, LP5, LP10, LP15, HP0, HP5, HP10 and HP15 (Table 3). Because the AA levels in the eight analysed diets were very close to the formulated levels, it followed that the diets had the formulated concentration of all AA and in particular of Lys.
Table 1 Composition of the low-protein (LP) and high-protein (HP) experimental diets used for determining the effect of diet digestible protein on lysine (Lys) requirements and retention efficiencies in rainbow trout fry
(Mean values and standard deviations)
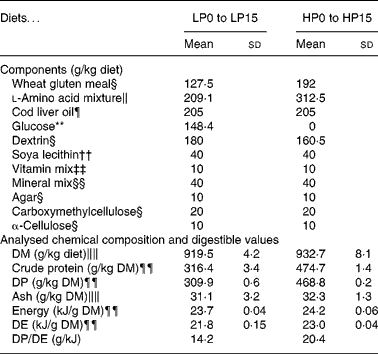
DE; digestible energy; DP, digestible protein.
§ Sigma (St Louis, MO, USA): wheat gluten meal g5004; dextrin (from corn) d2256; agar a5306; carboxymethylcellulose c4888; α-cellulose c8002.
‖ For composition, see Table 2.
¶ Federa (Brussels, Belgium).
** Merck (Darmstadt, Germany) 8337·5000.
†† Cereal (Beerzel, Belgium).
‡‡ Supplied the following (to provide g/kg premix): retinyl acetate (1 500 000 IU/g), 0·67; ascorbic acid, 120; cholecalciferol (4 000 000 IU/g), 0·1; tocopheryl acetate (1 000 IU/g), 34·2; phylloquinone, 2·2; thiamin, 5·6; riboflavin, 12; pyridoxine, 4·5; calcium-panthotenate, 14·1; p-aminobenzoic acid, 40; vitamin B12, 0·03; niacin, 30; biotin, 0·1; choline chloride, 300; folic acid, 1·5; inositol, 50; canthaxanthin, 7; butylated hydroxytoluene, 1·5; butylated hydroxyanisole, 1·5; α-cellulose, 323·8.
§§ Supplied the following (to provide g/kg mixture): CaHPO4·2H2O, 117·28; CaHPO4, 165·28; Ca(PO4)2·H2O, 236·03; NaHCO3, 100·44; Na2SO3, 0·011; KCl, 108·61; NaCl, 143·49; KI, 0·218; MgCl2, 101·88; MnSO4·H2O, 1·75; FeSO4·7H2O, 13·51; CuSO4·5H2O, 0·435; ZnSO4·7H2O, 10·88.
‖‖ Growth trial diets LP 0, 5 10 and 15 and HP 0, 5 10 and 15 were analysed in duplicates.
¶¶ Digestibility trial diets LP and HP (26 g Lys/kg DM) were tested or analysed in duplicates.
Table 2 Composition of l-amino acid mixtures (g/kg DM) used in the low-protein (LP) and high-protein (HP) experimental diets§
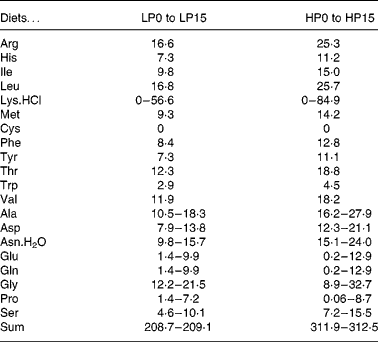
§ Ajinomoto Ltd (Tokyo, Japan).
Table 3 Crude protein (g nitrogen×6·25/kg) and amino acid (g/kg DM) content analysed in reference diets for rainbow trout fry

DAA, dispensable amino acid; HP, high-protein diet; IAA, indispensable amino acid; LP, low-protein diet.
§ According to the National Research Council(27).
‖ Methionine+cystine.
¶ Phenylalanine+tyrosine.
** Tryptophan could not be determined with the amino acid analysis method used. Values presented are calculated from the ingredients.
Fish and feeding
The Animal Welfare Commission of the Université catholique de Louvain approved the experiment in accordance with the EC directive concerning vertebrate laboratory animals.
Rainbow trout eyed embryonic eggs of domesticated origin were supplied to our laboratory hatchery (M. Huet Fish Culture Laboratory, Université catholique de Louvain, Louvain-la-Neuve, Belgium) by a commercial fish farm (La Fontaine aux Truites, Gérouville, Belgium) and then reared to the beginning of the experiment. After hatching, the fry were kept in a single tank and fed, to slight excess by an automatic feeder, an AquaBio Joosen-Luyckx (Turnhout, Belgium) commercial diet up to the start of the experiment. The daily mortality rate always stayed below 0·1 %.
After 36 h of feed deprivation and immediately prior to the experimental phase, the rainbow trout fry (mean initial body weight 0·78 (sd 0·01) g) were randomly distributed between thirty-four indoor aquaria (0·4 × 0·24 × 0·2 m) of 15 litres. There were sixty fish per aquarium and each experimental diet was randomly allocated to one aquarium (n 1). Thus, for each dietary protein level (LP and HP), there was one aquarium for every tested dietary Lys concentration. To serve as initial samples, the fish of two randomly chosen aquaria were weighed, anaesthetised with excess ethylene glycol monophenyl ether, counted and kept frozen ( − 20°C) until chemical analysis. Optimum conditions were maintained throughout the entire experiment as the aquaria were continuously aerated and supplied with freshwater (1 l/min) at 14·5–15·5°C. The fish were exposed to a photoperiod of 8 h of darkness and 16 h of light (100 lux measured at the water surface).
The fish were fed for 31 d, twice daily, at 09.00 and 22.00 hours, for three periods of 11, 10 and 10 d each. The duration of the experiment was chosen to ensure a tripling in body weight for the groups receiving a slightly sub-optimal Lys level (LP6 and HP6 and above). The fish were carefully fed manually to apparent satiety, which allowed the amount of feed distributed to each aquarium to be recorded after each meal. During the meals, it was ensured that the fish ate the pellets within a maximum of 15 s of contact with the water in order to minimise the leaching of nutrients into the water. Mortality, if present, was recorded daily. At the end of the experiment and after 72 h of food deprivation, the fish in each aquarium were weighed together, anaesthetised with excess ethylene glycol monophenyl ether, counted and frozen ( − 20°C). Initial and final fish whole bodies were freeze-dried, homogenised (Grindomix GM 200; Retsch, Haan, Germany) and kept frozen ( − 20°C) until chemical analysis.
Digestibility trial
A digestibility trial permitted the assessment of nutrient apparent digestibility for the experimental diets. LP diets were reground and mixed together in proportions so as to obtain a Lys concentration of 26 g Lys/kg DM. The same procedure was carried out with the HP diets in order to obtain one diet with a Lys level of 26 g Lys/kg DM. Chromic oxide served as the indigestible marker and was added at 10 g/kg in both diets. The diets were pelleted using a pellet mill (5 mm diameter) and stored at − 20°C.
Four groups of thirteen rainbow trout, weighing an average of 320 g per fish, were randomly allocated to four circular tanks with a water temperature of 14·4–15·8°C and a water flow of 4 l/min. The two diets (LP and HP) were each dispensed in two randomly chosen tanks. After an adaptation period of 3 d to the respective experimental diets and a fasting period of 4 d, the fish were under experiment for 16 d. Faeces were collected continuously with a rotating automatic faeces collector system(Reference Choubert, Delanoue and Luquet30) that ensures minimum contact of the faeces with the water. The exiting water carrying the faeces was filtered directly and continuously. Once a day we collected faeces from the trays and then fed the fish. Feed was collected in a basket for 1 h after feeding to prevent it from contaminating the faeces produced during that day. All the faeces collected per tank were mixed together, freeze-dried, ground and stored at − 20°C until analysis.
Sampling and chemical analysis
For the dose–response trial, the diets and fish were analysed for DM, crude protein (N × 6·25), crude ash and AA content (Tables 1 and 3). Proximate analyses of the samples were conducted as previously reported(Reference Nang Thu, Parkouda and De Saeger31). The same analyses were performed for the diets and faeces of the digestibility trial, as well as the determination of chromium III (trivalent) that involves digestion of organic matter, solubilisation of chromium and determination of chromium by simple photometry(Reference Czarnocki, Sibbald and Evans32, Reference Fenton and Fenton33). The crude energy content of the diets and of the faeces was determined with a bomb calorimeter (1241 Oxygen Bomb Calorimeter; Parr Instrument Company, IL, USA).
Calculations
The initial variables that were obtained or measured directly during and after the experiment were the following: DI is the dry diet intake per fish (g DM/fish) during the experimental period; NI is the N intake per fish (g N/fish); LysI is the Lys intake (g/kg MBW per d); n is the mean number of fish per aquarium, obtained by summing the number of fish per aquarium at the beginning and at the end of the experiment and then dividing by 2; Wf and Wi are the average final and initial fresh body weights (g) per fish; feedingd is the number of feeding days (31 for the present experiment); Nf and Ni are the mean N contents of the whole-body fry at the end and at the beginning of the experimental period (g N/g); mean MBW (in kg0·75/fish) was calculated as ((Wf/1000)0·75+(Wi/1000)0·75)/2; Lysf and Lysi are the Lys contents (in g/g total AA) of the whole-body fish proteins at the end and at the beginning of the experiment, respectively.
The following response criteria were calculated:




LIP is the lipid content in g/g body weight and it was calculated as:



Lys retention efficiency above maintenance = the slope of the linear relationship between Lys gain and Lys intake at marginal dietary Lys concentrations ( ≤ 10 g/kg DM)(Reference Fuller, McWilliam and Wang34, Reference Edwards, Baker and Fernandez35).
E is the Lys maintenance requirement in g/kg MBW per d. It was calculated as the x-intercept of the linear relationship between Lys intake (g Lys/kg MBW per d) and Lys gain (g Lys/kg MBW per d).
Data analysis
The linear model used was the BLM of Robbins et al. (Reference Robbins, Norton and Baker23):
where Y is the response criterion; P is the plateau value; R is the requirement; X is the independent variable (Lys dietary concentration in g/kg DM or Lys intake in g/kg MBW per d); U is the slope of the line; Z is a categorical variable which equals 1 when X < R and equals 0 otherwise; ɛ is the error term.
The x-intercept, I, is calculated as R − P/U. The Lys efficiency of utilisation was modelled with an inverse BLM which differs from the BLM in that Z equals 1 when X>R and equals 0 otherwise.
The non-linear model used was the SKM-4(Reference Morgan, Mercer and Flodin24, Reference Mercer36, Reference Mercer, May and Dodds37):
where X is the independent variable (Lys intake or Lys dietary concentration); Y is the response criterion; b is the intercept on the y-axis (for x = 0); k is the concentration for ymax/2; n is the apparent kinetic order; ymax is the maximum response; ɛ is the error term.
Three particular intake levels of interest are the intake at maximum slope (Xms), the intake of maximum efficiency (Xme), and the intake of zero response (I) which is only possible to calculate if b < 0(Reference Mercer36):
The Lys requirement was estimated at 0·95ymax and 0·90ymax(Reference Rodehutscord, Jacobs and Pack38).
Lys retention efficiency was modelled with the polynomial model of Heger & Frydrych(Reference Heger and Frydrych39):
where a, b, c and d are unknown coefficients.
Lys efficiency of utilisation was modelled with a composite model based on the BLM(Reference Robbins, Norton and Baker23) and the inverse exponential model(Reference Rodehutscord, Jacobs and Pack38).
where a, b, c and d are unknown coefficients; Z is a categorical variable applied separately for each Lys dose, it equals 1 when X is less than the breakpoint and equals 0 otherwise.
The model parameters were estimated by a classical least squares method for linear models and by iterative least squares procedures for non-linear and composite models. Calculations were carried out with the R statistical software package version 2.5.0 (University of Auckland, Auckland, New Zealand) and JMP statistical software package version 7 (SAS Institute, Cary, NC, USA)(Reference Venables and Ripley40). The level of significance chosen was P < 0·05. Models involving the two protein levels (HP and LP) were always estimated independently. Model parameters comparison was done with a Student's t test for classical cases and through bootstrap procedures when classical tests were not directly available. This was, for example, the case in the estimation of the difference between the Lys requirement for HP and LP protein levels: a bootstrap procedure(Reference Efron and Tibshirani41) on models residuals was applied to build 95 % CI on this difference.
Results
Digestibility trial
The proximate analyses of the experimental LP and HP diets for the digestibility trial (26 g Lys/kg DM) are found in Table 1. LP and HP diets did not have significantly different apparent digestible coefficient (ADC) values for Lys (mean 99·3 (se 0·12) %) or for ash (mean 53·2 (se 0·68) %). Because the Lys apparent digestible coefficient value was 99 %, the Lys of the LP and HP diets was considered completely absorbed and available for the trout fry in the present experiment. The apparent digestible coefficient values were significantly different for crude protein (98·0 (se 0·09) % for LP; 98·7 (se 0·09) % for HP), DM (88·4 (se 0·35) % for LP; 91·8 (se 0·35) % for HP), and crude energy (92·0 (se 0·32) % for LP; 94·9 (se 0·32) % for HP). Thus, digestible protein and digestible energy contents were of about 310 g/kg DM and 22 MJ/kg DM for LP diets and 469 g/kg DM and 23 MJ/kg DM for HP diets (Table 1). The differences in digestible energy content were considered minor, and the differences in digestible protein content were adequate for the purpose of the experiment.
Dose–response trial
In the dose–response trial, fry fed LP6 to LP15 diets or HP5 to HP15 diets increased their mean initial body weight (0·78 g/fish) by a factor of at least three by the end of the experiment (Table 4), thus showing good growth rates despite high concentrations of crystalline AA in the diets (66·4 % of crude protein for both LP and HP diets). A high mean mortality of thirteen fish per aquarium (22 %) was observed for the two diets with the lowest Lys concentrations at both protein levels (LP0, LP1, HP0, HP1). For the diets LP2 to LP15 and HP2 to HP15 the average mortality was of only one fish per aquarium (1·7 %).
Table 4 Final weight, body weight gain, daily growth coefficient (DGC; 1000×((final weight)1/3−(initial weight)1/3)/feeding days), feed efficiency (FE; wet weight gain/DM intake), protein productive value (PPV; 100×nitrogen gain/nitrogen intake), fat in weight gain, protein in weight gain, dry diet intake, lysine (Lys) intake, protein gain, Lys gain and Lys retention efficiency in rainbow trout fry fed on graded levels of Lys for 31 d §
(Values for one group of sixty fry)

HP, high-protein diet; LP, low-protein diet; MBW, metabolic body weight = ((initial body weight)0·75+(final body weight)0·75)/2.
§ For details of procedures and diets, see Materials and methods section and Table 1. The initial body weight was 0·78 (sd 0·01) g for the rainbow trout fry and they were kept at a temperature of 14·5–15·5°C.
Body weight gain, daily growth coefficient, feed efficiency, PPV, DM intake, protein gain and Lys gain (Table 4) were all plotted against the Lys dietary concentration and were fitted with the SKM-4 non-linear model (best fit model, see Table 5 for parameter values for body weight gain, protein gain and Lys gain). The ymax parameter was found to be significantly different between LP and HP diets for all criteria. For body weight gain, protein gain and Lys gain, the HP diets had a significantly greater ymax and inversely, for DM intake and PPV, it was the LP diets that had a significantly higher ymax (results not shown).
Table 5 Parameters estimated by fitting the non-linear model to the experimental data for the response criteria of body weight gain (g/kg metabolic body weight (MBW) per d), protein gain (g/kg MBW per d) and lysine (Lys) gain (g/kg MBW per d)§

b, y-intercept; HP, high-protein diet; I, x-intercept and intake of zero response; k, concentration for ymax/2; LP, low-protein diet; n, apparent kinetic order; R 0·90, requirement estimated as 0·90ymax; R 0·95, requirement estimated as 0·95ymax; RMSE, root mean square error; ymax, the maximum response; Xms, intake at maximum slope; Xme, intake of maximum efficiency.
Values of ymax were significantly different between LP and HP diet models: *P < 0·05. HPymax>LPymax.
§ For details of procedures and diets, see Materials and methods section and Table 1. MBW = ((initial body weight)0·75+(final body weight)0·75)/2.
The relative Lys requirement (expressed as g Lys/kg DM) for all three main response criteria (body weight gain, protein gain and Lys gain) was always greater for the HP diets than for the LP diets (Tables 6 and 7; Fig. 1). However, the significance of this difference (Table 7) depended upon the model used, the response criterion and the definition of the requirement (0·90ymax or 0·95ymax) for the SKM-4. For the BLM, the difference of relative Lys requirement between the LP and the HP diets was significant for all three response criteria. On the other hand, for the SKM-4, this difference was not significant for the criteria of protein gain and Lys gain when the 0·95ymax was used. As protein level was increased from LP to HP diets, the relative Lys requirement for optimal Lys gain increased from 16·8 to 23·4 g/kg DM, respectively, with the BLM (Table 7). When using 0·90ymax with the SKM-4, the relative Lys requirement increased from 19·6 to 24·5 g/kg DM for fish fed the LP and HP diets, respectively (Table 7). When estimating the requirement at 0·95ymax, with the SKM-4, the relative requirement increased from 24·5 to 29·4 g/kg DM with increasing protein level (LP and HP diets, respectively). When the relative Lys requirements were expressed in terms of dietary protein (g Lys/100 g protein), the difference between the LP and HP requirements was significant only for the SKM-4 using 0·90ymax and Lys gain as the response criterion (Table 7).
Table 6 Parameters estimated by fitting the broken-line model to the experimental data for the response criteria of body weight gain (g/kg metabolic body weight (MBW) per d), protein gain (g/kg MBW per d) and lysine (Lys) gain (g/kg MBW per d)§

HP, high-protein diet; I, x-intercept; LP, low-rotein diet; P, plateau; R, requirement; RMSE, root mean square error; U, slope.
§ For details of procedures and diets, see Materials and methods section and Table 1. MBW = ((initial body weight)0·75+(final body weight)0·75)/2.
Table 7 Comparison of the non-linear (NL) and the broken-line (BL) models for the relative lysine (Lys) requirement expressed in terms of diet DM (g/kg DM) and in terms of dietary protein (g/100 g protein), and the absolute Lys requirement expressed in terms of intake (g/kg metabolic body weight (MBW) per d) for the response criteria of body weight gain (g/kg MBW per d), protein gain (g/kg MBW per d) and Lys gain (g/kg MBW per d)§

HP, high-protein diet; LP, low-protein diet; NL 0·90, non-linear model requirement estimated as 0·90ymax; NL 0·95, non-linear model requirement estimated as 0·95ymax; Rq, lysine requirement; S, significant.
§ For details of procedures and diets, see Materials and methods section and Table 1. MBW = ((initial body weight)0·75+(final body weight)0·75)/2.
‖ For the difference between the HP and LP requirement estimates.

Fig. 1 The lysine (Lys) requirement for Lys gain expressed in g Lys/kg diet DM (a, c) and in g Lys intake/kg metabolic body weight (MBW) per d (b, d) estimated with a broken-line model (a, b) or a non-linear saturation kinetics model (SKM-4) (c, d) for low-protein (LP; Δ) and high-protein (HP; ○) diets. Each point represents one group of sixty fish (rainbow trout, 31 feeding d, initial body weight 0·78 g/fish). The vertical dotted lines represent the requirement. For the SKM-4 models, two small dotted lines (····) represent the requirement at 0·90ymax and 0·95ymax, from left to right, for the LP diets. The two larger dotted lines (––) represent the requirement at 0·90ymax and 0·95ymax, from left to right, for the HP diets. See Tables 5 and 6 for parameter values. MBW = ((initial body weight)0·75+ (final body weight)0·75)/2.
The Lys requirements were then expressed as an absolute value, that is, as Lys intake (g/kg MBW per d) instead of Lys concentration in the diet (Table 7). The absolute Lys requirement for the LP diets was sometimes greater than, sometimes less than and sometimes equal to the requirement for the HP diets. The difference between the absolute LP and HP requirements was only significant in the case of Lys gain with the BLM.
To bring to light the significance effect of the response criterion on the Lys requirement, the criteria may be classified as follows: the Lys requirement for weight gain is definitely smaller than the Lys requirement for protein gain which is smaller than or equal to the requirement for Lys gain (Table 7). For instance, the relative Lys requirements estimated with the BLM were 20·2, 22·3 and 23·4 g/kg DM for body weight gain, protein gain and Lys gain, respectively. This progression holds true for the two ways of expressing the Lys requirement, be it relative (as a dietary concentration) or absolute (as an intake).
In addition, the bootstrap procedure was applied on paired residuals for the BLM. For example, the difference in the LP relative requirement for body weight gain and the LP relative requirement for protein gain was calculated and its significance was tested. When this was done for LP and HP diets alike, twelve different tests (or pairs of values) were obtained (Table 8). In nine cases out of twelve the differences were significant which demonstrates clearly that the response criterion most likely has an influence on the value of the relative Lys requirement (g/kg DM). The three cases for which the differences were not significant concerned pairs between Lys gain and protein gain.
Table 8 The 95 % CI for the differences between the relative lysine (Lys) requirements expressed in terms of diet DM (g/kg DM) and between the absolute Lys requirements expressed in terms of intake (g/kg metabolic body weight (MBW) per d) for the response criteria of body weight gain (g/kg MBW per d), protein gain (g/kg MBW per d) and Lys gain (g/kg MBW per d) obtained with the broken-line model§

HP, high-protein diet; LP, low-protein diet.
§ For details of procedures and diets, see Materials and methods section and Table 1. MBW = ((initial body weight)0·75+ (final body weight)0·75)/2. Differences are considered significant when 0 is not contained in the interval of the two values.
The BLM and the SKM-4 fit the data about equally well since the r 2 was of about 0·98–1·00. In all cases for protein and Lys gains, the Lys requirement (in absolute and relative terms) estimated with the BLM was observed to be smaller than the requirement estimated with the non-linear model using 0·90ymax, as well as 0·95ymax (Table 7).
All the parameters of the SKM-4 were shown to be necessary. When the parameter b was removed, the residual standard error increased from 0·043 to 0·056, demonstrating that it had a role. The bootstrap procedure revealed that the SKM-4 and especially the use of 0·95ymax was quite unstable and so the uncertainty associated with its estimation was higher (Table 7). The Lys requirement (in absolute and relative terms) obtained with the SKM-4 using 0·90ymax was closer to the requirement obtained with the BLM than the requirement obtained using 0·95ymax.
The Lys maintenance requirement was estimated from the diets containing suboptimal concentrations of Lys (LP0 to LP6 or < 14 g Lys/kg DM and HP0 to HP5 or < 18 g Lys/kg DM). Lys gain (Y; g/kg MBW per d) (Table 4) was plotted against Lys intake (X; g/kg MBW per d) and a linear model was fitted (Fig. 2). Because the x-intercepts (P = 0·4) and slopes (P = 0·2) of these lines were not significantly different, a single line estimation was made (Y = 0·88 (se 0·02) X − 0·018 (se 0·002), n 13, r 2 0·99). The x-intercept was 0·0208 (se 0·002) g Lys intake/kg MBW per d and thus gave an estimate for the Lys maintenance requirement.

Fig. 2 The lysine (Lys) maintenance requirement estimated by linear regression of Lys gain against Lys intake for the suboptimal low-protein diets LP0 to LP6 (○; Y = 0·84 (se 0·04) X − 0·017 (se 0·003), n 7, r 2 0·99, x-intercept = 0·020 (se 0·0026) g Lys intake/kg metabolic body weight (MBW) per d) and high-protein diets HP0 to HP5 (●; Y = 0·91 (se 0·03) X − 0·019 (se 0·002), n 6, r 2 0·99, x-intercept = 0·021 (se 0·0020) g Lys intake/kg MBW per d). Each symbol represents one group of sixty rainbow trout fry (31 feeding d, initial body weight 0·78 g/fish). Neither the slopes (P = 0·2) nor the x-intercepts (P = 0·4) were significantly different. MBW = ((initial body weight)0·75+(final body weight)0·75)/2.
The Lys retention efficiency was modelled with the polynomial model of Heger & Frydrych(Reference Heger and Frydrych39) (Fig. 3). For the LP and HP diets, the curves rose sharply, reached a maximum at 70 and 73 % of Lys retention efficiency that corresponded to an intake of 94 and 109 mg Lys/kg MBW per d, for LP and HP diets, respectively. The Lys intakes at optimal protein gain (where the requirement is located at 0·95ymax) were of 0·295 and 0·275 mg Lys/kg MBW per d for LP and HP diets, respectively. Thus, the Lys intake needed to achieve maximum efficiency was situated at 32 and 40 %, for LP and HP diets, respectively, of the intake needed to obtain optimal protein gain (Tables 4 and 5).

Fig. 3 Lysine (Lys) retention efficiency represented as Lys gain plotted against Lys intake (each symbol represents one group of sixty rainbow trout fry) and modelled with a polynomial model for low-protein (LP; ○) and high-protein (HP; ●) diets (LP model: Y = − 2·89x− 1+135+ − 404x+399x2 +ɛ, root mean square error (RMSE) = 3·73) (HP model: Y = − 3·49x− 1+141+ − 355x+287x2 +ɛ, RMSE = 4·15). The diets LP0, LP1, HP0, HP1 were excluded from the model calculations because their retention efficiencies were negative (see Table 4). Metabolic body weight (MBW) = ((initial body weight)0·75+(final body weight)0·75)/2.
The efficiency of utilisation of both LP and HP diets was modelled with a composite model based on the BLM and the inverse exponential model (Fig. 4). The models began with very similar plateau values of 96 and 94 % for LP and HP diets, respectively, up to the break-off point at 0·10 and 0·14 g/kg MBW per d of Lys intake. Both inverse exponential curves decreased at very similar rates and remained parallel. The HP diets stayed above the LP diets.

Fig. 4 Plots for lysine (Lys) efficiency of utilisation (%) calculated as 100 × (Lys gain (g/kg metabolic body weight (MBW) per d)+Lys maintenance (0·0208 g/kg MBW per d)) divided by Lys intake (g/kg MBW per d). The efficiency of utilisation of both low-protein (LP; ○) and high-protein (HP; ●) diets was modelled with a composite model based on the broken-line and the inverse exponential model (LP model: Y = [15·4+124·7X exp( − 4·55X)] (Z − 1)2+95·3Z+ɛ, root mean square error (RMSE) = 3·41) (HP model: Y = [17·7+135·5X exp( − 4·41X)] (Z − 1)2+92·4Z+ɛ, RMSE = 2·81). Each symbol represents one group of sixty rainbow trout fry except for the first point for the LP and HP diets. It is the mean value for LP0 and LP1 or HP0 and HP1 diets. MBW = ((initial body weight)0·75+ (final body weight)0·75)/2.
The changes in fat gain (Table 4) followed a similar pattern for LP and HP diets, as did changes in protein gain (Table 4). The fat in weight gain started out at about 250–300 g/kg and then quickly levelled off to a plateau above a Lys dietary concentration of 5·7 g/kg DM. The plateaus were significantly different from one another (P < 0·0001) and were at 176 (se 4) and 146 (se 4) g/kg for LP and HP diets, respectively. The protein in weight gain values started out negative and rose to a plateau value for Lys concentrations above 11·7 g/kg DM. The plateaus were not significantly different from one another (P = 0·4) and were at 130 (se 4) and 134 (se 3) g/kg for LP and HP diets, respectively.
The N body composition (Table 9) showed no difference between LP- and HP-fed fry (P = 0·2). For both protein levels, the N body concentration increased with increasing Lys concentration in the diet (P = 0·002). The AA composition of the whole-body protein was significantly different between LP and HP diets for histidine and cystine (Table 9). For both LP and HP diets, histidine increased significantly and arginine decreased significantly, with increasing dietary Lys level. Lys whole-body protein composition increased significantly with increasing dietary Lys level for HP diets though it did not vary significantly for LP diets.
Table 9 Amino acid (AA) composition of whole-body protein (g/100 g AA) and nitrogen whole-body composition (g/100 g liveweight) in rainbow trout fry fed on different experimental diets containing graded levels of lysine (Lys) for 31 d
(Values for one group of sixty fry)§

HP, high-protein diet; LP, low-protein diet.
* Significant (P < 0·05) linear increase with increasing dietary Lys level.
† Significant (P < 0·05) linear decrease with increasing dietary Lys level.
‡ Significant (P < 0·05) difference between fry fed HP and LP diets for one amino acid.
§ For details of procedures and diets, see Materials and methods section and Table 1. The initial body weight of the rainbow trout fry was 0·78 (sd 0·01) g and water temperature was 14·5–15·5°C. Tryptophan could not be determined with the amino acid analysis method used.
To estimate the amount of Lys required to deposit 1 g body protein, the slope of the linear regression of protein gain (Y; g/kg MBW per d) (Table 4) against Lys intake (X; g/kg MBW per d) for the Lys-deficient diets ( < 14 g Lys/kg DM for LP0 to LP6 and < 18 g Lys/kg DM for HP0 to HP5) was calculated. The inverse value of the slopes ( × 1000) of these linear relationships (Y = − 0·17 (se 0·04)+10·64 (se 0·5) X, r 2 0·99, n 7 and Y = − 0·17 (se 0·03)+11·24 (se 0·4)X, r 2 0·99, n 6, for LP and HP diets, respectively) indicated that fry fed LP and HP diets required an intake of 94 (se 4·4) and 89 (se 3·2) mg Lys, respectively, to deposit 1 g body protein. Neither the x-intercepts (P = 0·4) nor the slopes (P = 0·2) of these linear relationships were significantly different and a single line estimation (Y = − 0·17 (se 0·03)+10·94 (se 0·3) X, r 2 0·99, n 13) gave a requirement estimate of 92 (se 2·5) mg Lys/g body protein accretion.
Discussion
The present study tested the effect of dietary protein level on the relative (g/kg DM or g/100 g protein) and absolute (g Lys intake/kg MBW per d) Lys requirements. The relative Lys requirement of trout fry markedly increased (+5·4 g/kg DM) when the digestible protein content increased from 310 to 469 g/kg DM (Table 7); therefore, we observed an increase in the relative Lys requirement of about 0·034 % for each 1 % increase in the protein level between 31 and 46·9 % protein. The relative Lys requirement difference was marginally influenced by the model or the response parameter selected for its estimation. Studies with warm-blooded animals also reported an increase of the relative Lys requirement (g/kg DM) with increasing dietary protein level(Reference Bressani and Mertz12–Reference Baker, Katz and Easter14, Reference Klay20). McWard et al. (Reference McWard, Becker and Norton13) working between 12·8 and 21·7 % protein in swine concluded that the relative Lys requirement (g/kg DM) increased by 0·023 % for each 1 % increase in dietary protein. Baker et al. (Reference Baker, Katz and Easter14) showed an increase in the relative Lys requirement (g/kg DM) of growing pigs of 0·02 % for each 1 % increase in dietary protein when working between 12 and 16 % dietary protein. The present results showed an even greater dependence in trout than in pigs between the relative Lys requirement (g/kg DM) and the protein level in the diet. This dependence is economically important and should not be ignored when formulating diets using crystalline Lys to replace part of the dietary protein. Hence, less total dietary Lys is needed in a Lys-supplemented LP diet than in an unsupplemented HP diet. It must be pointed out that the higher amount of digestible carbohydrates in the LP diets compared to the HP diets may have somewhat affected the present Lys requirement results. Indeed, salmonids have a limited capacity to metabolise glucose, though rainbow trout have a higher capacity to digest and absorb starches compared to Atlantic salmon(Reference Krogdahl, Sundby and Olli42, Reference Frøystad, Lilleeng and Sundby43). In rainbow trout, insulin-specific receptors were found(Reference Plisetskaya, Fabbri and Moon44, Reference Párrizas, Planas and Plisetskaya45) though their abundance was lower than in mammals(Reference Gutiérrez, Åsgård and Fabbri46). The excessive available carbohydrates may induce metabolic disturbances such as hyperglycaemia(Reference Wilson47), glucosuria(Reference Bucking and Wood48) or impaired liver function(Reference Hilton and Atkinson49–Reference Dixon and Hilton51). This may have influenced, in turn, the response variables used to estimate the Lys requirement. However, we believe this influence to be negligible in the present work for the following reasons: (1) LP-fed fish showed a higher voluntary feed intake and a higher PPV than the HP-fed fish, not indicating any metabolic disturbance; (2) the level of available carbohydrates is high in our LP diets but not excessive as dextrin digestibility reported in the literature is low in rainbow trout fry (44 %)(Reference Storebakken, Shearer and Refstie52) and the maximum recommended available carbohydrate level is 20 % for salmonids(Reference Wilson47); (3) this level of available carbohydrates has already been used before for similar LP diets in salmonids(Reference Rollin, Wauters and Bodin53).
The dietary protein level did not significantly affect the relative Lys requirement for Lys gain when expressed in terms of dietary protein. This confirms the relationship between the relative Lys requirement on an as-fed basis and the dietary protein level. In absolute terms (g Lys intake/kg MBW per d) the Lys requirements at 310 g protein/kg DM and at 469 g protein/kg DM were not significantly different. With the SKM-4 using 0·90ymax, for example, the Lys requirement for Lys gain was estimated to be 210 mg Lys intake/kg MBW per d for the LP and the HP diets alike. This optimum amount of absolute Lys intake corresponds to the LP9 and HP7 (197·9 and 203·3 mg Lys intake/kg MBW per d, respectively) diets. However, in terms of dietary DM consumption, the fry fed the LP9 diet ate more (+16 %) than the HP7-fed fry. In conclusion, to achieve the same absolute Lys intake (g/kg MBW per d) as the HP-fed fry, the LP fry had a greater voluntary feed intake. This is the primary reason why the Lys requirement when expressed in relative terms (g/kg DM) is lower for LP diets. Similar results were reported in work with pigs(Reference Baker, Katz and Easter14, Reference Klay20, Reference Katz, Baker and Sasse54) and rats(Reference Mercer, Watson and Ramlet55, Reference Finke, Defoliart and Benevenga56). Our interpretation of the data is further supported by the fact that the effect of the protein level on the Lys requirement virtually disappears when the requirement of Lys is expressed in absolute terms (g Lys intake/kg MBW per d) (Table 7), and the only exception is for Lys gain when the BLM is selected to interpret the present data. The latter observation is probably related to the occurrence of a second or third limiting AA in the LP diet, possibly methionine or histidine (Table 3), that may limit the response of the animals to Lys supplementation or lead to an underestimation of the Lys requirement. Alternatively, it could be related to the inadequacy of the BLM to evaluate the Lys requirement for the HP diets of the present study.
Calculating the percentage of difference between two requirement values (100 × (greatest value − smallest value)/smallest value) can sum up the effect of a factor on the Lys requirement estimation. Hauler & Carter(Reference Hauler and Carter2) found that the Lys requirements for rainbow trout expressed as a dietary concentration have an order of difference of 121 % which is typical of intra-species variation(Reference Tacon, Cowey, Tyler and Calow57). Hauler & Carter(Reference Hauler and Carter2) uphold that the wide variation of Lys requirements in the piscine literature cannot be explained by differences of protein level in the diets. In the present work, the effect of the protein level on the Lys requirement estimation can be assessed by comparing the two protein levels (LP − HP) for all response criteria (liveweight gain, protein gain and Lys gain), all models (BLM, SKM-4(0·90), SKM-4(0·95)) and all modes of expression (Lys concentration and Lys intake). Because the percentage of difference ranged from 1 to 39 %, we believe that protein level differences between studies have a role to play in explaining part of the relative Lys requirement variation observed in the piscine literature.
Model choice, another factor pinpointed as causing requirement variation, had an impact on the trout fry Lys requirement estimations in the present work. The BLM gave the lowest values compared to the SKM-4, especially when the requirement was defined as the Lys concentration or intake corresponding to 0·95 of the maximum response (0·95ymax). Lower values with the BLM compared to a non-linear model have also been previously reported in rainbow trout(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1, Reference Rodehutscord and Pack26). In a Lys requirement study, Encarnação et al. (Reference Encarnação, De Lange and Rodehutscord4) observed that relative dietary Lys requirement estimates obtained using the BLM resulted in a lower requirement value (18 g/kg diet) compared to a four-parameter logistic model used by Gahl et al. (Reference Gahl, Finke and Crenshaw58) (23 g/kg diet) that usually gives a very similar requirement estimate compared to the SKM-4 with four parameters(Reference Rodehutscord and Pack26). According to Bureau & Encarnação(Reference Bureau, Encarnação, Suárez, Marie, Salazar, López, Cavazos, Cruz and Ortega1), a value of 18 g Lys/kg diet recommended by the National Research Council(27) appears underestimated and this would be mainly a result of the fact that the National Research Council(27) based the AA fish requirement recommendations on studies that used the ANOVA or the BLM approaches. The present results clearly support the experimental evidence of Encarnação et al. (Reference Encarnação, De Lange and Rodehutscord4) and Rodehutscord et al. (Reference Rodehutscord, Becker and Pack59) that a Lys level of 18 g/kg is insufficient to ensure maximum response at an optimal protein concentration in trout, whatever the model used to interpret the data. Therefore, we suggest that the recommendations of the National Research Council(27) concerning the Lys requirements for trout as well as for salmon fry(Reference Rollin, Mambrini and Abboudi60) be re-evaluated.
Globally, both models fitted equally well the data (similar r 2). The Lys requirement estimation was less sensitive to small data modifications when estimated with the BLM or the SKM-4 with 0·90ymax. The requirement estimated with 0·95ymax had a larger uncertainty than with 0·90ymax due to the aspect of the curve, which is almost asymptotical in that area. In effect, for this particular part of the SKM-4 curve, a small variation in Y induces a large variation in X. For this reason, it is more difficult to estimate accurately the requirement with 0·95ymax as it is with 0·90ymax.
For specific parts of the response curve, such as for very low Lys intakes and for the portion around the optimum, the two models provided different fit for the data. At very low Lys intakes (between zero and the maintenance level), the dietary Lys intake is replacing the amount expended in obligatory metabolism which, in the case of insufficient dietary supply, is derived from body protein breakdown. In this zone, the SKM-4 describes the overall response of the animals as sigmoidal with a positive inflection at low intakes. Therefore, it suggests a small marginal response to the lowest AA intakes (the first derivative at zero intake is zero(Reference Fuller and Garthwaite61)). In the present study, however, the efficiency of utilisation of Lys in this zone seems to be constant and close to 100 %. Our group recently reported a similar conclusion in the study of the threonine requirement for maintenance in Atlantic salmon (Salmo salar) fry using either the graded supplementation technique(Reference Rollin, Wauters and Bodin53) or the diet dilution procedure(Reference Abboudi, Ooghe and Larondelle62). In view of this evidence and because it is in this intake range that the highest efficiency of utilisation is observed, we believe that the SKM-4 does not provide a good description of the fish response in this zone. Therefore, in this intake range, a linear model (BLM) seems more appropriate and it is for this reason that we used a linear regression to determine the Lys requirement for maintenance.
After the maintenance requirement to up to about 90 % of the maximum response, the animals in the present experiment responded to an increase in Lys intake and in Lys dietary concentration with a similar linear increase in protein and Lys gains at both protein levels. Both models were deemed adequate for this portion and for both LP and HP levels.
A diminishing returns portion of the response curve was apparent for Lys levels above 21 g/kg DM (diet HP7) for the HP diets. Therefore, the SKM-4 most accurately described this part of the response curve around the requirement at this protein level. However for the LP diets there was no evidence of diminishing returns in this part of the curve and the BLM fitted the data as well as the SKM-4. This difference in the form of the curve around the requirement between the HP and LP levels could be attributed to the suboptimal protein level of the LP diets. Indeed, the present study confirmed that the LP diets were suboptimal in terms of digestible protein concentration because, when Lys was supplied in sufficient quantities (above the total requirement for growth and maintenance), trout performances were higher for the HP diets compared to the LP diets in terms of weight gain, feed efficiency, protein gain and Lys gain. In the LP diets, another AA may become co-limiting, restraining abruptly the response of the animals. In this case, Lys would become in excess and consequently be oxidised, reducing the Lys utilisation efficiency (Fig. 3). In conclusion, neither of the two models that were tested seemed to provide an appropriate description of all parts of the response curve, although both provide a good fit to the data over one or two particular regions. To assess the possible influence the model choice can have on the Lys requirement estimation, the percentage of difference was calculated for the three model types between themselves (BLM − SKM-4(0·90), BLM − SKM-4(0·95) and SKM-4(0·90) − SKM-4(0·95)). This was done for all response criteria (liveweight gain, protein gain and Lys gain), all protein levels (LP and HP) and all modes of expression (Lys concentration and Lys intake). It led to a range of variation of 1–135 % and demonstrated clearly how great an influence the model choice may have.
The response criterion selection highly influenced the calculated Lys requirements in the present paper. In our study, 29·4 g Lys/kg DM were required to achieve 95 % of the maximum response in Lys gain whereas only 24 g/kg DM were required to achieve 95 % of the maximum response in body weight gain, for trout fed the HP diet and with the SKM-4. Several studies have demonstrated that the choice of the dependent variable is an important factor affecting the shape of the dose–response curve and hence the calculated AA requirement(Reference Finke, Defoliart and Benevenga63). In the present study, the Lys requirement varied with the selected response criterion (weight gain, protein gain or Lys gain) and suggests that body composition is affected by dietary Lys concentration. Indeed, the present results showed a linear increase of both nitrogen whole-body composition (g/100 g liveweight) and Lys concentration of whole-body protein (g/100 g AA) (Table 9) with dietary Lys concentration. This effect has already been reported in rainbow trout(Reference Encarnação, De Lange and Rodehutscord4, Reference Encarnação, De Lange and Bureau64), Atlantic salmon fry(Reference Rollin65), pigs(Reference Batterham, Andersen and Baigent66–Reference Gahl, Crenshaw and Benevenga68), chicks(Reference Edwards, Fernandez and Baker69) and rats(Reference Gahl, Finke and Crenshaw70).
Interestingly, in the present experiment the whole-body histidine concentration increased with increasing Lys level, at both protein concentrations. Recently, Bodin et al. (Reference Bodin, Mambrini and Wauters71) reported this observation with histidine when rainbow trout and Atlantic salmon fry were fed threonine-deficient diets. Their results suggest that these changes are not related specifically to individual AA deficiencies but are simply a consequence of slow growth. Therefore, whole-body histidine concentration appears to be a promising indicator of normal growth rate for fish. In addition, the data imply that the deficiency of an individual AA, such as Lys, does not necessarily entail a proportionate loss of body protein and a commensurately negative nitrogen balance. These changes presumably result from alterations in the relative amounts of different proteins, whose rates of synthesis or breakdown are in turn sensitive to the dietary AA supply(Reference Fuller and Garlick72). However, the identification of the proteins involved and the mechanism for the control of their turnover are yet to be discovered. The percentage of difference was also calculated for the three response criteria between themselves (liveweight gain, protein gain and Lys gain). This was done for all models (BLM, SKM-4(0·90), SKM-4(0·95), all protein levels (LP and HP) and all modes of expression (Lys concentration and Lys intake). It led to a range of variation of 4–48 % and showed the impact the response criterion may have on requirement estimation.
The manner of expressing the requirement is the last factor influencing Lys requirement estimations to be addressed. In the present paper, the differences in the Lys requirements between the different models used were more pronounced when Lys intake rather Lys concentration was used as the independent variable (Table 7). For example, when Lys gain (g/kg MBW per d) was plotted against Lys intake, the absolute Lys requirement was calculated to be 0·19 g/kg MBW per d with the BLM but 0·32 g/kg MBW per d with the SKM-4(0·95) at the HP level, i.e. a variation of 72 % (when calculated with seven decimals). These differences between the different models were considerably reduced (variation of 0·8 %) if the definition of the Lys requirement was the Lys concentration for 0·90 of the maximum response (0·90ymax). For rainbow trout, and concerning other ways of expressing the requirement, Hauler & Carter(Reference Hauler and Carter2) found more variation in the Lys requirement expressed as a percentage of the dietary protein (136 %) than as a percentage of the diet, while for other species, Cowey(Reference Cowey5) observed that AA requirements expressed as a percentage of dietary protein reduced the intra-species variation in the AA requirement estimations. We suggest that the best manner of expressing the Lys requirement depends on the available information. When the digestibility of the nutrients, the expected growth rates and the expected feed efficiency of a given diet are known (which is the case for most fish producers), the results of the present study demonstrate that the Lys requirement for rainbow trout fry is best expressed in absolute terms (g/kg MBW per d) since the dietary protein level did not influence significantly the absolute Lys requirement estimation. However, if the aforementioned parameters are not known (which is the case for most feed manufacturers), we suggest that Lys requirement be expressed in relative terms. Of the different possibilities, it is best expressed as a percentage of dietary protein since the dietary protein level did not significantly affect the relative Lys requirement estimation expressed in g/100 g protein for the rainbow trout fry in the present study. It would be interesting to undertake similar studies on other fish sizes and species in order to arrive at a consensus concerning the appropriate manner of expressing AA requirements.
The dietary protein levels did not affect the maintenance requirement for Lys in rainbow trout fry. In the present experiment and based on Lys accretion, the Lys requirement for maintenance of rainbow trout fry grown at 14·5–15·5°C was higher (21 (sd 2) mg Lys/kg MBW per d) than the reported value for rainbow trout juveniles (11 mg Lys/kg MBW per d(Reference Rodehutscord, Becker and Pack59)), but similar to the Lys requirement of Atlantic salmon fry (20 mg Lys/kg MBW per d, based on N accretion, or 28 mg Lys/kg MBW per d based on Lys accretion(Reference Abboudi, Mambrini and Ooghe28)) grown at 14·7°C in very similar conditions as the ones of the present study. In the present study, the estimate of the Lys requirement for maintenance in rainbow trout fry is in the range of values reported for terrestrial animals, i.e. pigs (25(Reference Baker, Becker and Norton73), 36(Reference Fuller, McWilliam and Wang34)), rats (34(Reference Said and Hegsted74), 10(Reference Dreyer75), 32(22)) or for man (33(Reference Rose76)). Since the protein requirement for maintenance is considerably higher (about five times) in these terrestrial animals(Reference Fuller, McWilliam and Wang34), it appears that the Lys maintenance requirement represents a much higher part of the protein maintenance requirement in trout fry(65) compared to terrestrial animals.
In conclusion, the present study shows that: (1) the relative Lys requirement of rainbow trout estimated with the BLM increased from 16·8 g/kg DM at LP level (310 g/kg DM) to 23·4 g/kg DM at HP level (469 g/kg DM); (2) the absolute Lys requirement expressed in terms of intake (g/kg MBW per d) and the relative Lys requirement expressed in terms of dietary protein (g/100 g protein) remained unaffected by the digestible protein content in the diet; (3) both the model and the response criterion chosen had a considerable impact on the relative Lys requirement; (4) the digestible protein content did not affect the Lys requirement for maintenance (21 mg Lys/kg MBW per d).
Acknowledgements
The authors thank Marc Michotte for expert technical assistance and Yves Beckers (Faculté universitaire des Sciences agronomiques de Gembloux, Gembloux, Belgium) for the use of the bomb calorimeter. X. R. designed the study. N. B. and B. G. did the data analysis. C. D. and S. D. S. did the AA analysis. N. B., X. R., Y. L. and T. A. contributed to the drafting of the paper. There are no financial or other contractual agreements that might cause conflicts of interest or be perceived as causing conflicts of interest. The authors are grateful to the Université catholique de Louvain for funding this project and to the helpful remarks of the anonymous referees.














