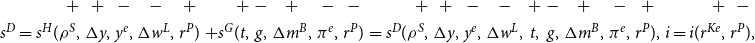2.1 Institutional balances

For the collective private household, H, at the current price level, P, nominal saving, Ps ^H , covers gross nominal investment, Pi, the holding of all newly supplied central bank issue, ΔM ^B , and the increment to the privately held portion of newly issued government debt, ΔD ^GP .

(1) \begin{align} P s^{H}=Pi+{\unicode{x0394}} M^{B}+{\unicode{x0394}} D^{GP}. \end{align}

${\unicode{x0394}} M^{B}$ is the period change in the monetary base. On the income side, H earns nominal, net factor income, Py, where y is the net volume of output of products. It also earns income from the creation of liquid assets, or money, by the private financial sector, which is the difference between the changes in money supply and the monetary base: ${\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B}$ . Finally, it earns debt service from the government at long maturity nominal yield $R^{G}$ . So H’s total nominal income must balance with H’s expenditures on consumption, assets and tax:

(2) \begin{align} P y+\left({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B}\right)+R^{G}D_{0}^{GP}=P c+P s^{H}+T=P c+\left(P i+{\unicode{x0394}} M^{B}+{\unicode{x0394}} D^{GP}\right)+T \end{align}

To complete the corresponding balance from the perspective of the government we need its incomings, which include overall debt increases (the sale of bonds to both the private sector and the central bank), ΔD ^G = ΔD ^GP +ΔD ^GCB , and central bank profits. We assume the central bank’s activities, including its money printing, incur negligible fixed and marginal cost. Its accounting profits, $\sqcap ^{CB}$ , therefore include seigniorage and central bank portfolio earnings, which here include only government bond returns: $\sqcap ^{CB}={\unicode{x0394}} M^{B}+R^{G}D_{0}^{GCB}$ .

Government outgoings comprise spending on products, G, and debt service at nominal yield R ^G . Equating incomings with outgoings we have:

(3) \begin{align} {\unicode{x0394}} D^{G}+\left({\unicode{x0394}} M^{B}+R^{G}D_{0}^{GCB}\right)+T=G+R^{G}D_{0}^{G}. \end{align}

Note, first, that ΔD ^G −ΔD ^GCB = ΔD ^GP in (3). Assume that the central bank implements “unconventional monetary policy” or quantitative easing, and so it prints money to acquire (without necessarily monopolising) government debt ( ${\unicode{x0394}} D^{GCB}={\unicode{x0394}} M^{B}$ ). These modifications allow us to substitute the adapted (3) for ΔD ^GP , in (2), with the result that:

\begin{equation*} P y+({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B})+R^{G}D_{0}^{GP}=P c+P i+T+{\unicode{x0394}} M^{B}+(G-T)+R^{G}D_{0}^{GP}-{\unicode{x0394}} M^{B}-{\unicode{x0394}} M^{B}. \end{equation*}

Eliminating internal exchanges, this simplifies to the expenditure identity in nominal terms, which equates nominal income, from the supply of products and new money, to total expenditure:

(4) \begin{align} P y+{\unicode{x0394}} M^{S}=GDP=P c+P i+G .\end{align}

2.2 Financial equilibrium

From (1) and (2) the source and distribution of nominal private saving is:

(5) \begin{align} P s^{H}=P y+\left({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B}\right)+R^{G}D_{0}^{GP}-T-P c=P i+{\unicode{x0394}} M^{B}+{\unicode{x0394}} D^{GP} .\end{align}

But real private consumption, c, and real investment, i, are both behavioural. Real private consumption is linked, in turn, to real private saving, which is what we formulate here. It depends on current, real private income, y, expected future real income, $y^{e}$ , the increment to the real wealth of the lower 90% of households by income, ${\unicode{x0394}} w^{L}$ , and the real, long maturity rate of return on portfolio assets, $r^{P}$ Footnote ¹³ :

(6) \begin{align} s^{H}=\left(a_{0}^{S}+\rho ^{S}\right)+a_{1}^{S}\,\left(y_{0}+{\unicode{x0394}} y\right)-a_{2}^{S}\,y^{e}-a_{3}^{S}{\unicode{x0394}} w^{L}+a_{4}^{S}\,r^{P}\, ,\end{align}

where ρ ^S is a shifter to represent the extent to which consumption is restricted by pandemic shutdowns and therefore real saving may be temporarily enlarged. The emphasis on the change in real wealth of the lower 90% of households reflects the fact that these households’ dominant asset is illiquid property. When the wealth embodied in this property rises it is well established that their consumption rises and their saving from disposable income declines. Very high-income households manage more liquid and diversified portfolios with smoothed consumption less affected by portfolio value changes (Luc et al., Reference Luc, Lamarche and Savignac2015). As we assume in the next section, a rise in their wealth, Δw ^H , affects their portfolio demand for money.Footnote ¹⁴

Real, net investment requires the issuance of private, long maturity, debt instruments. It depends positively on the expected real rate of return on capital net of depreciation, $r^{Ke}$ , and negatively on the real rate of return on long maturity assets in the collective portfolio, r ^P :

(7) \begin{align} i=a_{0}^{i}+a_{1}^{i}\,r^{Ke}-a_{2}^{i}\,r^{P}\,\hspace{0pt} \end{align}

From (4) nominal government saving is equal to its debt retirement, and private saving is from (5). Total nominal saving by source in the current period then emerges as nominal GDP (= Py + ΔM ^S ) less private consumption and government expenditure:

(8) \begin{align} P\left(s^{H}+s^{G}\right)& =\left[P y+\left({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B}\right)+R^{G}D_{0}^{GP}-T-P c\right]+\left[-{\unicode{x0394}} D^{G}\right] \nonumber\\& =\left[P y+\left({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B}\right)+R^{G}D_{0}^{GP}-T-P c\right]+\left[\left(T-G\right)+{\unicode{x0394}} M^{B}-R^{G}D_{0}^{GP}\right] \nonumber\\& =\left(P y+{\unicode{x0394}} M^{S}\right)-P c-G .\end{align}

The total saving on its LHS must be equal to the distribution of this saving—private acquisitions of physical capital (Pi), newly printed money (ΔM ^B ) and government debt, as well as government saving that takes the form of retiring its own debt:

(9) \begin{align} P\left(s^{H}+s^{G}\right)=\left(P y+{\unicode{x0394}} M^{S}\right)-P c-G=P i+{\unicode{x0394}} M^{B}-{\unicode{x0394}} D^{GCB}=Pi .\end{align}

Since the monetary expansion finances only the non-exclusive purchase by the central bank of newly issued government debt, we have, as in the previous section, ΔM ^B = ΔD ^GCB , and so (9) simplifies to the expenditure identity (4). From (2) we have that investment and consumption sum to disposable income, or the disposal identity for the private household: $P y+({\unicode{x0394}} M^{S}-{\unicode{x0394}} M^{B})+R^{G}D_{0}^{GP}=P c+P s^{H}+T$ . Using this to substitute for Pc in (9), we have:

\begin{equation*} P s^{H}-P i=G-T-{\unicode{x0394}} M^{B}+R^{G}D_{0}^{GP}=-P s^{G}={\unicode{x0394}} D^{G}. \end{equation*}

Then substituting the behavioural relationships for saving and investment on the LHS we have the financial market equilibrium condition:

\begin{equation*} \begin{array}{l} P\left[\left(a_{0}^{S}+\rho ^{S}\right)+a_{1}^{S}\,\left(y_{0}+{\unicode{x0394}} y\right)-a_{2}^{S}\,y^{e}-a_{3}^{S}{\unicode{x0394}} w^{L}+a_{4}^{S}\,r^{P}\right]-P\left[a_{0}^{i}+a_{1}^{i}\,r^{Ke}-a_{2}^{i}\,r^{P}\,\right]\\ \quad =G-T-{\unicode{x0394}} M^{B}+R^{G}D_{0}^{GP} \end{array} \end{equation*}

from which we can solve for the real yield on the private portfolio. Before doing so, however, we need to link the nominal yield on government debt to the real private portfolio yield. These differ by the safe asset discount factor, γ<1, and expected inflation, so that

(10) \begin{align}R^G = \gamma r^P + \pi^e.\end{align}

With this substituted in the final term we can divide through by the price level and express real variables in lower case. We can then place the two sources of saving on the LHS and investment on the RHS, expressing financial market equilibrium condition $s^{H}+s^{G}=i$ in terms of exogenous variables:

(11) \begin{align} & \left[\left(a_{0}^{S}+\rho ^{S}\right)+a_{1}^{S}\,\left(y_{0}+{\unicode{x0394}} y\right)-a_{2}^{S}\,y^{e}-a_{3}^{S}{\unicode{x0394}} w^{L}+a_{4}^{S}\,r^{P}\right]+\left[t-g+{\unicode{x0394}} m^{B}-d_{0}^{GP}\gamma r^{P}-d_{0}^{GP}\pi ^{e}\right] \nonumber\\& \quad =\left[a_{0}^{i}+a_{1}^{i}\,r^{Ke}-a_{2}^{i}\,r^{P}\,\right] \end{align}

An algebraic solution for the real portfolio yield, r ^P , is readily obtained in terms of all the exogenous variables and the change in the real value of the monetary base, Δm ^B . We offer this in an Appendix. Before interpreting this relationship, however, we note our intention that the change in the real monetary base should be endogenous, and so we require behaviour for it.

2.3 The market for money

The period increment to the real money supply, Δm ^S , must equal the increment to the demand to hold real money balances, Δm ^D , which meet both portfolio and transactions demand:

(12) \begin{align} {\unicode{x0394}} m^{D}={\unicode{x0394}} m^{P}+{\unicode{x0394}} m^{T}={\unicode{x0394}} m^{S} .\end{align}

Here real transaction demand, m ^T , is proportional to nominal output, ${\unicode{x0394}} m^{T}\approx \phi {\unicode{x0394}} y$ , so the nominal equivalent is ${\unicode{x0394}} M^{T}=\phi (Py-P_{0}y_{0})$ . We then require behaviour for the increment to portfolio money demand, Δm ^P . For this, we posit that the share of money in portfolios depends positively on the level of general volatility, v. This dependence arises from the well-known tendency for portfolios to rebalance toward safe assets, usually cash and short maturity government bonds, the more risky higher-returning, private assets become. Portfolio money holdings also depend on the change in the size of the high-income wealth portfolio, Δw ^H , measured as its purchasing power over goods, and the real yield spread between money and productive assets: $r^{Me}-r^{P}$ , where the expected real yield on money is $r^{Me}=P/P^{e}-1=-\pi ^{e}$ .

The dependence on real wealth is here intended to capture the difference in recent decades between the growth rates of real output and the purchasing power of the high-income real wealth portfolio at consumer product prices. A shock to real high-income wealth, w ^H , in the absence of a corresponding shock to real output and low-income wealth, w ^L , is therefore suggestive of a shift to greater inequality. It is our assumption that, where the wealth shock advantages high-income earners, it suggests a larger sized wealth portfolio and hence increased need for portfolio money to balance the liquid share (Agarwal et al., Reference Agarwal, Chua, Ghosh and Song2020; Lenza and Slacalek, Reference Lenza and Slacalek2019; Wei et al., Reference Wei, Wu and Zhang2019; Jawadi et al., Reference Jawadi, Sousa and Traverso2017).

To represent these behaviours in the portfolio money equation we adopt terms in general volatility, high-income real wealth and the spread between the real rates of return on money and returning assets:

(13) \begin{align} {\unicode{x0394}} m^{P}& =a_{0}^{P}+a_{1}^{P}v+a_{2}^{P}{\unicode{x0394}} w^{H}+a_{3}^{P}\left(r^{Me}-r^{P}\right)=a_{0}^{P}+a_{1}^{P}v+a_{2}^{P}{\unicode{x0394}} w^{H}-a_{3}^{P}\left(r^{P}+\pi ^{e}\right) \nonumber\\& =a_{0}^{P}+a_{1}^{P}v+a_{2}^{P}{\unicode{x0394}} w^{H}-a_{3}^{P}R^{P} ,\end{align}

where R ^P is the nominal yield on long maturity assets. Thus, we have the conventional dependence of the demand for real money balances on the nominal yield.Footnote ¹⁵ We can therefore write the change in the real money supply that meets demand as:

(14) \begin{align} {\unicode{x0394}} m^{D}={\unicode{x0394}} m^{S}=a_{0}^{P}+a_{1}^{P}v+a_{2}^{P}{\unicode{x0394}} w^{H}-a_{3}^{P}\left(r^{P}+\pi ^{e}\right)+\phi {\unicode{x0394}} y \end{align}

To complete the determination of the real equilibrium yield, r ^P , we require an expression for the change in the real monetary base, Δm ^B , to substitute into (11). This is the real value of period central bank purchases $(M^{B}/P-M_{0}^{B}/P_{0})\approx {\unicode{x0394}} M^{B}/P={\unicode{x0394}} m^{B}$ , where M ^B and m ^B are the nominal and real measures. The corresponding totals of safe, liquid assets available are the money supplies, M ^S and m ^S , which are traditionally larger than the monetary base by a factor equal to the money multiplier. This factor depends negatively on private cash holdings relative to deposits, and commercial bank liquidity reserves, both of which tend to rise when there is an increase in general financial market volatility, v. Here we achieve this effect linearly:

(15) \begin{align} {\unicode{x0394}} m^{S}-{\unicode{x0394}} m^{B}=a_{0}^{M}-a_{1}^{M}\nu,\ \text{so that}\ {\unicode{x0394}} m^{B}={\unicode{x0394}} m^{S}-a_{0}^{M}+a_{1}^{M}\nu .\end{align}

Expanding for Δm ^S from (14) then yields:

(16) \begin{align} {\unicode{x0394}} m^{B} & ={\unicode{x0394}} m^{P}+{\unicode{x0394}} m^{T}-a_{0}^{M}+a^{M}v=a_{0}^{P}+a_{1}^{P}v+a_{2}^{P}{\unicode{x0394}} w^{H}-a_{3}^{P}\left(r^{P}+\pi ^{e}\right)+\phi {\unicode{x0394}} y-a_{0}^{M}+a_{1}^{M}v \nonumber\\& =\left(a_{0}^{P}-a_{0}^{M}\right)+\left(a_{1}^{P}+a_{1}^{M}\right)v+a_{2}^{P}{\unicode{x0394}} w^{H}-a_{3}^{P}\left(r^{P}+\pi ^{e}\right)+\phi {\unicode{x0394}} y .\end{align}

Substituting this for Δm ^B in (11), yields the equilibrium real private portfolio rate of return, as detailed in the Appendix. The signs of the coefficients indicate that this relationship has the following structure:Footnote ¹⁶

(17) \begin{align} \begin{array}{rcccccccc} - & - & + & + & -& -& +& +& +\\ r^{P}=r^{P} [{\unicode{x0394}} y, & \rho ^{S}, & \left(g-t\right), &{\unicode{x0394}} w^{L}, & {\unicode{x0394}} w^{H},&v,& \pi ^{e}, & y^{e}, & r^{Ke} ] \end{array} .\end{align}

Bearing in mind that we seek the effects on the endogenous real yield of changing one exogenous variable while keeping all the others constant, we can readily explain the signs of these coefficients. The first, the real output shock, is negative because more real income shifts saving to the right and reduces the equilibrium yield. The second, a boost to saving because of consumption restrictions or taste changes, is negative because it shifts saving supply so as also to reduce the equilibrium yield. The third, the fiscal response indicated by the size of the fiscal deficit, is positive because of the usual crowding out effect of increased government expenditure raises $r^{P}$ . The fourth indicates that a positive shock to the real wealth of the lower 90% of households raises consumption, reduces saving and therefore raises the real yield. The fifth concerns the real wealth of the top 10% of households. Their restoration of liquidity balance requires a rise in portfolio money, which constrains investment in returning assets and therefore reduces the issue of assets, raises their prices and reduces their yields.

The sixth, which is general financial volatility, affects the real yield negatively, by two mechanisms. First, since it induces a retreat from investment in returning assets that reduces bond or equity issues, it raises asset prices and reduces the real yield. Second, by inducing cash holding, increased volatility raises the real monetary base relative to the chosen level of overall real money balances, which implies greater cash accumulation by commercial banks and households and hence less investment, reducing the real yield. The seventh, the expected rate of inflation, affects the real yield positively, again via two mechanisms. First, greater expected inflation raises the government’s nominal debt service burden and so reduces its own saving or raises the fiscal deficit. Second, greater expected inflation raises the opportunity cost of holding portfolio money, raising investment in physical capital and hence the demand for loanable funds. The eighth, the level of expected future real income, $y^{e}$ , is positive because a consumption-smoothing household reduces saving if expected future income rises. And the ninth, the effect of an increment to the expected real net yield on physical capital is to raise investment in such capital, which therefore raises the market real yield.

Figure 1. Global financial and money markets with a UMP money Shock.

Note: An unconventional (UMP) monetary expansion is represented. The saving, investment and money demand expressions are from (11) and (14) in the text, which have the following behaviour:

\begin{align*} \begin{array}{rcccc} +&+&-&-&+ \\ s^{D}=s^{H}(\rho ^{S},& {\unicode{x0394}} y,&y^{e},&{\unicode{x0394}} w^{L},&r^{P}) \end{array} \begin{array}{rcccc} +&-&+&-&- \\ +s^{G}(t,&g,&{\unicode{x0394}} m^{B},&\pi ^{e},&r^{P}) \end{array}\begin{array}{rcccccccc} +&+&-&-&+&-&+&-&+\\ =s^{D}(\rho ^{S},& {\unicode{x0394}} y,&y^{e},&{\unicode{x0394}} w^{L},&t,&g,&{\unicode{x0394}} m^{B},&\pi ^{e},&r^{P}) , \end{array}\begin{array}{rc} +&-\\ i=i(r^{Ke},&r^{P}) , \end{array} \end{align*}

\begin{align*} \begin{array}{rcccc} +&+&+&-&-\\ m^{D}=m_{0}^{D}+{\unicode{x0394}} m^{D}({\unicode{x0394}} y,&{\unicode{x0394}} w^{H},&v,&\pi ^{e},&r^{P}). \end{array} \end{align*}

The rightward shift in the saving curve is here due to the central bank’s acquisitions, which reduce the long maturity yield and raise real money balances, $m^{S}\uparrow$ . These acquisitions are financed by a nominal monetary expansion, $M^{B}\uparrow$ . From this shock alone, inflation only results if $\hat{P}=\hat{M}^{B}+\hat{\mu }-\hat{m}^{S}\gt 0$ , where μ is the money multiplier—that is, if the nominal expansion exceeds that in real money balances.

2.4 An almost conventional graphical representation

The financial equilibrium condition (11) suggests a conventional, graphical depiction of the financial market, or the market for loanable funds. The money market equilibrium condition (14) also suggests a graphical representation. Both are included in Figure 1, which depicts two interdependent asset markets: the global market for long-maturity assets and the corresponding global market for liquid assets that we call money. The vertical axis in both diagrams represents the real yield on the private, collective portfolio of primarily long maturity assets, $r^{P}$ , while the horizontal axes represent the levels of real saving, real investment and real money balances. In the market for money, we represent expected inflation as one of a number of shifters of the money demand curve, so that the two vertical axes are common.

In considering the effects of shocks graphically, it is best to begin with displacements of the two financial market curves, as indicated by the shifters noted below the diagram. These result in a changed real yield on the collective asset portfolio, $r^{P}$ , which then represents the opportunity cost of holding money in that portfolio. Real money balances then emerge from the level of this yield and the real money demand function. The figure illustrates a UMP expansion from which a resulting inflation is likely but not guaranteed. The ambiguity stems from the central bank’s acquisition of long maturity assets raising their price and suppressing their yield, causing a rise in the demand for real money balances. For an inflation to eventuate the associated nominal monetary expansion that finances the bond purchases must be proportionally larger.

Of course, we can imagine many other shocks to the shifting variables indicated at the foot of the diagram. One of these shocks is to inflation expectations. If agents expect deflation it further weighs against the monetary expansion, making deflation more likely in spite of it. To quantify this represented behaviour, and to see its effect on actual inflation, we require a corresponding formulation for real money balances.

2.5 The increment to the real monetary base

The period addition to the level of the real monetary base, given the exogenous conditions, is readily constructed by substituting (17) for $r^{P}$ into (16). We offer the complete solution in the Appendix. Its determinants can be signed as:

(18) \begin{align} \begin{array}{rcccccccc} +& +& -& -& +& +& -& -& -\\ {\unicode{x0394}} m^{B}= [{\unicode{x0394}} y, & \rho ^{S}, & \left(g-t\right), & {\unicode{x0394}} w^{L}, &{\unicode{x0394}} w^{H}, & v,& \pi ^{e},&y^{e},&r^{Ke}] \end{array} .\end{align}

Most significantly, relative to the corresponding expression for real, full money balances, this expression has a stronger positive response to general volatility.

Again, we can explain the emerging signs of the coefficients.Footnote ¹⁷ That of Δy is positive, since a rise in output also raises saving and reduces the real yield, which accommodates higher real money balances. A rise in the level of real transactions demand for money relative to real income bolsters this effect. That of consumption restriction, and therefore a rise in the saving shifter, ρ ^S , is also positive, since this also reduces the real yield and hence the opportunity cost of holding money. That of the fiscal deficit is negative. If the government deficit increases, the real yield rises, raising the opportunity cost of holding money and so implying decreased real money balances. A positive shock to the real wealth of the lower 90% of households raises consumption, reduces saving and therefore raises the real yield, raising the opportunity cost of holding money and reducing real money balances. A corresponding shock to the real wealth of the top 10% of households requires the restoration of their portfolio’s liquidity balance and therefore a rise in portfolio money. This constrains investment in returning assets and therefore reduces the issue of new debt or equity, raising their prices and reducing their yields.Footnote ¹⁸

That of general volatility, v, is positive. This reflects both the effect of volatility in discouraging investment and so reducing real yields and its direct effect on portfolio management that takes for form of a retreat to money holding. In the case of the period change to the real monetary base, it also reflects the tendency for worker households to hold more cash and commercial banks to hold greater liquidity reserves. That of $\pi ^{e}$ is negative. Beyond the effect on the real yield discussed previously, a positive shock to expected inflation increases the opportunity cost of holding money, causing a leftward shift in Figure 1’s real money demand curve. That of $y^{e}$ is negative, since if higher future income is expected, current saving decreases and the real yield rises, implying reduced real money balances. Finally, that of $r^{Ke}$ is negative, since investment optimism raises real investment demand. If current output stays constant, there is a higher real yield and this requires reduced real money balances. We can now assess the implications of these analytical results for future inflation rates.

2.6 The determinants of inflation

From (17) and (18) we have the signed determinants of the real long rate and the period change in the real monetary base. These pin down the real variables that represent the purchasing power of the monetary base over products. However, the actual rate of inflation, π, depends on the path of the nominal money supply, M ^S , and from a policy standpoint, on the path of the nominal monetary base, M ^B . By definition, $M^{S}=P m^{S}$ , but also $M^{B}=P m^{B}$ , so that $\pi =\hat{P}=\hat{M}^{B}-\hat{m}^{B}$ . Central banks can only affect $\hat{M}^{B}$ , and the period increment to the real monetary base is endogenous, from (18). Thus inflation depends on the rate of exogenous monetary expansion, $\hat{M}^{B}$ , and the endogenous change in the real monetary base:

\begin{align*} \pi \cong \frac{{\unicode{x0394}} P}{P_{0}}=\frac{{\unicode{x0394}} M^{B}}{M_{0}^{B}}-\frac{{\unicode{x0394}} m^{B}}{m_{0}^{B}}\cong \hat{M}^{B}-\hat{m}^{B}\left({\unicode{x0394}} y,\rho ^{S},\left(g-t\right),{\unicode{x0394}} w^{L},{\unicode{x0394}} w^{H},\,v,\, \pi ^{e},y^{e},r^{Ke}\right) .\end{align*}

This allows the consolidation and signing of determinants as:

(19) \begin{align} \begin{array}{rcccccccc} +\quad +\quad -& -& +& -& -& +& +& +\\ \pi =\hat{P}[\hat{M}^{B},\left(g-t\right),&{\unicode{x0394}} y,&\rho ^{S},&{\unicode{x0394}} w^{L},&{\unicode{x0394}} w^{H},&v,&\pi ^{e},&y^{e},&r^{Ke} ]\, \end{array} ,\end{align}

making clear that fiscal and monetary expansions are unambiguously inflationary as is a supply side contraction. Offsetting deflationary forces include a low-skill real wage decline, associated, for example, with technical change disadvantaging the low-skilled, and a similarly sourced high-skill wage increase. But then, the relaxation of demand restrictions, and declining output volatility would add to inflation, as would a return to optimism about future inflation, output and rates of return.Footnote ¹⁹

Apart from output recovery and the trend toward declines in real, low-skill wages, most of these deflationary drivers have not been observed for periods long enough for empirical testing. The global trend toward slower productivity and the widening of the real wage gap between the skilled and the low-skilled, has surely been a factor in the tendency to deflation in the years prior to the pandemic.Footnote ²⁰ Our focus here, however, is on the investigation of the relative strengths of the dependencies on monetised fiscal expansions and short run output changes, which are addressed in Section 3.

2.7 Implications of the shutdown and macro policy shocks for real yields and inflation

Consider the implications of combined fiscal and monetary expansions experienced worldwide during the COVID-19 epidemic. Unfortunately, ambiguity is pervasive. Even the primary shutdown shocks are ambiguous for inflation. The health policy response to the pandemic restricts both output and consumption, so the inflationary effects of output restrictions are offset, at least to some extent, by associated consumption restrictions:

\begin{equation*} \begin{array}{c} \,\qquad- \qquad-\\ \pi =\hat{P}[{\unicode{x0394}} y\downarrow ,\rho ^{S}\uparrow ] \end{array} .\end{equation*}

The effects of the pandemic on wealth and its distribution tend to suggest, at least thus far, that general housing wealth has declined while high-income portfolio wealth has increased, as suggested by persistently high equity prices. These are both deflationary forces, the first because less housing wealth causes less consumption and the second because increased portfolio wealth raises the demand for money holding and hence real money balances. By further opposing the inflationary effects of the supply shock, these additions therefore do nothing to address the ambiguity. Indeed, the outcome is made even murkier by the addition of a likely increase in general financial volatility, due possibly to the weakened accuracy of forecasts during the pandemic. This acts to cause a private retreat to money holding and conservative prudential behaviour by commercial banks, all of which is also deflationary:

\begin{equation*} \begin{array}{ccccc}\qquad -&\!\!\!\! -&\!\!\!\! +&\!\!\!\! -&\!\!\!\! -\\ \pi =\hat{P}[{\unicode{x0394}} y\downarrow ,&\rho ^{S}\uparrow , &{\unicode{x0394}} w^{L}\downarrow ,&{\unicode{x0394}} w^{H}\uparrow ,&v\uparrow ] \end{array} .\end{equation*}

When we add the macro policy changes, which include historically large fiscal and monetary expansions, since these both contribute to inflation, it is more likely that the net outcome includes some inflation, though ambiguity persists:

\begin{equation*} \begin{array}{ccccccc} \qquad+& \!\!\!\! +&\!\!\!\! -&\!\!\!\! +&\!\!\!\! -&\!\!\!\! -&\!\!\!\! -\\ \pi =\hat{P}[\hat{M}^{B}\uparrow ,&(g-t)\uparrow ,&{\unicode{x0394}} y\downarrow ,&{\unicode{x0394}} w^{L}\downarrow ,&{\unicode{x0394}} w^{H}\uparrow ,&\rho ^{S}\uparrow ,&v\uparrow ] \end{array} .\end{equation*}

Yet, key determining factors are whether expectations over inflation, future output and future returns are optimistic or pessimistic. If they remain pessimistic, they could cause deflation pressure that could, at least in theory, be large enough to offset the monetary and fiscal expansions:

\begin{equation*} \begin{array}{ccc} \qquad +&\!\!\!\! +& \!\!\!\! + \\ \pi \downarrow =\hat{P}[\pi ^{e}\downarrow ,&y^{e}\downarrow ,&r^{Ke}\downarrow ] \end{array} .\end{equation*}

Thus, inflation depends not only on the rate of expansion of the nominal monetary base, but also on the extent to which the primary shocks and their consequences for the wealth distribution and volatility, and the macro policy responses, have a net tendency to reduce real money balances. This leaves the scale of any inflationary response to pandemic shocks indeterminate, at least without numerical analysis.Footnote ^21,22

3.1 The econometric model

We estimate a structural panel vector auto-regression model using data from the Jordà-Schularick-Taylor Macrohistory Database, which suits our purpose because it covers a long time horizon that includes substantial shocks and associated fiscal policy changes. Indeed, during WWII many advanced economies experienced increases in sovereign debt that were of a similar magnitude to those during the recent pandemic.

The data over the entire period, since 1870, are illustrated in Figure 2. There are three particularly striking cases: Japan, Australia and the United States. For Japan, the public debt to GDP ratio exceeded two at the height of WWII and this coincided with a significant increase in broad money growth. By contrast, in the latter part of the sample, the mid-2000s saw Japan’s debt to GDP ratio approach 2.5, without any corresponding monetary expansion.Footnote ²⁴ By 2020, however, Japan’s broad money was expanding rapidly. In that year it grew 7.3%: approximately five percentage points higher than the rise in the previous year.Footnote ²⁵ A similar pattern is seen for the United States, where both the debt-to-GDP ratio and the growth rate of the broad money supply spiked during WWII. In 2020, the US money supply grew by 17.2%, an unprecedented rate since the 1940s. For Australia, debt levels rose both before and during WWII, whereas the broad money stock grew significantly during, but not immediately after, the war. Together, these patterns highlight the particular relevance of the 1940s as a reference period for our assessment of the post-pandemic recovery. Our empirical exercise uses the inflationary outcomes of the WWII period to infer likely changes associated with the recent pandemic, given similarities in the macroeconomic environments of many advanced economies in the two periods.

Figure 2. Pattern of real GDP growth, public debt to GDP ratio, broad money ratio and inflation in Australia, Japan and the US, (1870–2016).

Source: Constructed based on data from “Jordà-Schularick-Taylor Macrohistory Database”. The shaded bars indicate periods with output shocks: 1914–1918 (World War I), 1937–1950 (World War II), and 1973–1973 (1973 Oil Crisis).

The empirical model we employ is designed to test the relative strengths of the key determinants of inflation considered in the previous section, as summarised in equation (19). Given data limitations, we estimate a reduced system containing six variables from the microhistory database: real GDP, government revenue, public debt, private debt, broad money, and consumer price inflation. The use of a structural vector autoregression (SVAR) allows for the endogenous treatment of the inflation rate and an assessment of the role played by the key inflation drivers identified in (19). It also allows for the quantification of dynamic effects of shocks in system variables.Footnote ²⁶

In what follows, i indexes the countries in the sample and t indexes time (all data is at the annual frequency). The countries included in the database are Australia, Belgium, Canada, Denmark, Finland, France, Germany, Italy, Japan, Netherlands, Norway, Portugal, Spain, Sweden, Switzerland, UK, and USA. We first generate impulse response functions for the entire sample period (1870–2016) and then focus our attention on the WWII period. While the patterns we uncover are present for both sample periods, the magnitude of the effects are typically larger for the WWII period. Formally, the reduced-form model we estimate is

(20) \begin{align} y_{it}=a_{0}+A_{1}y_{i,t-1}+A_{2}y_{i,t-2}+\gamma _{i}+u_{i,t} ,\end{align}

where the matrices $A_{1}$ and $A_{2}$ comprise the estimated parameters of the system, $a_{0}$ is a vector of constants, $\gamma _{i}$ is a vector of country fixed effects and $u_{i,t}$ is a vector of reduced-form errors (which are linear combinations of the structural errors). The dependent variable, $y_{i,t}$ , is a vector of endogenous variables for country i at time t. Specifically,

(21) \begin{align} y_{i,t}=\left[g_{i,t}^{Y},g_{i,t}^{G},d_{i,t}^{G},d_{i,t}^{P},g_{i,t}^{M},\pi _{i,t}\right] ,\end{align}

where $g_{i,t}^{Y}$ is the real GDP growth rate, $g_{i,t}^{G}$ is the government revenue growth rate, $d_{i,t}^{G}$ is the growth rate of government debt, $d_{i,t}^{P}$ is the growth rate of private debt, $g_{i,t}^{M}$ is the growth rate of broad money and $\pi _{i,t}$ is the CPI inflation rate. All variables in $y_{i,t}$ are computed as year-on-year growth rates.

We assess the stationarity of the variables in the system via unit root tests, including the Augmented Dickey-Fuller Test, Im-Pesaran-Shin Test, Levin-Lin-Chu Test, and Phillips–Perron Test. For each variable, the null hypothesis of non-stationarity is rejected at the 1% significance level, suggesting that all variables in the SVAR model are stationary.Footnote ²⁷

We estimate this model on the balanced panel of 17 countries for the two aforementioned sample periods. Our final dataset contains growth rates of the macroeconomic variables in equation (21) across the 17 countries spanning the years 1870–2016. These countries have always been amongst the world’s most advanced, and so have had similar institutional structures and macro behaviour. The advantage of estimating a multi-country SVAR is therefore that it provides a significantly larger sample size compared to estimating the model using data from a single country, thereby increasing the precision of our estimates.Footnote ²⁸ The model’s lag order is selected using the Schwarz Information Selection Criterion (SIC), which yields a specification with two lags.

To identify the parameters of the SVAR, we impose a series of exclusion restrictions on the variables in the system. We rely on the theory in Section 2 to synthesise these identification restrictions.Footnote ²⁹ Specifically, following shocks to real GDP growth, government revenue growth adjusts simultaneously due to associated changes in tax revenue that occur on stable tax bases. Additionally, public debt and broad money growth also change simultaneously, reflecting the monetary financing of fiscal deficits. Inflation rates, public debt growth rates, and private debt growth rates also respond to changes in all other variables with a one-year lag. Under this set of identification assumptions, we estimate the Orthogonalized Impulse Response functions (OIRs) that identify the dynamic effects of shocks to one variable on the other variables in the system.Footnote ³⁰

3.2 The long term results

The interdependencies amongst real GDP growth rates, the public debt growth rates (which are proxies for fiscal expansions), broad money growth rates and inflation rates in Australia, Japan, and the US, have been noted previously from Figure 2. The positive correlation between public debt growth and broad money growth is further seen in Figure 3 where, for each country, the two variables are plotted against each other and a linear regression line is estimated on each country’s data. The linear regressions all show positive slopes, thus indicating the positive correlation between public debt growth and broad money growth.

Figure 3. Nominal public debt growth vs. nominal broad money growth.

Source: Constructed based on data from “Jordà-Schularick-Taylor Macrohistory Database”.

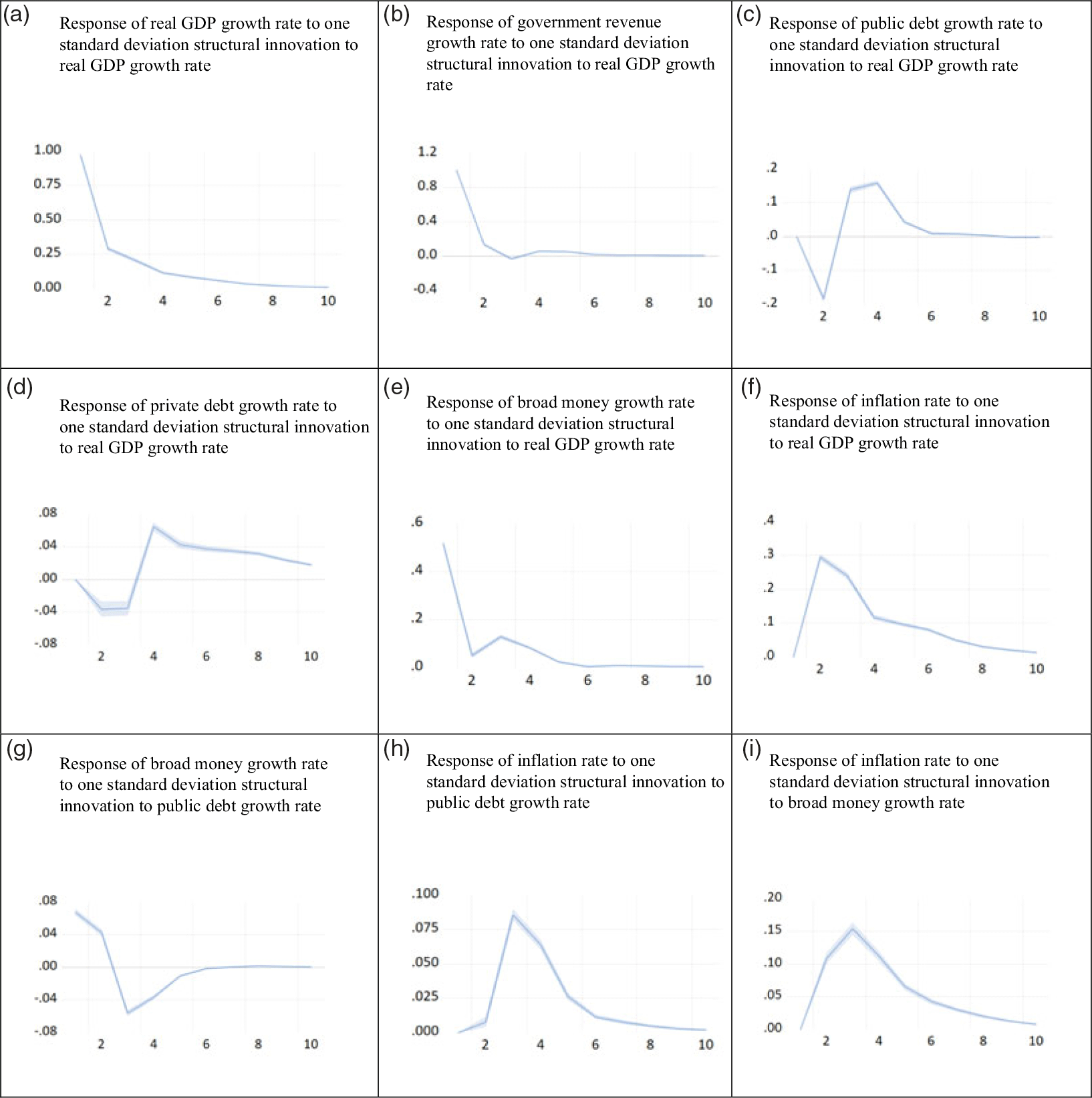
Moving to the formal estimation results, we first present the OIRs for the entire period of 1870–2016 (T = 147) in Figure 4. These show that, when real GDP contracts, government revenues decline, and both public and private debt levels rise. Broad money and inflation both rise when public debt rises, and so inflation rates increase when broad money growth accelerates. When real GDP growth rates fall, there are declines in both broad money growth rates and inflation rates, likely because of long run changes in the transactions demand for money. Superficially, this contrasts with our very short run theoretical analysis in the previous section, where greater product supply relative to the money stock tends to reduce the price level. But it occurs because money growth declines as well, and our theoretical result in (19) is ambiguous when both output and money grow simultaneously. The bottom line, however, is that in the long run inflation has tended to move in the same direction as real GDP growth.Footnote ³¹

Figure 4. Orthogonalized impulse response functions for the full sample period (1870–2016), with 95% confidence intervals.

Note: Each panel shows the orthogonalized impulse response (OIR) function over a ten-year period following a one standard deviation (positive) structural innovation to variables in the SVAR. The blue lines show the impulse response, while the shaded bands represent 95% confidence intervals.

Source: Authors’ estimation of the SVAR model using 1870–2016 data.

3.3 The WWII period

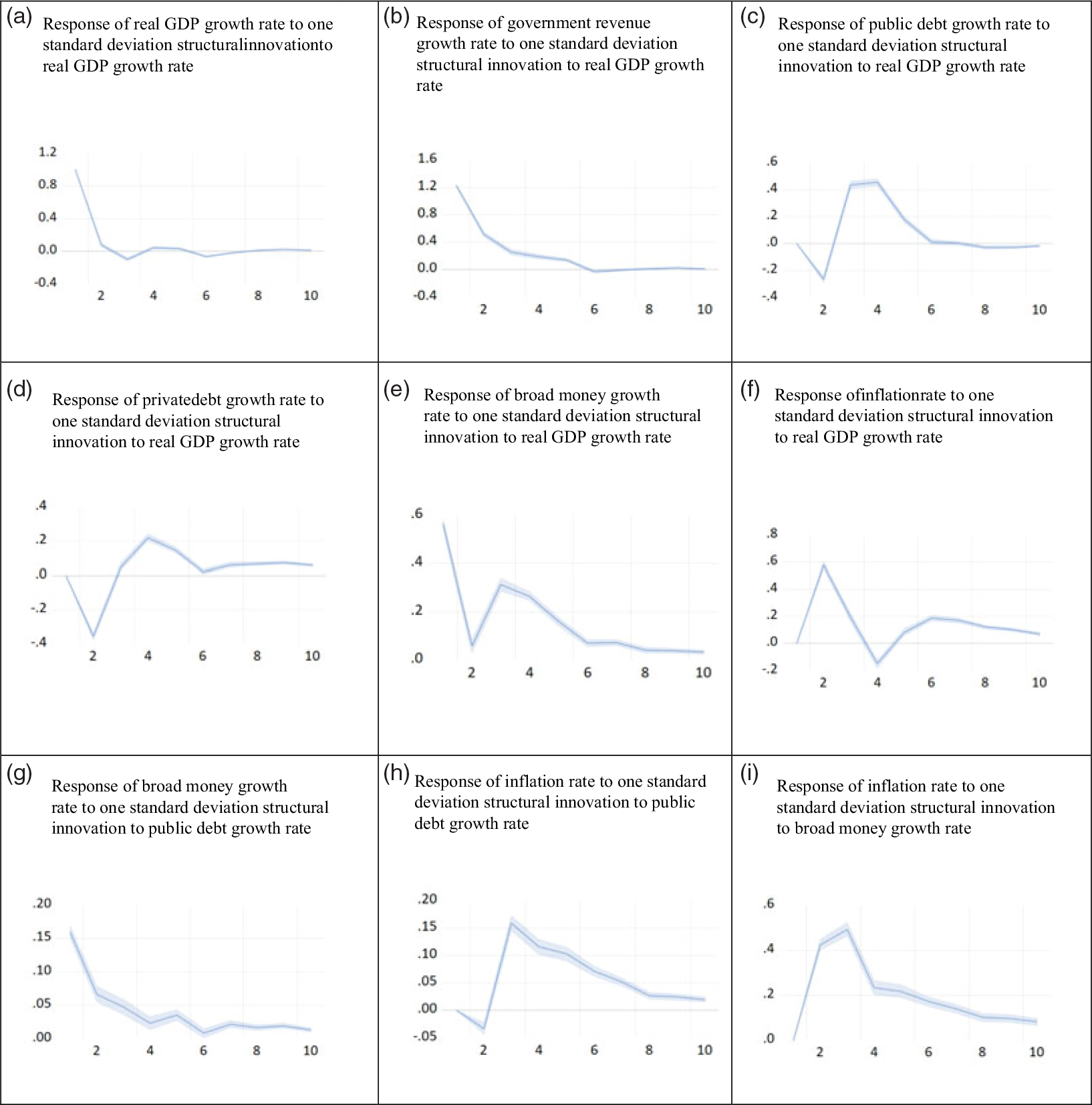
The long run patterns are found to prevail (and are exacerbated) if we limit our attention to the WWII period, during which the volatility levels of the variables in the system were much greater. To explore differences in the dynamics during this period, we re-estimate the model for the period 1937–1950 (T = 14). The OIRs of the SVAR for the WWII period (1937–1950) are presented in Figure 5.Footnote ³² They reveal similar relationships between the macroeconomic variables. In particular, a one standard deviation (SD) increase in the rate of public debt growth is associated with an approximately 0.2 SD increase in the rate of inflation after three years. Interestingly, inflation only seems to increase after two years, suggesting a considerable time lag between the initial public debt shock and the inflation response. Notably, this pattern is similar to the post-pandemic recovery period, during which the stimulus at the onset of the crisis seems only to have materialised in inflation statistics two years later.

Figure 5. Orthogonalized impulse response functions for the WWII period (1937–1950), with 95% confidence intervals.

Note: Each panel shows the orthogonalized impulse response (OIR) function over a ten-year period following a one standard deviation (positive) structural innovation to variables in the SVAR. The blue lines show the impulse response, while the shaded bands represent 95% confidence intervals.

Source: Authors’ estimation of the SVAR model using 1937–1950 data.

Another key result is the persistence of inflation for about eight years after the initial shock, suggesting that government intervention, while essential to avert a deep recession at the outset, may still cast a long shadow during the recovery period. Also notable is the amplified response of inflation to a one SD broad money growth shock. When the model is estimated on the full sample, innovations to broad money growth register approximately as a 0.15 SD increase in inflation after two years. When we focus on the WWII period, this rises to a 0.5 SD inflation increase. Taken together, the historical evidence shows that, consistent with our analysis in Section 2, when real GDP contracts, there are fiscal expansions so that public debt rises, and broad money supply rises as well. There is then upward pressure on the inflation rate. This relationship is of a greater magnitude during the WWII period compared with the entire period (1870–2016), suggesting greater strength when shocks are large and episodic.Footnote ³³

3.4 Forecasting based on the full sample

We conduct three sets of forecasts using the SVAR model estimated from the long-run sample. The three scenarios are: first, a baseline forecast using the estimated model without shocks; second, a forecast that incorporates the real GDP growth rate shocks due to the COVID-19 pandemic crisis; and third, a forecast that incorporates both the real GDP growth rate shocks and the public debt growth rate shocks due to the COVID-19 pandemic crisis. Drawing from the IMF’s forecasts of growth in advanced economies (IMF, 2021a), we specify the real GDP growth rate shocks as −7.1 percentage points, 2.1 percentage points, and 0.9 percentage points, for the years 2020, 2021, and 2022, respectively. Using information from the IMF’s Fiscal Monitor (IMF, 2021b), we specify the associated public debt growth rate shocks as 18 percentage points, 10 percentage points, and 5 percentage points, for the years 2020, 2021, and 2022, respectively.

Figure 6. Inflation rate, actual and forecast, various economies (actual: 2020–2019, forecast: 2020–2026). continued. Inflation rate, actual and forecast, various economies (actual: 2000–2019, forecast: 2020–2026). continued. Inflation rate, actual and forecast, various economies (actual: 2000–2019, forecast: 2020–2026).

Source: Authors’ forecasts based on estimated SVAR model using 1870–2016 data.

Figure 6 presents the inflation forecasts under the three scenarios for each of the 17 countries in our sample. We see that, when an economy experiences both a downturn in its real GDP growth rate and a rise in its public debt growth rate, inflation first declines and then increases to high levels before eventually reverting to the baseline levels. When there is a negative real GDP growth rate shock only, inflation declines significantly but converges back to the baseline trajectory without experiencing a strong pickup. These results suggest that it is mainly the rise in the public debt growth rate, accommodated by monetary expansions (its monetisation), that drives the observed post-crisis inflation surges. This offers strong evidence that monetary and fiscal shocks are comparatively powerful in generating subsequent inflation and that they have been important in driving the observed post-pandemic inflation surge.Footnote ³⁴