Introduction
Zirconia-based ceramics can experience a martensitic transformation between tetragonal and monoclinic phases under the stimulus of heat or external stress.[ Reference Garvie, Hannink and Pascoe 1 ] This transformation occurs rapidly in a crystallographic and reversible manner, and has been extensively studied in large part due to its beneficial effects as a toughening mechanism.[ Reference Hannink, Kelly and Muddle 2 , Reference Marshall, Ratto and Lange 3 ] More interestingly, the large reversible shear strain (~16%) associated with the martensitic transformation makes zirconia-based ceramics promising candidates as shape memory materials.[ Reference Chevalier, Gremillard, Virkar and Clarke 4 , Reference Sun, Huang, Ding, Zhao, Wang, Purnawali and Tang 5 ] Swain[ Reference Swain 6 ] first reported signatures of shape memory behavior in partially stabilized zirconia during thermal treatment in 1986. Reyes-Morel et al.[ Reference Reyes-Morel, Cherng and Chen 7 ] further demonstrated the shape memory effect (SME) and superelasticity (SE) in zirconia ceramics with macroscopic shape deformation and recovery under uniaxial compression in 1988. However, due to their polycrystalline nature, zirconia-based ceramics in bulk form suffer from microcracks along grain boundaries and other permanent structural damage during shape deformation, leading to limited macroscopic strain (<2%) and premature fracture.
The thermoelastic shape memory properties in zirconia-based ceramics are determined by the characteristic martensitic transformation temperatures (M s, M f, A s, A f—martensite start and finish, austenite start and finish, respectively),[ Reference Reyes-Morel, Cherng and Chen 7 ] which can be changed by tuning the concentration of tetragonal phase stabilizers added to zirconia, for example, Y2O3, CeO2, and MgO.[ Reference Scott 8 – Reference Porter and Heuer 10 ] Depending on the test temperature's value relative to the transformation temperatures, shape memory ceramics can exhibit either of two types of behavior: shape memory or SE. The former requires deformation and subsequent heating to trigger shape recovery, while the latter involves the automatic recovery of the shape once a martensite-inducing stress is released.[ Reference Miyazaki and Otsuka 11 ] Depending on doping, the four transformation temperatures can be tuned to permit shape memory ceramics to potentially operate over a wide temperature window, ranging from room temperature to high temperatures that are unavailable to metallic shape memory alloys.[ Reference Lai, Du, Gan and Schuh 12 ] Their characteristics of high strength and transformation stress, large transformation hysteresis, good environmental inertness, and a wide operation temperature window make zirconia-based ceramics promising for various applications in actuation, sensing, and mechanical energy damping.
Though extensive studies of transformation-toughening in zirconia provide a solid fundamental understanding of the reversible martensitic transformation, little effort has been devoted to their shape memory properties in the decades since their first discovery. This is essentially due to the very limited recoverable strain and premature fracture associated with the transformation in polycrystalline samples, which in addition to compromising technologic potential, also interfere with basic research in bulk samples. Recently, Lai et al. sidestepped this longstanding challenge by developing small-volume structures with no or limited grain boundaries, forming oligocrystalline or single-crystal structures.[ Reference Lai, Du, Gan and Schuh 12 ] The absence or reduction of grain boundaries is beneficial in reducing the number of locations experiencing transformation shape mismatch amongst neighboring grains, while the inflated prominence of free surfaces helps to relax what mismatch stresses might otherwise develop. As a result, large shape memory strains can be accommodated by the structure without leading to fracture.
An important goal of this prospective article is to describe the manner in which shape memory behaviors of zirconia-based ceramics reduced to micro-/submicro-scale dimensions differ from those of their bulk counterparts. Three zirconia-based systems including ceria-stabilized zirconia (CZ),[ Reference Du, Zeng, Liu, Schuh and Gan 13 ] ceria-yttria-stabilized zirconia (CYZ),[ Reference Du, Zeng, Liu, Lai, Amini, Miserez, Schuh and Gan 14 ] and yttria-titania-doped zirconia (YTDZ)[ Reference Zeng, Du, Schuh, Tamura and Gan 15 ] will be discussed as they all have demonstrated shape memory behaviors in the form of microscale pillars and particles. Some fundamental questions related to the structure—property connections of these materials will be addressed. Following that, we will discuss the cyclic SE of microscale particles and the associated processing science, which forms the basis for a number of potential scale-up pathways.
Shape memory, superelasticity, and the effect of composition
Martensitic transformation is characterized by the diffusionless and displacive transformation between austenite and martensite phases (which respectively correspond to tetragonal and monoclinic phases in the context of zirconia-based ceramics).[ Reference Orgeas and Favier 16 ] As noted above, four characteristic temperatures describe this transformation [Fig. 1(a)].[ Reference Kim, Ikehara, Kim, Hosoda and Miyazaki 17 ] For test temperatures in the fully austenitic state, i.e., for T ≥ A f, the material exhibits SE upon mechanical loading, experiencing a large strain plateau when the stress-induced tetragonal→monoclinic transformation is triggered, and full recovery because of the reverse martensitic monoclinic→tetragonal transformation during unloading [Fig. 1(b)]. For test temperatures below the austenite start, T ≤ A s, the material can demonstrate the SME; if deformed it can transform to martensite, and greater strains are accommodated by the reorientation of martensite variants toward those most favorable to those strains. Such deformation is not recovered on unloading, but upon heating one can trigger the reverse transformation to enable shape recovery [Fig. 1(c)].
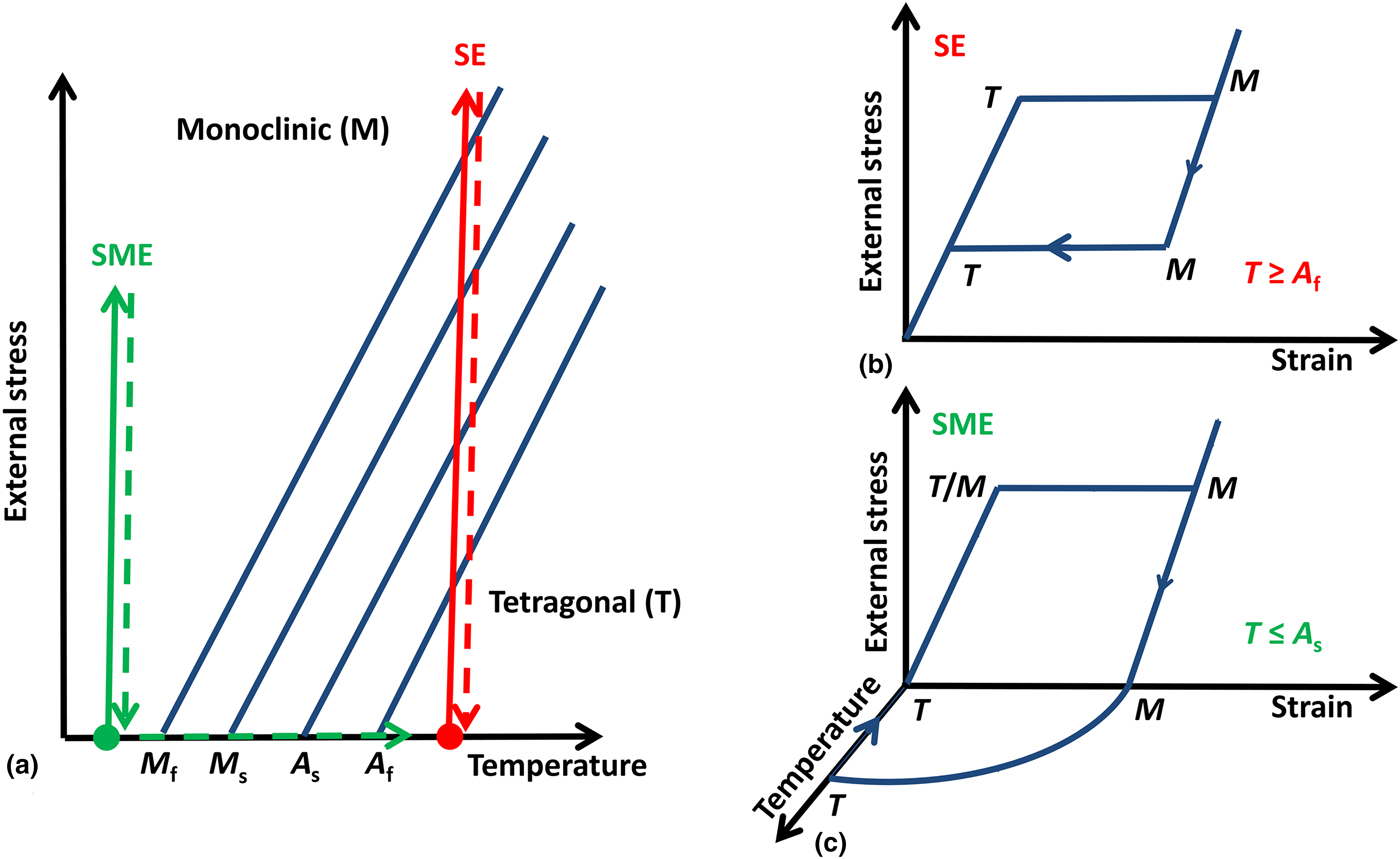
Figure 1. Schematic illustration of (a) shape memory effect (SME) and superelasticity (SE) with respect to the characteristic martensitic transformation temperatures (A s, A f, M s, and M f). Typical stress–strain behaviors of materials exhibiting (b) SE and (c) SME.
The characteristic martensitic transformation temperatures of zirconia-based ceramics can be obtained in an essentially stress-free condition from the endothermic and exothermic peaks in differential scanning calorimetry curves through one cycle of heating and cooling.[ Reference Zeng, Lai, Gan and Schuh 18 ] Direct structural characterization of the phase composition at temperature, such as by in situ x-ray diffraction analysis, has also been used. Based on such data, the four characteristic temperatures for the three systems (i.e., CZ, CYZ, YTDZ)[ Reference Lai, Du, Gan and Schuh 12 , Reference Zeng, Du, Schuh, Tamura and Gan 15 , Reference Zeng, Lai, Gan and Schuh 18 ] are summarized in Fig. 2. In this plot, only one dopant is varied in the ternary systems, i.e., yttria is maintained to be 0.5 mol% in the CYZ system and titania is maintained at 5 mol% in the YTDZ system. The transformation temperatures all tend to follow a linearly decreasing trend with dopant concentration, with a roughly similar transformation range spanning ~90 °C (A f–A s) during the forward transformation and ~60 °C (M f–M s) during the reverse transformation. The slope of these transformation temperatures with respect to composition reflects the effectiveness of the dopant in reducing the transformation temperatures. The relationship for A f as a function of the dopant concentration for the three systems can be empirically described as:
where T undoped = 1280.52 °C is the transformation temperature for pure zirconia. The doping slopes are α = 78.68 for ceria alone in zirconia; α = 74.59 for ceria and β = 382.90 for yttria in CYZ; α = 319.54 for yttria and β = 27.73 for titania in YTDZ.

Figure 2. The martensitic transformation temperatures (A s, A f, M s, and M f) with respect to the dopant concentration of ceria in CZ and CYZ (0.5 mol% yttria), and yttria in YTDZ (5 mol% titania).
The rescaled x-axes in Fig. 2 show the relative efficacies of these dopants upon the transformation temperatures; specifically, yttria is found 4–5 times as effective as ceria in terms of reducing the transformation temperatures. The stabilization of tetragonal zirconia is induced by the lattice distortion introduced by dopants with different ionic radii.[ Reference Fabris, Paxton and Finnis 19 ] Yttria is much more effective not only because the radius of Y3+ (0.1019 nm) is much larger than Zr4+ (0.084 nm),[ Reference Li and Chen 20 ] but also the doping of yttria introduces oxygen vacancies that further distort the lattice.[ Reference Fabris, Paxton and Finnis 19 ] Similarly, the transformation temperatures are less sensitive to ceria mainly because of the small difference in radius between Ce4+ (0.097 nm) and Zr4+ such that ceria introduces less significant distortion to the zirconia lattice.[ Reference Li and Chen 20 ] Ceria is therefore more suitable for fine tuning of the transformation temperatures in order to obtain the desired shape memory or superelastic properties at a target temperature, whereas yttria must be carefully controlled within tight tolerances.
Shape memory and SE have been explored in a range of compositions from among those in Fig. 2. For example, Du et al. reported that by tuning the ceria concentration between 16 and 14 mol% in CZ particles, a clear transition in the load–displacement curves from SE to SME could be obtained (Fig. 3).[ Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan 21 ] Fig. 3(a) shows the higher ceria content specimen, which is in the austenite (tetragonal phase) at room temperature, and thus reversibly transforms when loaded in compression. The plateaus in the load–displacement curve correspond to the forward and reverse transformations, and the inset images show the constancy of the unloaded particle shape through such a load cycle. Fig. 3(b) shows a similar experiment, but at the lower ceria concentration where the transformation to martensite (monoclinic phase) is no longer reversible on unloading. As shown in the inset, this particle remains deformed until it is reheated to obtain the austenite phase.
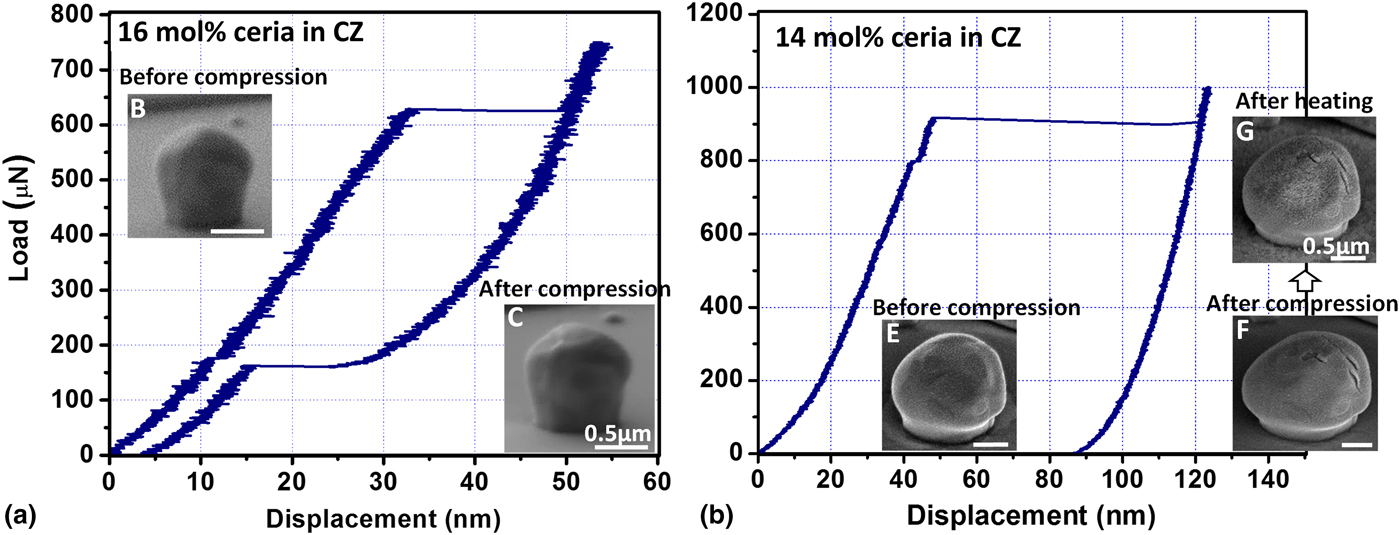
Figure 3. Load–displacement curves of single-crystal CZ particles with 16 and 14 mol% ceria doping, showing (a) superelasticity and (b) shape memory effect, respectively. A adapted with permission from Ref. Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan21.
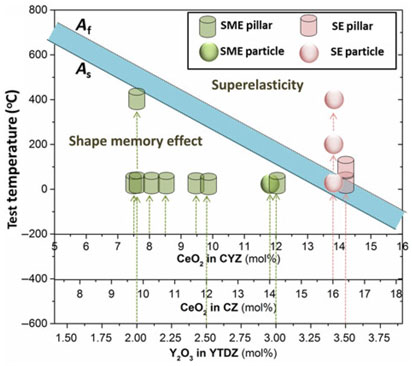
Summarizing across our previous work, the correlation between composition, test temperature, and mechanical behavior of zirconia-based ceramics are shown in Fig. 4. Some of these data are for particles (from the CZ system) such as shown in Fig. 3, and some are for micromachined pillars loaded in compression (from the CYZ and YTDZ systems). The test temperature in this figure refers to the temperature at which mechanical compression was carried out, not the heat treatment temperatures. The majority of the specimens were tested at room temperature, while some were compressed at higher temperatures of 200 and 400 °C. All specimens falling into the region below A s demonstrated SME regardless of the types of dopants they comprised; in other words, deformation at room temperature led to shape changes that were in every case found to be recoverable upon subsequent heating above A f. For pillars or particles showing SE, their transformation temperatures all fall in the region above A f. The data collectively show how the test temperature and ceramic composition are correlated parameters that work together to determine the mechanical behavior of zirconia-based ceramics. By selecting materials with test temperature–composition pairs in the vicinity of A s and A f, either SME or SE can be obtained for a wide range of operation temperatures.

Figure 4. Reported measurements of shape memory and superelasticity behaviors of zirconia-based ceramics, presented atop the map of transformation/test temperature versus composition. All data are obtained from Refs. Reference Lai, Du, Gan and Schuh12–Reference Zeng, Du, Schuh, Tamura and Gan15, Reference Zeng, Lai, Gan and Schuh18.
Size effects
Due to the brittle nature of polycrystalline ceramics, when the large strain of the martensitic transformation is triggered, it is common to exceed the strain/stress for microcracking if the strain cannot be accommodated. Microcracks commonly form at grain boundaries because of the mismatched transformation strains between neighboring grains with different orientations. As a consequence, the reduction or complete removal of grain boundaries can help minimize the nucleation and propagation of microcracks. Whereas grain boundary area can be reduced by inflating the grain size, d; increasing the surface area to accommodate shape change can also be effected by reduction of the characteristic sample size, D. By making pillars or particles with a sample size (D) approaching or equal to the grain size (d), so-called oligocrystalline structures can be produced, with limited grain boundary area and ideally no triple junctions; such structures can significantly suppress the occurrence of microcracks.
A systematic study by Du et al. showed this transition by preparing shape memory pillars with diameters spanning across the grain size of the specimen from which they were machined. As shown in Fig. 5(a),[ Reference Du, Zeng, Liu, Lai, Amini, Miserez, Schuh and Gan 14 ] an oligocrystalline structure achieves much larger recoverable strain and has a correspondingly lower critical stress for transformation; the grain constraints that lead to internal stresses and fracture are significantly reduced. Furthermore, similar studies on superelastic particles of different sizes [Fig. 5(b)] and relative polycrystallinity have drawn a similar conclusion that oligocrystalline or single-crystal structure is the key to obtain reliable and robust shape memory properties.[ Reference Du, Zeng, Liu, Schuh and Gan 13 ]

Figure 5. (a) The size effect of shape memory effect in CYZ pillars, reproduced (adapted) with permission from[ Reference Du, Zeng, Liu, Lai, Amini, Miserez, Schuh and Gan 14 ] copyright 2015 Scripta Materialia, (b) the size effect of superelasticity in CZ particles, reproduced (adapted) with permission from[ Reference Du, Zeng, Liu, Schuh and Gan 13 ] copyright 2017 Acta Materialia, (c) the size effect of single-crystal YTDZ pillars, reproduced (adapted) with permission from[ Reference Zeng, Lai, Gan and Schuh 18 ] copyright 2016 Acta Materialia.
If grain boundaries can be completely eliminated, there remains the possibility of sample size effects even in single-crystal structures, i.e., SME stresses and strains may be impacted by sample size D. While this issue requires a great deal more study and is a fertile area for future work, there are some preliminary suggestions that interesting physics may be at play during transformation of small zirconia structures. Zeng et al. studied sample size effects in YTDZ pillars for two different crystal orientations, over a narrow span of sample diameter from D = 1.2 to 2.5 µm.[ Reference Zeng, Lai, Gan and Schuh 18 ] It was found that the transformation stress follows an increasing trend with the pillar diameter, and the slopes of the stress-diameter curves may depend on crystal orientation [Fig. 5(c)]. While these data are the only ones of their kind of which we are aware, the presence of a trend is robust across multiple sample sizes within the tested range, and the magnitude of the critical stress change is dramatic (~GPa).
In single-crystalline zirconia, the crystal orientation is a predominant factor in the phase transformation that underlies shape memory properties.[ Reference Zeng, Lai, Gan and Schuh 18 ] Due to the displacive, diffusionless, and crystallographic nature of the tetragonal→monoclinic transformation, only a few variants, and thus a few strain orientations, are possible. Variant selection depends upon the orientation with respect to the applied stress direction, and the resulting shape memory strain is widely variable with orientation. A systematic study of the orientation dependence of transformation stress and strain in single-crystalline zirconia pillars is provided in Ref. Reference Zeng, Lai, Gan and Schuh18. That work, and the references therein on which it builds, suggests that some orientations must be avoided because they are likely to crack before they transform, and that others may be engineered for in future work to attain the optimum reversible strain.
Cyclic transformations
The above results show shape recovery of small-volume zirconia through a single cycle, either thermally or mechanically induced. However, one of the main advantages of the small-volume oligocrystalline forms of zirconia is the ability to sustain the transformation repeatedly; bulk zirconia typically fails after the first cycle, or at most after perhaps five or six cycles.[ Reference Reyes-Morel, Cherng and Chen 7 ] In contrast, reliable repeat transformation in fine pillars and particles opens the door to a variety of uses.
We recently explored cyclic superelastic loading in zirconia particles prepared by both sol–gel and spray drying.[ Reference Du, Zeng, Liu, Schuh and Gan 13 , Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan 21 ] The spray-dried particles exhibited good cyclic performance with repeatable load–displacement behavior up to 110 cycles [Fig. 6(a), (b)]. Sol–gel prepared particles demonstrated even better cycling performance with superelastic behavior remaining up to 412 cycles [Fig. 6(c)]. Differences between the sample processing methods remain an area for future study, as we expect that the defect structures of the as-prepared sol–gel and spray-dried particles are different. For example, raw nanopowders used in spray drying might contain impurities, whereas precipitated particles contained less heavy metal impurities. In addition, the shape of sol–gel prepared particles is more spherical as compared to spray-dried ones, indicating that the stress distribution might be more symmetric and better contact can be maintained during cyclic mechanical tests. Another possible origin of the difference is that the crystal orientations of the particles are not controlled during mechanical tests, leading to a variation of transformation crystallography. As reported by Zeng et al.,[ Reference Zeng, Lai, Gan and Schuh 18 ] crystal orientation plays a key role in determining the transformation stress and strain; samples with high transformation stresses close to the fracture stress are more sensitive to cracking during cyclic transformation and earlier fatigue is more likely to occur.
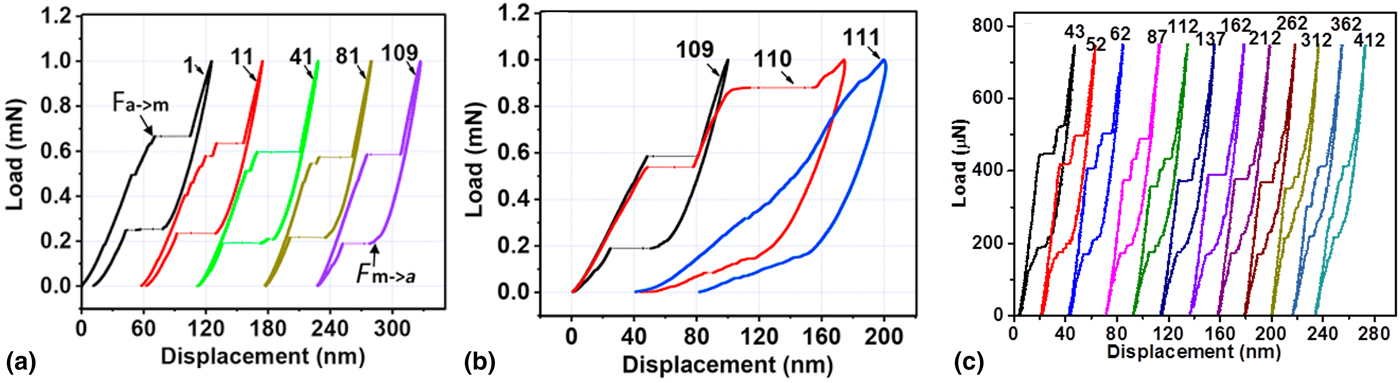
Figure 6. Cyclic load–displacement behaviors of (a) and (b) a spray-dried superelastic particle and (c) a sol-gel prepared superelastic particle. Adapted with permission from Refs. Reference Du, Zeng, Liu, Schuh and Gan13, Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan21.
In any event, the results in Fig. 6 are also similar to what has been reported in fine pillars of zirconia,[ Reference Lai, Du, Gan and Schuh 12 ] and shows that well-prepared samples can undergo the transformation hundreds of times; we are not aware of longer duration tests at the time of this writing, and this remains an area for future work. Among the possible uses for such repeatable transformations, reversible energy damping applications, or cyclic shock resistance, seem to present opportunities for ceramics used in a superelastic condition and subjected to reversible loading cycles. The loss factor for mechanical damping capacity is defined as:[ Reference San Juan, No and Schuh 22 ]
where W max is the maximum energy stored at the critical transformation stress during loading and ΔW is the area of the superelastic hysteresis loop. The typical merit index for damping is calculated as E 1/2 · η, where E is the Young's modulus.
The loss factor, Young's modulus, and merit index of superelastic single-crystal and oligocrystalline zirconia particles are compiled in Fig. 7, together with other bulk energy damping materials summarized by San Juan et al.,[ Reference San Juan, No and Schuh 22 ] including polymers, shape memory metal alloys, and energy damping composites. Superelastic zirconia stands out for being very stiff in the landscape of damping materials, and also exhibits a high loss factor of ~0.068–0.073, comparable to metals and composites. As a result, zirconia's merit index for damping is ~0.96–1.03 at 1 Hz, which ranks it the highest among all energy damping materials. It is worth noting here that the maximum strain amplitude for the materials reported in Fig. 7 varies significantly from 10−2 to 10−6, which signifies the extent of deformation and which is another advantage of shape memory materials vis-à-vis materials that flex only elastically. The applied stress level for elastic damping materials can be estimated roughly by multiplying the maximum strain amplitude with the Young's modulus, whereas the shape memory materials experience only about 1% elastic strain and much more superelastic strain that does not increase the applied stress level. However, it must be noted that although both bulk and small-volume zirconia exhibit this property, in bulk form it is sustained only over one or a few cycles of loading before cracking occurs. In fine oligocrystalline and single-crystalline particles, we have recorded this behavior over hundreds of cycles. The reliable SE of small-volume zirconia gives it strong potential for damping applications, especially when reversible or cyclic performance is of critical importance.

Figure 7. A comparison of loss factor, Young's modulus, merit index, and strain amplitude of superelastic CZ particle[ Reference Du, Zeng, Liu, Schuh and Gan 13 ] and various energy damping materials.[ Reference San Juan, No and Schuh 22 , Reference Reyes-Morel, Cherng and Chen 7 ]
Processing science of shape memory ceramics: particles and derivative architectures
The above sections alluded to the importance of processing science for fine-scale shape memory ceramics, and this is an area of significant need for future development. Although zirconia processing is well established, renewed focus on processing science with the explicit aim of optimizing shape memory and superelastic properties is certainly needed. We have taken a view that scaled-up production of small-volume shape memory ceramics is likely to begin from microscale particles, which benefit from the established methods of powder science and intrinsically access fine-scale oligocrystalline or single-crystalline structures. Above we noted that well-established methods such as spray drying, sol–gel, and hydrothermal processing methods have been used in work on shape memory zirconia particles. Given that a typical average grain size of zirconia-based ceramics after a thermal cycle would tend to lie in the micron-/submicron-scale, suitable particles that access oligocrystalline structures naturally would have a size of ~1–10 µm.
One straightforward processing approach that has been used to achieve such particles is spray drying. By spraying a slurry composed of zirconia and ceria nanoparticles at 135 °C with N2 gas, watery droplets were dried, and spherical- or donut-shaped particles with a size of ~1–20 µm were formed [Fig. 8(a)] in Ref. Reference Du, Zeng, Liu, Schuh and Gan13. Spray drying can also be easily scaled to high production volumes, although the resulting particles usually have a broad size distribution as there is limited control of size and shape during processing. An alternative approach is sol–gel processing, which can produce highly monodisperse spherical particles by controlled hydrolysis of the precursors [Fig. 8(b)].[ Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan 21 ] As compared to spray drying, the sol–gel method provides better control of the size and shape of the particles, albeit at lower production rates. The particle sizes prepared with sol–gel method range from ~0.8 to 2 µm, which can be fine-tuned via the acid/water ratio in the precursor, as has been discussed by Du et al.[ Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan 21 ] Judging from the resulting size similarity between the grains and particles, crystallized sol–gel particles are more likely to have single-crystalline or oligocrystalline structures with fewer grain boundaries, which is beneficial for shape memory properties.

Figure 8. The fabrication of shape memory particles with (a) spray drying[ Reference Du, Zeng, Liu, Schuh and Gan 13 ] and (b) sol–gel.[ Reference Du, Ye, Zeng, Schuh, Tamura, Zhou and Gan 21 ]
Shape memory ceramic particles can be assembled in a variety of ways to more macroscopic architectures, many of which maintain the desirable ratio of surface area to grain boundary area that would be oligocrystalline. For example, a granular packing of shape memory ceramic particles has been shown to retain all of the shape memory and superelastic properties of the particles, while easily increasing the scale of application by orders of magnitude.[ Reference Yu, Hassani-Gangaraj, Du, Gan and Schuh 23 ] Such packings offer a scalable approach to zirconia's use as an energy damping material (e.g., if a high operation temperature or high merit index is desired). The dissipated energy density of superelastic packings cyclically loaded was shown to gradually stabilize to ~2 J/g; while this is slightly smaller than measured in individual superelastic pillars and particles (~2–4 J/g),[ Reference Du, Zeng, Liu, Schuh and Gan 13 ] it is much larger than for shape memory alloys. From a random granular packing to more ordered colloidal crystal arrangements, we envision that monodisperse spheres could potentially be assembled into bulk powder compacts with an ordered structure.
Alternatively, the microscale features of shape memory ceramics could be scaled-up into foam structures. Zhao et al. reported the first demonstration of shape memory zirconia foams with an ice templating method.[ Reference Zhao, Lai and Schuh 24 ] Clear martensitic transformations were observed during multicycle thermal heating and up to 2% recoverable strain was obtained. Such non-uniform foam structures suffer from generally low macroscopic fracture stresses, and future work could address structural optimization, such as making an ordered inverse opal structure with controlled pore arrangement and size. Another potential approach is to use shape memory ceramic particles as reinforcements in adhesive matrices like polymers or metals; each particle can act as a shape memory or superelastic site whose transformation strain could be accommodated by (and transmitted through) the surrounding matrix.
In addition to the above approaches based on particles, other structural variations like fibers or thin films both admit potential oligocrystalline or even single-crystalline forms, which may be amenable to reproducible shape memory properties. Fibers are of particular interest for future work to extend the length of an oligocrystalline structure by orders of magnitude as compared with particles and pillars. Ribbons or fabrics made of fibers could also serve an alternative scaling-up approach with anisotropic properties in terms of strength and flexibility.
Summary
Zirconia-based ceramics exhibit significantly enhanced shape memory and SE properties when they are produced in small volumes with oligocrystalline or single-crystal structures. Their high transformation stresses, large recoverable strains, and highly tunable operation temperatures suggest a variety of possible applications for zirconia-based ceramics with shape memory properties. While micro-machined pillars offer scientific insight on the martensitic transformation mechanism, fine particles also exhibit the same sets of properties and are more amenable to large-scale production and have more practical implications. With good cyclic transformation performance, a large mechanical energy loss factor, and high merit index for damping, superelastic zirconia-based particles may see use in energy damping applications. The ability to magnify particles’ properties to larger scales through, e.g., granular materials, foams, or fibers, also suggests a variety of possible directions for future work.
Acknowledgments
The authors acknowledge the contributions of A. Lai, H. Z. Yu, and X. Zhao (MIT) to the previous works, which this paper has reviewed. C.A. Schuh acknowledges the support of the Institute for Soldier Nanotechnologies, funded at MIT by the US Army Research Office. The authors thank N. Tamura from Advanced Light Source (ALS), Lawrence Berkeley National Laboratory (LBNL) for the use of Synchrotron x-ray Microdiffraction (μSXRD) to confirm some of the transformation temperatures of CYZ ceramics.