The Russian School Twin Registry (RSTR) was established in 2012, supported by a grant from the Government of the Russian Federation (11.G34.31.003; PI — Dr YK). The main aim of the registry is to contribute to a program of research, called Progress in Education through Gene-Environment Studies (PROGRESS). Currently, the RSTR includes 500 twin pairs, but the formation of the registry has just begun and it is expected that most schools in the Russian Federation (approximately 50,000 schools) will contribute data to the registry. In addition, as a satellite project, we are establishing a twin registry in Kyrgyzia, for reasons explained later. With each school expected to have at least one to two twin pairs (age 7–18, see Table 1), the potential twin-sampling frame for the RSTR is greater than 100,000 pairs. The registry will include students from all existing schools in the primary and secondary educational sector, including public and private schools, gymnasiums, lyceums, external studies, schools specializing in specific subjects (e.g., languages, mathematics, art), and schools attached to specific university departments (e.g., physics, mathematics). This variety of school types will allow for important within-country and international comparisons. In addition to different school types, the comparisons will involve many aspects of culture across the diverse regions of the Russian Federation, including vast differences in geography, climate, linguistic factors, societal organization, family structure, and educational norms. PROGRESS includes four major (overlapping) stages, summarized in Table 2.
TABLE 1 Structure of the Formal Russian School Education

TABLE 2 Stages of the Project PROGRESS
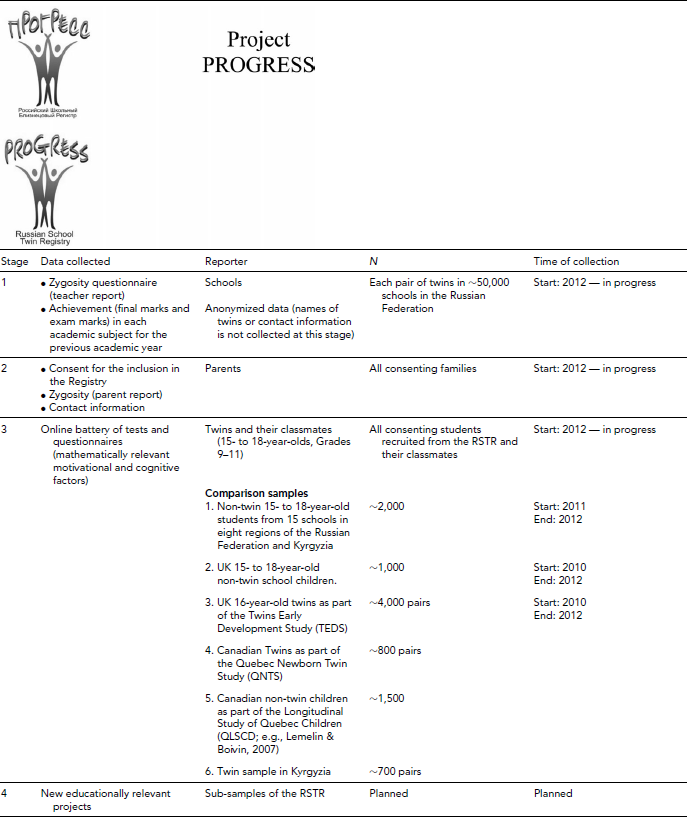
Stage 1: Anonymous Data from Schools
With the help of the Ministry of Science and Education of the Russian Federation, we are contacting schools with information about the project and a request to provide information about any twin pairs attending the school using an online form (http://www.protwins.ru/). The form includes a nine-item zygosity questionnaire (adapted from Goldsmith, Reference Goldsmith1991), and fields to provide the marks obtained by each twin in each semester and the final mark in all subjects studied in the previous academic year, as well as the mark for any State Examinations (Grades 9 and 11, see Table 1). At this stage of the project, the schools do not provide the names or contact information for the twins, but provide only the age and the year of study of the twin pairs.
Stage 2: Parental Consent and Information
As part of the first contact at Stage 1, the schools receive an information letter for the parents of twins, as well as a parental consent form, to be passed on to the parents of the twins in their schools. The parents are asked for their permission to enroll their children in the registry. The consent form also includes a nine-item twin zygosity questionnaire (adapted from Goldsmith, Reference Goldsmith1991) and a field to provide family contact information. The schools are asked to collect the signed parental consent forms and to post them to us, using prepaid envelopes provided. At this stage of the project, all the children for whom the consent has been given by their parents are enrolled in the RSTR.
Stage 3: Cross-Cultural Genetically Sensitive Investigation into the Sources of Individual Differences in Mathematical Ability, Motivation, and Achievement
The families of 15- to 18-year-old twins in the RSTR are contacted directly, with an invitation to take part in a project called Individual Differences in Mathematical Achievement. This large-scale investigation using the RSTR is already in progress and involves the study of the genetic and environmental influences on individual differences in mathematical ability, motivation, and achievement. A large battery of Web-based tests and questionnaires includes cognitive measures, as well as measures of the educational environment, motivation, and interest (see Appendix for the details). The unique feature of this investigation is that most of the twins’ classmates will also be assessed using the same battery. Moreover, over the past 2 years (2010–2012) this battery has already been administered to over 2,000 Russian and Kyrgyz singletons of the same ages, as well as almost 1,000 UK singletons of the same ages (as part of InLab Maths project; White et al., Reference White, Davidova, Sharafieva, Malykh and Kovas2012), 4,000 pairs of 16-year-old UK twins (as part of the Twins Early Development Study [TEDS]; Oliver & Plomin, Reference Oliver and Plomin2007), and is currently being administered to 800 Canadian twins, as part of the Quebec Newborn Twin Study (QNTS; Boivin et al., in press) and to 700 twin pairs in Kyrgyzstan.
Stage 4: Future Studies
This stage will include all future studies conducted on the basis of the RSTR. A series of neuroimaging, DNA, and behavioral studies are currently being planned. Parental consent will be sought for each specific study.
DNA Collection
DNA will be collected from twins at Stages 3 and 4. We have already piloted DNA collection from Russian school children using Oragene saliva kits (OG-500), as well as extraction and storage procedures. Separate informed consent will be sought from parents of twins in the registry for DNA collection, storage, and analyses.
Objectives, Planned Analyses, and Expected Outcomes
Stage 1 of the data collection will provide a wealth of anonymized data on school achievement of twins across the Russian formal school education years, and will allow for the first large-scale quantitative behavioral genetic analyses on academic achievement in this population. At the same time, a large-scale data collection is also in progress from non-twin school children of all ages across the Russian Federation and Kyrgyzia (currently N = 3,000), to enable the comparison between twin and non-twin children at each educational stage. We also plan to conduct multi-variate, genetically sensitive analyses on the links between cognitive and motivational factors and school achievement and performance in the State Examinations.
Stage 2 enables the establishment of the RSTR, containing contact information for families; information on the twins’ schools; teacher- and parent-reported zygosity for each pair; and information on academic attainment for the previous academic year for each twin. In accordance with the data protection policy, all identifying information, including name, address, and school, is stored separately from the questionnaire data. The data are confidential, linked to each participant only via an ID. This stage provides the foundation for the genetically sensitive, cross-cultural, educationally relevant research taking place at Stages 3 and 4.
Stage 3 of the project provides a large-scale, genetically sensitive cross-cultural investigation into the sources of the individual differences in mathematical ability, motivation, and achievement. The importance of mathematics in today's highly technologically driven societies cannot be overestimated. Mathematics is of great importance for economic success of nations, and improvements in mathematical ability throughout the distribution can lead to great benefits to individuals and countries overall (e.g., Butterworth et al., Reference Butterworth, Varma and Laurillard2011). Mathematics is also an extremely convenient phenotype to study cross-culturally as many relevant tasks can be easily adapted for administration in many different languages. For these reasons, we decided to focus on mathematically relevant traits in this first project of the RSTR.
The inclusion of the twins’ classmates will allow the examination of both within and between class/school variation. The cross-cultural design will allow us to examine the relative contribution of genes and environments to the variation in each examined trait, and to the co-variation among the traits in different cultures. The test battery used in this project has been developed, adapted, and validated for administration to 15- to 18-year-old students in Russia, the United Kingdom, Canada, the United States, and Kyrgyzia.
Examining the relative contribution of genes and environment to variation in educational phenotypes across these diverse populations can provide new insights into the sources of variation in these traits. Data collection on singleton and twin children in Kyrgyzia is of particular scientific interest: Kyrgyzia is the former Republic of the USSR and is currently the second poorest country in Central Asia. Despite following the Russian Educational System, children in Kyrgyzia show very low educational attainment results on average. For example, in mathematics, they have been reported to be at the bottom of the international comparison at age 15 (e.g., PISA, 2009). The reasons for such underachievement remain unclear.
Invitation for collaborative, genetically sensitive, educationally relevant cross-cultural research
We believe that cross-cultural genetically sensitive investigations offer great promise for education. Examining the extent to which the same genes are expressed in different cultures will provide new insights into the mechanisms of gene-environment interface. Cross-cultural comparisons have already yielded some important findings. Much recent data suggests that the patterns of genetic and environmental influences on many traits are similar across cultures. For example, the increase of heritability of general intelligence has been documented in many different countries (e.g., Haworth et al., Reference Haworth, Wright, Luciano, Martin, de Geus, van Beijsterveldt and Plomin2010; Malykh et al., Reference Malykh, Iskoldsky and Gindina2005).
Nevertheless, some etiological differences have also been documented. For example, several studies have found that some aspects of reading and mathematical ability are influenced by shared environment more than by genes in US school children (e.g., Petrill et al., Reference Petrill, Logan, Vincent, Hart, Thompson, Kovas and Plomin2011) than in UK children. The variation in school types and quality is much greater in the United States than in the United Kingdom, which might explain the observed differences in the relative contributions of genes and environments to educational phenotypes in these two countries. However, it is important to note that the average levels of academic performance of the population are not necessarily related to the relative contribution of genes and environments to the individual differences. For example, children in the United Kingdom and in the United States perform below average on the latest international comparisons of mathematical achievement (PISA, 2009). Another study specifically compared the relative influences of genes and environments on variation in early reading in response to differences in instruction, finding some etiological differences in the United States, Scandinavia, and Australia (Samuelsson et al., Reference Samuelsson, Byrne, Olson, Hulslander, Wadsworth, Corley and DeFries2008). Neither study provided adequate power to compare the influences of shared environment across the countries. In order to address important educational questions, very large samples are needed that will provide adequate power to detect ACE (genetic, shared, and non-shared environmental) differences between countries.
Cross-cultural differences could be driven both by average differences in the frequency of particular genetic variants across populations, and by average differences in the relevant environments, such as cultural norms or the structure of the school curricula. The same processes that are involved in cross-cultural differences may also be involved in individual variation within cultures, and in the group differences within countries. For example, even within a culture, heritability of the same trait can differ across generations or groups of society, reflecting economic and political changes, the societal organization, and cultural norms. Studying these processes using genetically sensitive cross-cultural approaches may help in the complex task of adapting education of the future to new demands.
The RSTR is designed to address many of these questions. First, diverse regions of the Russian Federation themselves provide a platform for some cross-cultural comparisons. For example, such ethnically and culturally distinct populations as Buryat or Tatar are included in the registry. Second, we already have begun collaborations with the twin registers in other countries and we are hoping to start new collaborations. At Stage 4 of our project we plan to design specific studies to address specific questions in collaboration with other registries. We invite all studies interested in education to collaborate with the RSTR.
Acknowledgments
The establishment of the Russian School Twin Registry is supported by the grant from the Government of the Russian Federation (grant 11.G34.31.003). The authors gratefully acknowledge the support from the Ministry of Science and Education of the Russian Federation for the assistance in the establishment of the registry.
Appendix Measures Included in Stage 3: cross-cultural genetically sensitive investigation into the sources of individual differences in mathematical ability, motivation, and achievement
The battery of tests used at Stage 3 has been developed for the online administration as part of the Twins Early Development Study assessment at age 16. The battery has then been adapted for the administration in Russia, and validated using a sample of singleton children in Russia (Tikhomirova & Kovas, Reference Tikhomirova and Kovas2012). Twins Early Development Study (TEDS) assessments have been carried out via the Internet since the wave of testing at age 10. This method of testing has proven to be reliable and less prone to human error due to immediate automatic data entry (Kovas et al., Reference Kovas, Haworth, Dale and Plomin2007). The battery is comprised of general cognitive ability measures, measures of specific numerical estimation ability, and measures of mathematical performance. The Web tests are designed to be carried out without supervision. Each test is provided with a set of instructions, an online tutorial, and practice trials. In order to maximize response, it is possible to complete the testing in more than one session, and for some tests it is possible to pause them to resume the testing at a later stage. The tests are available on a Web site where students are able to log in with a unique, anonymized username and password provided to them. The children's login is activated after parents give their consent. The following tests are included:
Tests of Symbolic and Non-Symbolic Numerical Estimation (Specific Numerical Ability)
-
1. Number Line: This task, assessing estimation of numerical magnitudes, was programmed and implemented online from a description obtained from Opfer and Siegler (Reference Opfer and Siegler2007). As documented in many studies (e.g., Booth & Siegler, 2006; Siegler & Booth, Reference Siegler and Booth2004), at 16 years most children rely on linear representations of numerical magnitudes on a mental number line from 0 to 1,000. For this reason, we opted for a number line estimation within this range. A line, with the left edge marked with ‘0’ and the right edge marked with ‘1000’ is presented in the middle of the screen with a numeral above the line. The task requires participants to indicate where they think the numeral should be, by dragging and releasing a red cursor along the line. Twenty-two numbers to be estimated are presented in the same order to all participants: 246, 179, 818, 78, 722, 150, 366, 122, 738, 5, 147, 938, 18, 606, 2, 34, 754, 100, 56, 163, 486, and 725. Total length of the line is 500 pixels with each unit 0.5 pixels long, therefore accuracy in response recorded to the nearest 0.5 units. The marks on the line were converted into numbers based on number of units (pixels); the scores are calculated as the mean of the deviations from the correct position of the numbers on the line. This test allows only one practice trial to reduce the effects of training/learning as this has been shown to positively affect estimation accuracy. At each screen participants are given the option to continue with the task or to resume it later. The program records the scores as described as well as response reaction time.
-
2. Dot Task: This task assesses the ability to discriminate numerosities. Stimuli and parameters were provided by the authors of the task and were an adaptation of the task described in Halberda et al. (Reference Halberda, Mazzocco and Feigenson2008). The stimuli consist of 150 static pictures with mixed arrays of yellow and blue dots. The number of dots ranges between 5 and 21 for each color, with ratios organized in eight bins, with the lowest ratio of each bin serving as the top boundary of the following bin. The bins ratio are organized as follows: 11 trials with a ratio randomly chosen between 8/7 and 7/6; 26 trials between 7/6 and 6/5; 28 trials between 6/5 and 5/4; 29 trials between 5/4 and 4/3; 26 trials between 4/3 and 3/2; 18 trials between 3/2 and 2; 8 trials between 2 and 3; 4 trials between 3 and 4. In all trials the average size of yellow dots is equal to the average size of blue dots. With this display, the array with more dots also occupies more area on the screen. The presentation order is the same for all participants. The stimulus flashes on the screen for 400 ms, and participants have to decide whether the array contained more yellow or blue dots. Response is given by pressing ‘Y’ for more yellow and ‘B’ for more blue dots. Maximum allowed response time is 8 seconds. If no answer is given during this time, the answer is recorded as wrong and a message appears on the screen to encourage pressing the space bar to see the next trial. The message disappears after 20 seconds and the next trial is displayed only after a press of the space bar. There is a two-item practice trial, with feedback and an option to repeat the practice if necessary. The task is divided in three blocks of 50 trials. At the end of each block it is possible to take a break and resume the test later. The test records accuracy and reaction time for each trial. A Weber Fraction score for each individual is derived using the method described in the supplementary information of Halberda et al. (Reference Halberda, Mazzocco and Feigenson2008). Weber Fraction is an amodal index of the ability to perceive changes in the appraised measure. In this task, the Weber Fraction indexes the ability to discriminate between the numbers of yellow and blue dots, with larger differences between the two arrays (i.e., larger ratios) being easier to discriminate. For example, given two arrays, one with 4 dots and one with 6 (ratio 2:3), the Weber Fraction is derived by dividing the difference of the two ratios by the smallest number in the ratio: (3 – 2)/2 = 0.5.
Tests of Mathematical Performance
-
1. Problem Verification Task: This Web-administered timed test of mathematical fluency is a shortened version (from 88 to 48 items) of the task described in Murphy and Mazzocco (Reference Murphy and Mazzocco2008). The items are arithmetic problems (24 fraction problems and 6 problems each for: addition, multiplication, subtraction, and division), appearing on the screen one at a time with an answer provided. Participants judge as quickly as possible whether the answer is correct or not. The proposed answer is correct in half of the trials. Response is given by pressing the keys F, J, or K, respectively, for correct, incorrect, and don't know. For every item, a reminder of which keys to press is shown at the bottom of the screen. Maximum time for response is 10 seconds and a time bar on the top-left corner of the screen reminds participants of the elapsing time. If no answer is given during this time the next trial follows. The next item is presented immediately following a response. One point is awarded for each correct response. Timed out and don't know responses receive zero points, therefore the maximum score for this task is 48. The test starts with a tutorial with visual and auditory instructions, and two practice items that can be repeated. After the 24th trial participants are presented with a screen with two buttons that give the option either to continue with the test or to take a break. The program records accuracy and response reaction time.
-
2. Number Game: This test assesses mathematical achievement according to the standards of the UK National Curriculum. Items of this task are problems selected from the Understanding Numbers component of the nferNelson booklets (level 1 to 8; nferNelson, 1994, 1999, 2001). The solution of the problems requires understanding of the relationship between numerical expressions and patterns of numbers, understanding of mathematical operations, as well as of relationships among mathematical operations (e.g., subtraction is the inverse of addition). The test is comprised of 18 items arranged in increasing level of difficulty. The level of difficulty was decided on the National Curriculum standardization sample (reported in the Group Record Sheets; nferNelson 1994, 1999, 2001) together with previous TEDS assessment data. The 18 questions were organized in three levels of six items each. Each level was further divided into three sub-levels of items with increasing difficulty. All participants start with the same question of medium difficulty. The subsequent presentation order is determined by participants’ answers: answering correctly to the problems of one level advances the test progressively to the more difficult questions; and items from the easier levels are credited as correct. If the problems within a level are answered incorrectly, the test branches down to easier levels. The test starts with a set of instructions and there is no practice trial. For some problems the answers need to be typed in; others have multiple-choice answers and response requires clicking on the correct answers. For some problems a simple calculator appears on the screen alongside the question. After response is given, participants have the choice to progress to the next question or take a break and resume the test later. Maximum response time is 5 minutes and prompts encourage participants to answer during this time. If no answer is given during the 5 minutes, participants are given the choice to go to the next question or take a break from the test. One point is awarded for each correct/credited answer; no points are given for timed out or incorrect answers, therefore maximum score on this test is 18. The program records accuracy and response reaction time.
Tests of General Cognitive Ability
Three tests of general cognitive ability were administered, measuring visuo-spatial working memory (Corsi Tapping Block), speed of processing (Reaction Time), and non-verbal intelligence (Raven's Progressive Matrices).
-
1. Corsi Tapping Block: This test was programmed and adapted for online administration from the pen and paper version described in Pagulayan et al. (Reference Pagulayan, Busch, Medina, Bartok and Krikorian2006). The number of items per trial was reduced from this version based on an internal validity analysis conducted on pilot testing. An image, depicting a black rectangle with nine small cubes-blocks arranged inside is shown on the screen. The cubes light up, turning yellow for 1 second in a patterned sequence, with a 1-second interval between each cube. Participants have to reproduce the sequence by clicking on the cubes with a mouse. Each cube has a number from 1 to 9 associated with it, so that each sequence can be identified with a numerical string (the numbers are not showing on the screen). Six difficulty levels are administered, with two sequences within each level. To make the test age appropriate to the sample, the test starts with four numbers in each sequence. The hardest level contains nine items in each sequence. Immediately after the last item of the sequence is presented, a text prompt appears on the screen inviting participants to start reproducing the sequence; they respond by clicking on the blocks in turn, using a mouse. As participants click on each block, it turns yellow and remains yellow until the next block is clicked. Clicks in the black areas between blocks are not registered. Responses are irreversible. After each response participants are presented with a screen with two buttons to choose either to continue with the test, or to come back to it later. The test has visual instructions and three-item practice trial that can be repeated until the participant is familiar with the task. If students correctly complete one or both sequences in a level, they progress to the first item of the next level. The test is terminated when both sequences in the same level are reproduced incorrectly. One point is assigned for each sequence correctly reproduced, with maximum score of 12. There is no time limit for response. The program records accuracy and reaction time for each trial.
-
2. Reaction Time: The task measures response reaction time and is programmed following the procedure described in Deary et al. (Reference Deary, Der and Ford2001). The numbers 1, 2, 3, 4 appear 10 times each in a randomized order with a random interval between 1 and 3 seconds. Participants have to press the key corresponding to the number on the screen as quickly as possible. Presentation of the stimuli is in the same randomized order for all participants. The interval of 1 second between presentations is repeated 14 times and the interval of 2 and 3 seconds is repeated 13 times each. The task started with a six-item practice trial. The practice trial can be repeated. Time out for responses is 8 seconds. If no response is given during this time the next trial follows and the question is recorded as incorrect. One point is assigned for each correct response for a maximum score of 40. The program records accuracy and response reaction time.
-
3. Raven Progressive Matrices: This computerized test of non-verbal (fluid) intelligence was adapted from Raven et al. (Reference Raven, Court and Raven1996). Participants are presented with a matrix of patterns with one piece missing from each pattern. The task requires the participant to select the missing pattern from a choice of eight by clicking on it with a mouse. The test consists of 30 items organized in three levels with 6 items each, and a fourth level with 12 items. There is a set of animated instructions and one practice trial that can be repeated at the discretion of the participant. The first three items of the first level are presented sequentially. Children progress within the same level if a correct response is given to at least one of the three items. If the first three items of the level are answered incorrectly, the following three items are skipped and the test advances to the next level. One point is assigned for each correct answer; the skipped items receive no points. The maximum score for this test is 30. If no answer is given within 5 minutes, the program returns to the main page of the Web site. When resuming the session the same question is presented. After each response, the next question follows immediately. Participants can, however, take a break at any point in the test. Accuracy and response reaction time are recorded by the program.
Questionnaires
The questionnaires included in the battery assess the following: (1) relationships with peers and school environment in general; (2) relationships with parents and home environment in general; (3) self-assessment of personality traits; and (4) mathematically relevant behavior.
The questions ask about peer relations, such as rejection and emotional acceptance (Mynard & Joseph, Reference Mynard and Joseph2000); relationship with the teacher, school resources, and well being in the classroom (Appleton et al., Reference Appleton, Christenson, Dongjin and Reschly2006); relationships with parents, including control, monitoring, and feelings on a scale from 1 to 5 (1 = never, 5 = very often; Deater-Deckard et al., Reference Deater-Deckard, Dodge, Bates and Pettit1998); and home environment (CHAOS: Confusion, Hubbub and Order Scale; Matheny et al., Reference Matheny, Wachs, Ludwig and Phillips1995). The self assessment of personality traits involves self-ratings on a scale from 1 to 5 (1 = very much like me, 5 = very much unlike me) of personality characteristics, such as aggressiveness, purposefulness, diligence, and discipline (Mullins-Sweatt et al., Reference Mullins-Sweatt, Jamerson, Samuel, Olson and Widiger2006).
The questions about mathematics were included from the Programme for International Student Assessment (PISA, 2009) questionnaires on mathematics. The questions assess four aspects of the children's relationship with mathematics: (1) time spent doing and exercising mathematics; (2) maths interest; (3) maths self-efficacy; and (4) attitude to academic subjects. The first aspect of the PISA maths questionnaire assesses the time spent doing mathematics: at school during regular lessons, outside school (e.g., tutors and additional maths activities), and studying mathematics by themselves. The second aspect of the PISA maths questionnaire looks at the individuals’ mathematical interests with three items: looking forward to mathematical lessons, doing maths out of enjoyment, and being interested in things learned in mathematics lessons. The third aspect of the PISA maths questionnaire looks at the individual's maths self-efficacy, including eight items, such as using train timetables, understanding graphs, and solving linear equations. The last aspect of the PISA questionnaire looks at the children's attitude toward academic subjects, rating Science, Mathematics, and English (Russian or French, depending on the sample) on a scale from 1 to 4 (1 = not important, 4 = very important).



