1 Introduction
DatalogMTL (Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) is an extension of the core rule-based language Datalog (Ceri et al. Reference Ceri, Gottlob and Tanca1989) with operators from metric temporal logic (MTL) (Koymans Reference Koymans1990) interpreted over the rational timeline. For example, the following DatalogMTL rule states that travellers can enter the US if they had a negative COVID-19 test sometime in the last
![]() $2$
days (
$2$
days (
![]() $\diamondsuit \!\!\!\!\!-_{[0,2]}$
) and have held fully vaccinated status continuously throughout the last
$\diamondsuit \!\!\!\!\!-_{[0,2]}$
) and have held fully vaccinated status continuously throughout the last
![]() $15$
days (
$15$
days (
![]() $\boxminus _{[0,15]}$
)
$\boxminus _{[0,15]}$
)
DatalogMTL is a powerful temporal knowledge representation language, which has recently found applications in ontology-based query answering (Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018; Kikot et al. Reference Kikot, Ryzhikov, Wałȩga and Zakharyaschev2018; Kalaycı et al. Reference Kalaycı, Xiao, Ryzhikov, Kalayci and Calvanese2018; Koopmann Reference Koopmann2019) and stream reasoning (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019 Reference Wałȩga, Kaminski and Cuenca Graub), amongst others (Nissl and Sallinger Reference Nissl and Sallinger2022; Mori et al. Reference Mori, Papotti, Bellomarini and Giudice2022). Reasoning in DatalogMTL is, however, of high complexity, namely ExpSpace-complete (Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) and PSpace-complete with respect to data size (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a), which makes reasoning in data-intensive applications challenging. Thus, theoretical research has focused on establishing a suitable trade-off between expressive power and complexity of reasoning, by identifying lower complexity fragments of DatalogMTL (Wałȩga et al. Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021,Reference Wałȩga, Zawidzki and Grau2023) and studying alternative semantics with favourable computational behaviour (Wałȩga et al. Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2020; Ryzhikov et al. Reference Ryzhikov, Wałȩga and Zakharyaschev2019).
The design and implementation of practical reasoning algorithms for DatalogMTL remains, however, a largely unexplored area – something that has so far prevented its widespread adoption in applications. Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) implemented a prototype reasoner based on query rewriting that is applicable only to non-recursive DatalogMTL programmes; in turn, the temporal extension of the Vadalog system (Bellomarini et al. Reference Bellomarini, Sallinger and Gottlob2018) described by Bellomarini et al. (Reference Bellomarini, Blasi, Nissl and Sallinger2022) implements the full DatalogMTL language, but without termination guarantees. The lack of available reasoners for DatalogMTL is in stark contrast with plain Datalog, for which a plethora of (both academic and commercial) systems have been developed and successfully deployed in practice (Motik et al. Reference Motik, Nenov, Piro, Horrocks and Olteanu2014; Bellomarini et al. Reference Bellomarini, Sallinger and Gottlob2018; Carral et al. Reference Carral, Dragoste, González, Jacobs, Krötzsch and Urbani2019).
In this paper, we present the first practical reasoning algorithm for the full DatalogMTL language, which is sound, complete, and terminating. Our algorithm combines materialisation (a.k.a. forward chaining) and automata-based reasoning. On the one hand, materialisation is the reasoning paradigm of choice in numerous Datalog systems (Bry et al. Reference Bry, Eisinger, Eiter, Furche, Gottlob, Ley, Linse, Pichler and Wei2007; Motik et al. Reference Motik, Nenov, Piro, Horrocks and Olteanu2014; Bellomarini et al. Reference Bellomarini, Sallinger and Gottlob2018; Carral et al. Reference Carral, Dragoste, González, Jacobs, Krötzsch and Urbani2019); facts logically entailed by an input programme and dataset are derived in successive rounds of rule applications (also called materialisation steps) until a fixpoint is reached or a fact of interest (or a contradiction) is derived; both this process and its output are often referred to as materialisation. A direct implementation of materialisation-based reasoning in DatalogMTL is, however, problematic since forward chaining may require infinitely many rounds of rule applications (Wałȩga et al. Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021,Reference Wałȩga, Zawidzki and Grau2023). An alternative to materialisation-based reasoning ensuring completeness and termination relies on constructing B FC;chi automata and checking non-emptiness of their languages (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a). This procedure, however, was mainly proposed for obtaining tight complexity bounds, and not with efficient implementation in mind; in particular, the constructed automata are of exponential size, which makes direct implementations impractical. Our approach deals with these difficulties by providing optimised materialisation-based algorithms together with an effective way of combining the scalability of materialisation-based reasoning and the completeness guaranteed by automata-based procedures, thus providing “the best of both worlds.”
After discussing related work in Section 2 and preliminary definitions for DatalogMTL in Section 3, we will present the following contributions of our work.
-
1. In Section 4 we recapitulate different techniques available for reasoning in DatalogMTL, which we will take as a starting point for the development of our approach. On the one hand, we present a variant of the (non-terminating) naïve materialisation procedure (Wałȩga et al. Reference Wałȩga, Zawidzki and Grau2023), and prove its soundness and completeness; on the other hand, we describe existing algorithms based on exponential reductions to reasoning in linear temporal logic (LTL) and to emptiness checking of B FC;chi automata.
-
2. In Section 5.1 we present a seminaïve materialisation procedure for DatalogMTL. In contrast to the naïve procedure provided in Section 4.1 and analogously to the classical seminaïve algorithm for plain Datalog (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995; Motik et al. Reference Motik, Nenov, Piro and Horrocks2019), our procedure aims at minimising redundant computation by keeping track of newly derived facts in each materialisation step and ensuring that rule applications in the following materialisation step involve at least one of these newly derived facts. In this way, each rule instance is considered at most once, and so our procedure is said to enjoy the non-repetition property.
-
3. In Section 5.2 we present an optimised variant of our seminaïve procedure which further reduces the number of redundant computations performed during materialisation by disregarding rules during the execution of the procedure as soon as we can be certain that their application will never derive new facts in subsequent materialisation steps.
-
4. In Section 5.3 we propose a practical reasoning algorithm combining optimised seminaïve materialisation and our realisation of the automata-based reasoning approach of (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a). Our algorithm is designed to delegate the bulk of the computation to the scalable materialisation component and resort to automata-based techniques only as needed to ensure termination and completeness.
-
5. We have implemented our approach in the MeTeoR (Metric Temporal Reasoner) system, which we have made publicly available.Footnote 1 In Section 6 we describe our implementation and present its evaluation on a temporal extension of the Lehigh University Benchmark (LUBM), the Weather Benchmark used by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), and the iTemporal benchmark generator developed by Bellomarini et al. (Reference Bellomarini, Blasi, Nissl and Sallinger2022). In Section 6.4 we describe the results of our evaluation and draw the following conclusions.
-
– Although completeness and termination in our approach can be ensured by relying on either automata construction or on a reduction to LTL satisfiability followed by the application of a LTL reasoner, our experiments show that automata construction yields superior performance and can be used to solve non-trivial problems; this justifies our choice of automata over LTL in MeTeoR.
-
– Our proposed seminaïve materialisation strategy offers significant performance and scalability gains over naïve materialisation, and it can be successfully applied to non-trivial programmes and datasets with tens of millions of temporal facts.
-
– The performance of MeTeoR is superior to that of the query rewriting approach proposed by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) on non-recursive programmes.
-
– The vast majority of queries for programmes generated by iTemporal can be answered using materialisation only. This supports the practicality of our approach since the bulk of the workload is delegated to the scalable materialisation component and the use of automata-based reasoning is only required in exceptional cases.
-
This paper is supplemented by a technical appendix containing all the proofs to our claims.
2 Related work
DatalogMTL was first introduced by Brandt et al. (Reference Brandt, Kalaycı, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017) and it has found applications in areas as diverse as temporal stream reasoning (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019b), temporal ontology-based data access (Brandt et al. Reference Brandt, Kalaycı, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017), specification and verification of banking agreements (Nissl and Sallinger Reference Nissl and Sallinger2022), fact-checking economic claims (Mori et al. Reference Mori, Papotti, Bellomarini and Giudice2022), and the description of human movements (Raheb et al. Reference Raheb, Mailis, Ryzhikov, Papapetrou and Ioannidis2017). The complexity of standard reasoning tasks in both the full language and its fragments has been investigated in depth (Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018; Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a,Reference Wałȩga, Zawidzki and Cuenca Grau2021; Bellomarini et al. Reference Bellomarini, Nissl and Sallinger2021). Alternative semantics to the standard continuous semantics over the rational timeline have also been considered; these include the semantics based on the integer timeline studied by Wałȩga et al. (Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2020) and the event-based semantics by Ryzhikov et al. (Reference Ryzhikov, Wałȩga and Zakharyaschev2019). DatalogMTL has also been recently extended with negation-as-failure under the stable model semantics, first for stratified programmes (Cucala et al. Reference Cucala, Wałȩga, Cuenca Grau and Kostylev2021) and subsequently for the general case (Wałȩga et al. Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021).
There have been numerous alternative proposals for extending Datalog with temporal constructs. For example, Datalog
![]() $_{1S}$
(Chomicki and Imielinski Reference Chomicki and Imielinski1988) is a prominent early extension, in which predicates are allowed to contain terms of an additional temporal sort and a single successor function symbol over this sort. A number of recent temporal extensions of Datalog feature operators from LTL (Artale et al. Reference Artale, Kontchakov, Kovtunova, Ryzhikov, Wolter and Zakharyaschev2015) as well as from the Halpern-Shoham logic of intervals (Kontchakov et al. Reference Kontchakov, Pandolfo, Pulina, Ryzhikov and Zakharyaschev2016). Extensions of DatalogMTL with non-monotonic negation are closely related to temporal extensions of answer set programming (ASP) (Aguado et al. Reference Aguado, Cabalar, Diéguez, Pérez, Schaub, Schuhmann and Vidal2021). Particularly relevant is a recently introduced extension of ASP with MTL operators (Cabalar et al. Reference Cabalar, Diéguez, Schaub and Schuhmann2020) as well as the LARS framework (Beck et al. Reference Beck, Dao-Tran and Eiter2018), which combines ASP and MTL operators for reasoning over data streams. It is worth observing, however, that all these temporal extensions of ASP are interpreted over the integer timeline. Finally, operators from MTL have also been exploited in temporal extensions of description logics (Gutiérrez-Basulto et al. Reference Gutiérrez-Basulto, Jung and Ozaki2016; Artale and Franconi Reference Artale and Franconi1998; Baader et al. Reference Baader, Borgwardt, Koopmann, Ozaki and Thost2017; Thost Reference Thost2018).
$_{1S}$
(Chomicki and Imielinski Reference Chomicki and Imielinski1988) is a prominent early extension, in which predicates are allowed to contain terms of an additional temporal sort and a single successor function symbol over this sort. A number of recent temporal extensions of Datalog feature operators from LTL (Artale et al. Reference Artale, Kontchakov, Kovtunova, Ryzhikov, Wolter and Zakharyaschev2015) as well as from the Halpern-Shoham logic of intervals (Kontchakov et al. Reference Kontchakov, Pandolfo, Pulina, Ryzhikov and Zakharyaschev2016). Extensions of DatalogMTL with non-monotonic negation are closely related to temporal extensions of answer set programming (ASP) (Aguado et al. Reference Aguado, Cabalar, Diéguez, Pérez, Schaub, Schuhmann and Vidal2021). Particularly relevant is a recently introduced extension of ASP with MTL operators (Cabalar et al. Reference Cabalar, Diéguez, Schaub and Schuhmann2020) as well as the LARS framework (Beck et al. Reference Beck, Dao-Tran and Eiter2018), which combines ASP and MTL operators for reasoning over data streams. It is worth observing, however, that all these temporal extensions of ASP are interpreted over the integer timeline. Finally, operators from MTL have also been exploited in temporal extensions of description logics (Gutiérrez-Basulto et al. Reference Gutiérrez-Basulto, Jung and Ozaki2016; Artale and Franconi Reference Artale and Franconi1998; Baader et al. Reference Baader, Borgwardt, Koopmann, Ozaki and Thost2017; Thost Reference Thost2018).
The first system with DatalogMTL support was an extension of the Ontop platform (Kalaycı et al. Reference Kalaycı, Xiao, Ryzhikov, Kalayci and Calvanese2018) restricted to non-recursive programmes and based on reasoning via rewriting into SQL. Very recently, the Vadalog reasoning system (Bellomarini et al. Reference Bellomarini, Sallinger and Gottlob2018) has also been extended with DatalogMTL support (Bellomarini et al. Reference Bellomarini, Blasi, Nissl and Sallinger2022); the algorithm implemented by this extension is, however, non-terminating in general. Fragments of DatalogMTL for which materialisation-based reasoning is guaranteed to terminate have been identified and studied by Wałȩga et al. (Reference Wałȩga, Zawidzki and Grau2023); these fragments, however, impose restrictions which effectively disallow programmes expressing “recursion through time.” Finally, there is a plethora of reasoners available for solving satisfiability checking problems in LTL, with techniques involving reduction to model checking, tableau systems, and automata-based techniques. Prominent recent examples of highly-optimised LTL reasoners include nuXmv (Cavada et al. Reference Cavada, Cimatti, Dorigatti, Griggio, Mariotti, Micheli, Mover, Roveri and Tonetta2014) and BLACK (Geatti et al. Reference Geatti, Gigante and Montanari2019), where the latter was our LTL reasoner of choice in the experiments reported in Section 6.
3 Preliminaries
In this section, we recapitulate the syntax, semantics, and key reasoning problems in DatalogMTL.
3.1 Syntax
We consider a timeline consisting of ordered rational numbers, denoted by
![]() $\mathbb{Q}$
, which we also call time points. A (rational) interval
$\mathbb{Q}$
, which we also call time points. A (rational) interval
![]() $\rho$
is a set of rational numbers that is either empty or such that
$\rho$
is a set of rational numbers that is either empty or such that
-
– for all
 $t_1,t_2, t_3 \in \mathbb{Q}$
satisfying
$t_1,t_2, t_3 \in \mathbb{Q}$
satisfying
 $t_1 < t_2 < t_3$
and
$t_1 < t_2 < t_3$
and
 $t_1,t_3 \in \rho$
, it must be the case that
$t_1,t_3 \in \rho$
, it must be the case that
 $t_2 \in \rho$
, and
$t_2 \in \rho$
, and -
– the greatest lower bound
 $\rho ^-$
and the least upper bound
$\rho ^-$
and the least upper bound
 $\rho ^+$
of
$\rho ^+$
of
 $\rho$
belong to
$\rho$
belong to
 $\mathbb{Q} \cup \{-\infty, \infty \}$
.Footnote
2
$\mathbb{Q} \cup \{-\infty, \infty \}$
.Footnote
2
The bounds
![]() $\rho ^-$
and
$\rho ^-$
and
![]() $\rho ^+$
are called the left and the right endpoints of
$\rho ^+$
are called the left and the right endpoints of
![]() $\rho$
, respectively. An interval is punctual if it contains exactly one time point. Intervals
$\rho$
, respectively. An interval is punctual if it contains exactly one time point. Intervals
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are union-compatible if
$\rho _2$
are union-compatible if
![]() $\rho = \rho _1 \cup \rho _2$
is also an interval. We represent a non-empty interval
$\rho = \rho _1 \cup \rho _2$
is also an interval. We represent a non-empty interval
![]() $\rho$
using the standard notation
$\rho$
using the standard notation
![]() $\langle \rho ^-,\rho ^+ \rangle$
, where the left bracket “
$\langle \rho ^-,\rho ^+ \rangle$
, where the left bracket “
![]() $\langle$
” is either “
$\langle$
” is either “
![]() $[$
” or “
$[$
” or “
![]() $($
”, and the right bracket
$($
”, and the right bracket
![]() $\rangle$
is either “
$\rangle$
is either “
![]() $]$
” or “
$]$
” or “
![]() $)$
”. We assume that each rational endpoint is given as a (not necessary reduced) fraction with an integer numerator and a positive integer denominator, both encoded in binary. As usual, the brackets “
$)$
”. We assume that each rational endpoint is given as a (not necessary reduced) fraction with an integer numerator and a positive integer denominator, both encoded in binary. As usual, the brackets “
![]() $[$
” and “
$[$
” and “
![]() $]$
” indicate that the corresponding endpoints are included in the interval, whereas “
$]$
” indicate that the corresponding endpoints are included in the interval, whereas “
![]() $($
” and “
$($
” and “
![]() $)$
” indicate that they are not included. Observe that every interval has multiple representations due to possibly non-reduced fractions. Each representation, however, uniquely determines an interval and so, if it is clear from the context, we will abuse notation and identify an interval representation with the unique interval it represents.
$)$
” indicate that they are not included. Observe that every interval has multiple representations due to possibly non-reduced fractions. Each representation, however, uniquely determines an interval and so, if it is clear from the context, we will abuse notation and identify an interval representation with the unique interval it represents.
We consider a signature consisting of pairwise disjoint countable sets of constants, variables, and predicates with non-negative integer arities. As usual, a term is either a constant or a variable. A relational atom is an expression of the form
![]() $P(\mathbf{s})$
, with
$P(\mathbf{s})$
, with
![]() $P$
a predicate and
$P$
a predicate and
![]() $\mathbf{s}$
a tuple of terms whose length matches the arity of
$\mathbf{s}$
a tuple of terms whose length matches the arity of
![]() $P$
. A metric atom is an expression given by the following grammar, where
$P$
. A metric atom is an expression given by the following grammar, where
![]() $P(\mathbf{s})$
is a relational atom,
$P(\mathbf{s})$
is a relational atom,
![]() $\top$
and
$\top$
and
![]() $\bot$
are logical truth and falsehood respectively, and
$\bot$
are logical truth and falsehood respectively, and
![]() $\diamondsuit \!\!\!\!\!-$
,
$\diamondsuit \!\!\!\!\!-$
,
![]() $\diamondsuit \kern -7.7pt{+}$
,
$\diamondsuit \kern -7.7pt{+}$
,
![]() $\boxminus$
,
$\boxminus$
,
![]() $\boxplus$
,
$\boxplus$
,
![]() $\mathcal{S}$
, and
$\mathcal{S}$
, and
![]() $\mathscr{U}$
are MTL operators that can be indexed with any intervals
$\mathscr{U}$
are MTL operators that can be indexed with any intervals
![]() $\rho$
containing only non-negative rationals:
$\rho$
containing only non-negative rationals:
We refer to
![]() $\diamondsuit \!\!\!\!\!-$
,
$\diamondsuit \!\!\!\!\!-$
,
![]() $\boxminus$
, and
$\boxminus$
, and
![]() $\mathscr{S}$
as past operators and we refer to
$\mathscr{S}$
as past operators and we refer to
![]() $\diamondsuit \kern -7.7pt{+}$
,
$\diamondsuit \kern -7.7pt{+}$
,
![]() $\boxplus$
, and
$\boxplus$
, and
![]() $\mathscr{U}$
as future operators. A rule is an expression of the form
$\mathscr{U}$
as future operators. A rule is an expression of the form
with each
![]() $M_i$
a metric atom, and
$M_i$
a metric atom, and
![]() $M'$
generated by the following grammar:
$M'$
generated by the following grammar:
The conjunction
![]() $M_1 \land \dots \land M_n$
in Expression (1) is the rule’s body and
$M_1 \land \dots \land M_n$
in Expression (1) is the rule’s body and
![]() $M'$
is the rule’s head. A rule mentioning
$M'$
is the rule’s head. A rule mentioning
![]() $\bot$
in the head is referred to as a
$\bot$
in the head is referred to as a
![]() $\bot$
-rule. A rule is forward-propagating (respectively backwards propagating) if it does not mention
$\bot$
-rule. A rule is forward-propagating (respectively backwards propagating) if it does not mention
![]() $\top$
or
$\top$
or
![]() $\bot$
, mentions only past (respectively, future) operators in the body, and only future (respectively, past) operators in the head. A rule is safe if each variable in its head also occurs in the body, and this occurrence is not in a left operand of
$\bot$
, mentions only past (respectively, future) operators in the body, and only future (respectively, past) operators in the head. A rule is safe if each variable in its head also occurs in the body, and this occurrence is not in a left operand of
![]() $\mathscr{S}$
or
$\mathscr{S}$
or
![]() $\mathscr{U}$
; for instance, a rule such as
$\mathscr{U}$
; for instance, a rule such as
![]() $P(x) \gets Q(x){\mathscr{S}}_{[0,0]} \top$
is not safe; in fact, it can be equivalently rewritten as
$P(x) \gets Q(x){\mathscr{S}}_{[0,0]} \top$
is not safe; in fact, it can be equivalently rewritten as
![]() $P(x) \gets \top$
(see the following section on DatalogMTL semantics). A programme is a finite set of safe rules; it is forward or backwards propagating if so are all its rules.
$P(x) \gets \top$
(see the following section on DatalogMTL semantics). A programme is a finite set of safe rules; it is forward or backwards propagating if so are all its rules.
An expression is ground if it mentions no variables. A fact is an expression of the form
![]() $M @ \rho$
with
$M @ \rho$
with
![]() $M$
a ground relational atom and
$M$
a ground relational atom and
![]() $\rho$
an interval; a dataset is a finite set of facts. The coalescing of facts
$\rho$
an interval; a dataset is a finite set of facts. The coalescing of facts
![]() $M@\rho _1$
and
$M@\rho _1$
and
![]() $M@\rho _2$
with union-compatible intervals
$M@\rho _2$
with union-compatible intervals
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
is the fact
$\rho _2$
is the fact
![]() $M@(\rho _1 \cup \rho _2)$
. The coalescing of a dataset
$M@(\rho _1 \cup \rho _2)$
. The coalescing of a dataset
![]() $\mathscr{D}$
, denoted by
$\mathscr{D}$
, denoted by
![]() $\mathsf{coal}({\mathscr{D}})$
, is the unique dataset obtained by iteratively coalescing facts in
$\mathsf{coal}({\mathscr{D}})$
, is the unique dataset obtained by iteratively coalescing facts in
![]() $\mathscr{D}$
until no more facts can be coalesced. The grounding
$\mathscr{D}$
until no more facts can be coalesced. The grounding
![]() $\mathsf{ground}(\Pi, {\mathscr{D}})$
of a programme
$\mathsf{ground}(\Pi, {\mathscr{D}})$
of a programme
![]() $\Pi$
with respect to a dataset
$\Pi$
with respect to a dataset
![]() $\mathscr{D}$
is the set of all ground rules that can be obtained by assigning constants in
$\mathscr{D}$
is the set of all ground rules that can be obtained by assigning constants in
![]() $\Pi$
or
$\Pi$
or
![]() $\mathscr{D}$
to variables in
$\mathscr{D}$
to variables in
![]() $\Pi$
.
$\Pi$
.
The dependency graph of a programme
![]() $\Pi$
is the directed graph
$\Pi$
is the directed graph
![]() $G_{\Pi }$
, with a vertex
$G_{\Pi }$
, with a vertex
![]() $v_P$
for each predicate
$v_P$
for each predicate
![]() $P$
in
$P$
in
![]() $\Pi$
and an edge
$\Pi$
and an edge
![]() $(v_Q, v_R)$
whenever there is a rule in
$(v_Q, v_R)$
whenever there is a rule in
![]() $\Pi$
mentioning
$\Pi$
mentioning
![]() $Q$
in the body and
$Q$
in the body and
![]() $R$
in the head. Programme
$R$
in the head. Programme
![]() $\Pi$
is recursive if
$\Pi$
is recursive if
![]() $G_{\Pi }$
has a cycle. A predicate
$G_{\Pi }$
has a cycle. A predicate
![]() $P$
is recursive in
$P$
is recursive in
![]() $\Pi$
if
$\Pi$
if
![]() $G_{\Pi }$
has a path ending in
$G_{\Pi }$
has a path ending in
![]() $v_P$
and including a cycle (the path can be a self-loop); otherwise, it is non-recursive. A metric atom is non-recursive in
$v_P$
and including a cycle (the path can be a self-loop); otherwise, it is non-recursive. A metric atom is non-recursive in
![]() $\Pi$
if so are all its predicates; otherwise it is recursive. The (non-)recursive fragment of
$\Pi$
if so are all its predicates; otherwise it is recursive. The (non-)recursive fragment of
![]() $\Pi$
is the subset of rules in
$\Pi$
is the subset of rules in
![]() $\Pi$
with (non-)recursive atoms in heads. Furthermore, for a predicate
$\Pi$
with (non-)recursive atoms in heads. Furthermore, for a predicate
![]() $P$
, a rule
$P$
, a rule
![]() $r$
is
$r$
is
![]() $P$
-relevant in
$P$
-relevant in
![]() $\Pi$
if there exists a rule
$\Pi$
if there exists a rule
![]() $r'$
in
$r'$
in
![]() $\Pi$
mentioning
$\Pi$
mentioning
![]() $P$
or
$P$
or
![]() $\bot$
in the head and a path in
$\bot$
in the head and a path in
![]() $G_{\Pi }$
starting from a vertex representing the predicate in the head of
$G_{\Pi }$
starting from a vertex representing the predicate in the head of
![]() $r$
and ending in a vertex representing some predicate from the body of
$r$
and ending in a vertex representing some predicate from the body of
![]() $r'$
.
$r'$
.
3.2 Semantics and reasoning problems
An interpretation
![]() $\mathfrak{I}$
is a function which assigns to each time point
$\mathfrak{I}$
is a function which assigns to each time point
![]() $t$
a set of ground relational atoms; if an atom
$t$
a set of ground relational atoms; if an atom
![]() $P(\mathbf{c})$
belongs to this set, we say that
$P(\mathbf{c})$
belongs to this set, we say that
![]() $P(\mathbf{c})$
is satisfied at
$P(\mathbf{c})$
is satisfied at
![]() $t$
in
$t$
in
![]() $\mathfrak{I}$
and we write
$\mathfrak{I}$
and we write
![]() ${\mathfrak{I}},t \models P(\mathbf{c})$
. This extends to arbitrary metric atoms as shown in Table 1.
${\mathfrak{I}},t \models P(\mathbf{c})$
. This extends to arbitrary metric atoms as shown in Table 1.
Table 1. Semantics of ground metric atoms

An interpretation
![]() $\mathfrak{I}$
satisfies a fact
$\mathfrak{I}$
satisfies a fact
![]() $M @ \rho$
if
$M @ \rho$
if
![]() ${\mathfrak{I}},t \models M$
for all
${\mathfrak{I}},t \models M$
for all
![]() $t \in \rho$
. Interpretation
$t \in \rho$
. Interpretation
![]() $\mathfrak{I}$
satisfies a ground rule
$\mathfrak{I}$
satisfies a ground rule
![]() $r$
if, whenever
$r$
if, whenever
![]() $\mathfrak{I}$
satisfies each body atom of
$\mathfrak{I}$
satisfies each body atom of
![]() $r$
at a time point
$r$
at a time point
![]() $t$
, then
$t$
, then
![]() $\mathfrak{I}$
also satisfies the head of
$\mathfrak{I}$
also satisfies the head of
![]() $r$
at
$r$
at
![]() $t$
. Interpretation
$t$
. Interpretation
![]() $\mathfrak{I}$
satisfies a (non-ground) rule
$\mathfrak{I}$
satisfies a (non-ground) rule
![]() $r$
if it satisfies each ground instance of
$r$
if it satisfies each ground instance of
![]() $r$
. Interpretation
$r$
. Interpretation
![]() $\mathfrak{I}$
is a model of a programme
$\mathfrak{I}$
is a model of a programme
![]() $\Pi$
if it satisfies each rule in
$\Pi$
if it satisfies each rule in
![]() $\Pi$
, and it is a model of a dataset
$\Pi$
, and it is a model of a dataset
![]() $\mathscr{D}$
if it satisfies each fact in
$\mathscr{D}$
if it satisfies each fact in
![]() $\mathscr{D}$
. Each dataset
$\mathscr{D}$
. Each dataset
![]() $\mathscr{D}$
has a unique least model
$\mathscr{D}$
has a unique least model
![]() ${\mathfrak{I}}_{\mathscr{D}}$
, and we say that dataset
${\mathfrak{I}}_{\mathscr{D}}$
, and we say that dataset
![]() $\mathscr{D}$
represents interpretation
$\mathscr{D}$
represents interpretation
![]() ${\mathfrak{I}}_{{\mathscr{D}}}$
. Programme
${\mathfrak{I}}_{{\mathscr{D}}}$
. Programme
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathscr{D}$
are consistent if they have a model, and they entail a fact
$\mathscr{D}$
are consistent if they have a model, and they entail a fact
![]() $M@ \rho$
if each model of both
$M@ \rho$
if each model of both
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
is a model of
$\mathscr{D}$
is a model of
![]() $M@ \rho$
.
$M@ \rho$
.
Consistency checking is the problem of checking whether a given programme and a dataset admit a common model. Fact entailment is the problem of checking whether a programme and a dataset entail a given relational fact. Consistency checking and fact entailment in
![]() $\textrm{DatalogMTL}$
reduce to the complements of each other. Specifically, to check whether a programme
$\textrm{DatalogMTL}$
reduce to the complements of each other. Specifically, to check whether a programme
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathscr{D}$
are inconsistent, it suffices to check whether they entail fact
$\mathscr{D}$
are inconsistent, it suffices to check whether they entail fact
![]() $P@0$
, for
$P@0$
, for
![]() $P$
a fresh proposition occurring neither in
$P$
a fresh proposition occurring neither in
![]() $\Pi$
nor in
$\Pi$
nor in
![]() $\mathscr{D}$
. In turn, to check whether
$\mathscr{D}$
. In turn, to check whether
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
entail a fact
$\mathscr{D}$
entail a fact
![]() $P(\mathbf{c})@\rho$
, it suffices to check whether the following programme and dataset are inconsistent, with
$P(\mathbf{c})@\rho$
, it suffices to check whether the following programme and dataset are inconsistent, with
![]() $P'$
a fresh predicate of the same arity as
$P'$
a fresh predicate of the same arity as
![]() $P$
,
$P$
,
![]() $\mathbf{x}$
a tuple of distinct variables, and
$\mathbf{x}$
a tuple of distinct variables, and
![]() $t$
an arbitrary time point belonging to the interval
$t$
an arbitrary time point belonging to the interval
![]() $\rho$
:
$\rho$
:
Intervals
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are constructed using
$\rho _2$
are constructed using
![]() $\rho$
and
$\rho$
and
![]() $t$
; for example, if
$t$
; for example, if
![]() $\rho =[ t_1,t_2 )$
, then
$\rho =[ t_1,t_2 )$
, then
![]() $\rho _1=[0,t-t_1]$
and
$\rho _1=[0,t-t_1]$
and
![]() $\rho _2=[0,t_2-t)$
, whereas if
$\rho _2=[0,t_2-t)$
, whereas if
![]() $t_2= \infty$
, then
$t_2= \infty$
, then
![]() $t_2-t$
stands for
$t_2-t$
stands for
![]() $\infty$
.
$\infty$
.
3.3 Fixpoint characterisation and the canonical interpretation
Each pair of a consistent programme
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathscr{D}$
admits a unique least model, which we refer to as their canonical interpretation
$\mathscr{D}$
admits a unique least model, which we refer to as their canonical interpretation
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
(Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018). As in plain Datalog, we can construct this interpretation by applying rules of
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
(Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018). As in plain Datalog, we can construct this interpretation by applying rules of
![]() $\Pi$
to
$\Pi$
to
![]() $\mathscr{D}$
in a forward-chaining manner until a fixpoint is reached. Unlike plain Datalog, however, the fixpoint in DatalogMTL may only be reachable after infinitely many materialisation steps; for example, given a fact
$\mathscr{D}$
in a forward-chaining manner until a fixpoint is reached. Unlike plain Datalog, however, the fixpoint in DatalogMTL may only be reachable after infinitely many materialisation steps; for example, given a fact
![]() $P@0$
, the rule
$P@0$
, the rule
![]() $\boxplus _1 P \gets P$
propagates
$\boxplus _1 P \gets P$
propagates
![]() $P$
to all positive integers, which requires
$P$
to all positive integers, which requires
![]() $\omega$
materialisation steps.
$\omega$
materialisation steps.
Materialisation is performed using the immediate consequence operator
![]() $T_{\Pi }$
; intuitively,
$T_{\Pi }$
; intuitively,
![]() $T_{\Pi }({\mathfrak{I}})$
can be seen as the interpretation obtained from
$T_{\Pi }({\mathfrak{I}})$
can be seen as the interpretation obtained from
![]() $\mathfrak{I}$
by adding all relational facts that can be derived by applying once all rules in
$\mathfrak{I}$
by adding all relational facts that can be derived by applying once all rules in
![]() $\Pi$
which are not
$\Pi$
which are not
![]() $\bot$
-rules in all possible ways to
$\bot$
-rules in all possible ways to
![]() $\mathfrak{I}$
. Formally, we define
$\mathfrak{I}$
. Formally, we define
![]() $T_{\Pi }$
, for a programme
$T_{\Pi }$
, for a programme
![]() $\Pi$
, as the operator mapping each interpretation
$\Pi$
, as the operator mapping each interpretation
![]() $\mathfrak{I}$
to the least interpretation containing
$\mathfrak{I}$
to the least interpretation containing
![]() $\mathfrak{I}$
and satisfying the following property for each ground instance
$\mathfrak{I}$
and satisfying the following property for each ground instance
![]() $r$
of a rule in
$r$
of a rule in
![]() $\Pi$
that is not a
$\Pi$
that is not a
![]() $\bot$
-rule: whenever
$\bot$
-rule: whenever
![]() $\mathfrak{I}$
satisfies each body atom of
$\mathfrak{I}$
satisfies each body atom of
![]() $r$
at a time point
$r$
at a time point
![]() $t$
, then
$t$
, then
![]() $T_{\Pi }({\mathfrak{I}})$
satisfies the head of
$T_{\Pi }({\mathfrak{I}})$
satisfies the head of
![]() $r$
at
$r$
at
![]() $t$
. Subsequent applications of
$t$
. Subsequent applications of
![]() $T_{\Pi }$
to the (least) model
$T_{\Pi }$
to the (least) model
![]() ${\mathfrak{I}}_{\mathscr{D}}$
of
${\mathfrak{I}}_{\mathscr{D}}$
of
![]() $\mathscr{D}$
define the following sequence of interpretations, for all ordinals
$\mathscr{D}$
define the following sequence of interpretations, for all ordinals
![]() $\alpha$
:
$\alpha$
:
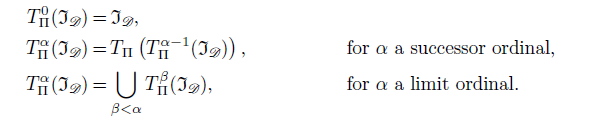 \begin{align*} T_{\Pi }^0({\mathfrak{I}}_{\mathscr{D}}) &={\mathfrak{I}}_{\mathscr{D}}, && \\ T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}}) & = T_{\Pi } \left ( T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{\mathscr{D}}) \right ), && \text{for } \alpha \text{ a successor ordinal}, \\ T_{\Pi }^{\alpha } ({\mathfrak{I}}_{\mathscr{D}}) &= \bigcup_{\beta < \alpha } T_{\Pi }^{\beta }({\mathfrak{I}}_{\mathscr{D}}), && \text{for } \alpha \text{ a limit ordinal}. \end{align*}
\begin{align*} T_{\Pi }^0({\mathfrak{I}}_{\mathscr{D}}) &={\mathfrak{I}}_{\mathscr{D}}, && \\ T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}}) & = T_{\Pi } \left ( T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{\mathscr{D}}) \right ), && \text{for } \alpha \text{ a successor ordinal}, \\ T_{\Pi }^{\alpha } ({\mathfrak{I}}_{\mathscr{D}}) &= \bigcup_{\beta < \alpha } T_{\Pi }^{\beta }({\mathfrak{I}}_{\mathscr{D}}), && \text{for } \alpha \text{ a limit ordinal}. \end{align*}
The canonical interpretation is obtained after at most
![]() $\omega _1$
(i.e. the first uncountable ordinal) applications of
$\omega _1$
(i.e. the first uncountable ordinal) applications of
![]() $T_{\Pi }$
; that is,
$T_{\Pi }$
; that is,
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}} = T_{\Pi }^{\omega _1}({\mathfrak{I}}_{\mathscr{D}})$
(Brandt et al. Reference Brandt, Kalaycı, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017); in turn, if
$\mathfrak{C}_{\Pi, {\mathscr{D}}} = T_{\Pi }^{\omega _1}({\mathfrak{I}}_{\mathscr{D}})$
(Brandt et al. Reference Brandt, Kalaycı, Kontchakov, Ryzhikov, Xiao and Zakharyaschev2017); in turn, if
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
are consistent then
$\mathscr{D}$
are consistent then
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is the least common model of
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is the least common model of
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. Furthermore,
$\mathscr{D}$
. Furthermore,
![]() $\bot$
-rules can be treated as constraints, and so
$\bot$
-rules can be treated as constraints, and so
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
are consistent if and only if
$\mathscr{D}$
are consistent if and only if
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is a model of all
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is a model of all
![]() $\bot$
-rules in
$\bot$
-rules in
![]() $\Pi$
.
$\Pi$
.
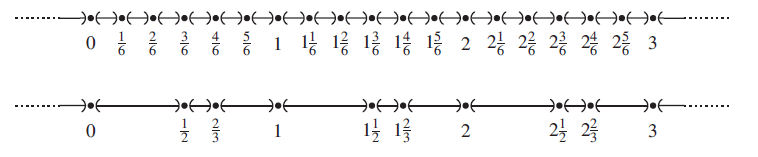
Although the timeline in DatalogMTL is dense, it can be divided into regularly distributed intervals which are uniform in the sense that, in the canonical interpretation, the same relational atoms hold in all time points belonging to the same interval. This observation was first exploited to partition the rational timeline, for a programme
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathscr{D}$
, into punctual intervals
$\mathscr{D}$
, into punctual intervals
![]() $[i\cdot d,i\cdot d]$
and open intervals
$[i\cdot d,i\cdot d]$
and open intervals
![]() $((i-1)\cdot d, i\cdot d)$
, for each
$((i-1)\cdot d, i\cdot d)$
, for each
![]() $i \in \mathbb{Z}$
, where
$i \in \mathbb{Z}$
, where
![]() $d$
is the greatest common divisor (gcd) of the numbers occurring as interval endpoints in
$d$
is the greatest common divisor (gcd) of the numbers occurring as interval endpoints in
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
(Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018). Later, an alternative partitioning of the timeline was proposed (Wałȩga et al. Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2019a), where punctual intervals of the form
$\mathscr{D}$
(Brandt et al. Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018). Later, an alternative partitioning of the timeline was proposed (Wałȩga et al. Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2019a), where punctual intervals of the form
![]() $[i\cdot d,i\cdot d]$
are replaced with punctual intervals
$[i\cdot d,i\cdot d]$
are replaced with punctual intervals
![]() $ [t + i \cdot d', t + i \cdot d']$
, for all rational numbers
$ [t + i \cdot d', t + i \cdot d']$
, for all rational numbers
![]() $t$
in
$t$
in
![]() $\mathscr{D}$
,
$\mathscr{D}$
,
![]() $i \in \mathbb{Z}$
, and
$i \in \mathbb{Z}$
, and
![]() $d'$
the gcd of numbers occurring in
$d'$
the gcd of numbers occurring in
![]() $\Pi$
; in turn, open intervals of the form
$\Pi$
; in turn, open intervals of the form
![]() $((i-1)\cdot d, i\cdot d)$
were replaced with open intervals located between the new punctual intervals. Below we present example partitionings of the timeline into intervals stemming from both discretisation methods, for the case where the only rationals occurring in
$((i-1)\cdot d, i\cdot d)$
were replaced with open intervals located between the new punctual intervals. Below we present example partitionings of the timeline into intervals stemming from both discretisation methods, for the case where the only rationals occurring in
![]() $\mathscr{D}$
are
$\mathscr{D}$
are
![]() $\frac{1}{2}$
and
$\frac{1}{2}$
and
![]() $\frac{2}{3}$
and the gcd of
$\frac{2}{3}$
and the gcd of
![]() $\Pi$
is 1 (therefore,
$\Pi$
is 1 (therefore,
![]() $d = \frac{1}{6}$
and
$d = \frac{1}{6}$
and
![]() $d'=1$
). The second partitioning has the advantage that the gcd is computed independently from
$d'=1$
). The second partitioning has the advantage that the gcd is computed independently from
![]() $\mathscr{D}$
; this was exploited to devise reasoning techniques with a better computational behaviour in data size (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a).
$\mathscr{D}$
; this was exploited to devise reasoning techniques with a better computational behaviour in data size (Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a).
4 Reasoning techniques for DatalogMTL
In this section we recapitulate different techniques available for reasoning in DatalogMTL, which we take as a starting point for the development of our approach; we present a variant of the naïve materialisation procedure (Wałȩga et al. Reference Wałȩga, Zawidzki and Grau2023,Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021), the reduction of DatalogMTL reasoning to LTL satisfiability proposed by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), and the automata-based procedure exploited by Wałȩga et al. Reference Wałȩga, Kaminski and Cuenca Grau2019a to establish optimal complexity bounds for reasoning.
Procedure 1: Naïve(
![]() $\Pi, {\mathscr{D}}, P(\mathbf{c})@\rho$
)
$\Pi, {\mathscr{D}}, P(\mathbf{c})@\rho$
)

4.1 Naïve materialisation
The fixpoint characterisation from Section 3.3 suggests the naïve materialisation-based approach specified in Procedure 1. For a programme
![]() $\Pi$
, a dataset
$\Pi$
, a dataset
![]() $\mathscr{D}$
, and a fact
$\mathscr{D}$
, and a fact
![]() $P(\mathbf{c})@\rho$
, the procedure applies the immediate consequence operator
$P(\mathbf{c})@\rho$
, the procedure applies the immediate consequence operator
![]() $T_\Pi$
to
$T_\Pi$
to
![]() ${\mathfrak{I}}_{\mathscr{D}}$
(Lines 3, 4, and 8) until one of the following holds:
${\mathfrak{I}}_{\mathscr{D}}$
(Lines 3, 4, and 8) until one of the following holds:
-
– the partial materialisation of
 $\Pi$
and
$\Pi$
and
 $\mathscr{D}$
yields inconsistency due to satisfaction of the body of some
$\mathscr{D}$
yields inconsistency due to satisfaction of the body of some
 $\bot$
-rule, in which case
$\bot$
-rule, in which case
 $\mathsf{inconst}$
is returned (Line 5),
$\mathsf{inconst}$
is returned (Line 5), -
– the partial materialisation entails the input fact
 $P(\mathbf{c})@\rho$
, in which case the truth value
$P(\mathbf{c})@\rho$
, in which case the truth value
 $\mathsf{true}$
and the obtained partial materialisation are returned (Line 6), or
$\mathsf{true}$
and the obtained partial materialisation are returned (Line 6), or -
– the application of
 $T_\Pi$
reaches a fixpoint and the obtained materialisation does not satisfy
$T_\Pi$
reaches a fixpoint and the obtained materialisation does not satisfy
 $P(\mathbf{c})@\rho$
nor yields an inconsistency, in which case the value
$P(\mathbf{c})@\rho$
nor yields an inconsistency, in which case the value
 $\mathsf{false}$
and the full materialisation are returned (Line 8).
$\mathsf{false}$
and the full materialisation are returned (Line 8).
Example 4.1.
As a running example, consider the input fact
![]() $R_1(c_1,c_2)@[4,4]$
, the dataset
$R_1(c_1,c_2)@[4,4]$
, the dataset
and the programme
![]() $\Pi _{\mathsf{ex}}$
consisting of the following rules:
$\Pi _{\mathsf{ex}}$
consisting of the following rules:
In naïve materialisation, rules are applied by first identifying the facts that can ground the rule body, and then determining the maximal intervals for which all the ground body atoms hold simultaneously. For instance, Rule
![]() $r_2$
in Example 4.1 is applied to
$r_2$
in Example 4.1 is applied to
![]() ${\mathscr{D}}_{\mathsf{ex}}$
by matching
${\mathscr{D}}_{\mathsf{ex}}$
by matching
![]() $R_2(c_1, c_2)$
and
$R_2(c_1, c_2)$
and
![]() $R_3(c_2,c_3)$
to the rule’s body atoms, and determining that
$R_3(c_2,c_3)$
to the rule’s body atoms, and determining that
![]() $[1,1]$
is the maximal interval in which the body atoms
$[1,1]$
is the maximal interval in which the body atoms
![]() $R_2(c_1, c_2)$
and
$R_2(c_1, c_2)$
and
![]() $\boxplus _{[1,2]} R_3(c_2,c_3)$
hold together. As a result, the head
$\boxplus _{[1,2]} R_3(c_2,c_3)$
hold together. As a result, the head
![]() $\boxplus _{[1,1]} R_5(c_2)@[1,1]$
holds, and so the fact
$\boxplus _{[1,1]} R_5(c_2)@[1,1]$
holds, and so the fact
![]() $ R_5(c_2)@[2,2]$
is derived. We formalise it below.
$ R_5(c_2)@[2,2]$
is derived. We formalise it below.
Definition 4.2. Let
![]() $r$
be a rule of the form
$r$
be a rule of the form
![]() $M' \leftarrow M_1 \land \dots \land M_n$
for some
$M' \leftarrow M_1 \land \dots \land M_n$
for some
![]() $n \geq 1$
, which is not a
$n \geq 1$
, which is not a
![]() $\bot$
-rule, and let
$\bot$
-rule, and let
![]() $\mathscr{D}$
be a dataset. The set of instances for
$\mathscr{D}$
be a dataset. The set of instances for
![]() $r$
and
$r$
and
![]() $\mathscr{D}$
is defined as follows:
$\mathscr{D}$
is defined as follows:
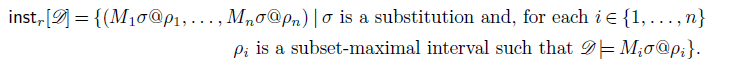 \begin{multline*} \mathsf{inst}_{r}[{\mathscr{D}}] = \big \{ ( M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n ) \mid \sigma \text{ is a substitution and, for each } i \in \{1, \dots, n\} \\ \rho _i \text{ is a subset-maximal interval such that }{\mathscr{D}} \models M_i\sigma @ \rho _i \big \}. \end{multline*}
\begin{multline*} \mathsf{inst}_{r}[{\mathscr{D}}] = \big \{ ( M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n ) \mid \sigma \text{ is a substitution and, for each } i \in \{1, \dots, n\} \\ \rho _i \text{ is a subset-maximal interval such that }{\mathscr{D}} \models M_i\sigma @ \rho _i \big \}. \end{multline*}
The set
![]() $r[{\mathscr{D}}]$
of facts derived by
$r[{\mathscr{D}}]$
of facts derived by
![]() $r$
from
$r$
from
![]() $\mathscr{D}$
is defined as follows:
$\mathscr{D}$
is defined as follows:
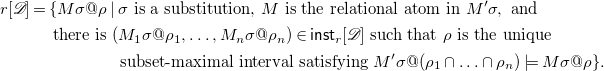 \begin{multline}{r[{\mathscr{D}}]} = \{M \sigma @ \rho \mid \sigma \text{ is a substitution, } M \text{ is the relational atom in } M' \sigma, \text{ and } \\ \text{there is } ( M_1 \sigma @\rho _1, \dots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[{\mathscr{D}}] \text{ such that } \rho \text{ is the unique} \\ \text{subset-maximal interval satisfying } M' \sigma @(\rho _1 \cap \ldots \cap \rho _n) \models M\sigma @ \rho \}. \end{multline}
\begin{multline}{r[{\mathscr{D}}]} = \{M \sigma @ \rho \mid \sigma \text{ is a substitution, } M \text{ is the relational atom in } M' \sigma, \text{ and } \\ \text{there is } ( M_1 \sigma @\rho _1, \dots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[{\mathscr{D}}] \text{ such that } \rho \text{ is the unique} \\ \text{subset-maximal interval satisfying } M' \sigma @(\rho _1 \cap \ldots \cap \rho _n) \models M\sigma @ \rho \}. \end{multline}
The set of facts derived from
![]() $\mathscr{D}$
by one-step application of
$\mathscr{D}$
by one-step application of
![]() $\Pi$
is
$\Pi$
is
By Definition 4.2, the set
![]() $\mathscr{N}$
of facts derived by Procedure 1 in Line 3 in the first iteration of the loop on our running example is
$\mathscr{N}$
of facts derived by Procedure 1 in Line 3 in the first iteration of the loop on our running example is
![]() $\Pi _{\mathsf{ex}}[{\mathscr{D}}_{\mathsf{ex}}] = \{R_1(c_1,c_2)@[1,2], R_4(c_2)@[0,2], R_5(c_2)@[2,2]\}.$
The partial materialisation
$\Pi _{\mathsf{ex}}[{\mathscr{D}}_{\mathsf{ex}}] = \{R_1(c_1,c_2)@[1,2], R_4(c_2)@[0,2], R_5(c_2)@[2,2]\}.$
The partial materialisation
![]() ${\mathscr{D}}_{\mathsf{ex}}^1$
that will be passed on to the next materialisation step is obtained in Line 4 as
${\mathscr{D}}_{\mathsf{ex}}^1$
that will be passed on to the next materialisation step is obtained in Line 4 as
![]() ${\mathscr{D}}_{\mathsf{ex}}^1 = \mathsf{coal}({\mathscr{D}}_{\mathsf{ex}} \cup \Pi _{\mathsf{ex}}[{\mathscr{D}}_{\mathsf{ex}}])$
where, as we described in Section 3.1,
${\mathscr{D}}_{\mathsf{ex}}^1 = \mathsf{coal}({\mathscr{D}}_{\mathsf{ex}} \cup \Pi _{\mathsf{ex}}[{\mathscr{D}}_{\mathsf{ex}}])$
where, as we described in Section 3.1,
![]() $\mathsf{coal}({\mathscr{D}})$
is the unique dataset obtained by exhaustively coalescing facts in
$\mathsf{coal}({\mathscr{D}})$
is the unique dataset obtained by exhaustively coalescing facts in
![]() $\mathscr{D}$
. In our example,
$\mathscr{D}$
. In our example,
![]() $R_1(c_1,c_2)@[0,1]$
in and
$R_1(c_1,c_2)@[0,1]$
in and
![]() $R_1(c_1,c_2)@[1,2]$
will be coalesced into
$R_1(c_1,c_2)@[1,2]$
will be coalesced into
![]() $R_1(c_1,c_2)@[0,2]$
. Thus,
$R_1(c_1,c_2)@[0,2]$
. Thus,
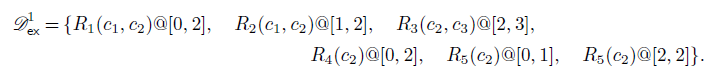 \begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^1 = \{R_1(c_1,c_2)@[0,2], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \quad \\ R_4(c_2)@[0,2], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2]\}. \end{multline*}
\begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^1 = \{R_1(c_1,c_2)@[0,2], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \quad \\ R_4(c_2)@[0,2], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2]\}. \end{multline*}
In the second round, rules are applied to
![]() ${\mathscr{D}}_{\mathsf{ex}}^1$
. The application of
${\mathscr{D}}_{\mathsf{ex}}^1$
. The application of
![]() $r_1$
derives
$r_1$
derives
![]() $R_1(c_1,c_2)@[1,3]$
(from
$R_1(c_1,c_2)@[1,3]$
(from
![]() $R_1(c_1, c_2)@[0,2]$
) and the application of
$R_1(c_1, c_2)@[0,2]$
) and the application of
![]() $r_2$
rederives a redundant fact
$r_2$
rederives a redundant fact
![]() $R_5(c_2)@[2,2]$
. In contrast to the previous step, Rule
$R_5(c_2)@[2,2]$
. In contrast to the previous step, Rule
![]() $r_4$
can now be applied to derive the new fact
$r_4$
can now be applied to derive the new fact
![]() $R_6(c_2)@[2,2]$
. Finally,
$R_6(c_2)@[2,2]$
. Finally,
![]() $r_3$
derives the new fact
$r_3$
derives the new fact
![]() $R_4(c_2)@[2,3]$
and rederives
$R_4(c_2)@[2,3]$
and rederives
![]() $R_4(c_2)@[0,2]$
. After coalescing, the second step of materialisation yields the following partial materialisation:
$R_4(c_2)@[0,2]$
. After coalescing, the second step of materialisation yields the following partial materialisation:
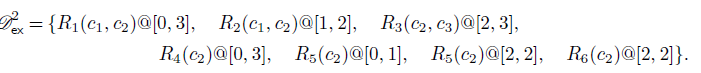 \begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^2 = \{R_1(c_1,c_2)@[0,3], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \\ R_4(c_2)@[0,3], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2], \quad R_6(c_2)@[2,2] \}. \end{multline*}
\begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^2 = \{R_1(c_1,c_2)@[0,3], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \\ R_4(c_2)@[0,3], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2], \quad R_6(c_2)@[2,2] \}. \end{multline*}
In the third materialisation step, rules are applied to
![]() ${\mathscr{D}}_{\mathsf{ex}}^2$
, and derive the new fact
${\mathscr{D}}_{\mathsf{ex}}^2$
, and derive the new fact
![]() $R_1(c_1,c_2)@[1,4]$
using Rule
$R_1(c_1,c_2)@[1,4]$
using Rule
![]() $r_1$
, as well as all facts which were already derived in the second materialisation step (with the only exception of
$r_1$
, as well as all facts which were already derived in the second materialisation step (with the only exception of
![]() $R_1(c_1,c_2)@[1,3]$
). After coalescing we obtain:
$R_1(c_1,c_2)@[1,3]$
). After coalescing we obtain:
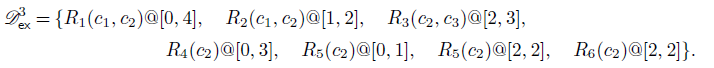 \begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^3 = \{R_1(c_1,c_2)@[0,4], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \\ R_4(c_2)@[0,3], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2], \quad R_6(c_2)@[2,2] \}. \end{multline*}
\begin{multline*}{\mathscr{D}}_{\mathsf{ex}}^3 = \{R_1(c_1,c_2)@[0,4], \quad R_2(c_1, c_2)@[1,2], \quad R_3(c_2,c_3)@[2,3], \\ R_4(c_2)@[0,3], \quad R_5(c_2)@[0,1], \quad R_5(c_2)@[2,2], \quad R_6(c_2)@[2,2] \}. \end{multline*}
At this point, the algorithm detects that
![]() ${\mathscr{D}}_{\mathsf{ex}}^3$
entails the input fact
${\mathscr{D}}_{\mathsf{ex}}^3$
entails the input fact
![]() $R_1(c_1,c_2)@[4,4]$
and stops.
$R_1(c_1,c_2)@[4,4]$
and stops.
Procedure 1 is both sound and complete. To show this, for each
![]() $k \in \mathbb{N}$
, let
$k \in \mathbb{N}$
, let
![]() $\mathscr{N}_k$
and
$\mathscr{N}_k$
and
![]() ${\mathscr{D}}_k$
denote the contents of, respectively,
${\mathscr{D}}_k$
denote the contents of, respectively,
![]() $\mathscr{N}$
and
$\mathscr{N}$
and
![]() $\mathscr{D}$
in Procedure 1 upon the completion of the
$\mathscr{D}$
in Procedure 1 upon the completion of the
![]() $k$
th iteration of the loop. Then we prove soundness by showing inductively on
$k$
th iteration of the loop. Then we prove soundness by showing inductively on
![]() $k\in \mathbb{N}$
, that
$k\in \mathbb{N}$
, that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T^k_\Pi ({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T^k_\Pi ({\mathfrak{I}}_{\mathscr{D}})$
.
Theorem 4.3 (Soundness). Consider Procedure 1 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. Upon the completion of the
$\mathscr{D}$
. Upon the completion of the
![]() $k$
th (for some
$k$
th (for some
![]() $k \in \mathbb{N}$
) iteration of the loop of Procedure 1, it holds that
$k \in \mathbb{N}$
) iteration of the loop of Procedure 1, it holds that
![]() ${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
By Theorem4.3, if the least model
![]() ${\mathfrak{I}}_{{\mathscr{D}}'}$
of
${\mathfrak{I}}_{{\mathscr{D}}'}$
of
![]() ${\mathscr{D}}'$
is not a model of a
${\mathscr{D}}'$
is not a model of a
![]() $\bot$
-rule in
$\bot$
-rule in
![]() $\Pi$
, then the canonical interpretation
$\Pi$
, then the canonical interpretation
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is also not a model of such a rule; thus, if the algorithm returns
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is also not a model of such a rule; thus, if the algorithm returns
![]() $\mathsf{inconst}$
, then
$\mathsf{inconst}$
, then
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
are inconsistent. Next, to show completeness, we prove inductively that
$\mathscr{D}$
are inconsistent. Next, to show completeness, we prove inductively that
![]() $T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
.
$T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
.
Theorem 4.4 (Completeness). Consider Procedure 1 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 1, it holds that
$k$
th iteration of the loop of Procedure 1, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
If
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
are inconsistent, the canonical interpretation
$\mathscr{D}$
are inconsistent, the canonical interpretation
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is not a model of some
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
is not a model of some
![]() $\bot$
-rule
$\bot$
-rule
![]() $r$
in
$r$
in
![]() $\Pi$
; thus, there is an ordinal
$\Pi$
; thus, there is an ordinal
![]() $\alpha$
such that
$\alpha$
such that
![]() $T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}})$
is also not a model of
$T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}})$
is also not a model of
![]() $r$
, in which case Theorem4.4 ensures that the algorithm returns
$r$
, in which case Theorem4.4 ensures that the algorithm returns
![]() $\mathsf{inconst}$
, as required.
$\mathsf{inconst}$
, as required.
Furthermore, if a fixpoint is reached without encountering an inconsistency, then our procedure ensures that the input fact is not entailed and also that we have obtained a representation of the full canonical interpretation which can be kept in memory and subsequently exploited for checking entailment of any other fact. The procedure is, however, not always terminating as reaching a fixpoint may require infinitely many rounds of rule applications.
4.2 Translation to LTL
The discretisation of the rational timeline described in Section 3.3 was exploited by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) to reduce reasoning in DatalogMTL to reasoning in LTL. The reduction transforms a programme
![]() $\Pi$
and a dataset
$\Pi$
and a dataset
![]() $\mathscr{D}$
into an LTL formula
$\mathscr{D}$
into an LTL formula
![]() $\varphi _{\Pi, {\mathscr{D}}}$
such that
$\varphi _{\Pi, {\mathscr{D}}}$
such that
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
are consistent if and only if
$\mathscr{D}$
are consistent if and only if
![]() $\varphi _{\Pi, {\mathscr{D}}}$
is LTL-satisfiable. Here, LTL is a propositional modal logic interpreted over the integer time points and equipped with temporal operators
$\varphi _{\Pi, {\mathscr{D}}}$
is LTL-satisfiable. Here, LTL is a propositional modal logic interpreted over the integer time points and equipped with temporal operators
![]() $\bigcirc _P$
for at the previous time point,
$\bigcirc _P$
for at the previous time point,
![]() $\Box _P$
for always in the past,
$\Box _P$
for always in the past,
![]() $\mathscr{S}$
for since,
$\mathscr{S}$
for since,
![]() $\bigcirc _F$
for at the next time point,
$\bigcirc _F$
for at the next time point,
![]() $\Box _F$
for always in the future, and
$\Box _F$
for always in the future, and
![]() $\mathscr{U}$
for until. An LTL formula
$\mathscr{U}$
for until. An LTL formula
![]() $\varphi$
is satisfiable if it holds at time point
$\varphi$
is satisfiable if it holds at time point
![]() $0$
in some LTL model.
$0$
in some LTL model.
Since, in contrast to DatalogMTL, the language of LTL is propositional, the first step in the translation is to ground
![]() $\Pi$
with all constants occurring in
$\Pi$
with all constants occurring in
![]() $\Pi$
or
$\Pi$
or
![]() $\mathscr{D}$
. Then, every relational atom
$\mathscr{D}$
. Then, every relational atom
![]() $P(\mathbf{c})$
occurring in the grounding of
$P(\mathbf{c})$
occurring in the grounding of
![]() $\Pi$
with constants from
$\Pi$
with constants from
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
is translated into a propositional symbol
$\mathscr{D}$
is translated into a propositional symbol
![]() $P^{\mathbf{c}}$
. Moreover, the MTL operators occurring in
$P^{\mathbf{c}}$
. Moreover, the MTL operators occurring in
![]() $\Pi$
are rewritten using LTL operators. Both the grounding of the input programme
$\Pi$
are rewritten using LTL operators. Both the grounding of the input programme
![]() $\Pi$
and the translation of the MTL operators (with binary-encoded numbers) into sequences of LTL operators yield an exponential blow-up. For instance, assume that
$\Pi$
and the translation of the MTL operators (with binary-encoded numbers) into sequences of LTL operators yield an exponential blow-up. For instance, assume that
![]() $\Pi$
mentions an atom
$\Pi$
mentions an atom
![]() $\boxminus _{[0,60)} A(x)$
, both
$\boxminus _{[0,60)} A(x)$
, both
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
mention constants
$\mathscr{D}$
mention constants
![]() $c_1, \dots, c_{n}$
, and that interval
$c_1, \dots, c_{n}$
, and that interval
![]() $(0,60)$
contains
$(0,60)$
contains
![]() $m$
intervals after discretising the timeline. Then
$m$
intervals after discretising the timeline. Then
![]() $\boxplus _{(0,60)} A(x)$
is translated to an LTL formula containing
$\boxplus _{(0,60)} A(x)$
is translated to an LTL formula containing
![]() $n$
conjuncts (one conjunct for each
$n$
conjuncts (one conjunct for each
![]() $c_i$
), each of the form
$c_i$
), each of the form
![]() $ \bigcirc _F A^{c_i} \land \bigcirc _F \bigcirc _F A^{c_i} \land \dots \land \underbrace{\bigcirc _F \dots \bigcirc _F }_{m} A^{c_i}.$
Consequently,
$ \bigcirc _F A^{c_i} \land \bigcirc _F \bigcirc _F A^{c_i} \land \dots \land \underbrace{\bigcirc _F \dots \bigcirc _F }_{m} A^{c_i}.$
Consequently,
![]() $\varphi _{\Pi, {\mathscr{D}}}$
is exponentially large. Since satisfiability checking in LTL is PSpace-complete, this approach provides a (worst-case optimal) ExpSpace reasoning procedure for DatalogMTL.
$\varphi _{\Pi, {\mathscr{D}}}$
is exponentially large. Since satisfiability checking in LTL is PSpace-complete, this approach provides a (worst-case optimal) ExpSpace reasoning procedure for DatalogMTL.
4.3 Automata-based reasoning
An alternative approach to exploit the time discretisation of DatalogMTL is to directly apply automata-based techniques, without the need of constructing an LTL formula. Such automata-based constructions are well-studied in the context of LTL, where checking satisfiability of a formula
![]() $\varphi$
reduces to checking non-emptiness of a generalised non-deterministic B FC;chi automaton where states are sets of formulas relevant to
$\varphi$
reduces to checking non-emptiness of a generalised non-deterministic B FC;chi automaton where states are sets of formulas relevant to
![]() $\varphi$
, the alphabet consists of sets of propositions, and the transition relation and accepting conditions ensure that words accepted by the automaton are exactly the models of
$\varphi$
, the alphabet consists of sets of propositions, and the transition relation and accepting conditions ensure that words accepted by the automaton are exactly the models of
![]() $\varphi$
(Baier and Katoen Reference Baier and Katoen2008).
$\varphi$
(Baier and Katoen Reference Baier and Katoen2008).
This technique can be adapted to the DatalogMTL setting (Wałȩga et al. Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021); each state now represents ground metric atoms holding at all time points within a fragment of the timeline called a window. Since the timeline can be discretised in DatalogMTL, each window can be finitely represented as a sequence consisting of sets of metric atoms which hold in the consecutive intervals from the window. Additionally, for such a sequence to be a state of the automaton, it is required that the involved metric atoms are locally consistent; for example, if
![]() $\boxplus _{[0,\infty )}A$
– which states that
$\boxplus _{[0,\infty )}A$
– which states that
![]() $A$
holds always in the future – holds in some interval
$A$
holds always in the future – holds in some interval
![]() $\rho$
, then
$\rho$
, then
![]() $\boxplus _{[0,\infty )}A$
needs to hold also in all the intervals in the window which are to the right of
$\boxplus _{[0,\infty )}A$
needs to hold also in all the intervals in the window which are to the right of
![]() $\rho$
in the timeline. The remaining components of the automaton are defined analogously to the case of LTL.
$\rho$
in the timeline. The remaining components of the automaton are defined analogously to the case of LTL.
Consistency checking in DatalogMTL reduces to checking non-emptiness of (pairs of) automata, and this reduction provides a PSpace upper bound for data complexity (Wałȩga et al. Reference Wałȩga, Tena Cucala, Kostylev and Cuenca Grau2021). In particular, automata states are polynomially large in the size of the dataset since windows can be chosen so that the number of intervals in each window is polynomially large. Moreover, the number of ground metric atoms that can hold in each of these intervals is also polynomially bounded. Thus, each state is polynomially representable and non-emptiness of the automata can be checked with the standard “on-the-fly” approach (Baier and Katoen Reference Baier and Katoen2008) in PSpace.
5 Our practical reasoning algorithm
In this section we propose a scalable approach for deciding both consistency and fact entailment in DatalogMTL. The key elements of our approach are as follows:
-
– an optimised materialisation procedure using a seminaïve strategy which efficiently applies the immediate consequence operator while minimising repeated inferences,
-
– a realisation of the automata-based reasoning approach, and
-
– an effective way of combining materialisation with automata-based reasoning that aims at resorting to materialisation-based reasoning whenever possible.
In the remainder of this section we discuss each of the key components of our approach in detail. For convenience of presentation, and without loss of generality, we will assume that input programmes do not contain rules whose body is vacuously satisfied (i.e. satisfied in the empty interpretation). Observe that each such rule can be formulated as a fact and added to the input dataset instead; for example, rule
![]() $P \gets \top$
is equivalent to a fact
$P \gets \top$
is equivalent to a fact
![]() $P@(-\infty, \infty )$
.
$P@(-\infty, \infty )$
.
5.1 Seminaïve materialisation
In this section we present a seminaïve materialisation procedure for DatalogMTL. Analogously to the classical seminaïve algorithm for plain Datalog (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995), the main idea behind our procedure is to keep track of newly derived facts in each materialisation step by storing them in a set
![]() $\Delta$
, and to make sure that each rule application in the following materialisation step involve at least one fact in
$\Delta$
, and to make sure that each rule application in the following materialisation step involve at least one fact in
![]() $\Delta$
. In this way, the procedure will consider each instance (for a rule and dataset, as we introduced in Definition 4.2) at most once throughout its entire execution, and so, such a procedure is said to enjoy the non-repetition property. The same fact, however, can still be derived multiple times by different instances; this type of redundancy is difficult to prevent and is not addressed by the standard seminaïve strategy.
$\Delta$
. In this way, the procedure will consider each instance (for a rule and dataset, as we introduced in Definition 4.2) at most once throughout its entire execution, and so, such a procedure is said to enjoy the non-repetition property. The same fact, however, can still be derived multiple times by different instances; this type of redundancy is difficult to prevent and is not addressed by the standard seminaïve strategy.
Our aim is to lift the seminaïve rule evaluation strategy to the setting of DatalogMTL. As we have seen in Section 4.1, a rule instance can be considered multiple times in the naïve materialisation procedure; for example, the instance
![]() $(\diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2])$
of Rule
$(\diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2])$
of Rule
![]() $r_3$
in Example 4.1 is considered by the naïve materialisation procedure in Section 4.1 both in the first and second materialisation steps to derive
$r_3$
in Example 4.1 is considered by the naïve materialisation procedure in Section 4.1 both in the first and second materialisation steps to derive
![]() $R_4(c_2)@[0,2]$
since the naïve procedure cannot detect that the fact
$R_4(c_2)@[0,2]$
since the naïve procedure cannot detect that the fact
![]() $R_5(c_2)@[0,1]$
used to instantiate
$R_5(c_2)@[0,1]$
used to instantiate
![]() $r_3$
in the second step had previously been used to instantiate
$r_3$
in the second step had previously been used to instantiate
![]() $r_2$
. Preventing such redundant computations, however, involves certain challenges. First, by including in
$r_2$
. Preventing such redundant computations, however, involves certain challenges. First, by including in
![]() $\Delta$
just newly derived facts as in Datalog, we may overlook information obtained by coalescing newly derived facts with previously derived ones. Second, restricting application to relevant rule instances requires consideration of the semantics of metric operators in rule bodies.
$\Delta$
just newly derived facts as in Datalog, we may overlook information obtained by coalescing newly derived facts with previously derived ones. Second, restricting application to relevant rule instances requires consideration of the semantics of metric operators in rule bodies.
Procedure 2 extends the seminaïve strategy to the setting of DatalogMTL while overcoming the aforementioned difficulties. Analogously to the naïve approach, each iteration of the main loop captures a single materialisation step consisting of a round of rule applications (Line 3) followed by the coalescing of relevant facts (Line 4); as before, dataset
![]() ${\mathscr{D}}'$
stores the partial materialisation resulting from each iteration and is initialised as the input dataset, whereas the dataset
${\mathscr{D}}'$
stores the partial materialisation resulting from each iteration and is initialised as the input dataset, whereas the dataset
![]() $\mathscr{N}$
stores the facts obtained as a result of rule application and is initialised as empty. Following the rationale behind the seminaïve strategy for Datalog, newly derived information in each materialisation step is now stored as a dataset
$\mathscr{N}$
stores the facts obtained as a result of rule application and is initialised as empty. Following the rationale behind the seminaïve strategy for Datalog, newly derived information in each materialisation step is now stored as a dataset
![]() $\Delta$
, which is initialised as the input dataset
$\Delta$
, which is initialised as the input dataset
![]() $\mathscr{D}$
and which is suitably maintained in each iteration (Line 5); furthermore, Procedure 2 ensures in Line 3 that only rule instances for which it is essential to involve facts from
$\mathscr{D}$
and which is suitably maintained in each iteration (Line 5); furthermore, Procedure 2 ensures in Line 3 that only rule instances for which it is essential to involve facts from
![]() $\Delta$
(as formalised in the following definition) are taken into account during rule application.
$\Delta$
(as formalised in the following definition) are taken into account during rule application.
Procedure 2: Seminaïve
![]() $\Pi,{\mathscr{D}},P(\mathbf{c})@\rho$
)
$\Pi,{\mathscr{D}},P(\mathbf{c})@\rho$
)

Definition 5.1. Let
![]() $r$
be a rule of the form
$r$
be a rule of the form
![]() $M' \leftarrow M_1 \land \dots \land M_n$
, for some
$M' \leftarrow M_1 \land \dots \land M_n$
, for some
![]() $n \geq 1$
, and let
$n \geq 1$
, and let
![]() $\mathscr{D}$
and
$\mathscr{D}$
and
![]() $\Delta$
be datasets. The set of instances for
$\Delta$
be datasets. The set of instances for
![]() $r$
and
$r$
and
![]() $\mathscr{D}$
relative to
$\mathscr{D}$
relative to
![]() $\Delta$
is defined as follows:
$\Delta$
is defined as follows:
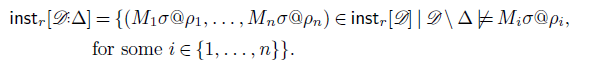 \begin{align*} & \mathsf {inst}_{r}[{\mathscr {D}} \substack {\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ] = \big \{ ( M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n ) \in \mathsf {inst}_{r}[{\mathscr {D}}] \mid {\mathscr {D}} \setminus \Delta \not \models M_i\sigma @\rho _i, \\ & \qquad\qquad\text { for some } i \in \{1, \dots, n \} \big \}. \end{align*}
\begin{align*} & \mathsf {inst}_{r}[{\mathscr {D}} \substack {\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ] = \big \{ ( M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n ) \in \mathsf {inst}_{r}[{\mathscr {D}}] \mid {\mathscr {D}} \setminus \Delta \not \models M_i\sigma @\rho _i, \\ & \qquad\qquad\text { for some } i \in \{1, \dots, n \} \big \}. \end{align*}
The set
![]() $r[{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
of facts derived by
$r[{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
of facts derived by
![]() $r$
from
$r$
from
![]() $\mathscr{D}$
relative to
$\mathscr{D}$
relative to
![]() $\Delta$
is defined analogously to
$\Delta$
is defined analogously to
![]() $r[{\mathscr{D}}]$
in Definition 4.2, with the exception that
$r[{\mathscr{D}}]$
in Definition 4.2, with the exception that
![]() $\mathsf{inst}_{r}[{\mathscr{D}}]$
is replaced with
$\mathsf{inst}_{r}[{\mathscr{D}}]$
is replaced with
![]() $\mathsf{inst}_{r}[{\mathscr{D}] \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta }$
in Expression (2). Finally, the set
$\mathsf{inst}_{r}[{\mathscr{D}] \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta }$
in Expression (2). Finally, the set
![]() $\Pi [{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
of facts derived from
$\Pi [{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
of facts derived from
![]() $\mathscr{D}$
by one-step seminaïve application of
$\mathscr{D}$
by one-step seminaïve application of
![]() $\Pi$
is defined as
$\Pi$
is defined as
![]() $\Pi [{\mathscr{D}}]$
in Expression (3), by replacing
$\Pi [{\mathscr{D}}]$
in Expression (3), by replacing
![]() $r[{\mathscr{D}}]$
with
$r[{\mathscr{D}}]$
with
![]() $r[{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
.
$r[{\mathscr{D}} \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]$
.
In each materialisation step, Procedure 2 exploits Definition 5.1 to identify as relevant those rule instances with some “new” element (i.e. one that cannot be entailed without the facts in
![]() $\Delta$
). The facts derived by such relevant rule instances in each iteration are stored in set
$\Delta$
). The facts derived by such relevant rule instances in each iteration are stored in set
![]() $\mathscr{N}$
(Line 3).
$\mathscr{N}$
(Line 3).
As in the naïve approach, rule application is followed by a coalescing step where the partial materialisation is updated with the facts derived from rule application (Line 4). In contrast to the naïve approach, however, Procedure 2 needs to maintain set
![]() $\Delta$
to ensure that it captures only new facts. This is achieved in Line 5, where a fact in the updated partial materialisation is considered new if it entails a fact in
$\Delta$
to ensure that it captures only new facts. This is achieved in Line 5, where a fact in the updated partial materialisation is considered new if it entails a fact in
![]() $\mathscr{N}$
that was not already entailed by the previous partial materialisation. The procedure terminates in Line 6 if an inconsistency has been derived, in Line 7 if the input fact has been derived, or in Line 8 if
$\mathscr{N}$
that was not already entailed by the previous partial materialisation. The procedure terminates in Line 6 if an inconsistency has been derived, in Line 7 if the input fact has been derived, or in Line 8 if
![]() $\Delta$
is empty. Otherwise, the procedure carries over the updated partial materialisation and the set of newly derived facts to the next materialisation step.
$\Delta$
is empty. Otherwise, the procedure carries over the updated partial materialisation and the set of newly derived facts to the next materialisation step.
We next illustrate the application of the procedure to
![]() ${\mathscr{D}}_{\mathsf{ex}}$
and
${\mathscr{D}}_{\mathsf{ex}}$
and
![]() $\Pi _{\mathsf{ex}}$
and our example fact
$\Pi _{\mathsf{ex}}$
and our example fact
![]() $R_1(c_1,c_2)@4$
from Example 4.1. In the first materialisation step, all input facts are considered as newly derived (i.e.
$R_1(c_1,c_2)@4$
from Example 4.1. In the first materialisation step, all input facts are considered as newly derived (i.e.
![]() $\Delta ={\mathscr{D}}$
) and hence
$\Delta ={\mathscr{D}}$
) and hence
![]() $\mathscr{N} ={\Pi [{\mathscr{D}}' \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]} = \Pi [{\mathscr{D}}']$
and the result of coalescing coincides with the partial materialisation computed by the naïve procedure (i.e.
$\mathscr{N} ={\Pi [{\mathscr{D}}' \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ]} = \Pi [{\mathscr{D}}']$
and the result of coalescing coincides with the partial materialisation computed by the naïve procedure (i.e.
![]() $\mathscr{C} ={\mathscr{D}}_{\mathsf{ex}}^1)$
. Then, the procedure identifies as new all facts in
$\mathscr{C} ={\mathscr{D}}_{\mathsf{ex}}^1)$
. Then, the procedure identifies as new all facts in
![]() ${\mathscr{D}}_{\mathsf{ex}}^1$
which are not entailed by
${\mathscr{D}}_{\mathsf{ex}}^1$
which are not entailed by
![]() ${\mathscr{D}}_{\mathsf{ex}}$
, namely:
${\mathscr{D}}_{\mathsf{ex}}$
, namely:
In the second step, rule evaluation is performed in Line 3; since
![]() $\Delta$
is used for this, the procedure no longer considers the redundant instance
$\Delta$
is used for this, the procedure no longer considers the redundant instance
![]() $( R_2(c_1,c_2)@[0,2],$
$( R_2(c_1,c_2)@[0,2],$
![]() $\boxplus _{[1,2]}R_3(c_2,c_3)@[1,2] )$
of
$\boxplus _{[1,2]}R_3(c_2,c_3)@[1,2] )$
of
![]() $r_2$
, since
$r_2$
, since
![]() $\boxplus _{[1,2]}R_3(c_2,c_3)@[1,2]$
is entailed already by
$\boxplus _{[1,2]}R_3(c_2,c_3)@[1,2]$
is entailed already by
![]() ${\mathscr{D}}_{\mathsf{ex}}^1 \setminus \Delta$
. Similarly, the redundant instance
${\mathscr{D}}_{\mathsf{ex}}^1 \setminus \Delta$
. Similarly, the redundant instance
![]() $(\diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2])$
of Rule
$(\diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2])$
of Rule
![]() $r_3$
is not considered, as
$r_3$
is not considered, as
![]() ${\mathscr{D}}_{\mathsf{ex}}^1 \setminus \Delta \models \diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2]$
. In contrast, all non-redundant facts derived by the naïve strategy are also derived by the seminaïve procedure and after coalescing dataset
${\mathscr{D}}_{\mathsf{ex}}^1 \setminus \Delta \models \diamondsuit \!\!\!\!\!-_{[0,1]}R_5(c_2)@[0,2]$
. In contrast, all non-redundant facts derived by the naïve strategy are also derived by the seminaïve procedure and after coalescing dataset
![]() $\mathscr{C} ={\mathscr{D}}_{\mathsf{ex}}^2$
. The set
$\mathscr{C} ={\mathscr{D}}_{\mathsf{ex}}^2$
. The set
![]() $\Delta$
is now updated as follows:
$\Delta$
is now updated as follows:
In particular, note that
![]() $\Delta$
contains the coalesced fact
$\Delta$
contains the coalesced fact
![]() $R_4(c_2)@[0,3]$
instead of fact
$R_4(c_2)@[0,3]$
instead of fact
![]() $R_4(c_2)@[2,3]$
derived from rule application. Datasets
$R_4(c_2)@[2,3]$
derived from rule application. Datasets
![]() $\Delta$
and
$\Delta$
and
![]() ${\mathscr{D}}' ={\mathscr{D}}_{\mathsf{ex}}^2$
are passed on to the third materialisation step, where all redundant computations identified in Section 4.1 are avoided with the only exception of fact
${\mathscr{D}}' ={\mathscr{D}}_{\mathsf{ex}}^2$
are passed on to the third materialisation step, where all redundant computations identified in Section 4.1 are avoided with the only exception of fact
![]() $R_6(c_2)@[2,2]$
, which is re-derived using the instance of
$R_6(c_2)@[2,2]$
, which is re-derived using the instance of
![]() $r_4$
consisting of
$r_4$
consisting of
![]() $R_1(c_2, c_2)@[0,3]$
,
$R_1(c_2, c_2)@[0,3]$
,
![]() $\boxminus _{[0,2]}R_4(c_2)@[2,3]$
, and
$\boxminus _{[0,2]}R_4(c_2)@[2,3]$
, and
![]() $R_5(c_2)@[2,2]$
. Note that this is a new instance which was not used in previous iterations, and hence it does not violate the non-repetition property. Note also that, as with the naïve strategy, our seminaïve procedure terminates on our running example in this materialisation step since input fact
$R_5(c_2)@[2,2]$
. Note that this is a new instance which was not used in previous iterations, and hence it does not violate the non-repetition property. Note also that, as with the naïve strategy, our seminaïve procedure terminates on our running example in this materialisation step since input fact
![]() $R_1(c_1,c_2)@[4,4]$
has been derived.
$R_1(c_1,c_2)@[4,4]$
has been derived.
We conclude this section by establishing correctness of our procedure, similarly as we did in Theorems4.3 and 4.4 for the naïve strategy from Procedure 1.
Theorem 5.2 (Soundness). Consider Procedure 2 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. Upon the completion of the
$\mathscr{D}$
. Upon the completion of the
![]() $k$
th (for some
$k$
th (for some
![]() $k \in \mathbb{N}$
) iteration of the loop of Procedure 2, it holds that
$k \in \mathbb{N}$
) iteration of the loop of Procedure 2, it holds that
![]() ${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
Completeness is proved by induction on the number
![]() $k$
of iterations of the main loop. In particular, we show that if
$k$
of iterations of the main loop. In particular, we show that if
![]() $ T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
satisfies a new fact
$ T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
satisfies a new fact
![]() $M@t$
, then there must be a rule
$M@t$
, then there must be a rule
![]() $r$
and an instance in
$r$
and an instance in
![]() $\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _k]$
witnessing the derivation of
$\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _k]$
witnessing the derivation of
![]() $M@t$
. Note that since
$M@t$
. Note that since
![]() $\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _k] \subseteq \mathsf{inst}_{r}[{\mathscr{D}}_k ]$
, it requires strengthening the argument from the proof of Theorem4.4, where it was sufficient to show that such an instance is in
$\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _k] \subseteq \mathsf{inst}_{r}[{\mathscr{D}}_k ]$
, it requires strengthening the argument from the proof of Theorem4.4, where it was sufficient to show that such an instance is in
![]() $\mathsf{inst}_{r}[{\mathscr{D}}_k ]$
. This will imply that each fact satisfied by
$\mathsf{inst}_{r}[{\mathscr{D}}_k ]$
. This will imply that each fact satisfied by
![]() $ T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
is derived in the
$ T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
is derived in the
![]() $k+1$
st iteration of our procedure.
$k+1$
st iteration of our procedure.
Theorem 5.3 (Completeness). Consider Procedure 2 with input programme
![]() $\Pi$
and input dataset
$\Pi$
and input dataset
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 2, it holds that
$k$
th iteration of the loop of Procedure 2, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
5.2 Optimised seminaïve evaluation
Although the seminaïve procedure enjoys the non-repetition property, it can still re-derive facts already obtained in previous materialisation steps; as a result, it can incur in a potentially large number of redundant computations. In particular, as discussed in Section 5.1, fact
![]() $R_6(c_2)@[2,2]$
is re-derived using Rule
$R_6(c_2)@[2,2]$
is re-derived using Rule
![]() $r_4$
in the third materialisation step of our running example, and (if the procedure did not terminate) it would also be re-derived in all subsequent materialisation steps (by different instances of Rule
$r_4$
in the third materialisation step of our running example, and (if the procedure did not terminate) it would also be re-derived in all subsequent materialisation steps (by different instances of Rule
![]() $r_4$
).
$r_4$
).
In this section, we present an optimised variant of our seminaïve procedure which further reduces the number of redundant computations performed during materialisation. The main idea is to disregard rules during the execution of the procedure as soon as we can be certain that their application will never derive new facts in subsequent materialisation steps. In our example, Rule
![]() $r_4$
can be discarded after the second materialisation step as its application will only continue to re-derive fact
$r_4$
can be discarded after the second materialisation step as its application will only continue to re-derive fact
![]() $R_6(c_2)@[2,2]$
in each subsequent materialisation step.
$R_6(c_2)@[2,2]$
in each subsequent materialisation step.
To this end, we will exploit the distinction between recursive and non-recursive predicates in a programme, as defined in Section 3. In the case of our Example 4.1, predicates
![]() $R_2$
,
$R_2$
,
![]() $R_3$
,
$R_3$
,
![]() $R_4$
, and
$R_4$
, and
![]() $R_5$
are non-recursive, whereas
$R_5$
are non-recursive, whereas
![]() $R_1$
and
$R_1$
and
![]() $R_6$
are recursive, since in the dependency graph of the programme
$R_6$
are recursive, since in the dependency graph of the programme
![]() $\Pi _{\mathsf{ex}}$
– depicted below – only vertices corresponding to
$\Pi _{\mathsf{ex}}$
– depicted below – only vertices corresponding to
![]() $R_1$
and
$R_1$
and
![]() $R_6$
can be reached by paths containing a cycle. Hence, Rules
$R_6$
can be reached by paths containing a cycle. Hence, Rules
![]() $r_2$
and
$r_2$
and
![]() $r_3$
are non-recursive in
$r_3$
are non-recursive in
![]() $\Pi _{\mathsf{ex}}$
since their heads mention non-recursive predicates, whereas
$\Pi _{\mathsf{ex}}$
since their heads mention non-recursive predicates, whereas
![]() $r_1$
and
$r_1$
and
![]() $r_4$
are recursive.
$r_4$
are recursive.
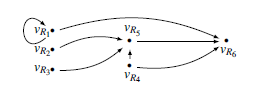
Now, in contrast to recursive predicates, for which new facts can be derived in each materialisation step, the materialisation of non-recursive predicates will be completed after linearly many materialisation steps; from then on, the rules will no longer derive any new facts involving these predicates. This observation can be exploited to optimise our seminaïve evaluation as follows. Assume that the procedure has fully materialised all non-recursive predicates in the input programme. At this point, we can safely discard all non-recursive rules; furthermore, we can also discard a recursive rule
![]() $r$
with a non-recursive body atom
$r$
with a non-recursive body atom
![]() $M$
if the current partial materialisation does not entail any grounding of
$M$
if the current partial materialisation does not entail any grounding of
![]() $M$
(in this case,
$M$
(in this case,
![]() $r$
cannot apply in further materialisation steps). An additional optimisation applies to forward-propagating programmes, where rules cannot propagate information “backwards” along the timeline; in this case, we can compute the maximal time points for which each non-recursive body atom in
$r$
cannot apply in further materialisation steps). An additional optimisation applies to forward-propagating programmes, where rules cannot propagate information “backwards” along the timeline; in this case, we can compute the maximal time points for which each non-recursive body atom in
![]() $r$
may possibly hold, select the minimum
$r$
may possibly hold, select the minimum
![]() $t_r$
amongst such values, and discard
$t_r$
amongst such values, and discard
![]() $r$
as soon as we can determine that the materialisation up to time point
$r$
as soon as we can determine that the materialisation up to time point
![]() $t_r$
has been fully completed.
$t_r$
has been fully completed.
In the case of our Example 4.1, materialisation of the non-recursive predicates
![]() $R_2$
,
$R_2$
,
![]() $R_3$
,
$R_3$
,
![]() $R_4$
, and
$R_4$
, and
![]() $R_5$
is complete after two materialisation steps. Hence, at this point we can disregard non-recursive Rules
$R_5$
is complete after two materialisation steps. Hence, at this point we can disregard non-recursive Rules
![]() $r_2$
and
$r_2$
and
![]() $r_3$
and focus on the recursive forward-propagating Rules
$r_3$
and focus on the recursive forward-propagating Rules
![]() $r_1$
and
$r_1$
and
![]() $r_4$
. Furthermore, the maximum time point at which the non-recursive predicates
$r_4$
. Furthermore, the maximum time point at which the non-recursive predicates
![]() $R_4$
and
$R_4$
and
![]() $R_5$
from
$R_5$
from
![]() $r_4$
can hold are
$r_4$
can hold are
![]() $3$
and
$3$
and
![]() $2$
, respectively, and hence
$2$
, respectively, and hence
![]() $t_{r_4} = 2$
; as upon the completion of the second materialisation step we can be certain that the remaining body atom of
$t_{r_4} = 2$
; as upon the completion of the second materialisation step we can be certain that the remaining body atom of
![]() $r_6$
, namely
$r_6$
, namely
![]() $R_1$
, has been materialised up to
$R_1$
, has been materialised up to
![]() $t_{r_6}$
, we can discard the rule
$t_{r_6}$
, we can discard the rule
![]() $r_6$
. In subsequent materialisation steps we can apply only Rule
$r_6$
. In subsequent materialisation steps we can apply only Rule
![]() $r_1$
, thus avoiding many redundant computations.
$r_1$
, thus avoiding many redundant computations.
Procedure 3 implements these ideas by extending our seminaïve materialisation from Lines 3–8. In particular, in each materialisation step, the procedure checks whether all non-recursive predicates have been fully materialised (Line 9), in which case it removes all non-recursive rules from the input programme as well as all recursive rules with an unsatisfied non-recursive body atom (Lines 10–12). It also sets the flag to
![]() $1$
, which activates the additional optimisation for forward-propagating programmes, which is applied in Lines 13–18.
$1$
, which activates the additional optimisation for forward-propagating programmes, which is applied in Lines 13–18.
Procedure 3: OptimisedSeminaïve
![]() $\Pi,{\mathscr{D}}, P(\mathbf{c})@\rho)$
)
$\Pi,{\mathscr{D}}, P(\mathbf{c})@\rho)$
)

We conclude this section by establishing correctness of our procedure. We first observe that, as soon as the algorithm switches the flag to
![]() $1$
, we can be certain that all facts with non-recursive predicates have been fully materialised.
$1$
, we can be certain that all facts with non-recursive predicates have been fully materialised.
Lemma 5.4. Consider Procedure 3 running on input programme
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathscr{D}$
. Whenever
$\mathscr{D}$
. Whenever
![]() $flag = 1$
, dataset
$flag = 1$
, dataset
![]() ${\mathscr{D}}'$
satisfies all facts over a non-recursive predicate in
${\mathscr{D}}'$
satisfies all facts over a non-recursive predicate in
![]() $\Pi$
that are entailed by
$\Pi$
that are entailed by
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
.
$\mathscr{D}$
.
This lemma shows us that once the
![]() $flag$
is changed to 1, Procedure 3 can safely ignore all the non-recursive rules, as they can no longer be used to derive any new facts. Thus, such rules are deleted from
$flag$
is changed to 1, Procedure 3 can safely ignore all the non-recursive rules, as they can no longer be used to derive any new facts. Thus, such rules are deleted from
![]() $\Pi$
in Line 12. The deletion of rules in Line 18, on the other hand, is based on a simple observation that a derivation of a new fact
$\Pi$
in Line 12. The deletion of rules in Line 18, on the other hand, is based on a simple observation that a derivation of a new fact
![]() $M@t$
by a forward-propagating programme is based only on facts holding at time points smaller-or-equal to
$M@t$
by a forward-propagating programme is based only on facts holding at time points smaller-or-equal to
![]() $t$
. Thus, if for a forward-propagating programme
$t$
. Thus, if for a forward-propagating programme
![]() $\Pi '$
(condition in Line 13) it holds that
$\Pi '$
(condition in Line 13) it holds that
![]() ${\mathfrak{I}}_{{\mathscr{D}}'}$
and
${\mathfrak{I}}_{{\mathscr{D}}'}$
and
![]() $T_{\Pi '}({\mathfrak{I}}_{{\mathscr{D}}'})$
satisfy the same facts within
$T_{\Pi '}({\mathfrak{I}}_{{\mathscr{D}}'})$
satisfy the same facts within
![]() $(-\infty, t_r]$
(condition in Line 18), then
$(-\infty, t_r]$
(condition in Line 18), then
![]() ${\mathfrak{I}}_{{\mathscr{D}}'}$
and
${\mathfrak{I}}_{{\mathscr{D}}'}$
and
![]() $T^\alpha _{\Pi '}({\mathfrak{I}}_{{\mathscr{D}}'})$
will coincide over
$T^\alpha _{\Pi '}({\mathfrak{I}}_{{\mathscr{D}}'})$
will coincide over
![]() $(-\infty, t_r]$
, for each ordinal number
$(-\infty, t_r]$
, for each ordinal number
![]() $\alpha$
. By the construction,
$\alpha$
. By the construction,
![]() $t_r$
is the maximum time point in which the body of rule
$t_r$
is the maximum time point in which the body of rule
![]() $r$
can hold, so if the above conditions are satisfied, we can safely delete
$r$
can hold, so if the above conditions are satisfied, we can safely delete
![]() $r$
from the programme in Line 18. Consequently, we obtain the following result.
$r$
from the programme in Line 18. Consequently, we obtain the following result.
Lemma 5.5. Whenever Procedure 3 removes a rule
![]() $r$
from
$r$
from
![]() $\Pi '$
in either Line 12 or 18,
$\Pi '$
in either Line 12 or 18,
![]() $\mathfrak{C}_{\Pi ', \mathscr{C}} = \mathfrak{C}_{\Pi '\setminus \{r\}, \mathscr{C}}$
.
$\mathfrak{C}_{\Pi ', \mathscr{C}} = \mathfrak{C}_{\Pi '\setminus \{r\}, \mathscr{C}}$
.
Finally, using Lemma 5.5 together with the soundness and completeness of our seminaïve evaluation (established in Theorems5.2 and 5.3), we can show soundness and completeness of the optimised version of the procedure.
Theorem 5.6 (Soundness and Completeness). Consider Procedure 3 with input programme
![]() $\Pi$
and input dataset
$\Pi$
and input dataset
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 2, it holds that
$k$
th iteration of the loop of Procedure 2, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
.
Note that our optimisation for forward-propagating programmes in Lines 13–18 can be adopted in a straightforward way for backwards-propagating programmes, as these cases are symmetric.
We conclude this section by recalling that Procedure 3 is non-terminating, as it is possible for the main loop to run for an unbounded number of iterations. In our approach, we will also exploit a terminating (but incomplete) variant of the procedure, which we call OptimisedSeminaïveHalt. This variant is obtained by adding an additional termination condition just before Line 19 which breaks the loop and returns
![]() $\Pi '$
and
$\Pi '$
and
![]() ${\mathscr{D}}'$
(without a truth value) if the flag has been set to 1. Thus, such a variant of the procedure ensures termination with a (partial) materialisation once all the non-recursive predicates in the input programme have been fully materialised, and also returns a subset of relevant rules in the programme.
${\mathscr{D}}'$
(without a truth value) if the flag has been set to 1. Thus, such a variant of the procedure ensures termination with a (partial) materialisation once all the non-recursive predicates in the input programme have been fully materialised, and also returns a subset of relevant rules in the programme.
5.3 Combining materialisation and automata
We are now ready to provide a practical and scalable reasoning algorithm combining optimised seminaïve materialisation and automata construction. Our algorithm delegates the bulk of the computation to the materialisation component and resorts to automata-based techniques only as needed to ensure termination and completeness.
Algorithm 4: Practical reasoning algorithm

Our approach is summarised in Algorithm 4. When given as input a programme
![]() $\Pi$
, a dataset
$\Pi$
, a dataset
![]() $\mathscr{D}$
, and a fact
$\mathscr{D}$
, and a fact
![]() $P(\mathbf{c})@\rho$
, the algorithm starts by identifying the subset
$P(\mathbf{c})@\rho$
, the algorithm starts by identifying the subset
![]() $\Pi '$
of the input rules and the subset
$\Pi '$
of the input rules and the subset
![]() ${\mathscr{D}}'$
of the input data that are relevant to deriving the input fact
${\mathscr{D}}'$
of the input data that are relevant to deriving the input fact
![]() $P(\mathbf{c})@\rho$
(Lines 1 and 2). This optimisation is based on the observation that a programme
$P(\mathbf{c})@\rho$
(Lines 1 and 2). This optimisation is based on the observation that a programme
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathscr{D}$
entail a fact of the form
$\mathscr{D}$
entail a fact of the form
![]() $P(\mathbf{c}) @ \rho$
if and only if so do the subset
$P(\mathbf{c}) @ \rho$
if and only if so do the subset
![]() $\Pi ^P$
of
$\Pi ^P$
of
![]() $P$
-relevant rules in
$P$
-relevant rules in
![]() $\Pi$
and the subset
$\Pi$
and the subset
![]() ${\mathscr{D}}^P$
of facts in
${\mathscr{D}}^P$
of facts in
![]() $\mathscr{D}$
mentioning only predicates from
$\mathscr{D}$
mentioning only predicates from
![]() $\Pi ^P$
. Then, the algorithm proceeds according to the following steps.
$\Pi ^P$
. Then, the algorithm proceeds according to the following steps.
-
1. Pre-materialise
 $\Pi '$
and
$\Pi '$
and
 ${\mathscr{D}}'$
using the terminating (but possibly incomplete) version of the seminaïve materialisation procedure OptimisedSeminaïveHalt discussed at the end of Section 5.2. If the procedure terminates because an inconsistency has been found, or the input fact has been derived, or a fixpoint has been reached, then we can terminate and report output (Line 5); otherwise, we have obtained a partial materialisation where non-recursive predicates have been fully materialised and we can proceed to the next stage.
${\mathscr{D}}'$
using the terminating (but possibly incomplete) version of the seminaïve materialisation procedure OptimisedSeminaïveHalt discussed at the end of Section 5.2. If the procedure terminates because an inconsistency has been found, or the input fact has been derived, or a fixpoint has been reached, then we can terminate and report output (Line 5); otherwise, we have obtained a partial materialisation where non-recursive predicates have been fully materialised and we can proceed to the next stage. -
2. Run two threads in parallel. In the first (possibly non-terminating) thread, continue performing optimised semi-naïve materialisation until the input fact (or an inconsistency) is derived or a fixpoint is reached. In turn, in the second thread we resort to automata-based techniques applied to the partial materialisation obtained in the first stage of the algorithm; in particular, this second thread applies in Line 10 the reduction from fact entailment to inconsistency checking as described in Section 3.2, and then applies in Line 11 the automata-based decision procedure of (Wałȩga et al. Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2019a), as described in Section 4.3.
It follows directly from the results proved earlier in this section and the theoretical results of Wałȩga et al. (Reference Wałȩga, Cuenca Grau, Kaminski and Kostylev2019a) that Algorithm 4 is sound, complete, and terminating. Furthermore, the algorithm is designed so that, on the one hand, materialisation is favoured over automata-based reasoning and, on the other hand, the automata construction relies on a recursive programme that is as small as possible as well as on a partial materialisation that is as complete as possible. The favourable computational behaviour of this approach will be confirmed by our experiments.
6 Implementation and evaluation
We have implemented our practical decision procedure from Algorithm 4 in a system called MeTeoR. Our system is implemented in Python 3.8 and does not depend on third-party libraries. MeTeoR is available for download and its demo can also be accessed via an online interface.Footnote 3 In this section, we describe the implementation choices made in MeTeoR and report the results of an extensive empirical evaluation on available benchmarks.
6.1 Implementation details
A scalable implementation of materialisation-based reasoning requires suitable representation and storage schemes for facts. In MeTeoR, we associate to each ground relational atom a list of intervals sorted by their left endpoints, which provides a compact account of all facts mentioning a given relational atom. Each ground relational atom is further indexed by a composite key consisting of its predicate and its tuple of constants. This layout is useful for fact coalescing and fact entailment checking; for instance, to check if a fact
![]() $M @ \rho$
is entailed by a dataset
$M @ \rho$
is entailed by a dataset
![]() $\mathscr{D}$
, it suffices to find and interval
$\mathscr{D}$
, it suffices to find and interval
![]() $\rho '$
such that
$\rho '$
such that
![]() $M @ \rho ' \in{\mathscr{D}}$
and
$M @ \rho ' \in{\mathscr{D}}$
and
![]() $\rho \subseteq \rho '$
; this can be achieved by first scanning the sorted list of intervals for
$\rho \subseteq \rho '$
; this can be achieved by first scanning the sorted list of intervals for
![]() $M$
using the index and checking if
$M$
using the index and checking if
![]() $\rho$
is a subset of one of these intervals. Additionally, each ground relational atom is also indexed by each of its term arguments to facilitate joins. Finally, when a fact is inserted into the dataset, the corresponding list of intervals is sorted to facilitate subsequent operations.
$\rho$
is a subset of one of these intervals. Additionally, each ground relational atom is also indexed by each of its term arguments to facilitate joins. Finally, when a fact is inserted into the dataset, the corresponding list of intervals is sorted to facilitate subsequent operations.
MeTeoR also implements an optimised version of (temporal) joins, which are required to evaluate rules with multiple body atoms. A naïve implementation of the join of metric atoms
![]() $M_1, \dots, M_n$
occurring in the body of a rule would require computing all intersections of intervals
$M_1, \dots, M_n$
occurring in the body of a rule would require computing all intersections of intervals
![]() $\rho _1, \dots, \rho _n$
such that
$\rho _1, \dots, \rho _n$
such that
![]() $M_i @ \rho _i$
occurs in the so-far constructed dataset, for each
$M_i @ \rho _i$
occurs in the so-far constructed dataset, for each
![]() $i \in \{1, \dots, n\}$
. Since each
$i \in \{1, \dots, n\}$
. Since each
![]() $M_i$
may hold in multiple intervals in the dataset, the naïve approach is ineffective in practice. In contrast, we implemented a variant of the classical sort-merge join algorithm: we first sort all
$M_i$
may hold in multiple intervals in the dataset, the naïve approach is ineffective in practice. In contrast, we implemented a variant of the classical sort-merge join algorithm: we first sort all
![]() $n$
lists of intervals corresponding to
$n$
lists of intervals corresponding to
![]() $M_1, \dots, M_n$
, and then scan the sorted lists to compute the intersections, which improves performance. Our approach to temporal joins can be seen as a generalisation of the idea sketched by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018, Section 5), which deals with two metric atoms at a time but has not been put into practice to the best of our knowledge.
$M_1, \dots, M_n$
, and then scan the sorted lists to compute the intersections, which improves performance. Our approach to temporal joins can be seen as a generalisation of the idea sketched by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018, Section 5), which deals with two metric atoms at a time but has not been put into practice to the best of our knowledge.
6.2 Baselines and machine configuration
We compared MeTeoR with two baselines: the query rewriting approach by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) and the reduction to LTL reasoning proposed by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) which was later implemented by Yang (Reference Yang2022). We could not compare our approach to the temporal extension of the Vadalog system recently proposed by Bellomarini et al. (Reference Bellomarini, Blasi, Nissl and Sallinger2022) as the system is not accessible.
The query rewriting approach by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) is based on rewriting a target predicate
![]() $P$
with respect to an input programme
$P$
with respect to an input programme
![]() $\Pi$
into an SQL query that, when evaluated over the input dataset
$\Pi$
into an SQL query that, when evaluated over the input dataset
![]() $\mathscr{D}$
, provides the set of all facts with maximal intervals over
$\mathscr{D}$
, provides the set of all facts with maximal intervals over
![]() $P$
entailed by
$P$
entailed by
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. The only implementation of this approach that we are aware of is the extension of the Ontop system described by Kalaycı et al. (Reference Kalaycı, Xiao, Ryzhikov, Kalayci and Calvanese2018); this implementation, however, is no longer availableFootnote
4
and hence we have produced our own implementation. Following Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), we used temporary tables (instead of subqueries) to compute the extensions of predicates appearing in
$\mathscr{D}$
. The only implementation of this approach that we are aware of is the extension of the Ontop system described by Kalaycı et al. (Reference Kalaycı, Xiao, Ryzhikov, Kalayci and Calvanese2018); this implementation, however, is no longer availableFootnote
4
and hence we have produced our own implementation. Following Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), we used temporary tables (instead of subqueries) to compute the extensions of predicates appearing in
![]() $\Pi$
on the fly, which has two implications. First, we usually have not just one SQL query but a set of queries for computing the final result; second, similarly to MeTeoR, the approach essentially works bottom-up rather than top-down. The implementation by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) provides two variants for coalescing: the first one uses standard SQL queries by Zhou et al. (Reference Zhou, Wang and Zaniolo2006), whereas the second one implements coalescing explicitly. For our baseline we adopted the standard SQL approach, which is less dependent on implementation details. Finally, we chose Postgresql 10.18 as the underpinning database for all our baseline experiments.
$\Pi$
on the fly, which has two implications. First, we usually have not just one SQL query but a set of queries for computing the final result; second, similarly to MeTeoR, the approach essentially works bottom-up rather than top-down. The implementation by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018) provides two variants for coalescing: the first one uses standard SQL queries by Zhou et al. (Reference Zhou, Wang and Zaniolo2006), whereas the second one implements coalescing explicitly. For our baseline we adopted the standard SQL approach, which is less dependent on implementation details. Finally, we chose Postgresql 10.18 as the underpinning database for all our baseline experiments.
As shown by Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), DatalogMTL reasoning can be reduced to LTL reasoning by means of an exponential translation. This approach has been implemented by Yang (Reference Yang2022) using BLACK (Geatti et al. Reference Geatti, Gigante and Montanari2019) as the LTL reasoner of choice, and we used their implementation as a baseline for our experiments.
All experiments have been conducted on a Dell PowerEdge R730 server with 512 GB RAM and two Intel Xeon E5-2640 2.6 GHz processors running Fedora 33, kernel version 5.8.17. In each experiment, we verified that the answers returned by MeTeoR and the baselines coincide.
6.3 Benchmarks
The Temporal LUBM Benchmark is an extension of the Lehigh University Benchmark (Guo et al. Reference Guo, Pan and Heflin2005) with temporal rules and data, which we developed (Wang et al. Reference Wang, Hu, Wałȩga and Grau2022
Reference Wang, Hu, Wałȩga and Graua). LUBM’s data generator, which provides means for generating datasets of different sizes, has been extended to randomly assign an interval to each generated fact; the rational endpoints of each interval belong to a range, which is a parameter. In addition, the plain Datalog rules from the OWL 2 RL fragment of LUBM have been extended with
![]() $29$
rules involving recursion and mentioning all metric operators in DatalogMTL. The resulting DatalogMTL programme is denoted by
$29$
rules involving recursion and mentioning all metric operators in DatalogMTL. The resulting DatalogMTL programme is denoted by
![]() $\Pi _L$
.
$\Pi _L$
.
The Weather Benchmark is based on freely available data with meteorological observations in the US (Maurer et al. Reference Maurer, Wood, Adam, Lettenmaier and Nijssen2002);Footnote
5
in particular, we used a dataset
![]() ${\mathscr{D}}_W$
consisting of 397 million temporal facts spanning over the years 1949–2010, and then considered smaller subsets of this dataset. Similar data was used in experiments of Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), however the format of data has slightly changed, so we adapted their (non-recursive) programme (consisting of 4 rules) for detecting US states affected by excessive heat and heavy wind, so that the programme matches the data. The obtained programme is still non-recursive and, in what follows, it is denoted by
${\mathscr{D}}_W$
consisting of 397 million temporal facts spanning over the years 1949–2010, and then considered smaller subsets of this dataset. Similar data was used in experiments of Brandt et al. (Reference Brandt, Kalaycı, Ryzhikov, Xiao and Zakharyaschev2018), however the format of data has slightly changed, so we adapted their (non-recursive) programme (consisting of 4 rules) for detecting US states affected by excessive heat and heavy wind, so that the programme matches the data. The obtained programme is still non-recursive and, in what follows, it is denoted by
![]() $\Pi _W$
.
$\Pi _W$
.
The iTemporal Benchmark provides a synthetic generator for DatalogMTL programmes and datasets (Bellomarini et al. Reference Bellomarini, Blasi, Nissl and Sallinger2022).Footnote
6
The benchmark can generate different types of DatalogMTL programmes and equips them with datasets. We used iTemporal to generate 10 recursive programmes
![]() $\Pi _I^1, \dots, \Pi _I^{10}$
with different structures and containing 20–30 rules each, as well as corresponding datasets of various size.
$\Pi _I^1, \dots, \Pi _I^{10}$
with different structures and containing 20–30 rules each, as well as corresponding datasets of various size.
6.4 Experiments
In this section, we describe experiments that we performed for benchmarking MeTeoR.Footnote 7
6.4.1 Automata vs LTL
Although MeTeoR utilises automata to ensure completeness and termination, we could have alternatively relied on the translation to LTL implemented by Yang (Reference Yang2022) together with BLACK (Geatti et al. Reference Geatti, Gigante and Montanari2019) as the LTL reasoner of choice. To determine which choice is favourable, we considered programmes
![]() $\Pi _I^1, \dots, \Pi _I^{10}$
from the iTempora benchmark, together with datasets containing
$\Pi _I^1, \dots, \Pi _I^{10}$
from the iTempora benchmark, together with datasets containing
![]() $1,000$
facts each. For each pair of a dataset and a programme, we constructed
$1,000$
facts each. For each pair of a dataset and a programme, we constructed
![]() $10$
query facts; these facts were generated by first randomly choosing a predicate that appears in a programme or in a dataset; second, constants are randomly chosen among those present in the programme and in the dataset; third, an interval for the fact is generated. Next, we performed fact entailment by first reducing to inconsistency checking and then either applying the automata-based approach or constructing an LTL formula and checking it’s satisfiability with BLACK. Average running times per 10 query facts for both approaches are reported in Figure 1 (left), where each point represents the running times for the automata-based approach (vertical coordinate) and LTL-based approach (horizontal coordinate) for a single programme and dataset. We can observe that the automata-based approach is consistently about an order of magnitude faster, which justifies our choice over an LTL-based reasoner.
$10$
query facts; these facts were generated by first randomly choosing a predicate that appears in a programme or in a dataset; second, constants are randomly chosen among those present in the programme and in the dataset; third, an interval for the fact is generated. Next, we performed fact entailment by first reducing to inconsistency checking and then either applying the automata-based approach or constructing an LTL formula and checking it’s satisfiability with BLACK. Average running times per 10 query facts for both approaches are reported in Figure 1 (left), where each point represents the running times for the automata-based approach (vertical coordinate) and LTL-based approach (horizontal coordinate) for a single programme and dataset. We can observe that the automata-based approach is consistently about an order of magnitude faster, which justifies our choice over an LTL-based reasoner.
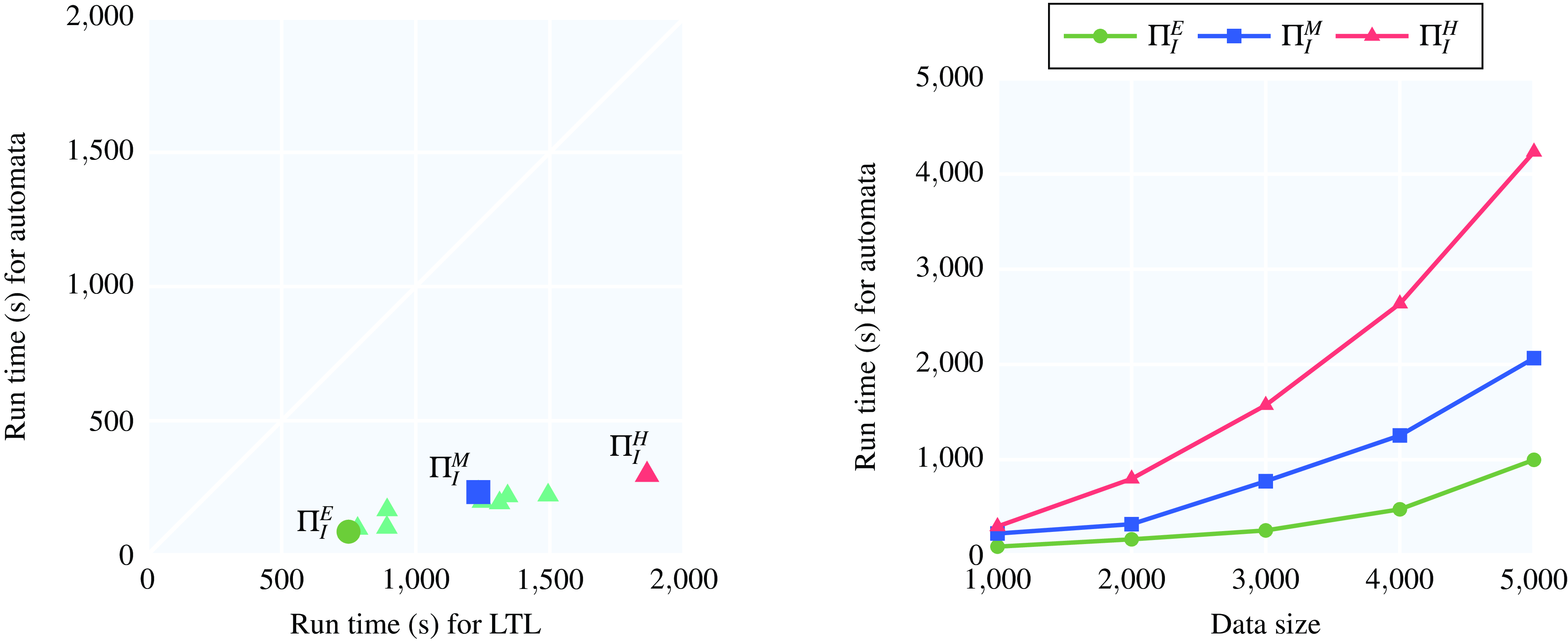
Fig. 1. Comparison of automata- and LTL-based approaches (left) and scalability of the automata approach (right).
6.4.2 Scalability of automata
We have conducted scalability experiments to understand the practical limitations of the automata-based approach. Based on the results from the previous experiment, we chose an “easy” programme
![]() $\Pi _I^E$
, a “medium” programme
$\Pi _I^E$
, a “medium” programme
![]() $\Pi _I^M$
, and a “hard” programme
$\Pi _I^M$
, and a “hard” programme
![]() $\Pi _I^H$
amongst programmes
$\Pi _I^H$
amongst programmes
![]() $\Pi _I^1, \dots, \Pi _I^{10}$
, as depicted in Figure 1 (left). We used iTemporal to generate increasing size datasets for these programmes and we randomly generated query facts as in the previous experiment. The runtimes of automata-based approach for such inputs are summarised in Figure 1 (right), where we observe that the automata-based procedure is able to solve non-trivial problems, but struggles to scale beyond datasets with a few thousand temporal facts.
$\Pi _I^1, \dots, \Pi _I^{10}$
, as depicted in Figure 1 (left). We used iTemporal to generate increasing size datasets for these programmes and we randomly generated query facts as in the previous experiment. The runtimes of automata-based approach for such inputs are summarised in Figure 1 (right), where we observe that the automata-based procedure is able to solve non-trivial problems, but struggles to scale beyond datasets with a few thousand temporal facts.
6.4.3 Comparison of materialisation strategies
We compared the naïve, seminaïve, and optimised seminaïve materialisation procedures described in Sections 4.1, 5.1, and 5.2, respectively. To this end, for each of the programmes
![]() $\Pi _i^{E}$
,
$\Pi _i^{E}$
,
![]() $\Pi _{i}^{M}$
, and
$\Pi _{i}^{M}$
, and
![]() $\Pi _i^{H}$
we used iTemporal to generate a dataset containing one million facts. In Figure 2 we present running time and memory consumption (measured as the maximum number of facts stored in memory) over the first 30 materialisation steps in each case. As we can see, the seminaïve procedure consistently outperforms the naïve approach both in terms of running time and memory consumption, especially as materialisation progresses. In turn, the optimised seminaïve approach disregards rules after
$\Pi _i^{H}$
we used iTemporal to generate a dataset containing one million facts. In Figure 2 we present running time and memory consumption (measured as the maximum number of facts stored in memory) over the first 30 materialisation steps in each case. As we can see, the seminaïve procedure consistently outperforms the naïve approach both in terms of running time and memory consumption, especially as materialisation progresses. In turn, the optimised seminaïve approach disregards rules after
![]() $6$
th,
$6$
th,
![]() $7$
th, and
$7$
th, and
![]() $8$
th materialisation steps for
$8$
th materialisation steps for
![]() $\Pi _I^{E}$
,
$\Pi _I^{E}$
,
![]() $\Pi _I^{M}$
, and
$\Pi _I^{M}$
, and
![]() $\Pi _I^{H}$
, respectively; from then onwards, the optimised procedure outperforms the basic seminaïve procedure. We can note that after several steps of materialisation the memory usage stabilises; the number of facts in memory stops increasing but their intervals keep growing. This behaviour seems to be specific to programmes we used in this experiment.
$\Pi _I^{H}$
, respectively; from then onwards, the optimised procedure outperforms the basic seminaïve procedure. We can note that after several steps of materialisation the memory usage stabilises; the number of facts in memory stops increasing but their intervals keep growing. This behaviour seems to be specific to programmes we used in this experiment.
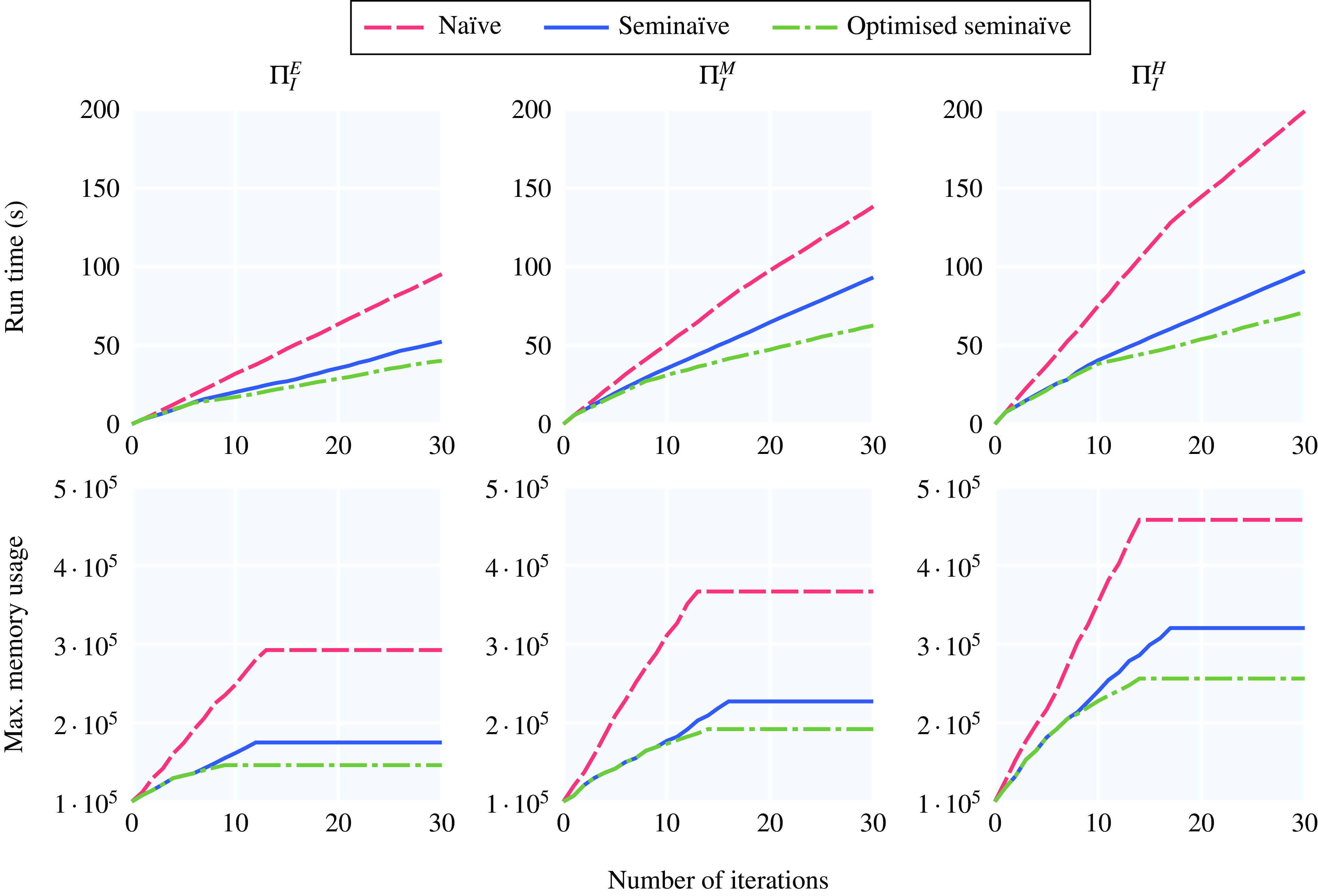
Fig. 2. Comparison of time and memory consumption in various materialisation strategies.
6.4.4 Scalability of optimised seminaïve materialisation
Our previous experiments provide evidence of the superiority of optimised seminaïve materialisation over the two alternative approaches. We further evaluated the scalability of optimised seminaïve materialisation as the size of the data increases. To this end, we considered the three iTemporal programmes
![]() $\Pi _I^{E}$
,
$\Pi _I^{E}$
,
![]() $\Pi _I^{M}$
, and
$\Pi _I^{M}$
, and
![]() $\Pi _I^{H}$
as well as programme
$\Pi _I^{H}$
as well as programme
![]() $\Pi _L$
from the Temporal LUBM Benchmark, and
$\Pi _L$
from the Temporal LUBM Benchmark, and
![]() $\Pi _W$
from the Weather Benchmark. In Figure 3 we show running times and memory consumption after the first
$\Pi _W$
from the Weather Benchmark. In Figure 3 we show running times and memory consumption after the first
![]() $10$
materialisation steps for datasets with up to
$10$
materialisation steps for datasets with up to
![]() $10$
million temporal facts. We note here that the programme
$10$
million temporal facts. We note here that the programme
![]() $\Pi _W$
is non-recursive and its full materialisation is obtained already after
$\Pi _W$
is non-recursive and its full materialisation is obtained already after
![]() $3$
materialisation steps; all other programmes are recursive. Our results suggest that the optimised seminaïve materialisation procedure exhibits favourable scalability behaviour as data size increases.
$3$
materialisation steps; all other programmes are recursive. Our results suggest that the optimised seminaïve materialisation procedure exhibits favourable scalability behaviour as data size increases.
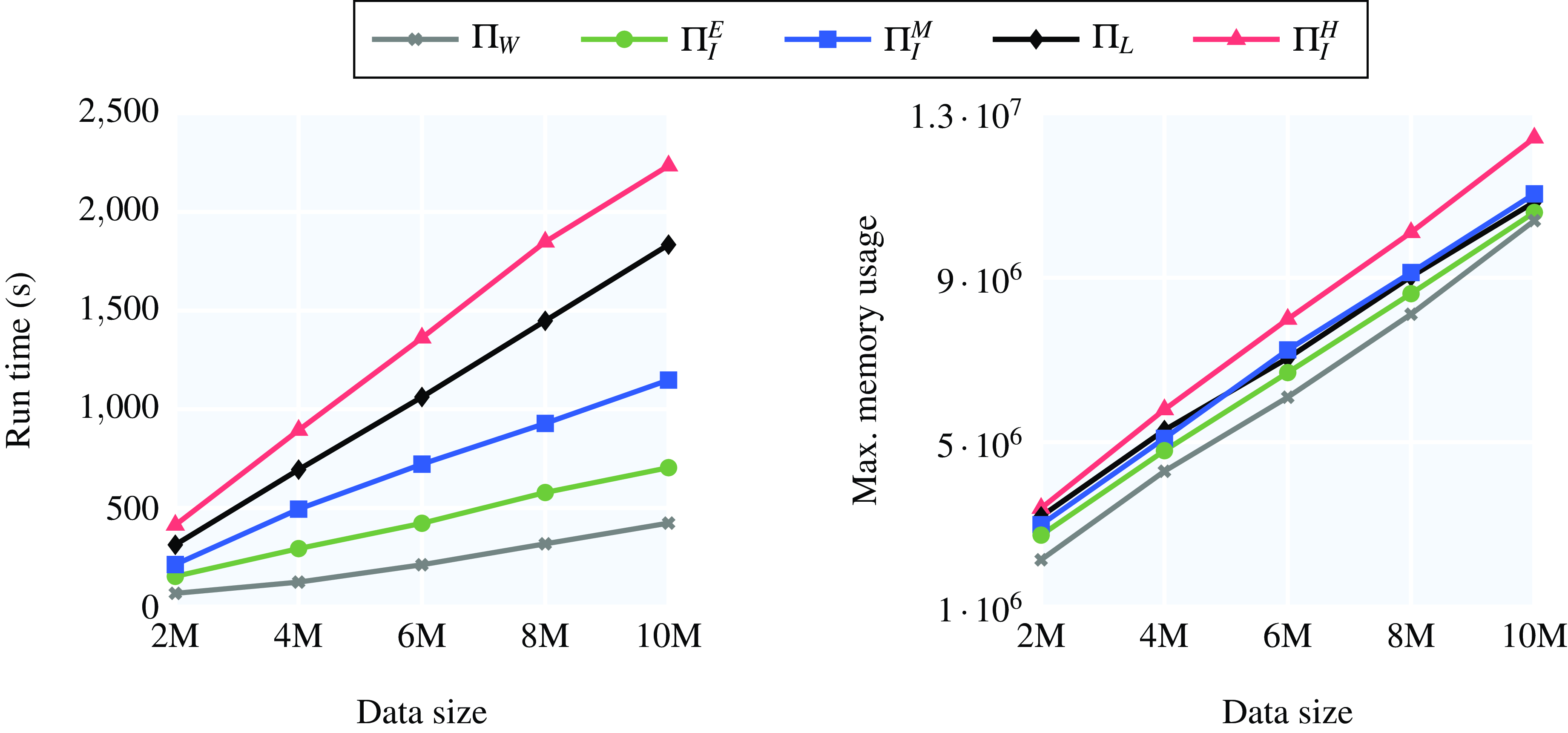
Fig. 3. Scalability of our optimised seminaïve materialisation.
6.4.5 Comparison with query rewriting
We compared the performance of MeTeoR with the query rewriting baseline. As the latter does not support recursive programmes, we considered non-recursive programmes only. For this, we generated non-recursive subsets of the programme
![]() $\Pi _L$
from the Temporal LUBM Benchmark and two subsets of the programme
$\Pi _L$
from the Temporal LUBM Benchmark and two subsets of the programme
![]() $\Pi _W$
from the Weather Benchmark. In particular, we considered fragments
$\Pi _W$
from the Weather Benchmark. In particular, we considered fragments
![]() $\Pi _L^{1}$
(with
$\Pi _L^{1}$
(with
![]() $5$
rules),
$5$
rules),
![]() $\Pi _L^{2}$
(
$\Pi _L^{2}$
(
![]() $10$
rules), and
$10$
rules), and
![]() $\Pi _L^{3}$
(
$\Pi _L^{3}$
(
![]() $21$
rules) of
$21$
rules) of
![]() $\Pi _L$
with rules relevant (see the end of Section 3.1 for the precise definition of this notion) to predicates
$\Pi _L$
with rules relevant (see the end of Section 3.1 for the precise definition of this notion) to predicates
![]() $\mathit{ResearchAssistant}$
,
$\mathit{ResearchAssistant}$
,
![]() $\mathit{Lecturer}$
, and
$\mathit{Lecturer}$
, and
![]() $\mathit{FullProfessorCandidate}$
, respectively. For the Weather Benchmark we used fragments
$\mathit{FullProfessorCandidate}$
, respectively. For the Weather Benchmark we used fragments
![]() $\Pi _W^1$
and
$\Pi _W^1$
and
![]() $\Pi _W^2$
(each with 2 rules) of
$\Pi _W^2$
(each with 2 rules) of
![]() $\Pi _W$
, with rules relevant to predicates
$\Pi _W$
, with rules relevant to predicates
![]() $\mathit{HeatAffectedState}$
and
$\mathit{HeatAffectedState}$
and
![]() $\mathit{HeavyWindAffectedState}$
, respectively. For each programme we generated a collection of datasets with
$\mathit{HeavyWindAffectedState}$
, respectively. For each programme we generated a collection of datasets with
![]() $100,000$
facts each and compared the runtime of MeTeoR with the baseline in the task of computing all entailed facts over the predicates mentioned above. Note that since the programmes are non-recursive, MeTeoR runs only (optimised seminaïve) materialisation without exploiting automata. Figure 4 presents results, where each point represents the running times for MeTeoR (vertical coordinate) and the baseline (horizontal coordinate) for particular pairs of a programme and a dataset; MeTeoR consistently outperformed the baseline.
$100,000$
facts each and compared the runtime of MeTeoR with the baseline in the task of computing all entailed facts over the predicates mentioned above. Note that since the programmes are non-recursive, MeTeoR runs only (optimised seminaïve) materialisation without exploiting automata. Figure 4 presents results, where each point represents the running times for MeTeoR (vertical coordinate) and the baseline (horizontal coordinate) for particular pairs of a programme and a dataset; MeTeoR consistently outperformed the baseline.
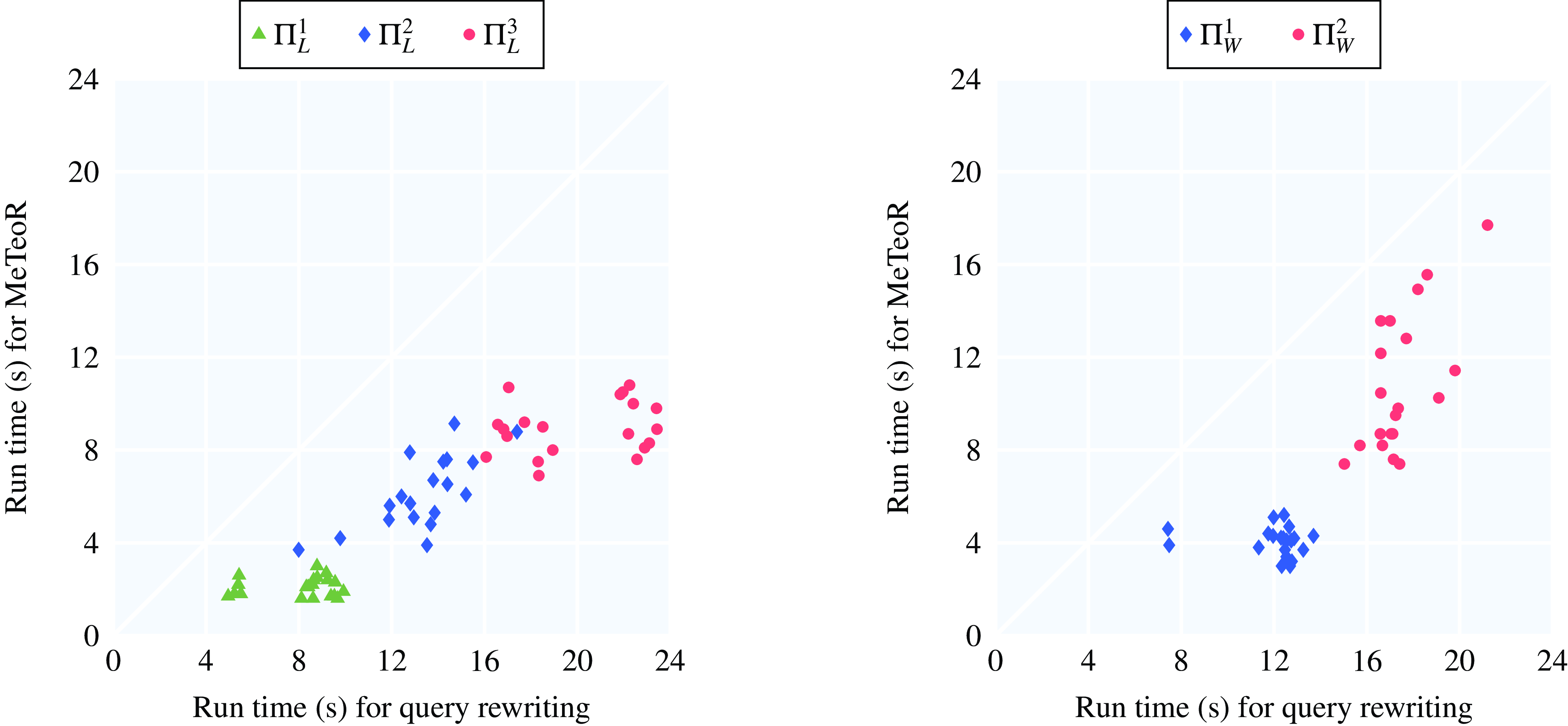
Fig. 4. Comparison between meTeoR and the query rewriting baseline.
6.4.6 Usage of materialisation and automata in meTeoR
Our previous experiments provide strong indication that the optimised seminaïve materialisation algorithm implemented in MeTeoR is more scalable than the automata-based component and that it can successfully deal with complex rules and datasets containing millions of temporal facts. Next, we assess whether Algorithm 4 is indeed effective in delegating most of the reasoning workload to the scalable materialisation component. To this end, we considered programmes
![]() $\Pi _I^1, \dots, \Pi _I^{10}$
generated by iTemporal together with their corresponding datasets with 1000 facts each. For each pair of a programme and a dataset we randomly generated 100 query facts and checked, for which facts entailment can be checked by MeTeoR using materialisation (i.e. Algorithm 4 terminates in either Line 3 or Line 8) and for which by the automata component (i.e. Algorithm 4 terminates in Line 12). It turned out that in
$\Pi _I^1, \dots, \Pi _I^{10}$
generated by iTemporal together with their corresponding datasets with 1000 facts each. For each pair of a programme and a dataset we randomly generated 100 query facts and checked, for which facts entailment can be checked by MeTeoR using materialisation (i.e. Algorithm 4 terminates in either Line 3 or Line 8) and for which by the automata component (i.e. Algorithm 4 terminates in Line 12). It turned out that in
![]() $99.7\%$
cases MeTeoR decided entailment using materialisation only, and so, only in
$99.7\%$
cases MeTeoR decided entailment using materialisation only, and so, only in
![]() $0.3\%$
cases the automata component was used. Although these results are obviously biased by the way iTemporal generates programmes and datasets, they do support our hypothesis that focusing on the materialisation component in MeTeoR can provide a practically efficient reasoning mechanism.
$0.3\%$
cases the automata component was used. Although these results are obviously biased by the way iTemporal generates programmes and datasets, they do support our hypothesis that focusing on the materialisation component in MeTeoR can provide a practically efficient reasoning mechanism.
7 Conclusions
In this paper, we presented a practical reasoning algorithm for full DatalogMTL, which combines materialisation with an automata-based approach. To achieve favourable performance, our algorithm delegates most of the computations to the materialisation component, which we optimised using seminaïve reasoning strategies. In turn, the computationally-expensive automata-based approach is used only to guarantee termination and completeness of reasoning. We have implemented our algorithm in the MeTeoR reasoner and made it publicly available. Our extensive evaluation supports our practicality and scalability claims.
We see many avenues for future research. First, DatalogMTL has been extended with stratified negation-as-failure (Cucala et al. Reference Cucala, Wałȩga, Cuenca Grau and Kostylev2021) and our seminaïve procedure could be extended accordingly. We are also working on blocking conditions that exploit the periodic structure of canonical models to ensure termination of materialisation-based reasoning. Finally, incremental materialisation-based reasoning has been studied in context of Datalog (Motik et al. Reference Motik, Nenov, Piro and Horrocks2019), and it would be interesting to lift such approaches to the DatalogMTL setting.
Acknowledgments
Our research was funded by the following EPSRC projects: OASIS (EP/S032347/1), and UK FIRES (EP/S019111/1), as well as by SIRIUS Centre for Scalable Data Access, Samsung Research UK, and NSFC grant No. 62206169. For the purpose of Open Access, the authors have applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission.
Appendix A Proofs
Theorem4.3: Consider Procedure 1 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. Upon the completion of the
$\mathscr{D}$
. Upon the completion of the
![]() $k$
th (for some
$k$
th (for some
![]() $k \in \mathbb{N}$
) iteration of the loop of Procedure 1, it holds that
$k \in \mathbb{N}$
) iteration of the loop of Procedure 1, it holds that
![]() ${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
Proof.
For each
![]() $k \in \mathbb{N}$
, we let
$k \in \mathbb{N}$
, we let
![]() $\mathscr{N}_k$
and
$\mathscr{N}_k$
and
![]() ${\mathscr{D}}_k$
denote the contents of, respectively,
${\mathscr{D}}_k$
denote the contents of, respectively,
![]() $\mathscr{N}$
and
$\mathscr{N}$
and
![]() $\mathscr{D}$
in Procedure 1 upon the completion of the
$\mathscr{D}$
in Procedure 1 upon the completion of the
![]() $k$
th iteration of the loop. Thus, it suffices to show, inductively on
$k$
th iteration of the loop. Thus, it suffices to show, inductively on
![]() $k\in \mathbb{N}$
, that
$k\in \mathbb{N}$
, that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T^k_\Pi ({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T^k_\Pi ({\mathfrak{I}}_{\mathscr{D}})$
.
In the base case, we have
![]() ${\mathscr{D}}_0 ={\mathscr{D}}$
. Moreover,
${\mathscr{D}}_0 ={\mathscr{D}}$
. Moreover,
![]() $T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{\mathscr{D}}$
, and so,
$T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{\mathscr{D}}$
, and so,
![]() ${\mathfrak{I}}_{{\mathscr{D}}_0} \subseteq T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}})$
, as required. For the inductive step, we assume that
${\mathfrak{I}}_{{\mathscr{D}}_0} \subseteq T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}})$
, as required. For the inductive step, we assume that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_{\Pi }^k({\mathfrak{I}}_{\mathscr{D}})$
, for some
${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_{\Pi }^k({\mathfrak{I}}_{\mathscr{D}})$
, for some
![]() $k \in \mathbb{N}$
, and that the procedure enters the
$k \in \mathbb{N}$
, and that the procedure enters the
![]() $k+1$
st iteration of the loop. If the
$k+1$
st iteration of the loop. If the
![]() $k+1$
st iteration of the loop breaks in Line 7, then
$k+1$
st iteration of the loop breaks in Line 7, then
![]() ${\mathscr{D}}_{k+1} ={\mathscr{D}}_{k}$
. By the inductive assumption we have
${\mathscr{D}}_{k+1} ={\mathscr{D}}_{k}$
. By the inductive assumption we have
![]() ${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}})$
, and therefore,
${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}})$
, and therefore,
![]() ${\mathfrak{I}}_{{\mathscr{D}}_{k+1} } \subseteq T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}})$
, and thus,
${\mathfrak{I}}_{{\mathscr{D}}_{k+1} } \subseteq T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}})$
, and thus,
![]() ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \subseteq T_\Pi ^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
. Now, assume that the
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \subseteq T_\Pi ^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
. Now, assume that the
![]() $k+1$
st iteration of the loop does not break in Line 7. Hence, by Lines 4 and 8, we have
$k+1$
st iteration of the loop does not break in Line 7. Hence, by Lines 4 and 8, we have
![]() ${\mathscr{D}}_{k+1} = \mathsf{coal}({\mathscr{D}}_{k} \cup \mathscr{N}_{k+1})$
. To show that
${\mathscr{D}}_{k+1} = \mathsf{coal}({\mathscr{D}}_{k} \cup \mathscr{N}_{k+1})$
. To show that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \subseteq T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
, we assume that
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \subseteq T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
, we assume that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
, for some relational fact
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
, for some relational fact
![]() $M@t$
. Hence, we have
$M@t$
. Hence, we have
![]() ${\mathscr{D}}_{k} \models M@t$
or
${\mathscr{D}}_{k} \models M@t$
or
![]() $\mathscr{N}_{k+1} \models M@t$
.
$\mathscr{N}_{k+1} \models M@t$
.
-
Case 1:
 ${\mathscr{D}}_{k} \models M@t$
. By the inductive assumption,
${\mathscr{D}}_{k} \models M@t$
. By the inductive assumption,
 ${\mathfrak{I}}_{{\mathscr{D}}_{k}} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
, so
${\mathfrak{I}}_{{\mathscr{D}}_{k}} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
, so
 $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
. Clearly,
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
. Clearly,
 $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
, and so,
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}})$
, and so,
 $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, as required.
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, as required. -
Case 2:
 $\mathscr{N}_{k+1} \models M@t$
. By Line 3 of Procedure 1, we obtain that
$\mathscr{N}_{k+1} \models M@t$
. By Line 3 of Procedure 1, we obtain that
 $\mathscr{N}_{k+1} = \Pi ({\mathscr{D}}_{k})$
. Thus, by Expression (3) from Definition 4.2, there exists a rule
$\mathscr{N}_{k+1} = \Pi ({\mathscr{D}}_{k})$
. Thus, by Expression (3) from Definition 4.2, there exists a rule
 $r \in \Pi$
, say of the form
$r \in \Pi$
, say of the form
 $ M' \gets M_1 \land \dots \land M_n$
, such that
$ M' \gets M_1 \land \dots \land M_n$
, such that
 $r[{\mathscr{D}}_k] \models M@t$
. Therefore, by Expression (2) from Definition 4.2, there are a substitution
$r[{\mathscr{D}}_k] \models M@t$
. Therefore, by Expression (2) from Definition 4.2, there are a substitution
 $\sigma$
and some intervals
$\sigma$
and some intervals
 $\rho _1, \dots, \rho _n$
such that
$\rho _1, \dots, \rho _n$
such that
 $(M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[D_k]$
and
$(M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[D_k]$
and
 $M'\sigma @(\rho _1 \cap \dots \cap \rho _n)\models M@t$
. Since
$M'\sigma @(\rho _1 \cap \dots \cap \rho _n)\models M@t$
. Since
 $(M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n)$
belongs to
$(M_1\sigma @\rho _1, \dots, M_n \sigma @\rho _n)$
belongs to
 $\mathsf{inst}_{r}[{\mathscr{D}}_k]$
, by Expression (2) from Definition 4.2, we obtain that
$\mathsf{inst}_{r}[{\mathscr{D}}_k]$
, by Expression (2) from Definition 4.2, we obtain that
 ${\mathscr{D}}_k \models M_i @ \rho _i$
, for each
${\mathscr{D}}_k \models M_i @ \rho _i$
, for each
 $i \in \{1, \dots, n \}$
. Therefore, by the definition of
$i \in \{1, \dots, n \}$
. Therefore, by the definition of
 $T_\Pi$
, we obtain that
$T_\Pi$
, we obtain that
 $T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \models M'\sigma @(\rho _1 \cap \dots \cap \rho _n)$
and so
$T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \models M'\sigma @(\rho _1 \cap \dots \cap \rho _n)$
and so
 $T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \models M@t$
. Finally, by the inductive assumption,
$T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \models M@t$
. Finally, by the inductive assumption,
 ${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_\Pi ^k({\mathfrak{I}}_{{\mathscr{D}}})$
, so
${\mathfrak{I}}_{{\mathscr{D}}_k} \subseteq T_\Pi ^k({\mathfrak{I}}_{{\mathscr{D}}})$
, so
 $T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \subseteq T_\Pi ^{k+1}({\mathfrak{I}}_{{\mathscr{D}}})$
, and therefore we obtain that
$T_\Pi ({\mathfrak{I}}_{{\mathscr{D}}_k}) \subseteq T_\Pi ^{k+1}({\mathfrak{I}}_{{\mathscr{D}}})$
, and therefore we obtain that
 $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
.
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
.
Theorem4.4: Consider Procedure 1 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 1, it holds that
$k$
th iteration of the loop of Procedure 1, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
Proof.
We use the same symbols
![]() $\mathscr{N}_k$
and
$\mathscr{N}_k$
and
![]() ${\mathscr{D}}_k$
as in the proof of Theorem4.3 and we define
${\mathscr{D}}_k$
as in the proof of Theorem4.3 and we define
![]() $\Delta _k$
analogously. We will show, inductively on natural numbers
$\Delta _k$
analogously. We will show, inductively on natural numbers
![]() $k$
, that
$k$
, that
![]() $T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
. The base case holds trivially, because we have
$T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
. The base case holds trivially, because we have
![]() ${\mathscr{D}}_0 ={\mathscr{D}}$
, and so,
${\mathscr{D}}_0 ={\mathscr{D}}$
, and so,
![]() $T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}_0}$
. For the inductive step assume that
$T_\Pi ^0({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}_0}$
. For the inductive step assume that
![]() $T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
, for some
$T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
, for some
![]() $k\in \mathbb{N}$
. Moreover, let
$k\in \mathbb{N}$
. Moreover, let
![]() $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
![]() $M@t$
. We will show that
$M@t$
. We will show that
![]() ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
. We have either
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
. We have either
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
or
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
or
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
.
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
.
-
Case 1:
 $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
. Then, by the inductive assumption,
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
. Then, by the inductive assumption,
 ${\mathfrak{I}}_{{\mathscr{D}}_k} \models M@t$
. Since
${\mathfrak{I}}_{{\mathscr{D}}_k} \models M@t$
. Since
 ${\mathscr{D}}_{k+1} \models{\mathscr{D}}_k$
, we obtain that
${\mathscr{D}}_{k+1} \models{\mathscr{D}}_k$
, we obtain that
 ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
.
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
. -
Case 2:
 $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
. Since
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
. Since
 $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, there exist a rule
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, there exist a rule
 $r\in \Pi$
, say of the form
$r\in \Pi$
, say of the form
 $M' \gets M_1 \land \dots \land M_n$
, and a time point
$M' \gets M_1 \land \dots \land M_n$
, and a time point
 $t'$
such that an application of
$t'$
such that an application of
 $r$
at
$r$
at
 $t'$
yields
$t'$
yields
 $M@t$
. More precisely, it means that there is a substitution
$M@t$
. More precisely, it means that there is a substitution
 $\sigma$
such that
$\sigma$
such that
 $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M_i \sigma @t'$
, for each
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \models M_i \sigma @t'$
, for each
 $i \in \{1, \dots, n \}$
, and
$i \in \{1, \dots, n \}$
, and
 $M'\sigma @ t' \models M@t$
. Therefore, by the fact that
$M'\sigma @ t' \models M@t$
. Therefore, by the fact that
 $T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
and by Expression (2) from Definition 4.2, there need to exist some intervals
$T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
and by Expression (2) from Definition 4.2, there need to exist some intervals
 $\rho _1, \dots, \rho _n$
such that
$\rho _1, \dots, \rho _n$
such that
 $t' \in \rho _1 \cap \dots \cap \rho _n$
and
$t' \in \rho _1 \cap \dots \cap \rho _n$
and
 $(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n) \in \mathsf{inst}_r[{\mathscr{D}}_k]$
. Thus, as
$(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n) \in \mathsf{inst}_r[{\mathscr{D}}_k]$
. Thus, as
 $M'\sigma @ t' \models M@t$
, we obtain by Definition 4.2 that
$M'\sigma @ t' \models M@t$
, we obtain by Definition 4.2 that
 $ r[{\mathscr{D}}_k] \models M@t$
, and so,
$ r[{\mathscr{D}}_k] \models M@t$
, and so,
 $ \Pi [{\mathscr{D}}_k] \models M@t$
. Finally, recall that
$ \Pi [{\mathscr{D}}_k] \models M@t$
. Finally, recall that
 ${\mathscr{D}}_{k+1} = \mathsf{coal}({\mathscr{D}}_{k} \cup \mathscr{N}_{k+1})$
and
${\mathscr{D}}_{k+1} = \mathsf{coal}({\mathscr{D}}_{k} \cup \mathscr{N}_{k+1})$
and
 $\mathscr{N}_{k+1} = \Pi [{\mathscr{D}}_k]$
. Therefore, the fact that
$\mathscr{N}_{k+1} = \Pi [{\mathscr{D}}_k]$
. Therefore, the fact that
 $\Pi [{\mathscr{D}}_k] \models M@t$
implies that
$\Pi [{\mathscr{D}}_k] \models M@t$
implies that
 ${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
.
${\mathfrak{I}}_{{\mathscr{D}}_{k+1}} \models M@t$
.
Theorem5.2: Consider Procedure 2 running on input
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
. Upon the completion of the
$\mathscr{D}$
. Upon the completion of the
![]() $k$
th (for some
$k$
th (for some
![]() $k \in \mathbb{N}$
) iteration of the loop of Procedure 2, it holds that
$k \in \mathbb{N}$
) iteration of the loop of Procedure 2, it holds that
![]() ${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
${\mathfrak{I}}_{{\mathscr{D}}'} \subseteq T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
.
Proof.
The proof relies on the observation that rule instances processed by seminaïve evaluation are also processed by the naïve evaluation. In particular, directly by Definition 5.1 we obtain that
![]() $\mathsf{inst}_{r}[{\mathscr{D}}' \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ] \subseteq \mathsf{inst}_{r}[{\mathscr{D}}']$
, for each
$\mathsf{inst}_{r}[{\mathscr{D}}' \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta ] \subseteq \mathsf{inst}_{r}[{\mathscr{D}}']$
, for each
![]() $r$
,
$r$
,
![]() ${\mathscr{D}}'$
, and
${\mathscr{D}}'$
, and
![]() $\Delta$
. Hence, in each loop iteration, the sets
$\Delta$
. Hence, in each loop iteration, the sets
![]() $\mathscr{N}$
and
$\mathscr{N}$
and
![]() $\mathscr{C}$
in Procedure 2 are subsets of the corresponding sets in Procedure 1. Consequently, the same holds for the set
$\mathscr{C}$
in Procedure 2 are subsets of the corresponding sets in Procedure 1. Consequently, the same holds for the set
![]() ${\mathscr{D}}'$
, and so, soundness follows from Theorem4.3.
${\mathscr{D}}'$
, and so, soundness follows from Theorem4.3.
Theorem5.3: Consider Procedure 2 with input programme
![]() $\Pi$
and input dataset
$\Pi$
and input dataset
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 2, it holds that
$k$
th iteration of the loop of Procedure 2, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}'}$
.
Proof.
We will use
![]() $\mathscr{N}_k$
,
$\mathscr{N}_k$
,
![]() $\Delta _k$
, and
$\Delta _k$
, and
![]() ${\mathscr{D}}'_k$
, for the contents of, respectively,
${\mathscr{D}}'_k$
, for the contents of, respectively,
![]() $\mathscr{N}$
,
$\mathscr{N}$
,
![]() $\Delta$
, and
$\Delta$
, and
![]() ${\mathscr{D}}'$
in Procedure 2 upon the completion of the
${\mathscr{D}}'$
in Procedure 2 upon the completion of the
![]() $k$
th iteration of the loop. Now, as in the proof of Theorem4.4, we will show inductively on natural numbers
$k$
th iteration of the loop. Now, as in the proof of Theorem4.4, we will show inductively on natural numbers
![]() $k$
, that
$k$
, that
![]() $T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
.
$T_\Pi ^k({\mathfrak{I}}_{\mathscr{D}}) \subseteq{\mathfrak{I}}_{{\mathscr{D}}_k}$
.
The only difference with respect to the proof of Theorem4.4 lies in Case 2, where we assume that
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
and
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) \not \models M@t$
and
![]() $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
![]() $M@t$
. By the inductive assumption, as in the proof of Theorem4.4, there needs to be an instance
$M@t$
. By the inductive assumption, as in the proof of Theorem4.4, there needs to be an instance
![]() $(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n)$
$(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n)$
![]() $\in \mathsf{inst}_{r}[{\mathscr{D}}_k]$
of some rule
$\in \mathsf{inst}_{r}[{\mathscr{D}}_k]$
of some rule
![]() $r$
of the form
$r$
of the form
![]() $M' \gets M_1 \land \dots \land M_n$
, and a time point
$M' \gets M_1 \land \dots \land M_n$
, and a time point
![]() $t' \in \rho _1 \cap \dots \cap \rho _n$
such that
$t' \in \rho _1 \cap \dots \cap \rho _n$
such that
![]() $M'\sigma @ t' \models M@t$
. Now, we argue that this instance is not only in
$M'\sigma @ t' \models M@t$
. Now, we argue that this instance is not only in
![]() $\mathsf{inst}_{r}[{\mathscr{D}}_k]$
, but also in
$\mathsf{inst}_{r}[{\mathscr{D}}_k]$
, but also in
![]() $\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _{k} ]$
, namely that
$\mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _{k} ]$
, namely that
![]() $(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _{k}]$
. To this end, by Definition 5.1, it suffices to show that there is
$(M_1 \sigma @\rho _1, \cdots, M_n \sigma @\rho _n) \in \mathsf{inst}_{r}[{\mathscr{D}}_k \substack{\cdot \\[-0.12cm]\cdot \\[-0.12cm]\cdot \\[0.05cm]} \Delta _{k}]$
. To this end, by Definition 5.1, it suffices to show that there is
![]() $i \in \{1, \dots, n \}$
such that
$i \in \{1, \dots, n \}$
such that
![]() ${\mathscr{D}}_k \setminus \Delta _k \not \models M_i \sigma @ \rho _i$
. We will consider two cases, namely, when
${\mathscr{D}}_k \setminus \Delta _k \not \models M_i \sigma @ \rho _i$
. We will consider two cases, namely, when
![]() $k=0$
and when
$k=0$
and when
![]() $k \gt 0$
.
$k \gt 0$
.
-
Case 2.1:
 $k=0$
. By the initialisation (Line 1) of the of Procedure 2,
$k=0$
. By the initialisation (Line 1) of the of Procedure 2,
 $\Delta _0 ={\mathscr{D}}$
, so
$\Delta _0 ={\mathscr{D}}$
, so
 ${\mathscr{D}}_0 \setminus \Delta _0 = \emptyset$
. Recall that we assumed in the paper that input programmes do not have rules with vacuously satisfied bodies, so there needs to exist
${\mathscr{D}}_0 \setminus \Delta _0 = \emptyset$
. Recall that we assumed in the paper that input programmes do not have rules with vacuously satisfied bodies, so there needs to exist
 $i \in \{1, \dots, n \}$
such that the empty interpretation does not satisfy
$i \in \{1, \dots, n \}$
such that the empty interpretation does not satisfy
 $M_i \sigma @\rho _i$
, that is,
$M_i \sigma @\rho _i$
, that is,
 ${\mathscr{D}}_0 \setminus \Delta _0 \not \models M_i \sigma @\rho _i$
.
${\mathscr{D}}_0 \setminus \Delta _0 \not \models M_i \sigma @\rho _i$
. -
Case 2.2:
 $k \gt 0$
. By Lines 9 and 4, we have
$k \gt 0$
. By Lines 9 and 4, we have
 ${\mathscr{D}}_k = \mathsf{coal}({\mathscr{D}}_{k-1} \cup \mathscr{N}_k)$
. Moreover, by the definition of
${\mathscr{D}}_k = \mathsf{coal}({\mathscr{D}}_{k-1} \cup \mathscr{N}_k)$
. Moreover, by the definition of
 $\Delta$
in Line 5, we obtain
$\Delta$
in Line 5, we obtain
 ${\mathscr{D}}_k = \mathsf{coal}({\mathscr{D}}_{k-1} \cup \Delta _k)$
. Thus
${\mathscr{D}}_k = \mathsf{coal}({\mathscr{D}}_{k-1} \cup \Delta _k)$
. Thus
 ${\mathfrak{I}}_{{\mathscr{D}}_k} ={\mathfrak{I}}_{{\mathscr{D}}_{k-1}} \cup{\mathfrak{I}}_{\Delta _{k}}$
, so
${\mathfrak{I}}_{{\mathscr{D}}_k} ={\mathfrak{I}}_{{\mathscr{D}}_{k-1}} \cup{\mathfrak{I}}_{\Delta _{k}}$
, so
 ${\mathfrak{I}}_{{\mathscr{D}}_k}\setminus{\mathfrak{I}}_{\Delta _k} ={\mathfrak{I}}_{{\mathscr{D}}_{k-1}} \setminus{\mathfrak{I}}_{\Delta _k}$
, and therefore
${\mathfrak{I}}_{{\mathscr{D}}_k}\setminus{\mathfrak{I}}_{\Delta _k} ={\mathfrak{I}}_{{\mathscr{D}}_{k-1}} \setminus{\mathfrak{I}}_{\Delta _k}$
, and therefore
 ${\mathfrak{I}}_{{\mathscr{D}}_k}\setminus{\mathfrak{I}}_{\Delta _k} \subseteq{\mathfrak{I}}_{{\mathscr{D}}_{k-1}}$
. Hence, to show that for some
${\mathfrak{I}}_{{\mathscr{D}}_k}\setminus{\mathfrak{I}}_{\Delta _k} \subseteq{\mathfrak{I}}_{{\mathscr{D}}_{k-1}}$
. Hence, to show that for some
 $i \in \{1, \dots, n \}$
we have that
$i \in \{1, \dots, n \}$
we have that
 ${{\mathscr{D}}_k \setminus \Delta _k \not \models }$
${{\mathscr{D}}_k \setminus \Delta _k \not \models }$
 $M_i \sigma @ \rho _i$
, it suffices to show that
$M_i \sigma @ \rho _i$
, it suffices to show that
 ${\mathscr{D}}_{k-1} \not \models M_i\sigma @\rho _i$
. Suppose towards a contradiction that
${\mathscr{D}}_{k-1} \not \models M_i\sigma @\rho _i$
. Suppose towards a contradiction that
 ${\mathscr{D}}_{k-1} \models M_i\sigma @\rho _i$
, for all
${\mathscr{D}}_{k-1} \models M_i\sigma @\rho _i$
, for all
 $i \in \{1, \dots, n \}$
. By Theorem5.2,
$i \in \{1, \dots, n \}$
. By Theorem5.2,
 $T_{\Pi }^{k-1}({\mathfrak{I}}_{{\mathscr{D}}}) \models M_i\sigma @\rho _i$
, for all
$T_{\Pi }^{k-1}({\mathfrak{I}}_{{\mathscr{D}}}) \models M_i\sigma @\rho _i$
, for all
 $i \in \{1, \dots, n \}$
. Thus,
$i \in \{1, \dots, n \}$
. Thus,
 $T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
, which raises a contradiction.
$T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
, which raises a contradiction.
Lemma 5.4: Consider Procedure 3 running on input programme
![]() $\Pi$
and dataset
$\Pi$
and dataset
![]() $\mathscr{D}$
. Whenever
$\mathscr{D}$
. Whenever
![]() $flag = 1$
, dataset
$flag = 1$
, dataset
![]() ${\mathscr{D}}'$
satisfies all facts over a non-recursive predicate in
${\mathscr{D}}'$
satisfies all facts over a non-recursive predicate in
![]() $\Pi$
that are entailed by
$\Pi$
that are entailed by
![]() $\Pi$
and
$\Pi$
and
![]() $\mathscr{D}$
.
$\mathscr{D}$
.
Proof.
In Procedure 3,
![]() $flag$
is initialised to 0 and once it is changed to 1 (in Line 10) its value cannot be reverted. Moreover, the consecutive contents of
$flag$
is initialised to 0 and once it is changed to 1 (in Line 10) its value cannot be reverted. Moreover, the consecutive contents of
![]() ${\mathscr{D}}'$
are obtained by coalescing the previous contents with facts in
${\mathscr{D}}'$
are obtained by coalescing the previous contents with facts in
![]() $\mathscr{N}$
(in Line 4), so once a fact is entailed by
$\mathscr{N}$
(in Line 4), so once a fact is entailed by
![]() ${\mathscr{D}}'$
, it will remain entailed by all the consecutive contents of
${\mathscr{D}}'$
, it will remain entailed by all the consecutive contents of
![]() ${\mathscr{D}}'$
. Therefore, to prove the lemma, it suffices to consider the step of computation in which
${\mathscr{D}}'$
. Therefore, to prove the lemma, it suffices to consider the step of computation in which
![]() $flag$
becomes 1. Let
$flag$
becomes 1. Let
![]() $k$
be this step and let
$k$
be this step and let
![]() ${\mathscr{D}}'_k$
, be the contents of
${\mathscr{D}}'_k$
, be the contents of
![]() ${\mathscr{D}}'$
upon the completion of the
${\mathscr{D}}'$
upon the completion of the
![]() $k$
th iteration of the loop. Hence, we need to show that
$k$
th iteration of the loop. Hence, we need to show that
![]() ${\mathscr{D}}'_k$
satisfies all the facts which are satisfied in
${\mathscr{D}}'_k$
satisfies all the facts which are satisfied in
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}}$
and which mention non-recursive predicates in
$\mathfrak{C}_{\Pi, {\mathscr{D}}}$
and which mention non-recursive predicates in
![]() $\Pi$
.
$\Pi$
.
For this, we observe that before
![]() $flag$
changes to 1, Procedure 3 works as Procedure 2 so, by Theorems5.2 and 5.3, we have
$flag$
changes to 1, Procedure 3 works as Procedure 2 so, by Theorems5.2 and 5.3, we have
![]() ${\mathfrak{I}}_{{\mathscr{D}}'_k} = T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
. Hence, as
${\mathfrak{I}}_{{\mathscr{D}}'_k} = T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
. Hence, as
![]() $\mathfrak{C}_{\Pi, {\mathscr{D}}} = T_{\Pi }^{\omega _1}({\mathfrak{I}}_{\mathscr{D}})$
, it suffices to show by a transfinite induction that, for each ordinal
$\mathfrak{C}_{\Pi, {\mathscr{D}}} = T_{\Pi }^{\omega _1}({\mathfrak{I}}_{\mathscr{D}})$
, it suffices to show by a transfinite induction that, for each ordinal
![]() $\alpha \geq k$
, the interpretations
$\alpha \geq k$
, the interpretations
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
and
$T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}})$
and
![]() $T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}})$
satisfy the same facts with non-recursive predicates in
$T_{\Pi }^{\alpha }({\mathfrak{I}}_{\mathscr{D}})$
satisfy the same facts with non-recursive predicates in
![]() $\Pi$
. For the base case assume that
$\Pi$
. For the base case assume that
![]() $T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
$T_{\Pi }^{k+1}({\mathfrak{I}}_{\mathscr{D}}) \models M@t$
, for some relational fact
![]() $M@t$
whose predicate is non-recursive in
$M@t$
whose predicate is non-recursive in
![]() $\Pi$
. Hence, there is a rule
$\Pi$
. Hence, there is a rule
![]() $r \in \mathsf{ground}(\Pi, {\mathscr{D}})$
and a time point
$r \in \mathsf{ground}(\Pi, {\mathscr{D}})$
and a time point
![]() $t'$
such that
$t'$
such that
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}})$
entails each body atom of
$T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}})$
entails each body atom of
![]() $r$
at
$r$
at
![]() $t'$
, and the head of
$t'$
, and the head of
![]() $r$
holding at
$r$
holding at
![]() $t'$
entails
$t'$
entails
![]() $M@t$
. Thus the head atom of
$M@t$
. Thus the head atom of
![]() $r$
has a non-recursive predicate in
$r$
has a non-recursive predicate in
![]() $\Pi$
; therefore, by the definition, each body atom in
$\Pi$
; therefore, by the definition, each body atom in
![]() $r$
also mentions only non-recursive predicates in
$r$
also mentions only non-recursive predicates in
![]() $\Pi$
. Now, as
$\Pi$
. Now, as
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}}) \not \models M@t$
, we obtain that
$T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}}) \not \models M@t$
, we obtain that
![]() $T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}})$
and
$T_{\Pi }^{k}({\mathfrak{I}}_{{\mathscr{D}}})$
and
![]() $T_{\Pi }^{k-1}({\mathfrak{I}}_{{\mathscr{D}}})$
do not satisfy the same relational facts with non-recursive predicates in
$T_{\Pi }^{k-1}({\mathfrak{I}}_{{\mathscr{D}}})$
do not satisfy the same relational facts with non-recursive predicates in
![]() $\Pi$
, which directly contradicts the condition from Line 9. The inductive step for a successor ordinal
$\Pi$
, which directly contradicts the condition from Line 9. The inductive step for a successor ordinal
![]() $\alpha$
uses the same argument; indeed, if
$\alpha$
uses the same argument; indeed, if
![]() $T_{\Pi }^{\alpha }({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
and
$T_{\Pi }^{\alpha }({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
and
![]() $T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
, for some relational fact
$T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{{\mathscr{D}}}) \models M@t$
, for some relational fact
![]() $M@t$
whose predicate is non-recursive in
$M@t$
whose predicate is non-recursive in
![]() $\Pi$
, then
$\Pi$
, then
![]() $T_{\Pi }^{\alpha }({\mathfrak{I}}_{{\mathscr{D}}})$
and
$T_{\Pi }^{\alpha }({\mathfrak{I}}_{{\mathscr{D}}})$
and
![]() $T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{{\mathscr{D}}})$
do not satisfy the same relational facts with non-recursive predicates, contradicting the inductive assumption. The inductive step for the transfinite ordinal
$T_{\Pi }^{\alpha -1}({\mathfrak{I}}_{{\mathscr{D}}})$
do not satisfy the same relational facts with non-recursive predicates, contradicting the inductive assumption. The inductive step for the transfinite ordinal
![]() $\alpha$
holds trivially as
$\alpha$
holds trivially as
![]() $T_{\Pi }^{\alpha } ({\mathfrak{I}}_{{\mathscr{D}}}) = \bigcup _{\beta < \alpha } T_{\Pi }^{\beta }({\mathfrak{I}}_{{\mathscr{D}}})$
.
$T_{\Pi }^{\alpha } ({\mathfrak{I}}_{{\mathscr{D}}}) = \bigcup _{\beta < \alpha } T_{\Pi }^{\beta }({\mathfrak{I}}_{{\mathscr{D}}})$
.
Theorem5.6: Consider Procedure 3 with input programme
![]() $\Pi$
and input dataset
$\Pi$
and input dataset
![]() $\mathscr{D}$
. For each
$\mathscr{D}$
. For each
![]() $k \in \mathbb{N}$
, upon the completion of the
$k \in \mathbb{N}$
, upon the completion of the
![]() $k$
th iteration of the loop of Procedure 2, it holds that
$k$
th iteration of the loop of Procedure 2, it holds that
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
.
Proof.
If for both Lines 12 and 18, the condition in the “if” statement never applies, then Procedure 3 works in the same way as Procedure 2. Hence, by Theorems5.2 and 5.3, we get
![]() $ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
. Otherwise, the loop from Procedure 3 works similarly as Procedure 2, except that it can delete in Lines 12 and 18 some rules. By Lemma 5.5, however, such rules can be safely deleted from the programme, without losing the properties established in Theorems5.2 and 5.3.
$ T_{\Pi }^{k}({\mathfrak{I}}_{\mathscr{D}}) ={\mathfrak{I}}_{{\mathscr{D}}'}$
. Otherwise, the loop from Procedure 3 works similarly as Procedure 2, except that it can delete in Lines 12 and 18 some rules. By Lemma 5.5, however, such rules can be safely deleted from the programme, without losing the properties established in Theorems5.2 and 5.3.














