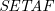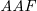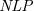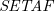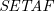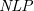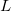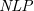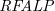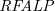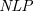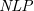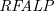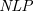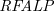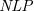1 Introduction
Argumentation and logic programming are two of the most successful paradigms in artificial intelligence and knowledge representation. Argumentation revolves around the idea of constructing and evaluating arguments to determine the acceptability of a claim. It models complex reasoning by considering various pieces of evidence and their interrelationships, making it a powerful tool for handling uncertainty and conflicting information. On the other hand, logic programming provides a formalism for expressing knowledge and defining computational processes through a set of logical rules.
In this scenario, the Abstract Argumentation Frameworks (
![]() $\mathit{AAF}$
s) proposed by Dung (Reference Dung1995b) in his seminal paper have exerted a dominant influence over the development of formal argumentation. We can depict such frameworks simply as a directed graph whose nodes represent arguments and edges represent the attack relation between them. Indeed, in
$\mathit{AAF}$
s) proposed by Dung (Reference Dung1995b) in his seminal paper have exerted a dominant influence over the development of formal argumentation. We can depict such frameworks simply as a directed graph whose nodes represent arguments and edges represent the attack relation between them. Indeed, in
![]() $\mathit{AAF}$
s, the content of these arguments is not considered, and the attack relation stands as the unique relation. The simplicity and elegance of
$\mathit{AAF}$
s, the content of these arguments is not considered, and the attack relation stands as the unique relation. The simplicity and elegance of
![]() $\mathit{AAF}$
s have made them an appealing formalism for computational applications.
$\mathit{AAF}$
s have made them an appealing formalism for computational applications.
In Dung’s proposal, the semantics for
![]() $\mathit{AAF}$
s are given in terms of extensions, which are sets of arguments satisfying certain criteria of acceptability. Naturally, different criteria of acceptability will lead to different extension-based semantics, including Dung’s original concepts of complete, stable, preferred, and grounded semantics (Dung Reference Dung1995b) and semi-stable semantics (Verheij Reference Verheij1996; Caminada Reference Caminada2006). A richer characterization based on labelings was proposed by Caminada and Gabbay (Reference Caminada and Gabbay2009) to describe these semantics. Differently from extensions, which explicitly regard solely the accepted arguments, the labeling-based approach permits a more fine-grained setting, where each argument is assigned a label
$\mathit{AAF}$
s are given in terms of extensions, which are sets of arguments satisfying certain criteria of acceptability. Naturally, different criteria of acceptability will lead to different extension-based semantics, including Dung’s original concepts of complete, stable, preferred, and grounded semantics (Dung Reference Dung1995b) and semi-stable semantics (Verheij Reference Verheij1996; Caminada Reference Caminada2006). A richer characterization based on labelings was proposed by Caminada and Gabbay (Reference Caminada and Gabbay2009) to describe these semantics. Differently from extensions, which explicitly regard solely the accepted arguments, the labeling-based approach permits a more fine-grained setting, where each argument is assigned a label
![]() $\mathtt{in}$
,
$\mathtt{in}$
,
![]() $\mathtt{out}$
, or
$\mathtt{out}$
, or
![]() $\mathtt{undec}$
. Intuitively, we accept an argument labeled as
$\mathtt{undec}$
. Intuitively, we accept an argument labeled as
![]() $\mathtt{in}$
, reject one labeled as
$\mathtt{in}$
, reject one labeled as
![]() $\mathtt{out}$
, and consider one labeled as
$\mathtt{out}$
, and consider one labeled as
![]() $\mathtt{undec}$
as undecided, meaning it is neither accepted nor rejected.
$\mathtt{undec}$
as undecided, meaning it is neither accepted nor rejected.
Despite providing distinct perspectives on reasoning and decision-making, argumentation and logic programming have clear connections. Indeed, we can see in Dung’s (Reference Dung1995b) work how to translate a Normal Logic Program (
![]() $\textit{NLP}$
) into an
$\textit{NLP}$
) into an
![]() $\mathit{AAF}$
. Besides, the author proved that stable models (resp., the well-founded model) of an
$\mathit{AAF}$
. Besides, the author proved that stable models (resp., the well-founded model) of an
![]() $\textit{NLP}$
correspond to stable extensions (resp., the grounded extension) of the associated
$\textit{NLP}$
correspond to stable extensions (resp., the grounded extension) of the associated
![]() $\mathit{AAF}$
. These results led to several studies concerning connections between argumentation and logic programming (Dung Reference Dung1995a; Nieves et al. Reference Nieves, Cortés and Osorio2008; Wu et al. Reference Wu, Caminada and Gabbay2009; Toni and Sergot Reference Toni and Sergot2011; Dvořák et al. Reference Dvořák, Gaggl, Wallner and Woltran2013; Caminada et al. Reference Caminada, Sá, Alcântara and Dvořák2015b, Reference Caminada, Harikrishnan and Sá2022). In particular, Wu et al. (Reference Wu, Caminada and Gabbay2009) established the equivalence between complete semantics and partial stable semantics. These semantics generalize a series of other relevant semantics for each system, as extensively documented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). However, one equivalence formerly expected to hold remained elusive: the correspondence between the semi-stable semantics (Caminada Reference Caminada2006) in
$\mathit{AAF}$
. These results led to several studies concerning connections between argumentation and logic programming (Dung Reference Dung1995a; Nieves et al. Reference Nieves, Cortés and Osorio2008; Wu et al. Reference Wu, Caminada and Gabbay2009; Toni and Sergot Reference Toni and Sergot2011; Dvořák et al. Reference Dvořák, Gaggl, Wallner and Woltran2013; Caminada et al. Reference Caminada, Sá, Alcântara and Dvořák2015b, Reference Caminada, Harikrishnan and Sá2022). In particular, Wu et al. (Reference Wu, Caminada and Gabbay2009) established the equivalence between complete semantics and partial stable semantics. These semantics generalize a series of other relevant semantics for each system, as extensively documented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). However, one equivalence formerly expected to hold remained elusive: the correspondence between the semi-stable semantics (Caminada Reference Caminada2006) in
![]() $\mathit{AAF}$
and the
$\mathit{AAF}$
and the
![]() $L$
-stable semantics in
$L$
-stable semantics in
![]() $\textit{NLP}$
(Eiter et al. Reference Eiter, Leone and Saccá1997) could not be attained. Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) even showed that with their proposed translation from
$\textit{NLP}$
(Eiter et al. Reference Eiter, Leone and Saccá1997) could not be attained. Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) even showed that with their proposed translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\mathit{AAF}$
s, there cannot be a semantics for
$\mathit{AAF}$
s, there cannot be a semantics for
![]() $\mathit{AAF}$
s equivalent to
$\mathit{AAF}$
s equivalent to
![]() $L$
-stable semantics.
$L$
-stable semantics.
Caminada and Schulz (Reference Caminada and Schulz2017) demonstrated how to translate Assumption-Based Argumentation (ABA) (Bondarenko et al. Reference Bondarenko, Dung, Kowalski and Toni1997; Dung et al. Reference Dung, Kowalski and Toni2009; Toni Reference Toni2014) to
![]() $\textit{NLP}$
s and how this translation can be reapplied for a reverse translation from
$\textit{NLP}$
s and how this translation can be reapplied for a reverse translation from
![]() $\textit{NLP}$
s to ABA. Curiously, the problematic direction here is from ABA to
$\textit{NLP}$
s to ABA. Curiously, the problematic direction here is from ABA to
![]() $\textit{NLP}$
. Caminada and Schulz (Reference Caminada and Schulz2017) proved that with their translation, there cannot be a semantics for
$\textit{NLP}$
. Caminada and Schulz (Reference Caminada and Schulz2017) proved that with their translation, there cannot be a semantics for
![]() $\textit{NLP}$
s equivalent to the semi-stable semantics (Schulz and Toni Reference Schulz and Toni2015; Caminada et al. Reference Caminada, Sá, Alcântara and Dvořák2015a) for ABA.
$\textit{NLP}$
s equivalent to the semi-stable semantics (Schulz and Toni Reference Schulz and Toni2015; Caminada et al. Reference Caminada, Sá, Alcântara and Dvořák2015a) for ABA.
Since then, a great effort has been made to identify paradigms where semi-stable and
![]() $L$
-stable semantics are equivalent. The strategy employed by Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) was to look for more expressive argumentation frameworks than
$L$
-stable semantics are equivalent. The strategy employed by Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) was to look for more expressive argumentation frameworks than
![]() $\mathit{AAF}$
s: Attacking Dialectical Frameworks, a support-free fragment of Abstract Dialectical Frameworks (Brewka and Woltran Reference Brewka and Woltran2010; Brewka et al. Reference Brewka, Ellmauthaler, Strass, Wallner and Woltran2013), a generalization of
$\mathit{AAF}$
s: Attacking Dialectical Frameworks, a support-free fragment of Abstract Dialectical Frameworks (Brewka and Woltran Reference Brewka and Woltran2010; Brewka et al. Reference Brewka, Ellmauthaler, Strass, Wallner and Woltran2013), a generalization of
![]() $\mathit{AAF}$
s designed to express arbitrary relationships among arguments. A translation from
$\mathit{AAF}$
s designed to express arbitrary relationships among arguments. A translation from
![]() $\textit{NLP}$
to
$\textit{NLP}$
to
![]() $\mathit{ADF}^+$
was proved by Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) to account for various equivalences between their semantics, including the definition of a semantics for
$\mathit{ADF}^+$
was proved by Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) to account for various equivalences between their semantics, including the definition of a semantics for
![]() $\mathit{ADF}^+$
corresponding to the
$\mathit{ADF}^+$
corresponding to the
![]() $L$
-stable semantics for
$L$
-stable semantics for
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
In a similar vein, other relevant proposals explored the equivalence between
![]() $L$
-stable and semi-stable semantics for Claim-augmented Argumentation Frameworks (
$L$
-stable and semi-stable semantics for Claim-augmented Argumentation Frameworks (
![]() $\mathit{CAF}$
s) (Dvořák et al. Reference Dvořák, Rapberger and Woltran2023; Rapberger Reference Rapberger2020; Rocha and Cozman Reference Rocha and Cozman2022b), which are a generalization of
$\mathit{CAF}$
s) (Dvořák et al. Reference Dvořák, Rapberger and Woltran2023; Rapberger Reference Rapberger2020; Rocha and Cozman Reference Rocha and Cozman2022b), which are a generalization of
![]() $\mathit{AAF}$
s where each argument is explicitly associated with a claim, and for Bipolar Argumentation Frameworks (
$\mathit{AAF}$
s where each argument is explicitly associated with a claim, and for Bipolar Argumentation Frameworks (
![]() $\mathit{BAF}$
s) with conclusions (Rocha and Cozman Reference Rocha and Cozman2022a), a generalization of
$\mathit{BAF}$
s) with conclusions (Rocha and Cozman Reference Rocha and Cozman2022a), a generalization of
![]() $\mathit{CAF}$
s with the inclusion of an explicit notion of support between arguments. In both frameworks, the equivalence with
$\mathit{CAF}$
s with the inclusion of an explicit notion of support between arguments. In both frameworks, the equivalence with
![]() $\textit{NLP}$
s does not just involve their semantics; it is also structural as there is a one-to-one mapping from them to
$\textit{NLP}$
s does not just involve their semantics; it is also structural as there is a one-to-one mapping from them to
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
Instead of looking for more expressive argumentation frameworks, the idea proposed by Sá and Alcântara (Reference Sá and Alcântara2021a) was to introduce more fine-grained semantics to deal with
![]() $\mathit{AAF}$
s. Then a five-valued setting was employed rather than the usual three-valued one. As in the previous cases, this approach also captures the correspondence between the semantics for
$\mathit{AAF}$
s. Then a five-valued setting was employed rather than the usual three-valued one. As in the previous cases, this approach also captures the correspondence between the semantics for
![]() $\mathit{AAF}$
s and
$\mathit{AAF}$
s and
![]() $\textit{NLP}$
s. Specifically, it captures the correspondence involving
$\textit{NLP}$
s. Specifically, it captures the correspondence involving
![]() $L$
-stable semantics.
$L$
-stable semantics.
The connections between
![]() $\mathit{ABA}$
and logic programming were later revisited by Sá and Alcântara (Reference Sá and Alcântara2019, Reference Sá and Alcântara2021b), where they proposed a new translation from
$\mathit{ABA}$
and logic programming were later revisited by Sá and Alcântara (Reference Sá and Alcântara2019, Reference Sá and Alcântara2021b), where they proposed a new translation from
![]() $\mathit{ABA}$
frameworks to
$\mathit{ABA}$
frameworks to
![]() $\textit{NLP}$
s. The correspondence between their semantics (including
$\textit{NLP}$
s. The correspondence between their semantics (including
![]() $L$
-stable) is obtained by selecting specific atoms in the characterization of the
$L$
-stable) is obtained by selecting specific atoms in the characterization of the
![]() $\textit{NLP}$
semantics.
$\textit{NLP}$
semantics.
In summary, in the connections between
![]() $\textit{NLP}$
and argumentation semantics, the Achilles’ heel is the relationship between
$\textit{NLP}$
and argumentation semantics, the Achilles’ heel is the relationship between
![]() $L$
-stable and semi-stable semantics.
$L$
-stable and semi-stable semantics.
In this paper, we focus on the relationship between logic programming and
![]() $\textit{SETAF}$
(Nielsen and Parsons Reference Nielsen and Parsons2006), an extension of Dung’s
$\textit{SETAF}$
(Nielsen and Parsons Reference Nielsen and Parsons2006), an extension of Dung’s
![]() $\mathit{AAF}$
s to allow joint attacks on arguments. Following the strategy adopted by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) and Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019), we resort to the characterization of the
$\mathit{AAF}$
s to allow joint attacks on arguments. Following the strategy adopted by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) and Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019), we resort to the characterization of the
![]() $\textit{SETAF}$
semantics in terms of labelings (Flouris and Bikakis Reference Flouris and Bikakis2019). As a starting point, we provide a mapping from
$\textit{SETAF}$
semantics in terms of labelings (Flouris and Bikakis Reference Flouris and Bikakis2019). As a starting point, we provide a mapping from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s (and vice versa) and show that
$\textit{SETAF}$
s (and vice versa) and show that
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s are pairwise equivalent under various semantics, including the equivalence between
$\textit{SETAF}$
s are pairwise equivalent under various semantics, including the equivalence between
![]() $L$
-stable and semi-stable. These results were inspired directly by two of our previous works: the equivalence between
$L$
-stable and semi-stable. These results were inspired directly by two of our previous works: the equivalence between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\mathit{ADF}^+$
s (Alcântara et al. Reference Alcântara, Sá and Acosta-Guadarrama2019), and the equivalence between
$\mathit{ADF}^+$
s (Alcântara et al. Reference Alcântara, Sá and Acosta-Guadarrama2019), and the equivalence between
![]() $\mathit{ADF}^+$
s and
$\mathit{ADF}^+$
s and
![]() $\textit{SETAF}$
s (Alcântara and Sá Reference Alcântara and Sá2021).
$\textit{SETAF}$
s (Alcântara and Sá Reference Alcântara and Sá2021).
Furthermore, we investigate a class of
![]() $\textit{NLP}$
s called Redundancy-Free Atomic Logic Programs (
$\textit{NLP}$
s called Redundancy-Free Atomic Logic Programs (
![]() $\textit{RFALP}$
s) (König et al. Reference König, Rapberger and Ulbricht2022). In
$\textit{RFALP}$
s) (König et al. Reference König, Rapberger and Ulbricht2022). In
![]() $\textit{RFALP}$
s, the translations from
$\textit{RFALP}$
s, the translations from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s and vice versa preserve the structure of each other’s theories. In essence, these translations become inverses of each other. Consequently, the equivalence results concerning
$\textit{SETAF}$
s and vice versa preserve the structure of each other’s theories. In essence, these translations become inverses of each other. Consequently, the equivalence results concerning
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s have deeper implications than the correspondence results between
$\textit{SETAF}$
s have deeper implications than the correspondence results between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\mathit{AAF}$
s: they encompass equivalence in both semantics as well as structure.
$\mathit{AAF}$
s: they encompass equivalence in both semantics as well as structure.
Some of these results are not new as recently they have already been obtained independently by König et al. (Reference König, Rapberger and Ulbricht2022). In fact, their translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s and vice versa coincide with ours, and the structural equivalence between
$\textit{SETAF}$
s and vice versa coincide with ours, and the structural equivalence between
![]() $\textit{RFALP}$
s and
$\textit{RFALP}$
s and
![]() $\textit{SETAF}$
s has also been identified there. However, their focus differs from ours. While their work establishes the equivalence between stable models and stable extensions, it does not explore equivalences involving labeling-based semantics or address the controversy relating semi-stable semantics and
$\textit{SETAF}$
s has also been identified there. However, their focus differs from ours. While their work establishes the equivalence between stable models and stable extensions, it does not explore equivalences involving labeling-based semantics or address the controversy relating semi-stable semantics and
![]() $L$
-stable semantics, which is a key motivation for this work. In comparison with König et al.’s work, the novelty of our proposal lies essentially in the aspects below:
$L$
-stable semantics, which is a key motivation for this work. In comparison with König et al.’s work, the novelty of our proposal lies essentially in the aspects below:
-
• Our proofs of these results follow a significantly distinct path as they are based on properties of argument labelings and are deeply rooted in the works of Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b); Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019); Alcântara and Sá (Reference Alcântara and Sá2021).
-
• We prove the equivalence between partial stable, well-founded, regular, stable, and semi-stable model semantics for
 $\textit{NLP}$
s and, respectively, complete, grounded, preferred, stable, and semi-stable labelings for
$\textit{NLP}$
s and, respectively, complete, grounded, preferred, stable, and semi-stable labelings for
 $\textit{SETAF}$
s. In particular, for the first time, an equivalence between
$\textit{SETAF}$
s. In particular, for the first time, an equivalence between
 $L$
-stable model semantics for
$L$
-stable model semantics for
 $\textit{NLP}$
s and semi-stable labelings for
$\textit{NLP}$
s and semi-stable labelings for
 $\textit{SETAF}$
s is established.
$\textit{SETAF}$
s is established. -
• We provide a more in-depth analysis of the relationship between
 $\textit{NLP}$
s and
$\textit{NLP}$
s and
 $\textit{SETAF}$
s. Going beyond just proving semantic equivalence, we define functions that map labelings to interpretations and interpretations to labelings. These functions allow us to see interpretations and labelings as equivalent entities, further strengthening the connections between
$\textit{SETAF}$
s. Going beyond just proving semantic equivalence, we define functions that map labelings to interpretations and interpretations to labelings. These functions allow us to see interpretations and labelings as equivalent entities, further strengthening the connections between
 $\textit{NLP}$
s and
$\textit{NLP}$
s and
 $\textit{SETAF}$
s. In substance, we demonstrate that the equivalence also holds at the level of interpretations/labelings.
$\textit{SETAF}$
s. In substance, we demonstrate that the equivalence also holds at the level of interpretations/labelings.
The strong connection we establish between interpretations and labelings opens doors for future exploration. This extends the applicability of our equivalence results to novel semantics beyond those investigated here, potentially even encompassing multivalued settings. This holds particular significance for the logic programming community. Well-established concepts from argumentation, such as argument strength (Beirlaen et al. Reference Beirlaen, Heyninck, Pardo and Straßer2018), can now be translated and investigated within the context of logic programming. This underscores the value of our decision to employ labelings instead of extensions as a more suitable approach to bridge the gap between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s.
$\textit{SETAF}$
s.
Our research offers another key contribution, particularly relevant to the logic programming community: it explores the expressiveness of
![]() $\textit{RFALP}$
s. We demonstrate that a specific combination (denoted by
$\textit{RFALP}$
s. We demonstrate that a specific combination (denoted by
![]() $\mapsto _{\textit{UTPM}}$
) of program transformations can transform any
$\mapsto _{\textit{UTPM}}$
) of program transformations can transform any
![]() $\textit{NLP}$
into an
$\textit{NLP}$
into an
![]() $\textit{RFALP}$
with exactly the same semantics. In simpler terms,
$\textit{RFALP}$
with exactly the same semantics. In simpler terms,
![]() $\textit{RFALP}$
s possess the same level of expressiveness as
$\textit{RFALP}$
s possess the same level of expressiveness as
![]() $\textit{NLP}$
s. Although each program transformation in
$\textit{NLP}$
s. Although each program transformation in
![]() $\mapsto _{\textit{UTPM}}$
was proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, 1999), the combination of these program transformations (to our knowledge) has not been investigated yet. Then we establish several properties of
$\mapsto _{\textit{UTPM}}$
was proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, 1999), the combination of these program transformations (to our knowledge) has not been investigated yet. Then we establish several properties of
![]() $\mapsto _{\textit{UTPM}}$
. Among other original contributions of our work related to
$\mapsto _{\textit{UTPM}}$
. Among other original contributions of our work related to
![]() $\mapsto _{\textit{UTPM}}$
, we highlight the following results:
$\mapsto _{\textit{UTPM}}$
, we highlight the following results:
-
• Given an
 $\textit{NLP}$
, if repeatedly applying
$\textit{NLP}$
, if repeatedly applying
 $\mapsto _{\textit{UTPM}}$
leads to a program where no further transformations are applicable (irreducible program), then the resulting program is guaranteed to be an
$\mapsto _{\textit{UTPM}}$
leads to a program where no further transformations are applicable (irreducible program), then the resulting program is guaranteed to be an
 $\textit{RFALP}$
.
$\textit{RFALP}$
. -
• We show that
 $\mapsto _{\textit{UTPM}}$
is confluent; that is, given an
$\mapsto _{\textit{UTPM}}$
is confluent; that is, given an
 $\textit{NLP}$
, it does not matter the order by which we apply repeatedly these program transformations; whenever we arrive at an irreducible program, they will always result in the same
$\textit{NLP}$
, it does not matter the order by which we apply repeatedly these program transformations; whenever we arrive at an irreducible program, they will always result in the same
 $\textit{RFALP}$
(and in the same corresponding
$\textit{RFALP}$
(and in the same corresponding
 $\textit{SETAF}$
). Hence, besides
$\textit{SETAF}$
). Hence, besides
 $\textit{NLP}$
s and
$\textit{NLP}$
s and
 $\textit{RFALP}$
s being equally expressive, each
$\textit{RFALP}$
s being equally expressive, each
 $\textit{NLP}$
is associated with a unique
$\textit{NLP}$
is associated with a unique
 $\textit{RFALP}$
.
$\textit{RFALP}$
. -
• The
 $\textit{SETAF}$
corresponding to an
$\textit{SETAF}$
corresponding to an
 $\textit{NLP}$
is invariant with respect to
$\textit{NLP}$
is invariant with respect to
 $\mapsto _{\textit{UTPM}}$
; that is, if
$\mapsto _{\textit{UTPM}}$
; that is, if
 $P_2$
is obtained from
$P_2$
is obtained from
 $P_1$
via
$P_1$
via
 $\mapsto _{\textit{UTPM}}$
(denoted by
$\mapsto _{\textit{UTPM}}$
(denoted by
 $P_1 \mapsto _{\textit{UTPM}} P_2$
), both
$P_1 \mapsto _{\textit{UTPM}} P_2$
), both
 $P_1$
and
$P_1$
and
 $P_2$
will be translated into the same
$P_2$
will be translated into the same
 $\textit{SETAF}$
.
$\textit{SETAF}$
. -
• We show that
 $\mapsto _{\textit{UTPM}}$
preserves the semantics for
$\mapsto _{\textit{UTPM}}$
preserves the semantics for
 $\textit{NLP}$
s studied in this paper: if
$\textit{NLP}$
s studied in this paper: if
 $P_1 \mapsto _{\textit{UTPM}} P_2$
, then
$P_1 \mapsto _{\textit{UTPM}} P_2$
, then
 $P_1$
and
$P_1$
and
 $P_2$
have the same partial stable models, well-founded models, regular models, stable models, and
$P_2$
have the same partial stable models, well-founded models, regular models, stable models, and
 $L$
-stable models.
$L$
-stable models.
The structure of the paper unfolds as follows: in Section 2, we establish the fundamental definitions related to
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{NLP}$
s. In Section 3, we adapt the procedure from Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) and Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) to translate
$\textit{NLP}$
s. In Section 3, we adapt the procedure from Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) and Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) to translate
![]() $\textit{NLP}$
s into
$\textit{NLP}$
s into
![]() $\textit{SETAF}$
s, and subsequently, in the following section, we perform the reverse translation from
$\textit{SETAF}$
s, and subsequently, in the following section, we perform the reverse translation from
![]() $\textit{SETAF}$
s to
$\textit{SETAF}$
s to
![]() $\textit{NLP}$
s. In both directions, we demonstrate that our labeling-based approach effectively preserves semantic correspondences, including the challenging case involving the equivalence between semi-stable semantics (on the
$\textit{NLP}$
s. In both directions, we demonstrate that our labeling-based approach effectively preserves semantic correspondences, including the challenging case involving the equivalence between semi-stable semantics (on the
![]() $\textit{SETAF}$
s side) and
$\textit{SETAF}$
s side) and
![]() $L$
-stable semantics (on the
$L$
-stable semantics (on the
![]() $\textit{NLP}$
s side). In Section 5, we focus on
$\textit{NLP}$
s side). In Section 5, we focus on
![]() $\textit{RFALP}$
s and reveal that, when restricted to them, the translation processes between
$\textit{RFALP}$
s and reveal that, when restricted to them, the translation processes between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s are each other’s inverse. Then, in Section 6, we guarantee that
$\textit{SETAF}$
s are each other’s inverse. Then, in Section 6, we guarantee that
![]() $\textit{RFALP}$
s are as expressive as
$\textit{RFALP}$
s are as expressive as
![]() $\textit{NLP}$
s. We conclude the paper with a discussion of our findings and outline potential avenues for future research endeavors.
$\textit{NLP}$
s. We conclude the paper with a discussion of our findings and outline potential avenues for future research endeavors.
The proofs for all novel results are provided in the Supplementary Material.
2 Preliminaries
2.1 SETAF
Nielsen and Parsons (Reference Nielsen and Parsons2006) proposed an extension of Dung’s (Reference Dung1995b) Abstract Argumentation Frameworks (
![]() $\mathit{AAF}$
s) to allow joint attacks on arguments. The resulting framework, called
$\mathit{AAF}$
s) to allow joint attacks on arguments. The resulting framework, called
![]() $\textit{SETAF}$
, is defined next:
$\textit{SETAF}$
, is defined next:
Definition 1 (SETAF (Nielsen and Parsons Reference Nielsen and Parsons2006)). A framework with sets of attacking arguments (
![]() $\mathit{SETAF}$
for short) is a pair
$\mathit{SETAF}$
for short) is a pair
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
, in which
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
, in which
![]() $\mathcal{A}$
is a finite set of arguments and
$\mathcal{A}$
is a finite set of arguments and
![]() $\mathit{Att} \subseteq ( 2^{\mathcal{A}} \setminus \left \{\emptyset \right \}) \times \mathcal{A}$
is an attack relation such that if
$\mathit{Att} \subseteq ( 2^{\mathcal{A}} \setminus \left \{\emptyset \right \}) \times \mathcal{A}$
is an attack relation such that if
![]() $(\mathcal{B}, a) \in \mathit{Att}$
, there is no
$(\mathcal{B}, a) \in \mathit{Att}$
, there is no
![]() $\mathcal{B}' \subset \mathcal{B}$
such that
$\mathcal{B}' \subset \mathcal{B}$
such that
![]() $(\mathcal{B}', a) \in \mathit{Att}$
; that is,
$(\mathcal{B}', a) \in \mathit{Att}$
; that is,
![]() $\mathcal{B}$
is a minimal set (w.r.t.
$\mathcal{B}$
is a minimal set (w.r.t.
![]() $\subseteq$
) attacking
$\subseteq$
) attacking
![]() $a$
Footnote 1. By
$a$
Footnote 1. By
![]() $\mathit{Att}(a) = \left \{\mathcal{B} \subseteq \mathcal{A} \mid (\mathcal{B}, a) \in \mathit{Att}\right \}$
, we mean the set of attackers of
$\mathit{Att}(a) = \left \{\mathcal{B} \subseteq \mathcal{A} \mid (\mathcal{B}, a) \in \mathit{Att}\right \}$
, we mean the set of attackers of
![]() $a$
.
$a$
.
In
![]() $\mathit{AAF}$
s, only individual arguments can attack arguments. In
$\mathit{AAF}$
s, only individual arguments can attack arguments. In
![]() $\textit{SETAF}$
s, the novelty is that sets of two or more arguments can also attack arguments. This means that
$\textit{SETAF}$
s, the novelty is that sets of two or more arguments can also attack arguments. This means that
![]() $\textit{SETAF}$
s
$\textit{SETAF}$
s
![]() $(\mathcal{A}, \mathit{Att})$
with
$(\mathcal{A}, \mathit{Att})$
with
![]() $|\mathcal{B}| = 1$
for each
$|\mathcal{B}| = 1$
for each
![]() $(\mathcal{B}, a) \in \mathit{Att}$
amount to (standard Dung)
$(\mathcal{B}, a) \in \mathit{Att}$
amount to (standard Dung)
![]() $\mathit{AAF}$
s.
$\mathit{AAF}$
s.
The semantics for
![]() $\textit{SETAF}$
s are generalizations of the corresponding semantics for
$\textit{SETAF}$
s are generalizations of the corresponding semantics for
![]() $\mathit{AAF}$
s (Nielsen and Parsons Reference Nielsen and Parsons2006) and can be defined equivalently in terms of extensions or labelings (Flouris and Bikakis Reference Flouris and Bikakis2019). Our focus here will be on their labeling-based semantics.
$\mathit{AAF}$
s (Nielsen and Parsons Reference Nielsen and Parsons2006) and can be defined equivalently in terms of extensions or labelings (Flouris and Bikakis Reference Flouris and Bikakis2019). Our focus here will be on their labeling-based semantics.
Definition 2 (Labelings (Flouris and Bikakis Reference Flouris and Bikakis2019)). Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\mathit{SETAF}$
. A labeling is a function
$\mathit{SETAF}$
. A labeling is a function
![]() $\mathcal{L} : \mathcal{A} \to \left \{\mathtt{in}, \mathtt{out}, \mathtt{undec}\right \}$
. It is admissible iff for each
$\mathcal{L} : \mathcal{A} \to \left \{\mathtt{in}, \mathtt{out}, \mathtt{undec}\right \}$
. It is admissible iff for each
![]() $a \in \mathcal{A}$
,
$a \in \mathcal{A}$
,
-
• If
 $\mathcal{L}(a) = \mathtt{in}$
, then for each
$\mathcal{L}(a) = \mathtt{in}$
, then for each
 $\mathcal{B} \in \mathit{Att}(a)$
, it holds
$\mathcal{B} \in \mathit{Att}(a)$
, it holds
 $\mathcal{L}(b) = \mathtt{out}$
for some
$\mathcal{L}(b) = \mathtt{out}$
for some
 $b \in \mathcal{B}$
.
$b \in \mathcal{B}$
. -
• If
 $\mathcal{L}(a) = \mathtt{out}$
, then there exists
$\mathcal{L}(a) = \mathtt{out}$
, then there exists
 $\mathcal{B} \in \mathit{Att}(a)$
such that
$\mathcal{B} \in \mathit{Att}(a)$
such that
 $\mathcal{L}(b) = \mathtt{in}$
for each
$\mathcal{L}(b) = \mathtt{in}$
for each
 $b \in \mathcal{B}$
.
$b \in \mathcal{B}$
.
A labeling
![]() $\mathcal{L}$
is called complete iff it is admissible and for each
$\mathcal{L}$
is called complete iff it is admissible and for each
![]() $a \in \mathcal{A}$
,
$a \in \mathcal{A}$
,
-
• If
 $\mathcal{L}(a) = \mathtt{undec}$
, then there exists
$\mathcal{L}(a) = \mathtt{undec}$
, then there exists
 $\mathcal{B} \in \mathit{Att}(a)$
such that
$\mathcal{B} \in \mathit{Att}(a)$
such that
 $\mathcal{L}(b) \neq \mathtt{out}$
for each
$\mathcal{L}(b) \neq \mathtt{out}$
for each
 $b \in \mathcal{B}$
, and for each
$b \in \mathcal{B}$
, and for each
 $\mathcal{B} \in \mathit{Att}(a)$
, it holds
$\mathcal{B} \in \mathit{Att}(a)$
, it holds
 $\mathcal{L}(b) \neq \mathtt{in}$
for some
$\mathcal{L}(b) \neq \mathtt{in}$
for some
 $b \in \mathcal{B}$
.
$b \in \mathcal{B}$
.
We write
![]() $\mathtt{in}(\mathcal{L})$
for
$\mathtt{in}(\mathcal{L})$
for
![]() $\left \{a \in \mathcal{A} \mid \mathcal{L}(a) = \mathtt{in}\right \}$
,
$\left \{a \in \mathcal{A} \mid \mathcal{L}(a) = \mathtt{in}\right \}$
,
![]() $\mathtt{out}(\mathcal{L})$
for
$\mathtt{out}(\mathcal{L})$
for
![]() $\{a \in \mathcal{A} \mid$
$\{a \in \mathcal{A} \mid$
![]() $\mathcal{L}(a) = \mathtt{out} \}$
, and
$\mathcal{L}(a) = \mathtt{out} \}$
, and
![]() $\mathtt{undec}(\mathcal{L})$
for
$\mathtt{undec}(\mathcal{L})$
for
![]() $\left \{a \in \mathcal{A} \mid \mathcal{L}(a) = \mathtt{undec}\right \}$
. As a labeling essentially defines a partition among the arguments, we sometimes write
$\left \{a \in \mathcal{A} \mid \mathcal{L}(a) = \mathtt{undec}\right \}$
. As a labeling essentially defines a partition among the arguments, we sometimes write
![]() $\mathcal{L}$
as a triple
$\mathcal{L}$
as a triple
![]() $(\mathtt{in}(\mathcal{L}), \mathtt{out}(\mathcal{L}), \mathtt{undec}(\mathcal{L}))$
. Intuitively, an argument labeled
$(\mathtt{in}(\mathcal{L}), \mathtt{out}(\mathcal{L}), \mathtt{undec}(\mathcal{L}))$
. Intuitively, an argument labeled
![]() $\mathtt{in}$
represents explicit acceptance; an argument labeled
$\mathtt{in}$
represents explicit acceptance; an argument labeled
![]() $\mathtt{out}$
indicates rejection; and one labeled
$\mathtt{out}$
indicates rejection; and one labeled
![]() $\mathtt{undec}$
is undecided; that is, it is neither accepted nor rejected. We can now describe the
$\mathtt{undec}$
is undecided; that is, it is neither accepted nor rejected. We can now describe the
![]() $\textit{SETAF}$
semantics studied in this paper:
$\textit{SETAF}$
semantics studied in this paper:
Definition 3 (Semantics (Flouris and Bikakis Reference Flouris and Bikakis2019)). Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\mathit{SETAF}$
. A complete labeling
$\mathit{SETAF}$
. A complete labeling
![]() $\mathcal{L}$
is called
$\mathcal{L}$
is called
-
• grounded iff
 $\mathtt{in}(\mathcal{L})$
is minimal (w.r.t.
$\mathtt{in}(\mathcal{L})$
is minimal (w.r.t.
 $\subseteq$
) among all complete labelings of
$\subseteq$
) among all complete labelings of
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
• preferred iff
 $\mathtt{in}(\mathcal{L})$
is maximal (w.r.t.
$\mathtt{in}(\mathcal{L})$
is maximal (w.r.t.
 $\subseteq$
) among all complete labelings of
$\subseteq$
) among all complete labelings of
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
• stable iff
 $\mathtt{undec}(\mathcal{L}) = \emptyset$
.
$\mathtt{undec}(\mathcal{L}) = \emptyset$
. -
• semi-stable iff
 $\mathtt{undec}(\mathcal{L})$
is minimal (w.r.t.
$\mathtt{undec}(\mathcal{L})$
is minimal (w.r.t.
 $\subseteq$
) among all complete labelings of
$\subseteq$
) among all complete labelings of
 $\mathfrak{A}$
.
$\mathfrak{A}$
.
Let us consider the following example:
Example 1. Consider the
![]() $\textit{SETAF}\ \mathfrak{A} = (\mathcal{A},\mathit{Att})$
below:
$\textit{SETAF}\ \mathfrak{A} = (\mathcal{A},\mathit{Att})$
below:

Fig. 1. A
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
.
$\mathfrak{A}$
.
Concerning the semantics of
![]() $\mathfrak{A}$
, we have
$\mathfrak{A}$
, we have
-
• Complete labelings:
 $\mathcal{L}_1 = (\emptyset, \emptyset, \left \{a,b,c,d,e\right \})$
,
$\mathcal{L}_1 = (\emptyset, \emptyset, \left \{a,b,c,d,e\right \})$
,
 $\mathcal{L}_2 =$
$\mathcal{L}_2 =$
 $(\left \{a\right \}, \left \{b\right \}, \left \{c,d,e\right \})$
and
$(\left \{a\right \}, \left \{b\right \}, \left \{c,d,e\right \})$
and
 $\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
;
$\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
; -
• Grounded labelings:
 $\mathcal{L}_1 = (\emptyset, \emptyset, \left \{a,b,c,d,e\right \})$
;
$\mathcal{L}_1 = (\emptyset, \emptyset, \left \{a,b,c,d,e\right \})$
; -
• Preferred labelings:
 $\mathcal{L}_2 =$
$\mathcal{L}_2 =$
 $(\left \{a\right \}, \left \{b\right \}, \left \{c,d,e\right \})$
and
$(\left \{a\right \}, \left \{b\right \}, \left \{c,d,e\right \})$
and
 $\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
;
$\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
; -
• Stable labelings: none;
-
• Semi-stable labelings:
 $\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
.
$\mathcal{L}_3 = (\left \{b\right \}, \left \{a,e\right \}, \left \{c,d\right \})$
.
2.2 Logic programs and semantics
Now, we take a look at propositional Normal Logic Programs. To delve into their definition and semantics, we will follow the presentation outlined by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), which draws from the foundation laid out by Przymusinski (Reference Przymusinski1990).
Definition 4 (Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b).) A rule
![]() $r$
is an expression
$r$
is an expression
where (
![]() $m, n \geq 0$
);
$m, n \geq 0$
);
![]() $c$
, each
$c$
, each
![]() $a_i$
(
$a_i$
(
![]() $1 \leq i \leq m$
) and each
$1 \leq i \leq m$
) and each
![]() $b_j$
(
$b_j$
(
![]() $1 \leq j \leq n$
) are atoms, and
$1 \leq j \leq n$
) are atoms, and
![]() $\mathtt{not}$
represents negation as failure. A literal is either an atom
$\mathtt{not}$
represents negation as failure. A literal is either an atom
![]() $a$
(positive literal) or a negated atom
$a$
(positive literal) or a negated atom
![]() $\mathtt{not\ } a$
(negative literal). Given a rule
$\mathtt{not\ } a$
(negative literal). Given a rule
![]() $r$
as above,
$r$
as above,
![]() $c$
is called the head of
$c$
is called the head of
![]() $r$
, which we denote as
$r$
, which we denote as
![]() ${\mathit{head}}(r)$
, and
${\mathit{head}}(r)$
, and
![]() $\mathit{body}(r) = \left \{a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}$
is called the body of
$\mathit{body}(r) = \left \{a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}$
is called the body of
![]() $r$
. Further, we divide
$r$
. Further, we divide
![]() $\mathit{body}(r)$
into two sets
$\mathit{body}(r)$
into two sets
![]() $\mathit{body}^+(r) = \left \{a_1, \ldots, a_m\right \}$
and
$\mathit{body}^+(r) = \left \{a_1, \ldots, a_m\right \}$
and
![]() $\mathit{body}^-(r) = \left \{\mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}$
. A fact is a rule where
$\mathit{body}^-(r) = \left \{\mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}$
. A fact is a rule where
![]() $m = n = 0$
. A Normal Logic Program (
$m = n = 0$
. A Normal Logic Program (
![]() $\mathit{NLP}$
) or simply a program
$\mathit{NLP}$
) or simply a program
![]() $P$
is a finite set of rules. If every
$P$
is a finite set of rules. If every
![]() $r \in P$
has
$r \in P$
has
![]() $body^{-}(r) = \emptyset$
,
$body^{-}(r) = \emptyset$
,
![]() $P$
is a positive program. The Herbrand Base of
$P$
is a positive program. The Herbrand Base of
![]() $P$
is the set
$P$
is the set
![]() ${\mathit{HB}}_{P}$
of all atoms appearing in
${\mathit{HB}}_{P}$
of all atoms appearing in
![]() $P$
.
$P$
.
A wide range of
![]() $\textit{NLP}$
semantics are based on the three-valued interpretations of programs (Przymusinski Reference Przymusinski1990):
$\textit{NLP}$
semantics are based on the three-valued interpretations of programs (Przymusinski Reference Przymusinski1990):
Definition 5 (Three-Valued Herbrand Interpretation (Przymusinski Reference Przymusinski1990)). A three-valued Herbrand Interpretation
![]() $\mathcal{I}$
(or simply interpretation) of an NLP
$\mathcal{I}$
(or simply interpretation) of an NLP
![]() $P$
is a pair
$P$
is a pair
![]() $\left\langle T, F \right \rangle$
with
$\left\langle T, F \right \rangle$
with
![]() $T, F \subseteq{\mathit{HB}}_P$
and
$T, F \subseteq{\mathit{HB}}_P$
and
![]() $T \cap F = \emptyset$
. The atoms in
$T \cap F = \emptyset$
. The atoms in
![]() $T$
are true in
$T$
are true in
![]() $\mathcal{I}$
, the atoms in
$\mathcal{I}$
, the atoms in
![]() $F$
are false in
$F$
are false in
![]() $\mathcal{I}$
, and the atoms in
$\mathcal{I}$
, and the atoms in
![]() ${\mathit{HB}}_P \setminus (T \cup F)$
are undefined in
${\mathit{HB}}_P \setminus (T \cup F)$
are undefined in
![]() $\mathcal{I}$
. For convenience, when the NLP
$\mathcal{I}$
. For convenience, when the NLP
![]() $P$
is clear from the context, we will refer to the set of undefined atoms in
$P$
is clear from the context, we will refer to the set of undefined atoms in
![]() ${\mathit{HB}}_P \setminus (T \cup F)$
simply as
${\mathit{HB}}_P \setminus (T \cup F)$
simply as
![]() $\overline{T \cup F}$
.
$\overline{T \cup F}$
.
Now we will consider the main semantics for
![]() $\textit{NLP}$
s. Let
$\textit{NLP}$
s. Let
![]() $\mathcal{I} = \left\langle T, F \right \rangle$
be a three-valued Herbrand interpretation of an
$\mathcal{I} = \left\langle T, F \right \rangle$
be a three-valued Herbrand interpretation of an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
; the reduct of
$P$
; the reduct of
![]() $P$
with respect to
$P$
with respect to
![]() $\mathcal{I}$
(written as
$\mathcal{I}$
(written as
![]() $P/\mathcal{I}$
) is the
$P/\mathcal{I}$
) is the
![]() $\textit{NLP}$
constructed using the following steps:
$\textit{NLP}$
constructed using the following steps:
-
1. Remove any
 $a \leftarrow a_1, \ldots, a_m,$
$a \leftarrow a_1, \ldots, a_m,$
 $\mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P$
such that
$\mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P$
such that
 $b_j \in T$
for some
$b_j \in T$
for some
 $j$
(
$j$
(
 $1 \leq j \leq n$
);
$1 \leq j \leq n$
); -
2. Afterward, remove any occurrence of
 $\mathtt{not\ } b_j$
from
$\mathtt{not\ } b_j$
from
 $P$
such that
$P$
such that
 $b_j \in F$
;
$b_j \in F$
; -
3. Then, replace any occurrence of
 $\mathtt{not\ } b_j$
left by a special atom
$\mathtt{not\ } b_j$
left by a special atom
 $\mathbf{u}$
(
$\mathbf{u}$
(
 $\mathbf{u} \not \in{\mathit{HB}}_P$
).
$\mathbf{u} \not \in{\mathit{HB}}_P$
).
In the above procedure,
![]() $\mathbf{u}$
is assumed to be an atom not in
$\mathbf{u}$
is assumed to be an atom not in
![]() ${\mathit{HB}}_{P}$
which is undefined in all interpretations of
${\mathit{HB}}_{P}$
which is undefined in all interpretations of
![]() $P$
(a constant). Note that
$P$
(a constant). Note that
![]() $P/\mathcal{I}$
is a positive program since all negative literals have been removed. As a consequence,
$P/\mathcal{I}$
is a positive program since all negative literals have been removed. As a consequence,
![]() $P/\mathcal{I}$
has a unique least three-valued model (Przymusinski Reference Przymusinski1990), obtained by the
$P/\mathcal{I}$
has a unique least three-valued model (Przymusinski Reference Przymusinski1990), obtained by the
![]() $\Psi$
operator:
$\Psi$
operator:
Definition 6 (
![]() $\Psi$
Operator (Przymusinski Reference Przymusinski1990)). Let
$\Psi$
Operator (Przymusinski Reference Przymusinski1990)). Let
![]() $P$
be a positive program and
$P$
be a positive program and
![]() $\mathcal{J} = \left\langle T, F \right \rangle$
be an interpretation. Define
$\mathcal{J} = \left\langle T, F \right \rangle$
be an interpretation. Define
![]() $\Psi _P(\mathcal{J}) = \left\langle T', F' \right \rangle$
, where
$\Psi _P(\mathcal{J}) = \left\langle T', F' \right \rangle$
, where
-
•
 $c \in T'$
iff
$c \in T'$
iff
 $c \in HB_P$
and there exists
$c \in HB_P$
and there exists
 $c \leftarrow a_1, \ldots, a_m \in P$
such that for all
$c \leftarrow a_1, \ldots, a_m \in P$
such that for all
 $i$
,
$i$
,
 $1 \leq i \leq m$
,
$1 \leq i \leq m$
,
 $a_i \in T$
;
$a_i \in T$
; -
•
 $c \in F'$
iff
$c \in F'$
iff
 $c \in HB_P$
and for every
$c \in HB_P$
and for every
 $c \leftarrow a_1, \ldots, a_m \in P$
, there exists
$c \leftarrow a_1, \ldots, a_m \in P$
, there exists
 $i$
,
$i$
,
 $1 \leq i \leq m$
, such that
$1 \leq i \leq m$
, such that
 $a_i \in F$
.
$a_i \in F$
.
The least three-valued model of
![]() $P$
is given by
$P$
is given by
![]() $ \Psi ^{\uparrow \ \omega }_P$
(Przymusinski Reference Przymusinski1990), the least fixed point of
$ \Psi ^{\uparrow \ \omega }_P$
(Przymusinski Reference Przymusinski1990), the least fixed point of
![]() $\Psi _P$
iteratively obtained as follows:
$\Psi _P$
iteratively obtained as follows:
 \begin{align*} \Psi ^{\uparrow \ 0}_P = & \left\langle \emptyset, {\mathit{HB}}_P \right \rangle \\[5pt] \Psi ^{\uparrow \ i + 1}_P = & \Psi _P(\Psi ^{\uparrow \ i}_P)\\[5pt] \Psi ^{\uparrow \ \omega }_P = & \left\langle \bigcup _{i \lt \omega } \left \{T_i \mid \Psi ^{\uparrow \ i}_P = \left\langle T_i, F_i \right \rangle \right \}, \bigcap _{i \lt \omega } \left \{F_i \mid \Psi ^{\uparrow \ i}_P = \left\langle T_i, F_i \right \rangle \right \} \right \rangle \end{align*}
\begin{align*} \Psi ^{\uparrow \ 0}_P = & \left\langle \emptyset, {\mathit{HB}}_P \right \rangle \\[5pt] \Psi ^{\uparrow \ i + 1}_P = & \Psi _P(\Psi ^{\uparrow \ i}_P)\\[5pt] \Psi ^{\uparrow \ \omega }_P = & \left\langle \bigcup _{i \lt \omega } \left \{T_i \mid \Psi ^{\uparrow \ i}_P = \left\langle T_i, F_i \right \rangle \right \}, \bigcap _{i \lt \omega } \left \{F_i \mid \Psi ^{\uparrow \ i}_P = \left\langle T_i, F_i \right \rangle \right \} \right \rangle \end{align*}
where
![]() $\omega$
denotes the first infinite ordinal.
$\omega$
denotes the first infinite ordinal.
We can now describe the logic programming semantics studied in this paper:
Definition 7. Let
![]() $P$
be an
$P$
be an
![]() $NLP$
and
$NLP$
and
![]() $\mathcal{I} = \left\langle T, F \right \rangle$
be an interpretation; by
$\mathcal{I} = \left\langle T, F \right \rangle$
be an interpretation; by
![]() $\Omega _P(\mathcal{I}) = \Psi ^{\uparrow \ \omega }_{\frac{P}{\mathcal{I}}}$
, we mean the least three-valued model of
$\Omega _P(\mathcal{I}) = \Psi ^{\uparrow \ \omega }_{\frac{P}{\mathcal{I}}}$
, we mean the least three-valued model of
![]() $\frac{P}{\mathcal{I}}$
. We say that
$\frac{P}{\mathcal{I}}$
. We say that
-
•
 $\mathcal{I}$
is a partial stable model of
$\mathcal{I}$
is a partial stable model of
 $P$
iff
$P$
iff
 $\Omega _P(\mathcal{I}) = \mathcal{I}$
(Przymusinski Reference Przymusinski1990).
$\Omega _P(\mathcal{I}) = \mathcal{I}$
(Przymusinski Reference Przymusinski1990). -
•
 $\mathcal{I}$
is a well-founded model of
$\mathcal{I}$
is a well-founded model of
 $P$
iff
$P$
iff
 $\mathcal{I}$
is a partial stable model of
$\mathcal{I}$
is a partial stable model of
 $P$
where there is no partial stable model
$P$
where there is no partial stable model
 $\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
$\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
 $P$
such that
$P$
such that
 $T' \subset T$
; that is,
$T' \subset T$
; that is,
 $T$
is minimal (w.r.t. set inclusion) among all partial stable models of
$T$
is minimal (w.r.t. set inclusion) among all partial stable models of
 $P$
(Przymusinski Reference Przymusinski1990).
$P$
(Przymusinski Reference Przymusinski1990). -
•
 $\mathcal{I}$
is a regular model of
$\mathcal{I}$
is a regular model of
 $P$
iff
$P$
iff
 $\mathcal{I}$
is a partial stable model of
$\mathcal{I}$
is a partial stable model of
 $P$
where there is no partial stable model
$P$
where there is no partial stable model
 $\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
$\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
 $P$
such that
$P$
such that
 $T \subset T'$
; that is,
$T \subset T'$
; that is,
 $T$
is maximal (w.r.t. set inclusion) among all partial stable models of
$T$
is maximal (w.r.t. set inclusion) among all partial stable models of
 $P$
(Eiter et al. Reference Eiter, Leone and Saccá1997).
$P$
(Eiter et al. Reference Eiter, Leone and Saccá1997). -
•
 $\mathcal{I}$
is a (two-valued) stable model of
$\mathcal{I}$
is a (two-valued) stable model of
 $P$
iff
$P$
iff
 $\mathcal{I}$
is a partial stable model of
$\mathcal{I}$
is a partial stable model of
 $P$
where
$P$
where
 $T \cup F ={\mathit{HB}}_P$
(Przymusinski Reference Przymusinski1990).
$T \cup F ={\mathit{HB}}_P$
(Przymusinski Reference Przymusinski1990). -
•
 $\mathcal{I}$
is an
$\mathcal{I}$
is an
 $L$
-stable model of
$L$
-stable model of
 $P$
iff
$P$
iff
 $\mathcal{I}$
is a partial stable model of
$\mathcal{I}$
is a partial stable model of
 $P$
where there is no partial stable model
$P$
where there is no partial stable model
 $\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
$\mathcal{I} ' = \left\langle T', F' \right \rangle$
of
 $P$
such that
$P$
such that
 $T \cup F \subset T' \cup F'$
; that is,
$T \cup F \subset T' \cup F'$
; that is,
 $T \cup F$
is maximal (w.r.t. set inclusion) among all partial stable models of
$T \cup F$
is maximal (w.r.t. set inclusion) among all partial stable models of
 $P$
(Eiter et al. Reference Eiter, Leone and Saccá1997).
$P$
(Eiter et al. Reference Eiter, Leone and Saccá1997).
Although some of these definitions are not standard in logic programming literature, their equivalence was proved by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). This format helps us to relate
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\textit{SETAF}$
semantics due to the structural similarities between Definition7 and Definitions2 and 3. We illustrate these semantics in the following example:
$\textit{SETAF}$
semantics due to the structural similarities between Definition7 and Definitions2 and 3. We illustrate these semantics in the following example:
Example 2. Consider the following logic program
![]() $P$
:
$P$
:
This program has
-
• Partial Stable Models:
 $\mathcal{M}_1 = \langle \emptyset, \emptyset \rangle$
,
$\mathcal{M}_1 = \langle \emptyset, \emptyset \rangle$
,
 $\mathcal{M}_2 = \langle \left \{ a \right \}, \left \{ b \right \} \rangle$
and
$\mathcal{M}_2 = \langle \left \{ a \right \}, \left \{ b \right \} \rangle$
and
 $\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
;
$\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
; -
• Well-founded model:
 $\mathcal{M}_1 = \langle \emptyset, \emptyset \rangle$
;
$\mathcal{M}_1 = \langle \emptyset, \emptyset \rangle$
; -
• Regular models:
 $\mathcal{M}_2 = \langle \left \{ a \right \}, \left \{ b \right \} \rangle$
and
$\mathcal{M}_2 = \langle \left \{ a \right \}, \left \{ b \right \} \rangle$
and
 $\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
;
$\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
; -
• Stable models: none;
-
•
 $L$
-stable model:
$L$
-stable model:
 $\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
.
$\mathcal{M}_3 = \langle \left \{ b \right \}, \left \{ a, e \right \} \rangle$
.
3. From
 $\textit{NLP}$
to
$\textit{NLP}$
to
 $\textit{SETAF}$
$\textit{SETAF}$
In this section, we revisit the three-step process of argumentation framework instantiation as employed by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) for translating an
![]() $\textit{NLP}$
into an
$\textit{NLP}$
into an
![]() $\mathit{AAF}$
. This method is based on the approach introduced by Wu et al. (Reference Wu, Caminada and Gabbay2009) and shares similarities with the procedures used in ASPIC (Caminada and Amgoud Reference Caminada and Amgoud2005, Reference Caminada and Amgoud2007) and logic-based argumentation (Gorogiannis and Hunter Reference Gorogiannis and Hunter2011). Its first step involves taking an
$\mathit{AAF}$
. This method is based on the approach introduced by Wu et al. (Reference Wu, Caminada and Gabbay2009) and shares similarities with the procedures used in ASPIC (Caminada and Amgoud Reference Caminada and Amgoud2005, Reference Caminada and Amgoud2007) and logic-based argumentation (Gorogiannis and Hunter Reference Gorogiannis and Hunter2011). Its first step involves taking an
![]() $\textit{NLP}$
and constructing its associated
$\textit{NLP}$
and constructing its associated
![]() $\mathit{AAF}$
. Then, we apply
$\mathit{AAF}$
. Then, we apply
![]() $\mathit{AAF}$
semantics in the second step, followed by an analysis of the implications of these semantics at the level of conclusions (step 3). In our case, starting with an
$\mathit{AAF}$
semantics in the second step, followed by an analysis of the implications of these semantics at the level of conclusions (step 3). In our case, starting with an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, we derive the associated
$P$
, we derive the associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $(\mathcal{A}_P, \mathit{Att}_P)$
. Unlike the construction described by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), rules with identical conclusions in
$(\mathcal{A}_P, \mathit{Att}_P)$
. Unlike the construction described by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), rules with identical conclusions in
![]() $P$
will result in a single argument in
$P$
will result in a single argument in
![]() $\mathcal{A}_P$
. This distinction is capital for establishing the equivalence results between
$\mathcal{A}_P$
. This distinction is capital for establishing the equivalence results between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s. Additionally, it simplifies steps 2 and 3, making them more straightforward to follow. We now detail this process.
$\textit{SETAF}$
s. Additionally, it simplifies steps 2 and 3, making them more straightforward to follow. We now detail this process.
3.1
 $\textit{SETAF}$
construction
$\textit{SETAF}$
construction
We will devise one translation from
![]() $\textit{NLP}$
to
$\textit{NLP}$
to
![]() $\textit{SETAF}$
that is sufficiently robust to guarantee the equivalence between various kinds of
$\textit{SETAF}$
that is sufficiently robust to guarantee the equivalence between various kinds of
![]() $\textit{NLP}$
s models and
$\textit{NLP}$
s models and
![]() $\textit{SETAF}$
s labelings. Specifically, our approach will establish the correspondence between partial stable models and complete labelings, well-founded models and grounded labelings, regular models and preferred labelings, stable models and stable labelings,
$\textit{SETAF}$
s labelings. Specifically, our approach will establish the correspondence between partial stable models and complete labelings, well-founded models and grounded labelings, regular models and preferred labelings, stable models and stable labelings,
![]() $L$
-stable models and semi-stable labelings. Our method is built upon a translation from
$L$
-stable models and semi-stable labelings. Our method is built upon a translation from
![]() $\textit{NLP}$
to
$\textit{NLP}$
to
![]() $\mathit{AAF}$
proposed by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), where
$\mathit{AAF}$
proposed by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), where
![]() $\textit{NLP}$
rules are directly translated into arguments. We will adapt this approach for
$\textit{NLP}$
rules are directly translated into arguments. We will adapt this approach for
![]() $\textit{SETAF}$
by employing the translation method outlined by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) to construct statements, and then statements corresponding to rules with the same head will be grouped to form a single argument. Taking an
$\textit{SETAF}$
by employing the translation method outlined by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) to construct statements, and then statements corresponding to rules with the same head will be grouped to form a single argument. Taking an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, we can start to construct statements recursively as follows:
$P$
, we can start to construct statements recursively as follows:
Definition 8 (Statements and Arguments). Let
![]() $P$
be an
$P$
be an
![]() $NLP$
.
$NLP$
.
-
• If
 $c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n$
is a rule in
$c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n$
is a rule in
 $P$
, then it is also a statement (say
$P$
, then it is also a statement (say
 $s$
) with
$s$
) with
-
—
 $\mathtt{Conc}(s) = c$
,
$\mathtt{Conc}(s) = c$
, -
—
 $\mathtt{Rules}(s) = \{ c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \}$
,
$\mathtt{Rules}(s) = \{ c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \}$
, -
—
 $\mathtt{Vul}(s) = \{ b_1, \ldots, b_n \}$
, and
$\mathtt{Vul}(s) = \{ b_1, \ldots, b_n \}$
, and -
—
 ${\mathtt{Sub}}(s) = \{ s \}$
.
${\mathtt{Sub}}(s) = \{ s \}$
.
-
• If
 $c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is a rule in
$c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is a rule in
 $P$
and for each
$P$
and for each
 $a_i$
(
$a_i$
(
 $1 \leq i \leq m$
) there exists a statement
$1 \leq i \leq m$
) there exists a statement
 $s_i$
with
$s_i$
with
 $\mathtt{Conc}(s_i) = a_i$
and
$\mathtt{Conc}(s_i) = a_i$
and
 $c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is not contained in
$c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is not contained in
 $\mathtt{Rules}(s_i)$
, then
$\mathtt{Rules}(s_i)$
, then
 $c \leftarrow (s_1),\ldots, (s_m),$
$c \leftarrow (s_1),\ldots, (s_m),$
 $\mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is a statement (say
$\mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n$
is a statement (say
 $s$
) with
$s$
) with
-
—
 $\mathtt{Conc}(s) = c$
,
$\mathtt{Conc}(s) = c$
, -
—
 $\mathtt{Rules}(s) = \mathtt{Rules}(s_1) \cup \ldots \cup \mathtt{Rules}(s_m)\cup$
$\mathtt{Rules}(s) = \mathtt{Rules}(s_1) \cup \ldots \cup \mathtt{Rules}(s_m)\cup$
 $ \{ c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n \}$
$ \{ c \leftarrow a_1,\ldots, a_m, \mathtt{not\ } b_1,\ldots, \mathtt{not\ } b_n \}$
-
—
 $\mathtt{Vul}(s) = \mathtt{Vul}(s_1)$
$\mathtt{Vul}(s) = \mathtt{Vul}(s_1)$
 $\cup \ldots \cup$
$\cup \ldots \cup$
 $\mathtt{Vul}(s_m)$
$\mathtt{Vul}(s_m)$
 $\cup$
$\cup$
 $\{b_1, \ldots, b_n \}$
, and
$\{b_1, \ldots, b_n \}$
, and -
—
 ${\mathtt{Sub}}(s) = \{ s \} \cup{\mathtt{Sub}}(s_1) \cup \ldots \cup{\mathtt{Sub}}(s_m)$
.
${\mathtt{Sub}}(s) = \{ s \} \cup{\mathtt{Sub}}(s_1) \cup \ldots \cup{\mathtt{Sub}}(s_m)$
.
By
![]() $\mathfrak S_P$
, we mean the set of all statements we can construct from
$\mathfrak S_P$
, we mean the set of all statements we can construct from
![]() $P$
as above. Then we define
$P$
as above. Then we define
![]() $\mathcal{A}_P = \left \{\mathtt{Conc}(s) \mid s \in \mathfrak S_P\right \}$
as the set of all arguments we can construct from
$\mathcal{A}_P = \left \{\mathtt{Conc}(s) \mid s \in \mathfrak S_P\right \}$
as the set of all arguments we can construct from
![]() $P$
. For an argument
$P$
. For an argument
![]() $c$
from
$c$
from
![]() $P$
(
$P$
(
![]() $c \in \mathcal{A}_P$
), we have that
$c \in \mathcal{A}_P$
), we have that
-
•
 $\mathtt{Conc}(c) = c$
, and
$\mathtt{Conc}(c) = c$
, and -
•
 $\mathtt{Vul}_P(c) = \left \{\mathtt{Vul}(s) \mid s \in \mathfrak S_P \textit{ and } \mathtt{Conc}(s) = c\right \}$
.
$\mathtt{Vul}_P(c) = \left \{\mathtt{Vul}(s) \mid s \in \mathfrak S_P \textit{ and } \mathtt{Conc}(s) = c\right \}$
.
If
![]() $c$
is an argument, then
$c$
is an argument, then
![]() $\mathtt{Conc}(c)$
is referred to as the conclusion of
$\mathtt{Conc}(c)$
is referred to as the conclusion of
![]() $c$
, and
$c$
, and
![]() $\mathtt{Vul}_P(c)$
is referred to as the vulnerabilities of
$\mathtt{Vul}_P(c)$
is referred to as the vulnerabilities of
![]() $c$
in
$c$
in
![]() $P$
. When the context is clear, we will write simply
$P$
. When the context is clear, we will write simply
![]() $\mathtt{Vul}(c)$
instead of
$\mathtt{Vul}(c)$
instead of
![]() $\mathtt{Vul}_P(c)$
.
$\mathtt{Vul}_P(c)$
.
Now we will clarify the connection between the existence of statements and the existence of a derivation in a reduct.
Lemma 1.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
,
$\textit{NLP}$
,
![]() $\mathcal{I} = \left\langle T, F \right \rangle$
an interpretation and
$\mathcal{I} = \left\langle T, F \right \rangle$
an interpretation and
![]() $\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
the least three-valued model of
$\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
the least three-valued model of
![]() $\frac{P}{\mathcal{I}}$
. It holds
$\frac{P}{\mathcal{I}}$
. It holds
-
(i)
 $c \in T'$
iff there exists a statement
$c \in T'$
iff there exists a statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
and
$\mathtt{Conc}(s) = c$
and
 $\mathtt{Vul}(s) \subseteq F$
.
$\mathtt{Vul}(s) \subseteq F$
. -
(ii)
 $c \in F'$
iff for every statement
$c \in F'$
iff for every statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
, we have
$\mathtt{Conc}(s) = c$
, we have
 $\mathtt{Vul}(s) \cap T \neq \emptyset$
$\mathtt{Vul}(s) \cap T \neq \emptyset$
We can prove both results in Lemma1 by induction. Assuming that
![]() $\Psi ^{\uparrow \ i}_{\frac{P}{\mathcal{I}}} = \left\langle T_i, F_i \right \rangle$
for each
$\Psi ^{\uparrow \ i}_{\frac{P}{\mathcal{I}}} = \left\langle T_i, F_i \right \rangle$
for each
![]() $i \in \mathbb{N}$
, we can prove the right-hand side of item 1 and the left-hand side of item 2 by induction on the value of
$i \in \mathbb{N}$
, we can prove the right-hand side of item 1 and the left-hand side of item 2 by induction on the value of
![]() $i$
after guaranteeing the following results:
$i$
after guaranteeing the following results:
-
• If
 $c \in T_i$
, then there exists a statement
$c \in T_i$
, then there exists a statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
and
$\mathtt{Conc}(s) = c$
and
 $\mathtt{Vul}(s) \subseteq F$
.
$\mathtt{Vul}(s) \subseteq F$
. -
• If
 $c \not \in F_i$
, then there exists a statement
$c \not \in F_i$
, then there exists a statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
and
$\mathtt{Conc}(s) = c$
and
 $\mathtt{Vul}(s) \cap T = \emptyset$
.
$\mathtt{Vul}(s) \cap T = \emptyset$
.
The remaining cases of Lemma1 can be proved by structural induction on the construction of a statement
![]() $s$
(see a detailed account of the proof of Lemma 1 in Supplementary Material).
$s$
(see a detailed account of the proof of Lemma 1 in Supplementary Material).
Lemma1 ensures that statements are closely related to derivations in a reduct. An atom
![]() $c$
is true in the least three-valued model of
$c$
is true in the least three-valued model of
![]() $\frac{P}{\mathcal{I}}$
iff we can construct a statement with conclusion
$\frac{P}{\mathcal{I}}$
iff we can construct a statement with conclusion
![]() $c$
and whose vulnerabilities are false according to
$c$
and whose vulnerabilities are false according to
![]() $\mathcal{I}$
; otherwise,
$\mathcal{I}$
; otherwise,
![]() $c$
is false in the least three-valued model of
$c$
is false in the least three-valued model of
![]() $\frac{P}{\mathcal{I}}$
iff for every statement whose conclusion is
$\frac{P}{\mathcal{I}}$
iff for every statement whose conclusion is
![]() $c$
, at least one of its vulnerabilities is true in
$c$
, at least one of its vulnerabilities is true in
![]() $\mathcal{I}$
. The next result is a direct consequence of Lemma1:
$\mathcal{I}$
. The next result is a direct consequence of Lemma1:
Corollary 2.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
.
$\textit{NLP}$
.
-
• Assume
 $\mathcal{I} = \left\langle \emptyset, {\mathit{HB}}_P \right \rangle$
and
$\mathcal{I} = \left\langle \emptyset, {\mathit{HB}}_P \right \rangle$
and
 $\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
. It holds that
$\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
. It holds that
 $c \in T'$
iff there exists a statement
$c \in T'$
iff there exists a statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
.
$\mathtt{Conc}(s) = c$
. -
• There is no statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
iff
$\mathtt{Conc}(s) = c$
iff
 $c \in F'$
for every interpretation
$c \in F'$
for every interpretation
 $\mathcal{I}$
with
$\mathcal{I}$
with
 $\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
.
$\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
.
The reduct of
![]() $P$
with respect to
$P$
with respect to
![]() $\left\langle \emptyset, {\mathit{HB}}_P \right \rangle$
gives us all the possible derivations of
$\left\langle \emptyset, {\mathit{HB}}_P \right \rangle$
gives us all the possible derivations of
![]() $P$
, and from these derivations, we can construct all the statements associated with
$P$
, and from these derivations, we can construct all the statements associated with
![]() $P$
. On the other hand, the atoms that are lost in the translation, that is, the atoms not associated with statements, are simply those that are false in the least three-valued model of every possible reduct of
$P$
. On the other hand, the atoms that are lost in the translation, that is, the atoms not associated with statements, are simply those that are false in the least three-valued model of every possible reduct of
![]() $P$
. Besides establishing connections between statements and derivations in a reduct, Lemma1 also plays a central role in the proof of Theorems4 and 5.
$P$
. Besides establishing connections between statements and derivations in a reduct, Lemma1 also plays a central role in the proof of Theorems4 and 5.
Apart from that, intuitively, we can see a statement as a tree-like structure representing a possible derivation of an atom from the rules of a program. In contrast, an argument for
![]() $c$
in
$c$
in
![]() $P$
is associated with the (derivable) atom
$P$
is associated with the (derivable) atom
![]() $c$
itself and can be obtained by collecting all the statements with the same conclusion
$c$
itself and can be obtained by collecting all the statements with the same conclusion
![]() $c$
(i.e., all the possible ways of deriving
$c$
(i.e., all the possible ways of deriving
![]() $c$
in
$c$
in
![]() $P$
).
$P$
).
Example 3. Consider the
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
below with rules
$P$
below with rules
![]() $\left \{r_1, \ldots, r_8\right \}$
:
$\left \{r_1, \ldots, r_8\right \}$
:
 \begin{equation*} \begin {array}{llcllcll} r_1: & a & & r_2: & b \leftarrow a & & r_3: & c \leftarrow \mathtt {not}\; c \\[5pt] r_4: & d \leftarrow b, \mathtt {not}\; a, \mathtt {not}\; d & & r_5: & d \leftarrow \mathtt {not}\; c, \mathtt {not}\; d & & r_6: & e \leftarrow b, c, \mathtt {not}\; e \\[5pt] r_7: & c \leftarrow f, \mathtt {not}\; g & & r_8: & f \leftarrow c, g & & \ & \ \end {array} \end{equation*}
\begin{equation*} \begin {array}{llcllcll} r_1: & a & & r_2: & b \leftarrow a & & r_3: & c \leftarrow \mathtt {not}\; c \\[5pt] r_4: & d \leftarrow b, \mathtt {not}\; a, \mathtt {not}\; d & & r_5: & d \leftarrow \mathtt {not}\; c, \mathtt {not}\; d & & r_6: & e \leftarrow b, c, \mathtt {not}\; e \\[5pt] r_7: & c \leftarrow f, \mathtt {not}\; g & & r_8: & f \leftarrow c, g & & \ & \ \end {array} \end{equation*}
According to Definition 8, we can construct the following statements from
![]() $P$
:
$P$
:
In the next table, we give the conclusions and vulnerabilities of each statement:

Alternatively, we can depict statements as possible derivations as in Figure 2:

Fig. 2. Statements constructed from
![]() $P$
.
$P$
.
The vulnerabilities of a statement
![]() $s$
are associated with the negative literals found in the derivation of
$s$
are associated with the negative literals found in the derivation of
![]() $s$
. If
$s$
. If
![]() $\mathtt{not}\; a$
is one of them, we know that
$\mathtt{not}\; a$
is one of them, we know that
![]() $a$
is one of its vulnerabilities. This means that if
$a$
is one of its vulnerabilities. This means that if
![]() $a$
is derived, then
$a$
is derived, then
![]() $\mathtt{Conc}(s)$
cannot be obtained via this derivation represented by
$\mathtt{Conc}(s)$
cannot be obtained via this derivation represented by
![]() $s$
. However, it can still be obtained via other derivations/statements. For instance, in the program
$s$
. However, it can still be obtained via other derivations/statements. For instance, in the program
![]() $P$
of Example 3, the derivation of
$P$
of Example 3, the derivation of
![]() $a$
suffices to prevent the derivation of
$a$
suffices to prevent the derivation of
![]() $d$
via statement
$d$
via statement
![]() $s_4$
(for that reason,
$s_4$
(for that reason,
![]() $a \in \mathtt{Vul}(s_4)$
), but we still can derive
$a \in \mathtt{Vul}(s_4)$
), but we still can derive
![]() $d$
via
$d$
via
![]() $s_5$
. Notice also that there are no statements with conclusions
$s_5$
. Notice also that there are no statements with conclusions
![]() $f$
and
$f$
and
![]() $g$
. From Corollary 2, we know that it is not possible to derive them in
$g$
. From Corollary 2, we know that it is not possible to derive them in
![]() $P$
as they are false in the least three-valued model of each reduct of
$P$
as they are false in the least three-valued model of each reduct of
![]() $P$
. In addition, to determine the vulnerabilities of an atom (and not only of a specific derivation leading to this atom), we collect these data about the statements with the same conclusions to give the conclusions and vulnerabilities of each argument. In our example, we obtain the following results:
$P$
. In addition, to determine the vulnerabilities of an atom (and not only of a specific derivation leading to this atom), we collect these data about the statements with the same conclusions to give the conclusions and vulnerabilities of each argument. In our example, we obtain the following results:

As the vulnerabilities of an atom/argument
![]() $a$
are a collection of the vulnerabilities of the statements whose conclusion is
$a$
are a collection of the vulnerabilities of the statements whose conclusion is
![]() $a$
, any set containing at least one atom in each of these statements suffices to prevent the derivation of
$a$
, any set containing at least one atom in each of these statements suffices to prevent the derivation of
![]() $a$
in
$a$
in
![]() $P$
. In our example, there are two statements with the same conclusion
$P$
. In our example, there are two statements with the same conclusion
![]() $d$
and
$d$
and
![]() $\mathtt{Vul}(d) = \left \{\left \{a, d\right \}, \left \{c, d\right \}\right \}$
. Thus any set of atoms containing
$\mathtt{Vul}(d) = \left \{\left \{a, d\right \}, \left \{c, d\right \}\right \}$
. Thus any set of atoms containing
![]() $\left \{d\right \}$
or
$\left \{d\right \}$
or
![]() $\left \{a, c\right \}$
prevents the conclusion of
$\left \{a, c\right \}$
prevents the conclusion of
![]() $d$
in
$d$
in
![]() $P$
. We will resort to these minimal sets to determine the attack relation:
$P$
. We will resort to these minimal sets to determine the attack relation:
Definition 9. Let
![]() $P$
be an
$P$
be an
![]() $NLP$
and let
$NLP$
and let
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $a$
be, respectively, a set of arguments and an argument in the sense of Definition 8. We say that
$a$
be, respectively, a set of arguments and an argument in the sense of Definition 8. We say that
![]() $(\mathcal{B}, a) \in \mathit{Att}_P$
iff
$(\mathcal{B}, a) \in \mathit{Att}_P$
iff
![]() $\mathcal{B}$
is a minimal set (w.r.t. set inclusion) such that for each
$\mathcal{B}$
is a minimal set (w.r.t. set inclusion) such that for each
![]() $V \in \mathtt{Vul}_P(a)$
, there exists
$V \in \mathtt{Vul}_P(a)$
, there exists
![]() $b \in \mathcal{B} \cap V$
.
$b \in \mathcal{B} \cap V$
.
For the arguments of Example3, it holds that both
![]() $a$
and
$a$
and
![]() $b$
are not attacked,
$b$
are not attacked,
![]() $c$
attacks itself,
$c$
attacks itself,
![]() $c$
attacks
$c$
attacks
![]() $e$
,
$e$
,
![]() $e$
attacks itself,
$e$
attacks itself,
![]() $d$
attacks itself,
$d$
attacks itself,
![]() $a$
and
$a$
and
![]() $c$
(collectively) attack
$c$
(collectively) attack
![]() $d$
. This strategy of extracting statements from
$d$
. This strategy of extracting statements from
![]() $\textit{NLP}$
s rules and then gathering those with identical conclusions into arguments is not novel; Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) proposed a translation from
$\textit{NLP}$
s rules and then gathering those with identical conclusions into arguments is not novel; Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019) proposed a translation from
![]() $\textit{NLP}$
s into Abstract Dialectical Frameworks (Brewka and Woltran Reference Brewka and Woltran2010; Brewka et al. Reference Brewka, Ellmauthaler, Strass, Wallner and Woltran2013) by following a similar path. Using the thus-defined notions of arguments and attacks, we define the
$\textit{NLP}$
s into Abstract Dialectical Frameworks (Brewka and Woltran Reference Brewka and Woltran2010; Brewka et al. Reference Brewka, Ellmauthaler, Strass, Wallner and Woltran2013) by following a similar path. Using the thus-defined notions of arguments and attacks, we define the
![]() $\textit{SETAF}$
associated with an
$\textit{SETAF}$
associated with an
![]() $\textit{NLP}$
.
$\textit{NLP}$
.
Definition 10. Let
![]() $P$
be an
$P$
be an
![]() $NLP$
. We define its associated
$NLP$
. We define its associated
![]() $SETAF$
as
$SETAF$
as
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
, where
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
, where
![]() $\mathcal{A}_P$
is the set of arguments in the sense of Definition 8 and
$\mathcal{A}_P$
is the set of arguments in the sense of Definition 8 and
![]() $\mathit{Att}_P$
is the attack relation in the sense of Definition 9.
$\mathit{Att}_P$
is the attack relation in the sense of Definition 9.
As an example, the
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P = (\mathcal{A}_P,\mathit{Att}_P)$
associated with the
$\mathfrak{A}_P = (\mathcal{A}_P,\mathit{Att}_P)$
associated with the
![]() $\textit{NLP}$
of Example3 is depicted in Figure 3
.
$\textit{NLP}$
of Example3 is depicted in Figure 3
.

Fig. 3. A
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P = (\mathcal{A}_P,\mathit{Att}_P)$
.
$\mathfrak{A}_P = (\mathcal{A}_P,\mathit{Att}_P)$
.
3.2 Equivalence results
Once the
![]() $\textit{SETAF}$
has been constructed, we show the equivalence between the semantics for an
$\textit{SETAF}$
has been constructed, we show the equivalence between the semantics for an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
and their counterpart for the associated
$P$
and their counterpart for the associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P$
. One distinguishing characteristic of our approach in comparison with König et al.’s (Reference König, Rapberger and Ulbricht2022) proposal is that it is more organic. We prove the equivalence results by identifying connections between fundamental notions used in the definition of the semantics for
$\mathfrak{A}_P$
. One distinguishing characteristic of our approach in comparison with König et al.’s (Reference König, Rapberger and Ulbricht2022) proposal is that it is more organic. We prove the equivalence results by identifying connections between fundamental notions used in the definition of the semantics for
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s. With this purpose, we introduce two functions:
$\textit{SETAF}$
s. With this purpose, we introduce two functions:
![]() $\mathcal{L}2\mathcal{I}_P$
associates an interpretation to each labeling while
$\mathcal{L}2\mathcal{I}_P$
associates an interpretation to each labeling while
![]() $\mathcal{I}2\mathcal{L}_P$
associates a labeling to each interpretation. We then investigate the conditions under which they are each other’s inverse and employ these results to prove the equivalence between the semantics. These functions essentially permit us to treat interpretations and labelings interchangeably.
$\mathcal{I}2\mathcal{L}_P$
associates a labeling to each interpretation. We then investigate the conditions under which they are each other’s inverse and employ these results to prove the equivalence between the semantics. These functions essentially permit us to treat interpretations and labelings interchangeably.
Definition 11 (
![]() $\mathcal{L}2\mathcal{I}_P$
and
$\mathcal{L}2\mathcal{I}_P$
and
![]() $\mathcal{I}2\mathcal{L}_P$
Functions). Let
$\mathcal{I}2\mathcal{L}_P$
Functions). Let
![]() $P$
be an
$P$
be an
![]() $NLP$
,
$NLP$
,
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be its associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be its associated
![]() $SETAF$
,
$SETAF$
,
![]() $\mathcal{I}\mathit{nt}$
be the set of all the three-valued interpretations of
$\mathcal{I}\mathit{nt}$
be the set of all the three-valued interpretations of
![]() $P$
and
$P$
and
![]() $\mathcal{L}\mathit{ab}$
be the set of all labelings of
$\mathcal{L}\mathit{ab}$
be the set of all labelings of
![]() $\mathfrak{A}_p$
. We introduce a function
$\mathfrak{A}_p$
. We introduce a function
![]() $\mathcal{L}2\mathcal{I}_P : \mathcal{L}\mathit{ab} \to \mathcal{I}\mathit{nt}$
such that
$\mathcal{L}2\mathcal{I}_P : \mathcal{L}\mathit{ab} \to \mathcal{I}\mathit{nt}$
such that
![]() $\mathcal{L}2\mathcal{I}_P(\mathcal{L}) = \left\langle T, F \right \rangle$
, in which
$\mathcal{L}2\mathcal{I}_P(\mathcal{L}) = \left\langle T, F \right \rangle$
, in which
-
•
 $T = \left \{c \in{\mathit{HB}}_P \mid c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{in}\right \}$
;
$T = \left \{c \in{\mathit{HB}}_P \mid c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{in}\right \}$
; -
•
 $F = \{c \in{\mathit{HB}}_P \mid c \not \in \mathcal{A}_P \textit{ or } c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{out} \}$
;
$F = \{c \in{\mathit{HB}}_P \mid c \not \in \mathcal{A}_P \textit{ or } c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{out} \}$
; -
•
 $\overline{T \cup F} = \left \{c \in{\mathit{HB}}_P \mid c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{undec}\right \}$
.
$\overline{T \cup F} = \left \{c \in{\mathit{HB}}_P \mid c \in \mathcal{A}_P \textit{ and } \mathcal{L}(c) = \mathtt{undec}\right \}$
.
We introduce a function
![]() $\mathcal{I}2\mathcal{L}_P : \mathcal{I}\mathit{nt} \to \mathcal{L}\mathit{ab}$
such that for any
$\mathcal{I}2\mathcal{L}_P : \mathcal{I}\mathit{nt} \to \mathcal{L}\mathit{ab}$
such that for any
![]() $\mathcal{I} = \left\langle T, F \right \rangle \in \mathcal{I}\mathit{nt}$
and any
$\mathcal{I} = \left\langle T, F \right \rangle \in \mathcal{I}\mathit{nt}$
and any
![]() $c \in \mathcal{A}_P$
,
$c \in \mathcal{A}_P$
,
-
•
 $\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{in}$
if
$\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{in}$
if
 $c\in T$
;
$c\in T$
; -
•
 $\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{out}$
if
$\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{out}$
if
 $c \in F$
;
$c \in F$
; -
•
 $\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{undec}$
if
$\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c) = \mathtt{undec}$
if
 $c \not \in T \cup F$
.
$c \not \in T \cup F$
.
![]() $\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c)$
is not defined if
$\mathcal{I}2\mathcal{L}_P(\mathcal{I})(c)$
is not defined if
![]() $c \not \in \mathcal{A}_P$
.
$c \not \in \mathcal{A}_P$
.
The correspondence between labelings and interpretations is clear for those atoms
![]() $c \in{\mathit{HB}}_P$
in which
$c \in{\mathit{HB}}_P$
in which
![]() $c \in \mathcal{A}_P$
. In this case, we have that
$c \in \mathcal{A}_P$
. In this case, we have that
![]() $c$
is interpreted as true iff
$c$
is interpreted as true iff
![]() $c$
is labeled as
$c$
is labeled as
![]() $\mathtt{in}$
;
$\mathtt{in}$
;
![]() $c$
is interpreted as false iff
$c$
is interpreted as false iff
![]() $c$
is labeled as
$c$
is labeled as
![]() $\mathtt{out}$
. In contradistinction, those atoms
$\mathtt{out}$
. In contradistinction, those atoms
![]() $c \in{\mathit{HB}}_P$
not associated with arguments (
$c \in{\mathit{HB}}_P$
not associated with arguments (
![]() $c \not \in \mathcal{A}_P$
) are simply interpreted as false. This will suffice to guarantee our results; next theorem assures us that
$c \not \in \mathcal{A}_P$
) are simply interpreted as false. This will suffice to guarantee our results; next theorem assures us that
![]() $\mathcal{I}2\mathcal{L}_P(\mathcal{L}2\mathcal{I}_P(\mathcal{L})) = \mathcal{L}$
:
$\mathcal{I}2\mathcal{L}_P(\mathcal{L}2\mathcal{I}_P(\mathcal{L})) = \mathcal{L}$
:
Theorem 3.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
![]() $\textit{SETAF}$
. For any labeling
$\textit{SETAF}$
. For any labeling
![]() $\mathcal{L}$
of
$\mathcal{L}$
of
![]() $\mathfrak{A}_P$
, it holds
$\mathfrak{A}_P$
, it holds
![]() $\mathcal{I}2\mathcal{L}_P(\mathcal{L}2\mathcal{I}_P(\mathcal{L})) = \mathcal{L}$
.
$\mathcal{I}2\mathcal{L}_P(\mathcal{L}2\mathcal{I}_P(\mathcal{L})) = \mathcal{L}$
.
In general,
![]() $\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{I}))$
is not equal to
$\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{I}))$
is not equal to
![]() $\mathcal{I}$
, because of those atoms
$\mathcal{I}$
, because of those atoms
![]() $c$
occurring in an
$c$
occurring in an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, but not in
$P$
, but not in
![]() $\mathcal{A}_P$
. However, when
$\mathcal{A}_P$
. However, when
![]() $\mathcal{M}$
is a partial stable model,
$\mathcal{M}$
is a partial stable model,
![]() $\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{M})) = \mathcal{M}$
:
$\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{M})) = \mathcal{M}$
:
Theorem 4.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
,
$\textit{NLP}$
,
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $\mathcal{M} = \left\langle T, F \right \rangle$
be a partial stable model of
$\mathcal{M} = \left\langle T, F \right \rangle$
be a partial stable model of
![]() $P$
. It holds that
$P$
. It holds that
![]() $\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{M})) = \mathcal{M}$
.
$\mathcal{L}2\mathcal{I}_P(\mathcal{I}2\mathcal{L}_P(\mathcal{M})) = \mathcal{M}$
.
This means that when restricted to partial stable models and complete labelings,
![]() $\mathcal{L}2\mathcal{I}_P$
and
$\mathcal{L}2\mathcal{I}_P$
and
![]() $\mathcal{I}2\mathcal{L}_P$
are each other’s inverse. From Lemma1, and Theorems3 and 4, we can obtain the following result:
$\mathcal{I}2\mathcal{L}_P$
are each other’s inverse. From Lemma1, and Theorems3 and 4, we can obtain the following result:
Theorem 5.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
![]() $\textit{SETAF}$
. It holds
$\textit{SETAF}$
. It holds
-
•
 $\mathcal{L}$
is a complete labeling of
$\mathcal{L}$
is a complete labeling of
 $\mathfrak{A}_P$
iff
$\mathfrak{A}_P$
iff
 $\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a partial stable model of
$\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a partial stable model of
 $P$
.
$P$
. -
•
 $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
 $P$
iff
$P$
iff
 $\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a complete labeling of
$\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a complete labeling of
 $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
.
Theorem5 is one of the main results of this paper. It plays a central role in ensuring the equivalence between the semantics for
![]() $\textit{NLP}$
and their counterpart for
$\textit{NLP}$
and their counterpart for
![]() $\textit{SETAF}$
:
$\textit{SETAF}$
:
Theorem 6.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
![]() $\textit{SETAF}$
. It holds
$\textit{SETAF}$
. It holds
-
1.
 $\mathcal{L}$
is a grounded labeling of
$\mathcal{L}$
is a grounded labeling of
 $\mathfrak{A}_P$
iff
$\mathfrak{A}_P$
iff
 $\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a well-founded model of
$\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a well-founded model of
 $P$
.
$P$
. -
2.
 $\mathcal{L}$
is a preferred labeling of
$\mathcal{L}$
is a preferred labeling of
 $\mathfrak{A}_P$
iff
$\mathfrak{A}_P$
iff
 $\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a regular model of
$\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a regular model of
 $P$
.
$P$
. -
3.
 $\mathcal{L}$
is a stable labeling of
$\mathcal{L}$
is a stable labeling of
 $\mathfrak{A}_P$
iff
$\mathfrak{A}_P$
iff
 $\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a stable model of
$\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is a stable model of
 $P$
.
$P$
. -
4.
 $\mathcal{L}$
is a semi-stable labeling of
$\mathcal{L}$
is a semi-stable labeling of
 $\mathfrak{A}_P$
iff
$\mathfrak{A}_P$
iff
 $\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is an
$\mathcal{L}2\mathcal{I}_P(\mathcal{L})$
is an
 $L$
-stable model of
$L$
-stable model of
 $P$
.
$P$
.
The following result is a direct consequence of Theorems4 and 6:
Corollary 7.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
$\mathfrak{A}_P = (\mathcal{A}_P, \mathit{Att}_P)$
be the associated
![]() $\textit{SETAF}$
. It holds
$\textit{SETAF}$
. It holds
-
1.
 $\mathcal{M}$
is a well-founded model of
$\mathcal{M}$
is a well-founded model of
 $P$
iff
$P$
iff
 $\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a grounded labeling of
$\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a grounded labeling of
 $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
. -
2.
 $\mathcal{M}$
is a regular model of
$\mathcal{M}$
is a regular model of
 $P$
iff
$P$
iff
 $\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a preferred labeling of
$\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a preferred labeling of
 $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
. -
3.
 $\mathcal{M}$
is a stable model of
$\mathcal{M}$
is a stable model of
 $P$
iff
$P$
iff
 $\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a stable labeling of
$\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a stable labeling of
 $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
. -
4.
 $\mathcal{M}$
is an
$\mathcal{M}$
is an
 $L$
-stable model of
$L$
-stable model of
 $P$
iff
$P$
iff
 $\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a semi-stable labeling of
$\mathcal{I}2\mathcal{L}_P(\mathcal{M})$
is a semi-stable labeling of
 $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
.
Next, we consider the
![]() $\textit{NLP}$
exploited by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) as a counterexample to show that in general,
$\textit{NLP}$
exploited by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b) as a counterexample to show that in general,
![]() $L$
-stable models and semi-stable labelings do not coincide with each other in their translation from
$L$
-stable models and semi-stable labelings do not coincide with each other in their translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\mathit{AAF}$
s:
$\mathit{AAF}$
s:
Example 4. Let
![]() $P$
be the
$P$
be the
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\mathfrak{A}_P$
be the associated
$\mathfrak{A}_P$
be the associated
![]() $\textit{SETAF}$
depicted in Figure 4:
$\textit{SETAF}$
depicted in Figure 4:

Fig. 4.
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
and its associated
$P$
and its associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P$
.
$\mathfrak{A}_P$
.
As expected from Theorems5 and 6, we obtain in Table 1 the equivalence between partial stable models and complete labelings, well-founded models and grounded labelings, regular models and preferred labelings, stable models and stable labelings,
![]() $L$
-stable models and semi-stable labelings. We emphasize the coincidence between
$L$
-stable models and semi-stable labelings. We emphasize the coincidence between
![]() $L$
-stable models and semi-stable labelings in Table 1 as it does not occur in the approach of Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). In their work, the associated
$L$
-stable models and semi-stable labelings in Table 1 as it does not occur in the approach of Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). In their work, the associated
![]() $\mathit{AAF}$
possesses two semi-stable labelings in contrast with the unique
$\mathit{AAF}$
possesses two semi-stable labelings in contrast with the unique
![]() $L$
-stable model
$L$
-stable model
![]() $\mathcal{M}_3$
of
$\mathcal{M}_3$
of
![]() $P$
. In the next two sections, we will show that this relation between
$P$
. In the next two sections, we will show that this relation between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s has even deeper implications.
$\textit{SETAF}$
s has even deeper implications.
4 From
 $\textit{SETAF}$
to
$\textit{SETAF}$
to
 $\textit{NLP}$
$\textit{NLP}$
Now we will provide a translation in the other direction, that is, from
![]() $\textit{SETAF}$
s to
$\textit{SETAF}$
s to
![]() $\textit{NLP}$
s. As in the previous section, this translation guarantees the equivalence between the semantics for
$\textit{NLP}$
s. As in the previous section, this translation guarantees the equivalence between the semantics for
![]() $\textit{NLP}$
s and their counterpart for
$\textit{NLP}$
s and their counterpart for
![]() $\textit{SETAF}$
s.
$\textit{SETAF}$
s.
Definition 12. Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\textit{SETAF}$
. For any argument
$\textit{SETAF}$
. For any argument
![]() $a \in \mathcal{A}$
, we will assume
$a \in \mathcal{A}$
, we will assume
![]() $\mathcal{V}_a = \{ V \mid V \textit{ is a minimal set (w.r.t. set inclusion) such that for each } \mathcal{B} \in \mathit{Att}(a), \textit{ there exists } b \in \mathcal{B} \cap V \}$
. We define the associated
$\mathcal{V}_a = \{ V \mid V \textit{ is a minimal set (w.r.t. set inclusion) such that for each } \mathcal{B} \in \mathit{Att}(a), \textit{ there exists } b \in \mathcal{B} \cap V \}$
. We define the associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
as follows:
$P_{\mathfrak{A}}$
as follows:
Example 5. Recall the
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
of Example 1 (it is the same as that in Figure 4
b). The associated
$\mathfrak{A}$
of Example 1 (it is the same as that in Figure 4
b). The associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
is
$P_{\mathfrak{A}}$
is
 \begin{equation*} \begin {array}{lcl} d \leftarrow \mathtt {not\ } d & & c \leftarrow \mathtt {not\ } c, \mathtt {not\ } d\\[5pt] a \leftarrow \mathtt {not\ } b & & b \leftarrow \mathtt {not\ } a\\[5pt] c \leftarrow \mathtt {not\ } c, \mathtt {not\ } a & & e \leftarrow \mathtt {not\ } e, \mathtt {not\ } b \end {array} \end{equation*}
\begin{equation*} \begin {array}{lcl} d \leftarrow \mathtt {not\ } d & & c \leftarrow \mathtt {not\ } c, \mathtt {not\ } d\\[5pt] a \leftarrow \mathtt {not\ } b & & b \leftarrow \mathtt {not\ } a\\[5pt] c \leftarrow \mathtt {not\ } c, \mathtt {not\ } a & & e \leftarrow \mathtt {not\ } e, \mathtt {not\ } b \end {array} \end{equation*}
Notice that
![]() $P_{\mathfrak{A}}$
and the
$P_{\mathfrak{A}}$
and the
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
of Example4 are the same. As it will be clear in the next section, this is not merely a coincidence. Besides, from Definition12, it is clear that
$P$
of Example4 are the same. As it will be clear in the next section, this is not merely a coincidence. Besides, from Definition12, it is clear that
![]() ${\mathit{HB}}_{P_{\mathfrak{A}}} = \mathcal{A}$
. Consequently, when considering a
${\mathit{HB}}_{P_{\mathfrak{A}}} = \mathcal{A}$
. Consequently, when considering a
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
and its associated
$\mathfrak{A}$
and its associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
, the definition of the function
$P_{\mathfrak{A}}$
, the definition of the function
![]() $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
(resp.,
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
(resp.,
![]() $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
), which associates labelings with interpretations (resp., interpretations with labelings), will be simpler than the definition of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
), which associates labelings with interpretations (resp., interpretations with labelings), will be simpler than the definition of
![]() $\mathcal{L}2\mathcal{I}_P$
(resp.,
$\mathcal{L}2\mathcal{I}_P$
(resp.,
![]() $\mathcal{I}2\mathcal{L}_P$
) presented in the previous section.
$\mathcal{I}2\mathcal{L}_P$
) presented in the previous section.
Definition 13 (
![]() $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
and
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
and
![]() $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
Functions). Let
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
Functions). Let
![]() $\mathfrak{A}$
be a
$\mathfrak{A}$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P$
be its associated
$P$
be its associated
![]() $\textit{NLP}$
,
$\textit{NLP}$
,
![]() $\mathcal{L}\mathit{ab}$
be the set of all labelings of
$\mathcal{L}\mathit{ab}$
be the set of all labelings of
![]() $\mathfrak{A}$
and
$\mathfrak{A}$
and
![]() $\mathcal{I}\mathit{nt}$
be the set of all the three-valued interpretations of
$\mathcal{I}\mathit{nt}$
be the set of all the three-valued interpretations of
![]() $P_{\mathfrak{A}}$
. We introduce the functions
$P_{\mathfrak{A}}$
. We introduce the functions
-
•
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}} : \mathcal{L}\mathit{ab} \to \mathcal{I}\mathit{nt}$
, in whichObviously
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}} : \mathcal{L}\mathit{ab} \to \mathcal{I}\mathit{nt}$
, in whichObviously \begin{equation*} \mathcal {L}2\mathcal {I}_{\mathfrak {A}}(\mathcal {L}) = \left\langle \mathtt {in}(\mathcal {L}), \mathtt {out}(\mathcal {L}) \right \rangle . \end{equation*}
\begin{equation*} \mathcal {L}2\mathcal {I}_{\mathfrak {A}}(\mathcal {L}) = \left\langle \mathtt {in}(\mathcal {L}), \mathtt {out}(\mathcal {L}) \right \rangle . \end{equation*}
 $\overline{\mathtt{in}(\mathcal{L}) \cup \mathtt{out}(\mathcal{L})} = \mathtt{undec}(\mathcal{L})$
.
$\overline{\mathtt{in}(\mathcal{L}) \cup \mathtt{out}(\mathcal{L})} = \mathtt{undec}(\mathcal{L})$
.
-
•
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}} : \mathcal{I}\mathit{nt} \to \mathcal{L}\mathit{ab}$
, in which for
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}} : \mathcal{I}\mathit{nt} \to \mathcal{L}\mathit{ab}$
, in which for
 $\mathcal{M} = \left\langle T, F \right \rangle \in \mathcal{I}\mathit{nt}$
,
$\mathcal{M} = \left\langle T, F \right \rangle \in \mathcal{I}\mathit{nt}$
, \begin{equation*} \mathcal {I}2\mathcal {L}_{\mathfrak {A}}(\mathcal {M}) = (T, F, \overline {T \cup F}). \end{equation*}
\begin{equation*} \mathcal {I}2\mathcal {L}_{\mathfrak {A}}(\mathcal {M}) = (T, F, \overline {T \cup F}). \end{equation*}
In contrast with
![]() $\mathcal{L}2\mathcal{I}_P$
and
$\mathcal{L}2\mathcal{I}_P$
and
![]() $\mathcal{I}2\mathcal{L}_P$
, the functions
$\mathcal{I}2\mathcal{L}_P$
, the functions
![]() $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
and
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}$
and
![]() $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
are each other’s inverse in the general case:
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}$
are each other’s inverse in the general case:
Table 1. Semantics for
![]() $P$
and
$P$
and
![]() $\mathfrak{A}_P$
$\mathfrak{A}_P$

Theorem 8.
Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P_{\mathfrak{A}}$
its associated
$P_{\mathfrak{A}}$
its associated
![]() $\textit{NLP}$
.
$\textit{NLP}$
.
-
• For any labeling
 $\mathcal{L}$
of
$\mathcal{L}$
of
 $\mathfrak{A}$
, it holds
$\mathfrak{A}$
, it holds
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})) = \mathcal{L}$
.
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})) = \mathcal{L}$
. -
• For any interpretation
 $\mathcal{I}$
of
$\mathcal{I}$
of
 $P_{\mathfrak{A}}$
, it holds
$P_{\mathfrak{A}}$
, it holds
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{I})) = \mathcal{I}$
.
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{I})) = \mathcal{I}$
.
A similar result to Theorem5 also holds here:
Theorem 9.
Let
![]() $\mathfrak{A}$
be a
$\mathfrak{A}$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P_{\mathfrak{A}}$
be its associated
$P_{\mathfrak{A}}$
be its associated
![]() $\textit{NLP}$
. It holds
$\textit{NLP}$
. It holds
-
•
 $\mathcal{L}$
is a complete labeling of
$\mathcal{L}$
is a complete labeling of
 $\mathfrak{A}$
iff
$\mathfrak{A}$
iff
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a partial stable model of
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a partial stable model of
 $P_{\mathfrak{A}}$
.
$P_{\mathfrak{A}}$
. -
•
 $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
 $P_{\mathfrak{A}}$
iff
$P_{\mathfrak{A}}$
iff
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a complete labeling of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a complete labeling of
 $\mathfrak{A}$
.
$\mathfrak{A}$
.
From Theorem9, we can ensure the equivalence between the semantics for
![]() $\textit{NLP}$
and their counterpart for
$\textit{NLP}$
and their counterpart for
![]() $\textit{SETAF}$
:
$\textit{SETAF}$
:
Theorem 10.
Let
![]() $\mathfrak{A}$
be a
$\mathfrak{A}$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P_{\mathfrak{A}}$
its associated
$P_{\mathfrak{A}}$
its associated
![]() $\textit{NLP}$
. It holds
$\textit{NLP}$
. It holds
-
1.
 $\mathcal{L}$
is a grounded labeling of
$\mathcal{L}$
is a grounded labeling of
 $\mathfrak{A}$
iff
$\mathfrak{A}$
iff
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a well-founded model of
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a well-founded model of
 $P_{\mathfrak{A}}$
.
$P_{\mathfrak{A}}$
. -
2.
 $\mathcal{L}$
is a preferred labeling of
$\mathcal{L}$
is a preferred labeling of
 $\mathfrak{A}$
iff
$\mathfrak{A}$
iff
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a regular model of
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a regular model of
 $P_{\mathfrak{A}}$
.
$P_{\mathfrak{A}}$
. -
3.
 $\mathcal{L}$
is a stable labeling of
$\mathcal{L}$
is a stable labeling of
 $\mathfrak{A}$
iff
$\mathfrak{A}$
iff
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a stable model of
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is a stable model of
 $P_{\mathfrak{A}}$
.
$P_{\mathfrak{A}}$
. -
4.
 $\mathcal{L}$
is a semi-stable labeling of
$\mathcal{L}$
is a semi-stable labeling of
 $\mathfrak{A}$
iff
$\mathfrak{A}$
iff
 $\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is an
$\mathcal{L}2\mathcal{I}_{\mathfrak{A}}(\mathcal{L})$
is an
 $L$
-stable model of
$L$
-stable model of
 $P_{\mathfrak{A}}$
.
$P_{\mathfrak{A}}$
.
The following result is a direct consequence of Theorems8 and 10:
Corollary 11.
Let
![]() $\mathfrak{A}$
be a
$\mathfrak{A}$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P_{\mathfrak{A}}$
its associated
$P_{\mathfrak{A}}$
its associated
![]() $\textit{NLP}$
. It holds
$\textit{NLP}$
. It holds
-
1.
 $\mathcal{M}$
is a well-founded model of
$\mathcal{M}$
is a well-founded model of
 $P_{\mathfrak{A}}$
iff
$P_{\mathfrak{A}}$
iff
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a grounded labeling of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a grounded labeling of
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
2.
 $\mathcal{M}$
is a regular model of
$\mathcal{M}$
is a regular model of
 $P_{\mathfrak{A}}$
iff
$P_{\mathfrak{A}}$
iff
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a preferred labeling of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a preferred labeling of
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
3.
 $\mathcal{M}$
is a stable model of
$\mathcal{M}$
is a stable model of
 $P_{\mathfrak{A}}$
iff
$P_{\mathfrak{A}}$
iff
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a stable labeling of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a stable labeling of
 $\mathfrak{A}$
.
$\mathfrak{A}$
. -
4.
 $\mathcal{M}$
is an
$\mathcal{M}$
is an
 $L$
-stable model of
$L$
-stable model of
 $P_{\mathfrak{A}}$
iff
$P_{\mathfrak{A}}$
iff
 $\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a semi-stable labeling of
$\mathcal{I}2\mathcal{L}_{\mathfrak{A}}(\mathcal{M})$
is a semi-stable labeling of
 $\mathfrak{A}$
.
$\mathfrak{A}$
.
Recalling the
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
and its associated
$\mathfrak{A}$
and its associated
![]() $P_{\mathfrak{A}}$
of Example5, we obtain the expected equivalence results related to their semantics (see Table 1). In the next section, we will identify a class of
$P_{\mathfrak{A}}$
of Example5, we obtain the expected equivalence results related to their semantics (see Table 1). In the next section, we will identify a class of
![]() $\textit{NLP}$
s in which the translation from a
$\textit{NLP}$
s in which the translation from a
![]() $\textit{SETAF}$
to an
$\textit{SETAF}$
to an
![]() $\textit{NLP}$
(Definition12) behaves as the inverse of the translation from an
$\textit{NLP}$
(Definition12) behaves as the inverse of the translation from an
![]() $\textit{NLP}$
to a
$\textit{NLP}$
to a
![]() $\textit{SETAF}$
(Definition10).
$\textit{SETAF}$
(Definition10).
5 On the relation between
 $\textit{RFALP}$
s and
$\textit{RFALP}$
s and
 $\textit{SETAF}$
s
$\textit{SETAF}$
s
We will recall a particular kind of
![]() $\textit{NLP}$
s, called Redundancy-Free Atomic Logic Programs
$\textit{NLP}$
s, called Redundancy-Free Atomic Logic Programs
![]() $(\textit{RFALP} s)$
. From an
$(\textit{RFALP} s)$
. From an
![]() $\textit{RFALP}$
$\textit{RFALP}$
![]() $P$
, we obtain its associated
$P$
, we obtain its associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P$
via Definition10; from
$\mathfrak{A}_P$
via Definition10; from
![]() $\mathfrak{A}_P$
, we obtain its associated
$\mathfrak{A}_P$
, we obtain its associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}_P}$
via Definition12. By following the other direction, from a
$P_{\mathfrak{A}_P}$
via Definition12. By following the other direction, from a
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
, we obtain its associated
$\mathfrak{A}$
, we obtain its associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
, and from
$P_{\mathfrak{A}}$
, and from
![]() $P_{\mathfrak{A}}$
, its associated
$P_{\mathfrak{A}}$
, its associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_{P_{\mathfrak{A}}}$
. An important result mentioned in this section is that
$\mathfrak{A}_{P_{\mathfrak{A}}}$
. An important result mentioned in this section is that
![]() $P = P_{\mathfrak{A}_P}$
and
$P = P_{\mathfrak{A}_P}$
and
![]() $\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}}}$
; that is, the translation from an
$\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}}}$
; that is, the translation from an
![]() $\textit{NLP}$
to a
$\textit{NLP}$
to a
![]() $\textit{SETAF}$
and the translation from a
$\textit{SETAF}$
and the translation from a
![]() $\textit{SETAF}$
to an
$\textit{SETAF}$
to an
![]() $\textit{NLP}$
are each other’s inverse. Next, we define
$\textit{NLP}$
are each other’s inverse. Next, we define
![]() $\textit{RFALP}$
s:
$\textit{RFALP}$
s:
Definition 14 (
![]() $\textit{RFALP}$
(König et al. Reference König, Rapberger and Ulbricht2022)). We define a Redundancy-Free Atomic Logic Program
$\textit{RFALP}$
(König et al. Reference König, Rapberger and Ulbricht2022)). We define a Redundancy-Free Atomic Logic Program
![]() $(\textit{RFALP})$
$(\textit{RFALP})$
![]() $P$
as an
$P$
as an
![]() $\textit{NLP}$
such that
$\textit{NLP}$
such that
-
1.
 $P$
is redundancy-free; that is,
$P$
is redundancy-free; that is,
 ${\mathit{HB}}_P = \left \{\mathit{head}(r) \mid r \in P\right \}$
, and if
${\mathit{HB}}_P = \left \{\mathit{head}(r) \mid r \in P\right \}$
, and if
 $c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P$
, there is no rule
$c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P$
, there is no rule
 $c \leftarrow \mathtt{not\ } c_1, \ldots, \mathtt{not\ } c_{n'} \in P$
such that
$c \leftarrow \mathtt{not\ } c_1, \ldots, \mathtt{not\ } c_{n'} \in P$
such that
 $\left \{c_1, \ldots, c_{n'}\right \} \subset \left \{b_1, \ldots, b_n\right \}$
.
$\left \{c_1, \ldots, c_{n'}\right \} \subset \left \{b_1, \ldots, b_n\right \}$
. -
2.
 $P$
is atomic; that is, each rule has the form
$P$
is atomic; that is, each rule has the form
 $c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n$
$c \leftarrow \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n$
 $(n \geq 0)$
.
$(n \geq 0)$
.
First, Proposition12 sustains that for any
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
, its associated
$\mathfrak{A}$
, its associated
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
will always be an
$P_{\mathfrak{A}}$
will always be an
![]() $\textit{RFALP}$
:
$\textit{RFALP}$
:
Proposition 12. Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\textit{SETAF}$
and
$\textit{SETAF}$
and
![]() $P_{\mathfrak{A}}$
its associated
$P_{\mathfrak{A}}$
its associated
![]() $\textit{NLP}$
. It holds
$\textit{NLP}$
. It holds
![]() $P_{\mathfrak{A}}$
is an
$P_{\mathfrak{A}}$
is an
![]() $\textit{RFALP}$
.
$\textit{RFALP}$
.
The following results guarantee that
![]() $\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}}}$
(Theorem13) and
$\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}}}$
(Theorem13) and
![]() $P = P_{\mathfrak{A}_P}$
(Theorem14):
$P = P_{\mathfrak{A}_P}$
(Theorem14):
Theorem 13.
Let
![]() $\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
$\mathfrak{A} = (\mathcal{A}, \mathit{Att})$
be a
![]() $\textit{SETAF}$
,
$\textit{SETAF}$
,
![]() $P_{\mathfrak{A}}$
its associated
$P_{\mathfrak{A}}$
its associated
![]() $\textit{NLP}$
, and
$\textit{NLP}$
, and
![]() $\mathfrak{A}_{P_{\mathfrak{A}}}$
the associated
$\mathfrak{A}_{P_{\mathfrak{A}}}$
the associated
![]() $\textit{SETAF}$
of
$\textit{SETAF}$
of
![]() $P_{\mathfrak{A}}$
. It holds that
$P_{\mathfrak{A}}$
. It holds that
![]() $\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}} }$
.
$\mathfrak{A} = \mathfrak{A}_{P_{\mathfrak{A}} }$
.
Theorem 14.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{RFALP}$
,
$\textit{RFALP}$
,
![]() $\mathfrak{A}_P$
its associated
$\mathfrak{A}_P$
its associated
![]() $\textit{SETAF}$
, and
$\textit{SETAF}$
, and
![]() $P_{\mathfrak{A}_P}$
the associated
$P_{\mathfrak{A}_P}$
the associated
![]() $\textit{NLP}$
of
$\textit{NLP}$
of
![]() $\mathfrak{A}_P$
. It holds that
$\mathfrak{A}_P$
. It holds that
![]() $P = P_{\mathfrak{A}_P}$
.
$P = P_{\mathfrak{A}_P}$
.
Remark 1. Minimality is crucial to ensure that the translation from an
![]() $\textit{NLP}$
to a
$\textit{NLP}$
to a
![]() $\textit{SETAF}$
and the translation from a
$\textit{SETAF}$
and the translation from a
![]() $\textit{SETAF}$
to an
$\textit{SETAF}$
to an
![]() $\textit{NLP}$
are each other’s inverse. If the minimality requirement in Definition 1 (and consequently in Definition 9) were dropped, any
$\textit{NLP}$
are each other’s inverse. If the minimality requirement in Definition 1 (and consequently in Definition 9) were dropped, any
![]() $\textit{SETAF}$
(among other combinations) in Figure 5 could be a possible candidate to be the associated
$\textit{SETAF}$
(among other combinations) in Figure 5 could be a possible candidate to be the associated
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P$
of the
$\mathfrak{A}_P$
of the
![]() $\textit{RFALP}$
$\textit{RFALP}$
![]() $P$
$P$

Fig. 5. Possible
![]() $\textit{SETAF}$
s associated with
$\textit{SETAF}$
s associated with
![]() $P$
.
$P$
.
As a result, Theorem 13 would no longer hold, and these translations would not be each other’s inverse. Notice also that the
![]() $\textit{SETAF}$
s in Figure 5 have the same complete labelings as non-minimal attacks are irrelevant and can be ignored when determining semantics based on complete labelings.
$\textit{SETAF}$
s in Figure 5 have the same complete labelings as non-minimal attacks are irrelevant and can be ignored when determining semantics based on complete labelings.
Theorems13 and 14 reveal that
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{RFALP}$
s are essentially the same formalism. The equivalence between them involves their semantics and is also structural: two distinct
$\textit{RFALP}$
s are essentially the same formalism. The equivalence between them involves their semantics and is also structural: two distinct
![]() $\textit{SETAF}$
s will always be translated into two distinct
$\textit{SETAF}$
s will always be translated into two distinct
![]() $\textit{RFALP}$
s and vice versa. In contradistinction, Theorem14 would not hold if we had replaced our translation from
$\textit{RFALP}$
s and vice versa. In contradistinction, Theorem14 would not hold if we had replaced our translation from
![]() $\textit{NLP}$
to
$\textit{NLP}$
to
![]() $\textit{SETAF}$
(Definition10) with that from
$\textit{SETAF}$
(Definition10) with that from
![]() $\textit{NLP}$
to
$\textit{NLP}$
to
![]() $\mathit{AAF}$
presented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). Thus, the connection between
$\mathit{AAF}$
presented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). Thus, the connection between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s is more robust than that between
$\textit{SETAF}$
s is more robust than that between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\mathit{AAF}$
s. In the forthcoming section, we will explore how expressive
$\mathit{AAF}$
s. In the forthcoming section, we will explore how expressive
![]() $\textit{RFALP}$
s can be; we will ensure they are as expressive as
$\textit{RFALP}$
s can be; we will ensure they are as expressive as
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
6 On the expressiveness of
 $\textit{RFALP}$
s
$\textit{RFALP}$
s
Dvořák et al. (Reference Dvořák, Fandinno and Woltran2019) comprehensively characterized the expressiveness of
![]() $\textit{SETAF}$
s. Now we compare the expressiveness of
$\textit{SETAF}$
s. Now we compare the expressiveness of
![]() $\textit{NLP}$
s with that of
$\textit{NLP}$
s with that of
![]() $\textit{RFALP}$
s. In the previous section, we established that
$\textit{RFALP}$
s. In the previous section, we established that
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{RFALP}$
s are essentially the same formalism. We demonstrated that from the
$\textit{RFALP}$
s are essentially the same formalism. We demonstrated that from the
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}_P$
associated with an
$\mathfrak{A}_P$
associated with an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, we can obtain
$P$
, we can obtain
![]() $P$
; and conversely, from the
$P$
; and conversely, from the
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_{\mathfrak{A}}$
associated with a
$P_{\mathfrak{A}}$
associated with a
![]() $\textit{SETAF}$
$\textit{SETAF}$
![]() $\mathfrak{A}$
, we can obtain
$\mathfrak{A}$
, we can obtain
![]() $\mathfrak{A}$
. Here, we reveal that this connection between
$\mathfrak{A}$
. Here, we reveal that this connection between
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{RFALP}$
s is even more substantial:
$\textit{RFALP}$
s is even more substantial:
![]() $\textit{RFALP}$
s are as expressive as
$\textit{RFALP}$
s are as expressive as
![]() $\textit{NLP}$
s when considering the semantics for
$\textit{NLP}$
s when considering the semantics for
![]() $\textit{NLP}$
s we have exploited in this paper. With this aim in mind, we transform any
$\textit{NLP}$
s we have exploited in this paper. With this aim in mind, we transform any
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
into an
$P$
into an
![]() $\textit{RFALP}$
$\textit{RFALP}$
![]() $P^*$
by resorting to a specific combination (denoted by
$P^*$
by resorting to a specific combination (denoted by
![]() $\mapsto _{\textit{UTPM}}$
) of some program transformations proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999). Although each program transformation in
$\mapsto _{\textit{UTPM}}$
) of some program transformations proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999). Although each program transformation in
![]() $\mapsto _{\textit{UTPM}}$
was proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999), the combination of these program transformations (as far as we know) has not been investigated yet. Then, we show that
$\mapsto _{\textit{UTPM}}$
was proposed by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999), the combination of these program transformations (as far as we know) has not been investigated yet. Then, we show that
![]() $P$
and
$P$
and
![]() $P^*$
share the same partial stable models. Since well-founded models, regular models, stable models, and
$P^*$
share the same partial stable models. Since well-founded models, regular models, stable models, and
![]() $L$
-stable models are all settled on partial stable models, it follows that both
$L$
-stable models are all settled on partial stable models, it follows that both
![]() $P$
and
$P$
and
![]() $P^*$
also coincide under these semantics. Based on Dunne et al.’s (Reference Dunne, Dvořák, Linsbichler and Woltran2015) work, where they define the notion of expressiveness of the semantics for
$P^*$
also coincide under these semantics. Based on Dunne et al.’s (Reference Dunne, Dvořák, Linsbichler and Woltran2015) work, where they define the notion of expressiveness of the semantics for
![]() $\mathit{AAF}$
s, we define formally expressiveness in terms of the signatures of the semantics for
$\mathit{AAF}$
s, we define formally expressiveness in terms of the signatures of the semantics for
![]() $\textit{NLP}$
s:
$\textit{NLP}$
s:
Definition 15 (Expressiveness). Let
![]() $\mathcal{P}$
be a class of
$\mathcal{P}$
be a class of
![]() $\textit{NLP}$
s. The signature
$\textit{NLP}$
s. The signature
![]() $\Sigma ^{\mathcal{P}}_{\mathit{PSM}}$
of the partial stable models associated with
$\Sigma ^{\mathcal{P}}_{\mathit{PSM}}$
of the partial stable models associated with
![]() $\mathcal{P}$
is defined as
$\mathcal{P}$
is defined as
where
![]() $\sigma (P) = \left \{\mathcal{I} \mid \mathcal{I} \textit{ is a partial stable model of } P\right \}$
is the set of all partial stable models of
$\sigma (P) = \left \{\mathcal{I} \mid \mathcal{I} \textit{ is a partial stable model of } P\right \}$
is the set of all partial stable models of
![]() $P$
.
$P$
.
Given two classes
![]() $\mathcal{P}_1$
and
$\mathcal{P}_1$
and
![]() $\mathcal{P}_2$
of
$\mathcal{P}_2$
of
![]() $\textit{NLP}$
s, we say that
$\textit{NLP}$
s, we say that
![]() $\mathcal{P}_1$
and
$\mathcal{P}_1$
and
![]() $\mathcal{P}_2$
have the same expressiveness for the partial stable models semantics if
$\mathcal{P}_2$
have the same expressiveness for the partial stable models semantics if
![]() $\Sigma ^{\mathcal{P}_1}_{\mathit{PSM}} = \Sigma ^{\mathcal{P}_2}_{\mathit{PSM}}$
$\Sigma ^{\mathcal{P}_1}_{\mathit{PSM}} = \Sigma ^{\mathcal{P}_2}_{\mathit{PSM}}$
In other words,
![]() $\mathcal{P}_1$
and
$\mathcal{P}_1$
and
![]() $\mathcal{P}_2$
have the same expressiveness if
$\mathcal{P}_2$
have the same expressiveness if
-
• For every
 $P_1 \in \mathcal{P}_1$
, there exists
$P_1 \in \mathcal{P}_1$
, there exists
 $P_2 \in \mathcal{P}_2$
such that
$P_2 \in \mathcal{P}_2$
such that
 $P_1$
and
$P_1$
and
 $P_2$
have the same set of partial stable models.
$P_2$
have the same set of partial stable models. -
• For every
 $P_2 \in \mathcal{P}_2$
, there exists
$P_2 \in \mathcal{P}_2$
, there exists
 $P_1 \in \mathcal{P}_1$
such that
$P_1 \in \mathcal{P}_1$
such that
 $P_1$
and
$P_1$
and
 $P_2$
have the same set of partial stable models.
$P_2$
have the same set of partial stable models.
Similarly, we can define when
![]() $\mathcal{P}_1$
and
$\mathcal{P}_1$
and
![]() $\mathcal{P}_2$
have the same expressiveness for the well-founded, regular, stable, and
$\mathcal{P}_2$
have the same expressiveness for the well-founded, regular, stable, and
![]() $L$
-stable semantics.
$L$
-stable semantics.
As the class of
![]() $\textit{RFALP}$
s is contained in the class of all
$\textit{RFALP}$
s is contained in the class of all
![]() $\textit{NLP}$
s, to show that these classes have the same expressiveness for these semantics, it suffices to prove that for every
$\textit{NLP}$
s, to show that these classes have the same expressiveness for these semantics, it suffices to prove that for every
![]() $\textit{NLP}$
, there exists an
$\textit{NLP}$
, there exists an
![]() $\textit{RFALP}$
with the same set of partial stable models. We will obtain this result by resorting to a combination of program transformations:
$\textit{RFALP}$
with the same set of partial stable models. We will obtain this result by resorting to a combination of program transformations:
Definition 16 (Program Transformation (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999)). A program transformation is any binary relation
![]() $\mapsto$
between
$\mapsto$
between
![]() $\textit{NLP}$
s. By
$\textit{NLP}$
s. By
![]() $\mapsto ^*$
we mean the reflexive and transitive closure of
$\mapsto ^*$
we mean the reflexive and transitive closure of
![]() $\mapsto$
.
$\mapsto$
.
Thus,
![]() $P \mapsto ^* P'$
means that there is a finite sequence
$P \mapsto ^* P'$
means that there is a finite sequence
![]() $P = P_1 \mapsto \cdots \mapsto P_n = P'$
. We are particularly interested in program transformations preserving partial stable models:
$P = P_1 \mapsto \cdots \mapsto P_n = P'$
. We are particularly interested in program transformations preserving partial stable models:
Definition 17 (Equivalence Transformation (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999)). We say a program transformation
![]() $\mapsto$
is a partial stable model equivalence transformation if for any
$\mapsto$
is a partial stable model equivalence transformation if for any
![]() $\textit{NLP}$
s
$\textit{NLP}$
s
![]() $P_1$
and
$P_1$
and
![]() $P_2$
with
$P_2$
with
![]() $P_1 \mapsto P_2$
, it holds
$P_1 \mapsto P_2$
, it holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_2$
.
$P_2$
.
From Definitions18 to 21, we focus on the following program transformations introduced by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999): Unfolding (it is also known as Generalized Principle of Partial Evaluation (GPPE)), elimination of tautologies, positive reduction, and elimination of non-minimal Rules. They are sufficient for our purposes.
Definition 18 (Unfolding (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999)). An
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_2$
results from an
$P_2$
results from an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_1$
by unfolding (
$P_1$
by unfolding (
![]() $P_1 \mapsto _U P_2$
) iff there exists a rule
$P_1 \mapsto _U P_2$
) iff there exists a rule
![]() $c \leftarrow a, a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P_1$
such that
$c \leftarrow a, a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P_1$
such that
 \begin{align*} P_2 = &\ (P_1 - \left \{c \leftarrow a, a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \})\\[5pt] & \hspace{5em} \cup \{c \leftarrow a_1', \ldots, a_p', a_1, \ldots, a_m, \mathtt{not\ } b_1', \ldots, \mathtt{not\ } b_q', \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \mid \\[5pt] & \hspace{6.675em} a \leftarrow a_1', \ldots, a_p', \mathtt{not\ } b_1', \ldots, \mathtt{not\ } b_q' \in P_1 \}. \end{align*}
\begin{align*} P_2 = &\ (P_1 - \left \{c \leftarrow a, a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \})\\[5pt] & \hspace{5em} \cup \{c \leftarrow a_1', \ldots, a_p', a_1, \ldots, a_m, \mathtt{not\ } b_1', \ldots, \mathtt{not\ } b_q', \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \mid \\[5pt] & \hspace{6.675em} a \leftarrow a_1', \ldots, a_p', \mathtt{not\ } b_1', \ldots, \mathtt{not\ } b_q' \in P_1 \}. \end{align*}
Definition 19 (Elimination of Tautologies (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999)). An
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_2$
results from an
$P_2$
results from an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_1$
by elimination of tautologies (
$P_1$
by elimination of tautologies (
![]() $P_1 \mapsto _T P_2$
) iff there exists a rule
$P_1 \mapsto _T P_2$
) iff there exists a rule
![]() $r \in P_1$
such that
$r \in P_1$
such that
![]() ${\mathit{head}}(r) \in \mathit{body}^+(r)$
and
${\mathit{head}}(r) \in \mathit{body}^+(r)$
and
![]() $P_2 = P_1 - \left \{r\right \}$
.
$P_2 = P_1 - \left \{r\right \}$
.
Definition 20 (Positive Reduction (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1999)). An
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_2$
results from an
$P_2$
results from an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_1$
by positive reduction (
$P_1$
by positive reduction (
![]() $P_1 \mapsto _P P_2$
) iff there exists a rule
$P_1 \mapsto _P P_2$
) iff there exists a rule
![]() $c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P_1$
such that
$c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n \in P_1$
such that
![]() $b \not \in \left \{{\mathit{head}}(r) \mid r \in P_1\right \}$
and
$b \not \in \left \{{\mathit{head}}(r) \mid r \in P_1\right \}$
and
 \begin{align*} P_2 = &\ (P_1 - \left \{c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \})\\[5pt] & \hspace{4.475em} \cup \left \{c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}. \end{align*}
\begin{align*} P_2 = &\ (P_1 - \left \{c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \})\\[5pt] & \hspace{4.475em} \cup \left \{c \leftarrow a_1, \ldots, a_m, \mathtt{not\ } b_1, \ldots, \mathtt{not\ } b_n\right \}. \end{align*}
Definition 21 (Elimination of Non-Minimal Rules (Brass and Dix, Reference Brass and Dix1994, Reference Brass and Dix1999)). An
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_2$
results from an
$P_2$
results from an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P_1$
by elimination of non-minimal rules (
$P_1$
by elimination of non-minimal rules (
![]() $P_1 \mapsto _M P_2$
) iff there are two distinct rules
$P_1 \mapsto _M P_2$
) iff there are two distinct rules
![]() $r$
and
$r$
and
![]() $r'$
in
$r'$
in
![]() $P_1$
such that
$P_1$
such that
![]() ${\mathit{head}}(r) ={\mathit{head}}(r')$
,
${\mathit{head}}(r) ={\mathit{head}}(r')$
,
![]() $\mathit{body}^+(r') \subseteq \mathit{body}^+(r)$
,
$\mathit{body}^+(r') \subseteq \mathit{body}^+(r)$
,
![]() $\mathit{body}^-(r') \subseteq \mathit{body}^-(r)$
and
$\mathit{body}^-(r') \subseteq \mathit{body}^-(r)$
and
![]() $P_2 = P_1 - \left \{r\right \}$
.
$P_2 = P_1 - \left \{r\right \}$
.
Now we combine these program transformations and define
![]() $\mapsto _{\textit{UTPM}}$
as follows:
$\mapsto _{\textit{UTPM}}$
as follows:
Definition 22 (Combined Transformation). Let
![]() $\mapsto _{\textit{UTPM}} = \mapsto _U \cup \mapsto _T \cup \mapsto _P \cup \mapsto _M$
.
$\mapsto _{\textit{UTPM}} = \mapsto _U \cup \mapsto _T \cup \mapsto _P \cup \mapsto _M$
.
We call an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
irreducible concerning
$P$
irreducible concerning
![]() $\mapsto$
if there is no
$\mapsto$
if there is no
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P' \neq P$
with
$P' \neq P$
with
![]() $P \mapsto ^* P'$
. Besides, we say
$P \mapsto ^* P'$
. Besides, we say
![]() $\mapsto$
is strongly terminating iff every sequence of successive applications of
$\mapsto$
is strongly terminating iff every sequence of successive applications of
![]() $\mapsto$
eventually leads to an irreducible
$\mapsto$
eventually leads to an irreducible
![]() $\textit{NLP}$
. As displayed by Brass and Dix (Reference Brass and Dix1998), not every program transformation is strongly terminating. For instance, in the
$\textit{NLP}$
. As displayed by Brass and Dix (Reference Brass and Dix1998), not every program transformation is strongly terminating. For instance, in the
![]() $\textit{NLP}$
$\textit{NLP}$
 \begin{equation*} \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \end{equation*}
\begin{equation*} \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \end{equation*}
if we apply unfolding
![]() $(\mapsto _U)$
to the third rule, this rule is replaced by
$(\mapsto _U)$
to the third rule, this rule is replaced by
![]() $c \leftarrow b, \mathtt{not\ } c$
. We can now apply unfolding again to this rule and get the original program; such an oscillation can repeat indefinitely. Thus we have a sequence of program transformations that do not terminate. However, if we restrict ourselves to fair sequences of program transformations, the termination is guaranteed:
$c \leftarrow b, \mathtt{not\ } c$
. We can now apply unfolding again to this rule and get the original program; such an oscillation can repeat indefinitely. Thus we have a sequence of program transformations that do not terminate. However, if we restrict ourselves to fair sequences of program transformations, the termination is guaranteed:
Definition 23 (Fair Sequences (Brass and Dix, Reference Brass and Dix1998)). A sequence of program transformations
![]() $P_1 \mapsto \cdots \mapsto P_n$
is fair with respect to
$P_1 \mapsto \cdots \mapsto P_n$
is fair with respect to
![]() $\mapsto$
if
$\mapsto$
if
-
• Every positive body atom occurring in
 $P_1$
is eventually removed in some
$P_1$
is eventually removed in some
 $P_i$
with
$P_i$
with
 $1 \lt i \leq n$
(either by removing the whole rule using a suitable program transformation or by an application of
$1 \lt i \leq n$
(either by removing the whole rule using a suitable program transformation or by an application of
 $\mapsto _U$
);
$\mapsto _U$
); -
• Every rule
 $r \in P_i$
such that
$r \in P_i$
such that
 ${\mathit{head}}(r) \in \mathit{body}^+(r)$
is eventually removed in some
${\mathit{head}}(r) \in \mathit{body}^+(r)$
is eventually removed in some
 $P_j$
with
$P_j$
with
 $i \lt j \leq n$
(either by applying
$i \lt j \leq n$
(either by applying
 $\mapsto _T$
or another suitable program transformation).
$\mapsto _T$
or another suitable program transformation).
The sequence above of program transformations is not fair, because it does not remove the positive body atoms occurring in the program. In contrast, the sequence of program transformations given by
 \begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
\begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
is not only fair but also terminates. The next result guarantees that it is not simply a coincidence:
Theorem 15.
The relation
![]() $\mapsto _{\textit{UTPM}}$
is strongly terminating for fair sequences of program transformations; that is, such fair sequences always lead to irreducible programs.
$\mapsto _{\textit{UTPM}}$
is strongly terminating for fair sequences of program transformations; that is, such fair sequences always lead to irreducible programs.
Theorem15 is crucial to obtain the following result:
Theorem 16.
For any
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, there exists an irreducible
$P$
, there exists an irreducible
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P^*$
such that
$P^*$
such that
![]() $P \mapsto ^*_{\textit{UTPM}} P^*$
.
$P \mapsto ^*_{\textit{UTPM}} P^*$
.
This means that from an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, it is always possible to obtain an irreducible
$P$
, it is always possible to obtain an irreducible
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P^*$
after successive applications of
$P^*$
after successive applications of
![]() $\mapsto _{\textit{UTPM}}$
. Indeed,
$\mapsto _{\textit{UTPM}}$
. Indeed,
![]() $P^*$
is an
$P^*$
is an
![]() $\textit{RFALP}$
:
$\textit{RFALP}$
:
Theorem 17.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $P^*$
be an
$P^*$
be an
![]() $\textit{NLP}$
obtained after applying repeatedly the program transformation
$\textit{NLP}$
obtained after applying repeatedly the program transformation
![]() $\mapsto _{\textit{UTPM}}$
until no further transformation is possible; that is,
$\mapsto _{\textit{UTPM}}$
until no further transformation is possible; that is,
![]() $P \mapsto ^*_{\textit{UTPM}} P^*$
and
$P \mapsto ^*_{\textit{UTPM}} P^*$
and
![]() $P^*$
is irreducible. Then
$P^*$
is irreducible. Then
![]() $P^*$
is an
$P^*$
is an
![]() $\textit{RFALP}$
.
$\textit{RFALP}$
.
From Theorems15 and 17, we can infer that for fair sequences, after applying repeatedly
![]() $\mapsto _{\textit{UTPM}}$
, we will eventually produce an
$\mapsto _{\textit{UTPM}}$
, we will eventually produce an
![]() $\textit{RFALP}$
. In fact, every
$\textit{RFALP}$
. In fact, every
![]() $\textit{RFALP}$
is irreducible:
$\textit{RFALP}$
is irreducible:
Theorem 18.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{RFALP}$
. Then
$\textit{RFALP}$
. Then
![]() $P$
is irreducible with respect to
$P$
is irreducible with respect to
![]() $\mapsto _{\textit{UTPM}}$
.
$\mapsto _{\textit{UTPM}}$
.
Theorems16 and 17 guarantee that every
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
can be transformed into an
$P$
can be transformed into an
![]() $\textit{RFALP}$
$\textit{RFALP}$
![]() $P^*$
by applying
$P^*$
by applying
![]() $\mapsto _{\textit{UTPM}}$
a finite number of times. It remains to show that
$\mapsto _{\textit{UTPM}}$
a finite number of times. It remains to show that
![]() $P$
and
$P$
and
![]() $P^*$
share the same partial stable models (and consequently, the same well-founded, regular, stable, and
$P^*$
share the same partial stable models (and consequently, the same well-founded, regular, stable, and
![]() $L$
-stable models). Before, however, note that
$L$
-stable models). Before, however, note that
![]() $\mapsto _{\textit{UTPM}}$
does not introduce new atoms; instead, it can eliminate the occurrence of existing atoms in an
$\mapsto _{\textit{UTPM}}$
does not introduce new atoms; instead, it can eliminate the occurrence of existing atoms in an
![]() $\textit{NLP}$
. For simplicity in notation, we assume throughout the rest of this section that
$\textit{NLP}$
. For simplicity in notation, we assume throughout the rest of this section that
![]() ${\mathit{HB}}_P ={\mathit{HB}}_{P'}$
whenever
${\mathit{HB}}_P ={\mathit{HB}}_{P'}$
whenever
![]() $P \mapsto _{\textit{UTPM}}^* P'$
. Next, we recall that these program transformations preserve the least models of positive programs:
$P \mapsto _{\textit{UTPM}}^* P'$
. Next, we recall that these program transformations preserve the least models of positive programs:
Lemma 19 (Brass and Dix, Reference Brass and Dix1995, Reference Brass and Dix1997). Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be positive programs such that
$P_2$
be positive programs such that
![]() $P_1 \mapsto _x P_2$
, in which
$P_1 \mapsto _x P_2$
, in which
![]() $x \in \left \{U,T,P,M\right \}$
. It holds
$x \in \left \{U,T,P,M\right \}$
. It holds
![]() $\mathcal{M}$
is the least model of
$\mathcal{M}$
is the least model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is the least model of
$\mathcal{M}$
is the least model of
![]() $P_2$
.
$P_2$
.
In the sequel, we aim to extend Lemma19 to
![]() $\textit{NLP}$
s. Notice, however, that we already have the result for the program transformation
$\textit{NLP}$
s. Notice, however, that we already have the result for the program transformation
![]() $\mapsto _U$
:
$\mapsto _U$
:
Theorem 20 (Aravindan and Minh Reference Aravindan and Minh1995). Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be
$P_2$
be
![]() $\textit{NLP}$
s such that
$\textit{NLP}$
s such that
![]() $P_1 \mapsto _U P_2$
. It holds
$P_1 \mapsto _U P_2$
. It holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_2$
.
$P_2$
.
It remains to guarantee the result for the program transformation
![]() $\mapsto _T$
,
$\mapsto _T$
,
![]() $\mapsto _P$
and
$\mapsto _P$
and
![]() $\mapsto _M$
:
$\mapsto _M$
:
Theorem 21.
Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be
$P_2$
be
![]() $\textit{NLP}$
s such that
$\textit{NLP}$
s such that
![]() $P_1 \mapsto _T P_2$
. It holds
$P_1 \mapsto _T P_2$
. It holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_2$
.
$P_2$
.
Theorem 22.
Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be
$P_2$
be
![]() $\textit{NLP}$
s such that
$\textit{NLP}$
s such that
![]() $P_1 \mapsto _P P_2$
. It holds
$P_1 \mapsto _P P_2$
. It holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_2$
.
$P_2$
.
Theorem 23.
Let
![]() $P_1$
and
$P_1$
and
![]() $P_2$
be
$P_2$
be
![]() $\textit{NLP}$
s such that
$\textit{NLP}$
s such that
![]() $P_1 \mapsto _M P_2$
. It holds
$P_1 \mapsto _M P_2$
. It holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_1$
iff
$P_1$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P_2$
.
$P_2$
.
Consequently, if
![]() $P_1 \mapsto _{\textit{UTPM}} P_2$
, then
$P_1 \mapsto _{\textit{UTPM}} P_2$
, then
![]() $P_1$
and
$P_1$
and
![]() $P_2$
share the same partial stable models. By repeatedly resorting to this result, we can even show that for any
$P_2$
share the same partial stable models. By repeatedly resorting to this result, we can even show that for any
![]() $\textit{NLP}$
, there exists an irreducible
$\textit{NLP}$
, there exists an irreducible
![]() $\textit{NLP}$
with the same set of partial stable models, well-founded models, regular models, stable models, and
$\textit{NLP}$
with the same set of partial stable models, well-founded models, regular models, stable models, and
![]() $L$
-stable models:
$L$
-stable models:
Theorem 24.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $P^*$
be an irreducible
$P^*$
be an irreducible
![]() $\textit{NLP}$
such that
$\textit{NLP}$
such that
![]() $P \mapsto ^*_{\textit{UTPM}} P^*$
. It holds
$P \mapsto ^*_{\textit{UTPM}} P^*$
. It holds
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P$
iff
$P$
iff
![]() $\mathcal{M}$
is a partial stable model of
$\mathcal{M}$
is a partial stable model of
![]() $P^*$
.
$P^*$
.
Corollary 25.
Let
![]() $P$
be an
$P$
be an
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $P^*$
be an irreducible
$P^*$
be an irreducible
![]() $\textit{NLP}$
such that
$\textit{NLP}$
such that
![]() $P \mapsto ^*_{\textit{UTPM}} P^*$
. It holds
$P \mapsto ^*_{\textit{UTPM}} P^*$
. It holds
![]() $\mathcal{M}$
is a well-founded, regular, stable,
$\mathcal{M}$
is a well-founded, regular, stable,
![]() $L$
-stable model of
$L$
-stable model of
![]() $P$
iff
$P$
iff
![]() $\mathcal{M}$
is, respectively, a well-founded, regular, stable,
$\mathcal{M}$
is, respectively, a well-founded, regular, stable,
![]() $L$
-stable model of
$L$
-stable model of
![]() $P^*$
.
$P^*$
.
As any irreducible
![]() $\textit{NLP}$
is an
$\textit{NLP}$
is an
![]() $\textit{RFALP}$
(Theorem17), the following result is immediate:
$\textit{RFALP}$
(Theorem17), the following result is immediate:
Corollary 26.
For any
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
, there exists an
$P$
, there exists an
![]() $\textit{RFALP}$
$\textit{RFALP}$
![]() $P^*$
such that
$P^*$
such that
![]() $\mathcal{M}$
is a partial stable, well-founded, regular, stable,
$\mathcal{M}$
is a partial stable, well-founded, regular, stable,
![]() $L$
-stable model of
$L$
-stable model of
![]() $P$
iff
$P$
iff
![]() $\mathcal{M}$
is, respectively, a partial stable, well-founded, regular, stable,
$\mathcal{M}$
is, respectively, a partial stable, well-founded, regular, stable,
![]() $L$
-stable model of
$L$
-stable model of
![]() $P^*$
.
$P^*$
.
Given that each
![]() $\textit{NLP}$
can be associated with an
$\textit{NLP}$
can be associated with an
![]() $\textit{RFALP}$
preserving the semantics above, it follows that
$\textit{RFALP}$
preserving the semantics above, it follows that
![]() $\textit{NLP}$
and
$\textit{NLP}$
and
![]() $\textit{RFALP}$
s have the same expressiveness for those semantics:
$\textit{RFALP}$
s have the same expressiveness for those semantics:
Theorem 27.
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{RFALP}$
s have the same expressiveness for partial stable, well-founded, regular, stable, and
$\textit{RFALP}$
s have the same expressiveness for partial stable, well-founded, regular, stable, and
![]() $L$
-stable semantics.
$L$
-stable semantics.
Another important result is that the
![]() $\textit{SETAF}$
corresponding to an
$\textit{SETAF}$
corresponding to an
![]() $\textit{NLP}$
is invariant with respect to
$\textit{NLP}$
is invariant with respect to
![]() $\mapsto _{\textit{UTPM}}$
:
$\mapsto _{\textit{UTPM}}$
:
Theorem 28.
For any
![]() $\textit{NLP}$
s
$\textit{NLP}$
s
![]() $P_1$
and
$P_1$
and
![]() $P_2$
, if
$P_2$
, if
![]() $P_1 \mapsto _{\textit{UTPM}} P_2$
, then
$P_1 \mapsto _{\textit{UTPM}} P_2$
, then
![]() $\mathfrak{A}_{P_1} = \mathfrak{A}_{P_2}$
$\mathfrak{A}_{P_1} = \mathfrak{A}_{P_2}$
This means that any
![]() $\textit{NLP}$
in a sequence of program transformations from
$\textit{NLP}$
in a sequence of program transformations from
![]() $\mapsto _{\textit{UTPM}}$
has the same corresponding
$\mapsto _{\textit{UTPM}}$
has the same corresponding
![]() $\textit{SETAF}$
. For instance, every
$\textit{SETAF}$
. For instance, every
![]() $\textit{NLP}$
in this sequence
$\textit{NLP}$
in this sequence
 \begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
\begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
leads to the same corresponding
![]() $\textit{SETAF}$
, constituted by a unique (unattacked) argument:
$\textit{SETAF}$
, constituted by a unique (unattacked) argument:
Theorem28 also suggests an alternative way to find the
![]() $\textit{SETAF}$
corresponding to an
$\textit{SETAF}$
corresponding to an
![]() $\textit{NLP}$
$\textit{NLP}$
![]() $P$
: instead of resorting directly to Definition8 to construct the arguments, we can apply (starting from
$P$
: instead of resorting directly to Definition8 to construct the arguments, we can apply (starting from
![]() $P$
)
$P$
)
![]() $\mapsto _{\textit{UTPM}}$
successively by following a fair sequence of program transformations. By Theorems15 and 17, we know that eventually, we will reach an
$\mapsto _{\textit{UTPM}}$
successively by following a fair sequence of program transformations. By Theorems15 and 17, we know that eventually, we will reach an
![]() $\textit{RFALP}$
whose corresponding
$\textit{RFALP}$
whose corresponding
![]() $\textit{SETAF}$
is identical to that of the original program
$\textit{SETAF}$
is identical to that of the original program
![]() $P$
(Theorem28). Then, we apply Definition8 to this
$P$
(Theorem28). Then, we apply Definition8 to this
![]() $\textit{RFALP}$
to obtain the arguments and Definition9 for the attack relation. Notably, when
$\textit{RFALP}$
to obtain the arguments and Definition9 for the attack relation. Notably, when
![]() $P$
is an
$P$
is an
![]() $\textit{RFALP}$
, Definition8 becomes considerably simpler, requiring only its first item to characterize the statements.
$\textit{RFALP}$
, Definition8 becomes considerably simpler, requiring only its first item to characterize the statements.
In addition, from the same
![]() $\textit{NLP}$
, various fair sequences of program transformations can be conceived. Recalling the
$\textit{NLP}$
, various fair sequences of program transformations can be conceived. Recalling the
![]() $\textit{NLP}$
$\textit{NLP}$
 \begin{equation*} \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \end{equation*}
\begin{equation*} \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \end{equation*}
exploited above, we can design the following alternative fair sequence
 \begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _M \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & b\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} a & \leftarrow & b\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
\begin{equation*} \small { \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & a\\[5pt] c & \leftarrow & a, \mathtt {not\ } c\\[5pt] c \end {array} \mapsto _M \begin {array}{rcl} a & \leftarrow & a\\[5pt] b & \leftarrow & a\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} a & \leftarrow & b\\[5pt] b & \leftarrow & b\\[5pt] c \end {array} \mapsto _T \begin {array}{rcl} a & \leftarrow & b\\[5pt] c \end {array} \mapsto _U \begin {array}{rcl} c \end {array} } \end{equation*}
This sequence produced the same
![]() $\textit{RFALP}$
as before; it is not a coincidence. Apart from being strongly terminating for fair sequences of program transformations, the relation
$\textit{RFALP}$
as before; it is not a coincidence. Apart from being strongly terminating for fair sequences of program transformations, the relation
![]() $\mapsto _{\textit{UTPM}}$
has an appealing property; it is also confluent:
$\mapsto _{\textit{UTPM}}$
has an appealing property; it is also confluent:
Theorem 29.
The relation
![]() $\mapsto _{\textit{UTPM}}$
is confluent; that is, for any
$\mapsto _{\textit{UTPM}}$
is confluent; that is, for any
![]() $\textit{NLP}$
s
$\textit{NLP}$
s
![]() $P$
,
$P$
,
![]() $P'$
and
$P'$
and
![]() $P''$
, if
$P''$
, if
![]() $P \mapsto _{\textit{UTPM}}^* P'$
and
$P \mapsto _{\textit{UTPM}}^* P'$
and
![]() $P \mapsto _{\textit{UTPM}}^* P''$
and both
$P \mapsto _{\textit{UTPM}}^* P''$
and both
![]() $P'$
and
$P'$
and
![]() $P''$
are irreducible, then
$P''$
are irreducible, then
![]() $P' = P''$
.
$P' = P''$
.
By confluent
![]() $\mapsto _{\textit{UTPM}}$
, we mean that it does not matter the path we take by repeatedly applying
$\mapsto _{\textit{UTPM}}$
, we mean that it does not matter the path we take by repeatedly applying
![]() $\mapsto _{\textit{UTPM}}$
, if it ends, it will always lead to the same irreducible
$\mapsto _{\textit{UTPM}}$
, if it ends, it will always lead to the same irreducible
![]() $\textit{NLP}$
. In addition, as any irreducible
$\textit{NLP}$
. In addition, as any irreducible
![]() $\textit{NLP}$
is an
$\textit{NLP}$
is an
![]() $\textit{RFALP}$
(Theorem17), and the translations from
$\textit{RFALP}$
(Theorem17), and the translations from
![]() $\textit{SETAF}$
to
$\textit{SETAF}$
to
![]() $\textit{RFALP}$
s and conversely, from
$\textit{RFALP}$
s and conversely, from
![]() $\textit{RFALP}$
s to
$\textit{RFALP}$
s to
![]() $\textit{SETAF}$
are each other’s inverse (Theorems13 and 14), we obtain that two distinct
$\textit{SETAF}$
are each other’s inverse (Theorems13 and 14), we obtain that two distinct
![]() $\textit{SETAF}$
s will always be associated with two distinct
$\textit{SETAF}$
s will always be associated with two distinct
![]() $\textit{NLP}$
s. The confluence of
$\textit{NLP}$
s. The confluence of
![]() $\mapsto _{\textit{UTPM}}$
is of particular significance from the logic programming perspective as it guarantees that the ordering of the transformations in
$\mapsto _{\textit{UTPM}}$
is of particular significance from the logic programming perspective as it guarantees that the ordering of the transformations in
![]() $\textit{UTPM}$
does not matter: we are free to choose always the “best” transformation, which maximally reduces the program. Consequently, Theorem29 also sheds light on the search for efficient implementations in
$\textit{UTPM}$
does not matter: we are free to choose always the “best” transformation, which maximally reduces the program. Consequently, Theorem29 also sheds light on the search for efficient implementations in
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
From the previous section, we know that the equivalence between
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{RFALP}$
s is not only of a semantic nature but also structural: two distinct
$\textit{RFALP}$
s is not only of a semantic nature but also structural: two distinct
![]() $\textit{SETAF}$
s will always be translated into two distinct
$\textit{SETAF}$
s will always be translated into two distinct
![]() $\textit{RFALP}$
s and vice versa. Now we enhance our understanding of this result still more by establishing that
$\textit{RFALP}$
s and vice versa. Now we enhance our understanding of this result still more by establishing that
-
•
 $\textit{RFALP}$
s are as expressive as
$\textit{RFALP}$
s are as expressive as
 $\textit{NLP}$
s.
$\textit{NLP}$
s. -
• The
 $\textit{SETAF}$
corresponding to an
$\textit{SETAF}$
corresponding to an
 $\textit{NLP}$
is invariant with respect to
$\textit{NLP}$
is invariant with respect to
 $\mapsto _{\textit{UTPM}}$
; that is, if
$\mapsto _{\textit{UTPM}}$
; that is, if
 $P_1 \mapsto _{\textit{UTPM}} P_2$
, then
$P_1 \mapsto _{\textit{UTPM}} P_2$
, then
 $\mathfrak{A}_{P_1} = \mathfrak{A}_{P_2}$
.
$\mathfrak{A}_{P_1} = \mathfrak{A}_{P_2}$
. -
• Each
 $\textit{NLP}$
$\textit{NLP}$
 $P$
leads to a unique
$P$
leads to a unique
 $\textit{RFALP}$
$\textit{RFALP}$
 $P^*$
via the relation
$P^*$
via the relation
 $\mapsto _{\textit{UTPM}}$
. Besides,
$\mapsto _{\textit{UTPM}}$
. Besides,
 $P$
and
$P$
and
 $P^*$
have the same partial stable, grounded, regular, stable, and
$P^*$
have the same partial stable, grounded, regular, stable, and
 $L$
-stable models.
$L$
-stable models.
Beyond revealing the connections between
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{NLP}$
s, the results in this paper also enhance our understanding of
$\textit{NLP}$
s, the results in this paper also enhance our understanding of
![]() $\textit{NLP}$
s themselves. To give a concrete example, let us consider the following issue: in the sequence of program transformations in
$\textit{NLP}$
s themselves. To give a concrete example, let us consider the following issue: in the sequence of program transformations in
![]() $\mapsto _{\textit{UTPM}}$
, atoms can be removed. Are these atoms underivable and set to false in the partial stable models of the program or true/undecided atoms can be removed in this sequence? Such questions can be answered by considering some results from Section 3 and the current section. In more formal terms, let
$\mapsto _{\textit{UTPM}}$
, atoms can be removed. Are these atoms underivable and set to false in the partial stable models of the program or true/undecided atoms can be removed in this sequence? Such questions can be answered by considering some results from Section 3 and the current section. In more formal terms, let
![]() $P$
and
$P$
and
![]() $P^*$
be
$P^*$
be
![]() $\textit{NLP}$
s such that
$\textit{NLP}$
s such that
![]() $P \mapsto ^*_{\textit{UTPM}} P^*$
and
$P \mapsto ^*_{\textit{UTPM}} P^*$
and
![]() $P^*$
is irreducible. We have
$P^*$
is irreducible. We have
-
•
 $P^*$
is an
$P^*$
is an
 $\textit{RFALP}$
(Theorem17), and the set of atoms occurring in
$\textit{RFALP}$
(Theorem17), and the set of atoms occurring in
 $P^*$
is
$P^*$
is
 $\left \{\mathit{head}(r) \mid r \in P^*\right \}$
(Definition14);
$\left \{\mathit{head}(r) \mid r \in P^*\right \}$
(Definition14); -
•
 $\mathcal{A}_{P^*} = \left \{\mathit{head}(r) \mid r \in P^*\right \}$
is the set of all arguments we can construct from
$\mathcal{A}_{P^*} = \left \{\mathit{head}(r) \mid r \in P^*\right \}$
is the set of all arguments we can construct from
 $P^*$
(Definition8), and
$P^*$
(Definition8), and
 $\mathfrak{A}_P = \mathfrak{A}_{P^*}$
(Theorem28), that is,
$\mathfrak{A}_P = \mathfrak{A}_{P^*}$
(Theorem28), that is,
 $\mathcal{A}_P = \mathcal{A}_{P^*}$
;
$\mathcal{A}_P = \mathcal{A}_{P^*}$
; -
• Thus
 $c$
occurs in
$c$
occurs in
 $P$
, but does not occur in
$P$
, but does not occur in
 $P^*$
iff there is no statement
$P^*$
iff there is no statement
 $s$
constructed from
$s$
constructed from
 $P$
such that
$P$
such that
 $\mathtt{Conc}(s) = c$
. According to Corollary2,
$\mathtt{Conc}(s) = c$
. According to Corollary2,
 $c \in F'$
for every interpretation
$c \in F'$
for every interpretation
 $\mathcal{I}$
with
$\mathcal{I}$
with
 $\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
.
$\Omega _P(\mathcal{I}) = \left\langle T', F' \right \rangle$
.
Consequently, every atom occurring in
![]() $P$
, but not occurring in
$P$
, but not occurring in
![]() $P^*$
is set to false in the least three-valued model of each disjunct of
$P^*$
is set to false in the least three-valued model of each disjunct of
![]() $P$
. In particular, they will be false in its partial stable models.
$P$
. In particular, they will be false in its partial stable models.
Supported by the findings presented in the current section, we can argue that
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{RFALP}$
s are essentially the same paradigm, and both are deeply connected with
$\textit{RFALP}$
s are essentially the same paradigm, and both are deeply connected with
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
7 Conclusion and future works
This paper investigates the connections between frameworks with sets of attacking arguments (
![]() $\textit{SETAF}$
s) and Normal Logic Programs (
$\textit{SETAF}$
s) and Normal Logic Programs (
![]() $\textit{NLP}$
s). Building on the research of Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019); Alcântara and Sá (Reference Alcântara and Sá2021), we employ the characterization of the
$\textit{NLP}$
s). Building on the research of Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019); Alcântara and Sá (Reference Alcântara and Sá2021), we employ the characterization of the
![]() $\textit{SETAF}$
semantics in terms of labelings (Flouris and Bikakis Reference Flouris and Bikakis2019) to establish a mapping from
$\textit{SETAF}$
semantics in terms of labelings (Flouris and Bikakis Reference Flouris and Bikakis2019) to establish a mapping from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s (and vice versa). We further demonstrate the equivalence between partial stable, well-founded, regular, stable, and
$\textit{SETAF}$
s (and vice versa). We further demonstrate the equivalence between partial stable, well-founded, regular, stable, and
![]() $L$
-stable models semantics for
$L$
-stable models semantics for
![]() $\textit{NLP}$
s and, respectively, complete, grounded, preferred, stable, and semi-stable labelings for
$\textit{NLP}$
s and, respectively, complete, grounded, preferred, stable, and semi-stable labelings for
![]() $\textit{SETAF}$
s.
$\textit{SETAF}$
s.
Our translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s offers a key advantage over the translation from
$\textit{SETAF}$
s offers a key advantage over the translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\mathit{AAF}$
s presented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). Our approach captures the equivalence between semi-stable labelings for
$\mathit{AAF}$
s presented by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b). Our approach captures the equivalence between semi-stable labelings for
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $L$
-stable models for
$L$
-stable models for
![]() $\textit{NLP}$
s. In addition, their translation is unable to preserve the structure of the
$\textit{NLP}$
s. In addition, their translation is unable to preserve the structure of the
![]() $\textit{NLP}$
s. While an
$\textit{NLP}$
s. While an
![]() $\textit{NLP}$
can be translated to an
$\textit{NLP}$
can be translated to an
![]() $\mathit{AAF}$
, recovering the original
$\mathit{AAF}$
, recovering the original
![]() $\textit{NLP}$
from the corresponding
$\textit{NLP}$
from the corresponding
![]() $\mathit{AAF}$
is generally not possible. In contradistinction, we have revisited a class of
$\mathit{AAF}$
is generally not possible. In contradistinction, we have revisited a class of
![]() $\textit{NLP}$
s called Redundancy-Free Atomic Logic Programs (
$\textit{NLP}$
s called Redundancy-Free Atomic Logic Programs (
![]() $\textit{RFALP}$
s). For
$\textit{RFALP}$
s). For
![]() $\textit{RFALP}$
s, the translations from
$\textit{RFALP}$
s, the translations from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s and from
$\textit{SETAF}$
s and from
![]() $\textit{SETAF}$
s to
$\textit{SETAF}$
s to
![]() $\textit{NLP}$
s also preserve their structures as they are each other’s inverse. Hence, when compared to the relationship between
$\textit{NLP}$
s also preserve their structures as they are each other’s inverse. Hence, when compared to the relationship between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\mathit{AAF}$
s, the relationship between
$\mathit{AAF}$
s, the relationship between
![]() $\textit{NLP}$
s and
$\textit{NLP}$
s and
![]() $\textit{SETAF}$
s is demonstrably more robust. It extends beyond semantics to encompass structural aspects.
$\textit{SETAF}$
s is demonstrably more robust. It extends beyond semantics to encompass structural aspects.
Some of these results are not new as they have already been obtained independently by König et al. (Reference König, Rapberger and Ulbricht2022). In fact, their translation from
![]() $\textit{NLP}$
s to
$\textit{NLP}$
s to
![]() $\textit{SETAF}$
s and vice versa coincide with ours, and the structural equivalence between
$\textit{SETAF}$
s and vice versa coincide with ours, and the structural equivalence between
![]() $\textit{RFALP}$
s and
$\textit{RFALP}$
s and
![]() $\textit{SETAF}$
s has also been identified there. Notwithstanding, our proofs of these results stem from a significantly distinct path as they are based on properties of argument labelings and are deeply rooted in the works of Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b); Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019); Alcântara and Sá (Reference Alcântara and Sá2021). For instance, our equivalence results are settled on two important aspects:
$\textit{SETAF}$
s has also been identified there. Notwithstanding, our proofs of these results stem from a significantly distinct path as they are based on properties of argument labelings and are deeply rooted in the works of Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b); Alcântara et al. (Reference Alcântara, Sá and Acosta-Guadarrama2019); Alcântara and Sá (Reference Alcântara and Sá2021). For instance, our equivalence results are settled on two important aspects:
-
• Properties involving the maximization/minimization of labelings adapted from Caminada et al.’s (Reference Caminada, Sá, Alcântara and Dvořák2015b) work to deal with labelings for
 $\textit{SETAF}$
s.
$\textit{SETAF}$
s. -
• Again inspired by Caminada et al. (Reference Caminada, Sá, Alcântara and Dvořák2015b), we proposed a mapping from interpretations to labelings and a mapping from labelings to interpretations. We also showed that they are each other’s inverse.
In contrast, König et al. (Reference König, Rapberger and Ulbricht2022) demonstrated the equivalence between the semantics in terms of extensions. They also have not tackled the controversy between semi-stable and
![]() $L$
-stable, one of our leading motivations for developing this work.
$L$
-stable, one of our leading motivations for developing this work.
In addition to showing this structural equivalence between
![]() $\textit{RFALP}$
s and
$\textit{RFALP}$
s and
![]() $\textit{SETAF}$
s, we have also investigated the expressiveness of
$\textit{SETAF}$
s, we have also investigated the expressiveness of
![]() $\textit{RFALP}$
s. To demonstrate that they are as expressive as
$\textit{RFALP}$
s. To demonstrate that they are as expressive as
![]() $\textit{NLP}$
s, we proved that any
$\textit{NLP}$
s, we proved that any
![]() $\textit{NLP}$
can be transformed into an
$\textit{NLP}$
can be transformed into an
![]() $\textit{RFALP}$
with the same partial stable models through repeated applications of the program transformation
$\textit{RFALP}$
with the same partial stable models through repeated applications of the program transformation
![]() $\mapsto _{\textit{UTPM}}$
. It is worth noticing that
$\mapsto _{\textit{UTPM}}$
. It is worth noticing that
![]() $\mapsto _{\textit{UTPM}}$
results from the combination of the following program transformations presented by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999): unfolding, elimination of tautologies, positive reduction, and elimination of non-minimal rules. In the course of our investigations, we also have obtained relevant findings as follows:
$\mapsto _{\textit{UTPM}}$
results from the combination of the following program transformations presented by Brass and Dix (Reference Brass and Dix1994, Reference Brass and Dix1997, Reference Brass and Dix1999): unfolding, elimination of tautologies, positive reduction, and elimination of non-minimal rules. In the course of our investigations, we also have obtained relevant findings as follows:
-
•
 $\textit{RFALP}$
s are irreducible with respect to
$\textit{RFALP}$
s are irreducible with respect to
 $\mapsto _{\textit{UTPM}}$
: the application of
$\mapsto _{\textit{UTPM}}$
: the application of
 $\mapsto _{\textit{UTPM}}$
to an
$\mapsto _{\textit{UTPM}}$
to an
 $\textit{RFALP}$
will result in the same program.
$\textit{RFALP}$
will result in the same program. -
• The mapping from
 $\textit{NLP}$
s to
$\textit{NLP}$
s to
 $\textit{SETAF}$
s is invariant with respect to the program transformation
$\textit{SETAF}$
s is invariant with respect to the program transformation
 $\mapsto _{\textit{UTPM}}$
; that is, if an
$\mapsto _{\textit{UTPM}}$
; that is, if an
 $\textit{NLP}$
$\textit{NLP}$
 $P_2$
is obtained from an
$P_2$
is obtained from an
 $\textit{NLP}$
$\textit{NLP}$
 $P_1$
via
$P_1$
via
 $\mapsto _{\textit{UTPM}}$
, then the
$\mapsto _{\textit{UTPM}}$
, then the
 $\textit{SETAF}$
corresponding to
$\textit{SETAF}$
corresponding to
 $P_1$
is the same corresponding to
$P_1$
is the same corresponding to
 $P_2$
.
$P_2$
. -
• The program transformation
 $\mapsto _{\textit{UTPM}}$
is confluent: any
$\mapsto _{\textit{UTPM}}$
is confluent: any
 $\textit{NLP}$
will lead to a unique
$\textit{NLP}$
will lead to a unique
 $\textit{RFALP}$
after repeatedly applying
$\textit{RFALP}$
after repeatedly applying
 $\mapsto _{\textit{UTPM}}$
. Consequently, two distinct
$\mapsto _{\textit{UTPM}}$
. Consequently, two distinct
 $\textit{RFALP}$
s will always be associated with two distinct
$\textit{RFALP}$
s will always be associated with two distinct
 $\textit{NLP}$
s.
$\textit{NLP}$
s.
In summary,
![]() $\textit{RFALP}$
s (which are as expressive as
$\textit{RFALP}$
s (which are as expressive as
![]() $\textit{NLP}$
s) and
$\textit{NLP}$
s) and
![]() $\textit{SETAF}$
s are essentially the same formalism. Roughly speaking, we can consider a
$\textit{SETAF}$
s are essentially the same formalism. Roughly speaking, we can consider a
![]() $\textit{SETAF}$
as a graphical representation of an
$\textit{SETAF}$
as a graphical representation of an
![]() $\textit{RFALP}$
and an
$\textit{RFALP}$
and an
![]() $\textit{RFALP}$
as a rule-based representation of a
$\textit{RFALP}$
as a rule-based representation of a
![]() $\textit{SETAF}$
. Any change in one formalism is mirrored by a corresponding change in the other. Thus,
$\textit{SETAF}$
. Any change in one formalism is mirrored by a corresponding change in the other. Thus,
![]() $\textit{SETAF}$
s emerge as a natural candidate for representing argumentation frameworks corresponding to
$\textit{SETAF}$
s emerge as a natural candidate for representing argumentation frameworks corresponding to
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
Regarding the significance and potential impact of our results, we highlight that by pursuing this line of research, one gains insight into what forms of non-monotonic reasoning can and cannot be represented by formal argumentation. In particular, by enlightening these connections between
![]() $\textit{SETAF}$
s and
$\textit{SETAF}$
s and
![]() $\textit{NLP}$
s, many approaches, semantics, and techniques naturally developed for the former may be applied to the latter, and vice versa. While
$\textit{NLP}$
s, many approaches, semantics, and techniques naturally developed for the former may be applied to the latter, and vice versa. While
![]() $\textit{SETAF}$
s serve as an inspiration for defining
$\textit{SETAF}$
s serve as an inspiration for defining
![]() $\textit{RFALP}$
s, the representation of
$\textit{RFALP}$
s, the representation of
![]() $\textit{NLP}$
s as
$\textit{NLP}$
s as
![]() $\textit{SETAF}$
s is an alternative for intuitively visualizing logic programs.
$\textit{SETAF}$
s is an alternative for intuitively visualizing logic programs.
In addition, our results associated with the confluence of
![]() $\mapsto _{\textit{UTPM}}$
are of particular significance from the logic programming perspective as they guarantee that the ordering of the transformations in
$\mapsto _{\textit{UTPM}}$
are of particular significance from the logic programming perspective as they guarantee that the ordering of the transformations in
![]() $\mapsto _{\textit{UTPM}}$
does not matter: we are free to choose always the “best” transformation, which maximally reduces the program. Consequently, our paper also sheds light on the search for efficient implementations in
$\mapsto _{\textit{UTPM}}$
does not matter: we are free to choose always the “best” transformation, which maximally reduces the program. Consequently, our paper also sheds light on the search for efficient implementations in
![]() $\textit{NLP}$
s.
$\textit{NLP}$
s.
Natural ramifications of this work include an in-depth analysis of other program transformations beyond those studied here and their impact on
![]() $\textit{SETAF}$
and argumentation in general. Given the close relationship between argumentation and logic programming, a possible line of research is to investigate how Argumentation can benefit from these program transformations in the development of more efficient algorithms. The structural connection involving
$\textit{SETAF}$
and argumentation in general. Given the close relationship between argumentation and logic programming, a possible line of research is to investigate how Argumentation can benefit from these program transformations in the development of more efficient algorithms. The structural connection involving
![]() $\textit{RFALP}$
s and
$\textit{RFALP}$
s and
![]() $\textit{SETAF}$
s gives rise to exploiting other extensions of Dung
$\textit{SETAF}$
s gives rise to exploiting other extensions of Dung
![]() $\mathit{AAF}$
s; in particular, we are interested in identifying which of them are robust enough to preserve the structure of logic programs. Along this same line of research, it is also our aim to study connections between extensions of
$\mathit{AAF}$
s; in particular, we are interested in identifying which of them are robust enough to preserve the structure of logic programs. Along this same line of research, it is also our aim to study connections between extensions of
![]() $\textit{NLP}$
s (including their paraconsistent semantics) and Argumentation.
$\textit{NLP}$
s (including their paraconsistent semantics) and Argumentation.
Competing interests
The authors declare none.
Supplementary material
To view supplementary material for this article, please visit http://doi.org/10.1017/S1471068424000188.