Article contents
Integrating Cardinality Constraints into Constraint Logic Programming with Sets
Published online by Cambridge University Press: 09 November 2021
Abstract
Formal reasoning about finite sets and cardinality is important for many applications, including software verification, where very often one needs to reason about the size of a given data structure. The Constraint Logic Programming tool 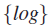 $$\{ log\} $$ provides a decision procedure for deciding the satisfiability of formulas involving very general forms of finite sets, although it does not provide cardinality constraints. In this paper we adapt and integrate a decision procedure for a theory of finite sets with cardinality into
$$\{ log\} $$ provides a decision procedure for deciding the satisfiability of formulas involving very general forms of finite sets, although it does not provide cardinality constraints. In this paper we adapt and integrate a decision procedure for a theory of finite sets with cardinality into 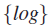 $$\{ log\} $$. The proposed solver is proved to be a decision procedure for its formulas. Besides, the new CLP instance is implemented as part of the
$$\{ log\} $$. The proposed solver is proved to be a decision procedure for its formulas. Besides, the new CLP instance is implemented as part of the 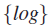 $$\{ log\} $$ tool. In turn, the implementation uses Howe and King’s Prolog SAT solver and Prolog’s CLP(Q) library, as an integer linear programming solver. The empirical evaluation of this implementation based on +250 real verification conditions shows that it can be useful in practice.
$$\{ log\} $$ tool. In turn, the implementation uses Howe and King’s Prolog SAT solver and Prolog’s CLP(Q) library, as an integer linear programming solver. The empirical evaluation of this implementation based on +250 real verification conditions shows that it can be useful in practice.
Under consideration in Theory and Practice of Logic Programming (TPLP)
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 6
- Cited by


