Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lisi, Francesca A.
and
Esposito, Floriana
2008.
Inductive Logic Programming.
Vol. 5194,
Issue. ,
p.
158.
Lisi, Francesca A.
and
Esposito, Floriana
2009.
Knowledge Discovery Enhanced with Semantic and Social Information.
Vol. 220,
Issue. ,
p.
3.
Greco, Sergio
and
Lisi, Francesca A.
2010.
A 25-Year Perspective on Logic Programming.
Vol. 6125,
Issue. ,
p.
183.
Lehmann, Jens
Auer, SSren
BBhmann, Lorenz
and
Tramp, Sebastian
2010.
Class Expression Learning for Ontology Engineering.
SSRN Electronic Journal ,
LISI, FRANCESCA A.
2010.
Inductive Logic Programming in Databases: From Datalog to .
Theory and Practice of Logic Programming,
Vol. 10,
Issue. 3,
p.
331.
Lisi, Francesca A.
2011.
AL-QuIn.
International Journal on Semantic Web and Information Systems,
Vol. 7,
Issue. 3,
p.
1.
Danyaro, Kamaluddeen Usman
Jaafar, Jafreezal
and
Liew, Mohd Shahir
2011.
Tractability method for ontology development of Semantic Web.
p.
34.
Lehmann, Jens
Auer, Sören
Bühmann, Lorenz
and
Tramp, Sebastian
2011.
Class expression learning for ontology engineering.
Journal of Web Semantics,
Vol. 9,
Issue. 1,
p.
71.
Auer, Sören
Lehmann, Jens
and
Ngonga Ngomo, Axel-Cyrille
2011.
Reasoning Web. Semantic Technologies for the Web of Data.
Vol. 6848,
Issue. ,
p.
1.
Groppe, Sven
2011.
Data Management and Query Processing in Semantic Web Databases.
p.
7.
Zhu, Man
2011.
The Semantic Web – ISWC 2011.
Vol. 7032,
Issue. ,
p.
373.
Auer, Sören
2011.
Creating knowledge out of interlinked data.
p.
1.
Tran, An C.
Dietrich, Jens
Guesgen, Hans W.
and
Marsland, Stephen
2012.
Rules on the Web: Research and Applications.
Vol. 7438,
Issue. ,
p.
302.
Bühmann, Lorenz
and
Lehmann, Jens
2012.
Knowledge Engineering and Knowledge Management.
Vol. 7603,
Issue. ,
p.
57.
Lisi, Francesca A.
2013.
Semantic Web.
p.
52.
Auer, Sören
Lehmann, Jens
Ngonga Ngomo, Axel-Cyrille
and
Zaveri, Amrapali
2013.
Reasoning Web. Semantic Technologies for Intelligent Data Access.
Vol. 8067,
Issue. ,
p.
1.
Galárraga, Luis Antonio
Teflioudi, Christina
Hose, Katja
and
Suchanek, Fabian
2013.
AMIE.
p.
413.
Bühmann, Lorenz
and
Lehmann, Jens
2013.
Advanced Information Systems Engineering.
Vol. 7908,
Issue. ,
p.
33.
Suchanek, Fabian M.
and
Preda, Nicoleta
2014.
Semantic culturomics.
Proceedings of the VLDB Endowment,
Vol. 7,
Issue. 12,
p.
1215.
Ngomo, Axel-Cyrille Ngonga
Auer, Sören
Lehmann, Jens
and
Zaveri, Amrapali
2014.
Reasoning Web. Reasoning on the Web in the Big Data Era.
Vol. 8714,
Issue. ,
p.
1.
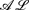 -log that integrates the description logic
-log that integrates the description logic 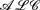 and the function-free Horn clausal language Datalog. In this paper, we consider the problem of automating the acquisition of these rules for the Semantic Web. We propose a general framework for rule induction that adopts the methodological apparatus of Inductive Logic Programming and relies on the expressive and deductive power of
and the function-free Horn clausal language Datalog. In this paper, we consider the problem of automating the acquisition of these rules for the Semantic Web. We propose a general framework for rule induction that adopts the methodological apparatus of Inductive Logic Programming and relies on the expressive and deductive power of 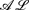 -log. The framework is valid whatever the scope of induction (description versus prediction) is. Yet, for illustrative purposes, we also discuss an instantiation of the framework which aims at description and turns out to be useful in Ontology Refinement.
-log. The framework is valid whatever the scope of induction (description versus prediction) is. Yet, for illustrative purposes, we also discuss an instantiation of the framework which aims at description and turns out to be useful in Ontology Refinement.
