Published online by Cambridge University Press: 20 September 2019
Answer Set Programming (ASP) is a logic programming paradigm featuring a purely declarative language with comparatively high modeling capabilities. Indeed, ASP can model problems in NP in a compact and elegant way. However, modeling problems beyond NP with ASP is known to be complicated, on the one hand, and limited to problems in 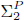 $\[\Sigma _2^P\]$ on the other. Inspired by the way Quantified Boolean Formulas extend SAT formulas to model problems beyond NP, we propose an extension of ASP that introduces quantifiers over stable models of programs. We name the new language ASP with Quantifiers (ASP(Q)). In the paper we identify computational properties of ASP(Q); we highlight its modeling capabilities by reporting natural encodings of several complex problems with applications in artificial intelligence and number theory; and we compare ASP(Q) with related languages. Arguably, ASP(Q) allows one to model problems in the Polynomial Hierarchy in a direct way, providing an elegant expansion of ASP beyond the class NP.
$\[\Sigma _2^P\]$ on the other. Inspired by the way Quantified Boolean Formulas extend SAT formulas to model problems beyond NP, we propose an extension of ASP that introduces quantifiers over stable models of programs. We name the new language ASP with Quantifiers (ASP(Q)). In the paper we identify computational properties of ASP(Q); we highlight its modeling capabilities by reporting natural encodings of several complex problems with applications in artificial intelligence and number theory; and we compare ASP(Q) with related languages. Arguably, ASP(Q) allows one to model problems in the Polynomial Hierarchy in a direct way, providing an elegant expansion of ASP beyond the class NP.