Article contents
An ASP approach for reasoning in a concept-aware multipreferential lightweight DL
Published online by Cambridge University Press: 21 September 2020
Abstract
In this paper we develop a concept aware multi-preferential semantics for dealing with typicality in description logics, where preferences are associated with concepts, starting from a collection of ranked TBoxes containing defeasible concept inclusions. Preferences are combined to define a preferential interpretation in which defeasible inclusions can be evaluated. The construction of the concept-aware multipreference semantics is related to Brewka’s framework for qualitative preferences. We exploit Answer Set Programming (in particular, asprin) to achieve defeasible reasoning under the multipreference approach for the lightweight description logic ξ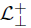 $\mathcal L_ \bot ^ + $.
$\mathcal L_ \bot ^ + $.
Information
- Type
- Original Article
- Information
- Theory and Practice of Logic Programming , Volume 20 , Issue 5: 36th International Conference on Logic Programming Special Issue I , September 2020 , pp. 751 - 766
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 9
- Cited by


